注:本文包含 AI 辅助创作
- 参考链接:
Paper Summary
- 核心内容:
- 本综述很长,核心内容探讨了 LLM 作为评判的复杂性
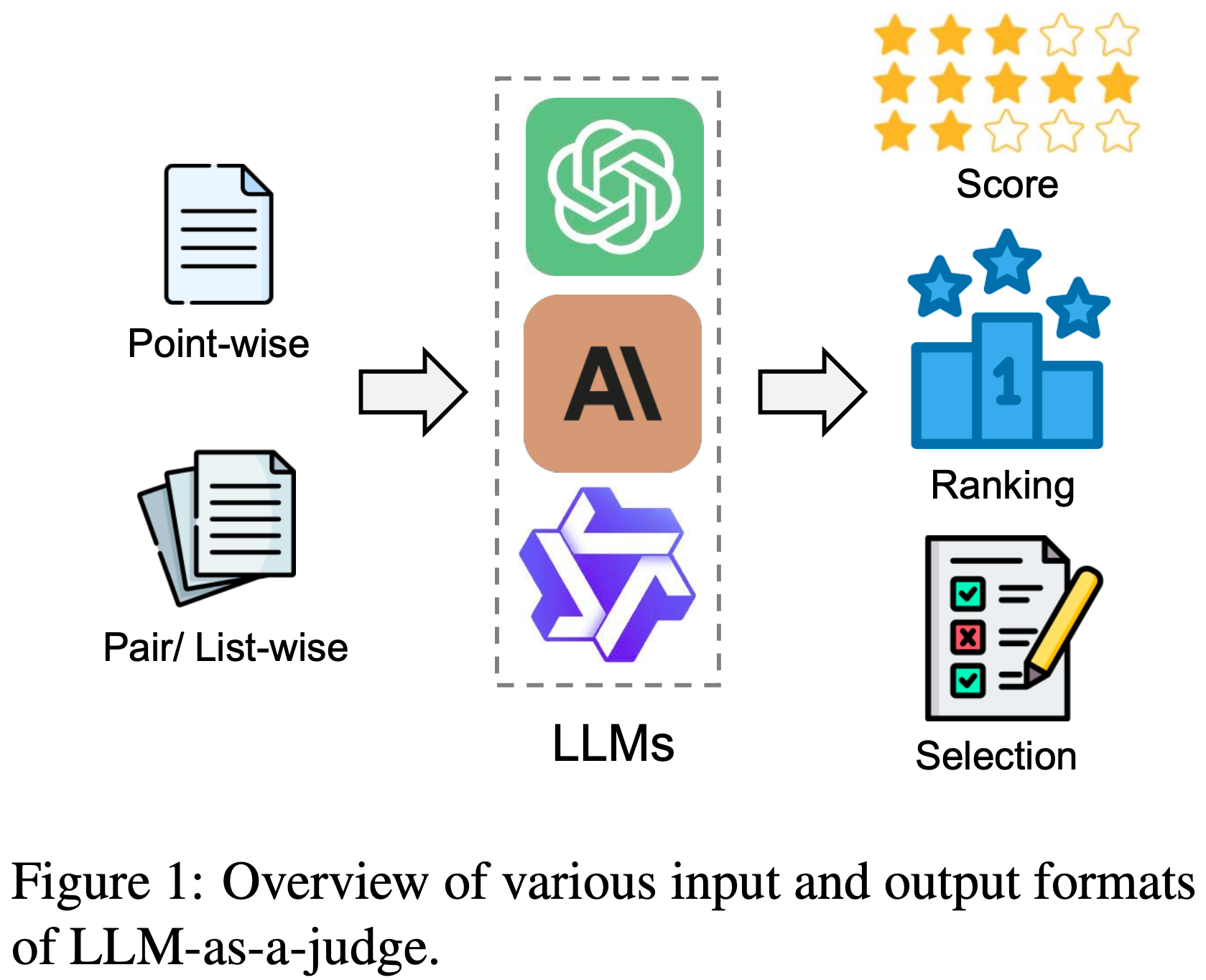
- 作者根据输入格式( Pointwise 、 Pairwise 和 Listwise )和输出格式(评分、排名和选择)对现有 LLM-based 评判方法进行分类
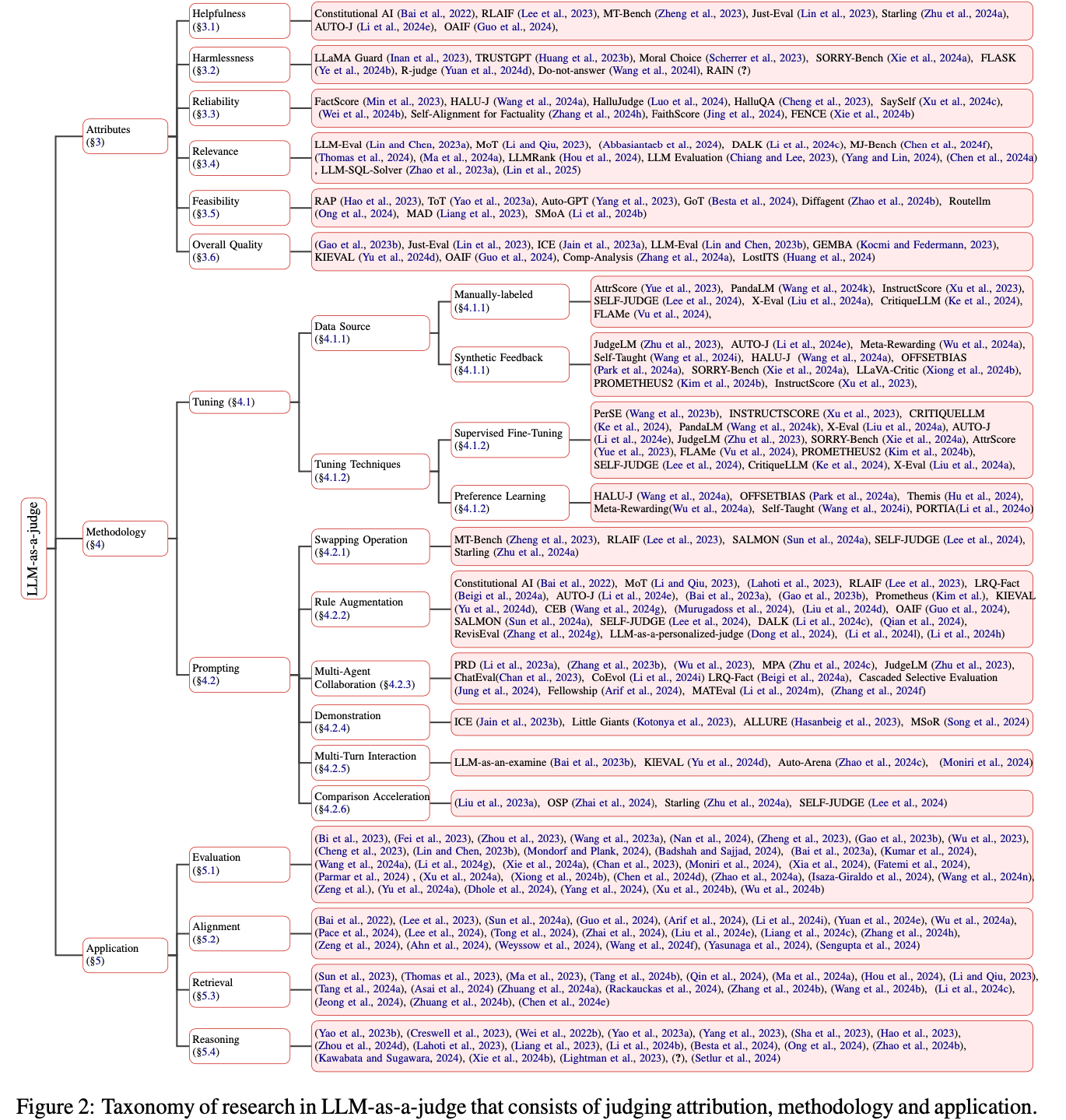
- 然后,论文为 LLM 作为评判提出了一个全面的分类法,涵盖评判属性、方法论和应用
- 在此之后,论文介绍了 LLM 作为评判的基准的详细集合,并伴随着对当前挑战和未来方向的深思熟虑的分析,旨在为这一新兴领域的未来工作提供更多资源和见解
- 问题提出:
- 评估(Assessment)与评价(Evaluation) 长期以来一直是 AI 和 NLP 领域的关键挑战
- 传统方法(基于匹配 or 基于 Embedding),往往在评判(Judging)细微属性和提供令人满意的结果方面存在不足
- LLM 的最新进展启发了“LLM-as-a-judge”范式,即利用 LLM 在各种任务和应用中执行评分、排序或选择
- 论文对 LLM-based 评判和评估进行了全面综述
- 首先从输入和输出的角度给出详细定义
- 然后引入一个全面的分类法(taxonomy),从 what to judge, how to judge and where to judge(评判什么,如何评判,在哪里评判) 三个维度探讨 LLM-as-a-judge 的问题
Introduction and Discussion
- 评估与评价长期以来一直是机器学习和自然语言处理(NLP)中必不可少但颇具挑战性的任务,尤其是对给定候选列表的各种属性(如质量、相关性和有用性)进行评分和比较(2022;2024)
- 传统评估方法依赖于静态指标,如 BLEU(双语评估辅助工具)(2002)和 ROUGE(摘要评价指标)(2004)
- 这些指标通过计算输出与参考文本之间的词重叠来衡量质量
- 这些自动指标计算效率高,并在许多生成应用中得到使用(2022, 2023a, 2024c)
- 但是,它们对 n-gram 匹配(n-gram matching)和基于参考设计(reference-based designs)的依赖严重限制了它们在动态和开放式场景中的适用性(2016;Reiter, 2018)
- 随着深度学习模型(2019;2019)的兴起,许多基于 Embedding 的评估方法(如 BERTScore(2020)和 BARTScore(2021))也应运而生
- 尽管这些基于小模型的指标从词级表示转向了 Embedding 级表示,并提供了更大的灵活性,但它们仍然难以捕捉相关性之外的细微属性(2024),如有用性和无害性
- 最近先进的 LLM,如 GPT-4(2023)和 o1,在指令遵循、查询理解和响应生成方面表现出了惊人的性能
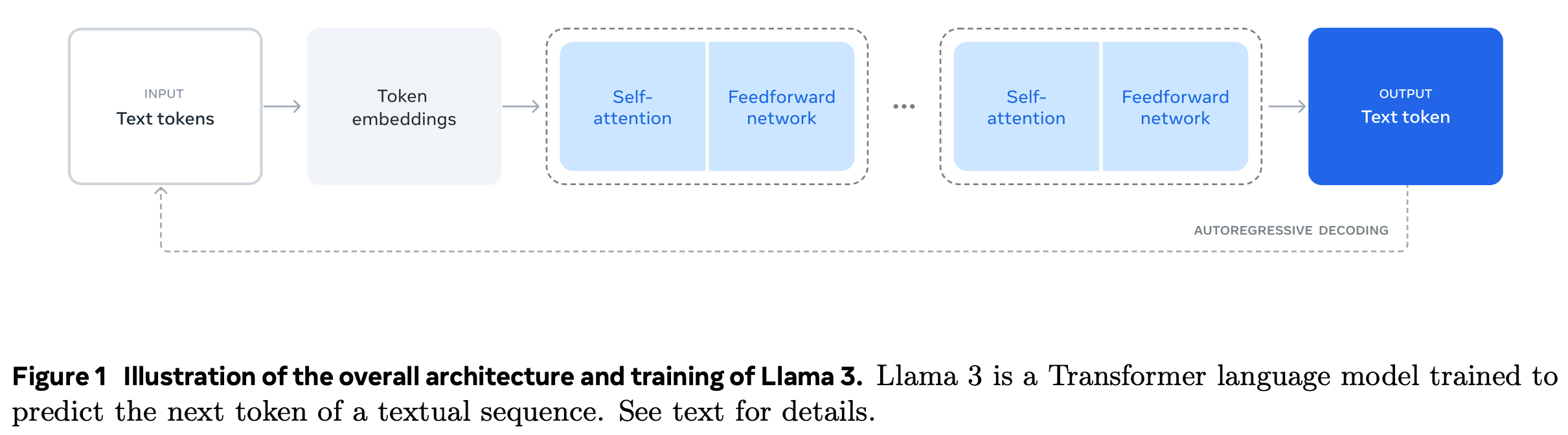
- 这一进展促使研究人员提出了“LLM-as-a-judge ”的概念(2023),即利用强大的 LLM 对一组候选进行评分、排序和选择(图 1)
- LLM 的强大性能(2020)与精心设计的评估 Pipeline (2023a;2024b;2023a)相结合,能够对各种评估应用进行细粒度和详细的评判,显著解决了传统评估方法的局限性,为 NLP 评估设定了新的标准
- 除了评估之外,LLM-as-a-judge 还被广泛应用于整个 LLM 生命周期,包括对齐(2022;2023)、检索(2023;2024c)和推理(2023;2024b)等任务
- 它赋予 LLM 一系列高级能力,如自我进化(2024a)、主动检索(2024c)和决策(2023),推动它们从传统模型向智能代理(2024)转变
- 然而,随着 LLM-as-a-judge 的快速发展,评判偏差(judging bias)和脆弱性(vulnerability)等挑战(2023a;2024a;2024)也逐渐显现
- 因此,对当前技术和未来挑战进行系统回顾对于推进 LLM-based 评判方法具有重要价值
- 在本综述中,论文深入探讨了 LLM-as-a-judge 的细节,旨在全面概述 LLM-based 评判
- 论文首先通过讨论其各种输入和输出格式(第 2 节)对 LLM-as-a-judge 进行正式定义
- 接下来,论文提出了一个深入而全面的分类法,以解决三个关键问题(第 3-5 节):
- 属性(Attribute) :评判什么? 论文深入研究 Judge LLM 评估的具体属性,包括帮助性、无害性、可靠性、相关性、可行性和整体质量
- Methodology :如何评判? 论文探索了 LLM-as-a-judge 系统的各种调优和提示技术,包括手动标记数据、合成反馈、监督微调、偏好学习、交换操作、规则增强、多智能体协作、演示、多轮交互和比较加速
- 应用(Application) :在哪里评判? 论文调查了 LLM-as-a-judge 已被应用的领域,包括评估、对齐、检索和推理
- 此外,论文在第 6 节中收集了从不同角度评估 LLM-as-a-judge 的现有基准
- 最后,论文在第 7 节中提出了当前的挑战和未来研究的有前途方向,包括偏差与脆弱性、动态与复杂评判、自我评判和人机共判
Differences from Other LLM-related Surveys
- 近年来,LLM 已成为热门研究领域,涌现出诸多相关综述文献(2023b;2024;2024a)
- 尽管已有若干综述专注于 LLM-based 自然语言生成(NLG)评估(2024a;2024n),但本研究旨在系统梳理”LLM-as-a-judge”这一方法论
- 如前所述,”LLM-as-a-judge”的应用范畴已远超评估领域,因此有必要建立全局视角进行归纳与分类
- 此外,现有综述多聚焦 LLM 赋能的具体应用场景
- 如 LLM-based 数据标注(2024b)、数据增强(2024e)以及自我修正(2024)
- 但目前仍缺乏针对”LLM-as-a-judge”范式的系统性与全面性综述研究
Preliminary
- 在本节中,论文旨在提供 LLM-as-a-judge 的详细定义,分别在 2.1 节和 2.2 节讨论各种输入和输出格式
Input
- 给定一个 Judge LLM \(J\),评估过程可以表示为:
$$R = J\left(C_{1}, \ldots, C_{n}\right). \tag{1}$$- 这里 \(C_{i}\) 是第 \(i\) 个待评判的候选,\(R\) 是评判结果
- 在本节中,论文根据候选数量 \(n\) 将输入格式分为两种类型:
- ** Pointwise (Point-Wise)** :当 \(n = 1\) 时,成为逐点评判,此时 Judge LLM 将只关注一个候选样本(2023b)
- 成对/ Listwise (Pair/List-Wise) :当 \(n \geq 2\) 时,成为成对(\(n = 2\))或 Listwise (\(n > 2\))评判,此时提供多个候选样本供 Judge LLM 比较并进行综合评估(2023;2024)
Output
- 在本节中,论文根据 \(R\) 的不同格式讨论评判的三种输出类型:
- 分数(Score) :当每个候选样本被分配一个连续或离散的分数时,\(R = \{C_{1}: S_{1}, \ldots, C_{n}: S_{n}\}\),这成为基于分数的评判
- 这是最常见和广泛使用的协议,利用 LLM 进行评分以进行定量比较(2024a)或属性检测(2024a)
- 排名(Ranking) :在基于排名的评判中,输出是每个候选样本的排名,表示为 \(R = \{C_{i} > \ldots > C_{j}\}\)
- 这种比较方法在需要建立候选之间排名顺序的场景中很有用(2023a)
- 选择(Selection) :在基于选择的评判中,输出涉及选择一个或多个最优候选,表示为 \(R = \{C_{i}, \ldots, C_{j}\} > \{C_{1}, \ldots, C_{n}\}\)
- 这种方法在决策(2023a)或内容过滤(2024c)场景中特别有用
- 分数(Score) :当每个候选样本被分配一个连续或离散的分数时,\(R = \{C_{1}: S_{1}, \ldots, C_{n}: S_{n}\}\),这成为基于分数的评判
Attribute
- 在本节中,论文从属性角度对当前 LLM-as-a-judge 的研究进行分类。图 3 概述了 Judge LLM 可以评估的方面

Helpfulness
- 现代最先进的 LLM 经过指令调整和对齐过程,能够遵循用户指令并有效响应
- 这一对齐步骤依赖于大量有用和无害的数据,通常作为人类偏好数据收集,然后用于对齐训练的强化学习
- 鉴于获取此类对齐数据的成本很高,最近的工作探索了使用 LLM 来标记帮助性,以及生成或评估对齐数据(2022)
- (2024)的作者以在线方式使用 LLM 来获取偏好 ,以直接对齐另一个 LLM
- 最近的一些工作表明,来自 AI 的帮助性反馈,即 LLM 的反馈与人类反馈相当(2023)
- 也有一些成功的 LLM(2024a)通过 AI 反馈数据进行了微调,从而证明了这种方法的可行性和有用性
- 除了这些对齐方面的工作,利用 LLM 作为评估器的通用框架在评估候选响应的帮助性方面也至关重要(2023;2023;2024e)
Harmlessness
- 评估文本数据的无害性对于内容审核和创建或管理合成数据集都很重要
- 鉴于人类标注工作既昂贵又耗时,并且受先前研究中 Embedding 在 LLM 中的道德信念的启发(2023),许多最近的工作研究了使用 LLM 来评估无害性
- 最先进的 LLM 能够有效地用于内容审核,要么在遵循一些政策指导方针的情况下现成使用,要么在安全/不安全数据上进行微调(2023;2024g)
- Ye 等人 (2024b) 探索了使用 LLM 以细粒度方式评估无害性等属性的可行性,并发现专有模型的表现比开源模型好得多
- Wang 等人 (2024l) 使用 OpenAI 的 GPT-4 来评估无害性,并进一步将其性能与针对该特定任务微调的较小预训练语言模型进行比较。此外,Bai 等人 (2022) 使用原则来指导 LLM 进行无害性评估以用于对齐目的,他们将这种范式称为“宪法 AI”(Constitutional AI)
- (2023)使用相同的 LLM 来评估其响应是否有害,并为 GPT-3.5 和 Llama-2 提供了见解和最佳实践
- Xie 等人 (2024a) 在 LLM 安全拒绝基准上对几个 LLM 进行了全面比较,发现小型 LLM 在微调设置下是有效的安全评判
- 在推理时,(2023b) 提出了可回退自回归推理(RAIN),允许 LLM 进行自我评估和回退以确保 AI 安全
Reliability
- 可靠性是指,LLM 能够生成事实性和忠实的内容 ,同时也能表达不确定性或承认对某些主题的知识空白(2024)
- 关于事实性,Wang 等人 (2024a) 引入了 HALU-J,这是一个基于批判的幻觉评判(critique-based hallucination judge),通过选择相关证据并提供详细批判来增强事实性评估
- Cheng 等人 (2023) 设计了一种使用 GPT-4 的自动评估方法,用于评判模型的输出是否是幻觉
- 此外,一些工作采用 Judge LLM 进行长文本事实性评估
- 在对话上下文中,Luo 等人 (2024) 收集了一个大规模的基准,用于自动对话级幻觉评估
- 基于此数据集,他们引入了 HalluJudge,一个专门用于评估对话级幻觉的评判语言模型
- Min 等人 (2023) 开发了 FactScore,一种细粒度的方法,用于评估长文本生成的事实性,首先将内容拆分为原子级句子,然后从维基百科检索相关语料库以评估其事实性
- 在此基础上,Wei 等人 (2024b) 提出为 Judge LLM 配备 Google 搜索 API,以实现更灵活和高效的事实性评估
- Jing 等人 (2024) 将这种细粒度的可靠性评估扩展到多模态领域,并引入了 FaithScore
- Zhang 等人 (2024h) 在 LLM 对齐中采用了类似的策略,创建了一个合成对齐数据集,其中涉及使用声明提取和自我评判技术对每个生成的样本进行评估和过滤
- Xie 等人 (2024b) 训练了一个外部基于批判的 LLM-as-a-judge,在生成阶段提供声明级的事实性反馈,以提高响应的事实性
- 对于不确定性评判,Xu 等人 (2024c) 提出了 SaySelf,这是一个新的训练框架,通过自我一致性提示和基于组的校准训练,教 LLM 表达更细粒度的置信度估计(1-46, 1-50)
Relevance
- 相关性衡量生成或检索的内容与原始查询的一致程度
- 传统的相关性评估方法通常依赖于关键字匹配(2009)或语义相似度(2021),这些方法难以捕捉上下文中的细微差异或细微差别
- 使用 Judge LLM 进行相关性评估已被探索并验证为在各种应用中更细粒度和有效的方式(2023;2024;2024b)
- 在对话评估中,Lin 和 Chen (2023a) 首先提出用 LLM 评判来取代昂贵且耗时的人类注释,用于相关性评估,为 Judge LLM 提供对话上下文和生成的响应进行评估
- 类似地,Abbasiantaeb 等人 (2024) 将 LLM-as-a-judge 应用于对话搜索,与人类注释者合作解决与不完整相关性评判相关的问题。在检索增强生成(RAG)场景中,Li 和 Qiu (2023) 利用 LLM 来确定哪些历史记忆最适合解决当前问题
- 遵循这一概念,Li 等人 (2024c) 还提议采用 LLM 作为重新排序器,以评判和过滤子知识图中的噪声和不相关知识
- 最近,LLM-as-a-judge 也被用于多模态应用中的相关性评判(2025;2024i;2024b;2024;2024b;2024;2024m;2024)
- Yang 和 Lin (2024) 以及 Chen 等人 (2024a) 都采用多模态 LLM 来构建自动评估基准
- 相比之下,Chen 等人 (2024f) 使用多模态奖励模型来评估文本到图像生成中的相关性
- 在 SQL 生成评估中,(2023a) 提出利用 LLM 来确定 SQL 等价性
- 此外,LLM-as-a-judge 还在许多传统检索应用中探索了相关性评估,如搜索(2024)、检索(2024a)和推荐(2024)
Feasibility
- 复杂且设计良好的推理 Pipeline 可以进一步释放 LLM 的潜力
- 在这些代理式 LLM 中,评估候选动作或步骤的可行性对于规划、推理和决策的成功至关重要
- 虽然一些工作利用指标或外部工具进行这种可行性评估(2023a;Yuan 等人),但许多其他工作利用 LLM 本身来选择最适当和合理的动作来执行
- Hao 等人 (2023) 首先提出提示 LLM 进行自我评估,并生成可行性评判作为奖励信号来执行蒙特卡洛树搜索(MCTS)
- 类似地,Yao 等人 (2023a) 建议在其提出的“思维树”(ToT)框架中采用 LLM 作为状态评估器,用于潜在步骤搜索
- Besta 等人 (2024) 将先前研究中使用的树结构替换为图结构,并使用 LLM 根据每个思维的可行性或正确性为其分配分数
- 在多智能体协作系统中,Liang 等人 (2023)、Li 等人 (2024b) 和 Wang 等人 (2024d) 提议利用 Judge LLM 在多个候选响应中选择最可行和合理的解决方案
- 此外,还有一些工作采用 Judge LLM 在 API 选择(2024b)、工具使用(2023)和 LLM 路由(2024)中进行可行性评估
Overall Quality
- 如前所述,LLM-as-a-judge 可用于在各种任务和应用中执行多方面和细粒度的评估
- 然而,在许多情况下,仍然需要一个综合评估来表示候选的整体质量,以进行比较或排名
- 获得此整体分数的一种直接方法是计算特定方面分数的平均值或加权平均值(2023;2023b;Saad-2024)
- 此外,其他一些研究呈现每个属性的评估结果,并提示 LLM 评判生成整体质量评判(2024d;2024;2024a)
- 除了从多个属性总结整体质量外,其他研究专注于直接产生整体评判
- 例如,在摘要(2023b;2023a;2024a;2024d,h)和机器翻译(2024;2023;2024)等传统 NLP 任务中,与更开放式的长文本生成任务相比,评估维度较少
- 因此,在这些情况下,LLM-as-a-judge 通常用于直接提示 LLM 生成整体评判
Methodology
- 在本节中,论文介绍 LLM-as-a-judge 常用的方法和技巧,将其分为调优方法(4.1 节)和提示策略(4.2 节)
Tuning
- 为了增强通用 LLM 的评判能力,不同研究采用了各种调优技术
- 在本节中,论文从两个角度讨论 LLM-as-a-judge 的调优方法:
- 数据来源(4.1.1 节)
- 训练方法(4.1.2 节)
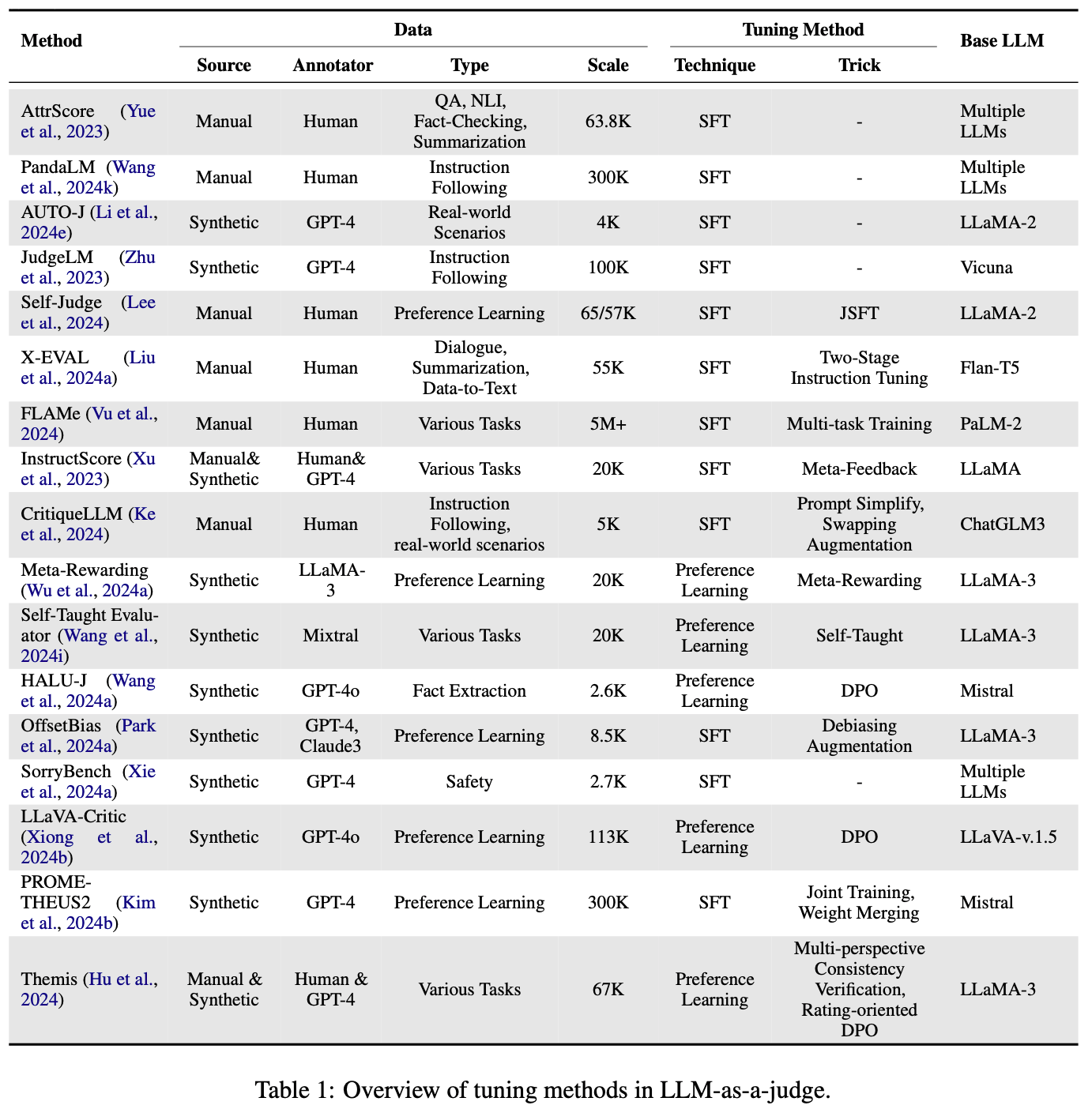
- 表 1 收集了所有专注于调优 Judge LLM 的研究论文
Data Source
- 手动标注数据(Manually-labeled Data) :为了训练具有类似人类标准的 Judge LLM,一种直观的方法是收集手动标注的样本和相应的评判
- 许多先前的工作已经利用并整合现有资源来构建全面的数据集,用于调优 Judge LLM
- Vu 等人(2024)构建了一个大型且多样化的集合,包含超过 100 个质量评估任务,涵盖超过 500 万个人类评判,这些评判通过整理和标准化先前研究中公开的人类评估得到
- 类似地,Wang 等人(2024k)提出了 PandaLM,并收集了多样化的人类标注测试数据,其中所有上下文均为人类生成,标签与人类偏好一致
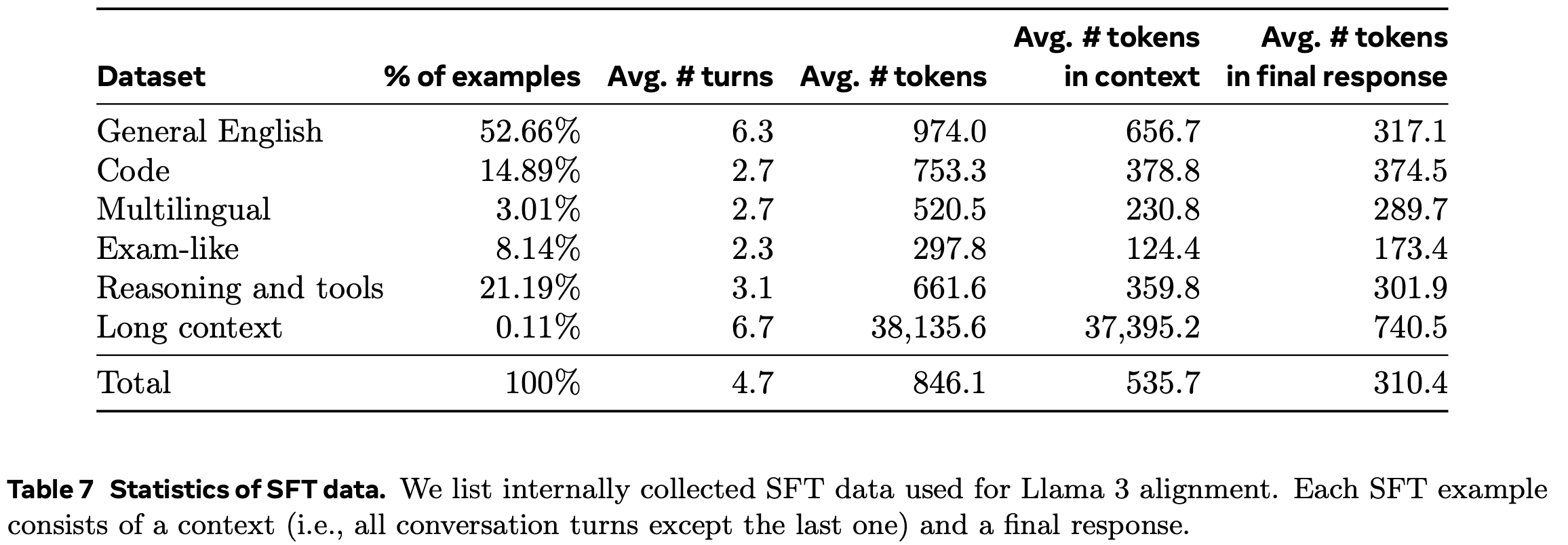
- 为了增强策略在对齐数据合成中的评判能力,Lee 等人(2024)通过成对评判任务扩充了 SFT数据集 ,该任务的指令是从一组选项中选择所选响应
- 还有一些工作收集数据集用于细粒度的评判反馈(2024)
- Xu 等人(2023)引入了 InstructScore,一种可解释的文本生成评估指标,并策划了 MetricInstruct 数据集,该数据集涵盖六个文本生成任务和 23 个数据集
- Liu 等人(2024a)收集了 ASPECTINSTRUCT,这是第一个专为多方面 NLG 评估设计的指令调优数据集,跨越 65 个任务的 27 个不同评估方面
- Yue 等人(2023)首先提出了属性评估,并使用来自相关任务(如问答、事实核查、自然语言推理和摘要)的数据对 Judge LLM 进行微调
- Ke 等人(2024)采用了一种独特的方法,首先提示 GPT-4 生成反馈,并手动检查其为每个用户查询生成的文本,必要时进行修订以提高质量
- 合成反馈(Synthetic Feedback) :尽管手动标注的反馈质量高且能准确反映人类评判偏好,但其在数量和覆盖范围上存在局限性
- 一些研究人员将合成反馈作为调优 Judge LLM 的数据源。这一方向的一种方法依赖于 Judge LLM 自身生成合成反馈
- Wu 等人(2024a)通过提示策略 LLM 评估自己的评判来构建成对反馈,以增强评判能力
- Wang 等人(2024i)提示 LLM 生成原始指令的“noisy”版本 ,并将对该损坏指令的相应响应作为较差响应
- Wang 等人(2024a)提示 GPT-4-Turbo 为每个实例基于原始证据生成多条证据,将其分类为完全不相关证据、部分不相关证据和高度相关证据,以训练幻觉评判 LLM
- 一些研究人员将合成反馈作为调优 Judge LLM 的数据源。这一方向的一种方法依赖于 Judge LLM 自身生成合成反馈
- Park 等人(2024a)构建了 OFFSETBIAS,这是一个成对偏好数据集 ,利用 GPT-4 生成不良、离题和错误的响应 ,并进行难度过滤
- 对于安全评判,Xie 等人(2024a)采用 GPT-4 作为分类器,将每个数据点映射到预定义的安全类别,以训练自动化评估器
- 与先前工作不同,Li 等人(2024e)采用 GPT-4 合成成对和逐点数据,以训练生成式 Judge LLM
- 对于逐点数据,他们采用“分而治之”的策略,从 GPT-4 收集单个响应的两条批评意见,将其合并为更全面的批评,并提供最终评分
- 紧随其后,Kim 等人(2024b)使用 GPT-4 用详细的人类评估标准和口头反馈扩充偏好学习数据集
- 在多模态领域,Xiong 等人(2024b)提出了 LLaVA-Critic,并采用 GPT-4o 生成给定分数或偏好评判背后的原因,用于训练数据构建
- 此外,通过利用人类显式指令和 GPT-4 的隐式知识,Xu 等人(2023)基于 LLaMA 微调了一个 Judge LLM,为生成的文本同时生成分数和人类可读的诊断报告
- Zhu 等人(2023)引入了 JudgeLM,并提出了一个全面、大规模、高质量的数据集,包含任务种子、LLM 生成的答案和 GPT-4 生成的评判,用于微调高性能评判
Tuning Techniques
- SFT : SFT 是最常用的方法,用于帮助 Judge LLM 从成对(2024k;2024e;2023b;2023)或逐点(2024a;2023b;2023)评判数据中学习
- 在采用 SFT 的众多工作中,Vu 等人(2024)提出了一种监督多任务训练方法,用于在各种任务的多个混合数据集上微调其基础大型自动评分模型(FLAMe)
- 为了使 Judge LLM 同时具备成对和逐点评判能力,Kim 等人(2024b)在调优阶段新颖地提出了联合训练和权重合并方法,并发现后者在大多数情况下并未提高评估性能
- 为了获得不仅能生成响应还能比较成对偏好的评判模型,Lee 等人(2024)设计了 Judge 增强监督微调( Judge-augmented Supervised Fine-tuning,JSFT),使用扩充的偏好学习数据集
- 在训练阶段,Ke 等人(2024)通过添加简化提示来区分输入的不同部分,并通过交换两个生成文本的顺序和交换批评中的相应内容来扩充成对训练数据,从而增强他们的模型
- Xu 等人(2023)进一步在自我生成的输出上微调其 INSTRUCTSCORE 模型,以优化反馈分数,生成与人类评判更好对齐的诊断报告
- Liu 等人(2024a)还提出了两阶段监督微调方法,首先应用普通指令调优,使模型具备遵循指令进行各种评估的能力,然后使用辅助方面进行进一步调优,以丰富训练过程,纳入额外的指令调优阶段,利用与目标评估方面的潜在连接
- 偏好学习(Preference Learning) :偏好学习与评判和评估任务密切相关,尤其是比较和排名评判
- 除了直接采用或扩充偏好学习数据集用于监督微调 Judge LLM 的工作外,一些研究还应用偏好学习技术来增强 LLM 的评判能力
- 为了提高 HALU-J 提供的评判质量,Wang 等人(2024a)在多证据设置下的 SFT 阶段后,使用定向偏好优化(DPO)(2023)进一步对其进行调优
- 类似地,Park 等人(2024a)将 DPO 与包含关键错误但具有评判模型偏好的风格质量的合成“bad”响应一起应用,帮助减轻 Judge LLM 中的偏差
- Wu 等人(2024a)新颖地提出了元奖励,利用策略 LLM 来评判自己评判的质量,并生成成对信号以增强 LLM 的评判能力
- 这一概念也被 Wang 等人(2024i)采用,他们提出了自教评估器,使用损坏的指令生成次优响应作为偏好学习的劣质示例
- 最近,Hu 等人(2024)提出了 Themis,一种专注于 NLG 评估的 LLM,其训练采用了设计的多视角一致性验证和面向评分的偏好对齐方法
- Li 等人(2024o)提出了 PORTIA,一种基于对齐的方法,旨在以有效方式模拟人类比较行为,以校准位置偏差
Prompting
- 在推理阶段设计适当的提示策略和 Pipeline 可以提高评判准确性并减轻偏差
- 在本节中,论文总结和分类 LLM-as-a-judge 的现有提示策略(图 4)
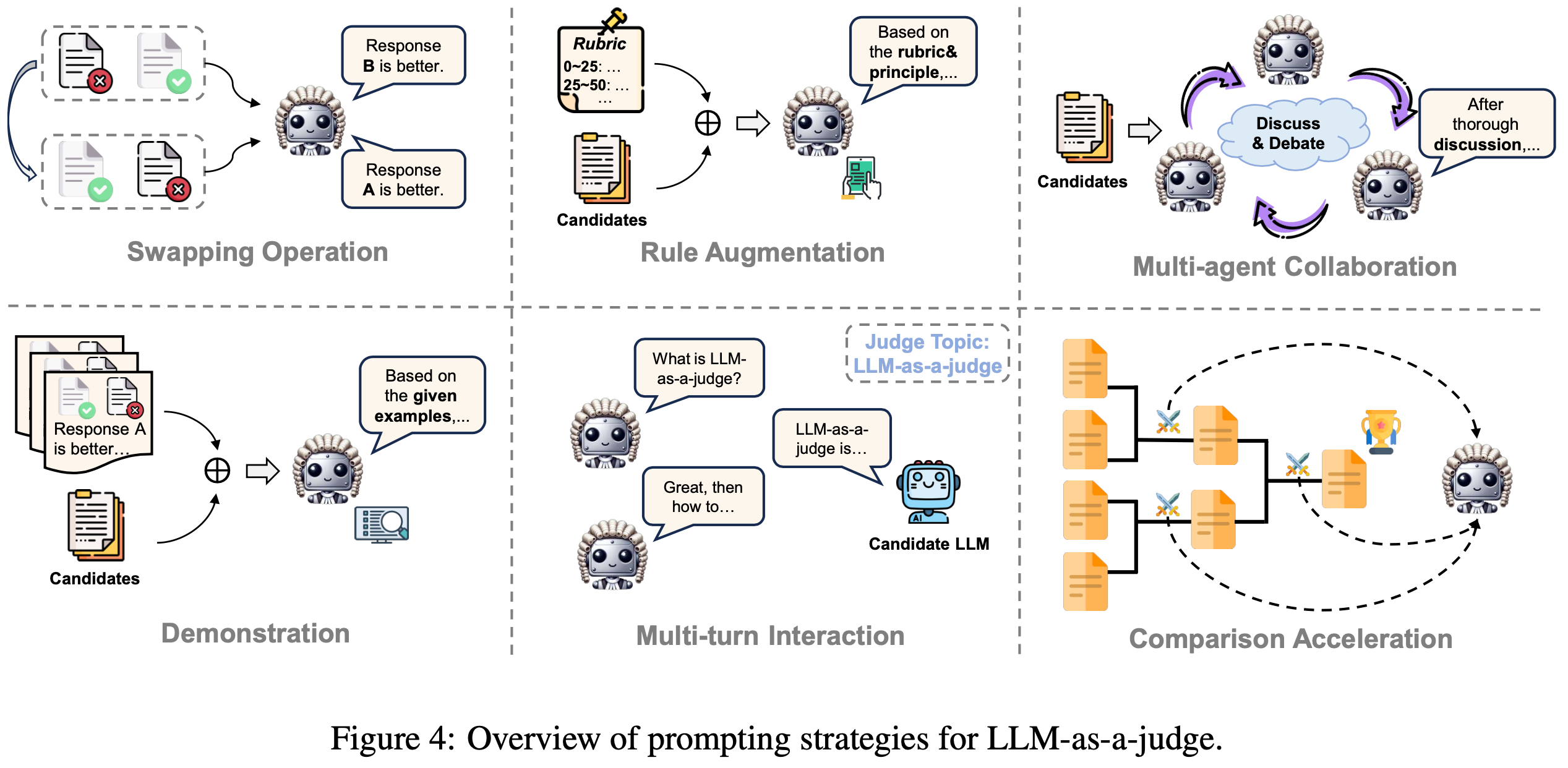
Swapping Operation
- 先前的研究表明, LLM-based 评判对候选的位置敏感,候选响应的质量排名很容易通过仅改变其在上下文中的顺序来操纵(2023c;2024;2023)
- 为了减轻这种位置偏差并建立更公平的 LLM 评判系统,交换操作(2023)已被引入并广泛采用
- 该技术涉及调用 Judge LLM 两次,在每个实例中交换两个候选的顺序
- 在评估中,如果交换后的结果不一致,则标记为“平局(tie)” ,表明 LLM 无法自信地区分候选的质量(2023)
- 几项研究还在自我对齐(2023;2024a;2024)中纳入了交换操作,以从 Judge LLM 获得更准确的成对反馈
- Zhu 等人(2024a)提出了一种类似思维链(CoT-like)的提示技术,通过要求模型首先提供所有成对排名,然后用排名列表进行总结来减轻位置偏差
Rule Augmentation
- 规则增强提示(Rule-augmented prompting)是指将一系列原则、参考依据和评估准则直接嵌入到 judge LLM 的提示指令中的方法
- 这种方法通常用于 LLM-based 评估,其中引导 Judge LLM 评估特定方面(2024e;2023a;2024d;2024),并为其提供详细的标准(2023b;2024g;2024;2024l,h;2024c)以确保公平比较
- Liu 等人(2024d)采用了一种独特的方法,提示 Judge LLM 通过对一组少样本示例的上下文学习来生成自己的评分标准。为了与 LLM-as-a-judge 保持一致,Bai 等人(2022)首先提出引入一系列原则(如帮助性、无害性、诚实性),使 Judge LLM 能够更精确和有方向地比较两个候选
- 紧随其后,后续工作(2023, 2024;2024;2024a;2024a)通过为原则或标准的每个方面纳入更详细的解释来增强这种基于原则的提示
- 此外,Li 和 Qiu(2023)以及 Li 等人(2024c)都提出提示 LLM 根据候选在解决特定问题中的帮助性来检索适当的演示/知识三元组
- 为了从 LLMs 获得多样化的响应,Lahoti 等人(2023)提示多个 LLM 评判每个候选的多样性,并选择最多样化的一个进行进一步优化
- Zhang 等人(2024g)提出了 RevisEval,其利用 LLM 的自我纠正能力自适应地修改响应,然后将修改后的文本作为后续评估的原则
- 最近,一些工作研究了 LLM 作为个性化评判的可靠性(2024;2024;2024),将 persona 作为原则的一部分提供给 LLMs,以进行个性化评判
Multi-agent Collaboration
- 由于 LLM 固有的各种偏差(2023c;2024;2023;2023a;2023c),访问单个 LLM 评判的结果可能不可靠
- 为了解决这一限制,Li 等人(2023a)引入了 Peer Rank(PR)算法,该算法考虑每个对等 LLM 对所有答案对的成对偏好,并生成模型的最终排名
- 在此基础上,出现了几种多智能体 LLM 的架构和技术,包括智能体混合(2023b)、角色扮演(2023)、辩论(2023;2024f;2024b)和投票(2024c;2024)。Jung 等人(2024)提出了级联选择性评估,其中成本较低的模型作为初始评判,仅在必要时升级到更强的模型(2024a)
- 此外,一些工作将多智能体协作应用于对齐数据合成,利用多个 LLM 评判来完善响应(2024)或提供更准确的成对反馈(2024i)
- 最近,(2024m)提出了 MATEval,其中所有智能体均由 GPT-4 等 LLM 扮演
- MATEval 框架模仿人类协作讨论方法,整合多个智能体的交互以评估开放式文本
Demonstration
- 上下文中的样本或演示(2020;2023;Agarwal 等人)为 LLM 提供了可遵循的具体示例,并已被证明是 LLM 上下文学习成功的关键因素
- 几项研究引入了人类评估结果作为 LLM-as-a-judge 的演示,旨在引导 LLM 从几个具体的上下文中学习评估标准
- Jain 等人(2023b)是第一个探索大型语言模型作为多维评估器在上下文学习中的功效的研究,无需大量训练数据集
- Kotonya 等人(2023)对各种提示技术进行了系统实验,包括标准提示、基于注释器指令的提示和思维链提示,将这些方法与零样本和一样本学习相结合,以最大化评估效果
- 为了提高 LLM 评估的鲁棒性,Hasanbeig 等人(2023)提出了 ALLURE,一种通过迭代纳入显著偏差的演示来增强评估器鲁棒性的方法
- 此外,Song 等人(2024)引入并研究了两种多样本上下文学习(ICL)提示,使用两种版本的多样本 ICL 模板来帮助减轻 LLM 中的潜在偏差
Multi-turn Interaction
- 在评估中,单个响应可能无法为 LLM 评判提供足够的信息来全面和公平地评估每个候选的表现
- 为了解决这一限制,多轮交互通常被采用以提供更全面的评估
- 通常,该过程从初始查询或主题开始,随后在 Judge LLM 和候选模型之间进行动态交互
- Bai 等人(2023b)提出了一种多轮设置,其中评估器扮演面试官的角色,根据模型的先前答案提出越来越复杂的后续问题
- 类似地,Yu 等人(2024d)引入了 KIEval,一种基于知识的交互式评估框架,其新颖地纳入了一个 LLM 驱动的交互器,以实现动态、抗污染的评估
- 此外,一些方法促进候选之间的多轮辩论
- 例如,Zhao 等人(2024c)设计了一个框架,其中两个 LLM 围绕查询进行多轮 peer battle ,使它们的真实性能差异得以显现
- Moniri 等人(2024)提出了一个自动化基准系统,其中 LLM 进行辩论,最终评估由另一个 LLM 评判执行
Comparison Acceleration
- 在 LLM-as-a-judge 的各种比较格式中(如 Pointwise 和 Listwise ),成对比较是直接比较两个模型或生成成对反馈的最常用方法
- 然而,当需要对多个候选进行排名时(注:需要凉凉进行排列),这种方法可能非常耗时(2024)
- 为了减轻计算开销,Zhai 等人(2024)提出了一种排名配对方法,所有候选首先与空白基线响应进行比较 ,然后根据每个候选与基线的比较表现确定其排名
- Zhu 等人(2024a)提出了一种类似 CoT 的提示技术,通过强制模型首先提供所有成对排名,然后用列表总结这些成对排名来减轻位置偏差
- 此外,Lee 等人(2024)在推理期间利用基于 tournament 的方法(2023a;2023c)进行拒绝采样,以加速成对比较
- 他们构建了一个 tournament 树,其中叶节点表示采样的响应,非叶节点根据子节点之间的评判结果进行选择
Application
- 尽管“LLM-as-a-judge ”最初是为评估应用而提出的,但其使用范围已大幅扩展到许多其他场景,如对齐、检索和推理
- 因此,如图 5 所示,论文将全面介绍 LLM-as-a-judge 如何应用于各种领域
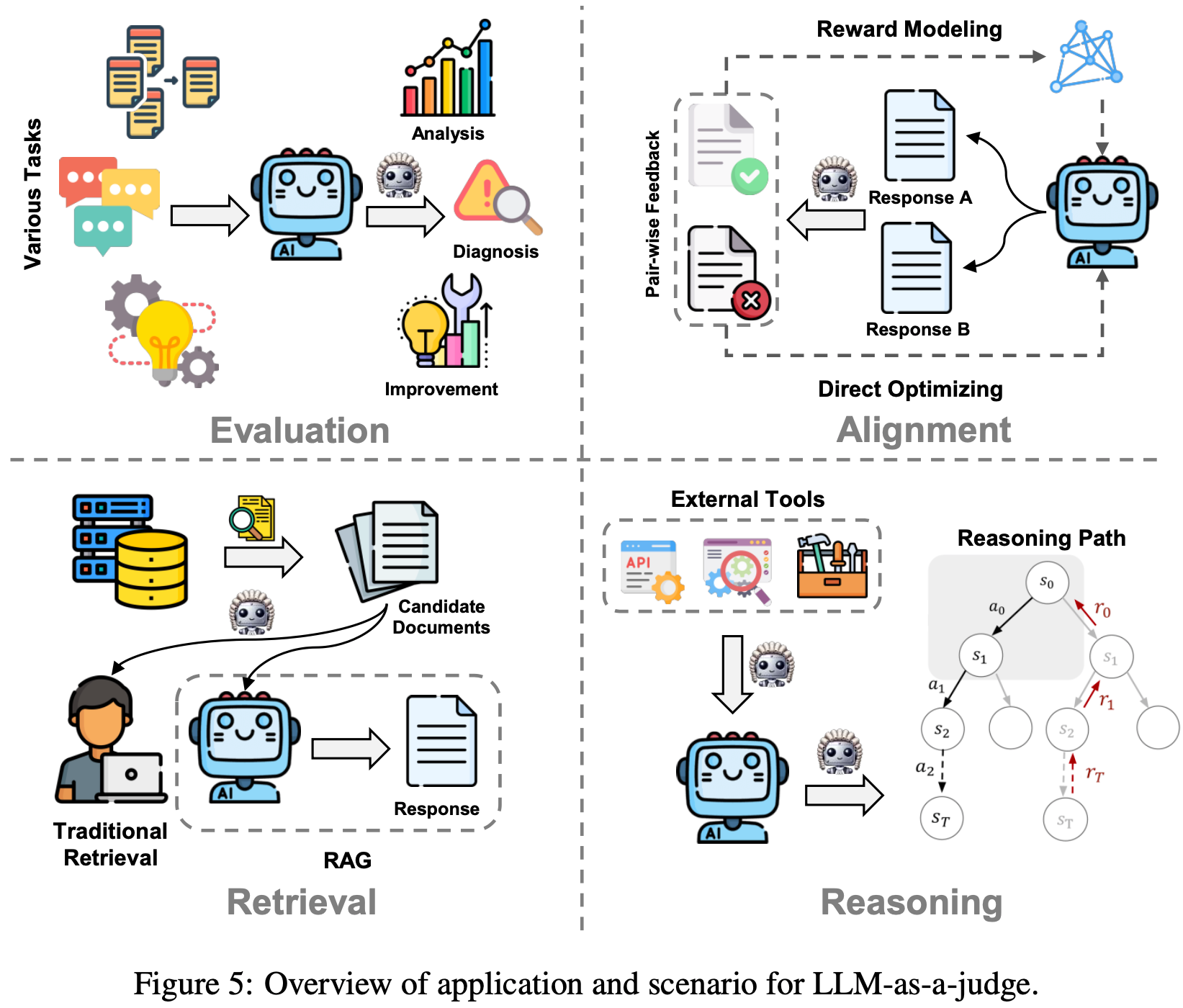
Evaluation
- 自然语言处理中的传统评估依赖于预定义标准,通常通过指标来评估机器生成文本的质量
- 一些著名的指标,如 BLEU、ROUGH 和 BERTScore 已在该领域广泛使用
- 然而,基于指标的评估过度强调词汇重叠和相似性,当需要考虑许多有效响应和更细微的语义属性时,可能会显得不足(Post, 2018;2022)
- 为解决这些局限性,LLM-as-a-judge 已被用于充当自动化评判,以增强许多任务的评估(2023b;2024)
- LLM-as-a-judge 能够进行类似人类的定性评估,而不仅仅是对机器生成输出与 ground truth 的匹配程度进行简单的定量比较
- 本节将讨论 LLM-as-a-judge 如何被用于评估开放式生成、推理和更多新兴 NLP 任务
Open-ended Generation Tasks
- 开放式生成指的是生成内容应安全、准确且上下文相关的任务,尽管没有单一的“正确”答案
- 此类任务包括对话响应生成、摘要、故事生成和创意写作(2024;2023a;2024;2024;Bermejo, 2024)。与传统的基于指标的评估方法不同,LLM-as-a-judge 提供了更细致、适应性更强的定制化评估
- 正如 Zheng 等人 (2023) 所指出的,像 GPT-4 这样的 LLM 在评判开放式文本生成方面表现得可与人类媲美
- 在实践中,LLM-as-a-judge 已被应用于评估单个模型的输出,以及在竞争环境中比较多个模型的输出
- 例如,Gao 等人 (2023b) 使用 ChatGPT 进行类似人类的摘要评估
- 同样,Wu 等人 (2023) 提出了一个基于比较的框架,让 LLMs 充当具有多种角色扮演的评判,以特定维度评估摘要质量并生成评估结果
- 现代 LLM 擅长生成详细的长文本响应。然而,随着输出长度的增加,产生幻觉的可能性也随之增加
- 为了更好地理解这一现象,Cheng 等人 (2023) 和 Zhang 等人 (2024d) 引入了一种评估方法,使用 GPT-4 来评判生成的输出是否包含逻辑结构合理但无意义的陈述
- Wang 等人 (2024a) 提出了一个基于批判的评判系统,通过选择相关证据并提供深入批判来评估幻觉
- 除了幻觉之外,LLM 生成有害(如鼓励自杀)和不安全(如指导非法活动)响应的问题也备受关注
- 针对这一问题,Li 等人 (2024g) 引入了 MD-Judge 和 MCQ-Judge,用于评估与安全相关的问答对,尤其关注旨在引发不安全响应的查询。这种方法支持无缝且可靠的评估
- 然而,对不安全查询过于谨慎的态度可能导致过度拒绝响应,从而阻碍正常功能并对用户体验产生负面影响
- 为了探讨这一问题,Xie 等人 (2024a) 对各种 LLM-as-a-judge 的框架进行了元评估,评估了当前 LLMs 对潜在不安全查询的拒绝倾向
- 此外,(2024a) 引入了一个 LLM-based 答案提取器,以准确确定开放式生成中答案的关键部分
- 另外,An 等人 (2023) 提出了 L-Eval,这是一个 LLM-as-a-judge 的框架,旨在为长上下文语言模型建立更标准化的评估
- 这一概念得到了 Bai 等人 (2024) 的跟进,他们提议利用 LLM-as-a-judge 来过滤长上下文 LLMs 的评估数据
- 最近的研究还利用 LLM-as-a-judge 来评估生成模型的通用能力
- 这种方法通常采用基于辩论的框架,其中多个 LLMs 生成响应,随后由单独的 Judge LLM 进行评估
- 例如,Chan 等人 (2023) 引入了一个多智能体辩论框架,旨在促进自主讨论并评估开放式文本生成任务中不同 LLMs 生成响应的质量
- 类似地,Moniri 等人 (2024) 提出了一个自动化辩论框架,该框架不仅根据领域知识评估 LLMs,还评估它们在问题定义和不一致识别方面的能力
Reasoning Tasks
- LLMs 的推理能力可以通过它们在特定推理任务上的中间思维过程和最终答案来评估(2024;2024;2024c)
- 最近,LLM-as-a-judge 已被用于评估模型中间推理路径的逻辑进展、深度和连贯性
- 对于数学推理任务,Xia 等人 (2024) 引入了一个自动评估框架,使用专门设计的 Judge LLM 来评估问题解决过程中推理步骤的质量
- LLM-as-a-judge 还可以应用于更复杂的推理任务,如时间推理,其中模型需要理解不同事件在时间上的关系
- Fatemi 等人 (2024) 构建了合成数据集,专门用于评估 LLMs 在各种场景下的时间推理能力,测试它们在时间有序事件的序列、因果关系和依赖关系方面的推理熟练程度
- 大量的训练数据带来了一个挑战,即如何确定模型是通过深度逻辑理解进行推理,还是仅仅利用记忆模式(2024)
- Wang 等人 (2023a) 设计了一个辩论式框架来评估 LLMs 的推理能力。给定一个特定问题,LLM 和用户采取对立立场并讨论该主题,以达成正确的决策
- Nan 等人 (2024) 开发了一个多智能体评估框架,模拟学术同行评审过程
- 该框架让 LLM-as-a-judge 参与协作评审,为数据驱动任务中 LLMs 的推理能力提供了更细致的理解
Emerging Tasks
- 随着 LLMs 能力的快速发展,机器越来越多地被用于以前被认为是人类专属的任务,尤其是在特定上下文领域
- 一个突出的任务是社交智能,其中模型面临复杂的社交场景,需要理解文化价值观、伦理原则和潜在的社会影响
- 例如,Xu 等人 (2024a) 评估了 LLMs 的社交智能,强调尽管这些模型在学术问题解决能力方面取得了进步,但在社交智能方面仍明显落后
- 同样,Zhou 等人 (2023) 引入了 SOTOPIA 和 SOTOPIA-EVAL,以模拟 LLM 智能体之间的复杂社交互动并评估它们的社交智能
- 在他们的工作中,GPT-4 被用作人类评判的代理,以评估模拟互动中的目标完成度、财务管理和关系维护
- 另一项研究致力于评估大型多模态模型(LMMs)和大型视觉语言模型(LVLMs)
- 例如,Xiong 等人 (2024b) 探索了 LMM 作为评判来评估多模态模型的性能,提供最终分数和评估的基本原理,以提高透明度和一致性
- Chen 等人 (2024d) 提出了第一个用于 LVLMs 自动评估的基准,专门针对自动驾驶的边缘情况
- 他们发现,由 LLMs 作为评判进行的评估比由 LVLMs 作为评判进行的评估更符合人类偏好
- 最近,论文看到 LLM-as-a-judge 的更定制化应用,用于评估新兴任务,如
- 代码理解(2024a;2025;2024c;2024a;2024a;2024)
- 法律知识(2023)
- 游戏开发(Isaza-2024)
- 海洋科学(2023)
- 医疗对话(2024n)
- 辩论评判(2024a)
- 检索增强生成(2024)
- 跨能力(cross ability,2024)
- 人机交互(HCI)(2024j;2025;2024)
- 角色扮演(2024c)
- RAG(2024)
- 语音合成(2024b)
- 反语音生成(counterspeech generation,2025b,a)等
- 这一趋势反映了 LLM-as-a-judge 在评估多样化和专业领域方面的适应性日益增强
Alignment
- 对齐调优(2022a;2022)是使 LLMs 与人类偏好和价值观保持一致的重要技术
- 这一过程的一个关键组成部分是收集高质量的成对反馈,这对于奖励建模(2017)或直接偏好学习(2023)至关重要
- 最近,越来越多的研究兴趣集中在通过在对齐调优中采用 LLM-as-a-judge 来自动化这种成对反馈机制
Larger Models as Judges
- 在对齐调优中采用 LLM-as-a-judge 的一个直观想法是利用更大、更强的 LLMs 的反馈来指导较小、能力较弱的模型
- (2022) 首先提出利用 AI 的反馈来构建无害的 AI 助手
- 他们使用基于预训练语言模型偏好的合成偏好数据来训练奖励模型
- 在此基础上,Lee 等人 (2023) 发现,即使 LLM 评判不够强大,RLAIF 方法也能通过 RLHF 取得可比的性能
- 他们还引入了 DIRECT-RLAIF,直接使用现成的 LLM-as-a-judge 模型,以减轻奖励模型中的奖励陈旧问题
- 为了避免对齐中的奖励欺骗,Sun 等人 (2024a) 设计了一个可指示的奖励模型,该模型在合成偏好数据上训练
- 它使人类能够在 RL 时间进行干预,以更好地使目标策略与人类价值观保持一致
- 除了上述研究之外,Guo 等人 (2024) 引入了在线 AI 反馈(OAIF),直接利用注释模型的偏好信号来训练目标模型
- 还有一些工作利用多智能体合作来在对齐调优中获得更好的评判
- Arif 等人 (2024) 和 (2024) 使用多智能体工作流构建合成偏好优化数据集,并采用具有各种提示策略和 Pipeline 的 LLMs 作为评判
- 类似地,(2024i) 利用多个 LLMs 相互辩论,迭代提高响应质量,同时创建一个 Judge LLM 来选择偏好的响应,以增强指令调优
- 为了使生成的代码与人类偏好保持一致,Weyssow 等人 (2024) 引入了 CodeUltraFeedback,这是一个使用 LLM-as-a-judge 方法构建的偏好编码数据集
- 这个合成数据集后来被用于使用 SFT 和 DPO 对小型代码 LLMs 进行微调和对齐
- 最近,Wang 等人 (2024f) 提出了 BPO,使用 GPT-4 作为评判,并在对齐过程中构建合成成对反馈,以实现知识深度和广度的平衡
Self-Judging
- 另一类工作旨在利用同一 LLM 的偏好信号来自我改进
- Yuan 等人 (2024e) 首先提出了自我奖励 LLM 的概念,其中通过让 LLM 自身充当评判来构建成对数据
- 紧随其后,Wu 等人 (2024a) 引入了元奖励,对 LLMs 的评判进行评判,并使用反馈来改进它们的评判技能
- 他们的 LLM 作为元评判的方法显著增强了模型评估和遵循指令的能力
- 为了提高合成数据质量:
- Pace 等人 (2024) 结合了 Best-of-N 和 Worst-of-N 采样策略,并引入了 West-of-N 方法
- Lee 等人 (2024) 设计了 Judge 增强监督微调(Judge augmented Supervised Fine-Tuning,JSFT),以训练单个模型同时充当策略和评判
- 为了充分利用这个评判模型,他们还提出了通过 tournament 进行自我拒绝的方法,以在推理时选择最佳响应
- 与上述使用 LLM-as-a-judge 来构建成对数据的方法不同,Tong 等人 (2024) 将 LLM-as-a-judge 应用于自我过滤方法,以确保对齐任务中合成数据对的质量,用于推理
- 为了减少成对评判中的计算开销,Zhai 等人 (2024) 提出了一种用于自我偏好语言模型的排名配对方法,通过测量每个响应相对于基线的强度来加速比较过程
- Liu 等人 (2024e) 引入了元排名(meta-ranking),使较弱的 LLMs(2024b)能够充当可靠的评判并提供可信赖的反馈。他们还将元排名方法应用于 SFT 后训练,将其与 Kahneman-Tversky 优化(KTO)结合使用,以改进对齐
- 为了提高合成指令调优数据的质量,Liang 等人 (2024c) 引入了迭代自我增强范式(I-SHEEP)。在训练期间,他们采用 LLM-as-a-judge 来为合成响应评分,并设置阈值来收集高质量的查询-响应对,用于后续训练迭代
- 最近,Yasunaga 等人 (2024) 提出将 LLM-as-a-judge 与数据合成相结合,并成功构建了只需少量注释即可与人类对齐的 LLMs
- 几项工作还在特定领域或针对特定属性采用了 LLM-as-a-judge
- Zhang 等人 (2024h) 提出了一种自我评估机制,通过生成问答对来评判响应的事实性。然后,他们利用这些自我注释的响应通过 DPO 算法对模型进行微调,以提高事实性
- 在机器人技术中,Zeng 等人 (2024) 利用 LLMs 的自我排名响应来迭代更新奖励函数,从而在没有人类监督的情况下提高学习效率
- 在多模态领域,Ahn 等人 (2024) 提出了迭代自我回顾评判(iterative self-retrospective judgment, i-SRT),该方法采用自我反思来改进响应生成和偏好建模
Retrieval
- LLM-as-a-judge 在检索中的作用包括传统文档排名和更动态的、上下文自适应的检索增强生成(Retrieval-Augmented Generation,RAG)方法
- 在传统检索中,LLMs 通过先进的提示技术提高排名准确性,使它们能够在几乎没有标记数据的情况下按相关性对文档进行排序
- 作为补充,RAG 框架利用 LLMs 生成内容的能力,这些内容由检索到的信息引导,支持需要复杂或不断发展的知识整合的应用
- 这些技术共同强调了 LLMs 作为检索任务评判的适应性,从基础排名到特定领域的知识增强应用
Traditional Retrieval
- 最近的研究探索了 LLMs 作为评判在信息检索中对文档进行排名的作用,旨在提高排名精度并减少对大量训练数据的依赖
- Sun 等人 (2023) 探索了像 GPT-4 这样的生成式 LLMs 在信息检索中进行相关性排名的潜力
- 他们提出了一种基于排列的方法来按相关性对段落进行排名,指示 LLMs 输出段落的有序排列,从而提高排名精度
- 作为补充,Zhuang 等人 (2024a) 引入了一种方法,将细粒度的相关性标签 Embedding 到 LLM 提示中,使模型能够区分细微的相关性变化并产生更精细的文档排序
- Listwise 排名的进一步创新由 Ma 等人 (2023) 展示,他们提出了使用大型语言模型的 Listwise 重新排序器(LRL),这是一种直接对文档标识符进行重新排序的工具,无需依赖特定任务的训练数据。此外,Zhuang 等人 (2024b) 提出了一种适用于零样本排名的集合式提示策略,通过减少 LLM 推理频率和标记使用来简化排名操作,在不牺牲性能的情况下提高了效率
- Sun 等人 (2023) 探索了像 GPT-4 这样的生成式 LLMs 在信息检索中进行相关性排名的潜力
- 为了解决位置偏差(这是 Listwise 排名任务中的常见挑战),Tang 等人 (2024b) 引入了排列自我一致性技术,该技术对多个列表顺序进行平均,以产生与顺序无关的排名。这种方法有效减少了位置偏差,这在 LLM 驱动的 Listwise 排名中是一个特别成问题的问题
- 最后,Qin 等人 (2024) 批评了现有方法中点式和 Listwise 排名提示的局限性,指出典型的 LLMs 往往缺乏理解复杂排名任务的深度
- 为了缓解这一问题,他们提出了使用中等规模开源 LLMs 的成对排名提示(PRP),作为更昂贵的大型专有模型的有效且经济的替代方案
- 除了一般检索任务之外,LLMs 还证明了它们作为专门应用评判的实用性。例如,Ma 等人 (2024a) 概述了一个少样本工作流程,该流程使用通用 LLM 进行法律信息检索中的相关性评判。该模型通过将任务分解为多个阶段,实现了与专家注释的高度一致性,促进了专家推理的整合,以提高法律环境中相关性评估的准确性
- 在推荐系统中,Hou 等人 (2024) 研究了 LLMs 将项目排名视为条件排名任务的潜力。该框架考虑了用户交互历史以及候选项目,解决了 LLMs 已知的偏差,例如倾向于偏爱流行或排名靠前的项目。采用了专门的提示和引导技术来纠正这些偏差并提高解释准确性
- 最后,在搜索系统领域,Thomas 等人 (2023) 发现 LLMs 在预测搜索者偏好方面的表现可与人类标注者相媲美,使它们成为识别高性能系统和标记具有挑战性查询的有价值工具。这项研究强调了 LLMs 作为复杂检索任务评判的有效性,能够在各种应用中实现更细致和准确的相关性评估
Retrieval-Augmented Generation, RAG
- 检索增强生成(RAG)的最新发展探索了 LLMs 自我评估和自我改进的能力,无需注释数据集或参数调整(2024e)
- Li 和 Qiu (2023) 引入了思维记忆(MoT)框架,这是一个两阶段自我反思模型,自主增强 LLM 的推理能力
- 在第一阶段,模型在未标记数据集上生成高置信度推理,将其存储为记忆
- 在测试阶段,模型通过评判每个记忆与当前问题的相关性来回忆这些记忆,并选择最相关的记忆作为演示
- 类似地,Tang 等人 (2024a) 提出了自我检索,这是一种创新架构,通过自然语言索引将信息检索(IR)能力整合到单个 LLM 中,以将语料库内化。这种方法将检索转变为文档生成和自我评估过程,在单个模型中实现了完全端到端的 IR 工作流程
- 此外,Asai 等人 (2024) 提出了 SELF-RAG(Self-Reflective Retrieval-Augmented Generation,自我反思检索增强生成),该模型通过检索和自我反思循环提高 LLM 响应的质量和事实性。通过使用“反思标记”来指导适应性响应,SELF-RAG 使模型能够根据特定任务要求动态评判和调整其响应
- 在问答领域,LLMs 越来越多地被用作评估代理,以实时评估答案的相关性、质量和实用性
- Rackauckas 等人 (2024) 引入了一个 LLM-based 评估框架,该框架从实际用户交互和特定领域文档生成合成查询
- 在这个框架中,LLMs 充当评判,评估检索到的文档并通过 RAGElo(一种基于 Elo 的自动竞争)对 RAG 智能体变体进行排名
- 这种结构为 QA 系统中的质量控制提供了可扩展的解决方案
- Rackauckas 等人 (2024) 引入了一个 LLM-based 评估框架,该框架从实际用户交互和特定领域文档生成合成查询
- 此外,Zhang 等人 (2024b) 对 LLMs 评估开放域 QA 中相关性与实用性的能力进行了广泛研究。他们的发现表明,LLMs 可以有效区分两者,并且在呈现反事实段落时具有高度适应性
- 这种实用性评估能力使 LLMs 能够在评估过程中提供更细致和上下文相关的响应
- 针对特定领域的 RAG 系统揭示了 LLMs 通过整合专业知识结构来导航复杂查询的潜力
- 在特定领域检索中,Wang 等人 (2024b) 提出了 BIORAG,这是一种先进的 RAG 框架,通过分层知识结构增强向量检索
- BIORAG 采用自我意识评估检索器来持续评判其收集信息的充分性和相关性,从而提高检索文档的准确性
- 对于生物医学研究,Li 等人 (2024c) 引入了 DALK(LLMs 和知识图谱的动态协同增强),这是一种新颖的系统,将 LLM 与从科学文献中派生的不断发展的阿尔茨海默病(AD)知识图谱相结合
- 使用新颖的自我意识知识检索方法,DALK 利用 LLMs 的评判能力进行噪声过滤,增强 LLM 在 AD 相关查询中的推理性能
- 类似地,Jeong 等人 (2024) 提出了 SelfBioRAG,这是一种将 RAG 原理应用于生物医学应用的框架
- Self-BioRAG 采用 LLM 来选择最佳证据并基于所选证据和编码知识生成答案
- 最近,(Déjean, 2024) 提炼了一个 LLM-as-a-judge ,从 LLMs 的参数记忆中提取检索结果
Reasoning
- 释放 LLMs 的推理能力提供了一种缓解缩放定律局限性的方法,仅靠缩放定律可能无法充分揭示模型的潜力
- 推理是 LLMs 的一个关键方面,因为它直接影响它们解决复杂问题、做出决策和提供准确的上下文感知响应的能力
- 最近,许多关于 LLMs 推理能力的研究都集中在如何利用 LLM-as-a-judge 来选择推理路径(5.4.1 节)和利用外部工具(5.4.2 节)
Reasoning Path Selection
- Wei 等人 (2022b) 引入了思维链(CoT)提示的概念,以鼓励模型生成逐步推理过程。虽然已经提出了其他更复杂的认知结构(2023a;2023)来增强 LLMs 的推理能力,但一个关键挑战是如何为 LLMs 选择合理且可靠的推理路径或轨迹以遵循
- 为了解决这个问题,许多工作采用了 LLM-as-a-judge
- 一些工作专注于推理过程中的样本级选择
- (2023a) 引入了策略评估器,以在验证集上进一步评估候选策略
- (2024) 引入了 REPS(Rationale Enhancement through Pairwise Selection, 通过成对选择增强理由),通过使用 LLMs 进行成对自我评估来评判和选择有效理由,并基于这些数据训练验证器(verifier)
- LLMs 的另一个推理路径选择问题是多样性,Lahoti 等人 (2023) 发现 LLMs 掌握了多样性的概念,并且可以识别响应缺乏多样性的方面。通过选择和聚合多个批评意见,LLMs 可以取得类似的收益,与多次批评和修订迭代相比
- 在多智能体协作框架中,Liang 等人 (2023) 提出了多智能体辩论(multi-agent debating,MAD),这是一种促进多个智能体之间辩论和讨论的新范式。他们利用 Judge LLM 在辩论过程结束时选择最合理的响应作为最终输出
- 类似地,Li 等人 (2024b) 在基于层的多智能体协作中提出了新角色,采用 Judge LLM 来选择高质量和合理的响应,从而显著提高整个系统的标记利用效率
- 此外,还有许多工作专注于步骤级推理路径选择,利用 Judge LLM 作为过程奖励模型(process reward model,PRM)来评估状态分数。Creswell 等人 (2023) 将推理过程分解为选择和推理。在选择步骤中,他们利用 LLM 本身来评判和评估每个潜在的推理轨迹,选择合适的轨迹用于后续推理步骤
- Xie 等人 (2024b) 提出了 Kwai-STaR 框架,该框架将 LLMs 转变为状态转换推理器,以在数学推理中为自己评判和选择最佳推理状态。Lightman 等人 (2023) 训练 LLM 作为 PRM 来进行推理时监督,并在推理阶段执行 Best-of-N 采样策略
- 紧随其后,Setlur 等人 (2024) 进一步提出了过程优势验证器(process advantage verifiers,PAVs),基于未来产生正确响应的可能性变化生成奖励。其他工作模拟高级认知结构作为推理过程
- Hao 等人 (2023) 采用 LLMs 作为世界模型来模拟环境状态,并执行蒙特卡洛树搜索(Monte Carlo Tree Search,MCTS)以提高需要谨慎路径选择的任务的性能
- Besta 等人 (2024) 将 LLMs 生成的输出视为任意图(arbitrary graph)
- LLM 思维被建模为顶点,而边是思维之间的依赖关系
- 该框架能够对每个推理状态的连贯性和逻辑推理进行系统评判
- Yao 等人 (2023a) 提出了思维树(ToT),其中每个思维都作为解决问题的中间步骤
- 它将推理分解为多个步骤,在每个状态进行自我评估和评判进展,并使用带有 LMs 的搜索算法通过前瞻和回溯来评判思维路径
- 此外,还有一些研究训练基于批评的 LLM 评判(2024;2024b;2024e;2024b;2024;2024),这些评判提供细粒度的口头反馈以促进推理过程
Reasoning with External Tools
- Yao 等人 (2023b) 首先提出以交错方式使用 LLMs 来生成推理轨迹和特定任务的动作
- 推理轨迹帮助模型评判和更新动作计划,而动作使其能够与外部源交互
- 随后,Auto-GPT 由 (2023) 引入,通过将 LLM-as-a-judge 用于工具使用,提供更准确的信息
- 通过配备一系列外部复杂工具,LLMs 变得更加通用和有能力,通过评判和推理使用哪些工具来提高规划性能
- Sha 等人 (2023) 探索了 LLMs 在推理和评判方面的潜力,将它们用作需要人类常识理解的复杂自动驾驶场景的决策组件
- Zhou 等人 (2024d) 利用自我发现过程,其中 LLMs 根据给定的查询进行评判,并选择最可行的推理结构用于后续推理阶段
- 尽管 LLMs 在各种工具的评判能力方面表现出色,但选择使用哪个模型或 API 通常涉及性能和成本之间的权衡
- 更强大的模型虽然有效,但成本也更高,而能力较弱的模型则更具成本效益
- 为了解决这个难题,(2024) 的作者提出了一个路由模型,该模型可以在评判过程中动态选择较强或较弱的 LLM ,旨在平衡成本和响应质量
- 出于效率考虑,类似地,Zhao 等人 (2024b) 引入了 DiffAgent,作为一种旨在根据用户特定提示评判和选择不同文本到图像 API 的智能体
- DiffAgent 的评判与人类偏好更一致,优于传统的 API 选择方法
Benchmark: Judging LLM-as-a-judge
- 对 LLM 作为评判的评估需要强大且目标明确的基准,以捕捉这一任务的多方面性质
- 论文将现有基准按以下维度分类:通用性能、偏差量化、领域特定性能、多模态评估、多语言能力、评估指令遵循、脆弱性评估和挑战性任务性能
- 这一分类法展示了LLM作为评判评估框架的多样化目标,为分析其设计、范围和影响提供了结构化视角
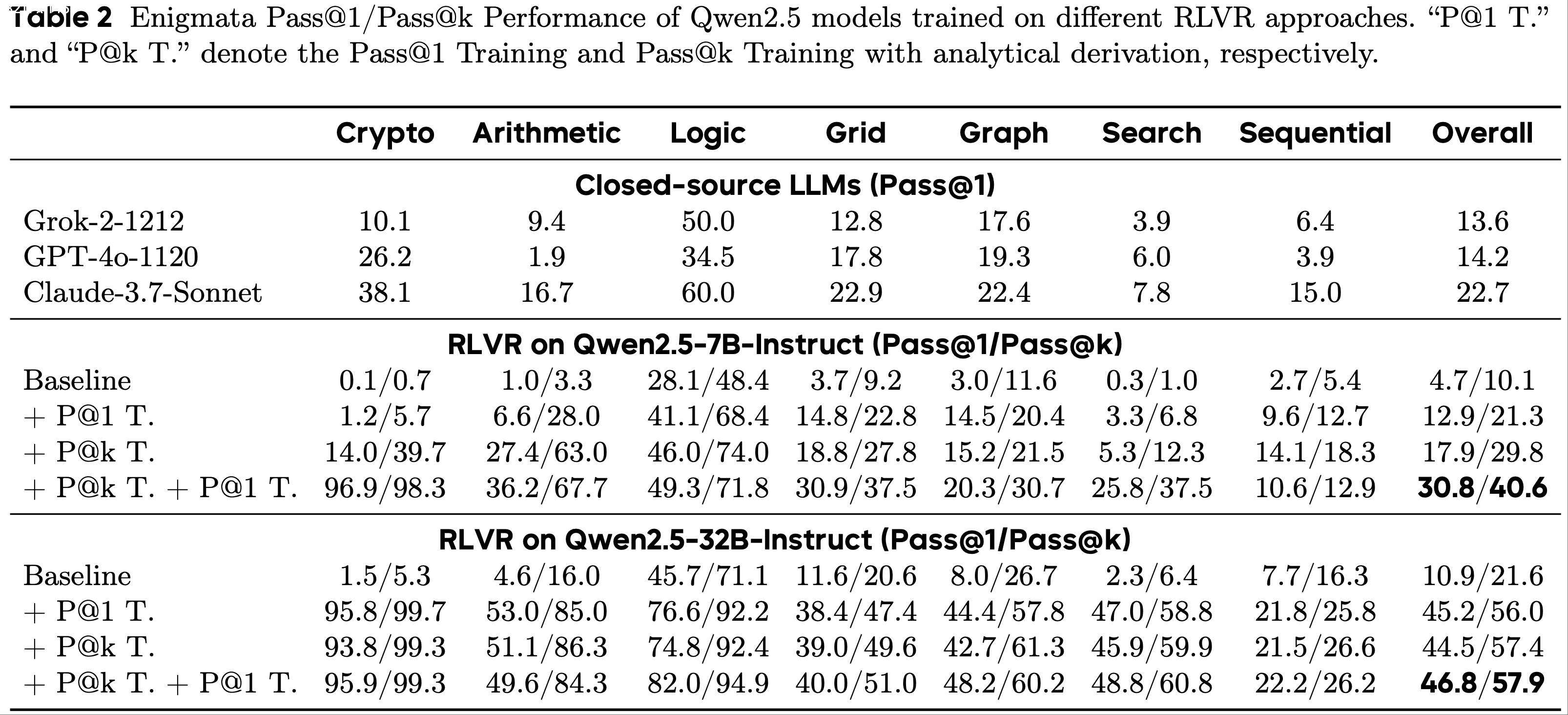
- 表 2 展示了LLM作为评判的各种基准和数据集的集合
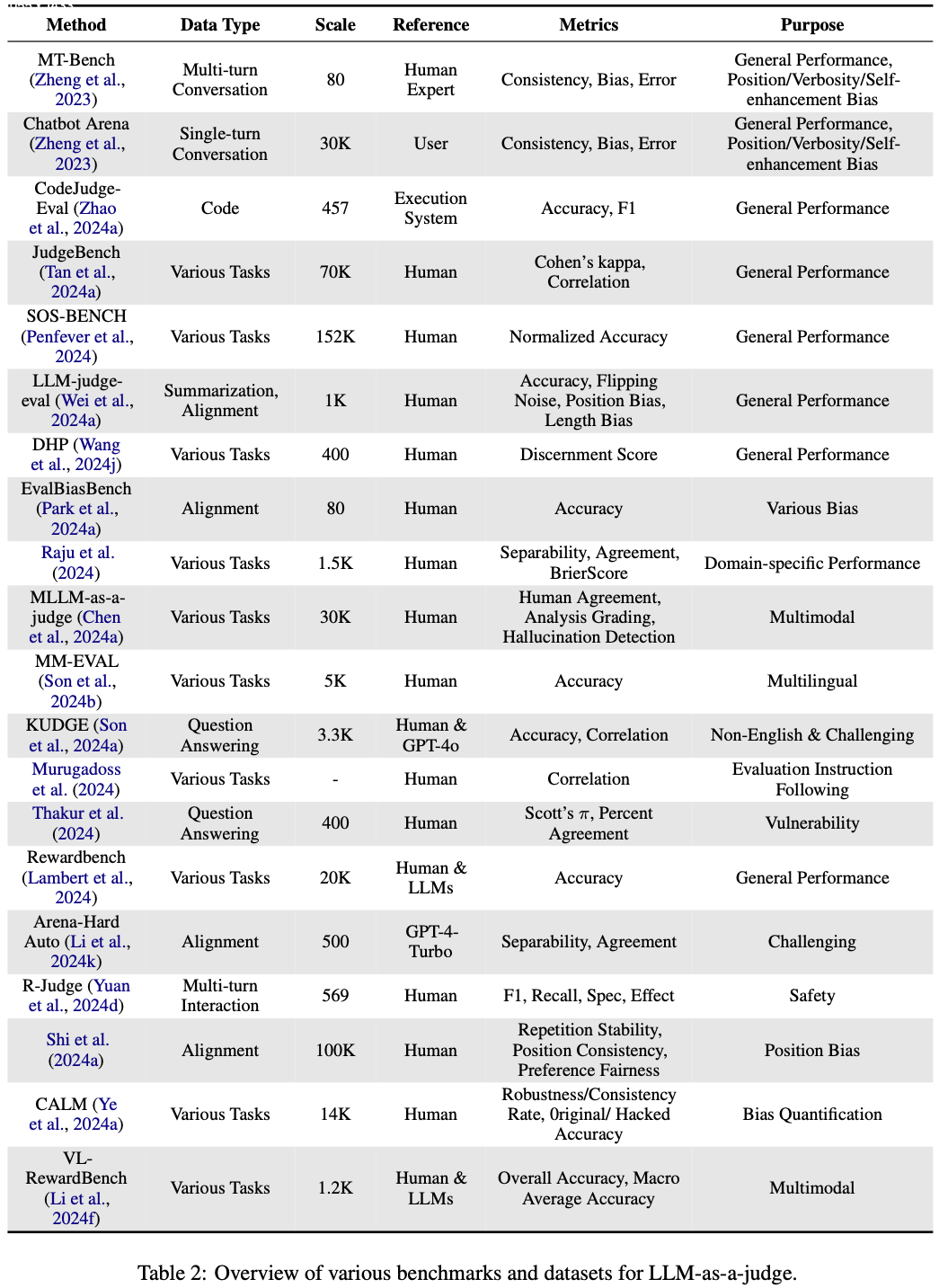
General Performance
- 专注于通用性能的基准旨在评估LLM在各种任务中的整体能力。这些基准通常测量与人类评判的一致性、准确性和相关性
- 值得注意的例子包括:
- MT-Bench和Chatbot Arena(2023),使用一致性、偏差和错误等指标评估对话场景
- 这些基准进一步探索特定偏差,包括位置偏差、冗长偏差和自我增强倾向
- JUDGE-BENCH(2024a)、DHP(2024j)、RewardBench(2024)、SOS-BENCH(2024)和JuStRank(2024),它们在更大规模上运行,使用Cohen’s kappa、辨别分数和标准化准确性等指标来基准化通用LLM性能
- LLM-judge-eval(2024a),评估摘要和对齐等任务,并使用额外指标如翻转噪声和长度偏差
- MT-Bench和Chatbot Arena(2023),使用一致性、偏差和错误等指标评估对话场景
Bias Quantification
- 减轻LLM评判中的偏差对于确保公平性和可靠性至关重要(Schroeder和Wood-Doughty, 2024)。典型基准包括EvalBiasBench 和CALM(2024a),它们明确专注于量化偏差,包括从对齐中出现的偏差和对抗条件下的鲁棒性偏差。此外,Shi等人 (2024a) 在问答任务中评估位置偏差和一致性百分比等指标
Challenging Task Performance
- 为困难任务设计的基准推动了LLM评估的边界。例如
- Arena-Hard Auto(2024k)、JudgeBench(2024a)和Yuan等人 (2024b) 分别针对对话式QA和各种推理任务,根据LLM的表现选择更难的问题
- CALM(2024a)探索对齐和挑战性场景,使用可分离性、一致性和破解准确性等指标,评估在手动识别的硬数据集上的性能
Domain-Specific Performance
- 领域特定基准提供了针对特定上下文的任务评估,以评估LLM的有效性
- 具体而言,Raju等人 (2024) 测量跨任务的可分离性和一致性,利用 Brier 分数等指标,深入了解编码、医疗、金融、法律和数学等特定领域
- CodeJudge-Eval(2024a)专门评估 LLM 对代码生成的评判,使用以执行为中心的指标如准确性和 F1 分数
- 这一想法也被后续代码摘要和生成评估的多项工作所采用(2024b;2024;2024;2024;2024;2024e;2024)(1-172, 1-173)
Other Evaluation Dimensions
- 除了通用性能和偏差量化,一些基准还解决了使用 LLM 作为评判的其他关键评估维度:
- 多模态(Multimodal) :MLLM-as-a-judge(2024a)将评估框架扩展到涉及多种数据模态的任务,专注于与人类评判的一致性、分析评分和幻觉检测
- 多语言(Multilingual) :MM-EVAL(2024b)和KUDGE(2024a)等基准评估多语言和非英语性能,测量准确性和相关性等指标,尤其在挑战性场景中
- 指令遵循(Instruction Following) :Murugadoss等人 (2024) 检查LLM遵循特定评估指令的程度,使用相关性指标量化性能
Challenges & Future Works
- 在本节中,论文概述了LLM作为评判的当前挑战和值得探索的未来方向,包括偏差与脆弱性、动态与复杂评判、自我评判以及人机协同评判
Bias & Vulnerability
- LLM 作为评判本质上将评估构建为生成任务,引入了与偏差和脆弱性相关的重大挑战
- 这些偏差通常源于模型的训练数据,其中常常嵌入(embeds)了与种族、性别、宗教、文化和意识形态等人口身份相关的社会刻板印象(2021)
- 当LLM被部署于多样化的评判任务时,此类偏差会显著损害公平性和可靠性
- 除了这些一般性偏差,当LLM充当评判时还会出现特定的评估偏差
- 位置偏差(Order Bias) 是一个突出问题,候选的顺序会影响偏好(2023;2023c;2023a;2024b)
- 这种偏差会扭曲评估结果,尤其是在成对比较中,当竞争响应之间的质量差距较小时更为明显(2024b;2023c)
- 自我中心偏差(Egocentric Bias) 出现时,LLM会偏爱同一模型生成的输出,损害客观性(2023c;2023a;2024;2024)
- 当评估指标使用同一模型设计时,这一问题尤为突出,会导致对源自该模型的输出评分虚高(2023c)
- 长度偏差(Length Bias) 是另一个普遍挑战,评估会不成比例地偏爱更长或更短的响应,而不论质量如何(2023;2023a)
- 其他偏差进一步复杂化了 LLM 评估,如:
- 错误信息忽视偏差(Misinformation Oversight Bias) :比如,错误信息忽视偏差反映了忽略事实性错误的倾向
- 权威偏差(Authority Bias) :比如,权威偏差偏爱来自所谓权威来源的陈述
- 美观偏差(Beauty Bias) :比如,美观偏差优先考虑视觉吸引力内容而非实质质量(2024b,e;2024)
- 冗长偏差(Verbosity Bias) 表现为偏爱更长的解释,通常将冗长等同于质量,这可能误导评判过程(2024c)
- 情感偏差(Sentiment Bias) 会使评估因情感基调而倾斜,偏爱带有积极表述的响应(2024a)
- 位置偏差(Order Bias) 是一个突出问题,候选的顺序会影响偏好(2023;2023c;2023a;2024b)
- LLM评判还极易受到对抗性操纵
- 诸如 JudgeDeceiver 等技术凸显了基于优化的提示注入攻击的风险,精心设计的对抗序列可操纵 LLM 评判以偏爱特定响应(2024a;2024;2024a;2024b)
- 同样,通用对抗短语可在绝对评分范式中大幅抬高分数,揭示了零样本评估设置的脆弱性(2023;2024;2024)
- 这些操纵引发了对 LLM 评判在排行榜、学术或法律评估等高风险场景中的可靠性的担忧(2024a;2024;2024e;2024)
- 为解决这些偏差和脆弱性,诸如 CALM(2024a)和 BWRS(2024b)等框架提供了系统的偏差量化和缓解方法
- 多重证据校准(Multiple Evidence Calibration, MEC)、平衡位置校准(Balanced Position Calibration, BPC)和人机协同校准(Human-in-the-Loop Calibration, HITLC)等技术已被证明在使模型评判与人类评估一致的同时减少位置偏差和其他偏差方面有效(2023c)
- 此外,认知偏差基准如 COBBLER 已识别出需要在 LLM 评估中系统缓解的六种关键偏差,包括显著性偏差和从众效应(2023b)
- 未来方向(Future Direction) :
- 未来研究的一个有希望的方向是将检索增强生成(RAG)框架集成到 LLM 评估过程中(2024e)
- 通过结合生成和检索能力,这些框架可通过将评估基于外部可验证的数据源来减少自我偏好和事实性问题等偏差
- 另一个有前景的途径是使用偏差感知数据集 ,如 OFFSETBIAS,以系统地解决 LLM 作为评判系统中的固有偏差(2024a)
- 将此类数据集纳入训练 Pipeline 可使 LLM 更好地区分表面特质与实质正确性,从而增强公平性和可靠性
- 探索微调 LLM 作为可扩展评判,如 JudgeLM 框架所示,代表了另一个有趣的方向(2023)
- 该框架中 Embedding 的交换增强和参考支持等技术可系统地减轻偏差,提高评估一致性,并将基于LLM的评判的适用性扩展到开放式任务
- 此外,推进零样本(zero-shot)比较评估框架具有重要前景(2023)
- 这些框架可完善成对比较技术并实施去偏策略,提高跨不同评估领域的公平性和可靠性,而无需广泛的提示工程或微调
- 最后,需要进一步探索抗 JudgeDeceiver 校准和对抗短语检测策略,以保护 LLM 作为评判框架免受攻击(2024a;2024;2024b;2024d;2024c)
- 未来研究的一个有希望的方向是将检索增强生成(RAG)框架集成到 LLM 评估过程中(2024e)
Dynamic & Complex Judgment
- 早期关于 LLM 作为评判的工作通常采用静态和直接的方法,直接提示评判 LLM 执行评估(2023)
- 最近,已提出更多动态和复杂的评判 Pipeline 来解决各种限制,提高LLM作为评判的鲁棒性和有效性
- 一个方向上的方法遵循“LLM-as-a-examiner”的概念,系统根据候选 LLM 的表现动态交互地生成问题和评判(2024d;2023a;2024a)
- 其他工作专注于基于两个或更多候选 LLM 的对抗和辩论结果进行评判(2024;2024c)
- 这些动态评判方法极大地提高了评判 LLM 对每个候选的理解,并可能防止 LLM 评估中的数据污染问题(2024)
- 此外,构建复杂和精密的评判 Pipeline 或智能体是另一个流行的研究领域(2023a;2023;2024;2024)
- 这些方法通常涉及多智能体协作,以及精心设计的规划和记忆系统,使评判 LLM 能够处理更复杂和多样化的评判场景
- 未来方向(Future Direction) :
- 未来研究的一个有希望的方向是赋予 LLM 类似人类的评判能力(2024c;2024b;2024)
- 这些设计可借鉴人类评判时的行为,如锚定与比较、后见之明与反思,以及元评判(meta-judgment)
- 另一个有趣的途径是开发使用 LLM 的自适应难度评估系统(adaptive difficulty assessment system, 2024)
- 该系统将根据候选的当前表现调整问题难度
- 这种自适应和动态系统可解决 LLM 评估中的一个重大限制,因为静态基准通常无法准确评估具有不同能力的LLM
Self-Judging
- LLM-based 评估器,如 GPT-4,广泛用于评估输出,但面临重大挑战:
- 尤其是自我中心偏差(Egocentric Bias) ,即模型偏爱自己的响应而非外部系统的响应(2023b;2023a;2023;2025)
- 这种自我偏好破坏了公正性,造成了“先有鸡还是先有蛋”的困境:强大的评估器对开发强大的 LLM 至关重要,而推进 LLM 又依赖于无偏的评估器
- 其他问题包括自我增强偏差(Self-Enhancement Bias) ,模型会高估自己的输出(2023a),以及奖励欺骗(Reward Hacking),对特定信号的过度优化导致评估的泛化能力降低(2024a)
- 此外,对静态奖励模型的依赖(Static Reward Models)限制了适应性,而位置(Positional)和冗长(Verbosity)等偏差通过偏爱响应顺序或长度而非质量来扭曲评判(2024e;2024i)
- 人类注释的高成本和有限可扩展性进一步复杂化了动态和可靠评估系统的创建(2022;2022)
- 尤其是自我中心偏差(Egocentric Bias) ,即模型偏爱自己的响应而非外部系统的响应(2023b;2023a;2023;2025)
- 未来方向(Future Direction) :
- 未来研究的一个有希望的方向是开发如 Peer Rank and Discussion(PRD)(2023a)这样的协作评估框架
- 这些框架利用多个 LLM 集体评估输出,使用加权成对评判和多轮对话来减少自我增强偏差,并使评估更接近人类标准
- 另一个有趣的途径是采用自教评估器框架,生成合成偏好对和推理轨迹,以迭代改进模型评估能力(2024i)
- 这种方法消除了对昂贵人类注释的依赖,同时确保评估标准适应不断发展的任务和模型
- 集成自我奖励语言模型(Self-Rewarding Language Models, SRLM)提供了另一条有前景的路径(2024e)
- 通过采用如直接偏好优化(DPO)等迭代机制,这些模型持续改进其指令遵循和奖励建模能力,缓解奖励欺骗和过拟合问题
- 在 SRLM 的基础上,使用元奖励机制引入元评判角色,以评估和改进评判质量(2024a)
- 这一迭代过程解决了冗长和位置等偏差,增强了对齐和评估复杂任务的能力
- 最后,利用合成数据创建生成对比响应为训练评估器提供了可扩展的解决方案(2024i)
- 通过在合成偏好对上迭代改进评估,模型可逐步提高其鲁棒性和适应性
- 将这些方法与多样化基准(2022;2022)、多方面评估标准(2020)和人类反馈(2023;2022)相结合,可确保评估在各个领域公平、可靠且与人类期望一致
- 未来研究的一个有希望的方向是开发如 Peer Rank and Discussion(PRD)(2023a)这样的协作评估框架
Human-LLMs Co-judgement
- 如前所述,LLM 作为评判中的偏差和脆弱性可通过人类参与评判过程进行进一步干预和校对来解决。然而,仅有少数研究关注这一方法
- Wang 等人 (2023c) 引入了人机协同校准,采用平衡位置多样性熵来衡量每个示例的难度,并在必要时寻求人类协助
- 在相关性评判背景下,Faggioli等人 (2023) 提出了人机协作光谱,根据人类依赖机器的程度对不同相关性评判策略进行分类
- 未来方向(Future Direction)*
- 随着数据选择(2023;2024)成为提高 LLM 训练和推理效率的日益流行的研究领域,它也有望提升 LLM 评估
- LLM 作为评判可从数据选择中汲取灵感,使评判 LLM 能够作为关键样本选择器,根据特定标准(如代表性或难度)选择一小部分样本供人类注释者评估
- 此外,人机协同评判的发展可受益于其他领域成熟的人机交互解决方案,如数据标注(2024b)和主动学习(2023)


















](/Notes/NLP/NLP——开源大模型结构汇总/Llama-Architecture1.jpg)

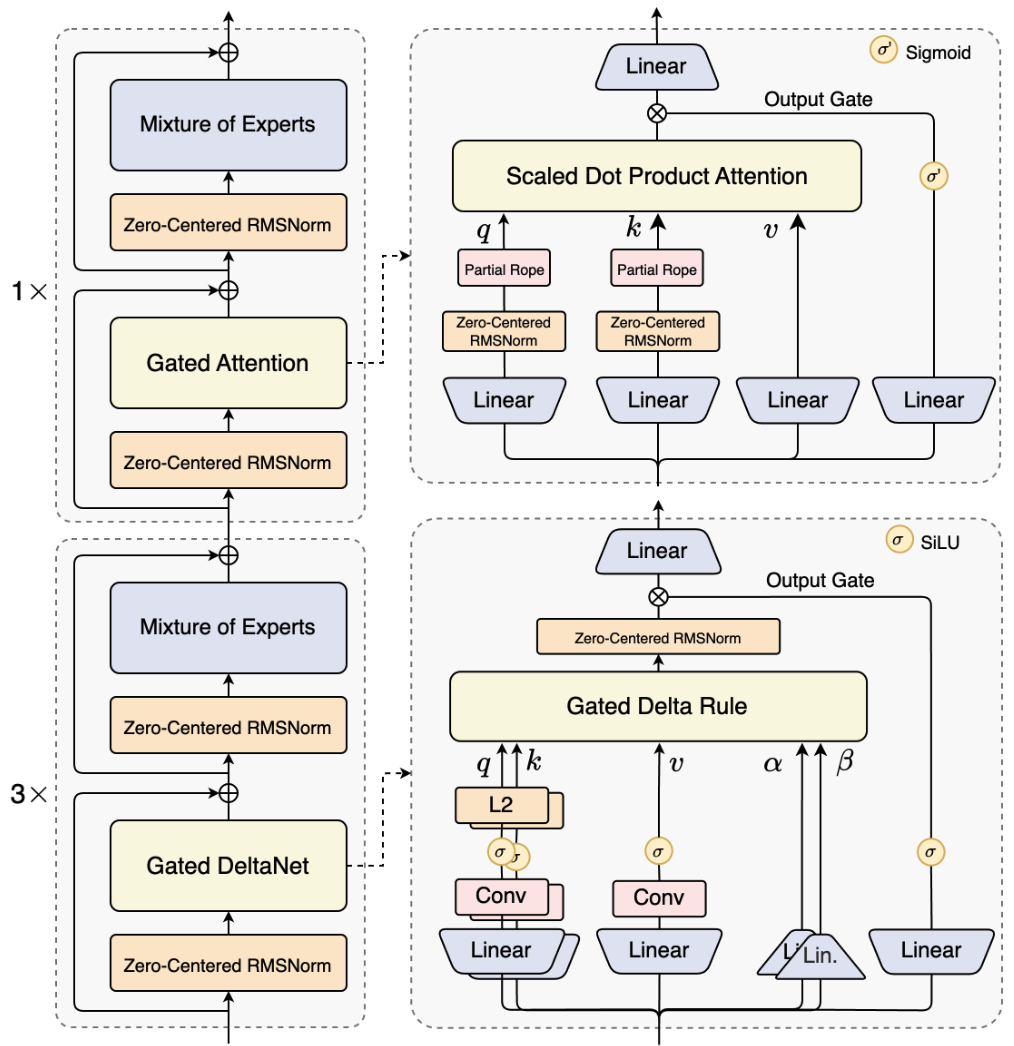
](/Notes/NLP/NLP——开源大模型结构汇总/Gated-Attention-Figure1.png)










![来源于:[[张量/序列并行]📚图解 DeepSpeed-Ulysses & Megatron-LM TP/SP](https://zhuanlan.zhihu.com/p/5750410146)](/Notes/NLP/LLM-Infra/NLP——Megatron各种并行总结/TP-Row-and-Column-Parallel.png)
/Megatron-LM-3-Figure5.png)