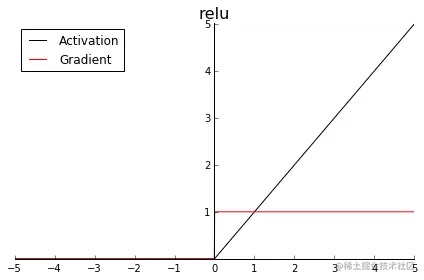
ReLU
修正线性单元(Rectified Linear Unit)
- 表达式:
$$\text{ReLU}(x)=
\begin{cases}
0& \text{x<=0}\\
x& \text{x>0}
\end{cases}$$ - 函数图像:
x 为 0 时的导数问题
- 在实际场景中,x 为 0 的概率非常低
- 实际场景中,当 x 为 0 时,原函数不可导,可以给此时的导数制定一个值,如0,或1
- 神经元永久死亡问题:https://www.zhihu.com/question/67151971
- 当对于任意的训练样本,某一个神经元输出都小于0时,该神经元的反向梯度为0,所以神经元上层与神经元相连接的所有节点梯度都为0(链式法则,梯度相乘),也就是对所有的训练样本,这些节点相关的参数都不会被更新(因为梯度为0),下一次正向计算到这些节点时值都不会变
- 一个常见的疑问:如果当前神经元上层的神经元其他参数发生改变而导致当前神经元的输入数据发生改变呢?
- 回答:可能有这种情况,一个神经元的反向梯度为0以后,所有只与该层该神经元相关的参数都不会变了,但与该层其他神经元相关的节点参数还是会变的!【需要进一步探讨这个问题】
- 补充回答:可以确定的是,如果当前层的其他神经元不影响该神经元上层的相关参数,那么,这个神经元将永久性死亡
- 所以正确的描述是:对于任意的输入(不管当前层输入为何值时,当前神经元的输出都等于0,也就是说,虽然上层的输入可能会变,但是当前节点的输出已经不会变化了!),都有当前神经元的输出等于0,此时反向梯度永远为0
- 注意:这不是说神经元从开始就怎么样,而是神经元相关的参数偏向太多,导致当前神经元的值永远为0
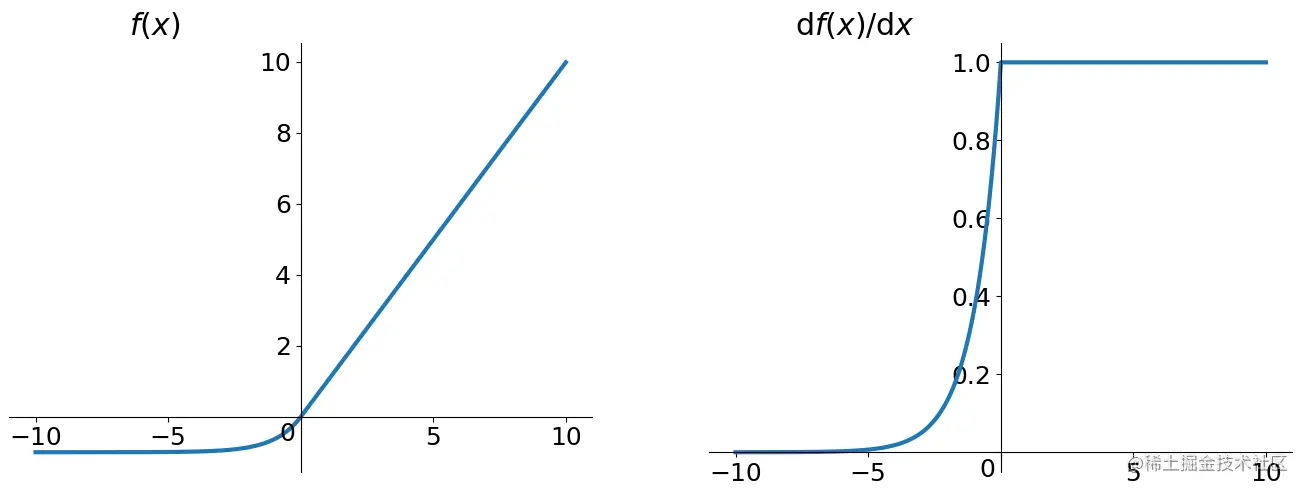
ELU
Exponential Linear Units
- 表达式:
$$\text{ELU}(x)=
\begin{cases}
x, & \text{if } x > 0 \\
\alpha(e^x - 1), & \text{otherwise}
\end{cases}
$$ - 函数图像:
Leaky ReLU
Leaky ReLU
- 表达式:
$$\text{Leaky-ReLU}(x)=
\begin{cases}
\alpha \cdot x& \text{x<=0} \\
x& \text{x>0}
\end{cases}$$ - 函数图像:
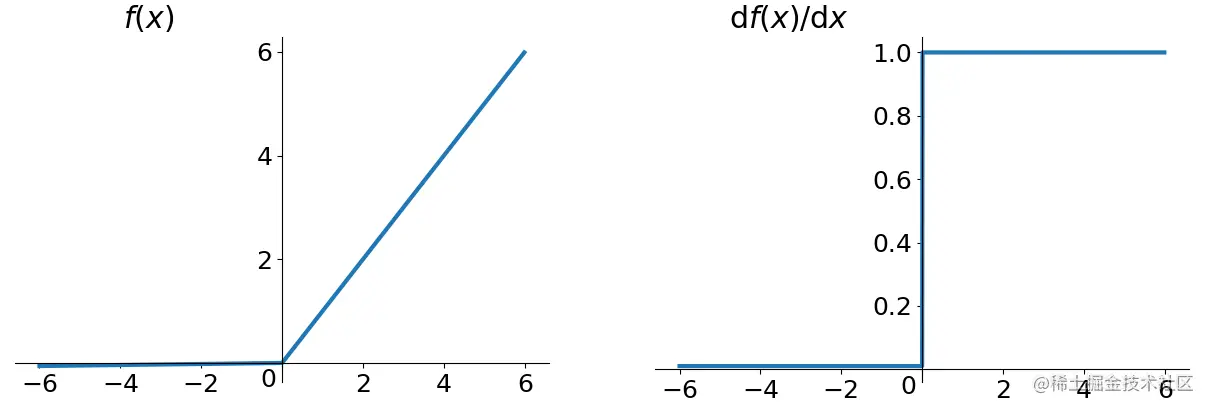
- 函数实现
1
2
3
4
5def leaky_relu(x, alpha=0.01):
return np.where(x >= 0, x, alpha * x)
def leaky_relu_derivative(x, alpha=0.01):
return np.where(x >= 0, 1, alpha)
PReLU
Parametric ReLU(PReLU)
- 表达式(虽然表达式与Leaky ReLU相同,但是其中的参数是可学习的):
$$\text{PReLU}_{\alpha}(x)=
\begin{cases}
\alpha \cdot x& \text{x<=0} \\
x& \text{x>0}
\end{cases}$$ - 函数图像:

- 函数实现
1
2
3
4
5def prelu(x, alpha):
return np.where(x >= 0, x, alpha * x)
def prelu_derivative(x, alpha):
return np.where(x >= 0, 1, alpha)
Softplus
表达式:
$$ \text{Softplus}(x) = \ln(1+e^x) $$函数图像:
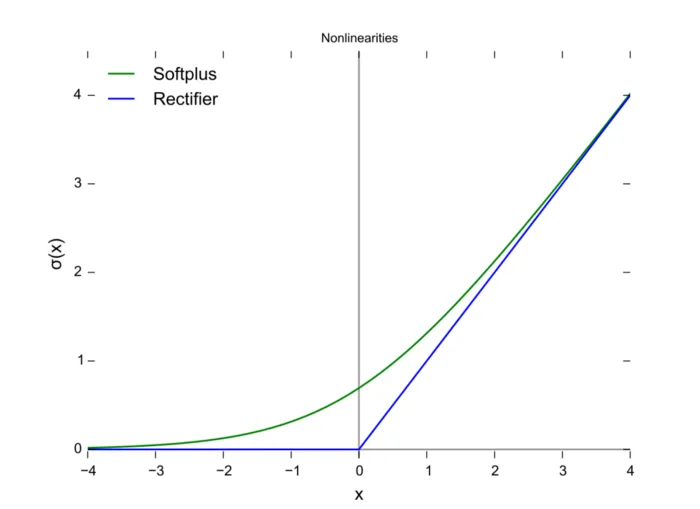
torch实现
1
x = F.softplus(x)
Sigmoid
- 表达式:
$$ \text{Sigmoid}(x) = \frac{1}{1+e^{-x}} $$ - 函数图像:
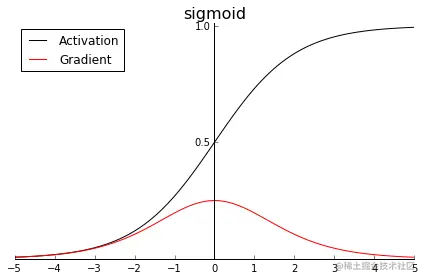
Tanh
- 表达式:
$$
\begin{align}
\tanh (x)&=\frac{e^x-e^{-x}}{e^x+e^{-x}} \\
\tanh (x)&=\frac{2}{1+e^{-2x}} - 1 \\
\tanh (x)&=2\cdot \text{Sigmoid}(2x) - 1 \\
\end{align}
$$ - 函数图像:
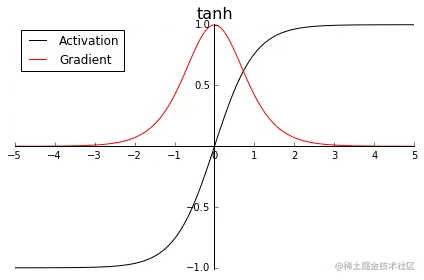
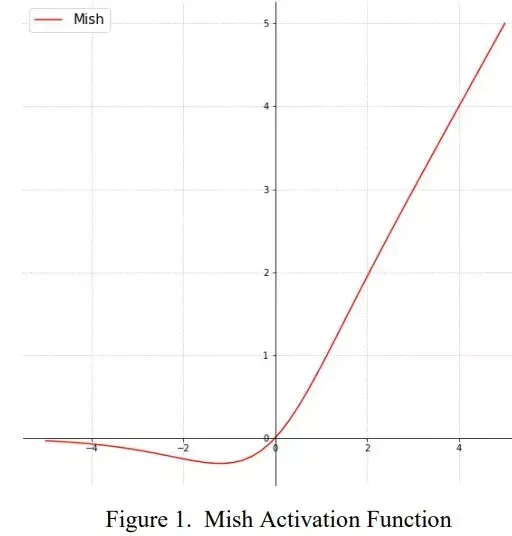
Mish
Mish: A Self Regularized Non-Monotonic Neural Activation Function
- 表达式:
$$ Mish(x) = x\cdot \text{tanh}(\ln(1+e^x))$$ - 函数图像