趣味题——绳子剪三段后能构成三角形的概率

初始题目为1米长的绳子剪成三段后能够构成三角形的概率，实际上绳子的长度可以是任意的，解法都一样

题目描述

  • 一根绳子长度为 n，剪三段后能构成三角形的概率是多少？
  • 由于长度与概率无关，所以接下来我们把绳子当做长度为 1 米来处理

解决方案

  • 三段绳子的长度分别为 x，y，1-x-y
  • 首先需要满足
    $$
    \begin{align}
    x &> 0 \\
    y &> 0\\
    1-x-y &> 0 \\
    \end{align}
    $$
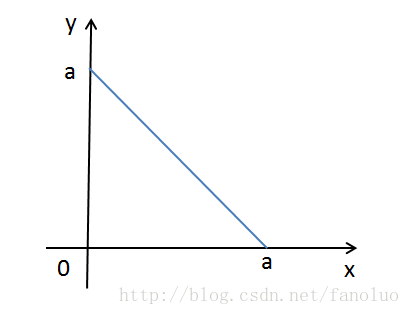
    • 以 x 为横坐标，y 为纵坐标画图得到阴影区域面积为 \(\frac{1}{2}\)
  • 图片来源于：https://blog.csdn.net/fanoluo/article/details/40374571*
  • 进一步分析三段绳子能生成组成三角形的概率
    $$
    \begin{align}
    x+y &> 1-x-y \\
    y + 1-x-y &> x\\
    x + 1-x-y &> y \\
    \end{align}
    $$
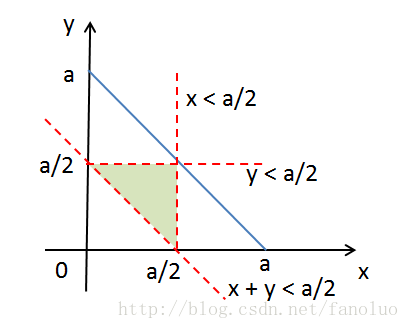
    • 进一步分析得到阴影部分面积为 \(\frac{1}{8}\)
  • 图片来源于：https://blog.csdn.net/fanoluo/article/details/40374571*
  • 所以有
    $$P = \frac{1/8}{1/2} = \frac{1}{4}$$