本文主要介绍 LLM 对齐微调的 RLHF(即 PPO)训练方式,论文参考了一些优秀的技术博客,然后加入了自己的理解
注:本文包含 AI 辅助创作
- 参考链接:
- 图解大模型RLHF系列之:人人都能看懂的PPO原理与源码解读
- OPENAI原始论文:Training language models to follow instructions with human feedback
- 论文补充材料:补充材料包含很多细节,比如奖励的定义就在附属材料中
- 微软RLHF论文:ALIGNING LARGE MULTIMODAL MODELS WITH FACTUALLY AUGMENTED RLHF
概念
- 对齐微调(Alignment tuning):为了避免模型输出一些不安全或者不符合人类正向价值观的回复
- 人类偏好对齐:基于人类反馈的对齐微调(Alignment tuning)方法,如RLHF
- AI偏好对齐:基于AI反馈的对齐微调方法,如RLAIF
- RLHF,Reinforcement Learning from Human Feedback,即基于人类反馈的强化学习方法
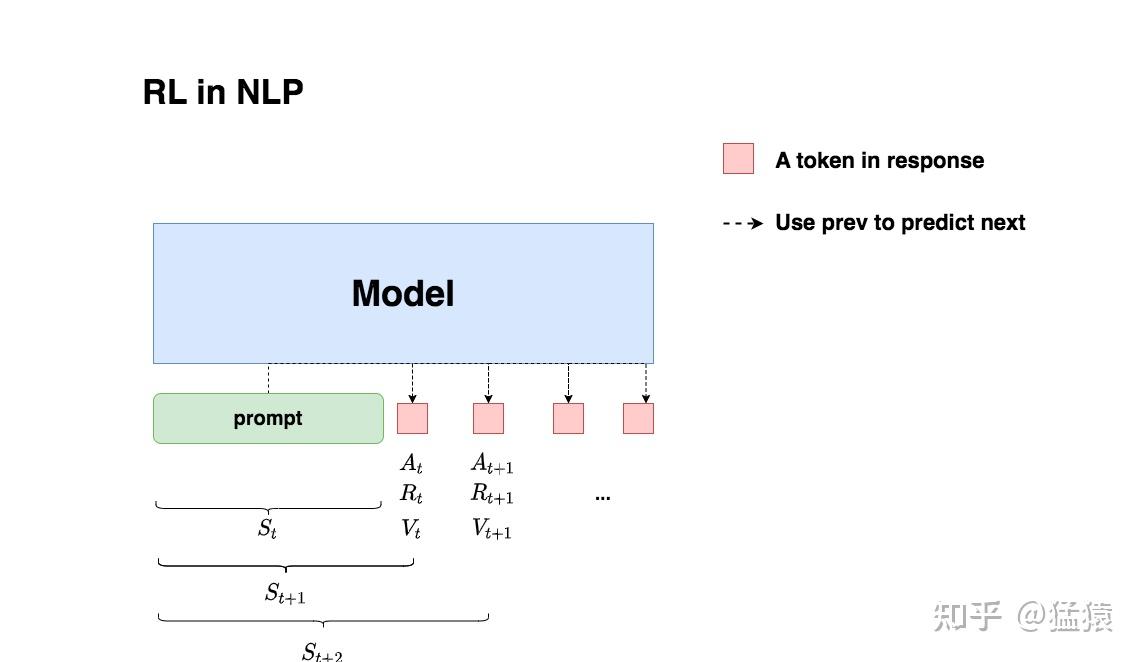
RLHF 的 MDP 过程
- 一个response就是一个trajectory:
RLHF 整体框架
- RLHF的一般框架如下:
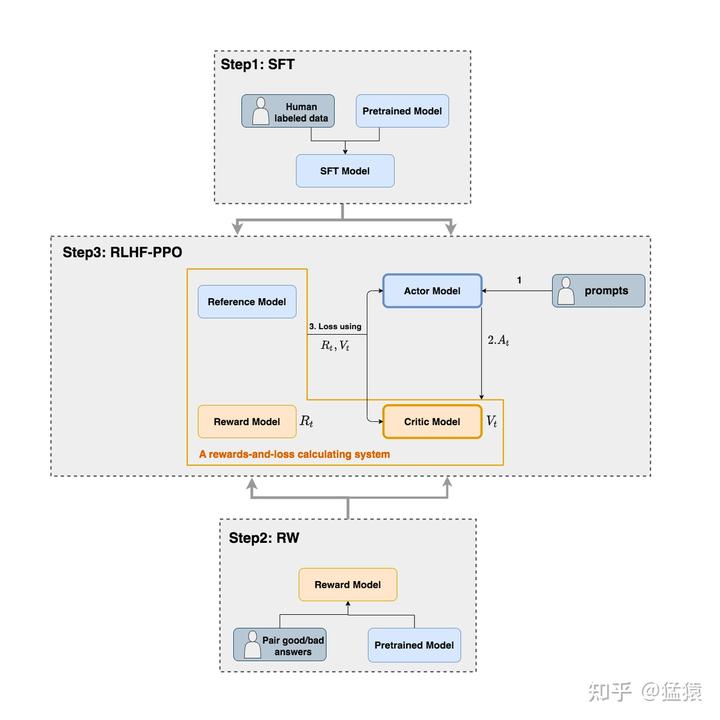
- Actor Model :被训练的目标语言模型LLM
- Critic Model :AC强化学习中的Critic角色,用于估计 \(V_t\)
- Reward Model :奖励模型,它的作用是计算收益 \(R_t\) ,实际实现一个response仅预估一次
- Reference Model :参考模型,它的作用是在RLHF阶段给语言模型增加一些“约束”,防止语言模型训歪(朝不受控制的方向更新,效果可能越来越差)
- Actor/Critic Model在RLHF阶段是需要训练的(图中给这两个模型加了粗边,就是表示这个含义);
- Reward/Reference Model是参数冻结的
- Critic/Reward/Reference Model共同组成了一个“奖励-loss”计算体系(图解大模型RLHF系列之:人人都能看懂的PPO原理与源码解读作者自己命名的,为了方便理解),我们综合它们的结果计算loss,用于更新Actor
不同角色的细节
Actor Model
Actor Model的整体图示如下:
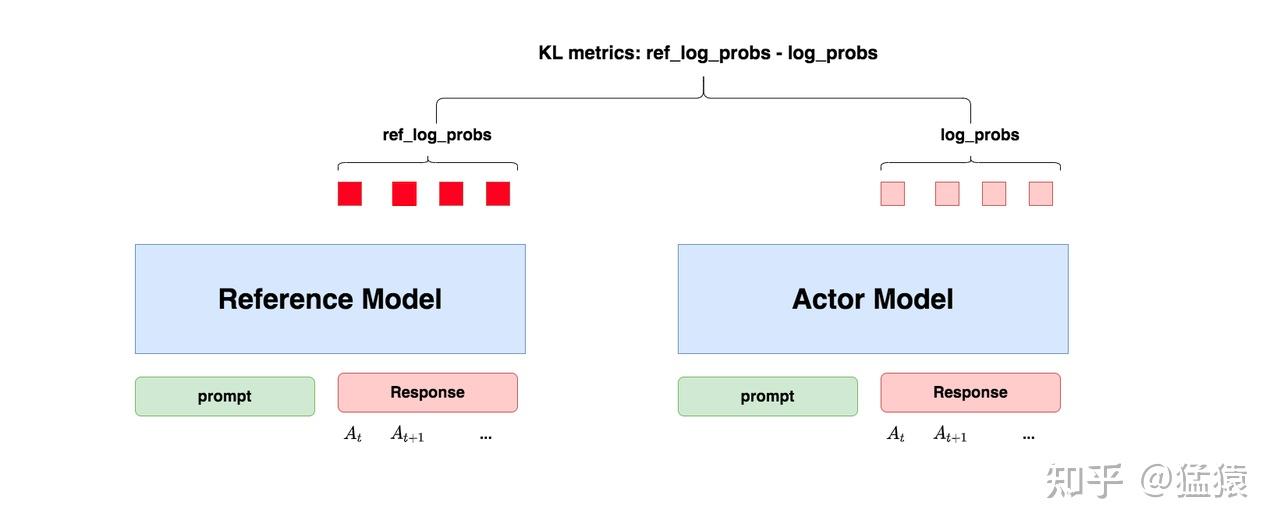
Actor的目标是:在不太偏离Reference Model的情况下,最大化reward,其定义可以写为如下形式(注意不是最终损失函数)
$$
\max_{\pi_\theta} \mathbb{E}_{x\sim D, y\sim \pi_\theta(y|x)} [r_{RM}(x,y)]-\beta \mathbb{D}_{KL}[\pi_\theta(y|x)||\pi_{ref}(y|x)]
$$- \(r_{RM}(x,y)\) 是Reward Model的返回值
- 上面是一个简单的示例,可以暂且理解为 \(x\) 表示 Prompt,用 \(y\) 表示 response,实际上真实场景中 \(x\) 表示 Prompt+截止到目前的输出 tokens,用 \(y\) 表示 下一个 token
- 可以使用Reward Engineering来实现这个目标,可在不修改其他公式的情况下,使用下面的Reward来实现上述目标:
$$
r(x,y) = r_{RM}(x,y) - \beta(\log\pi_\theta(y|x) - \log\pi_{ref}(y|x) )
$$ - 上述Reward常常也写作下面的形式(使用 token 形式精确表达):
$$
r_{t}=r_{\varphi}(q,o_{\leq t})-\beta\log\frac{\pi_{\theta}(o_{t}|q,o_{ < t})}{\pi_{ref}(o_{t}|q,o_{ < t})}
$$- \(r_{\varphi}(q, o_{\leq t})\) 是外部奖励模型给出的原始奖励
- \(\beta \log\frac{\pi_{\theta}(o_{t}|q,o_{ < t})}{\pi_{ref}(o_{t}|q,o_{ < t})}\) 是 KL散度惩罚项,\(\beta\) 是一个正的超参数,本质是一个去除期望的KL散度
- 实际上,可直接将负的Actor-Reference KL加入到reward中,仅在最后一个时间步加入Reward:
$$
R_t=
\begin{cases}
-k\log\frac{\pi_\theta(A_t|S_t)}{\pi_\text{ref}(A_t|S_t)} & t < T\\
-k\log\frac{\pi_\theta(A_t|S_t)}{\pi_\text{ref}(A_t|S_t)} + R_t & t = T
\end{cases}
$$- 其中,仅在response最后一步 \(t=T\) 时取 \(R_t\) 的值,因为Reward Model训练时也是一整个Response作为一个样本训练的,这也很好理解,因为一次回答中间的结果无法评估好坏,需要整个回答完成后才知道这次Response是否合理
- \(\frac{\pi_\theta(A_t|S_t)}{\pi_\text{ref}(A_t|S_t)}\) 不一定是正数,但是由于动作 \(A_t\) 是从Actor策略中采样的(具体来说,是从 \(\pi_{\theta_\text{old}}\) 中采样的,PPO下可以近似认为两者相等),而 \(\mathbb{E}_{A_t \sim \pi_\theta}[\log\frac{\pi_\theta(A_t|S_t)}{\pi_\text{ref}(A_t|S_t)}]\) 是KL散度,值一定大于0,所以最大化带KL散度后的 \(R_t\) 就可以最小化KL散度,让Actor不要偏离Reference Model太多
- 在实现时,取模型输出的概率取对数再做减法即可:
$$
R_t=
\begin{cases}
k (ref\_log\_probs-log\_probs) & t < T\\
k (ref\_log\_probs-log\_probs) + R_t & t = T
\end{cases}
$$
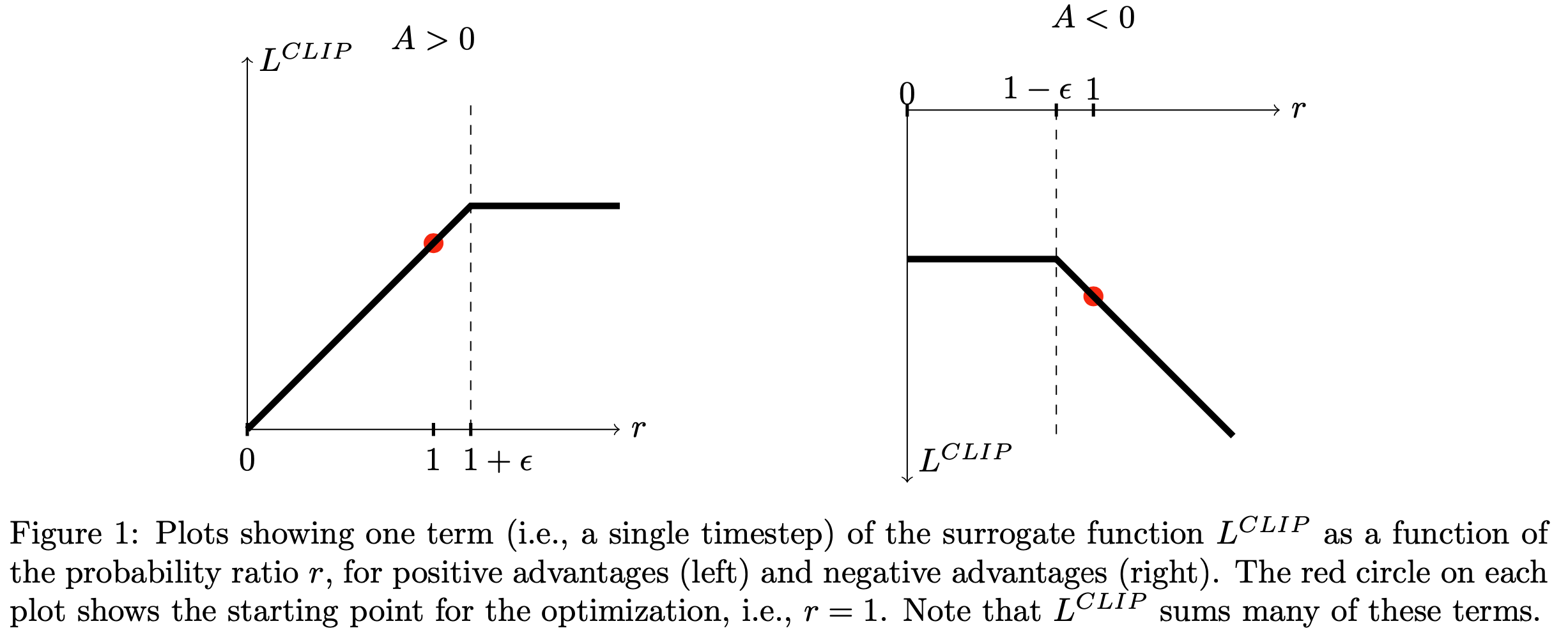
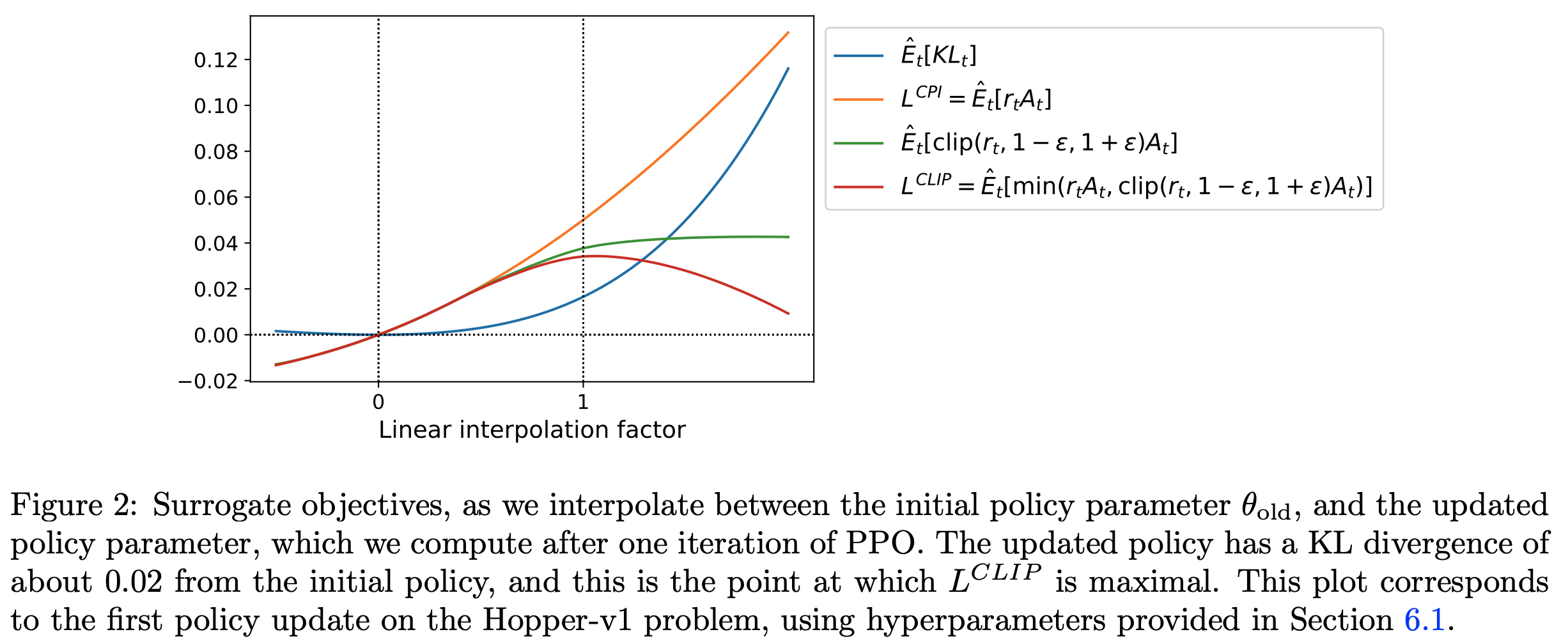
PPO-loss定义(这里是Clip版本,引入拉格朗日对偶性的Adaptive KL Penalty版本不太常用,这里没有给出),对于一个完整的response生成后(等价于一次完整的trajectory),损失函数如下:
$$
\mathcal{J}_{\textit{PPO}}(\theta)=\mathbb{E}_\left[q\sim P(Q),o\sim\pi_{\theta_{old}}(O|q)\right]\frac{1}{|o|}\sum_{t=1}^{|o|}\min\left[\frac{\pi_{\theta}(o_ {t}|q,o_{<t})}{\pi_{\theta_{old}}(o_{t}|q,o_{<t})}A^{\pi_\text{old}}_{t},\textrm{clip}\left( \frac{\pi_{\theta}(o_{t}|q,o_{<t})}{\pi_{\theta_{old}}(o_{t}|q,o_{<t})},1-\epsilon ,1+\epsilon\right)A^{\pi_\text{old}}_{t}\right],
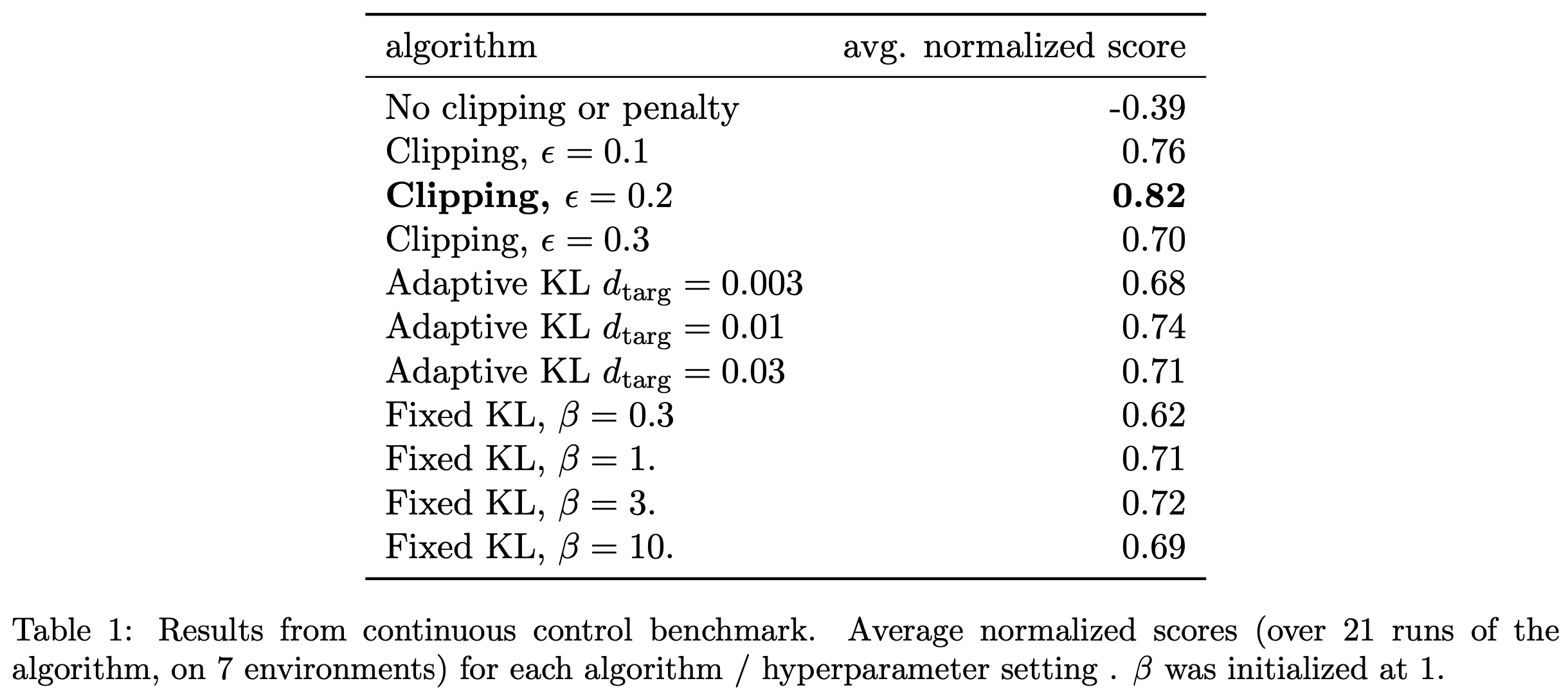
$$- 实践中PPO通常设置 \(\epsilon=0.2\)
- 优势函数 \(A^{\pi_\text{old}}_t\) 是通过广义优势估计GAE计算得到的(注:计算优势函数使用的Reward是经过KL散度修正的)
优势函数的优化(GAE):
- 可以使用GAE,可以累加实现优势函数 \(A^{Actor_{old}}(S_t, A_t)\) 的计算:
$$
\begin{align}
\delta_t &= R_t + \gamma V_{t+1} - V_t \\
A^{Actor_{old}}(S_t, A_t) &= \sum_{l=0}^{T-t} (\gamma \lambda)^l \delta_{t+l}
\end{align}
$$ - 在一些文章中还会写成下面的等价形式(两者的等价性很容易证明),然后从后往前累加(动态规划的思想)
$$
A^{Actor_{old}}(S_t, A_t) = \delta_t + \gamma\lambda A^{Actor_{old}}(S_{t+1}, A_{t+1})
$$
- 可以使用GAE,可以累加实现优势函数 \(A^{Actor_{old}}(S_t, A_t)\) 的计算:
最终,通过把负Actor-Reference KL 添加到 \(R_t\) 中,Actor loss的形式与PPO-loss的形式完全一致
Critic Model
- Critic Model的整体图示如下:
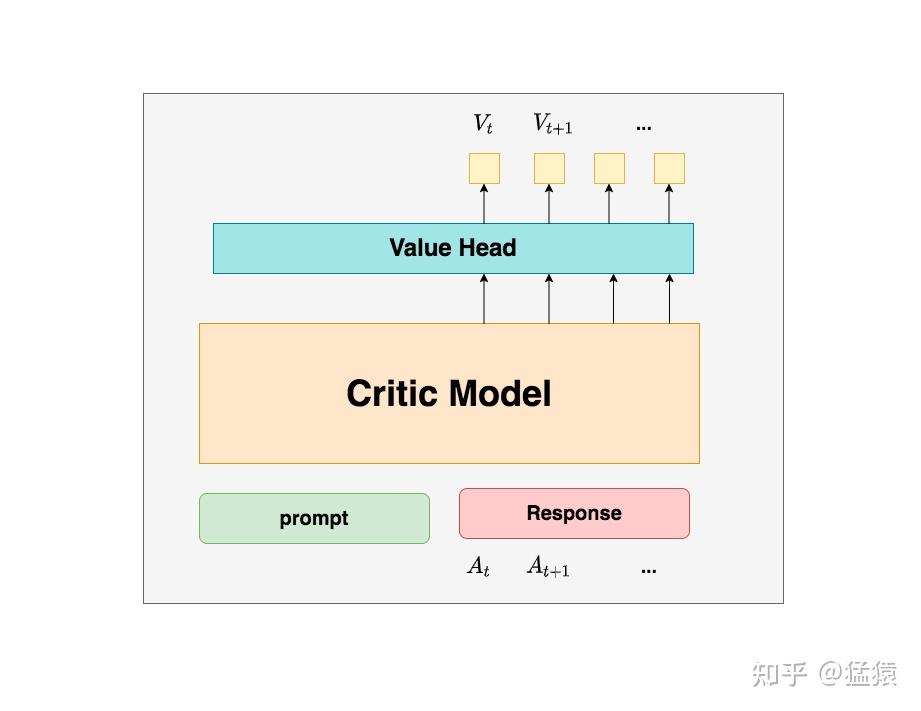
- 在强化学习阶段,用到的Reward Model和Critic Model都使用同一个模型初始化,因此在训练Reward Model的过程中,也是在训练Critic Model
- Critic loss,MSE损失函数(其中 \(R_t\) 是一个经过KL散度修正的奖励):
$$
loss = (R_t + \gamma V_{t+1} - V_t)^2
$$
Reward Model
Reward Model的整体图示如下(问题:这个图有点问题,Reward Model对一个response仅需要预估一个最终的Reward即可吧?):
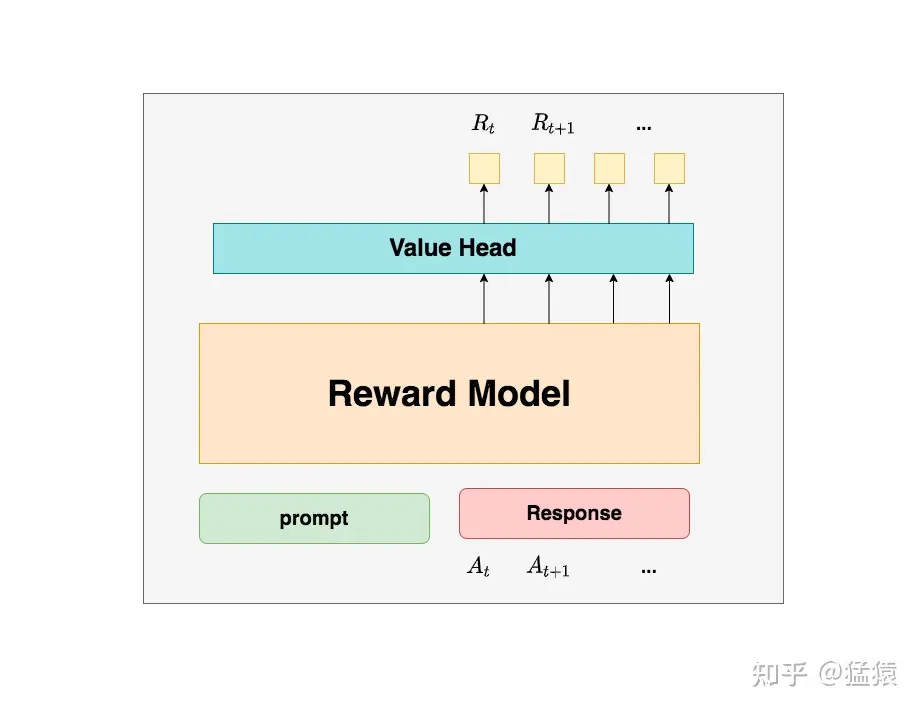
Reward Model的训练流程如下:
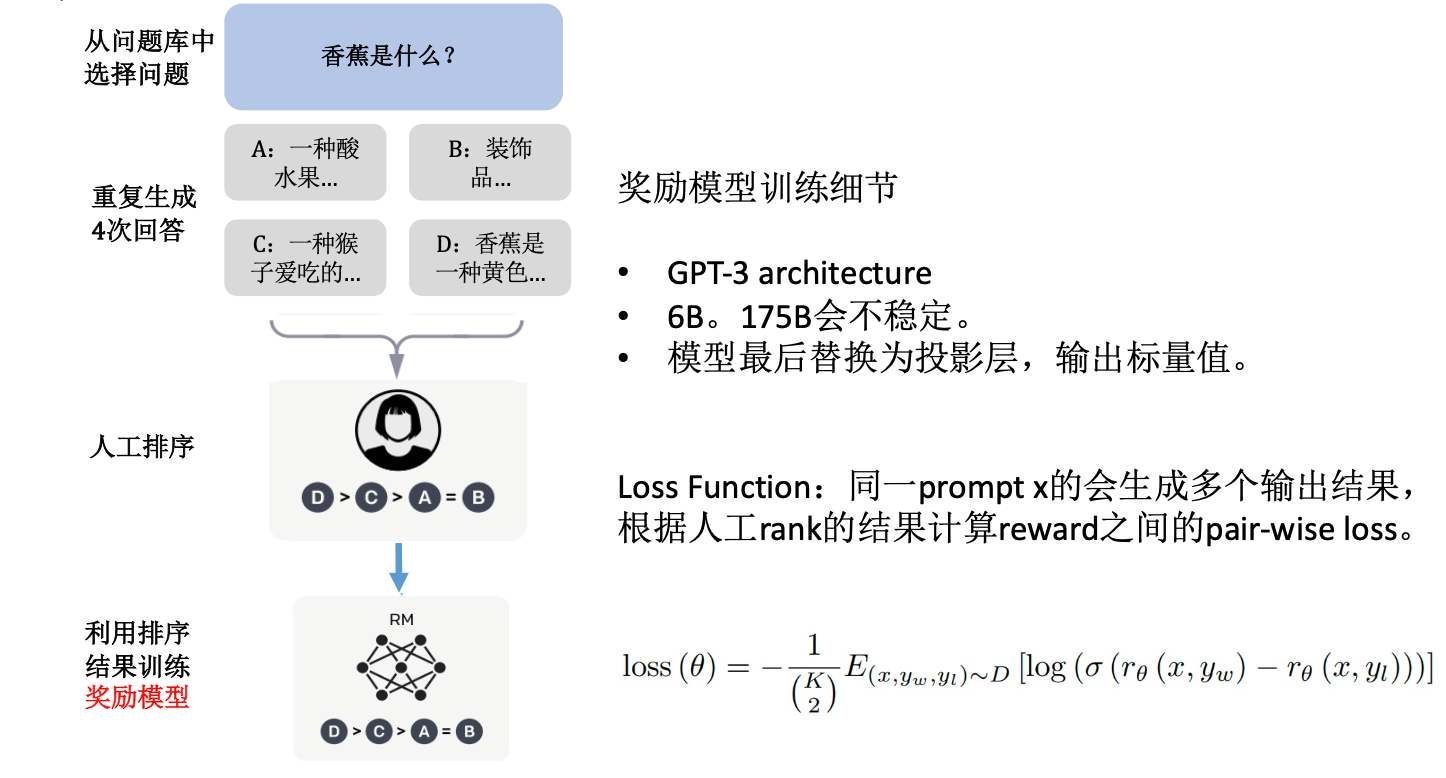
- 使用SFT模型对每个Prompt \(x\) 重复生成多个不同Response \(y\),记为 \(y_a, y_b, y_c, y_d\)
- 让人类对回答进行排序打分: \(y_a \succ y_b \succ y_c \succ y_d\),最终可获得数据集 \(D = \{x^{(i)}, y^{(i)}_w, y^{(i)}_l\}_{i=1}^N\),实际上,对于一个 \(x\) 对应K个 \(y\) 的情况,可以拆开成 \(C_K^2\) 个样本
- 这里有一些标注平台,可用于便捷式打分,方便人类操作,比如GitHub:label-studio提供了一个开源标注服务,GitHub:transformers_tasks提供了一个简单的模型生成数据到可视化打标的工具
- 使用收集的数据训练Reward Model,目标是让输入Prompt \(x\) 时排序越高的Response \(y\) 打分 \(r_\theta(x,y)\) 越高
- Reward Model通常比Actor Model小,deepspeed的示例中,语言大模型66B,奖励模型只有350M)
- 也可以使用SFT后的LM模型后面接一层线性层作为Reward Model
- 奖励模型训练优化采用pair-wise loss,即同时输入模型关于同一个问题的两个回答,让模型学会这两个句子哪个分高哪个分低,原始论文给出的损失函数如下(其中是否需要乘以 \(\frac{1}{C_K^2}\) 有待考证,感觉不需要,因为后面是期望,相当于已经做过归一化了):
$$
Loss_{\text{RM}}(\theta) = -\frac{1}{C_K^2} \mathbb{E}_{(x,y_w,y_l)\sim D}[\log \sigma(r_\theta(x, y_w) - r_\theta(x, y_l))]
$$ - \((x,y_w,y_l)\sim D\) 表示从数据集中随机抽取胜者和败者两个回答进行配对
- Reward Model通常比Actor Model小,deepspeed的示例中,语言大模型66B,奖励模型只有350M)
损失函数的推导过程:
- 对于任意的Prompt \(x\) 和两个不同的Response \(y_w, y_l\),人类偏好是 \(y_w \succ y_l\),假设这些偏好是由一个最优的打分模型 \(r^{*}(x,y)\) 确定,我们用一个神经网络 \(r_\theta(x,y)\) 来表示打分模型,按照Bradley-Terry (BT)方法(详情见DPO论文:Direct Preference Optimization: Your Language Model is Secretly a Reward Model),我们可将人类偏好分布表示为:
$$
p(y_w \succ y_l|x) = \frac{e^{r_\theta(x,y_w)}}{e^{r_\theta(x,y_w)} + e^{r_\theta(x,y_l)}}
$$ - 进一步地,为了最大化数据集 \(D = \{x^{(i)}, y^{(i)}_w, y^{(i)}_l\}_{i=1}^N\) 中人类偏好出现的概率,我们有:
$$
\begin{align}
\theta^{*} &= \arg\max \prod p(y_w \succ y_l|x) \\
&= \arg\max \prod \frac{e^{r_\theta(x,y_w)}}{e^{r_\theta(x,y_w)} + e^{r_\theta(x,y_l)}} \\
&= \arg\max \sum log \frac{e^{r_\theta(x,y_w)}}{e^{r_\theta(x,y_w)} + e^{r_\theta(x,y_l)}} \\
&= \arg\max \sum log \frac{1}{1+\frac{e^{r_\theta(x,y_l)}}{e^{r_\theta(x,y_w)}}} \\
&= \arg\max \sum log \frac{1}{1+e^{r_\theta(x,y_l) - r_\theta(x,y_w)}} \\
&= \arg\max \sum log \frac{1}{1+e^{-(r_\theta(x,y_w) - r_\theta(x,y_l))}} \\
&= \arg\max \sum log \sigma(r_\theta(x,y_w) - r_\theta(x,y_l)) \\
\end{align}
$$
- 对于任意的Prompt \(x\) 和两个不同的Response \(y_w, y_l\),人类偏好是 \(y_w \succ y_l\),假设这些偏好是由一个最优的打分模型 \(r^{*}(x,y)\) 确定,我们用一个神经网络 \(r_\theta(x,y)\) 来表示打分模型,按照Bradley-Terry (BT)方法(详情见DPO论文:Direct Preference Optimization: Your Language Model is Secretly a Reward Model),我们可将人类偏好分布表示为:
打分归一化:为了确保打分函数具有较低的方差(不同输入Prompt的打分可能会差距非常大),实际训练中还可以对打分进行归一化,即对所有 \(x\)
\(\mathbb{E}_{x,y\sim D}[r_\theta(x,y)] = 0\)- 问题,是分别对不同 \(x\) 做多次归一化,还是所有 \(x\) 一起做N次归一化,直观来看,是不是分别对不同 \(x\) 做N次归一化会更好?(论文没有明说,代码也没看到)
实现代码示例,参考自博客GitHub:transformers_tasks:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29def compute_rank_list_loss(rank_rewards_list: List[List[torch.tensor]], device='cpu') -> torch.Tensor:
"""
通过给定的有序(从高到低)的ranklist的reward列表,计算rank loss
所有排序高的句子的得分减去排序低的句子的得分差的总和,并取负
Args:
rank_rewards_list (torch.tensor): 有序(从高到低)排序句子的reward列表,e.g. ->
[
[torch.tensor([0.3588]), torch.tensor([0.2481]), ...],
[torch.tensor([0.5343]), torch.tensor([0.2442]), ...],
...
]
device (str): 使用设备
Returns:
loss (torch.tensor): tensor([0.4891], grad_fn=<DivBackward0>)
"""
if type(rank_rewards_list) != list:
raise TypeError(f'@param rank_rewards expected "list", received {type(rank_rewards)}.')
loss, add_count = torch.tensor([0]).to(device), 0
for rank_rewards in rank_rewards_list:
for i in range(len(rank_rewards)-1): # 遍历所有前项-后项的得分差
for j in range(i+1, len(rank_rewards)):
diff = F.sigmoid(rank_rewards[i] - rank_rewards[j]) # sigmoid到0~1之间
loss = loss + diff
add_count += 1
loss = loss / add_count
return -loss
Reference Model
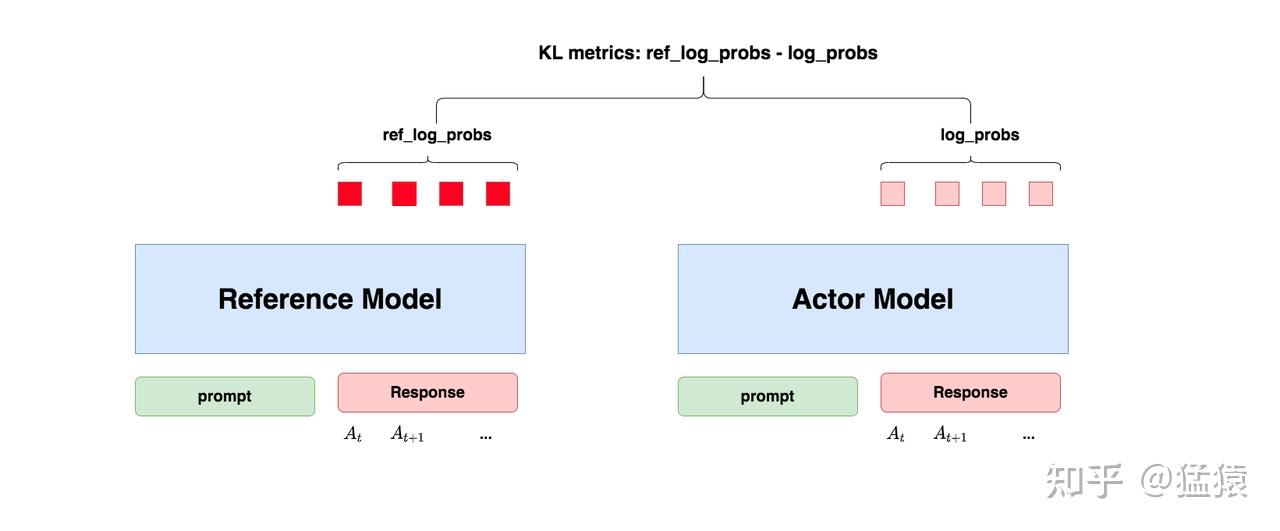
- 基本思想:为了防止Actor偏离SFT的结果(Reference Model)太多,导致丧失Pretrain和SFT的优秀能力, 在训练过程中保证Actor和Reference的动作分布差异不要太大(KL散度)
- Reference Model可以防止Reward Hacking问题 ,参考LLMs 奖励剥削 RLHF: Reward hacking
- 在强化学习中,Reward Hacking问题通常是指智能体在学习过程中发现并利用奖励函数的漏洞,为了获得最大reward而偏离训练者的目标的情况
- 在RLHF中,Reward Hacking问题是指没有Reference Model的情况下,Actor为了实现最大化reward,会越来越偏离原来的SFT模型,这不是我们想要的
- KL散度公式:
$$
\begin{align}
D_{KL}(Actor(S)||Ref(S)) &= \mathbb{E}_{a \sim Actor(s)} [\log \frac{Actor(S)}{Ref(S)}] \\
&= \mathbb{E}_{a \sim Actor(s)} [\log Actor(S) - \log Ref(S)] \\
&\approx log\_probs - ref\_log\_probs\\
\end{align}
$$- 公式中最后一步用 \(\approx\) 的原因是因为需要保证生成 \(log\_probs\) 和 \(ref\_log\_probs\) 的样本是按照策略 \(Actor\) 来进行采样的(即按照Actor执行动作)
- 思考:保证Actor和Reference两者策略足够接近,即KL散度足够接近有两种方法:
- 方法一:按照Actor采样样本,并且在训练Actor的loss中直接加入KL散度 ,loss越小越好 => KL散度越小越好
- 方法二:即按照Actor采样样本,并且在Reward中加入负的KL散度 ,Reward越大越好 => KL散度越小越好
- 方法二是Reward Engineering过程,通过修改Reward来避免Reward Hacking问题
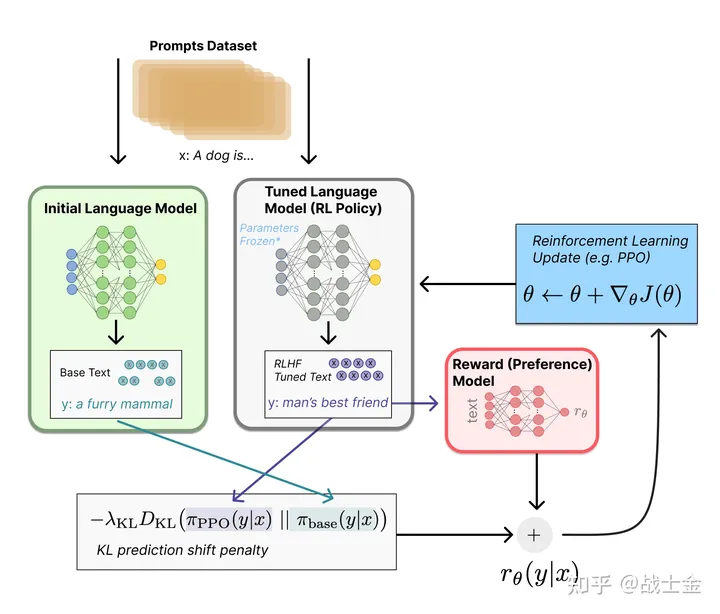
- 目前已知的方案中,一般是加入到Reward中(如下图来自微软RLHF论文:ALIGNING LARGE MULTIMODAL MODELS WITH FACTUALLY AUGMENTED RLHF),其实还可以有其他方案

RLHF中的奖励设计
在RLHF(从人类反馈中进行强化学习)的真实训练中,KL散度会在强化学习的优化目标中作为额外的正则化项出现,对Reward Model给出的奖励进行修正
$$
r_{t}=r_{\varphi}(q,o_{\leq t})-\beta\log\frac{\pi_{\theta}(o_{t}|q,o_{ < t})}{\pi_{ref}(o_{t}|q,o_{ < t})},
$$其中,\(r_{\varphi}\) 是奖励模型的输出,\(\pi_{ref}\) 是参考模型(通常是初始的SFT模型),\(\beta\) 是KL惩罚的系数
注意:虽然这里写的 KL 散度计算是 \(\pi_{\theta}\) 和 \(\pi_{ref}\) 的 KL 散度,但是实际训练中,在 off-policy 场景下,应该是 \(\pi_{\theta_\text{old}}\) 和 \(\pi_{ref}\) 的 KL 散度
- 因为 GAE 仅计算一次,多次更新时也不会重新计算 GAE,接着就是其他的计算,实现中(比如Hand-on-RL TRPO & PPO)还会使用
.detach()以防止梯度反传回去(奖励仅仅是梯度的权重比例,不参与梯度更新) - 补充:最近看到的博客 The critical implementation detail of KL loss in GRPO 中也强调了这一点
- 因为 GAE 仅计算一次,多次更新时也不会重新计算 GAE,接着就是其他的计算,实现中(比如Hand-on-RL TRPO & PPO)还会使用
注意:仅对每个 Response 的最后一个 Token 上有 Reward ,其他地方都是 0,实现如下:
1
2for j in range(batch_size):
rewards[j, start:ends[j]][-1] += reward_from_model[j] # 假定 start 是 prompt 的长度,ends 是 padding 前的最后一个 index- 注:许多文章不明所以,会错误表述为每个 Token 都有 Reward,实际上,不针对所有输出Token,很难对单个Token评估奖励
理解:以上Reward的本质是想要限制KL散度,KL散度的原始公式是:
$$
KL = \mathbb{E}_{o_t \sim \pi_{\theta}(o_{t}|q,o_{ < t})} \Big[\log\frac{\pi_{\theta}(o_{t}|q,o_{ < t})}{\pi_{ref}(o_{t}|q,o_{ < t})}\Big]
$$更详细的讨论见论文附录
KL散度的作用
KL散度(Kullback-Leibler Divergence)在RLHF中主要用于防止策略模型偏离初始模型(参考模型)太远 ,从而避免模型生成不合理或极端的输出
KL散度的计算 :
$$
\text{KL}(\pi_\theta || \pi_{\text{ref}}) = \mathbb{E}_{y \sim \pi_\theta} \left[ \log \frac{\pi_\theta(y|x)}{\pi_{\text{ref}}(y|x)} \right]
$$- 其中 \( \pi_\theta \) 是当前策略模型,\( \pi_{\text{ref}} \) 是参考模型(如初始预训练模型)
KL散度的作用 :
- 防止模型过度优化奖励,导致输出偏离人类期望
- 保持生成内容的多样性和合理性
强化学习的优化目标
- 在RLHF中,强化学习的优化目标通常结合了奖励模型的输出和KL散度正则化项。具体形式如下:
$$
\max_{\pi_\theta} \mathbb{E}_{(x, y) \sim \pi_\theta} \left[ R(x, y) - \beta \cdot \text{KL}(\pi_\theta || \pi_{\text{ref}}) \right]
$$ - 其中:
- \( R(x, y) \) 是Critic网络预测的奖励值
- \( \beta \) 是KL散度的权重系数,用于控制正则化的强度
其他相关RLHF的描述
- 其他框架表达形式:
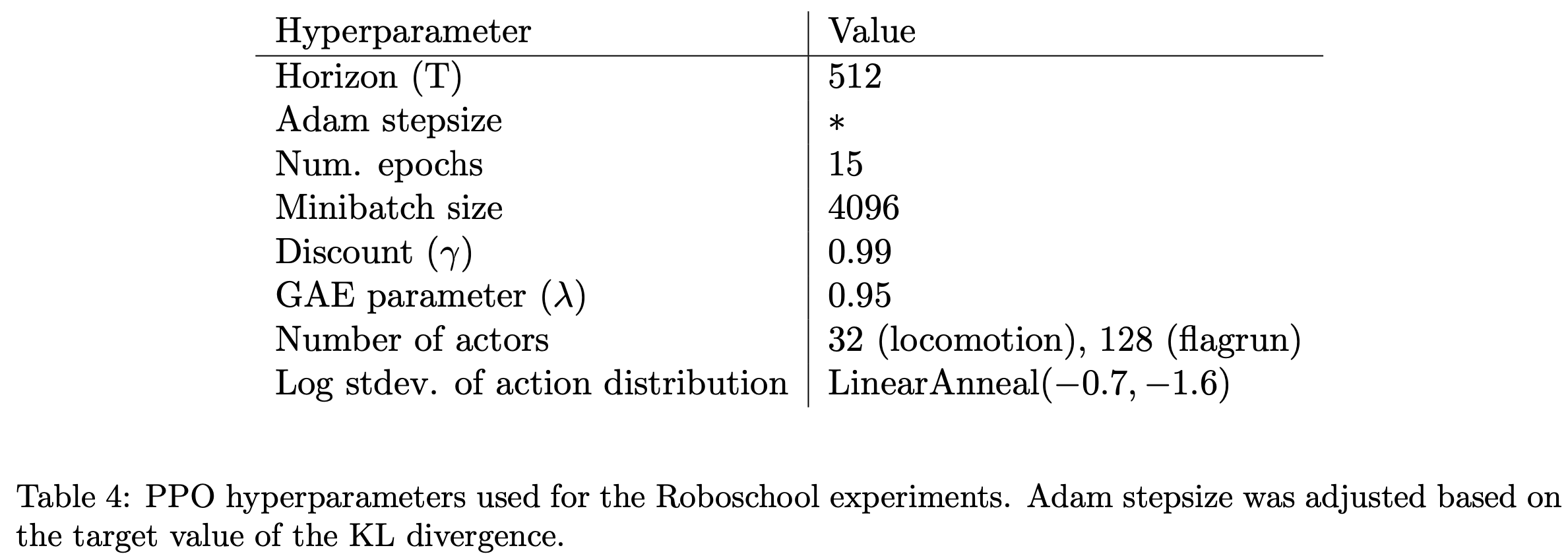
- 训练流程,来自OPENAI原始论文:Training language models to follow instructions with human feedback
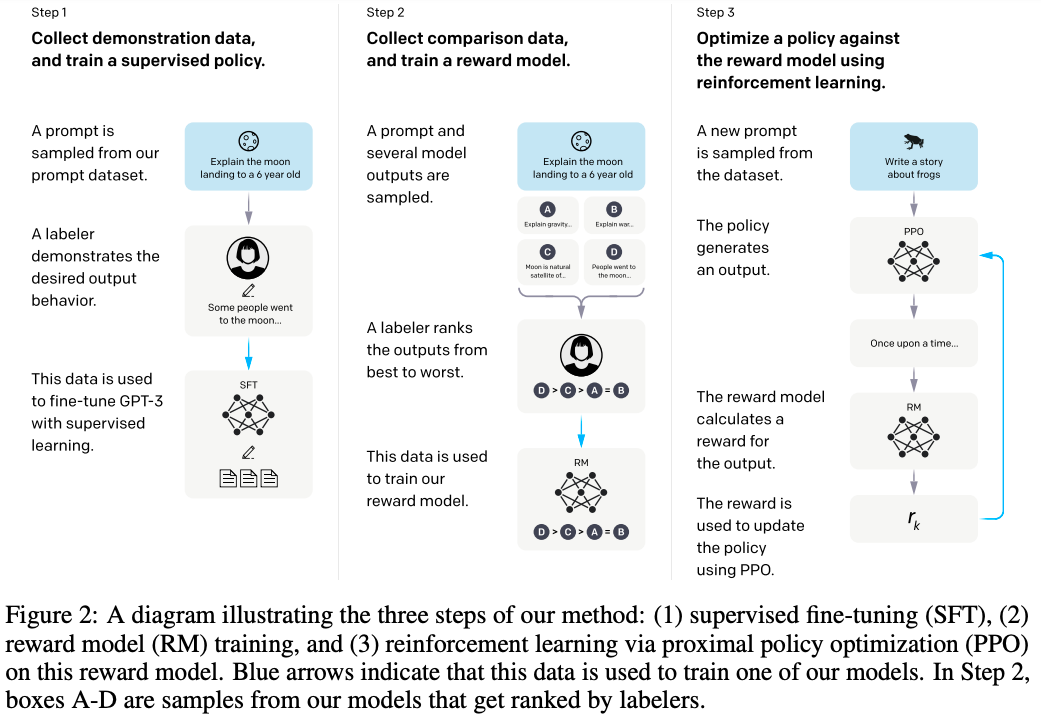
附录:Reward 的 KL 散度为什么可以将期望消去
- 奖励函数的定义 :
$$
r_t = r_{\varphi}(q, o_{\leq t}) - \beta \log \frac{\pi_\theta(o_t|q, o_{ < t})}{\pi_{ref}(o_t|q, o_{ < t})}
$$- \(r_{\varphi}(q, o_{\leq t})\) 是外部奖励模型给出的原始奖励
- \(\beta \log \frac{\pi_\theta}{\pi_{ref}}\) 是 KL散度惩罚项,\(\beta\) 是一个正的超参数,本质是一个去除期望的KL散度
理论理解(目前 OK)
- 由于动作 \(o_t\) 是从 \(\pi_\theta\) 策略中采样的(具体来说,是从 \(\pi_{\theta_\text{old}}\) 中采样的,PPO下可以近似认为两者相等),而 \(\mathbb{E}_{o_t \sim \pi_\theta(o_t|q,o_{ < t})}\Big[\log\frac{\pi_\theta(o_t|q,o_{ < t})}{\pi_\text{ref}(o_t|q,o_{ < t})}\Big]\) 是KL散度,值一定大于0,所以最大化带KL散度后的 \(r_t\) 就可以最小化KL散度,让Actor不要偏离Reference Model太多
- 在策略更新时,本质就是按照 \(o_t \sim \pi_\theta(o_t|q,o_{ < t})\) 采样得到的样本更新的,也就是在更新 \(\log\frac{\pi_\theta(o_t|q,o_{ < t})}{\pi_\text{ref}(o_t|q,o_{ < t})}\) 在分布 \(o_t \sim \pi_\theta(o_t|q,o_{ < t})\) 下的期望 \(\mathbb{E}_{o_t \sim \pi_\theta(o_t|q,o_{ < t})}\Big[\log\frac{\pi_\theta(o_t|q,o_{ < t})}{\pi_\text{ref}(o_t|q,o_{ < t})}\Big]\)
- 注:在许多实现中都有类似操作,比如SpinningUp项目的PPO的实现中,有
approx_kl = (logp_old - logp).mean().item()语句来表示近似KL散度,这里样本都是从 \(\pi_{\theta_\text{old}}\) 策略中采样得到的,所以:
$$
\begin{align}
D_{\text{KL}}(\pi_{\theta_\text{old}}||\pi_{\theta}) &= \mathbb{E}_{a \sim \pi_{\theta_\text{old}}} \left[\log\frac{\pi_{\theta_\text{old}}(a|s)}{\pi_{\theta}(a|s)}\right] &\\
&\approx \frac{1}{N} \log\frac{\pi_{\theta_\text{old}}(a|s)}{\pi_{\theta}(a|s)} \\
&= \frac{1}{N} (\log \pi_{\theta_\text{old}}(a|s)- \log\pi_{\theta}(a|s))
\end{align}
$$
直观理解(暂未想通)
- \(\log \frac{\pi_\theta}{\pi_{ref}}\) 带来的行为 :
- 当 \(\pi_\theta(o_t|q, o_{ < t}) > \pi_{ref}(o_t|q, o_{ < t})\) 时,\(\frac{\pi_\theta}{\pi_{ref}} > 1\),因此 \(\log \frac{\pi_\theta}{\pi_{ref}} > 0\)
- 当 \(\pi_\theta(o_t|q, o_{ < t}) < \pi_{ref}(o_t|q, o_{ < t})\) 时,\(\frac{\pi_\theta}{\pi_{ref}} < 1\),因此 \(\log \frac{\pi_\theta}{\pi_{ref}} < 0\)
- 当 \(\pi_\theta(o_t|q, o_{ < t}) = \pi_{ref}(o_t|q, o_{ < t})\) 时,\(\log \frac{\pi_\theta}{\pi_{ref}} = 0 \)
- \(\log \frac{\pi_\theta}{\pi_{ref}}\) 对奖励的影响 :
- 当 \(\pi_\theta > \pi_{ref}\) 时 :\(\log \frac{\pi_\theta}{\pi_{ref}} > 0\),因此惩罚项 \(-\beta \log \frac{\pi_\theta}{\pi_{ref}} < 0\),会导致奖励 \(r_t\) 降低
- 当 \(\pi_\theta \lt \pi_{ref}\) 时 :\(\log \frac{\pi_\theta}{\pi_{ref}} < 0\),因此惩罚项 \(-\beta \log \frac{\pi_\theta}{\pi_{ref}} > 0\),会导致奖励 \(r_t\) 增加
- 当 \(\pi_\theta = \pi_{ref}\) 时 :
\(\log \frac{\pi_\theta}{\pi_{ref}} = 0\),惩罚项为 0,奖励 \(r_t\) 仅由外部奖励 \(r_{\varphi}\) 决定
- 为什么 \(\pi_\theta < \pi_{ref}\) 时奖励应该增加?
- 与直觉相反 :当 \(\pi_\theta < \pi_{ref}\) 时,\(\log \frac{\pi_\theta}{\pi_{ref}} < 0\),因此惩罚项 \(-\beta \log \frac{\pi_\theta}{\pi_{ref}} > 0\),这确实会导致奖励 \(r_t\) 增加
- 直观理解有问题不太(还需要思考):
- 鼓励策略采取保守行为 :当 \(\pi_\theta\) 生成某个 token 的概率低于 \(\pi_{ref}\) 时,模型的行为更加保守,RLHF在鼓励这种保守行为,这种保守其实很奇怪,本质是在鼓励降低 \(o_t\) 出现的概率
- 问题:这也会导致模型概率往负向偏离原始参考模型吧?
- 直观理解的疑惑总结 :
- 当 \(\pi_\theta < \pi_{ref}\) 时,\(\log \frac{\pi_\theta}{\pi_{ref}} < 0\),惩罚项 \(-\beta \log \frac{\pi_\theta}{\pi_{ref}} > 0\),奖励 \(r_t\) 会增加,这种设计是为了鼓励模型的行为更加保守(注:保守其实很奇怪,本质是在鼓励降低 \(o_t\) 出现的概率)
- 当 \(\pi_\theta > \pi_{ref}\) 时,惩罚项为负,奖励会降低(此时是符合常识的),从而防止模型过度自信地生成偏离参考策略的内容
- 其他说明:在GRPO中,有一种全新的KL散度近似公式,该公式下,近似值永远大于等于0,就不存在上面的问题了





/Algorithm1.png)
/Figure2.png)
/Figure3.png)
/Figure4.png)
/Figure6.png)
/Figure7.png)
/Figure8.png)
/Figure9.png)
/Figure10.png)
/Figure11.png)
/Figure12.png)
/Figure13.png)
/Figure14.png)
/Figure15.png)
/Figure16.png)
/Figure17.png)
/Figure18.png)
/Figure19.png)
/Table4.png)
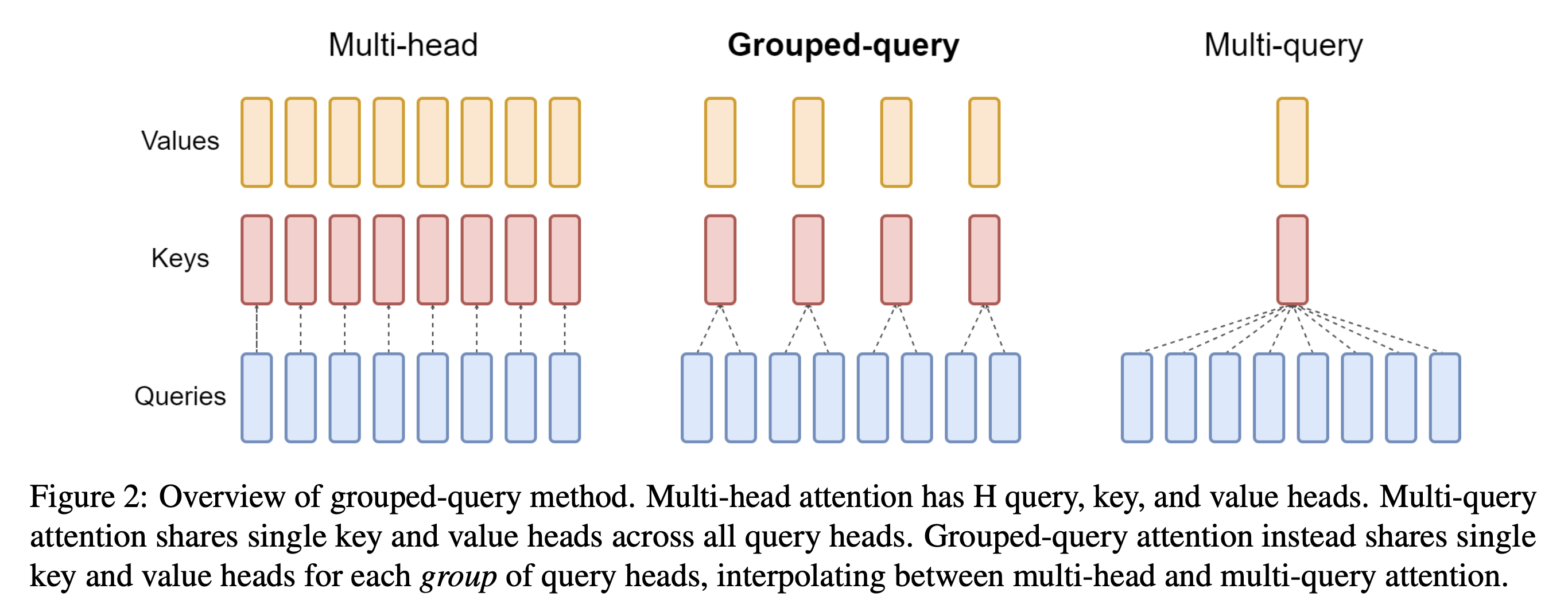
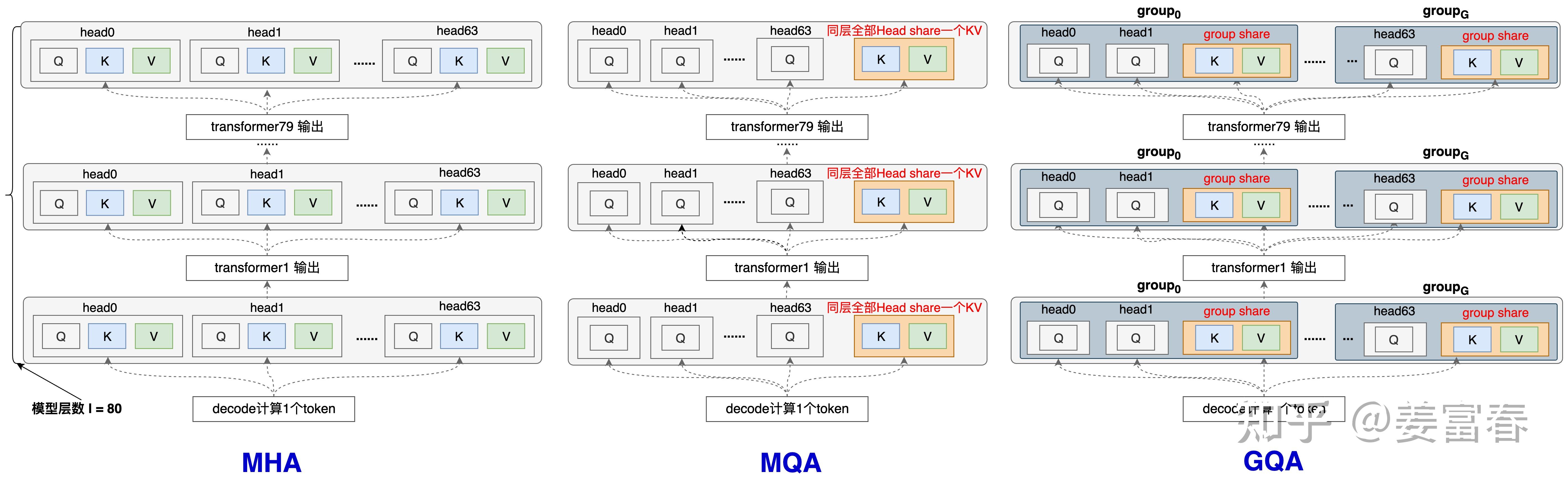
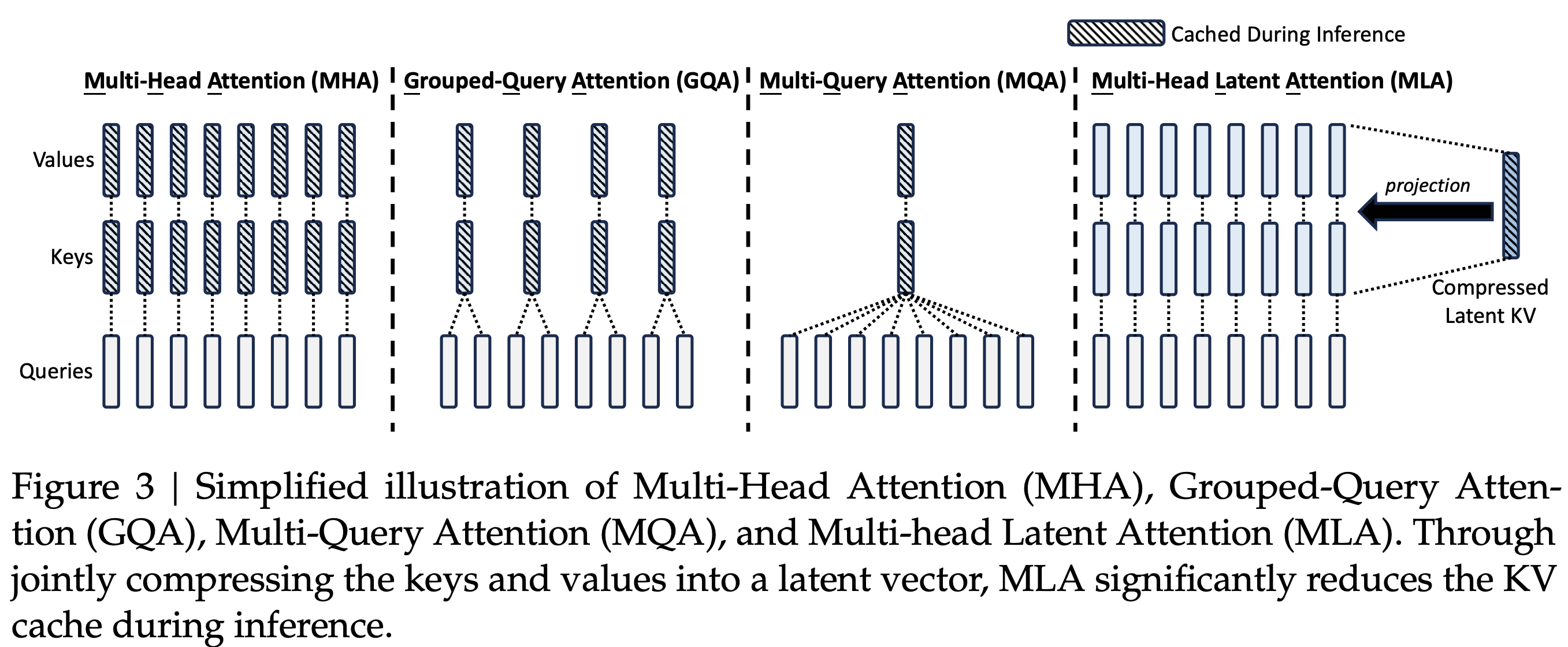
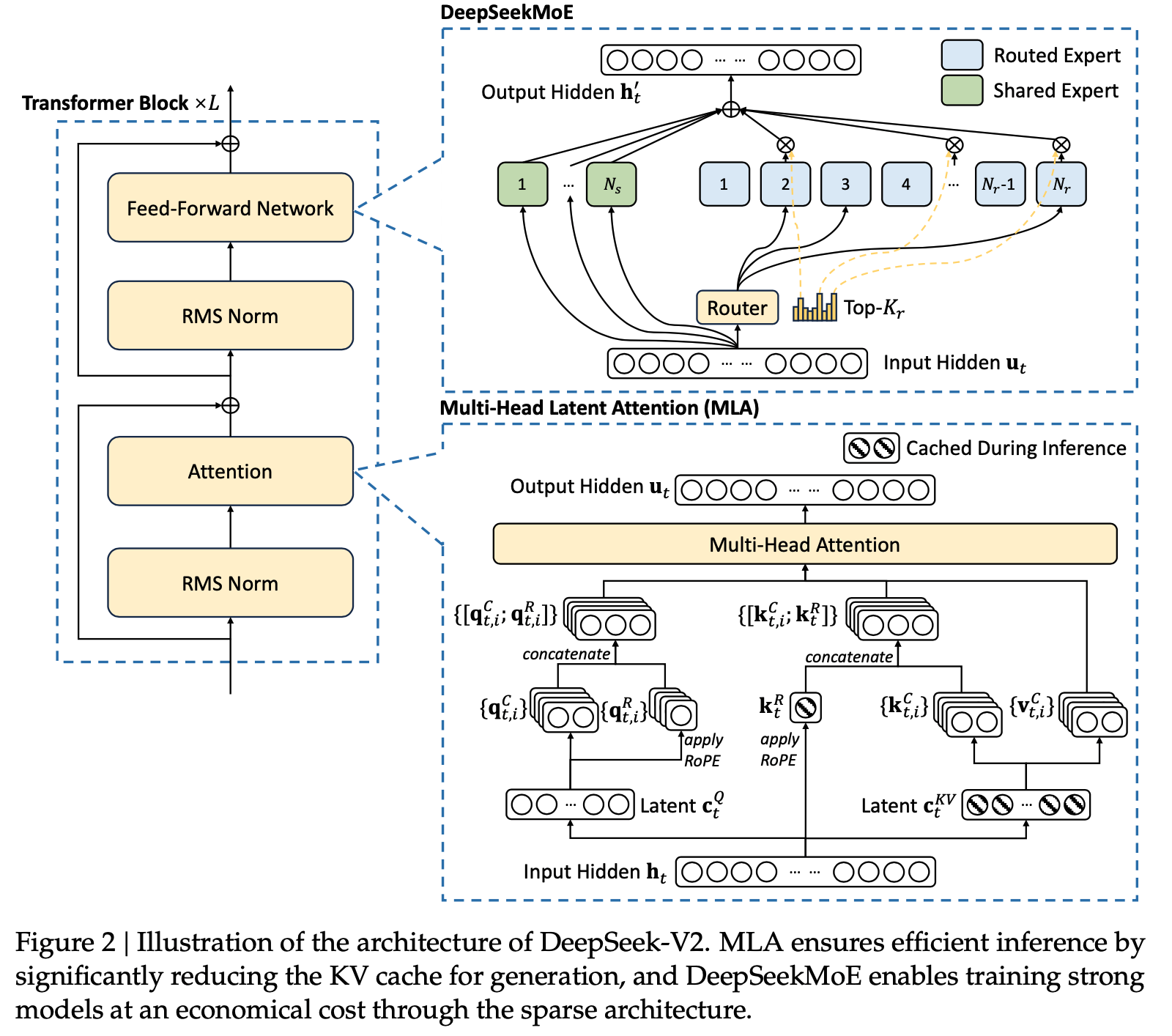 * 核心,MLA 将 Q 和 K 拆开成 引入 RoPE 和 不引入 RoPE(NoPE)两部分,两者的 q 和 k 分别做 concat,本质是 qk 相乘以后做加法
* 核心,MLA 将 Q 和 K 拆开成 引入 RoPE 和 不引入 RoPE(NoPE)两部分,两者的 q 和 k 分别做 concat,本质是 qk 相乘以后做加法

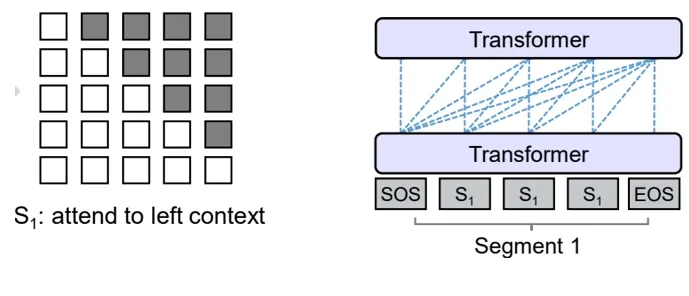
](/Notes/NLP/NLP——LLM相关名词/prefix-causal-encoder_decoder-mask-overview.png)
](/Notes/NLP/NLP——LLM相关名词/MHA-MQA-GQA-Overview.png)