本文介绍几种采样的方法
计算机能做什么样的采样
Uniform
- 本质上来讲,计算机只能实现对均匀分布(Uniform Distribution)的采样
numpy.random模块功能介绍
numpy.random是用来实现随机数生成的库
- 生成随机数
random - 生成某个随机数的随机样本
random_sample - 对序列做随机
shuffle,choice等
numpy.random模块的采样
numpy.random模块下实现了很多常见分布的采样函数(他们本质上都是计算机通过多次均匀分布采样实现的)
单变量分布
beta:beta分布binomial:二项分布chisquare:卡方分布exponential:指数分布- 还有更多…
多变量分布
dirichlet: Multivariate generalization of Beta distribution. 狄利克雷分布multinomial: Multivariate generalization of the binomial distribution. 多项分布multivariate_normal: Multivariate generalization of the normal distribution. 多变量正太(高斯)分布
标准分布
standard_cauchy: Standard Cauchy-Lorentz distribution.standard_exponential: Standard exponential distribution.standard_gamma: Standard Gamma distribution.standard_normal: Standard normal distribution.standard_t: Standard Student’s t-distribution.
复杂分布的采样方式
在实践中,往往有很多复杂的分布,复杂到我们无法直接对他进行采样
有些时候我们甚至不知道目标函数的分布函数
逆变换采样
Inverse Transform Sampling
目标函数: \(p(x)\)
相关补充:
- 求函数的累积分布函数 \(\Phi(x) = \int_{- \infty}^{x}p(t)d_{t}\)
- 求累计分布函数的逆函数(反函数) \(\Phi^{-1}(x)\)
采样步骤:
- 均匀分布采样: \(u_{i} \sim U(0,1)\)
- 计算: \(x_{i} = \Phi^{-1}(u_{i})\),其中 \(\Phi^{-1}(\cdot)\) 是 \(p(x)\) 的累积分布函数(CDF)的逆函数
- \(x_{i}\) 服从 \(p(x)\) 分布
优缺点:
- 优点:
- 仅需进行一个均匀分布采样即可
- 缺点:
- 需要求解累积分布函数的逆函数
- 累积分布函数的逆函数不一定容易求解,有些甚至无法求解
- 优点:
证明:
- 示意图如下:
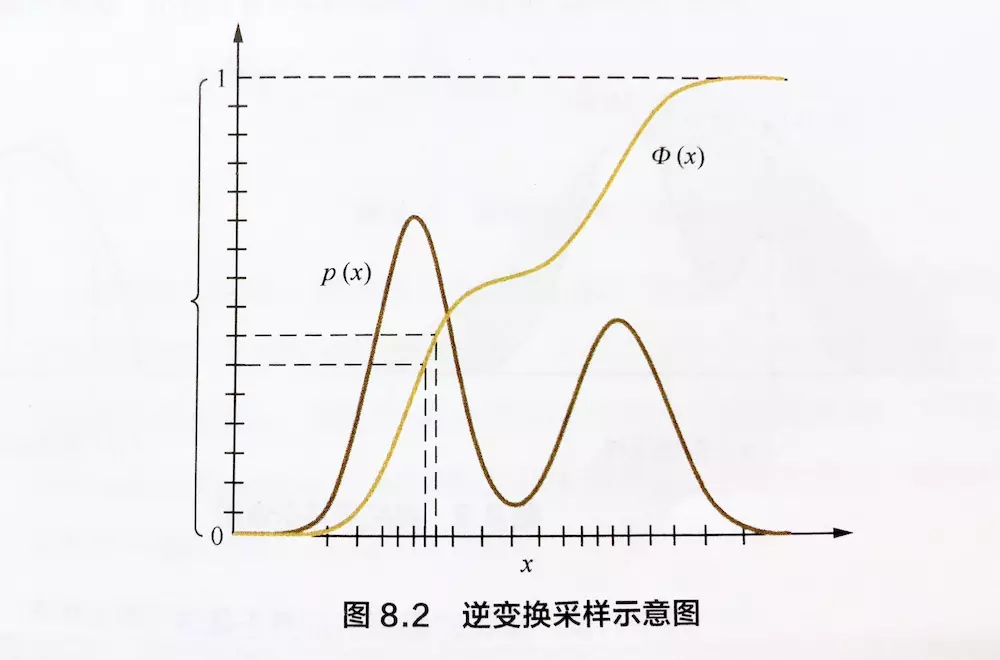
- 图中纵轴就是均匀分布采样的结果,然后丛纵轴对应到的累计分布函数 \(\Phi(x)\) 的曲线上概率越大的地方实际上也就是累积分布函数的导数(原始分布函数 \(p(x)\))最大的地方
- 这个对应过程等价于我们将 \(x\) 轴和 \(y\) 轴互换,也就是求累积分布函数的逆函数即可
- 示意图如下:
拒绝采样
别名: Accept-Reject Sampling, 接受-拒绝采样
目标函数: \(p(x)\)
相关补充:
- (参考分布寻找) : 寻找一个容易采样的分布 \(q(x)\),满足 \(p(x) \leq M\cdot q(x)\)
- 一般选择正太分布等
- \(M > 1\),从后面的证明可以知道, M越小越好
采样步骤:
- 参考分布采样: \(x_{i} \sim q(x)\)
- 均匀分布采样: \(u_{i} \sim U(0,1)\)
- 判断是否接受: 如果 \(u_{i} < \frac{p(x_{i})}{M\cdot q(x_{i})}\),则接受采样,否则拒绝本次采样(丢弃本次采样的 \(x_{i}\))
- \(x_{i}\) 服从 \(p(x)\) 分布(不包括被拒绝的样本)
证明:
- 由采样步骤得到,最终得到的分布服从$$q(x)\cdot \frac{p(x)}{M\cdot q(x)} = \frac{1}{M}p(x)$$
- 对上述分布进行归一化即可得到采样的样本服从 \(p(x)\)
- 从 \(\frac{1}{M}p(x)\) 这里也可以看出来采样的效率由M值的大小决定,M越小,采样效率越高
优缺点:
- 优点:
- 复杂分布变成简单分布采样+一个均匀分布,有时候甚至可以将参考分布也使用均匀分布
- 缺点:
- 参考分布 \(q(x)\) 的选择很难的
- 不合适的参考分布可能导致采样效率低下
- 优点:
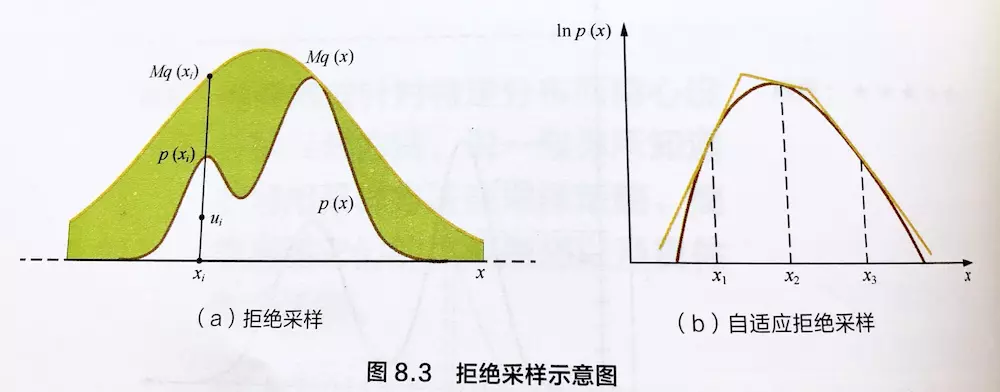
解决 \(q(x)\) 难以寻找的一种解决方案: 自适应拒绝采样(Adaptive Rejection Sampling)
- 只适用于目标函数为凸函数
- 使用分段线性函数来覆盖目标函数
- 下面是示意图片(图片来源: https://www.jianshu.com/p/3fb6f4d39c60)
重要性采样
Importance Sampling
- 重要性采样与前面两者不同,重要性采样解决的问题是在求一个函数的关于原始分布的期望时
- 目标定义: \(\mathbb{E}_{x\sim p(x)}[f(x)] = \int_{x}f(x)p(x)d_{x}\)
- 直接对 \(p(x)\) 采样可能存在的两个问题:
- \(p(x)\) 可能难以采样
- \(p(x)\) 采样到的样本大多都在 \(f(x)\) 比较小的地方,即 \(f(x)\) 与 \(p(x)\) 的差别太大导致有限次采样无法正确评估原始期望,采样次数不够大的话偏差可能很大
- 这里一种解决方案是采样足够多的次数,多花点时间保证所有样本量足够,降低偏差
- 解决方案:
- 引入一个容易采样的参考分布 \(q(x)\),满足
$$
\begin{align}
\mathbb{E}_{x\sim p(x)}[f(x)] &= \int_{x}f(x)p(x)d_{x} \\
&= \int_{x}f(x)\frac{p(x)}{q(x)}q(x)d_{x} \\
&= \int_{x}f(x)w(x)q(x)d_{x} \\
\end{align}
$$ - 其中 \(w(x) = \frac{p(x)}{q(x)}\) 称为样本 \(x\) 的重要性权重(Importance Weight),不同样本的重要性权重不同
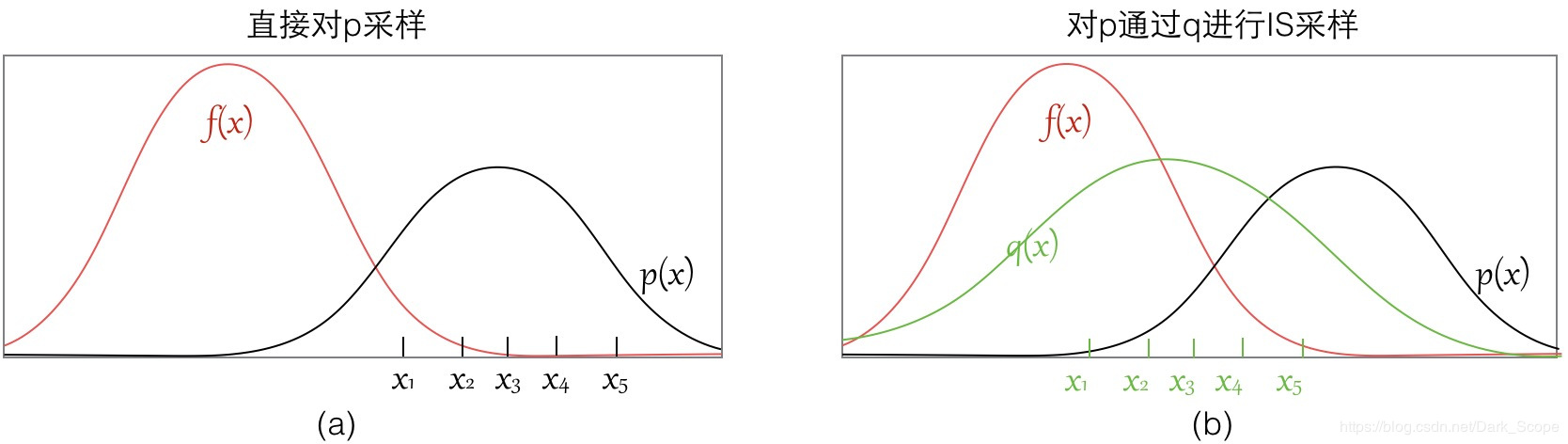
- 与直接从 \(p(x)\) 中采样相比,相同采样次数,最终得到期望偏差会更小,因为 \(p(x)\) 会增大在 \(f(x)\) 大但是 \(p(x)\) 极小处的样本被采样的概率,然后调低这个样本的权重
- 引入一个容易采样的参考分布 \(q(x)\),满足
- 示意图片:
总结
- 逆采样和拒绝采样都是在通过简单分布采样来采样原始分布的样本,最终的样本就是服从原始分布的样本 \(x_{i}\sim p(x)\)
- 重要性采样本质上是通过简单分布来采样和重要性权重来估计某个函数在原始分布上的期望 \(\mathbb{E}_{x\sim p(x)}[f(x)] = \int_{x}f(x)p(x)d_{x}\)
- 对于高维空间中的随机向量,拒绝采样和重要性采样经常难以找到合适的参考分布,容易导致采样效率低下(样本的接受概率太小或者重要性权重太低),此时可以考虑马尔可夫蒙特卡罗采样法(MCMC),MCMC中常见的有两种,MH(Metropolis-Hastings)采样法和Gibbs采样法,关于MCMC详情可参考我的博客ML——MCMC采样