RS——推荐系统综述

推荐系统分类(基于推荐依据分类)

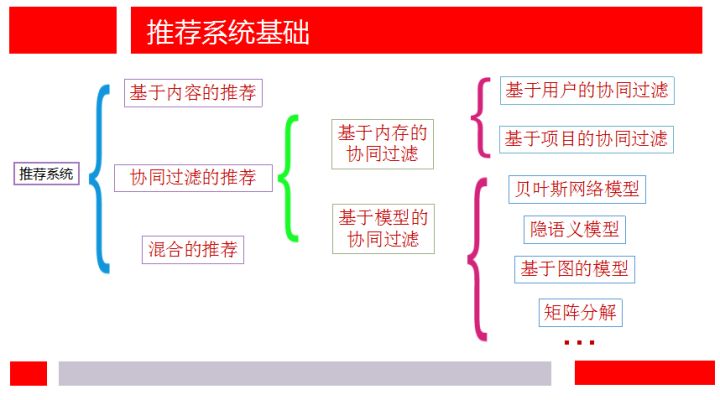
[待更新]

基于内容的推荐

Content-based recommenders

  • 推荐和用户曾经喜欢的商品相似的商品
  • 主要是基于商品属性信息和用户画像信息的对比
  • 核心问题是如何刻画商品属性和用户画像以及效用的度量
  • 使用一个效用函数(utility function)来评价特定用户\(c \in C\)对特定项目\(s_{c}’ \in S\)的评分, \(UserProfit(c), ItemProfit(s)\)分别表示用户和商品的收益函数(Profit Function)[存疑: 待更新]
    $$u(c,s) = score(UserProfit(c), ItemProfit(s))$$
    • 基于启发式的方法(Heuristic-based method):
      • 特征构建: 基于关键字提取等方法,使用TF-IDF等指标提取关键字作为特征
      • 效用的度量: 使用启发式cosine等相似性指标, 衡量商品特征和用户画像的相似性,相似性越高,效用越大
    • 基于机器学习的方法(Machine learning-based mehod):
      • 特征构建: 使用机器学习算法来构建用户和商品的维度特征,例如建模商品属于某个类别,得到商品的刻画属性
      • 效用的度量: 直接使用机器学习算法拟合效用函数
  • 对于任意的用户\(c \in C\),我们可以通过选择商品\(s_{c}’ \in S\)来得到最大化的效用函数
    $$\forall c \in C, s_{c}’ = \arg\max_{s \in S} u(c,s)$$

基于协同过滤的推荐

Collaborative filtering recommenders

基于内存的推荐
  • 直接对User-Item矩阵进行研究
    • User-based CF: 推荐给特定用户列表中还没有发生过行为、而在相似用户列表中产生过行为的高频商品
    • Item-based CF: 推荐给特定用户列表中还没有发生过行为、并且和当前用户已经发生过行为的商品相似的商品
基于模型的推荐
损失函数+正则项(Loss Function)
神经网络+层(Neural Network)
图模型+圈(Graph Model)
基于矩阵分解的推荐
  • Traditional SVD
    • 传统的SVD分解
      $$R_{m\times n} = U_{m \times k} \Sigma_{k \times k} V_{k \times n}^T$$
    • 缺点:
      • 普通SVD分解时矩阵必须是稠密的,即每个位置都必须有值
      • 如果矩阵是稀疏的,有空值,那么需要先用均值或者其他统计学方法来填充矩阵
      • 计算复杂度高,空间消耗大
  • FunkSVD
    • 分解为两个低秩矩阵而不是三个矩阵
      $$\hat{r}_{u,i} = q_i^T p_u$$
      • \(\hat{r}_{u,i}\)指用户对商品的评分
      • \(q_{i}\)是商品\(i\)在隐空间的隐向量表示
      • \(p_{u}\)是用户\(u\)在隐空间的隐向量表示
    • 不使用传统的矩阵分解方式,定一个损失函数(针对\(\hat{r}_{u,i}\)未缺失的地方,\(\hat{r}_{u,i}\)缺失的地方训练时不用管),然后用梯度下降法进行参数优化
      • 优化问题(最小化损失函数)定义如下
        $$q^{\star}, p^{\star} = \min_{q, p} \sum_{(u,i) \in R_{train}} (r_{u,i} - q_i^T p_u)^2 + \lambda (||q_i||^2 + ||p_u||^2 )$$
        • 正则项是两个参数的L2正则
        • \(R_{train}\)是评分矩阵中可观测的数据对构成的集合, 缺失值不参与训练, 缺失值是需要我们最终预测的
  • BiasSVD
    • BiasSVD是FunkSVD诸多变形版本的一个相对成功的方法
    • 带有偏执项的SVD分解
    • 基于假设:
      • 关于用户的假设: 天生存在偏好,有的喜欢给商品好评,有的喜欢给商品差评
        • 这些用户的固有属性与商品无关
      • 关于商品的假设: 天生存在优劣,有的容易被人给好评,有的容易被人给差评
        • 这些商品的固有属性与用户无关
    • 优化问题(最小化损失函数)定义
      $$
      \begin{align}
      &\hat{r}_{ui} = \mu + b_u + b_i + q_i^Tp_u \\
      &min \sum_{r_{ui} \in R_{train}} \left(r_{ui} - \hat{r}_{ui} \right)^2 + \lambda\left(b_i^2 + b_u^2 + ||q_i||^2 + ||p_u||^2\right)
      \end{align}
      $$
    • 梯度下降更新公式
      $$
      \begin{align}
      \begin{split}b_u &\leftarrow b_u &+ \gamma (e_{ui} - \lambda b_u) \\
      b_i &\leftarrow b_i &+ \gamma (e_{ui} - \lambda b_i)\\
      p_u &\leftarrow p_u &+ \gamma (e_{ui} \cdot q_i - \lambda p_u)\\
      q_i &\leftarrow q_i &+ \gamma (e_{ui} \cdot p_u - \lambda q_i)\end{split}
      \end{align}
      $$
      • \(e_{ui} = r_{ui} - \hat{r}_{ui}\)
      • \(b_{u}\)[待更新]
      • \(b_{i}\)[待更新]
      • \(u\)[待更新]
  • SVD++
    • SVD++是对BiasSVD进行改进的
    • 基于假设:
      • 除了显示的评分行为以外，用户对于商品的浏览记录或购买记录（隐式反馈）也可以从侧面反映用户的偏好。相当于引入了额外的信息源，能够解决因显示评分行为较少导致的冷启动问题
    • 优化问题定义[待更新]
  • TimeSVD++
    • 之前的模型都是静态的,这里TimeSVD++是动态的,每个时间段学习一个参数,不同时间段使用该时间段的训练数据进行学习
    • 优化问题定义[待更新]
  • BiasSVDwithU
  • NMF
  • 非负矩阵分解Nonnegative Matrix Factorization*
  • PMF
  • 概率矩阵分解Probabilistic Matrix Factorization*
  • WRMF
  • weighted regularized matrix factorization*

混合的推荐

  • 基于混合的推荐，顾名思义，是对以上算法的融合
  • 淘宝上就既有基于内容的推荐也有协同过滤的推荐
  • 对模型的融合可以参考集成学习的三种集成方式ML——Ensemble-集成学习

推荐系统分类(基于推荐的最终输出形式分类)

评分预测模型

Rating prediction

  • 核心目的: 填充User-Item矩阵中的缺失值
  • 模型衡量指标: 均方根误差(RMSE, Root Mean Squard Error), 平均绝对误差(MAE, Mean Absolute Error)

排序预测模型

Ranking prediction (top-n recommendation)

  • 核心目的: 给定一个用户,推荐一个有序的商品列表
  • 模型衡量指标: Precision@K, Recall@K等

分类模型

Classification

  • 核心目的: 将候选商品分类,然后用于推荐
  • 模型衡量指标: Accuracy