本文主要介绍因子分解机(FM, Factorization Machine)
FM模型
- 最早于2010年提出,目标是解决稀疏特征下的特征组合问题
模型推导
- 假设训练数据为:\(\{(x, y)\}\)
- \(x\)特征维度为n(One-Hot编码后的维度), 初始时维度比较小,但是特征中含有特殊的字符串或者对象类型等,我们使用One-Hot编码来拓展每个特殊特征(如果一个特征有m个可能的取值,那么One-Hot编码下每个特征将被扩展为m个维度)
- 由于用One-Hot来编码,所以实际上特征是非常稀疏的(某些特征很多样本都为0,只有少数的样本为1)
- \(y_{i}\)是样本的标签,表示是否点击(Clicked?), 1表示点击,0表示未点击
- \(x\)特征维度为n(One-Hot编码后的维度), 初始时维度比较小,但是特征中含有特殊的字符串或者对象类型等,我们使用One-Hot编码来拓展每个特殊特征(如果一个特征有m个可能的取值,那么One-Hot编码下每个特征将被扩展为m个维度)
- 一般模型建模
$$y(x) = w_0+ \sum_{i=1}^n w_i x_i \label{eq:poly}\tag{1}$$- 未挖掘到特征之间的关联关系,
- 如“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征，对用户的点击有着正向的影响
- 如“化妆品”类商品与“女”性，“球类运动配件”的商品与“男”性，“电影票”的商品与“电影”品类偏好等
- 未挖掘到特征之间的关联关系,
- FM建模
$$ y(x) = w_0+ \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n w_{ij} x_i x_j $$- n是样本的特征数量
- \(x_{i}\)是样本的第\(i\)个特征,不是第\(i\)个样本
- \(w_{0}, w_{i}, w_{ij}\)都是模型参数
- 显然模型组合特征的参数数量为\(\frac{n(n-1)}{2}\),且任意两个参数独立
- 存在问题: 在数据稀疏性普遍存在的实际应用场景中，二次项参数的训练是很困难的
- 原因: 每个参数\(w_{ij}\) 的训练需要大量\(x_{i}\) 和\(x_{j}\) 都非零的样本；由于样本数据本来就比较稀疏，满足“\(x_{i}\)和\(x_{j}\)都非零”的样本将会非常少。训练样本的不足，很容易导致参数\(w_{ij}\)不准确，最终将严重影响模型的性能
- 解决问题的灵感
- 基于模型的协同过滤中,一个User-Item的评分(rating)矩阵可以分解为User和Item两个矩阵,每个用户和商品都可以用一个隐向量表示
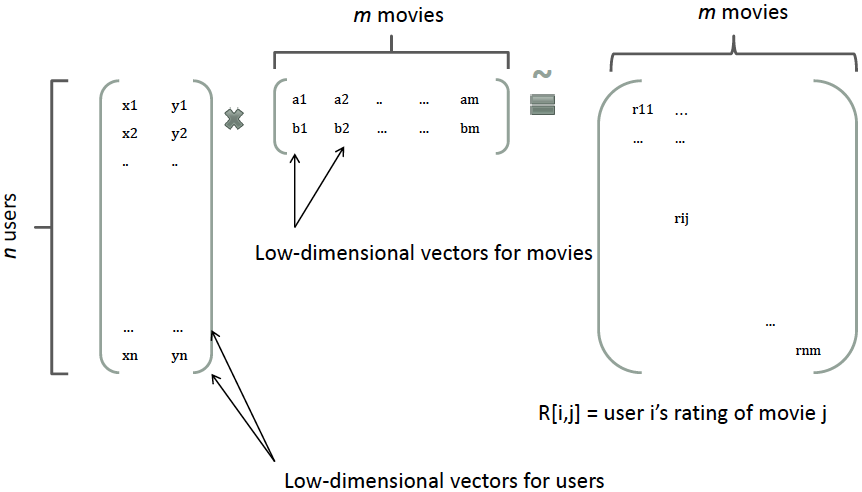
- 基于模型的协同过滤中,一个User-Item的评分(rating)矩阵可以分解为User和Item两个矩阵,每个用户和商品都可以用一个隐向量表示
- FM解决问题的方法:
- 用一个对称矩阵\(W\)代表所有二次项参数\(w_{ij}\),矩阵的两边对称的是参数,中间填充正实数
- 矩阵\(W\)可分解为
$$W=V^{T}V$$- \(V\)的第 \(j\) 列就是第 \(j\) 维特征的隐向量
- \(V\)是\(k x n\)维的向量(\(k << n\))
- 此时有
$$w_{ij} = \boldsymbol{v}_i^T \boldsymbol{v}_j$$
$$ y(x) = w_0+ \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n \boldsymbol{v}_i^T \boldsymbol{v}_j x_{i} x_{j} $$ - \(v_{i}\cdot v_{j}\)是两个隐向量的内积
- 此时\(w_{ij}\)和\(w_{mj}\)之间不在是独立的,他们有相同的内积项\(v_{j}\),这意味着所有包含“\(x_{i}\)的非零组合特征”(存在某个\(j\neq i\)，使得 \(x_{i}x_{j}\neq 0\))的样本都可以用来学习隐向量\(v_{i}\)(从而学习到\(w_{ij}\)), 这很大程度上避免了数据稀疏性造成的影响
- 问题: 以前不能用来学习吗?
- 回答: 以前的时候 \(w_{ij}\) 参数只能靠 \(x_{i}, x_{j}\) 均为1的样本 \(x\) 来训练,现在 \(w_{ij}\) 能由 \(v_{j}, v_{j}\) 生成,而 \(x_{i}\) 不为0的所有 \(x\) 都可以用来训练 \(v_{i}\),(当然,这里还需要存在某个 \(j\neq i\) ，使得 \(x_{i}x_{j}\neq 0\) , 只要当前样本不是只有\(x_{i}\)这个维度为1,这个条件肯定是成立的)
- 当前的式子运算复杂度是\(O(kn^2)\),这意味着我们训练和预测时计算\(y(x)\)的值都需要\(O(n^2)\)的时间
- 考虑到上面的公式主要是复杂在二次项的计算,我们考虑对二次项进行化简
$$
\sum_{i=1}^{n-1}\sum_{j=i+1}^n(v_i^T v_j)x_ix_j = \frac{1}{2}\left(\sum_{i=1}^n\sum_{j=1}^n(v_i^T v_j)x_ix_j-\sum_{i=1}^n(v_i^T v_i)x_ix_i\right)
$$
$$
\begin{align}
&=\frac{1}{2}\left(\sum_{i=1}^n\sum_{j=1}^n\sum_{l=1}^kv_{il}v_{jl}x_ix_j-\sum_{i=1}^n\sum_{l=1}^k v_{il}^2x_i^2\right)\\
&=\frac{1}{2}\sum_{l=1}^k\left(\sum_{i=1}^n(v_{il}x_i)\sum_{j=1}^n(v_{jl}x_j)-\sum_{i=1}^nv_{il}^2x_i^2\right)\\
&=\frac{1}{2}\sum_{l=1}^k\left(\left(\sum_{i=1}^n(v_{il}x_i)\right)^2-\sum_{i=1}^n (v_{il}x_i)^2\right)\\
\end{align}
$$
- 上式中：
- 现在二次项的复杂度是\(O(nk)\),最终模型的计算复杂度也是\(O(nk)\),注意这里是计算复杂度,不是参数数量(虽然FM模型的二次项参数数量碰巧也是\(nk\)个)
- 意味着我们可以在线性时间内对FM模型进行训练和预测,是非常高效的
- \(v_i, v_j\)分别表示\(\boldsymbol{v}_i, \boldsymbol{v}_j\)
参数数量
- 整体模型的参数一共是\(1+n+nk\)个
- 偏执项一个\(w_{0}\)
- 一次项 \(n\) 个\((w_{1},\dots,w_{n})\)
- 二次项 \(nk\) 个\(v_{ij}\),其中\(i=1,2,\dots,n\), \(j=1,2,\dots,k\)
和其他模型的对比
- FM较为灵活,通过一些合适的特征变换,可以用来模拟二阶多项式核的(SVM,MF模型,SVD++模型)等
- 相比SVM的二阶多项式而言,FM在样本稀疏的情况下有优势?什么优势?[待更新],
- 能想到的其中一个优势是FM训练/预测是线性复杂度,而二阶多项式核SVM需要计算核矩阵[待更新,关于核矩阵的理解?],所以复杂度是\(O(n^2)\)
- MF相当于只有 \(u,i\) 两类特征的FM模型[待更新:MF的详细推导]
- 而FM模型中我们还可以加入任意多的特征,比如user的历史购买平均值,item的历史购买平均值等,但是MF只能局限在两类特征中
- 为什么MF相当于只有 \(u,i\) 两类特征的FM模型?
- 证明,将MF中的每一项评分(rating)改写为:
$$r_{ui} \sim \beta_{u} + \gamma_i + x_u^Ty_i$$ - 显然可得结论
- 证明,将MF中的每一项评分(rating)改写为:
- SVD++与MF类似,都是矩阵分解方法,在特征的扩展性上也不如FM模型[待更新: SVD++的推导和理解]
- FFM是FM的改进模型,加入了Field的概念,参考RS——FMM模型