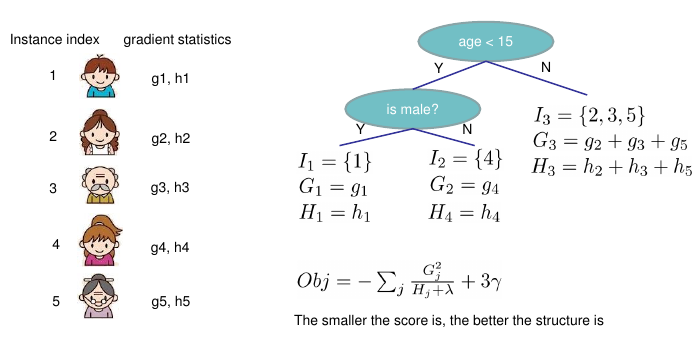
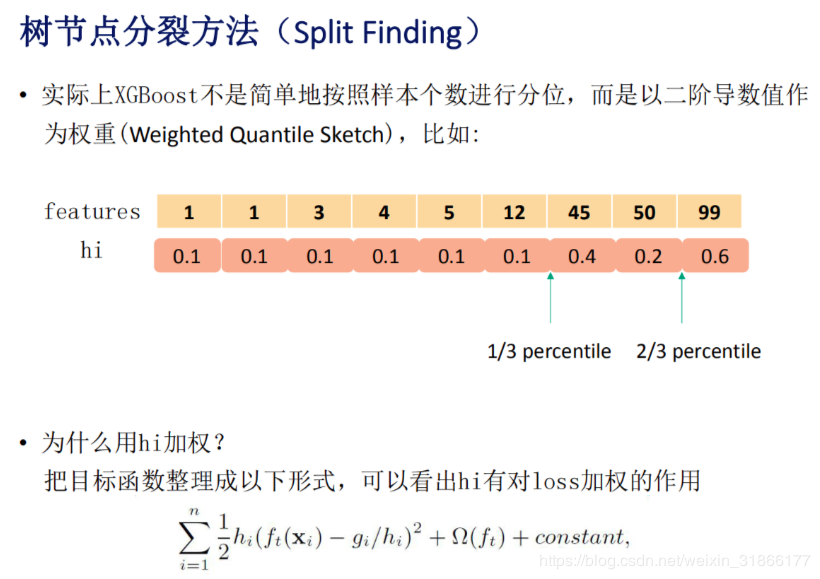
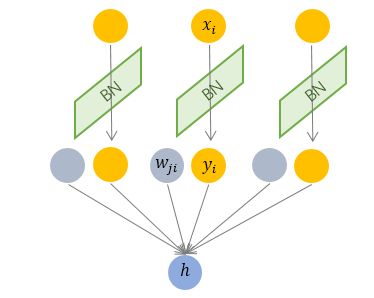
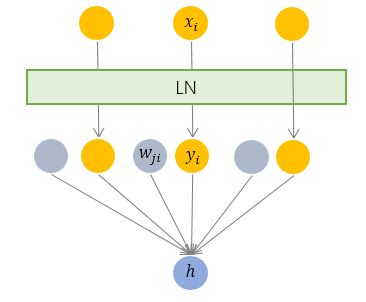
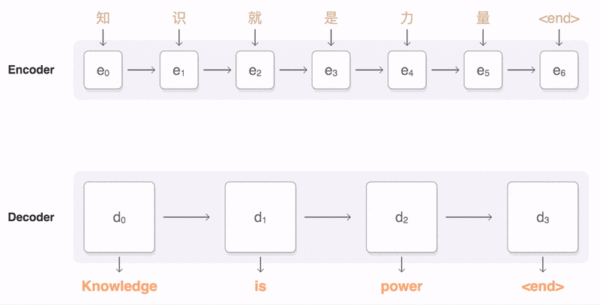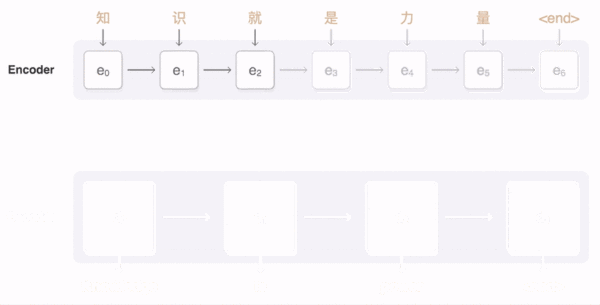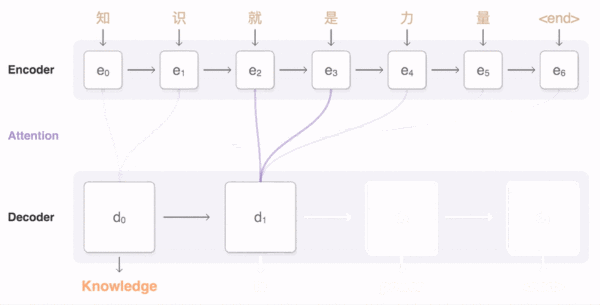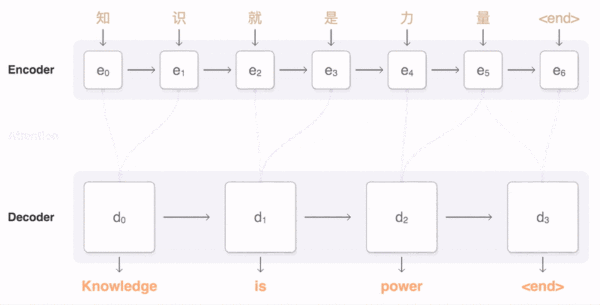
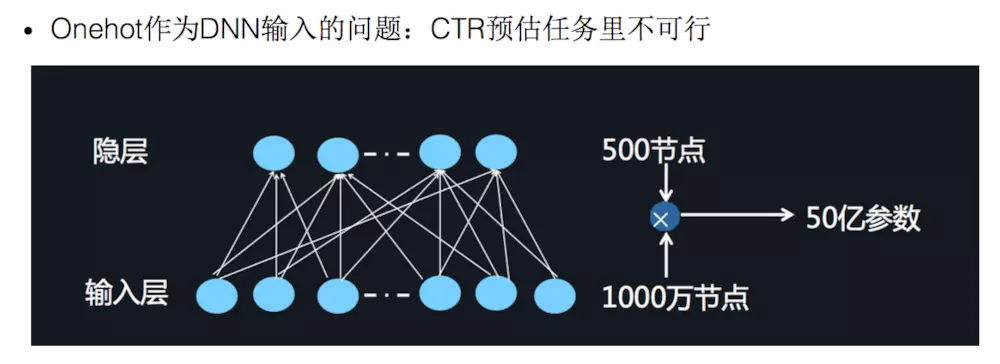
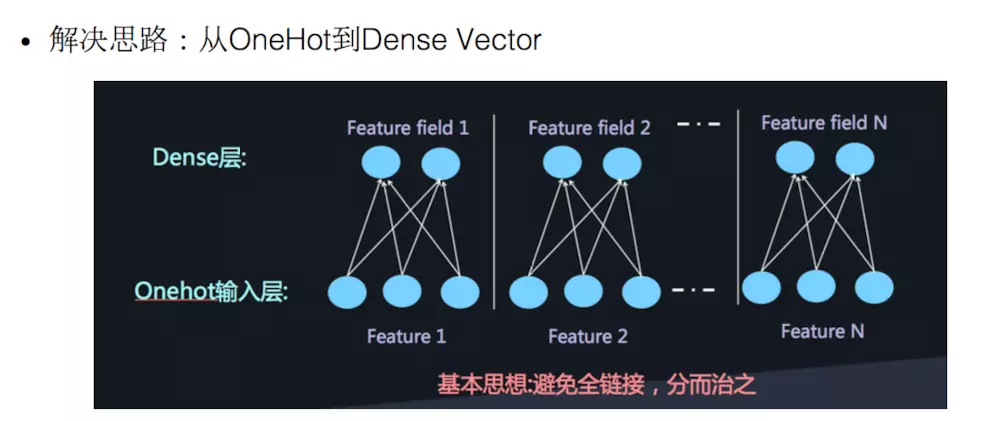
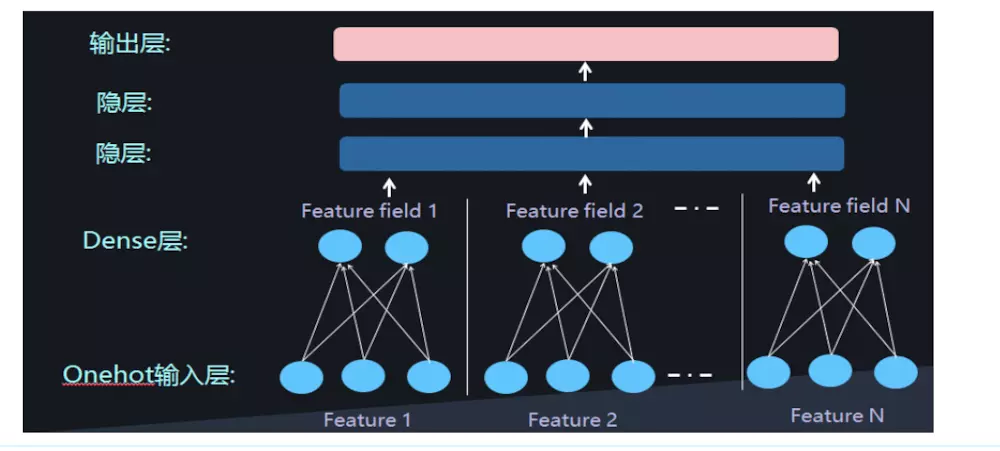
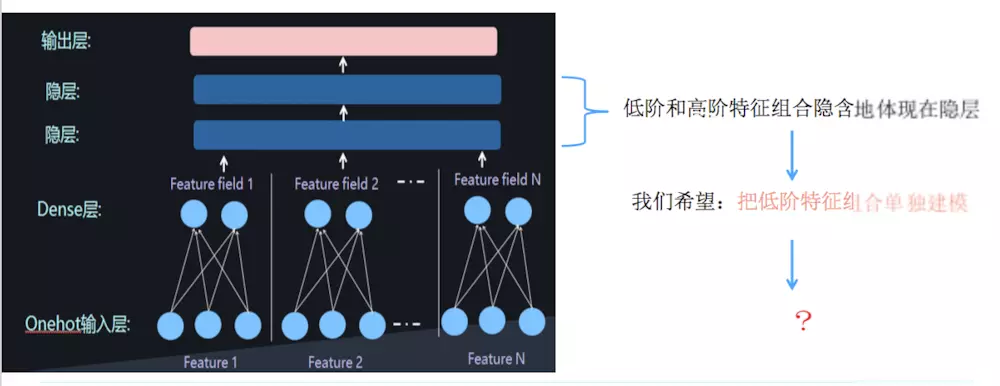
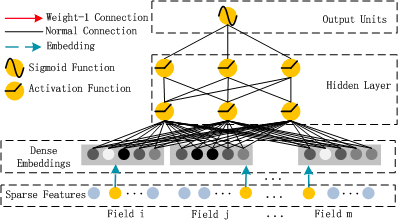
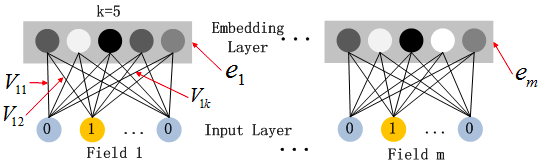
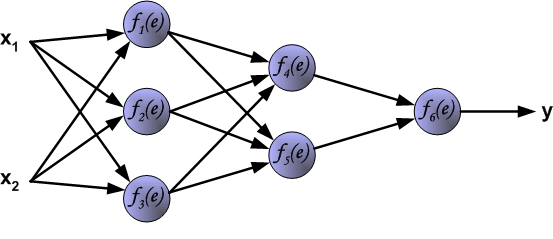
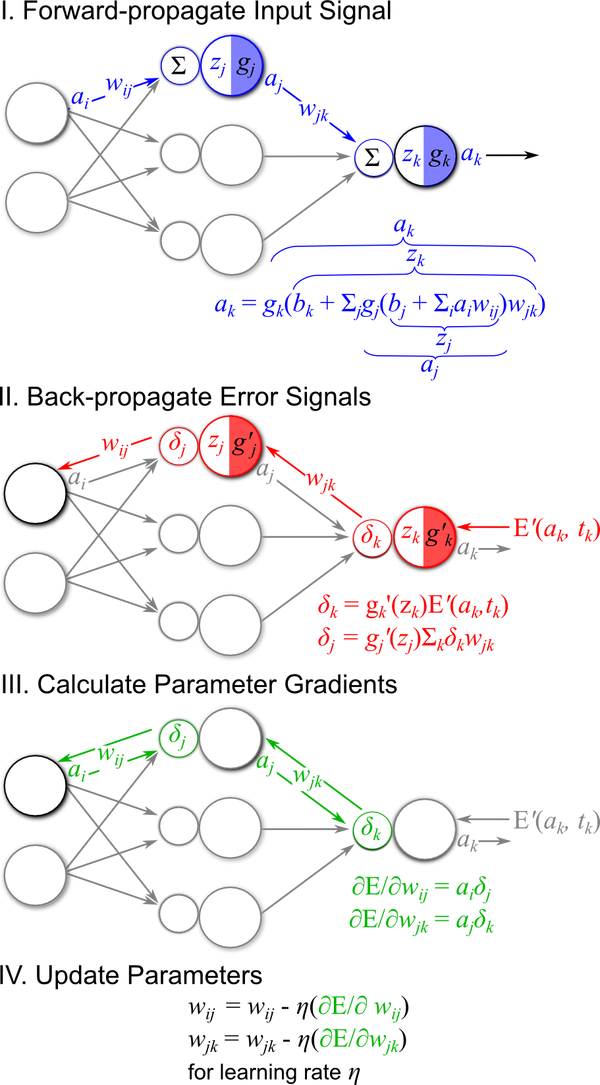
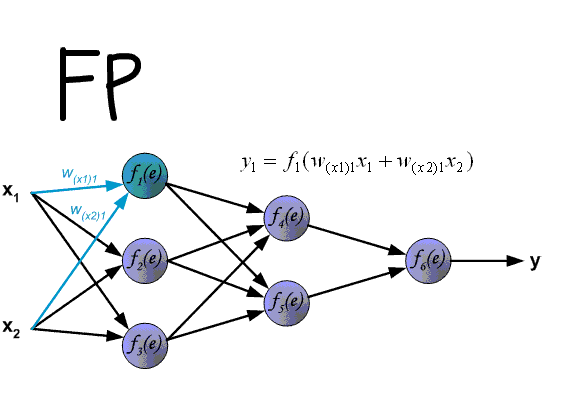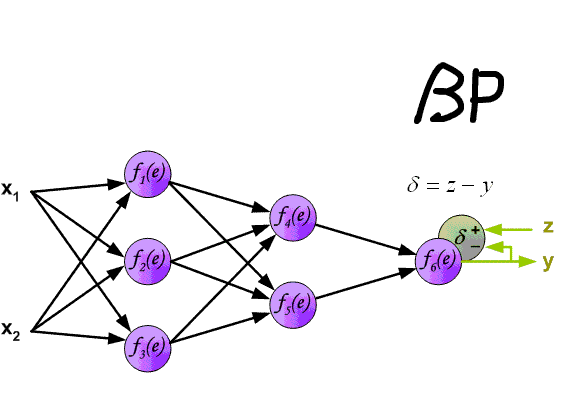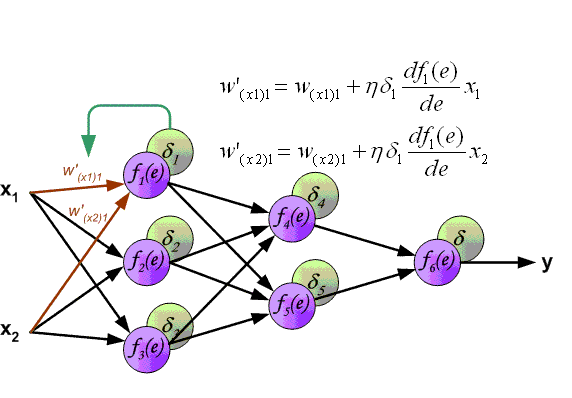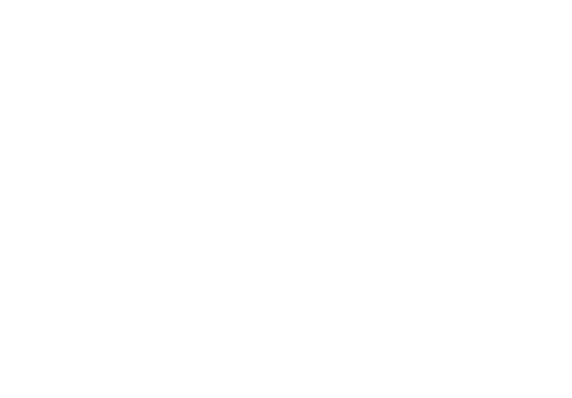
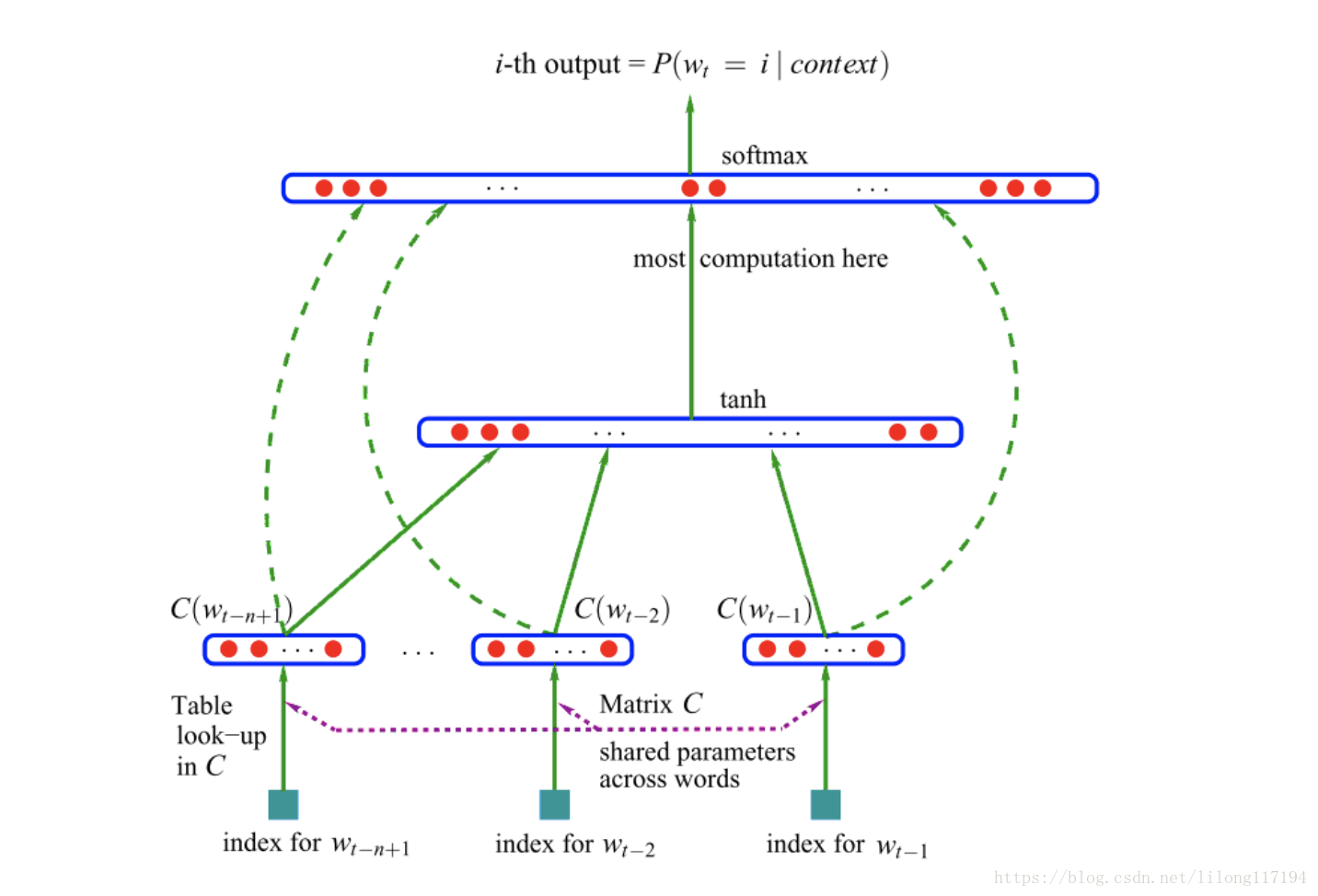
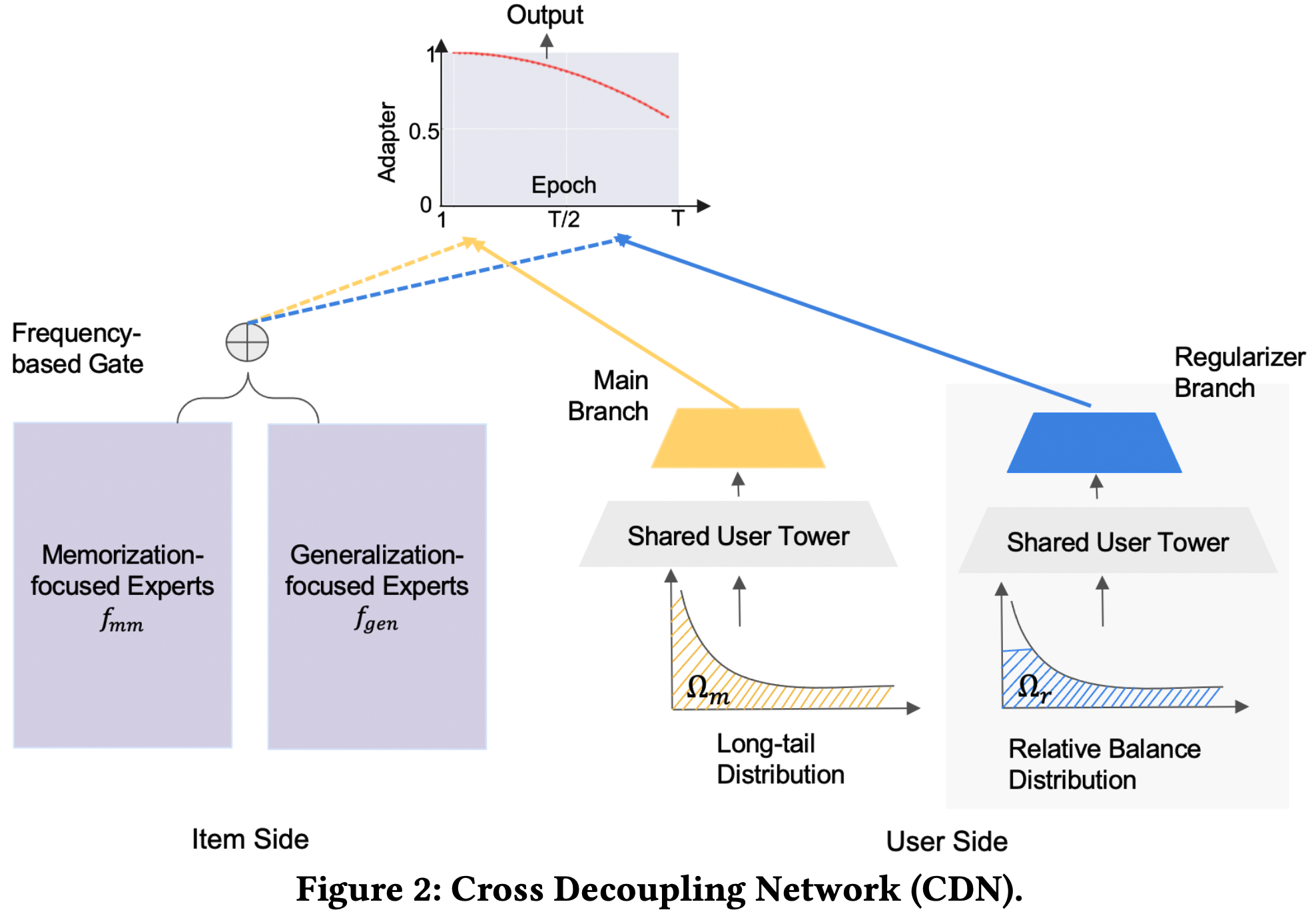
本文主要广告计算领域用于CTR,CVR预估的模型

计算广告领域的术语

一些术语

• CPA(Cost Per Action):
  • 一种广告计费模式
  • 按照行为(Action)来计费
  • 这里的行为可以是注册,咨询,放入购入车等
• CPC(Cost Per Click)
  • 一种广告计费模式
  • 按照点击(Click)次数

衡量指标

• 点击率CTR(click-through rate), 又名点击通过率:
  $$CTR = \frac{Count_{click}}{Count_{show}} $$
  • 分母是广告的实际展示次数
  • 分子是广告的实际点击次数
• 转化率CVR(conversion rate), 一种CPA衡量指标
  $$CVR= \frac{Count_{conversion}}{Count_{click}}$$
  • 分母是广告的实际点击次数
  • 分子是广告的转化次数,不同场景对转化成功的定义不同,比如手机号码注册用户为一次有效转化,那么这里CVR统计的就是所有点击了广告的人中有多少进行了实际的手机号注册

预估CTR,CVR的模型

人工特征工程+LR

• 人工提取当前广告的特征
• LR模型预估用户是否会点击该广告或者注册该网站(二分类)

GBDT+LR

• 参考博客: https://www.jianshu.com/p/96173f2c2fb4
• Facebook paper中的一个例子
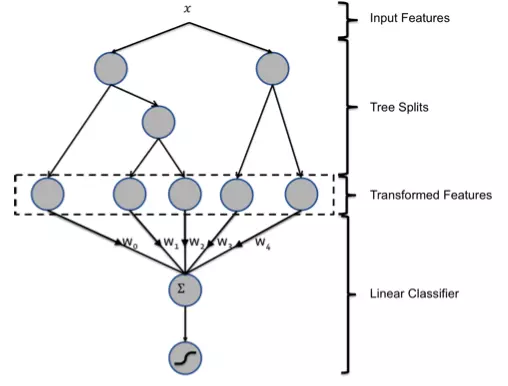
  • 图中的GBDT只包含两棵树,实际上使用时可包含更多
  • LR的特征数量(样本维度)就是所有树的叶节点树,样本落到当前叶节点则,当前叶节点对应的特征值为1,否则为0
  • 用于LR训练的特征维度共num_trees * num_leaves(也就是所有树叶节点的总数)
  • 由于有多棵树,每个原始样本在每棵树都会落到一个叶节点上,所以得到的新样本中可能有很多个特征值为1
  • 实践中原始输出时可能维度是树的棵数,每个数表示当前树中样本落到第几个叶节点上,对每棵树分别使用OneHot编码即可的到上面的 (num_trees * num_leaves) 维数据

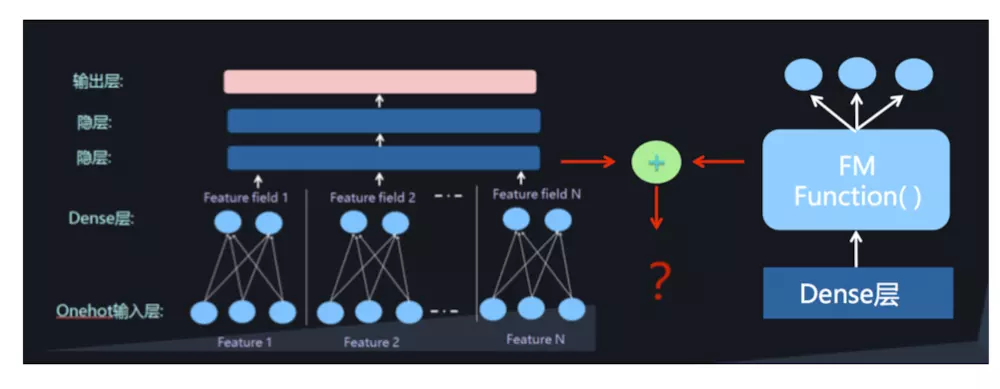
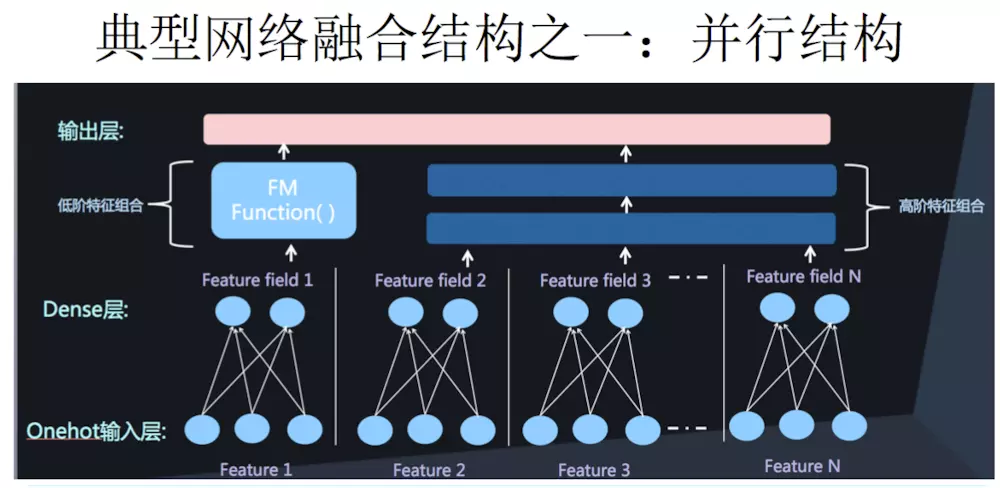
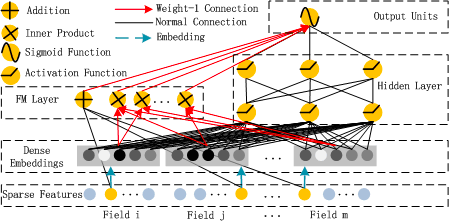
FM

• 参考博客RS——FM-因子分解机

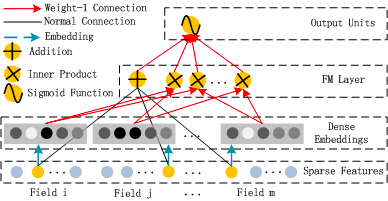
FFM

• 参考博客RS——FMM模型

XGBoost,全称: Extreme Gradient Boosting

概述

• CART回归树是XGBoost的基分类器

XGBoost模型推导(假设回归树的结构确定)

模型 \(F\) 的加法定义：

$$
\begin{align}
F(x;w) = \sum_{k=0}^{K} f_{k}(x;w_{k})
\end{align}
$$

• 其中, \(x\) 为输入样本, \(f_{k}\) 为分类回归树,可以是分类回归树空间中的任意一棵树, \(w_{k}\) 是树 \(f_{k}\) 的参数

定义损失函数

$$
\begin{align}
L^{t} &= \sum_{i=1}^{n}l(y_{i},\hat{y}_{i}^{t}) + \Omega(f_{t}) \\
&= \sum_{i=1}^{n}l(y_{i},\hat{y}_{i}^{t-1} + f_{t}(x_{i})) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2
\end{align}
$$

• \(L^{t}\)： 第 \(t\) 轮迭代的损失函数
• \(l(y_{i},\hat{y}_{i}^{t})\) 表示单个样本的损失函数定义
• \(\hat{y}_{i}^{t} = \hat{y}_{i}^{t-1} + f_{t}(x_{i})\) 表示第 \(t\) 轮 \(x_{i}\) 样本的预测值
  • 加法模型: 第 \(t\) 轮预测值 = 第 \(t-1\) 轮预测值 + 第 \(t\) 棵(轮)决策树的预测值
• \(\Omega(f_{t})\) 表示正则项
  • \(n\) 表示样本的个数
  • \(T\) 表示叶子结点的个数
  • \(w_{j}\) 表示叶节点分数 ， 即任意样本落到第 \(t\) 棵(轮)决策树的第 \(j\) 叶子结点时的预测值(可称为第 \(t\) 棵(轮)决策树的第 \(j\) 叶子结点的预测值)
  • \(\gamma\) 和 \(\lambda\) 都是正则项参数

第 \(t\) 轮训练的目标

• 找到一个最优的分类器 \(f_t^{\star}(x)\)，满足
  $$
  \begin{align}
  f_t^{\star}(x) &= \mathop{\arg\max}_{f_t(x)}L^{t} \\
  &= \mathop{\arg\max}_{f_t(x)}\left(\sum_{i=1}^{n}l(y_{i},\hat{y}_{i}^{t}) + \Omega(f_{t})\right) \\
  &= \mathop{\arg\max}_{f_t(x)}\left(\sum_{i=1}^{n}l(y_{i},\hat{y}_{i}^{t-1} + f_{t}(x_{i})) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2 \right)
  \end{align}
  $$

最小化损失函数推导

损失函数二阶泰勒展开

• 回忆传统泰勒展开:
  $$
  \begin{aligned}
  f(x) &= f(x_0) + f’(x_0)(x-x_0) + \frac{f’’(x_0)}{2!}(x-x_0)^2 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \\
  & = \sum\limits_{n=0}^{\infty}\frac{f^{(n)}x_0}{n!}(x - x_0)^n
  \end{aligned}
  $$

• 二阶泰勒展开公式
  $$
  \begin{align}
  f(x+\Delta x) \approx f(x) + f’(x)\Delta x + \frac{1}{2}f’’(x)\Delta x^2
  \end{align}
  $$

• 在我们的场景中,令

  • \(x = \hat{y}_{i}^{t-1}\)
  • \(\Delta x = f_{t}(x_{i})\)

• 则有对单个样本能得到
  $$
  \begin{align}
  l(y_{i},\hat{y}_{i}^{t-1} + f_{t}(x_{i})) \approx l(y_i,\hat{y}_i^{t-1}) + l’(y_i,\hat{y}_i^{t-1})f_t(x_i) + \frac{1}{2}l’’(y_i,\hat{y}_i^{t-1})f_t^2(x_i)
  \end{align}
  $$

  • \(l’(y_i,\hat{y}_i^{t-1})\) 是 \(l(y_i,\hat{y}_i)\) 对 \(\hat{y}_i\) 的一阶导数在 \(\hat{y}_i = \hat{y}_i^{t-1}\) 处的值
  • \(l’’(y_i,\hat{y}_i^{t-1})\) 是 \(l(y_i,\hat{y}_i)\) 对 \(\hat{y}_i\) 的二阶导数在 \(\hat{y}_i = \hat{y}_i^{t-1}\) 处的值

• 我们第 \(t\) 轮的目标是找到一个最优的分类器 \(f_t^{\star}(x)\) 最小化损失函数 \(L^{t}\)
  $$
  \begin{align}
  L^{t} \approx \sum_{i=1}^{n}\left(l(y_i,\hat{y}_i^{t-1}) + l’(y_i,\hat{y}_i^{t-1})f_t(x_i) + \frac{1}{2}l’’(y_i,\hat{y}_i^{t-1})f_t^2(x_i)\right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2
  \end{align}
  $$

• 显然上面式子中的 \(l(y_i,\hat{y}_i^{t-1})\) 与 \(f_t(x_i)\) 无关,可以移除,于是有
  $$
  \begin{align}
  L^{t} \approx \sum_{i=1}^{n}\left(l’(y_i,\hat{y}_i^{t-1})f_t(x_i) + \frac{1}{2}l’’(y_i,\hat{y}_i^{t-1})f_t^2(x_i)\right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2
  \end{align}
  $$

• 令:

  • \(g_i = l’(y_i,\hat{y}_i^{t-1})\) 为 \(l(y_i,\hat{y}_i)\) 对 \(\hat{y}_i\) 的一阶导数在 \(\hat{y}_i = \hat{y}_i^{t-1}\) 处的值
  • \(h_i = l’’(y_i,\hat{y}_i^{t-1})\) 是 \(l(y_i,\hat{y}_i)\) 对 \(\hat{y}_i\) 的二阶导数在 \(\hat{y}_i = \hat{y}_i^{t-1}\) 处的值

• 则有:
  $$
  \begin{align}
  L^{t} \approx \sum_{i=1}^{n}\left(g_if_t(x_i) + \frac{1}{2}h_if_t^2(x_i)\right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2
  \end{align}
  $$

• 做一个重要的转换 :
  $$f_t(x_i) = w_j, \quad s.t. \ x_i \in I_j$$

  • 上面的式子前半部分成立的条件是 \(x_i\) 落在叶子结点 \(j\) 上
  • 我们将条件 \(x_i\) 落在叶子结点 \(j\) 上表示为 \(\ x_i \in I_j\)

• 于是: 我们可以将前面对样本的累加变成对叶子结点的累加
  $$
  \begin{align}
  L^{t} &\approx \sum_{j=1}^{T}\left((\sum_{i \in I_j}g_i)w_j + \frac{1}{2}(\sum_{i \in I_j}h_i)w_j^2\right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2 \\
  &\approx \sum_{j=1}^{T}\left((\sum_{i \in I_j}g_i)w_j + \frac{1}{2}(\sum_{i \in I_j}h_i + \lambda)w_j^2\right) + \gamma T
  \end{align}
  $$

• 令:

  • \(G_j = \sum_{i \in I_j}g_i\)
  • \(H_j = \sum_{i \in I_j}h_i\)

• 则有
  $$
  \begin{align}
  L^{t} \approx \sum_{j=1}^{T}\left(G_jw_j + \frac{1}{2}(H_j + \lambda)w_j^2\right) + \gamma T
  \end{align}
  $$

• \(L^t\) 对 \(w_j\) 求偏导有
  $$
  \begin{align}
  \frac{\partial L^{t}}{\partial w_j} = G_j + (H_j + \lambda)w_j
  \end{align}
  $$

• 令导数 \(\frac{\partial L^{t}}{\partial w_j} = 0\) 可得
  $$
  \begin{align}
  w_j^{\star} = -\frac{G_j}{H_j+\lambda}
  \end{align}
  $$

• 同时
  $$
  \begin{align}
  L^{\star^t} &\approx min(L^t) \\
  &\approx \sum_{j=1}^{T}\left(G_j\cdot (-\frac{G_j}{H_j+\lambda}) + \frac{1}{2}(H_j + \lambda)\cdot(-\frac{G_j}{H_j+\lambda})^2\right) + \gamma T \\
  &\approx -\frac{1}{2}\sum_{j=1}^{T}\left(\frac{G_j^2}{H_j+\lambda}\right) + \gamma T
  \end{align}
  $$

• 目标函数的计算示例: 目标分数越小越好

  

结论

• 在第 \(t\) 轮回归树的结构确定后 ，我们得到的最优叶节点分数与结构无关 \(w_j^{\star} = -\frac{G_j}{H_j+\lambda}\)
• 最小损失与第 \(t\) 轮回归树的结构的复杂度(叶节点数量)相关
• 我们还需要确定第 \(t\) 轮回归树的结构

回归树的结构确定

普通决策树树结构的确定

• 详细情况可参考: ML——DT-决策树

ID3

• 最大化信息增益来选择分裂特征

C4.5

• 最大化信息增益比来选择分裂特征

CART

分类树

• 最小化基尼指数来选择分裂特征

回归树

• 最小化平方误差来选择分裂特征

XGBoost结点分裂前后的信息增益

• 信息增益应该与前面的损失函数相关, 损失越小越好
• 原始损失函数为
  $$
  \begin{align}
  L^{\star^t} \approx -\frac{1}{2}\sum_{j=1}^{T}\left(\frac{G_j^2}{H_j+\lambda}\right) + \gamma T
  \end{align}
  $$
• 显然,要使得损失函数最小,我们需要使得下面的式子最大:
  $$
  \begin{align}
  \frac{G_j^2}{H_j+\lambda}
  \end{align}
  $$
• 一个结点分裂后的信息为
  $$
  \begin{align}
  \frac{G_L^2}{H_L+\lambda} + \frac{G_R^2}{H_R+\lambda}
  \end{align}
  $$
  • 左子树的信息 + 右子树的信息
• 一个结点分裂前信息为
  $$
  \begin{align}
  \frac{(G_L + G_R)^2}{H_L+ H_R + \lambda}
  \end{align}
  $$
• 从而我们定义一个结点分列前后的信息增益为:
  $$
  \begin{align}
  Gain = \frac{G_L^2}{H_L+ \lambda} + \frac{G_R^2}{H_R+ \lambda} - \frac{(G_L + G_R)^2}{H_L+ H_R + \lambda} - \gamma
  \end{align}
  $$
  • Gain 越大说明当前结点的当前分裂方式越好
  • 其中 \(\gamma\) 是一个超参数用于防止过拟合 ，可以理解为有两层含义:
    • 用于对叶节点数目进行控制
    • 用于增大分裂前后Gain的阈值
    • 事实上 \(\gamma\) 不是凭空来的,开始的定义中 \(\gamma\) 就是L1正则化(叶节点数量)的系数, 这里分裂后叶节点数量多了1个, 我们希望树的叶节点越少越好(模型越简单越好),而这个的信息增益越大越好, 所以减去 \(\gamma\) 值,防止结点分裂得太多
    • 对于每个特征的每个分裂点, \(\gamma\) 值都相同,所以 \(\gamma\) 值对特征和分裂点的选择没有影响,只是影响了某个结点是否能够被分裂(信息增益太小或者为负时我们可以选择不分裂)

XGBoost树节点分裂

精确分裂算法

• 单个叶节点精确计算信息增益分裂流程(特征和特征分裂取值的选择, 假设一共m个特征)
  • 注意: 每次只对叶节点分裂,已经分裂了的就不是叶节点了,不能二次分裂
  • 原图来自: https://www.cnblogs.com/massquantity/p/9794480.html

近似分裂算法

• 将每个特征的取值划分为多个分位点
• 每次考察特征时值考察分位点,减少计算复杂度
• 其他的步骤与前面的精确分裂算法相同,包括分数计算和选择最大分数等

分桶策略与GBDT的不同

• 传统的GBDT分桶时每个样本的权重都是相同的
• XGBoost中每个样本的权重为损失函数在该样本点的二阶导数(对不同的样本,计算得到的损失函数的二阶导数是不同的), 这里优点AdaBoost的思想,重点关注某些样本的感觉
• 这里影响的是划分点的位置(我们划分划分点[桶]时都是均匀划分样本到桶里面,当不同样本的权重不同时,每个桶里面的样本数量可能会不同)
• 下图是一个示例
• 详细推导解释,为什么选择损失函数在当前样本的二阶导数作为权重?
  $$
  \begin{align}
  L^{t} &\approx \sum_{i=1}^{n}\left(g_if_t(x_i) + \frac{1}{2}h_if_t^2(x_i)\right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2 \\
  &\approx \sum_{i=1}^{n}\frac{1}{2}h_i\left(2\frac{g_i}{h_i}f_t(x_i) + f_t^2(x_i)\right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2 \\
  &\approx \sum_{i=1}^{n}\frac{1}{2}h_i\left(f_t(x_i) - \frac{g_i}{h_i}\right)^2 + \sum_{i=1}^{n}\left ( \frac{g_i^2}{2h_i} - 2g_if_t(x_i) \right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2 \\
  \end{align}
  $$
  • 上面的式子中第二项在原文中用constant来表示,可以被看成某种正则项
  • 第一项是一个平方误差表达式,样本 \(x_i\) 对应的输出值为 \(\frac{g_i}{h_i}\)，而样本权重就是 \(h_i\)
  • 权重代表概率,概率越大说明该点出现的次数或者该点附近的值出现的次数就越多.
• XGBoost分桶流程
  • [待更新]

XGBoost整棵树分裂流程

• 初始化 \(f^0(x)\)
• for t=1 to M:
  • 计算损失函数对每个训练样本点的一阶导数 \(g_i\)，二阶导数 \(h_i\)
  • 递归对叶子节点运用树分裂算法生成一颗决策树 \(f^t(x)\)，
    • (这一步包括叶子节点的分数 \(w_j\) 也都确定下来)
    • (这一步可以使用近似分裂算法加快训练速度)
  • 把新生成的决策树加入到模型中, \(\hat{y}^t = \hat{y}^{t-1} + f_m(x)\)

传统GDBT与XGBoost的比较

• 参考博客: ML——XGBoost-vs-传统GBDT

本文介绍各种不同的Normalization方法

• BN: Batch Normalization
• LN: Layer Normalization
• IN: Instance Normalization
• GN: Group Normalization
• LRN: Local Response Normalization
• WN: Weight Normalization

Normalization总体介绍

• BN,LN,IN的归一化的步骤都是使用下面的公式:
  $$
  \begin{align}
  u &= \frac{1}{m}\sum_{k\in S}x_k \\
  \sigma &= \sqrt{\frac{1}{m}\sum_{k\in S}(x_k-u) + \epsilon} \\
  \hat{x} &= \frac{1}{\sigma}(x-u) \\
  y &= \gamma \hat{x} + \beta
  \end{align}
  $$
  • \(u\) 为均值
  • \(\sigma\) 为标准差
  • \(\gamma\) 和 \(beta\) 是可以训练的参数
  • \(\epsilon\) 是平滑因子, 防止分母为0
  • BN,LN,IN三种不同的归一化方法, 对应的数据集 \(S\) 不同
    • BN对同一批数据进行归一化, 不管其他神经元, 只针对某个神经元的Mini Batch个样本输出值做归一化
    • LN对同一个样本的同一层输出进行归一化, 不依赖其他样本, 每次只依赖当前样本本身

BN

Batch Normalization

• 对一批数据实行归一化

• 对某个具体的神经元的Mini Batch个样本输出做归一化, 与其他神经元的输出无关

  

• 代码:

  1 2 3 4

  mu = np.mean(x,axis=0) sigma2 = np.var(x,axis=0) x_hat = (x-mu)/np.sqrt(sigma2+eps) out = gamma*x_hat + beta

• 特别说明：TensorFlow在BN训练过程中（trainable=True）使用的是当前批次的均值和方差归一化，同时将均值和方法以滑动平均的方式更新并存储下来。最终，在预估/推断(trainable=False)阶段，则直接使用滑动平均的结果

  • 隐藏问题：当使用BN时，如果更新的轮次不够（训练global step太少），会导致均值和方差滑动平均的结果并未贴近真实的均值和方差，会导致训练时模型输出正常，预测时模型输出异常的情况，且这种问题比较隐晦，难以排查
  • 解决方案：
    • 当训练的轮次较少时，要注意动量不要设置太大，否则更新不足，此时设置小的动量可以缓解BN均值方差更新不足的问题（不建议使用这种方式，原因是：一般来说，动量太小会导致最终的均值方差仅被最近的Batch决定，模型效果波动大）
    • 建议在使用BN时，设置较大的动量，且注意保证足够的训练轮次，充分更新动量和方法

LN

Layer Normalization

• 对单个训练样本的同一层所有神经元的输入做归一化
• 与其他样本无关

BN的作用和说明

• Batch Normalization把网络每一层的输出Y固定在一个变化范围的作用
• BN都能显著提高训练速度
• BN可以解决梯度消失问题
  • 归一化操作将每一层的输出从饱和区拉到了非饱和区(导数),从而解决了梯度消失问题
• 普通的优化器加上BN后效果堪比Adam
  $$ ReLU + Adam \approx ReLU + SGD + BN$$
• 如果对于具有分布极不平衡的二分类测试任务, 不要使用BN
• BN一定程度上有归一化作用
  • BN本身就能提高网络模型的泛化能力
  • 使用BN后,不用太依赖Dropout, L2正则化等,可以将L2正则化的参数变小一点

WN

Weight Normalization

• 对参数做归一化
• 与数据无关

总结

BN和WN对比

• BN是对对一个mini batch的数据在同一个神经元计算均值和方差
• WN对网络的网络权值 W 进行归一化(L2归一化)

BN和LN对比

• BN高度依赖于mini-batch的大小，实际使用中会对mini-Batch大小进行约束，不适合类似在线学习（mini-batch为1）情况；
• BN不适用于RNN网络中normalize操作：
  • BN实际使用时需要计算并且保存某一层神经网络mini-batch的均值和方差等统计信息，对于对一个固定深度的前向神经网络（DNN，CNN）使用BN，很方便；
  • 但对于RNN来说，sequence的长度是不一致的，换句话说RNN的深度不是固定的，不同的time-step需要保存不同的statics特征，可能存在一个特殊sequence比其的sequence长很多，这样training时，计算很麻烦
• 但LN可以有效解决上面这两个问题
• LN适用于LSTM的加速，但用于CNN加速时并没有取得比BN更好的效果

问题描述

requires_grad=True

等价于requires_grad=a, a为任意非0整数,不能为浮点数
浮点数会报错: TypeError: integer argument expected, got float

• 测试代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

  import torch from torch.autograd import Variable tensor = torch.ones(1) variable = Variable(tensor, requires_grad=True) print(tensor) print(variable) print("type1: ", type(tensor), type(variable)) print(tensor.data) print(variable.data) print("type2: ", type(tensor.data), type(variable.data)) print(tensor.data.numpy()) print(variable.data.numpy()) print("type3: ", type(tensor.data.numpy()), type(variable.data.numpy())) print(tensor.numpy()) print(variable.numpy()) print("type4: ", type(tensor.numpy()), type(variable.numpy())) # Output: tensor([1.]) tensor([1.], requires_grad=True) ('type1: ', <class 'torch.Tensor'>, <class 'torch.Tensor'>) tensor([1.]) tensor([1.]) ('type2: ', <class 'torch.Tensor'>, <class 'torch.Tensor'>) [1.] [1.] ('type3: ', <type 'numpy.ndarray'>, <type 'numpy.ndarray'>) [1.] Traceback (most recent call last): File "/home/jiahong/JupyterWorkspace/test.py", line 16, in <module> print(variable.numpy()) RuntimeError: Can't call numpy() on Variable that requires grad. Use var.detach().numpy() instead.

• 从上面的测试用例可以看出:

  • Variable和Tensor在判断类型时都是torch.Tensor
    • type(tensor) == type(variable) == torch.Tensor
  • 几乎所有操作都相同
    • tensor.data == variable.data
    • tensor.data.numpy() == varible.data.numpy()
  • 直接输出变量结果不相同
    • tensor输出时没有requires_grad=True
    • variable输出时有requires_grad=True
  • variable不能直接调用函数variable.numpy(),会报异常
    • 异常描述为: 当前Variable变量要求requires grad,也就是requires_grad属性为真时,变量不能直接使用

requires_grad=False

等价于requires_grad=0
不等价于requires_grad=None, None会报错: TypeError: an integer is required

• 测试代码:

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  import torch from torch.autograd import Variable tensor = torch.ones(1) variable = Variable(tensor, requires_grad=False) print(tensor) print(variable) print("type1: ", type(tensor), type(variable)) print(tensor.data) print(variable.data) print("type2: ", type(tensor.data), type(variable.data)) print(tensor.data.numpy()) print(variable.data.numpy()) print("type3: ", type(tensor.data.numpy()), type(variable.data.numpy())) print(tensor.numpy()) print(variable.numpy()) print("type4: ", type(tensor.numpy()), type(variable.numpy())) # Output: tensor([1.]) tensor([1.]) ('type1: ', <class 'torch.Tensor'>, <class 'torch.Tensor'>) tensor([1.]) tensor([1.]) ('type2: ', <class 'torch.Tensor'>, <class 'torch.Tensor'>) [1.] [1.] ('type3: ', <type 'numpy.ndarray'>, <type 'numpy.ndarray'>) [1.] [1.] ('type4: ', <type 'numpy.ndarray'>, <type 'numpy.ndarray'>)

• 从上面的测试用例可以看出:

  • 当variable变量的requires_grad=False时,variable完全退化为tensor
    • 直接输出变量时没有requires_grad=False属性
    • 可以直接使用variable.numpy()函数

Variable的三种等价定义

下面三种定义的Variable类型变量varible等价

• requires_grad=False

  1	variable = Variable(tensor, requires_grad=False)

• 没有requires_grad参数

  1	variable = Variable(tensor)

• requires_grad=True,然后variable = variable.detach()

  1 2	variable = Variable(tensor, requires_grad=True) variable = variable.detach()

• 上面三种定义都等价于原始的tensor

  • 这里的等价并未经过详细测试,但是至少以下方面等价:
    • 自身类型相同type, 类型为torch.Tensor
    • 可以调用属性.data,类型为torch.Tensor
    • 可以调用.grad,只不过都为None
    • 直接输出对象完全相同,都不包含requires_grad=True属性
    • 可以调用相同的函数.numpy(), 类型为numpy.ndarray
    • 可以调用相同的函数.data.numpy(), 类型为numpy.ndarray

本文主要介绍Attention的原理和变种

• 参考博客(其中有些错误，本文已经修正): https://zhuanlan.zhihu.com/p/47063917
• 参考论文: An Introductory Survey on Attention Mechanisms in NLP Problems
• 强烈推荐一篇写得非常好的动画讲解: 基于Attention的Seq2Seq可视化神经机器翻译机
• 另一篇不错的Attention和Transformer讲解自然语言处理中的自注意力机制(Self-Attention Mechanism)
• 这个博客中有李宏毅老师的讲解：Self Attention详解——知乎

RNN的局限: Encoder-Decoder模型

• RNN 结构
• Encoder-Decoder结构

Attention机制的引入

• Attention机制的根本优势在于对不同的
• 引入Attention前后的Encoder和Decoder对比图
  • 使用 Attention 前: \(\vec{h_{t}^{out}} = f(\vec{h_{t-1}^{out}},\vec{y_{t-1}})\)
  • 使用 Attention 后: \(\vec{h_{t}^{out}} = f(\vec{h_{t-1}^{out}},\vec{y_{t-1}}, \vec{c_{t}})\)
    • \(\vec{c_{t}} = q(\vec{h_{1}^{in}}, \dots, \vec{h_{T}^{in}})\)
    • \(q\) 是个多层的运算,有多重不同实现,详情参考后面的讲解
• 动态图理解 Attention 机制
  • 图中线条越清晰说明对当前结点的影响越大,不清晰说明影响较小

• 进一步看结构图
• 上图中Encoder使用的是双层双向的RNN
  • 第一层倒序从后 \(X_T\) 到前 \(X_1\) 生成, 反方向编码器
  • 第二层正序从前 \(X_1\) 到后 \(X_T\) 生成, 正方向编码器
  • 二者combine为一个更高维度的向量, 这个更高维度的向量整个作为Encoder的隐藏层
• 流程说明:
  • 利用 RNN 结构得到 Encoder中的 Hidden State (\(\vec{h_1}, \vec{h_2},\dots, \vec{h_T}\))
  • 假设当前 Decoder 的Hidden State 是 \(\vec{s_{t-1}}\)，计算每一个 \(\vec{h_j}\) 与当前输入位置的关联性 \(e_{ij} = a(\vec{s_{t-1}}, \vec{h_j})\)，得到向量 \(\vec{e_t} = (a(\vec{s_{t-1}}, \vec{h_1}), \dots, a(\vec{s_{t-1}}, \vec{h_T})) \)
    • 这里的 \(a\) 是相关性的(函数)运算符, 常用的可以用向量内积(点成),加权点乘等
      • 内积点乘: \(e_{tj} = \vec{s_{t-1}}^T\cdot\vec{h_j}\)
      • 加权点乘: \(e_{tj} = \vec{s_{t-1}}^TW\vec{h_j}\) (一般使用这个)
      • 更复杂的: \(e_{tj} = \vec{v}^Ttanh(W_1\vec{s_{t-1}}^T + W_2\vec{h_j})\)
  • 对 \(\vec{e_t}\) 进行 softmax 操作,将其归一化得到 Attention 的分布, \(\vec{\alpha_t} = softmax(\vec{e_t})\)
  • 利用 \(\vec{\alpha_t}\)，我们可以进行加权求和得到相应的上下文向量(context verctor) \(\vec{c_t} = \sum_{j=1}^T\alpha_{tj}\vec{h_j}\)
  • 计算 Decoder 的下一个 Hidden State \(\vec{s_t} = f_h(\vec{s_{t-1}}, \vec{y_{j-1}}, \vec{c_t})\)

Attention的变种

这里的总结参考博客Attention

• 基于强化学习的注意力机制：选择性的Attend输入的某个部分
• 全局&局部注意力机制：其中，局部注意力机制可以选择性的Attend输入的某些部分
• 多维度注意力机制：捕获不同特征空间中的Attention特征
• 多源注意力机制：Attend到多种源语言语句
• 层次化注意力机制：word->sentence->document
• 注意力之上嵌一个注意力：和层次化Attention有点像
• 多跳注意力机制：和前面两种有点像，但是做法不太一样。且借助残差连接等机制，可以使用更深的网络构造多跳Attention。使得模型在得到下一个注意力时，能够考虑到之前的已经注意过的词
• 使用拷贝机制的注意力机制：在生成式Attention基础上，添加具备拷贝输入源语句某部分子序列的能力
• 基于记忆的注意力机制：把Attention抽象成Query，Key，Value三者之间的交互；引入先验构造记忆库
• 自注意力机制：自己和自己做attention(这里的自己只每个文档自身)，使得每个位置的词都有全局的语义信息，有利于建立长依赖关系

广义的Attention机制

参考博客: https://www.sohu.com/a/226596189_500659

• Attention的本质:
  • 一个Attention函数可以被描述为一个把查询(Query)和键-值(Key-Value)对集合变换成输出(Attention Value)的映射
  • 简单的讲就是一个把 (Query,[Key-Value]s) 映射成一个 Attention Value (输出)
  • An attention function can be described as Mapping aquery and a set of key-value pairs to an output
• 表示成数学公式如下
• 如上图所示,在计算 Attention 时主要分为三步
  • 第一步是将 Query 和每个 Key 进行相似度计算得到权重，常用的相似度函数有点积，拼接，感知机等
  • 第二步一般是使用一个 Softmax 函数对这些权重进行归一化
  • 第三步将权重和相应的键值 Value 进行加权求和得到最后的 Attention
• Attention过程还可以大致分为两步理解:
  • 1. *将Query和Key经过相似度计算(某种数学运算)的结果通过 Softmax 激活函数激活得到上文所说的权重得分布 \(\vec{\alpha} = (\alpha_1\dots \alpha_n)\) *
       • 变换一般包括
         • 点乘(Dot): \(f(Q,K_i) = Q^TK_i\)
         • 加权点乘(General): \(f(Q,K_i) = Q^TW_{\alpha}K_i\)， \(W_{\alpha}\) 对不同的 \(\alpha_i\)
         • 拼接(Concat): \(f(Q,K_i) = W[Q^T;K_i]\)
         • 感知机(Perceptorn): \(f(Q,K) = \boldsymbol{v}^T tanh(W_Q, UK_i)\)
       • Query和Key在不同任务中是不同的东西
         • 在阅读理解中: Query指的是问题,Key指的是文档
         • 在简单的文本分类中: Query和Key可以是同一个句子(这也就是Self Attention), 也就是句子自己和自己做两个词之间的相似度计算的到权重分布
  • 2. 将权重分布 \(\vec{\alpha} = (\alpha_1\dots \alpha_n)\) 对Value做加权求和得到最终的特征表示
       • 在当前NLP任务中, 基本上 Key == Value
       • 阅读理解任务中, Value指的就是前面的Key, 是文档
       • 简单文本分类中, Value指句子
       • 在 Self Attention 机制中, 由于之前提到过, Query == Key ， 所以有Key == Value == Query
         • 输入一个句子，那么里面的每个词都要和该句子中的所有词进行 Attention 计算, 然后Softmax得到当前句子中每个词的权重,进而对句子中的词求和, 输出当前句子在当前模型中的Attention表示(Attention Value), 即$$\boldsymbol{Y_{AttentionOutput}} = Self Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = Attention(\boldsymbol{X},\boldsymbol{X},\boldsymbol{X})$$

对Attention的直观解释是

请求为向量时

• 现有查询向量 q
• 想从 Value 矩阵(每列对应一个样本) 中按照比例选择样本进行加权求和得到与 q 相关的查询结果
  • 要求是样本与 q 越相关，权重越大
• Value 中的每个样本都有 Key 矩阵 中的一个样本与之对应(NLP中 Key 往往是 Value 自己)
• 将 q 与 Key 的每个样本做相关性计算，得到其与 Key 中每个样本的相关性
• 对 q 与 Key 的所有相关性做归一化，得到权重比例
• 按照这个比例将 Value 中的样本加权输出结果
• 该结果就是 Value 经过 \(F(q, Key)\) 加权求和后的结果
• 也就是 q 对应的结果

请求为矩阵时

• 现有查询矩阵 Query， 包含 m 个查询向量
• 相当于重复 m 次做单个请求为向量的运算
• 每个 q 都能得到一个结果
• 在实际计算时，可以将整个矩阵一起计算，主要注意归一化是对单个 q 向量与 Key 矩阵生成的结果即可

更多分析

• 当 Key 与 Value 相同时
  • 其实是说计算 Value 每个样本的权重就用自己去与 q 计算即可
  • NLP中一般都是这样的
• 当 Key 与 Query 相同时，
  • 其实是找自身不同样本间的相关性
  • 然后根据不同样本的对应其他样本的相关性对其他样本进行加权求和得到自己对应的结果
  • NLP中Self-Attention是这样的
• Self-Attention是 Key == Value == Query 的情况

Attention研究发展趋势

文本介绍DeepFM的理论和实现

• 原始论文: DeepFM: A Factorization-Machine based Neural Network for CTR Prediction, IJCAI 2017
• 参考博客: https://www.jianshu.com/p/6f1c2643d31b

回顾特征组合的问题

传统解决方案

• FM: (Factorization Machines, FM)因子分解机
• FMM: (Field Factorization Machines, FFM)

存在问题

• 只能二阶特征组合,无法做到高阶特征组合
  • 理论上来讲FM经过简单的拓展后可以组合高阶特征,但是那样的话参数会爆炸增加,所以实际上使用时一般只是二阶特征.

DNN建模高阶组合特征

优点

• 理论上DNN建模高阶组合特征是可行的

缺点

• 由于离散特征中我们使用One-Hot编码,会导致输入维度增加,网络参数很多

解决方案

• 利用FFM中的思想,特征分为不同的Field
• 基本思想是从One-Hot编码换成Dense Vector
• 进一步加上两个全连接层(隐藏层),让刚刚学到的Dense Vector进行组合,于是得到高阶组合特征
• 此时,高阶和低阶的特征体现在隐藏层中,我们希望把低阶特征组合单独建模,然后融合高阶特征组合
• 将DNN与FM进行一个合理的融合
• 二者的融合分两种方式: 串行结构和并行结构

DeepFM

• 是一种并行化的解决方案

  

• 包含 FM 和 DNN 两个部分, FM 负责低阶组合特征的提取,DNN 负责高阶组合特征的提取,两部分共享同样的输入

• DeepFM的预测结果可以表示为如下的形式
  $$\hat{y} = sigmoid(y_{FM} + y_{DNN})$$

FM部分

• FM的输入仅仅包含稀疏特征，连续特征不包含在FM部分
• 输出如下
  $$ y(x) = w_0+ \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n w_{ij} x_i x_j $$

DNN部分

• DNN的输入包含Combine(稀疏特征，连续特征)
• DNN部分是一个前馈神经网络
• 与图像语音的区别:
  • 图像语音输入为连续且密集的
  • CTR中使用的一般是稀疏的
• 在进入隐藏层之前,使用一个嵌入层(DenseEmbeddings): 将高维稀疏输入向量压缩为低维稠密向量

多层感知机(Multi-Layer Perception， MLP)及其BP(Back Propagation)算法，本文记录一些有趣的图

多层感知机

• 图示如下

BP算法

推导

以一维输出(二分类)为例

详细流程

• 动图

References

References:

• http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html
• https://www.cnblogs.com/ooon/p/5577241.html
• https://blog.csdn.net/guotong1988/article/details/52096724

神经网络语言模型(Nerual Network Language Model, NNLM)

参考论文: A Neural Probabilistic Language Model
参考博客: 神经网路语言模型(NNLM)的理解

概率模型

• 传统的 \(n\) 元语言模型：
  $$(p(w_{t}|w_{t-(n-1)},…,w_{t-1}))$$
• 一般来说可以通过前 \(n-1\) 个词将预测第 \(n\) 个词的概率分布

NNLM模型原理

• NNLM 模型直接通过一个神经网络结构对 \(n\) 元条件概率进行评估

模型结构

• NNLM 网络结构图如下：

数据集预处理

• 对于给定的预料库，我们需要生成训练数据集(大量训练样本的集合)，单个样本如下是长度为n的序列 \((w_{1},…,w_{n})\)，其中 \((w_{1},…,w_{n-1})\) 对应训练样本特征值，训练样本标记为 \(w_{n}\)，通常可以用One-Hot编码(一个维度为|V|的向量)

模型分析

模型分析主要介绍前向传播过程

输入与输出

• 将构造的数据集作为训练样本集
• 其中每个样本输入为 \((w_{1},…,w_{n-1})\)，输出为一个向量(维度为 |V|)，向量代表词的分布，该分布应该与词 \(w_{n}\) 的 One-Hot 编码（也是一个 |V| 维向量）尽量匹配，输出误差就是这两个向量的差异大小（不同损失函数均通过将上述两个向量作为输入，输出一个标量等（也可能 \(n\) 为向量，此时按照不同维度分别计算，或者是其他的值）从而实现当前样本损失的计算

模型结构分析

• \(x=(C_{j|w_{j}=w_{1}};…;C_{j|w_{j}=w_{n-1}})\)

  • \(x\) 为输入向量， \(x\in R^{(n-1)m}\)，\(x\) 是词序列 \((w_{1},…,w_{n-1})\) 对应的拼接向量，其中每个词都会先被矩阵C映射成一个m维的向量，将 \((n-1)\) 维的向量拼接起来就得到了 \(x\)

• \(y=b+Wx+Utanh(d+Hx)\)

  • \(y\) 为输出向量， \(y\in R^{|V|}\)， \(y_{i}\) 表示 \(w_{i}\) 是第 \(n\) 个单词的概率

模型参数分析

• C：映射矩阵 \(C\in R^{|V|\times m}\)，其中矩阵的第 \(j\) 行 \(C_{j}\) 是词 \(w_{j}\) 对应的特征向量， \(m\) 为特征向量的维度

• H：输入层到隐含层的权重矩阵 \(H\in R^{(n-1)m\times h}\)，其中 \(h\) 为隐含层神经元的数量

• W：输入层到输出层的权重矩阵 \(W\in R^{(n-1)m\times |V|}\)， \(W\) 是可选参数，对应模型结构图中的绿色虚线，如果输入层输出层不直接相连，则直接令 \(W=0\) 即可

• U：隐含层到输出层的权重矩阵 \(U\in R^{h\times |V|}\)

• b：输出层的偏执参数

• d：隐含层的偏执参数

模型训练

损失函数

• 似然函数：\(L(\theta)=\prod_{t=1}^{T} p(w_{t-(n-1)},…,w_{t-1},w_{t}|\theta)+R(\theta)\)
  • T 为训练集 D 中的样本总数，即 \(T=|D|\)
  • \(R(\theta)\) 是正则项
• 对数似然函数：\(L(\theta)=\sum_{t=1}^{T}\log(p(w_{t-(n-1)},…,w_{t-1},w_{t})|\theta) + R(\theta)\)，其中T为训练集 D 中的样本总数，即 \(T=|D|\)
• 我们选择优化对数似然函数，原因如下：
  • 似然函数连乘操作造成浮点数溢出，乘积越来越小（概率值都在[0,1]之间）
  • 似然函数连乘操作耗时大于对数似然函数的连加操作
  • 取对数的操作可以同时把函数中其他的指数项（比如出现在正则项 \(R(\theta)\) 中）中的处理成连加，减少运算量
  • 对数似然函数的单调性与似然函数相同，最大化对数似然函数等价于最大化似然函数（最重要的一点）

训练目标

• 最大化对数似然函数（等价于最大化似然函数）

参数迭代

• 使用梯度上升法，每轮迭代时朝着正梯度方向移动
  • \(\theta=\theta+\lambda\frac{\partial L(\theta)}{\partial\theta}\)
  • \(\lambda\) 为步长

总结

• NNLM 模型使用了低维连续的词向量对上文进行表示，这解决了词袋模型带来的数据稀疏、语义鸿沟等问题
• 相比传统模型，NNLM 是一种更好的n元语言模型（NNLM的 \(n\) 元不是由神经元决定，而是在根据语料库生成训练数据时单个训练样本中包含的词数，也就是窗口大小）
  • n元模型指的是跟军前 \(n-1\) 个词预测第 \(n\) 个词的语言模型，而不是根据前 \(n\) 个词生成第 \(n+1\) 个词的模型
• 根据相似的上下文语境，NNLM 模型可以预测出相似的目标词，而传统模型无法做到这一点

关键词：Softmax梯度，Softmax求导

softmax函数定义

• 对于输入向量 \( x = [x_1, x_2, \dots, x_n] \)，softmax函数将其映射为概率分布：
  $$
  \sigma(x)_i = \frac{e^{x_i} }{\sum_{j=1}^n e^{x_j} }
  $$
  • 其中 \( \sigma(x)_i \) 表示第 \( i \) 个元素的输出，满足 \( \sum_{i=1}^n \sigma(x)_i = 1 \)

求导推导（分情况讨论）

• 设 \( s_i = \sigma(x)_i \)，目标是计算 \( \frac{\partial s_i}{\partial x_j} \)，分两种情况

情况1：\( i = j \)（自变量对自身求导）

• 展开表达式：
  $$
  s_i = \frac{e^{x_i} }{\sum_{k=1}^n e^{x_k} } = \frac{e^{x_i} }{S}, \quad \text{其中 } S = \sum_{k=1}^n e^{x_k}
  $$
• 利用商数法则求导：
  $$
  \frac{\partial s_i}{\partial x_i} = \frac{e^{x_i} \cdot S - e^{x_i} \cdot e^{x_i} }{S^2} = \frac{e^{x_i}(S - e^{x_i})}{S^2} = \frac{e^{x_i} }{S} \cdot \frac{S - e^{x_i} }{S} = s_i(1 - s_i)
  $$

情况2：\( i \neq j \)（自变量对其他元素求导）

• 此时 \( x_j \) 出现在分母 \( S \) 中，分子与 \( x_j \) 无关：
  $$
  \frac{\partial s_i}{\partial x_j} = \frac{0 \cdot S - e^{x_i} \cdot e^{x_j} }{S^2} = -\frac{e^{x_i} e^{x_j} }{S^2} = -\frac{e^{x_i} }{S} \cdot \frac{e^{x_j} }{S} = -s_i s_j
  $$

矩阵形式（向量求导）

• 若输入为向量 \( \mathbf{x} \)，输出为向量 \( \mathbf{s} = \sigma(\mathbf{x}) \)，则其雅可比矩阵为：
  $$
  \frac{\partial \mathbf{s} }{\partial \mathbf{x}^T} = \left[ \frac{\partial s_i}{\partial x_j} \right] = \mathbf{S} - \mathbf{s s}^T
  $$
  • \( \mathbf{S} \) 是对角矩阵，对角线元素为 \( s_i \)；
  • \( \mathbf{s s}^T \) 是外积矩阵
• 对角矩阵 \(\mathbf{S}\) ：
  $$
  \mathbf{S} = \begin{bmatrix}
  s_1 & 0 & \cdots & 0 \\
  0 & s_2 & \cdots & 0 \\
  \vdots & \vdots & \ddots & \vdots \\
  0 & 0 & \cdots & s_n
  \end{bmatrix}
  $$
• 外积矩阵 \(\mathbf{s s}^T\) ：
  $$
  \mathbf{s s}^T =
  \begin{bmatrix}
  s_1 \\
  s_2 \\
  \vdots \\
  s_n
  \end{bmatrix}
  \begin{bmatrix}
  s_1 & s_2 & \cdots & s_n
  \end{bmatrix} =
  \begin{bmatrix}
  s_1 s_1 & s_1 s_2 & \cdots & s_1 s_n \\
  s_2 s_1 & s_2 s_2 & \cdots & s_2 s_n \\
  \vdots & \vdots & \ddots & \vdots \\
  s_n s_1 & s_n s_2 & \cdots & s_n s_n
  \end{bmatrix}
  $$
• 最终梯度形式 ：
  $$
  \frac{\partial \mathbf{s} }{\partial \mathbf{x}^T} = \mathbf{S} - \mathbf{s s}^T = \begin{bmatrix}
  s_1 & 0 & \cdots & 0 \\
  0 & s_2 & \cdots & 0 \\
  \vdots & \vdots & \ddots & \vdots \\
  0 & 0 & \cdots & s_n
  \end{bmatrix} -
  \begin{bmatrix}
  s_1 s_1 & s_1 s_2 & \cdots & s_1 s_n \\
  s_2 s_1 & s_2 s_2 & \cdots & s_2 s_n \\
  \vdots & \vdots & \ddots & \vdots \\
  s_n s_1 & s_n s_2 & \cdots & s_n s_n
  \end{bmatrix}
  $$

一些总结

• softmax 函数的矩阵形式导数可表示为 对角矩阵与外积矩阵的差
  • 核心结论：“对角线元素为 \(s_i-s_i s_i\)，非对角线元素为 \(-s_i s_j\)”的规律
• 越接近 one-hot 的预估，其梯度越接近于 0

本文分析UserID（User ID）和ItemID（Item ID）特征的及其常见处理方法

• 参考链接：
  • 深度学习推荐算法中user-id和item-id是否需要放入模型中作为特征进行训练呢？ - 杨木易的回答 - 知乎
  • Empowering Long-tail Item Recommendation through Cross Decoupling Network (CDN), Google, KDD 2023

UserID和ItemID类特征有什么特点？

• UserID和ItemID可训练的交互数据一般服从长尾分布。从UserID视角看，头部UserID占据了样本的大多数；从ItemID视角看，头部ItemID占据了样本的大多数
• 头部的ID对应的Embedding可以得到充分学习，但是尾部的ID由于数据不够，他们的Embedding往往得不到充足的学习（一轮数据训练完成，Embedding几乎没有被更新过，那就与随机初始化参数无异了）
• 通常UserID和ItemID是高维稀疏特征，如果表示成One-Hot特征的话，会出现几千万甚至上亿维度的向量中，只有一个维度为1的情况
• 这部分特征样本区分度很高，常常称为“记忆性”特征，他们没有什么泛化能力，但是可以记住某些交互行为（比如用户A购买过物品B）

是否应该加入模型？

• 基本理念 ：适合加入的情况应该是大部分ID训练样本充足的情况，且线上serving时遇到的新ID不能太多
• 数据量要求：
  • 基本思路：每个ID取值下，平均样本量越少的场景越不建议加入ID特征，如果数据过于集中于极少数头部ID，还需要看看长尾情况，长尾商家（样本不足的商家）越多，越不建议加入ID特征
  • 理解：ID是否能用还是要看是否有充足的数据量训练ID对应的Embedding
• 冷起要求：
  • 基本思路：ItemID更新越频繁（即物品池频繁汰换）的场景越不建议加入ItemID特征；新用户占比越高的场景越不建议加入UserID特征
  • 理解：新ID过多时，新的ID都是模型没有见过的，模型效果会衰减的非常快，现实生活中，可以通过使用 T+N 的数据集作为测试集验证是否有衰减问题

加入模型的哪个位置？

• 数据充足时 ：每个ID数据充足的场景，可以将这些ID特征当做普通特征对待，直接Embedding后加入模型
• 数据不足时 ：
  • 可以考虑使用特征粒度Dropout（直接按照Embedding维度Dropout）的方式来增强泛化性【TOOD：如何理解？】
  • 可以考虑将这部分特征放到一个独立的塔，然后其他特征在另一个塔，引入一个门控网络来控制两个塔对最终预估结果的影响。可参考谷歌的Empowering Long-tail Item Recommendation through Cross Decoupling Network (CDN)，其网络结构图如下：