ML——XGBoost-vs-传统GBDT

本文主要介绍XGBoost和其他传统GBDT的比较的优劣
XGBoost又叫(Newton Boosting Tree)

GBDT推导: ML——GBDT-梯度提升树-推导过程
XGBoost推导: ML——XGBoost-推导过程

XGBoost的优点

参考博客: https://www.cnblogs.com/massquantity/p/9794480.html

XGBoost损失函数是二阶泰勒展开(与牛顿法对应),GBDT是一阶泰勒展开(与梯度下降法对应)
- 传统 GBDT 在优化时只用到一阶导数信息, 所以传统GBDT也叫 (Gradient Boosting)
- XGBoost 则对目标函数进行了二阶泰勒展开，同时用到了一阶和二阶导数, 所以XGBoost又叫(Newton Boosting Tree)
XGBoost加了正则项,普通的GBDT没有,所以XGBoost学出来的模型更简单,能防止过拟合,提高模型的泛化性能
XGBoost Shrinkage(缩减)
- 每次进行完一次迭代后,将叶子节点的权重乘以该系数(一般叫做eta$\eta$)
- 可以理解为这里Shrinkage是将学习速率调小,从而需要的迭代次数增多
- 减小学习率实际上是减弱了每棵树对整体的影响,从而让后面的树有更多的学习空间
- 下面的表述还有待确定:
  - 进一步惩罚决策树叶节点的值(惩罚的意思是叶节点越大,惩罚越多,损失函数越大)
  - 对叶节点的惩罚本身可以理解为一个正则化
结点分裂的增益计算公式不同
- 传统 GBDT 一般采用的是最小二乘法作为内部分裂的增益计算指标(因为用的都是回归树)
  - 注意: 这里论文中描述的最小绝对偏差回归(LAD)是第一步损失函数的定义,不是这一步中的信息增益计算
  - 查看源码: sklearn.ensemble.GradientBoostingClassifier在分裂结点时可以选择三种方式:
    - friedman_mse(默认), mean squared error with improvement score by Friedman
    - mse: mean squared error
    - mae: mean absolute error
- 而 XGBoost 使用的是经过优化推导后的式子
  $$
  \begin{align}
  Gain = \frac{G_L^2}{H_L+ \lambda} + \frac{G_R^2}{H_R+ \lambda} - \frac{(G_L + G_R)^2}{H_L+ H_R + \lambda} - \gamma
  \end{align}
  $$
  - 注意: XGBoost中的信息增益计算形式固定为上面的计算方式,但是具体的值与损失函数的定义相关(因为 $g_i$ 和 $h_i$ 的是损失函数的一阶和二阶梯度)

XGBoost支持自定义的损失函数,支持一阶和二阶可导就行

注意,这里的损失函数指的是 $l(y_i,\hat{y}_i)$, 单个样本预测值与目标值的差异, 也就是单个样本的损失函数
从ML——XGBoost-推导过程中可知:
- $g_i = l’(y_i,\hat{y}_i^{t-1})$ 为 $l(y_i,\hat{y}_i)$ 对 $\hat{y}_i$ 的一阶导数在 $\hat{y}_i = \hat{y}_i^{t-1}$ 处的值
- $h_i = l’’(y_i,\hat{y}_i^{t-1})$ 是 $l(y_i,\hat{y}_i)$ 对 $\hat{y}_i$ 的二阶导数在 $\hat{y}_i = \hat{y}_i^{t-1}$ 处的值
XGBoost中只要损失函数二次可微分即可得到 $g_i$ 和 $h_i$
- $g_i$ 和 $h_i$ 本身与损失函数的定义形式无关, 只要求损失函数二阶可微分即可
只要有了 $g_i$ 和 $h_i$ 我们即可
- 根据预先推导的叶子节点分数表达式 $w_j^{\star} = -\frac{G_j}{H_j+\lambda}$ 求得叶子结点的分数
- 根据预先推导的信息增益公式 $Gain = \frac{G_L^2}{H_L+ \lambda} + \frac{G_R^2}{H_R+ \lambda} - \frac{(G_L + G_R)^2}{H_L+ H_R + \lambda} - \gamma$ 确定分裂特征和分裂点

GBDT 损失函数关系一般选择最小二乘回归或者最小绝对偏差回归

最小方差回归: (Least-Squares Regression, LSR)
$$\begin{align} L(y,F(x)) = \frac{1}{2}(y-F(x))^{2} \end{align}$$
最小绝对偏差回归: (Least Absolute Deviation Regression, LAD)
$$\begin{align} L(y,F(x)) = |y-F(x)| \end{align}$$

查看源码: sklearn.ensemble.GradientBoostingClassifier的损失函数是定义好的, 不能自己定义, 详细如下源码

LOSS_FUNCTIONS = {'ls': LeastSquaresError,
                  'lad': LeastAbsoluteError,
                  'huber': HuberLossFunction,
                  'quantile': QuantileLossFunction,
                  'deviance': None,    # for both, multinomial and binomial
                  'exponential': ExponentialLoss,
                  }


_SUPPORTED_LOSS = ('deviance', 'exponential')
....

if (self.loss not in self._SUPPORTED_LOSS
                or self.loss not in LOSS_FUNCTIONS):
            raise ValueError("Loss '{0:s}' not supported. ".format(self.loss))

XGBoost 借鉴了随机森林的做法，支持列采样，不仅能降低过拟合，还能减少计算量，这也是 XGBoost 异于传统 GBDT 的一个特性
- 列采样: 这借鉴于随机森林中的做法,每棵树不使用所有特征,而是部分特征参与训练
- 可以减少计算量,同时还能降低过拟合,简直优秀
XGBoost 有缺失值自动处理, 在计算分裂增益时不会考虑带有缺失值的样本，这样就减少了时间开销,在分裂点确定了之后，将带有缺失值的样本分别放在左子树和右子树，比较两者分裂增益，选择增益较大的那一边作为默认分裂方向
- 进一步理解稀疏数据的支持: [待更新]
并行化处理：由于 Boosting 本身的特性，传统 GBDT 无法像随机森林那样树与树之间的并行化
- XGBoost 的并行主要体现在特征粒度上，在对结点进行分裂时，由于已预先对特征排序并保存为block 结构，每个特征的增益计算就可以开多线程进行，极大提升了训练速度
剪枝策略不同
- 传统 GBDT 在损失不再减少时会停止分裂，这是一种预剪枝的贪心策略，容易欠拟合
- XGBoost采用的是后剪枝的策略，先分裂到指定的最大深度 (max_depth) 再进行剪枝
  - 而且和一般的后剪枝不同， XGBoost 的后剪枝是不需要验证集的[待更新:XGBoost剪枝的策略是怎样的?只依赖信息增益指标吗?]
  - 和博客作者指出的一样,我这里并不是”纯粹的”后剪枝,因为提前设定了最大深度
基分类器的选择不同:
- 传统GBDT中原始论文使用树回归,论文见Firedman 1999,后来作者提出可以使用逻辑回归,论文见Friedman 2000
- XGBoost后面的各种损失计算等都包含着树模型的复杂度,叶子节点分类等,所以是只能用CART,不能使用逻辑回归的
- (从函数空间定义和后面的公式推导来看)XGBoost中基函数只使用CART回归树，不能使用逻辑回归
- 但是事实上XGBoost的实现中是支持线性分类器作为基分类器的, 参数booster[default='gbtree'],可选为booster=gblinear
  - 使用线性分类器作为基分类器时, XGBoost相当于带有L1正则化和L2正则化的:
    - Logistic回归(分类问题)
    - 线性回归(回归问题)
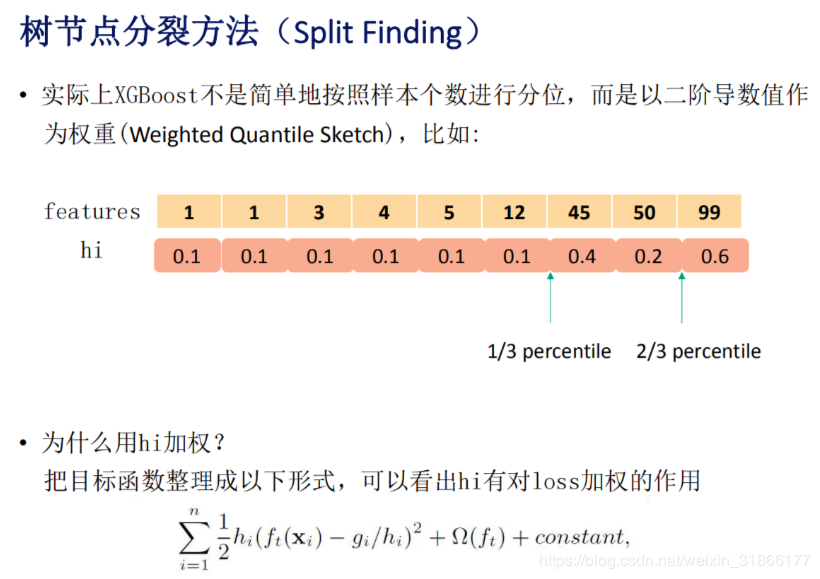
分桶策略算法不同
- 传统的GBDT分桶时每个样本的权重都是相同的
- XGBoost中每个样本的权重为损失函数在该样本点的二阶导数(对不同的样本,计算得到的损失函数的二阶导数是不同的), 这里优点AdaBoost的思想,重点关注某些样本的感觉
- 这里影响的是划分点的位置(我们划分划分点[桶]时都是均匀划分样本到桶里面,当不同样本的权重不同时,每个桶里面的样本数量可能会不同)
- 下图是一个示例

XGBoost的缺点

注意这里是

空间消耗大
- 因为要在训练之前先对每个特征进行预排序并将结果存储起来，所以空间消耗较大
- GBDT无需预排序,但是每次重新排序很耗时间
速度慢
- 虽然XGBoost速度比传统 GBDT 快了不少, 但是不如 LightGBM 快, 且 LightGBM 占用内存更低

XGBoost为什么能够并行?

而GBDT是不能并行的，原因是：https://www.136.la/shida/show-187480.html

GBDT不能并行的原因是没有预排序（XGB的预排序结果会存储到block结构）等，在有了预排序结果后，同一个特征的切割方式可以并行尝试计算增益
决策树最耗时间(包括GBDT)的步骤是对特征值的排序
- 用于确定最佳分割点
XGBoost训练前,预先对数据进行了排序,称为预排序
- 将预先排序的结果保存为block结构, 后面迭代的时候重复使用这个结构,从而实现一次排序,多次使用,大大减少计算量
这个结构减少计算量的同时还为并行化提供了可能([待更新]实际上不用预排序也能并行的吧?只是每次需要先使用一个单一线程排序,然后再多个线程并行?只是不够并行)
- 进行结点的分裂时,需要计算每个特征的增益,然后选择增益最大的那个特征分裂
- 这里我们可以同时使用多个线程计算不同特征的增益, 从而实现并行化
总结为三方面的并行, ([待更新]但是具体实现了哪些并行不确定)
- 同一层级的结点间每个结点的分裂可以并行
- 同一个结点内部不同特征增益的计算可以并行
- 同一个结点同一个特征的不同分裂点的增益计算可以并行

GBDT为什么不能自定义损失函数?

GBDT为什么不能像XGBoost一样自定义损失函数?

查看sklearn.ensemble.GradientBoostingClassifier的源码发现, 确实不支持自定义的损失函数
[待更新],因为涉及到后面的参数更新方式?

XGBoost如何使用自定义的损失函数?

模型直接调用fit函数无法传入自定义的损失函数, 需要在模型开始定义的时候传入或者使用xgb.train函数调用

使用方法1:

1
2
3

from xgboost import XGBClassifier

clf = XGBClassifier(objective=MyLossFunction)

使用方法2:

import xgboost as xgb
from xgboost import XGBClassifier

clf = XGBClassifier()
xgb.train(xgb_model=clf, obj=MyLossFunction)