DL——Attention

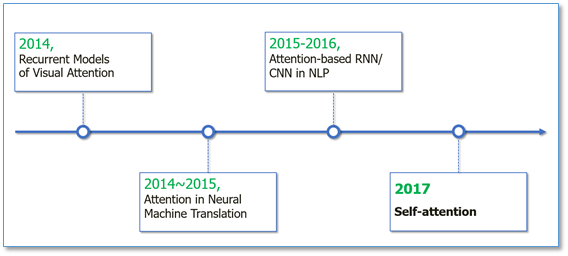
本文主要介绍Attention的原理和变种

RNN的局限: Encoder-Decoder模型

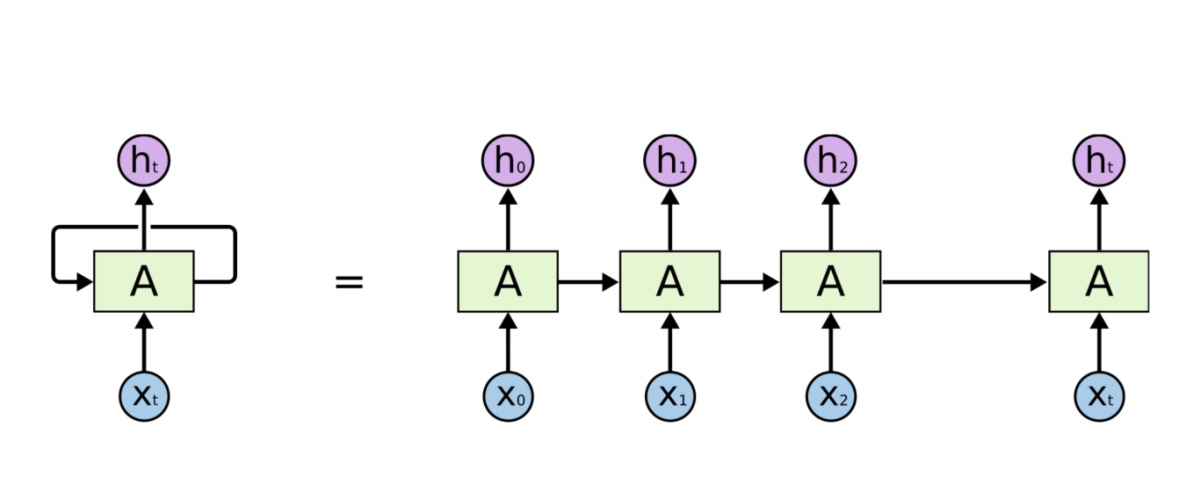
  • RNN 结构
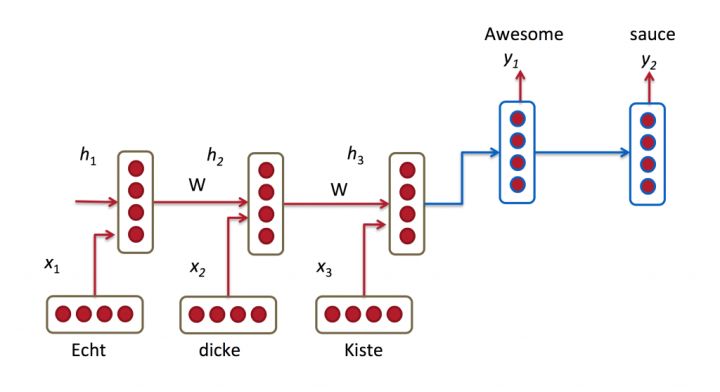
  • Encoder-Decoder结构

Attention机制的引入

  • Attention机制的根本优势在于对不同的
  • 引入Attention前后的Encoder和Decoder对比图
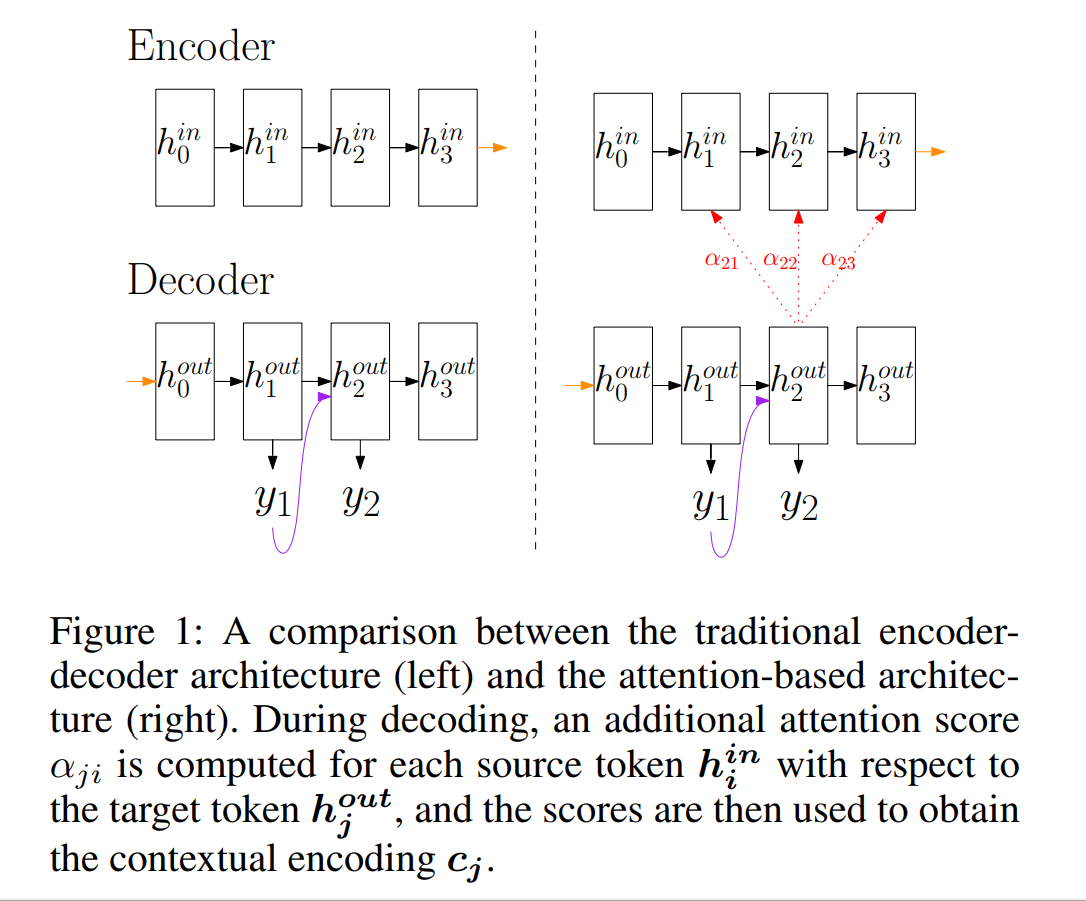
    • 使用 Attention 前: \(\vec{h_{t}^{out}} = f(\vec{h_{t-1}^{out}},\vec{y_{t-1}})\)
    • 使用 Attention 后: \(\vec{h_{t}^{out}} = f(\vec{h_{t-1}^{out}},\vec{y_{t-1}}, \vec{c_{t}})\)
      • \(\vec{c_{t}} = q(\vec{h_{1}^{in}}, \dots, \vec{h_{T}^{in}})\)
      • \(q\) 是个多层的运算,有多重不同实现,详情参考后面的讲解
  • 动态图理解 Attention 机制
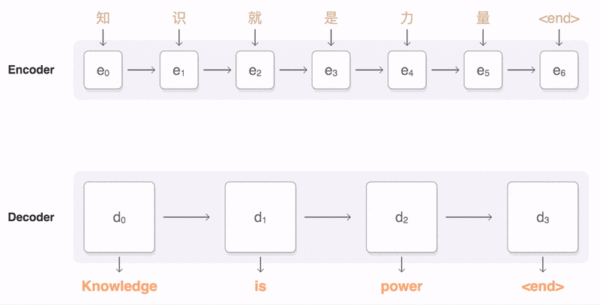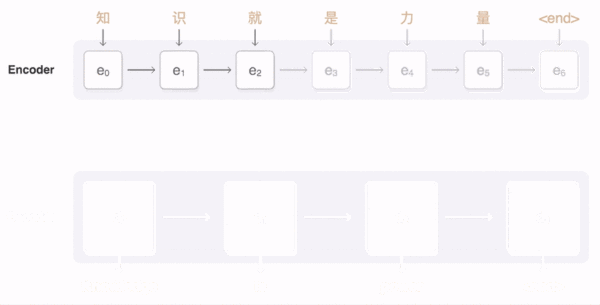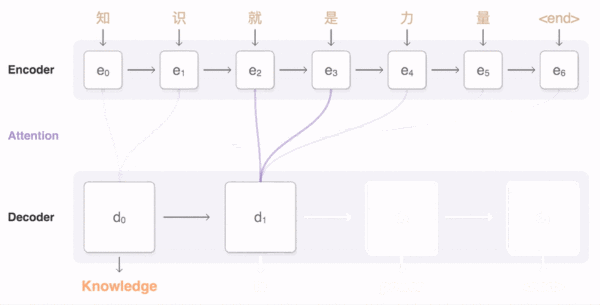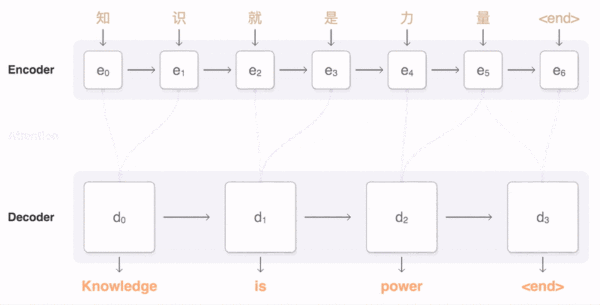
    • 图中线条越清晰说明对当前结点的影响越大,不清晰说明影响较小
  • 进一步看结构图
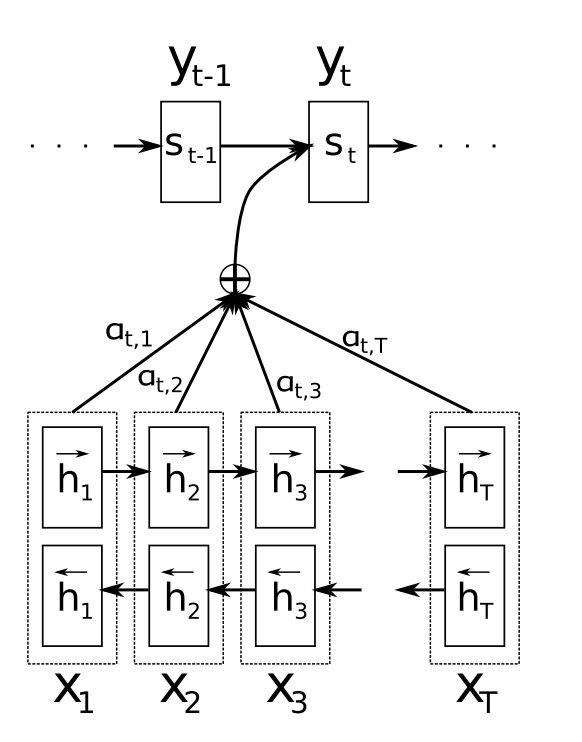
  • 上图中Encoder使用的是双层双向的RNN
    • 第一层倒序从后\(X_T\)到前\(X_1\)生成, 反方向编码器
    • 第二层正序从前\(X_1\)到后\(X_T\)生成, 正方向编码器
    • 二者combine为一个更高维度的向量, 这个更高维度的向量整个作为Encoder的隐藏层
  • 流程说明:
    • 利用 RNN 结构得到 Encoder中的 Hidden State (\(\vec{h_1}, \vec{h_2},\dots, \vec{h_T}\))
    • 假设当前 Decoder 的Hidden State 是 \(\vec{s_{t-1}}\), 计算每一个 \(\vec{h_j}\) 与当前输入位置的关联性 \(e_{ij} = a(\vec{s_{t-1}}, \vec{h_j})\), 得到向量 \(\vec{e_t} = (a(\vec{s_{t-1}}, \vec{h_1}), \dots, a(\vec{s_{t-1}}, \vec{h_T})) \)
      • 这里的 \(a\) 是相关性的(函数)运算符, 常用的可以用向量内积(点成),加权点乘等
        • 内积点乘: \(e_{tj} = \vec{s_{t-1}}^T\cdot\vec{h_j}\)
        • 加权点乘: \(e_{tj} = \vec{s_{t-1}}^TW\vec{h_j}\) (一般使用这个)
        • 更复杂的: \(e_{tj} = \vec{v}^Ttanh(W_1\vec{s_{t-1}}^T + W_2\vec{h_j})\)
    • 对 \(\vec{e_t}\) 进行 softmax 操作,将其归一化得到 Attention 的分布, \(\vec{\alpha_t} = softmax(\vec{e_t})\)
    • 利用 \(\vec{\alpha_t}\), 我们可以进行加权求和得到相应的上下文向量(context verctor) \(\vec{c_t} = \sum_{j=1}^T\alpha_{tj}\vec{h_j}\)
    • 计算 Decoder 的下一个 Hidden State \(\vec{s_t} = f_h(\vec{s_{t-1}}, \vec{y_{j-1}}, \vec{c_t})\)

Attention的变种

这里的总结参考博客Attention

  • 基于强化学习的注意力机制：选择性的Attend输入的某个部分
  • 全局&局部注意力机制：其中，局部注意力机制可以选择性的Attend输入的某些部分
  • 多维度注意力机制：捕获不同特征空间中的Attention特征。
  • 多源注意力机制：Attend到多种源语言语句
  • 层次化注意力机制：word->sentence->document
  • 注意力之上嵌一个注意力：和层次化Attention有点像。
  • 多跳注意力机制：和前面两种有点像，但是做法不太一样。且借助残差连接等机制，可以使用更深的网络构造多跳Attention。使得模型在得到下一个注意力时，能够考虑到之前的已经注意过的词。
  • 使用拷贝机制的注意力机制：在生成式Attention基础上，添加具备拷贝输入源语句某部分子序列的能力。
  • 基于记忆的注意力机制：把Attention抽象成Query，Key，Value三者之间的交互；引入先验构造记忆库。
  • 自注意力机制：自己和自己做attention(这里的自己只每个文档自身)，使得每个位置的词都有全局的语义信息，有利于建立长依赖关系。

广义的Attention机制

参考博客: https://www.sohu.com/a/226596189_500659

  • Attention的本质:
    • 一个Attention函数可以被描述为一个把查询(Query)和键-值(Key-Value)对集合变换成输出(Attention Value)的映射
    • 简单的讲就是一个把 (Query,[Key-Value]s) 映射成一个 Attention Value (输出)
    • An attention function can be described as Mapping aquery and a set of key-value pairs to an output
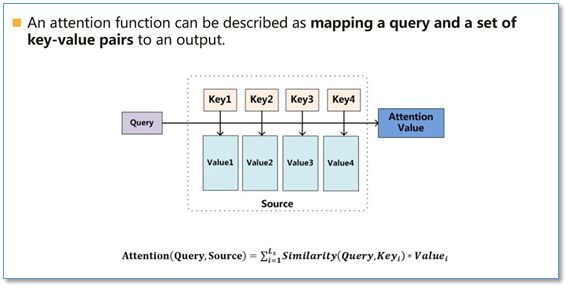
  • 表示成数学公式如下
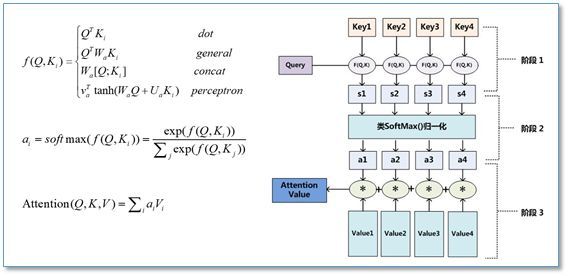
  • 如上图所示,在计算 Attention 时主要分为三步
    • 第一步是将 Query 和每个 Key 进行相似度计算得到权重，常用的相似度函数有点积，拼接，感知机等
    • 第二步一般是使用一个 Softmax 函数对这些权重进行归一化
    • 第三步将权重和相应的键值 Value 进行加权求和得到最后的 Attention
  • Attention过程还可以大致分为两步理解:
      1. 将Query和Key经过相似度计算(某种数学运算)的结果通过 Softmax 激活函数激活得到上文所说的权重得分布 \(\vec{\alpha} = (\alpha_1\dots \alpha_n)\)
        • 变换一般包括
          • 点乘(Dot): \(f(Q,K_i) = Q^TK_i\)
          • 加权点乘(General): \(f(Q,K_i) = Q^TW_{\alpha}K_i\), \(W_{\alpha}\) 对不同的 \(\alpha_i\)
          • 拼接(Concat): \(f(Q,K_i) = W[Q^T;K_i]\)
          • 感知机(Perceptorn): \(f(Q,K) = \boldsymbol{v}^T tanh(W_Q, UK_i)\)
        • Query和Key在不同任务中是不同的东西
          • 在阅读理解中: Query指的是问题,Key指的是文档
          • 在简单的文本分类中: Query和Key可以是同一个句子(这也就是Self Attention), 也就是句子自己和自己做两个词之间的相似度计算的到权重分布
      1. 将权重分布 \(\vec{\alpha} = (\alpha_1\dots \alpha_n)\) 对Value做加权求和得到最终的特征表示
        • 在当前NLP任务中, 基本上 Key == Value
        • 阅读理解任务中, Value指的就是前面的Key, 是文档
        • 简单文本分类中, Value指句子
        • 在 Self Attention 机制中, 由于之前提到过, Query == Key, 所以有Key == Value == Query
          • 输入一个句子，那么里面的每个词都要和该句子中的所有词进行 Attention 计算, 然后Softmax得到当前句子中每个词的权重,进而对句子中的词求和, 输出当前句子在当前模型中的Attention表示(Attention Value), 即$$\boldsymbol{Y_{AttentionOutput}} = Self Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = Attention(\boldsymbol{X},\boldsymbol{X},\boldsymbol{X})$$

对Attention的直观解释是

请求为向量时

  • 现有查询向量 q
  • 想从 Value 矩阵(每列对应一个样本) 中按照比例选择样本进行加权求和得到与 q 相关的查询结果
    • 要求是样本与 q 越相关，权重越大
  • Value 中的每个样本都有 Key 矩阵 中的一个样本与之对应(NLP中 Key 往往是 Value 自己)
  • 将 q 与 Key 的每个样本做相关性计算，得到其与 Key 中每个样本的相关性
  • 对 q 与 Key 的所有相关性做归一化，得到权重比例
  • 按照这个比例将 Value 中的样本加权输出结果
  • 该结果就是 Value 经过 \(F(q, Key)\)加权求和后的结果
  • 也就是 q 对应的结果

请求为矩阵时

  • 现有查询矩阵 Query， 包含 m 个查询向量
  • 相当于重复 m 次做单个请求为向量的运算
  • 每个 q 都能得到一个结果
  • 在实际计算时，可以将整个矩阵一起计算，主要注意归一化是对单个 q 向量与 Key 矩阵生成的结果即可

更多分析

  • 当 Key 与 Value 相同时
    • 其实是说计算 Value 每个样本的权重就用自己去与 q 计算即可
    • NLP中一般都是这样的
  • 当 Key 与 Query 相同时，
    • 其实是找自身不同样本间的相关性
    • 然后根据不同样本的对应其他样本的相关性对其他样本进行加权求和得到自己对应的结果
    • NLP中Self-Attention是这样的
  • Self-Attention是 Key == Value == Query 的情况

Attention研究发展趋势