f-divergence定义
- \( f \)-散度(\( f \)-divergence)是概率论和信息论中的一种概念,用于衡量两个概率分布之间的差异。它是由Imre Csiszár引入的,并且在统计学、机器学习以及信息理论等领域有着广泛的应用
- 形式上,对于两个概率分布 \( P \) 和 \( Q \),定义在一个共同的样本空间上, \( f \)-散度可以被定义为:
$$ D_f(P|Q) = \int_{\Omega} q(x) f\left(\frac{p(x)}{q(x)}\right) dx $$- \( \Omega \) 是样本空间
- \( p(x) \) 和 \( q(x) \) 分别是 \( P \) 和 \( Q \) 的概率密度函数
- \( f \) 是一个凸函数,满足 \( f(1) = 0 \),这是为了保证当 \( P = Q \) 时 \( D_f(P|Q) = 0 \)
- \( f \)-散度的一个重要性质是它是非负的,即 \( D_f(P|Q) \geq 0 \),并且只有当 \( P = Q \) 时等号成立。这意味着 \( f \)-散度可以作为两个概率分布之间距离的一种度量,尽管它不满足距离的所有公理(比如对称性)
常见的f-divergence例子
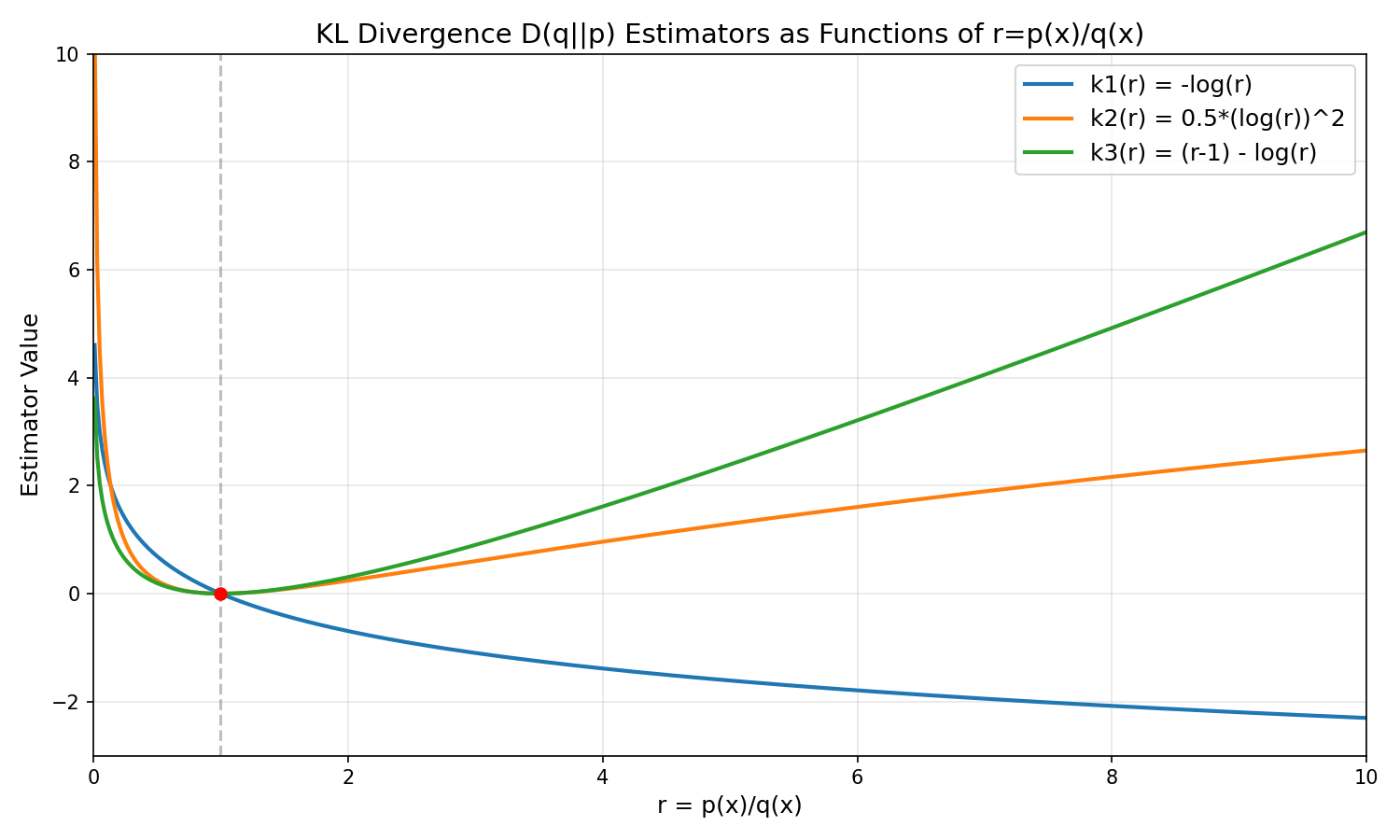
- Kullback-Leibler散度 (KL散度),其中 \( f(u) = u \log u \)
- 注意带入以后可以消去分母得到KL散度的最终公式
- Hellinger距离,这里 \( f(u) = (\sqrt{u} - 1)^2 \)
- 总变差距离,此时 \( f(u) = |u - 1| \)
- χ²散度,使用 \( f(u) = \frac{(u - 1)^2}{u} \)
附录:KL散度的非负性证明
- 核心,利用Jensen不等式证明 Kullback-Leibler(KL)散度是非负的
- 对于两个概率分布 \( P \) 和 \( Q \) 在同一空间 \( \mathcal{X} \) 上,KL 散度定义为:
$$
D_{\text{KL} }(P \parallel Q) = \sum_{x \in \mathcal{X} } P(x) \log \frac{P(x)}{Q(x)}
$$- 注意 KL 散度的积分权重和分子是相同的(这是由其含义和非负性决定的,详情见附录),若对换分子分母,得到的是 KL 的负数值
- 对于连续变量,定义为:
$$
D_{\text{KL} }(P \parallel Q) = \int_{-\infty}^{\infty} p(x) \log \frac{p(x)}{q(x)} , dx
$$- 其中 \( p(x) \) 和 \( q(x) \) 分别是 \( P \) 和 \( Q \) 的概率密度函数
- 进一步地,KL散度可以表示为:
$$
D_{\text{KL} }(P \parallel Q) = \mathbb{E}_{P} \left[ \log \frac{P(x)}{Q(x)} \right]
$$- 即 \( \log \frac{P(x)}{Q(x)} \) 在分布 \( P \) 下的期望
应用Jensen不等式求负KL散度
- 由于 \( \log(x) \) 是一个凹函数(伞状),根据Jensen不等式,对于凹函数有:
$$
\mathbb{E}_[\log X] \leq \log \mathbb{E}_[X]
$$- 令 \( X = \frac{Q(x)}{P(x)} \),则:
$$
\mathbb{E}_{P} \left[ \log \frac{Q(x)}{P(x)} \right] \leq \log \left( \mathbb{E}_{P} \left[ \frac{Q(x)}{P(x)} \right] \right)
$$
- 令 \( X = \frac{Q(x)}{P(x)} \),则:
- 计算期望:
$$
\mathbb{E}_{P} \left[ \frac{Q(x)}{P(x)} \right] = \sum_{x} P(x) \cdot \frac{Q(x)}{P(x)} = \sum_{x} Q(x) = 1
$$ - 因此:
$$
\mathbb{E}_{P} \left[ \log \frac{Q(x)}{P(x)} \right] \leq \log(1) = 0
$$
推导KL散度的非负性
- 注意到:
$$
\mathbb{E}_{P} \left[ \log \frac{Q(x)}{P(x)} \right] = -D_{\text{KL} }(P \parallel Q)
$$ - 因此:
$$
-D_{\text{KL} }(P \parallel Q) \leq 0 \implies D_{\text{KL} }(P \parallel Q) \geq 0
$$ - 当且仅当 \( P(x) = Q(x) \) 对所有 \( x \) 成立时,\( \frac{P(x)}{Q(x)} = 1 \),此时:
$$
D_{\text{KL} }(P \parallel Q) = \sum_{x} P(x) \log 1 = 0
$$ - KL散度始终满足:
$$
D_{\text{KL} }(P \parallel Q) \geq 0
$$ - 且 \( D_{\text{KL} }(P \parallel Q) = 0 \) 当且仅当 \( P = Q \)
附录:KL 散度=交叉熵与熵的差 推导
- KL 散度本质上是交叉熵与熵的差,反映了用错误模型编码时的“额外信息量”
熵 \(H(P)\) 和 交叉熵 \(H(P, Q)\) 的定义
- 对于离散分布 \(P(x)\),熵定义为:
$$
H(P) = -\sum_x P(x) \log P(x)
$$- 它表示在分布 \(P\) 下,平均需要多少信息量(比特或 nats)来编码事件
- 交叉熵定义为:
$$
H(P, Q) = -\sum_x P(x) \log Q(x)
$$- 它表示在真实分布是 \(P\) 时,如果用分布 \(Q\) 来编码,平均需要的信息量
KL 散度=两者的差
- 交叉熵与熵的差:
$$
\begin{align}
H(P, Q) - H(P) &= \left[ -\sum_x P(x) \log Q(x) \right] - \left[ -\sum_x P(x) \log P(x) \right] \\
&= -\sum_x P(x) \log Q(x) + \sum_x P(x) \log P(x) \\
&= \sum_x P(x) \left[ \log P(x) - \log Q(x) \right] \\
&= \sum_x P(x) \log \frac{P(x)}{Q(x)} \\
&= D_{\mathrm{KL} }(P | Q)
\end{align}
$$
理解
- 熵 \(H(P)\) :理想编码长度
- 交叉熵 \(H(P, Q)\) :用错误分布 \(Q\) 编码的平均长度
- KL 散度 :额外的编码长度,也就是交叉熵比真实熵多出来的部分