- 参考链接:
- PPO 一作的博客:Approximating KL Divergence, 2020,在博客中解释了作者使用一些近似方法,本文主要参考该博客的内容,有一些自己的总结和思考
KL散度的定义
- KL散度定义为:
$$
D_\text{KL}(q||p) = \sum_x q(x) \log \frac{q(x)}{p(x)} = \mathbb{E}_{x \sim q} \left[ \log \frac{q(x)}{p(x)} \right]
$$- 很多地方也常常写为 \(D_\text{KL}(q,p)\) 或 \(KL[q,p]\)
- 注意:这里使用的 \(p,q\) 顺序可能和常规的文章可能不同
一些假设
- 作者假设可以计算任意 \(x\) 的概率(或概率密度) \(p(x)\) 和 \(q(x)\),但无法解析地计算关于 \(x\) 的和(即期望)
- 现实场景中,无法解析计算的原因是有:
- 精确计算需要过多计算资源或内存
- 不存在闭式表达式
- 为了简化代码,仅存储对数概率而非整个分布。如果KL散度仅用作诊断(如强化学习中常见的情况),这是一个合理的选择
好的估计量应该是怎样的?
- 好的估计量应具有无偏性(期望相同)和低方差
- 比如对于来自 \(q\) 的样本, \(\log \frac{q(x)}{p(x)}\) 就是一个无偏估计,但它的方差很高
- 问题:为什么说这个式子方差高?
- 回答:一个直观的理解是 因为对于一半样本它是负值,而KL散度总是正值,后续会通过实验验证
- 注意 KL 散度的积分权重和分子是相同的(这是由其含义和非负性决定的),若对换分子分母,得到的是 KL 的负数值
一些前置定义
- 定义 一个 比例 \(r\) :
$$r = \frac{p(x)}{q(x)}$$- 特别注意 :这里的定义与 KL 散度中括号内的分子分母相反,对应到原始 KL 散度中,值为:
$$
\begin{align}
D_\text{KL}(q||p) &= \mathbb{E}_{x \sim q} \left[ \log \frac{q(x)}{p(x)} \right] \\
&= \mathbb{E}_{x \sim q} \left[ - \log \frac{p(x)}{q(x)} \right] \\
&= \mathbb{E}_{x \sim q} \left[ - \log r \right]
\end{align}
$$
- 特别注意 :这里的定义与 KL 散度中括号内的分子分母相反,对应到原始 KL 散度中,值为:
朴素估计量(\(k_1\))
- 朴素估计量(\(k_1\)) 表达式:
$$
k_1 = -\log r = \log \frac{q(x)}{p(x)}
$$ - 无偏 : \(\mathbb{E}[k_1] = D_\text{KL}(q||p)\)
- 高方差 :因 \(\log r\) 在 \(r>1\) 时为负, \(r<1\) 时为正,导致样本间波动大
- 适用场景 :理论分析或对无偏性要求严格的场景,但实际应用中可能因高方差不稳定
二次估计量(\(k_2\))
- 二次估计量(\(k_2\)) 表达式:
$$
k_2 = \frac{1}{2} (\log r)^2
$$ - 有偏(低偏差) : \(\mathbb{E}[k_2] \approx D_\text{KL}(q||p) + O(\theta^3)\),当 \(p \approx q\) 时偏差极小(如实验中的0.2%)
- 低方差 :因平方项强制为正,减少了样本间的波动
- 适用场景 : \(p\) 和 \(q\) 接近时的高效估计,适合作为诊断指标(如强化学习中的策略评估)
- 理解:这里的诊断主要是指仅仅作为判断条件,而不是作为损失函数的主要优化目标
为什么说估计量 \(k_2\) 具有低偏差?
- 它的期望是一个 \(f\)-散度。 \(f\)-散度定义为:
$$D_f(p,q) = \mathbb{E}_{x \sim q} \left[ f\left( \frac{p(x)}{q(x)} \right) \right]$$- 其中 \(f\) 是凸函数
- KL散度和其他许多著名的概率距离都是 \(f\)-散度, KL 散度中 \(f(\cdot) = -\log (\cdot)\)(\(\log(\cdot)\) 是凹函数,凹函数取负号就是凸函数)
- 当 \(q\) 接近 \(p\) 时,所有具有可微 \(f\) 的 \(f\)-散度在二阶近似下都类似于KL散度。具体来说,对于参数化分布 \(p_\theta\) :
$$
D_f(p_0, p_\theta) = \frac{f’’(1)}{2} \theta^T F \theta + O(\theta^3)
$$- 其中 \(F\) 是 \(p_\theta\) 在 \(p_\theta = p_0\) 处评估的Fisher信息矩阵
- \(\mathbb{E}_q[k_2] = \mathbb{E}_q \left[ \frac{1}{2}(\log r)^2 \right]\) 对应 \(f(x) = \frac{1}{2}(\log x)^2\) 的 \(f\)-散度,而 \(D_\text{KL}(q||p)\) 对应 \(f(x) = -\log x\)。容易验证两者都有 \(f’’(1)=1\),因此对于 \(p \approx q\),两者看起来像相同的二次距离函数
- \(k_2\) 的取值总是大于等于0,可以通过求导证明:当 \(x>0\) 时,有 \(x - \log x - 1 \ge 0\) 恒成立,最小值在 \(x=1,y=0\)处,其函数图像如下:
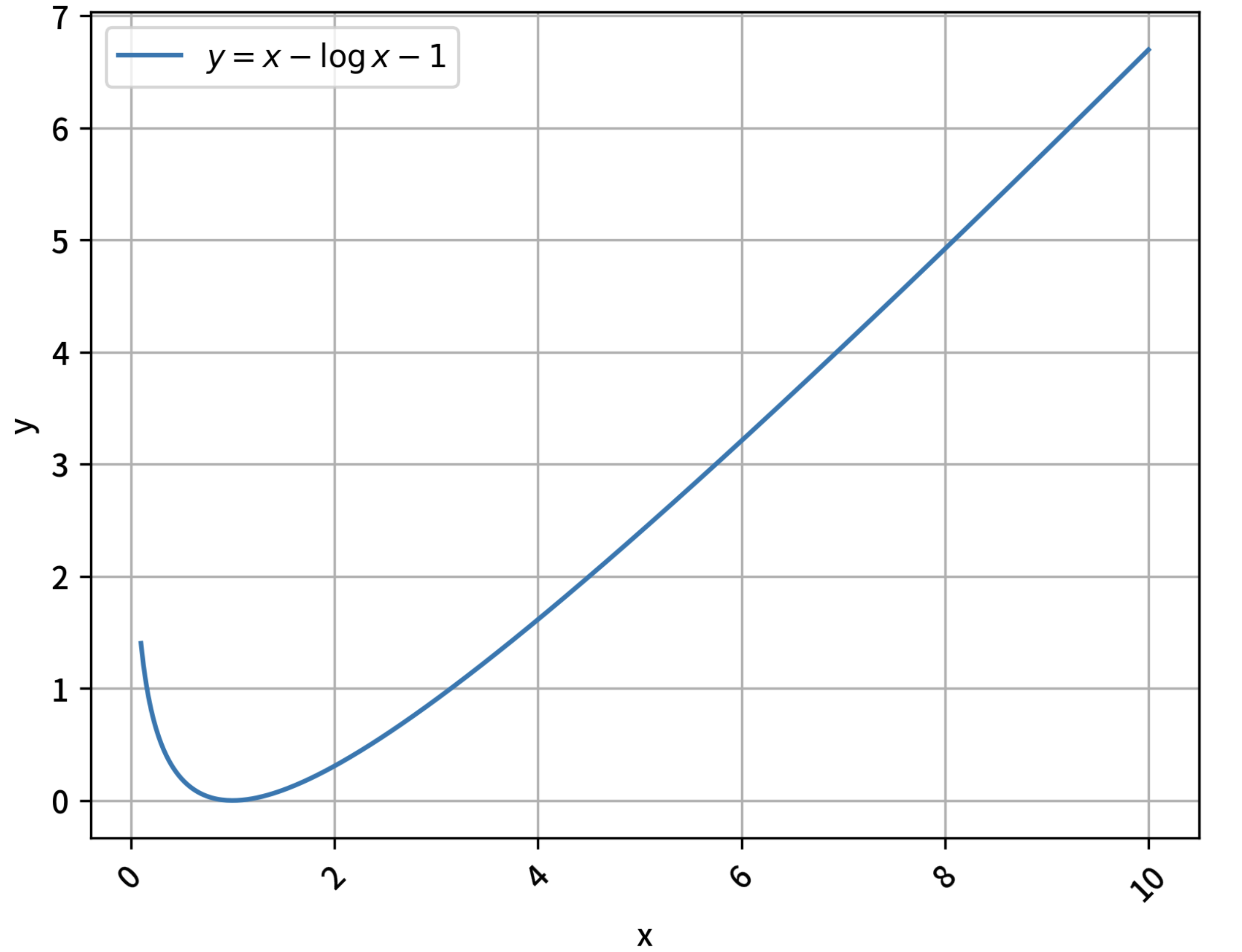
Bregman散度估计量(\(k_3\))
- Bregman散度估计量(\(k_3\)) 表达式:
$$
k_3 = (r - 1) - \log r
$$ - 无偏 : \(\mathbb{E}[k_3] = D_\text{KL}(q||p)\)
- 最低方差 :结合了 \(r-1\) 的线性项与 \(\log r\) 的校正,进一步降低波动
- 适用场景 :对无偏性和低方差同时要求的场景(如精确的梯度估计或敏感的参数优化)
Bregman散度估计量(\(k_3\)) 是怎么设计出来的?
- 我们的目标:是找到一个无偏且低方差的KL散度估计量
- 降低方差的通用方法是使用控制变量:取 \(k_1\) 并加上一个期望为零但与 \(k_1\) 负相关的量
- 幸运的是,作者发现 \(\frac{p(x)}{q(x)} - 1 = r - 1\) 是一个期望为0的量),于是,对于任意 \(\lambda\),下面的表达式都是 \(D_\text{KL}(q||p)\) 的无偏估计量:
$$-\log r + \lambda(r - 1)$$- 注:作者可以通过计算最小化这个估计量的方差来求解 \(\lambda\)。但不幸的是,作者得到的表达式依赖于 \(p\) 和 \(q\),并且难以解析计算
- 所以,作者使用更简单的策略选择一个好的 \(\lambda\)
- 作者注意到由于 \(\log\) 是凹函数,有 \(\log(x) \leq x - 1\)
- 因此,如果作者设 \(\lambda=1\),上述表达式保证为正。它测量了 \(\log(x)\) 与其切线之间的垂直距离
- 于是作者提出了估计量 \(k_3 = (r - 1) - \log r\)
更多扩展和思考
- 这种通过观察凸函数与其切平面之间的差异来测量距离的思想出现在许多地方。它被称为Bregman散度 ,具有许多优美的性质
- 可以推广上述思想,为任何 \(f\)-散度得到一个良好的、总是正的估计量
- 另一个KL散度是 \(KL[p,q]\)(注意这里 \(p\) 和 \(q\) 交换了位置 ,与 \(D_\text{KL}(q||p)\) 不同)
- 由于 \(f\) 是凸函数,且 \(\mathbb{E}_q[r] = 1\),以下表达式是 \(f\)-散度的估计量:
$$f(r) - f’(1)(r - 1)$$ - 这个量总是正的,因为它是 \(f\) 在 \(r=1\) 处与切线的距离,而凸函数位于其切线上方。现在 \(KL[p,q]\) 对应 \(f(x) = x \log x\),它有 \(f’(1) = 1\),于是有估计量 \(r \log r - (r - 1)\)
- 总结一下,作者提出以下估计量(对于样本 \(x \sim q\),且 \(r = \frac{p(x)}{q(x)}\)):
$$
\begin{align}
D_\text{KL}(p||q): &\quad r \log r - (r - 1)\\
D_\text{KL}(q||p): &\quad (r - 1) - \log r
\end{align}
$$- 注意上面的 KL 散度先后顺序,KL 散度不是对称的
Experiments
- 现在让我们比较三个 \(D_\text{KL}(q||p)\) 估计量的偏差和方差
- 定义 \(q = \mathcal{N}(0,1)\), \(p = \mathcal{N}(0.1,1)\)(此时真实的KL散度为0.005)
统计量/真实值 \(k_1\) \(k_2\) \(k_3\) 偏差(期望与真实值差) 0 0.002 0 标准差 20 1.42 1.42 - 注意到 \(k_2\) 的偏差在这里极低:仅为0.2%
- 以上标准差是使用 KL 单独作归一化后的(除以 KL 散度)
- 定义 \(p = \mathcal{N}(1,1)\) (此时真实KL散度为0.5)
统计量/真实值 \(k_1\) \(k_2\) \(k_3\) 偏差(期望与真实值差) 0 0.25 0 标准差 2 1.73 1.7 - 这里 \(k_2\) 的偏差大得多
- \(k_3\) 在保持无偏的同时甚至比 \(k_2\) 具有更低的标准差,因此它似乎是一个严格更好的估计量
- 作者给出的上述实验的代码:
1
2
3
4
5
6
7
8
9
10
11
12import torch.distributions as dis
p = dis.Normal(loc=0, scale=1)
q = dis.Normal(loc=0.1, scale=1)
x = q.sample(sample_shape=(10_000_000,))
truekl = dis.kl_divergence(p, q)
print("true", truekl)
logr = p.log_prob(x) - q.log_prob(x)
k1 = -logr
k2 = logr ** 2 / 2
k3 = (logr.exp() - 1) - logr
for k in (k1, k2, k3):
print((k.mean() - truekl) / truekl, k.std() / truekl)
一些总结和思考
- 三种估计量的对比如下:
估计量 无偏性 方差 偏差(当 \(p \neq q\)) 计算复杂度 适用场景 \(k_1\) 无偏 高 0 低 理论分析,高精度需求 \(k_2\) 有偏(低) 中低 随 \(KL\) 增大而增加 低 \(p \approx q\) 时的一些近似判别 \(k_3\) 无偏 最低 0 中(需算 \(r\)) 高精度需求(如优化算法) - 方差排序 : \(k_3 < k_2 < k_1\)
- 偏差权衡 :
- 若 \(p \approx q\), \(k_2\) 的偏差可忽略,且计算简单
- 若 \(KL\) 较大(如 \(p,q\) 差异显著), \(k_3\) 是唯一同时满足无偏和低方差的选项
- 实践建议 :
- 使用 \(k_3\) 作为默认选择(尤其对敏感任务)
- 在快速迭代或 \(p \approx q\) 时,可用 \(k_2\) 作为轻量替代
不同估计值的函数图像
- 函数图像如下:
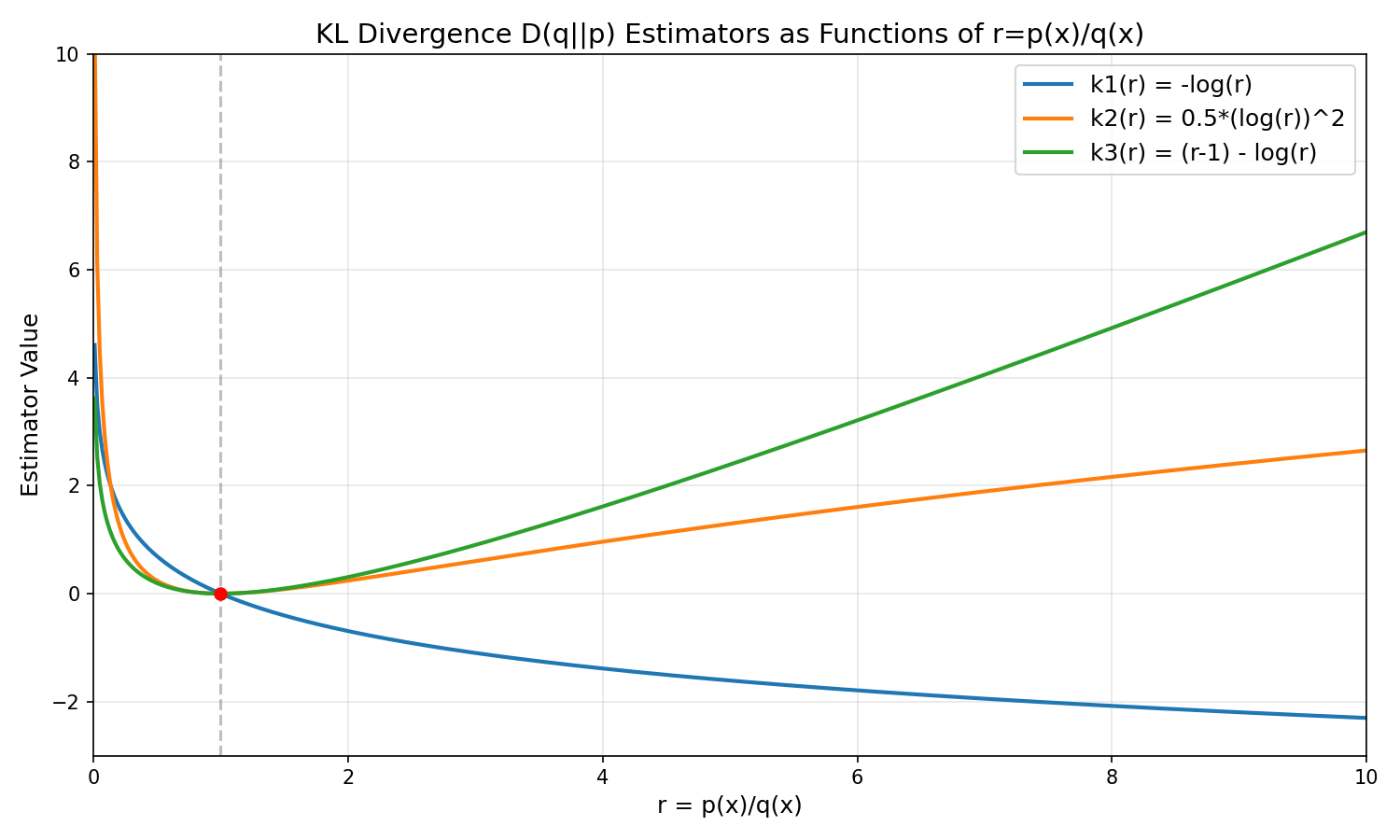
- 补充讨论:
- 背景:从图中看,不管是 k1,k2 还是 k3,当 kl 散度为 0.1 的时候(VeRL 的默认 kl_target 值),其实 ratio 波动已经不小了(以 k1 为例,此时的比值 r 为 \(e^{-0.1} \approx 0.9\))
- 问题:为什么体感上,模型整体偏差又还好?
- 回答(暂为个人思考推测,不严谨):
- 一方面,因为均值会被一些大的 ratio 带偏:真实观察来看,实际上 k1_kl 的均值会是中位数的两倍左右(说明少量的异常值主导了大的 kl,许多 Token 的 kl 其实没有变化太多)
- 另一方面,一些 Token 的概率变化成了 0.9 其实也还好(比如原始 0.2 的,现在变成 0.18,似乎对整体分布的变化也还好)
- 补充:上述图片的生成代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45import numpy as np
import matplotlib.pyplot as plt
# Define the functions
def k1(r):
return -np.log(r)
def k2(r):
return 0.5 * (np.log(r))**2
def k3(r):
return (r - 1) - np.log(r)
x_max = 10
# Generate r values (avoid r=0 for log)
r = np.linspace(0.01, x_max, 500)
# Calculate function values
k1_vals = k1(r)
k2_vals = k2(r)
k3_vals = k3(r)
# Create plot
plt.figure(figsize=(10, 6))
plt.plot(r, k1_vals, label='k1(r) = -log(r)', linewidth=2)
plt.plot(r, k2_vals, label='k2(r) = 0.5*(log(r))^2', linewidth=2)
plt.plot(r, k3_vals, label='k3(r) = (r-1) - log(r)', linewidth=2)
# Add special points and lines
plt.axvline(1, color='gray', linestyle='--', alpha=0.5)
plt.plot(1, 0, 'ro') # All functions equal 0 at r=1
# Plot formatting
plt.title('KL Divergence Estimators as Functions of r=p(x)/q(x)', fontsize=14)
plt.xlabel('r = p(x)/q(x)', fontsize=12)
plt.ylabel('Estimator Value', fontsize=12)
plt.legend(fontsize=12)
plt.grid(True, alpha=0.3)
plt.xlim(0, x_max)
plt.ylim(-3, 10)
# Show plot
plt.tight_layout()
plt.show()
附录:回顾凹函数和凸函数定义
凸函数(Convex Function)
- 若函数 \( f \) 的定义域为某个凸集(如区间),且对定义域内任意两点 \( x_1, x_2 \) 和任意 \( \lambda \in [0, 1] \),满足:
$$
f(\lambda x_1 + (1-\lambda) x_2) \leq \lambda f(x_1) + (1-\lambda) f(x_2)
$$ - 则称 \( f \) 为凸函数
- 直观理解:函数图像上任意两点间的线段始终位于函数图像上方(或重合),形如“碗状”或“线性”
- 举例: \( f(x) = x^2 \)、\( f(x) = e^x \))
凹函数(Concave Function)
- 若函数 \( f \) 的定义域为凸集,且对任意两点 \( x_1, x_2 \) 和 \( \lambda \in [0, 1] \),满足:
$$
f(\lambda x_1 + (1-\lambda) x_2) \geq \lambda f(x_1) + (1-\lambda) f(x_2)
$$ - 则称 \( f \) 为凹函数
- 直观理解:函数图像上任意两点间的线段始终位于函数图像下方(或重合),形如“拱形”或“线性”
- 举例:\( f(x) = -x^2 \)、\( f(x) = \ln x \)(定义域 \( x > 0 \))
补充说明
- 线性函数既是凸的也是凹的(因不等式取等号)
- 凹凸性反转 :若 \( f \) 是凸函数,则 \( -f \) 是凹函数,反之亦然
- 严格凸/凹 :当不等式在 \( x_1 \neq x_2 \) 且 \( \lambda \in (0,1) \) 时严格成立(如 \( < \) 或 \( > \)),则称函数为严格凸或严格凹
附录:LLM 训练中的 k1,k2,k3
LLM 中训练时,发现一个反常的现象:k3 估计值的波动远大于 k1
- 这与本文代码的评估结果相反
原因如下:
- 当分布接近时(本文中的两个分布比较接近),采样点的比值接近 \(r \approx 1\),即 \(\log r \approx 0\),此时对 k3 可以泰勒展开,变化为:
$$
\begin{align}
k3 &= (r-1) - \log r \\
&= (e^{\log r}-1) - \log r \\
&= (1+ \log r + (\log r)^2 + o((\log r)^2) - 1) - \log r \\
&= (\log r)^2 + o((\log r)^2)
\end{align}
$$- 显然,原始 k1 = \(- \log r\) 是一次项,这里是二次项,当 \(\log r \approx 0\),二次项的方差显然更小
- 当分布存在差异较大的点时(如 LLM 的高维空间中,两个分布的比值可能出现较大差异)k3 中包含的 \(r\) 相当于是:
$$ r = e^{\log r} $$- 可以看到 k3 的 \(r\) 相对 k1, k2 的 \(\log r\) 来说,本质是指数项,相对来说会放大对数比值的量级,导致出现波动较大的情况
- 具体来说,由于 \(r = \frac{\pi_{\theta_\text{ref}}}{\pi_\theta}\),所以,当 \(\pi_\theta\) 变得很小时会发生 \(r\) 被无限放大的情况(即异常值)
- 当分布接近时(本文中的两个分布比较接近),采样点的比值接近 \(r \approx 1\),即 \(\log r \approx 0\),此时对 k3 可以泰勒展开,变化为:
复现 k3 出现较大值的情况:
设定一:两个分布应该有一定的差异,即允许原始分布较大的值,在当前分布上较小的点出现
设定二:同时打印 k1, k2, k3 的最大值(即异常值)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42# 作者原始测试代码:
import torch.distributions as dis
p = dis.Normal(loc=0, scale=1)
q = dis.Normal(loc=0.1, scale=1)
x = q.sample(sample_shape=(10_000_000,))
truekl = dis.kl_divergence(p, q)
print("true", truekl)
logr = p.log_prob(x) - q.log_prob(x)
k1 = -logr
k2 = logr ** 2 / 2
k3 = (logr.exp() - 1) - logr
for k in (k1, k2, k3):
print((k.mean() - truekl) / truekl, k.std() / truekl, k.max()) # 微改,增加 k.max()
# true tensor(0.0050)
# tensor(-0.0014) tensor(20.0019) tensor(0.5416)
# tensor(0.0027) tensor(1.4182) tensor(0.1467)
# tensor(0.0001) tensor(1.4169) tensor(0.1412)
# 微改上述代码:
import torch.distributions as dis
p = dis.Normal(loc=0, scale=1) # old 策略
# q = dis.Normal(loc=0.1, scale=1) # 之前作者的定义
q = dis.Normal(loc=1, scale=1) # new 策略,这里假设偏移了较多了,注意:LLM 中是 Categorical 分布,其实变化应该比 正太分布大多了(正太分布太规范了)
x = q.sample(sample_shape=(10_000_000,)) # 保持作者之前的采样方式,样本点都是从当前策略 q 中采样得到的,跟线上 LLM 对齐
# x = dis.Normal(0,1).sample(sample_shape=(10_000_000,))
truekl = dis.kl_divergence(p, q)
print("true", truekl)
logr = p.log_prob(x) - q.log_prob(x) # p 是 old 策略
# logr = logr.double()
print("mean_ratio", logr.exp().mean())
k1 = -logr
k2 = logr ** 2 / 2
k3 = (logr.exp() - 1) - logr
for k in (k1, k2, k3):
print((k.mean() - truekl) / truekl, k.std() / truekl, k.max())
# true tensor(0.5000)
# mean_ratio tensor(1.0002)
# tensor(-0.0005) tensor(1.9999) tensor(5.9776)
# tensor(0.2497) tensor(1.7324) tensor(17.8657)
# tensor(-0.0001) tensor(1.6956) tensor(124.3422) # 这里可以看到,k3 估计器标准差最小,但是 k3 的最大值明显大于 k1 和 k2,若分布点再变化大一些,这个值会更离谱;原因就是因为 k3 包含了 r=e^{log(r)},而 k1 和 k2 都是 log(r)- 可以看到,当分布差异明显时,k3 的最大值确实是更大的,这也是一些 Batch 中看到 k3 非常离谱的原因
实际上,在 LLM 中,是多项式分布的,如果当前 Token 对应的 概率降低了非常多,就会导致异常的 k3 出现,且概率降低的倍数就是 k3 的值的量级
$$ k3 \approx r = \frac{\pi_{\theta_\text{ref}}}{\pi_\theta}, \quad \text{when } r \text{ is big}$$- 一般来说 k3 应该不会出现非常大的异常值
- 加上 Token 是当前策略或临近的策略采样得到的,当前策略一般很难采样到概率极低的 Token
- 如果是个位数是比较 OK 的,如果出现几百甚至几千(现实中遇到过上万),此时就要小心了,应该是推理出错了导致的
- 实际训练时,看到了一些
cur_policy_log_prob = -12的 Token,这些 Token 的采样概率本应该很低(甚至不应该采样出来才对) - 修复这个问题:
- 使用
min_p,保证太低概率的 Token 不要采样出来 - 减少 Rollout 和 Megatron 策略的 diff, Rollout 时 概率较大的 Token,在 Megatron 计算后概率也有偏小的可能性
- 使用
- 一般来说 k3 应该不会出现非常大的异常值
补充:k3 的梯度推导
- 首先有:
$$
\begin{align}
r = \frac{\pi_{\theta_\text{ref}}}{\pi_{\pi_\theta}}\\
Loss_{k3} = r - 1 - \log r
\end{align}
$$ - 要计算 Loss 对模型输出(Logits)的梯度
- 令 \(u = \log \pi_{\pi_\theta}\)(这是模型直接输出的东西)
- 那么 \(\log r = \log \pi_{\theta_\text{ref}} - u\)
- 所以 \(r = e^{\log \pi_{\theta_\text{ref}} - u} = C \cdot e^{-u}\) (\(C\) 是常数)
- 代入 Loss 公式:
$$L(u) = C \cdot e^{-u} - 1 - (\log C - u) = C \cdot e^{-u} - 1 - \log C + u$$ - 现在对 \(u\) 求导(计算梯度):
$$
\begin{align}
\frac{\partial L}{\partial u} &= C \cdot e^{-u} \cdot (-1) + 0 - 0 + 1 \\
\frac{\partial L}{\partial u} &= 1 - r
\end{align}
$$ - 最终得到:梯度是
$$(1 - r) \nabla_\theta u_\theta = (1 - r) \nabla_\theta \log \pi_{\pi_\theta} $$- 注:这与 REINFORCE++ 中附录公式 (14) 中的推导结果一致
问题:GRPO 中,当 k3 估计下的 kl_loss 很大时,梯度会很大吗?
- 从上面可以知道,梯度是:
$$ (1 - r) \nabla_\theta \log \pi_{\pi_\theta} $$- 显然,当 Loss 很大是因为 \(r\) 很大导致的时,梯度是很大的
- 注:另一种可能是 Loss 很大是因为 \(r\) 无限趋近于 0 导致的
- 但这种情况需要 \(r\) 非常非常小才会导致,比如即使小如 \(r= 1e-10\) 时:
$$- \log r = - ln(1e-10) \approx 23$$ - 而且这种情况下,当 k3 很大时, k1 和 k2 也会很大
- 但这种情况需要 \(r\) 非常非常小才会导致,比如即使小如 \(r= 1e-10\) 时:
问题:什么情况下会出现 k1,k2 平缓,但 k3 发生 spike 的问题?
- k3 和 k1,k2 的主要区别在于:
- k1, k2 仅拥有 \(\log r\) 或 \((\log r)^2\)
- k3 同时拥有 \(\log r\) 和 \(r\)
- 当 \(\log r\) 没有问题,但 \(r\) 很大时,会出现 k1,k2 平缓,但 k3 发生 spike
- 此时 说明当前策略 Token 的概率相对 Reference 策略的概率小很多(小 \(r\) 倍)
附录:Reverse KL Divergence vs Forward KL Divergence
- 正向 KL 散度和反向 KL 散度
两种 KL 散度的定义
- KL 散度(Kullback–Leibler Divergence)衡量两个概率分布 \( P \) 和 \( Q \) 之间的差异(非对称):
Forward KL
- Forward KL 从 真实分布 \(P\) 中采样,惩罚 \(Q\) 给 \(P\) 的高概率事件分配低概率(即“覆盖模式(Mode-covering)”)
$$
D_{KL}(P | Q) = \mathbb{E}_{x \sim P} \left[ \log \frac{P(x)}{Q(x)} \right]
$$
Reverse KL
- Reverse KL 从 近似分布 \(Q\) 中采样,惩罚 \(Q\) 给自身的样本分配高概率,而 \(P\) 却认为这些样本概率很低(即“避免零概率陷阱”或“模式寻求”)
$$
D_{KL}(Q | P) = \mathbb{E}_{x \sim Q} \left[ \log \frac{Q(x)}{P(x)} \right]
$$
两者的区别
- 假设真实分布 \(P\) 是一个双峰分布(两个分离的高峰),而论文的模型分布 \(Q\) 是一个单峰分布(如高斯分布)
- 最小化前向 KL 散度 \(D_{KL}(P | Q)\)
- 优化目标是让 \(Q\) 覆盖 \(P\) 的所有高概率区域
- \(Q\) 会尝试覆盖两个峰,变成一个宽而平的分布 ,覆盖两个模式,但无法精确匹配任何一个(均值覆盖,模糊拟合)
- 核心是 避免遗漏(avoid missing modes)
- 最小化反向 KL 散度 \(D_{KL}(Q | P)\)
- 优化目标是让 \(Q\) 只放在 \(P\) 的某一个高概率区域 ,并尽量让 \(Q\) 自身的概率集中
- \(Q\) 会选择其中一个峰 ,并紧密拟合它,完全忽略另一个峰(模式寻求(Mode-seeking),尖锐拟合)
- 核心 避免生成低概率样本(avoid generating low-probability samples)