文本介绍CTR预估模型STAR

• 参考链接：
  • 原始论文：One Model to Serve All: Star Topology Adaptive Recommender for Multi-Domain CTR Prediction, CIKM 2021, Alibaba
  • 博客：CIKM 2021 | 多场景下的星型CTR预估模型STAR

Background

• 随着业务场景的多样化，单一场景下的CTR预估模型已经不能满足需求，因此出现了针对多场景联合建模的需求。STAR（Star Topology Adaptive Recommender）模型正是为了解决这一问题而设计的

STAR 模型概述

• STAR模型的设计目的是为了同时学习不同业务场景中的共性和差异性。它通过一种星形拓扑结构来实现这一点，这种结构允许模型在共享某些参数的同时，也为每个特定场景保留一些私有参数。这样做不仅能够利用跨场景的信息来提升长尾小场景的学习效果，同时也确保了对各个场景特性的精确捕捉

STAR 的核心组成部分

• 模型结构

  

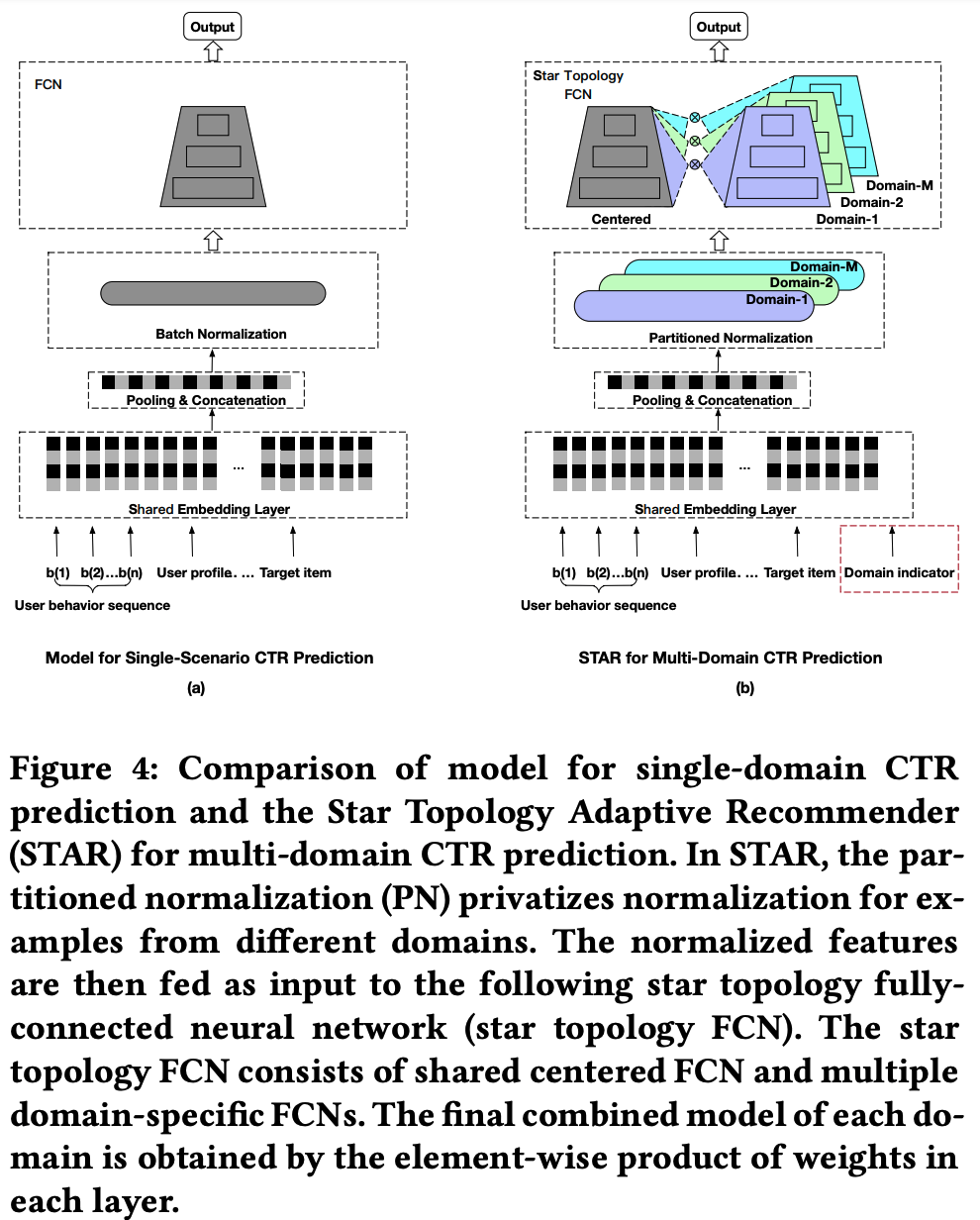
• STAR模型主要包括三个核心部分：

  • 星型拓扑全连接网络（STAR Topology Fully-Connected Network） ：这是STAR的核心架构，它由两大部分组成——一个所有业务场景共享的中心网络和每个业务场景独有的独立网络。对于每一层FC（Fully Connected），都有一个中心的共享参数和场景特有的私有参数。这些参数通过逐元素乘法（element-wise product）结合在一起，从而为每个场景生成最终的参数。这种方式使得共享参数可以被所有场景的数据更新，以学习到跨场景的共同特征；而场景私有参数则仅由该场景内的数据更新，以捕捉场景特有的特征
  • Partitioned Normalization (PN) ：在多场景背景下，传统的Batch Normalization (BN)假设所有样本都是独立同分布的，并使用相同的统计量进行归一化处理。然而，在实际应用中，不同场景的数据分布往往存在显著差异，这就要求我们采用不同的归一化策略。为此，STAR引入了Partitioned Normalization，即对不同域（domain）的样本采用不同的归一化统计量，以更好地适应各场景的独特性
    • 普通BN的公式为：
      $$ \text{BN}(x) = \gamma \left( \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} \right) + \beta $$
    • PN的公式为：
      $$ \text{PN}_d(x) = (\gamma \cdot \gamma_p) \left( \frac{x - \mu_{p}}{\sqrt{\sigma_{p}^2 + \epsilon}} \right) + (\beta+\beta_p) $$
  • 辅助网络 ：

• 关于STAR Topology Fully-Connected Network的说明

  
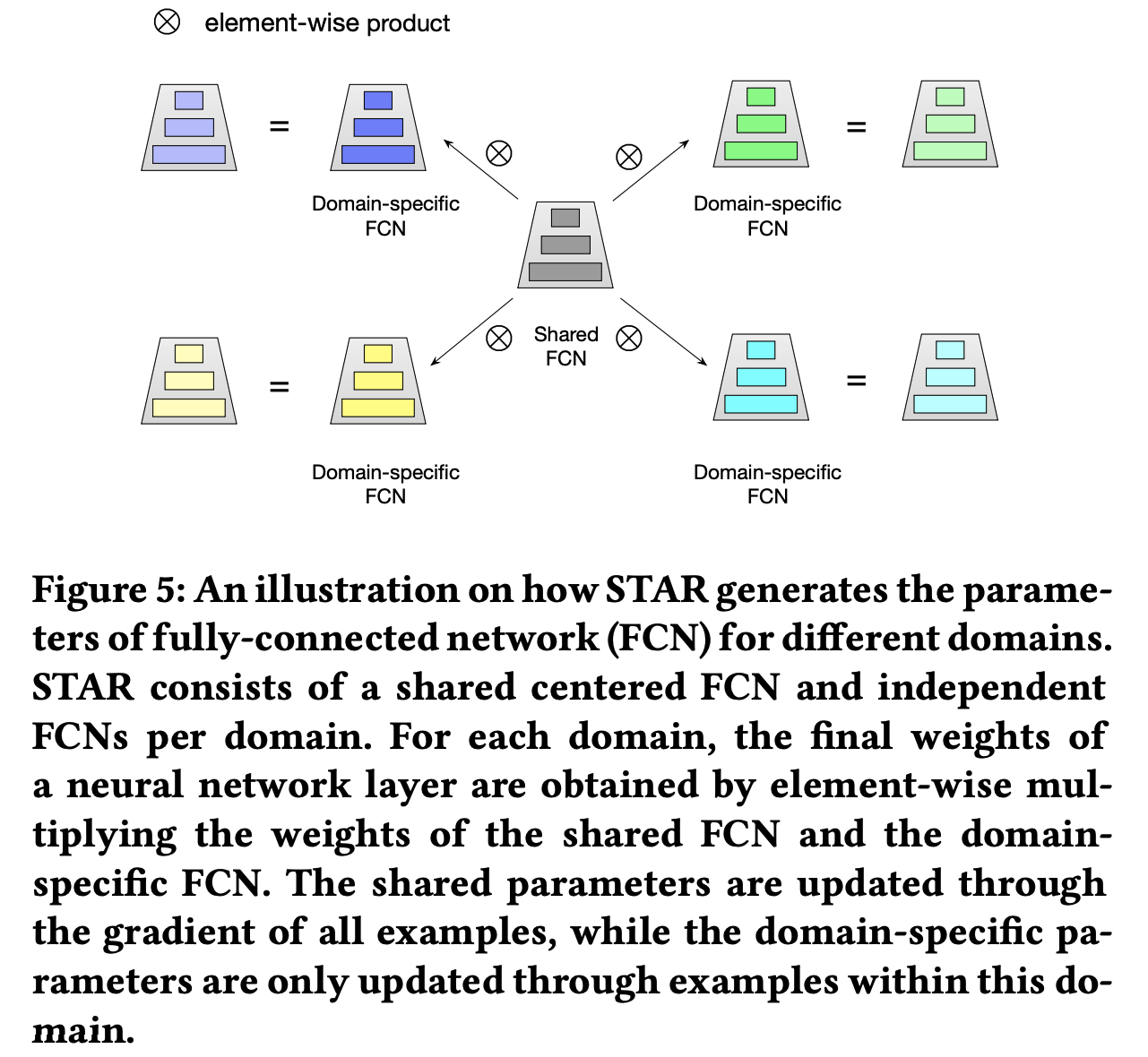
  • 每个域的参数都是与通过中心共享参数和私有参数按照按位相乘的到的，其中权重和Bias参数的计算方式不同:
    $$
    W_{p}^{\star} = W_{p} \otimes W, \quad b_{p}^{\star} = b_{p} + b
    $$
    • \(W_{p}^{\star}\) ：这是第 \(p\) 个领域的最终权重矩阵，通过将共享的中心网络的权重 \(W\) 和特定领域的权重 \(W_{p}\) 进行逐元素相乘（ \(\otimes\) ）得到
    • \(b_{p}^{\star}\) ：这是第 \(p\) 个领域的最终偏置向量，通过将共享的中心网络的偏置 \(b\) 和特定领域的偏置 \(b_{p}\) 进行相加得到
    • \(W\) 和 \(b\) ：这些是共享的中心网络的权重和偏置，它们从所有领域的数据中学习，捕捉跨领域的共性
    • \(W_{p}\) 和 \(b_{p}\) ：这些是特定领域的权重和偏置，它们只从第 \(p\) 个领域的数据中学习，捕捉该领域的特性
    • 通过这种结合方式，STAR模型能够在共享的共性知识和特定领域的特性之间找到一个平衡，从而更好地适应多领域的CTR预测任务
  • 最终输出：
    $$
    out_{p} = \phi((W_{p}^{\star})^{\top} in_{p} + b_{p}^{\star})
    $$
    • \(out_{p}\) ：这是第 \(p\) 个领域的输出，表示该领域的CTR预测结果
    • \(in_{p}\) ：这是第 \(p\) 个领域的输入特征向量
    • \(\phi\) ：这是激活函数，用于引入非线性
    • \((W_{p}^{\star})^{\top} in_{p}\) ：这是将输入特征 \(in_{p}\) 与最终权重矩阵 \(W_{p}^{*}\) 进行矩阵乘法操作，得到线性变换后的结果
    • \(b_{p}^{\star}\) ：这是最终偏置向量，加到线性变换的结果上
    • \(\phi((W_{p}^{\star})^{\top} in_{p} + b_{p}^{\star})\) ：这是将线性变换后的结果加上偏置，并通过激活函数 \(\phi\) 进行非线性变换，得到最终的输出

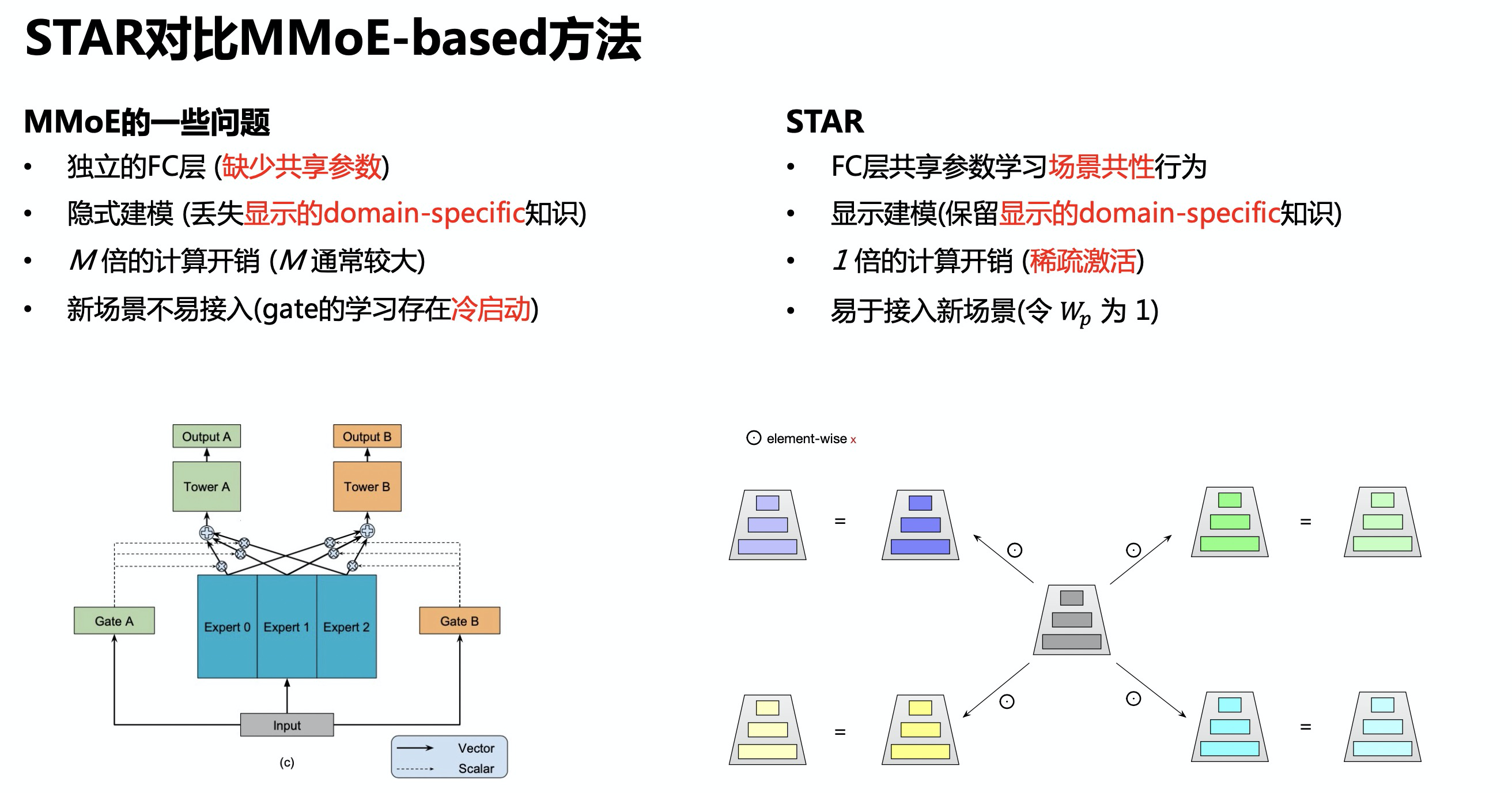
STAR与MMoE对比

• 对比如下，图来自 CIKM 2021 | 多场景下的星型CTR预估模型STAR：

文本介绍DDIM（Denoising Diffusion Implicit Models）的理论介绍

• 参考链接：
  • 原始论文：DENOISING DIFFUSION IMPLICIT MODELS, ICLR 2021
  • 一文带你看懂DDPM和DDIM（含原理简易推导，pytorch代码） - Deja vu的文章 - 知乎
  • 一文读懂DDIM凭什么可以加速DDPM的采样效率
  • 一个视频看懂DDIM凭什么加速采样|扩散模型相关

---

DDPM为什么慢？

• 采样步数不能太小，否则单次破坏力度过大，不容易恢复？
• 不能跳步，否则不遵循马尔可夫过程

---

推导过程

• 核心是在DDPM的基础上，增加一些设定，解决马尔可夫性导致的无法跳步采样的问题

• 直观理解

  

• 放弃马尔可夫性假设后，我们假设分布 \(p(x_{t-1}|x_t, x_0)\) 服从高斯分布：
  $$
  \begin{align}
  p(x_{t-1}|x_t, x_0) &\sim \mathcal{N}(kx_0+mx_t, \sigma^2) \\
  x_{t-1} &= kx_0+mx_t + \sigma \epsilon, \ \epsilon \sim \mathcal{N}(0,\boldsymbol{I})
  \end{align}
  $$

• 在 \( x_t\) 加噪过程中有（详情参见DDPM推导）：
  $$ x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1-\bar{\alpha}_t} \epsilon, \ \epsilon \sim \mathcal{N}(0,\boldsymbol{I})$$

• 将 \(x_t\) 带入原始假设分布，并合并同类项有(下面的推导使用到两个高斯分布的混合)：
  $$
  \begin{align}
  x_{t-1} &= kx_0+m(\sqrt{\bar{\alpha}_t} x_0 + \sqrt{1-\bar{\alpha}_t} \epsilon’) + \sigma \epsilon, \ \text{where} \ \epsilon,\epsilon’ \sim \mathcal{N}(0,\boldsymbol{I}) \\
  x_{t-1} &= (k+m\sqrt{\bar{\alpha}_t})x_0 + \sqrt{m^2(1-\bar{\alpha}_t) + \sigma^2}\epsilon, \ \epsilon \sim \mathcal{N}(0,\boldsymbol{I})
  \end{align}
  $$

• 在 \( x_{t-1}\) 加噪过程中有（详情参见DDPM推导）：
  $$ x_{t-1} = \sqrt{\bar{\alpha}_{t-1}} x_0 + \sqrt{1-\bar{\alpha}_{t-1}} \epsilon, \ \epsilon \sim \mathcal{N}(0,\boldsymbol{I})$$

• 于是，对照两个等式，让对应项相等可得以下方程：
  $$
  \begin{align}
  k+m\sqrt{\bar{\alpha}_t} &= \sqrt{\bar{\alpha}_{t-1}}\\
  \sqrt{m^2(1-\bar{\alpha}_t) + \sigma^2} &= \sqrt{1-\bar{\alpha}_{t-1}}
  \end{align}
  $$

• 解方程可得：
  $$
  \begin{align}
  m &= \frac{\sqrt{1-\bar{\alpha}_{t-1}-\sigma^2}}{\sqrt{1-\bar{\alpha}_t}} \\
  k &= \sqrt{\bar{\alpha}_{t-1}} - \frac{\sqrt{1-\bar{\alpha}_{t-1}-\sigma^2}}{\sqrt{1-\bar{\alpha}_t}}\sqrt{\bar{\alpha}_t}
  \end{align}
  $$

• 将结果带回原始假设分布可得：
  $$
  \begin{align}
  x_{t-1} &= (\sqrt{\bar{\alpha}_{t-1}} - \frac{\sqrt{1-\bar{\alpha}_{t-1}-\sigma^2}}{\sqrt{1-\bar{\alpha}_t}}\sqrt{\bar{\alpha}_t})x_0+(\frac{\sqrt{1-\bar{\alpha}_{t-1}-\sigma^2}}{\sqrt{1-\bar{\alpha}_t}})x_t + \sigma \epsilon, \ \epsilon \sim \mathcal{N}(0,\boldsymbol{I}) \\
  x_{t-1} &= \sqrt{\bar{\alpha}_{t-1}}x_0 - \sqrt{1-\bar{\alpha}_{t-1}-\sigma^2} \frac {x_t - \sqrt{\bar{\alpha}_t}x_0}{\sqrt{1-\bar{\alpha}_t}} + \sigma \epsilon, \ \epsilon \sim \mathcal{N}(0,\boldsymbol{I}) \\
  \end{align}
  $$

• 由加噪过程中关系，用 \(x_t\) 表示 \(x_0\) 有（详情见DDPM推导）：
  $$
  \begin{align}
  x_0 = \frac{x_t - \sqrt{1-\bar{\alpha}_t} \epsilon_t}{\sqrt{\bar{\alpha}_t} } \\
  \epsilon_t = \frac{x_t - \sqrt{\bar{\alpha}_t}x_0}{\sqrt{1-\bar{\alpha}_t}}
  \end{align}
  $$

• 将上述结果带入上一步的结论可得：
  $$ x_{t-1} = \sqrt{\bar{\alpha}_{t-1}}\frac{x_t - \sqrt{1-\bar{\alpha}_t} \epsilon_t}{\sqrt{\bar{\alpha}_t} } - \sqrt{1-\bar{\alpha}_{t-1}-\sigma^2} \epsilon_t + \sigma \epsilon, \ \epsilon \sim \mathcal{N}(0,\boldsymbol{I}) $$

  • 其中 \(\epsilon_t = \epsilon_\theta(x_t, t)\)，为了跟许多论文对齐，我们后续也可以写成 \(\epsilon_t = \epsilon_\theta(x_t, t) = \epsilon_\theta^{(t)}(x_t)\)

• 至此，我们还差 \(\sigma\) 的值没有确定：

  • 考虑上式可以写成：
    $$
    q_\sigma(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)
    = \mathcal{N}(\mathbf{x}_{t-1}; \sqrt{\bar{\alpha}_{t-1}} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \epsilon^{(t)}_\theta(\mathbf{x}_t), \sigma_t^2 \boldsymbol{I})
    $$
  • 且 \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\boldsymbol{\mu}}(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t \boldsymbol{I})\)
  • 于是有：
    $$ \tilde{\beta}_t = \sigma_t^2 = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t $$
  • 实际实验时，可以改写为： \(\sigma_t^2 = \eta’ \cdot \tilde{\beta}_t\) 或直接使用 \(\sigma_t^2 = \eta \cdot \beta_t\)，详情见论文实验部分

• 推导过程中没有一定要求 \(x_{t-1}\) 是 \(x_t\) 的上一步，所以可以用 \(x_s\) 替换 \(x_{t-1}\)：
  $$q_{\sigma, s < t}(\mathbf{x}_s \vert \mathbf{x}_t, \mathbf{x}_0)
  = \mathcal{N}(\mathbf{x}_s; \sqrt{\bar{\alpha}_s} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_s - \sigma_t^2} \epsilon^{(t)}_\theta(\mathbf{x}_t), \sigma_t^2 \boldsymbol{I})$$

• 最后，我们可以得到推导结果：

  
  • 当采样方差 \(\sigma\) 满足一定条件时，上面的式子会满足马尔可夫过程，即等价于DDPM（注：DDIM采样公式中， \(x_t\) 前面的系数展开以后和DDPM是是一样的）

• 图示跳步采样（生成）的原理：

  

---

训练和推理

DDPM的训练和推理

DDIM的训练和推理

• 训练过程与DDPM基本一致，但DDIM只需要采样固定间隔的步数即可

  • 如果已经有训练好的DDPM，可以直接用，因为DDPM的训练时间步包含了DDIM的训练时间步

• 推理过程

  

• 推理时，一般会设置 \(\sigma=0\)，即DDIM是确定性的，这是DDIM中区别于DDPM的很大的点

---

实验结果

• 实验设置
• 结果展示
• 结果分析
• 从图中可以得出结论
  • \(\sigma\) 越小（ \(\eta\) 越小，方差越小），即方差越小，效果越好，DDIM最好（DDIM对应 \(\eta=0\) 且 \(\sigma=0\) ）
  • 当 \(T=1000\) 时（或者 \(T\) 非常大时），DDPM效果最好（DDPM对应 \(\eta=1\) 且 \(\sigma = \hat{\sigma}\) ）
  • 小节：当采样步数少时（即间隔大时），使用DDIM效果更好，DDPM效果非常差；当采样步数很大时，DDPM效果微微好于DDIM

---

代码亲测

• 各种 \(\alpha,\beta\) 的定义技巧：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14

  num_steps = 100 betas = torch.linspace(-6,6,num_steps) betas = torch.sigmoid(betas)*(0.5e-2 - 1e-5)+1e-5 # beta逐步递增 alphas = 1-betas print("alphas: %s" % alphas) alphas_prod = torch.cumprod(alphas,0) # 连乘 alphas_bar = alphas_prod alphas_prod_p = torch.cat([torch.tensor([1]).float(),alphas_prod[:-1]],0) # previous连乘 alphas_bar_sqrt = torch.sqrt(alphas_bar) one_minus_alphas_bar_log = torch.log(1 - alphas_bar) one_minus_alphas_bar_sqrt = torch.sqrt(1 - alphas_bar) # 模型定义：model(x, t) # 采样方式：torch.randn_like(x)

• 实现细节(为了清晰表达，对原始采样公式有所修改)：
  $$
  x_s = \sqrt{\bar{\alpha}_s}\left(\frac{x_k-\sqrt{1-\bar{\alpha}_k}\epsilon_{\theta}(x_k,k)}{\sqrt{\bar{\alpha}_k}}\right) + \sqrt{1-\bar{\alpha}_s-a_1\sigma_k^2}\epsilon_{\theta}(x_k,k) + a_2\sigma_k \epsilon
  $$

  • 其中： \(\sigma_k^2 = \beta_t\)
  • 注意： \(a_1,a_2\) 是新加的，拆开 \(a_1,a_2\) 的原因是实验发现两者可以设置不同值，且有以下现象：
    • \(a_2=0,a_1=1.0\) 时，此时表示不采样，整个生成过程中没有添加随机值（除了初始样本为随机值外），不影响样本的生成质量，相对有随机值生成效果甚至更好
    • \(a_1=0\) 时，无论 \(a_2\) 值为多少，生成的样本均是类似乱码的图
    • \(a_1>0.5\) 时，无论 \(a_2\) 值是否为0，生成的样本均不错（ \(a_1\) 的值不能太小，否则效果会不好）

• 亲测实验结果与论文有偏差的原因分析:

  • 如果采样步数较少，效果也不好，但当采样间隔为2时，即跳一步采样，效果还可以（不如间隔为1）
    • 采样步数越多，效果越好（与原始论文结果一样）
  • 为什么本人实现的DDIM采样步数不能太少？（跳步10步时效果较差，与原始论文结果不一致）
    • DDIM可能对模型要求很高，本人尝试环境中模型过于简单？训练样本过少？
  • 为什么 \(a_1=0\) 时，效果非常差？
    • 待解答

---

DDIM对比DDPM

• DDIM训练流程与DDPM完全相同，只是推理(采样)过程不同
• DDIM主要解决DDPM采样慢的问题
  • DDPM有符合马尔可夫假设，需要一步步采样，效率慢
  • DDIM没有马尔可夫假设，可以跳步生成图片，且可以不采样（标准的DDIM就是不采样的，论文中，噪音的方差越小，得到的效果越好）
• DDIM中Implicit名字的来源是什么？
  • Implicit的含义是表示“隐式的”，原论文的DDIM就是特指 \(\sigma_t=0\) 的情形，意思这是一个隐式的概率模型，因为跟其他选择所不同的是，此时从给定的 \(\boldsymbol{x}_T = \boldsymbol{z}\) 出发，得到的生成结果 \(\boldsymbol{x}_0\) 是不带随机性的生成扩散模型漫谈（四）：DDIM = 高观点DDPM，科学空间
• 可以推导：在DDIM的结果中，如果方差 \(\sigma_t\) 取值满足一定条件时，跨度为1的DDIM采样过程会变成DDPM

---

一些问题和解答

• DDPM采样时不能去掉噪音，为什么DDIM可以？
  • 回答：因为DDIM采样中，噪音的方差 \(\sigma\) 是通过实验发现效果比较好的
  • 具体原因？
• 为什么DDPM和DDIM训练逻辑基本一致，但DDPM推断必须遵循马尔可夫性，而DDIM不需要？
  • 回答：
    • 训练时：DDIM和DDPM训练过程都遵循马尔可夫过程。DDIM可以按照一定间隔采样时间步，但实际上也是经过在满足马尔可夫过程的情况下推导出来的，DDPM和DDIM的训练采样公式都是因为方差可以累加实现跳跃采样的
    • 推断时：因为DDPM的采样公式是在满足马尔可夫过程情况下推导出来的， 而DDIM的采样公式是在非马尔可夫过程情况下推导出来的，所以使用DDPM采样公式时，不能跳步；使用DDIM采样公式时（注意：实际上DDIM不采样，直接确定性生成），可以跳步

---

附录：其他快速推导方式

• 参考自：What are Diffusion Models?
  $$
  \begin{aligned}
  \mathbf{x}_{t-1}
  &= \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1}}\boldsymbol{\epsilon}_{t-1} & \\
  &= \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \boldsymbol{\epsilon}_t + \sigma_t\boldsymbol{\epsilon} & \\
  &= \sqrt{\bar{\alpha}_{t-1}} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \epsilon^{(t)}_\theta(\mathbf{x}_t) + \sigma_t\boldsymbol{\epsilon} \\
  q_\sigma(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)
  &= \mathcal{N}(\mathbf{x}_{t-1}; \sqrt{\bar{\alpha}_{t-1}} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \epsilon^{(t)}_\theta(\mathbf{x}_t), \sigma_t^2 \boldsymbol{I})
  \end{aligned}
  $$

---

附录：DDIM和ODE的关系

• 常微分方程（Ordinary Differential Equation，ODE）典型的形式表达如下：
  $$ dy = f(x,y) dx $$
• 由之前的推导已经有：
  $$\mathbf{x}_{t-1} = \sqrt{\bar{\alpha}_{t-1}} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \epsilon^{(t)}_\theta(\mathbf{x}_t) + \sigma_t\boldsymbol{\epsilon}$$
• 此时令 \(\sigma_t = 0\)，可得：
  $$
  \begin{align}
  \mathbf{x}_{t-1} = \sqrt{\bar{\alpha}_{t-1}} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_{t-1}} \epsilon^{(t)}_\theta(\mathbf{x}_t) \\
  \end{align}
  $$
• 经过变换有：
  $$
  \begin{align}
  \frac{\mathbf{x}_{t-1}}{\sqrt{\bar{\alpha}_{t-1}}} = \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \frac{\sqrt{1 - \bar{\alpha}_{t-1}}}{\sqrt{\bar{\alpha}_{t-1}}} \epsilon^{(t)}_\theta(\mathbf{x}_t) \\
  \frac{\mathbf{x}_{t-1}}{\sqrt{\bar{\alpha}_{t-1}}} = \frac{\mathbf{x}_t}{\sqrt{\bar{\alpha}_t}} - \frac{\sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} + \frac{\sqrt{1 - \bar{\alpha}_{t-1}}}{\sqrt{\bar{\alpha}_{t-1}}} \epsilon^{(t)}_\theta(\mathbf{x}_t) \\
  \frac{\mathbf{x}_{t-1}}{\sqrt{\bar{\alpha}_{t-1}}} = \frac{\mathbf{x}_t}{\sqrt{\bar{\alpha}_t}} + \Big(\frac{\sqrt{1 - \bar{\alpha}_{t-1}}}{\sqrt{\bar{\alpha}_{t-1}}} - \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\bar{\alpha}_t}}\Big) \epsilon^{(t)}_\theta(\mathbf{x}_t) \\
  \end{align}
  $$
• 当 \(T\) 足够大时，相邻距离 \(t-1\) 可以用 \(t-\Delta t\) 表示，于是有：
  $$
  \begin{align}
  \frac{\mathbf{x}_{t-\Delta t}}{\sqrt{\bar{\alpha}_{t-\Delta t}}} = \frac{\mathbf{x}_t}{\sqrt{\bar{\alpha}_t}} + \Big(\frac{\sqrt{1 - \bar{\alpha}_{t-\Delta t}}}{\sqrt{\bar{\alpha}_{t-\Delta t}}} - \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\bar{\alpha}_t}}\Big) \epsilon^{(t)}_\theta(\mathbf{x}_t) \\
  \end{align}
  $$
• 进一步作变量替换 \(\sigma = \frac{\sqrt{1-\bar{\alpha}}}{\sqrt{\bar{\alpha}}}\) 和 \(\bar{\mathbf{x}} = \frac{\mathbf{x}}{\sqrt{\bar{\alpha}}}\)，则有：
  $$
  \begin{align}
  \bar{\mathbf{x}}_{t-\Delta t} = \bar{\mathbf{x}}_{t} + \Big(\sigma_{t-\Delta t} - \sigma_{t}\Big) \epsilon^{(t)}_\theta(\mathbf{x}_t) \\
  \end{align}
  $$
• 进一步变换有：
  $$
  \begin{align}
  \bar{\mathbf{x}}_{t} - \bar{\mathbf{x}}_{t-\Delta t} = \Big(\sigma_{t} - \sigma_{t-\Delta t}\Big) \epsilon^{(t)}_\theta(\mathbf{x}_t) \\
  \end{align}
  $$
• 写成微分形式有：
  $$
  \begin{align}
  d \bar{\mathbf{x}}_{t} = \epsilon^{(t)}_\theta(\mathbf{x}_t) d\sigma_t \\
  \end{align}
  $$
• 进一步将 \(\epsilon^{(t)}_\theta(\mathbf{x}_t)\) 中的 \(\mathbf{x}_t\) 替换为 \(\bar{\mathbf{x}_t}\)：
  $$
  \begin{align}
  \bar{\alpha} &= \frac{1}{\sigma_t^2 + 1} \\
  \mathbf{x}_t &= \bar{\mathbf{x}} \sqrt{\bar{\alpha}} = \frac{\bar{\mathbf{x}}_t}{\sqrt{\sigma_t^2 + 1}}
  \end{align}$$
• 最终我们可以得到微分方程如下：
  $$
  \begin{align}
  d \bar{\mathbf{x}}_{t} = \epsilon^{(t)}_\theta\Big(\frac{\bar{\mathbf{x}}_t}{\sqrt{\sigma_t^2 + 1}}\Big) d\sigma_t \\
  \end{align}
  $$
• 表达成时间的函数形式有：
  $$
  \begin{align}
  d \bar{\mathbf{x}}(t) = \epsilon^{(t)}_\theta\Big(\frac{\bar{\mathbf{x}}(t)}{\sqrt{(\sigma(t))^2 + 1}}\Big) d\sigma(t) \\
  \end{align}
  $$
• 所以，在给定初始状态为 \(x_T \sim \mathcal{N}(0,\boldsymbol{I})\) 的情况下，求解 \(x_0\) 的过程 \(\mathbf{x}_{t-1} = \sqrt{\bar{\alpha}_{t-1}} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_{t-1}} \epsilon^{(t)}_\theta(\mathbf{x}_t)\) 可以等价于利用欧拉方法迭代求解常微分方程 \(d \bar{\mathbf{x}}(t) = \epsilon^{(t)}_\theta\Big(\frac{\bar{\mathbf{x}}(t)}{\sqrt{(\sigma(t))^2 + 1}}\Big) d\sigma(t)\) 离散点的过程，以下描述来自生成扩散模型漫谈（四）：DDIM = 高观点DDPM：

  而DDPM或者DDIM的迭代过程，对应于该常微分方程的欧拉方法。众所周知欧拉法的效率相对来说是最慢的，如果要想加速求解，可以用Heun方法、R-K方法等。也就是说，将生成过程等同于求解常微分方程后，可以借助常微分方程的数值解法，为生成过程的加速提供更丰富多样的手段

---

附录：欧拉方法

• 欧拉方法是求解常微分方程（Ordinary Differential Equation，ODE）数值解的一种基础且直观的方法。其核心思想是利用给定点处的斜率来预测下一个点的位置。这种方法特别适用于那些难以找到解析解或解析解过于复杂的问题
• （回顾）常微分长程典型的形式表达如下：
  $$ dy = f(x,y) dx $$

欧拉方法的形式及推导

• 为了理解欧拉方法的工作原理，我们可以从泰勒展开的角度出发。假设我们有一个初值问题：
  $$
  \begin{cases}
  y’(t) = f(t, y(t)), & t \in [a, b] \\
  y(a) = y_0 & \text{; initial }
  \end{cases}
  $$
• 对于任意一点 \(t_n\)，如果我们想要求得 \(t_{n+1} = t_n + h\) 处的 \(y_{n+1}\)，可以通过对 \(y(t)\) 在 \(t_n\) 点进行一阶泰勒展开近似得到：
  $$
  y(t_{n+1}) \approx y(t_n) + hy’(t_n) = y(t_n) + hf(t_n, y(t_n))
  $$
• 这里 \(h\) 是步长，即相邻两个时间点之间的距离。因此，欧拉方法的迭代公式可以写作（下面迭代公式的等号是赋值的意思）下面的形式：
  $$
  y_{n+1} = y_n + hf(t_n, y_n), \quad n=0, 1, 2, \ldots
  $$
  • 这便是向前欧拉公式的定义。通过这种方式，我们可以递归地计算出后续各点的函数值
• 同理，欧拉公式也可以按照后项定义如下：
  $$
  y_{n} = y_{n+1} - hf(t_n, y_n), \quad n=0, 1, 2, \ldots
  $$

欧拉方法求解函数离散点示例

• 使用欧拉方法解决实际问题时，首先需要确定的是微分方程的形式以及初始条件。然后选择合适的步长 \(h\) 并应用上述迭代公式逐步计算未来的值。例如，考虑一个简单的例子：
  $$
  y’(t) = \lambda y(t), \quad y(0) = 1
  $$
• 如果我们设定 \(\lambda = -1\) 和 \(h = 0.1\)，那么根据欧拉公式，我们可以写出如下代码片段来实现这个过程：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  import numpy as np def euler_method(f, y0, t): """Simple implementation of Euler's method.""" y = np.zeros_like(t) y[0] = y0 for i in range(1, len(t)): y[i] = y[i-1] + (t[i] - t[i-1]) * f(t[i-1], y[i-1]) return y def f(t, y): return -1 * y t = np.linspace(0, 5, 51) # 50 steps from 0 to 5 y0 = 1 # Initial condition # Solve using Euler's method y_euler = euler_method(f, y0, t) print(y_euler[-1]) # Print the last computed value

其他扩展概念

• 与常微分方程对应的还有一个概念是随机微分方程（Stochastic Differential Equation，SDE），随机微分方程在常微分方程的基础上加入了随机过程作为其中一项，本质也是一个随机过程，示例如下：
  $$\mathrm{d}X_t = \mu(t, X_t)\mathrm{d}t + \sigma(t, X_t)\mathrm{d}W_t$$
• 这里， \(\mu(t, X_t)\) 被称为漂移系数，表示系统的确定性变化趋势；而 \(\sigma(t, X_t)\) 是扩散系数，反映了系统受随机波动的影响程度； \(W_t\) 用来模拟不可预测的随机扰动。

文本介绍IDDPM（Improved Denoising Diffusion Probabilistic Models）的理论介绍

• 参考链接：
  • 原始论文：Improved Denoising Diffusion Probabilistic Models, ICML 2021
  • 源码：Improved Denoising Diffusion Probabilistic Models

---

整体说明

• IDDPM提供了对DDPM的一些优化，许多内容是基于DDPM原始论文Denoising Diffusion Probabilistic Models, NeurIPS 2020的

---

可学习的逆向过程方差 \(\Sigma_\theta(x_t,t)\)

• DDPM中逆向过程方差 \(\Sigma_\theta(x_t,t)\) 设置：
  • DDPM中的方差设置为固定值： \(\mathbf{\Sigma}_\theta(\mathbf{x}_t, t) = \sigma^2_t \boldsymbol{I}\)，其中 \(\sigma_t = \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t\)，或者直接使用 \(\sigma_t = \beta_t\) （实验上，两种设置效果差不多）
  • DDPM中作者通过实验发现，如果将 \(\Sigma_\theta(x_t,t)\) 设置为可学习的，模型会不容易收敛，采样效果会变差
• IDDPM中的改进：
  • 采用一种插值的方法表示 \(\Sigma_\theta(x_t,t)\)： \(\mathbf{\Sigma}_\theta(\mathbf{x}_t, t) = \exp(\mathbf{v} \log \beta_t + (1-\mathbf{v}) \log \tilde{\beta}_t)\)
    • 其中 \(\mathbf{v} \) 是可以学习的向量（注意 \(\beta_t\) 是标量，而 \(\mathbf{v} \) 是向量，DDPM中的协方差矩阵是 \(\sigma^2_t \boldsymbol{I}\) 中实际上假设了各个维度的方差都相同，都是 \(\sigma^2_t\)，IDDPM中则通过引入 \(\mathbf{v} \) 来实现不同维度方差不同），注意协方差 \(\Sigma_\theta(x_t,t)\) 在这里是对角矩阵，即假设不同变量之间相互独立
      • \(\mathbf{v}_{\theta}(x_t, t)\) 是从模型输出出来的（详情见improved_diffusion源码:模型定义和improved_diffusion源码:向量使用），的维度是与 \(\mathbf{x}_t\) 相同的
    • 能够这样插值的一个思路是因为 \(\sigma_t\) 的取值范围在 \([\beta_t, \tilde{\beta}_t]\) （详情见Improved Denoising Diffusion Probabilistic Models (IDDPM) - 妖妖的文章 - 知乎）。
    • 虽然理论上应该对 \(\mathbf{v} \) 进行限制，但是IDDPM实验中也没有对 \(\mathbf{v} \) 进行限制，实验结果证明了即使不限制 \(\mathbf{v} \) 范围，也不会超过插值范围
  • 传统DDPM的损失函数 \(L_{\text{simple}}\) 不依赖 \(\Sigma_\theta(x_t,t)\)，所以优化传统的损失函数不能更新到 \(\mathbf{v} \)，为了更新到 \(\mathbf{v} \)，IDDPM在传统损失函数上增加了一项，最终IDDPM损失函数为：
    $$ L_\text{hybrid} = L_\text{simple} + \lambda L_\text{VLB} $$
    • 其中 \(L_\text{VLB} = L_T + L_{T-1} + \dots + L_0\)，详情见：Denoising Diffusion Probabilistic Models, NeurIPS 2020
    • 设置 \(\lambda=0.001\)，用于防止 \(L_\text{VLB}\) 过于强势，影响 \(L_\text{simple}\) 的学习
    • 设置 \(L_\text{VLB}\) 对 \(\mu_\theta(x_t, t)\) 是停止梯度回传的（stop_gradient），确保 \(\mu_\theta(x_t, t)\) 还是主要由 \(L_\text{simple}\) 学习
    • 问题： \(L_\text{VLB}\) 对 \(\mu_\theta(x_t, t)\) 都停止梯度回传了，还需要设置 \(\lambda=0.001\) 这么小吗？

---

Improving the Noise Schedule

优化前向过程中的方差 \(\{\beta_t\}_{t=1}^T\) 安排

• DDPM中前向过程的方差安排设置:
  • DDPM实现中是使用线性的固定值，也就是说扩散过程 \(q\) 都是不可学习的参数。具体来说，DDPM实验时设置了 \(T=1000\) 该固定值使用的是 \([10^{-4}, 0.02]\) 之间的线性的固定值（即 \(\beta_1 = 10^{-4} \ \text{to} \ \beta_T = 0.02\) ）
  • 在DDPM中曾经提到方差 \(\beta_t\) 是可以通过重参数法学习的，也可以设置为固定值
• IDDPM中的改进：
  • IDDPM将 \(\beta_t\) 从线性机制改成余弦机制，具体来说，通过 \(\bar{\alpha}_t\) 反推 \(\beta_t\)
    $$ \beta_t = \text{clip}(1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}, 0.999) \quad\bar{\alpha}_t = \frac{f(t)}{f(0)}\quad\text{where }f(t)=\cos\Big(\frac{t/T+s}{1+s}\cdot\frac{\pi}{2}\Big)^2 $$
    • 其中 \(s\) 是一个非常小的数字，用于防止 \(t\) 太小的时候 \(\beta_t\) 取值太小，实验中，取 \(s=0.008\)
  • 改进前后的取值比较

---

基于重要性采样训练 \(L_\text{VLB}\)

• DDPM中，训练时时间步时均匀采样得到的，但是不同的时间步 \(L_\text{VLB}\) 的Loss值不同，所以使用重要性采样来使得Loss大的地方得到更多的训练，详情见Improved Denoising Diffusion Probabilistic Models (IDDPM) - 妖妖的文章 - 知乎：
  $$ L_\text{VLB} = \mathbb{E}_{t \sim p_t}\Big[\frac{L_t}{p_t}\Big] \quad \text{where } p_t \propto \sqrt{\mathbb{E}[L_t^2]} \ \text{and} \ \sum_t p_t = 1$$
  • Loss不均匀示意图：
  • 改进后的效果示意图：
  • 这里的改进不常用，文章写的有点晦涩难懂，需要时再来好好理解一下

---

加速采样

• 与DDIM相似

文本介绍DDPM（Denoising Diffusion Probabilistic Models）的理论介绍

• 参考链接：
  • 原始论文：Denoising Diffusion Probabilistic Models, NeurIPS 2020
  • What are Diffusion Models?：Lilian Weng的博客
  • 54、Probabilistic Diffusion Model概率扩散模型理论与完整PyTorch代码详细解读
    • 视频中有部分小bug，评论区已修复
  • 一文解决你关于扩散模型ddpm的所有疑惑，回答了很多疑惑
    • 一个视频看懂扩散模型DDPM原理推导|AI绘画底层模型，

---

推导过程

这部分推导参考自由浅入深了解Diffusion Model - ewrfcas的文章 - 知乎和What are Diffusion Models?

Diffusion前向过程

前向过程的整体描述

• 给定真实图片 \(x_0 \sim q(x_0)\)，Diffusion前向过程通过 \(T\) 次对其添加高斯噪声，得到 \(x_T\)，第 \(t\) 次加噪后得到的样本为 \(x_t\)
• 加噪过程是增加一个服从高斯分布的误差，每一步中高斯分布方差的超参数是提前设定的 \(\{\beta_t \in (0,1)\}_{t=1}^T\)
• 前向过程由于每个时刻 \(t\) 只与 \(t-1\) 时刻有关，所以也可以看做马尔可夫过程
  $$
  \begin{align}
  q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t\boldsymbol{I}) \\
  q(x_{1:T}|x_0) = \prod_{t=1}^T q(x_t|x_{t-1}) \\
  \end{align}
  $$
• 实际实现中 \(\{\beta_t \in (0,1)\}_{t=1}^T\) 中的元素是递增的，即 \(\beta_1 < \beta_2 < \cdots < \beta_T\)，DDPM实验时设置了 \(T=1000\)，且 \(\beta_t\) 是 \([0.0001, 0.02]\) 之间的线性的固定值，即 \(\beta_1 = 0.0001 \ \text{to} \ \beta_T = 0.02\)
• 加噪过程中，随着加噪时间步骤 \(t\) 的增加， \(x_t\) 越来越接近纯随机噪声，且 \(T \rightarrow \infty\) 时， \(x_T\) 完全是噪声

可以用 \(x_0\) 和方差 \(\beta\) 来表示 \(x_t\)

• 即 \(\forall t, \ x_t = f(x_0, \{\beta_i\}_{i=1}^t)\) \(x_t\)
• 引入新变量 \(\alpha_t = 1- \beta_t\)，且 \(\bar{\alpha}_t = \prod_{i=1}^t\alpha_i\) （理解： \(\alpha_t\) 和 \(\bar{\alpha}_t\) 都随着扩散时间步逐步变小）
• 将 \(x_t\) 进行展开可得得到用 \(x_0\) 和方差 \(\beta\) 来表示 \(x_t\)：
  $$
  \begin{align}
  \mathbf{x}_t
  &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\mathbf{\epsilon}_{t-1} \quad \quad \quad \quad \quad \quad \quad \quad \text{ ;where } \mathbf{\epsilon}_{t-1}, \mathbf{\epsilon}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I}) \\
  &= \sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}\mathbf{x}_{t-2} + \sqrt{1 - \alpha_{t-1}}\mathbf{\epsilon}_{t-2}) + \sqrt{1 - \alpha_t}\mathbf{\epsilon}_{t-1} \\
  &= \sqrt{\alpha_t \alpha_{t-1}}\mathbf{x}_{t-2} + (\sqrt{\alpha_t(1 - \alpha_{t-1})}\mathbf{\epsilon}_{t-2} + \sqrt{1 - \alpha_t}\mathbf{\epsilon}_{t-1}) \\
  &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\mathbf{\epsilon}}_{t-2} \quad \quad \quad \quad \text{ ;where } \bar{\mathbf{\epsilon}}_{t-2} \text{ merges two Gaussians (*).} \\
  &\quad \vdots \\
  &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\mathbf{\epsilon} \\
  q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\boldsymbol{I})
  \end{align}
  $$
  • 推导中两个高斯分布的合并使用使用到： \(\mathcal{N}(\mu_1,\sigma_1^2\boldsymbol{I}) + \mathcal{N}(\mu_2,\sigma_2^2\boldsymbol{I}) \sim \mathcal{N}\Big((\mu_1+\mu_2),(\sigma_1^2+\sigma_2^2)\boldsymbol{I}\Big)\)
  • 显然，当 \(T \rightarrow \infty\) 时， \(x_T\) 完全是噪声，因为 \(\sqrt{\bar{\alpha}_T} \rightarrow 0,\ \sqrt{1-\bar{\alpha}_T} \rightarrow 1\)
  • Merge后的噪声 \(\epsilon\) 也是高斯噪声，且服从标准正态分布 \(\epsilon \sim \mathcal{N}(0,\boldsymbol{I})\)
• 同时，也可以用 \(x_t\) 和方差 \(\beta\) 来表示 \(x_0\)：
  $$ x_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(x_t - \sqrt{1-\bar{\alpha}_t}\epsilon) $$

• 问题：为什么前向过程的需要使用 \(\sqrt{1-\beta_t}x_{t-1}\) 来表示均值？
  • 回答：因为这样可以使得 \(x_T\) 的均值中不含有原始样本 \(x_0\) 的信息，也就是说，这样使得 \(x_T\) 接近噪声
  • 补充问题：使用其他小于0的数 \(k_t\) 替代 \(\sqrt{1-\beta_t}\) 吗？答案是可以的，但是使用 \(\sqrt{1-\beta_t}\) 是为了满足 \((\sqrt{1-\beta_t})^2+\beta_t = 1\) 这样的形式，方便后续的推导，如果不使用这样的形式，推导起来会更复杂些，详情见苏神的博客生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼

Diffusion逆向过程

• 符号定义 ：为了与其他文章常用习惯保持一致，论文在前向过程中使用 \(q(x_t|x_0)\)，逆向过程中 \(q(x_0|x_t)\)，需要按照区分前后下标大小来区分前向过程和后向过程

• 逆向过程的目标 ：逆向过程是前向过程的相反过程，其目标是从随机噪声 \(x_T \sim \mathcal{N}(0, \boldsymbol{I})\) 中一步步恢复得到原始样本 \(x_0\)

  • 思考 ：如果能够得到 \(q(x_{t-1}|x_t)\)，则可以一步步恢复出来原始样本 \(x_0\)
  • 注：可以证明，如果 \(q(x_t|x_{t-1})\) 是高斯分布且方差 \(\beta_t\) 足够小，那么 \(q(x_{t-1}|x_t)\) 也还是一个高斯分布【TODO: On the theory of stochastic processes, with particular reference to applications.?】

• 逆向过程的拟合 ：我们使用 \(p_\theta(x_{t-1}|x_t)\) 来拟合逆向分布，由于 \(p_\theta(x_{t-1}|x_t)\) 是高斯分布，所以可以拆解成建模均值 \(\mu_\theta(x_t, t)\) 和方差 \(\Sigma_\theta(x_t, t)\) 即可
  $$
  \begin{align}
  p_\theta(\mathbf{x}_{0:T}) &= q(\mathbf{x}_T) \prod^T_{t=1} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \\
  p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) &= \mathcal{N}(\mathbf{x}_{t-1}; \mathbf{\mu}_\theta(\mathbf{x}_t, t), \mathbf{\Sigma}_\theta(\mathbf{x}_t, t))
  \end{align}
  $$

• 难题 ：实际上，我们是无法直接得到 \(q(x_{t-1}|x_t)\) 的（理解：不知道 \(x_0\) 的情况下，噪声并不知道要朝着什么方向去生成 \(x_0\) ）

• 如果 \(x_0\) 已知，结合 \(x_t \sim q(x_t|x_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\boldsymbol{I})\)，则可以通过贝叶斯公式求得 \(q(x_{t-1}|x_t,x_0)\)：
  $$q(x_{t-1}|x_t,x_0) = \mathcal{N}(x_{t-1};\tilde{\mu}(x_t, x_0), \tilde{\beta}_t\boldsymbol{I})$$

  • \(\tilde{\mu}(x_t,x_0)\) 是均值，是 \(x_t,x_0\) 的函数，而 \(\tilde{\beta}_t\) 是方差，与 \(x_t,x_0\) 无关，仅与时间片有关

• 目标是均值和方差 ：至此，我们的目标是求得 \(\tilde{\mu}(x_t, x_0)\) 和 \(\tilde{\beta}_t\)，为了这个目标，我们首先将 \(q(x_{t-1}|x_t,x_0)\) 展开：
  $$
  \begin{aligned}
  q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)
  &= \frac{q(x_{t-1},x_t,x_0)}{q(x_t, x_0)} \\
  &= \frac{q(x_t|x_{t-1},x_0) \cdot q(x_{t-1},x_0)}{q(x_t, x_0)} \\
  &= q(x_t|x_{t-1},x_0) \frac{q(x_{t-1}|x_0) \cdot q(x_0)}{q(x_t| x_0) \cdot q(x_0)} \\
  &= q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \\
  &= q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \quad \quad \quad \quad \text{；马尔可夫性}\\
  &\propto \exp \Big(-\frac{1}{2} \big(\frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\
  &= \exp \Big(-\frac{1}{2} \big(\frac{\mathbf{x}_t^2 - 2\sqrt{\alpha_t} \mathbf{x}_t \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \alpha_t} \color{red}{\mathbf{x}_{t-1}^2} }{\beta_t} + \frac{ \color{red}{\mathbf{x}_{t-1}^2} \color{black}{- 2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0} \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \bar{\alpha}_{t-1} \mathbf{x}_0^2} }{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\
  &= \exp\Big( -\frac{1}{2} \big( \color{red}{(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})} \mathbf{x}_{t-1}^2 - \color{blue}{(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)} \mathbf{x}_{t-1} \color{black} + C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big)
  \end{aligned}
  $$

  • 其中 \(C(\mathbf{x}_t, \mathbf{x}_0)\) 是与 \(x_{t-1}\) 无关的常数，在指数上，可以变成乘法，所以能忽略

• 转换为高斯分布 ，上面的结果本质是在用等式表达一个高斯分布来，回顾高斯分布的概率密度函数的指数部分是 \(\exp\Big( -\frac{(x-\mu)^2}{2\sigma^2} \Big) = \exp\Big( -\frac{1}{2}(\frac{1}{\sigma^2}x^2 - \frac{2\mu}{\sigma^2}x + \frac{\mu^2}{\sigma^2})\Big) \)，上面的推导结果可以进一步得到 \(\tilde{\mu}(x_t, x_0)\) 和 \(\tilde{\beta}_t\)：

  • 方差的推导：
    $$
    \begin{aligned}
    \frac{1}{\sigma^2} &= \frac{1}{\tilde{\beta}_t} = (\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) \\
    \color{red}{\tilde{\beta}_t} &= 1/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})
    = 1/(\frac{\alpha_t - \bar{\alpha}_t + \beta_t}{\beta_t(1 - \bar{\alpha}_{t-1})})
    = \color{red}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} ;
    \end{aligned}
    $$
  • 均值的推导：
    $$
    \begin{aligned}
    \frac{2\mu}{\sigma^2} &= \frac{2\tilde{\mu}(x_t,x_0)}{\tilde{\beta}_t} = \frac{2\sqrt{\alpha_t}} {\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \\
    \color{red}{\tilde{\boldsymbol{\mu}} (\mathbf{x}_t, \mathbf{x}_0)} &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) \\
    &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0) \color{red}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\
    &= \color{red}{\frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0} \\
    \end{aligned}
    $$

• 去掉结果中的\(\boldsymbol{x_0}\)，结合用 \(x_t\) 和方差 \(\beta\) 来表示 \(x_0\) 的公式 ： \(x_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(x_t - \sqrt{1-\bar{\alpha}_t}\epsilon) \) ，我们可以进一步可以将 \(\tilde{\mu}(x_t,x_0)\) 中的 \(x_0\) 替换为 \(x_t\)，得到 \( \tilde{\mu}(x_t,x_0) = \tilde{\mu}(x_t)\)：
  $$
  \begin{aligned}
  \color{red}{\tilde{\boldsymbol{\mu}}(x_t)}
  &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}) \\
  &= \color{red}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon} \Big)}
  \end{aligned}
  $$

  • 其中 \(\epsilon\) 是使用深度学习预测得到的混合噪声，表示 \(x_0 \rightarrow x_t\) 过程中添加的 \(t\) 个噪声的Merge结果（仍然是一个高斯噪声且服从标准正太分布），可以表示为 \(\epsilon_\theta(x_t, t)\)

• 最终得到逆向推导结果 ：我们已经求得了 \(\tilde{\mu}(x_t, x_0) = \tilde{\mu}(x_t)\) 和 \(\tilde{\beta}_t\)，即可根据下面的方式采样：
  $$q(x_{t-1}|x_t,x_0) = \mathcal{N}(x_{t-1};\tilde{\mu}(x_t, x_0), \tilde{\beta}_t\boldsymbol{I})$$

  • 将 \(x_0\) 替换为 \(x_t\) 后得到：
    $$q(x_{t-1}|x_t,x_0) = q(x_{t-1}|x_t) = \mathcal{N}(x_{t-1};\tilde{\mu}(x_t), \tilde{\beta}_t\boldsymbol{I})$$
  • 进一步地带入详细表征形式有（其中 \(z_t \sim N(0,\boldsymbol{I})\)）：
    $$
    \begin{align}
    x_{t-1} &= \tilde{\mu}(x_t) + \sqrt{\tilde{\beta}_t} z_t \\
    \color{red}{x_{t-1}} &= \color{red}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(x_t, t) \Big)} + \color{blue}{\sqrt{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t}} \cdot z_t
    \end{align}
    $$

• 对推导结果进行简化 ：采样（生成）过程可以总结为如下的流程（下面的流程表示已知 \(x_t\) 和时间步 \(t\) 时采样 \(x_{t-1}\) 的步骤）：

  • 计算均值 \(\tilde{\boldsymbol{\mu}}(x_t, t)\)：将 \(x_t\) 和时间步 \(t\) 输入神经网络预测 \(x_0 \rightarrow x_t\) 过程中添加的 \(t\) 个噪声的Merge结果 \(\epsilon_\theta(x_t, t)\)，接着将 \(\epsilon_\theta(x_t, t)\) 带入 \(\tilde{\boldsymbol{\mu}}(x_t) = \color{red}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(x_t, t) \Big)}\) 得到均值
  • 计算方差 \(\boldsymbol{\Sigma}_\theta(x_t,t)\)：在DDPM中，使用固定值作为方差 \(\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) = \sigma^2_t \boldsymbol{I}\)，此时所有 \(\mathbf{x}_t\) 中所有维度的变量共享同一个方差 ，同时在实践中，使用 \(\color{blue}{\sigma_t^2 = \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t \approx \beta_t} \)，即简单实现下可以取 \(\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) = \beta_t \boldsymbol{I}\)
    • 其他有些文章会使用可学习的神经网络表示 \(\Sigma_\theta(x_t, t)\)，此时不同维度的变量方差可能不同，但是一般仍然假设不同维度变量独立 ，即始终保持 \(\Sigma_\theta(x_t, t)\) 是对角矩阵，比如[GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models]和[Improved Denoising Diffusion Probabilistic Models, ICML 2021]等
  • 采样 \(x_{t-1} \sim \mathcal{N}(\tilde{\boldsymbol{\mu}}(x_t, t), \Sigma_\theta(x_t,t))\)

• 一些符号说明 ：在数学中，常用 \(\sigma\) 表示标准差、 \(\Sigma\) 表示方差或协方差矩阵（多变量情况下，如果变量间独立，则有 \(\Sigma\) 矩阵上每个元素是 \(\sigma_i^2\) ），Diffusion相关的文章也沿用了这种表示。同时，由于特定的设定在Diffusion中， \(\beta\) 常常等于方差，所以常常也会用 \(\beta\) 直接表达方差含义

Diffusion模型训练目标函数推导

• 之前已经知道了，我们Diffusion模型的目标是通过训练学习 \(\mu_\theta(x_t,t)\) 和 \(\Sigma_\theta(x_t,t)\)，这个模型训练时的目标是在已知数据集中数据出现的概率最大（极大似然法），即优化在分布 \(x_0 \sim q(x_0)\) 下 \(p_\theta(x_0)\) 的交叉熵：
  $$ L(\theta) = \mathbb{E}_{x_0 \sim q(x_0)}[-\log p_\theta(x_0)] = \mathbb{E}_{q(x_0)}[-\log p_\theta(x_0)] $$

• 其中(下面的推导使用了Jenson不等式)：
  $$
  \begin{aligned}
  - \log p_\theta(\mathbf{x}_0)
  &\leq - \log p_\theta(\mathbf{x}_0) + D_\text{KL}(q(\mathbf{x}_{1:T}\vert\mathbf{x}_0) | p_\theta(\mathbf{x}_{1:T}\vert\mathbf{x}_0) ) \\
  &= -\log p_\theta(\mathbf{x}_0) + \mathbb{E}_{\mathbf{x}_{1:T}\sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T}) / p_\theta(\mathbf{x}_0)} \Big] \\
  &= -\log p_\theta(\mathbf{x}_0) + \mathbb{E}_{\mathbf{x}_{1:T}\sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} + \log p_\theta(\mathbf{x}_0) \Big] \\
  &= \mathbb{E}_{\mathbf{x}_{1:T}\sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\
  \text{Let }L_\text{VLB}
  &= \mathbb{E}_{\mathbf{x}_{0:T} \sim q(\mathbf{x}_{0:T})} \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \geq - \mathbb{E}_{x_0 \sim q(\mathbf{x}_0)} [\log p_\theta(\mathbf{x}_0)]
  \end{aligned}
  $$

• 交叉熵损失函数(下面的推导使用到了重积分中的Fubini定理和Jenson不等式)
  $$
  \begin{aligned}
  L_\text{CE}
  &= - \mathbb{E}_{x_0 \sim q(\mathbf{x}_0)} \Big[\log p_\theta(\mathbf{x}_0) \Big]\\
  &= - \mathbb{E}_{x_0 \sim q(\mathbf{x}_0)} \Big[\log \Big( \int p_\theta(\mathbf{x}_{0:T}) d\mathbf{x}_{1:T} \Big)\Big] \\
  &= - \mathbb{E}_{x_0 \sim q(\mathbf{x}_0)} \Big[\log \Big( \int q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} d\mathbf{x}_{1:T} \Big)\Big] \\
  &= - \mathbb{E}_{x_0 \sim q(\mathbf{x}_0)} \Big[\log \Big( \mathbb{E}_{\mathbf{x}_{1:T} \sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} \Big)\Big] \\
  &\leq - \mathbb{E}_{x_0 \sim q(\mathbf{x}_0)} \Big[\mathbb{E}_{\mathbf{x}_{1:T} \sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)}\Big[ \log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})}\Big]\Big] \\
  &= - \mathbb{E}_{\mathbf{x}_{0:T} \sim q(\mathbf{x}_{0:T})} \Big[\log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} \Big]\\
  &= \mathbb{E}_{\mathbf{x}_{0:T} \sim q(\mathbf{x}_{0:T})}\Big[\log \frac{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})}{p_\theta(\mathbf{x}_{0:T})} \Big] = L_\text{VLB}
  \end{aligned}
  $$

• 进一步推导：
  $$
  \begin{aligned}
  L_\text{VLB}
  &= \mathbb{E}_{\mathbf{x}_{0:T} \sim q(\mathbf{x}_{0:T})} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\
  &= \mathbb{E}_{\mathbf{x}_{0:T} \sim q(\mathbf{x}_{0:T})} \Big[ \log\frac{\prod_{t=1}^T q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{ p_\theta(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) } \Big] \\
  &= \mathbb{E}_{\mathbf{x}_{0:T} \sim q(\mathbf{x}_{0:T})} \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=1}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} \Big] \\
  &= \mathbb{E}_{\mathbf{x}_{0:T} \sim q(\mathbf{x}_{0:T})} \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\
  &= \mathbb{E}_{\mathbf{x}_{0:T} \sim q(\mathbf{x}_{0:T})} \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \Big( \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)}\cdot \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1}\vert\mathbf{x}_0)} \Big) + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\
  &= \mathbb{E}_{\mathbf{x}_{0:T} \sim q(\mathbf{x}_{0:T})} \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1} \vert \mathbf{x}_0)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\
  &= \mathbb{E}_{\mathbf{x}_{0:T} \sim q(\mathbf{x}_{0:T})} \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{q(\mathbf{x}_1 \vert \mathbf{x}_0)} + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\
  &= \mathbb{E}_{\mathbf{x}_{0:T} \sim q(\mathbf{x}_{0:T})} \Big[ \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_T)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \Big] \\
  &= \mathbb{E}_{\mathbf{x}_{0:T} \sim q(\mathbf{x}_{0:T})} [\underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} + \sum_{t=2}^T \underbrace{D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))}_{L_{t-1}} \underbrace{- \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} ]
  \end{aligned}
  $$

• 我们可以进一步将上面的表达式简化写为下面的形式：
  $$
  \begin{aligned}
  L_\text{VLB} &= L_T + L_{T-1} + \dots + L_0 \\
  \text{where } L_T &= D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T)) \\
  L_t &= D_\text{KL}(q(\mathbf{x}_t \vert \mathbf{x}_{t+1}, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_t \vert\mathbf{x}_{t+1})) \text{ for }1 \leq t \leq T-1 \\
  L_0 &= - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)
  \end{aligned}
  $$

  • \(L_T\)：由于前向过程 \(q(x_T|x_0)\) 没有可学习参数，且 \(x_T\) 是纯粹的高斯噪声，所以优化参数 \(\theta\) 时 \(L_T\) 可以当做常数忽略
  • \(L_0\)： \(\mathcal{N}(\mathbf{x}_0; \boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \boldsymbol{\Sigma}_\theta(\mathbf{x}_1, 1))\) , \(L_0\) 是扩散模型训练过程中变分下界的一部分，定义为 \(-\log p_{\theta}(x_0 | x_1)\) ，与反向过程的最后一项有关。实际上，虽然 \( L_0 \) 确实与模型参数 \( \theta \) 有关，但在论文的推导和训练过程中，作者通过离散解码器的设计和简化训练目标，将 \( L_0 \) 视为一个相对不重要的常数项。这种做法简化了训练过程，并且实验结果表明，这种简化并不会显著影响模型的生成质量。更多讨论见附录
  • \(L_t\)： \(L_t\) 可以看做是两个高斯分布的KL散度， \(q(x_{t-1}|x_t,x_0) = \mathcal{N}(x_{t-1};\tilde{\mathbf{\mu}}(x_t,x_0),\tilde{\beta}_t\boldsymbol{I})\) 和 \(p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))\)，其中 \(\tilde{\boldsymbol{\mu}}(x_t,t) = \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)\)
    • 参照 \(\tilde{\boldsymbol{\mu}}(x_t,t) = \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)\) 的定义，可以将 \(\mu_\theta(x_t,t)\) 定义为如下形式（也就是说，只需要学习噪声 \(\epsilon_\theta(x_t, t)\) 即可）：
      $$
      \begin{aligned}
      \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) &= \color{red}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big)} \\
      \text{Thus }\mathbf{x}_{t-1} &= \mathcal{N}(\mathbf{x}_{t-1}; \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))
      \end{aligned}
      $$
    • 使得KL散度最小，可以直接使得两者的均值和方差尽可能相等，其中均值目标可以进一步优化为（DDPM中方差直接使用固定值）
      $$\begin{aligned}
      L_t
      &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 | \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) |^2_2} | \color{blue}{\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - \color{green}{\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} |^2 \Big] \\
      &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 |\boldsymbol{\Sigma}_\theta |^2_2} | \color{blue}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} - \color{green}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) \Big)} |^2 \Big] \\
      &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) | \boldsymbol{\Sigma}_\theta |^2_2} |\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)|^2 \Big] \\
      &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) | \boldsymbol{\Sigma}_\theta |^2_2} |\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)|^2 \Big]
      \end{aligned}
      $$

• 最终训练时的目标函数可以表示为：
  $$
  \begin{aligned}
  L_t^\text{simple}
  &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)|^2 \Big] \\
  &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)|^2 \Big]
  \end{aligned}
  $$

• 如果考虑 \(L_T\) 和 \(L_0\)，则有：
  $$ L_\text{simple} = L_t^\text{simple} + C $$

---

训练和推理

• 训练和推理伪代码：
• 训练过程：
  • 从数据集中挑选出一个样本 \(x_0 \sim q(x_0)\)
  • 均匀采样，随机选择一个扩散时间步 \(t \sim \text{Uniform}(\{ 1,\cdots,T \})\) （扩散时间步的总长度是提前设置的）
  • 从标准正态分布采样误差 \(\epsilon \sim \mathcal{N}(0, \boldsymbol{I})\)，注意这里的误差跟样本 \(x_0\) 维度相同
  • 使用梯度下降训练Diffusion的误差模型 \(\epsilon_\theta(x_t,t)\)： \(L(\theta) = \mathbb{E}_{t,x_0,\epsilon}[|\epsilon - \epsilon_\theta(\sqrt{\bar{\alpha}}x_0+\sqrt{1-\bar{\alpha}}\epsilon, t)|]^2 \)
• 采样过程：
  • 从标准正态分布采样加噪后的样本 \(x_T\)： \(x_T \sim \mathcal{N}(0, \boldsymbol{I})\)，注：可以这样采样的原因是实际上加噪后的样本可以看做是已经变成了随机值了
  • 逆向过程包含 \(T\) 步， \(t = T,\cdots,1\)：
    • 如果 \(t > 0\)，则采样 \(z \sim \mathcal{N}(0, \boldsymbol{I})\)，否则 \(z = 0\)
    • 恢复 \(x_{t-1}\)： \(x_{t-1} = \frac{1}{\sqrt{\alpha_t}}\Big( x_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta(x_t, t) \Big) + \sigma_t z\)
      • 其中 \(\epsilon_\theta(x_t, t)\) 的含义是在预测从 \(x_0 \rightarrow x_t\) 的过程中加入的 \(t\) 个混合噪声， \(\sigma_t\) 是方差，DDPM中直接取近似值 \(\sigma_t = \beta_t\)
      • \(z\) 是为了添加生成图片的随机性加入的，与 \(\epsilon_\theta(x_t, t)\) 没有任何关系，如果在每一步中保持 \(z=0\)，对于相同的噪声 \(x_T\)，生成的图片 \(x_0\) 将是固定的，且图片质量往往不好

---

一些问题和思考

为什么学习的是 Merge噪声 \(\epsilon_{\theta}(x_t, t)\)

• 训练时预估的 \(\epsilon_{\theta}(x_t, t)\) 的含义是什么？学到的是从 \(x_0\) 到 \(x_t\) 加的噪声，还是从 \(x_{t-1}\) 到 \(x_t\) 加的噪声？
  • 回答：是从 \(x_0\) 到 \(x_t\) 加的噪声，本质是多个噪声Merge以后得结果(还是高斯噪声)，因为从训练流程的公式就可以看出， \(\epsilon_{\theta}(x_t, t)\) 中的 \(x_t=\sqrt{\bar{\alpha}_{t}}x_0 + \sqrt{1-\bar{\alpha}_{t}}\epsilon\)，其中 \(\epsilon\) 就是从 \(x_0\) 到 \(x_t\) 加的噪声，而损失函数的目标就是让 \(\epsilon_{\theta}\rightarrow\epsilon\)
• 在推理时，既然 \(\epsilon_{\theta}(x_t, t)\) 是从 \(x_0\) 到 \(x_t\) 加的累计噪声，为什么可以使用 \(\epsilon_{\theta}(x_t, t)\) 来完成从 \(x_{t}\) 到 \(x_{t-1}\) 的过程？
  • 回答：因为这里从 \(x_{t}\) 到 \(x_{t-1}\) 的本质也是分两步的，第一步是从 \(x_{t}\) 到 \(x_{0}\) (由 \(x_t=\sqrt{\bar{\alpha}_{t}}x_0 + \sqrt{1-\bar{\alpha}_{t}}\epsilon_{\theta}\) 反推即可得到 \(x_0 = \frac{1}{\sqrt{\bar{\alpha}_{t}}}(x_t-\sqrt{1-\bar{\alpha}_{t}}\epsilon_{\theta})\)，注意这里得到的 \(x_0\) 可能质量不太好，不能直接作为最终结果)；第二步是已知从 \(x_{t}\) 和 \(x_{0}\) 后，可以得到 \(x_{t-1}\) 的分布 \(q(x_{t-1}|x_t,x_0)\)，进一步对分布进行采样，就能得到一个 \(x_{t-1}\) 的实例。两步合并以后就是DDPM的采样伪代码中的公式

为什么不能一步到位得到 \(x_0\)?

• 补充一步到位的公式 ：\(x_0 = \frac{1}{\sqrt{\bar{\alpha}_{t}}}(x_t-\sqrt{1-\bar{\alpha}_{t}}\epsilon_{\theta})\)
• 回答1（训练损失函数视角）：可以，但效果不好。从训练的损失函数看，这样做可以，但是效果不一定好（实践来看效果不好，效果不好的原因是一步到位难度较高？），此时相当于简单的把Diffusion模型作为一个单步去噪器了，甚至不需要采样过程
• 回答2（一种直观理解）：为什么效果不好？ ：模型直接学习 \(q(x_0|x_t)\) 是困难的，即误差 \(\epsilon_\theta(x_t,t)\) 虽然可以用于直接恢复 \(x_0\)，但是不太精确（相当于是“粗略预估”），为了得到较好的 \(x_0\)，在预估误差 \(\epsilon_\theta(x_t,t)\) 后，我们需要进行“修正”，所以，逐步采样的过程就是逐步“粗略预估”，逐步“修正”的过程（“预估”+“修正”的视角来自生成扩散模型漫谈（十）：统一扩散模型（理论篇））
  • 更进一步的理解：可以将多步采样看做是一个ensemble的过程，可以提升效果
• 回答3（一种理论视角的讨论，待商榷）：不可以。在整个推导过程中，我们有 \(q(x_t|x_0) = \mathcal{N}(x_t;\sqrt{\bar{\alpha}_{t}}x_0, (1-\bar{\alpha}_{t})\boldsymbol{I})\) （这里是通过高斯过程的叠加实现的，整个过程遵循马尔可夫过程），所以才有公式 \(x_t=\sqrt{\bar{\alpha}_{t}}x_0 + \sqrt{1-\bar{\alpha}_{t}}\epsilon\)，这不代表我们可以通过 \(x_0 = \frac{1}{\sqrt{\bar{\alpha}_{t}}}(x_t-\sqrt{1-\bar{\alpha}_{t}}\epsilon_{\theta})\) 来得到 \(x_0\)，因为此时的 \(x_0\) 是无法一步导出的（即 \(q(x_0|x_t)\) 是未知的，未知的原因是不遵循马尔可夫过程，训练时使用的损失函数是在满足马尔可夫过程假设的情况下推导出来的，推理时也不能违背该假设），必须遵循马尔可夫过程（即 \(q(x_{t-1}|x_t)\) ）
  • \(q(x_t|x_0)\) 已知但是 \(q(x_0|x_t)\) 未知的原因是因为采样是不可逆的
  • 既然 \(x_0 = \frac{1}{\sqrt{\bar{\alpha}_{t}}}(x_t-\sqrt{1-\bar{\alpha}_{t}}\epsilon_{\theta})\) 不准确（不遵循马尔可夫过程），为什么按照 \(x_0 = \frac{1}{\sqrt{\bar{\alpha}_{t}}}(x_t-\sqrt{1-\bar{\alpha}_{t}}\epsilon_{\theta})\) 的到的 \(x_0\) 可以作为中间变量来帮助生成 \(x_{t-1}\) 呢？公式推导带入的时候使用了这个式子，本质上也说明推导过程不遵循马尔可夫过程了吧？（一种理解是中间使用的 \(x_0 = \frac{1}{\sqrt{\bar{\alpha}_{t}}}(x_t-\sqrt{1-\bar{\alpha}_{t}}\epsilon_{\theta})\) 本质是 \(x_0\) 的一个不精确近似，使用这个来作为条件引导生成可行【引导需要的准确度不高】，但是直接用来作为最终的 \(x_0\) 则效果不太行）

DDPM可以不加入噪声吗？

• 实践1 ：不可以，图片生成质量会特别差
• 实践2 ：不加入噪声，没有随机性，生成图片的多样性受损
• 理解1 ：可以类比LLM采样不能使用纯贪心策略（argmax），因为这样可能生成的是重复的无意义文本，噪音反而能一定程度跳开重复
• 理解2 ：类似于随机梯度下降（SGD）中的噪声帮助跳出局部最优解，扩散模型的噪声让生成过程有机会“绕开”累积的预测偏差
• 理解3 ：扩散模型的生成是一个多步迭代过程，如果每一步仅依赖预测的均值（不加噪声），前一步的误差会逐步累积，最终偏离真实数据分布。通过加入噪声，模型能够在后续步骤中修正误差，提升生成稳定性
• 理解4 ：扩散模型的推导基于随机微分方程（SDE）或变分推断。在反向过程中，噪声项的引入是数学推导的自然结果。例如，在基于分数的生成模型（Score-Based Models）中，采样过程需要引入朗之万动力学（Langevin Dynamics）的随机性，对应扩散模型中的噪声添加
• 其他参考：一个视频看懂DDIM凭什么加速采样|扩散模型相关【这个观点无法解释DDIM为什么可以直接生成，DDIM（DDIM生成时不加入噪声）生成1000步效果也不会太差】

为什么模型不直接拟合 \(x_t\rightarrow x_{t-1}\) 的噪音？

• DDPM现状 ：目前DDPM训练时模拟拟合的是从 \(x_0\) 到 \(x_t\) 加的噪声，本质是多个噪声Merge以后得结果(还是高斯噪声)
• 原因（效率视角） ：如果直接一步步采样，会导致没张图片都要采样T次（T一般很大）才能训练，训练效率较低，都2023年了，我不允许你还不懂DDPM！ - Defa Zhu的文章 - 知乎 中是这个观点
• 原因（理论视角） ：因为逆向过程实际上是 \(q(x_{t-1}|x_t,x_0)\)，而 \(q(x_{t-1}|x_t)\) 是在近似拟合 \(q(x_{t-1}|x_t,x_0)\)，噪音应该是与 \(x_0\) 相关的，只是在推导过程中用 \(x_t\) 和 Merge噪声 把 \(x_0\) 替换了
  • 特别注意： \(q(x_{t-1}|x_t)\) 本身可以被预估误差，但是本质上是无法直接求解的（一个采样的逆过程，没有梯度，也无法求解），只有 \(q(x_{t-1}|x_t,x_0)\) 可以求解
• 如果不考虑效率，直接拟合 \(x_t\rightarrow x_{t-1}\) 的噪音是否可行呢？
  • 直观感觉是可行的，但是预估结构可能无法保障，此时相当于假设了 \(q(x_{t-1}|x_t)\) 是一个高斯分布，是否还能继续在采样过程中加入随机有待实践考证
• 参考：为什么DDPM反向去噪时不直接用q(x_t|x_{t-1})从x_t反推回x_{t-1}？ - gpenai的回答 - 知乎 是一个知乎回答，不一定准确，但可以参考看一下

---

附录：为什么\(L_0\)可以舍弃？

• 结论：不论是否丢弃 \(L_0\)，最终求出来的损失函数形式是一样的，都是 MSE 的形式；
  • 一方面：通过其他推导方式（生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼或 DDPM 推导视频），可以做到不丢弃任何项得到相同的最终结果
  • 另一方面：最小化 \(\mathcal{N}(\mathbf{x}_0; \boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \boldsymbol{\Sigma}_\theta(\mathbf{x}_1, 1))\) 等价于最小化 \(\vert x_0 - \boldsymbol{\mu}_\theta(\mathbf{x}_1, 1)\vert^2\)，进一步推导后可得 \(t=1\) 时刻的最终形式和以上化简后的最优目标函数其实是相同的
• 在论文中，损失函数的变分下界（VLB）被分解为多个项，其中 \( L_0 \) 是最后一项，表示在给定 \(\mathbf{x}_1\) 的情况下，模型对原始数据 \( \mathbf{x}_0 \) 的重建误差。具体来说，\( L_0 \) 的形式如下：
  $$
  L_0 = -\log p_{\theta}(\mathbf{x}_0 | \mathbf{x}_1)
  $$
  • 进一步可表达为：\(\mathcal{N}(\mathbf{x}_0; \boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \boldsymbol{\Sigma}_\theta(\mathbf{x}_1, 1))\)
• 在论文的推导中，有一些误区
  • 问题一 ：作者提到 \( L_0 \) 可以被视为常数，这实际上是一种简化，不是严谨的表达，因为 \( L_0 \) 显然与模型参数 \( \theta \) 有关，直接说是化简不合适
  • 问题二（问题一的扩展）：虽然 \( L_0 \) 确实与模型参数 \( \theta \) 有关，但在论文的推导和训练过程中，作者认为自己通过离散解码器的设计和简化训练目标，将 \( L_0 \) 视为一个相对不重要的常数项，这种做法简化了训练过程，并且实验结果表明，这种简化并不会显著影响模型的生成质量
    • 实际上作者使用的损失函数已经是最优的了，且训练会采样到 \(t=1\) 的样本，所以不存在丢弃或者简化的操作
  • 问题三 ：作者声称自己丢弃了 \(p_\theta(x_0|x_1)\) 的损失学习，如果真的是丢弃，是否会导致采样到最后一步的时候模型不知道应该如何从 \(x_1\) 生成 \(x_0\)？实验证明是不会的（从理论上来看也不会，因为作者其实没丢弃 \(p_\theta(x_0|x_1)\) 的损失学习），具体原因是：
    • 从目标函数看：简化后的训练的目标函数为：
      $$
      L_\text{simple} = \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)|^2 \Big]
      $$
      • 当训练时遇到 \(t=1\) 时（训练采样时 \(t\in \{1,2,\cdots,T\}\)，所以可以遇到这种样本），这里这个损失函数的目标是建模误差就是 \(\epsilon_\theta(x_1, 1)\)，即已知 \(x_1\) 时，自然可以恢复 \(x_0\)
    • 考虑到最小化 \(\mathcal{N}(\mathbf{x}_0; \boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \boldsymbol{\Sigma}_\theta(\mathbf{x}_1, 1))\) 等价于让 \(\vert x_0 - \boldsymbol{\mu}_\theta(\mathbf{x}_1, 1)\vert^2\) 最小化，进一步推导后得到 \(t=1\) 时刻的最终形式和以上化简后的最优目标函数其实是相同的（这在苏神的博客 生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼 中给出了证明）
• 苏神的博客中，从另一个视角推导(不一定很严谨)，得到了简化的目标函数，详情参考：生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼，这说明 \(L_0\) 的简化是合理的
• DDPM 推导视频 也提供了另一种推导方式，在不丢弃任何一项的情况下，最终目标函数是一样的

---

附录：其他推导过程参考

• 参考链接：
  • 原始论文：GPipe: Easy Scaling with Micro-Batch Pipeline Parallelism, 2019, Google

Paper Summary

• 已有结论：模型越大，模型效果上限越高
• 模型容量超过单个加速器（GPU 或 TPU）的内存限制时，需要开发特殊算法和工程设计（这些解决方案通常是针对特定架构设计的，难以迁移）
• 论文提出了 GPipe
  • 是一个 流水线并行（Pipeline Parallelism）库
  • 能够扩展任何可表示为层序列的网络
  • 高效且任务无关的模型并行
• GPipe 将不同的层子序列分配到不同的加速器上流水执行
  • 可以灵活高效地将多种网络扩展至超大规模
• GPipe 采用了一种新颖的批次分割流水线算法 ，在模型跨多个加速器分区时实现了近乎线性的加速比
• 论文通过训练两种不同任务的大规模神经网络来展示 GPipe 的优势，这些任务具有截然不同的网络架构：
  • (i) 图像分类（Image Classification） ：
    • 训练了一个包含 5.57 亿参数的 AmoebaNet 模型，在 ImageNet-2012 上达到了 84.4% 的 top-1 准确率；
  • (ii) 多语言神经机器翻译（Multilingual Neural Machine Translation） ：
    • 在涵盖 100 多种语言的语料库上训练了一个包含 60 亿参数、128 层的 Transformer 模型，其质量优于所有双语模型
    • 实验表明，该模型在 100 种语言对上的性能优于单独训练的 3.5 亿参数双语 Transformer Big 模型 (2017)
• 评价：
  • Google 出品，必属精品，GPipe 已成为各种框架的加速选项

---

Introduction and Discussion

• 近年来深度学习的巨大进步部分归功于神经网络有效容量扩展方法的发展
• 这一趋势在图像分类任务中最为明显，例如 ImageNet 的准确率随着模型容量的增加而提升（图 0(a)）
  • 类似现象也出现在自然语言处理领域（图 0(b)），简单的浅层句子表示模型 (2017; 2018) 被更深、更大的模型 (2018; 2019) 超越
• 更大的模型为多个领域带来了显著的性能提升，但扩展神经网络也带来了实际的挑战
  • 硬件限制（包括加速器（GPU 或 TPU）的内存和通信带宽）迫使用户将大模型分割为多个分区，并将不同分区分配到不同的加速器上
  • 高效的模型并行算法设计和实现极为困难，通常需要用户在扩展容量、灵活性（或对特定任务和架构的适应性）以及训练效率之间做出艰难抉择
  • 大多数高效的模型并行算法都是针对特定架构和任务的
  • 随着深度学习应用的不断增加，对可靠且灵活的基础设施的需求日益增长
• 为解决这些挑战，论文提出了 GPipe，一个灵活的库，支持高效训练大规模神经网络
  • GPipe 通过将模型分配到不同加速器上并支持在每个加速器上重新计算中间结果 (2000; 2016)，能够突破单个加速器的内存限制 ，扩展任意深度神经网络架构
  • GPipe 中，每个模型可以表示为层序列，连续的层组可以划分为单元（cell），每个单元分配到单独的加速器上
• 基于这种分区设置，论文提出了一种新颖的批次分割流水线并行算法
  • 首先，论文将训练样本的小批次（mini-batch）分割为更小的微批次（micro-batch） ，然后在单元上流水执行每组微批次
  • 训练采用同步小批次梯度下降，梯度在所有微批次中累积，并在小批次结束时统一更新
  • GPipe 的梯度更新与分区数量无关，保证了训练的一致性 ，使研究人员能够通过部署更多加速器轻松训练更大的模型
  • GPipe 还可以与数据并行结合，进一步扩展训练规模

---

GPipe 库（The GPipe Library）

• 论文现在描述 GPipe 的接口和主要设计特性
• 该开源库是在 Lingvo（2019）框架下实现的
• GPipe的核心设计特性具有通用性，可以为其他框架（2017; 2018; 2019）实现

Interface

• 任何深度神经网络都可以定义为一个由 \(L\) 个层组成的序列
  • 每个层 \(L_i\) 由一个前向计算函数 \(f_i\) 和对应的参数集 \(w_i\) 组成
• GPipe 允许用户指定一个可选的计算成本估计函数 \(c_i\)
• 在给定分区数量 \(K\) 的情况下，可以将 \(L\) 个层的序列划分为 \(K\) 个复合层或单元（cell）
  • 设复合单元 \(p_k\) 由层 \(i\) 到层 \(j\) 之间的连续层组成
  • 与复合单元 \(p_k\) 对应的参数集等价于 \(w_i, w_{i+1}, \ldots, w_j\) 的并集，其前向函数为 \(F_k = f_j \circ \ldots \circ f_{i+1} \circ f_i\)
  • 对应的反向传播函数 \(B_k\) 可以通过自动符号微分从 \(F_k\) 计算得到
  • 成本估计器 \(C_k\) 设置为 \(\Sigma^{j}_{l=i}c_l\)
• GPipe 的接口非常简单直观，要求用户指定：
  • (i) 模型分区数量 \(K\)
  • (ii) 微批次（micro-batch）数量 \(M\)
  • (iii) 定义模型的 \(L\) 个层的序列和定义
• 具体示例请参见补充材料

Algorithm

• 当用户通过模型参数 \(w_i\) 、前向计算函数 \(f_i\) 和成本估计函数 \(c_i\) 定义网络中层的序列后，GPipe 将网络划分为 \(K\) 个单元，并将第 \(k\) 个单元放置在第 \(k\) 个加速器上
• 在分区边界处自动插入通信原语，以允许相邻分区之间的数据传输
• 分区算法最小化所有单元的估计成本方差，以通过同步所有分区的计算时间来最大化流水线的效率
• 在前向传播期间：
  • GPipe 首先将每个大小为 \(N\) 的小批次（mini-batch）划分为 \(M\) 个相等的微批次
  • 这些微批次通过 \(K\) 个加速器进行流水线处理
• 在反向传播期间：
  • 每个微批次的梯度基于前向传播使用的相同模型参数计算
  • 在每个小批次结束时，所有 \(M\) 个微批次的梯度被累积并应用于更新所有加速器上的模型参数
• 这一系列操作如图1(c)所示
• 如果网络中使用了 Batch Normalization（BatchNorm），则训练期间输入的充分统计量（Sufficient Statistic）是在每个微批次上计算的 ，并在需要时在副本上计算（2017）
  • 论文还跟踪整个小批次上充分统计量的移动平均值，以用于评估
    • 注：充分统计量的介绍见附录
  • 理解：使用 GPipe 时，对 BatchNorm 不太友好，因为太小的微批次会导致训练时使用的均值和方差波动太大（注：BatchNorm 训练时始终使用的是当前微批次的统计值）

Performance Optimization

• 为了减少激活内存需求，GPipe 支持重计算（re-materialization）（2016）
  • 在前向计算期间，每个加速器仅存储分区边界处的输出激活
  • 在反向传播期间，第 \(k\) 个加速器重新计算复合前向函数 \(F_k\)
• 峰值激活内存需求减少到
  $$O(N + \frac{L}{K} \times \frac{N}{M})$$
  • 其中 \(\frac{N}{M}\) 是微批次大小
  • \(\frac{L}{K}\) 是每个分区的层数
• 如果不使用重计算和分区，内存需求将为
  $$ O(N \times L)$$
  • 因为计算梯度 \(b_i\) 需要上层梯度 \(b_{i+1}\) 和缓存的激活 \(f_i(x)\)
• 如图2(c)所示，分区会在每个加速器上引入一些空闲时间，论文称之为气泡（bubble）开销
  • 这种气泡时间在微步骤数量 \(M\) 上平均为 \(O(\frac{K-1}{M+K-1})\)
  • 在论文的实验中，当 \(M \geq 4 \times K\) 时，气泡开销可以忽略不计
  • 这部分也是因为反向传播期间的重计算可以更早调度，而无需等待来自上层的梯度
• GPipe 还引入了低通信开销，因为论文只需在加速器之间传递分区边界处的激活张量
  • 即使在没有高速互连的加速器上，也可以实现高效的扩展性能
• 图2(c)假设分区是均匀平衡的
  • 但不同层的内存需求和计算浮点操作往往非常不平衡
  • 在这种情况下，不完美的分区算法可能导致负载不平衡
  • 更好的分区算法可能会在论文的启发式方法基础上进一步提升性能

---

Performance Analyses

• 通过两种模型架构评估 GPipe 的性能（研究它们的可扩展性、效率和通信成本）：
  • AmoebaNet（2018）卷积模型
  • Transformer（2017）Sequence2Sequence模型
• 论文预计重计算和流水线并行都会有益于内存利用，从而使训练巨型模型成为可能
• 在表1中，报告了在合理大的输入大小下 GPipe 可以支持的最大模型大小
• 对于 AmoebaNet 模型 ，在每个加速器内存为 8GB 的 Cloud TPUv2 上运行实验
  • 使用固定的输入图像大小 \(224 \times 224\) 和小批次大小 128
  • 在没有 GPipe 的情况下，受设备内存限制，单个加速器最多可以训练 8200万 参数的 AmoebaNet，
  • 利用反向传播中的重计算和批次分割：
    • GPipe 将中间激活内存需求从 6.26GB 减少到 3.46GB，从而在单个加速器上支持 3.18亿 参数的模型
  • 通过模型并行
    • 能够在 8 个加速器上将 AmoebaNet 扩展到 18亿 参数 ，比不使用 GPipe 时多25倍
    • 在这种情况下，最大模型大小没有完全线性扩展，因为 AmoebaNet 中不同层的模型参数分布不平衡
• 对于 Transformer 模型 ，每个加速器核心内存为 16GB 的 Cloud TPUv3 训练
  • 模型配置如下：
    • 使用固定的词汇大小 32k
    • 序列长度 1024 和批次大小 32
    • 每个Transformer层的模型维度为2048
    • 前馈隐藏维度为 8192
    • 注意力头数量为 32
  • 注：论文通过改变层数量来扩展模型
  • 重计算允许在单个加速器上训练比原来大 2.7 倍的模型
  • 通过 128 个分区，GPipe 可以将 Transformer 扩展到 839亿 参数，比单个加速器上可能的规模增加 298 倍
  • 与 AmoebaNet 不同，Transformer 的最大模型大小随加速器数量线性扩展，因为每个层具有相同数量的参数和输入大小
• 表2给出了 GPipe 的训练效率效率（主要评估 AmoebaNet-D 和 Transformer-48 的标准化训练吞吐量）
  • 使用不同数量的分区和不同数量的微批次
  • 每个分区分配给一个独立的加速器
• 一些结论：
  • 当微批次数量 \(M\) 至少是分区数量 \(K\) 的 4 倍时，气泡开销几乎可以忽略不计
    • 换算一下可以知道，就以 4 倍为例
    • 气泡量是（注：气泡总数仅与 \(K\) 有关，与 \(M\) 无关）
      $$ 6 + 6 = 12 $$
    • 总的小区域数量是
      $$ (16+3) \times 4 = 76$$
    • 气泡率约为：
      $$12 / 76 \approx 15.8%$$
    • 且微批次数量 \(M\) 越大，气泡开销越小，因为气泡总数是固定的
  • 对于 Transformer 模型，当分区数量增加 4 倍时，速度提升 3.5 倍
  • 由于计算在 Transformer 层之间均匀分布，训练吞吐量几乎随设备数量线性扩展
  • 由于计算在 AmoebaNet模型上分布不平衡，训练吞吐量仅实现了次线性加速
  • 当 微批次数量 \(M\) 相对较小时，气泡开销不再可以忽略
  • 当 微批次数量 \(M\) 为 1 时，实际上没有流水线并行
    • 论文观察到训练吞吐量相对恒定，无论使用多少加速器，这表明任何时候只有一个设备在主动计算
• 为了测量 GPipe 的通信开销影响，论文在没有 NVLink 的多个 NVIDIA P100 GPU 的单个主机上运行实验
  • 跨 GPU 的数据传输必须通过 PCI-E 进行相对较慢的设备到主机和主机到设备传输
  • 微批次数量固定为 32
• 如表3所示，当分区数量从 2 增加到 8 时：
  • AmoebaNet-D 的速度提升 2.7 倍
  • 对于 24 层 Transformer，速度提升为 3.3 倍
• 与配备高速互连的 TPU 上观察到的情况类似，存在类似的线性加速
  • 由于 GPipe 仅在分区边界传输激活张量，设备之间的通信带宽不再是模型并行的瓶颈

---

Image Classification

• 作为概念验证，本节首先使用 GPipe 扩展 AmoebaNet
  • 增加了 AmoebaNet 的通道数，并将输入图像尺寸扩展到 \(480 \times 480\)
  • 在 ImageNet 2012 数据集上训练了这个包含 5.57 亿参数的 AmoebaNet-B 模型，使用的超参数与 (2018) 中描述的相同
  • 该网络被划分为 4 个分区
  • 这一单一模型在单次裁剪下实现了 84.4% 的 top-1 准确率和 97% 的 top-5 验证准确率
• 论文进一步通过迁移学习 (2022, 2023) 证明了巨型卷积网络在其他图像数据集上的有效性
  • 使用预训练的 ImageNet 模型在多个目标数据集上进行微调，这些数据集涵盖了一般分类到细粒度分类任务
  • 将最后一个 softmax 分类层的输出单元数更改为目标数据集的类别数，并随机初始化新的 softmax 层
  • 其余所有层均从 ImageNet 预训练中初始化
  • 训练期间，输入网络的图像被调整为 \(480 \times 480\) ，并随机水平翻转，同时使用 cutout (2017) 进行数据增强
  • 训练超参数与 ImageNet 训练时相同（详细的训练设置见补充材料）
• 在表4 中，论文报告了每个目标数据集 5 次微调运行的平均单次裁剪测试准确率
  • 巨型模型在所有目标数据集上均取得了具有竞争力的结果
    • CIFAR-10 的错误率降至 1%
    • CIFAR-100 的错误率降至 8.7%
  • 这些结果验证了 Kornblith 等人 (2018) 的发现，即更好的 ImageNet 模型具有更好的迁移能力

---

Massively Multilingual Machine Translation

• 本节还通过扩展用于 NLP 的模型来展示 GPipe 的灵活性，论文在一个大规模多语言 NMT 任务上继续 GPipe 的实验
  • 因为并行语料库的丰富性，神经机器翻译（NMT）已成为评估 NLP 架构的基准任务 (2017, 2018, 2019)
• 论文使用包含 102 种语言与英语的平行文档语料库，总计 250 亿训练样本，每种语言的样本量从 \(10^4\) 到 \(10^9\) 不等 (2019)
  • 该数据集通过涵盖从低资源到高资源的多样化语言，为可扩展性实验提供了真实的测试环境
  • 论文首次在机器翻译中证明，足够大的 NMT 模型可以同时学习超过 100 种语言对的映射，并且在所有语言上均优于双语模型性能
  • 这进一步凸显了高效且灵活的模型并行工具的重要性
• 论文的比较基于在该语料库上所有语言对训练的单一 Transformer (2017) 的性能
  • 通过两个维度扩展架构以强调 GPipe 的灵活性：
    • (i) 通过增加模型的层数扩展深度；
    • (ii) 通过增加前馈层的隐藏维度以及多头注意力层中的注意力头数（和注意力通道数）扩展宽度
    • 类似于 Shazeer 等人 (2018) 的方法（数据集、基线、训练配置和优化超参数的详细描述见补充材料）
• 论文从标准的 4 亿参数 Transformer Big 模型 \(T(6,8192,16)\) （如 Chen 等人 (2018) 所述）开始，词汇量为 64k
  • 注：论文用 \(T(L,\ H,\ A)\) 表示 \(T(层数，FFN隐藏层维度，Attention头数)\)
• 在图3 中，论文将其性能与下列模型进行了比较：
  • 13 亿参数的深层模型 \(T(24,\ 8192,\ 16)\)
  • 13 亿参数的宽模型 \(T(12,\ 16384,\ 32)\)
  • 30 亿参数模型 \(T(32,\ 16384,\ 32)\)
  • 60 亿参数模型 \(T(64,\ 16384,\ 32)\)
• 所有模型均使用基于温度的多语言 BERT (2018) 采样方法在所有语言对上同时训练
  • \(T(12,\ 16384,\ 32)\) 、 \(T(24,\ 8192,\ 32)\) 、 \(T(32,\ 16384,\ 32)\) 和 \(T(64,\ 16384,\ 32)\) 分别被划分为 2、4、8 和 16 个加速器
• 从图3 中可以看出
  • 将模型容量从 4 亿参数增加到 13 亿参数显著提升了所有语言的性能
  • 将模型从 13 亿参数扩展到 60 亿参数进一步提升了性能，尤其是高资源语言
    • 注：从 13 亿到 30 亿和 60 亿参数时出现了收益递减现象
• 以下是论文基于这些大规模实验的一些实证发现：
  • 深度-宽度权衡（Depth-Width Trade-off） ：
    • 论文研究了多语言设置中深度与宽度的权衡，并比较了 13 亿参数的宽模型 \(T(12,\ 16384,\ 32)\) 和 13 亿参数的深模型 \(T(24,\ 8192,\ 16)\) 的性能
    • 虽然这两种模型在高资源语言（图3 左侧）上的质量非常接近，但深层模型在低资源语言上的表现显著优于宽模型 ，这表明增加模型深度可能更有利于泛化
      • 注：图3是 100+ 种语言按照数据量从左到右逆序排序的结果（high-resource language 代表数据量较大的语言），每个点代表当前语言上的表现？
    • 与 4 亿参数模型相比，13 亿参数深层模型在低资源语言（图3 右侧）上的质量提升几乎与高资源语言相当，这表明增加深度可能会增强对低资源任务的迁移效果
  • 深层模型的训练挑战（Trainability Challenges with Deep Models） ：
    • 深度增加了神经网络的表示能力，但也使优化问题复杂化
    • 在大规模实验中，论文遇到了由尖锐激活（sharp activations）且是正峰度的（positive kurtosis）和数据集噪声组合引起的严重训练问题
    • 在训练几千步后，模型预测会变得极其尖锐且对噪声敏感，这通常会导致非有限或大梯度，最终破坏学习进程
    • 为了解决这些问题，论文采用了两种方法：
      • (i) 遵循 Zhang 等人 (2019) 的方法，按层数比例缩小所有 Transformer 前馈层的初始化；
      • (ii) 当 logit 预测（softmax 预激活）的幅度超过特定值时，对其进行裁剪
      • 这两种方法的结合缓解了因模型深度扩展带来的训练不稳定性
  • 大批量训练（Large Batches） ：
    • 数据并行使用简单，是扩展神经网络训练的主导方法 (2016, 2017)
    • 论文通过显著增加标准 Transformer Big 训练的批量大小来测试大批量训练的极限
    • 从每批 26 万词开始，论文将有效批量增加到 400 万词，并观察高资源语言对（德语-英语）的验证损失和 BLEU 分数（其他语言对也观察到类似趋势）
      • 此处使用的优化参数与之前实验相同
      • 据论文所知，400 万词每批是文献中迄今为止用于训练 NMT 模型的最大批量 (2018)
    • 表5 显示，随着批量增加，两项指标均显著改善
    • 作者相信进一步增加批量可能会带来更多改进

---

Design Features and Trade-Offs

• 已有多种方法用于实现高效的大规模模型并行，但每种方法都有其特定的权衡，使其适用于特定硬件约束下的特定架构扩展
• 本节将重点讨论多种模型并行方法的设计选择与权衡，并比较它们与 GPipe 在灵活性、可扩展性以及不同硬件约束和架构变体下的效率
• 模型并行的核心思想是将网络划分为不同的计算单元，然后将这些单元分配到不同的设备上（2014; 2014; 2017; 2012）
  • 从概念上讲，这种方法支持将多种模型扩展至巨大规模
  • 但这些方法通常面临硬件利用率低和设备间通信瓶颈的问题
• 单程序多数据（Single Program Multiple Data, SPMD）和流水线并行被提出以应对这些挑战
  • Mesh-Tensorflow（2018）遵循 SPMD 范式
    • 将数据并行中使用的单指令多数据（Single Instruction Multiple Data, SIMD）方法扩展到其他张量维度
  • SPMD 允许将每个计算拆分到多个设备上，从而使用户能够将单个矩阵乘法（以及单个层的模型参数）的大小随加速器数量线性扩展
    • 但这也引入了设备间的高通信开销，因为需要大量类似 AllReduce 的操作来合并每个并行化矩阵乘法的输出
      • 限制了该方法在配备高速互联的加速器场景下的适用性
    • SPMD 限制了可高效扩展的操作类型，使其仅适用于特定网络架构和机器学习任务
      • 例如，在该范式下沿卷积层的通道维度拆分效率较低，因为通道实际上是全连接的，而沿空间维度拆分则需要复杂的技术来处理边缘区域（halo regions）
    • 尽管 SPMD 允许通过使每个操作更小来扩展模型深度，但它需要将每个层拆分到更多加速器上，这进一步增加了设备间的通信开销
• 其他方法尝试利用基于流水线并行的技术来扩展神经网络（1993; 2017），最近应用于神经网络训练的流水线并行迭代是 PipeDream（2018）
  • PipeDream 的目标是减少参数服务器（2014）的通信开销
  • PipeDream 通过流水线化前向传播的执行，并将其与反向传播交错，以最大化硬件利用率
  • 这种设计因异步反向更新引入的权重陈旧性（weight staleness）而受到影响
  • 为了避免权重陈旧性导致的优化问题，PipeDream 需要在每个加速器上维护多个版本化的模型参数副本以准确计算梯度更新 ，从而限制了用户扩展至更大模型的能力
• GPipe 引入了一种新型流水线并行技术
  • 在应用整个小批量（mini-batch）的同步梯度更新之前，对微批次（micro-batches）的执行进行流水线化
  • 论文的新型批拆分流水线并行算法与重计算（re-materialization）相结合，支持扩展到大量微批次
    • 这最小化了“气泡”（bubble）开销，同时无需异步梯度更新
  • GPipe 使用户能够将模型大小随加速器数量线性扩展
    • 与 SPMD 不同，流水线并行在扩展模型时引入的额外通信开销极少
  • 设备间通信仅在每个微批次的划分边界发生，且引入的通信开销可以忽略不计，这使得 GPipe 在缺乏高速设备互联的场景下仍然适用
• 待提升点：
  • GPipe 目前假设单个层可以适配单个加速器的内存限制
    • 注：突破这一限制的一种可行方法是：将单次矩阵乘法拆分为多个更小的矩阵运算，并依次分散到多个网络层中执行（注：即张量并行）
  • 微批次拆分需要复杂的策略来支持跨批次计算的层（例如，BatchNorm 在训练时使用微批次的统计量，但在评估时累积小批次的统计量）

---

Conclusion

• 论文介绍了 GPipe，一个用于训练巨型神经网络的可扩展模型并行库
• 论文提出并实现了一种新型批拆分流水线并行算法，该算法使用同步梯度更新，实现了高硬件利用率和训练稳定性的模型并行
• 论文利用 GPipe 训练了大规模卷积和基于 Transformer 的模型，并在图像分类和多语言机器翻译任务上展示了强大的实证结果
• 论文重点强调了 GPipe 库的三个关键特性：
  • 1）高效性（Efficiency） ：通过新型批拆分流水线算法，GPipe 实现了几乎随设备数量线性增长的速度提升
  • 2）灵活性（Flexibility） ：GPipe 支持任何可以表示为层序列的深度网络
  • 3）可靠性（Reliability） ：GPipe 使用同步梯度下降，并保证无论划分数量多少，训练结果一致

---

附录1：GPipe GPipe Example Usage

• GPipe 库的用户首先需要将他们的神经网络表示为 \(L\) 层的顺序列表
  • 任何计算图都可以被划分为一系列子图
• 示例基础层包括卷积(convolution)、池化(pooling)、批量归一化(batch normalization)、dropout、transformer、softmax 以及其他层
• 可以按顺序或并行连接的层可以被组合成一个新的复合层
• 用户可以以任意方式组合任意数量的层，只要正确定义了复合前向函数
• 图1展示了 GPipe 库的一个示例用例
  • 这是一个用于验证训练一致性的单元测试，它验证了在这个示例网络中，所有梯度的范数在数值误差范围内是相同的，无论分区数量如何

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46

    import tensorflow as tf from lingvo.core import base_layer from lingvo.core import layers from lingvo.core import py_utils from TensorPipe import TensorPipeLayer def BuildDummyTensorPipeLayer( num_layers=16, num_splits=4, num_mirco_batches=8): assert num_layers % num_splits == 0 layers = [] # Construct a dummy layer with 16 3x3 conv layers for i in range(num_layers): layers.append(layers.Conv2DLayer.Params().Set( name=’layer_{}’.format(i)), filter_shape=(3, 3, 1, 1), filter_stride=(1, 1)) # Evenly distribute layers to partitions. partitions = [] layers_per_split = num_layers // num_splits for split in range(num_splits): sub = layers[split * layers_per_split: (split + 1) * layers_per_split] partitions.append(sub) # Build pipeline parallelism model using TensorPipe p = TensorPipeLayer.Params().Set(name=’TensorPipe’, num_mirco_batches=num_mirco_batches , partitions=partitions) layer = p.cls(p) return layer class DummyTensorPipeTest(tf.test.TestCase): def _verify_consistent_training(self, num_splits): g = tf.Graph() with g.as_default(): py_utils.GetOrCreateGlobalStep() tf.set_random_seed(88888888) inputs = tf.random_uniform([16, 8, 8, 1]) net = BuildDummyTensorPipeLayer(num_splits=num_splits) logits = net.FPropDefaultTheta(inputs) loss = tf.reduce_mean(logits) grads = tf.gradients(loss, tf.trainable_variables()) grad_norm = tf.sqrt( py_utils.SumSquared(grads)) with self.session(graph=g) as sess: sess.run(tf.global_variables_initializer()) grad_norm_val , = sess.run([grad_norm]) # Verify grad norm is the same regardless of # the number of splits self.assertNear(grad_norm_val , 0.269997 , err=1.0e-6) def testDummyPipelineCnnOneSplit(self): self._verify_timestep_counts(num_splits=1) def testDummyPipelineCnnTwoSplits(self): self._verify_timestep_counts(nu2m_splits=2) def testDummyPipelineCnnFourSplits(self): self._verify_timestep_counts(num_splits=4)

---

附录2：图像分类训练细节 (2 Image Classification Training Details)

Training Hyperparameters

• 论文在 ImageNet ILSVRC-2012 数据集上训练了一个具有 \(557\) 百万模型参数和输入图像尺寸为 \(480\times 480\) 的 AmoebaNet-B 模型
• 论文遵循 (2018) 中描述的超参数和输入预处理方法来训练 AmoebaNet-B
  • 衰减率为 \(0.9\)
  • \(\epsilon=0.1\) 的 RMSProp 优化器
  • \(L^{2}\) 正则化系数 \(\lambda=4\times 10^{-5}\)
  • 标签平滑系数 \(0.1\)
  • 权重为 \(0.4\) 的辅助头
  • 对中间层应用了与 NasNet (2018) 中相同的 drop-path 调度，并对最终层应用了概率为 \(0.5\) 的 dropout
  • 使用了学习率调度，该调度每 \(3\) 个周期以 \(0.97\) 的速率衰减，初始学习率为 \(0.00125\) 乘以批量大小
• 在附录表1中，论文报告了每个迁移学习数据集使用的超参数
  • 从集合 \(\{0.0125,0.00375,0.075,0.115,0.15\}\) 中选择学习率
  • 从集合 \(\{0,4e-8,4e-7,4e-6,4e-5\}\) 中选择 \(L^{2}\) 权重衰减
  • 选择基于训练数据的保留子集（20%）
  • 论文应用选定的超参数进行最终训练，并重复五次
• 表1中：
  • 论文为每个数据集在训练数据集的保留子集上选择了学习率和 \(L^{2}\) 权重正则化参数
  • 对于其他超参数，论文使用了与 ImageNet 训练中相同的参数

Consistent Training

• GPipe 在微批次（micro-batches）上执行同步训练
• 在本节中，验证了以下假设：
  • 使用 GPipe 的端到端收敛精度在统计误差范围内是相同的，无论分区数量如何
• 实验过程：
  • 多次训练 AmoebaNet-D (6, 256) 模型 35 个 epoch，并在 ImageNet 上测量最终的验证准确率
  • 选择 AmoebaNet-D (6, 256) 是因为它是 DAWNBench 竞赛 (2018) 中训练成本最优的图像模型
  • 采用了 DAWNBench 中报告的超参数和训练流程
  • 作为基线，使用官方开源实现训练了 AmoebaNet-D (6, 256) 5 次，并计算了最终准确率的均值和标准差
  • 使用相同的超参数和训练流程，分别用 1、2、4 和 8 个分区通过 GPipe 训练了相同的网络
• 结果发现，最终的准确率落在均值 1.6 倍标准差范围内，符合预期

---

附录3：Machine Translation Training Details

• 论文研究了大规模多语言神经机器翻译（Neural Machine Translation, NMT），使用的语料库通过从网页爬取并提取平行句子构建
• 图 2 展示了论文研究的 102 种语言的数据分布情况

Baselines

• 在双语实验中，论文使用了 Transformer 架构（2017）的变体
• 对于大多数双语实验，论文采用了一个包含 3.75 亿参数的大型 Transformer Big 模型，并使用了共享的源-目标句子片段模型（SentencePiece Model, SPM）词汇表，包含 32k 个词符
• 论文根据每种语言对的数据集大小调整了不同的 dropout 值
  • 理解：这里说明是训练了很多个双语 Transformer 模型
  • 问题：图3中的模型是如何和基线比较的呢？想说明什么呢？
    • 理解：基线是谁不重要，重点是实验模型不同配置之间（不同宽度，深度之间）互相比较能拿到结论
• 对于大多数中低资源语言，论文还尝试了 Transformer Base 模型
  • 注：数据量大对应高资源，数据量小对应低资源
• 所有模型均采用 Adafactor 优化器（2018）和动量因子化，学习率调度为 \( (3.0, 40\text{K}) \)，并设置了每参数范数裁剪阈值为 1.0
• 对于 Transformer Base 模型，学习率调度为 \( (2.0, 8\text{K}) \)
• BLEU 分数基于验证集上表现最佳的检查点计算，输出和参考文本均为真实大小写形式

Multilingual Baselines

• 接下来，论文描述训练多语言模型的方法
• 由于训练数据集的严重不平衡（图 2），论文首先设计了一种采样策略，以同时在 200 多个语言对上训练单一模型
  • 直接从数据分布中采样会导致高资源语言表现良好，但低资源语言表现较差；
  • 平等采样所有语言对会显著提升低资源语言的翻译性能，但高资源语言的表现会明显低于其双语基线
• 为了平衡高资源和低资源语言对，论文采用了训练多语言 BERT（2018）时使用的基于温度的采样策略
  • 对于语言对 \( l \)，设 \( D_l \) 为可用平行语料库的大小
  • 若从数据集的并集中采样，样本来自语言 \( l \) 的概率为 \( p_l = \frac{1}{S_l D_l} \)
  • 论文将采样分布的概率设置为与 \( p_l^{\frac{1}{T} } \) 成正比，其中 \( T \) 为采样温度
    • 当 \( T = 1 \) 时，对应真实数据分布；
    • 当 \( T = 100 \) 时，几乎对每种语言采样数量相等
  • 论文的多语言模型采用了 \( T = 5 \)
• 在所有多语言实验中，论文使用与双语模型相同的超参数，训练了一个同时在所有语言上训练的单一 Transformer 模型
• 论文采用了共享的 SPM 词汇表，包含 64k 个词符，生成时使用了与训练相同的采样分布（\( T = 5 \)）
• 论文设置了字符覆盖率为 0.999995，以确保词汇表涵盖所有 103 种语言的大部分字母

Effects of Large Batch Size

• 由于数据并行（Data Parallelism）的简单性，它成为扩展神经网络训练的主要方法（2016, 2017）
• 论文通过显著增加标准 Transformer Big 训练的批量大小来测试大批量训练的极限
• 从每批 260k 词符开始，论文将有效批量增加到 400 万，并观察高资源语言对（德英）的验证损失和 BLEU 分数（其他语言对也呈现相似趋势）
• 优化参数与此前的实验相同
• 据论文所知，400 万词符每批是文献中迄今为止用于训练 NMT 模型的最大批量（2018）
• 表 2 显示，随着批量增加，两项指标均显著提升
• 作者认为进一步增加批量可能带来更多改进

---

附录4：Discussion

• 拥有一个灵活的大规模深度学习实验框架，为理解大规模模型的底层机制和原理提供了令人兴奋的机会
• 本节中，论文将实验结果与深度学习领域的最新研究联系起来，并与从业者分享一些额外的实证发现
• 表达力与泛化（Expressivity and Generalization） ：
  • 深度学习理论的最新发现（2018, 2018）假设，随着网络表达能力的增长，泛化性能也会提升
    • 论文在此通过实验进行实证验证
    • 论文通过增加深度作为提高网络表达能力（2017）的手段，同时控制批量大小
      • 论文能够观察到网络在以往从未实验过的规模上的泛化行为
    • 从 6 层 Transformer Big（编码器+解码器共 12 层）开始，论文逐步将深度增加到 64 层（共 128 层）
      • 论文发现，64 层模型的表现几乎呈现出与 6 层模型相同的上升趋势，而中间深度模型的表现介于两者之间
    • 尽管结果支持理论，但论文也观察到收益递减现象，这引发了可训练性的担忧
    • 论文可能尚未掌握进一步降低训练误差的工具或技术，理解可训练性挑战对进一步发展是必要的
• 深度-宽度权衡（Depth-Width Trade-off） ：
  • 另一个吸引深度学习理论研究者关注的领域是模型宽度和深度对泛化的影响（2018, 2019）
  • 接下来，论文在多语言设置中研究深度与宽度的权衡，并比较 13 亿参数的宽模型 \( T(12, 16384, 32) \) 和 13 亿参数的深模型 \( T(24, 8192, 16) \) 的性能
  • 虽然这两种模型在高资源语言上的表现非常相似 ，但深模型在低资源语言上的表现显著优于宽模型 ，这表明增加模型深度可能更有利于泛化
  • 将 13 亿参数深模型与 4 亿参数模型进行比较时，低资源语言（图3 右侧）的性能提升几乎与高资源语言相当，这表明增加深度还可能扩大对低资源任务的迁移效果
• 深度加速收敛（Faster Convergence with Depth） ：
  • 论文报告了一个与模型深度相关的有趣现象
  • 在保持有效批量大小、优化器超参数和模型宽度不变的情况下 ，增加模型深度会优化加速 ，如附录图3 所示
    • 注：层数越深，损失下降越快
  • 此前报道类似现象的工作推测，深度通过过参数化实现了预条件（2018）
• 尽管论文主要关注与扩展神经网络相关的系统挑战，但为了更好地解决泛化和可训练性问题，对深度神经网络的理论理解需求日益增长
  • 作者相信，像 GPipe 这样灵活的扩展工具对于弥合深度学习理论与实践的差距至关重要
  • 希望论文的实证发现和讨论能够激励更多研究沿着这一方向展开

---

附录：Sufficient Statistic(充分统计量)

• 在统计学中，充分统计量 的本质是对原始样本数据的“压缩”
  • 即在保留所有关于未知参数的信息的前提下，将复杂的样本数据简化为更简洁的统计量
• 这种简化不会丢失用于推断未知参数的任何关键信息，因此是统计推断中简化数据、提高效率的重要工具

定义

• 假设
  • 总体的概率分布依赖于未知参数 \(\theta\)（\(\theta\)可以是单参数或多参数，比如分布的均值）
  • \(X_1, X_2, \dots, X_n\)是来自该总体的样本
• 若
  • 一个统计量\(T = T(X_1, X_2, \dots, X_n)\) 满足：给定\(T\)的取值后，样本\(X_1, \dots, X_n\)的条件分布不再依赖于\(\theta\)
• 则
  • 称\(T\)是参数\(\theta\)的充分统计量
• 简单来说：一旦知道了充分统计量 \(T\) 的值，原始样本中就不再包含任何关于 \(\theta\) 的额外信息
  • 例如，伯努利分布中，\(T = \sum x_i\) 和样本均值 \(\bar{X} = T/n\)（因\(n\) 固定，二者一一对应）都是\(p\)的充分统计量

充分统计量的总结

• 充分统计量的核心思想是：“压缩数据但不丢失信息”**
• 统计推断的核心是利用样本信息推断未知参数 \(\theta\)
  • 原始样本往往包含大量冗余信息（例如，100个数据点中可能有重复或无关细节）
• 充分统计量的作用是：
  • 简化数据 ：将高维样本（如 \(n\) 个数据）压缩为低维统计量（如1个或2个值）；
  • 保留信息 ：压缩后的统计量包含推断 \(\theta\) 所需的全部信息，原始样本的其他细节对推断 \(\theta\) 无意义
• 注：充分统计量不唯一性 ：一个参数可能有多个充分统计量
  • 例如，伯努利分布中，\(T = \sum x_i\) 和样本均值 \(\bar{X} = T/n\)（因 \(n\) 固定，二者一一对应）都是 \(p\) 的充分统计量

---

附录：其他流水线策略介绍

各种流水线整体介绍

• 三种流水线策略（pipeline strategies），Gpipe, PipeDream 1F1B, Interleaved 1F1B
• PipeDream 1F1B 论文：
  • PipeDream: Fast and Efficient Pipeline Parallel DNN Training, 2018, Microsoft ：第一篇，主要介绍概念等
  • PipeDream: Generalized Pipeline Parallelism for DNN Training, SOSP 2019, Microsoft：第二篇，包含更多细节
  • PipeDream 1F1B 也叫做经典 1F1B（One-Forward-One-Backward），也称为 1F1B 或 PipeDream 1F1B
• Interleaved 1F1B（Megatron-2）论文：Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM, SC 2021, NVIDIA
• 下图来自 Interleaved 1F1B（Megatron-2）论文：Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM, SC 2021, NVIDIA
• 上图中内容解读：
  • 图中数字表示不同 micro-batch 的过程（共 8 个 micro-batches 和 4 张 GPU），颜色区分前向后向过程，Interleaved 1F1B 中的灰色和深色则表示多分出来的虚拟 Stage
  • 核心要诀：
    • 对每个 micro-batch，前向过程是必须 GPU 正序进行的
    • 对每个 micro-batch，后向过程是必须 GPU 逆序进行的
    • 对任意 micro-batch，需要一个完整的 Stage 完成前向过程，才能开始后向过程
    • 需要所有 micro-batch 都走完后向过程，才能执行一次梯度更新（所以叫做 1F1B）
      • 吐槽：实际上 Gpipe 也是一次正向一次反向的，也可以叫做 1F1B？
    • Interleaved 1F1B 中，同一个 Stage 内部的 Stage 分片是按照模型切分，所以需要以大的 Stage 为单位遵循上面的过程
      • 比如：对每个 micro-batch，需要所有的虚拟 Stage 分片完成前向过程，才能开始后向过程
    • Interleaved 1F1B 中，对同一个 Stage 内部的分片来说，理论上同一个 Stage 内部的 Stage 分片是按照模型切分，所以也是有依赖顺序的
    • 对每个 micro-batch，1F1B 保证激活值在反向结束后立即释放，降低缓存

GPipe -> 1F1B -> Interleaved 1F1B

• TLDR：Interleaved 1F1B 是在经典 1F1B（PipeDream 1F1B）流水线并行调度基础上，把“模型纵向切成更多 Stage ，再循环交错地放到 GPU 上”，用更细粒度、更紧凑的时序进一步压缩“流水线气泡（bubble）”，从而提升 GPU 利用率与训练吞吐，同时保持 1F1B 的低显存优势
  • 注意：切割的是模型
• GPipe, 1F1B, Interleaved 1F1B 三种流水线并行调度对比

  方案	层划分方式	执行顺序	主要优点	主要缺点
  GPipe	连续层，每 GPU 一个 Stage	先跑完所有 micro-batch 的 Forward，再依次跑 Backward	易实现、等价性好	激活值全保留，显存爆炸；气泡大
  1F1B	同上	每个 Stage 交替执行 1 Forward / 1 Backward	激活值及时释放，省显存；气泡已减半	气泡仍随 Stage 数线性增加
  Interleaved 1F1B	把原 Stage 均分 v 份，循环交错地放到 GPU 上	仍然是 1F1B 顺序，但 Stage 粒度变细	气泡进一步缩小；通信-计算可重叠	代码/通信更复杂；micro-batch 数需为 v·pp 的整数倍

  • 气泡比例（p 为 Pipeline Stage 数量，即物理 GPU 数， m 为 micro-batch 数量）
    • GPipe：(p−1) / m
    • 1F1B：(p−1) / m
    • Interleaved 1F1B： (p−1) / (v·m)
• Interleaved 1F1B 的特点：
  • 时间轴上，Forward/Backward 任务被拆得更碎，空隙（bubble）被其他 micro-batch 的计算填满
  • 仍然遵守“1 Forward -> 1 Backward”的稳态节奏，保证激活值在反向结束后立即释放
  • 由于 Stage 变细，单个 micro-batch 在每个 GPU 上的停留时间变短，更多 micro-batch 可以同时在流水线上“滑动” ，
  • 当前 micro-batch 的 Backward 计算 与 下一个 micro-batch 的 P2P 接收 无依赖，可并行；
  • 当前 Send-Forward 与 下一次循环的 Forward 计算 也无依赖，可并行
  • 在带宽充足时，通信几乎被计算完全掩盖

Interleaved 1F1B 的优缺点

• Interleaved 1F1B显存：与 1F1B 相同，稳态下每 GPU 最多保存 v 份激活 ，仍远低于 GPipe
• 吞吐：Megatron-LM 实验显示，在 1T+ 参数模型、1024 GPU 上，Interleaved 1F1B 比 1F1B 提升 8~15% 吞吐；

其他相关细节

• Megatron-LM 中 Interleaved 1F1B 叫做 interleaved schedule

最新技术：Zero Bubble Pipeline Parallelism

• Zero Bubble Pipeline Parallelism（ZB），即 零气泡流水线并行
• 参考链接：
  • 原始论文：Zero Bubble Pipeline Parallelism, arXiv 2023, Sea AI Lab
  • 开源地址：github.com/sail-sg/zero-bubble-pipeline-parallelism
• 基本思路是让 GPU 不要停止，让气泡消失
  • 首先，如下图所示，将原始 1F1B 的后向过程拆开为 B 和 W 来表示（B 表示 对输入 \(x\) 求梯度，W 表示对权重 \(W\) 求梯度）

文本介绍随机微分方程（SDE）视角下的Diffusion的相关知识

• 参考链接：
  • 原始论文1：(NCSN)Generative Modeling by Estimating Gradients of the Data Distribution, Stanford, 2020 ，Score-based 模型NCSN
  • 原始论文2：Score-based generative modeling through stochastic differential equations, Stanford & Google, 2021：随机微分方程的视角，将DDPM，SDE，ODE，Score-based模型等概念串起来
  • 其他参考1：深度学习（生成式模型）——score-based generative modeling through stochastic differential equations
  • 其他参考2：生成扩散模型漫谈（五）：一般框架之SDE篇，苏剑林，2022
  • 其他参考3：论文学习笔记SDE：从EBM到Score-Matching，随机微分方程视角下的Diffusion大一统

---

写在前面

• 论文Score-based generative modeling through stochastic differential equations, Stanford & Google, 2021发表于2021年，这篇文章将DDPM，SDE，ODE等概念串起来了，论文在苏神博客生成扩散模型漫谈（五）：一般框架之SDE篇，苏剑林，2022的基础上，以这篇论文为主分析SDE视角下的DDPM

---

ODE的定义

• 常微分长程（Ordinary Differential Equation，ODE），其典型的形式表达如下：
  $$ dy = f(x,y) dx $$
  • 一种更常见的表达为： \(\frac{dy}{dx} = f(x,y)\)
  • 理解：导数 \(\frac{dy}{dx}\) 可以表示因变量 \(y\) 关于 \(x\) 的变化率
• 常微分方程的离散形式：
  $$ y(x + \Delta x) = y(x) + f(x, y(x)) \Delta x $$
  • 理解：即在任意一点 \((x_0,y_0)\) 处，有： \(y(x_0 + \Delta x) = y(x_0) + f(x_0, y_0) \Delta x \)，即当 \(x\) 增加 \(\Delta x\) 时， \(y\) 增加大约 \(f(x_0,y_0)\Delta x\)
• 常微分方程一般可以直接求解，解析解是一系列差值为常数的函数，在给定某个点函数初始值的情况下，也可以使用欧拉（Euler）方法等方法迭代求解数值解

---

SDE的定义

• 随机微分方程（Stochastic Differential Equation, SDE）是数学中的一个分支，它描述了含有随机过程的系统随时间变化的行为。与普通的微分方程不同，SDE中除了包含确定性的微分项外，还包含了随机项，这些随机项通常由布朗运动（Brownian motion，也称为Wiener过程，一种连续时间随机过程）或其他类型的随机过程表示

SDE基本形式

• 一个典型的随机微分方程可以表示为：
  $$ dX_t = \mu(X_t,t)dt + \sigma(X_t,t)dW_t $$
• 对SDE方程的理解：
  • \(X_t\) 是随机过程
  • \(\mu(X_t,t)\) 是漂移系数 ，表示了过程的平均变化率，类似于常微分方程里面的一阶导数 \(\frac{dX_t}{dt}\) 。漂移项 \(\mu(X_t,t)dt\) 描述了在没有随机影响的情况下， \(X_t\) 随时间的变化趋势
  • \(dW_t\) 是布朗运动的增量，代表了随机扰动
  • \(\sigma(X_t,t)\) 是扩散系数，表示了过程的波动程度。扩散项 \(\sigma(X_t,t)dW_t\) 描述了随机因素对 \(X_t\) 的影响。其中 \(dW_t\) 代表了布朗运动的一个小增量，它可以看做是一个均值为0，方差为 \(dt\) 的正态分布随机变量。 \(\sigma(X_t,t)dW_t\) 整体表示

    参考自：《随机过程》布朗运动基本假设与实验结果不符 - 高宏的文章 - 知乎
    《随机过程》布朗运动理论是描述和揭示质点随机运动现象及规律的科学理论，其基本假设（公理）是：布朗粒子在 \(t\) 时刻的位移 \(x_t\) 服从 \(\mathcal{N}(0, \sigma^2 t)\) 的正态分布
    但是，实际布朗粒子位移观测实验结果表明：布朗粒子位移不服从正态分布，实验证明《随机过程》布朗运动基本假设不成立

• 与ODE的对比 ：相对ODE方程 \(dy = f(x,y) dx\) 形式（对应 \(dX_t = \mu(X_t,t)dt \) ），SDE增加了一项随机项 \(dX_t = \mu(X_t,t)dt + \color{red}{\sigma(X_t,t)dW_t}\)
• SDE的离散形式：
  $$ X_{t+\Delta} - X_t = \mu(X_t,t)\Delta t + \sigma(X_t,t)\sqrt{\Delta t} \epsilon, \ \epsilon \sim \mathcal{N}(0,1) $$
  • 在这里，原始形式中的 \(dW_t\) 可表示成服从均值为0，方差为 \(\Delta t\) 的高斯分布的随机变量 \(\epsilon’ \sim \mathcal{N}(0, \Delta t)\) 。同理， \(\sigma(X_t,t)dW_t\) 则可表示成一个服从均值为0，方差为 \(\sigma^2(X_t,t)\Delta t\) 的高斯分布的随机变量 \(\epsilon’ \sim \mathcal{N}(0, \sigma^2(X_t,t)\Delta t)\)
  • 理解：在任意点 \((t_0,X_{t_0})\) 处，有：
    $$ X_{t_0+\Delta} = X_{t_0} + \mu(X_{t_0},t_0)\Delta t + \sigma(X_{t_0},t_0)\sqrt{\Delta t} \epsilon, \ \epsilon \sim \mathcal{N}(0,1) $$
    • 在任意点 \((t_0,X_{t_0})\) 处， \(X_{t_0+\Delta}\) 约等于 服从均值为 \(X_{t_0} + \mu(X_{t_0},t_0)\Delta t\)，方差为 \(\sigma^2(X_{t_0},t_0)\Delta t\) 的正太分布，写成分布采样形式有：
      $$ X_{t_0+\Delta} \sim \mathcal{N}(X_{t_0} + \mu(X_{t_0},t_0)\Delta t, \sigma^2(X_{t_0},t_0)\Delta t) $$
• 注：更一般的SDE，随机项不一定是服从正态分布，比如跳-扩散过程（Jump-Diffusion Process）模型： \(dX_t = \mu X_t dt + \sigma X_t dW_t + \color{red}{dJ_t} \) 中可以是包含其他随机项 \(dJ_t\) 表示复合泊松过程，代表价格中的突然跳跃

SDE求解方法

• 求解随机微分方程的方法包括解析方法和数值方法。由于大多数SDE没有闭式解，因此数值方法如Euler-Maruyama方法（类似于ODE中的欧拉（Euler）方法）

---

EBM

• 基于能量的生成模型（Energy-Based Model，EBM），是一种独立于GANs（Generative Adversarial Networks），VAEs（Variational Autoencoders），Diffusion之外的生成模型基于能量的生成模型。EBMs不直接建模概率密度函数，而是通过能量函数间接地表示数据分布，相关论文可见：Implicit Generation and Modeling with Energy Based Models, OpenAI, NeurIPS 2019
• 假设真实样本服从分布 \(x \sim p_{\text{data}}(x)\)，一般的生成模型，比如GAN或者VAE都使用一个神经网络取拟合一个分布 \(p_\theta(x)\) 来逼近真实分布，而EBM不直接拟合真实分布，而是使用玻尔兹曼分布来建模原始分布，并使用神经网络取拟合能量函数 \(E_\theta(x)\)，即：
  $$ p_\theta(x) = \frac{1}{Z(\theta)}e^{-E_\theta(x)} $$
• 此时如果使用极大似然法优化 \(p_\theta(x)\)，则需要最小化以下负对数似然目标：
  $$ L_\text{ML}(\theta) = \mathbb{E}_{x \sim p_{D}}[-\log p_\theta(x)] = \mathbb{E}_{x \sim p_{D}}[E_\theta(x) - \log Z(\theta)]$$
• 由于 \(Z(\theta)\) 很难求解，所以我们一般不使用极大似然法，幸运的是，生成模型的最终目标是生成一个 \(x\)，之前的研究给出了一种通过Langevin dynamics采样来近似得到 \(x_T\) 的方案，该方案重复使用下面的迭代来采样：
  $$ x_t = x_{t-1} - \frac{\lambda}{2}\nabla_x E_\theta(x_{t-1}) + \sqrt{\lambda} \varepsilon, \ \epsilon \sim \mathcal{N}(0, 1) $$
  • 如果将这种建模方式可以假设为对应分布 \(q_\theta(x)\)，可以证明，当 \(T \rightarrow +\infty\) 时，有 \(q_\theta(x) \approx p_\theta(x)\)，也就是说，迭代的次数够多就能生成接近于真实分布的样本 \(x\)
• 虽然得到了采样的方式，但是，学习 \( E_\theta(x) \) 的参数依然需要使用到极大似然法，此时仍然要面对无法求解的 \(Z(\theta)\)，幸运的是，为了避开 \(Z(\theta)\)，可以进一步使用下面的方式来近似梯度：
  $$ \nabla_\theta L_\text{ML} \approx \mathbb{E}_{x^+\sim p_{D}}[\nabla_\theta E_\theta(x^+)] - \mathbb{E}_{x^-\sim q_\theta(x)}[\nabla_\theta E_\theta(x^-)] $$
  • \(x^+ \sim p_D(x)\)
  • \(x^- \sim q_\theta(x)\) 是按照Langevin dynamics采样过程中得到的中间样本
• 详细训练流程如下（其中 \(\Omega(\cdot)\) 表示停止梯度回传）：
• 注：EBM的效果比较一般

---

Score-Matching

• 本节许多推导参考自：有没有谁通俗的讲一下Denoising score matching? - kkkkkkk的回答 - 知乎
• Score-Matching方法也把生成样本对应的分布建模为玻尔兹曼分布，但不同于EBM使用近似梯度来避开求解 \(Z(\theta)\)，Score-Matching使用Score-based方法
• Score-based方法中，我们考虑 \(Z(\theta)\) 与 \(x\) 无关，于是我们考虑先对 \(x\) 求导，于是我们可以定义得分函数 \(s(x;\theta)\) 如下：
  $$ s(x;\theta) = \nabla_x \log p_\theta(x) = - \nabla_x E_\theta(x) $$
• 得分函数 \(s(x;\theta)\) 的本质是对数概率函数关于 \(x\) 的梯度，如果我们能让 \(s(x;\theta)\) 尽量接近真实对数概率关于 \(x\) 的梯度，即可实现和极大似然法相似的效果，即最大化已知数据出现的概率，真实的对数概率关于 \(x\) 的梯度 \(s_\text{real}(x)\) 可以定义为：
  $$ s_\text{real}(x) = \nabla_x \log p_\text{real}(x) = - \nabla_x E_\text{real}(x) $$
• Score-Matching的过程就是 \(s(x;\theta)\) 和 \(s_\text{real}(x)\) 匹配的过程，也就是最小化下面的目标函数 \(J(\theta)\)：
  $$
  \begin{align}
  J(\theta) &= \mathbb{E}_{x\sim p_\text{real}} [\Vert s(x;\theta) - s_\text{real}(x) \Vert^2] \\
  &= \int_{x\in \mathbb{R}^n} p_\text{real}(x) \Vert s(x;\theta) - s_\text{real}(x) \Vert^2 dx
  \end{align}
  $$
  • 当两个得分函数相同时，他们的积分值会相差一个常数
• 至此，我们还不知道 \(s_\text{real}(x)\)，为了求解上面的式子，我们进一步展开 \(\Vert s(x;\theta) - s_\text{real}(x) \Vert^2\) 并去除与参数 \(\theta\) 无关的部分，于是有（接下来的推导中，为了方便，我们先把 \(x\) 当做一维的情况来推导）：
  $$
  \begin{align}
  \mathop{\arg\max}_\theta J(\theta) &= \mathop{\arg\max}_\theta \int_{x\in \mathbb{R}^n} p_\text{real}(x) \Vert s(x;\theta) - s_\text{real}(x) \Vert^2 dx \\
  &= \mathop{\arg\max}_\theta \int_{x\in \mathbb{R}^n} p_\text{real}(x) \Big( (s(x;\theta))^2 - 2 s(x;\theta) s_\text{real}(x)+ (s_\text{real}(x))^2 \Big) dx \\
  &= \mathop{\arg\max}_\theta \int_{x\in \mathbb{R}^n} p_\text{real}(x) \Big( (s(x;\theta))^2 - 2 s(x;\theta) s_\text{real}(x) \Big) dx \\
  \end{align}
  $$
  • 其中 \( (s_\text{real}(x))^2\) 与 \(\theta\) 无关，可以丢掉
• 可以进一步消掉 \(s(x;\theta) s_\text{real}(x)\) 中的 \(s_\text{real}(x)\)：
  $$
  \begin{align}
  \int_{x\in \mathbb{R}^n} p_\text{real}(x) s(x;\theta) s_\text{real}(x) dx &= \int_{x\in \mathbb{R}^n} p_\text{real}(x) s(x;\theta) \nabla_x p_\text{real}(x) dx \\
  &= \int_{x\in \mathbb{R}^n} p_\text{real}(x) s(x;\theta) \nabla_x \log p_\text{real}(x) dx \\
  &= \int_{x\in \mathbb{R}^n} p_\text{real}(x) s(x;\theta) \frac{\nabla_x p_\text{real}(x)}{p_\text{real}(x)} dx \\
  &= \int_{x\in \mathbb{R}^n} s(x;\theta) \nabla_x p_\text{real}(x) dx \\
  &= s(x;\theta) p_\text{real}(x) - \int_{x\in \mathbb{R}^n} p_\text{real}(x) \nabla_x s(x;\theta) dx \\
  \end{align}
  $$
  • 其中用到了分部积分：\(\int u(x) dv(x) = u(x)v(x) - \int v(x) du(x)\) 的展开形式 \(\int u(x) v’(x) dx = u(x)v(x) - \int v(x)u’(x) dx\)
• 接下来，Estimation of Non-Normalized Statistical Models by Score Matching-Theorem 1, 2005文章做了一些假设，这些假设下，可以得到下面的结论（问题：为什么在 \(x \to \infty\) 时等于0就可以继续证明？）：
  $$ \lim_{x \to \infty }s(x;\theta) p_\text{real}(x) = 0$$
• 于是有 \(\int_{x\in \mathbb{R}^n} p_\text{real}(x) s(x;\theta) s_\text{real}(x) dx = - \int_{x\in \mathbb{R}^n} p_\text{real}(x) \nabla_x s(x;\theta) dx\)，带入原始目标函数变成如下：
  $$
  \begin{align}
  \mathop{\arg\max}_\theta J(\theta) &= \mathop{\arg\max}_\theta \int_{x\in \mathbb{R}^n} p_\text{real}(x) (s(x;\theta))^2 + 2 \nabla_x s(x;\theta) dx \\
  &= \mathop{\arg\max}_\theta \mathbb{E}_{x \sim p_\text{real}(x)} [(s(x;\theta))^2 + 2 \nabla_x s(x;\theta)] \\
  &= \mathop{\arg\max}_\theta \mathbb{E}_{x \sim p_\text{real}(x)} [\nabla_x s(x;\theta) + \frac{1}{2}(s(x;\theta))^2 ] \\
  \end{align}
  $$
• 上面的表达中，先把 \(x\) 当做一维的情况来推导只是为了推导方便，实际上，\(x\) 是多维的，因此 \(\nabla_x s(x;\theta)\) 是一个向量，此时需要使用如下将所有维度的梯度值的和的形式（原始论文中就是这样）：
  $$
  \begin{align}
  \mathop{\arg\max}_\theta J(\theta) &= \mathop{\arg\max}_\theta \mathbb{E}_{x \sim p_\text{real}(x)}[\sum_{i=1}^k(\nabla_{x_i} s(x;\theta) + \frac{1}{2}(s(x;\theta))^2)] \\
  \end{align}
  $$
• 至此，已经消掉了 \(s_\text{real}(x)\)，上面的形式就是我们常见的Score-Matching形式

---

DDPM中的SDE

• SDE形式：
  $$\begin{equation}d\boldsymbol{x} = \boldsymbol{f}_t(\boldsymbol{x}) dt + g_t d\boldsymbol{w}\end{equation}$$
• 写成离散形式：
  $$\begin{equation}\boldsymbol{x}_{t+\Delta t} - \boldsymbol{x}_t = \boldsymbol{f}_t(\boldsymbol{x}_t) \Delta t + g_t \sqrt{\Delta t}\boldsymbol{\varepsilon},\quad \boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})\end{equation}$$
• 进一步移项可得：
  $$\boldsymbol{x}_{t+\Delta t} = \boldsymbol{x}_t + \boldsymbol{f}_t(\boldsymbol{x}_t) \Delta t + g_t \sqrt{\Delta t}\boldsymbol{\varepsilon},\quad \boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$$
• 变换成高斯分布采样形式：
  $$\boldsymbol{x}_{t+\Delta t} \sim \mathcal{N} (\boldsymbol{x}_t + \boldsymbol{f}_t(\boldsymbol{x}_t) \Delta t, g_t^2 \Delta t) $$
• 前向过程条件概率的微分形式可以表示为：
  $$\begin{equation}\begin{aligned}
  p(\boldsymbol{x}_{t+\Delta t}|\boldsymbol{x}_t) =&\ \mathcal{N}\left(\boldsymbol{x}_{t+\Delta t};\boldsymbol{x}_t + \boldsymbol{f}_t(\boldsymbol{x}_t) \Delta t, g_t^2\Delta t \boldsymbol{I}\right)\\
  \propto&\ \exp\left(-\frac{\Vert\boldsymbol{x}_{t+\Delta t} - \boldsymbol{x}_t - \boldsymbol{f}_t(\boldsymbol{x}_t) \Delta t\Vert^2}{2 g_t^2\Delta t}\right)
  \end{aligned}\end{equation}$$
• 经过一系列推导（参见：生成扩散模型漫谈（五）：一般框架之SDE篇，苏剑林，2022），可以得到反向过程的微分方程形式如下：
  $$\begin{equation}\begin{aligned}
  p(\boldsymbol{x}_t|\boldsymbol{x}_{t+\Delta t}) \propto&\ \exp\left(-\frac{\Vert\boldsymbol{x}_{t+\Delta t} - \boldsymbol{x}_t - \left[\boldsymbol{f}_t(\boldsymbol{x}_t) - g_t^2\nabla_{\boldsymbol{x}_t}\log p(\boldsymbol{x}_t) \right]\Delta t\Vert^2}{2 g_t^2\Delta t}\right) \\
  \approx&\exp\left(-\frac{\Vert \boldsymbol{x}_t - \boldsymbol{x}_{t+\Delta t} + \left[\boldsymbol{f}_{t+\Delta t}(\boldsymbol{x}_{t+\Delta t}) - g_{t+\Delta t}^2\nabla_{\boldsymbol{x}_{t+\Delta t}}\log p(\boldsymbol{x}_{t+\Delta t}) \right]\Delta t\Vert^2}{2 g_{t+\Delta t}^2\Delta t}\right)
  \end{aligned}\end{equation}
  $$
  • 上面的 \(\approx\) 是一种近似，下面是苏神的回答：

    本就不是严格的推导，“随意”是必然的。这里约等号的原因是 \(\boldsymbol{f}_{t+\Delta t}(\boldsymbol{x}_{t+\Delta t})\Delta t
    \) 与 \(\boldsymbol{f}_t(\boldsymbol{x}_t)\Delta t\) 具有相同的一阶近似精度

• 最终可得到反向过程 \(p(\boldsymbol{x}_t|\boldsymbol{x}_{t+\Delta t})\) 近似一个均值为 \(\boldsymbol{x}_{t+\Delta t} - \left[\boldsymbol{f}_{t+\Delta t}(\boldsymbol{x}_{t+\Delta t}) - g_{t+\Delta t}^2\nabla_{\boldsymbol{x}_{t+\Delta t}}\log p(\boldsymbol{x}_{t+\Delta t}) \right]\Delta t\)，协方差为 \(g_{t+\Delta t}^2\Delta t\ \boldsymbol{I}\) 的正太分布，即：
  $$ p(\boldsymbol{x}_t|\boldsymbol{x}_{t+\Delta t}) = \mathcal{N}(p(\boldsymbol{x}_t|\boldsymbol{x}_{t+\Delta t}); \underbrace{\boldsymbol{x}_{t+\Delta t} - \left[\boldsymbol{f}_{t+\Delta t}(\boldsymbol{x}_{t+\Delta t}) - g_{t+\Delta t}^2\nabla_{\boldsymbol{x}_{t+\Delta t}}\log p(\boldsymbol{x}_{t+\Delta t}) \right]\Delta t}_{\mu}, \underbrace{g_{t+\Delta t}^2\Delta t\ \boldsymbol{I}}_{\Sigma}) $$
• 采样形式是：
  $$
  \begin{align}
  \boldsymbol{x}_t &= \boldsymbol{x}_{t+\Delta t} - \left[\boldsymbol{f}_{t+\Delta t}(\boldsymbol{x}_{t+\Delta t}) - g_{t+\Delta t}^2\nabla_{\boldsymbol{x}_{t+\Delta t}}\log p(\boldsymbol{x}_{t+\Delta t}) \right]\Delta t - g_{t+\Delta t} \sqrt{\Delta t}\boldsymbol{\varepsilon},\quad \boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})
  \end{align}
  $$
• 变换一下形式可得：
  $$
  \begin{align}
  \boldsymbol{x}_{t+\Delta t} - \boldsymbol{x}_t &= \left[\boldsymbol{f}_{t+\Delta t}(\boldsymbol{x}_{t+\Delta t}) - g_{t+\Delta t}^2\nabla_{\boldsymbol{x}_{t+\Delta t}}\log p(\boldsymbol{x}_{t+\Delta t}) \right]\Delta t + g_{t+\Delta t} \sqrt{\Delta t}\boldsymbol{\varepsilon},\quad \boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}) \\
  \end{align}
  $$
• 写成SDE的形式为（注意：\(d\boldsymbol{x} = \boldsymbol{x}_{t+\Delta t} - \boldsymbol{x}_t\)）：
  $$\begin{equation}d\boldsymbol{x} = \left[\boldsymbol{f}_t(\boldsymbol{x}) - g_t^2\nabla_{\boldsymbol{x}}\log p_t(\boldsymbol{x}) \right] dt + g_t d\boldsymbol{w}\end{equation}$$
  • \(\log p_t(\boldsymbol{x})\) 中带着下标 \(t\)，表示是 \(t\) 时刻的分布，这里虽然SDE形式一样，但是不同时刻的分布是不同的

---

Score-Matching Loss

• 回顾DDPM反向过程的SDE形式：
  $$\begin{equation}d\boldsymbol{x} = \left[\boldsymbol{f}_t(\boldsymbol{x}) - g_t^2\nabla_{\boldsymbol{x}}\log p_t(\boldsymbol{x}) \right] dt + g_t d\boldsymbol{w}\end{equation}$$
• 由于前向过程是已知的，所以 \(\boldsymbol{f}_t(\boldsymbol{x})\) 和 \(g_t\) 都是已知项。所以在反向过程SDE形式中，唯一的未知项是 \(\nabla_x \log p_\theta(x)\)，即得分函数（按照得分函数的定义 ： \(s(x;\theta) = \nabla_x \log p_\theta(x)\) 可知）
• 我们使用神经网络 \(s_\theta(x_t,t)\) 去拟合 \(t\) 时刻的得分函数 \(s(t) = \nabla_{x_t} \log p(x_t)\)，DDPM对应的Score-Matching应该是（最小化 \(s_\theta(x_t,t)\) 和 \(s(t)\) 之间的距离）：
  $$
  \begin{align}
  J(\theta) &= \int_{x_t} p(x_t) \Vert s_\theta(x_t,t) - \nabla_{x_t} \log p(x_t)\Vert^2 dx_t \\
  &= \mathbb{E}_{x_t \sim p(x_t)} [\Vert s_\theta(x_t,t) - \nabla_{x_t} \log p(x_t)\Vert^2] \\
  \end{align}
  $$
• 接下来的任务是求解 \(\nabla_x \log p(x)\)，此时我们，在实际场景中，我们已知的数据是 \(x_0\)，基于前向过程扩散可以得到任意时刻的数据 \(x_t\)，所以前向过程中 \(x_t\) 也是已知的（或者说 \(p(\boldsymbol{x_t}|\boldsymbol{x_0})\) 是有解析解的）：
  $$ \begin{equation}p(\boldsymbol{x}_t) = \int p(\boldsymbol{x}_t|\boldsymbol{x}_0)\tilde{p}(\boldsymbol{x}_0)d\boldsymbol{x}_0=\mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0)}\left[p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right]\end{equation} $$
  • 其中 \(\tilde{p}(x_0) = p_\text{D}(x_0) = p_\text{real}(x_0)\)，表示 \(x_0\) 的真实分布
• 按照对数概率求导的方法，于是有：
  $$ \begin{equation}\nabla_{\boldsymbol{x}_t}\log p(\boldsymbol{x}_t) = \frac{\mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0)}\left[\nabla_{\boldsymbol{x}_t} p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right]}{\mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0)}\left[p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right]} = \frac{\mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0)}\left[p(\boldsymbol{x}_t|\boldsymbol{x}_0)\nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right]}{\mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0)}\left[p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right]}\end{equation} $$
• 经过推导可以得到最小化目标函数等价于最小化下面的形式：
  $$
  \begin{align}
  \mathbb{E}_{x_t \sim p(x_t)} [\Vert s_\theta(x_t,t) - \nabla_{x_t} \log p(x_t)\Vert^2] &= \mathop{\arg\min}_\theta \left\Vert \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - \frac{\mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0)}\left[p(\boldsymbol{x}_t|\boldsymbol{x}_0)\nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right]}{\mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0)}\left[p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right]}\right\Vert^2 \\
  &= \mathop{\arg\min}_\theta \frac{\mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0)}\left[p(\boldsymbol{x}_t|\boldsymbol{x}_0)\left\Vert \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right\Vert^2\right]}{\mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0)}\left[p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right]} \\
  &= \mathop{\arg\min}_\theta \mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0)}\left[p(\boldsymbol{x}_t|\boldsymbol{x}_0)\left\Vert \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right\Vert^2\right]
  \end{align}
  $$
  • 上面的第二个等号可以通过推导证明 \(\forall \boldsymbol{f}(\boldsymbol{x}), g(\boldsymbol{x}), \quad \mathop{\arg\min}_\boldsymbol{\mu} \mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x}) \cdot \left\Vert
    \boldsymbol{\mu} - \boldsymbol{f}(\boldsymbol{x})
    \right\Vert^2 \right] = \frac { \mathbb{E}_{\boldsymbol{x}}[g(\boldsymbol{x}) \cdot \boldsymbol{f}(\boldsymbol{x})] }{ \mathbb{E}_{\boldsymbol{x}}[g(\boldsymbol{x})] } \) 得到，详细证明见附录：证明加权均方误差形式
  • 第三个等号是因为上式的分母与参数 \(\theta\) 无关，可以消掉
• 进一步对 \(x_t\) 进行积分（相当于对每个 \(x_t\) 都做最小化），最终可以得到下面的结论：
  $$
  \begin{align}
  J(\theta)&= \int_{\boldsymbol{x}_t} \mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0)}\left[p(\boldsymbol{x}_t|\boldsymbol{x}_0)\left\Vert \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right\Vert^2\right] d\boldsymbol{x}_t \\
  &=\ \mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0),\boldsymbol{x}_t \sim p(\boldsymbol{x}_t|\boldsymbol{x}_0)}\left[\left\Vert \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right\Vert^2\right]
  \end{align}
  $$

---

DDPM和Score-based模型的关系

扩散模型的一般流程总结

• 第一步：前向过程，定义如下的SDE：
  $$\begin{equation}d\boldsymbol{x} = \boldsymbol{f}_t(\boldsymbol{x}) dt + g_t d\boldsymbol{w}\end{equation}$$
• 第二步：求解得到 \(p(x_t|x_0)\) 的表达式
  $$ p(\boldsymbol{x}_{t+\Delta t}|\boldsymbol{x}_t) =\ \mathcal{N}\left(\boldsymbol{x}_{t+\Delta t};\boldsymbol{x}_t + \boldsymbol{f}_t(\boldsymbol{x}_t) \Delta t, g_t^2\Delta t \boldsymbol{I}\right)$$
• 第三步：Score-Matching，使用下面的损失函数训练得分函数模型 \(s_\theta(x_t, t)\)
  $$ J(\theta) =\ \mathbb{E}_{\boldsymbol{x}_0 \sim \tilde{p}(x_0),\boldsymbol{x}_t \sim p(\boldsymbol{x}_t|\boldsymbol{x}_0)}\left[\left\Vert \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{x}_t|\boldsymbol{x}_0)\right\Vert^2\right] $$
• 第四步：将 \(s_\theta(x_t, t)\) 作为 \(\nabla_{\boldsymbol{x}_{t+\Delta t}}\log p(\boldsymbol{x}_{t+\Delta t})\) 的近似值带入下面的式子采样生成样本 $$ p(\boldsymbol{x}_t|\boldsymbol{x}_{t+\Delta t}) = \mathcal{N}(p(\boldsymbol{x}_t|\boldsymbol{x}_{t+\Delta t}); \underbrace{\boldsymbol{x}_{t+\Delta t} - \left[\boldsymbol{f}_{t+\Delta t}(\boldsymbol{x}_{t+\Delta t}) - g_{t+\Delta t}^2\nabla_{\boldsymbol{x}_{t+\Delta t}}\log p(\boldsymbol{x}_{t+\Delta t}) \right]\Delta t}_{\mu}, \underbrace{g_{t+\Delta t}^2\Delta t\ \boldsymbol{I}}_{\Sigma}) $$
• 在DDPM中，有 \(t+\Delta t = t+1\)，即 \(x_{t+\Delta t} = x_{t+1}\)

DDPM损失函数与Score-Based损失函数的区别

• 正太分布 \(\mathbf{x} \sim \mathcal{N}(\mathbf{\mu}, \sigma^2 \boldsymbol{I})\) 的梯度计算如下：
  $$\nabla_{\mathbf{x}}\log p(\mathbf{x}) = \nabla_{\mathbf{x}} \Big(-\frac{1}{2\sigma^2}(\mathbf{x} - \boldsymbol{\mu})^2 \Big) = - \frac{\mathbf{x} - \boldsymbol{\mu}}{\sigma^2} = - \frac{\boldsymbol{\epsilon}}{\sigma}$$
• 结合 \(q(\mathbf{x}_t \vert \mathbf{x}_0) \sim \mathcal{N}(\sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\boldsymbol{I})\)，可得：
  $$
  \mathbf{s}_\theta(\mathbf{x}_t, t)
  \approx \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t)
  = \mathbb{E}_{q(\mathbf{x}_0)} [\nabla_{\mathbf{x}_t} q(\mathbf{x}_t \vert \mathbf{x}_0)]
  = \mathbb{E}_{q(\mathbf{x}_0)} \Big[ - \frac{\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)}{\sqrt{1 - \bar{\alpha}_t}} \Big]
  = - \frac{\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)}{\sqrt{1 - \bar{\alpha}_t}}
  $$
• Score-based模型中用神经网络建模并学习 \(\mathbf{s}_\theta(\mathbf{x}_t, t) \)，DDPM中神经网络建模并学习 \(\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\)

---

附录：玻尔兹曼分布

• 玻尔兹曼分布（Boltzmann distribution），也称为吉布斯分布（Gibbs distribution），是统计力学中的一个核心概念，它描述了在热力学平衡状态下，一个系统处于各种可能状态的概率。该分布给出了粒子占据某个量子态的概率与该状态的能量以及系统的温度之间的关系
• 玻尔兹曼分布可以表示为：
  $$ p_i \propto e^{-\frac{\varepsilon_i}{kT}} $$
  • \( p_i \) 是系统处于状态 \( i \) 的概率
  • \( \varepsilon_i \) 是状态 \( i \) 的能量
  • \( k \) 是玻尔兹曼常数
  • \( T \) 是系统的绝对温度（热力学温度）
  • 符号 \( \propto \) 表示正比例关系
  • 实际使用中概率可以定义为： \(p_i = \frac{1}{Q}e^{-\frac{\varepsilon_i}{kT}}\)，其中\(Q\)是归一化因子，用于确保概率和为1
• 这意味着，在较高的温度下，不同能量状态之间的概率差异会减小；而在较低的温度下，低能量状态将比高能量状态更有可能被占用
• 更一般的情况下，我们所说的玻尔兹曼分布，形式上有所变化，更像是Softmax形式，比如假定能量函数为 \(\{E_i\}_{i=1}^N\)，玻尔兹曼分布可以定义为 \(p_i \propto e^{\frac{1}{\beta} E_i}\)：
  $$ p_i = \frac{e^{\frac{1}{\beta} E_i}}{\sum_i e^{\frac{1}{\beta} E_i}} $$
  • \(\frac{1}{\beta}\) 是温度系数

---

附录：Langevin dynamics方法

• Langevin dynamics 是一种用于模拟分子系统中粒子运动的方法，它结合了经典力学和随机过程。这种方法得名于法国物理学家保罗·朗之万（Paul Langevin），他提出了描述布朗运动的方程

---

附录：证明加权均方误差形式

注：以下证明参考自生成扩散模型漫谈（五）：一般框架之SDE篇，shyoshyo评论

• 目标是证明：
  $$ \begin{aligned}
  \forall \boldsymbol{f}(\boldsymbol{x}), g(\boldsymbol{x}), \quad \mathop{\arg\min}_\boldsymbol{\mu} \mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x}) \cdot \left\Vert
  \boldsymbol{\mu} - \boldsymbol{f}(\boldsymbol{x})
  \right\Vert^2 \right] = \frac { \mathbb{E}_{\boldsymbol{x}}[g(\boldsymbol{x}) \cdot \boldsymbol{f}(\boldsymbol{x})] }{ \mathbb{E}_{\boldsymbol{x}}[g(\boldsymbol{x})] }
  \end{aligned}
  $$
• 证明过程：
  $$\begin{aligned}
  \mathop{\arg\min}_\boldsymbol{\mu} \mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x}) \cdot \left\Vert
  \boldsymbol{\mu} - \boldsymbol{f}(\boldsymbol{x})
  \right\Vert^2 \right] = & \mathop{\arg\min}_\boldsymbol{\mu} \mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x}) \cdot \left( \left\Vert
  \boldsymbol{\mu} \right\Vert^2 - 2 \boldsymbol{\mu} \cdot \boldsymbol{f}(\boldsymbol{x}) + \left\Vert
  \boldsymbol{ \boldsymbol{f}(\boldsymbol{x})} \right\Vert^2 \right) \right] \\
  = & \mathop{\arg\min}_\boldsymbol{\mu} \mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x}) \cdot \left( \left\Vert
  \boldsymbol{\mu} \right\Vert^2 - 2 \boldsymbol{\mu} \cdot \boldsymbol{f}(\boldsymbol{x}) \right) \right] \\
  = & \mathop{\arg\min}_\boldsymbol{\mu} \left( \left\Vert
  \boldsymbol{\mu} \right\Vert^2 \cdot \mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x}) \right] - 2 \boldsymbol{\mu} \cdot \mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x})\cdot\boldsymbol{f}(\boldsymbol{x}) \right] \right) \\
  = & \mathop{\arg\min}_\boldsymbol{\mu} \left( \left\Vert
  \boldsymbol{\mu} \right\Vert^2 - 2 \boldsymbol{\mu} \cdot \frac{\mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x})\cdot\boldsymbol{f}(\boldsymbol{x}) \right]}{\mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x}) \right]} \right) \\
  = & \mathop{\arg\min}_\boldsymbol{\mu} \left( \left\Vert
  \boldsymbol{\mu} \right\Vert^2 - 2 \boldsymbol{\mu} \cdot \frac{\mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x})\cdot\boldsymbol{f}(\boldsymbol{x}) \right]}{\mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x}) \right]} +
  \left\Vert \frac{\mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x})\cdot\boldsymbol{f}(\boldsymbol{x}) \right]}{\mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x}) \right]}\right\Vert^2 \right) \\
  = & \mathop{\arg\min}_\boldsymbol{\mu} \left\Vert
  \boldsymbol{\mu} - \frac{\mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x})\cdot\boldsymbol{f}(\boldsymbol{x}) \right]}{\mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x}) \right]}\right\Vert^2 \\
  = & \frac{\mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x})\cdot\boldsymbol{f}(\boldsymbol{x}) \right]}{\mathbb{E}_{\boldsymbol{x}}\left[ g(\boldsymbol{x}) \right]}
  \end{aligned}
  $$

文本介绍xDeepFM的理论介绍,包括阅读论文后自己的理解

• 上篇博客参考: DeepFM
• 原始论文: xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems, KDD 2018

xDeepFM结构图

• 显然, 上图中除了 CIN 部分以外,其他跟 DeepFM 基本是相同的, 所以我们论文主要讲述 CIN 组件部分, 其他的嵌入层等可参考我之前的博客DeepFM

CIN组件

Compressed Interaction Network

• 论文中首先提出的就是这个CIN网络(Compressed Interaction Network)
• 结构图如下:
• 理解
  • 每个隐藏层都与一个池化操作连接到一起
  • 特征阶数与网络层数相关
  • 可以与 RNN 对应着看, 当前网络层由上一个隐藏层和一个额外输入确定
  • 确切的说: CIN 中当前层输入是前一层的隐藏层 + 原来的特征向量

---

整体说明

• TLDR：对比学习（Contrastive Learning）是自监督学习中的一种方法，其核心思想是通过学习数据样本之间的相似性和差异性 ，使得相似样本在表示空间（embedding space）中靠近，不相似样本相互远离，从而学习一个表示空间
• 对比学习的目标是：学习一个表示空间（embedding space），使得在这个表示空间中，满足下面的条件
  • 正样本对（相似的样本）的表示距离尽可能近
  • 负样本对（不相似的样本）的表示距离尽可能远
• 注：通过这种对比机制，模型无需人工标注即可从数据中自动学习有意义的特征表示

---

详细方法说明

正负样本构造

• 正样本 ：同一数据的不同增强视图（如裁剪、旋转、颜色变换后的同一图像），或语义相似的样本
• 负样本 ：随机选择的其他数据样本，或显式定义的 dissimilar 样本
  • 常用的策略有：同一batch内的其他样本、动态队列（历史batch中的样本）等
  • 一些特殊的模型，比如BYOL（Bootstrap Your Own Latent）提出了 免负样本策略 ，详情见附录

常用损失函数

• InfoNCE Loss（Noise Contrastive Estimation）：
  $$
  \mathcal{L} = -\log \frac{\exp(sim(q, k_+) / \tau)}{\sum_{i=0}^K \exp(sim(q, k_i) / \tau)}
  $$
  • \(q\)：查询样本的表示
  • \(k_+\)：正样本表示，\(k_i\) 为负样本表示
  • \(\tau\)：温度系数，控制分布的尖锐程度
  • \(sim(\cdot)\)：相似度函数（如余弦相似度）
• Triplet Loss ：（三元组损失）
  $$
  \mathcal{L} = \max(d(a, p) - d(a, n) + \text{margin}, 0)
  $$
  • \(a\)：锚点（Anchor）样本
  • \(p\)：为正（Positive）样本
  • \(n\)：为负（Negative）样本
  • 三元组损失的含义也就是 \(<a,p,n>\) 三元组
  • \(\text{margin}\) 是超参数，用于控制正负样本之间的最小间隔

模型网络架构

• 通常使用双分支网络，两个分支可共享权重或不共享

---

对比学习的优势

• 无监督/自监督：无需人工标注，利用数据自身结构学习
• 迁移能力强：预训练的表示可泛化到下游任务（如分类、检测）
• 鲁棒性：通过数据增强学习到不变性特征（如CV中的光照、旋转不变性）

---

应用场景

• 计算机视觉：图像分类（SimCLR）、目标检测（MoCo）
• 自然语言处理：句子表示学习（SimCSE）
• 多模态学习：图文匹配（CLIP）、视频-文本对齐

---

附录：BYOL 的免负样本策略

• 原始论文：Bootstrap Your Own Latent A New Approach to Self-Supervised Learning, NeurIPS 2020, Google DeepMind
• 比如BYOL（Bootstrap Your Own Latent）提出了 免负样本策略 ，其中Target网络的参数通过指数移动平均（EMA）从Online网络缓慢更新（动量更新），模型学习目标是最小化同一图像的不同增强视图（正样本对，分别输入Target网络和Online网络中）的表示距离
• BYOL模型的整体架构图如下：
• 一种更容易理解的架构图：

---

附录：NCE 和 InfoNCE 损失

• InfoNCE 和 NCE 的核心区别可以一句话概括为：
  • NCE 用“二分类”把真实样本从 K 个噪声里挑出来；
  • InfoNCE 用“K+1 类 Softmax”把真实样本从 K 个负样本里挑出来，并直接最大化互信息下界
• 下面给出各自的损失函数（公式均为单样本版本，可简单批平均得到最终损失）

Noise Contrastive Estimation (NCE)

• 目标：估计归一化常数 Z，同时学习打分函数 \(s_\theta(x)\)
• NCE 损失（对一条真实样本 \(x\) 和 K 条噪声 \(x’\sim q\)）：
  $$
  \mathcal L_{\text{NCE} } = -\log \frac{e^{s_\theta(x)} }{e^{s_\theta(x)} + K e^{s_\theta(x’)}/Z} - \sum_{k=1}^K \log \frac{e^{s_\theta(x’_k)}/Z}{e^{s_\theta(x)} + K e^{s_\theta(x’_k)}/Z}
  $$
  • 实际实现时通常把 Z 也当可学习参数，上式退化为二分类交叉熵：
    • 正类 logits 为 \(s_\theta(x)-\log Z\)
    • 负类 logits 为 \(s_\theta(x’)-\log Z\)

InfoNCE

• InfoNCE 又称“对比预测编码”损失（Contrastive Predictive Coding Loss），也可简称为 CPC Loss
• 目标：最大化互信息 \(I(x; c)\) 的下界，其中 \(c\) 为上下文/表征
• 对一条正样本 \((x, c)\) 和 K 条负样本 \(\{(x’_k, c)\}\)：
  $$
  \mathcal L_{\text{InfoNCE} } = -\log \frac{e^{f(x,c)/\tau} }{\displaystyle e^{f(x,c)/\tau} + \sum_{k=1}^K e^{f(x’_k,c)/\tau} }
  $$
  • 这里 \(f(\cdot,\cdot)\) 是兼容函数（通常用内积或余弦相似度），\(\tau>0\) 为温度超参
  • 当 \(K\rightarrow\infty\) 时，该损失给出的下界趋于真实的互信息，因此得名 InfoNCE

互信息 与 InfoNCE 的关联

• 互信息衡量了两个分布的依赖程度，当两个分布完全独立，他们的互信息为 0，当两个分布完全依赖，他们的互信息为其中一个分布的熵
• InfoNCE 损失的设计目标是最大化互信息的下界 ，而非直接计算互信息
• 当负样本数量 \(K\rightarrow\infty\) 时，InfoNCE 损失对应的下界会收敛到真实的互信息 \(I(X;Y)\)，这也是该损失函数命名的核心原因

• 参考链接：
  • 原始论文 Training Deep Nets with Sublinear Memory Cost, MIT, 2016：论文以这篇文章的内容为主进行介绍，后续会补充一些 transformer 场景下的梯度检查点技术

---

整体总结

• 梯度检查点（Gradient Checkpointing）技术广泛应用于当前大规模深度学习模型训练中，能有效降低显存的使用
• 梯度检查点技术也叫做 重计算（re-materialization）技术
• Training Deep Nets with Sublinear Memory Cost, MIT, 2016这篇文章的核心贡献是：
  • 提出并系统化了一种 “用计算换内存”的通用方法（在自动微分领域也被称为梯度检查点技术）
  • 通过分段和重计算，巧妙地将深度学习训练过程中的内存瓶颈从 \(O(n)\) 降低到 \(O(\sqrt{n})\)，甚至理论上的 \(O(\log n)\)，极大地拓展了论文使用现有硬件能够训练的模型规模和深度

---

核心问题：为什么训练深度网络如此消耗内存？

• 在训练神经网络时，标准的训练流程包含两个步骤：
  • 前向传播 (Forward Pass) ：
    • 输入数据从网络的第一层开始，逐层计算，直到最后一层得到输出
    • 在这个过程中，每一层的输出（称为“激活”或“特征图”）都需要被保存下来
  • 反向传播 (Backward Pass) ：
    • 计算输出的损失（预测值与真实值的差距），然后从最后一层开始，反向逐层计算梯度
    • 为了计算某一层参数的梯度，通常需要用到该层在前向传播时产生的激活值
• 问题出现：
  • 为了进行反向传播，必须在内存中保留网络中每一层的激活值
  • 如果一个网络有 \(n\) 层，那么内存消耗就大致与 \(n\) 成正比 ，即内存成本为 \(O(n)\)
  • 对于现在动辄成百上千层的深度模型（如 ResNet），这笔内存开销会迅速占满顶配 GPU 的几十 GB 显存，从而限制了探索更深、更复杂模型的能力

---

传统内存优化方法（治标不治本）

• 论文首先提到了一些已有的内存优化技术，这些技术主要通过分析计算图 (Computation Graph) 来实现
  • 原地操作 (In-place Operation) ：
    • 如果一个操作的输入值在后续计算中不再需要，那么其输出可以直接覆盖输入的内存空间
    • 例如，y = relu(x)，如果 x 后面用不到了，y 的结果可以直接写在 x 的内存里
  • 内存共享 (Memory Sharing) ：
    • 分析所有变量的“生命周期”，将生命周期不重叠的变量共享同一块内存
• 这些方法能将内存占用降低2到3倍，但无法改变内存消耗随网络层数线性增长的趋势，当网络深到一定程度时，内存瓶颈依然存在

---

梯度检查点：用计算换内存 (Trade Computation for Memory)

• 既然保存所有中间结果是内存消耗的根源，那么论文提出的核心思想非常直接：
  • 不保存所有中间结果，只保存其中一部分
  • 当反向传播需要用到某个被丢弃的中间结果时，再临时重新计算它
• 这是一种典型的“用时间换空间”的策略
  • 虽然会增加一些计算量（因为需要重新执行部分前向计算），但可以极大地降低内存峰值

---

工作原理一：\(O(\sqrt{n})\) 内存成本算法（实用策略）

• 这是论文提出的主要实用算法
• \(O(\sqrt{n})\) 内存成本算法原理如下：
  • 1）分段 (Segmenting) ：将一个包含 \(n\) 层的网络链条，切分成 \(k\) 个小段（segment）
  • 2）前向传播 ：在正常的前向传播过程中，只保存每个分段的最终输出 ，而丢弃每个分段内部的所有中间激活值
  • 3）反向传播 ：
    • 当反向传播进行到第 \(i\) 段时，由于计算该段的梯度需要其内部的激活值（这些值已经被丢弃了），算法会执行一次“局部前向传播”：
      • 利用保存的第 \(i-1\) 段的输出作为输入，重新计算一次第 \(i\) 段的前向传播，以得到所有需要的激活值
    • 计算完梯度后，这些临时重新计算的激活值可以立即被丢弃

关键推导：为什么是 \(O(\sqrt{n})\)？

• 内存成本分析：假设网络总共有 \(n\) 层，被均匀地切分成 \(k\) 段，那么每一段的长度就是 \(n/k\)层
• 总内存成本主要由两部分构成：
  • 1）段间内存 (Inter-segment Memory) ：用于存储 \(k\) 个分段的输出，以便在反向传播时作为“检查点”(checkpoint)
    • 这部分的成本是 \(O(k)\)
  • 2）段内内存 (Intra-segment Memory) ：在对任何一段进行反向传播时，需要临时重新计算并存储该段内部的所有激活值
    • 由于所有段中最大的内存开销决定了峰值，这部分的成本是 \(O(n/k)\)
• 因此，总的内存成本可以表示为：
  $$\text{Cost}(n, k) = O(k) + O(n/k)$$
• 为了让总成本最低，论文需要让这两部分达到一个平衡。一个简单的优化方法是让它们的量级相等（实际上等价于导数为 0 的推导）：
  $$k \approx \frac{n}{k} \implies k^2 \approx n \implies k = \sqrt{n}$$
• 当选择 \(k=\sqrt{n}\) 时，总内存成本为：
  $$\text{Cost} = O(\sqrt{n}) + O(n/\sqrt{n}) = O(\sqrt{n}) + O(\sqrt{n}) = O(\sqrt{n})$$
• 至此，我们就成功地将内存成本从线性 \(O(n)\) 降到了亚线性 \(O(\sqrt{n})\)
• 作为代价，整个训练过程大约需要额外进行一次完整的前向传播计算（因为每个分段都被重新计算了一次），使得训练时间增加了约 30%
  • 问题：30% 的计算时间怎么来的呢？
  • 回答：反向传播的时间复杂度大约是前向传播的 2~3 倍，折合计算以后大致能算出这个数字（增加了一次前向传播计算），详情见附录

---

工作原理二：\(O(\log n)\) 内存成本算法（理论极限）

• 论文进一步展示，通过递归 (Recursion) 的方式，可以实现更低的内存成本
• 我们可以把一个分段本身看作一个“超级操作符”
• 对这个超级操作符内部的计算，作者同样可以再次应用分段和重计算的策略

关键推导：\(O(\log n)\) 的递推关系

• 让 \(g(n)\) 表示训练一个 \(n\) 层网络所需的内存
• 假设将这个网络分成 \(k+1\) 个子问题，每个子问题的规模是 \(n/(k+1)\)
• 为了连接这些子问题，需要存储 \(k\) 个中间结果
• 那么，\(g(n)\) 可以表示为递推公式：
  $$g(n) = k + g\left(\frac{n}{k+1}\right)$$
  • 这是一个典型的对数关系
  • \(k\) 是存储这 \(k\) 个结果的成本
  • \(g\left(\frac{n}{k+1}\right)\) 是解决其中一个子问题所需的成本
  • 注：这里使用 \(k+1\) 或 \(k\) 不影响最终结果
• 通过解这个递推公式，我们可以得到：
  $$g(n) = k \cdot \log_{k+1}(n)$$
• 作为一个特例，如果每次只将问题一分为二，即只存储一个中间结果（\(k=1\)），那么递推关系变为 \(g(n) = 1 + g(n/2)\)，解得：
  $$g(n) = \log_2(n)$$
  • 注：简单理解一下，展开 \(g(n)\) 后，大致共有 \(\log_2(n)\) 个 1
• 这揭示了一个终极的理论可能性：
  • 训练一个 \(n\) 层网络的内存成本可以降低到 \(O(\log n)\)
  • 不过，这种方法的计算开销会大得多（需要 \(O(\log n)\) 次额外的前向传播，因此在实践中不如 \(O(\sqrt{n})\) 策略常用

---

实验效果与结论

• 作者通过在深度残差网络 (ResNet) 和长短期记忆网络 (LSTM) 上的实验，验证了该方法的有效性
  • 对于一个 1000层 的 ResNet，标准优化方法需要 48GB 显存，而使用亚线性算法后仅需 7GB
  • 在 LSTM 上，该方法同样带来了 超过4倍 的内存节省
  • 代价是训练速度降低了大约30%，这对于能够训练原本无法训练的模型来说，是一个非常值得的交换

---

Transformer 中的梯度检查点

• Transformer中的梯度检查点（Gradient Checkpointing）与上述论文中的基本原理上是完全相同的 ，但其应用方式和带来的收益上，针对Transformer 的结构有更多特点
• 无论是用于CNN、RNN还是Transformer，梯度检查点的核心思想始终是：
  • 目标 ：打破模型训练时内存消耗与网络深度（层数）之间的线性关系
  • 方法 ：在前向传播时，不再保存所有中间层的激活值，而是只保存少数几个关键节点（检查点）
  • 代价 ：在反向传播时，当需要用到被丢弃的激活值时，就从最近的一个检查点开始，重新进行一小段前向计算来恢复它们
  • 权衡 ：本质上都是“用计算换内存”的策略

针对 Transformer 结构的应用说明

• Transformer的独特结构使得梯度检查点的应用非常直接，且效果尤其显著
• 1. 应用位置非常明确
  • 一个标准的 Transformer 模型是由一个个完全相同的 Transformer Block 堆叠而成的
    • 每个块通常包含一个多头自注意力（Multi-Head Self-Attention）层和一个前馈神经网络（Feed-Forward Network, FFN）层
  • 最自然、最常见的应用方式就是 将每一个Transformer块作为一个分段（Segment）
    • 前向传播时 ：
      • 当数据流经第 \(i\) 个Transformer块时，只保留送入这个块的输入（也就是第 \(i-1\) 块的输出）
      • 在块内部计算过程中产生的所有中间结果，例如注意力分数矩阵（Attention Scores）、注意力权重（Attention Weights）、FFN层的中间激活等，计算完毕后立即被丢弃
    • 反向传播时 ：
      • 当反向传播回第 \(i\) 个块时，算法会利用之前保存的输入，重新执行一次该块的前向计算，从而得到计算梯度所必需的那些中间结果
• 2. 带来的收益为何对 Transformer 尤其显著
  • 梯度检查点能极大缓解Transformer在两个维度上的内存压力：
  • 深度（层数 \(L\)） ：
    • 现代的大型语言模型（如GPT、LLaMA）可以有几十甚至上百层
    • 如果没有梯度检查点，内存消耗会随着层数 \(L\) 线性暴增。梯度检查点将这个成本从 \(O(L)\) 降到了 \(O(\sqrt{L})\) ，使得训练极深的Transformer 成为可能
  • 序列长度（Sequence Length \(S\)） ：这是Transformer最独特的内存瓶颈
    • 注意力矩阵的二次方开销 ：
      • 自注意力机制的核心是计算一个注意力分数矩阵，其大小为 (序列长度 x 序列长度)
      • 这意味着内存开销与序列长度成二次方关系 ，即 \(O(S^2)\)
      • 当序列很长时（例如4096、8192甚至更长），这个矩阵会变得异常巨大
    • 梯度检查点的作用 ：
      • 梯度检查点不能改变单次注意力计算需要 \(O(S^2)\) 内存峰值的事实
      • 但它能确保不必同时在内存中保留每一层的这个巨大矩阵
      • 在没有检查点的情况下，内存中需要为 \(L\) 个注意力矩阵的激活值（或其相关值）分配空间
      • 有了检查点，在任何时候，只需要为当前正在重计算的那一个块的注意力矩阵分配内存
      • 这极大地降低了总体的内存占用

---

附录：梯度检查点技术增加了多少训练成本？

• 论文中 “训练时间增加了约30%” 这个数字主要是一个经验性的测量结果 ，来源于作者在特定硬件上进行的基准测试，并且这个结果也与理论上的计算开销分析相符

实验测量结果（经验来源）

• 作者在论文的第5.4节 （Impact on Training Speed） 和 图7 专门讨论了这个问题
  • 测试方法 ：
    • 作者在单个 Titan X GPU 上对不同的内存分配策略进行了速度基准测试
    • 测量了在 ResNet 和 LSTM 两种模型上，处理一个批次（batch）数据所需的实际运行时间（秒）
  • 对比对象 ：
    • 比较了采用标准内存优化（论文中称为 “sharing”）的策略和采用亚线性内存成本（”sublinear plan”）策略的速度
  • 测量结论 ：
    • 实验结果图表（图7）直观地显示，”sublinear plan” 的时间成本曲线始终在 “sharing” 曲线之上
    • 论文在图7的说明文字和正文中明确指出，使用亚线性内存方案会带来“大约30%的额外运行时成本”

理论计算分析（理论支撑）

• 训练一个批次的主要计算量如下：
  • 标准训练流程 ：包含一次完整的前向传播（Forward Pass）和一次完整的反向传播（Backward Pass）：
    $$ 总计算量 \approx 1F + 1B $$
  • 亚线性方案的流程 ：它在反向传播过程中需要重新计算前向传播，因此:
    $$ 总计算量 \approx 1F + (1F_recompute + 1B) = 2F + 1B $$
• 论文中提到，通常一次反向传播的计算量大约是前向传播的两倍（\(B \approx 2F\)）
  • 实际上是大约 2~3 倍的样子
• 基于上述这个假设，我们可以估算增加的计算开销：
  • 标准流程计算量 ：
    $$T_{standard} = T_F + T_B \approx T_F + 2T_F = 3T_F$$
  • 亚线性方案计算量 ：
    $$T_{sublinear} = 2T_F + T_B \approx 2T_F + 2T_F = 4T_F$$
• 增加的运行时间百分比约为：
  $$\frac{T_{sublinear} - T_{standard}}{T_{standard}} = \frac{4T_F - 3T_F}{3T_F} = \frac{1T_F}{3T_F} = \frac{1}{3} \approx 33.3%$$
• 这个理论计算出的 33.3% 与实验中测量到的 约30% 基本吻合（考虑到反向传播大致是前向传播的 2~3 倍，那就基本符合了）

文本介绍Conditional Diffusion的相关知识

• 参考链接：
  • 生成扩散模型漫谈（九）：条件控制生成结果：论文的证明大多参考自苏神的博客
  • What are Diffusion Models?：Lilian Weng的博客
  • Diffusion Models Beat GANs on Image Synthesis, OpenAI, 2021：第一篇条件扩散模型的文章，Classifier Guidance 方法；
    • 文章附录：Supplemental中有相关推导
    • 实现讲解：sunlin-ai.github.io/guided-diffusion
  • Classifier-Free Diffusion Guidance, Google Research, Brain team, 2022：第一篇使用Classifier-free Guidance方法的文章
  • Score-based generative modeling through stochastic differential equations, Stanford & Google, 2021：随机微分方程的视角
  • 【笔记】扩散模型（五）：Classifier-Free Guidance 理论推导与代码实现

---

整体概述

• 在图像生成领域，条件一般可以分成类别标签或者是一段文本
• 从方法上来看，条件控制生成的方式主要分两种：Classifier Guidance 和 Classifier-free Guidance
  • Classifier Guidance ：先训练无条件的模型，训练后在生成时引入条件分类器（Classifier）。这种方式灵活，无需重新训练，但是生成效果较差
  • Classifier-free Guidance：训练时引入条件，生成时无需Classifier。这种方式需要重新训练Diffusion模型，但生成效果更好些

---

前置推导

• 正太分布 \(\mathbf{x} \sim \mathcal{N}(\mathbf{\mu}, \sigma^2 \boldsymbol{I})\) 的梯度计算如下：
  $$\nabla_{\mathbf{x}}\log p(\mathbf{x}) = \nabla_{\mathbf{x}} \Big(-\frac{1}{2\sigma^2}(\mathbf{x} - \boldsymbol{\mu})^2 \Big) = - \frac{\mathbf{x} - \boldsymbol{\mu}}{\sigma^2} = - \frac{\boldsymbol{\epsilon}}{\sigma}$$
• 结合 \(q(\mathbf{x}_t \vert \mathbf{x}_0) \sim \mathcal{N}(\sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\boldsymbol{I})\)，可得：
  $$
  \mathbf{s}_\theta(\mathbf{x}_t, t)
  \approx \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t)
  = \mathbb{E}_{q(\mathbf{x}_0)} [\nabla_{\mathbf{x}_t} q(\mathbf{x}_t \vert \mathbf{x}_0)]
  = \mathbb{E}_{q(\mathbf{x}_0)} \Big[ - \frac{\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)}{\sqrt{1 - \bar{\alpha}_t}} \Big]
  = - \frac{\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)}{\sqrt{1 - \bar{\alpha}_t}}
  $$
  • 其中 \(\mathbf{s}_\theta(\mathbf{x}_t, t) \) 是Noise Conditional Score Network (NCSN)，详情参见论文：(NCSN)Generative Modeling by Estimating Gradients of the Data Distribution, Stanford, 2020

---

Classifier Guidance 方法

Classifier Guidance Diffusion的直观理解

• 参考自：通俗理解Classifier Guidance 和 Classifier-Free Guidance 的扩散模型

  2021年OpenAI在「Diffusion Models Beat GANs on Image Synthesis」中提出Classifier Guidance，使得扩散模型能够按类生成。后来「More Control for Free! Image Synthesis with Semantic Diffusion Guidance」把Classifier Guidance推广到了Semantic Diffusion，使得扩散模型可以按图像、按文本和多模态条件来生成，例如，风格化可以通过content和style两者共同进行引导，这些都是通过梯度引导来实现

  • Classifier Guidance可以通过Score function（问题：Score function是什么？）直观地解释，用贝叶斯定理将条件生成概率进行对数分解：
    $$
    \begin{align}
    \nabla_{x_t} \log p(x_t|y) &= \nabla_{x_t} \log \Big( \frac{p(x_t)p(y|x_t)}{p(y)}\Big) \\
    &= \nabla_{x_t} \log p(x_t) + \nabla_{x_t} \log p(y|x_t) - \nabla_{x_t} \log p(y) \\
    &= \underbrace{\nabla_{x_t} \log p(x_t)}_{\text{unconditional score}} + \underbrace{\nabla_{x_t} \log p(y|x_t)}_{\text{classifier gradient}}
    \end{align}
    $$
  • 从上式可以看到，Classifier Guidance条件生成只需额外添加一个classifier的梯度来引导。从成本上看，Classifier Guidance 需要训练噪声数据版本的classifier网络，推理时每一步都需要额外计算classifier的梯度

• 以上是简单的理解，推导不严谨，论文接下来对DDPM和DDIM对应的Classifier Guidance Diffusion方法进行详细推导

Conditional Diffusion Process

• 本小节相关推导参考自：Diffusion Models Beat GANs on Image Synthesis, OpenAI, 2021——Supplemental

  • 其他参考：深度学习（生成式模型）——Classifier Guidance Diffusion

• 条件扩散模型相关定义 ：

  • 参考普通扩散模型的前向过程 \(q(x_{t+1}|x_{t})\) 和后向过程为 \(q(x_{t}|x_{t+1})\)
  • 定义带条件的扩散模型的前向过程 \(\hat{q}(x_{t+1}|x_{t}, y)\) 和后向过程为 \(\hat{q}(x_t|x_{t+1}, y)\)

• 设定：条件扩散模型的前向过程与普通扩散模型的前向过程一致，与条件无关
  $$
  \begin{align}
  \hat{q}(x_0) &:= q(x_0) \\
  \hat{q}(y|x_0) &:= \text{Known labels per sample} \\
  \hat{q}(x_{t+1}|x_t,y) &:= q(x_{t+1}|x_t) \\
  \hat{q}(x_{1:T}|x_0,y) &:= \prod_{t=1}^T \hat{q}(x_{t}|x_{t-1}, y) \\
  \end{align}
  $$

  • 直观理解：上式表名前向过程中对 \(x_0\) 如何增加噪音(\(\epsilon \sim \mathcal{N}(0,1)\))确实与 \(x_0\) 类别无关

• 进一步地，我们可以推导得到，前向过程中的每一步加噪都与条件无关（以下内容详细推导可见论文：Diffusion Models Beat GANs on Image Synthesis, OpenAI, 2021——Supplemental）：
  $$
  \begin{align}
  \hat{q}(x_{t+1}|x_{t}) &= \hat{q} (x_{t+1}|x_{t},y) \\
  \hat{q}(x_{1:T}|x_0) &= q(x_{1:T}|x_0) \\
  \hat{q}(x_t) &= q(x_t) \\
  \hat{q}(y|x_t, x_{t+1}) &= \hat{q}(y|x_t) \\
  \hat{q}(x_{t}|x_{t+1}) &= q(x_{t}|x_{t+1}) \\
  \end{align}
  $$

  • 注意，其中： \(\hat{q}(x_{t}|x_{t-1})\) 中不含有条件，实际是一个边际分布（或边缘分布）：
    • \(\hat{q}(x_{t}|x_{t-1}) = \mathbb{E}_{y}[\hat{q}(x_{t}, y|x_{t-1})]\)
    • 同理有： \(\hat{q}(x_t) = \mathbb{E}_{y}[\hat{q}(x_t,y)] = \mathbb{E}_{y}[\mathbb{E}_{x_{0:t-1}}[\hat{q}(y,x_0,\cdots,x_{t})]]\)
    • 或： \(\hat{q}(x_t) = \mathbb{E}_{x_{0:t-1}}[\hat{q}(x_0,\cdots,x_{t})] = \mathbb{E}_{x_{0:t-1}}[\mathbb{E}_{y}[\hat{q}(y,x_0,\cdots,x_{t})]]\)
  • 关于 \(\hat{q}(y|x_t, x_{t+1}) = \hat{q}(y|x_t)\) 的理解：因为 \(x_{t+1}\) 是 \(x_t\) 增加前向噪音得到的，而前向过程不依赖于条件，该式子的证明如下：
    $$
    \begin{align}
    \hat{q}(y|x_{t},x_{t+1}) &= \frac{\hat{q}(y,x_{t},x_{t+1})}{\hat{q}(x_{t},x_{t+1})} = \frac{\hat{q}(x_{t+1}|y,x_{t})\hat{q}(y|x_{t})\hat{q}(x_{t})}{\hat{q}(x_{t+1}|x_{t})\hat{q}(x_{t})} \\
    &= \hat{q} (x_{t+1}|x_{t}, y) \frac{\hat{q}(y|x_{t})}{\hat{q}(x_{t+1}|x_{t})} \\
    &= \hat{q} (x_{t+1}|x_{t}) \frac{\hat{q}(y|x_{t})}{\hat{q}(x_{t+1}|x_{t})}\\
    &= \hat{q}(y|x_{t}) \\
    \end{align}
    $$
    • 其他补充说明 ：因为前向过程与条件无关 ，可以理解为已知 \(x_t\) 时，条件 \(y\) 就与反向过程的前一步 \(x_{t+1}\) 无关了，故可以消掉 \(x_{t+1}\) ；但由于反向过程依赖条件 \(y\)，不能消掉 \(x_t\)，即 \(\hat{q}(y|x_t, x_{t+1}) \neq \hat{q}(y|x_{t+1})\)，可理解为在相同的 \(x_{t+1}\) 下， \(x_t\) 与条件 \(y\) 相关（ \(x_{t+1}\) 想通的条件下不同的条件 \(y\) 会生成不同的 \(x_t\) ）
  • 关于 \(\hat{q}(x_{t}|x_{t+1}) = q(x_{t}|x_{t+1})\) 的理解：，该式子的证明如下：
    $$
    \begin{align}
    \hat{q}(x_{t}|x_{t+1}) &= \frac{\hat{q}(x_{t+1}|x_{t})\hat{q}(x_{t})}{\hat{q}(x_{t+1})} = \frac{q(x_{t+1}|x_{t})q(x_{t})}{q(x_{t+1})} = q(x_t|x_{t+1})
    \end{align}
    $$

• 接下来我们到了最终目标：推导条件扩散模型的反向过程
  $$
  \begin{align}
  \hat{q}(x_{t}|x_{t+1},y) &= \frac{\hat{q}(x_{t},x_{t+1},y)}{\hat{q}(x_{t+1},y)} = \frac{\hat{q}(y|x_{t},x_{t+1})\hat{q}(x_{t}|x_{t+1})\hat{q}(x_{t+1})}{\hat{q}(y|x_{t+1})\hat{q}(x_{t+1})} \\
  &= \frac{\hat{q}(y|x_{t},x_{t+1})\hat{q}(x_{t}|x_{t+1})}{\hat{q}(y|x_{t+1})} \\
  &= \frac{\hat{q}(y|x_{t})\hat{q}(x_{t}|x_{t+1})}{\hat{q}(y|x_{t+1})} \\
  &= \frac{q(x_{t}|x_{t+1})\hat{q}(y|x_{t})}{\hat{q}(y|x_{t+1})} \\
  \end{align}
  $$

• 至此，在已知 \(x_{t+1}\) 时，在条件 \(y\) 下，为了采样生成 \(x_t\)，我们可以按照带条件的后向过程的概率 \(\hat{q}(x_{t}|x_{t+1},y) = \frac{q(x_{t}|x_{t+1})\hat{q}(y|x_{t})}{\hat{q}(y|x_{t+1})}\) 采样来实现。其中 \(\hat{q}(y|x_{t+1})\) 与 \(x_t\) 无关，可以设置为常数；于是可按照下面的形式采样(这里使用 \(\frac{1}{Z}\) 更容易理解)：
  $$ x_t \sim \frac{1}{Z} q(x_{t}|x_{t+1})\hat{q}(y|x_{t}) $$

  • 具体场景下， \(q(x_{t}|x_{t+1})\) 是无条件的Diffusion后向过程，可以通过无条件的Diffusion网络 \(p_\theta(x_{t}|x_{t+1})\) 来实现； \(\hat{q}(y|x_{t})\) 则可通过在扰动后的数据集 \(x_t \sim q(x_t)\) 上训练一个分类器（Classifier）来实现；故最终采样形式可以表示如下形式：

Classifier Guidance DDPM

• 本小节相关推导参考自：Diffusion Models Beat GANs on Image Synthesis, OpenAI, 2021——Supplemental，论文附录有其他相关推导可做参考

• 推导过程：

  
  • 推导过程中使用到一个技巧，在高斯分布相关的推导中，将指数函数临时取对数来进行推导，推导完成后得到的仍然可以看做一个高斯分布的指数部分（在论文附录中提供的另一种推导方法没有使用到这个点）

• 其他说明：在Diffusion Models Beat GANs on Image Synthesis, OpenAI, 2021中，作者发现，在分类器上增加一个梯度缩放参数 \(s\) （gradient scale \(s\) ）可以更好的调节生成效果：
  $$
  \begin{equation}\boldsymbol{x}_{t-1} = \boldsymbol{\mu}(\boldsymbol{x}_t) \color{red}{+} {\color{red}{\underbrace{ \color{black}{s} \sigma_t^2 \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)}_{\text{新增项}}}} + \sigma_t\boldsymbol{\varepsilon},\quad \boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})\end{equation}
  $$

  • 当 \(s > 1\) 时，生成过程中将更多由Classifier主导，提升生成结果和条件 \(y\) 的相关性，降低生成结果的多样性（没有改变方差，实际上多样性不会变化吧？）；反之，则会降低生成结果的相关性，增加多样性
  • 关于 \(s\) 这个参数还有更多理解和推导，讨论详情可见：生成扩散模型漫谈（九）：条件控制生成结果：
    • \(s\) 可以理解为在概率函数上的指数，用来控制图片的聚焦程度， \(s\) 越大，下面的条件概率 \(\tilde{p}(\boldsymbol{y}|\boldsymbol{x}_t)\) 越趋近于one-hot
      $$\begin{equation}\tilde{p}(\boldsymbol{y}|\boldsymbol{x}_t) = \frac{p^{s}(\boldsymbol{y}|\boldsymbol{x}_t)}{Z(\boldsymbol{x}_t)},\quad Z(\boldsymbol{x}_t)=\sum_{\boldsymbol{y}} p^{s}(\boldsymbol{y}|\boldsymbol{x}_t)\end{equation}$$

• 其他证明方式见附录

Classifier Guidance DDIM

• 本小节相关推导参考自：Diffusion Models Beat GANs on Image Synthesis, OpenAI, 2021——Supplemental，论文附录有其他相关推导可做参考

• 推导过程：

  
  • 上图第一个公式中的梯度证明见论文的“前置推导”
  • 推导过程中使用了一个技巧，通过求解梯度的相似形式来对比得到最终结果
  • 公式(58)中 \(p_\theta(x_t)p_\phi(y|x_t)\) 没有直接来源，但可以从下面的推导看出，\(\nabla_{x_t} \log (p_\theta(x_t)p_\phi(y|x_t)) = \nabla_{x_t} \log p(x_t|y)\)
    $$
    \begin{align}
    \nabla_{x_t} \log p(x_t|y) &= \nabla_{x_t} \log p(x_t) +\nabla_{x_t} \log p(y|x_t) - \nabla_{x_t} \log p(y) \\
    &= \nabla_{x_t} \log p(x_t) +\nabla_{x_t} \log p(y|x_t) \\
    &= \nabla_{x_t} \log (p(x_t)p(y|x_t)) \\
    \end{align}
    $$

• 其他说明，这里也可以在分类器的梯度上增加一个权重 \(w\)，调节条件相关性和多样性：
  $$ \hat{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) = \boldsymbol{\epsilon}_\theta(x_t, t) - \sqrt{1 - \bar{\alpha}_t} w \nabla_{\mathbf{x}_t} \log p_\phi(y \vert \mathbf{x}_t) $$

• 其他证明方式见附录

基于Classifier Guidance的DDPM和DDIM的采样过程

• Classifier Guidance DDPM和DDIM下伪代码如下：

  
  • 其中 \(\Sigma\) 表示协方差矩阵，有不同的实现方式，IDDPM中，使用了 \(\mathbf{\Sigma}_\theta(\mathbf{x}_t, t) = \exp(\mathbf{v} \log \beta_t + (1-\mathbf{v}) \log \tilde{\beta}_t)\)， \(\mathbf{v}_{\theta}(x_t, t)\) 维度是与 \(\mathbf{x}_t\) 相同的，（详情见improved_diffusion源码:模型定义和improved_diffusion源码:向量使用）
  • 问题：矩阵 \(\Sigma\) 和梯度向量相乘的结果是向量，这里梯度向量是列向量才能相乘

---

Classifier-free Guidance

• Classifier-free Guidance的方法直接讲条件添加到原始Diffusion模型中，从而使得模型在训练时就能感知到条件，因此，在采样（生成）时，不需要额外训练Classifier了
• 一个直观的解释是：
  • 在原始分布 \(p(x_{t-1}|x_t)\) 增加条件 \(y\)，则原始分布变成 \(p(x_{t-1}|x_t,y)\)
    $$
    \begin{equation}
    p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{y}) = \mathcal{N}(\boldsymbol{x}_{t-1}; \boldsymbol{\mu}(\boldsymbol{x}_t, \boldsymbol{y}),\sigma_t^2\boldsymbol{I})
    \end{equation}$$
  • 接着，在训练时，噪声网络上也增加输入 \(y\)，即 \(\epsilon_\theta(x_t, y, t)\)
  • 最后，可以使用下面的式子来实现加权
    $$\begin{equation}\tilde{\boldsymbol{\epsilon}}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, \boldsymbol{y}, t) = (1 + w)\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, \boldsymbol{y}, t) - w \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\end{equation}
    $$
    • 其中，无条件的 \(\epsilon_\theta(x_t, t)\) 通过设置一个特定的条件 \(\varnothing\) 获得，即 \(\epsilon_\theta(x_t, t) = \epsilon_\theta(x_t, \varnothing, t)\)
    • \(w\) 也叫做 guidance scale，用于调整生成条件相关性和多样性
• 接下来我们介绍详细推导过程，首先，回顾条件概率转换：
  $$
  \begin{align}
  \nabla_{x_t} \log p(x_t|y) &= \nabla_{x_t} \log \Big( \frac{p(x_t)p(y|x_t)}{p(y)}\Big) \\
  &= \nabla_{x_t} \log p(x_t) + \nabla_{x_t} \log p(y|x_t) - \nabla_{x_t} \log p(y) \\
  &= \underbrace{\nabla_{x_t} \log p(x_t)}_{\text{unconditional score}} + \underbrace{\nabla_{x_t} \log p(y|x_t)}_{\text{classifier gradient}}
  \end{align}
  $$
• 于是有：
  $$ \nabla_{\mathbf{x}_t} \log p(y \vert \mathbf{x}_t) = \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t \vert y) - \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t) $$
• 进一步地，有（以下推导来自What are Diffusion Models?的推导）：
  $$
  \begin{aligned}
  \nabla_{\mathbf{x}_t} \log p(y \vert \mathbf{x}_t)
  &= \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t \vert y) - \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t) \\
  &= - \frac{1}{\sqrt{1 - \bar{\alpha}_t}}\Big( \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big) \\
  \end{aligned}
  $$
• 回顾DDIM Classifier Guidance里面的推导有：
  $$
  \begin{aligned}
  \bar{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t, y)
  &= \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - \sqrt{1 - \bar{\alpha}_t} \ w \nabla_{\mathbf{x}_t} \log p(y \vert \mathbf{x}_t) \\
  &= \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) + w \big(\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \big) \\
  &= (w+1) \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - w \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)
  \end{aligned}
  $$
• 采样时，利用将DDPM或者DDIM中的 \(\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\) 替换为 \(\bar{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t, y)\)， 正常采样即可
• 总结一下，Classifier-free Guidance方法的训练流程和采样流程如下：

---

Classifier-free Guidance和Classifier Guidance谁更好？

• GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models, OpenAI, 2022对CLIP Guidance和Classifier-free Guidance两种策略进行实验，结果发现Classifier-free Guidance效果更好

  The guided diffusion model, GLIDE (Nichol, Dhariwal & Ramesh, et al. 2022), explored both guiding strategies, CLIP guidance and classifier-free guidance, and found that the latter is more preferred. They hypothesized that it is because CLIP guidance exploits the model with adversarial examples towards the CLIP model, rather than optimize the better matched images generation.

---

附录：DDPM和DDIM加入条件以后的采样形式为什么不同呢？

• 可以证明，在设置DDPM中协方差矩阵 \(\Sigma\) 使用固定值后，DDPM和DDIM的Classifier Guidance 形式基本是非常相似的，都可以看做是用梯度 \(\nabla_{x_t}\log p_\phi(y|x_t)\) 对 \(\mathbf{\epsilon}_\theta(x_t, t)\) 进行修正【有时间时可以详细推导一下】

• 补充对比：

  • 带条件的训练形式：

    

  • 原始DDPM采样形式
    $$ x_{t-1} = \frac{1}{\sqrt{\alpha_t}}\Big( x_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta(x_t, t) \Big) + \sigma_t z $$

  • 原始DDIM采样形式
    $$x_s = \sqrt{\bar{\alpha}_s}\left(\frac{x_k-\sqrt{1-\bar{\alpha}_k}\epsilon_{\theta}(x_k,k)}{\sqrt{\bar{\alpha}_k}}\right) + \sqrt{1-\bar{\alpha}_s-a_1\sigma_k^2}\epsilon_{\theta}(x_k,k) + a_2\sigma_k \epsilon$$

---

附录：其他推导-Classifier Guidance DDPM

• 下面的推导参考苏神生成扩散模型漫谈（九）：条件控制生成结果的推导
• 在推导过程中，在原始分布 \(p(x_{t-1}|x_t)\) 增加条件 \(y\)，则原始分布变成 \(p(x_{t-1}|x_t,y)\)
• 根据贝叶斯公式有：
  $$\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{y}) = \frac{p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)p(\boldsymbol{y}|\boldsymbol{x}_{t-1}, \boldsymbol{x}_t)}{p(\boldsymbol{y}|\boldsymbol{x}_t)}\label{eq:bayes-1}\end{equation}$$
• 由于前向过程与条件无关， \(x_t\) 是由 \(x_{t-1}\) 加上与条件无关的噪声得到的，所以 \(p(\boldsymbol{y}|\boldsymbol{x}_{t-1}, \boldsymbol{x}_t) = p(\boldsymbol{y}|\boldsymbol{x}_{t-1})\)，这在前文已经得到证明
• 于是有：
  $$ \begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{y}) = \frac{p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)p(\boldsymbol{y}|\boldsymbol{x}_{t-1})}{p(\boldsymbol{y}|\boldsymbol{x}_t)} = p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \exp({\log p(\boldsymbol{y}|\boldsymbol{x}_{t-1}) - \log p(\boldsymbol{y}|\boldsymbol{x}_t)})\label{eq:bayes-2}\end{equation} $$
• 接下来我们要求解 \(\log p(\boldsymbol{y}|\boldsymbol{x}_{t-1}) - \log p(\boldsymbol{y}|\boldsymbol{x}_t)\) 这一项，首先做一下近似，当 \(T\) 足够大时，有 \(x_t\) 和 \(x_{t-1}\) 非常接近，故而可以用泰勒展开来近似：
  $$ \begin{equation}\log p(\boldsymbol{y}|\boldsymbol{x}_{t-1}) - \log p(\boldsymbol{y}|\boldsymbol{x}_t)\approx (\boldsymbol{x}_{t-1} - \boldsymbol{x}_t)\cdot\nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)\end{equation}$$
  • 其中 \(\nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)\) 是一种简写形式，实际上有 \(\nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t) = \nabla_{\boldsymbol{x}} \log p(\boldsymbol{y}|\boldsymbol{x})\vert_{\boldsymbol{x} = \boldsymbol{x}_t}\)，表示函数在 \(\boldsymbol{x}_t\) 处的梯度
• 假设 \(p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)=\mathcal{N}(\boldsymbol{x}_{t-1};\boldsymbol{\mu}(\boldsymbol{x}_t),\sigma_t^2\boldsymbol{I})\propto \exp({-\frac{\Vert \boldsymbol{x}_{t-1} - \boldsymbol{\mu}(\boldsymbol{x}_t)\Vert^2}{2\sigma_t^2}})\)，则有
  $$
  \begin{aligned}
  p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{y}) =&\ p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \exp({\log p(\boldsymbol{y}|\boldsymbol{x}_{t-1}) - \log p(\boldsymbol{y}|\boldsymbol{x}_t)}) \\
  \propto&\ \exp\Big({-\frac{\Vert \boldsymbol{x}_{t-1} - \boldsymbol{\mu}(\boldsymbol{x}_t)\Vert^2}{2\sigma_t^2} + (\boldsymbol{x}_{t-1} - \boldsymbol{x}_t)\cdot\nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)}\Big) \\
  \propto&\ \exp\Big(\frac{-\Vert \boldsymbol{x}_{t-1} - \boldsymbol{\mu}(\boldsymbol{x}_t) - \sigma_t^2 \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)\Vert^2}{2\sigma_t^2}\Big)
  \end{aligned}
  $$
  • 其中 \(\exp\Big({-\frac{\Vert \boldsymbol{x}_{t-1} - \boldsymbol{\mu}(\boldsymbol{x}_t)\Vert^2}{2\sigma_t^2} + (\boldsymbol{x}_{t-1} - \boldsymbol{x}_t)\cdot\nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)}\Big) \propto\ \exp\Big(\frac{-\Vert \boldsymbol{x}_{t-1} - \boldsymbol{\mu}(\boldsymbol{x}_t) - \sigma_t^2 \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)\Vert^2}{2\sigma_t^2}\Big) \) 是指数中配方后，略去了与 \(\boldsymbol{x}_{t-1}\) 无关的项，所以使用的是“正比于”（在指数部分，包括 \(\boldsymbol{x}_{t}\) 也与 \(\boldsymbol{x}_{t-1}\) 无关，可以略去，因为分布仅留下与 \(\boldsymbol{x}_{t-1}\) 相关的部分即可，注：标准的正太分布概率密度函数为 \(p(x) = \frac{1}{\sqrt{2\pi}\sigma} \exp(-\frac{(x-\mu)^2}{2\sigma^2}) \propto \exp(-\frac{(x-\mu)^2}{2\sigma^2})\)，只关注与 \(x\) 有关的项即可）
• 将上面的形式转换成正太分布，有：
  $$ \mathcal{N}(\boldsymbol{x}_{t-1};\boldsymbol{\mu}(\boldsymbol{x}_t) + \sigma_t^2 \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t),\sigma_t^2\boldsymbol{I})$$
• 也就是说按照下面形式采样即可实现条件的加入：
  $$
  \begin{equation}\boldsymbol{x}_{t-1} = \boldsymbol{\mu}(\boldsymbol{x}_t) \color{red}{+} {\color{red}{\underbrace{\sigma_t^2 \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)}_{\text{新增项}}}} + \sigma_t\boldsymbol{\varepsilon},\quad \boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})\end{equation}
  $$
• 在原始论文Diffusion Models Beat GANs on Image SynthesisClassifier Guidance DDPM的采样形式为：
  $$\begin{equation}\sigma_t^2 \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)|_{\boldsymbol{x}_t=\boldsymbol{\mu}(\boldsymbol{x}_t)}\end{equation}$$
  • 这个形式与论文推导结果不同，生成扩散模型漫谈（九）：条件控制生成结果中指出两者差不多（问题：零阶近似是指在 \(x_t=\mu(x_t)\) 处进行泰勒展开吗？需要进一步理解）：

    论文中梯度项在 \(\boldsymbol{\mu}(\boldsymbol{x}_t)\) 处的结果而非 \(\boldsymbol{x}_t\) 处，而一般情况下 \(\boldsymbol{\mu}(\boldsymbol{x}_t)\) 的零阶近似正是 \(\boldsymbol{x}_t\)，所以两者结果是差不多的

  • 理解：梯度的位置决定了建模价值模型时使用 \(\boldsymbol{x}_t\) 还是 \(\boldsymbol{\mu}(\boldsymbol{x}_t)\)，直观上理解，应该是在 \(\boldsymbol{\mu}(\boldsymbol{x}_t)\) 上进行梯度偏移，所以应该是在 \(\boldsymbol{\mu}(\boldsymbol{x}_t)\) 的梯度才对
    • Diffuser中代码实现比较奇怪，与论文伪代码不同：这部分实现的Diffuser详细代码可见Diffuser源码-采样函数
    • 其他代码实现参考：

---

附录：其他推导-Classifier Guidance DDIM

本小节推导主要参考自What are Diffusion Models?

• 由[(NCSN)Generative Modeling by Estimating Gradients of the Data Distribution, Stanford, 2020]和[Score-based generative modeling through stochastic differential equations, Stanford & Google, 2021]可以知道，只需要求得目标分布的对数概率梯度即可按照该梯度进行采样，原始分布的对数概率梯度为（详细证明见论文“前置推导”）:
  $$ \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) = - \frac{1}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) $$
• 增加条件以后的联合概率梯度为（此时的 \(\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t, y)\) 与 \(\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t\vert y)\) 是等价的，因为 \(\nabla_{\mathbf{x}_t}\log q(y)=0\) ）：
  $$
  \begin{aligned}
  \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t, y)
  &= \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) + \nabla_{\mathbf{x}_t} \log q(y \vert \mathbf{x}_t) \\
  &\approx - \frac{1}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) + \nabla_{\mathbf{x}_t} \log f_\phi(y \vert \mathbf{x}_t) \\
  &= - \frac{1}{\sqrt{1 - \bar{\alpha}_t}} (\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) - \sqrt{1 - \bar{\alpha}_t} \nabla_{\mathbf{x}_t} \log f_\phi(y \vert \mathbf{x}_t))
  \end{aligned}
  $$
• 对照两个概率的梯度形式，可以得到 \(\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\) 变成如下形式即可将 \(q(\mathbf{x}_t)\) 替换为带条件的 \(q(\mathbf{x}_t, y)\)：
  $$\bar{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) = \boldsymbol{\epsilon}_\theta(x_t, t) - \sqrt{1 - \bar{\alpha}_t} \nabla_{\mathbf{x}_t} \log f_\phi(y \vert \mathbf{x}_t)$$
• 为了权衡Classifier Guidance的强度，可以添加一个权重 \(w\)：
  $$ \bar{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) = \boldsymbol{\epsilon}_\theta(x_t, t) - \sqrt{1 - \bar{\alpha}_t} w \nabla_{\mathbf{x}_t} \log f_\phi(y \vert \mathbf{x}_t) $$

---

附录：问题汇总

• Classifier Guidance方法在训练Classifier时，需要包含随机扰动后的数据吧？
• DDPM推导时（附录和正文）得到了两种不同的梯度位置 \(x_t\) 和 \(\mu_t\)，实现时应该是用哪个呢？
• Classifier Guidance方法训练过程中有哪些需要注意的？
• Classifier-free Guidance方法训练过程中有哪些需要注意的？