Paper Summary
- 已有结论:模型越大,模型效果上限越高
- 模型容量超过单个加速器(GPU 或 TPU)的内存限制时,需要开发特殊算法和工程设计(这些解决方案通常是针对特定架构设计的,难以迁移)
- 论文提出了 GPipe
- 是一个 流水线并行(Pipeline Parallelism)库
- 能够扩展任何可表示为层序列的网络
- 高效且任务无关的模型并行
- GPipe 将不同的层子序列分配到不同的加速器上流水执行
- 可以灵活高效地将多种网络扩展至超大规模
- GPipe 采用了一种新颖的批次分割流水线算法 ,在模型跨多个加速器分区时实现了近乎线性的加速比
- 论文通过训练两种不同任务的大规模神经网络来展示 GPipe 的优势,这些任务具有截然不同的网络架构:
- (i) 图像分类(Image Classification) :
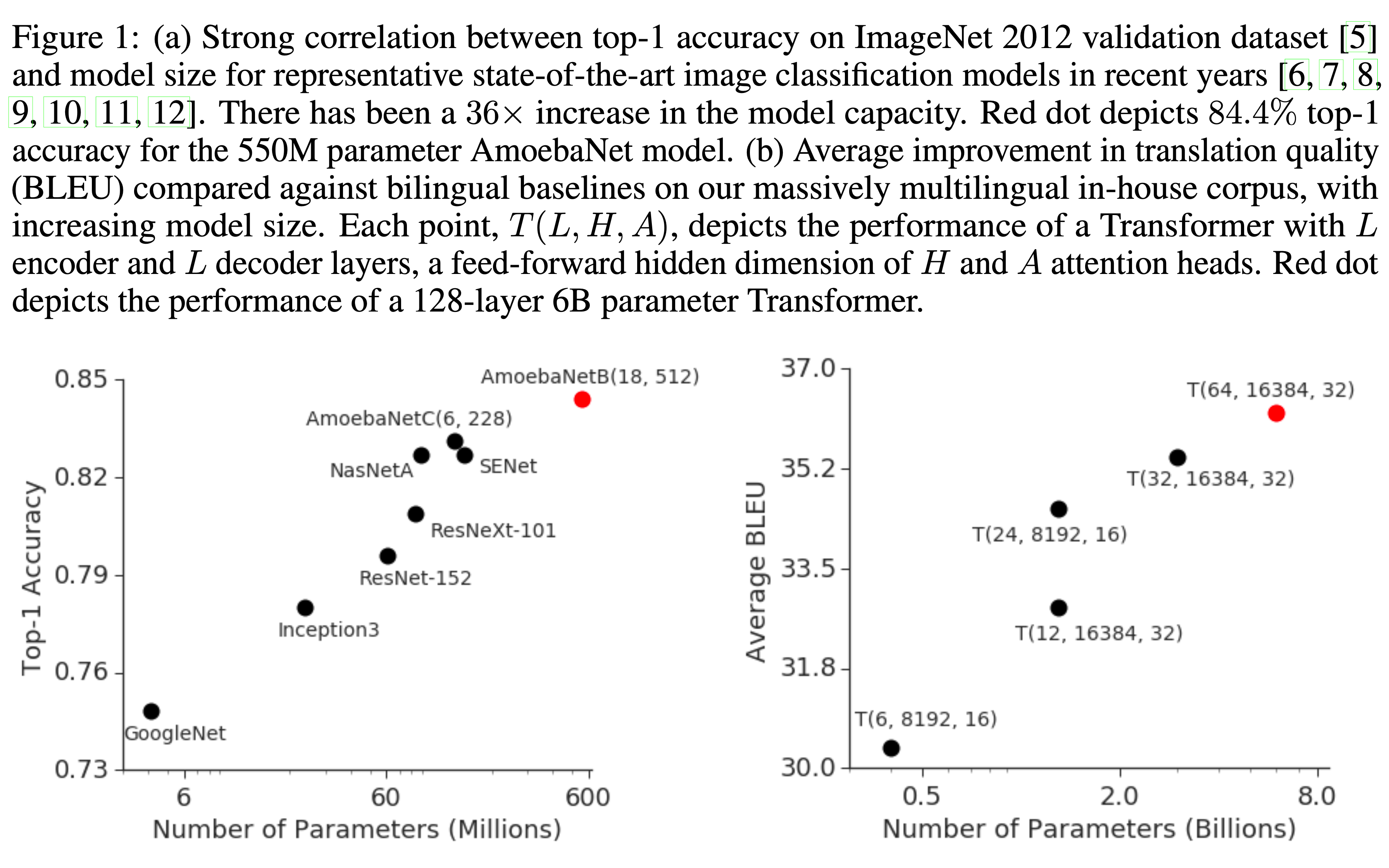
- 训练了一个包含 5.57 亿参数的 AmoebaNet 模型,在 ImageNet-2012 上达到了 84.4% 的 top-1 准确率;
- (ii) 多语言神经机器翻译(Multilingual Neural Machine Translation) :
- 在涵盖 100 多种语言的语料库上训练了一个包含 60 亿参数、128 层的 Transformer 模型,其质量优于所有双语模型
- 实验表明,该模型在 100 种语言对上的性能优于单独训练的 3.5 亿参数双语 Transformer Big 模型 (2017)
- (i) 图像分类(Image Classification) :
- 评价:
- Google 出品,必属精品,GPipe 已成为各种框架的加速选项
Introduction and Discussion
- 近年来深度学习的巨大进步部分归功于神经网络有效容量扩展方法的发展
- 这一趋势在图像分类任务中最为明显,例如 ImageNet 的准确率随着模型容量的增加而提升(图 0(a))
- 类似现象也出现在自然语言处理领域(图 0(b)),简单的浅层句子表示模型 (2017; 2018) 被更深、更大的模型 (2018; 2019) 超越
- 更大的模型为多个领域带来了显著的性能提升,但扩展神经网络也带来了实际的挑战
- 硬件限制(包括加速器(GPU 或 TPU)的内存和通信带宽)迫使用户将大模型分割为多个分区,并将不同分区分配到不同的加速器上
- 高效的模型并行算法设计和实现极为困难,通常需要用户在扩展容量、灵活性(或对特定任务和架构的适应性)以及训练效率之间做出艰难抉择
- 大多数高效的模型并行算法都是针对特定架构和任务的
- 随着深度学习应用的不断增加,对可靠且灵活的基础设施的需求日益增长
- 为解决这些挑战,论文提出了 GPipe,一个灵活的库,支持高效训练大规模神经网络
- GPipe 通过将模型分配到不同加速器上并支持在每个加速器上重新计算中间结果 (2000; 2016),能够突破单个加速器的内存限制 ,扩展任意深度神经网络架构
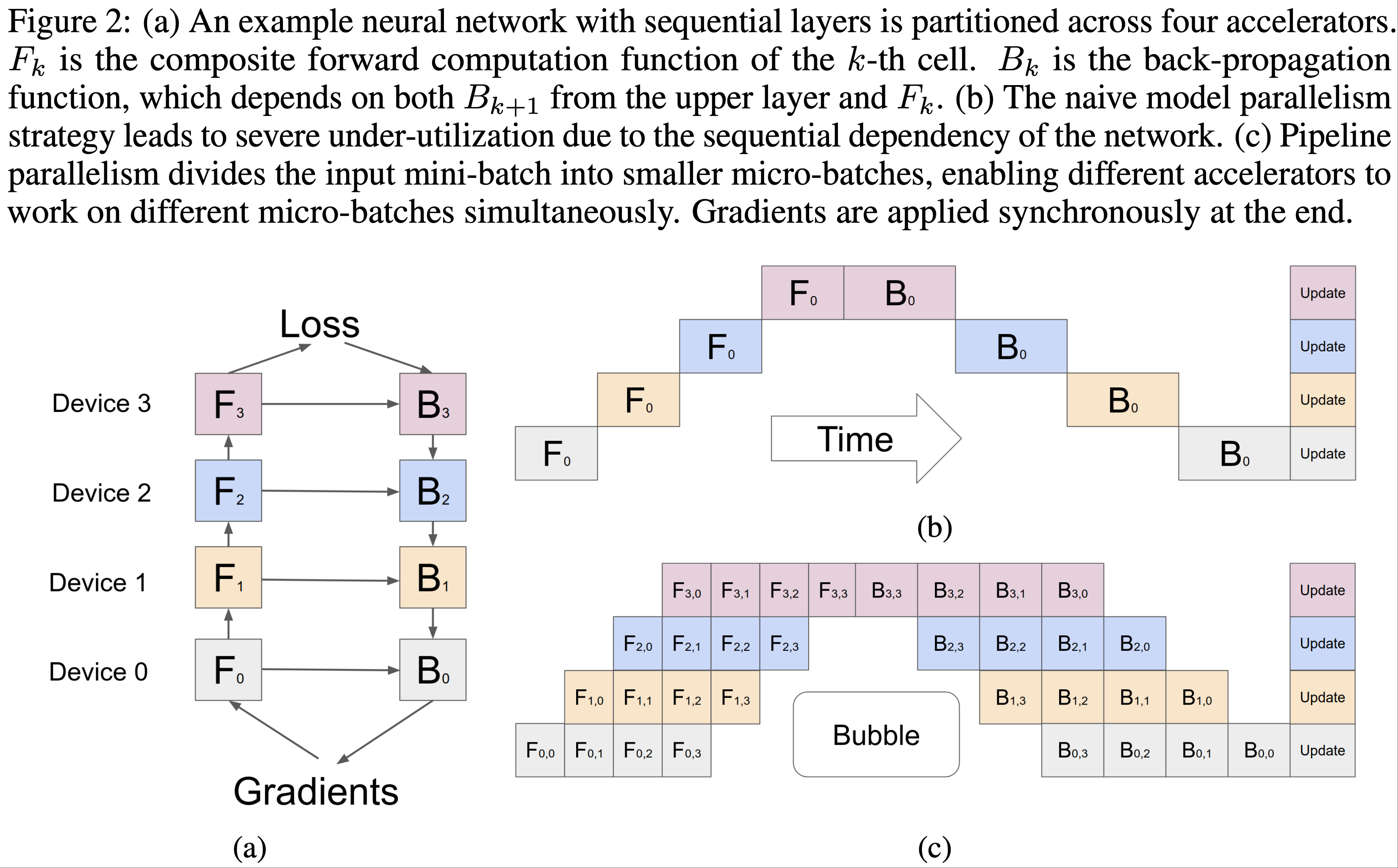
- GPipe 中,每个模型可以表示为层序列,连续的层组可以划分为单元(cell),每个单元分配到单独的加速器上
- 基于这种分区设置,论文提出了一种新颖的批次分割流水线并行算法
- 首先,论文将训练样本的小批次(mini-batch)分割为更小的微批次(micro-batch) ,然后在单元上流水执行每组微批次
- 训练采用同步小批次梯度下降,梯度在所有微批次中累积,并在小批次结束时统一更新
- GPipe 的梯度更新与分区数量无关,保证了训练的一致性 ,使研究人员能够通过部署更多加速器轻松训练更大的模型
- GPipe 还可以与数据并行结合,进一步扩展训练规模
GPipe 库(The GPipe Library)
- 论文现在描述 GPipe 的接口和主要设计特性
- 该开源库是在 Lingvo(2019)框架下实现的
- GPipe的核心设计特性具有通用性,可以为其他框架(2017; 2018; 2019)实现
Interface
- 任何深度神经网络都可以定义为一个由 \(L\) 个层组成的序列
- 每个层 \(L_i\) 由一个前向计算函数 \(f_i\) 和对应的参数集 \(w_i\) 组成
- GPipe 允许用户指定一个可选的计算成本估计函数 \(c_i\)
- 在给定分区数量 \(K\) 的情况下,可以将 \(L\) 个层的序列划分为 \(K\) 个复合层或单元(cell)
- 设复合单元 \(p_k\) 由层 \(i\) 到层 \(j\) 之间的连续层组成
- 与复合单元 \(p_k\) 对应的参数集等价于 \(w_i, w_{i+1}, \ldots, w_j\) 的并集,其前向函数为 \(F_k = f_j \circ \ldots \circ f_{i+1} \circ f_i\)
- 对应的反向传播函数 \(B_k\) 可以通过自动符号微分从 \(F_k\) 计算得到
- 成本估计器 \(C_k\) 设置为 \(\Sigma^{j}_{l=i}c_l\)
- GPipe 的接口非常简单直观,要求用户指定:
- (i) 模型分区数量 \(K\)
- (ii) 微批次(micro-batch)数量 \(M\)
- (iii) 定义模型的 \(L\) 个层的序列和定义
- 具体示例请参见补充材料
Algorithm
- 当用户通过模型参数 \(w_i\) 、前向计算函数 \(f_i\) 和成本估计函数 \(c_i\) 定义网络中层的序列后,GPipe 将网络划分为 \(K\) 个单元,并将第 \(k\) 个单元放置在第 \(k\) 个加速器上
- 在分区边界处自动插入通信原语,以允许相邻分区之间的数据传输
- 分区算法最小化所有单元的估计成本方差,以通过同步所有分区的计算时间来最大化流水线的效率
- 在前向传播期间:
- GPipe 首先将每个大小为 \(N\) 的小批次(mini-batch)划分为 \(M\) 个相等的微批次
- 这些微批次通过 \(K\) 个加速器进行流水线处理
- 在反向传播期间:
- 每个微批次的梯度基于前向传播使用的相同模型参数计算
- 在每个小批次结束时,所有 \(M\) 个微批次的梯度被累积并应用于更新所有加速器上的模型参数
- 这一系列操作如图1(c)所示
- 如果网络中使用了 Batch Normalization(BatchNorm),则训练期间输入的充分统计量(Sufficient Statistic)是在每个微批次上计算的 ,并在需要时在副本上计算(2017)
- 论文还跟踪整个小批次上充分统计量的移动平均值,以用于评估
- 注:充分统计量的介绍见附录
- 理解:使用 GPipe 时,对 BatchNorm 不太友好,因为太小的微批次会导致训练时使用的均值和方差波动太大(注:BatchNorm 训练时始终使用的是当前微批次的统计值)
- 论文还跟踪整个小批次上充分统计量的移动平均值,以用于评估
Performance Optimization
- 为了减少激活内存需求,GPipe 支持重计算(re-materialization)(2016)
- 在前向计算期间,每个加速器仅存储分区边界处的输出激活
- 在反向传播期间,第 \(k\) 个加速器重新计算复合前向函数 \(F_k\)
- 峰值激活内存需求减少到
$$O(N + \frac{L}{K} \times \frac{N}{M})$$- 其中 \(\frac{N}{M}\) 是微批次大小
- \(\frac{L}{K}\) 是每个分区的层数
- 如果不使用重计算和分区,内存需求将为
$$ O(N \times L)$$- 因为计算梯度 \(b_i\) 需要上层梯度 \(b_{i+1}\) 和缓存的激活 \(f_i(x)\)
- 如图2(c)所示,分区会在每个加速器上引入一些空闲时间,论文称之为气泡(bubble)开销
- 这种气泡时间在微步骤数量 \(M\) 上平均为 \(O(\frac{K-1}{M+K-1})\)
- 在论文的实验中,当 \(M \geq 4 \times K\) 时,气泡开销可以忽略不计
- 这部分也是因为反向传播期间的重计算可以更早调度,而无需等待来自上层的梯度
- GPipe 还引入了低通信开销,因为论文只需在加速器之间传递分区边界处的激活张量
- 即使在没有高速互连的加速器上,也可以实现高效的扩展性能
- 图2(c)假设分区是均匀平衡的
- 但不同层的内存需求和计算浮点操作往往非常不平衡
- 在这种情况下,不完美的分区算法可能导致负载不平衡
- 更好的分区算法可能会在论文的启发式方法基础上进一步提升性能
Performance Analyses
- 通过两种模型架构评估 GPipe 的性能(研究它们的可扩展性、效率和通信成本):
- AmoebaNet(2018)卷积模型
- Transformer(2017)Sequence2Sequence模型
- 论文预计重计算和流水线并行都会有益于内存利用,从而使训练巨型模型成为可能
- 在表1中,报告了在合理大的输入大小下 GPipe 可以支持的最大模型大小
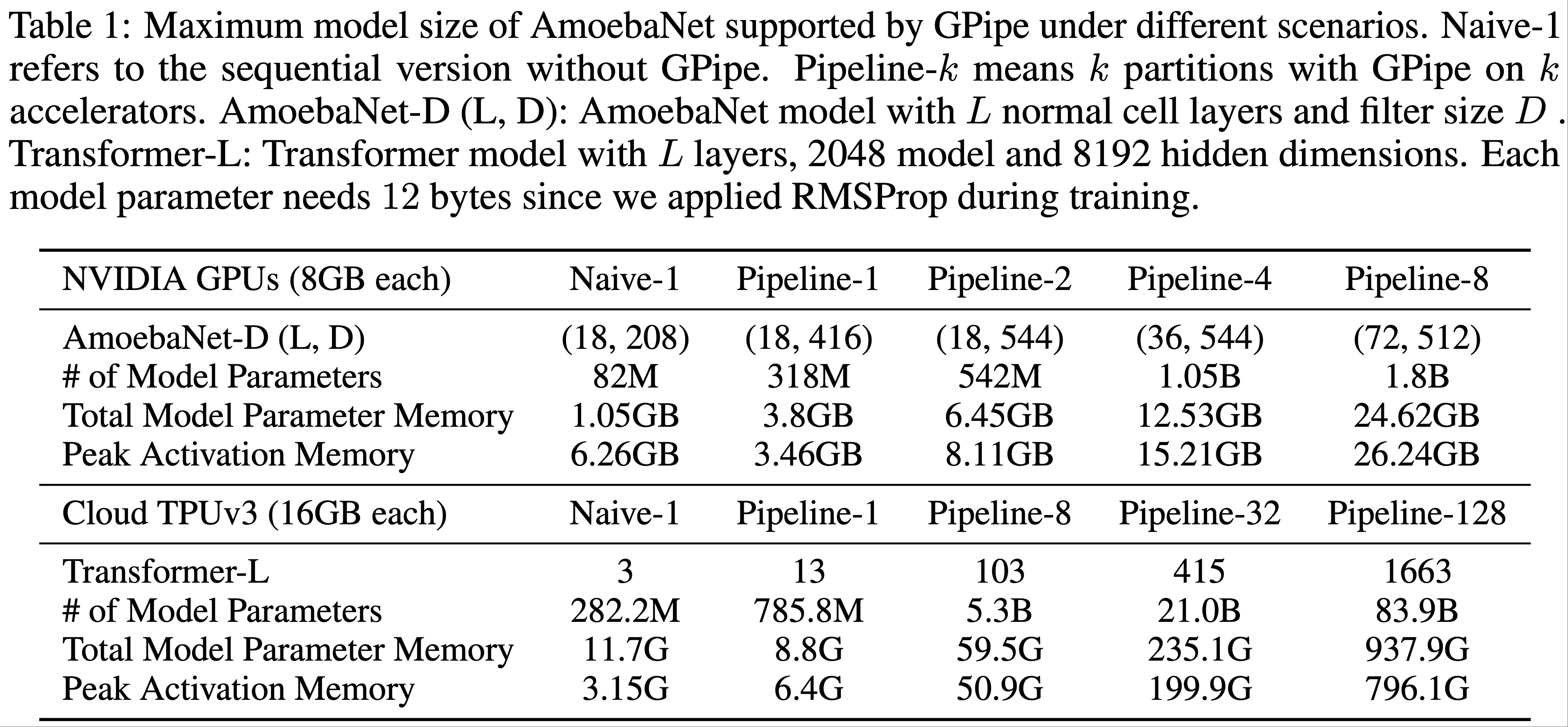
- 对于 AmoebaNet 模型 ,在每个加速器内存为 8GB 的 Cloud TPUv2 上运行实验
- 使用固定的输入图像大小 \(224 \times 224\) 和小批次大小 128
- 在没有 GPipe 的情况下,受设备内存限制,单个加速器最多可以训练 8200万 参数的 AmoebaNet,
- 利用反向传播中的重计算和批次分割:
- GPipe 将中间激活内存需求从 6.26GB 减少到 3.46GB,从而在单个加速器上支持 3.18亿 参数的模型
- 通过模型并行
- 能够在 8 个加速器上将 AmoebaNet 扩展到 18亿 参数 ,比不使用 GPipe 时多25倍
- 在这种情况下,最大模型大小没有完全线性扩展,因为 AmoebaNet 中不同层的模型参数分布不平衡
- 对于 Transformer 模型 ,每个加速器核心内存为 16GB 的 Cloud TPUv3 训练
- 模型配置如下:
- 使用固定的词汇大小 32k
- 序列长度 1024 和批次大小 32
- 每个Transformer层的模型维度为2048
- 前馈隐藏维度为 8192
- 注意力头数量为 32
- 注:论文通过改变层数量来扩展模型
- 重计算允许在单个加速器上训练比原来大 2.7 倍的模型
- 通过 128 个分区,GPipe 可以将 Transformer 扩展到 839亿 参数,比单个加速器上可能的规模增加 298 倍
- 与 AmoebaNet 不同,Transformer 的最大模型大小随加速器数量线性扩展,因为每个层具有相同数量的参数和输入大小
- 模型配置如下:
- 表2给出了 GPipe 的训练效率效率(主要评估 AmoebaNet-D 和 Transformer-48 的标准化训练吞吐量)
- 使用不同数量的分区和不同数量的微批次
- 每个分区分配给一个独立的加速器
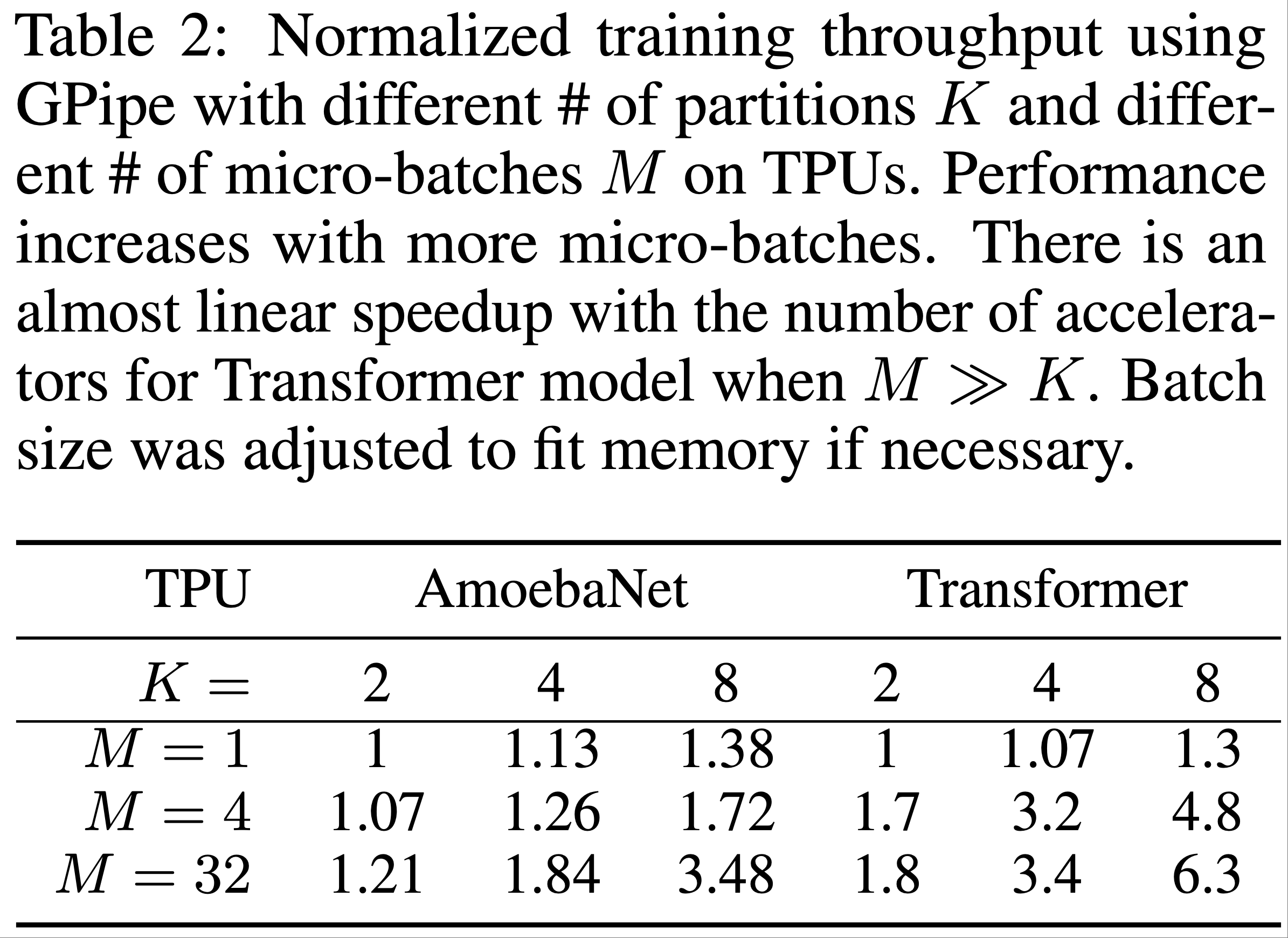
- 一些结论:
- 当微批次数量 \(M\) 至少是分区数量 \(K\) 的 4 倍时,气泡开销几乎可以忽略不计
- 换算一下可以知道,就以 4 倍为例
- 气泡量是(注:气泡总数仅与 \(K\) 有关,与 \(M\) 无关)
$$ 6 + 6 = 12 $$ - 总的小区域数量是
$$ (16+3) \times 4 = 76$$ - 气泡率约为:
$$12 / 76 \approx 15.8%$$ - 且微批次数量 \(M\) 越大,气泡开销越小,因为气泡总数是固定的
- 对于 Transformer 模型,当分区数量增加 4 倍时,速度提升 3.5 倍
- 由于计算在 Transformer 层之间均匀分布,训练吞吐量几乎随设备数量线性扩展
- 由于计算在 AmoebaNet模型上分布不平衡,训练吞吐量仅实现了次线性加速
- 当 微批次数量 \(M\) 相对较小时,气泡开销不再可以忽略
- 当 微批次数量 \(M\) 为 1 时,实际上没有流水线并行
- 论文观察到训练吞吐量相对恒定,无论使用多少加速器,这表明任何时候只有一个设备在主动计算
- 当微批次数量 \(M\) 至少是分区数量 \(K\) 的 4 倍时,气泡开销几乎可以忽略不计
- 为了测量 GPipe 的通信开销影响,论文在没有 NVLink 的多个 NVIDIA P100 GPU 的单个主机上运行实验
- 跨 GPU 的数据传输必须通过 PCI-E 进行相对较慢的设备到主机和主机到设备传输
- 微批次数量固定为 32
- 如表3所示,当分区数量从 2 增加到 8 时:
- AmoebaNet-D 的速度提升 2.7 倍
- 对于 24 层 Transformer,速度提升为 3.3 倍
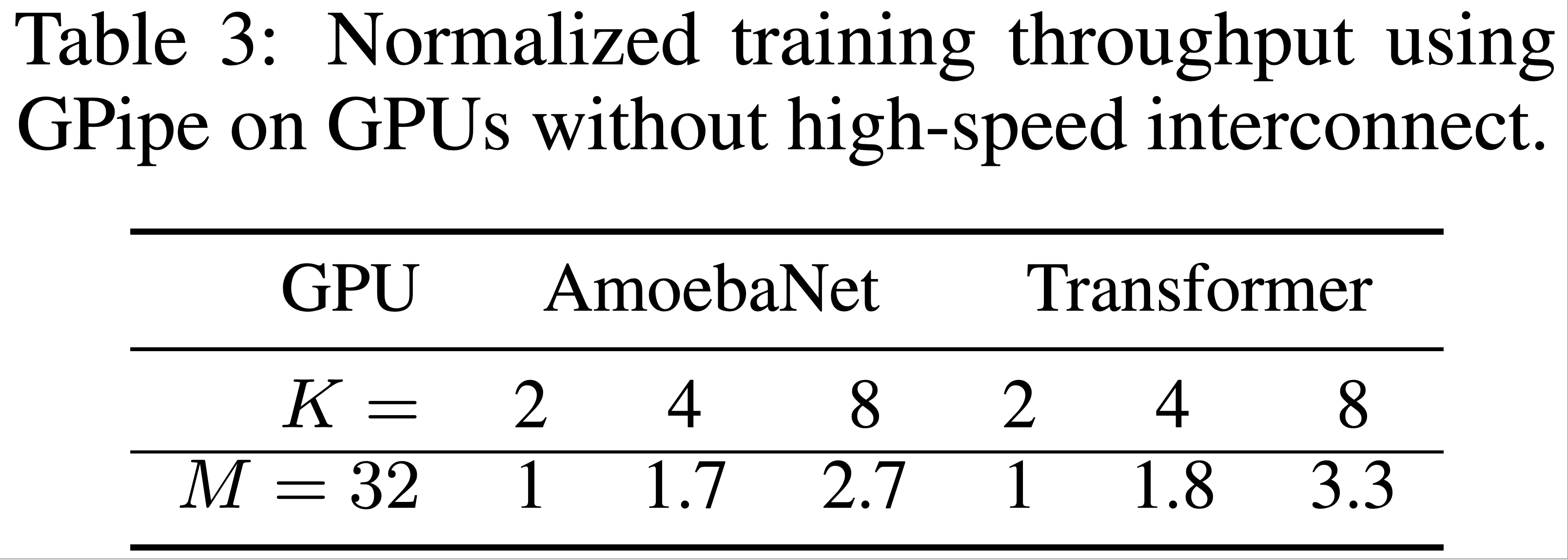
- 与配备高速互连的 TPU 上观察到的情况类似,存在类似的线性加速
- 由于 GPipe 仅在分区边界传输激活张量,设备之间的通信带宽不再是模型并行的瓶颈
Image Classification
- 作为概念验证,本节首先使用 GPipe 扩展 AmoebaNet
- 增加了 AmoebaNet 的通道数,并将输入图像尺寸扩展到 \(480 \times 480\)
- 在 ImageNet 2012 数据集上训练了这个包含 5.57 亿参数的 AmoebaNet-B 模型,使用的超参数与 (2018) 中描述的相同
- 该网络被划分为 4 个分区
- 这一单一模型在单次裁剪下实现了 84.4% 的 top-1 准确率和 97% 的 top-5 验证准确率
- 论文进一步通过迁移学习 (2022, 2023) 证明了巨型卷积网络在其他图像数据集上的有效性
- 使用预训练的 ImageNet 模型在多个目标数据集上进行微调,这些数据集涵盖了一般分类到细粒度分类任务
- 将最后一个 softmax 分类层的输出单元数更改为目标数据集的类别数,并随机初始化新的 softmax 层
- 其余所有层均从 ImageNet 预训练中初始化
- 训练期间,输入网络的图像被调整为 \(480 \times 480\) ,并随机水平翻转,同时使用 cutout (2017) 进行数据增强
- 训练超参数与 ImageNet 训练时相同(详细的训练设置见补充材料)
- 在表4 中,论文报告了每个目标数据集 5 次微调运行的平均单次裁剪测试准确率
- 巨型模型在所有目标数据集上均取得了具有竞争力的结果
- CIFAR-10 的错误率降至 1%
- CIFAR-100 的错误率降至 8.7%
- 这些结果验证了 Kornblith 等人 (2018) 的发现,即更好的 ImageNet 模型具有更好的迁移能力
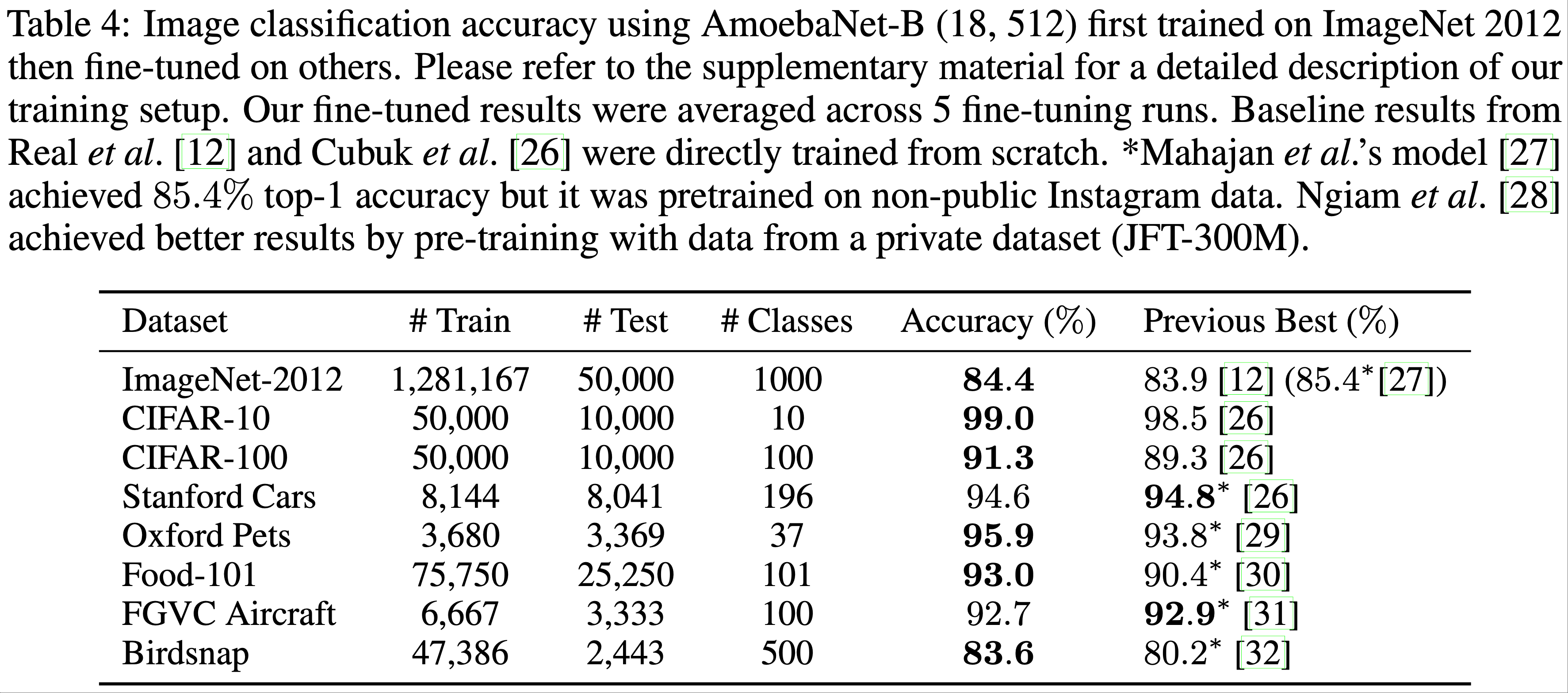
- 巨型模型在所有目标数据集上均取得了具有竞争力的结果
Massively Multilingual Machine Translation
- 本节还通过扩展用于 NLP 的模型来展示 GPipe 的灵活性,论文在一个大规模多语言 NMT 任务上继续 GPipe 的实验
- 因为并行语料库的丰富性,神经机器翻译(NMT)已成为评估 NLP 架构的基准任务 (2017, 2018, 2019)
- 论文使用包含 102 种语言与英语的平行文档语料库,总计 250 亿训练样本,每种语言的样本量从 \(10^4\) 到 \(10^9\) 不等 (2019)
- 该数据集通过涵盖从低资源到高资源的多样化语言,为可扩展性实验提供了真实的测试环境
- 论文首次在机器翻译中证明,足够大的 NMT 模型可以同时学习超过 100 种语言对的映射,并且在所有语言上均优于双语模型性能
- 这进一步凸显了高效且灵活的模型并行工具的重要性
- 论文的比较基于在该语料库上所有语言对训练的单一 Transformer (2017) 的性能
- 通过两个维度扩展架构以强调 GPipe 的灵活性:
- (i) 通过增加模型的层数扩展深度;
- (ii) 通过增加前馈层的隐藏维度以及多头注意力层中的注意力头数(和注意力通道数)扩展宽度
- 类似于 Shazeer 等人 (2018) 的方法(数据集、基线、训练配置和优化超参数的详细描述见补充材料)
- 通过两个维度扩展架构以强调 GPipe 的灵活性:
- 论文从标准的 4 亿参数 Transformer Big 模型 \(T(6,8192,16)\) (如 Chen 等人 (2018) 所述)开始,词表为 64k
- 注:论文用 \(T(L,\ H,\ A)\) 表示 \(T(层数,FFN隐藏层维度,Attention头数)\)
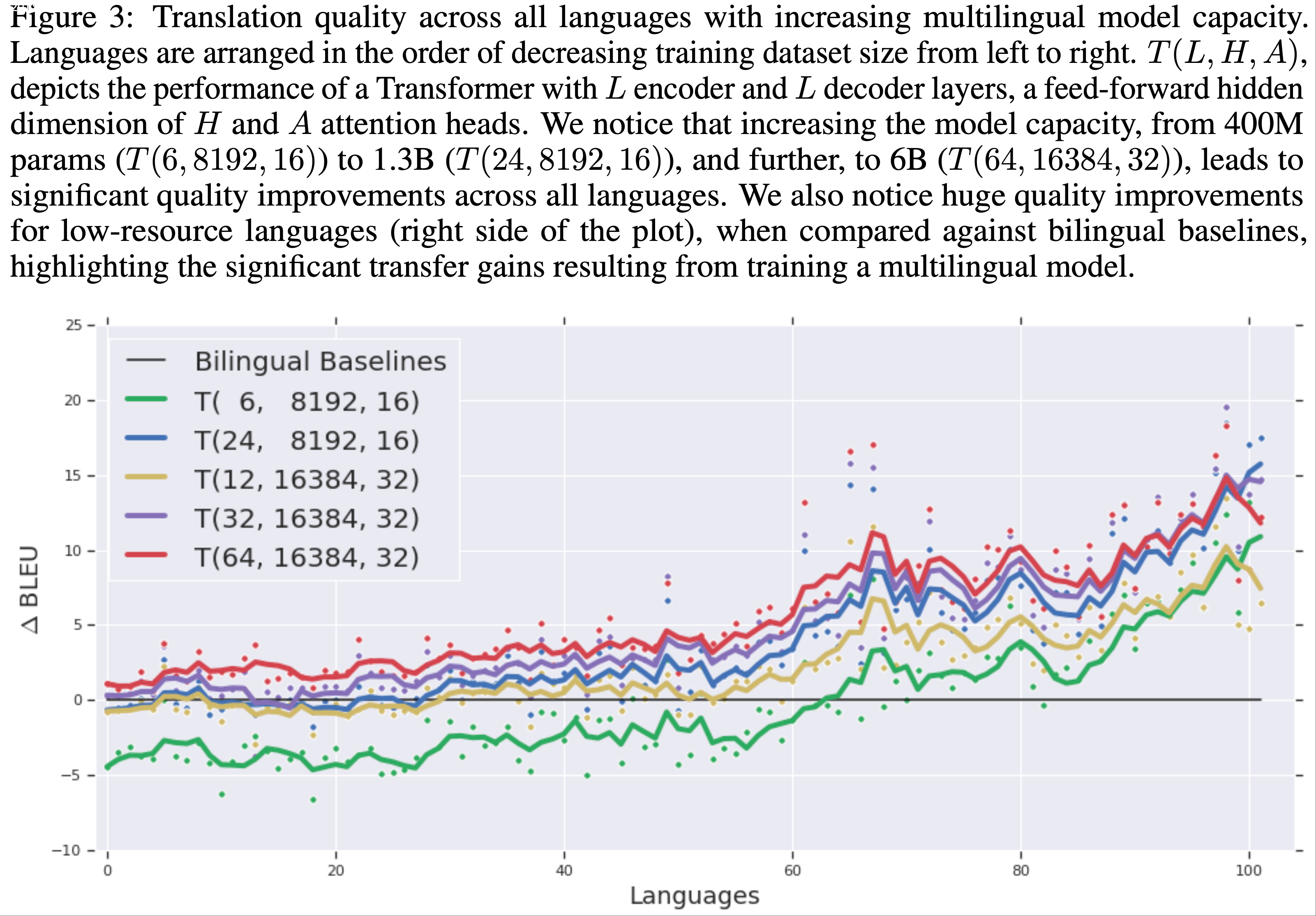
- 在图3 中,论文将其性能与下列模型进行了比较:
- 13 亿参数的深层模型 \(T(24,\ 8192,\ 16)\)
- 13 亿参数的宽模型 \(T(12,\ 16384,\ 32)\)
- 30 亿参数模型 \(T(32,\ 16384,\ 32)\)
- 60 亿参数模型 \(T(64,\ 16384,\ 32)\)
- 所有模型均使用基于温度的多语言 BERT (2018) 采样方法在所有语言对上同时训练
- \(T(12,\ 16384,\ 32)\) 、 \(T(24,\ 8192,\ 32)\) 、 \(T(32,\ 16384,\ 32)\) 和 \(T(64,\ 16384,\ 32)\) 分别被划分为 2、4、8 和 16 个加速器
- 从图3 中可以看出
- 将模型容量从 4 亿参数增加到 13 亿参数显著提升了所有语言的性能
- 将模型从 13 亿参数扩展到 60 亿参数进一步提升了性能,尤其是高资源语言
- 注:从 13 亿到 30 亿和 60 亿参数时出现了收益递减现象
- 以下是论文基于这些大规模实验的一些实证发现:
- 深度-宽度权衡(Depth-Width Trade-off) :
- 论文研究了多语言设置中深度与宽度的权衡,并比较了 13 亿参数的宽模型 \(T(12,\ 16384,\ 32)\) 和 13 亿参数的深模型 \(T(24,\ 8192,\ 16)\) 的性能
- 虽然这两种模型在高资源语言(图3 左侧)上的质量非常接近,但深层模型在低资源语言上的表现显著优于宽模型 ,这表明增加模型深度可能更有利于泛化
- 注:图3是 100+ 种语言按照数据量从左到右逆序排序的结果(high-resource language 代表数据量较大的语言),每个点代表当前语言上的表现?
- 与 4 亿参数模型相比,13 亿参数深层模型在低资源语言(图3 右侧)上的质量提升几乎与高资源语言相当,这表明增加深度可能会增强对低资源任务的迁移效果
- 深层模型的训练挑战(Trainability Challenges with Deep Models) :
- 深度增加了神经网络的表示能力,但也使优化问题复杂化
- 在大规模实验中,论文遇到了由尖锐激活(sharp activations)且是正峰度的(positive kurtosis)和数据集噪声组合引起的严重训练问题
- 在训练几千步后,模型预测会变得极其尖锐且对噪声敏感,这通常会导致非有限或大梯度,最终破坏学习进程
- 为了解决这些问题,论文采用了两种方法:
- (i) 遵循 Zhang 等人 (2019) 的方法,按层数比例缩小所有 Transformer 前馈层的初始化;
- (ii) 当 logit 预测(softmax 预激活)的幅度超过特定值时,对其进行裁剪
- 这两种方法的结合缓解了因模型深度扩展带来的训练不稳定性
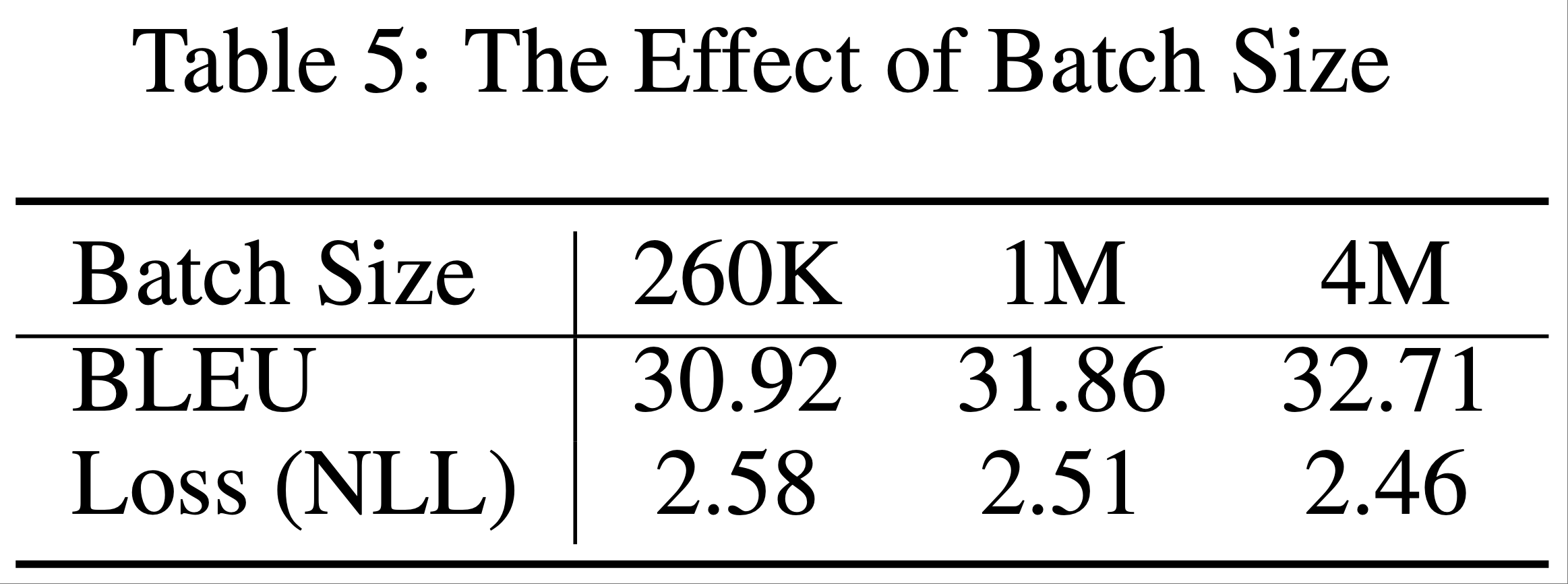
- 大批量训练(Large Batches) :
- 数据并行使用简单,是扩展神经网络训练的主导方法 (2016, 2017)
- 论文通过显著增加标准 Transformer Big 训练的批量大小来测试大批量训练的极限
- 从每批 26 万词开始,论文将有效批量增加到 400 万词,并观察高资源语言对(德语-英语)的验证损失和 BLEU 分数(其他语言对也观察到类似趋势)
- 此处使用的优化参数与之前实验相同
- 据论文所知,400 万词每批是文献中迄今为止用于训练 NMT 模型的最大批量 (2018)
- 表5 显示,随着批量增加,两项指标均显著改善
- 作者相信进一步增加批量可能会带来更多改进
- 深度-宽度权衡(Depth-Width Trade-off) :
Design Features and Trade-Offs
- 已有多种方法用于实现高效的大规模模型并行,但每种方法都有其特定的权衡,使其适用于特定硬件约束下的特定架构扩展
- 本节将重点讨论多种模型并行方法的设计选择与权衡,并比较它们与 GPipe 在灵活性、可扩展性以及不同硬件约束和架构变体下的效率
- 模型并行的核心思想是将网络划分为不同的计算单元,然后将这些单元分配到不同的设备上(2014; 2014; 2017; 2012)
- 从概念上讲,这种方法支持将多种模型扩展至巨大规模
- 但这些方法通常面临硬件利用率低和设备间通信瓶颈的问题
- 单程序多数据(Single Program Multiple Data, SPMD)和流水线并行被提出以应对这些挑战
- Mesh-Tensorflow(2018)遵循 SPMD 范式
- 将数据并行中使用的单指令多数据(Single Instruction Multiple Data, SIMD)方法扩展到其他张量维度
- SPMD 允许将每个计算拆分到多个设备上,从而使用户能够将单个矩阵乘法(以及单个层的模型参数)的大小随加速器数量线性扩展
- 但这也引入了设备间的高通信开销,因为需要大量类似 AllReduce 的操作来合并每个并行化矩阵乘法的输出
- 限制了该方法在配备高速互联的加速器场景下的适用性
- SPMD 限制了可高效扩展的操作类型,使其仅适用于特定网络架构和机器学习任务
- 例如,在该范式下沿卷积层的通道维度拆分效率较低,因为通道实际上是全连接的,而沿空间维度拆分则需要复杂的技术来处理边缘区域(halo regions)
- 尽管 SPMD 允许通过使每个操作更小来扩展模型深度,但它需要将每个层拆分到更多加速器上,这进一步增加了设备间的通信开销
- 但这也引入了设备间的高通信开销,因为需要大量类似 AllReduce 的操作来合并每个并行化矩阵乘法的输出
- Mesh-Tensorflow(2018)遵循 SPMD 范式
- 其他方法尝试利用基于流水线并行的技术来扩展神经网络(1993; 2017),最近应用于神经网络训练的流水线并行迭代是 PipeDream(2018)
- PipeDream 的目标是减少参数服务器(2014)的通信开销
- PipeDream 通过流水线化前向传播的执行,并将其与反向传播交错,以最大化硬件利用率
- 这种设计因异步反向更新引入的权重陈旧性(weight staleness)而受到影响
- 为了避免权重陈旧性导致的优化问题,PipeDream 需要在每个加速器上维护多个版本化的模型参数副本以准确计算梯度更新 ,从而限制了用户扩展至更大模型的能力
- GPipe 引入了一种新型流水线并行技术
- 在应用整个小批量(mini-batch)的同步梯度更新之前,对微批次(micro-batches)的执行进行流水线化
- 论文的新型批拆分流水线并行算法与重计算(re-materialization)相结合,支持扩展到大量微批次
- 这最小化了“气泡”(bubble)开销,同时无需异步梯度更新
- GPipe 使用户能够将模型大小随加速器数量线性扩展
- 与 SPMD 不同,流水线并行在扩展模型时引入的额外通信开销极少
- 设备间通信仅在每个微批次的划分边界发生,且引入的通信开销可以忽略不计,这使得 GPipe 在缺乏高速设备互联的场景下仍然适用
- 待提升点:
- GPipe 目前假设单个层可以适配单个加速器的内存限制
- 注:突破这一限制的一种可行方法是:将单次矩阵乘法拆分为多个更小的矩阵运算,并依次分散到多个网络层中执行(注:即张量并行)
- 微批次拆分需要复杂的策略来支持跨批次计算的层(例如,BatchNorm 在训练时使用微批次的统计量,但在评估时累积小批次的统计量)
- GPipe 目前假设单个层可以适配单个加速器的内存限制
Conclusion
- 论文介绍了 GPipe,一个用于训练巨型神经网络的可扩展模型并行库
- 论文提出并实现了一种新型批拆分流水线并行算法,该算法使用同步梯度更新,实现了高硬件利用率和训练稳定性的模型并行
- 论文利用 GPipe 训练了大规模卷积和基于 Transformer 的模型,并在图像分类和多语言机器翻译任务上展示了强大的实证结果
- 论文重点强调了 GPipe 库的三个关键特性:
- 1)高效性(Efficiency) :通过新型批拆分流水线算法,GPipe 实现了几乎随设备数量线性增长的速度提升
- 2)灵活性(Flexibility) :GPipe 支持任何可以表示为层序列的深度网络
- 3)可靠性(Reliability) :GPipe 使用同步梯度下降,并保证无论划分数量多少,训练结果一致
附录1:GPipe GPipe Example Usage
- GPipe 库的用户首先需要将他们的神经网络表示为 \(L\) 层的顺序列表
- 任何计算图都可以被划分为一系列子图
- 示例基础层包括卷积(convolution)、池化(pooling)、批量归一化(batch normalization)、dropout、transformer、softmax 以及其他层
- 可以按顺序或并行连接的层可以被组合成一个新的复合层
- 用户可以以任意方式组合任意数量的层,只要正确定义了复合前向函数
- 图1展示了 GPipe 库的一个示例用例
- 这是一个用于验证训练一致性的单元测试,它验证了在这个示例网络中,所有梯度的范数在数值误差范围内是相同的,无论分区数量如何
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46import tensorflow as tf
from lingvo.core import base_layer
from lingvo.core import layers
from lingvo.core import py_utils
from TensorPipe import TensorPipeLayer
def BuildDummyTensorPipeLayer( num_layers=16, num_splits=4, num_mirco_batches=8):
assert num_layers % num_splits == 0
layers = []
# Construct a dummy layer with 16 3x3 conv layers
for i in range(num_layers):
layers.append(layers.Conv2DLayer.Params().Set( name=’layer_{}’.format(i)), filter_shape=(3, 3, 1, 1), filter_stride=(1, 1))
# Evenly distribute layers to partitions.
partitions = []
layers_per_split = num_layers // num_splits
for split in range(num_splits):
sub = layers[split * layers_per_split: (split + 1) * layers_per_split]
partitions.append(sub)
# Build pipeline parallelism model using TensorPipe
p = TensorPipeLayer.Params().Set(name=’TensorPipe’, num_mirco_batches=num_mirco_batches , partitions=partitions)
layer = p.cls(p)
return layer
class DummyTensorPipeTest(tf.test.TestCase):
def _verify_consistent_training(self, num_splits):
g = tf.Graph()
with g.as_default():
py_utils.GetOrCreateGlobalStep() tf.set_random_seed(88888888)
inputs = tf.random_uniform([16, 8, 8, 1])
net = BuildDummyTensorPipeLayer(num_splits=num_splits) logits = net.FPropDefaultTheta(inputs)
loss = tf.reduce_mean(logits)
grads = tf.gradients(loss, tf.trainable_variables()) grad_norm = tf.sqrt(
py_utils.SumSquared(grads))
with self.session(graph=g) as sess:
sess.run(tf.global_variables_initializer())
grad_norm_val , = sess.run([grad_norm])
# Verify grad norm is the same regardless of # the number of splits
self.assertNear(grad_norm_val , 0.269997 , err=1.0e-6)
def testDummyPipelineCnnOneSplit(self):
self._verify_timestep_counts(num_splits=1)
def testDummyPipelineCnnTwoSplits(self):
self._verify_timestep_counts(nu2m_splits=2)
def testDummyPipelineCnnFourSplits(self):
self._verify_timestep_counts(num_splits=4)
- 这是一个用于验证训练一致性的单元测试,它验证了在这个示例网络中,所有梯度的范数在数值误差范围内是相同的,无论分区数量如何
附录2:图像分类训练细节 (2 Image Classification Training Details)
Training Hyperparameters
- 论文在 ImageNet ILSVRC-2012 数据集上训练了一个具有 \(557\) 百万模型参数和输入图像尺寸为 \(480\times 480\) 的 AmoebaNet-B 模型
- 论文遵循 (2018) 中描述的超参数和输入预处理方法来训练 AmoebaNet-B
- 衰减率为 \(0.9\)
- \(\epsilon=0.1\) 的 RMSProp 优化器
- \(L^{2}\) 正则化系数 \(\lambda=4\times 10^{-5}\)
- 标签平滑系数 \(0.1\)
- 权重为 \(0.4\) 的辅助头
- 对中间层应用了与 NasNet (2018) 中相同的 drop-path 调度,并对最终层应用了概率为 \(0.5\) 的 dropout
- 使用了学习率调度,该调度每 \(3\) 个周期以 \(0.97\) 的速率衰减,初始学习率为 \(0.00125\) 乘以批量大小
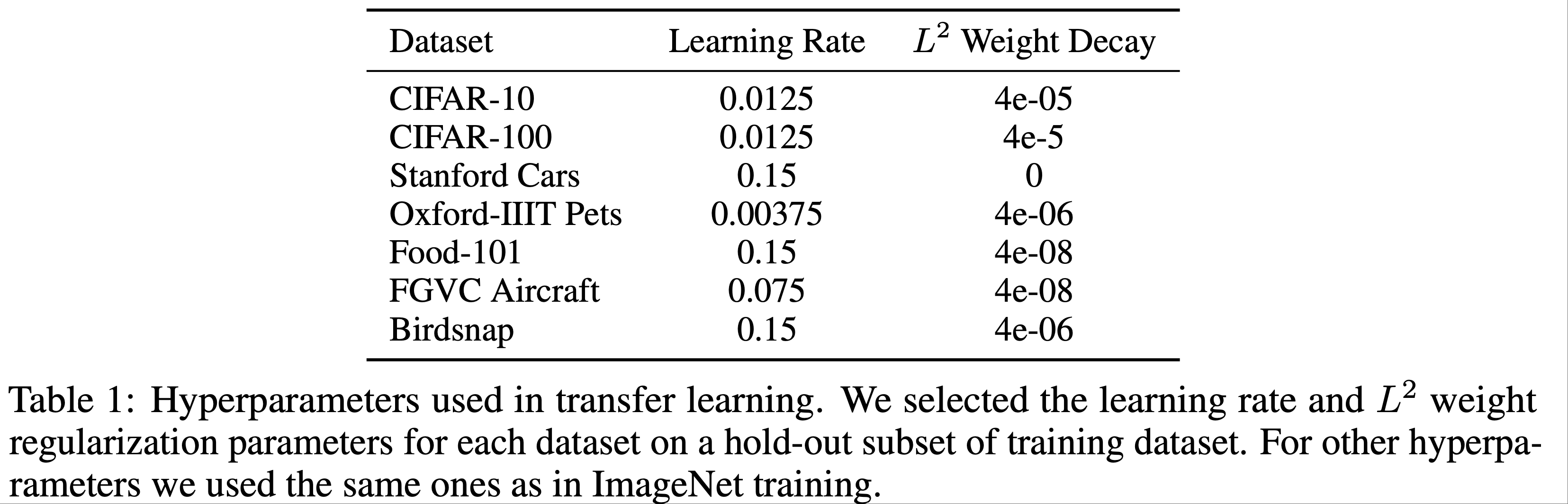
- 在附录表1中,论文报告了每个迁移学习数据集使用的超参数
- 从集合 \(\{0.0125,0.00375,0.075,0.115,0.15\}\) 中选择学习率
- 从集合 \(\{0,4e-8,4e-7,4e-6,4e-5\}\) 中选择 \(L^{2}\) 权重衰减
- 选择基于训练数据的保留子集(20%)
- 论文应用选定的超参数进行最终训练,并重复五次
- 表1中:
- 论文为每个数据集在训练数据集的保留子集上选择了学习率和 \(L^{2}\) 权重正则化参数
- 对于其他超参数,论文使用了与 ImageNet 训练中相同的参数
Consistent Training
- GPipe 在微批次(micro-batches)上执行同步训练
- 在本节中,验证了以下假设:
- 使用 GPipe 的端到端收敛精度在统计误差范围内是相同的,无论分区数量如何
- 实验过程:
- 多次训练 AmoebaNet-D (6, 256) 模型 35 个 epoch,并在 ImageNet 上测量最终的验证准确率
- 选择 AmoebaNet-D (6, 256) 是因为它是 DAWNBench 竞赛 (2018) 中训练成本最优的图像模型
- 采用了 DAWNBench 中报告的超参数和训练流程
- 作为基线,使用官方开源实现训练了 AmoebaNet-D (6, 256) 5 次,并计算了最终准确率的均值和标准差
- 使用相同的超参数和训练流程,分别用 1、2、4 和 8 个分区通过 GPipe 训练了相同的网络
- 结果发现,最终的准确率落在均值 1.6 倍标准差范围内,符合预期
附录3:Machine Translation Training Details
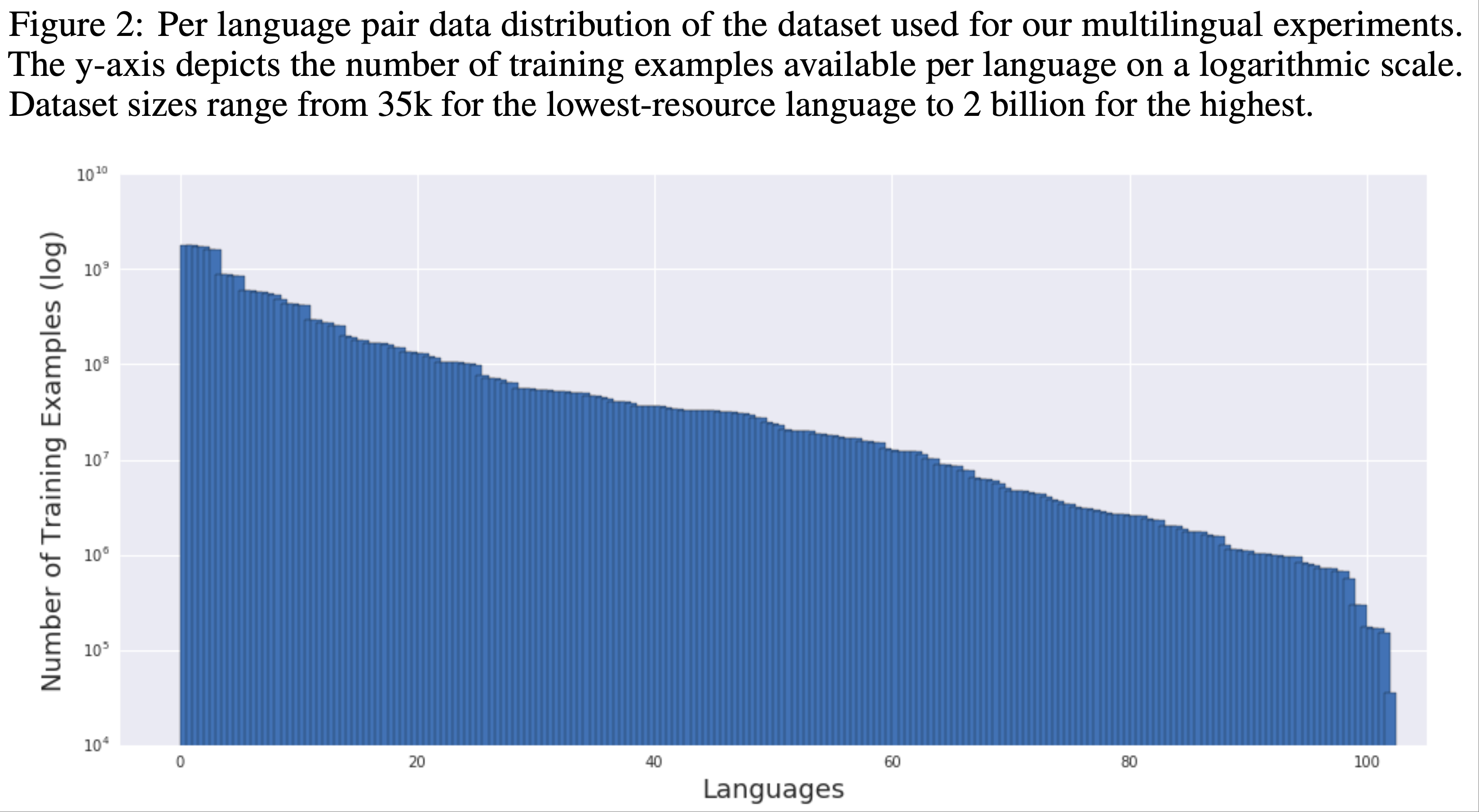
- 论文研究了大规模多语言神经机器翻译(Neural Machine Translation, NMT),使用的语料库通过从网页爬取并提取平行句子构建
- 图 2 展示了论文研究的 102 种语言的数据分布情况
Baselines
- 在双语实验中,论文使用了 Transformer 架构(2017)的变体
- 对于大多数双语实验,论文采用了一个包含 3.75 亿参数的大型 Transformer Big 模型,并使用了共享的源-目标句子片段模型(SentencePiece Model, SPM)词汇表,包含 32k 个词符
- 论文根据每种语言对的数据集大小调整了不同的 dropout 值
- 理解:这里说明是训练了很多个双语 Transformer 模型
- 问题:图3中的模型是如何和基线比较的呢?想说明什么呢?
- 理解:基线是谁不重要,重点是实验模型不同配置之间(不同宽度,深度之间)互相比较能拿到结论
- 对于大多数中低资源语言,论文还尝试了 Transformer Base 模型
- 注:数据量大对应高资源,数据量小对应低资源
- 所有模型均采用 Adafactor 优化器(2018)和动量因子化,学习率调度为 \( (3.0, 40\text{K}) \),并设置了每参数范数裁剪阈值为 1.0
- 对于 Transformer Base 模型,学习率调度为 \( (2.0, 8\text{K}) \)
- BLEU 分数基于验证集上表现最佳的检查点计算,输出和参考文本均为真实大小写形式
Multilingual Baselines
- 接下来,论文描述训练多语言模型的方法
- 由于训练数据集的严重不平衡(图 2),论文首先设计了一种采样策略,以同时在 200 多个语言对上训练单一模型
- 直接从数据分布中采样会导致高资源语言表现良好,但低资源语言表现较差;
- 平等采样所有语言对会显著提升低资源语言的翻译性能,但高资源语言的表现会明显低于其双语基线
- 为了平衡高资源和低资源语言对,论文采用了训练多语言 BERT(2018)时使用的基于温度的采样策略
- 对于语言对 \( l \),设 \( D_l \) 为可用平行语料库的大小
- 若从数据集的并集中采样,样本来自语言 \( l \) 的概率为 \( p_l = \frac{1}{S_l D_l} \)
- 论文将采样分布的概率设置为与 \( p_l^{\frac{1}{T} } \) 成正比,其中 \( T \) 为采样温度
- 当 \( T = 1 \) 时,对应真实数据分布;
- 当 \( T = 100 \) 时,几乎对每种语言采样数量相等
- 论文的多语言模型采用了 \( T = 5 \)
- 在所有多语言实验中,论文使用与双语模型相同的超参数,训练了一个同时在所有语言上训练的单一 Transformer 模型
- 论文采用了共享的 SPM 词汇表,包含 64k 个词符,生成时使用了与训练相同的采样分布(\( T = 5 \))
- 论文设置了字符覆盖率为 0.999995,以确保词汇表涵盖所有 103 种语言的大部分字母
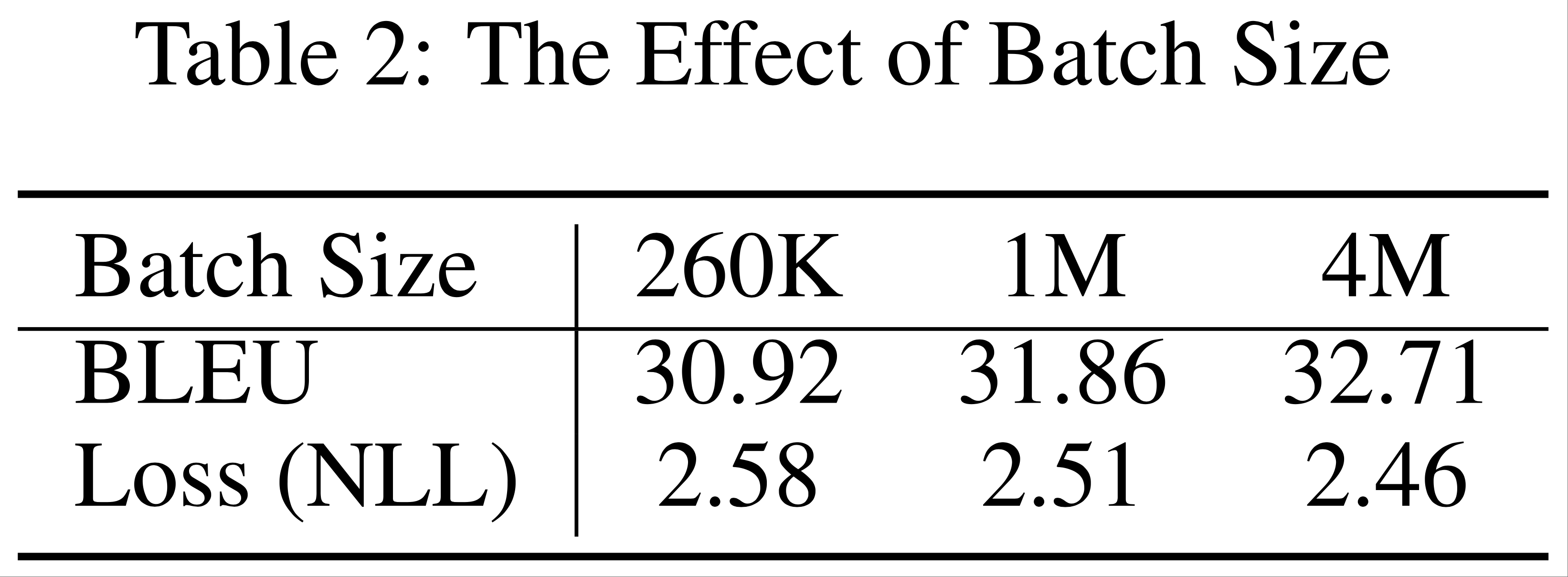
Effects of Large Batch Size
- 由于数据并行(Data Parallelism)的简单性,它成为扩展神经网络训练的主要方法(2016, 2017)
- 论文通过显著增加标准 Transformer Big 训练的批量大小来测试大批量训练的极限
- 从每批 260k 词符开始,论文将有效批量增加到 400 万,并观察高资源语言对(德英)的验证损失和 BLEU 分数(其他语言对也呈现相似趋势)
- 优化参数与此前的实验相同
- 据论文所知,400 万词符每批是文献中迄今为止用于训练 NMT 模型的最大批量(2018)
- 表 2 显示,随着批量增加,两项指标均显著提升
- 作者认为进一步增加批量可能带来更多改进
附录4:Discussion
- 拥有一个灵活的大规模深度学习实验框架,为理解大规模模型的底层机制和原理提供了令人兴奋的机会
- 本节中,论文将实验结果与深度学习领域的最新研究联系起来,并与从业者分享一些额外的实证发现
- 表达力与泛化(Expressivity and Generalization) :
- 深度学习理论的最新发现(2018, 2018)假设,随着网络表达能力的增长,泛化性能也会提升
- 论文在此通过实验进行实证验证
- 论文通过增加深度作为提高网络表达能力(2017)的手段,同时控制批量大小
- 论文能够观察到网络在以往从未实验过的规模上的泛化行为
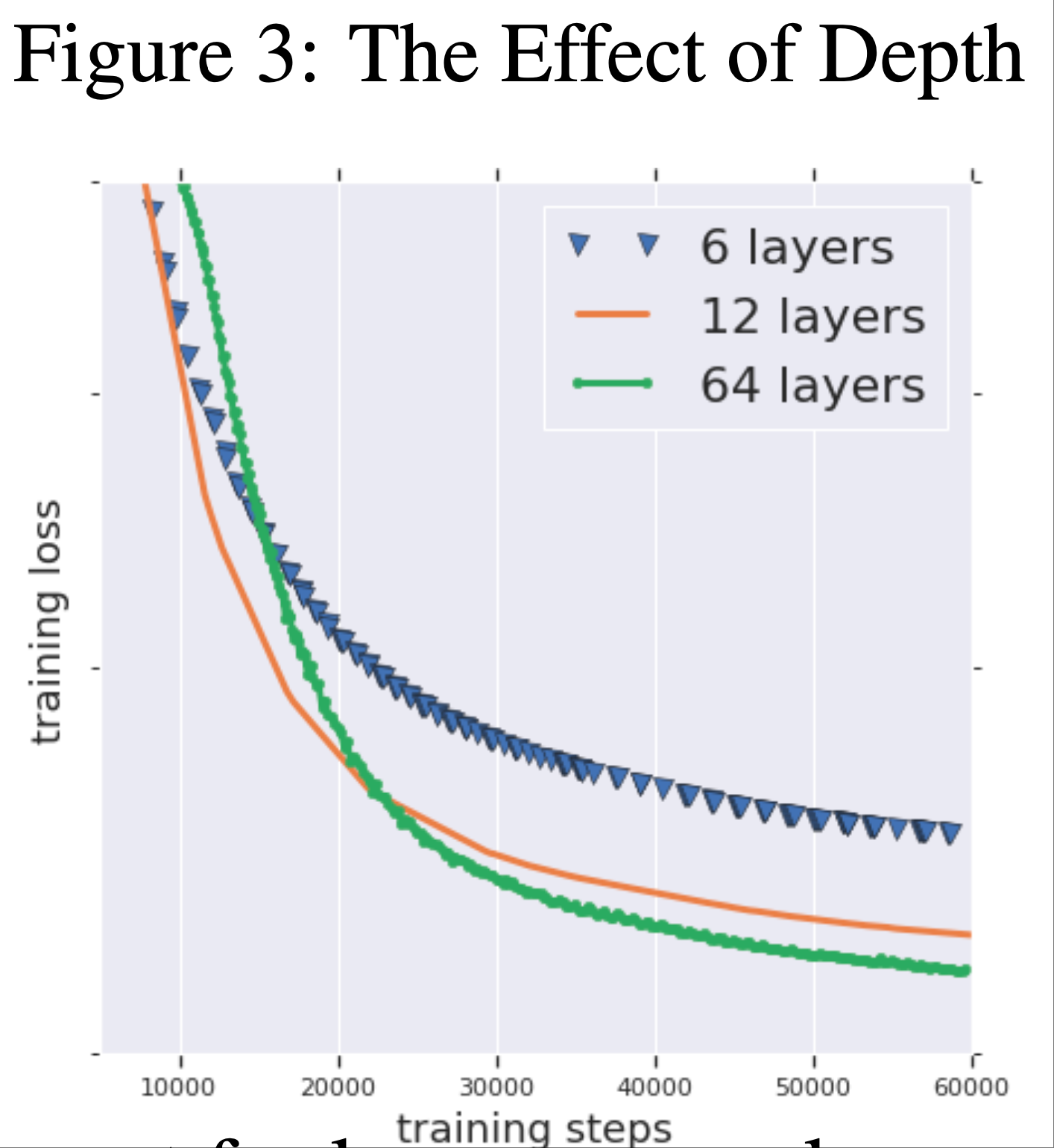
- 从 6 层 Transformer Big(编码器+解码器共 12 层)开始,论文逐步将深度增加到 64 层(共 128 层)
- 论文发现,64 层模型的表现几乎呈现出与 6 层模型相同的上升趋势,而中间深度模型的表现介于两者之间
- 尽管结果支持理论,但论文也观察到收益递减现象,这引发了可训练性的担忧
- 论文可能尚未掌握进一步降低训练误差的工具或技术,理解可训练性挑战对进一步发展是必要的
- 深度学习理论的最新发现(2018, 2018)假设,随着网络表达能力的增长,泛化性能也会提升
- 深度-宽度权衡(Depth-Width Trade-off) :
- 另一个吸引深度学习理论研究者关注的领域是模型宽度和深度对泛化的影响(2018, 2019)
- 接下来,论文在多语言设置中研究深度与宽度的权衡,并比较 13 亿参数的宽模型 \( T(12, 16384, 32) \) 和 13 亿参数的深模型 \( T(24, 8192, 16) \) 的性能
- 虽然这两种模型在高资源语言上的表现非常相似 ,但深模型在低资源语言上的表现显著优于宽模型 ,这表明增加模型深度可能更有利于泛化
- 将 13 亿参数深模型与 4 亿参数模型进行比较时,低资源语言(图3 右侧)的性能提升几乎与高资源语言相当,这表明增加深度还可能扩大对低资源任务的迁移效果

- 深度加速收敛(Faster Convergence with Depth) :
- 论文报告了一个与模型深度相关的有趣现象
- 在保持有效批量大小、优化器超参数和模型宽度不变的情况下 ,增加模型深度会优化加速 ,如附录图3 所示
- 注:层数越深,损失下降越快
- 此前报道类似现象的工作推测,深度通过过参数化实现了预条件(2018)
- 尽管论文主要关注与扩展神经网络相关的系统挑战,但为了更好地解决泛化和可训练性问题,对深度神经网络的理论理解需求日益增长
- 作者相信,像 GPipe 这样灵活的扩展工具对于弥合深度学习理论与实践的差距至关重要
- 希望论文的实证发现和讨论能够激励更多研究沿着这一方向展开
附录:Sufficient Statistic(充分统计量)
- 在统计学中,充分统计量 的本质是对原始样本数据的“压缩”
- 即在保留所有关于未知参数的信息的前提下,将复杂的样本数据简化为更简洁的统计量
- 这种简化不会丢失用于推断未知参数的任何关键信息,因此是统计推断中简化数据、提高效率的重要工具
定义
- 假设
- 总体的概率分布依赖于未知参数 \(\theta\)(\(\theta\)可以是单参数或多参数,比如分布的均值)
- \(X_1, X_2, \dots, X_n\)是来自该总体的样本
- 若
- 一个统计量\(T = T(X_1, X_2, \dots, X_n)\) 满足:给定\(T\)的取值后,样本\(X_1, \dots, X_n\)的条件分布不再依赖于\(\theta\)
- 则
- 称\(T\)是参数\(\theta\)的充分统计量
- 简单来说:一旦知道了充分统计量 \(T\) 的值,原始样本中就不再包含任何关于 \(\theta\) 的额外信息
- 例如,伯努利分布中,\(T = \sum x_i\) 和样本均值 \(\bar{X} = T/n\)(因\(n\) 固定,二者一一对应)都是\(p\)的充分统计量
充分统计量的总结
- 充分统计量的核心思想是:“压缩数据但不丢失信息”**
- 统计推断的核心是利用样本信息推断未知参数 \(\theta\)
- 原始样本往往包含大量冗余信息(例如,100个数据点中可能有重复或无关细节)
- 充分统计量的作用是:
- 简化数据 :将高维样本(如 \(n\) 个数据)压缩为低维统计量(如1个或2个值);
- 保留信息 :压缩后的统计量包含推断 \(\theta\) 所需的全部信息,原始样本的其他细节对推断 \(\theta\) 无意义
- 注:充分统计量不唯一性 :一个参数可能有多个充分统计量
- 例如,伯努利分布中,\(T = \sum x_i\) 和样本均值 \(\bar{X} = T/n\)(因 \(n\) 固定,二者一一对应)都是 \(p\) 的充分统计量
附录:其他流水线策略介绍
各种流水线整体介绍
- 三种流水线策略(pipeline strategies),Gpipe, PipeDream 1F1B, Interleaved 1F1B
- PipeDream 1F1B 论文:
- PipeDream: Fast and Efficient Pipeline Parallel DNN Training, 2018, Microsoft :第一篇,主要介绍概念等
- PipeDream: Generalized Pipeline Parallelism for DNN Training, SOSP 2019, Microsoft:第二篇,包含更多细节
- PipeDream 1F1B 也叫做经典 1F1B(One-Forward-One-Backward),也称为 1F1B 或 PipeDream 1F1B
- Interleaved 1F1B(Megatron-2)论文:Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM, SC 2021, NVIDIA
- 下图来自 Interleaved 1F1B(Megatron-2)论文:Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM, SC 2021, NVIDIA
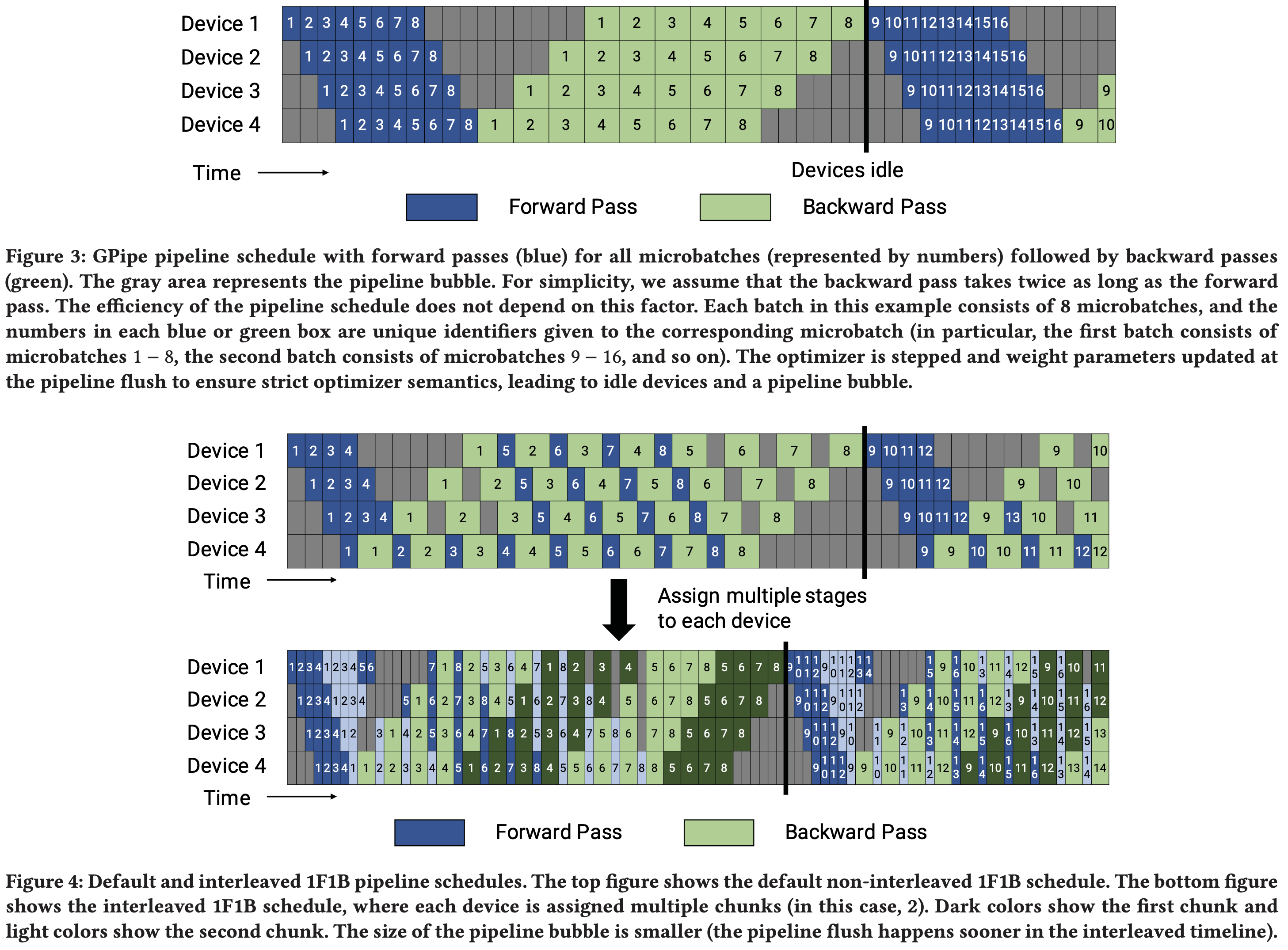
- 上图中内容解读:
- 图中数字表示不同 micro-batch 的过程(共 8 个 micro-batches 和 4 张 GPU),颜色区分前向后向过程,Interleaved 1F1B 中的灰色和深色则表示多分出来的虚拟 Stage
- 核心要诀:
- 对每个 micro-batch,前向过程是必须 GPU 正序进行的
- 对每个 micro-batch,后向过程是必须 GPU 逆序进行的
- 对任意 micro-batch,需要一个完整的 Stage 完成前向过程,才能开始后向过程
- 需要所有 micro-batch 都走完后向过程,才能执行一次梯度更新(所以叫做 1F1B)
- 吐槽:实际上 Gpipe 也是一次正向一次反向的,也可以叫做 1F1B?
- Interleaved 1F1B 中,同一个 Stage 内部的 Stage 分片是按照模型切分,所以需要以大的 Stage 为单位遵循上面的过程
- 比如:对每个 micro-batch,需要所有的虚拟 Stage 分片完成前向过程,才能开始后向过程
- Interleaved 1F1B 中,对同一个 Stage 内部的分片来说,理论上同一个 Stage 内部的 Stage 分片是按照模型切分,所以也是有依赖顺序的
- 对每个 micro-batch,1F1B 保证激活值在反向结束后立即释放,降低缓存
GPipe -> 1F1B -> Interleaved 1F1B
- TLDR:Interleaved 1F1B 是在经典 1F1B(PipeDream 1F1B)流水线并行调度基础上,把“模型纵向切成更多 Stage ,再循环交错地放到 GPU 上”,用更细粒度、更紧凑的时序进一步压缩“流水线气泡(bubble)”,从而提升 GPU 利用率与训练吞吐,同时保持 1F1B 的低显存优势
- 注意:切割的是模型
- GPipe, 1F1B, Interleaved 1F1B 三种流水线并行调度对比
方案 层划分方式 执行顺序 主要优点 主要缺点 GPipe 连续层,每 GPU 一个 Stage 先跑完所有 micro-batch 的 Forward,再依次跑 Backward 易实现、等价性好 激活值全保留,显存爆炸;气泡大 1F1B 同上 每个 Stage 交替执行 1 Forward / 1 Backward 激活值及时释放,省显存;气泡已减半 气泡仍随 Stage 数线性增加 Interleaved 1F1B 把原 Stage 均分 v 份,循环交错地放到 GPU 上 仍然是 1F1B 顺序,但 Stage 粒度变细 气泡进一步缩小;通信-计算可重叠 代码/通信更复杂;micro-batch 数需为 v·pp 的整数倍 - 气泡比例(p 为 Pipeline Stage 数量,即物理 GPU 数, m 为 micro-batch 数量)
- GPipe:(p−1) / m
- 1F1B:(p−1) / m
- Interleaved 1F1B: (p−1) / (v·m)
- 气泡比例(p 为 Pipeline Stage 数量,即物理 GPU 数, m 为 micro-batch 数量)
- Interleaved 1F1B 的特点:
- 时间轴上,Forward/Backward 任务被拆得更碎,空隙(bubble)被其他 micro-batch 的计算填满
- 仍然遵守“1 Forward -> 1 Backward”的稳态节奏,保证激活值在反向结束后立即释放
- 由于 Stage 变细,单个 micro-batch 在每个 GPU 上的停留时间变短,更多 micro-batch 可以同时在流水线上“滑动” ,
- 当前 micro-batch 的 Backward 计算 与 下一个 micro-batch 的 P2P 接收 无依赖,可并行;
- 当前 Send-Forward 与 下一次循环的 Forward 计算 也无依赖,可并行
- 在带宽充足时,通信几乎被计算完全掩盖
Interleaved 1F1B 的优缺点
- Interleaved 1F1B显存:与 1F1B 相同,稳态下每 GPU 最多保存 v 份激活 ,仍远低于 GPipe
- 吞吐:Megatron-LM 实验显示,在 1T+ 参数模型、1024 GPU 上,Interleaved 1F1B 比 1F1B 提升 8~15% 吞吐;
其他相关细节
- Megatron-LM 中 Interleaved 1F1B 叫做 interleaved schedule
最新技术:Zero Bubble Pipeline Parallelism
- Zero Bubble Pipeline Parallelism(ZB),即 零气泡流水线并行
- 参考链接:
- 基本思路是让 GPU 不要停止,让气泡消失
- 首先,如下图所示,将原始 1F1B 的后向过程拆开为 B 和 W 来表示(B 表示 对输入 \(x\) 求梯度,W 表示对权重 \(W\) 求梯度)
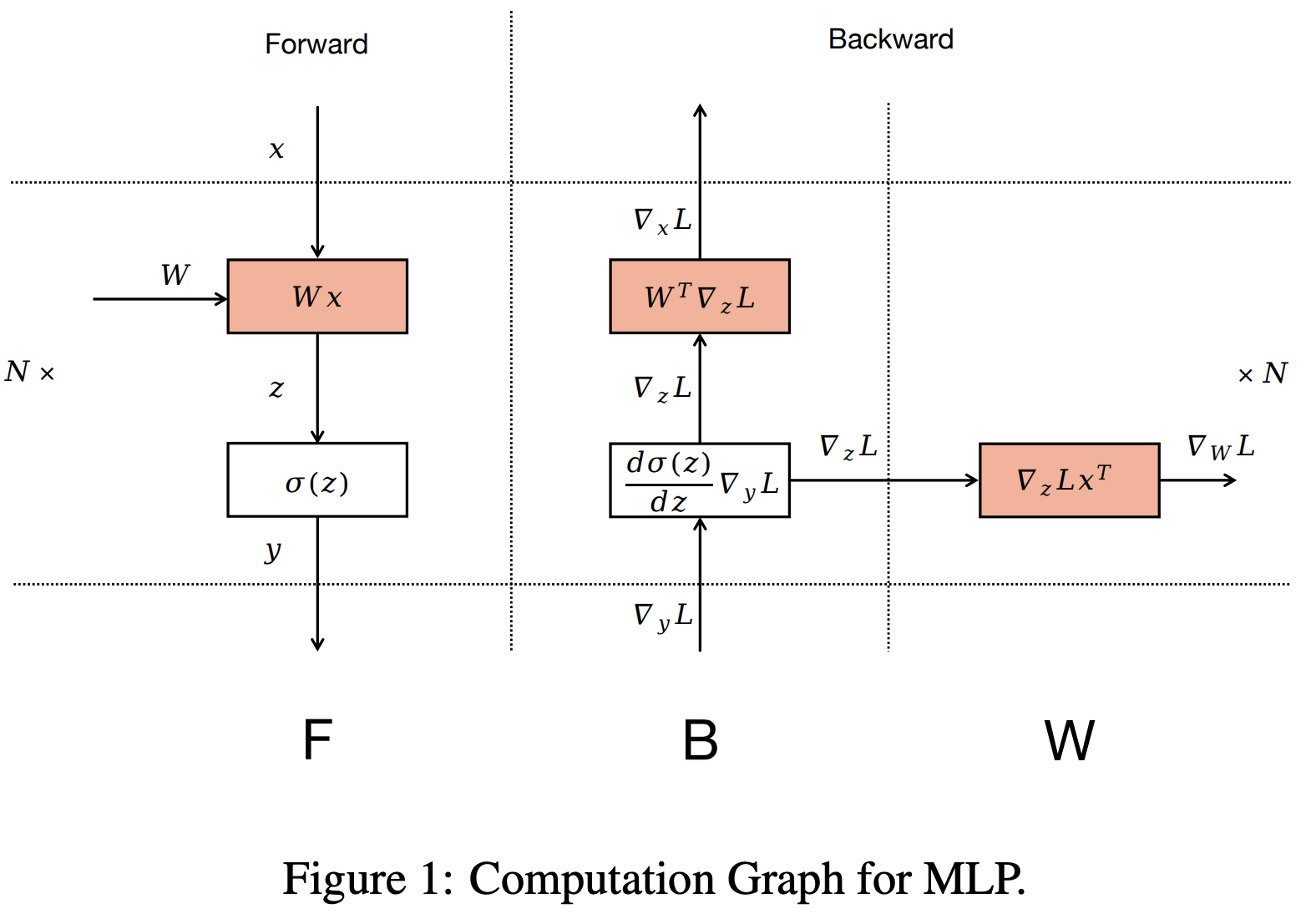
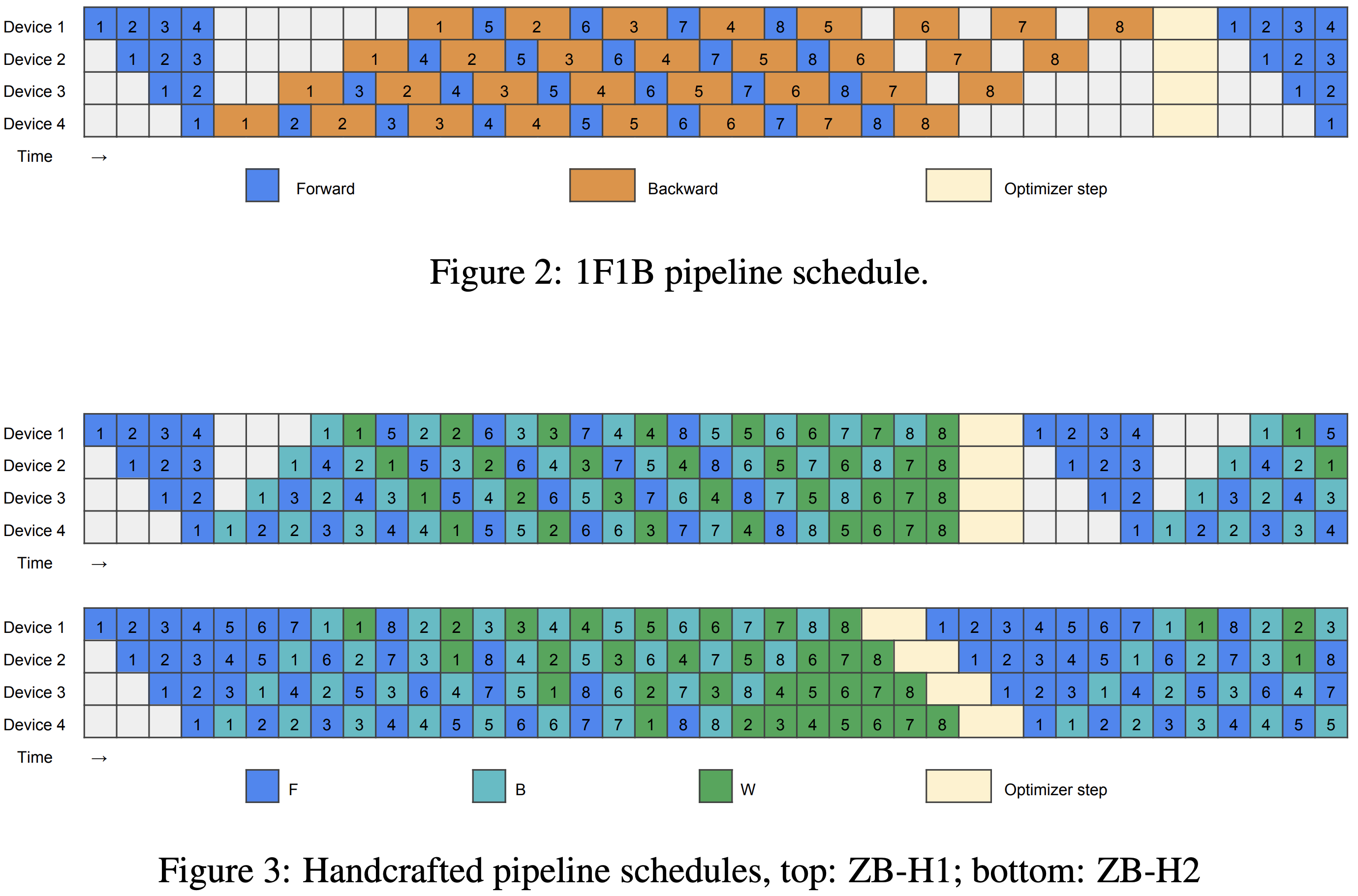
- 首先,如下图所示,将原始 1F1B 的后向过程拆开为 B 和 W 来表示(B 表示 对输入 \(x\) 求梯度,W 表示对权重 \(W\) 求梯度)