文本介绍IDDPM(Improved Denoising Diffusion Probabilistic Models)的理论介绍
- 参考链接:
整体说明
- IDDPM提供了对DDPM的一些优化,许多内容是基于DDPM原始论文Denoising Diffusion Probabilistic Models, NeurIPS 2020的
可学习的逆向过程方差 \(\Sigma_\theta(x_t,t)\)
- DDPM中逆向过程方差 \(\Sigma_\theta(x_t,t)\) 设置:
- DDPM中的方差设置为固定值: \(\mathbf{\Sigma}_\theta(\mathbf{x}_t, t) = \sigma^2_t \boldsymbol{I}\),其中 \(\sigma_t = \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t\),或者直接使用 \(\sigma_t = \beta_t\) (实验上,两种设置效果差不多)
- DDPM中作者通过实验发现,如果将 \(\Sigma_\theta(x_t,t)\) 设置为可学习的,模型会不容易收敛,采样效果会变差
- IDDPM中的改进:
- 采用一种插值的方法表示 \(\Sigma_\theta(x_t,t)\): \(\mathbf{\Sigma}_\theta(\mathbf{x}_t, t) = \exp(\mathbf{v} \log \beta_t + (1-\mathbf{v}) \log \tilde{\beta}_t)\)
- 其中 \(\mathbf{v} \) 是可以学习的向量(注意 \(\beta_t\) 是标量,而 \(\mathbf{v} \) 是向量,DDPM中的协方差矩阵是 \(\sigma^2_t \boldsymbol{I}\) 中实际上假设了各个维度的方差都相同,都是 \(\sigma^2_t\),IDDPM中则通过引入 \(\mathbf{v} \) 来实现不同维度方差不同),注意协方差 \(\Sigma_\theta(x_t,t)\) 在这里是对角矩阵,即假设不同变量之间相互独立
- \(\mathbf{v}_{\theta}(x_t, t)\) 是从模型输出出来的(详情见improved_diffusion源码:模型定义和improved_diffusion源码:向量使用),的维度是与 \(\mathbf{x}_t\) 相同的
- 能够这样插值的一个思路是因为 \(\sigma_t\) 的取值范围在 \([\beta_t, \tilde{\beta}_t]\) (详情见Improved Denoising Diffusion Probabilistic Models (IDDPM) - 妖妖的文章 - 知乎)。
- 虽然理论上应该对 \(\mathbf{v} \) 进行限制,但是IDDPM实验中也没有对 \(\mathbf{v} \) 进行限制,实验结果证明了即使不限制 \(\mathbf{v} \) 范围,也不会超过插值范围
- 其中 \(\mathbf{v} \) 是可以学习的向量(注意 \(\beta_t\) 是标量,而 \(\mathbf{v} \) 是向量,DDPM中的协方差矩阵是 \(\sigma^2_t \boldsymbol{I}\) 中实际上假设了各个维度的方差都相同,都是 \(\sigma^2_t\),IDDPM中则通过引入 \(\mathbf{v} \) 来实现不同维度方差不同),注意协方差 \(\Sigma_\theta(x_t,t)\) 在这里是对角矩阵,即假设不同变量之间相互独立
- 传统DDPM的损失函数 \(L_{\text{simple}}\) 不依赖 \(\Sigma_\theta(x_t,t)\),所以优化传统的损失函数不能更新到 \(\mathbf{v} \),为了更新到 \(\mathbf{v} \),IDDPM在传统损失函数上增加了一项,最终IDDPM损失函数为:
$$ L_\text{hybrid} = L_\text{simple} + \lambda L_\text{VLB} $$- 其中 \(L_\text{VLB} = L_T + L_{T-1} + \dots + L_0\),详情见:Denoising Diffusion Probabilistic Models, NeurIPS 2020
- 设置 \(\lambda=0.001\),用于防止 \(L_\text{VLB}\) 过于强势,影响 \(L_\text{simple}\) 的学习
- 设置 \(L_\text{VLB}\) 对 \(\mu_\theta(x_t, t)\) 是停止梯度回传的(
stop_gradient),确保 \(\mu_\theta(x_t, t)\) 还是主要由 \(L_\text{simple}\) 学习 - 问题: \(L_\text{VLB}\) 对 \(\mu_\theta(x_t, t)\) 都停止梯度回传了,还需要设置 \(\lambda=0.001\) 这么小吗?
- 采用一种插值的方法表示 \(\Sigma_\theta(x_t,t)\): \(\mathbf{\Sigma}_\theta(\mathbf{x}_t, t) = \exp(\mathbf{v} \log \beta_t + (1-\mathbf{v}) \log \tilde{\beta}_t)\)
Improving the Noise Schedule
优化前向过程中的方差 \(\{\beta_t\}_{t=1}^T\) 安排
- DDPM中前向过程的方差安排设置:
- DDPM实现中是使用线性的固定值,也就是说扩散过程 \(q\) 都是不可学习的参数。具体来说,DDPM实验时设置了 \(T=1000\) 该固定值使用的是 \([10^{-4}, 0.02]\) 之间的线性的固定值(即 \(\beta_1 = 10^{-4} \ \text{to} \ \beta_T = 0.02\) )
- 在DDPM中曾经提到方差 \(\beta_t\) 是可以通过重参数法学习的,也可以设置为固定值
- IDDPM中的改进:
- IDDPM将 \(\beta_t\) 从线性机制改成余弦机制,具体来说,通过 \(\bar{\alpha}_t\) 反推 \(\beta_t\)
$$ \beta_t = \text{clip}(1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}, 0.999) \quad\bar{\alpha}_t = \frac{f(t)}{f(0)}\quad\text{where }f(t)=\cos\Big(\frac{t/T+s}{1+s}\cdot\frac{\pi}{2}\Big)^2 $$- 其中 \(s\) 是一个非常小的数字,用于防止 \(t\) 太小的时候 \(\beta_t\) 取值太小,实验中,取 \(s=0.008\)
- 改进前后的取值比较
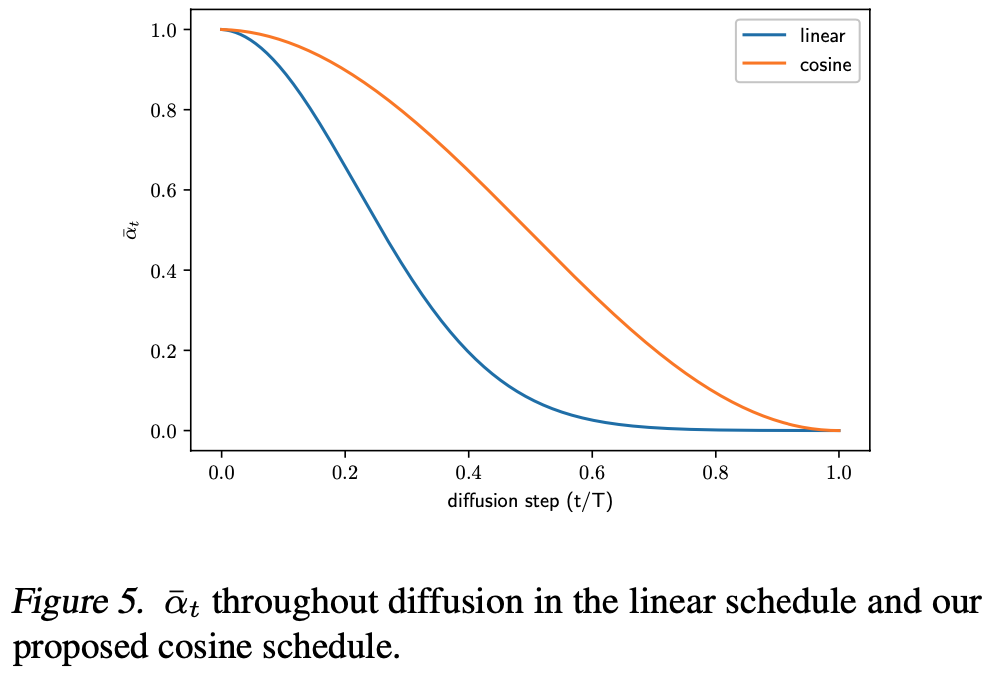
- IDDPM将 \(\beta_t\) 从线性机制改成余弦机制,具体来说,通过 \(\bar{\alpha}_t\) 反推 \(\beta_t\)
基于重要性采样训练 \(L_\text{VLB}\)
- DDPM中,训练时时间步时均匀采样得到的,但是不同的时间步 \(L_\text{VLB}\) 的Loss值不同,所以使用重要性采样来使得Loss大的地方得到更多的训练,详情见Improved Denoising Diffusion Probabilistic Models (IDDPM) - 妖妖的文章 - 知乎:
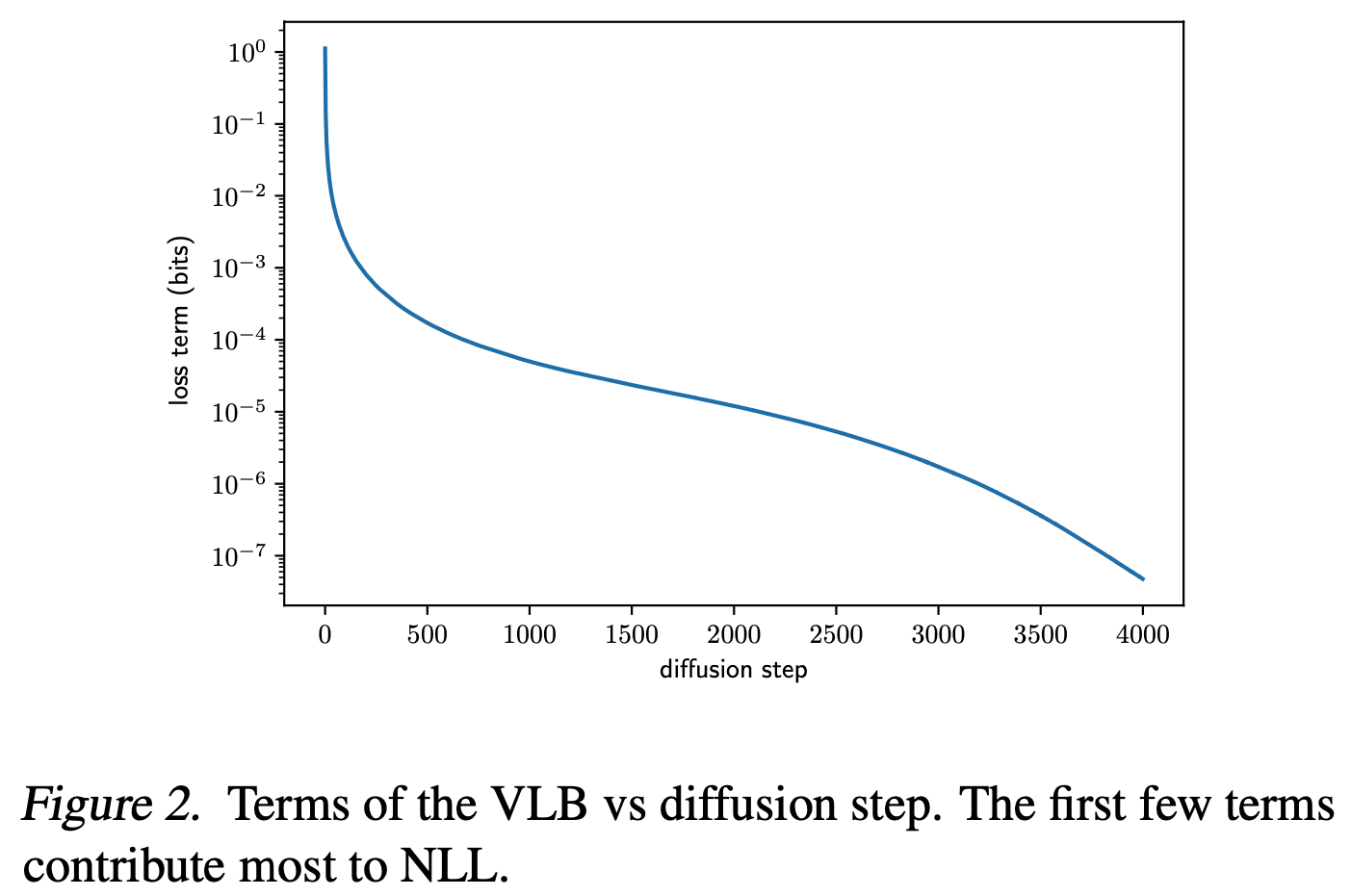
$$ L_\text{VLB} = \mathbb{E}_{t \sim p_t}\Big[\frac{L_t}{p_t}\Big] \quad \text{where } p_t \propto \sqrt{\mathbb{E}[L_t^2]} \ \text{and} \ \sum_t p_t = 1$$- Loss不均匀示意图:
- 改进后的效果示意图:
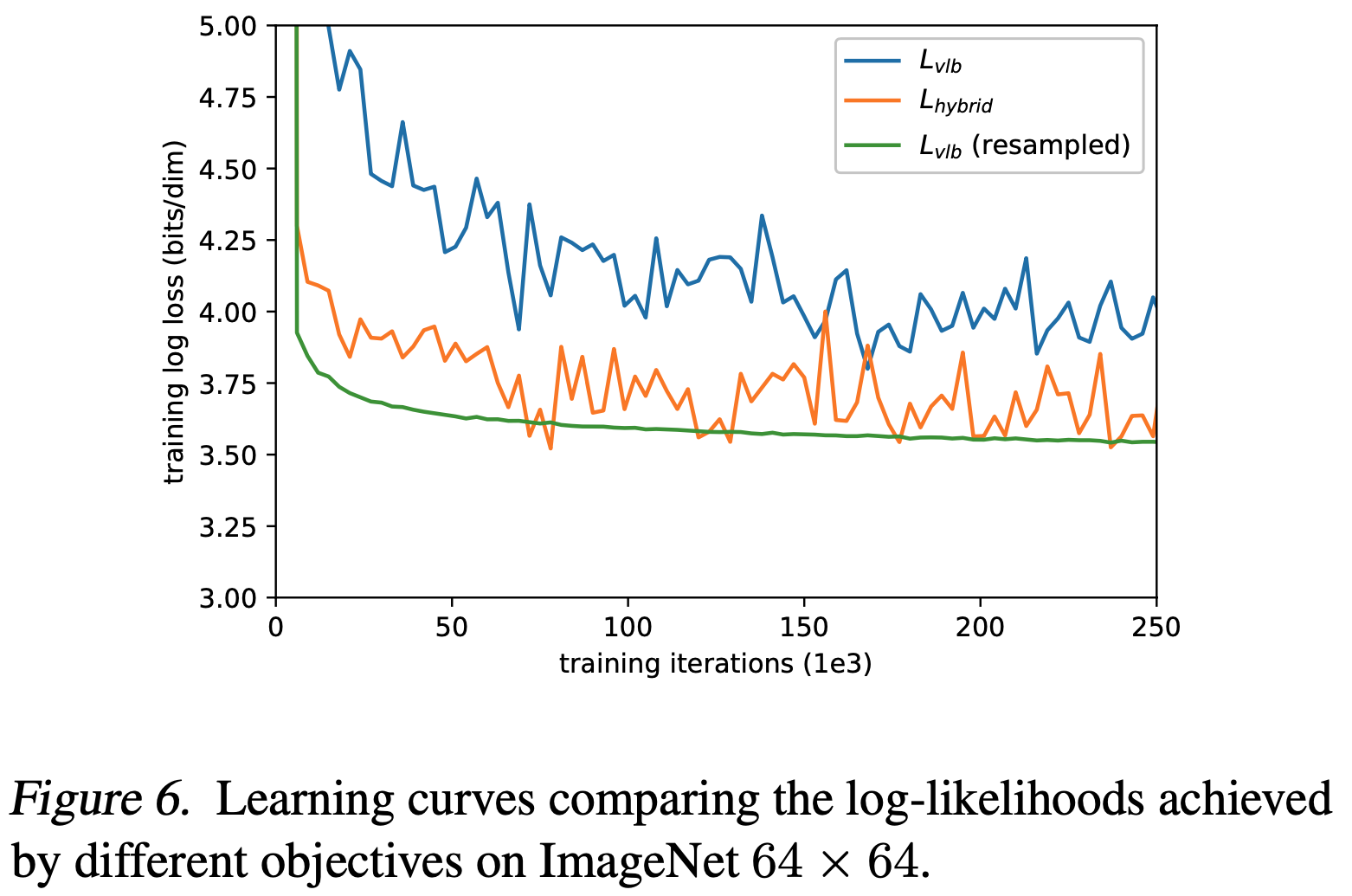
- 这里的改进不常用,文章写的有点晦涩难懂,需要时再来好好理解一下
- Loss不均匀示意图:
加速采样
- 与DDIM相似