文本介绍DDIM（Denoising Diffusion Implicit Models）的理论介绍
- 参考链接：
DDPM为什么慢？
- 采样步数不能太小，否则单次破坏力度过大，不容易恢复？
- 不能跳步，否则不遵循马尔科夫过程
推导过程
- 核心是在DDPM的基础上，增加解决马尔科夫问题
- 直观理解
- 推导结果，推导流程有时间再补充
- 当采样方差\(\sigma\)满足一定条件时，上面的式子会满足马尔科夫过程，即等价于DDPM
- 图示跳步采样（生成）的原理：
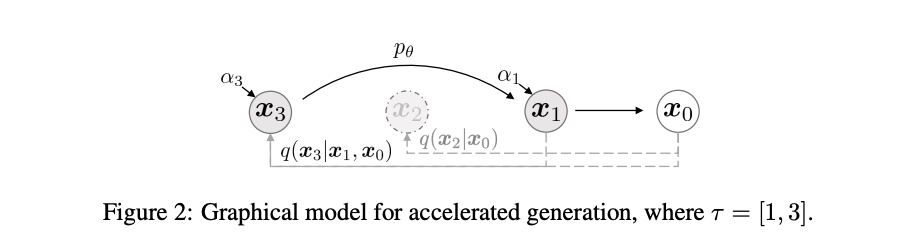
训练和推理
DDPM的训练和推理
DDIM的训练和推理
训练过程与DDPM基本一致，但DDIM只需要采样固定间隔的步数即可
- 如果已经有训练好的DDPM，可以直接用，因为DDPM的训练时间步包含了DDIM的训练时间步
推理过程
推理时，一般会设置\(\sigma=0\)，即DDIM是确定性的，也就是DDIM中I(Implicit)区别于DDPM中(Probabilistic)的原因
实验结果
- 实验设置
- 结果展示
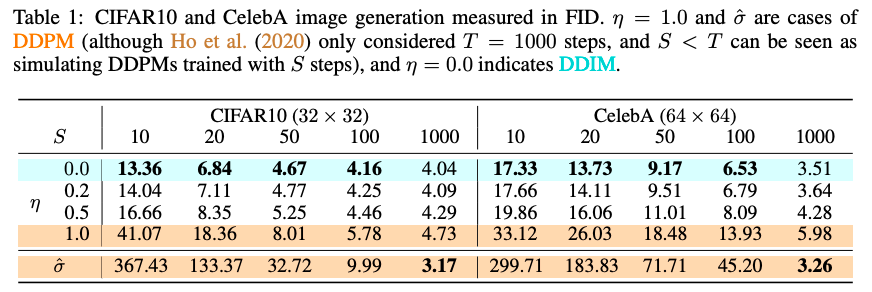
- 结果分析
- 从图中可以得出结论
- \(\sigma\)越小（\(\eta\)越小，方差越小），即方差越小，效果越好，DDIM最好（DDIM对应\(\eta=0\)且\(\sigma=0\)）
- 当\(T=1000\)时（或者\(T\)非常大时），DDPM效果最好（DDPM对应\(\eta=1\)且\(\sigma = \hat{\sigma}\)）
- 小节：当采样步数少时（即间隔大时），使用DDIM效果更好，DDPM效果非常差；当采样步数很大时，DDPM效果微微好于DDIM
代码亲测
各种\(\alpha,\beta\)的定义技巧：
1
2
3
4
5
6
7
8
9
10
11
12
13
14num_steps = 100
betas = torch.linspace(-6,6,num_steps)
betas = torch.sigmoid(betas)*(0.5e-2 - 1e-5)+1e-5 # beta逐步递增
alphas = 1-betas
print("alphas: %s" % alphas)
alphas_prod = torch.cumprod(alphas,0) # 连乘
alphas_bar = alphas_prod
alphas_prod_p = torch.cat([torch.tensor([1]).float(),alphas_prod[:-1]],0) # previous连乘
alphas_bar_sqrt = torch.sqrt(alphas_bar)
one_minus_alphas_bar_log = torch.log(1 - alphas_bar)
one_minus_alphas_bar_sqrt = torch.sqrt(1 - alphas_bar)
# 模型定义：model(x, t)
# 采样方式：torch.randn_like(x)实现细节(为了清晰表达，对原始采样公式有所修改)：
$$
x_s = \sqrt{\bar{\alpha}_s}\left(\frac{x_k-\sqrt{1-\bar{\alpha}_k}\epsilon_{\theta}(x_k,k)}{\bar{\alpha}_k}\right) + \sqrt{1-\bar{\alpha}_s-a_1\sigma_k^2}\epsilon_{\theta}(x_k,k) + a_2\sigma_k \epsilon
$$- 其中：\(\sigma_k^2 = \beta_t\)
- 注意：\(a_1,a_2\)是新加的，拆开\(a_1,a_2\)的原因是实验发现两者可以设置不同值，且有以下现象：
- \(a_2=0,a_1=1.0\)时，此时表示不采样，整个生成过程中没有添加随机值（除了初始样本为随机值外），不影响样本的生成质量，相对有随机值生成效果甚至更好
- \(a_1=0\)时，无论\(a_2\)值为多少，生成的样本均是类似乱码的图
- \(a_1>0.5\)时，无论\(a_2\)值是否为0，生成的样本均不错（\(a_1\)的值不能太小，否则效果会不好）
亲测实验结果与论文有偏差的原因分析:
- 如果采样步数较少，效果也不好，但当采样间隔为2时，即跳一步采样，效果还可以（不如间隔为1）
- 采样步数越多，效果越好（与原始论文结果一样）
- 为什么本人实现的DDIM采样步数不能太少？（跳步10步时效果较差，与原始论文结果不一致）
- DDIM可能对模型要求很高，本人尝试环境中模型过于简单？训练样本过少？
- 为什么\(a_1=0\)时，效果非常差？
- 待解答
- 如果采样步数较少，效果也不好，但当采样间隔为2时，即跳一步采样，效果还可以（不如间隔为1）
DDIM对比DDPM
- DDIM训练流程与DDPM完全相同，只是推理(采样)过程不同
- DDIM主要解决DDPM采样慢的问题
- DDPM有符合马尔科夫假设，需要一步步采样，效率慢
- DDIM没有马尔科夫假设，可以跳步生成图片，且可以不采样（标准的DDIM就是不采样的，论文中，噪音的方差越小，得到的效果越好）
一些问题和解答
- DDPM采样时不能去掉噪音，为什么DDIM可以？
- 回答：因为DDIM采样中，噪音的方差\(\sigma\)是通过实验发现效果比较好的
- 具体原因？
- 为什么DDPM和DDIM训练逻辑基本一致，但DDPM推断必须遵循马尔科夫性，而DDIM不需要？
- 回答：
- 训练时：DDIM和DDPM训练过程都遵循马尔科夫过程。DDIM可以按照一定间隔采样时间步，但实际上也是经过在满足马尔科夫过程的情况下推导出来的，DDPM和DDIM的训练采样公式都是因为方差可以累加实现跳跃采样的
- 推断时：因为DDPM的采样公式是在满足马尔科夫过程情况下推导出来的， 而DDIM的采样公式是在非马尔科夫过程情况下推导出来的，所以使用DDPM采样公式时，不能跳步；使用DDIM采样公式时（注意：实际上DDIM不采样，直接确定性生成），可以跳步
- 回答：