整体说明
- TLDR:对比学习(Contrastive Learning)是自监督学习中的一种方法,其核心思想是通过学习数据样本之间的相似性和差异性 ,使得相似样本在表示空间(embedding space)中靠近,不相似样本相互远离,从而学习一个表示空间
- 对比学习的目标是:学习一个表示空间(embedding space),使得在这个表示空间中,满足下面的条件
- 正样本对(相似的样本)的表示距离尽可能近
- 负样本对(不相似的样本)的表示距离尽可能远
- 注:通过这种对比机制,模型无需人工标注即可从数据中自动学习有意义的特征表示
详细方法说明
正负样本构造
- 正样本 :同一数据的不同增强视图(如裁剪、旋转、颜色变换后的同一图像),或语义相似的样本
- 负样本 :随机选择的其他数据样本,或显式定义的 dissimilar 样本
- 常用的策略有:同一batch内的其他样本、动态队列(历史batch中的样本)等
- 一些特殊的模型,比如BYOL(Bootstrap Your Own Latent)提出了 免负样本策略 ,详情见附录
常用损失函数
- InfoNCE Loss(Noise Contrastive Estimation):
$$
\mathcal{L} = -\log \frac{\exp(sim(q, k_+) / \tau)}{\sum_{i=0}^K \exp(sim(q, k_i) / \tau)}
$$- \(q\):查询样本的表示
- \(k_+\):正样本表示,\(k_i\) 为负样本表示
- \(\tau\):温度系数,控制分布的尖锐程度
- \(sim(\cdot)\):相似度函数(如余弦相似度)
- Triplet Loss :(三元组损失)
$$
\mathcal{L} = \max(d(a, p) - d(a, n) + \text{margin}, 0)
$$- \(a\):锚点(Anchor)样本
- \(p\):为正(Positive)样本
- \(n\):为负(Negative)样本
- 三元组损失的含义也就是 \(<a,p,n>\) 三元组
- \(\text{margin}\) 是超参数,用于控制正负样本之间的最小间隔
模型网络架构
- 通常使用双分支网络,两个分支可共享权重或不共享
对比学习的优势
- 无监督/自监督:无需人工标注,利用数据自身结构学习
- 迁移能力强:预训练的表示可泛化到下游任务(如分类、检测)
- 鲁棒性:通过数据增强学习到不变性特征(如CV中的光照、旋转不变性)
应用场景
- 计算机视觉:图像分类(SimCLR)、目标检测(MoCo)
- 自然语言处理:句子表示学习(SimCSE)
- 多模态学习:图文匹配(CLIP)、视频-文本对齐
附录:BYOL 的免负样本策略
- 原始论文:Bootstrap Your Own Latent A New Approach to Self-Supervised Learning, NeurIPS 2020, Google DeepMind
- 比如BYOL(Bootstrap Your Own Latent)提出了 免负样本策略 ,其中Target网络的参数通过指数移动平均(EMA)从Online网络缓慢更新(动量更新),模型学习目标是最小化同一图像的不同增强视图(正样本对,分别输入Target网络和Online网络中)的表示距离
- BYOL模型的整体架构图如下:
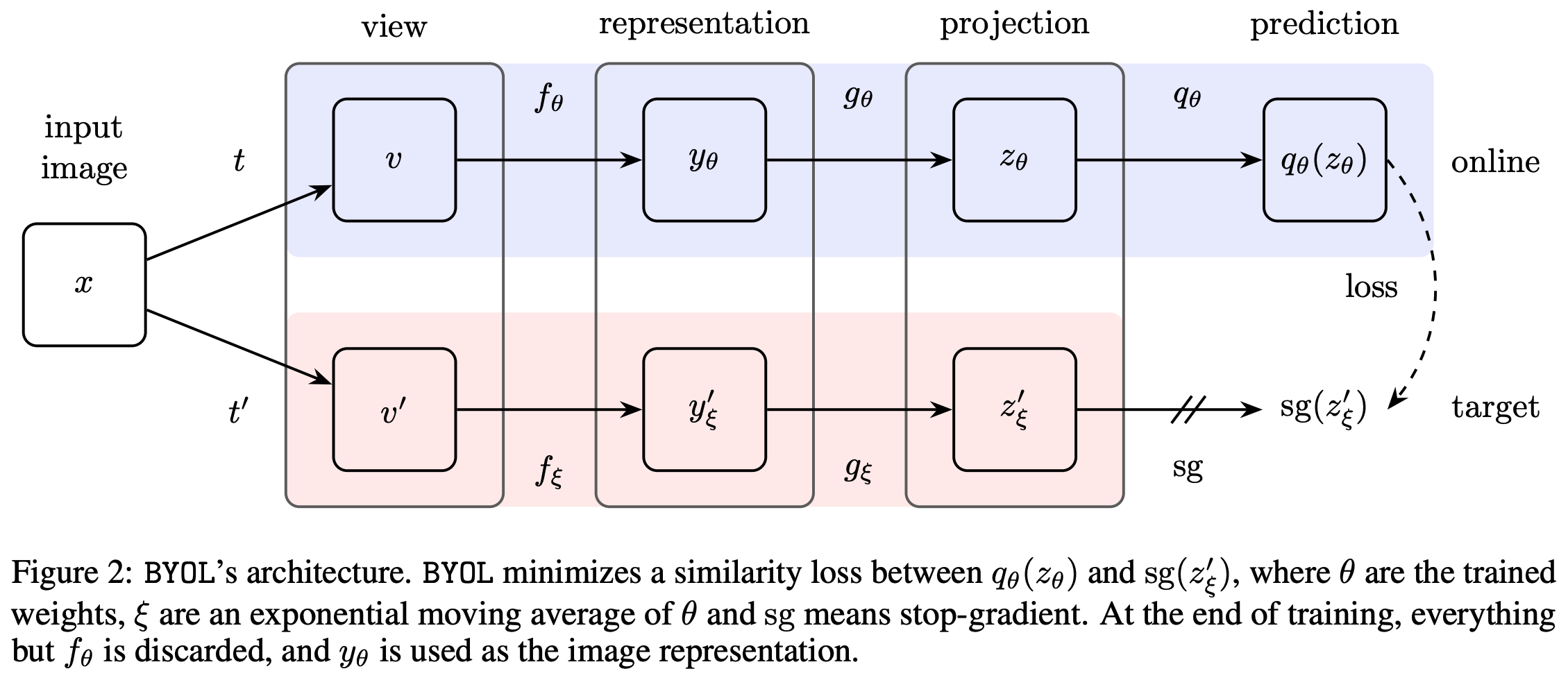
- 一种更容易理解的架构图:
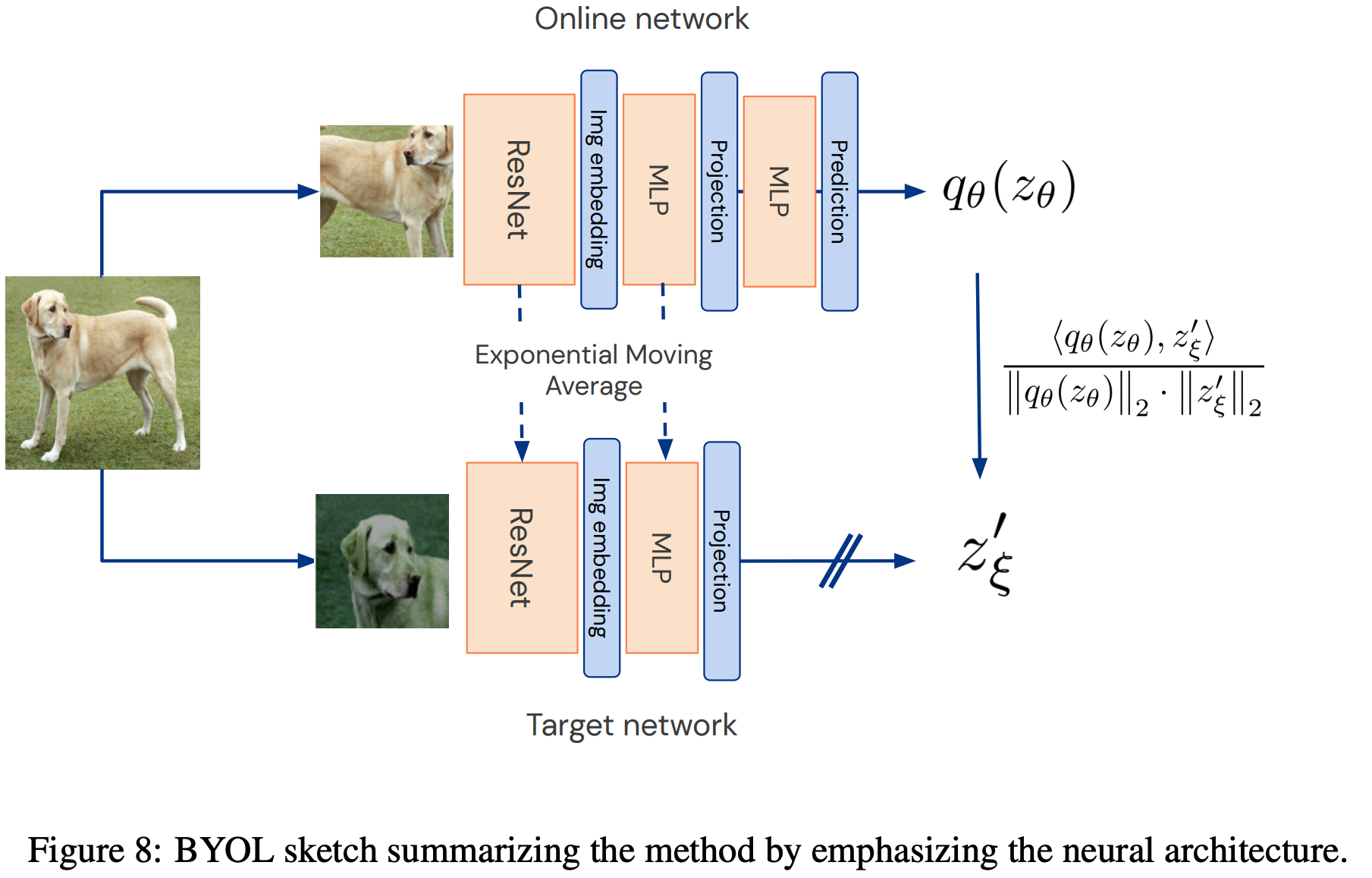
附录:NCE 和 InfoNCE 损失
- InfoNCE 和 NCE 的核心区别可以一句话概括为:
- NCE 用“二分类”把真实样本从 K 个噪声里挑出来;
- InfoNCE 用“K+1 类 Softmax”把真实样本从 K 个负样本里挑出来,并直接最大化互信息下界
- 下面给出各自的损失函数(公式均为单样本版本,可简单批平均得到最终损失)
Noise Contrastive Estimation (NCE)
- 目标:估计归一化常数 Z,同时学习打分函数 \(s_\theta(x)\)
- NCE 损失(对一条真实样本 \(x\) 和 K 条噪声 \(x’\sim q\)):
$$
\mathcal L_{\text{NCE} } = -\log \frac{e^{s_\theta(x)} }{e^{s_\theta(x)} + K e^{s_\theta(x’)}/Z} - \sum_{k=1}^K \log \frac{e^{s_\theta(x’_k)}/Z}{e^{s_\theta(x)} + K e^{s_\theta(x’_k)}/Z}
$$- 实际实现时通常把 Z 也当可学习参数,上式退化为二分类交叉熵:
- 正类 logits 为 \(s_\theta(x)-\log Z\)
- 负类 logits 为 \(s_\theta(x’)-\log Z\)
- 实际实现时通常把 Z 也当可学习参数,上式退化为二分类交叉熵:
InfoNCE
- InfoNCE 又称“对比预测编码”损失(Contrastive Predictive Coding Loss),也可简称为 CPC Loss
- 目标:最大化互信息 \(I(x; c)\) 的下界,其中 \(c\) 为上下文/表征
- 对一条正样本 \((x, c)\) 和 K 条负样本 \(\{(x’_k, c)\}\):
$$
\mathcal L_{\text{InfoNCE} } = -\log \frac{e^{f(x,c)/\tau} }{\displaystyle e^{f(x,c)/\tau} + \sum_{k=1}^K e^{f(x’_k,c)/\tau} }
$$- 这里 \(f(\cdot,\cdot)\) 是兼容函数(通常用内积或余弦相似度),\(\tau>0\) 为温度超参
- 当 \(K\rightarrow\infty\) 时,该损失给出的下界趋于真实的互信息,因此得名 InfoNCE
互信息 与 InfoNCE 的关联
- 互信息衡量了两个分布的依赖程度,当两个分布完全独立,他们的互信息为 0,当两个分布完全依赖,他们的互信息为其中一个分布的熵
- InfoNCE 损失的设计目标是最大化互信息的下界 ,而非直接计算互信息
- 当负样本数量 \(K\rightarrow\infty\) 时,InfoNCE 损失对应的下界会收敛到真实的互信息 \(I(X;Y)\),这也是该损失函数命名的核心原因