RL——IMPALA

注：本文包含 AI 辅助创作

参考链接
- 原始论文：IMPALA: Scalable Distributed Deep-RL with Importance Weighted Actor-Learner Architectures
- 补充材料（附录）：IMPALA Supplemental Material
- 其他参考博客：【强化学习 44】IMPALA/V-trace - 张海抱的文章 - 知乎

Paper Summary

论文的目标是使用一个具有单一参数集的单一强化学习智能体来解决大量任务
- 一个关键挑战是处理增加的数据量和延长的训练时间
论文开发了一种新的分布式智能体 IMPALA（重要性加权 Actor-Learner 架构，Importance Weighted Actor-Learner Architecture），
- IMPALA 不仅能在单机训练中更有效地使用资源，而且可以扩展到数千台机器，同时不牺牲数据效率或资源利用率
论文通过将解耦的执行与学习相结合，并采用一种称为 V-trace 的新型 Off-policy 校正方法，实现了高吞吐量下的稳定学习
论文在 DMLab-30（来自 DeepMind Lab 环境 (2016) 的 30 个任务集）和 Atari-57（Arcade Learning Environment (2013b) 中所有可用的 Atari 游戏）上展示了 IMPALA 在多任务强化学习中的有效性
论文的结果表明，IMPALA 能够用更少的数据实现比先前智能体更好的性能，并且由于其多任务方法，关键地展示了任务间的正向迁移

Introduction and Discussion

深度强化学习方法通过试错学习掌握了多种领域 (2015; 2016; 2017; 2013a; 2014)
- 虽然在围棋 (2016) 和 Atari 游戏 (2015) 等任务上的改进是显著的，但进展主要是在单任务性能上，即每个任务分别训练一个智能体
论文感兴趣的是开发能够同时掌握多种多样任务的新方法，以及适合评估此类方法的环境
在多个任务上同时训练单个智能体的一个主要挑战是可扩展性
- 由于当前最先进的方法如 A3C (2016) 或 UNREAL (2017) 可能需要多达十亿帧数据和数天时间来掌握一个单一领域，同时在数十个领域上训练它们就太慢而不实用
论文提出了如图 1 所示的重要性加权 Actor-Learner 架构（Importance Weighted Actor-Learner Architecture, IMPALA）
IMPALA 能够扩展到数千台机器，同时不牺牲训练稳定性或数据效率
- 与流行的基于 A3C 的智能体（其工作进程向中央参数服务器通信关于策略参数的梯度）不同，IMPALA 的执行者（actor）将经验轨迹（状态、动作和奖励的序列）通信给一个集中化的 Learner
  - 由于 IMPALA 中的 Learner 可以访问完整的经验轨迹，论文使用 GPU 对轨迹的小批量进行更新，同时积极并行化所有时间无关的操作
- 这种解耦架构可以实现非常高的吞吐量
然而，因为在梯度计算时，用于生成轨迹的策略可能落后于 Learner 上的策略若干次更新，学习就变成了 Off-policy 的
- 因此，论文引入了 V-trace Off-policy Actor-Critic 算法来校正这种有害的差异
结合可扩展架构和 V-trace，IMPALA 实现了每秒 250,000 帧的极高数据吞吐率，使其比单机 A3C 快 30 多倍
关键的是，IMPALA 也比基于 A3C 的智能体更具数据效率，并且对超参数值和网络架构更具鲁棒性，使其能够更好地利用更深的神经网络
论文通过在 DMLab-30（一个新的挑战集，包含在 3D DeepMind Lab (2016) 环境中的 30 个多样化认知任务）上训练单个智能体来解决多任务问题，以及在 Atari-57 任务集中的所有游戏上训练单个智能体，来展示 IMPALA 的有效性

最早扩展深度强化学习的尝试依赖于具有多个工作进程的分布式异步随机梯度下降（SGD）(2012)
- 比如分布式 A3C (2016) 和 Gorila (2015)（深度 Q 网络 (2015) 的分布式版本）
最近用于强化学习的异步 SGD 的替代方案
- 包括使用进化过程 (2017)、分布式 BA3C (2018) 和 Ape-X (2018)（其具有分布式回放但同步 Learner ）
也有多项工作通过利用 GPU 来扩展强化学习
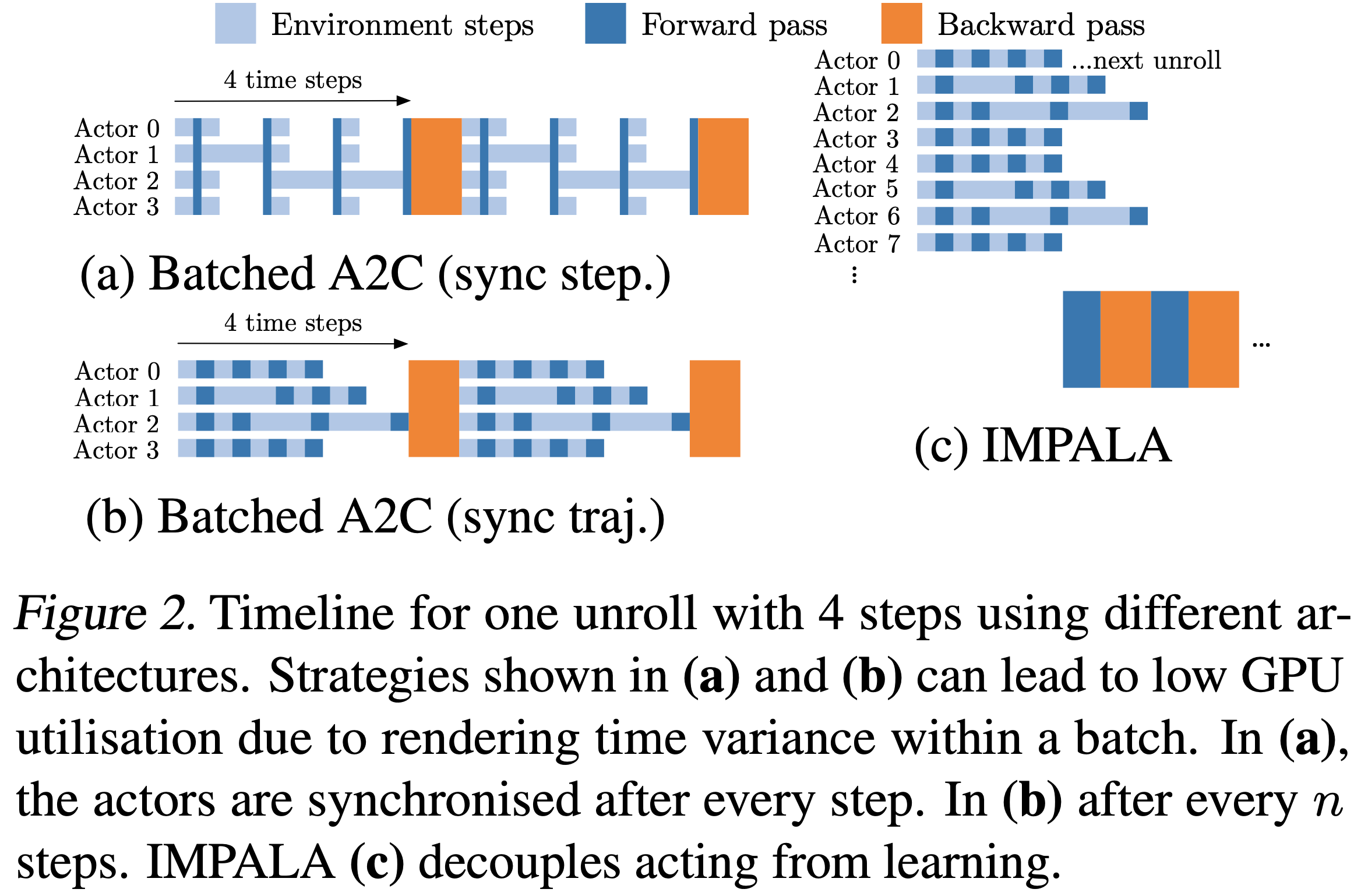
- 其中最简单的方法之一是批处理 A2C (2017)
  - 在每一步，批处理 A2C 产生一批动作并将其应用于一批环境
  - 每批中最慢的环境决定了执行整批步骤所需的时间（见图 1(a) 和 1(b)）
  - 换句话说，环境速度的高方差会严重限制性能
- 批处理 A2C 在 Atari 环境中特别有效，因为与强化学习智能体执行的昂贵张量操作相比，渲染和游戏逻辑在计算上非常便宜
  - 但视觉或物理上更复杂的环境可能模拟速度较慢，并且每一步所需的时间可能具有高方差
  - 环境也可能具有可变长度的（子）片段，导致初始化片段时速度减慢
与 IMPALA 最相似的架构是 GA3C (2016)，它也使用异步数据收集来更有效地利用 GPU
- GA3C 通过使用动态批处理将执行/前向传递与梯度计算/后向传递解耦
- GA3C 中的 Actor/Learner 异步性导致学习期间的不稳定性，(2016) 仅通过在策略梯度估计期间向动作概率添加一个小常数来部分缓解
- 相比之下，IMPALA 使用了更原则性的 V-trace 算法
先前关于 Off-policy 强化学习的相关工作包括 (2000, 2001); (2009); (2014); (2017) 和 (2016)
- 与论文工作最接近的是 Retrace 算法 (2016)，它引入了多步强化学习的 Off-policy 校正，并已在多种智能体架构中使用 (2017); (2018)
- Retrace 需要学习状态-动作值（state-action-value）函数 $Q$ 以进行 Off-policy 校正
- 然而，许多 Actor-Critic 方法（如 A3C）学习状态值（state-value）函数 $V$ 而不是状态-动作值函数 $Q$
- V-trace 基于状态值函数

IMPALA

IMPALA (图 1) 使用 Actor-Critic 设置来学习一个策略 $\pi$ 和一个基线函数 $V^{\pi}$
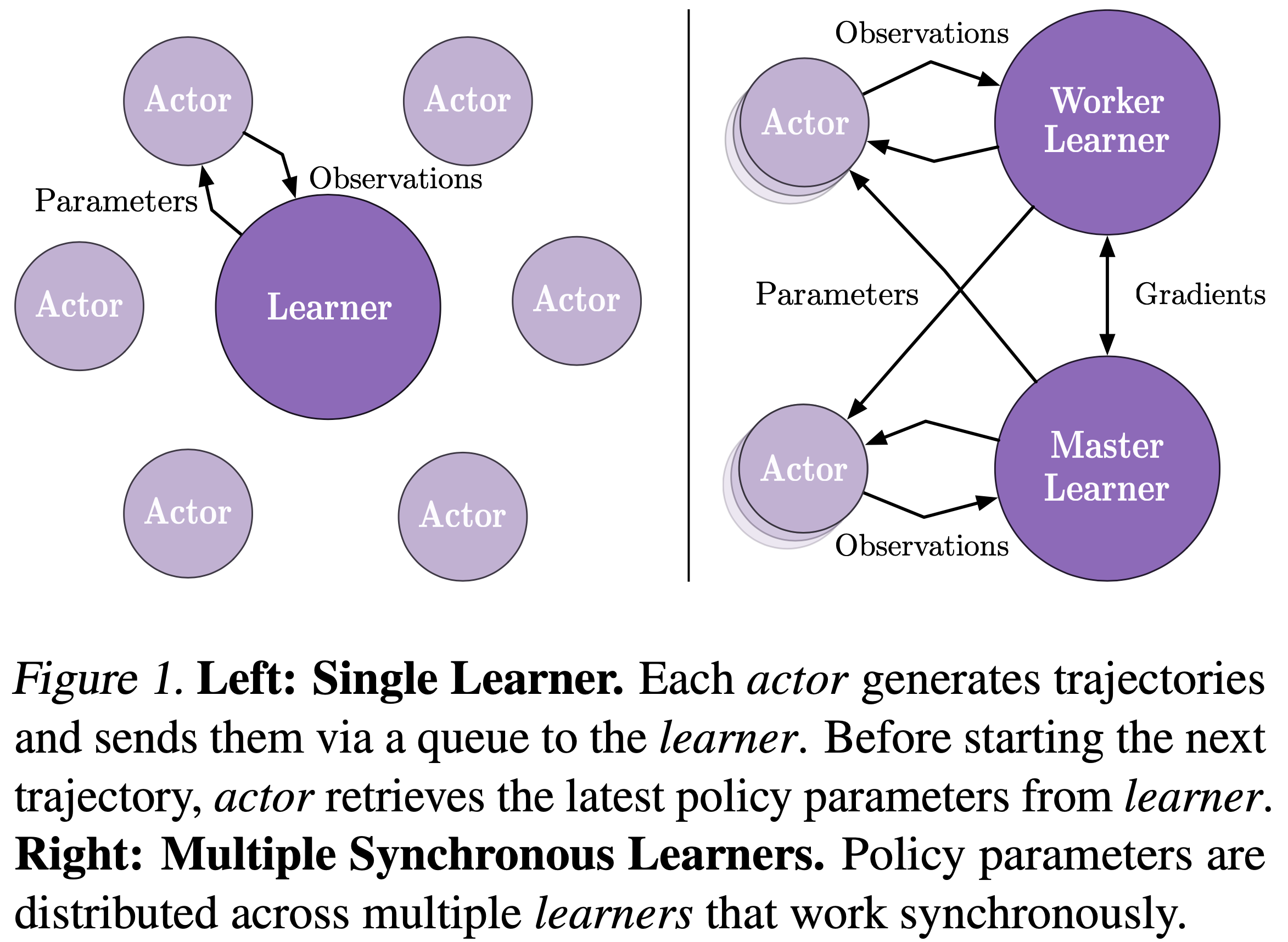
生成经验的过程与学习 $\pi$ 和 $V^{\pi}$ 的参数是解耦的
该架构由一组 Actor 和一个或多个 Learner 组成， Actor 反复生成经验轨迹， Learner 使用 Actor 发送的经验来 Off-policy 地 (off-policy) 学习 $\pi$
- 在每个轨迹开始时，一个 Actor 会将其自身的本地策略 $\mu$ 更新为最新的 Learner 策略 $\pi$ （$\mu \leftarrow \pi$），并在其环境中运行 $n$ 步
- 在 $n$ 步之后， Actor 将状态、动作和奖励的轨迹 $x_{1},a_{1},r_{1},\ldots,x_{n},a_{n},r_{n}$ 连同相应的策略分布 $\mu(a_{t}|x_{t})$ 和初始 LSTM 状态通过一个队列发送给 Learner
- Learner 持续地在来自许多 Actor 的轨迹批次上更新其策略 $\pi$
这种简单的架构使得 Learner 能够使用 GPU 进行加速，并且 Actor 可以轻松地分布在多台机器上
- 但在更新时， Learner 策略 $\pi$ 可能比 Actor 的策略 $\mu$ 领先若干次更新，因此在 Actor 和 Learner 之间存在策略滞后 (policy-lag)
V-trace 算法校正了这种滞后，从而在保持数据效率的同时实现了极高的数据吞吐量
- 使用 Actor-Learner 架构，提供了像分布式 A3C 那样的容错能力，但通常具有更低的通信开销，因为 Actor 发送的是观测值而不是参数/梯度
随着模型架构越来越深，单个 GPU 的速度常常成为训练期间的 limiting factor (限制因素)
如图 1 所示，IMPALA 可以与分布式的 Learner 集合一起使用，以高效地训练大型神经网络
参数分布在各个 Learner 之间， Actor 并行地从所有 Learner 检索参数，同时只将观测值发送给单个 Learner
IMPALA 使用同步参数更新，这在扩展到多台机器时对于保持数据效率至关重要 (2016)

Efficiency Optimisations

GPU 和 many-core CPU 通过运行少量大型、可并行化的操作而不是许多小操作而受益匪浅
由于 IMPALA 中的 Learner 在整个轨迹批次上执行更新，因此它能够比像 A3C 这样的在线智能体并行化更多的计算
- 例如，一个典型的深度 RL 智能体包含一个卷积网络，后接一个长短期记忆网络 (Long Short-Term Memory, LSTM) (1997) 和一个在 LSTM 之后的全连接输出层
- IMPALA Learner 通过将时间维度折叠到批次维度中，将卷积网络并行地应用于所有输入
类似地，一旦所有 LSTM 状态计算完毕，它也将输出层并行地应用于所有时间步
- 这种优化将有效批次大小增加到数千
- 基于 LSTM 的智能体还通过利用网络结构依赖性和操作融合 (2016) 在 Learner 上获得了显著的加速
最后，论文还利用了 TensorFlow (2017) 中提供的几种现成的优化，例如在执行计算的同时为 Learner 准备下一批数据、使用 XLA（一个 TensorFlow 即时编译器）编译部分计算图，以及优化数据格式以从 cuDNN 框架 (2014) 获得最大性能

V-trace

在解耦的分布式 Actor-Learner 架构中， Off-policy 学习非常重要，因为 Actor 生成动作与 Learner 估计梯度之间存在滞后
为此，论文为 Learner 引入了一种新颖的 Off-policy Actor-Critic 算法，称为 V-trace
论文考虑马尔可夫决策过程 (Markov Decision Processes, MDP) (1994; 1998) 中的 discounted infinite-horizon 强化学习问题，目标是找到一个策略 $\pi$，以最大化未来折扣奖励的期望和：
$$ V^{\pi}(x)\stackrel{ {\mathrm{def} } }{ {=} }\mathbb{E}_{\pi}\big{[} \sum_{t\geq 0}\gamma^{t}r_{t}\big{]} $$
- 其中 $\gamma\in[0,1)$ 是折扣因子，$r_{t}=r(x_{t},a_{t})$ 是时间 $t$ 的奖励，$x_{t}$ 是时间 $t$ 的状态（初始化为 $x_{0}=x$），$a_{t}\sim\pi(\cdot|x_{t})$ 是通过遵循某个策略 $\pi$ 生成的动作
Off-policy RL 算法的目标是使用由某个策略 $\mu$（称为行为策略 (behaviour policy)）生成的轨迹，来学习另一个策略 $\pi$（可能与 $\mu$ 不同，称为目标策略 (target policy)）的价值函数 $V^{\pi}$

V-trace 目标 (V-trace target)

考虑一个由 Actor 遵循某个策略 $\mu$ 生成的轨迹 $(x_{t},a_{t},r_{t})_{t=s}^{t=s+n}$
- 论文为 $V(x_{s})$（论文在状态 $x_{s}$ 的价值近似值）定义 $n$-step V-trace 目标为：
  $$v_{s}\stackrel{ {\mathrm{def} } }{ {=} } V(x_{s})+\sum_{t=s}^{s+n-1}\gamma^{t-s}\Big{(}\prod_{i=s}^{t-1 }c_{i}\Big{)}\delta_{t}V \tag{1}$$
  - 理解：这里是贝尔曼目标而不是 Advantage，类似 $r_t + V(s_t)$ 的角色
  - 其中 $\delta_{t}V$ 是 $V$ 的时序差分：
    $$ \delta_{t}V\stackrel{ {\mathrm{def} } }{ {=} }\rho_{t}\big{(}r_{t}+ \gamma V(x_{t+1})-V(x_{t})\big{)} $$
  - $\rho_{t}$ 和 $c_{i}$ 是截断的重要性采样 (Importance Sampling, IS) 权重（论文使用符号约定 $\prod_{i=s}^{t-1}c_{i}=1$ 当 $s=t$）
    $$
    \rho_{t}\stackrel{ {\mathrm{def} } }{ {=} }\min\big{(}\bar{\rho},\frac {\pi(a_{t}|x_{t})}{\mu(a_{t}|x_{t})}\big{)} \\
    c_{i}\stackrel{ {\mathrm{def} } }{ {=} }\min\big{(}\bar{c},\frac{\pi(a_{ t}|x_{t})}{\mu(a_{t}|x_{t})}\big{)}
    $$
  - 此外，论文假设截断水平满足 $\bar{\rho}\geq\bar{c}$
在 On-policy 的情况下（当 $\pi=\mu$），并假设 $\bar{c}\geq 1$，那么所有的 $c_{i}=1$ 且 $\rho_{t}=1$，因此 (1) 式重写为
$$
\begin{align}
v_{s} &=V(x_{s})+\sum_{t=s}^{s+n-1}\gamma^{t-s}\big{(}r_{t}+\gamma V(x_{t +1})-V(x_{t})\big{)}\\
&=\sum_{t=s}^{s+n-1}\gamma^{t-s}r_{t}+\gamma^{n}V(x_{s+n})
\end{align} \tag{2}
$$
- 这是 On-policy $n$-step Bellman 目标
- 因此，在 On-policy 情况下，V-trace 简化为 On-policy $n$-step Bellman 更新
  - 这个属性（是 Retrace (2016) 所不具备的）允许人们对离线和 On-policy 数据使用相同的算法
（截断的）IS 权重 $c_{i}$ 和 $\rho_{t}$ 扮演不同的角色
权重 $\rho_{t}$ 出现在时序差分 $\delta_{t}V$ 的定义中，并定义了此更新规则的固定点
- 在表格情况下，即函数可以被完美表示时，此更新的固定点（即，当对所有状态都有 $V(x_{s})=v_{s}$ 时），其特征是在期望下（在 $\mu$ 下）$\delta_{t}V$ 等于零，它是某个策略 $\pi_{\bar{\rho} }$ 的价值函数 $V^{\pi_{\bar{\rho} } }$，该策略由下式定义：
  $$\pi_{\bar{\rho} }(a|x)\stackrel{ {\mathrm{def} } }{ {=} }\frac{\min\big{(}\bar{\rho}\mu(a|x),\pi(a|x)\big{)} }{\sum_{b\in A}\min\big{(}\bar{\rho}\mu(b|x ),\pi(b|x)\big{)} } \tag{3}$$
- （参见附录 A 中的分析）
- 所以当 $\bar{\rho}$ 是无限的（即没有对 $\rho_{t}$ 进行截断）时，这就是目标策略 $\pi$ 的价值函数 $V^{\pi}$
- 然而，如果论文选择一个截断水平 $\bar{\rho}<\infty$，论文的固定点就是策略 $\pi_{\bar{\rho} }$ 的价值函数 $V^{\pi_{\bar{\rho} } }$，该策略介于 $\mu$ 和 $\pi$ 之间
- 在 $\bar{\rho}$ 接近零的极限情况下，论文得到行为策略 $\mu$ 的价值函数 $V^{\mu}$
- 在附录 A 中，论文证明了相关 V-trace 算子的收缩性以及相应在线 V-trace 算法的收敛性
权重 $c_{i}$ 类似于 Retrace 中的“迹切割”系数
- 它们的乘积 $c_{s}\dots c_{t-1}$ 衡量了在时间 $t$ 观察到的时序差分 $\delta_{t}V$ 对先前时间 $s$ 的价值函数更新的影响程度
- $\pi$ 和 $\mu$ 越不相似（论文越是 Off-policy ），该乘积的方差就越大
- 论文使用截断水平 $\bar{c}$ 作为一种方差缩减技术
- 但请注意，这种截断不会影响论文收敛到的解（该解仅由 $\bar{\rho}$ 表征）
因此，论文看到截断水平 $\bar{c}$ 和 $\bar{\rho}$ 代表了算法的不同特征：
- $\bar{\rho}$ 影响 IMPALA 收敛到的价值函数的性质
- $\bar{c}$ 影响 IMPALA 收敛到该函数的速度
Remark 1 ：V-trace 目标可以递归地计算：
$$v_{s}=V(x_{s})+\delta_{s}V+\gamma c_{s}\big{(}v_{s+1}-V(x_{s+1})\big{)}.$$
Remark 2 ：
- 与 Retrace$(\lambda)$ 类似，也可以在 V-trace 的定义中考虑一个额外的折扣参数 $\lambda\in[0,1]$，通过设置 $c_{i}=\lambda\min\big{(}\bar{c},\frac{\pi(a_{i}|x_{i})}{\mu(a_{i}|x_{i})}\big{)}$ 来实现
- 在 On-policy 情况下，当 $n=\infty$ 时，V-trace 则简化为 TD$(\lambda)$

Actor-Critic algorithm

策略梯度 (Policy gradient)

在 On-policy 情况下，价值函数 $V^{\mu}(x_{0})$ 关于策略 $\mu$ 的某个参数的梯度是
$$\nabla V^{\mu}(x_{0})=\mathbb{E}_{\mu}\Big{[}\sum_{s\geq 0}\gamma^{s}\nabla\log \mu(a_{s}|x_{s})Q^{\mu}(x_{s},a_{s})\Big{]},$$
- 其中 $Q^{\mu}(x_{s},a_{s})\stackrel{ {\textrm{def} } }{ {=} }\mathbb{E}_{\mu} \big{[}\sum_{t\geq s}\gamma^{t-s}r_{t}|x_{s},a_{s}\big{]}$ 是策略 $\mu$ 在 $(x_{s},a_{s})$ 的状态-动作价值
- 这通常通过随机梯度上升来实现，该上升沿 $\mathbb{E}_{a_{s}\sim\mu(\cdot|x_{s})}\Big{[}\nabla\log\mu(a_{s}|x_{s})q_{s}|x_ {s}\Big{]}$ 的方向更新策略参数，其中 $q_{s}$ 是 $Q^{\mu}(x_{s},a_{s})$ 的一个估计值，并在某个行为策略 $\mu$ 下访问到的一组状态 $x_{s}$ 上取平均
现在，在论文考虑的 Off-policy 设置中，我们可以使用被评估的策略 $\pi_{\bar{\rho} }$ 和行为策略 $\mu$ 之间的 IS 权重，沿以下方向更新论文的策略参数
$$\mathbb{E}_{a_{s}\sim\mu(\cdot|x_{s})}\Big{[}\frac{\pi_{\bar{\rho} }(a_{s}|x_{s })}{\mu(a_{s}|x_{s})}\nabla\log\pi_{\bar{\rho} }(a_{s}|x_{s})q_{s}\big{|}x_{s} \Big{]} \tag{4}$$
- 其中 $q_{s}\stackrel{ {\textrm{def} } }{ {=} }r_{s}+\gamma v_{s+1}$ 是从下一个状态 $x_{s+1}$ 的 V-trace 估计 $v_{s+1}$ 构建的 $Q^{\pi_{\bar{\rho} } }(x_{s},a_{s})$ 的估计值
- 论文使用 $q_{s}$ 而不是 $v_{s}$ 作为论文的 Q 值 $Q^{\pi_{\bar{\rho} } }(x_{s},a_{s})$ 的目标的原因是：
  - 假设论文的价值估计在所有状态下都是正确的，即 $V=V^{\pi_{\bar{\rho} } }$，那么论文有 $\mathbb{E}[q_{s}|x_{s},a_{s}]=Q^{\pi_{\bar{\rho} } }(x_{s},a_{s})$（而如果论文选择 $q_{t}=v_{t}$ 则不具备此性质）。有关分析请参见附录 A，关于估计 $q_{s}$ 的不同方法的比较请参见附录 E.3
为了降低策略梯度估计 (4) 的方差，论文通常从 $q_{s}$ 中减去一个依赖于状态的基线，例如当前的价值近似值 $V(x_{s})$
最后请注意，(4) 式估计的是 $\pi_{\bar{\rho} }$ 的策略梯度，这是在使用截断水平 $\bar{\rho}$ 时 V-trace 算法所评估的策略
- 然而，假设偏差 $V^{\pi_{\bar{\rho} } }-V^{\pi}$ 很小（例如，如果 $\bar{\rho}$ 足够大），那么我们可以期望 $q_{s}$ 为论文提供 $Q^{\pi}(x_{s},a_{s})$ 的良好估计
- 考虑到这些 Remarks，论文推导出以下规范的 V-trace Actor-Critic 算法

V-trace actor-critic algorithm

考虑价值函数 $V_{\theta}$ 和当前策略 $\pi_{\omega}$ 的参数化表示
轨迹是由 Actor 遵循某个行为策略 $\mu$ 生成的
V-trace 目标 $v_{s}$ 由 (1) 定义
在训练时间 $s$，价值参数 $\theta$ 通过梯度下降法在 $l2$ 损失上朝着目标 $v_{s}$ 更新，即，沿着下面的方向更新
$$\big{(}v_{s}-V_{\theta}(x_{s})\big{)}\nabla_{\theta}V_{\theta}(x_{s})$$
而策略参数 $\omega$ 则沿着策略梯度的方向更新：
$$\rho_{s}\nabla_{\omega}\log\pi_{\omega}(a_{s}|x_{s})\big{(}r_{s}+\gamma v_{s+1}- V_{\theta}(x_{s})\big{)}$$
为了防止过早收敛，我们可以像在 A3C 中那样，沿着以下方向添加一个熵奖励 (entropy bonus)
$$-\nabla_{\omega}\sum_{a}\pi_{\omega}(a|x_{s})\log\pi_{\omega}(a|x_{s})$$
总的更新是通过将这三个梯度按适当的系数重新缩放后相加得到的，这些系数是算法的超参数

Experiments

论文研究了 IMPALA 在多种设置下的性能
为了评估数据效率、计算性能和 Off-policy 校正的有效性，论文观察了在单个任务上训练的 IMPALA 智能体的学习行为
对于多任务学习，论文在一个新引入的包含 30 个 DeepMind Lab 任务的集合以及 Atari 学习环境 (2013a) 的所有 57 个游戏上训练智能体，每个智能体对所有任务使用同一组权重
在所有实验中，论文使用了两种不同的模型架构：
- 一个类似于 (2016) 的浅层模型，在策略和价值函数之前有一个 LSTM（如图 3（左）所示）；
- 一个更深的残差模型 (2016)（如图 3（右）所示）
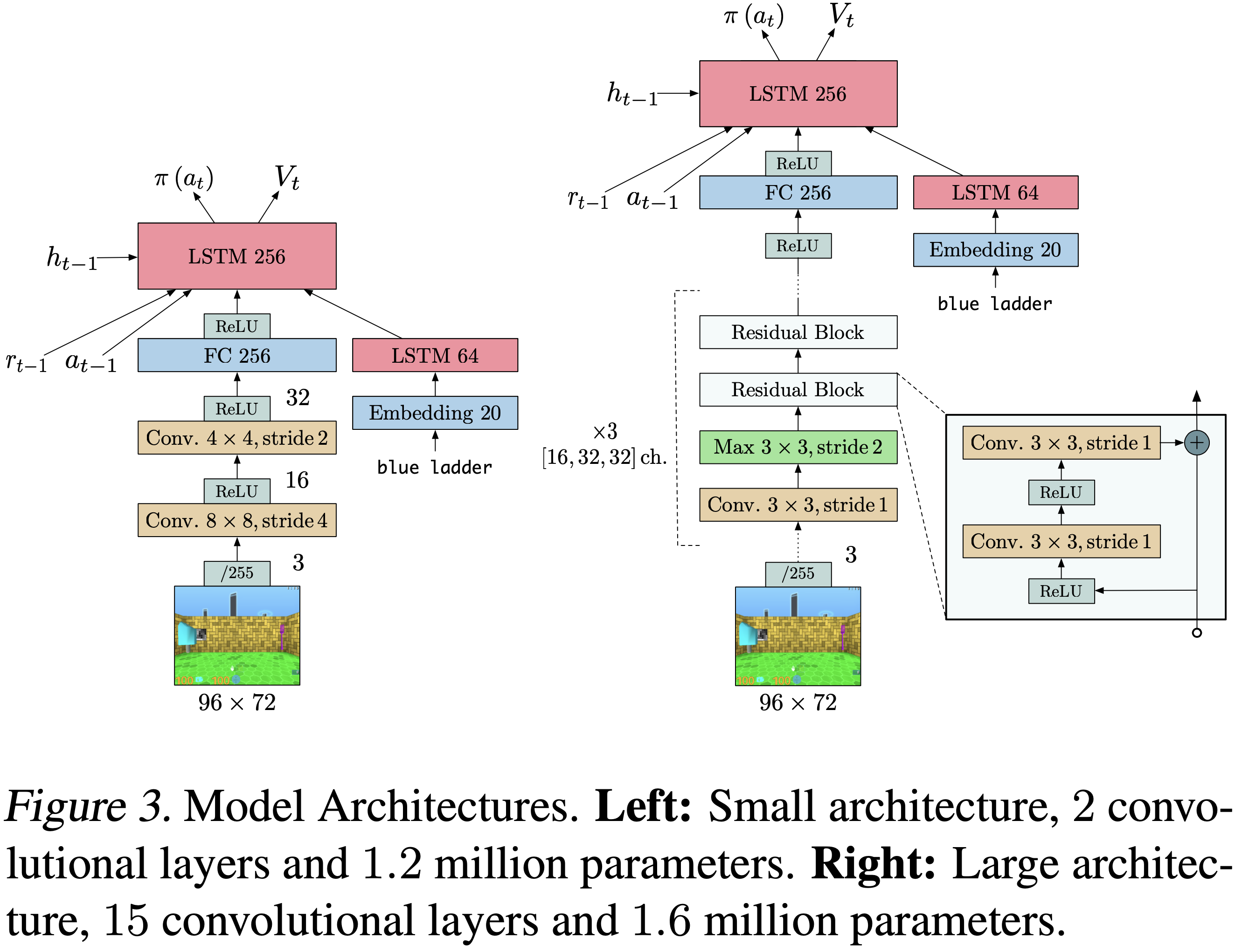
对于有语言通道的任务，论文使用了一个以文本嵌入作为输入的 LSTM

计算性能 (Computational Performance)

高吞吐量、计算效率和可扩展性是 IMPALA 的主要设计目标
为了证明 IMPALA 在这些指标上优于当前算法，论文比较了 A3C (2016)、批处理 A2C 变体以及具有各种优化的 IMPALA 变体
- 对于使用 GPU 的单机实验，论文在前向传播中使用动态批处理来避免多次批大小为 1 的前向传播
- 论文的动态批处理模块由专门的 TensorFlow 操作实现，但在概念上类似于 GA3C 中使用的队列
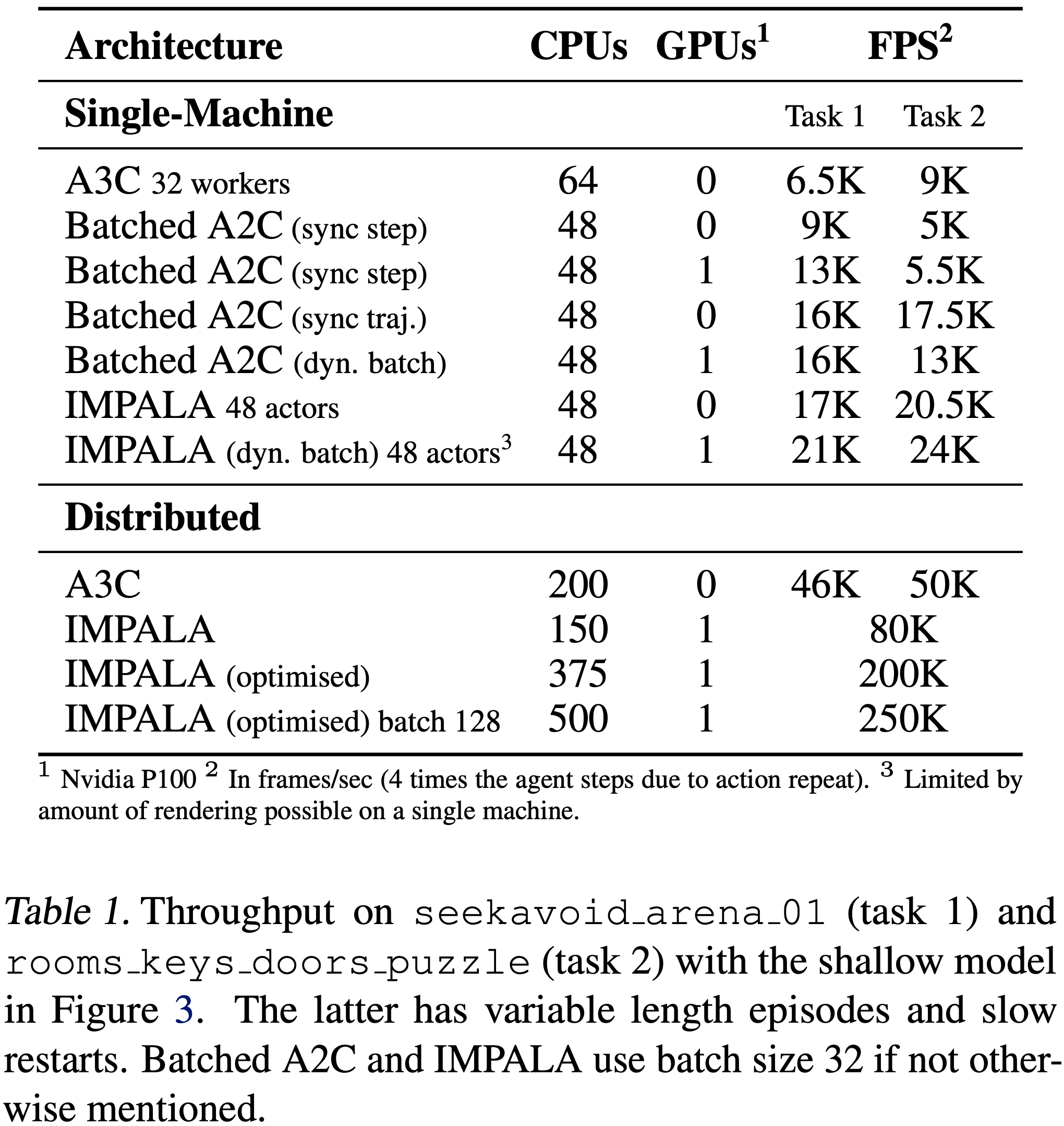
表 1 详细列出了使用图 3 中浅层模型的单机和多机版本的结果
- 在单机情况下，IMPALA 在两个任务上都实现了最高性能，领先于所有批处理 A2C 变体以及 A3C
- 且分布式多机设置才是 IMPALA 真正展示其可扩展性的地方
- 通过第 3.1 节中的优化来加速基于 GPU 的学习器，IMPALA 智能体实现了 250,000 帧/秒或 210 亿帧/天的吞吐率
- 为了减少每个学习器所需的执行器数量，可以使用辅助损失、来自经验回放的数据或其他仅在学习器上进行的昂贵计算

单任务训练 (Single-Task Training)

为了研究 IMPALA 的学习动态，论文采用了单任务场景，在 5 个不同的 DeepMind Lab 任务上分别训练智能体
- 该任务集包括一个规划任务、两个迷宫导航任务、一个带有脚本机器人的激光标签任务和一个简单的水果收集任务
论文对熵正则化的权重、学习率和RMSProp epsilon进行了超参数扫描
- 对于每个实验，论文使用一组相同的 24 个从附录 D.1 范围内预采样的超参数组合
- 其他超参数固定为附录 D.3 中指定的值

收敛性与稳定性 (Convergence and Stability)

图 4 显示了 IMPALA、A3C 和使用图 3 中浅层模型的批处理 A2C 之间的比较
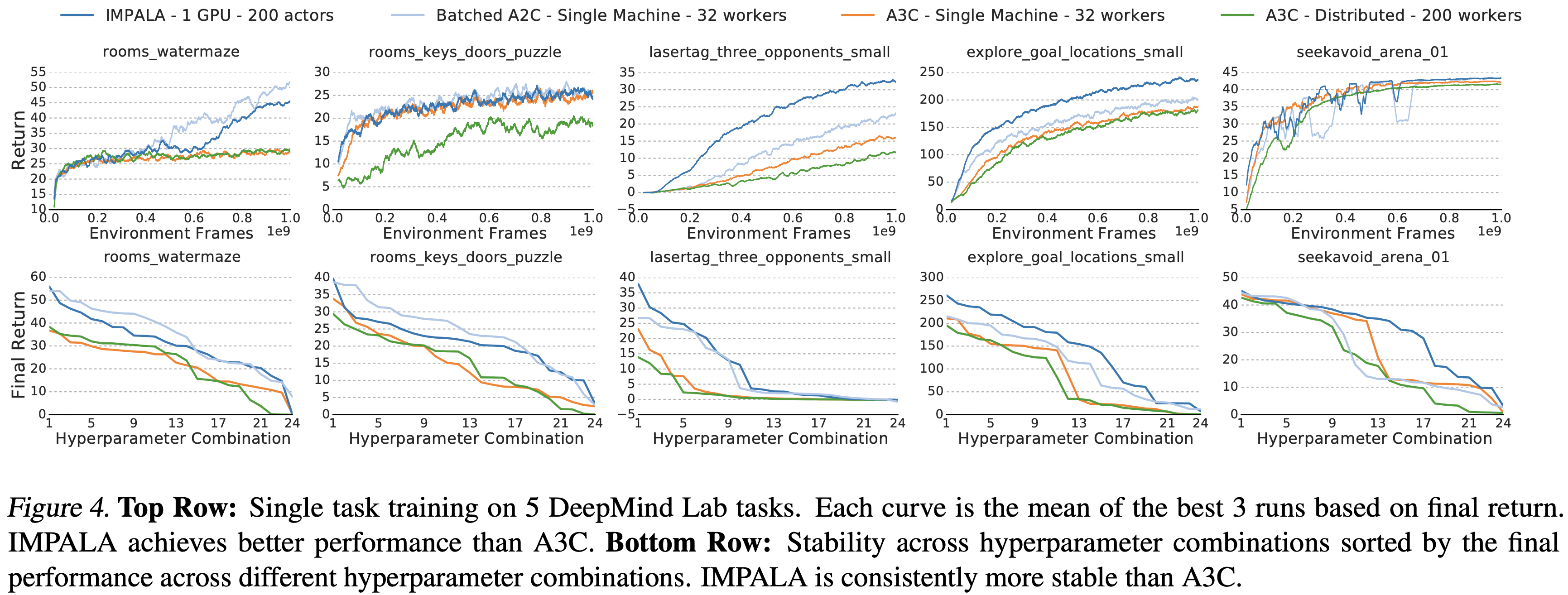
在所有 5 个任务中，要么是批处理 A2C 要么是 IMPALA 达到了最佳最终平均回报
- 并且在除 seekavoid_arena_01 之外的所有任务中，它们在整个训练过程中都领先于 A3C
- 理解：
  - A2C 是严格 On-policy 的，且参数是同步更新，所以是理论上的性能最优；
  - 对比来看，虽然 A3C 是 On-policy 的，但是存在参数的异步更新（有一定的滞后性），会导致一定的导致不稳定性
IMPALA 在 5 个任务中的 2 个上优于同步批处理 A2C，同时实现了更高的吞吐量（见表 1）
- 论文推测这种行为可能源于
  - 1）V-trace Off-policy 校正的作用类似于广义优势估计 (2016)
  - 2）异步数据收集产生了更多样化的经验批次
除了达到更好的最终性能外，IMPALA 对超参数选择的鲁棒性也比 A3C 更强
图 4 比较了上述方法在不同超参数组合下的最终性能，这些组合按平均最终回报从高到低排序
- IMPALA 在更多的组合上取得了更高的分数

V-trace 分析 (V-trace Analysis)

为了分析 V-trace，论文研究了四种不同的算法：
- 1. 无校正 (No-correction) ：无 Off-policy 校正
- 2. $\varepsilon$-校正 ($\varepsilon$-correction) ：在梯度计算期间添加一个小的常数值（$\varepsilon=1e-6$），以防止 $\log\pi(a)$ 变得非常小并导致数值不稳定，类似于 (2016)
- 3. 1-step 重要性采样 (1-step importance sampling) ：优化 $V(x)$ 时不进行 Off-policy 校正
  - 对于策略梯度，将每个时间步的优势（advantage）乘以相应的重要性采样权重
  - 此变体类似于没有“迹（traces）”的 V-trace，包含它是为了研究“迹”在 V-trace 中的重要性
- 4. V-trace ：如第 4 节所述
对于 V-trace 和 1-step 重要性采样，论文将每个重要性权重 $\rho_{t}$ 和 $c_{t}$ 裁剪为 $1$（即 $\bar{c}=\bar{\rho}=1$）
- 这降低了梯度估计的方差但引入了偏差
- 在 $\bar{\rho}\in[1,10,100]$ 中，论文发现 $\bar{\rho}=1$ 效果最好
论文在上一节的 5 个 DeepMind Lab 任务集上评估了所有算法
- 论文还在学习器上添加了一个经验回放缓冲区，以增加 $\pi$ 和 $\mu$ 之间的 Off-policy 差距
- 在经验回放实验中，论文从回放缓冲区中均匀随机抽取每批中 50% 的项目
表 2 分别显示了每种算法在有回放和无回放情况下的最终性能
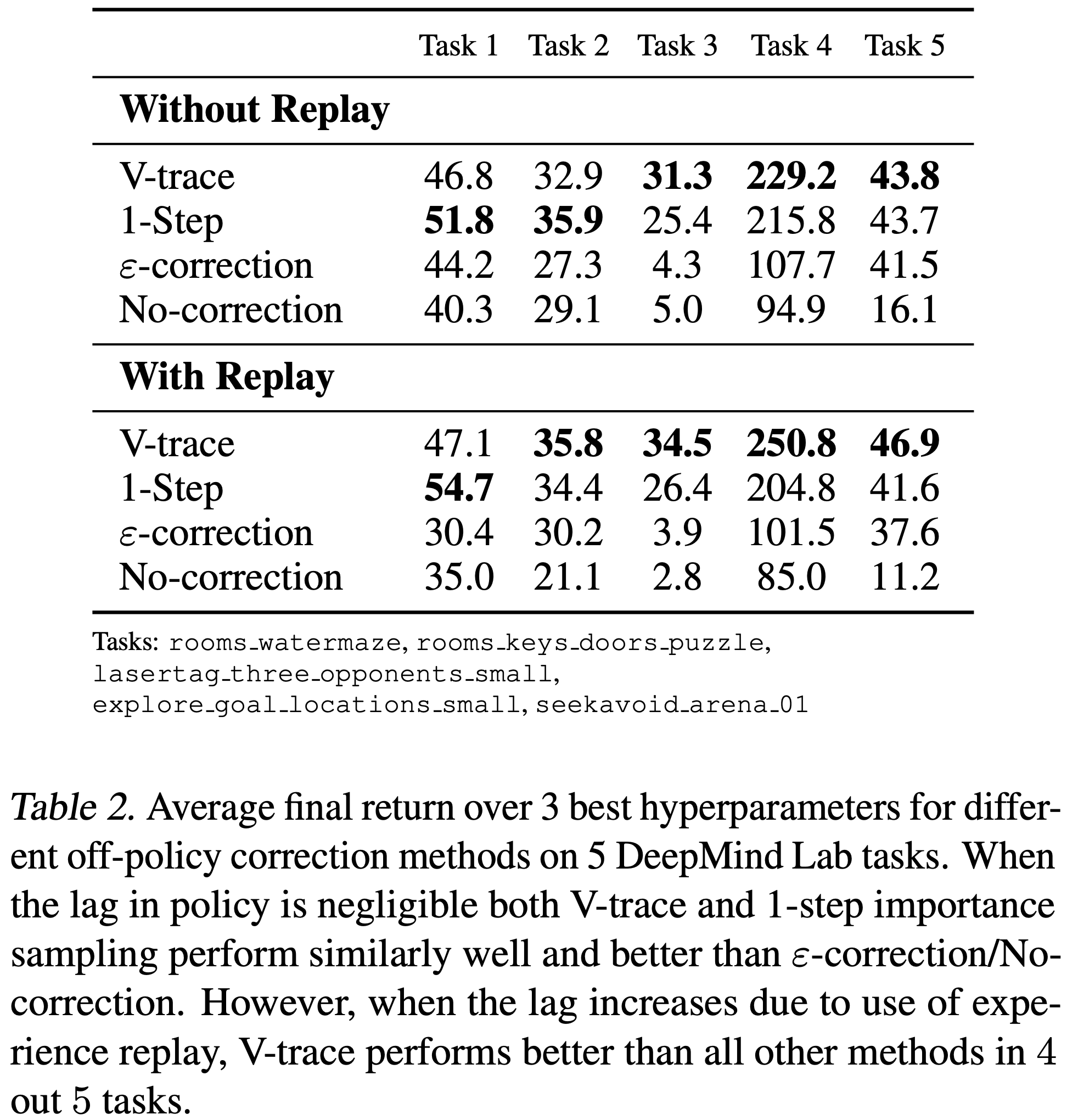
在无回放设置中，V-trace 在 5 个任务中的 3 个上表现最佳，其次是 1-step 重要性采样、$\varepsilon$-校正和无校正
- 尽管 1-step 重要性采样在无回放设置中表现与 V-trace 相似，但在使用经验回放时，在 5 个任务中的 4 个上差距扩大了
  - 这表明，当目标策略和行为策略偏离更严重时，粗糙的 1-step 重要性采样近似变得不足
- 还要注意，V-trace 是唯一一个始终受益于添加经验回放的变体
- $\varepsilon$-校正在两个任务上比无校正有显著改进，但远远落后于基于重要性采样的方法，特别是在使用经验回放的更 Off-policy 的设置中
- 图 E.1 显示了更详细分析的结果
- 图 E.2 显示基于重要性采样的方法在所有超参数下也表现更好，并且通常更鲁棒

多任务训练 (Multi-Task Training)

IMPALA 的高数据吞吐量和数据效率使论文不仅可以在一个任务上训练，还可以在多个任务上并行训练，只需对训练设置进行最小更改
论文没有在所有执行器上运行相同的任务，而是将固定数量的执行器分配给多任务套件中的每个任务
注意，模型不知道它正在被训练或评估的是哪个任务

DMLab-30

为了测试 IMPALA 在多任务设置中的性能，论文使用 DMLab-30，这是一个基于 DeepMind Lab 构建的包含 30 个多样化任务的集合
该套件中的众多任务类型包括具有自然外观地形的视觉复杂环境、基于指令的接地语言任务 (2017)、导航任务、认知任务 (2018) 以及以脚本机器人作为对手的第一人称标签任务
DMLab-30 和任务的详细描述可在 github.com/deepmind/lab 和 deepmind.com/dm-lab-30 获取
论文比较了多种 IMPALA 变体与分布式 A3C 实现
- 除了使用基于群体的训练 (Population-Based Training, PBT) (2017a) 的智能体外，所有智能体都在附录 D.1 给出的相同范围内进行了超参数扫描
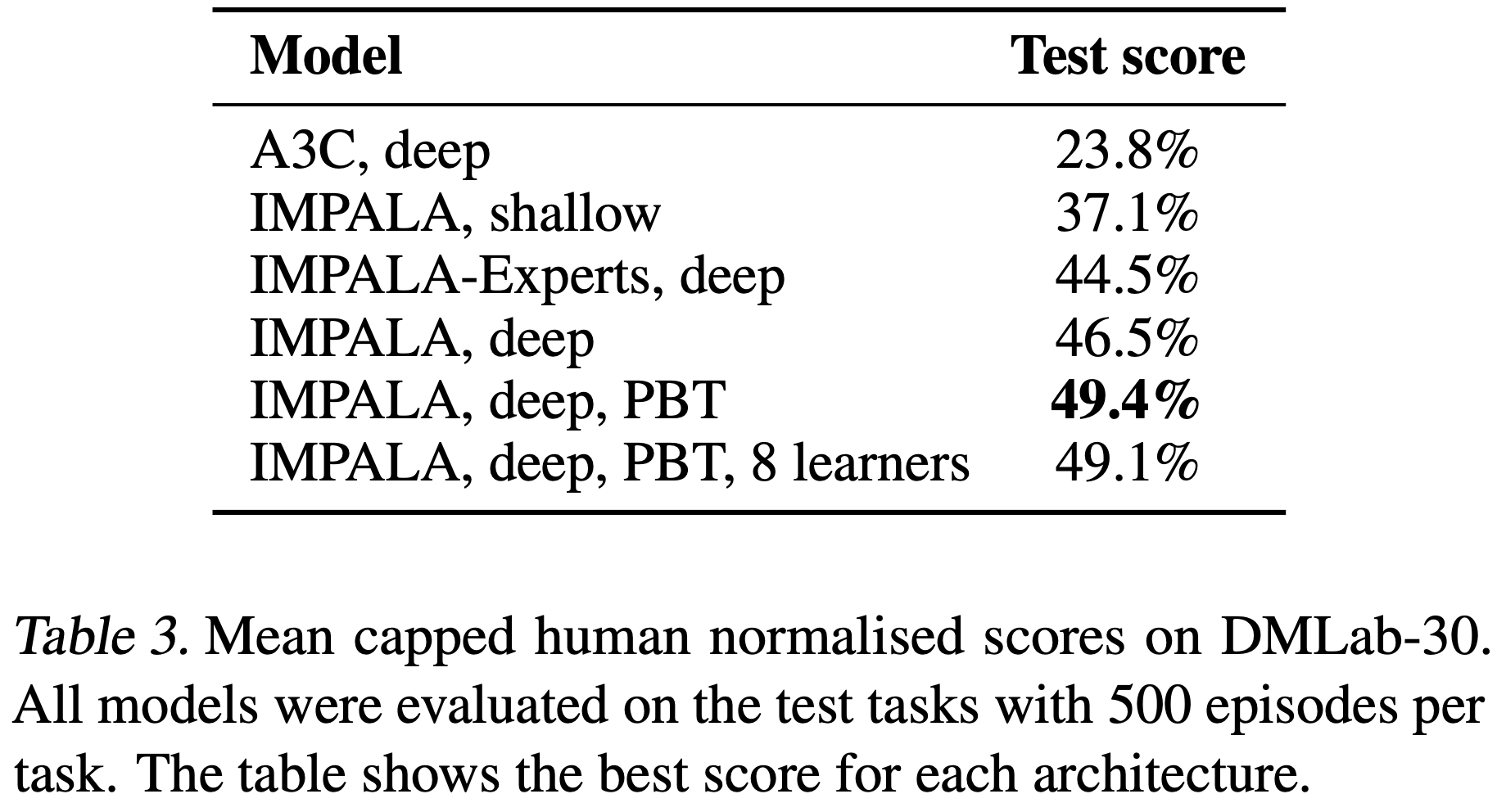
- 论文报告了平均上限人类标准化分数（mean capped human normalised score），其中每个任务的分数上限为 100%（见附录 B）
- 使用平均上限人类标准化分数强调了解决多个任务的需要，而不是专注于在单个任务上变得超人类
- 对于 PBT，论文使用平均上限人类标准化分数作为适应度函数，并调整熵成本、学习率和 RMSProp $\varepsilon$
- PBT 设置的具体细节见附录 F
具体来说，论文比较了以下智能体变体
- A3C,deep ，一个具有 210 个工作者（每个任务 7 个）的分布式实现，采用深度残差网络架构（图 3（右））
- IMPALA,shallow 具有 210 个执行器
- IMPALA,deep 具有 150 个执行器，两者都使用单个学习器
- IMPALA,deep,PBT ，与 IMPALA,deep 相同，但额外使用 PBT (2017a) 进行超参数优化
- IMPALA,deep,PBT,8 learners ，它利用 8 个学习器 GPU 来最大化学习速度
论文还在专家设置中训练了 IMPALA 智能体，IMPALA-Experts,deep ，其中每个任务训练一个单独的智能体
- 在这种情况下，论文没有为每个任务单独优化超参数，而是在训练 30 个专家智能体的所有任务上进行了优化
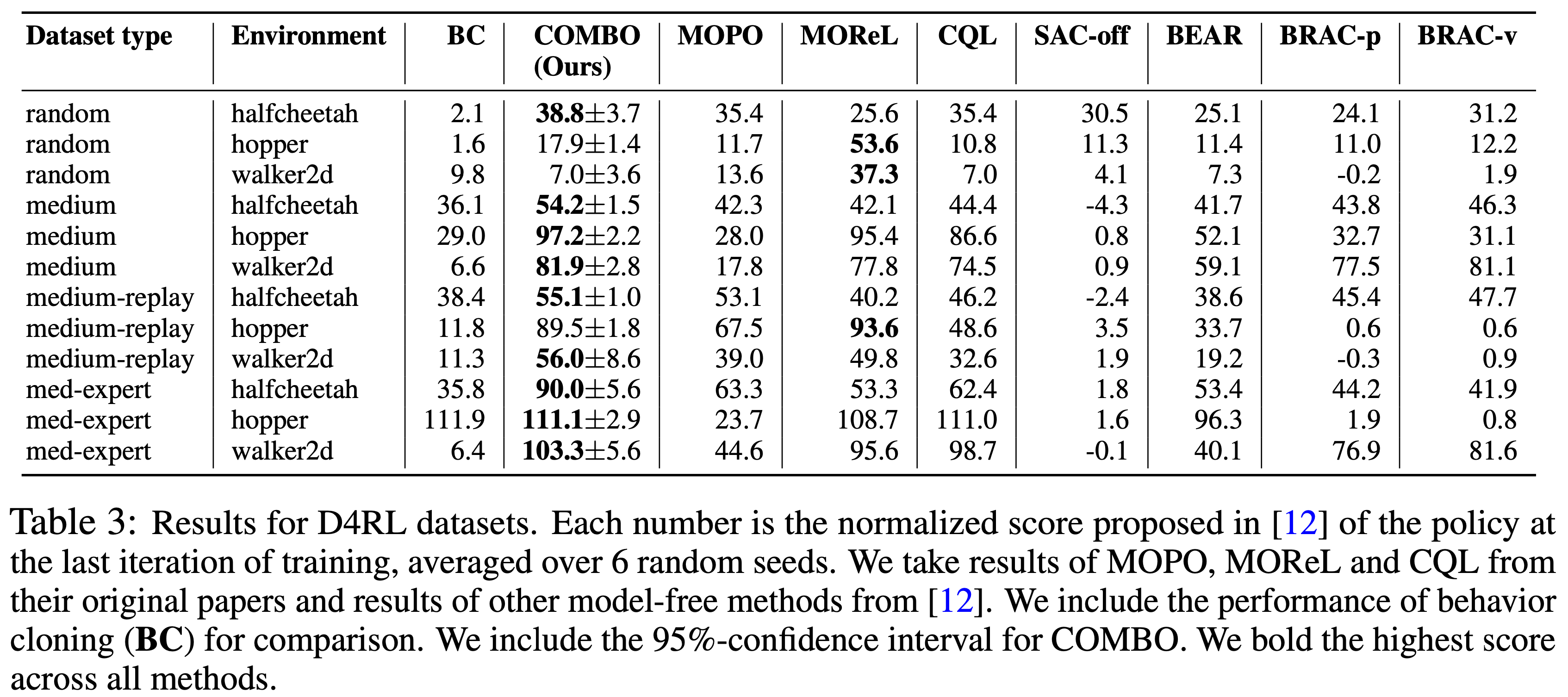
表 3 和图 5 显示所有 IMPALA 变体的性能都远优于深度分布式 A3C
- 此外，深度 IMPALA 变体不仅在最终性能上优于浅层网络版本，而且在整个训练过程中都表现更好
- 注意在表 3 中， IMPALA,deep,PBT,8 learners 虽然提供了更高的吞吐量，但在相同步数下达到了与 1 GPU 的 IMPALA,deep,PBT 相同的最终性能
特别地，在每个任务上单独训练的IMPALA-Experts 与同时在所有任务上训练的 IMPALA,deep,PBT 之间的差距
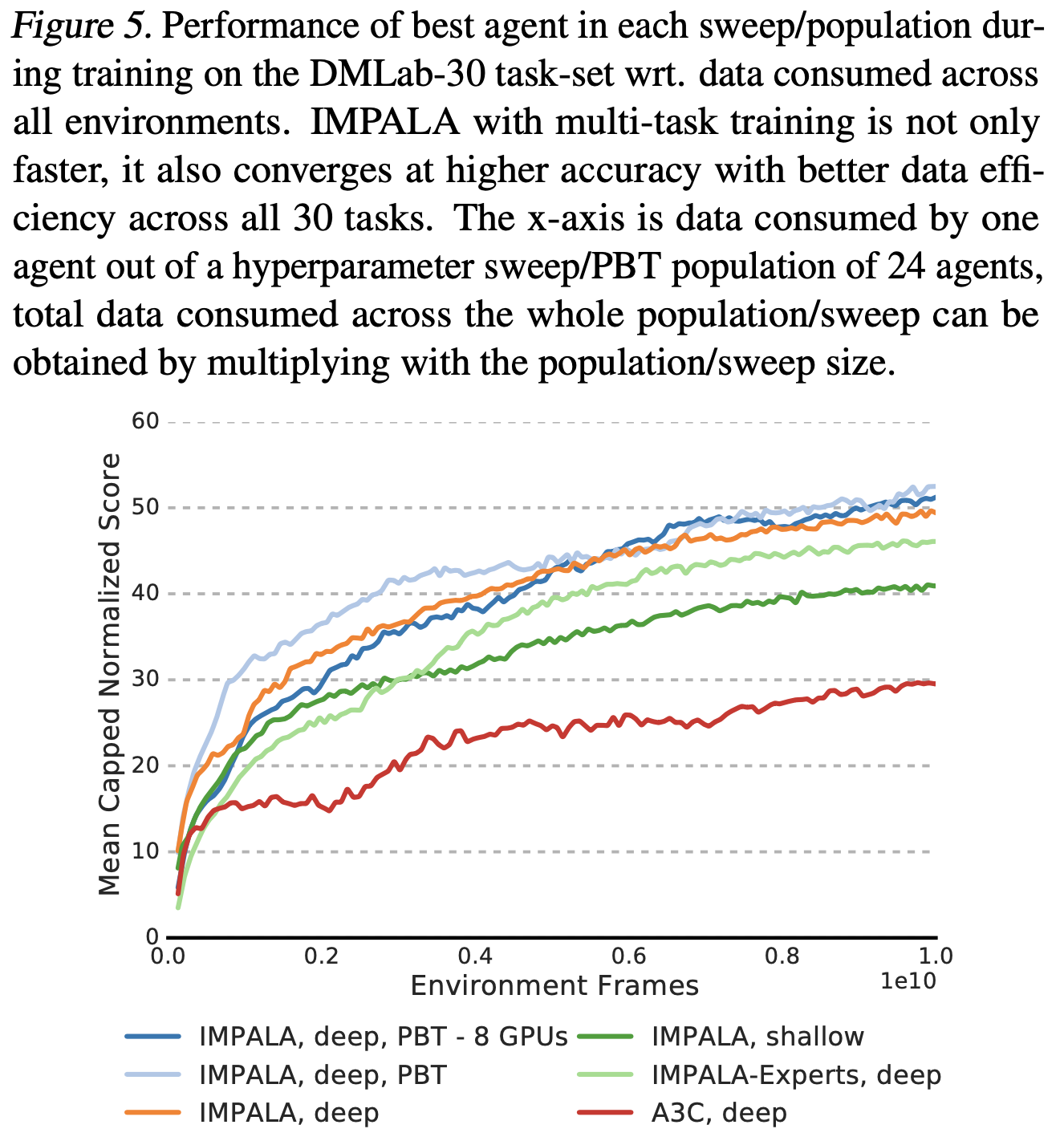
- 如图 5 所示，多任务版本在整个训练过程中都优于IMPALA-Experts ，附录 B 中的个体分数细分显示在语言任务和激光标签任务等任务上存在正向迁移（positive transfer）
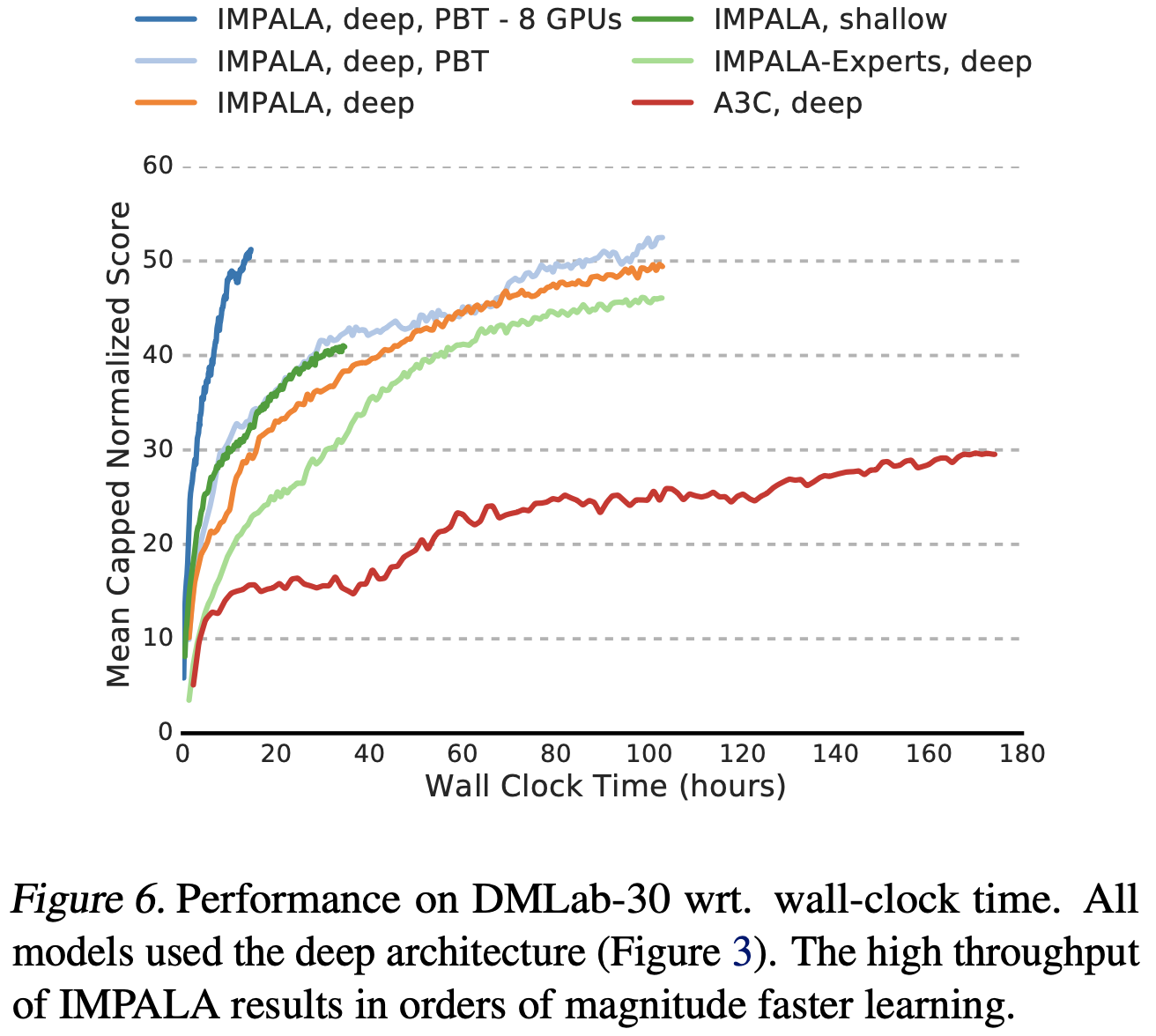
将 A3C 与 IMPALA 在挂钟时间（wall clock time）上进行比较（图 6）进一步凸显了两种方法之间的可扩展性差距
- 使用 1 个学习器的 IMPALA 仅需约 10 小时即可达到 A3C 在 7.5 天后才接近的性能
- 使用 8 个学习器 GPU 而不是 1 个，将深度模型的训练速度进一步提高了 7 倍，达到 210K 帧/秒，高于原来的 30K 帧/秒

Atari

Atari 学习环境 (ALE) (2013a) 是大多数近期深度强化学习智能体的测试平台
- Atari 中的 57 个任务提出了具有挑战性的强化学习问题，包括探索、规划、反应性游戏和复杂的视觉输入
- 大多数游戏具有非常不同的视觉效果和游戏机制，这使得该领域对多任务学习尤其具有挑战性
论文在每个游戏上单独训练 IMPALA 和 A3C 智能体，并使用第 5 节介绍的深度网络（不含 LSTM）比较它们的性能
论文还提供了使用浅层网络的结果，该网络等效于 (2016) 中使用的前馈网络，包含三个卷积层
- 该网络通过在每个步骤堆叠最近的 4 个观察值来提供短期历史信息
- 有关预处理和超参数设置的详细信息，请参阅附录 G
除了使用固定超参数集训练 2 亿帧的个体每游戏专家外，论文还训练了一个 IMPALA Atari-57 智能体（一个智能体，一组权重），同时在所有 57 个 Atari 游戏上训练，每个游戏 2 亿帧，总计 114 亿帧
对于 Atari-57 智能体，论文使用群体大小为 24 的基于群体的训练，在整个训练过程中调整熵正则化、学习率、RMSProp $\varepsilon$ 和全局梯度范数裁剪阈值
论文比较了所有算法在 57 个 Atari 游戏上的中位数人类标准化分数
- 评估遵循标准协议，每个游戏分数是 200 个评估回合的平均值，每个回合开始时执行随机数量的无操作动作（从 [1, 30] 中均匀选择）以对抗 ALE 环境的确定性
如表 4 所示，IMPALA 专家在深度和浅层配置下都提供了比其 A3C 对应物更好的最终性能和数据效率
- 正如在论文的 DeepMind Lab 实验中一样，深度残差网络比浅层网络导致更高的分数，与使用的强化学习算法无关
- 浅层 IMPALA 实验在不到一小时内完成了超过 2 亿帧的训练
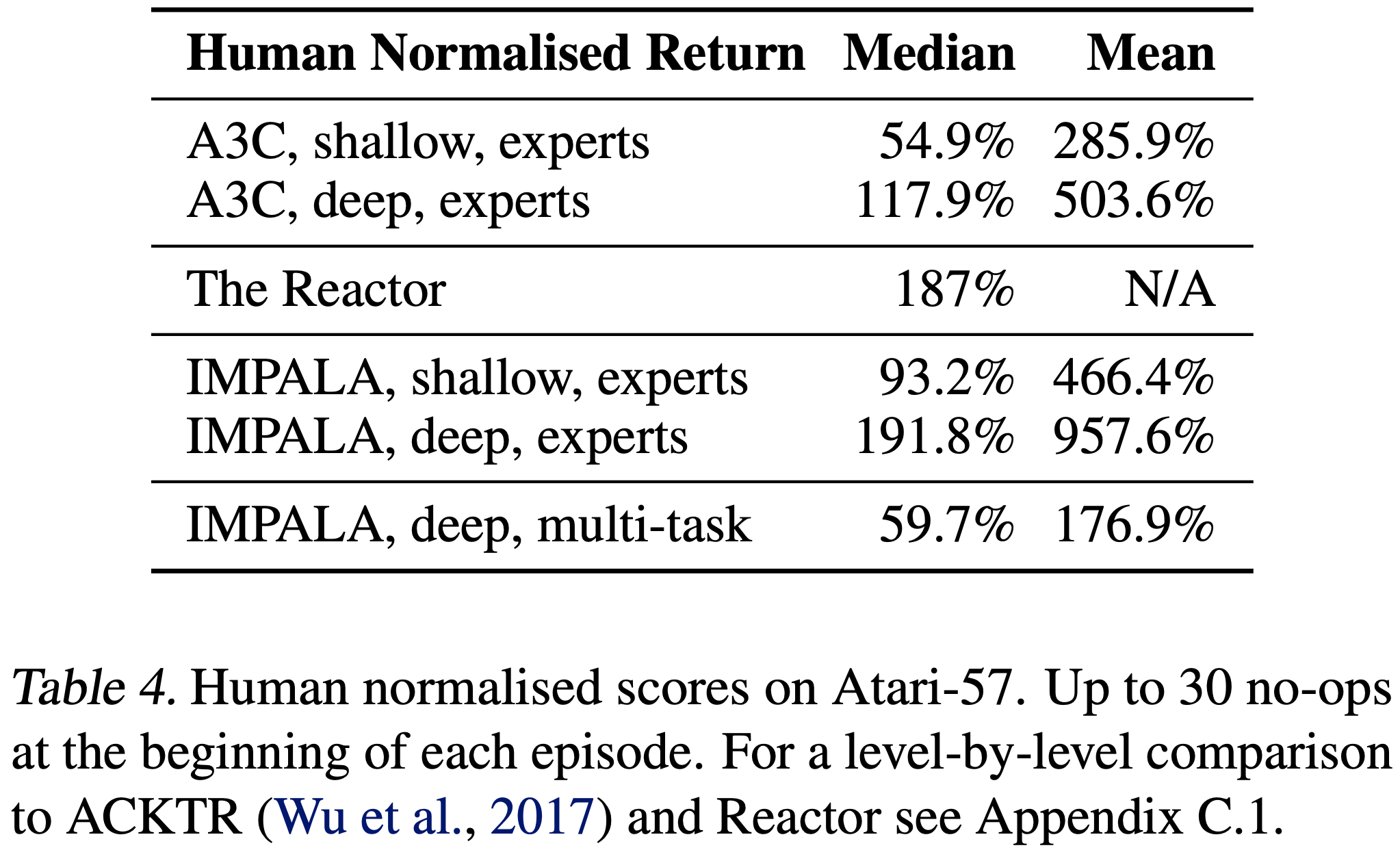
作者特别强调，IMPALA, deep, multi-task ，一个同时在所有 57 个 ALE 游戏上训练的单一智能体，达到了 59.7% 的中位数人类标准化分数
- 尽管 ALE 套件内的视觉外观和游戏机制具有高度多样性，IMPALA 多任务版本仍然设法与相关工作中常用作基线的 A3C, shallow, experts 保持竞争力
- ALE 通常被认为是一个困难的多任务环境，常常伴随着任务间的负迁移（negative transfer）(2016)
- 据论文所知，IMPALA 是第一个在 ALE 所有 57 个游戏的多任务设置下进行训练、并能与标准专家基线竞争的智能体

Conclusion

论文引入了一种新的高度可扩展的分布式智能体 IMPALA 以及一种新的 Off-policy 学习算法 V-trace
- 凭借其简单但可扩展的分布式架构，IMPALA 能够高效地利用小规模和大规模场景下的可用计算资源
- 这直接转化为研究新想法时非常快的周转时间，并开启了未被探索的机会
V-trace 是一种通用的 Off-policy 学习算法，与其他用于 Actor-Critic 智能体的 Off-policy 校正方法相比，它更加稳定和鲁棒
论文已经证明，在数据效率、稳定性和最终性能方面，IMPALA 实现了比 A3C 变体更好的性能
论文进一步在新的 DMLab-30 任务集和 Atari-57 任务集上评估了 IMPALA
据论文所知，IMPALA 是第一个在此类大规模多任务设置中成功测试的深度强化学习（Deep-RL）智能体，并且与基于 A3C 的智能体相比，它显示出卓越的性能（在 DMLab-30 上，标准化人类分数为 49.4% 对比 23.8%）
最重要的是，论文在 DMLab-30 上的实验表明，在多任务设置中，个体任务之间的正向迁移（positive transfer）使得 IMPALA 实现了比专家训练设置更好的性能
作者相信，IMPALA 为构建更好的深度强化学习智能体提供了一个简单、可扩展且鲁棒的框架，并具有激发新挑战研究的潜力

附录：【待补充】

补充材料（附录）：IMPALA Supplemental Material

RL——AC、A2C和A3C

策略梯度法的推导结论

策略梯度法推导结论是
$$
\begin{align}
\nabla_\theta J(\theta) &= \mathbb{E}_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla_\theta \log p_\theta(\tau)] \\
& = \mathbb{E}_{\tau \sim p_\theta(\tau)} \left[\sum_t \nabla_\theta \log \pi_\theta(a_t|s_t) R(\tau) \right] \\
& = \mathbb{E}_{\tau \sim p_\theta(\tau)} \left[\sum_t \psi_t \nabla_\theta \log \pi_\theta(a_t|s_t) \right] \\
\end{align}
$$
- 推导详情见RL——策略梯度法推导
- $\psi_t$ 来替换 $R(\tau)$ 的理由是可以考虑用一个与时间相关的变量来替换与时间无关的累计收益
进一步地，其中的 $\psi_t$ 可以换成不同的形式，包括：
- $\sum_{t’=0}^T \gamma^t r_{t’}$：完成的轨迹收益
- $\sum_{t’=t}^T \gamma^{t’-t} r_{t’}$：从第 $t$ 步开始的轨迹收益，理由是策略主要影响的是 $t$ 步开始收益，对前面步骤的收益影响不大
- $\sum_{t’=t}^T \gamma^{t’-t} r_{t’} - b(s_t)$：进一步降低方差，详细证明见RL——策略梯度法
- $Q^{\pi_\theta}(s_t,a_t)$：动作价值函数，是 $\sum_{t’=t}^T \gamma^{t’-t} r_{t’}$ 的估计值
- $A^{\pi_\theta}(s_t,a_t)$：优势函数，仅考虑当前状态 $s_t$ 下不同动作带来的收益，忽略状态本身的价值
- $ r_t + \gamma V^{\pi_\theta}(s_{t+1}) - V^{\pi_\theta}(s_{t}) $： V 值的TD-Error形式，即贝尔曼残差，本质等价于优势函数
问题：将 $\psi_t$ 换成 $ r_t + \gamma Q^{\pi_\theta}(s_{t+1}, a_{t+1}) - Q^{\pi_\theta}(s_{t}, a_t) $ 可以吗？
- 答案是不可以。理由是 $ r_t + \gamma Q^{\pi_\theta}(s_{t+1}, a_{t+1}) - Q^{\pi_\theta}(s_{t}, a_t) $ 本身不是优势函数 $A(s,a)$，也不是 $Q(s,a)$ 没有别的含义，只有 Q 值自身更新时的TD-Error
- 证明：如果 $a_{t+1} \sim \pi_\theta$，则 $Q^{\pi_\theta}(s_{t+1}, a_{t+1}) = V^{\pi_\theta}(s_{t+1})$ ；但是因为 $Q^{\pi_\theta}(s_{t}, a_t) \neq V^{\pi_\theta}(s_{t})$ （因为 $a_t$ 是已经发生的事实），故而 $ r_t + \gamma Q^{\pi_\theta}(s_{t+1}, a_{t+1}) - Q^{\pi_\theta}(s_{t}, a_t) $ 本身不是优势函数，也能等价于优势函数
- 改进：如果非要用 Q 值来作为 Actor Critic 的价值网络，则需要求解策略 $\pi_{\theta^*} = \mathop{\arg\max}_{\pi_\theta} \mathbb{E}_{a_t \sim \pi_\theta(\cdot|s_t)} [Q(s_t, a_t)]$，比如DDPG就是如此

AC 算法

普通 AC（Actor Critic）算法一般是直接使用 $Q(s_t,a_t)$ 来替换 $\psi_t$

Critic 网络的更新

Critic 网络更新方式
$$
Loss_{\text{critic}} = \sum (r_t + \gamma Q^{\bar{w}}(s_{t+1}, a_{t+1}) - Q^{w}(s_{t}, a_t)) ^ 2
$$
- 这里要求 $a_{t+1} \sim \pi_\theta$（实际上是 SARSA 的更新方式）， $Q^{w}$ 值拟合的目标是策略 $\pi_\theta$ 对应的 Q 值 $Q^{\pi_\theta}(s_{t}, a_t)$
这里虽然使用 Target 网络的表达，但 AC 算法一般不需要 Target 网络，加入 Target 网络可能会导致收敛变慢
Critic 网络往往可以使用比 Actor 网络更大的学习率或更多的更新次数，这称为双时间尺度 AC 算法（Two-time Scale Actor-Critic Algorithms），该算法中，使用两种不同的学习速率（或时间尺度）来更新 Actor 和 Critic

Actor 网络的更新

Actor 网络的损失函数
$$
\begin{align}
Loss_{\text{actor}} &= \sum Q^{w}(s_{t}, a_t) \log \pi_\theta(a_t|s_t) \\
Q^{w}(s_{t}, a_t) &= \text{Stop_Gradient}(Q^{w}(s_{t}, a_t))
\end{align}
$$
这里面的 $Q^{w}(s_{t}, a_t)$ 是不参与 Actor 参数的更新的
$a_t \sim \pi_\theta(\cdot|s_t)$

AC 算法的问题

AC 算法虽然是直接优化策略的，但是由于它是 on-policy 的，样本利用率很低，导致训练缓慢

A2C 算法

A2C（Advantage Actor Critic）算法引入了优势函数（Advantage），这也是 A2C 名字的由来
- 即使用 $ r_t + \gamma V^{\pi_\theta}(s_{t+1}) - V^{\pi_\theta}(s_{t}) $ 来替换 $\psi_t$ 的方法
很多书籍里面会直接默认使用 A2C 算法作为 AC 算法的等价表述

Critic 网络的更新

Critic 网络的损失函数：
$$
Loss_{\text{critic}} = \sum (r_t + \gamma V^{\bar{w}}(s_{t+1}) - V^{w}(s_{t})) ^ 2
$$
这里 V 值拟合的目标是策略 $\pi_\theta$ 对应的 V 值 $V^{\pi_\theta}$
这里虽然使用 Target 网络的表达，但A2C 算法一般不需要 Target 网络，加入 Target 网络可能会导致收敛变慢
Critic 网络往往可以使用比Actor 网络更大的学习率或更多的更新次数

Actor 网络的更新

Actor 网络损失函数：
$$
\begin{align}
Loss_{\text{actor}} &= \sum \delta \log \pi_\theta(a_t|s_t) \\
\delta &= \text{Stop_Gradient}(r_t + \gamma V^{w}(s_{t+1}) - V^{w}(s_{t}))
\end{align}
$$
这里面的 $r_t + \gamma V^{w}(s_{t+1}) - V^{w}(s_{t})$ 是不参与 Actor 参数的更新的

A2C 算法的问题

A2C 算法是同步更新的，需要每个 Worker 都收集完成数据才能执行一次更新，很多时候数据交互完成的时间是很不一致的，训练也较慢

A3C 算法

A3C（Asynchronous Advantage Actor Critic），是 Actor Critic 方法的异步版本
注意：这里的异步是参数更新的异步，类似 PS 架构，不会导致 A3C 变成 Off-Policy 的
- 也就是说：A3C 始终是 On-Policy 的

A3C 的主要优化点

异步训练框架优化：

一个全局网络（包括V网络和Actor 网络）和多个相互独立的 Local 网络（即 Worker）
训练时：使用多个 Worker 并行的和环境分别交互，各自收集数据、计算梯度、异步更新全局网络参数
inference 时：仅适用全局网络中的 Actor 网络就可以

A3C 的“异步”更新流程

A3C 的“异步”特指 “多线程并行更新全局网络的方式” ，而非“采样策略与更新策略的分离”
- 其核心逻辑是通过“多个本地线程独立采样+异步向全局网络传梯度”提升训练效率
A3C 具体流程如下：
- 全局网络（Global Network） ：
  - 存储共享的策略参数$ \theta $（Actor和Critic共享一套参数），是最终需要优化的目标网络
- Local Workers ：通常有多个独立线程，每个线程的工作流程是：
  - 同步参数 ：先从全局网络复制当前最新的参数$ \theta $到本地（此时本地策略=全局策略）；
  - 采样轨迹 ：用本地策略$ \pi_\theta $与环境交互，采样一段短轨迹（如n-step，5~20步）；
  - 计算梯度 ：基于采样轨迹计算 Actor（策略）和 Critic（价值）的损失梯度（此时本地行为策略=本地待更新策略）；
    - 注意：这一步计算梯度时是在行为策略的基础上计算的，所以是 On-policy，不是 Off-policy
  - 异步更新 ：将本地梯度发送给全局网络，全局网络用这些梯度更新参数$ \theta $（无需等待其他线程，即“异步”）；
  - 重置本地参数 ：下一轮循环前，再次从全局网络同步最新的$ \theta $，覆盖本地旧参数
注：A3C 的“异步”仅描述“多个本地线程与全局网络的交互方式”，不改变“每个线程采样时用的策略=当前待更新的全局策略”这一核心事实

策略更新损失增加熵

增加熵的损失函数定义如下：
$$
\begin{align}
Loss_{\text{actor}} &= \sum \delta \log \pi_\theta(a_t|s_t) + c H(\pi_\theta(a|s)) \\
\delta &= \text{Stop_Gradient}(r_t + \gamma V^{w}(s_{t+1}) - V^{w}(s_{t}))
\end{align}
$$
增加熵相当于是一种正则，与 SAC 思想相似

AC/A2C/A3C的区别

AC（Actor-Critic）、A2C（Advantage Actor-Critic）和 A3C（Asynchronous Advantage Actor-Critic）三者可以从名字上看出来算法的区别

AC（Actor-Critic）

Actor-Critic 方法结合了值函数方法和策略梯度方法的优点。它由两部分组成：一个称为“actor”的网络负责学习采取什么行动；另一个称为“critic”的网络评估采取的动作的好坏，即这个动作的价值

A2C（Advantage Actor-Critic）

关键词：Advantage
A2C 是 Actor-Critic 方法的一个变种，它引入了优势函数（advantage function）的概念来代替直接使用价值函数
优势函数 (A(s, a)) 定义为执行特定动作相对于遵循当前策略下的平均行为所能获得的优势或劣势。这种方法有助于更准确地估计哪些动作比其他动作更好，从而提高学习效率

更新方式 ：A2C 使用同步的方式更新参数，可以考虑使用多个网Actor分别于环境进行交互，然后共同的样本一起同步更新主网络 ，这意味着所有代理（agents）共享同一个模型，并且在每个训练步骤结束时同步更新模型权重

A3C（Asynchronous Advantage Actor-Critic）

关键词：Asynchronous
A3C 是 A2C 的异步版本，它允许多个代理同时在不同的环境中学习
更新方式 ：每个代理都有自己的环境副本和局部模型副本，它们独立地探索环境并收集经验。然后，这些经验被用来异步地更新全局模型，这样可以增加数据多样性并加快学习速度
优点：通过异步更新，A3C 可以有效利用多核处理器的能力，实现更快的学习速度和更好的性能

附录：为什么 A3C 不需要重要性采样？

标准 A3C 不需要重要性采样，因为其 “本地线程采样的策略” 与 “全局网络待更新的策略” 完全一致，无分布偏差
A3C 的“异步”是工程实现层面的并行更新方式 ，解决“单线程采样慢”的问题；
“On/Off-policy” 是算法理论层面的策略更新逻辑 ，解决“采样数据是否匹配目标策略”的问题
A3C 中“异步（Asynchronous）”与“Off-policy”的概念辨析
- A3C 的“异步”是“更新方式的异步”，而非“采样与更新策略的偏离（即Off-policy）”
- 正因为 A3C 本质上仍是On-policy（同策略） 算法，所以依然不需要重要性采样
对 A3C 而言，每个本地线程的采样过程完全满足 On-policy：
- 1）线程在采样前，会强制同步全局网络的最新参数$ \theta $到本地采样用的策略$ \pi_\theta $，就是当前全局网络正在优化的“目标策略”；
- 2）采样得到的轨迹，仅用于更新“产生该轨迹的策略$ \pi_\theta $”（即全局网络的$ \theta $）；
  - 旧轨迹不会被重复用于更新新策略
- 3）A3C 的异步可以保证每个 Local Worker 上计算得到的梯度是 On-policy 的，但是这个参数更新的异步会导致更新使用的参数是过期的（比如使用到上一个版本的 Actor 计算的梯度来更新这个版本）
  - 再次强调：这里不是 Off-policy，只是参数梯度更新存在一定的滞后性，这是 A3C 为了效率使用异步导致的，是可以容忍的

RL——COMBO

本文简单介绍COMBO模型

参考链接：
- 原始论文：COMBO: Conservative Offline Model-Based Policy Optimization, Stanford & UC Berkeley & Facebook AI Research, NeurIPS 2021

COMBO 基本思想

主要用于解决Offline RL的问题，属于Model-based方法
COMBO是结合了CQL思想的一种Model-based方法

原始 CQL 的更新公式

策略评估更新公式：
$$\hat{Q}^{k+1} = \mathop{\arg\min}_Q \alpha \left(\mathbb{E}_{\color{red}{s\sim \mathcal{D}, a\sim \mu(a\vert s)}}[Q(s, a)] - \mathbb{E}_{\color{blue} {s\sim \mathcal{D}, a\sim\hat{\pi}_\beta(a\vert s)}}[Q(s, a)] \right) + \frac{1}{2} \mathbb{E}_{\color{red} {\mathbf{s}, \mathbf{a}, \mathbf{s’} \sim \mathcal{D}}}\left[\left(Q(\mathbf{s}, \mathbf{a})-\hat{\mathcal{B}}^{\pi} \hat{Q}^{k}(\mathbf{s}, \mathbf{a})\right)^{2}\right]$$
注，以上更新公式并不直接用于CQL的训练，是损失函数的中间结果

COMBO 的训练流程

COMBO 训练代码：
模型的训练：
- 模型输入是 $s,a$，预估目标是 $s’,r$，上面的训练代码中将输出建模成表达成高斯分布的形式（适用于连续型的场景），如果是离散型的场景，可以使用分类模型
策略评估更新公式：
$$\hat{Q}^{k+1} = \mathop{\arg\min}_Q \color{red}{\beta} \left(\mathbb{E}_{\color{red} {s,a\sim\rho(s,a)}}[Q(s, a)] - \mathbb{E}_{\color{blue} {s,a\sim\mathcal{D}}}[Q(s, a)] \right) + \frac{1}{2} \mathbb{E}_{\color{red} {\mathbf{s}, \mathbf{a}, \mathbf{s’} \sim \mathcal{d_f}}}\left[\left(Q(\mathbf{s}, \mathbf{a})-\hat{\mathcal{B}}^{\pi} \hat{Q}^{k}(\mathbf{s}, \mathbf{a})\right)^{2}\right]$$
以上红色部分是COMBO和CQL的核心区别，蓝色部分表达不同，但是本质是相同的，都是从离线的数据集中采样样本
- 第一部分：$\rho(s,a) = \color{red}{\mathcal{d}^\pi_{\hat{\mathcal{M}}}(s)}\pi(a|s)$，其中 $\color{red}{\mathcal{d}^\pi_{\hat{\mathcal{M}}}(s)}$ 表示策略 $\pi$ 与模型 $\hat{\mathcal{M}}$ 交互时的状态 $s$ 的访问概率
  - 注意这里只有状态的概率 $\color{red}{\mathcal{d}^\pi_{\hat{\mathcal{M}}}(s)}$ 选取与CQL的 $\color{red}{\mathcal{D}}$ 不同，后面的策略还是当前策略 $\pi(a|s)$，策略这个点与CQL是相同的
- 第二部分：$\mathcal{d}^\mu_f := f\ \mathcal{d}(s,a) + (1-f)\ \mathcal{d}^\mu_{\hat{\mathcal{M}}}(s,a)$，其中 $f\in [0,1]$ 表示数据混合比例
  - CQL中使用的全是真实数据集，在COMBO中则使用到了部分当前策略与模型交互生成的结果
  - COMBO论文中关于 $f$ 的选取一般在0.5或0.8不等，个人理解：在真实数据集较多的场景，这个混合比例不宜过低

实验结果

COMBO实验结果

RL——DDPG和TD3

参考链接：
- 强化学习之图解PPO算法和TD3算法

DPG

原始论文：Deterministic Policy Gradient Algorithms（论文中详细描述了 SGD，DPG 两种算法的 off-policy，on-policy 版本的分析）

Stochastic Actor-Critic Algorithms

Critic 网络损失函数
$$
Loss_{\text{critic}} = \sum_t (r_t + \gamma Q^{\bar{w}}(s_{t+1}, a_{t+1}) - Q^{w}(s_{t}, a_t)) ^ 2
$$
- 这里要求 $a_{t+1} \sim \pi_\theta$， $Q^w(s_t,a_t)$ 值拟合的目标是策略 $\pi_\theta$ 对应的Q值 $Q^{\pi_\theta}(s_{t}, a_t)$ ，代码中使用next_action = self.actor(next_states)代替动作即可
- 这里训练使用的 $(s_t,a_t,s_{t+1})$ 是当前策略采样到的数据（实际上，Q值的学习样本保证 $a_{t+1}$ 的采样策略即可，样本可以是任意策略采样的，当然，用当前策略采样的会更好些）
Actor 网络优化梯度：
$$
\nabla_\theta J(\pi_\theta) = \mathbb{E}_{s\sim \rho^{\pi},a\sim\pi_\theta}\left[ \nabla_\theta \log \pi_\theta(a|s)Q^w(s,a) \right]
$$
- 问题： $s\sim \rho^{\pi}$ 中的 $\pi$ 必须是 $\pi_\theta$ 吗？
  - 回答：是的，原始推导中，回合 $\tau$ 必须是来自当前策略的

Off-Policy Actor Critic

Critic 网络损失函数
$$
Loss_{\text{critic}} = \sum_t (r_t + \gamma Q^{\bar{w}}(s_{t+1}, a_{t+1}) - Q^{w}(s_{t}, a_t)) ^ 2
$$
- 这里要求 $a_{t+1} \sim \pi_\theta$， $Q^w(s_t,a_t)$ 值拟合的目标是策略 $\pi_\theta$ 对应的Q值 $Q^{\pi_\theta}(s_{t}, a_t)$ ，代码中使用next_action = self.actor(next_states)代替动作即可
- 这里训练使用的 $(s_t,a_t,s_{t+1})$ 是当前其他行为策略采样到的数据
Actor 网络优化梯度：
$$
\nabla_\theta J(\pi_\theta) = \mathbb{E}_{s\sim \rho^\beta,a\sim \beta}\left[ \frac{\pi_\theta(a|s)}{\beta_\theta(a|s)} \nabla_\theta \log \pi_\theta(a|s)Q^w(s,a) \right]
$$
- 问题：动作的偏移通过重要性采样 $\frac{\pi_\theta(a|s)}{\beta_\theta(a|s)} $ 来解决，但是状态也可以吗？
  - 回答：不可以，这里状态采用行为策略采样是因为off-policy场景下，策略梯度的目标就是在行为策略采样的状态上最大化目标函数（这样得到的不是最优策略，线上serving时的状态分布肯定与当前行为策略采样的状态不一致，所以是一个妥协的次优解）
- 思考：off-policy AC 与 DQN 的区别
  - 对于DQN，我们通过在每一个状态上让Q值拟合到最优策略对应的Q值（与状态分布无关，任意的状态我们都可以找到最优策略对应的Q值），然后通过 $\mathop{\arg\max}_a Q(s,a)$ 来找到最优策略
  - 对于off-policy AC，如果不考虑状态的分布，这里带来的偏差是从优化目标上出现的，即off-policy AC最大化的目标是，在行为策略采样的状态分布下，寻找一个策略，最大化累计策略收益期望。这里的目标显然与on-policy的原始目标不同了，状态分布线上线下不一致问题会导致天然的偏差
  - 问题：为什么不可以理解为与DQN一样？任意给定的状态我都做到策略最大化了，实际上就已经求到了最优策略了？（按照这个理解，除了off-policy都会遇到的训练评估数据分布不一致外，没有别的问题？）
    - 回答：不可以，因为DQN的目标是拟合 $Q^*(s,a)$，与状态分布无关；而策略梯度法的目标找到一个最优策略 $\pi^*$，最大化策略该策略下的累计收益，这里要求状态分布和动作分布均来自求解到的最优策略 $\pi^*$ ，off-policy AC下的状态分布是行为策略的，存在偏差
注：off-policy AC方法中，若使用n-step回报，则每一步都需要重要性采样，使用连乘方式将新旧策略的重要性采样比值乘上去即可
off-policy AC方法不常用，因为从目标上天然旧带着偏差

Off-Policy AC如何对混合策略采样的样本进行重要性采样？

在 Replay Buffer 中记录下每个样本的采样策略（代码示例），并在更新时逐个样本计算动作概率比值（代码示例），参见：

## 策略记录
memory.append(state, action, reward, policy.detach()) 

## 动作概率比值计算
if off_policy:
    rho = policies[i].detach() / old_policies[i]
else:
    rho = torch.ones(1, action_size)

上面的代码是 ACER（Actor-Critic with Experience Replay）方法的样例
- ACER 基于 Actor-Critic 框架
- ACER 利用经验回放技术来提高样本效率
- ACER 使用通过重要性采样权重来修正策略更新时的偏差，确保梯度估计的无偏性

On-Policy Deterministic Actor-Critic

优化目标
$$ J(\theta) = \int_\mathcal{S} \rho^{\mu_\theta}(s) Q^{\mu_\theta}(s, \mu_\theta(s)) ds $$
- 其中 $\rho^{\mu_\theta}(s’) = \int_\mathcal{S} \sum_{k=1}^\infty \gamma^{k-1} \rho_0(s) \rho^\mu(s \to s’, k) ds$
确定性梯度定理：
$$
\begin{aligned}
\nabla_\theta J(\theta)
&= \int_\mathcal{S} \rho^{\mu_\theta}(s) \nabla_a Q^{\mu_\theta}(s, a) \nabla_\theta \mu_\theta(s) \rvert_{a=\mu_\theta(s)} ds \\
&= \mathbb{E}_{s \sim \rho^{\mu_\theta}} [\nabla_a Q^{\mu_\theta}(s, a) \nabla_\theta \mu_\theta(s) \rvert_{a=\mu_\theta(s)}]
\end{aligned}
$$
确定性策略看作是随机策略的一种特殊形式，也就是策略的概率分布仅在某一个动作上有非零概率(该动作概率为1)
实际上，在 DPG 的论文中，作者指出：如果对随机策略，通过确定性策略和一个随机变量进行重参数化(re-parameterize)，那么随机策略最终会在方差 $\sigma=0$ 时与确定性策略等价
- 由于随机策略需要对整个状态和动作空间进行积分，我们可以预计随机策略的学习需要比确定性策略更多的样本（这里只是猜测，没有证据证明）

Off-Policy Deterministic Actor-Critic

优化目标
$$ J_\beta(\theta) = \int_\mathcal{S} \rho^\beta(s) Q^{\mu_\theta}(s, \mu_\theta(s)) ds $$
- 其中 $\rho^\beta(s)$ 是行为策略上采样得到的样本状态分布，这里直接导致了优化目标不是在最优策略下的回合（回合包含状态和动作）分布下的奖励期望最大，相对on-policy Deterministic AC算是次优解
推导结果：
$$
\begin{aligned}
\nabla_\theta J_\beta(\theta) &= \mathbb{E}_{s \sim \rho^\beta(s)} \left[\nabla_a Q^{\mu_\theta}(s, a) \nabla_\theta \mu_\theta(s) \rvert_{a=\mu_\theta(s)} \right]
\end{aligned}
$$

Critic 网络更新（TD-Error）
$$
Loss_{\text{critic}} = \sum_t (r_t + \gamma Q^{\bar{w}}(s_{t+1}, a_{t+1}) - Q^{w}(s_{t}, a_t)) ^ 2
$$

这里要求 $a_{t+1} = \mu_\theta(s_{t+1})$， $Q^w(s_t,a_t)$ 值拟合的目标是策略 $\mu_\theta$ 对应的Q值 $Q^{\mu_\theta}(s_{t}, a_t)$，实际更新中常使用Target网络 $\bar{\theta}$ 一个简单的实现示例如下（参考自《动手学强化学习书籍》）：

1
2
3

next_q_values = self.target_critic(next_states, self.target_actor(next_states))
q_targets = rewards + self.gamma * next_q_values * (1 - dones)
critic_loss = torch.mean(F.mse_loss(self.critic(states, actions), q_targets))

这里训练使用的 $(s_t,a_t,s_{t+1})$ 是行为策略采样到的数据（Q值 $Q^{\mu_\theta}(s_{t}, a_t)$ 的学习样本保证 $a_{t+1}$ 的采样策略是 $\mu_\theta$ 即可，样本可以是任意策略采样的，当然，用当前策略采样的会更好些）

Actor 网络更新
$$
\begin{aligned}
Loss_{\text{actor}} = - \mathbb{E}_{s_t \sim \rho^\beta(s)} [Q_w(s_t,\mu_\theta(s_t))]
\end{aligned}
$$
- 上面的Loss求导就可以得到梯度是 $\mathbb{E}_{s \sim \rho^\beta(s)} \left[\nabla_a Q^{\mu_\theta}(s, a) \nabla_\theta \mu_\theta(s) \rvert_{a=\mu_\theta(s)} \right]$，与之前推导结论一致
- 直观上理解，这里的目标是对于任意给定的状态 $s_t$ 下（这个状态样本是行为策略采样得到的），找到一个最大最大化当前 $Q_w(s_t,\mu_\theta(s_t)) $ 的动作参数 $\mu_\theta$

DDPG

Deep Deterministic Policy Gradient Algorithms，是 DPG 的 Deep 网络版本，原始论文地址CONTINUOUS CONTROL WITH DEEP REINFORCEMENT LEARNING

DDPG训练流程

伪代码如下（其中 $\theta^{\mu’}$ 和 $\theta^{Q’}$ 分别表示策略 $\mu’$ 和价值 $Q’$ 的参数）：
随机探索 ：做选择动作 $a_t$ 时，添加一个随机噪声，可以增强探索能力，使得模型更加鲁棒，如果没有随机噪声，可能会很快收敛到局部最优
软更新 ：Target网络的更新选择软更新，DQN中是硬更新

DDPG 为什么可以是 off-policy 的？

DDPG 是 off-policy 的，原因如下：
- Q函数的学习 ：DQN 和 DDPG 本质都是基于贝尔曼最优公式迭代Q值的，因为 Q 函数都是在学习某个策略 $\pi_0$ （$\pi_0$ 实际上就是截止到当前的最优策略）下对应的 Q 值，只要 TD-Error中的 Q 值目标 $r(s,a)+\gamma Q(s’,a’) - Q(s, a)$ 中的 $a’$ 是策略 $\pi_0$ 采样的，即服从策略 $a\sim\pi_0(\cdot|s’)$ 即可保证学到的Q值是 $Q^{\pi_0}(s,a)$，与 $(s,a,s’)$ 本身的采样策略无关
- 策略的学习 ：在保证Q函数预估的是当前策略（即截止到目前的最优策略）对应的Q值以后，我们只需要求解一个策略，保证当前策略对应的动作分布下的Q值最大即可，此时有：
  - DDPG如何找到最优策略？ ：目标是找到一个确定性策略 $\pi_\theta(s)$，最大化 $Q(s,\pi_\theta(s))$ （本质可以理解为Q值在策略下的期望 $\pi_\theta(s)$，确定性策略的期望就是这个策略对应的Q值），可采用梯度直接回传的方式链式求导；
  - 注意：DDPG/SAC等方法中 ，策略学习的目标是找到使得当前 $Q(s,a)|a\sim\pi_\theta(s)$ 值最大的策略 $\pi_\theta$，学习时状态 $s$ 是从什么策略采样来的无关，即任意给我一个状态 $s$，目标策略都能使得该状态下的 $Q$ 值最大化（这里的Q值在学习中拟合目标是在当前策略下的Q值）；但普通的AC方法中 ，Actor是直接对Reward的期望求梯度来更新的，这个期望是需要在当前策略下的期望，故而状态和动作都需要是当前状态下采样得到的，否则梯度有偏，而DDPG/SAC中则因为直接最大化Q值(该Q值是当前策略下的Q值)来实现了，绕过了必须保证状态 $s$ 是当前策略采样得到的这一步了
更多详情讨论可参考：RL——强化学习相关笔记

TD3

TD3 是对 DDPG 的改进，全称为 Twin Delayed Deep Deterministic Policy Gradient Algorithm，原始论文：Addressing Function Approximation Error in Actor-Critic Methods，ICML 2018，Google Research, Brain Team，代码地址：github.com/sfujim/TD3
有两个改进包含在名字中，Twin和Delayed
其他改进是在Actor 的target网络输出中，增加噪声

TD3 训练流程

伪代码如下（其中， $t \ \text{mod} \ d$ 表示策略更新比Q值更新慢一些， $d$ 次Q值更新对应一次策略更新）：

改进1：Twin

采用双Critic网络（训练网络和target网络均为双网络），缓解Q值高估问题

改进2：Delayed

Actor的目标是在Q值更新时，寻找最优的策略，如果Q值更新太快，容易波动，可以让Q值比较稳定了再更新Actor网络
具体做法，Critic网络更新 $d$ 次再更新一次Actor

改进3：Target 策略网络增加噪声

在Actor 的target策略网络输出的策略中，增加噪声，可以缓解Q值高估问题

TD3+BC（TD3 with behavior cloning，for Offline RL）

原始论文(与TD3同一个作者)：A Minimalist Approach to Offline Reinforcement Learning，NeurIPS 2021，Google Research, Brain Team，开源代码：github.com/sfujim/TD3_BC
TD3+BC，在 TD3 的基础上，增加策略模仿，即对策略进行迭代时，损失函数中增加 $loss_{\text{BC}} = (\pi_{\theta}(s) - a)^2$
论文中提到三个改进点：
- 加入带权重的 BC 正则项
- 状态归一化（不一定很重要）
- 提出对权重的一种设定方式
DDPG 是 Online RL 的算法，TD3+BC 是 Offline RL 的算法

RL——HER技术

Hindsight Experience Replay，简称HER，一种用于解决奖励稀疏问题的方法

参考链接：
- 原始论文：Hindsight Experience Replay，NIPS 2017，OpenAI
- 论文解读：Hindsight Experience Replay，Kenvnn’s Blog，论文的许多笔记参考自该博客

Background

在机器人领域，要想使强化学习训练它完美执行某任务，往往需要设计合理的奖励函数，但是设计这样的奖励函数工程师不仅需要懂得强化学习的领域知识，也需要懂得机器人、运动学等领域的知识。而且，有这些知识也未必能设计出很好的奖励函数供智能体进行学习
因此，如果可以从简单的奖励函数（如二分奖励）学习到可完成任务的模型，那就不需要费心设计复杂的奖励函数了

HER 技术思路

奖励函数的设计往往需要很强的先验知识，且往往比较难，特别在稀疏奖励和二分奖励场景中
- 系数奖励：完成目标的episode太少或者完成目标的步数太长，导致负奖励的样本数过多
- 二分奖励：完成目标时，奖励为A值，完不成目标时，奖励为B值
一句话说：通过在经验池中引入“Hindsight”（事后聪明）来解决稀疏奖励和二分奖励中的问题
- Hindsight的理解：hind表示“后面的”，sight则表示“看见；视力；视野等”，综合起来表示“事后聪明；事后的领悟”。与Foresight表示“先见之明”对比来看，翻译Hindsight为“后见之明”可能更为合适
可以用于所有Off-policy方法中

A motivating example

一个来自HER论文中的例子：bit-flipping environment
- 状态空间 $\mathcal{S}=\left \{ 0,1 \right \}^{n}$，维度为n
- 动作空间 $\mathcal{A}=\left \{ 0,1,\cdots,n-1 \right \}$，动作空间大小也为n
- 规则：对于每个episode，给定目标状态 $s_{g}$，从任意初始状态 $s_{0}$ （如 $n=5，s_{0}=10101$ ）每一步从动作空间中选取一个动作 $a$，翻转 $s_{0}$ 第 $a$ 个位置的值，如 $a=1\Rightarrow s_{1}=11101$，直到回合结束或者翻转后的状态与 $s_{g}$ 相同
- 奖励函数： $r_{g}(s,a)=-\left [ s \neq g \right ]$，即达到目标状态则为0，未达到目标状态则为-1。（ $s \neq g \Rightarrow true \doteq 1，s = g \Rightarrow false \doteq 0$ ）
- 注：后续将目标状态 $s_{g}$ 简化为 $g$
数组长度越长，反馈越稀疏，当 $n>40$ 时，几乎没有除了-1以外的奖励，标准的强化学习算法很难求解该问题。即使使用一些探索技术也不行，因为这个问题完全不是缺乏探索，而是状态太多，探索不完，导致奖励极其稀疏，算法根本不知道需要优化的目标在哪里

解决方法

reward shaping

将reward设计成某些变量的函数，如 $r_{g}(s,a)=-\left || s-g \right ||^{2}$，将训练的算法逐步引导至奖励函数增大的决策空间
- 该方案在这种场景中可以使用，但是不通用，无法应用到其他更加复杂的现实问题中

任务分解

将目标分解成多个粒度更小的，更容易解决的任务，使用类似层次强化学习（Hierarchical reinforcement learning）的方法去解决
这个文章中没有提到，一些书籍会提到

HER的做法

HER的主要思想就是：
- 通过修改目标简化问题，从而让奖励变得稠密。具体地，假定序列为 $s_{0},s_{1},s_{2}, \cdots ,s_{T}$，目标为 $g$，如果将目标状态 $g$ 修改为 $s_{T}$，即 $g=s_{T}$，那么这样看来智能体就可以获得奖励了
- 利用这个思想对经验池进行扩充即可，可以将稀疏奖励问题给转化成非稀疏奖励，使得奖励变得稠密
HER具体做法：
- 将经验池中的状态 $s$ 改为 $s||g$，也就是tf.concat(s,g)
- 训练算法的输入也是 $s||g$，也就是需要在当前状态后边连结上每个episode的目标状态，每个episode的目标状态可能不同
- HER对经验池进行了扩充，不仅存入实际采样得到的transition/experience， $\left ( s_{t}||g,a_{t},r_{t},s_{t+1}||g \right )$，也要在回合结束时重新设置目标状态，得到相应的奖励值（在二分奖励问题中，只有在 $s=g$ 时奖励才需要更改），存入“事后”（当初如果这样就好啦！）的经验 $\left ( s_{t}||g’,a_{t},r_{t}’,s_{t+1}||g’ \right )$，详见伪代码，这个事后经验究竟存入多少份、多少种，由超参数 $k$ 控制，下文讲解
- HER更适合解决多目标问题，多目标的意思为，目标点非固定，每个episode的目标状态可以不相同。详见实验部分
HER的几种扩展方式：
- 未来模式——future：在一个序列 $s_{0},s_{1},s_{2},\cdots,s_{T}$ 中，如果遍历到状态 $s_{2}$，则在 $s_{3},\cdots,s_{T}$ 之间随机抽取 $k$ 个状态作为目标状态 $g’$，并依此向经验池中存入 $\left ( s_{2}||g’,a_{2},r_{2}’,s_{3}||g’ \right )$，特点：一个episode的后续部分
- 回合模式——episode：在一个序列 $s_{0},s_{1},s_{2},…,s_{T}$ 中，如果遍历到状态 $s_{2}$，则在整个序列中随机抽取 $k$ 个状态作为目标状态 $g’$，并依此向经验池中存入 $\left ( s_{2}||g’,a_{2},r_{2}’,s_{3}||g’ \right )$，特点：一个episode
- 随机模式——random：在一个序列 $s_{0},s_{1},s_{2},…,s_{T}$ 中，如果遍历到状态 $s_{2}$，则在多个序列 $\tau_{0},\tau_{1},\tau_{2},\cdots$ 中随机抽取 $k$ 个状态作为目标状态 $g’$，并依此向经验池中存入 $\left ( s_{2}||g’,a_{2},r_{2}’,s_{3}||g’ \right )$，特点：多个episode
- 最终模式——final：在一个序列 $s_{0},s_{1},s_{2},\cdots,s_{T}$ 中，如果遍历到状态 $s_{2}$，则之间令 $g’=s_{T}$，并向经验池中存入 $\left ( s_{2}||g’,a_{2},r_{2}’,s_{3}||g’ \right )$，特点：一个episode的最后一个状态，如果设置k，则存入k个相同的经验
- 注：上面的 $s_{T}$ 不一定是当前episode的最终目标值，因为此时我们拟合的本意已经变成了“任意给定一个起始状态 $s_0$ 和目标状态 $s_i$，找到一个动作来实现将动作从 $s_0$ 变化到 $s_i$ ”
伪代码及其解析
- $r(s,a,g)$ 表示奖励不仅仅与当前状态和动作有关，还与最终的目标状态有关
- 伪代码中没有提到超参数 $k$，其实在循环条件 $\textbf{for} \ g’ \in G \ \textbf{do}$ 中循环执行了 $k$ 次
- $||$ 操作为连结操作，简言之，将两个长度为5的向量合并成一个长度为10的向量
- $G:=\mathbb{S}(\textbf{current episode})$ 即为上文提到的四种扩展模式：future、episode、random、final
- 奖励函数 $r(s,a,g)=-\left [ f_{g}(s)=0 \right ]$ 即为前文提到的 $r_{g}(s,a)=-\left [ s \neq g \right ]$，即完成为0，未完成为-1，具体奖励函数可以根据我们的使用环境设计
- $a_{t} \leftarrow \pi_{b}(s_{t}||g)$ 表示神经网络的输入为当前状态与目标状态的连结
HER的优点
- 可解决稀疏奖励、二分奖励问题
- 可适用于所有的Off-Policy算法
- 提升了数据采样效率

如何选择 HER 的模式？

实验结果：
- 效果：future>final>episode>random>no HER
- 稳定性：final(好)=no-HER(差)>future>episode>random

超参数的设置

$k$ 值不能太大，太大了会导致数据集中真实样本减少，出现问题

其他理解

问题：HER从 $s_{2}$ 扩展成 $s_{2}||g’$ 的过程中，相当于增加了MDP的数量（虽然MDP可能变得更短了），是否会导致MDP数量太多，模型难以收敛呢？

RL——MBPO

本文简单介绍 MBPO（Model-Based Policy Optimization）模型

参考链接：
- 原始论文：When to Trust Your Model: Model-Based Policy Optimization, UC Berkeley, NeurIPS 2019

MBPO 基本思想

主要用于解决 Online RL 的问题，属于 Model-based 方法

MBPO 方法详情

MBPO 训练代码
- 在收集到的奖励上减去一个误差项
- 训练时，Policy Optimization使用的是SAC方法：
其中，关键变量定义如下：

$\eta[\pi]$ denotes the returns of the policy in the true MDP, whereas $\hat{\eta}[\pi]$ denotes the returns of the policy under our model. Such a statement guarantees that, as long as we improve by at least C under the model, we can guarantee improvement on the true MDP.
- $\eta[\pi]$ 定义为真实MDP的累计折扣收益：
  $$ \eta[\pi] = \mathbb{E}_\pi\Big[ \sum_{t=0}^\infty \gamma^t r(s_t, a_t) \Big]$$
- $\hat{\eta}[\pi]$ 定义为模型返回的累计折扣收益
- $\eta[\pi]$ 和 $\hat{\eta}[\pi]$ 的关系：
  $$ \eta[\pi] \gt \hat{\eta}[\pi] - C $$
- 关于 $C(\epsilon_m, \epsilon_\pi)$ 的定义：
- $\epsilon_m$ : 模型误差
  $$ \epsilon_m = \max_t\mathbb{E}_{s\sim \pi_\text{D,t}} [D_{TV}(p(s’,r|s,a)\Vert p_\theta(s’,r|s,a))] $$
  - $s\sim \pi_\text{D,t}$ 表示时间步 $t$ 采样到状态 $s$
- $ \epsilon_\pi$ : 策略偏移
  $$ \max_s D_{TV}(\pi \Vert \pi_\text{D}) \lt \epsilon_\pi $$

附录：动手学强化学习中介绍的 MBPO

训练流程
- 没有考虑减去误差项

RL——MCTS

参考文献：
- Survey参考：A Survey of Monte Carlo Tree Search Methods, 2012

整体说明

蒙特卡洛树搜索（Monte Carlo Tree Search, MCTS）是一种基于随机模拟的强化学习决策方法 ，尤其在复杂决策问题（如围棋、游戏等）中表现出色。它通过智能地平衡探索（Exploration）和利用（Exploitation） ，逐步构建搜索树并优化策略
MCTS决策方法常用于围棋（AlphaGo）、即时战略游戏、扑克等场景中，目前在LLM领域也有所应用
优势：适用于高维、稀疏奖励问题；无需预先知识，仅依赖模拟；可并行化，扩展性强
局限：初期模拟可能低效（依赖随机探索）；需大量模拟才能收敛

MCTS 的核心思想

MCTS通过反复模拟（Simulation）从当前状态出发的可能路径，逐步构建一棵非对称的搜索树
MCTS树的节点代表游戏状态，边代表动作
MCTS的核心优势在于：
- 无需完整模型 ：仅需模拟环境（如游戏规则）即可
- 适应大规模状态空间 ：通过选择性扩展树，避免穷举
- 异步更新 ：模拟结果反向传播，动态优化策略

MCTS 每次迭代的四个阶段

MCTS过程概览（图片来源于 A Survey of Monte Carlo Tree Search Methods, 2012）

第一步：选择（Selection）

目标：从根节点（当前状态）出发，递归选择子节点，直到到达一个可扩展的状态节点（即存在未尝试的动作的状态节点），返回这个被选择的节点
策略：使用树策略（如UCT算法或PUCT算法）平衡探索与利用
UCT（Upper Confidence Bound applied to Trees）算法 ：
$$
\textit{UCT}(s, a) = Q(s, a) + c \sqrt{\frac{\ln N(s)}{N(s, a)} }
$$
- $Q(s, a)$：动作$a$的平均回报
- $N(s)$：状态$s$的访问次数，$N(s, a)$：动作$a$的访问次数（注：如果分母不会为0，此时所有节点都是完整探索过的，不存在为0的情况）
- $c$：探索系数（通常设为$\sqrt{2}$），当$c=\sqrt{2}$时，UCT的累计遗憾（Regret）有对数上界
- 探索时选择动作为： $a^* = \arg\max_a \textit{UCT}(s, a)$
PUCT（Predictor UCT）算法 ：
$$
\textit{PUCT}(s, a) = Q(s, a) + c_\textit{puct}\cdot P(s,a)\cdot \frac{\sqrt{N(s)}}{1+N(s, a)}
$$
- $P(s,a)$：即 $\pi(a|s)$，是先验策略网络（Policy Network）给出的先验概率（表示动作 $a$ 的初始偏好）
- $c_\text{puct}$：探索系数（控制先验权重，AlphaZero中常设为1~2）
- $1+N(s,a)$：（不用为了避免除0操作而增加1吧，毕竟此时所有节点都是完整探索过的，不存在为0的情况）
- 探索时选择动作为：探索时选择 $a^* = \arg\max_a \textit{PUCT}(s, a)$
- 基本思想：采样次数 $N(s, a)$ 少时，按照策略 $\pi(a|s)$ 为主探索；采样次数 $N(s, a)$ 多时，按照价值 $Q(s, a)$ 为主探索
- PUCT被使用到了AlphaZero和MuZero中
  - 注：MuZero是由DeepMind开发的一种通用强化学习模型，它能够在不知道环境规则的情况下，通过自我学习和规划，掌握多种复杂游戏和任务，MuZero采用模型预测控制（Model-Based RL） ，并结合了MCTS

第二步：扩展（Expansion）

前提条件 ：第一步完成后，我们选择到了一个未完全展开的节点（即存在未尝试的动作的节点）时，扩展该节点
节点扩展 ：添加一个新子节点（随机执行一个未尝试的动作，将环境反馈的新状态作为新子节点）

第三步：模拟（Simulation）

在一些资料中，这一步也称为评估，相当与对一个动作的价值评估
模拟：从新节点开始，按照随机策略（或其他基于简单策略）Rollout 模拟至终止状态（如游戏结束），最终获得本次模拟的奖励（如胜利/失败）

第四步：回溯（Backpropagation）

回溯：将模拟结果（奖励）反向传播到路径上的所有节点
- 更新访问次数 $N(s)$ 和 $N(s, a)$
- 更新动作价值 $Q(s, a)$（如累加奖励的平均值）

MCTS的终止与决策

终止条件 ：达到预设时间、计算资源或迭代次数
最终决策 ：选择根节点下访问次数最多或价值最高的动作（如AlphaGo选择访问次数最多的动作）
- 问题：为什么是访问次数最多而不是价值最高的动作作为决策？

一些理解与讨论

棋局中，对手策略如何模拟？
- AlphaGo中，使用策略网络 $\pi(a|s)$ 来模拟对手策略
为什么MCTS第三步中使用随机策略模拟采样？
- 传统的MCTS确实是按照随机采样的，但从直观上看，使用当前策略来模拟采样决策是否才是符合预期的；
- AlphaGo的做法：
  - 实际上是使用策略网络来模拟决策的
  - 为了加快速度，AlphaGo还训练了一个较小的策略网络专门用来在MCTS的第三步中模拟决策
  - 为了提升稳定性，AlphaGo的价值评估结合了价值网络的输出和MCTS模拟奖励结果 $V(s_{t+1}) = \frac{1}{2}(reward + V_\theta(s_{t+1}))$
- 在LLM等场景中，随机采样是毫无意义的，也需要基于LLM来采样决策
为什么AlphaGo决策时选择访问最多的动作而不是价值最高的动作？
- 理解：实际上访问最多的动作往往也是价值最高的动作，即使不是价值最高的，也不会太差，且价值最高的动作可能是因为波动带来的，访问最多的动作更置信
- 节点被访问的次数越多，说明MCTS对其进行了更充分的探索，其Q值的置信度越高。选择高访问次数的动作，相当于选择被反复验证过的最优策略，避免因偶然性导致的风险

附录：MCTS在围棋中的流程

第一步-选择 ：从当前棋盘状态出发，递归选择UCT值最高的落子点
第二步-扩展 ：当遇到一个未尝试的合法落子时，扩展新节点
第三步-模拟 ：随机落子至终局，判断胜负
第四步-回溯 ：若胜利，路径上所有节点的胜利次数+1
决策：经过数万次迭代后，选择根节点下胜率最高的落子

RL——TD误差和优势函数的区别

参考链接：
- TD误差 vs 优势函数 vs贝尔曼误差

TD 误差

时间差分误差，TD error
定义如下：
$$
\delta_{\theta}(s, a, s’) = R(s, a, s’) + \gamma v_{\theta}(s’) - v_{\theta}(s)
$$
$R(s,a,s’)=r(s,a,s’)$，表示从状态 $s$ 执行 $a$ 之后转移到 $s’$ 获得的立即回报
TD error是针对确定的 $s’$ 来说的

优势函数

优势函数，Advantage Function
$$
A_{\theta}(s,a) = \mathbb{E}_{s’\sim P}[\delta_{\theta}(s, a, s’)] = \mathbb{E}_{s’\sim P}[R(s, a, s’) + \gamma v_{\theta}(s’)] - v_{\theta}(s) = Q_{\theta}(s,a) - v_{\theta}(s)
$$
优势函数是TD误差关于状态 $s’$ 的期望，即从状态 $s$ 执行 $a$ 之后关于状态 $s’$ 的期望

贝尔曼误差

贝尔曼误差
$$
\epsilon_{\theta}(s) = \mathbb{E}_{a\sim \pi} [A_{\theta}(s,a)] = \mathbb{E}_{a\sim \pi,s’\sim P}[\delta_{\theta}(s, a, s’)] = \mathbb{E}_{a \sim \pi, s’\sim P}[R(s, a, s’) + \gamma v_{\theta}(s’)] - v_{\theta}(s)
$$
贝尔曼误差是优势函数关于动作 $a$ 的期望

期望贝尔曼误差

期望贝尔曼误差
$$
\mathbb{E}_{s\sim \mu} [\epsilon_{\theta}(s)] = \mathbb{E}_{s\sim \mu}[\mathbb{E}_{a \sim \pi, s’\sim P}[R(s, a, s’) + \gamma v_{\theta}(s’)]] - \mathbb{E}_{s\sim \mu}[ v_{\theta}(s)]
$$
贝尔曼误差是优势函数关于动作 $a$ 的期望

RL——Q-learning与DQN收敛性证明

前言

在数学中，函数、泛函、算子都是映射
函数：是从一个集合的元素映射到另一个集合的元素
泛函：是从一个函数空间映射到数值空间（如实数或复数集）
算子：是从一个函数空间映射到另一个函数空间

Q-learning 和 DQN 的收敛性讨论

DQN基本原理 ：DQN的核心是使用一个深度神经网络来逼近Q-learning的Q函数
Q-learning有严格的收敛性证明（贝尔曼最优算子是压缩映射），但DQN没有（DQN虽然也按照贝尔曼最优算子更新，但还增加了一个神经网络近似）
- 贝尔曼算子和贝尔曼最优算子都是压缩映射；神经网络近似是收敛的，但是贝尔曼最优算子+神经网络近似不一定能保证收敛
本文主要针对Q-learning证明其收敛性，同时附带证明了贝尔曼算子和贝尔曼最优算子都是压缩映射

压缩映射定理（Contraction Mapping Theorem）

压缩映射定理也称为Banach不动点定理
压缩映射的定义
定义：设 $(X, d)$ 是一个完备的度量空间（即所有柯西序列都收敛）， $\mathcal{T}: X \to X$ 是一个映射。如果存在一个常数 $\gamma \in (0, 1)$ ，使得对于所有的 $x_1, x_2 \in X$ ，都有满足下面的式子，则称 $\mathcal{T}$ 是一个压缩映射 ：
$$ \color{red}{d}(\mathcal{T}(x_1), \mathcal{T}(x_2)) \leq \color{blue}{\gamma} \color{red}{d}(x_1, x_2) $$
- 其中 $ d $ 表示度量（metric） ，即度量空间中用于衡量两个点之间距离的函数
直观理解 ：
- 压缩映射会将空间中的点逐渐拉近，使得它们之间的距离不断缩小。由于这种收缩性质，压缩映射在完备度量空间中必然存在一个唯一的不动点
- $\mathcal{T}$ 将任意两点之间的距离压缩至少 $\gamma$ 倍
- 即构造序列 ${x_n}$ ，其中 $x_{n + 1} = \mathcal{T}(x_n)$，则随着 $n \rightarrow \infty$, 序列 ${x_n}$ 会收敛到压缩映射的不动点 $x^*$

压缩映射定理（Contraction Mapping Theorem）

不动点（Fixed-Point）定义 ：对于一个映射 $\mathcal{T}: X \to X$ ，如果存在一个点 $x^* \in X$ ，使得 $\mathcal{T}(x^*) = x^*$ ，那么 $x^*$ 就被称为 $\mathcal{T}$ 的不动点
压缩映射定理（Banach不动点定理） ：设 $(X, d)$ 是一个完备的度量空间（即所有柯西序列都收敛），$\mathcal{T}: X \to X$ 是一个压缩映射。则：
- $\mathcal{T}$ 在 $X$ 中存在唯一的不动点 $x^*$（即 $\mathcal{T}(x^*) = x^*$）
- 对于任意初始点 $x_0 \in X$，通过迭代 $x_{n+1} = \mathcal{T}(x_n)$ 生成的序列 ${x_n}$ 收敛于 $x^*$
- 收敛速度的估计：
  $$
  d(x_n, x^*) \leq \frac{k^n}{1 - k} d(x_0, x_1)
  $$
  - 即，误差以指数速度衰减

压缩映射定理的简单证明

存在性 ：从任意 $x_0$ 出发，构造序列 $x_{n+1} = \mathcal{T}(x_n)$。利用压缩性可证明 ${x_n}$ 是柯西序列，由完备性可知其收敛到某点 $x^*$。再证明 $x^*$ 是不动点
唯一性 ：假设有两个不动点 $x^*$ 和 $y^*$，利用压缩性导出矛盾

贝尔曼算子与压缩映射

贝尔曼方程定义 ：在强化学习中，贝尔曼方程用于描述最优值函数（如最优Q函数）的递归关系。对于一个马尔可夫决策过程（MDP），贝尔曼最优性方程可以表示为：
$$Q^*(s, a)=\mathbb{E}_{s^{\prime}}\left[r(s, a, s^{\prime})+\gamma \max _{a^{\prime}} Q^*(s^{\prime}, a^{\prime})\right]$$
- $\gamma$ 是折扣因子， $Q^*(s, a)$ 是最优Q函数，表示在状态 $s$ 执行动作 $a$ 的最优价值
贝尔曼算子与压缩映射 ：贝尔曼方程定义了一个从Q函数空间到自身的映射 $\mathcal{T}$ （函数空间到函数空间的映射也称为算子，这里也称为贝尔曼算子），即：
$$\mathcal{T}Q(s, a)=\mathbb{E}_{s^{\prime}}\left[r(s, a, s^{\prime})+\gamma \max _{a^{\prime}} Q(s^{\prime}, a^{\prime})\right]$$
- 可以证明，在无穷范数度量下（即度量 $d$ 为无穷范数（$ \Vert \cdot\Vert_\infty $））时，有贝尔曼算子 $\mathcal{T}$ 是一个压缩映射
- 实际上，在无穷范数度量下，贝尔曼最优算子和贝尔曼算子都是压缩映射 ，详情见附录证明

附录：度量的完整定义

度量的定义

给定一个集合 $ X $，若函数 $ d: X \times X \to \mathbb{R} $ 满足以下性质，则称 $ d $ 为 $ X $ 上的度量：
- 非负性 ：
  $$ d(x, y) \geq 0 \quad \text{且} \quad d(x, y) = 0 \iff x = y. $$
- 对称性 ：
  $$ d(x, y) = d(y, x). $$
- 三角不等式 ：
  $$ d(x, z) \leq d(x, y) + d(y, z). $$
此时，二元组 $ (X, d) $ 称为度量空间
在压缩映射定理中:
$$ d(\mathcal{T}(x_1), \mathcal{T}(x_2)) \leq \gamma \cdot d(x_1, x_2) \quad (\gamma \in [0, 1)), $$
- $ d(x_1, x_2) $ 表示两点 $ x_1 $ 和 $ x_2 $ 的原始距离
- $ d(\mathcal{T}(x_1), \mathcal{T}(x_2)) $ 表示它们经过映射 $\mathcal{T}$ 后的像之间的距离
- 不等式表明，$\mathcal{T}$ 将距离压缩了至少 $ \gamma $ 倍（$ \gamma < 1 $）

附录：贝尔曼算子是压缩映射的证明

证明目标：贝尔曼算子（Bellman Operator）和贝尔曼最优算子（Bellman Optimality Operator）在适当的条件下都是无穷范数（$ \Vert \cdot\Vert_\infty $）下的压缩映射 ，但它们的压缩性质依赖于折扣因子 $ \gamma \in [0, 1) $ 和 MDP 的结构。

贝尔曼算子 $ \mathcal{T}^\pi $（Policy Evaluation）

对于给定的策略 $ \pi $，贝尔曼算子定义为：
$$
(\mathcal{T}^\pi V)(s) = \sum_{a} \pi(a|s) \left( r(s, a) + \gamma \sum_{s’} P(s’|s, a) V(s’) \right)
$$
对于任意两个值函数 $ V_1, V_2 $，有：
$$
\begin{align}
\Vert \mathcal{T}^\pi V_1 - \mathcal{T}^\pi V_2 \Vert_\infty &= \max_s \left| \sum_{a} \pi(a|s) \gamma \sum_{s’} P(s’|s, a) (V_1(s’) - V_2(s’)) \right| \\
&\leq \gamma \max_s \sum_{a} \pi(a|s) \sum_{s’} P(s’|s, a) |V_1(s’) - V_2(s’)| \\
&\leq \gamma \max_s \sum_{a} \pi(a|s) \sum_{s’} P(s’|s, a) \Vert V_1 - V_2 \Vert_\infty \\
&= \gamma \Vert V_1 - V_2 \Vert_\infty \quad (\text{注： } \sum_{a} \pi(a|s) \sum_{s’} P(s’|s, a) = 1)
\end{align}
$$
也就是说，下面的式子成立：
$$
\Vert \mathcal{T}^\pi V_1 - \mathcal{T}^\pi V_2 \Vert_\infty \leq \gamma \Vert V_1 - V_2 \Vert_\infty
$$
至此，我们证得结论：贝尔曼算子 $ \mathcal{T}^\pi $ 是无穷范数下的压缩映射（$ \gamma $-压缩），压缩因子为 $ \gamma $

贝尔曼最优算子 $ \mathcal{T}^* $（Optimal Control）

贝尔曼最优算子定义为：
$$
(\mathcal{T}^* V)(s) = \max_{a} \left( r(s, a) + \gamma \sum_{s’} P(s’|s, a) V(s’) \right)
$$
对于任意两个值函数 $ V_1, V_2 $，设 $ a^*_1 $ 和 $ a^*_2 $ 分别是 $ \mathcal{T}^* V_1 $ 和 $ \mathcal{T}^* V_2 $ 的最优动作：
$$
\begin{align}
\mathcal{T}^* V_1(s) - \mathcal{T}^* V_2(s) &= \left( r(s, a^*_1) + \gamma \sum_{s’} P(s’|s, a^*_1) V_1(s’) \right) - \left( r(s, a^*_2) + \gamma \sum_{s’} P(s’|s, a^*_2) V_2(s’) \right) \\
&\leq \left( r(s, a^*_1) + \gamma \sum_{s’} P(s’|s, a^*_1) V_1(s’) \right) - \left( r(s, a^*_1) + \gamma \sum_{s’} P(s’|s, a^*_1) V_2(s’) \right) \\
&= \gamma \sum_{s’} P(s’|s, a^*_1) (V_1(s’) - V_2(s’)) \\
&\leq \gamma \Vert V_1 - V_2 \Vert_\infty
\end{align}
$$
同理可得：
$$
\mathcal{T}^* V_2(s) - \mathcal{T}^* V_1(s) \leq \gamma \Vert V_1 - V_2 \Vert_\infty
$$
进一步将上面两个结论转换为绝对值，也就是说，下面的式子成立：：
$$
| \mathcal{T}^* V_1(s) - \mathcal{T}^* V_2(s) | \leq \gamma \Vert V_1 - V_2 \Vert_\infty
$$
对绝对值取最大值，即得到无穷范数：
$$
\Vert \mathcal{T}^* V_1 - \mathcal{T}^* V_2 \Vert_\infty \leq \gamma \Vert V_1 - V_2 \Vert_\infty
$$
至此，我们证得结论：贝尔曼最优算子 $ \mathcal{T}^* $ 是无穷范数下的压缩映射（$ \gamma $-压缩），压缩因子为 $ \gamma $

比较两者的不动点

贝尔曼算子 $ \mathcal{T}^\pi $ ：用于策略评估（Policy Evaluation） ，计算给定策略 $ \pi $ 的值函数 $ V^\pi $
$$ (\mathcal{T}^\pi V)(s) = \mathbb{E}_{a \sim \pi} [ r + \gamma \mathbb{E}_{s’} V(s’) ] $$
- 收敛到 $ V^\pi $，即 $ \mathcal{T}^\pi V^\pi = V^\pi $，且 $ V^\pi $ 是唯一不动点
贝尔曼最优算子 $ \mathcal{T}^* $ ：用于最优控制（Optimal Control） ，计算最优值函数 $ V^* $
$$(\mathcal{T}^* V)(s) = \max_a [ r + \gamma \mathbb{E}_{s’} V(s’) ] $$
- 收敛到 $ V^* $，即 $ \mathcal{T}^* V^* = V^* $，且 $ V^* $ 是唯一不动点

一些补充思考

折扣因子 $ \gamma < 1 $ 是关键，否则压缩性可能不成立（如无折扣问题 $ \gamma = 1 $ 时，可能不收敛）
无穷范数 保证了压缩性，其他范数（如 $ L^2 $）不一定成立
随机策略 vs. 确定性策略 ：$ \mathcal{T}^\pi $ 适用于随机策略，而 $ \mathcal{T}^* $ 隐含地使用了确定性策略（取 max）

附录：神经网络近似的本质讨论

神经网络近似本身可以看做是一种算子 $\mathcal{\Pi}$：
$$ (\mathcal{\Pi} q)(s,a) = \arg\min_{q’\in\Omega} \frac{1}{2}\Vert q(s,a) - q’(s,a)\Vert^2_2 $$
（未经过严格证明）一些讨论中会提到这种算子也是一种压缩映射。（注：即便如此，两个压缩映射（贝尔曼最优算子+神经网络近似）组合以后得映射也无法证明为压缩映射 ，即无法证明DQN的收敛性）

RL——MOPO

本文简单介绍 MOPO（Model-Based Offline Policy Optimization）模型

参考链接：
- 原始论文：MOPO: Model-based Offline Policy Optimization, Stanford & UC Berkeley, NeurIPS 2020
- 论文附录：MOPO-Supplemental
- 源码地址：github.com/tianheyu927/mopo

MOPO基本思想

主要用于解决Offline RL的问题，属于Model-based方法
使用一个模型预估状态转移和奖励，同时使用训练一个误差评估器，在真实使用奖励时，使用误差评估器对奖励进行修正

MOPO方法详情

MOPO训练Framework
- 基本思路是在原始Reward上给与一定的修正，对方差大的Reward采取更多的惩罚，防止高估问题发生
MOPO训练代码（这里是Ensemble Uncertainty形式，即Ensemble Penalty形式，其他还包括No Penalty和True Penalty形式）
- 在收集到的静态数据集上训练 N 个模型（Probabilistic Dynamics）
- 每次需要与环境交互时，随机选择一个模型（Dynamics）来交互
- 修正这个Reward时，使用所有模型的方差的 F 范数中的最大值作为惩罚项，其中矩阵 F 范数的定义为：$\Vert A \Vert_F = \sqrt{\sum_{i=1}^N\sum_{i=1}^M|a_{ij}|^2}$
  - 也可以用均值而不是最大值: $u^{\text{mean}}(s,a) = \frac{1}{N}\sum_{i=1}^N\Vert\Sigma_\phi^i \Vert_F$

关键代码（https://github.com/tianheyu927/mopo/blob/master/mopo/models/fake_env.py#L80-L102）

if self.penalty_coeff != 0:
    if not self.penalty_learned_var:
        ensemble_means_obs = ensemble_model_means[:,:,1:]
        mean_obs_means = np.mean(ensemble_means_obs, axis=0)     # average predictions over models
        diffs = ensemble_means_obs - mean_obs_means
        normalize_diffs = False
        if normalize_diffs:
            obs_dim = next_obs.shape[1]
            obs_sigma = self.model.scaler.cached_sigma[0,:obs_dim]
            diffs = diffs / obs_sigma
        dists = np.linalg.norm(diffs, axis=2)   # distance in obs space # np.linalg.norm 函数默认情况下会计算向量或矩阵的二范数（欧几里得范数），也可通过增加参数来实现计算不同的范数
        penalty = np.max(dists, axis=0)         # max distances over models
    else:
        penalty = np.amax(np.linalg.norm(ensemble_model_stds, axis=2), axis=0)

    penalty = np.expand_dims(penalty, 1)
    assert penalty.shape == rewards.shape
    unpenalized_rewards = rewards
    penalized_rewards = rewards - self.penalty_coeff * penalty
else:
    penalty = None
    unpenalized_rewards = rewards
    penalized_rewards = rewards

Joe Zhou

Stay Hungry. Stay Foolish.

GitHub E-Mail

Introduction and Discussion

Related Work

IMPALA

Efficiency Optimisations

V-trace

V-trace 目标 (V-trace target)

Actor-Critic algorithm

策略梯度 (Policy gradient)

V-trace actor-critic algorithm

Experiments

计算性能 (Computational Performance)

单任务训练 (Single-Task Training)

收敛性与稳定性 (Convergence and Stability)

V-trace 分析 (V-trace Analysis)

多任务训练 (Multi-Task Training)

DMLab-30

Atari

Conclusion

附录：【待补充】

策略梯度法的推导结论

AC 算法

Critic 网络的更新

Actor 网络的更新

AC 算法的问题

A2C 算法

Critic 网络的更新

Actor 网络的更新

A2C 算法的问题

A3C 算法

A3C 的主要优化点

异步训练框架优化：

A3C 的“异步”更新流程

策略更新损失增加熵

AC/A2C/A3C的区别

AC（Actor-Critic）

A2C（Advantage Actor-Critic）

A3C（Asynchronous Advantage Actor-Critic）

附录：为什么 A3C 不需要重要性采样？

COMBO 基本思想

原始 CQL 的更新公式

COMBO 的训练流程

实验结果

DPG

Stochastic Actor-Critic Algorithms

Off-Policy Actor Critic

Off-Policy AC如何对混合策略采样的样本进行重要性采样？

On-Policy Deterministic Actor-Critic

Off-Policy Deterministic Actor-Critic

DDPG

DDPG训练流程

DDPG 为什么可以是 off-policy 的？

TD3

TD3 训练流程

改进1：Twin

改进2：Delayed

改进3：Target 策略网络增加噪声

TD3+BC（TD3 with behavior cloning，for Offline RL）

Background

HER 技术思路

A motivating example

解决方法

reward shaping

任务分解

HER的做法

如何选择 HER 的模式？

超参数的设置

其他理解

MBPO 基本思想

MBPO 方法详情

附录：动手学强化学习中介绍的 MBPO

整体说明

MCTS 的核心思想

MCTS 每次迭代的四个阶段

第一步：选择（Selection）

第二步：扩展（Expansion）

第三步：模拟（Simulation）

第四步：回溯（Backpropagation）

MCTS的终止与决策

一些理解与讨论

附录：MCTS在围棋中的流程