PyTorch——backward函数详细解析

本文主要介绍PyTorch中backward函数和grad的各种用法

梯度的定义

\(y\) 对 \(x\) 的梯度可以理解为: 当 \(x\) 增加1的时候, \(y\) 值的增加量
如果 \(x\) 是矢量(矩阵或者向量等),那么计算时也需要看成是多个标量的组合来计算,算出来的值表示的也是 \(x\) 当前维度的值增加1的时候, \(y\) 值的增加量

backward基础用法

tensorflow是先建立好图，在前向过程中可以选择执行图的某个部分(每次前向可以执行图的不同部分，前提是，图里必须包含了所有可能情况)
pytorch是每次前向过程都会重新建立一个图，反向(backward)的时候会释放，每次的图可以不一样, 所以在Pytorch中可以随时使用if, while等语句
- tensorflow中使用if, while就得在传入数据前(构建图时)告诉图需要构建哪些逻辑,然后才能传入数据运行
- PyTorch中由于不用在传入数据前先定义图(图和数据一起到达,图构建的同时开始计算数据?)
backward操作会计算梯度并将梯度直接加到变量的梯度上，所以为了保证梯度准确性，需要使用optimizer.zero_grad()清空梯度

计算标量对标量的梯度

结构图如下所示

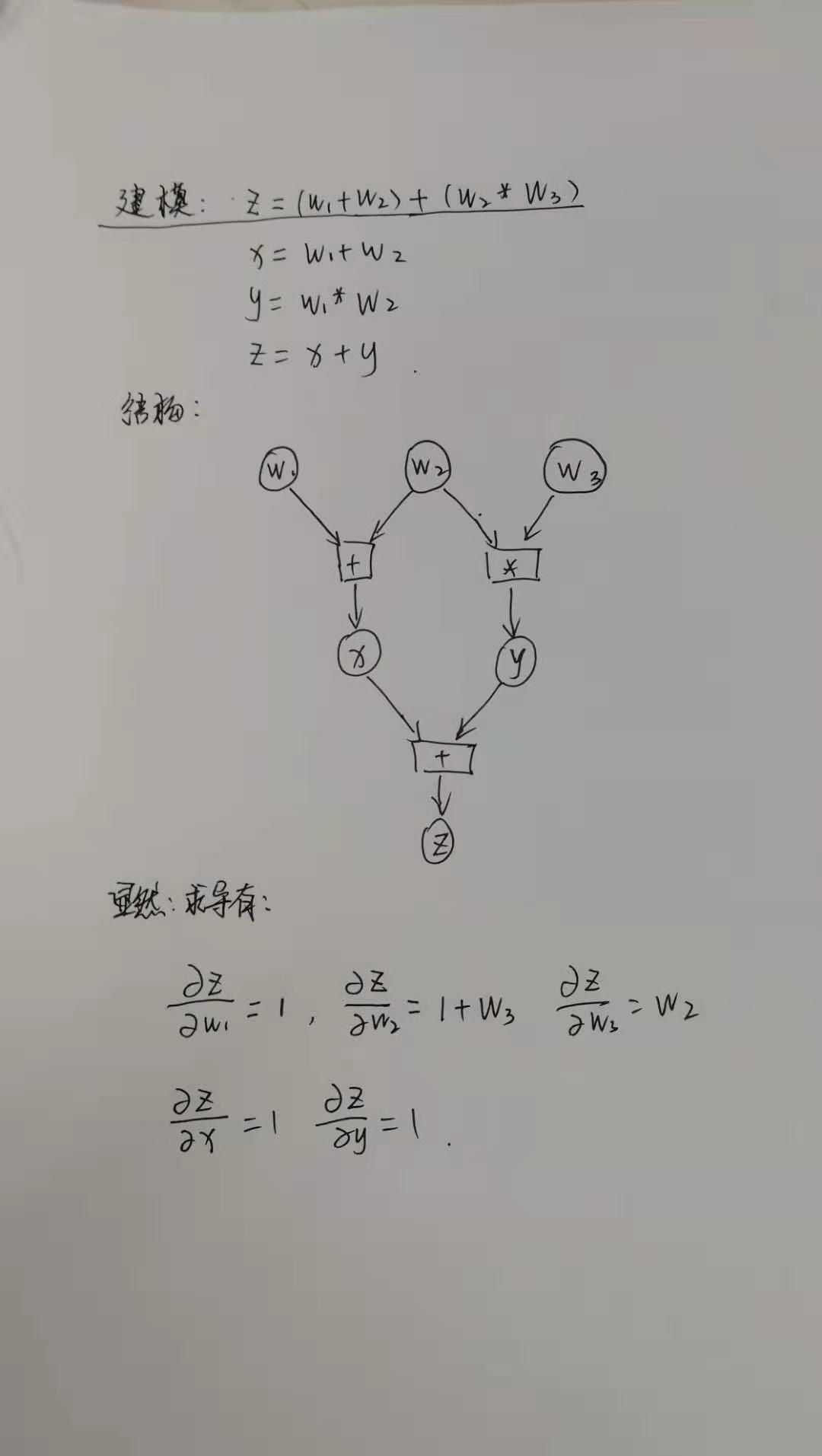
上面图的代码构建如下

import torch
from torch.autograd import Variable

w1 = Variable(torch.Tensor([2]),requires_grad=True)
w2 = Variable(torch.Tensor([3]),requires_grad=True)
w3 = Variable(torch.Tensor([5]),requires_grad=True)
x = w1 + w2
y = w2*w3
z = x+y
z.backward()
print(w1.grad)
print(w2.grad)
print(w3.grad)
print(x.grad)
print(y.grad)

# output:
tensor([1.])
tensor([6.])
tensor([3.])
None
None

从图中的推导可知,梯度符合预期
\(x, y\) 不是叶节点,没有梯度存储下来,注意可以理解为梯度计算了,只是没有存储下来,PyTorch中梯度是一层层计算的

计算标量对矢量的梯度

修改上面的构建为
- 增加变量 \(s = z.mean\)，然后直接求取 \(s\) 的梯度
结构图如下:

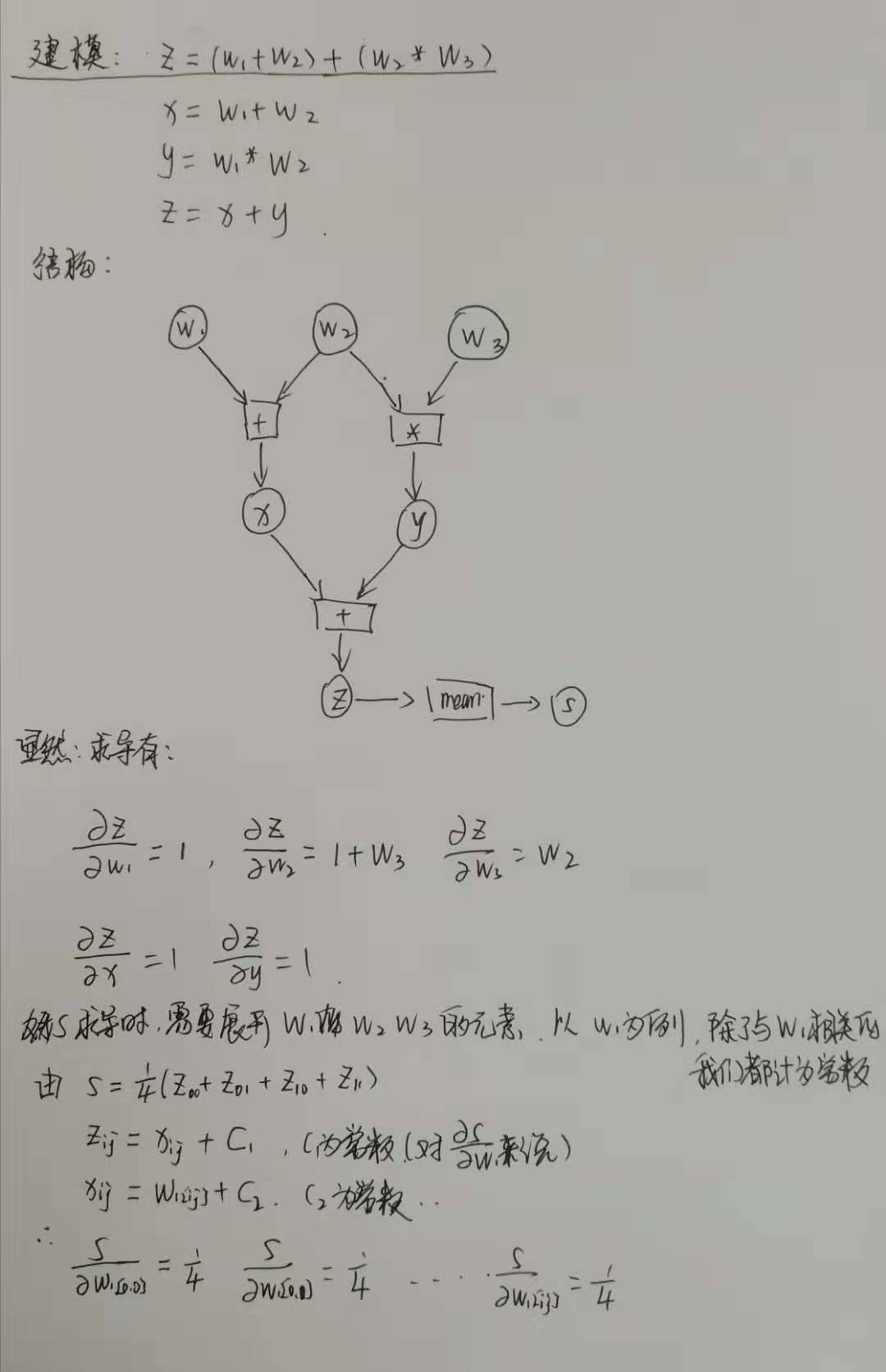
代码如下:

import torch
from torch.autograd import Variable

w1 = Variable(torch.ones(2,2)*2,requires_grad=True)
w2 = Variable(torch.ones(2,2)*3,requires_grad=True)
w3 = Variable(torch.ones(2,2)*5,requires_grad=True)
x = w1 + w2
y = w2*w3
z = x+y
# z.backward()
s = z.mean()
s.backward()
print(w1.grad)
print(w2.grad)
print(w3.grad)
print(x.grad)
print(y.grad)
# output:
tensor([[0.2500, 0.2500],
		[0.2500, 0.2500]])
tensor([[1.5000, 1.5000],
		[1.5000, 1.5000]])
tensor([[0.7500, 0.7500],
		[0.7500, 0.7500]])
None
None

显然推导结果符合代码输出预期
梯度的维度与原始自变量的维度相同,每个元素都有自己对应的梯度,表示当当前元素增加1的时候, 因变量值的增加量

计算矢量对矢量的梯度

还以上面的结构图为例
直接求中间节点 \(z\) 关于自变量的梯度

代码如下

import torch
from torch.autograd import Variable

w1 = Variable(torch.ones(2,2)*2, requires_grad=True)
w2 = Variable(torch.ones(2,2)*3, requires_grad=True)
w3 = Variable(torch.ones(2,2)*5, requires_grad=True)
x = w1 + w2
y = w2*w3
z = x+y
z_w1_grad = torch.autograd.grad(outputs=z, inputs=w1, grad_outputs=torch.ones_like(z))
print(z_w1_grad)

在因变量是矢量时,grad_outputs参数不能为空,标量时可以为空(grad_outputs为空时和grad_outputs维度为1时等价)
grad_outputs的维度必须和outputs参数的维度兼容

关于autograd.grad函数

参考博客: https://blog.csdn.net/qq_36556893/article/details/91982925

`grad_outputs`参数详解

在因变量是矢量时,grad_outputs参数不能为空,标量时可以为空(grad_outputs为空时和grad_outputs维度为1时等价)
grad_outputs的维度必须和outputs参数的维度兼容
[待更新]

backward 对计算图的清空

在 PyTorch 中，backward() 方法在计算反向梯度后，不仅不会保存中间节点（非叶子张量）的梯度，还会释放对应的计算图
- 所以，多次调用 backward() 方法是会报错的 RuntimeError: Trying to backward through the graph a second time
如果想要多次调用 backward() 方法，需要使用 backward(retain_graph=True)

多次调用 backward() 的错误示例：

import torch

x = torch.tensor(2.0, requires_grad=True)
y = x**3
z = y + 1

z.backward()  # 第一次调用，正常运行
z.backward()  # 报错：RuntimeError: Trying to backward through the graph a second time...

多次调用 backward() 的正确示例：

import torch

x = torch.tensor(2.0, requires_grad=True)
y = x**3
z = y + 1

z.backward(retain_graph=True)  # 第一次调用，保留计算图
print(x.grad)  # 输出：tensor(12.)

z.backward()  # 第二次调用，此时可以不保留计算图
print(x.grad)  # 输出：tensor(24.)，梯度累加了

自定义算子的前向后向实现

PyTorch 中，自定义算子适用于一些 PyTorch 内置函数无法满足的场景：
- 实现个性化运算算子：当需要使用 PyTorch 未内置的数学运算（如特殊激活函数、自定义卷积等），且需支持自动求导时
- 优化计算效率：对特定操作手动编写前向 / 反向逻辑，可能比内置函数更高效（如简化冗余计算）
- 整合外部库：可用于将 C++、CUDA 或其他语言实现的算法接入 PyTorch，并支持自动求导
自定义算子是 Function 类需继承 torch.autograd.Function，并实现两个静态方法 ：
- forward()：定义前向传播逻辑，输入为张量，输出为计算结果
- backward()：定义反向传播梯度计算逻辑，输入为上游梯度，输出为各输入的梯度

PyTorch 自定义实现代码 Demo：

import torch

class SquareSumFunction(torch.autograd.Function):
	@staticmethod
	def forward(ctx, x, y):
		"""
		:param ctx: 可用于保存需要在反向传播中使用的张量，torch.autograd.function.BackwardCFunction 的实例
		:param x: 输入张量
		:param y: 输入张量
		:return: 输出张量
		"""
		ctx.save_for_backward(x, y) # ctx 用于存储反向传播所需的中间变量
		output = x **2 + y **2
		return output

	@staticmethod
	def backward(ctx, grad_output): # backward 输入参数和 forward 输出参数数量一致
		"""
		:param ctx: 获取在 forward() 中保存的中间变量
		:param grad_output: 上游梯度，计算到当前算子的梯度后，链式法则乘上这个梯度就行，形式为torch.Tensor，第一次反向操作传入值为常量1
		:return: 返回多个值，依次对齐 forward 过程输入的张量的梯度
		"""
		x, y = ctx.saved_tensors  # 取出前向保存的变量
		grad_x = grad_output * 2 * x  # 计算这个算子的 forward 输出 对x的梯度，然后按照链式法则乘上上游梯度
		grad_y = grad_output * 2 * y
		return grad_x, grad_y # backward 输出 和 forward 输入参数一一对齐

x = torch.tensor([2.0], requires_grad=True)
y = torch.tensor([3.0], requires_grad=True)
z = SquareSumFunction.apply(x, y)  # 通过 apply 调用
z.backward() # 计算梯度
print(x.grad, y.grad)  # 输出：tensor([4.]) tensor([6.])，符合预期
print(z.grad_fn)
# 若计算图没有被清空，可以用下面的式子主动调用算子的 backward 函数（注意这里不会自动给 x.grad和y.grad赋值）
# print(z.grad_fn.apply(1)) # 传入常量1作为上游梯度 `grad_output`，会返回两个梯度值+grad_fn的 tuple (tensor([4.], grad_fn=<MulBackward0>), tensor([6.], grad_fn=<MulBackward0>))，

梯度的定义

backward基础用法

计算标量对标量的梯度

计算标量对矢量的梯度

计算矢量对矢量的梯度

关于autograd.grad函数

grad_outputs参数详解

backward 对计算图的清空

自定义算子的前向后向实现

`grad_outputs`参数详解