本文介绍各种不同的Normalization方法
- BN: Batch Normalization
- LN: Layer Normalization
- IN: Instance Normalization
- GN: Group Normalization
- LRN: Local Response Normalization
- WN: Weight Normalization
Normalization总体介绍
- BN,LN,IN的归一化的步骤都是使用下面的公式:
$$
\begin{align}
u &= \frac{1}{m}\sum_{k\in S}x_k \\
\sigma &= \sqrt{\frac{1}{m}\sum_{k\in S}(x_k-u) + \epsilon} \\
\hat{x} &= \frac{1}{\sigma}(x-u) \\
y &= \gamma \hat{x} + \beta
\end{align}
$$- \(u\) 为均值
- \(\sigma\) 为标准差
- \(\gamma\) 和 \(beta\) 是可以训练的参数
- \(\epsilon\) 是平滑因子, 防止分母为0
- BN,LN,IN三种不同的归一化方法, 对应的数据集 \(S\) 不同
- BN对同一批数据进行归一化, 不管其他神经元, 只针对某个神经元的Mini Batch个样本输出值做归一化
- LN对同一个样本的同一层输出进行归一化, 不依赖其他样本, 每次只依赖当前样本本身
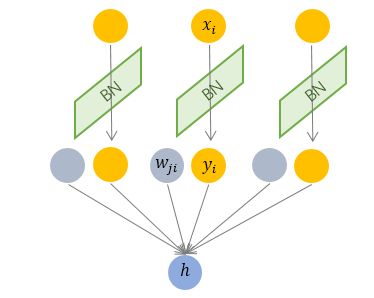
BN
Batch Normalization
对一批数据实行归一化
对某个具体的神经元的Mini Batch个样本输出做归一化, 与其他神经元的输出无关
代码:
1
2
3
4mu = np.mean(x,axis=0)
sigma2 = np.var(x,axis=0)
x_hat = (x-mu)/np.sqrt(sigma2+eps)
out = gamma*x_hat + beta特别说明:TensorFlow在BN训练过程中(trainable=True)使用的是当前批次的均值和方差归一化,同时将均值和方法以滑动平均的方式更新并存储下来。最终,在预估/推断(trainable=False)阶段,则直接使用滑动平均的结果
- 隐藏问题:当使用BN时,如果更新的轮次不够(训练global step太少),会导致均值和方差滑动平均的结果并未贴近真实的均值和方差,会导致训练时模型输出正常,预测时模型输出异常的情况,且这种问题比较隐晦,难以排查
- 解决方案:
- 当训练的轮次较少时,要注意动量不要设置太大,否则更新不足,此时设置小的动量可以缓解BN均值方差更新不足的问题(不建议使用这种方式,原因是:一般来说,动量太小会导致最终的均值方差仅被最近的Batch决定,模型效果波动大)
- 建议在使用BN时,设置较大的动量,且注意保证足够的训练轮次,充分更新动量和方法
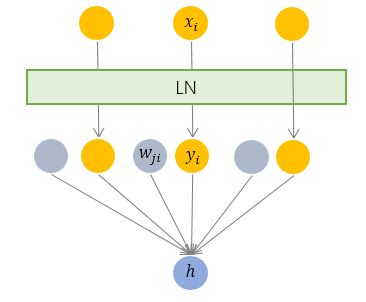
LN
Layer Normalization
- 对单个训练样本的同一层所有神经元的输入做归一化
- 与其他样本无关
BN的作用和说明
- Batch Normalization把网络每一层的输出Y固定在一个变化范围的作用
- BN都能显著提高训练速度
- BN可以解决梯度消失问题
- 归一化操作将每一层的输出从饱和区拉到了非饱和区(导数),从而解决了梯度消失问题
- 普通的优化器加上BN后效果堪比Adam
$$ ReLU + Adam \approx ReLU + SGD + BN$$ - 如果对于具有分布极不平衡的二分类测试任务, 不要使用BN
- BN一定程度上有归一化作用
- BN本身就能提高网络模型的泛化能力
- 使用BN后,不用太依赖Dropout, L2正则化等,可以将L2正则化的参数变小一点
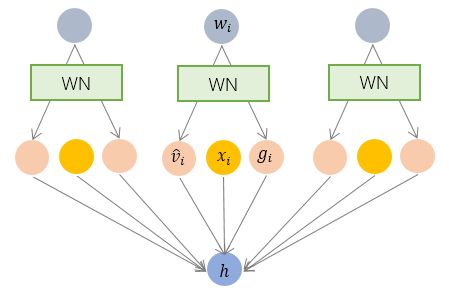
WN
Weight Normalization
- 对参数做归一化
- 与数据无关
总结
BN和WN对比
- BN是对对一个mini batch的数据在同一个神经元计算均值和方差
- WN对网络的网络权值 W 进行归一化(L2归一化)
BN和LN对比
- BN高度依赖于mini-batch的大小,实际使用中会对mini-Batch大小进行约束,不适合类似在线学习(mini-batch为1)情况;
- BN不适用于RNN网络中normalize操作:
- BN实际使用时需要计算并且保存某一层神经网络mini-batch的均值和方差等统计信息,对于对一个固定深度的前向神经网络(DNN,CNN)使用BN,很方便;
- 但对于RNN来说,sequence的长度是不一致的,换句话说RNN的深度不是固定的,不同的time-step需要保存不同的statics特征,可能存在一个特殊sequence比其的sequence长很多,这样training时,计算很麻烦
- 但LN可以有效解决上面这两个问题
- LN适用于LSTM的加速,但用于CNN加速时并没有取得比BN更好的效果