NLP——样本packing与权重讨论

整体总结

样本 packing 训练可以大幅提升模型训练速度
由此引发的训练样本的组织方式和 loss 权重有多种组合形式
本文对样本 packing 和 packing 后的样本权重（packing weight）相关的各种情况进行总结

packing 模式的一些结论

下面两个数据处理方式在算法理论层面不等价（特别是在 tool 等 prompt 很长，response 很短的场景）：
- 数据处理方案一：将多轮拆成多个单轮样本训练
- 数据处理方案二：保留多轮，即多轮本身是一个样本，但训练计算损失时每个轮次视作一个样本（即按照轮次处理 Loss 归一化）
上述两种训练方式不等价的原因包括：
- 样本训练时的分布不等价
- 样本训练时的权重不等价
多轮拆单轮/保留多轮的数据处理方式暂无法简单从算法层面实现等价
- 除非 GBS 无穷大，达到所有样本一次过完

非 packing 下的训练模式（与 packing 无关的朴素模式）

数据集内所有 token 权重相等训练模式

具体实现方式为：
$$
\begin{align}
\text{Loss}(\text{batch}) &= \sum_{\text{token}_i \in \text{batch}} \text{loss}_{\text{token}_i} \\
\text{Loss}(\text{batch}) &= \frac{1}{\text{GBS}} \sum_{\text{token}_i \in \text{batch}} \text{loss}_{\text{token}_i}
\end{align}
$$
- 每个 token 的 loss 直接累加，不做任何归一化或仅除以 Global Batch 内样本数 GBS（一般对同一次训练来说是固定值）
这种方式可以确保训练的整个过程中，所有 token 的权重都是相同的
可能会导致部分短序列得到的关注度不够高
预训练中就应该使用这种方式，每个 Token 是等权的

Global Batch 内部每个 token 权重相等训练模式（Global Batch 间的 token 权重可能不相等）

具体实现方式：
$$
\text{Loss}(\text{batch}) = \frac{1}{\text{GBS_Token_Num}} \sum_{\text{token}_i\in \text{batch}} \text{loss}_{\text{token}_i}
$$
- 每个 token 的 loss 累加，除以 Global Batch 内的 token 总数
这种方式可以确保同一个 Global Batch 内部的 token 权重相等
不同 Global Batch 内部的权重可能是不相同的，跟 Global Batch 内部的 token 总数有关
学习率相同的情况下，不同 Global Batch 对模型训练的贡献相等
当 Global Batch Size 非常大时，这个实现方式几乎等价于 数据集所有 token 权重相等训练模式

样本内部每个 token 权重相等训练模式（样本间的 token 权重可能不相等）

具体实现方式：
$$
\begin{align}
\text{Loss}(\text{batch}) &= \sum_{\text{sample} \in \text{batch}} \frac{1}{|\text{sample}|} \sum_{\text{token}_i \in \text{sample}}\text{loss}_{\text{token}_i} \\
\text{Loss}(\text{batch}) &= \frac{1}{\text{GBS}} \sum_{\text{sample} \in \text{batch}} \frac{1}{|\text{sample}|} \sum_{\text{token}_i \in \text{sample}} \text{loss}_{\text{token}_i}
\end{align}
$$
- 每个 token 的 loss 累加，除以样本内的 token 总数，同时样本间不做任何归一化或除以 Global Batch 内样本数 GBS
这种情况下可以防止长序列样本权重过高，让不同样本对训练的影响权重相同
长序列样本中的 Token 可能因为平均后权重过低而学不好
很多框架实现中的目标就是实现这样的方式，想要保证样本粒度的 Loss 贡献相同

样本 packing 下的训练模式

数据集内所有 token 权重相等训练模式

具体实现方式：
$$
\begin{align}
\text{Loss}(\text{batch}) &= \sum_{\text{token}_i \in \text{batch}} \text{loss}_{\text{token}_i} \\
\text{Loss}(\text{batch}) &= \frac{1}{\text{GBS}} \sum_{\text{token}_i \in \text{batch}} \text{loss}_{\text{token}_i}
\end{align}
$$
- 每个 token 的 loss 直接累加，不做任何归一化或除以 Global Batch 内样本数 GBS（一般对同一次训练来说是固定值）
这种方式下，与非 packing 的训练方式相同
注：如果想要与非 packing 情况下的 数据集内所有 token 权重相等训练模式 完全等价，自回归下 Attention 时需要对前面的样本做 mask 才可以
预训练中就应该使用这种方式

Global Batch 内部每个 token 权重相等训练模式（Global Batch 间的 token 权重可能不相等）

具体实现方式：
$$\text{Loss}(\text{batch}) = \frac{1}{\text{GBS_Token_Num}} \sum_{\text{token}_i\in \text{batch}} \text{loss}_{\text{token}_i}$$
- 每个 token 的 loss 累加，除以 Global Batch 内的 token 总数
此时已经是 packing 以后的样本，但理论上仍然与非 packing 下的训练方式相同
注：如果想要完全等价于非 packing 模式下的 Global Batch 内部每个 token 权重相等训练模式 ，自回归下 Attention 时需要对前面的样本做 mask 才可以

packing 样本内部每个 token 权重相等训练模式（样本间的 token 权重可能不相等）

具体实现方式：
$$
\begin{align}
\text{Loss}(\text{batch}) &= \sum_{\text{sample} \in \text{batch}} \frac{1}{|\text{sample}|} \sum_{\text{token}_i \in \text{sample}}\text{loss}_{\text{token}_i} \\
\text{Loss}(\text{batch}) &= \frac{1}{\text{GBS}} \sum_{\text{sample} \in \text{batch}} \frac{1}{|\text{sample}|} \sum_{\text{token}_i \in \text{sample}} \text{loss}_{\text{token}_i}
\end{align}
$$
- 每个 token 的 loss 累加，除以样本内的 token 总数，同时样本间不做任何归一化或除以 Global Batch 内样本数 GBS
这种情况下由于短序列样本被 packing 为固定长度的样本，所以与非 packing 下的样本内部平均完全不同 ，无法做到每个样本贡献度一致了（长样本占优）

真实样本内部每个 token 权重相等训练模式

每个 token 的 loss 累加，除以真实样本（需要特殊手段去识别）内的 token 总数，同时有归一化有三种实现方式：
方式一：样本间不做任何归一化
$$
\text{Loss}(\text{batch}) = \sum_{\color{red}{\text{sample}_{true}} \in \text{batch}} \frac{1}{|\color{red}{\text{sample}_{true}}|} \sum_{\text{token}_i \in \color{red}{\text{sample}_{true}}}\text{loss}_{\text{token}_i}
$$
方式二：除以 Global Batch 内样本数 GBS
$$
\text{Loss}(\text{batch}) = \frac{1}{\text{GBS}} \sum_{\color{red}{\text{sample}_{true}} \in \text{batch}} \frac{1}{|\color{red}{\text{sample}_{true}}|} \sum_{\text{token}_i \in \color{red}{\text{sample}_{true}}} \text{loss}_{\text{token}_i}
$$
方式三：除以 Global Batch 内真实样本数 GBS_true
$$
\text{Loss}(\text{batch}) = \frac{1}{\color{red}{\text{GBS_true}}} \sum_{\color{red}{\text{sample}_{true}} \in \text{batch}} \frac{1}{|\color{red}{\text{sample}_{true}}|} \sum_{\text{token}_i \in \color{red}{\text{sample}_{true}}} \text{loss}_{\text{token}_i}
$$
特别注意，此时除以 GBS 和除以 GBS_true 是不同的，为了保证真实样本间的权重一致，应该除以 GBS_true

多轮场景的训练思考

有时候想要将多轮中的每一轮单独看做一个样本（即一次回复一个样本）
- 这种思路的基础逻辑是认为一次回复就应该是一个样本
- 实际上，评估指标中，可能涉及多轮回复只对应一个分数，即多轮回复对整体评估的贡献跟单轮回复权重一样，这时候要注意训练指标和评估指标的一致性问题
多轮场景下，即使不做样本 packing，也相当于隐含的存在样本 packing 了，如果想要做到轮次间权重一致，可以参考 真实样本内部每个 token 权重相等训练模式 的实现，这种实现方式可以分为两种：
方式一：将多轮拆成多个样本，labels 仅保留最后一个回复，再使用用样本平均的方式实现
- 注：这种拆开的方式会引入一些特别的变化，且是不可恢复的
  - 这种拆开会导致重复计算一些 prompt ，且会将同一个多轮样本分散到不同的 Batch 上学习，是不可恢复的
  - 这种拆开还会导致 拆单轮 情况 vs 不拆单轮 情况的单个 Batch 内数量和分布不一致，导致一些差异，也是不可恢复的
    - 这里的影响应该还好，主要强调的是不可恢复性
- 总结：拆开的方式虽然方便，但与合并训练的方式相比，无论如何也无法恢复到真实水平
方式二：不管是否 packing，都将单个轮次识别为当个真实样本做归一化和学习
- 此时不管是否 packing，都可以做到轮次即样本，两者基本等价

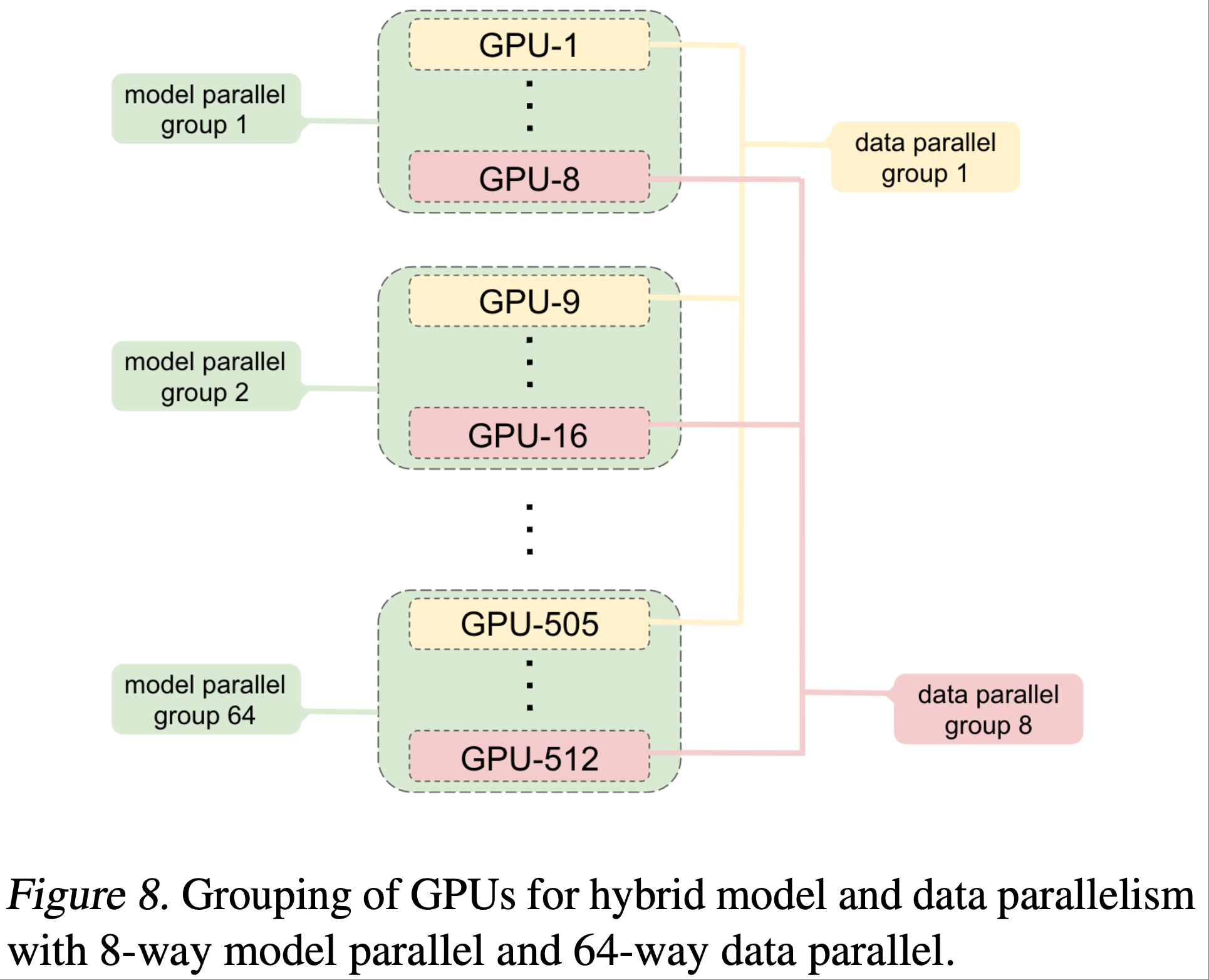
在 DP 不为 1 的情况思考

在 DP 不为 1 的情况下，每个 DP 内部是独立计算梯度的，所以需要先做归一化

NLP——LoRA-Without-Regret

注：本文包含 AI 辅助创作

参考链接：
- 原始博客：LoRA Without Regret, 20250929, Thinking Machines

Blog Summary

本文是 Thinking Machines 发布的一篇博客，核心是研究 LoRA 在 LLM 中的作用以及的各超参的详细影响
本文包含非常详细的实验细节，讨论了各种 LoRA 相关超参数（学习率和 Rank 等）设置技巧，是一篇非常实在的技术博客，值得深读

Introduction

如今主流的语言模型（Language Model）包含超过一万亿（1T）个参数，这些模型在数十万亿个 Token 上进行预训练
基础模型（Base Model）的性能随着规模的扩大而不断提升，因为这万亿级别的参数对于学习和表征人类书面知识中的所有模式至关重要
In contrast， Post-Traning 使用的数据集规模更小，且通常聚焦于更狭窄的知识领域和行为范围
- 用万亿比特（Terabit）级别的权重来表征来自十亿比特（Gigabit）或百万比特（Megabit）级训练数据的更新，似乎存在资源浪费
- 这种直觉推动了参数高效微调（Parameter-Efficient Fine-Tuning, PEFT）技术的发展，该技术通过更新一组规模小得多的参数来调整大型网络
目前主流的参数高效微调方法是 LoRA（Low-Rank Adaptation）
- LoRA 将原始模型中的每个权重矩阵 $ W $ 替换为经过修改的版本 $ W’ = W + \gamma BA $，其中矩阵 $ B $ 和 $ A $ 加起来的参数数量远少于 $ W $，而 $ \gamma $ 是一个常数缩放因子
- 实际上，LoRA 为微调所带来的更新创建了一个低维表征
LoRA 在 Post-Traning 的成本和速度方面可能具有优势，此外，从操作角度来看，相比全参数微调（Full Fine-Tuning，以下简称 FullFT），选择 LoRA 还有几个理由：
- 多租户服务（Multi-Tenant Serving） ：
  - 由于 LoRA 仅训练一个 Adapter （即矩阵 $ A $ 和 $ B $），同时保持原始权重不变，因此单个推理服务器可以在内存中存储多个 Adapter （不同的模型版本），并以批量方式同时从中采样
  - 现代推理引擎（如 vLLM 和 SGLang）已实现此功能（2023）
- 训练 Layout 大小（Layout Size for Training） ：
  - 对整个模型进行微调时，优化器状态需要与原始权重一起存储，且通常需要更高的精度
  - FullFT 通常比对同一模型进行采样所需的加速器数量多一个数量级，进而需要不同的 Layout (理解：这里的 Layout 应该是指显存？)
    - 注：在训练过程中，除了存储权重外，通常还需要存储所有权重的梯度和优化器动量；而且，这些变量的存储精度（float32）通常高于推理时权重的存储精度（bfloat16 或更低）
  - 由于 LoRA 训练的权重数量少得多，占用的内存也少得多，因此其训练所需的 Layout 仅比采样所需的 Layout 略大
  - 这使得训练更容易实现，且通常效率更高
- 加载与迁移便捷性（Ease of Loading and Transfer） ：
  - 由于需要存储的权重更少，LoRA Adapter 的设置速度更快、更便捷，也更容易在不同机器之间迁移
上述原因足以解释自 2021 年 LoRA 原始论文发表以来，该技术日益普及的现象（2021）
- 但现有文献中关于 LoRA 与 FullFT 性能对比的结论尚不明确
研究界普遍认为，在类似预训练的场景下，LoRA 性能表现较差（2024）
- 即当数据集规模极大，超出 LoRA 参数的存储限制时，LoRA 会处于劣势
但对于 Post-Traning 中常见的数据集规模，LoRA 具备足够的容量来存储关键信息
- 不过，这一事实并不能保证 LoRA 在样本效率和计算效率上的表现
核心问题在于：LoRA 是否能达到全参数微调的性能水平？如果可以，需要满足哪些条件？
论文实验发现，当正确把握几个关键细节时，LoRA 的样本效率确实与 FullFT 相同，并且能达到相同的最终性能

What Matters for LoRA（什么最关键？）

论文介绍了论文开展的一系列 SFT 和 RL 实验，旨在确定 LoRA 与 FullFT 效率匹配的条件
为此，论文的实验方法与以往关于 LoRA 的实验存在以下几点不同：
- 1）论文研究了训练集大小与 LoRA 参数数量之间的一般关系 ，而非聚焦于特定的数据集和任务
- 2）在监督学习中，论文测量的是对数损失（Log Loss） ，而非采用基于采样的评估方法（Sampling-Based Evals），这样做同样是为了保证结论的通用性
  - 对数损失测量能在不同训练步骤和训练参数范围内，提供清晰的结果和缩放定律（Scaling Laws）
论文的研究发现如下：
- 在中小型指令微调（Instruction-Tuning）和推理数据集（Reasoning Dataset）上进行 SFT 时，LoRA 的性能与全参数微调相同
- 当数据集规模超出 LoRA 的容量时，LoRA 性能会低于 FullFT
  - 此时，LoRA 并非会达到一个无法突破的损失下限（Distinct Floor）
  - 而是其训练效率会下降 ，且下降程度取决于模型容量与数据集大小之间的关系
  - 理解：这里的意思是训练慢，但是多训练一段时间，也能达到不错的效果
- 在某些场景下，LoRA 对大批量大小（Large Batch Size）的容忍度低于 FullFT（当批量大小超过某个阈值后，LoRA 的损失 penalty 会更大）
  * 增加 LoRA 的 Rank 无法缓解这种 penalty ，这是矩阵乘积参数化（Product-of-Matrices Parametrization）的固有属性，该参数化方式的 Training Dynamics 与优化原始权重矩阵的 Training Dynamics 不同
  - 注：Training Dynamics 指的是训练过程中模型的各种属性随时间或迭代轮数的变化情况，包括但不限于损失函数值、准确率、模型参数的更新、梯度的分布等属性
  - 问题：这里的意思是 Batch Size 太大，不适合 LoRA?
- 即使在小数据场景下，将 LoRA 应用于所有权重矩阵（尤其是 MLP 和 MoE 层）时，其性能也会更优
  - 仅将 LoRA 应用于注意力层（Attention-Only LoRA）的性能较差，即便通过提高 Rank 来匹配可训练参数的数量，结果依然如此
- 在强化学习中 ，即使使用较小的 Rank ，LoRA 的性能也能与 FullFT 相当
  - 论文发现强化学习所需的容量非常低 ，这一结果与论文基于信息论的推断一致
论文还研究了 LoRA 超参数对其学习率（相对于 FullFT 学习率）的影响
- 论文分析了初始缩放（Init Scales）、乘数（Multipliers）等超参数的一些不变性，并解释了为何 $ \frac{1}{r} $ 预因子能使最优学习率（LR）大致独立于 Rank
- 论文还通过实验展示了 LoRA 的最优学习率与 FullFT 最优学习率之间的关系
论文的实验结果明确了“低遗憾区间（Low-Regret Regime）”的特征
- 在该区间内，LoRA 在数据集大小和参数数量方面的性能与 FullFT 相近
- 论文发现该区间涵盖了大多数 Post-Traning 场景，这为在众多应用中使用高效微调技术开辟了道路

Methods and Results

论文设计实验的目的是，在不同条件下详细测量 LoRA 相对于 FullFT 的性能。以下是实验设置的一些细节：
- 论文将 LoRA 的 Rank 在三个数量级范围内变化（ Rank 的取值为 1 到 512），并将这些不同 Rank 的 LoRA 与全参数微调进行对比
- 为了排除因使用非最优学习率可能带来的干扰，论文针对每个实验条件都进行了学习率扫描（LR Sweep）
  - 论文采用恒定学习率调度（Constant Learning Rate Schedule），不进行预热（Warmup）或冷却（Cooldown）
- 实验使用的模型为 Llama 3 系列模型（2024）和 Qwen3 模型（2025），其中包括一个 MoE 模型
- 主要的监督学习实验使用了 Tulu3（2024）和 OpenThoughts3（2025）数据集，分别聚焦于指令遵循（Instruction Following）和推理任务
  - 这两个数据集在范围、结构和应用场景上存在显著差异，这有助于验证论文结果的通用性
- 强化学习实验使用数学推理任务，以答案的正确性作为奖励（Reward）

LoRA Rank

论文在 Tulu3 数据集和 OpenThoughts3 数据集的一个子集上进行了单轮训练（Single Epoch）
针对每个数据集和模型大小，论文都对 LoRA 的 Rank 和学习率进行了扫描
在下图中，每条彩色线条代表一个特定的 Rank ，线条是通过在每个训练步骤中取所有学习率对应的最小点得到的：
论文观察到，FullFT 和高 Rank LoRA 具有相似的训练曲线，损失随训练步骤对数的增加而线性下降
- 当训练步骤达到某个与 Rank 相关的阈值时，中低 Rank LoRA 会偏离最小损失训练曲线
- 从直觉上看，当 Adapter 达到容量上限时，学习速度会减慢，而容量上限由 Rank 决定
接下来，论文绘制了损失随学习率变化的曲线，以验证论文的扫描是否覆盖了每个 Rank 对应的最优学习率
- 理解：LoRA 比 FullFT 需要更大的最优学习率
论文发现，FullFT 的最优学习率比高 Rank LoRA 的最优学习率低一个数量级（即 1/10）（2024）
- 论文将在后面讨论 LoRA 超参数时再次提及这一点
所有不同 Rank 的 LoRA 运行对应的最优学习率似乎相近（论文将在下文从理论角度解释这一发现）
- 不过，最优学习率确实存在一定的 Rank 依赖性（Rank 为 1 时的最优学习率低于更高 Rank LoRA 的最优学习率）
- 在 Rank 为 4 到 512 的范围内，最优学习率的变化因子小于 2

Batch Size Effects

论文发现，在某些设置下，LoRA 对大批量大小的容忍度低于 FullFT
随着批量大小的增加，两者的性能差距会扩大，且这种差距与 Rank 无关
在接下来的实验中，论文使用了 OpenThoughts3 数据集中一个包含 10,000 个样本的小子集
图 3 中的左图显示
- 在大批量大小时，LoRA（虚线）与 FullFT（实线）的训练曲线之间存在持续的差距
- 而在批量大小为 32（较小批量）时，这种差距更小，且会随着训练的进行而缩小
- 问题：左图是不是少了些其他的曲线？
右图展示了最终损失随批量大小变化的情况
- 随着批量大小的增加，LoRA 与 FullFT 之间的损失差距越来越大
大批量下的性能差距似乎与 Rank 无关，而是 LoRA 的固有属性
- 其可能原因是，在该数据集上，矩阵乘积参数化（$ BA $）的优化 Dynamics 不如全矩阵（$ W $）的优化 Dynamics 有利
- 不过，LoRA 和 FullFT 在较小批量大小时都能达到最佳损失，因此在实际应用中，这种差距可能不会产生太大影响
问题：为什么 Batch Size 对最终结果的影响这么大，是因为 Batch Size 和学习率没有对应调优吧！
- 理解：理论上，Batch Size 对于训练不应该有那么大的差异才是

Layers Where LoRA Is Applied（LoRA 应用的层）

论文研究了将 LoRA 应用于网络中不同层所产生的影响
Hu 等人的原始论文建议仅将 LoRA 应用于注意力矩阵（Attention Matrix），此后许多论文也遵循了这一做法
- 但最近的趋势是将 LoRA 应用于所有层
与论文的结果类似，QLoRA 论文也发现，仅将 LoRA 应用于注意力层的性能低于应用于 MLP 层或同时应用于 MLP 层与注意力层的性能
- 不过该论文发现“MLP 层+注意力层 > MLP 层 > 注意力层”，而论文发现 MLP 层+注意力层 和 MLP 层 的性能大致相当
- 事实上，当论文将 LoRA 应用于所有层（尤其是 MLP 层，包括 MoE 层）时，取得了好得多的结果
- 实际上，将 LoRA 应用于注意力矩阵，相比仅将其应用于 MLP 层，并没有带来额外的收益（2024）
  - 理解：虽然加入注意力层没有带来额外收益，博客最终还是使用了所有层都微调，其实有些矛盾
仅应用于注意力层的 LoRA 性能较差，并非因为参数数量少
- 在特定案例中， Rank 为 256 的仅注意力层 LoRA，其参数数量与 Rank 为 128 的仅 MLP 层 LoRA 大致相同，但前者的性能却低于后者（可对比下表中的粗体数字）
  
  LoRA Configuration Params
  
  mlp, rank=256 0.49B
  
  attn, rank=256 0.25B
  
  all, rank=256 0.70B
  
  mlp, rank=128 0.24B
在 MoE 实验中，论文为每个专家（Expert）训练了一个单独的 LoRA，每个 LoRA 的 Rank 等于总 Rank 除以活跃专家（Active Expert）的数量（Qwen3 MoE 模型的活跃专家数量为 8）
- 这种缩放方式使得 MoE 层中 LoRA 参数与 FullFT 参数的比例，与其他层中两者的比例保持一致
- 理解：这可以保证最终激活的 Rank 数是一致的
论文还在另外两个场景中进行了类似实验，比较不同 LoRA 应用层的效果：
- （1）在 OpenThoughts3 数据集的一个小子集上进行 Rank 为 256 的监督学习；
- （2）在 MATH 数据集上进行强化学习
- 论文将在下一节描述实验设置
在这些场景中，仅注意力层的 LoRA 性能依然低于仅 MLP 层的 LoRA（后者与“MLP 层+注意力层”的 LoRA 性能相近）

LoRA Configuration	Params
mlp, rank=256	0.49B
attn, rank=256	0.25B
all, rank=256	0.70B
mlp, rank=128	0.24B

RL

论文的实验得出一个关键发现：在使用策略梯度算法（Policy Gradient Algorithm）进行强化学习时，即使 LoRA 的 Rank 低至 1，其学习性能也能完全匹配 FullFT
在这些实验中，论文使用了一种带有重要性采样校正（Importance Sampling Correction）的基础策略梯度算法，其目标函数为（2024）：
$$ \text{objective} = \sum_t \frac{p_{\text{learner} } }{p_{\text{sampler} } } Adv_t $$
论文采用了类似 GRPO 的中心化方案（2024），即针对每个问题采样多个补全结果（Completion），并减去每组的平均奖励
下图（图 6）展示了在 MATH（2021）和 GSM（2021）数据集上的学习率扫描结果，每个数据集都使用了典型的超参数
- 论文使用 Llama-3.1-8B 基础模型进行实验，因为正如 Qwen 技术报告（2024）所描述的，Qwen2.5 和 Qwen3 模型的预训练数据已提升了其数学性能，这会使得论文难以衡量仅在强化学习阶段学到的内容
- LoRA 具有更广泛的有效学习率范围，并且能达到与 FullFT（黑线）相同的峰值性能，至少在强化学习的噪声所允许的精度范围内是如此
这一结果与信息论的推断一致（注意：下面是重点，需要重点理解）
- 监督学习每个样本（Episode）可提供约 $ O(\text{ Token 数量}) $ 比特的信息
- 在策略梯度方法中，学习由优势函数（Advantage Function）驱动 ，每个样本仅能提供 $ O(1) $ 比特的信息
- 当每个样本包含数千个 Token 时，强化学习在训练过程中每 Token 吸收的信息约为监督学习的 1/1000
我们可以根据实验数据给出更精确的数值
- 在 MATH 数据集的实验中，论文在约 10,000 个问题上进行训练，每个问题采样 32 次
- 假设每个补全结果提供 1 比特信息，那么整个训练过程仅需吸收 320,000 比特信息
- Llama-3.1-8B 模型的 Rank 为 1 的 LoRA 已有 300 万个参数（论文通过对模型中所有权重矩阵求和 $ \text{rank}\cdot d_{\text{in} } $（矩阵 $ A $ 的参数数量）和 $ \text{rank} \cdot d_{\text{out} } $（矩阵 $ B $ 的参数数量）计算得出），几乎是所需信息比特数的 10 倍
  - 问题：信息和信息比特数可以直接比较吗？
- 即便 Rank 为 1，LoRA 也拥有足够的容量来吸收训练过程中提供的所有信息
作为另一个对比案例，DeepSeek-R1-Zero 模型在 5.3M 个样本上进行了训练（训练共进行 10,400 步，每步包含 32 个独特问题，每个问题采样 16 次），这对应着 5.3M 比特的信息
- 这一数量少于低 Rank LoRA 的参数数量，因此论文预测，使用 LoRA 也能复现该模型的训练结果
为了进一步验证 LoRA 在推理强化学习中有效性的发现，论文使用 Qwen3-8b-base 模型在 DeepMath 数据集（2025）上进行了更大规模的实验
- DeepMath 数据集比 MATH 数据集大得多，且通常包含更难的问题
- 为了加快实验速度，论文将训练和评估的样本长度限制为 8192 个 Token
- 这个长度足以支持回溯（Backtracking）和推理过程，但与更长的思维链（Chain-of-Thought）相比，会限制模型性能
论文观察到，当为每种设置选择最优学习率后，不同大小的 LoRA 和 FullFT 的训练过程几乎完全一致
- 此外，在预留的 AIME 2024 和 AIME 2025 测试集上评估模型时，论文也得到了类似的结果
- 而且，论文发现 LoRA 和 FullFT 的训练过程表现出相似的定性行为：
  - 两者都发展出了先进的推理能力，如回溯、自我验证（Self-Verification）和上下文内探索（In-Context Exploration），这一点可以从模型思维链长度的增加中看出

Setting LoRA Hyperparameters

LoRA 应用的一个障碍是需要选择最优超参数，而这些超参数与为 FullFT 优化的超参数不同
在本节中，论文将说明这个问题并不像最初看起来那么棘手，并讨论论文在超参数选择方面的发现

Optimal Learning Rate and Rank

参照 Hu 等人的研究，论文采用以下参数化方式表示 LoRA：
$$ W’ = W + \frac{\alpha}{r} BA $$
- 其中，$ r $ 是 LoRA 的 Rank
- $ \alpha $ 是 LoRA 的缩放因子（论文遵循其他实现的标准做法，设置 $ \alpha = 32 $）
- $ A $ 和 $ B $ 是 LoRA 的权重矩阵（ Rank 为 $ r $）
$ \frac{1}{r} $ 缩放因子使得最优学习率大致独立于 Rank
- 事实上，存在一个更强的条件：训练初期的学习曲线完全相同，与 Rank 无关
- 这一现象非常显著，在实验中，不同 Rank 的学习曲线如此接近，以至于论文曾担心是程序漏洞导致 Rank 参数未被正确使用
- 由此可见，在短期训练中，最优学习率也与 Rank 无关
- 然而，正如论文在之前的学习率-损失图（图 2）中所展示的，在长期训练中，最优学习率会表现出一定的 Rank 依赖性
我们可以通过分析训练首次更新后 LoRA 矩阵的预期更新来部分解释这一结果（注：即解释 $ \frac{1}{r} $ 缩放因子使得最优学习率大致独立于 Rank 这个事实）
- 我们可以将 LoRA 矩阵乘积 $ BA $ 表示为 $ r $ 个 Rank-1 外积的和：
  $$ BA = \sum_{i=1}^r b_i a_i^T = \sum_{i=1}^r \Delta_i $$
  - 其中论文定义 $ \Delta_i = b_i a_i^T $
  - 这里，所有 $ i $ 对应的 $ \frac{\partial \text{Loss}}{\partial \Delta_i} $ 都是相同的；
  - 但梯度 $ \frac{\partial \text{Loss}}{\partial b_i} $ 和 $ \frac{\partial \text{Loss}}{\partial a_i} $ 会依赖于初始化（例如，$ \frac{\partial \text{Loss}}{\partial b_i} $ 依赖于 $ a_i $）
  - 由于 $ a_i $ 和 $ b_i $ 的初始化与 Rank 无关，因此所有 $ i $ 对应的 $ \mathbb{E}[\Delta_i] $ 都是相同的，且与 Rank 无关
  - 在训练的第一步，每个外积项的预期更新是相等的，且与 Rank 无关
  - 由此可知，$ (\frac{1}{r}) \sum_{i=1}^r \Delta_i $ 本质上是 $ r $ 个具有相同期望的项的样本均值，因此该均值的期望（即 Adapter $ (\frac{1}{r})BA $ 的变化量）与 Rank 无关

Parametrization Invariances（参数化不变性）

LoRA 可能涉及四个超参数：
- 1）缩放因子 $ \alpha $（出现在 $ \alpha/r $ 中）
- 2）下投影矩阵 $ A $ 的学习率 $ LR_A $
- 3）上投影矩阵 $ B $ 的学习率 $ LR_B $
- 4）矩阵 $ A $ 的初始化缩放 $ \text{init}_A $
  - 对于随机初始化，这是 $ A $ 初始元素的标准差
  - 矩阵 $ B $ 初始化为零，因此无需定义 $ \text{init}_B $
调整这四个参数似乎难度较大，但 Training Dynamics 的不变性意味着其中两个参数是冗余的，学习行为仅由两个参数决定
- 问题：如何理解这里的 Training Dynamics 的不变性
论文通过以下分析说明这种不变性：
在使用 Adam 优化器且 $ \varepsilon = 0 $ 时（我们可以将此结果扩展到 $ \varepsilon > 0 $ 的情况；此时需要将 $ \varepsilon $ 按 $ 1/q $ 缩放，因为梯度会按该因子缩放），优化过程在以下两参数变换下保持不变
- 对于 $ p, q > 0 $，满足：
  - $ \alpha \rightarrow \frac{1}{pq} \cdot \alpha $
  - $ \text{init}_A \rightarrow p \cdot \text{init}_A $
  - $ LR_A \rightarrow p \cdot LR_A $
  - $ LR_B \rightarrow q \cdot LR_B $
由于四个参数中的两个自由度不影响学习过程，因此实际需要调整的参数空间为二维
我们可以为这个二维空间选择不同的基，例如以下具有直观解释的基：
- 1）$ \alpha \cdot \text{init}_A \cdot LR_B $：
  - 该参数决定初始更新的规模，或者说学习曲线的初始斜率
  - 由于 $ B $ 初始化为零，$ LR_A $ 和 $ A $ 的初始更新在此阶段无关紧要
- 2）$ \text{init}_A / LR_A $：
  - 由于 Adam 优化器每步对 $ A $ 元素的更新量约为 $ LR_A $，因此这个时间尺度参数决定了 $ A $ 从初始状态发生显著变化所需的步数
我们可以用这个基来重新解释以往关于 LoRA 的一些研究提案：
- LoRA+（2024）提出对 $ A $ 和 $ B $ 使用不同的学习率，且 $ B $ 的学习率更高。用上述基表示，提高 $ LR_B $ 等价于提高 $ \text{init}_A / LR_A $，从而使 $ A $ 的变化时间尺度更长
- Unsloth 的 LoRA 超参数指南建议对高 Rank LoRA 使用更大的 $ \alpha $ 值（例如，避免 $ \frac{1}{r} $ 缩放）
  - 这也等价于提高 $ \text{init}_A / LR_A $
  - 当论文提高 $ \alpha $ 时，需要相应降低 $ LR_A $ 和 $ LR_B $ 以保持更新规模不变，这反过来会使 $ LR_A $ 相对于 $ \text{init}_A $ 更小
在论文的实验中，论文采用了 Hugging Face PEFT 库（2022）中 Hu 等人提出的标准参数化方式：
- $ A $ 采用均匀分布初始化（缩放因子为 $ 1/\sqrt{d_{\text{in} } } $）
- $ B $ 初始化为零，$ A $ 和 $ B $ 使用相同的学习率，且 $ \alpha = 32 $
- 在实验中，论文未能找到比这些超参数更优的设置

Optimal Learning Rates for LoRA vs. FullFT（最优学习率对比）

论文的实验表明，无论是在监督学习还是强化学习中，LoRA 的最优学习率始终是同一应用场景下 FullFT 最优学习率的 10 倍
- 这一规律在所有以性能（损失或奖励）为纵轴、学习率为横轴的 U 型图中都能体现
- 这一发现应能简化从 FullFT 到 LoRA 的学习率超参数迁移过程
目前，论文尚未对这一现象做出充分的理论解释
- 论文尝试从“LoRA 最优学习率与 Rank 无关”和“满 Rank LoRA 可直接与 FullFT 对比”这两个事实出发推导该结果，但分析得出的学习率比例为“模型隐藏层大小除以 $ 2 \cdot \alpha $”，这与“最优比例固定为 10（与基础模型无关）”的实验结果不符
在实证分析中，论文在 Tulu3 数据集上对 14 个不同的 Llama 和 Qwen 模型进行了 LoRA 和 FullFT 的学习率扫描
- 基于这些扫描结果，论文拟合了一个函数，该函数可根据模型的隐藏层大小和模型类型（Llama 或 Qwen）预测最优学习率。所用函数形式如下：
  $$ LR = M_{\text{LoRA} } \cdot \left( \frac{2000}{\text{hidden size} } \right)^{\text{model pow} + \text{LoRA pow} } $$
  - 其中：
    - $ M_{\text{LoRA} } $ 是使用 LoRA 时的乘数（使用 FullFT 时为 1）
    - $ \text{model pow} $ 是针对不同模型来源（Llama 和 Qwen）分别计算的指数调整项
    - $ \text{LoRA pow} $ 是针对 LoRA 的额外指数调整项
    - $ \text{hidden size} $ 是模型残差流（Residual Stream）的维度
论文通过线性插值基于扫描数据预测损失，以此对预测的学习率进行评分，并通过对 14 个模型的预测损失求和来评估参数
优化结果显示：
- LoRA 相对于 FullFT 的乘数为 9.8；
- Qwen3 和 Llama 模型对隐藏层大小的依赖不同，但 LoRA 学习率对隐藏层大小的依赖与 FullFT 相同（即优化结果显示 $ \text{LoRA pow} = 0 $）

Learning Rates in Short and Long Runs

LoRA 的典型初始化会导致有效学习率产生一个隐含的变化过程，这使得短期训练和长期训练存在差异，且学习曲线的形状与 FullFT 也有所不同
在训练初期，$ B $ 初始化为零
- 当 $ B $ 非常小时，$ A $ 的变化对 Adapter $ BA $（将被添加到原始网络权重中）的影响可忽略不计
- 随着 $ B $ 逐渐增大，$ A $ 的更新对网络输出的影响开始变大
  - 当 $ B $ 的规模接近 $ A $ 时，有效学习率会在训练过程中逐渐提高
- 论文发现，在 Tulu3 和 OpenThoughts 数据集上完成完整训练后，$ B $ 矩阵的谱范数（Spectral Norm）最终会大于 $ A $ 矩阵的谱范数
这意味着，对于短期训练，应设置更高的最优学习率
- 初步证据表明，短期训练（根据经验，约 100 步以内）的最优乘数约为 FullFT 的 15 倍 ，而对于长期训练，该乘数会收敛到前文提到的 10 倍

Discussion

除了实证结果外，论文还希望探讨与 LoRA 性能和适用性相关的更广泛问题，这些问题对研究人员和工程实践者都具有参考价值
首先，论文深入分析核心结论，LoRA 与 FullFT 性能相近的两个条件：
- 1）LoRA 应用于网络的所有层，尤其是参数占比最高的 MLP/MoE 层
- 2）LoRA 未受容量限制，即可训练参数数量超过待学习信息的总量（可根据数据集大小估算）
当条件（1）满足时，训练初期 LoRA 的学习 Dynamics 与 FullFT 相似；
然后，在条件（2）的保障下，LoRA 会继续保持与 FullFT 相近的性能，直到达到容量限制

Why LoRA Might Be Needed on All Layers（Why LoRA 需要应用在所有层上）

正如论文之前所展示的，若仅将 LoRA 应用于注意力层，即使在小数据场景下，学习速度也会变慢
一种可能的解释来自对经验神经正切核（Empirical Neural Tangent Kernel, eNTK）的分析（该核可用于近似少量微调时的模型行为（2022））
- eNTK 基于梯度的点积，具体而言，梯度：
  $$ g_i = \partial/\partial \theta \log p(\text{token}_i \mid \text{prefix}_i) $$
- 且 $ K(i,j) = g_i \cdot g_j $
- 因此，参数数量最多的层通常对核的影响最大
该论文还指出，当对所有层进行训练时，LoRA 的 eNTK 与 FullFT 的 eNTK 大致相同，因此:
$$\text{LoRA training} \approx \text{eNTK(LoRA)}\approx \text{eNTK(FullFT)} \approx \text{FullFT} $$
- 而 “$\text{eNTK(LoRA)}\approx \text{eNTK(FullFT)}$” 这一近似关系仅在将 LoRA 应用于“构成梯度点积的主要参数所在层”时成立

How Much Capacity Is Needed by Supervised and Reinforcement Learning?

监督学习与强化学习需要多少容量？
- 注：这里指参数容量
以往的研究（2024）表明，神经网络每个参数可存储 2 比特信息
- 但该结果针对的是长期训练极限下模型可吸收的最大信息量，而非计算效率或学习速度
“每个参数 2 比特”的结论基于精心构建的合成数据集（这些数据集包含精确的信息量）
- 对于现实学习任务，估算所需的信息量则更为复杂
一个经典结论是：
- 在最小化对数损失时，首轮训练的总对数损失可用于衡量数据集的描述长度，即记忆该数据集所需比特数的上限
- LLM 数据集的损失通常约为每 Token 1 比特（0.69 纳特），具体数值因数据集和模型大小而异
  
  One classic observation is that when minimizing log-loss, the total log-loss measured during the first epoch of training provides a measurement of the dataset’s description length. That is, an upper bound for the number of bits required to memorize the dataset
该估算值衡量的是“完美记忆数据集”所需的容量，而这一数值高估了“降低测试集对数损失”的泛化学习所需的实际容量
目前，监督学习的容量需求及其与可训练参数数量的关系仍是有待未来研究的开放问题
对于强化学习，作者认为，由于每个样本的末尾仅有一个奖励值，策略梯度算法每个样本大致仅学习 1 比特信息
- 但这并非强化学习的固有属性，其他算法可能从每个样本中学习更多信息
- 例如，基于模型的强化学习（Model-Based RL）算法会训练智能体预测观测结果并构建世界模型（World Model），从而可能从每个样本中提取更多信息
- “每个样本 1 比特”的结论可能仅适用于策略梯度算法
- 注：这里每个样本仅 1 比特的理论不敢苟同，因为强化学习的信号也可以不止是 0-1 信号，可以是 Reward 啊，此时就不再是 1 比特能够表达的了吧？
我们可以从信息论角度更精确地阐述比特计数论证
- 考虑一个样本（包含轨迹 $ \tau $ 和最终奖励）作为一条消息（即一个噪声信道），该消息包含关于未知奖励函数 $ R $ 的部分信息
- 论文基于当前策略和训练历史，分析策略梯度估计量与 $ R $ 之间的互信息
- REINFORCE 算法的更新公式为
  $$ G = S \cdot \text{Adv} $$
  - 其中 $ S = \nabla \log p_\theta(\tau) $
- 在给定历史的情况下，$ S $ 与 $ R $ 无关，因此唯一依赖 $ R $ 的部分是标量优势函数（Advantage）
根据数据处理不等式：
$$ I(G; R \mid \text{history}) \leq I((S, \text{Adv}); R \mid \text{history}) = I(\text{Adv}; R \mid S, \text{history}) \leq H(\text{Adv}) $$
若将优势函数量化为 $ B $ 个区间，则 $ H(\text{Adv}) \lesssim \log(B) $
- 即每个样本可获取的有效信息比特数为 $ O(1) $，与模型大小无关
- 这些比特信息告诉论文，当前面对的是离散奖励函数集合（或等效的最优策略类别集合）中的哪一个
- 这种互信息分析与一些优化算法的理论分析方法一致（2009）
需要注意的是，该估算值是训练可吸收信息量的上限，实际学习到的信息量会依赖于策略初始化和其他细节
- 例如，若初始化的策略无法获得任何奖励，则优势函数的熵为 0（而非 $ \log(B) $），模型无法学习到任何内容

Compute Efficiency Advantage of LoRA

上述实验通过训练步数衡量学习进度，但论文也关注不同方法的计算效率
论文计算得出，LoRA 每轮前向-反向传播所需的浮点运算数（FLOPs）略多于 FullFT 的 2/3
- 因此，总体而言，LoRA 的计算效率通常会优于 FullFT
论文通过分析给定权重矩阵上“前向-反向传播”操作的 FLOPs 来推导这一 2/3 比例，这些操作占据了神经网络模型中绝大部分的 FLOPs。论文使用以下符号：
- $ W \in \mathbb{R}^{N \times N} $：权重矩阵
- $ x \in \mathbb{R}^N $：输入向量
- $ y = Wx \in \mathbb{R}^N $：输出向量
- $ \bar{x}, \bar{y} \in \mathbb{R}^N $：损失分别对 $ x $ 和 $ y $ 的梯度（在反向传播中计算）
- $ \bar{W} \in \mathbb{R}^{N \times N} $：损失对 $ W $ 的梯度
全参数微调（FullFT）执行以下操作：
- 1）前向传播（Forward）
  - $ y = Wx $（需 $ N^2 $ 次乘加运算）
- 2）反向传播（Backward）
  - $ \bar{x} = W^T \bar{y} $（需 $ N^2 $ 次乘加运算）
  - $ \bar{W} += x \bar{y}^T $（需 $ N^2 $ 次乘加运算）
- 前向传播需 $ N^2 $ 次乘加运算，反向传播需额外 $ 2 \cdot N^2 $ 次乘加运算，总计 $ 3N^2 $ 次
  - 因此，包含前向和反向传播的训练过程，其 FLOPs 是仅前向推理的 3 倍
在 LoRA 中，论文将 $ W $ 替换为 $ W + BA $，其中 $ B \in \mathbb{R}^{N \times R} $、$ A \in \mathbb{R}^{R \times N} $，且 $ R \ll N $
- 由于论文仅更新 $ \bar{A} $ 和 $ \bar{B} $，因此无需执行 FullFT 中“更新 $ \bar{W} $”的第三步，而是替换为代价低得多的操作
- $ A $ 和 $ B $ 均为 $ N \cdot R $ 规模的矩阵，因此各自的“前向-反向传播”完整计算需 $ 3NR $ 次乘加运算，而非 FullFT 中 $ W $ 所需的 $ 3N^2 $ 次；两者合计需 $ 6NR $ 次乘加运算
- 同时，论文仍需对 $ Wx $ 和 $ \bar{x} $ 执行前向-反向传播（等效于 FullFT 的前两步）
- 因此，LoRA 总乘加运算次数为 $ 2N^2 + 6NR $
- 由于 $ R \ll N $，该数值略多于 FullFT 总运算量（$ 3N^2 $）的 2/3
若论文以 FLOPs（而非训练步数）为横轴绘制 LoRA 性能曲线（本分析未包含注意力机制的 FLOPs，在长上下文场景中，注意力 FLOPs 可能占比显著），LoRA 相对于 FullFT 的优势将更为明显

Open Questions

关于论文的研究结果，仍有几个问题有待未来探索：
- 1）细化 LoRA 性能预测 ：论文已大致描述了 LoRA 与 FullFT 性能相当的区间，并能通过 Token 或样本数量估算所需容量，但尚未能做出精确预测
  - 未来需进一步明确 LoRA 性能的预测方法及与 FullFT 匹配的具体条件
- 2）LoRA 学习率与 Training Dynamics 的理论解释 ：目前论文对 LoRA 学习率和 Training Dynamics 的理论理解仍有限
  - 若能建立完整理论解释 LoRA 与 FullFT 学习率的比例关系，将具有重要价值
- 3）LoRA 变体的性能评估 ：如 PiSSA（2024）等 LoRA 变体，若采用论文方法评估，其性能表现如何？
- 4）MoE 层的 LoRA 应用方案 ：将 LoRA 应用于 MoE 层有多种可选方案
  - 未来需研究不同方案的性能，以及每种方案与“张量并行”“专家并行”等大型 MoE 模型关键技术的兼容性

Closing Thoughts

在 Thinking Machines，作者相信微调技术能提升人工智能在多个专业领域的实用性
论文对 LoRA 的关注，源于让这种技术“广泛可及”并“易于定制以满足特定需求”的目标
除实际应用价值外，LoRA 研究还促使论文深入探索模型容量、数据集复杂度和样本效率等基础问题
通过分析“学习速度与性能如何依赖容量”，论文获得了研究机器学习基础问题的新视角
论文期待未来能进一步推进这一领域的研究

NLP——GShard

注：本文包含 AI 辅助创作

参考链接：
- 专家并行论文：GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding, 2020, Google

Paper Summary

评价：
- 本文是 2020 年的文章，是非常重要的 Scaling 方向的作品，对模型规模的扩展意义重大
- 核心思路：
  - 条件计算（Conditional Computation）：采用了稀疏门控混合专家（Sparsely-Gated MoE）架构
  - 自动分片（Automatic Sharding）：通过轻量级标注 API（replicate/split/shard）和 XLA 编译器扩展，实现张量的自动分布式划分
  - SPMD 编译优化：提出单程序多数据（SPMD）编译范式（替代传统多程序多数据（MPMD）模式），为所有设备生成单一程序，编译时间与设备数量无关
- Google 出品，必属精品
GShard 是一个由一组轻量级标注接口（API）和 XLA 编译器扩展组成的模块
- Gshard 提供了一种简洁的方式，只需对现有模型代码进行少量修改，就能实现多种并行计算模式
- Gshard 解决了神经网络扩展过程中的计算成本、编程便捷性以及在并行设备上的高效实现等问题
作者使用 GShard 将带有稀疏门控混合专家层的多语言神经机器翻译 Transformer 模型扩展到了 600B 参数以上（应该是当时第一次有这么大的模型）
论文的实验表明：
- 这样一个巨型模型能够在 2048 个 TPU v3 加速器上高效训练 4 天，在 100 种语言到英语的翻译任务中，取得了远超现有技术水平的翻译质量

Introduction and Discussion

在各类机器学习问题中，神经网络扩展都带来了显著的质量提升
- 在计算机视觉领域，提升模型容量使得多种计算机视觉架构在图像分类和检测精度上有了更好的表现
- 在自然语言处理领域，Transformer 模型的扩展在语言理解任务（2018, 2019）、跨语言下游迁移任务（2018, 2019）以及（大规模）多语言神经机器翻译任务（2019）中都实现了稳定的性能提升
这种普遍趋势促使近期研究开始深入探究影响扩展成功的关键因素（2017, 2019, 2020），其中包括过往研究发现的训练数据量、模型大小和计算资源利用率等
尽管研究发现最终模型质量与数据量、计算资源和模型大小呈幂律关系（2017, 2020），但更大模型带来的显著质量提升也伴随着各种实际挑战
训练效率便是其中至关重要的挑战之一，论文将其定义为：为获得优于现有最佳系统的模型质量所消耗的计算资源和训练时间 ，而这一指标往往被忽视
图1：
- 多语言翻译质量（与双语基线模型相比的平均 $\delta$ BLEU 值）随着混合专家（MoE）模型规模增长到 600B 参数而不断提升，而端到端训练成本（以 TPU v3 核心年为单位）仅呈亚线性增长
- 将模型规模从 37.5B 参数扩大到 600B 参数（16 倍），计算成本仅从 6 个核心年增加到 22 个核心年（3.6倍）
- 达到最佳翻译质量的 600B 参数模型，使用 2048 个 TPU v3 核心训练了 4 天，总成本为 22 个 TPU v3 核心年
- 相比之下，训练所有 100 个双语基线模型则需要 29 个 TPU v3 核心年
- 论文训练的最佳质量密集型单一 Transformer 模型（2.3B 参数）， $\delta$ BLEU 值为 6.1，该模型使用 GPipe（2019）在 2048 个 TPU v3 核心上训练了 6 周，总成本达 235.5 个 TPU v3 核心年

Practical Challenges for Scaling（扩展面临的实际挑战）

本节将列举在训练超大规模模型时面临的主要实际挑战，这类模型的规模远超单个加速器内存（如 GPU 或 TPU）的容量限制
特定架构的模型并行支持问题 ：在 TensorFlow（2016）和 PyTorch（2017）等常用深度学习框架中，缺乏对高效模型并行算法的支持
- 框架虽支持基于图分割的简单模型并行，但由于网络的顺序依赖性和基于梯度的优化方式，这种并行方式会导致设备利用率严重不足
- 为了高效扩展现有模型，用户通常需要投入大量工程工作，例如将模型代码迁移到专门的框架中（2018, 2019）
计算成本与模型规模的超线性扩展问题 ：通过增加网络深度或宽度来直接扩展模型规模（2018, 2019），通常会导致训练步长时间至少呈线性增长
- 为解决这一问题，通常需要通过在多个设备间分割层权重和计算过程来实现模型并行，但这会带来网络通信开销和设备利用率不足的问题
- 设备利用率不足源于神经网络底层计算任务分配不均衡以及存在顺序依赖关系
- 这种计算成本与模型规模之间的超线性关系，无法通过简单增加设备数量来解决，使得训练超大规模模型变得不切实际
巨型模型表示的基础设施扩展性问题 ：对于分布在数千个设备上的超大规模模型，简单的图表示可能会成为深度学习框架及其优化编译器的瓶颈
- 例如，通过操作间分割（inter-op partitioning）增加 D 倍的层数，或通过操作内分割（intra-op partitioning）在 D 个设备上增加模型维度，都可能导致图节点数量大幅增加
- 设备间的通信通道可能会进一步使图大小增加（例如，分割聚合或转置操作时）
- 对于超大规模模型而言，图大小的这种增长会导致图构建和编译时间达到无法实现的程度
实现分片策略的复杂工作 ：将模型高效地分割到多个设备上运行具有挑战性，因为这需要协调设备间的通信
- 在图级分割方面，需要复杂的算法（2019, 2018）来减少因不同设备上分配的图分割部分之间存在顺序依赖而引入的开销
- 在算子级并行方面，不同分割后的算子会有不同的通信模式，这取决于算子的语义，例如是否需要累积部分结果或重新排列数据分片
- 根据论文的经验，由于 TensorFlow 等框架包含大量具有特殊语义的算子，在模型中手动处理这些问题需要耗费大量精力
- 在所有情况下，实现模型分片对研究人员和工程师来说都是一项负担，因为改变模型架构就需要修改底层的设备通信逻辑，从而产生连锁反应

Design Principles for Efficient Training at Scale

论文展示了如何通过构建一个拥有 600B 参数、带有稀疏门控混合专家层（Sparsely-Gated Mixture-of-Experts layers）的 sequence-to-sequence Transformer 模型，来克服上述挑战
- 该模型的计算成本呈亚线性增长，编译时间为 $O(1)$
- 论文在 2048 个 TPU v3 设备上，针对多语言机器翻译任务训练该模型 4 天，最终实现了单个非集成模型在 100 种语言到英语翻译任务中远超现有技术的翻译质量
- 论文对不同规模的模型进行了实验，结果发现，随着模型规模增大，翻译质量不断提升，而训练总耗时（wall-time）相对于模型规模仅呈亚线性增长，如图1所示
为构建如此庞大的模型，论文做出了以下关键设计选择
- 亚线性扩展（Sub-linear Scaling） ：首先，模型架构的设计应确保计算和通信需求相对于模型容量呈亚线性增长
  - 条件计算（2015, 2019, 2020, 2020）通过在每个输入样本的基础上激活一个子网络，使论文能够兼顾训练和推理效率
  - 通过在基于循环神经网络（RNN）的机器翻译和语言模型中添加位置感知稀疏门控混合专家层（Position-wise Sparsely Gated Mixture-of-Experts, MoE）（2019），可以在实现最先进性能的同时，使计算成本呈亚线性增长
  - 因此，论文将在第2节中详细介绍如何用混合专家层扩展 Transformer 架构
- 抽象的力量（The Power of Abstraction） ：其次，模型描述应与分片实现和优化相分离
  - 这种关注点分离使模型开发人员能够专注于网络架构，并灵活地改变分片策略，而底层系统则负责执行语义保持转换并实现高效的并行执行
  - 为此，论文提出了 GShard 模块，用户只需在模型中对少数关键张量标注分片策略即可
  - 该模块包含一组简单的标注接口，以及一个用于自动并行化的 XLA（2019）编译器扩展
  - 模型开发人员可以像在一个拥有超大内存和计算能力的单一设备上编写模型，编译器会根据标注信息和自身的启发式算法，自动为目标设备分割计算任务
  - 论文将在3.2节中提供更多标注示例
- 可扩展编译器（Scalable Compilers） ：第三，包括计算表示和编译在内的系统基础设施，必须能够支持数千个设备的并行执行
  - 例如，图2 展示了在 4 个设备上分割点积运算（用颜色编码）的两种不同方式
  - 需要注意的是，图2a 中常用的 MPMD（多程序多数据，Multiple Program Multiple Data）方法在扩展性方面面临挑战
    - 因为图中的节点数量会随着设备数量的增加而线性增长
  - 相反，论文开发了一种用于 SPMD（单程序多数据，Single Program Multiple Data）转换的编译器技术
    - 该技术生成一个可在所有设备上运行的单一程序，使得编译时间与设备数量无关，保持恒定，如图2b所示
    - 论文将在3.3节中详细讨论 SPMD 框架
论文其余部分的结构如下：
- 第2节详细描述带有稀疏门控混合专家层的 Transformer 架构；
- 第3节介绍论文开发的 GShard 模块；
- 第4节展示混合专家模型在100个语言对的多语言机器翻译任务中的应用；
- 第5节对实现的性能和内存使用情况进行评估；
- 第6节讨论相关工作
图2：
- 在4个设备上对点积算子（ $[M, K] \times [K, N] = [M, N]$ ）进行 MPMD 分片与论文提出的 SPMD 分片的对比
- 在该示例中，两个操作数均沿收缩维度 K 进行分片，每个设备计算本地结果后，通过 AllReduce 操作进行全局合并
- MPMD 分片会为每个设备生成独立的算子，限制了其扩展性；
- 而 SPMD 分片则生成一个可在所有设备上运行的程序
- 需要注意的是，使用论文提出的 SPMD 分片时，编译时间与所使用的设备数量无关

Model

Sparse scaling of the Transformer architecture

Transformer架构（2017）已被广泛应用于自然语言处理领域，成为许多 sequence-to-sequence 任务（如机器翻译）的事实标准
Transformer 包含两个计算模块，即 Encoder 和 Decoder，两者均通过堆叠多个 Transformer 层实现
Transformer Encoder 层由两个连续的层组成，即自注意力层（self-attention layer）之后紧跟一个位置感知前馈层（position-wise feed-forward layer）
Decoder 则额外增加了第三个交叉注意力层（cross-attention layer），该层会关注 Encoder 的输出
论文通过条件计算（conditional computation）对 Transformer 进行稀疏扩展，在 Encoder 和 Decoder 中，每隔一个前馈层就用一个位置感知混合专家层（Position-wise Mixture of Experts, MoE）（2019）替代，该混合专家层采用了一种改进的 top-2 门控机制（图3）
论文通过改变 Transformer 层的数量和每个混合专家层中专家的数量来调整模型容量
每个训练样本由一对子词 Token（subword tokens）序列组成
在训练和推理过程中，每个 Token 都会激活混合专家 Transformer 的一个子网络
子网络的大小大致与每个混合专家层中的专家数量无关，这使得计算成本能够像前一节所述的那样呈亚线性增长
3.1节将进一步分析计算复杂度，5节将分析训练性能

Position-wise Mixture-of-Experts Layer

论文模型中使用的混合专家（MoE）层基于文献（2019）的设计，并在稀疏门控函数和辅助损失函数方面进行了改进
Transformer 的混合专家层由 E 个前馈网络（FFN）组成，其计算过程如下：

$$ g_{s,e} = \text{GATE}(x_s) \quad \tag{1} $$

$$ \text{FFN}_e(x_s) = w o_e \cdot \text{ReLU}(w i_e \cdot x_s) \quad \tag{2} $$

$$ y_s = \sum_{e=1}^{E} g_{s,e} \cdot \text{FFN}_e(x_s) $$

其中：
- $x_s$ 是混合专家层的输入 Token
- $w i_e$ 和 $w o_e$ 分别是前馈层（即一个专家）的输入投影矩阵和输出投影矩阵
- 向量 $g_{s,e}$ 由门控网络计算得到
- $g_{s,e}$ 中每个专家对应一个非负值，其中大部分值为零，这意味着该 Token 不会被分配给对应的专家
  - 每个 Token 仅被分配给极少数专家，论文设定每个 Token 最多被分配给两个专家
- $g_{s,e}$ 中对应的值非零，表示该专家对最终网络输出的贡献程度
- 每个专家 $\text{FFN}_e$ 都采用含 ReLU 激活函数（2010）的两层全连接网络对 $x_s$ 进行处理
- 混合专家层的输出 $y_s$ 是所有被选中专家输出的加权平均值
门控函数 $\text{GATE}(\cdot)$ 是混合专家层的核心，它采用 softmax 激活函数来表示每个专家在处理输入 Token 时的权重，即表示某个专家处理该输入 Token 的适合程度
此外，门控函数必须满足以下两个目标：
- 负载均衡（Balanced load） ：对于给定的 Token ，混合专家层最好能稀疏地激活专家
  - 一种简单的方案是根据 softmax 概率分布选择前k个专家，但研究表明这种方法会导致训练中的负载不均衡问题（2019）：训练过程中看到的大多数 Token 会被分配给少数几个专家，导致这几个（繁忙的）专家的输入缓存变得极大，而其他专家则处于未充分训练的状态，从而减慢训练速度
    - 问题：分配给少数专家也不一定会导致训练速度变慢吧，除非有 EP （专家并行）？
  - 同时，许多其他专家根本无法得到充分训练
  - 因此，门控函数需要设计得更合理，以实现所有专家间处理负载的更均匀分配
- 大规模下的效率（Efficiency at scale） ：如果门控函数采用顺序执行方式，实现负载均衡相对容易
  - 但对于输入批次中所有 N 个 Token 和 E 个专家 ，仅门控函数的计算成本就至少为 $O(N \cdot E)$
  - 在论文的研究中，N 达到数百万量级，E达到数千量级，若门控函数采用顺序实现，会导致大部分计算资源在大部分时间处于空闲状态
  - 因此，论文需要一种高效的并行门控函数实现方式，以充分利用多个设备的计算能力
为满足上述要求，论文在门控函数 $\text{GATE}(\cdot)$ 中设计了以下机制（细节如算法1所示）：
- 专家容量限制（Expert capacity） ：为确保负载均衡，论文强制每个专家处理的 Token 数量不超过某个统一的阈值，论文将该阈值定义为专家容量
  - 假设一个训练批次中的 Token 总数为 N，每个 Token 最多被分配给两个专家，那么专家容量设置为 $\frac{2N}{E}$
  - 门控函数 $\text{GATE}(\cdot)$ 会为每个专家维护一个计数器 $c_e$ ，用于记录分配给该专家的 Token 数量
  - 当一个 Token 选中的两个专家都已超过其容量限制时，该 Token 被视为溢出 Token ，此时 $g_{s,e}$ 退化为零向量
  - 这类 Token 的表示会通过残差连接传递到下一层
    - 问题：这里是说专家容量限制也传递到下一层？
- 本地组分配（Local group dispatching） ：
  - 门控函数 $\text{GATE}(\cdot)$ 将训练批次中的所有 Token 均匀划分为 G 个组，即每个组包含 $S = \frac{N}{G}$ 个 Token ，所有组独立并行处理
  - 每个组被分配到每个专家的部分容量为 $\frac{2N}{G \cdot E}$
  - 每个组会确保分配给每个专家的 Token 数量不超过该部分容量
  - 通过这种方式，既能保证专家容量限制得到遵守，又能实现整体负载均衡
- 辅助损失（Auxiliary loss） ：门控函数不应总是选择相同的几个专家，否则会导致仅少数专家出现容量溢出，而其余专家利用率不足（这一点至关重要）
  - 借鉴文献（2019）的方法，论文定义了一个辅助损失项来强制执行这一约束
  - 该辅助损失项以一个常数系数 k 添加到模型的总损失函数中
  - 算法1第13行中辅助损失项的具体形式基于以下考虑：
    - $\frac{c_e}{S}$ 表示分配给每个专家的输入 Token 比例，作者希望最小化 $\frac{c_e}{S}$ 的均方值
    - 但由于 $c_e$ 是通过 top-2 操作得到的，不具有可微性，因此论文使用每个专家的平均门控值作为可微近似，并用 $m_e \cdot \frac{c_e}{S}$ 替代 $(\frac{c_e}{S})^2$ ，这样就可以通过梯度下降法对其进行优化
- 随机路由（Random routing） ：
  - 直观上，由于 $y_s$ 是所选专家输出的加权平均值，如果第二个专家的权重非常小，我们可以直接忽略该专家 ，以节省整体专家容量
  - 因此，除了遵守专家容量约束外，门控函数 $\text{GATE}(\cdot)$ 还会以与第二个最佳专家权重 $g_2$ 成比例的概率，将 Token 分配给该专家

Highly Parallel Implementation using GShard（高度并行化）

本节将介绍第2节中模型在张量处理单元（TPU）设备集群上的高效运行实现方案
实现的第一步是将模型用线性代数运算表示，因为论文的软件栈（TensorFlow（2016））和硬件平台（TPU）在这类运算上经过了高度定制和优化
- 与原始 Transformer 模型类似，将模型的大部分部分用线性代数运算编写非常容易
- 但由于混合专家层（MoE Layer），尤其是算法1 中提出的 $\text{GATE}(\cdot)$ 函数具有顺序执行特性，要用线性代数运算表示该层则需要额外付出努力，论文将在3.1节详细介绍相关细节
接下来，论文对线性代数计算进行标注，以体现并行性
通过3.2节中的分片接口（sharding APIs），可以对计算中的每个张量进行标注，指定其在设备集群中是采用复制（replication）还是分布（distribution）方式存储
分片标注能够实现模型描述与高效并行实现的关注点分离，让用户可以灵活地表达各种并行化策略；例如：
- （1）注意力层（attention layer）通过沿批次维度（batch dimension）分割并将权重复制到所有设备上来实现并行化；
- （2）由于混合专家层中专家（expert）的规模极大，无法在所有设备上进行复制，因此唯一可行的策略是将专家分片存储到多个设备中
- 此外，整个模型会在这两种模式（1）-（2）之间切换
- 通过标注，模型开发人员无需关注系统优化工作，也不必将并行实现细节和底层细节融入模型代码中
最后，编译器基础设施会接收（部分）标注后的线性代数计算，并生成可在数千个设备上高效运行的并行程序
如3.3节所述，编译器会应用单程序多数据（SPMD，Single Program Multiple Data）分片转换来表示每个设备的计算任务，插入必要的跨设备通信操作，处理非规则模式（如非均匀分片），最终生成一个可在所有设备上启动并执行并行计算的单一程序

Positions-wise Mixture-of-Expert Layer Expressed in Linear Algebra（线性代数）

论文的模型实现（算法2）将整个加速器集群视为一个单一设备，并用少量与集群具体配置无关的张量运算来表示其核心数学算法
- 爱因斯坦求和符号（Einstein summation notation）（1923）（即tf.einsum）是一种能够简洁表示模型的强大工具，论文在实现中大量使用了该符号
- softmax 门控计算可以通过一个爱因斯坦求和运算（einsum）后紧跟 softmax 函数来轻松表示；
- 将输入分配给选定专家的操作，可以通过分配掩码（dispatching mask）与输入之间的单次爱因斯坦求和运算来表示；
- 所有 $\text{FFN}_e$ 的权重被组合成单个三维张量 $wi$ 和 $wo$
- $\text{FFN}_1 \dots \text{FFN}_E$ 的计算则通过三个算子（两个爱因斯坦求和运算和一个relu运算）来表示；
- 最后，对所有专家输出进行加权平均以得到最终输出的操作，也可以通过另一个爱因斯坦求和运算来表示
算法2中的 Top2Gating 计算了算法1中所有组本地（group-local）门控决策的并集
- combine_weights是一个四维张量，形状为[G, S, E, C]
- 其中，combine_weights[g, s, e, c] 非零时，表示组 g 中的输入 Token s被发送到专家 e 的输入缓存中，且位于缓存位置 c
- 对于特定的 g 和 s，combine_weight 切片中最多包含两个非零值
- 通过将所有非零值设为 1，可由 combine_weights 生成二进制分配掩码（binary dispatch_mask）
论文需要合理选择组数（G）和专家数量（E），以确保该算法能够在包含D个设备的集群上实现扩展
- 有必要分析在一个包含 N 个 Token 的训练批次中，该算法在一个训练步骤内的整体计算复杂度（浮点运算总数）

算法2 ：位置感知混合专家层的前向传播（Forward pass of the Positions-wise MoE layer），下划线字母（如G和E）表示张量将沿该维度进行分片

1: gates = softmax(einsum("GSM, ME -> GSE", inputs, wg))
2: combine_weights, dispatch_mask = Top2Gating(gates)
3: dispatched_expert_inputs = einsum("GSEC, GSM -> EGCM", dispatch_mask, reshaped_inputs)
4: h = einsum("EGCM, EMH -> EGCH", dispatched_expert_inputs, wi)
5: h = relu(h)
6: expert_outputs = einsum("EGCH, EHM -> GECM", h, wo)
7: outputs = einsum("GSEC, GECM -> GSM", combine_weights, expert_outputs)

在分析算法2的计算复杂度随设备数量D的扩展情况时，论文做出以下假设：
- a）每个设备上的 Token 数量 $\frac{N}{D}=O(1)$ (在实际应用中，为避免设备内存溢出，这一假设通常是必要的)，且保持恒定；
- b） $G=O(D)$ 、 $S=O(1)$ ；
- c） $H=O(1)$ ；
- d） $E=O(D)$ ；
- e） $C=O(\frac{2S}{E})=O(\frac{1}{D})$ ，且 $D< S$ ，D 为正整数

算法2中的浮点运算总数计算如下：
$$
\begin{align}
\text{FLOPS}_{\text{Softmax} } + \text{FLOPS}_{\text{Top2Gating} } + \text{FLOPS}_{\text{Dispatch/Combine} } + \text{FLOPS}_{\text{FFN} } &= \\
O(G S M E) + O(G S E) + O(G S M E C) + O(G E C H) &= \\
O(D \cdot 1 \cdot 1 \cdot D) + O(D \cdot 1 \cdot D) + O(D \cdot 1 \cdot 1 \cdot D \cdot \frac{1}{D}) + O(D \cdot D \cdot \frac{1}{D} \cdot 1) &= \\
O(D^2) + O(D^2) + O(D) + O(D)
\end{align}
$$
- 因此，每个设备的浮点运算量为 $O(D)$
- 每个设备上 softmax 的计算复杂度 $\text{FLOPS}_{\text{Softmax} } / D = O(D)$ 与设备数量呈线性关系，但实际上，由于 $D< S$ ，该复杂度会被其他项主导，因此可将整体复杂度视为 $O(1)$ ，满足亚线性扩展的设计要求
- 5节通过实验验证了这一分析结果
除计算成本外，跨设备通信成本并非恒定，但如5节所述，当设备数量增加时，通信成本仅以 $O(\sqrt{D})$ 的温和速率增长

GShard Annotation API for Parallel Execution

由于算法1中张量的规模和计算需求极大，论文必须在多个设备上对该算法进行并行化处理
算法2中带下划线的字母展示了对每个张量进行分片的一种直接方案
GShard 中的分片接口允许论文对程序中的张量进行标注，选择性地指定其分片方式
这些信息会传递给编译器，以便编译器自动应用转换以实现并行执行
在论文的研究中，使用了 TensorFlow/Lingvo（2019）中的以下接口
- replicate(tensor)：对张量进行标注，使其在各个分片（partition）中复制，并返回标注后的张量。该接口通常用于模型中的非混合专家层（non-MoE layers），以实现权重复制
- split(tensor, split_dimension, num_partitions)：对张量进行标注，使其沿split_dimension维度进行分片，并返回标注后的张量。第i个分片会被放置在第i个设备上，且num_partitions（分片数量）不得超过系统中的设备数量
- shard(tensor, device_assignment)：是split()接口的泛化形式，支持对多个维度进行分片，并指定每个分片的放置位置。附录A.3对该接口进行了更详细的描述
需要注意的是，调用split或shard接口仅会添加标注，不会改变用户程序中张量的逻辑形状。用户仍可使用完整形状的张量进行操作，无需担心非均匀分片等问题
GShard 具有良好的通用性，其简单接口可同样应用于所有维度
根据具体应用场景，分片维度可以包括批次维度（数据并行）、特征维度、专家维度，甚至图像模型中的空间维度
此外，由于分片标注是基于每个张量单独进行的，模型的不同部分可以采用不同的分片方式
这种灵活性使论文能够对巨型混合专家层权重进行分片，并在混合专家层和非混合专家层之间切换分片模式，同时也支持论文未涉及的其他应用场景，例如对大型图像进行空间分片（2019）（附录A.4）

通过上述分片接口，可以将算法2中所示的分片策略表示如下：

输入张量沿第一个维度（组维度G）进行分片，门控权重张量（wg）采用复制方式存储

计算得到分配后的专家输入（dispatched expert inputs）后，应用split接口将分片维度从组维度（G）切换为专家维度（E）。其中，D为设备数量

1: # 沿组维度（G）对输入进行分片
2: inputs = split(inputs, 0, D)
3: # 复制门控权重
4: wg = replicate(wg)
5: gates = softmax(einsum("GSM, ME -> GSE", inputs, wg))
6: combine_weights, dispatch_mask = Top2Gating(gating_logits)
7: dispatched_expert_inputs = einsum("GSEC, GSM -> EGCM", dispatch_mask, reshaped_inputs)
8: # 沿专家维度（E）对分配后的输入进行分片
9: dispatched_expert_inputs = split(dispatched_expert_inputs, 0, D)
10: h = einsum("EGCM, EMH -> EGCH", dispatched_expert_inputs, wi)

Per-tensor sharding assignment

如上述示例所示，用户无需对程序中的每个张量都进行标注
通常只需对模型中的少数重要算子（如爱因斯坦求和算子）进行标注，编译器会通过自身的启发式算法推断出其余张量的分片方式
- 注：由于反向传播计算通常由前端框架自动生成，用户无法访问这些张量，因此编译器推断缺失的分片信息也非常重要
- 例如，由于输入张量沿组维度（G）进行分片，而权重张量采用复制方式存储，编译器会选择沿相同维度（组维度G）对爱因斯坦求和运算的输出进行分片（第5行）
- 类似地，由于输入分配的爱因斯坦求和运算（第7行）的两个输入均沿组维度（G）进行分片，因此输出的分片方式会被推断为沿组维度（G）进行分片，之后论文通过添加split标注将输出的分片维度切换为专家维度（E）
- 上述示例中的某些标注（如replicate(wg)）也可由编译器自动确定，但建议对计算的初始输入张量和最终输出张量进行标注
目前，编译器采用迭代数据流分析（iterative data-flow analysis），从用户标注的算子开始，将分片信息传播到其相邻算子（操作数和使用者）
- 该分析通过对齐相邻算子的分片决策，尽量减少重分片（resharding）的需求
- 虽然还可以采用整数规划或机器学习等其他方法，但改进自动分片分配并非论文的重点，论文将其留作未来的研究工作

Mixing manual and automatic sharding（手动分片与自动分片结合）

在常见情况下，通过分片标注实现自动分片通常已足够，但GShard也支持灵活地将手动分片算子与自动分片算子结合使用
这让用户能够更好地控制算子的分片方式，例如当用户掌握算子语义之外的运行时知识时
例如，XLA 和 TensorFlow 的 Gather 算子定义均未包含输入中不同范围的索引边界信息，但用户可能知道某个特定的 Gather 算子仅在每个分片内对数据进行重排
在这种情况下，用户只需缩小维度大小并执行本地 Gather 操作，即可轻松对该算子进行分片；
否则，编译器需要对索引范围采取保守处理，并添加不必要的通信开销
例如，算法2中使用独热矩阵（one-hot matrix）分配输入的爱因斯坦求和算子（第3行），也可以通过手动分片的 Gather 算子来实现，而模型的其余部分仍采用自动分片方式

以下伪代码展示了该应用场景

1: # 输入形状为[G, S, M]，split()不改变逻辑形状
2: input = split(input, 0, num_devices)
3: # s_indices形状为[E, G, C, 1]，值为输入中S维度的索引
4: s_indices = split(s_indices, 1, num_devices)
5: 
6: # 开始手动分片
7: # partitioned_input形状为[G/num_devices, S, M]
8: partitioned_input = auto_to_manual_spmd_partition(input)
9: # partitioned_s_indices形状为[E, G/num_devices, C, 1]
10: partitioned_s_indices = auto_to_manual_spmd_partition(s_indices)
11: # 在partitioned_input中拼接G维度的索引：在G维度上生成Iota张量
12: partitioned_gs_indices = concat(
13:     iota([E, G/num_devices, C, 1], 1), 
14:     partitioned_s_indices, 
15:     3
16: )
17: # partitioned_data形状为[E, G/num_devices, C, M]
18: partitioned_data = gather(partitioned_input, partitioned_gs_indices)
19: 
20: # 切换回自动分片
21: # data形状为[E, G, C, M]
22: data = manual_to_auto_spmd_partition(partitioned_data)
23: ...

The XLA SPMD Partitioner for GShard

本节将介绍基于分片标注自动对计算图进行分片的编译器基础设施
分片标注告知编译器每个张量应如何在设备间分布
SPMD（单程序多数据，Single Program Multiple Data）分片器（简称“分片器”）是编译器的一个组件，它将计算图转换为可在所有设备上并行执行的单一程序
- 注：另一种方案是MPMD（多程序多数据，Multiple Program Multiple Data），如图2所示，该方案的扩展性较差
这使得编译时间几乎与分片数量无关，从而支持论文将模型扩展到数千个分片⁴
论文在 XLA 编译器（2019）中实现了该分片器
TensorFlow、JAX、PyTorch 和 Julia 等多个前端框架已具备将其图表示转换为 XLA HLO 图的降级逻辑（lowering logic）
与 TensorFlow 等流行前端框架相比，XLA 的算子数量要少得多，这在不影响通用性的前提下降低了实现分片器的负担，因为现有前端的降级过程已实现了强大的表达能力
- 尽管论文在 XLA 中开发了该基础设施，但论文介绍的技术也可应用于其他机器学习框架的中间表示（如 ONNX（2019）、TVM Relay（2018）、Glow IR（2018））
XLA 将计算表示为数据流图（dataflow graph），其中节点表示算子，边表示在算子之间流动的张量
分片器的核心是对每个算子进行处理，根据输入和输出指定的分片方式，将全尺寸算子转换为分片尺寸算子
对计算进行分片时，会引入各种跨设备数据传输模式
为了在大规模场景下最大化性能，定义一组核心通信原语（communication primitive）并针对目标平台对其进行优化至关重要

Communication Primitives，通信原语

由于分片器强制所有设备运行相同的程序，通信模式也具有规律性，XLA 定义了一组集合算子（collective operator）来执行类似 MPI（2009）的通信操作
下面列出了论文在 SPMD 分片器中使用的常见通信原语
- CollectivePermute ：该算子指定一组源-目标设备对（source-destination pairs），源设备的输入数据会发送到对应的目标设备
  - 它主要用于两个场景：改变分片张量在各分片间的设备顺序，以及本节后续讨论的 Halo Exchange
- AllGather ：该算子按照指定顺序将所有参与设备的张量连接起来，用于将分片张量转换为复制张量
- AllReduce ：该算子对所有参与设备的输入执行按元素归约（如求和）操作，用于合并来自不同分片的部分归约中间张量
  - 在 TPU 设备网络中，当分片数量增加时，AllReduce 的成本保持恒定（5.2节）
  - 它也是一种在其他类型网络拓扑中具有高效实现的常用原语（2019）
- AllToAll ：该算子从逻辑上沿某个维度对每个参与设备的输入进行分割，然后将每个数据片段发送到不同的参与设备
  - 每个设备在接收来自其他设备的数据片段后，会将这些片段连接起来生成结果
  - AllToAll 用于将分片张量从一个维度重分片到另一个维度
  - 在 TPU 设备网络中，AllToAll 是实现此类重分片的高效方式，其成本随分片数量的增加呈亚线性增长（5.2节）

Per-Operator SPMD Partitioning

分片器的核心是根据指定的分片方式，对每个算子进行从全尺寸到分片尺寸的转换
虽然某些算子（如按元素算子）的分片支持非常简单，但论文将讨论需要跨分片通信的几种常见情况
一般情况下，存在一些重要的技术挑战，论文将在3.3.3节中介绍
为了使讨论与混合专家模型更相关，本节将重点关注爱因斯坦求和算子（Einsum）的分片，以展示几种通信模式
为简化讨论，此处假设所有张量均采用均匀分片方式，即待分片维度的大小是分片数量的整数倍

Einsum Case Study

爱因斯坦求和算子是实现混合专家模型的最关键算子
在 XLA HLO 中，它们被表示为点积（Dot）运算，其中每个操作数（左操作数 LHS 或右操作数 RHS）包含三种类型的维度：
- 批次维度（Batch dimensions） ：是易并行化维度（embarrassingly parallel dimensions）。所有左操作数、右操作数和输出都必须包含相同的批次维度集合，且输出中的每个元素仅依赖于左操作数和右操作数中对应的批次元素
- 收缩维度（Contracting dimensions） ：仅存在于操作数中。左操作数和右操作数必须包含相同的收缩维度集合，这些维度在输出中会被求和并压缩
- 非收缩维度（Non-contracting dimensions） ：也是并行维度，存在于某个操作数和输出中。左操作数和右操作数分别具有自己的非收缩维度集合，这些维度会被输出继承
分片传播（Sharding propagation）优先选择在左操作数、右操作数和输出的批次维度上采用相同的分片方式，因为这样可以避免任何跨分片通信
但在实际情况中，这并不总是可行的，以下三种情况需要跨分片通信：
- 1）重分片（Resharding） ：在论文构建的混合专家模型中，专家分配逻辑（算法2第3行）需要在爱因斯坦求和运算后切换分片维度。由于使用AllToAll可以高效实现重分片（5.2节），论文首先在本地执行爱因斯坦求和运算，然后将结果重分片到目标维度，如图4a所示
- 2）累积部分结果（Accumulating partial results） ：如果输入沿收缩维度进行分片，本地计算得到的结果只是部分结果，需要使用AllReduce将这些部分结果合并以生成最终结果，如图4b所示
- 3）循环切片（Slicing in a loop） ：在某些场景下，论文还实现了一种类似于Cannon算法（1969）的方法，以限制每个分片上张量的大小。例如，如果两个操作数均沿非收缩维度进行分片，由于操作数的非收缩维度不同，无法直接在本地执行爱因斯坦求和运算。复制其中一个操作数不会导致冗余计算，但需要确保被复制的操作数能够放入设备内存
  - 因此，如果操作数的规模过大，论文会保持两个操作数的分片状态，通过循环迭代计算结果的每个切片，并使用 CollectivePermute 来传输输入切片（图4c）
图4：带有跨设备通信的爱因斯坦求和算子分片示例：
- （a）分片爱因斯坦求和算子
  - 彩色字母（G和E）表示每个张量的分片维度
  - 分片器决定首先沿G维度执行批次并行爱因斯坦求和运算，然后将结果重分片到E维度。（注：图中省略了S和M维度）
- （b）在收缩维度上分片的简单爱因斯坦求和算子（矩阵乘法）
  - 每个分片计算部分结果，然后通过AllReduce合并得到完整结果
- （c）在循环中使用CollectivePermute的爱因斯坦求和算子（矩阵乘法）
  - 通过循环每次计算一个切片，整个过程中不会出现全尺寸张量

Supporting a Complete Set of Operators

为了使 SPMD 分片器能够支持完整的算子集合，且不对张量形状或算子配置施加额外限制，论文解决了若干额外挑战
这些挑战通常涉及分片间的非对称计算或通信模式，而由于单一程序需要对所有分片都具有通用性，这些模式在 SPMD 中尤其难以表达
论文不能简单地根据运行时设备ID在单一程序中创建多个分支，因为这会导致程序规模激增

Static shapes and uneven partitioning

XLA要求张量形状是静态的（注：中间表示中有限的动态性对于高效适配加速器通常是必要的）
然而，对计算进行分片时，由于维度大小可能无法被分片数量整除，并非所有分片的输入/输出形状都相同
在这种情况下，会将形状大小向上取整到分片数量的下一个整数倍，填充区域（padded region）中的数据可以是任意值
在计算算子时，为了保证正确性，可能需要在填充区域中填充已知值
- 例如，对 Reduce-Add 算子进行分片时，需要使用单位元0作为填充值
- 考虑一个示例：待分片维度大小为 15，无法被 2（分片数量）整除，因此分片1比所需大小多一列
- 论文生成一个范围为 [0, 8) 的 Iota 算子，加上分片偏移量（由分片 ID×8 计算得到），并与全尺寸偏移量（15）进行比较。根据比较得到的谓词值（predicate value），选择从操作数中取值或从 0 中取值，最终得到掩码操作数（masked operand）

Static operator configurations

XLA算子具有静态配置，例如卷积（Convolution）中定义的填充（padding）、步幅（stride）和扩张（dilation）
但不同分片可能不会使用相同的算子配置
- 例如，对于卷积算子，最左侧的分片会在其左侧应用填充，而最右侧的分片会在其右侧应用填充
- 在这种情况下，分片器可能会选择让某些分片生成略多于所需的数据，然后切分出无关部分
附录A.4讨论了卷积和类似算子的示例

Halo Exchange

某些算子具有一种通信模式，需要与相邻分片交换部分数据，论文称之为 Halo Exchange
论文使用 CollectivePermute 算子在分片间交换 Halo 数据
Halo Exchange 最典型的应用场景是对基于窗口的算子（如卷积、ReduceWindow）进行分片，因为相邻分片可能需要重叠的输入数据（图5a）
在实际应用中，由于窗口配置（扩张、步幅和填充）的复杂使用以及非均匀 Halo 大小，这些算子的 Halo Exchange 通常需要结合适当的填充、切片和掩码操作
- 论文在附录A.4中描述了各种场景
Halo Exchange 的另一个应用场景是改变形状大小的数据格式化算子（data formatting operator）
- 例如，经过 Slice 或 Pad 算子后，张量的形状会发生变化，分片间的边界也会随之改变
- 这需要论文重新对齐不同分片上的数据，而这可以通过 Halo Exchange 的形式来处理（图5b）
其他数据格式化算子（尽管在逻辑上不改变形状大小）也可能需要 Halo Exchange ，这主要是由于静态形状约束和非均匀分片
- 例如，Reverse 算子会反转张量中元素的顺序，但如果对其进行非均匀分片，需要在分片间移动数据，以确保填充在逻辑上位于结果张量的右侧
- 另一个示例是Reshape算子：
  - 考虑将形状为 [3, 2] 的张量重塑为 [6]，其中输入在第一个维度上采用2种非均匀分片方式（分片形状为 [2, 2]），输出也采用2种分片方式（分片形状为[3]）
  - 由于非均匀分片，输入中存在填充，但重塑后输出张量不再有填充；因此，需要采用与Slice类似的 Halo Exchange 方式（图5c）

Compiler optimizations

SPMD 分片器会创建各种数据格式化算子，以执行切片、填充、连接、掩码和 Halo Exchange 操作
为解决这一问题，论文利用了 XLA 在 TPU 上的融合能力（fusion capabilities），以及针对切片和填充的代码移动优化（code motion optimizations），在很大程度上隐藏了数据格式化的开销
因此，即使在大量使用掩码和填充的卷积网络中，运行时开销通常也可以忽略不计

Massively Multilingual, Massive Machine Translation, M4

待补充

Performance and Memory Consumption

待补充

NLP——Megatron-LM原始论文解读-第一篇

注：本文包含 AI 辅助创作

参考链接：
- 官网主页：Megatron Core User Guide
- GitHub开源地址：github.com/NVIDIA/Megatron-LM
- Megatron 系列目前公认的三篇核心论文如下，它们分别对应了张量并行、3D 并行 与 序列并行/激活重计算优化 三大阶段：
- 第一篇：Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism, arXiv 2019, NVIDIA
  - 核心贡献：提出 张量并行（Tensor Parallelism） ，将 Transformer 的 Attention 头与 FFN 权重按列/按行切分，实现层内模型并行，首次在 GPU 集群上训练出 8.3 B 参数的 GPT-2 模型
- 第二篇：Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM, SC 2021, NVIDIA
  - 核心贡献：提出 3D 并行（数据 + 张量 + 流水线），并给出 interleaved 1F1B 流水线调度，显著降低流水线气泡；在 3072 块 A100 上训练出 530 B 参数的 GPT-3 级模型，GPU 利用率达到 76 %
- 第三篇：Reducing Activation Recomputation in Large Transformer Models, MLSys 2023, NVIDIA
  - 核心贡献：提出 序列并行（Sequence Parallelism） 与 选择性激活重计算 ，将激活显存占用再降 3–5 倍，支持更长序列与更大批训练；与 Flash-Attention 思想互补，现已成为 Megatron-Core 默认配置
- 以上三篇即社区常说的“Megatron 三篇论文”，覆盖了从单层切分、多层多维并行到显存优化的完整技术路线，本文介绍第一篇论文

Paper Summary

整体总结：
- 本文是 Megatron-LM原始论文解读-第一篇
- 论文的核心贡献：提出 张量并行（Tensor Parallelism） ，将 Transformer 的 Attention 头与 FFN 权重按列/按行切分，实现层内模型并行，首次在 GPU 集群上训练出 8.3 B 参数的 GPT-2 模型
- 论文通过对现有 PyTorch Transformer 实现仅进行少量修改来实现模型并行，成功突破了传统的单 GPU 单模型训练的限制
- 论文在 512 块 NVIDIA V100 GPU 上使用 8 路模型并行高效训练了高达 8.3B 参数的基于 Transformer 的模型，并在整个应用中实现了高达 15.1 PetaFLOPs 的持续性能
- 论文表明，对于 BERT 模型，随着模型规模的增长，类 BERT 模型中 Layer Normalization 的位置对准确率的提升至关重要
- 论文研究了模型规模对下游任务准确率的影响，在下游任务上取得了远超现有水平的结果，并在 WikiText103、LAMBADA 和 RACE 数据集上建立了新的最佳结果（SOTA）
- 非常值得称赞的是：论文开源了论文的代码，以支持未来基于模型并行 Transformer 的研究工作
背景 & 问题提出：
- Transformer 模型推动了 NLP 技术发展，但内存限制，导致超大型模型的训练难度极大
方法内容：
- 论文提出了训练超大型 Transformer 模型的技术，并实现了一种简单、高效的层内模型并行（intra-layer model parallel）方法，该方法能够训练具有数十亿参数的 Transformer 模型
- 本方法不需要新的编译器或库修改，与流水线模型并行（pipeline model parallelism）相互独立且互补，完全可以通过在原生 PyTorch 中插入少量通信操作来实现
论文通过使用 512 个 GPU 训练出高达 8.3B 参数的 Transformer 模型验证了该方法的有效性
- 与单个GPU基准（可持续 39 TeraFLOPs，达到峰值浮点运算的 30%）相比，论文在整个应用中实现了 15.1 PetaFLOPs 的性能，扩展效率为76%
- ${39 \times 512 / 1000}{39} \approx 76%$
为了证明 LLM 能进一步推动技术发展，论文训练了一个与 GPT-2 类似的 8.3B 参数 Transformer 语言模型和一个与 BERT 类似的 3.9B 参数模型
- 论文发现，对于类 BERT 模型，随着模型规模的增长， Layer Normalization的位置对性能提升至关重要
- 使用 GPT-2 模型，论文在 WikiText103 数据集和 LAMBADA 数据集上取得了最佳结果
  - WikiText103 数据集：困惑度为 10.8（之前最佳困惑度为 15.8）
  - LAMBADA 数据集：准确率为 66.5%（之前最佳准确率为63.2%）
- 使用 BERT 模型，论文在在 RACE 数据集上取得了最佳结果
  - RACE 数据集：准确率为 90.9%（之前最佳准确率为 89.4%）

Introduction and Discussion

NLP 正在快速发展，部分原因是可用计算资源和数据集规模的增加
- 丰富的计算资源和数据使得通过无监督预训练（unsupervised pretraining）训练越来越大的语言模型成为可能（2018；2019）
实证证据表明，更大的语言模型在文章补全、问答和自然语言推理等 NLP 任务中更有用（2019；2019）
- 近期研究显示，在下游自然语言任务上对这些预训练语言模型进行微调（finetuning），可以取得最佳结果（2018；2017；2016；2019b；）
模型规模的增长超出了现代处理器的内存限制，需要额外的内存管理技术，如激活检查点（activation checkpointing）（2016）
- ADAM 等广泛使用的优化算法（optimization algorithms）需要为每个参数额外分配内存来存储动量（momentum）和其他优化器状态，这限制了可有效训练的模型规模
- 几种模型并行（model parallelism）方法通过对模型进行分区来克服这一限制，使得权重及其相关的优化器状态无需同时驻留在处理器上，比如：
  - GPipe（2018）和 Mesh-Tensorflow（2018）提供了不同类型的模型并行框架
  - 但它们需要重写模型，并依赖仍在开发中的自定义编译器和框架
论文使用层内模型并行（intra-layer model-parallelism）实现了一种简单高效的模型并行方法
论文利用基于 Transformer 的语言模型的固有结构，实现了一种简单的模型并行方案，该方案能在 PyTorch 中高效训练，无需自定义 C++ 代码或编译器
- 这种方法与 GPipe（2018）等方法所倡导的基于流水线的模型并行相互独立
为了证明论文方法的可扩展性，论文建立了一个基准：在单个 NVIDIA V100 32GB GPU 上训练 1.2B 参数的模型，可持续 39 TeraFLOPs
- 这相当于 DGX-2H 服务器中配置的单个 GPU 理论峰值浮点运算的 30%，因此是一个很强的基准
- 通过 8路模型并行在 512 个 GPU 上训练 8.3B 参数的模型，论文在整个应用中实现了高达 15.1 PetaFLOPs 的持续性能
  - 与单GPU情况相比，这一扩展效率为76%
- 图1显示了更详细的扩展结果
为了分析模型规模扩展对准确率的影响：
- 论文训练了从左到右的 GPT-2（2019）语言模型和 BERT（2018）双向 Transformer，并在多个下游任务上对它们进行了评估
  - 论文发现，现有 BERT 架构会随着规模的增加而导致模型性能下降
  - 论文通过重新排列 Transformer 层中的 Layer Normalization 和残差连接（residual connection）克服了这一挑战，并表明通过这种修改，下游任务在开发集上的结果会随着模型规模的增加而单调提升
- 论文的模型在 WikiText103 测试集、LAMBADA 的完形填空预测准确率（cloze-style prediction accuracy）和阅读理解 RACE 数据集上取得了最佳结果
总结来看：论文的贡献如下：
- 通过对现有 PyTorch Transformer 实现仅进行少量有针对性的修改，实现了一种简单高效的模型并行方法
- 对模型和数据并行技术进行了深入的实证分析，并证明了在 512 个 GPU 上的扩展效率高达 76%
- 论文实验表名：对于类 BERT 模型，随着模型规模的增长， Layer Normalization 的位置对准确率的提升至关重要
- 论文证明：模型规模的扩展会提高 GPT-2（研究到 8.3B 参数）和 BERT（研究到 3.9B 参数）模型的准确率
- 展示了论文的模型在测试集上取得了最佳结果：WikiText103的困惑度（10.8 ppl）、LAMBADA 的准确率（66.5%）和 RACE 的准确率（90.9%）
- 开源了论文的代码以及训练和评估流水线，地址为 github.com/NVIDIA/Megatron-LM

Background and Challenges

Neural Language Model Pretraining

预训练语言模型已成为 NLP 研究人员工具包中不可或缺的一部分
- 利用大型语料库预训练来学习稳健的语言神经表征是过去十年中一个活跃的研究领域
预训练和迁移语言神经表征的早期例子表明，预训练的词嵌入表（word embedding tables）比从头学习的词嵌入表能更好地提升下游任务结果（2013；2014；2010）
后来的研究通过学习和迁移能捕捉单词上下文表征（contextual representations）的神经模型推进了这一领域（2016；2018；2017；2019）
近期的相关研究（2016；2018；2019b；）进一步基于这些思想，不仅迁移语言模型来提取上下文单词表征，还在下游任务上对语言模型进行端到端微调
通过这些工作，技术发展已经从仅迁移词嵌入表发展到迁移整个数十亿参数的语言模型
这种方法的发展使得需要能够高效大规模运行并满足日益增长的计算需求的硬件、系统技术和框架
论文的工作旨在提供必要的工具，以推动这一趋势向前迈出又一步

Transformer Language Models and Multi-Head Attention

当前 NLP 研究趋势是使用 Transformer 模型（2017），因为它们具有更高的准确率和计算效率
原始 Transformer 结构被设计为机器翻译架构，它使用 Encoder 和 Decoder 两部分将输入序列转换为另一个输出序列
近期利用 Transformer 进行语言建模的研究（如BERT（2018）和GPT-2（2019））根据其需求仅使用 Encoder 或 Decoder
本研究探讨了 Decoder 架构 GPT-2 和 Encoder 架构 BERT
图2显示了论文使用的模型示意图
- 有关模型架构的详细描述，论文建议读者参考先前的研究（2017；2018；2019）
- 特别地，GPT-2 和 BERT都使用 GeLU（2016）非线性激活函数和 Layer Normalization （2016），并将其应用于多头注意力（multi-head attention）和前馈层（feed forward layers）的输入，而原始 Transformer （2017）使用 ReLU 非线性激活函数，并将 Layer Normalization 应用于输出

Data and Model Parallelism in Deep Learning

将深度神经网络训练扩展到多个硬件加速器有两种核心范式：数据并行（data parallelism）（1990）和模型并行（model parallelism）
- 数据并行是将训练小批量（minibatch）分配到多个工作节点（workers）
- 模型并行是将模型的内存使用和计算分配到多个工作节点
通过与可用工作节点数量成比例地增加批量大小（即弱扩展），可以观察到训练数据吞吐量接近线性扩展
- 但大批量训练会给优化过程带来复杂性，可能导致准确率下降或收敛时间延长，从而抵消训练吞吐量增加带来的好处（2017）
- 进一步的研究（2017；2017；2019）开发了缓解这些影响的技术，并缩短了大型神经网络的训练时间
- 为了进一步扩展训练，相关研究（2016）将数据并行与激活检查点相结合 ：
  - 在反向传播（backward pass）中重新计算激活（activations），而不在前向传播（forward pass）中存储它们，以减少内存需求
以上这些技术在处理问题规模上有一个根本限制：模型必须完全适合单个工作节点
- 随着 BERT 和 GPT-2 等语言模型规模和复杂性的增加，神经网络已经接近现代硬件加速器的内存容量
- 解决这一问题的一种方法是使用参数共享（parameter sharing）来减少模型的内存占用（2019），但这会限制模型的整体容量
- 论文的方法是利用模型并行将模型分配到多个加速器上
  - 这不仅减轻了内存压力，还独立于微批量（microbatch）大小增加了并行性
在模型并行中，还有两种进一步的范式：分层流水线并行（layer-wise pipeline parallelism）和更通用的分布式张量计算（distributed tensor computation）
- 在流水线模型并行中，一组操作在一个设备上执行，然后将输出传递到流水线中的下一个设备，在那里执行另一组操作
  - 一些方法（2018；2018）将参数服务器（parameter server）（2014）与流水线并行结合使用，但这些方法存在不一致问题
  - TensorFlow 的 GPipe 框架（2018）通过使用同步梯度下降（synchronous gradient decent）克服了这一不一致问题
    - GPipe 需要额外的逻辑来处理这些通信和计算操作的高效流水线，并且会受到流水线气泡（pipeline bubbles）的影响而降低效率，或者需要修改优化器本身，从而影响准确率
- 分布式张量计算是一种独立且更通用的方法，它将张量操作分配到多个设备上，以加速计算或增加模型规模
  - FlexFlow（2018）是一个协调这种并行计算的深度学习框架，它提供了一种选择最佳并行策略的方法
  - Mesh-TensorFlow（2018）引入了一种在 TensorFlow（2015）中指定通用分布式张量计算类别的语言
    - 用户在该语言中指定并行维度，然后使用适当的集合原语（collective primitives）编译生成的图
论文利用与 Mesh-TensorFlow 中类似的见解，并利用 Transformer 注意力头（attention heads）计算中的并行性来并行化论文的 Transformer 模型
- 论文没有为模型并行实现框架和编译器，而是仅对现有 PyTorch Transformer 实现进行了少量有针对性的修改
- 论文的方法简单，不需要任何新的编译器或代码重写，并且可以通过插入一些简单的原语来完全实现，如下一节所述

Model Parallel Transformer s

论文利用 Transformer 网络的结构，通过添加一些同步原语（synchronization primitives），实现了一种简单的模型并行方案
如图2所示：一个 Transformer 层由一个自注意力块（self attention block）和一个两层的多层感知器（multi-layer perceptron, MLP）组成
- 论文分别在这两个块中引入模型并行
首先详细介绍 MLP 块
- MLP 块的第一部分是一个通用矩阵乘法（general matrix multiplication, GEMM），后跟一个 GeLU 非线性激活函数：
  $$Y=GeLU(X A) \tag{1}$$
- 并行化 GEMM 的一种方法是将权重矩阵 $A$ 按行拆分，将输入 $X$ 按列拆分，如下所示：
  $$X=\left[X_{1}, X_{2}\right], A=\left[\begin{array}{l}A_{1} \\ A_{2}\end{array}\right] \tag{2}$$
- 这种划分将导致
  $$ Y=GeLU(X_{1} A_{1}+X_{2} A_{2}) $$
- 由于 GeLU 是一个非线性函数
  $$ GeLU(X_{1} A_{1}+X_{2} A_{2}) \neq GeLU(X_{1} A_{1})+GeLU(X_{2} A_{2})$$
- 因此这种方法需要在 GeLU 函数之前设置一个同步点
另一种方法是将 $A$ 按列拆分 $A=[A_{1}, A_{2}]$
- 这种划分允许 GeLU 非线性激活函数独立应用于每个划分的 GEMM 输出：
  $$\left[Y_{1}, Y_{2}\right]=\left[GeLU\left(X A_{1}\right), GeLU\left(X A_{2}\right)\right]$$
- 这一方法的优势在于消除了同步点
- 论文以这种列并行的方式划分第一个 GEMM，并将第二个 GEMM 按行拆分，使其可以直接接收 GeLU 层的输出，而无需任何通信（如图3a所示）
- 然后，第二个 GEMM 的输出在多个 GPU 之间进行归约（reduce），之后再传递到 dropout 层
- 这种方法将 MLP 块中的两个 GEMM 都拆分到多个 GPU 上，并且在正向传播中只需要一个 $g$ 算子，在反向传播中只需要一个全归约（all-reduce）（ $f$ 算子）
  - 这两个算子是共轭的，可以用 PyTorch 中的几行代码实现
- 例如， $f$ 算子的实现如下：
  1
  2
  3
  4
  5
  6
  class f(torch.autograd.Function):
  def forward(ctx, x):
  return x
  def backward(ctx, gradient):
  all_reduce(gradient)
  return gradient
- $g$ 与 $f$ 类似，只是在正向传播中执行全归约，在反向传播中执行恒等操作
如图3b所示
- 对于自注意力块，利用多头注意力操作中固有的并行性 ，将与 $K$、 $Q$ 和 $V$ 相关的 GEMM 以列并行的方式划分 ，这样每个注意力头对应的矩阵乘法都在单个 GPU 上本地完成
- 这使得我们可以将每个注意力头的参数和计算负载分配到多个 GPU 上，并且不需要立即通信就能完成自注意力计算
- 自注意力之后的输出线性层（output linear layer）的 GEMM 按行并行化，可以直接接收并行注意力层的输出，无需 GPU 之间的通信
- 这种针对 MLP 层和自注意力层的方法融合了两组 GEMM，消除了它们之间的同步点，从而实现了更好的扩展性
- 这使得论文能够在一个简单的 Transformer 层中，仅在正向传播和反向传播中各使用两次全归约来执行所有 GEMM（见图4）
Transformer 语言模型的 Output Embedding 维度为隐藏层大小（ $H$ ）乘以词汇表大小（ $v$ ）
- 现代语言模型的词汇表大小通常在数万个 token 量级（例如，GPT-2 使用的词汇表大小为 50257），因此并行化 Output Embedding 的 GEMM 是有益的
- 但在 Transformer 语言模型中， Output Embedding 层与 Input Embedding 层共享权重，这需要对两者都进行修改
- 对于 Input Embedding 权重矩阵 $E_{H \times v}$ 沿词汇表维度按列拆分：
  $$ E=[E_{1}, E_{2}]$$
  - 由于每个分区现在只包含一部分嵌入，因此在 Input Embedding 之后需要一个 $g$ 算子
- 对于 Output Embedding ：
  - 一种方法是执行下面的并行 GEMM 以获得 logits
    $$ [Y_{1}, Y_{2}]=[X E_{1}, X E_{2}] $$
    - 然后添加一个全收集（all-gather）操作 $$ Y = \text{all-gather}([Y_{1}, Y_{2}])$$
    - 再将结果传递给交叉熵损失函数（cross-entropy loss function）
    - 但这种情况下，全收集操作将传递 $b \times s \times v$ 个元素（ $b$ 是批大小， $s$ 是序列长度），由于词汇表大小很大，这一数据量非常庞大
  - 为了减少通信量，论文将并行 GEMM 的输出 $[Y_{1}, Y_{2}]$ 与交叉熵损失融合，这将维度减少到 $b \times s$
  - 传递标量损失而不是 logits 大大减少了通信量，提高了论文模型并行方法的效率
论文的模型并行方法在很大程度上可以概括为旨在减少通信并使 GPU 保持计算受限（compute bound）的技术
论文选择在多个 GPU 上复制计算，而不是让一个 GPU 计算 dropout、 Layer Normalization 或残差连接的一部分，然后将结果广播到其他 GPU
具体来说：
- 论文在每个 GPU 上维护 Layer Normalization 参数的副本
- 并对模型并行区域的输出执行 dropout 和残差连接
- 然后将其作为输入馈送到下一个模型并行区域
- 问题：如何理解这里的每个 GPU 独立维持 Layer Normalization 参数的副本？
为了优化模型，论文允许每个模型并行工作节点优化自己的一组参数
- 由于所有值要么在 GPU 上本地存储，要么在 GPU 上复制，因此在这种形式中不需要通信更新后的参数值
关于混合模型并行与数据并行以及随机数生成的处理，论文在附录B中提供了更多细节
总之，如上所述，论文的方法易于实现，只需要在正向传播和反向传播中添加少量额外的全归约操作
- 它不需要编译器，并且与 GPipe（2018）等方法所倡导的流水线模型并行相互独立且互补

Setup

预训练语言理解模型是自然语言处理和语言理解中的核心任务
语言建模有多种形式，论文重点关注 GPT-2（2019）（一种基于 Transformer 的从左到右生成式语言模型）和 BERT（2018）（一种基于掩码语言模型的双向 Transformer 模型）
论文在以下部分解释这些模型的配置，并建议读者参考原始论文以获取更多细节

Training Dataset

为了收集具有长期依赖关系的大型多样化训练集，论文聚合了几个最大的语言建模数据集
论文创建的聚合数据集包括 Wikipedia（2018）、CC-Stories（2018）、RealNews（2019）和 OpenWebtext（2019）
为了避免训练集数据泄露到下游任务中
- 移除了 WikiText103 测试集（2016）中存在的 Wikipedia 文章
- 还移除了 CC-Stories 语料库中因预处理 artifacts 引入的不必要换行
对于 BERT 模型，论文在训练数据集中包含了 BooksCorpus（2015），但由于该数据集与 LAMBADA 任务重叠，因此在 GPT-2 训练中排除了该数据集
论文合并了所有数据集，然后做了以下操作：
- 从聚合数据集中过滤掉内容长度小于 128 个 token 的所有文档
- （聚合数据集中可能存在重复的相似内容），论文使用局部敏感哈希（locality-sensitive hashing, LSH）对 Jaccard 相似度大于 0.7 的内容进行去重
最终的聚合语料库包含 174 GB 的去重文本

Training Optimization and Hyperparameters

为了高效训练论文的模型，论文利用混合精度训练（mixed precision training）和动态损失缩放（dynamic loss scaling），以充分利用 V100 的Tensor Core（2017；2018）
使用简单的正态分布初始化权重 $W$ ：
$$ W \sim N(0,0.02)$$
在残差层（residual layers）之前立即按下面的比例缩放权重：
$$ \frac{1}{\sqrt{2 N} } $$
- 其中 $N$ 是由自注意力和 MLP 块组成的 Transformer 层数
使用带权重衰减（weight decay）（2019）的 Adam 优化器（2014），其中 $\lambda=0.01$
使用全局梯度范数裁剪（global gradient norm clipping）为 1.0，以提高大型模型训练的稳定性
dropout 率均设置为 0.1
在每个 Transformer 层之后使用激活检查点（2016）
对于 GPT-2 模型
- 所有训练都使用 1024 个子词单元（subword units）的序列
- 批大小为 512
- 共训练 300K 次迭代
- 初始学习率为 1.5e-4（3k 次迭代的预热期（warmup period））
- 剩余的 297K 次迭代中遵循单周期余弦衰减（single cycle cosine decay）至最小学习率 1e-5
对于 BERT 模型
- 在很大程度上遵循（2019）中描述的训练过程
- 论文使用原始 BERT 词典，词汇表大小为 30522
- 按照（2019）的建议，用句子顺序预测（sentence order prediction）替换了下一句预测（next sentence prediction）头，并使用（2019）的全词 n-gram 掩码（whole word n-gram masking）
- 批大小设置为 1024
- 学习率为 1.0e-4
- 在 10k 次迭代中预热，然后在 2M 次迭代中线性衰减
- 其他训练参数与（2018）保持一致

Experiments

论文所有的实验都使用了多达 32 台 DGX-2H 服务器（总共 512 块 Tesla V100 SXM3 32GB GPU）
论文的基础设施针对多节点深度学习应用进行了优化，服务器内部的 GPU 之间通过 NVSwitch 实现 300 GB/秒的带宽，服务器之间通过每台服务器配备的 8 个 InfiniBand 适配器实现 100 GB/秒的互联带宽

Scaling Analysis

为了测试论文实现方案的可扩展性，论文考虑了四组参数的 GPT-2 模型，详情见表1
为了使自注意力层中的通用矩阵乘法（GEMM）大小保持一致，每个注意力头的隐藏层大小固定为 96，通过调整注意力头数和层数来获得参数规模从 1B 到 8B 的配置
- 1.2B 参数的配置可以在单个 GPU 上运行，而 8B 参数的模型则需要 8 路模型并行（8 块 GPU）
- 将原始词汇表大小从 50257 填充为 51200，原因如下：
  - 为了使 logit 层的通用矩阵乘法（GEMM）更高效，每个 GPU 上的词汇表大小最好是 128 的倍数
  - 论文的模型并行最多为 8 路，因此论文将词汇表填充为可被 $128 \times 8 = 1024$ 整除的大小，最终填充后的词汇表大小为 51200
- 论文研究了模型并行和模型+数据并行两种扩展性
  - 对于模型并行扩展性，所有配置都使用固定的批大小 8
  - 数据并行扩展对于训练许多最先进的模型是必要的，这些模型通常使用更大的全局批大小
  - 在模型+数据并行的情况下，论文所有实验的全局批大小都固定为 512，这对应于 64 路数据并行

Model and Data Parallelism

本节展示模型并行和模型+数据并行情况下，相对于模型参数的弱扩展性
弱扩展性通常通过扩展批大小来实现，但这种方法无法解决训练无法在单个 GPU 上运行的大型模型的问题，而且会导致大批量训练的收敛性下降
论文不同，在这里使用弱扩展性来训练原本无法实现的更大模型
所有扩展性数据的基准是表1中的第一种配置（1.2B 参数）在单个 GPU 上的运行情况
- 这是一个很强的基准，因为它在整个训练过程中达到了 39 TeraFLOPs，相当于 DGX-2H 服务器中单个 GPU 理论峰值浮点运算的 30%
图5显示了模型并行和模型+数据并行的扩展性数值：论文在两种设置下都观察到了优异的扩展性。例如，
- 8.3B 参数的模型在 8 路（8 块 GPU）模型并行下实现了 77% 的线性扩展效率
- 模型+数据并行由于需要额外的梯度通信，扩展性数值略有下降
- 但即使是在 512 块 GPU 上运行的最大配置（8.3B 参数），相对于 1.2B 参数在单个 GPU 上的强基准配置，论文也实现了 74% 的线性扩展效率
- 更多扩展性分析见附录D

Language Modeling Results Using GPT-2

为了证明大型语言模型能进一步推动技术发展，论文考虑训练表2中列出的不同规模和配置的 GPT-2 模型
- 355M 参数的模型与 BERT-Large 模型（2018）的规模和配置相当
- 2.5B 参数的模型比之前最大的 GPT-2 模型更大，而据论文所知，8.3B 参数的模型比任何已训练的从左到右的 Transformer 语言模型都要大
论文使用第4节中描述的流程来训练和评估论文的语言模型
表2还列出了完成一个 epoch 所需的时间，一个 epoch 相当于 68507 次迭代
- 例如， 8.3B 参数的模型在 512 块 GPU 上，每个 epoch 大约需要两天
- 与表1中用于扩展性研究的配置相比：
  - 2.5B 参数的模型是相同的
  - 8.3B 参数的模型有 24 个注意力头（而不是 32 个）
  - 355M 参数的模型比之前的任何模型都小，但仍使用 64 块 GPU 进行训练，因此每个 epoch 的时间短得多
图6显示了验证集困惑度（perplexity）随迭代次数的变化
- 随着模型规模的增加，验证集困惑度降低， 8.3B 参数的模型达到 9.27 的验证集困惑度
表3报告了训练后的模型在 LAMBADA 和 WikiText103 数据集上的零样本评估结果
- 有关评估方法的更多细节，请参见附录E
论文观察到，随着模型规模的增加，WikiText103 上的困惑度降低，LAMBADA 上的完形填空准确率（cloze accuracy）提高
- 论文的 8.3B 参数模型在 WikiText103 测试集上实现了 10.81 的调整后困惑度，达到了最佳水平
- 8.3B 参数的模型在 LAMBADA 任务上的准确率为 66.51%，同样超过了之前的完形填空准确率结果
- 附录C 中包含了 8.3B 参数模型生成的样本
最近，微软的研究人员与 NVIDIA 合作，使用 Megatron 训练了一个 17B 参数的 GPT-2 模型，称为 Turing-NLG（微软，2020），并表明随着模型规模的扩大，准确率进一步提高，凸显了更大模型的价值
为了确保论文的训练数据中不包含任何测试集数据
- 论文计算了测试集中的 8-grams 在训练集中出现的百分比，就像之前的工作（2019）所做的那样
- WikiText103 测试集的重叠率最多为 10.8%，LAMBADA 测试集（2016）的重叠率最多为 1.4%
- WikiText103 测试集与 WikiText103 训练集的重叠率已经达到 9.09%（2019）
- 由于这些结果与之前的工作一致，论文有信心训练数据中没有无意中包含任何测试数据的文档

Bi-directional Transformer Results Using BERT

在本节中，论文将论文的方法应用于类 BERT（BERT-style）的 Transformer 模型，并研究模型扩展对多个下游任务的影响
先前的工作（2019）发现，当模型规模超过 336M 参数的 BERT-large 时，会出现意想不到的模型性能下降
- 为了解决这种下降，该工作的作者（2019）引入了参数共享，并表明他们的模型比原始 BERT 模型的扩展性好得多
论文进一步研究了这种现象，并通过实证证明，如图7所示，重新排列 Layer Normalization 和残差连接（residual connections）的顺序，对于使类 BERT 模型能够扩展到超过 BERT-Large 的规模至关重要
图7中的架构（b）消除了使用原始BERT架构（a）时观察到的不稳定性，并且具有更低的训练损失
据论文所知，论文是第一个报告这种修改能够训练更大 BERT 模型的研究
使用图7（b）中的架构修改，论文考虑了表4中详细列出的三种情况
- 336M 参数的模型与 BERT-large 的规模相同
- 1.3B 参数的模型与之前被证明比 336M 参数的 BERT-large 模型结果更差的 BERT-xlarge 配置相同（2019）
- 论文通过同时增加隐藏层大小和层数，将 BERT 模型进一步扩展到 3.9B 参数的情况
- 在所有情况下，每个注意力头的隐藏层大小都固定为 64
- 336M 和 1.3B 参数的模型训练了 2M 次迭代，而 3.9B 参数的模型训练了 1.5M 次迭代，目前仍在训练中
在 3% 的保留集上，336M、1.3B和 3.9B 参数的模型分别实现了 1.58、1.30 和 1.16 的验证集困惑度 ，随着模型规模的增加而单调下降
论文在多个下游任务上对训练后的模型进行微调，包括 GLUE 基准（2019）中的 MNLI 和 QQP，斯坦福问答数据集（2016；2018）中的 SQuAD 1.1 和 SQuAD 2.0，以及阅读理解 RACE 数据集（2017）
- 微调时，论文遵循（2019b）中的相同流程
- 论文首先对批大小和学习率进行超参数调优
- 获得最佳值后，论文报告 5 个不同随机种子初始化的开发集结果的中值
- 每个模型和任务使用的超参数见附录A
表5显示了 MNLI、QQP、SQuAD 1.1 和 SQuAD 2.0 的开发集结果，以及 RACE 的测试集结果
- 对于 RACE 的测试集结果，论文首先使用开发集找到在 5 个随机种子上给出中值分数的检查点，然后报告该检查点在测试集上的结果
- 论文还报告了 SQuAD 开发集和 RACE 测试集的 5 路集成（ensemble）结果
从表5中论文观察到：
- （a）随着模型规模的增加，所有情况下的下游任务性能都有所提高；
- （b）论文的 3.9B 参数模型在开发集上建立了比其他基于 BERT 的模型更好的最佳结果；
- （c）论文的 3.9B 参数模型在 RACE 测试集上同时实现了单模型和集成模型的最佳结果

Future Work

未来的工作有几个方向
- 继续扩大预训练规模是一个很有前景的研究方向，这将进一步考验现有的深度学习硬件和软件
  - 为了实现这一点，需要提高优化器的效率和减少内存占用
  - 此外，训练超过16B 参数的模型将需要比 DGX-2H 服务器的16块GPU更多的内存
  - 对于此类模型，混合层内和层间模型并行以及节点间模型并行将更合适
- 其他三个研究方向包括：
  - （a）预训练不同的模型系列（XLNet、T5）；
  - （b）评估大型模型在更多更困难和更多样化的下游任务（如生成式问答、摘要和对话）上的性能；
  - （c）使用知识蒸馏（knowledge distillation）从这些大型预训练教师模型（teacher models）中训练小型学生模型（student models）

A. BERT Finetuning Hyperparameters

表6展示了每个模型和任务在微调过程中使用的超参数

B. Model Parallel Supplementary Material

在本节中，论文将详细介绍混合模型并行与数据并行以及随机数生成的处理方法

B.1 Hybrid Model and Data Parallelism

模型并行与数据并行是相互独立的，因此我们可以同时使用这两种方法，在合理的时间内训练大型模型
图8展示了用于混合模型并行与数据并行的 GPU 分组方式
同一服务器内的两块或多块 GPU 组成模型并行组（例如图8中的 GPU 1 至 8），这些 GPU 共同分布运行一个模型实例
其余的 GPU（可能位于同一服务器内，但更常见的是位于其他服务器中）运行额外的模型并行组
每个模型并行组中处于相同位置的 GPU（例如图8 中的 GPU 1、9、……、505）组成数据并行组，因此数据并行组内的所有GPU都持有相同的模型参数
在反向传播过程中，论文并行运行多个梯度全归约（gradient all-reduce）操作，以在每个不同的数据并行组内归约权重梯度
所需的 GPU 总数是模型并行组数与数据并行组数的乘积
例如，对于 8.3B 参数的模型，论文每个模型并行组使用 8 块 GPU，并采用 64 路数据并行，因此总共需要 512 块 GPU
所有通信都是在 PyTorch 中通过 Python 调用 NCCL 实现的
每个模型并行组内的 GPU 在组内所有 GPU 之间执行全归约操作
对于数据并行，每个全归约操作都在每个模型并行组中的一块 GPU 之间进行

B.2 Model Parallel Random Number Generation

诸如 dropout 等利用随机数生成的技术是现代深度学习训练中的重要组成部分
Transformer 在模型并行区域之外的残差连接之前以及模型并行区域内的自注意力块中都有 dropout 层
由于一些 dropout 层位于模型并行区域内，而另一些则不在，因此论文需要谨慎处理随机数生成，以确保 dropout 正常工作
为了在模型并行工作节点之间同步残差连接 dropout，论文在训练开始时使用相同的种子初始化随机数生成器
这使得所有模型并行工作节点的 dropout 模式完全相同
然而，模型并行区域内的 dropout 应该为每个工作节点生成不同的随机模式，以实现整个操作的随机性
- 为了实现这一点，论文为模型并行区域内的 dropout 维护一个单独的随机数生成器
- 每个模型并行工作节点的这个随机数生成器都有唯一的种子

C. Text Samples

本节展示了 Megatron-LM 使用上下文提示生成的一些文本样本

D. Further Scaling Analysis

在本节中，论文研究注意力头数对扩展性结果的影响
论文还展示了 1.2B 参数模型的强扩展性结果

D.1 Attention Heads and Scaling

本节研究注意力头数对模型并行扩展性的影响
为此，论文考虑 8.3B 参数配置（采用8路模型并行），并将注意力头数从 16 调整到 32
结果如表7所示
- 随着注意力头数的增加 ，自注意力层内的一些通用矩阵乘法（GEMMs）会变小 ，自注意力 softmax 中的元素数量也会增加
  - 这导致扩展性效率略有下降
- 未来的研究在设计平衡模型速度和准确率的大型 Transformer 模型时，应注意这个超参数

D.2 Strong Scaling

论文的模型并行主要是为了能够训练规模超过单个 GPU 内存的模型，但它也可以在不增加批大小的情况下加速较小模型的训练
为了衡量这种加速效果，论文训练了一个固定的 1.2B 参数模型
论文使用每次迭代 8 个样本的固定批大小，并通过模型并行增加 GPU 数量
结果如表8所示
- 使用两块GPU可使训练速度提高 64%
- 超过这个数量后，论文看到收益递减，因为每个 GPU 的计算量减少，内存带宽和通信开销开始占据主导地位

E. 使用 WikiText103 和 LAMBADA 评估语言模型（Evaluating Language Models Using WikiText103 and LAMBADA）

在本节中，论文详细介绍了 WikiText103 数据集（2016）和 LAMBADA 数据集（2016）上完形填空式预测准确率的评估方法

E.1 Wikitext103 困惑度（Wikitext103 Perplexity）

WikiText103 困惑度是过去几年中被广泛研究的评估标准，困惑度是语料库平均交叉熵的指数（2011）。是语言模型的自然评估指标，因为语言模型表示整个句子或文本的概率分布：
$$\text{PPL}=\exp \left(-\frac{1}{T_{o} } \sum_{t}^{T} \log P(t | 0: t-1)\right) \tag{4}$$
为了计算式（4）中的困惑度
- 论文根据子词词汇表对 WikiText103 测试语料库进行分词，并对每个 token $[0, T]$ 的交叉熵损失求和
- 然后，论文通过原始分词方案中的 token 数量 $T_{0}$ 对交叉熵损失进行归一化
WikiText103 测试语料库已经过预处理，采用单词级分词，先前的研究使用这种分词来计算困惑度
为了在公平的环境下与先前的研究比较论文模型的困惑度，论文必须通过原始 token 数量 $T_{0}$ 进行归一化，而不是输入到论文模型中的实际分词数据的 token 数量 $T$
这种预分词还会在文本中引入训练数据中不存在的 artifacts
为了缓解这种分布不匹配，论文首先使用可逆的去分词器对 WikiText103 测试数据集进行预处理，以去除与标点符号和空格相关的各种 artifacts
$T_{0}$ 的值是在这种预处理之前计算的
对于WikiText103的测试集， $T_{o}=245566$ ， $T=270329$
论文还必须对困惑度计算进行一项特定于 Transformer 的修改
- 与基于 RNN 的语言模型不同， Transformer 在固定的窗口输入大小上运行
- 因此，它们无法完全计算 $P(t | 0: t-1)$ ，只能计算 $P(t | t-w: t-1)$ ，其中 $w$ 是论文的上下文大小：1024 个 token
- 但为数据集中的每个 token 计算这个值的成本过高，因为论文必须对 $w$ 大小的上下文进行大约 $T$ 次评估
- 为了高效地评估论文的模型，论文采用了一种称为重叠评估（overlapping evaluation）的折中方法，每次滑动窗口前进一定的重叠量 $o$ ，只计算窗口最后 $o$ 个 token 的交叉熵损失
- 在论文的实验中，论文使用 32 的重叠量 $o$ ，并以这种方式对所有滑动窗口计算损失

E.2 LAMBADA Cloze Accuracy

处理长期上下文的能力对于最先进的语言模型至关重要，也是长文本生成和基于文档的问答等问题的必要前提
像 LAMBADA 这样的完形填空式数据集旨在衡量模型在这些类型的长期上下文中运行和推理的能力
完形填空式阅读理解使用单词 token 的上下文 $x=x_{1: t}$ ，其中一个 token $x_{j}$ 被掩码；
- 模型的目标是正确预测缺失的第 $j$ 个 token
为了准确预测缺失的 token，模型需要深入理解周围的上下文以及在这种上下文中应如何使用语言
LAMBADA 使用完形填空式阅读理解来测试生成式从左到右语言模型，它构建了 45 个句子的示例，其中上下文 $x_{t}$ 的最后一个单词被掩码
论文的模型使用子词单元，因此在 LAMBADA 评估中，论文使用原始的、未处理的 LAMBADA 数据集，并要求论文的模型预测组成单词 token 的多个子词token
论文使用教师强制（teacher forcing），只有当所有输出预测都正确时，才认为答案正确
- 这种形式与原始的单词 token 预测任务等效

NLP——Megatron-LM原始论文解读-第三篇

注：本文包含 AI 辅助创作

参考链接：
- Megatron 系列目前公认的有三篇核心论文如下，它们分别对应了 张量并行、3D 并行 与 序列并行/激活重计算优化 三大阶段，本文是第三篇的解读
- 第三篇：(Megatron-LM-3)Reducing Activation Recomputation in Large Transformer Models, MLSys 2023, NVIDIA
  - 核心贡献：提出 序列并行（Sequence Parallelism） 与 选择性激活重计算 ，将激活显存占用再降 3–5 倍，支持更长序列与更大批训练；与 Flash-Attention 思想互补，现已成为 Megatron-Core 默认配置
- 论文补充材料：Supplementary Material of Megatron-LM-3

Paper Summary

整体内容总结：
- 论文提出了 序列并行（Sequence Parallelism） 与 减少激活重计算（Reducing Activation Recomputation）
- 论文证明了将 SP (Sequence Parallelism) 与 TP (Tensor Parallelism) 结合使用可以显著减少所需的激活内存
- 结合选择性激活重计算 (Selective Activation Recomputation)，论文证明了可以实现内存占用减少 $5\times$，并且恢复了使用完全激活重计算 (Full Activation Recomputation) 所引入的计算开销的 90% 以上
  - 传统上实现：通过不存储激活值，而是在反向传播时按需要重新计算它们，节省了内存但增加了冗余计算
  - 论文表明大部分这种冗余计算是不必要的，因为我们可以有选择的保存部分激活值
补充：结合张量并行 (tensor parallelism， TP)，这些技术几乎消除了重计算激活的需要
论文在规模 高达一万亿参数 的语言模型上评估了论文的方法，结果表明：
- 论文的方法将激活内存减少了 $5\times$，同时将激活重计算带来的执行时间开销降低了 90% 以上
在 2240 个 NVIDIA A100 GPU 上训练一个 530B 参数的 GPT-3 风格模型 (2022) 时，论文实现了 54.2% 的模型浮点运算利用率 (Model Flops Utilization, MFU)，这比使用重计算实现的 42.1% 快了 29%

Introduction and Discussion

随着 Transformer 模型规模向万亿参数扩展，需要模型并行 (model parallelism) 来将模型参数、激活值和优化器状态分布到多个设备上，以便它们能够放入设备内存并在现实的时间量内可训练
虽然模型并行线性地减少了每个设备的参数数量（例如，当模型并行规模加倍时，每个设备的参数数量减半），但模型并行的扩展是有限度的
- 张量级模型并行 (Tensor-level model parallelism, TP) 增加了通信需求并引入了更小且性能较差的矩阵乘法，使得将模型分割到大量设备上效率低下
  - 因此，TP 通常仅限于通过高速带宽连接（例如 DGX 服务器内通过 NVLink 连接的 GPU）的相对较小的 GPU 组
- 流水线并行 (Pipeline parallelism， PP) 需要存储几个微批次 (microbatches) 的激活值以减少流水线气泡 (pipeline bubble) (2021)
  - 因此， PP 只能帮助减少存储模型参数和优化器状态所需的内存，无法在保持高设备利用率的同时减少激活值所需的内存
- 因此，激活值的存储迅速成为扩展大型 Transformer 模型的关键问题
  - 问题：实际上，对于不适用 Activation Recomputation 的场景，PP 也减少激活存储了；但是对于 Activation Recomputation 的场景，每一层存储的激活基本都还在，所以相当于此时 PP 对激活存储是没有节省的
为了量化这一点，图 1 显示了从 22B 参数到 1 万亿（1T）参数的四种模型配置所需的内存（模型配置的详细信息在表 3 中提供）
- 可以看出，对于所有这些情况，基线情况所需的内存都超过了 NVIDIA A100 GPU 提供的 80GB 内存
- 缓解这种内存压力的标准方法是简单地不存储大部分激活值，并在反向传播 (backward pass) 期间根据需要重新计算它们以计算梯度 (2016)
  - 这种方法通常称为“梯度检查点 (gradient checkpointing)”或“激活重计算 (activation recomputation)”，会带来严重降低训练效率的代价
- 对于 Transformer 架构，大多数先前的工作在 Transformer 层边界处检查点（或存储）激活值，并在反向传播中重新计算其余必要的激活值
- 在论文中，论文将这种方法称为“完全激活重计算 (full activation recomputation)”
- 在论文的训练运行中，论文观察到当使用完全激活重计算时 ，会产生 $30-40\%$ 的执行时间开销
论文提出了新技术，帮助缓解存储激活值的内存压力，从而减少重计算激活值的需求
- 这些技术特定于 Transformer 架构，并且易于实现，对计算效率没有影响或影响非常小
正如论文在第 2 节中详细说明的那样，还有其他几种技术可以减少训练大型模型的内存需求，例如：
- 跨数据并行 Rank (data parallel ranks) 分区各种数据
- 将数据卸载到 CPU 内存 (2020; 2021)
以上这些技术与论文提出的技术是互补的，可以额外采用以获得更大的内存节省；但通常这些其他技术比论文提出的技术具有更高的实现成本和对计算效率的更大影响
将这些技术与论文的技术进行比较的分析超出了论文的范围，留待未来工作
论文工作内容包括：
- 首先论文简要回顾 Transformer 架构，然后建立一个近似公式，用于存储 Single Stack Transformer 模型前向传播 (forward pass) 中激活值所需的内存
  - 使用这个公式，我们可以研究不同形式的模型并行如何影响激活内存需求
- 然后论文引入序列并行 (sequence parallelism) 与 TP (tensor parallelism) 结合，以防止在不适合标准 TP 的区域中冗余存储激活值
  - 论文表明，通过有选择地保存哪些激活值以及重新计算哪些激活值，我们可以消除大部分重计算成本，同时仅使用不进行重计算时所需内存的一小部分
- 最后论文提出了几个实验，测量这些技术对训练各个组成部分以及完整训练吞吐量的改进

模型并行 (model parallelism) 使得能够跨多个 GPU 训练非常大的模型
- 模型参数以及这些模型相关的优化器状态需要大量内存，无法容纳在单个 GPU 上
- 即使能够将模型放入单个 GPU（例如，通过在主存和设备内存之间交换参数 (2021)），所需的高计算操作数量可能导致不切实际的长训练时间
- 结论：需要并行化
两种常用的模型并行形式用于将模型参数分布到 GPU 上：
- 1） TP (tensor parallelism)，其中每层的参数分布在许多设备上 (2018; 2019; 2021)；
- 2） PP (pipeline parallelism)，其中模型沿网络的层维度分割 (2019; 2021a; 2019)
一些最近的方法结合了两种类型的模型并行，以支持训练高达 1T 参数的大型模型 (2021)
- 模型并行的替代方案是结合一些训练技术与数据并行 (data parallelism)，以实现大规模模型训练 (2020; 2021;)
  - 这种方法基于将优化器状态、梯度和参数跨数据并行 Rank 进行分片 (sharding)
- 最近的一个扩展 (2021) 使用 CPU 卸载技术，使得能够在少量 GPU 上训练数万亿参数的模型
  - 与模型并行相比，这些基于数据并行的技术效率较低，并且不能很好地扩展到大量 GPU (2021)，因此更适合在资源受限的环境中进行模型微调 (finetuning)
- 论文仅关注模型并行优化，将这些技术与论文的技术进行比较的分析超出了论文的范围
此外，Megatron-LM (2019) 中引入的 TP 在一定程度上帮助减少了激活内存
- 在这种方法中，Transformer 的某些部分激活值没有在 TP Rank 之间分割，增加了激活内存开销
Li 等 (2021a) 提出的序列并行 (sequence parallelism)，其中激活值沿序列维度分区贯穿整个网络可以缓解这个问题
- 但他们的方法类似于数据并行，要求在所有设备上复制参数和优化器状态，这使得它不适合大型模型训练
Sagemaker (2021) 和 GSPMD (2021) 提出了内存高效的 TP 版本，这些版本在整个网络中沿隐藏维度 (hidden dimension) 在设备之间分割激活值
- 这些方法的主要缺点是它们包含多设备层归一化 (multi-device layer normalization)，这在计算/通信上非常低效
  - LayerNorm 操作需要沿隐藏维度顺序计算均值和方差
  - 如果 LayerNorm 沿隐藏维度分割（即使用 TP），它将增加两个额外的全规约 (all-reduce) 操作
  - 而且 LayerNorm 反向传播需要两个额外的 sequential reductions（即另外两个 all-reduce）
- 与 LayerNorm 计算时间相比，每个 Transformer 层的这 4 次通信将引入显著的开销
- LayerNorm 操作的这种通信开销可以通过 SP 来避免
在论文中，论文提出了一种新技术，它利用了 TP 和 SP 的优点，而没有先前方法的任何缺点
- 换句话说，论文的技术结合了 TP 和 SP ，显著减少了激活内存，而没有任何额外的计算、通信或内存开销
论文的论文特别侧重于研究 Transformer 架构，因为作者相信它是一个重要且广泛使用的架构，足以证明手动检查各个层以了解其内存和计算贡献并推导最佳并行化方案是合理的
通过分析建模，论文表明内存（包括激活值和参数）在设备之间均匀分区
- 换句话说，论文的并行化策略在内存需求方面是最优的
- Transformer 网络被广泛使用，足以高度利用这种手动搜索和验证最佳并行化策略的方法
- 自动搜索 (2019; 2019) 有可能找到这种最优策略，但据论文所知，论文尚未看到这些方法应用于 Transformer 网络的任何已发表结果
与并行化方案类似，论文提出的选择性激活重计算 (selective activation recomputation) 是基于手动搜索 Transformer 模型在激活内存需求和重计算之间的最佳权衡
探索自动方法 (2021) 是否可以补充并可能改进这种权衡是未来工作的一个有趣方向

Transformer Architecture

论文考虑一个具有 $L$ 层的 Single Stack Transformer 编码器或解码器，如图 2 所示
符号定义：$s$ 是序列长度 (sequence length)，$h$ 是隐藏维度大小 (hidden dimension size)，$v$ 是词汇表大小 (vocabulary size)
在网络的开始，输入 Tokens 被送入一个词嵌入表(word embedding table)：
$$v\times h$$
Token 嵌入与学习到的位置嵌入(positional embeddings) 相结合：
$$s\times h$$
嵌入层的输出，即 Transformer 块的输入，是一个 3 维张量：
$$s\times b\times h$$
- 其中 $b$ 是微批次大小 (microbatch size)
每个 Transformer 层由一个具有 $a$ 个注意力头 (attention heads) 的自注意力块 (self-attention block) 和一个具有两层的多层感知器 (MLP) 组成，该 MLP 将隐藏大小增加到 $4h$，然后将其减小回 $h$
每个 Transformer 层的输入和输出具有相同的大小
$$ s\times b\times h $$
最后一个 Transformer 层的输出被投影回词汇表维度以计算交叉熵损失 (cross-entropy loss)
- 论文假设词嵌入和输出层权重是共享的
论文相关变量名称列于表 1 中以供参考：

Activation Memory

论文推导出一个近似公式，用于计算如图 2 所示的 Single Stack Transformer 模型在前向传播中存储激活所需的内存
请注意，论文中的 “激活（activations）” 指的是 在前向传播中创建并在反向传播期间梯度计算所必需的任何张量
- 注：不包括模型的主要参数和优化器状态，但包括 Dropout 操作使用的掩码
论文只考虑内存的主要贡献者，而忽略小的缓冲区
- 小的缓冲区包括 LayerNorm 输入的均值和方差（$2sb$）以及 GEMM 操作的偏置（$O(h)$）
- 总的来说，这些缓冲区占激活内存的比例远小于 1%，因为隐藏维度（$h$）和序列维度（$s$）的数量级都是数千，因此与 GEMM 和 LayerNorm 激活的 $O(sbh)$ 大小相比，$2sb$ 和 $O(h)$ 都缺少了其中一个因子
论文还假设网络和激活以 16-bit 浮点格式存储，因此每个元素需要 2 字节的存储空间
- 唯一的例外是 Dropout 掩码，每个元素只需要 1 个字节
请注意，除非明确提及，本节中报告的所有大小均以字节（Bytes）为单位，而不是元素数量

Activations Memory Per Transformer Layer

如图 2 所示，每个 Transformer 层包含一个注意力块和一个 MLP 块，通过两个 LayerNorm 连接
下面，论文推导存储这些元素激活所需的内存：
注意力块 (Attention block)：
- 包括自注意力操作，后跟一个线性投影和注意力 Dropout
- 线性投影存储其输入激活，大小为 $2sbh$，注意力 Dropout 需要一个大小为 $sbh$ 的掩码
- 图 3 所示的自注意力包含几个元素：
  - Query ($Q$), Key ($K$), and Value ($V$)矩阵乘法 (matrix multiplies)： 论文只需要存储它们共享的输入，大小为 $2sbh$
  - $QK^{T}$ 矩阵乘法 (matrix multiply)： 需要存储 $Q$ 和 $K$，总大小为 $4sbh$
  - Softmax： 反向传播需要存储 Softmax 输出，大小为 $2as^{2}b$
  - Softmax Dropout： 只需要一个大小为 $as^{2}b$ 的掩码
    - 问题：Softmax 也有 Dropout 吗？
    - 理解：在 Softmax 之后施加 Dropout，随机将部分注意力权重置为 0，目的是防止模型过度依赖某些特定的注意力权重，减少过拟合风险，提高模型的泛化能力，但原始 Transformer 论文中，没看到这部分的 dropout，只有 Residual Dropout（$P_\text{drop} = 0.1$）
  - 注意力作用于值（$V$）(Attention over Values ($V$))： 论文需要存储 Dropout 输出（$2as^{2}b$）和值（$2sbh$），因此需要 $2as^{2}b+2sbh$ 的存储空间
- 将上述值相加，注意力块总共需要 $11sbh+5as^{2}b$ 字节的存储空间
MLP：
- 两个线性层存储它们的输入，大小分别为 $2sbh$ 和 $8sbh$
- GeLU 非线性操作也需要其输入（大小为 $8sbh$）用于反向传播
- 最后，Dropout 存储其掩码，大小为 $sbh$
- MLP 块总共需要 $19sbh$ 字节的存储空间
LayerNorm：
- 每个 LayerNorm 存储其输入，大小为 $2sbh$，因此论文总共需要 $4sbh$ 的存储空间
最终，将注意力、MLP 和 LayerNorm 所需的内存相加，存储 Transformer 网络单层激活所需的内存为：
$$\text{Activations memory per layer}=sbh\left(34+5\frac{as}{h}\right) \tag{1}$$
上述方程适用于未应用任何形式模型并行的情况

Model Parallelism

论文先量化 TP 对每层所需激活内存的影响，然后介绍一种将 SP 与 TP 相结合的新方法，以进一步减少每层激活所需的内存
在本小节的最后，论文还讨论了 PP 对激活内存的影响，并推导了激活所需总内存的公式

TP (Tensor Parallelism)

论文使用 Shoeybi 等人 (2019) 开发的 TP ，并按照图 4 所示并行化注意力块和 MLP 块
- 这种形式的并行性引入了两个额外的通信操作 $f$ 和 $\bar{f}$
- 更多细节，请参阅该论文 (2019)
TP 不仅并行化了注意力块和 MLP 块内的模型参数和优化器状态，还并行化了这些块内部的激活
- 这些块的输入激活（例如，输入到 $Q$、$K$ 和 $V$ 矩阵乘法的输入，或输入到 $h \to 4h$ 线性层的输入）没有被并行化，只有每个块内的激活在 TP 组内被划分
- 假设采用 $t$ 路 TP ，存储激活所需的每层内存从公式 1 减少到：
  $$\text{Activations memory per layer}=sbh\left(10+\frac{24}{t}+5\frac{as}{ht}\right) \tag{2}$$

SP (Sequence Parallelism)

如图 4 所示， TP 并行化了 Transformer 层中训练过程中最耗时的部分，因此它在计算上是高效的
但它保留了 LayerNorm 以及注意力块和 MLP 块之后的 Dropout 操作不变，因此 LayerNorm 和 Dropout 在 TP 组内是复制的（单卡上需要完整保留所有参数和激活）
这些元素不需要大量计算，但需要相当数量的激活内存
定量地说，公式 2 中的 $10sbh$ 部分就是由于这些复制操作造成的，因此它们没有除以 TP 大小 $t$
论文注意到，在 Transformer 层的非 TP 区域中，操作在序列维度上是独立的
- 这一特性允许论文沿序列维度 $s$ 划分这些区域
- 沿序列维度划分减少了激活所需的内存
这种额外的并行性级别在 $f$ 之前和 $\bar{f}$ 之后引入了新的通信集合，这些操作将充当 SP 区域和 TP 区域之间的转换器
- 例如，在前向传播中，论文需要在图 4 中的操作符 $f$ 之前进行一次额外的 All-Gather
- 这些额外的通信会引入开销并减慢训练速度
为了避免这些额外的通信，论文将这些操作与 $f$ 和 $\bar{f}$ 操作符结合起来，并引入新的操作 $g$ 和 $\bar{g}$，如图 5 所示
- 可以看出，$g$ 和 $\bar{g}$ 是 SP 区域和 TP 区域之间的转换器
- 论文在本小节的剩余部分推导这些操作
论文使用 MLP 块详细说明 $g$ 和 $\bar{g}$ 的推导。在非并行形式中，如图 2 所示，LayerNorm 后接 MLP 块可以表述为：
$$
\begin{align}
Y &=\text{LayerNorm}(X), \\
Z &=\text{GeLU}(YA), \\
W &=ZB, \\
V &=\text{Dropout}(W),
\end{align}
$$
- 其中：
  - $X$ 是 LayerNorm 的输入，大小为 $s\times b\times h$
  - $A$ 和 $B$ 是线性层的权重矩阵，大小分别为 $h\times 4h$ 和 $4h\times h$
上述操作的张量和 SP 组合形式如图 6 所示
下标表示在加速器间的划分（注：理解为 Rank），上标表示划分所沿的维度 ，例如：
- $X_{1}^{s}$ 是 $X$ 在第一个加速器上的部分，沿 $s$ 维度（序列维度）划分
- $Z_{2}^{h}$ 是 $Z$ 在第二个加速器上的部分，沿 $h$ 维度（隐藏维度）划分
LayerNorm 的输入沿序列维度并行化
$$ X=[X_{1}^{s},X_{2}^{s}]$$
因此，LayerNorm 的输出也将沿序列维度并行
$$Y=[Y_{1}^{s},Y_{2}^{s}]$$
带有 GeLU 非线性的线性层需要完整的输入 $Y$，因此论文需要执行一次 All-Gather
- 这意味着 $g$ 在前向传播中是一个沿序列维度的 All-Gather 操作
通过将 $A$ 沿其列划分（$A_{1}^{c}$ 和 $A_{2}^{c}$），将 $B$ 沿其行划分（$B_{1}^{r}$ 和 $B_{2}^{r}$），论文避免了通信（更多细节请参见 (2019)）并得到 $W_{1}$ 和 $W_{2}$
- 这两个张量不再是并行的，需要在输入到 Dropout 层之前求和为 $W=W_{1}+W_{2}$ (对应 Reduce 操作)
- 但 Dropout 需要其输入在序列维度 $s$ 上是并行的（对应 Scatter 操作）
论文不是先求和再在序列维度上并行化，而是将这两个操作合并为一个 Reduce-Scatter 操作
- 因此，$\bar{g}$ 在前向传播中可以是一个单一的 Reduce-Scatter 操作
综上所述，论文得到：
$$
\begin{align}
[Y_{1}^{s},Y_{2}^{s}] &=\text{LayerNorm}([X_{1}^{s},X_{2}^{s}]) \\
Y &=g(Y_{1}^{s},Y_{2}^{s}), \\
[Z_{1}^{h},Z_{2}^{h}] &=[\text{GeLU}(YA_{1}^{c}),\ \text{GeLU}(YA_{2}^{c})],\\
W_{1} &=Z_{1}^{h}B_{1}^{r}\ \text{ and }\ W_{2}=Z_{2}^{h}B_{2}^{r},\\
[W_{1}^{s},W_{2}^{s}] &=\bar{g}(W_{1},W_{2}),\\
[V_{1}^{s},V_{2}^{s}] &=[\text{Dropout}(W_{1}^{s}),\ \text{Dropout}(W_{2}^{s})]
\end{align}
$$
如果论文对反向传播进行类似的分解，论文会发现 $g$ 和 $\bar{g}$ 是彼此共轭的（Conjugate）
- $g$ 在前向传播中是 All-Gather，在反向传播中是 Reduce-Scatter；
- $\bar{g}$ 在前向传播中是 Reduce-Scatter，在反向传播中是 All-Gather
对 Transformer 层的 LayerNorm 后接注意力部分进行类似的分解，得到图 5
TP 在单次前向和反向传播中需要四次 All-Reduce，而 TP 与 SP 结合在单次前向和反向传播中需要四次 All-Gather 和四次 Reduce-Scatter
- 乍一看，似乎张量与 SP 比 TP 需要更多的通信
- 但论文注意到，Ring All-Reduce 由两个步骤组成：
  - 一个 Reduce-Scatter 后接一个 All-Gather
- 因此，TP 与张量加 SP 所使用的通信带宽是相同的
  - 问题：Reduce-Scatter 和 All-Gather 只有在无缝连着的时候才能说等价于 Ring All-Reduce 吧
  - 理解：是的，但是无论是否无缝连着，Reduce-Scatter + All-Gather 的通信都等于 Ring All-Reduce，因为都是 Reduce，然后 Scatter，继而 Gather
    - 补充：论文后面的 6.2 章节也提到了：reduce-scatter 和 all-gather 组合的执行速度比单独的 all-reduce 慢
- 所以， SP 不会引入任何通信开销！
根据公式 3， SP 与 TP 结合，将反向传播所需的所有激活沿并行维度划分
- 注：第一个线性操作所需的张量 $Y$）不会被划分
- 为了缓解这个问题，论文不存储完整的张量 $Y$ 用于反向传播，只在第 $i$ 个 TP Rank 上存储 $Y_{i}^{s}$ 部分，并在反向传播中执行一次额外的 All-Gather
- 为了消除这个额外 All-Gather 引入的延迟，论文将此通信与计算 $Y$ 梯度所需的计算重叠，从而减少了开销
使用 SP 与 TP 结合，存储每个 Transformer 层激活所需的内存从公式 2 减少到：
$$
\begin{align}
\text{Activations memory per layer} &= sbh\left(\frac{10}{t}+\frac{24}{t}+5\frac{as}{ht}\right) \\
&=\frac{sbh}{t}\left(34+5\frac{as}{h}\right) \tag{4}
\end{align}
$$
上述方程现在是公式 1 除以 TP 大小
- 这意味着使用张量和 SP ，我们可以在 TP 组内分布激活，并将所需内存减少 TP 大小 $t$ 倍

PP (Pipeline Parallelism)

PP 简单地将 Transformer 的 $L$ 层划分为 $\frac{L}{p}$ 组层，其中 $p$ 是 PP 大小
- 但 PP 并不会将激活所需的总内存均匀地除以 $p$
- 这是由于 PP 调度引入了重叠（overlapping）以减少流水线气泡 (2021)
  - 注：overlap 意味着对应的激活需要同时在内存中
为了量化这一点，论文考虑 PipeDream (2020) 中开发的 1F1B 流水线调度
- 具有最小化流水线气泡的调度对流水线的第一个阶段施加最大的内存压力
  - 流水线的第一阶段指的是第一个 $\frac{L}{p}$ 层组，也包括输入嵌入
- 激活内存随流水线阶段变化的可视化图见附录 B
- 为了保持流水线加压并避免额外的空闲时间，第一阶段必须存储 $p$ 个微批次的激活（更多细节参见 (2021) 的图 4-top）
- 每个阶段包含 $\frac{L}{p}$ 层，因此第一阶段必须存储激活层为：
  $$p \times \frac{L}{p} = L$$
  - 注：（与 PP 大小 $p$ 无关）
- 因此，第一阶段存储激活所需的总内存为：
  $$\text{Total activations memory of 1st stage}=\frac{sbhL}{t}\left(34+5\frac{as}{h}\right) \tag{5}$$
对于其他流水线调度，所需的总内存会略有不同
- 例如，Megatron-LM (2021) 中开发的交错调度需要存储 $L(1+\frac{p-1}{pm})$ 层的激活，其中 $m$ 是交错阶段的数量
  - 因此，如果使用交错调度，则总激活内存应乘以 $(1+\frac{p-1}{pm})$

Total Activations Memory

总的激活内存的大部分由公式 5 提供，但该公式未包括输入嵌入、最后一个 LayerNorm 和输出层所需的激活内存，如图 2 所示
位置和词嵌入不需要存储任何大量的激活用于反向传播，但 Dropout 需要存储
- 嵌入层中的 Dropout 也沿序列维度并行化
- 因此，它将需要 $\frac{sbhp}{t}$ 的存储空间
- 注意，因子 $p$ 来自 PP 以及论文需要存储 $p$ 个微批次的事实（见第 4.2.3 节）
输出层之前的 LayerNorm 也使用 SP ，因此需要 $\frac{2sbh}{t}$ 的存储空间
输出层投影到词汇维度需要存储其输入，大小为 $\frac{2sbh}{t}$
交叉熵损失需要存储以 32 位浮点数计算的 logits，因此需要 $\frac{4sbv}{t}$ 的存储空间
请注意，由于论文只考虑流水线第一阶段的激活，上述激活（即总共 $\frac{4sbh}{t} \cdot (1+\frac{v}{h})$）仅在没有 PP （$p=1$）的情况下被计入
加上上述内存，由于输入嵌入、最后一个 LayerNorm 和输出层产生的额外内存为：
$$\frac{sbhL}{t}\left(\frac{p}{L}+\delta_{p=1}\frac{4}{L}\left(1+\frac{v}{h}\right)\right)$$
- 其中 $\delta_{p=1}$ 是一个 0-1 函数，在 $p=1$ 时为 1，否则为 0
论文注意到，与公式 5 中的项 $34+5\frac{as}{h}$ 相比，$\frac{p}{L}$ 和 $\frac{4}{L}\cdot (1+\frac{v}{h})$ 都是可以忽略的
- 例如，对于一个具有 22B 参数的模型，这些额外项占总激活内存需求的比例小于 $0.01\%$
- 问题：$\frac{v}{h}$ 对不同配置也不算小吧，也有几十了
因此，公式 5 是总所需激活内存的一个良好近似，论文将在论文的其余部分使用它

选择性激活重计算，Selective Activation Recomputation

公式 (5) 给出的总激活内存需求对于大型模型而言仍然相当可观
激活重计算 (2016) 通过存储（或 checkpoint）一组层的输入激活，并在反向传播期间使用额外的前向传递重新计算其他所需的激活，来克服这一内存限制（论文中称之为完全激活重计算）
假设检查组仅包含单个层，并忽略 Transformer 层之外的激活，该方法将激活所需的总内存减少到
$$ 2sbhL $$
- 论文也注意到，如果论文只在每个 TP Rank 上存储部分激活，这个所需内存可以进一步减少到
  $$ \frac{2sbhL}{t} $$
  - 但这种方法需要每层额外的 all-gather 操作 ，会增加通信开销，因此论文不考虑这种方法
与存储所有激活（公式 (5)）相比，检查（checkpointing）所有 Transformer 层显著减少了训练模型所需的内存量
- 这种减少确实是以重计算（一次额外的前向传递）为代价的，这可能会带来高达 $ 30-40\% $ 的计算时间开销
为了平衡内存节省和计算开销，理想的做法是：仅仅 Checkpointing 足够的激活，使得给定的模型并行配置能够在设备内存的限制下进行训练
SP 提供的内存节省使得比以往更多的配置可以在不进行重计算的情况下进行训练，但大型模型的最佳模型并行配置通常仍然需要存储和重计算部分激活
选择存储与重计算的激活量的一种简单方法是仅 checkpoint 部分 Transformer 层，并存储其他所有层的激活
- 这种方法对于大型模型的扩展性并不好；
  - 例如，在训练 MT-NLG 时，每个设备只有三层，限制了平衡内存与计算的粒度
- 此外，论文注意到并非所有激活都需要相同数量的操作来重新计算，因此在选择存储哪些激活和重计算哪些激活时更智能是有益的
论文不是 checkpoint 和重计算完整的 Transformer 层，而是建议仅 checkpoint 和重计算每个 Transformer 层中占用大量内存但重新计算计算成本不高的部分 ，即选择性激活重计算（Selective Activation Recomputation）
为此，论文注意到公式 (5) 中的项 $ \frac{5as}{h} $ 是由于在通过计算 Q、K 和 V 值的线性层增加了网络宽度之后的注意力操作（after the width of the network is increased by the linear layer calculating the Q, K, and V values）；
- 即如图 3 所示的 $ QK^{T} $ 矩阵乘法、softmax、softmax dropout 和注意力作用于 $ V $
- 这些操作通常具有大的输入尺寸，因此激活也很大，然而，每个输入元素的浮点操作数非常低
- Transformer 层的其余部分对应公式 (5) 中的常数项 34
- 因此，对于 $ \frac{5as}{h}>34 $ 的大型模型，如果论文 checkpoint 并重计算 Transformer 层的这一部分，论文存储的激活不到一半，并且重计算那些未存储的激活只需付出适度的成本
为了量化这一点，让论文考虑 GPT-3 (2020) 和 MT-NLG (2022) 模型，这些是迄今为止训练过的一些最大模型
- 对于 GPT-3，$ a=96 $，$ s=2048 $，$ h=12288 $，因此 $ \frac{5as}{h}=80 $
- 对于 MT-NLG，$ a=128 $，$ s=2048 $，$ h=20480 $，所以 $ \frac{5as}{h}=64 $
将这些数字与常数项 34（即该层其余部分的因子）进行比较，我们可以看到这些激活占总激活的很大一部分
- 因此，通过使用选择性激活重计算，我们可以分别为 GPT-3 和 MT-NLG 模型节省 $ 70\% $ 和 $ 65\% $ 的激活内存需求
- 这些激活的重计算仅为这两个模型引入了 $ 2.7\% $ 和 $ 1.6\% $ 的 FLOPs 开销
- 有关 FLOPs 计算的更多细节，请参见附录 A
随着序列长度的增加，序列长度与隐藏大小的比率 $ (\frac{s}{h}) $ 将增加，执行选择性部分重计算的相对成本也会增加，从而使选择性激活重计算更加昂贵
作者认为，对于任何实际的 $ \frac{s}{h} $ 比率，选择性激活重计算仍然是平衡内存节省和计算的最佳重计算策略
使用这种形式的选择性激活重计算，存储激活所需的内存从公式 (5) 减少到：
$$
\text{Total required memory}=34\frac{sbhL}{t}.
$$
- 上述公式表明，使用选择性激活重计算使得所需的激活内存随序列长度线性缩放，并且与注意力头的数量无关
- 如第 4.2.3 节所述，在使用交错流水线调度的情况下，上述公式需要乘以 $ (1+\frac{p-1}{pm}) $
当使用 PP 时，如第 4.2.3 节所述，尽管给定设备只有 $ \frac{L}{p} $ 层，但第一阶段仍然必须存储相当于 $ L $ 层的激活，因为它必须存储 $ p $ 个微批次的激活以保持流水线压力
- 在这种情况下，可以采用一种额外技术来降低重计算成本，即根据可用设备内存尽可能多地存储所有微批次的激活，并对其余部分进行完全或选择性重计算
- 实际上，论文发现应用 SP 和选择性激活重计算后，重计算开销已经足够小，以至于这种额外技术带来的改进非常有限
- 该技术在附录 C 中有更详细的描述和分析

Evaluations

在本节中，论文评估了论文提出的方法对内存使用和训练执行速度的影响
表 3 列出了评估中使用的模型配置
论文考虑了参数规模高达一万亿的模型，对于所有这些模型，TP 大小设置为 8
对于 175B 和 530B 模型，论文使用具有三个交错阶段 ($ m=3 $) 的交错调度
在所有情况下，序列长度设置为 $ s=2048 $，词汇表大小设置为 $ v=51200 $
论文还注意到，在这些评估中没有考虑数据并行，因为论文的方法与数据并行无关
因此，论文分析中使用的批大小远低于端到端训练中使用的批大小
论文的所有结果都是在 Selene 超级计算机上使用混合精度运行的
每个集群节点有 8 个 NVIDIA 80GB A100 GPU，通过 NVLink 和 NVSwitch 相互连接
每个节点有八个 NVIDIA Mellanox 200Gbps HDR Infiniband HCA 用于应用程序通信

Memory Usage

论文通过借助前向和后向钩子在运行的不同时间点跟踪 GPU 活跃内存和 GPU 总内存（在 PyTorch 中可用）来验证内存消耗模型
论文验证了测量的内存使用情况与论文的分析模型密切匹配
表 2 的第一列总结了论文讨论的不同技术所需的内存
为了量化这一点，图 7 显示了不同技术使用的激活内存，表示为在所有 TP Rank 上保持所有激活所需内存的百分比，即公式 (2)
单独来看，两种技术都将内存需求减少了近一半，结合使用则提供了 5 倍的减少，将内存需求降至 20% 以下。这仅是完全激活重计算（基线水平的 10%）的约 $ \sim 2\times $
如果没有 SP 和选择性重计算共同提供的内存节省，这些模型都无法装入内存
- 请注意，所有这些结果都包括了附录 B 中描述的内存优化

Execution Time per Layer

表 2 的第二列和第三列总结了论文讨论的不同技术下每个 Transformer 层的计算量（FLOPs）和通信字节数
为了量化这一点，表 4 显示了针对 22B 模型的各种实验下，执行一个 Transformer 层前向和后向传递的时间
- 前两行显示， SP 对完成一个 Transformer 层所需的时间提供了适度的改进，将前向时间从 7.7ms 减少到 7.2ms，加速了 6%
  - 这种改进来自于 LayerNorm 和 Dropout 层在 $ \frac{1}{t} $ 的数据上执行
- 论文还发现，尽管移动的数据量是相同的 ，但 reduce-scatter 和 all-gather 组合的执行速度比单独的 all-reduce 慢 ，这降低了 SP 带来的改进
  - 请注意，这种加速是使用 SP 主要优势之外的额外好处，其主要优势是节省内存，从而减少激活的重计算
表 4 的后两行显示，如果论文在重计算哪些操作上具有选择性（由于 SP ，我们可以在更多配置中做到这一点），我们可以显著减少后向传递中重计算的开销
- 选择性重计算的开销是 $ 1.3 $ms，占 11.9ms 基线的 $ 11\% $，而重计算整个层的开销是 $ 7.6 $ms 或 $ 64\% $
- 对于前向和后向总时间，开销是 $ 7\% $ 对比 $ 39\% $
- 请注意，重计算整个层的开销为 $ 39\% $（而非预期的 $ 33\% $）是由于后向传递中的一项优化，论文将 all-reduce 通信与线性层权重的梯度计算重叠
- 正如论文后面将看到的，这种好处随着模型大小的增加而增加
- 表 4 的最后一行显示了选择性重计算和 SP 结合的好处：当两种技术一起使用时，开销降至仅 $ 4\% $
图 8 显示了所有测试案例的相同细分
- 论文看到，随着模型规模的增长，开销的减少也在增加
- 对于 $ 530 $B 和 $ 1 $T 的情况，开销仅为 $ 2\% $，而完全重计算的开销为 $ 36\% $

End-to-End Iteration Time

表 5 列出了表 3 中列出的四种配置中每一种的完整端到端迭代时间
- 论文发现，对于所有测试的配置，论文提出的技术相比不使用 SP 的完全重计算，在吞吐量上提供了介于 $ 29.0\% $ 和 $ 32.1\% $ 之间的改进。这些节省将直接转化为更短的训练时间
论文定义了模型 FLOPs 利用率（MFU）和硬件 FLOPs 利用率（HFU） ，定义方式与 Chowdhery 等 (2022) 类似
- 模型 FLOPs 是执行单次前向和后向传递（单次迭代）所需的浮点操作数（不包括激活值），与实现方式和硬件限制无关
  - 因此，模型 FLOPs 是硬件和实现无关的，仅取决于底层模型
  - 注：但模型 FLOPs 利用率（MFU）的分母是理论最大峰值 FLOPs，是与硬件有关的
- 硬件 FLOPs 表示硬件上每次迭代实际执行的浮点操作
  - 因此，如果实现需要激活重计算（例如论文的实现），那么硬件 FLOPs 将大于模型 FLOPs
  - 理解：因为增加了一些激活重计算的操作，这里的硬件主要强调的是实际计算量（包括激活重计算的操作量）
  - 注：硬件 FLOPs 利用率（HFU）的分母是也是理论最大峰值 FLOPs
- 论文在附录 A 中提供了模型和硬件 FLOPs 的严格下界公式
- 对于论文的方法，硬件 FLOPs 与模型 FLOPs 的比率约为 $ 1+\frac{s}{18h} $
随后，论文分别将模型和硬件每秒 FLOPs 定义为模型和硬件 FLOPs 除以迭代时间
- 使用这些定义，MFU 和 HFU 分别定义为模型和硬件每秒 FLOPs 除以加速器的理论峰值每秒 FLOPs
  $$
  \begin{align}
  MFU &= \frac{\text{observed throughput (tokens-per-second) }}{\text{theoretical peak FLOPs of device}} \\
  HFU &= \frac{\text{observed FLOPs}}{\text{theoretical peak FLOPs of device}}
  \end{align}
  $$
- 以上定义参考自：PaLM: Scaling Language Modeling with Pathways, 2022, Google
表 5 提供了所有四种配置的 MFU 和 HFU
- 随着模型规模的增加，论文实现了更好的 GPU 利用率，对于一万亿参数模型，论文分别达到了 $ 56.3\% $ 和 $ 57.0\% $ 的 MFU 和 HFU
虽然论文的分析中没有考虑初始化、评估、检查点等时间，但这些时间与迭代时间乘以迭代次数（这主导了端到端训练时间）相比可以忽略不计
- 用于训练大型语言模型的迭代次数根据训练目标而有很大差异
- 因此，作者认为论文报告的迭代时间（即吞吐量），包括了所有必要的操作，如数据加载和优化器步骤，是大型语言模型端到端训练时间的一个良好代理
- 论文还发现迭代时间在整个训练过程中是一致的，因此对吞吐量进行采样可以准确衡量预期结果
特别说明：表 5 中的结果没有使用任何数据并行
- 数据并行会由于数据并行组之间所需的梯度 all-reduce 而引入一些开销
- 但对于大型 Transformer 模型，这种开销并不大
  - 例如，如果论文将 530B 模型扩展到 8 路数据并行（2240 个 GPU），同时保持每个模型实例的批大小不变（即批大小也乘以数据并行大小）每次迭代的时间从 $ 37.83 $ 秒略微增加到 $ 39.15 $ 秒
  - 这导致 MFU 从 $ 56.0\% $ 下降到 $ 54.2\% $，下降幅度不大
- 论文注意到论文没有使用任何梯度 all-reduce 与反向传播的重叠，而高效的重叠几乎可以完全消除迭代时间的增加

Future Work

作者未来计划通过解决由大批次 (Large Microbatches) 导致的内存碎片化问题以及由 PP (Pipeline Parallelism) 导致的非均匀内存分配问题，来进一步减少激活内存
作者准备研究能够减轻流水线第一级 (First Stage of the Pipeline) 内存压力的方法

附录：论文补充材料

详情见论文补充材料：Supplementary Material of Megatron-LM-3

NLP——Megatron-LM原始论文解读-第二篇

注：本文包含 AI 辅助创作

参考链接：
- Megatron 系列目前公认的有三篇核心论文如下，它们分别对应了张量并行、3D 并行 与 序列并行/激活重计算优化 三大阶段，本文是第二篇的解读
- 第二篇：(Megatron-LM-2)Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM, SC 2021, NVIDIA
  - 核心贡献：提出 3D 并行（数据 + 张量 + 流水线），并给出 interleaved 1F1B 流水线调度，显著降低流水线气泡；在 3072 块 A100 上训练出 530 B 参数的 GPT-3 级模型，GPU 利用率达到 76 %

Paper Summary

整体说明：
- 本文是 Megatron-LM原始论文解读-第二篇
- 论文展示了如何将 PTD-P（节点间 PP、节点内 TP 和 DP ）组合起来，以在训练具有万亿参数的大模型时实现高聚合吞吐量
- 论文首次实现了端到端训练能够在合理的时间内完成（万亿参数模型的估计时间约为 3 个月）
- 论文通过分析讨论了与每种并行类型相关的各种权衡，以及在组合使用时需要仔细考虑它们之间的相互作用
- 论文中的很多思想是与加速器无关：
  - 1）智能地划分模型训练计算图以在保持设备活跃的同时最小化通信量的思想
  - 2）通过算子融合和仔细的数据布局来最小化内存受限的内核数量
  - 3）其他领域特定的优化（例如，散射-聚集优化）
背景 & 问题：
- 高效地训练 LLM 模型具有挑战性，原因在于：
  - 1）GPU 内存容量有限，使得即使是在多 GPU 服务器上也无法容纳大型模型；
  - 2）所需的计算操作数量可能导致不切实际的长训练时间
之前的工作：
- 之前已经提出了 TP （Tensor Parallelism, TP）和 PP （Pipeline Parallelism, PP），但这些方法的简单使用会在数千个 GPU 上导致扩展性问题
本文的核心方法贡献：
- 论文展示了如何组合使用 TP 、PP 和 DP （Data Parallelism, DP），以扩展到数千个 GPU
- 论文提出了一种新颖的交错流水线调度方法，在内存占用与现有方法相当的情况下，可以将吞吐量提高 10% 以上
特别亮眼的表现：论文的方法使得论文能够在 3072 个 GPU 上以 502 petaFLOP/s 的速度对具有 1 万亿参数的模型执行训练迭代（每 GPU 吞吐量达到理论峰值的 52%）
- 注意：这是在 2021 年实现的，而本文的方法已经是家喻户晓

Introduction and Discussion

NLP 中基于 Transformer 的语言模型近年来推动了快速进展，因为大规模计算变得更加可用且数据集变得更大
最近的工作 (2020) 表明，大语言模型是有效的零样本或少样本学习者，在许多 NLP 任务和数据集上具有高准确率
这些大语言模型有许多令人兴奋的下游应用，例如客户反馈摘要、自动对话生成、语义搜索和代码自动补全 (2021;)
最先进的 NLP 模型中的参数数量呈指数级增长（图 1）
训练此类模型具有挑战性，原因有二：
- (a) 即使使用最大的 GPU（NVIDIA 最近发布了 80GB A100 卡），也无法将这些模型的参数容纳在其主内存中；
- (b) 即使论文能够将模型装入单个 GPU（例如，通过在主机和设备内存之间交换参数 (2021)），所需的大量计算操作可能导致不切实际的长训练时间（例如，使用单个 NVIDIA V100 GPU 训练具有 175B 参数的 GPT-3 (2020) 将需要大约 288 年）
所以需要并行化， DP 扩展通常效果良好，但受到两个限制：
- a）超过某个点后，每 GPU 批大小变得太小，降低了 GPU 利用率并增加了通信成本；
- b）可使用的最大设备数量等于批大小，限制了可用于训练的加速器数量
为了应对这两个挑战，已经提出了各种模型并行技术
- 一些工作 (2019; 2020) 展示了如何使用张量（层内）模型并行（即将每个 Transformer 层内的矩阵乘法拆分到多个 GPU 上）来克服这些限制
- 尽管这种方法对于在 NVIDIA DGX A100 服务器（配备 8 个 80GB A100 GPU）上训练大小达 20B 参数的模型效果良好，但对于更大的模型则会失效
- 更大的模型需要拆分到多个多 GPU 服务器上，这会导致两个问题：
  - (a) TP 所需的全局归约（All-Reduce）通信需要通过服务器间链路进行，这些链路比多 GPU 服务器内可用的高带宽 NVLink (2020) 慢；
  - (b) 高度的模型并行可能会产生小的矩阵乘法（GEMM），可能降低 GPU 利用率
PP (2019; 2020; 2021) 是另一种支持训练大模型的技术，它将模型的层分布到多个 GPU 上
一个批次被分割成更小的微批次（microbatch），执行过程在这些微批次之间进行流水线化
- 层可以以各种方式分配（assigned）给工作节点，并且可以使用各种输入的前向传播和后向传播调度策略
- 层分配（layer assignment）和调度策略会导致不同的性能权衡
无论采用何种调度，为了保持严格的优化器语义，优化器步骤需要在设备间同步，这导致在每个批次结束时进行一次 流水线刷新（pipeline flush） ，此时允许微批次完成执行（并且不注入新的微批次）
- flushing the pipeline 可能会花费多达 50% 的时间（取决于注入流水线的微批次数量）
- 微批次数量与流水线规模（阶段数）的比率越大，花费在流水线刷新上的时间就越少
- 为了实现高效率，通常需要更大的批大小
- 在这项工作中，论文还引入了一种新的流水线调度方案，该方案提高了小批大小下的效率
这些技术可以组合使用，但组合这些技术会导致 non-trivial 的相互作用，需要仔细推理才能获得良好的性能
在论文中，论文解决了以下问题：
- 在给定批大小并保持严格优化器语义的前提下，应如何组合并行技术以最大化大模型的训练吞吐量？
具体来说，论文展示了如何组合 PP 、TP 和 DP，论文称之为 PTD-P（pipeline, tensor, and data parallelism）的技术，以在数千个 GPU 上以良好的计算性能（达到设备峰值吞吐量的 52%）训练大语言模型
论文的方法利用跨多 GPU 服务器的 PP 、多 GPU 服务器内的 TP 以及 DP 的组合，在实际中训练具有万亿参数的模型，并在具有服务器内和服务器间 GPU 高速链路的优化集群环境中实现优雅的扩展
给定更多的训练资源，也可以使用类似的思想来训练更大的模型
在论文的实验中，论文在一个具有万亿参数的 GPT 模型 (2020) 上，使用混合精度，展示了接近线性的扩展到 3072 个 A100 GPU，实现了每 GPU 163 teraFLOP/s 的端到端训练吞吐量（包括通信、数据处理和优化），以及 502 petaFLOP/s 的总吞吐量
- 这个吞吐量使得实际的训练时间成为可能：论文估计该模型的端到端训练大约需要 3 个月
作者相信这是针对该规模模型实现的最快训练吞吐量：过去的系统 (2019; 2020) 无法训练如此大的模型，因为它们没有结合 PP 和 TP
论文还将论文的方法与 ZeRO (2019) 进行了比较，发现由于跨节点通信更少，论文的方法对于 175B 和 530B 参数的模型比 ZeRO-3 性能高出 70%
- 这些模型太大，无法容纳在单个多 GPU 服务器上
在大规模下实现这种吞吐量需要在多个方面进行创新和精心的工程：
- 高效的内核实现使得大部分计算是计算受限而非内存受限的
- 在设备间智能划分计算图以减少通过网络链路发送的字节数同时限制设备空闲时间
- 领域特定的通信优化以及快速的硬件（最先进的 GPU 以及服务器内和服务器间的高速链路）
作者希望论文开源的软件（可在 github.com/nvidia/megatron-lm 获取）将使其他团队能够高效地大规模训练大型 NLP 模型
论文通过实验和尽可能的分析，研究了影响吞吐量的各个组件之间的相互作用
基于这些研究，论文提供以下关于如何配置分布式训练的指导原则 ：
- 不同形式的并行化以 non-trivial 的方式相互作用：
  - 并行化策略会影响通信量和内核执行的计算效率，还会影响工作节点上的气泡时间（因流水线刷新（气泡）所花费的空闲时间）
    - 例如，在论文的实验中，论文发现，即使服务器间有高带宽网络链路，次优的 TP 和 PP 组合也可能导致吞吐量降低多达 2 倍；
    - TP 在多 GPU 服务器内是有效的 ，但对于更大的模型必须使用 PP
- 用于 PP 的调度方案会影响通信量、流水线气泡大小以及用于存储激活值的内存
  - 论文提出了一种新颖的交错调度方案，与先前提出的调度方案 (2019; 2020) 相比，在内存占用相当的情况下，可以将吞吐量提高多达 10%
- 微批次大小等超参数的值会影响内存占用、工作节点上执行的内核的算术效率以及流水线气泡大小
  - 在论文的实验中，微批次大小的最优值是问题相关的，并且可以将吞吐量提高 15%
- 在大规模下，分布式训练是通信密集型的
  - 当在 3072 个 GPU 上训练一个万亿参数模型时，论文的实现用于 PP 通信的有效二分带宽为 892 GB/s，用于 DP 通信的有效二分带宽为 13 TB/s
  - 使用较慢的节点间互连或通信更密集的划分会阻碍扩展性能
论文不会自动探索并行策略的搜索空间（例如 FlexFlow (2018), PipeDream (2019), Tarnawski 等 (2020), 和 DAPPLE (2021)），而是提出论文在实践中发现效果很好的启发式方法（在章节3 中）

Models of Parallelism

论文关注单个 GPU 无法装下的大型模型进行高效训练的并行技术
论文将 PP (pipeline model parallelism) 和 TP (tensor model parallelism)（组合如图 2 所示）与 DP (data parallelism) 结合起来（论文将其简称为 PTD-P）

DP (Data Parallelism)

使用 DP (2021) 时，每个工作节点 (worker) 都拥有完整模型的一个副本，输入数据集被分片，工作节点定期聚合它们的梯度，以确保所有权重版本一致
对于无法放在单个工作节点上的大型模型，可以在较小的模型分片上使用 DP

PP (Pipeline Model Parallelism)

使用 PP 时，模型的层被分片到多个设备上
当用于具有重复相同 Transformer 块的模型时，可以为每个设备分配相同数量的 Transformer 层
论文不考虑更不对称的模型架构 ，因为将层分配给流水线阶段更为困难；论文将这个问题留给相关工作 (2021;) 来解决
一个批次 (batch) 被分割成更小的微批次 (microbatch)；然后跨微批次进行流水线执行
- 流水线方案需要确保输入在前向传播和后向传播中看到一致的权重版本，以获得明确定义的同步权重更新语义
具体来说，简单的流水线可能导致一个输入在后向传播中看到在前向传播中未见的权重更新
- 为了精确保持严格的优化器语义，论文引入了周期性的流水线刷新 (pipeline flush)，以便跨设备同步优化器步骤
- 在每个批次的开始和结束时，设备处于空闲状态，论文将此空闲时间称为流水线气泡 (pipeline bubble)，并希望使其尽可能小
诸如 PipeMare、PipeDream 和 PipeDream-2BW (2019; 2020; 2021) 之类的异步和有界陈旧度 (bounded-staleness) 方法完全取消了刷新，但放宽了权重更新语义
- 论文将对此类方案的考虑留待未来工作
有多种可能的方式来跨设备调度前向和后向微批次；每种方法在流水线气泡大小、通信量和内存占用之间提供了不同的权衡
论文将在本节讨论两种这样的方法

Default Schedule

GPipe 提出了一种调度方案，即首先执行一个批次中所有微批次的前向传播（如图 3 所示），然后是所有微批次的后向传播
我们可以量化 GPipe 的流水线气泡大小 ($t_{pb}$)
- 用一个批次中的微批次数量记为 $m$，流水线阶段数（用于 PP 的设备数量）记为 $p$，每次迭代的理想时间为 $t_{id}$（假设完美或理想缩放），执行单个微批次的前向和后向传播的时间记为 $t_{f}$ 和 $t_{b}$
- 在此调度中，流水线气泡包括批次开始时的 $p-1$ 次前向传播和批次结束时的 $p-1$ 次后向传播
  - 理解：图 3 中，对于 PP=4 的场景，即每个设备都要有 3 个完整的前向和后向传播气泡
- 花费在流水线气泡中的总时间为：
  $$t_{pb}=(p-1)\cdot(t_{f}+t_{b})$$
- 该批次的理想处理时间为：
  $$t_{id}=m\cdot(t_{f}+t_{b})$$
- 因此，理想计算时间中花费在流水线气泡中的比例为：
  $$\text{Bubble time fraction (pipeline bubble size)} =\frac{t_{pb} }{t_{id} }=\frac{p-1}{m}.$$
  - 理解：这里分母上算少了，分母上应该再加上分子才对
为了使气泡时间比例变小，一般需要 $m\gg p$，但对于如此大的 $m$，这种方法具有很高的内存占用，因为它需要在一次训练迭代的整个生命周期内，将所有 $m$ 个微批次的暂存中间激活值（或者在使用激活重计算时，仅为每个流水线阶段的输入激活值）保存在内存中
论文使用 PipeDream-Flush 调度 (2021)
- 论文首先进入一个预热阶段，工作节点执行不同数量的前向传播，如图 4（顶部）所示
  - 此调度将进行中的微批次（其后向传播尚未完成且需要维护激活值的微批次）的数量限制为流水线的深度，而不是一个批次中的微批次数量
- 预热阶段之后，每个工作节点进入稳定状态，每个工作节点执行一次前向传播，然后执行一次后向传播（简称 1F1B）
- 最后，在批次结束时，论文完成所有剩余进行中微批次的后向传播
- 这种新调度花费在气泡中的时间是相同的，但对于 PipeDream-Flush 调度，未完成的前向传播数量最多为流水线阶段数
- 因此，此调度需要为 $p$ 个或更少的微批次暂存激活值（相比之下，GPipe 调度需要为 $m$ 个微批次暂存）
- 因此，当 $m\gg p$ 时，PipeDream-Flush 比 GPipe 内存效率高得多

Schedule with Interleaved Stages

为了减小流水线气泡的大小，每个设备可以执行多个层子集（称为模型块, model chunk）的计算，而不是单个连续的层集
例如，如果之前每个设备有 4 层（即设备 1 有第 1-4 层，设备 2 有第 5-8 层，依此类推），我们可以让每个设备执行两个模型块（每个有 2 层）的计算，即设备 1 有第 1, 2, 9, 10 层；设备 2 有第 3, 4, 11, 12 层；依此类推
- 使用这种方案，流水线中的每个设备被分配多个流水线阶段（每个流水线阶段的计算量比之前少）
- 像之前一样，我们可以使用此调度方案的“全部前向，全部后向”版本，但这具有很高的内存占用（与 $m$ 成正比）
论文开发了一种交错调度 (interleaved schedule) ，它适配了之前的内存高效 1F1B 调度
- 这种新调度如图 4 所示，并要求一个批次中的微批次数量是 PP 度（流水线中的设备数量）的整数倍
- 例如，对于 4 个设备，一个批次中的微批次数量必须是 4 的倍数
如图 4 所示，相同批次大小的流水线刷新在新调度中发生得更早
- 如果每个设备有 $v$ 个阶段（或模型块），那么每个阶段或块的微批次的前向和后向时间现在将是 $t_{f}/v$ 和 $t_{b}/v$
因此，流水线气泡时间减少到
$$t_{pb}^{\text{int.} }=\frac{(p-1)\cdot(t_{f}+t_{b})}{v}$$
- 气泡时间比例则为：
  $$\text{Bubble time fraction (pipeline bubble size)} =\frac{t_{pb}^{\text{int.} } }{t_{id} }=\frac{1}{v}\cdot\frac{p-1}{m}.$$
这意味着新调度将气泡时间减少了 $v$ 倍
- 但这种减小的流水线气泡大小并非没有代价：此调度需要额外的通信
- 定量地说，通信量也增加了 $v$ 倍
在下一节中，论文将讨论如何利用多 GPU 服务器（例如 DGX A100 节点）中的 8 个 InfiniBand 网络卡来减少这种额外通信的影响

TP (Tensor Model Parallelism)

使用 TP 时，模型的各个层在多个设备上进行划分
在论文中，论文使用 Megatron (2019) 针对语言模型基础 Transformer 层所使用的特定划分策略
也可以将类似的思想应用于其他类型的模型，如 CNN
论文简要概述此策略，如图 5 所示
一个 Transformer 层由一个自注意力块 (self-attention block) 和一个两层的多层感知机 (MLP) 组成
MLP 块：MLP 块包含两个 GEMM（通用矩阵乘法，General Matrix Multiply）和一个 GeLU 非线性：
$$Y=\text{GeLU}(XA).\quad Z=\text{Dropout}(YB).$$
- 第一个权重矩阵 $A$ 按列划分，即 $A=[A_{1}, A_{2}]$
  - 这种划分允许将 GeLU 非线性独立应用于每个划分后 GEMM 的输出：
    $$[Y_{1},Y_{2}]=\left[\text{GeLU}(XA_{1}),\text{GeLU}(XA_{2})\right].$$
  - 这样做的好处是它消除了同步的需要（如果 $A$ 沿其行划分则需要同步，因为 GeLU 是非线性的）
- 第二个权重矩阵 $B$ 的按行划分，以消除 GEMM 之间的任何通信需要（如图 4(a) 所示），如下所示：
  $$B=\begin{bmatrix}B_{1}\ B_{2}\end{bmatrix}, Y=[Y_{1},Y_{2}].$$
- 第二个 GEMM 的输出然后在 Dropout 层之前跨 GPU 进行归约 (reduce)
自注意力块：利用多头注意力操作中固有的并行来划分自注意力块（如图 4(b) 所示）
- 键 ($K$)、查询 ($Q$) 和值 ($V$) 矩阵可以以列并行 (column-parallel) 的方式进行划分（每个设备上负责不同的注意力头，并行计算）
- 输出线性层然后可以直接在注意力操作的划分输出上运行（权重矩阵跨行划分，不需要 GPU 同步通信）
TP 将 MLP 和自注意力块中的 GEMM 拆分到多个 GPU 上，同时在前向传播中仅需要两次全归约 (All-Reduce) 操作（$g$ 运算符），在后向传播中需要两次全归约操作（$f$ 运算符）
论文用几行代码实现了 $f$ 和 $g$

Performance Analysis of Parallelization Configurations

考虑将 PP (pipeline parallelism) 和 TP (tensor model parallelism) 与 DP (data parallelism) 结合使用的性能影响
给定固定的 GPU 预算和批次大小 (batch size)，可以使用 PTD-P 中不同维度的并行类型来训练模型；
每个维度都在内存占用 (memory footprint)、设备利用率 (device utilization) 和通信量之间进行权衡
论文将在本节剩余部分讨论这些权衡，并在 5.4 节展示实证结果
- 论文在分析流水线气泡 (pipeline bubble) 大小时会提供分析模型
- 论文定性地描述通信时间的行为，并提供通信量的成本模型；但是，论文不提供通信时间的直接成本模型，因为对于层次化网络拓扑（同一服务器上 GPU 之间的互连带宽高于服务器之间的互连带宽）来说，通信时间更难建模
据论文所知，这是首个分析这些并行化维度性能交互作用的工作

Notation

论文在本节中使用以下符号表示：
- $ (p, t, d) $：并行化维度
  - $ p $ 表示 PP 大小 (pipeline-model-parallel size)，$ t $ 表示 TP 大小 (tensor-model-parallel size)，$ d $ 表示 DP 大小 (data-parallel size)
- $ n $：GPU 数量，论文要求 $ p \cdot t \cdot d = n $
- $ B $：全局批次大小 (global batch size)（作为输入提供）
- $ b $：微批次大小 (microbatch size)
- $ m = \frac{1}{b} \cdot \frac{B}{d} $：每个流水线 (per pipeline) 中一个批次内的微批次数量

TP 和 PP（Tensor and Pipeline Model Parallelism）

TP 和 PP 均可以用于在多个 GPU 对模型的参数进行分区
正如前文所述，使用带有周期性刷新（periodic flushes）的 PP 会产生下面大小的流水线气泡（pipeline bubble）：
$$\frac{p-1}{m}$$
假设 DP 规模 $d=1$（ DP 大小，data-parallel size），那么此时总 GPU 数量满足
$$ t \cdot p = n; \quad \text{s.t.} \ d=1 $$
基于 TP 规模 $t$ 的流水线气泡大小可表示为：
$$
\frac{p-1}{m} = \frac{n/t - 1}{m}
$$
- 说明：在固定批次大小 $B$、微批次大小 $b$ 以及固定 $d$（此时 $m = \frac{B}{b \cdot d}$ 也保持固定）的前提下，随着 TP 规模 $t$ 的增大，流水线气泡会逐渐减小
不同 GPU 之间的通信量同样会受到 PP 规模 $p$ 和 TP 规模 $t$ 的影响
- PP 的特点是点到点通信（point-to-point communication）成本更低；TP 则需要使用 All-Reduce communication
  - TP：正向传播（forward pass）需执行两次归约操作；反向传播（backward pass）也需执行两次归约操作（详见第2.3节）
- 在 PP 中，对于每个微批次，每对 PP 相邻设备之间需要执行的PP 通信总量为（一次点对点通信）：
  $$ bsh $$
  - 其中 $s$ 代表序列长度（sequence length），$h$ 代表隐藏层大小（hidden size）
  - 正向传播和反向传播各需要一次点对点通信，所以总共是 $$ 2bsh $$
- 在 TP 中，对于每个层，总大小为 $bsh$ 的张量需在 $t$ 个模型副本（model replicas）间，正向传播和反向传播各两次通信，这使得每个设备、每个微批次、每个层的 TP 通信总量为
  $$8bsh \cdot \frac{t-1}{t}$$
  - 理解：TP 参数通信量估计详情
    - MLP 正向和反向各需要一次 TP 通信（All-Reduce），一次 All-Reduce 通信是 $2\Phi_\text{TP} = 2bsh$（使用 Ring All-Reduce，一次通信使用 $2\Phi\frac{t-1}{t}$ 的通信量），单层模型上， MLP TP 累计通讯量是：
      $$ 4\Phi\frac{t-1}{t} = 4bsh\frac{t-1}{t} $$
    - Attention 部分正向和反向也各需要一次 TP 通信（All-Reduce），单层模型上，Attention TP 累计通讯量是：
      $$ 4\Phi\frac{t-1}{t} = 4bsh\frac{t-1}{t} $$
    - 注：上述通信量评估详情见：图解大模型训练之：张量模型并行(TP)，Megatron-LM - 猛猿的文章 - 知乎
- 通常每个设备会负责多个层的计算（TP 中，每个层都需要分别与其他设备交互），因此对于每个设备、每个微批次， TP 的总通信量可表示为
  $$l^{stage} \cdot (8bsh \cdot \frac{t-1}{t})$$
  - 其中 $l^{stage}$ 代表一个流水线阶段（pipeline stage）中包含的层数，即一个设备负责的层数
由此可见，TP 会增加设备间的通信量
- 因此，当 TP 规模 $t$ 大于单个节点（node）中的 GPU 数量时，跨节点链路（inter-node links）的传输速度较慢，此时在这类链路上执行 TP 的开销会变得难以承受
- 这一结果已在第5.4节的实验中得到验证
Takeaway #1 ：TP 不跨节点
- 对于使用每个节点 $g$ 个 GPU 的服务器时， TP 的规模通常应不超过 $g$；若要在多台服务器间扩展以训练更大的模型，则可使用 PP
- 理解：这里指的是单台机器的 GPU 数为 $g$，TP 规模 $t$ 大于 $g$ 时会导致跨节点的 TP 通信，开销难以接受

DP Data and Model Parallelism

注：这里的模型并行（Model Parallelism）包括了 PP（Pipeline Model Parallelism）和 TP（Tensor Model Parallelism）
论文还需要考虑 DP （data parallelism）与两种模型并行（ TP 和 PP ）之间的相互作用
- 为简化分析，本节将分别对这些相互作用进行讨论

PP （Pipeline Model Parallelism）

假设 TP 规模 $t=1$（tensor-model-parallel size），则每个流水线的微批次数量为
$$ m = \frac{B}{d \cdot b} = \frac{b’}{d}$$
- 其中：
  - $ b $ 是微批次大小 (microbatch size)
  - $b’ = \frac{B}{b}$ 表示每个 Global Step 的微批次数量；
- 注：每个流水线的微批次数量 $m$ 与 DP 大小 $d$ 成反比
在总 GPU 数量为 $n$ 的情况下，流水线阶段的数量为
$$ p = \frac{n}{(t \cdot d)} = \frac{n}{d} $$
此时流水线气泡大小可表示为：
$$
\frac{p-1}{m} = \frac{n/d - 1}{b’/d} = \frac{n - d}{b’}
$$
- 随着 DP 规模 $d$ 的增大，$n - d$ 会逐渐减小，因此流水线气泡也会随之变小
图6展示了在不同 $d$、$n$ 和 $b’$（批次大小与微批次大小的比值，$b’ = \frac{B}{b}$）下，流水线气泡大小的变化趋势
- 需要注意的是，并非所有模型都能将 $d$ 增大到 $n$，因为部分模型的完整训练内存占用（full training memory footprint）可能超过单个加速器（accelerator）的内存容量
若 DP 所需的归约通信量未随 $d$ 的增大而大幅增加，那么整体吞吐量（throughput）会随之提升
- 这一假设是成立的，因为基于环形实现（ring-based implementation，即 Ring All-Reduce）的通信时间与 $\frac{d-1}{d} = 1 - \frac{1}{d}$ 呈正相关
论文还可以分析批次大小 $B$ 增大带来的影响
- 在特定的并行配置下，随着批次大小 $B$ 的增加，$b’ = \frac{B}{b}$ 会增大，进而导致流水线气泡大小 $\frac{n - d}{b’}$ 减小，最终使吞吐量提升
- 此外，DP 所需的归约通信频率会随 $B$ 的增大而降低，这也会进一步提升吞吐量
  - 理解：这里是指相同的数据量和 epoch 下，$B$ 越大，需要更新的总步数越少？

DP Data and Tensor Model Parallelism

TP 中，每个微批次都需要执行归约通信，而跨多 GPU 服务器执行此类通信的成本较高
DP 仅需在每个批次执行一次高成本的归约通信
而且，在 TP 中，每个模型并行进程（model-parallel rank）仅负责模型每层计算中的一部分；
- 若层的规模不够大，现代 GPU 执行这些子矩阵（sub-matrix）计算时可能无法达到峰值效率（peak efficiency）
Takeaway #2 ：
- 在同时使用 DP 和模型并行时，应将模型并行的总规模设为
  $$M = t \cdot p$$
  - 其中 $t$ 为 TP 规模，$p$ 为 PP 规模，以确保模型的参数和中间元数据（intermediate metadata）能够放入 GPU 内存；
  - 问题：模型并行的总规模本来就是：$M = t \cdot p$ 吧，还需要什么特殊处理吗？
- 而 DP 则可用于扩展训练规模，以适配更多的 GPU

Microbatch Size

微批次大小 $ b $ 的选择也会影响模型训练吞吐量
例如，论文在图 7 中看到，在单个 GPU 上，使用较大的微批次大小，每 GPU 吞吐量最多可提高 1.3 倍
本节回答：确定给定并行配置 $ (p, t, d) $ 和批次大小 $ B $ 时，最优微批次大小 $ b $ 是多少呢？
无论微批次大小如何， DP 通信量将是相同的
给定函数 $ t_{f}(b) $ 和 $ t_{b}(b) $ 它们将微批次大小映射到单个微批次的前向和后向计算时间，则处理一个微批次的总计算时间（忽略通信成本）为（如前所述，定义 $ b’ $ 为 $ \frac{B}{d} $）：
$$ \left(\frac{b’}{b} + p - 1\right) \cdot \left(t_{f}(b) + t_{b}(b)\right). $$
- 因此，微批次大小既影响操作的算术强度 (arithmetic intensity)，也影响流水线气泡大小（通过影响 $ m $）
  - 理解：随着 microbatch size $b$ 增大，气泡占比变小，处理一个微批次的总时间减少，但总微批次数量增加
- 注：进一步分析总的时间为：
  $$ b \cdot \left(\frac{b’}{b} + p - 1\right) \cdot \left(t_{f}(b) + t_{b}(b)\right). $$
  - 显然，上述式子存在一个处于最大值和最小值中间的最优点（类似二次函数）
图 8 显示了一个具有十亿参数且 $ (p, t) = (8, 8) $ 的 GPT 模型的估计吞吐量（使用方程 (1) 估计处理时间）
- 对于两种批次大小，最优的 $ b $ 都是 4
Takeaway #3：
- 最优微批次大小 $ b $ 取决于模型的吞吐量和内存占用特性，以及流水线深度 $ p $、 DP 大小 $ d $ 和批次大小 $ B $

激活重计算，Activation Recomputation

激活重计算 (activation recomputation) (2016; 2000; 2019; 2020) 是一种可选技术，通过仅存储给定流水线阶段的输入激活，而不是存储整个中间激活集，后者要大得多，来权衡增加执行的计算操作数量以换取更少的内存占用
- 注：成本是后向传递之前需要按需再次运行前向传递
为了在可接受的低内存占用下训练合理的大模型，需要使用激活重计算
之前的工作如 PipeDream-2BW (2021) 已经研究了激活重计算的性能影响
- 激活检查点 (activation checkpoint) 的数量不影响吞吐量，但影响内存占用
- 设 $ A^{\text{input} } $ 为一层的输入激活大小，$ A^{\text{intermediate} } $ 为每层的中间激活大小
- 如果一个模型阶段有 $ l $ 层，并且有 $ c $ 个检查点，则总内存占用将为
  $$ c \cdot A^{\text{input} } + \frac{l}{c} \cdot A^{\text{intermediate} } $$
  - $\frac{l}{c} \cdot A^{\text{intermediate} }$ 为每个时刻在使用的激活大小
- 当 $ c = \sqrt{l \cdot (A^{\text{intermediate} }/A^{\text{input} })} $ 时，该函数取得最小值
- 在实践中，论文通过经验测量 $ A^{\text{intermediate} } $
- 在大多数情况下，每 1 或 2 个 Transformer 层设置一个检查点是最优的
其他技术，如激活分区 (activation partitioning) (2020)，也可以与 TP 结合使用，以进一步减少由激活引起的内存占用

Implementation

论文将 PTD-P 作为 Megatron-LM 代码库的一个扩展来实现
论文的实现基于 PyTorch (2017)
论文使用 NCCL (2018) 进行设备间的通信
为了获得良好的性能，论文实施了针对通信和计算的优化，下面将概述这些优化

Communication Optimizations

当使用 PP 时，作者希望并行地发送和接收前向和后向传播的张量
每个 DGX A100 节点配备了 8 个 InfiniBand (IB) 网络卡
- 不幸的是，发送和接收是点对点的，并且只发生在两个服务器上的一对 GPU 之间，这使得很难在流水线内的单个通信调用中利用所有 8 张卡
然而，我们可以利用同时使用 TP 和 PP 这一事实来降低跨节点通信的开销
特别地，论文注意到每个 Transformer 层的输出在 TP Rank 之间是复制的（在 MLP 块中的 $g$ 操作之后，见图 5(a)）
- 因此，在执行 TP 的两个连续流水线阶段中的 Rank ，会发送和接收完全相同的张量集合（图 5(a)）
对于足够大的模型，论文使用大小为 8 的 TP
- 这意味着论文在相邻的多 GPU 服务器上的对应 GPU 之间发送相同的张量集合 8 次
- 为了减少这种冗余，我们可以在发送端将张量分割成大小相等的块，然后只将一个块发送到下一个节点上的对应 Rank ，使用该 Rank 自己的 InfiniBand 卡（例如，在图 9 中， Rank 1 发送给 Rank 3， Rank 2 发送给 Rank 4）
对于 8 个 TP Rank ，每个块的大小将减小为原来的八分之一
然后，在接收端，我们可以通过 NVLink 执行一个 all-gather 操作（这比 InfiniBand 互连快得多）来重新构建完整的张量（如图 5(b) 所示）
论文称之为 分散/聚集通信优化 (scatter/gather communication optimization)
- 这种优化有助于更好地利用 DGX A100 服务器上的多个 IB 卡，并使诸如交错调度这样通信密集的调度变得可行
量化来看，通过分散-聚集通信优化，每对连续阶段之间需要执行的总通信量减少到 $\frac{bsh}{t}$，其中 $t$ 是 TP 大小，$s$ 是序列长度，$h$ 是隐藏层大小（在论文的实验中 $t=8$）

Computation Optimizations

论文对计算图实施了三个模型特定的优化以获得高性能
第一，论文改变了 Transformer 层中的数据布局，以避免内存密集的转置操作，并启用跨步批处理 GEMM 内核
- 具体来说，论文将数据布局从 $[b, s, a, h]$ 改为 $[s, b, a, h]$，其中 $b$、$s$、$a$ 和 $h$ 分别是批处理大小、序列长度、注意力头数和隐藏层大小的维度
第二，论文使用 PyTorch JIT (2016) 为一序列逐元素操作（偏置 + GeLU 以及偏置 + Dropout + 加法）生成了融合内核
第三，论文创建了两个自定义内核来实现缩放、掩码和 Softmax（归约）操作的融合：
- 一个支持通用掩码（用于如 BERT 的模型），另一个支持隐式因果掩码（用于如 GPT 的自回归模型）
论文将在下一节量化这些优化的效果

Evaluation

在本节中，论文试图回答以下问题：
- PTD-P 的性能如何？它是否能够满足现实的端到端训练时间？
- 对于给定的模型和批处理大小， PP 的扩展性如何？交错调度对性能有多大影响？
- 不同的并行化维度如何相互作用？微批处理大小等超参数的影响是什么？
- 分散-聚集通信优化的影响是什么？在规模上运行训练迭代时，论文对硬件施加了哪些类型的限制？
论文所有的结果都是在 Selene 超级计算机 (Selene, 2000) 上使用混合精度运行的
- 每个集群节点有 8 个 NVIDIA 80-GB A100 GPU (2018)，通过 NVLink 和 NVSwitch (2018) 相互连接
- 每个节点有八个 NVIDIA Mellanox 200Gbps HDR InfiniBand HCA 用于应用通信，另外每个节点还有两个 HCA 用于专用存储
- 节点通过具有 850 个交换机的三级（叶子、脊柱、核心）胖树拓扑连接
- 这种拓扑支持高效的 All-Reduce 通信（深度学习训练中的主导通信模式）
- 集群使用全 NVME 共享并行文件系统进行高性能数据访问和存储
一个具有 16 位精度的 A100 GPU 的峰值设备吞吐量为 312 teraFLOP/s
对于论文的大部分结果，论文报告每个 GPU 的吞吐量
总吞吐量可以通过乘以使用的 GPU 数量来计算
在论文的实验中，论文使用适当大小的 GPT 模型
- 特别地，对于任何给定的微基准测试，模型需要能够适应实验中使用的模型并行 GPU 的数量
- 适当的时候，论文使用标准的模型架构，如 GPT-3 (2016)

End-to-End Performance

论文考虑了论文的系统在参数量从十亿到一万亿的 GPT 模型上的端到端性能，使用了张量、流水线和 DP （使用第 3 节中描述的启发式方法选择维度）
特别地，论文使用了启用了分散/聚集优化的交错流水线调度
所有模型使用词汇表大小（表示为 $V$）为 51,200（1024 的倍数）和序列长度（表示为 $s$）为 2048
- 论文改变隐藏层大小（$h$）、注意力头数和层数（$l$）
- 模型中的参数量 $P$ 可以计算为：
  $$P=12lh^{2}\left(1+\frac{13}{12h}+\frac{V+s}{12lh}\right). \tag{2}$$
随着模型大小的增加，论文也增加批处理大小（$B$）和 GPU 的数量（$n$）
模型中大部分的浮点运算是在 Transformer 层和 logit 层中的矩阵乘法（GEMMs）中执行的
- 仅考虑这些 GEMMs，每次迭代的 FLOPs 数量为（更多细节见附录）：
  $$F=96Bslh^{2}\left(1+\frac{s}{6h}+\frac{V}{16lh}\right). \tag{3}$$
- 这是真实 FLOP 计数的下限，但应接近实际值
- 论文将 FLOP 计为浮点运算，无论精度如何
- 方程 (3) 假设了激活重计算，并考虑了与额外前向传播相关的浮点运算
表 1 显示了模型配置以及实现的 FLOP/s（包括每个 GPU 的和所有 GPU 的总和）
- 论文看到在 3072 个 A100 GPU（384 个 DGX A100 节点）上实现了超线性扩展，因为随着模型变大（更大的矩阵乘法），GPU 利用率提高，而通信时间相对于计算时间没有显著增加
- 吞吐量是针对端到端训练测量的，即包括所有操作，包括数据加载、优化器步骤、通信和日志记录
- 对于最大的模型，论文达到了峰值设备吞吐量的 52%，对于最小的模型，达到了峰值设备吞吐量的 44%

训练时间估算

给定这些吞吐量，论文还可以估算在 $T$ 个 Token 上进行端到端训练所需的总时间
- 训练需要 $I=\frac{T}{B\cdot s}$ 次迭代（$s$ 为序列长度）
- 使用方程 (3) 中的 $F$ 值和表 1 中的经验端到端吞吐量（表示为 X），我们可以估算总训练时间
- 对于表 1 中的配置，论文有 $12lh \gg (V+s)$ 和 $16lh \gg V$
将这些观察结果与方程 (2) 和 (3) 结合，论文得到：
$$\text{End-to-end training time}\approx\frac{8TP}{nX}.$$
- 其中：
  - $n$ 为 GPU 数量；
  - $X$ 为每个 GPU 的吞吐量；
  - $T$ 为 Token 数量
  - $P$ 为模型参数量
让论文以具有 $P=$ 175B 参数的 GPT-3 模型为例
- 该模型在 $T=3000$ 亿个 Token 上进行了训练
  - 在 $n=1024$ 个 A100 GPU 上使用批处理大小 1536，论文实现了每个 GPU $X=140$ teraFLOP/s 的吞吐量
  - 因此，训练该模型所需的时间为 34 天
- 对于 1 万亿参数模型，论文假设端到端训练需要 450B 个 Token
- 使用 3072 个 A100 GPU，我们可以实现每个 GPU 163 teraFLOP/s 的吞吐量，端到端训练时间为 84 天
- 作者认为这些训练时间（使用合理数量的 GPU）是可行的

Comparison to ZeRO-3

论文在表 2 和图 10 中将 PTD-P 与 ZeRO-3 (2020; 2021) 进行了比较（针对标准的 GPT-3 模型架构以及表 1 中的 530B 参数模型）
- 这些结果提供了一个与不使用模型并行的方法的对比点
- 论文使用 DeepSpeed Python 库 (2020) 将 ZeRO 集成到论文的代码库中
- 当论文增加 GPU 数量时，论文保持全局批处理大小不变
- 在 GPU 数量较少且微批处理大小为 4 的情况下，PTD-P 对于 175B 和 530B 参数模型的吞吐量分别高出 6% 和 24%
- 随着论文增加 GPU 数量，PTD-P 比单独使用 ZeRO-3 扩展得更优雅（见图 10）
  - 例如，通过将 GPU 数量加倍（保持批处理大小不变），由于跨节点通信更少，PTD-P 对两个模型的性能均优于 ZeRO-3 70%
- 论文只考虑了不使用 TP 的 ZeRO-3
- ZeRO-3 可以与模型并行结合，以潜在地改善其扩展行为

PP (Pipeline Parallelism)

论文现在单独评估 PP 的弱扩展性能，并将非交错调度与交错调度的性能进行比较

Weak Scaling

论文使用弱扩展设置、一个具有 128 个注意力头和隐藏层大小为 20480 的 GPT 模型以及微批处理大小为 1 来评估默认非交错 PP 调度的扩展性
随着论文增加流水线阶段的数量，论文也按比例增加模型中的层数来增加模型的大小
- 例如，当 PP 大小为 1 时，论文使用具有 3 个 Transformer 层和 15B 参数的模型，当 PP 大小为 8 时，论文使用具有 24 个 Transformer 层和 121B 参数的模型
论文对所有配置使用 TP 大小为 8，并改变使用的 A100 GPU 总数，从 8 到 64
图 11 显示了两种不同批处理大小下每个 GPU 的吞吐量，以说明流水线气泡的影响，其行为符合 $\frac{p-1}{m}$（第 2.2.1 节）
- 正如预期的那样，较高的批处理大小扩展性更好，因为流水线气泡被分摊到更多的微批处理上

Interleaved versus Non-Interleaved Schedule

图 12 显示了在具有 175B 参数（96 层，96 个注意力头，隐藏层大小为 12288）的 GPT-3 (2020) 模型上，交错和非交错调度每个 GPU 的吞吐量
- 带有分散/聚集通信优化的交错调度比非交错（默认）调度具有更高的计算性能
- 随着批处理大小的增加，这个差距会缩小，原因有二：
  - (a) 随着批处理大小的增加，默认调度中的气泡大小减小
  - (b) 流水线内的点对点通信量与批处理大小成正比，因此随着通信量的增加，非交错调度会赶上（交错调度每个样本的通信量更多）
- 在没有分散/聚集优化的情况下，默认调度在较大批处理大小下表现优于交错调度（未显示）

Comparison of Parallel Configurations

在本小节中，论文展示了结合不同并行化维度所带来的各种权衡
特别地，论文展示了对于给定模型和多个批处理大小，使用相同数量 GPU 的并行配置的性能

TP 与 PP (Tensor versus Pipeline Parallelism)

论文评估了对于给定模型和批处理大小，流水线和 TP 对性能的影响
图 13 中的实证结果显示了结合使用张量和 PP 来训练一个 161B 参数 GPT 模型（32 个 Transformer 层以支持 PP 大小为 32，128 个注意力头，隐藏层大小为 20480）的重要性，以实现低通信开销和高计算资源利用率
论文观察到
- TP 在一个节点（DGX A100 服务器）内效果最好，因为其 All-Reduce 通信开销大
- PP 使用成本低得多的点对点通信，可以在节点之间进行，而不会成为整个计算的瓶颈
- 使用 PP 时，可能会在流水线气泡中花费大量时间：
  - 因此，流水线阶段的总数应受到限制，使得流水线中的微批处理数量是流水线阶段数量的合理倍数
- 当 TP 大小等于单个节点中的 GPU 数量（对于 DGX A100 节点为 $8$）时，达到了峰值性能
这一结果表明，无论是单独使用 TP （由 Megatron (2019) 使用）还是单独使用 PP （由 PipeDream (2019) 和其他人使用），都无法与结合使用这两种技术的性能相媲美

PP 与 DP (Pipeline versus Data Parallelism)

论文在图 14 中评估了数据和 PP 对一个具有 59 亿参数（32 个 Transformer 层，32 个注意力头，隐藏层大小为 3840）的 GPT 模型性能的影响
论文使用比之前更小的模型，因为论文想展示当模型并行大小仅为 $2$ 时模型能够容纳的性能
为简单起见，论文在这些实验中保持微批处理大小等于 $1$
论文看到，对于每个批处理大小，吞吐量随着 PP 大小的增加而降低，这与论文在第 3.3 节中的分析模型相符
PP 应主要用于支持训练无法容纳在单个工作器上的大模型，而 DP 应用于扩展训练规模

TP 与 DP (Tensor versus Data Parallelism)

论文在图 15 中评估了数据和 TP 对同一个 59 亿参数 GPT 模型性能的影响（使用较小模型的原因同上）
如前所述，论文最初保持微批处理大小等于 $1$
在较大的批处理大小和微批处理大小为 1 的情况下， DP 通信不频繁；
TP 中所需的 all-to-all 通信需要对批次中的每个微批处理执行
这种 TP 的 all-to-all 通信主导了端到端训练时间，特别是当通信需要在多 GPU 节点之间执行时
随着 TP 大小的增加，论文在每个 GPU 上执行更小的矩阵乘法，降低了每个 GPU 的利用率
尽管 DP 可以导致高效的扩展，但不能单独使用 DP 来处理具有有限训练批处理大小的非常大的模型，原因是
- a）内存容量不足
- b） DP 的扩展限制
  - 例如，GPT-3 是以 1536 的批处理大小训练到收敛的
  - 因此， DP 仅支持扩展到 1536 个 GPU；然而，大约使用了 $10,000$ 个 GPU 来在合理的时间内训练该模型

Microbatch Size

论文在图 16 中评估了微批处理大小对结合流水线和 TP 的并行配置性能的影响（针对一个具有 91B 参数（$(t,p)=(8,8)$）的模型）
论文看到：
- 对于这个模型，最佳微批处理大小是 $2$；
- 对于其他模型，最佳微批处理大小是不同的（图中未显示）并且是模型依赖的
对于给定的批处理大小，
- 增加微批处理大小会减少流水线中的微批处理数量（$m$），导致更大的流水线气泡；
- 但增加微批处理大小也可以通过增加执行内核的算术强度来提高 GPU 利用率
- 以上这两个因素是相互矛盾的，这使得选择最佳微批处理大小具有挑战性
论文来自第 3.3 节的分析模型合理地近似了真实性能，并且可以作为代理来确定如何为各种训练配置和模型选择此超参数值

Activation Recomputation

图 17 显示了对于具有 145B 参数（80 个 Transformer 层，96 个注意力头，隐藏层大小为 12288）的 GPT 模型，在使用 128 个 A100 GPU、$(t,p)=(8,16)$ 以及一系列批处理大小的情况下，使用和不使用激活重计算的吞吐量
- 对于小批处理大小，由于在反向传播期间需要执行额外的前向传播，激活重计算导致吞吐量（以每秒序列数计）降低高达 33%
- 但激活重计算是支持更大批处理大小所必需的
由于流水线气泡更小，使用激活重计算的大批处理大小的吞吐量比不使用激活重计算（对于较小批处理大小）实现的最佳吞吐量高出 up to 2$\times$

Scatter-Gather Optimization

图 18 显示了对于具有 175B 参数的 GPT-3 模型，使用和不使用（未优化）分散/聚集通信优化时每个 GPU 的吞吐量
论文看到，通过减少跨节点链路上的通信量，对于通信密集的调度（大批处理大小带交错），吞吐量提高了 up to 11%

Fused Operators（融合操作）

论文还评估了第 4.2 节中描述的操作符融合对性能的影响
对于 GPT-3 模型（175B 参数），通过融合，吞吐量提高了 19%（从每个 GPU 113 teraFLOP/s 到每个 GPU 135 teraFLOP/s）
对于更大的 530B 参数 GPT 模型（图 1 中的模型配置），吞吐量提高了 11%（从每个 GPU 133 teraFLOP/s 到每个 GPU 148 teraFLOP/s）

Inter-Node Communication Bandwidth

论文强劲的结果是优化软件和硬件栈共同使用的副产品
特别地，论文利用了同一服务器内和跨服务器的 GPU 之间的高带宽通信链路
在具有 3072 个 GPU 的万亿参数模型上，论文观察到流水线阶段之间点对点通信的有效二分带宽为 892 GB/s，而 DP 副本之间 All-Reduce 操作的有效二分带宽为 12.9 TB/s
跨设备的操作符分区若优化不足，会导致更多的节点间通信，从而阻碍扩展性能

Checkpoint Loading and Saving

训练大模型的一个重要实际考虑是加载和保存模型检查点，对于论文中考虑的模型，检查点尤其大
例如，万亿参数模型的检查点大小为 13.8 TB
- 问题：如果仅考虑参数，换算后不太对，1000000000000*4/1000/1000/1000/1000 = 4 TB，若考虑激活值才会到 12 TB
所有 384 个节点（3072 个 GPU）对万亿参数模型的检查点初始加载达到了 1TB/s 的峰值读取带宽，这是并行文件系统可能的最大读取吞吐量
检查点保存达到了峰值写入带宽的 40%（273 GB/s）

Parallelism for Large Models

PP（Pipeline model parallelism）是一种用于训练大模型的常用技术
PP 有几种不同的模式：
- 论文讨论的模式使用流水线刷新（flush）来确保严格（strict）的优化器语义
- TeraPipe (2021) 为像 GPT 这样的自回归模型（auto-regressive models）在单个训练序列的 token 之间暴露了细粒度的 PP
- PipeTransformer (2021) 通过冻结具有“稳定”权重的层，弹性地调整 PP 和 DP 的程度，并将资源专用于训练剩余的“活跃”层
- HetPipe (2020) 在一组异构加速器上结合使用了流水线和 DP
- PP 也可以使用松弛的语义来实现：
  - PipeDream-2BW (2021) 维护两个权重版本，并保证权重更新延迟为 1，而无需昂贵的流水线刷新；
  - PipeMare (2021) 和 Kosson 等人 (2021) 使用异步 PP
- 与论文考虑的带有流水线刷新的技术相比，这些技术提高了吞吐量，但可能以收敛速度或最终精度为代价
- 此外，单独的 PP 仍然只能扩展到与模型中层数相等数量的设备，这对于某些模型架构来说是有限的
PipeDream (2019) 以一种原则性的方式结合了 PP 和 DP ，以减少跨设备通信
- DeepSpeed (2021) 将 PP 与 TP 和 DP 结合起来，以训练高达万亿参数规模的模型，但吞吐量低于论文所示的结果（峰值利用率的 52% 对比 36%），原因有几个：
  - 通过算子融合使大部分算子图保持计算受限（compute-bound）、使用更高效的 PP 调度以最小化流水线气泡（pipeline bubble）大小、快速的硬件（A100 与 V100 GPU 以及同一服务器内和不同服务器间 GPU 的高带宽链路）以及扩展到更多 GPU 的能力
- 作者希望强调，这种更高的吞吐量使得估计的训练时间更加实用（约 3 个月）；37.6 petaFLOP/s 的总吞吐量将需要大约 40 个月来训练一个同等规模的模型
  - 也可以扩展到更大的模型，但需要更多的 GPU 来保持训练时间的实用性
Mesh-TensorFlow (2018) 提出了一种语言，用于轻松指定结合数据和模型并行的并行化策略
- Switch Transformers (2021) 使用 Mesh-Tensorflow 训练了一个具有 1.6 万亿参数的稀疏激活（sparsely activated）的基于专家（expert-based）的模型，其预训练速度比 T5-11B 模型 (2019) 有所提高

Sharded Data Parallelism（分片 DP）

作为 MLPerf 0.6 (2019) 性能优化的一部分，引入了分片 DP （sharded data parallelism）(2019, 2020)，其中优化器状态（optimizer state）在 DP 工作节点（data-parallel workers）上进行分片
这种方法有两个优点：
- (a) 它不会在原始 DP （vanilla data parallelism）的基础上引入额外的通信；
- (b) 它将优化器的计算和内存成本分摊到 DP 分区中
ZeRO (2019, 2021) 扩展了这个思想：
- 权重参数和梯度也在 DP 工作节点上进行分片，工作节点在执行计算前从其“拥有”相应状态的工作节点获取相关状态
  - 这增加了额外的通信，但可以通过仔细重叠计算和通信来部分隐藏
  - 但如果不使用 TP 或者批大小不够大以隐藏额外的通信开销，这会变得困难（图 10）
ZeRO-Infinity (2021) 使用 NVMe 来高效地交换参数，使得能够在少量 GPU 上训练非常大的模型
论文注意到，使用少量 GPU 训练非常大的模型会导致不切实际训练时间（例如，收敛需要数千年）

Automatic Partitioning（自动分区）

FlexFlow (2018)、PipeDream (2019)、DAPPLE (2021) 和 Tarnawski 等人 (2020) 都借助成本模型（cost models）在多个设备上自动分区模型训练图
然而，这些方法都没有考虑论文考虑的所有并行维度：流水线和 TP、DP、微批大小（microbatch size）、以及像激活重计算（activation recomputation）这样的内存节省优化对训练大于加速器内存容量的模型的影响
这些增加的维度扩大了需要探索的搜索空间
Gholami 等人 (2018) 展示了如何对数据和模型并行组合的通信成本进行建模

高性能计算（HPC for Model Training）

Goyal 等人 (2017) 和 You 等人 (2018) 都展示了使用高性能计算（High Performance Computing, HPC）技术在几分钟内训练高精度 ImageNet 模型
但所考虑的图像分类模型可以轻松地放在单个加速器上，使得模型并行变得不必要；
它们支持非常大的批大小（$>32k$），允许将 DP 扩展到大量工作节点，且通信不频繁；
- 并且它们由紧凑的卷积层组成，这些层本身就很适合 DP 通信

NLP——AReaL

注：本文包含 AI 辅助创作

参考链接：
- 原始论文：(AReaL)AREAL: A Large-Scale Asynchronous Reinforcement Learning System for Language Reasoning, arXiv 20250604, THU & Ant Research & HKUST：蚂蚁研究院和港科大也参与了
- 开源地址：github.com/inclusionAI/AReaL/

Paper Summary

核心内容总结：
- 论文提出了是一个专为高效大规模 RL 训练设计的完全异步（fully asynchronous ）系统 AReaL
- 论文还提出了多项算法创新，包括陈旧感知训练和解耦 PPO 目标 ，使异步环境中的 PPO 训练既高效又稳定
背景：RL 已成为训练 LLM 的一种流行范式，尤其在推理任务中，有效的 LLM 强化学习需要大规模并行化，因此亟需高效的训练系统
现有的大规模 RL 系统多为同步（synchronous）设计，即在批量设置中交替进行生成和训练，每个训练批次的样本由同一（或最新）模型生成 ，这种设计的优缺点如下：
- 优点：稳定
- 缺点：存在严重的系统效率问题，即生成阶段必须等待批次中最长的输出完成后才能更新模型，导致 GPU 利用率低下
论文提出 AReaL ，一种完全异步的 RL 系统 ，彻底解耦生成与训练
- AReaL 的 Rollout Worker无需等待即可持续生成新输出
- 训练 Worker （training worker）在收集到足够数据后立即更新模型
AReaL 还引入了一系列系统级优化，显著提高了 GPU 利用率
- 为稳定 RL 训练，AReaL 通过平衡生成与训练 Worker 的负载控制数据陈旧性（staleness），并采用一种改进的 PPO（Proximal Policy Optimization）变体以更好地处理过时样本
实验结论：在数学和代码推理基准测试中，AReaL 相比同步系统实现了高达 2.77 倍的训练加速，同时保持甚至提升了最终性能

Introduction and Discussion

RL 作为一种新的扩展范式，通过赋予 LLM 思考能力（thinking abilities）来增强其性能 (2022)
- 给定一个提示（prompt），RL 允许 LLM 在输出最终答案前生成思考 Token（thinking tokens），从而实现测试时扩展（test-time scaling）(2024; 2025)
- 这类具备思考能力的 LLM 被称为大型推理模型（Large Reasoning Model, LRM） ，在 challenging reasoning problems 上表现出色
  - 即数学 (2021; 2021; 2023)、编程 (2021; 2023; 2023)、逻辑谜题（logic puzzles） (2025) 和智能体任务（agentic tasks） (2024) 等
有效的 RL 训练通常需要大规模并行化，以获取足够探索的大批量生成样本（rollouts），这是实现最优模型性能的关键
- 例如，PPO (2017) 和 GRPO (2024) 等流行 RL 算法通常需要数千个输出的有效训练批次 (2025; 2025; 2025)
- 此外，LRM 可能为每个输入提示生成数万个思考 Token (2025)，这进一步凸显了对高效训练系统的迫切需求
开发高效的大规模 RL 系统具有挑战性，表现在：
- RL 系统需要频繁切换 LLM 生成与训练，若缺乏精心优化，会引入显著的系统开销
- 对于 LRM，训练模型的输出长度因提示不同而变化巨大，导致生成和训练的工作负载不断变化，常引发高性能硬件的空闲时间，造成计算浪费
- 经典的大规模 RL 算法（如 PPO 或 GRPO）通常需要 on-policy 训练数据（即由最新模型生成的样本）以确保最佳性能，这带来了额外的系统挑战
  - 理解：on-policy 限制了最新模型生成的样本，导致效率进一步降低
基于以上原因，现有的大多数大规模 RL 系统采用完全同步设计 (2024; 2024; 2025; 2025)，严格交替执行 LLM 生成与训练，确保模型始终基于最新输出进行训练以获得最佳性能
- 在这种同步设计中，生成阶段必须等待批次中最长的输出完成后才能开始训练
- 由于 LRM 的输出长度变化较大，同步 RL 系统会遭受严重的训练效率损失
最近，也有研究尝试并行生成与训练 (2025; 2024; 2025)，这些工作使用先前模型版本生成的输出来更新当前模型
- 为保障性能，生成所用的模型版本仅允许比当前模型早一到两步
- 然而，这些系统仍 Following 批量生成设置，即一个训练批次内的所有样本来自同一模型版本，因此生成阶段的系统效率问题仍未解决
为从根本上解决系统设计问题，论文开发了 AReaL，一种完全异步的 LRM RL 训练系统 ，彻底解耦生成与训练且不影响最终性能
- AReaL 以流式方式（streaming manner）运行 LLM 生成，每个 Rollout Worker 无需等待即可持续生成新输出，从而实现高 GPU 利用率
- AReaL 的训练 Worker 在从 Rollout Worker 收集到训练批次后立即并行更新模型
  - 模型更新后，系统会同步各 Rollout Worker 的模型权重
- 在这种异步设计中，AReaL 的每个训练批次可能包含来自不同模型版本的样本
  - 因此，AReaL 结合了改进的 PPO 目标函数，能够利用更旧模型版本生成的样本且不会降低性能
- AReaL 还通过数据过滤过程（data filtering process）确保每个训练样本的陈旧性（staleness）得到控制
- AReaL 还引入了多项系统级优化，进一步提升了整体训练吞吐量，包括：
  - 可中断的 Rollout Worker（interruptible rollout workers）
  - 可变长度输出的动态批处理（dynamic batching for variable-length outputs）
  - 并行奖励服务（parallel reward service）
论文在 32B 参数的模型上对 AReaL 进行了数学推理和代码生成任务的评估
- 相比 SOTA 同步系统（synchronous systems），AReaL 实现了高达 2.57 倍的训练吞吐量提升，并在 512 个 GPU 上展现出线性扩展效率
- 特别说明：不止加速，还带来了任务求解准确率的提升 ，表明 AReaL 在显著提高效率的同时并未牺牲模型性能（甚至增强了模型性能）

Background

Preliminaries about RL Training

RL Formulation and PPO

论文将问题形式化为马尔可夫决策过程（Markov Decision Process, MDP）(1994)
- 定义为元组 $ \langle \mathcal{S}, \mathcal{A}, r, P, \gamma, H \rangle $
  - 其中，$ \mathcal{S} $ 表示状态空间，$ \mathcal{A} $ 表示动作空间，$ P $ 是转移模型，$ r: \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R} $ 是奖励函数，$ \gamma $ 是折扣因子，$ H $ 是时间范围
- LRM（Large Reasoning Model）实现了一个参数化策略 $ \pi_{\theta}: \mathcal{S} \rightarrow \mathcal{A} $，每个动作 $ a_t \in \mathcal{A} $ 对应词汇表中的一个文本标记
- 状态 $ s_t \in \mathcal{S} $ 由问题 $ s_1 = q $ 和之前生成的响应标记 $ (a_1, \ldots, a_{t-1}) $ 组成
- 转移是确定性的：$ s_{t+1} = \text{concat}(s_t, a_t) $
- 给定问题分布 $ \mathcal{D} $，论文优化以下目标：
  $$
  J(\theta) = \mathbb{E}_{q \sim \mathcal{D}, a_t \sim \pi_{\theta}(\cdot|q, a_{ < t})} \left[ \sum_{t=1}^{H} \gamma^{t-1} r(s_t, a_t) \right]. \tag{1}
  $$
Following 常见实践 (2025)，论文使用基于规则的奖励函数 ，仅在最终动作提供非零反馈（表示答案正确性），并设 $ \gamma = 1 $。论文使用近端策略优化（Proximal Policy Optimization, PPO）(2017) 来优化这一目标：
$$
J_{\text{PPO} }(\theta) = \mathbb{E}_{q \sim \mathcal{D}, a_t \sim \pi_{\text{old} }(\cdot|q, a_{ < t})} \left[ \sum_{t=1}^{H} \min \left( u_t(\theta) \hat{A}(s_t, a_t), \text{clip} \left( u_t(\theta), 1-\epsilon, 1+\epsilon \right) \hat{A}(s_t, a_t) \right) \right], \tag{2}
$$
- $ u_t(\theta) = \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\text{old} }(a_t|s_t)} $ 表示重要性比率（importance ratio）
- $ \hat{A}(s_t, a_t) $ 是估计的优势函数 (2016)
Following RL 的标准实践 (2017, 2022)，论文将全局批次划分为小批次以进行顺序参数更新（sequential parameter updates）

Distributed Systems for LRM Training

论文的工作专注于在 SFT 后增强 LRM 的推理能力，不同于激励（incentivize）预训练基模型推理的方法 (2025)
经过 SFT 的 LRM 生成长推理序列（例如 32K 标记），通常需要较大的全局批大小（例如每个问题 128 个响应）以实现稳定的 RL 训练 (2025, 2024)
在同步 RL 系统中，两个阶段交替执行：生成（ rollout）和训练
- 生成阶段使用最新的模型参数为训练批次中的每个查询生成多个推理轨迹
- 训练阶段则基于生成的轨迹更新模型参数
- 这些阶段在同一 GPU 上迭代执行

Motivation for Asynchronous RL System

论文总结了同步 RL 系统的两个主要局限性：
- 1） 推理设备利用率低（Inference devices are underutilized） ：
  - 如图 1（左）所示，生成必须等待批次中最长序列完成后才能开始训练
  - 这导致 GPU 解码长度不均匀，从而浪费计算资源
- 2） 同步 RL 系统的可扩展性差（Scalability is poor in synchronous RL systems） ：
  - 同步系统在所有设备上分配生成任务，降低了每 GPU 的解码批大小，使解码过程进入 memory-IO-bound 状态 (2024)，此时增加设备无法提高吞吐量

System Architecture

3.2节中提到的局限性促使论文设计一个将生成（generation）和训练（training）完全解耦的系统 ，使其具备硬件高效性、可扩展性 ，并支持定制化的 RL 工作流
论文在 AReaL 中实现了这些原则，这是一个专为高效大规模 LRM 训练设计的异步 RL 系统

System Overview

图2 展示了 AReaL 的架构和数据流
如图2 所示，AReaL系统包含4个核心组件：
可中断的 Rollout Worker（Interruptible Rollout Worker） 处理两种请求：
- 1） generate request ：根据提示生成响应
- 2） 权重更新请求（update_weights request） ：中断所有正在进行的生成任务，并加载新版本的参数
  - 中断后， Rollout Worker 会丢弃由旧权重计算的 KV 缓存，并使用新权重重新计算
    - 理解：注意这里没有抛弃之前已经生成的片段（已经生成的 token 会保留，只是从中断点开始使用新的权重（包括 KV 缓存也抛弃））
  - 之后， Rollout Worker 继续解码未完成的序列，直到下一次中断或终止
  - 需要注意的是，这种中断和权重更新会导致轨迹由不同模型版本生成的片段组成 ，这将带来新的算法挑战（详见第5节）
Reward Service 评估模型生成响应的准确性
- 例如，在编码任务中，该服务会提取代码并执行单元测试以验证其正确性
Trainer Workers
- 持续从回放缓冲区（replay buffer）中采样数据 ，直到达到配置的训练批次大小
- 执行 PPO 更新 ，并将结果参数存储在分布式存储中
- 为确保数据新鲜度，回放缓冲区中的数据仅使用一次
Rollout Controller 承担以上三者（ Rollout Worker、奖励服务和训练 Worker）之间的桥梁的角色，在训练过程如下：
- Step1（生成响应 by Rollout Worker）：控制器从数据集中读取数据并调用 Rollout Worker 的生成请求，获取生成
- Step2（生成奖励 by 奖励服务器）：控制器将生成的响应发送给奖励服务，奖励服务返回奖励给控制器
- Step3（储存缓冲区 for 训练 Worker）：轨迹和奖励一起存入回放缓冲区，等待训练 Worker 处理
- Step4（训练 Worker 参数更新）：当训练 Worker 更新参数后，控制器会调用 Rollout Worker 的权重更新请求
图3 展示了生成和训练的管理流程。这种异步流水线设计确保了生成和训练资源的持续高效利用

Algorithmic Challenges

异步系统设计虽然通过提高设备利用率显著加速了训练，但也引入了需要算法解决的技术挑战
挑战1：数据陈旧性（Data Staleness）
- 由于AReaL的异步特性，每个训练批次包含来自多个先前策略版本的数据
- 已有研究表明，这种陈旧性会降低 RLHF 和游戏环境中的学习性能 (2024; 2019)
- 在 LRM 的异步强化学习训练中，由于解码时间较长，这一问题可能更加严重
挑战2：策略版本不一致（Inconsistent Policy Versions）
- 如第4.1节所述，生成的轨迹可能包含由不同策略版本生成的片段
- 这种不一致性从根本上违背了标准 PPO 的假设（公式2），即所有动作均由单一策略 $\pi_{\text{old} }$ 生成
- 理解：注意这里是同一个轨迹中的不同片段可能是不同策略采样得到的
在下一节中，论文将详细介绍克服这些挑战的技术创新，同时保留异步系统的效率优势

Addressing the Algorithmic Challenges in AReaL

Staleness-Aware Training

为避免因训练数据过于陈旧而导致性能下降，论文引入了一个超参数 $\eta$，表示 每个训练批次中允许的最大陈旧性
- 具体来说，当 $\eta=0$ 时，系统退化为同步强化学习，所有训练样本均由当前策略生成
- 论文在系统中通过动态控制生成请求的吞吐量来实现陈旧性控制
- 给定当前策略版本 $i$、生成的轨迹总数 $N_r$ 和每个训练步骤的训练批次大小 $B$，论文在提交新生成请求时强制执行以下公式：
  $$
  \lfloor(N_r - 1)/B \rfloor \leq i + \eta. \tag{3}
  $$
- 理解：这也不能完全解决问题吧，只能是缓解问题？而且需要考虑数据的采样策略，从而计算重要性权重
论文还优先从数据缓冲区中选择较旧的轨迹组成训练批次
- 在系统实现中，生成控制器跟踪参数服务器中的生成样本数 $N_r$ 和策略版本 $i$，并拒绝可能违反陈旧性约束的新生成请求
- 问题：为什么是优先选择旧的，因为每个数据仅使用一次；
- 思考：优先使用旧的会导致模型总是使用不到最新的策略生成的样本吧
需要注意的是，这种速率限制协议在实践中是一种简单而有效的设计选择
- 但是，当 $\eta$ 过小时，生成吞吐量可能会因某些极长轨迹的生成而降低
- 因此，论文建议在实践中采用较大的 $\eta$ 值以获得最佳系统吞吐量
- 这一系统级实践也促使论文采用一种增强算法，能够有效利用更陈旧的数据进行强化学习训练

Decoupled PPO Objective

论文采用了一种解耦的 PPO 目标 (2022)，将 行为策略（behavior policy） $\pi_{\text{behav} }$ 和 近端策略（proximal policy） $\pi_{\text{prox} }$ 分离
- 行为策略 用于采样轨迹
- 近端策略 作为最近的目标（用于正则化策略 $\pi_\theta$ 的更新）
- 通过对采样轨迹应用重要性采样，论文推导出适用于异步强化学习训练的解耦 PPO 目标：
  $$
  \begin{align}
  J(\theta) &= \mathbb{E}_{q \sim \mathcal{D}, a_t \sim \pi_{\text{behav} } } \left[ \sum_{t=1}^H \min \left( \underbrace{\color{red}{\frac{\pi_\theta}{\pi_{\text{behav} } }}}_{\text{Importance Ratio} } \hat{A}_t, \overbrace{\color{red}{\frac{\pi_{\text{prox} } }{\pi_{\text{behav} } }} \text{clip} \left( \underbrace{\color{red}{\frac{\pi_\theta}{\pi_{\text{prox} } }}}_{T_{\text{Trust Region Center} } } , 1-\epsilon, 1+\epsilon \right)}^{\text{Importance Ratio} } \hat{A}_t \right) \right] \tag{4} \\
  &= \mathbb{E}_{q \sim \mathcal{D}, a_t \sim \pi_\text{behav} } \left[ \sum_{t=1}^H \color{red}{\frac{\pi_{\text{prox} } }{\pi_{\text{behav} } }} \min \left( \color{red}{u^{\text{prox} }_t(\theta)} \hat{A}_t, \text{clip}(\color{red}{u^{\text{prox} }_t(\theta)}, 1-\epsilon, 1+\epsilon) \hat{A}_t \right) \right], \tag{5}
  \end{align}
  $$
  - 其中 $\color{red}{u^{\text{prox} }_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\text{prox} }(a_t|s_t)}}$ 是相对于近端策略的重要性比率
  - 为简洁起见，论文省略了状态-动作项（state-action terms）
  - 理解：重要性采样还是针对了行为策略的，这本身没有问题，$\min$ 操作的第二项中，本质是通过增加一个中间概率 $\pi_\text{prox}$ 实现了重要性采样比值
    $$ \color{red}{\frac{\pi_\theta}{\pi_{\text{behav} } } = \frac{\pi_{\text{prox} } }{\pi_{\text{behav} } } \cdot \frac{\pi_\theta}{\pi_{\text{prox} } }}$$
异步 PPO 目标（公式5）与标准 PPO 目标（公式2）的主要区别在于用于正则化模型更新的近端策略 $\pi_{\text{prox} }$
- 在异步 PPO 训练中，使用行为策略作为近端策略会将最新策略 $\pi_\theta$ 拉向旧版本和低质量策略，从而减缓模型改进
- 通过采用最近的策略作为近端策略 ，模型更新发生在高质量近端策略 $\pi_{\text{prox} }$ 的信任区域内，从而稳定训练
公式5 中的解耦 PPO 目标具有一个天然优势：它放宽了训练批次中所有数据必须由单一策略生成的要求
- 这一特性在将可中断生成与策略更新结合时，对保持算法正确性至关重要
论文提出以下命题：命题1（Proposition 1） ：
- 对于由策略序列 $(\pi_\theta, \ldots, \pi_{\theta+k})$ 生成的任何序列 $(q, a_1, \ldots, a_H)$，其中 $\pi_{\theta+i}$ 生成 Token $(a_{t_i}, \ldots, a_{t_{i+1} })$，且 $1 = t_0 < \cdots < t_{k+1} = H$，存在一个行为策略 $\pi_{\text{behav} }$，使得中断生成等效于完全从 $\pi_{\text{behav} }$ 采样
- 问题：实际代码中，如何得到行为策略 $\pi_{\text{behav} }$？需要存储每次采样时的策略或推理 logits 吧！
实践经验 ：
- 虽然 Hilton 等人 (2022) 采用参数的指数移动平均作为 $\pi_{\text{prox} }$，但这种方法对 LRM 来说计算成本过高
- 因此，论文简单地使用每次模型更新前的参数作为 $\pi_{\text{prox} }$
- 公式5 通过在每次训练步骤中重新计算 Token 概率来实现

Implementation

论文基于 Real_HF 框架 (2024)，使用 Python 和 PyTorch (2019) 实现了 AReaL
论文的系统设计到以下框架：
- SGLang (2024) v0.4.6（用于生成服务）
- Megatron-Core (2019) v0.11.0（作为训练后端）
- 通过 SLURM (2003) 进行资源调度
为了最大化生成和训练阶段的吞吐量，论文实现了多项关键的系统级优化，解决了流水线中的瓶颈问题
AReaL 将 GPU 计算与 CPU 操作（如基于规则的奖励计算和基于 TCP 的数据传输）解耦
通过在单独线程中执行这些操作并将工作流流水线化，论文将奖励计算和数据传输与后续生成请求重叠
论文使用 asyncio 协程在 Rollout Worker 中并发运行多个请求，以避免相互阻塞等待
为了处理可变长度序列的训练，论文采用了一种无填充的序列打包策略，并结合动态分配算法（见算法1）
- 该算法在固定内存约束下平衡微批次间的 Token 分布，最大化 GPU 内存利用率，同时最小化所需的前向-反向传播次数

Experiments

论文的评估包含三个部分：
- (1) 在不同模型规模下与最先进的开源框架进行全面对比；
- (2) 在不同计算资源下的强扩展性分析；
- (3) 通过消融实验验证论文的设计选择

Experiment Setup

论文在具有挑战性的数学和代码任务上评估 AReaL
论文使用来自 DeepSeek-R1 (2025) 的蒸馏 Qwen2 模型系列（即 R1-Distilled-Qwen）作为基础模型，参数规模从 1.5B 到 32B
对于每个任务-模型组合，论文固定 PPO 更新次数进行训练，并评估最终检查点
数学任务的评估 Following Qwen 评估协议 (2024; 2024)，而代码模型则在 LiveCodeBench (2025) 上使用官方协议进行评估
除非另有说明，否则代码任务的最大陈旧度 $\eta$ 设为 4，数学任务设为 8，并采用 7.2 节中的训练配置，其他超参数详见附录 A
实验在配备 64 个节点（每个节点 8 块 H800 GPU）的集群上进行
- 集群通过 NVLink 实现节点内连接，通过 RoCE（带宽 3.2Tbps）实现节点间通信
- 为确保快速收敛，论文为完整实验分配至少 16 个节点作为基准配置
- 模型规模增大时，论文按比例扩展节点数量，最终使用 48 个节点训练最大的 32B 参数模型
- 这种扩展策略使论文能够在保持高效资源利用的同时并行运行不同规模的实验
对于 AReaL，论文保持推理设备与训练设备的固定比例，将四分之三的设备分配给推理
- 这一配置是基于早期实验中 75-25 分配方案显示出更高训练吞吐量而选择的
- 尽管论文采用这一启发式配置，但最佳分配比例可能因不同设置而异，甚至可能受益于训练期间的动态调整，如第 8 节所述

End-to-End Comparison

论文使用同步 RL 系统建立了两个最先进的基线：
- 针对 1.5B 模型数学推理任务的 DeepScaleR (2025)
- 针对 14B 模型代码生成任务的 DeepCoder (2024)
- 两者均使用 verl (2025) 进行训练
对于更大的 7B 和 32B 模型，由于缺乏可比基线，论文使用 AReaL 的同步变体从头开始训练
- 训练完成后，数学模型在 AIME24 基准上评估，代码模型在 LiveCodeBench (2025) 基准上评估
- 其他基准的评估结果见附录 B
表 1 展示了主要结果
- 由于之前 SOTA 模型的代码可能过时，论文使用最新 verl 代码测量吞吐量并估算训练时长以确保公平对比
- AReaL 在性能不降的前提下，显著加速训练，端到端训练时间相比同步系统最多减少 $2.77 \times$

Scalability

论文比较了 AReaL 与最先进的同步 RL 系统 verl (2025) 在不同模型规模和上下文长度下的扩展性
对于 7B 模型和 32k 上下文长度，论文选择 verl 不出现 OOM 问题时的最小 GPU 数量，然后根据模型规模按比例调整 GPU 数量
论文测量训练的有效吞吐量，定义为 PPO 更新期间消耗生成 token 的速率（经过适当预热步骤后）
图 4 展示了 16k 和 32k 上下文长度的结果。此处上下文长度指提示长度与生成长度之和，最大提示长度限制为 1k
在所有设置中，AReaL 展现出近似线性的扩展趋势，而同步系统通常无法有效扩展
AReaL 的吞吐量在大多数设置中超过基线，最高可实现 $2.5 \times$ 加速
对于较短的上下文长度，AReaL 的优势可能较小，因为生成吞吐量无法匹配训练吞吐量
尽管生成了许多序列，但它们未被训练过程有效消耗
AReaL 对生成长度的鲁棒性更强，因为异步和可中断的生成可以将长响应的生成完全隐藏在关键路径中，因此延长生成长度不会显著影响 AReaL 的有效训练吞吐量

Algorithm Ablations

论文通过消融实验验证第 5 节的算法创新，使用 1.5B LRM 在数学任务上进行训练
Following DeepScaleR 的基本实验设置，并逐步增加 $\eta$ 值进行消融
具体来说，论文改变最大允许陈旧度 $\eta$，并比较是否使用解耦 PPO 目标的配置
图 5a 和图 5b 展示了 250 训练步后的学习曲线
表 2 展示了多个数学推理基准上的最终评估性能
论文 Following PPO 的常见实践，在每个训练步内执行多次小批量更新
需要强调的是，$\eta$ 限制了训练步级别的训练批次陈旧度
图 5a 显示，朴素 PPO 无法匹配同步 RL 的性能（即 $\eta=0$ 时的性能）
- 即使轻微的陈旧度也会因不恰当的裁剪中心和可中断生成期间策略变化而显著降低最终性能
- 此外，增加数据陈旧度会持续降低学习性能，这与之前在其他领域的研究观察一致 (2022; 2024)
- 如图 5b 与图 5a 的对比所示，解耦 PPO 目标在处理陈旧数据时显著提高了训练稳定性，这与游戏领域的研究发现一致 (2022)
- 即使使用解耦目标，无界陈旧度（最大陈旧度 $\rightarrow \infty$）的性能仍低于零陈旧度的基准
- 在适当约束下，中等陈旧度（如 $\eta \leq 8$）对最终性能影响极小，同时通过异步流水线显著加速训练（如图 5c 和表 2 所示）
- 这些结果验证了论文将受控陈旧度与解耦 PPO 目标结合用于高效异步 RL 训练的方法

System Ablations

可中断生成（Interruptible Generation）
- 论文消融可中断生成功能，生成吞吐量结果如图 6 所示
- 若不可中断生成，控制器必须等待最长响应完成
- 具体而言，在 4 节点上，可中断生成使 1.5B 和 7B 模型的吞吐量分别提升 12% 和 17%，验证了论文的架构设计选择
动态微批次分配（Dynamic Microbatch Allocation）
论文通过对比动态批处理与标准微批处理策略的 PPO 训练吞吐量，验证动态批处理的有效性
标准微批处理策略可能导致多个长序列分配到同一微批次，通常需要足够多的微批次以防止内存不足
实验中，论文为标准设置配置 32 个微批次，为动态批处理方法设置每微批次 32,768 token 的预算
如图 7 所示，动态批处理在不同模型规模下平均提升 30% 吞吐量

RL for LLMs

RL 已成为增强 LLM 推理能力的主要范式 (2022)
现有的 RL 方法通常聚焦于具有明确定义奖励函数（well-defined reward functions）的任务，包括数学推理 (2021)、代码生成 (2021)、科学问题求解 (2023) 以及工具使用 (2024)
在训练过程中，模型通过逐步扩展 CoT 轨迹来学习推理 (2022)
最近的开源项目通过小型蒸馏模型展示了显著的成功 (2024, 2025)
论文的工作基于这一研究方向，与 preference-based RLHF (2022) 和零样本（zero-shot）推理方法 (2025) 不同
- zero-shot 推理方法试图从预训练模型中直接获取推理能力，而无需任务特定的微调

Asynchronous RL

解耦的异步 RL （decoupled asynchronous RL）架构 (2018, 2020) 结合相应的算法创新 (2018, 2019)，在游戏应用中取得了显著成功 (2019, 2021)
尽管类似的异步方法已用于 LLM 训练，但它们通常关注短上下文场景（如 RLHF）(2024) 或仅支持一到两步的生成-训练重叠 (2024, 2025)
论文的研究扩展了这些工作，并在第 5 节展示了更灵活的陈旧性与训练速度之间的权衡
- 与并发工作 (2025) 追求系统级效率最大化（maximizes system-level efficiency）不同，论文采用算法-系统协同设计方法，同时提供了表达性强的系统和实用的算法实现
论文的可中断生成技术（interruptible generation technique）与同步 RL 系统中的部分轨迹生成 (2025) 概念相似
- 不同于固定长度预算，AReaL 动态中断生成，同时通过缓冲保持训练批大小的稳定性，从而确保 PPO 的稳定性
- 与先前方法 (2024, 2025) 相比，论文在异步设置中的算法创新能够容忍更高的数据陈旧性，并与可中断生成兼容

LLM Training and Inference

论文的研究聚焦于 Dense Transformer 模型 (2017)
RL 训练主要包括生成（推理）和训练两个阶段
- 生成阶段涉及自回归解码，需要高效的 KV 缓存管理 (2023) 和优化的解码内核 (2024)
- 训练阶段则需要精心设计数据、张量和流水线并行策略 (2020, 2023)
传统的同步系统在同一硬件资源上顺序执行生成和训练，但二者需要不同的最优并行化策略
最近的研究提出了上下文切换 (context switching，2024) 或权重重分配技术 (weight resharding techniques，2024, 2025) 来解决这种不匹配问题
AReaL 通过解耦生成和训练 ，完全消除了关键训练路径（critical training path）中的重分配开销（resharding overhead） ，从而超越了同步 RL 系统

附录 A 实现细节

A.1 PPO Details

论文禁用了 PPO 中的 Critic Model 和 Reference Model
GAE 中的优势估计参数 $\lambda$ 和强化学习的折扣因子 $\gamma$ 固定为 1
- 问题：没有 Critic Model 如何评估 GAE？使用 GRPO 的评估方式吗？
如果答案正确，则在最后一个 token 处奖励为 5，否则为 -5
论文在全局批次中采用优势归一化（Advantage Normalization）以稳定训练
其他与学习相关的超参数和配置见表 3

A.2 Dataset Details

对于数学任务，论文使用了 DeepScaleR (2025) 的开源数据
对于代码训练，论文使用了 DeepCoder (2025) 发布的数据集
所有对比方法均使用相同的数据集

A.3 Dynamic Batching

动态批处理算法如算法 A.1 所示：

A.4 Baselines

在论文的实验中，论文使用 verl (2025) 的最新版本（20250507日的主分支）来评估图 4 中的训练吞吐量和表 1 中的训练时长
对于大多数结果，论文使用 SGLang (2024) v0.4.6 作为生成后端，并使用 PyTorch FSDP (2023) 作为训练后端
在少数情况下（例如 32B 模型或 64 节点的实验），如果 SGLang 报错，论文使用 vLLM (2023) v0.8.4 作为替代

附录 B Additional Results

文在更多数学基准上评估了使用 AReaL 训练的模型，结果列于表 4

附录 C Proof of Proposition 1

命题 1 ：对于任何由策略序列 $(\pi_\theta, \ldots, \pi_{\theta+k})$ 生成的序列 $(q, a_1, \ldots, a_H)$，其中 $\pi_{\theta+i}$ 生成 tokens $(a_{t_i}, \ldots, a_{t_{i+1} })$，且 $1 = t_0 < \cdots < t_{k+1} = H$，存在一个行为策略 $\pi_{\text{behav} }$，使得中断生成等价于完全从 $\pi_{\text{behav} }$ 采样
证明：对于问题 $q$，设 $\mathcal{S}_i(q)$ 表示策略序列在步骤 $t$ 遇到的状态。由于对于 $i \neq j$ 有 $\mathcal{S}_{t_i}(q) \cap \mathcal{S}_{t_j}(q) = \emptyset$（理解：因为在 LLM 中，响应序列长度和时间步 $t$ 唯一确定），我们可以构造：
$$
\pi_{\text{behav} }(\cdot|s) =
\begin{cases}
\pi_{\theta+j}(\cdot|s) & \text{if } \quad t_j \leq t \leq t_{j+1} \text{ and } s \in \mathcal{S}_t(q) \\
\text{arbitrary} & \text{otherwise}
\end{cases}
$$

附录 D Limitations and Future Work

论文的工作存在一些局限性，为未来研究提供了方向
首先，推理设备与训练设备的比例可以针对特定训练设置进一步优化
此外，这一比例可能受益于训练期间的动态调整，尤其是在微调预训练基础模型时，上下文长度通常会增加
虽然论文的评估集中在单步数学和编码任务上 ，但 AReaL 架构并不局限于这些领域
- 理解：这也算缺点？
论文将多轮交互和智能体场景的探索留给未来工作

NLP——DeepCoder

注：本文包含 AI 辅助创作

参考链接：
- 原始博客链接：DeepCoder: A Fully Open-Source 14B Coder at O3-mini Level
  - 作者：Agentica 团队与 Together AI 的联合合作
- 其他链接：官网 | GitHub | Hugging Face 模型 | Hugging Face 数据集 | Wandb | 评估日志

Paper Summary

核心内容：
- 论文推出了 14B 模型 Deepcoder-14B-Preview（DeepCoder 是一款完全开源达到 o3-mini 水平的编程模型）
  - 基于 Deepseek-R1-Distilled-Qwen-14B 并通过分布式强化学习微调而成的代码推理模型
  - 在 LiveCodeBench 中实现了与 o3-mini 模型相当的性能，Pass@1（单次尝试通过率）准确率达60.6%
- 重点：构建了高质量、可验证的代码数据集，并引入了算法与系统层面的优化，以实现高效的 RL 训练
- Deepcoder-14B-Preview 是该方向上的第二个重要里程碑，其研发建立在作者之前的首款模型DeepScaleR-1.5B-Preview（聚焦数学推理任务）奠定的基础之上
- 论文完整共享数据集、代码及训练方案
该模型在 LiveCodeBench 上取得了令人印象深刻的 60.6% Pass@1 准确率（+8% 提升），以仅 14B 参数的规模，性能匹敌 o3-mini-2025-01-031 (Low) 和 o1-2024-12-17
作者已将数据集、代码、训练日志和系统优化全部开源，旨在推动基于强化学习的智能扩展与加速

DeepCoder-14B-Preview 性能概览

整体性能概览表：

模型	LiveCodeBench (Pass@1) (2024年8月1日 - 2025年2月1日)	Codeforces 评分	Codeforces 百分位
DeepCoder-14B-Preview	60.6	1936	95.3
DeepSeek-R1-Distill-Qwen-14B	53.0	1791	92.7
O3-Mini-2025-1-31 (Low)	60.9	1918	94.9
O1-2024-12-17 (Low)	59.5	1991	96.1

图 1： DeepCoder 在训练过程中的 LiveCodeBench (LCB) 分数。在第 180 步时，上下文长度扩展至 32K。最佳的 32K 检查点用于推理时扩展至 64K，最终实现 60.6% 的 LCB 分数——性能与 o3-mini 相当
近年来，我们见证了通过 RL 在数学领域（例如 DeepScaleR、AReaL、Light-R1、DAPO）显著提升了推理模型的扩展能力。然而，编程领域的进展相对滞后，主要原因是构建具有可靠、可验证奖励的高质量数据集存在挑战
在这篇博客中，作者将公开训练一个小型模型成为强大竞争性编程选手的“配方”，使用强化学习技术使其达到与 o3-mini 相当的水平
- 作者介绍了 DeepCoder-14B-Preview，该模型在 32 块 H100 GPU 上，利用 2.4 万个可验证的编程问题训练了 2.5 周，其表现达到甚至超越了 OpenAI 的 o3-mini 在多个编程基准测试上的成绩
- 作者还开源了 verl-pipe，这是对 verl 后训练系统的扩展，包含多项系统优化，可将端到端训练速度提升 2 倍

数据集构建

在数学领域，先前的研究表明，使用可验证奖励进行强化学习可以显著增强模型的推理能力。然而，与互联网上存在大量高质量、可验证数据的数学领域不同，编程领域面临此类数据相对稀缺的问题
在早期实验中，作者评估了几个流行的编程数据集，包括 APPS、TACO、CodeContests、KodCode 和 LeetCode，作者发现：
- 有些数据集对于论文的模型来说太简单（如 KodCode、LeetCode）
- 另一些数据集则存在噪声或包含有缺陷或缺失测试用例的不可验证问题
- 这些问题通常会产生无效或误导性的奖励信号，最终导致 RL 训练不稳定
为克服这些限制，作者精心策划了一个高质量的训练集，包含：
- TACO 验证过的问题
- PrimeIntellect 的 SYNTHETIC-1 数据集中经过验证的问题
- 2023 年 5 月 1 日至 2024 年 7 月 31 日期间提交的 LiveCodeBench 问题
为了确保数据质量以实现有效的 RL 训练，作者实施了严格的过滤流程：
- 1）程序化验证 ：每个问题都使用外部官方解决方案自动验证
  - 论文只保留那些官方解决方案能通过所有单元测试的问题
  - 此过程在 tests/rewards/test_code_batch.py 中自动化完成
- 2）测试用例过滤 ：每个问题必须至少包含 5 个单元测试
  - 论文发现，测试用例较少的问题容易引发 “Reward Hacking” 行为 ，即模型学会通过识别常见测试用例来直接打印出记忆的答案
- 3）去重：论文移除了跨数据集的重复问题，以避免污染
  - 论文对三个训练数据集（Taco Verified、PrimeIntellect SYNTHETIC-1 和 LCB (05/01/23-07/31/24)）进行了去重，并验证了测试数据集（LCB (08/01/24-02/01/25) 和 57 场 Codeforces 比赛）中没有污染
经过过滤后，论文得到了 2.4 万个高质量的编程问题用于 RL 训练，其中包括：
- 7500 个来自 TACO Verified 的问题
- 1.6 万个来自 PrimeIntellect 的 SYNTHETIC-1 的问题
- 600 个来自 LiveCodeBench 的问题

代码沙箱环境

为了计算代码 RL 训练的奖励，我们必须在代码沙箱中运行模型生成代码的单元测试
在每次 RL 迭代中，论文的训练批次需要在 1024 个问题上进行评估，每个问题都包含多个单元测试（大于等于 5 个）
这种繁重的工作负载要求并行扩展 100 多个代码沙箱，以确保在合理时间内准确验证大语言模型生成的代码
目前，论文使用两种沙箱，下面分别进行介绍

Together Code Interpreter

这是一个快速、高效的环境，与论文的 RL 训练直接兼容，每个问题的成本仅为 3 美分
论文一直在努力将 Together Code Interpreter 可靠地扩展到 100 多个并发沙箱和每分钟 1000 多次沙箱执行
这些沙箱暴露了 stdout、stdin 和代码输出的最后一行，同时安全地限制执行并将代码与主机系统隔离
Together Code Interpreter 目前处于测试阶段；详细信息请参阅 Together Code Interpreter 文档，集成示例代码可在论文的代码仓库中找到

Local Code Sandbox

启动一个独立的、有防护的 Python 子进程作为本地沙箱，通过 stdin 接收测试用例输入，并将答案打印到 stdout
论文的本地沙箱遵循官方 LiveCodeBench 仓库的相同评估代码，确保论文的结果与现有排行榜一致

奖励函数

论文的奖励函数采用稀疏的结果奖励模型（ORM）
论文避免分配部分奖励，例如思维链惩罚，或如果 K/N 个测试通过则分配 K/N 的奖励，因为这可能导致 “Reward Hacking” 行为，即大语言模型学会直接打印出公共测试的答案，或错误地收敛于通过简单的边缘情况
1 ：生成的代码必须通过所有采样的单元测试
- 由于一些问题包含数百个测试，使得完全验证不切实际，论文为每个问题采样 15 个最具挑战性的测试，这些测试由其输入字符串的长度确定
0 ：如果大语言模型的代码至少在一个测试用例上失败，或者答案格式不正确（即缺少 python [CODE]），则不给予奖励
- 每个测试用例的超时时间为 6-12 秒

训练配方

GRPO+：GRPO 的稳定版本

图 2： GRPO+ 和 GRPO 在 16K 运行中的平均训练奖励。GRPO 的奖励曲线最终崩溃。由于 Clip High，GRPO+ 的曲线保持稳定
图 3： 由于长序列过滤，GRPO+ 的响应长度随时间稳步增长
图 4： Clip High 和无熵损失确保了 GRPO+ 的 token 级熵不会崩溃，并鼓励足够的探索
论文通过整合 DAPO 的见解，增强了原始的 GRPO 算法，以实现更稳定的训练：
- 无熵损失 ：论文观察到包含熵损失项常常导致不稳定，熵会呈指数级增长并最终导致训练崩溃。为缓解此问题，论文完全消除了熵损失
- 无 KL 损失 (来自 DAPO) ：消除 KL 损失可以防止大语言模型被约束在原始 SFT 模型的信任区域内。这一移除也免去了计算参考策略的对数概率的需要，从而加速了训练
- 长序列过滤 (来自 DAPO) ：为了保留长上下文推理能力，论文对截断的序列屏蔽损失。这项技术使 DeepCoder 能够推广到 64K 上下文的推理，尽管它是在 32K 上下文下训练的。如图 3 所示，这种方法允许响应长度自然增长而不受截断惩罚
- Clip High (来自 DAPO) ：通过增加 GRPO/PPO 代理损失的上限，论文鼓励更多探索并稳定熵。图 4 表明，这种调整带来了更稳定的训练和改进的模型性能

迭代式上下文延长：开箱即用的泛化能力

在论文最初的 DeepScaleR 博客文章中，论文介绍了迭代式上下文延长，这是一种训练技术，使语言模型能够先在较短的上下文长度下学习有效思考，然后推广到更长的上下文
这种方法帮助论文的 1.5B 参数模型在将其上下文窗口从 8K -> 16K -> 24K 扩展时，下游性能稳步提升，在 AIME 上的准确率从 33% -> 38% -> 43%，最终达到 O1-preview 的性能
然而，在将此技术应用于论文的 14B 参数模型时，论文遇到了新的挑战：
- 14B 参数模型已经比 1.5B 参数模型拥有显著更强的推理能力，这意味着进一步的改进需要解决更难的问题
- 这些更难的问题自然需要比小模型使用的 8K 起始点更长的上下文窗口
- 从短上下文开始并惩罚模型超出该窗口的行为产生了负面影响——导致初始性能下降、响应变短以及模型在长上下文上推理能力的退化
为了在实现高效训练的同时保留长上下文推理能力，论文采用了来自 DAPO 的长序列过滤技术
- 该技术在训练期间屏蔽截断的序列，因此模型不会因生成超出当前上下文限制的深思熟虑但冗长的输出而受到惩罚
- 结果是，模型在较短的上下文中训练时仍然可以“长思考”
论文将迭代式上下文延长应用于论文的 DeepCoder-14B-Preview，将上下文窗口从 16K 扩展到 32K。在 LiveCodeBench 上，该模型实现了：
- 16K 和 32K 上的准确率分别为 54% -> 58%，
- 在 64K 上下文评估时达到 60.6%，展示了超越其训练上下文的强大泛化能力
这种泛化能力与像 DeepSeek-R1-Distill-Qwen-14B 这样的基础蒸馏模型形成鲜明对比，后者在其训练上下文长度之外会达到性能瓶颈：

模型 16K 32K 64K

DeepCoder-14B-Preview 45.6 57.9 60.6

DeepSeek-R1-Distill-Qwen-14B 50.2 53.0 53.0
虽然由于其更长的平均响应长度导致截断和分数惩罚，DeepCoder 在 16K 的原始性能较低，但它最终在 64K 上凭借其在更长上下文中推理的能力超越了其他模型
图 5： DeepCoder 在训练过程中的平均响应长度和训练奖励。平均响应长度从 8K 增加到 17.5K 上下文长度 > Baby, there ain't no mountain high enough. Ain't no context long enough. — Inspired by Marvin Gaye & Tammi Terrell
DeepCoder 的成功直接源于将迭代式上下文延长与长序列过滤相结合。如图 5 所示，在整个训练过程中，模型的平均响应长度从 8K 稳步增长到 17.5K，同时平均奖励从 0.6 提升到 0.7——这清晰地表明，模型正在逐步学习更具可扩展性和连贯性的思考模式

模型	16K	32K	64K
DeepCoder-14B-Preview	45.6	57.9	60.6
DeepSeek-R1-Distill-Qwen-14B	50.2	53.0	53.0

评估

论文在多个编程基准上评估了Deepcoder-14B-Preview，包括 LiveCodeBench (LCB)、Codeforces 和 HumanEval+ 以及AIME2024
拥有 14B 参数的模型在整个编程基准测试中展示了强大的性能，LiveCodeBench 达到了 60.6%，Codeforces 评分为 1936 分，与o3-mini（低配置版）和o1的表现相当
此外，尽管该模型没有专门针对数学任务进行训练，但其从编程任务中获得的推理能力很好地推广到了数学领域
- 这在其 AIME2024 得分 73.8% 上体现出来，比基础模型提高了 4.1%
- 总体而言，论文的模型在编程和数学领域都表现出色

评估结果如下：

Model	LCB (8/1/24-2/1/25)	Codeforces Rating*	Codeforces Percentile*	HumanEval+Pass@1	AIME 2024
DeepCoder-14B-Preview (ours)	*60.6*	*1936*	*95.3*	*92.6*	73.8
DeepSeek-R1-Distill-Qwen-14B	53.0	1791	92.7	92.0	69.7
O1-2024-12-17 (Low)	59.5	1991	96.1	90.8	74.4
O3-Mini-2025-1-31 (Low)	60.9	1918	94.9	92.6	60.0
O1-Preview	42.7	1658	88.5	89	40.0
Deepseek-R1	62.8	1948	95.4	92.6	79.8
Llama-4-Behemoth**	49.4	-	-	-

* 表示由于 DeepSeek 和 OpenAI 对 Codeforces 的评估为内部流程，有关 Codeforces 评估的更多细节，可参考附录A
** 表示非推理型模型

图6：LiveCodeBench Pass@1准确率与模型规模对比。DeepCoder仅需14B 参数，性能便已与前沿推理模型o1和o3-mini（低配置版）持平

训练后阶段的系统优化

采用长上下文强化学习训练大型语言模型十分耗时，需要在长上下文环境中反复进行采样和训练
若缺乏系统级优化，完整的训练流程可能需要数周甚至数月，论文针对 14B 参数模型的编程任务训练，每一步便需 1200-2500 秒，总训练时长更是长达2.5周
为此，论文开发并开源了 verl-pipeline ，这是基于开源强化学习人类反馈（RLHF）库 verl 的优化扩展版本
- 该扩展通过多项系统级改进，实现了端到端强化学习训练的加速，较基础版 verl 实现最高可提升2.5倍训练速度
- 论文将这些全新的系统优化方案应用于 DeepCoder-1.5B-Preview 模型的训练，使其在 LCB 测试集上的通过率达到 25%，较Deepseek-R1-Distill-Qwen-1.5B模型提升了 8%
作者诚邀整个社区（包括verl开发团队及其他新兴项目团队）采用这些优化方案，并在此基础上进一步开发创新

采样器是性能瓶颈

图7：Verl的PPO/GRPO训练流程。每个强化学习迭代周期均包含采样、奖励函数计算和训练三个环节。其中，采样是性能瓶颈；训练速度受限于生成长序列的“滞后采样器”（straggler samplers）
在训练后阶段的系统中，采样时间往往是主要瓶颈，使用 vLLM、SGLang 等推理引擎生成超长序列（最长可达32K tokens）会产生较高延迟
如图7所示的 Verl PPO/GRPO 流程中，响应长度的不一致会导致部分采样器成为“滞后采样器”
- 这些滞后采样器会拖延训练进度，而已完成任务的采样器则处于闲置状态，最终导致 GPU 利用率低下

基础解决方案：Minibatch Pipelining

图8：小批量流水线流程。采样器与训练器分属不同的工作组。当采样器完成小批量（用于PPO/GRPO）生成并输出后，训练器工作组会异步处理这些数据。在一个迭代周期结束时，训练器会将权重广播至采样器
为减少训练后阶段的设备闲置时间，作者将采样与训练流程进行流水线处理，允许训练器在采样器继续生成下一批数据的同时，提前对已生成的小批量数据进行更新。这种并行重叠操作有助于掩盖采样过程中的延迟
然而，该方案存在三个关键局限性：
- 1）首先，小批量数据的平均序列长度会随时间推移而增加，这会延长后续小批量数据的训练时间。最终，最后几批数据的训练往往会在采样完成后才结束，从而限制了流水线方案的收益
- 2）其次，流水线方案需要在采样器和训练器之间分配GPU资源，这会减少可用于采样的设备数量。与Verl不同（Verl可在同一GPU资源池内动态切换采样器和训练器角色），这种静态资源分配方式会因采样器数量减少，导致端到端采样时间延长
- 3）最后，奖励函数计算可能需要较长时间（尤其对于编程类任务而言，每个强化学习迭代周期可能需要运行数千次单元测试）。在默认的Verl流程中，奖励计算需在采样完成后，由主节点（head node）统一执行
尽管存在上述限制，我们仍在代码库的 ray_trainer_pipeline.py 文件中实现了小批量流水线方案，并发现通过微批量（microbatching）技术可进一步改进流水线性能

论文的解决方案：One-Off Pipelining

图9：一次性流水线流程。采样器提前一个迭代周期生成数据批次，而训练器则使用上一个迭代周期的数据更新梯度。其次，奖励函数计算与采样过程交叉进行。该方案不会为GRPO/PPO的在策略（on-policy）算法引入异步离策略（off-policy）样本
为实现训练、奖励计算与采样的完整流水线化，我们提出了 一次性流水线（One-Off Pipelining） 方案。其核心思路十分简洁：
- 牺牲第一个强化学习迭代周期，仅用于采样；
- 在下一个迭代周期中，再使用上一周期采样得到的数据进行训练
- 这种设计能让采样与训练并行进行，彻底消除采样完成后训练器的闲置时间
其次，作者将奖励计算与采样过程交叉结合，一旦某个请求处理完成，便立即对其进行奖励计算
- 这一改进减少了奖励评估的额外开销，尤其适用于编程类等计算密集型任务（如测试用例执行）
作者在 verl 分支的 ray_trainer_async.py 文件中实现了一次性流水线方案

端到端性能

在图10 中，我们针对数学和编程两类任务负载，分别评估了 verl 基础版、微批量流水线方案和一次性流水线方案的性能
为保证公平性，所有基准方案均通过 Python 线程池并行计算奖励；而 verl 官方版本对每个样本的奖励计算为串行执行，这对于编程任务而言耗时过长，不具备实际可行性
作者在8台A100设备上对Deepcoder-1.5B-Preview模型进行评估，并调整采样器与训练器的比例，以更好地平衡两者的运行时间
在数学任务中，一次性流水线方案将每个强化学习迭代周期的时间缩短了1.4倍。需说明的是，数学任务的奖励计算时间几乎为零，因为其仅涉及基础的sympy检查。具体而言，一次性流水线方案完全掩盖了训练器的运行时间，而微批量流水线方案中最后一批数据的训练仍会出现延迟
在编程任务中，奖励计算需在每个强化学习迭代周期内运行数千次测试，是一个耗时过程。一次性流水线方案同时掩盖了训练器和奖励计算的时间，最终将端到端训练时间缩短了2倍
图10：一次性流水线方案完全掩盖了训练器和奖励计算的时间，使数学任务的训练时间缩短1.4倍 ，编程任务的训练时间缩短2倍
最重要的是，一次性流水线方案不仅有效，还能扩展应用于复杂的编程任务
- 作者使用 ray_trainer_async.py 训练出 DeepCoder-1.5B-Preview 模型，其 LCB 得分较基础蒸馏模型提升了 8%
具体数据为：

Model LCB(8/1/24-2/1/25) Codeforces Rating Codeforces Percentile HumanEval+

DeepCoder-1.5B-Preview 25.1 963 28.5 73.0

Deepseek-R1-Distill-Qwen-1.5B 16.9 615 1.9 58.3

Model	LCB(8/1/24-2/1/25)	Codeforces Rating	Codeforces Percentile	HumanEval+
DeepCoder-1.5B-Preview	25.1	963	28.5	73.0
Deepseek-R1-Distill-Qwen-1.5B	16.9	615	1.9	58.3

附录

附录 A. 训练基础设施与成本

DeepCoder-14B-Preview 的训练在 Together AI 提供的云平台上进行，使用了 32 块 NVIDIA H100 GPU
- 整个训练过程持续了 2.5 周
论文采用了高效的分布式训练框架和优化的通信策略，以最大化 GPU 利用率
- 得益于 verl-pipe 系统中的多项优化（包括梯度检查点、混合精度训练和高效的批处理调度），端到端的强化学习训练速度相比基线提升了 2 倍
单次完整训练的成本主要由 GPU 小时和沙箱验证费用构成：
- GPU 计算成本 ：约 $45,000
- Together Code Interpreter 沙箱成本 ：约 $720 （基于 3¢/problem 和总计 24,000 个问题计算）
- 总估算成本 ：约 $45,720

附录 B. 可复现性指南

为确保研究结果的可复现性，作者在 GitHub 仓库中提供了详细的文档和脚本：
- 1）数据准备 ：scripts/download_and_filter_datasets.py 脚本自动化了从原始来源下载、验证和过滤数据集的全过程
- 2）环境配置 ：environment.yml 文件定义了精确的 Python 依赖环境
- 3）训练启动 ：launch_training.sh 脚本包含了启动 GRPO+ 训练的所有参数和配置
- 4）评估流程 ：eval/ 目录下的脚本可用于在 LiveCodeBench、Codeforces 和 AIME2024 等基准上复现我们的评估结果
强烈建议使用者参考 README.md 中的“快速开始”部分来部署和运行模型

附录 C. 局限性与未来工作

尽管 DeepCoder-14B-Preview 取得了显著成果，但仍存在一些局限性：
- 领域专注 ：模型在竞争性编程任务上表现出色，但在真实世界软件工程任务（如调试大型代码库、理解复杂 API）上的泛化能力有待验证
- 语言覆盖 ：当前版本主要针对 Python 代码生成进行了优化，对其他编程语言的支持较弱
- 推理延迟 ：由于其长上下文推理能力，在 64K 上下文下生成答案的延迟较高，可能不适用于对实时性要求极高的场景
未来的工作将集中在解决这些局限性，并探索将此框架应用于更广泛的智能体任务，例如自主代理和复杂决策系统

NLP——DeepScaleR

注：本文包含 AI 辅助创作

参考链接：
- 原始博客链接：DeepScaleR: Surpassing O1-Preview with a 1.5B Model by Scaling RL, 2025
- 其他链接：网站 | GitHub | HF 模型 | HF 数据集 | Wandb 日志 | 评估日志

Blog Summary

核心内容：
- 作者的目标是在揭示强化学习对 LLM 的扩展效应，并使其为每个人所用（作者特别推崇开源）
- DeepScaleR-1.5B-Preview 以 43.1% 的 Pass@1 准确率超越了 o1-preview
RL 的魔力正在显现！论文推出了 DeepScaleR-1.5B-Preview，这是一个基于 Deepseek-R1-Distilled-Qwen-1.5B，使用简单的 RL 进行微调的语言模型
DeepScaleR-1.5B-Preview 在 AIME2024 上取得了 43.1% 的 Pass@1 准确率（相比基础模型提升了14.3%），仅凭 1.5B 参数就超越了 OpenAI 的 o1-preview 的性能
论文已将数据集、代码和训练日志开源，以便每个人都能在通过RL扩展智能的道路上取得进展

DeepScaleR-1.5B-Preview 整体评估效果如下：

模型	AIME 2024	MATH 500	AMC 2023	Minerva Math	Olympiad Bench	平均
DeepScaleR-1.5B-Preview	43.1	87.8	73.6	30.2	50.0	57.0
DeepSeek-R1-Distill-Qwen-1.5B	28.8	82.8	62.9	26.5	43.3	48.9
O1-Preview	40.0	81.4	-	-	-	-

图1： DeepScaleR在AIME2024上的Pass@1准确率随训练进展的变化。在第 1040 步和第 1520 步，上下文长度分别扩展到 16K 和 24K
在这篇博客中，论文将逐步揭示利用 RL 将小型模型转变为强大推理模型的秘诀
DeepScaleR-1.5B-Preview 在 40K 高质量数学问题上进行了训练，耗时 3,800 个 A100 GPU 小时（约4500美元），在多个竞赛级数学基准测试上超越了 OpenAI 的 o1-preview

Introduction: 迈向 LLM 强化学习的民主化（Towards Democratizing RL for LLMs）

Deepseek-R1 的近期开源发布（一个可与 OpenAI 的 o1 相媲美的模型）标志着在推理模型民主化方面迈出了重要一步
但其确切的训练配方、超参数和底层系统仍然不可用
在这项工作中，论文朝着实现一个完全开放配方的、可扩展的推理模型强化学习迈出了重要一步
扩展强化学习的最大挑战之一是高昂的计算成本
- 例如，论文发现直接复制 DeepSeek-R1 的实验（上下文长度 $\ge$32K，约 8000 步）至少需要 70,000 个 A100 GPU 小时（即使对于一个 1.5B 的模型也是如此）
为了解决这个问题，论文利用了一个蒸馏模型，并引入了一种新颖的 RL 迭代延长方案，将计算需求减少到仅 3,800 个 A100 GPU 小时（减少了 18.42 倍），同时实现了仅凭 1.5B 模型就超越 OpenAI 的 o1-preview 的性能
论文的工作表明，通过强化学习开发定制化推理模型既可以扩展，又具有成本效益
在接下来的博客中，论文将介绍论文的数据集整理和训练方法，展示评估结果，并分享从论文的发现中获得的关键见解

DeepScaleR’s Recipe

Dataset Curation

对于论文的训练数据集，论文整理了 1984-2023 年的 AIME 问题和 2023 年之前的 AMC 问题，以及来自 Omni-MATH 和 Still 数据集的问题
- 这些数据集包含了来自各种国家和国际数学竞赛的问题
论文的数据处理流程包括三个关键步骤：
- 1）提取答案 ：对于 AMC 和 AIME 等数据集，论文使用 gemini-1.5-pro-002 从官方 AoPS 解决方案中提取答案
- 2）删除冗余问题 ：论文使用基于 sentence-transformers/all-MiniLM-L6-v2 嵌入的 RAG 来消除重复的问题
  - 为了防止数据污染，论文还检查了训练集和测试集之间的重叠
- 3）过滤无法评分的问题 ：一些数据集，如 Omni-MATH，包含无法使用 sympy 评估并需要 LLM judge 的问题
  - 由于使用 LLM judge 可能会减慢训练速度并引入嘈杂的奖励信号，论文应用了一个额外的过滤步骤来删除这些无法评分的问题
经过去重和过滤后，论文的最终训练数据集包含大约 40,000 个唯一的问题-答案对
- 论文将在未来的运行中扩展论文的数据集

Reward Function

正如 Deepseek-R1 所倡导的，论文采用结果奖励模型（ORM）而不是过程奖励模型（PRM）来避免奖励作弊。简而言之，论文的奖励函数返回：
- 1 ：如果 LLM 的答案通过了基本的 LaTeX/Sympy 检查
- 0 ：如果 LLM 的答案错误或格式不正确（例如缺少<think>、</think>分隔符）

Iterative Context Lengthening: Think Shorter, then Longer

图2： DeepScaleR的平均响应长度和训练奖励随训练进展的变化。曲线显示了100个窗口大小的移动平均值
在推理任务中扩展强化学习的一个关键挑战是选择最佳的上下文窗口进行训练
- 推理工作负载的计算量非常大，因为它们生成的输出比标准任务长得多，从而减慢了轨迹采样和策略梯度更新
- 将上下文窗口大小加倍至少会使训练计算量增加 2 倍
这引入了一个根本性的权衡：
- 更长的上下文为模型提供了更多的思考空间，但会显著减慢训练速度；
- 更短的上下文可以加速训练，但可能会限制模型解决需要长上下文的更难问题的能力
- 因此，在效率和准确性之间取得适当的平衡至关重要
简而言之，论文采用 Deepseek 的 GRPO 算法的训练配方遵循两个步骤：
- 1）首先，论文使用8K最大上下文进行强化学习训练，以实现更有效的推理和高效的训练
- 2）接着，论文将训练扩展到16K和24K上下文，使模型能够解决更具挑战性、之前未解决的问题

引导有效的 CoT（Bootstrapping effective CoT）with 8K context

在启动论文的完整训练运行之前，论文在 AIME2024 上评估了 Deepseek-R1-Distilled-Qwen-1.5B 并分析了轨迹统计
平均而言，错误的响应包含的 token 数量是正确响应的三倍（20,346 vs. 6,395）
- 这表明更长的响应往往会导致错误的结果
- 因此，立即使用长上下文窗口进行训练可能是低效的，因为大多数 token 实际上被浪费了
- 此外，论文在评估日志中观察到，长响应表现出重复的模式，表明它们对有效的思维链（CoT）推理没有实质性贡献
鉴于这一见解，论文以 8K 上下文启动训练，在 AIME2024 上取得了 22.9% 的初始准确率，仅比原始模型低 6%
- 这种策略被证明是有效的：在训练过程中，平均训练奖励从 46% 增加到 58%，而平均响应长度从 5,500 减少到 3,500 个 token（见图2）
更重要的是，将输出限制在 8K token 使模型能够更有效地利用上下文

如表所示，论文的模型为正确和错误答案生成的响应都显著缩短，同时在AIME准确率上超过了基础模型 5%（仅使用了三分之一的 token）

	基础模型	DeepScaleR-1.5b-8k	变化
AIME Pass@1	28.9%	33.9%	+5%
正确响应的平均 token 数	6396.0	3661.2	-2734.8
错误响应的平均 token 数	20346.3	6976.8	-13369.5
总体平均 token 数	16335.6	5850.9	−10484.7

Extending to 16K context at the turning point

在大约 1,000 步之后，论文的 8K 运行出现了一个有趣的变化：响应长度开始再次增加
- 但这导致了收益递减，准确率趋于平稳并最终下降
- 与此同时，响应截断率从 4.2% 上升到 6.5%，表明有更多响应在上下文限制处被截断
图3： 在 1000 步之后，8K 运行的响应长度再次上升，但训练奖励最终下降
图4： 在 8K 上下文运行中，1000 步之后响应长度截断率上升
这些结果表明，模型试图通过“思考更长时间”来提高训练奖励。但当它生成更长的响应时，越来越多地遇到 8K 上下文窗口的上限，从而限制了进一步的改进
认识到这是一个自然的过渡点，论文决定“打开笼子，让鸟儿飞翔（set the cage free and let the bird fly.）”
- 论文取了第 1,040 步的检查点（此时响应长度开始呈上升趋势），并以 16K 上下文窗口重新启动训练
- 这种两阶段方法比从一开始就以 16K 进行训练要高效得多：8K 的引导将平均响应长度保持在 3,000 个token，而不是 9,000 个，使这一阶段的训练速度至少快2倍。在此切换之后，论文观察到训练奖励、响应长度和AIME准确率稳步提高。在额外的500步之后，平均响应长度从3500增加到5500个token，AIME2024的Pass@1准确率达到38%

Surpassing O1-preview with the 24K magic

在 16K 上下文上再训练 500 步后，论文注意到性能开始趋于平稳（平均训练奖励收敛在 62.5%）
- AIME 24 Pass@1准确率在 38% 左右徘徊，响应长度再次开始下降
- 同时，最大响应截断率逐渐上升到 2%
为了向 o1 级别的性能发起最后的冲刺，论文决定施展 “24k 魔法”（将上下文窗口增加到 24K）
- 论文取 16K 运行在第 480 步的检查点，并以 24K 上下文窗口重新启动训练运行
- 有了扩展的上下文窗口，模型终于得以突破
- 大约 50 步后，论文的模型终于超过了 40% 的 AIME 准确率，并在第 200 步达到 43%
- 24K的魔法完全生效了！
总的来说，论文的训练运行大约包含 1,750 步
- 初始的 8K 阶段在 8 个 A100 GPU 上训练
- 16K 和 24K 阶段将训练扩展到 32 个 A100 GPU
- 总共：训练耗时约 3,800 个 A100 GPU 小时，相当于在 32 个 A100 上运行约5天，计算成本约为 4500 美元

Evaluation

论文在竞赛级数学基准上评估了论文的模型，包括 AIME 2024、AMC 2023、MATH-500、Minerva Math 和 OlympiadBench

以下报告的是 Pass@1 准确率，每个问题平均 16 个样本。论文运行以验证分数的基线已加下划线

模型	AIME 2024	MATH 500	AMC 2023	Minerva Math	OlympiadBench	平均
Qwen-2.5-Math-7B-Instruct	13.3	79.8	50.6	34.6	40.7	43.8
rStar-Math-7B	26.7	78.4	47.5	-	47.1	-
Eurus-2-7B-PRIME	26.7	79.2	57.8	38.6	42.1	48.9
Qwen2.5-7B-SimpleRL	26.7	82.4	62.5	39.7	43.3	50.9
DeepSeek-R1-Distill-Qwen-1.5B	28.8	82.8	62.9	26.5	43.3	48.9
Still-1.5B	32.5	84.4	66.7	29.0	45.4	51.6
DeepScaleR-1.5B-Preview	43.1	87.8	73.6	30.2	50.0	57.0
O1-Preview	40.0	81.4	-	-	-	-

图5： AIME 准确率与模型大小，DeepScaleR实现了性能和尺寸之间最帕累托最优的组合
论文将 DeepScaleR 与论文使用的基础 DeepSeek 模型以及近期探索用于推理任务的强化学习的学术作品进行了比较
- DeepScaleR 在所有基准测试上都显著优于基础模型，在 AIME2024 上取得了 14.4% 的绝对增益，整体提升了 8.1%
- DeepScaleR 超越了近期如 rSTAR、Prime 和 SimpleRL 等学术作品，这些作品都是从 7B 模型微调而来
- 如图5所示，DeepScaleR 仅凭 1.5B 参数就达到了 o1-preview 级别的性能（这是一个显著的效率提升）

Key Takeaways

强化学习扩展也适用于小型模型（RL scaling can manifest in small models as well）
- Deepseek-R1 表明，直接在小型模型上应用强化学习不如蒸馏有效
- 他们的消融实验显示，对 Qwen-32B 进行强化学习在 AIME 上达到 47%，而仅蒸馏就能达到 72.6%
- 一个常见的误解是强化学习扩展只对大模型有益，但通过从大模型蒸馏出的高质量 SFT 数据，小型模型也可以通过强化学习更有效地学习推理
- 论文的结果证实了这一点：强化学习扩展将 AIME 准确率从 28.9% 提高到了 43.1%！这些发现表明，SFT 或 RL 单独都不够
  - 相反，通过结合高质量的 SFT 蒸馏和强化学习扩展 ，我们才能真正释放 LLM 的推理潜力
迭代延长实现了更有效的长度扩展（Iterative lengthening enables more effective length scaling）
- 先前的研究[1, 2]表明，直接在 16K 上下文上训练强化学习与 8K 相比没有显著改进，这可能是因为计算量不足以让模型充分利用扩展的上下文
  - Demystifying Long Chain-of-Thought Reasoning in LLMs, arXiv 20250205, THU & CMU
  - T1: Advancing Language Model Reasoning through Reinforcement Learning and Inference Scaling, arXiv 20250113, THU & ZhipuAI
- 最近的一项工作[3]表明，更长的响应长度包含冗余的自我反思，导致错误结果（论文的实验与这些发现一致）
  - https://github.com/sail-sg/oat-zero: (oat-zero)There May Not be Aha Moment in R1-Zero-like Training — A Pilot Study
- 通过首先在较短的上下文（8K）上优化推理，论文为后续的 16K 和 24K 运行实现了更快、更有效的训练
  - 这种迭代方法在扩展到更长上下文之前，使模型建立在有效的思维模式上，从而使基于强化学习的长度扩展更加高效

NLP——LLM-Reasoning-Coconut

注：本文包含 AI 辅助创作

参考链接：
- 原始论文：(Coconut)Training Large Language Models to Reason in a Continuous Latent Space, Meta, 20251104

Paper Summary

核心内容：
- 论文介绍了一种在连续潜在空间中进行推理的新范式 Coconut，创新性很强，可能是未来的一个趋势，有可能开一个先河
- Coconut 在潜在空间中进行推理产生了新行为，即 Continuous Thought 可以表示多个备选的后续步骤
- Coconut 使得模型能够对可能的推理路径执行 BFS，而不是像语言空间 CoT 推理那样过早地承诺一条单一的确定性轨迹
LLM 被限制在“语言空间（Language Space）”中进行推理，通常通过 CoT 来表达推理过程以解决复杂的推理问题
作者认为语言空间对于推理而言可能并非总是最优的
- 如大多数 Token 主要是为了确保文本连贯性，对推理并非必需
- 一些关键 Token 则需要复杂的规划，并对 LLM 构成了巨大挑战
为了探索 LLM 在不受限制的潜在空间（Latent Space）中进行推理的潜力（而不是使用自然语言），论文引入了一个新范式 Coconut（连续思维链，Chain of Continuous Thought）
- 利用 LLM 的最后一个隐藏状态作为推理状态的表示（称为“ Continuous Thought”）
论文不是将其解码为一个 Token ，而是直接在连续空间中将其作为后续的输入嵌入反馈给 LLM
- 这种 Latent Reasoning 范式导致了一种高级推理模式的出现：** Continuous Thought 可以对多个备选的后续推理步骤进行编码** ，使得模型能够执行广度优先搜索（Breadth-First Search, BFS）来解决问题，而不是像思维链那样过早地承诺单一的确定性路径
- Coconut 在某些需要大量搜索规划的逻辑推理任务上优于思维链，并在准确性和效率之间展现了更好的权衡

Introduction and Discussion

LLM 已经展现出卓越的推理能力，这源于对人类语言的大规模预训练 (2024; 2023)
虽然 Next Token Prediction 是一个有效的训练目标，但它对 LLM 作为一个推理机器施加了一个基本限制：
- LLM 的显式推理过程必须用 Token 生成
- 例如 CoT 推理 (2022)，涉及提示或训练 LLM 使用自然语言逐步生成解决方案，但这与某些人类认知研究结果形成鲜明对比
  - 神经影像学研究一致表明，在各种推理任务中，负责语言理解和产生的脑区集合（语言网络）大部分保持不活跃状态 (2019; 2012, 2007, 2009; 2011)
- 进一步的证据表明，人类语言是为沟通而非推理而优化的 (2024)
当 LLM 使用语言进行推理时，一个显著的问题出现了：
- 每个特定 Token 所需的推理量差异很大，然而当前的 LLM 架构为预测每个 Token 分配了几乎相同的计算预算
  - 理解：有些 Token 需要思考，有些 Token 是不需要的
- 推理链中的大多数 Token 仅仅是为了流畅性而生成的，对实际的推理过程贡献甚微
  - 另一些关键 Token 则需要复杂的规划，并对 LLM 构成了巨大挑战
- 先前的工作试图通过 Prompting LLM 生成简洁的推理链 (2022)，或者在生成一些关键 Token 之前执行额外的推理 (2024) 来修复这些问题
  - 但这些解决方案仍然局限于语言空间内，并未解决根本问题
- 理想的情况是： LLM 能够不受任何语言约束地自由推理，然后仅在必要时将其发现转化为语言
论文引入一个新范式 Coconut（连续思维链，Chain of Continuous Thought）来探索 LLM 在潜在空间中的推理
- Coconut 对传统思维链过程做了简单修改：
  - Coconut 不使用语言模型头和嵌入层在隐藏状态和语言 Token 之间进行映射，而是直接将最后一个隐藏状态（一个 Continuous Thought）作为下一个 Token 的输入 Embedding（图 1）
- 这种修改将推理从语言空间中解放出来，并且系统可以通过梯度下降进行端到端优化，因为 Continuous Thought 是完全可微分的
- 为了增强 Latent Reasoning 的训练，论文采用了受 (2024) 启发的多阶段训练策略，该策略有效地利用语言推理链来指导训练过程
论文提出的范式给出了一种高效的推理模式
- 对比基于语言的推理，Coconut 的 Continuous Thought 可以同时编码多个潜在的后续步骤，允许进行类似于 BFS 的推理过程
  - 理解：离散化本身是一个采样过程，会丢失一些信息，相当于在选择一条确定的路，而 Continuous Thought 则保留了未采样的分布信息
- 虽然模型最初可能不会做出正确的决策，但它可以在 Continuous Thought 中保持许多可能的选择，并在某些隐式价值函数的指导下，通过推理逐步消除不正确的路径
- 这种高级推理机制超越了传统的思维链，尽管模型并未像先前工作 (2023; 2023) 中那样被明确训练或指示以这种方式操作
  - 问题：如何理解上面这句话？
实验表名：Coconut 成功增强了 LLM 的推理能力
- 对于数学推理（GSM8k, 2021）任务， Continuous Thought 对推理准确性有益
  - 这表明通过链接更多 Continuous Thought 来扩展和解决更具挑战性问题的潜力
- 在逻辑推理方面，包括 ProntoQA (2022) 和论文新提出的需要更强规划能力的 ProsQA（第 4 节）
  - Coconut 及其一些变体甚至超越了基于语言的思维链方法，同时在推理过程中生成的 Token 数量显著减少
  - 作者相信这些发现强调了 Latent Reasoning 的潜力，并可能为未来的研究提供宝贵的见解

Coconut： Continuous Thought 链 (Coconut: Chain of Continuous Thought)

本节介绍新范式 Coconut（Chain of Continuous Thought），在不受约束的潜在空间中进行推理

Background

对于输入序列 $x=(x_{1},…,x_{T})$，标准的 LLM $\mathcal{M}$ 可以描述为：
$$
\begin{align}
H_{t} =\text{Transformer}(E_{t}) \\
\mathcal{M}(x_{t+1}\mid x_{\leq t}) =\text{softmax}(Wh_{t})
\end{align}
$$
- $E_{t}=[e(x_{1}),e(x_{2}),…,e(x_{t})]$ 是直到位置 $t$ 的 Token 嵌入序列；
- $H_{t}\in\mathbb{R}^{t\times d}$ 是直到位置 $t$ 的所有 Token 的最后一个隐藏状态矩阵；
- $h_{t}$ 是位置 $t$ 的最后一个隐藏状态，即 $h_{t}=H_{t}[t,:]$；$e(\cdot)$ 是 Token 嵌入函数；$W$ 是语言模型头的参数

Method Overview

在语言模式下，模型作为标准语言模型运行，自回归地生成下一个 Token
在 Coconut 中， LLM 在“语言模式”和“潜在模式”之间切换（图 1）
- 直接使用最后一个隐藏状态作为下一个输入嵌入
- 这个最后一个隐藏状态代表了当前的推理状态，被称为“ Continuous Thought ”
使用特殊 Token <bot> 和 <eot> 分别 Token Latent Thought 模式的开始和结束
举例：假设 Latent Reasoning 发生在位置 $i$ 和 $j$ 之间，即 $x_{i}=
$ 且 $x_{j}=
$
- 当模型处于潜在模式时（$i < t < j$），论文使用前一个 Token 的最后一个隐藏状态来替换输入嵌入，即
  $$ E_{t}=[e(x_{1}),e(x_{2}),…,e(x_{t}),h_{i},h_{i+1},…,h_{t-1}]$$
- 在潜在模式结束后（$t\geq j$），输入恢复为使用 Token 嵌入，即
  $$ E_{t}=[e(x_{1}),e(x_{2}),…,e(x_{t}),h_{i},h_{i+1},…,h_{j-1},e(x_{j}),…,e( x_{t})] $$
- It is worth noting that 最后一个隐藏状态已经经过最终归一化层处理，因此它们的幅度不会太大
  - 当 $i < t < j$ 时，$\mathcal{M}(x_{t+1}\mid x_{\leq t})$ 未定义，因为 Continuous Thought 不打算映射回语言空间
  - 但出于探测目的，仍然可以计算 softmax($Wh_{t}$)（见第 5 节）

Training Procedure

论文专注于一个问题解决场景，其中模型接收一个问题作为输入，并期望通过推理过程生成一个答案
论文利用语言思维链数据，通过实施受 (2024) 启发的多阶段训练课程来监督 Continuous Thought
如图 2 所示
- 在初始阶段，模型在常规的思维链实例上进行训练
- 在后续阶段中，在第 $k$ 个阶段，思维链中的前 $k$ 个推理步骤被替换为 $k\times c$ 个 Continuous Thought（如果语言推理链短于 $k$ 步，那么所有的语言思维都将被移除）
  - 其中 $c$ 是一个超参数，控制替换单个语言推理步骤的 Latent Thought 数量
  - 问题：这里的推理步骤是如何定义和划分的？
- 遵循 (2024)，论文在训练阶段切换时也重置优化器状态
- 论文插入 <bot> 和 <eot> Token （不计入 $c$）来封装 Continuous Thought
在训练过程中，优化标准的负对数似然损失，但屏蔽问题和 Latent Thought 上的损失
It is important to note that 目标并不鼓励 Continuous Thought 去压缩被移除的语言思维 ，而是去促进对未来推理的预测
- 因此， LLM 有可能学习到比人类语言更有效的推理步骤表示

Training Details

Continuous Thought 是完全可微分的，并允许反向传播
在当前训练阶段安排了 $n$ 个 Latent Thought 时，论文执行 $n+1$ 次前向传播，每次传播计算一个新的 Latent Thought ，最后进行一次额外的前向传播以获得剩余文本序列上的损失
虽然可以通过使用 KV 缓存来节省任何重复计算，但多次前向传播的顺序性质对并行性提出了挑战
进一步优化Coconut 的训练效率仍然是未来研究的一个重要方向

Inference Process

Coconut 的推理过程类似于标准的语言模型解码，除了在潜在模式下，直接将最后一个隐藏状态作为下一个输入嵌入
一个挑战在于确定何时在潜在模式和语言模式之间切换
论文专注于问题解决场景
- 在问题 Token 之后立即插入一个 <bot> Token
- 对于 <eot>，论文考虑两种潜在策略（或关系）：
  - a）在 Latent Thought 上训练一个二元分类器，使模型能够自主决定何时终止 Latent Reasoning
  - b）总是将 Latent Thought 填充到恒定长度
- 作者发现两种方法效果相当
- 在实验中，除非另有说明，论文出于简单性使用第二个选项

Continuous Space Enables Latent Tree Search（连续空间使得我们可以使用Latent 树搜索）

本节提供了一个概念验证，证明了在连续潜在空间中进行推理的优势
在 ProsQA 这个需要强大规划能力的新数据集上，Coconut 的表现优于语言空间的 CoT 推理
Interestingly，论文的分析表明，推理的连续表示可以编码多个备选的后续推理步骤
- 这使得模型能够执行广度优先搜索来解决问题，而不是像语言 CoT 那样过早地承诺一条单一的确定性路径
4.1 节：介绍实验设置
4.2 节：通过利用 Coconut 在语言和潜在空间推理之间切换的能力，论文能够控制模型在完全 Latent Reasoning 和完全语言推理之间进行插值，并测试它们的性能
4.3 节：作者将 Latent Reasoning 过程解释为树搜索（tree search）
4.4 节：基于树搜索的视角，作者解释了为什么 Latent Reasoning 能帮助 LLM 做出更好的决策

Experimental Setup

Dataset

论文引入了 ProsQA（Proof with Search Question-Answering），一个新的逻辑推理数据集
- 一个可视化的例子如图 4 所示
ProsQA 中的每个实例都由一个概念间逻辑关系的有向无环图组成，以自然语言语句的形式呈现
该任务要求模型通过在此图中找到有效路径来确定逻辑关系，这需要复杂的规划和搜索策略
与之前的逻辑推理数据集（如 ProntoQA (Saparov and He, 2022)）不同，ProsQA 的 DAG 结构引入了复杂的探索路径，使得模型识别正确的推理链特别具有挑战性
关于数据集构建和特征的更全面细节可以在附录 A 中找到

Setup

论文使用预训练的 GPT-2 模型作为所有实验的基础模型
学习率设置为 $1\times 10^{-4}$，有效批次大小为 128
作者按照第 3 节的训练过程训练一个 Coconut 模型
由于 ProsQA 中的最大推理步数为 6，论文在训练过程中将训练阶段数设置为 $N=6$
在每个阶段，论文训练模型 5 个 Epoch ，并在最后一个阶段保持训练直到总共 50 个 Epoch
使用最后一个阶段中准确率最高的检查点进行评估
作为参考，论文报告了以下基线的性能：
- (1) CoT：模型使用 CoT 数据进行训练，在推理过程中，模型会生成完整的推理链来解决问题
- (2) no-CoT：模型仅使用问题和答案对进行训练，没有任何推理步骤
为了理解 Latent Reasoning 空间和语言推理空间的特性，论文通过手动设置 <eot> Token 在推理过程中的位置，来操纵模型在完全 Latent Reasoning 和完全语言推理之间切换
当强制 Coconut 使用 $k$ 个 Continuous Thought 时，模型需要从第 $k+1$ 步开始，以语言形式输出剩余的推理链
在论文的实验中，论文在 ProsQA 上测试了 Coconut 的变体，其中 $k\in \{0,1,2,3,4,5,6\}$
- 请注意，所有这些变体仅在推理时有所不同，而共享相同的模型权重

Metrics

论文应用了两套评估指标
- 一套基于 最终答案 的正确性，而不考虑推理过程。这也是后面章节（第 5.3 节）使用的主要指标
- 为了对 ProsQA 进行细粒度分析，论文定义了另一个关于 推理过程 的指标
论文将推理链分类为：
- (1) 正确路径 (Correct Path) ：输出是到达正确答案的最短路径之一
- (2) 更长路径 (Longer Path) ：正确回答问题但比最短路径长的有效路径
- (3) 幻觉 (Hallucination) ：路径包含不存在的边或是不连通的
- (4) 错误目标 (Wrong Target) ：图中的有效路径，但目标节点不是被问及的节点
这四类自然地适用于 Coconut ($k=0$) 和 $CoT$ 的输出，它们生成完整路径
对于仅输出部分语言路径（初始步骤为连续推理）的 Coconut ($k>0$)，如果存在一个有效的解释可以补全该路径，论文将其推理归类为正确路径
- 类似地，作者也为部分路径定义了更长路径和错误目标
如果没有有效的解释可以补全该路径，则归类为幻觉
在 no-CoT 和具有较大 $k$ 的 Coconut 中，模型可能只输出最终答案而没有任何部分路径，这属于
- (5) 正确标签 (Correct Label) 或
- (6) 错误标签 (Incorrect Label)
以上这六个类别涵盖了所有情况且没有重叠

Overall Results

图 3 展示了在 ProsQA 上评估的各种推理方法的比较分析
- 使用 $CoT$ 训练的模型经常幻觉出不存在的边或输出导致错误目标的路径，导致答案准确率较低
- 利用连续空间推理的 Coconut 随着使用 Continuous Thought 数量的增加，表现出更高的准确率
- 正确推理过程（由“正确标签”和“正确路径”表示）的比例显著增加
- “幻觉”和“错误目标”的情况显著减少，这些问题通常在模型在推理过程早期犯错时出现
图 4 所示的案例研究直观地展示了在语言空间进行推理的局限性
- 如图所示，在语言空间操作的模型常常无法提前规划或回溯
  - 一旦它们承诺了一条错误的路径，它们要么幻觉出不支持的边，要么以不相关的结论终止
- Latent Reasoning 通过使模型能够在多个推理步骤中迭代地优化其决策，避免了这种过早的承诺
  - 这种灵活性允许模型逐步淘汰不正确的选项并收敛到正确答案，最终实现更高的准确率

Interpreting the Latent Reasoning as Tree Search（将 Latent Reasoning 解释为树搜索）

为了更好地理解 Coconut，论文通过在中间 Continuous Thought 之后强制模型显式生成语言推理步骤来探测 Latent Reasoning 过程（图 5）
- 使用图 4 中展示的例子，在初始推理步骤，模型必须选择接下来考虑“Alex”的哪个直接子节点，具体是从集合 {“lempus”, “sterpus”, “zhorpus”, “grimpus”} 中选择
- 这些候选下一步的分布如图 5 左侧所示
- 在随后的推理步骤中，这些节点进一步扩展为一组扩展的潜在路径，包括“Alex”的所有孙节点（图 5 右侧）
论文将 Continuous Thought 之后某个概念的预测概率定义为一个价值函数（图 5），用于估计每个节点到达正确目标的潜力
Interestingly，Coconut 采用的推理策略并非贪婪搜索：
- 虽然在第一个推理步骤中“lempus”最初具有最高的价值 ($0.33$)（图 5 左侧），但模型随后将最高价值 ($0.87$) 分配给了“grimpus”的子节点“corpus”，而不是跟随“lempus”（图 5 右侧）
- 这个特性类似于广度优先搜索方法，与传统的 CoT 方法典型的贪婪解码形成鲜明对比
- 连续表示能够编码多个候选路径的固有能力使模型能够避免立即做出确定性决策
- Importantly，这种树搜索模式并不仅限于所展示的例子，而是构成了在 Coconut 中使用较大 $k$ 值时观察到的一致改进的基本机制
图 6 展示了模型在第一和第二个思维中 Latent Reasoning 并行性的分析
- 对于第一个思维（左图），计算了前 1、前 2 和前 3 候选节点的累积价值，并针对它们在测试集中的相应百分位数进行绘制
- 三条线之间的明显差距表明，模型在此阶段在其推理路径中保持了显著的多样性，表明了对替代可能性的广泛探索
- In contrast，第二个思维（右图）显示这些差距在缩小
  - 这种趋势表明，模型在第二个 Latent Reasoning 步骤中从并行探索转向更集中的推理，很可能是因为它对最有希望的路径获得了更多的确定性

Why is Latent Space Better for Planning?

基于树搜索的视角，作者进一步研究了为什么 Latent Reasoning 有益于规划任务
- 具体来说，为什么保持多个候选路径并推迟确定性决策能提高推理性能
作者的假设是，在早期推理阶段探索的节点本质上更难以准确评估，因为它们距离最终的目标节点更远
- In contrast，位置更接近潜在目标的节点，由于后续探索的可能性较少，可以以更高的置信度进行准确评估
为了系统地测试这一点，论文定义了一个节点的高度为其到任何叶节点的最短距离，并分析了节点高度与模型估计价值之间的关系
理想情况下，一个正确的节点（即能够通向目标节点的节点）应该获得较高的估计价值，而一个不正确的节点（即不能通向目标节点的节点）应该获得较低的价值
在整个测试集上的实证结果（图 7）支持了作者的假设：
- 高度较低的节点持续获得更准确和明确的概率评估
- Conversely，高度较大的节点表现出更模糊的评估，反映了不确定性的增加
这些发现强调了潜在空间推理的优势
- 通过延迟确定性决策并允许探索向终端状态进行， Latent Reasoning 显著增强了模型区分正确路径和错误路径的能力，从而在复杂的、规划密集的任务上相比传统的贪婪方法提高了性能

Coconut Empirical Results with Coconut

在分析了 Coconut 有前景的并行搜索模式之后，论文通过更全面的实验验证了在连续潜在空间中进行 LLM 推理的可行性，突出了其相对于语言空间更好的推理效率，以及通过测试时缩放增强模型表达能力的潜力

Experimental Setup

Math Reasoning

论文使用 GSM8k (2021) 作为数学推理的数据集
- 它包含小学水平的数学问题
为了训练模型，论文使用 (2023) 生成的合成数据集
论文对每个推理步骤使用两个 Continuous Thought （即 $c=2$）
模型除了初始阶段外，还经历了 3 个阶段
然后论文增加一个额外的阶段，该阶段仍像前一个阶段一样使用 $3\times c$ 个 Continuous Thought ，但移除所有剩余的语言推理链
这处理了推理链长度超过 3 步的长尾分布
论文在初始阶段训练模型 6 个 Epoch ，在其余每个阶段训练 3 个 Epoch

Logical Reasoning

逻辑推理涉及正确应用已知条件，使用逻辑规则来证明或反驳一个结论
论文使用 ProntoQA (Saparov and He, 2022) 数据集和论文新提出的 ProsQA 数据集，后者由于有更多干扰分支而更具挑战性
论文对每个推理步骤使用一个 Continuous Thought （即 $c=1$）
模型除了初始阶段外，还经历了 6 个训练阶段，因为这两个数据集中的最大推理步数为 6
然后模型在最后一个阶段完全使用 Continuous Thought 来解决问题
论文在每个阶段训练模型 5 个 Epoch
对于所有数据集，在标准调度之后，模型停留在最终训练阶段，直到达到 50 个 Epoch
论文根据验证集上的准确率选择检查点
对于推理，论文手动设置 Continuous Thought 的数量，以与其最终训练阶段保持一致
所有实验均使用贪婪解码

Coconut Baselines and Variants of Coconut

论文考虑了以下基线：
- (1) CoT
- (2) No-CoT
- (3) iCoT (2024)：模型使用语言推理链进行训练，并遵循一个精心设计的、用于“内化” CoT 的调度
  - 随着训练的进行，推理链开头的 Token 被逐渐移除，直到只剩下答案
  - 在推理过程中，模型直接预测答案
- (4) Pause token (2023)：模型仅使用问题和答案（没有推理链）进行训练
  - 与 No-CoT 不同，在问题和答案之间插入了特殊的 <pause> Token ，这为模型提供了额外的计算能力来推导答案
  - <pause> Token 的数量设置为与 Coconut 中的 Continuous Thought 数量相同
论文还评估了 Coconut 的一些变体：
- (1) w/o curriculum： 直接在最后一个阶段训练模型
  - 模型使用 Continuous Thought 来解决整个问题
- (2) w/o thought： 论文保留多阶段训练，但不添加任何连续 Latent Thought
  - 虽然这与 iCoT 的高层思想相似，但为了进行严格比较，其确切的训练调度设置为与 Coconut 一致，而不是 iCoT
- (3) pause as thought：论文使用特殊的 <pause> Token 替换 Continuous Thought ，并应用与 Coconut 相同的多阶段训练课程

Results and Discussion

在表 1 中展示了总体结果
- 使用 Continuous Thought 有效地增强了 LLM 推理能力，超过了 No-CoT 基线
- 例如，通过使用 6 个 Continuous Thought ，Coconut 在 GSM8k 上达到了 34.1% 的准确率，显著优于 No-CoT (16.5%)

“链接” Continuous Thought 增强了推理能力

语言 CoT 被证明可以增加 LLM 的有效深度并增强其表达能力 (2023)
因此，生成更多 Token 是推理时缩放的一种方式 (2025; 2024)
这个理想的特性自然也适用于 Coconut
在 GSM8k 上，Coconut 的表现优于使用类似策略训练的其他架构，包括 Coconut (pause as thought) 和 Coconut ( w/o thought )
- 特别是，它超过了最新的基线 iCoT (2024)，后者需要更精心设计的训练调度
此外，论文尝试调整超参数 $c$，它控制对应于一个语言推理步骤的 Latent Thought 数量（图 8, II）
- 随着论文将 $c$ 从 0 增加到 1 再到 2，模型的性能稳步提高
- 这进一步验证了 Continuous Thought 能够扩展到更困难问题的潜力
在另外两个合成任务中，论文发现 Coconut 的变体（ w/o thoughts 或 pause as thought）以及 iCoT 基线也取得了令人印象深刻的准确率
- 这表明在这些任务中，模型的计算能力可能不是瓶颈
- 相比之下，GSM8k 涉及更复杂的上下文理解和建模，对计算能力提出了更高的要求

Continuous Thought 是高效的推理表示

与传统的 CoT 相比，Coconut 在 ProntoQA 和 ProsQA 上生成的 Token 更少，同时实现了更高的准确率（表 1）
尽管 Coconut 在 GSM8k 上没有超过 CoT ，但它在推理效率和准确率之间提供了更优的权衡（图 8, I）
为了说明这一点，论文训练了一系列 CoT 模型，这些模型逐步“内化”(2024) 了初始的 $m=\{0,1,2,3,\textrm{ALL}\}$ 个推理步骤，并绘制了它们的准确率与生成 Token 数量的关系图（在图中 Token 为“语言”）
这些模型在跳过更多推理步骤时迅速失去准确率
相比之下，通过应用 Coconut 训练策略——用两个 Continuous Thought 替换每个语言推理步骤——准确率的下降得到了显著缓解，即使在生成更少 Token 时也能保持更高的性能
另一个有趣的观察是，当论文解码第一个 Continuous Thought 时，它通常对应于计算中可能的中间变量（图 9）
这也表明 Continuous Thought 是更高效的推理表示

LLM 仍然需要指导来学习 Latent Reasoning

在理想情况下，模型应该通过关于问题和答案的梯度下降自动学习最有效的 Continuous Thought （即 Coconut$w/o$$curriculum$）
然而，从实验结果中，论文发现以这种方式训练的模型表现并不比 no-CoT 更好
相反，通过多阶段课程学习，Coconut 能够在各种任务中达到顶尖性能
多阶段训练也能与 pause tokens 很好地结合（Coconut-pause as thought）
尽管使用相同的架构和相似的多阶段训练目标，论文观察到：
- $iCoT$ 和 Coconut ($w/o$$thoughts$) 的性能之间存在微小差距
- $iCoT$ 中更细粒度的移除调度（逐个 Token ）和其他一些技巧可能使训练过程更容易
论文将结合 $iCoT$ 和 Coconut 作为未来的工作
虽然用于 Coconut 的多阶段训练已被证明是有效的，但肯定需要进一步的研究来开发更好、更通用的策略，以在潜在空间中学习推理，特别是在没有语言推理链监督的情况下

CoT 推理

论文广义地使用思维链这个术语来指代在输出最终答案之前，用语言生成中间推理过程的方法
- 这包括 Prompting LLM (2022; 2022; 2022)，或者通过监督微调 (2023; 2023) 或强化学习 (2024; 2024; 2024; 2024b) 来训练 LLM 生成推理链
- Madaan and Yazdanbakhsh (2022) 将思维链中的 Token 分类为符号、模式和文本，并基于对其角色的分析提出引导 LLM 生成简洁的思维链
- 最近的理论分析从模型表达能力的角度证明了思维链的有用性 (2023; 2023; 2024)
- 思维链使得 Transformer 的有效深度增加了，生成的输出被循环回输入 (2023)
这些分析，结合思维链已确立的有效性，促使作者设计了将 Continuous Thought 反馈给 LLM 作为输入嵌入的方案
- 虽然思维链已被证明对某些任务有效，但其自回归生成的性质使得在更复杂的问题上模仿人类推理具有挑战性 (2022; 2023)，这些问题通常需要规划和搜索
- 有一些工作为 LLM 配备了显式的树搜索算法 (2023; 2023; 2024)，或者在搜索动态和轨迹上训练 LLM (2024; 2024; 2024)
- 作者分析发现，在移除语言空间的约束后，即使模型没有经过明确的训练，也会出现一种类似于广度优先搜索的新推理模式

LLM 中的 Latent Reasoning

先前的工作大多将 LLM 中的 Latent Reasoning 定义为 Transformer 中的隐藏计算 (2024; 2024)
- Yang 等 (2024) 构建了一个双跳推理问题的数据集，并发现从隐藏表示中恢复中间变量是可能的
- Biran 等 (2024) 进一步提出通过“反向修补”隐藏表示来干预 Latent Reasoning
- Shalev 等 (2024) 在 LLM 中发现了并行的 Latent Reasoning 路径
另一项工作发现，即使模型生成思维链进行推理，模型实际上可能利用的是不同的 Latent Reasoning 过程
- 这种现象被称为思维链推理的不忠实性 (2022; 2024)
为了增强 LLM 的 Latent Reasoning ，先前的研究提出用额外的 Token 来增强它
- Goyal 等 (2023) 通过在训练语料库中随机插入一个可学习的 <pause> Token 来预训练模型
  - 这提高了 LLM 在各种任务上的性能，特别是在随后使用 <pause> Token 进行监督微调时
- Pfau 等 (2024) 进一步探索了填充 Token （例如“…”）的使用，并得出结论它们对于高度可并行化的问题效果很好
  - 但Pfau 等 (2024) 提到这些方法不像思维链那样扩展 LLM 的表达能力；因此，它们可能无法扩展到更一般和复杂的推理问题
- Wang 等 (2023) 提出在生成下一个推理步骤之前预测一个规划 Token 作为离散潜在变量
最近还发现可以通过知识蒸馏 (2023) 或逐渐缩短思维链的特殊训练课程 (2024) 将思维链推理“内化”到 Transformer 的 Latent Reasoning 中
- Yu 等 (2024b) 也提出从使用复杂推理算法生成的数据中蒸馏出一个能够进行 Latent Reasoning 的模型
这些训练方法可以结合到论文的框架中：
- 具体来说，作者发现，受 iCoT (2024) 启发，将 Continuous Thought 的学习分解为多个阶段对训练非常有益
- 其他工作探索了用于 Latent Reasoning 的替代架构，包括循环 Transformer (2023; 2024)，句子嵌入空间中的扩散模型 (2024)
与这些工作不同，论文专注于一般的多步推理任务 ，并旨在研究 Latent Reasoning 与语言空间相比的独特属性
除了推理任务，Pham 等 (2023) 也探索了使用连续空间进行多智能体通信
- 基于 Coconut，Zhu 等 (2025b) 开发了一个理论框架，证明通过将多个推理路径编码在叠加状态中， Continuous Thought 链在某些任务上可以比离散思维链更高效
- Zhu 等 (2025a) 分析了训练动态，以解释这种叠加是如何在 Coconut 训练目标下出现的

附录 A：数据集 Datasets

附录 A.1：示例 Examples

示例：

附录 A.2： Construction of ProsQA

附录 A.3：统计数据 Statistics

附录 B：Clock-Time Reasoning Efficiency Metric

论文提供了一个时钟时间比较来评估推理效率
报告的值代表了在 Nvidia A100 GPU 上测量的、批次大小为 1 时每个测试案例的平均推理时间（以秒为单位）
对于 no-CoT 和 CoT 基线，论文使用了 transformers 库中的标准生成方法。论文的结果表明，时钟时间通常与新生成的 Token 数量成正比，详见表 1

附录 C：更多讨论 More Discussion

C.1 使用更多 Continuous Thought Using More Continuous Thoughts

在图 8 (II) 中，论文展示了 Coconut 在 GSM8k 上使用 $c\in\{0,1,2\}$ 的性能
当试验 $c=3$ 时，论文观察到性能略有下降，同时方差增大
对训练日志的分析表明，一次性添加三个 Continuous Thought（尤其是在最后阶段转换期间）会导致训练损失急剧上升，从而引发不稳定性
未来的工作将探索更细粒度的调度方案，例如像 iCoT (2024) 那样，逐步一次添加一个 Continuous Thought ，同时移除更少的语言 Token
此外，将语言推理和 Latent Reasoning 相结合（例如，用语言生成推理骨架，并在潜在空间中完成推理过程）可能为提高性能和稳定性提供一个有前景的方向

C.2 使用更大模型的 Coconut Coconut with Larger Models

论文在 GSM8k 上使用 Llama 3.2-3B 和 Llama 3-8B (2024) 以及 $c=1$ 对 Coconut 进行了实验。论文在阶段 0 训练 3 个 Epoch ，随后每个后续阶段训练 1 个 Epoch
结果如表 5 所示
论文观察到，与 no-CoT 基线相比，在 Llama 3.2-3B 和 Llama 3-8B 模型上都取得了一致的性能提升，尽管这些改进不如之前使用 GPT-2 所展示的那么显著
- 一个可能的原因是更大的模型已经经历了广泛的语言焦点预训练，使得向 Latent Reasoning 的转变更具挑战性
We emphasize that 论文的主要目标是突出潜在空间推理的有前景特性，并在这个新方向上启动探索
要普遍超越基于语言的 CoT，很可能需要致力于潜在空间预训练的大量研究工作
论文受到该领域近期进展 (2025; 2024; 2025) 的鼓舞
虽然这些最近的模型为潜在表示学习提供了可扩展的方法，但潜在空间尚未被明确优化用于推理
将这些最新进展与 Coconut 相结合，为未来的研究提供了一个令人兴奋且有前景的途径

Joe Zhou

Stay Hungry. Stay Foolish.

GitHub E-Mail