NLP——LoRA-Without-Regret

注：本文包含 AI 辅助创作

参考链接：
- 原始博客：LoRA Without Regret, 20250929, Thinking Machines

Blog Summary

本文是 Thinking Machines 发布的一篇博客，核心是研究 LoRA 在 LLM 中的作用以及的各超参的详细影响
本文包含非常详细的实验细节，讨论了各种 LoRA 相关超参数（学习率和 Rank 等）设置技巧，是一篇非常实在的技术博客，值得深读

Introduction

如今主流的语言模型（Language Model）包含超过一万亿（1T）个参数，这些模型在数十万亿个 Token 上进行预训练
基础模型（Base Model）的性能随着规模的扩大而不断提升，因为这万亿级别的参数对于学习和表征人类书面知识中的所有模式至关重要
In contrast， Post-Traning 使用的数据集规模更小，且通常聚焦于更狭窄的知识领域和行为范围
- 用万亿比特（Terabit）级别的权重来表征来自十亿比特（Gigabit）或百万比特（Megabit）级训练数据的更新，似乎存在资源浪费
- 这种直觉推动了参数高效微调（Parameter-Efficient Fine-Tuning, PEFT）技术的发展，该技术通过更新一组规模小得多的参数来调整大型网络
目前主流的参数高效微调方法是 LoRA（Low-Rank Adaptation）
- LoRA 将原始模型中的每个权重矩阵 $ W $ 替换为经过修改的版本 $ W’ = W + \gamma BA $，其中矩阵 $ B $ 和 $ A $ 加起来的参数数量远少于 $ W $，而 $ \gamma $ 是一个常数缩放因子
- 实际上，LoRA 为微调所带来的更新创建了一个低维表征
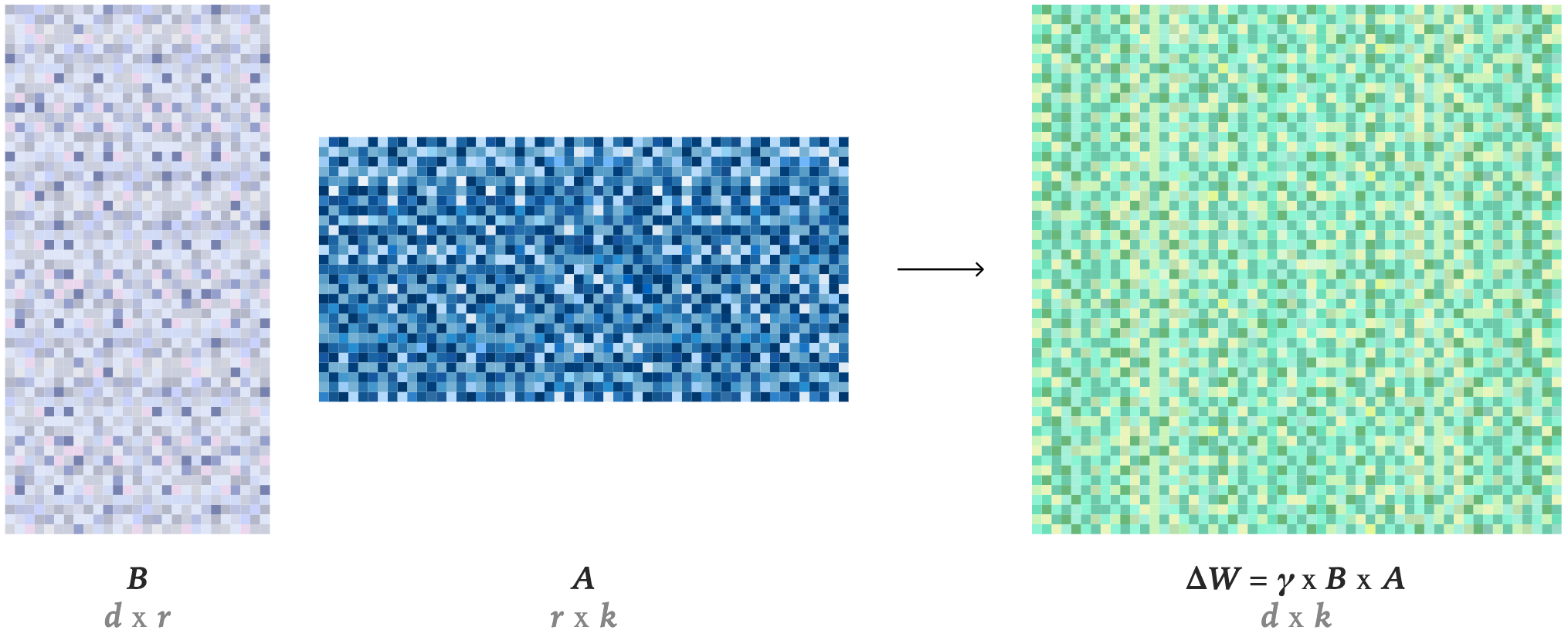
LoRA 在 Post-Traning 的成本和速度方面可能具有优势，此外，从操作角度来看，相比全参数微调（Full Fine-Tuning，以下简称 FullFT），选择 LoRA 还有几个理由：
- 多租户服务（Multi-Tenant Serving） ：
  - 由于 LoRA 仅训练一个 Adapter （即矩阵 $ A $ 和 $ B $），同时保持原始权重不变，因此单个推理服务器可以在内存中存储多个 Adapter （不同的模型版本），并以批量方式同时从中采样
  - 现代推理引擎（如 vLLM 和 SGLang）已实现此功能（2023）
- 训练 Layout 大小（Layout Size for Training） ：
  - 对整个模型进行微调时，优化器状态需要与原始权重一起存储，且通常需要更高的精度
  - FullFT 通常比对同一模型进行采样所需的加速器数量多一个数量级，进而需要不同的 Layout (理解：这里的 Layout 应该是指显存？)
    - 注：在训练过程中，除了存储权重外，通常还需要存储所有权重的梯度和优化器动量；而且，这些变量的存储精度（float32）通常高于推理时权重的存储精度（bfloat16 或更低）
  - 由于 LoRA 训练的权重数量少得多，占用的内存也少得多，因此其训练所需的 Layout 仅比采样所需的 Layout 略大
  - 这使得训练更容易实现，且通常效率更高
- 加载与迁移便捷性（Ease of Loading and Transfer） ：
  - 由于需要存储的权重更少，LoRA Adapter 的设置速度更快、更便捷，也更容易在不同机器之间迁移
上述原因足以解释自 2021 年 LoRA 原始论文发表以来，该技术日益普及的现象（2021）
- 但现有文献中关于 LoRA 与 FullFT 性能对比的结论尚不明确
研究界普遍认为，在类似预训练的场景下，LoRA 性能表现较差（2024）
- 即当数据集规模极大，超出 LoRA 参数的存储限制时，LoRA 会处于劣势
但对于 Post-Traning 中常见的数据集规模，LoRA 具备足够的容量来存储关键信息
- 不过，这一事实并不能保证 LoRA 在样本效率和计算效率上的表现
核心问题在于：LoRA 是否能达到全参数微调的性能水平？如果可以，需要满足哪些条件？
论文实验发现，当正确把握几个关键细节时，LoRA 的样本效率确实与 FullFT 相同，并且能达到相同的最终性能

What Matters for LoRA（什么最关键？）

论文介绍了论文开展的一系列 SFT 和 RL 实验，旨在确定 LoRA 与 FullFT 效率匹配的条件
为此，论文的实验方法与以往关于 LoRA 的实验存在以下几点不同：
- 1）论文研究了训练集大小与 LoRA 参数数量之间的一般关系 ，而非聚焦于特定的数据集和任务
- 2）在监督学习中，论文测量的是对数损失（Log Loss） ，而非采用基于采样的评估方法（Sampling-Based Evals），这样做同样是为了保证结论的通用性
  - 对数损失测量能在不同训练步骤和训练参数范围内，提供清晰的结果和缩放定律（Scaling Laws）
论文的研究发现如下：
- 在中小型指令微调（Instruction-Tuning）和推理数据集（Reasoning Dataset）上进行 SFT 时，LoRA 的性能与全参数微调相同
- 当数据集规模超出 LoRA 的容量时，LoRA 性能会低于 FullFT
  - 此时，LoRA 并非会达到一个无法突破的损失下限（Distinct Floor）
  - 而是其训练效率会下降 ，且下降程度取决于模型容量与数据集大小之间的关系
  - 理解：这里的意思是训练慢，但是多训练一段时间，也能达到不错的效果
- 在某些场景下，LoRA 对大批量大小（Large Batch Size）的容忍度低于 FullFT（当批量大小超过某个阈值后，LoRA 的损失 penalty 会更大）
  * 增加 LoRA 的 Rank 无法缓解这种 penalty ，这是矩阵乘积参数化（Product-of-Matrices Parametrization）的固有属性，该参数化方式的 Training Dynamics 与优化原始权重矩阵的 Training Dynamics 不同
  - 注：Training Dynamics 指的是训练过程中模型的各种属性随时间或迭代轮数的变化情况，包括但不限于损失函数值、准确率、模型参数的更新、梯度的分布等属性
  - 问题：这里的意思是 Batch Size 太大，不适合 LoRA?
- 即使在小数据场景下，将 LoRA 应用于所有权重矩阵（尤其是 MLP 和 MoE 层）时，其性能也会更优
  - 仅将 LoRA 应用于注意力层（Attention-Only LoRA）的性能较差，即便通过提高 Rank 来匹配可训练参数的数量，结果依然如此
- 在强化学习中 ，即使使用较小的 Rank ，LoRA 的性能也能与 FullFT 相当
  - 论文发现强化学习所需的容量非常低 ，这一结果与论文基于信息论的推断一致
论文还研究了 LoRA 超参数对其学习率（相对于 FullFT 学习率）的影响
- 论文分析了初始缩放（Init Scales）、乘数（Multipliers）等超参数的一些不变性，并解释了为何 $ \frac{1}{r} $ 预因子能使最优学习率（LR）大致独立于 Rank
- 论文还通过实验展示了 LoRA 的最优学习率与 FullFT 最优学习率之间的关系
论文的实验结果明确了“低遗憾区间（Low-Regret Regime）”的特征
- 在该区间内，LoRA 在数据集大小和参数数量方面的性能与 FullFT 相近
- 论文发现该区间涵盖了大多数 Post-Traning 场景，这为在众多应用中使用高效微调技术开辟了道路

Methods and Results

论文设计实验的目的是，在不同条件下详细测量 LoRA 相对于 FullFT 的性能。以下是实验设置的一些细节：
- 论文将 LoRA 的 Rank 在三个数量级范围内变化（ Rank 的取值为 1 到 512），并将这些不同 Rank 的 LoRA 与全参数微调进行对比
- 为了排除因使用非最优学习率可能带来的干扰，论文针对每个实验条件都进行了学习率扫描（LR Sweep）
  - 论文采用恒定学习率调度（Constant Learning Rate Schedule），不进行预热（Warmup）或冷却（Cooldown）
- 实验使用的模型为 Llama 3 系列模型（2024）和 Qwen3 模型（2025），其中包括一个 MoE 模型
- 主要的监督学习实验使用了 Tulu3（2024）和 OpenThoughts3（2025）数据集，分别聚焦于指令遵循（Instruction Following）和推理任务
  - 这两个数据集在范围、结构和应用场景上存在显著差异，这有助于验证论文结果的通用性
- 强化学习实验使用数学推理任务，以答案的正确性作为奖励（Reward）

LoRA Rank

论文在 Tulu3 数据集和 OpenThoughts3 数据集的一个子集上进行了单轮训练（Single Epoch）
针对每个数据集和模型大小，论文都对 LoRA 的 Rank 和学习率进行了扫描
在下图中，每条彩色线条代表一个特定的 Rank ，线条是通过在每个训练步骤中取所有学习率对应的最小点得到的：
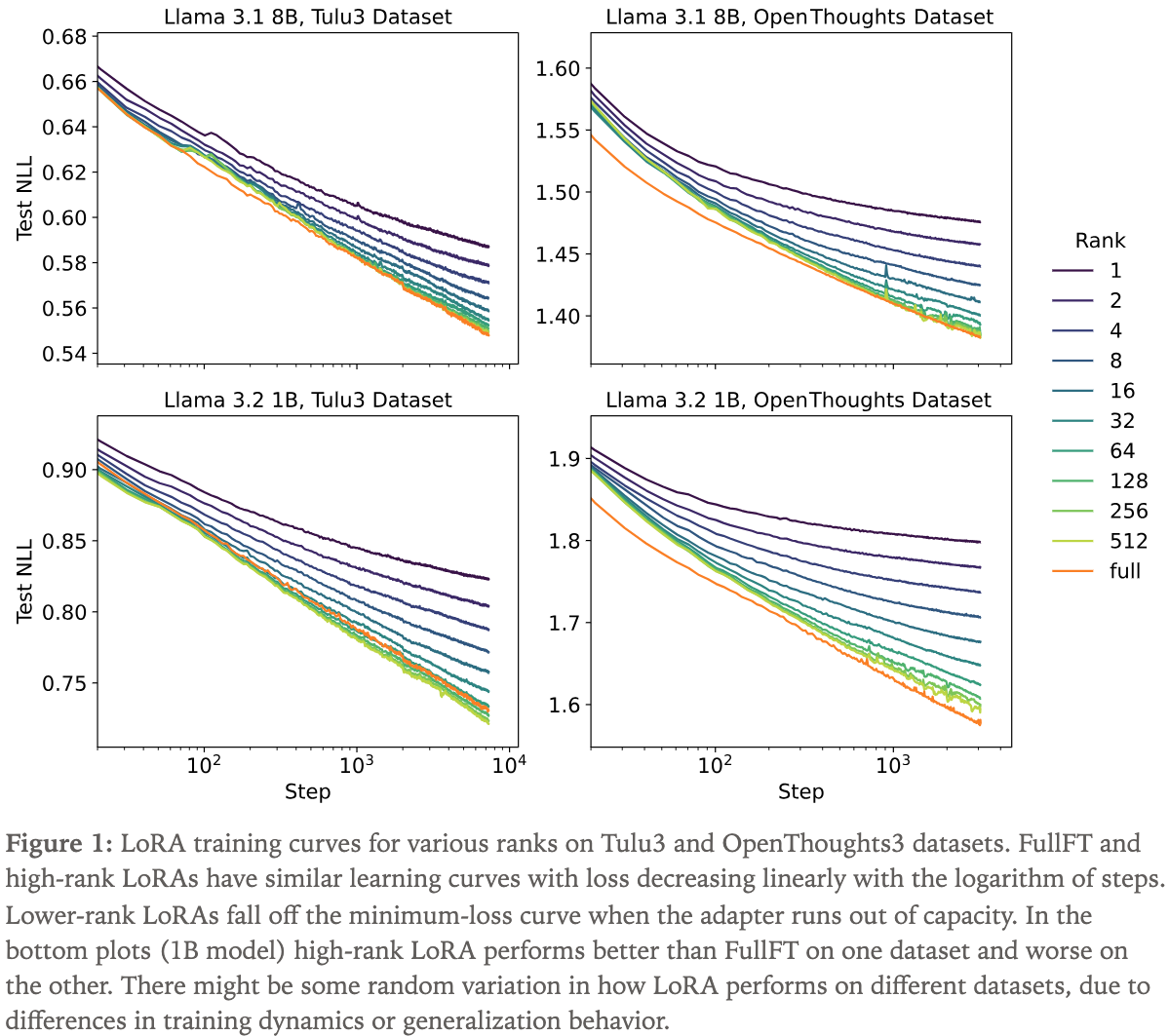
论文观察到，FullFT 和高 Rank LoRA 具有相似的训练曲线，损失随训练步骤对数的增加而线性下降
- 当训练步骤达到某个与 Rank 相关的阈值时，中低 Rank LoRA 会偏离最小损失训练曲线
- 从直觉上看，当 Adapter 达到容量上限时，学习速度会减慢，而容量上限由 Rank 决定
接下来，论文绘制了损失随学习率变化的曲线，以验证论文的扫描是否覆盖了每个 Rank 对应的最优学习率
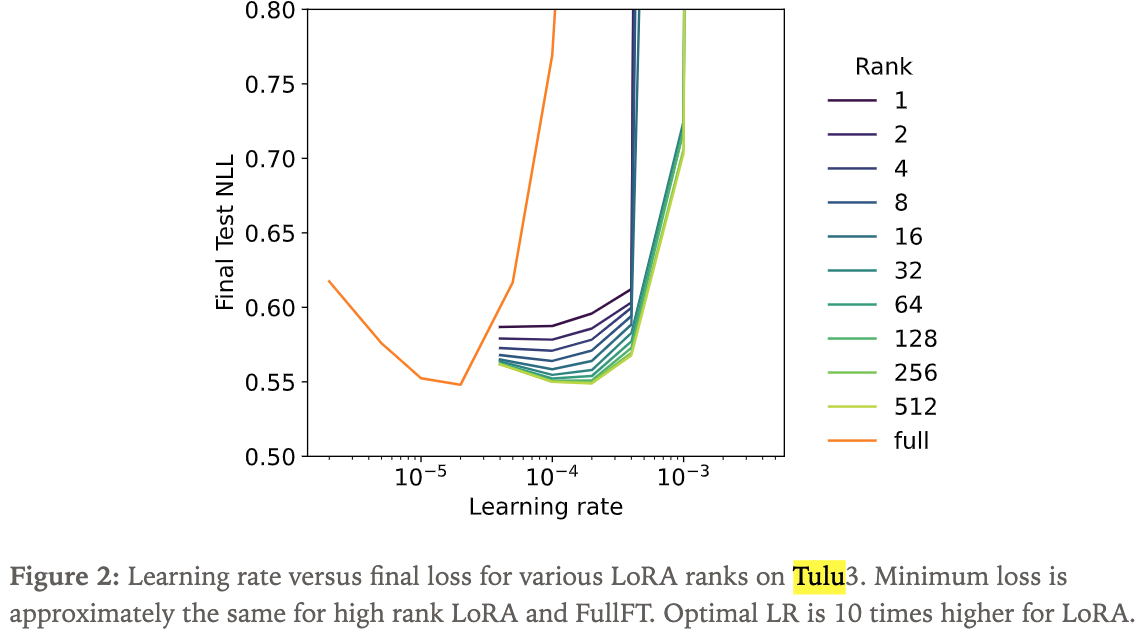
- 理解：LoRA 比 FullFT 需要更大的最优学习率
论文发现，FullFT 的最优学习率比高 Rank LoRA 的最优学习率低一个数量级（即 1/10）（2024）
- 论文将在后面讨论 LoRA 超参数时再次提及这一点
所有不同 Rank 的 LoRA 运行对应的最优学习率似乎相近（论文将在下文从理论角度解释这一发现）
- 不过，最优学习率确实存在一定的 Rank 依赖性（Rank 为 1 时的最优学习率低于更高 Rank LoRA 的最优学习率）
- 在 Rank 为 4 到 512 的范围内，最优学习率的变化因子小于 2

Batch Size Effects

论文发现，在某些设置下，LoRA 对大批量大小的容忍度低于 FullFT
随着批量大小的增加，两者的性能差距会扩大，且这种差距与 Rank 无关
在接下来的实验中，论文使用了 OpenThoughts3 数据集中一个包含 10,000 个样本的小子集
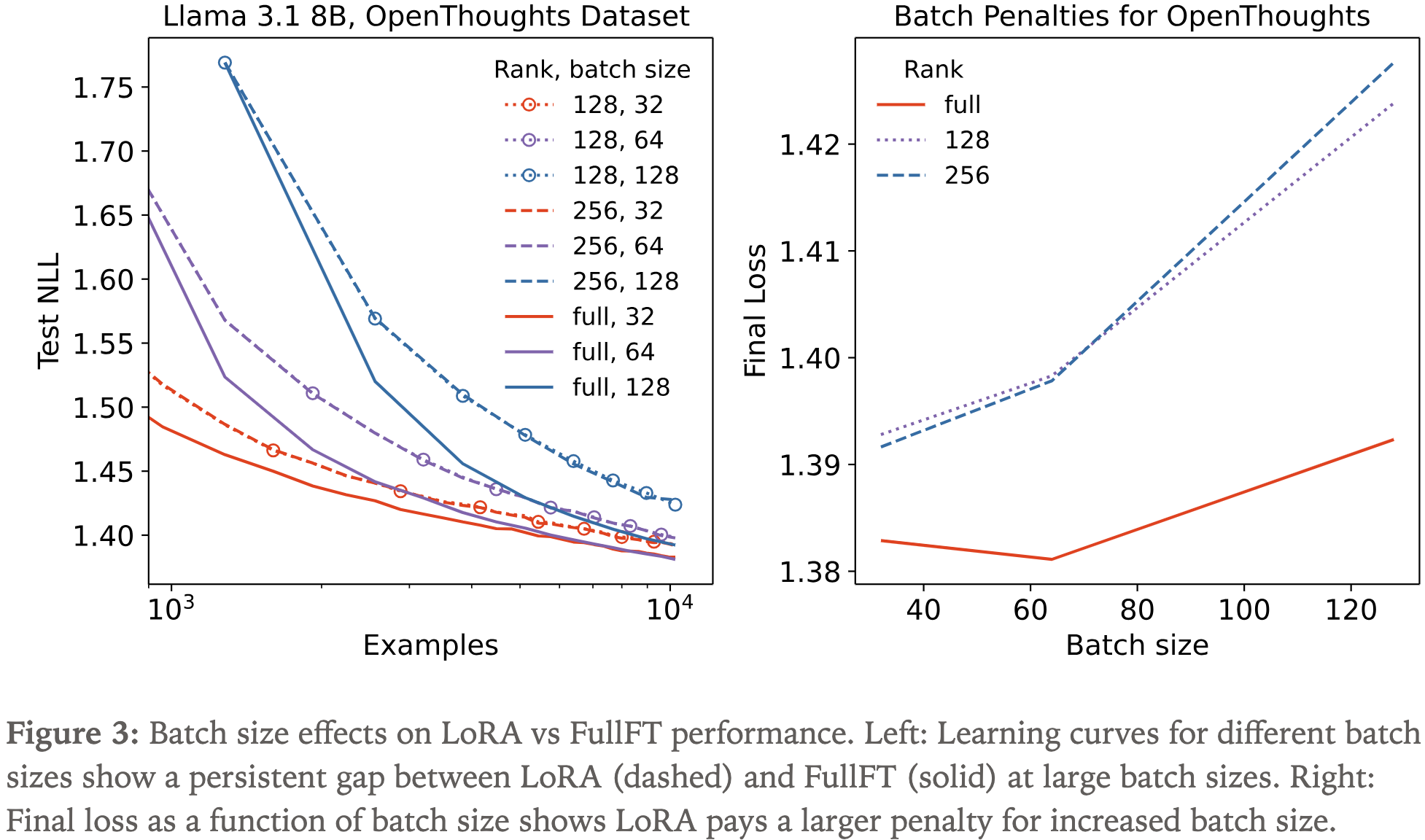
图 3 中的左图显示
- 在大批量大小时，LoRA（虚线）与 FullFT（实线）的训练曲线之间存在持续的差距
- 而在批量大小为 32（较小批量）时，这种差距更小，且会随着训练的进行而缩小
- 问题：左图是不是少了些其他的曲线？
右图展示了最终损失随批量大小变化的情况
- 随着批量大小的增加，LoRA 与 FullFT 之间的损失差距越来越大
大批量下的性能差距似乎与 Rank 无关，而是 LoRA 的固有属性
- 其可能原因是，在该数据集上，矩阵乘积参数化（$ BA $）的优化 Dynamics 不如全矩阵（$ W $）的优化 Dynamics 有利
- 不过，LoRA 和 FullFT 在较小批量大小时都能达到最佳损失，因此在实际应用中，这种差距可能不会产生太大影响
问题：为什么 Batch Size 对最终结果的影响这么大，是因为 Batch Size 和学习率没有对应调优吧！
- 理解：理论上，Batch Size 对于训练不应该有那么大的差异才是

Layers Where LoRA Is Applied（LoRA 应用的层）

论文研究了将 LoRA 应用于网络中不同层所产生的影响
Hu 等人的原始论文建议仅将 LoRA 应用于注意力矩阵（Attention Matrix），此后许多论文也遵循了这一做法
- 但最近的趋势是将 LoRA 应用于所有层
与论文的结果类似，QLoRA 论文也发现，仅将 LoRA 应用于注意力层的性能低于应用于 MLP 层或同时应用于 MLP 层与注意力层的性能
- 不过该论文发现“MLP 层+注意力层 > MLP 层 > 注意力层”，而论文发现 MLP 层+注意力层 和 MLP 层 的性能大致相当
- 事实上，当论文将 LoRA 应用于所有层（尤其是 MLP 层，包括 MoE 层）时，取得了好得多的结果
- 实际上，将 LoRA 应用于注意力矩阵，相比仅将其应用于 MLP 层，并没有带来额外的收益（2024）
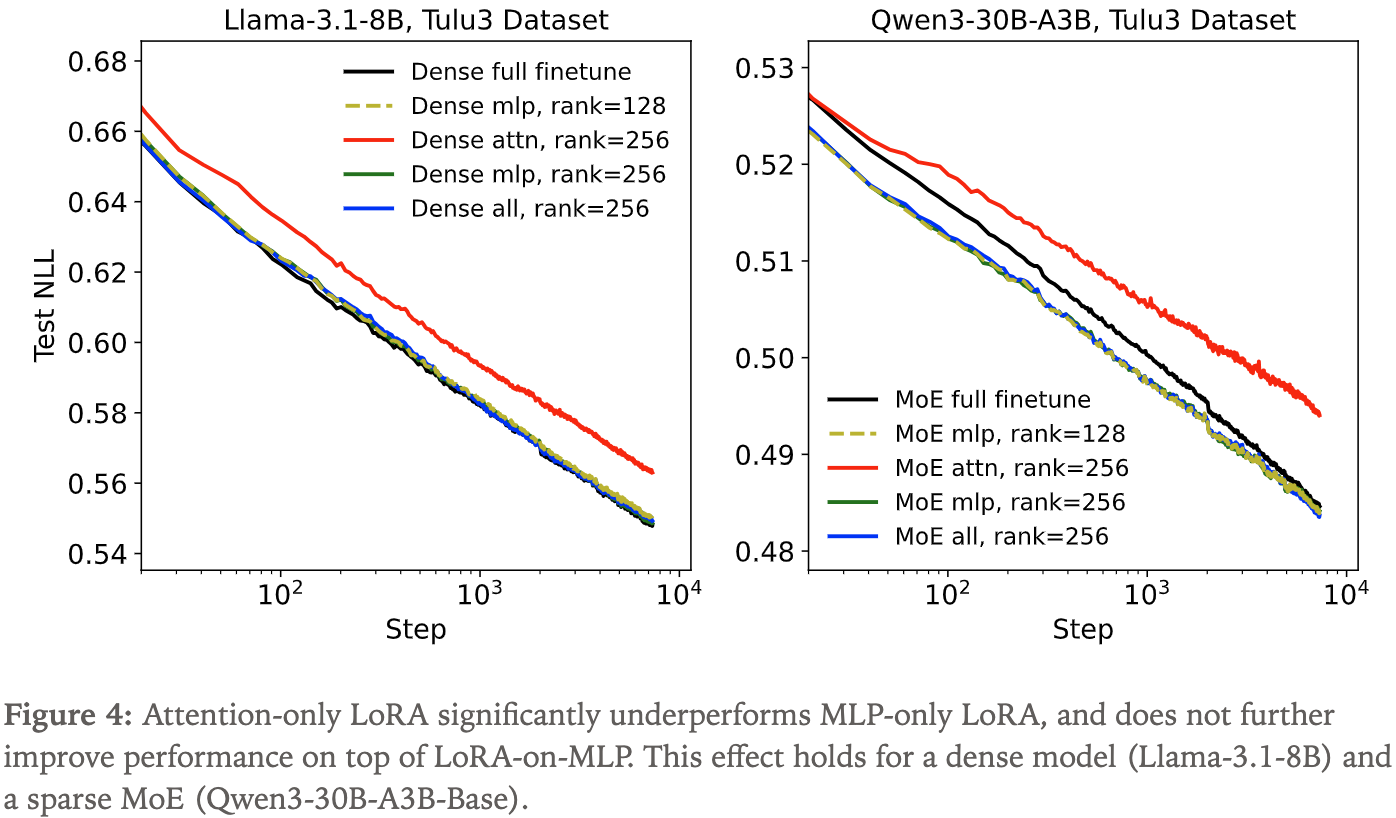
  - 理解：虽然加入注意力层没有带来额外收益，博客最终还是使用了所有层都微调，其实有些矛盾
仅应用于注意力层的 LoRA 性能较差，并非因为参数数量少
- 在特定案例中， Rank 为 256 的仅注意力层 LoRA，其参数数量与 Rank 为 128 的仅 MLP 层 LoRA 大致相同，但前者的性能却低于后者（可对比下表中的粗体数字）
  
  LoRA Configuration Params
  
  mlp, rank=256 0.49B
  
  attn, rank=256 0.25B
  
  all, rank=256 0.70B
  
  mlp, rank=128 0.24B
在 MoE 实验中，论文为每个专家（Expert）训练了一个单独的 LoRA，每个 LoRA 的 Rank 等于总 Rank 除以活跃专家（Active Expert）的数量（Qwen3 MoE 模型的活跃专家数量为 8）
- 这种缩放方式使得 MoE 层中 LoRA 参数与 FullFT 参数的比例，与其他层中两者的比例保持一致
- 理解：这可以保证最终激活的 Rank 数是一致的
论文还在另外两个场景中进行了类似实验，比较不同 LoRA 应用层的效果：
- （1）在 OpenThoughts3 数据集的一个小子集上进行 Rank 为 256 的监督学习；
- （2）在 MATH 数据集上进行强化学习
- 论文将在下一节描述实验设置
在这些场景中，仅注意力层的 LoRA 性能依然低于仅 MLP 层的 LoRA（后者与“MLP 层+注意力层”的 LoRA 性能相近）

LoRA Configuration	Params
mlp, rank=256	0.49B
attn, rank=256	0.25B
all, rank=256	0.70B
mlp, rank=128	0.24B

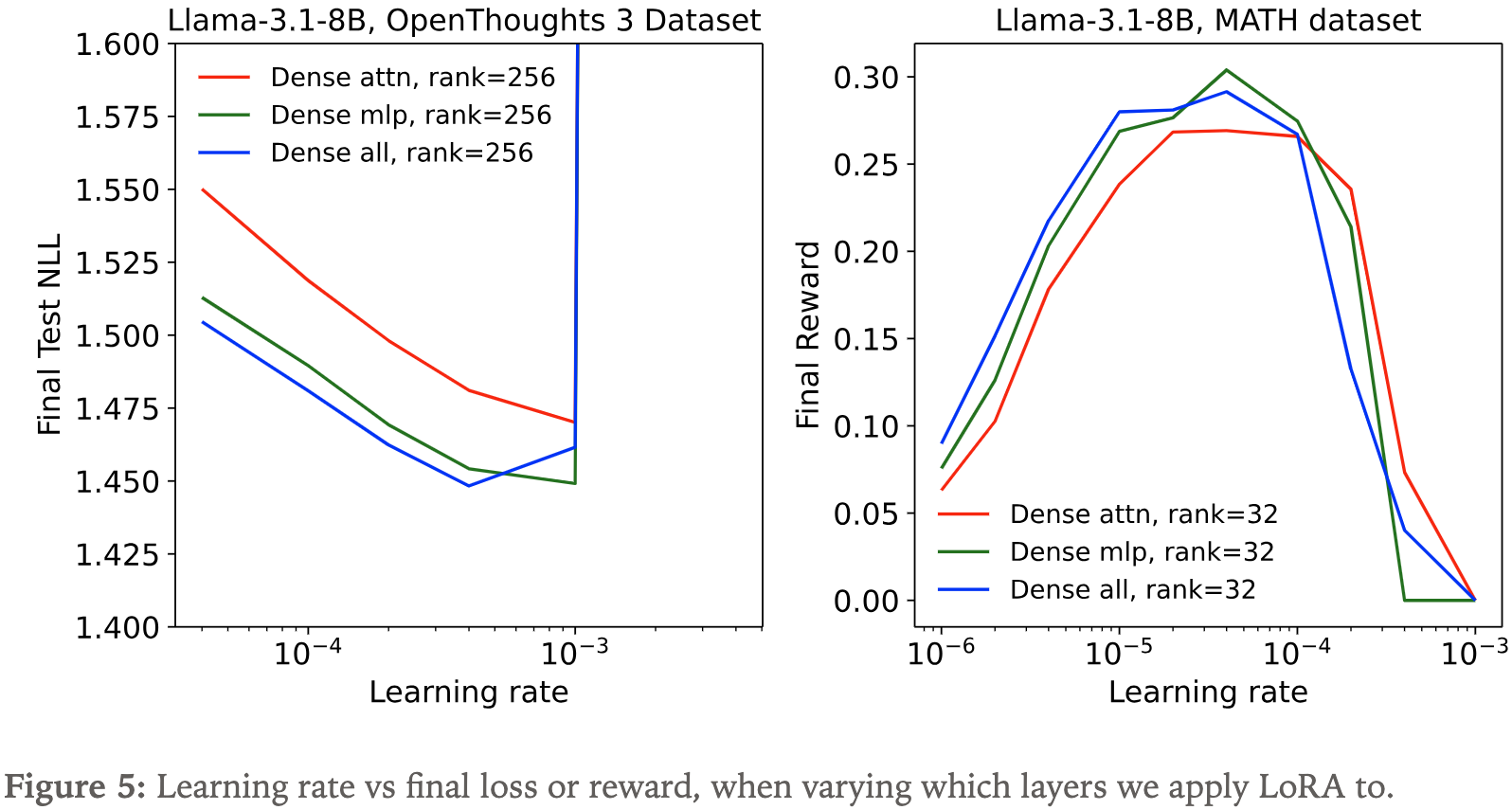
RL

论文的实验得出一个关键发现：在使用策略梯度算法（Policy Gradient Algorithm）进行强化学习时，即使 LoRA 的 Rank 低至 1，其学习性能也能完全匹配 FullFT
在这些实验中，论文使用了一种带有重要性采样校正（Importance Sampling Correction）的基础策略梯度算法，其目标函数为（2024）：
$$ \text{objective} = \sum_t \frac{p_{\text{learner} } }{p_{\text{sampler} } } Adv_t $$
论文采用了类似 GRPO 的中心化方案（2024），即针对每个问题采样多个补全结果（Completion），并减去每组的平均奖励
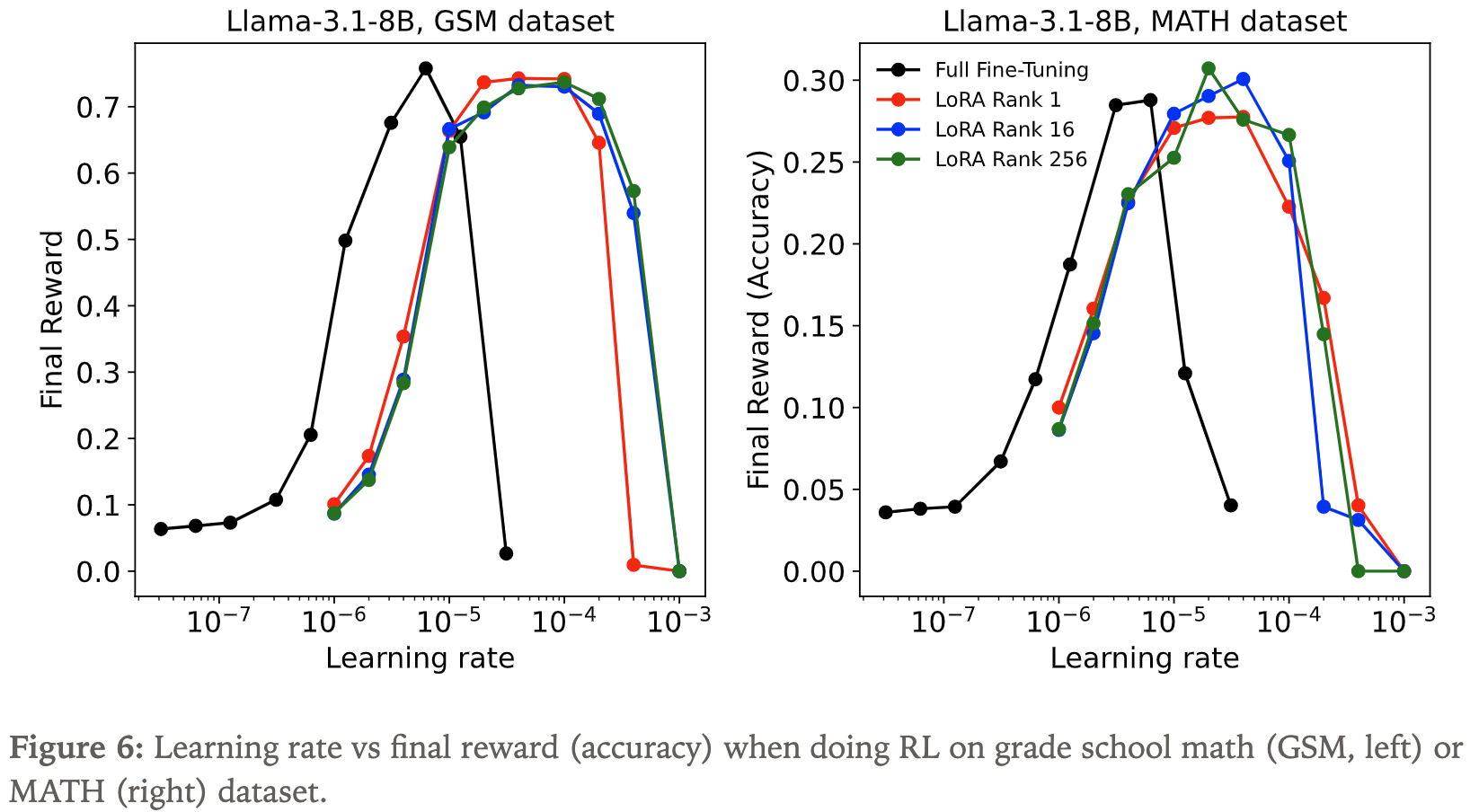
下图（图 6）展示了在 MATH（2021）和 GSM（2021）数据集上的学习率扫描结果，每个数据集都使用了典型的超参数
- 论文使用 Llama-3.1-8B 基础模型进行实验，因为正如 Qwen 技术报告（2024）所描述的，Qwen2.5 和 Qwen3 模型的预训练数据已提升了其数学性能，这会使得论文难以衡量仅在强化学习阶段学到的内容
- LoRA 具有更广泛的有效学习率范围，并且能达到与 FullFT（黑线）相同的峰值性能，至少在强化学习的噪声所允许的精度范围内是如此
这一结果与信息论的推断一致（注意：下面是重点，需要重点理解）
- 监督学习每个样本（Episode）可提供约 $ O(\text{ Token 数量}) $ 比特的信息
- 在策略梯度方法中，学习由优势函数（Advantage Function）驱动 ，每个样本仅能提供 $ O(1) $ 比特的信息
- 当每个样本包含数千个 Token 时，强化学习在训练过程中每 Token 吸收的信息约为监督学习的 1/1000
我们可以根据实验数据给出更精确的数值
- 在 MATH 数据集的实验中，论文在约 10,000 个问题上进行训练，每个问题采样 32 次
- 假设每个补全结果提供 1 比特信息，那么整个训练过程仅需吸收 320,000 比特信息
- Llama-3.1-8B 模型的 Rank 为 1 的 LoRA 已有 300 万个参数（论文通过对模型中所有权重矩阵求和 $ \text{rank}\cdot d_{\text{in} } $（矩阵 $ A $ 的参数数量）和 $ \text{rank} \cdot d_{\text{out} } $（矩阵 $ B $ 的参数数量）计算得出），几乎是所需信息比特数的 10 倍
  - 问题：信息和信息比特数可以直接比较吗？
- 即便 Rank 为 1，LoRA 也拥有足够的容量来吸收训练过程中提供的所有信息
作为另一个对比案例，DeepSeek-R1-Zero 模型在 5.3M 个样本上进行了训练（训练共进行 10,400 步，每步包含 32 个独特问题，每个问题采样 16 次），这对应着 5.3M 比特的信息
- 这一数量少于低 Rank LoRA 的参数数量，因此论文预测，使用 LoRA 也能复现该模型的训练结果
为了进一步验证 LoRA 在推理强化学习中有效性的发现，论文使用 Qwen3-8b-base 模型在 DeepMath 数据集（2025）上进行了更大规模的实验
- DeepMath 数据集比 MATH 数据集大得多，且通常包含更难的问题
- 为了加快实验速度，论文将训练和评估的样本长度限制为 8192 个 Token
- 这个长度足以支持回溯（Backtracking）和推理过程，但与更长的思维链（Chain-of-Thought）相比，会限制模型性能
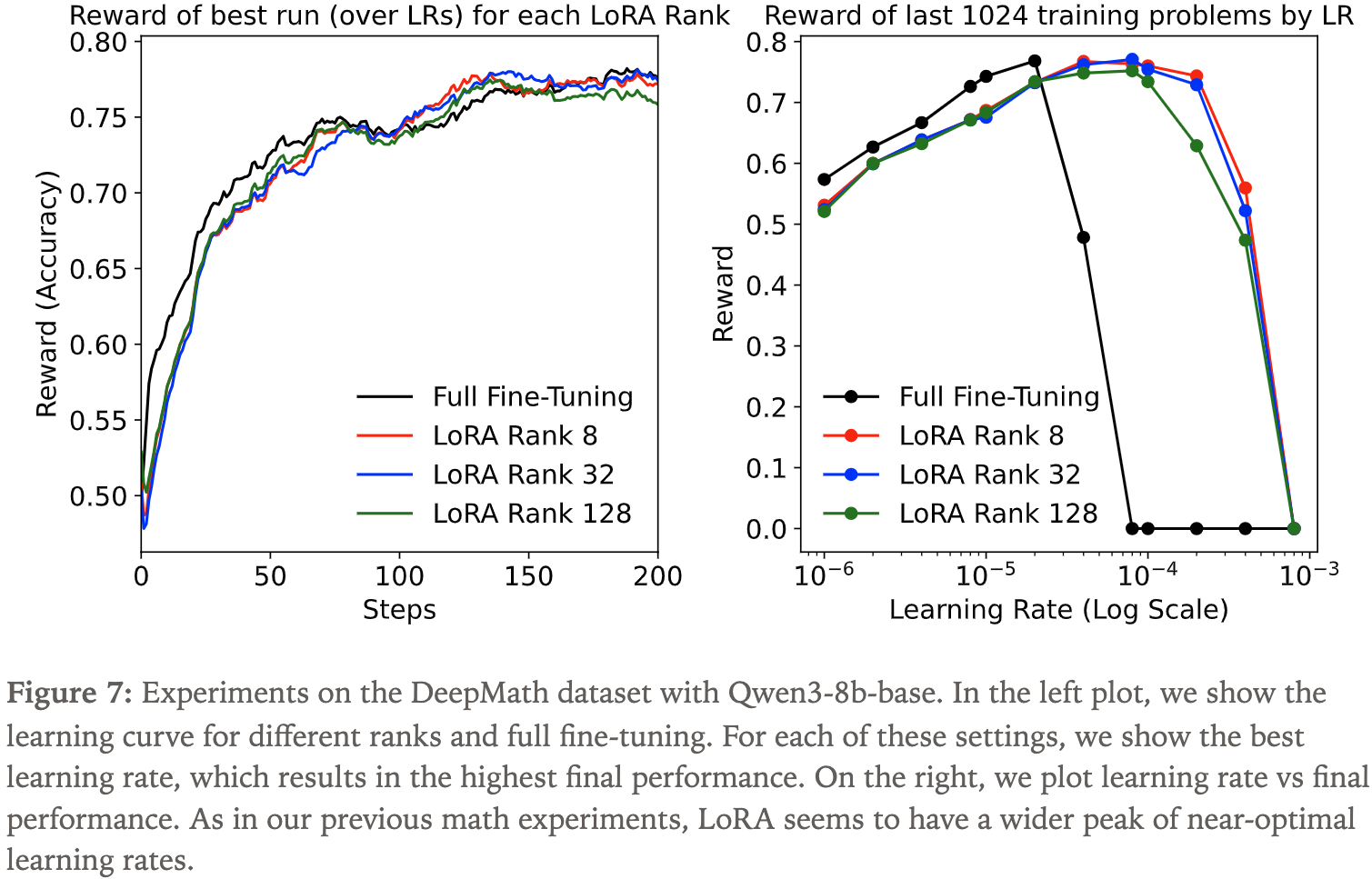
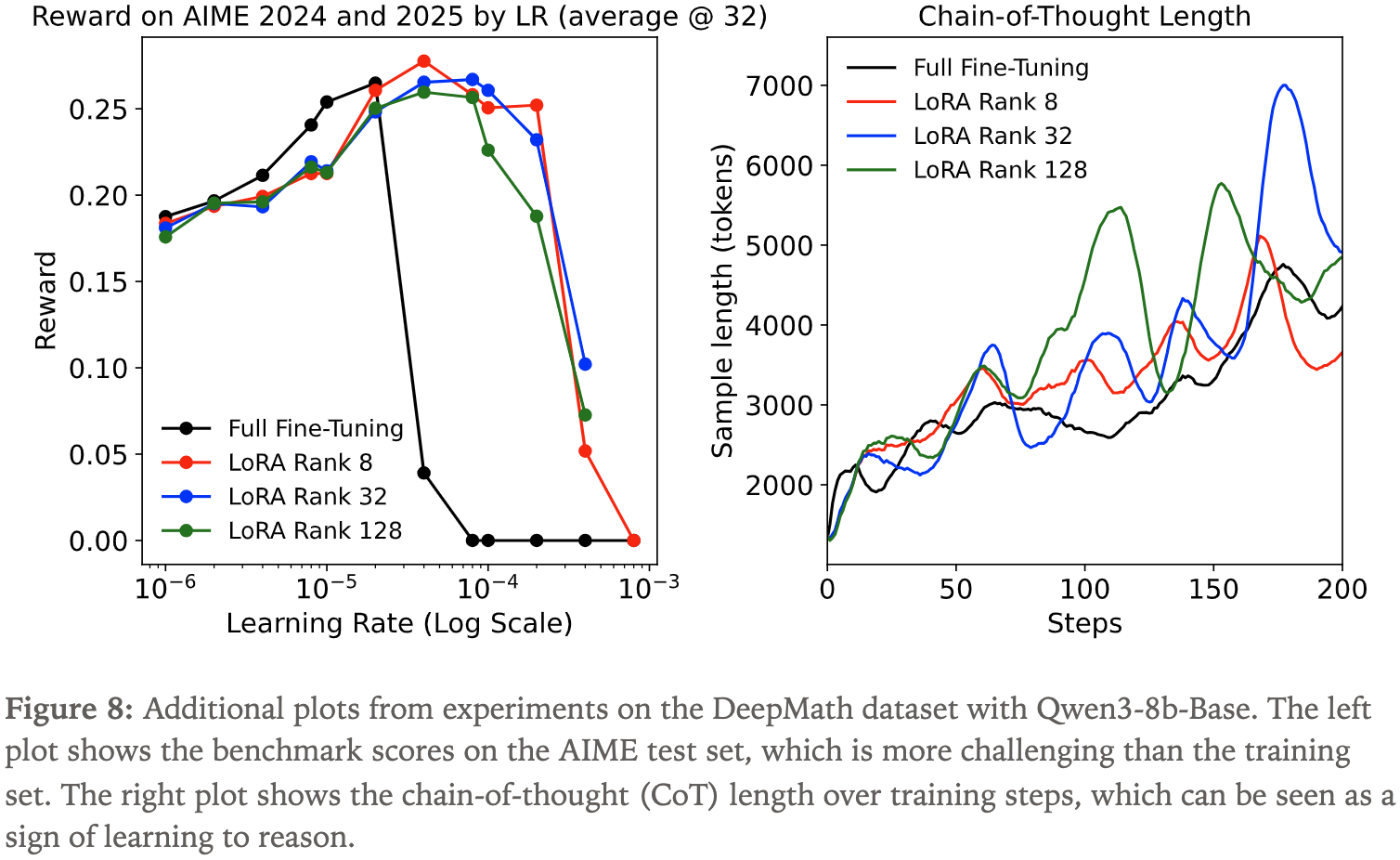
论文观察到，当为每种设置选择最优学习率后，不同大小的 LoRA 和 FullFT 的训练过程几乎完全一致
- 此外，在预留的 AIME 2024 和 AIME 2025 测试集上评估模型时，论文也得到了类似的结果
- 而且，论文发现 LoRA 和 FullFT 的训练过程表现出相似的定性行为：
  - 两者都发展出了先进的推理能力，如回溯、自我验证（Self-Verification）和上下文内探索（In-Context Exploration），这一点可以从模型思维链长度的增加中看出

Setting LoRA Hyperparameters

LoRA 应用的一个障碍是需要选择最优超参数，而这些超参数与为 FullFT 优化的超参数不同
在本节中，论文将说明这个问题并不像最初看起来那么棘手，并讨论论文在超参数选择方面的发现

Optimal Learning Rate and Rank

参照 Hu 等人的研究，论文采用以下参数化方式表示 LoRA：
$$ W’ = W + \frac{\alpha}{r} BA $$
- 其中，$ r $ 是 LoRA 的 Rank
- $ \alpha $ 是 LoRA 的缩放因子（论文遵循其他实现的标准做法，设置 $ \alpha = 32 $）
- $ A $ 和 $ B $ 是 LoRA 的权重矩阵（ Rank 为 $ r $）
$ \frac{1}{r} $ 缩放因子使得最优学习率大致独立于 Rank
- 事实上，存在一个更强的条件：训练初期的学习曲线完全相同，与 Rank 无关
- 这一现象非常显著，在实验中，不同 Rank 的学习曲线如此接近，以至于论文曾担心是程序漏洞导致 Rank 参数未被正确使用
- 由此可见，在短期训练中，最优学习率也与 Rank 无关
- 然而，正如论文在之前的学习率-损失图（图 2）中所展示的，在长期训练中，最优学习率会表现出一定的 Rank 依赖性
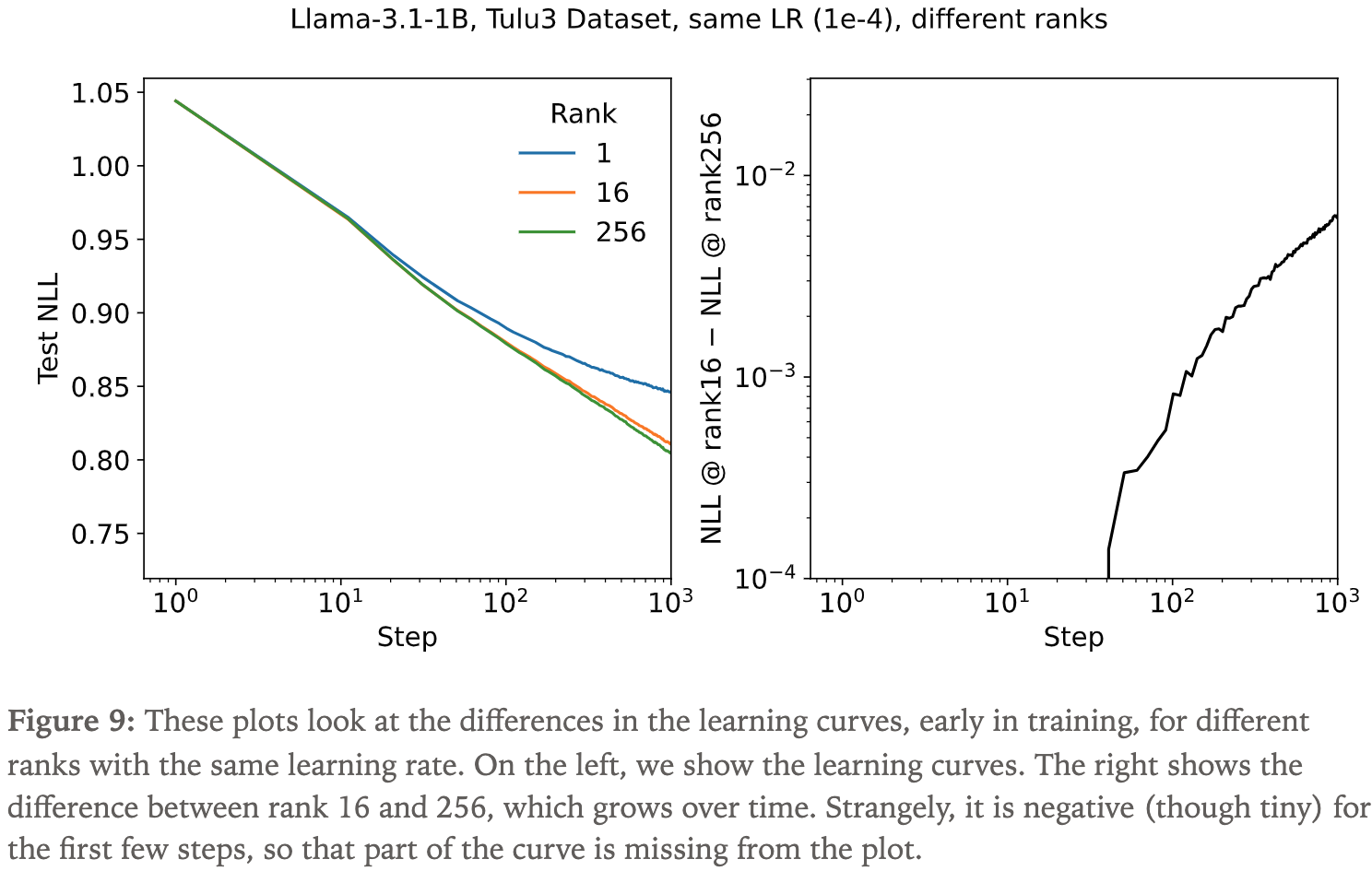
我们可以通过分析训练首次更新后 LoRA 矩阵的预期更新来部分解释这一结果（注：即解释 $ \frac{1}{r} $ 缩放因子使得最优学习率大致独立于 Rank 这个事实）
- 我们可以将 LoRA 矩阵乘积 $ BA $ 表示为 $ r $ 个 Rank-1 外积的和：
  $$ BA = \sum_{i=1}^r b_i a_i^T = \sum_{i=1}^r \Delta_i $$
  - 其中论文定义 $ \Delta_i = b_i a_i^T $
  - 这里，所有 $ i $ 对应的 $ \frac{\partial \text{Loss}}{\partial \Delta_i} $ 都是相同的；
  - 但梯度 $ \frac{\partial \text{Loss}}{\partial b_i} $ 和 $ \frac{\partial \text{Loss}}{\partial a_i} $ 会依赖于初始化（例如，$ \frac{\partial \text{Loss}}{\partial b_i} $ 依赖于 $ a_i $）
  - 由于 $ a_i $ 和 $ b_i $ 的初始化与 Rank 无关，因此所有 $ i $ 对应的 $ \mathbb{E}[\Delta_i] $ 都是相同的，且与 Rank 无关
  - 在训练的第一步，每个外积项的预期更新是相等的，且与 Rank 无关
  - 由此可知，$ (\frac{1}{r}) \sum_{i=1}^r \Delta_i $ 本质上是 $ r $ 个具有相同期望的项的样本均值，因此该均值的期望（即 Adapter $ (\frac{1}{r})BA $ 的变化量）与 Rank 无关

Parametrization Invariances（参数化不变性）

LoRA 可能涉及四个超参数：
- 1）缩放因子 $ \alpha $（出现在 $ \alpha/r $ 中）
- 2）下投影矩阵 $ A $ 的学习率 $ LR_A $
- 3）上投影矩阵 $ B $ 的学习率 $ LR_B $
- 4）矩阵 $ A $ 的初始化缩放 $ \text{init}_A $
  - 对于随机初始化，这是 $ A $ 初始元素的标准差
  - 矩阵 $ B $ 初始化为零，因此无需定义 $ \text{init}_B $
调整这四个参数似乎难度较大，但 Training Dynamics 的不变性意味着其中两个参数是冗余的，学习行为仅由两个参数决定
- 问题：如何理解这里的 Training Dynamics 的不变性
论文通过以下分析说明这种不变性：
在使用 Adam 优化器且 $ \varepsilon = 0 $ 时（我们可以将此结果扩展到 $ \varepsilon > 0 $ 的情况；此时需要将 $ \varepsilon $ 按 $ 1/q $ 缩放，因为梯度会按该因子缩放），优化过程在以下两参数变换下保持不变
- 对于 $ p, q > 0 $，满足：
  - $ \alpha \rightarrow \frac{1}{pq} \cdot \alpha $
  - $ \text{init}_A \rightarrow p \cdot \text{init}_A $
  - $ LR_A \rightarrow p \cdot LR_A $
  - $ LR_B \rightarrow q \cdot LR_B $
由于四个参数中的两个自由度不影响学习过程，因此实际需要调整的参数空间为二维
我们可以为这个二维空间选择不同的基，例如以下具有直观解释的基：
- 1）$ \alpha \cdot \text{init}_A \cdot LR_B $：
  - 该参数决定初始更新的规模，或者说学习曲线的初始斜率
  - 由于 $ B $ 初始化为零，$ LR_A $ 和 $ A $ 的初始更新在此阶段无关紧要
- 2）$ \text{init}_A / LR_A $：
  - 由于 Adam 优化器每步对 $ A $ 元素的更新量约为 $ LR_A $，因此这个时间尺度参数决定了 $ A $ 从初始状态发生显著变化所需的步数
我们可以用这个基来重新解释以往关于 LoRA 的一些研究提案：
- LoRA+（2024）提出对 $ A $ 和 $ B $ 使用不同的学习率，且 $ B $ 的学习率更高。用上述基表示，提高 $ LR_B $ 等价于提高 $ \text{init}_A / LR_A $，从而使 $ A $ 的变化时间尺度更长
- Unsloth 的 LoRA 超参数指南建议对高 Rank LoRA 使用更大的 $ \alpha $ 值（例如，避免 $ \frac{1}{r} $ 缩放）
  - 这也等价于提高 $ \text{init}_A / LR_A $
  - 当论文提高 $ \alpha $ 时，需要相应降低 $ LR_A $ 和 $ LR_B $ 以保持更新规模不变，这反过来会使 $ LR_A $ 相对于 $ \text{init}_A $ 更小
在论文的实验中，论文采用了 Hugging Face PEFT 库（2022）中 Hu 等人提出的标准参数化方式：
- $ A $ 采用均匀分布初始化（缩放因子为 $ 1/\sqrt{d_{\text{in} } } $）
- $ B $ 初始化为零，$ A $ 和 $ B $ 使用相同的学习率，且 $ \alpha = 32 $
- 在实验中，论文未能找到比这些超参数更优的设置

Optimal Learning Rates for LoRA vs. FullFT（最优学习率对比）

论文的实验表明，无论是在监督学习还是强化学习中，LoRA 的最优学习率始终是同一应用场景下 FullFT 最优学习率的 10 倍
- 这一规律在所有以性能（损失或奖励）为纵轴、学习率为横轴的 U 型图中都能体现
- 这一发现应能简化从 FullFT 到 LoRA 的学习率超参数迁移过程
目前，论文尚未对这一现象做出充分的理论解释
- 论文尝试从“LoRA 最优学习率与 Rank 无关”和“满 Rank LoRA 可直接与 FullFT 对比”这两个事实出发推导该结果，但分析得出的学习率比例为“模型隐藏层大小除以 $ 2 \cdot \alpha $”，这与“最优比例固定为 10（与基础模型无关）”的实验结果不符
在实证分析中，论文在 Tulu3 数据集上对 14 个不同的 Llama 和 Qwen 模型进行了 LoRA 和 FullFT 的学习率扫描
- 基于这些扫描结果，论文拟合了一个函数，该函数可根据模型的隐藏层大小和模型类型（Llama 或 Qwen）预测最优学习率。所用函数形式如下：
  $$ LR = M_{\text{LoRA} } \cdot \left( \frac{2000}{\text{hidden size} } \right)^{\text{model pow} + \text{LoRA pow} } $$
  - 其中：
    - $ M_{\text{LoRA} } $ 是使用 LoRA 时的乘数（使用 FullFT 时为 1）
    - $ \text{model pow} $ 是针对不同模型来源（Llama 和 Qwen）分别计算的指数调整项
    - $ \text{LoRA pow} $ 是针对 LoRA 的额外指数调整项
    - $ \text{hidden size} $ 是模型残差流（Residual Stream）的维度
论文通过线性插值基于扫描数据预测损失，以此对预测的学习率进行评分，并通过对 14 个模型的预测损失求和来评估参数
优化结果显示：
- LoRA 相对于 FullFT 的乘数为 9.8；
- Qwen3 和 Llama 模型对隐藏层大小的依赖不同，但 LoRA 学习率对隐藏层大小的依赖与 FullFT 相同（即优化结果显示 $ \text{LoRA pow} = 0 $）

Learning Rates in Short and Long Runs

LoRA 的典型初始化会导致有效学习率产生一个隐含的变化过程，这使得短期训练和长期训练存在差异，且学习曲线的形状与 FullFT 也有所不同
在训练初期，$ B $ 初始化为零
- 当 $ B $ 非常小时，$ A $ 的变化对 Adapter $ BA $（将被添加到原始网络权重中）的影响可忽略不计
- 随着 $ B $ 逐渐增大，$ A $ 的更新对网络输出的影响开始变大
  - 当 $ B $ 的规模接近 $ A $ 时，有效学习率会在训练过程中逐渐提高
- 论文发现，在 Tulu3 和 OpenThoughts 数据集上完成完整训练后，$ B $ 矩阵的谱范数（Spectral Norm）最终会大于 $ A $ 矩阵的谱范数
这意味着，对于短期训练，应设置更高的最优学习率
- 初步证据表明，短期训练（根据经验，约 100 步以内）的最优乘数约为 FullFT 的 15 倍 ，而对于长期训练，该乘数会收敛到前文提到的 10 倍

Discussion

除了实证结果外，论文还希望探讨与 LoRA 性能和适用性相关的更广泛问题，这些问题对研究人员和工程实践者都具有参考价值
首先，论文深入分析核心结论，LoRA 与 FullFT 性能相近的两个条件：
- 1）LoRA 应用于网络的所有层，尤其是参数占比最高的 MLP/MoE 层
- 2）LoRA 未受容量限制，即可训练参数数量超过待学习信息的总量（可根据数据集大小估算）
当条件（1）满足时，训练初期 LoRA 的学习 Dynamics 与 FullFT 相似；
然后，在条件（2）的保障下，LoRA 会继续保持与 FullFT 相近的性能，直到达到容量限制

Why LoRA Might Be Needed on All Layers（Why LoRA 需要应用在所有层上）

正如论文之前所展示的，若仅将 LoRA 应用于注意力层，即使在小数据场景下，学习速度也会变慢
一种可能的解释来自对经验神经正切核（Empirical Neural Tangent Kernel, eNTK）的分析（该核可用于近似少量微调时的模型行为（2022））
- eNTK 基于梯度的点积，具体而言，梯度：
  $$ g_i = \partial/\partial \theta \log p(\text{token}_i \mid \text{prefix}_i) $$
- 且 $ K(i,j) = g_i \cdot g_j $
- 因此，参数数量最多的层通常对核的影响最大
该论文还指出，当对所有层进行训练时，LoRA 的 eNTK 与 FullFT 的 eNTK 大致相同，因此:
$$\text{LoRA training} \approx \text{eNTK(LoRA)}\approx \text{eNTK(FullFT)} \approx \text{FullFT} $$
- 而 “$\text{eNTK(LoRA)}\approx \text{eNTK(FullFT)}$” 这一近似关系仅在将 LoRA 应用于“构成梯度点积的主要参数所在层”时成立

How Much Capacity Is Needed by Supervised and Reinforcement Learning?

监督学习与强化学习需要多少容量？
- 注：这里指参数容量
以往的研究（2024）表明，神经网络每个参数可存储 2 比特信息
- 但该结果针对的是长期训练极限下模型可吸收的最大信息量，而非计算效率或学习速度
“每个参数 2 比特”的结论基于精心构建的合成数据集（这些数据集包含精确的信息量）
- 对于现实学习任务，估算所需的信息量则更为复杂
一个经典结论是：
- 在最小化对数损失时，首轮训练的总对数损失可用于衡量数据集的描述长度，即记忆该数据集所需比特数的上限
- LLM 数据集的损失通常约为每 Token 1 比特（0.69 纳特），具体数值因数据集和模型大小而异
  
  One classic observation is that when minimizing log-loss, the total log-loss measured during the first epoch of training provides a measurement of the dataset’s description length. That is, an upper bound for the number of bits required to memorize the dataset
该估算值衡量的是“完美记忆数据集”所需的容量，而这一数值高估了“降低测试集对数损失”的泛化学习所需的实际容量
目前，监督学习的容量需求及其与可训练参数数量的关系仍是有待未来研究的开放问题
对于强化学习，作者认为，由于每个样本的末尾仅有一个奖励值，策略梯度算法每个样本大致仅学习 1 比特信息
- 但这并非强化学习的固有属性，其他算法可能从每个样本中学习更多信息
- 例如，基于模型的强化学习（Model-Based RL）算法会训练智能体预测观测结果并构建世界模型（World Model），从而可能从每个样本中提取更多信息
- “每个样本 1 比特”的结论可能仅适用于策略梯度算法
- 注：这里每个样本仅 1 比特的理论不敢苟同，因为强化学习的信号也可以不止是 0-1 信号，可以是 Reward 啊，此时就不再是 1 比特能够表达的了吧？
我们可以从信息论角度更精确地阐述比特计数论证
- 考虑一个样本（包含轨迹 $ \tau $ 和最终奖励）作为一条消息（即一个噪声信道），该消息包含关于未知奖励函数 $ R $ 的部分信息
- 论文基于当前策略和训练历史，分析策略梯度估计量与 $ R $ 之间的互信息
- REINFORCE 算法的更新公式为
  $$ G = S \cdot \text{Adv} $$
  - 其中 $ S = \nabla \log p_\theta(\tau) $
- 在给定历史的情况下，$ S $ 与 $ R $ 无关，因此唯一依赖 $ R $ 的部分是标量优势函数（Advantage）
根据数据处理不等式：
$$ I(G; R \mid \text{history}) \leq I((S, \text{Adv}); R \mid \text{history}) = I(\text{Adv}; R \mid S, \text{history}) \leq H(\text{Adv}) $$
若将优势函数量化为 $ B $ 个区间，则 $ H(\text{Adv}) \lesssim \log(B) $
- 即每个样本可获取的有效信息比特数为 $ O(1) $，与模型大小无关
- 这些比特信息告诉论文，当前面对的是离散奖励函数集合（或等效的最优策略类别集合）中的哪一个
- 这种互信息分析与一些优化算法的理论分析方法一致（2009）
需要注意的是，该估算值是训练可吸收信息量的上限，实际学习到的信息量会依赖于策略初始化和其他细节
- 例如，若初始化的策略无法获得任何奖励，则优势函数的熵为 0（而非 $ \log(B) $），模型无法学习到任何内容

Compute Efficiency Advantage of LoRA

上述实验通过训练步数衡量学习进度，但论文也关注不同方法的计算效率
论文计算得出，LoRA 每轮前向-反向传播所需的浮点运算数（FLOPs）略多于 FullFT 的 2/3
- 因此，总体而言，LoRA 的计算效率通常会优于 FullFT
论文通过分析给定权重矩阵上“前向-反向传播”操作的 FLOPs 来推导这一 2/3 比例，这些操作占据了神经网络模型中绝大部分的 FLOPs。论文使用以下符号：
- $ W \in \mathbb{R}^{N \times N} $：权重矩阵
- $ x \in \mathbb{R}^N $：输入向量
- $ y = Wx \in \mathbb{R}^N $：输出向量
- $ \bar{x}, \bar{y} \in \mathbb{R}^N $：损失分别对 $ x $ 和 $ y $ 的梯度（在反向传播中计算）
- $ \bar{W} \in \mathbb{R}^{N \times N} $：损失对 $ W $ 的梯度
全参数微调（FullFT）执行以下操作：
- 1）前向传播（Forward）
  - $ y = Wx $（需 $ N^2 $ 次乘加运算）
- 2）反向传播（Backward）
  - $ \bar{x} = W^T \bar{y} $（需 $ N^2 $ 次乘加运算）
  - $ \bar{W} += x \bar{y}^T $（需 $ N^2 $ 次乘加运算）
- 前向传播需 $ N^2 $ 次乘加运算，反向传播需额外 $ 2 \cdot N^2 $ 次乘加运算，总计 $ 3N^2 $ 次
  - 因此，包含前向和反向传播的训练过程，其 FLOPs 是仅前向推理的 3 倍
在 LoRA 中，论文将 $ W $ 替换为 $ W + BA $，其中 $ B \in \mathbb{R}^{N \times R} $、$ A \in \mathbb{R}^{R \times N} $，且 $ R \ll N $
- 由于论文仅更新 $ \bar{A} $ 和 $ \bar{B} $，因此无需执行 FullFT 中“更新 $ \bar{W} $”的第三步，而是替换为代价低得多的操作
- $ A $ 和 $ B $ 均为 $ N \cdot R $ 规模的矩阵，因此各自的“前向-反向传播”完整计算需 $ 3NR $ 次乘加运算，而非 FullFT 中 $ W $ 所需的 $ 3N^2 $ 次；两者合计需 $ 6NR $ 次乘加运算
- 同时，论文仍需对 $ Wx $ 和 $ \bar{x} $ 执行前向-反向传播（等效于 FullFT 的前两步）
- 因此，LoRA 总乘加运算次数为 $ 2N^2 + 6NR $
- 由于 $ R \ll N $，该数值略多于 FullFT 总运算量（$ 3N^2 $）的 2/3
若论文以 FLOPs（而非训练步数）为横轴绘制 LoRA 性能曲线（本分析未包含注意力机制的 FLOPs，在长上下文场景中，注意力 FLOPs 可能占比显著），LoRA 相对于 FullFT 的优势将更为明显

Open Questions

关于论文的研究结果，仍有几个问题有待未来探索：
- 1）细化 LoRA 性能预测 ：论文已大致描述了 LoRA 与 FullFT 性能相当的区间，并能通过 Token 或样本数量估算所需容量，但尚未能做出精确预测
  - 未来需进一步明确 LoRA 性能的预测方法及与 FullFT 匹配的具体条件
- 2）LoRA 学习率与 Training Dynamics 的理论解释 ：目前论文对 LoRA 学习率和 Training Dynamics 的理论理解仍有限
  - 若能建立完整理论解释 LoRA 与 FullFT 学习率的比例关系，将具有重要价值
- 3）LoRA 变体的性能评估 ：如 PiSSA（2024）等 LoRA 变体，若采用论文方法评估，其性能表现如何？
- 4）MoE 层的 LoRA 应用方案 ：将 LoRA 应用于 MoE 层有多种可选方案
  - 未来需研究不同方案的性能，以及每种方案与“张量并行”“专家并行”等大型 MoE 模型关键技术的兼容性

Closing Thoughts

在 Thinking Machines，作者相信微调技术能提升人工智能在多个专业领域的实用性
论文对 LoRA 的关注，源于让这种技术“广泛可及”并“易于定制以满足特定需求”的目标
除实际应用价值外，LoRA 研究还促使论文深入探索模型容量、数据集复杂度和样本效率等基础问题
通过分析“学习速度与性能如何依赖容量”，论文获得了研究机器学习基础问题的新视角
论文期待未来能进一步推进这一领域的研究