- 参考链接:
- (TIGER)Recommender Systems with Generative Retrieval, NeurIPS 2023, Google: 一篇比较早,也比较基础的工作
- OneRec: Unifying Retrieve and Rank with Generative Recommender and Preference Alignment, 202502, KuaiShou
- (COBRA)Sparse Meets Dense: Unified Generative Recommendations with Cascaded Sparse-Dense Representations, 202503, Baidu
- (RARE)Real-time Ad retrieval via LLM-generative Commercial Intention for Sponsored Search Advertising, 202504, Tencent
- 相关博客:腾讯搜索广告生成式检索
- 一文汇总:LLM应用到推荐系统的各类玩法总结
- Slow Thinking for Sequential Recommendation, 2025, RUC
- LEARN: Knowledge Adaptation from Large Language Model to Recommendation for Practical Industrial Application, AAAI 2025, Kuaishou
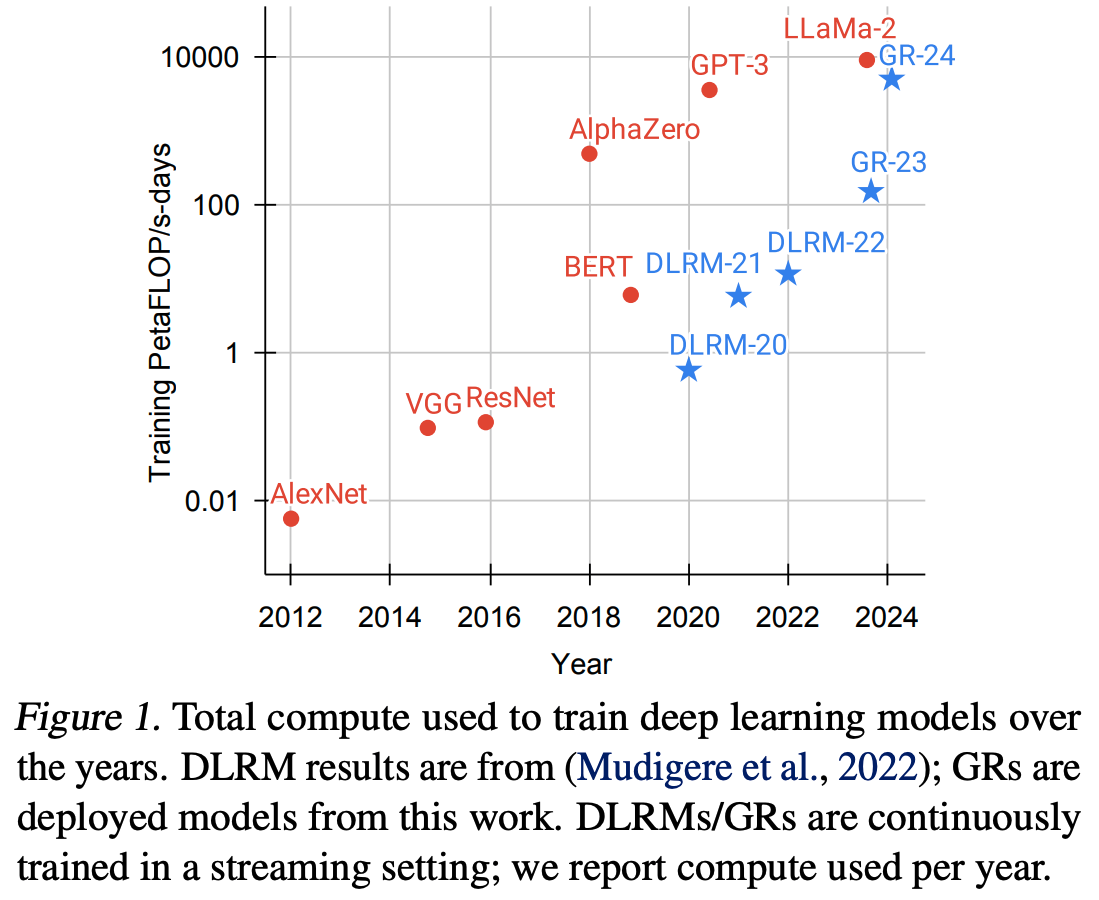
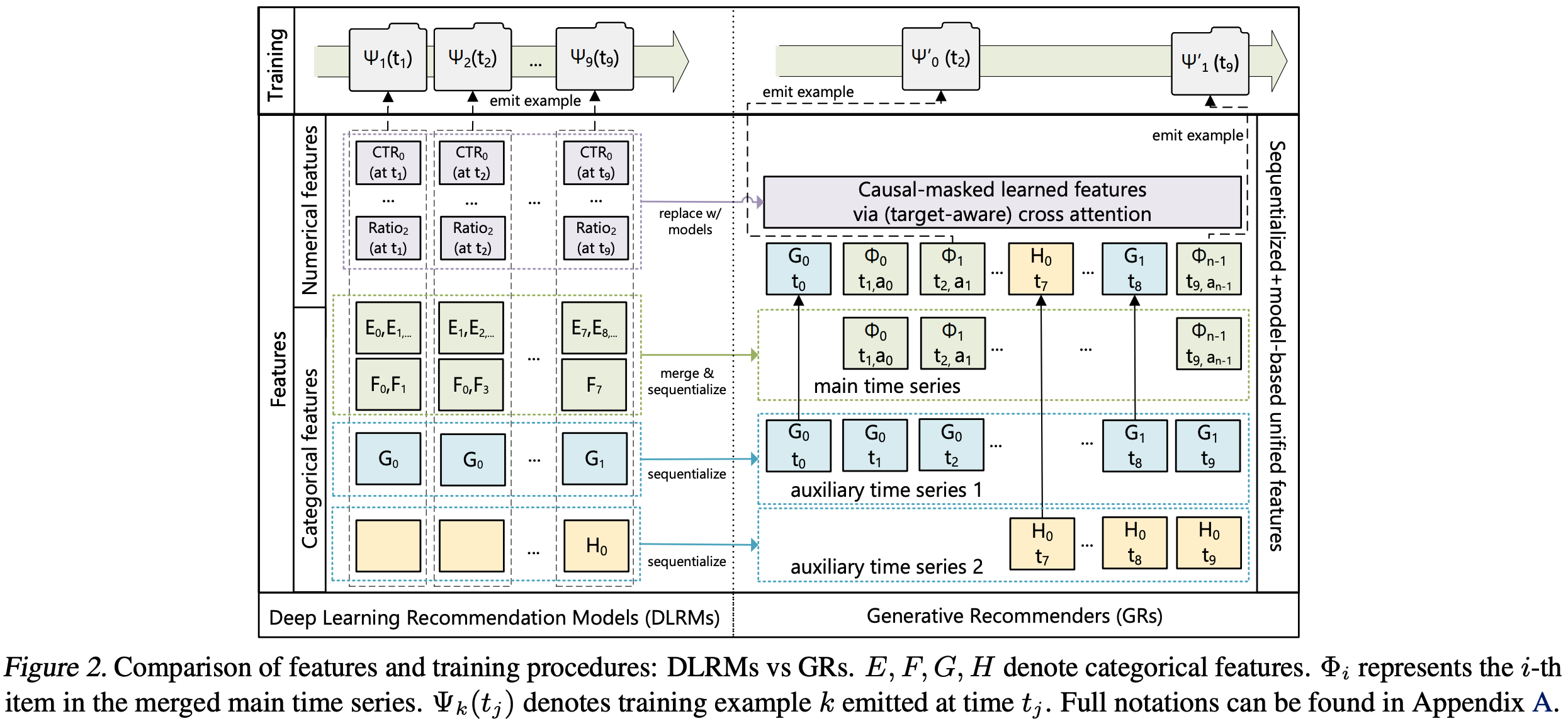
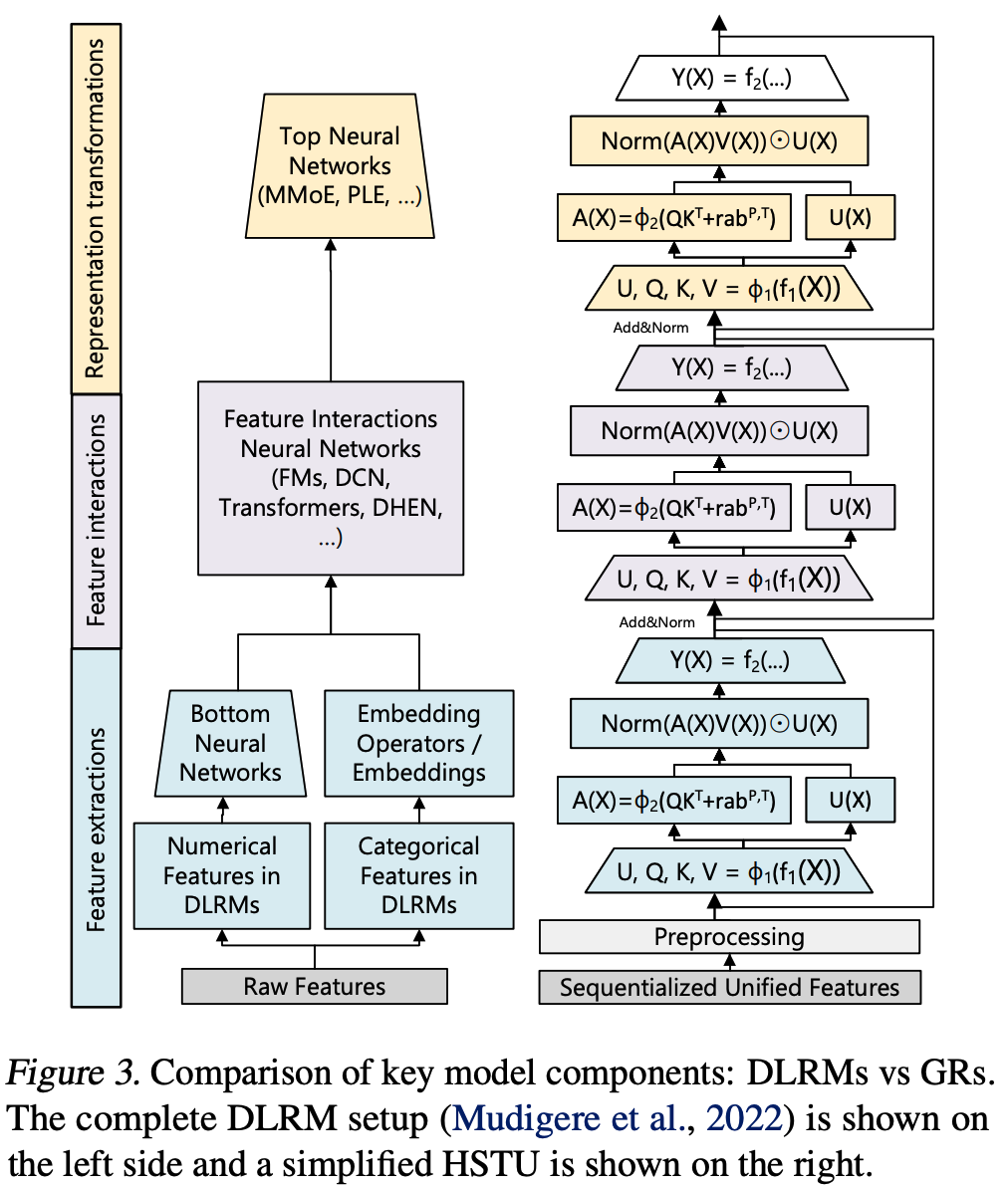
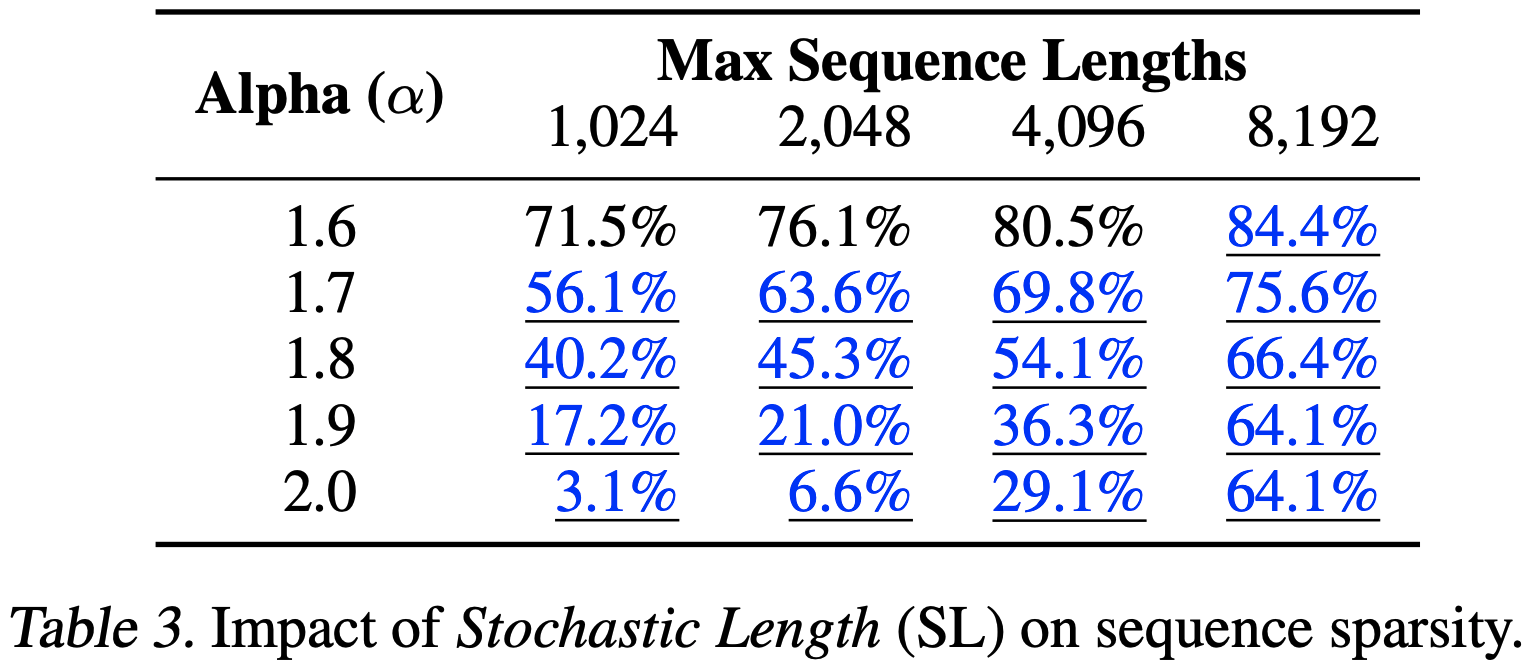
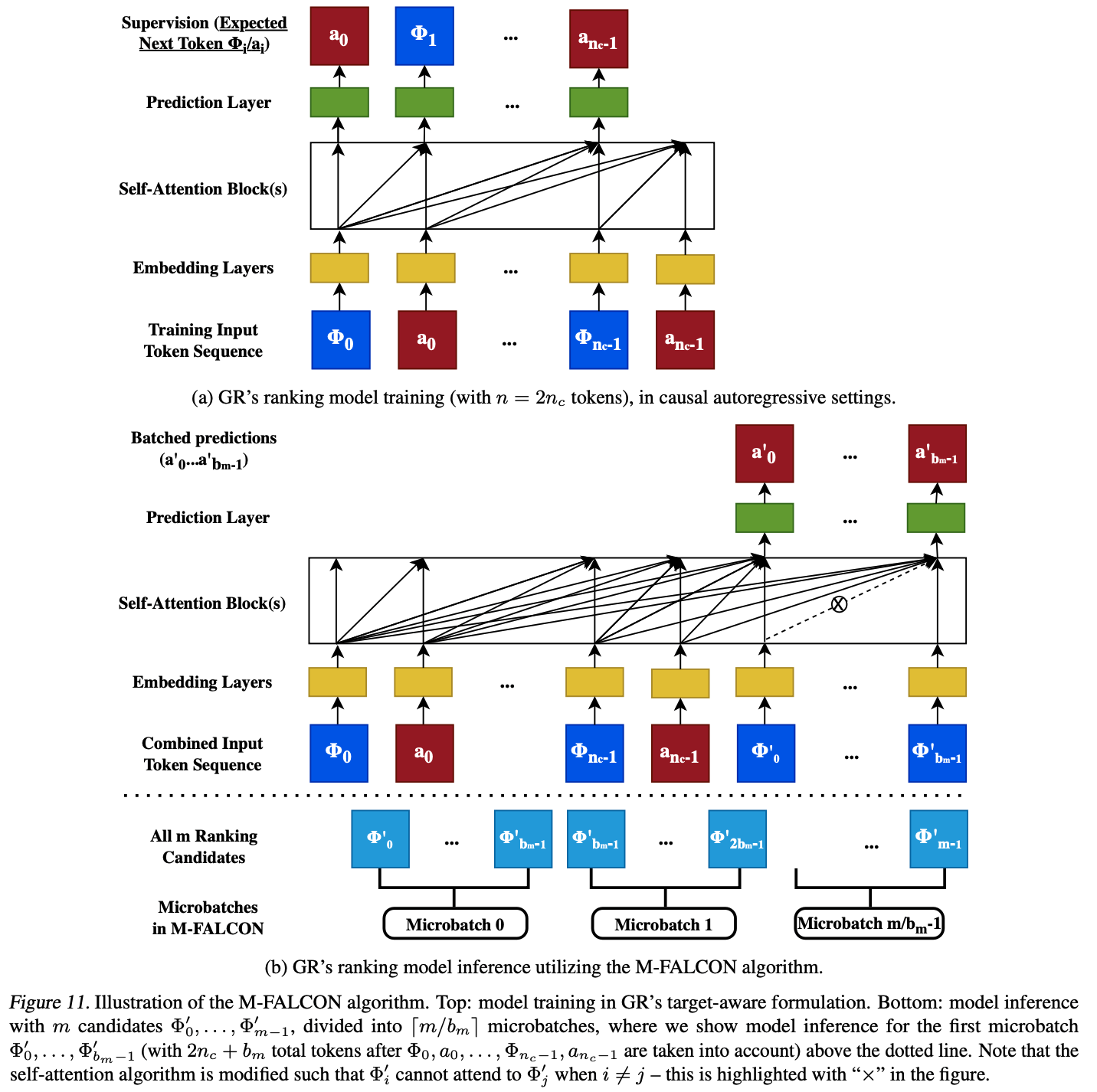
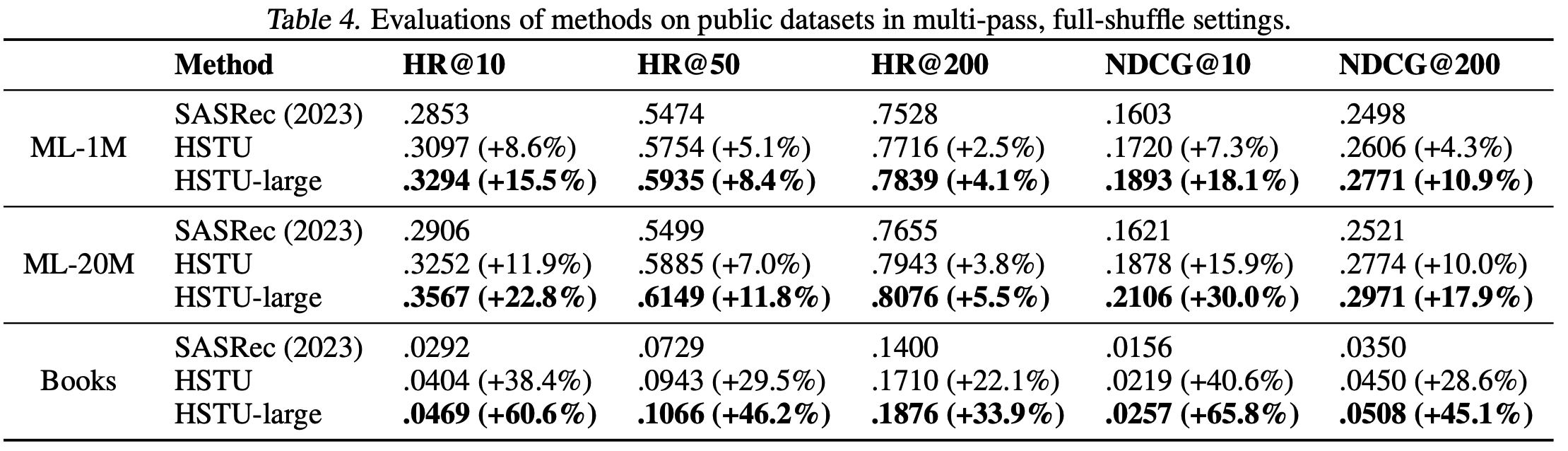
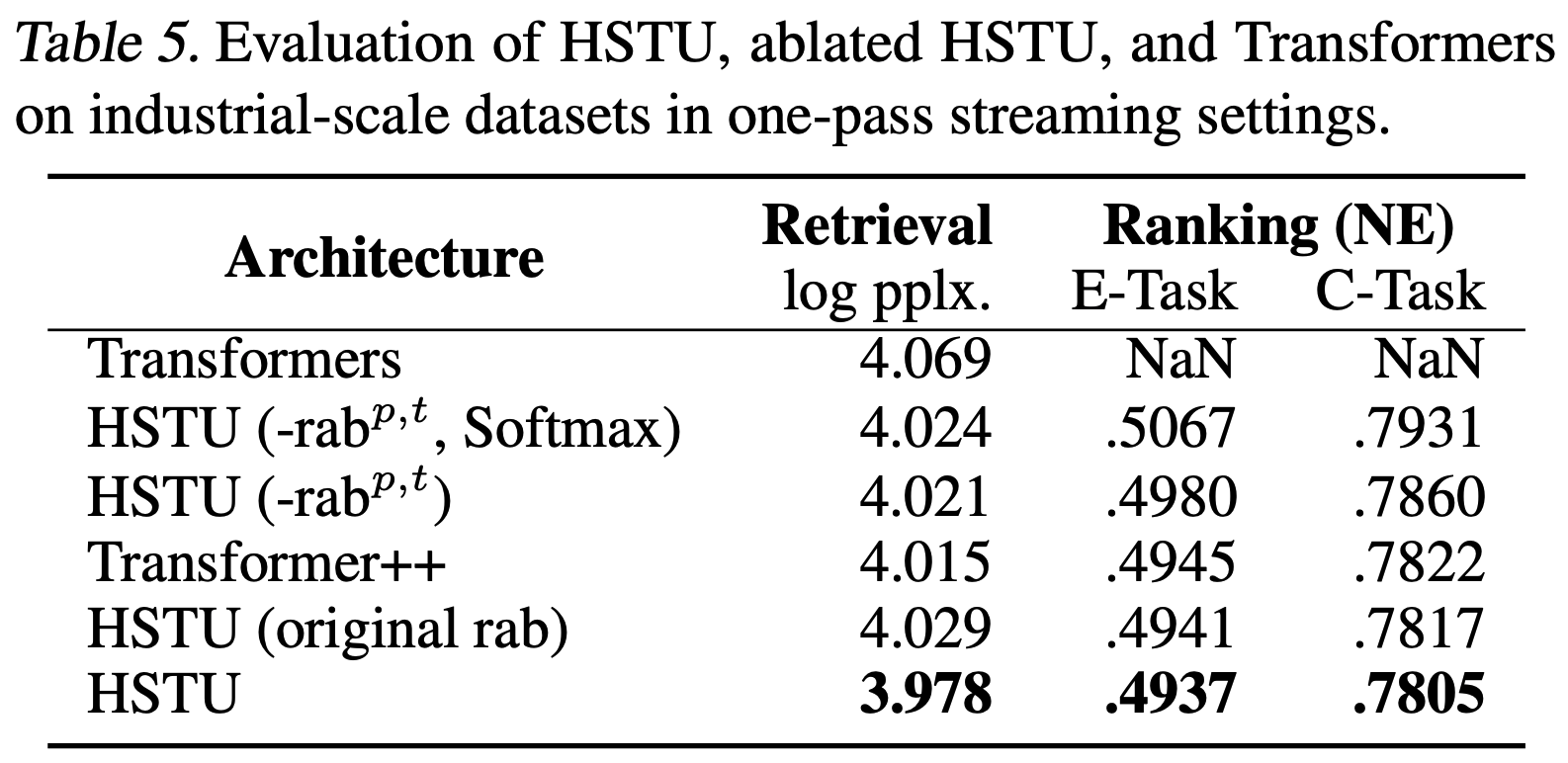
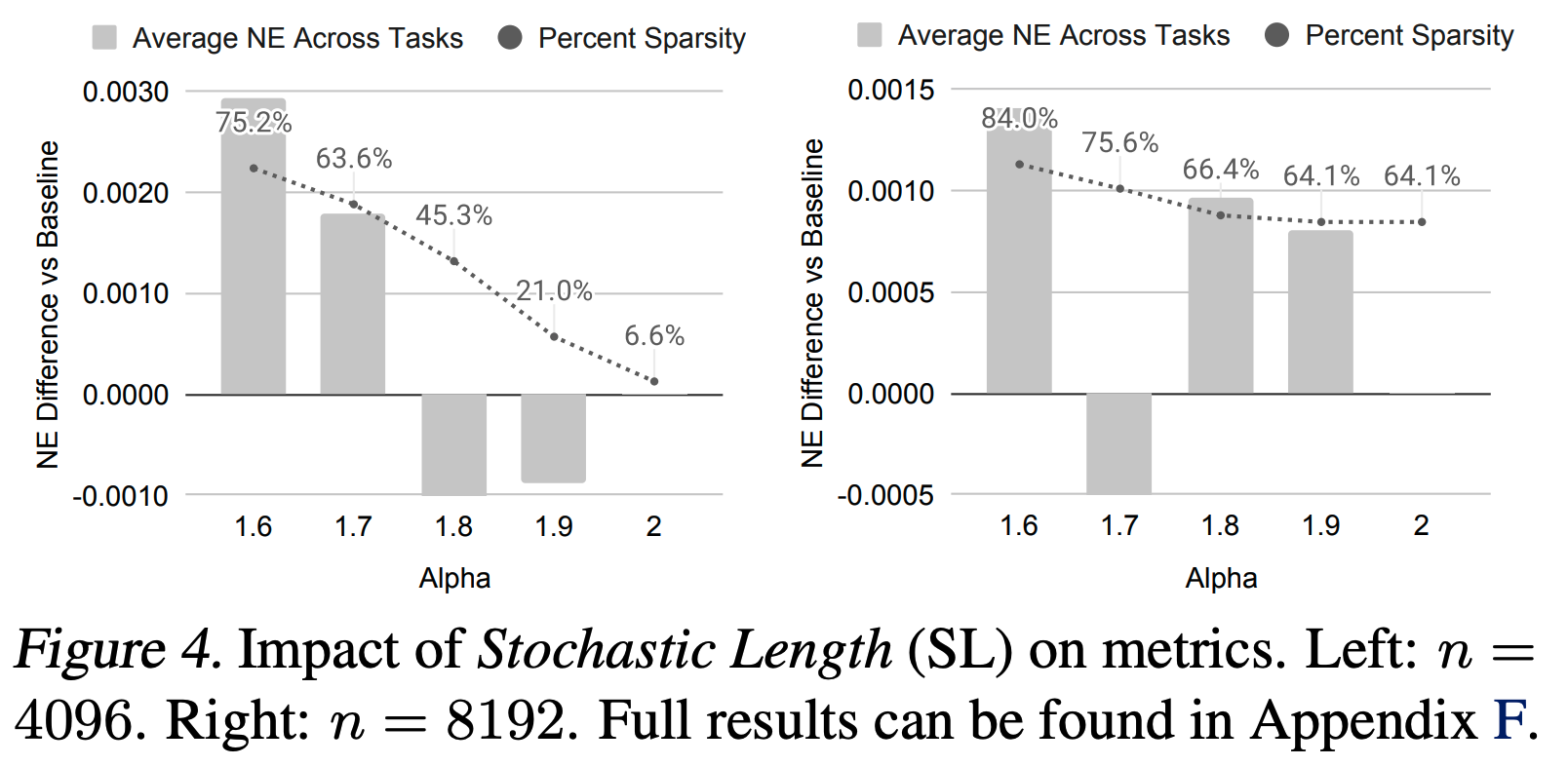
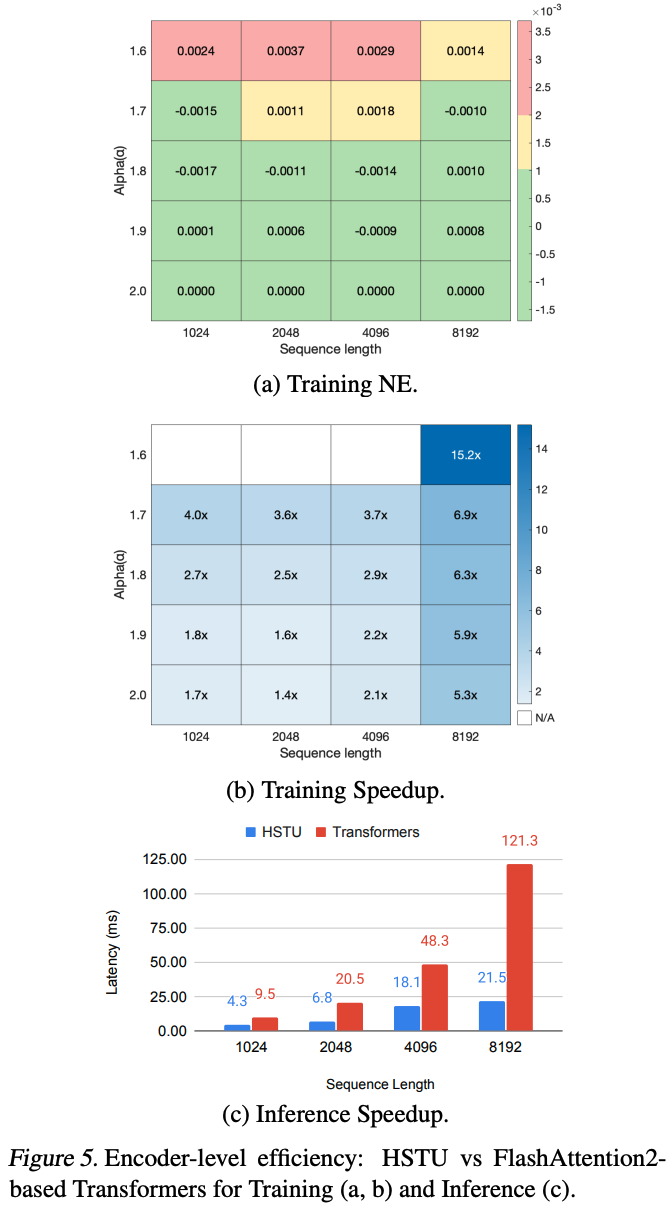
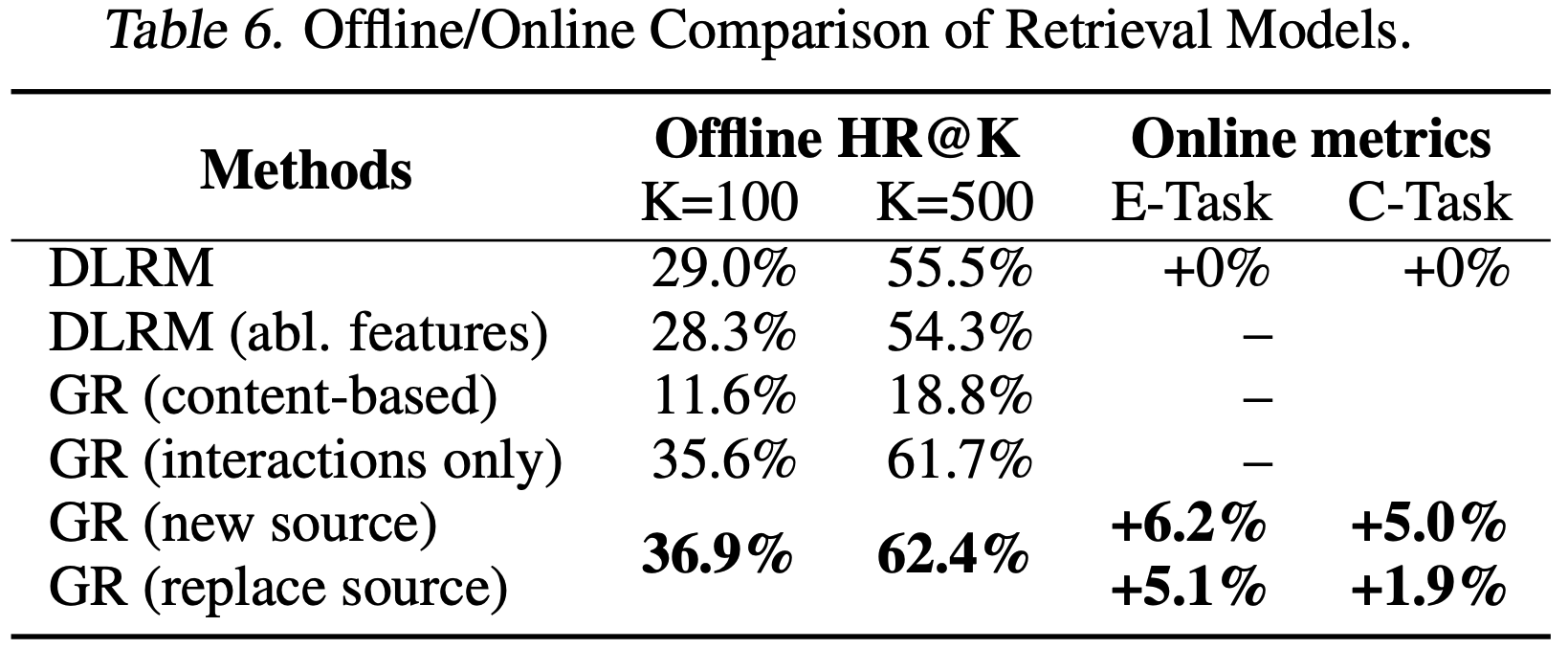
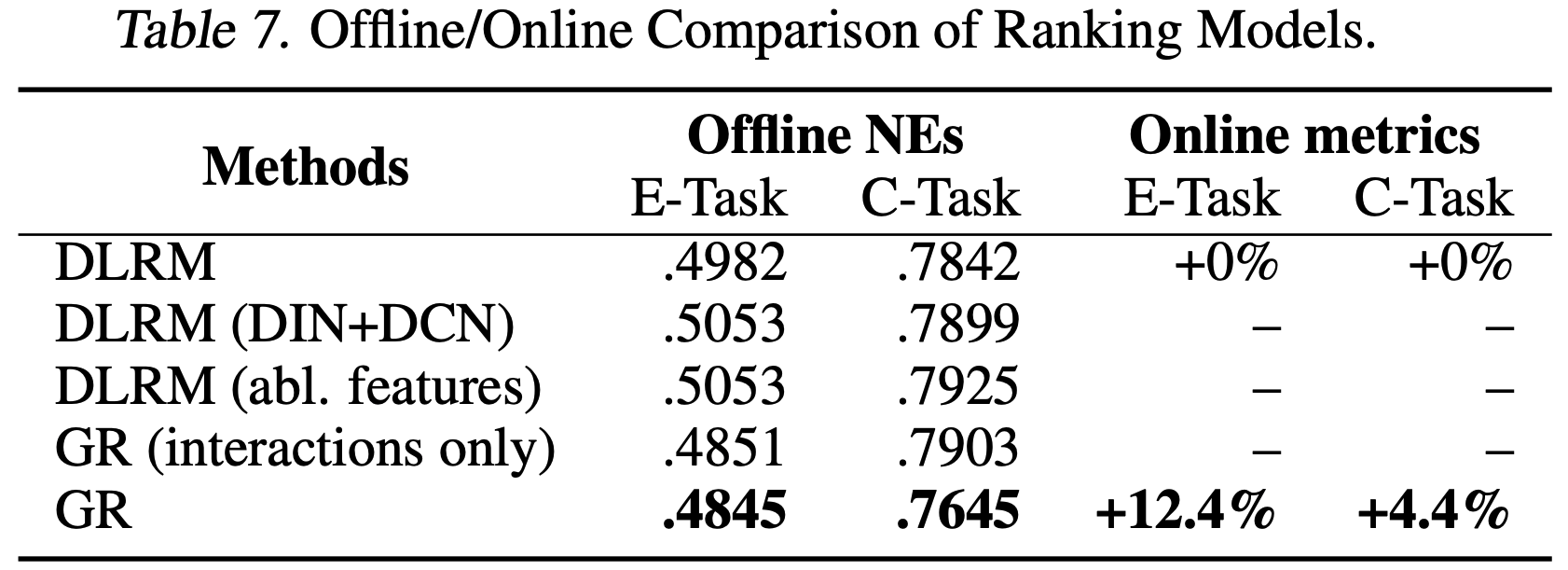
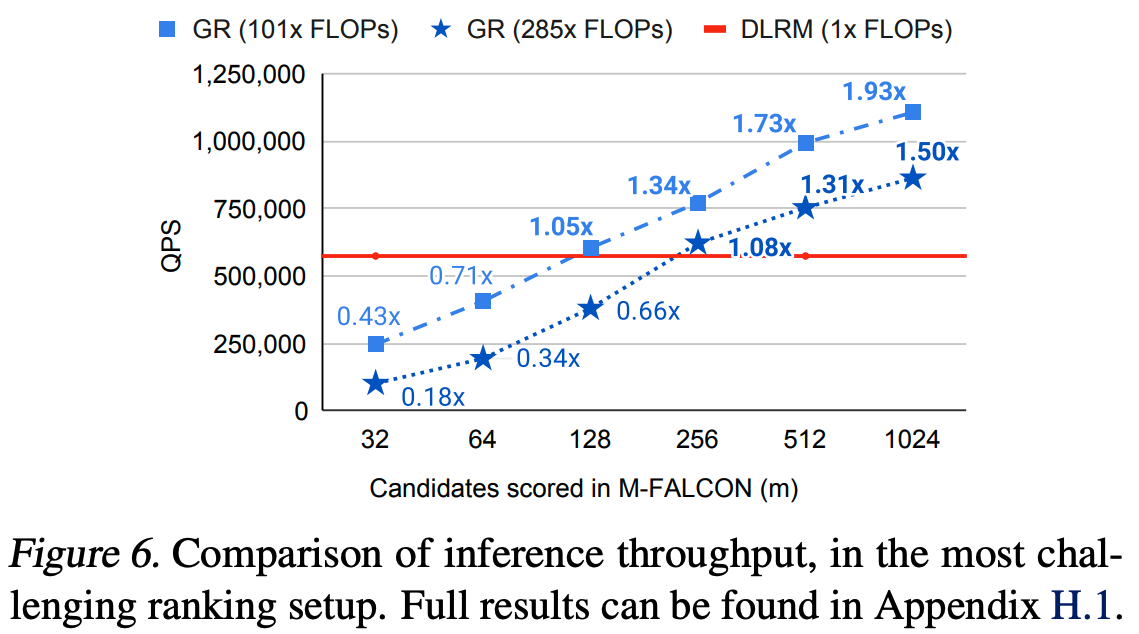
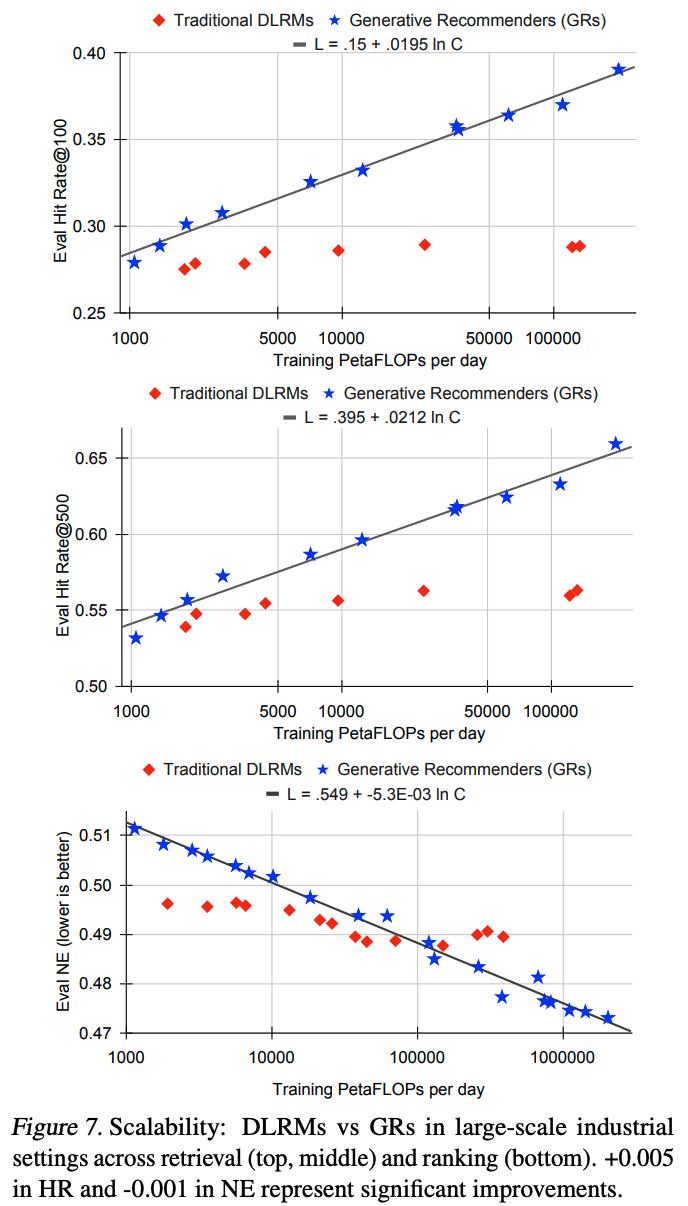
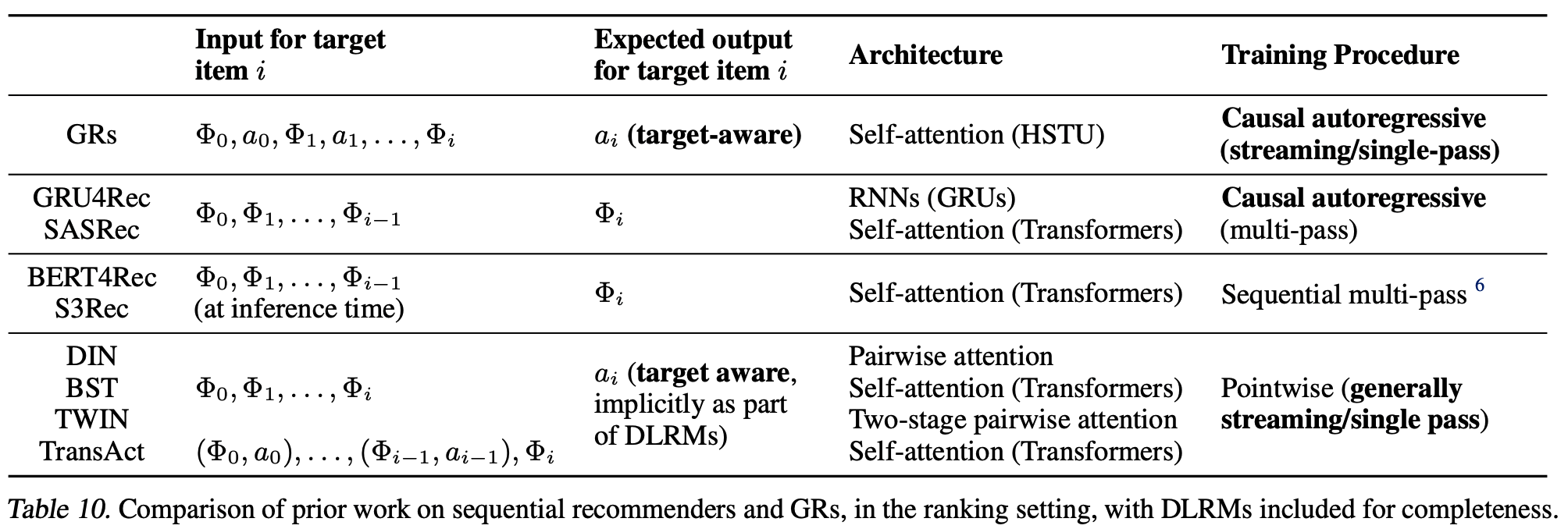
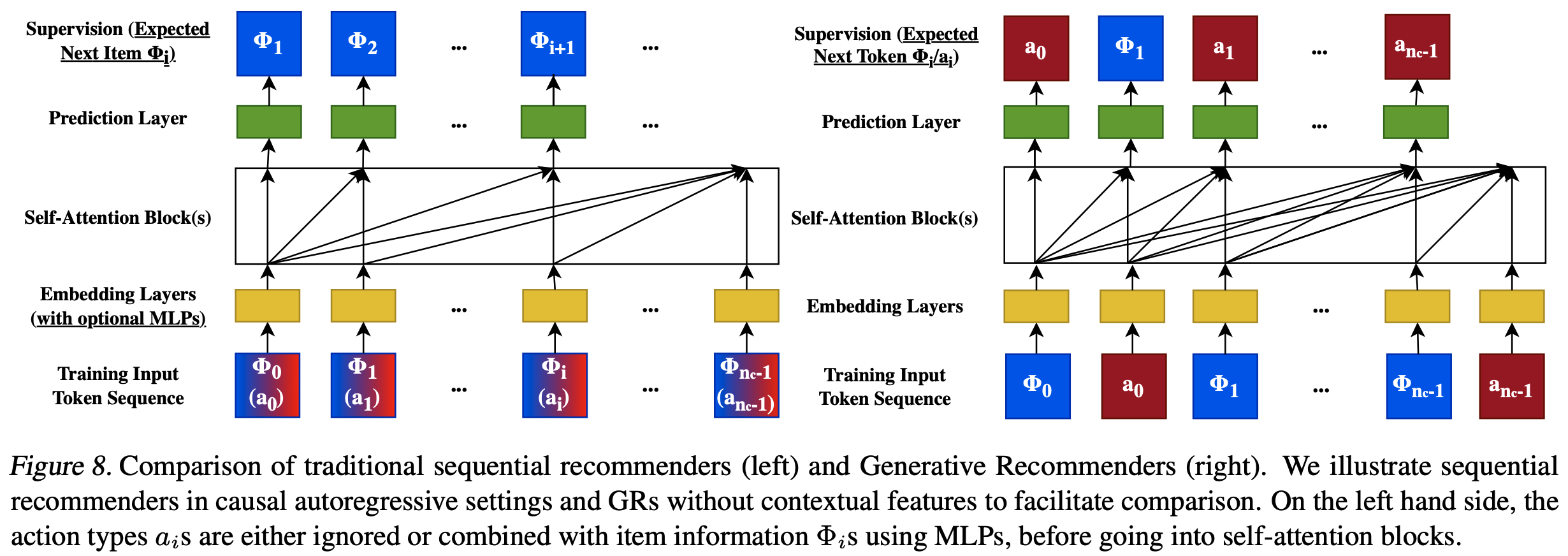
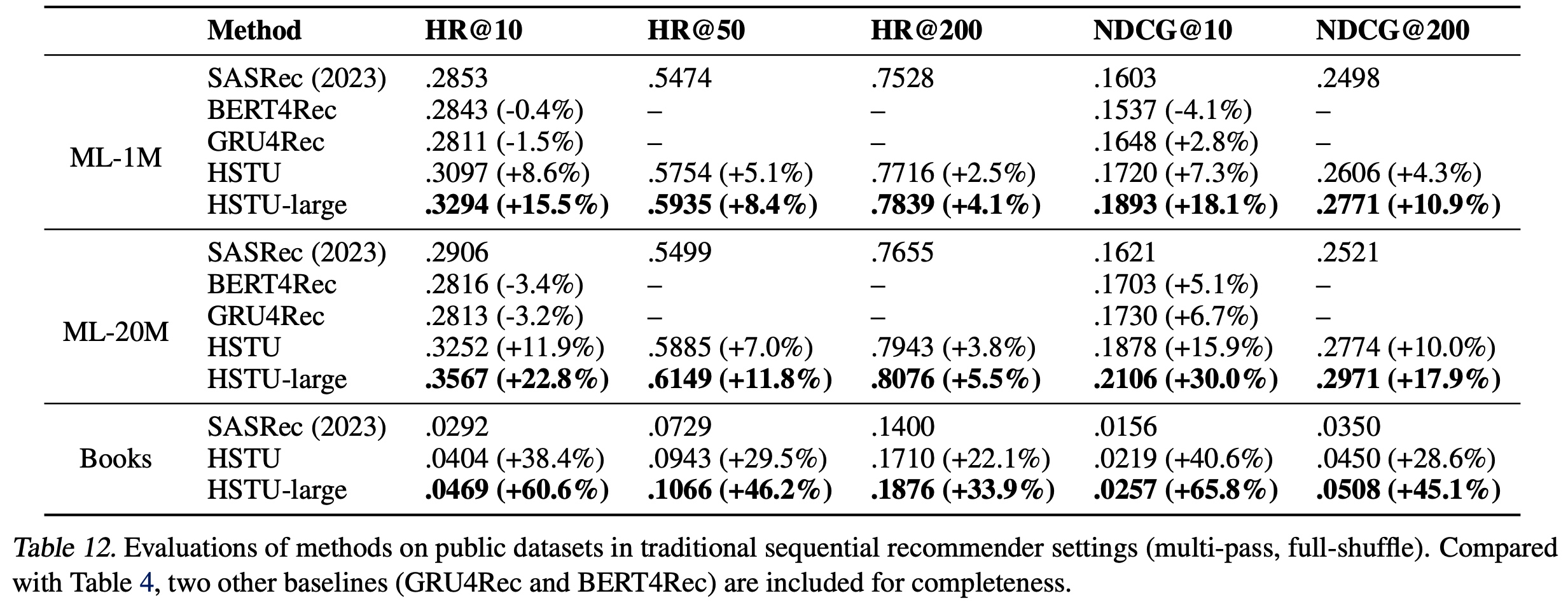
- Actions Speak Louder than Words: Trillion-Parameter Sequential Transducers for Generative Recommendations
- HLLM: Enhancing Sequential Recommendations via Hierarchical Large Language Models for Item and User Modeling, 202409, ByteDance
- Unlocking Scaling Law in Industrial Recommendation Systems with a Three-step Paradigm based Large User Model, 202502, Alibaba
整体说明
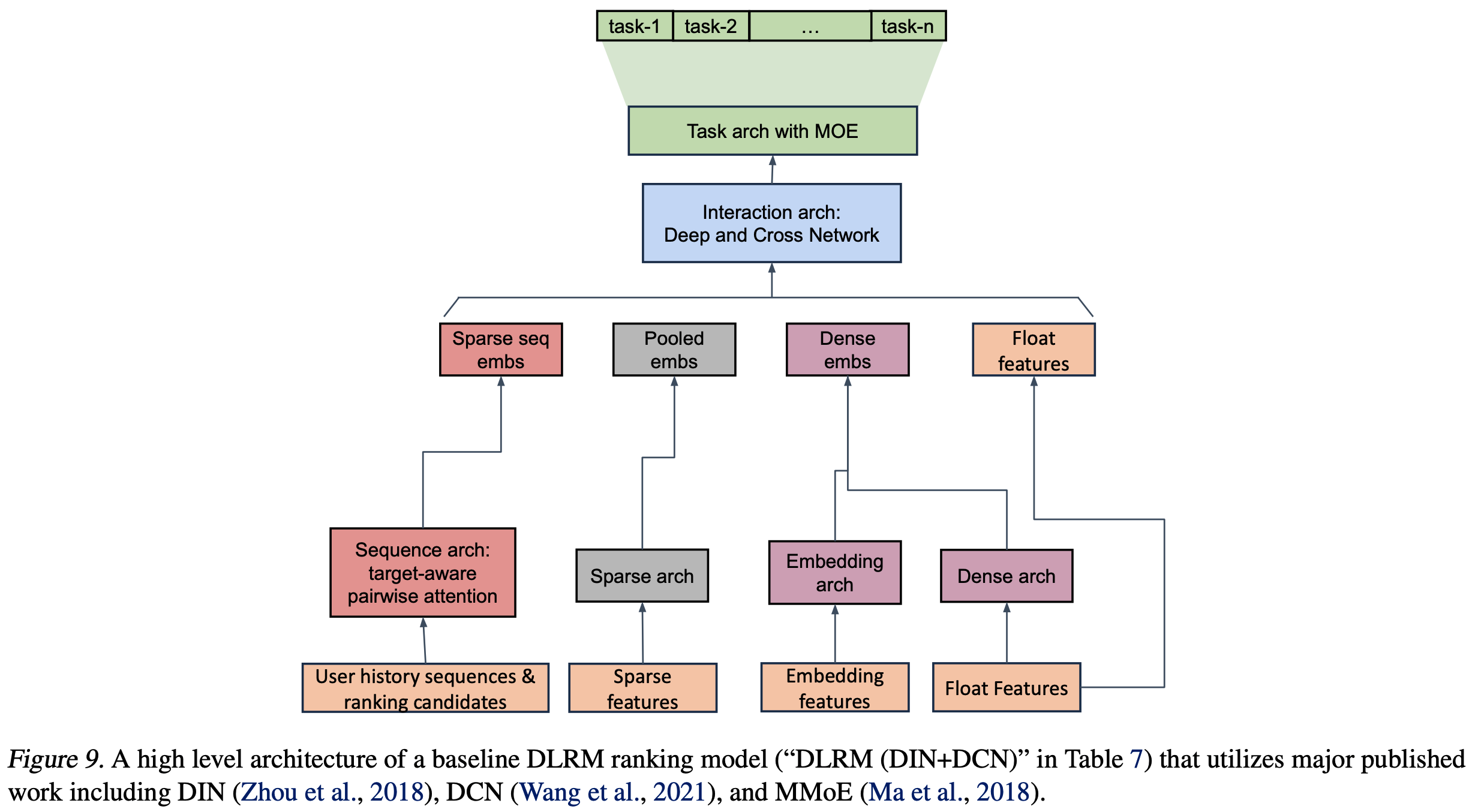
- 传统深度学习推荐模型(Deep Learning Recommendation Models,DLRMs)范式主要是“Retrieval-Ranking”模式
- 目前大模型在推荐领域的实践大致分为三类:
- 第一类:保留 DLRMs 范式,仅利用通用的 LLM 做知识增强,或从领域数据中提取表征信息等
- 第二类:仍保留 DLRMs 范式,部分重构 Retrieval 阶段或者 Ranking 阶段(或者在 Retrieval 阶段增加一路生成式召回通道)
- 第二类:直接修改 DLRMs 范式,将输入和输出都重新构造为 LLM 模式,直接利用重构后的领域数据做预训练和微调











/EfficientAttention-Survey-Figure1.png)
/EfficientAttention-Survey-Table1.png)
/EfficientAttention-Survey-Figure2.png)
/EfficientAttention-Survey-Figure3.png)
/EfficientAttention-Survey-Figure4.png)