Git——rebase

Git rebase命令的使用

rebase可以将某个目标分支上的提交作为基础，并将当前分支与目标分支不同的提交合并后放到后面
合并完成后，commit的名称不变，但hash值发生了变化
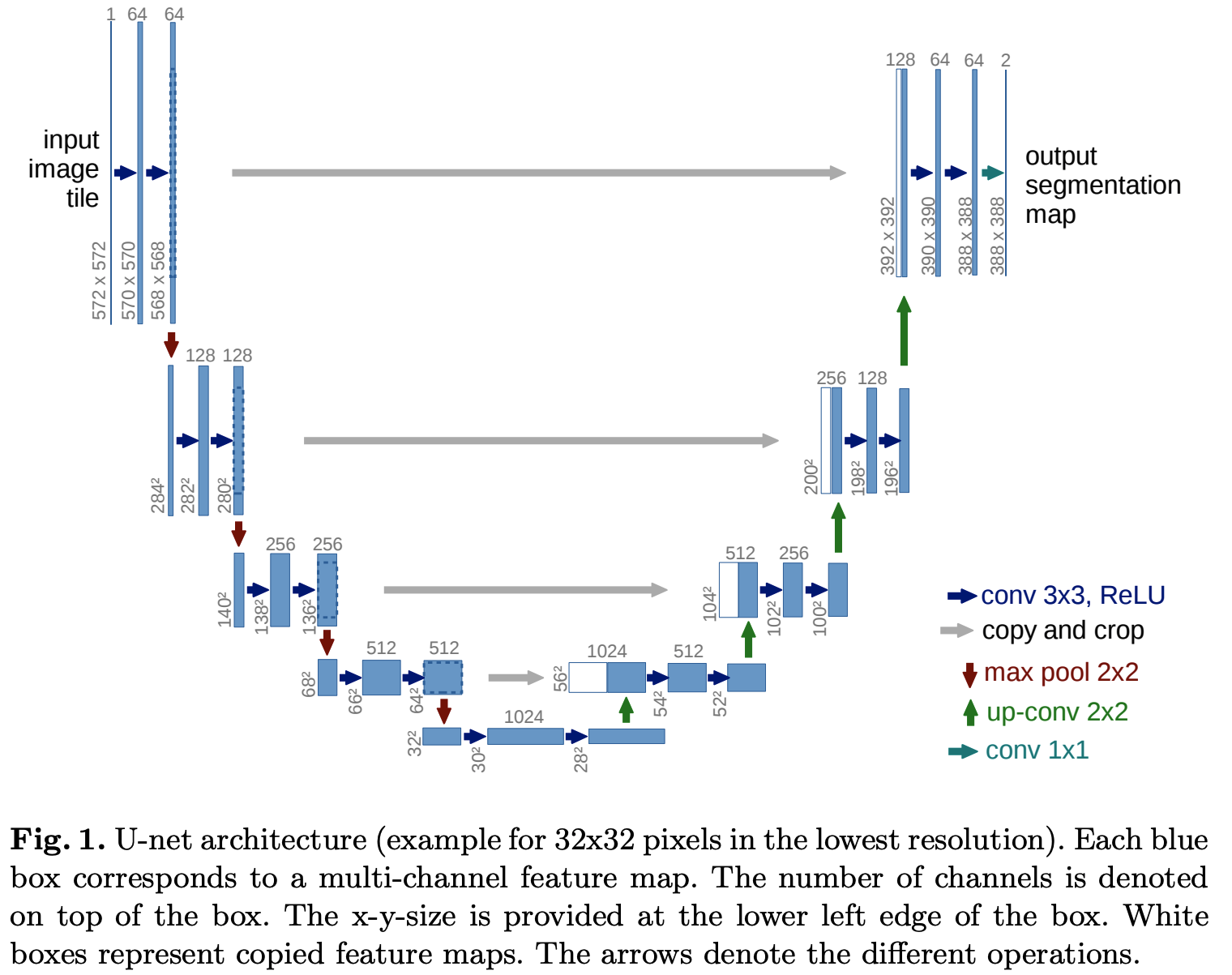
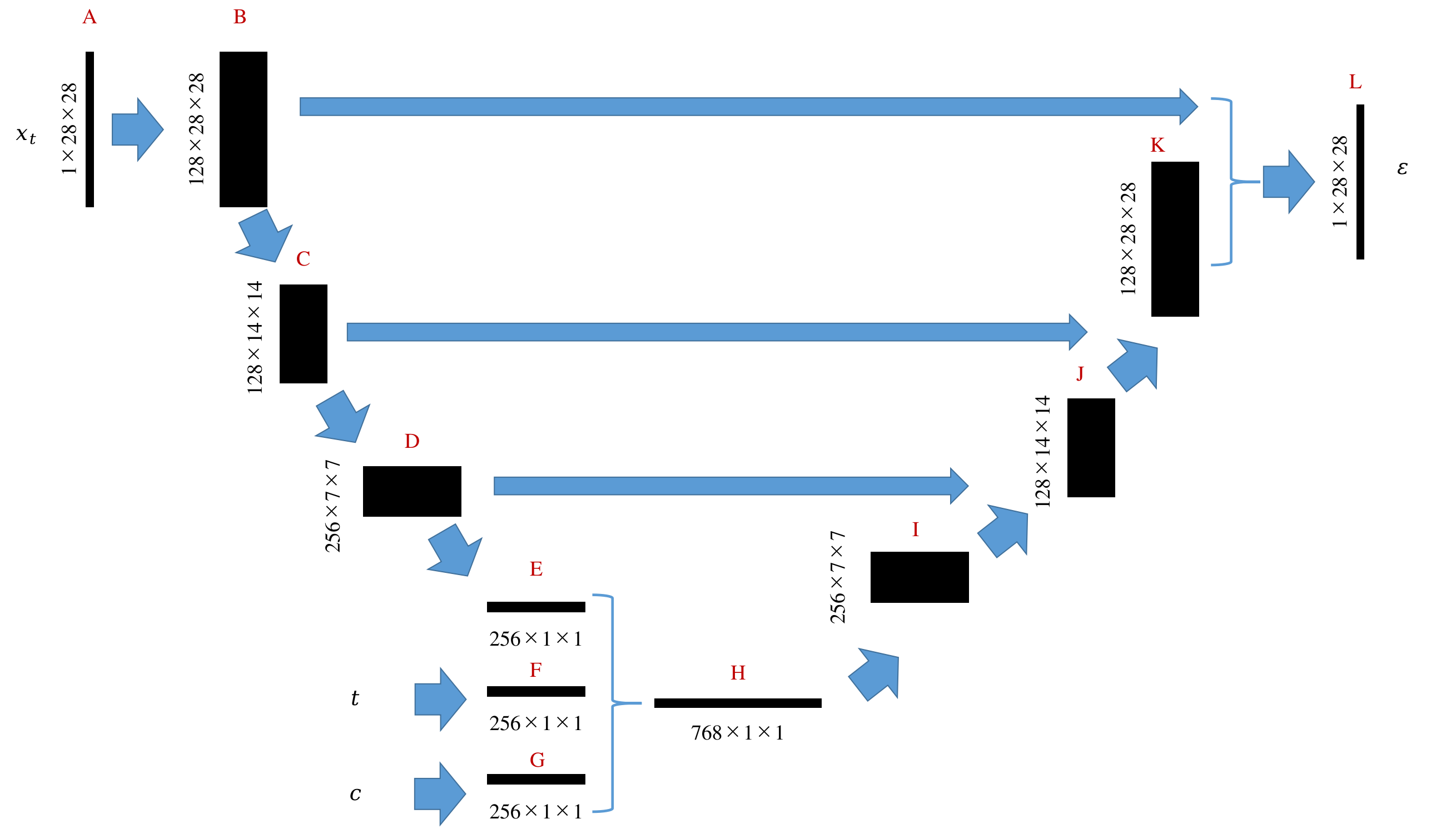
可视化描述：
- master分支开始创建两个分支A，B
- 分支A: master->A1->A2-A3
- 分支B: master->B1->B2
- 在分支A上rebase目标分支B执行git rebase B
- 解决冲突【缺陷是这里的分支冲突好像无法使用IDEA的工具检查，只能自己搜索查看】
  - rebase时git rebase target_branch会一个个文件出现冲突
  - 使用git rebase --skip可以跳过当前冲突对应的文件的当前分支的修改，保留别人target_branch的修改，慎用
- 解决冲突的文件使用git add file或者git rm file标记为已解决
- 所有文件都解决以后使用git rebase --continue完成rebase操作【注意，这个过程不可逆，不像merge一样可以回退】
  - 解决冲突并git rebase --continue后会出现下一个冲突，直到没有冲突
- 此时的分支情况
  - 分支A: master->B1->B2->A1’->A2’-A3’
    - A1’和A1 commit的名称相同，但是hash值不同，已经不是同一个提交了，是融合了B1,B2的提交
    - A2’和A2 以及 A3’和A3 commit的情况相似
  - 分支B: master->B1->B2
- 中途取消rebase操作可以使用git rebase --abort回退到原始分支的【但一旦git rebase --continue提交成功后无法回退】

rebase和merge的区别

rebase
- 操作后当前分支的commit【从相同commit开始往后的】都被修改了，所以无法回退到当前分支和目标分支的交叉之间的commit
- 在version control工具上看不出来是哪些线合并的，只保留一条线，看起来就像是从未有过分支一样
- rebase时git rebase target_branch会一个个文件出现冲突，解决冲突并git rebase --continue后会出现下一个，直到全部完成，而merge时git merge target_branch是所有文件的冲突一起出现的
merge
- 操作后是保留了所有分支的commit，新创建了一个commit用于合并分支，还能从当前分支回退到之前的版本
- 在version control工具上看起来就是两条线合并到了一起
如果想使用IDEA进行冲突解决，需要从IDEA上提交rebase或merge请求

Python——函数重载overload

整体说明

Python 本身不支持传统意义上的函数重载（overload）（即同名函数根据参数个数/类型自动匹配调用）
- 因为 Python 是动态类型语言，函数定义时不指定参数类型，且同名函数会直接覆盖前一个定义
虽然 Python 无原生函数重载，但可通过“参数判断”“singledispatch”“multipledispatch”模拟效果
- 简单场景用“手动判断参数”，按类型重载用 singledispatch，复杂多参数重载用 multipledispatch
Python 不允许同名函数并存（后定义的会覆盖前一个），因此“模拟重载”的本质是：
- 在同一个函数中，通过判断参数个数（*args/`kwargs`）** 或参数类型 ，分支执行不同逻辑

Python 不支持原生重载的原因

动态类型 ：Python 变量无类型声明，函数参数类型由运行时传入的值决定，无法在定义时区分“同名不同类型”的函数
命名空间机制 ：函数定义后会存入当前命名空间，同名函数会直接覆盖前一个（后定义的函数地址覆盖前一个）

例如，以下代码中，后定义的 foo 会覆盖前一个，调用时只会执行第二个：

def foo(a):
    print(f"1个参数：{a}")

def foo(a, b):
    print(f"2个参数：{a}, {b}")

foo(1)    # 报错：foo() missing 1 required positional argument: 'b'（第一个 foo 已被覆盖）

方式 1：手动判断参数个数/类型

通过 *args 接收可变参数，再根据参数长度/类型分支执行

def calculate(a, b=None, c=None):
    """根据参数个数，实现加法/乘法/幂运算的重载效果"""
    # 1. 传入 1 个参数：计算 a 的平方（a^2）
    if b is None and c is None:
        return a **2
    # 2. 传入 2 个参数：计算 a + b
    elif c is None:
        return a + b
    # 3. 传入 3 个参数：计算 a * b * c
    else:
        return a * b * c

# 测试不同参数调用
print(calculate(5))      # 1 个参数：5^2 = 25
print(calculate(2, 3))   # 2 个参数：2+3 = 5
print(calculate(2, 3, 4))# 3 个参数：2*3*4 = 24

方式 2：使用 `functools.singledispatch`（按参数类型重载）

Python 3.4+ 提供的 functools.singledispatch 装饰器，可实现“基于第一个参数的类型”的重载（单分派重载）

from functools import singledispatch

# 基函数（默认实现）
@singledispatch
def process_data(data):
    """处理任意类型数据（默认逻辑）"""
    return f"未知类型数据：{data}"

# 重载 1：处理 int 类型
@process_data.register(int)
def _(data):
    return f"整数类型：{data}，平方为 {data**2}"

# 重载 2：处理 str 类型
@process_data.register(str)
def _(data):
    return f"字符串类型：{data}，长度为 {len(data)}"

# 重载 3：处理 list 类型
@process_data.register(list)
def _(data):
    return f"列表类型：{data}，元素和为 {sum(data)}"

# 测试不同类型参数
print(process_data(10))          # 整数类型：10，平方为 100
print(process_data("hello"))     # 字符串类型：hello，长度为 5
print(process_data([1,2,3,4]))   # 列表类型：[1,2,3,4]，元素和为 10
print(process_data(3.14))        # 未知类型数据：3.14（触发默认实现）

方式 3：使用第三方库 `multipledispatch`（支持多参数类型/个数重载）

第三方库 multipledispatch 支持更灵活的重载（如根据多个参数的类型、个数匹配）

multipledispatch 是第三方库，需先安装 pip install multipledispatch

from multipledispatch import dispatch

# 两个 int 类型参数：加法
@dispatch(int, int)
def add(a, b):
    return f"int + int = {a + b}"

# 一个 int + 一个 str 类型：拼接
@dispatch(int, str)
def add(a, b):
    return f"int + str = {str(a) + b}"

# 三个 int 类型参数：求和
@dispatch(int, int, int)
def add(a, b, c):
    return f"int + int + int = {a + b + c}"

# 两个 list 类型参数：合并
@dispatch(list, list)
def add(a, b):
    return f"list + list = {a + b}"

# 测试不同参数组合
print(add(2, 3))                # int + int = 5
print(add(2, "苹果"))           # int + str = 2苹果
print(add(1, 2, 3))             # int + int + int = 6
print(add([1,2], [3,4]))        # list + list = [1,2,3,4]

附录：`@overload` 装饰器

Python 中使用 @overload 装饰器的类型提示重载，但不是真正的运行时重载，而是 静态类型提示重载
- 仅用于给类型检查工具（如 mypy）、IDE（如 PyCharm）提供类型信息，帮助开发者避免类型错误，运行时仍需一个 实际实现函数 来处理所有参数情况
Python 3.5+ 引入的 typing.overload 装饰器，作用是：
- 为同一个函数的不同参数组合（类型/个数/关键字参数要求）提供明确的类型注解
- 不影响运行时逻辑（运行时会忽略 @overload 装饰的函数体，只执行最后一个 实际实现函数）
- 解决 动态类型语言的类型模糊问题 ，让 IDE 能精准提示参数类型，类型检查工具能发现类型错误

Python——内置函数总结

整体说明

Python 中，内置函数是可以直接使用的（无需额外导入任何模块）
Python 的内置函数完整列表可参考官方文档：Built-in Functions — Python 3.9.16 documentation
本文内容总结自非官方分类，部分内容非规范写法

基础数据类型相关

int() ：转换为整数
float() ：转换为浮点数
str() ：转换为字符串
bool() ：转换为布尔值（True 或 False）
list() ：创建或转换为列表
tuple() ：创建或转换为元组
dict() ：创建字典
set() ：创建集合
complex() ：转换为复数

数学运算相关

abs(x) ：返回绝对值
round(x, n) ：四舍五入到指定小数位数
pow(x, y) ：返回 x 的 y 次幂（等价于 x**y）
sum(iterable) ：计算可迭代对象中所有元素的和
min(iterable) 和 max(iterable) ：返回最小值/最大值

类型检查与帮助相关

type(obj) ：返回对象的类型
isinstance(obj, class) ：检查对象是否是某个类的实例
help(obj) ：显示对象的帮助文档
dir(obj) ：返回对象的所有属性和方法

输入输出相关

print(*objects) ：打印对象到标准输出
input(prompt) ：从标准输入读取用户输入
open(file, mode) ：打开文件并返回文件对象

迭代与序列处理相关

len(obj) ：返回对象的长度（元素个数）
range(start, stop, step) ：生成不可变的整数序列
sorted(iterable) ：返回新的已排序列表
reversed(seq) ：返回反向迭代器
enumerate(iterable) ：返回索引-值对的枚举对象
zip(*iterables) ：将多个可迭代对象的元素打包成元组

函数与对象操作相关

map(func, iterable) ：对可迭代对象的每个元素应用函数
filter(func, iterable) ：过滤可迭代对象中的元素
reduce(func, iterable) ：（需从 functools 导入）累积计算可迭代对象的元素
lambda args: expression ：创建匿名函数
getattr(obj, name) 和 setattr(obj, name, value) ：获取/设置对象的属性

一些其他常用函数

id(obj) ：返回对象的唯一标识符（内存地址）
hash(obj) ：返回对象的哈希值（如果可哈希）
chr(i) ：将整数转换为对应的 Unicode 字符
ord(c) ：返回字符的 Unicode 码点
bin(x)、oct(x)、hex(x) ：转换为二进制、八进制、十六进制字符串
eval(expression) ：执行字符串表达式并返回结果
exec(code) ：执行字符串形式的 Python 代码

Python——pickle

Python pickle

关于pickle模块

Python的一个序列化与反序列化模块,支持Python基本数据类型
可以处理自定义的类对象,方法等

内存中使用

import pickle

origin = [1, 2, 3, [4, 5, 6]]
print "origin: %s" % origin
temp = pickle.dumps(origin)
print "temp: %s" % temp
new = pickle.loads(temp)
print "new: %s" % new

## output:
# origin: [1, 2, 3, [4, 5, 6]]
# temp: (lp0
# I1
# aI2
# aI3
# a(lp1
# I4
# aI5
# aI6
# aa.
# new: [1, 2, 3, [4, 5, 6]]

硬盘中使用

import pickle

origin = [1, 2, 3, [4, 5, 6]]
print "origin: %s" % origin
# open a binary and write the result
pickle.dump(origin, open('temp', 'wb'))
# open a binary and read the original object
new = pickle.load(open('temp', 'rb'))
print "new: %s" % new

## output
# origin: [1, 2, 3, [4, 5, 6]]
# new: [1, 2, 3, [4, 5, 6]]

Numpy——random模块

库名: np.random

RandomState()

np.random.RandomState(seed)

seed 相同时两个不同的RandomState对象会产生相同的随机数据序列

seed 默认值为None,此时不同的RandomState对象产生不同的随机数据序列,此时RandomState将从/dev/urandom 或者从clock otherwise读取seed值

print np.random.RandomState(1).randint(1, 100010)
print np.random.RandomState(1).randint(1, 100000)
print np.random.RandomState(1).randint(1, 100000)
print np.random.RandomState().randint(1, 100000)
print np.random.RandomState().randint(1, 100000)
print np.random.RandomState().randint(1, 100000)
print np.random.RandomState(1) is np.random.RandomState(1)
print np.random.RandomState() is np.random.RandomState()

输出如下:

98540
98540
98540
38317
42305
70464
False
False

关于初始化向量的维度

不是行向量也不是列向量
1
2
np.random.randn(5)
# [1,2,3,4,5]
- shape为(5,)
- 是一个特殊的数据结构
- 是一个一维向量，不是矩阵，不是行向量，也不是列向量

列向量

np.random.randn(5,1)
# [[1]
   [2]
   [3]
   [4]
   [5]]

shape为(5,1)
是一个矩阵

行向量
1
2
np.random.randn(1,5)
# [[1,2,3,4,5]]
- shape为(1,5)
- 是一个矩阵
一个好的习惯是使用向量时用Assert语句确保维度
1
assert(a.shape == (3,4))

Numpy——使用笔记

整体说明

Numpy 包含很多高效的函数，能够替换普通的循环，实现非常快
比如累加变成向量运算等

批量运算提效

普通用法

import numpy as np
a = np.zeros((n, 1))
b = np.zeros((n, 1))

for i in range(n):
	b[i] = math.exp(a[i])

高效用法

1
2
3

import numpy as np
a = np.zeros((n, 1))
b = np.exp(a)

相似的还有 log,abs 等函数

广播机制(broadcasting)

当两个向量（numpy的对象）的维度不同时，Python会将维度小的一个拓展（复制）成与维度大的相同，以便于计算
举例
1
2
a = np.zeros((n, 1))
b = a + 10

广播规则

形式1

1
2
3

(m,n) [+-*/] (m,1) 
<===>
(m,n) [+-*/] (m,n) # 按列复制第二个n次

形式2

1
2
3

(m,n) [+-*/] (1,n) 
<===>
(m,n) [+-*/] (m,n) # 按行复制第二个m次

形式3

1
2
3

(m,n) [+-*/] r # r为实数，维度为1
<===>
(m,n) [+-*/] (m,n) # 复制r m*n 次

形式4

1
2
3

(m,1) [+-*/] (1,n) 
<===>
(m,n) [+-*/] (m,n) # 按行复制第二个m次,并按列复制第一个n次

广播机制需要注意

广播机制使得书写更加美观，代码更加简洁
但广播机制往往会出现用户意想不到的微妙bug, 需要开发者注意

附录：一些笔记

axis=i表示第i维计算后将会消失或变化（该维度的size变成1）
多使用 reshape 函数
- reshape 函数复杂度是常数的(O(1))
- reshape 函数可确保我们的程序正确，不用随意猜测矩阵的维度

附录：使用 numpy 包为 Python 内置对象提效

numpy 包可以直接操作 list 等对象

# # 一维数组
import numpy as np

arr = np.array([1, 2, 3, 4, 5])
mean = np.mean(arr)
print(mean)  # 输出：3.0，整数数组计算均值默认返回浮点数（如 int32 数组返回 float64）；若指定 dtype=np.int32，结果会向下取整

# # 二维数组
arr = np.array([[1, 2, 3], 
				[4, 5, 6]])

# 沿轴0（列方向）计算均值：每列的均值
mean_axis0 = np.mean(arr, axis=0)
print(mean_axis0)  # 输出：[2.5 3.5 4.5]

# 沿轴1（行方向）计算均值：每行的均值
mean_axis1 = np.mean(arr, axis=1)
print(mean_axis1)  # 输出：[2. 5.]

# 全局均值（展平后）
mean_all = np.mean(arr)
print(mean_all)  # 输出：3.5

注意事项：
- 若数组包含 np.nan，np.mean 会返回 nan，需用 np.nanmean 忽略缺失值
- 对空数组调用 np.mean 会抛出 RuntimeWarning，并返回 nan
np.mean 支持多维数组、指定轴计算，且效率远高于 Python 内置的 statistics.mean（statistics 是 Python 内置库）

DL——PPNet-and-PEPNet

参考链接：

LHUC

LHUC（Learning Hidden Unit Contributions），最早应用于语音识别中
LHUC的基本思路是在语音识别中，用一个网络建模说话者的特点，这个网络输出用于修改主网络上的隐藏向量，其模型结构见下图（参考自PPNET参考链接：推荐模型简介之快手PPENT - Shard Zhang的文章 - 知乎）：

PPNet

快手2019年将LHUC的思想使用到推荐系统中，并将该方法命名为PPNet（Parameter Personalized Net），据说2019年全量后取得了很不错的收益
推荐系统中的一般的LHUC结构图（参考自PPNET参考链接：推荐模型简介之快手PPENT - Shard Zhang的文章 - 知乎）：
快手的PPNet结构图如下：

如上图3所示，PPNet的左侧是目前常见的DNN网络结构，由稀疏特征(sparse features)、嵌入层(embedding layer)、多神经网络层(neural layer)组成
右侧是PPNet特有的模块，包括Gate NN 和只给Gate NN作为输入的id特征。其中uid，pid，aid分别表示user id，photo id，author id。即bias embedding
左侧的所有特征的embedding会同这3个id特征（uid，pid，aid）的embedding拼接到一起作为所有Gate NN的输入。需要注意的是，左侧所有特征的embedding并不接受Gate NN的反传梯度，这样操作的目的是减少Gate NN对现有特征embedding收敛产生的影响。Gate NN的数量同左侧神经网络的层数一致，其输出同每一层神经网络的输入做element-wise product来做用户的个性化偏置
Gate NN是一个2层神经网络，其中第二层网络的激活函数是 2 * sigmoid，目的是约束其输出的每一项在[0, 2]范围内，并且默认值为1。当Gate NN输出是默认值时，PPNet同左侧部分网络是等价的
经实验对比，通过Gate NN为神经网络层输入增加个性化偏置项，可以显著提升模型的目标预估能力。PPNet通过Gate NN来支持DNN网络参数的个性化能力，来提升目标的预估能力，理论上来讲，可以用到所有基于DNN模型的预估场景，如个性化推荐，广告，基于DNN的强化学习场景等
快手PPNet实现的几个核心点：
- 输入Gate NN的特征是包含了所有特征的，包括左边主塔的输入特征和用户ID特征等
- Gate NN的梯度不影响左侧的embedding特征（embedding不接受Gate NN的反向梯度）
  - 问题：左边的MLP是否接受来自Gate NN的梯度呢？
  - 回答：从论文PEPNet: Parameter and Embedding Personalized Network for Infusing with Personalized Prior Information中看是可以接受的，当然真实场景中，训练时可以尝试测一下不同方案

PEPNet

PEPNet（Parameter and Embedding Personalized Network），包含EPNet和PPNet两个核心逻辑：
- EPNet（Embedding Personlized Network）：主要用于做不同场景(domain)的个性化
- PPNet（Parameter Personlized Network）：做用户维度的个性化，详情见上文
详细框架图如下：
- 特点：多场景、多任务、千人千模

DL——RQ-VAE

参考链接：
- 原始论文：Autoregressive Image Generation using Residual Quantization, CVPR 2022, Kakao Brain：韩国科技巨头的作品

整体说明

VQ-VAE的问题 ：自回归（autoregressive，AR）模型在高分辨率图像生成中，向量量化（vector quantization，VQ）通过将图像表示为离散编码序列来实现建模。较短的序列长度可降低处理编码间的长程交互的计算成本，作者认为现有VQ方法在率失真权衡下无法同时实现序列缩短和高保真图像生成
论文提出了一种两阶段框架 ：包括RQ-VAE（Residual-Quantized VAE）和 RQ-Transformer ，以高效生成高分辨率图像
- 在固定码本大小下，RQ-VAE能精确近似图像特征图，并将其表示为多层离散编码的堆叠图
- RQ-Transformer通过学习预测下一位置的量化特征向量（即预测下一组编码）来生成图像。得益于RQ-VAE的精确近似，256×256图像可表示为8×8分辨率的特征图，从而显著降低RQ-Transformer的计算成本
实验表明，该框架在无条件与有条件图像生成任务中均优于现有AR模型，且采样速度显著提升

文章引言

向量量化（vector quantization，VQ） 已成为自回归（autoregressive，AR）模型生成高分辨率图像的基础技术。具体而言，图像特征图经VQ量化和顺序重排（如光栅扫描）后，被表示为离散编码序列。量化完成后，AR模型通过顺序预测编码序列生成图像，从而避免直接预测所有像素
较短的序列能显著降低AR模型的计算成本（因为AR模型需利用历史编码预测后续编码）。然而，现有方法在率失真权衡下难以缩减序列长度。例如，VQ-VAE需指数级增长的码本以降低特征图分辨率并保持重建质量，但大码本会导致参数激增和码本坍缩（Codebook Collapse）问题，使训练不稳定
本研究提出RQ-VAE（Residual-Quantized VAE），通过残差量化（residual quantization，RQ）精确近似特征图并降低其空间分辨率：
- RQ在固定码本大小下递归量化特征图，以粗到细的方式生成多层离散编码堆叠图。经D次迭代后，特征图可表示为D层编码的堆叠。由于RQ能组合码本大小的D次方个向量，RQ-VAE无需大码本即可精确近似特征图。例如，RQ-VAE可将256×256图像的特征图分辨率降至8×8
此外，论文提出RQ-Transformer来预测RQ-VAE提取的编码。RQ-Transformer将量化特征图转换为特征向量序列，并预测下一位置的D个编码。得益于RQ-VAE降低的分辨率，RQ-Transformer能显著减少计算成本并更易学习长程交互。论文还提出软标签和随机采样技术，缓解训练中的暴露偏差问题
主要贡献包括：
- 1）提出RQ-VAE ，以多层编码堆叠图表示图像并实现高保真重建；
- 2）提出RQ-Transformer及其训练技术以解决暴露偏差；
- 3）在图像质量、计算成本和采样速度上显著优于现有AR模型

整体方法（两阶段）

论文提出了一个由残差量化变分自编码器（RQ-VAE）和RQ-Transformer组成的两阶段框架，用于图像的自回归建模：
RQ-VAE利用码本将图像表示为由D个离散编码堆叠而成的映射。随后，论文的RQ-Transformer通过自回归方式预测下一个空间位置的D个编码。论文还介绍了RQ-Transformer如何解决自回归模型训练中的曝光偏差问题

第一阶段：残差量化变分自编码器（RQ-VAE）

本节首先介绍向量量化（VQ）和VQ-VAE的公式化表示，随后提出RQ-VAE。RQ-VAE能够在无需增加码本大小的情况下精确逼近特征映射，并解释RQ-VAE如何将图像表示为离散编码的堆叠映射

VQ与VQ-VAE的公式化表示

设码本$\mathcal{C}$为一个有限集合$\{(k,\mathbf{e}(k))\}_{k\in[K]}$，其中包含编码$k$与其对应的编码嵌入$\mathbf{e}(k)\in\mathbb{R}^{n_{z} }$的配对，$K$为码本大小，$n_{z}$为编码嵌入的维度。给定向量$\mathbf{z}\in\mathbb{R}^{n_{z} }$，$\mathcal{Q}(\mathbf{z};\mathcal{C})$表示对$\mathbf{z}$的向量量化，即选择嵌入与$\mathbf{z}$最接近的编码：
$$
\mathcal{Q}(\mathbf{z};\mathcal{C})=\operatorname*{arg,min}_{k\in[K]}|\mathbf{z}-\mathbf{e}(k)|^{2}_{2}.
$$
VQ-VAE将图像编码为离散编码映射后，再从编码映射中重建原始图像。设$E$和$G$分别为VQ-VAE的编码器和解码器。给定图像$\mathbf{X}\in\mathbb{R}^{H_{o}\times W_{o}\times 3}$，VQ-VAE提取特征映射$\mathbf{Z}=E(\mathbf{X})\in\mathbb{R}^{H\times W\times n_{z} }$，其中$(H,W)=(H_{o}/f,W_{o}/f)$为$\mathbf{Z}$的空间分辨率，$f$为下采样因子。通过对每个位置的每个特征向量应用VQ，VQ-VAE量化$\mathbf{Z}$并返回其编码映射$\mathbf{M}\in[K]^{H\times W}$和量化特征映射$\hat{\mathbf{Z} }\in\mathbb{R}^{H\times W\times n_{z} }$：
$$
\mathbf{M}_{hw}=\mathcal{Q}(\mathbf{Z}_{hw};\mathcal{C}),\\
\hat{\mathbf{Z} }_{hw}=\mathbf{e}(\mathbf{M}_{hw}),
$$
- 其中$\mathbf{Z}_{hw}\in\mathbb{R}^{n_{z} }$为位置$(h,w)$处的特征向量，$\mathbf{M}_{hw}$为其编码。最终，输入图像被重建为$\hat{\mathbf{X} }=G(\hat{\mathbf{Z} })$
论文注意到，降低$\hat{\mathbf{Z} }$的空间分辨率$(H,W)$对自回归建模非常重要，因为自回归模型的计算成本随$HW$增加。然而，由于VQ-VAE对图像进行了有损压缩，降低$(H,W)$与保留图像信息之间存在权衡。具体而言，码本大小为$K$的VQ-VAE使用$HW\log_{2}K$比特表示图像的编码。根据率失真理论[38]，最佳重建误差取决于比特数。因此，若要将$(H,W)$进一步降低至$(H/2,W/2)$并保持重建质量，VQ-VAE需要大小为$K^{4}$的码本。然而，大码本会导致码本崩溃问题[8]和不稳定的训练

残差量化（RQ）

论文采用残差量化（Residual-Quantized，RQ）来离散化向量$\mathbf{z}$，而非增加码本大小。给定量化深度$D$，RQ将$\mathbf{z}$表示为有序的$D$个编码：
$$
\mathcal{RQ}(\mathbf{z};\mathcal{C},D)=(k_{1},\cdots,k_{D})\in[K]^{D},
$$
- 其中$\mathcal{C}$为大小为$|\mathcal{C}|=K$的码本；$k_{d} = 1,\cdots,K$为深度$d$处的编码（离散值）；$d=1,\cdots,D$
- 从第0个残差$\mathbf{r}_{0}=\mathbf{z}$开始，RQ递归计算编码$k_{d}$（残差$\mathbf{r}_{d-1}$的编码）和下一个残差$\mathbf{r}_{d}$：
  $$
  k_{d}=\mathcal{Q}(\mathbf{r}_{d-1};\mathcal{C}),\\
  \mathbf{r}_{d}=\mathbf{r}_{d-1}-\mathbf{e}(k_{d}), \tag{4}
  $$
  - $k_{d}=\mathcal{Q}(\mathbf{r}_{d-1};\mathcal{C})$ 表示从 codebook $\mathcal{C}$ 中搜索到残差向量 $\mathbf{r}_{d-1}$ 的最近邻向量的索引（或编码） $k_{d}$，该索引对应的编码向量为 $\mathbf{e}(k_{d})$
  - 定义$\hat{\mathbf{z} }^{(d)}=\sum_{i=1}^{d}\mathbf{e}(k_{i})$为前$d$个编码嵌入的部分和，RQ的递归量化以从粗到细的方式逼近向量。$\hat{\mathbf{z} }^{(1)}$是码本中最接近$\mathbf{z}$的编码嵌入$\mathbf{e}(k_{1})$，随后的编码被依次选择以减少量化误差。因此，部分和$\hat{\mathbf{z} }^{(d)}$随着$d$的增加提供更精细的逼近
  - 最终：$\hat{\mathbf{z} }:=\hat{\mathbf{z} }^{(D)}$为$\mathbf{z}$的量化向量
理解：开始的残差比较大，随着不断地用残差最最近邻匹配，随着匹配次数的增加，残差越来越小，越来越精细
每层共享codebook ：尽管可以为每个深度$d$单独构建码本，但论文为所有量化深度使用单一的共享码本$\mathcal{C}$。共享码本有两个优势：一是避免了为每个深度确定码本大小的超参数搜索，二是所有编码嵌入在每个深度均可使用，从而最大化其效用
RQ与VQ的讨论 ：值得注意的是，在码本大小相同的情况下，RQ比VQ能更精确地逼近向量。VQ将整个向量空间$\mathbb{R}^{n_{z} }$划分为$K$个簇，而深度为$D$的RQ最多将向量空间划分为$K^{D}$个簇。因此，RQ的划分能力与码本大小为$K^{D}$的VQ相当

RQ-VAE

论文提出RQ-VAE以精确量化图像的特征映射。RQ-VAE同样采用VQ-VAE的编码器-解码器架构，但将VQ模块替换为上述RQ模块。具体而言，深度为$D$的RQ-VAE将特征映射$\mathbf{Z}$表示为编码的堆叠映射$\mathbf{M}\in[K]^{H\times W\times D}$，并提取深度$d$处的量化特征映射$\hat{\mathbf{Z} }^{(d)}\in\mathbb{R}^{H\times W\times n_{z} }$：
$$
\mathbf{M}_{hw}=\mathcal{RQ}(E(\mathbf{X})_{hw};\mathcal{C},D),\\
\hat{\mathbf{Z} }_{hw}^{(d)}=\sum_{d^{\prime}=1}^{d}\mathbf{e}(\mathbf{M}_{hwd^{\prime} }). \tag{5}
$$
- $E(\mathbf{X})$ 表示编码器将输入 $\mathbf{X}$ 编码后输出为 $H\times W$ 维度的矩阵，$E(\mathbf{X})_{hw}$ 则表示矩阵中的一个向量（索引为$h,w$）
为简洁起见，深度$D$处的量化特征映射$\hat{\mathbf{Z} }^{(D)}$也记为$\hat{\mathbf{Z} }$。最终，解码器$G$从$\hat{\mathbf{Z} }$重建输入图像：$\hat{\mathbf{X} }=G(\hat{\mathbf{Z} })$
RQ-VAE能够以较低计算成本高效生成高分辨率图像。对于固定的下采样因子$f$，RQ-VAE比VQ-VAE能生成更真实的图像重建，因为RQ-VAE可以利用给定的码本大小精确逼近特征映射。此外，RQ-VAE允许进一步增加$f$和降低$(H,W)$，同时保持重建质量，从而降低自回归模型的计算成本、提高图像生成速度，并更好地学习编码间的长程交互
RQ-VAE的训练 ：通过梯度下降训练编码器$E$和解码器$G$，损失函数为$\mathcal{L}=\mathcal{L}_{\textrm{recon} }+\beta\mathcal{L}_{\textrm{commit} }$，其中$\beta>0$为乘性因子。重建损失（reconstruction loss）$\mathcal{L}_{\textrm{recon} }$和承诺损失（commitment loss）$\mathcal{L}_{\textrm{commit} }$定义为：
$$
\mathcal{L}_{\textrm{recon} }=|\mathbf{X}-\hat{\mathbf{X} }|_{2}^{2},\\
\mathcal{L}_{\textrm{commit} }=\sum_{d=1}^{D}\left|\mathbf{Z}-\operatorname{sg}\left[\hat{\mathbf{Z} }^{(d)}\right]\right|_{2}^{2},
$$
- 其中$\operatorname{sg}[\cdot]$为停止梯度操作，通过RQ模块的反向传播使用直接估计器[40]。承诺损失是所有深度$d$的量化误差之和，而非单一项$|\mathbf{Z}-\operatorname{sg}[\hat{\mathbf{Z} }]|_{2}^{2}$，目的是使$\hat{\mathbf{Z} }^{(d)}$随$d$增加逐步减少量化误差，从而实现从粗到细的逼近并保持训练稳定。码本$\mathcal{C}$通过聚类特征的指数移动平均更新[40]

RQ-VAE的对抗训练

RQ-VAE还通过对抗学习提升重建图像的感知质量，使用基于块的对抗损失[20]和感知损失[21]，具体细节见补充材料

第二阶段：RQ-Transformer

本节提出RQ-Transformer ，用于自回归预测RQ-VAE提取的编码堆叠。在形式化RQ-VAE编码的自回归建模后，介绍RQ-Transformer如何高效学习离散编码的堆叠映射，并提出训练技术以解决自回归模型中的曝光偏差问题

深度为D的编码自回归建模

RQ-VAE提取编码映射$\mathbf{M}\in[K]^{H\times W\times D}$后，通过光栅扫描顺序(raster scan order)[30]将其空间索引重排为2D编码数组$\mathbf{S}\in[K]^{T\times D}$，其中$T=HW$。即，$\mathbf{S}_{t}$（$\mathbf{S}$的第$t$行）包含$D$个编码：
$$
\mathbf{S}_{t}=(\mathbf{S}_{t1},\cdots,\mathbf{S}_{tD})\in[K]^{D}\quad\textrm{for }t\in[T].
$$
将$\mathbf{S}$视为图像的离散隐变量，自回归模型学习$p(\mathbf{S})$，其自回归分解为：
$$
p(\mathbf{S})=\prod_{t=1}^{T}\prod_{d=1}^{D}p(\mathbf{S}_{td},|,\mathbf{S}_{<t,d},\mathbf{S}_{t,<d}).
$$

RQ-Transformer架构

一种朴素方法是将$\mathbf{S}$展开为长度为$TD$的序列并输入传统Transformer[41]，但这既未利用RQ-VAE减少的序列长度$T$，也未降低计算成本。因此，论文提出RQ-Transformer以高效学习RQ-VAE提取的深度为$D$的编码。如图2所示，RQ-Transformer由Spatial Transformer和Depth Transformer组成
Spatial Transformer ：Spatial Transformer是一组掩码自注意力块，用于提取汇总先前位置信息的上下文向量。输入$\mathbf{u}_{t}$定义为：
$$
\mathbf{u}_{t}=\mathrm{P}\mathrm{E}_{T}(t)+\sum_{d=1}^{D}\mathbf{e}(\mathbf{S}_{t-1,d})\quad\textrm{for }t>1,
$$
- 其中$\mathrm{P}\mathrm{E}_{T}(t)$为空间位置$t$的位置嵌入，第二项为量化特征向量（见式5）。第一位置的输入$\mathbf{u}_{1}$为可学习嵌入，表示序列起始。Spatial Transformer处理后，上下文向量$\mathbf{h}_{t}$编码$\mathbf{S}_{ < t}$的所有信息：
  $$
  \mathbf{h}_{t}=\text{SpatialTransformer}(\mathbf{u}_{1},\cdots,\mathbf{u}_{t}).
  $$
Depth Transformer ：基于上下文向量$\mathbf{h}_{t}$，Depth Transformer自回归预测位置$t$的$D$个编码$(\mathbf{S}_{t1},\cdots,\mathbf{S}_{tD})$。输入$\mathbf{v}_{td}$定义为：
$$
\mathbf{v}_{td}=\text{PE}_{D}(d)+\sum_{d^{\prime}=1}^{d-1}\mathbf{e}(\mathbf{S}_{td^{\prime} })\quad\textrm{for }d>1,
$$
- 其中$\text{PE}_{D}(d)$为深度$d$的位置嵌入，所有位置$t$共享。对于$d=1$，使用$\mathbf{v}_{t1}=\text{PE}_{D}(1)+\mathbf{h}_{t}$。Depth Transformer预测条件分布$\mathbf{p}_{td}(k)=p(\mathbf{S}_{td}=k|\mathbf{S}_{<t,d},\mathbf{S}_{t,<d})$：
  $$
  \mathbf{p}_{td}=\text{DepthTransformer}(\mathbf{v}_{t1},\cdots,\mathbf{v}_{td}).
  $$
RQ-Transformer的训练目标是最小化负对数似然损失$\mathcal{L}_{AR}$：
$$
\mathcal{L}_{AR}=\mathbb{E}_{\mathbf{S} }\mathbb{E}_{t,d}\left[-\log p(\mathbf{S}_{td}|\mathbf{S}_{<t,d},\mathbf{S}_{t,<d})\right].
$$
计算复杂度 ：RQ-Transformer的计算复杂度远低于朴素方法（展开为1D序列）。Transformer处理长度为$TD$的序列时，计算复杂度为$O(NT^{2}D^{2})$[41]。而RQ-Transformer的空间和Depth Transformer的计算复杂度分别为$O(N_{\text{spatial} }T^{2})$和$O(N_{\text{depth} }TD^{2})$，总复杂度为$O(N_{\text{spatial} }T^{2}+N_{\text{depth} }TD^{2})$，显著低于$O(NT^{2}D^{2})$。第4.3节显示，RQ-Transformer的图像生成速度更快

软标签与随机采样

曝光偏差[34]会因训练与推理间的预测差异导致误差累积，从而降低自回归模型性能。在推理中，预测误差会随深度$D$累积，因为更精细的特征向量估计难度增加
为此，论文提出软标签和随机采样以缓解曝光偏差。基于RQ-VAE编码嵌入的几何关系，定义分类分布$\mathcal{Q}_{\tau}(k|\mathbf{z})$：
$$
\mathcal{Q}_{\tau}(k|\mathbf{z})\propto e^{-||\mathbf{z}-\mathbf{e}(k)||_{2}^{2}/\tau}\quad\textrm{for }k\in[K],
$$
- 其中$\tau>0$为温度参数。当$\tau$趋近于0时，$\mathcal{Q}_{\tau}$退化为单点分布$\mathcal{Q}_{0}(k|\mathbf{z})=\mathbf{1}[k=\mathcal{Q}(\mathbf{z};C)]$
目标编码的软标签 ：基于编码嵌入的距离，软标签通过显式监督编码间的几何关系改进RQ-Transformer的训练。对于位置$t$和深度$d$，使用软化分布$\mathcal{Q}_{\tau}(\cdot|\mathbf{r}_{t,d-1})$替代单点标签$\mathcal{Q}_{0}(\cdot|\mathbf{r}_{t,d-1})$
RQ-VAE编码的随机采样 ：通过从$\mathcal{Q}_{\tau}(\cdot|\mathbf{r}_{t,d-1})$采样选择编码$\mathbf{S}_{td}$，替代RQ的确定性编码选择（式4）。随机采样在$\tau\to 0$时等价于原始RQ编码选择，为给定特征映射提供不同的编码组合

DL——RectifiedFlow

参考链接：
- 原始论文：Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow, 202209，虽然原理很简单，但是原始论文证明比较详细，且伪代码不够清晰（包含一些数据内容），所以显得晦涩难懂

Rectified Flow 整体说明

Rectified Flow 是一种基于常微分方程（ODE）的生成模型，旨在通过“直线化”轨迹实现高效采样。其核心思想是通过优化一个速度场（velocity field）来最小化传输映射的误差，从而将源分布（如高斯噪声）转换为目标分布（如图像数据）
Rectified Flow 的训练通过优化速度场和 Reflow 技术逐步拉直轨迹，而采样则通过 ODE 求解实现高效生成。其核心贡献在于简化扩散模型的复杂推导 ，并通过直线化路径实现快速采样 ，适用于生成、迁移等多种任务

Rectified Flow 训练过程

Rectified Flow 的训练分为两个主要阶段：初始训练（1-Rectified Flow）和轨迹优化（Reflow）

初始训练（1-Rectified Flow）

目标：学习一个速度场 $ v(X_t, t) $，使得从源分布 $ \pi_0 $（如高斯噪声）到目标分布 $ \pi_1 $（如真实图像）的传输路径尽可能直线化
数据配对 ：随机采样 $ X_0 \sim \pi_0 $ 和 $ X_1 \sim \pi_1 $，并假设它们之间通过线性插值连接：
$$
X_t = t X_1 + (1-t) X_0, \quad t \in [0,1]
$$
损失函数 ：最小化速度场 $ v $ 与理想直线方向 $ (X_1 - X_0) $ 的均方误差：
$$
\min_v \int_0^1 \mathbb{E}_{X_0, X_1} \left[ | (X_1 - X_0) - v(X_t, t) |^2 \right] dt
$$
- 其中 $ X_t $ 是插值点

Reflow（轨迹优化，可选，可多次执行）

问题：初始训练中 $ X_0 $ 和 $ X_1 $ 是随机配对的，导致轨迹可能交叉或弯曲，影响采样效率
解决方案 ：使用已训练的 1-Rectified Flow 生成新的配对数据 $ (X_0, \text{Flow}_1(X_0)) $，再训练一个新的速度场（2-Rectified Flow）。这样，轨迹会变得更直，减少交叉
数学表达 ：
$$
\min_v \int_0^1 \mathbb{E}_{X_0 \sim \pi_0, X_1 \sim \text{Flow}_1(X_0)} \left[ | (X_1 - X_0) - v(X_t, t) |^2 \right] dt
$$
迭代优化 ：可以多次应用 Reflow ，逐步拉直轨迹，提高采样效率
可理论证明这是 Reflow 的单调改进

采样过程

Rectified Flow 的采样过程通过数值求解 ODE 实现，通常使用欧拉法（Euler method）或更高阶的数值积分器

标准采样（多步）

从 $ Z_0 \sim \pi_0 $ 开始，逐步计算：
$$
Z_{t+\Delta t} = Z_t + v(Z_t, t) \cdot \Delta t
$$
- 其中 $ \Delta t = 1/N $，$ N $ 是步数
- 由于轨迹已被 Reflow 拉直，即使步数较少（如 10-20 步），也能生成高质量样本
- 采样时 $t = 0 \rightarrow 1$

一步生成（蒸馏）

经过 Reflow 后，轨迹足够直，可以尝试一步生成：
$$
Z_1 = Z_0 + v(Z_0, 0)
$$
- 这一步相当于直接预测 $ X_1 - X_0 $，但需要高质量的 Reflow 训练

Rectified Flow 对比传统 Diffusion 模型

Rectified Flow 采样更高效 ：相比传统扩散模型（如 DDPM），Rectified Flow 的直线化轨迹允许更少的采样步数，甚至一步生成
Rectified Flow 应用范围更广 ：Rectified Flow 的本质是拟合一个分布到另一个分布，不仅可用于生成模型（噪声到图像），还可用于域迁移（如猫脸到人脸）
其他说明 ：使用 Reflow 能不断降低传输代价，使轨迹越来越直，可理论证明这是 Reflow 的单调改进
采样时 $t$ 的取值不同，但都表示从噪声到真实图片的生成过程：
- Diffusion Model 是 $t = T \rightarrow 1$，逐渐减小
- Rectified Flow 是 $t = 0 \rightarrow 1$，逐渐增大，详情见附录代码示例输出结果
  - 注：这是由于训练时使用的混合值方式不同造成的，微改一下混合方式，$t$ 的取值也可以逐渐变小

Rectified Flow 应用场景

Stable Diffusion 3 采用了 Rectified Flow 的改进版本，结合 Transformer 架构，在高分辨率文本到图像生成中表现优异

Rectified Flow 的证明过程

待补充

附录：Rectified Flow 代码示例

一个简单的 Rectified Flow 训练和采样代码示例

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
from torch.utils.data import Dataset, DataLoader
from sklearn.datasets import make_moons

# 可兼容旧版本PyTorch的SiLU实现，新版本中直接使用 nn.SiLU即可
if hasattr(nn, 'SiLU'):
    SiLU = nn.SiLU
else:
    class SiLU(nn.Module):
        def forward(self, x):
            return x * torch.sigmoid(x)

# 设置随机种子
torch.manual_seed(42)
np.random.seed(42)

# 超参数
batch_size = 512
lr = 1e-3
epochs = 2000
num_samples = 10000  # 生成的数据点数量
dim = 2  # 数据维度

# 创建一个简单的 2D 数据集 (两个半圆月亮)
class MoonsDataset(Dataset):
    def __init__(self, n_samples):
        X, _ = make_moons(n_samples=n_samples, noise=0.05)
        self.x = torch.tensor(X, dtype=torch.float32)

    def __len__(self):
        return len(self.x)

    def __getitem__(self, idx):
        return torch.FloatTensor(self.x[idx])


# 创建一个简单的 2D 数据集 (两个半圆拼凑成一个圆形)
class CircleDataset(Dataset):
    def __init__(self, num_samples):
        theta = np.random.uniform(0, np.pi, num_samples)
        self.x = np.stack([
            np.concatenate([np.cos(theta), np.cos(theta)]),
            np.concatenate([np.sin(theta), -np.sin(theta)])
        ], axis=1)
        self.x = self.x + 0.1 * np.random.randn(*self.x.shape)  # 添加噪声

    def __len__(self):
        return len(self.x)

    def __getitem__(self, idx):
        return torch.FloatTensor(self.x[idx])

# 定义一个简单的 MLP 作为流模型
class FlowModel(nn.Module):
    def __init__(self, dim=2, hidden_dim=128):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(dim + 1, hidden_dim),  # +1 对应时间 t
            SiLU(),
            nn.Linear(hidden_dim, hidden_dim),
            SiLU(),
            nn.Linear(hidden_dim, dim)
        )

    def forward(self, x, t):
        # x: (batch_size, dim), t: (batch_size, 1)
        t = t.view(-1, 1)
        inputs = torch.cat([x, t], dim=1)
        return self.net(inputs)

# 训练函数
def train(model, dataloader, optimizer, epochs):
    model.train()
    loss_history = []
    for epoch in range(epochs):
        total_loss = 0
        for x1 in dataloader:
            x1 = x1.to(device) # 真实数据 x1
            t = torch.rand(x1.size(0), device=device).view(-1,1) # 随机采样时间 t ~ Uniform(0, 1)
            x0 = torch.randn_like(x1) # 采样噪声 x0 ~ N(0, 1)
            x_t = t * x1 + (1-t) * x0 # 计算插值: x_t = t*x1 + (1-t)*x0
            v_pred = model(x_t, t) # 模型预测速度场

            loss = torch.mean(torch.sum(((x1 - x0) - v_pred)**2, dim=1)) # 计算损失: || (x1 - x0) - v ||^2
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            total_loss += loss.item()
        avg_loss = total_loss / len(dataloader)
        loss_history.append(avg_loss)
        if epoch % 100 == 0:
            print(f"Epoch {epoch}, Loss: {avg_loss:.4f}")
    return loss_history

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
dataset = CircleDataset(num_samples) # 圆形数据
# dataset = MoonsDataset(num_samples) # 双月形数据
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)
model = FlowModel(dim=dim).to(device)
optimizer = optim.Adam(model.parameters(), lr=lr)

loss_history = train(model, dataloader, optimizer, epochs) # 训练模型

# 绘制训练损失
plt.plot(loss_history)
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("Training Loss")
plt.show()

# 采样函数
def sample(model, num_samples, dim, steps=100):
    model.eval()
    with torch.no_grad():
        z = torch.randn(num_samples, dim, device=device) # 采样初始噪声
        dt = 1.0 / steps # 时间离散化为 delta 值
        traj = [z.cpu().numpy()] # 轨迹存储（可选，用于展示生成过程）
        for i in range(0,steps,1):
            t = torch.ones(num_samples, device=device) * (i*1.0 / steps)
            v = model(z, t) # 计算速度场
            z = z + v * dt # 欧拉方法更新求解常微分方程： z_{t+dt} = z_t + v * dt
            if i % 10 == 0:
                traj.append(z.cpu().numpy())
        return z.cpu().numpy(), traj

samples, traj = sample(model, 10000, dim) # 采样新数据

# 绘制结果
plt.figure(figsize=(12, 5))
x_min, x_max, y_min, y_max = -2, 3, -2, 3

# 绘制原始数据
plt.subplot(1, 2, 1)
plt.scatter(dataset.x[:, 0], dataset.x[:, 1], s=1, alpha=0.5)
plt.xlim(x_min, x_max)  # 设置横轴的上下界
plt.ylim(y_min, y_max)  # 设置纵轴的上下界
plt.title("Original Data")

# 绘制生成样本
plt.subplot(1, 2, 2)
plt.scatter(samples[:, 0], samples[:, 1], s=1, alpha=0.5)
plt.xlim(x_min, x_max)  # 设置横轴的上下界
plt.ylim(y_min, y_max)  # 设置纵轴的上下界
plt.title("Generated Samples")

plt.tight_layout()
plt.show()

# 可选: 绘制轨迹变化过程（用颜色来区分）
def plot_trajectory(traj):
    plt.figure(figsize=(8, 8))
    for i, t in enumerate(np.linspace(0, len(traj)-1, 5, dtype=int)):
        plt.scatter(traj[t][:, 0], traj[t][:, 1], s=1, label=f"t={t/len(traj):.1f}")
    plt.xlim(x_min, x_max)  # 设置横轴的上下界
    plt.ylim(y_min, y_max)  # 设置纵轴的上下界
    plt.legend()
    plt.title("Sampling Trajectory")
    plt.show()
plot_trajectory(traj)

训练 Loss 变化趋势
真实值（左）对比采样值（右）：
采样过程展示（从图中可看出，随着 $t$ 从 0 到 1 逐渐增大，采样到的点从最开始的随机分布，到后来越来越趋近于目标分布（圆形））

DL——UNet

UNet最早应用与图像分割领域，目前随着Diffusion模型的应用，使用越来越广泛

参考链接：
- 原始论文：U-Net: Convolutional Networks for Biomedical Image Segmentation, 2015

最早的UNet

最早的UNet网络是用作图片分割的，其输入是572x572像素，并且输出一个较小尺寸（388x388）的分割图，UNet架构图如下：
可以按照编码器-解码器思想来理解UNet
编码器部分：
- 可以看到，原始的UNet网络没有用Padding，所以每次卷积（3x3的卷积）后，图片尺寸（长和宽）会缩小2，在实际实现时，可以使用Padding，保证卷积的输入和输出图片尺寸不变
- 在编码过程中，Max Pooling操作和卷积操作使得样本长和宽逐步缩小（输入尺寸是572x572,编码结果最小尺寸为28x28），卷积输出通道逐步增加的（输入Channel为1，编码结果最大增加到1024）

解码器部分：

核心组件是上卷积：up-conv 2x2，该网络将通道减少为原来的 $\frac{1}{2}$，同时将尺寸变化成原来的2倍，实际实现时，是通过上采样+带padding的卷积实现扩大尺寸为原来的两倍的

class up_conv(nn.Module):
    """
    Up Convolution Block
    """
    def __init__(self, in_ch, out_ch):
        super(up_conv, self).__init__()
        self.up = nn.Sequential(
            nn.Upsample(scale_factor=2),
            nn.Conv2d(in_ch, out_ch, kernel_size=3, stride=1, padding=1, bias=True),
            nn.BatchNorm2d(out_ch),
            nn.ReLU(inplace=True)
        )

    def forward(self, x):
        x = self.up(x)
    return x

跳跃连接：在每次进行上卷积以后，都将编码器的中间结果Clip并Concat过来
最终输出维度是388x388的，通道数为2

Diffusion模型中的UNet

一个简单的Conditional Diffusion实现代码：github.com/TeaPearce/Conditional_Diffusion_MNIST
以下内容参考自：扩散模型U-Net可视化理解
- 整体框架图示：
- 架构图解读：
  
  扩散模型中的U-net结构如上图所示，1X28X28表示通道数为1，长宽为28的图片。在实际训练中不是一个三阶张量而是一个四阶张量128X1X28X28，其中128表示批处理数，即128张图片同时在GPU上完成一次训练迭代
  整个计算流程如下：输入图片（A）被提取出128张特征图（B），经过第一次下采样图像缩小一半（C），经过第二次下采样图像进一步缩小为一半（D），经过平均池化得到一个向量（E），这个向量包含了图片中的所有必要特征信息。至此，输入图片已被编码。除了图片以外，时间标签、其他条件变量也可使用全链接网络进行编码，得到两个向量（F和G），为了确保后续上采样顺利，E、F、G的长度应当相同。接下来，将E、F、G合并为一个更长的向量H。H经过上采用不断恢复出I、J、K直到L。L即为最终期望输出的噪声图。用这个噪声图即可实现对图片的去噪
- 时间片和条件信息是在编码完成后加入的，且加入时先Embedding，再将Embedding向量Concat添加到图片编码结果上

Joe Zhou

Stay Hungry. Stay Foolish.

GitHub E-Mail

Git rebase命令的使用

rebase和merge的区别

整体说明

Python 不支持原生重载的原因

方式 1：手动判断参数个数/类型

方式 2：使用 functools.singledispatch（按参数类型重载）

方式 3：使用第三方库 multipledispatch（支持多参数类型/个数重载）

附录：@overload 装饰器

整体说明

基础数据类型相关

数学运算相关

类型检查与帮助相关

输入输出相关

迭代与序列处理相关

函数与对象操作相关

一些其他常用函数

关于pickle模块

内存中使用

硬盘中使用

RandomState()

关于初始化向量的维度

整体说明

批量运算提效

广播机制(broadcasting)

广播规则

广播机制需要注意

附录：一些笔记

附录：使用 numpy 包为 Python 内置对象提效

LHUC

PPNet

PEPNet

整体说明

文章引言

相关工作

整体方法（两阶段）

第一阶段：残差量化变分自编码器（RQ-VAE）

VQ与VQ-VAE的公式化表示

残差量化（RQ）

RQ-VAE

第二阶段：RQ-Transformer

深度为D的编码自回归建模

RQ-Transformer架构

软标签与随机采样

Rectified Flow 整体说明

Rectified Flow 训练过程

初始训练（1-Rectified Flow）

Reflow（轨迹优化，可选，可多次执行）

采样过程

标准采样（多步）

一步生成（蒸馏）

Rectified Flow 对比传统 Diffusion 模型

Rectified Flow 应用场景

Rectified Flow 的证明过程

附录：Rectified Flow 代码示例

最早的UNet

Diffusion模型中的UNet

方式 2：使用 `functools.singledispatch`（按参数类型重载）

方式 3：使用第三方库 `multipledispatch`（支持多参数类型/个数重载）

附录：`@overload` 装饰器