DL——RectifiedFlow

• 参考链接：
  • 原始论文：Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow, 202209，虽然原理很简单，但是原始论文证明比较详细，且伪代码不够清晰（包含一些数据内容），所以显得晦涩难懂

---

Rectified Flow 整体说明

• Rectified Flow 是一种基于常微分方程（ODE）的生成模型，旨在通过“直线化”轨迹实现高效采样。其核心思想是通过优化一个速度场（velocity field）来最小化传输映射的误差，从而将源分布（如高斯噪声）转换为目标分布（如图像数据）
• Rectified Flow 的训练通过优化速度场和 Reflow 技术逐步拉直轨迹，而采样则通过 ODE 求解实现高效生成。其核心贡献在于简化扩散模型的复杂推导 ，并通过直线化路径实现快速采样 ，适用于生成、迁移等多种任务

---

Rectified Flow 训练过程

• Rectified Flow 的训练分为两个主要阶段：初始训练（1-Rectified Flow）和轨迹优化（Reflow）

初始训练（1-Rectified Flow）

• 目标 ：学习一个速度场 \( v(X_t, t) \)，使得从源分布 \( \pi_0 \)（如高斯噪声）到目标分布 \( \pi_1 \)（如真实图像）的传输路径尽可能直线化
• 数据配对 ：随机采样 \( X_0 \sim \pi_0 \) 和 \( X_1 \sim \pi_1 \)，并假设它们之间通过线性插值连接：
  $$
  X_t = t X_1 + (1-t) X_0, \quad t \in [0,1]
  $$
• 损失函数 ：最小化速度场 \( v \) 与理想直线方向 \( (X_1 - X_0) \) 的均方误差：
  $$
  \min_v \int_0^1 \mathbb{E}_{X_0, X_1} \left[ | (X_1 - X_0) - v(X_t, t) |^2 \right] dt
  $$
  • 其中 \( X_t \) 是插值点

Reflow（轨迹优化，可选，可多次执行）

• 问题 ：初始训练中 \( X_0 \) 和 \( X_1 \) 是随机配对的，导致轨迹可能交叉或弯曲，影响采样效率
• 解决方案 ：使用已训练的 1-Rectified Flow 生成新的配对数据 \( (X_0, \text{Flow}_1(X_0)) \)，再训练一个新的速度场（2-Rectified Flow）。这样，轨迹会变得更直，减少交叉
• 数学表达 ：
  $$
  \min_v \int_0^1 \mathbb{E}_{X_0 \sim \pi_0, X_1 \sim \text{Flow}_1(X_0)} \left[ | (X_1 - X_0) - v(X_t, t) |^2 \right] dt
  $$
• 迭代优化 ：可以多次应用 Reflow ，逐步拉直轨迹，提高采样效率
• 可理论证明这是 Reflow 的单调改进

---

采样过程

• Rectified Flow 的采样过程通过数值求解 ODE 实现，通常使用欧拉法（Euler method）或更高阶的数值积分器

标准采样（多步）

• 从 \( Z_0 \sim \pi_0 \) 开始，逐步计算：
  $$
  Z_{t+\Delta t} = Z_t + v(Z_t, t) \cdot \Delta t
  $$
  • 其中 \( \Delta t = 1/N \)，\( N \) 是步数
  • 由于轨迹已被 Reflow 拉直，即使步数较少（如 10-20 步），也能生成高质量样本
  • 采样时 \(t = 0 \rightarrow 1\)

一步生成（蒸馏）

• 经过 Reflow 后，轨迹足够直，可以尝试一步生成：
  $$
  Z_1 = Z_0 + v(Z_0, 0)
  $$
  • 这一步相当于直接预测 \( X_1 - X_0 \)，但需要高质量的 Reflow 训练

---

Rectified Flow 对比传统 Diffusion 模型

• Rectified Flow 采样更高效 ：相比传统扩散模型（如 DDPM），Rectified Flow 的直线化轨迹允许更少的采样步数，甚至一步生成
• Rectified Flow 应用范围更广 ：Rectified Flow 的本质是拟合一个分布到另一个分布，不仅可用于生成模型（噪声到图像），还可用于域迁移（如猫脸到人脸）
• 其他说明 ：使用 Reflow 能不断降低传输代价，使轨迹越来越直，可理论证明这是 Reflow 的单调改进
• 采样时 \(t\) 的取值不同，但都表示从噪声到真实图片的生成过程：
  • Diffusion Model 是 \(t = T \rightarrow 1\)，逐渐减小
  • Rectified Flow 是 \(t = 0 \rightarrow 1\)，逐渐增大，详情见附录代码示例输出结果
    • 注：这是由于训练时使用的混合值方式不同造成的，微改一下混合方式，\(t\) 的取值也可以逐渐变小

---

Rectified Flow 应用场景

• Stable Diffusion 3 采用了 Rectified Flow 的改进版本，结合 Transformer 架构，在高分辨率文本到图像生成中表现优异

---

Rectified Flow 的证明过程

• 待补充

---

附录：Rectified Flow 代码示例

• 一个简单的 Rectified Flow 训练和采样代码示例

  import torch
  import torch.nn as nn
  import torch.optim as optim
  import numpy as np
  import matplotlib.pyplot as plt
  from torch.utils.data import Dataset, DataLoader
  from sklearn.datasets import make_moons
  
  # 可兼容旧版本PyTorch的SiLU实现，新版本中直接使用 nn.SiLU即可
  if hasattr(nn, 'SiLU'):
      SiLU = nn.SiLU
  else:
      class SiLU(nn.Module):
          def forward(self, x):
              return x * torch.sigmoid(x)
  
  # 设置随机种子
  torch.manual_seed(42)
  np.random.seed(42)
  
  # 超参数
  batch_size = 512
  lr = 1e-3
  epochs = 2000
  num_samples = 10000  # 生成的数据点数量
  dim = 2  # 数据维度
  
  # 创建一个简单的 2D 数据集 (两个半圆月亮)
  class MoonsDataset(Dataset):
      def __init__(self, n_samples):
          X, _ = make_moons(n_samples=n_samples, noise=0.05)
          self.x = torch.tensor(X, dtype=torch.float32)
  
      def __len__(self):
          return len(self.x)
  
      def __getitem__(self, idx):
          return torch.FloatTensor(self.x[idx])
  
  
  # 创建一个简单的 2D 数据集 (两个半圆拼凑成一个圆形)
  class CircleDataset(Dataset):
      def __init__(self, num_samples):
          theta = np.random.uniform(0, np.pi, num_samples)
          self.x = np.stack([
              np.concatenate([np.cos(theta), np.cos(theta)]),
              np.concatenate([np.sin(theta), -np.sin(theta)])
          ], axis=1)
          self.x = self.x + 0.1 * np.random.randn(*self.x.shape)  # 添加噪声
  
      def __len__(self):
          return len(self.x)
  
      def __getitem__(self, idx):
          return torch.FloatTensor(self.x[idx])
  
  # 定义一个简单的 MLP 作为流模型
  class FlowModel(nn.Module):
      def __init__(self, dim=2, hidden_dim=128):
          super().__init__()
          self.net = nn.Sequential(
              nn.Linear(dim + 1, hidden_dim),  # +1 对应时间 t
              SiLU(),
              nn.Linear(hidden_dim, hidden_dim),
              SiLU(),
              nn.Linear(hidden_dim, dim)
          )
  
      def forward(self, x, t):
          # x: (batch_size, dim), t: (batch_size, 1)
          t = t.view(-1, 1)
          inputs = torch.cat([x, t], dim=1)
          return self.net(inputs)
  
  # 训练函数
  def train(model, dataloader, optimizer, epochs):
      model.train()
      loss_history = []
      for epoch in range(epochs):
          total_loss = 0
          for x1 in dataloader:
              x1 = x1.to(device) # 真实数据 x1
              t = torch.rand(x1.size(0), device=device).view(-1,1) # 随机采样时间 t ~ Uniform(0, 1)
              x0 = torch.randn_like(x1) # 采样噪声 x0 ~ N(0, 1)
              x_t = t * x1 + (1-t) * x0 # 计算插值: x_t = t*x1 + (1-t)*x0
              v_pred = model(x_t, t) # 模型预测速度场
  
              loss = torch.mean(torch.sum(((x1 - x0) - v_pred)**2, dim=1)) # 计算损失: || (x1 - x0) - v ||^2
              optimizer.zero_grad()
              loss.backward()
              optimizer.step()
              total_loss += loss.item()
          avg_loss = total_loss / len(dataloader)
          loss_history.append(avg_loss)
          if epoch % 100 == 0:
              print(f"Epoch {epoch}, Loss: {avg_loss:.4f}")
      return loss_history
  
  device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
  dataset = CircleDataset(num_samples) # 圆形数据
  # dataset = MoonsDataset(num_samples) # 双月形数据
  dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)
  model = FlowModel(dim=dim).to(device)
  optimizer = optim.Adam(model.parameters(), lr=lr)
  
  loss_history = train(model, dataloader, optimizer, epochs) # 训练模型
  
  # 绘制训练损失
  plt.plot(loss_history)
  plt.xlabel("Epoch")
  plt.ylabel("Loss")
  plt.title("Training Loss")
  plt.show()
  
  # 采样函数
  def sample(model, num_samples, dim, steps=100):
      model.eval()
      with torch.no_grad():
          z = torch.randn(num_samples, dim, device=device) # 采样初始噪声
          dt = 1.0 / steps # 时间离散化为 delta 值
          traj = [z.cpu().numpy()] # 轨迹存储（可选，用于展示生成过程）
          for i in range(0,steps,1):
              t = torch.ones(num_samples, device=device) * (i*1.0 / steps)
              v = model(z, t) # 计算速度场
              z = z + v * dt # 欧拉方法更新求解常微分方程： z_{t+dt} = z_t + v * dt
              if i % 10 == 0:
                  traj.append(z.cpu().numpy())
          return z.cpu().numpy(), traj
  
  samples, traj = sample(model, 10000, dim) # 采样新数据
  
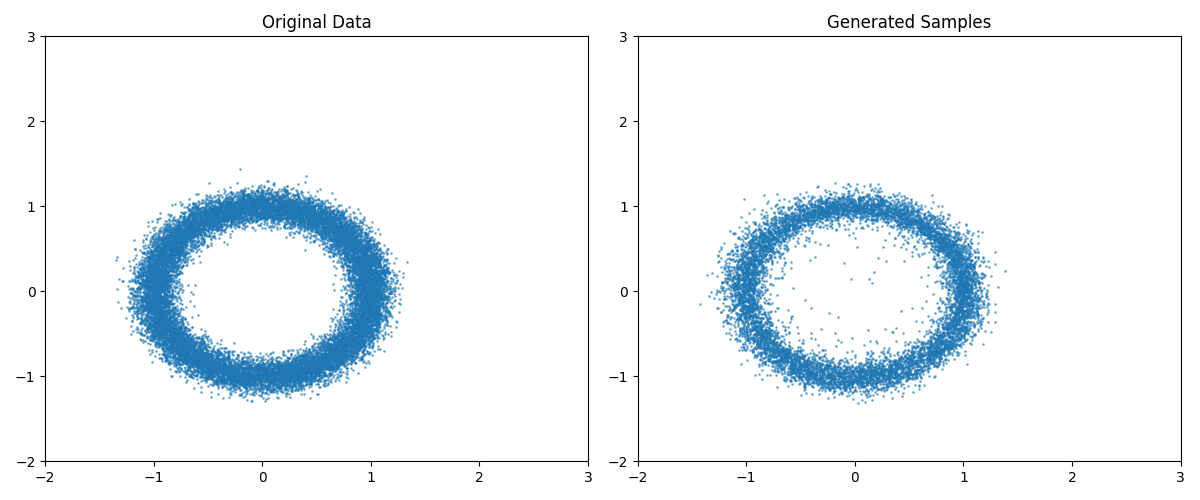
  # 绘制结果
  plt.figure(figsize=(12, 5))
  x_min, x_max, y_min, y_max = -2, 3, -2, 3
  
  # 绘制原始数据
  plt.subplot(1, 2, 1)
  plt.scatter(dataset.x[:, 0], dataset.x[:, 1], s=1, alpha=0.5)
  plt.xlim(x_min, x_max)  # 设置横轴的上下界
  plt.ylim(y_min, y_max)  # 设置纵轴的上下界
  plt.title("Original Data")
  
  # 绘制生成样本
  plt.subplot(1, 2, 2)
  plt.scatter(samples[:, 0], samples[:, 1], s=1, alpha=0.5)
  plt.xlim(x_min, x_max)  # 设置横轴的上下界
  plt.ylim(y_min, y_max)  # 设置纵轴的上下界
  plt.title("Generated Samples")
  
  plt.tight_layout()
  plt.show()
  
  # 可选: 绘制轨迹变化过程（用颜色来区分）
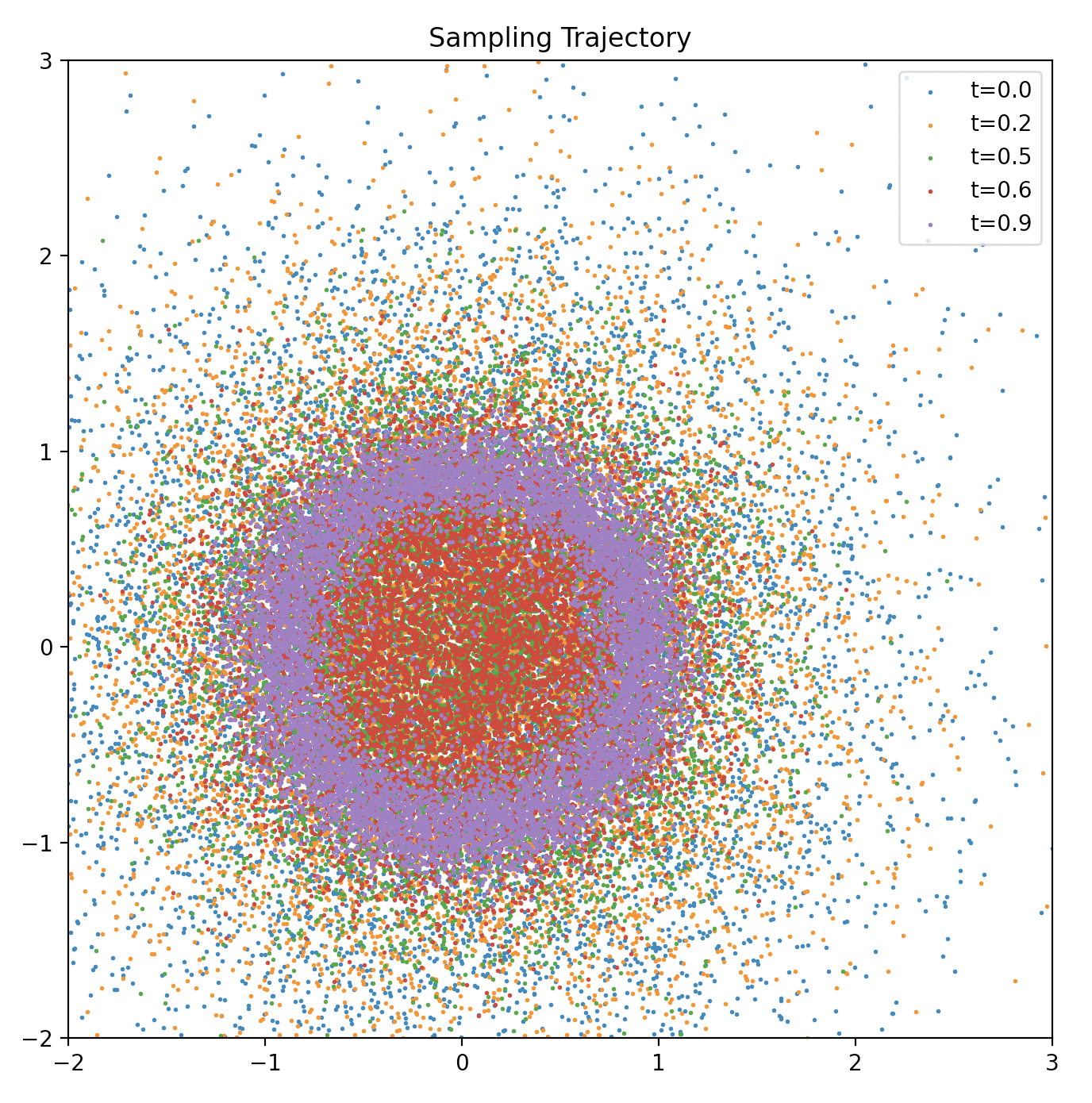
  def plot_trajectory(traj):
      plt.figure(figsize=(8, 8))
      for i, t in enumerate(np.linspace(0, len(traj)-1, 5, dtype=int)):
          plt.scatter(traj[t][:, 0], traj[t][:, 1], s=1, label=f"t={t/len(traj):.1f}")
      plt.xlim(x_min, x_max)  # 设置横轴的上下界
      plt.ylim(y_min, y_max)  # 设置纵轴的上下界
      plt.legend()
      plt.title("Sampling Trajectory")
      plt.show()
  plot_trajectory(traj)

• 训练 Loss 变化趋势

  

• 真实值（左）对比采样值（右）：

  

• 采样过程展示（从图中可看出，随着 \(t\) 从 0 到 1 逐渐增大，采样到的点从最开始的随机分布，到后来越来越趋近于目标分布（圆形））