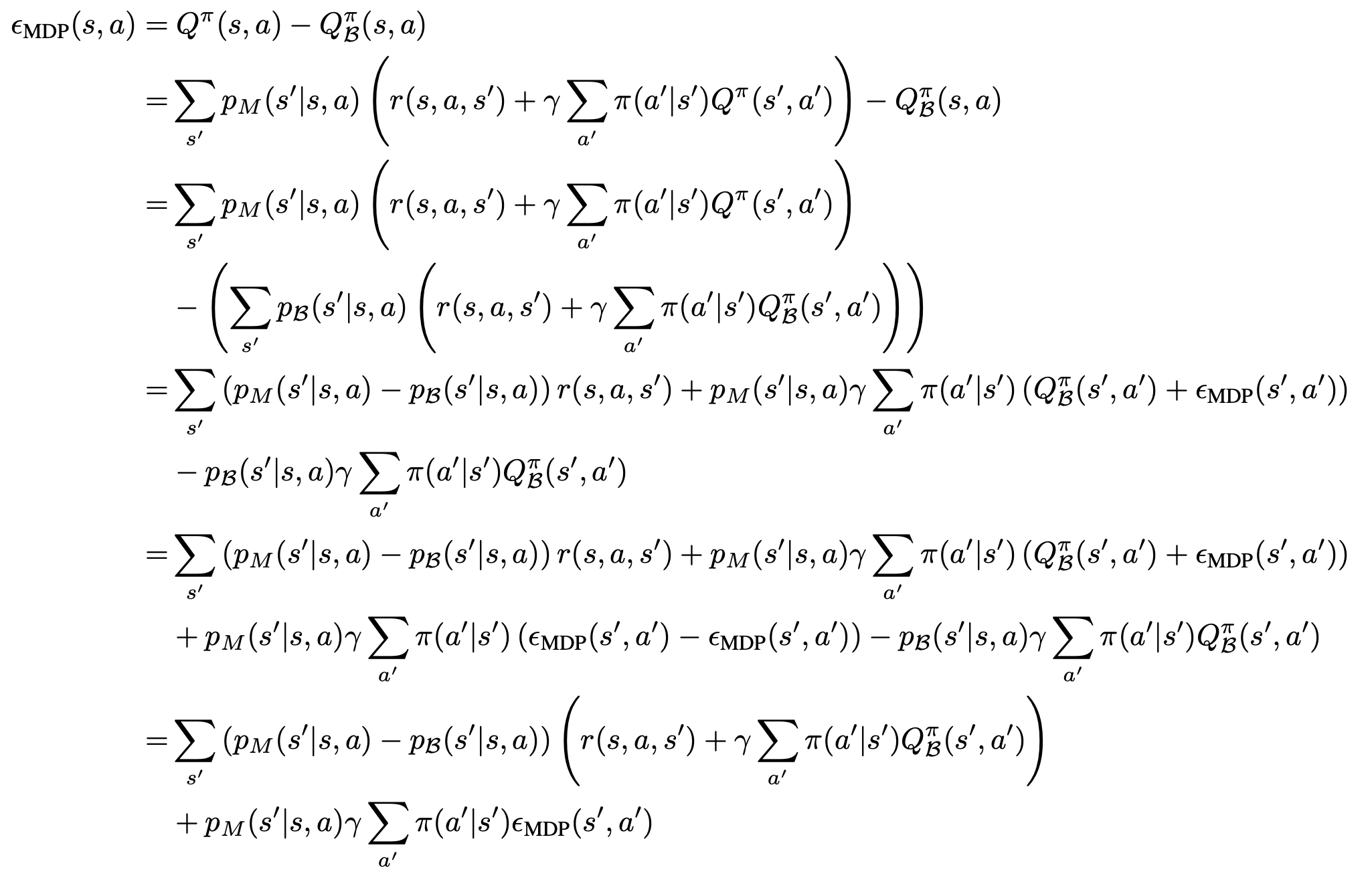- 参考文献:
离线强化学习是什么?
- 一句话描述:不与环境进行交互,只在固定数据集上进行策略学习的强化学习,也称为 Offline RL 或 Batch RL,自2020年以后基本都叫做Offline RL
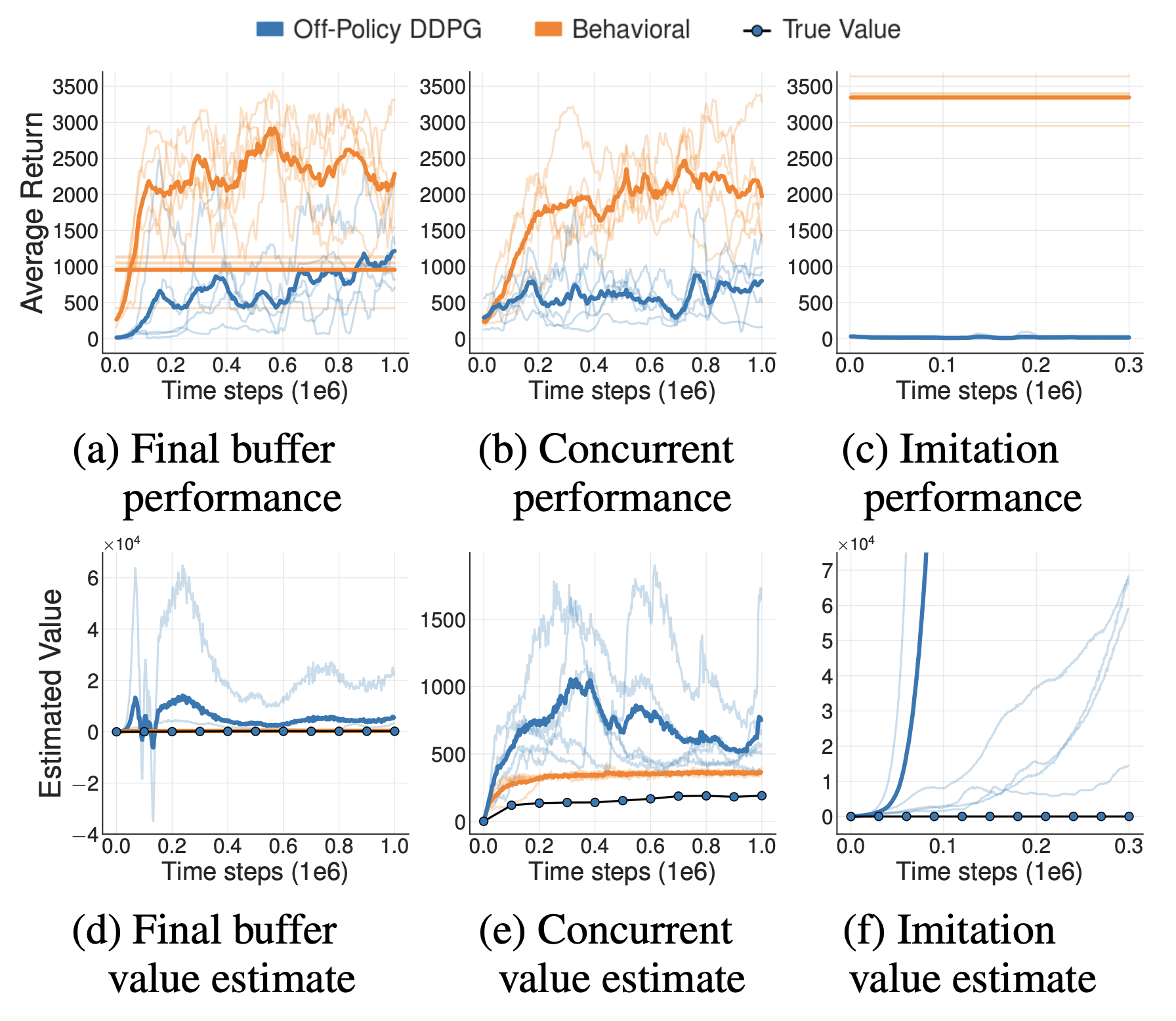
- 直接将off-policy方法使用到Offline RL场景会面临的核心问题是外推误差 ,外推误差(Extrapolation Error)的定义:off-policy值学习中,当前策略真实状态动作访问分布和数据集中的状态动作分布不匹配导致的一种误差,具体来说,包括Absent Data(状态动作对缺失),Training Mismatch(训练预测分布不一致),Model Bias(随机MDP的状态转移概率有偏差)等问题
离线强化学习的优缺点
- 优点:
- 应用安全:不需要与真实环境交互,能防止未知风险;
- 训练高效:样本利用率高;
- 缺点:
- 外推误差:容易面临外推误差问题,导致策略学不好;
- 样本限制:样本量多和行为策略探索性强的数据集较好,对于基于模仿学习的离线强化学习方法,一般需要行为策略是专家策略(本质也于外推误差相关,如果样本量太少,或者行为策略过于局限,都可能只收集到固定的某个局部状态或动作,加重外推误差问题)
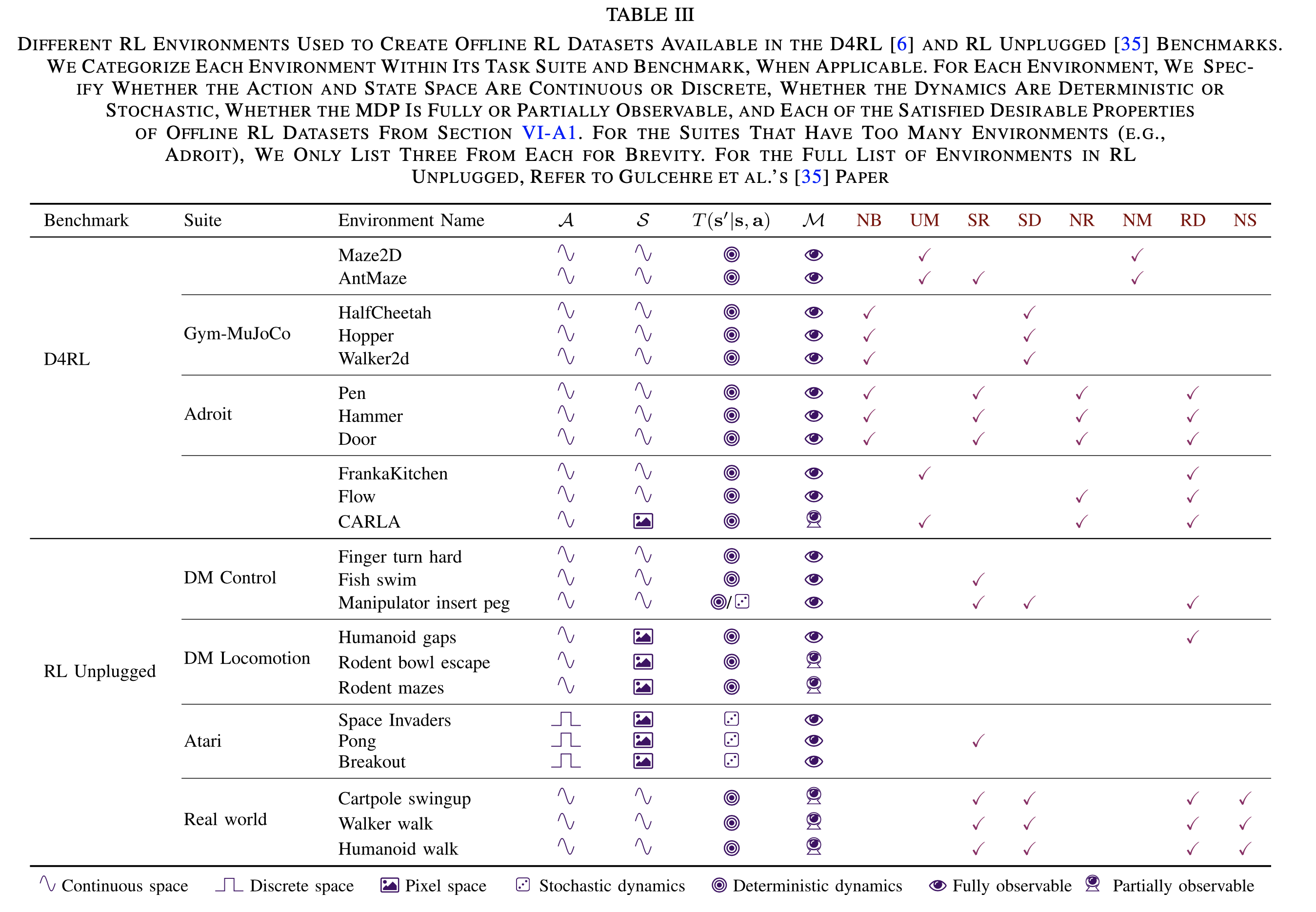
离线强化学习数据集D4RL
- 数据集原始论文:D4RL: Datasets for Deep Data-Driven Reinforcement Learning
- D4RL的一些介绍:
- 数据集安装:离线强化学习(Offline RL)系列2: (环境篇)D4RL数据集简介、安装及错误解决 - Jensen Wang的文章 - 知乎,直接安装D4RL会遇到一些问题,需要逐步解决
- 数据集一般都会包含一些特性:
- Narrow and Biased Data Distributions (NB) :少量且有偏数据集,即OOD问题可能很严重的数据
- Undirected and Multitask Data (UM) :无方向和多任务数据,即当前收集到的数据不是为了解决问题而收集的。(理解:比如要出找到出口,但是行为策略不找出口而是随机开门关门打开柜子等操作)
- Sparse Rewards (SR) :系数奖励,即奖励稀疏的场景
- Suboptimal Data (SD) :次优数据,即使用次优策略收集的数据
- Nonrepresentable Behavior Policies (NR) :不可表示的行为策略。(理解:当函数逼近器(function approximator)很难完全捕捉基础行为的复杂性时,策略难以被神经网络或其他函数逼近器表示出来)
- Non-Markovian Behavior Policies (NM) :非马尔可夫行为策略,一般出现在人类Agent或者手动工程控制中?不遵循马尔可夫性?【TODO:待补充】
- Realistic Domains (RD) :现实领域。即现实数据,不是模拟数据,可能会出现噪声等信息
- Nonstationarity (NS) :非平稳性,即不稳定的MDP过程。在这个数据集中,Agent可能会遇到传感器故障、执行器退化或奖励函数更新的情况,导致随时间变化的MDP中的扰动(例如,泵的效率随时间下降)
- D4RL和RL Unplugged环境
离线强化学习的分类
说明:目前没有非常官方的离线强化学习分类方法,本文的分类方法来源于论文A Survey on Offline Reinforcement Learning: Taxonomy, Review, and Open Problems(2022,最新更新2024年8月,持续更新)
- 本文按照修改类型分类(Modification Types),即按照离线强化学习方法在标准多步AC(Multi-step Actor Critic)的基础上做了哪些修改(注:修改类型的对照基线模型是标准Multi-step AC方法),可以将修改类型分成以下几类
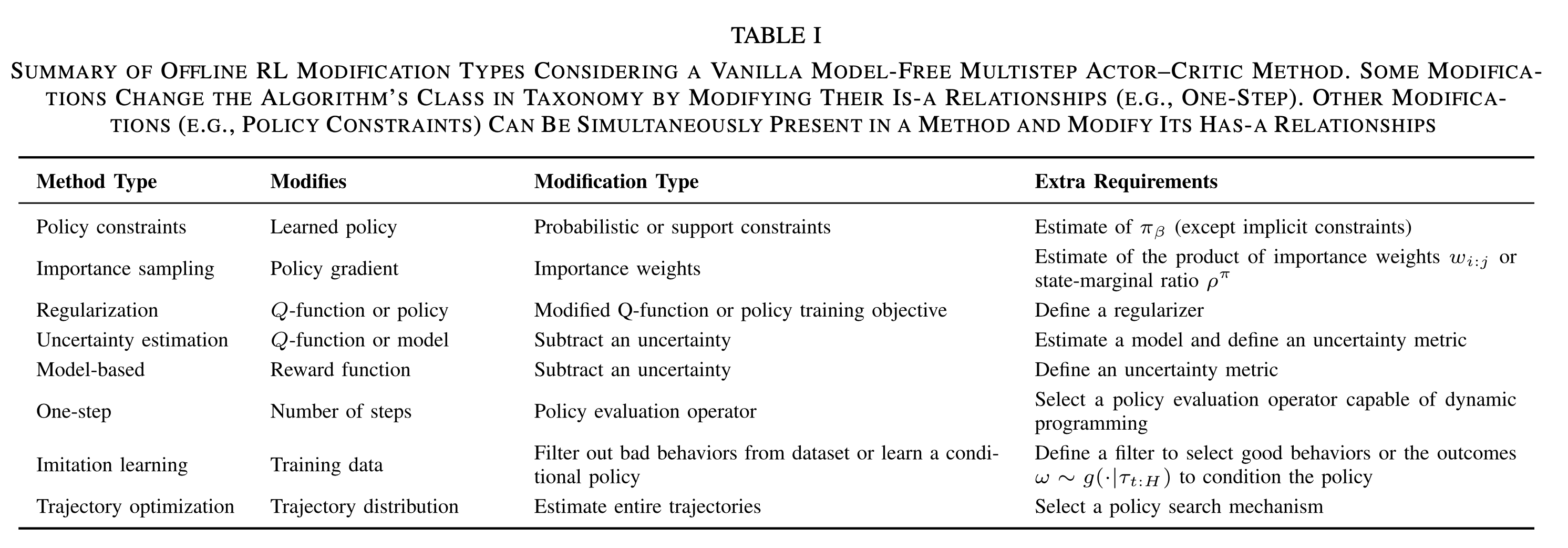
- 各种修改类型的一些图示
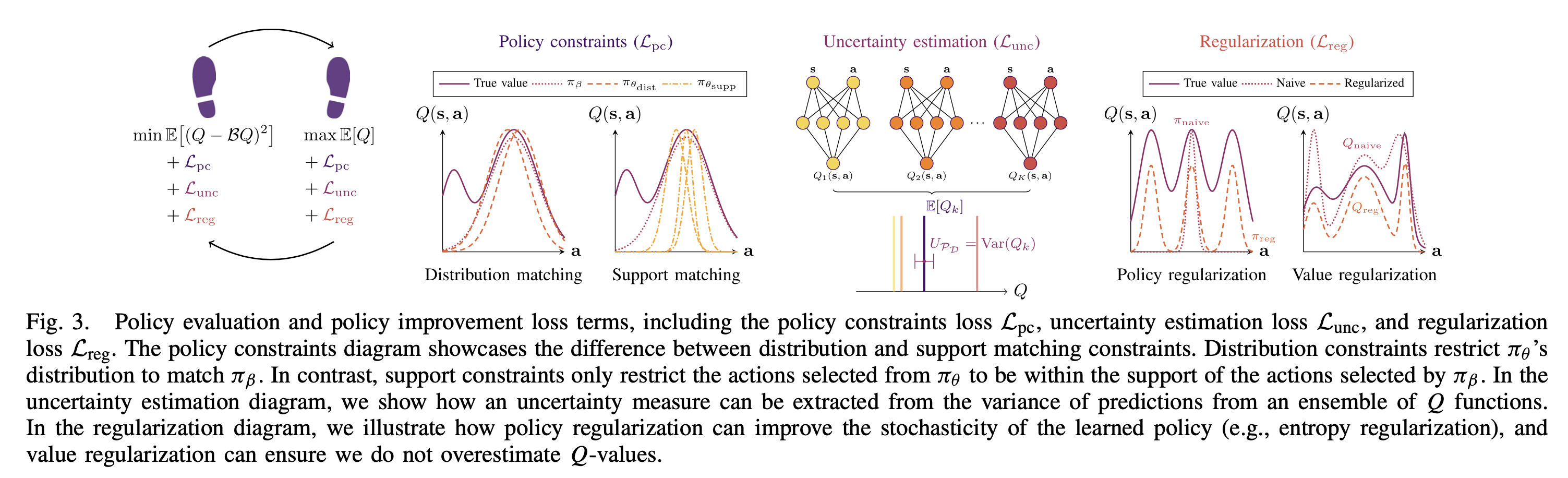
- 不同算法的修改类型归属(同一个算法可能同时使用多个修改类型)
Policy Constraints
- 策略约束分为直接策略约束(Direct Policy Constriants)和隐式策略约束(Implicit Policy Constraints)两种
- 直接策略约束方法 :学习策略 \(\pi_\theta\) 的同时估计行为策略 \(\pi_\beta\),同时限制策略 \(\pi_\theta\) 贴近行为策略 \(\pi_\beta\)
$$
\begin{align}
J(\theta) &= \mathbb{E}_{s\sim d^{\pi_\theta}, a\sim\pi_\theta(\cdot\vert s)}[Q^{\pi}(s,a)] \\
\text{s.t.} &\ D(\pi_\theta(\cdot\vert s), \hat{\pi}_\beta(\cdot\vert s)) \le \epsilon
\end{align}
$$- 其中D表示某个距离评估指标,一般常用KL散度
- 需要直接评估行为策略,如果行为策略评估不准确,这种方式效果会比较差
- 隐式策略约束方法 :不显示的估计行为策略 \(\pi_\beta\),只依赖于样本(行为策略 \(\pi_\beta\) 收集来的样本),通过修改目标函数来隐式的约束策略 \(\pi_\theta\),实现不评估行为策略 \(\pi_\beta\) 的同时对策略 \(\pi_\theta\) 施加约束
- 首先通过策略提升推导得到如下目标函数:
$$
\begin{align}
\mathcal{L}(\pi,\lambda) &= \mathbb{E}_{s\sim d^{\pi_\beta}(\cdot)}[\mathbb{E}_{ a\sim\pi(\cdot\vert s)}[\hat{A}^{\pi}(s,a)] + \lambda (\epsilon - D_{\text{KL}}(\pi(\cdot\vert s), \hat{\pi}_\beta(\cdot\vert s)))]
\end{align}
$$ - 然后进一步求解优化问题的解如下:
$$ \pi^*(a|s) = \pi_\beta(a|s)exp(\frac{1}{\lambda}\hat{A}^{\pi}(s,a)) $$ - 进一步地,最小化 \(\pi_\theta\) 和 \(\pi^*\) 的KL散度,可以最终推导得到如下的目标函数:
$$ J(\theta) = \mathbb{E}_{(s,a) \sim \mathcal{D}} \log \pi_\theta(a|s)exp(\frac{1}{\lambda}\hat{A}^{\pi}(s,a)) $$ - 以上方式相当于一种加权极大似然估计(Weighted Maximum Likelihood),根据以上公式,我们不再需要显示的学习行为策略 \(\pi_\beta\),可以直接从 \((s,a)\) 中学习到最优策略
- 首先通过策略提升推导得到如下目标函数:
- 策略约束有两种形式,一种是Distribution Matching Constraints(也称为Distribution Constraints),一种是Support Matching Constraints(也称为Support Constraints)
- Distribution Constraints:指限制 \(\pi_\theta\) 和 \(\pi_\beta\) 这两个策略的分布足够接近
- Support Constraints:不要求 \(\pi_\theta\) 和 \(\pi_\beta\) 这两个策略的分布足够接近,只需要限制从 \(\pi_\theta\) 采样的动作在 \(\pi_\beta\) 采样动作的支持集里面即可(支持集即 \(\pi_\beta(a|s)\) 分配了正概率的所有动作 \(a\) 的集合)
Importance Sampling
- 通过重要性采样实现
$$
\mathbb{E}_{\tau\sim \pi_\beta}\Big[ w_{0:H}\sum_{t=0}^H\nabla_\theta\gamma^t \log \pi_\theta(a_t|s_t)\hat{Q}^{\pi}(s_t,a_t) \Big]
$$- 其中 \(w_{0:H}\) 是重要性权重 \(w_t = \frac{\pi(a_t|s_t)}{\hat{\pi}_\beta(a_t|s_t)}\) 的乘积
Regularization
- 基本思路是在优化目标上增加一个正则项,分为策略正则(Policy Regularization)和值正则(Values Regularization)
- 策略正则(Policy Regularization)
$$ J(\theta) = \mathbb{E}_{(s,a) \sim \mathcal{D}} [\hat{Q}^{\pi_\theta}(s_t,a_t)] + \mathcal{R}(\theta) $$ - 值正则(Values Regularization)
$$ J(\phi) = \mathbb{E}_{(s,a,s’) \sim \mathcal{D}}\Big[(r(s,a) + \gamma \mathbb{E}_{a’\sim\pi_{\text{off}}(\cdot|s)}[Q_\phi^\pi(s’,a’)] - Q_\phi^\pi(s,a))^2\Big] + \mathcal{R}(\phi) $$
Uncertainty Estimation
- 基本思路是在保守(Conservative)RL和原始(Native)RL上做一些Trade off,基于我们对泛化能力的信任程度不同,可以选择不同程度的保守策略,对策略做不同程度的放松;这里的不确定性评估可以是对策略、值和模型的评估
$$ J(\theta) = \mathbb{E}_{(s,a) \sim \mathcal{D}}\Big[ \mathbb{E}_{Q^\pi\sim\mathcal{P}_{\mathcal{D}}(\cdot)} [Q^\pi(s,a)] - \alpha U_{\mathcal{P}_{\mathcal{D}}} (\mathcal{P}_{\mathcal{D}}(\cdot)) \Big] $$- \(\mathcal{P}_{\mathcal{D}}(Q^\pi)\) 表示在数据集 \(\mathcal{D}\) 中,Q函数的分布
- 其中 \(U_{\mathcal{P}_{\mathcal{D}}}(\cdot)\) 是对 \(\mathcal{P}_{\mathcal{D}}\) 的不确定性评估(这里的 \(\mathcal{P}_{\mathcal{D}}\) 是下角标)
- 理解:在对数据集 \(\mathcal{D}\) 上对某个变量进行不确定性评估,这个变量也是与数据集相关的,所以 \(U_{\mathcal{P}_{\mathcal{D}}} (\mathcal{P}_{\mathcal{D}}(\cdot))\) 中数据集出现了两次
Model-based
- 首先通过标准的监督学习回归方法构建模型预测状态转移概率 \(T_{\psi_T}(s_{t+1}|s_t,a_t)\) 和奖励函数 \(r_{\psi_r}(s_t,a_t)\)
- 使用学习到的状态转移概率和奖励函数模型作为真实环境的一个代理,与策略交互
- 在数据覆盖面广(探索足够充分)时,Model-based方法效果比较容易学习
- Model-based方法也可以用到Online RL场景,在Offline RL场景中,由于无法与环境交互,所以无法修正一些错误的预估值,一种解决这个问题的方法是采用保守策略,类似于Uncertainty Estimation思想对奖励函数进行修正
$$ \tilde{r}_{\psi_r}(s,a) = r_{\psi_r}(s,a) + \lambda U_r(s,a) $$- \(U_r(s,a)\) 表示不确定度,在数据集中出现过的 \((s,a)\),对应的不确定性较小,没有出现过的不确定性较大
One-step
- 多步策略评估和策略提升出现OOD问题的原因是需要对策略 \(\pi_{\text{off}}\) 做策略评估,在选择动作评估目标Q值时,不可避免的容易出现 \(\pi_\beta\) 没有见过的动作
- One-step方法的思想:先对策略 \(\pi_\beta\) 做策略评估得到准确的 \(Q^{\pi_\beta}(s,a)\),此时不会出现OOD,因为 \(a’\) 都是来自 \(\pi_\beta\) 的;接着从 \(Q^{\pi_\beta}(s,a)\) 中进行一步策略提取,找到最优策略
- 在One-step的方法下,不需要担心OOD问题,因为我们从不需要访问OOD的状态动作对
Imitation Learning
- 模仿学习是一类学习方法,这类方法的思路是通过模仿行为策略的行为来实现策略学习
- 离线强化学习中的模仿学习常见的有行为克隆(Behavior Clone,BC)及其改进版本
- BC方法要求行为策略是专家策略,BC的基本目标如下:
$$ J(\theta) D(\pi_\theta(\cdot\vert s), \hat{\pi}_\beta(\cdot\vert s)) $$- \(D(\cdot,\cdot)\) 是f-divergence,可以是交叉熵等
- 其他说明:行为策略本身比较优质时BC能学到较好的效果
- 改进版本不要求行为策略是专家策略,常常通过丢弃劣质动作或者对高收益动作进行加权实现
- 动作挑选 :通过Q值或者一些启发式方法识别劣质和优质的动作
- 动作加权 :设计特殊的目标函数,让策略决策到高收益动作的概率更高,比如AWR的优化目标
- 条件策略(Conditional Policy) :学习一个条件生成网络和条件策略网络,条件生成网络可在给定轨迹 \(\tau\) 下生成条件,条件策略网络会根据给定条件和状态来生成策略,该策略的目标就是使得决策能够最终生成给定轨迹 \(\tau\) ?【TODO:待补充】
Trajectory optimization
- 直接建模状态动作的联合分布,即轨迹分布,然后在这些分布里面规划出优质的轨迹,轨迹里面就包含了动作
- 给定任意的 \(s_0\),先试探性规划多步,找到最优轨迹,然后选择最优轨迹上的动作决策一步即可(注意,为了避免误差累计,一次规划仅进行一次决策)
Off-policy Evaluation (OPE)
- 目标:给定待评估策略 \(\pi\) 和评估数据集 \(\mathcal{D}_e\),希望定义一个可以评估效果的OPE目标 \(\hat{J}(\pi)\)
- 方法包含Model-based,Importance Sampling和Fit Q Evaluation
- 为什么需要OPE?
- 现实世界中,许多领域里面,直接使用真实环境预测去交互以评估策略效果是危险且成本高昂(包括时间成本和资源成本)的,而OPE提供了一个不需要与环境交互就可以评估策略效果的方案(虽然有时候不是很准确)
- OPE可以用作超参数的选择
Model-based Approach
- 类似Model-based强化学习方法,通过标准的监督学习回归方法构建模型预测状态转移概率 \(T_{\psi_T}(s_{t+1}|s_t,a_t)\) 和奖励函数 \(r_{\psi_r}(s_t,a_t)\)
- 评估结果为:
$$\hat{J}(\pi) = \mathbb{E}_{\tau\sim p_{\phi_T}(\cdot)}\Big[ \sum_{t=0}^H\gamma^t r_{\psi_r}(s_t,a_t) \Big]$$- 其中 \(p_{\phi_T}(\cdot)\) 表示按照策略 \(\pi\) 在环境 \(T_{\psi_T}(s_{t+1}|s_t,a_t)\) 中采样得到的trajectory分布
Importance Sampling (IS)
- 利用重要性采样的性质完成评估
$$\hat{J}(\pi) = \mathbb{E}_{\tau\sim p_{\hat{\pi}_\beta(\cdot)}}\Big[ w_{0:H}\sum_{t=0}^H\gamma^t r(s_t,a_t) \Big]$$- 其中 \( w_{i:j}\) 是重要性采样的权重乘积
$$ w_{i:j} = \frac{\prod_{t=i}^j\pi(a_t|s_t)}{\prod_{t=i}^j\hat{\pi}_\beta(a_t|s_t)} $$ - 其中每一项 \(w_t = \frac{\pi(a_t|s_t)}{\hat{\pi}_\beta(a_t|s_t)}\),实际上 \( w_{i:j}\) 也可以写为:
$$ w_{i:j} = \prod_{t=i}^j w_t = \prod_{t=i}^j\frac{\pi(a_t|s_t)}{\hat{\pi}_\beta(a_t|s_t)} $$
- 其中 \( w_{i:j}\) 是重要性采样的权重乘积
Fit Q Evaluation (FQE)
- 先使用策略评估方法学习一个Q值 \(Q_\phi^\pi\) (最小化贝尔曼误差即可),然后在数据集上评估该Q值的累计值
$$ \hat{J}(\pi) = \mathbb{E}_{(s,a)\sim \mathcal{D}_e}[Q_\phi^\pi(s,a)] $$
离线强化学习方法补充
AWR(Advantage-Weighted Regression)
- 参考链接:ADVANTAGE-WEIGHTED REGRESSION: SIMPLE AND SCALABLE OFF-POLICY REINFORCEMENT LEARNING, UC Berkeley, arXiv 2019
- AWR 训练流程

BCQ
CQL
IQL
BRAC(Behavior-Regularized Actor-Critic)
XQL(Extreme Q-Learning)
- 参考链接:Extreme Q-Learning: MaxEnt RL without entropy, ICLR 2023, Google
- 也称为 \(\mathcal{X}\)-QL
- XQL 训练流程

SQL(Sparse Q-Learning)
- 参考链接:[待确认]
- 参考链接:Sparse Q-learning with Mirror Descent, University of Massachusetts, arXiv 2012
- 参考链接:SPARSE Q-LEARNING: OFFLINE REINFORCEMENT LEARNING WITH IMPLICIT VALUE REGULARIZATION, Offline RL Workshop 2023
RWR(Reward-Weighted Regression)
- 参考链接:待确认
EDAC(Ensemble Diversity Actor-Critic)
- 参考链接:待确认
AWAC(Advantage-Weighted Actor-Critic)
- 参考链接:AWAC: Accelerating Online Reinforcement Learning with Offline Datasets, UC Berkeley, arXiv 2020
- AWAC 整体方案介绍(Offline + Online 的训练方式)
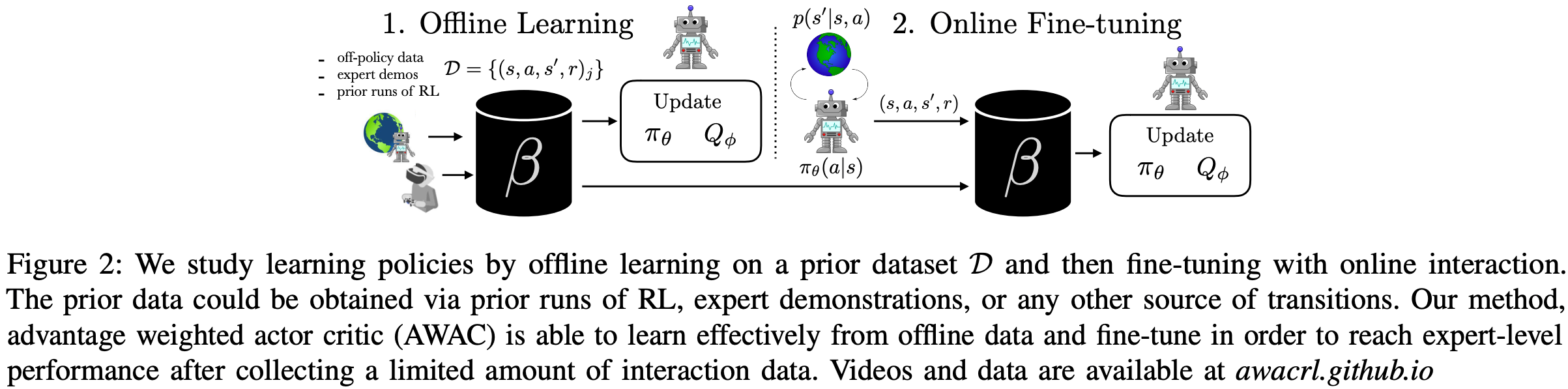
- AWAC 训练流程