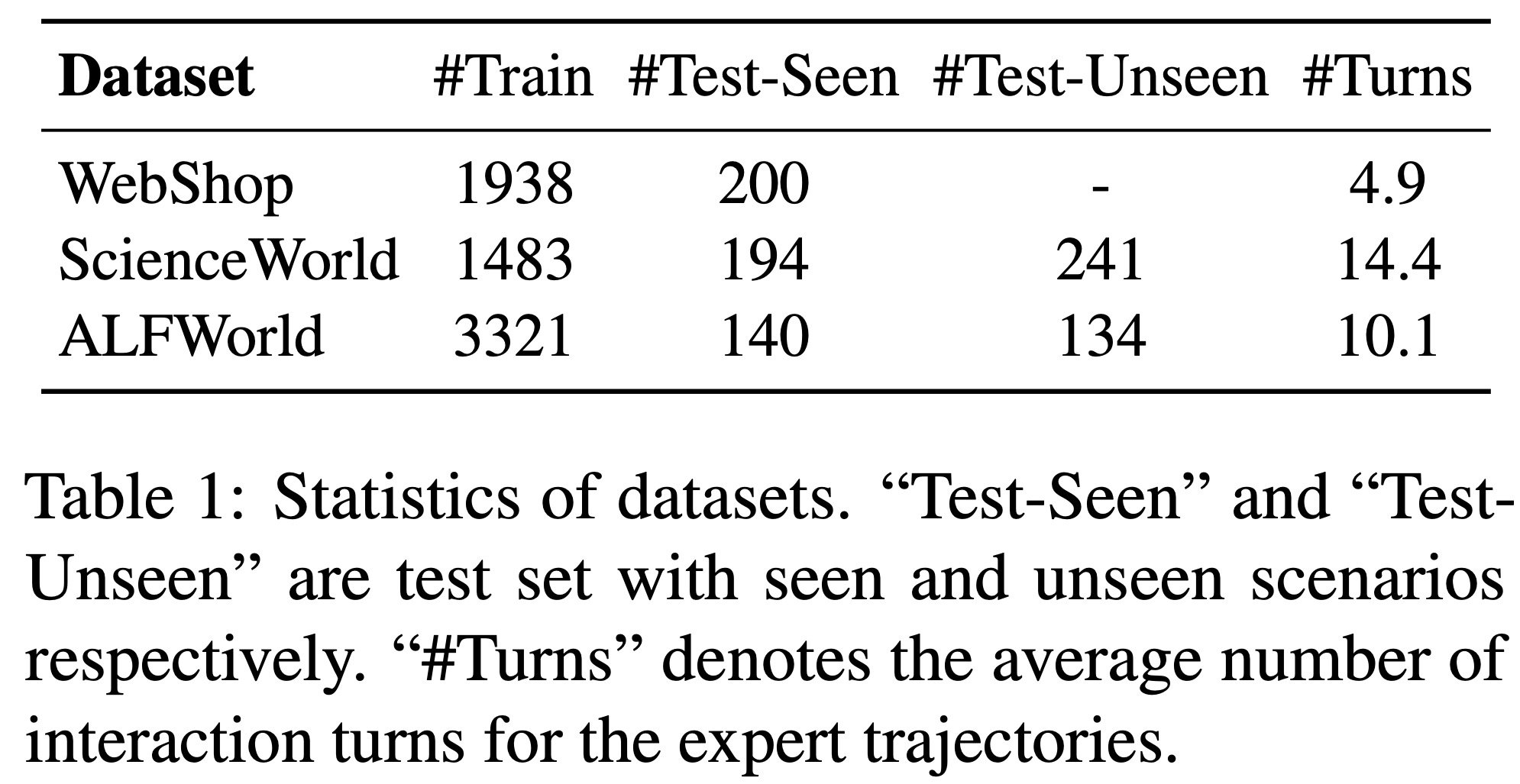
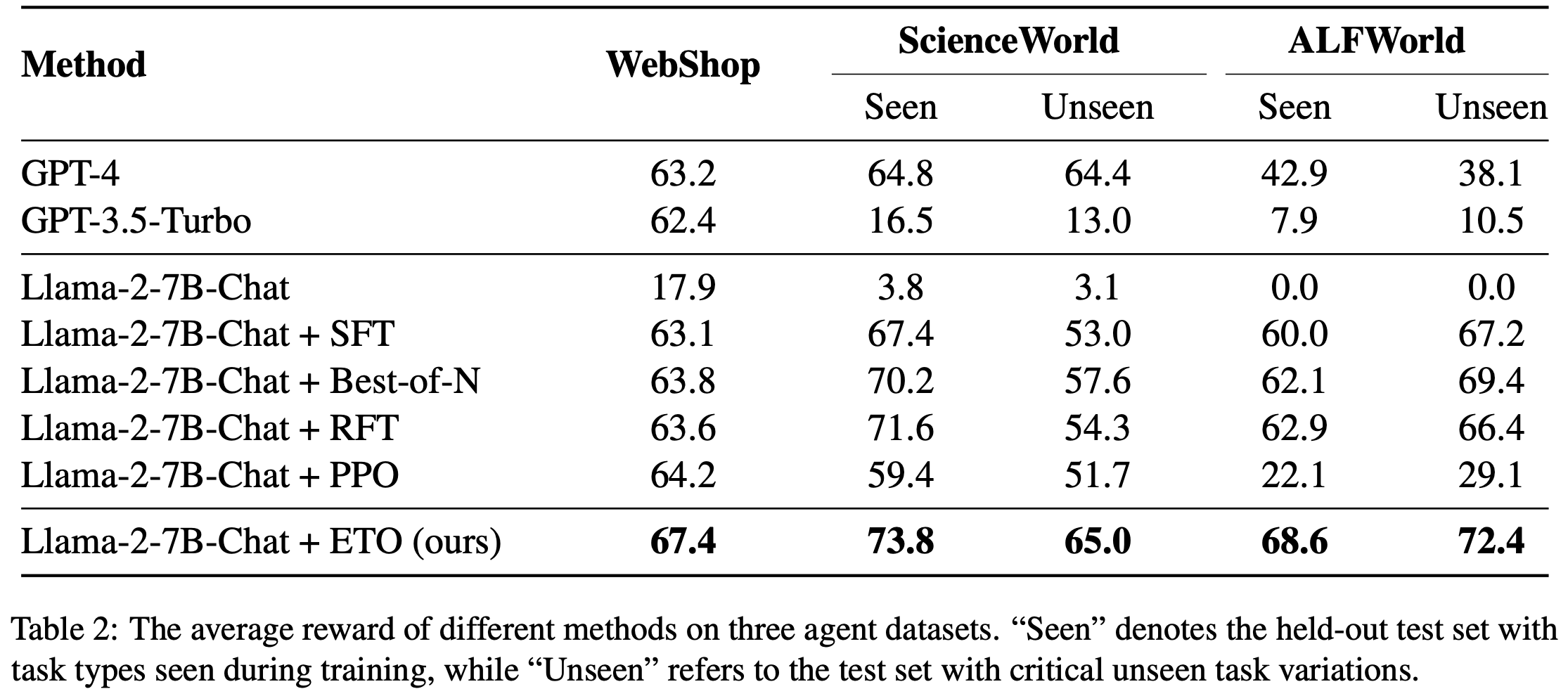
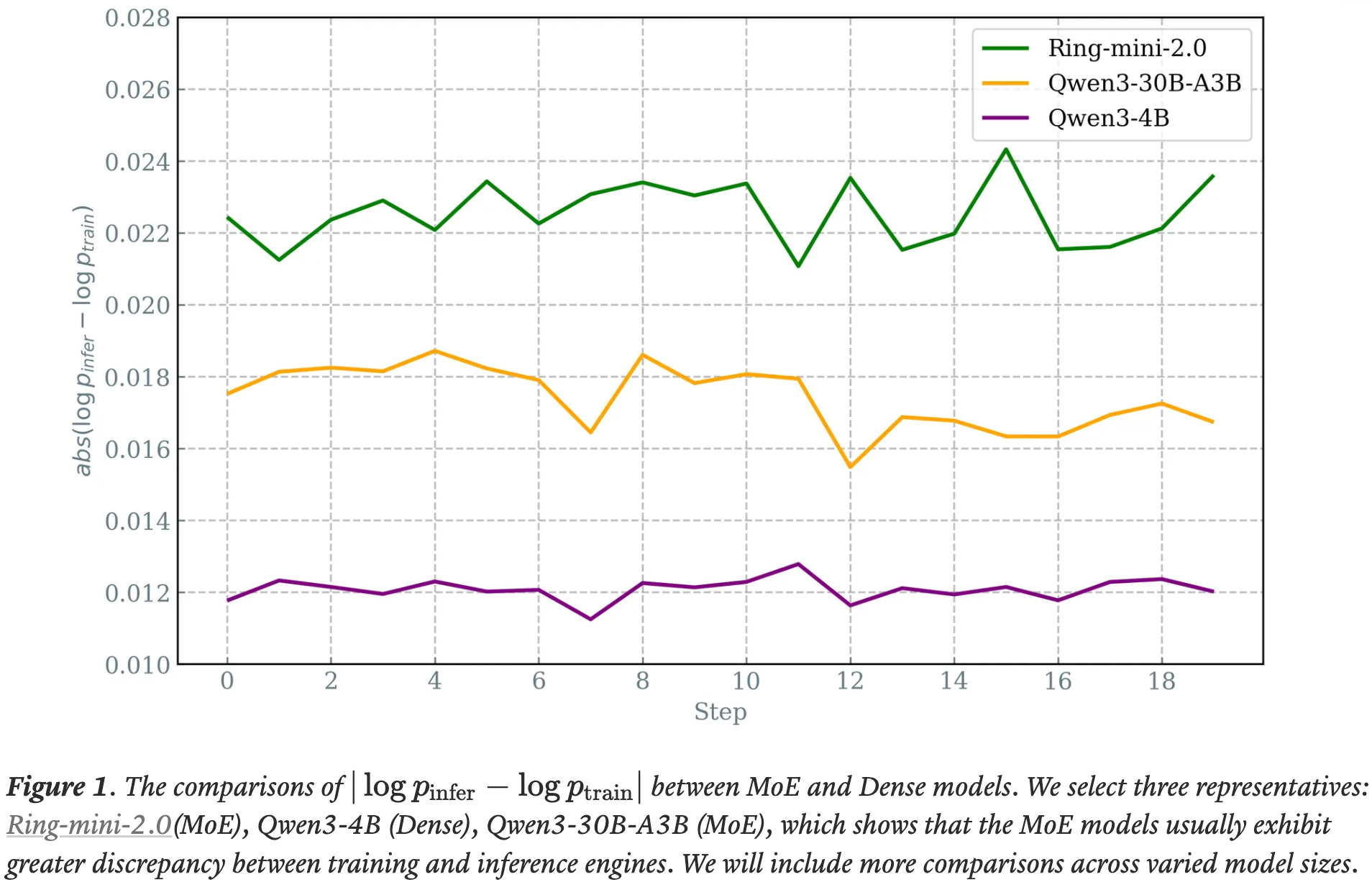
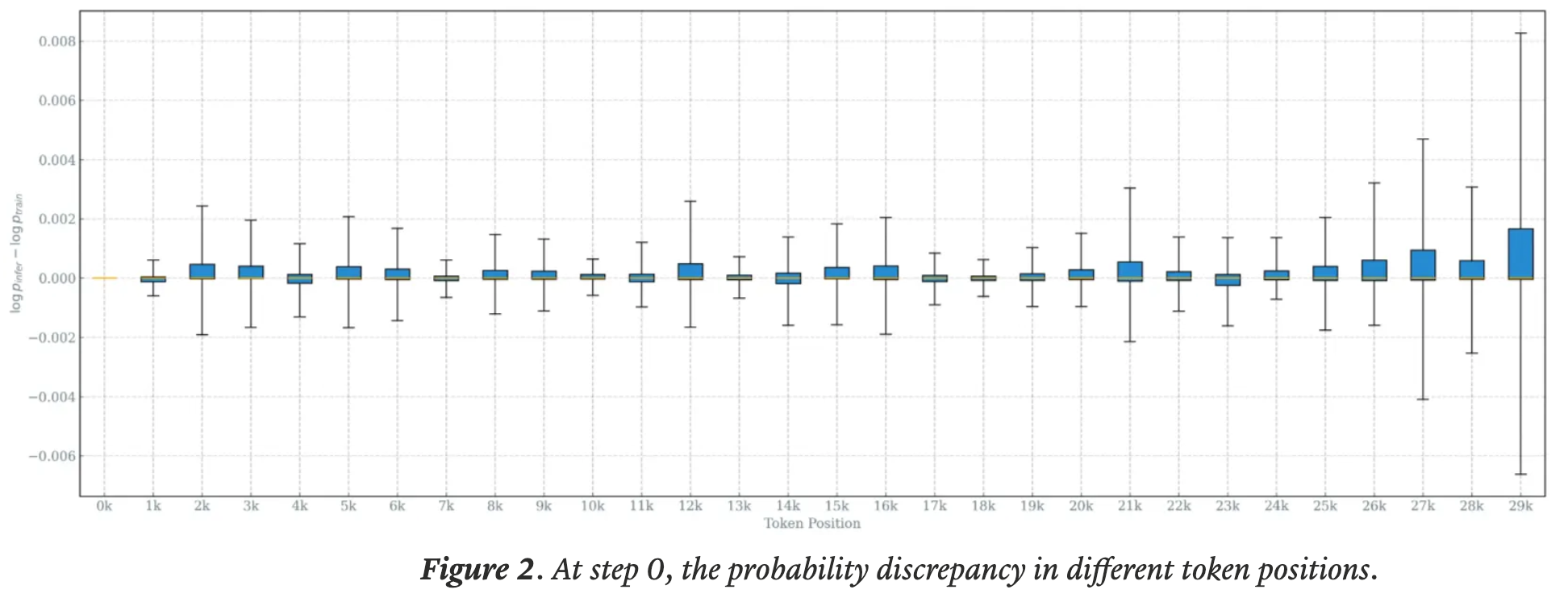
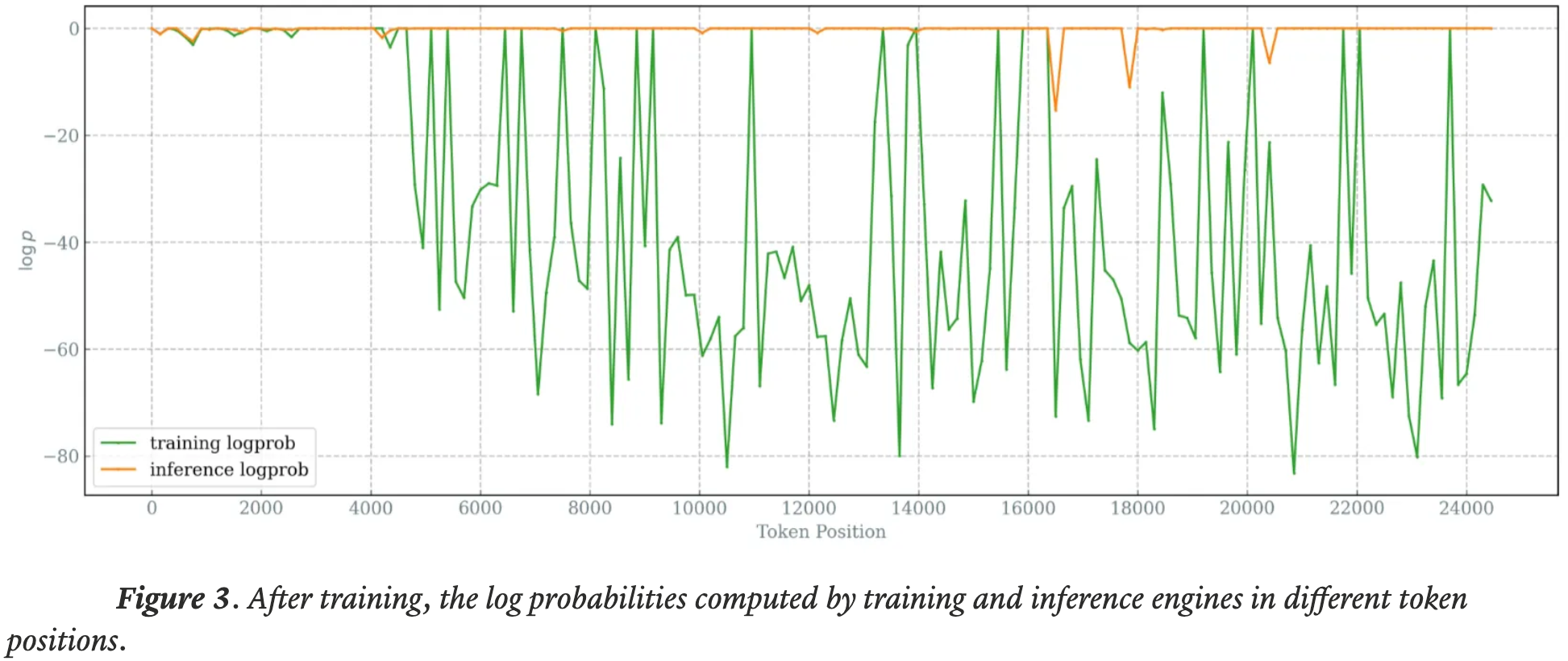
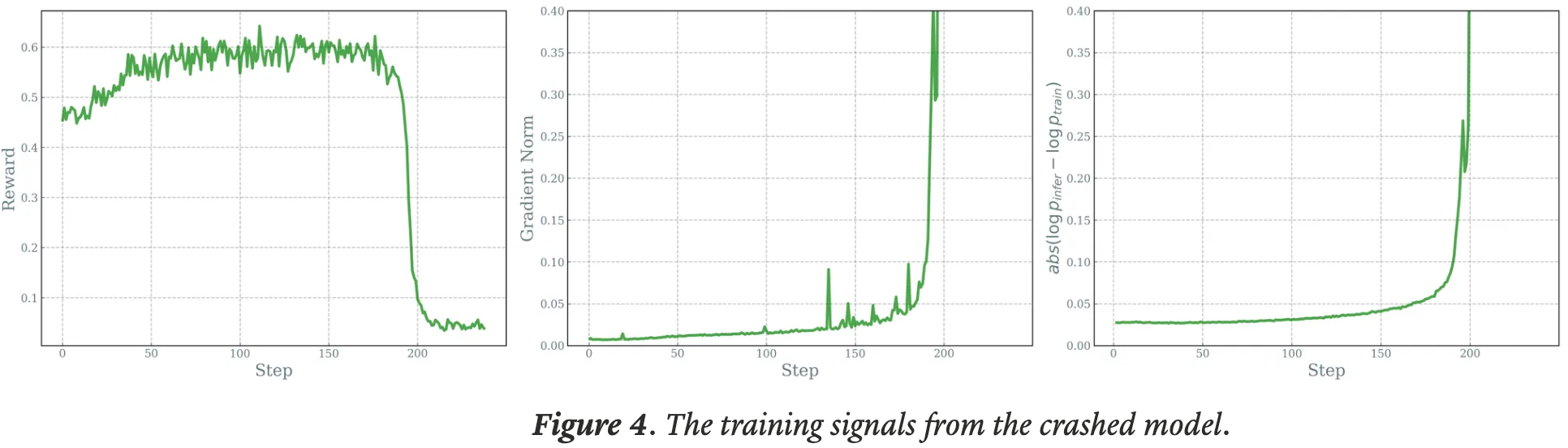
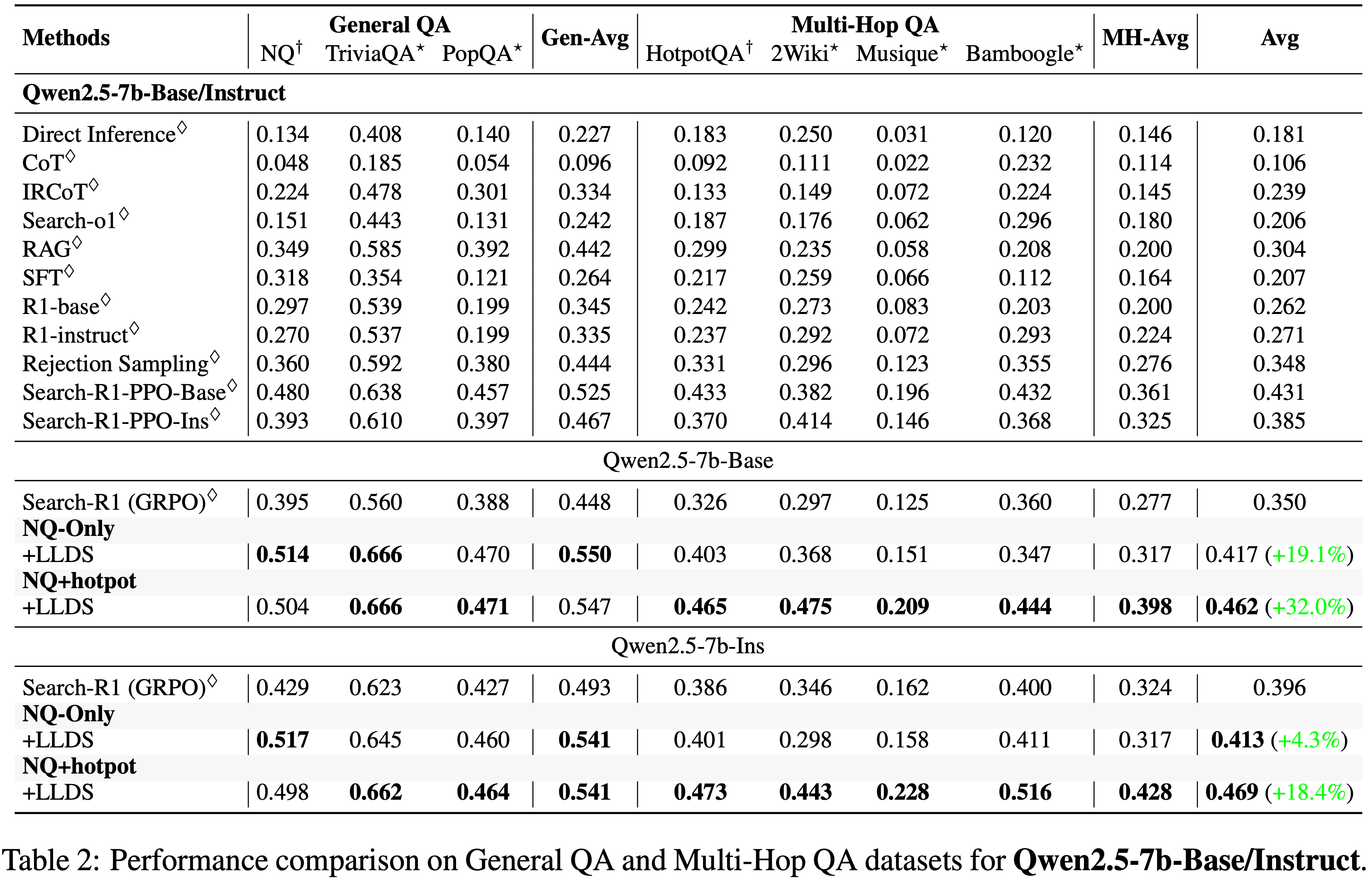
注:本文包含 AI 辅助创作
- 参考链接:
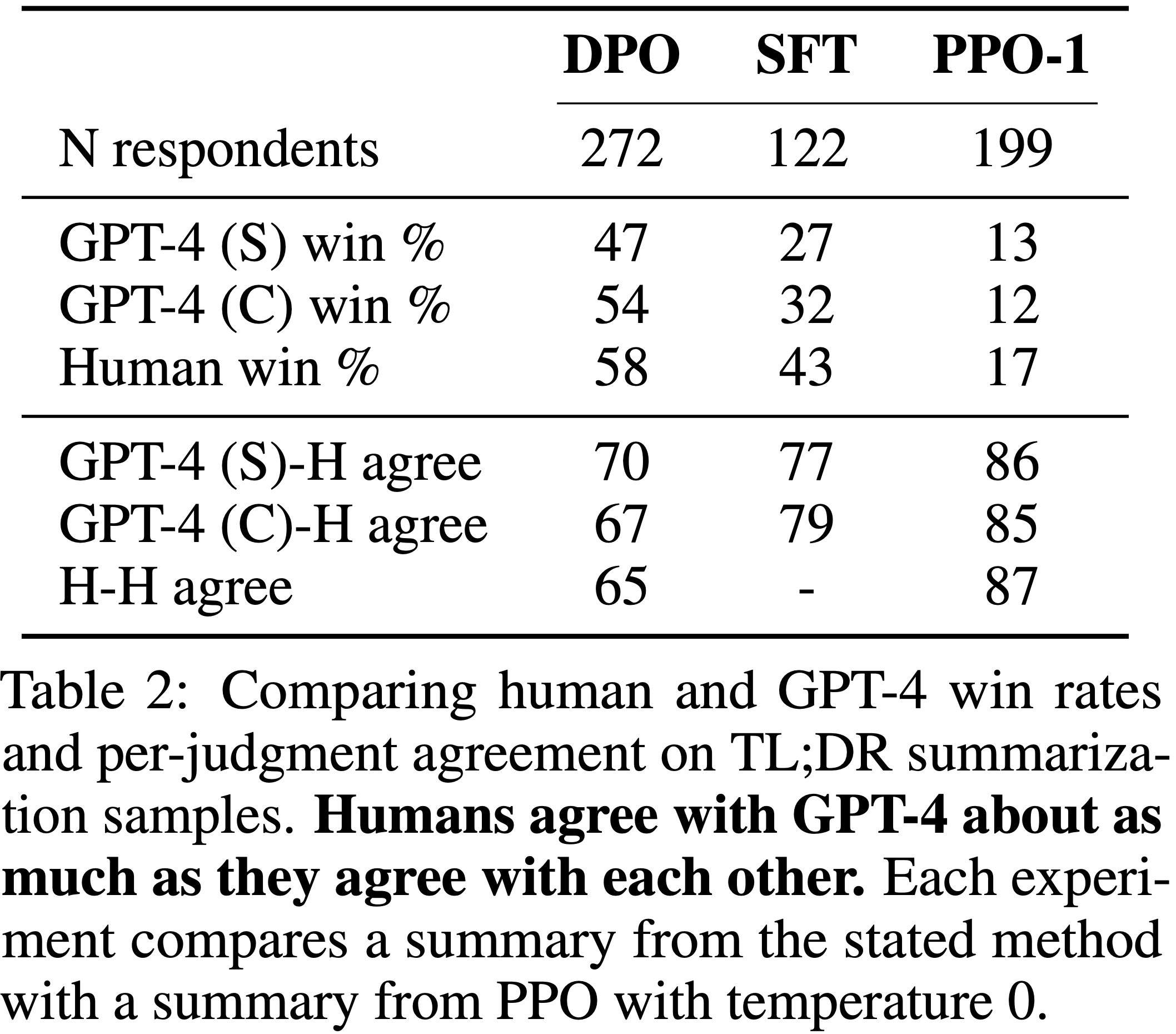
Paper Summary
- 整体总结:
- 论文以批判性视角审视了用于 R1-Zero-like 训练的 Base Models 和用于 RL 的算法
- 作者揭示了预训练偏差如何影响 RL 结果,以及像 GRPO 这样的优化选择如何无意中塑造模型行为
- 论文提出的 Dr.GRPO 提供了一个简单的修正,在保持推理性能的同时提高了 token 效率(目前在很多场景上已经被广泛应用,各大 RL 框架均有实现)
- PS:scaling RL can be both effective and efficient,sometimes, less really is more
- 背景:
- DeepSeek-R1-Zero 已证明:大规模 RL(无需SFT)即可直接增强 LLM 的推理能力
- 分析:
- 论文从 Base Model 和 RL 对 R1-Zero-like 训练进行了批判性审视
- 研究了包括 DeepSeek-V3-Base 在内的多种 Base Models ,以理解预训练特性如何影响 RL 性能
- 分析表明:
- 预训练偏差:DeepSeek-V3-Base 已展现出“顿悟时刻”(Aha moment);Qwen2.5 Base Models无需提示模板也表现出强大的推理能力
- GRPO 存在优化偏差:GRPO 会在训练过程中人为增加响应长度(尤其是错误输出)
- 主要工作:
- 提出一种无偏优化方法 Dr.GRPO,在保持推理性能的同时提升 token 效率(token efficiency)
- 继而论文提出了一种极简的 R1-Zero 方案,使用 7B Base Models 在 AIME 2024 上达到 43.3% 的准确率,创造了新的 SOTA
- 注:给出的很多评估测试指标和数据集都有很明确的引用 ,很方便查找各种指标来源 ,论文不会清晰展示,详情可以看论文原文
Introduction and Discussion
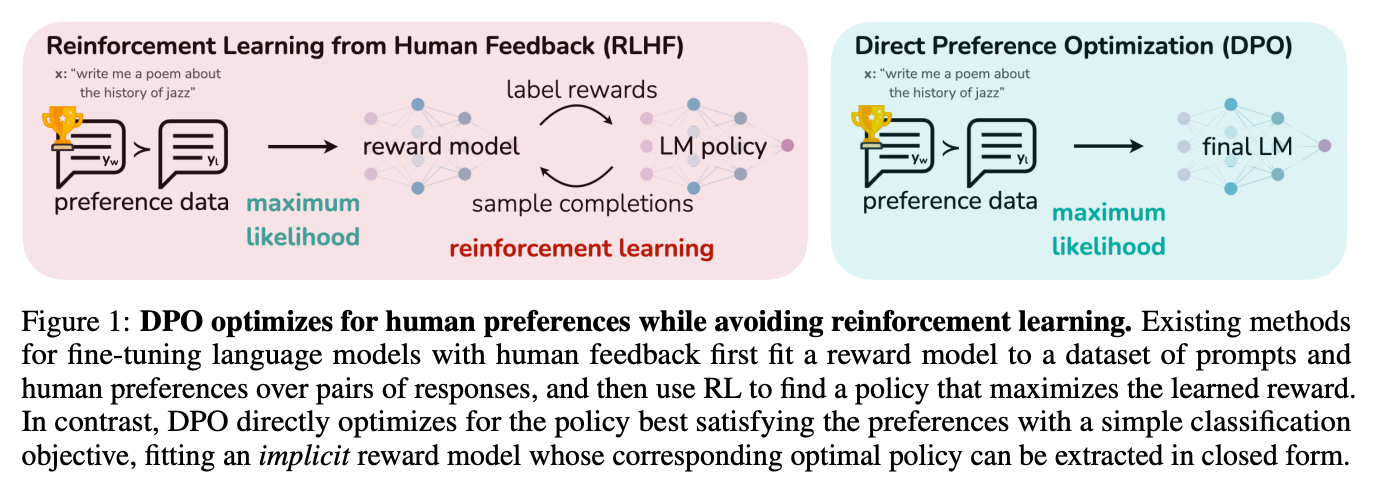
- DeepSeek-R1-Zero 通过引入R1-Zero式训练范式 ,彻底改变了 LLM 的后训练流程:
- 即:无需依赖 SFT 作为前置步骤,直接将 RL 应用于基础 LLM
- 这一新范式因其简洁性和展示的 RL scaling phenomenon 而备受关注:
- 模型的推理能力随着响应长度的持续增加而提升
- 这一现象还伴随着“Aha moment”的出现,即模型通过学习涌现出自我反思等高级技能
- 论文旨在通过研究两个关键组件(Base Models和RL),来理解 R1-Zero-like 训练
- 第一部分,论文探讨 Base Models 的各种属性,重点关注 Qwen2.5 模型家族,该家族被用于近期尝试复现 R1-Zero 的研究,以及 DeepSeek-V3-Base ,真正的 R1-Zero 模型正是基于后者通过 RL 调优得到的
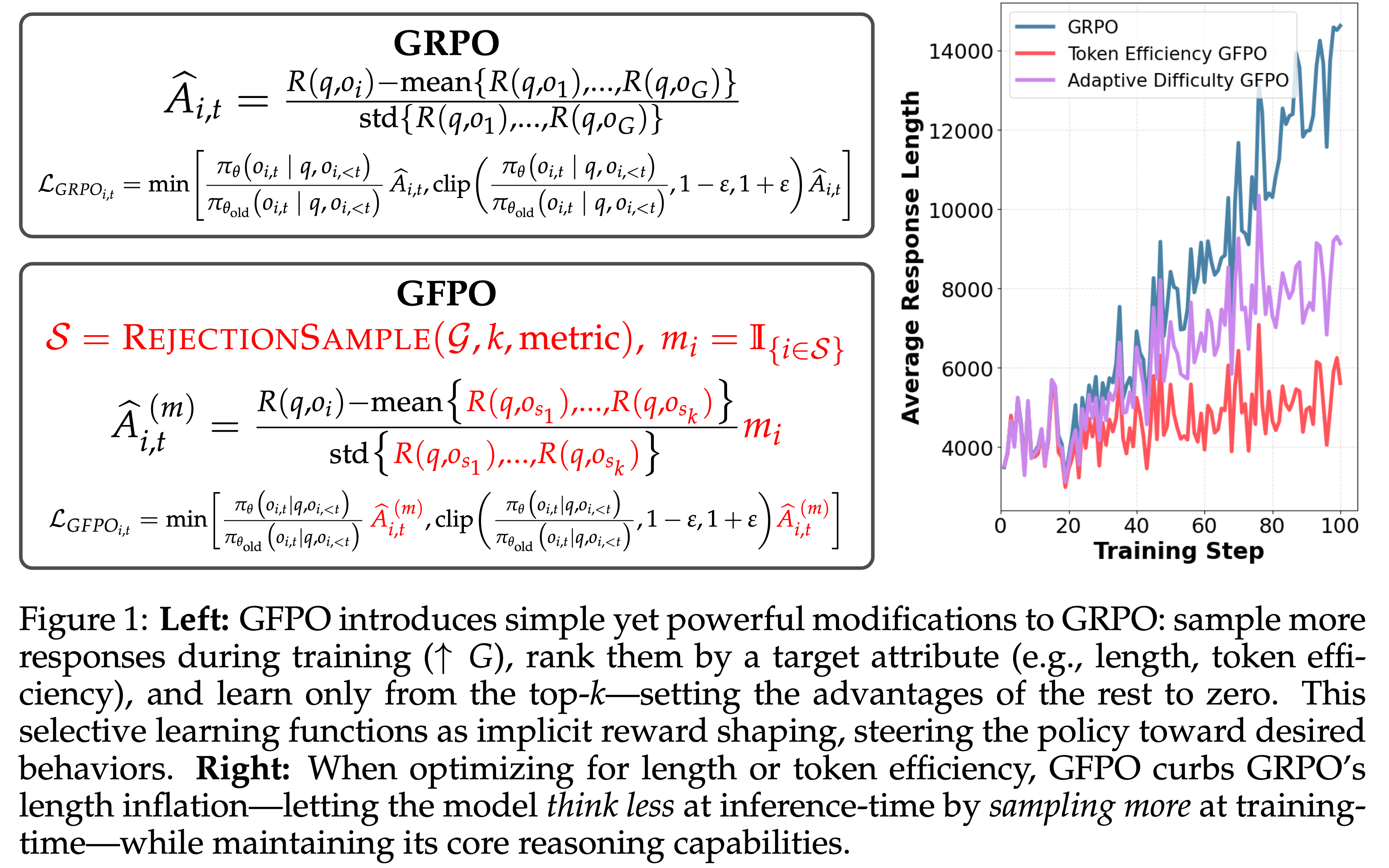
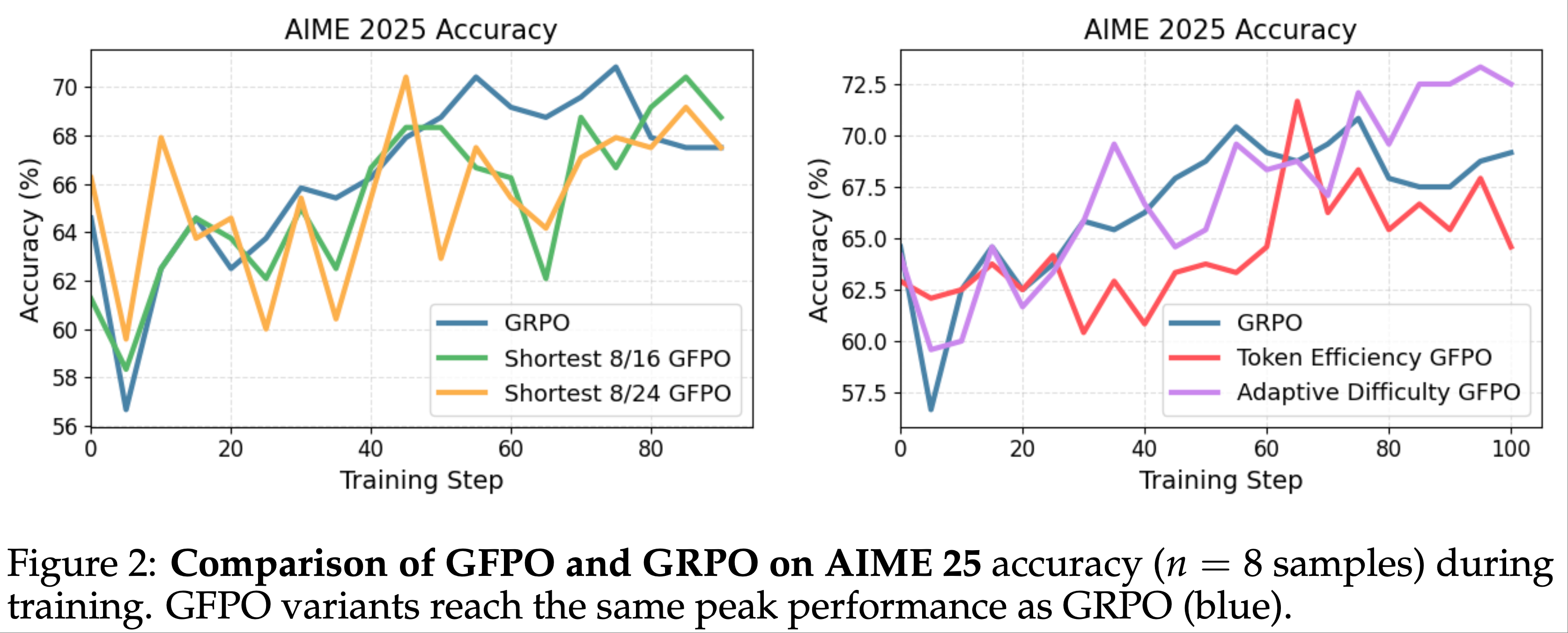
- 第二部分,论文揭示了 GRPO 优化中的偏差(Shao等,2024),该偏差可能导致错误响应逐渐变长。为此,论文提出了一种简单修改以消除偏差,即“正确实现的GRPO”(Dr.GRPO),从而获得 better token efficiency(如图1所示)
- 理解:这里的 better token efficiency 是指用更短的 Token 序列获得更高的奖励
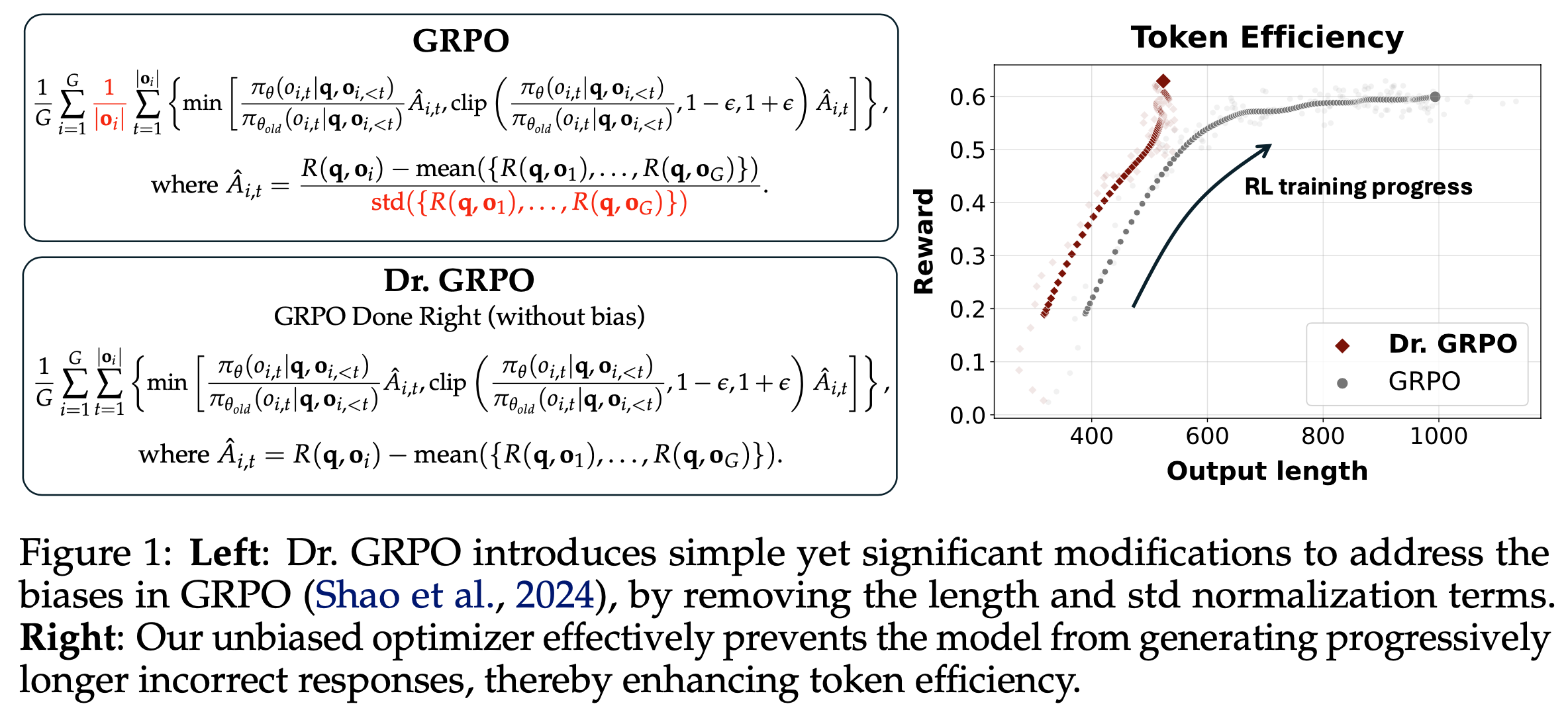
- 理解:这里的 better token efficiency 是指用更短的 Token 序列获得更高的奖励
- 通过对 Base Models 和 RL 的分析,论文提出了 R1-Zero-like 训练的极简方案(minimalist recipe) :
- 使用(无偏的)Dr.GRPO 算法在 MATH level 3-5(详情见原论文引用) 问题上对 Qwen2.5-Math-7B 进行 RL 调优,并采用 Qwen-Math 模板,仅需 8 块 A100 GPU 运行 27 小时即达到最先进的性能(图2)。作者希望论文的发现、发布的模型和开源代码库能为该领域的未来研究提供帮助
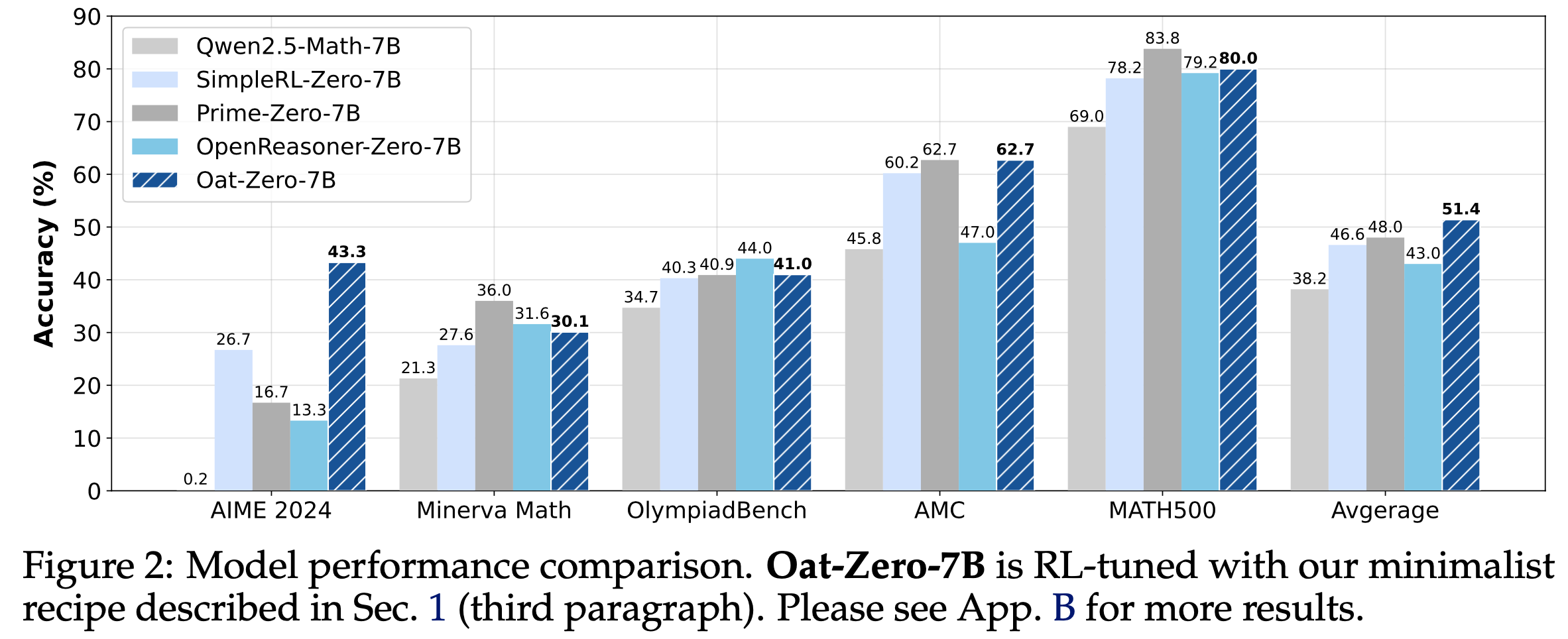
- 使用(无偏的)Dr.GRPO 算法在 MATH level 3-5(详情见原论文引用) 问题上对 Qwen2.5-Math-7B 进行 RL 调优,并采用 Qwen-Math 模板,仅需 8 块 A100 GPU 运行 27 小时即达到最先进的性能(图2)。作者希望论文的发现、发布的模型和开源代码库能为该领域的未来研究提供帮助
- 论文的核心结论概述(TLDR):
- (第2.1节)模板可以让 Base Models 回答问题而非补全句子;所有 Base Models 在 RL 之前已具备数学解题能力
- (第2.2节)Qwen-2.5 Base Models 不使用模板时性能立即提升约 60% ,论文推测其在模型构建过程中可能预训练了 concatanated Question-Answer 文本
- (第2.3节)几乎所有 Base Models (包括 DeepSeek-V3-Base)均已展现出“Aha moment”
- (第3.1-3.2节)Dr.GRPO 有效修正了 GRPO 的优化偏差,实现了 better token efficiency
- (第3.3节)模型与模板的不匹配可能破坏推理能力,而 RL 会重建这种能力
- (第3.4节)Llama-3.2-3B 的数学预训练提升了其 RL 性能上限
Analysis on Base Models
- 本节论文深入研究了多种 Base Models ,包括 Qwen-2.5家族、Llama-3.1 和 DeepSeek系列
- 论文从 MATH(Hendrycks等,2021)训练集中抽取 500 个问题,分析这些模型的响应
R1-Zero Trainability: Templates Construct Exploratory Base Policies(R1-Zero 可训练性分析)
- 由于从 Base Models 开始训练是 R1-Zero 式范式的基本设定,论文首先研究广泛使用的开源 Base Models(通常训练用于句子补全,即 \(p_{\theta}(\mathbf{x})\))是否能够通过适当的模板有效激发其问答能力,从而作为问答基础策略 \(\pi_{\theta}(\cdot|\mathbf{q})\)
- 问题:句子补全为什么是 \(p_{\theta}(\mathbf{x})\)?
- 回答:这里应该是强调与 Question-Answer 数据不同,区别于 \(p_{\theta}(\mathbf{o}|\mathbf{q})\)
- 除了Guo等(2025)中的R1模板(模板1),论文还考虑了Zeng等(2025)使用的 Qwen-Math 模板(模板2)以及无模板(模板3):
- Template 1 (R1 template):
A conversation between User and Assistant. The User asks a question, and the Assistant solves it. The Assistant first thinks about the reasoning process in the mind and then provides the User with the answer. The reasoning process is enclosed within <think> </think> and answer is enclosed within <answer> </answer> tags, respectively, i.e., <think> reasoning process here </think> <answer> answer here </answer>.\nUser: {question}\nAssistant: <think>
- Template 2 (Qwen-Math template)
<|im_start|>system\nPlease reason step by step, and put your final answer within \\boxed{}.<|im_end|>\n<|im_start|>user\n{question}<|im_end|>\n<|im_start|>assistant\n
- Template 3 (No template)
{question}
- Template 1 (R1 template):
- 实验设置 :
- 论文测试了 Qwen2.5-Math-1.5B、Qwen2.5-Math-7B、Qwen2.5-7B、Llama-3.1-8B、DeepSeek-Math-7B 和 DeepSeek-V3-Base-685B
- 对每个模型,
- 首先应用无模板获取响应,然后让 GPT-4o-mini 判断响应是问答格式(无论质量)还是句子补全模式。记录倾向于回答问题的响应百分比作为指标
- 然后应用R1模板和Qwen-Math模板获取响应,并根据指标确定每个模型的最适合模板。最后,评估每个模型在对应模板下的 pass@8 准确率,以判断基础策略是否能探索出有利于 RL 改进的轨迹
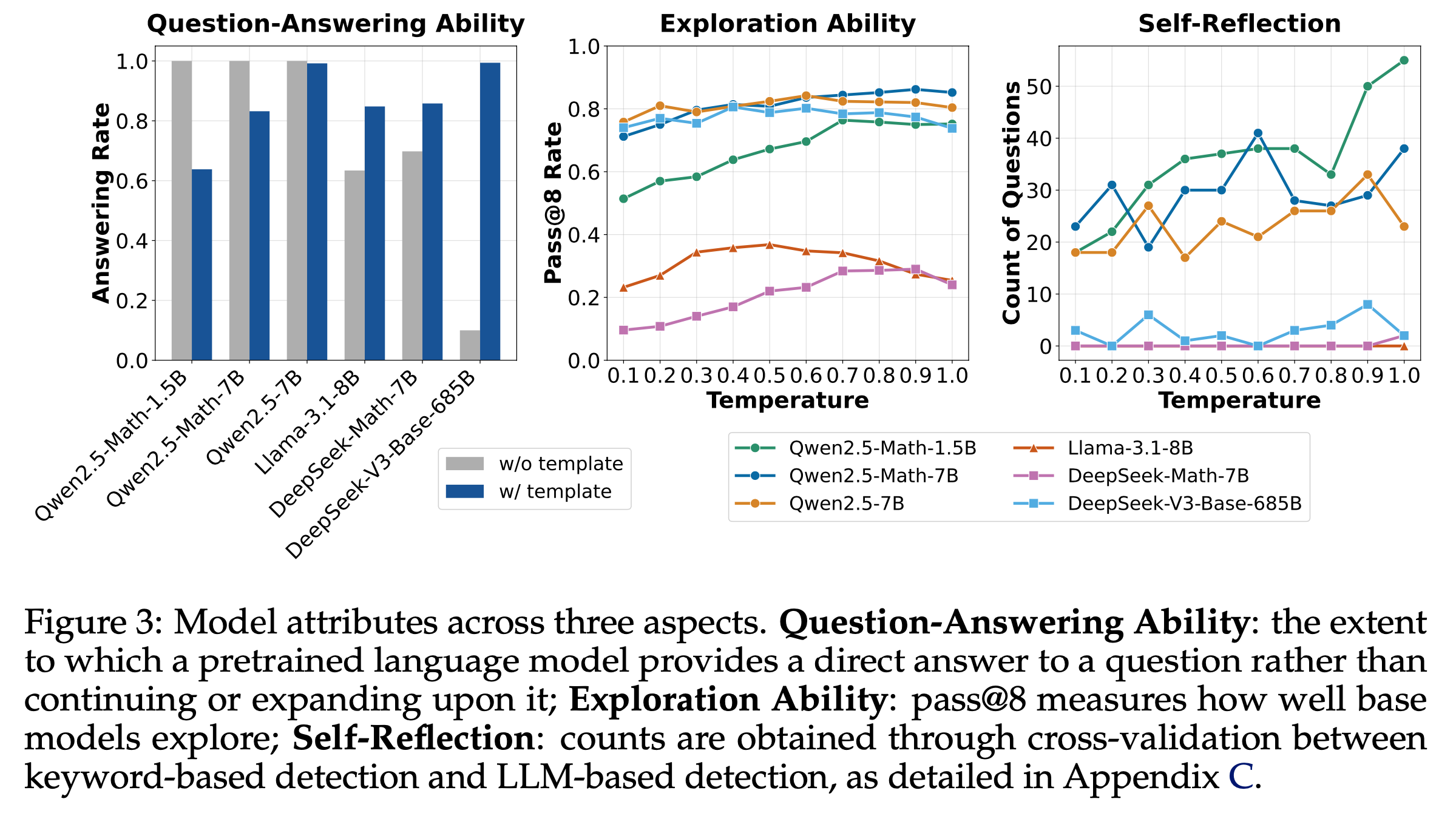
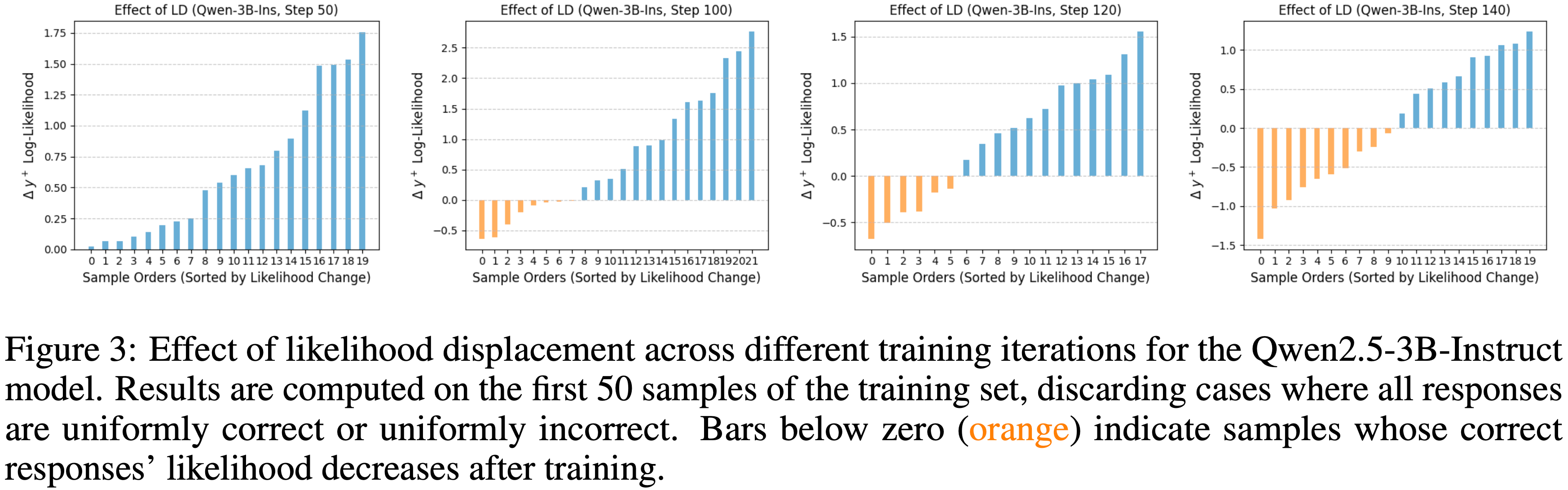
- 结果 :图3(左)展示了 Base Models (使用或不使用模板)回答问题的能力,论文发现:
- 不同 Base Models 使用模板后的提升不一致 :Llama 和 DeepSeek 模型通过使用适当模板(R1 模板)显著提升了问答能力,但Qwen2.5 模型在不使用模板时表现最佳(问答率100%)
- 这一有趣特性促使论文进一步研究(见第2.2节)
- DeepSeek-V3-Base 在无模板时问答率最低,表明它是一个近乎纯净的 Base Models
- 这一观察促使论文探索纯净 Base Models (如DeepSeek-V3-Base)是否展现出 Aha moment(第2.3节)
- 图3(中)展示了不同 Base Models(使用模板)在不同采样温度下的 pass@8 准确率
- 该指标可作为基础策略探索能力的指标
- 例如,若基础策略无法采样出任何导致正确答案的轨迹,RL 将无法改进策略,因为缺乏奖励信号
- 结果表明,所有测试模型均具备探索能力(适合 RL),其中 Qwen2.5 模型表现最佳(甚至超越 DeepSeek-V3-Base)。这可能部分解释了为何多数 R1-Zero 项目(Zeng等,2025;Hu等,2025)基于 Qwen2.5 模型
- 不同 Base Models 使用模板后的提升不一致 :Llama 和 DeepSeek 模型通过使用适当模板(R1 模板)显著提升了问答能力,但Qwen2.5 模型在不使用模板时表现最佳(问答率100%)
Qwen-2.5 Models Unlock the Best Performance When Discarding Template
- 论文进一步探究了图3(左)中的有趣现象:所有 Qwen2.5 Base Models 即使不使用任何模板,也能直接作为聊天模型
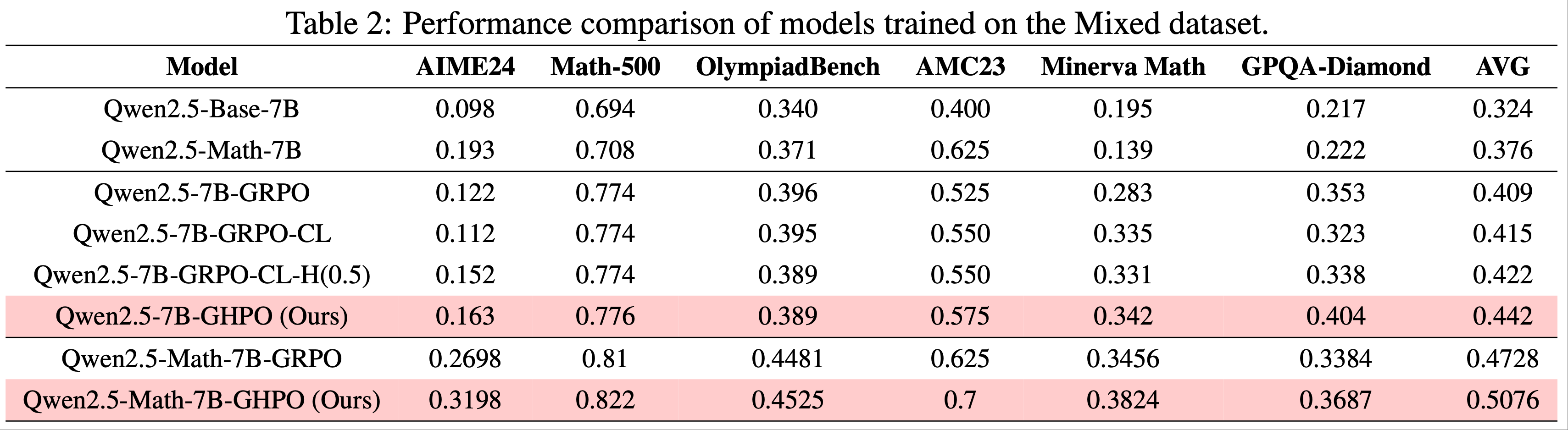
- 论文在五个标准基准上评估 Qwen2.5-Math 模型的推理能力:AIME 2024、AMC、MATH500、Minerva Math 和 OlympiadBench
- 采用贪婪解码,采样 token 限制为 3000
- 如表1所示,不使用任何模板可显著提升 Qwen2.5-Math 模型平均性能,相比传统的 4-shot prompting 提升约 60%
- 理解:没有模板效果反而最好,说明模板需要一定的格式遵循能力,这会让模型解决问题的能力有所降低!
- 问题:传统的 4-shot prompting 也是无模板吧?为什么给了 4-shot 效果反而变差了?
- 回答:猜测是因为增加了太多上下文反而让模型有点混乱了?就像要遵循模板一样,降低了模型解决问题的能力
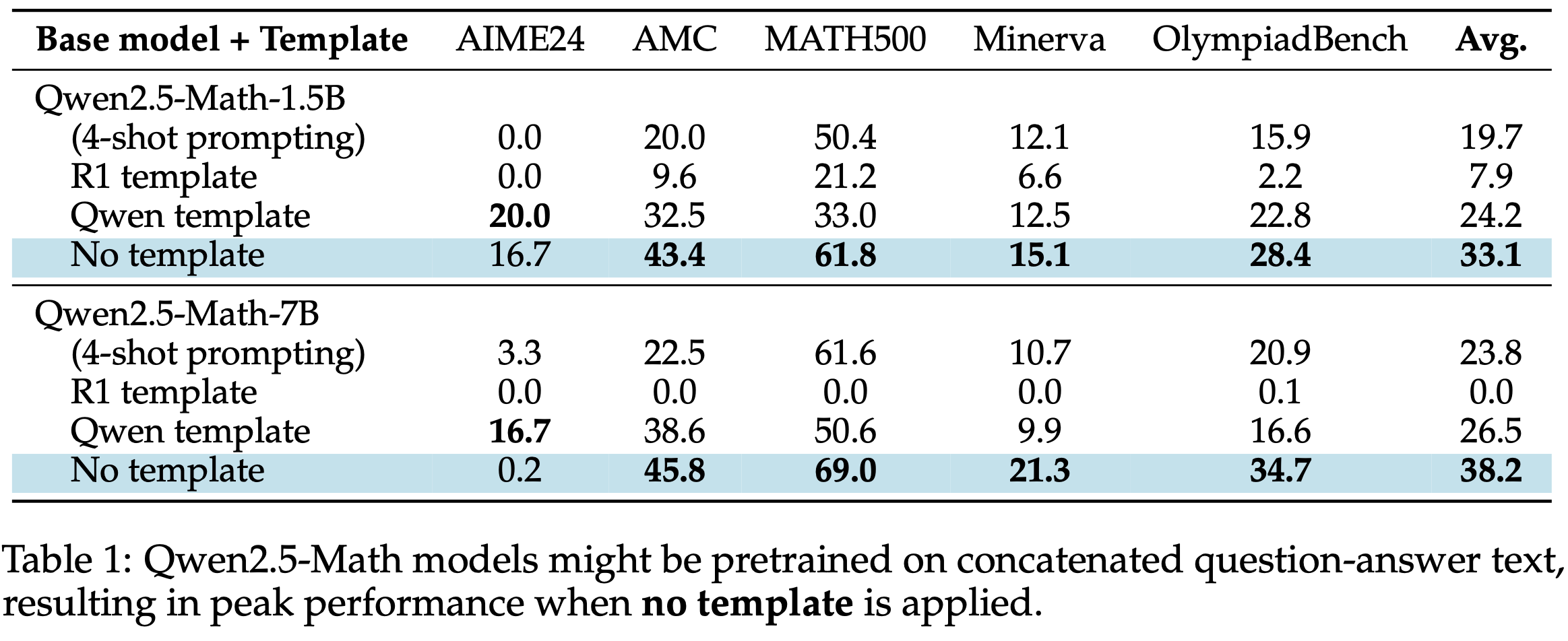
- 回答:猜测是因为增加了太多上下文反而让模型有点混乱了?就像要遵循模板一样,降低了模型解决问题的能力
- 由于 Qwen2.5-Math(2024)在预训练阶段使用了聊天模型数据(Question-Answer 对),论文推测其可能直接预训练拼接文本以最大化 \(\log p_{\theta}(\mathbf{q};\mathbf{o})\)
- 若假设成立,使用 Qwen2.5 模型复现 DeepSeek-R1-Zero 时需更加谨慎,因为这些 Base Models 即使无模板也已类似 SFT 模型
Aha moment 已出现在包括 DeepSeek-V3-Base 的 Base Models 中
- DeepSeek-R1-Zero 最引人注目的成果之一是通过纯 RL 训练涌现出自我反思行为(即Aha moment)
- 一些前期研究(Liu等,2025b;Yeo等,2025)指出,开源 R1 复现可能不存在 Aha moment,因为它们使用的 Base Models 已包含 self-reflection keywords
- 然而,这些研究未测试真正的 R1-Zero 模型所基于的 DeepSeek-V3-Base。论文通过自行托管 DeepSeek-V3-Base-685B 并分析其对 500个 MATH 问题的响应(使用 R1 模板)填补了这一空白。从图3(右)可见,DeepSeek-V3-Base 也生成了相当数量的自我反思,进一步验证了Liu等(2025b)的观点。图4 展示了 DeepSeek-V3-Base 生成“Aha”、“wait”和“verify the problem”等关键词的案例
- 问题:Liu等(2025b)的观点是什么?

- 问题:Liu等(2025b)的观点是什么?
- 另一个重要问题是自我反思行为是否与 RL 训练后模型性能提升相关。论文使用 DeepSeek-R1-Zero 模型并分析其对相同 MATH 问题的响应。虽然 R1-Zero 中自我反思行为更频繁,但这些行为未必意味着更高的准确率。详细分析见附录D
Analysis on Reinforcement Learning
- 语言模型的生成过程可以形式化为一个 token-level 的马尔可夫决策过程(MDP)\(\mathcal{M}=(\mathcal{S},\mathcal{A},r,p_Q)\)
- 在每一步生成 \(t\) 时,状态 \(s_t \in \mathcal{S}\) 是输入问题和已生成输出的拼接:\(s_t = \mathbf{q};\mathbf{o}_{ < t} = [q_1,\ldots,q_M,o_1,\ldots,o_{t-1}]\)
- 策略 \(\pi_\theta(\cdot|s_t)\) 会从词汇表 \(\mathcal{A}\) 中选择 next token \(o_t\),确定性地转移到下一个状态 \(s_{t+1} = s_t;[o_t]\)
- 生成过程从初始状态 \(s_1 = \mathbf{q} \sim p_Q\) 开始,当自回归策略生成 [eos] token 或耗尽 Budget 时停止
- 通常,论文最大化以下熵正则化目标(2017a):
$$
\mathcal{J}(\pi_\theta) = \mathbb{E}_{\mathbf{q}\sim p_Q} \left[\mathbb{E}_{\mathbf{o}\sim \pi_\theta(\cdot|\mathbf{q})}[R(\mathbf{q},\mathbf{o})] - \beta \mathbb{D}_{KL}[\pi_\theta(\cdot|\mathbf{q})||\pi_{\text{ref} }(\cdot|\mathbf{q})]\right], \tag{1}
$$- \(\pi_{\text{ref} }\) 是参考策略
- \(R(\mathbf{q},\mathbf{o}) = \sum_{t=1}^{|\mathbf{o}|} r(s_t,o_t)\) 是轨迹 \(\mathbf{q};\mathbf{o}\) 的回报(Sutton, 2018)
- 其中 \(r\) 是从 \(\pi_{\text{ref} }\) 收集的数据中学习的奖励模型
- KL 正则项通常用于 RLHF,以防止 \(\pi_\theta\) 偏离奖励模型准确的分布(类似 OOD 问题)
- 在调整推理模型时,通常使用 Rule-based Verifiers 作为奖励模型 \(r\)(2024),消除了分布偏移的担忧
- 这使得我们可以移除 KL 项 ,不仅节省了训练时 \(\pi_{\text{ref} }\) 的内存和计算需求,还可能为 R1-Zero-like 训练带来更好的性能(2025)
- 论文全文中,我们将假设 \(\beta = 0\)
- 问题:为什么说Rule-based Verifiers 作为奖励模型可以消除分布偏移的担忧?
- 理解:作者的思路是这样的
- 第一:奖励模型 \(r\) 是从 \(\pi_{\text{ref} }\) 收集的数据中学习的
- 第二:KL 正则项是为了防止 \(\pi_\theta\) 偏离奖励模型准确的分布(偏离太多会导致奖励模型估不准)
- 第三:Rule-based Verifiers 作为奖励模型后,无论策略分布怎么变化,其实都不会出现奖励模型无法评估的情况,也就不存在分布偏移问题
- 补充说明:这里可能理解是有误的:
- 首先,奖励模型不一定是从 \(\pi_{\text{ref} }\) 收集的数据中学习的(当然,从 \(\pi_{\text{ref} }\) 收集会更好,可保证策略和奖励模型都是基于 \(\pi_{\text{ref} }\) 分布的);
- 其次,个人认为是 KL 散度还可以防止模型 Reward Hacking 跑飞了或遗忘了之前的知识。当然,实际是否有效需要实操,都有各自的道理
- 这使得我们可以移除 KL 项 ,不仅节省了训练时 \(\pi_{\text{ref} }\) 的内存和计算需求,还可能为 R1-Zero-like 训练带来更好的性能(2025)
策略优化算法
- 为了优化上述目标(式 (1) 中 \(\beta = 0\)),近端策略优化(PPO)(2017b)最大化以下替代目标:
$$
\begin{align}
\mathcal{J}_{\text{PPO} }(\pi_\theta) &= \mathbb{E}_{\mathbf{q}\sim p_Q,\mathbf{o}\sim \pi_{\theta_{\text{old} } }(\cdot|\mathbf{q})} \\
&\sum_{t=1}^{|\mathbf{o}|} \left\{\min\left[\frac{\pi_\theta(o_t|\mathbf{q},\mathbf{o}_{ < t})}{\pi_{\theta_{\text{old} } }(o_t|\mathbf{q},\mathbf{o}_{ < t})}\hat{A}_t, \text{clip}\left(\frac{\pi_\theta(o_t|\mathbf{q},\mathbf{o}_{ < t})}{\pi_{\theta_{\text{old} } }(o_t|\mathbf{q},\mathbf{o}_{ < t})},1-\epsilon,1+\epsilon\right)\hat{A}_t\right]\right\},
\end{align} \tag{2}
$$- \(\pi_{\theta_{\text{old} } }\) 是更新前的策略
- \(\hat{A}_t\) 是第 \(t\) 个 token 的优势函数估计(注意:PPO 的优势函数估计使用的奖励函数中包含了 KL 散度, GRPO 的奖励函数不包含 KL 散度)
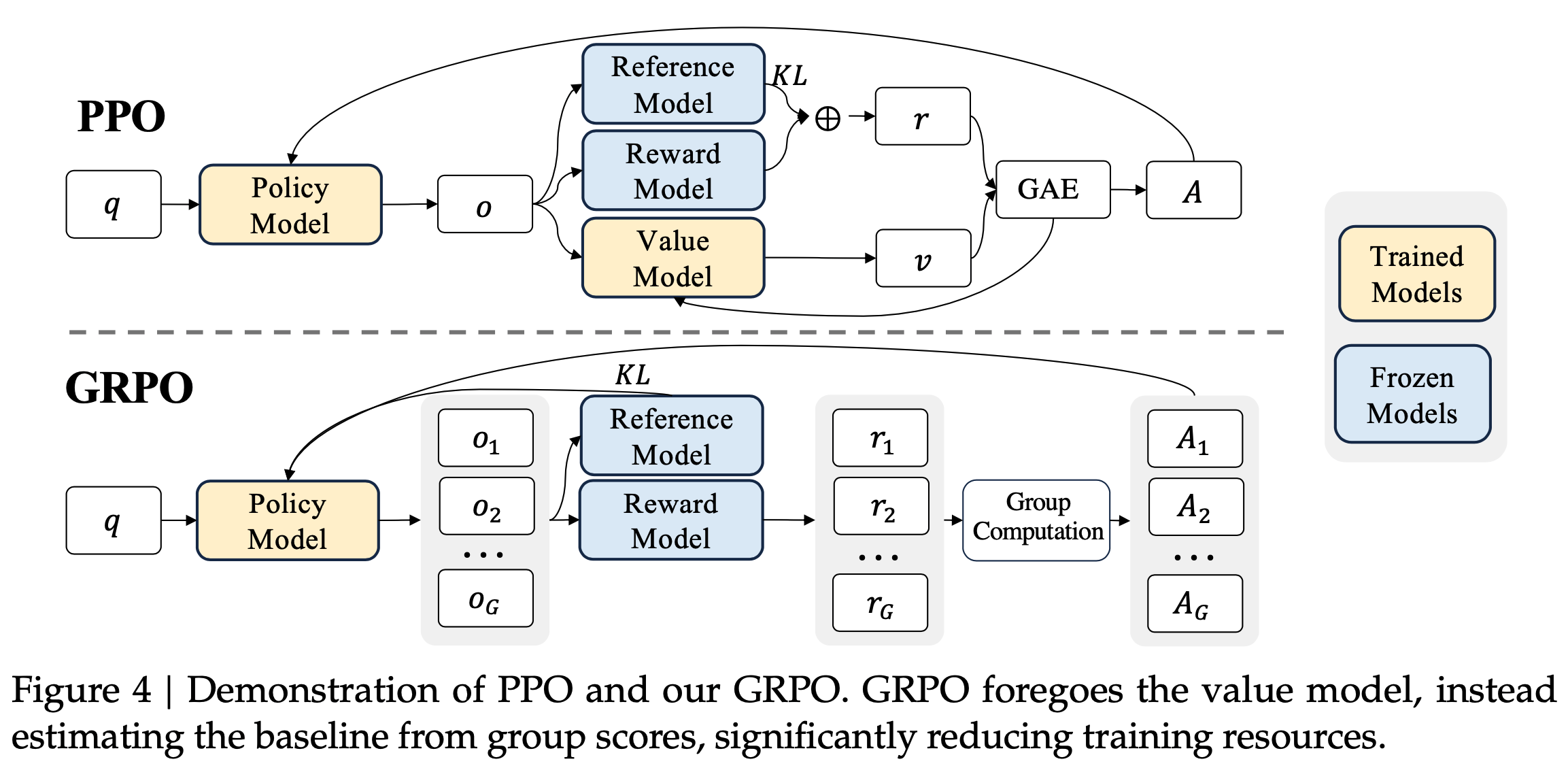
- 标准方法是通过学习的价值模型 \(V_\phi\) 计算广义优势估计(GAE)(2015)。然而,在 LLM 调整的背景下,学习价值模型计算成本高,因此更倾向于无需 \(V_\phi\) 的方法
- 例如:GRPO 首先对每个问题采样一组响应 \(\{\mathbf{o}_1,\ldots,\mathbf{o}_G\}\) 并计算其回报 \(\mathbf{R} = \{R_1,\ldots,R_G\}\),然后将 \(\mathbf{o}_i\) 的所有 token 优势设为
$$\hat{A}_t = \frac{R_i - \text{mean}(\mathbf{R})}{\text{std}(\mathbf{R})}$$
- 例如:GRPO 首先对每个问题采样一组响应 \(\{\mathbf{o}_1,\ldots,\mathbf{o}_G\}\) 并计算其回报 \(\mathbf{R} = \{R_1,\ldots,R_G\}\),然后将 \(\mathbf{o}_i\) 的所有 token 优势设为
GRPO 导致优化偏差
- 在 Deepseek-R1-Zero(2025)中,一个显著趋势是训练过程中响应长度的持续增加。这常被解释为高级推理能力(如自我反思)的发展
- 近期研究(2025; 2025; 2025)使用不同算法和实现复现了这一现象
- 但作者认为观察到的响应长度增加可能是 GRPO(2024)目标函数中的固有偏差导致:
$$
\begin{align}
\mathcal{J}_{\text{GRPO} }(\pi_\theta) &= \mathbb{E}_{\mathbf{q}\sim p_Q, \{\mathbf{o}_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|\mathbf{q})} \\
&\frac{1}{G} \sum_{i=1}^G \color{red}{\frac{1}{|\mathbf{o}_i|}} \sum_{t=1}^{|\mathbf{o}_i|} \left\{\min\left[\frac{\pi_\theta(o_{i,t}|\mathbf{q},\mathbf{o}_{i,<t})}{\pi_{\theta_{\text{old} } }(o_{i,t}|\mathbf{q},\mathbf{o}_{i,<t})}\hat{A}_{i,t}, \text{clip}\left(\frac{\pi_\theta(o_{i,t}|\mathbf{q},\mathbf{o}_{i,<t})}{\pi_{\theta_{\text{old} } }(o_{i,t}|\mathbf{q},\mathbf{o}_{i,<t})},1-\epsilon,1+\epsilon\right)\hat{A}_{i,t}\right]\right\}
\end{align} \tag{3}
$$- 其中
$$
\hat{A}_{i,t} = \frac{R(\mathbf{q},\mathbf{o}_i) - \text{mean}(\{R(\mathbf{q},\mathbf{o}_1),\ldots,R(\mathbf{q},\mathbf{o}_G)\})}{\color{red}{\text{std}(\{R(\mathbf{q},\mathbf{o}_1),\ldots,R(\mathbf{q},\mathbf{o}_G)\})}},
$$ - 且回报 \(R(\mathbf{q},\mathbf{o}_i)\) 通常仅包含 LLM 推理中的可验证结果奖励(outcome verifiable reward)
注:该分析同样适用于过程奖励情况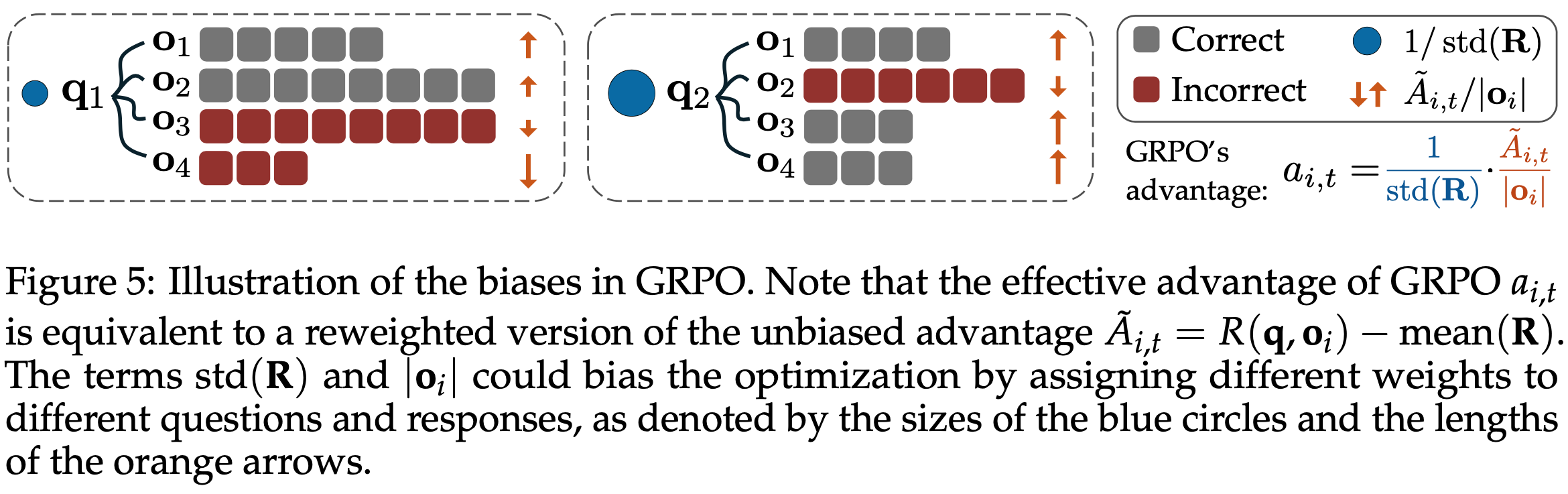
- 其中
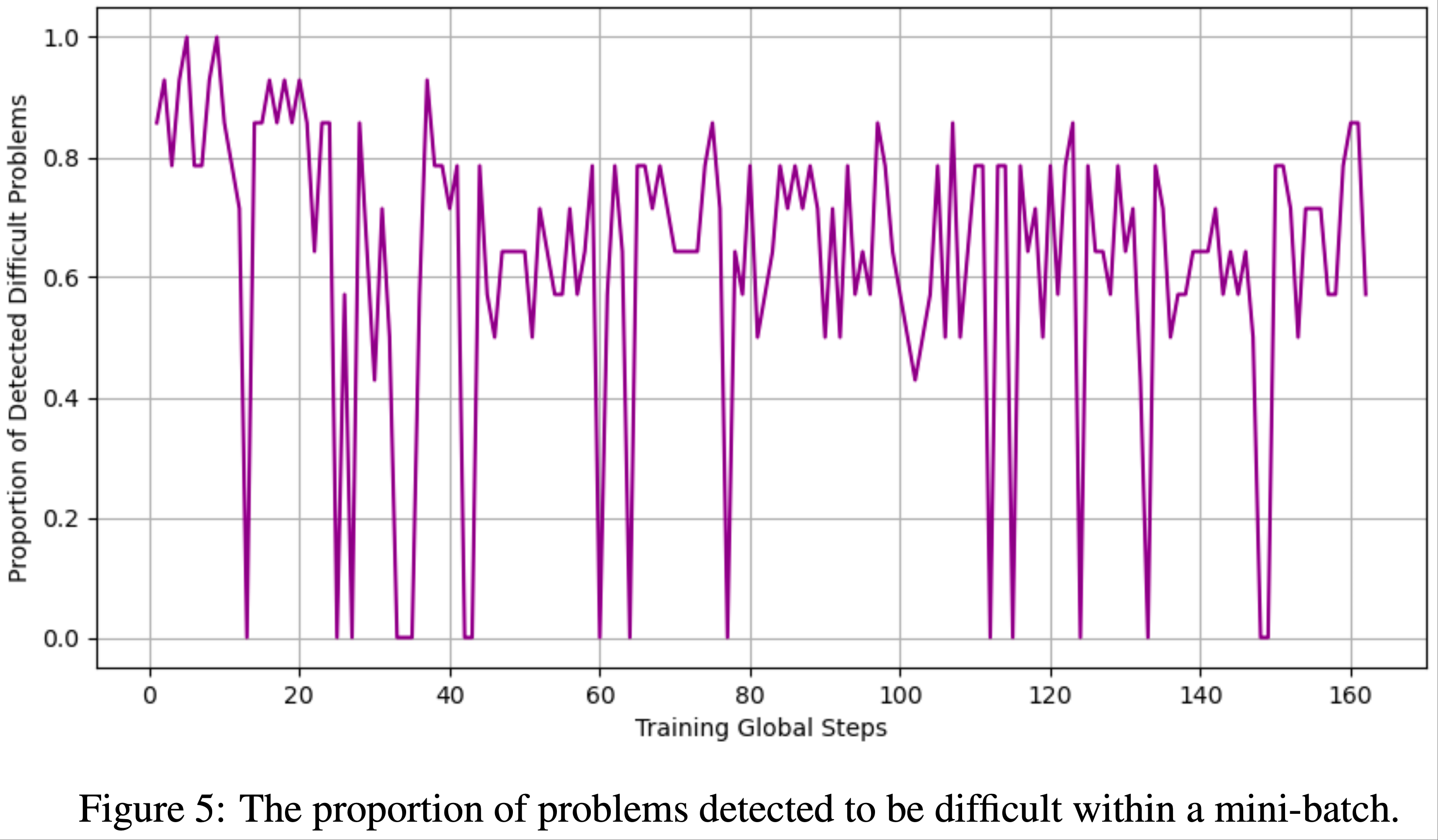
- 与式 (2) 相比,GRPO 引入了两种偏差(见图5):
- Response-level length bias :由除以 \(|\mathbf{o}_i|\) 引起
- 对于正优势(\(\hat{A}_{i,t} > 0\),表示正确响应),此偏差导致对较短响应的梯度更新更大,使策略倾向于简短的正确回答
- 对于负优势(\(\hat{A}_{i,t} < 0\),表示错误响应),较长响应的惩罚较小(因为其 \(|\mathbf{o}_i|\) 较大),导致策略在错误响应中偏好更长的回答
- 思考:常规的 RL 场景中,存在另一种(结束状态奖励一致,但时间步不一致导致)的问题,这时候 RL 更倾向于时间步短的轨迹。这与 GRPO 不同
- GRPO 的奖励是有正有负的,且同一个轨迹上的每个 token 奖励都一致
- GRPO 对同一轨迹的 token 求平均计算 loss 的做法会在奖励为负和为正时都缩小长轨迹上 token 的 Loss 权重
- 所以模型会倾向于 简短的正确回答 和 较长的错误回答
- 问题:在 \(\color{red}{\frac{1}{|\mathbf{o}_i|}}\) 前面还有 \(\sum_{t=1}^{|\mathbf{o}_i|}\),似乎并不会导致本论文中所说的问题,\(\color{red}{\frac{1}{|\mathbf{o}_i|}} \sum_{t=1}^{|\mathbf{o}_i|}\) 相当于是一个平均而已
- 这里理解有误,\(\sum_{t=1}^{|\mathbf{o}_i|}\) 只是损失函数累计到一起的动作(可以看做是一个 Batch 的多个样本一起更新模型), \(\color{red}{\frac{1}{|\mathbf{o}_i|}}\) 则是相当于给所有样本都加了一个权重 \(\color{red}{\frac{1}{|\mathbf{o}_i|}}\)
- 这个权重与 \(\color{red}{\mathbf{o}_i}\) 有关,对不同长度的 response 的 Token 是不公平的,此时,长序列的回复梯度会被缩小(不论正负都会被缩小)),导致模型会倾向于 简短的正确回答 和 较长的错误回答
- Question-level difficulty bias :由将中心化结果奖励除以 \(\text{std}(\{R(\mathbf{q},\mathbf{o}_1),\ldots,R(\mathbf{q},\mathbf{o}_G)\})\) 引起
- 标准差较低的问题(如过于简单或困难,结果奖励几乎全为 1 或 0)在策略更新时被赋予更高权重
- 尽管优势归一化是 RL 中的常见技巧(2021),但通常在整批数据上计算
- 相比之下,Question-level 归一化导致不同问题在目标中权重不同,从而在优化中引入难度偏差
- Response-level length bias :由除以 \(|\mathbf{o}_i|\) 引起
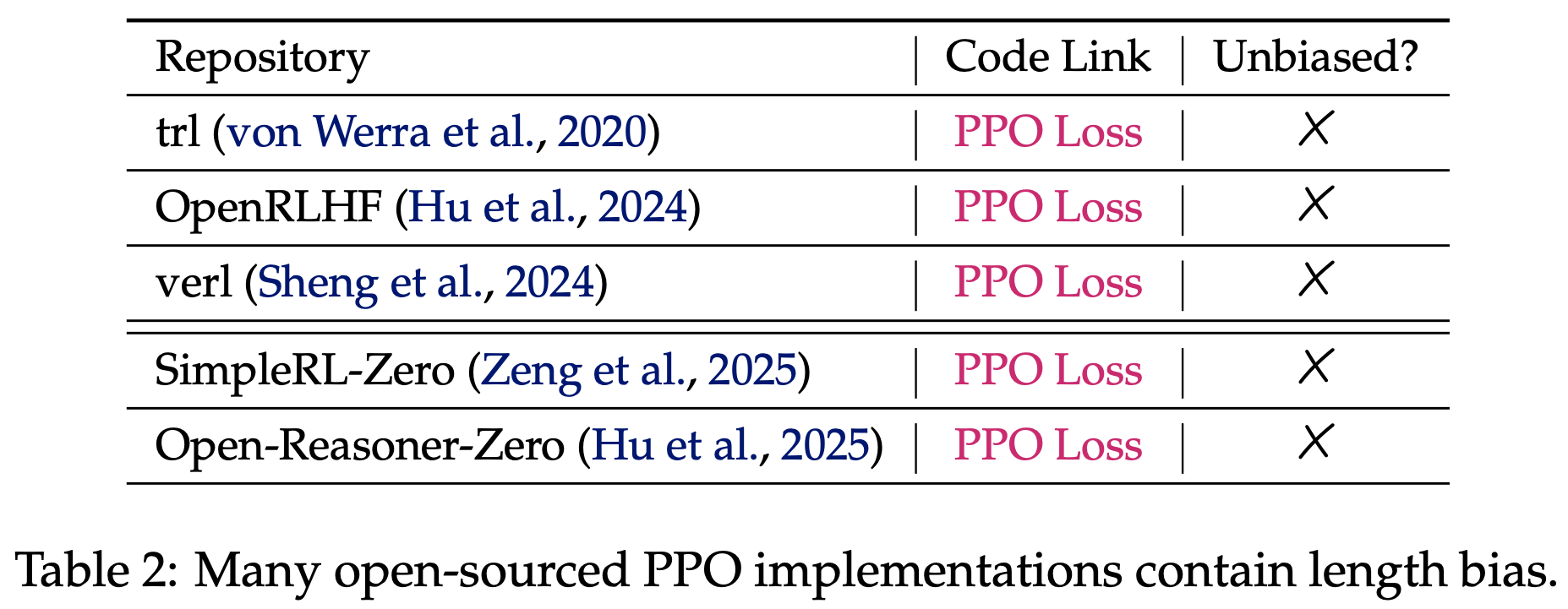
- 特别说明:开源 PPO 实现中同样存在长度偏差
- 论文还检查了几种流行的开源 PPO 实现
- 令人惊讶的是,所有这些实现都通过响应长度对损失进行归一化(见表2),这与式 (2) 中定义的 PPO 目标不一致
- 这种公式与实现的错配甚至在 GRPO 发表之前就已存在
- 论文推测这种错配可能源于预训练阶段(2019),其中所有 token 被打包到固定长度的上下文中,通过上下文长度归一化损失(即计算
loss.mean(-1))提高了数值稳定性 - 然而,在 RL-tuning stage,典型实现(2020)通过响应长度归一化损失,而响应长度非常量,从而引入了意外的长度偏差
Dr.GRPO:修正 GRPO 的优化偏差(Dr.GRPO: GRPO Done Right)
- 为避免上述 GRPO 的优化偏差,论文提出简单地移除 \(\frac{1}{|\mathbf{o}_i|}\) 和 \(\text{std}(\{R(\mathbf{q},\mathbf{o}_1),\ldots,R(\mathbf{q},\mathbf{o}_G)\})\) 归一化项
- 同时,为了忠实实现无偏优化目标(unbiased optimization objective,这里的无偏是指上述两个偏差Response-level length bias 和 Question-level difficulty bias),我们可以将 listing 1 中
masked mean函数的mask.sum(axis=dim)替换为常数值(如 Generation Budget ,论文使用最大输出 Token 数),如绿色行所示
- 特别说明:实际上 verl 库中实现的 DAPO 其实已经没有按照不同回复的 response 长度作为分母了(分母位置如果直接 sum 所有,相当于按照整个 Batch 的总 Token 做归一化),详情见:verl/xxx/masked_mean
- 这些简单修改恢复了式 (2) 中的 PPO 目标,优势通过蒙特卡洛回报和无偏基线估计(Sutton 2018)。详细推导见附录 A。论文将新优化算法称为 Dr.GRPO ,并通过实验验证其有效性
- 问题:如何理解这里的代码?
- 实验设置 :论文使用 Oat(2025a)实现算法,采用 Qwen2.5-1.5B Base Models 和 R1 模板(模板 1)进行 online RL-tuning。论文使用 Math-Verify 实现基于验证的奖励函数,规则如下:
$$
R(\mathbf{q},\mathbf{o}) = \begin{cases}
1 & \text{if } \mathbf{o} \text{ 包含 } \mathbf{q} \text{ 的正确答案} \\
0 & \text{else}
\end{cases}
$$- 论文从 MATH(2021)训练数据集中采样问题运行 RL,比较原始 GRPO 和提出的 Dr.GRPO
- 论文在五个基准测试上评估在线模型:AIME2024、AMC、MATH500、Minerva Math 和 OlympiadBench
- 更多实验细节和超参数见开源代码库
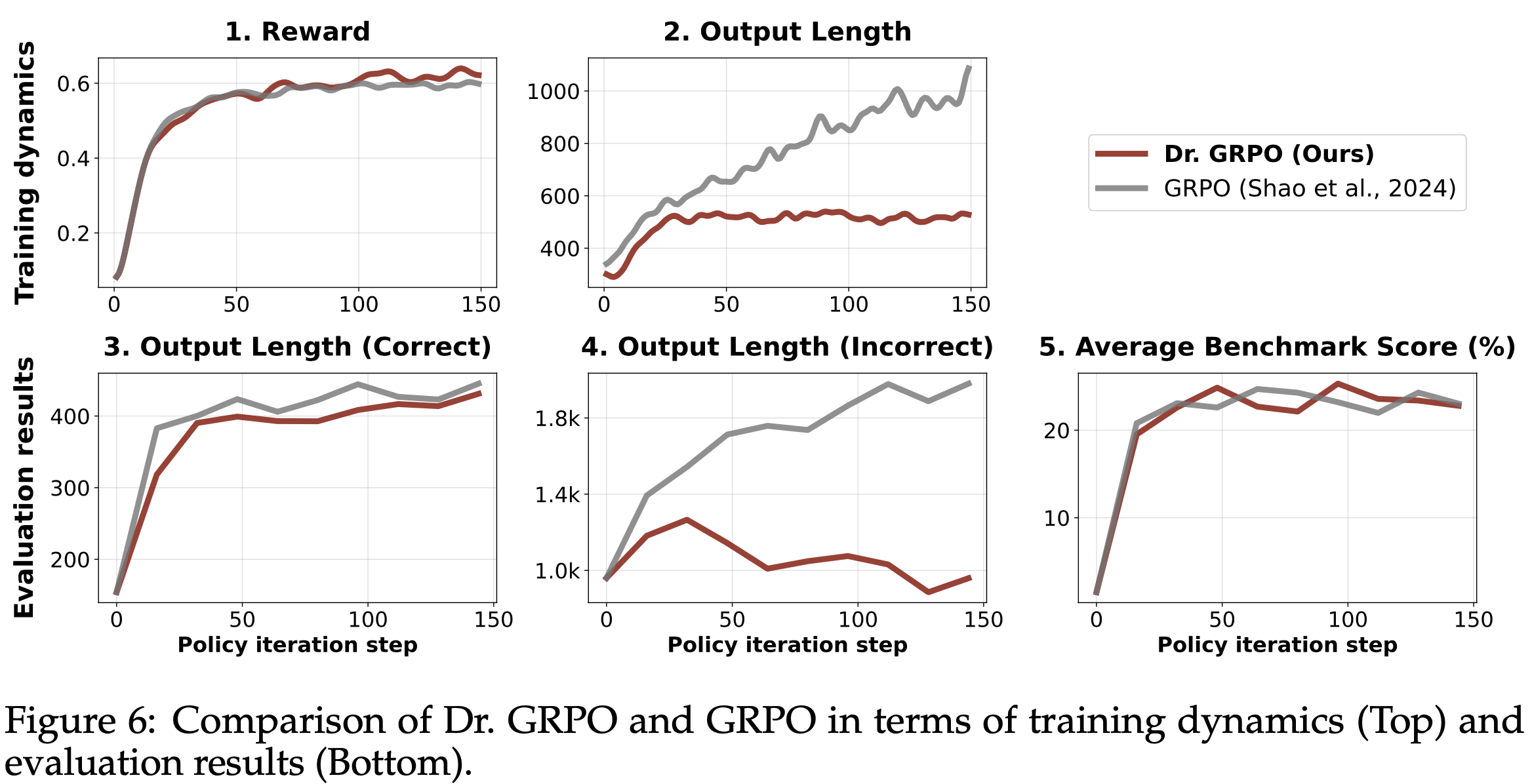
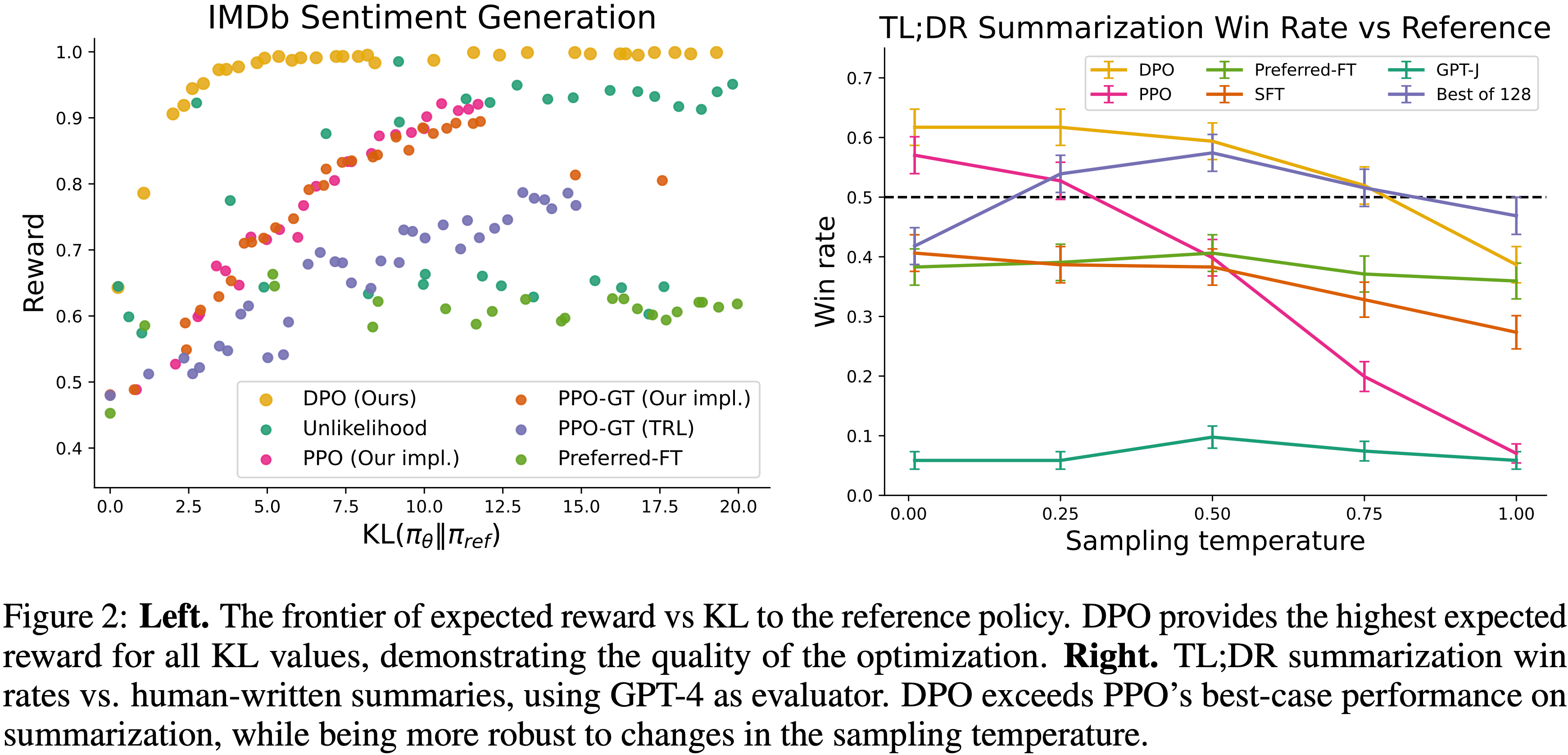
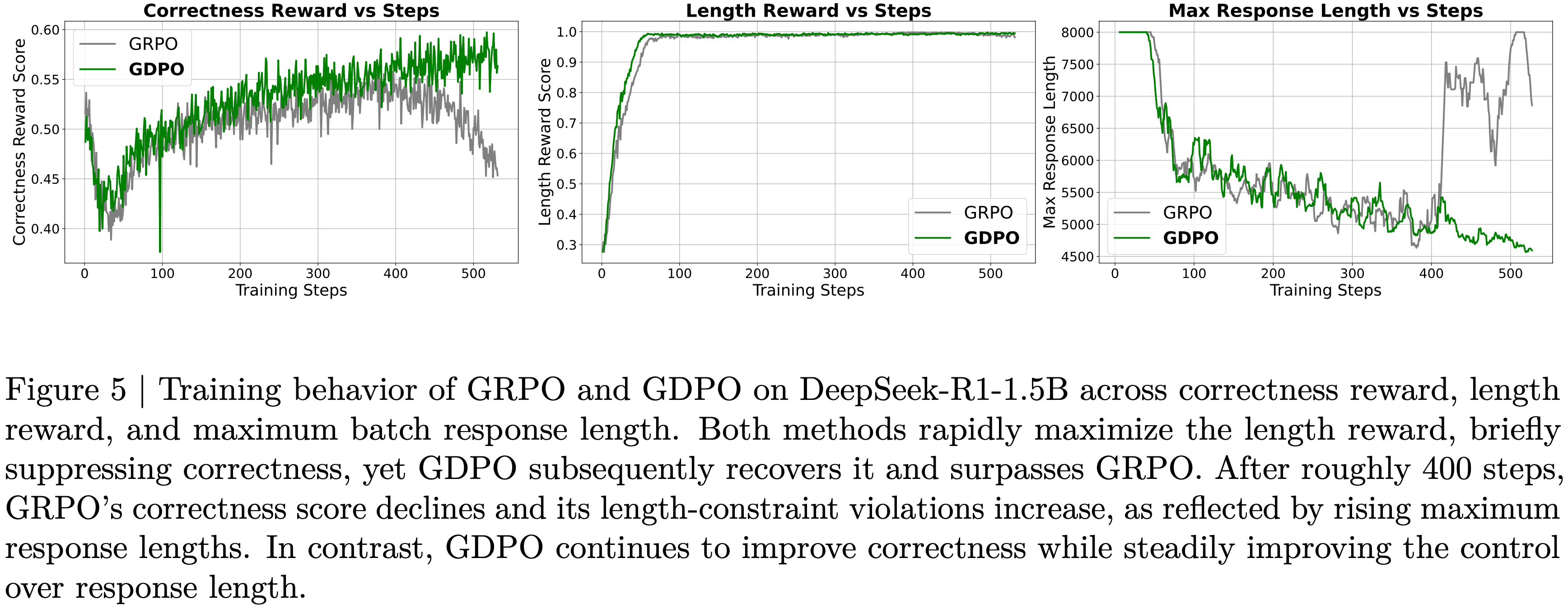
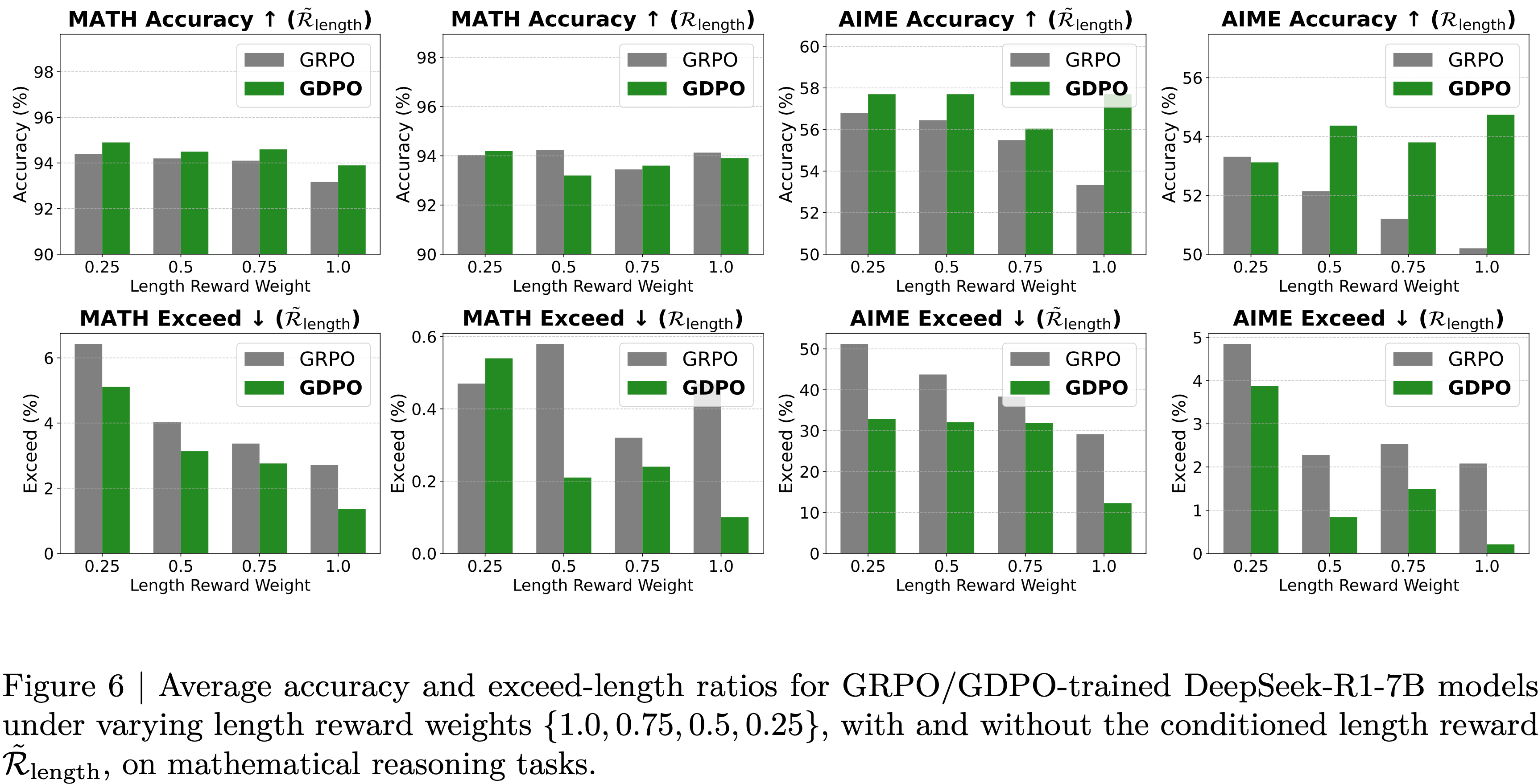
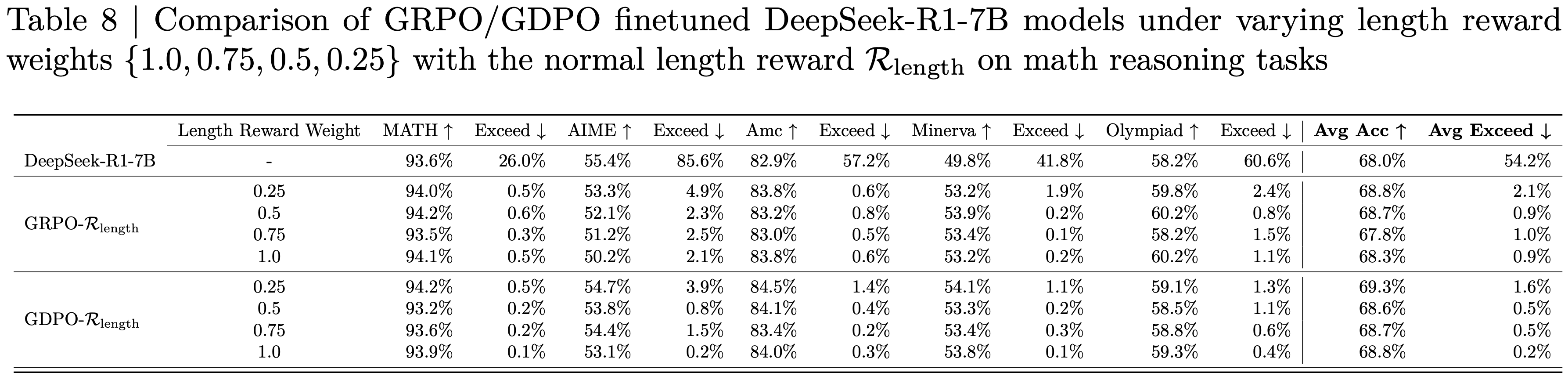
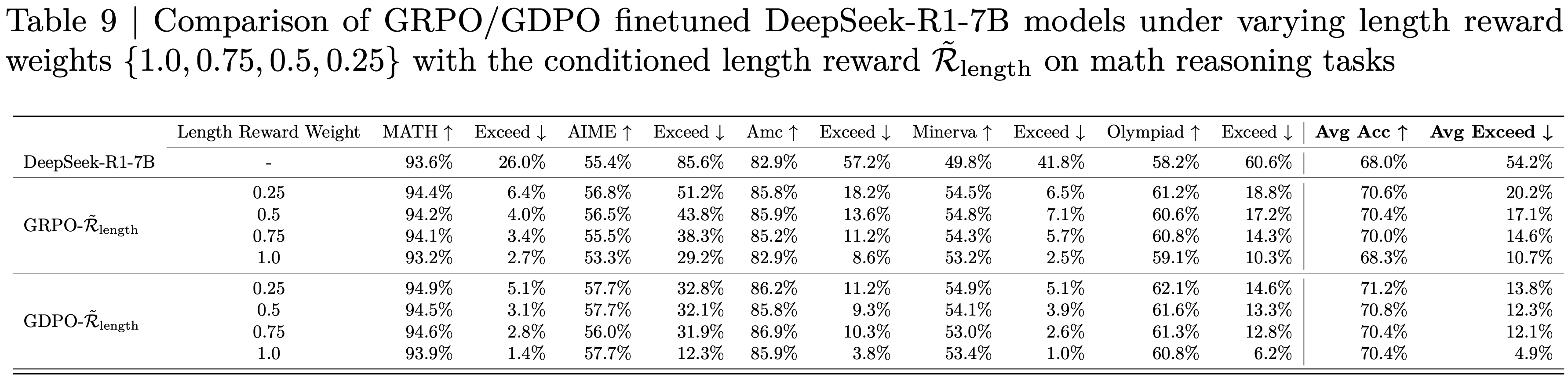
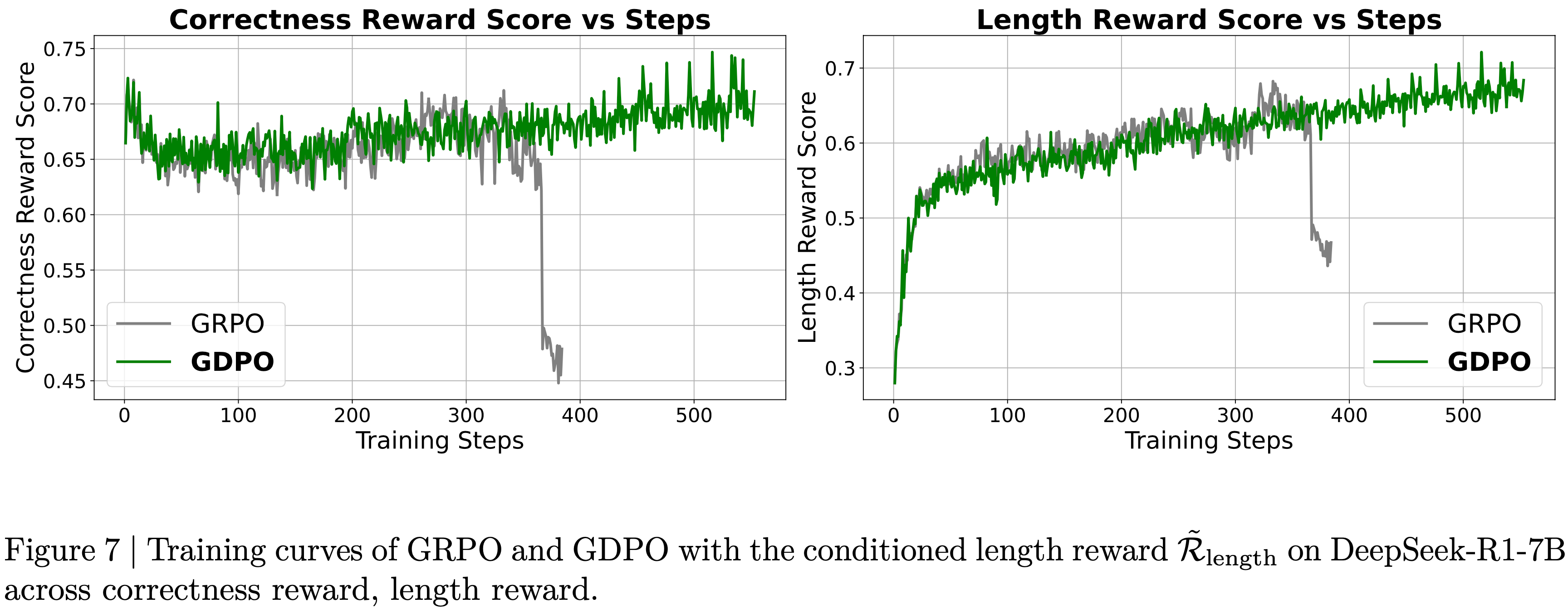
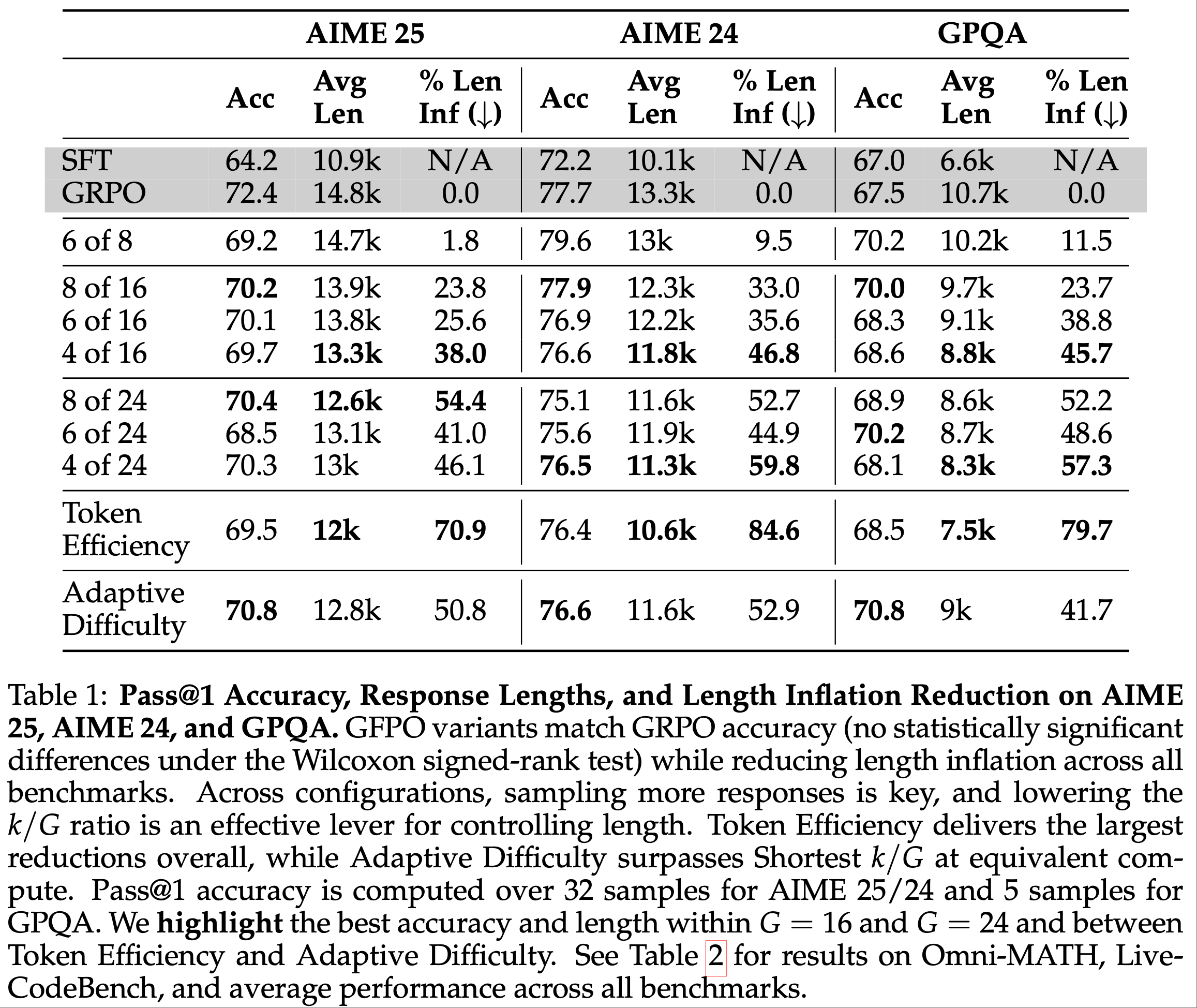
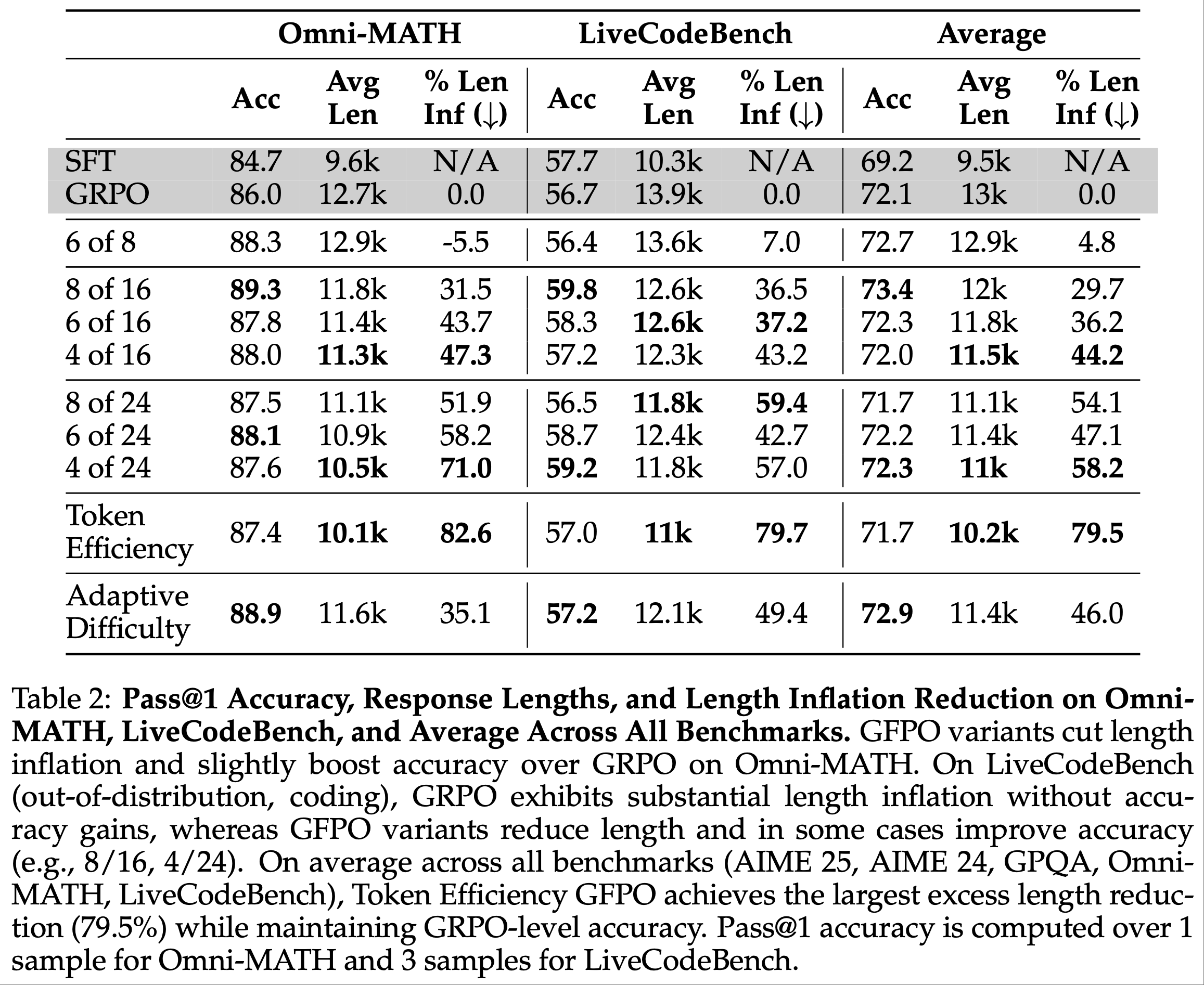
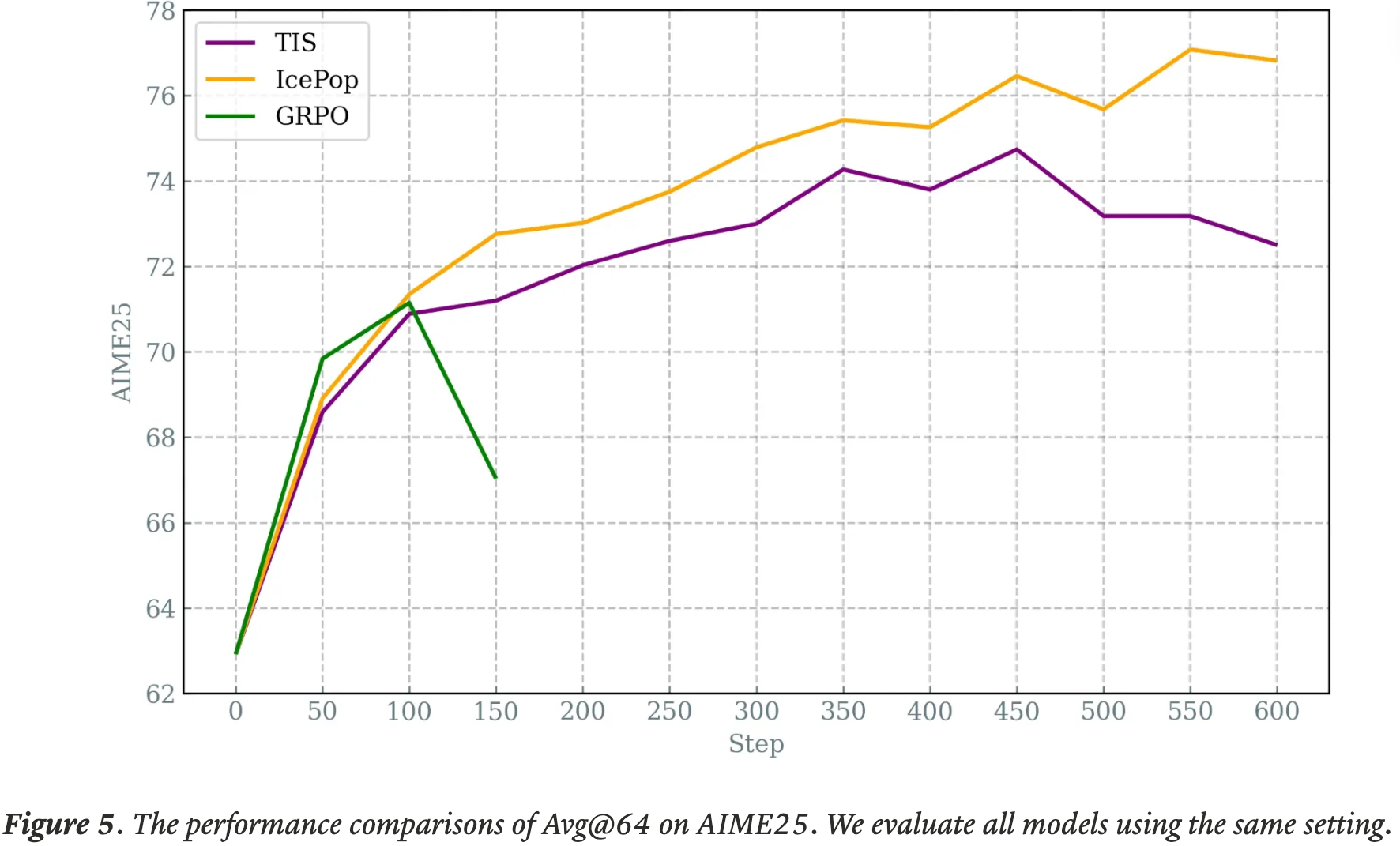
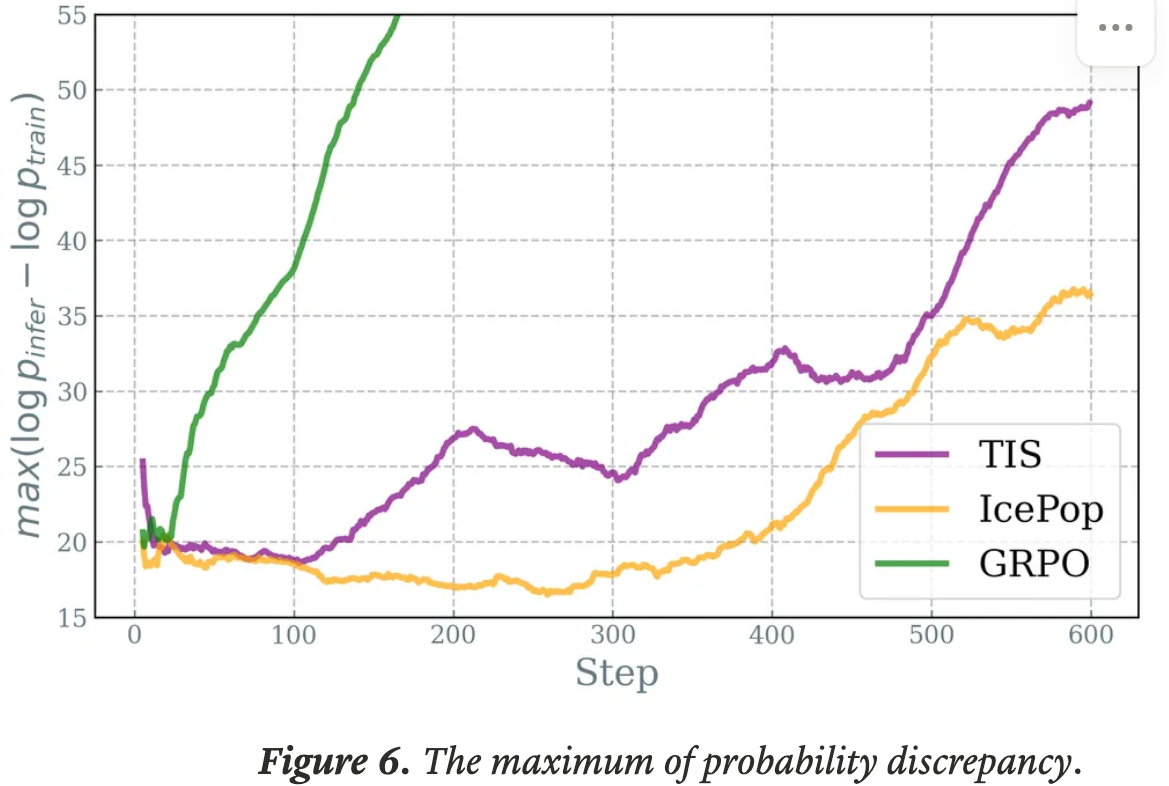
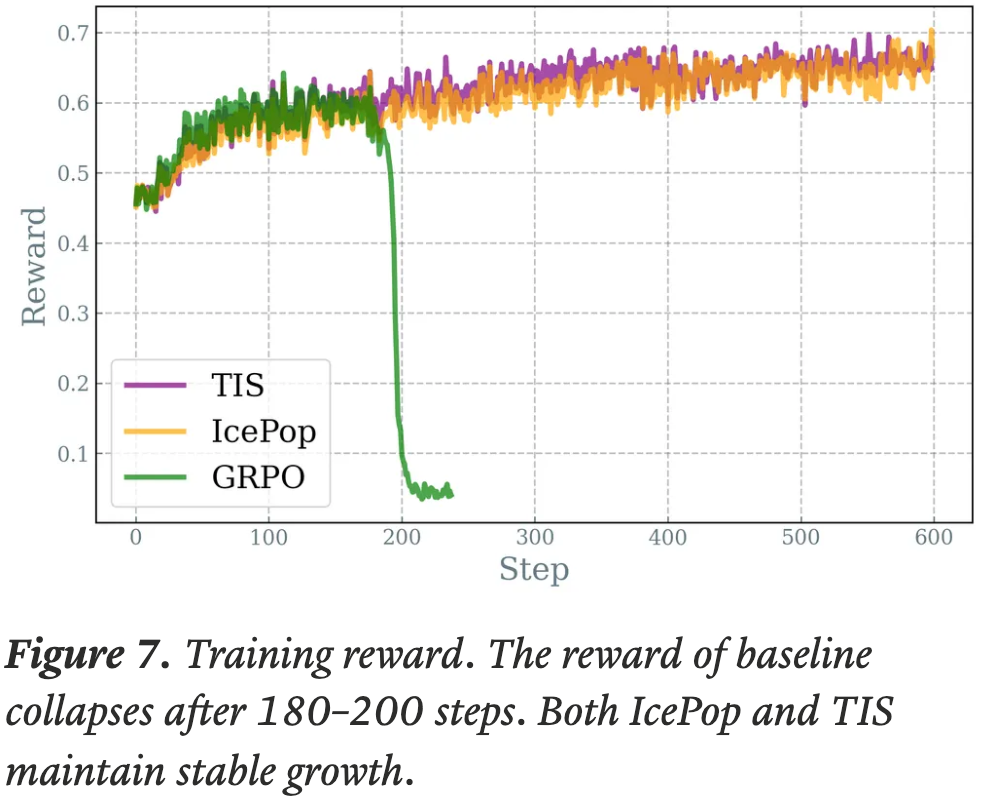
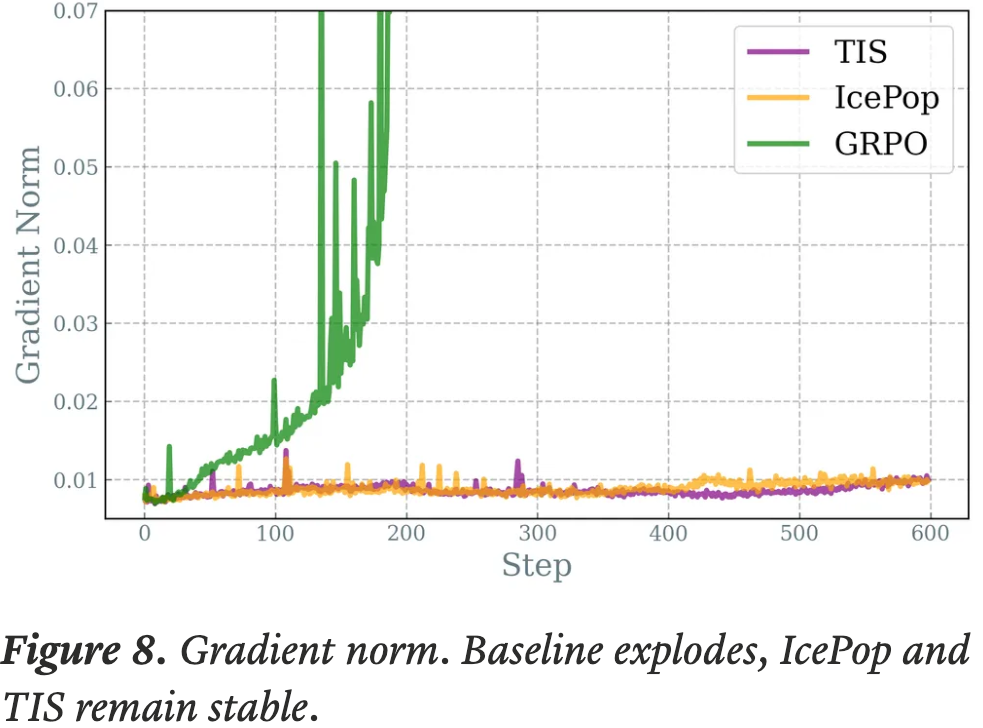
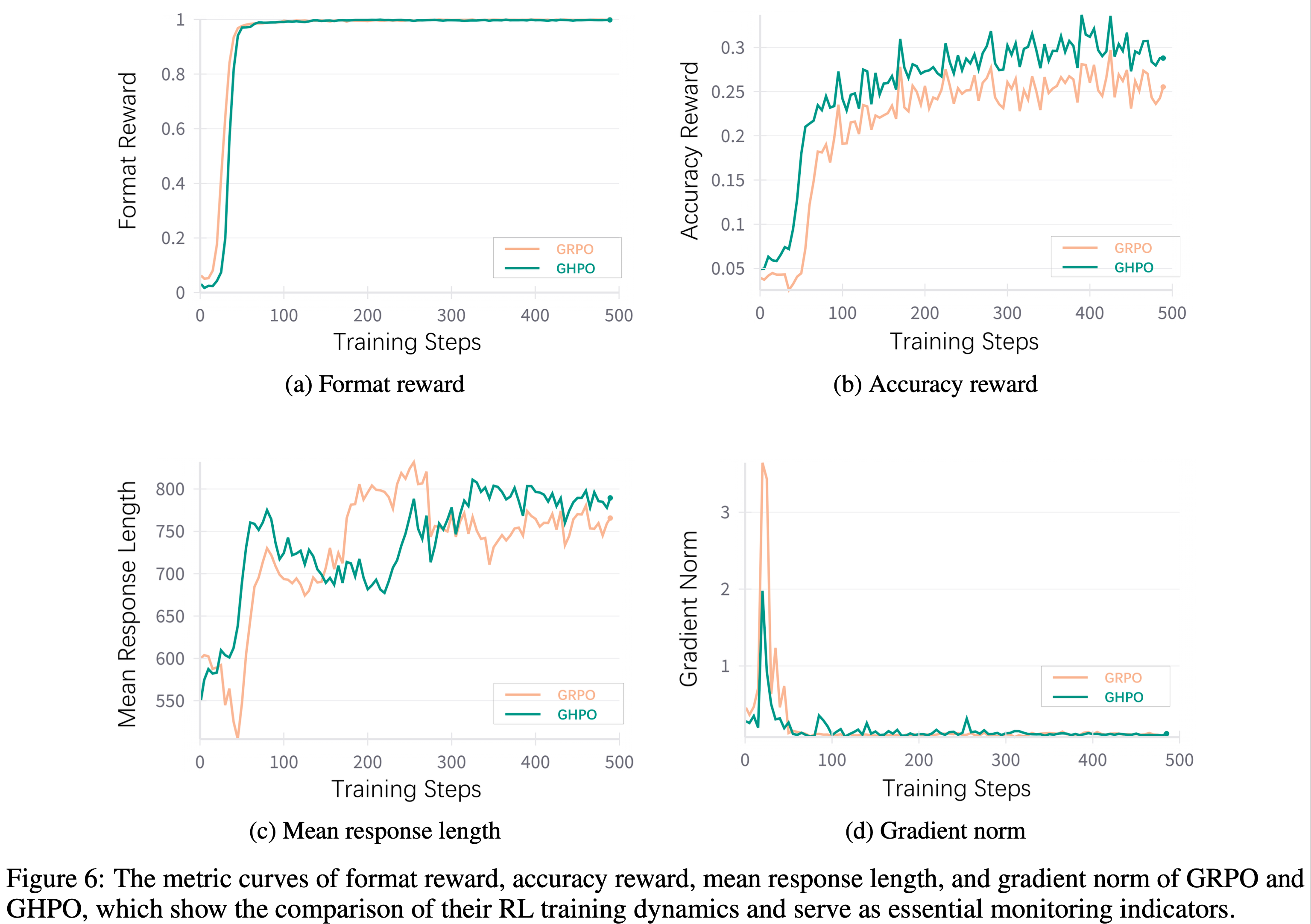
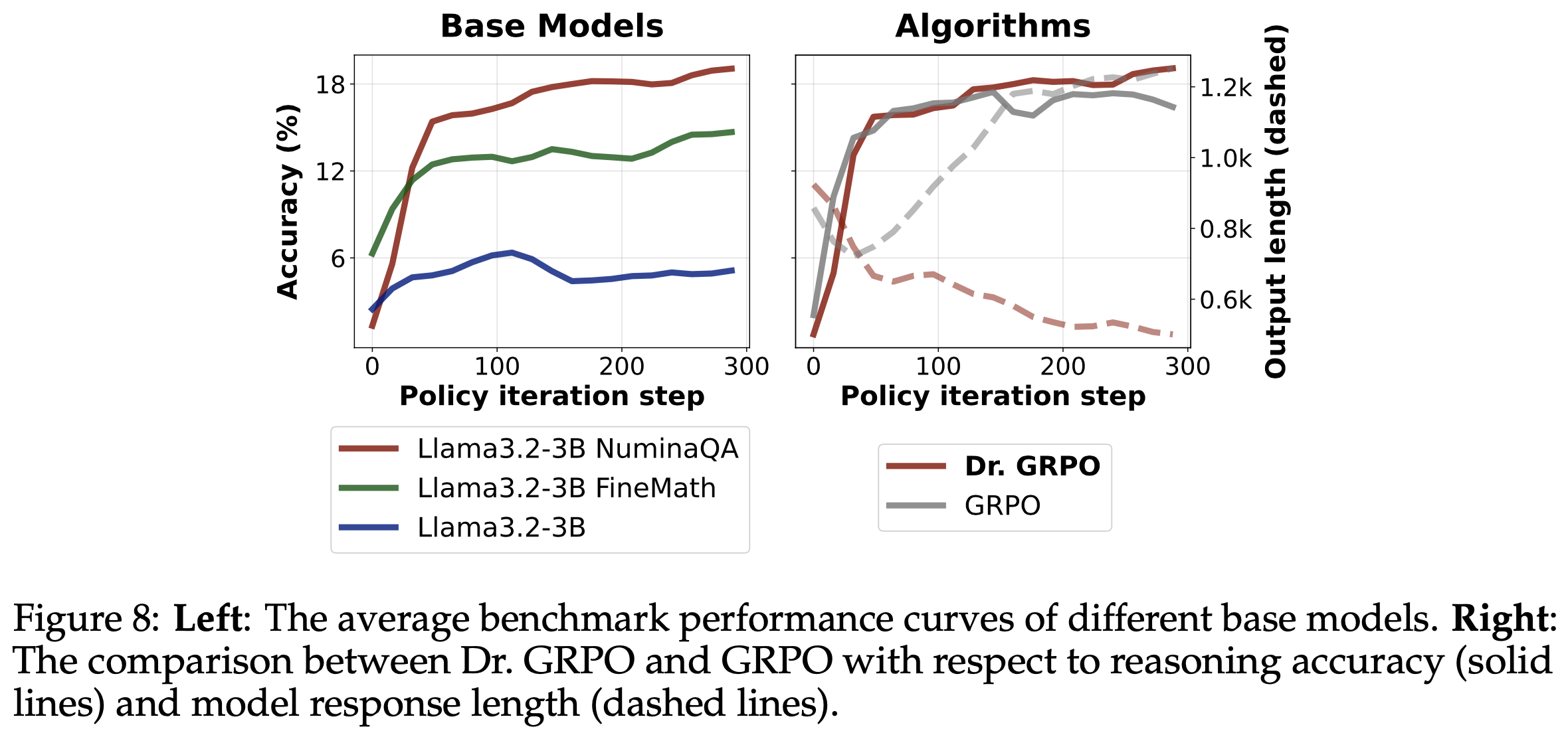
- 结果 :图6 展示了 Dr.GRPO 能有效减轻优化偏差并提升 token 效率
- 论文发现 GRPO 和 Dr.GRPO 均表现出与 DeepSeek-R1-Zero(2025)相似的趋势,即响应长度随训练奖励增加(图1 & 2)
- GRPO 在奖励提升放缓时仍持续生成长响应(图2)
- 尽管这种现象常被称为 RL 中长链式思维的“涌现”(2025 等),作者认为这也与优化中的响应级长度偏差(3.1 节)有关
- 相比之下,通过计算无偏策略梯度,Dr.GRPO 防止了训练中响应长度的无限制增长(图2)
- 此外,在评估基准上,Dr.GRPO 显著减少了错误响应的长度(图4),表明无偏优化器还能减轻过度思考(Chen 等, 2024)
A Duet of Template and Question Set Coverage in RL dynamics(模板与问题集覆盖在 RL Dynamics 中的双重作用)
- 回想 Qwen2.5-Math Base Models 无需任何提示模板即可高准确率回答问题(2.2 节)
- 基于这一有趣现象,论文研究不同模板如何影响 RL 训练
- 鉴于普遍认为更大的问题集覆盖能带来更好性能(2025 等),论文还研究了不同模板与不同问题集覆盖水平的交互

- 实验设置 :从 Qwen2.5-Math-1.5B Base Models 出发,分别应用 R1 模板、Qwen-Math 模板和无模板运行 Dr.GRPO 的 RL。所有实验针对表3 中不同问题集重复进行
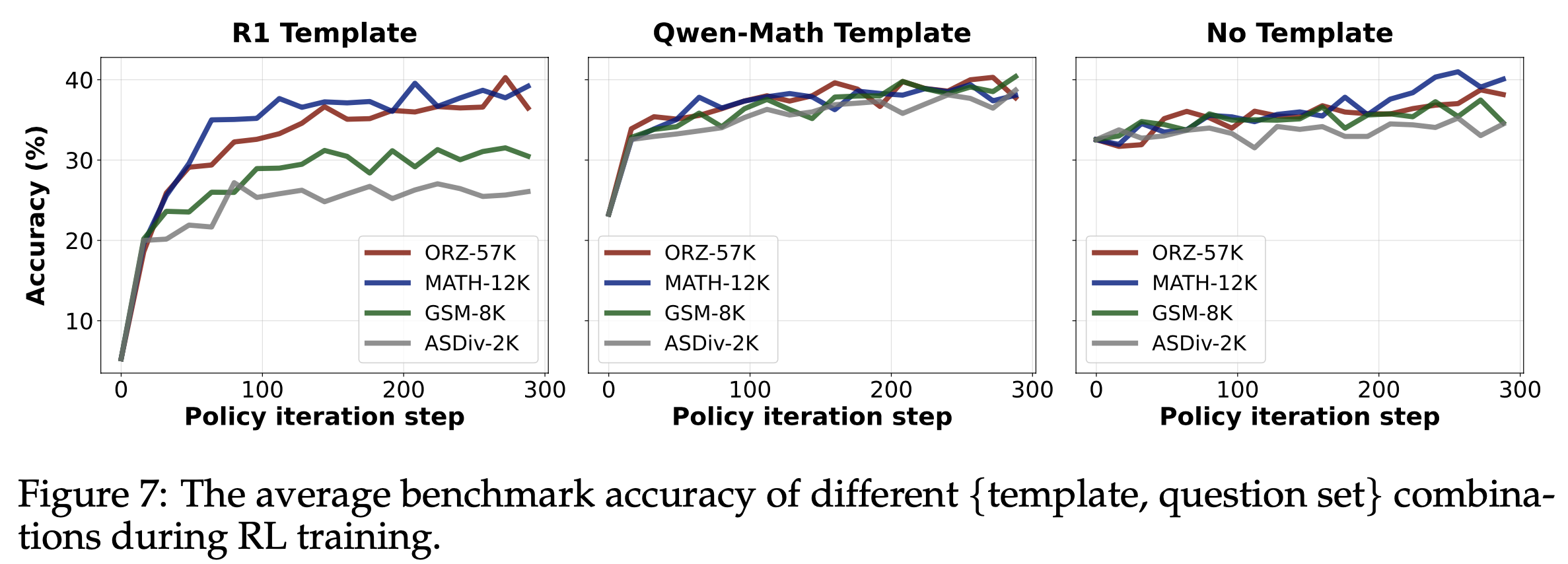
- 结果 :图7 展示了不同设定下的 RL 曲线(注:图中的数据集是训练集,不是测试集),论文得出以下观察:
- 1)模板决定初始策略性能,但 RL 可将所有策略提升至约 40%(给定合适问题集);
- 2)使用 R1 模板时,问题集对 RL 动态影响显著,覆盖过窄会导致较低的平台性能;使用 Qwen-Math 模板时,最佳最终性能通过在 GSM-8K 为训练集的 RL 实现,表明在更简单(且分布外)问题上训练可大幅提升(近翻倍)困难问题的测试准确率
- 由此论文得出以下见解:
- Qwen2.5-Math-1.5B Base Models 已具备强大数学求解能力(见图7 右图起点)。应用模板实际上会破坏此能力,RL 可以重建这个能力。这意味着我们在宣称纯 RL 带来的巨大增益时应更加谨慎
- 当 Base Models 与模板严重不匹配(如 R1 模板与 Qwen2.5-Math-1.5B),策略改进主要来自 RL-tuning ,因此需要问题集具有良好的覆盖(图7 左图)。
- 当 Base Models 与模板匹配时:即使是 Completely OOD 的小问题集也能通过强化正确推理行为(而非灌输新知识)同样有效地诱导推理能力
When there is a large mismatch between base models and templates (e.g., R1 template mismatches Qwen2.5-Math-1.5B), the policy improvement mainly comes from RL- tuning, thus requiring question set to have good coverage (left plot of Fig. 7). Otherwise, even a small and completely o.o.d. question set could induce the reasoning ability equally well, by reinforcing correct reasoning behaviors instead of infusing new knowledge.
- 理解:这里是在说,RL 主要是在激活模型的推理能力,如果模板匹配,则我们进需要很少的数据集就能激活这个能力;但如果不匹配,则需要较为全面的数据来重构这个能力
- 质疑:这里训练步数太少了,看着大家的效果都还没有收敛呢
Domain-Specific Pretraining Improves RL Ceiling
- 近期成功的 R1-Zero-like 数学推理复现大多采用 Qwen2.5 Base Models 作为初始策略(2025等),这些模型已是强大的数学求解器并表现出自我反思模式(2.2 和 2.3 节)
- 本节我们探索另一面:
- R1-Zero-like 训练能否在原本较弱(数学推理方面)的 Base Models 上成功?
- 回答是肯定的 ,论文还观察到数学预训练会提高 RL 的上限
- 实验设置 :论文以 Llama-3.2-3B Base Models 为起点,分别用不同数据集进行预训练得到不同的领域模型,然后使用无偏 Dr.GRPO 算法和 R1 模板进行 RL-tuning
- Llama-3.2-3B :基础模型
- Llama-3.2-3B-FineMath :在 FineMath 数据集(2025)上对 Llama-3.2-3B 持续预训练(continual pretrained model,CPT)得到的模型
- 论文假设领域特定预训练有助于 RL,因此特意训练了 Llama-3.2-3B-FineMath
- Llama-3.2-3B-NuminaQA :在基于 NuminaMath-1.5 的 concatanated Question-Answer 文本数据集上以学习率 1e-5 对 Llama-3.2-3B-FineMath 持续预训练 2 轮
- 理解:论文假设了 Qwen2.5 模型可能预训练于 concatanated Question-Answer 文本,所以类似地利用 NuminaMath-1.5(2024)数据集生成 concatanated 数据集来训练一个基础模型用于测试 RL
- 理解:论文假设了 Qwen2.5 模型可能预训练于 concatanated Question-Answer 文本,所以类似地利用 NuminaMath-1.5(2024)数据集生成 concatanated 数据集来训练一个基础模型用于测试 RL
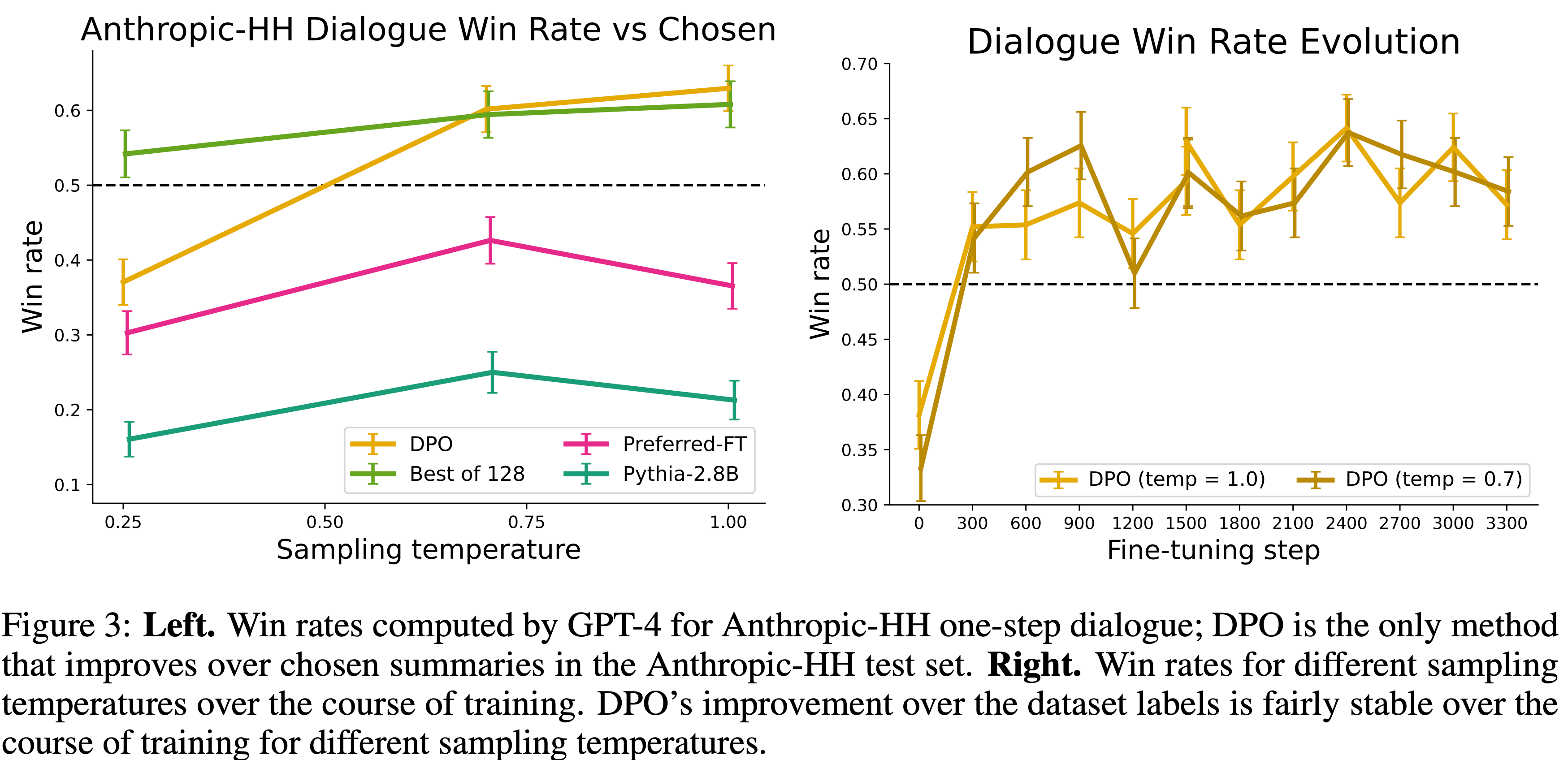
- 结果 :图8 左图展示了不同 Base Models 的 RL 曲线
- 论文发现 RL 甚至能改进原始 Llama Base Models,但增益有限
- 理解:增益有限的原因是因为 Llama Based 模型较差,难以生成正确回复
- 通过持续预训练(及 concatanated 持续预训练)嵌入数学领域知识后,Llama 模型展现出更强的 RL 性能,验证了论文的假设(假设是基础模型决定了 RL 上限)
- 论文还用 Llama Base Models(Llama-3.2-3B-NuminaQA)重新审视 GRPO 的优化偏差
- 图8 右图比较了 GRPO 和 Dr.GRPO 在模型性能和响应长度上的表现
- 可以清晰看到 GRPO 会产生“double-increase”现象(性能和输出长度),可能导致在 Llama 模型上数学预训练后长链式思维“涌现”的误解
- 遗憾的是,长度增加可能源于优化偏差(3.1 节),而提出的 Dr.GRPO 能有效缓解此问题(3.2 节和图8 右图)
- 论文发现 RL 甚至能改进原始 Llama Base Models,但增益有限
附录A:策略梯度推导
- 在 LLM 后训练的 RL 中,论文通常最大化以下目标函数:
$$
\mathcal{J}(\pi_{\theta}) = \mathop{\mathbb{E} }_{\mathbf{q}\sim p_{Q} } \left[\mathop{\mathbb{E} }_{\mathbf{o}\sim \pi_{\theta}(\cdot|\mathbf{q})}[R(\mathbf{q}, \mathbf{o})]\right], \tag{4}
$$- \( R(\mathbf{q}, \mathbf{o}) = \sum_{t=1}^{|\mathbf{o}|} r(\mathbf{q}, \mathbf{o}_{ < t}) \) 是轨迹 \(\mathbf{q};\mathbf{o}\) 的回报(Sutton 2018),而 \( r(\mathbf{q}, \mathbf{o}_{ < t}) \) 表示响应 \(\mathbf{o}\) 中第 \( t \) 个 token 的 token-level 奖励
- 方程(4)的蒙特卡洛策略梯度(Sutton 2018)为:
$$
\begin{split}
\nabla_{\theta}\mathcal{J}(\pi_{\theta}) &= \mathop{\mathbb{E} }_{\mathbf{q}\sim p_{Q} } \left[\mathop{\mathbb{E} }_{\mathbf{o}\sim \pi_{\theta}(\cdot|\mathbf{q})}[\nabla_{\theta} \log \pi_{\theta}(\mathbf{o}|\mathbf{q}) R(\mathbf{q}, \mathbf{o})]\right] \\
&= \mathop{\mathbb{E} }_{\mathbf{q}\sim p_{Q} } \left[\mathop{\mathbb{E} }_{\mathbf{o}\sim \pi_{\theta}(\cdot|\mathbf{q})}[\nabla_{\theta} \sum_{t=1}^{|\mathbf{o}|} \log \pi_{\theta}(o_{t}|\mathbf{q}, \mathbf{o}_{ < t}) R(\mathbf{q}, \mathbf{o})]\right] \\
&= \mathop{\mathbb{E} }_{\mathbf{q}\sim p_{Q} } \left[\mathop{\mathbb{E} }_{\mathbf{o}\sim \pi_{\theta}(\cdot|\mathbf{q})}[\sum_{t=1}^{|\mathbf{o}|} \nabla_{\theta} \log \pi_{\theta}(o_{t}|\mathbf{q}, \mathbf{o}_{ < t}) \sum_{t’=t}^{|\mathbf{o}|} r(\mathbf{q}, \mathbf{o}_{\leq t’})]\right] \\
&= \mathop{\mathbb{E} }_{\mathbf{q}\sim p_{Q} } \left[\mathop{\mathbb{E} }_{\mathbf{o}\sim \pi_{\theta}(\cdot|\mathbf{q})} \left[\sum_{t=1}^{|\mathbf{o}|} \nabla_{\theta} \log \pi_{\theta}(o_{t}|\mathbf{q}, \mathbf{o}_{ < t}) \left( \sum_{t’=t}^{|\mathbf{o}|} r(\mathbf{q}, \mathbf{o}_{\leq t’}) - B(\mathbf{q}, \mathbf{o}_{ < t}) \right)\right]\right],
\end{split} \tag{5}
$$- 其中 \( B(\mathbf{q}, \mathbf{o}_{ < t}) \) 是一个减少方差的项,其相对于 \( o_{t} \) 不变,因此:
$$
\begin{split}
\mathop{\mathbb{E} }_{o_{t}\sim \pi_{\theta}(\cdot|\mathbf{q}, \mathbf{o}_{ < t})}[\nabla_{\theta} \log \pi_{\theta}(o_{t}|\mathbf{q}, \mathbf{o}_{ < t}) B(\mathbf{q}, \mathbf{o}_{ < t})] &= \mathop{\mathbb{E} }_{o_{t}\sim \pi_{\theta}(\cdot|\mathbf{q}, \mathbf{o}_{ < t})}[\nabla_{\theta} \log \pi_{\theta}(o_{t}|\mathbf{q}, \mathbf{o}_{ < t})] B(\mathbf{q}, \mathbf{o}_{ < t}) \\
&= [\sum_{o_{t} } \pi_{\theta}(o_{t}|\mathbf{q}, \mathbf{o}_{ < t}) \nabla_{\theta} \log \pi_{\theta}(o_{t}|\mathbf{q}, \mathbf{o}_{ < t})] B(\mathbf{q}, \mathbf{o}_{ < t}) \\
&= [\sum_{o_{t} } \nabla_{\theta} \pi_{\theta}(o_{t}|\mathbf{q}, \mathbf{o}_{ < t})] B(\mathbf{q}, \mathbf{o}_{ < t}) \\
&= [\nabla_{\theta} \sum_{o_{t} } \pi_{\theta}(o_{t}|\mathbf{q}, \mathbf{o}_{ < t})] B(\mathbf{q}, \mathbf{o}_{ < t}) \\
&= [\nabla_{\theta} 1] B(\mathbf{q}, \mathbf{o}_{ < t}) = 0.
\end{split}
$$- 理解:这里证明主要是证明了策略梯度法中,对累计奖励减去任意与动作无关的值都可以保证原始策略梯度是无偏的
- 其中 \( B(\mathbf{q}, \mathbf{o}_{ < t}) \) 是一个减少方差的项,其相对于 \( o_{t} \) 不变,因此:
- 通常,论文设 \( B(\mathbf{q}, \mathbf{o}_{ < t}) = \mathop{\mathbb{E} }_{\mathbf{o}_{\geq t’} \sim \pi_{\theta}(\cdot|\mathbf{q}, \mathbf{o}_{ < t})}[\Sigma_{t’=t}^{|\mathbf{o}|} r(\mathbf{q}, \mathbf{o}_{\leq t’})] \),即当前状态的期望累积奖励(也称为当前状态的价值),并定义 \( A(o_{t}|\mathbf{q}, \mathbf{o}_{ < t}) = \sum_{t’=t}^{|\mathbf{o}|} r(\mathbf{q}, \mathbf{o}_{\leq t’}) - B(\mathbf{q}, \mathbf{o}_{ < t}) \) 为优势。在结果奖励的情况下,\( \Sigma_{t’=t}^{|\mathbf{o}|} r(\mathbf{q}, \mathbf{o}_{\leq t’}) = \sum_{t=1}^{|\mathbf{o}|} r(\mathbf{q}, \mathbf{o}_{\leq t}) = R(\mathbf{q}, \mathbf{o}) \)
- 通过设 \( B(\mathbf{q}, \mathbf{o}_{ < t}) = \text{mean}(\{R(\mathbf{q}, \mathbf{o}_{1}), \ldots, R(\mathbf{q}, \mathbf{o}_{G})\}) \),方程(5)的策略梯度变为:
$$
\nabla_{\theta}\mathcal{J}(\pi_{\theta}) = \mathop{\mathbb{E} }_{\mathbf{q}\sim p_{Q} } \left[\mathop{\mathbb{E} }_{\{\mathbf{o}_{i}\}_{i=1}^{G} \sim \pi_{\theta}(\cdot|\mathbf{q})}[\frac{1}{G} \sum_{i=1}^{G} \sum_{t=1}^{|\mathbf{o}|} \nabla_{\theta} \log \pi_{\theta}(o_{i,t}|\mathbf{q}, \mathbf{o}_{i,<t}) \tilde{A}_{i,t}]\right], \tag{6}
$$- 其中:
$$
\tilde{A}_{i,t} = R(\mathbf{q}, \mathbf{o}_{i}) - \text{mean}(\{R(\mathbf{q}, \mathbf{o}_{1}), \ldots, R(\mathbf{q}, \mathbf{o}_{G})\})
$$- 注:以上公式分母上是删除了原始 GRPO 中的的分母,作为对照,补充原始 GRPO 的优势函数估计为:
$$
\tilde{A}_{i,t} = \frac{R(\mathbf{q}, \mathbf{o}_{i}) - \text{mean}(\{R(\mathbf{q}, \mathbf{o}_{1}), \ldots, R(\mathbf{q}, \mathbf{o}_{G})\})}{\color{gray}{\color{red}{\text{std}(\{R(\mathbf{q}, \mathbf{o}_{1}), \ldots, R(\mathbf{q}, \mathbf{o}_{G})\})}}}.
$$
- 注:以上公式分母上是删除了原始 GRPO 中的的分母,作为对照,补充原始 GRPO 的优势函数估计为:
- 其中:
- 论文采用 PPO(2017b)目标计算方程(6):
$$
\begin{split}
\mathcal{J}(\pi_{\theta}) &= \mathbb{E}_{\mathbf{q} \sim p_{Q}, \{\mathbf{o}_{i}\}_{i=1}^{G} \sim \pi_{\theta_{old} }(\cdot|\mathbf{q})} \\
&\quad \left[\frac{1}{G} \sum_{i=1}^{G} \sum_{t=1}^{|\mathbf{o_i}|} \left\{\min \left[\frac{\pi_{\theta}(o_{i,t}|\mathbf{q}, \mathbf{o}_{i,<t})}{\pi_{\theta_{old} }(o_{i,t}|\mathbf{q}, \mathbf{o}_{i,<t})} \tilde{A}_{i,t}, \text{clip} \left(\frac{\pi_{\theta}(o_{i,t}|\mathbf{q}, \mathbf{o}_{i,<t})}{\pi_{\theta_{old} }(o_{i,t}|\mathbf{q}, \mathbf{o}_{i,<t})}, 1 - e, 1 + e \right) \tilde{A}_{i,t} \right]\right\}\right],
\end{split}
$$- 注意:上述公式中与原始 GRPO 的不同是移除了 \(\color{red}{\frac{1}{|\mathbf{o_i}|}}\)
- 由此论文得出结论:RL 目标中不应出现 std 和 \(|\mathbf{o}|\)
- \(\tilde{A}_{i,t}\)的无偏性 :论文注意到,上述计算的 \(\tilde{A}_{i,t}\) 与 REINFORCE Leave-One-Out(RLOO)(Ahmadian 等, 2024; Kool 等, 2019)的优势函数等价,仅差一个比例因子,该因子可以归入学习率而不影响RL动态。具体来说:
$$
\frac{G}{G-1} \cdot \tilde{A}_{i,t} = \frac{G}{G-1} R(\mathbf{q}, \mathbf{o}_{i}) - \frac{G}{G-1} \frac{1}{G} \sum_{j=1}^{G} R(\mathbf{q}, \mathbf{o}_{j}) = \tilde{A}^{\text{RLOO} }_{i,t}.
$$
附录B:详细基准测试结果
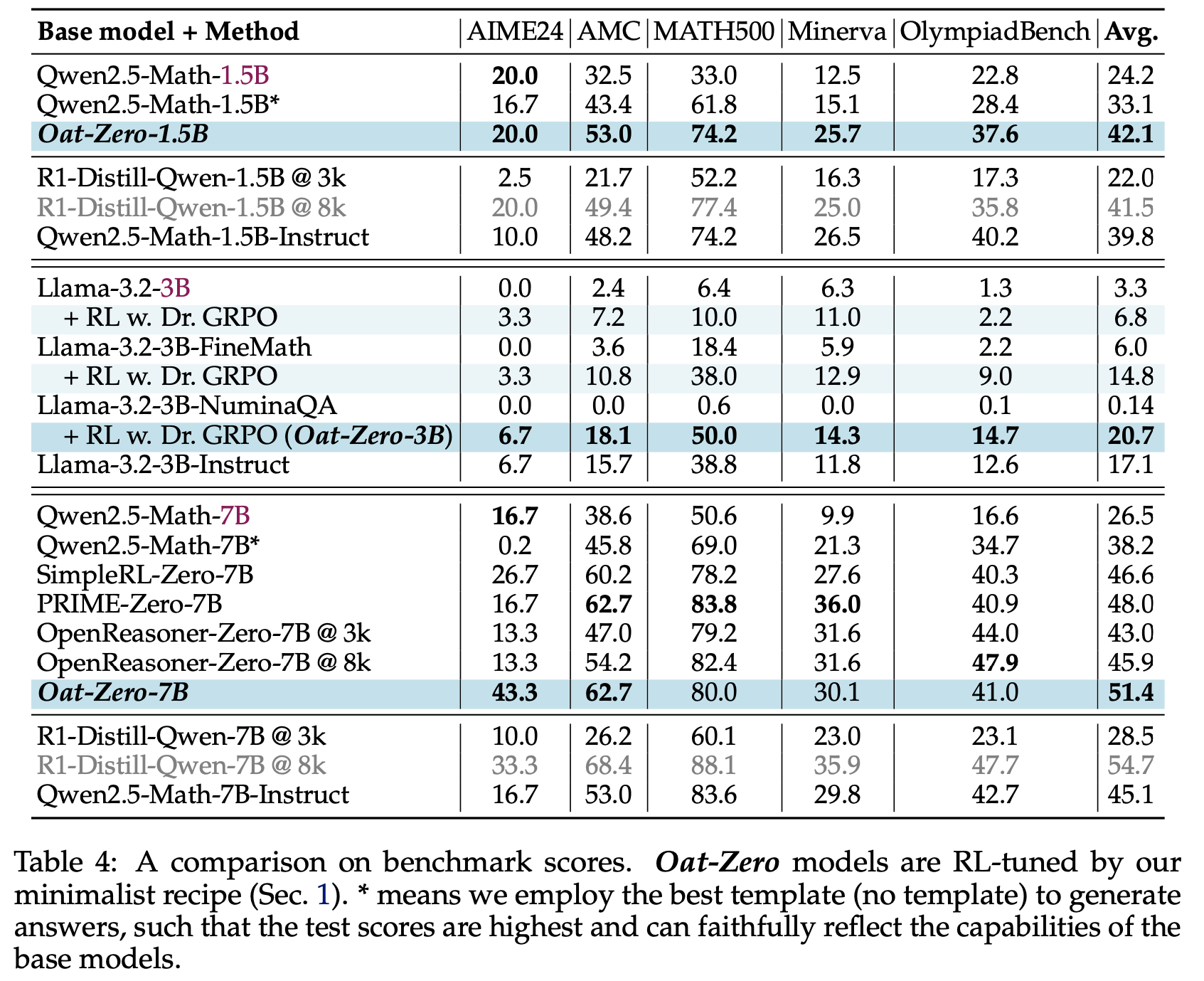
- 论文在表4中展示了三种规模(1.5B、3B和7B)的详细基准测试结果。论文还包含了同规模的指令模型和 R1-Distill 模型作为比较。由于论文使用了上下文长度为 4k 的 Qwen2.5-Math Base Models ,因此将所有基线的 Generation Budget 限制为 3k。对于训练了更长上下文的模型(如OpenReasoner-Zero和R1-Distill-Qwen),论文还 Report 了它们在 8k Generation Budget 下的性能
附录C:基于关键词和 LLM 的自我反思行为检测
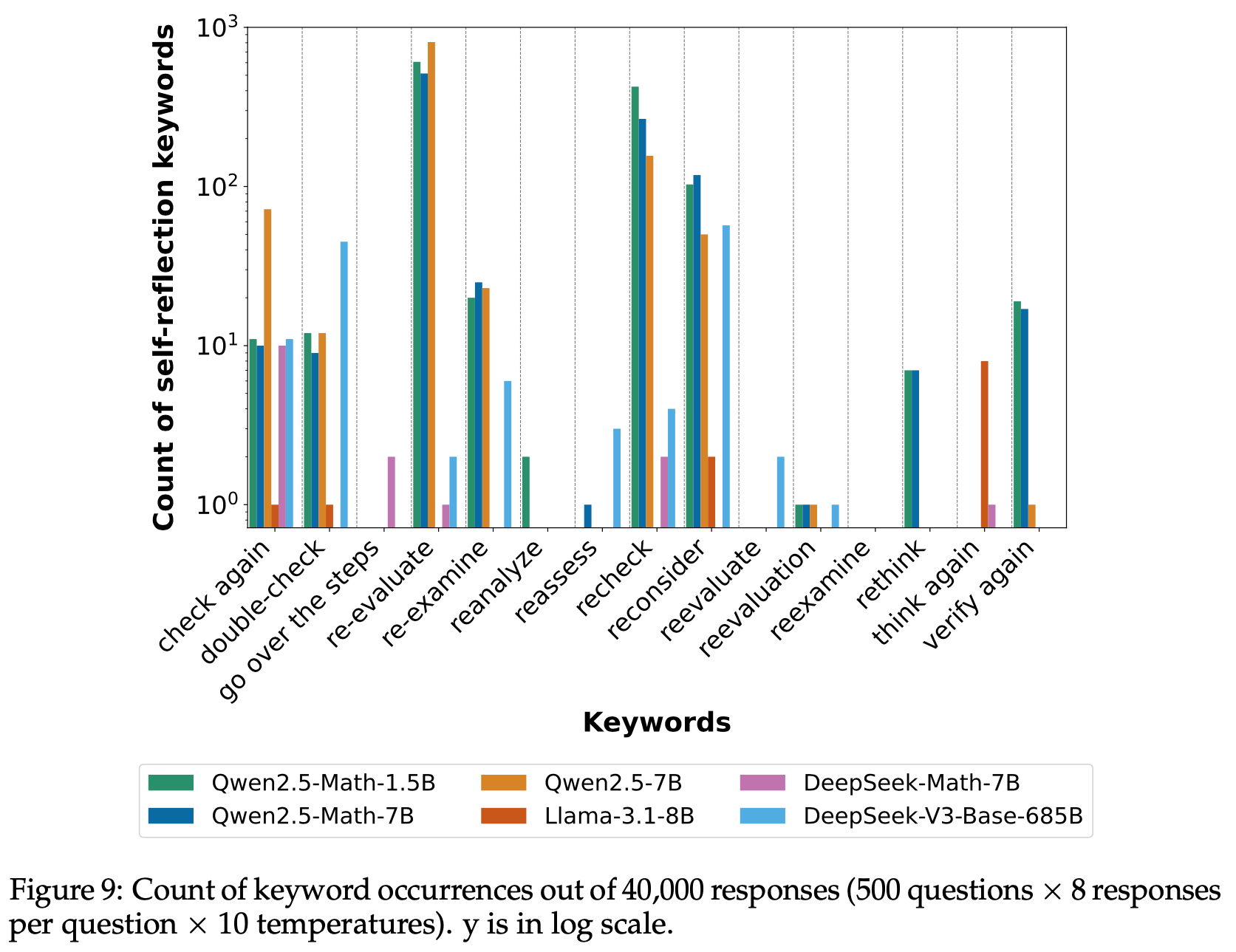
- 论文构建了一个精心选择的关键词和短语池,用于识别 LLM 响应中的自我反思行为。然而,LLM 生成的响应通常包含幻觉和无关内容,导致简单或模糊的关键词可能并不代表真正的自我反思。例如,“wait”和“try again”等术语经常导致误检。为了减少误报,论文保持了一个高度选择性且规模较小的关键词池,仅包含强烈指示自我反思的术语。在论文的实验中,关键词池包括:recheck、rethink、reassess、reevaluate、re-evaluate、reevaluation、re-examine、reexamine、reconsider、reanalyze、double-check、check again、think again、verify again 和 go over the steps
- 我们在图9中展示了不同模型生成回答中各类关键词的出现情况。有趣的是,不同模型家族会侧重不同的关键词。例如:
- “check again”(再次检查)、”double-check”(复核)、”re-evaluate”(重新评估)、”re-examine”(重新审视)、”recheck”(复查)、”reconsider”(重新考虑)以及”verify again”(再次验证)等短语在 Qwen2.5 家族中出现频率最高
- DeepSeek 家族的回复中从未出现”re-evaluate”、”re-examine”和”verify again”等表达
- Llama 模型则频繁使用”think again”(重新思考)这一短语
- 我们推测这种现象源于预训练数据的差异,尤其是与逻辑推理和数学相关的内容部分
- 尽管论文精心选择了关键词池,但仍可能不足以识别某些不包含特定关键词的隐式自我反思行为。此外,它仍可能导致误报,如图10中的案例(a)所示。为了更准确地评估 Base Models 的自我反思能力,论文利用更强的LLM(实验中为gpt-4o-mini)分析响应,判断其是否表现出显式或隐式的自我反思行为。这种方法有助于区分真正的自我反思行为与表面或偶然使用相关术语的情况

- 尽管LLM检测能有效过滤关键词检测的误报并识别隐式自我反思行为,但它仍可能对冗长复杂的响应产生误分类。例如,图10中的案例(b)展示了LLM检测的误报,其中响应被归类为自我反思,但实际上并未表现出自我反思行为。通过关键词检测和 LLM 检测的交叉验证,论文增强了检测的鲁棒性。图11展示了结合两种方法的检测结果
- 问题:Qwen2.5-Math-1.5B 为什么比 Qwen2.5-Math-7B 反思能力还强?
- 理解:Qwen2.5 系列模型并不是针对反思训练的,反思多不代表模型性能更好?
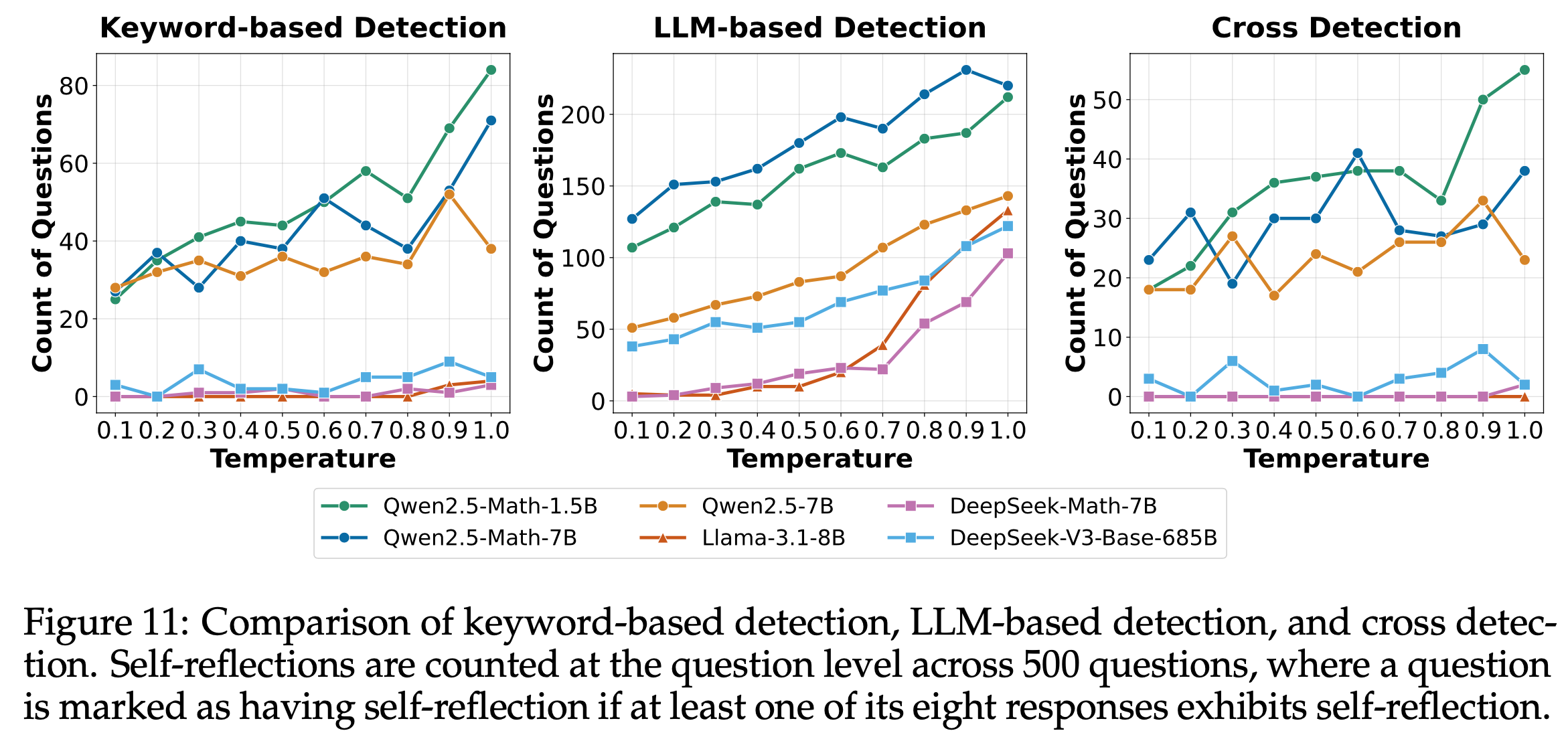
- 理解:Qwen2.5 系列模型并不是针对反思训练的,反思多不代表模型性能更好?
- 问题:Qwen2.5-Math-1.5B 为什么比 Qwen2.5-Math-7B 反思能力还强?
附录D:DeepSeek-V3-Base 与 DeepSeek-R1-Zero 的比较
- 论文分析了 DeepSeek-V3-Base 和 DeepSeek-R1-Zero,以理解 R1-Zero 训练期间模型行为的变化。图12展示了 500 个 MATH 问题在不同难度级别上的响应分类结果。结果表明,大多数错误响应在 RL 训练后被修正,证明了 R1-Zero 训练带来的显著性能提升。同时,论文发现未格式化响应的数量有所增加 ,这与Liu等人(2025b)的观察一致
- 问题:未格式化响应的数量有所增加 是指 RL 训练反而导致 V3-Base 模型的格式遵循能力下降了吗?
- 理解:格式遵循是基础模型就有的能力,并不需要 RL 来训练,RL 时将格式作为奖励的一部分,主要是防止格式下降?

- 理解:格式遵循是基础模型就有的能力,并不需要 RL 来训练,RL 时将格式作为奖励的一部分,主要是防止格式下降?
- 问题:未格式化响应的数量有所增加 是指 RL 训练反而导致 V3-Base 模型的格式遵循能力下降了吗?
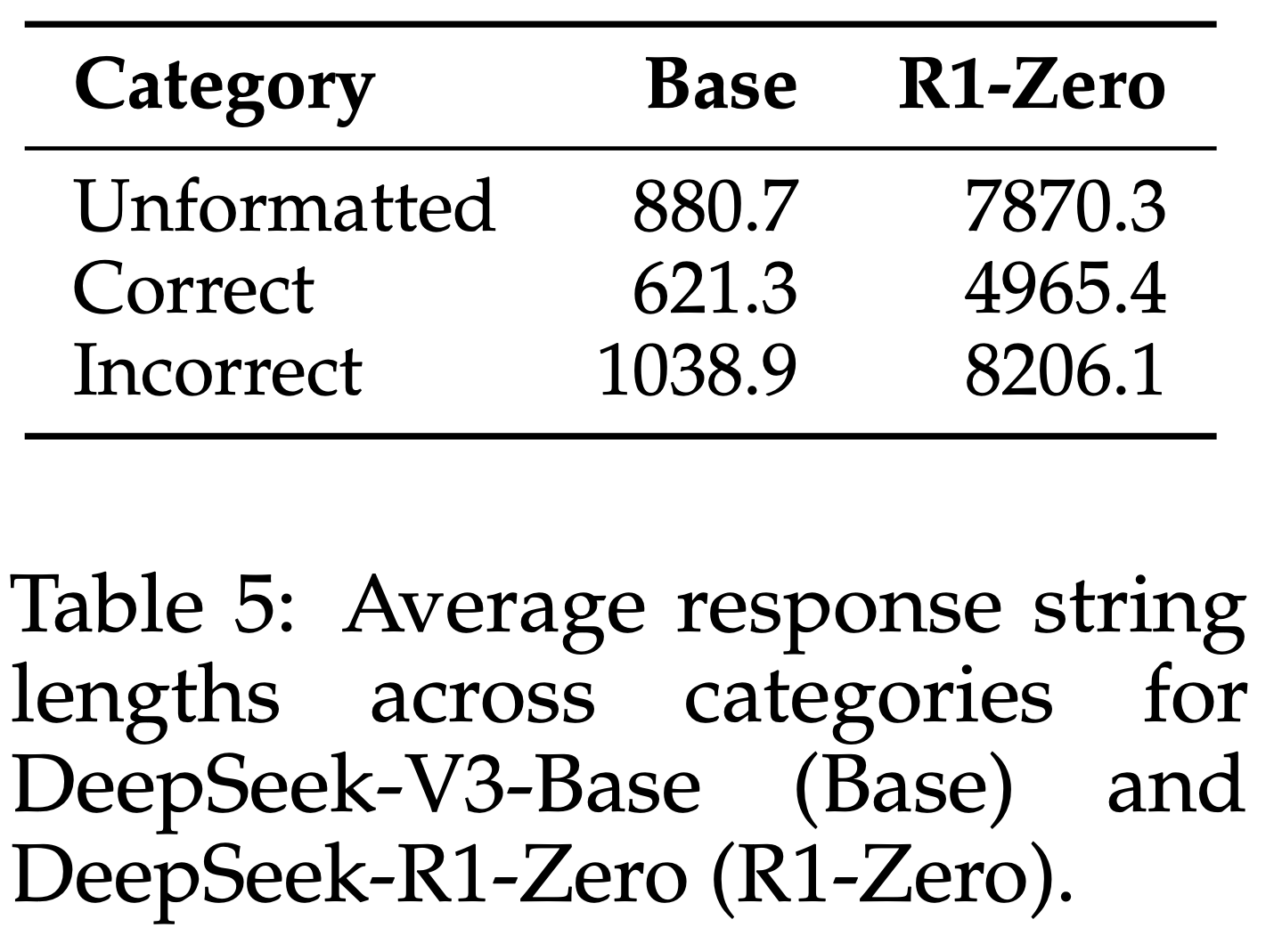
- 表5 Report 了各类别的平均响应长度。结果显示,所有类别的响应长度均显著增加,包括正确响应,这与Guo等人(2025)的图3结果一致。然而,错误响应的平均长度明显长于正确响应。论文猜测这是因为更具挑战性的问题通常需要更长的响应,而错误响应更可能来自较难的问题,从而导致更长的平均长度
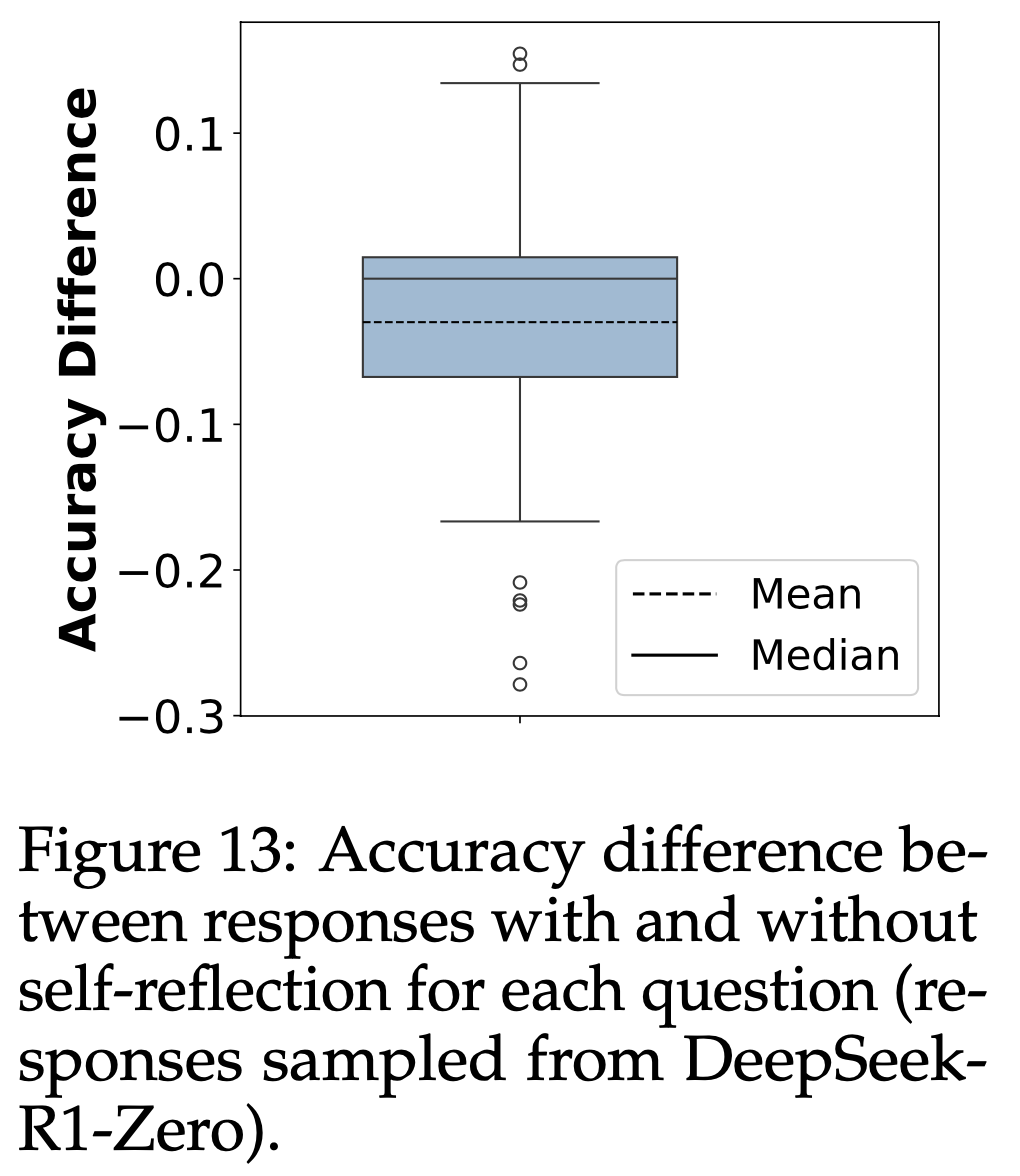
- 自我反思并不一定意味着更高的准确性 :为了研究自我反思行为是否与推理阶段的准确性相关,论文分析了 DeepSeek-R1-Zero 在八次试验中至少引发一次自我反思的问题。对于每个问题,论文采样 100 个响应,并将其分为有自我反思和无自我反思两组。图13展示了每组在每个问题上的准确性差异。结果表明,近一半的自我反思响应并未比无自我反思的响应实现更高的准确性,这表明自我反思并不一定意味着 DeepSeek-R1-Zero 在推理阶段的准确性更高
附录E:Prompts Used for GPT-As-A-Judge
用于检测自我反思行为的 LLM 提示:

上述 Prompt 的基本目标就是使用 GPT 来评估模型是否在自我反思(Self-Reflection),其中文简单总结如下
1
2
3
4
5
6
7我将发送一个数学问题及其详细回答。您的任务是判断回答是否试图解决问题。如果回答偏离主题、包含幻觉、随机内容或其他无关信息,则标记为0。否则,评估回答是否表现出自我反思
分类规则:
1. 类别0:回答偏离主题、无意义、不连贯、过度重复或缺乏逻辑推理
2. 类别1:回答试图解决问题,但未表现出自我反思
3. 类别2:回答表现出任何形式的自我反思(显式或隐式)
4. 类别3:回答仅包含用于计算的Python代码,无自我反思
输出格式:简要说明后跟单个类别编号(0、1、2或3)用于检查模型问答能力的提示:

上述 Prompt 其中文简单总结如下:
1
2
3
4我将发送一个问题和一个由LLM生成的长回答。您的任务是判断输出是否试图回答问题。输出可能包含无关内容、幻觉或随机回答
输出格式:以单个整数(0或1)开头,后跟简要说明
* 返回0:输出未尝试回答问题
* 返回1:输出尝试回答问题(无论是否完整或正确)