注:本文包含 AI 辅助创作
Paper Summary
- 核心总结:
- 论文提出了一种专为训练多轮 LLM-based Agent 设计的创新强化学习算法:ARPO
- 基于作者的前置实验表明,LLM 在工具使用后表现出高 Token 熵
- ARPO 提出基于熵的自适应 Rollout 机制(entropy-based adaptive rollout mechanism),平衡全局和逐步采样,鼓励在高熵工具使用阶段的多样化探索
- ARPO 集成优势归因估计(Advantage Attribution Estimation),使 LLM 能够内化逐步工具使用交互中的优势差异
- 实验表明,在计算推理、知识推理和深度搜索领域的 13 个挑战性基准测试中,ARPO consistently 优于传统 Trajectory-level 强化学习算法
- 特别注意:ARPO 仅需现有方法一半的工具使用训练预算即可实现卓越性能
- 背景:
- 目前已经有大量的工作证明了大规模RLVR 在释放 LLM 处理单轮推理任务潜力方面 的有效性
- 问题提出:
- 在现实推理场景中,LLM 通常可以利用外部工具辅助任务解决过程,但当前的强化学习算法未能充分平衡模型内在的长程推理(long-horizon reasoning)能力与多轮工具交互的熟练度(proficiency)
- 为弥补以上差距,论文提出了一种专为训练 LLM-based 多轮 Agent 设计的新型 Agentic RL 算法:智能体强化策略优化(Agentic Reinforced Policy Optimization, ARPO)
- ARPO 使用基于熵的自适应 Rollout 机制 :
- 通过初步实验,论文观察到 LLM 在与外部工具交互后 ,往往会表现出高度不确定的行为 ,其特征是生成 Token 的熵分布增加
- 受此启发,ARPO 引入了一种基于熵的自适应 Rollout 机制 ,动态平衡全局轨迹采样和 Step-level 采样,从而在工具使用(tool-use)后的高不确定性步骤中促进探索
- ARPO 使用优势归因估计 ,使 LLM 能够内化逐步工具交互中的优势差异
- ARPO 使用基于熵的自适应 Rollout 机制 :
- 实验结论:
- 论文在计算推理、知识推理和深度搜索领域的 13 个挑战性基准测试中验证了 ARPO 的优越性
- 而且,ARPO 仅需现有方法一半的工具使用预算即可实现性能提升,为 LLM-based Agent 与实时动态环境对齐提供了可扩展的解决方案
Introduction and Discussion
- RLVR 展现了释放前沿 LLM 潜力的强大能力,在各类单轮推理任务中表现出色(2024; 2025;)
- 但在开放式推理场景中(2024; 2020;),LLM 不仅需要培养长程规划和自适应决策技能,还需参与与外部工具环境的动态多轮交互
- 为应对这些挑战,智能体强化学习(Agentic Reinforcement Learning, Agentic RL)(2025; 2025)作为一种有前景的训练范式应运而生,将 LLM 训练从静态任务解决转向动态智能体-环境推理的领域(2017; 2025; 2024; 2025; 2025; 2025)
- 当前的 Agentic RL 方法通常采用 Trajectory-level 算法,如 GRPO 或 DAPO(2024; 2025;)
- 这些方法通过预定义的特殊 Token 独立采样完整的工具使用轨迹(tool-use trajectories),并基于最终输出提供奖励信号
- 为解决工具过度使用和稀疏奖励问题(2025),一些研究尝试设计更优雅的奖励函数以更好地对齐工具使用行为(2025;)
- 尽管取得了一定进展,但这些优化往往忽略了训练 LLM-based Agent 的一个关键方面:LLM 与工具环境之间的多轮交互循环(2025;)
- 与单轮推理范式不同,多轮工具交互循环为 LLM 提供了实时多样且信息丰富的反馈
- 这一特性凸显了发现有效逐步工具使用行为的必要性
- 为深入理解 LLM 的 Step-level 工具使用行为,论文受到一系列基于熵的强化学习研究启发(2025; 2025; 2025),并量化了深度搜索任务中 LLM-based 搜索 Agent 在生成 Token 的熵分布变化
- 如图 1(左)所示,LLM 在接收每轮工具调用反馈后生成的初始 Token 始终表现出高熵
- 这表明外部工具调用显著引入了 LLM 推理过程的不确定性,揭示了 LLM-based Agent 中尚未充分探索的潜在行为(2023; 2024; 2025;)
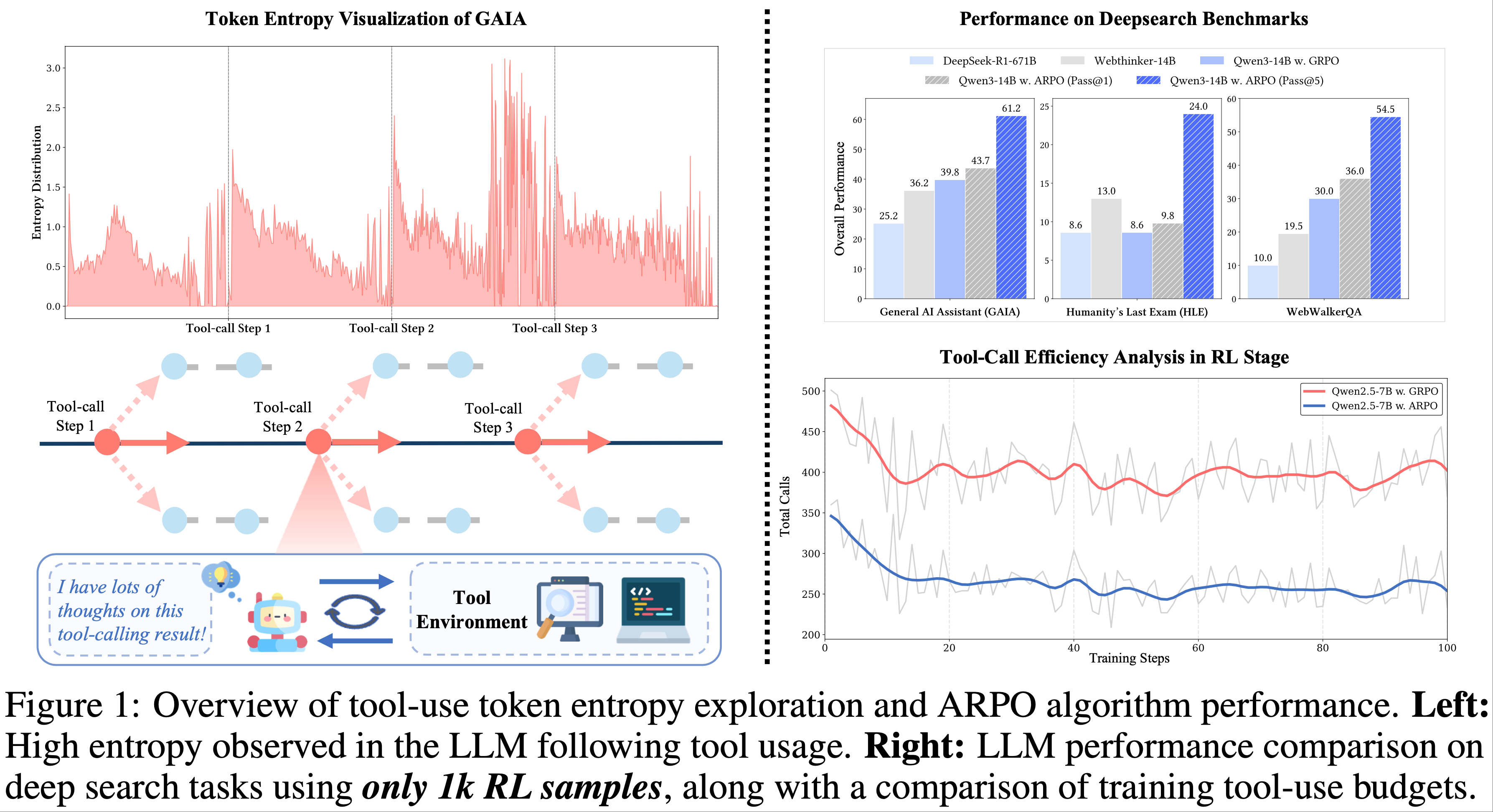
- 遗憾的是,当前的 Trajectory-level 强化学习方法往往过度强调完整 Rollout 采样的比较,而忽视了每个工具使用步骤中细粒度行为的探索(2024; 2024; 2025)
- 这种忽视限制了对齐(更好的)工具使用行为所需的多样性和范围
- 因此,有必要开发一种与智能体-环境交互特性相符的 Agentic RL 算法 ,以充分发挥 LLM-based Agent 潜力
- 论文提出了 ARPO ,专为训练 LLM-based 多轮 Agent 设计的强化学习算法
- ARPO 的核心原则是鼓励策略模型在高熵工具调用轮次中自适应分支采样,从而高效对齐 Step-level 工具使用行为:
- 论文提出了一种基于熵的自适应 Rollout 机制,整合了全局和局部采样视角
- 在 Rollout 阶段,LLM 首先执行多次全局采样,记录每个样本的初始熵分布
- 每次工具调用后,论文进一步监测实时 Token 熵变化,并将其作为分支标准
- 若熵变化超过预定义阈值,模型将执行额外的局部采样以探索更多样化的工具集成推理行为
- 这一设计使 ARPO 能够有效扩展原始采样空间,同时平衡全局和 Step-level 工具使用行为的学习
- 为充分利用自适应采样的优势,论文引入了优势归因估计 :
- 论文探索了 ARPO 的硬优势和软优势设置,为同一推理路径上的 Token 分配共享优势值,而分支路径上的 Token 则分配不同的优势值
- 这一机制鼓励模型内化 stepwise 工具使用行为中的优势差异
- 论文的实验全面评估了计算推理(computational reasoning)、知识推理(knowledge reasoning)和Deep Search三大领域的 13 个数据集
- 图 1(右)展示了深度搜索任务的总体结果
- ARPO 在智能体训练中 consistently surpasses traditional sample-level RL algorithms in agentic training
- ARPO 仅需轨迹级强化学习方法(trajectory-level RL methods)一半的工具调用预算即可达成这一目标,在准确性和效率之间实现了 optimal balance(进一步的扩展分析验证了 ARPO 以可扩展方式增强 LLM 智能体推理的能力)
- 论文的关键贡献如下:
- Token Entropy Quantification(量化分析) :论文量化了 LLM 在智能体推理过程中的 Token 熵变化,揭示了轨迹级强化学习算法(trajectory-level RL algorithms)在对齐 LLM-based 智能体时的固有局限性
- ARPO 算法设计(ARPO Algorithm Design) :
- ARPO 算法使用了基于熵的自适应 Rollout 机制(entropy-based adaptive rollout mechanism),在保持全局采样(global sampling)的同时,鼓励在高熵工具使用步骤进行分支采样(branch sampling);
- ARPO 采用优势归因估计(Advantage Attribution Estimation),帮助 LLM 更好地内化逐步工具使用行为中的优势差异
- Theoretical Foundation :作者从理论上证明了 ARPO 算法在 LLM-based 智能体训练中的适用性:
- Empirical Validation :在 13 个具有挑战性的基准测试中,ARPO 优于主流强化学习算法,同时仅需一半的工具使用训练预算,这为探索智能体强化学习算法提供了 practical insights
Preliminary
Agentic RL
- 论文将 Agentic RL 的训练目标表述为:
$$
\max_{\pi_{\theta} }\mathbb{E}_{x\sim\mathcal{D},y\sim\pi_{\theta}(\cdot|x;T)} \left[r_{\phi}(x,y)\right]-\beta\mathbb{D}_{\text{RL} }\left[\pi_{\theta}(y \mid x;T),|,\pi_{\text{ref} }(y \mid x;T)\right],
$$- \(T\) 表示可用工具集合
- \(\pi_{\theta}\) 表示策略 LLM
- \(\pi_{\text{ref} }\) 是参考 LLM
- \(r_{\phi}\) 表示奖励函数
- \(\mathbb{D}_{\text{RL} }\) 表示 KL 散度
- \(x\) 是输入,从数据集 \(\mathcal{D}\) 中采样
- \(y\) 是对应的输出,可能穿插工具调用反馈
- 与传统强化学习方法仅依赖 LLM Rollout 不同, Agentic RL 在推理过程中整合了工具调用反馈(2023; 2024; 2025;)。 Rollout 采样可分解为:
$$
P_{\theta}(\mathcal{R},y \mid x;T) = \underbrace{\prod_{t=1}^{t_{\mathcal{R} } }P_{\theta}(\mathcal{R}_{t}\mid\mathcal{R}_{ < t},x;T)}_{\text{Agentic Reasoning} } \cdot \underbrace{\prod_{t=1}^{t_{y} }P_{\theta}(y_{t}\mid y_{ < t},\mathcal{R},x;T)}_{\text{Answer Generation} }, \tag{2}
$$- \(\mathcal{R}\) 是长度为 \(t_{\mathcal{R} }\) 的推理轨迹,穿插工具调用反馈
- \(y\) 是长度为 \(t_{y}\) 的最终答案
- 论文的 ARPO 基于规则化强化学习算法(如 GRPO(2024)、Reinforce++(2025))设计,旨在优化 LLM-based Agent
Analyzing Token Entropy in Agentic Reasoning
- Token 熵计算(Calculation) :根据近期基于熵的强化学习研究(2025; ),论文在步骤 \(t\) 计算 Token-level 生成熵:
$$
H_{t}=-\sum_{j=1}^{V}p_{t,j}\log p_{t,j}, \quad \text{ where } {\boldsymbol{p} }_{t}=\pi_{\theta}\left(\cdot \mid \mathcal{R}_{ < t},x;T\right)=\text{Softmax}\left(\frac{ {\boldsymbol{z} }_{t} }{\tau}\right). \tag{3}
$$- \(V\) 是词汇量大小
- \({\boldsymbol{z} }_{t}\in\mathbb{R}^{V}\) 是 softmax 前的 logits
- \(\tau\) 是解码温度
- 特别注意:此熵反映的是 Token 生成分布的不确定性 ,而非特定 Token 的不确定性
- Token 熵的初步实验(Pilot Experiment on Token Entropy) :为深入理解 LLM-based 工具使用智能体的推理过程,论文进行了初步研究,涉及两类智能体:
- 一类使用搜索引擎处理知识密集型任务;另一类使用 Python 解释器处理计算任务
- 论文测量了推理过程中 Token 熵的变化以评估不确定性
- 如图 2 所示,论文的关键观察如下:
- 1)每次工具调用后的前 10-50 个 Token 中,熵急剧上升;
- Ob.1 归因:外部反馈与模型内部推理之间的分布偏移
- 2)在早期推理阶段,熵趋于增加,但仍低于接收工具调用反馈后的水平;
- Ob.2 归因:偏移引入的不确定性通常超过原始输入的不确定性
- 3)搜索反馈比 Python 反馈引入更多不确定性
- Ob.3 归因:搜索引擎通常返回信息丰富的文本内容 ,而 Python 输出由确定性数字组成 ,导致前者熵波动更大(Ob.3)
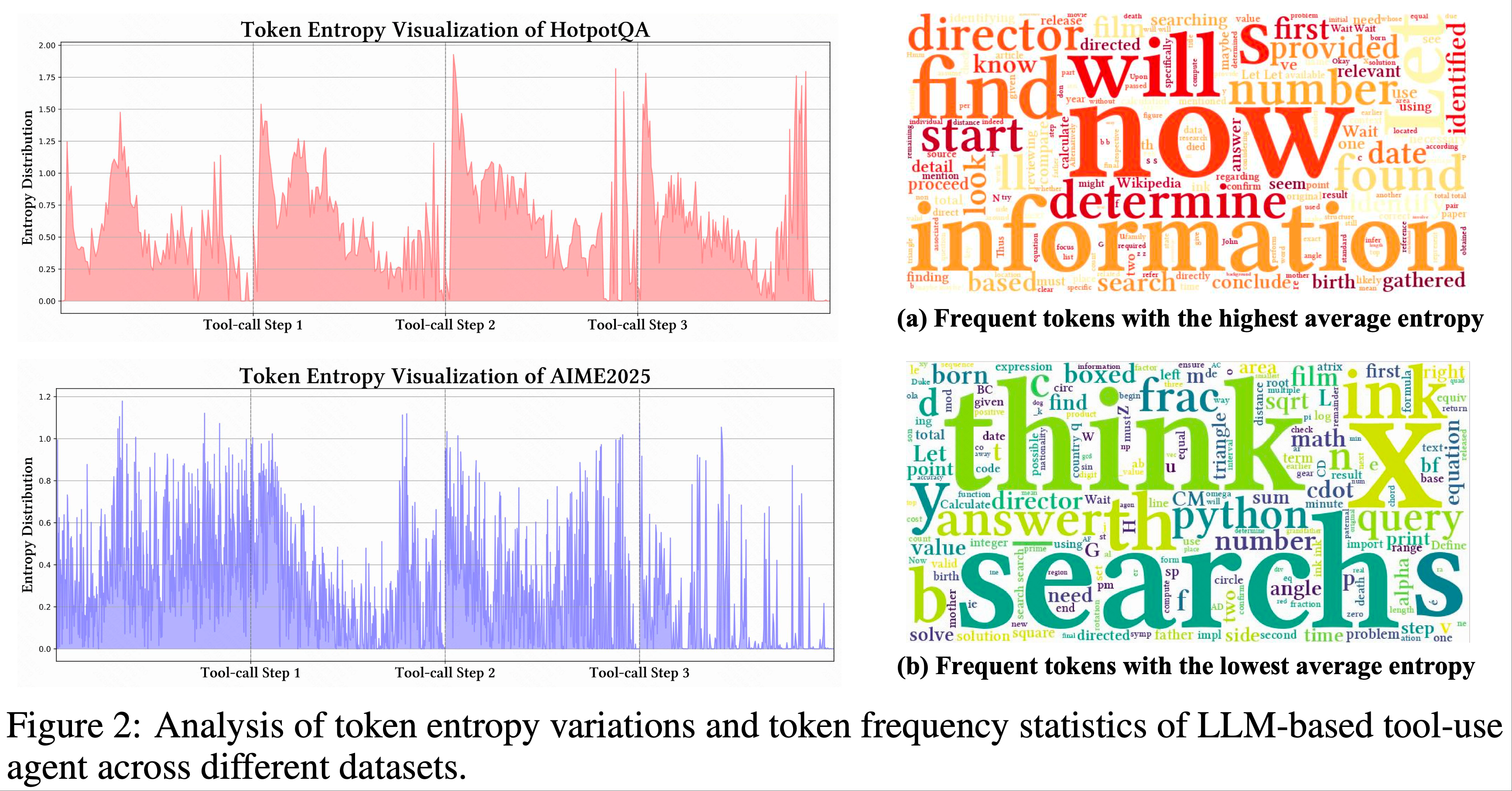
- Ob.3 归因:搜索引擎通常返回信息丰富的文本内容 ,而 Python 输出由确定性数字组成 ,导致前者熵波动更大(Ob.3)
- 1)每次工具调用后的前 10-50 个 Token 中,熵急剧上升;
- 这些发现凸显了 Trajectory-level 强化学习方法的局限性,其关注初始推理而忽视了工具调用反馈引入的不确定性
- 论文提出的 ARPO 算法通过结合基于熵的探索来解决这一问题,该探索专为 LLM 智能体训练定制
Agentic Tool Design
- 在本工作中,论文主要关注优化 LLM-based 工具使用智能体的训练算法
- 通过对 Agentic RL 研究(2025;)进行全面回顾后,论文确定了三个代表性工具来实证评估 ARPO 的有效性:
- Search Engine :通过执行网络查询来检索相关信息
- Web Browser Agent :访问并解析搜索引擎返回的相关网页链接,提取并总结关键内容
- 代码解释器(Code Interpreter) :自动执行语言模型生成的代码,返回执行结果(执行成功)或编译器错误信息(执行失败)
ARPO(Agentic Reinforced Policy Optimization)
- ARPO 算法 旨在通过基于熵的引导,指导 LLM 探索逐步的工具使用行为,如图 3 和图 4 所示:
- Entropy-based Adaptive Rollout :受初步实验(章节2.2)中观察到的熵变化启发,ARPO 扩展了传统的 Rollout 过程,不仅进行 Trajectory-level 采样,还在高熵的工具使用步骤进行分支采样
- 通过平衡全局和局部采样,ARPO 鼓励更广泛的工具使用行为探索
- 优势归因估计(Advantage Attribution Estimation) :为了更好地适应自适应 Rollout 机制,论文提出了优势归因估计,使模型能够更有效地内化逐步工具使用行为的优势差异
- Theoretical Analysis :为了建立 ARPO 的理论基础,论文提供了一个形式化分析,证明 ARPO 在多轮训练场景中对 LLM-based Agent 具有良好的适应性
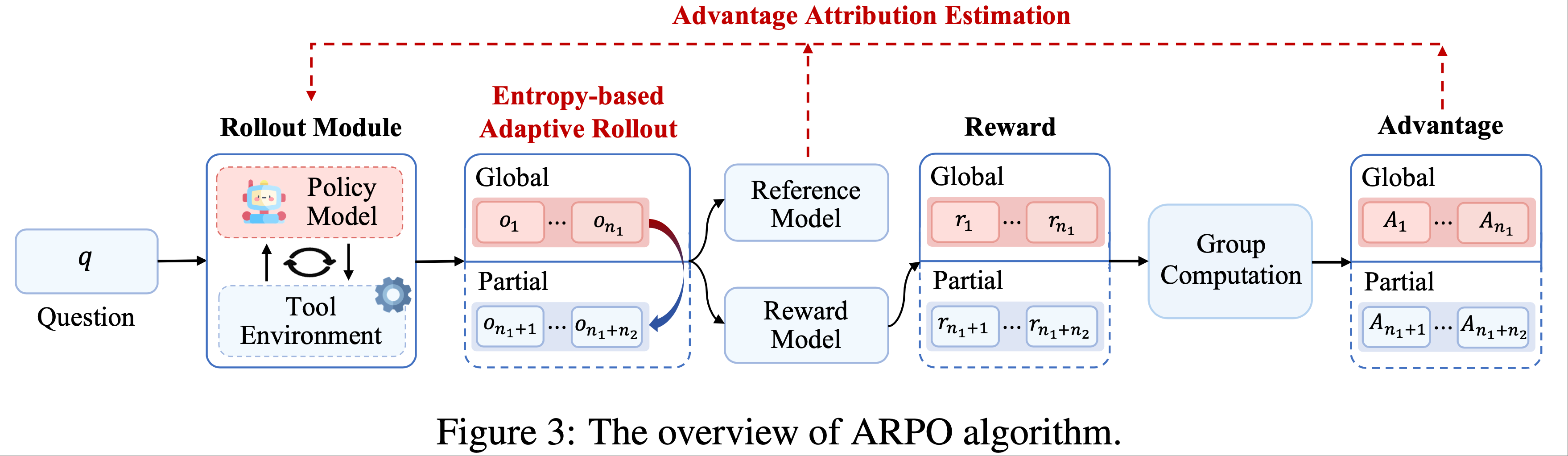
- Entropy-based Adaptive Rollout :受初步实验(章节2.2)中观察到的熵变化启发,ARPO 扩展了传统的 Rollout 过程,不仅进行 Trajectory-level 采样,还在高熵的工具使用步骤进行分支采样
- 以下论文将详细介绍论文的方法
Entropy-based Adaptive Rollout
- 受初步实验(章节2.2)的启发,论文在 Rollout 阶段同时引入 Trajectory-level 采样和基于熵的局部采样,以覆盖更全面的采样范围
- 该机制的设计包含以下四个核心步骤:
- (1) Rollout Initialization :给定全局 Rollout 大小为 \( M \),LLM 首先基于输入问题 \( q \) 通过 Trajectory-level 采样生成 \( N \) 条轨迹,剩余的 \( M-N \) 条轨迹预算保留用于局部采样
- 随后,论文使用公式 3 计算每条轨迹中前 \( k \) 个 Token 的熵,形成初始熵矩阵 \( H_{\text{initial} } \in \mathbb{R}^{1 \times k} \)
- (2) 熵变化监测(Entropy Variation Monitoring) :记录初始熵后,模型按照公式 2 的定义与工具进行 Agent 推理
- 为了持续监测每次工具调用后的熵动态变化,论文允许模型在拼接工具调用响应后生成额外的 \( k \) 个 Token
- 对于工具调用步骤 \( t \),论文计算 Step-level 熵矩阵 \( H_t \in \mathbb{R}^{1 \times k} \),并通过以下公式量化相对于初始状态的归一化熵变化:
$$
\Delta H_t = \text{Normalize}(H_t - H_{\text{initial} })
$$ - 其中归一化表示将所有 \( \Delta H \) 的值除以词汇量大小 \( V \) 求和,正值表示工具调用步骤 \( k \) 后不确定性增加,负值则表示不确定性降低
- 问题:为什么归一化要除以 词汇量大小 \( V \)?
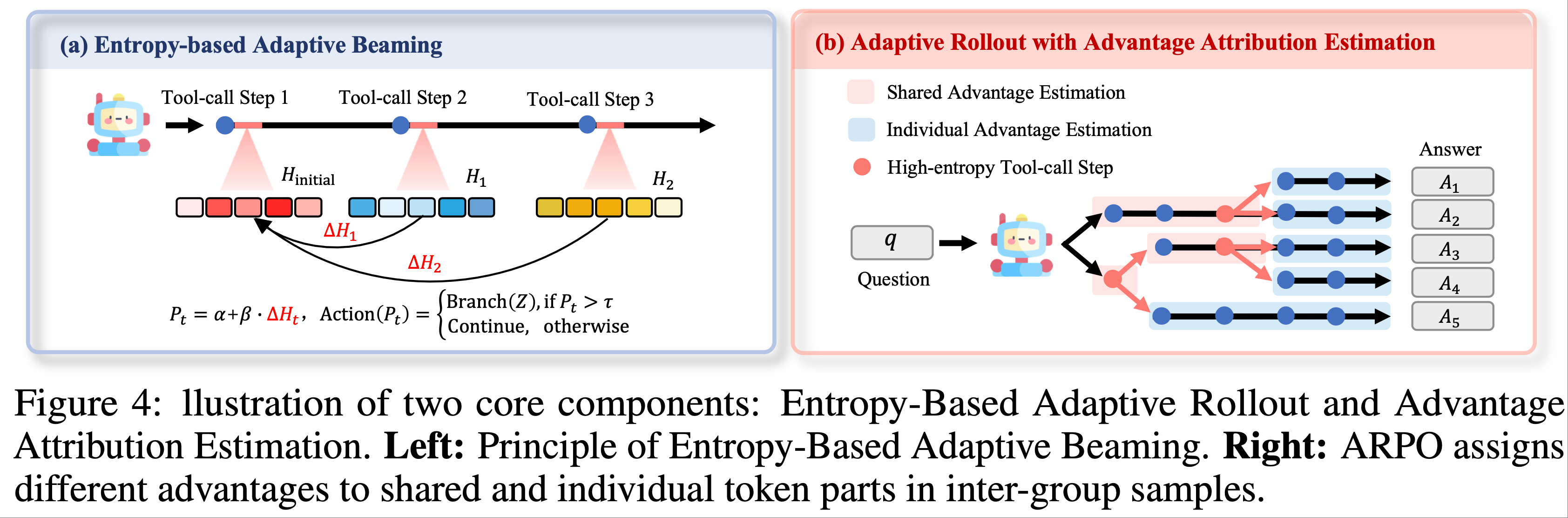
- (3) Entropy-based Adaptive Beaming(束搜索) :为了鼓励在具有有益熵变化的工具使用路径上进行自适应探索,论文定义工具调用步骤 \( t \) 的局部采样概率如下:
$$
P_t = \alpha + \beta \cdot \Delta H_t, \quad \text{Action}(P_t) =
\begin{cases}
\text{Branch}(Z), & \text{if } P_t > \tau \\
\text{Continue}, & \text{otherwise}
\end{cases}
$$- \( \alpha \) 是基础采样概率
- \( \beta \) 是稳定性熵值(stability entropy value)
- 如图 4(a) 所示,模型使用 \( P_t \) 决定其分支行为:
- 当 \( P_t \) 超过预定义阈值 \( \tau \) 时,从当前节点启动 \( \text{Branch}(Z) \),分出来(branching) \( Z \) 条局部推理路径;
- 否则继续沿当前轨迹推进
- 这一机制使模型能够自适应地将探索资源分配到推理空间中信息丰富的区域(推理空间中熵上升的步骤);
- 注:推理空间中熵上升,则表明其潜在信息丰富,这里就是指将探索资源分配到熵上升的 步骤 上
- (4) 终止条件(Termination) :该过程迭代直到满足以下条件之一:
- (1) 如果分叉路径总数 \( \hat{Z} \) 达到局部采样预算 \( M-N \),则停止分支并继续采样直到生成最终答案;
- (2) 如果所有路径在达到 \( M-N \) 前终止,则补充 \( M-N-\hat{Z} \) 条额外的 Trajectory-level 样本以满足条件 (1)
- (1) Rollout Initialization :给定全局 Rollout 大小为 \( M \),LLM 首先基于输入问题 \( q \) 通过 Trajectory-level 采样生成 \( N \) 条轨迹,剩余的 \( M-N \) 条轨迹预算保留用于局部采样
- 通过利用这种高效的 Rollout 机制,ARPO 促进了不确定性感知的探索,使 LLM 能够更有效地识别逐步工具调用行为
- 假设全局扩展大小和每条轨迹的 Token 数为 \( n \),ARPO 将每次 Rollout 的计算复杂度从 Trajectory-level RL 的 \( O(n^2) \) 降低到介于 \( O(n \log n) \) 和 \( O(n^2) \) 之间
Advantage Attribution Estimation(优势归因估计)
- 论文的基于熵的自适应 Rollout 机制自然地生成了包含共享推理 Token 段(segments)和不同束路径的轨迹(图 4),这促使论文探索一种更有原则的 Agent RL 策略更新策略
- 为此,论文考虑以下两种优势分配设置:
- 硬优势估计(Hard Advantage Estimation) :如图 4(b) 所示,一种直接的方法是在优势级别明确区分每条轨迹的共享部分和独立部分,从而鼓励模型捕获逐步工具使用行为
- 独立 Token 的优势 :给定 \( d \) 条共享某些 Token 但在其他部分分叉的轨迹,论文使用归一化奖励 \( R_i \) 计算独立 Token 的优势:
$$
\hat{A}_{i,t} = \frac{r_t - \text{mean}(\{R_i\}_{i=1}^G)}{\text{std}(\{R_i\}_{i=1}^G)}
$$- 注意:\(r_t \) 是步骤 \(t\) 对应的奖励
- 共享 Token 的优势 :对于共享 Token ,论文分配包含共享段的 \( d \) 条轨迹的平均优势:
$$
\hat{A}_{i,t}^{\text{shared} } = \frac{1}{d} \sum_{i=1}^d \hat{A}_{i,t}
$$
- 独立 Token 的优势 :给定 \( d \) 条共享某些 Token 但在其他部分分叉的轨迹,论文使用归一化奖励 \( R_i \) 计算独立 Token 的优势:
- 软优势估计(Soft Advantage Estimation) :硬优势分配的一种优雅替代方案是在策略优化过程中隐式整合共享和独立 Token 段的区别
- 对于每个输入问题 \( x \),GRPO 使参考策略 \( \pi_{\text{ref} } \) 生成一组响应 \( \{y_1, y_2, \ldots, y_G\} \),并通过最大化以下目标优化策略:
$$
J_{\text{GRPO} }(\theta) = \mathbb{E}_{(q,a)\sim D,\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|q)} \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \min \left( r_{i,t}(\theta) \hat{A}_{i,t}, \text{clip} \left( r_{i,t}(\theta), 1-\epsilon, 1+\epsilon \right) \hat{A}_{i,t} \right) - \beta D_{\text{KL} }(\pi_{\theta} \parallel \pi_{\text{ref} }) \right]
$$ - GRPO 目标通过重要性采样比 \( r_{i,t}(\theta) \) 整合了共享和独立 Token 的区别:
$$
r_{i,t}(\theta) = \frac{\pi_{\theta}(y_{i,t} \mid x, y_{i,< t})}{\pi_{\text{ref} }(y_{i,t} \mid x, y_{i,< t})}, \quad
\begin{cases}
r_{i,t}(\theta) = r_{j,t}(\theta), & \text{if } y_{i,< t} = y_{j,< t} \text{ (i.e., shared tokens)} \\
r_{i,t}(\theta) \neq r_{j,t}(\theta), & \text{if } y_{i,< t} \neq y_{j,< t} \text{ (i.e., individual tokens)}
\end{cases}
$$ - 如上述公式所示,当轨迹 \( y_i \) 和 \( y_j \) 在 Token \( t \) 处进行部分 Rollout 时,它们共享相同的响应前缀 Token ,即 \( y_{i,< t} = y_{j,< t} \)
- 两条轨迹中的共享前缀 Token 被分配相同的重要性权重 \( r_{i,t}(\theta) \)
- 在 GRPO 公式中,数学解释是策略更新由每组内 Token 的平均优势指导,作为损失信号
- 论文在附录 D.1 中为上述论点提供了详细证明
- 问题:软优势估计是直接复用 GRPO 的损失函数吗?是否不需要考虑优势估计了?
- 对于每个输入问题 \( x \),GRPO 使参考策略 \( \pi_{\text{ref} } \) 生成一组响应 \( \{y_1, y_2, \ldots, y_G\} \),并通过最大化以下目标优化策略:
- 在实践中,论文进一步比较了 RL 训练中硬优势估计和软优势估计的奖励变化
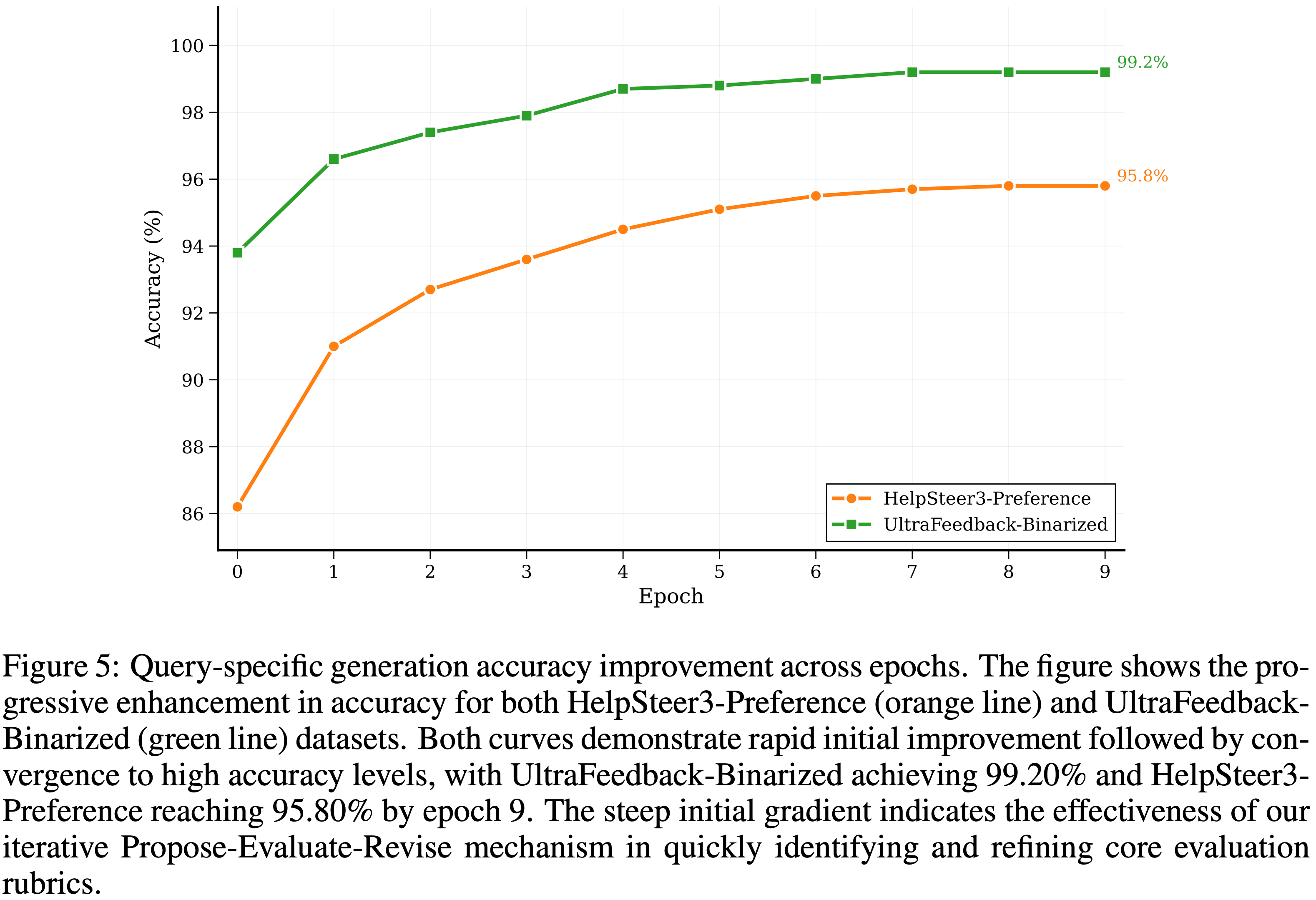
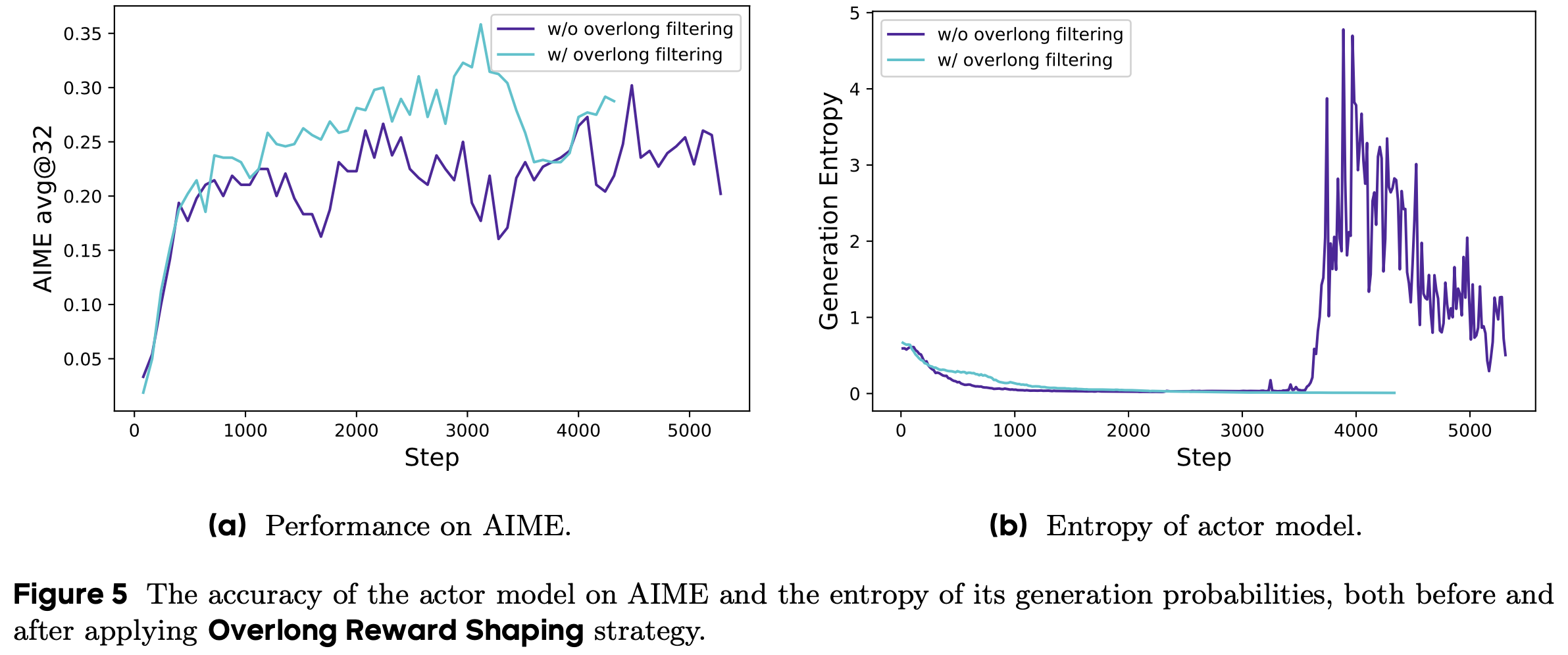
- 如图 5 所示,软优势估计在 ARPO 训练期间实现了更稳定的更高奖励(因此,论文的 ARPO 默认使用软优势估计)
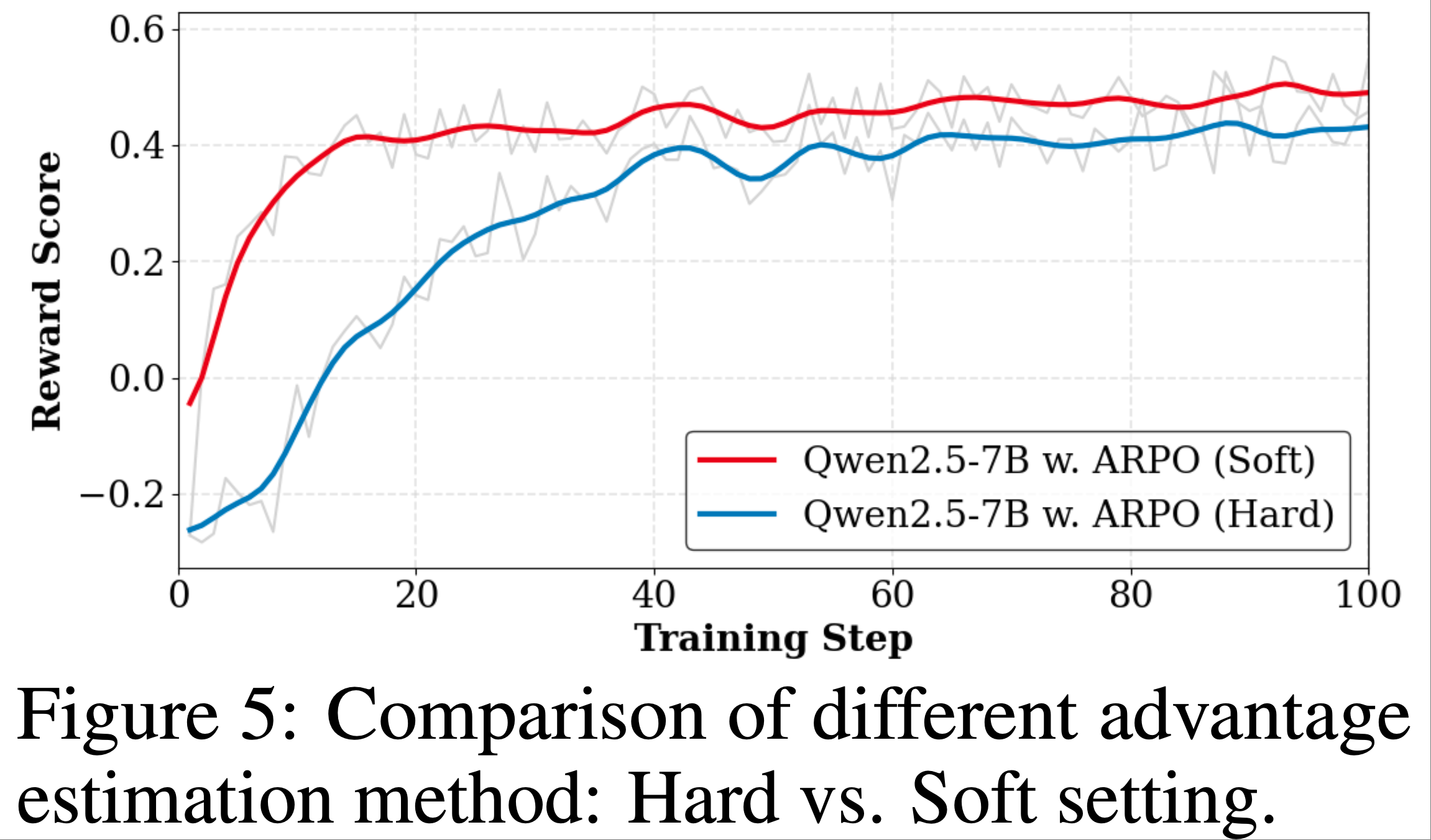
- 如图 5 所示,软优势估计在 ARPO 训练期间实现了更稳定的更高奖励(因此,论文的 ARPO 默认使用软优势估计)
- Hierarchical Reward Design :奖励函数作为优化目标,指导策略模型在训练期间的行为
- 论文遵循 Tool-Star (2025),同时考虑正确性和格式奖励,以及多工具协作奖励机制
- 当模型生成正确答案、遵循正确的工具调用格式、并在推理过程中使用多个工具(即 [search] 和 [python])时,会给予额外奖励 \( r_M \)
- 总体奖励 \( R \) 正式定义为:
$$
\begin{align}
R =
&\begin{cases}
\max(\text{Acc.} + r_{\text{M} }, \text{Acc.}), & \text{ If Format is Good & } \text{Acc.} > 0 \\
0, & \text{ If Format is Good & } \text{Acc.} = 0 \\
-1, & \text{ Otherwise }
\end{cases}, \\
r_{\text{M} } =
&\begin{cases}
0.1, & \text{If } \exists(\text{search} > \text{python}) \\
0, & \text{ Otherwise}
\end{cases}
\end{align}
$$
- ARPO 算法的详细流程图见算法 1
Theoretical Foundation
- 论文的方法利用了自适应部分 Rollout 机制,该机制涉及在高熵工具使用步骤进行分支
- 本节的目标是阐明这一机制背后的原理
- 如图 4 所示,自适应部分 Rollout 机制(adaptive partial rollout mechanism)将 Transformer-based 策略的输出 Token \( <OT_1, OT_2, \ldots, OT_{|output|}> \) 动态分割为 \( K \) 段
- 每段定义为一个宏动作 \( MA_i \triangleq <OT_m, OT_{m+1}, \ldots, OT_{m+n}> \)
- 对应的宏状态定义为 \( MS_1 \triangleq <IT_1, IT_2, \ldots, IT_{|input|}> \) 和 \( MS_i \triangleq <MS_{i-1}, MA_{i-1}> \)
- 这种分割使论文能够推导出适用于所有 Transformer-based 策略的广义策略梯度(Generalized Policy Gradient, GPG)定理:
$$
\nabla_{\theta} J(\theta) = \mathbb{E}_{\tau \sim \pi_{\theta} } \left\{ \sum_{T=1}^K \left[ \nabla_{\theta} \log \pi_{\theta}(MA_T | MS_T) A_T(\tau) \right] \right\}
$$- \( T \) 表示宏步骤
- \( A_T(\tau) \) 表示轨迹 \( \tau \) 的优势
- 如图 4 所示,自适应部分 Rollout 机制(adaptive partial rollout mechanism)将 Transformer-based 策略的输出 Token \( <OT_1, OT_2, \ldots, OT_{|output|}> \) 动态分割为 \( K \) 段
- GPG 定理断言,对于任何可微的 Transformer-based 策略 \( \pi_{\theta} \) 和任何目标函数 \( J(\theta) \),可以使用宏动作(即部分 Rollout 段)有效地进行优化
- 这一概括涵盖了传统的策略梯度定理 (1999),即:
$$ \nabla_{\theta} J(\theta) = \mathbb{E}_{\tau \sim \pi_{\theta} } \left\{ \sum_{t=1}^H \left[ \nabla_{\theta} \log \pi_{\theta}(a_t | s_t) A_t(\tau) \right] \right\} $$- 其中 \( a_t \) 是 Transformer 的单个输出 Token
- 以上是更广泛的 GPG 框架的一个特定实例
- 这一概括涵盖了传统的策略梯度定理 (1999),即:
- 作为 GPG 定理的高级实现,ARPO 提供了一个坚实的理论基础
- GPG 定理的形式化证明见附录 D.2
Experiment
Datasets
- 为了全面评估 ARPO 算法在训练 LLM-based 工具使用智能体方面的有效性,论文在以下三类长程推理任务上进行了实验:
- 1)Mathematical Reasoning :包括 AIME2024、AIME2025、MATH500 (2024)、MATH (2021) 和 GSM8K
- 2)知识密集型推理(Knowledge-Intensive Reasoning) :包括 WebWalker (2025b)、HotpotQA (2018)、2WikiMultihopQA (2020)、Musique (2022) 和 Bamboogle (2023)
- 3)Deep Search :包括 GAIA (2024)、WebWalker (2025b)、Humanity’s Last Exam (HLE, 2025) 和 xbench (2025a)
- 为确保一致性,论文遵循 Tool-Star (2025) 的测试集划分方式处理数学和知识推理基准,而对于深度搜索基准,则采用 Webbinker 和 HIRA (2025b; 2025a) 的 Deepsearch 测试集划分
Baselines
- 为有效评估 ARPO 的效果,论文选择了以下三类基线方法:
- 1)直接推理(Direct Reasoning) :对于数学和知识推理任务,论文评估了 Qwen2.5 (2024) 和 Llama3.1 (2024) 系列的指导版本模型。由于 Qwen3 系列 (2025) 在数学任务上表现优异,论文使用其作为深度搜索任务的测试主干模型。同时,论文还参考了 QwQ (2024c)、DeepSeek-R1 (2025)、GPT-4o (2024) 和 o1-preview (2024) 等强推理模型
- 2)Trajectory-level RL Algorithms :论文将 ARPO 与常见的 Trajectory-level 强化学习算法进行比较,包括 GRPO (2024)、DAPO (2025) 和 REINFORCE++ (2025)
- 3)LLM-based 搜索智能体(LLM-based Search Agent) :对于深度搜索任务,论文纳入了 GRPO 和一系列开源的工作流搜索智能体作为参考,例如 Vanilla RAG (2020)、Search o1 (2025d)、Webthinker (2025e) 和 ReAct (2022)
Training Guideline
- 本研究的目标是 在算法层面验证 ARPO 相较于传统强化学习在训练 LLM 智能体上的有效性,而非单纯追求性能提升
- 为确保可复现性,所有训练框架和数据集均来自公开资源
- 具体实验遵循冷启动 SFT 与强化学习结合的范式 (2025; 2025),以避免初始强化学习阶段的奖励崩溃问题
- 1)冷启动微调阶段(Cold-Start Finetuning Phase) :使用 LLaMAFactory (2024) 框架,基于 Tool-Star 开源的 54K 训练样本数据集。为丰富数学推理数据质量,论文额外引入了 STILL 数据集 (0.8K),灵感来自 CORT (2025a)
- 2)强化学习阶段(RL Phase) :为评估 ARPO 在不同场景下的表现,论文探索了以下领域:
- 深度推理任务(Deep Reasoning Tasks) :包括计算推理(如 AIME24、MATH500)和多跳知识推理(如 HotpotQA、Bamboogle)
- 论文使用 Tool-Star 开源的 10K 强化学习训练样本进行算法比较
- 深度搜索任务(Deep Search Tasks) :这类任务需要广泛的网络探索和信息整合,涉及长上下文和频繁的工具交互
- 论文仅使用 SimpleDeepSearcher (2025b) 和 WebSailor (2025c) 的 1K 混合硬搜索样本进行训练
- 深度推理任务(Deep Reasoning Tasks) :包括计算推理(如 AIME24、MATH500)和多跳知识推理(如 HotpotQA、Bamboogle)
- 为加速强化学习阶段,论文整合了 Bing 搜索引擎的前 10 条摘要作为搜索结果,在沙箱环境中使用 Python 编译器,并以 token-level F1 分数作为正确性信号
- 问题:如何理解这里的 token-level F1 分数作为正确性信号?
Evaluation Metric
- 在评估阶段,论文使用具备浏览器功能的搜索引擎以对齐标准推理性能
- 对于准确性,知识密集型推理中的四个问答任务采用 F1 分数作为指标,其他任务则使用 Qwen2.5-72B-instruct 在 LLM-as-Judge 设置下评估
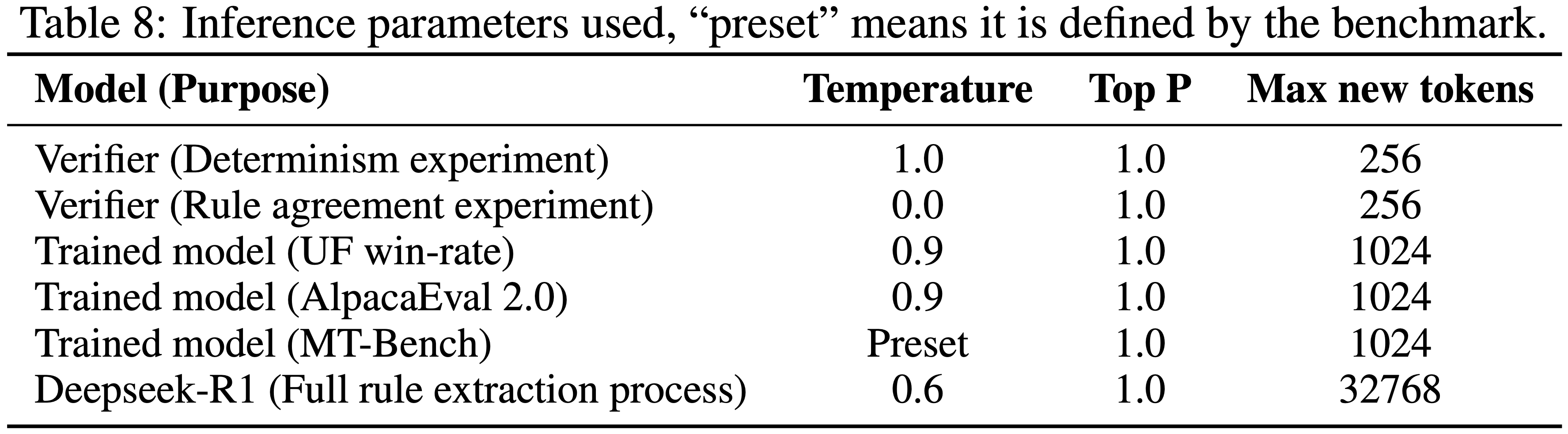
- 论文采用非零温度的 pass@1 评估,将温度和 top-p 分别设为 0.6 和 0.95
- 对于所有任务,论文遵循先前工作 (2025c) 的设定,从模型输出中提取 \box{} 内的答案
- 问题:这里的 非零温度 是什么意思?
- 回答:这里的反面不是指温度真的为 0,而是无穷小;温度为 0 时,对应的是贪心策略;这里相当于是说使用的不是贪心策略(而是有一定随机性的策略)
Main Results
Results on Mathematical & Knowledge-Intensive Reasoning
- 表 1 展示了主要结果
- 在公平设置下,ARPO 始终优于所有 Trajectory-level 强化学习算法,确立了其优越性
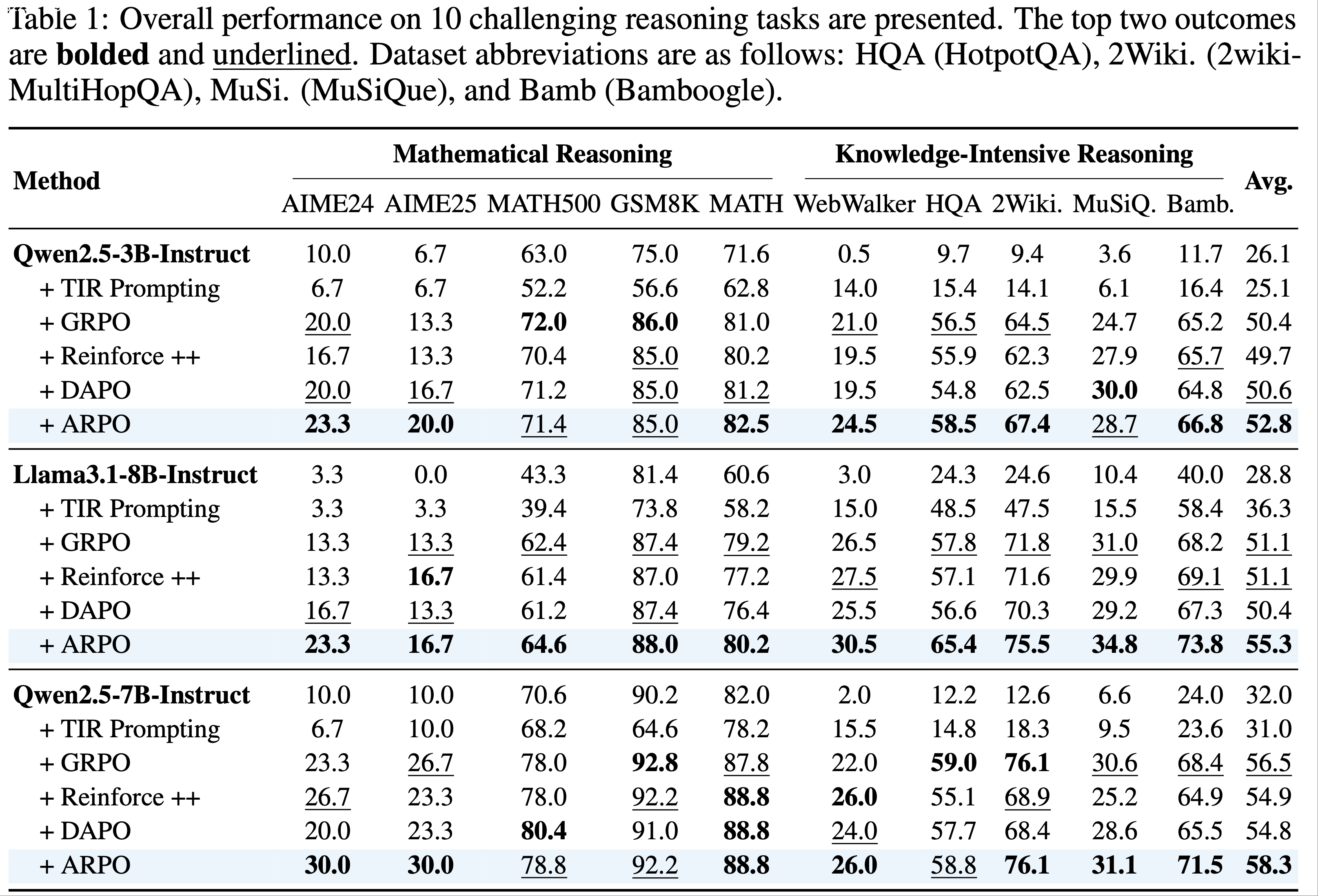
- 在公平设置下,ARPO 始终优于所有 Trajectory-level 强化学习算法,确立了其优越性
- 此外,作者还强调他们的以下发现:
- 提示方法的无效性(Ineffectiveness of Prompting Methods) :工具集成提示(Tool-integrated prompting,TIR)方法 (2025c) 未能有效探索更优的工具使用行为
- 对于 Qwen 和 Llama 系列模型,TIR 提示的性能提升有限,甚至低于直接推理
- 这表明仅依赖提示工程不足以引导 LLM 实现最佳工具行为 ,甚至可能破坏其固有推理能力
- Trajectory-level 强化学习的局限性(Limitations of Trajectory-Level RL) :与 ARPO 相比,三种经典 Trajectory-level 强化学习算法未能有效利用工具集成推理的潜力
- DAPO 在单轮推理任务中表现优异 ,但在多轮工具调用交互中表现不佳(尤其是在知识密集型场景中)
- 这与论文的初步观察一致,即 Trajectory-level 强化学习算法难以激发 LLM 学习细粒度的工具使用行为
- ARPO 的稳健性能(Robust Performance of ARPO) :在相同实验设置下,ARPO 在 10 个数据集上始终优于其他强化学习算法,平均准确率提升 4%,同时在各个领域保持竞争力
- ARPO 在 Qwen 和 Llama 系列等不同主干模型上均表现出显著提升
- 这些结果凸显了 ARPO 的高效性、强适应性以及在不同模型主干和任务上的广泛适用性
- 提示方法的无效性(Ineffectiveness of Prompting Methods) :工具集成提示(Tool-integrated prompting,TIR)方法 (2025c) 未能有效探索更优的工具使用行为
Results on Deep Search Tasks
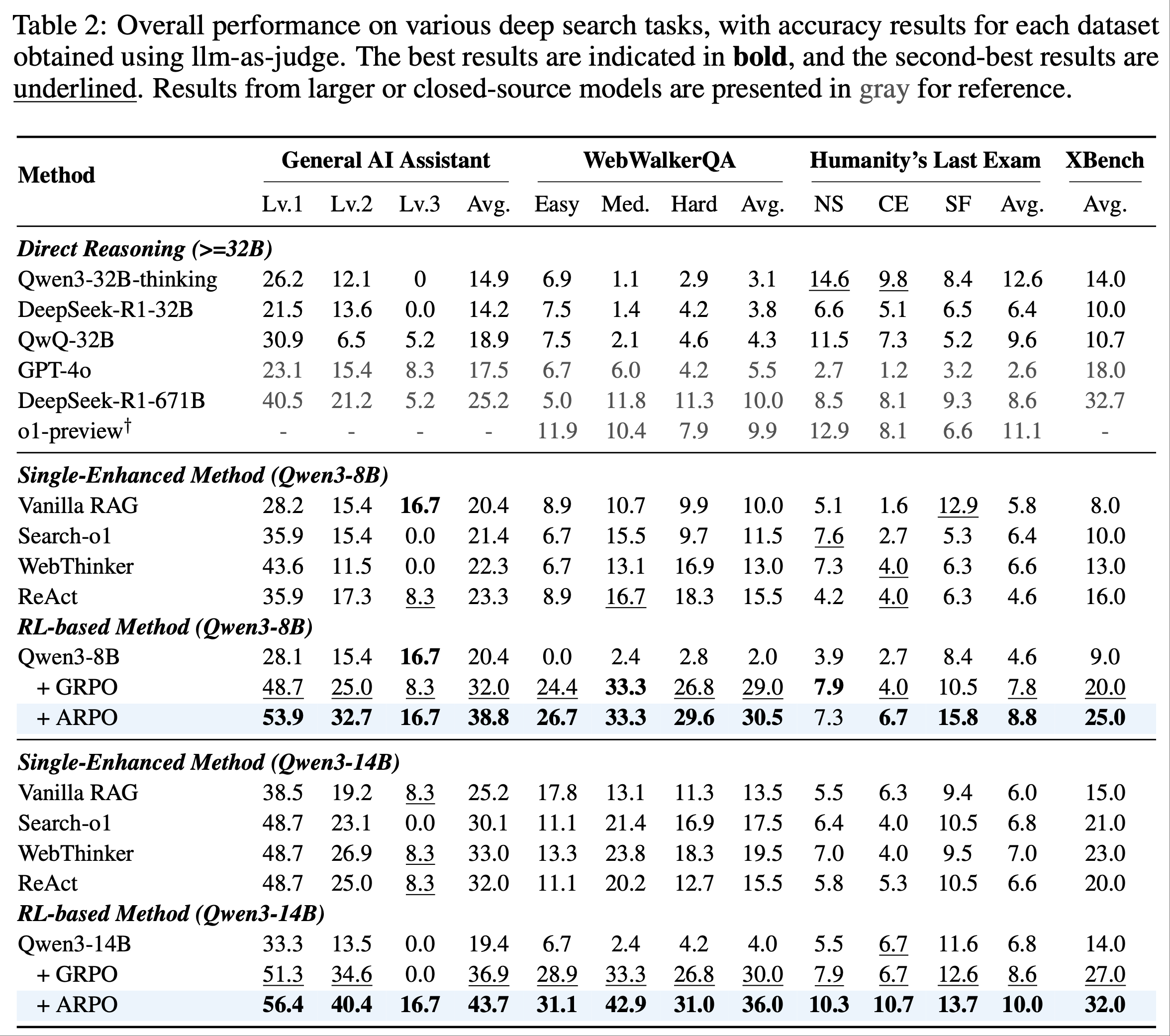
- 为验证 ARPO 在挑战性深度搜索场景中的有效性,论文比较了 Qwen3 系列模型(仅用 1K 强化学习样本训练)与一系列强基线方法的表现
- 论文的观察如下:
- ARPO 在深度搜索领域的泛化能力(Generalization of ARPO in Deep Search Domain) :在深度搜索场景中,即使是最先进的 LLM(如 GPT-4o 和 DeepSeek-R1-671B)表现也有限,在 HLE 基准上分别仅得 2% 和 8.6%
- 相比之下,ARPO 仅使用 Qwen3-8B 和 14B 模型就取得了显著性能,在 HLE 和 GAIA 基准上分别达到 pass@1 分数 10.0% 和 43.2%
- 特别地,在强化学习阶段,ARPO 仅使用开源网络搜索数据集的 1K 样本进行训练,展示了其在工具集成推理能力上的高效性
- 探索分步工具使用行为的重要性(Importance of Step-Level Tool Use Behavior Exploration) :ARPO 在平均性能和单个基准上均优于 GRPO,尤其在 GAIA 和 WebwalkerQA 基准上提升了 6%
- 这凸显了 ARPO 算法设计的核心价值:通过平衡全局和分步采样,促进 LLM 在高熵工具使用步骤中探索多样化行为 ,这对涉及频繁工具调用的深度搜索场景至关重要
- ARPO 在深度搜索领域的泛化能力(Generalization of ARPO in Deep Search Domain) :在深度搜索场景中,即使是最先进的 LLM(如 GPT-4o 和 DeepSeek-R1-671B)表现也有限,在 HLE 基准上分别仅得 2% 和 8.6%
Quantitative Analysis(定量分析)
- 规模化采样分析(Analyzing Sampling at Scale)
- 由于深度搜索评估的动态性和多轮交互特性,pass@1 不足以捕捉模型的工具使用潜力
- 因此,论文进一步对 pass@3 和 pass@5 进行了采样分析(如图 6 所示)
- 8B 和 14B 模型在 ARPO 对齐阶段后均表现出稳定的提升和扩展趋势
- 论文的 Qwen-14B 结合 ARPO 在 pass@5 上取得了显著性能,GAIA 达到 61.2%,HLE 达到 24.0%,xbench-DR 达到 59%
- 这种在 pass@K 上的稳定提升主要归功于 ARPO 能够更高效地探索细粒度工具使用行为,从而扩展采样空间,实现推理效率和采样多样性的平衡
- 原文注释:由于 xbench-DR 完全由中文问题组成,论文使用中文提示分析 pass@k 结果,导致性能相较于表 2 有所提升
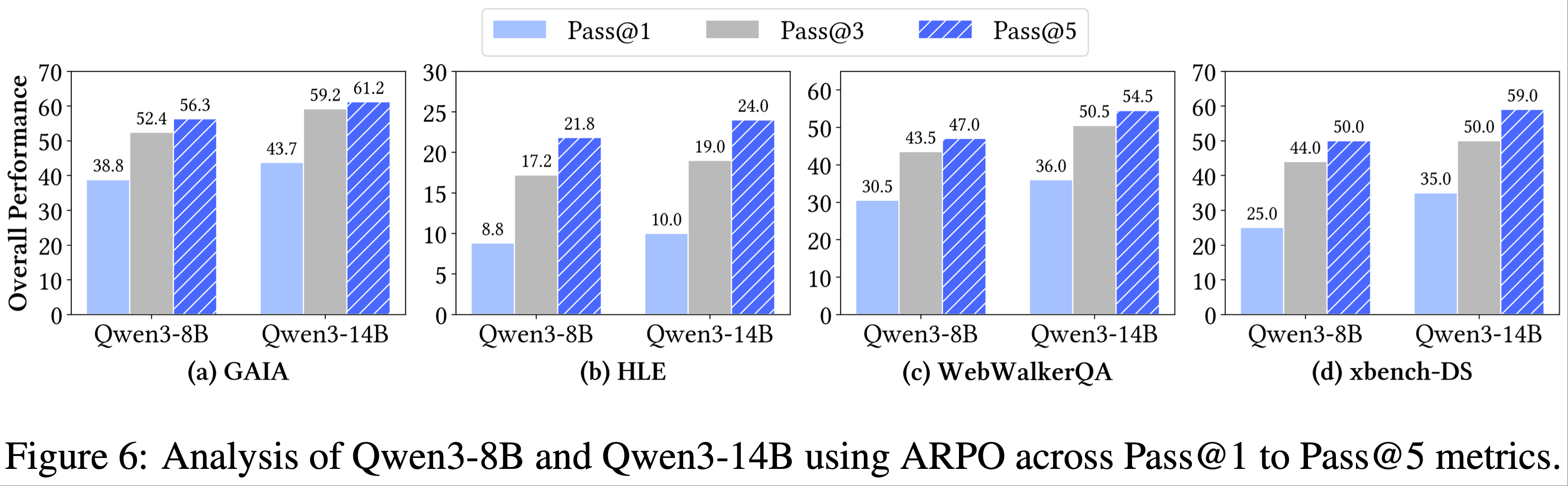
- 原文注释:由于 xbench-DR 完全由中文问题组成,论文使用中文提示分析 pass@k 结果,导致性能相较于表 2 有所提升
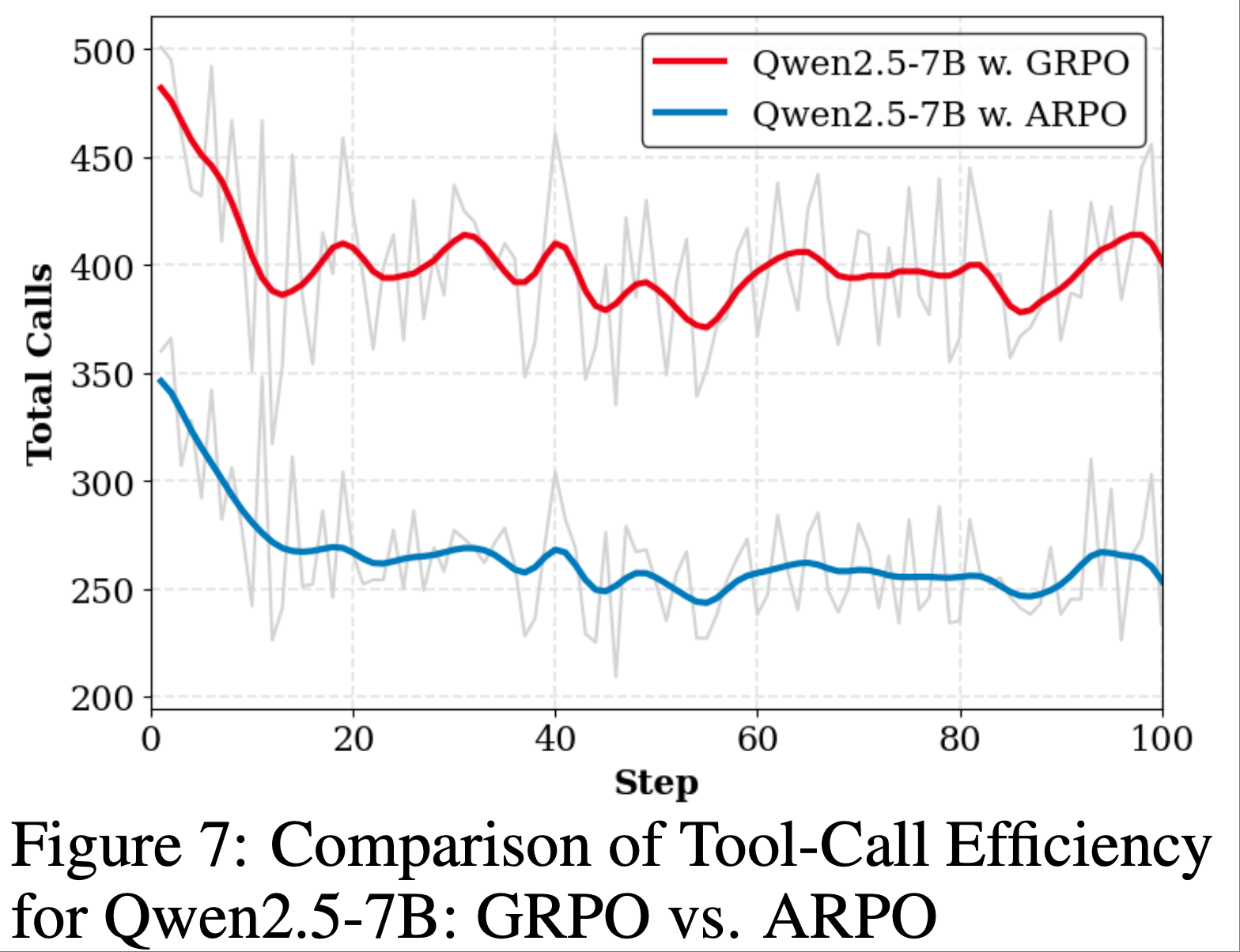
- Tool-Call Efficiency Analysis
- 在 Agentic RL 训练中,增加工具调用次数通常会导致高昂成本
- 因此,有效的 Agentic RL 算法必须确保工具使用效率
- 为评估 ARPO 在训练中的工具使用效率,论文将其与 GRPO 在 Qwen2.5-7B 上进行比较
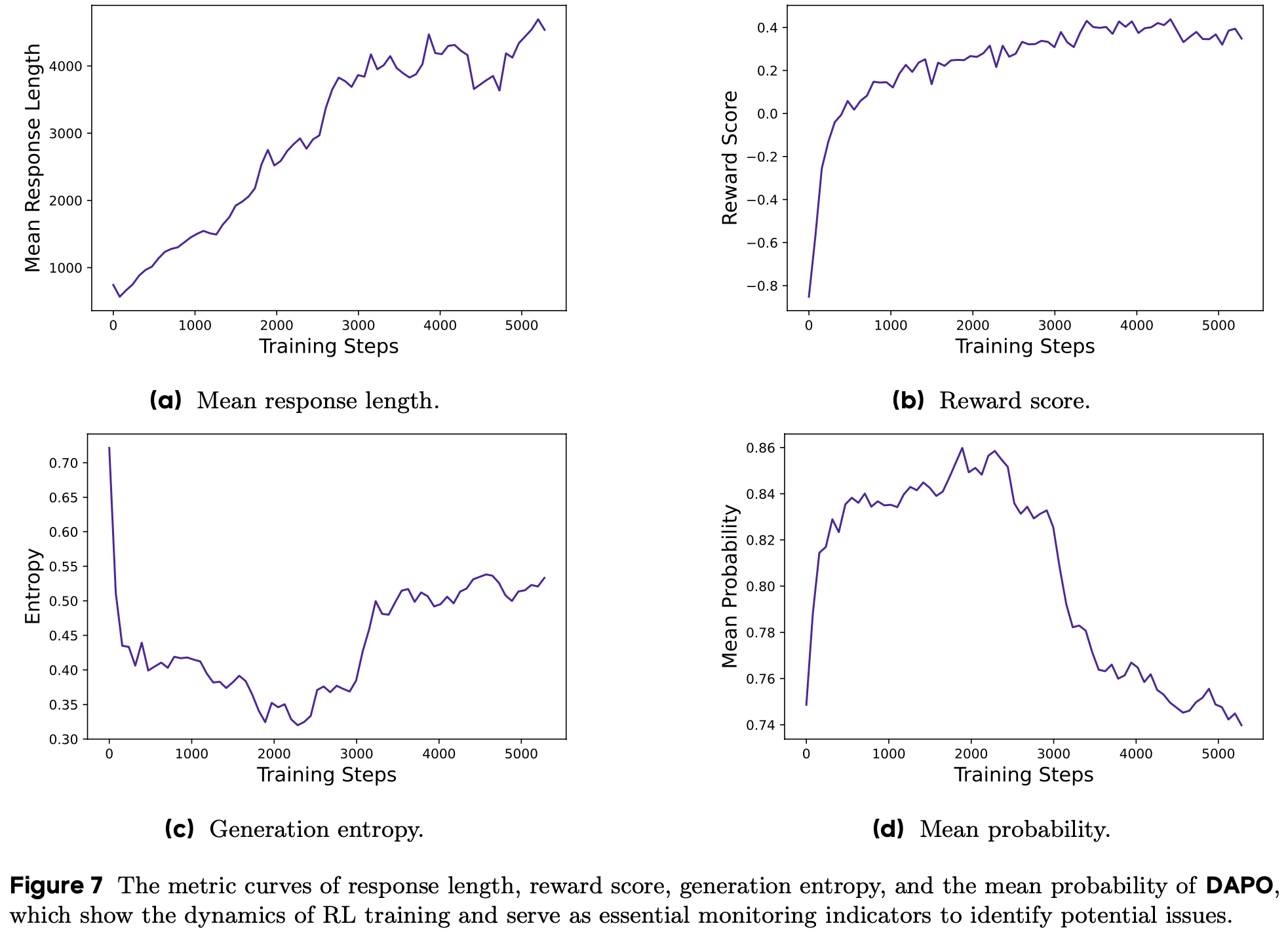
- 如图 7 所示,ARPO 在仅使用 GRPO 一半工具调用次数的情况下实现了更优的整体准确率
- 这种效率归功于 ARPO 独特的基于熵的自适应采样机制,仅在工具调用步骤的高熵阶段选择性探索分支,显著扩展了工具行为的探索空间,同时大幅减少了工具调用次数
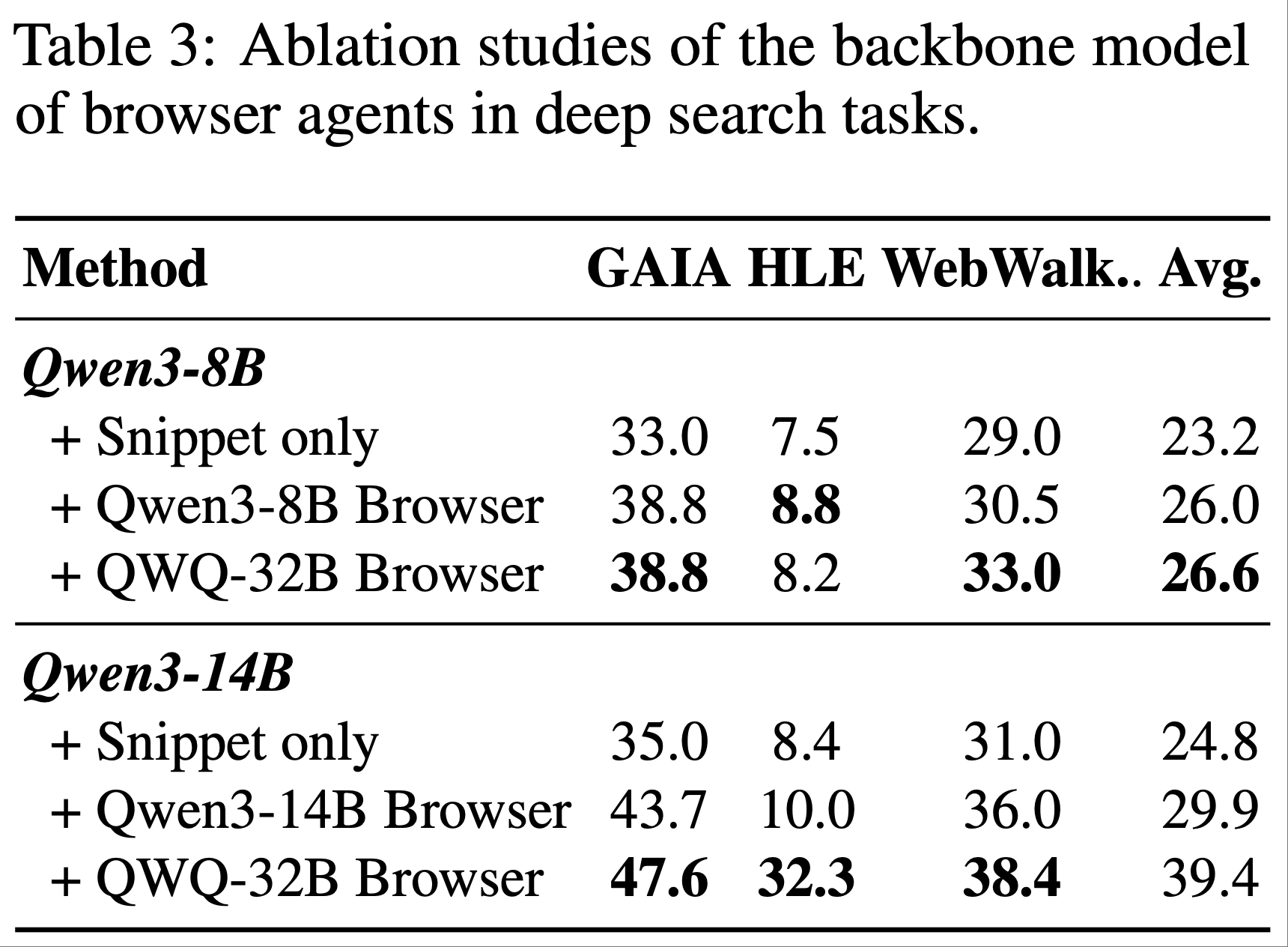
- Ablations of Browser Agents
- 为进一步研究浏览器智能体在深度搜索任务中的重要性,论文设计了三种浏览器设置,按能力从弱到强排序:
- 1)无浏览器,仅使用摘要;
- 2)与推理模型规模相似的浏览器智能体;
- 3)更大参数的浏览器智能体
- 如表 3 所示:
- 无浏览器的场景表现最差 ,表明仅依赖规则生成的网页摘要无法为深度搜索任务提供必要的信息支持
- 随着浏览器智能体能力的提升,模型性能显著提高,证明更强大的搜索智能体能更有效地整合信息并提取与问题相关的关键细节
- 结论:外部浏览器智能体的能力与深度搜索任务的准确性高度相关,且随着其规模扩大呈现明显上升趋势
- 为进一步研究浏览器智能体在深度搜索任务中的重要性,论文设计了三种浏览器设置,按能力从弱到强排序:
Scaling Analysis of ARPO
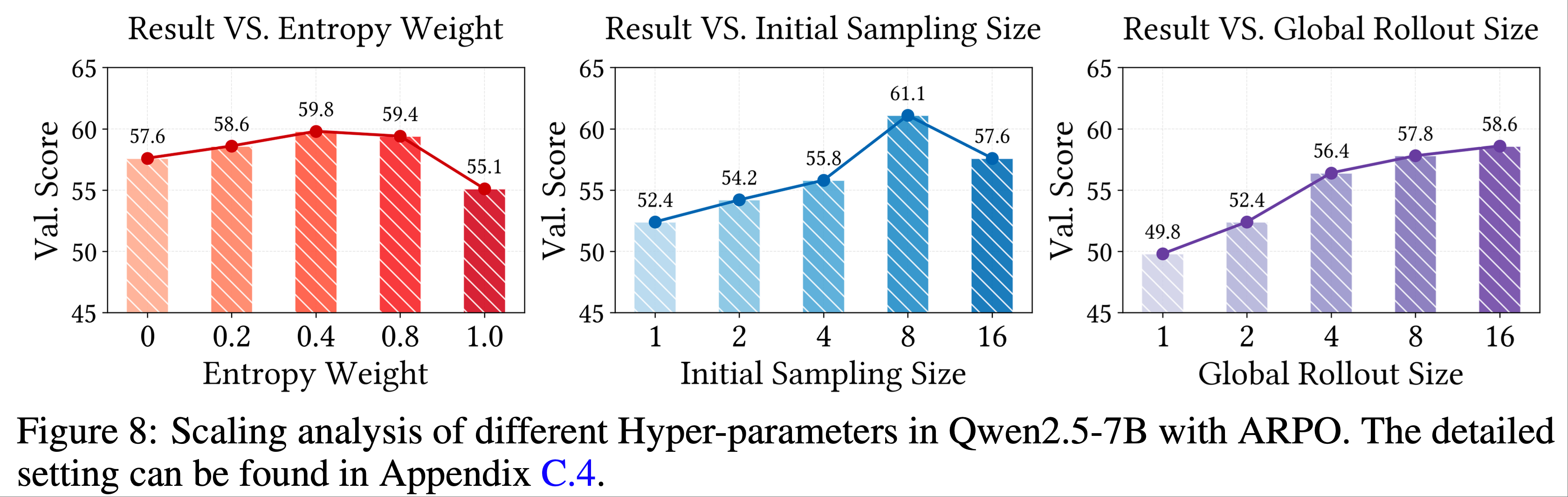
- 为验证 ARPO 的可扩展性并深入理解其特性,论文以 Qwen2.5-7B 模型为 Backbone,对三个核心参数进行了规模化分析:熵值(\(\Delta H_t\))、全局采样大小(\(M\))和初始采样大小(\(N\))
- 论文的观察如下:
- 1)熵值(\(\Delta H_t\)) :如图 8(左)所示,模型性能随熵值增加而提升,在 0.4 处达到峰值
- 这表明将适量熵值作为部分采样的线索能显著增强模型探索罕见工具使用行为的能力,从而改善训练效果
- 但当熵值达到 1.0 时,性能下降,表明熵值在采样中的权重需要权衡,过度依赖熵值可能降低采样多样性,验证了 ARPO 中平衡基础采样概率 \(\alpha\) 与熵值的必要性
- 2)初始采样大小(\(N\)) :图 8(中)显示,随着初始采样大小增加,模型性能提升,在 8 处达到峰值
- 全局采样大小为 16 时,将初始采样大小从 0 增加到 8 会将全局与部分采样的比例从 1:15 调整为 1:1,这凸显了平衡采样比例对提升性能的重要性
- 如预期所示,将初始采样大小增至 16 会导致性能大幅下降,因为这会导致完全全局采样,破坏动态采样平衡
- 3)全局采样大小(\(M\)) :如图 8(右)所示,增加全局采样大小能提升模型性能
- 表明 ARPO 算法具有可扩展性,且能通过更大规模的采样提升泛化性能
- 表明 ARPO 算法具有可扩展性,且能通过更大规模的采样提升泛化性能
- 1)熵值(\(\Delta H_t\)) :如图 8(左)所示,模型性能随熵值增加而提升,在 0.4 处达到峰值
Related Work
RLVR(Reinforcement Learning with Verifiable Reward)
- 近年来,RLVR 已成为 RLHF 领域的重要方法,尤其在提升数学和编程推理能力方面表现突出(2024; 2025;)
- OpenAI 的 o1 模型(2024)首次展示了强化学习在大规模推理任务中的有效性
- 随后,DeepSeek R1(2025)、QwQ(2025)和 Kimi k1.5(2025)等模型致力于复现并超越其性能
- 为了提升强化学习算法的性能和稳定性,研究人员开发了 DAPO(2025)和 SimpleRIZoo(2025)等模型,探索了强化学习模块的多样化设计(2019; 2024; 2025)
- Lin 等人发现关键 Token 对模型行为的影响,并表明替换这些 Token 可以改变模型行为
- 研究(2025; 2025)指出 RLVR 主要学习格式而非内容,而另一些工作(2025; 2025; 2025; 2025)则通过高熵 Token 探索强化学习的本质
- 但专门针对 LLM 智能体的 RLVR 算法仍未被充分探索
- 论文利用熵作为标准,研究适用于 LLM 智能体行为的强化学习算法
Agentic RL
- 强化学习对于使 LLM 智能体适应动态开放环境至关重要(2025; 2020; 2024)
- 奠基性工作如 DQN(2015)和 AlphaZero(2017)表明,基于自我对弈的强化学习可以为智能体赋予从自然语言理解到策略游戏的能力(2015)
- 在此基础上,基于价值的强化学习方法被用于增强硬件控制和复杂游戏任务中的智能体能力(2024; 2017; 2019)
- 近期研究以 RAGEN(2025; 2024)为例,将推理状态和环境交互整合到回合级响应中,使用 Trajectory-level 强化学习
- 为了提升工具集成推理能力,研究(2025; 等)采用基于规则的强化学习,教导 LLM 如何自主调用外部工具(如搜索引擎、Python 编译器)以提高推理准确性
- 进一步研究包括 ToolRL(2025)、Tool-Star(2025)和 OTC(2025),探索多工具集成和工具使用效率
- Kimi Deepresearcher 和 Websailor(2025)等系列工作优化强化学习算法,以更好地适应深度搜索的长上下文场景
- 大多数研究通过奖励设计和滚动机制改进工具调用,但简单地应用 Trajectory-level 强化学习无法有效捕捉 LLM-based Agent 在多回合、长视野行为中的特征
- 这促使论文提出 ARPO,尝试学习逐步工具使用行为模式
附录 A:Datasets
A.1 Mathematical Reasoning Benchmarks
- AIME24 是一个用于评估模型数学推理能力的数据集,包含 30 道具有挑战性的数学问题
- 这些问题均来自美国数学邀请赛(American Invitational Mathematics Examination)
- AIME24 数据集中的问题涵盖了代数方程、几何谜题等多种数学领域
- 由于其题目难度和类型的丰富性,该数据集已成为评估模型推理性能的热门基准,并被广泛应用于多项相关研究实验中
- AIME25 包含 30 道具有挑战性的数学问题,直接选自 2025 年 2 月新发布的美国数学邀请赛(AIME I & II)真题
- AIME25 的知识领域极为广泛,深度覆盖了代数、几何、数论和组合数学等核心数学分支
- 这一特点使得 AIME25 数据集能够有效区分不同模型的数学推理能力
- MATH500 (2024) 由 OpenAI 从 MATH 评估数据集中精选而出,包含 500 道高难度数学问题
- 这些问题涵盖代数、几何、微积分和数论等多个数学领域,难度接近或超过大学水平
- 在学术研究中,MATH500 数据集常被用于评估各种推理模型的性能
- MATH (2021) 是一个重要的学术数据集,旨在测试和提升模型的数学推理能力
- 它涵盖了抽象代数、微积分和离散数学等广泛的数学领域
- 该数据集将训练数据分为三个级别,有助于有效评估模型在不同阶段的表现
- GSM8K (2021) 是 OpenAI 发布的小学数学问题数据集
- 这些问题需要通过 2 到 8 步的基本计算得出最终答案
- 该数据集主要用于测试模型的逻辑和数学能力,并已在多项基准测试中得到应用
A.2 Knowledge-Intensive Reasoning Benchmarks
- HotPotQA (2018) 是一个多跳问答数据集
- 所有文档均来自维基百科,为数据集提供了丰富的知识库和相对结构化的信息
- 是评估 LLM 理解复杂搜索任务能力的重要基准
- 2WikiMultihopQA (2020) 是一个专为多跳问答任务设计的数据集
- 旨在测试和评估自然语言处理模型回答需要多步推理和整合不同文档信息的问题的能力
- Musique (2022) 是一个专为多跳问答任务设计的问答数据集
- Musique 旨在成为一个具有挑战性的基准
- 用于评估模型的多跳问答能力,推动模型从简单信息检索向更深层次的语义理解和逻辑推理发展
A.3 Deep Search Benchmarks
- GAIA (2024) 旨在评估大语言模型在现实世界任务中的综合能力
- 该数据集包含 466 道精心设计的问题,用于测试人工智能系统在推理、网页浏览和工具使用等基本能力方面的表现
- GAIA 的提出为通用人工智能助手的评估提供了新框架
- HLE (2025) 是一个新兴且极具挑战性的基准数据集,旨在深度评估大语言模型在面对需要深度理解和复杂推理的复杂问题时的表现
- 该数据集涵盖了大量边缘性、跨学科问题,需要高度抽象的思维来解决
- 与传统基准不同,HLE 旨在模拟对人工智能智能水平的终极测试
- WebWalker (2025b) 是一个用于评估大语言模型在网页遍历任务中表现的数据集
- 该数据集包含 680 组问答对,旨在解决大语言模型在处理复杂信息时的局限性,并提升模型在多跳推理和动态网页结构方面的能力
- xbench-DeepSearch (2025a) 是一个用于评估 AI 智能体深度搜索能力的测试集
- 该数据集充分考虑了搜索空间的广度和推理的深度
- 与现有的知识搜索基准不同,xbench-DeepSearch 更能检验智能体的高阶能力
附录 B: Baselines
B.1 Direct Reasoning
- Qwen2.5 系列 (2024) 是阿里巴巴团队开发的一系列大语言模型,包括通用语言模型 Qwen2.5、编程专用模型 Qwen2.5-Coder 和数学专用模型 Qwen2.5-Math
- Qwen2.5 系列模型已在大规模数据集上进行了预训练
- 与过去的 Qwen 系列模型相比,Qwen2.5 系列拥有更丰富的知识储备,同时在编程、数学和指令遵循等各种任务中表现出色
- Llama3.1 系列 (2024) 是 Meta 推出的一系列自然语言生成模型,包括 8B、70B 和 405B 三种规格
- 这些模型能够处理更长的文本输入,并生成更连贯的长文本输出
- 该系列模型在多语言任务中也表现优异
- Llama 3.1 系列模型已在 150 多个基准数据集上进行了性能测试,其大规模模型在一系列任务中与领先的基础模型具有竞争力,而较小的 8B 和 70B 模型在与参数量相近的闭源和开源模型的比较中也表现突出
- Qwen 3 系列 (2025) 是阿里巴巴开发的一系列开源模型
- Qwen3 系列模型包括 2 个混合专家(Mixture-of-Experts, MoE)模型和 6 个 Dense 模型,参数量从 0.6B 到 235B 不等
- Qwen3 原生支持思考模式和非思考模式:
- 在思考模式下,模型逐步推理,适合处理复杂问题;
- 非思考模式可提供快速、近乎即时的响应,适合简单问题
- Qwen3 基于约 36T token 构建了训练语料库,确保了模型的强大能力和灵活性
- QwQ (Team, 2024c) 是阿里巴巴团队推出的开源推理模型,专注于提升 AI 在数学、编程和复杂逻辑推理方面的能力
- QwQ-32B 是一个拥有 320 亿参数的 Dense 模型,在数学推理和代码生成能力等核心任务上超越了大多数现有模型
- QwQ-32B 通过创新的多阶段强化学习实现了突破,其核心训练方法在于逐步扩展通用能力的同时巩固专业优势
- DeepSeek-R1 (DeepSeek-2025) 是 DeepSeek-AI 开发的推理模型
- DeepSeek-R1 使用强化学习进行训练,推理过程涉及大量反思和验证,思维链长度可达数万 token
- 它在数学、代码和各种复杂逻辑推理任务中表现卓越
- GPT-4o (2024) 是 OpenAI 发布的多模态大语言模型
- GPT-4o 可以接受文本、音频和图像的任意组合作为输入,并生成文本、音频和图像的任意组合作为输出
- GPT-4o 在文本、推理和编码等方面的表现与 GPT-4 Turbo 相当,同时在多语言、音频和视觉功能的性能评分上创下了新高
- o1-preview (2024) 是 OpenAI 推出的 o1 系列大语言模型的预览版本,代表了推理领域的重要突破
- o1-preview 基于 GPT-4 架构,通过强化学习训练,旨在增强复杂任务的推理能力和实际问题的解决能力
- 在需要深度推理的任务中,它可以展现出强大的能力
B.2 Trajectory-level RL Algorithms
- GRPO (2024) 是一种基于策略优化的强化学习算法,旨在解决传统策略优化方法在稳定性、样本效率和理论保证之间的平衡问题
- 通过引入相对优势的概念,它在保持策略改进理论保证的同时简化了计算
- GRPO 算法适用于连续和离散动作空间中的强化学习任务
- DAPO (2025) 是字节跳动实验室开发的大语言模型强化学习算法,旨在解决大规模强化学习训练的关键挑战
- DAPO 在数学推理和代码生成等复杂任务中表现突出
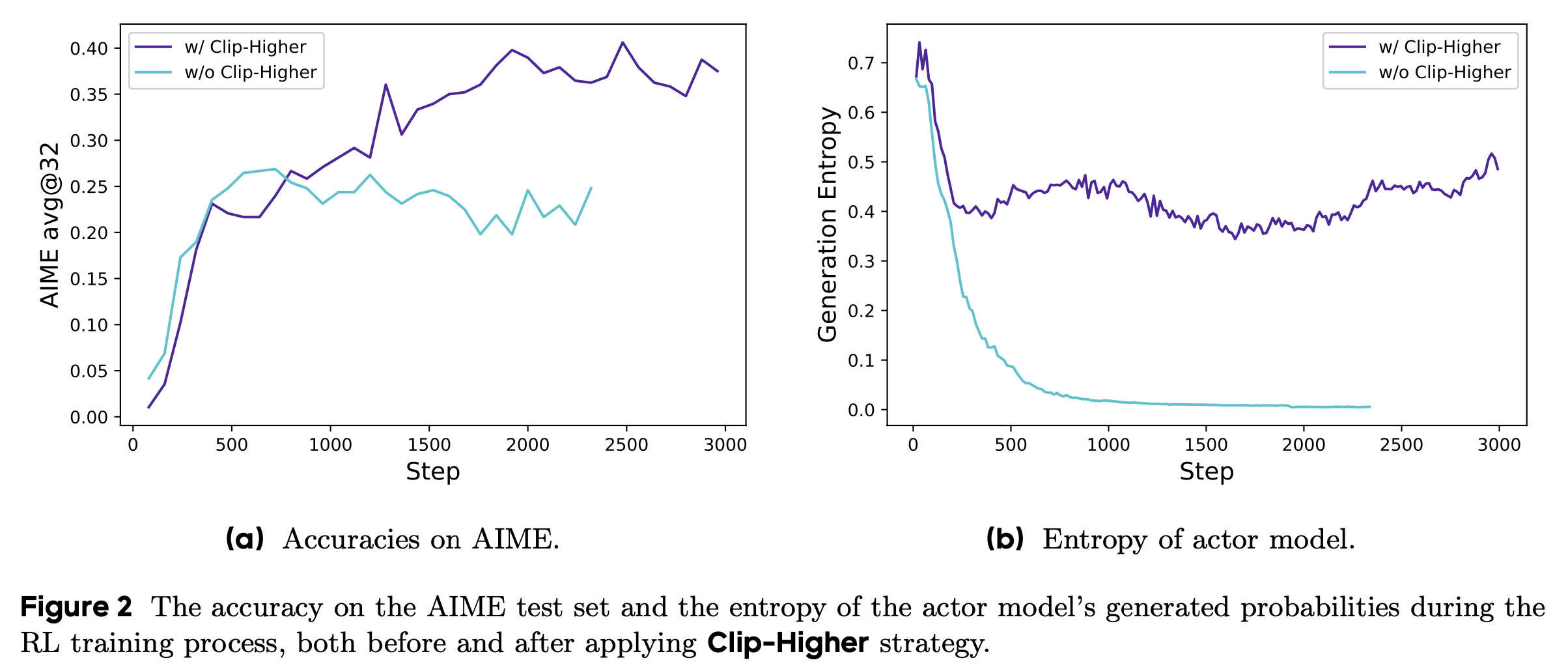
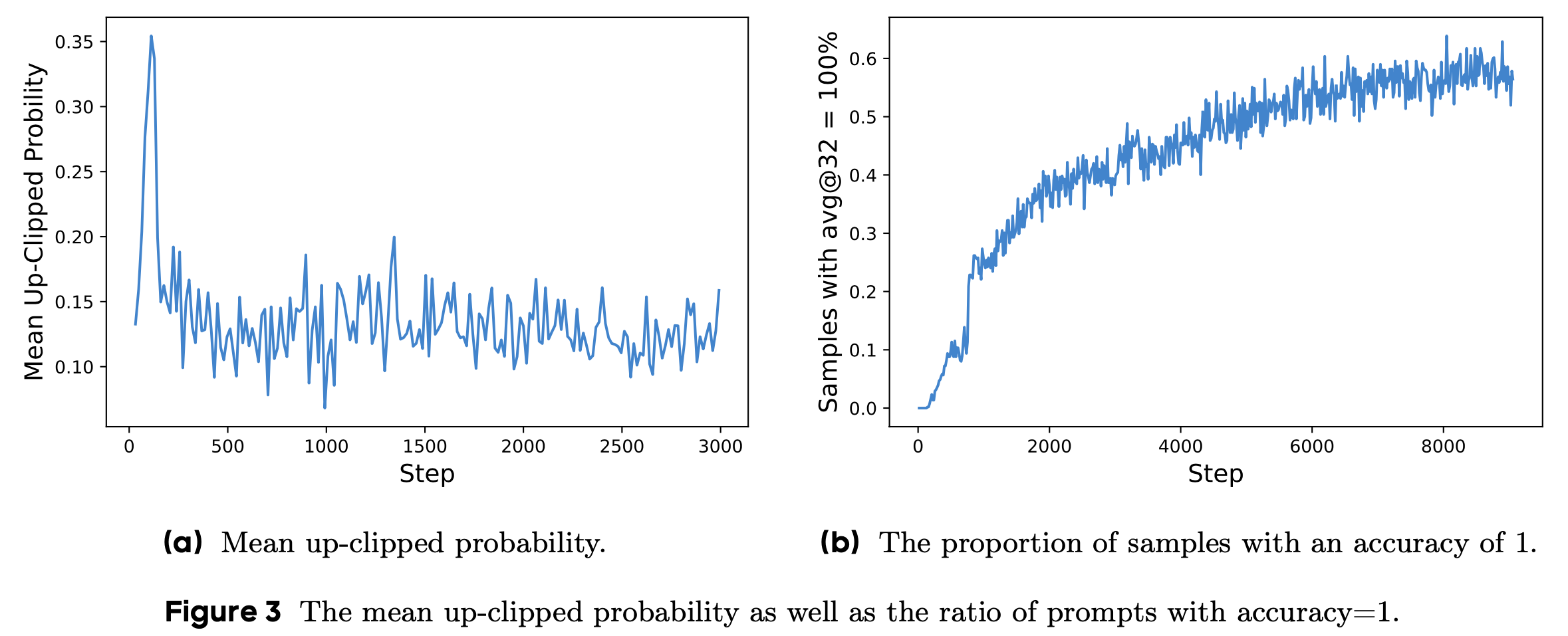
- DAPO 提出的 Clip-Higher 策略有效提高了熵值,有助于生成更多样化的样本
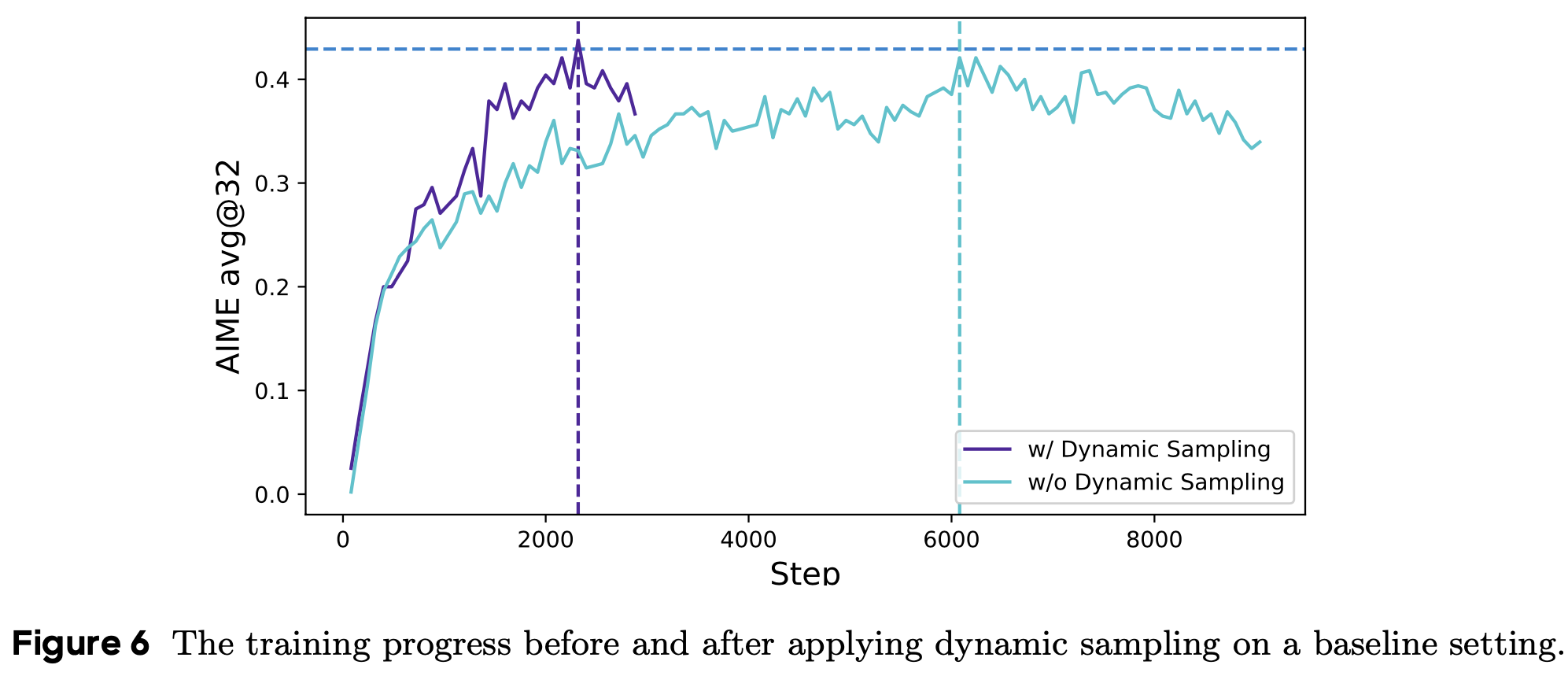
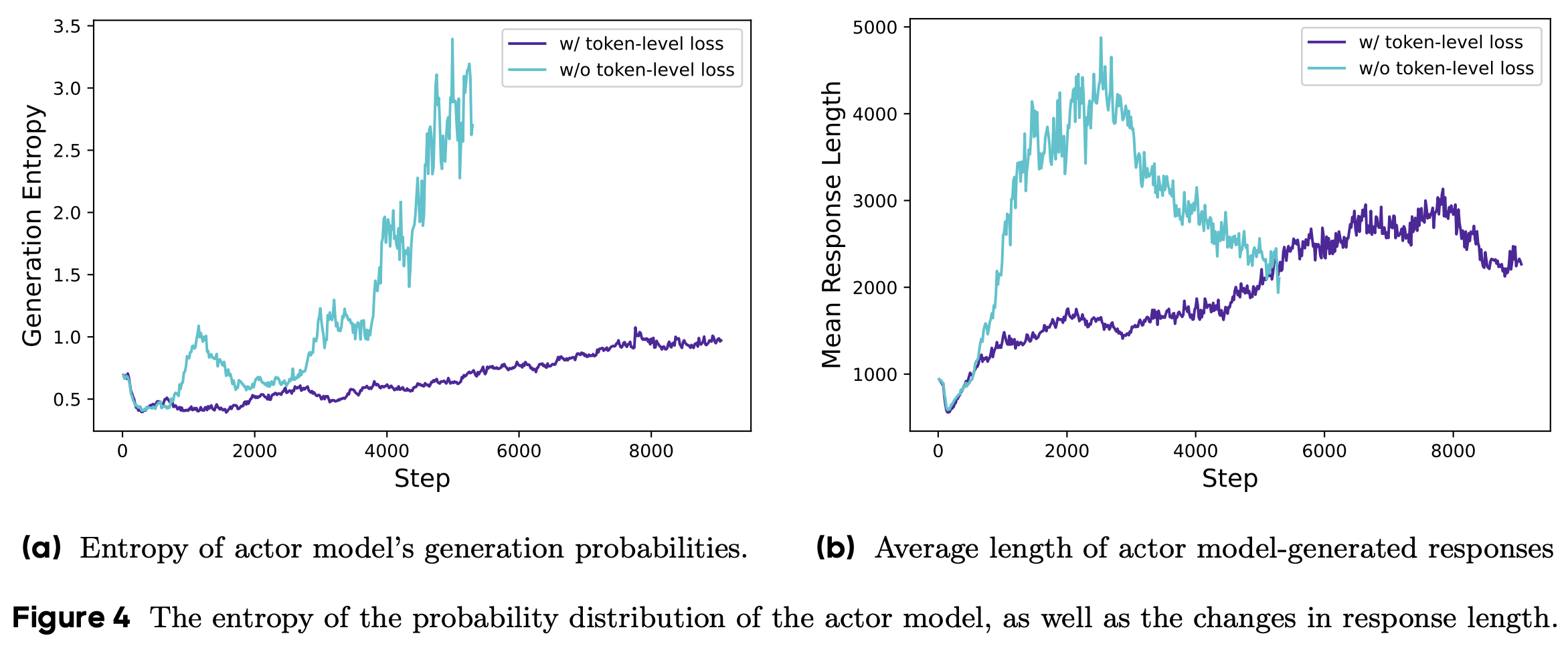
- DAPO 还引入了动态采样、Token-Level 策略梯度损失计算和过长奖励塑形等机制以稳定训练过程
- REINFORCE++ (Hu, 2025) 是经典 REINFORCE 算法的改进版本新算法
- REINFORCE++ 的核心目标是解决原始 REINFORCE 的局限性,并通过整合多种优化策略来提升性能
- REINFORCE++ 通常通过引入基线函数来减少方差,同时支持增量更新
- REINFORCE++ 还通过熵正则化避免策略过早僵化
B.3 LLM-based Search Agent
- RAG (2020)(检索增强生成)是一种将信息检索与生成模型相结合的技术方法,旨在提高生成模型输出的准确性、可靠性和时效性
- RAG 核心思想是:在生成答案之前,先从外部知识库中检索与问题相关的信息,然后让模型根据检索到的内容生成响应
- RAG 在一定程度上可以解决模型内部知识不足或幻觉的问题
- Search-o1 (2025d) 是一个基于智能体的搜索增强推理模型框架 ,主要用于解决推理过程中存在的知识不足问题
- 通过整合智能体 RAG 机制和文档内推理模块,它提高了模型推理的准确性、连贯性和可靠性
- 实验表明,Search-o1 在复杂推理任务中优于原生推理和传统 RAG 方法
- WebThinker (2025e) 是中国人民大学推出的开源深度研究框架,赋予 LRM 自主搜索、深度探索网页和撰写研究报告的能力
- WebThinker 开发了一种基于直接偏好优化的训练策略,通过迭代合成工具使用偏好数据来增强 LRM 的工具利用能力
- ReAct (2022) 是一种结合推理和行动的 AI 方法 ,旨在通过类似人类“边做边想”的模式让模型更有效地解决复杂任务
- ReAct 核心思想是打破传统模型的限制,允许模型在决策过程中主动生成推理步骤并调用外部工具(如搜索引擎、数据库等),最终通过迭代优化获得答案
附录 C: Implementation Details
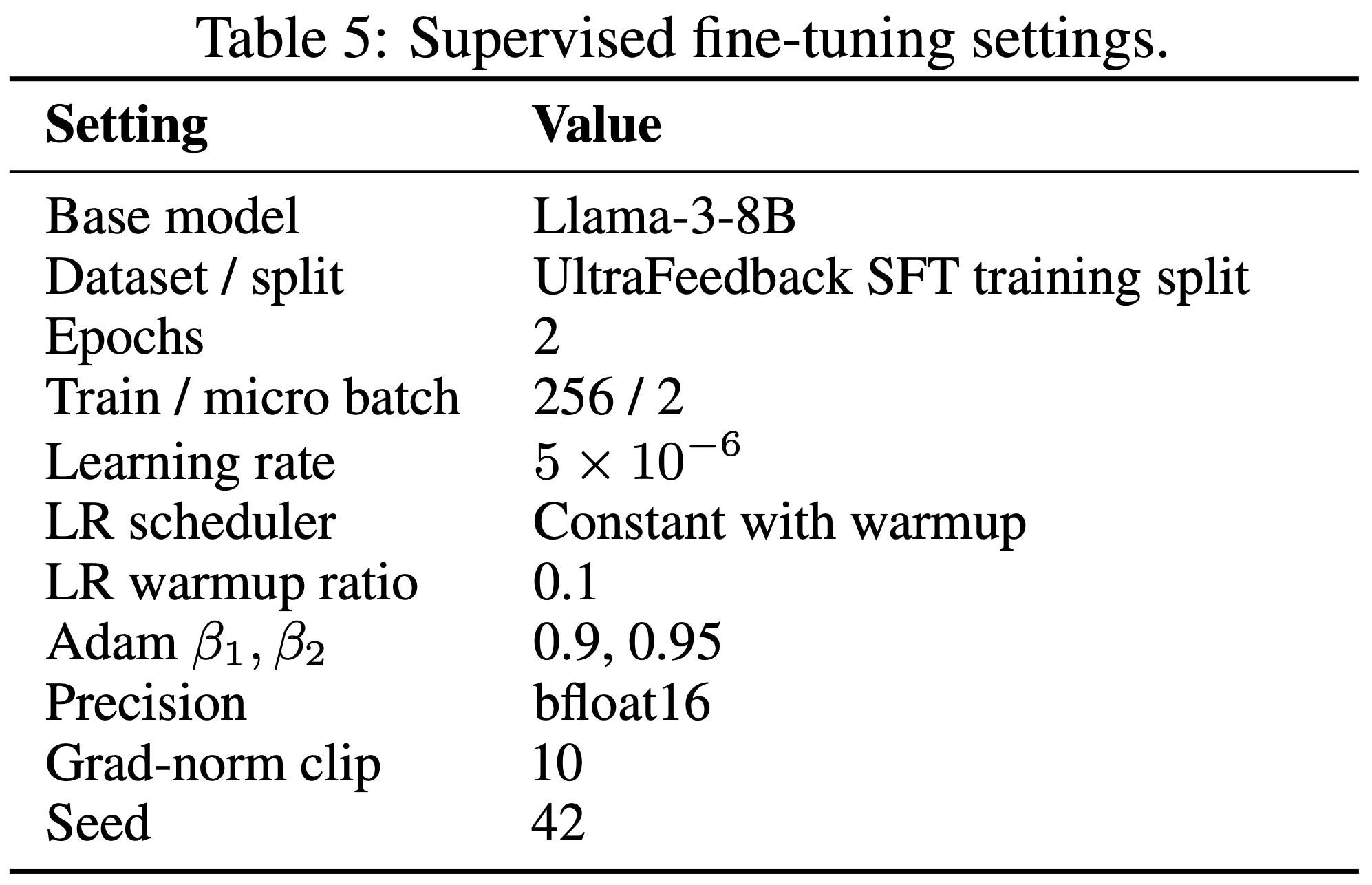
C.1 SFT
- 如第 4.3 节所述,在监督微调阶段,论文使用 Llama Factory 框架以 \(7 \times 10^{-6}\) 的学习率训练 Qwen2.5-3B-Instruct 模型
- 论文采用 DeepSpeed ZeRO-3 (2020) 和 FlashAttention2 (Dao, 2023) 进行优化
- 批量大小设置为 128,权重衰减为 0.1,模型训练 3 个周期
- 论文使用 BF16 混合精度,最大输入长度为 4096 token
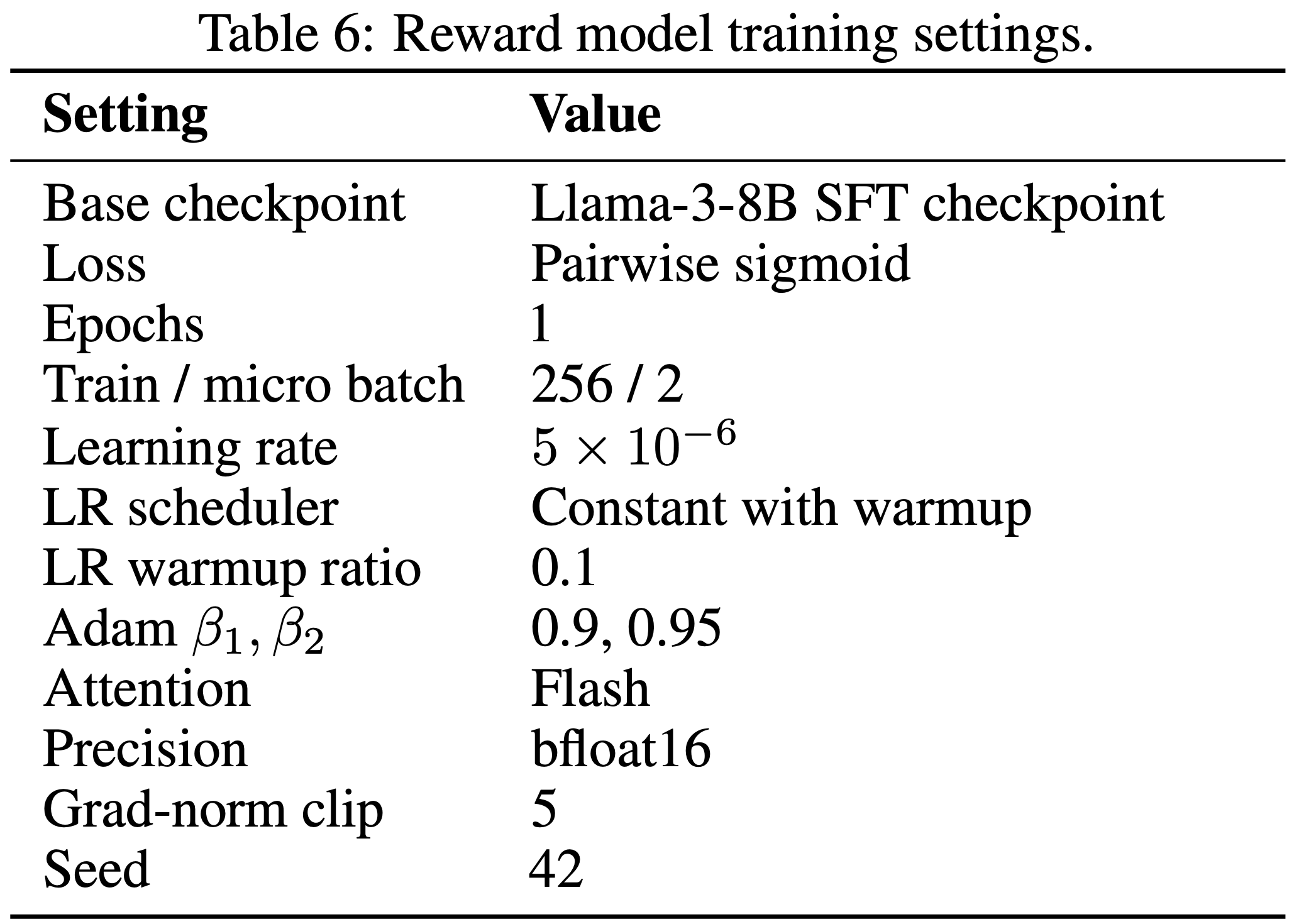
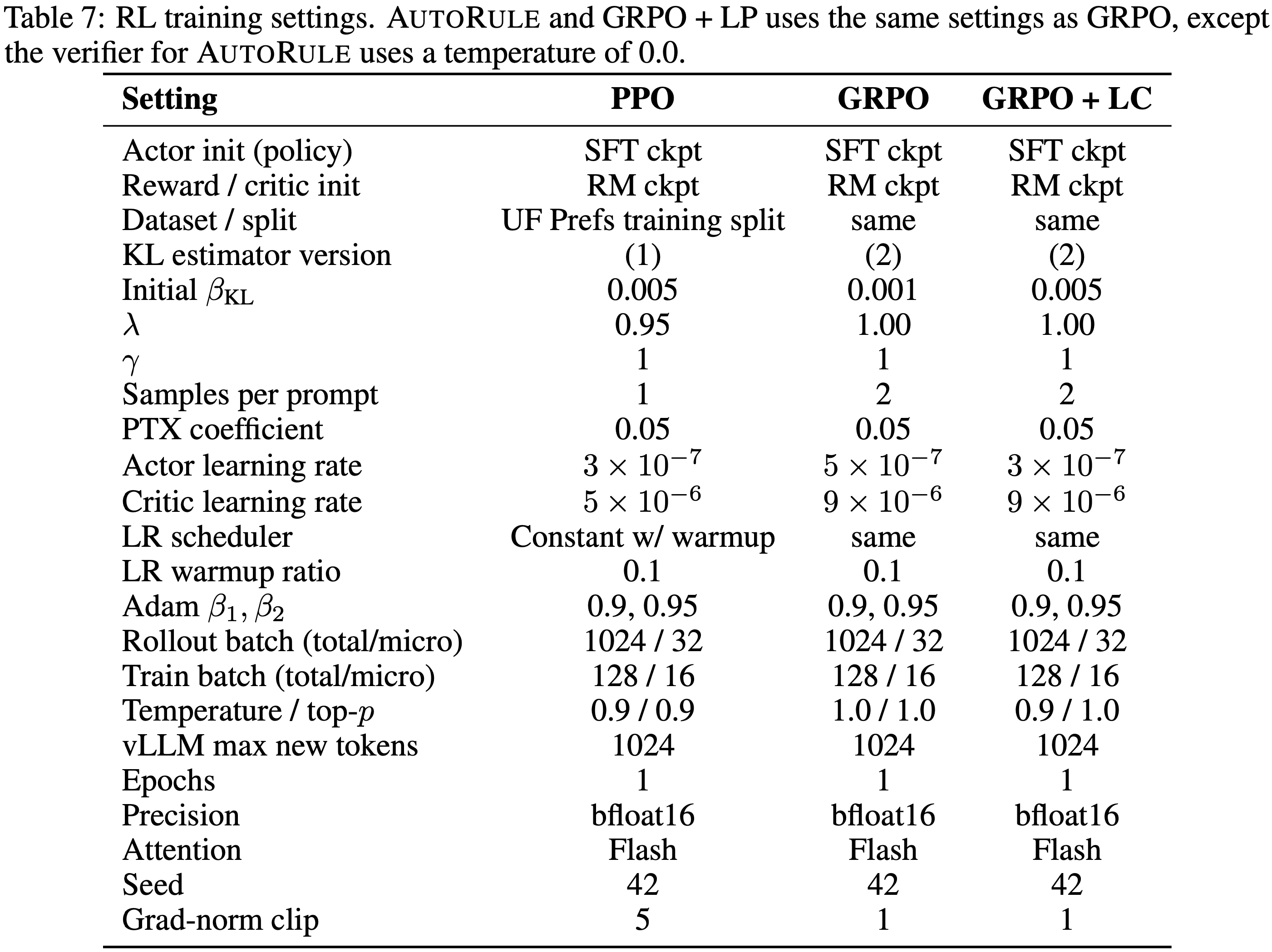
C.2 Reinforcement learning
- 在 ARPO 阶段,论文基于 VERL 框架 (2024) 实现了 ARPO 算法
- 值得注意的是,所有工具调用结果均被排除在损失计算之外 ,以避免对工具输出的偏向
- 损失计算仅考虑参与文本推理和工具请求的 token
- 论文对深度推理任务和深度搜索任务进行了差异化设置:
- 1. 深度推理任务(Deep Reasoning Tasks):
- 对于 7B 参数的模型,无论是使用 ARPO 还是其他 Trajectory-level 强化学习方法,论文的标准设置包括:
- 总训练批量大小为 128
- PPO 小批量大小为 16
- 全局 rollout 大小为 16
- 初始采样大小为 8
- 每次交互的响应长度上限为 4096 token
- 对于 ARPO rollout:
- 熵权重设置为 0.2
- 参数 \(a\) 设置为 0.5
- 阈值为 0.5
- 为了稳定训练,GRPO 中的 KL 散度系数设置为 0(问题:为什么设置为 0 反而稳定?)
- 强化学习阶段持续 2 个 epoch ,在 8 张 NVIDIA H800 GPU 上进行
- 对于 7B 参数的模型,无论是使用 ARPO 还是其他 Trajectory-level 强化学习方法,论文的标准设置包括:
- 2. 深度搜索任务(Deep Search Tasks):
- 对于 8B 参数的模型,论文保持与深度推理任务相同的设置,只是每次交互的响应长度延长至 8192 token
- 对于 14B 模型,使用相同的参数,但在 16 张 NVIDIA H800 GPU 上进行实验
- 由于数据集仅含 1K 样本,强化学习阶段持续 5 个 epoch
C.3 Details of Search
- 在训练和测试阶段,论文使用 Bing Web Search API 作为检索器,配置为美国英语(US-EN)区域
- 遵循一系列与 RAG 相关的工作 (2024; 2024b; 2024b, 2024e),论文为每个查询检索 10 个网页作为支持文档
- 对于数学和知识推理任务 ,论文仅使用 Top-10 Snippets 进行评估
- 对于深度搜索任务,论文从 URL 中获取每个页面最多 6000 tokens ,并使用与推理模型相同规模的模型作为浏览器 Agent 来提炼信息
C.4 Scaling Experiment Setup
- 在论文的扩展实验中,论文与上述设置保持一致:
- 总训练批量大小为 128
- PPO 小批量大小为 16
- 全局 rollout 大小为 16
- 初始采样大小为 8
- 对于 ARPO rollout
- 熵权重为 0.2
- \(a\) 为 0.5
- 阈值为 0.5
- 论文针对特定实验调整某些参数,同时保持其他参数不变
附录 D:Theoretical Analysis and Proofs
D.1 Theoretical Analysis of Soft Advantage Estimation
- 本节对软优势估计(Soft Advantage Estimation)进行详细的理论分析
- 首先,论文给出经典的 GRPO 优化目标:
$$
J_{\text{GRPO} }(\theta) = \mathbb{E}_{(q,a)\sim D,\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|q)} \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \min \left( r_{i,t}(\theta) \hat{A}_{i,t}, \text{clip} \left( r_{i,t}(\theta), 1-\epsilon, 1+\epsilon \right) \hat{A}_{i,t} \right) - \beta D_{\text{KL} }(\pi_\theta \parallel \pi_{\text{ref} }) \right]
$$ - 对于每个单独的问题,论文定义优化目标为:
$$
J^q_{\text{GRPO} }(\theta) = \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \min \left( r_{i,t}(\theta), \text{clip} \left( r_{i,t}(\theta), 1 \pm \epsilon \right) \right) \hat{A}_{i,t} - \beta D_{\text{KL} }(\pi_\theta \parallel \pi_{\text{ref} })
$$- 问题:\(\hat{A}_{i,t}\) 的正负影响了 \(\min\) 操作的取值,不能提出来吧?
- 因此,经典的 GRPO 优化目标可以表示为:
$$
J_{\text{GRPO} }(\theta) = \mathbb{E}_{(q,a)\sim D,\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|q)} [J^q_{\text{GRPO} }(\theta)]
$$ - 随后,论文重点分析 \( J^q_{\text{GRPO} }(\theta) \)。假设对于问题 \( q \) 的推理,部分 Rollout (partial rollout)操作从第 \( l \) 个 Token 开始。论文定义两个重要性采样比率(importance sampling ratio):
$$
r_{i,t}(\theta)^{<l} = \frac{\pi_\theta(y_{i,t} \mid x, y_{i,< t})}{\pi_{\text{ref} }(y_{i,t} \mid x, y_{i,< t})}, \\
r_{i,t}(\theta)^{>l} = \frac{\pi_\theta(p \mid x, q)}{\pi_{\text{ref} }(p \mid x, q)} \frac{\pi_\theta(y_{i,t} \mid x, q, p, y_{i,< t})}{\pi_{\text{ref} }(y_{i,t} \mid x, q, p, y_{i,< t})},
$$- \( r_{i,t}(\theta)^{< l} \) 表示第 \( l \) 个 Token 之前的重要性采样比率
- \( r_{i,t}(\theta)^{>l} \) 表示第 \( l \) 个 Token 之后的重要性采样比率
- \( q \) 表示输入问题
- \( p \) 表示共享 Token
- 而公式 (14) 中的 \( y_{i,< t} \) 表示从共享 Token 到第 \( t \) 个 Token 之前的序列
- 此外,论文定义 \( o^i_l \) 为第 \( i \) 个序列的第 \( l \) 个 Token
- 此时 \( J^q_{\text{GRPO} }(\theta) \) 可以表示为:
$$
J_{\text{GRPO} }(\theta) = \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \left[ \sum_{t=1}^{|o^i_l|} \min \left( r_{i,t}(\theta)^{<l}, \text{clip} \left( r_{i,t}^{<l}(\theta), 1 \pm \epsilon \right) \right) \hat{A}_{i,t} + \sum_{t=|o^i_l|}^{|y_i|} \min \left( r_{i,t}^{>l}(\theta), \text{clip} \left( r_{i,t}^{>l}(\theta), 1 \pm \epsilon \right) \right) \hat{A}_{i,t} \right] - \beta D_{\text{KL} }(\pi_\theta \parallel \pi_{\text{ref} })
$$- 原文有对本式继续化简,详情见论文
- 论文进一步定义:
$$
J_i^{\leq l} = \frac{1}{|o_l|} \sum_{t=1}^{|o^i_l|} \min \left( r_{i,t}(\theta)^{<l}, \text{clip} \left( r_{i,t}^{<l}(\theta), 1 \pm \epsilon \right) \right) \hat{A}_{i,t}, \\
J_i^{>l} = \frac{1}{|o_{l:i}|} \sum_{t=|o^i_l|}^{|y_i|} \min \left( r_{i,t}^{>l}(\theta), \text{clip} \left( r_{i,t}^{>l}(\theta), 1 \pm \epsilon \right) \right) \hat{A}_{i,t}, \\
J_{\text{GRPO} }^{>l} = \frac{1}{G} \sum_{i=1}^G \frac{1}{|o_{l:i}|} \left[ \sum_{t=|o^i_l|}^{|y_i|} \min \left( r_{i,t}^{>l}(\theta), \text{clip} \left( r_{i,t}^{>l}(\theta), 1 \pm \epsilon \right) \right) \hat{A}_{i,t} \right],
$$- \( J_i^{< l} \) 表示第 \( i \) 条链共享 Token 部分的优化目标
- \( J_i^{>l} \) 表示第 \( i \) 条链部分 Rollout 后的优化目标
- \( J_{\text{GRPO} }^{>l} \) 表示从第 \( l \) 个位置开始直接执行经典 GRPO 采样操作的优化目标
- 此时,原始优化目标 \( J_{\text{GRPO} }(\theta) \) 可以表示为:
$$
J_{\text{GRPO} }(\theta) = \frac{1}{G} \sum_{i=1}^G \frac{|o_l|}{|y_i|} [J_i^{<l} - J_i^{>l}] + J_{\text{GRPO} }^{>l} - \beta D_{\text{KL} }(\pi_\theta \parallel \pi_{\text{ref} })
$$- 在这种情况下,软优势估计下的 GRPO 优化目标可以表示为一个标准 GRPO 目标(从部分 Rollout 位置开始)与前后两点目标加权差值的总和
- 每个差值的权重与其对应推理链的长度密切相关
D.2 Theoretical Proof of GPG Theorem
D.2.1 Transformer-based Policy
- Transformer-based 策略 \( \pi_\theta(a_t|s_t) \),通过应用链式法则,论文有以下关系:
$$
\begin{aligned}
&\pi_\theta(OT_1 | IT_1, IT_2, …, IT_{|\text{input}|}) \times \\
&\pi_\theta(OT_2 | IT_1, IT_2, …, IT_{|\text{input}|}, OT_1) \times \\
&\pi_\theta(OT_3 | IT_1, IT_2, …, IT_{|\text{input}|}, OT_1, OT_2) \times \\
& … \\
&\pi_\theta(OT_{|\text{output}|} | IT_1, …, IT_{|\text{input}|}, OT_1, …, OT_{|\text{output}|-1}) \\
= &\pi_\theta(OT_1, OT_2, …, OT_{|\text{output}|} & | IT_1, IT_2, …, IT_{|\text{input}|}) \\
= &\pi_\theta(MA | MS_1)
\end{aligned}
$$- \( IT_i \) 和 \( OT_i \) 分别是输入 Token 和输出 Token ;
- \( MS_1 \triangleq <IT_1, IT_2, …, IT_{|\text{input}|}> \) 表示宏状态(macro state)
- \( MA \triangleq <OT_1, OT_2, …, OT_{|\text{output}|}> \) 表示宏动作(macro action)
- 在更一般的形式中,我们可以将完整的输出 \( OT_1, OT_2, …, OT_{|\text{output}|} \) 分割为 \( K \) 个片段,并得到广义的宏状态和宏动作,即 \( MS_i \triangleq <MS_{i-1}, MA_{i-1}> \) 和 \( MA_i \triangleq <OT_m, OT_{m+1}, …, OT_{m+n}> \)
- 此时,论文有以下关系:
$$
\begin{aligned}
&\pi_\theta(MA | MS_1) \\
= &\pi_\theta(MA_1 | MS_1) \times \\
&\pi_\theta(MA_2 | MS_1, MA_1) \times \\
& … \\
&\pi_\theta(MA_K | MS_1, MA_1, MA_2, …, MA_{K-1}) \\
= &\pi_\theta(MA_1 | MS_1) \times \\
&\pi_\theta(MA_2 | MS_2) \times \\
& … \\
&\pi_\theta(MA_K | MS_K) \\
= &\prod_{T=1}^K \pi_\theta(MA_T | MS_T)
\end{aligned}
$$- 其中 \( T \) 表示宏时间步(macro timestep)
D.2.2 Derivation of the GPG Theorem
- 基于上述定义的宏状态和宏动作,我们可以得到广义策略梯度定理(Generalized Policy Gradient Theorem, GPG)(适用于 Transformer-based 策略):
$$
\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left\{ \sum_{T=1}^K [\nabla_\theta \log \pi_\theta (MA_T | MS_T) \Phi_T] \right\}
$$ - GPG 定理的一个关键优势是它允许对任意长度的宏动作进行分割。这种灵活性使得该定理具有高度的实用性:
- 例如,能够基于特殊 Token 对轨迹进行分割
- 证明如下:
$$
\begin{aligned}
\nabla_\theta J(\theta) &= \nabla_\theta \mathbb{E}_{\tau \sim \pi_\theta} [R(\tau)] \\
&= \nabla_\theta \sum_\tau P(\tau; \theta) R(\tau) \\
&= \sum_\tau \nabla_\theta P(\tau; \theta) R(\tau) \\
&= \sum_\tau P(\tau; \theta) \frac{\nabla_\theta P(\tau; \theta)}{P(\tau; \theta)} R(\tau) \\
&= \sum_\tau P(\tau; \theta) \nabla_\theta \log P(\tau; \theta) R(\tau) \\
&= \sum_\tau P(\tau; \theta) \nabla_\theta \left[ \log \mu(s_1) \prod_{t=1}^H \pi_\theta (a_t | s_t) P(s_{t+1} | s_t, a_t) \right] R(\tau) \\
&= \sum_\tau P(\tau; \theta) \nabla_\theta \left[ \log \prod_{t=1}^H \pi_\theta (a_t | s_t) P(s_{t+1} | s_t, a_t) \right] R(\tau) \\
&= \sum_\tau P(\tau; \theta) \nabla_\theta \left[ \log \prod_{t=1}^H \pi_\theta (a_t | s_t) \right] R(\tau) \\
&= \sum_\tau P(\tau; \theta) \nabla_\theta \left[ \log \prod_{T=1}^K \pi_\theta (MA_T | MS_T) \right] R(\tau) \\
&= \sum_\tau P(\tau; \theta) \left[ \sum_{T=1}^K \nabla_\theta \log \pi_\theta (MA_T | MS_T) \right] R(\tau) \\
&= \sum_\tau P(\tau; \theta) \left[ \sum_{T=1}^K \nabla_\theta \log \pi_\theta (MA_T | MS_T) R(\tau) \right] \\
&= \mathbb{E}_{\tau \sim \pi_\theta} \left\{ \sum_{T=1}^K [\nabla_\theta \log \pi_\theta (MA_T | MS_T) R(\tau)] \right\} \\
&= \mathbb{E}_{\tau \sim \pi_\theta} \left\{ \sum_{T=1}^K [\nabla_\theta \log \pi_\theta (MA_T | MS_T) \Phi_T] \right\}
\end{aligned}
$$ - 证明中的关键步骤如下:
- 1)从公式 (30) 到公式 (31),这是因为对于 Transformer-based 策略,\( s_{t+1} = [s_t, a_t] \),因此 \( P(s_{t+1} | s_t, a_t) = 1 \)
- 2)从公式 (31) 到公式 (32),这是因为对于 Transformer-based 策略,\( s_{t+1} = [s_t, a_t] \),因此我们可以进行以下推导:
$$
\begin{aligned}
\prod_{t=1}^H \pi_\theta (a_t | s_t) \\
&= \pi_\theta (a_1 | s_1) \times \pi_\theta (a_2 | s_2) \times … \times \pi_\theta (a_H | s_H) \\
&= \pi_\theta (a_1 | s_1) \times \pi_\theta (a_2 | s_1, a_1) \times … \times \pi_\theta (a_H | s_0, a_0, a_1, …, a_{H-1}) \\
&= \pi_\theta (a_1, a_2, …, a_H | s_1) \\
&= \pi_\theta (MA | MS_1) \\
&= \pi_\theta (MA_1 | MS_1) \times \\
& \pi_\theta (MA_2 | MS_1, MA_1) \times \\
& … \\
& \pi_\theta (MA_K | MS_1, MA_1, MA_2, …, MA_{K-1}) \\
&= \prod_{T=1}^K \pi_\theta (MA_T | MS_T)
\end{aligned}
$$ - 3)从公式 (35) 到公式 (36),这与从策略梯度定理(Policy Gradient Theorem)到策略梯度定理的一般形式(即从传统优势函数到 GAE)的转换类似
附录 E:The Algorithm Workflow of ARPO
- ARPO 的训练流程见算法 1

附录 F:Case Study
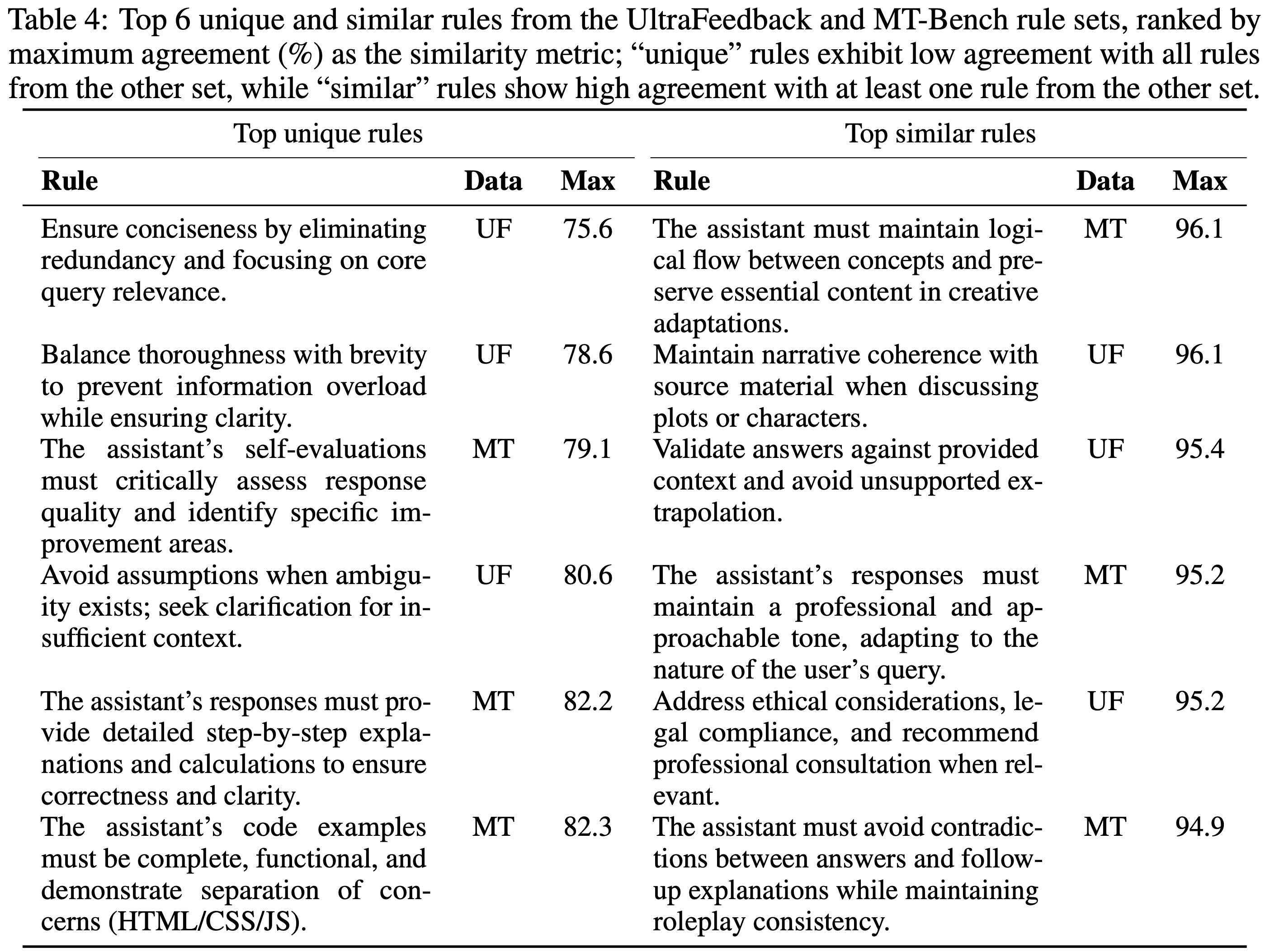
- 详情见原始论文(以下仅展示表 4,原文中还有多个 Case 可供参考)





/AdvancedIF-Figure1.png)
/AdvancedIF-Figure2.png)
/AdvancedIF-Table1.png)
/AdvancedIF-Table2.png)
/AdvancedIF-Table3.png)
/AdvancedIF-Figure3.png)
/AdvancedIF-Figure4.png)
/AdvancedIF-Table4.png)
/AdvancedIF-Table5.png)
/AdvancedIF-Table6.png)
/AdvancedIF-Table7.png)
/AdvancedIF-Table7-p2.png)