CA——(MIAA)Deep-Automated-Mechanism-Design-for-Integrating-Ad-Auction-and-Allocation-in-Feed

参考链接：
- 原始论文：Deep Automated Mechanism Design for Integrating Ad Auction and Allocation in Feed, SIGIR 2024, Meituan

整体思路说明（摘要）

电子商务平台通常会在每个用户的页面浏览请求中展示一个有序列表，其中包含多个自然商品和一个广告。这个列表是广告拍卖和分配过程的结果，直接影响平台的广告收入和商品交易总额（GMV）。具体来说，广告拍卖决定了展示哪个广告以及相应的支付金额，而广告分配则决定了广告和自然商品的展示位置
目前普遍的方法将广告拍卖和分配分为两个独立的阶段，面临两个问题：
- 1）广告拍卖没有考虑外部性，例如实际展示位置和上下文对广告点击率（CTR）的影响；
- 2）广告分配利用拍卖获胜广告的支付金额动态决定展示位置，但无法保持广告的激励兼容性（IC）。例如，在使用传统广义第二价格（GSP）的拍卖阶段，即使获胜广告提高出价，其支付金额也不会改变。这意味着广告无法获得更好的位置，从而失去了在后续广告分配阶段实现更高效用的机会
以往的研究通常只关注其中一个阶段，忽略了这两个阶段的问题，可能导致次优结果
论文提出了一种深度自动化机制：
- 将广告拍卖和分配集成在一起，确保在存在外部性的情况下同时满足IC和个体合理性（IR），并最大化收入和GMV
- 该机制以候选广告和自然商品的有序列表作为输入
  - 对于每个候选广告，通过在自然商品列表的不同位置插入广告生成多个候选分配
  - 对于每个候选分配，列表模型将整个分配作为输入，并输出每个广告和自然商品的预测结果，以建模全局外部性
  - 最后，通过深度神经网络建模的自动化拍卖机制执行，选择最优分配
- 因此，该机制同时决定了广告的排名、支付金额和展示位置
论文机制在离线实验和在线A/B测试中比最先进的基线方法实现了更高的收入和GMV

Introduction and Discussion

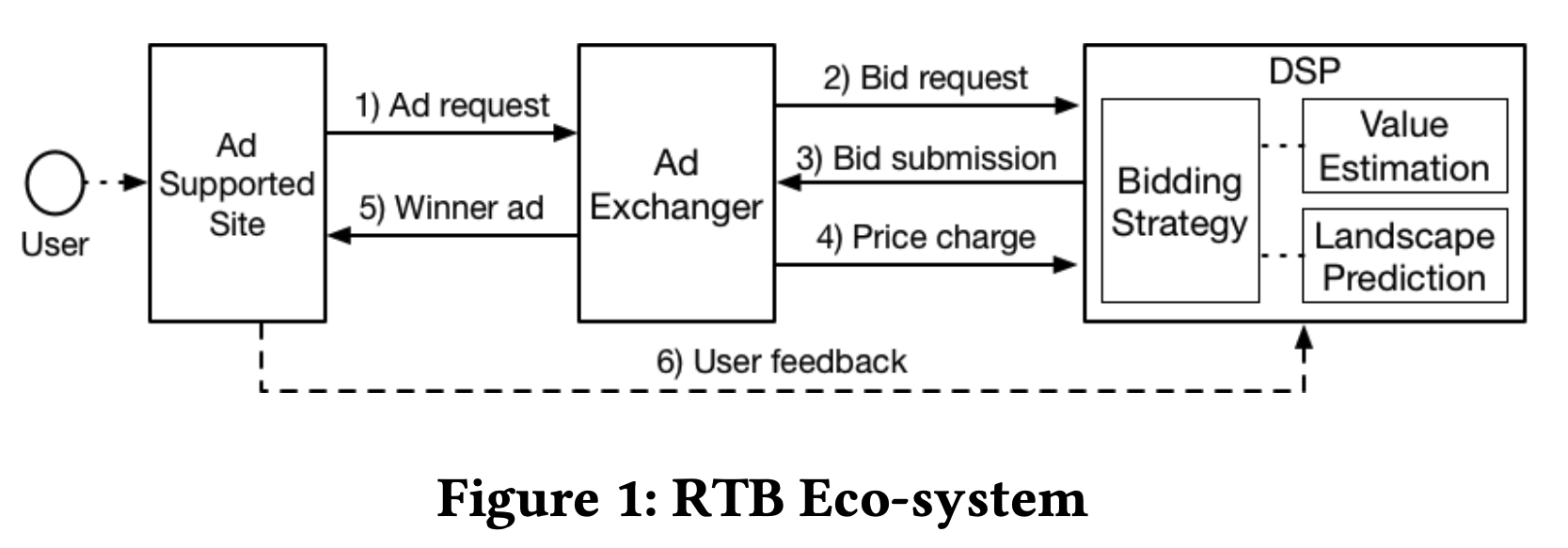
在许多电子商务信息流中，每个用户的页面浏览请求都会展示一个有序列表，其中包含多个自然商品和一个按点击付费的广告（如果用户点击广告，平台将向相应的广告主收费，这是平台收入的关键来源。同时，如果用户购买了自然商品或广告中的产品，平台的商品交易总额（GMV）将增加
实际上，这个列表由广告拍卖和分配过程生成，直接决定了平台的收入和GMV
- 广告拍卖 ：决定了展示哪个广告以及广告的支付金额
- 广告分配 ：决定了广告和自然商品在信息流中的展示位置
- 广告拍卖和分配是相互影响的
引出问题 ：设计广告拍卖和分配机制以最大化平台收入和GMV成为一个非常有意义且具有挑战性的问题
传统广告拍卖和位置分配方法 ：将广告拍卖和分配分为两个阶段
- 首先，在广告拍卖中，例如经典的GSP，候选广告通过eCPM（预计每千次展示收入）进行排名，eCPM由广告的预测点击率（pCTR）和出价计算得出，eCPM最高的广告获胜，其支付金额为下一个排名广告的eCPM除以其自身的pCTR。显然，获胜广告的支付金额取决于下一个排名广告的出价，而不是其自身的出价。同时，自然商品列表按估计的GMV排序
- 随后，广告分配算法动态地将拍卖获胜的广告插入到有序的自然商品列表中，其中获胜广告的支付金额用于位置决策，旨在最大化收入和GMV
从广告机制设计的角度来看，传统这种将广告拍卖和分配分为两个独立阶段的方法面临以下两个问题：
- 广告拍卖未考虑外部性。广告外部性通常指其展示位置和上下文对其CTR的影响。传统拍卖，包括GSP，通常不考虑外部性，并基于分离的CTR假设获得稳定的结果。然而，在实际中，广告被自然商品包围时的CTR受其实际展示位置和上下文的影响。外部性导致广告主之间复杂的战略竞争，阻碍了稳定结果和社会福利优化。因此，在考虑外部性时，传统拍卖并不适用。（比如：在美团零售配送平台上，信息流中的广告“乐事薯片”与外部自然商品一起展示给用户。用户是否点击广告很容易受到广告位置和上下文的影响）
- 广告分配无法保持激励兼容性（IC）。广告分配利用拍卖获胜广告的支付价格动态确定显示位置，无法保持广告的激励兼容性。例如，在使用传统GSP的拍卖阶段，即使获胜广告增加其出价，其支付价格仍保持不变。这意味着广告无法获得更好的位置，从而失去了在后续广告分配阶段实现更高效用的机会
  - 个人理解：不激励兼容可以理解为，用户在和自然竞争时，拿到更好或者更坏的位置，价格不会发生变化，即广告位置分配与出价无关导致了不激励兼容
以往的研究通常只关注其中一个阶段，忽略了这两个阶段的问题，这可能导致次优结果。因此，论文提出了一种深度自动化机制，将广告拍卖和分配整合在一起，确保在存在外部性的情况下同时满足激励兼容性（IC）和个体合理性（IR） ，并最大化收入和GMV
- 该机制以候选广告和有机商品的有序列表作为输入。对于每个候选广告，通过在有机商品列表的不同位置插入广告生成多个候选分配；对于每个候选分配，列表模型将整个分配作为输入，并输出每个广告和有机商品的预测结果，以建模全局外部性；最后，执行由深度神经网络建模的自动化拍卖机制，以选择最佳分配
- 也就是说，该机制同时决定了广告的排名、支付价格和显示位置
最后：论文所提出的机制在离线实验和在线A/B测试中比最先进的基线方法实现了更高的收入和GMV
注：论文旨在设计一种深度自动化机制，集成信息流中的广告拍卖和分配，在存在外部性的情况下同时满足IC和IR，并最大化收入和GMV

Preliminary

广告拍卖与分配的场景设置

论文考虑在信息流中集成按点击付费广告拍卖和分配的机制设计。对于每个用户的页面浏览请求，有 $m$ 个可用位置用于放置广告和自然商品。有 $n$ 个广告主竞争一个广告位置，其他 $m-1$ 个位置由自然商品填充。由于平台业务划分的限制，论文假设这些自然商品已根据估计的GMV进行了排序。在后续过程中，自然商品的相对排名不会被修改，但它们的CTR和GMV将被重新预测。论文的主要符号总结在表1中
每个广告主 $i\in[n]$ 对其广告有一个私有的点击价值 $v_{i}\in\mathcal{B}\subseteq R^{+}$ ，并提交一个点击出价 $b_{i}\in\mathcal{B}\subseteq R^{+}$ 进行拍卖。论文假设自然商品的点击价值和出价为0。设 $\mathbf{v}=(v_{1},v_{2},\ldots,v_{n})\in\mathcal{B}^{n}$ 和 $\mathbf{b}=(b_{1},b_{2},\ldots,b_{n})\in\mathcal{B}^{n}$ 分别为所有广告的价值分布和出价分布。论文使用 $\mathbf{v}_{-i}$ 和 $\mathbf{b}_{-i}$ 表示除广告 $i$ 之外的所有广告的价值分布和出价分布。广告分配可以表示为 $\mathbf{a}=\mathit{a}(i,j)$ ，其中 $\mathit{a}(i,j)$ 表示广告 $i$ 被插入到第 $j$ 个位置。设 $j=\sigma(i)$ 表示广告 $i$ 在分配中的位置索引。所有可能分配的集合表示为 $\mathcal{A}=\{\mathit{a}(i,j):\forall i\in[n],j\in[m]\}$
形式上，一个分配（具体某个分配）就是一个包含多个自然商品和一个广告的有序列表。在建模全局外部性的影响时，CTR预测需要考虑多个方面，例如广告本身的属性、广告的位置和上下文以及周围自然商品的属性。论文将分配 $\mathbf{a}$ 中第 $j$ 个项目的pCTR表示为 $q_{j}(\mathbf{a})$ 。设 $g_{j}(\mathbf{a})$ 为分配中第 $j$ 个项目的估计每点击商品交易额。为了方便起见，论文使用 $e_{j}\in\mathcal{E}\subseteq R$ 表示分配中第 $j$ 个项目的外部性，如CTR和GMV

问题公式化

给定广告主的出价和有序的自然商品列表，论文表示一个广告拍卖与分配机制 $\mathcal{M}\langle\mathcal{R},\mathcal{P}\rangle$ ，其中：
- $\mathcal{R}(\mathbf{b};\mathbf{e}):\mathcal{B}^{n}\times\mathcal{E}^{m}\to \mathcal{A}$ 是广告分配规则，用于从 $n$ 个广告主中选择一个获胜广告，并将其插入到自然商品列表的某个位置
- $\mathcal{P}(\mathbf{b};\mathbf{e})$ 是支付规则， $p_{i}(\mathbf{b};\mathbf{e})$ 是广告主 $i$ 的按点击支付价格
对于机制 $\mathcal{M}\langle\mathcal{R},\mathcal{P}\rangle$ ：
- 广告主 $i$ 的预期效用为：
  $$u_{i}^{\mathcal{M}}(v_{i};\mathbf{b};\mathbf{e})=(v_{i}-p_{i}(\mathbf{b}; \mathbf{e}))\times q_{\sigma(i)}\left(\mathcal{R}(\mathbf{b};\mathbf{e})\right),$$
- 平台的预期收入和GMV为：
  $$\begin{align}
  \text{Rev}^{\mathcal{M}}(\mathbf{b};\mathbf{e}) =\sum_{i=1}^{n}p_{i}(\mathbf{b};\mathbf{e}))\times q_{\sigma(i)} \left(\mathcal{R}(\mathbf{b};\mathbf{e})\right)\\
  \text{Gmv}^{\mathcal{M}}(\mathbf{b};\mathbf{e}) =\sum_{j=1}^{m}g_{j}(\mathcal{R}(\mathbf{b};\mathbf{e}))\times q _{j}(\mathcal{R}(\mathbf{b};\mathbf{e}))
  \end{align}
  $$
对于广告拍卖机制的设计，IC和IR是必须考虑的标准经济约束。一个拍卖机制 $\mathcal{M}\langle\mathcal{R},\mathcal{P}\rangle$ 是IC的，如果每个广告主如实报告其出价 $b_{i}=v_{i}$ ，则其效用最大化。形式上，对于任何 $\mathbf{e}$ ，对于每个 $i$ ，有
$$u_{i}(v_{i};v_{i},\mathbf{b}_{-1};\mathbf{e})\geq u_{i}(v_{i};b_{i}, \mathbf{b}_{-1};\mathbf{e}),\forall b_{i}\in\mathcal{B},$$
一个拍卖机制 $\mathcal{M}\langle\mathcal{R},\mathcal{P}\rangle$ 是IR的，如果每个广告主不会被收取超过其出价的分配费用。形式上，对于任何 $\mathbf{e}$ ，对于每个 $i$ ，有
$$p_{i}(\mathbf{b};\mathbf{e})\leq b_{i}.$$
论文的目标是设计一个机制 $\mathcal{M}\langle\mathcal{R},\mathcal{P}\rangle$ ，在存在外部性的情况下同时满足IC和IR，并最大化平台的收入和GMV，如下所示：
$$
\begin{align}
\max_{\mathcal{M}}\inf_{z\in\mathbf{e}} z \mathbb{E}_{\mathbf{a}\in\mathcal{A}}&[\text{Rev}(\mathbf{b};\mathbf{e})+ \alpha\text{Gmv}(\mathbf{b};\mathbf{e})],\\
\text{s.t.} \quad &\textit{IC and IR constraint}
\end{align}
$$
- 其中 $\alpha$ 是平台设置的权重系数，用于平衡收入和GMV

自动化机制设计

形式上，广告拍卖与分配的集成可以看作广告和自然商品的组合拍卖（CA），其中自然商品的点击私有价值和出价可以假设为0。Sandholm和Likhodedov提出了一种基于VCG的自动化机制AMA，用于最大化收入的组合拍卖。AMA定义如下
- 每个投标人 $j$ 提交一个估值函数 $v_{j}$ 。分配 $\mathbf{a}^{*}$ 被计算为最大化
  $$\text{SW}^{\mu}_{\lambda}(\mathbf{a})=\sum_{j=1}^{m}\mu_{j}v_{j }(\mathbf{a})+\lambda(\mathbf{a}),$$
- 其中 $\mu_{j}$ 是一个正数，与投标人 $j$ 的价值分布相关，但与分配无关，同时 $\lambda(\mathbf{a})$ 是分配的任意函数。支付为:
  $$p_{j}(\mathbf{a}^{*})=\frac{1}{\mu_{j}}\Big[\text{SW}^{\mu}_{ \lambda}(\mathbf{a}^{*}_{-j})-\sum_{i\neq j}\mu_{i}v_{i}(\mathbf{a}^{*})- \lambda(\mathbf{a}^{*})\Big],$$
- 其中 $\mathbf{a}^{*}_{-j}$ 是投标人 $j$ 不存在时的最佳分配:
  $$\mathbf{a}^{*}_{-j}=\max_{\mathbf{a}\in\mathcal{A}}\lim_{i\to \infty}z\in\text{SW}^{\mu}_{\lambda}(\mathbf{a}).$$
AMA是一系列机制，由向量 $\mu$ 和 $\lambda$ 参数化。VCG是特殊情况，其中对于所有投标人 $j$ 和任何分配， $\mu_{j}=1$ 且 $\lambda(\cdot)=0$ 。 $\mu_{j}$ 和 $\lambda(\cdot)$ 通过自动化搜索理论求解以最大化收入。Roberts等和Lavi等已经证明，只有AMA在所有CA设置中都是IC和IR的。因此，受AMA启发，论文将其应用扩展到集成广告拍卖与分配。与搜索理论不同，论文中 $\mu_{j}$ 和 $\lambda(\cdot)$ 被建模为深度神经网络，并通过端到端学习方法进行训练

MIAA拍卖机制

在本节中，论文介绍了集成信息流中广告拍卖与分配的深度自动化机制MIAA的细节，该机制在存在外部性的情况下同时满足IC和IR，并最大化收入和GMV。如图2所示，MIAA以候选广告和有序的自然商品列表作为输入，并通过三个模块输出最优分配。MIAA的三个模块是外部性感知预测模块（ Externality-aware Prediction Module，EPM）、自动化拍卖模块（Automated Auction Module，AAM）和可微分排序模块（Differentiable Sorting Module，DSM）
- EPM以分配为输入，建模全局外部性的影响，并输出每个广告和自然商品的预测结果
- AAM使用两个深度神经网络来建模机制参数 $\mu_{j}$ 和 $\lambda(\cdot)$ ，旨在提高该自动化机制的表达能力，同时保证IC和IR
- DSM使用多分类模型softmax对机制中的排序操作进行连续松弛，并输出表示每个候选分配获胜概率的向量
平台的预期收入和GMV可以通过端到端学习方式可微分地计算和优化

外部性感知预测模块（EPM）

外部性感知预测模块（ Externality-aware Prediction Module，EPM）

在大多数传统拍卖机制中，广告的位置和上下文信息只能在拍卖后得知，因此CTR预测模型无法提前获取这些信息。然而，拍卖依赖于预测模型的pCTR。为了解决这种相互依赖问题并获得稳定的分配结果，机制设计基于分离的CTR假设，即广告的最终CTR等于其自身内容的CTR与其位置的CTR的乘积，忽略了上下文商品的影响。因此，在这种假设下，通常使用点模型来预测CTR，该模型不考虑广告展示位置和广告与自然商品之间的相互作用的影响。一些模型相继提出，捕捉局部外部性，仅关注广告的展示位置或广告的局部上下文。为此，论文使用列表预测模块显式建模全局外部性，为每个项目输出更准确的pCTR
第一步 ，对于每个候选广告，通过在有序自然商品列表的不同位置插入广告生成多个候选分配。此步骤对应的时间复杂度为 $O(m\times n)$ 。在实际生产过程中， $m$ 的值通常不大于5，这在平台性能方面是可以接受的
第二步 ，EPM对所有候选分配采用参数共享结构。这里论文以分配 $\mathbf{a}$ 为例进行说明。如图2所示，EPM以分配 $\mathbf{a}$ 和两种类型的公共信息（即请求信息、当前请求中的用户画像）作为输入，并输出分配中每个项目的pCTR。论文首先使用嵌入层从原始稀疏特征中提取嵌入，然后将密集特征与嵌入连接起来，形成第 $j$ 个项目的 $d$ 维特征向量 $\mathbf{z}_{j}\in\mathbb{R}^{d}$ 。分配 $\mathbf{a}$ 的特征矩阵表示为 $\mathbf{Z}^{\mathbf{a}}\in\mathbb{R}^{m\times d}$ ，而请求信息和用户画像的特征向量分别表示为 $\mathbf{z}^{\prime\prime}$ 和 $\mathbf{z}^{\prime}$
第三步 ，论文使用自注意力单元来建模候选分配中广告与自然商品之间的相互作用：
$$\mathbf{H}^{\mathbf{a}}=\text{SelfAtt}\left(\mathbf{Q}^{\mathbf{a}},\mathbf{K}^{ \mathbf{a}},\mathbf{V}^{\mathbf{a}}\right)=\text{softmax}\left(\frac{\mathbf{Q}^ {\mathbf{a}}(\mathbf{K}^{\mathbf{a}})^{\top}}{\sqrt{d}}\right)\mathbf{v}^{ \mathbf{a}},$$
- 其中 $\mathbf{Q}^{\mathbf{a}}$ 、 $\mathbf{K}^{\mathbf{a}}$ 、 $\mathbf{V}^{\mathbf{a}}$ 分别表示查询、键和值。这里查询、键和值从分配 $\mathbf{a}$ 的特征信息线性变换而来，如下所示：
  $$\mathbf{Q}^{\mathbf{a}}=\mathbf{Z}^{\mathbf{a}}\mathbf{W}^{Q},\mathbf{K}^{ \mathbf{a}}=\mathbf{Z}^{\mathbf{a}}\mathbf{W}^{K},\mathbf{V}^{\mathbf{a}}= \mathbf{Z}^{\mathbf{a}}\mathbf{W}^{V}.$$
第四步 ，论文将 $\mathbf{H}^{\mathbf{a}}$ 重塑为一个向量 $\mathbf{h}^{\mathbf{a}}\in\mathbb{R}^{md}$ ，并将 $\mathbf{z}^{u}$ 、 $\mathbf{z}^{r}$ 连接起来，放入多层感知机（MLP）中以建模全局外部性：
$$\hat{q}_{j}=q_{j}(\mathbf{a})=\text{Sigmoid}\left(\text{FC}_{j} \left(\text{MLP}^{\mathbf{c}}\left(\mathbf{h}^{\mathbf{a}}|\mathbf{z}^{u}|\mathbf{z}^{r}\right)\right)\right),;\forall j\in[m],$$
- 其中 $q_{j}(\mathbf{a})$ 表示分配中第 $j$ 个项目的pCTR。在EPM中，通过每个项目的真实点击行为计算交叉熵损失来训练该列表模型：
  $$\text{Loss}_{\text{ec}}=-\sum_{j=1}^{m}\left(y_{j}\text{log}(q_{j}(\mathbf{a})) +(1-y_{j})\text{log}(1-q_{j}(\mathbf{a}))\right).$$
  - 其中 $y_{j}\in{0,1}$ 表示用户是否点击了分配中的第 $j$ 个项目
外部性感知预测模块（EPM）以候选分配为输入，并输出分配中每个位置的pCTR。它是独立构建和训练的，不与下游模块耦合。EPM是一个通用框架，可以轻松扩展到多个目标预测，如转化率（CVR）和GMV。下文中的 $g_{j}(\mathbf{a})$ 可以在EPM中同时预测，无需进一步阐述。与点模型相比，列表模型捕捉了全局外部性并输出了更准确的结果，这有助于后续模块实现更好的性能

自动化拍卖模块（AAM）

自动化拍卖模块（Automated Auction Module，AAM）

该模块从所有可能的候选分配中选择最优分配，同时决定广告的排名、支付金额和展示位置。将AMA扩展为深度自动化机制， $\mu$ 和 $\lambda(\cdot)$ 被建模为深度神经网络 $\mu$ -网络和 $\lambda$ -网络，以提高排名公式的表达能力，同时保证IC和IR属性
$\mu$ 表示项目出价能力的强度，与分配无关（Kumar等，2019）。因此，更具体地说，广告的价值分布信息、请求信息的特征、用户画像和项目的特征是 $\mu$ -网络的主要输入特征。设 $\mathbf{x}_{j}$ 表示分配中第 $j$ 个项目的价值分布信息向量。 $\mu$ -网络可以形式化表示为：
$$f_{j}^{\mu}=\text{Sigmoid}\left(\text{MLP}^{\mu}(\mathbf{x}_{j}|\mathbf{z}^{\mu}| \mathbf{z}^{r})\right),\forall j\in[m],$$
- 其中sigmoid函数确保输出为正。每个项目都有一个 $f_{j}^{\mu}$ 来表示其竞争能力
$\lambda$ 是分配 $\mathbf{a}$ 的任意函数。分配 $\mathbf{a}$ 中每个项目的特征被连接起来以表示整个分配，分配 $\mathbf{a}$ 的 $\lambda$ -网络为：
$$f^{\lambda}(\mathbf{a})=\text{MLP}^{\lambda}\left(\mathbf{o}_{1}|\mathbf{o}_{2}| \dots|\mathbf{o}_{m}|\mathbf{z}^{\mu}|\mathbf{z}^{r}\right),$$
- 其中 $\mathbf{o}_{j}=\mathbf{x}_{j}|g_{j}(\mathbf{a})|g_{j}(\mathbf{a})$
分配 $\mathbf{a}$ 的社会福利计算为：
$$\text{SW}_{\lambda}^{\mu}(\mathbf{a})=\sum_{j=1}^{m}f_{j}^{\mu}\times\text{eCPM}_ {j}(\mathbf{a})+f^{\lambda}(\mathbf{a}),$$
- 其中 $\text{eCPM}_{j}(\mathbf{a})=b_{j}\times q_{j}(\mathbf{a})$ 是分配 $\mathbf{a}$ 中第 $j$ 个项目的估值函数
最优分配 $\mathbf{a}^{*}$ 被计算为最大化 $\text{SW}_{\lambda}^{\mu}(\cdot)$ 。分配 $\mathbf{a}^{*}$ 中第 $\sigma(i)$ 个位置的广告 $i$ 的按点击支付为
$$p_{i}(\mathbf{a}^{*})=\frac{1}{f_{\sigma(i)}^{\mu}(\mathbf{a}^{*})}\left[\text{ SW}_{\lambda}^{\mu}(\mathbf{a}^{*}_{-i})-\text{SW}_{\lambda}^{\mu}(\mathbf{a}^{* })_{-i}\right]\times\frac{1}{q_{\sigma(i)}(\mathbf{a}^{*})},$$
- 其中 $\mathbf{a}^{*}_{-i}$ 是广告 $i$ 不存在时的最优分配， $\text{SW}_{\lambda}^{\mu}(\mathbf{a}^{*})_{-i}=\sum_{j\neq\sigma(i)}f_{j}^{\mu} \cdot b_{j}\cdot q_{j}(\mathbf{a}^{*})+f^{\lambda}(\mathbf{a}^{*})$ 。因为分配中只有一个广告，且每个自然商品的出价为0，所以 $\text{SW}_{\lambda}^{\mu}(\mathbf{a}^{*})_{-i}=f^{\lambda}(\mathbf{a}^{*})$
显然，该过程保持了AMA的IC和IR属性。 $\mu$ -网络和 $\lambda$ -网络在下一个模块DSM中通过端到端学习进行训练

可微分排序模块（DSM）

可微分排序模块（Differentiable Sorting Module，DSM）

AMA（Kumar等，2019）中用于求解 $\mu$ 和 $\lambda$ 参数的搜索理论效率低下。论文旨在通过端到端学习方式提高解决该机制问题的效率和有效性。然而，论文面临两个挑战，第一个是拍卖中排序过程的不可微性，第二个是缺乏用户真实行为反馈
在AAM中，获取最优分配的排序操作导致整个过程的不可微性。受Liu等（Liu等，2020）提出的可微分排序引擎启发，论文使用多分类模型softmax对机制中的排序操作进行连续松弛。给定分配集 $\mathbf{SW}=[\text{SW}_{\lambda}^{\mu}(\mathbf{a}_{1}),\dots,\text{SW}_{\lambda }^{\mu}(\mathbf{a}_{mn})]$ ，分配向量 $\mathbf{Pr}$ 通过softmax函数映射：
$$\mathbf{Pr}=\text{softmax}(\frac{\mathbf{SW}}{\tau})=[Pr(\mathbf{a}_{1}),Pr( \mathbf{a}_{2}),\dots,Pr(\mathbf{a}_{mn})],$$
- 其中 $\tau$ 是温度参数。直观上， $\mathbf{Pr}$ 可以解释为所有分配的获胜概率
论文使用pCTR和预测GMV（pGMV）指标来模拟用户行为，并计算分配的性能指标，然后用于反馈训练。因此，分配的预期收入和GMV通过公式(2)计算为：
$$\begin{split}\mathbf{Rev}=&[\text{Rev}(\mathbf{a}_{ 1}),\text{Rev}(\mathbf{a}_{2}),\dots,\text{Rev}(\mathbf{a}_{mn})],\ \mathbf{Gmv}=&[\text{Gmv}(\mathbf{a}_{1}),\text{Gmv}( \mathbf{a}_{2}),\dots,\text{Gmv}(\mathbf{a}_{mn})].\end{split}$$
具体来说，只有获胜分配的收入大于0，而非获胜分配的收入为0。最后，整体优化目标是最大化 $\text{Reward}_{\lambda}^{\mu}$ ，即最小化
$$\text{Loss}=-\text{Reward}_{\lambda}^{\mu}=-\sum_{k=1}^{mn}Pr(\mathbf{a}_{k}) \left(\text{Rev}(\mathbf{a}_{k})+\alpha\text{Gmv}(\mathbf{a}_{k})\right).$$
该损失为训练 $\mu$ -网络和 $\lambda$ -网络提供了直接反馈，这是一种部分可微的方法。该训练过程高度依赖于pCTR和pGMV的准确性，这可能导致该机制的离线和在线效果不一致。因此，有必要提高EPM中pCTR和pGMV的预测性能，并对它们进行列表校准（Bernstein等，2018）

训练与在线服务

每个请求中的数据（例如候选广告集、自然商品列表、真实展示的有序列表等）应记录下来用于MIAA的训练。AAM中 $\mu$ -网络和 $\lambda$ -网络的训练依赖于EPM中列表模型的预测输出。因此，EPM中的列表模型首先需要单独训练，使用真实展示的有序列表数据。然后，对于每个请求记录，基于候选广告和自然商品列表生成所有可能的分配。接下来，EPM中训练好的列表模型为每个分配提供pCTR和pGMV的预测结果，这些结果将用于后续AAM中 $\mu$ -网络和 $\lambda$ -网络的训练。该训练过程无法获得真实的用户行为反馈，因此依赖于预测数据来评估模型性能
EPM和AAM中训练好的模型同时部署在线，并按照以下过程提供在线服务：
- 步骤1 ：生成所有可能的分配
- 步骤2 ：通过EPM预测每个分配的pCTR和pGMV
- 步骤3 ：通过AAM从所有可能的分配中选择最优分配
- 步骤4 ：返回获胜广告及其位置

Experiments

在本节中，论文评估了所提出的机制MIAA的有效性，旨在回答以下问题：
- Q1 ：与点模型pCTR相比，论文的列表模型在CTR预测方面的表现如何？
- Q2 ：与工业平台中广泛使用的广告拍卖和分配机制相比，论文的机制在平台收入和GMV方面的表现如何？
论文在公共和工业数据集上进行了广泛的离线实验，并在美团零售配送平台上进行了在线A/B测试

Experiment Setup

数据集

在离线实验中，论文在公共和工业数据集上提供了论文机制有效性的实证证据。两个数据集的统计信息总结在表2中，详细描述如下：
- Avito1。公共数据集是用于Kaggle的Avito上下文广告点击竞赛的Avito数据集。它是avito.ru上至少连续26天内先前选择的用户搜索的随机样本。在每个搜索结果页面中，仅记录了位置1、2、6、7、8中的五个项目。并且只有第1和第7位置的项目（即上下文广告）标记了用户是否点击。对于后续实验，论文基于第1和第7位置的点击行为模拟用户是否点击第2和第6位置的项目。设CTR ${}_{j}$ 表示位置 $j$ 的CTR。CTR ${}_{1}$ 和CTR ${}_{7}$ 可以通过统计分析获得。然后，CTR ${}_{2}$ 被模拟为遵循正态分布 $N(0.8\text{CTR}_{1}+0.2\text{CTR}_{7},0.1\text{CTR}_{1})$ ，而CTR ${}_{6}$ 被模拟为遵循正态分布 $N(0.2\text{CTR}_{1}+0.8\text{CTR}_{7},0.1\text{CTR}_{7})$ 。公共信息包括搜索ID、用户ID和搜索日期，而项目信息包括广告ID、位置ID、类别ID和标题。对于每个样本，论文选择第1和第7位置的项目作为候选广告，其余三个项目被视为自然商品。因此，每个候选分配由一个候选广告和这三个自然商品组成。这里论文使用20150425到20150517的数据作为训练集，20150518到20150520的数据作为测试集，以避免数据泄露
- 美团数据 ：工业数据集是在2023年12月期间在美团零售配送平台上使用GSP拍卖和固定位置收集的。从每个信息流请求转换而来，每个样本包含由候选广告和自然商品组成的所有可能候选分配，以及最终获胜的最优分配。每个候选分配由一个候选广告和三个自然商品组成。在每个候选分配中，每个项目的信息包括出价、稀疏特征（例如ID、类别、品牌等）、密集特征（例如历史CTR、销售量、价值分布信息等）。此外，生产环境中的点模型pCTR被记录下来用于后续性能比较。根据数据收集的日期，论文将数据集按8:2的比例划分为训练集和测试集

评估指标

论文基于pCTR和pGMV构建了一个离线模拟系统，以评估MIAA的有效性。每个实验使用不同的随机种子重复5次，每个结果以均值±标准差的形式呈现。论文的离线实验和在线A/B测试中使用了以下评估指标
- 点击率 ：CTR = $\frac{\sum click}{\sum impression}$
- AUC ：AUC代表曲线下面积，通常用于评估机器学习模型的性能。AUC值越接近1，模型表现越好
- PCOC ：PCOC代表预测CTR与后验CTR之比，是预测准确性的度量。如果PCOC值接近1，则表示预测准确性高
- 每千次展示收入 ：RPM = $\frac{\sum click\times payment}{\sum impression}\times 1000$
- 每千次展示GMV ：GPM = $\frac{\sum GMV}{\sum impression}\times 1000$

基线

在外部性建模方面，论文将所提出的列表模型的pCTR与点模型的pCTR进行比较。在平台收入和GMV方面，论文将MIAA与以下四种常见的拍卖和分配机制进行比较：
- GSP和固定位置 ：这是一种将广告拍卖和分配分为两个阶段的机制。首先，使用GSP机制选择获胜广告，然后将该广告展示在固定位置
- GSP和Cross DQN ：GSP中的获胜广告与自然商品形成多个候选位置的组合，通过Cross DQN进行评估和选择，最终确定广告的展示位置
- Score-Weighted VCG ：Score-Weighted VCG框架将最优拍卖设计分解为两部分：设计单调评分函数和基于匹配的分配算法。但它没有考虑平台GMV及其激励效果
- IAS ：IAS将自然商品视为出价为0的特殊广告，并将广告和自然商品集成到最优拍卖中以获得它们的排名

离线实验

外部性建模的性能比较（Q1）

在公共Avito数据集上，论文需要构建EPM的点模型和列表模型。点模型是一个具有多个全连接层 $256\times 128\times 64\times 32\times 1$ 的深度神经网络。对于每个请求，提取第1、2、6和7位置的项目以形成列表，用于构建EPM的列表模型。如前所述，该列表中只有第1和第4位置有真实的用户点击行为数据，可用于评估这两个模型的性能。Avito数据集上的详细实验结果如表3所示。对于分配中的所有位置，EPM中的列表模型pCTR比点模型pCTR提高了0.0036的AUC，并且其PCOC更接近1。在每个位置，EPM中列表模型的预测结果优于点模型
在美团工业数据集上，生产环境中已经包含了DIN[34]模型的点模型pCTR。因此，论文只需要构建EPM的列表模型来预测CTR，然后与前者进行比较。美团工业数据集上的详细实验结果如表4所示。从结果来看，EPM中的列表模型显著提高了所有位置的AUC，从点模型的0.6485提高到0.7077，并且所有位置的PCOC更接近1。考虑到位置外部性，EPM中的列表模型解决了点模型在第一位置预测低的问题
显然，考虑到外部性（例如广告的展示位置和上下文），EPM中的列表模型在公共Avito数据集和美团工业数据集上的AUC和PCOC指标上表现优于点模型

机制的性能比较（Q2）

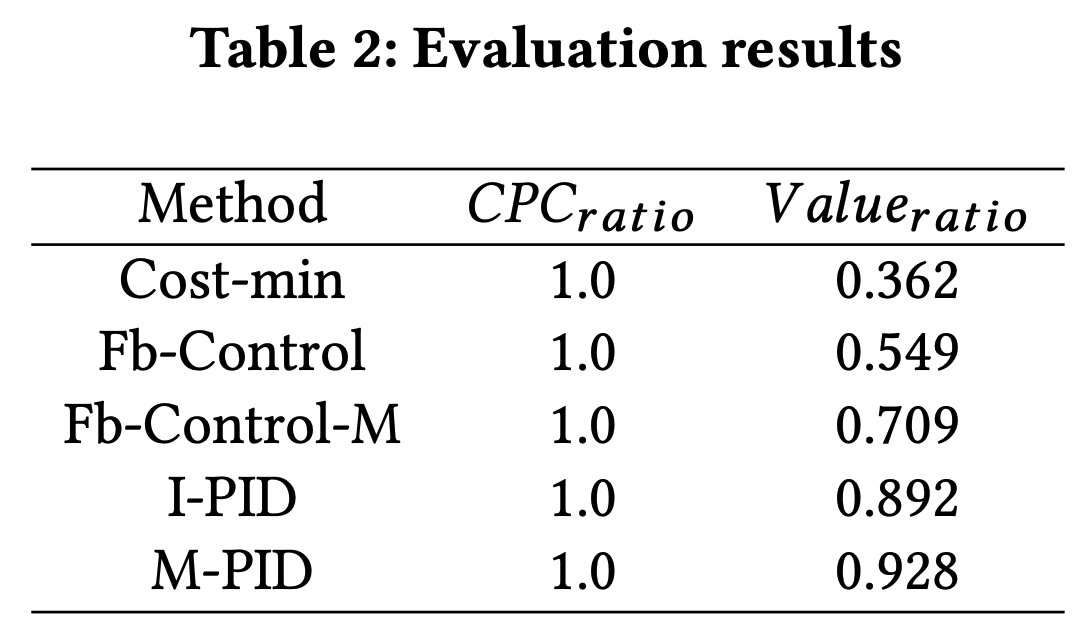
为了验证所提出机制在提高平台收入和GMV方面的有效性，论文在两个数据集上实现了GSP和固定位置、GSP和Cross DQN、Score-Weighted VCG和IAS进行比较分析。在公共Avito数据集上，论文选择第1和第7位置的项目作为候选广告，其余三个项目被视为自然商品。此外，论文为每个广告提供模拟出价，并为每个项目提供模拟的每点击pGMV。每个广告的出价独立地从0.5到1.0的均匀分布中采样。同时，自然商品的每点击pGMV独立地从3.5到6.0的均匀分布中采样，广告的每点击pGMV独立地从2.0到4.0的均匀分布中采样。在这两个数据集上，GSP和固定位置基线中的固定位置设置为2。特别指出的是，由于离线模拟系统无法获得不同机制下的实际用户行为数据，这些实验的有效性评估是基于用户对项目的pCTR和pGMV统计得出的。考虑到商业数据的保密性，美团数据集上的实验结果基于GSP和固定位置呈现。公共和工业数据集上的详细实验结果如表5所示
从实验结果可以看出，MIAA在所有基线机制中实现了最高的收入和GMV。与GSP和固定位置相比，MIAA实现了显著改进，因为具有更高eCPM或GMV的项目获得了更好的位置，并且广告的支付金额增加。MIAA考虑到自然商品对广告的激励效果，与GSP和Cross DQN相比，实现了更高的pRPM。Score-Weighted VCG在不考虑GMV损失的情况下实现了最大的pRPM。与IAS相比，MIAA考虑到外部性，实现了更高的pRPM和pGMV

在线结果

论文通过在美团零售配送平台上部署所提出的机制来展示在线实验。在信息流的生产环境中，对于每个页面请求，系统返回一个包含一个广告和三个自然商品的有序列表。有两个基线，一个是GSP和固定位置（即广告插入在第二位置），另一个是GSP和Cross DQN，其中广告被动态分配到某个位置
为了展示所提出机制的性能，论文在2023年10月15日至2023年12月15日期间使用5%的生产流量进行了在线A/B测试。在实际生产环境中，论文无法基于广告主进行A/B测试。使用基于用户的流量进行A/B测试使得难以评估所提出机制对广告主出价的激励效果。因此，论文只关注实验中的收入、GMV、RPM和GPM的表现。为了在生产流量中公平高效地比较不同基线，论文将实验组中的广告展示次数与基线中的广告展示次数相等。在线A/B测试的实验结果如表6所示。从结果可以看出，与GSP和固定位置以及GSP和Cross DQN相比，所提出的机制在收入、GMV、RPM和GPM方面实现了最高的提升

CA——BCB出价推导

本文主要记录BCB出价的推导

其他参考链接：
- 智能出价——BCB求解
- 互联网广告算法漫谈——浅谈广告中的出价技术：包含许多公式的详细推导

BCB介绍

预算约束的出价，Budget Constrained Bidding（简称BCB），广告主的出价目标是设置一定预算，拿到最多的流量（点击或者订单）

问题定义

一般BCB优化问题的定义:
$$
\begin{align}
\max_{x_{ij}} \sum^N_{i=1} x_{ij} v_{ij} \\
\text{s.t. } \quad\sum^N_{i=1} x_{ij} c_{ij} \le B \\
\sum^M_{j=1} x_{ij} = 1 \\
x_{ij} \in {0, 1}
\end{align}
$$

解法一

根据 RL-MPCA 给出的方案，可以解得最终结果为（求解过程参见RL-MPCA论文）：
$$ j^* = \mathop{\arg\max}_{j} (v_{ij} - \lambda c_{ij}) $$

解法二

如果只有一个广告位置，且使用二价计费 ，原始问题可化简为
$$
\begin{align}
\max_{x_{i}} \sum^N_{i=1} x_{i} v_{i} \\
\text{s.t. } \quad \sum^N_{i=1} x_{i} c_{i} \le B \\
x_{i} \in {0, 1}
\end{align}
$$
最终可解得结果为(求解参考链接：智能出价——BCB求解)：
$$ bid = \frac{v_i}{\lambda} $$

关于两种解法的结果分析

本质上，两种解法结果应该是完全相同的，第一种解法中，如果只有一个广告位置，且使用二价计费，求解到的结果本质于第二种解法结果一致
- 当 $v_{i} > \lambda \cdot Price_{win} $ 时($Price_{win} = c_{i}$，表示净胜价格), 此时选择 $bid > Price_{win}$ 的出价即可获得本次竞拍，此时不管是解法一(取 $v_{ij} - \lambda * c_{ij}$ 最大的动作)还是解法二($bid=v_i/\lambda$)都会选择执行竞拍动作
- 反之，当当 $v_{i} < \lambda \cdot Price_{win}$ 时, 此时选择 $bid < Price_{win}$ 的出价即可获得本次竞拍，此时不管是解法一还是解法二都会选择执行不竞拍动作
解法一适用于任何场景，解法二则仅适用于只有一个广告位置，且使用二价计费的场景
解法二的结果使用起来会更简单：
- 解法一需要预估不同出价下的收益，实际上，在只有一个广告位置，且使用二价计费的场景，不竞争当前广告位置的价值为0，计费为0，若竞争，则价值为 $v_i$，计费为 $c_i$，所以仅需要预估价值 $v_i$，计费 $c_i$
- 解法二则可直接预估一个值 $v_i$ 即可，不需要预估 $c_i$，即在线不需要预估净胜价格
  - 但是离线流量回放求解 $\lambda$ 时，理论上也需要预估一个净胜价格，或者在给出一个价格时，需要知道是否会竞争成功。 $c_i$ 已经隐含在求解到的 $\lambda$ 中
- 若对于任意竞拍，都给定净胜价格，那么解法一和解法二等价，都只需要预估 $v_i$ 一个值即可

CA——(RegretNet)Optimal-Auctions-through-Deep-Learning

参考链接：
- 原始论文：Optimal Auctions through Deep Learning，ICML 2019，London School of Economics & Harvard University
- 博客：【论文阅读】Optimal Auctions Through Deep Learning

整体概述

最优拍卖（收益最大化拍卖） ：激励兼容且能最大化预期收益的拍卖机制（这种机制一般称为最优拍卖(Optimal Aucion)机制），这种机制很复杂，很难设计
Myerson拍卖 ：Myerson 在1981年一篇具有开创性的论文中提出了单一物品下的最优拍卖机制
问题提出 ：然而，即使经过了30-40年的深入研究，对于看似简单的多竞拍者、多物品拍卖场景 ，这个问题仍然没有得到解决
论文的内容 ：
- 创新性方法 ：论文开启了利用深度学习工具自动设计最优拍卖机制的探索。将拍卖建模为一个多层神经网络，把最优拍卖设计框架构建为一个带约束的学习问题，并展示了如何使用标准流程来解决它
- 方法论证 ：论文证明了泛化边界，并进行了大量实验，在多物品拍卖场景中，论文基本上恢复了过去已知的所有解析解，并且在最优机制未知的场景中获得了新的拍卖机制

论文设计思路

最优拍卖（Optimal auction）设计是经济理论的基石之一，具有重要的实际意义。在标准的独立私人估值模型中，每个竞拍者对物品子集都有一个估值函数，这些估值函数独立地从不一定相同的分布中抽取。假设拍卖人知道这些分布，并且能够（也会）在设计拍卖机制时利用这些信息。设计拍卖机制的一个主要困难在于，估值是私人信息 ，需要激励竞拍者如实报告他们的估值。目标是找到一种激励兼容的拍卖机制，以实现收益最大化
Myerson 解决了单一物品拍卖时的最优拍卖设计问题（ Myerson ，1981）。但该方案仅限于单物品拍卖，直到30-40年后的今天，即使是对于有两个竞拍者和两个物品的简单场景，这个问题也没有完全解决。今年来的研究中，大多数适用于较弱的贝叶斯激励兼容（BIC）概念
- 贝叶斯激励兼容（BIC） ：
论文的重点是设计满足占优策略激励兼容（DSIC）的拍卖机制，这是一种更稳健、更理想的激励兼容概念

论文的贡献

论文提供了第一个通用的端到端方法来解决多物品拍卖设计问题。使用多层神经网络对拍卖机制进行编码，将竞拍者的估值作为输入，将物品分配和支付决策作为输出。然后，论文使用从估值分布中抽取的样本来训练网络，以便在满足激励兼容约束的情况下最大化预期收益
为了能够使用标准流程来解决这个问题，论文将激励兼容约束重新表述为要求拍卖的预期事后遗憾为零。论文采用增广拉格朗日方法来解决由此产生的约束优化问题，在每次迭代中，论文通过求解一个内部优化问题来找到每个竞拍者和估值 profile 的最优虚报值，从而通过遗憾项推送梯度
论文描述了针对具有加性、单位需求和组合估值的竞拍者的网络架构（注：这几个概念的详细定义见后面的内容），并进行了大量实验，结果表明：
- 理论保障 ：论文的方法能够恢复过去30-40年中多物品拍卖场景下几乎所有的解析解。通过找到收益几乎最优且遗憾极小的拍卖机制，其分配和支付规则与理论上最优拍卖的规则匹配度非常高
- 最优拍卖 ：在最优拍卖未知的场景中，论文的方法能找到收益高且遗憾可忽略不计的拍卖机制，其性能与当前最先进的计算结果相当或更优
- 多竞拍者多物品 ：目前分析文献中研究的最大场景是有2个竞拍者和2个物品，而论文的方法可以为更大的场景学习拍卖机制，例如5个竞拍者、10个物品的场景。在这些场景中，最优拍卖很难设计，而论文的方法能找到遗憾低且收益比强基线更高的拍卖机制
- 注：（其他理论证明）论文还证明了一个新的泛化边界，这意味着，对于论文的架构，在训练数据上的高收益和低遗憾很有可能转化为在新抽取的估值上的高收益和低遗憾

论文中的一些讨论

事后遗憾非论文创新 ：通过关注预期事后遗憾（expected ex post regret），论文采用了对占优策略激励兼容的一种可量化的松弛，这一概念最早在（迪廷等人，2014）中提出。论文的实验表明，这种松弛是逼近最优DSIC拍卖的有效工具
论文的方法更高效 ：虽然最初关于自动拍卖设计的工作将该问题表述为线性规划（LP）（2002；2004），但后续研究已经认识到这种方法存在严重的可扩展性问题，因为它需要的约束和变量数量与参与者和物品的数量呈指数关系（2010）。论文发现，即使对于有2个竞拍者和3个物品的小场景（并且将每个物品的价值离散化为5个区间），LP也需要69个小时才能完成，因为LP需要处理约 $10^5$ 个决策变量和约 $4×10^6$ 个约束。对于相同的场景，论文的方法在9个多小时内就找到了一个遗憾更低的拍卖机制（见表1）

Auction Design as a Learning Problem

拍卖设计基础及符号说明

论文考虑一个有一组 $n$ 个竞拍者 $N = \{1, \ldots, n\}$ 和 $m$ 个物品 $M = \{1, \ldots, m\}$ 的场景。每个竞拍者 $i$ 都有一个估值函数 $v_i: 2^M \to \mathbb{R}_{\geq0}$ ，其中 $v_i(S)$ 表示竞拍者对物品子集 $S \subseteq M$ 的估值。在最简单的情况下，竞拍者可能具有加性估值 ，即她对 $M$ 中单个物品有一个价值，并且她对物品子集 $S \subseteq M$ 的价值为 $v_i(S) = \sum_{j \in S} v_i(\{j\})$。竞拍者 $i$ 的估值函数独立地从分布 $F_i$ 中抽取，取值包含在价值取值空间 $V_i$ 中。论文将估值 profile 写为 $v = (v_1, \ldots, v_n)$ ，并表示 $V = \prod_{i = 1}^{n} V_i$
拍卖人知道分布 $F = (F_1, \ldots, F_n)$ ，但不知道竞拍者实际的估值 $x$ 。竞拍者报告他们的估值（可能不真实），然后拍卖决定将物品分配给哪些竞拍者，并向他们收取费用。论文将拍卖 $(g, p)$ 表示为一对分配规则 $g_i: V \to 2^M$ 和支付规则 $p_i: V \to \mathbb{R}_{\geq0}$ （这些规则可以是随机化的）。给定出价 $b = (b_1, \ldots, b_n) \in V$ ，拍卖计算出分配 $g(b)$ 和支付 $p(b)$
一个估值为 $v_i$ 的竞拍者对出价配置文件 $b$ 的效用为 $u_i(v_i, b) = v_i(g_i(b)) - p_i(b)$ 。竞拍者是策略性的，他们试图最大化自己的效用，可能会报告与他们真实估值不同的出价。令 $v_{-i}$ 表示不包含元素 $v_i$ 的估值 profile $v = (v_1, \ldots, v_n)$ ，类似地定义 $b_{-i}$ ，并令 $V_{-i} = \prod_{j \neq i} V_j$ 表示除竞拍者 $i$ 之外其他竞拍者可能的估值 profile 。如果无论其他竞拍者报告什么，每个竞拍者如实报告时其效用最大，那么这个拍卖就是占优策略激励兼容（DSIC）的。换句话说，对于每个竞拍者 $i$ 、每个估值 $v_i \in V_i$ 、每个出价 $b_i \in V_i$ 以及其他竞拍者的所有出价 $b_{-i} \in V_{-i}$ ，都有 $u_i(v_i, (v_i, b_{-i})) \geq u_i(v_i, (b_i, b_{-i}))$ 。如果每个竞拍者都能获得非零效用，即对于所有 $i \in N$ 、 $v_i \in V_i$ 和 $b_{-i} \in V_{-i}$ ，都有 $u_i(v_i, (v_i, b_{-i})) \geq 0$ ，那么这个拍卖就是（事后）个体理性（IR）的
在DSIC拍卖中，如实报告对每个竞拍者来说是最有利的，因此在估值 profile $v$ 上的收益是 $\sum_{i} p_i(v)$ 。最优拍卖设计旨在找到一个DSIC拍卖，以最大化预期收益

表述为 Learning Problem

论文将最优拍卖设计问题表述为一个学习问题，在这里，论文不使用衡量与目标标签误差的损失函数，而是采用从 $F$ 中抽取的估值上的负预期收益。论文给定一个参数化的拍卖类 $(g^w, p^w) \in \mathcal{M}$ ，其中参数 $w \in \mathbb{R}^d$ （ $d \in \mathbb{N}$ ），以及一个从 $F$ 中独立同分布抽取的竞拍者估值 profile 样本 $S = \{v^{(1)}, \ldots, v^{(L)}\}$ 。目标是在所有满足激励兼容性的拍卖中，找到一个使负预期收益 $-\sum_{i \in N} p_i^w(v)$ 最小的拍卖
特别地，论文在学习问题中引入约束，以确保所选的拍卖满足激励兼容性。为此，论文定义每个竞拍者的事后遗憾，来衡量拍卖违反激励兼容性的程度。固定其他竞拍者的出价，一个竞拍者的事后遗憾是她考虑所有可能的非如实出价时，效用的最大增加量。论文关注竞拍者 $i$ 的预期事后遗憾：
$$rgt_i(w) = \mathbb{E}_{v\sim F}\left[\max_{v_i’ \in V_i} u_i^w(v_i; (v_i’, v_{-i})) - u_i^w(v_i; (v_i, v_{-i}))\right]$$
- 其中期望是对 $v \sim F$ 取的，并且对于给定的模型参数 $w$ ， $u_i^w(v_i, b) = v_i(g_i^w(b)) - p_i^w(b)$ 。论文假设 $F$ 在估值取值空间 $V$ 上具有完全支撑，并且认识到遗憾是非负的，一个拍卖满足DSIC当且仅当对于所有 $i \in N$ ， $rgt_i(w) = 0$
- 特别说明：$V_{i \cdot }$ 是估值取值空间（估值空间，包含所有可能得估值集合）
- 个人理解：$rgt_{i \cdot } \geq 0 $ 可衡量一个机制的满足 DSIC 条件的程度。任意一个 $\boldsymbol{v}$ 都是一个包含所有竞拍者真实私有价值 ，$u_{i \cdot }$ 则与机制 $\mathcal{M}(g,p)$ 有关，由于 $\boldsymbol{v}$ 是竞拍者真实私有估值（相当于都在说真话），此时满足 DSIC 条件的机制下，应该有事后遗憾 $rgt_{i \cdot } = 0 $。从更加广义的松弛视角看，机制越满足 DSIC 条件，则事后遗憾值应该越小，最小值为0
- 模型训练中，$rgt_{i \cdot }$ 越小的机制越满足 DSIC 条件
鉴于此，论文将学习问题重新表述为最小化预期损失，即在每个竞拍者的预期事后遗憾为0的条件下，最小化预期负收益：
$$\min_{w \in \mathbb{R}^d} \mathbb{E}_{v \sim F}\left[-\sum_{i \in N} p_i^w(v)\right] \\ \text{ s.t. } rgt_i(w) = 0, \forall i \in N$$
给定一个来自 $F$ 的 $L$ 个估值 profile 的样本 $S$ ，论文估计竞拍者 $i$ 的经验事后遗憾为：
$$\hat{rgt}_i(w) = \frac{1}{L} \sum_{\ell = 1}^{L} \max_{v_i’ \in V_i} u_i^w(v_i^{(\ell)}; (v_i’, v_{-i}^{(\ell)})) - u_i^w(v_i^{(\ell)}; v^{(\ell)})$$
并寻求在所有竞拍者的经验遗憾为零的条件下，最小化经验损失：
$$\min_{w \in \mathbb{R}^d} -\frac{1}{L} \sum_{\ell = 1}^{L} \sum_{i = 1}^{n} p_i^w(v^{(\ell)}) \\ \text{ s.t. } \hat{rgt}_i(w) = 0, \forall i \in N$$

个体理性

论文还将要求设计的拍卖满足个体理性，这可以通过将搜索空间限制在一类参数化拍卖 $(g^w, p^w)$ 中来实现，这类拍卖向任何竞拍者收取的费用都不超过她对分配的预期效用。在第3节中，论文将分配和支付规则建模为神经网络，并在架构中纳入个体理性要求

泛化边界（TODO）

论文根据抽取的估值 profile 数量来界定预期遗憾和经验遗憾之间的差距。论文对收益也展示了类似的结果。论文的边界适用于从有限容量类中选择的任何拍卖，这意味着用大样本求解（2）式会得到一个预期收益接近最优且预期遗憾接近零的拍卖（论文注意到，在实践中，论文可能无法精确求解（2）式）
论文使用排名文献中使用的覆盖数定义来衡量拍卖类的容量（鲁丁和沙皮尔，2009）。论文定义拍卖 $(g, p)$ ， $(g’, p’) \in \mathcal{M}$ 之间的 $\ell_{\infty, 1}$ 距离为 $\max_{v \in V} \sum_{i, j}|g_{ij}(v) - g_{ij}’(v)| + \sum_{i}|p_i(v) - p_i’(v)|$ 。对于任何 $\epsilon > 0$ ，令 $N_{\infty}(\mathcal{M}, \epsilon)$ 是在 $\ell_{\infty, 1}$ 距离下覆盖 $\mathcal{M}$ 所需的半径为 $\epsilon$ 的最小球数
定理1 ：对于每位竞拍者 $i$，不失一般性地假设其估值函数 $v_{i}(S)\leq1$，其中 $\forall S\subseteq M$。设 $\mathcal{M}$为满足个体理性的拍卖类别。固定 $\delta\in(0,1)$。从 $F$中抽取 $L$个估值 profile 样本 $s$，至少以 $1-\delta$的概率，对于任何 $(g^{w}, p^{w})\in\mathcal{M}$，有：
$$\mathbb{E}_{v\sim F}\left[-\sum_{i\in N}p_{i}^{w}(v)\right]\leq -\frac{1}{L}\sum_{\ell = 1}^{L}\sum_{i = 1}^{n}p_{i}^{w}(v^{(\ell)})+2n\Delta_{L}+Cn\sqrt{\frac{\log(1/\delta)}{L}}$$
- 并且
  $$\frac{1}{n}\sum_{i = 1}^{n}rgt_{i}(w)\leq\frac{1}{n}\sum_{i = 1}^{n}\widehat{rgt}_{i}(w)+2\Delta_{L}+C’\sqrt{\frac{\log(1/\delta)}{L}}$$
  - 其中 $\Delta_{L}=\inf_{\epsilon>0}\left\{\frac{\epsilon}{n}+2\sqrt{\frac{2\log(N_{\infty}(\mathcal{M},\epsilon/2))}{L}}\right\}$，$C$、$C’$为与分布无关的常数
- 证明见附录。若上述边界中的 $\Delta_{L}$项随着样本量 $L$的增加而趋于 0，则当 $L\rightarrow\infty$时，上述边界也趋于 0。在第 3 节的定理 2 中，论文给出了论文所提出神经网络架构的 $\Delta_{L}$上界

神经网络架构

论文描述用于对多物品拍卖进行建模的神经网络架构，称为RegretNet。论文考虑具有加性、单位需求和一般组合估值的竞拍者。该架构包含两个逻辑上不同的组件：分配网络和支付网络

加性估值下的网络架构

如果竞拍者对物品束（bundle of item） $S\subseteq M$的价值是她对 $S$中单个物品价值的总和，即 $v_{i}(S)=\sum_{j\in S}v_{i}(j)$，则该竞拍者具有加性估值。在这种情况下，竞拍者仅报告他们对单个物品的估值。此场景下的架构对随机分配网络 $g^{w}:\mathbb{R}^{nm}\to[0,1]^{nm}$和支付网络 $p^{w}:\mathbb{R}^{nm}\to\mathbb{R}_{\geq0}^{n}$进行建模，这两个网络均被建模为具有双曲正切（tanh）激活函数的前馈全连接网络。网络的输入层由表示竞拍者 $i$对物品 $j$估值的出价 $b_{ij}$组成
分配网络为每个物品 $j\in[m]$输出一个分配概率向量 $z_{1j}=g_{1j}(b),\cdots,z_{nj}=g_{nj}(b)$。为确保可行性，即物品被分配的概率至多为 1，分配概率通过softmax激活函数计算，使得对于所有物品 $j$，$\sum_{i = 1}^{n}z_{ij}\leq1$。为适应物品未分配给任何竞拍者的可能性，论文在softmax计算中引入一个虚拟节点，用于保留剩余的分配概率。由于将物品分配给同一竞拍者的输出单元可能相关，因此可以实现物品捆绑
支付网络 ：为每个竞拍者输出一个支付金额，表示该竞拍者针对此特定出价配置文件的预期支付金额。为确保拍卖满足个体理性，即向竞拍者收取的费用不超过其对分配的预期价值，网络首先使用sigmoid单元为每个竞拍者 $i$计算一个分数支付 $\tilde{p}_{i}\in[0,1]$，并输出支付 $p_{i}=\tilde{p}_{i}\sum_{j = 1}^{m}z_{ij}b_{ij}$，其中 $z_{ij}$是分配网络的输出。架构概述见图1，其中收益和遗憾是根据分配网络和支付网络的参数计算得出的

单位需求估值下的网络架构

（这部分比较晦涩，待进一步理解）

当竞拍者对物品束 $S\subseteq M$ 的价值是她对束中单个物品分配的最大价值时（理解：说明至多只能分配一个物品），即 $v_{i}(S)=\max_{j\in S}v_{i}(j)$，该竞拍者具有单位需求估值。单位需求竞拍者的分配网络是图2所示的前馈网络。在这个场景中为实现收益最大化，可以证明考虑为每个竞拍者分配至多一个物品的分配规则就足够了。在随机分配规则的情况下，这要求每个竞拍者的总分配至多为1，即 $\sum_{j}z_{ij}\leq1$，$\forall i\in[n]$。论文还要求任何物品都不会被过度分配，即 $\sum_{i}z_{ij}\leq1$，$\forall j\in[m]$
- 因此，论文设计的分配网络其输出概率矩阵 $[z_{ij}]_{i,j = 1}^{n}$是双随机的（注：doubly stochastic matrix，双随机矩阵是指每行每列之和为1 ，且单个元素值大于0的矩阵，论文中似乎将行列之和放松为小于等于1了）
具体来说，论文让分配网络计算两组分数 $s_{ij}$和 $s_{ij}’$，第一组分数按行归一化，第二组分数按列归一化。这两组归一化都可以通过将分数输入softmax函数来实现。然后，竞拍者 $i$对物品 $j$的分配计算为相应归一化分数中的最小值：
$$z_{ij}=\varphi_{ij}^{DS}(s,s’)=\min\left\{\frac{e^{s_{ij}}}{\sum_{k = 1}^{n + 1}e^{s_{kj}}},\frac{e^{s_{ij}’}}{\sum_{k = 1}^{m + 1}e^{s_{jk}’}}\right\}$$
- 其中索引 $n + 1$和 $m + 1$表示虚拟输入，分别对应物品未分配给任何竞拍者以及竞拍者未分配到任何物品的情况
引理1 ：对于 $\forall s$，$s’\in\mathbb{R}^{nm}$，$\varphi^{DS}(s,s’)$是双随机的。对于任何双随机分配 $z\in[0,1]^{nm}$，存在 $s$，$s’\in\mathbb{R}^{nm}$，使得 $z=\varphi^{DS}(s,s’)$
- 注：双随机矩阵式行和列的和都等于1的矩阵，论文将双随机矩阵的行列和定义为小于等于1 ，所以引理1才能成立，否则是不成立的
支付网络与图1中的相同

组合估值下的网络架构

论文还考虑具有一般组合估值的竞拍者。在本研究中，论文仅针对少量物品开发了这种架构
在这种情况下，每个竞拍者 $i$针对每个物品束 $S\subseteq M$（空束除外，其估值视为零）报告一个出价 $b_{i,S}$。分配网络为每个竞拍者 $i$和物品束 $S$输出一个 $z_{i,S}\in[0,1]$，表示该竞拍者被分配到该物品束的概率。为防止物品被过度分配，论文要求物品出现在分配给某个竞拍者的物品束中的概率至多为1。论文还要求分配给每个竞拍者的物品束总量至多为1（约束（3）和约束（4））：
$$\sum_{i\in N}\sum_{S\subseteq M:j\in S}z_{i,S}\leq1,\forall j\in M \\
\sum_{S\subseteq M}z_{i,S}\leq1,\forall i\in N$$
- 论文将满足上述约束（3）和（4）的分配称为组合可行分配。为强制执行这些约束，论文让分配网络为每个物品计算一组分数，并为每个竞拍者计算一组分数。具体而言，对于每个竞拍者 $i\in N$，有一组竞拍者相关分数 $s_{i,S}$，$\forall S\subseteq M$；对于每个物品 $j\in M$，有一组物品相关分数 $s_{i,S}^{(j)}$，$\forall i\in N$，$S\subseteq M$。每组分数都使用softmax函数进行归一化：$\bar{s}_{i,S}=\frac{\exp(s_{i,S})}{\sum_{S’}\exp(s_{i,S’})}$和 $\bar{s}_{i,S}^{(j)}=\frac{\exp(s_{i,S}^{(j)})}{\sum_{i’,S’}\exp(s_{i’,S’}^{(j)})}$。竞拍者 $i$对物品束 $S\subseteq M$的分配定义为 $i$的归一化竞拍者相关分数 $\bar{s}_{i,S}$与 $S$中每个物品 $j$的归一化物品相关分数 $\bar{s}_{i,S}^{(j)}$中的最小值：
  $$z_{i,S}=\varphi_{i,S}^{CF}(s,s^{(1)},\cdots,s^{(m)})=\min\left\{\bar{s}_{i,S},\bar{s}_{i,S}^{(j)}:j\in S\right\}$$
引理2 ：对于 $\forall s$，$s^{(1)},\cdots,s^{(m)}\in\mathbb{R}^{n2^{m}}$，$\varphi^{CF}(s,s^{(1)},\cdots,s^{(m)})$是组合可行的。对于任何组合可行分配 $z\in[0,1]^{n2^{m}}$，存在 $s$，$s^{(1)},\cdots,s^{(m)}\in\mathbb{R}^{n2^{m}}$，使得 $z=\varphi^{CF}(s,s^{(1)},\cdots,s^{(m)})$
图2（b）展示了有2个竞拍者和2个物品场景下的网络架构。为便于说明，论文在讨论中忽略空物品束。对于每个竞拍者 $i\in\{1,2\}$，网络为她可能被分配的每个物品束计算三个分数 $s_{i,\{1\}}$，$s_{i,\{2\}}$和 $s_{i,\{1,2\}}$，并使用softmax函数对其进行归一化。网络还为物品1计算四个分数：$s_{1,\{1\}}^{1}$，$s_{2,\{1\}}^{1}$，$s_{1,\{1,2\}}^{1}$和 $s_{2,\{1,2\}}^{1}$，即物品1存在于每个分配中的分数，类似地，为物品2计算四个分数：$s_{1,\{2\}}^{2}$，$s_{2,\{2\}}^{2}$，$s_{1,\{1,2\}}^{2}$和 $s_{2,\{1,2\}}^{2}$。然后，每组分数都通过单独的softmax函数进行归一化。每个竞拍者的最终分配为：$z_{i,\{1\}}=\min\{\bar{s}_{i,\{1\}},\bar{s}_{i,\{1\}}^{1}\}$，$z_{i,\{2\}}=\min\{\bar{s}_{i,\{2\}},\bar{s}_{i,\{2\}}^{2}\}$，$z_{i,\{1,2\}}=\min\{\bar{s}_{i,\{1,2\}},\bar{s}_{i,\{1,2\}}^{1},\bar{s}_{i,\{1,2\}}^{2}\}$
组合竞拍者的支付网络与图1中的结构相同，使用sigmoid单元为每个竞拍者 $i$计算一个分数支付 $\tilde{p}_{i}\in[0,1]$，并输出支付 $p_{i}=\tilde{p}_{i}\sum_{S\subseteq M}z_{i,S}b_{i,S}$，其中 $z_{i,S}$是分配网络的输出

覆盖数边界

论文现在为上述神经网络在定理1的泛化边界中界定 $\Delta_{L}$项
定理2 ：对于具有 $R$个隐藏层、每个隐藏层有 $K$个节点、分配网络有 $d_{a}$个参数、支付网络有 $d_{p}$个参数且所有模型参数向量 $|w|_{1}\leq W$的RegretNet，对于不同竞拍者估值类型，$\Delta_{L}$项的边界如下：
加性估值 ：
$$\Delta_{L}\leq O\left(\sqrt{\frac{R(d_{a}+d_{p})\log(LW\max\{K,mn\})}{L}}\right)$$
单位需求估值 ：
$$\Delta_{L}\leq O\left(\sqrt{\frac{R(d_{a}+d_{p})\log(LW\max\{K,mn\})}{L}}\right)$$
组合估值 ：
$$\Delta_{L}\leq O\left(\sqrt{\frac{R(d_{a}+d_{p})\log\left(LW\max\left\{K,n2^{m}\right\}\right)}{L}}\right)$$
证明见附录。随着样本量 $L\rightarrow\infty$，$\Delta_{L}\rightarrow0$。上述结果对网络层数、节点数和参数的依赖与神经网络的标准覆盖数边界类似（安东尼和巴特利特，2009）。注意，组合估值边界中的对数项抵消了对物品数量 $m$的指数依赖

优化与训练

论文使用增广拉格朗日方法在神经网络参数 $w$的空间上求解（2）式中的约束训练问题。首先，论文为优化问题定义拉格朗日函数，并添加一个用于惩罚违反约束的二次项：
$$\mathcal{C}_{\rho}(w;\lambda)=-\frac{1}{L}\sum_{\ell = 1}^{L}\sum_{i\in N}p_{i}^{w}(v^{(\ell)})+\sum_{i\in N}\lambda_{i}\widehat{rgt}_{i}(w)+\frac{\rho}{2}\left(\sum_{i\in N}\widehat{rgt}_{i}(w)\right)^{2}$$
- 其中 $\lambda\in\mathbb{R}^{n}$是拉格朗日乘子向量，$\rho>0$是一个固定参数，用于控制二次惩罚项的权重。求解器在每次迭代中对模型参数和拉格朗日乘子进行以下交替更新：
  - （a）$w^{new}\in\arg\min_{w}\mathcal{C}_{\rho}(w^{old};\lambda^{old})$；
  - （b）$\lambda_{i}^{new}=\lambda_{i}^{old}+\rho\widehat{rgt}_{i}(w^{new})$，$\forall i\in N$
- 理解：对于 regret 约束，给了一次项惩罚和二次项惩罚
- 问题：在训练时如何计算 $\widehat{rgt}_{i}(w)$ ?
  - 回答：计算公式为
    $$\hat{rgt}_i(w) = \frac{1}{L} \sum_{\ell = 1}^{L} \max_{v_i’ \in V_i} u_i^w(v_i^{(\ell)}; (v_i’, v_{-i}^{(\ell)})) - u_i^w(v_i^{(\ell)}; v^{(\ell)})$$
    - 其中 $V_i$ 出价可能的取值集合（即取值空间），猜测可以通过随机采样几个值 ，或提前定义几个按照固定间隔采样取值，再取他们对应效用函数中的最大值即可作为近似最大效用函数
具体训练流程如下：
求解器如算法1所示。论文将训练样本 $s$划分为大小为 $B$的 minibatch，并对训练样本进行多次遍历（每次遍历后对数据进行随机洗牌）。论文将第 $t$次迭代时收到的 minibatch 记为 $S_{t}=\{u^{(1)},\cdots,u^{(B)}\}$。对模型参数的更新（a）涉及对 $\mathcal{C}_{\rho}$关于 $w$的无约束优化，使用基于梯度的优化器进行。令 $\tilde{rgt}_{i}(w)$表示在 minibatch $S_{t}$上计算的经验遗憾（见（1）式）。对于固定的 $\lambda^{t}$，$\mathcal{C}_{\rho}$关于 $w$的梯度为：
$$\nabla_{w}\mathcal{C}_{\rho}(w;\lambda^{t})=-\frac{1}{B}\sum_{\ell = 1}^{B}\sum_{i\in N}\nabla_{w}p_{i}^{w}(v^{(\ell)})+\sum_{i\in N}\sum_{\ell = 1}^{B}\lambda_{i}^{t}g_{\ell,i}+\rho\sum_{i\in N}\sum_{\ell = 1}^{B}\tilde{rgt}_{i}(w)g_{\ell,i}$$
- 其中
  $$g_{\ell,i}=\nabla_{w}\left[\max_{v_{i}’\in V_{i}}u_{i}^{w}(v_{i}^{(\ell)};(v_{i}’,v_{-i}^{(\ell)})) - u_{i}^{w}(v_{i}^{(\ell)};v^{(\ell)})\right]$$
- 注意，$rgt$和 $g_{\ell,i}$项涉及对每个竞拍者 $i$和估值 profile $\ell$的虚报值求 “最大值”。论文使用另一个基于梯度的优化器求解关于虚报值的内部最大化问题，并通过最优虚报值处的效用差异推送梯度。具体来说，论文为每个 $i$和估值 profile $\ell$维护虚报值 $v_{i}^{(\ell)}$。对于模型参数 $w^{t}$的每次更新，执行 $R$次梯度更新以计算最优虚报值：$v_{i}^{(\ell)}=v_{i}^{\prime(\ell)}+\gamma\nabla_{v_{i}’}u_{i}^{w}(v_{i}^{(\ell)};(v_{i}^{\prime(\ell)},v_{-i}^{(\ell)}))$，其中 $\gamma>0$。在论文的实验中，论文使用Adam优化器（金马和巴，2014）对模型 $w$和 $v_{i}^{(\ell)}$进行更新
由于论文试图解决的优化问题是非凸的，求解器不能保证达到全局最优解。然而，在论文的实验中，论文的方法非常有效。学习到的拍卖机制产生的遗憾非常低，并且在已知最优拍卖结构的场景中，与最优拍卖结构非常匹配

实验结果

论文证明了论文的方法能够在几乎所有已知最优解的场景中找到接近最优的拍卖方案，并且在没有已知解析解的场景中发现新的拍卖方案。论文在附录中给出了完整的实验集，这里展示部分具有代表性的结果

Experiment Setup

框架：论文使用TensorFlow深度学习库实现了论文的框架
架构：所有网络均采用Glorot均匀初始化，隐藏节点使用tanh激活函数
数据集 ：在所有实验中，论文使用640,000个估值 profile 的样本进行训练，10,000个配置文件的样本进行测试
超参数设置 ：增广拉格朗日求解器最多运行80个轮次（epoch）， minibatch （minibatch）大小为128。增广拉格朗日中的超参数ρ初始值设为1.0 ，每2个轮次增加一次。每次 minibatch 更新时，使用学习率为0.001的Adam优化器更新w。每次更新w时，论文以0.1的学习率运行25次虚报更新步骤。在25次更新结束时，当前 minibatch 的优化虚报值会被缓存，并用于下一轮次相同 minibatch 的虚报值初始化。每100个 minibatch 更新一次拉格朗日乘子λ（即Q = 100）
硬件环境 ：论文的实验在配备NVIDIA GPU核心的计算集群上运行

评估指标

除了在测试集上评估学习到的拍卖机制的收益外，论文还评估所有竞拍者和测试估值 profile 上的平均遗憾值，计算公式为 $rgt = \frac{1}{n} \sum_{i = 1}^{n} \widehat{rgt}_{i}(f, p)$。每个 $\widehat{rgt}_{i}$ 都涉及在竞拍者估值 $v_{i}’ \in V_{i}$ 上对效用函数取“最大值”（见公式(1)）。论文通过对 $v_{i}’$ 进行2000次步长为0.1的梯度上升操作来评估这些项（论文测试1000个不同的随机初始 $v_{i}’$，并报告产生最大遗憾值的那个）

单个竞拍者

即使在单竞拍者拍卖的简单场景中，也只有在特殊情况下才有解析解。论文给出了第一种能够处理一般设计问题的计算方法，并与现有的解析结果进行比较。结果表明，论文不仅能够学习到收益接近最优的拍卖机制，而且能够学习到与理论最优规则惊人相似的分配规则
- 场景（I） ：单个竞拍者对2个物品具有加性估值，物品价值从均匀分布U[0,1]中抽取。最优拍卖方案由Manelli & Vincent (2006)给出
- 场景（II） ：单个竞拍者对2个物品具有单位需求估值，物品价值从均匀分布U[2,3]中抽取。最优机制由Pavlov (2011)给出
图3（a）展示了为场景（I）和（II）学习到的最终拍卖机制在测试集上的收益和遗憾值，所使用的网络架构有两个隐藏层，每层100个节点。学习到的拍卖机制的收益非常接近最优收益，遗憾值可忽略不计。在某些情况下，学习到的拍卖机制实现的收益略高于最优激励兼容拍卖。这是因为它们产生了很小的非零遗憾值。图4（a） - （b）中学习到的分配规则可视化结果表明，论文的方法也能很好地还原最优拍卖的结构。图3（c）展示了收益和遗憾值随训练轮次变化的曲线。求解器自适应地调整遗憾值上的拉格朗日乘子，在初始迭代中关注收益，在后续迭代中关注遗憾值

多个竞拍者

接下来，论文将论文的结果与Sandholm和Likhodedov（Sandholm & Likhodedov, 2015）在最优拍卖未知场景下的最先进计算结果进行比较。这些拍卖是通过在一类参数化的激励兼容拍卖中搜索得到的。与这些先前的方法不同，论文不需要在特定的激励兼容拍卖类中搜索，仅受所使用网络的表达能力限制。结果表明，这能产生新颖的拍卖设计，其性能与现有最先进机制相当甚至更优
- 场景（III） ：2个加性估值的竞拍者和2个物品，竞拍者对每个物品的价值从U[0,1]中抽取
- 场景（IV） ：2个竞拍者和2个物品，其中$v_{1,1}, v_{1,2}, v_{2,1}, v_{2,2} \sim U[1,2]$，$v_{1,\{1,2\}} = v_{1,1} + v_{1,2} + C_{1}$，$v_{2,\{1,2\}} = v_{2,1} + v_{2,2} + C_{2}$，$C_{1}, C_{2} \sim U[-1,1]$
- 场景（V） ：2个竞拍者和2个物品，其中$v_{1,1}, v_{1,2} \sim U[1,2]$，$v_{2,1}, v_{2,2} \sim U[1,5]$，$v_{1,\{1,2\}} = v_{1,1} + v_{1,2} + C_{1}$，$v_{2,\{1,2\}} = v_{2,1} + v_{2,2} + C_{2}$，$C_{1}, C_{2} \sim U[-1,1]$
论文采用与场景（I） - （II）相同的实验设置。将训练得到的机制与来自VVCA和 $AMA_{bsym}$ 系列的激励兼容拍卖的最优拍卖方案进行比较（Sandholm & Likhodedov, 2015）。图3（b）总结了论文的结果。论文的方法带来了显著的收益提升，且遗憾值极小。与图3（a）相比，场景（I）中0.004（即0.72%）的遗憾值带来了收益优势，但在这些先前结果的对比下，这种微小的非零遗憾似乎不太可能解释论文方法在收益上的优势

扩展性测试

论文还考虑了多达5个竞拍者和10个物品的场景。由于问题的指数性质，这比现有分析文献所能处理的问题复杂几个数量级。在论文研究的场景中，在竞拍者数量趋于无穷时，对每个物品分别进行Myerson拍卖是最优的（Palfrey, 1983）。这提供了一个很强但仍可改进的基准
- 场景（VI） ：3个加性估值的竞拍者和10个物品，竞拍者对每个物品的价值从U[0,1]中抽取
- 场景（VII） ：5个加性估值的竞拍者和10个物品，竞拍者对每个物品的价值从U[0,1]中抽取
对于场景（VI），论文在图5（a）中展示了使用不同架构在10,000个配置文件的验证样本上学习到的拍卖机制的收益和遗憾值。这里 $(R, K)$ 表示具有R个隐藏层和每层K个节点的架构。在上述两种场景中，(5, 100)架构在所有100节点的网络中遗憾值最低。图5（b）表明，与基线相比，最终学习到的拍卖机制产生了更高的收益（遗憾值极小）

与线性规划（LP）的比较

论文还将论文算法的运行时间与Conitzer和Sandholm（2002; 2004）提出的LP方法进行比较。为了能够完整运行LP，论文考虑一个较小的场景，即2个加性估值的竞拍者和3个物品，物品价值从U[0,1]中抽取。使用商业求解器Gurobi求解LP。论文通过将每个物品的价值离散化为5个区间来处理连续估值（这会产生约 $10^5$ 个决策变量和约 $4×10^6$ 个约束），然后将连续的输入估值 profile 四舍五入到最接近的离散配置文件进行评估。关于LP的进一步讨论见附录
结果如表1所示。论文还报告了LP在测试集上违反个体理性（IR）约束的情况；对于L个估值 profile ，其计算方式为 $\frac{1}{Ln} \sum_{\ell = 1}^{L} \sum_{i \in N} \max(u_{i}(v^{(\ell)}), 0)$。由于粗粒度的离散化，LP方法存在显著的IR约束违反情况（因此产生了更高的收益）。对于更精细的离散化，论文无法在一周以上的计算时间内运行LP。相比之下，论文的方法在大约9小时内就产生了低得多的遗憾值，并且没有IR约束违反情况（因为神经网络在设计上满足IR）。实际上，即使对于更大的场景（VI） - （VII），论文算法的运行时间也不到13小时

附录：双随机矩阵（doubly stochastic matrix）

双随机矩阵（doubly stochastic matrix），在数学中，是一种特殊的方阵，其满足以下条件：
- 非负性：矩阵中的每个元素都是非负的。这意味着对于任意的元素 $P_{ij}$ 来说，都有 $P_{ij} \geq 0$
- 行和为1：每一行的所有元素之和都等于1。即对于所有的行索引 $i$，有 $\sum_j P_{ij} = 1$
- 列和为1：每一列的所有元素之和也都等于1。即对于所有的列索引 $j$，有 $\sum_i P_{ij} = 1$
- 随机这两个字的理解：随机是指概率，也就是行列都可以单抽出来作为一个概率的矩阵
一句话定义 ：每行的元素加起来是1，而且每列的元素加起来也是1，并且所有元素都是非负数，那么这个矩阵就是双随机矩阵
注：论文中对双随机矩阵定义有修改，论文中将双随机矩阵的定义修改为了行列和小于等于1

CA——Deep-Neural-Auction(DNA)

Deep Neural Auction, 简称 DNA

参考链接：
- 原始论文：Neural Auction: End-to-End Learning of Auction Mechanisms for E-Commerce Advertising, Alibaba, KDD 2021
- 博客：KDD 2021 | Neural Auction: 电商广告中的端到端机制优化方法

问题定义

和 DeepGSP 类似，DNA拍卖问题形式化定义为：
$$
\begin{align}
\mathop{\text{maximize}}_{\mathbf{\mathcal{M}}} &\mathbb{E}_{\mathbf{b} \sim \mathcal{D}}\Big[\sum_{j=1}^L \lambda_j\times f_j(\mathbf{b};\mathbf{\mathcal{M}})\Big]\\
\text{s.t.} &\text{Incentive Compatibility (IC) constraint}, \\
&\text{Individual Rationality (IR) constraint},
\end{align}
$$
- $\mathbf{b}$：广告主出价向量
- $L$：优化目标数
- $\mathcal{D}$：广告主出价分布, $\mathbf{b}$ 是从分布 $\mathcal{D}$ 中采样得到的
- $\lambda_j$：目标权重，是用于控制目标之间重要性的权重因子，可调整目标重要性
- 注：相对 DeepGSP 论文的定义，这里增加了激励兼容(IC)和个体理性约束(IR)，其中个体理性约束是指竞拍者的效用不为负 $u_i = v_i - p_i \ge 0$

Deep Neural Auction 基本思路

分配规则和计费规则

基本思路：按照经典GSP的基本原理，先按照 Rank Score 进行非递减的顺序排序，然后竞胜者按照获得该位置所需要的最小价格计费
分配规则 $\mathcal{R}$ ：按照 Rank Score 排序(Rank Score 是关于出价 bid 非递减的函数)，$r_i(b_i)$，排序中最靠前的 Top-K 个广告主赢得 K 个广告位
计费规则 $\mathcal{P}$ ： $p_i = r_i^{-1}(r_{i+1}(b_{i+1}))$

DNA与传统拍卖模型的区别

DNA与传统拍卖模型的区别对照示意图

经济学属性

Definition 2.1 (Incentive Compatibility)

原始论文表述：

An auction mechanism is IC if it is in the best interest of each advertiser $i$ to truthfully reveal her maximum willing-to-pay price, i.e., $b_i = m_i$.
理解：一个拍卖机制是激励兼容的，意味着每个广告主的最佳利益就是真实的表达他愿意支付的最大出价
注：最大愿意支付价格，即 maximum willing-to-pay price，用 $m_i$ 表示

Definition 2.2 (Value Maximizer)

论文中，作者引入了价值最大化类型广告主（Value Maximizer），同时讨论了，价值最大化类型广告主和效用最大化类型广告主的区别（Utility Maximizer）
讨论：传统经典的拍卖机制，比如 VCG 拍卖或者 Myerson 拍卖，都假定了广告主是效用最大化的类型（Utility Maximizer），即广告主的目标是为了最大化其拟线性效用（Quasi-linear Utility），形式化的定义为： $u_i = v_i - p_i$。然而，作者观察到工业界的电商平台中，这种效用最大化模型不再能建模广告主的行为范式，比如，淘宝广告平台中，oCPC 和 MCB 这两种广告主，他们的目标都是在指定约束下，最大化他们的点击量/转化量，这种类型的广告主会使用自动出价服务，基于当前竞拍环境，为每个请求/PV计算并报告他们的最大 willing-to-pay 价格，这种行为范式可以建模为价值最大化（Value Maximizer）
- 注：MCB一般是指多约束，论文中主要指预算约束+PPA（pay-per-acquisition）或PPC（pay-per-click）约束
原文定义表述：

A value maximizer $i$ optimizes value $v_i$ while keeping payment $p_i$ below her maximum willing-to-pay $m_i$; when value is equal, a lower $p_i$ is preferred
理解：价值最大化类型的竞拍者的目标是在愿意支付的成本约束下（$p_i \le m_i$），最大化拿量；当量相等时，更倾向于更低的价格
在多位置拍卖系统中，在计费不超过最大愿意支付价格 $m_i$ 的情况下，广告主会更喜欢争取更高的位置；同时，在价值量 $v_i$ 相同的情况下，广告主更倾向于支付更低的价格
个人理解：Value Maximizer 只是表象，本质上，广告主的最终目标应该也是 Utility Maximizer（即利润最大化），只是这个效用包含了广告主毛利等私有信息，这部分信息是未知的

IC和IR

激励兼容满足等价于下面两个约束满足：
- Monotonicity: An advertiser would win the same or a higher slot if she reports a higher bid;
- Critical price: The payment for the winning advertiser is the minimum bid that she needs to report to maintain the same slot
个体理性约束：当满足IC要求的两个约束时，个体理性约束自然满足的，因为IC约束中隐含着 $p_i \le m_i$

Deep Neural Auction

整体架构

整体架构图
整体包含三个主要部分：Set Encoder, Context-Aware Rank Score Function, Differentiable Sorting Engine

Set Encoder

用于从整个竞价队列中提取特征，Set Encoder的输出会作为特征输入后续的其他模块
可以用于解决 ambiguity issue，该问题的定义是：在同一个拍卖中，相同的特征可能获得不同的结果：

The second challenge is data efficiency. The current learningbased approaches [20, 39] usually require a large number of samples to learn the optimal auction due to an ambiguity issue we observed in the data from auctions. It is a common case that an advertiser with the same feature profile can result in different outcomes in distinct auctions, e.g., wins in one auction but loses in another, due to the change of the auction context, e.g., the competition from the other advertisers.
编码过程
$$
\begin{align}
h_i &= \sigma(\phi_1(\mathbf{x}_i)) \\
\mathbf{h} &=\{h_i\}_{i=1}^N \\
h_i^\prime &= \sigma(\phi_2(\text{avgpool}(\mathbf{h}_{-i})))
\end{align}
$$
- 其中 $\{\mathbf{x}_i\}_{i=1}^N$ 表示候选广告， $\mathbf{h}_{-i}$ 表示出去广告 $i$ 后的其他广告特征

Context-Aware Rank Score Function

分配规则

输入是单个广告特征和Set Encoder输出的降价队列特征，用于计算 Rank Score 分数
其网络表示如下：
$$rankScore = r(b_i, \mathbf{x}_i^\prime)$$
- 其中 $\mathbf{x}_i^\prime = (\mathbf{x}_i, h_i^\prime)$
为了保证单调性，使用了一种两层的 MinMax 网络：设置 Q 组函数，每次包含 Z 个线性函数：
$$ r_i = \min_{q\in[Q]} \max_{z \in [Z]} (e^{w_{qz}}\times b_i + w^\prime_{qz}\times \mathbf{x}_i^\prime + \alpha_{qz})$$
- 单调性保证：任意给定 $w$ 和 $z$，都存在一个线性函数 $f_{qz}$：$f_{qz}(b_i, \mathbf{x}_i^\prime) = e^{w_{qz}} \times b_i + w^\prime_{qz}\times \mathbf{x}_i^\prime + \alpha_{qz}$，显然该线性函数关于出价 $b_i$ 单调，此时对多个单调的线性函数取 Max 操作不会改变单调性，继续取 Min 操作也不会改变单调性（ $b_i$ 增加时，任意函数 $f_{qz}(b_i, \mathbf{x}_i^\prime)$ 的最大最小值也都在增加）
- 函数拟合能力：上面的 MIN-MAX 函数理论上可以近似任意的函数（详情见：Monotone and partially monotone neural networks）

计费规则

计费逻辑如下：
$$ p_i = \max_{z\in[Z]}\min_{q\in[Q]} e^{-w_{qz}}(r_{i+1} -\alpha_{qz} - w_{qz}^\prime \times \mathbf{x}_i^\prime) $$
问题：这里的反函数是错的，理论上应该是下面的表达才对(TODO：待确认)：
$$ p_i = \min_{z\in[Z]}\max_{q\in[Q]} e^{-w_{qz}}(r_{i+1} -\alpha_{qz} - w_{qz}^\prime \times \mathbf{x}_i^\prime) $$
- 可以举例并画出函数图像说明： $f(x) = \max(2x, x+1)$ 的反函数是 $f^{-1}(y) = \min(\frac{1}{2}y, y-1)$

Differentiable Sorting Engine

输入 Rank Score 分数，进行可微分排序，并执行计费操作，包含 Differentialble Sorting Operator 和 Allocation & Pricing 两部分
设未排序的 Rank Score 分数集合为 $\mathbf{r} = [r_1, r_2, \cdots, r_N]^T$，令 $\text{argsort}(\mathbf{r})$ 为 $\mathbf{r}$ 降序排列的序号，则可以定义排列矩阵 $M_r \in \{0,1\}^{N\times N}$：
$$M_r[k,i]=
\begin{cases}
1& \text{if}\ i=\text{argsort}(\mathbf{r})[k]\\
0& \text{otherwise}
\end{cases}$$
进一步地，可以用下面的等价形式表示：
$$M_r[k,i]=
\begin{cases}
1& \text{if}\ i=\text{argmax}(c_k)\\
0& \text{otherwise}
\end{cases}$$
- 其中 $c_k = (N+1-2k)\mathbf{r} - A_r\mathbb{I}$, $A_r[i,j] = |r_i - r_j|$ 表示两个元素对之间的 Rank Score 差的绝对值， $\mathbb{I}$ 表示值全为1的列向量 $\mathbb{I}=[1,1,\cdots,1]^T$
- 这一步表述来自论文：Stochastic Optimization of Sorting Networks via Continuous Relaxations, Stanford University, ICLR 2019 的 Corollary 3 和附录 B.1 B.2，详细验证代码见附录
于是，对 $\text{argmax}$ 进一步做放松（放松为 $\text{softmax}$ ），则有
$$\hat{M}_r[k,:] = \text{softmax}(\frac{c_k}{\tau})$$
- $\tau > 0$ 表示温度系数，当 $\tau \to 0$ 时，$\hat{M}_r \to M_r$
- 理解：用 $\text{softmax}$ 来替换 $\text{argmax}$ 做放松可以理解为将 100% 的确定性选择概率变成了带随机性的选择概率
- $\hat{M}_r$ 也被作者称为行随机的排列矩阵（ row-stochastic permutation matrix ）
此时，如果将按照 Rank Score 降序排列后，按照反函数计费规则计费的结果表达为 $\mathbf{p} = [p_1, p_2, \cdots, p_N]^T$ ，则有 Top-K 广告的付费金额为：
$$ f_{\text{pay}} = \hat{M}_r[1:K,:]\cdot \mathbf{p} $$
- 理解：这里 $f_{\text{pay}}$ 是一个 K 行的向量，分别代表 Top-K 的支付值

端到端训练实现

主要损失函数

前K个位置拍卖的性能指标可以表达为：
$$
\begin{align}
\text{整体性能指标} &= \hat{M}_r[1:k,:] \cdot F_{\text{all}} \\
F_{\text{all}} &= [\sum_{l=1}^L\lambda_l\times f_l^1,\sum_{l=1}^L\lambda_l\times f_l^2,\cdots,\sum_{l=1}^L\lambda_l\times f_l^N]^T
\end{align}
$$
- 其中 $F_{\text{all}}$ 表示所有广告的性能指标向量
- 理解：$\hat{M}_r[1:k,:]$ 表示前 K 个位置展示 $N$ 个广告的概率，$\hat{M}_r[1:k,:] \cdot F_{\text{all}}$ 是一个 K 维向量，表示前 K 个位置的性能指标
因此，训练时最小化前K个位置的负目标性能指标和，即下面整体目标损失函数即可：
$$\mathcal{L}_{\text{tgt}} = \sum_{i=1}^K \hat{M}_r[i,:] \cdot F_{\text{all}}$$
- 注：由于排序改变会影响计费（论文中也称计费为 Revenue），作者使用 $f_{\text{pay}} = \hat{M}_r[1:K,:]\cdot \mathbf{p}$ 来近似代替前 K 个位置的计费（问题：这个计费的 Top-K 排序也是按照 Rank Score 降序排列得到的吧，一旦 Rank Score 发生了变化， Top-K 广告也要变化的，计费不用变化吗？）
- 无论如何都会出现不稳定问题(计费 Revenue 的值依赖着 Rank Score 的求逆)，以下是来自阿里官方账号的讲解 KDD 2021 | Neural Auction: 电商广告中的端到端机制优化方法的内容：
  
  仔细观察这两个 loss 的形式不难发现，$\mathcal{L}_{\text{tgt}}$ 的优化其实就是使网络产生的 rankscore 与在用户真实行为上计算出的多目标最优排序一致，但由于 revenue 的计算还是依赖于网络 rankscore 的求逆，导致 rankscore 之间的 distance 又会被显式优化，这给模型训练带来了一些不稳定的因素（离线实验中我们也确实观察到了）；而 $\mathcal{L}_{\text{ce}}$ 由于只纠正序的准确性，不涉及广告 rankscore 之间 distance 的学习，它的训练过程较为稳定。我们的经验是：如果优化目标仅有 revenue，那么 $\mathcal{L}_{\text{tgt}}$ 任务可以独立训练，最终会收敛（尽管其 learning curve 存在一些毛刺）；如果优化多个目标之间权衡，那么 $\mathcal{L}_{\text{tgt}}$ 的权重要和 $\mathcal{L}_{\text{ce}}$ 在同一水平，或者先全局优化 $\mathcal{L}_{\text{ce}}$ 学好 allocation，再引入 $\mathcal{L}_{\text{tgt}}$ 精细化优化 revenue
  值得注意的是，工业界广告系统的真实反馈通常是稀疏的，算法日志中有用户行为的数据占比可能较低。为了使训练信号更加稠密、提高模型学习的效率，我们将用户反馈与预估值进行了融合，在有用户行为的数据上使用后验校准技术来纠正预估值，再进一步构造两个 loss，提高了训练的稳定性

辅助损失函数

借助用户真实反馈来构建辅助损失，让出现最优排序的概率越大越好，辅助损失函数的形式如下：
$$ \mathcal{L}_{\text{ce}} = -\frac{1}{N} \sum_{k=1}^N \sum_{i=1}^N \mathbb{I}{(M_y[k,i]=1)} \log \hat{M}_r[k,i] $$
- 其中 $\mathbb{I}(\cdot) $ 是指示函数
- 注：$M_y[k,i]$ 表示按照真实反馈算出来的 ground-truth 排序矩阵（问题：无法观察到同一个请求不同排列的反馈吧，使用如何确定这个是最优的排列？除非用预估值或模拟器，如果用预估值的话，和普通GSP分配方式有何区别？）

附录：可微分排序argsort到argmax转换证明

证明

参考论文 Stochastic Optimization of Sorting Networks via Continuous Relaxations, Stanford University, ICLR 2019 的 Corollary 3 和附录 B.1 B.2

代码验证

验证代码如下：

import numpy as np

def generate_rank_matrix_original(r):
    """
    通过 argsort 生成排列矩阵 M_r^{(1)}
    """
    N = len(r)
    # argsort 返回的是从小到大排序的索引，我们需要降序排序
    sorted_indices = np.argsort(-r)
    Mr = np.zeros((N, N), dtype=int)
    for k in range(N):
        i = sorted_indices[k]
        Mr[k, i] = 1
    return Mr

def generate_rank_matrix_equiv(r):
    """
    通过等价定义生成排列矩阵 M_r^{(2)}
    """
    N = len(r)
    # 计算 A_r 矩阵: |r_i - r_j|
    A_r = np.abs(r.reshape(-1, 1) - r.reshape(1, -1))  # Shape: (N, N)
    # print(A_r)
    # 生成全1向量 I
    I = np.ones(N)

    Mr = np.zeros((N, N), dtype=int)

    for k in range(1, N + 1):
        # 计算 (N +1 - 2k)*r
        term1 = (N + 1 - 2 * k) * r
        # 计算 A_r @ I
        term2 = A_r @ I
        # 计算 c_k
        c_k = term1 - term2
        # 找到 argmax(c_k)
        # 如果有多个最大值，argmax 返回第一个
        i_max = np.argmax(c_k)
        Mr[k - 1, i_max] = 1
    return Mr

def verify_equivalence(r):
    Mr_original = generate_rank_matrix_original(r)
    Mr_equiv = generate_rank_matrix_equiv(r)
    print("Rank Score Vector r:")
    print(r)
    print("\n排列矩阵 M_r^{(1)} (原始定义):")
    print(Mr_original)
    print("\n排列矩阵 M_r^{(2)} (等价定义):")
    print(Mr_equiv)
    print("\n是否相同:", np.array_equal(Mr_original, Mr_equiv))
    print("-" * 50)

def main():
    np.random.seed(42)  # 为了结果可重复

    # # 测试案例1: 简单的已排序向量
    # r1 = np.array([5, 4, 3, 2, 1])
    # verify_equivalence(r1)

    # 测试案例2: 随机向量
    # r2 = np.random.rand(10)
    # verify_equivalence(r2)
    #
    # # 测试案例4: 含有负数的向量
    # r4 = np.array([3, -1, 4, -5, 2])
    # verify_equivalence(r4)

if __name__ == "__main__":
    main()

测试结果

Rank Score Vector r:
[ 3 -1  4 -5  2]

排列矩阵 M_r^{(1)} (原始定义):
[[0 0 1 0 0]
[1 0 0 0 0]
[0 0 0 0 1]
[0 1 0 0 0]
[0 0 0 1 0]]

排列矩阵 M_r^{(2)} (等价定义):
[[0 0 1 0 0]
[1 0 0 0 0]
[0 0 0 0 1]
[0 1 0 0 0]
[0 0 0 1 0]]

是否相同: True

说明两者确实等价

CA——DeepGSP

参考链接：
- 原始论文：Optimizing Multiple Performance Metrics with Deep GSP Auctions for E-commerce Advertising, Alibaba, WSDM 2021
- 博客：Deep GSP ：面向多目标优化的工业界广告智能拍卖机制

核心贡献

端到端拍卖机制
能保证单广告位下的激励兼容（Incentive Compatibility, IC）和多广告位下的对称纳什均衡（Symmetric Nash equilibrium, SNE）
离线+在线验证

问题建模

定义拍卖问题为多目标优化问题：
$$ \mathop{\text{maximize}}_{\mathbf{\mathcal{M}}} \mathbb{E}_{\mathbf{b} \sim \mathcal{D}}\Big[\sum_{j=1}^L w_j\times f_j(\mathbf{b};\mathbf{\mathcal{M}})\Big]$$
- $\mathbf{b}$：广告主出价向量
- $L$：优化目标数
- $\mathcal{D}$：广告主出价分布, $\mathbf{b}$ 是从分布 $\mathcal{D}$ 中采样得到的
- $w_j$：目标权重，是用于控制目标之间重要性的权重因子，可调整目标重要性
- 注：实际上，还应该加上激励兼容和个体理性的约束才完整

一些重要的理论

Theorem 1：IC，激励兼容

单位置拍卖机制 $\mathcal{M}<\mathcal{R},\mathcal{R}>$ 是激励兼容（Incentive-Compatible）的，当且仅当满足两个规则：
- 分配规则（Allocation Scheme） $\mathcal{R}$ 是单调的（即出价越高，竞拍获胜的概率越大，改规则也称为Monotone Allocation）；
- 计费规则（Pricing Rule） $\mathcal{P}$ 是竞胜者支付其需要保持竞胜状态所需要的最低报价（该价格也称为Critical Bid，该规则也称为Critical Bid based Pricing）：
  $$
  \begin{align}
  \mathcal{R}_i(z, \mathbf{b}_{-i}) &> \mathcal{R}_i(b_i, \mathbf{b}_{-i}) \ \text{if} \ z > b_i \text{(Monotone Allocation)} \\
  \mathcal{P}_i &= \text{inf}_{z \vert \mathcal{R}_i(z, \mathbf{b}_{-i}) = \mathcal{R}_i(b_i, \mathbf{b}_{-i})} \ \text{(Critical Bid based Pricing)}
  \end{align}
  $$
注意：Theorem 1 仅针对单位置（single slot）拍卖场景

Theorem 2: SNE，对称纳什均衡

拍卖机制 $\mathcal{M}<\mathcal{R},\mathcal{R}>$ 满足对称纳什均衡（Symmetric Nash equilibrium，SNE），当且仅当：
- 竞拍者在均衡状态下更喜欢他当前的分配到位置（相对其他位置而言，更喜欢当前位置）
  $$ \beta_i(v_i - p_i) \ge \beta_j(v_j - p_j) $$
  - 其中 $\beta_i$ 表示当前位置固有的CTR预估值（理解：$\beta_i(v_i - p_i)$ 表示当前位置点击的概率乘以点击价值和付出点击成本的差值
  - 个人理解：这里仅针对CPC计费场景，广告主针对点击来估计流量的点击价值，付费也在点击上，此时不同位置之间的最大价值差异在CTR上
注意：Theorem 2 可扩展到针对多位置（multi-slot）拍卖场景

Deep GSP Auction

分配规则和计费规则设计

分配规则 $\mathcal{R}$ ：按照 Rank Score 排序(Rank Score 是关于出价 bid 非递减的函数)，$r_i = R_\theta(b_i, \mathbf{x}_i)$，排序中最靠前的 Top-K 个广告主赢得 K 个广告位
- 这里参照了经典的GSP拍卖机制实现，选择了一个非单调递减的排序分数
计费规则 $\mathcal{P}$ ： $p_i = R_\theta^{-1}(r_{i+1},\mathbf{x}_i)$
- 用后一位广告主的分数，通过逆运算计算当前广告主的价格

Point-wise Monotonicity Loss

用于引导分配规则的单调性，思路是在损失函数中增加惩罚非单调的部分
单调损失部分呢定义如下：
$$ \mathcal{L}_{\text{mono}} = \sum_{i=1}^N \max(0, -\nabla_b R_\theta(b_i, \mathbf{x}_i)) $$
- 理解：非单调则说明梯度小于0，惩罚梯度小于0的部分即可引导 Rank Score 分数 $R_\theta(b_i, \mathbf{x}_i)$ 关于出价 $b_i$ 的梯度 $\nabla_b R_\theta(b_i, \mathbf{x}_i) \ge 0$，这种单调是不严格的，智能引导，不能强保障

Approximate Inverse Operation

用于近似计算计费规则中的逆运算操作
第一步：将 Rank Score 分数 $R_\theta(b_i, \mathbf{x}_i)$ 拆解为：
$$ r_i = R_\theta(b_i, \mathbf{x}_i) = b_i \times \pi_\theta(b_i, \mathbf{x}_i) $$
- 理解：$\pi_\theta(b_i, \mathbf{x}_i)$ 是关于 $b_i$ 的非线性函数
第二步：单调损失函数对应变为：
$$ \mathcal{L}_{\text{mono}} = \sum_{i=1}^N \max(0, -(\pi_\theta(b_i, \mathbf{x}_i) + b_i\nabla_b \pi_\theta(b_i, \mathbf{x}_i))) $$
- 复合函数求导展开
第三步：近似逆运算操作
$$ p_i = \frac{r_{i+1}}{\pi_\theta(b_i, \mathbf{x}_i)} $$
- 这里假定了 $\pi_\theta(b_i, \mathbf{x}_i)$ 是关于 $b_i$ 的一个函数，这样的好处是逆运算会变得非常简单，准确求解逆运算是需要推理神经网络（神经网络函数难以定义明确的反函数吧？）
- 论文中提到，通过观察看到了 $\pi_\theta(b_i, \mathbf{x}_i)$ 关于 bid 的变化是不敏感的
  
  We have observed from an industrial data set that the non-linear function $\pi_\theta(b_i, \mathbf{x}_i)$ is not so sensitive to the bid (please refer to the experiment results in Section 4.2.3 for more details). Thus, in payment calculation, we regard $\pi_\theta(b_i, \mathbf{x}_i)$ as a constant w.r.t. $b_i$

Deep GSP的一些讨论

Theorem 3：Deep GSP的纳什均衡

Deep GSP Auction存在对称纳什均衡状态的非空集合

Theorem 3. There exists a non-empty set of Symmetric Nash Equilibrium (SNE) states in the Deep GSP auction.
理解：Deep GSP Auction拍卖下，至少存在一个状态是满足对称纳什均衡的

Deep GSP 实现

思考：考虑到一些指标是难以通过精确数学公式定义的，所以考虑使用反馈来学习

As introduced in Section 2.2, some performance metrics are not feasible to have rigorous mathematical analyses, and we can only evaluate these metrics via actual feedback from the system after deploying the auction mechanism.

强化学习建模

状态：
- 广告信息
- 广告主信息
- 用户特征等
动作：
- 深度 Rank Score 模型的输出就是动作（连续动作），策略就是深度 Rank Score 模型本身，即策略就是 $R_\theta$
奖励：
$$ re_i = F(\mathbf{b};\mathcal{M}) - \eta \times \max(0, (1-\epsilon)\mu_i(\mathcal{M_0}) - \mu_i(\mathcal{M})) $$
- 理解：
  - $F(\mathbf{b};\mathcal{M})$ 部分是原始目标；
  - $- \eta \times \max(0, (1-\epsilon)\mu_i(\mathcal{M_0}) - \mu_i(\mathcal{M}))$ 部分表示希望引导 $\mu_i(\mathcal{M}) \ge (1-\epsilon)\mu_i(\mathcal{M_0})$ 成立
状态转移 ：
- 模型训练是单步的是单步决策问题，无需要考虑状态转移

强化学习实现更多细节

强化学习的目标是：
$$ R_\theta^* = \mathop{\arg\max}_{R_\theta} \mathbb{E}_{\mathbf{b}\sim \mathcal{D}}[re_i|R_\theta] $$
使用DDPG来训练，Critic 网络和 Policy 网络损失函数如下：
$$
\begin{align}
\text{Critic Net:} \quad \mathcal{L}(Q_\theta) &= \frac{1}{N}\sum_i(y_i - Q_\theta(s_i, a_i))^2 \\
\text{Policy Net:} \quad \mathcal{L}(R_\theta) &= \frac{1}{N}\sum_i(-Q_\theta(s_i, R_\theta(s_i)) + \gamma \times \mathcal{L}_{\text{mono}})
\end{align}
$$
- 其中 $y_i = re_i$
实现时，与原始的DDPG有两点不同：
- Deep GSP 是一个单步决策问题
DeepGSP强化框架(Figure 2)：

实验指标设置

一般业务指标

Revenue Per Mille (RPM), Add-to-Cart Rate (ACR), CTR, CVR, GMV Per Mille (GPM)等等

单调性指标

计算出价和其对应的 Deep Rank 模型输出之间的单调性关系，该指标定义为：
$$ \mathcal{T}_m = \frac{1}{n}\sum \rho_{rank_{bids}},\rho_{rank_{outputs}} $$
- 其中斯皮尔曼秩相关系数（Spearman’s rank correlation coefficient）系数的定义为：
  $$ \rho = 1 - \frac{6 \sum d_i^2}{n(n^2-1)} $$
  - $d_i$ 表示每一对样本之间的等级差异。当排序一致时，等级差异为0，此时 $\rho$ 取得最大值 1；当排序相反时，可以证明，$\rho$ 取得最小值 -1

计费错误率

计费错误率（Payment Error Rate，PER），近似计费可能引入误差，作者首先使用二分查找去搜索精确的计费 $p_i^*$，使用 $\frac{p_i}{p_i^*}$ 来表示PER

激励兼容性

作者使用 Individual Stage-IC (i-SIC) 指标来量化激励兼容性(该指标参考自A Data-Driven Metric of Incentive Compatibility)，其定义为：假设广告主的效用是 $\hat{u}(b) = b \times x(b) - p(b)$ （其中 $x(\cdot)$ 是分配概率），同时广告主的价值分布满足 $F$。则 i-SIC 可以定义为：
$$ \text{i-SIC} = \lim_{\alpha \to 0} \frac{\mathbb{E}_{v\sim F}[\hat{u}((1+\alpha)v)] - \mathbb{E}_{v\sim F}[\hat{u}((1-\alpha)v)] }{2\alpha \times \mathbb{E}_{v \sim F}[v \times x(v)]} $$
- i-SIC 通过对出价进行微小扰动并评估给竞拍者带来的效用以量化激励兼容性，可通过在拍卖日志上的黑盒模拟直接计算
- i-SIC 取值为0到1（一价拍卖对应0，二价拍卖对应1），值越大，说明激励兼容性越好
  
  We now utilize the i-SIC metric [7] to evaluate incentive compatibility (IC) of Deep GSP. The i-SIC metric is between 0 and 1, and the larger value means the better IC property
  - 可以证明：一价计费下，i-SIC的值为0；二价计费下，i-SIC 的值为1
    - 一价计费时，由于竞拍者的出价等于商户的计费，在 $\lim_{\alpha \to 0}$ 时
      - 分配概率为 $x((1+\alpha)v) = x((1-\alpha)v) = x(v)$
      - 计费为 $p((1+\alpha)v) = (1+\alpha)v \times x(v) $ 和 $ p((1-\alpha)v) = (1-\alpha)v \times x(v)$，故而有
        $$
        \begin{align}
        \mathbb{E}_{v\sim F}[&\hat{u}((1+\alpha)v)] - \mathbb{E}_{v\sim F}[\hat{u}((1-\alpha)v)] \\
        &= \mathbb{E}_{v\sim F}[(1+\alpha)v \times x(v) - (1+\alpha)v \times x(v) - ((1-\alpha)v \times x(v)-(1-\alpha)v\times x(v))] \\
        &= \mathbb{E}_{v\sim F}[0] \\
        &= 0
        \end{align}
        $$
    - 二价计费时，若竞拍者赢得拍卖，在 $\lim_{\alpha \to 0}$ 时
      - 分配概率为 $x((1+\alpha)v) = x((1-\alpha)v) = x(v)$
      - 计费为 $p((1+\alpha)v) = p((1-\alpha)v) = p(v)$，故而有:
        $$
        \begin{align}
        \mathbb{E}_{v\sim F}[\hat{u}((1+\alpha)v)] - \mathbb{E}_{v\sim F}[\hat{u}((1-\alpha)v)] &= \mathbb{E}_{v\sim F}[(1+\alpha)v \times x(v) - (1-\alpha)v \times x(v)] \\
        &= \mathbb{E}_{v\sim F}[2\alpha v \times x(v) ] \\
        &= 2\alpha \mathbb{E}_{v\sim F}[ v \times x(v) ]
        \end{align}
        $$

对照基线

GSP

Generalized Second Price auction (GSP). 排序规则是通过 expected Cost Per Milles (eCPM) 排序，支付规则时使用下一位的排序分反算计费

uGSP

Utility-based Generalized Second Price auction (uGSP)，最早提出于论文 Optimising trade-offs among stakeholders in ad auctions, Microsoft Research, 2014. 是对GSP的一种扩展，其分配规则中的排序公式为：
$$ r_i(b_i) = \lambda_1 \times b_i \times pCTR_i + o_i $$
- 其中 $o_i$ 表示其他效用指标，比如作者使用了 $o_i = \lambda_2 \times pCTR_i + \lambda_3 \times pCVR_i$
支付规则与GSP相同，都是通过下一位的排序分反算计费

附录：Smooth Transition是什么？

以下内容参考自：基于深度学习的广告拍卖机制论文阅读笔记（1）

平滑切换（Smooth Transition），即多目标优化中的各指标权重发生变化时，广告主侧的优化目标不会有明显的波动；
理解：不是“广告主的优化目标”不会有明显波动，应该是“广告主效果指标”不会有明显波动
原始论文内容：

As the importance of different performance metrics can vary over time due to business needs, we further introduce the smooth transition constraint to ensure the advertiser performance metrics not fluctuate too much when the auction mechanism switches among candidate mechanisms to achieve different optimization objectives

Another desirable property we want to achieve is Smooth Transition (ST). As discussed in Section 1, the performance objectives of the ad platform may vary due to the change of the business logic. If the new optimization objective is quite different from the previous one, the resulting auction mechanism would significantly affect the advertisers’ utilities [2]. This introduces the chaos of the auction environment. To stabilize advertisers’ utility change under different mechanisms, we choose a benchmark mechanism $\mathcal{M}_0$, and require advertisers’ utility under the new mechanism should not be less than $1-\epsilon$ of that under $\mathcal{M}_0$. The benchmark mechanism $\mathcal{M}_0$ could be the currently deployed mechanism.
$$ \mu_i(\mathcal{M}) \ge (1-\epsilon)\mu_i(\mathcal{M_0}) $$
where we set a lower bound for advertiser $i$’s utility $\mu_i$ when selecting a new auction mechanism $\mathcal{M}$. The lower bound $\bar{\mu}(\mathcal{M}_0)$ could be set as the average utility over a certain period under the benchmark mechanism $\mathcal{M}_0$. The parameter $\epsilon$ is a tolerant utility loss ratio for advertisers (0 ≤ $\epsilon$ ≤ 1). By choosing an appropriate $\epsilon$, the advertiser’s utility would not fluctuate too much when the auction mechanism is switched towards optimizing another objective.
个人理解：在切换不同候选拍卖机制去实现不同的优化目标时，广告主效果波动不大(相对之前的基线不能负向太多)，相当于能比较平滑的迁移拍卖机制

CA——GAVE

参考链接：
- 原始论文：Generative Auto-Bidding with Value-Guided Explorations, SIGIR 2025, Kuaishou

整体思路

现有自动出价方法 ：通常采用 rule-based strategies 或 RL 技术，这些方法存在一些问题：
- rule-based strategies ：缺乏适应时变市场条件的灵活性
- RL-based methods ：在 MDP 框架中难以捕捉重要的历史依赖关系和观测结果
- 通用问题 ：
  - 目前切换的适应性问题 ：在 ensuring strategy adaptability across diverse advertising objectives 方面常常面临挑战
  - Offline问题 ：随着越来越多地采用离线训练方法来促进稳定在线策略的部署和维护，在固定离线数据集上进行训练所导致的行为模式记录和行为崩溃问题变得日益突出
为解决这些局限性，论文提出了基于价值引导探索的离线生成式自动出价框架（offline Generative Auto-bidding framework with Value-Guided Explorations，GAVE）
- 通过 Score-based未来回报（Return-To-Go, RTG）模块适应各种广告目标
- 将动作探索机制与基于 RTG 的评估方法相结合，在探索新动作的同时确保保持稳定性的更新
- 设计了一个可学习的价值函数来指导动作探索的方向，并减轻 OOD（Out-of-Distribution）问题
实验：离线+在线
- 注：论文方法在 NeurIPS 2024 竞赛 “AIGB赛道 ：使用生成模型学习自动出价智能体” 中荣获第一名
其他：实现代码已开源 Applied-Machine-Learning-Lab/GAVE

一些讨论

自动出价的重要性 ：自动出价凭借其在动态竞争的在线环境中优化出价决策的强大能力，已成为广告平台的关键策略，有助于企业触达目标受众并提高销售额
出价需求 ：现代广告系统非常复杂（市场条件的波动、用户行为的多样性），这要求出价策略能够适应这些变化并与广告商的多样化目标保持一致。此外，大量需要实时处理的广告竞价进一步加剧了这一需求，在这种情况下，人为干预既不切实际，也往往无法实现最佳广告效果
现有解决方案主要发展为两类：
- rule-based strategies ：计算量小且易于部署，但其静态特性导致其不适合动态市场，也无法满足广告商的多样化需求
- RL-based methods ：虽然采用 MDP 来适应环境变化并获得更好的性能，但面临一个关键的结构性制约：
  - MDP 状态独立性假设本质上忽略了出价序列中的时间依赖关系和观测结果。这一限制阻碍了对不断变化的行为模式和市场波动的识别，大大削弱了RL在高度波动的实时出价环境中的实际适用性
  - 个人理解：这里对 RL 无法建模波动主要体现在无法预知快速变化的流量趋势（特别是与历史趋势不一致时）；特别地，出价场景可能是 POMDP 问题，常规 RL 方法将难以解决问题，将历史序列都作为输入才能缓解
DT 在出价上的前景 ：Decision Transformer（DT）作为一个强大的框架，能够有效捕捉时间依赖关系和历史上下文（temporal dependencies and historical context），因此，将 DT 应用于离线出价建模为改进策略提供了一个有前景的方向，其优点有：
- 适配Offline RL场景 ：通过采用离线训练范式，DT 规避了在线训练的风险和实施挑战，确保了在各种场景中的更广泛适用性
- 时间依赖和上下文建模 ： DT 的生成式建模基础进一步使其能够明确捕捉时间依赖关系和历史出价上下文，实现与现实世界广告环境的动态特性相匹配的自适应决策
DT 的面临问题 ：
- 首先，实际部署需要适应复杂的广告目标 ：其评估指标不仅限于总点击量或转化率等基本指标，这些目标通常涉及许多复杂函数（包含相互依赖的参数，如 CPA 或 CPC 约束等），这要求 DT 建模具有自适应优化目标 ，以符合多样化的运营标准
- 其次，在离线环境中直接训练 DT 模型可能会局限于已记录的行为模式 ，并遭受行为崩溃问题，这需要在稳定更新的同时加强动作探索
论文提出了一个统一框架 GAVE，用于增强 DT 在离线生成式自动出价中的应用
- 首先，为适应复杂的广告目标，论文设计了一个 Score-based RTG 模块，其分数函数可定制，通过可微编程实现对各种目标要求（如CPA约束）的自适应建模
- 其次，提出了一种动作探索机制以及基于 RTG 的评估方法，用于在固定数据集之外探索和评估动作，同时确保探索动作与原始动作之间的稳定更新
  - 在如此敏感的出价环境中，动作空间大，通过随机探索学习有益策略并避免分布外（OOD）风险颇具挑战。因此，论文引入了一个可学习的价值函数来指导动作探索过程，将探索导向潜在的最优动作。该机制将探索锚定在合理区域内，同时实现可控的外推（extrapolation），从而促进策略改进并进一步减轻OOD问题
论文的贡献：
- 引入了创新框架 GAVE ，利用 DT 优化自动出价策略，旨在无缝适应各种现实场景，提出了三项技术创新：
  - （1）一个 Score-based RTG 模块，通过可微编程实现针对各种广告目标的可定制函数；
  - （2）一种动作探索机制，结合基于 RTG 的评估，确保稳定更新；
  - （3）一个可学习的价值函数，将探索锚定在合理区域，从而减轻OOD风险，并实现可控外推以改进策略
- 实验：离线+在线，AIGB 出价赛道第一名

一些基础知识

自动出价问题

考虑在离散时间段 $i = 1, \cdots, I$ 内到达的一系列 $I$ 个曝光机会。广告商通过为这些曝光提交出价 $\{b_{i}\}_{i = 1}^{I}$ 参与实时竞争
拍卖机制遵循以下规则：
- 如果广告商的出价 $b_{i}$ 超过其他参与者的最高竞争出价 $b_{i}^{-}$，则该广告商赢得曝光 $i$
- 获胜的广告商随后会产生成本 $c_{i}$，该成本由拍卖机制确定，按照行业标准做法，论文采用 GSP 拍卖机制
广告商的目标 ：在指定时间段内通过赢得的曝光最大化总获取价值。这个优化问题可以正式表示为：
$$\max \sum_{i = 1}^{I} x_{i} v_{i}$$
- 其中 $v_{i} \in \mathbb{R}^{+}$ 表示广告商对曝光 $i$ 的私人估值（例如转化率或点击率），$x_{i} \in \{0, 1\}$ 表示指示拍卖结果的二元决策变量：
  $$x_{i}= \begin{cases}1 & \text{如果 } b_{i}>b_{i}^{-} \ 0 & \text{否则} \end{cases}$$
同时，广告商必须满足多个约束条件以确保有效的广告计划（campaign）管理。基本约束是总预算限制：
$$\sum_{i = 1}^{I} x_{i} c_{i} \leq B$$
- 其中 $B \in \mathbb{R}^{+}$ 表示广告商的总预算。其他关键绩效指标（KPI）约束，以每次获取成本（CPA）为例，可以表示如下：
  $$\frac{\sum_{i = 1}^{I} x_{i} c_{i} }{\sum_{i = 1}^{I} x_{i} v_{i} } \leq C \tag{4}$$
  - 其中 $C \in \mathbb{R}^{+}$ 表示最大允许的CPA。这个比率量化了广告支出相对于价值创造的效率。由于大多数其他KPI约束可以类似地建模，为简单起见，论文仅考虑CPA约束。然而，与由拍卖平台直接管理的预算约束不同，这些KPI约束在实际场景中通常并不严格。这是因为计算这些约束需要广告商对所有出价曝光的 $v_{i}$，因此只有在整个出价过程结束后才能确定真正的CPA。尽管如此，论文仍然希望在建模中将它们作为软约束使用
因此，整个出价过程可以表示为：
$$\begin{aligned} \max_{b_{1}, \cdots, b_{I} } & \sum_{i} x_{i} v_{i} \ \text{s.t.} & \sum_{i} x_{i} c_{i} \leq B \ & \frac{\sum_{i} x_{i} c_{i} }{\sum_{i} x_{i} v_{i} } \leq C \end{aligned} \tag{5}$$
解决这个优化问题存在固有的挑战，这源于曝光的高基数以及对未来拍卖表现的基本不确定性。先前的研究将这个问题重新表述为一个线性规划问题，以得出简化的最优出价策略：
$$b_{i}^{*}=\lambda_{0}^{*} v_{i}-\sum_{j} \lambda_{j}^{*}\left(q_{i j}\left(1-\mathbb{1}_{C R_{j} }\right)-\mathbb{k}_{j} \mathbb{p}_{i j}\right) \tag{6}$$
- 其中 $b_{i}^{*}$ 表示曝光 $i$ 的理论最优出价，$q_{ij}$ 可以是任何性能指标或常数，$\mathbb{1}_{C R_{1} }$ 是指示约束 $j$ 是否与成本相关的指标函数。$P_{i j}$ 和 $k_{j}$ 可以视为在多个KPI条件下公式（5）中 $v_{i}$ 和 $c$ 的扩展表达式。这种重新表述将自动出价问题转化为确定满足所有约束的最优 $\lambda_{0}^{*}$ 和 $\lambda_{j}^{*}$。通过将公式（6）代入公式（5），令 $j = 1$，$\mathbb{1}_{C R_{j} } = 1$，$\mathbb{P}_{i j} = v_{i}$，$k_{j} = C$ 且 $q_{i j}$ 为任何性能指标或常数，我们可以得到：
  $$b_{i}^{*}=\left(\lambda_{0}^{*}+\lambda_{1}^{*} C\right) v_{i}=\lambda^{*} v_{i} \tag{7}$$
  - 其中 $\lambda^{*}=\lambda_{0}^{*}+\lambda_{1}^{*} C$ 作为统一的出价参数。因此，许多近期研究试图通过在出价过程中迭代确定最优的 $\lambda^{*}$ 来解决出价问题。此外，值得注意的是，当根据公式（7）解决出价问题时，第一个条件，即 $\sum_{i} x_{i} c_{i} \leq B$ 总是满足的。这是因为当广告商的预算不足时，拍卖平台会自动控制 $x_{1}$，以确保广告商不欠款。然而，第二个条件并不总是满足，因为论文预测的 $\lambda$ 与最优的 $\lambda^{*}$ 之间存在差距。解决这个问题的一个简单方法是在评估阶段为模型选择在公式（7）的目标函数中添加一个关于CPA条件的惩罚项，这将在3.2节中进一步讨论

基于 DT 的自动出价

为解决自动出价问题，现有方法采用基于规则的策略或RL方法进行优化。然而，基于规则的策略通常无法适应现实出价环境的高度动态性，而RL方法依赖于由 $s_{t + 1} = f(s_{t}, a_{t})$ 定义的状态转换，这使得对拍卖生态系统中固有的重要时间依赖关系和历史观测进行建模变得复杂
Transformer架构的最新进展催生了 DT，使其成为顺序决策的最先进方法。DT 在捕捉长程依赖关系方面表现出色，使其非常适合拍卖结果显示出显著时间相关性的出价环境。基于这个框架，论文将自动出价视为 DT 设置下的序列建模任务。出价期被划分为离散的时间步，每个时间步在特定的环境设置下进行配置：
- 状态 $s_{t}$ ：状态向量 $s_{t}$ 包含一系列特征，用于描述时间步 $t$ 的出价条件。对于广告场景，这些特征可以是剩余时间、未使用的预算、历史出价统计信息等
- 动作 $a_{t}$ ：动作 $a_{t}$ 表示在整个出价期内可以迭代调整的出价变量。在论文中，根据公式（7），最优动作是 $a = \lambda^{*}$。因此，论文将时间步 $t$ 的实际动作表示为： $a_{t}=\lambda_{t}$
- 奖励 $rw_{t}$ ：假设有 $N_{t}$ 个候选曝光在时间步 $t$ 到 $t + 1$ 之间到达。奖励 $rw_{t}$ 可以定义为： $rw_{t}=\sum_{n = 0}^{N_{t} } x_{n_{t} } v_{n_{t} }$，其中 $x_{n_{t} }$ 和 $v_{n_{t} }$ 是时间步 $t$ 第 $n$ 个曝光的二元指示符和价值
- 未来回报（Return-To-Go, RTG） $r_{s}$ ： RTG 值表示在未来时间步中要获得的总奖励： $r_{t}=\sum_{t’ = t}^{T} rw_{t’}$，其中 $T$ 是最后一个时间步
这些设置导致了以下轨迹表示，非常适合自回归训练和推理：
$$\tau=\left(r_{1}, s_{1}, a_{1}, r_{2}, s_{2}, a_{2}, \cdots, r_{T}, s_{T}, a_{T}\right)$$

GAVE 整体框架介绍

GAVE概述

GAVE整体架构：
如图1所示，GAVE采用 DT 架构，其中 RTG、状态和动作对构成输入序列，即时间戳 $t$ 处的 $(r_{t}, s_{t}, a_{t})$。与传统 DT 不同，GAVE引入了几个关键创新，以实现自适应优化、增强稳定性并促进策略改进，这些创新包括
- 自适应的 RTG ：用于与多样化广告目标对齐的 Score-based RTG （图1（a.1））
- 配备基于 RTG 评估机制的动作探索模块（图1（a.2）），用于发现和评估新动作并稳定更新
- 一个可学习的价值函数（图1（a.3）），用于引导探索以改进策略 ，同时减轻分布外（OOD）风险。GAVE的训练遵循离线范式（图1（b）），使用序列样本作为输入生成预测标签
- 为进行评估，采用模拟出价环境（图1（c）），其中测试模型与固定策略智能体进行交互
GAVE的预测过程如下所示：
$$\left\{\begin{array}{l} \left(\hat{\beta}_{t}, \hat{a}_{t}, \hat{V}_{t+1}\right)=GAVE(r_{t-M},s_{t-M},a_{t-M},\cdots ,r_{t},s_{t})\\ \hat {r}_{t+1}=GAVE(r_{t-M},s_{t-M},a_{t-M},\cdots ,r_{t},s_{t},a_{t})\\ \tilde {a}_{t}=\hat {\beta }_{t}a_{t}\end{array} \right.$$
- 其中 $M$ 是一个超参数，表示具有 $M + 1$ 个输入时间步的序列
GAVE采用自适应的 Score-based RTG 函数 ，可以使优化目标与不同的广告目标保持一致：在时间步 $t$ 的动作探索过程中，除了预测动作 $\hat{a}_{t}$ 之外，GAVE还预测以下内容：
- 一个系数 $\hat{\beta}_{t}$
  - 问题：$\hat{\beta}_{t}$ 的训练依赖 $\tilde {a}_{t}$，继而依赖 $\tilde {r}_{t}$，损失函数见文章后面的公式（22）？是否在图1（a.2）中还需要接一个网络预估 $\tilde{r}_{t}$ 才能反传损失函数吗？
  - 回答：从源码看，是的，且使用的是和主网络相同的同一个 transformer 网络
    - transformer 网络过程见：CAVE/…/dt.py：$\tilde {a}_{t}\rightarrow \tilde {r}_{t}$ 定义
    - 损失函数见：CAVE/…/dt.py：$L_v$ 定义
- 一个用于估计可学习价值函数 $V_{t + 1}$ 的 $\hat{V}_{t + 1}$（注：文章后面会介绍，损失函数是分位点回归）
- 一个 RTG 值 $\hat{r}_{t + 1}$ （注：文章后面会介绍，拟合目标是真实的 RTG $r_{t+1}$）
以下创新共同使GAVE能够实现更好的性能和鲁棒性：
- 通过使用基于 RTG 的评估方法评估探索动作 $\tilde{a}_{t}$ 和动作标签 $a_{t}$，GAVE应用平衡更新策略来协调 $\tilde{a}_{t}$ 和 $a_{t}$。这确保了一个保持稳定性的更新过程
- 引入可学习的价值函数 $V_{t + 1}$ 来引导模型朝着潜在的最优策略改进，同时进一步降低OOD风险

Score-based RTG

如2.1节所述，直接优化赢得曝光的累积价值可能会导致每次行动成本（CPA）约束显著超出其限制范围。为解决这个问题，可以构建包含惩罚项的目标函数作为评估指标，从而能够依据特定的广告目标调整对CPA限制的重视程度
- 这种方式有助于对最优模型进行评估和筛选。例如，先前的研究工作[44]提出在测试阶段使用分数 $S$ 来评估模型的实际性能，进而能够挑选出性能更优的模型。该分数整合了针对CPA约束的惩罚项，用于评估整个出价周期内出价模型的整体表现，公式如下：
  $$\begin{cases}
  CPA = \frac{\sum_{i} x_{i} c_{i} }{\sum_{i} x_{i} v_{i} } \\
  \mathbb{P}(CPA; C) = \min\left\{\left(\frac{C}{CPA}\right)^{\gamma}, 1\right\} \\
  S = \mathbb{P}(CPA; C) \cdot \sum_{i} x_{i} v_{i}
  \end{cases} \tag{13}$$
- 注：前文已经定义过，$C$ 是允许的最大 $CPA$
- 理解： $CPA > C$ 时，$\mathbb{P}(CPA; C) < 1$ 成立，此时原始收益会变小
在论文中，论文将约束条件直接融入训练阶段，不再仅仅依赖于预训练模型的选择来提升评估分数（如何理解？）
- 为了使训练与各种广告目标的评估指标保持一致，论文提出在 GAVE 中采用带约束的分数函数（而非无约束的 $\sum_{i = 1}^{I} x_{i} v_{i}$）来进行 RTG 建模，如图1（a.1）所示。例如，基于公式（13）所定义的评估指标，可以利用以下 Score-based RTG 函数来使训练与评估同步：
  $$\begin{cases}
  CPA_{t} = \frac{\sum_{i}^{I_{t} } x_{i} c_{i} }{\sum_{i}^{I_{t} } x_{i} v_{i} } \\
  \mathbb{P}(CPA_{t}; C) = \min\left\{\left(\frac{C}{CPA_{t} }\right)^{\gamma}, 1\right\} \\
  S_{t} = \mathbb{P}(CPA_{t}; C) \cdot \sum_{i}^{I_{t} } x_{i} v_{i} \\
  r_{t} = S_{T} - S_{t - 1}
  \end{cases} \tag{14}$$
- $I_{t}$ 表示从时间步0到时间步 $t$ 的曝光数量
- $S_{t}$ 代表时间步 $t$ 的广义分数函数
- $T$ 表示出价周期中的最后一个时间步
- 通过将分数计算推广到每个时间步，推导出 RTG $r_{t}$，以表示尚未获得的未来分数，进而引导GAVE的优化方向
此外，在实际应用中，不同的广告目标对CPA约束的依赖程度可能有所不同，从而产生不同的评估指标。尽管如此，通过以类似的方式将分数推广到每个时间步（即 $S_{t}$），训练和评估仍可保持一致，公式如下：
$$r_{t} = S_{T} - S_{t - 1} \tag{15}$$
这种 Score-based RTG 函数增强了 GAVE 的灵活性，确保其能够适用于各种不同的广告目标
问题：在推理阶段，广告曝光次数等是未知的，如何设计对应的 RTG？

Action Explorations

本节的主要目标是在训练过程中探索新的动作，以发现离线数据集中可能缺失的策略，从而实现更好的模型优化，但离线环境动作探索面临以下问题：
- 不探索面临的问题 ：在离线环境中，由于无法与环境进行交互，仅从固定的数据集中学习可能会导致模型局限于已记录的行为模式
- 探索面临的问题 ：但在数据集之外探索动作可能会引入固有的分布转移，进而可能导致行为崩溃[6, 21]（与实际动作标签相比，探索出的动作对模型性能的影响可能是有益的，也可能是有害的，这给开发保持稳定性的更新过程带来了巨大挑战）
为应对这些挑战，GAVE 引入了一种全新的动作探索机制，并结合基于 RTG 的评估方法，如图1（a.2）所示。这使得GAVE能够通过识别动作的重要性，自适应地调整动作的探索和更新方向，从而实现保持稳定性的更新
- 具体而言，在时间步 $t$，GAVE预测一个与 $a_{t}$ 维度相同的系数 $\hat{\beta}_{t}$，以生成一个新的动作 $\tilde{a}_{t}$。该过程的正式表达式为：
  $$\begin{cases}
  \hat{\beta}_{t} = \sigma(FC_{\beta}( DT (r_{t - M}, s_{t - M}, a_{t - M}, \cdots, r_{t}, s_{t}))) \\
  \tilde{a}_{t} = \hat{\beta}_{t}a_{t}
  \end{cases}$$
  - 如前文所述，$M$ 是一个超参数，表示具有 $M + 1$ 个输入时间步的序列
其中，$ DT (\cdot)$ 表示 DT backbone（主干网络），$FC_{\beta}(\cdot)$ 表示全连接层，$\sigma$ 是缩放函数。为减轻分布外（OOD）问题，缩放函数定义为：
$$\sigma(x) = Sigmoid(x) + 0.5$$
- 该公式将 $\hat{\beta}_{i}$ 限制在区间 $[0.5, 1.5]$ 内，确保探索出的动作 $\tilde{a}_{t}$ 与动作标签 $a_{t}$ 保持接近
为了在训练过程中最小化分布转移并实现保持稳定性的更新，论文并未直接使用 $\tilde{a}_{t}$ 来生成新样本，而是将其作为额外标签，与原始标签 $a_{t}$ 共同平衡动作更新
- 这种方法需要估计 $\tilde{a}_{t}$ 和 $a_{t}$ 的相对重要性，以确定预测动作 $\hat{a}_{t}$ 的最优更新方向
- 根据强化学习的惯例[21, 39, 41]，论文将 $a_{t}$ 的动作价值定义为 $r_{t + 1}$ （时间步 $t + 1$ 的 RTG），因为它 代表了执行动作 $a_{t}$ 后 未来的累积回报
论文设计了如图1（b.1）所示的 $w_{t}$，以平衡更新方向：
$$\begin{cases}
\tilde{r}_{t + 1} = GAVE(r_{t - M}, s_{t - M}, a_{t - M}, \cdots, r_{t}, s_{t}, \tilde{a}_{t}) \\
\hat{r}_{t + 1} = GAVE(r_{t - M}, s_{t - M}, a_{t - M}, \cdots, r_{t}, s_{t}, a_{t}) \\
w_{t} = Sigmoid(\alpha_{r} \cdot (\tilde{r}_{t + 1} - \hat{r}_{t + 1}))
\end{cases} \tag{18}$$
- 其中，$\tilde{r}_{t + 1}$ 和 $\hat{r}_{t + 1}$ 分别表示 $\tilde{a}_{t}$ 和 $a_{t}$ 的估计 RTG
- 问题：$\alpha_{r}$ 是超参数吗？如何设置？
- 相应的动作探索损失函数定义为：
  $$\begin{cases}
  L_{r} = \frac{1}{M + 1} \sum_{t - M}^{t}(\hat{r}_{t + 1} - r_{t + 1})^{2} \\
  L_{a} = \frac{1}{M + 1} \sum_{t - M}^{t}((1 - w_{t}’) \cdot (\hat{a}_{t} - a_{t})^{2} + w_{t}’ \cdot (\hat{a}_{t} - \tilde{a}_{t}’)^{2})
  \end{cases} \tag{19}$$
  - $w’$ 和 $\tilde{a}_{t}’$ 表示梯度冻结后的 $w$ 和 $\tilde{a}_{t}$
  - $\hat{a}_t$ 是预测动作，也是 $L_{a}$ 的学习目标
  - 通过 $L_{r}$，GAVE 确保了 RTG 预测的准确性，能够可靠地估计 $\tilde{a}_{t}$ 和 $a_{t}$ 的 RTG
  - 通过 $L_{a}$，GAVE 在 $\tilde{a}_{t}$ 和 $a_{t}$ 之间维持了平衡且保持稳定性的更新过程，当 $w_{t} > 0.5$ 时，更新方向朝着 $\tilde{a}_{t}$ ；否则，朝着 $a_{t}$，以此减轻OOD问题以及探索可能带来的负面影响
    - 理解：当 $w_{t} > 0.5$ 时，说明探索动作 $\tilde{a}_{t}$ 预估的 RTG $\tilde{r}_{t + 1}$ 比真实动作 $a_{t}$ 预估的 RTG $\hat{r}_{t + 1}$ 好的比较多，值得让 $\hat{a}_t$ 朝探索动作 $\tilde{a}_{t}$ 更新一些

Learnable Value Function

虽然动作探索机制确保了在数据集之外进行探索并实现保持稳定性的更新过程，但随机生成的 $\tilde{a}_{t}$ 并不能保证提升模型性能。为解决这一局限性，论文提出了一种可学习价值函数，如图1（a.3）所示，该函数有助于发现更优的动作以改进策略。具体而言，受强化学习惯例[21, 39, 41]的启发，论文提出了一个序列价值函数 $V_{t + 1}$，类似于强化学习中的最优状态价值函数，它表示 $r_{t + 1}$ 的上限，公式如下：
$$V_{t + 1} = \underset{a_{t} \in \mathbb{A} }{\arg \max} \ r_{t + 1} \tag{20}$$
- $\mathbb{A}$ 表示可用动作空间
- 由于动作空间广泛，且离线数据集中的实际动作有限，直接对 $V_{t + 1}$ 进行统计计算并不可行。论文使用 $r_{t + 1}$ 的期望分位数回归过程来学习这个值：
  $$\begin{align}
  L_{e} &= \frac{1}{M + 1} \sum_{t - M}^{t}(L_{2}^{\tau}(r_{t + 1} - \hat{V}_{t + 1})) \\
  &= \frac{1}{M + 1} \sum_{t - M}^{t}(\left|\tau - \mathbb{1}((r_{t + 1} - \hat{V}_{t + 1}) < 0)\right|(r_{t + 1} - \hat{V}_{t + 1})^{2})
  \end{align} \tag{21}$$
  - $\hat{V}_{t + 1}$ 表示 $V_{t + 1}$ 的预测值
  - $L_{2}^{\tau}(y - m(x))$ 表示使用模型 $m(x)$ 预测标签 $y$ 的期望分位数 $\tau \in (0, 1)$ 时的损失函数[21]。根据公式（20），论文将 $\tau = 0.99$，以学习 $r_{t + 1}$ 的上限，从而有效地估计 $V_{t + 1}$
通过使用 $\hat{V}_{t + 1}$ 估计 $V_{t + 1}$，并利用它来指导 $\tilde{r}_{t + 1}$ 的更新方向，GAVE隐式地将探索出的 $\tilde{a}_{t}$ 的更新方向引导向潜在的最优动作。这一过程如图1（b.2）所示，可正式表示为：
$$L_{v} = \frac{1}{M + 1} \sum_{t - M}^{t}(\tilde{r}_{t + 1} - \hat{V}_{t + 1}’)^{2} \tag{22}$$
- 其中，$\hat{V}_{t + 1}’$ 表示梯度冻结后的 $\hat{V}_{t + 1}$。通过应用 $L_{v}$，GAVE将 $\tilde{a}_{t}$ 的 RTG 锚定在 $\hat{V}_{t + 1}$ 附近，从而隐式地将 $\tilde{a}_{t}$ 的更新方向引导向最优动作。这种方法减轻了OOD风险，并实现了可控的外推以改进策略

Optimization Algorithm

通过上述机制，GAVE实现了一个离线生成式自动出价框架，该框架结合了价值引导的探索，以增强策略学习能力。综合损失函数由公式（19）、（21）和（22）中定义的各个组件加权组合而成：
$$L_{o} = \alpha_{1} \cdot L_{r} + \alpha_{2} \cdot L_{a} + \alpha_{3} \cdot L_{e} + \alpha_{4} \cdot L_{v} \tag{23}$$
- 其中，${\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4} }$ 是超参数，用于控制每个损失组件的相对贡献
GAVE的完整优化过程在算法1中详细列出，训练过程如图1（b）所示
在推理过程中，如图1（c）所示，GAVE处理每个输入序列以预测 $\hat{a}_{t} = \lambda_{t}$，它作为时间步 $t$ 的出价参数。然后，根据公式（7），时间步 $t$ 第 $n$ 个曝光的出价计算为 $b_{t n} = \lambda_{t} v_{t n}$，从而实现实时出价模拟

离线实验

在本节中，论文在两个公共数据集上进行实验，以研究以下问题：
- RQ1 ：与最先进的自动出价基线方法相比，GAVE 的性能如何？
- RQ2 ：GAVE 能否适应多样化的广告目标？
- RQ3 ：可学习价值函数在促进动作探索方面的效果如何？
- RQ4 ：GAVE 中所提出的组件对最终出价性能有何贡献？

Experiment Setup

数据集 ：先前的自动出价研究主要依赖于专有出价日志进行评估，问题的表述往往针对特定场景。这种评估方法的异质性阻碍了不同方法之间进行公平、系统的比较。最近，阿里巴巴妈妈推出了AuctionNet，这是行业内首个标准化的大规模模拟出价基准，能够在一致的条件下对模型进行全面评估。在本研究中，论文使用AuctionNet框架中的两个数据集：
- （i）AuctionNet：主要数据集，包含全面的出价轨迹；
- （ii）AuctionNet-Sparse：AuctionNet的稀疏变体，具有较低的转化率
- 以上这两个数据集都包含约 50 万个出价轨迹，收集自 1 万个不同的投放期，每个投放期由 48 个时间步组成，并且包含来自数百万个曝光机会的交互数据。详细统计信息见表1
评估协议 ：论文的评估方法遵循AuctionNet基准，并采用模拟环境来模拟现实世界的广告系统，如图1（c）所示
- 评估涵盖一个 24 小时的投放期，离散化为 48 个均匀的时间步，在此期间，预测动作用于出价（$(\hat{a}_{t} = a_{t})$）
- 在这个模拟环境中，48个具有不同策略的出价智能体竞争即将到来的（incoming）曝光机会，性能使用公式（13）（$\gamma = 2$）进行衡量。为确保全面评估，论文采用循环测试策略：测试模型依次替换48个智能体中的每一个，在每一轮中与其余智能体竞争。最终性能计算为所有评估的平均得分，从而提供了对模型有效性的可靠衡量
基线方法 ：为评估GAVE的有效性，论文将其与多种基线方法进行全面比较：
- DiffBid：应用扩散框架来模拟出价轨迹并对出价序列进行建模
- USCB：在在线RL出价环境中动态调整出价参数以实现最优出价性能
- CQL：学习一个保守的价值函数，以减轻 Offline RL 中的高估问题
- IQL：应用期望分位数回归方法，在不评估超出范围动作的情况下实现策略改进
- BCQ：在典型的 Offline RL 学习过程中对动作空间施加限制
- DT：采用transformer架构进行顺序决策建模，并使用行为克隆方法从数据集中学习平均策略
- CDT：尝试在离线设置中训练一个约束满足策略，以平衡安全性和任务性能
- GAS：尝试通过在建模中应用蒙特卡洛树搜索（MCTS）来构建一个基于 DT 的离线出价框架，并进行训练后搜索
实现细节 ：根据先前的研究，论文使用原始数据集中不同的预算比率进行评估。性能使用以下评分指标衡量：
$$S = \mathbb{P}(CPA; C) \cdot \sum_{i} x_{i} v_{i}$$
该指标如公式（13）所定义，其中 $Y = 2$。所有实验均在NVIDIA H100 GPU上进行，使用固定的批量大小128，最大训练步数为40万步。GAVE的实现采用具有8层和16个注意力头的因果transformer架构。模型参数使用AdamW优化器进行优化，学习率为 $1e^{-5}$。其他超参数通过全面的网格搜索确定，以最大化性能。为确保统计显著性，论文使用最优参数配置进行10次独立运行，并报告平均性能指标

整体性能（RQ1）

论文在不同预算设置下对GAVE和各种基线方法进行了全面比较，结果汇总在表2中
实验分析揭示了几个关键发现：
- GAVE在所有预算和数据集配置下均表现出色，始终优于现有方法。这种优越性可归因于论文新颖的动作探索方法，该方法在价值函数的指导下，能够在离线数据集之外发现新颖的、潜在的最优动作，同时通过平衡探索收益和风险的稳定更新过程保持稳健的训练
- 在所有基线方法中，基于 DT 的方法（GAS、 DT 和 CDT）表现较为突出，这凸显了 DT 结构在捕捉时间依赖关系和促进出价场景中的顺序决策方面的有效性。值得注意的是，GAS比 DT 和 CDT 取得了更好的结果，验证了其MCTS实现对策略优化的有效性。DiffBid在数据集上的表现不佳，可能是由于长序列和高度动态的环境给DiffBid准确预测轨迹和从反向过程中学习带来了额外挑战

一致性分析（RQ2）

如3.2节所述，广告目标可能需要不同的评估指标。为解决这一问题，GAVE采用了 Score-based自适应 RTG 建模方法，该方法能够适应各种优化目标，从而使训练目标与评估指标保持一致，如公式（15）所示。在本节中，论文探究GAVE在不同 RTG 和评估指标配置下的性能，以回答RQ2。具体而言，论文考虑以下三种评估指标：
$$\begin{cases}
S_{1}=\sum_{i} x_{i} v_{i} \\
S_{2}=\min\left\{\left(\frac{C}{CPA}\right)^{2}, 1\right\} \cdot \sum_{i} x_{i} v_{i} \\
S_{3}=\min\left\{\left(\frac{C}{CPA}\right)^{5}, 1\right\} \cdot \sum_{i} x_{i} v_{i}
\end{cases}$$
- 其中，$S_{1}$ 仅考虑获得的总曝光价值，代表对CPA条件限制较为宽松的业务场景。$S_{2}$ 是论文的优化目标和评估分数，它对CPA约束添加了惩罚项。$S_{3}$ 进一步提高了CPA的惩罚系数，代表对CPA条件限制严格的业务场景。这些指标既可以在训练期间用于 RTG 建模，也可以在测试期间用作评估标准。结果如表3所示
从表3中可以观察到，当训练 RTG 与用作评估指标的函数一致时，GAVE始终能取得最高性能。这一发现强调了通过论文 Score-based RTG 方法使训练目标与特定评估指标保持一致的重要性
注：表3体现不出来自适应能力吧，毕竟没有对照，靠衰减不多来说明目标变化时的有效性吗？

参数分析（RQ3）

为回答RQ3，论文对权重 $w_{t}$ 进行参数分析，如图1（b.1）所示，以阐明训练过程中 $\tilde{a}_{t}$ 和 $a_{t}$ 之间的差异。具体而言，图2曝光了训练步骤中平均总损失 $L_{o}$ 和权重 $w_{t}$ 的变化情况，使论文能够监测 $\tilde{r}_{t + 1}$ 和 $\hat{r}_{t + 1}$ 之间的差异。$w_{t}$ 越大，表明 $\tilde{r}_{t + 1}$ 对 $\hat{r}_{t + 1}$ 的影响越大，进而证明 $\tilde{a}_{t}$ 优于 $a_{t}$。这一结果凸显了价值函数在指导动作探索方面的有效性
从图2中明显可以看出，随着训练的进行，参数 $w_{t}$ 从约0.5增加到稳定高于0.5的位置。该稳定位置受数据集分布和模型超参数的共同影响。这一趋势证实了可学习价值函数在指导动作探索方面的有效性。在价值函数的引导下，模型持续探索具有更高 RTG 值 $\tilde{r}_{t + 1}$ 且接近估计最优值 $\hat{V}_{t + 1}$ 的动作 $\tilde{a}_{t}$。这种方法有助于学习潜在的最优策略，同时减轻OOD问题

消融研究（RQ4）

为进一步阐明GAVE中每个模块的贡献以回答RQ4，论文进行了消融研究，评估以下修改版本的GAVE：
GAVE-V ：不包含3.4节中描述的可学习价值函数。在此配置下，损失函数 $L_{v}$ 和 $L_{e}$ 被以下更新规则取代，以确保探索出的动作通过提高其 RTG 值 $\tilde{r}_{t + 1}$ 总体上优于原始标签：
$$L_{w}=1 - Sigmoid\left(\alpha_{r} \cdot \left(\tilde{r}_{t + 1}-\hat{r}_{t + 1}’\right)\right)$$
- 其中，$\hat{r}_{t + 1}’$ 是 $\hat{r}_{t + 1}$ 的梯度冻结版本。然而，由于没有价值函数，$\tilde{r}_{t + 1}$ 的更新方向变得无界，导致OOD问题和次优性能
GAVE-VA ：既不包含3.4节中的价值函数，也不包含3.3节中详细介绍的动作探索机制
DT ：移除所有与GAVE相关的设计模块，包括3.4节、3.3节和3.2节中描述的模块。因此，此配置与纯 DT 框架一致，使用 $S=\sum_{i} x_{i} v_{i}$ 进行 RTG 建模
图3曝光了评估结果。结果表明：
- （i）使用 Score-based RTG 建模使优化目标与评估指标保持一致，这使得GAVE-VA的性能优于 DT，证明了训练中目标一致性的重要性；
- （ii）GAVE-V中融入动作探索机制和基于 RTG 的评估，使模型能够发现离线数据集之外的潜在策略，并评估其重要性以实现稳定更新过程，从而比GAVE-VA取得更好的性能；
- （iii）GAVE中完全集成价值函数以指导动作探索，利用了潜在的最优策略，进一步缓解了OOD问题并提高了整体性能

在线部署

论文通过在两个工业实时出价场景（Nobid 和 Costcap）中的A/B测试来评估GAVE的有效性。Nobid 旨在在每日预算内最大化转化次数，Costcap 旨在在CPA/ROI限制下最大化转化次数。实验设置如下：
- 状态：20步的序列，特征包括预算、CPA限制、预测值、流量/成本速度、时间分段预算、剩余时间和窗口平均出价系数
- 动作：为稳定出价结果，出价系数 $\lambda$ 基于前两小时包含 $E$ 个时间步的窗口平均值确定，$\lambda_{t}=a_{t}+\frac{1}{|E|} \sum_{t’=t-E}^{t-1} \lambda_{t’}$，其中 $a_{t}$ 是GAVE在时间步 $t$ 的输出动作
- 未来回报（RTG） ：鉴于实际转化的稀疏性，论文在训练期间使用预期总转化次数 $\sum_{i} pcvr_{i}$，其中 $pcvr_{i}$ 是赢得流量 $i$ 的预测转化率。在推理时，整个序列的 RTG 设置为前一天广告计划的总预期转化次数
论文将GAVE与目前正在实际应用中的离线强化学习算法IQL进行比较
- 评估指标包括成本、转化次数、目标成本和CPA有效率，出价策略侧重于在预算和CPA约束下最大化转化次数
- 为考虑不同的广告计划目标，目标成本作为一种价值加权的转化度量，对于 Costcap 广告计划，转化价值等于CPA限制；对于 Nobid 广告计划，使用总流量的平均实际 CPA
- 如果 Costcap 广告计划的 CPA 保持在限制以下，则认为其 CPA 有效，该指标仅针对 Costcap 广告计划进行评估。论文进行了为期五天的在线A/B测试，将每个广告计划25%的预算和流量分配给基线出价模型和GAVE，结果汇总在表4中
对于 Nobid 和 Costcap 广告计划，GAVE均改善了成本和转化次数指标。在 Nobid 广告计划中，GAVE使成本增加了0.8%，转化次数增加了8.0%，目标成本增加了3.2%。在 Costcap 广告计划中，广告收入和广告商价值有所提升，同时CPA有效性显著改善，成本增加2.0%，转化次数增加3.6%，目标成本增加2.2%，有效CPA率增加1.9%

结论

论文提出了GAVE，通过价值引导探索来增强 DT 在离线生成式自动出价中的应用
- 为适应复杂的广告目标，论文设计了一种可定制的 Score-based RTG 机制，能够对各种优化目标进行自适应建模，以匹配不同的评估指标
- 论文将动作探索机制与基于 RTG 的评估方法相结合，在离线数据集之外探索动作的同时，确保稳定的更新过程
- 为进一步引导探索并减轻 OOD 风险，论文采用了可学习价值函数，将 RTG 更新锚定在分布合理的区域，同时允许可控的外推以改进策略
大量实验、在线部署和 NeurIPS 竞赛结果表明，论文的 GAVE 框架在增强自动出价策略的适应性和性能方面是有效的，为在动态环境中优化数字广告计划提供了一种通用解决方案

CA——Generative-Auto-bidding(GAS)

参考链接：
- 原始论文：GAS: Generative Auto-bidding with Post-training Search, WWW 2025, Kuaishou

GAS 整体思路说明

自动竞价通过代表广告主自动出价，对促进在线广告至关重要
生成式模型及优点 ：生成式自动竞价利用如 Transformer 和 Diffuser 等模型，根据可调节条件生成出价，因其能够直接从数据中学习最优策略并灵活适应偏好 ，近年来成为一种新趋势
生成式模型的不足 ：
- 生成式模型面临低质量数据导致的条件（condition，生成式强化中也就是return to go，也称为剩余回报）与真实动作价值不匹配的问题，尤其是在长序列决策中
- 数据集中的多数偏好可能阻碍模型对少数广告主偏好的泛化能力。虽然可以通过收集高质量数据并针对不同偏好重新训练多个模型来解决，但高昂的成本使其难以实现，阻碍了自动竞价进入大型基础模型时代
论文提出了一种灵活且实用的，基于训练后搜索（post-training Search）的生成式自动竞价方案（Generative Auto-bidding scheme using post-training Search），称为GAS
- 可用于优化基础策略模型的输出并适应多种偏好
- 论文采用弱到强（weak-to-strong）的搜索对齐方法，训练针对不同偏好的小型 Critic 模型，并利用蒙特卡洛树搜索（MCTS）的启发式搜索优化模型输出
- 具体而言，一种基于 Transformer 的 Critic 模型结合策略指示的新型投票机制可提升搜索对齐性能
- 论文还针对高频偏好场景或计算效率敏感场景提供了一种微调方法
- 在真实数据集和快手广告平台的在线A/B测试中进行的广泛实验证明了GAS的有效性，例如目标消耗提升了1.554%

Background

自动出价问题引入 ：随着商业的快速数字化，在线广告平台的覆盖范围和重要性显著扩大，成为企业吸引目标受众和提升销售的重要工具。面对海量的展示机会，手动调整出价以在预算和KPI约束下优化成本是不现实的。为此，广告平台现在提供自动竞价服务，利用高级策略自动化出价过程。这些策略考虑了即时或历史竞价信息中的多种因素，例如展示机会的分布和剩余预算（Wang等，2020）。此外，根据广告主类型的不同，策略还需考虑其偏好差异。例如，品牌广告主以长期增长和品牌认知为目标，通常希望在平均每展示成本等约束下向尽可能多的人展示广告；而效果广告主以最大化获胜展示的价值为目标，希望在每次转化的成本约束下最大化转化量（Xiao等，2017）。为满足这些多样化需求，谷歌、Facebook和阿里巴巴等广告平台为客户提供了多种定制化的竞价策略（Zhang等，2019；Zhang等，2020；Xiang等，2020）。此外，面对动态变化的广告环境，策略需要定期优化以紧密贴合客户偏好，从而帮助其实现长期商业利益（Zhang等，2020）
智能出价中的强化学习方法 ： RL 长期以来是通过广告模拟器或离线广告日志训练代理以优化自动竞价策略的主要方法。然而，RL方法主要基于马尔可夫决策过程（MDP），假设未来状态仅由当前单步状态和动作决定
- 最近的统计分析（Zhang等，2020）对自动竞价中的这一假设提出了质疑，揭示了历史状态序列长度与后续状态之间的强相关性。这一发现表明，在不可预测的在线广告环境中，仅依赖最近状态可能导致策略不稳定
- 此外，RL策略的偏好不易控制。USCB（Xiao等，2017）提出基于历史数据计算多约束下的最优解，然后训练RL优化策略。然而，一旦部署，策略的偏好即固定，限制了交互性和可控性
因此，基于条件生成模型（如Transformer和Diffuser）的生成式自动竞价方法成为新趋势
- 这些方法通过表示偏好的向量条件直接输出动作甚至轨迹，无需MDP假设。例如，决策Transformer（Chen等，2021）可以利用丰富的历史信息进行决策；Diffuser（Ajay等，2023）可直接根据条件生成规划轨迹
- 更重要的是，生成式模型通过简单修改条件值即可灵活控制偏好
随着基于生成式模型的大型基础模型在自然语言处理和计算机视觉等领域的显著进展（如ChatGPT和Stable Diffusion），可以预见自动竞价领域也将迈向基础模型时代，即开发决策基础模型以直接从大规模数据中学习最优决策策略
生成式自动竞价方法在应用中存在两大挑战 ：
- 首先，生成式竞价方法的性能受数据集质量显著影响，其中收集的条件（即 return to go ）无法反映动作的真实价值。例如，一个好的动作 $a_t$ 后接一个糟糕的未来动作 $a_{t+1}$ 可能导致 $a_t$ 的 return to go 较低，反之亦然。因此，由于训练中条件与真实动作价值不匹配，学习到的策略难以达到最优
- 其次，实际竞价任务通常涉及随时间变化的偏好，但生成式方法总是倾向于模仿多数偏好（Navigli等，2023），需要重新训练以适应新的少数偏好。然而，随着自动竞价领域模型规模的扩大，基于Transformer等基础模型的竞价模型会变得越来越大，重新训练一组大型决策Transformer以适应不同偏好的成本高昂且不切实际，阻碍了自动竞价进入大型基础模型时代。因此，论文提出一个问题：“能否仅用一个策略模型高效实现多种偏好下的最优策略？”
论文方案 ：论文提出了一种基于 post-training Search 的生成式自动竞价方案GAS ，通过优化单一基础策略模型的输出并高效适应多种偏好
- 论文采用弱到强的搜索对齐思想，即通过小型模型优化大型基础模型的输出（Burns等，2024）。具体而言，论文训练一组小型 Critic 模型评估不同偏好的价值，然后利用蒙特卡洛树搜索（MCTS）启发的方法优化模型输出（Kocsis和Szepesvári，2006）。在此方案中，条件值与真实动作价值之间的不匹配（通过基于Q学习的 Critic 模型近似）将得到缓解。这是因为基于 Bellman Backup 的Q学习仅需当前奖励，不受未来轨迹影响。此外，通过多样化策略收集的大规模数据集有助于训练 Critic 模型，使其能够评估不同质量的动作，缓解域外高估问题（Kostrikov等，2022）。该方案还可在不重新训练或微调模型的情况下，通过 Critic 引导的动作优化实现与不同偏好的更好对齐
论文的贡献总结如下：
- 提出了一种灵活实用的框架，利用 post-training Search 方法优化生成式自动竞价模型并适应多种偏好，为自动竞价基础模型打开了大门
- 为提升搜索过程的准确性，论文利用基于Transformer的 Critic 模型，通过历史竞价序列感知底层策略，并引入新型投票机制以增强搜索过程中价值反向传播阶段的价值近似准确性
- 除了在测试时执行搜索外，论文还为高频偏好场景或计算效率敏感场景提供了一种微调方法
- 在真实世界的大规模数据集和快手广告平台的在线A/B测试中进行的广泛实验证明了所提生成式自动竞价方案的有效性

Preliminary

问题描述

在一个时间段内，假设有 $H$ 个展示机会依次到达并编号为 $i$。在竞价平台中，广告主提交出价以竞争每个展示机会。若广告主的出价 $b_i$ 高于其他广告主，则赢得该展示。获胜后，广告主需支付成本 $c_i$，通常在第二价格拍卖中为其他广告主的最高出价。在此期间，广告主的目标是最大化获胜展示的总价值 $\sum_{i}o_{i}v_{i}$，其中 $v_{i}$ 为展示 $i$ 的价值， $o_{i}$ 为广告主是否赢得展示 $i$ 的二元指标。此外，预算和多种KPI约束（He等，2021）对广告主控制广告投放效果至关重要。预算约束为 $\sum_{i}o_{i}c_{i}\leq B$，其中 $B$ 为预算。其他KPI约束更为复杂，可分为两类：成本相关（CR，cost-related）约束（如CPC和CPA）和非成本相关（NCR， non-cost-related）约束（如CTR和CPI）。为简化问题，论文考虑带成本相关约束的自动竞价，其统一形式为 $\frac{\sum_{i}c_{ij}o_{i} }{\sum_{i}p_{ij}o_{i} }\leq C_{j}$，其中 $C_{j}$ 为广告主提供的第 $j$ 个约束上限。给定 $J$ 个约束，多约束竞价（MCB）问题可表述为：
$$
\begin{aligned}
\max & \quad \sum_{i}o_{i}v_{i} \\
\text{s.t.} & \quad \sum_{i}o_{i}c_{i}\leq B \\
& \quad \frac{\sum_{i}c_{ij}o_{i} }{\sum_{i}p_{ij}o_{i} }\leq C_{j}, \quad \forall j \\
& \quad o_{i}\in\{0,1\}, \quad \forall i
\end{aligned} \tag{1}
$$
已有研究（USCB）表明其最优解为：
$$
b_{i}^{*}=\lambda_{0}v_{i}+\sum_{j=1}^{J}\lambda_{j}p_{ij}C_{j},
$$
- 其中 $\lambda_{j}$ 为最优竞价参数。然而，由于广告环境的不确定性和动态性，这些参数难以直接计算。不同类型的广告主可能通过不同约束组合表达偏好，例如，仅考虑预算约束的最大回报竞价广告主和同时考虑预算与CPA约束的目标CPA竞价广告主

自动竞价的决策过程

由于广告环境高度动态，最优竞价参数需定期调整以最大化整个时间段内的总价值。因此，自动竞价任务可建模为序列决策问题。论文考虑标准决策设置：自动竞价代理与广告环境 $E$ 在离散时间步中交互。在每个时间步 $t$，代理接收描述实时广告状态的状态 $s_{t}\in\mathcal{S}$，并输出动作 $a_{t}\in\mathcal{A}$ 以确定最终出价。广告环境具有未知状态转移动态 $\mathcal{T}$。在MDP假设下，转移动态可表示为 $\mathcal{T}:s_{t}\times a_{t}\to s_{t+1}$，即下一状态 $s_{t+1}\in\mathcal{S}$ 由当前状态 $s_{t}$ 和动作 $a_{t}$ 决定。此时，代理的策略为 $\pi(a_{t}|s_{t})$。若无MDP假设，下一状态可能由更多因素（如历史轨迹 $\tau$ ）决定。转移到下一状态后，环境会发出奖励 $r_{t}$，表示时间步 $t$ 内对目标的贡献价值。重复此过程直到竞价周期结束（例如一天），自动竞价代理的目标是最大化整个周期内的总价值
如公式1所述。具体建模如下：
- $s_{t}$ ：状态是描述广告活动状态的信息集合，包括剩余时间、剩余预算、预算消耗速度、当前KPI比率等
- $a_{t}$ ：对竞价参数 $\lambda_{j}$ 的调整，建模为 $(a_{t}^{\lambda_{0} },\ldots,a_{t}^{\lambda_{J} })$
- $r_{t}$ ：时间步 $t$ 内候选展示集合 $C$ 对目标的贡献价值

基于搜索的生成式自动竞价

本节首先介绍如何开发MCTS启发的 post-training Search 过程以优化基础策略模型的输出动作，然后介绍两种应用此搜索的实用范式

MCTS启发的 post-training Search

由于决策Transformer广泛用于生成式决策，论文将其作为自动竞价的 backbone 模型，策略生成动作的公式为：
$$
a_{t}\sim\pi_{dt}=\text{DT}_{\theta}(a|s_{\leq t},a_{ < t},R_{\leq t}),
$$
- 其中条件 $R_{t}$ 为时间步 $t$ 的 return to go ：
  $$
  R_{t}=\sum_{i=t}^T\gamma^{i-t}r(s_{i},a_{i}),
  $$
- 其中 $\gamma$ 为折扣因子， $r(s_{i},a_{i})$ 为表示偏好的奖励函数（如仅考虑价值时，可表示为 $o_{i}v_{i}$ ）
搜索方案的目的是找到更优动作以更好对齐偏好（如更高价值）。将典型MCTS方法应用于决策过程需在每步包含四部分：
- 选择：从根状态节点 $s_{t}$ 出发，在探索预算 $i = 1\sim N$ 内随机选择连续有效子动作节点 $a^i_{t}$
- 扩展：除非子动作节点结束竞价过程，否则根据转移动态 $s^i_{t+1}\sim\mathcal{T}$ 创建子状态节点 $s^i_{t+1}$
- 模拟：从节点 $s^i_{t+1}$ 出发，根据策略 $\pi(a|s)$ 完成一次推演至结束
- 反向传播 ：利用推演结果更新节点 $a^i_{t}$ 的价值信息
完成四部分后，可根据探索与利用平衡原则选择最终动作 $a^i_{t}$。然而，与围棋不同，竞价是部分可观测MDP（POMDP）任务，其他广告主行为不可预测，因此无法模拟所有可能动作。为此，论文通过增强的基于Transformer的Q值函数近似扩展和模拟过程，无需实际模拟。以下分三部分介绍GAS实现（图1(a)）：选择、扩展与模拟、反向传播

选择

给定决策Transformer策略 $\text{DT}_{\theta}$，首先生成基础动作 $a^i_{t}$，然后通过乘以90%至110%的随机因子生成 $N-1$ 个随机动作 $\{a^i_{t}\}_{i=1:N-1}$ ：
$$
a^i_{t}=a_{t}*\varepsilon,\varepsilon\sim\mathcal{U}(90\%,110\%).
$$
保留初始基础动作 $a_{t}$，得到 $N$ 个动作提议（proposals） $\{a^i_{t}\}_{i=1:N}=\{a^i_{t}\}_{i=1:N-1}\oplus a_{t}$。选择过程即从这些动作提议中选择

扩展和模拟

由于无法在模拟器或真实环境中推演，需直接通过Q值函数估计动作提议 $a^i_{t}$ 在状态 $s_{t}$ 下的价值：
$$
Q_{\phi}(s_{t},a^i_{t};\pi)=r(s_{t},a^i_{t})+\mathbb{E}_{s_{t+1}\sim \mathcal{T},a_{t+1}\sim \pi}Q_{\phi}(s_{t+1},a_{t+1};\pi). \tag{6}
$$
- 问题：$s_{t+1} \sim P(s_{t+1}|s_t, \color{red}{a^i_{t}})$ 还是 $s_{t+1} \sim P(s_{t+1}|s_t, \color{red}{a^{t}})$ 呢？
论文采用IQL方法（Kostrikov等，2022）学习 $Q_{\phi}$，引入额外价值网络 $V_{\psi}(s)$ 以避免分布偏移导致的高估问题：
$$
\mathcal{L}_{\mathcal{V} }(\psi)=\mathbb{E}_{(s,a)\sim \mathcal{D} }[L^{x}_{2}(\mathcal{Q}_{\hat{\phi} }(s,a)-V_{\psi}(s))],
$$
- 其中 $L^{x}_{2}(u)=|\tau-1(u<0)|u^{2}$ 为期望回归损失。价值网络用于Q值学习：
  $$
  \mathcal{L}_{\mathcal{Q} }(\phi)=\mathbb{E}_{(s_{t},a_{t},s_{t+1})\sim \mathcal{D} }[(r(s_{t},a_{t})+\gamma V_{\psi}(s_{t+1})- \mathcal{Q}_{\phi}(s_{t},a_{t}))^{2}].
  $$
如公式6所示， $Q$ 与底层策略 $\pi$ 在后项期望中耦合。然而， $Q_{\phi}(s_{t},a_{t})$ 仅接收单状态-动作对而无策略指示，导致价值预测基于实际收集数据集的策略 $\pi_{\beta}$，与生成式自动竞价中由不同条件指示的策略 $\pi_\epsilon$ 产生策略差距
通过QT推演（Rollout via QT） ：为通过历史轨迹表示实际策略 $\pi_\epsilon$，论文利用Transformer的序列建模能力进行Q值学习，称为 $QT$：
$$
Q^{\pi_\epsilon }_{\phi}(s_{t},a^i_{t})=Q_{\phi}(s_{t},a^i_{t};\pi_\epsilon)=\textrm{QT}_{\phi}(s_{t},a^i_{t};s_{ < t},a_{ < t}).
$$
大规模预训练集（包含多样化策略收集的轨迹）有助于通过历史轨迹预测未来轨迹，即 rollout $\{s_{\leq t},a_{\leq t}\}\rightarrow\{s_{t+1:T},a_{t+1:T}\}$。训练后， $\textrm{QT}_{\phi}(s_{t},a^i_{t};s_{ < t},a_{ < t})$ 可返回竞价结束前推演价值的近似值

反向传播

由于Q值函数的高估问题，不准确的推演价值估计会导致反向传播为动作节点 $a^i_{t}$ 提供不准确的价值，从而执行不良动作。为缓解此问题，论文提出基于共识启发式的Q投票机制
通过Q投票的价值反向传播 ：鉴于离线RL的成功（Q值用于学习改进行为策略的策略），论文可直观认为不同随机训练的Q值网络能以高概率对真实最佳动作赋予更高价值达成一致。此外，由于高估是偶然错误，对特定动作赋予更高价值不会达成一致。形式上，若用不同随机种子独立训练 $M$ 个Q值网络 $\{Q^{\pi_\epsilon }_{\phi_{k} }\}_{k=1:M}$，且有 $N$ 个动作提议 $\{a^i_{t}\}_{i=1:N}$ 及真实最佳动作 $a^j_{t}$，论文通过概率密度函数 $p(a|Q)$ 建模共识启发式：
$$
\textbf{Consensus:}\ p(a^j_{t}|Q_{\phi_{k} }^{\pi_\epsilon})>p(a_{t}^{i\neq j}|Q_{\phi_k}^{\pi_\epsilon}),\forall k\in\{1,…,M\}.
$$
因此，若仅使用单一Q，选择 $a^j_{t}$ 的最终胜率为：
$$
\mathcal{R}^{k}:=\frac{p(a^j_{t}|Q_{\phi_{k} }^{\pi_\epsilon })}{\sum_{i\neq j}p(a^i_{t}|Q_{\phi_{k} }^{\pi_\epsilon })}.
$$
基于此共识，可采用多数投票方法提高胜率 $\mathcal{R}^{k}$。为简洁起见，假设所有 $k\in\{1,…,M\}$ 的 $p(a^i_{t}|Q_{\phi_{k} }^{\pi_\epsilon })$ 相同。通过多数投票选择动作 $a^i_{t}$ 为最终动作的概率为：
$$
p(a^i_{t}|\{Q_{\phi_{k} }^{\pi_\epsilon }\}_{k=1:M})=\sum_{l=\left\lfloor \frac{M}{2} \right\rfloor+1}^{M}\binom{M}{l}p(a^i_{t}|Q_{\phi_{k} }^{\pi_\epsilon })^{l}(1-p(a^i_{t}|Q_{\phi_{k} }^{\pi_\epsilon }))^{M-l}.
$$
应用Condorcet’s Jury theorem（Boland，1989），可得：
$$
\mathcal{R}^{1:M}=\frac{p(a^i_{t}|\{Q_{\phi_k }^{ {\pi_\epsilon } }\}_{k=1:M})}{\sum_{i\neq j}p(a^i_{t}|\{Q_{\phi_k }^{ {\pi_\epsilon } }\}_{k=1:M})}>\mathcal{R}^{k}.
$$
- 为简化理解，我们假设 $p(a^1_{t}|Q_{\phi_{k} }^{\pi_\epsilon }) = 0.4$, $p(a^2_{t}|Q_{\phi_{k} }^{\pi_\epsilon }) = 0.3$，$p(a^3_{t}|Q_{\phi_{k} }^{\pi_\epsilon }) = 0.3$，则有对于 $\forall k$，有 $\mathcal{R}^{1:3} = 0.81 > \mathcal{R}^k = 0.67$
为避免无效多数投票结果（即无动作获得比其他动作更多的票数），论文提出基于Q值的软多数投票机制（Q投票），分两步实现：
- 第一步 ：对每个 $Q_{\phi_{k} }^{\pi_\epsilon }$，基于所有 $a^i_{t}$ 的min-max归一化投票为：
  $$
  v(a^i_{t}|Q_{\phi_{k} }^{\pi_\epsilon })=\frac{Q_{\phi_{k} }^{\pi_\epsilon }(s_{t},a^i_{t})-\min_{n}\{Q_{\phi_{k} }^{\pi_\epsilon }(s_{t},a^i_{t})\} }{\max_{n}\{Q_{\phi_{k} }^{\pi_\epsilon }(s_{t},a^i_{t})\}-\min_{n}\{Q_{\phi_{k} }^{\pi_\epsilon }(s_{t},a^i_{t})\} }\in[0,1].
  $$
- 第二步 ：动作 $a^i_{t}$ 的最终总票数为：
  $$
  v(a^i_{t}|\{Q_{\phi_{k} }^{\pi_\epsilon }\}_{k=1:M})=\sum_{k=1}^{M}v(a^i_{t}|Q_{\phi_{k} }^{\pi_\epsilon }).
  $$
完成上述MCTS启发搜索后，可得到比 $a_{t}$ 具有更高偏好价值的优化动作 $a^n_{t}$

基于GAS的竞价

GAS有两种应用方式：i）在测试时搜索，ii）利用搜索微调基础策略模型。两种方法均需训练表示不同偏好的 Critic 模型
偏好表示 ：偏好通过奖励函数设置表达，例如：
- 仅考虑预算约束的最大回报竞价偏好： $r_{t}=o_{t}v_{t}$ ；
- 综合考虑价值和KPI约束的偏好： $r_{t}=o_{t}v_{t}\cdot\frac{1}{J}\sum_{j}\min\left\{\big(\frac{C_{j} }{c_{tj}o_{t}/p_{tj}o_{t} }\big)^{\beta},1\right\},\beta>1$ ；
  - 问题：是加法吧？
- 通过更大可控权重 $w$ 更偏好KPI约束的偏好： $r_{t}=o_{t}v_{t}+\frac{w}{J}\sum_{j}\min\left\{(\frac{C_{j} }{c_{tj}o_{t}/p_{tj}o_{t} })^{\beta},1\right\},\beta>1$
基于公式8，可利用这些奖励函数训练 Critic 模型

基于搜索的推理

在推理的每个时间步重复第3.1节的搜索过程，得到测试时版本的方法_GAS-infer_，可直接与基础策略模型和多个 Critic 模型部署。详细流程见算法1

基于搜索的微调

由于搜索方法能够围绕基础动作找到更优动作（尤其是基础动作质量差或与偏好不对齐时），可利用搜索增强训练数据并微调基础策略模型。首先，对数据集中的每个数据点 $\{s_{t},a^{\beta}_{t}\}$ 进行搜索，得到更优动作 $a^{\rho}_{t}$。然后，基于监督微调（sfft）损失训练DT ${}_{\theta}$ ：
$$
\mathcal{L}_{\text{DT} }^{\text{sft} }(\theta)=mse(a_{t},a^{\rho}_{t}).
$$
尽管存在更多偏好对齐方法（如DPO和RLHF），但它们通常基于轨迹级查询数据集且稳定性较差，因此留作未来工作

Experiments

Experiment Setup

数据集 ：与以往从非开源的广告自动出价系统中收集私有竞价日志的数据集准备方法不同，论文采用了阿里巴巴[43]发布的新公开大规模真实世界竞价数据集AIGB。据论文所知，这是目前最大的公开数据集，包含超过200万条轨迹，并提供了一个稀疏版本以应对更具挑战性的场景。更多细节见附录A
评估指标 ：为简化评估，论文采用以下三个指标衡量性能：
- 价值（Value） ：竞价期间获得的总价值，计算公式为$\sum_{i} o_{i} v_{i}$；
- KPI约束超限率（ER） ：引入二元指示函数$I(x^{h}_{j}, C_{j})$，判断在周期$h$内的最终KPI表现$x^{h}_{j} = \Sigma_{i} c_{ij} o_{i} / \Sigma_{i} p_{ij} o_{i}$是否超过给定约束$C_{j}$。假设共有$H$个周期，KPI约束超限率定义为：
  $$
  ER = \frac{1}{H} \sum\nolimits_{h=1}^{H} \sum\nolimits_{j=1}^{J} \mathbb{I}(x^{h}_{j}, C_{j}).
  $$
- 综合得分（Score） ：引入惩罚项
  $$
  penalty_{j} = \min\left\{\left(\frac{C_{j} }{\Sigma_{i} c_{ij} o_{i} / \Sigma_{i} p_{ij} o_{i} }\right)^{\beta}, 1\right\}, \beta=2,
  $$
- 综合得分是价值与KPI约束的平衡，计算公式为：
  $$
  score = \left(\sum_{i} o_{i} v_{i}\right) \times \min\{penalty_{j}\}_{j=1}^{J}.
  $$
基线方法 ：论文对比了多种基于 RL 和生成模型的方法：
- USCB[18]：一种在线RL方法，动态调整参数至最优出价；
- BCQ[14]：典型的离线RL方法，仅通过固定数据集更新策略；
- CQL[23]：通过正则化Q值学习保守价值函数的离线RL方法；
- IQL[22]：无需查询样本外动作即可实现多步动态规划更新的离线RL方法；
- DiffBid[17]：基于扩散模型的生成方法，根据条件生成竞价轨迹；
- DT[7]：基于Transformer的序列决策生成方法；
- CDT[26]：考虑多约束向量的DT改进方法；
- DT-score ：采用同时考虑获胜价值和KPI约束的奖励函数的DT方法
实现细节 ：基线方法的超参数参考原论文默认值，并进一步调优以优化性能。GAS包含两个组件：基础策略模型和多个QT网络。基础策略模型可任选，论文选择DT-score ，其超参数参考[43]提供的官方代码，微调时学习率设为$1e^{-5}$。QT网络采用6个注意力层，每层8个头，隐藏层大小为512，总计1400万参数，轻量高效。总训练步数为40万步，使用AdamW优化器[27]，学习率为$1e^{-4}$，批量大小为128。训练基于PyTorch框架，在两块NVIDIA H100 GPU上完成。QT网络的详细超参数见表6（附录B）

与基线方法的性能对比

本实验在多种设置下对比各基线方法的性能，包括不同数据集（AIGB-2M及其稀疏版本AIGB-sparse）和MCB竞价中的不同预算约束（最大允许预算的50%、75%、100%、125%、150%）。结果以综合得分衡量，如表1所示
结果显示，GAS-infer和GAS-sft在所有预算设置下均优于其他方法，得分最高。其他生成方法如DT、CDT和DT-score表现也较好，体现了生成模型相较于传统RL方法（如IQL）的优势。DiffBid在此大规模任务中表现不佳，可能原因是预测长轨迹和学习逆动态模型引入了额外挑战。稳定性方面，如图2(d)所示，GAS优于基础策略模型。GAS-sft性能略低于GAS-infer，可能因其将 Critic 与原始模型融合，导致评论能力模糊化。需注意的是，Q-voting过程可并行执行，每步耗时约0.1秒，远小于30分钟的竞价间隔，表明GAS-infer在大规模自动竞价任务中极具效率

偏好对齐性能

为验证搜索方法能否通过不同偏好的 Critic 提升基础策略模型的对齐性能，论文在表2中进行了偏好对齐实验。评估了三种偏好范式（Score-first、Value-first、ER-first）下GAS-infer和GAS-sft与基础模型DT-score的对齐效果。结果显示，两种搜索方法在所有偏好下均优于基础模型，证明了搜索在偏好对齐中的有效性

消融实验

搜索范围 ：搜索范围直接影响探索（尝试新动作）与利用（聚焦已知优质动作）的平衡。较小的范围可能遗漏优质动作，但能更精确评估；较大的范围增加发现最优动作的概率，但评估准确性可能下降。极端情况下可搜索整个动作空间，但效率低下。基于计算效率考虑，论文在±10%范围内随机搜索5个动作，结果如图2(c)所示。实验表明，10%的搜索范围性能最佳，扩大范围收益递减，而最小-最大方法因动作预算有限效果最差。值得注意的是，10%的小范围即可实现最优性能，表明基于基础策略模型的微调已足够高效
Critic 数量 ：如Q-voting机制所述，更多 Critic 可提升价值评估的准确性。论文固定搜索范围为±10%，随机选择5个动作进行价值评估，结果如图2(b)所示。 Critic 数量从1增至7时性能显著提升，超过7后改善不明显，表明当前任务中7个 Critic 已足够
搜索预算 ：增加动作采样数量可能提升找到最优动作的概率。本实验未使用原始基础动作，结果如图2(a)所示。动作数量从1增至5时性能显著提升，超过5后趋于稳定，表明5个动作已能覆盖近优解
QT的有效性 ：由于跳过了实际模拟过程，Q值函数对预期收益的预测准确性至关重要。若缺乏历史轨迹信息，仅凭状态$s_t$和动作$a_t$预测模拟过程具有高度随机性。表3结果显示，结合历史轨迹的QT性能远超基于普通状态-动作对的Q值函数
论文还对比了无Q值函数的其他方法（贪婪搜索、随机/均值选择）以验证MCTS搜索的有效性。贪婪搜索选择即时奖励最高的动作，随机方法随机选择动作，均值方法取5个随机动作的平均值。如表3所示，论文的方法显著优于其他方法

线上实验

为验证GAS的实际效果，论文将其部署在快手广告系统中（见图1(b)），场景为多约束竞价（MCB）。由于线上测试资源有限且可能影响广告主收益，仅对比了GAS-infer与当前生产环境的基线模型DT。实验设置如下：
- 状态：预算、成本、基于时间的预算分配、成本速度、预测转化率、实时CPA/ROI状态等；
- 动作：调整上一时刻的竞价系数$\lambda_t = \lambda_{t-1} + a_t$（见公式2）；
- 训练后搜索 ： Critic 以获胜印象的总价值训练，搜索在Value-first偏好下进行，动作范围仍为基动作的±10%，采样5个点
线上A/B测试持续5天，每个MCB活动分配25%预算和流量给基线模型和GAS。结果如表4所示，GAS在展示量（+0.934%）、成本（+0.953%）、目标成本（+1.554%）和整体ROI（+0.595%）上均显著提升

结论

论文提出了一种灵活实用的生成式自动竞价框架GAS，通过 post-training Search 方法优化生成式自动竞价策略模型以适应多种广告主偏好。所提方法利用基于Transformer的 Critic 模型和投票机制提升价值近似准确性，为自动竞价基础模型的应用开辟了新途径，解决了无需多次昂贵训练过程即可使单一模型适应多样化偏好的挑战
然而，本研究存在一些局限性。首先，MCTS过程的简化（如近似扩展和模拟步骤）可能未完全捕捉现实竞价场景的复杂性（其他广告主行为不可预测且系统转移动态随时间变化）。其次，GAS的微调版本虽计算效率更高，但性能仍有限，需更先进有效的微调方法。

CA——M-PID

参考链接：
- 原始论文：Bid Optimization by Multivariable Control in Display Advertising, KDD 2019, Alibaba

整体思路介绍

实时竞价（RTB）是展示广告中的重要范式，广告主利用需求方平台（DSP）提供的信息和算法来提升广告效果
- DSP面临的一个常见问题是在预算约束下帮助广告主获取最大价值
- 实际场景中，广告主通常会添加某些关键绩效指标（KPI）约束，广告 campaign 必须满足这些约束
论文研究广告主旨在最大化转化量并将每次点击成本（CPC）作为KPI约束的常见情况
- 论文将此问题转化为线性规划问题，并利用 primal-dual 方法推导出最优竞价策略
- 为了解决适用性问题，论文提出了一种基于反馈控制的解决方案，并设计了多变量控制系统
基于淘宝网真实数据的实证研究验证了论文的方法相比行业最新实践的有效性和优越性

一些讨论

在在线展示广告中，广告主为展示广告的机会支付一定费用。实时竞价（RTB）是展示广告中最流行的范式。RTB允许广告主在展示级别对广告机会进行竞价，出价最高的广告主赢得展示其广告的机会（每个广告机会的竞价价格可以跟随其效用和成本而改变，这使得广告主能够利用DSP提供的扩展信息和算法）
DSP面临的一个常见问题是在预算约束下帮助广告主获取尽可能多的价值。已有一些竞价策略和算法被提出，用于在预算约束下最大化广告价值。因此，广告主只需设置广告 campaign 的预算，DSP会代表广告主计算竞价价格
除了预算约束外，广告主通常会添加某些关键绩效指标（key performance indicator，KPI）约束，广告 campaign 必须满足这些约束
- KPI设置的必要性 ：广告主设置此类KPI约束是因为仅具有单一预算约束的广告 campaign 可能会受到竞价环境波动导致的流量巨大变化的影响。例如，某些日期的广告机会可能变得非常昂贵，以至于广告主无法承担所有预算
- 解决方案1 ：一种解决方案是不断调整每日预算以控制投资，这对广告主来说成本高昂甚至不切实际
- 解决方案2 ：另一种解决方案是设置某些KPI约束，每千次展示成本（CPM）和每次点击成本（CPC）约束，对广告投放的总成本有很强的影响
  - 通过设置此类KPI约束，广告主可以对总成本施加限制，并在广告机会不值得时避免花费所有预算，从而免去频繁调整广告 campaign 设置的繁重工作
  - 此外，KPI约束还作为实时代理来调节广告效果。在大多数情况下，广告主最终希望获得转化。然而，转化是稀疏且延迟的，这使得广告主无法实时评估广告效果。因此，广告主使用DSP提供的KPI来评估广告的预期价值 ，并将其设置为约束以确保广告效果可控
- 论文重点关注CPC约束 ，这是最常见的KPI约束之一。论文的方法可以推广到其他与成本相关的KPI约束 ，如CPM约束
论文提出了在预算和CPC约束下最大化广告转化量的最优竞价策略。在这项工作中，竞价优化被表述为一个线性规划问题，并利用 primal-dual 方法推导出最优竞价策略
论文提出了基于最优竞价策略的多变量控制系统 ，以解决适用性问题，特别是在工业应用中面临的动态环境
- PID控制系统 ：基于对竞价策略中超参数的分析，论文声称这些超参数在实现相应约束方面具有强大的控制能力，并设计了独立的PID控制系统
- 模型预测控制系统 ：考虑到耦合效应，论文通过提出模型预测控制系统进一步提高了系统的性能
论文所提出的系统已在真实工业数据集上实现和评估。基于淘宝网真实数据的实验表明，这些系统在实现约束方面具有强大的控制能力。论文还将论文的方法与行业最新实践进行了比较，结果显示了论文方法的优越性。论文工作的主要贡献可以总结如下：
- 论文提出了在预算和CPC约束下最大化转化量的最优竞价策略
- 论文设计了多变量控制系统 ，以应对在工业应用中应用竞价策略时的动态环境
- 进行了广泛的实验，结果证明了论文方法的优势

竞价策略

在本节中，论文首先回顾RTB生态系统的一些基础知识，然后提出竞价优化问题。接着，论文推导最优竞价策略，并讨论竞价策略的特性

RTB生态系统

RTB的工作流程如图1所示，每一步如下：
- 1）用户访问一个支持广告的网站，网站向广告交换平台发送广告请求
- 2）广告交换平台发起拍卖并向DSP请求竞价
- 3）DSP代表广告主向广告交换平台提交竞价价格和广告
- 4）广告交换平台进行拍卖并向获胜的DSP收取广告机会费用
- 5）获胜者的广告被发送到网站
- 6）用户的后续反馈会被发送回相应的DSP
当DSP从广告交换平台接收到竞价请求时，它会通过其竞价策略为广告主计算竞价价格。由于转化是大多数广告主的目标事件 ，几乎所有竞价策略（包括论文的策略）都严重依赖于学习模型的能力来估计广告点击率（CTR）和转化率（CVR）。此外，一些DSP还可能基于对获胜价格（竞价环境预测）的预测来制定竞价策略。论文假设估计和预测问题已经解决，点击和转化的预期概率可以分别通过CTR和CVR量化
当DSP在拍卖中赢得展示广告的机会时，它会被收取一个价格。在广义第二价格（GSP）拍卖机制下，该价格等于第二高的竞价价格，该机制在工业平台中被广泛采用。还有一些其他拍卖机制，如Vickrey-Clarke-Groves拍卖机制（VCG）。在论文中，不失一般性，论文基于最常见的GSP拍卖机制进行讨论和建模
用户对广告的任何反馈，如点击和转化，都会被发送回相应的DSP。DSP可以利用这些反馈来训练预测模型，并及时调整其竞价策略。此外，这些反馈会被DSP整合并暴露给广告主。在论文提出的系统中，论文利用这些反馈，并在广告 campaign 的生命周期中持续微调竞价策略

问题建模

假设一天中有 $N$ 个广告机会，论文按生成顺序将每个广告机会索引为 $opportunity_i$ 。每个广告机会对广告主具有不同的价值，论文用 $v_i = CTR_i \cdot CVR_i$ 表示 $opportunity_i$ 对广告主的价值。基于 $v_i$ ，计算竞价价格 $bid_i$ 并提交给广告交换平台。每个广告机会有一个获胜价格 $wp_i$ 。从广告主的角度来看， $wp_i$ 等于其他广告主的最高竞价价格。如果 $bid_i$ 高于 $wp_i$ ，这意味着广告主将赢得广告机会并在GSP拍卖机制下被收取 $wp_i$ ，论文将 $x_i$ 设为1，否则设为0。广告 campaign 的总价值和总成本如公式（1）和公式（2）所示
$$
Value = \sum_{i=1\ldots N} x_i \cdot v_i \\
Cost = \sum_{i=1\ldots N} x_i \cdot wp_i
$$
论文在公式（3）中定义CPC。值得注意的是，论文用CTR替换了实际点击，这为论文提供了更简洁的公式。这种替换在很大程度上促进了论文的理论分析，并且对后续的实际系统设计影响很小
$$CPC = \frac{\sum_{i=1\ldots N} x_i \cdot wp_i}{\sum_{i=1\ldots N} x_i \cdot CTR_i} \tag{3}$$
转化是广告主最终希望的结果。因此，论文通过 $CTR_i \cdot CVR_i$ 量化 $v_i$ 。请注意，必须考虑 $CTR_i$ ，因为只有在点击后才能生成转化，而CVR是以点击为条件的。论文将问题总结如下，并将其建模为（LP1，包含约束（4）和约束（5）），论文在预算 $B$ 下最大化广告转化量，并保证CPC不超过给定值 $C$ ：
$$
\begin{align}
\max_{x_i} \sum_{i=1\ldots N} x_i \cdot CTR_i \cdot &CVR_i \text{(LP1)}\\
\text{s.t.} \quad \quad \sum_{i=1\ldots N} x_i \cdot wp_i &\leq B \\
\frac{\sum_{i=1\ldots N} x_i \cdot wp_i}{\sum_{i=1\ldots N} x_i \cdot CTR_i} &\leq C \\
0 \leq x_i &\leq 1, \forall i
\end{align}
$$

最优竞价策略

问题（LP1）实际上是一个线性规划问题，即在线性约束下找到最优的 $x_i$ 以最大化目标函数。已有许多算法直接解决此类问题，但论文的目标是推导最优竞价策略而非分配策略。换句话说，论文本质上并不关心 $x_i$ 的值，而是关心内在影响 $x_i$ 的竞价策略。基于此考虑，论文创造性地采用 primal-dual 方法。每个线性规划问题（称为原始问题）都可以转换为对偶问题。此外，根据对偶定理（duality theorem），最优原始解可以通过相应的对偶解获得。这些数学特性为论文提供了一些启示，论文整合原始空间和对偶空间，推导出以下定理：
定理2.1 ：最优竞价策略的公式为：
$$bid_i = \frac{1}{p + q} \cdot CTR_i \cdot CVR_i + \frac{q}{p + q} \cdot CTR_i \cdot C \tag{6}$$
- 最优竞价策略在公式（6）中给出，其中 $p$ 和 $q$ 是从对偶空间引入的超参数，对应于最优对偶解。论文将在后续章节中研究 $p$ 和 $q$ 的性质。现在，论文给出定理2.1的证明
证明：（LP1）被转换为对偶问题：
$$
\begin{align}
\min_{p, q, r_i} B \cdot p + \sum_{i=1\ldots N} r_i \quad &\text{(LP2)} \\
\text{s.t.} wp_i \cdot p + (wp_i - CTR_i \cdot C) q + r_i &\geq CTR_i \cdot CVR_i, \forall i \\
p &\geq 0,\\ q &\geq 0,\\ r_i &\geq 0, \forall i
\end{align}
$$
- 假设原始问题（LP1）的最优解为 $x_i^*, \forall i = 1, \ldots, n$ ，对应的对偶问题（LP2）的最优解为 $p^*, q^*, \{r_i^* | i = 1, \ldots, n\}$ 。根据互补松弛定理，论文得到：
  $$x_i^* \cdot (CTR_i \cdot CVR_i - wp_i \cdot p - (wp_i - CTR_i \cdot C) q - r_i) = 0, \forall i \\
  (x_i^* - 1) \cdot r_i^* = 0, \forall i \tag{8&9}$$
- 论文巧妙地设最优出价形式为：
  $$\color{red}{bid_i^* = \frac{1}{p^* + q^*} CTR_i \cdot CVR_i + \frac{q^*}{p^* + q^*} C \cdot CTR_i}$$
  - 特别说明 ：这里的公式形式是有规律的，直接对原始问题构造拉格朗日函数，然后令原始拉格朗日函数对 $x_i$ 的偏导数为0，即可得到 $wp_i$ 的形式，其他类似约束问题也可以这样求解最优出价形式
- 最优出价形式的验证 ：
  - 将公式（8）转换为公式（10）：
    $$x_i^* \cdot ((bid_i^* - wp_i)(p^* + q^*) - r_i^*) = 0, \forall i \tag{10}$$
  - 根据公式（10）：
    - 如果广告 campaign 赢得 $opportunity_i$ ，即 $\color{red}{x_i^* > 0}$ ，则 $(bid_i^* - wp_i)(p^* + q^*) - r_i^* = 0$ 。同时， $p^* \geq 0, q^* \geq 0, r_k \geq 0$ ，因此 $\color{red}{bid_i^* \geq wp_i}$
    - 如果广告 campaign 失去 $opportunity_i$ ，即 $\color{red}{x_i^* = 0}$ ，我们可以从公式（9）推导出 $r_i^* = 0$ 。因此，根据公式（7），论文得到 $(bid_i^* - wp_i)(p^* + q^*) < 0$ ，即 $\color{red}{bid_i^* \leq wp_i}$
综上所述，对于任何 $opportunity_i$ ，竞价策略将保证 $x_i$ 是最优的，从而得到（LP1）的最优解。也就是说，当最优 $x_i$ 为1（广告 campaign 应赢得 $opportunity_i$ ）时，基于最优竞价策略的竞价价格 $bid_i$ 高于 $wp_i$ ，这将保证广告 campaign 赢得 $opportunity_i$ 。当最优 $x_i$ 为0时，推理相同。因此，广告 campaign 只需按照公式（6）中的最优竞价策略进行竞价，总广告价值将在约束条件下最大化。
关于 $p$ 和 $q$ 的讨论 ：公式（6）并未明确给出 $p$ 和 $q$ 的值。实际上，通过使用成熟的线性规划算法求解对偶问题，可以轻松推导出最优的 $p$ 和 $q$ 。此类工作对论文的理解没有贡献，因此论文在此不讨论如何计算 $p$ 和 $q$ 的值
引入点击出价 $c\_bid_i$ 变量 ：论文将（LP1）的最优竞价策略重新表述为两个阶段，如公式（11）、公式（12）和图2所示，其中 $c\_bid_i$ 可以视为点击的竞价价格。当一个广告机会到来时，论文首先确定点击的竞价价格，即 $c\_bid_i$ 。在确定 $c\_bid_i$ 后，最终竞价价格通过将 $c\_bid_i$ 与 $CTR_i$ 相乘来计算，这一过程可以自动完成，并在后续讨论中省略
$$c\_bid_i = \frac{1}{p + q} \cdot CVR_i + \frac{q}{p + q} \cdot C \tag{11}$$
进一步地，有曝光出价为：
$$
\begin{align}
bid_i &= c\_bid_i \cdot CTR_i \\
&= \left( \frac{1}{p + q} \cdot CVR_i + \frac{q}{p + q} \cdot C \right) \cdot CTR_i \tag{12}
\end{align}
$$
此外，在GSP拍卖机制下，点击的成本自然不高于点击的竞价价格，因此 $c\_bid_i$ 直接与CPC相关。因此，为了便于演示，论文将讨论重点放在点击的竞价价格（ $c\_bid_i$ ）上，而非最终竞价价格
论文以一些明显的事实开始讨论最优竞价策略，如图2a所示
- 第一，点击的竞价价格与 $CVR_i$ 严格正相关。这很有道理：论文应该为更有价值的点击提供更高的竞价价格，为价值较低的点击提供较低的价格
- 第二，竞价价格相对于 $CVR_i$ 是线性的。这是一个自然的结果，因为论文要最大化价值的和，而价值是相对于 $CVR_i$ 本身的线性函数
- 第三，竞价策略肯定会穿过图中强调的两个点。论文将在后续分析中详细讨论这一点
- CVR为0时，点击出价不为0 ：论文中有一个不寻常的事实：与广泛采用的竞价策略不同，该函数不一定通过原点。具体来说，即使广告机会对广告主没有价值，竞价价格也可能非零。论文为一个没有价值的广告机会出非零价格有点反直觉
  - 论文陈述原因如下：考虑到给定CPC约束 ，竞价策略试图赢得一些廉价的广告机会，即使没有任何价值，以降低整体CPC ，从而赢得一些具有高CPC的有价值广告机会

系统设计

在本节中，论文解决了竞价策略在工业场景中的适用性问题，并提出了基于反馈控制的解决方案。基于对最优竞价策略中超参数的分析，论文提出了多变量控制系统

适用性问题

如（LP2）所示，为了求解线性规划问题并获得最优竞价策略，论文需要准确知道一天中每个广告机会的信息，包括获胜价格、CTR和CVR。然而，在现实世界中，这些信息直到一天结束时才能获得，而最优竞价策略需要在广告 campaign 开始前确定
除了在广告 campaign 开始前难以精确预测所有这些信息之外，如何预测一天中的广告机会本身仍然是一个开放性问题 ，因为动态环境（dynamic environment）
- 有人可能认为有许多统计算法可以解决此类问题：可以从足够的历史数据中推导出最优解，并应用于未来（此类算法的一个强假设是变量的分布是平稳的）。然而，在动态RTB环境中，不仅广告机会的分布 ，其他因素如获胜价格、CTR和CVR的分布也不是平稳的。因此，基于历史数据推导的最优竞价策略对未来不再最优 ，甚至可能打破CPC约束

基于反馈控制的解决方案

如上一节所述，由于动态竞价环境，论文基于历史数据推导的竞价策略可能不可靠。因此，论文需要利用实时信息来调整竞价策略。反馈控制通过从系统输出和外部噪声中处理动态系统(dynamic system)（Kumar等，2014），因其鲁棒性和有效性而在工业中被广泛采用。反馈控制系统(feedback control problem)通过基于系统输出的反馈调整系统输入来实现理想的性能
在论文的场景中，论文自然可以将竞价策略和RTB环境集成为一个动态系统 ，并将竞价策略的超参数 $p$ 和 $q$ 视为系统的输入。通过这样做，问题被转化为反馈控制问题
仍然有一个问题：什么是理想的性能，因此论文应该关心输出的哪些反馈？首先，论文的目标是最大化广告价值并控制CPC。其次，为了最大化广告价值，论文应该在时间上分散预算支出以赢得有价值的广告机会。因此，论文需要同时控制预算支出和CPC。论文提出以下反馈解决方案：为了提高广告性能，论文基于实时反馈控制预算支出和CPC
关于控制器的介绍 ：论文简要介绍标准的反馈控制系统。反馈控制系统的框图如图3所示。输出的期望值称为参考值 ，根据具体任务预先设定。传感器从系统输出中测量变量的实际值，并将其传输给控制器。通过比较测量值和参考值 ，控制器会根据其预定义的算法或策略调整系统输入，以减小它们之间的差异
- 比例-积分-微分（Proportional-Integral-Derivative，PID）控制器（Bennett，1993）是工业中最广泛采用的反馈控制器。已知PID控制器在缺乏对底层过程了解的情况下提供最佳性能（Åström和Hägglund，1995）
- PID控制器用法介绍 ：PID控制器在每个时间步 $t$ 连续计算测量值 $y(t)$ 和参考值 $r(t)$ 之间的误差 $e(t)$ ，并基于误差的比例、积分和微分项的组合产生控制信号 $u(t)$ 。控制信号 $u(t)$ 然后被发送以通过执行器模型 $\phi(x(0), u(t))$ 调整系统输入 $x(t)$ 。在在线广告场景中，使用离散时间步 $(t_1, t_2, \ldots)$ 是实际和常见的，因此PID的过程可以表示为以下公式，其中 $k_p$ 、 $k_i$ 和 $k_d$ 是PID控制器的权重参数

$$e(t) = r(t) - y(t) \tag{13}$$

$$u(t) = k_p e(t) + k_i \sum_{k=1\ldots t} e(k) + k_d (e(t) - e(t-1)) \tag{14}$$

$$x(t+1) = \phi(x(0), u(t)) \tag{15}$$

超参数分析

多变量下的控制方法 ：论文已经将问题转化为反馈控制问题，并在上一节中确定了动态系统（竞价策略和RTB）、输入参数（ $p$ 和 $q$ ）和输出变量（预算支出和CPC）。挑战在于如何通过调整 $p$ 和 $q$ 同时控制预算支出和CPC。由于多输入参数和多输出变量，论文不能直接在论文的场景中应用PID控制器（PID是单输入参数和单输出变量系统设计的）。已有一些多变量控制方法，如模型预测控制（Rawlings和Mayne，2009），用于处理此类系统，论文将在下一节的设计中利用其基本思想。在本节中，论文重新审视公式（11）中的最优竞价策略，并分享论文设计多变量控制系统的想法
回顾最优点击出价公式：
$$c\_bid_i = \frac{1}{p + q} \cdot CVR_i + \frac{q}{p + q} \cdot C \tag{11}$$
论文分析超参数 $p$ 和 $q$ 如何对公式（11）中的竞价策略做出贡献。请回顾 $p$ 和 $q$ 是由约束（4）和（5）引入的对偶变量，论文探讨它们与相应约束的关系
图4显示了在固定 $q$ 的情况下 ， $p$ 分别减小、增大、等于0和等于 $\infty$ 时的最优竞价策略。值得注意的是，竞价价格将直接影响预期成本：更高的竞价价格会导致更多成本，因为广告 campaign 可能赢得更多广告机会。如图4所示，随着 $p$ 的增加或减少，竞价价格通常会降低或提升
- 当论文增加 $p$ 时 ，竞价策略将围绕点 $(-q \cdot C, 0)$ 顺时针旋转。结果是：高于零的竞价价格将降低 ，低于零的竞价价格将提升（注：低于零的价格图上没有画出来，实际上，低于0时不会出价），从而预期成本将减少。以 $p = \infty$ 和 $p = 0$ 作为极端例子。当 $p = \infty$ 时，广告 campaign 的竞价价格始终为零，因此永远不会被收费。当 $p = 0$ 时，预算不再是一个约束。竞价价格不会无限高，因为仍然存在CPC约束，并且竞价策略的斜率完全由 $q$ 控制。如果论文同时将 $q$ 设为0，这意味着CPC约束也被移除，竞价价格将无限高，广告 campaign 将赢得所有广告机会。根据图示，论文声称 $p$ 对预算支出具有直接和有效的控制能力，并且可以明确降低预算支出速度
以类似的方式，论文固定 $p$ 并将 $q$ 分别设为减小、增大、等于0和等于 $\infty$ 。如图5所示， $q$ 对最优竞价策略的影响与 $p$ 的影响显著不同
- 当论文增加 $q$ 时 ，竞价策略将围绕点 $(p \cdot C, C)$ 顺时针旋转。增加 $q$ 时，高于 $C$ 的竞价价格将降低，低于 $C$ 的竞价价格将提升。因此，广告 campaign 将赢得更多CPC低于 $C$ 的广告机会，而减少CPC高于 $C$ 的广告机会。综合结果是CPC更有可能低于 $C$ 。在极端情况下，当 $q = \infty$ 时，CPC将保证低于 $C$ 。当 $q$ 设为0时，意味着CPC约束被移除，竞价策略由 $p$ 决定 ，并退化为（Perlich等，2012；Zhang等，2016）中的最优预算约束竞价策略。基于分析，论文声称CPC可以通过 $q$ 明确控制。论文提出以下两个陈述：
  - 1）超参数 $p$ 对预算支出具有直接和有效的控制能力，并且在任何 $q$ 值下，预算支出速度都可以通过 $p$ 明确降低
  - 2）超参数 $q$ 对CPC具有直接和有效的控制能力，并且在任何 $p$ 值下，CPC约束都可以通过调整 $q$ 明确实现

多变量控制

如上一节所述，预算支出和CPC可以分别通过 $p$ 和 $q$ 明确控制。换句话说， $p$ 和 $q$ 可以用于独立控制预算支出和CPC，并将彼此视为外部噪声。因此，我们可以将多变量反馈控制问题分解为两个单变量反馈控制问题。通过这样做，PID控制器可以轻松部署，论文提出了图6中的独立PID设计，其中论文稍微滥用下标 $p$ 和 $q$ 以区分两个控制器
进一步，论文重新审视之前的分析。如图4所示，增加 $p$ 通常会降低竞价价格并减少预算支出速度。增加 $p$ 引起的另一个 non-trivial 影响是预期CPC也会降低。根据这些观察，调整 $p$ 实际上会对CPC产生影响。类似地，调整 $q$ 也会对预算支出产生了影响。尽管论文的独立PID控制系统可以处理这种耦合效应（控制器将其视为外部噪声），但通过解决此类问题，可以进一步提高系统的性能。然而，由于论文对动态系统没有明确的了解，这种耦合效应难以量化和补偿
为了解决上述问题，论文利用模型预测控制（MPC）（Rawlings和Mayne，2009）的基本思想来预测和补偿耦合效应。值得注意的是，论文没有直接在控制系统中应用MPC ，因为建模高度非线性的RTB环境成本高昂甚至不切实际。在论文的设计中，结合人类知识，模型预测模块仅需预测耦合效应，这可以通过线性模型近似。如图7所示，在PID控制器之后部署了一个模型预测模块，通过解决耦合效应来调节控制信号
MPC最重要的组成部分之一是表示动态系统行为的模型。在论文的案例中，论文针对成本和CPC对竞价环境进行建模：
- 如公式（16）所示，其中 $\mathbf{X}$ 是一个 $2 \times 2$ 矩阵， $\mathbf{b}$ 是一个 $2 \times 1$ 矩阵
- 在从反馈中获得预期的 $\Delta cost$ 和 $\Delta CPC$ 后，我们可以通过求解公式（17）中的方程来调整 $p$ 和 $q$ ，并推导出如公式（18）所示的结果
- 公式（18）表明， $p$ 和 $q$ 的控制信号应该是成本和CPC变化的线性组合
- 因此，论文通过公式（19）定义模型预测模块：
  - 其中 $\Delta cost$ 和 $\Delta CPC$ 分别由 $u_p(t)$ 和 $u_q(t)$ 量化，
  - 而 $[\mathbf{X}]^{-1}$ 由 $\alpha$ 和 $\beta$ 确定的 $2 \times 2$ 矩阵近似
  - 通过近似 $[\mathbf{X}]^{-1}$ ，我们可以简单地将 $\alpha$ 和 $\beta$ 视为两个权重参数，并在训练集中搜索其最佳值
    - 尽管这种近似削弱了表示系统的能力，但它使控制器在变化的环境中更加鲁棒和稳定
    - 问题： $\alpha$ 和 $\beta$ 的最佳值如何搜索？是类似PID的参数 $K_p,K_i,K_d$ 等一样搜索吗？
- 值得注意的是，论文提出了矩阵 $\mathbf{X}$ 和 $\mathbf{b}$ 来建模动态系统，然而，这些矩阵的确切值并不明确需要。如公式（19）所示，论文利用这些矩阵来解决耦合效应，并获得仅由 $\alpha$ 和 $\beta$ 确定的近似函数

$$\begin{bmatrix}
cost \\
CPC
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{X} & \mathbf{b}
\end{bmatrix}
\begin{bmatrix}
p \\
q \\
1
\end{bmatrix}
\tag{16}$$

$$\begin{bmatrix}
\Delta cost \\
\Delta CPC
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{X}
\end{bmatrix}
\begin{bmatrix}
\Delta p \\
\Delta q
\end{bmatrix}
\tag{17}$$

$$\begin{bmatrix}
\Delta p \\
\Delta q
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{X}
\end{bmatrix}^{-1}
\begin{bmatrix}
\Delta cost \\
\Delta CPC
\end{bmatrix}
\tag{18}$$

$$\begin{bmatrix}
u’_p(t) \\
u’_q(t)
\end{bmatrix}
=
\begin{bmatrix}
\alpha & 1 - \alpha \\
1 - \beta & \beta
\end{bmatrix}
\begin{bmatrix}
u_p(t) \\
u_q(t)
\end{bmatrix}
\tag{19}$$

实证研究

在本节中，论文进行了全面的实验，以证明论文的陈述和多变量控制系统的优势
论文在示例广告 campaign 上进行了实验，以证明超参数的控制能力
为了展示论文系统的优越性，论文在大量广告 campaign 上将论文的方法与行业最新实践进行了比较

Experiment Setup

数据集

论文基于淘宝网的真实数据集进行实验。数据集包含40个广告 campaign 在连续多天的数据，总计2000万条竞价日志。根据日期将其分为训练数据集和测试数据集。从特定广告 campaign 的角度来看，数据集的关键信息可以总结为表1
论文主要使用获胜价格、CTR和CVR的信息。每个广告机会的获胜价格在每次在线拍卖结束后记录。由于淘宝网也是一个发布商，即使广告主在在线拍卖中错过了广告机会，也可以观察到获胜价格。CTR和CVR由在线部署的模型估计，这些模型利用了用户和广告的广泛实时和历史信息。有关在线部署的估计模型的详细信息，请参阅（Zhou等，2018）

指标

竞价策略和系统的目标是最大化赢得广告机会的总价值，并将CPC控制在给定阈值以下。论文通过 $CTR \cdot CVR$ 的总和量化广告价值，这对应于转化的预期结果。值得注意的是，论文将 $CTR \cdot CVR$ 视为价值，而非实际转化事件，以排除估计模型不准确带来的影响（注：尽管一些先前的工作通过实际转化评估竞价策略，但作者认为估计误差实际上对结果产生了 non-trivial 影响）。所以，具有固定竞价策略的广告 campaign 可能仅通过优化估计模型就获得更多点击/转化，因此论文将 $CTR \cdot CVR$ 视为真实转化以减少这种影响
- (1) $R$ 表示广告 campaign 的广告价值
- (2) $R^*$ 表示广告 campaign 在预算和CPC约束下可以实现的最高广告价值
- (3) $R/R^*$ 可用于评估广告性能与理想结果的接近程度
- (4) $CPC_{ratio}$ 是满足CPC约束（允许10%的超调）的广告 campaign 比例，可用于在大量广告 campaign 上比较不同方法时评估CPC控制能力
- (5) $Value_{ratio}$ 是在CPC约束成立的广告 campaign 上的平均 $R/R^*$ ，用于评估广告价值的实现。对于那些打破CPC约束的广告 campaign ，论文在计算 $Value_{ratio}$ 时排除了它们的 $R/R^*$ ，因为在论文的场景中，通过打破CPC约束赢得更多价值是不允许的

实现细节

论文在PID控制器和基线策略中采用了公式（20）所示的执行器，其中 $u(t)$ 的符号取决于输入参数和输出变量之间的关系
$$x(t+1) = x(0) \cdot \exp(-u(t)) \tag{20}$$
此外，需要注意的是，论文实际上关心的是广告 campaign 结束时的累计CPC，而每个时间步的实时CPC对累计CPC的贡献不同，因为每个时间步的点击量不同。传统的PID误差无法解决论文场景中的不同权重问题，因此论文通过点击量对误差进行加权，并修改 $q$ 的控制信号，如公式（21）和公式（22）所示，其中 $u(t)$ 由公式（14）计算， $click(t)$ 表示时间步 $t$ 的点击量。通过这种修改，PID控制器将不断增加其对累计CPC的关注，并为每个时间步赋予不同的权重：
$$e_q(t) = click(t) \cdot (r(t) - y(t)) \tag{21}$$

$$u_q(t) = \frac{1}{\sum_{i=1\ldots t}^T click(t)} \cdot u(t) \tag{22}$$

$$u(t) = k_p e(t) + k_i \sum_{k=1\ldots t} e(k) + k_d (e(t) - e(t-1)) \tag{14}$$

针对上述公式的理解：
- $e(t) = click(t) \cdot (r(t) - y(t))$ 表示当前时间片 $t$ 的累计收入差异（注意：这样得到的是目标消耗和真实消耗的差异）
  $$
  \begin{align}
  e(t) &= click(t) \cdot (r(t) - y(t)) \\
  &= click(t) \cdot (\frac{targetCharge(t)}{click(t)} - \frac{realCharge(t)}{click(t)}) \\
  &= targetCharge(t) - realCharge(t)
  \end{align}
  $$
- 从上面的推导进一步可以得到，经过这样处理的后的积分项 $\sum_{k=1\ldots t} e(k)$ 表示全天截止到当前目标消耗与真实消耗的差异，在一些无法分时间片做特征的场景中，可以用这一项去替换这个值
  - 补充思考 ：考虑到越到后面，积分项影响越大，比例项影响越小，真实场景中如果没有的话，甚至可以不使用比例项
为了确定PID控制器的权重参数以及权重参数 $\alpha$ 和 $\beta$ ，论文在训练数据集上网格搜索最佳设置，并将其应用于测试数据集。论文将每小时视为一个时间步，因此最大时间步 $T$ 等于24
参考值设定 ：如论文在前面章节中讨论的，PID控制器需要一个参考值（目标值）。在论文的实验中，广告主给出的CPC被设为控制 $q$ 的恒定参考值。考虑到广告机会和获胜价格对成本有直接影响，并且在时间步上表现出不同的统计特征，成本参考值应根据时间步定制（如果目标就是全天达到商家的某个固定目标值呢？）。论文计算训练数据集上的成本分布，即每天每个时间步的理想成本归一化为总成本，作为成本参考
论文的实验流程步骤如下：
- 1）在训练数据集上计算最优的 $p$ 和 $q$ ；
- 2）在测试数据集上模拟竞价过程，其中计算出的 $p$ 和 $q$ 作为初始超参数应用；
- 3）当广告 campaign 预算耗尽或没有更多广告机会时，模拟结束

控制能力

在本节中，论文进行实验以证明论文的陈述，即预算支出和CPC可以分别通过 $p$ 和 $q$ 独立控制。论文同时调整两个超参数，而不使用模型预测模块，并在示例广告 campaign 上分别展示预算支出和CPC的控制性能。控制性能如图8和图9所示：
如图8所示，由 $p$ 控制的每个时间步的成本围绕成本参考值波动，累计成本相对于累计成本参考值得到了良好控制。如图9所示，每个时间步的CPC迅速被限制在可容忍的范围内，累计CPC成功控制在给定的参考值以下。值得注意的是，实时CPC在时间步上表现出可观察的波动，因为论文对实时CPC的关注逐渐减少（因为积分项的影响会逐渐增大）。与实时CPC相比，累计CPC表现出稳定的性能，如图9b所示。根据实验，尽管 $p$ 和 $q$ 相互干扰，但它们可以独立调整以控制相应的输出变量

性能评估

在本节中，论文将论文的方法与行业最新实践进行比较。论文首先介绍基线策略，并在真实数据集上评估它们

基线策略

Cost-min ：Cost-min（Kitts等，2017）是一种在广告场景中解决多约束的通用算法，可以应用于论文的场景如下。采用竞价策略公式（23）。论文通过PID控制器根据成本参考值调整 $b_0$ ，并将 $c\_bid_i$ 的上限设为 $C$ 。由于截断的竞价价格，广告 campaign 的CPC约束将始终成立。论文将给定的CPC除以广告 campaign 所有竞价日志的平均CVR来初始化 $b_0$
$$ c\_bid_i = b_0 \cdot CVR_i \tag{23} $$
Fb-Control ：Zhang等提出了一种动态调整竞价以控制CPC的反馈控制机制（Zhang等，2016）。在他们的工作中，他们采用了广义竞价策略，如公式（24）所示，并通过PID控制器根据CPC的反馈不断调整 $b_0$ 。给定的CPC被设为 $b_0$ 的初始值。为简单起见，论文将他们的方法称为Fb-Control
$$ c\_bid_i = b_0 \tag{24} $$
Fb-Control-M ：Fb-Control没有考虑点击的价值（即CVR），这对提高广告性能很重要。因此，论文修改了他们的竞价策略以更好地适应论文的场景，如公式（23）所示，其中 $b_0$ 通过PID控制器根据论文的成本参考值进行调整，而 $c\_bid_i$ 的上限通过独立的PID控制器根据CPC的反馈进行控制。上限由给定的CPC初始化，将在每次竞价时截断 $c\_bid_i$

评估结果

论文在40个广告 campaign 上评估了所有方法，并计算了 $CPC_{ratio}$ 和 $Value_{ratio}$ 。结果总结在表2中。从表2可以看出，所有方法都能成功控制CPC，因为它们的 $CPC_{ratio}$ 均为1.0。然而，论文的方法在广告价值实现方面显著优于基线策略。具体来说，独立PID控制系统（I-PID）和模型预测PID控制系统（M-PID）分别实现了0.892和0.928的 $Value_{ratio}$ ，而最佳基线策略Fb-Control-M仅实现了0.709。此外，M-PID的性能优于I-PID，这表明模型预测模块通过解决耦合效应进一步提高了系统的性能

附录：相关工作（原文直译）

注：为方便check，这里均保留引用信息

论文的工作与在线广告中的竞价策略和反馈控制密切相关。在线广告中的竞价策略已被广泛研究（Wang和Yuan，2015）。Zhang等（Zhang等，2014）提出了一种在预算约束下最大化点击量的最优竞价策略。Perlich等（Perlich等，2012）提出了一种基于库存评分的竞价策略。Lee等（Lee等，2013）提出了一种在预算平滑约束下的实时竞价优化方法。Zhang等（Zhang等，2016）提出了一种广义竞价策略，并通过反馈控制机制动态调整竞价以控制CPC。论文的工作与他们的不同之处在于，论文同时考虑了预算和KPI约束，并推导出最优竞价策略
馈控制在在线广告中的应用也得到了广泛研究（Karlsson和Zhang，2013）。Jamali等（Jamali等，2012）提出了一种基于控制理论的推荐系统。Zhang等（Zhang等，2016）提出了一种基于反馈控制的竞价策略。论文的工作与他们的不同之处在于，论文设计了一个多变量控制系统，以同时控制预算支出和CPC
此外，论文的工作还与线性规划和 primal-dual 方法相关。线性规划已被广泛应用于在线广告中的资源分配问题（Agrawal等，2014）。 primal-dual 方法已被用于解决在线线性规划问题（Buchbinder等，2007）。论文的工作与他们的不同之处在于，论文采用这种方法推导最优竞价策略而非分配策略。为了解决动态环境问题，论文利用了反馈控制理论，该理论已被许多工作证明在多种场景中有效（Jamali等，2012；Karlsson和Zhang，2013；Zhang等，2016）。其他相关工作包括点击率估计（McMahan等，2013；Zhou等，2018）、转化率估计（Lee等，2012；Yang，2017）、获胜价格预测（Wang等，2016；Wu等，2018）和预算平滑（Xu等，2015；Song等，2017）。

CA——Optimal-Auction-Design论文阅读

Background

本文是论文Optimal Auction Design, 1981的阅读笔记
本文参考了：Optimal Auction Design 最优拍卖论文笔记, CSDN
《拍卖理论》第五章也有相关证明（表示符号不同，问题定义和推导结果相同）

Introduction

Tips：论文的机制也称为 Myerson 拍卖（迈尔森拍卖）机制
论文针对单物品拍卖下，Seller 如何获得最大的收益的问题
- 单物品拍卖即一个 Seller 有一个物品（Object）, 多个竞价者（Bidder）参与拍卖
论文提出一种单物品拍卖下，保证DSIC的收益最大化的机制
- Tips：单物品拍卖下，二价拍卖是社会福利最大化的DSIC拍卖机制，但不是收益最大化拍卖
- Tips：单物品拍卖下，假设竞拍者私有估值独立同分布，则带保留价的二价拍卖是等价于Myerson拍卖

Basic Definitions and Assumptions

（本节阐述基本定义和假设）

约定一个Seller 准备出售某个商品 (Object)，有 $n$ 个 Bidders。每个Bidder $i$ 对该Object有一个估计的价值 $t_i$ ($i$ ‘s value estimate)，也即其最大可承担的竞价
名词约定：
- 假设 $t_i$ 的上下限为 $a_i, b_i$，竞拍者 $i$ 的私有估值分布（value estimate distribute）即出价分布函数为 $f_i$， $f_i(t_i) > 0$，而且 $f_i$ 为一个在区间 $[a_i, b_i]$ 上连续的函数
- 对应的累计密度函数 $F_i$ 即： $F_i(t_i) = \int_{a_i}^{t_i} f_i(s_i)d s_i$ $F_i(t_i)$ 也是Seller 对竞拍者Bidder $i$ 的竞价 $f_i(s_i) \le t_i$ 的估计概率
- $T$ 表示Bidders 对估计价值 $t_i$ 的所有可能组合： $i [a_1, b_1] \times [a_2, b_2] \times .. \times [a_n, b_n] $
- $T_{-i}$ 表示除去Bidder $i$ 之外对所有bidders 的估计价值的组合之和 $T_{-i} = \mathop{\times}\limits_{j \in N, j \neq i}[a_j, b_j] $
- 假设所有 $n$ 个竞价者是相互独立对随机变量，即其联合概率分布为所有 $f_i(t_i)$ 的乘积 $f_t = \prod \limits_{j \in N} f_j(t_j)$
- 各个竞拍者出价独立的两个主要因素【如何理解？】：
  - 1，偏好不确定，此时竞拍者 $i$ 了解到对竞拍者 $j$ 的出价信息不影响 $i$ 去修改自己的出价，
  - 2，对商品的质量（价值）的估计不确定 (quality uncertainly)，此时竞拍者 $i$ 了解到对竞拍者 $j$ 的出价信息后会修改自身的出价
- 假设存在 $n$ 个出价调整函数 $e_j$ : $[a_i, b_i]$， $e_j(t_j)$ 表示其他竞拍者 $i$ 获知到竞拍者 $j$ 对商品的价值估计 $t_j$ 后修改自身出价的调整幅度（注意，这里假设了知道竞拍者 $j$ 的出价信息后，任何一个非 $j$ 竞拍者修正自己出价的幅度都是相同的 $e_j(t_j)$ ），即竞拍者出价变为 $t_i - e_j(t_j)$ 。一般假设 $e_j(t_j) = 0$ 即对竞拍者知道其他竞拍者的估值后不影响自己的原始出价。如果 $i$ 获知了全部 $t = (t_1,..,t_n)$ 的出价信息后， $i$ 将修改其对商品的估计价值为（公式 2.7）：
  $$
  \begin{align}
  v_i(t) = t_i + \sum \limits_{j \in N, j \neq i}e_j(t_j)
  \end{align}
  $$
  - 相应的，Seller 获得N个竞价者对出价后重新调整其对自身的估价为（公式 2.8）：
    $$
    \begin{align}
    v_0(t) = t_0 + \sum \limits_{j \in N}e_j(t_j)
    \end{align}
    $$
  - 一般假设： $e_j(t_j)$ 为0

小结：

$f(t_i)$ 即竞拍者 $i$ 对商品的价值估计为 $t_i$ 的概率分布函数
$v_i(t)$ 即竞拍者 $i$ 考虑其他竞拍者对商品的价值估计后，修正的价格估计

Feasible Auction Mechanisms

（本节阐述可行性拍卖机制的基本条件）

以直接报价机制(direct revelation mechanisms) 为例展开
给定估计报价 $t = (t_1,..,t_n)$，直接报价机制的支出函数outcome functions $(p,x)$，其中 $p_i(t)$ 即竞拍者 $i$ 商品竞拍成功的概率， $x_i(t)$ 即此时 $i$ 给Seller 的期望付费金额
约定Seller 和所有竞拍者都是中性风险倾向的，对商品有各自的独立的收益函数(utility function)，竞拍者 $i$ 的期望效用函数是（公式 3.1）：

$$
\begin{align}
U_i(p,x,t) = \int_{T_{-i}} \left( v_i(t)p_i(t)-x_i(t) \right) f_{-i}(t_{-i})dt_{-i}
\end{align}
$$
- 其中 $dt_{-i} = dt_1…dt_{i-1}dt_{t+1}dt_n$
- 其中 $f_{-i}$ 即竞拍者 $i$ 和 Seller 估计除去 $i$ 之外的各竞拍者的出价的联合概率分布（独立，独立分布的乘积），之所以不包含自身的出价概率分布函数，是因为假定竞拍者已经按给定的出价 $t_i$ 以给定的概率 $p_i$ 获得商品为一确定性事件
- 解释：即竞拍者对商品本身估计的价值收益 $v_i(t)p_i(t)$ - 竞拍者为这个商品付出的成本 $x_i(t)$ 的累计积分
与之相对应，Seller 对这次竞拍的期望收益为（公式 3.2）：
$$
\begin{align}
U_0(p,x) = \int_{T}\left( v_0(t)\left(1-\sum_{j \in N}p_j(t)\right) + \sum_{j \in N}x_j(t)\right)f(t)dt
\end{align}
$$
- 其中 $dt_{i} = dt_1…dt_n$
- 解释：即庄家不出售商品时，自身对其的价值估计为 $v_0$，不出售的概率为 $1-\sum_{j \in N}p_j(t)$，则不出售收益部分 $v_0(t)\left(1-\sum_{j \in N}p_j(t)\right) $ + 出售商品时从竞拍者处获得的支付收益 $\sum_{j \in N}x_j(t)$ 的累计
我们的最优化问题目标就是最大化 $U_0(p,x)$ (定义见：公式3.2），同时对 $(p, x)$ 有一些约束条件：
- 公式3.3：（概率约束 probability constraints）由于每次只有一个商品拍卖，所以有：
  $$
  \begin{align}
  \sum_{j \in N}p_j(t) \le 1 \quad \text{and} \quad p_i(t) \ge 0, \quad \forall i \in N, \forall t \in T
  \end{align}
  $$
- 公式3.4：（个体理性约束 individual-rationality constraints）由于Seller不能强制竞拍者参加，所以需要保证每个竞拍者参与进来的收益非负才有动力参加，即：
  $$
  \begin{align}
  U_i(p,x,t_i) \ge 0, \quad \forall i \in N, \forall t_i \in [a_i, b_i]
  \end{align}
  $$
- 假设竞拍者有隐瞒自己的估计从而期望获得额外收益，这时候应该保证诚实报价的状态是一种纳什均衡状态。假设竞拍者 $i$ 声称 $s_i$ 是他的声称估计而 $t_i$ 是他的真实估价，那么他的期望效益函数为：
  $$
  \begin{align}
  \int_{T_{-i}} \left( v_i(t)p_i(t_{-i}, s_i)-x_i(t_{-i}, s_i) \right) f_{-i}(t_{-i})dt_{-i}
  \end{align}
  $$
- 说明：竞拍者 $i$ 获得物品的概率变成受两个因素的影响 $p_i(t_{-i}, s_i)$，为拍得商品支付的成本 $x_i$ 也是 $x_i(t_{-i}, s_i)$
- 公式3.5：（激励相容约束 incentive-compatibility constraints）从而，为保证每个竞拍者都没有动力隐瞒报价，需要满足如下的激励相容的条件（隐瞒后的期望收益更小）：
  $$
  \begin{align}
  U_i(p,x,t_i) \ge \int_{T_{-i}} \left( v_i(t)p_i(t_{-i}, s_i)-x_i(t_{-i}, s_i) \right) f_{-i}(t_{-i})dt_{-i}, \quad \forall i \in N, \forall t_i \in [a_i, b_i], \forall s_i \in [a_i, b_i]
  \end{align}
  $$
- 论文称满足以上3个条件的拍卖机制是可行的feasible。that is, if the seller plans to allocate the Object according to p and to demand monetary payments from bidders according to x, then the scheme can be implemented, with all bidders willing to participate honesty.
在一个一般性的拍卖中，每个Bidder有一些候选策略 $\Theta_i$，以及其对应的收益函数：
$$
\begin{align}
\hat{p}: \Theta_1 \times … \times \Theta_n \rightarrow \mathbb{R}^n \quad \hat{x}: \Theta_1 \times … \times \Theta_n \rightarrow \mathbb{R}^n
\end{align}
$$
一个拍卖机制auction mechanism 涉及到各个竞拍者使用的一系列strategic plans 参与游戏中。a strategic plan即一个 $[a_i, b_i] \rightarrow \Theta_i$ 的规则函数， $\Theta_i$ 即当竞拍者对商品的估价是 $t_i$ 时采取的竞拍策略。Direct revelation mechanisms直接报价机制即 $\Theta_i = t_i$ 。
定理1：给定任何的可行拍卖机制，总存在一个等价的可行的直接报价机制，可以给Seller和所有竞拍者带来与之相同的收益

小结：可行拍卖的3个条件：竞拍成功的概率非负、竞拍者的效用函数非负(挣的比花的多)、激励相容(鼓励说真话)

Analysis of the problem

*（本节展开拍卖机制的更多属性，确定具体的竞拍标准和计费标准） *

定义Bidder $i$ 在 $(p,x)$ 的拍卖机制下，当 $i$ 的估价是 $t_i$ 时竞拍成功的条件概率为（公式4.1）：
$$
\begin{align}
Q_i(p,t_i) = \int_{T_{-i}}p_i(t)f_{-i}(t_{-i})dt_{-i}
\end{align}
$$
- 如何理解？
此处省略许多推导…

Optimal auctions in the regular case

(本节给出正则问题下的最优拍卖机制)

对任意竞拍者 $i$，定义新的变量（其他地方也称为虚拟估值）：
$$
\begin{align}
c_i(t_i) = t_i -e_i(t_i) - \frac{1-F_i(t_i)}{f_i(t_i)}
\end{align}
$$
- 如果对所有竞拍者 $i$，均有 $c_i(t_i)$ 是 $t_i$ 的严格单调递增函数，则称原始问题为正则问题
- 算法博弈论中也称满足 $v - \frac{1-F(v)}{f(v)}$ 是关于 $v$ 的非减函数的分布 $F$ 为正则分布。在实际应用中，一般假设 $e_j(t_j) = 0$ 。 $e_j(t_j)$ 表示其他竞拍者 $i$ 获知到竞拍者 $j$ 对商品的价值估计 $t_j$ 后修改自身出价的调整幅度（注意，这里假设了知道竞拍者 $j$ 的出价信息后，任何一个非 $j$ 竞拍者修正自己出价的幅度都是相同的 $e_j(t_j)$ ），即竞拍者出价变为 $t_i - e_j(t_j)$ 。一般假设 $e_j(t_j) = 0$ 即对竞拍者知道其他竞拍者的估值后不影响自己的原始出价
- 正则的分布包括：正太分布(normal distribution)，对数正太分布(lognormal distribution)，均匀分布(uniform distribution)，指数分布(exponential distribution)
  - 对数正态分布的介绍可参考对数正态分布（Log-Normal Distribution）
  - 指数分布的介绍可参考指数分布（定义、期望、方差）
- 非正则的分布包括：多峰分布和长尾分布
正则问题的最优拍卖机制对应的分配规则为：
$$
\begin{align}
p_i(t) > 0 \quad \text{implies} \quad c_i(t_i) = \max \limits_{j \ in N}\left(c_j(t_j) \right) \ge t_0
\end{align}
$$
- 个人理解：上述公式包含下面几个逻辑：
  - 分配函数：将商品卖给 $c_i(t_i)$ 最大的人，实际实现时可以采用按照 $c_i(t_i)$ 排序的方式实现
    - 对应到广告中，则可以用 $ RankScore_i = c_i(bid_i^{cpc}) * CTR $ 排序
    - 考虑GMV时，也可以扩展为用 $RankScore_{i} = c_i(bid_i^{cpc}) * CTR + k \cdot GMV$ 排序
  - 保留价：当所有人的虚拟估值都低于Seller 对商家的估值 $t_0$ 时，流拍。在广告系统中，广告位不卖出去一般没有收益（忽略不出广告带来的用户体验提升），即估值为0，也就是 $t_0=0$，此时保留价一般定义为，对任意竞拍者 $i$，有 $Bid_{reserve} = c_i^{-1}(t_0) = c_i^{-1}(0)$
正则问题的最优拍卖机制对应的支付规则为：
$$
\begin{align}
x_i(t) = p_i(t)v_i(t) - \int_{a_i}^{t_i}p_i(t_{-i}, s_i)ds_i
\end{align}
$$
- 其中 $v_i(t) = t_i + \sum \limits_{j \in N, j \neq i}e_j(t_j)$
- 个人理解：上述公式包含下面几个逻辑：
  - 直观解释支付规则：竞拍者 $i$ 的支付价格为其对商品估值（修改后的估值）减去其出价较低时累计概率和【如何理解减去累计概率和是表达声明，是不是写错了？】
- 由于 $v_i(t) = t_i + \sum \limits_{j \in N, j \neq i}e_j(t_j)$，原始支付规则可进一步转化为：
  $$
  \begin{align}
  x_i(t) = p_i(t)\left( t_i + \sum \limits_{j \in N, j \neq i}e_j(t_j)\right) - \int_{a_i}^{t_i}p_i(t_{-i}, s_i)ds_i
  \end{align}
  $$
进一步定义如下新变量 $z_i(t_{-i})$ ：
$$
\begin{align}
z_i(t_{-i}) = \inf\{s_i|c_i(s_i) \ge t_0 \quad \text{and} \quad c_i(s_i) \ge c_j(t_j), \forall j \neq i\}.
\end{align}
$$
- 个人对上述新变量 $z_i(t_{-i})$ 的理解：
  - $z_i(t_{-i})$ 是一个满足下列条件的 $s_i$ 的最小值：
    - 满足 $s_i$ 的虚拟估值 $c_i(s_i)$ 大于Seller对商品估值 $t_0$
    - 满足 $s_i$ 的虚拟估值 $c_i(s_i)$ 大于等于其他所有竞拍者的真实估值对应虚拟估值 $c_j(t_j)$
  - 论文原文： $z_i(t_{-i})$ is the infimum of all winning bids for i against $t_{-i}$ . ($z_i(t_{-i})$ 是竞拍者 $i$ 对 $t_{-i}$ 的所有出价的下确界值)
  - $z_i(t_{-i})$ 本质上是除竞价者 $i$ 以外的 $c_j(t_j)$ 最高的值 $c_{j^*}(t_{j^*}) = \max \limits_{j \neq i} c_j(t_j)$ 对应的逆函数值 $c_i^{-1}(c_{j^*}(t_{j^*}))$ 和 $c_i(t_0)$ 的最大值
  - 也就是说，对于任意的竞价者 $i$， $z_i(t_{-i})$ 是在其他商家出价为 $t_{-i}$ 时， $i$ 获胜的最低出价，也是其获胜后的计费价格
- 当修正函数为0（即 $e_i(t_i) = 0$ ），则可以得到：
  $$
  \begin{align}
  x_i(t) &= z_i(t_{-i}) \\
  &= \max \left \{c_i^{-1}(t_0), \max \limits_{j \neq i} c_i^{-1}(c_j(t_j))\right\} \\
  &= c_i^{-1}\left(\max\left\{t_0, \max \limits_{j \neq i} c_j(t_j)\right\}\right) \\
  \end{align}
  $$
  - 实际使用时，若 $RankScore_{i} = c_i(bid_i^{cpc}) * CTR + k \cdot GMV$，则是：
    $$
    \begin{align}
    x_i(t) &= z_i(t_{-i}) \\
    &= c_i^{-1}\left(\max \left\{t_0, \frac{RankScore_{next} - k \cdot GMV}{CTR}\right\}\right)
    \end{align}
    $$
- 进一步地，如果问题是正则的，且是对称的（即所有竞拍者的估值分布是一样的）那么有：
  $$
  \begin{align}
  x_i(t) =z_i(t_{-i}) = \max \left \{c_i^{-1}(t_0), \max \limits_{j \neq i} t_j \right \}.
  \end{align}
  $$
  - 公式理解：
    - 当所有竞拍者的估值分布一致时（即 $\forall i,j$，有 $F_i = F_j = F$ ），此时 $c_i = c_j = c$ 成立， $c_i^{-1}(c_j(t_j)) = c^{-1}(c(t_j)) = t_j$ 成立
    - 此时表示，如果问题是正则且对称的，那么带保留价的二价拍卖($Bid_{reserve} = c_i^{-1}(t_0)$)就是最优机制
分配规则也可表示为：
$$
\begin{align}
p_i(t_{-i},s)=
\begin{cases}
0& 1 \ if \ s_i \gt z_i(t_{-i}), \\
1& 0 \ if \ s_i \lt z_i(t_{-i}).
\end{cases}
\end{align}
$$
- 分配规则的理解：
  - 如果一个竞拍者 $i$ 的出价大于除他以外的所有竞拍者的虚拟估值最大值的逆且大于Seller对商品估值的逆，则获胜
  - 更直观的理解：虚拟估值 $c_i(s_i)$ 最高的竞拍者获胜，若最高虚拟估值低于Seller对商品估值（ $t_0$ ），则流拍
计费规则也可表示为：
$$
\begin{align}
x_i(t)=
\begin{cases}
0& z_i(t_{-i}) + \sum \limits_{j \in N, j \neq i}e_j(t_j) &\ if \ p_i(t)=1, \\
1& 0 &\ if \ p_i(t)=0.
\end{cases}
\end{align}
$$
- 其中 $\sum \limits_{j \in N, j \neq i}e_j(t_j)$ 通常为0，故更简洁的计费规则形式为：
  $$
  \begin{align}
  x_i(t)=
  \begin{cases}
  0& z_i(t_{-i}) &\ if \ p_i(t)=1, \\
  1& 0 &\ if \ p_i(t)=0.
  \end{cases}
  \end{align}
  $$

小结

Myerson拍卖问题的建模为：
$$
\begin{align}
\max U_0(p,x) &= \int_{T}\left( v_0(t)\left(1-\sum_{j \in N}p_j(t)\right) + \sum_{j \in N}x_j(t)\right)f(t)dt \\
s.t. \sum_{j \in N}p_j(t) \le 1 \quad \text{and} \quad p_i(t) \ge 0 &, \quad \forall i \in N, \forall t \in T \\
U_i(p,x,t_i) \ge 0 &, \quad \forall i \in N, \forall t_i \in [a_i, b_i] \\
U_i(p,x,t_i) \ge \int_{T_{-i}} \left( v_i(t)p_i(t_{-i}, s_i)-x_i(t_{-i}, s_i) \right) f_{-i}(t_{-i})dt_{-i} &, \quad \forall i \in N, \forall t_i \in [a_i, b_i], \forall s_i \in [a_i, b_i]
\end{align}
$$
若以上问题为正则问题（即当对任意的竞拍者 $i$，对商品的估值分布 $F_i$ 是正则函数）时，有最优拍卖机制 $(p,x)$ 为：
- 原始形式：
  - 分配规则 $p$ ：
    - 按照 $RankScore_i = c_i(t_i) = t_i - \frac{1-F_i(t_i)}{f_i(t_i)}$ 对竞拍者进行排序，取 $RankScore_i$ 最高的竞拍者 $RankScore_i^*$
    - 若 $RankScore_i^*\ \ge t_0$ （等价于 $t_{i*} \ge c_{i^*}^{-1}(t_0)$ ），则竞拍者 $i^*$ 获胜，否则流拍
  - 支付规则 $x$ ：
    $$
    \begin{align}
    x_i(t) &= z_i(t_{-i}) \\
    &=c_i^{-1}\left(\max\left\{t_0, \max \limits_{j \neq i} c_j(t_j)\right\}\right)
    \end{align}
    $$
- 在真实广告系统中，往往需要考虑 $GMV$ 等指标，此时一般可定义 $RankScore_{i} = c_i(bid_i^{cpc}) * CTR + k \cdot GMV$，则
  - 分配规则是：
    - 按照 $RankScore_{i} = c_i(bid_i^{cpc}) * CTR + k \cdot GMV$ 对竞拍者进行排序
    - 取 $RankScore_i$ 最高的竞拍者 $i^*$，其对应的排序分数为 $RankScore_i^*$
    - 若 $\frac{RankScore_{i^*} - k \cdot GMV}{CTR} \ge t_0$ （等价于 $bid_{i^*}^{cpc} \ge c_{i^*}^{-1}(t_0)$ ），则竞拍者 $i^*$ 获胜，否则流拍
      - 注意：当竞拍者的出价分布不同时，其对应的保留价也不同，一般广告中实现时会考虑数据稀疏问题等，将同以区域(一般为蜂窝粒度)商家出价分布假定为独立同分布的，即同一区域内所有商家保留价相同
  - 支付规则是：
    $$
    \begin{align}
    x_i(t) &= z_i(t_{-i}) \\
    &= c_i^{-1}\left(\max \left\{t_0, \frac{RankScore_{next} - k \cdot GMV}{CTR}\right\}\right)
    \end{align}
    $$

Optimal auctions in the general case

(本节给出一般情况下的最优拍卖机制)

The independence assumption

Implementation

其他讨论

缺点：
- 无法避免Bidders串谋调低价格
- 可能出现Seller雇佣托儿太高价格（即保留价）【Seller没有动力吧】
- 无法避免同一个Bidder用多个身份竞拍【Bidder没有动力吧】

CA——Neural-Multi-slot-Auctions(NMA)

参考链接：
- 原始论文：NMA: Neural Multi-slot Auctions with Externalities for Online Advertising, 2022, ArXiv preprint, Meituan

整体总结

其他已有机制盘点

广义第二价格拍卖（GSP）（也包括uGSP），因其易于解释和部署，几乎已成为广告拍卖机制的基准。但GSP拍卖机制忽略了外部性（假设了用户点击仅依赖于广告本身）
深度神经拍卖（DNA） ，通过深度神经网络升级GSP，并在一定程度上建模了局部外部性(注：DNA忽略了广告的顺序和展示位置)，然而，它仅考虑了拍卖中的集合级上下文，忽略了广告的顺序和展示位置，仍然不够
Vickrey-Clarke-Groves（VCG） ，与GSP和DNA相比，代表性的真实拍卖Vickrey-Clarke-Groves（VCG）考虑了外部item的影响，并在理论上可以建模全局外部性。然而，VCG导致平台收入下降，这对大多数工业界广告平台来说是不可接受的
加权Vickrey-Clarke-Groves（WVCG） ，可以建模全局外部性，并在一定程度上解决了VCG的收入下降问题。然而，参数求解的高复杂性使其难以在工业场景中实际应用

关键挑战提出

通过分析上述代表性拍卖机制的问题，作者认为在设计具有外部性的多槽位拍卖机制时面临三个关键挑战：
- i）大多数拍卖机制要么仅建模局部外部性，要么低效地建模全局外部性。如何高效地建模全局外部性已成为关键点
- ii）平台收入和社会福利（SW）是设计拍卖机制的核心指标。大多数现有工作要么专注于平台收入的最大化，要么专注于社会福利的最大化，缺乏对两者的有效平衡
- iii）一些方法专注于理论拍卖设置，缺乏大规模工业部署的洞察

方案概述

神经多槽位拍卖（NMA） ：一种端到端学习的多槽位拍卖机制，以在最大化平台收入的同时减少社会福利的下降。包括四个部分：
- 所有候选分配通过上下文感知的列表预测模块输入，该模块有效地建模了全局外部性
- List深度排序模块，通过将参数建模为神经网络，使得复杂的拍卖机制可以端到端训练
- List可微分排序模块，通过真实系统奖励反馈有效地训练级联的深度神经网络
- 社会福利的辅助损失，以在最大化收入的同时有效减少其下降
主要贡献总结如下：
- 多槽位拍卖的新框架 ：论文提出了一种名为NMA的端到端学习框架，能够准确建模全局外部性，并有效平衡设计拍卖机制的关键指标
- 建模全局外部性的优越方法 ：论文采用精心设计的神经网络来建模每个分配的列表级信息和拍卖中的公共信息，大大提高了全局外部性建模的有效性和预测值的准确性
- 平衡收入和社会福利的有效方法 ：论文设计了社会福利最大化的辅助损失，能够有效平衡平台收入和社会福利
- 详细的工业实践经验 ：论文成功将NMA部署在美团外卖平台上。离线模拟和在线A/B实验的结果表明，与GSP、DNA、VCG和WVCG相比，NMA在点击率和平台收入方面带来了显著提升

问题建模

多槽位拍卖场景

电子商务广告中典型的多槽位拍卖场景中，形式上，当用户发起页面浏览请求时，电子商务平台向用户展示 $J$ 个item，其中包含 $K(K\leq J)$ 个广告。 $N$ 个广告主竞争 $K(K\leq N)$ 个广告位，每个广告主 $a_{i}$ 根据私有信息（如PCTR等）提交一个出价 $b_{i}$ 。论文通过 $\mathcal{M}(\mathcal{R},\mathcal{P})$ 表示拍卖机制。 $\mathcal{R}$ 是广告分配方案，用于从 $N$ 个候选广告主中选择 $K$ 个获胜广告，并按顺序展示在相应的 $K$ 个固定广告位上。 $\mathcal{P}$ 是支付规则，用于计算获胜广告的支付，并经过精心设计以保证拍卖机制的经济属性和收入

问题公式化建模

在多槽位拍卖中，论文将广告集合表示为 $\mathcal{A}={a_{1},\ldots,a_{N}}$ ，广告位集合表示为 $\mathcal{K}={1,\ldots,K}$ 。然后，分配 $\theta$ 定义为从 $N$ 个候选中选择 $K$ 个广告并按顺序放置在 $K$ 个广告位上。给定广告主的出价和预测的点击率，论文的目标是设计具有外部性的多槽位拍卖机制 $\mathcal{M}(\mathcal{R},\mathcal{P})$ ，以在基本假设下最大化平台收入并减少社会福利的下降，如下所示：
$$
\begin{align}
\underset{\mathcal{M}}{\text{maximize}} &\mathbb{E}_{\theta\in\Theta}[\sum_{a_{j}\in\text{ads}(\theta)}p(\theta,a_{j})\cdot\hat{q}(\theta,a_{j})],\\
\text{s.t.}\quad &\textit{Incentive Compatibility (IC) constraint,}\\
&\textit{Individual Rationality (IR) constraint,}\\
&\textit{Social Welfare (SW) constraint,}
\end{align}
$$
- 其中 $\Theta$ 是所有可能分配的集合， $\theta^{*}$ 是最佳分配， $\text{ads}(\theta)$ 是分配 $\theta$ 中的广告子集， $p(\theta,a_{j})$ 是分配 $\theta$ 中广告 $a_{j}$ 的支付， $\hat{q}(\theta,a_{j})$ 是分配 $\theta$ 中广告 $a_{j}$ 的预测点击率
- IC和IR约束保证了广告主会如实报告出价，并且不会为其分配支付超过其最大愿意支付的价格。社会福利是在线广告的关键指标，因为它衡量了广告主和用户匹配的效率，也是广告平台总收入的上限。SW约束定义如下：
  $$
  1-\frac{\textit{SW}(\theta^{*},\mathbf{b})}{\textit{SW}^{*}}<\varepsilon,
  $$
  - 其中 $\textit{SW}(\theta^{*},\mathbf{b})$ 是最佳分配 $\theta^{*}$ 的社会福利， $\textit{SW}^{*}$ 是 $\Theta$ 中的最大社会福利， $\varepsilon$ 是根据业务场景制定的社会福利下降阈值

$\mathcal{M}(\mathcal{R},\mathcal{P})$ 中的分配方案和支付规则如下：
- 分配方案 $\mathcal{R}:\times_{a_{j}\in\mathcal{A}}\mathcal{V}_{j}\longrightarrow\Theta$
- 每个广告的支付规则 $\mathcal{P}:\times_{a_{j}\in\mathcal{A}}\mathcal{B}_{j}\longrightarrow\mathbb{R }^{+}$，
- 其中 $\mathcal{V}_{j}$ 是广告 $a_{j}$ 的可能价值集合，$\mathcal{B}_{j}$ 是广告 $a_{j}$ 的可能出价集合。具体来说，论文将广告 $a_{i}$ 的实际点击价值表示为 $v_{i}$，广告 $a_{j}$ 的提交点击价值表示为 $b_{j}$
如果拍卖机制是激励相容的（IC），那么每个广告主如实揭示其最大愿意支付价格是最有利的，即 $b_{j}=v_{j}$。如果拍卖机制是个体理性的（IR），那么广告主 $a_{j}$ 的支付金额不会超过其报告的价值，即如果广告 $a_{j}$ 被展示并点击，则 $p(\theta,a_{j})\lt b_{j}$；否则不支付任何费用。有了这两个属性，广告主不需要花费精力计算出价策略，并且可以无风险地参与拍卖。在线平台也能获得真实可靠的广告主价值。由于论文遵循了 WVCG 的理论基础，WVCG 已被证明是 IC 和 IR 的 [Kumar et al., 2019]，因此论文用 $b_{i}$ 表示第 $i$ 个广告主的实际点击价值
为了清晰起见，论文在表 1 中列出了论文中使用的关键符号

NMA拍卖方案

整体方案图：
- 如图2所示，NMA将所有候选广告列表（即每个广告列表代表一个分配 $\theta$ ）和三种类型的公共信息作为输入，并使用三个模块来选择获胜广告列表
  - 上下文感知列表预测模块（CLPM）：CLPM建模每个广告列表的位置依赖外部性和广告依赖外部性，并根据请求的公共信息和广告列表的上下文信息预测每个广告的列表级pCTR
  - 列表深度排序模块（LDRM）：LDRM将拍卖机制与深度学习相结合，并使用子网络建模每个广告列表的信息，旨在提高排序公式的表达能力，同时保证IC和IR属性
  - 列表可微分排序模块（LDSM）：LDSM对拍卖中的排序操作进行连续松弛，并输出一个行随机的置换矩阵。我们可以使用这个行随机置换矩阵来表达预期收入，并端到端学习最优列表
  - 其他辅助损失：社会福利最大化的辅助损失，以满足社会福利约束并减少社会福利的下降

上下文感知列表预测模块

大多数传统的广告拍卖机制使用点级pCTR来计算分配和支付过程中的排序分数。然而，点级pCTR不仅缺乏对拍卖中公共信息的利用，还未能考虑一个列表中广告之间的交互。最近，Liu等人考虑了广告的交互，并提出了一个名为集合编码器的模块来自动建模拍卖中的集合级信息。但它仅建模了局部外部性，因此仍然不够优化。为此，论文提出了上下文感知列表预测模块，以显式建模全局外部性，输出每个广告在列表中的更准确的列表级pCTR
CLPM采用参数共享结构处理所有候选广告列表。这里论文以广告列表 $\theta$ 为例进行说明。如图2所示，CLPM将广告列表 $\theta$ 和三种类型的公共信息（即请求信息、用户画像和当前请求中的Organic Item）作为输入，并输出列表中每个广告的列表级pCTR。论文首先使用嵌入层从原始输入中提取嵌入。广告列表和Organic Item列表的嵌入矩阵分别表示为 $\mathbf{E}_{\text{ad}}\in\mathbb{R}^{K\times d}$ 和 $\mathbf{E}_{\text{oi}}\in\mathbb{R}^{M\times d}$ ，其中 $K$ 是 $\theta$ 中的广告数量， $M$ 是当前请求中Organic Item的数量， $d$ 是嵌入的维度。同时，用户画像和请求信息的嵌入分别表示为 $\mathbf{e}^{\text{u}}$ 和 $\mathbf{e}^{\text{r}}$
使用自注意力单元（SAU）来建模Organic Item列表的序列信息：
$$
\mathbf{H}_{\text{oi}}=\text{Self-Att}(\mathbf{Q}_{\text{oi}},\mathbf{K}_{\text{oi}},\mathbf{V}_{\text{oi}})=\text{soft max}(\frac{\mathbf{Q}_{\text{oi}}\mathbf{K}_{\text{oi}}^{\top}}{\sqrt{d}})\mathbf{V}_{\text{oi}},
$$
- 其中 $\mathbf{Q}_{\text{oi}},\mathbf{K}_{\text{oi}},\mathbf{V}_{\text{oi}}$ 分别表示查询、键和值。这里查询、键和值是从Organic Item的嵌入矩阵线性变换得到的，如下所示：
  $$
  \mathbf{Q}_{\text{oi}}=\mathbf{E}_{\text{oi}}\mathbf{W}_{\text{oi}}^{O}, \mathbf{K}_{\text{oi}}=\mathbf{E}_{\text{oi}}\mathbf{W}_{\text{oi}}^{K}, \mathbf{V}_{\text{oi}}=\mathbf{E}_{\text{oi}}\mathbf{W}_{\text{oi}}^{V}.
  $$
接下来，使用目标注意力单元（TAU）来编码Organic Item与广告列表中每个广告之间的交互：
$$
\begin{align}
\mathbf{h}_{j}^{\text{ad}} &=\text{Tgt-Att}\big(\mathbf{e}_{j}^{\text{ad}},(\mathbf{h}_{i}^{\text{oi}})_{i=1}^{M}\big) \\
&=\mathbf{e}_{j}^{\text{ad}}\cdot\text{MLP}_{\text{att}}(\mathbf{e}_{j}^{\text{ad}}|\mathbf{h}_{i}^{\text{oi}})+\cdots+\mathbf{e}_{j}^{\text{ad}}\cdot\text{MLP}_{\text{att}}(\mathbf{e}_{j}^{\text{ad}}|\mathbf{h}_{M}^{\text{oi}}),\forall j\in[K],
\end{align}
$$
- 其中 $|$ 表示连接， $\mathbf{e}_{j}^{\text{ad}}$ 是广告列表 $\theta$ 中第 $j$ 个广告的嵌入，MLP ${}_{\text{att}}$ 是一个多层感知器（MLP），它将广告和Organic Item对的嵌入作为输入并输出一个注意力权重， $\mathbf{h}_{i}^{\text{oi}}$ 是从前一个单元生成的有序item列表中第 $i$ 个Organic Item的表示
  $$
  \mathbf{e}^{\text{list}}=\text{MLP}_{\text{list}}\Big{(}(\mathbf{e}_{1}^{\text{ad}}|\mathbf{h}_{1}^{\text{ad}}|\text{CTR}_{1}^{\text{ad}})|\cdots|(\mathbf{e}_{K}^{\text{ad}}|\mathbf{h}_{K}^{\text{ad}}|\text{CTR}_{K}^{\text{ad}})\Big{)},
  $$
然后，将第 $j$ 个广告的表示与其对应的嵌入和点级pCTR连接起来，作为其最终表示。广告列表 $\theta$ 中所有广告的表示被输入到一个MLP中，以建模全局外部性：
$$
\hat{q}(\theta,a_{j})=\sigma\Big{(}\text{FC}_{j}(\mathbf{e}^{\text{list}}|\mathbf{e}^{u}|\mathbf{e}^{r})\Big{)},\forall j\in[K],
$$
- 其中CTR表示点级pCTR， $\sigma$ 表示sigmoid函数， $\hat{q}(\theta,a_{j})$ 表示广告列表 $\theta$ 中第 $j$ 个广告的列表级pCTR。为了使CLPM更好地收敛，论文基于每个广告的真实反馈提出了CLPM的辅助损失：
  $$
  L_{list}=\sum_{j=1}^{K}\Big{(}-y_{j}^{\text{ad}}\log(\hat{q}(\theta,a_{j}))-(1-y_{j}^{\text{ad}})\log(1-\hat{q}(\theta,a_{j}))\Big{)},
  $$
  - 其中 $y_{j}^{\text{ad}}\in{0,1}$ 表示用户是否点击了广告列表 $\theta$ 中的第 $j$ 个广告。通过CLPM，我们可以有效地建模全局外部性，输出广告列表的列表级pCTR。与点级pCTR相比，列表级pCTR能够建模位置依赖的外部性，并且更准确，这有助于NMA实现更好的性能。需要注意的是，这里论文仅以CTR为例。通过建模全局外部性来提高预测值准确性的CLPM框架可以轻松转移到其他预测问题，如CVR预测、订单价格预测等

列表深度排序模块

LDRM拍卖机制与深度学习相结合，以提高排序公式的表达能力，同时保证IC和IR属性。首先，论文提取广告列表中广告的出价、嵌入和列表级pCTR作为输入。根据拍卖理论，论文设计了一个子网络（即 $\mu$-Net）来计算每个广告列表的排序分数。 $\mu$-Net的输出对应于WVCG中的权重，用作增加收入的加权因子。然而，WVCG的MAB方法在高工业场景中难以优化。因此，论文升级了深度神经网络以进行端到端优化，它具有丰富的表达能力，可以自动优化仿射参数
数学上，论文将 $\mu$-Net表示为 $f_{\mu}(\cdot)$ ，它将每个广告的分配无关特征作为输入以确保IC，并输出相应广告的私有价值：
$$
f_{\mu}(a_{j})=\sigma\Big{(}\text{MLP}_{\mu}(\mathbf{e}_{j}^{\text{ad}})\Big{)},\forall j\in[K].
$$
然后，广告列表 $\theta$ 的排序分数计算如下：
$$
\mathcal{RS}(\theta,\mathbf{b})=\sum_{a_{j}\in\text{ads}(\theta)}f_{\mu}(a_{j})\cdot b_{j}\cdot\hat{q}(\theta,a_{j})
=\sum_{j=1}^{K}f_{\mu}(a_{j})\cdot b_{j}\cdot\hat{q}(\theta,a_{j}).
$$
最佳广告列表 $\theta^{*}$ 的支付规则为：
$$
p(\theta,a_{j})=\frac{1}{\int_{\Omega}(a_{j})\cdot\hat{q}(\theta,a_{j})}\left[RS(\theta^{*}_{-j},\mathbf{b}_{-j})-RS_{-j}(\theta^{*},\mathbf{b})\right], \forall j\in[K],
$$
- 其中 $a_{j}\in\text{ads}(\theta^{*})$ 且 $\theta^{*}_{-j}$ 是当 $a_{j}$ 不存在时的最佳广告列表
显然，给定支付规则，每个广告的支付低于其出价，这保证了NMA的IR。广告列表 $\theta$ 的预期收入计算如下：
$$
r(\theta)=\sum_{j=1}^{K}\hat{q}(\theta,a_{j})\cdot p(\theta,a_{j}).
$$
为了研究此问题对IC属性的影响，论文在第5.2.1节中进行了综合实验，以计算NMA的数据驱动IC指标。论文将NMA在复杂拍卖场景中的严格IC保留为未来工作的一个有趣开放问题

列表可微分排序模块

LDRM可以有效地计算不同广告列表的排序分数，并选择最佳广告列表进行支付。然而，将分配和支付置于模型学习之外（即作为不可知环境）在某种程度上不适合深度学习。也就是说，分配和支付的过程（实际上是排序操作）本身是不可微分的。Liu等人提出了一个可微分排序引擎来解决这个问题。但在基于VCG的拍卖中，论文对不同的广告列表进行排序，而不是对广告进行排序，这使得之前的可微分排序解决方案在论文的场景中不适用。为此，论文提出了列表可微分排序模块，它将可微分排序从点级广告排序升级到列表级广告列表排序，使得复杂的拍卖机制可以端到端训练
给定集合 $\text{RS}=\left[\text{RS}(\theta_{1},\mathbf{b}),\text{RS}(\theta_{2},\mathbf{b}),\cdots,\text{RS}(\theta_{N_{L}},\mathbf{b})\right]^{T}$ ，论文将argsort操作符定义为从 $N_{L}$ 维实向量 $\text{RS}\in\mathbb{R}^{\tilde{N}_{L}}$ 到 $N_{L}$ 个广告列表的排列的映射，其中置换矩阵 $M_{rs}$ 表示为：
$$
M_{rs}[j,i]=\begin{cases}1&\text{如果 }i=\text{argsort}(\text{RS})\lfloor j\rfloor\\
0&\text{Otherwise}\end{cases},
$$
- 其中 $M_{rs}[j,i]$ 表示 $\text{RS}(\theta_{i},\mathbf{b})$ 是否是RS中广告列表的第 $j$ 大排序分数。结果来自[15]显示了恒等式：
  $$
  M_{rs}[j,i]=\begin{cases}1&\text{如果 }i=\text{argmax}(c_{j})\\
  0&\text{Otherwise}\end{cases},
  $$
其中 $c_{j}=(N_{L}+1-2j);\text{RS}-\text{A}_{\text{RS}}\mathbf{I},$ $\text{A}_{\text{RS}}[m,n]$ 表示元素的绝对成对差异， $\mathbf{I}$ 表示全1列向量。根据之前的工作[15, 25]，论文将Eq. (14)中的argmax操作符松弛如下：
$$
\hat{M}_{rs}[j,:]=\text{softmax}(\frac{c_{j}}{r}),
$$
- 其中 $r$ 是温度参数。直观上， $M_{rs}$ 的第 $j$ 行可以解释为在所有广告列表上获得第 $j$ 个最佳广告列表的选择概率
论文将由Eq. (12)计算的所有广告列表的预期收入表示为 $\text{R}=\left[r(\theta_{1}),r(\theta_{2}),…,r(\theta_{N_{L}})\right]^{T}$ ，然后多槽位拍卖的端到端学习问题可以表述为最小化前1预期收入的总和：
$$
L_{tgt}=-\hat{M}_{rs}[1,:]\cdot\text{R}.
$$

社会福利最大化辅助损失

如Eq. (16)所述，广告收入仅与获胜广告列表相关，这使得端到端过程难以学习，并导致社会福利下降。因此，论文设计了一个社会福利最大化的辅助损失，以加速学习过程并减少社会福利的下降
具体来说，广告列表 $\theta$ 的社会福利定义为：
$$
SW(\theta,\mathbf{b})=\sum_{j=1}^{K}b_{j}\cdot\hat{q}(\theta,a_{j}).
$$
- 请注意，论文在Eq 17中有 $v_{j}=b_{j}$ 。由于论文遵循WVCG的理论基础，它被证明是IC的
显然，具有最大社会福利的广告列表是VCG的结果，其中 $f_{p}(\cdot)=1$ 。这里论文首先形成一个置换矩阵 $M_{y}$ ，它通过排序所有广告列表的社会福利来计算。然后，论文使用真实置换矩阵和预测的行随机置换矩阵之间的行级交叉熵（CE）来构建社会福利最大化辅助损失：
$$
L_{ce}=\frac{1}{N_{L}}\sum_{k=1}^{N_{L}}\sum_{j=1}^{N_{L}}\mathbb{I}(M_{y}[k,j]=1)\log\hat{M}_{rs}[k,:].
$$
社会福利最大化辅助损失可以帮助预测的行随机置换矩阵 $\hat{M}_{rs}$ 向最大化社会福利的方向收敛，并有效减少社会福利的下降
然后，NMA的最终训练损失为：
$$
L=L_{tgt}+\alpha_{1}L_{ce}+\alpha_{2}L_{list},
$$
- 其中 $\alpha_{1},\alpha_{2}$ 是用于平衡三个损失的系数。我们可以通过调整这两个参数的值来平衡NMA的性能，并确保NMA满足社会福利约束

Experiments

在本节中，论文在公共和工业数据集上进行了广泛的离线实验，并在美团外卖平台上进行了在线A/B测试，旨在回答以下研究问题：
- RQ1 ：与工业平台上广泛使用的拍卖机制相比，NMA在平台收入和社会福利方面的表现如何？
- RQ2 ：不同模块（即CLPM、LDRM、LDSM、社会福利最大化辅助损失）如何影响NMA的性能？
- RQ3 ：不同的关键超参数设置（即 $\alpha_{1},\alpha_{2}$ ）如何影响NMA的性能？

Experiment Setup

数据集

在离线实验中，论文在公共和工业数据集上提供了NMA有效性的经验证据。两个数据集的统计信息总结在表2中，论文详细描述这两个数据集如下：
- Avito ：公共Avito数据集来自avito.ru的用户搜索日志随机样本。每次搜索对应一个包含五个item的搜索页面，其中两个item有标签并被视为展示广告，其他三个被视为Organic Item。对于每个样本，论文构建候选广告集合 $\mathcal{A}$ ，其中包含用户点击的N-2个item和当前搜索中的2个展示广告，并通过全排列算法生成集合 $\Theta$ 。公共信息包括用户ID、搜索ID和搜索日期。每个item的特征包括itemID、类别ID和标题。每个广告的出价独立地从0.5到1.5的均匀分布中采样。这里论文使用20150428到20150515的数据作为训练集，20150516到20150520的数据作为测试集，以避免数据泄露
- Meituan ：工业Meituan数据集是在2022年4月期间在美团外卖平台上通过GSP拍卖收集的。每个请求转换的样本包括两部分：特征和标签。特征包括所有候选广告列表的信息和公共信息。这些候选广告列表是通过对展示广告集合进行全排列算法生成的。在一个广告列表中，每个广告的信息包括其出价和稀疏特征（如ID、类别、品牌等）。标签包括最终展示的广告列表、该列表的广告收入以及列表中每个广告的二进制点击标签。根据数据收集的日期，论文将数据集按8:2的比例划分为训练集和测试集

评估指标

论文构建了一个离线模拟系统，以确保离线和在线性能趋势一致。每个实验重复5次，使用不同的随机种子，每个结果以均值±标准差的形式呈现。论文在离线实验和在线A/B测试中考虑了以下指标。对于论文中的所有实验，实验结果都归一化到相同的尺度
- 点击率（CTR） ：CTR = $\frac{\sum click}{\sum impression}$
- 每千次展示收入（RPM） ：RPM = $\frac{\sum click\times payment}{\sum impression}\times 1000$
- 每千次展示社会福利（SWPM） ：SWPM = $\frac{\sum click\times bid}{\sum impression}\times 1000$
- 社会福利最大化比率（SWMR） ：SWMR = $\frac{\text{SWPM}}{\text{SWPM}^{+}}\times 100%$ ，其中SWPM ${}^{+}$ 是VCG的SWPM。论文优先考虑收入指标，同时也考虑社会福利指标，因为它是收入的上限。尽管VCG具有最高的社会福利，但其收入非常低。在实际工业场景中，社会福利可以在一定范围内减少，以确保最大收入。需要注意的是，由于实际广告收入与平台的隐私相关，论文转换了出价和支付的绝对值，仅显示RPM和SWPM的相对趋势
除了上述指标外，论文还评估了论文设计的多槽位拍卖机制在IC属性上的有效性

超参数

在Avito和Meituan数据集中，论文使用每个PV请求中展示的top- $K$ 广告（即 $K$ 槽位拍卖）的设置，并根据业务需求将 $\epsilon$ 设置为0.05。论文使用网格搜索尝试了NMA中的不同超参数。由于篇幅限制，论文仅展示最佳结果。在Avito数据集中， $d$ 为8， $\alpha_{1}$ 为0.2， $\tau$ 为1， $\alpha_{2}$ 为0.01，学习率为 $10^{-3}$ ，优化器为Adam，批量大小为1,024，MLP ${}_{\text{list}}$ 和MLP ${}_{\mu}$ 的隐藏层大小分别为 $(32,16,8)$ 和 $(32,8,1)$ 。在Meituan数据集中， $d$ 为8， $\tau$ 为0.1， $\alpha_{1}$ 为0.4， $\alpha_{2}$ 为0.3，学习率为 $10^{-3}$ ，优化器为Adam，批量大小为8,192，MLP ${}_{\text{list}}$ 和MLP ${}_{\mu}$ 的隐藏层大小分别为 $(60,32,10)$ 和 $(32,8,1)$ 。需要注意的是，实验中的广告数量 $N$ 和Organic Item数量 $M$ 被截断以简化。因此，在Avito数据集中， $K$ 为2， $N$ 为10， $M$ 为4；在Meituan数据集中， $K$ 为4， $N$ 为20， $M$ 为50。但显然，NMA可以扩展到具有更多广告和Organic Item的场景

基线

论文将NMA与以下四种代表性的拍卖机制进行比较，这些机制在工业广告平台上广泛使用：
- 广义第二价格拍卖（GSP） ：经典GSP中的排序分数简单地是出价乘以pCTR，即有效每千次展示成本（eCPM）。论文表示第 $i$ 个广告的排序分数为 $rs_{i}=bid_{i}\times pCTR_{i}$ 。其支付为 $p_{i}=rs_{i}^{-1}(rs_{i+1}(b+1))$ ，其中 $rs_{i+1}(b+1)$ 是下一个最高广告主的排序分数， $rs_{i}^{-1}$ 是 $r_{i}(\cdot)$ 的反函数
- 深度神经拍卖（DNA） ：DNA是基于GSP的端到端神经拍卖机制。DNA可以使用历史拍卖结果的真实反馈优化多个性能指标。在论文中，论文统一优化eCPM以确保DNA和NMA的公平比较。但值得注意的是，论文的实验结论很容易类比到具有多个性能指标的实验
- Vickrey-Clarke-Groves（VCG） ：具有外部性的VCG使用社会福利评估所有分配。具有最大社会福利的分配获胜，其支付规则为：获胜分配中的每个广告因其导致的社会福利损失而被收费，即没有该广告的最佳分配的社会福利与获胜分配的社会福利之间的差异
- 加权Vickrey-Clarke-Groves（WVCG） ：WVCG通过参数线性加权每个分配的社会福利，并使用MAB求解参数

离线实验

性能比较（RQ1）

论文构建了一个离线模拟系统，以确保离线和在线性能趋势一致。每个离线实验重复5次，使用不同的随机种子，每个结果以均值±标准差的形式呈现。论文在公共和工业数据集上的详细实验结果总结在表3中。与代表性拍卖机制相比，论文从实验结果中得出以下观察：i）直观上，NMA在两种数据集上的所有三个指标上都比DNA和GSP有显著改进。一个合理的解释是，NMA可以有效地建模全局外部性，而DNA仅建模了局部外部性。ii）与VCG相比，NMA在广告收入和社会福利之间有更好的平衡，这意味着NMA在较小的社会福利下降下实现了更高的广告收入。这也表明VCG以广告收入为代价最大化社会福利，这对大多数工业实践来说是不可接受的。iii）显然，WVCG在RPM方面被NMA压倒。这一实验结果验证了NMA强大的表达能力和高效的端到端学习能力
此外，论文还应用IC-R（表示效用最大化者的事后遗憾）来量化NMA的IC。IC-R的较大值表示广告主可以通过操纵出价获得更大的效用。例如，表4中的0.309表示广告主可以通过修改其出价在GFP拍卖中增加约30.9%的效用。具体来说，论文每次在Avito上进行 $2000\times 10$ 次测试，在Meituan上进行 $2000\times 25$ 次测试，其中2000是测试拍卖的数量，10（或25）是每次拍卖的广告数量。对于广告 $a_{i}$ ，论文仅将其出价 $b_{i}$ 替换为 $\beta\times b_{i}$ ，其中 $\beta\in{0.1,0.3,0.5,\cdots,1.9}$ 是乘法扰动因子。该拍卖中其他广告的所有特征和出价保持不变。基于上述设置，论文随机抽样数据并重复实验20次，以观察三种拍卖的IC-R。如表4所示，NMA与VCG具有相同的性能——两者都优于广义第一价格（GFP），这验证了NMA有效地满足了IC约束

消融研究（RQ2）

为了验证不同模块（即CLPM、LDRM、LDSM、社会福利最大化辅助损失）的影响，论文在Meituan数据集上研究了NMA的三个消融变*
- NMA (-CLPM) ：不使用上下文感知列表预测模块，并使用原始点级pCTR计算排序分数。对于具有相同排序分数的分配，论文随机选择一个作为获胜广告列表
- NMA (-LDRM-LDSM) ：同时屏蔽列表深度排序模块和列表可微分排序模块，并使用WVCG计算每个分配的排序分数和支付
- NMA (-SW Aux Loss) ：移除社会福利最大化的辅助损失，即 $\alpha_{2}=0$
从表6中的实验结果来看，论文有以下发现：i）没有CLPM的变体表现不如NMA。这一现象证明了论文提出的CLPM可以有效地建模全局外部性，并帮助NMA实现更好的性能。ii）NMA(-LDRM-LDSM)的实验结果在所有三个指标上都比NMA差。这支持了训练升级可以促进性能提升的观点。iii）有和没有社会福利最大化辅助损失的SWPM性能差距明显。这表明辅助损失使论文能够在最大化广告收入的同时减少社会福利的下降
此外，论文还观察了有和没有CLPM的AUC和Logloss指标，以验证CLPM在CTR预测方面的改进。如表5所示，CLPM在Avito和Meituan上分别比原始点级pCTR结果提高了0.006和0.016的AUC，这说明CLPM能够有效地建模全局外部性，并提高预测值的准确性

超参数分析（RQ3）

论文分析了两个超参数的敏感性： $\alpha_{1}$ 和 $\alpha_{2}$ 。具体来说， $\alpha_{1}$ 和 $\alpha_{2}$ 分别是社会福利最大化辅助损失和CLPM辅助损失的系数。RPM和SWPM的曲线如图3所示，论文有以下发现：i）随着 $\alpha_{1}$ 的增加，NMA的SWPM增加，但RPM下降。这一现象表明，论文的社会福利最大化辅助损失有助于NMA在广告收入和社会福利之间实现更好的平衡。当 $\alpha_{1}$ 增加时，论文更关注社会福利。当 $\alpha_{1}$ 减少时，论文更关注广告收入。ii）在一定范围内增加 $\alpha_{2}$ 可以提高性能。但如果 $\alpha_{2}$ 过大，会导致性能下降。一个可能的解释是，CLPM的辅助损失可以在一定范围内有效地引导NMA朝着目标方向学习。但如果辅助任务的权重过大，可能会导致学习方向被该任务主导，从而导致整体性能下降

在线结果

论文将NMA与GSP进行比较，并通过在线A/B测试将两种拍卖机制部署在美团外卖平台上。对于候选广告列表，论文使用全排列算法在线获取所有候选广告列表，超参数 $K$ 、 $N$ 、 $M$ 与离线相同。需要注意的是，在论文的基于位置的服务（LBS）场景中，广告数量 $N$ 非常少。因此，论文还将NMA扩展到具有大量广告的场景，以验证其可行性，其中论文使用一些列表生成算法来减少时间复杂度并近似生成候选广告列表
论文从2022年5月20日到2022年6月20日（一个月）进行了在线A/B测试，使用了1%的生产流量。在长期观察下，性能稳定。结果发现，CTR、RPM和SWPM分别增加了6.37%、10.88%和6.22% ，这表明NMA可以实现更高的平台收入和社会福利。值得注意的是，离线实验中的增加值为6.97%、11.20%和6.49%。绝对值差异的一些可能原因是数据分布的差异和离线评估中的小误差

结论

一句话总结 ：论文提出了具有外部性的神经多槽位拍卖（NMA），旨在为在线广告学习端到端的多槽位拍卖机制，并在减少社会福利下降的同时获得更高的收入
细节简述 ：具体来说，论文通过上下文感知列表预测模块有效地建模了全局外部性。论文设计了一个列表深度排序模块，以确保端到端学习中的IC；论文还提出了一个社会福利最大化的辅助损失，以在最大化收入的同时有效减少社会福利的下降
应用情况 ：作者已将NMA机制部署在美团外卖平台上。离线实验结果和在线A/B测试表明，NMA显著优于其他现有的拍卖机制基线
一些讨论 ：论文中提到，全排列可以替换为列表生成模块 ，如启发式方法，这可以满足工业部署需求（全排列需要搜索的空间大，耗时长），但这可能会对有效性产生影响
未来：未来需要进一步优化以提高方案线上serving的效率

Joe Zhou

Stay Hungry. Stay Foolish.

GitHub E-Mail