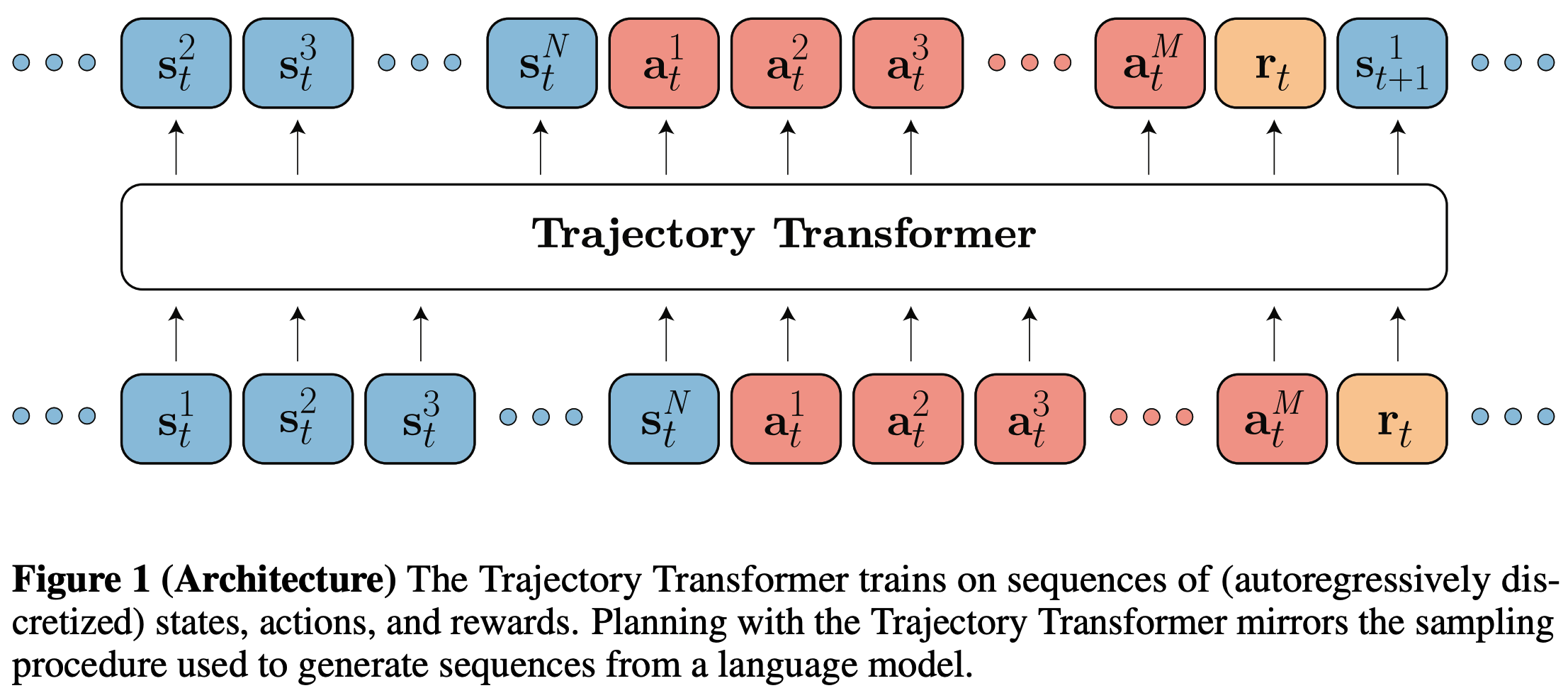
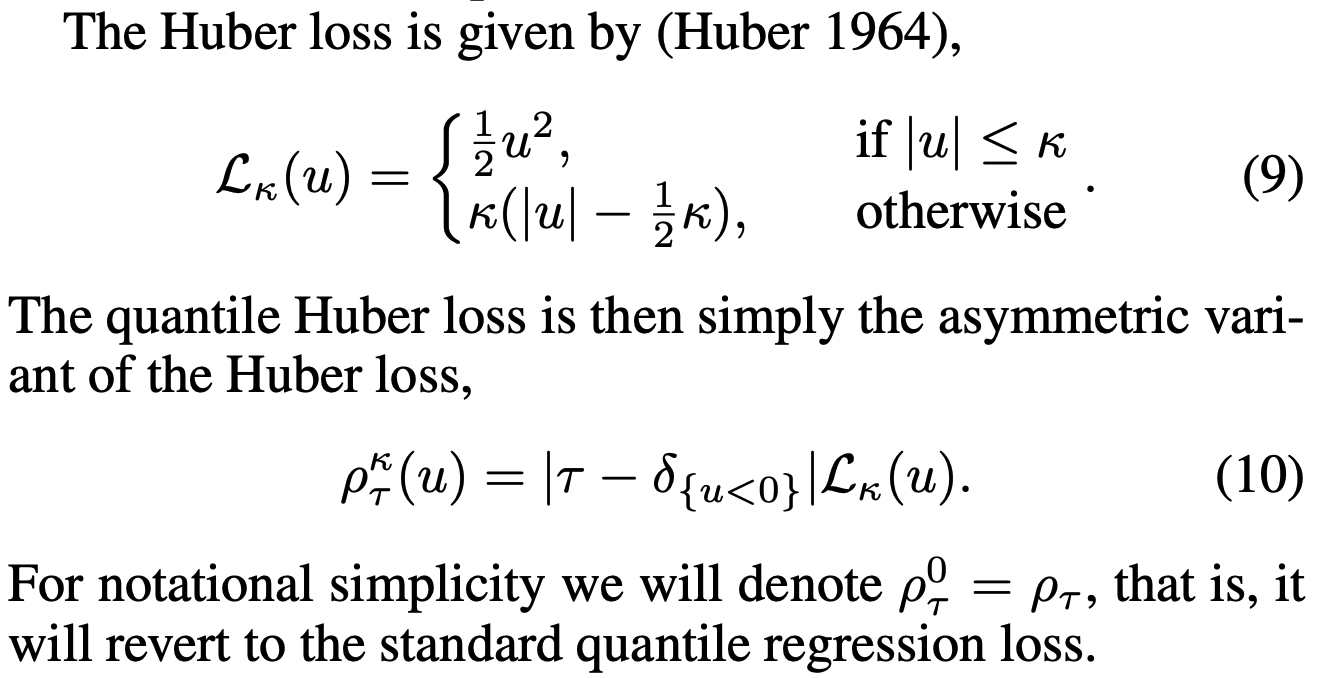SAC
- 原始论文:
- 论文1(2V+2Q+1策略, 2018,UC Berkeley):Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor
- 论文2(4Q+1策略,自适应温度系数,2019,UC Berkeley):Soft Actor-Critic Algorithms and Applications
相关推导
- 目标定义
$$ J(\phi) = \sum_{t=0}^T \mathbb{E}_{(s_t, a_t) \sim \rho_{\pi_\phi}} [r(s_t, a_t) + \alpha \mathcal{H}(\pi_\phi(\cdot \vert s_t))] $$- 这里目标中增加的熵就是Soft名字的来源
- Q值V值定义
$$
\begin{aligned}
Q(s_t, a_t) &= r(s_t, a_t) + \gamma \mathbb{E}_{s_{t+1} \sim p(\cdot|s_t,a_t)} [V(s_{t+1})] \\
V(s_t) &= \mathbb{E}_{a_t \sim \pi} [Q(s_t, a_t) - \alpha \log \pi(a_t \vert s_t)] \\
\end{aligned}
$$
SAC(2V+2Q+1策略)
- 原始论文:Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor
- 目标定义见上面部分,由于温度系数 \(\alpha\) 是一个固定的超参数,于是,当我们可以通过将Reward乘以 \(\frac{1}{\alpha}\) 来Rescaling Reward,使得熵的系数为1,所以本论文后面的推导都可以将 \(\alpha=1\) 来推导
- 网络结构
- 一个V网络及其对应的一个Target V网络,两个Q网络(Twin Q),一个策略网络
- 由于存在V网络和Target V网络,不需要Q网络的Target Q网络了
- 训练流程

- 原始论文的伪代码中没有强调Twin Q的使用,但源码实现更新V网络时有使用Twin Q的思想,更新V网络时使用的是两个Q网络中各个动作上的较小者,用于防止V的估计过高
- 引申问题:策略更新时是否需要使用Twin Q中的较小者计算损失函数呢?
- SAC作者开源的源码中没有使用Twin Q(SAC(V)-原论文开源实现),包括强化学习之图解SAC算法中也没有使用Twin Q,都仅使用了一个Q网络计算策略损失函数,但其他开源实现中许多都取Twin Q的最小值作为损失函数
- 注:Target V网络为软更新
Soft Policy Evaluation
- V值更新:
$$
\begin{aligned}
J_V(\psi) &= \mathbb{E}_{s_t \sim \mathcal{D}} [\frac{1}{2} \big(V_\psi(s_t) - \mathbb{E}_{a_t \sim \pi_\phi}[Q_\theta(s_t, a_t) - \log \pi_\phi(a_t \vert s_t)] \big)^2] \\
\nabla_\psi J_V(\psi) &= \nabla_\psi V_\psi(s_t)\big( V_\psi(s_t) - Q_\theta(s_t, a_t) + \log \pi_\phi (a_t \vert s_t) \big)
\end{aligned}
$$ - Q值更新:
$$
\begin{aligned}
J_Q(\theta) &= \mathbb{E}_{(s_t, a_t) \sim \mathcal{D}} [\frac{1}{2}\big( Q_\theta(s_t, a_t) - (r(s_t, a_t) + \gamma \mathbb{E}_{s_{t+1} \sim p(\cdot|s_t,a_t)}[V_{\bar{\psi}}(s_{t+1})]) \big)^2] \\
\nabla_\theta J_Q(\theta) &= \nabla_\theta Q_\theta(s_t, a_t) \big( Q_\theta(s_t, a_t) - r(s_t, a_t) - \gamma V_{\bar{\psi}}(s_{t+1})\big)
\end{aligned}
$$- 策略评估(Q值和V值的更新过程统称为策略评估过程)的收敛性证明 :
- 定义回报为 \(r_\pi(s_t, a_t) \triangleq r(s_t, a_t) + \alpha \mathbb{E}_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}[\mathcal{H}(\pi(\cdot\vert s_{t+1}))]\) (注意:其中 \(p(s_{t+1}|s_t,a_t)\) 在论文中常简写为 \(p\) 或 \(p(\cdot|s_t,a_t)\),在不影响理解的情况下,可以混用)
- 则有: \(Q(s_t, a_t) = r_\pi(s_t, a_t) + \gamma \mathbb{E}_{s_{t+1}\sim p(s_{t+1}|s_t,a_t), a_{t+1}\sim\pi}[Q(s_{t+1},a_{t+1})]\)
- 此时有贝尔曼算子(Bellman backup operator) \(\mathcal{T}^\pi\) 为: \(\mathcal{T}^\pi Q(s_t, a_t) \triangleq r(s_t, a_t) + \gamma \mathbb{E}_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}[V(s_{t+1})]\)
- 其中 \(V(s_{t}) = \mathbb{E}_{a_t \sim \pi}[Q(s_t, a_t) - log\pi(a_t|s_t)]\)
- 贝尔曼算子 \(\mathcal{T}^\pi\) 是一种操作符,它表示对当前的价值函数集Q利用贝尔曼方程进行更新
- Lemma 1 (Soft Policy Evaluation) : 按照上式定义的 \(\mathcal{T}^\pi\),当动作维度 \(|\mathcal{A}|<\infty\) 时, \(Q^{k+1} = \mathcal{T}^\pi Q^{k}\) 会收敛到策略 \(\pi\) 对应的soft Q-value
- 问题这里的动作维度有限,是否说明连续动作是不可以的?证明中哪里用到了动作有限?
- Lemma 1 (Soft Policy Evaluation)中引用的论文证明需要保证动作空间有限,从而保证熵是有界的,此时可以保证加入熵以后的reward还是可以收敛的
apply the standard convergence results for policy evaluation (Sutton & Barto, 1998). The assumption |A| < ∞ is required to guarantee that the entropy augmented reward is bounded.
- 连续动作的熵如果是有界的理论上也可以?
- Lemma 1 (Soft Policy Evaluation)中引用的论文证明需要保证动作空间有限,从而保证熵是有界的,此时可以保证加入熵以后的reward还是可以收敛的
- 问题这里的动作维度有限,是否说明连续动作是不可以的?证明中哪里用到了动作有限?
- 策略评估(Q值和V值的更新过程统称为策略评估过程)的收敛性证明 :
Soft Policy Improvement
策略更新目标推导(新策略本质是在拟合函数Q的玻尔兹曼分布,后续有相关证明这种方式得到的新策略一定优于旧策略):
$$
\begin{aligned}
\pi_\text{new}
&= \mathop{\arg\min}_{\pi’ \in \Pi} \mathbb{E}_{s_t \sim \mathcal{D}} \Big[ D_\text{KL} \Big( \pi’(\cdot\vert s_t) | \frac{\exp(Q^{\pi_\text{old}}(s_t, \cdot))}{Z^{\pi_\text{old}}(s_t)} \Big) \Big] \\[6pt]
&= \mathop{\arg\min}_{\pi’ \in \Pi} \mathbb{E}_{s_t \sim \mathcal{D}} \Big[ D_\text{KL} \big( \pi’(\cdot\vert s_t) | \exp(Q^{\pi_\text{old}}(s_t, \cdot) - \log Z^{\pi_\text{old}}(s_t)) \big) \Big] \\[6pt]
\text{目标函数: } J_\pi(\phi) &= \mathbb{E}_{s_t \sim \mathcal{D}} \Big[ D_\text{KL} \big( \pi_\phi(\cdot\vert s_t) | \exp(Q_\theta(s_t, \cdot) - \log Z_w(s_t)) \big) \Big] \\[6pt]
&= \mathbb{E}_{s_t \sim \mathcal{D}, a_t\sim\pi_\phi} \Big[ \log \big( \frac{\pi_\phi(a_t \vert s_t)}{\exp(Q_\theta(s_t, a_t) - \log Z_w(s_t))} \big) \Big] \\[6pt]
&= \mathbb{E}_{s_t \sim \mathcal{D}, a_t\sim\pi_\phi} [ \log \pi_\phi(a_t \vert s_t) - Q_\theta(s_t, a_t) + \log Z_w(s_t) ]
\end{aligned}
$$- Lemma 2 (Soft Policy Improvement),详细证明见附录:
- 若新策略 \(\pi_\text{new}\) 定义为 \(
\pi_\text{new} = \mathop{\arg\min}_{\pi’ \in \Pi} D_\text{KL} \Big( \pi’(\cdot\vert s_t) | \frac{\exp(Q^{\pi_\text{old}}(s_t, \cdot))}{Z^{\pi_\text{old}}(s_t)} \Big)\) - 则有 \(Q^{\pi_\text{new}}(s_t, a_t) \ge Q^{\pi_\text{old}}(s_t, a_t), \quad \forall (s_t, a_t) \in \mathcal{S} \times \mathcal{A}\)
- 若新策略 \(\pi_\text{new}\) 定义为 \(
- Lemma 2 (Soft Policy Improvement),详细证明见附录:
由于 \(\log Z_w(s_t)\) 与参数 \(\phi\) 无关,梯度为0,故而可以消掉 \(\log Z_w(s_t)\),最终得到SAC离散策略的的更新目标(实现时,离散版本是可以直接按照动作概率加权求和得到期望的):
$$
J_\pi(\phi) = \mathbb{E}_{s_t \sim \mathcal{D}, a_t\sim\pi_\phi} [ \log \pi_\phi(a_t \vert s_t) - Q_\theta(s_t, a_t) ]
$$SAC连续动作的策略更新目标 ,首先需要采用重参数法建模连续动作 \(a_t = f_\phi(\epsilon_t; s_t)\),然后有:
$$
J_\pi(\phi) = \mathbb{E}_{s_t \sim \mathcal{D}, \epsilon_t \sim \mathcal{N}}[\log \pi_\phi(f_\phi(\epsilon_t;s_t)\vert s_t) - Q_\theta(s_t, f_\phi(\epsilon_t; s_t))]
$$- \(f_\phi(\epsilon_t;s_t)\) 是中按照策略 \(\pi_\phi\) 输出的均值方差通过采样(重参数化技术)得到的,可以回传梯度
- \(\log \pi_\phi(f_\phi(\epsilon_t;s_t)\vert s_t)\) 是概率密度函数 \(\pi_\phi(\cdot|s_t)\) 的对数,也可以回传梯度,注意这里的梯度回传包含了 \(\pi_\phi\) 和 \(f_\phi\) 都需要回传回去,由于只需要定义一个 \(f_\phi\) 后, \(\pi_\phi\) 自然也就被定义出来了,无需重新定义参数,所以 \(\pi_\phi\) 和 \(f_\phi\) 共用了参数
- 上述损失函数的近似梯度(移除期望)可以是:
$$ \hat{\nabla}_\phi J_\pi(\phi) = \nabla_\phi \log \pi_\phi(\mathbf{a_t} \vert s_t) + (\nabla_{\mathbf{a_t}} \log \pi_\phi(\mathbf{a_t} \vert s_t) - \nabla_{\mathbf{a_t}} Q(s_t, \mathbf{a_t})) \nabla_\phi f_\phi(\epsilon_t; s_t) $$- 论文中伪代码没有显示指定 \(\nabla_{\mathbf{a_t}} Q(s_t, \mathbf{a_t})\) 中的Q是什么值,实际上实现时,使用的是Twin Q的最小值
Soft Policy Iteration
- Theorem 1 (Soft Policy Iteration). 重复应用上面的Soft Policy Evaluation 和 Soft Policy Improvement,最终策略 \(\pi\) 会收敛到最优策略 \(\pi^*\),使得 \(Q^{\pi^*}(s_t, a_t) \ge Q^{\pi}(s_t, a_t)\) 对所有的 \(\pi \in \Pi\) 和 \((s_t, a_t) \in \mathcal{S} \times \mathcal{A}\) 成立
- 原始论文中有证明,实际上可以表述为“单调有界,所以收敛:Soft Q单调有界,所以会收敛到一个最优的Soft Q,对应的就是最优策略”
SAC(4Q+1策略)
原始论文:Soft Actor-Critic Algorithms and Applications
- 本论文是第一篇论文的改进版本,主要改进是允许温度系数 \(\alpha\) 变得可学习
- 由于 \(\alpha\) 是一个是可学习的变量,所以不再可以像之前的论文一样,通过将Reward乘以 \(\frac{1}{\alpha}\) 来Rescaling Reward,使得熵的系数为1。所以本论文后面的推导都可以将带着 \(\alpha\)
网络结构
- 两个Q网络(Twin Q)及其分别对应的Target Q网络,一个策略网络
- 两个Q网络分别迭代,有各自的Target Q网络
训练流程(下图中,离散策略更新使用的损失函数是 \(\color{red}{Q(s_t,a_t)}\) 而不是 \(\color{blue}{Q(s_t,s_t)}\))

- 注:Target Q网络为软更新
Q值更新:
$$
\begin{aligned}
J_Q(\theta) &= \mathbb{E}_{(s_t, a_t) \sim \mathcal{D}} [\frac{1}{2}\big( Q_\theta(s_t, a_t) - (r(s_t, a_t) + \gamma \mathbb{E}_{s_{t+1} \sim p, a_{t+1} \sim \pi_\phi}(Q_\bar{\theta}(s_{t+1}, a_{t+1}) - \alpha \log \pi_\phi(a_{t+1} \vert s_{t+1}))) \big)^2] \\
\end{aligned}
$$- 论文中没有明确,但实际实现时, \(Q_\bar{\theta}(s_{t+1}, a_{t+1})\) 使用的是Twin Q中的较小值
策略更新(在前一篇文章的基础上,增加 \(\alpha\) 即可):
- SAC离散策略的的更新目标 :
$$
J_\pi(\phi) = \mathbb{E}_{s_t \sim \mathcal{D}, a_t\sim\pi_\phi} [ \alpha \log \pi_\phi(a_t \vert s_t) - Q_\theta(s_t, a_t) ]
$$ - SAC连续动作的策略更新目标 ,首先需要采用重参数法建模连续动作 \(a_t = f_\phi(\epsilon_t; s_t)\),然后有:
$$
J_\pi(\phi) = \mathbb{E}_{s_t \sim \mathcal{D}, \epsilon_t \sim \mathcal{N}}[\alpha \log \pi_\phi(f_\phi(\epsilon_t;s_t)\vert s_t) - Q_\theta(s_t, f_\phi(\epsilon_t; s_t))]
$$ - \(f_\phi(\epsilon_t;s_t)\) 是中按照策略 \(\pi_\phi\) 输出的均值方差通过采样(重参数化技术)得到的,可以回传梯度
- \(\log \pi_\phi(f_\phi(\epsilon_t;s_t)\vert s_t)\) 是概率密度函数 \(\pi_\phi(\cdot|s_t)\) 的对数,也可以回传梯度,注意这里的梯度回传包含了 \(\pi_\phi\) 和 \(f_\phi\) 都需要回传回去,由于只需要定义一个 \(f_\phi\) 后, \(\pi_\phi\) 自然也就被定义出来了,无需重新定义参数,所以 \(\pi_\phi\) 和 \(f_\phi\) 共用了参数
- 上述损失函数的近似梯度(移除期望)可以是:
$$ \hat{\nabla}_\phi J_\pi(\phi) = \nabla_\phi \alpha \log \pi_\phi(\mathbf{a_t} \vert s_t) + (\nabla_{\mathbf{a_t}} \alpha \log \pi_\phi(\mathbf{a_t} \vert s_t) - \nabla_{\mathbf{a_t}} Q(s_t, \mathbf{a_t})) \nabla_\phi f_\phi(\epsilon_t; s_t) $$- 论文中伪代码没有显示指定 \(\nabla_{\mathbf{a_t}} Q(s_t, \mathbf{a_t})\) 中的Q是什么值,实际上实现时,使用的是Twin Q的最小值
- SAC离散策略的的更新目标 :
温度系数 \(\alpha\) 自动更新:
将强化学习的目标改成:
$$
\begin{align}
\max_{\pi_0, \dots, \pi_T} \mathbb{E}_{\rho_\pi} &\Big[ \sum_{t=0}^T r(s_t, a_t)\Big] \\
\text{s.t. } \forall t\text{, } &\mathcal{H}(\pi_t) \geq \mathcal{H}_0 \\
\end{align}
$$即:
$$
\begin{align}
\max_{\pi_0, \dots, \pi_T} \mathbb{E}_{\rho_\pi} &\Big[ \sum_{t=0}^T r(s_t, a_t)\Big] \\
\text{s.t. } \forall t\text{, } \mathbb{E}_{(s_t, a_t) \sim \rho_{\pi_t}}&[-\log(\pi_t(a_t|s_t))] \geq \mathcal{H}_0
\end{align}
$$- 其中 \(\mathcal{H}_0 \) 是一个期望的最小熵阈值
经过一系列的数学推导,可得 \(\alpha\) 的更新目标为:
$$J(\alpha) = \mathbb{E}_{a_t \sim \pi_t} [-\alpha \log \pi_t(a_t \mid s_t) - \alpha \mathcal{H}_0]$$实践:
从实践经验来看,可以设置 \(\mathcal{H}_0 = -dim(\mathcal{A})\),跟动作空间维度相关(注意不是动作的数量,而是动作的维度,单维的离散动作维度应该是1,单维连续动作的维度也应该是1,比如HalfCheetah-v1动作对应六个关节的扭矩控制输入,故而动作维度是6)
1
2
3
4### 连续动作:
target_entropy = - env.action_space.shape[0]
### 离散动作:
target_entropy = -1温度系数自动调整方案不一定优于固定温度系数方案,在不同场景下效果不同,详情见原始论文
SAC连续动作与离散动作的实现有什么区别
建模方式
策略网络 :连续动作需要使用 \(\mu_\phi,\sigma_\phi\) 表示均值和方差,连续分布下,每个动作的概率理论上都是0,但借助概率密度函数的含义,可以通过计算概率密度来使用
采样方式 :采样时需要创建分布来采样,由于需要梯度回传,所以需要使用重参数法
log_prob的计算 :借助概率密度函数定义完成log值的抽取
连续策略对应的动作采样和对数概率计算:1)重参数法;2)tanh转换;3)对数概率计算
1
2
3
4
5
6
7
8
9
10
11
12def forward(self, x):
x = F.relu(self.fc1(x))
mu = self.fc_mu(x)
std = F.softplus(self.fc_std(x))
dist = Normal(mu, std)
normal_sample = dist.rsample() # rsample()是重参数化采样
log_prob = dist.log_prob(normal_sample)
action = torch.tanh(normal_sample)
# 计算tanh_normal分布的对数概率密度
log_prob = log_prob - torch.log(1 - torch.tanh(action).pow(2) + 1e-7)
action = action * self.action_bound
return action, log_prob这里关于
log_prob = log_prob - torch.log(1 - torch.tanh(action).pow(2) + 1e-7)是一个推导得到的,若 \(y = tanh(x)\),那么有 \(\log p(y) = \log p(x) - \log(1-(tanh(x))^2)\)使用
action = torch.tanh(normal_sample)的原因是想将原来的值放缩到 \([-1,1]\) 之间,防止原始高斯分布采样到非常离谱的动作
Critic网络 :连续动作下,需要将动作放到输入侧,输出维度为1;离散动作下,可以像连续时一样处理,也可以不输入动作,同时输出维度为动作维度
计算损失函数
熵+目标的计算(最大化Q值)的计算 :
连续场景下(最大化动作下的Q值,梯度直接包含在重参数法采样的动作中;熵则仅使用对数概率,因为连续分布下,难以积分,虽然状态不同,但多个动作自然一起优化,自然就有期望熵的含义了)
1
2
3
4
5new_actions, log_prob = self.actor(states) # 重参数法
entropy = -log_prob
q1_value = self.critic_1(states, new_actions)
q2_value = self.critic_2(states, new_actions)
actor_loss = torch.mean(-self.log_alpha.exp() * entropy - torch.min(q1_value, q2_value))离散场景下(用策略输出的分布计算Q值期望;熵也是完整的期望版本)
1
2
3
4
5
6
7
8probs = self.actor(states)
log_probs = torch.log(probs + 1e-8)
# 直接根据概率计算熵
entropy = -torch.sum(probs * log_probs, dim=1, keepdim=True) #
q1_value = self.critic_1(states)
q2_value = self.critic_2(states)
min_qvalue = torch.sum(probs * torch.min(q1_value, q2_value), dim=1, keepdim=True) # 直接根据概率计算期望
actor_loss = torch.mean(-self.log_alpha.exp() * entropy - min_qvalue)
SAC的连续和离散动作的思考
- SAC的一个核心创新是使用玻尔兹曼分布去作为策略分布,这使得SAC可以拟合多峰情况,但是对于连续动作的场景中,SAC选择了输出一个高斯分布,也就是让高斯趋近于玻尔兹曼分布。高斯是一个单峰的分布,这意味着连续动作的SAC本质上还是单峰(Unimodal)的算法,而不是soft q-learning的多峰(Multi-modal)
- 离散情况下,确实可以拟合多峰分布
SAC必须是随机策略吗?
- 是的,确定性策略熵太小,SAC适用于随机策略
- 问题一:如果SAC直接像DQN一样按照 \(\mathop{\arg\max}_a Q(s,a)\) 选择动作而不是玻尔兹曼分布会怎样?
- 回答:确定性动作的熵为0,所以熵不再有用,整个SAC会退化成DQN
- 问题二:如果DQN像SAC一样做玻尔兹曼分布会怎样?
- 回答:得到的策略不再是最优的,决策到的不再是Q值最大的动作【TODO】
为什么最大熵能带来收益呢?
- 所有可能的模型中熵最大的模型是最好的模型 :这意味着在给定的信息下,模型的选择应该尽可能地保持不确定性,即不做不必要的假设
- 熵与正则化 :机器学习/深度学习模型容易过拟合,主要原因是数据不足,建模太复杂等,增加一些正则可以降低过拟合,最大熵可以理解为一种正则
- 在普通机器学习中收益来源 :主要是防止过拟合(不做不必要的假设)
- 在强化学习中收益来源 :一方面是防止过拟合,另一方面是让探索更加充分
SAC vs AC中添加entropy loss?
- SAC将原始AC的目标修改了,理论上目标就是让熵和reward一起最优,Critic网络和策略网络学习的目标都包含了最大化熵
- AC 中加入 entropy loss则只是一种正则,在损失函数上对熵进行了一些约束,此时Critic网络学不到熵的信息(此时AC的Actor目标和Critic目标不完全一致)
DSAC(Distributional SAC)
- 背景:SAC是基于值学习的方法,值学习方法往往存在值过估计问题,即算法倾向于高估某些状态-动作对的价值,从而影响学习性能
- DSAC通过引入值分布的方法来解决值过估计问题
- DSAC 还引入了三个重要改进,包括:
- Expected Value Substituting
- Variance-Based Critic Gradient Adjusting
- Twin Value Distribution Learning
附录:新策略一定优于旧策略的证明
- 证明目标(Lemma 2 (Soft Policy Improvement)):
- 若新策略 \(\pi_\text{new}\) 定义为:
$$
\pi_\text{new} = \mathop{\arg\min}_{\pi’ \in \Pi} D_\text{KL} \Big( \pi’(\cdot\vert s_t) | \frac{\exp(Q^{\pi_\text{old}}(s_t, \cdot))}{Z^{\pi_\text{old}}(s_t)} \Big)
$$ - 则有:
$$
Q^{\pi_\text{new}}(s_t, a_t) \ge Q^{\pi_\text{old}}(s_t, a_t), \quad \forall (s_t, a_t) \in \mathcal{S} \times \mathcal{A}
$$
- 若新策略 \(\pi_\text{new}\) 定义为:
- 证明:
- 由之前的定义我们有:
$$
\begin{align}
\pi_\text{new}
&= \mathop{\arg\min}_{\pi’ \in \Pi} D_\text{KL} \Big( \pi’(\cdot\vert s_t) | \frac{\exp(Q^{\pi_\text{old}}(s_t, \cdot))}{Z^{\pi_\text{old}}(s_t)} \Big) \\[6pt]
&= \mathop{\arg\min}_{\pi’ \in \Pi} D_\text{KL} \big( \pi’(\cdot\vert s_t) | \exp(Q^{\pi_\text{old}}(s_t, \cdot) - \log Z^{\pi_\text{old}}(s_t)) \big) \\[6pt]
&= \mathop{\arg\min}_{\pi’ \in \Pi} \mathbb{E}_{a_t\sim\pi’} \Big[ \log \big( \frac{\pi’(a_t \vert s_t)}{\exp(Q^{\pi_\text{old}}(s_t, a_t) - \log Z^{\pi_\text{old}}(s_t))} \big) \Big] \\[6pt]
&= \mathop{\arg\min}_{\pi’ \in \Pi} \mathbb{E}_{a_t\sim\pi’} [ \log \pi’(a_t \vert s_t) - Q^{\pi_\text{old}}(s_t, a_t) + \log Z^{\pi_\text{old}}(s_t) ]
\end{align}
$$ - 于是有:
$$
\mathbb{E}_{a_t\sim\pi_\text{new}} [ \log \pi_\text{new}(a_t \vert s_t) - Q^{\pi_\text{old}}(s_t, a_t) + \log Z^{\pi_\text{old}}(s_t) ] \le \mathbb{E}_{a_t\sim\pi_\text{old}} [ \log \pi_\text{old}(a_t \vert s_t) - Q^{\pi_\text{old}}(s_t, a_t) + \log Z^{\pi_\text{old}}(s_t) ]
$$ - 由于 \(\log Z^{\pi_\text{old}}(s_t)\) 与策略无关,仅与状态有关,所以可以消掉,于是有:
$$
\begin{align}
\mathbb{E}_{a_t\sim\pi_\text{new}} [ \log \pi_\text{new}(a_t \vert s_t) - Q^{\pi_\text{old}}(s_t, a_t)] &\le \mathbb{E}_{a_t\sim\pi_\text{old}} [ \log \pi_\text{old}(a_t \vert s_t) - Q^{\pi_\text{old}}(s_t, a_t)] \\
- \mathbb{E}_{a_t\sim\pi_\text{new}} [ \log \pi_\text{new}(a_t \vert s_t) - Q^{\pi_\text{old}}(s_t, a_t)] &\ge - \mathbb{E}_{a_t\sim\pi_\text{old}} [ \log \pi_\text{old}(a_t \vert s_t) - Q^{\pi_\text{old}}(s_t, a_t)] \\
\mathbb{E}_{a_t\sim\pi_\text{new}} [Q^{\pi_\text{old}}(s_t, a_t) - \log \pi_\text{new}(a_t \vert s_t)] &\ge \mathbb{E}_{a_t\sim\pi_\text{old}} [Q^{\pi_\text{old}}(s_t, a_t) - \log \pi_\text{old}(a_t \vert s_t) ] \\
\mathbb{E}_{a_t\sim\pi_\text{new}} [Q^{\pi_\text{old}}(s_t, a_t) - \log \pi_\text{new}(a_t \vert s_t)] &\ge V^{\pi_\text{old}}(s_t)\\
\end{align}
$$ - 于是,将 \(Q^{\pi_\text{old}}(s_t, a_t)\) 展开后,并将上面的式子 \(V^{\pi_\text{old}}(s_t) \le \mathbb{E}_{a_t\sim\pi_\text{new}} [Q^{\pi_\text{old}}(s_t, a_t) - \log \pi_\text{new}(a_t \vert s_t)]\) 不断地带入下面的式子有:
$$
\begin{align}
Q^{\pi_\text{old}}(s_t, a_t) &= r(s_t, a_t) + \gamma \mathbb{E}_{s_{t+1} \sim p} [V^{\pi_\text{old}}(s_t)] \\
&\le r(s_t, a_t) + \gamma \mathbb{E}_{s_{t+1} \sim p} \big[\mathbb{E}_{a_{t+1}\sim\pi_\text{new}} [Q^{\pi_\text{old}}(s_{t+1}, a_{t+1}) - \log \pi_\text{new}(a_{t+1} \vert s_{t+1})]\big] \\
&\cdots \\
&\le Q^{\pi_\text{new}}(s_t, a_t)
\end{align} \\
$$- 不断带入 \(V^{\pi_\text{old}}(s_t) \le \mathbb{E}_{a_t\sim\pi_\text{new}} [Q^{\pi_\text{old}}(s_t, a_t) - \log \pi_\text{new}(a_t \vert s_t)]\),最后所有的采样策略都会变成新策略,对应的值也就是 \(Q^{\pi_\text{new}}(s_t, a_t)\) 了
- 证毕.
- 由之前的定义我们有:
附录:证明tanh变换后的对数概率密度
- 为了证明给定的关系式 \(\log p(y) = \log p(x) - \log(1-(\tanh(x))^2)\),我们需要理解这个关系式的背景。这里 \(p(x)\) 和 \(p(y)\) 分别表示随机变量 \(X\) 和 \(Y\) 的概率密度函数(PDF),其中 \(Y = \tanh(X)\)
- 根据概率论中的变换法则,如果我们有一个随机变量 \(X\) 和一个单调可微的函数 \(g\),那么新的随机变量 \(Y = g(X)\) 的概率密度函数 \(p_Y(y)\) 可以通过原随机变量 \(X\) 的概率密度函数 \(p_X(x)\) 以及变换函数 \(g\) 的导数来计算。具体来说,有:
$$ p_Y(y) = p_X(x) \left| \frac{dx}{dy} \right| $$- 上面的式子可以通过概率论推导得到:
- 概率累积分布定义: \( F_Y(y) = P(Y \leq y) = P(g(X) \leq y) \)
- 如果 \(g\) 是单调增加的,则 \(P(g(X) \leq y) = P(X \leq g^{-1}(y))\) ;如果 \(g\) 是单调减少的,则 \(P(g(X) \leq y) = P(X \geq g^{-1}(y))\) 。这里假设 \(g\) 是单调增加的,因此: \( F_Y(y) = P(X \leq g^{-1}(y)) = F_X(g^{-1}(y))\)
- 所以有:
$$
\begin{align}
p_Y(y) &= \frac{d}{dy} F_Y(y) = \frac{d}{dy} F_X(g^{-1}(y)) \\
&= f_X(g^{-1}(y)) \cdot \frac{d}{dy} g^{-1}(y) = f_X(x) \cdot \frac{d}{dy} x \\
&= f_X(x) \cdot \frac{dx}{dy}
\end{align}
$$- 其中 \(x = g^{-1}(y)\) 是反函数,这里的 \(\frac{dx}{dy}\) 中,实际上 \(x\) 是 \(y\) 的函数,即写成 \(\frac{dx(y)}{dy}\) 更合适
- 对于不确定 \(g\) 是否单调的情况,需要加绝对值符号
- 上面的式子可以通过概率论推导得到:
- 在这个特定的情况下, \(g(x) = \tanh(x)\),所以 \(y = \tanh(x)\) 。为了找到 \(p_Y(y)\),我们需要计算 \(g\) 的导数,即 \(\tanh(x)\) 的导数:
$$ \frac{d}{dx}\tanh(x) = 1 - \tanh^2(x) $$ - 因此,我们可以将上述变换法则应用于此情况:
$$ p_Y(y) = p_X(x) \left| \frac{dx}{dy} \right| $$ - 因为 \(y = \tanh(x)\),所以 \(x = \tanh^{-1}(y)\),从而:
$$ \frac{dx}{dy} = \frac{d}{dy}\tanh^{-1}(y) = \frac{1}{1-y^2} $$- \(\frac{dx}{dy}\) 表示x对y求导,也是x对y的斜率(所以时除法),所以有 \(\frac{dy}{dx} = 1 - \tanh^2(x) \) 推出 \(\frac{dx}{dy} = \frac{1}{1 - \tanh^2(x)} = \frac{1}{1 - y^2}\)
- 代入上面的概率密度变换公式中,我们得到:
$$ p_Y(y) = p_X(x) \left| \frac{1}{1-\tanh^2(x)} \right| $$ - 由于 \(1 - \tanh^2(x)\) 总是正的(对于所有实数 \(x\) ),我们可以去掉绝对值符号:
$$ p_Y(y) = \frac{p_X(x)}{1-\tanh^2(x)} $$ - 取对数两边,得到:
$$ \log p_Y(y) = \log p_X(x) - \log(1-\tanh^2(x)) $$ - 这正是我们要证明的等式:
$$ \log p(y) = \log p(x) - \log(1-(\tanh(x))^2) $$ - 证毕.
SAC为什么可以是off-policy的?
- SAC与DQN,DDPG一样,思路是一致的。详情参考:RL——强化学习相关笔记