注:本文包含 AI 辅助创作
- 参考链接:
Paper Summary
- 整体总结:
- Rubrics as Rewards (RaR) 是一个使用结构化、清单式 rubrics 作为奖励信号来对语言模型进行后训练的框架
- Rubric-guided 的训练在各个领域都实现了强劲的性能,显著优于基于 Likert 的基线,并达到或超过了基于参考的奖励生成方法的性能
- 背景 & 问题提出:
- 其他工作已证明 RLVR 对具有明确正确性信号(如数学和编码)的复杂推理任务有效
- 但将其扩展到现实世界的推理任务具有挑战性
- 因为评估依赖于微妙、多标准的判断,而非二元正确性(n, multi-criteria judgments rather than binary correctness)
- Instance-specific rubrics 最近被用于评估基准中以捕捉此类判断,但尚未充分探索奖 Rubrics 用于 On-policy 后训练的奖励信号
- 论文介绍了一种 On-policy 强化学习方法 Rubrics as Rewards(RaR)
- 通过使用 Rubric-based 反馈,将 RLVR 扩展到可验证领域之外
- 在医学和科学领域,论文评估了多种将 Rubric 反馈聚合成奖励的策略
- 最佳的 RaR 变体在 HealthBench 上实现了高达 31% 的相对提升,在 GPQA-Diamond 上相比流行的、依赖直接 Likert-based 奖励的 LLM-as-judge 基线提升了 7%
- 问题:这里的 Likert-based 奖励是人工专家打分吗?
- 这些结果表明,RaR 训练的策略能很好地适应不同的评估格式,在 Rubric-based 任务和多项选择题任务上都表现强劲
- Moreover,论文发现使用 Rubrics 作为结构化的奖励信号能更好地对齐较小的 Judge 模型,并减少跨不同规模 Judge 的性能方差
Introduction and Discussion
- RLVR 使得 LLM 能够在具有明确可验证结果的任务上激发复杂推理
- 这在数学和代码等领域尤其有效,其中奖励模型可以被评分函数或自动验证正确性的测试用例所取代(2019, 2025, 2025)
- 但是,将 RLVR 扩展到非结构化的现实世界推理具有挑战性
- 因为此类任务缺乏易于验证的答案
- 常见的解决方案是使用基于偏好的奖励模型,但它们倾向于过拟合表面的伪影(artifacts)(例如, Response 长度、格式怪癖、标注者偏见)(2023, 2024, 2024, 2024, 2024, 2024),并且需要大量的成对比较(2022)
- Instance-specific rubrics 最近在专家领域用于细微评估(nuanced evaluation)(2025),但将它们在用于专家级推理的(expert-level reasoning) On-policy 训练中的应用很大程度上尚未被探索
- 为填补这一空白(To address this gap),论文探索了一种范式转变,它在可验证奖励的简单性和偏好排序(preference rankings)的表达能力之间引入了一个中间地带(middle ground)
- 偏好排序后者常常伴随人工伪影和操作开销
- 论文引入了一个用于 On-policy 强化学习的框架Rubrics as Rewards(RaR)
- 使用结构化标准或 Rubric 作为核心奖励机制
- 论文不仅仅将 Rubric 用于评估(2025, 2025),而是将其视为清单式(checklist-style)的监督,为 On-policy RL 产生奖励信号
- 每个 Rubric 由模块化、可解释的子目标组成,提供与专家意图一致的可自动化反馈
- 通过将”什么是好的 Response “分解为具体、人类可解释的标准,Rubric 在二元正确性信号和粗略偏好排序之间提供了一个中间地带
- 先前的工作训练生成式奖励模型来学习用可解释的分数评估推理或最终输出(2025, 2025, 2025, 2025, 2025),有些甚至使用模型内部置信度估计作为奖励的代理(2025)
- 最近的工作已将可验证数据集扩展到 STEM 领域之外,拓宽了 RLVR 方法对更广泛任务的适用性(2025, 2025)
- 但仍没有找到通用方法实现 指定可靠奖励信号(specifying reliable reward signals),尤其是在没有单一正确答案、需要同时考虑主观和客观标准的任务中
- In Contrast,论文将 Rubric 视为 Instance-Specific 、可重用的奖励函数
- Rubric 提供可解释和可自动化的监督,可以一致地应用于新的生成 Rollouts,为 On-policy 学习中的不透明奖励建模提供了可扩展且透明的替代方案
- 最近的并行工作探索了用于偏好调整和 LLM 安全性的清单和原则性 Rubric 标准(2025, 2025, 2025),突显了向结构化监督发展的趋势
- 相比之下,论文将 Rubric 转化为用于 On-policy RL 的奖励函数,目标是专家推理和应用现实世界领域
- 这完成了从 Rubric 到学习的闭环,并提高了在 Rubric 指导的评估和具有可验证答案的任务上的性能
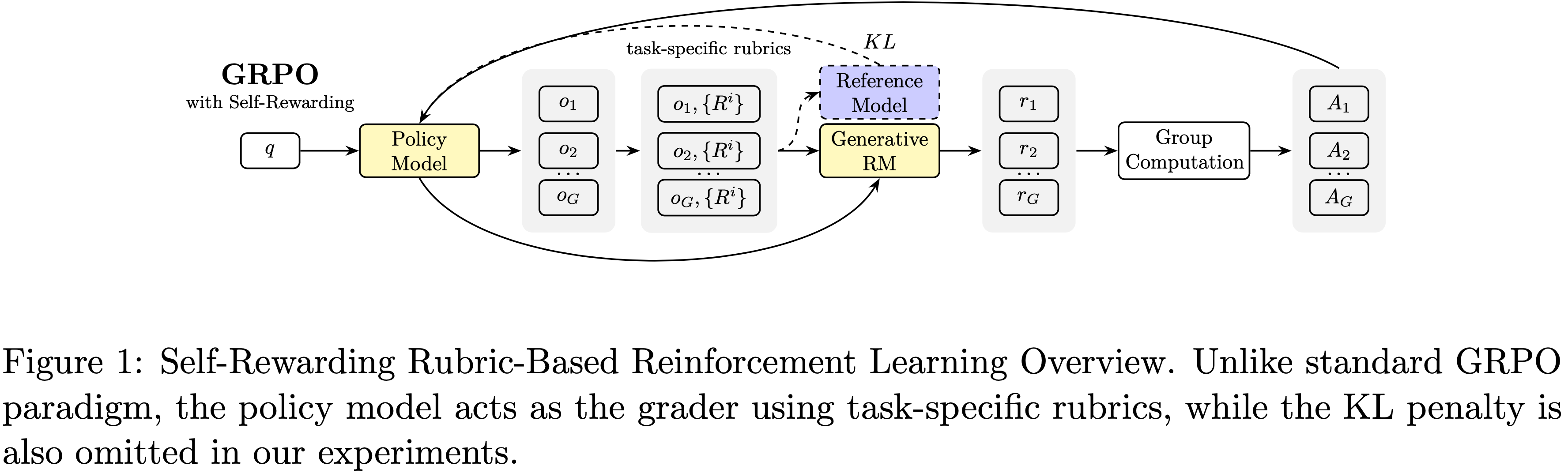
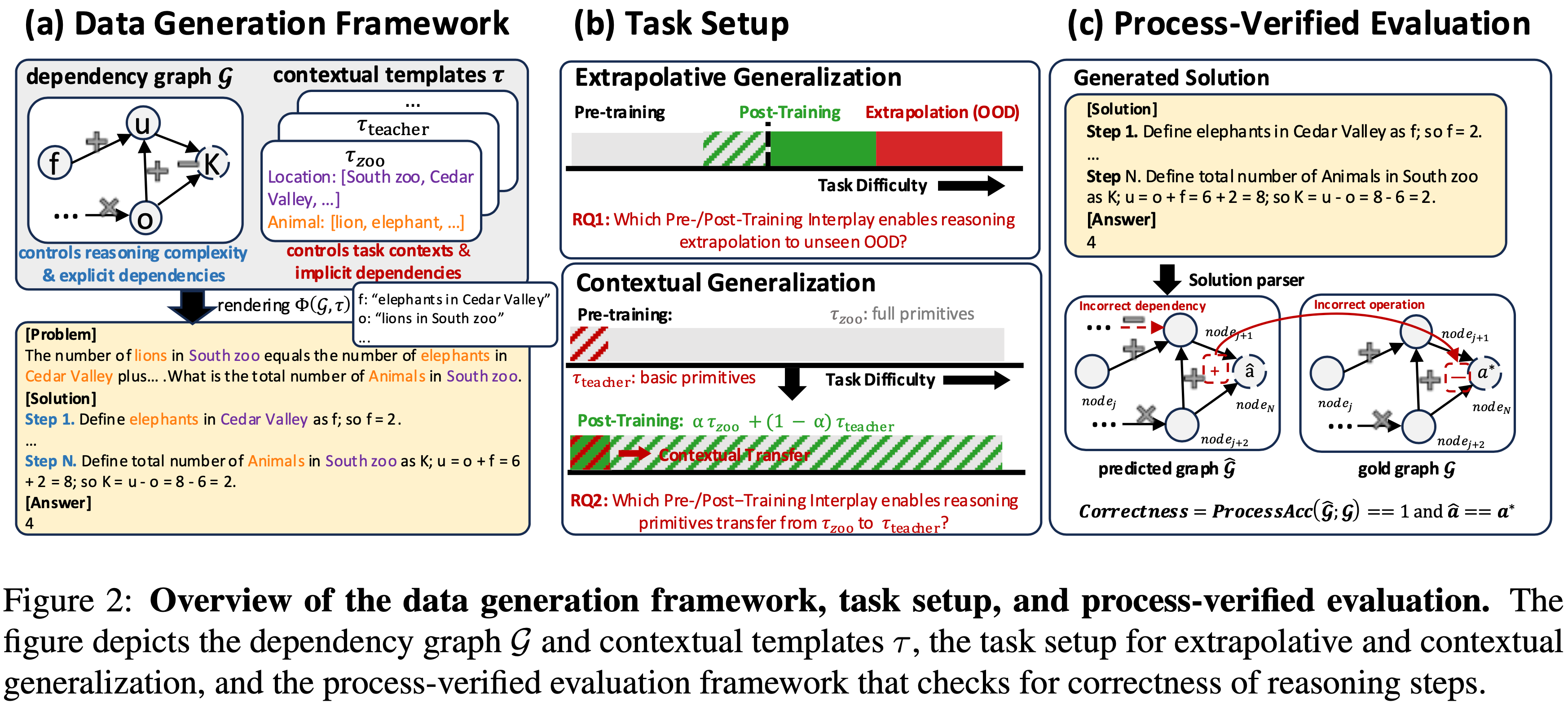
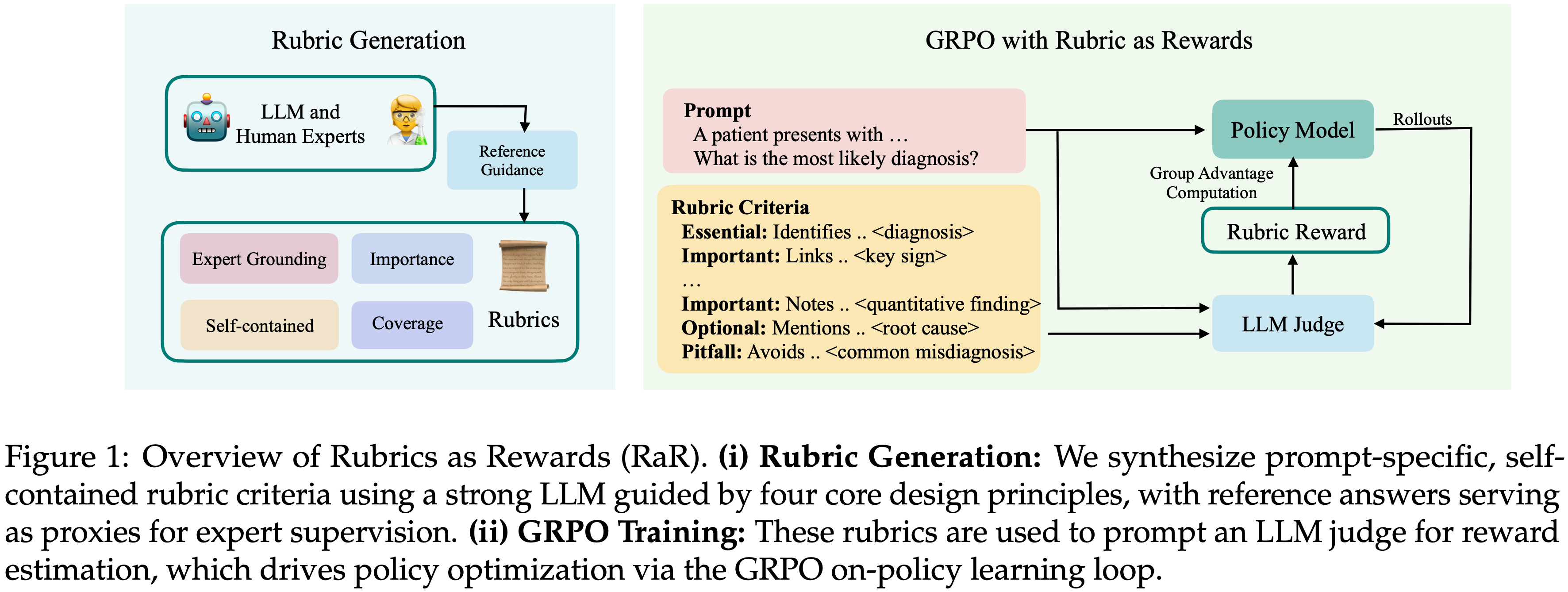
- 图 1 展示了论文的框架(图 1: RaR 概述)
- (i) Rubric 生成(Rubric Generation): 论文使用一个强大的 LLM,以四个核心设计原则为指导,合成了 Prompt 特定、自包含的 Rubric 标准,参考答案作为专家监督的代理
- (ii) GRPO训练(GRPO Training): 这些 Rubric 用于 Prompt 一个 LLM-as-judge 进行奖励估计,通过 GRPO On-policy 学习循环驱动策略优化
- 论文的主要贡献如下:
- (i) 论文引入了一个 On-policy 强化学习框架 Rubrics as Rewards(RaR)
- 使用清单式 Rubric 为推理和现实世界领域提供多标准监督
- (ii) 论文为医学和科学合成了 Instance-specific rubrics ,并发布了相应的训练集 RaR-Medicine 和 RaR-Science
- (iii) RaR 训练的模型持续优于强基线,并产生稳定、可泛化的训练信号,在 Rubric 评分和可验证的多项选择评估设置上都取得了收益
- (iv) 论文的结果表明, Rubric-based 奖励提供了跨 Judge 模型规模的稳定监督,帮助较小的模型有效地与人类偏好对齐,并保持从小型到大型 Judge 的稳健评估性能
- (i) 论文引入了一个 On-policy 强化学习框架 Rubrics as Rewards(RaR)
Rubrics as Rewards
Problem Formulation
- 令 \(x\) 表示输入 Prompt ,\(\hat{y}\sim\pi_{\theta}(\cdot \mid x)\) 为来自参数化模型 \(\theta\) 的采样 Response
- 在没有单一正确答案或自动正确性信号的领域,使用 Instance-specific rubrics 标准定义结构化奖励函数
- 每个 Prompt \(x\) 与一组 \(k\) 个 Rubric 项 \(\{(w_{j},c_{j})\}_{j=1}^{k}\) 相关联
- 其中 \(w_{j}\in\mathbb{R}\) 表示标准 \(j\) 的权重,\(c_{j}:(x,\hat{y})\mapsto\{0,1\}\) 是一个二元正确性函数
- 指示给定 Prompt 下 Response \(\hat{y}\) 是否满足该标准
Reward Aggregation Strategies
- 论文研究了两种将 Rubric 反馈组合成标量奖励的互补方法
- 显式聚合(Explicit Aggregation):每个标准使用 LLM-as-judge 独立评估,最终的归一化奖励计算为:
$$r(x,\hat{y})=\frac{\sum_{j=1}^{k}w_{j}\cdot c_{j}(x,\hat{y})}{\sum_{j=1}^{k}w_{j} } \tag{1}$$- 归一化使得奖励在不同 Rubric 数量或权重的 Prompt 之间具有可比性
- 尽管论文在实验中对 \(c_{j}\) 使用了二元检查,但该公式可以扩展到连续值分数
- 隐式聚合(Implicit Aggregation):所有 Rubric 标准连同分类权重一起传递给一个 LLM-as-judge ,将聚合委托给模型本身以产生单个标量奖励:
$$r_{\text{implicit} }(x,\hat{y})=f_{\phi}(x,\hat{y},\{d_{j}\}_{j=1}^{k}) \tag{2}$$- 这里,\(f_{\phi}\) 表示一个 LLM-based Judge,它将 Prompt \(x\)、 Response \(\hat{y}\) 和 Rubric 标准集合 \(\{d_{j}\}\) 作为输入
- 这个公式允许模型直接计算一个整体的奖励分数,避免了手动调整 Rubric 权重的需要
- 每种方法使用的 Prompt 详见附录 A.6
Generalization of RLVR with Rubrics as Rewards(使用 Rubric 作为奖励对 RLVR 的泛化)
- Rubric-based 强化学习通过支持多维、 Prompt 特定的评估标准,扩展了标准的 RLVR Setting
- 论文在下面形式化这种关系
Remark 1:Rubrics as Rewards subsumes RLVR(把 RLVR 归入 RaR )
- RLVR setting 是公式 1 中定义的基于 Rubric 奖励的一个特例,其中 \(k=1\),\(w_{1}=1\),并且 \(c_{1}(x,\hat{y})\) 简化为一个单一的可验证正确性函数,将模型输出 \(\hat{y}\) 与已知正确答案 \(y\) 进行比较
- 例如,这可能涉及精确匹配或测试用例执行,形式上:
$$r_{\text{RLVR} }(x,\hat{y})=\text{match}(y,\hat{y}) \tag{3}$$ - 其中 \(\text{match}(y,\hat{y})\in\{0,1\}\) 指示 Response 是否满足可验证正确性条件
- 例如,这可能涉及精确匹配或测试用例执行,形式上:
- Rubric-based 奖励函数通过实现多维监督、跨标准的灵活加权以及结合 Response 质量的客观和主观方面,泛化了 RLVR
- 这种形式化强调 RLVR 可以看作是具有单一基本标准的 Rubric 指导 RL(rubric-guided RL)的一个受限实例(restricted instance)
- In Contrast, Rubric-based 奖励进一步使得在正确性是多方面(multifaceted)且可能无法严格验证的 Settings 中实现结构化监督
Rubric Generation
Desiderata(必要条件)
- 一个 Rubric 规定了高质量 Response 的标准,并提供人类可解释的监督
- 论文确定了有效 Rubric 生成的四个必要条件(desiderata):
- 基于专家指导(Grounded in Expert Guidance)
- Rubric 应通过捕捉正确性所必需的基本事实、推理步骤和结论来反映领域专业知识
- 理想情况下(Ideally),这种基础来自于人类专家或其高质量代理
- 全面覆盖(Comprehensive Coverage)
- Rubric 应涵盖 Response 质量的多个维度,包括事实准确性、逻辑连贯性、完整性、风格和安全性
- 负面标准(pitfalls,即陷阱)有助于识别损害整体质量的常见或高风险错误
- 标准重要性(Criterion Importance)
- Rubric 应反映 Response 质量的某些维度比其他维度更关键
- 例如,事实正确性必须优先于次要方面,如风格清晰度
- 为标准分配权重确保了这种优先级排序,无论是通过简单的分类标签、明确的数值还是学习到的加权方案
- Rubric 应反映 Response 质量的某些维度比其他维度更关键
- 自包含评估(Self-Contained Evaluation)
- 每个 Rubric 项应是独立可操作的,允许人类标注者或自动化 Judge 无需外部上下文或领域特定知识即可独立评估
- 基于专家指导(Grounded in Expert Guidance)
Rubrics Creation
- 论文将这些必要条件应用于医学和科学领域的推理任务数据集
- 鉴于这些领域人类标注的 Rubric 数据集稀缺,论文使用 LLM 从 Golden Reference Answer 中大规模生成 Instance-specific rubrics,从而能够在没有昂贵人工标注的情况下研究结构化奖励
Given the scarcity of human-annotated rubric datasets in these domains, we use LLMs to generate instance-specific rubrics from golden reference answers at scale, enabling the study of structured rewards without costly human annotation.
- 对于每个 Prompt ,一个 LLM 生成一个 Rubric,这个 Rubric 包含 7-20 个自包含项 (self-contained items)
- 每个项被分配一个数值权重和一个分类权重,以反映其相对重要性
- 虽然数值权重提供了细粒度的优先级排序,但在论文的实验中,为便于在受控设置中实现和解释,论文采用分类标签(Essential(必需)、Important(重要)、Optional(可选)、Pitfall(陷阱))
- 生成的 Rubric 随后通过显式聚合(公式 1)或隐式聚合(第2.2节)直接用作奖励函数
- 在实践中,论文使用 OpenAI 的 o3-mini 和 GPT-4o 生成 Rubric ,其生成过程以基础数据集中的参考答案为条件,以近似专家基础
- 生成的集合 RaR-Medicine 和 RaR-Science 已公开发布供使用
- 这些 Rubric 集使用显式和隐式奖励聚合,在 GRPO 下监督较小的策略
Experiments
Datasets
- 论文在两个推理领域,医学(Medicine)和 科学(Science)中研究了 Rubrics as Rewards(RaR)的效用
- RaR-Medicine:
- 一个包含20k个 Prompt 的数据集
- 来源于不同的医学推理来源
- 包括 medical-o1-reasoning-natural_reasoning (2025),SCP-116K (2025),以及 GeneralThought-430K (2025)
- 该数据集的 Instance-specific rubrics 使用 GPT-4o 生成(见附录A.1)
- RaR-Science:
- 一个包含约20k个 Prompt 的数据集,旨在与 GPQA-Diamond 类别对齐
- Prompt 来源于 natural_reasoning (2025),SCP-116K (2025),以及 GeneralThought-430K (2025),涵盖了广泛的科学推理任务(附录A.2)
- 该数据集的 Rubric 使用 o3-mini 合成
Training Details
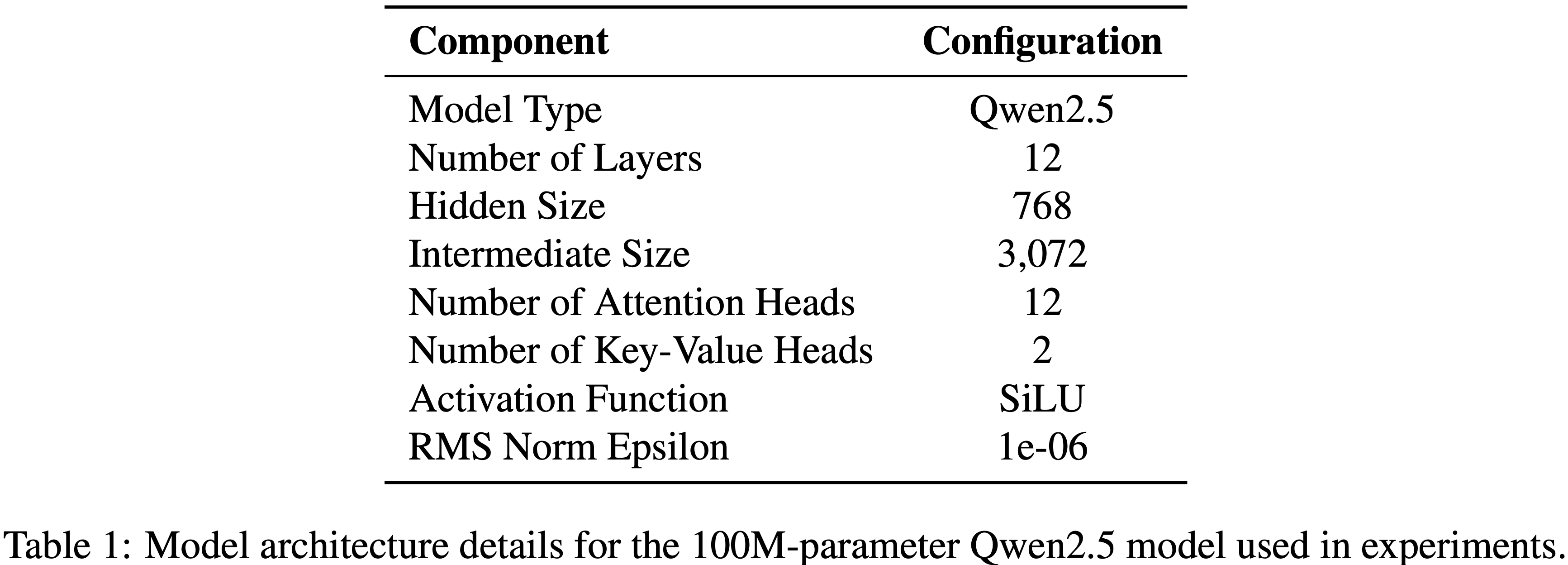
- 论文使用 GRPO 算法进行 On-policy 强化学习的所有实验,以 Qwen2.5-7B 作为基础策略
- 模型训练超参:Batch Size=96、学习率=\(5\times 10^{-6}\)、带有 10% 线性预热的恒定调度器(constant schedule with 10% linear warmup)
- 完整的超参数设置列在附录 A.3 中
- 训练运行在配备 8 个 NVIDIA H100 GPU 的单个计算节点上执行
- 论文的训练流程由以下关键组件组成:
- Response Generation:
- 对于每个 Prompt \(q\),论文从当前策略 \(\pi_{\theta}\) 采样 \(k=16\) 个 Response ,使用 3584 的上下文长度和 1.0 的采样温度
- 使用 Rubric 计算奖励(Reward Computation with Rubrics):
- 论文使用 gpt-4o-mini 作为 Judge 模型,为采样的 Response 分配奖励 \(R_{q}\)
- 论文尝试了第 4.3 和 4.4 节 进一步描述的各种奖励计算和聚合策略
- 策略更新(Policy Update):
- 策略权重基于计算出的奖励,使用 GRPO 进行更新
- Response Generation:
Rubric-Free Baselines
- 论文考虑了各种 Rubric-free 基线和现成的后训练模型
- Rubric-free 基线以 Qwen2.5-7B 作为基础策略进行训练
- 现成模型(OFF-THE-SHELF): 对于现成基线,论文评估 Qwen2.5-7B 的性能
- 论文还包括了 Qwen2.5-7B-Instruct 的性能,以与基础策略的指令调优变体进行比较
- 理解:不经过任何训练的原始开源模型
- 直接 Likert(DIRECT-LIKERT):
- 一个 LLM-as-judge 对每个
Response-Prompt对提供 1-10 Likert 量表上的直接评估(2024, 2023),并归一化到 \([0,1]\) 范围 - 得到的分数直接用作训练奖励信号
- 一个 LLM-as-judge 对每个
- 参考 Likert(REFERENCE-LIKERT):
- 一个 LLM-as-judge 将生成的 Response 与参考答案(由专家或更强的 LLM 编写)进行比较,并分配一个 1-10 的 Likert 分数(2023),归一化到 \([0,1]\) 范围
- 这个参考指导的分数被用作策略更新的奖励信号
- 每个
Prompt-Response-Reference三元组的奖励定义为:
$$R_{\text{ref} }(q,x)=\text{Norm}(\text{LikertScore}(q,x,x^{*}))$$- 其中 \(x^{*}\) 表示参考答案
Rubric-guided Methods
- RaR-预定义(RaR-PREDEFINED):
- 此方法对所有 Prompt 使用一组固定的通用 Rubric (例如,Response 简洁,Response 包含正确信息)
- 它采用显式聚合方法(公式 1),所有标准权重均匀(见附录 A.5)
- RaR-显式(RaR-EXPLICIT):
- 此变体也使用加权和的显式聚合(公式 1),但将其应用于第 3 节中的 Instance-specific rubrics
- 论文根据生成的分类标签手动分配数值权重:
{"Essential": 1.0, "Important": 0.7, "Optional": 0.3, "Pitfall": 0.9} - 注:陷阱 Rubric 以正面形式表述(例如,“Response 避免了错误信息”),因此满足它们对分数有积极贡献
- 如果未满足陷阱,则相应的奖励会减少或受到惩罚
- RaR-隐式(RaR-IMPLICIT):
- 此变体使用隐式聚合方法(公式 2)
- 利用 Prompt-specific Rubrics, Judge 模型整体评估 Response 以分配单个 Likert 评分(1-10),避免了手动调整权重的需要
- 奖励在训练期间归一化到 \([0,1]\) 范围
Evaluation Setup
- Rubric-based 评估(Rubric-Based Evaluation)
- 论文在HealthBench (2025) 上评估使用 RaR-Medicine 训练的模型,这是一个包含 5,000 个临床对话的基准,旨在评估模型在真实医学场景中的安全性和有用性
- 性能使用详细的、由医生编写的 Rubric 进行测量
- 论文使用贪婪解码(
temperature=0)生成 Response ,并按照原始设置报告总体分数和每轴分数 - 对于消融研究,论文采样了 1,000 个 Prompt 的子集(下称 HealthBench-1k),其余用于训练
- 多项选择评估(Multiple-Choice Evaluation)
- 每个模型在 10 次独立运行中进行评估,使用贪婪解码(
temperature=0)为每个 Prompt 采样一个 Response- 问题:模型训练 10 次的成本是否过高了,是因为数据量很少吗?
- 答案选项在每个示例中随机排列以减少位置偏差,并解析输出以寻找框选的答案格式(例如,boxed{A})
- 如果提取失败,论文回退到 GPT-4o 验证器,检查 Response 是否包含正确的选项字母或文本(见附录 A.4)
- 最终准确率报告为 10 次运行的平均值,论文包括 95% 置信区间以考虑运行间的方差
- 每个模型在 10 次独立运行中进行评估,使用贪婪解码(
- LLM Judge 对齐评估(LLM-Judge Alignment Evaluation)
- 特别注意:这里是评估 LLM-Judge 本身!
- 为了衡量 LLM Judge 与人类偏好的对齐程度,论文从大约 3,000 个 HealthBench Prompt 构建了一个成对评估集
- 对于每个 Prompt ,论文将从业者认可的答案作为 偏好(preferred) Response ,并通过受控编辑创建一个 扰动(perturbed) 替代项(见附录 A.9 获取用于扰动和 Prompt 选择的方法)
- 度量标准是 成对偏好准确率(pairwise preference accuracy),即偏好的 Response 获得更高分数的配对比例,报告于不同规模的 Judge 模型之间
Results
- 本节展示本研究的主要发现
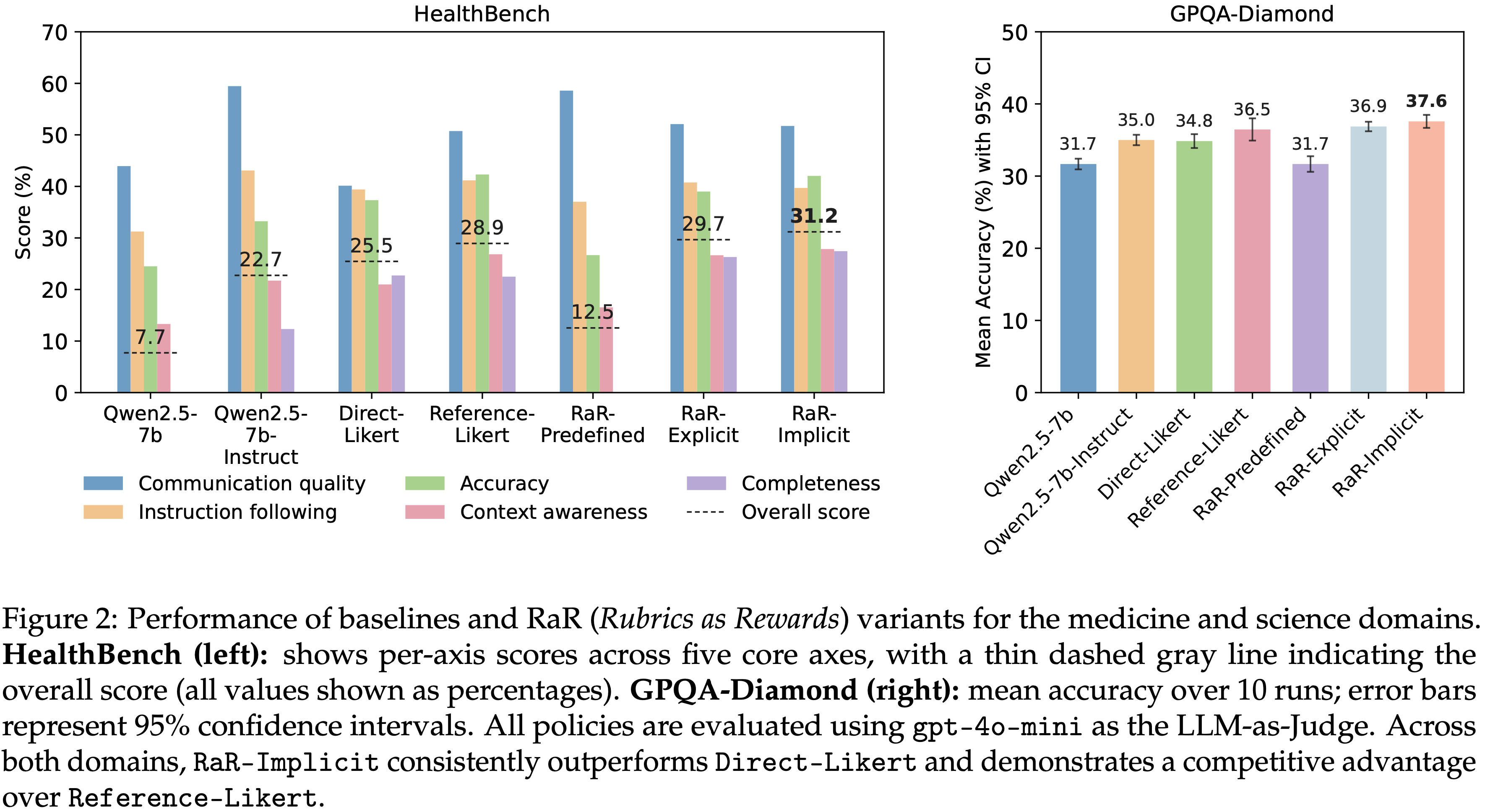
- 图 2:医学和科学领域基线及 RaR(Rubrics as Rewards)变体的性能
- HealthBench(左): 显示了五个核心轴上的各轴分数,灰色虚线表示总分(所有值以百分比显示)
- GPQA-Diamond(右): 10 次运行的平均准确率;误差线代表 95% 置信区间
- 所有策略均使用 gpt-4o-mini 作为 LLM-as-Judge 进行评估
- 在两个领域中,RaR-Implicit 始终优于 Direct-Likert,并对 Reference-Likert 展现出竞争优势
Rubrics as Rewards shows strong gains across evaluation settings(性能显著提升)
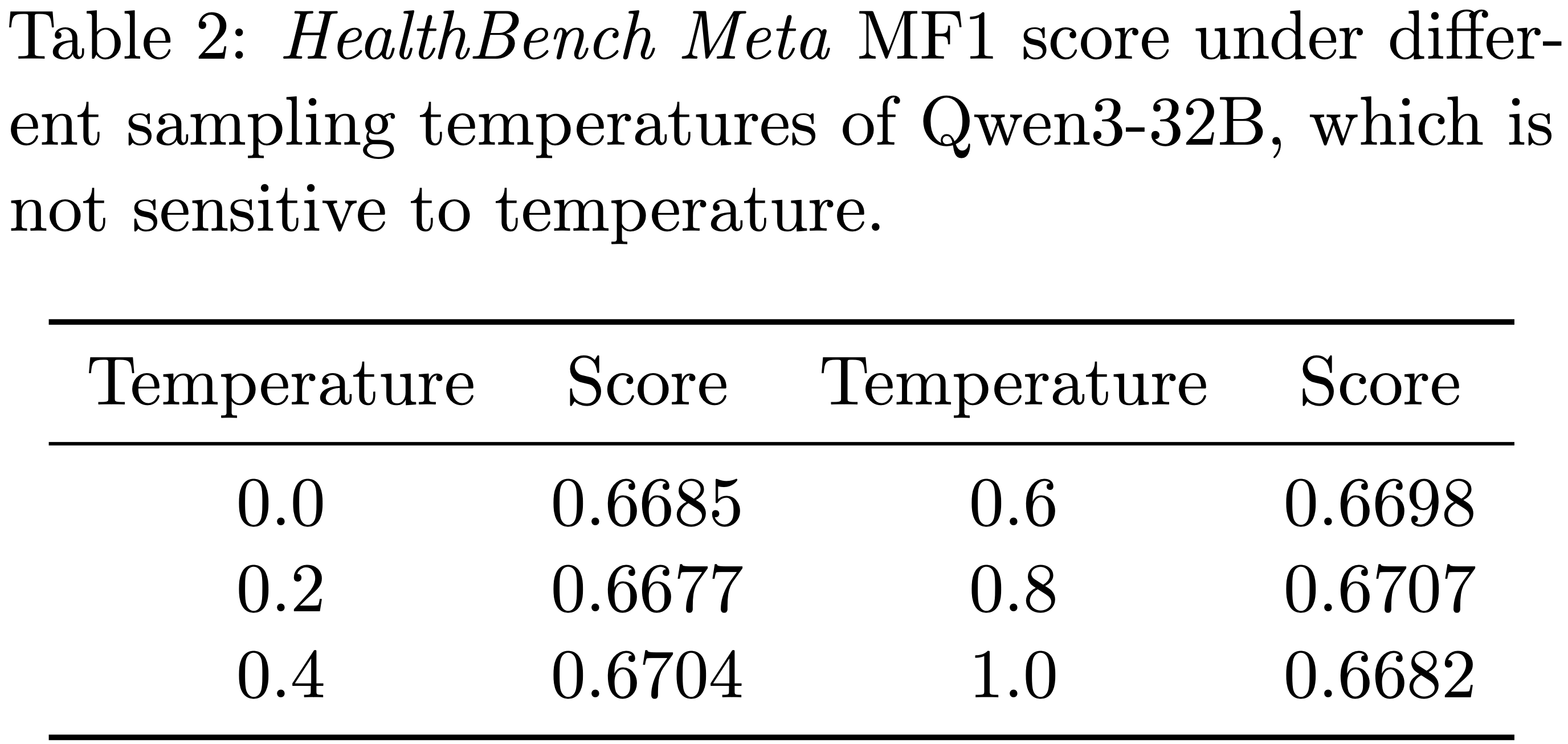
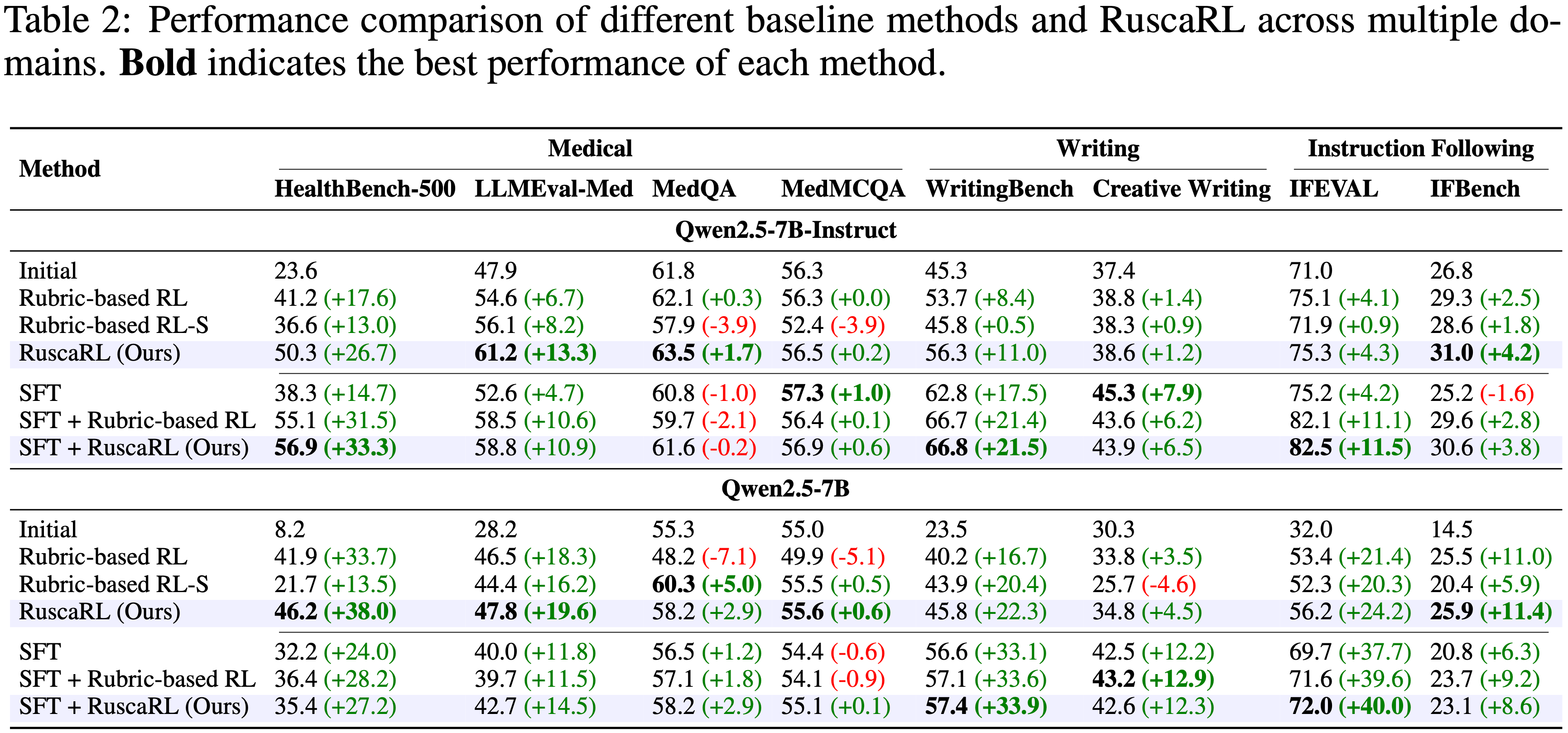
- 表 2 报告了在 HealthBench(基于 rubrics、自由形式)和 GPQA-Diamond(多项选择)上的结果
- RaR-Implicit 始终优于 Direct-Likert,在 HealthBench 上相对提升高达 31%,在 GPQA 上提升 7%
- 两种 Rubric-guided 的变体都比基础策略和指令调优策略获得了更高的分数
- 在 GPQA-Diamond 上的提升表明,由 rubrics 诱导的技能可以泛化到基于 rubric 的评估之外
- RaR-Predefined 变体(对每个 Prompt 应用固定的通用 rubrics 列表,不进行 Instance-Specific 生成)表现不佳,因为通用标准会错过特定 Prompt 的要求和常见失败模式,从而产生错位的奖励信号
- 因此,有效的训练需要 Instance-Specific rubrics 生成,因为它们能更好地捕捉任务上下文和典型失败模式
- RaR-Implicit 始终优于 Direct-Likert,在 HealthBench 上相对提升高达 31%,在 GPQA 上提升 7%
- 除了这些提升之外(Beyond these gains),RaR-Implicit 也比 Reference-Likert 显示出虽小但一致的提升
- 在论文的设置中,rubrics 是由更强的 LLM 使用参考答案作为专家监督的代理生成的 ,因此 rubric 质量受参考质量影响
- 即便如此(Even so),将开放式答案转换为明确的标准,也能产生有效且良好对齐的奖励信号
- 在两种 Rubric-guided 的方法中
- RaR-Implicit 总体上取得了最强的结果
- RaR-Explicit 中的固定加权求和提供了更多的控制,但可能很脆弱
- 显式加权可能难以调优,但提供了更强的可解释性;
- 作者认为 RaR-Implicit 和 RaR-Explicit 的选择取决于具体应用,并将其留给实践者
- 未来的工作可以探索学习或动态的权重策略,在保持可解释性的同时提高适应性
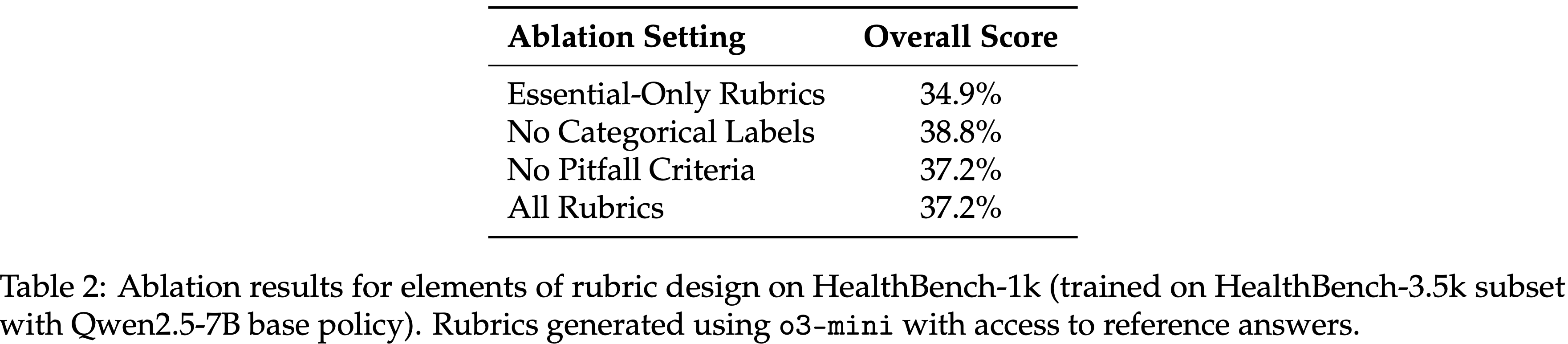
- 表 2:在 HealthBench-1k(使用 Qwen2.5-7B 基础策略在 HealthBench-3.5k 子集上训练)上关于 rubric 设计要素的消融结果
- Rubrics 使用能访问参考答案的 o3-mini 生成
- Rubrics 使用能访问参考答案的 o3-mini 生成
Rubrics enhance alignment with human preferences across model scales(Rubrics 增强了不同规模模型与人类偏好的对齐)
- 论文通过让不同规模的 LLM judges 在两个设置下对 HealthBench-1k 中选中的与被拒绝的 Response 在 1-10 分制上进行评分,来评估与人类的对齐度:
- (i) Rubric-guided(RaR-IMPLICIT),其中提供了 Instance-Specific rubric;
- (ii) Rubric-free(DIRECT-LIKERT),其中仅显示 Prompt 和答案
- 图 3 报告了成对偏好准确率 (pairwise preference accuracy)(即首选 Response 获得更高分数的配对比例)
- Rubric-guided 提高了每个 Judge 规模的准确率,对小 Judge 的提升最大,缩小了与大模型的差距
- 这表明,明确、上下文特定的标准比直接的 Likert 评分更能帮助 Judge 区分细微的质量差异
- 关于 Judge 规模对 GRPO 训练影响的进一步分析详见附录 A.8
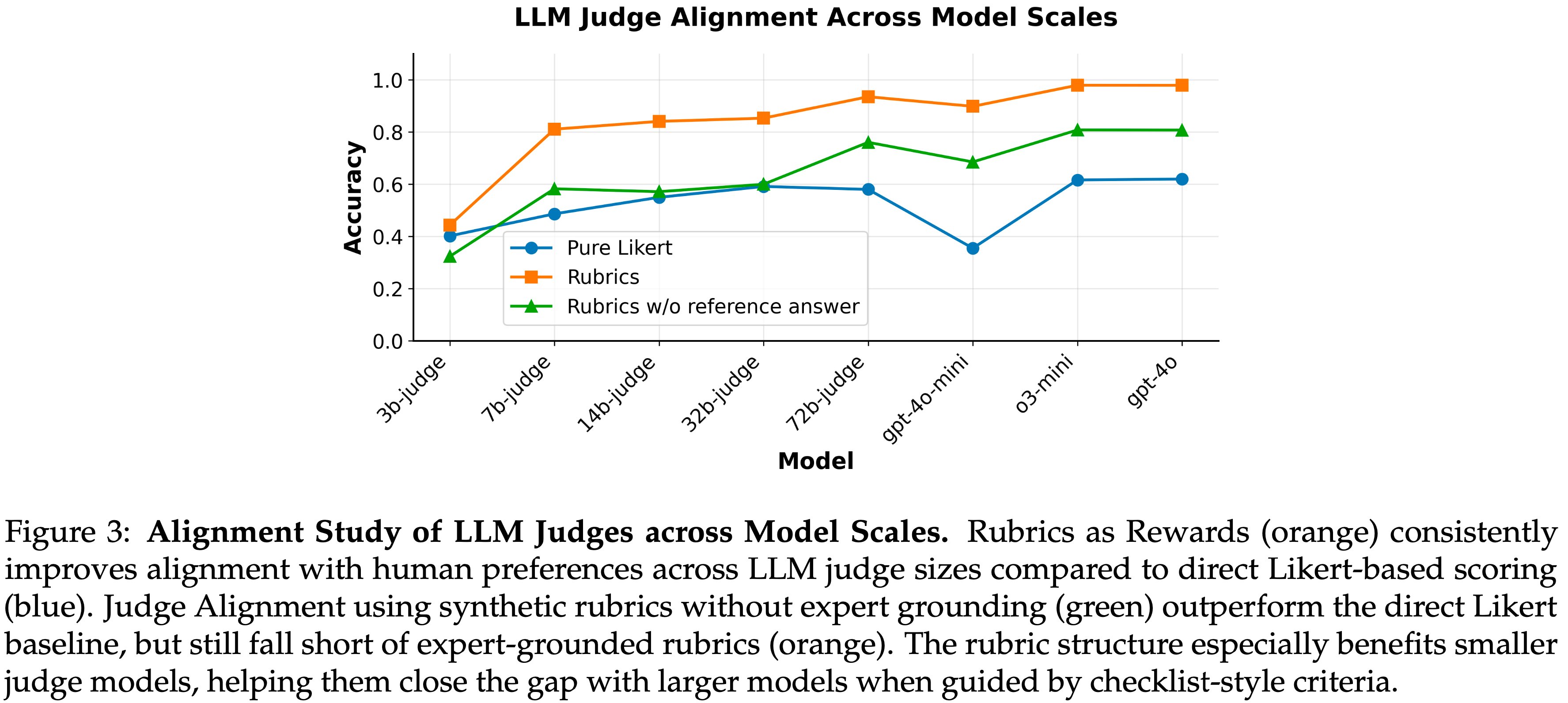
- 图 3:LLM Judge 在不同模型规模下的对齐研究 (Alignment Study of LLM Judges across Model Scales)
- 与直接的基于 Likert 的评分(蓝色)相比,Rubrics as Rewards(橙色)始终提高了不同 LLM Judge 规模下与人类偏好的对齐度
- 使用无专家基础的合成 rubrics 的 Judge 对齐(绿色)表现优于直接的 Likert 基线,但仍不及基于专家基础的 rubrics(橙色)
- Rubric 结构尤其有利于较小的 Judge 模型,当它们受到清单式标准引导时,有助于缩小与较大模型的差距
Expert guidance is crucial for synthetic rubric generation(专家指导的重要性)
- 人工指导显著影响了 rubrics 在捕捉细微人类偏好方面的有效性
- 图 3 突出显示了包含参考答案和不包含参考答案的基于 rubric 的评估之间的性能差异
- 数据显示,使用参考答案开发的 rubrics 达到了更高的准确率,强调了在 rubric 生成过程中整合的人类洞察力能够实现更细粒度的标准,并改善与人类偏好的对齐
Ablations
Impact of Rubric Generation Strategies in Real-World Domains(现实世界领域中 Rubric 生成策略的影响)
- Rubric 生成方法如何影响在具有挑战性的现实世界设置中的下游训练?为了研究这一点,论文保留 HealthBench-1k 用于评估,并使用剩余的 HealthBench 池中的 3.5k 个 Prompt 来生成用于训练的 rubrics,因为它可以访问人工生成的 rubrics
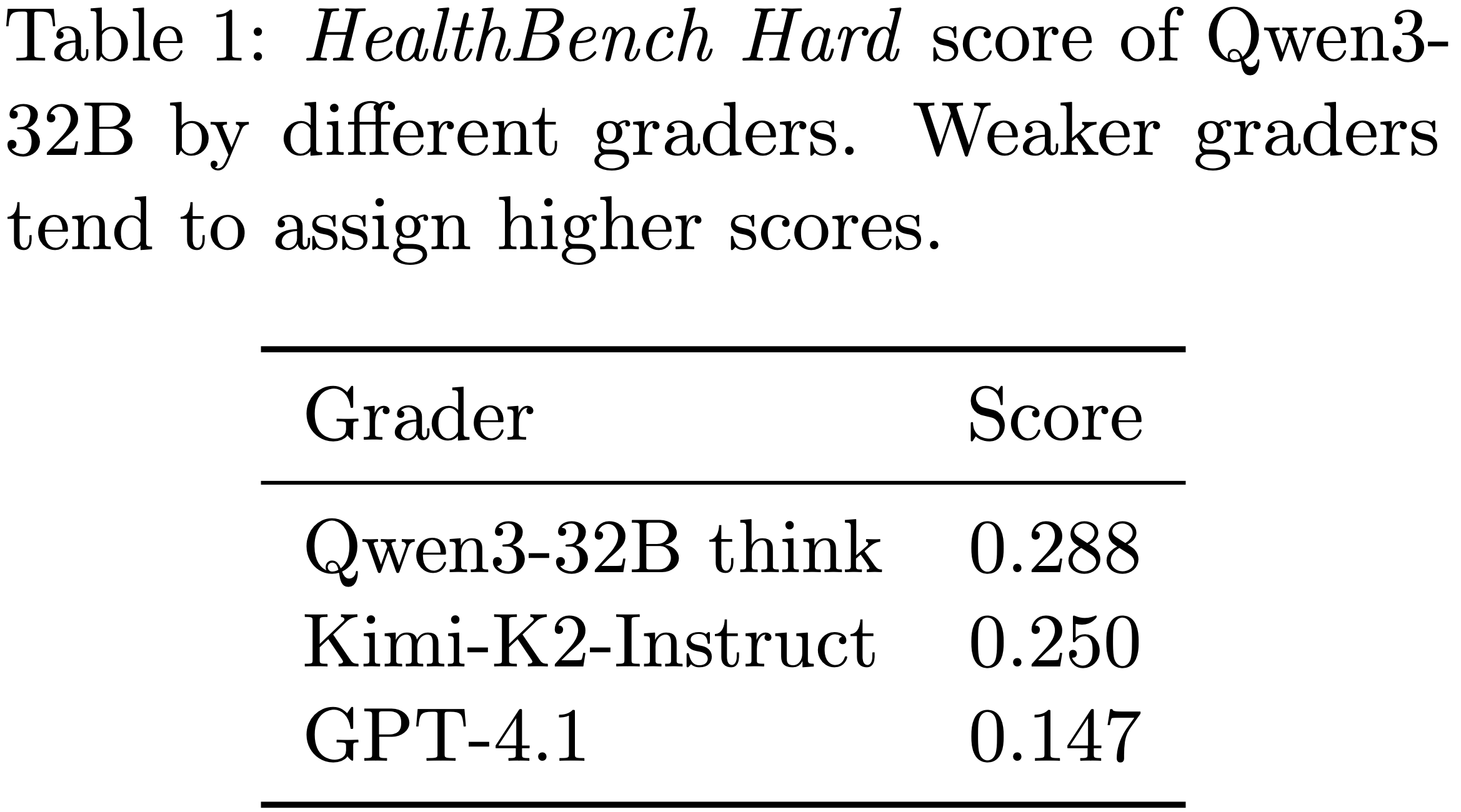
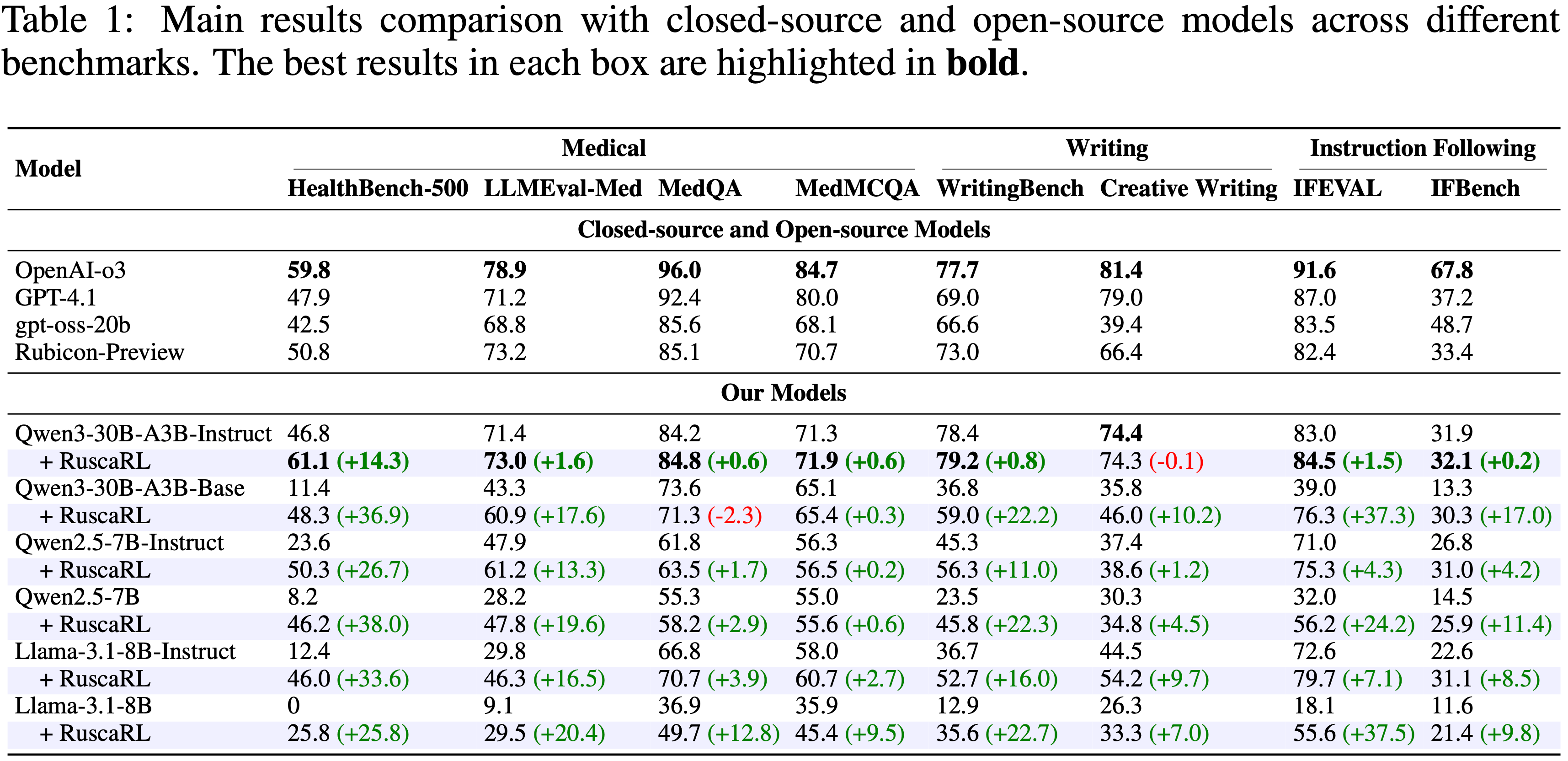
- 结果总结在表 1 中
- 在 HealthBench-1k 上的域内测试放大了 RaR 的增益:
- 每个基于 Instance-specific rubrics 的方法都优于 Rubric-free s 基线
- 值得注意的是,即使最弱的 RaR 变体也显著超越了 Reference-Likert,这突显了在医疗保健等主观、开放式领域中结构化监督的优势
- 论文将此归因于 rubrics 在分配奖励时提供了更精细的粒度和清晰度(尤其是在正确性不是二元,且答案在语气、完整性或安全性相关性方面可能有所不同时)
- 此外,论文发现 rubric 质量至关重要(注:参考答案是 Rubrics 的一部分):
- 在参考答案指导下生成的合成 rubrics 始终优于没有参考答案生成的 rubrics
- 这突显了融入专家信号(无论是通过人在回路标注还是高质量的参考答案)对于生成有效且对齐的 rubrics 的重要性
- 纯粹合成的 rubrics,虽然可扩展,但目前在高风险领域用于稳健训练所需的细微标准捕捉方面仍有不足
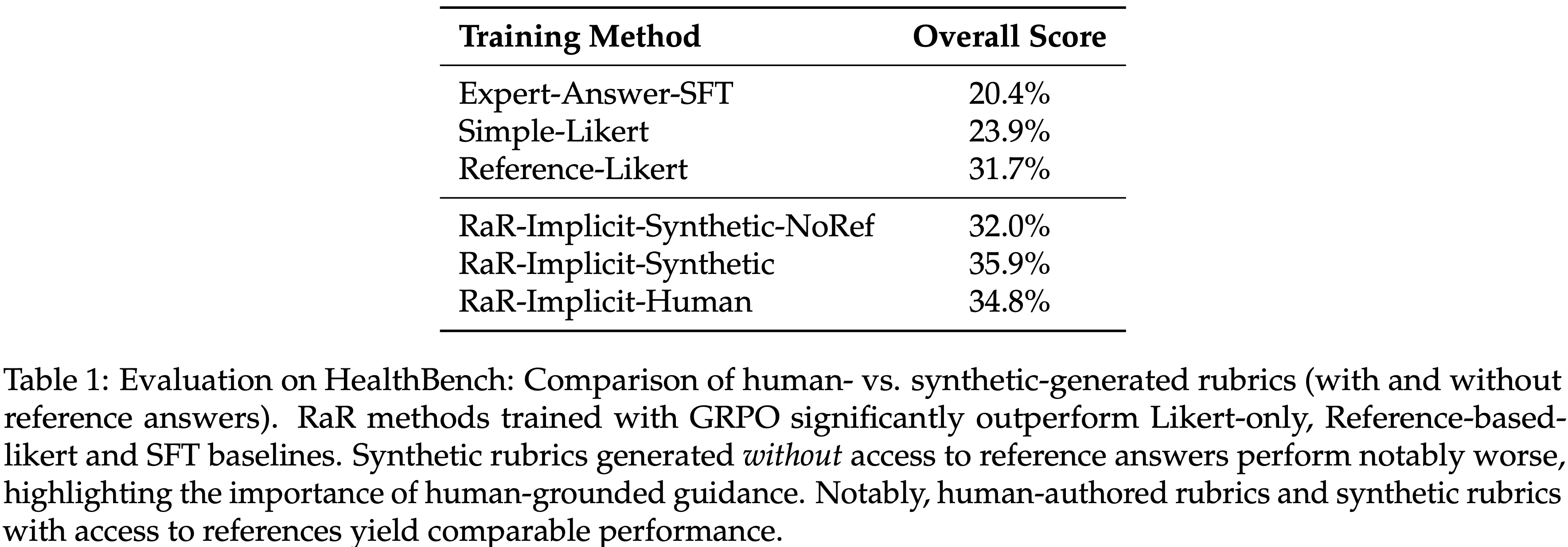
- 表 1:在 HealthBench 上的评估:人工生成与合成生成 rubrics(有和无参考答案)的比较
- 使用 GRPO 训练的 RaR 方法显著优于仅用 Likert、基于参考的 Likert 和 SFT 基线
- 无法访问参考答案生成的合成 rubrics 表现明显较差,突显了基于人类指导的重要性
- 值得注意的是,人工编写的 rubrics 和能访问参考的合成 rubrics 产生了可比的性能
Elements of Rubric Design(设计的要素)
- 这项消融研究检查了合成 rubrics 的结构和权重如何影响在 HealthBench-1k 上的下游性能
- 如表 2 所示,包含更广泛标准的 rubrics 优于仅限于基本检查的 rubrics,这表明更丰富的评估信号能带来更好的学习
- 有趣的是,论文观察到在训练期间包含 rubric 权重或 pitfalls 标准时,性能差异很小
- 一种可能的解释是,有效合成 pitfalls 标准本身就很困难,因为它需要预见到模型最常见或最关键的错误模式,这通常需要人类的直觉和领域专业知识
- 因此,这些合成的负面标准可能缺乏有效惩罚不良 Response 所需的具体性或相关性

Impact of LLM Expertise on Rubric Quality(LLM 专业能力对 Rubric 质量的影响)
- 为了评估 rubric 生成 LLM 的能力如何影响下游性能,论文在无法访问参考答案的情况下生成合成 rubrics,并用它们在 HealthBench 上训练策略
- 这隔离了 LLM 质量对无参考 rubrics 效用的影响
- 具体来说,论文在 HealthBench-1k 子集上进行评估,使用在 HealthBench 剩余 4k 训练样本生成的 rubrics 上训练的模型
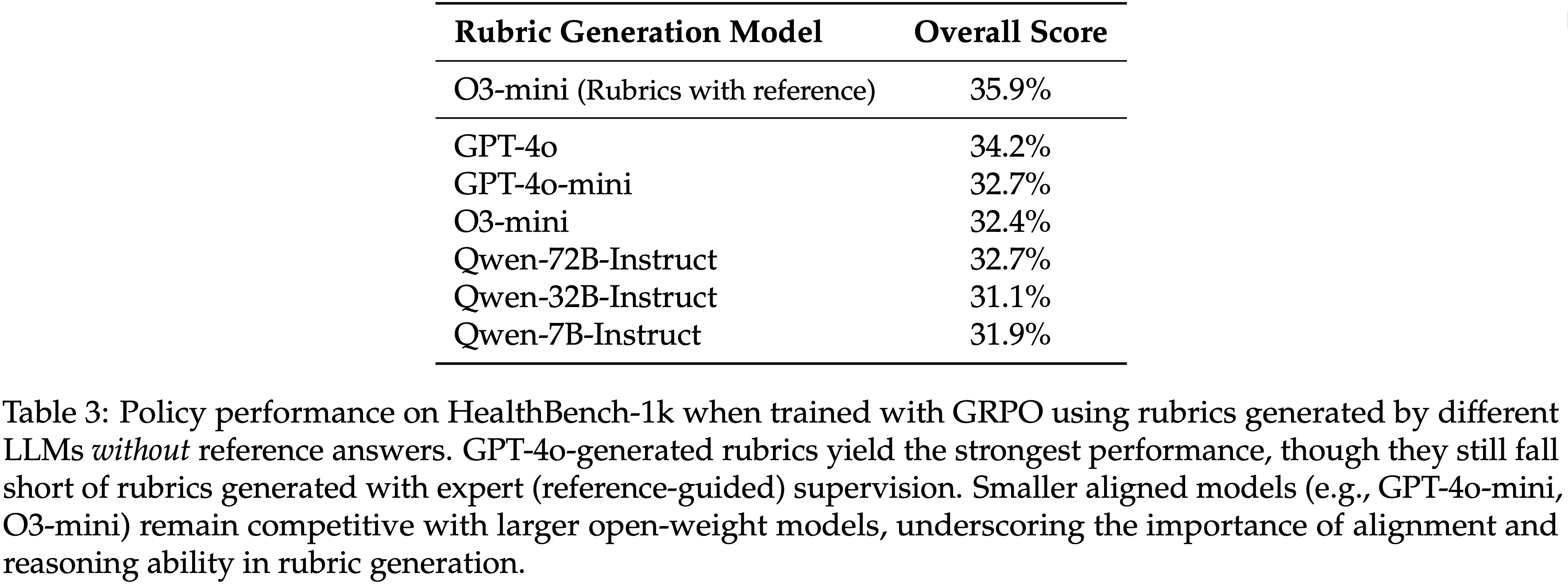
- 如表 3 所示
- 更大或能力更强的 LLM 通常能产生更有效的 rubrics,其中 GPT-4o 在无参考模型中产生了最佳性能
- 但所有这些模型的性能仍然低于在有参考指导下生成的 rubrics(例如,能访问参考答案的 O3-mini)
- 此外,指令调优和推理能力等模型属性在 rubric 生成的有效性中起着关键作用
- 更大或能力更强的 LLM 通常能产生更有效的 rubrics,其中 GPT-4o 在无参考模型中产生了最佳性能
- 表 3:当使用由不同 LLM 不依赖参考答案生成的 rubrics 进行 GRPO 训练时,策略在 HealthBench-1k 上的性能
- GPT-4o 生成的 rubrics 产生了最强的性能,尽管它们仍然不及在专家(参考引导)监督下生成的 rubrics
- 较小的对齐模型(例如,GPT-4o-mini、O3-mini)仍然与较大的开放权重模型竞争,突显了在 rubric 生成中对齐和推理能力的重要性
Related Work
RLVR across domains
- 使用可验证奖励的强化学习 (RLVR) 正在扩展到数学和代码之外
- General-Reasoner 在一个涵盖物理、金融和政策的 200k 混合语料库上进行训练,并报告在 GRPO 微调后 MMLU-Pro 提高了 10 分 (2025)
- 后续工作将 RLVR 扩展到医学、化学、心理学和经济学领域,表明一个单一的跨领域奖励模型可以在无需特定任务调整的情况下监督所有四个领域 (2025)
- 在医疗保健领域,Med-RLVR 将类似方法应用于多项选择临床 QA,在从 3B 基础模型引出思维链的同时,提高了相对于监督基线的准确率 (2025)
- 这些结果表明了稳步进展,然而稀疏的信号、验证器的可靠性以及有限的基准覆盖范围仍然是开放的挑战
Rubrics for evaluation and training
- 特定任务的 rubrics 越来越多地用于在难以验证的领域中评估 LLMs (2024, 2025, 2025)
- Pathak 等人 (2025) 表明,rubric Prompt 的 LLM 评分器比与问题无关的清单更准确、更一致
- HealthBench 在医学领域扩展了这一想法,将 48k 临床医生编写的标准与 GPT-4 Judge 配对,以评估各个轴 (2025)
- 除了评估之外,rubrics 还被用于为 DPO 创建偏好对(CPT (2025))以及指导安全、遵循指令和创意写作设置中基于清单的偏好调优 (2025, 2025, 2025)
- 这些工作主要使用 rubrics 来对输出进行评分或用于构建偏好数据,通常用于安全、指令遵循或创意写作等非推理领域
- 相比之下,论文直接将 rubric 标准用作专家推理和现实世界领域中进行 on-policy RL 的奖励信号
Learning from feedback signals
- RLHF 使用大量人工比较来训练策略,这引入了主观性并可能导致奖励黑客攻击 (2022)
- RLVR 通过使用可编程检查来减少这些问题,从 GSM8K 和 MATH 上的精确匹配到 General-Reasoner 和 Cross-Domain RLVR 中的混合域验证器 (2025, 2025),尽管信号可能稀疏
- 过程监督 (2023) 通过步骤级标签提供更密集的指导,而 MCTS 生成的标注或生成式奖励模型(如 ThinkPRM)提高了性能,但标注成本很高 (2025, 2025)
- 基于 Rubric 的 RL 通过将多个 rubric 标准转化为结构化验证器并将其标量分数用作更密集的奖励,找到了一个中间地带
Limitations and Future Work
- 论文的工作专注于医学和科学,以便进行受控实验
- 这一选择使论文能够进行受控实验,但在对话、工具使用或其他智能体任务上进行更广泛的验证仍然是一个重要的方向
- 论文仅评估了两种奖励聚合策略,隐式和显式,因为它们捕捉了灵活性和控制力的互补极端;
- 未来的工作可以探索更先进的 rubric 标准组合方式,例如学习每个标准的连续权重,或在训练过程中动态调整权重以模拟课程学习
- 例如,早期优先考虑基本正确性,然后逐渐强调更微妙的品质,如风格或安全性
- 最后,论文使用现成的 LLM 作为 Judge ,以实现可访问性和可重复性;探索具有更强推理能力或生成式奖励模型的专门评估器可能会带来进一步的收益
A.1 RaR-Medicine 数据集的细节
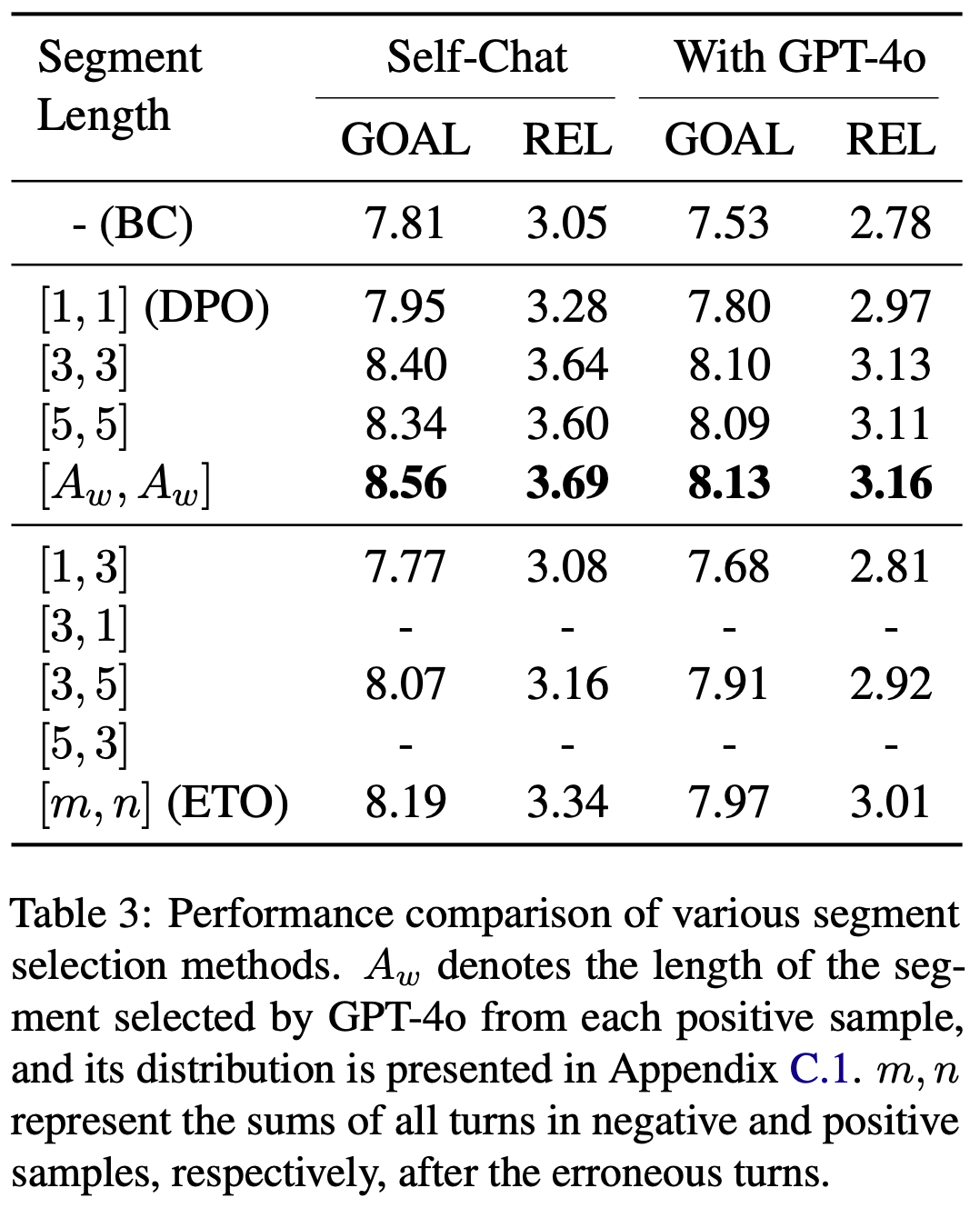
- 以下是来自 RaR-Medicine 数据集的一个示例,其中包含更多关于统计信息和评分标准类别分布的详细信息,详见表 4 和表 6
- 英文原始示例(RaR-Medicine Example)

- 中文概述(RaR-Medicine 示例):
问题 (Question). 一位 50 岁男性患者体重 65 kg,pH 值为 7.05,PCO2 为 15 mmHg,HCO3 为 5 mEq/L,碱缺乏为 -40 mEq/L。为纠正其代谢性酸中毒,在最初 4 小时内应给予多少碳酸氢钠?
参考答案 (Reference Answer). 为治疗这位 50 岁患者(体重 65 kg)的严重代谢性酸中毒(pH 7.05),必须谨慎处理以避免过度矫正带来的并发症。碱缺乏为 -40 mEq/L,表明存在显著的酸碱平衡紊乱
通常,碳酸氢钠给药的计算公式为:
$$\text{碳酸氢钠需要量} = \text{碱缺乏}(\text{mEq}/\text{L}) \times \text{体重}({\text{kg} }) \times 0.3$$
代入数值:
$$40,\text{mEq}/\text{L} \times 65,{\text{kg} } \times 0.3 = 780,\text{mEq}$$
然而,标准做法是先进行部分矫正,以确保安全和逐步改善。因此,在最初 4 小时内给予约 150 mEq 的碳酸氢钠是审慎的做法。此剂量符合严重代谢性酸中毒初始治疗的安全临床指南,确保患者开始稳定之路,同时避免因快速矫正带来的风险
评分标准 (Rubric,核对清单及权重).- 碳酸氢钠计算 (Bicarbonate Calculation) (\(w\)=5): 必须标准 (Essential Criteria): Response 必须正确识别并应用公式(碱缺乏 × 体重 × 0.3)来确定碳酸氢钠需要量
- 安全剂量推荐 (Safe Dosing Recommendation) (\(w\)=5): 必须标准 (Essential Criteria): Response 必须明确提出建议,即在最初 4 小时内给予约 150 mEq 的碳酸氢钠
- 部分矫正的理由 (Partial Correction Justification) (\(w\)=4): 重要标准 (Important Criteria): Response 应解释最初仅进行部分矫正以避免快速过度矫正的并发症
- 分步计算 (Step-by-Step Calculation) (\(w\)=3): 重要标准 (Important Criteria): Response 必须详细说明计算步骤,显示 40 mEq/L × 65 kg × 0.3 等于 780 mEq,然后注明出于安全考虑调整剂量
- 碱缺乏的解读 (Base Deficit Interpretation) (\(w\)=2): 可选标准 (Optional Criteria): Response 可以提及 -40 mEq/L 的碱缺乏表明需要谨慎治疗的严重代谢性酸中毒
- 患者数据准确性 (Patient Data Accuracy) (\(w\)=3): 重要标准 (Important Criteria): Response 必须准确地将患者的体重 65 kg 以及关键的 pH、PCO2 和 HCO3 值纳入解释
- 避免过度矫正风险 (Avoid Overcorrection Risk) (\(w\)=-1): 缺陷标准 (Pitfall Criteria): 若未提及仅按计算出的全部碳酸氢钠量给药时,与快速矫正代谢性酸中毒相关的风险
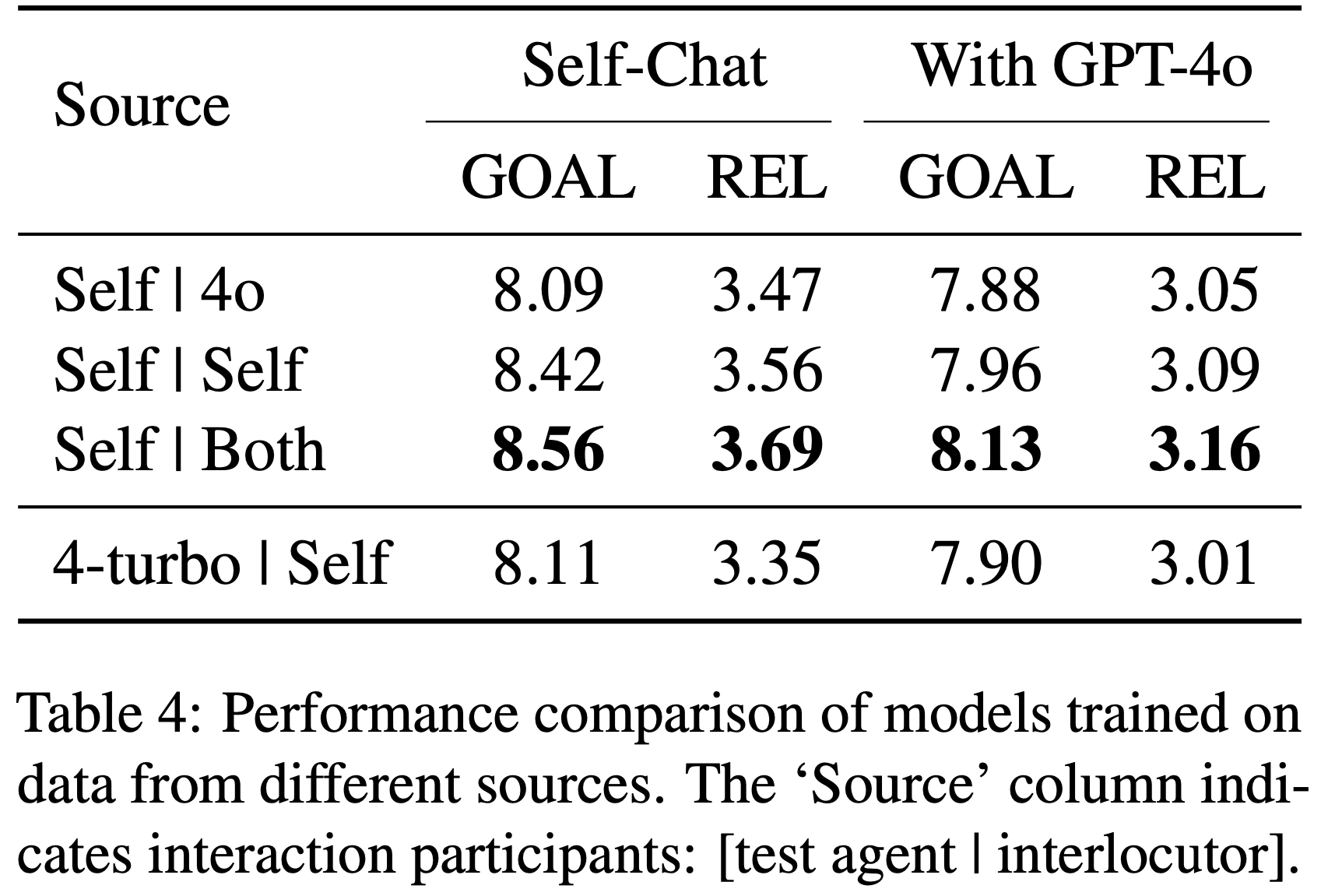
- Table 4: Aggregate statistics for the RaR-Medicine dataset (train and validation) dataset
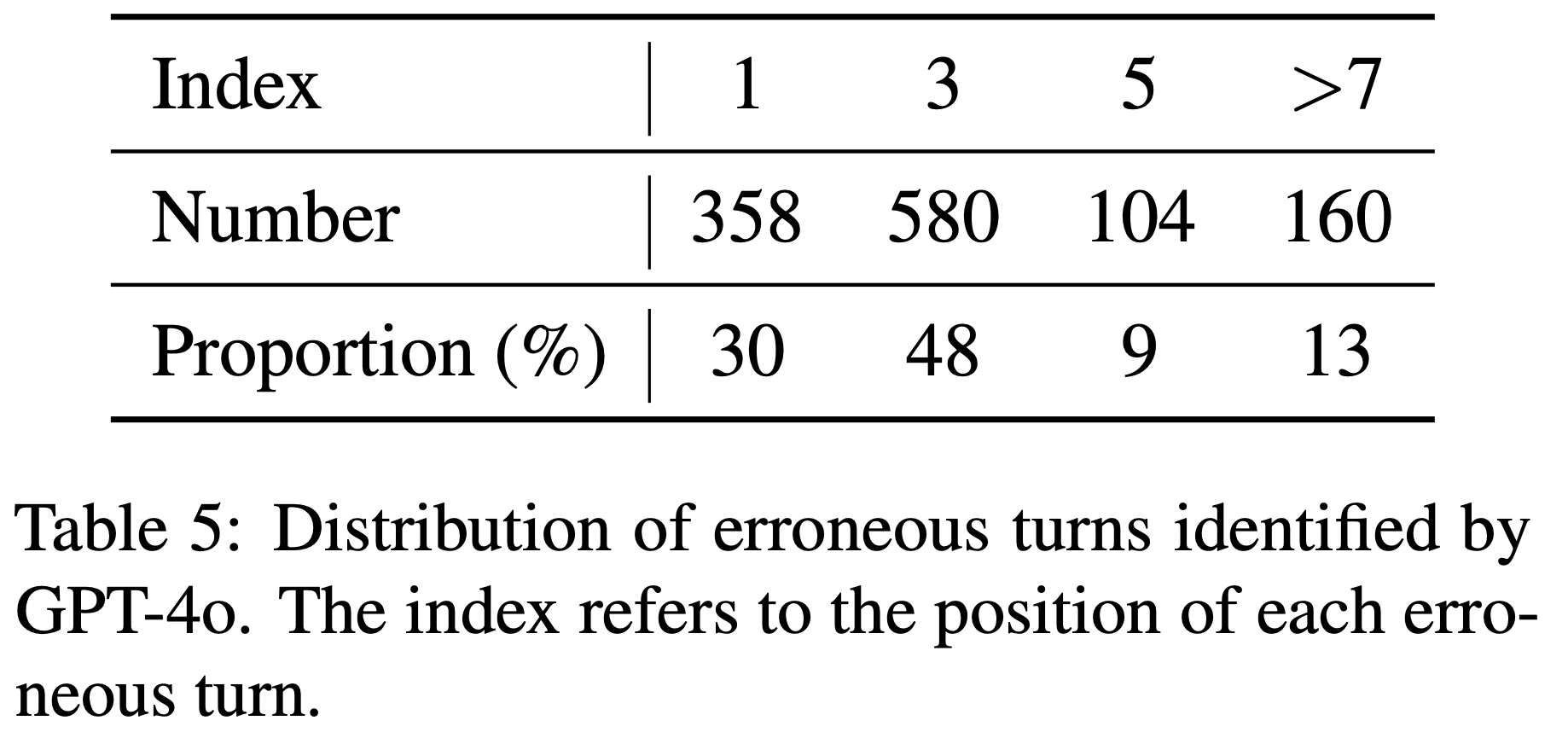
Metric Value 总样本数 (Total examples) 20,166 每问题平均评分标准数 (Avg. rubrics per question) 7.5 平均问题长度(词数) (Avg. question length (words)) 45.0 - Table 5: Rubric-type distribution across all 20,166 examples.
Rubric Type Count Percent 重要 (Important) 52,748 34.1 必须 (Essential) 47,584 30.7 可选 (Optional) 34,261 22.1 缺陷 (Pitfall) 20,215 13.1 - Table 6: 医学训练和验证数据集中的主题分布(Distribution of topics in the medical training and validation dataset)
Topics Count Percent 总样本数 (Total examples) 20,166 100.0 医学诊断 (Medical Diagnosis) 10,147 50.3 医学治疗 (Medical Treatment) 3,235 16.0 医学知识 (Medical Knowledge) 2,557 12.7 医学诊断与管理 (Medical Diag. and Mngmnt) 2,033 10.1 医学生物学 (Medical Biology) 770 3.8 其他 (Other) 428 2.1 医学伦理学 (Medical Ethics) 377 1.9 健康物理学 (Health Physics) 276 1.4 流行病学与公共卫生 (Epidemiology & Pub. Health) 216 1.1 普通医学 (General Medicine) 113 0.6 法医学 (Forensic Medicine) 14 0.1
A.2 RaR-Science 数据集的细节
- 本节展示 RaR-Science 数据集的一个示例,其中包含更多关于统计信息和评分标准类别分布的详细信息,详见表 7、8、9
- 原始英文示例:

- 中文说明(RaR-Science 示例)
问题 (Question). 根据“相似相溶”原理和 \(K_{sp}\) 值的作用,确定硼酸(\(H_3BO_3\))在乙醇(\(C_2H_5OH\))中的溶解度与在苯 (\(C_6H_6\)) 中的溶解度相比如何。解释你的推理,并提供增溶剂如何影响物质在不同溶剂中溶解度的例子
参考答案 (Reference Answer). 硼酸在乙醇中的溶解度高于在苯中的溶解度
评分标准 (Rubric,核对清单及权重).- 正确溶解度方向 (Correct Solubility Direction) (\(w=5\)): 必须标准 (Essential Criteria): Response 必须明确指出硼酸在乙醇中的溶解度高于在苯中
- 极性原理 (Polarity Principle) (\(w=5\)): 必须标准 (Essential Criteria): 答案应通过对比乙醇的极性与苯的非极性特征来解释“相似相溶”原理如何应用
- Ksp 上下文 (Ksp Context) (\(w=4\)): 重要标准 (Important Criteria): Response 应考虑 Ksp 值的作用,讨论它们通常与溶解度的相关性,尽管硼酸是共价化合物而非离子化合物
- 增溶剂解释 (Immulcifier Explanation) (\(w=4\)): 重要标准 (Important Criteria): 答案应解释增溶剂如何改变溶解度,提供一个例子说明它们对不同溶剂中溶剂化的影响
- 化学性质 (Chemical Properties) (\(w=4\)): 重要标准 (Important Criteria): Response 应分析硼酸和溶剂的固有化学性质,以证明观察到的溶解度差异
- 避免离子假设 (Avoid Ionic Assumptions) (\(w=-1\)): 缺陷标准 (Pitfall Criteria): 答案不得错误地假设离子化合物的 Ksp 值直接决定了像硼酸这样的共价酸的溶解度
- 增强细节 (Enhanced Detail) (\(w=2\)): 可选标准 (Optional Criteria): Response 可以包含额外的例子或对溶剂化动力学的简要解释,以进一步说明溶解度如何受影响
- Table 7: 完整医学数据集(训练和验证)的汇总统计数据
Metric Value 总样本数 (Total examples) 20,625 每问题平均评分标准数 (Avg. rubrics per question) 7.5 平均问题长度(词数) (Avg. question length (words)) 52.6 - Table 8: 所有 20,625 个样本的评分标准类型分布
Rubric Type Count Percent 重要 (Important) 52,315 34.8 必要 (Essential) 42,739 28.4 可选 (Optional) 33,622 22.3 缺陷 (Pitfall) 21,808 14.5 - Table 9: STEM(科学、技术、工程、数学)训练和验证数据集中的主题分布
Topics Count Percent 总样本数 (Total examples) 20625 100.0 普通化学 (General Chemistry) 3163 15.3 量子力学 (Quantum Mechanics) 3158 15.3 物理化学 (Physical Chemistry) 2761 13.4 统计力学 (Statistical Mechanics) 2530 12.3 有机化学 (Organic Chemistry) 2059 10.0 普通物理学 (General Physics) 1439 7.0 凝聚态物理学 (Condensed Matter Physics) 1387 6.7 遗传学 (Genetics) 1378 6.7 分子生物学 (Molecular Biology) 815 4.0 天体物理学 (Astrophysics) 409 2.0 无机化学 (Inorganic Chemistry) 407 2.0 分析化学 (Analytical Chemistry) 398 1.9 电磁学 (Electromagnetism) 239 1.2 光学 (Optics) 143 0.7 高能物理学 (High Energy Physics) 116 0.6 电磁理论 (Electromagnetic Theory) 105 0.5 电磁学 (Electromagnetics) 72 0.3 相对论力学 (Relativistic Mechanics) 46 0.2
A.3 训练细节
- 训练超参数描述见表 10(用于医学和科学领域的 GRPO 超参数设置)
Hyperparameters num_rollouts_per_prompt 16 batch_size (effective) 96 sampling_temperature 1.0 warmup_ratio 0.1 learning_rate 5.0e-06 lr_scheduler_type constant_with_warmup max_length 3584 num_train_steps 300
A.4 评估 Prompt
- GPQA Evaluation Prompt
1
2
3
4
5
6
7
8
9Determine whether the following model response matches the ground truth answer.
## Ground truth answer##: Option {correct_answer} or {correct_answer_text}
## Model Response ##: {response_text}
A response is considered correct if it’s final answer is the correct option letter (A, B, C, or D),
or has the correct answer text. Please respond with only "Yes" or "No" (without quotes).
Do not include a rationale.
A.5 预定义的静态评分标准
- 用于 RaR-静态方法的预定义静态评分标准 (Predefined Static Rubrics for RaR-Static Method)
1
2
3
4* The response contains correct information without factual errors, inaccuracies, or hallucinations that could mislead the user.
* The response fully answers all essential parts of the question and provides sufficient detail where needed.
* The response is concise and to the point, avoiding unnecessary verbosity or repetition.
* The response effectively meets the user’s practical needs, provides actionable information, and is genuinely helpful for their situation.
A.6 LLM-Judge Prompt
Prompt for RAR-IMPLICIT Method
- Prompt 详情:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33# System Prompt:
You are an expert evaluator. Given a user prompt, a generated response, and a list of quality rubrics,
please rate the overall quality of the response on a scale of 1 to 10 based on how well it satisfies the rubrics.
Consider all rubrics holistically when determining your score. A response that violates multiple rubrics should receive a lower score,
while a response that satisfies all rubrics should receive a higher score.
Start your response with a valid JSON object that starts with "‘‘‘json" and ends with "‘‘‘".
The JSON object should contain a single key "rating" and the value should be an integer between 1 and 10.
Example response:
‘‘‘json
{
"rating": 7
}‘‘‘
# User Prompt Template:
Given the following prompt, response, and rubrics, please rate the overall quality of the response on a scale of 1 to 10 based on how well it satisfies the rubrics.
<prompt>
{prompt}
</prompt>
<response>
{response}
</response>
<rubrics>
{rubric_list_string}
</rubrics>
Your JSON Evaluation:
Prompt for DIRECT-LIKERT Baseline
- Prompt 详情
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25# System Prompt:
You are an expert evaluator. Given a user prompt and a generated response, please rate the overall quality of
the response on a scale of 1 to 10, where 1 is very poor and 10 is excellent.
Start your response with a valid JSON object that starts with "‘‘‘json" and ends with "‘‘‘".
The JSON object should contain a single key "rating" and the value should be an integer between 1 and 10.
Example response:
‘‘‘json
{
"rating": 8
}‘‘‘
# User Prompt Template:
Given the following prompt, and response, please rate the overall quality of the response on a scale of 1 to 10.
<prompt>
{prompt}
</prompt>
<response>
{response}
</response>
Your JSON Evaluation:
Prompt for REFERENCE-LIKERT Baseline
- Prompt 内容:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31# System Prompt:
You are an expert evaluator. Given a user prompt, a reference response, and a generated response,
please rate the overall quality of the generated response on a scale of 1 to 10 based on how well it compares to the reference response.
Consider factors such as accuracy, completeness, coherence, and helpfulness when comparing to the reference.
The reference response represents a high-quality answer that you should use as a benchmark.
Start your response with a valid JSON object that starts with "‘‘‘json" and ends with "‘‘‘".
The JSON object should contain a single key "rating" and the value should be an integer between 1 and 10.
Example response: ‘‘‘json
{
"rating": 8
} ‘‘‘
# User Prompt Template:
Given the following prompt, reference response, and generated response, please rate the overall quality of
the generated response on a scale of 1 to 10 based on how well it compares to the reference.
<prompt>
{prompt}
</prompt>
<reference_response>
{reference}
</reference_response>
<generated_response>
{response}
</generated_response>
Your JSON Evaluation:
A.7 合成偏好集生成
- 论文利用公开发布的 HealthBench (2025) 语料库,其中包含 5,000 个与健康相关的 Prompt ,并附有专家撰写的答案
- 其中,4,203 个数据点已包含经执业临床医生审查的理想(ideal)补全内容
- 对于每一个这样的 Prompt-ideal 配对,论文使用 o3 自动生成一个扰动(perturbed)副本,采用下面展示的结构化模板
- 该模板强制模型
- (i) 阐明一个降低质量的[推理]计划
- (ii) 输出降级后的[扰动补全]
- (iii) 记录精确的[新增文本块]和[移除文本块]
- 只有在人工筛选确认扰动版本客观上更差 ,至少在医学准确性、完整性、清晰度、安全性、特异性、结构或语气中的至少一个维度上更差,同时保持连贯且不包含危险建议后,才会接受该扰动
- 论文进一步排除了用于消融研究的 HealthBench-1k 中的 Prompt
- 此过程产生了一个平衡的评估集,包含 3,027 个优选 和 3,027 个扰动 响应(总计 6,054 个),论文在第 5 节的评分标准与 Likert 对比实验中使用了该集合
- 用于此生成的 Prompt 详见图 A.9
A.8 Judge 质量对后训练的影响
- 论文评估了在用于 GRPO 训练时,评分标准引导的评估与无评分标准的 Likert 评分相比,是否提高了 Judge 的有效性
- 表 11 报告了 Judge 在合成医学数据上的准确性,所有策略均使用 Qwen2.5-7B 进行训练,并采用不同的 Judge 模型

A.9 扰动数据集生成(注:用于评估 LLM-Judge 本身)
- 健康响应扰动的 Prompt (Prompt for Health Response Perturbation)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36You are tasked with creating perturbed versions of health-related responses to generate training data for evaluating model robustness.
Given an original health prompt and an ideal completion, you must generate a perturbed version that is strictly worse than the ideal response but still plausible.
**Input Format:**
[prompt]: prompt
[ideal_completion]: ideal_completion
**Task Instructions:**
For the perturbed version, follow this exact process:
[reasoning]: Explain your strategy for making the response worse. Consider these perturbation approaches:
- Medical Accuracy: Introduce subtle medical inaccuracies or outdated information - Completeness: Remove crucial information or context
- Clarity: Make explanations less clear or more confusing
- Safety: Reduce appropriate medical disclaimers or caveats
- Specificity: Replace specific advice with vague generalizations
- Structure: Disorganize the logical flow of information - Tone: Make the response less empathetic or more dismissive
[perturbed_completion]: Create the modified response based on your reasoning strategy.
[chunks_added]: List any new text segments you added (even if they're incorrect or unhelpful)
[chunks_removed]: List any text segments you removed from the ideal response
**Quality Guidelines:**
- Ensure Degradation: Each perturbed response must be objectively worse than the ideal response
- Maintain Plausibility: The perturbed responses should still seem like reasonable attempts (not obviously nonsensical)
- Vary Approaches: Use different perturbation strategies for each version
- Track Changes Precisely: Be specific about what text was added or removed
- Health Context Sensitivity: Be mindful that health misinformation can be harmful
- focus on subtle degradations rather than dangerous advice
**Example Perturbation Strategies:**
- Remove important safety warnings or medical disclaimers
- Add outdated medical information that was once accepted but is now known to be incorrect
- Remove specific dosage information or timing details
- Add overly general statements that replace specific guidance
- Remove context about when to seek professional medical help
- Add confusing or contradictory information
- Remove step-by-step instructions and replace with vague advice
- Add unnecessarily complex medical jargon without explanation