注:本文包含 AI 辅助创作
- 参考链接:
Paper Summary
- 整体总结:
- 论文作者分析了 DPO 应用于多轮任务时,由于无法消去配分函数(partition function) 而带来了的挑战
- 论文提出了一种简单且鲁棒的损失函数 DMPO(是 DPO 的一种改进),可以直接优化多轮智能体任务的强化学习目标
- 通过将策略约束替换为状态-动作占用度量(SAOM)约束,并在 BT 模型中引入长度归一化,论文消除了 BT 模型中的配分函数,并推导出了 DMPO 损失函数
- 背景:
- 直接偏好优化(Direct Preference Optimization, DPO)是一种缓解复合错误(compounding errors)的有前景的技术,能够直接优化 RL 目标
- 问题提出:
- 将 DPO 应用于多轮任务时,由于无法消去配分函数(partition function) ,带来了挑战,解决这个问题需要使配分函数独立于当前状态,并解决偏好轨迹与非偏好轨迹之间的长度差异问题
- 论文提出了一种名为 DMPO 的新型损失函数,用于多轮智能体任务,并提供了理论解释
- 在强化学习目标中用状态-动作占用度量(state-action occupancy measure, SAOM)约束替换策略约束
- 并在 Bradley-Terry(BT)模型中引入长度归一化(length normalization)
- 在三个多轮智能体任务数据集上的广泛实验验证了 DMPO 损失的有效性和优越性
Introduction and Discussion
- 开发能够解决复杂任务的通用智能体一直是人工智能领域的核心目标(2022;2024)
- 近年来,语言智能体(Language agents)(2022a)成为一个重要的研究方向
- Language agents 其利用 LLM 的巨大潜力来解决涉及指令跟随(2022)、动作规划(2022)和工具使用(2024)的复杂任务
- 然而,LLM 的预训练任务与智能体任务需求之间的巨大差距表明,语言智能体能力仍有很大的提升空间
- 行为克隆(Behavioral Cloning, BC)(1991)是一种常用的方法,通过专家智能体轨迹对 LLM 进行微调,以弥合领域差距
- 近期关于 BC 的研究(2023)涉及对最优状态-动作对进行SFT
- 尽管这些方法能够快速将 LLM 适配到智能体任务中,但 BC 对复合错误(compounding errors)尤为敏感——学习者的微小错误会在智能体与环境的交互过程中累积,导致在非确定性环境中性能下降(2011)
- 在缓解复合错误方面,直接偏好优化(Direct Preference Optimization, DPO)(2023b)因其简单实现和鲁棒性,在单轮偏好对齐任务中取得了显著成功
- DPO 通过最大化偏好响应相对于非偏好响应的似然来优化强化学习目标,避免了与传统强化学习算法相关的持续环境交互和训练不稳定性(2023;2024)
- 尽管已有初步尝试将 DPO 损失应用于智能体任务的 LLM(2024),但其性能欠佳,因为它是专为单轮(single-turn) Bandit设置设计的,不适合( ill-suited)多轮(multi-turn)智能体任务
- 本研究旨在开发一种鲁棒的损失函数,能够直接优化多轮场景下的强化学习目标。这一目标的关键在于消除 Bradley-Terry(BT)模型(Bradley and Terry, 1952)中的配分函数。具体来说,需要确保配分函数独立于当前状态,并消除偏好与非偏好轨迹长度差异的影响
- 论文在强化学习目标中用状态-动作占用度量( state-action occupancy measure,SAOM)(2000)约束替换策略约束
- 并在 BT 模型中引入长度归一化
- 这些调整最终形成了一种新的简单损失函数 DMPO,用于多轮智能体任务
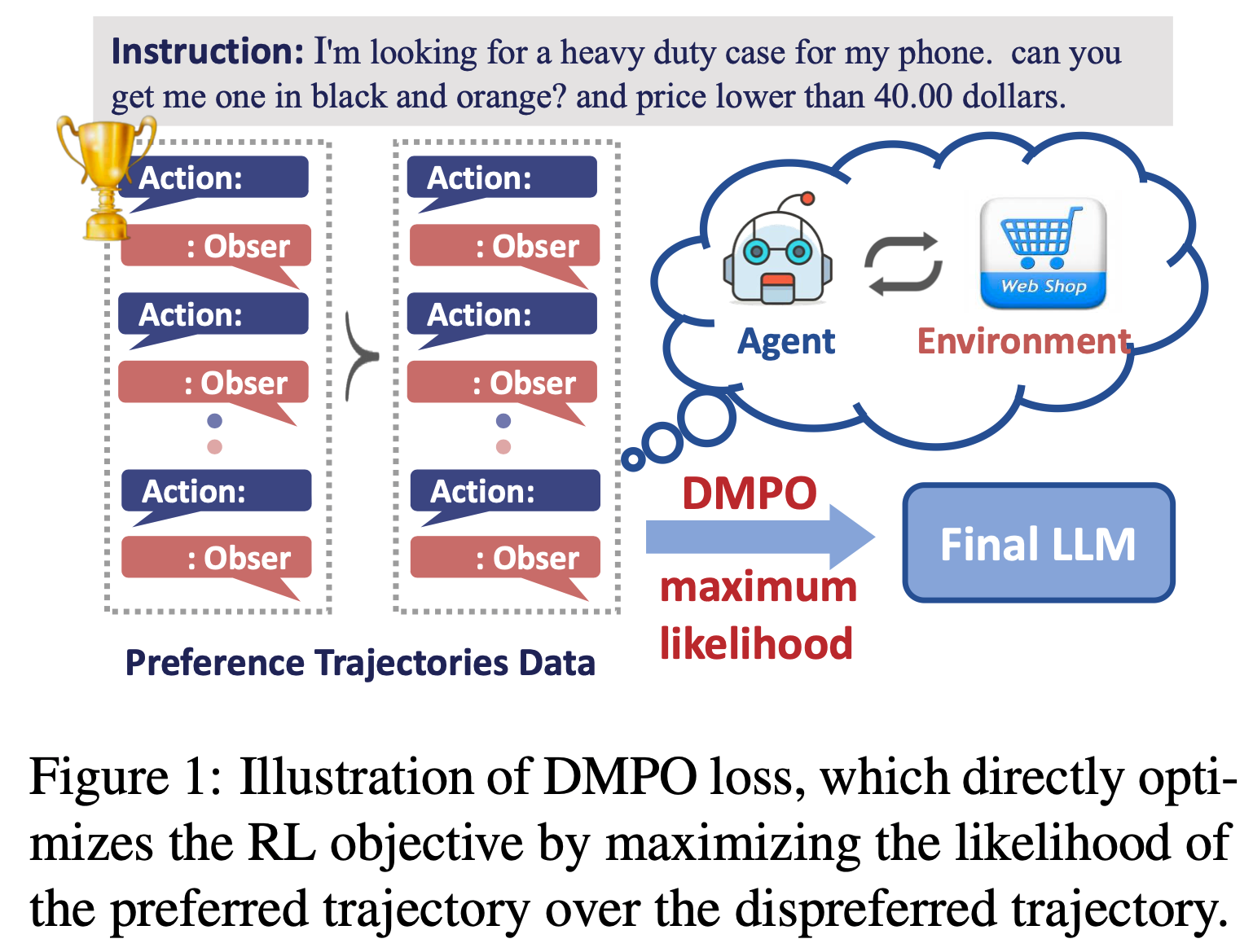
- 如图1 所示,DMPO 通过最大化偏好(“win”)轨迹相对于非偏好(“loss”)轨迹的似然,直接优化强化学习目标
- 值得注意的是,与策略约束相比,SAOM 约束在缓解复合错误方面具有优势(2020)
- 此外,该推导为长度归一化技术在 DPO 损失中的有效性提供了理论依据(2024)
- 总结而言,论文的贡献如下:
- 提出了一种名为 DMPO 的新型损失函数,可直接优化多轮场景下的强化学习目标,从而缓解 BC 方法中的复合错误
- 为长度归一化技术的有效性提供了理论解释,说明其如何消除 BT 模型中的配分函数并提升性能
- 在三个多轮智能体任务数据集上的广泛实验验证了 DMPO 损失函数的有效性和优越性
Related Work
- 本节首先介绍语言智能体的上下文学习方法(in-context learning)和微调方法(fine-tuning),然后回顾基于偏好的强化学习(preference-based RL)相关文献
- 上下文学习 :受 LLM 强大的上下文学习能力启发(2023),研究人员设计了多种指令提示(instruction prompts),配备记忆模块(2024)、工具包(2024)和各种工作流(2023),以构建适用于不同现实领域任务的语言智能体
- ReAct(2022b)将 CoT 推理(2022)融入动作生成中
- Reflexion(2024)和 PROMST(2024)利用环境反馈优化提示
- 然而,这些上下文学习方法未能充分发挥 LLM 的潜力,因为大多数 LLM 并未专门针对智能体任务进行训练
- 本研究专注于通过微调将 LLM 适配到智能体任务
- 智能体微调 :近期研究,如 FireAct(2023)、AgentTuning(2023)、Lumos(2023)、MIMIR(2024)、AUTOACT(2024)和 \(\alpha\)-UMi(2024),通过自指令或专家轨迹对 LLM 进行监督微调
- 但此类 BC 方法在与动态环境交互时会受到复合错误的影响
- 更进一步,Pangu(2023)和 CMAT(2024)利用强化学习技术进一步微调 LLM,但这可能导致训练过程复杂且不稳定
- 为了简化流程,ETO(2024)和 EMMA(2024)直接采用 DPO 损失(2023b)优化智能体任务的强化学习目标,然而,DPO 损失是为单轮 Bandit 设置设计的,不适合多轮场景
- 沿着这一方向,本研究将 DPO 损失扩展到多轮场景,并推导出 DMPO 损失
- 基于偏好的强化学习 :在多轮场景中,基于偏好的强化学习通常首先从偏好数据中显式学习奖励函数,然后对其进行优化(2012)
- 然而,这种两阶段学习过程在训练效率和稳定性方面存在挑战,本研究提出了一种使用 DMPO 损失的单阶段策略学习方法,直接优化策略以满足偏好
- 尽管 IPL(2024)和 CPL(2023)与本研究在消除奖励学习阶段方面有相似思路,但其损失函数仅限于长度相等的轨迹对,极大地限制了其适用性
Preliminaries
- 在本节中,论文将介绍多轮智能体任务的数学形式,并简要介绍直接偏好优化(Direct Preference Optimization, DPO)损失函数
任务描述
- 智能体任务可以建模为一个马尔可夫决策过程(Markov Decision Process, MDP),一个 MDP 是一个五元组 \((\mathcal{S}, \mathcal{A}, \mathcal{T}, \mathcal{R}, \gamma)\)
- \(\mathcal{S}\) 表示状态空间
- \(\mathcal{A}\) 表示动作空间
- \(\mathcal{T}\) 表示动态转移函数 \(\mathcal{S} \times \mathcal{A} \rightarrow \mathcal{S}\)
- \(\mathcal{R}\) 表示奖励函数 \(\mathcal{S} \times \mathcal{A} \rightarrow [0,1]\)
- \(\gamma \in [0,1)\) 是折扣因子
- 智能体的目标是在每个时间步选择动作,以最大化期望的未来折扣奖励
$$\mathbf{E} \left[\sum_{t=0}^{T-1} \gamma^{t} r(s_{t}, a_{t})\right]$$- 其中 \(T\) 是轨迹长度
- 在语言智能体(Language Agents)的设置中,状态空间和动作空间都是语言空间的子集
- 初始状态 \(s_{0} \in \mathcal{S}\) 包含任务指令和提示
- 在每个时间步 \(t\), LLM 根据策略 \(\pi_{\theta}(a_{t}|s_{t})\) 生成动作 \(a_{t}\),其中 \(\theta\) 是参数
- 随后,环境会返回动态反馈 \(o_{t}\) 并将状态转移到 \(s_{t+1}\)
- 需要注意的是,新状态 \(s_{t+1}\) 仅仅是 \(s_{t}\)、\(a_{t}\) 和 \(o_{t}\) 的简单组合,而轨迹为
$$ \tau = (s_{0}, a_{0}, s_{1}, a_{1}, \cdots, s_{T}, a_{T}) $$
DPO
- DPO 损失的目标是通过在策略函数上施加 KL 散度约束,直接优化 RL 目标:
$$
\max_{\pi_{\theta} } \mathbb{E}_{\tau}\left[ \sum_{t=0}^{T-1} \gamma^{t} r(s_{t}, a_{t})\right] - \beta \mathbb{D}_{KL}\left[\pi_{\theta}(a_{t}|s_{t}) || \pi_{ref}(a_{t}|s_{t})\right],
$$- \(\mathbb{E}\) 是期望函数
- \(\mathbb{D}_{KL}[\cdot || \cdot]\) 表示两个分布之间的 KL 散度
- \(\pi_{ref}\) 表示参考策略
- \(\beta\) 是控制与参考策略 \(\pi_{ref}\) 偏离程度的参数
- DPO 损失专为单轮偏好对齐任务设计,其中轨迹长度 \(T\) 限制为 1
- 值得注意的是,奖励函数是通过布拉德利-特里(Bradley-Terry, BT)模型学习的:
$$
p(a_{0}^{w} \succ a_{0}^{l}|s_{0}) = \frac{\exp(r(s_{0}, a_{0}^{w}))}{\exp(r(s_{0}, a_{0}^{w})) + \exp(r(s_{0}, a_{0}^{l}))}, \tag{2}
$$- 该模型给出了在给定状态 \(s_{0}\) 下,“win”动作 \(a_{0}^{w}\) 优于“loss”动作 \(a_{0}^{l}\) 的概率
- 随后,DPO 利用单轮强化学习问题的闭式解:
$$
\pi^{*}(a|s) = \frac{1}{Z(s)} \pi_{ref}(a|s) e^{r(s,a)},
$$- 其中 \(\pi^{*}\) 表示最优策略,\(Z(s)\) 是归一化的配分函数
- 我们可以轻松地重新整理上式并将其代入 BT 模型,得到关于策略的 BT 模型:
$$
p(a_{0}^{w} \succ a_{0}^{l}|s_{0}) = \sigma \left( \beta \log \frac{\pi_{\theta}(a_{0}^{w}|s_{0})}{\pi_{ref}(a_{0}^{w}|s_{0})} - \beta \log \frac{\pi_{\theta}(a_{0}^{l}|s_{0})}{\pi_{ref}(a_{0}^{l}|s_{0})} \right),
$$- 其中配分函数 \(Z(s)\) 从 BT 模型中消去,\(\sigma\) 是 sigmoid 函数
- DPO 损失通过最大化似然函数来获得最优策略 \(\pi_{\theta}^{*}\):
$$
\mathcal{L}_{DPO} = -\mathbb{E}_{(s_{0}, a_{0}^{w}, a_{0}^{l}) \sim D} \log \left[ p(a_{0}^{w} \succ a_{0}^{l}|s_{0}) \right],
$$- 其中 \(D\) 表示偏好数据集
- 然而,这种简洁而优雅的推导仅适用于单轮偏好优化任务。如式 (3) 所示,配分函数 \(Z(s)\) 依赖于当前状态 \(s\),因此在多轮设置中无法通过策略约束消去
论文方法细节
- 在本节中,论文将首先介绍状态-动作占用度量(State-Action Occupancy Measure, SAOM)的定义及其优势
- 随后,论文将提出两项调整以推导 DMPO 损失函数。最后,论文将深入分析 DMPO 损失的特性
State-Action Occupancy Measure(状态-动作占用度量)
- 策略 \(\pi\) 的折扣状态-动作占用度量 \(d^{\pi}(s,a)\) 描述了智能体在策略 \(\pi\) 下访问状态-动作对的分布:
$$
d^{\pi}(s,a) = \frac{1 - \gamma}{1 - \gamma^T} \sum_{t=0}^{T-1} \gamma^t \mathbb{P}(s_t = s, a_t = a | \pi),
$$- 其中 \(\mathbb{P}(\cdot)\) 表示概率,系数 \((1 - \gamma)/(1 - \gamma^T)\) 用于归一化概率分布
- 首先,论文将直观解释 SAOM 约束如何减少复合误差(compounding errors)。在模仿学习(imitation learning)中,传统的 SFT 学习目标是最小化专家策略与当前策略之间的 KL 散度:
$$
\min_{\pi_{\theta} } \mathbb{E}_{(s,a) \sim d^E} \left[ \mathbb{D}_{KL}(\pi_E(a|s) || \pi_{\theta}(a|s)) \right] = -\max_{\pi_{\theta} } \mathbb{E}_{(s,a) \sim d^E} \left[ \log(\pi_{\theta}(a|s)) \right],
$$- 其中 \(\pi_E\) 是专家策略,\(d^E\) 是策略 \(\pi_E\) 的 SAOM
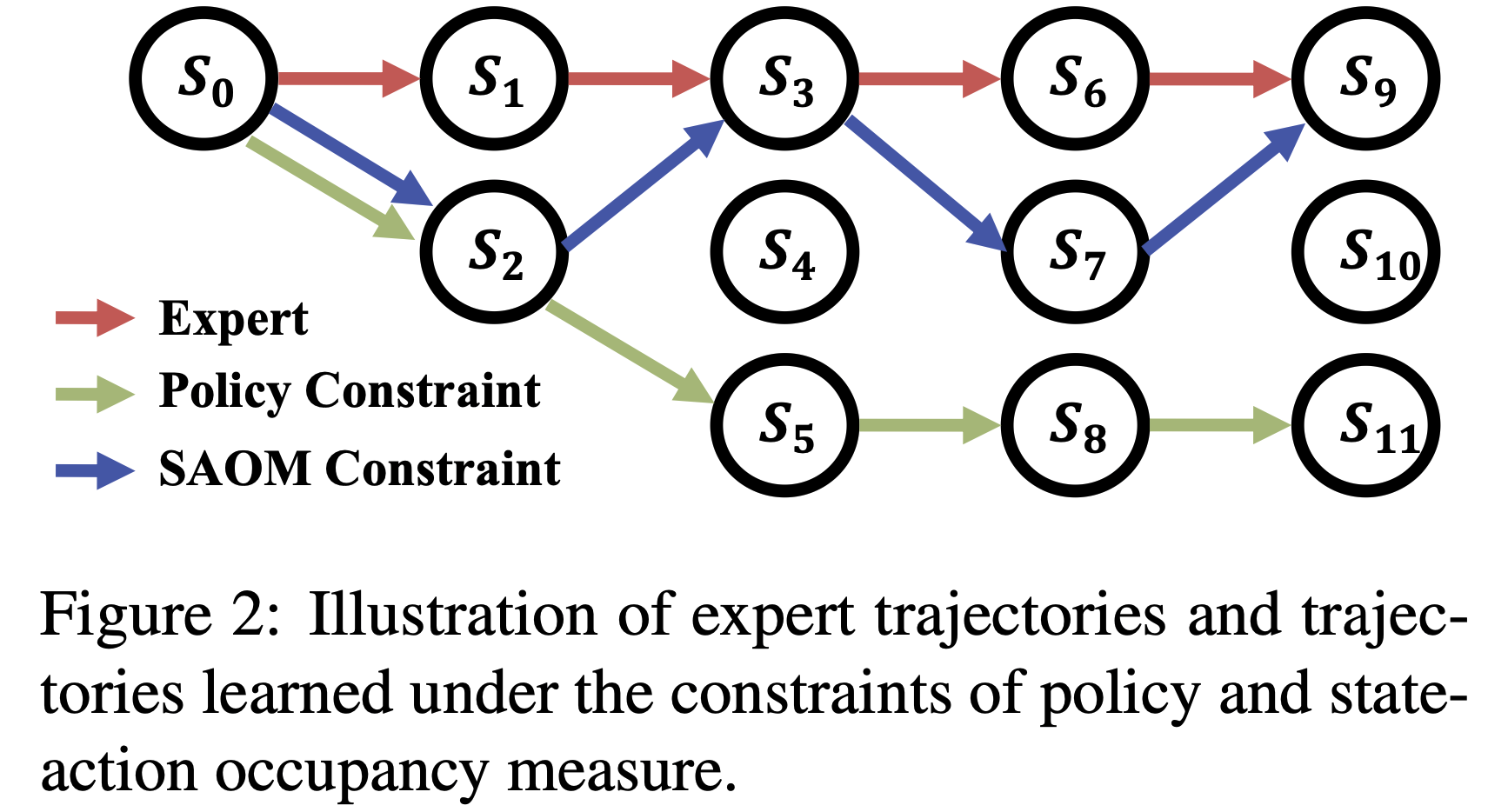
- 如图2 所示,在策略约束下学习的轨迹容易受到显著的复合误差影响
- 这种脆弱性源于专家数据集无法全面覆盖所有可能的状态
- 因此,SFT 损失会导致模型在专家数据集中未出现的状态下选择随机动作,从而在初始错误后逐渐偏离专家轨迹,这就是所谓的复合误差现象
- 为了缓解复合误差,后续的模仿学习研究(2004;2020;2016)采用了 SAOM 约束:
$$
\min_{\pi_{\theta} } \mathbb{E}_{(s,a) \sim d^E} \left[ \mathbb{D}_{(\cdot)}(d^{\pi_{\theta} }(a|s) || d^{\pi_E}(a|s)) \right],
$$- 其中不同的方法使用了不同的分布距离度量 \(\mathbb{D}_{(\cdot)}\)
- SAOM 约束的优势在于,它能够引导动作选择向模仿专家状态-动作对的方向靠近,尤其是在专家数据集中未探索的状态下
- 如图2 所示,在状态 \(s_2\) 下,策略约束会导致模型均匀选择动作,而 SAOM 约束则旨在引导模型选择能将下一状态带回专家轨迹的动作,从而有效缓解复合误差并提升累积奖励
DMPO
- 受模仿学习的启发,论文将公式(1)中的策略约束替换为 SAOM 约束,得到以下强化学习目标:
$$
\max_{\pi_{\theta} } \mathbb{E}_{(s,a) \sim d^{\pi_{\theta} }(s,a)} \left[ r(s,a) \right] - \beta \mathbb{D}_{KL} \left[ d^{\pi_{\theta} }(s,a) || d^{\pi_{ref} }(s,a) \right], \tag{9}
$$- 其中 \(\pi_{ref}\) 表示参考策略。类似于 Rafailov 等(2023b),可以证明公式(9)的 RL 目标的最优解形式为:
$$
d^{\pi^{*} }(s,a) = \frac{1}{Z} d^{\pi_{ref} }(s,a) \exp \left( \frac{1}{\beta} r(s,a) \right), \tag{10}
$$- 其中 \(\pi^{*}\) 表示最优策略,\(Z\) 是归一化概率的配分函数。值得注意的是,由于 \(d^{\pi}(s,a)\) 是 \((s,a)\) 对的函数,归一化后配分函数 \(Z\) 与当前状态 \(s\) 无关。因此,\(Z\) 对所有 \((s,a)\) 对保持恒定,这为论文提供了消除它的机会。我们可以轻松地将公式(10)整理为:
$$
r(s,a) = \beta \log \frac{d^{\pi^{*} }(s,a)}{d^{\pi_{ref} }(s,a)} + \beta \log Z. \tag{11}
$$
- 其中 \(\pi^{*}\) 表示最优策略,\(Z\) 是归一化概率的配分函数。值得注意的是,由于 \(d^{\pi}(s,a)\) 是 \((s,a)\) 对的函数,归一化后配分函数 \(Z\) 与当前状态 \(s\) 无关。因此,\(Z\) 对所有 \((s,a)\) 对保持恒定,这为论文提供了消除它的机会。我们可以轻松地将公式(10)整理为:
- 其中 \(\pi_{ref}\) 表示参考策略。类似于 Rafailov 等(2023b),可以证明公式(9)的 RL 目标的最优解形式为:
- 类似于公式(2),论文通过 Bradley-Terry(BT)模型学习多轮场景的奖励函数:
$$
p(\tau^w \succ \tau^l | s_0) = \sigma \left( \sum_{t=0}^{T_w - 1} \gamma^t r(s_t^w, a_t^w) - \sum_{t=0}^{T_l - 1} \gamma^t r(s_t^l, a_t^l) \right), \tag{12}
$$- 其中 \(\tau^w\) 和 \(\tau^l\) 分别表示“win”和“lose”轨迹,\(T_w\) 和 \(T_l\) 分别表示“win”和“lose”轨迹的长度。然而,由于 \(T^w \neq T^l\),配分函数 \(Z\) 无法直接在公式(12)中消除
- 为了克服这一障碍,论文在公式(12)中引入了长度归一化技术:
$$
p(\tau^w \succ \tau^l | s_0) = \sigma \left( \frac{1 - \gamma}{1 - \gamma^{T_w} } \sum_{t=0}^{T_w - 1} \gamma^t r(s_t^w, a_t^w) - \frac{1 - \gamma}{1 - \gamma^{T_l} } \sum_{t=0}^{T_l - 1} \gamma^t r(s_t^l, a_t^l) \right). \tag{13}
$$ - 通过这种方式,我们可以通过将公式(11)中的奖励函数 \(r(s,a)\) 代入公式(13)来消除配分函数 \(Z\)。然后,论文最大化似然并得到:
$$
L_\text{DMPO} = -\mathbb{E}_{(s_0, \tau^w, \tau^l) \sim D} \log \sigma \left[ \frac{1 - \gamma}{1 - \gamma^{T_w} } \sum_{t=0}^{T_w - 1} \beta \gamma^t \log \frac{d^{\pi_{\theta} }(s_t^w, a_t^w)}{d^{\pi_{ref} }(s_t^w, a_t^w)} - \frac{1 - \gamma}{1 - \gamma^{T_l} } \sum_{t=0}^{T_l - 1} \beta \gamma^t \log \frac{d^{\pi_{\theta} }(s_t^l, a_t^l)}{d^{\pi_{ref} }(s_t^l, a_t^l)} \right], \tag{14}
$$- 其中 \(d^{\pi}(s_t, a_t)\) 可以进一步表示为:
$$
d^{\pi}(s = s_t^w, a = a_t^w) = \gamma^t \cdot P(s_0) \cdot \prod_{k=0}^{t-1} \pi(a_k^w | s_k^w) P(s_{k+1}^w | s_k^w, a_k^w), \tag{15}
$$- 其中 \(P(s_0)\) 表示初始状态 \(s_0\) 的概率,\(P(s_{k+1} | s_k, a_k)\) 表示转移函数。通常情况下,获取 SAOM \(d^{\pi}(s_t, a_t)\) 具有挑战性,因为论文在动态环境中不知道转移函数 \(P(s_{k+1} | s_k, a_k)\)。然而,在公式(16)中,论文只需计算当前 SAOM \(d^{\pi_{\theta} }(s_t, a_t)\) 与参考 SAOM \(d^{\pi_{ref} }(s_t, a_t)\) 的比率。值得注意的是,两者的转移函数保持一致,因此可以相互抵消
- 其中 \(d^{\pi}(s_t, a_t)\) 可以进一步表示为:
- 通过将公式(15)代入公式(14),我们可以得到 DMPO 损失函数:
$$
L_\text{DMPO} = -\mathbb{E}_{(s_0, \tau^w, \tau^l) \sim D} \log \sigma \left[ \sum_{t=0}^{T_w - 1} \beta \phi(t, T_w) \log \frac{\pi_{\theta}(a_t^w | s_t^w)}{\pi_{ref}(a_t^w | s_t^w)} - \sum_{t=0}^{T_l - 1} \beta \phi(t, T_l) \log \frac{\pi_{\theta}(a_t^l | s_t^l)}{\pi_{ref}(a_t^l | s_t^l)} \right],
$$- 其中折扣函数 \(\phi(t, T) = \gamma^t \cdot (1 - \gamma^{T - t}) / (1 - \gamma^T)\)。值得注意的是,DMPO 通过折扣函数 \(\phi(t, T)\) 对不同步骤的状态-动作对进行重新加权
深入分析
- 在本小节中,论文将探讨 DMPO 损失的优势,并提出一些引理和观察结果
- 推论 4.0.1(Corollary 4.0.1) :DMPO 损失为早期步骤的状态-动作对分配更高的权重,其中权重与折扣因子 \(\gamma\) 相关
- 证明 :为了证明该引理,论文分析损失函数 \(L_\text{DMPO}\) 关于 \(\theta\) 的梯度:
$$
\nabla_{\theta} L_\text{DMPO} = -\mathbb{E}_{(s_0, \tau^w, \tau^l) \sim D} \sigma \left[ \Phi(\tau^l) - \Phi(\tau^w) \right] \left[ \sum_{t=0}^{T_w - 1} \beta \phi(t, T_w) \nabla_{\theta} \log \pi_{\theta}(a_t^w | s_t^w) - \sum_{t=0}^{T_l - 1} \beta \phi(t, T_l) \nabla_{\theta} \log \pi_{\theta}(a_t^l | s_t^l) \right],
$$- 其中函数 \(\Phi(\tau) = \sum_{t=0}^{T-1} \beta \phi(t, T) \log \frac{\pi_{\theta}(a_t | s_t)}{\pi_{ref}(a_t | s_t)}\),且 \(\phi(t, T) = \gamma^t \cdot (1 - \gamma^{T - t}) / (1 - \gamma^T)\)。折扣函数 \(\phi(t, T)\) 随着 \(t\) 的增加而减小,并与折扣因子 \(\gamma\) 相关。证明完成
- 推论 4.0.2(Corollary 4.0.2) :当折扣因子 \(\gamma\) 趋近于零时,DMPO 损失退化为单轮 DPO 损失
- 证明 :当 \(\gamma\) 等于 0 时,函数 \(\phi(t, T)\) 在 \(t = 0\) 时为 1,其余情况下为 0,这等价于单轮 DPO 损失
- 基于上述分析,论文得出以下观察结果:
- 观察 4.0.1(Observation 4.0.1) :与 DPO 损失类似,DMPO 损失增加了偏好轨迹 \(\tau_w\) 的似然,同时降低了非偏好轨迹 \(\tau_l\) 的似然
- 观察 4.0.2(Observation 4.0.2) :如果策略 \(\pi_{\theta}\) 对非偏好轨迹的奖励 \(\Phi(\tau_l)\) 估计过高,则权重 \(\sigma \left[ \Phi(\tau^l) - \Phi(\tau^w) \right]\) 会更大
- 长度归一化解释 :在 SimPO(Meng 等,2024)中,长度归一化技术的有效性已通过实验验证,但未提供理论解释。论文的推导表明,它有助于消除 BT 模型中的配分函数。如果在公式(13)中不使用长度归一化,BT 模型中会出现一个与长度相关的偏置项,随着偏好和非偏好样本之间轨迹长度差异的增加,模型性能会下降
- 进一步讨论 :如 4.2 节所述,公式(9)的 RL 目标的最优解形式为公式(10)。然而,有人认为,在语言智能体设置中,对于任意奖励函数 \(r(s,a)\),实现最优解可能并不总是可行。这种限制源于新状态 \(s_{t+1}\) 定义为 \(s_t\)、\(a_t\) 和 \(o_t\) 的组合,这引入了状态之间转移函数的内在约束。总体而言,在多轮动态环境中,没有损失函数能够严格优化 RL 目标,而 DMPO 损失是一个良好的近似。在许多情况下,DMPO 损失可以精确优化公式(9)中的 RL 目标
相关实验
- 在本节中,论文在三个智能体任务上进行了广泛的实验,以验证所提出的 DMPO 损失函数的有效性。论文的实验旨在回答以下问题:
- RQ1 :DMPO 损失函数能否对噪声训练轨迹数据表现出鲁棒性,并减轻复合错误?
- RQ2 :与其他基线方法相比,DMPO 损失函数的表现如何?
- RQ3 :折扣因子 \(\gamma\) 和轨迹长度对 DMPO 损失函数有何影响?
Experiment Setup
- 数据集(Datasets) :遵循先前的工作(2024),论文在三个代表性的智能体数据集上进行了实验,包括 WebShop(2022a)、ScienceWorld(2022)和 ALFWorld(2020b)
- WebShop :一个模拟购物网站环境,智能体根据自然语言指令中的规格查找并购买产品。最终奖励 \(r \in [0,1]\) 基于购买产品与指定标准的匹配程度计算
- ScienceWorld :一个交互式文本环境,测试智能体在基础科学实验中的科学推理能力,包含 10 种任务类型。最终奖励 \(r \in [0,1]\) 基于智能体在每个任务中成功完成的子目标数量计算
- ALFWorld :一个基于文本的模拟环境,智能体需要完成 ALFRED 基准测试(2020a)中的家庭任务。最终奖励为二元值,表示任务的完成状态
这三个环境均可形式化为马尔可夫决策过程(MDP),并由语言智能体执行。数据集的统计细节如表1 所示。遵循 Song 等 (2024),除了分布内的“已见”测试集外,ScienceWorld 和 ALFWorld 还包含分布外的“未见”测试集,用于评估不同智能体的泛化能力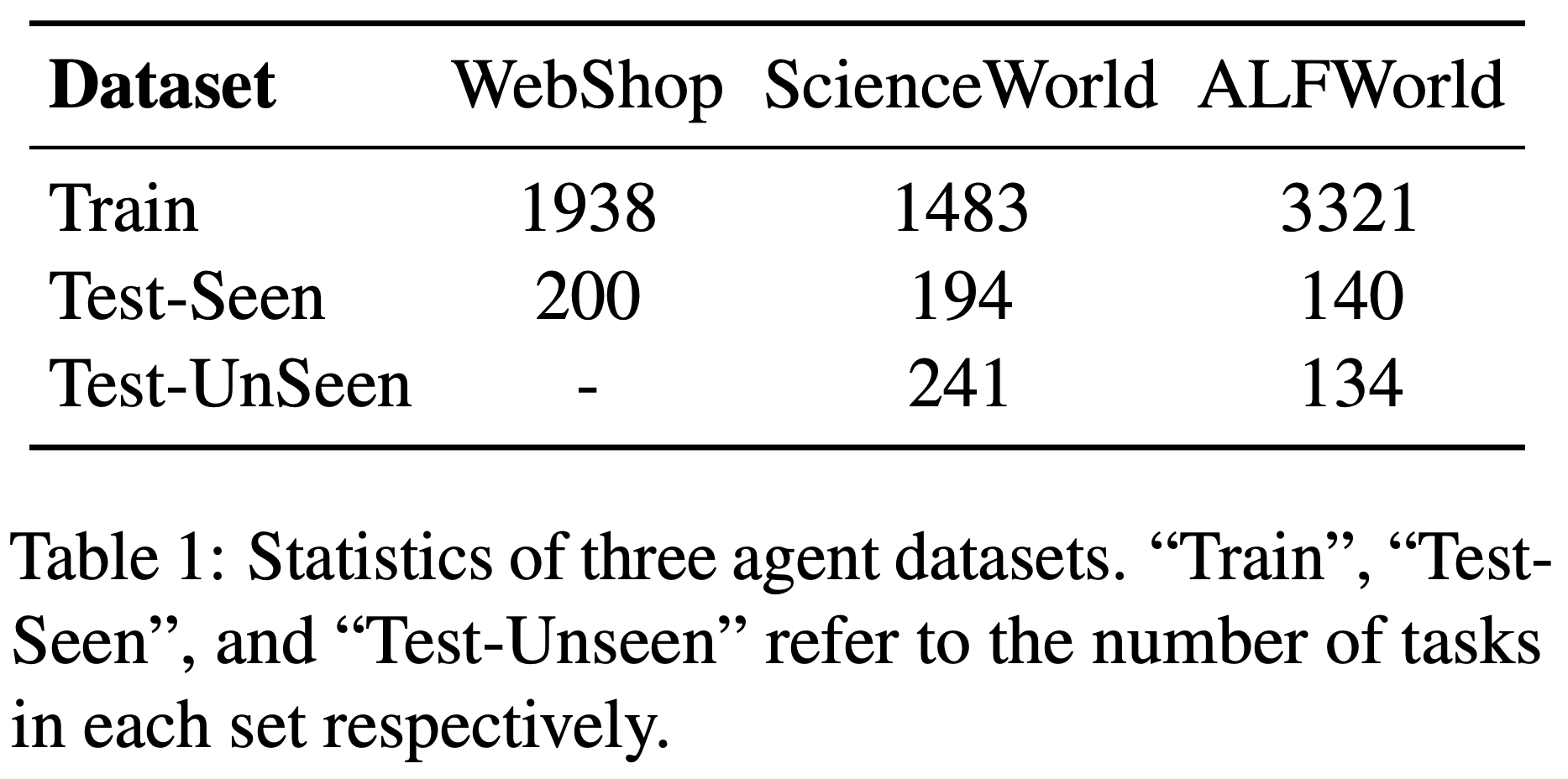
- 训练设置(Training Settings) :论文通过两种不同的训练场景评估 DMPO 损失函数的鲁棒性和有效性:噪声设置(Noisy setting)和干净设置(Clean setting)
- 遵循 Song 等 (2024),在噪声设置和干净设置中,论文均使用专家轨迹作为“win”轨迹构建偏好轨迹数据
- 论文使用经过专家轨迹微调的 LLM 在训练集上生成新轨迹。观察到 LLM 倾向于生成包含重复动作或无意义词语的轨迹
- 在噪声设置中,这些噪声轨迹被用作“lose”轨迹构建偏好数据;
- 在干净设置中,论文剔除噪声轨迹,使用剩余的轨迹作为“lose”轨迹
- 参数设置(Parameter Settings) :本研究使用了两个不同的基础模型:Llama-2-7B-Chat(2023)和 Mistral-7B-Instruct-v0.2(2023)来构建语言智能体。其他超参数设置遵循 Song 等 (2024):
- 使用 AdamW 优化器
- 在监督微调基础模型以获取参考模型时,批量大小设为 64,学习率从 \(\{1e-5, 2e-5, 3e-5\}\) 中选择,预热比例为 3%,并采用余弦调度器
- 在使用 DMPO 损失函数优化智能体时,批量大小设为 32,超参数 \(\beta\) 和 \(\gamma\) 分别在 \(\{0.1, 0.2, …, 0.9\}\) 和 \(\{0.1, 0.2, …, 0.9, 0.99\}\) 范围内调优
- 所有实验均在 8 块 NVIDIA A100 GPU 上完成
- 评估设置(Evaluation Setting ) :遵循 Song 等 (2024),论文使用 ReAct 风格的交互格式(Yao 等, 2022b)评估所有方法,该格式会交错生成推理轨迹和动作。对于每个任务,论文添加 1-shot 示例,具体可参考 Song 等 (2024)。除非另有说明,解码生成温度设为 0.0
RQ1:噪声设置结果
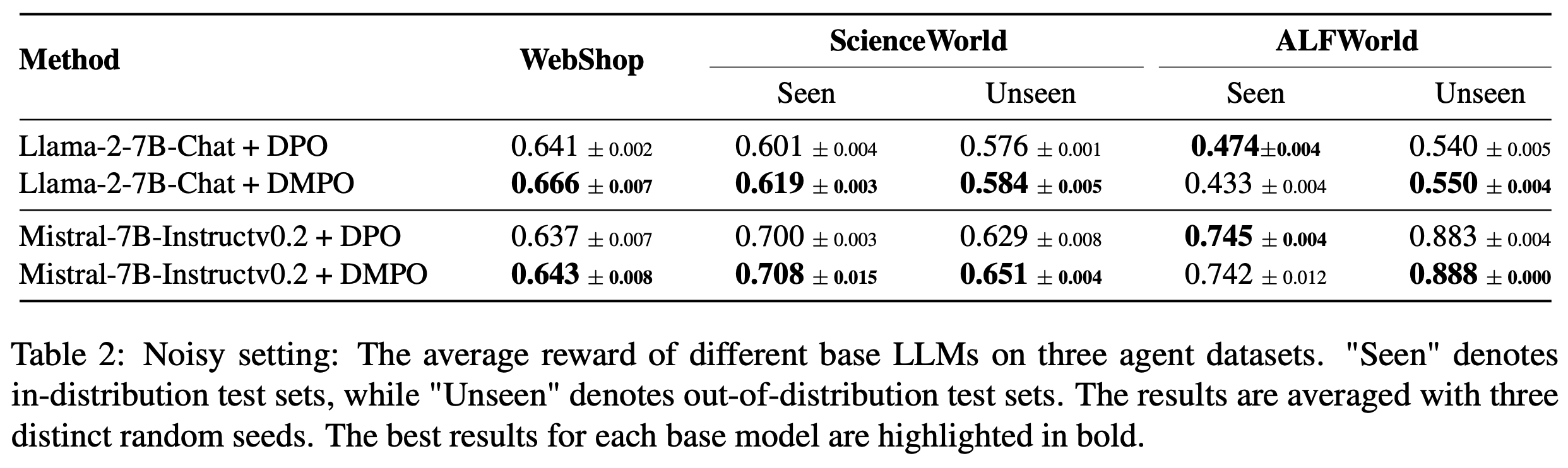
- 在噪声设置中,论文使用噪声轨迹作为“lose”轨迹构建偏好数据,以研究 DMPO 损失函数的鲁棒性。如表2 所示,论文在两个不同的基础模型上评估了 DMPO 损失函数在两个代表性智能体任务上的表现,观察到以下现象:
- 在所有未见测试集和大多数已见测试集中,DMPO 损失函数的表现优于 DPO 损失函数。这种优势源于 DMPO 对初始状态-动作对赋予更高权重,优先学习早期阶段的高质量专家动作,并减少后期噪声“lose”动作的影响。这减轻了噪声的影响,增强了模型的泛化能力。而 DPO 损失函数不适用于多轮设置,无法在 BT 模型中消除配分函数,因此表现较差
- Mistral-7B-Instruct-v0.2 在 ScienceWorld 和 ALFWorld 上的表现显著优于 Llama-2-7B-Chat。这表明基础模型的有效性与使用 DMPO 损失函数微调后的性能提升呈正相关
RQ2:干净设置结果
- 在干净设置中,论文过滤掉噪声轨迹,选择高质量轨迹作为“lose”轨迹构建偏好数据,以充分发挥 DMPO 损失函数的潜力
- 基线方法 :遵循 Song 等 (2024),论文将使用 DMPO 损失函数训练的模型与以下代表性基线进行比较:
1) Base :未经调优的默认 LLM
2) SFT :通过监督学习在专家轨迹上微调的 LLM
3) Best-of-N :使用基于 SFT 的智能体采样,并从 N 个样本中选择奖励最高的轨迹,此处 N=10
4) RFT(拒绝采样微调,Yuan 等, 2023):通过添加成功轨迹扩展专家轨迹数据集,随后在扩展数据集上训练智能体
5) PPO(近端策略优化,Schulman 等, 2017):直接优化强化学习目标以最大化累积奖励
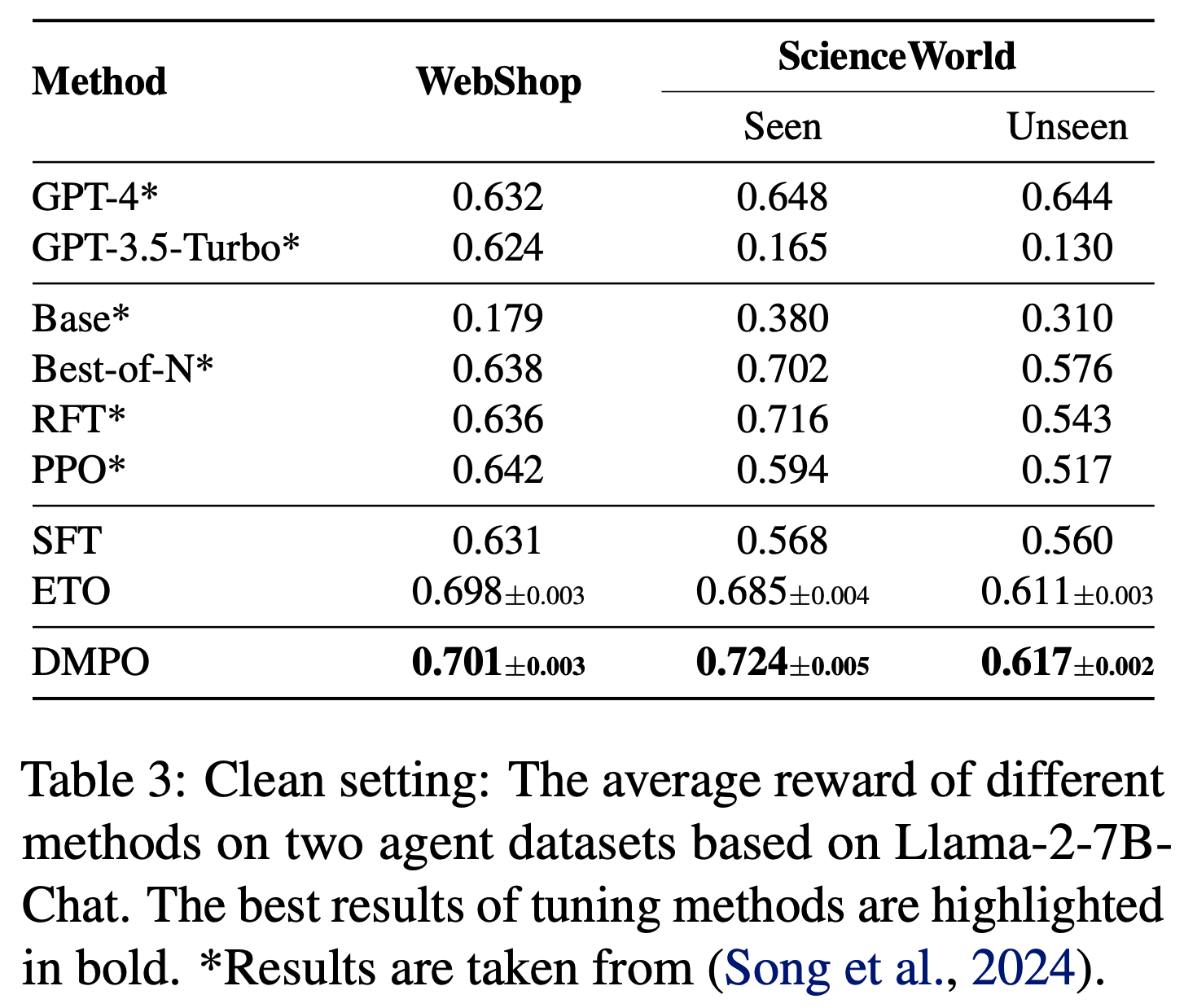
6) ETO(基于探索的轨迹优化,Song 等, 2024):通过迭代探索环境增强训练偏好数据,并使用 DPO 损失从偏好数据中学习 - 结果 :基于 Llama-2-7B-Chat 模型,论文在干净设置下的对比结果如表3 所示。值得注意的是:
- 所有微调方法在两个数据集上的表现均显著优于基础模型,提升幅度至少为 49%。在 WebShop 上,它们甚至超越了先进闭源 LLM 的表现。这表明 LLM 的预训练任务与智能体任务之间存在显著差距,通过微调 LLM,语言智能体具有巨大的改进潜力
- 使用 DMPO 损失函数训练的模型在两个数据集上均取得了最佳性能,凸显了 DMPO 损失函数从偏好数据中学习的有效性。与 SFT 模型相比的改进表明,DMPO 减少了复合错误,从而获得了更高的奖励
- 与噪声设置相比,使用 DMPO 损失函数训练的模型在性能上有显著提升,WebShop 平均提升 5.2%,ScienceWorld 平均提升 11.3%。这表明在构建偏好数据时选择高质量的“lose”轨迹非常重要,选择此类轨迹能够带来更优的性能
RQ3:消融研究
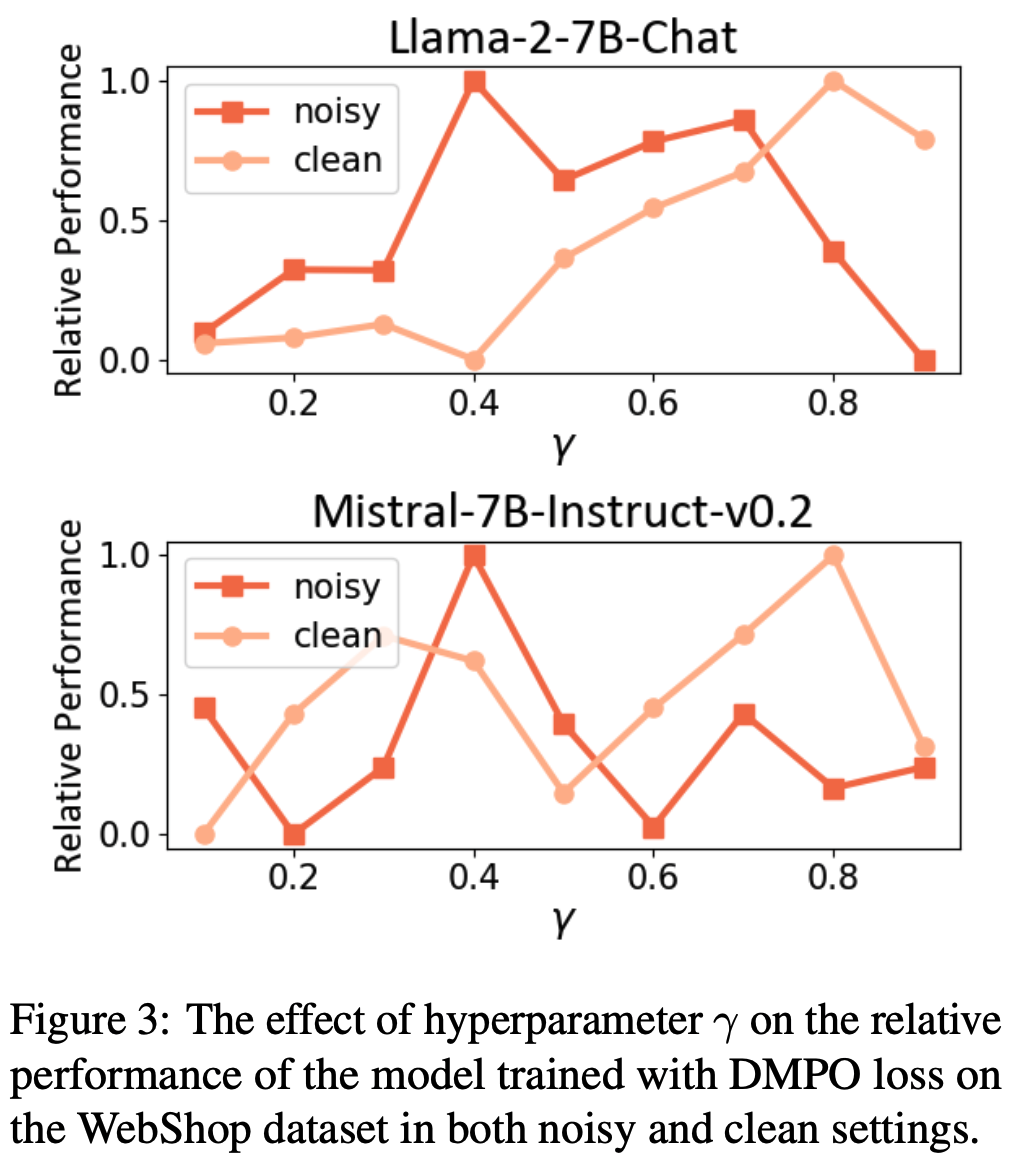
- 超参数分析 :为了验证公式(17)中重加权函数 \(\phi(t,T)\) 的影响,论文在 WebShop 上调整超参数 \(\gamma\),结果如图3 所示。论文发现,在噪声设置中,较小的 \(\gamma\) 能使两个基础模型达到最佳性能;而在干净设置中,较大的 \(\gamma\) 表现更优。根据公式(17),较小的 \(\gamma\) 意味着 DMPO 损失函数对后期步骤的状态-动作对赋予较低权重。这表明 DMPO 可以通过调整参数 \(\gamma\) 平衡噪声的影响。面对噪声“lose”轨迹时,选择较小的 \(\gamma\) 可以减轻噪声影响;而面对高质量“lose”轨迹时,选择较大的 \(\gamma\) 可以更好地从后期状态-动作对中学习策略
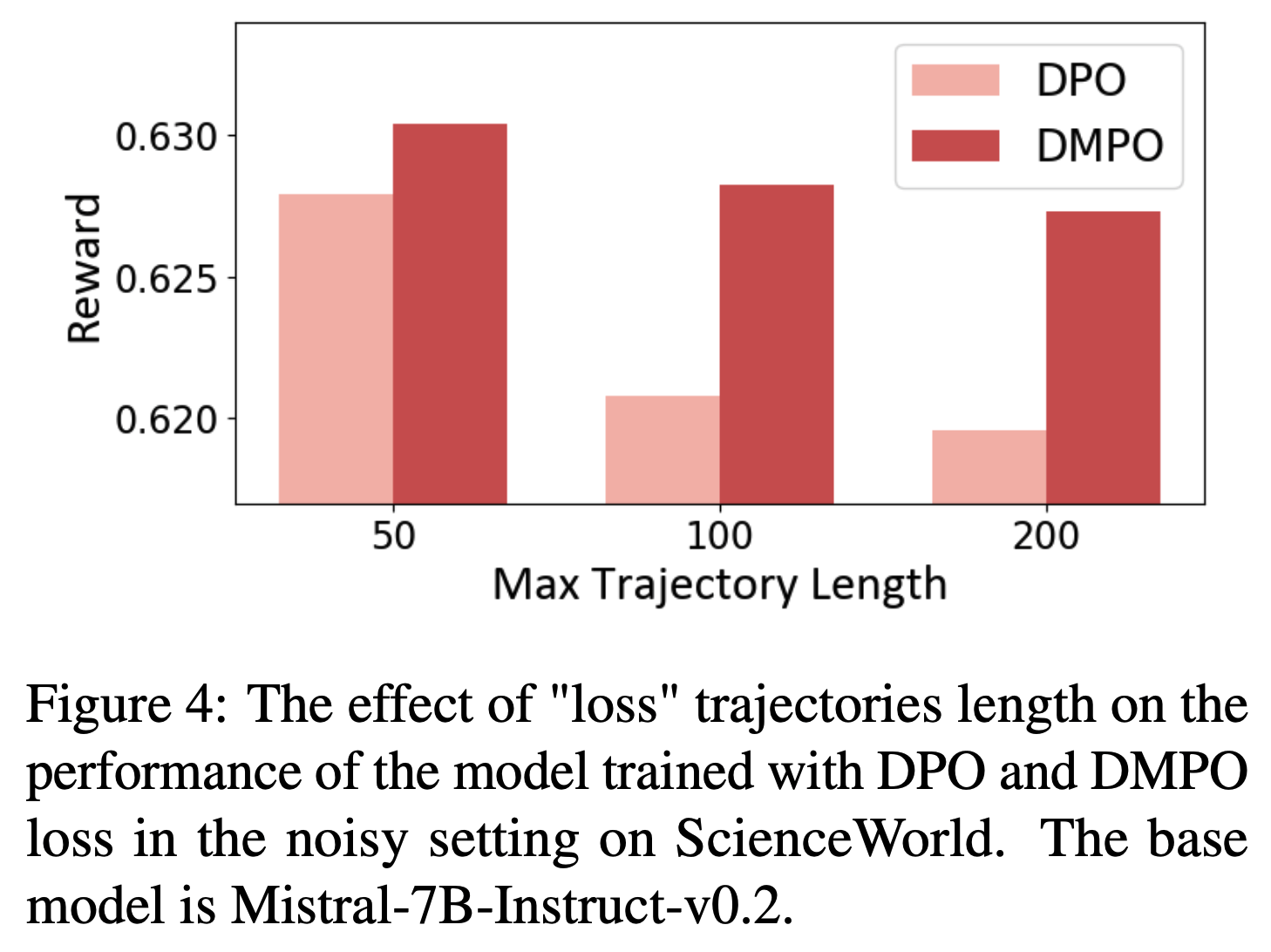
- 长度分析 :为了研究轨迹长度对模型性能的影响,论文根据噪声轨迹的最大长度将其分为三组,并确保每组偏好数据的数量相同。如图4 所示,论文观察到,使用 DPO 损失函数训练的模型性能随着噪声“lose”轨迹长度的增加而迅速下降;而使用 DMPO 损失函数训练的模型对噪声“lose”轨迹长度表现出鲁棒性。这归功于 DMPO 损失中采用的长度归一化技术,它减轻了“win”和“lose”轨迹长度不一致的影响
Limitation
- 论文主要关注在智能体任务上微调 LLM 时的问题,并提出了一种简单且鲁棒的损失函数
- 论文的研究存在以下局限性:
- 1)论文仅关注了轮次级别的任务形式化,这导致 LLM 的奖励稀疏。未来可以探索如 Rafailov 等 (2024b) 所建议的 token-level 任务形式化
- 2)本研究的实验基于 7B 规模的模型和模拟数据集。未来可以在更大模型和数据集上进行实验,以进一步验证论文的结论
附录A 案例研究
- 在本节中,论文通过一个来自 WebShop 的示例比较 DPO 和 DMPO 的性能。在该示例中,DPO 在回答的第一步丢失了所需的价格信息。相比之下,DMPO 在初始步骤提供了全面的回答,从而取得了成功的结果

附录B MT-Bench 评估
- 在本节中,论文使用 MT-bench(2023)评估并比较了在不同数据集上使用 DMPO 和 DPO 训练的模型,结果如表4所示
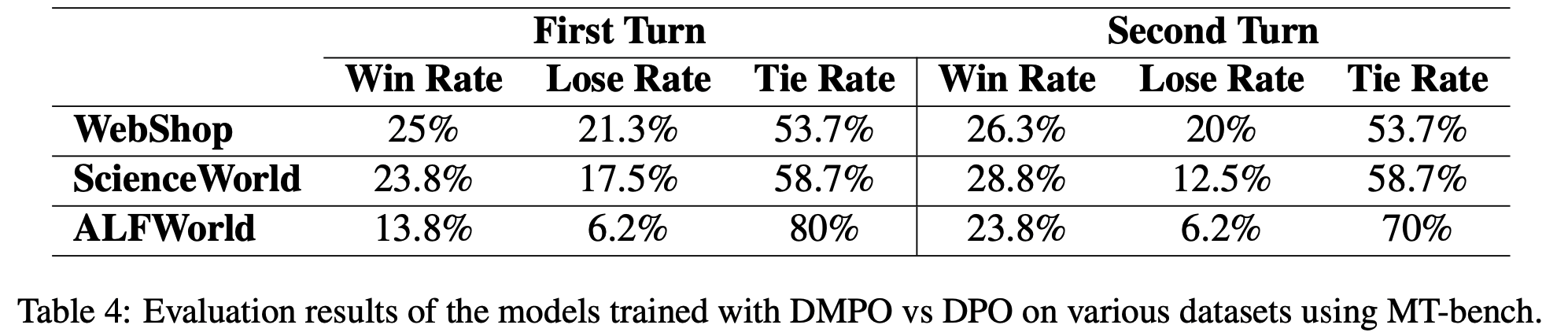
- 表中胜率分析表明,DMPO 在 MT-bench 的所有训练数据集上均优于 DPO。值得注意的是,DMPO 在 MT-bench 的第二轮评估中胜率显著高于 DPO,这证明了 DMPO 的有效性