本文简单主要记录 DPO 的改进,记录各种类 DPO 类的方法,更详细的介绍见论文的其他讲解
注:本文包含 AI 辅助创作
- 参考链接:
- (DPO)Direct Preference Optimization: Your Language Model is Secretly a Reward Model, NeurIPS 2023, Stanford University
- (DPOP)Smaug: Fixing Failure Modes of Preference Optimisation with DPO-Positive, 2024, Abacus.AI
- SLiC-HF: Sequence Likelihood Calibration with Human Feedback, 2023, Google Deepmind
- (TDPO)Token-level Direct Preference Optimization, ICML 2024, UCAS
- KTO: Model Alignment as Prospect Theoretic Optimization, ICML 2024, Contextual AI
- (IPO)A General Theoretical Paradigm to Understand Learning from Human Preferences, 202312, Google DeepMind
- 一篇容易误解为 IPO 方法的文章:IPO: Your Language Model is Secretly a Preference Classifier, 202502, Indian Institute of Technology Roorkee & Lossfunk,这篇文章不是常说的 IPO 方法,是印度一所理工大学 25 年发的比较新的方法
- Self-Play Fine-Tuning Converts Weak Language Models to Strong Language Models, ICML 2024, UCLA
- Insights into Alignment: Evaluating DPO and its Variants Across Multiple Tasks, 202502, Arizona State University
- SDPO: Segment-Level Direct Preference Optimization for Social Agents, 202502, Nankai, Alibaba
- (ODPO)Direct Preference Optimization with an Offset, 2024
- SimPO: Simple Preference Optimization with a Reference-Free Reward, 2024
回顾 DPO 的损失函数
- DPO 的损失函数 :
$$
Loss_{\text{DPO}}(\pi_\theta;\pi_\text{ref}) = - \mathbb{E}_{(x,y_w,y_l) \sim D}\left [ \log \sigma \left( \color{red}{\beta}\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} - \color{red}{\beta}\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} \right)\right ]
$$
DPOP(DPO-Positive)
- DPO 中存在的问题 :
- DPO 中的损失函数要求的是 \(\left(\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} -\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} \right) \) 变大;实际上,模型可能学习到的是,让 \(\pi_\theta(y_w|x)\) 和 \(\pi_\theta(y_w|x)\) 同时变小,只要正样本变小的幅度较小即可
- DPOP 的改进 :
$$
Loss_{\text{DPOP}}(\pi_\theta;\pi_\text{ref}) = - \mathbb{E}_{(x,y_w,y_l) \sim D}\left [ \log \sigma \left( \color{red}{\beta}\left(\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} - \log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} - \lambda\cdot \max\left( 0, \log\frac{\pi_\text{ref}(y_w|x)}{\pi_\theta(y_w|x)} \right) \right) \right)\right ]
$$- \(\lambda\) 是一个大于 0 的超参数
- 在 DPOP 中会加入额外损失函数 \(- \lambda\cdot \max\left( 0, \log\frac{\pi_\text{ref}(y_w|x)}{\pi_\theta(y_w|x)} \right)\) 保证 \(\pi_\theta(y_w|x) > \pi_\text{ref}(y_w|x)\)
- 核心思路可以一句话总结为:让模型生成正样本的概率高于参考模型生成正样本的概率
SLiC(Sequence Likelihood Calibration)
- 注:原始论文中的损失函数不够清晰,这里为了跟 DPO 风格统一,我们参考其他论文的表达,SLiC 的损失函数为:
$$ L_{SLiC}(\pi_{\theta}) = \mathbb{E}_{(x,y_w,y_l) \sim D, y_\text{ref} \color{red}{\sim \pi_\text{ref}(x)}} \left[ \max\left(0, \delta - \log \pi_{\theta}(y_w|x) + \log \pi_{\theta}(y_l|x)\right) - \lambda \log \pi_{\theta}(y_\text{ref}|x) \right] $$- \(\max\left(0, \beta - \log \pi_{\theta}(y_w|x) + \log \pi_{\theta}(y_l|x)\right)\) 是 对比学习逻辑 :
- 通过 \(\log \pi_{\theta}(y_w|x)\)(正样本条件概率的对数)和 \(\log \pi_{\theta}(y_l|x)\)(负样本条件概率的对数)的差,衡量模型对正负样本的区分能力;
- 边界参数 \(\delta\) :
- 当正样本对数概率与负样本对数概率的差小于 \(\delta\) 时(说明大的不够多),损失项为 \(\delta - (\log \pi_{\theta}(y_w|x)\log \pi_{\theta}(y_l|x))\)
- 否则,正样本对数概率与负样本对数概率的差大于 \(\delta\) 时 ,损失为 0,此时正样本概率比负样本概率大的够多了,不需要惩罚了
- 这类似于 hinge 损失;
- 正则化项 \(-\lambda \log \pi_{\theta}(y_\text{ref}|x)\):
- \(\lambda\) 为正则化系数,用于平衡主体损失和正则化强度;
- \(\log \pi_{\theta}(y_\text{ref}|x)\) 鼓励模型对参考样本 \(y_\text{ref}\) 赋予高概率,避免过拟合或增强对特定参考的拟合能力
- \(\max\left(0, \beta - \log \pi_{\theta}(y_w|x) + \log \pi_{\theta}(y_l|x)\right)\) 是 对比学习逻辑 :
- 文章也同时提出了 SLiC-HF 方法,允许使用多轮迭代来加入人类反馈
- 注:DPO 方法理论上早于 SLiC,但是 SLiC 没有引用 DPO 方法,也没有与之作比较
TDPO(Token-level Direct Preference Optimization)
- TDPO1 损失函数
$$
\mathcal{L}_{\text{TDPO1} } = -\mathbb{E}_{(x,y_w,y_l) \sim D}\left [\log \sigma \left( \beta \log \frac{\pi_\theta(y_w|x)}{\pi_{\text{ref} }(y_w|x)} - \beta \log \frac{\pi_\theta(y_l|x)}{\pi_{\text{ref} }(y_l|x)} - \beta \left( D_{\text{SeqKL} }(x, y_l; \pi_{\text{ref} } | \pi_\theta) - D_{\text{SeqKL} }(x, y_w; \pi_{\text{ref} } | \pi_\theta) \right) \right) \right]
$$- \(D_{\text{SeqKL} }(x, y; \pi_{\text{ref} } | \pi_\theta)\) 是序列KL散度,定义为 Token-level KL 散度的和
$$D_{SeqKL}(x, y; \pi_{\text{ref}} \parallel \pi_\theta) = \sum_{t=1}^{T} D_{KL}\left(\pi_{\text{ref}}(\cdot | [x, y^{ < t}]) \parallel \pi_\theta(\cdot | [x, y^{ < t}])\right)$$
- \(D_{\text{SeqKL} }(x, y; \pi_{\text{ref} } | \pi_\theta)\) 是序列KL散度,定义为 Token-level KL 散度的和
- TDPO2 损失函数
$$
\mathcal{L}_{\text{TDPO2} } = -\mathbb{E}_{(x,y_w,y_l) \sim D}\left [\log \sigma \left( \beta \log \frac{\pi_\theta(y_w|x)}{\pi_{\text{ref} }(y_w|x)} - \beta \log \frac{\pi_\theta(y_l|x)}{\pi_{\text{ref} }(y_l|x)} - \alpha \left( \beta D_{\text{SeqKL} }(x, y_l; \pi_{\text{ref} } | \pi_\theta) - \text{sg} \left( \beta D_{\text{SeqKL} }(x, y_w; \pi_{\text{ref} } | \pi_\theta) \right) \right) \right) \right]
$$- \(\text{sg}(\cdot)\) 表示 stop_gradient 操作,主要思想是停止 \(y_w\) 样本上的 KL 散度项
- 相对 TDPO1,TDPO2 还增加了 \(\alpha\) 参数,用于权衡序列 KL 散度的重要性
- \(\alpha\) 和 \(\beta\) 是算法超参数
- 补充:来自原始论文的图示

- 说明:实验证明 TDPO2 效果更好,可实现在 KL 散度更小的情况下,实现更大的 Reward,详情见原论文图3
KTO(Kahneman-Tversky Optimization)
- KTO 不需要对比样本,仅需要有标签的样本数据即可,每个 Prompt 可只有一个或正(Desirable)或负(Undesirable)的标签即可
- KTO 从 Kahneman & Tversky’s prospect theory 中得到启发,定义了一个损失函数家族,称为 human-aware losses (HALOs),不需要对比样本,仅需要有标签的样本数据即可学习
- KTO 损失函数定义为:
$$
L_{KTO}(\pi_{\theta}, \pi_\text{ref}) = \mathbb{E}_{x,y \sim D}[\lambda_y - v(x, y)] \quad (8)
$$- 可以看出,该损失函数在最大化 \(v(x, y)\),其定义为:
$$
v(x, y) =
\begin{cases}
\lambda_D \sigma(\beta(r_{\theta}(x, y) - z_0)) & \text{if } y \sim y_{\text{desirable} }|x \\
\lambda_U \sigma(\beta(z_0 - r_{\theta}(x, y))) & \text{if } y \sim y_{\text{undesirable} }|x
\end{cases}
$$- 直观理解:最大化 Desirable 样本的概率,最小化 Undesirable 样本的概率
- 其他符号含义:
$$
r_{\theta}(x, y) = \log \frac{\pi_{\theta}(y|x)}{\pi_\text{ref}(y|x)} \\
z_0 = \text{KL}(\pi_{\theta}(y’|x) \parallel \pi_\text{ref}(y’|x))
$$- \(z_0\) 是对分布的 KL 散度估计(注意:不针对特定样本进行估计),估计两个分布的KL散度时,需要从原始空间中随机采样任意样本进行估计
- \(y’\) 是从原始空间中采样的 \(\mathcal{Y}\) 任意输出
- \(\lambda_y, \lambda_D, \lambda_U\) 均为超参数
- 可以看出,该损失函数在最大化 \(v(x, y)\),其定义为:
- 实际实践中,实际训练中,由于直接计算完整分布的期望不现实,采样 microbatch 方法对 KL 散度进行估计:
$$ \hat{z}_0 = \max\left(0, \frac{1}{m} \sum_{1 \leq i \leq m} \log \frac{\pi_{\theta}(y_j|x_i)}{\pi_\text{ref}(y_j|x_i)}\right) $$- 其中 \(j = (i+1) \mod m\),表示输入 \(x_i\) 和输出 \(y_j\) 进行错位匹配
- 已进行 SFT 的情况 :若 KTO 前已用相同数据进行 SFT,且将 SFT 模型作为 \(\pi_\text{ref}\),则 KL 估计值 \(\hat{z}_0\) 会快速趋近于零(随机样本下,目标策略和参考策略的分布基本相同),此时可直接设 \(\hat{z}_0 = 0\),避免额外计算
- 未进行 SFT 的情况 :当 KTO 前未进行 SFT,或 SFT 数据与 KTO 数据不重叠时,必须估计 \(\hat{z}_0\) 以确保损失函数的有效性
IPO(Indentity Preference Optimisation, Indentity-PO)
注:原始论文中作者使用了很多新的符号,很影响理解,这里会对部分符号进行讲解
- IPO 中,作者移除了 DPO 中在概率差上添加激活函数的做法
- IPO 论文中,作者推导了一个通用的偏好优化目标函数 \(\Psi\)PO ,通过引入一个非递减函数 \(\Psi\),平衡偏好概率的非线性函数最大化与 KL 正则化项,鼓励策略接近参考策略。其表达式为:
$$\max_{\pi} \underset{\substack{x \sim \rho \\ y \sim \pi(\cdot| x) \\ y’ \sim \mu(\cdot| x)} }{\mathbb{E} }\left[\Psi\left(p^{*}\left(y \succ y’ | x\right)\right)\right]-\tau D_{KL}\left(\pi | \pi_\text{ref}\right)$$- \(y’\) 跟 DPO 中的 \(y_l\) 含义一致
- \(\mu(\cdot|x)\) 是行为策略(用作偏好数据对收集),与 \(\pi_\text{ref}\) 不同(用作 KL 正则化约束)
- IPO 是在 \(\Psi\)PO 的基础上,将 \(\Psi\) 设定为恒等映射得到的一种特殊形式,其目标函数为:
$$\max_{\pi} p_{\rho}^{*}(\pi \succ \mu)-\tau D_{KL}\left(\pi | \pi_\text{ref}\right)$$- \(\tau\) 为正则化参数,用于平衡偏好优化与策略正则化
- \(p_{\rho}^{*}(\pi \succ \mu)\) 表示在给定上下文 \(x\) 的条件下,采样 \(y_w \sim \pi(\cdot|x), y_l \sim \mu(\cdot|x)\) 后,人类真实偏好 \(y_w \succ y_l\) 的概率
- \(p^*\) 是真实概率,\(p\) 是预估概率,是对真实概率的估计值
- 经推导得到 IPO 损失函数公式如下:
$$
L(\pi) = \underset{y, y’ \sim \mu}{\mathbb{E} } \left[ \left( h_{\pi}(y, y’) - \frac{p^{*}(y \succ \mu) - p^{*}(y’ \succ \mu)}{\tau} \right)^2 \right]
$$- \(p^{*}(y \succ \mu)\) 表示在上下文 \(x\) 下,动作 \(y\) 优于分布 \(\mu\) 的真实偏好概率:
$$ p^{*}(y \succ \mu) = \mathbb{E}_{y’\sim\mu(\cdot|x)}[p^{*}(y \succ y’|x)] $$- \(p^{*}(y \succ y’|x)\) 表示在给定上下文 \(x\) 后,人类对 \(y\) 的偏好优于 \(y’\) 的真实概率;给定 \(y,y’\) 后,这个值与模型策略无关,比如在伯努利分布下就取值为 0 或 1
- \(h_{\pi}(y, y’)\) 表示策略 \(\pi\) 与参考策略 \(\pi_{\text{ref} }\) 的对数似然比差异
$$ h_{\pi}(y, y’) = \log \left( \frac{\pi(y) \pi_{\text{ref} }(y’)}{\pi(y’) \pi_{\text{ref} }(y)} \right) $$- 理解:进一步地,该值还可以写成其他形式
$$ h_{\pi}(y, y’) = \log \left( \frac{\pi(y)}{\pi_{\text{ref} }(y)} \right) - \log \left( \frac{\pi(y’)} {\pi_{\text{ref} }(y’)}\right) $$
- 理解:进一步地,该值还可以写成其他形式
- Bradley-Terry 模型中,有:
$$ p^*(y \succ y’) = \sigma(r(y) - r(y’)) $$
- \(p^{*}(y \succ \mu)\) 表示在上下文 \(x\) 下,动作 \(y\) 优于分布 \(\mu\) 的真实偏好概率:
基于伯努利采样的 IPO 损失函数
- 基于伯努利采样的 IPO 损失函数
$$
\underset{y, y’ \sim \mu}{\mathbb{E} } \left[ \left( h_{\pi}(y, y’) - \tau^{-1} I(y, y’) \right)^2 \right]
$$- 其中 \(I(y, y’)\) 是伯努利分布采样的偏好指示变量:当 \(y\) 优于 \(y’\) 时取1,否则取0,其均值为 \(p^{*}(y \succ y’)\)
给定数据集上的 IPO 损失函数(其他博客中最常见的形式)
- 给定数据集上的 IPO 损失函数
$$
\underset{(y_w, y_l) \sim D}{\mathbb{E} } \left[ \left( h_{\pi}(y_w, y_l) - \frac{\tau^{-1} }{2} \right)^2 \right]
$$- \(D\) 为经验偏好数据集,包含成对的偏好样本 \((y_w, y_l)\)(\(y_w\) 为偏好动作,\(y_l\) 为非偏好动作)
- 该表达式通过对称采样(即同时考虑 \((y_w, y_l, 1)\) 和 \((y_l, y_w, 0)\))简化了方差,并最终转化为对对数似然比的回归优化
- 正则化强度 \(\tau\) 的取值分析(论文中测试时取值为 \(\tau = 0.1,0.5,1.0\)):
- 当 \(\tau \to +\infty\) 时,\(\tau^-1 \to +0\) ,\(\pi^*\) 收敛到均匀策略 \(\pi_{\text{ref} }\);
- 当 \(\tau \to 0^+\) 时,\(\tau^-1 \to +\infty\),\(\pi^*(y_1) \to 1\) 且 \(\pi^*(y_2) \to 0\),即收敛到确定性最优策略
- 给定数据集上的 IPO 的训练伪代码为:

SPIN(Self-Play fIne-tuNing)
- SPIN(Self-Play Fine-Tuning)是一种无需额外人类标注数据(仅 SFT 数据即可),就能将弱语言模型转化为强语言模型的微调方法,其核心是通过语言模型与自身迭代版本进行自我博弈(Self-Play),逐步提升模型性能
- SPIN 受游戏领域自我博弈(如 AlphaGo Zero)的启发,让语言模型在迭代过程中与自身的旧版本进行“对抗”:
- 自我博弈过程 :当前模型(主玩家)需要区分人类标注数据与旧版本模型生成的数据,而旧版本模型(对手玩家)则试图生成与人类数据难以区分的响应。通过这种动态博弈,模型逐步逼近目标数据分布
- 核心目标 :使模型的生成分布 \( p_{\theta}(y|x) \) 最终与人类标注数据的分布 \( p_{data}(y|x) \) 一致
训练过程(非正式流程,仅作为理解)
- SPIN 的迭代过程包含两个关键步骤,以第 \( t+1 \) 次迭代为例:
- 训练主玩家(区分器)
- 利用旧版本模型 \( p_{\theta_t} \) 生成 synthetic 数据 \( y’ \),主玩家 \( f_{t+1} \) 的目标是最大化人类数据 \( y \) 与旧模型生成数据 \( y’ \) 的期望差异。基于积分概率度量(IPM),目标函数定义为:
$$
f_{t+1} = \underset{f \in \mathcal{F}_t}{\text{argmax} } , \mathbb{E}_{ x \sim q(\cdot),y \sim p_{data}(\cdot|x), y’ \sim p_{\theta_t}(\cdot|x)}\left[ f(x, y) - f(x, y’) \right]
$$- 其中 \( \mathcal{F}_t \) 是函数类,为避免目标无界,通常采用逻辑损失函数:
$$ \ell(t) = \log(1 + \exp(-t)) $$ - 由此原始问题可转化为:
$$
f_{t+1} = \underset{f \in \mathcal{F}_t}{\text{argmin} } , \mathbb{E}_{ x \sim q(\cdot),y \sim p_{data}(\cdot|x), y’ \sim p_{\theta_t}(\cdot|x)} \left[ \ell(f(x, y) - f(x, y’)) \right]
$$
- 其中 \( \mathcal{F}_t \) 是函数类,为避免目标无界,通常采用逻辑损失函数:
- 利用旧版本模型 \( p_{\theta_t} \) 生成 synthetic 数据 \( y’ \),主玩家 \( f_{t+1} \) 的目标是最大化人类数据 \( y \) 与旧模型生成数据 \( y’ \) 的期望差异。基于积分概率度量(IPM),目标函数定义为:
- 更新对手玩家(生成器)
- 基于训练好的主玩家 \( f_{t+1} \),更新旧模型 \( p_{\theta_t} \) 以生成更接近人类数据的响应。引入 KL 正则化项以稳定训练,优化目标为:
$$
\underset{p}{\text{argmax} } , \mathbb{E}_{x \sim q(\cdot), y \sim p(\cdot|x)}\left[ f_{t+1}(x, y) \right] - \lambda \mathbb{E}_{x \sim q(\cdot)} \text{KL}\left( p(\cdot|x) || p_{\theta_t}(\cdot|x) \right)
$$ - 其闭式解为:
$$
\hat{p}(y|x) \propto p_{\theta_t}(y|x) \exp\left( \lambda^{-1} f_{t+1}(x, y) \right)
$$
- 基于训练好的主玩家 \( f_{t+1} \),更新旧模型 \( p_{\theta_t} \) 以生成更接近人类数据的响应。引入 KL 正则化项以稳定训练,优化目标为:
端到端训练目标(正式流程)
- 将上述两步整合为端到端的迭代更新规则,第 \( t+1 \) 次迭代的参数 \( \theta_{t+1} \) 由以下目标函数确定:
$$
L_{\text{SPIN} } = \mathbb{E}\left[ \ell\left( \lambda \log\frac{p_{\theta}(y|x)}{p_{\theta_t}(y|x)} - \lambda \log\frac{p_{\theta}(y’|x)}{p_{\theta_t}(y’|x)} \right) \right]
$$- 其中期望同上,\( \ell \) 为逻辑损失函数。该过程不断迭代,直至模型分布收敛到 \( p_{data}(\cdot|x) \)
- SPIN 训练伪代码为:

- 注:GAN 的判别器和生成器是独立模型,而SPIN 的主玩家和对手玩家均为同一模型的不同迭代版本
- 收敛性证明 :在损失函数 \( \ell \) 单调递减且凸的假设下(如逻辑损失),SPIN 的全局最优解当且仅当 \( p_{\theta}(y|x) = p_{data}(y|x) \) 时达到。此时,模型无法区分自身生成数据与人类数据
- 数据效率 :仅使用 SFT 数据集的 50k 子集(Ultrachat200k),SPIN 迭代 0 次时效果略微不如 DPO,迭代 1 次即可达到甚至超过 DPO 使用 62k 新偏好数据的性能,详情见原始论文 6.2 和图3
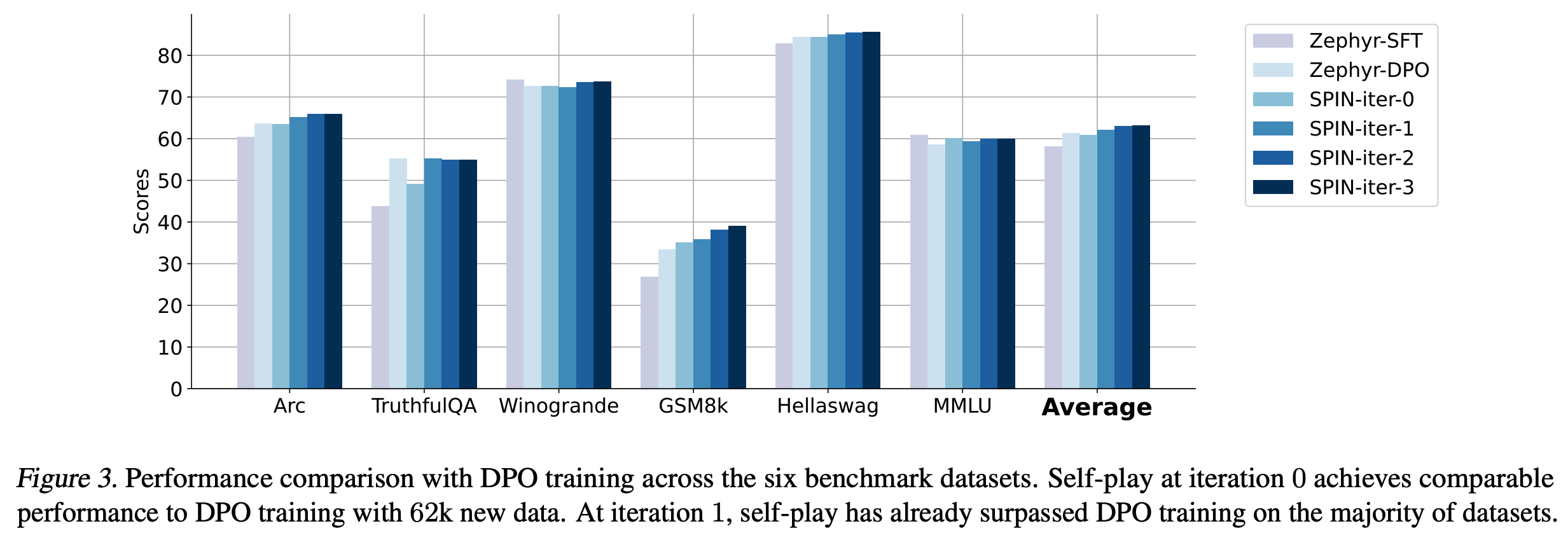
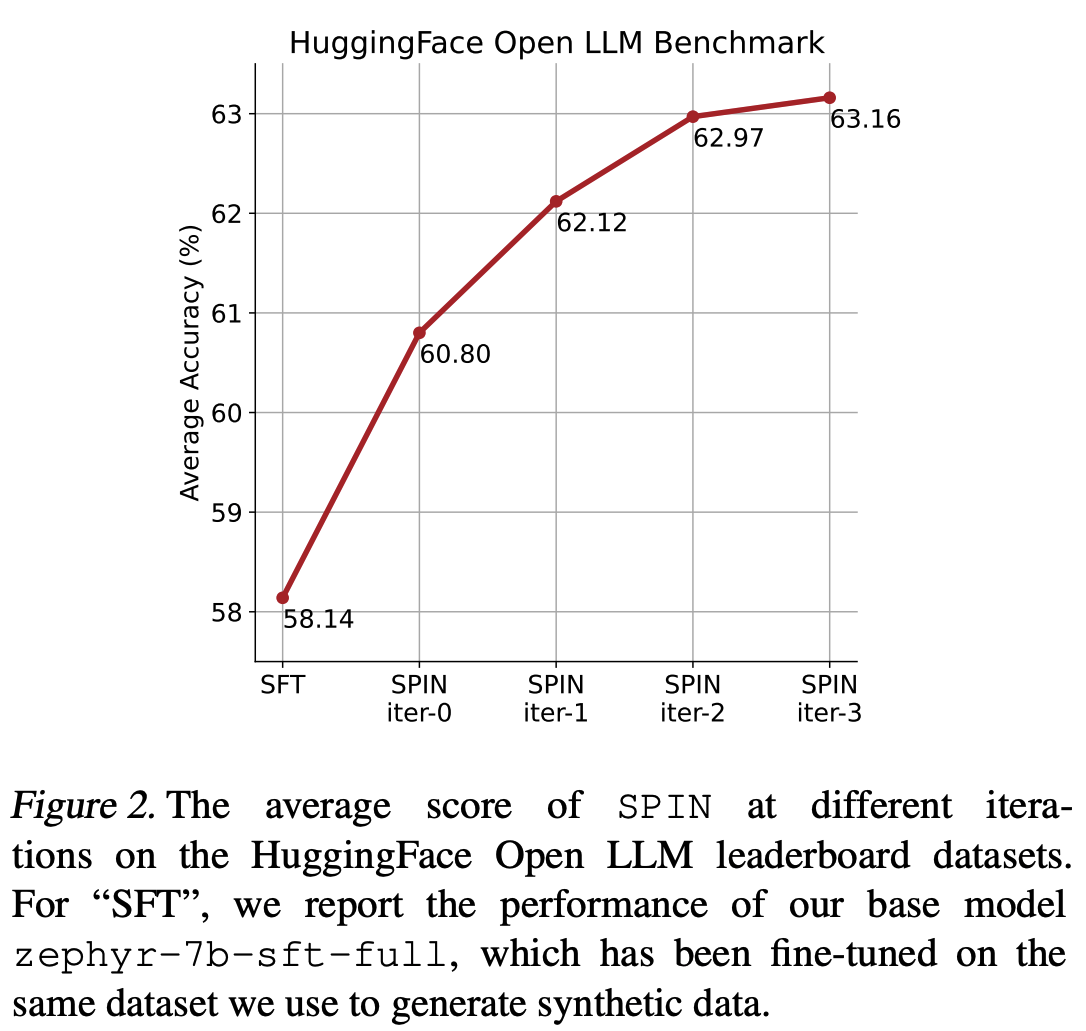
- 迭代必要性 :论文中通过实验证明了,迭代多轮是必要的(对数曲线),原论文图2
SDPO(Segment-Level Direct Preference Optimization)
- 原始论文:SDPO: Segment-Level Direct Preference Optimization for Social Agents, 20250227, Tongyi Lab
- 详细介绍链接:NLP——LLM对齐微调-SDPO
sDPO(stepwise DPO)
SimPO
- 详细介绍链接:NLP——LLM对齐微调-SimPO
ODPO(Offset DPO)
- 原始论文:(ODPO)Direct Preference Optimization with an Offset, 20240606
- Offset DPO(ODPO)是DPO的泛化变体,核心是为偏好对引入偏移量以区分偏好强度,让模型按偏好差异优化生成概率,在奖励与KL散度的帕累托前沿表现更优,尤其适合偏好数据有限或偏好强度差异大的场景:
$$ \mathcal{L}_{\text{ODPO}} = -\mathbb{E}_{(x,y^+,y^-)} \left[ \log \sigma \left( \beta \left( \log \frac{\pi_\theta(y^+|x)}{\pi_{\text{ref}}(y^+|x)} - \log \frac{\pi_\theta(y^-|x)}{\pi_{\text{ref}}(y^-|x)} \right) - \Delta \right) \right] + \lambda \cdot \text{KL}(\pi_\theta \parallel \pi_{\text{ref}}) $$- 通过 \(\Delta\) 量化偏好差异,实现差异化优化,提升对齐精度
rDPO(Robust DPO)
- 原始论文:Provably Robust DPO: Aligning Language Models with Noisy Feedback, Microsoft, 20240412
- 目标是提升 DPO 稳定性:
- rDPO :在优化过程中考虑标签可能被随机翻转的情况
- Label Flip(Label 翻转):标签被错误标注为相反结果,主要用于建模偏好数据中的噪声
- cDPO :利用 Label Smoothing 处理噪声偏好标签,使优化更稳健
- Label Smoothing:将硬标签平滑成概率分布,缓解过拟合并提升鲁棒性
- rDPO :在优化过程中考虑标签可能被随机翻转的情况
- 上述思想最早在 Secrets of RLHF in Large Language Models Part II: Reward Modeling, Fudan, 202401 中提到的思想