NLP——LLM对齐微调-DAPO

注：本文包含 AI 辅助创作

• 参考链接：
  • 原始论文：DAPO: An Open-Source LLM Reinforcement Learning System at Scale, THU, ByteDance, 202503
  • verl库原始论文：HybridFlow: A Flexible and Efficient RLHF Framework, EuroSys 2025, HKU & ByteDance

Paper Summary

• 总结：
  • DAPO 作为 GRPO 的扩展算法，其提出的众多改进方式已经成为了 GRPO 方法的默认 Features
  • DAPO 算法共包含了四项关键技术，具体内容详见原文第3节：
    • Clip-Higher ：提升系统多样性，避免熵崩溃；
    • 动态采样 ：提高训练效率和稳定性；
    • 词级策略梯度损失 ：在长思维链RL场景中至关重要；
    • 过长奖励调整 ：减少奖励噪声，稳定训练
• 推理能力的扩展使 LLM 具备了前所未有的推理能力，而 RL 是激发复杂推理的核心技术
• 然而，当前最先进的推理型 LLM 的关键技术细节（例如 OpenAI 的博客和 DeepSeek R1 技术报告中所述）并未公开，因此学术界仍难以复现其 RL 训练结果
• 论文工作总结如下：
  • 提出了解耦裁剪与动态采样策略优化（Decoupled Clip and Dynamic sAmpling Policy Optimization，DAPO）算法
  • 开源了一个基于 Qwen2.5-32B 基础模型的大规模 RL 系统，该系统在 AIME 2024 上达到了50分的成绩
    • 与以往隐瞒训练细节的研究不同，论文介绍了算法中的 4 项关键技术 ，这些技术使得大规模 LLM 的 RL 训练成为可能
  • 论文还开源了基于 verl 框架的训练代码，以及经过精心整理和处理的数据集
• 这些开源组件增强了研究的可复现性，并为未来大规模 LLM RL 研究提供了支持
• 补充：项目主页网址为 https://dapo-sia.github.io/

---

Introduction and Discussion

• Test-time scaling 技术：
  • 如 OpenAI 的 o1 和 DeepSeek-R1 等 Test-time scaling 为 LLM 带来了深刻的范式转变
  • Test-time scaling 能够支持更长的思维链（Chain-of-Thought）推理，并激发复杂推理行为，使模型在竞争性数学和编程任务（如 AIME 和 Codeforces）中表现卓越
• 推动这一变革的核心技术是大规模 RL ，它能够激发诸如自我验证（self-verification）和迭代优化等复杂推理行为
• 但现有推理模型的技术报告中并未公开可扩展RL训练的实际算法和关键方法
• 论文揭示了大规模 RL 训练中的主要障碍（obstacles），并开源了一个可扩展的 RL 系统，包括完全公开的算法、训练代码和数据集，为学术界提供了工业级 RL 结果的民主化解决方案
• 论文以 Qwen2.5-32B 作为 RL 训练的预训练模型进行实验。在初始的 GRPO 实验中，模型在 AIME 上的得分仅为 30 分，远低于 DeepSeek 的 RL 结果（47分）
  • 深入分析表明，朴素的 GRPO 基线存在熵崩溃、奖励噪声和训练不稳定等关键问题
  • 学术界在复现 DeepSeek 的结果时也遇到了类似挑战，这表明 R1 论文中可能遗漏了开发工业级、大规模且可复现RL系统所需的关键训练细节
• 为填补这一空白，论文开源了一个基于 Qwen2.5-32B 模型的大规模 LLM RL 系统，该系统在 AIME 2024 上达到了 50 分的成绩，优于 DeepSeek-R1-Zero-Qwen-32B 的 47 分，且训练步数减少了 50%（图1）
  • 问题：图1 中的 cons@32 是什么指标？
  • 回答：猜测是类似多数投票的结果（补充已经证实，就是多数投票的结果（cons 表示 consensus，即 共识）：详情见 NLP——技术报告解读-DeepSeek-R1）
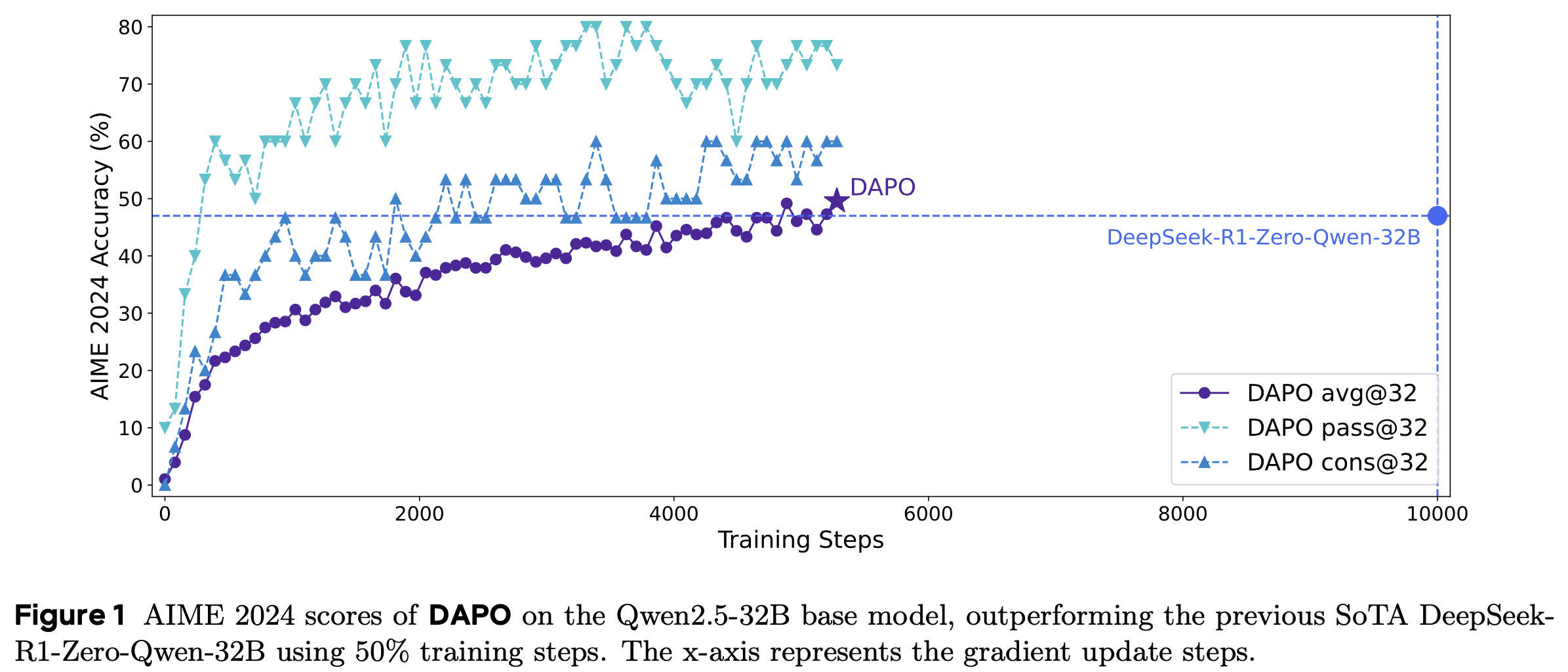
• 论文的实现基于 verl 框架。通过完全开源包括训练代码和数据在内的最先进 RL 系统，作者希望为大规模 LLM RL 研究提供有价值的见解，造福更广泛的学术界

---

Preliminary

PPO

• PPO 引入了一种裁剪替代目标函数用于策略优化。通过裁剪重要性采样比率将策略更新限制在先前策略的近端区域内，PPO能够稳定训练并提高样本效率。具体而言，PPO通过最大化以下目标函数更新策略：
  $$
  \mathcal{J}_{\textrm{PPO} }(\theta)=\mathbb{E}_{(\mathbf{q},\mathbf{a})\sim\mathcal{D},o_{\leq t}\sim\pi_{\theta_\textrm{old} }(\cdot|q)}\left[\min\left(\frac{\pi_{\theta}(o_{t}\mid q,o_{ < t})}{\pi_{\theta_\textrm{old} }(o_{t}\mid q,o_{ < t})}\hat{A}_{t},\operatorname{clip}\left(\frac{\pi_{\theta}(o_{t}\mid q,o_{ < t})}{\pi_{\theta_\textrm{old} }(o_{t}\mid q,o_{ < t})},1-\varepsilon,1+\varepsilon\right)\hat{A}_{t}\right)\right],
  $$
  • \((\mathbf{q},\mathbf{a})\) 是数据分布 \(\mathcal{D}\) 中的 question-answer 对
  • \(\varepsilon\) 是重要性采样比率的裁剪范围
  • \(\hat{A}_{t}\) 是时间步 \(t\) 的优势估计值： 给定价值函数 \(V\) 和奖励函数 \(R\)，\(\hat{A}_{t}\) 通过广义优势估计（GAE）计算：
    $$
    \hat{A}_{t}^{\textrm{GAE}(\gamma,\lambda)}=\sum_{l=0}^{\infty}(\gamma\lambda)^{l}\delta_{t+l},
    $$
    • 其中：
      $$
      \delta_{l}=R_{l}+\gamma V(s_{l+1})-V(s_{l}),\quad 0\leq\gamma,\lambda\leq 1.
      $$

Group Relative Policy Optimization（GRPO）

• 与 PPO 相比，GRPO 省去了价值函数，并以组相对方式估计优势，对于特定 question-answer 对 \((\mathbf{q},\mathbf{a})\)，行为策略 \(\pi_{\theta_{old} }\) 采样一组 \(G\) 个独立响应 \(\{o_{i}\}_{i=1}^{G}\)。随后，第 \(i\) 个响应的优势通过对组级奖励 \(\{R_{i}\}_{i=1}^{G}\) 归一化计算：
  $$
  \hat{A}_{i,t}=\frac{r_{i}-\mathrm{mean}(\{R_{i}\}_{i=1}^{G})}{\mathrm{std}(\{R_{i}\}_{i=1}^{G})}.
  $$
• 与 PPO 类似，GRPO 采用裁剪目标函数，并直接引入 KL 惩罚项：
  $$
  \begin{split}
  \mathcal{J}_{\mathrm{GRPO} }(\theta) &=\mathbb{E}_{(\mathbf{q},\mathbf{a})\sim\mathcal{D},\{o_{i}\}_{i=1}^{G}\sim\pi_{\theta_{old} }(\cdot|q)} \\
  &\left[\frac{1}{G}\sum_{i=1}^{G}\frac{1}{|\mathbf{o}_i|}\sum_{t=1}^{|\mathbf{o}_i|}\Bigg{(}\min\Big{(}r_{i,t}(\theta)\hat{A}_{i,t},\mathrm{clip}\Big{(}r_{i,t}(\theta),1-\varepsilon,1+\varepsilon\Big{)}\hat{A}_{i,t}\Big{)}-\beta D_{\mathrm{KL} }(\pi_{\theta}|\pi_{\mathrm{ref} })\Bigg{)}\right],
  \end{split}
  $$
  • 其中
    $$
    r_{i,t}(\theta)=\frac{\pi_{\theta}(o_{i,t}\mid q,\mathbf{o}_{i,<t})}{\pi_{\theta_{old} }(o_{i,t}\mid q,\mathbf{o}_{i,<t})}.
    $$
• 特别注意：GRPO 在样本级别计算目标函数
  • GRPO 首先计算每个生成样本序列内的平均损失 ，再对不同样本的损失取平均
  • 如第3.3节所述，这种差异可能对算法性能产生影响。

Removing KL Divergence

• KL 惩罚项用于调节在线策略与冻结参考策略之间的差异
• 在 RLHF 场景[23]中，RL 的目标是在不偏离初始模型太远的情况下对齐模型行为
• 但在训练长思维链推理模型时，模型分布可能与初始模型显著偏离，因此这种限制并非必要
• 因此，论文将从提出的算法中排除 KL 项
• 理解：容易把模型训崩溃了吧，毕竟 Reward 中已经没有了 KL 散度了，保留 KL 散度项，适当降低权重是否就足够了？

Rule-based Reward Modeling

• 使用奖励模型通常会遇到奖励破解（Reward Hacking）问题。相反，论文直接使用可验证任务的最终准确率作为结果奖励，通过以下规则计算：
  $$
  R(\hat{y},y)=\begin{cases}1,&\texttt{is_equivalent}(\hat{y},y)\\ -1,&\text{otherwise}\end{cases}
  $$
  • 其中 \(y\) 是真实答案， \(\hat{y}\) 是预测答案
• 这种方法已被证明能够有效激活基础模型的推理能力，并在多个领域（如自动定理证明、计算机编程和数学竞赛）中表现出色

---

DAPO 算法

• DAPO 为每个问题 \(q\) 及其对应答案 \(a\) 采样一组输出 \(\{\mathbf{o}_i\}_{i=1}^G\)，并通过以下目标函数优化策略：
  $$
  \begin{align}
  \mathcal{J}_{\mathrm{GRPO} }(\theta) &=\mathbb{E}_{(\mathbf{q},\mathbf{a})\sim\mathcal{D},\{o_{i}\}_{i=1}^{G}\sim\pi_{\theta_{old} }(\cdot|q)} \\
  &\left[\frac{1}{\color{red}{\sum_{i=1}^G|\mathbf{o}_i|}}\color{red}{\sum_{i=1}^{G}\sum_{t=1}^{|\mathbf{o}_i|}}\min\Big{(}r_{i,t}(\theta)\hat{A}_{i,t},\mathrm{clip}\Big{(}r_{i,t}(\theta),1-\color{red}{\varepsilon_\text{low}},1+\color{red}{\varepsilon_\text{high}}\Big{)}\hat{A}_{i,t}\Big{)}\right] \\
  \text{s.t.}\quad &\color{red}{0 < \left|\{\mathbf{o}_i \mid \texttt{is_equivalent}(\mathbf{a}, \mathbf{o}_i)\}\right| < G}
  \end{align}
  $$
  • 其中：
    $$
    r_{i,t}(\theta) = \frac{\pi_{\theta}(o_{i,t} \mid q, \mathbf{o}_{i,<t})}{\pi_{\theta_{\text{old} } }(o_{i,t} \mid q, \mathbf{o}_{i,<t})}, \quad \hat{A}_{i,t} = \frac{R_i - \text{mean}(\{R_i\}_{i=1}^G)}{\text{std}(\{R_i\}_{i=1}^G)}.
    $$
• 完整算法如算法1所示

Raise the Ceiling: Clip-Higher

• 在初步实验中，论文发现使用原始 PPO 或 GRPO 时会出现熵崩溃现象：随着训练进行，策略的熵迅速下降（图2(b)）。某些组内的采样响应几乎完全相同，这表明探索能力受限和策略过早确定性化，从而阻碍了模型性能的提升
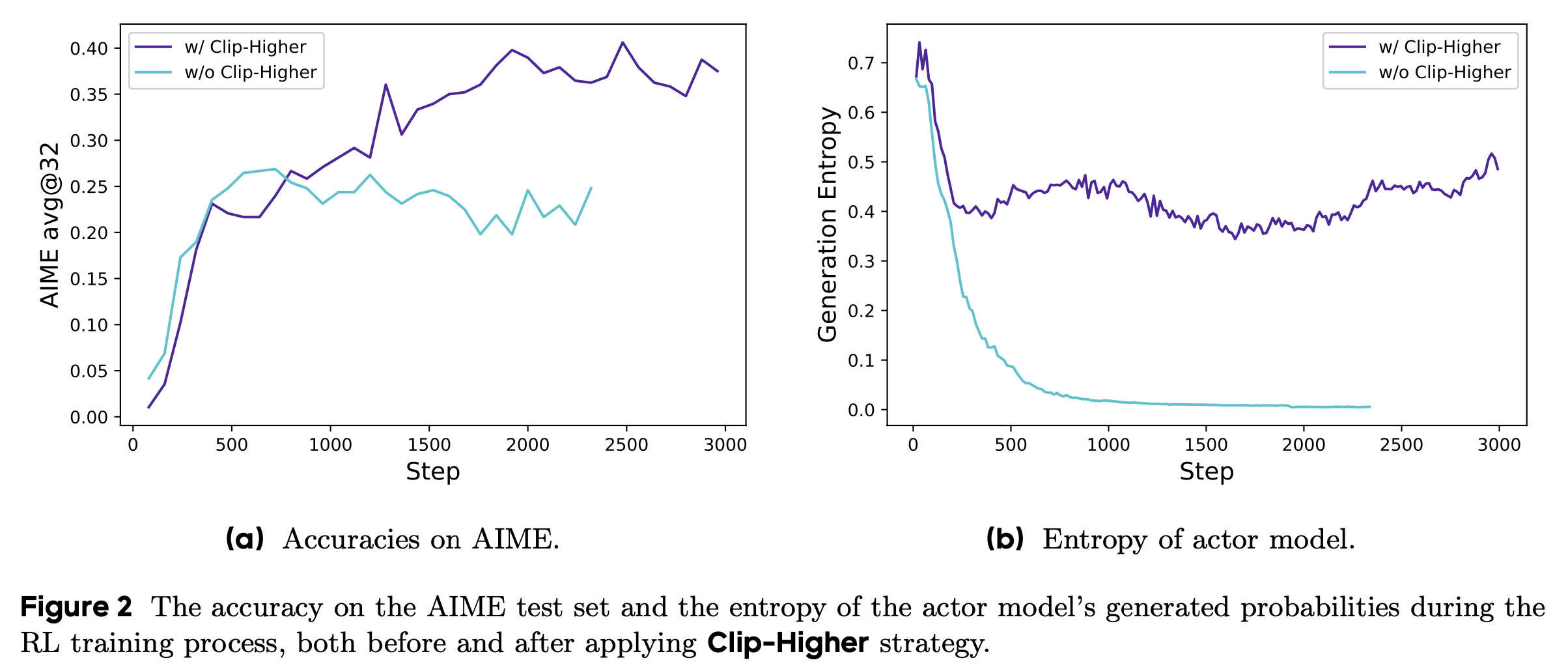
• 为解决这一问题，论文提出了Clip-Higher策略。裁剪重要性采样比率（PPO-Clip）的目的是通过限制信任区域来增强 RL 训练的稳定性。论文发现，上限裁剪会限制策略的探索能力。具体来说，提升高概率 token（“利用token”）的概率比提升低概率 token（“探索token”）的概率更容易
  • 理解：原始 PPO 对称 Clip 设定下，确实存在提升高概率 token 的概率比提升低概率 token 的概率更容易的现象
• 论文中给了一个例子：
  • 当 \(\varepsilon = 0.2\) （大多数算法的默认值）时，考虑两个动作的概率分别为 \(\pi_{\theta_{\text{old} } }(\mathbf{o}_i \mid q) = 0.01\) 和 \(0.9\) ，更新后的最大概率 \(\pi_{\theta}(\mathbf{o}_i \mid q)\) 分别为 \(0.012\) 和 \(1.08\)
  • 以上现象意味着高概率 token（如 \(0.9\) ）受到的约束较小，而低概率 token 的概率提升则更为困难
• 实验数据显示，裁剪后 token 的最大概率约为 \(\pi_{\theta}(\mathbf{o}_i \mid q) < 0.2\) （图3(a)），这证实了上限裁剪确实限制了低概率 token 的概率提升，从而可能降低系统的多样性
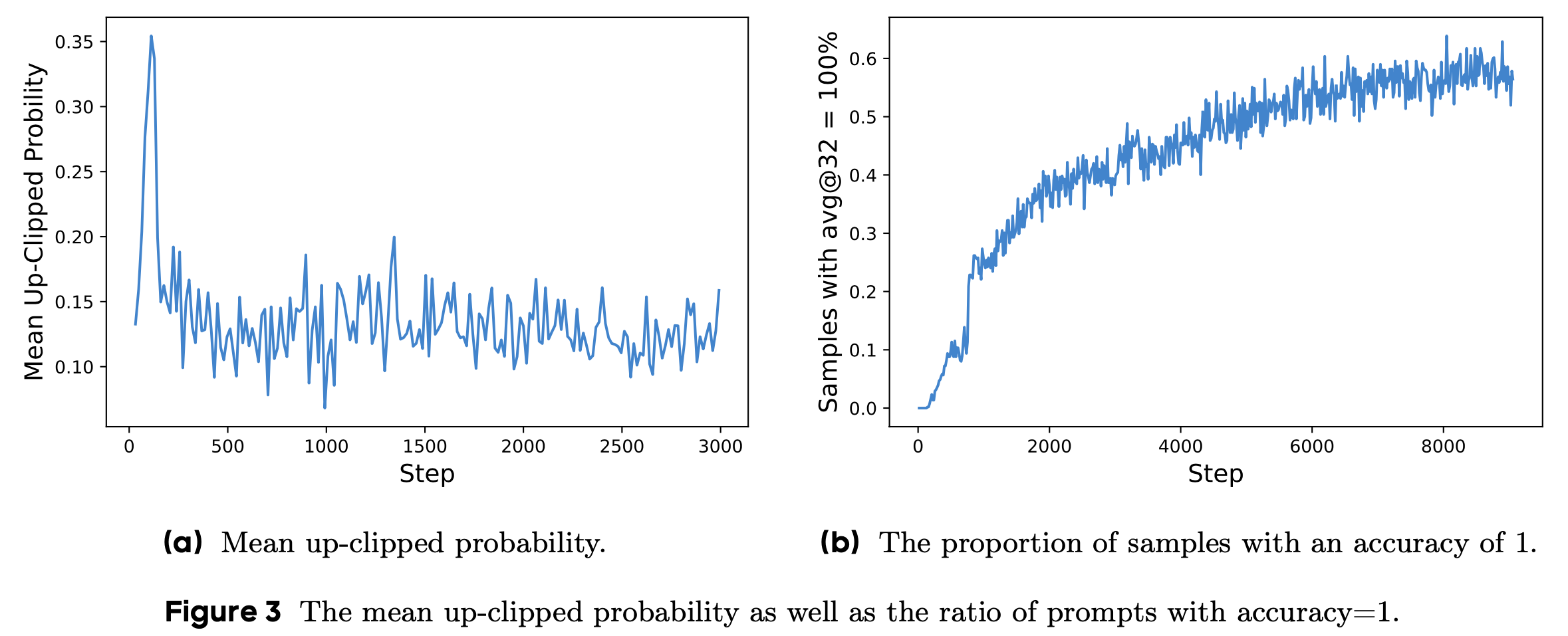
• 问题：这里说的最大概率是什么？是真实概率还是概率提升比例？
  • 回答：猜测是指触碰到最大上界的样本的比例
• 基于 Clip-Higher 策略，论文将裁剪范围解耦为下限 \(\varepsilon_{\text{low} }\) 和上限 \(\varepsilon_{\text{high} }\) ，如公式10所示：
  $$
  \begin{align}
  \mathcal{J}_{\mathrm{GRPO} }(\theta) &=\mathbb{E}_{(\mathbf{q},\mathbf{a})\sim\mathcal{D},\{o_{i}\}_{i=1}^{G}\sim\pi_{\theta_{old} }(\cdot|q)} \\
  &\left[\frac{1}{\sum_{i=1}^G|\mathbf{o}_i|}\sum_{i=1}^{G}\sum_{t=1}^{|\mathbf{o}_i|}\min\Big{(}r_{i,t}(\theta)\hat{A}_{i,t},\mathrm{clip}\Big{(}r_{i,t}(\theta),1-\color{red}{\varepsilon_\text{low}},1+\color{red}{\varepsilon_\text{high}}\Big{)}\hat{A}_{i,t}\Big{)}\right] \\
  \text{s.t.}\quad &0 < \left|\{\mathbf{o}_i \mid \texttt{is_equivalent}(\mathbf{a}, \mathbf{o}_i)\}\right| < G
  \end{align}
  $$
• 论文通过增大 \(\varepsilon_{\text{high} }\) 为低概率 token 的概率提升留出更多空间
• 如图2所示，这一调整有效提升了策略的熵，并促进了更多样化的采样。同时，论文保持 \(\varepsilon_{\text{low} }\) 较小，因为增大它会将这些 token 的概率压制到 0，导致采样空间崩溃

The More the Merrier: Dynamic Sampling

• 标题为“多多益善：动态采样”，思路是通过动态采样来过滤全正或全负的 Prompt（样本）
• 现有 RL 算法在部分 Prompt 的准确率为 1 时会面临梯度消失问题
  • 例如，在 GRPO 中，如果某一组所有输出 \(\{\mathbf{o}_i\}_{i=1}^G\) 均正确且奖励为1，则该组的优势值为零
  • 零优势值会导致策略更新无梯度，从而降低采样效率
• 实验数据显示，准确率为 1 的样本数量持续增加（图3(b)），这意味着每批次中有效 Prompt 数量不断减少，可能导致梯度方差增大并削弱训练信号
• 为此，论文提出动态采样策略，通过过采样并过滤掉准确率为 1 或 0 的 Prompt （如公式11所示），确保批次中所有 Prompt 均具有有效梯度，并保持 Prompt 数量稳定。在训练前，论文持续采样直至批次中所有样本的准确率均不为 0 或 1
  $$
  \begin{align}
  \mathcal{J}_{\mathrm{GRPO} }(\theta) &=\mathbb{E}_{(\mathbf{q},\mathbf{a})\sim\mathcal{D},\{o_{i}\}_{i=1}^{G}\sim\pi_{\theta_{old} }(\cdot|q)} \\
  &\left[\frac{1}{\sum_{i=1}^G|\mathbf{o}_i|}\sum_{i=1}^{G}\sum_{t=1}^{|\mathbf{o}_i|}\min\Big{(}r_{i,t}(\theta)\hat{A}_{i,t},\mathrm{clip}\Big{(}r_{i,t}(\theta),1-\varepsilon_\text{low},1+\varepsilon_\text{high}\Big{)}\hat{A}_{i,t}\Big{)}\right] \\
  \text{s.t.}\quad &\color{red}{0 < \left|\{\mathbf{o}_i \mid \texttt{is_equivalent}(\mathbf{a}, \mathbf{o}_i)\}\right| < G}
  \end{align} \tag{11}
  $$
  • 理解：这里是按照 Prompt 为维度进行过滤的，也就是说只有当一个 Prompt 所有的回答都对或者都错时才会被计算梯度，否则这个 Prompt 不参与梯度计算
  • \(\color{red}{0 < \left|\{\mathbf{o}_i \mid \texttt{is_equivalent}(\mathbf{a}, \mathbf{o}_i)\}\right| < G}\) 的含义是 保留符合以下要求的 Prompt：
    • 对每个 Prompt，采样 \(G\) 个答案 \(\mathbf{o}_i\)，要求这些答案不全对也不全错（因为不管是全对还是全错都会导致没有梯度）
    • 注：模型输出 \(\mathbf{o}_i\) 与 标准答案 \(a\) 等价意味着 \(\texttt{is_equivalent}(\mathbf{a}, \mathbf{o}_i) = 1\)
• 需要注意的是，这一策略不会显著影响训练效率，因为生成时间主要由长尾样本的生成决定（前提是 RL 系统同步且生成阶段未流水线化）
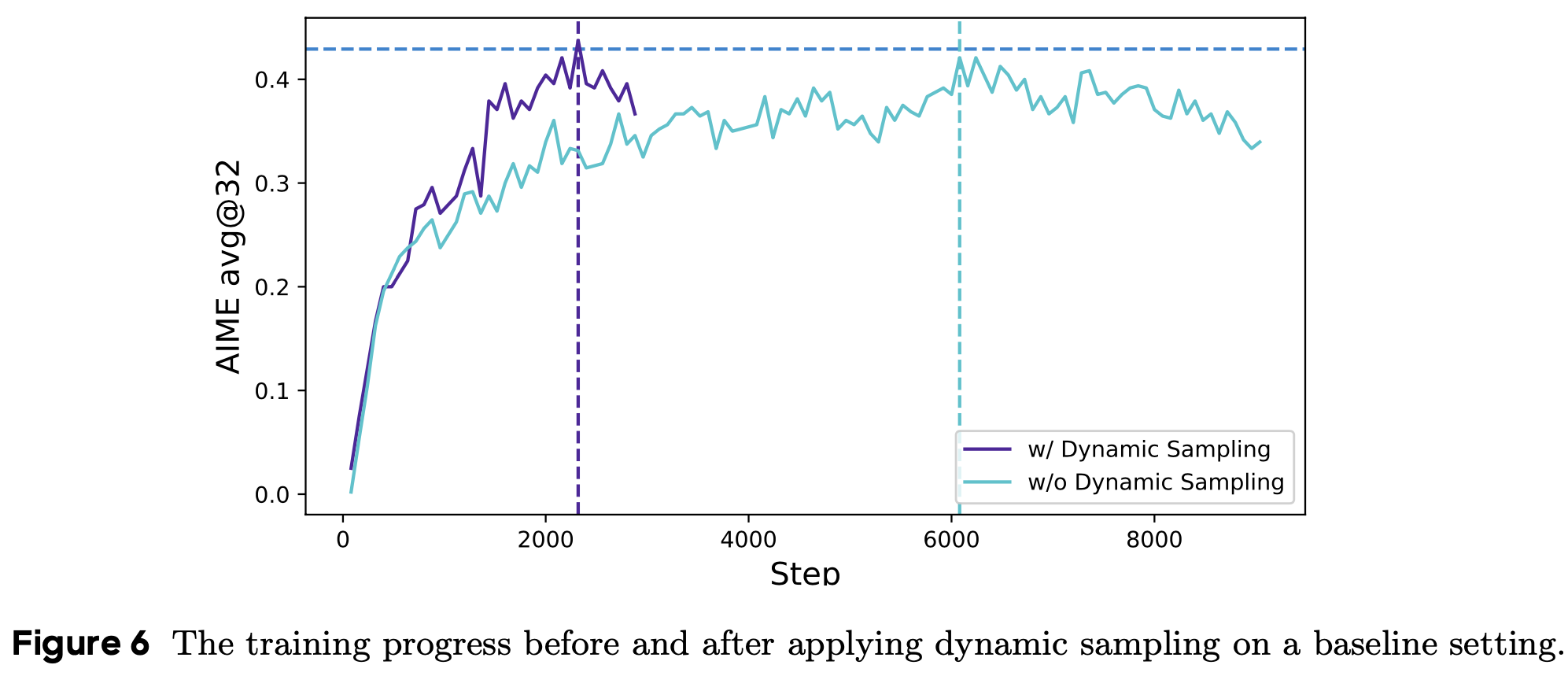
• 此外，实验表明动态采样能以更少的训练步骤达到相同性能（图6）

Rebalancing Act: Token-Level Policy Gradient Loss

• 原始 GRPO 算法采用样本级损失计算，即先在每个样本内按 token 平均损失，再在样本间聚合损失
• 这种方法为每个样本分配了相同的权重。然而，论文发现这种损失计算方式在长链式思维（long-CoT）RL场景中会带来以下问题：
  • 由于所有样本在损失计算中权重相同，长响应中的 token 对整体损失的贡献可能被低估
  • 这会导致两种负面影响：
    • 第一，对于高质量的长样本，模型难以从中学习推理相关的模式；
    • 第二，论文观察到过长的样本通常包含低质量模式（如无意义重复）
  • 样本级损失计算无法有效惩罚这些长样本中的不良模式，从而导致熵和响应长度不健康增长（图4(a)和图4(b)）
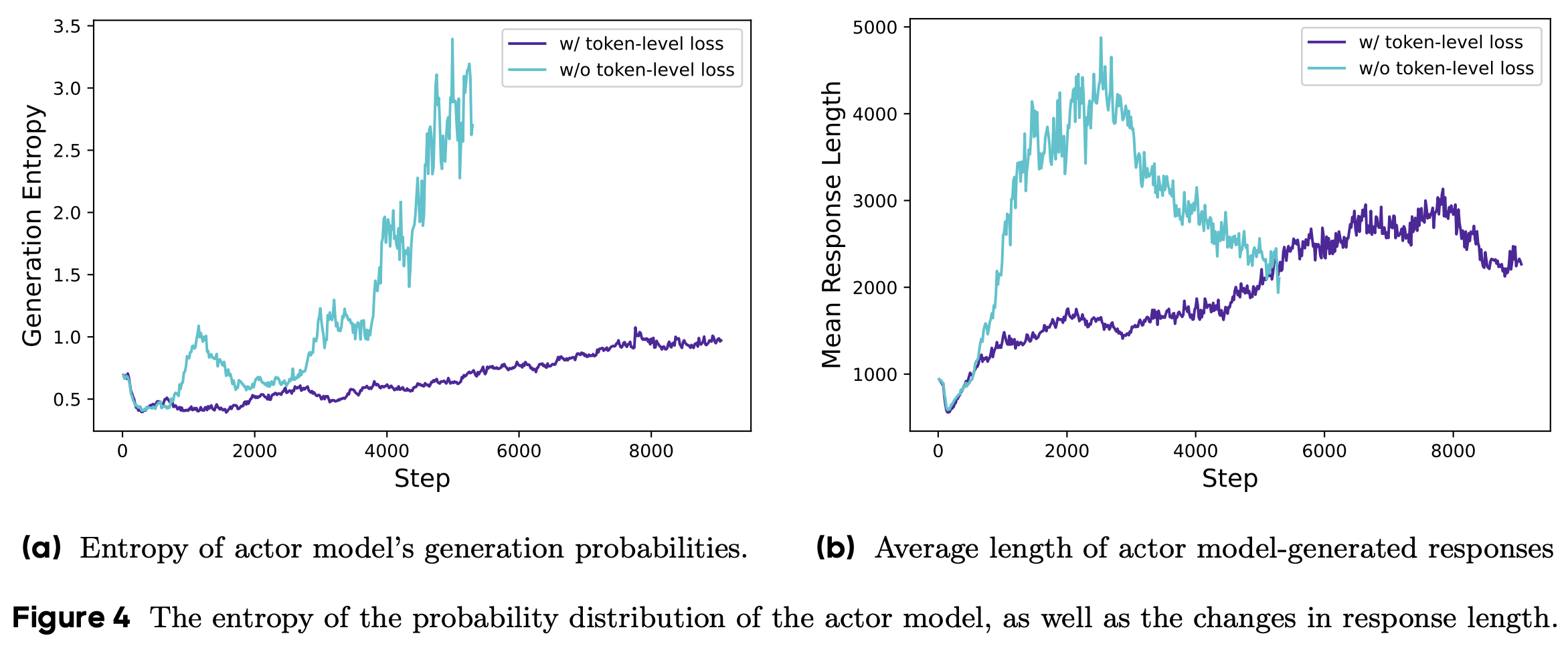
• 为解决这一问题，论文在长链式思维RL场景中引入了Token-Level Policy Gradient Loss ：
  $$
  \begin{align}
  \mathcal{J}_{\mathrm{GRPO} }(\theta) &=\mathbb{E}_{(\mathbf{q},\mathbf{a})\sim\mathcal{D},\{o_{i}\}_{i=1}^{G}\sim\pi_{\theta_{old} }(\cdot|q)} \\
  &\left[\frac{1}{\color{red}{\sum_{i=1}^G|\mathbf{o}_i|}}\color{red}{\sum_{i=1}^{G}\sum_{t=1}^{|\mathbf{o}_i|}}\min\Big{(}r_{i,t}(\theta)\hat{A}_{i,t},~\mathrm{clip}\Big{(}r_{i,t}(\theta),1-\varepsilon_\text{low},1+\varepsilon_\text{high}\Big{)}\hat{A}_{i,t}\Big{)}\right] \\
  \text{s.t.}\quad &0 < \left|\{\mathbf{o}_i \mid \texttt{is_equivalent}(\mathbf{a}, \mathbf{o}_i)\}\right| < G
  \end{align}
  $$
• 在这种设置下，长序列对整体梯度更新的影响更大
• 从单个 token 的角度看，如果某种生成模式能够增加或减少奖励，无论其出现在多长的响应中，都会被同等程度地促进或抑制

Hide and Seek: Overlong Reward Shaping

• 在 RL 训练中，论文通常设置生成的最大长度，超长样本会被截断
  • 论文发现，对截断样本的不当奖励设计会引入噪声并严重干扰训练过程
• 默认情况下，研究人员会为截断样本分配惩罚性奖励（punitive reward）
  • 这种方式可能会在训练中引入噪声，因为一些正确的推理过程可能仅因长度过长而受到惩罚 ，从而混淆模型对其推理有效性的判断
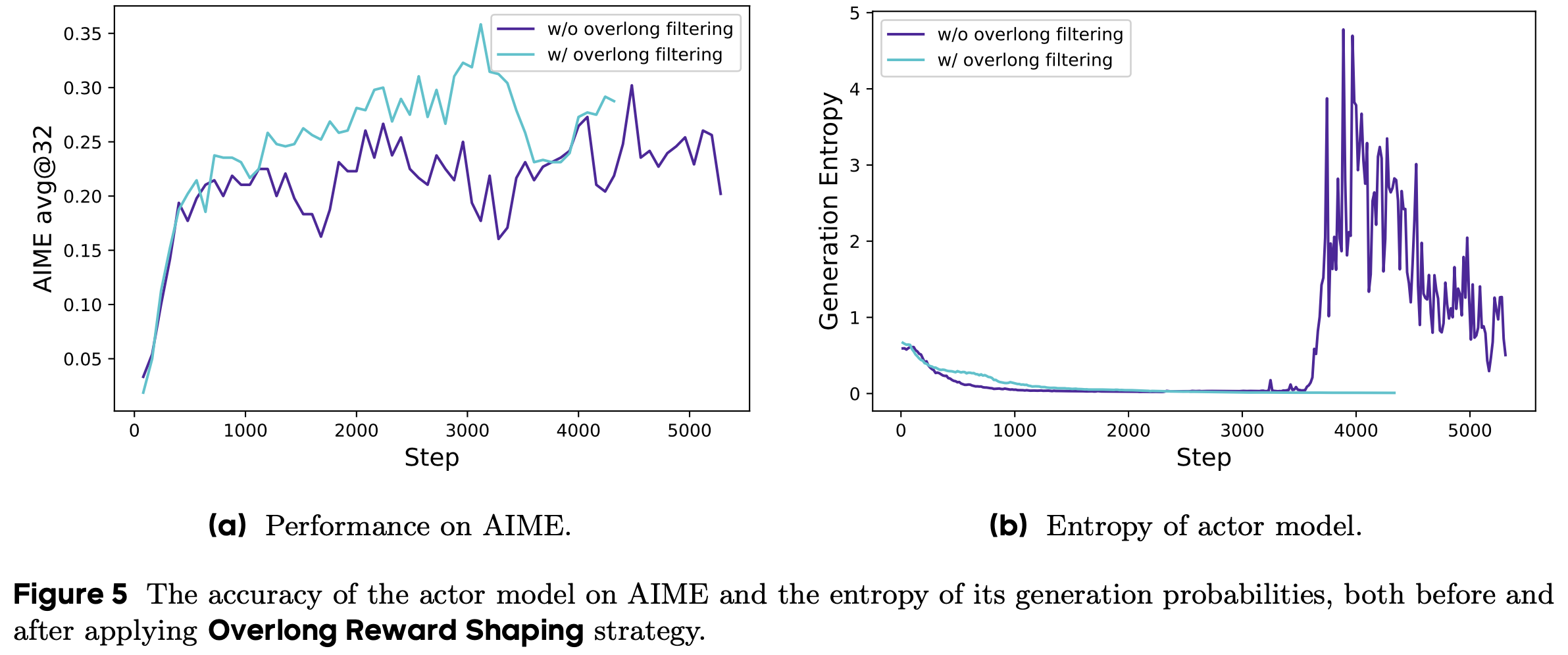
• 为研究这种奖励噪声的影响，论文首先采用超长过滤（Overlong Filtering）策略，屏蔽截断样本的损失（实验表明，这种方法显著提升了训练稳定性和性能（图5））
  • 问题：超长过滤策略为什么可以屏蔽阶段样本的损失？
  • 答案：太长的样本就直接过滤掉（而不是截断），因为截断了就是错误（会回传负奖励），而过滤掉则不会回传梯度
• 此外，论文提出了软超长惩罚（Soft Overlong Punishment）机制（公式13），这是一种基于长度的惩罚方法，用于重塑截断样本的奖励
  $$
  R_{\text{length} }(y) =
  \begin{cases}
  0, & |y| \leq L_{\max} - L_{\text{cache} } \\
  \frac{(L_{\max} - L_{\text{cache} }) - |y|}{L_{\text{cache} } }, & L_{\max} - L_{\text{cache} } < |y| \leq L_{\max} \\
  -1, & L_{\max} < |y|
  \end{cases} \tag{13}
  $$
  • 当响应长度超过预设最大值时，论文定义一个惩罚区间，区间内响应越长，惩罚越大
  • 该惩罚会叠加到原始基于正确性的规则奖励上，从而引导模型避免生成过长的响应
  • 理解：\(L_{\max} - L_{\text{cache} } < |y| \leq L_{\max}\) 时，有：
    $$\frac{(L_{\max} - L_{\text{cache} }) - |y|}{L_{\text{cache} } } \color{red}{\in (-1, 0)}$$
    • 这是一种软性的惩罚，更适合放到模型里面
• 个人理解：
  • 原始的超长样本截断（阶段后答案就是错误，奖励是负的）本身也具有惩罚超长样本的能力吧？

---

DAPO 相关实验

Training Details

• 在本工作中，论文专注于数学任务来评估论文的算法，该算法可以轻松迁移到其他任务
• 论文采用 verl 框架进行训练，并以 naive GRPO 作为基线算法，使用组奖励归一化（group reward normalization）来估计优势
• 在超参数设置上：
  • 论文使用 AdamW 优化器
  • 恒定学习率为 \(1 \times 10^{-6}\)
  • 在 20 个 rollout 步骤中进行线性预热（预热后使用恒定学习率）
    • 问题：这里 20 个 rollout 是指每个 Prompt 都 rollout 20 次，然后进行训练吗？
  • 对于 rollout， Prompt 的批次大小为 512，每个 Prompt 采样 16 个响应
  • 训练时，小批次大小设置为 512，即每个 rollout 步骤进行 16 次梯度更新
  • 对于过长奖励调整（Overlong Reward Shaping） ，论文将预期最大生成长度设置为 16,384 个 token，并额外分配 4,096 个 token 作为软惩罚缓存，因此生成的最大 token 数为 20,480
  • 对于Clip-Higher机制，论文将裁剪参数 \(\varepsilon_{\text{low} }\) 设置为 0.2， \(\varepsilon_{\text{high} }\) 设置为 0.28 ，以有效平衡探索与利用的权衡
  • 在 AIME 评估中，论文将评估集重复 32 次，并报告 avg@32 以确保结果稳定性
    • 问题：avg@32 是代表同一个 Prompt 使用 32 次采样，每次采样取最大概率的回复，然后对所有回复求均值吗？
    • 回答：是的，参见文中图3对采样回答全对的描述
  • 推理超参数设置为 temperature 1.0 和 topp 0.7

实验结果

• 在 AIME 2024 上的实验表明，DAPO 成功地将 Qwen-32B 基础模型训练为一个强大的推理模型，其性能优于 DeepSeek 在 Qwen2.5-32B 上使用 R1 方法的结果
• 如 图1 所示，论文在 AIME 2024 上观察到性能的显著提升，准确率从接近 0% 提高到 50%。值得注意的是，这一提升仅使用了 DeepSeek-R1-Zero-Qwen-32B 所需训练步骤的 50%
• 论文在 表1 中详细分析了每种训练技术对结果的贡献
  • 这些改进证明了这些技术在 RL 训练中的有效性，每种技术都为 AIME 2024 的准确率提升贡献了若干百分点
  • 在 native GRPO 设置下，Qwen2.5-32B 基础模型的准确率仅能达到 30%
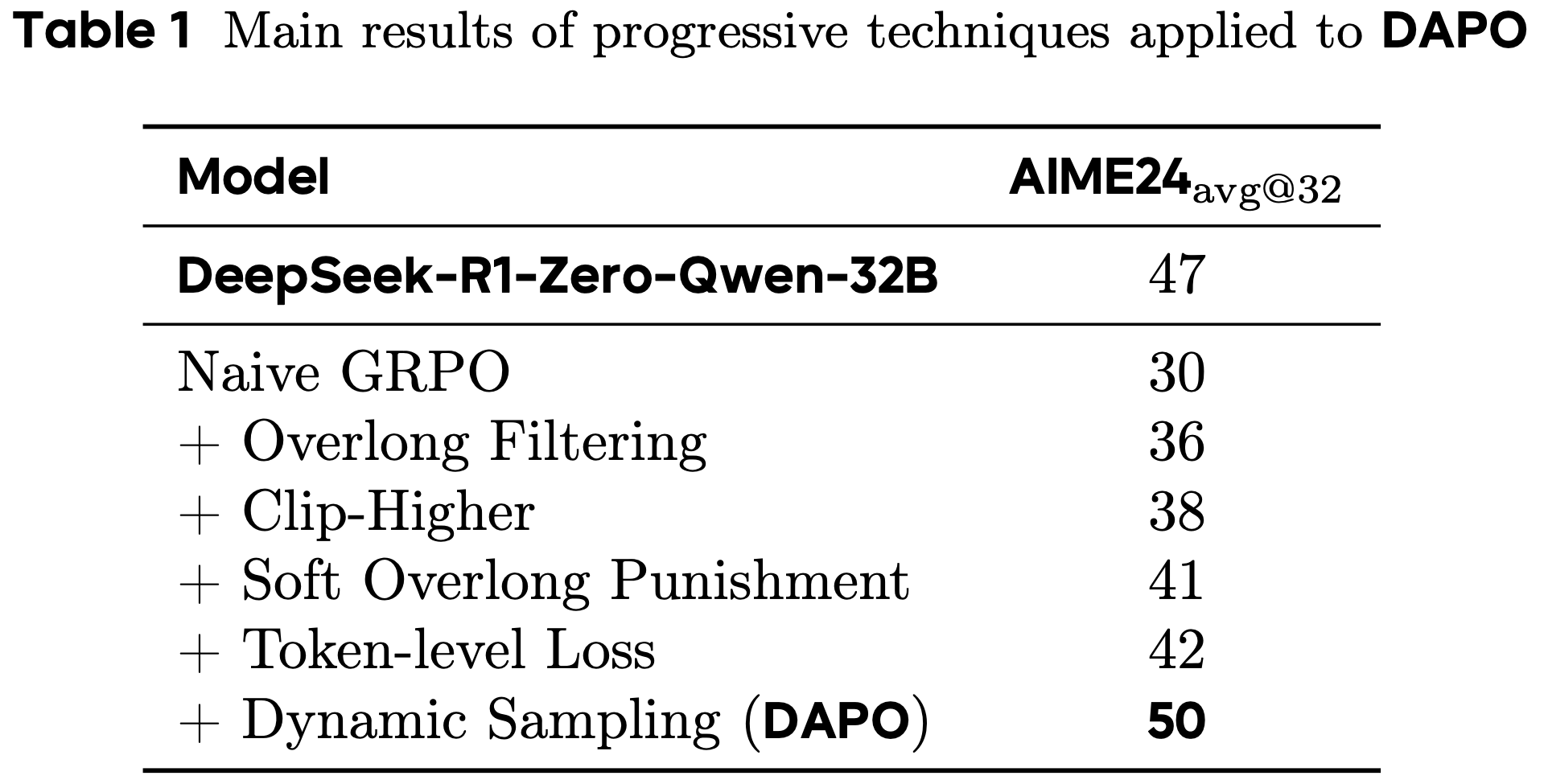
• 对于 token-level 损失，尽管其带来的性能提升较小，但论文发现它增强了训练的稳定性，并使生成长度的增长更加健康
• 在应用动态采样时，尽管由于过滤掉零梯度数据需要采样更多数据，但整体训练时间并未受到显著影响
  • 如图 6 所示，尽管采样实例数量增加，但由于所需训练步骤减少，模型的收敛时间甚至有所缩短

Training Dynamics（训练动态监控）

• 大型语言模型的强化学习不仅是一个前沿研究方向，也是一个内在复杂的系统工程挑战，其特点是各子系统之间的相互依赖
• 对任何子系统的修改都可能通过系统传播，并由于这些组件之间的复杂相互作用而导致不可预见的后果
• 即使是初始条件的微小变化（如数据和超参数的差异），也可能通过迭代强化学习过程放大，从而在结果中产生显著偏差
• 这种复杂性常常使研究人员陷入两难境地：即使经过细致分析并有充分理由认为某项修改会提升训练过程的某些方面，实际结果却往往与预期轨迹不符
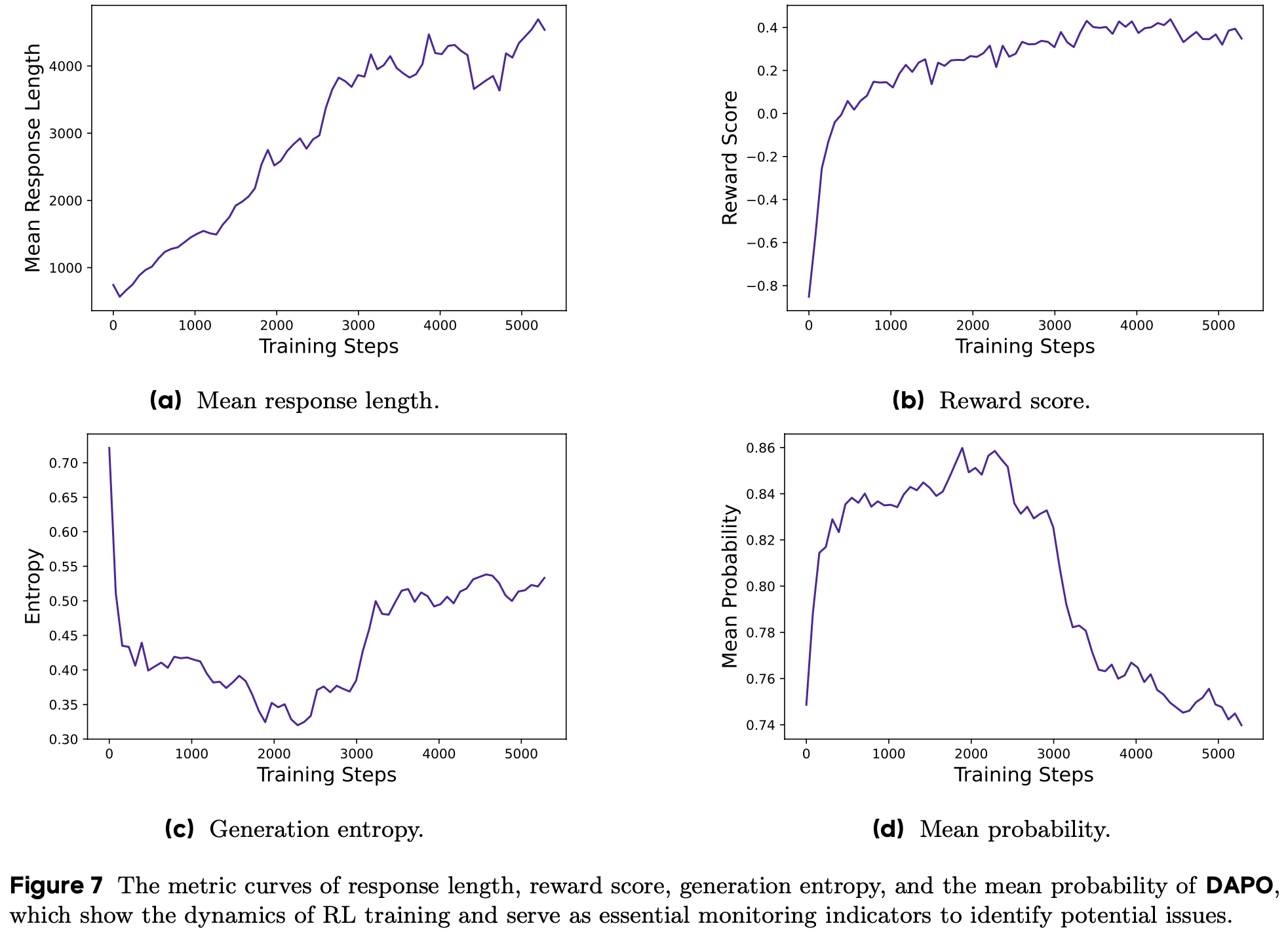
• 因此，在实验过程中监控关键中间结果对于快速识别差异来源并最终优化系统至关重要，监控指标包括下面三种：
• 生成响应的长度（The Length of Generated Responses） ：
  • 与训练稳定性和性能密切相关的指标，如图7(a) 所示
  • 长度的增加为模型提供了更大的探索空间，允许采样更复杂的推理行为，并通过训练逐步强化
  • 需要注意的是，长度在训练过程中并不总是保持持续上升趋势：在某些较长的阶段，它可能表现出停滞甚至下降的趋势，这在 Deepseek-r1: Incentivizing reasoning capability in llms via reinforcement learning 中也有所体现
  • 论文通常将长度与验证准确率结合使用，作为评估实验是否恶化的指标
• 训练期间的奖励动态（The Dynamics of Reward）
  • 强化学习中的关键监控指标之一，如图 7(b) 所示
  • 在大多数实验中，奖励的增长趋势相对稳定，不会因实验设置的调整而出现显著波动或下降
  • 这表明，在可靠的奖励信号下，语言模型能够稳健地拟合训练集的分布
  • 过拟合发现 ：论文发现训练集的最终奖励与验证集的准确率往往相关性较低，这表明模型对训练集存在过拟合
• Actor Model 的熵 & 生成概率
  • 熵与模型的探索能力相关，是论文实验中密切监控的关键指标
  • 直观上，模型的熵需要保持在适当范围内：熵过低表明概率分布过于尖锐，导致探索能力丧失；而熵过高通常与过度探索问题（如胡言乱语和重复生成）相关
    • 生成概率则与熵相反，生成概率越大，对应的熵可能越小
  • 如第 3.1 节所示，通过应用 Clip-Higher 策略，论文有效解决了熵崩溃问题
  • 在后续实验中，论文发现保持熵的缓慢上升趋势有助于模型性能的提升 ，如图 7(c) 和图 7(d) 所示

Case Study

• 在 RL 训练过程中，论文观察到一个有趣的现象：Actor Model 的推理模式会随时间动态演变
• RL 算法不仅会强化那些有助于正确解决问题的现有推理模式，还会逐渐催生最初不存在的全新推理模式
• 这一发现揭示了 RL 算法的适应性和探索能力，并为模型的学习机制提供了新的见解
• 观察到的现象示例：在模型训练的早期阶段 ，几乎没有出现对模型之前输出推理步骤的检查和反思行为；随着训练的进行，模型表现出明显的反思和回溯行为，如表2 所示（这一观察为未来研究 RL 中推理能力的涌现提供了新的方向）

---

附录A 数据集转换示例

• 以下展示了一个数据转换的示例，包括原始问题、转换后的问题以及模型在转换过程中的输出（原始内容为 Markdown 文本，已为可读性进行渲染）
  • 问题：转换是谁做的？提前人工转换的？
• 为确保模型能高精度完成此任务，论文的目标是使其进行全面的推理，同时避免幻觉
• 为此，论文提供了一个清晰的思维框架，鼓励深入推理，采用思维链（CoT）推理，并定义四个明确的步骤：
  • 提取答案格式
  • 重写问题陈述（问题：按照什么目标来重写？写的更简单，还是难？）
  • 解决修改后的问题
  • 提供整数作为最终答案
• 在每个步骤中，论文提供少量示例解决方案或详细指南，以引导模型的推理过程
• 通过这种方法，论文观察到在大多数情况下，LLM 生成的重新表述在格式和质量上都能令人满意

---

附录B 一个补充示例

• 反思性行为涌现的一个示例