NLP——Does-RL-Incentivize-Reasoning-Capacity

注：本文包含 AI 辅助创作

• 参考链接：
  • 原始论文：Does Reinforcement Learning Really Incentivize Reasoning Capacity in LLMs Beyond the Base Model?, Leap Lab of THU & SJTU, 20250418-20251124
  • GitHub 项目地址：limit-of-RLVR.github.io

Paper Summary

• 论文内容总结：
  • 论文发布以来，在业内广受认可，非常值得一读
  • 论文系统地研究了当前 RLVR 方法对 LLM 推理能力边界的影响
  • 论文的研究结果表明
    • 当前的 RLVR 很少激发根本性的新推理模式；
    • RLVR 训练模型的推理能力仍然受限于其 Base Model 的能力
    • 当前的 RLVR 方法尚未完全实现 RL 通过探索和利用来激发 LLM 新推理能力的潜力
    • 注：这种局限性可能源于论文第 5 节讨论的在巨大语言空间中缺乏有效的探索策略
  • 在高级抽象中进行探索、细粒度的信用分配以及多轮智能体-环境互动可能缓解这个问题
  • 本研究的结论不一定保真，因为论文的研究有些设定问题：
    • 作者已经尽量评估尽可能多的强大的、公开可用的纯 RLVR 模型，但是仍然有问题
    • 目前能力最强的模型和训练流程仍然是私有的，所以作者无法分析内部的细节（论文的分析需要这些细节）
    • 目前的技术发展很快，其实已经有一些文章对论文的结论提出了一些挑战
      • 论文的作者最终版本更新的论文中，比较谦逊，已经意识到了这些实际限制
• RLVR 近期在提升 LLM 的推理性能方面取得了显著成功，尤其是在数学和编程任务中
  • 人们普遍认为，与传统 RL 帮助智能体探索和学习新策略类似，RLVR 能够使 LLMs 持续自我改进，从而获得超越对应 Base Model 能力的新型推理能力
• 在本研究中，论文通过对 RLVR 训练的 LLMs 在不同的模型家族、 RL 算法和数学/代码/视觉推理基准测试中进行系统性的推理能力边界探测，并采用大 \(k\) 值下的 pass@\(k\) 作为评估指标，对 RLVR 的当前状态（the current state of RLVR） 进行了批判性审视
• 虽然 RLVR 提高了采样正确路径的效率，但论文惊奇地发现，当前的训练 极少（rarely） 能激发出根本性的新推理模式
  • 论文观察到，尽管 RLVR 训练的模型在较小的 \(k\) 值（例如 \(k\)=1）下优于其 Base Model ，但在 \(k\) 值较大时， Base Model 反而能达到更高的 pass@\(k\) 分数
• Moreover，论文发现 LLMs 的推理能力边界常常随着 RLVR 训练的进行而变窄（narrows）
• 进一步的覆盖率和困惑度（perplexity）分析表明，RLVR 模型生成的推理路径已经包含在 Base Model 的采样分布中
  • 这表明它们的推理能力源自 Base Model 并 受限于（bounded by） Base Model
• 从这个视角出发，将 Base Model 视为一个上界，论文的定量分析表明：
  • 六种流行的 RLVR 算法表现相似，并且远未达到充分利用 Base Model 潜力的最优状态
• In Contrast，论文发现蒸馏（distillation）能够从教师模型中引入新的推理模式，并真正扩展模型的推理能力
• Taken together，论文的研究结果表明，当前的 RLVR 方法尚未完全实现 RL 激发 LLMs 真正新颖推理能力的潜力
  • 这突显了改进 RL 范式的必要性，例如有效的探索机制、更审慎和大规模的数据管理、细粒度的过程信号以及多轮智能体交互，以释放这种潜力

---

Introduction and Discussion

• 专注于推理的大型语言模型（reasoning-centric LLMs）的发展极大地推动了 LLM 能力的前沿
  • 例如 OpenAI-o1 (2024)、DeepSeek-R1 (2025) 和 Kimi-1.5 (2025)，
  • 特别是在解决涉及数学和编程的复杂逻辑任务方面
• 与传统依赖于人工标注指令（instruction-tuned）的方法（2023; 2024）相比，这一飞跃背后的关键驱动力是大规模的 RLVR (2024; 2025)
  • RLVR 从一个预训练的 Base Model 或经过长链思维（chain of thought，CoT）数据微调的模型开始，基于简单的、可自动计算的奖励通过 RL 对其进行优化
  • 这些奖励取决于模型的输出在数学问题上是否匹配真实解，或在代码问题上是否通过单元测试，从而无需人工标注即可实现规模化
  • RLVR 框架因其简单性和实际有效性而备受关注
• 在传统的 RL 设置中，例如游戏（如 Atari，Go），智能体通常通过自我改进自主发现新策略并超越甚至达到人类水平 (2015; 2017)
  • 受此成功启发，人们普遍认为 RLVR 同样能使 LLMs 自主发展出新的推理模式，包括枚举、自我反思和迭代优化，从而超越其 Base Model 的能力 (2025)
• Consequently，RLVR 被视为实现 LLMs 持续自我进化、可能使论文更接近更强大智能的一条有希望的途径 (2025)
  • However，尽管取得了经验上的成功，当前 RLVR 的根本有效性仍未得到充分检验
  • 这引出了一个根本性问题：当前 RLVR 是否真正使 LLMs 获得了新的推理能力，类似于传统 RL 通过探索发现新策略，还是仅仅利用了 Base Model 中已有的推理模式？
• 为了严格回答这个问题，论文首先必须评估 Base Model 和 RLVR 训练模型的推理能力边界
  • 传统的评估指标依赖于贪心解码（greedy decoding）或核采样（nucleus sampling）(2020) 的平均分，这反映了平均情况下的行为
  • However，这些指标可能会低估模型的真实潜力，尤其是在尝试次数有限的情况下模型在难题上失败时，尽管它有能力通过更多采样解决这些问题
• 为了克服这一限制，论文采用 pass@\(k\) 指标 (2024)，即如果 \(k\) 个采样输出中任意一个是正确的，则认为问题已解决
  • 通过允许多次尝试，pass@\(k\) 揭示了模型是否具备解决问题的潜力
  • 数据集的平均 pass@\(k\) 分数因此反映了模型在 \(k\) 次尝试内可能解决的问题比例，为其推理边界提供了更稳健的视角
    • 这为 RLVR 训练是否能产生根本性的超越能力、使模型能够解决 Base Model 无法解决的问题提供了严格检验
• 使用 pass@\(k\) 指标，论文在多个基准测试中进行了广泛的实验，涵盖了多个 LLM 家族、模型大小和 RLVR 算法，以比较 Base Model 与其 RLVR 训练的对应模型
• 图 1 内容：
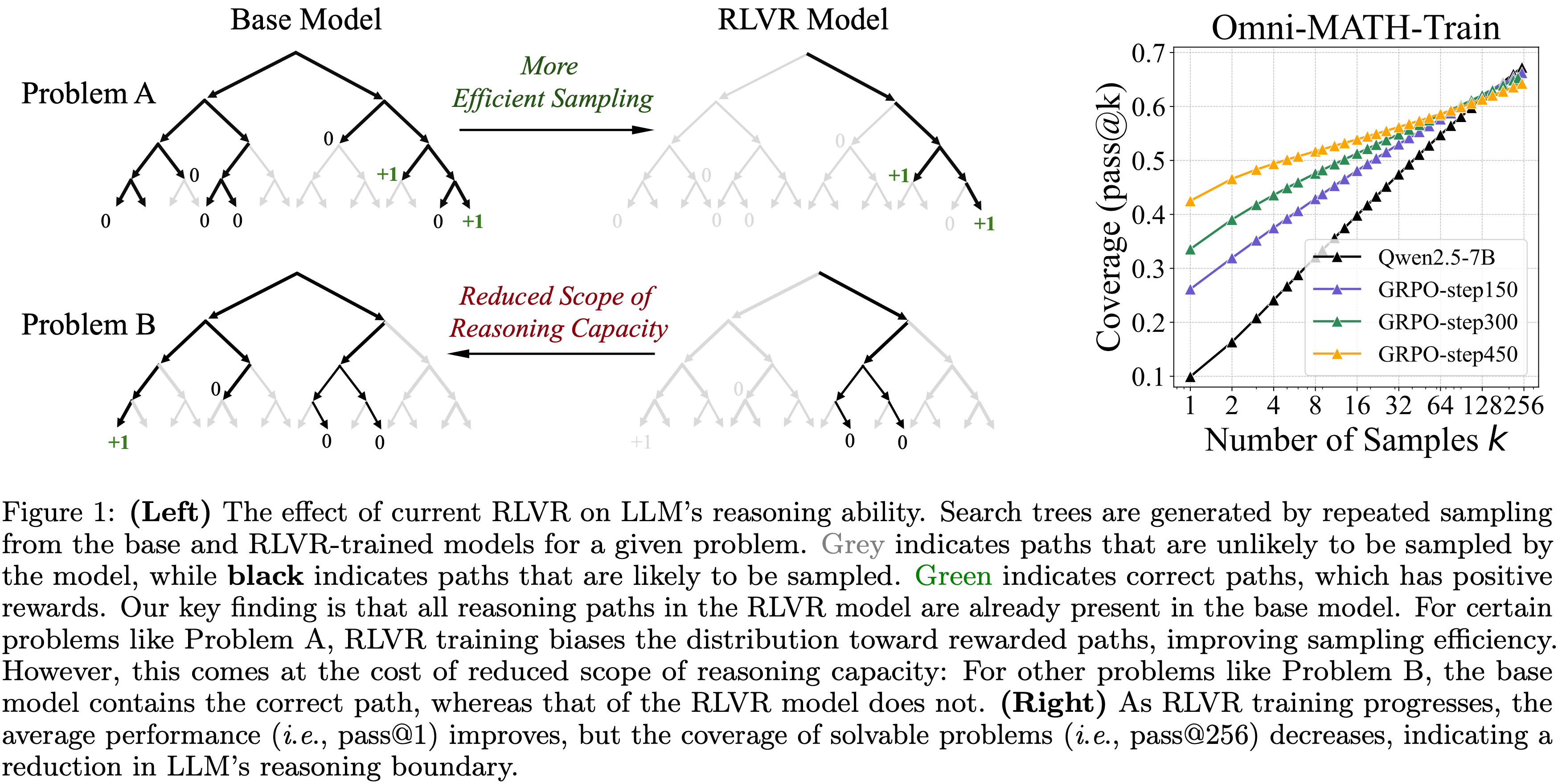
  • Left：当前 RLVR 对 LLM 推理能力的影响
    • 搜索树（search tree）通过对给定问题从 Base Model 和 RLVR 训练模型中重复采样生成
    • 灰色表示模型不太可能采样的路径，而 黑色 表示模型可能采样的路径
    • 绿色表示具有正奖励的正确路径
    • 论文的关键发现是，RLVR 模型中的所有推理路径都已存在于 Base Model 中
    • 对于某些问题，如问题 A，RLVR 训练使分布偏向奖励路径，提高了采样效率
      • However，这是以减少推理能力范围为代价的：
        • 对于其他问题如问题 B， Base Model 包含正确路径，而 RLVR 模型则没有
  • Right：随着 RLVR 训练的进行，平均性能（即 pass@1）提高，但可解问题（solvable problem）的覆盖率（即 pass@256）下降，表明 LLM 的推理边界在缩小

---

Preliminaries

• 本节首先概述 RLVR 的基础知识，然后介绍用于评估推理边界的 pass@\(k\) 指标，并解释为什么它比最佳采样（best-of-\(N\)）等替代方案更受青睐

RLVR（Reinforcement Learning with Verifiable Rewards）

Verifiable Rewards

• 设 \(\pi_{\theta}\) 为一个具有参数 \(\theta\) 的 LLM，它在自然语言 Prompt \(x\) 的条件下生成一个 Token 序列 \(\mathbf{y}=(y_{1},\ldots,y_{T})\)
• 一个确定性的 ** Verifier** \(\mathcal{V}\) 返回一个二元奖励：
  $$ r=\mathcal{V}(x,\mathbf{y})\in\{0,1\}$$
  • 当且仅当模型的最终答案完全正确时 \(r=1\)
• 也可以添加格式奖励以鼓励模型明确地将推理过程与最终答案分开
• RL 的目标是学习一个策略以最大化期望奖励：
  $$ J(\theta)=\mathbb{E}_{x\sim\mathcal{D} }\left[\mathbb{E}_{\mathbf{y}\sim\pi_{\theta}(\cdot|x)}[r]\right] $$
  • 其中 \(\mathcal{D}\) 是 Prompt 的分布

RLVR Algorithms

• 近端策略优化（Proximal Policy Optimization，PPO）(2017) 提出使用以下裁剪替代目标（clipped surrogate）来最大化目标函数：
  $$\mathcal{L}_{\text{CLIP} }=\mathbb{E}\left[\min(r_{t}(\theta)A_{t},\text{clip}(r_{t}(\theta),1-\epsilon,1+\epsilon)A_{t})\right],$$
  • 其中 \(r_{t}(\theta)=\frac{\pi_{\theta}(y_{t}|x,\mathbf{y}_{ < t})}{\pi_{\theta_{\text{old} } }(y_{t}|x,\mathbf{y}_{ < t})}\)，\(A_{t}\) 是由价值网络 \(V_{\phi}\) 估计的优势（advantage）
• 可选地应用 KL 散度项（KL divergence term），以约束模型偏离原始策略的程度
• 更多算法介绍见 C.5 节

Policy Gradient

• PPO 及其变体属于 RL 的策略梯度类（policy gradient class）(1992; 1998)
• 这些方法仅从 On-policy samples 中学习，即由当前 LLM 生成的样本
• 在可验证奖励的背景下，训练目标通常是 最大化正确答案样本的对数似然，并最小化错误答案样本的似然

Zero RL Training

• Zero RL Training 将 RL 直接应用于 Base Model ，无需任何 SFT (2025)
• 为了清晰研究 RLVR 的效果
  • 对所有数学任务
    • 遵循 Zero-RL 设置，使用预训练模型作为起始模型
  • 对于 Coding 和视觉推理（Visual Reasoning）任务
    • 使用微调模型作为起始模型，比较微调模型与其 RLVR 训练的对应模型
  • 补充：对于 Coding 和视觉推理（Visual Reasoning）任务，开源工作通常使用指令微调模型作为起点
    • 主要是由于使用纯 Zero-RL 设置存在训练不稳定性和有限的有效性
    • 遵循此惯例，论文比较微调模型与其 RLVR 训练的对应模型，以专注于 RLVR 的效果
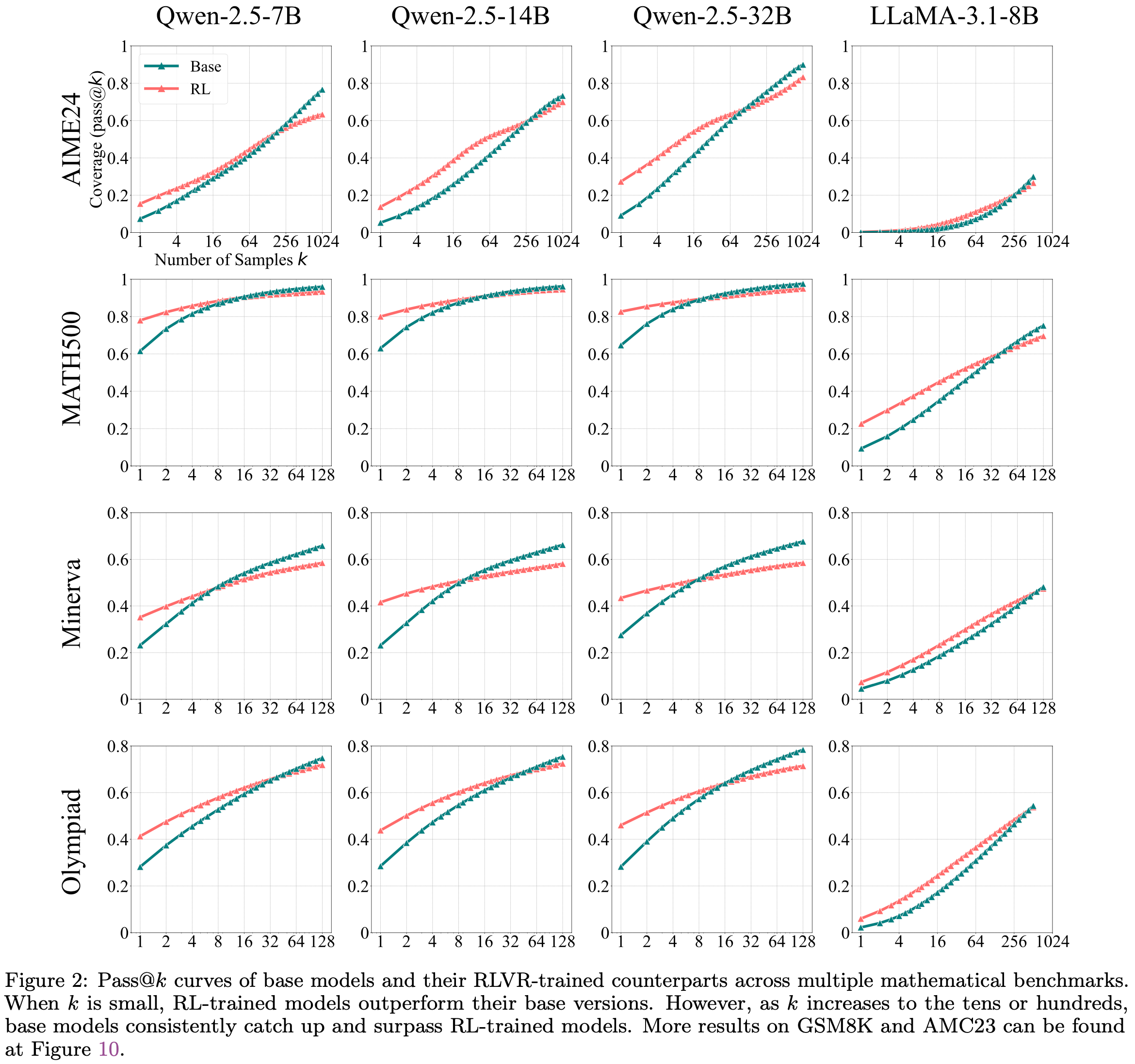
• 图 2 ： Base Model 及其 RLVR 训练对应模型在多个数学基准测试上的 Pass@\(k\) 曲线
  • 当 \(k\) 较小时， RL 训练的模型优于其基础版本
  • However，当 \(k\) 增加到数十或数百时， Base Model 持续赶上并超越 RL 训练的模型
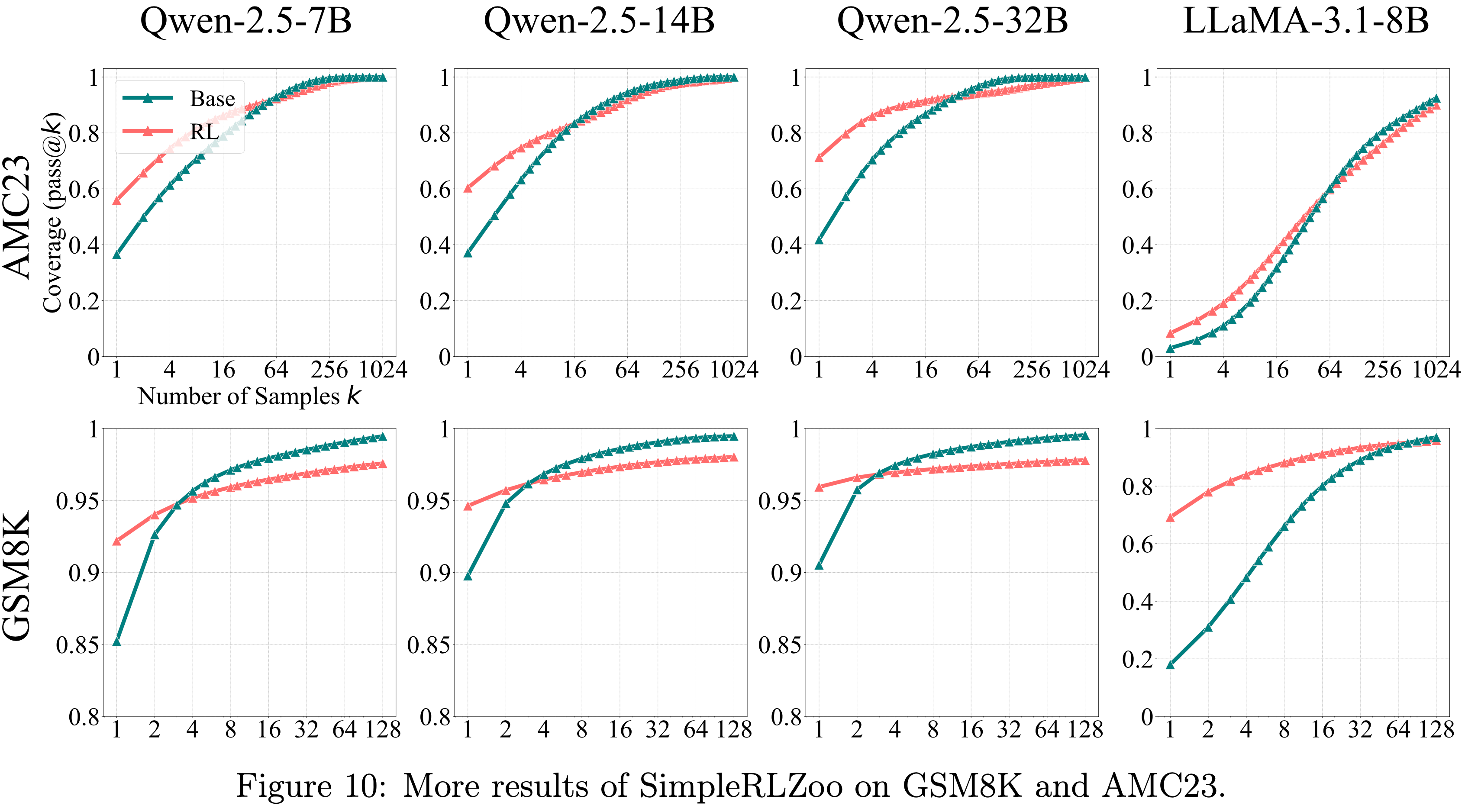
  • GSM8K 和 AMC23 的更多结果见图 10

Metrics for LLM Reasoning Capacity Boundary

Pass@\(k\) Metrics

• 准确测量 Base 和 RL 模型的推理能力边界具有挑战性，因为贪心解码或核采样的平均值 (2020) 等方法仅反映平均情况下的性能
• 为了准确测量推理能力边界，论文将代码生成中常用的 pass@\(k\) 指标 (2021) 扩展到所有具有可验证奖励的任务
• 给定一个问题，论文从模型采样 \(k\) 个输出
  • 如果至少有一个样本通过验证，则该问题的 pass@\(k\) 值为 1；否则为 0
  • 问题：这里的模型采样可能会重复吗？
• 数据集的平均 pass@\(k\) 值反映了模型在 \(k\) 次尝试内可以解决的数据集中问题比例，为 LLMs 的推理能力覆盖范围提供了严格评估
• 论文采用一种无偏、低方差的估计器（unbiased, low-variance estimator）来计算 pass@\(k\)，详见 A.2 节

Comparison with Best-of-\(N\) and Majority Voting

• Best-of-\(N\) (2021) 和 Majority Voting 是选择正确答案的实用方法，但它们可能忽略了模型的全部推理潜力
• In Contrast，论文使用 pass@\(k\) 不是为了评估实际效用 ，而是为了探究推理能力的边界
  • 如果模型在任意 \(k\) 个样本中产生了一个正确解，论文将该问题视为在其潜在范围内
  • Thus，如果 RL 增强了推理能力， RL 训练的模型应该比 Base Model 在更多此类问题上成功
• 如果 Verifier 或投票未选择正确答案，像 Best-of-\(N\) 或多数投票这样的方法可能会错过这些成功

Random Guessing Issue

• 对于 Coding 任务，使用编译器和预定义的单元测试用例作为 Verifier ，pass@\(k\) 值可以准确反映模型是否能解决问题
• 在 Mathematics 中，“猜测”问题可能随着 \(k\) 的增加而变得显著，即模型可能生成不正确的 CoT 但仍偶然得出正确答案
• 为了解决这个问题，论文对模型输出的一个子集手动检查 CoT 的正确性 ，详见 3.1 节
• 通过结合数学上手动检查的结果和 Coding 的结果，论文严格评估了 LLM 推理能力的范围
• 另一个注意事项是（Another caveat is that），如果 \(k\) 值极大，即使是 Token 字典（Dictionary）上的均匀采样也会偶然发现正确的推理路径
  • 尽管这在当今的时间和计算资源预算下是不可行的
• Crucially，论文发现 Base Model 在实际的 \(k\) 值（\(k=128\) 或 1024）下已经能产生正确的输出，这完全在实用资源限制内
  • 理解：这里也是最早本人的担忧，这里作者相当于给了比较合适的回答了，但依然是论文的一个核心讨论点，因为采样次数足够多，任何模型都能成功

---

RLVR’s Effect on Reasoning Capacity Boundary

• 前文建立了推理边界评估指标
• 本节现在通过广泛的实验对基础和 RLVR 模型进行全面评估
• 论文的分析按任务类别组织，涵盖三个代表性领域：数学、代码生成和视觉推理
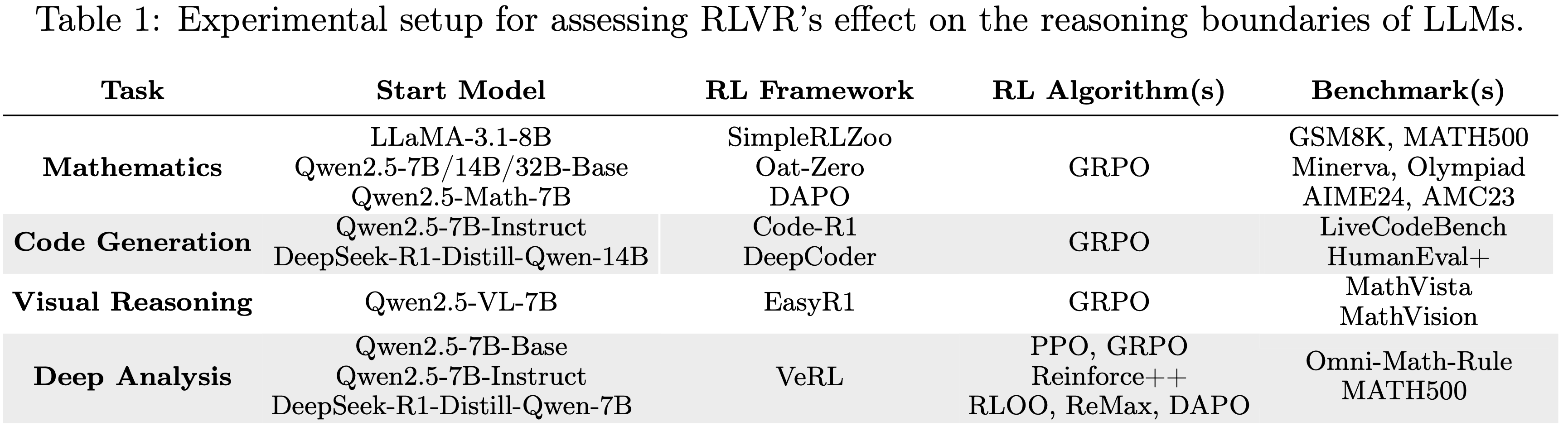
• 整体实验设置总结在表 1 中（表 1 ：评估 RLVR 对 LLMs 推理边界影响的实验设置）
• 评估协议（Evaluation Protocol）
  • 对于 Base Model 和 RLVR 模型的采样过程，论文使用温度 temperature=0.6 和 top-\(p\) 值 0.95，允许最大生成 16,384 个 Token
    • 论文在图 17 中还展示了不同温度设置的效果
  • 对于 Base Model 的评估，一种常见做法是在 Prompt 中包含少量示例（few-shot examples）以引导输出 (2024; 2024; 2024)
    • However，为了确保公平和无偏见的比较，论文特意避免为 Base Model 使用少量 Prompt （few-shot prompts），以消除上下文示例可能对推理造成的任何潜在混杂影响
  • 为了评估 Base Model 和 RLVR 模型，论文使用与 RLVR 训练相同的零样本 Prompt （zero-shot prompt），或基准测试提供的默认 Prompt ，确保两种模型之间设置一致
    • Interestingly，尽管 Base Model 在没有少量指导的情况下经常产生未格式化或无意义的 Response ，但论文观察到，只要有足够的采样，它们仍然能够生成正确格式化的输出并成功解决复杂问题
    • 训练和评估的 Prompt 模板在附录 D 节中提供

RLVR for Mathematical Reasoning

Models and Benchmarks

• 在数学问题中，模型需要生成一个推理过程（即 CoT）以及最终答案
• 为了确保结论的稳健性，论文实验了多个 LLM 家族，主要是 Qwen2.5 (7B/14B/32B 基础变体) (2024) 以及额外的 LLaMA-3.1-8B (2024)
• 论文采用由 SimpleRLZoo (2025) 发布的 RLVR 模型，这些模型使用 GRPO 在 GSM8K 和 MATH 训练集上训练 Zero RL 模型，仅使用正确性奖励，排除任何基于格式的奖励
• 论文在不同难度的基准测试上比较 Base 和 Zero RL 模型的 pass@\(k\) 曲线：
  • GSM8K (2021)、MATH500 (2021)、Minerva (2022)、Olympiad (2024)、AIME24 和 AMC23
• Additionally，论文还包括 RLVR 模型 Oat-Zero-7B 和 DAPO-32B (2025a; 2025)
  • 这两个模型的特点是在具有挑战性的 AIME24 基准测试上表现出色

The Effect of RLVR: Increased Likelihood of Correct Samples, Decreased Coverage of Solvable Problems（增加正确样本的可能性，减少可解问题的覆盖范围）

• 如图 2 所示，论文一致地观察到小 \(k\) 值和大 \(k\) 值之间的对比趋势
  • 当 \(k\) 较小时（例如 \(k=1\)，相当于平均准确率）， RL 训练的模型优于其基础对应模型
    • 这与 RL 提升性能的常见观察相符，表明 RLVR 使模型采样正确 Response 的可能性显著增加
  • 随着 \(k\) 增加，曲线变得更陡峭，在所有基准测试中， Base Model 持续赶上并最终超越 RL 训练的模型
    • 表明 Base 模型对可解问题的覆盖范围更广
    • 例如，在 Minerva 基准测试上使用 32B 大小模型时， Base Model 在 \(k=128\) 时比 RL 训练的模型高出约 9%，这意味着它可以在验证集中解决大约多 9% 的问题
• 论文进一步检查了使用 Oat-Zero 和 DAPO 训练的 RL 模型
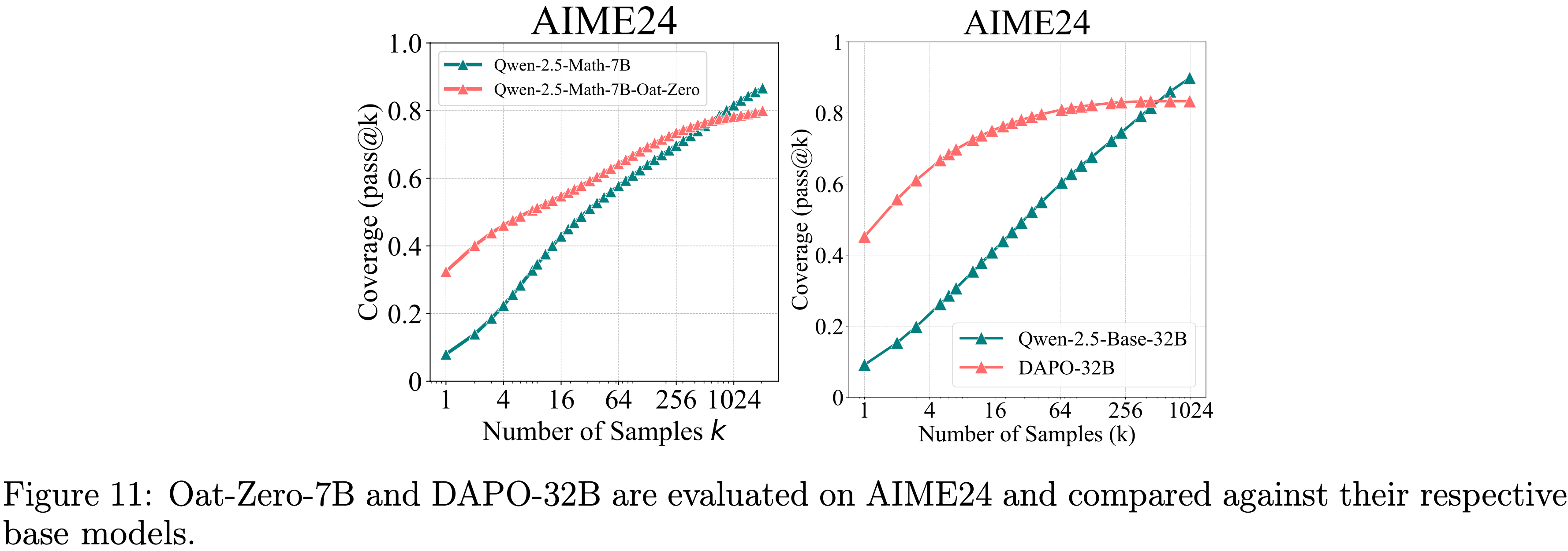
  • 如图 11 所示，尽管 RL 模型最初表现出强劲性能，比 Base Model 高出近 30%，但最终被 Base Model 超越
• 基于这些结果，论文得出结论：RLVR 在低 \(k\) 时增加了采样正确 Response 的可能性，但缩小了模型的整体覆盖范围
• 论文在 4.1 节进一步分析了这种现象的根本原因

CoT Case Analysis

• 论文在图 20 和图 21 中展示了从 Base Model 中采样的正确 CoT，这些是从 AIME24 最难问题的 2048 次采样中手动选择的
• Base Model 的 Response 往往是较长的 CoT 并表现出反思行为，突显了 Base Model 内在的强大推理能力

Validityof Chain-of-Thought

• 对于数学问题，常见的评估仅基于最终答案的正确性，存在 hacking 风险
• 为了使用 pass@\(k\) 准确反映推理能力边界，重要的是评估有多少已解决的问题是源于采样到真正正确的 CoT，而非幸运猜测
• 遵循 (2024)，论文手动检查了 GSM8K 数据集中最具挑战性的可解问题（平均准确率低于 5% 但高于 0%）中导致（led to）正确答案的所有 CoT
  • Base Model 回答了 25 个这样的问题，其中 24 个包含 至少一个（at least one） 正确的 CoT
  • Similarly， RL 训练的模型回答了 25 个问题，其中 23 个包含 至少一个 正确的 CoT
• 论文还手动检查了具有挑战性的 AIME24 基准测试中平均准确率低于 5% 的问题的 CoT（详情见 C.2 节）
  • Base Model 回答了 7 个这样的问题，其中 5 个（共 6 个，排除一个因跳过推理步骤而正确性模糊的情况）包含 至少一个 正确的 CoT
  • 类似地， RL 训练的模型回答了 6 个问题，其中 4 个包含 至少一个 正确的 CoT
• 这些结果表明， Base Model 可以采样有效的推理路径来解决问题
  • 理解：这里是挑选最可能因为随机猜对答案（而 CoT 是错的）的问题进行人工 check，看起来 check 结果也是符合预期的（Base Model 回答对的情况跟 RL 模型差不多或更好）

RLVR for Code Generation

Models and Benchmarks

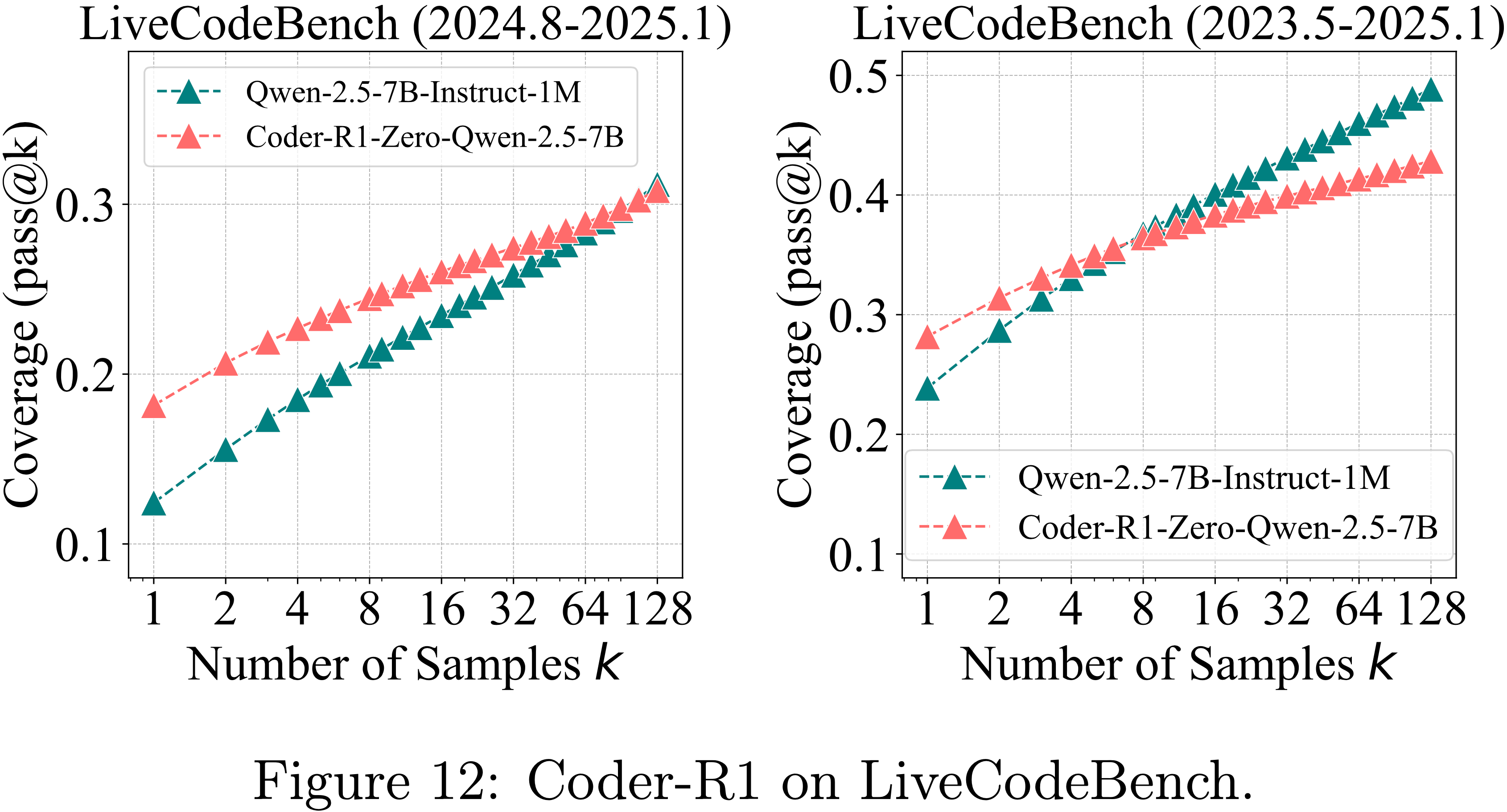
• 论文采用了开源的、经过 RLVR 训练的模型 CodeR1-Zero-Quen2.5-7B (2025)
  • 该模型基于 Quen2.5-7B-Instruct-1M (2025b)，在 12K 个 LeetCode 和 TACO 样本上训练了 832 步
• For Evaluation，模型在 LiveCodeBench v5 上进行评估（assessed）
  • 该 LiveCodeBench v5 基准包含从 2024 年 8 月到 2025 年 1 月的 279 个问题 (2025)，同时还使用了 HumanEval+ 和 MBPP+ (2023)
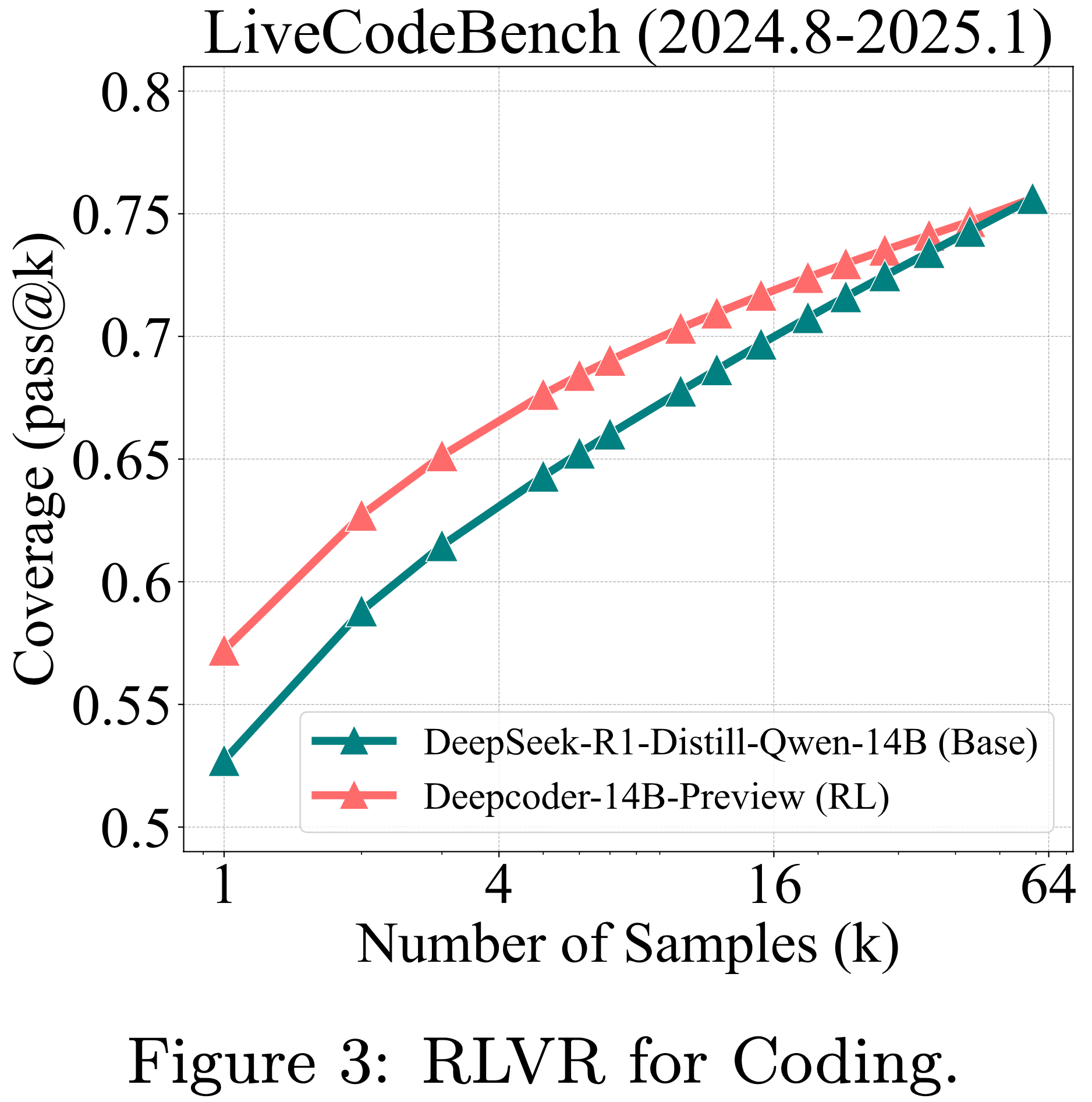
• 论文还评估了最强大的开源 RLVR 训练代码 LLM DeepCoder-14B (2025)，它基于 DeepSeek-R1-Distill-Quen-14B 构建
  • 这两个模型的 Response 长度均为 32k
  • 由于其高昂的计算成本，论文仅在 LiveCodeBench 上对它们进行评估，作为代表性基准

The Effect of RLVR

• 由于通过猜测几乎不可能通过所有单元测试，因此 pass@(k) 可以可靠地衡量模型的推理边界
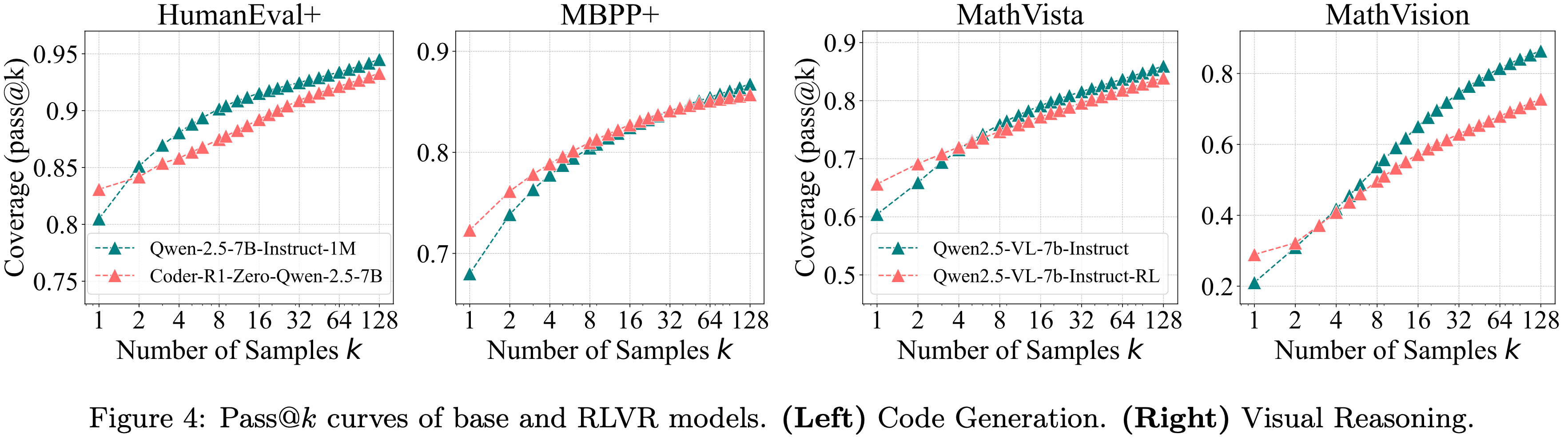
• 如图 3、图 12 和图 4（左）所示，RLVR 在三个代码生成基准上的影响趋势与在数学基准上观察到的趋势高度一致

RLVR for Visual Reasoning

Models and Benchmarks

• 在视觉推理任务中，模型必须共同解释视觉和文本输入以解决复杂的推理问题
• 自 LLM 推理兴起以来，这已在多模态社区中获得极大关注 (2025a; 2025; 2025)
• 在我们的实验中，我们选择视觉情境下的数学问题作为代表性任务
• 我们使用 EasyR1 框架 (2025) 在 Geometry3K (2021) 上训练 Quen2.5-VL-7B (2025)，并在经过筛选的 MathVista-TestMini (2024) 和 MathVision-TestMini (2024) 上评估其视觉推理能力，其中移除了多项选择题

The Effect of RLVR

• 如图 4（右）所示，RLVR 对视觉推理的影响与在数学和代码基准上观察到的结果高度一致
• 这表明，即使在多模态任务中，原始模型对可解问题也具有更广泛的覆盖范围

Validity of Chain-of-Thought

• Similarly，作者手动检查了最具挑战性的问题子集，即平均准确率低于 5% 的问题
  • 作者发现，对于原始模型和 RL 模型，8 个问题中有 7 个问题至少包含一条正确的思维链
• 这些结果支持了思维链的有效性

---

Deep Analysis

• 本节对当前 RLVR 训练的效果进行了更深入的分析
• 另外，论文也强调了蒸馏技术与 RLVR 的显著不同特征
• In Addition，论文设计了对照实验来考察不同 RL 算法和设计选择的影响

Reasoning Paths Already Present in Base Models

Accuracy Distribution Analysis

• 第 3 节的实验揭示了一个令人惊讶的趋势： Base Model 比 RLVR 训练后的模型覆盖了更广范围的可解问题
• 为了更好地理解这一点，论文分析了 RLVR 训练前后准确率分布的变化
  • 如图 5 所示，RLVR 增加了接近 1.0 的高准确率频次，并减少了低准确率（例如 0.1, 0.2）的频次
  • However，与这一趋势偏离的是在准确率为 0 处的频次增加（这表明 RLVR 导致了更多不可解的问题）
  • 这也解释了 RLVR 在平均分数上的提升，这种提升并非源于解决新问题，而是源于在 Base Model 已经可解的问题上提高了采样效率
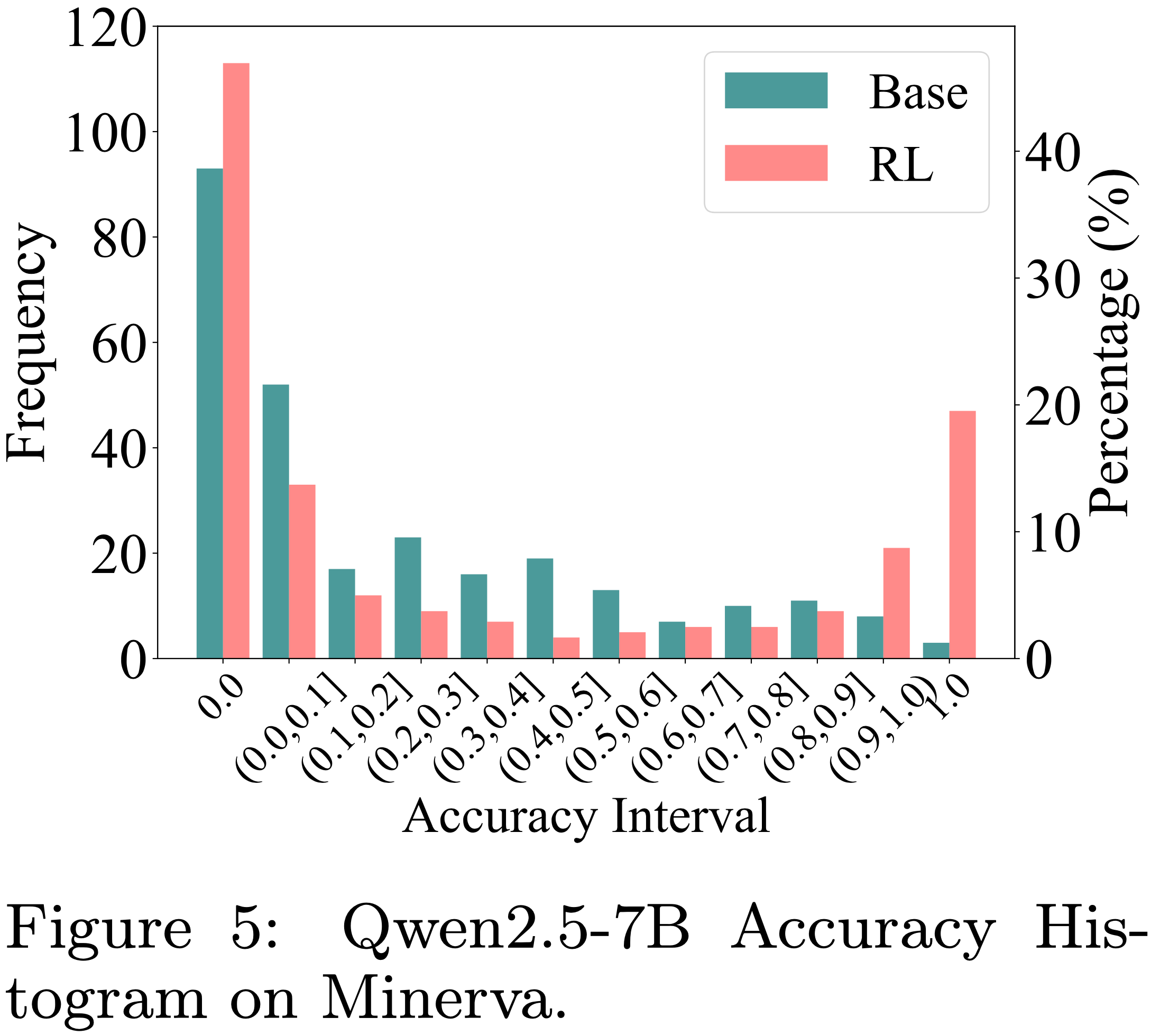
• 更多准确率直方图参见图14

Solvable-Problem Coverage Analysis

• 为了进一步研究，论文在 AIME24 和 MATH500 上比较了 Base Model 及其对应的 RL 训练版本的可解问题集合
• 论文发现，存在许多 Base Model 能解决而 RLVR 模型失败的情况，而 RLVR 成功但 Base Model 失败的案例极少，如表 2 所示
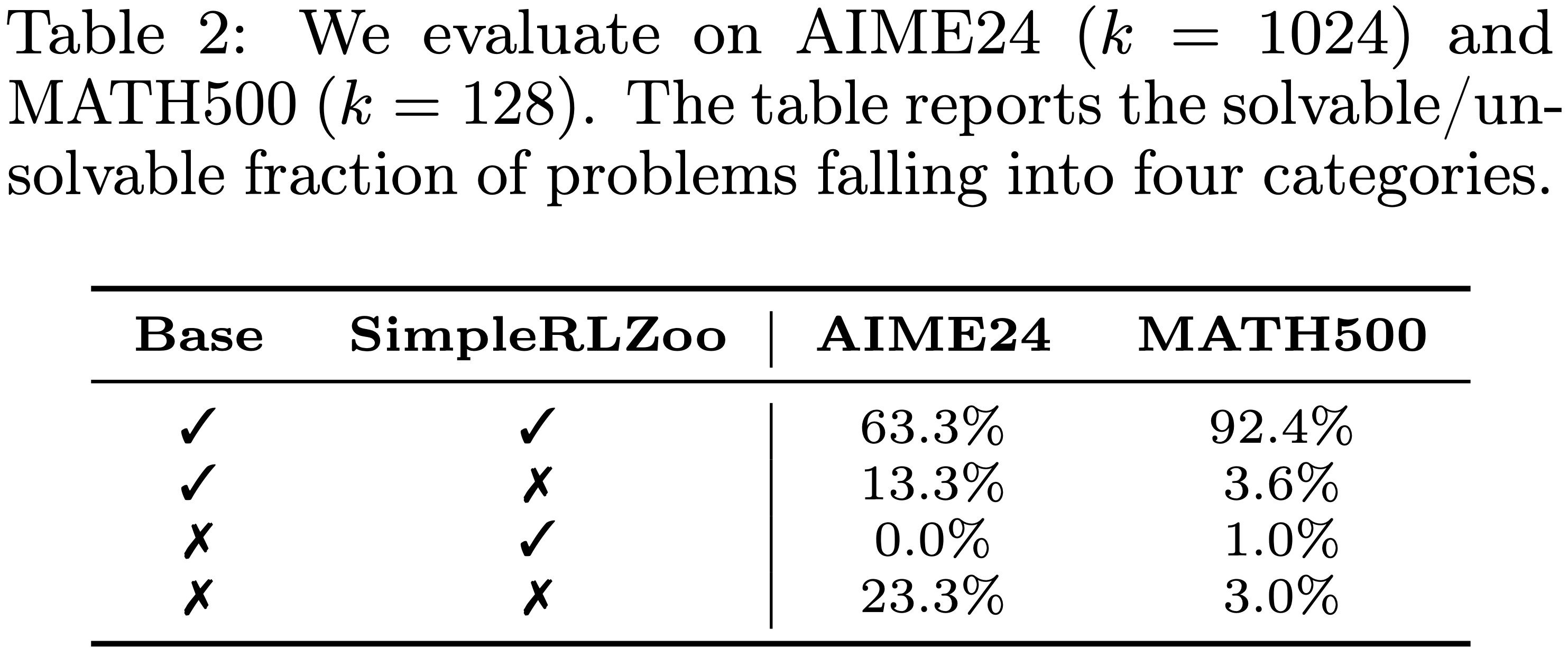
• 详细情况见第 C.7 节
  • 如表 5 所示，RL 训练模型解决的可解问题集合几乎是 Base Model 可解问题集合的一个子集
  • 如表 6 所示， Coding 任务中也观察到了类似的趋势
• 这引发了一个自然的问题：RL 训练模型生成的所有推理路径是否已经存在于其 Base Model 的输出分布中？

Perplexity Analysis

• 上文中我们提出了 RL 训练模型生成的所有推理路径是否已经存在于其 Base Model 的输出分布中？ 这个问题
• 为了回答这个问题，论文使用了 困惑度 (perplexity, PPL) 这一指标
  • 给定一个模型 \(m\)、一个问题 \(x\) 和一个 Response \(\mathbf{Y}=(y_{1},\ldots,y_{T})\)（可以由同一模型、另一模型或人类生成），PPL 定义为序列的负对数似然平均的指数形式：
    $$
    \texttt{PPL}_{m}(\mathbf{Y}|x)=\exp\left(-\frac{1}{T}\sum_{t=1}^{T}\log P(y_{t}|x,y_{1},\ldots,y_{t-1})\right),
    $$
  • 它反映了模型在给定 Prompt \(x\) 的条件下预测给定 Response \(\mathbf{Y}\) 的能力
  • 更低的困惑度表明模型生成此 Response 的可能性更高
• 论文从 AIME24 中随机抽取两个问题，并分别使用 Qwen2.5-7B-Base 和 SimpleRL-Qwen2.5-7B-Base 为每个问题生成 16 个 Response ，分别记为 \(\mathbf{Y}_{\text{Base} }\) 和 \(\mathbf{Y}_{\text{RL} }\)
• 论文还让 OpenAI-o1 (2024) 生成了 8 个 Response ，记为 \(\mathbf{Y}_{\text{GT} }\)
• 如图 6 所示，\(\textrm{PPL}_{\text{Base} }(\mathbf{Y}_{\text{RL} }|x)\) 的分布与 \(\textrm{PPL}_{\text{Base} }(\mathbf{Y}_{\text{Base} }|x)\) 分布的下部紧密匹配，对应于 Base Model 倾向于生成的 Response
• 这表明 RL 训练模型的 Response 极有可能被 Base Model 生成。在第 C.4 节中，论文展示了 \(\textrm{PPL}_{\text{Base} }(\mathbf{Y}_{\text{RL} }|x)\) 随着 RL 训练的进行逐渐降低，表明 RLVR 主要是在 Base Model 先验内部锐化了分布，而不是扩展超出其范围

Summary

• 结合上述分析，论文得出三个关键观察
  • First，RLVR 模型解决的问题 Base Model 也能解决；观察到的平均分数提升源于在这些已经可解的问题上进行更有效的采样，而不是学会了解决新问题
  • Second，在 RLVR 训练后，模型通常表现出比其 Base Model 更窄的推理覆盖率
  • Third，RLVR 模型利用的所有推理路径已经存在于 Base Model 的采样分布中
• 这些发现表明 RLVR 并未引入根本性的新推理能力，训练模型的推理能力仍然受限于其 Base Model

Distillation Expands the Reasoning Boundary

• 除了直接 RL 训练之外，提升小型 Base Model 推理能力的另一个有效方法是从强大的推理模型进行蒸馏 (2025)
  • 蒸馏过程类似于训练后阶段的 Instruction-Following Fine-tuning
  • 蒸馏使用的训练数据不是使用简短的 Instruction-Response 对，而是由教师模型生成的长链式推理轨迹组成
• 鉴于当前 RLVR 在扩展推理能力方面的局限性，很自然地要问蒸馏是否表现出类似的行为
  • 一个代表性模型是 DeepSeek-R1-Distill-Qwen-7B，它是在 Qwen2.5-Math-7B 上，使用 DeepSeek-R1 蒸馏的
• 论文将其与 Base Model Qwen2.5-Math-7B 及其 RL 训练对应物 Qwen2.5-Math-7B-Oat-Zero 进行比较，并加入 Qwen2.5-Math-7B-Instruct 作为额外基线
• 如图7所示，蒸馏模型的 pass@\(k\) 曲线始终显著高于 Base Model
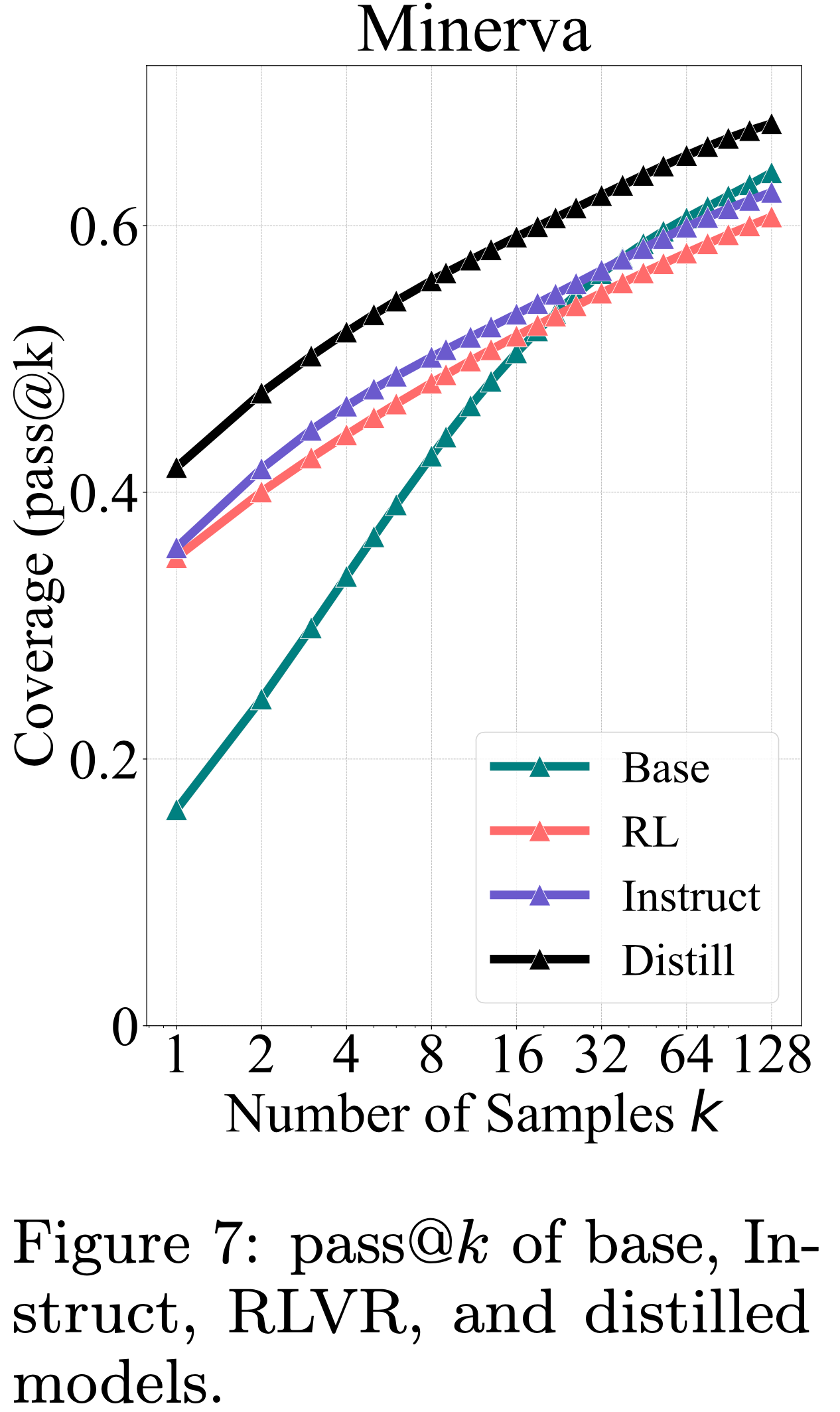
• 这表明，与本质上受 Base Model 推理能力限制的 RL 不同，蒸馏引入了从更强的教师模型学习到的新推理模式
  • As a result，蒸馏模型能够超越 Base Model 的推理边界

Effects of Different RL Algorithms

• As discussed previously，RL 的主要效果是提高采样效率，而不是扩展模型的推理能力
• 为了量化这一点，论文提出了采样效率差距 (Sampling Efficiency Gap) （\(\Delta_{\text{SE} }\)）
  • 定义为 RL 训练模型的 pass@1 与 Base Model 的 pass@\(k\) 之间的差值（在论文的评估中使用 \(k=256\)）
  • \(\Delta_{\text{SE} }\) 越低越好
• 在这里，论文进行了干净的实验来研究不同 RL 算法在提高采样效率方面的效果

Experiment Setup

• 为了公平比较，论文使用 VeRL 框架 (2024) 重新实现了流行的 RL 算法，包括 PPO (2017)、GRPO (2024)、Reinforce++ (2025)、RLOO (2024)、ReMax (2024) 和 DAPO (2025)
• 遵循 DAPO (2025) 和 Oat-Zero (2025) 的做法，论文移除了 KL 项以避免限制模型学习
• 在训练期间，论文使用 AdamW 优化器 (2017)，恒定学习率为 \(10^{-6}\)
• 对于 rollout，论文使用 Prompt Batch Size 为 256，每个 Prompt 生成 8 个 Response
• 最大 rollout 长度设置为 8,192 个 Token ，采样温度设置为 1.0
• 论文使用的 PPO Mini-Batch Size 为 256
• 为了评估 RLVR 下的领域内和领域外泛化能力，论文将 Omni-MATH 的一个子集 Omni-MATH-Rule（包含可验证问题）分成训练集（2,000 个样本）和领域内测试集（821 个样本），并使用 MATH500 作为领域外基准

Results

• 如图 8（顶部）所示，尽管不同的 RL 算法在 pass@1 和 pass@256 上表现出微小的差异，但这些差异并非根本性的
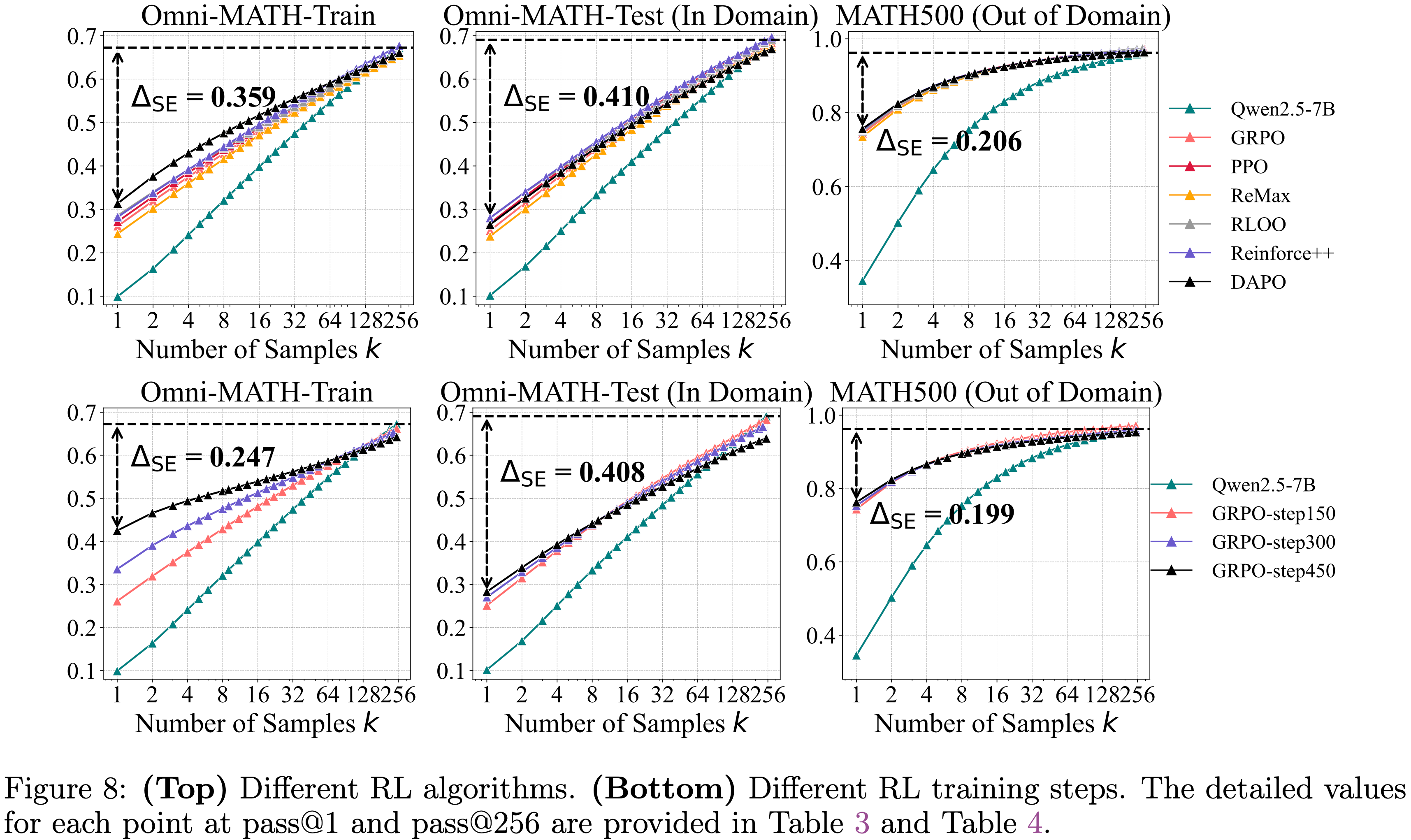
• 不同的 RL 算法产生略微不同的 \(\Delta_{\text{SE} }\) 值（例如，在领域内测试集上，从 GRPO 的 43.9 到 RLOO 最佳值 42.6 之间）
• Furthermore，论文观察到 \(\Delta_{\text{SE} }\) 在不同算法中始终保持在 40 分以上，突出现有 RL 方法距离实现最优采样效率仍然很远
• 这表明可能需要新的 RL 算法或全新的范式来接近上界
• 更多观察结果见第 C.5 节

Effects of RL Training

Asymptotic Effects

• 基于第 4.3 节的设置，论文研究了训练步数对模型渐近性能的影响
• 如图 1（右）所示，随着 RL 训练的进行，训练集上的 pass@1 从 26.1 持续提升到 42.5
• However，随着 RLVR 训练的进行，pass@256 逐渐下降，表明推理边界在缩小

每次 Prompt 的 Rollout 数量 \(n\) 的影响 (Effect of Number of Rollouts \(n\))

• 训练超参数 \(n\)（每个 Prompt 的 Response 数量）可以通过在训练期间实现更广泛的探索来影响 pass@\(k\)
  • 论文将 \(n\) 从 8 增加到 32
  • 如图 16 所示，pass@\(k\) 比 \(n=8\) 时略有改善，但 RL 训练模型最终仍然被 Base Model 超越
    • 注：在 Math500 上，n=32 的始终不如 n=8 的；但实际上 n=32 实际上只训练了 220 steps（并没有跟 n=8 的对齐 steps）
    • KL 散度的训练 Rollout Number 配置是 8
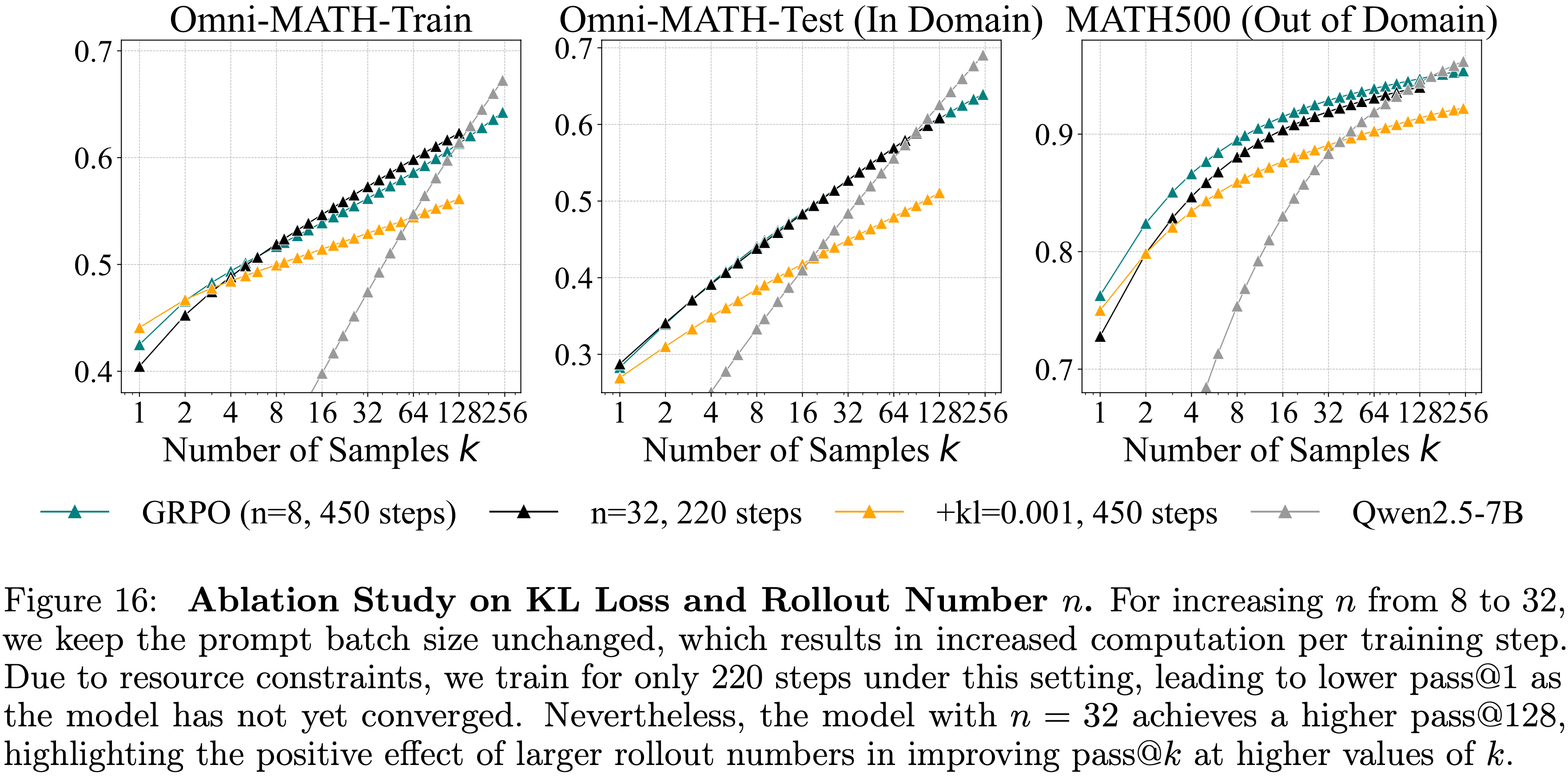
• 论文将扩大 RLVR 训练是否最终能超越 Base Model 的问题留给未来研究

Effect of KL Loss

• 为了控制模型偏差，一些先前的工作添加了 KL 惩罚项
• 论文通过应用系数为 0.001 的 KL 项来进行消融实验
• 如图 16 所示，带有 KL 正则化的模型在不使用 KL 的 GRPO 基础上实现了相似的 pass@1，但 pass@128 低得多

Effects of Entropy

• 随着 RL 训练的进行，模型的输出熵通常会降低 (2025)，这可能由于输出多样性减少而导致推理边界缩小
• 为了研究这个因素，论文提高了 RLVR 训练模型的生成温度，以匹配 Base Model 在 \(T=0.6\) 时的输出熵
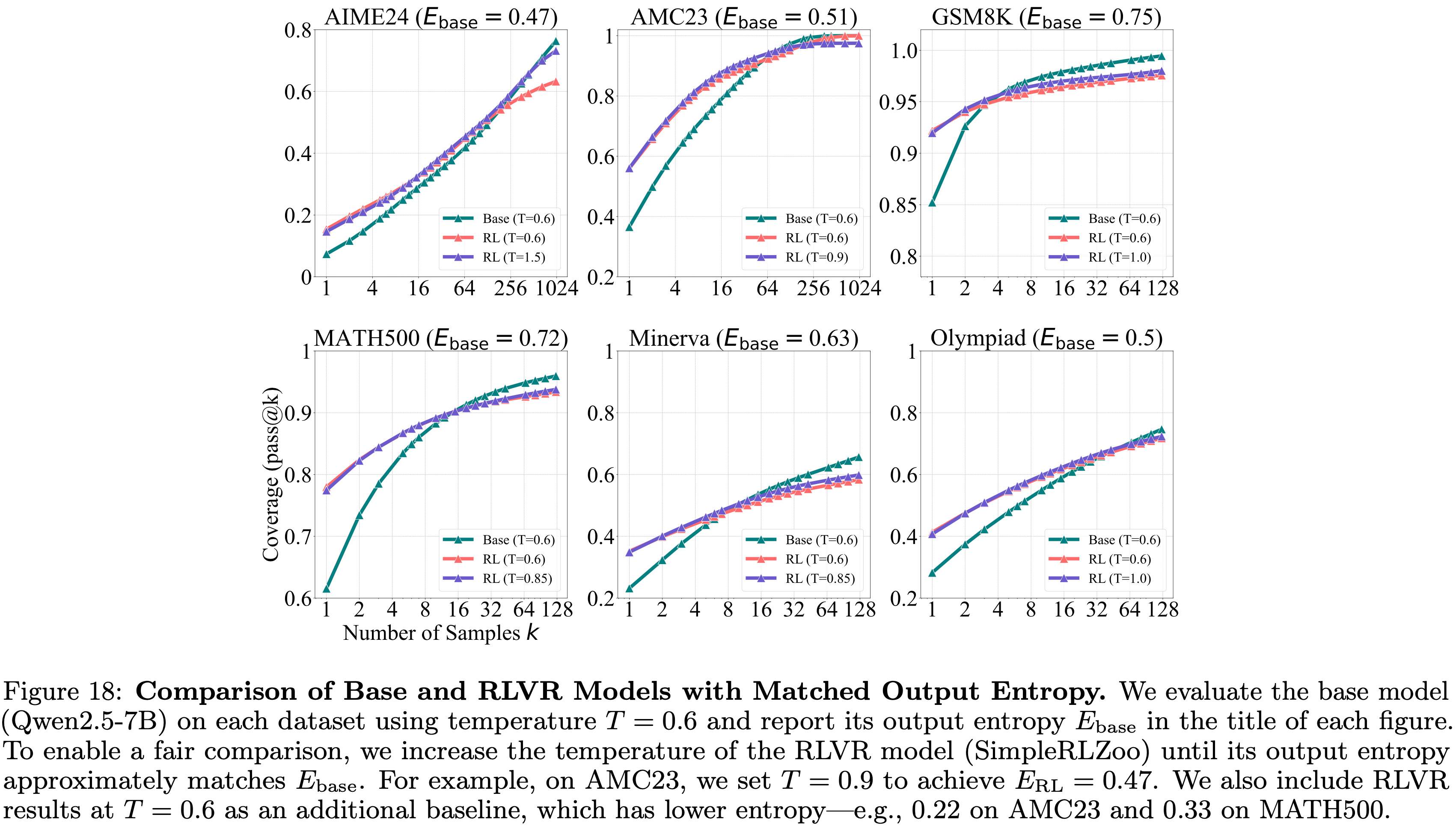
• 如图 18 所示，尽管 RLVR 模型在更高温度下相比其自身在 \(T=0.6\) 时的表现，pass@\(k\) 略有改善，但在整个 pass@\(k\) 范围内仍然表现不如 Base Model
• 这表明，虽然熵的降低导致了推理边界的缩小，但这并不是唯一的原因

Effects of Model Size Scaling

• Scaling 在当代 LLM 的能力中扮演着核心角色
  • 随着模型规模的增加，（论文）所得出的结论是否继续成立仍然是一个重要问题
• 对于许多大型模型，分离（isolating） RLVR 的影响是不可行的（即难以拿到 RLVR 过程前后的模型）
  • For Example
    • 对于 GPT-o1，其 Base Model 并非公开可访问
    • Qwen3-235B (2025) 通过多个阶段进行训练，包括 RLVR 和长上下文 CoT 监督微调，这使得无法单独分离 RLVR 的影响
    • 对于 Deepseek-R1-Zero，由于没有公开托管的 API，论文被迫自行托管模型，但在最大序列长度为 32k 的情况下，吞吐量被限制在每秒约 50 个 Token ，使得 pass@\(k\) 评估目前不可行
  • 作为一个更可行的替代方案，论文选择了 Magistral-Medium-2506 API 进行初步实验
    • 该模型使用纯 RL 训练，以 Mistral-Medium-3-2505 作为 starting model（起始模型，2025）
      • 尽管模型规模未公开，但 Magistral-Medium 的性能与 Deepseek-R1 相当，在推理能力方面定位接近前沿
• 论文按照原论文的做法，使用最大 40k 的上下文长度查询模型
  • 论文再次观察到，RLVR 在低 \(k\) 值时提供了显著的增益，但在更高的 \(k\) 值下改善很小或没有改善
  • Specifically，在 \(k=1\) 时，与他的 Base Version 相比，RLVR 增强的模型在 AIME24 上多解决了大约 7 个问题，在 AIME25 上多解决了大约 8 个问题
  • However，随着 \(k\) 的增加，性能差距稳步缩小
• 这些观察结果表明，即使对于当前高度强大、接近前沿的推理模型，论文的结论仍然成立
• 随着更多计算（例如预训练规模预算）投入到 RL 训练中，这一趋势是否会持续下去，仍然是 LLM 推理未来的一个关键问题

---

Discussion

• 在第 3 节和第 4 节中，论文确定了 RLVR 在提升 LLM 推理能力方面的关键局限性
• 在本节中，论文探讨可能解释为什么 RLVR 仍然受限于 Base Model 推理能力的潜在因素

Discussion 1: 传统 RL 与 LLM 的 RLVR 之间的关键区别在于巨大的动作空间和预训练先验

• Key Differences Between Traditional RL and RLVR for LLMs are Vast Action Space and Pretrained Priors
• 传统 RL，如 AlphaGo Zero 和 DQN 系列 (2017, 2015, 2023)，可以在围棋和 Atari 游戏等环境中没有显式上界（without an explicit upper bound）地持续改进策略性能
• 传统 RL 与 LLM 的 RLVR 之间存在两个关键区别
  • First，语言模型中的动作空间比围棋或 Atari 游戏的动作空间指数级更大 (2023)
    • RL 算法最初并非设计用于处理如此巨大的动作空间，如果从零开始训练，几乎不可能有效探索奖励信号
  • Therefore， The Second Distinction is LLM 的 RLVR 从一个具有有用先验的预训练 Base Model 开始，而 Atari 和 GO 游戏中的传统 RL 通常是从零开始
  • 这种预训练先验指导 LLM 生成合理的 Response ，使得探索过程显著更容易，并且策略可以获得正向奖励反馈

Discussion 2: 在这个巨大动作空间中，先验是一把双刃剑

• Priors as a Double-Edged Sword in This Vast Action Space
• 由于 Response 的采样受到预训练先验的引导，策略可能难以探索超出先验已经提供内容的新推理模式
• Specifically，在如此复杂且高度组合的空间中，通过朴素的 Token-level 采样探索（naive token-level sampling exploration）生成的大多数 Response 都受到 Base Model 先验的限制
  • 任何偏离先验的样本都极有可能产生无效或无意义的输出，从而导致负的结果奖励 (Negative outcome reward)
• 如第 2.1 节所讨论的，策略梯度算法旨在最大化在先验内获得正奖励的 Response 的对数似然，同时最小化在先验外获得负奖励的 Response 的似然
  • As a result，训练后的策略倾向于产生已经存在于先验中的 Response ，将其推理能力限制在 Base Model 的边界内
• 从这个角度看，从蒸馏模型开始训练 RL 模型可能暂时提供一个有益的解决方案，因为蒸馏有助于注入更好的先验
  • 理解：但蒸馏也会大幅度改变模型之前的分布，从而导致模型在其他方面的能力受到影响

Possible Future Work

• 如上所述，巨大动作空间中的低效探索机制以及对二元结果奖励的依赖，可能是当前 RLVR 设置中所观察到局限性的根本原因
• 为了从根本上应对这些挑战，以下几个方向可能值得探索：
  • 在高级抽象中进行高效探索策略 (Efficient exploration strategies in high-level abstraction)
    • 高级别的探索机制，例如在程序级抽象空间中进行自我演化的 AlphaEvolve (2025)，可能对于驾驭巨大的动作空间至关重要
    • 此类策略可以促进发现先验外的推理模式和以前未见的知识结构
  • 通过课程学习扩展数据规模 (Data scale via curriculum)
    • 课程学习可以从训练较简单的子问题开始，使模型提高采样效率并获得必要的元技能
    • 通过在处理更难问题之前提高简单任务的成功率，这种课程可以分层减少探索空间，并在具有挑战性的父任务上使性能从接近零提升到非零，从而使 RLVR 能够获得有意义的奖励 (2025, 2025)
    • 尽管当前 RLVR 训练数据中偶尔会出现这种层次关系的痕迹，并且最近的工作中已经观察到了它们的效果 (2025)，但要实现其全部潜力，将需要一个更加审慎、大规模的数据-RL 迭代流程，确保对元技能以及简单与困难问题之间适当关系的充分覆盖
  • 过程奖励和细粒度信用分配 (Process reward and fine-grained credit assignment)
    • 与纯粹的二元结果奖励相比，结合中间信号来指导推理轨迹可能会显著提高探索效率，并将探索引导向更有希望的解决方案路径
  • Agentic RL (理解：即基于经验探索的 RL)
    • 当前的 RLVR 推理仅限于单轮 Response ，而基于反馈的迭代细化对于 IMO 级别的推理至关重要 (2025)
    • 当前的 RLVR 推理也缺乏通过使用搜索工具或进行实验来主动收集新信息的能力
    • 一个多轮智能体 RL 范式，具有与环境反馈的更丰富交互，可以让模型生成新颖的经验并从中学习
    • 这个新兴的智能体框架被描述为“经验时代（era of experience）”的开端 (2025) Silver, D. and Sutton, R. S. Welcome to the era of experience. Google AI, 2025

---

Related Work

• 论文在此总结了关于 RLVR 分析的关键相关工作，并在附录 B 中提供了更全面的讨论
• 尽管最近的 RLVR 方法取得了令人印象深刻的经验结果 (2025, 2024)，但其对推理的根本影响仍未得到充分探索
  • 一些研究 (2025, 2025, 2025) 表明，RLVR 模型中的反思行为源于 Base Model ，而不是通过 RL 学到的
  • Dang 等人 (2025) 观察到 RLVR 训练后 pass@\(k\) 性能下降，但他们的分析范围有限
    • More Importantly，他们没有探索 Base Model 与 RL 模型之间的关系
  • Deepseek-Math (2024) 也观察到了类似的趋势，但其研究仅限于单个指令微调模型和两个数学基准
• In Contrast，论文的工作系统地调查了（systematically investigates）广泛的模型、任务和 RL 算法，以准确评估当前 RLVR 方法和模型的效果
• 论文进一步提供了深入的分析，包括准确率分布、推理覆盖率、困惑度趋势以及与蒸馏模型的比较，提供了对 RLVR 能力和局限性的全面理解

---

附录 A：Implementation Details

A.1 RLVR Algorithms

• 为了减少内存和计算开销，人们提出了几种无需 Critic 的变体
  • GRPO (2024) 通过同一问题的一组 Response 内的归一化奖励来估计优势值：
    $$ A_i = \frac{r_i - \text{mean}(\mathbf{r})}{\text{std}(\mathbf{r})}$$
    • 其中 \(\mathbf{r} = \{r_1, \ldots, r_G\}\) 表示一组 \(G\) 个采样 Response 的奖励集合
  • RLOO (2024) 则在每个批次 \(\mathcal{B}\) 内采用留一法（leave-one-out）基线
    • 其优势值定义为
      $$ A_i = r_i - \frac{1}{|\mathcal{B}|-1} \sum_{j \neq i} r_j$$

A.2 Low-Variance pass@k Estimation

• 直接使用每个问题仅 \(k\) 个采样输出来计算 pass@\(k\) 可能会导致高方差
• 为了缓解这个问题，论文遵循 Chen 等人 (2021) 提出的无偏估计方法
• Specifically，对于评估数据集 \(\mathcal{D}\) 中的每个问题 \(x_i\)，论文生成 \(n\) 个样本 (\(n \geq k\))，并将正确样本的数量记为 \(c_i\)
• 数据集中 pass@\(k\) 的无偏估计量由下式给出：
  $$
  \text{pass@}k := \mathbb{E}_{x_i \sim \mathcal{D} } \left[1 - \frac{\binom{n-c_i}{k} }{\binom{n}{k} } \right]
  $$
  • 通过这个公式，我们可以轻松地以低方差估计所有 \(k \leq n\) 的 pass@\(k\) 值
• 在论文的实验中，将 \(n\) 设置为 pass@\(k\) 曲线中最大的（即最右边的） \(k\) 值，通常是 128、256 或 1024
  • 例如，在图2中
    • 论文对 MATH500、Minerva 和 GSM8K 使用 \(n=128\)
    • 对 AMC23 和 AIME24 使用 \(n=1024\)
    • 对于 Olympiad 基准测试，由于 Base Model 能力相对较低
      • 论文为 Qwen 模型设置 \(n=128\)
      • 为 LLaMA-3.1-8B 设置 \(n=1024\)
  • 问题：这里其实说明在评估最大的 \(k\) 时， \(k\) 和 \(n\) 是相同的，此时方差应该不小

---

附录 B：More Related Works

Reinforcement Learning for LLM Reasoning

• 自从 LLM 出现以来，Post-Training 阶段已被证明对于增强问题解决和推理能力至关重要 (2022)
• Post-Training 阶段通常分为三个主要类别：
  • 使用人工整理或蒸馏数据进行监督微调 (2023)，supervised fine-tuning using human-curated or distilled data
  • 自我改进迭代 (2022; 2023)，self-improvement iteration
  • RL (2022)
• Previously，人们使用奖励模型或 Response 对之间的偏好进行奖励建模 (2022; 2023)
• Recently，RLVR 作为一种提高 LLM 在数学和编程等领域推理能力的方法，获得了显著的关注 (2024; 2024)
  • 一个鼓舞人心的里程碑工作是 OpenAI 的 o1 模型 (2024)
    • 这是首批大规模应用 RL 进行推理的模型之一，在发布时达到了当时的先进水平（achieving state-of-the-art results）
• Following this，Deepseek-R1 (2025) 成为首个性能匹配或超越 o1 的开放权重模型
  • R1 引入的一个重要创新是 “Zero” 设置，即直接对 Base LLM 应用 RL ，绕过任何中间的监督调优
  • 这种方法启发了一波旨在复制或扩展 R1 方法并改进 RL 算法的开源努力 (2025; 2025a; 2025; 2025; 2025a; 2025)
• 与此同时（In Parallel）， RL 在多模态领域也获得了关注，推动了多模态推理（multimodal reasoning）的进步 (2025a; 2025; 2025)

Analysis of RLVR

• 尽管在 RLVR 领域有许多优秀的开源工作和算法设计，但关于 RLVR 对 LLM 推理能力的根本影响及其从 Base Model 开始的局限性，仍然缺乏深入的理解
  • 几项研究 (2025a; 2025b; 2025) 强调，在 R1 类模型中观察到的反思行为实际上源于 Base Model ，而不是由 RLVR 训练引入的
  • Dang等人 (2025) 观察到了与论文的发现类似的现象：Pass@k 性能在 RL 后迅速恶化且无法恢复，但这仅限于一个有限的实验设置（在 GSM8K 上使用 Qwen-2.5-0.5B 模型）
  • More Importantly，他们没有探究 Base Model 与 RL 模型之间的关系
• In Contrast，论文的论文通过系统和严谨的实验表明，不仅是反思行为，所有推理路径都早已嵌入在 Base Model 中
  • 论文进一步证明，RLVR 并未引出超越 Base Model 的新推理能力

---

附录 C：Detailed Experimental Results

C.1 More Results on Mathematics and Coding

• 图 11：在AIME24上评估 Oat-Zero-7B 和 DAPO-32B，并与各自的 Base Model 进行比较
• 图10：SimpleRLZoo 在 GSM8K 和 AMC23 上的更多结果

C.2 Validity of Chain-of-Thought on AIME24

• 论文手动检查了最具挑战性的 AIME24 基准测试中的思维链
• To Begin，论文引入一种过滤机制，旨在消除容易猜测的问题
  • Specifically，论文 Prompt Qwen2.5-7B-Base 模型直接回答问题，不使用思维链推理，并多次采样答案
  • 如果一个问题能够以低但非零的概率（例如，< 5%）被正确回答，论文将其视为可猜测并移除
  • 那些能以高概率直接正确回答的问题则保留，因为它们很可能更容易，并且可以通过有效的思维链解决
• Base Model 和 RL 模型在这个经过过滤的 AIME24 数据集上的 pass@\(k\) 曲线在图 13 中，显示出与之前结果相似的趋势
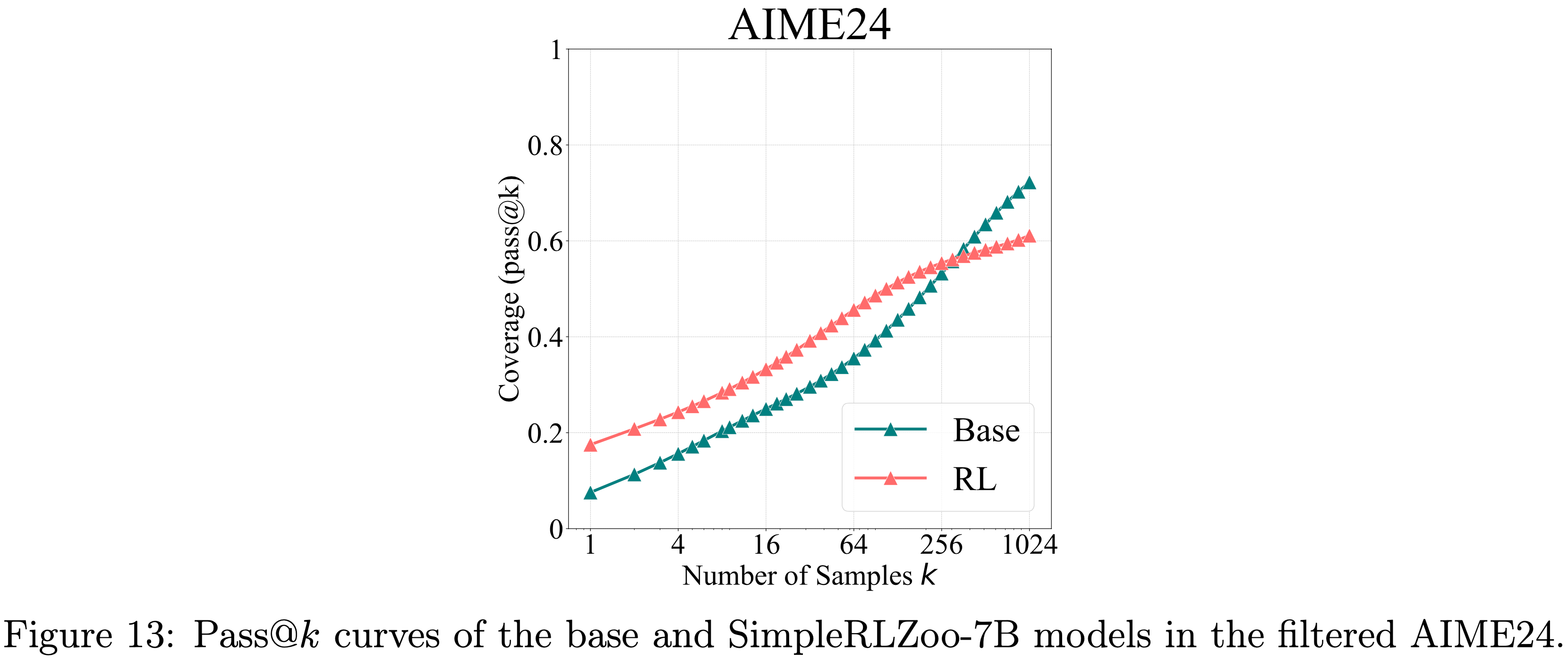
• 尽管这种过滤方法是启发式的，但它被证明是有效的
• 将其应用于 AIME24（共 30 个问题）后，得到一个包含 18 个问题的子集
• 然后论文 Prompt 模型使用思维链推理来回答这些过滤后的问题
• 接着，论文手动检查了所有导致难题（平均正确率低于5%）得出正确答案的思维链
  • Base Model 回答了 7 个此类问题，其中 5/6 的问题包含至少一个正确的思维链（排除一个因跳过推理步骤而正确性模糊的情况）
  • Similarity，经过 RL 训练的模型回答了 6 个问题，其中 4 个包含至少一个正确的思维链
• 这些结果表明，即使对于AIME24中最具挑战性的难题， Base Model 也能采样出有效的推理路径来解决问题

C.3 Accuracy Distribution Visualization

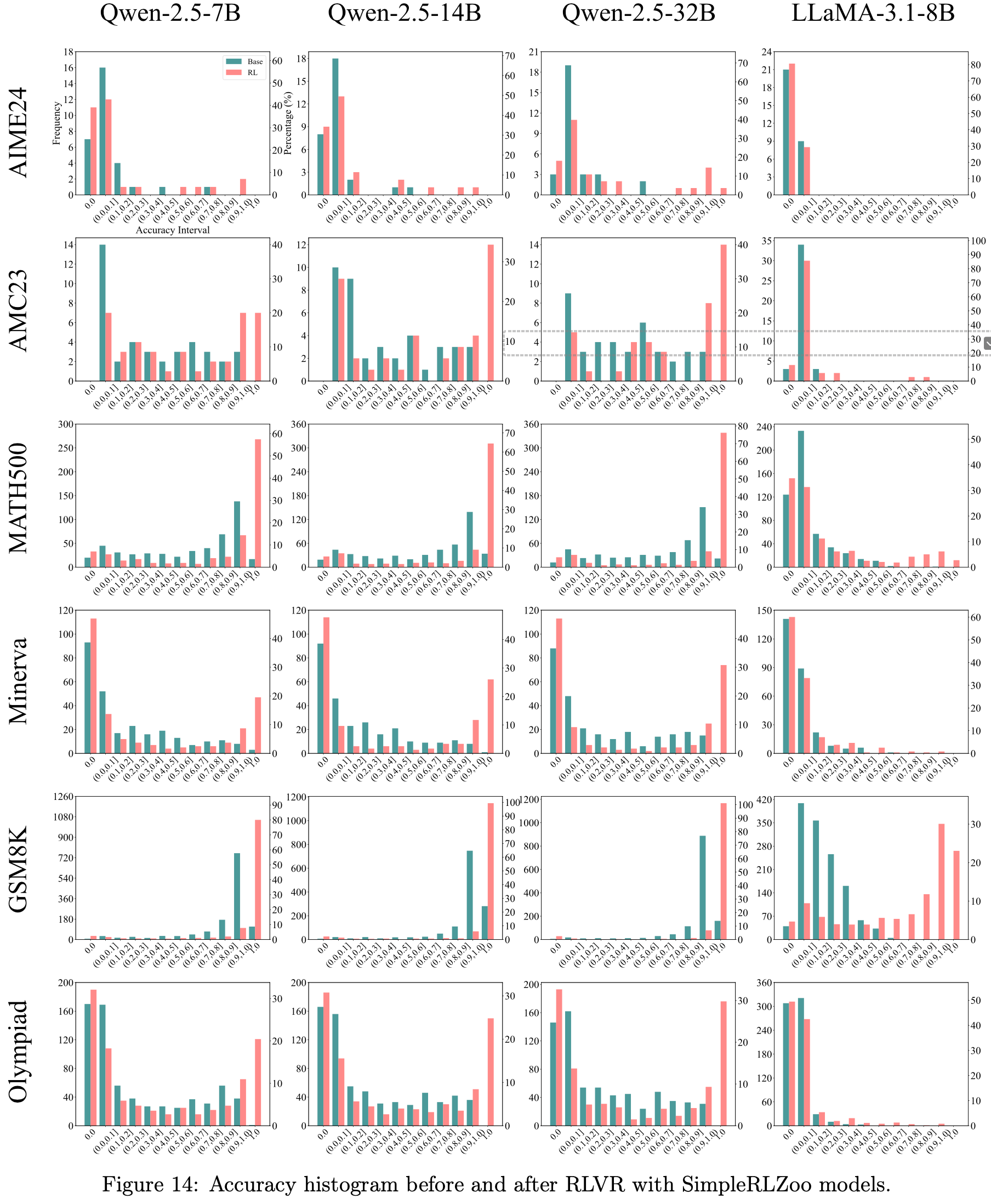
• 图14：在使用 SimpleRLZoo 模型进行 RLVR 训练前后的准确率直方图

C.4 Perplexity Analysis

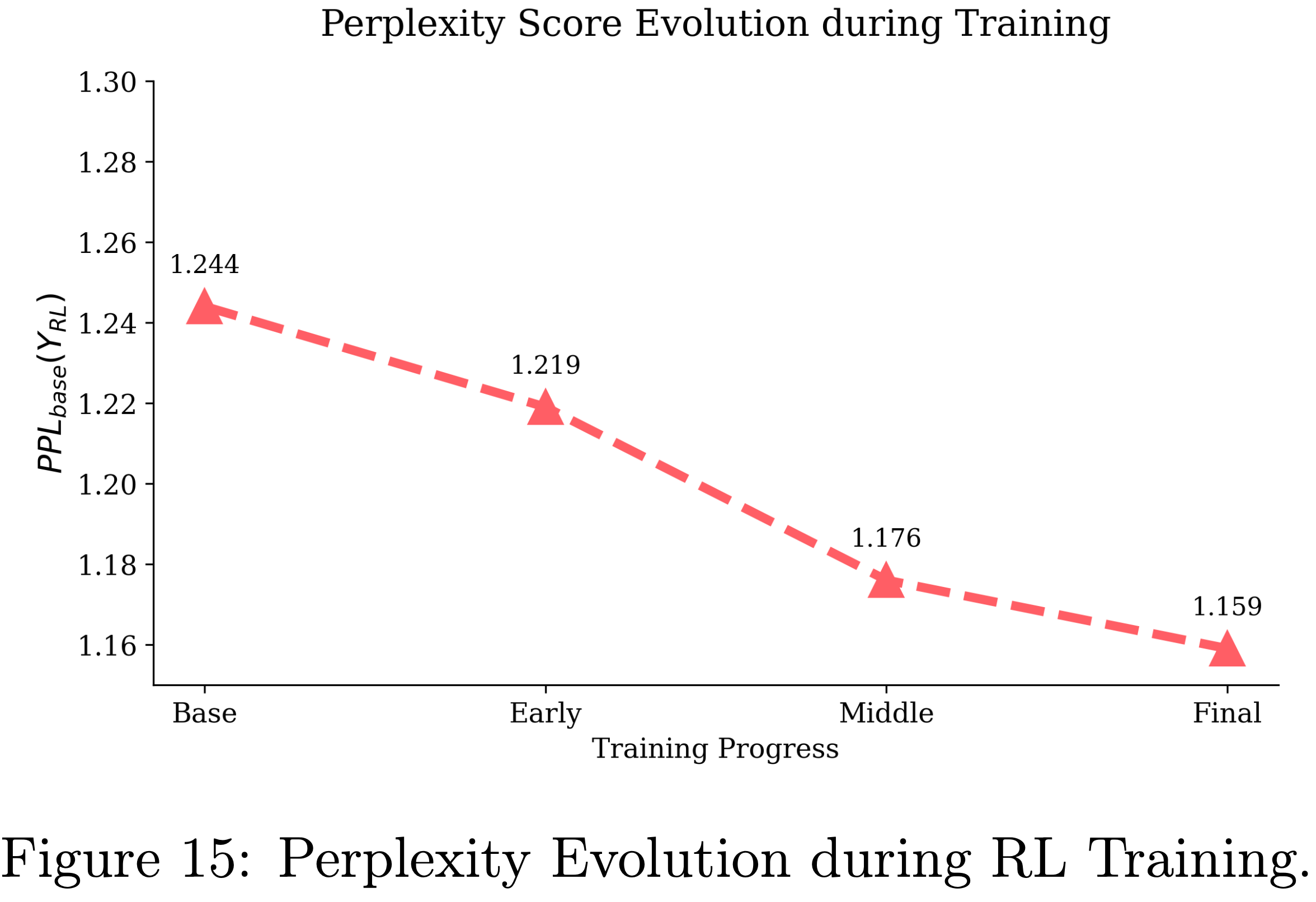
• 为了分析困惑度在 RLVR 训练过程中如何演变，论文在第 4.3 节提到的 RL 训练过程中评估了三个 RLVR 检查点：早期、中期和最终（early, middle, and final）
• 对于每个检查点，论文针对每个问题采样 32 个 Response ，计算 32 个困惑度值的中位数，并在表格中报告前 10 个问题的平均值
• 正如预期的那样，论文观察到：
  • 随着 RL 训练的进行，\(\text{PPL}_{\text{Base} }(\boldsymbol{\mathbf{Y} }_{\text{RL} }|x)\) 逐渐降低
  • 这表明 RLVR 主要是锐化了 Base Model 先验分布内的分布，而不是扩展到其之外
• 图15：RL训练期间的困惑度演变

C.5 Different RLVR Algorithms

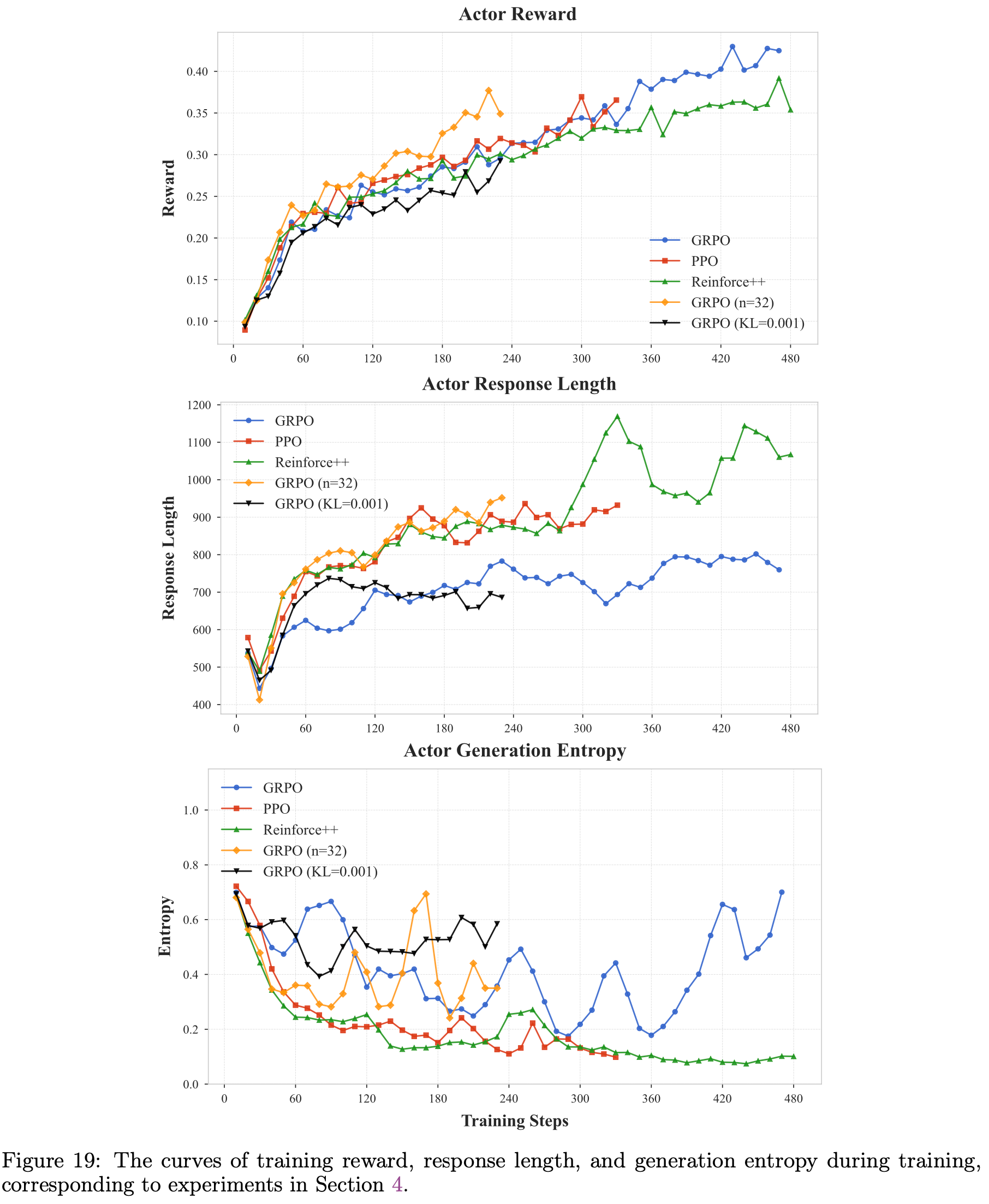
• 论文在图 8 中报告了关于不同 RLVR 算法的几个额外观察结果
• First，DAPO 在所有三个数据集上都取得了略高的 pass@1 分数；
  • However，其动态采样策略在训练期间每批次所需的样本量比其他算法多大约 \(3 \sim 6\) 倍
  • Moreover，其在 \(k=256\) 时的性能显著下降
• Second，RLOO 和 Reinforce++ 在整个 \(k\) 范围（从1到256）内表现一致良好，同时保持了高效的训练成本，在效果和效率之间取得了良好的平衡
• Third，ReMax 在 pass@1 和 pass@256 上都表现出较低的性能
  • 论文推测（hypothesize）这是由于它使用了贪婪 Response 的奖励作为优势基线，而在 RLVR 设置中奖励是二元的（0 或 1）且高度可变
• 这很可能导致训练期间梯度更新不稳定
• 表 4：图 1（右）中不同 RL 训练步骤在 pass@1 和 pass@256 的详细数值

C.6 Effects of KL and Rollout Number

• 图 16：关于 KL 损失和 Rollout Number \(n\) 的消融研究
  • 对于将 \(n\) 从8增加到32的情况，论文保持 Prompt 批次大小不变，这导致了每个训练步骤的计算量增加
  • 由于资源限制，论文在此设置下仅训练了220步，导致 pass@1 较低，因为模型尚未收敛
  • 尽管如此，\(n=32\) 的模型实现了更高的 pass@128，突显了较大的 Rollout Number 在提高较大 \(k\) 值时的 pass@\(k\) 性能方面的积极影响
  • 注：KL 散度的训练 Rollout Number 配置是 8
• 表 5：AIME24 中可解决问题（从0开始）的索引
  • 可以观察到近似的子集关系：RL模型解决的大多数问题也都能被 Base Model 解决
• 表 6：LiveCodeBench（范围从400到450，从0开始）中可解决问题的索引

C.7 Solvable Problem Coverage Analysis

• 表2 统计了问题按四类情形划分的占比：
  • （1）两个模型均至少成功求解一次该问题
  • （2）仅基准模型成功求解
  • （3）仅RLVR模型成功求解
  • （4）在 \(k\) 次采样中，两个模型均未成功求解该问题
• 结果表明，存在大量“基准模型可求解、但 RLVR 模型求解失败”的情形（情形 2），而 “RLVR 模型可求解、但基准模型求解失败” 的情形（情形 3）则极为罕见
• 即便在情形 (3) 的少数案例中（例如在 MATH500 数据集里占比 1%，约对应 5 个问题），当采样次数提升至 1024 次时，基准模型也能完成所有这类问题的求解
• 上述结果印证了我们的结论：RLVR模型很少能求解基准模型无法解决的问题，且通常会导致任务覆盖范围下降

C.8 Temperature and Entropy Analysis

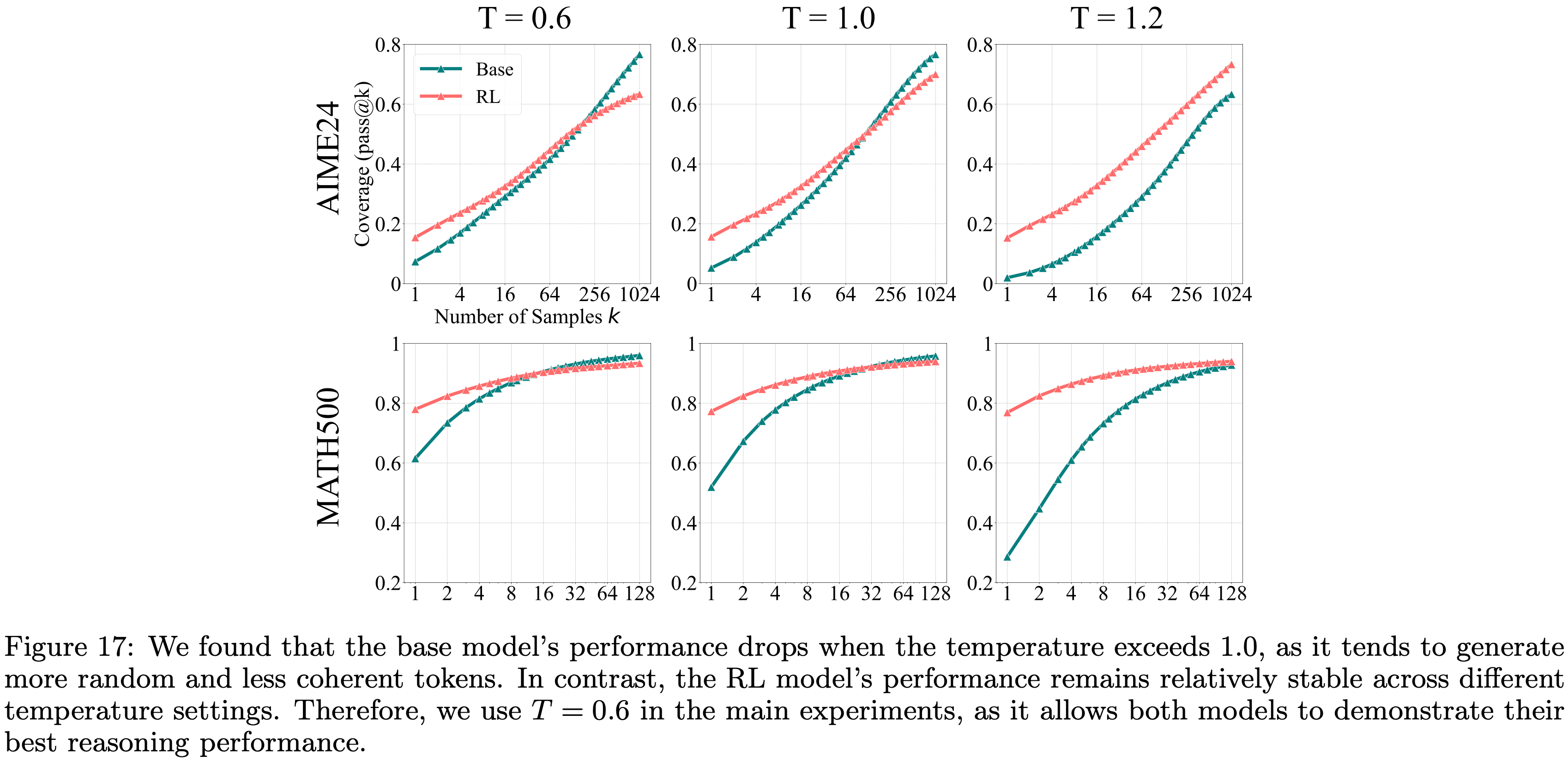
• 图17：论文发现当温度超过 1.0 时， Base Model 的性能会下降，因为它倾向于生成更随机、更不连贯的 Token
  • In Contrast，RL 模型的性能在不同温度设置下保持相对稳定
  • Therefore，论文在主要实验中使用 \(T=0.6\)，因为它允许两个模型都展示其最佳的推理性能
• 图18：输出熵匹配的 Base Model 与 RLVR 模型比较
  • 论文使用温度 \(T=0.6\) 评估 Base Model (Qwen2.5-7B) 在每个数据集上的表现，并在每个图的标题中报告其输出熵 \(E_{\text{base} }\)
  • 为了进行公平比较，论文增加 RLVR 模型 (SimpleRLZoo) 的温度，直到其输出熵近似匹配 \(E_{\text{base} }\)
  • For Example，在 AMC23 上，论文设置 \(T=0.9\) 以实现 \(E_{\text{RL} }=0.47\)
  • 论文还将 RLVR 在 \(T=0.6\) 时的结果作为额外基线，其熵更低（e.g., 在 AMC23 上为 0.22，在 MATH500 上为 0.33）

C.9 Training Dynamics

• 图19：训练过程中的训练奖励、 Response 长度和生成熵曲线，对应于第 4 节的实验

附录 C.10 CoT Case Analysis

• 图 20：Owen2.5-Base-7B 正确 Response - 案例 1
• 图 21：Owen2.5-Base-7B 正确 Response - 案例 2

---

附录 D：Prompt Templates

• 论文提供了实验中用于训练和评估的 Prompt 模板
• 用于 SimpleRL 训练和评估的 Prompt 如图 22 所示
• 用于 Oat-Zero 的 Prompt 如图 23 所示
• 对于 Code-R1 训练，采用图 24 中的 Prompt
• 对于 Code-R1 评估，论文遵循原始代码库，并采用基准测试的默认模板（核心：LiveCodeBench 需要添加 Prompt “```python” 作为结尾），包括 LiveCodeBench Prompt （图25）、HumanEval+ 和 MBPP+ Prompt （图26）
• 用于 EasyR1 训练和评估的 Prompt 如图 27 所示
• 对于使用 VeRL 训练的 RL 模型，如第 4.3 节和第 4.4 节所讨论的，训练和评估 Prompt 如图 28 所示
• 对于在 AIME24/25 上评估 Mistral 和 Magistral 模型， Prompt 如图 29 所示
  • 为确保公平比较， Base Model 在评估时使用与其对应的 RL 训练模型相同的 Prompt

---

附录 E：Broader Impacts

• 论文的方法的潜在负面社会影响与通常与通用 LLM 推理技术相关的那些影响一致
• 论文强调在 LLM 系统中遵守公平和安全部署原则的重要性