注:本文包含 AI 辅助创作
Paper Summary
- 解读说明:
- 论文是实验室师兄的论文,提出了一种很 makesense 的方案,将传统 RL 中的 Q-Learning 思路放到了 LLM 的记忆上来
- 论文使用了类似 Q-Learning 的方案,且使用非参数的方式建模 Q 值(类似于动态 Q 值表格的概念)
- Q 值的更新方式重点看 4.3 节
- 整体流程可见 4.5.1,图 4
- 背景介绍:
- 人类智能的标志在于通过 建构式情景模拟(Constructive Episodic Simulation)
- 即检索过去经验以合成新任务解决方案,来掌握新技能的能力
- 问题提出:
- 虽然LLM 具备强大的推理能力,但它们难以模仿这种自我演化(emulate this self-evolution)
- 微调计算成本高昂且容易导致灾难性遗忘,而现有的基于记忆的方法(memory-based methods)依赖被动的语义匹配(passive semantic matching),常常检索到噪声
- 论文提出了一个能够让智能体通过在情景记忆上进行非参数强化学习来实现自我演化的框架:MemRL
- MemRL 明确地将冻结大语言模型(frozen LLM)的稳定推理与可塑的、演化的记忆分离开来
- 与传统方法不同, MemRL 采用一种两阶段检索机制(Two-Phase Retrieval)
- 先通过语义相关性筛选候选记忆,然后基于学习到的 Q 值(效用)进行选择
- 这些效用值通过试错方式从环境反馈中持续优化,使得智能体能够区分高价值策略与相似噪声
- 在 HLE、BigCodeBench、ALFWorld 和 Lifelong Agent Bench 上的大量实验表明, MemRL 显著优于现有 SOTA 基线方法
- 论文的分析实验证实, MemRL 有效调和了 稳定性-可塑性困境(stability-plasticity dilemma) ,实现了无需权重更新的持续运行时改进
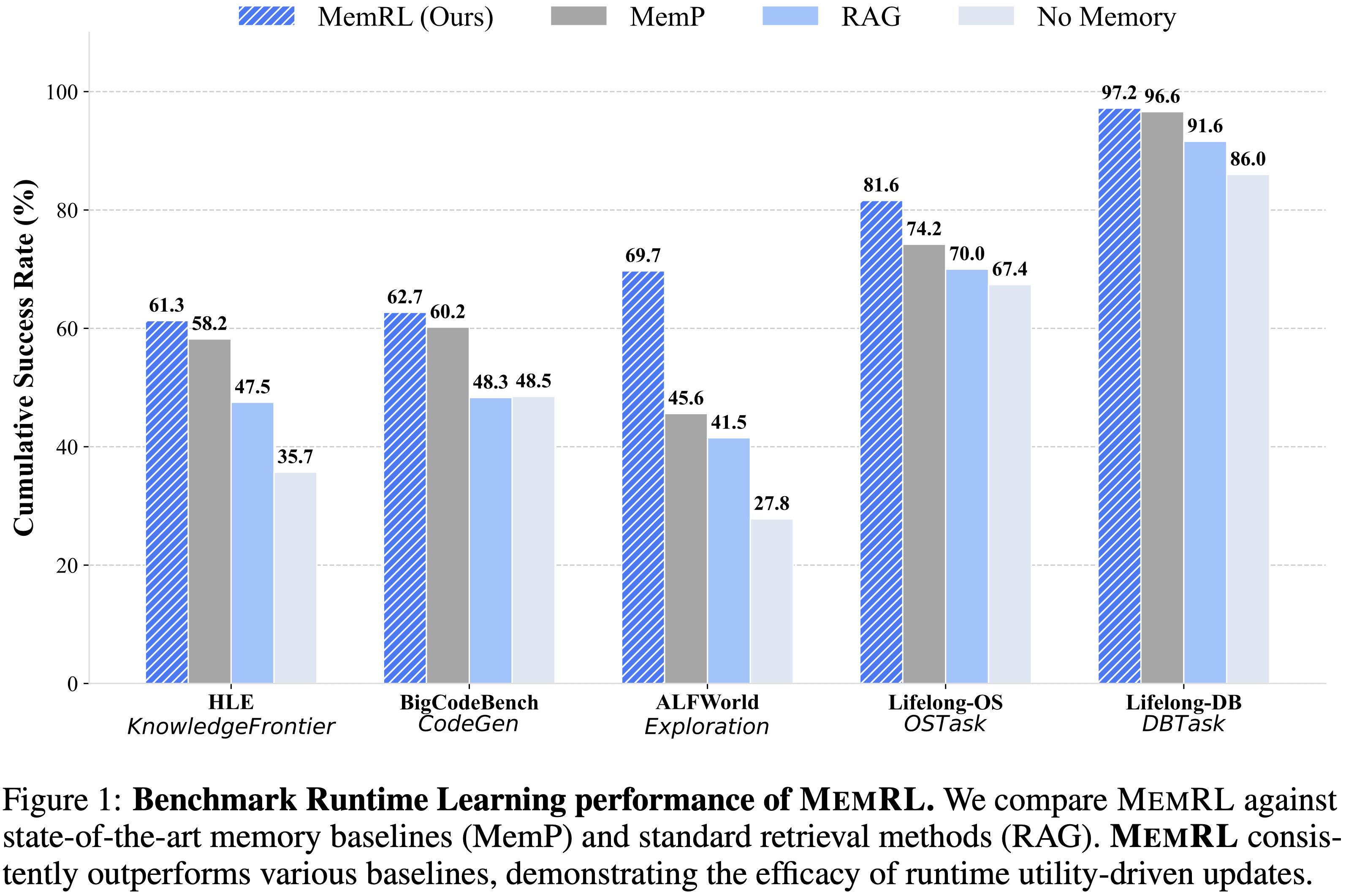
- 图 1: MemRL 的基准运行时学习性能
- 论文将 MemRL 与 SOTA 记忆基线方法 (MemP) 和标准检索方法 (RAG) 进行对比
- MemRL 持续优于各种基线,证明了运行时效用驱动更新的有效性
Introduction and Discussion
- 人类智能的标志在于认知推理的稳定性(stability) 与情景记忆的可塑性(plasticity) 之间的微妙平衡 (Grossberg, 2013; 1995; 2016)
- 这是一种被称为建构式情景模拟(Constructive Episodic Simulation) 的机制
- 它允许在不重新连接神经回路的情况下进行适应 (2007; 2007; 2012; 1980)
- 虽然 LLM 展现出令人印象深刻的推理能力,但现有范式难以模仿这种动态的、解耦的自我演化 (2022; 2022; 2023; 2023)
- 一方面,微调方法试图通过修改模型权重来内化经验 (2022; 2020; 2023; 2024),但通常容易遭受灾难性遗忘和高昂的计算成本 (2017; 2024; 2024)
- 另一方面,检索增强生成(Retrieval-Augmented Generation, RAG) (2020) 提供了一种非参数的替代方案,但其根本上是被动的;
- RAG 仅基于语义相似性检索信息,而不评估其实际效用 (2020; 2023)
- 由于缺乏一种机制来区分高价值的过去策略与相似噪声,当前的 RAG 智能体难以有效地从运行时反馈中学习以随时间优化其性能
- 这一限制突显了一个关键的研究问题:
- 如何能让一个智能体在部署后持续改进其性能,同时不损害其预训练 Backbone Model 的稳定性?
- 论文的目标是实现一个能随着持续使用而演化,并在部署后快速适应新任务的智能体,这被称为运行时持续学习(Runtime Continuous Learning) (2023; 2025; 2019; 2024),同时保持 Backbone Model 冻结以防止灾难性遗忘 (2017; 2025)
- 为应对这一挑战,受人类建构式模拟认知机制的启发,论文提出了 MemRL
- 这是一个通过显式解耦模型稳定的认知推理与动态的情景记忆来促进自我演化智能体的框架
- 图 2 展示了论文提出的 MemRL 的概念框架
- 借鉴强化学习 (Reinforcement Learning, RL) 中估计预期经验效用的值迭代方法 (2018),论文将冻结大语言模型与外部记忆之间的交互形式化为一个马尔可夫决策过程(Markov Decision Process, MDP) (Puterman, 2014)
- 与优化 Backbone Model 权重的方法不同, MemRL 优化记忆使用策略以最大化预期效用
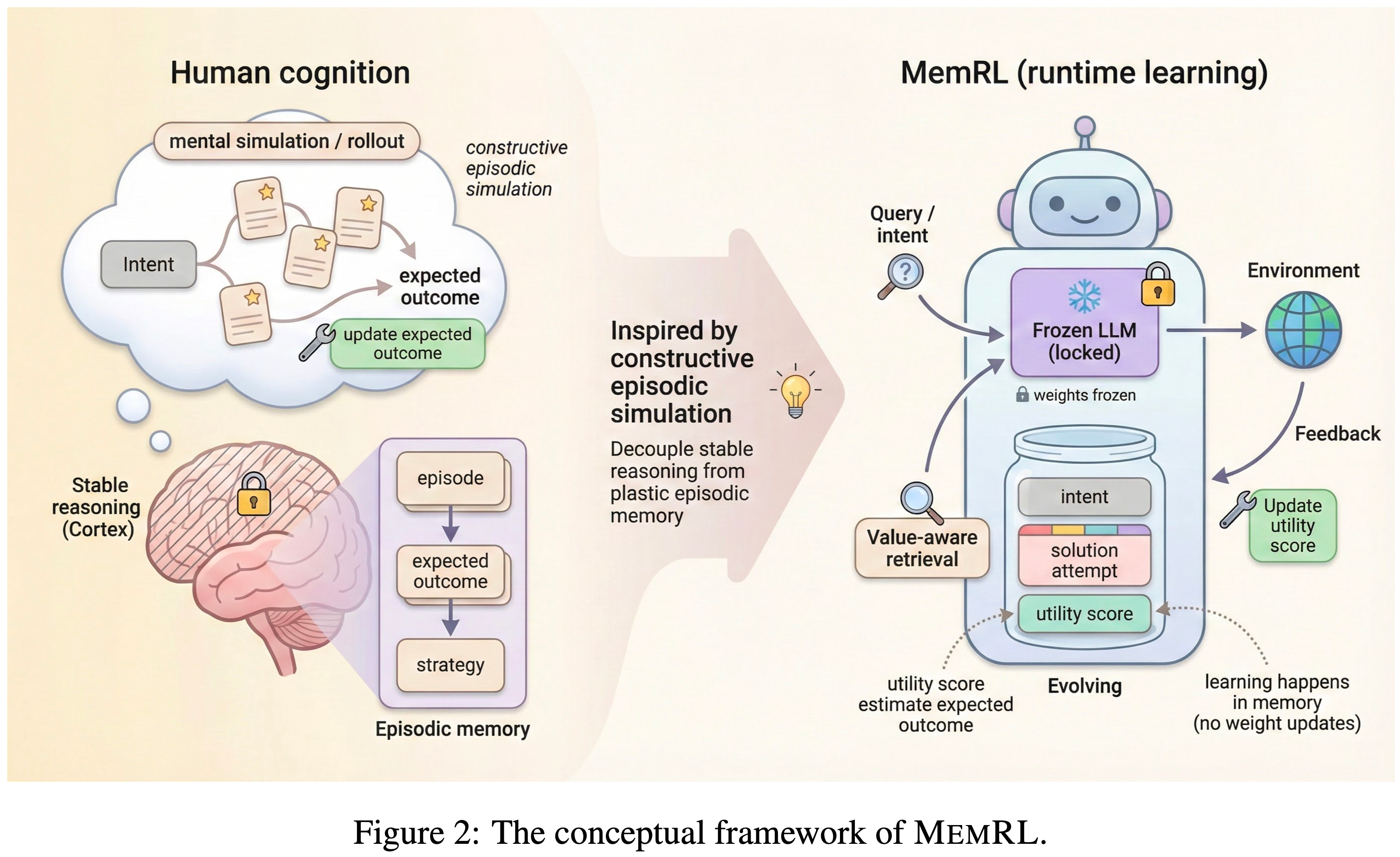
- MemRL 将记忆组织成结构化的意图-经验-效用三元组(Intent-Experience-Utility triplet)
- 这种结构将检索从一个被动的语义匹配任务转变为一个主动的决策过程:
- 值感知检索(Value-Aware Retrieval) 根据学习到的 Q 值选择经验,反映预期效用而非仅仅语义相似性 (1992);
- 效用驱动更新(Utility-Driven Update) 通过环境反馈和贝尔曼备份 (Bellman backup) (Bellman, 1966) 来优化这些 Q 值
- 这个闭环循环使智能体能够区分高价值策略与相似噪声,有效地从成功和失败中学习,而无需承担与权重更新相关的计算成本或灾难性遗忘风险
- 这种结构将检索从一个被动的语义匹配任务转变为一个主动的决策过程:
- 论文在四个不同的基准测试上验证了 MemRL
- 包括 HLE、BigCodeBench、ALFWorld 和 Lifelong Agent Bench
- 论文的结果表明其始终优于基线方法,在探索密集的环境中实现了相对改进
- 论文的深入分析揭示了学习到的效用与任务成功之间存在强相关性,进一步证实了 MemRL 的有效性
- In Summary,论文的贡献有三方面:
- 论文提出了一种基于模型-记忆解耦(Model-Memory decoupling) 和意图-经验-效用三元组(Intent-Experience-Utility triplet) 的运行时学习框架
- 它通过使智能体无需参数更新即可学习,从而调和了 Stability-plasticity 困境
- 论文引入了 MemRL ,一种实现值感知检索(Value-Aware Retrieval) 和效用驱动记忆管理(Utility-Driven Memory Curation) 的非参数强化学习算法
- 这使得智能体能够通过优化记忆效用来自我演化,建立了一种增强智能体能力的新范式
- 论文进行了广泛的评估,并提供了对 MemRL 工作机制的深入洞察
- 论文分析了它如何确保复杂任务中的结构完整性,并通过贝尔曼收缩 (Bellman contraction) 从理论上证实了其稳定性,探索了效用驱动更新如何最小化灾难性遗忘同时最大化正向迁移 (positive transfer)
- 论文提出了一种基于模型-记忆解耦(Model-Memory decoupling) 和意图-经验-效用三元组(Intent-Experience-Utility triplet) 的运行时学习框架
Problem Formulation
- 在本节中,论文正式定义记忆增强生成的问题,并建立智能体策略与记忆检索之间的理论联系
- 论文采用基于记忆的马尔可夫决策过程(Memory-Based Markov Decision Process, M-MDP) (2025) 的形式化定义,并用论文的非参数强化学习框架来解决它
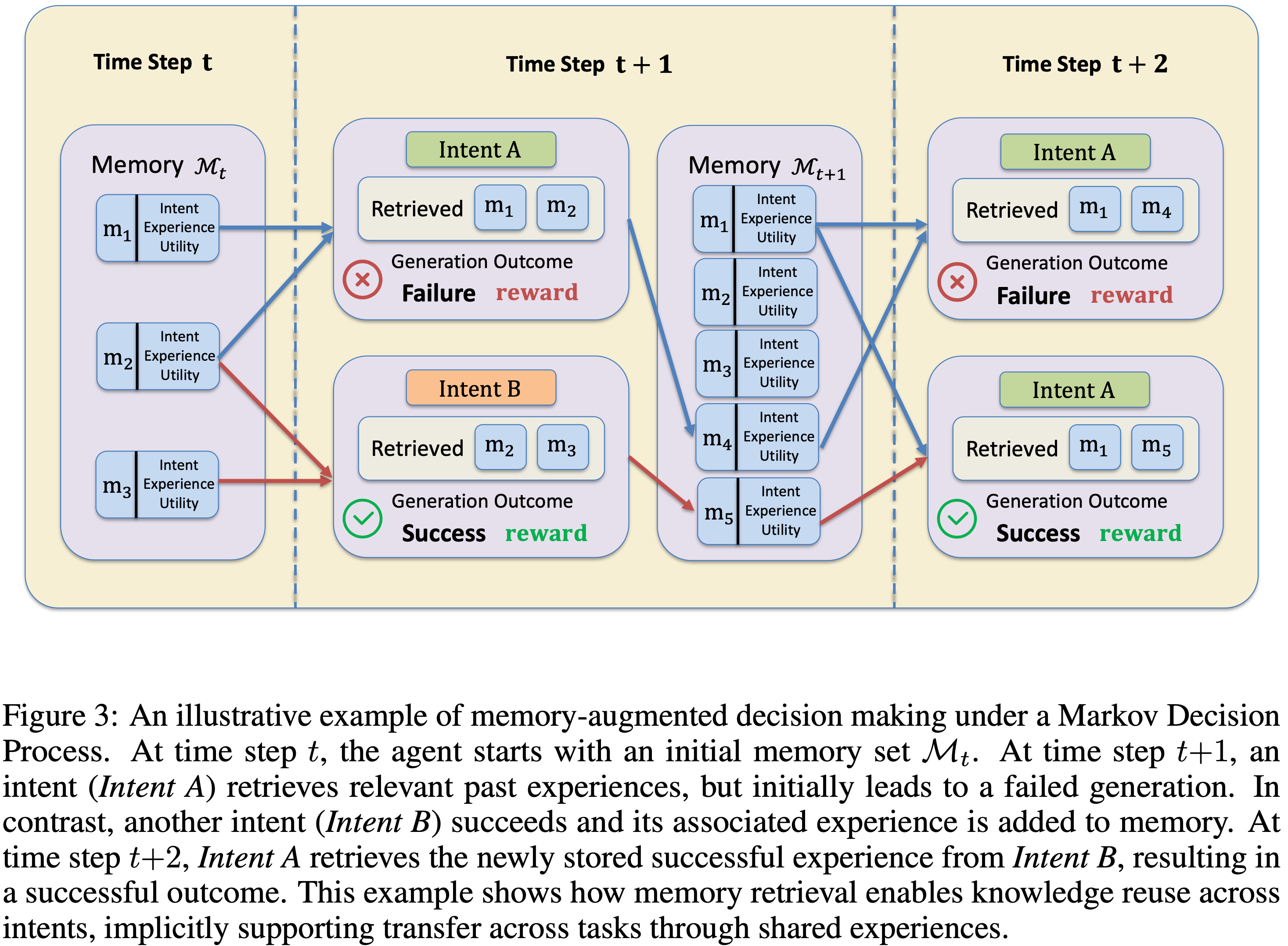
- 图 3 提供了一个记忆增强决策过程的示例,展示了检索结果和记忆演化如何随时间步骤展开
- 图 3:马尔可夫决策过程中记忆增强决策的示例
- 在时间步 \(t\):智能体以初始记忆集 \(\mathcal{M}_t\) 开始
- 在时间步 \(t + 1\)
- 意图 A 检索相关的过去经验,但最初导致生成失败
- 意图 B 成功,其相关经验被添加到记忆中
- 在时间步 \(t + 2\) ,意图 A 从意图 B 检索新存储的成功经验,resulting in 成功的结果
- 这个例子展示了记忆检索如何实现跨意图的知识重用,通过共享经验隐式支持跨任务迁移
Memory-Augmented Agent Policy
- 为了使智能体能够自我演化,论文继承 M-MDP 作为问题形式化 (2025)
- M-MDP 被正式定义为一个元组
$$ \langle S, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma , \mathcal{M} \rangle$$- 其中:
- \(S\) 表示状态空间
- \(\mathcal{A}\) 表示 Action 空间
- \(\mathcal{P}: S \times \mathcal{A} \to \mathbb{R}\) 表示转移动态
- \(\mathcal{R}: S \times \mathcal{A} \to \mathbb{R}\) 表示奖励函数
- \(\gamma \in [0, 1)\) 表示折扣因子
- \(\mathcal{M} = (S \times \mathcal{A} \times \mathbb{R})^*\) 表示包含过去经验的演化记忆空间 (2025)
- 在此 Setting 中,策略 \(\pi\) 不仅生成 token,而且首先根据检索分布 \(\mu (\cdot |s,M)\) 选择一个记忆上下文 \(m\) ,允许智能体利用历史数据在下游任务中获得更好的性能
- 其中:
- 论文考虑一个通用智能体在离散时间步上与环境或用户交互
- 在每个时间步 \(t\) ,智能体接收一个状态 \(s_t\) (例如用户 Query 或任务描述),并可以访问外部 Memory Bank \(\mathcal{M}\)
- 智能体的目标是生成一个响应 \(y_t\) 以最大化奖励信号
- 遵循此形式化,记忆增强智能体的行为可以分为两个不同的阶段:检索(Retrieve) 和生成
- 联合策略 \(\pi (y_t|s_t,\mathcal{M}_t)\) 被定义为所有可能检索到的记忆项上的边际概率(marginal probability) (2025):
$$\pi (y_t|s_t,\mathcal{M}_t) = \sum_{m\in \mathcal{M}_t}\underbrace{\mu(m|s_t,\mathcal{M}_t)}_{\text{Retrieval Policy} }\cdot \underbrace{p_{\text{LLM} }(y_t|s_t,m)}_{\text{Inference Policy} } \tag{1}$$- 注:这里的 \(\mathcal{M}_t\) 指的是时间步 \(t\) 时的 Memory Bank
- \(\mu (m|s_t,\mathcal{M}_t)\) 表示检索策略(Retrieval Policy) ,它根据当前状态 \(s_t\) 从 Memory Bank \(\mathcal{M}_t\) 中为选择特定记忆上下文 \(m\) (由过去的意图和经验组成)分配概率
- \(p_{\text{LLM} }(y_t|s_t,m)\) 表示推理策略(Inference Policy) ,通常由一个冻结的大语言模型参数化。它模拟了在给定 Query \(s_t\) 和检索到的上下文 \(m\) 的条件下生成输出 \(y_t\) 的可能性
- 在之前的 RAG 或基于记忆的智能体范式中,检索策略 \(\mu\) 通常由固定的向量相似性度量决定,例如嵌入向量的余弦相似度
- 虽然对于语义匹配有效,但此类策略未能考虑记忆的效用,即检索(retrieving) \(m\) 是否真正导致成功的结果 \(y_t\)
Non-Parametric RL
- 为了克服静态 Similarity-based 检索的局限性,论文通过将记忆检索形式化为一个 Value-based 决策过程来操作 M-MDP 框架
- 与通过权重更新优化 \(\pi_{\text{LLM} }\) 的参数化方法不同,论文的目标是直接在记忆空间内优化检索策略 \(\mu (m|s,M)\)
- 论文将抽象的 M-MDP 组件映射到一个特定的意图-经验-效用结构:
From Semantic Matching to Decision Making
- 论文将状态 \(s\) 实例化为用户意图(User Intent) ,由当前 Query 的嵌入表示封装(encapsulated by the embedding of the current query) (2020)
- 因此, Action 空间 \(\mathcal{A}_t\) 变得动态且离散,对应于从当前 Memory Bank \(\mathcal{M}_t\) 中选择特定的 \(m\)
- 注意:这里说的是 Action 空间是离散的(且动态变化的),状态空间是 Embedding,理论上是连续的,空间无限
- 问题:Embedding 是连续的吧?状态空间是否过大了?
- 在此形式化下,从记忆中检索不再是一个被动的匹配任务,而是一个主动的 Action \(a_t = m\) ,用于增强生成器 (2025)
Defining Utility via Q-Values
- 论文框架的核心是从估计语义相关性转向估计功能效用
- 论文将 State-Action 值函数 \(Q(s,m)\) 定义为对与 \(s\) 相似的意图应用检索到的上下文 \(m\) 的预期效用
- MemRL 的目标是学习一个最优的检索策略 \(\mu^*\) ,该策略选择最大化此预期效用的上下文:
$$\mu^{*}(m|s,M) = \arg \max_{m\in \mathcal{M} }Q(s,m) \tag{2}$$ - 这个 Q 值充当一个 Critic ,区分高价值策略与可能具有高语义相似性的不相关噪声
- MemRL 的目标是学习一个最优的检索策略 \(\mu^*\) ,该策略选择最大化此预期效用的上下文:
Non-Parametric Learning
- 由于在论文的 Setting 中,检索策略 \(\mu\) 的 Action 空间与大语言模型的生成空间解耦,我们可以在不修改大语言模型权重的情况下进行学习
- 在接收到环境反馈 \(r\) (例如执行成功)后,我们可以使用时序差分 (Temporal-Difference, TD) 误差 (Sutton, 1988) 来更新检索到的记忆上下文的 Q 值:
$$Q(s,m)\gets Q(s,m) + \alpha [r + \gamma \max Q(s’,m’) - Q(s,m)] \tag{3}$$- 其中 \(\alpha\) 是学习率
- 这种贝尔曼式 (Bellman-style) 备份允许效用估计随时间收敛到真实的预期回报 (Bellman, 1966)
- 通过在记忆结构中显式地维护和更新这些 Q 值, MemRL 提供了一种具有理论保证的非参数学习方式,使智能体能够通过交互自我演化其能力
- 问题:状态空间无穷大的情况下,不能使用 TD-Error 更新吧
MemRL
- 基于第 3 节定义的 M-MDP 公式,论文提出了 MemRL,一个使冻结的 LLM 能够通过非参数强化学习进行自我演进的框架
- MemRL 不修改模型权重 \(\theta\),而是在演进的记忆空间内优化检索策略 \(\mu (m|s, \mathcal{M})\)
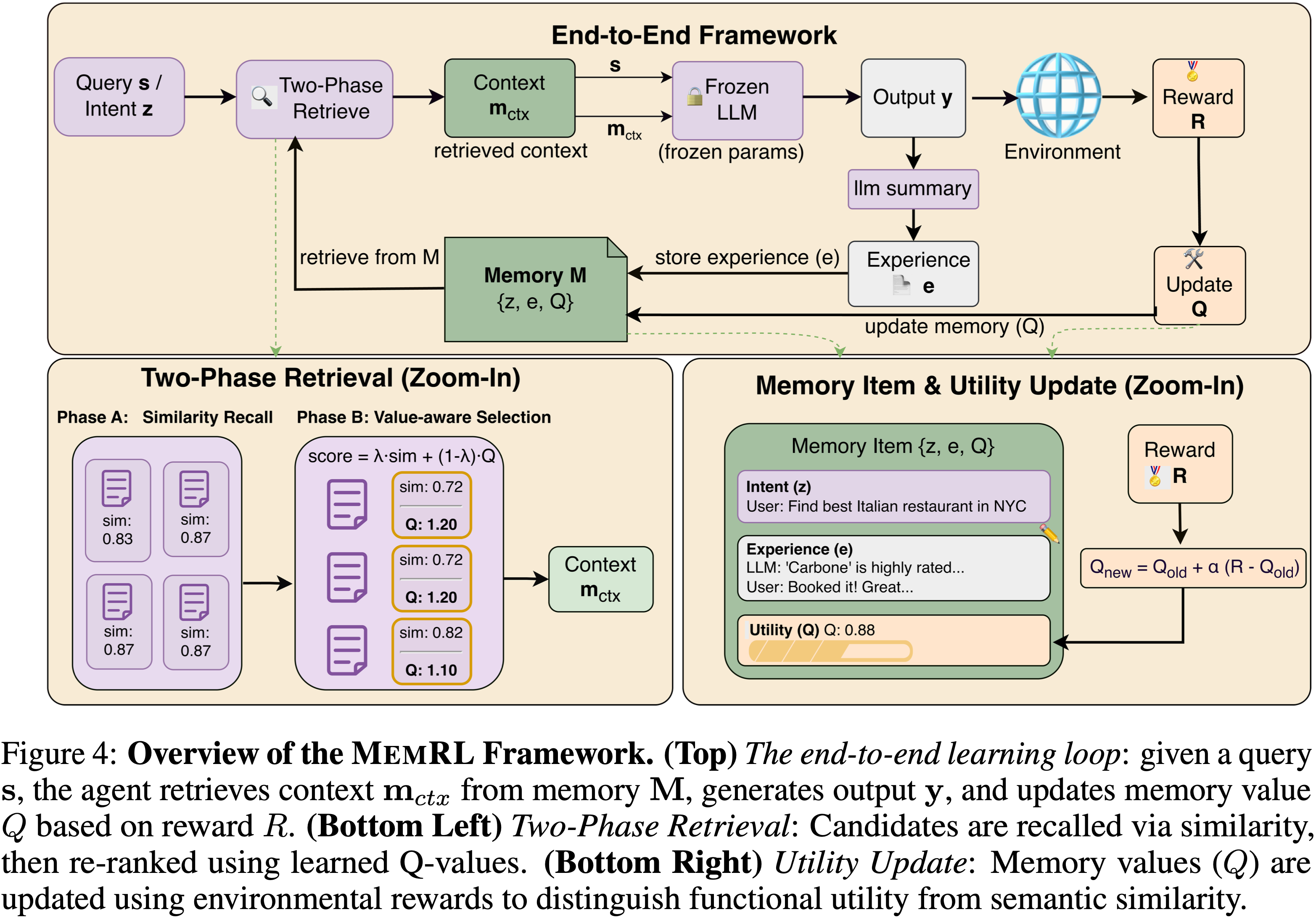
- 如图 4 所示,该框架由三个核心组件组成:
- (i) 一个结构化的意图-经验-效用 Memory Bank
- (ii) 一个将语义召回与价值感知选择解耦的两阶段检索机制
- (iii) 一个稳定 Q 值估计的运行时效用更新规则
- 图 4:MemRL 框架概览
- (Top)端到端学习循环:给定 Query \(s\),智能体从记忆 \(\mathcal{M}\) 中检索上下文 \(\mathbf{m}_{c t x}\) ,生成输出 \(y\),并基于奖励 \(R\) 更新记忆值 \(Q\)
- (Bottom Left)两阶段检索:候选者通过相似性被召回,然后使用学习到的 Q 值重新排序
- (Bottom Right)效用更新:记忆值 \(Q\) 使用环境奖励进行更新,以区分功能效用和语义相似性
Memory Structure: The Intent-Experience-Utility Triplet
- 为了支持 Value-based 决策,论文将外部记忆 \(\mathcal{M}\) 结构化为不仅仅是键值对,而是一组三元组:
$$
\mathcal{M} = \{(z_i,e_i,Q_i)\}_{i = 1}^{|\mathcal{M}|}, \tag{4}
$$- \(z_{i}\) 代表意图嵌入(Intent Embedding)(例如, Query 或任务描述的向量表示)
- \(e_{i}\) 存储原始经验(Experience)(例如,成功的解决方案轨迹)
- \(Q_{i} \equiv Q(z_{i}, e_{i})\) 表示习得的效用(Utility)
- \(Q_{i}\) 近似于将经验 \(e_{i}\) 应用于与 \(z_{i}\) 相似的意图的预期回报,在 RL 公式中充当 Critic
- 理解:这里强调是相似意图,不是意图本身,蕴含了后续是基于相似度来检索意图的(类似 RAG)
Two-Phase Retrieval: From Semantic Recall to Value-Aware Seletion
- 标准的 RAG 或记忆系统仅依赖于语义相似性,隐含地假设“相似意味着有用”
- 但在智能体任务中,语义相关的上下文可能编码了脆弱、特定于环境的例程,无法泛化 (2025; 2024; 2024; 2024)
- 为了解决这个问题,MemRL 实施了一种两阶段检索策略,首先通过相关性过滤候选,然后再通过效用过滤
Phase A: Similarity-Based Recall
- 给定当前 Query 状态 \(s\),论文首先隔离(isolate)一个语义一致的经验候选池 \(C(s)\),以确保检索在上下文上是相关的
- 具体方法是计算余弦相似度 \(sim(s,z_i)\) 并过滤 Memory Bank :
$$
\mathcal{C}(s) = \text{TopK}_{k_1}(\{i|sim(s,z_i) > \delta \} ,\text{by}sim) \tag{5}
$$- 其中 \(\delta\) 是一个稀疏度阈值
- 此阶段充当粗过滤器,将搜索空间从整个记忆 \(\mathcal{M}\) 缩小到相关子集 \(\mathcal{C}(s)\)
- 值得注意的是,如果 \(\mathcal{C}(s) = \emptyset\), MemRL 不注入任何记忆,仅依赖冻结的 LLM 进行更广泛的探索
Phase B: Value-Aware Selection
- 为了从 \(\mathcal{C}(s)\) 中选择最优上下文,论文纳入了习得的效用 \(Q\)
- 论文定义了一个复合评分函数,以平衡探索(通过语义匹配)和利用(通过高效用历史):
$$
\text{score}(s,z_i,e_i) = (1 - \lambda)\cdot \hat{sim}(s,z_i) + \lambda \cdot \hat{Q}(z_i,e_i) \tag{6}
$$- Remind:
- \(z_{i}\) 代表 Intent Embedding ,即之前已经存储下来的意图
- \(e_{i}\) 存储原始 Experience ,即待检索的候选 Memory
- 其中 \(\hat{\cdot}\) 表示在候选池内进行 z-score 归一化,\(\lambda \in [0,1]\) 调节权衡
- 当 \(\lambda \rightarrow 1\) 时,策略优先考虑已验证的效用;
- 当 \(\lambda \rightarrow 0\) 时,它恢复到标准的 Similarity-based 检索
- 最终的上下文 \(\mathcal{M}_{ctx}(s)\) 由最大化此分数的前 \(k_{2}\) 项组成:
$$
\mathcal{M}_{ctx}(s) = \text{TopK}_{k_2}(\mathcal{C}(s),\text{by score}). \tag{7}
$$ - 这种机制有效地过滤掉了“干扰性”记忆,那些语义相似但历史上产生低回报(低 Q 值)的记忆
- Remind:
- 论文将在第 5.3.3 节进一步验证归一化和相似度阈值的必要性,证明 z-score 归一化和严格的相似度阈值对于过滤噪声和在自我演进过程中保持低遗忘率至关重要
Runtime Learning: Non-Parametric RL on Memory
- MemRL 的核心是基于环境反馈持续改进 Q 值,使智能体能够“记住”有效的方法
- 在运行时, MemRL 完全在记忆空间中进行学习
- 重点1:奖励信号获取:
- 完成一项任务后,智能体收到 环境奖励信号 \(r\)(例如,执行成功、用户反馈或标量任务分数)
- 重点2:对于已有记忆的价值更新:
- 对于实际注入到上下文 \(\mathcal{M}_{ctx}(s)\) 中的记忆 ,论文使用蒙特卡洛风格的规则更新其三元组中的效用:
$$
Q_{\text{new} }\leftarrow Q_{\text{old} } + \alpha \big(r - Q_{\text{old} }\big). \tag{8}
$$- 理解:上面式子的更新是针对 已有(被检索出来)的 Memory 的
- 通过将 \(s’\) 设为终止状态,公式 8 作为公式 3 的自然简化版本,与 (2025) 共享相似的单步 MDP 公式
- 此更新驱动 \(Q_{\text{new} }\) 趋近于在相似意图下使用经验 \(e_i\) 的经验预期回报
- 对于实际注入到上下文 \(\mathcal{M}_{ctx}(s)\) 中的记忆 ,论文使用蒙特卡洛风格的规则更新其三元组中的效用:
- 重点3:对于新采样轨迹的添加:
- 对于每个采样的轨迹,论文使用 LLM 来总结经验 (理解:经验是通过 LLM 总结出来的,不是原始的 Rollout)
- 将其作为新的三元组 \((z(s),e_{\text{new} },Q_{\text{init} })\) 写回 Memory Bank ,从而在不断扩展经验的同时保持 LLM 参数不变
- 注:这里的 \(z(s)\) 表示从 \(s\) 中提出取来的意图
Cognitive Interpretation
- MemRL 提供了建构性情景模拟的算法类比 (2007)
- 阶段 A 通过回忆语义相似的过去事件来实施类比迁移 (1983)
- 阶段 B 类似于心理预演 (2004),通过使用习得的效用估计在回忆的候选中进行选择,有效地倾向于预期带来更高回报的策略
- 最后,公式 8 实现了一种记忆再巩固形式 (2016):
- 一旦记忆被检索和应用,其效用会根据后续结果得到强化或减弱
- 这些组件共同实现了 Stability-plasticity 平衡:
- 冻结的 LLM 保持稳定的认知推理,而演进的记忆效用则为持续适应提供了可塑性的渠道
Stability Analysis
- 论文从强化学习的角度分析 MemRL 的稳定性,重点关注存储在记忆中的效用估计的收敛行为
- 与经典的值迭代不同, MemRL 使用恒定步长更新进行非参数运行时学习
- 论文表明,在温和且现实的假设下,习得的效用值在期望上收敛于记忆有效性的稳定估计,且方差有界
Setup
- 在每个时间步 \(t\),智能体观察一个意图状态 \(s_{t}\),检索一个记忆项 \(m_{t} \in \mathcal{M}_{t}\),生成一个输出 \(y_{t}\),并接收一个标量奖励 \(r_{t} \in [- 1,1]\) 指示任务成功或失败
- 生成策略遵循公式 1 中定义的分解,其中 \(\mu\) 表示检索策略,\(p_{\text{LLM} }\) 是冻结的推理策略
- 对于每个检索到的记忆, MemRL 使用公式 8 中表述的指数移动平均规则更新其效用,学习率为 \(\alpha \in (0,1]\)
- 为了分析清晰,论文考虑一个固定的状态-记忆对 \((s,m)\) 并记 \(Q_{t} \equiv Q_{t}(s,m)\)
Stationary Reward Assumption
- 论文在固定数据集上分析学习过程,并提出两个确保环境稳定性的关键条件:
- 1)冻结推理策略(Frozen Inference Policy) :\(p_{\text{LLM} }(y|s,m)\) 的参数和评估器的标准是固定的
- 2)固定任务分布(Fixed Task Distribution) :任务 \(s\) 是从一个固定数据集的平稳分布中抽取的
- 这些假设保证了学习目标是明确定义的:任何特定任务-记忆对(specific task-memory pair)的预期奖励是时不变的(time-invariant)
- 因此,论文有:
$$
\mathbb{E}{[r_t|s_t = s,\mathcal{M}_t = m]} = \beta (s,m). \tag{9}
$$
Expected Convergence of Utility Estimates
Theorem 1
- 令 \(\{Q_{t}\}\) 根据公式 8 中的规则更新,恒定步长 \(\alpha \in (0,1]\)
- 如果公式 9 成立且对 \((s,m)\) 无限次更新,则:
$$
\lim_{t\to \infty}\mathbb{E}{[Q_t]} = \mathbb{E}{[r_t|s_t = s,\mathcal{M}_t = m]} = \beta (s,m). \tag{10}
$$ - 此外,收敛速率是指数级的:
$$
\mathbb{E}{[Q_t]} - \beta (s,m) = (1 - \alpha)^t (Q_0 - \beta (s,m)). \tag{11}
$$
Proof of Theorem 1
- 定义估计误差
$$ e_{t} \triangleq Q_{t} - \beta (s,m) $$ - 基于公式 8 的更新规则,误差递推关系为:
$$
e_{t + 1} = (1 - \alpha)e_{t} + \alpha (r_{t} - \beta (s,m)).
$$ - 给定 历史 \(\mathcal{F}_{t}\) 的条件期望并利用公式 9,论文得到:
$$
\mathbb{E}{[e_{t + 1}|\mathcal{F}_t]} = (1 - \alpha)e_t.
$$- 注:附录 A.1 中会提到,其中 \(\mathcal{F}_{t}\) 定义为截至时间 \(t\) 的 filtration (history)
- 取完全期望(full expectation)得:
$$
\mathbb{E}{[e_{t + 1}]} = (1 - \alpha)\mathbb{E}{[e_t]}.
$$ - 迭代递归得 \(\mathbb{E}{[e_t]} = (1 - \alpha)^t e_0\),当 \(t \to \infty\) 时收敛于零
- 论文在附录 A.1 中提供了收敛证明的详细推导
Bounded Variance and Stability
- 如果奖励方差 \(\text{Var}(r_t|s,m) < \infty\),则 \(Q_{t}\) 的方差保持有界:
$$
\lim_{t\to \infty}\text{Var}(Q_t)\leq \frac{\alpha}{2 - \alpha}\text{Var}(r_t|s,m). \tag{12}
$$ - 因此,恒定步长更新不会引起无界振荡;
- 相反,它们产生稳定的效用估计,这些估计跟踪预期的记忆有效性,同时过滤高频噪声
- 论文在附录 A.2 中明确推导了方差界限,以证明在任务聚类下估计量的全局稳定性
Global Stability via EM Convergence
- 局部估计(定理 1)的稳定性扩展到全局记忆效用 \(Q(m)\)。根据期望的线性性质,\(Q(m)\) 充当蒙特卡洛积分器,力图收敛于:
$$
\lim_{t\to \infty}\mathbb{E}{[Q_t(m)]} = \mathbb{E}{[r|m]} = \sum_{s\in \mathcal{S}(m)}\frac{\mathbb{E}{[r|s,m]}}{\text{Stationary} }\frac{\text{Pr}(s|m)}{\text{Retr}\text{ive}\text{-}\text{Dep}\text{end}\text{ent} }. \tag{13}
$$- 其中 \(\mathcal{S}(m) \triangleq \{s \in \mathcal{S} | \text{sim}(s, z_m) \geq \tau_A \}\) 表示记忆 \(m\) 的有效支持集,包含所有与记忆意图嵌入 \(z_m\) 足够相似以满足阶段 A 检索准则的任务意图 \(s\)
- 这里出现了一个理论挑战:权重项 \(\text{Pr}(s|m)\) 是一个由检索策略 \(\mu (m|s; \mathcal{M})\) 支配的潜在变量,而该策略本身随着 \(Q\) 值的演变而变化
- 为了证明尽管存在这种依赖关系仍然收敛,论文将 MemRL 分析为一个广义期望最大化过程 (1977; 1998)
- 从变分的角度来看,该系统在全局目标函数 \(\mathcal{J}(Q, \mu)\)(预期奖励的变分下界)上执行坐标上升:
- (i) E 步(策略改进) :阶段 B 的排序更新检索策略 \(\mu\) 以与当前估计保持一致,相对于 \(\mu\) 单调增加 \(\mathcal{J}\);
- (ii) M 步(值更新) :效用更新(公式 8)相对于 \(Q\) 增加 \(\mathcal{J}\)
- 根据单调改进定理 (1998),这种交替优化保证了系统收敛到一个平稳点,在该点检索策略稳定 \((\mu_{t + 1} \approx \mu_t)\)
- 因此,诱导的分布 \(\text{Pr}(s|m)\) 变得时不变,确保公式 13 成立,并通过将更新锚定在稳定策略上来有效防止灾难性遗忘
- 更多细节可在附录 B 中找到
Experiments
Experimental Setup
Baselines
- 论文在统一的冻结主干模型设置(a unified frozen-backbone setting)下,将 MemRL 与一套全面的记忆增强基线方法进行比较,以分离出记忆机制的贡献:
- 1)RAG-based Approaches :RAG (2020) 和 Self-RAG (2023),分别代表标准的语义检索和基于批判的过滤
- 2)智能体记忆(Agentic Memory) :MemO (2025) 和 MemP (2025),它们引入了结构化的读/写操作或过程性记忆蒸馏
- 3)Test-Time Scaling: :Pass@k 和 Reflexion (2023),后者在 \( k \) 轮内应用迭代式的自我精炼
Benchmarks
- 论文在四个多样化的基准测试上评估 MemRL 和基线方法:
- 用于代码生成的 BigCodeBench (2025)
- 用于具身导航的 ALFWorld (2021)
- 用于操作系统/数据库交互的 Lifelong Agent Bench (2025)
- 用于多学科复杂推理的 Humanity’s Last Exam (HLE) (2025)
- 论文在两种不同的设置下评估论文的 MemRL 和基线方法:
- 运行时学习(Runtime Learning) ,评估在训练会话中学习和适应的能力;
- 迁移学习(Transferring) ,评估习得记忆在未见任务上的泛化能力
Runtime Learning Results
- 表 1 报告了超过10个训练周期的最终 Epoch 准确率(Last Epoch Accuracy)和累计成功率(Cumulative Success Rate, CSR)
- MemRL 在所有领域均持续优于所有基线方法
- 这验证了非参数价值估计能够有效引导自我进化
- 价值感知检索(value-aware retrieval)的优势在 ALFWorld 这类探索密集型环境中最为显著
- 在 ALFWorld 上,MemRL 取得了 0.507 的优异最终 Epoch 准确率,相对于 MemP(0.324)和“无记忆”基线(0.278)分别实现了约 56% 和 82% 的相对提升
- ALFWorld 中高达 0.697 的 CSR 表明,RL 组件有效地鼓励了智能体去探索并发现复杂任务的解决方案,而 Similarity-based 检索方法通常无法解决这些任务
- 在具有挑战性的 Knowledge Frontier HLE 基准测试中,相较于 MemP 的 0.528,MemRL 将最终准确率提升至 0.573,其 CSR 甚至达到了惊人的 61.3%
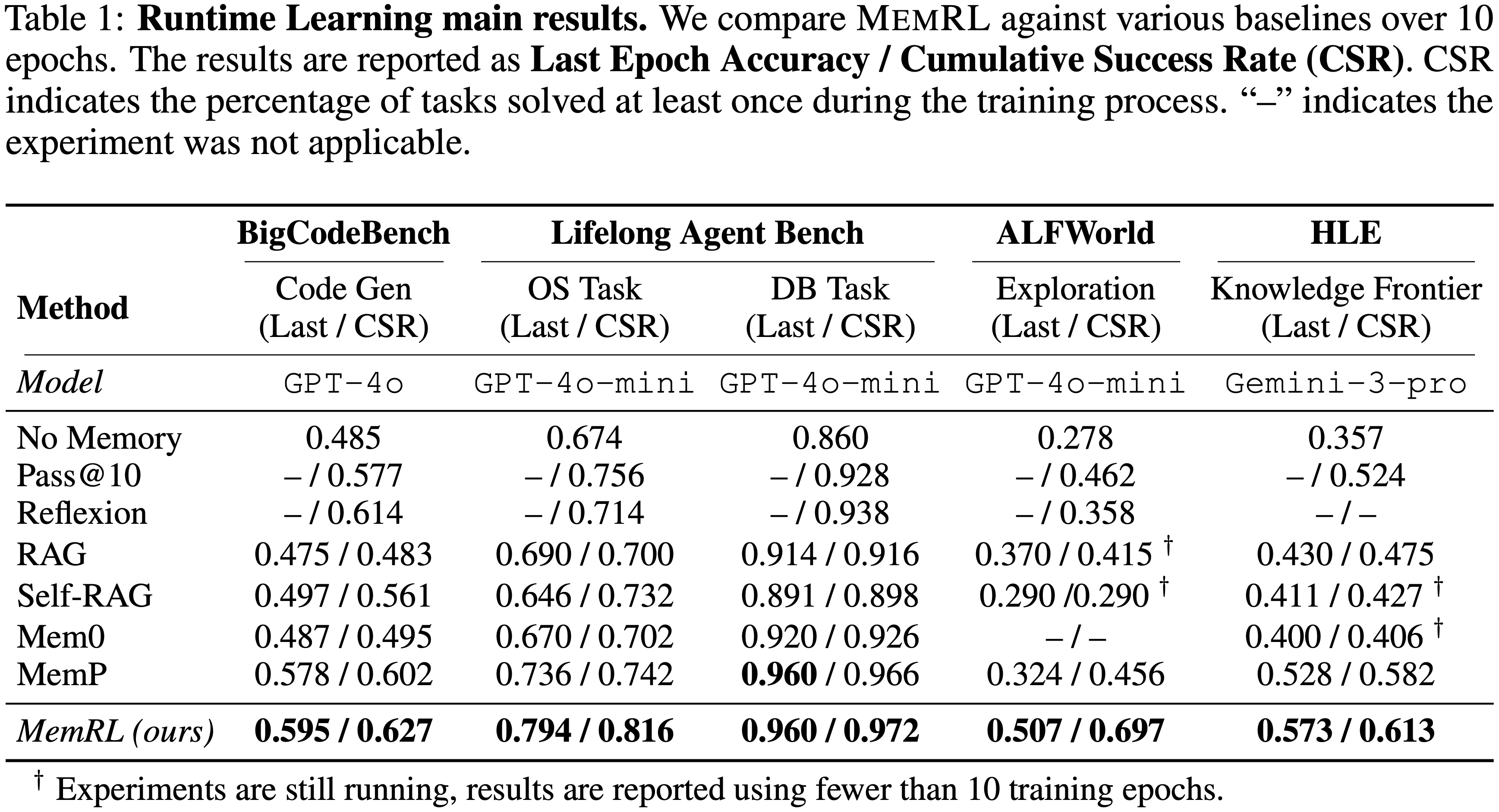
- MemRL 在所有领域均持续优于所有基线方法
- 将这些收益与 BigCodeBench 等单轮任务进行比较,揭示了一个重要趋势:性能提升与任务结构复杂性相关
- MemRL 的优势在以深度探索和高过程可转移性(procedural transferability)为特征的环境中(例如 ALFWorld)最大化,而在结构复用较少的任务中,优势幅度则较窄
- 这表明我们的价值驱动机制特别擅长从探索轨迹(exploratory trajectories)中提炼并迁移复杂的问题解决模式
- Overall,CSR 和最终准确率的同时提升表明,MemRL 不仅在探索过程中发现了高质量的解决方案,而且能够有效地保留和检索它们,以实现稳定的性能
Transferring Results
- 通过在训练后冻结记忆库并在保留集(30% split)上进行测试来评估记忆的可迁移性
- 如表 2 所示,与基线方法相比,MemRL 展现出更优异的泛化能力
- 在 BigCodeBench 上,MemRL 达到了 0.508 的最高准确率,优于 Self-RAG(0.500)和标准 MemP(0.494)等高级检索方法
- 在操作系统控制任务(Lifelong Agent Bench)中,MemRL 获得了 0.746 的准确率,相比标准 RAG 基线(0.713)有显著提升
- 与运行时结果一致,在 ALFWorld 中收益显著,MemRL 达到了 0.479,明显优于 MemP(0.421)和 RAG(0.336)
- 这些结果验证了 MemRL 中的价值感知检索(Value-Aware Retrieval)和非参数强化学习机制并不仅仅是过拟合训练实例;
- instead,它过滤了低价值记忆,保留了高效用经验,从而促进了向未见任务的泛化
Ablations
Effectiveness of Runtime RL
- 为了分离出运行时强化学习的效果,论文在操作系统交互环境中,比较了带有和不带有强化学习组件(即 MemP 对比 MemRL 以及 RAG 对比 MemRL (RAG))的记忆机制
- 图 5a 展示了成功率随训练轮次的变化情况
- 虽然强化学习增强(enhancement)在初始阶段带来的增益有限,但随着训练的进行,性能差异明显扩大
- MemRL 在后续轮次中持续优于原始的 MemP 基线,表现出更平滑的学习曲线和更少的性能回退
- 这种稳定性表明,强化学习驱动的价值函数有效缓解了噪声记忆的干扰,而噪声记忆常常困扰基于静态相似性的检索方法
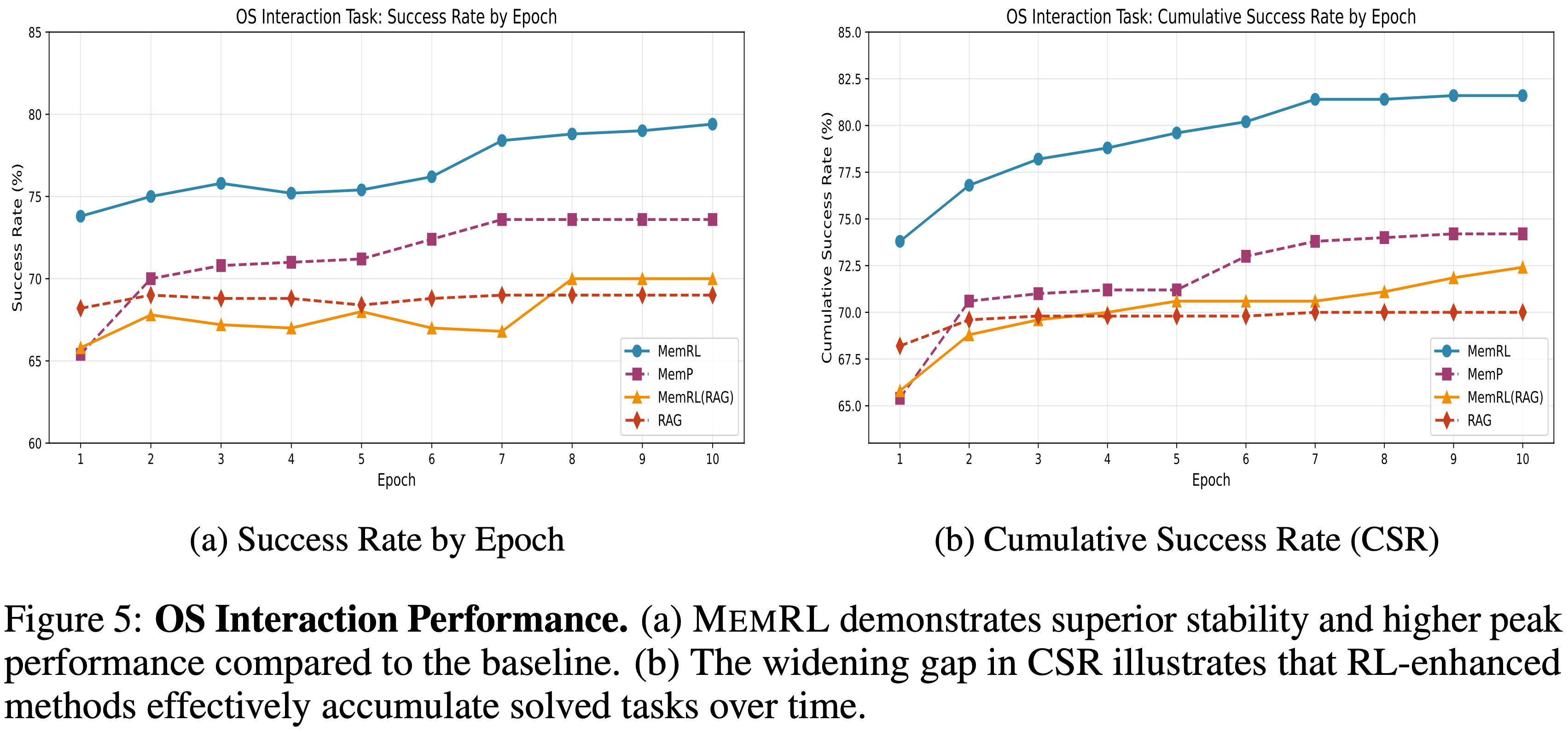
- 论文进一步分析了图 5b 中的 CSR Cumulative Success Rate ,它衡量了智能体在训练过程中至少成功解决过一次不同任务的能力
- 在这里,强化学习的好处更加明显
- MemRL 和 MemRL (RAG) 最终达到的 CSR 分别优于其对应方法 MemP 和 RAG
- 图 5a 中性能差距的单调扩大表明,运行时强化学习显著增强了智能体从早期失败中恢复的能力
- 通过优先考虑具有高期望效用的记忆,智能体有效减轻了噪声记忆的干扰,并巩固了成功的经验,将短暂的探索转化为稳健、可重复的能力
Impact of Q-value Weighting
- 为了理解语义检索和强化学习之间的相互作用,论文分析了评分函数(即公式6)中 Q 值加权因子 \( \lambda \) 的影响:
- 论文将 平衡设置(balanced configuration) \( (\lambda = 0.5) \) 与两种极端情况进行比较:
- 纯语义检索(pure semantic retrieval baseline) \( (\lambda = 0) \)
- 纯贪婪强化学习(pure RL setting) \( (\lambda = 1) \)
- 论文将 平衡设置(balanced configuration) \( (\lambda = 0.5) \) 与两种极端情况进行比较:
- 如图 6 所示,平衡配置始终产生更优的性能
- 这表明语义基础 semantic grounding 和效用驱动排序 utility-driven ranking 的结合能有效地引导智能体找到高质量的解决方案,同时保持上下文相关性
- 此外,纯语义检索基线提供了一个稳定的起点,但缺乏过滤语义相似但功能错误的次优记忆的机制
- 因此,其性能很快进入平台期,这凸显了强化学习信号对于持续改进的必要性
- 另一方面,纯强化学习设置揭示了忽视语义上下文的风险,表现出显著的不稳定性和较差的初始性能
- 论文将这种不稳定性归因于上下文脱离 context detachment :
- 在没有语义相似性约束的情况下,智能体可能会检索到与当前任务无关的高 \( Q \) 值记忆(在其他上下文下是成功的)
- 这证实了语义相似性必须作为检索的锚点,而强化学习则为优化记忆选择提供了必要的梯度
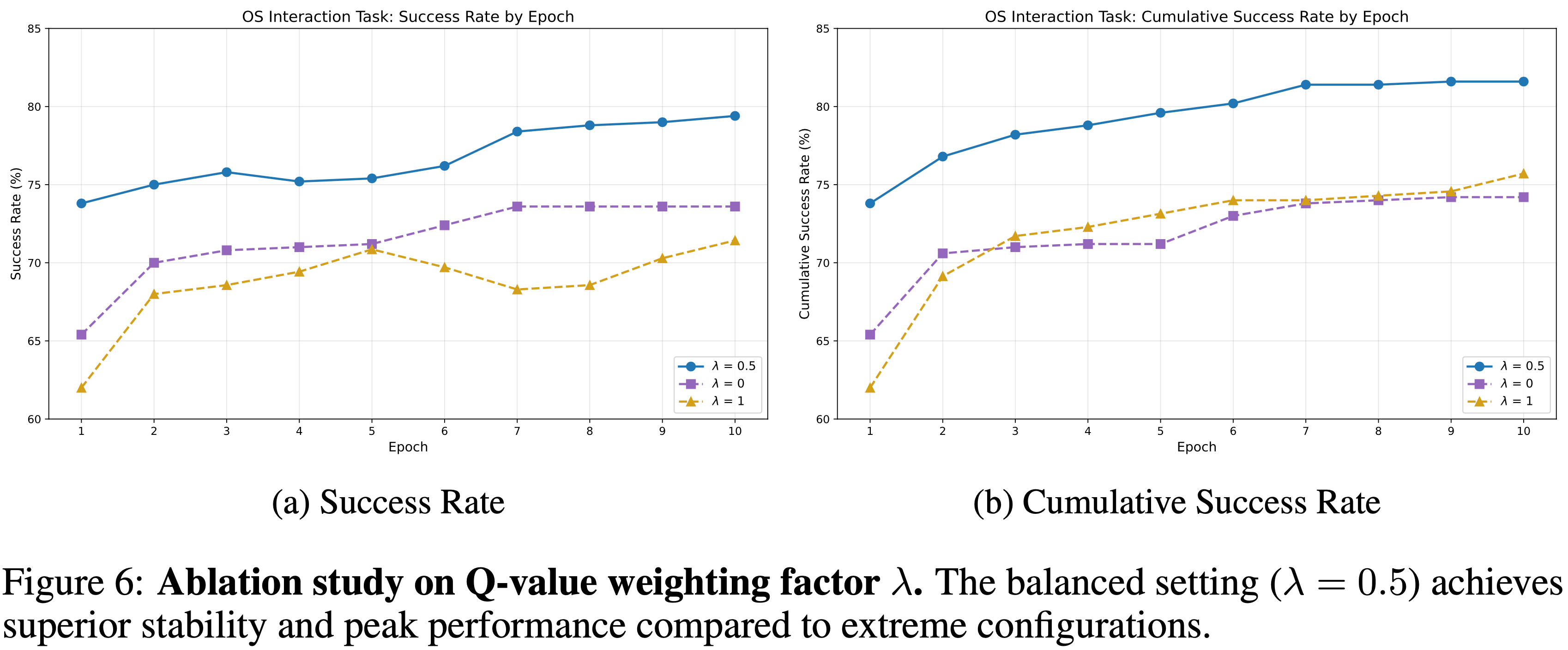
- 论文将这种不稳定性归因于上下文脱离 context detachment :
- 这表明语义基础 semantic grounding 和效用驱动排序 utility-driven ranking 的结合能有效地引导智能体找到高质量的解决方案,同时保持上下文相关性
Sensitivity to Retrieval size
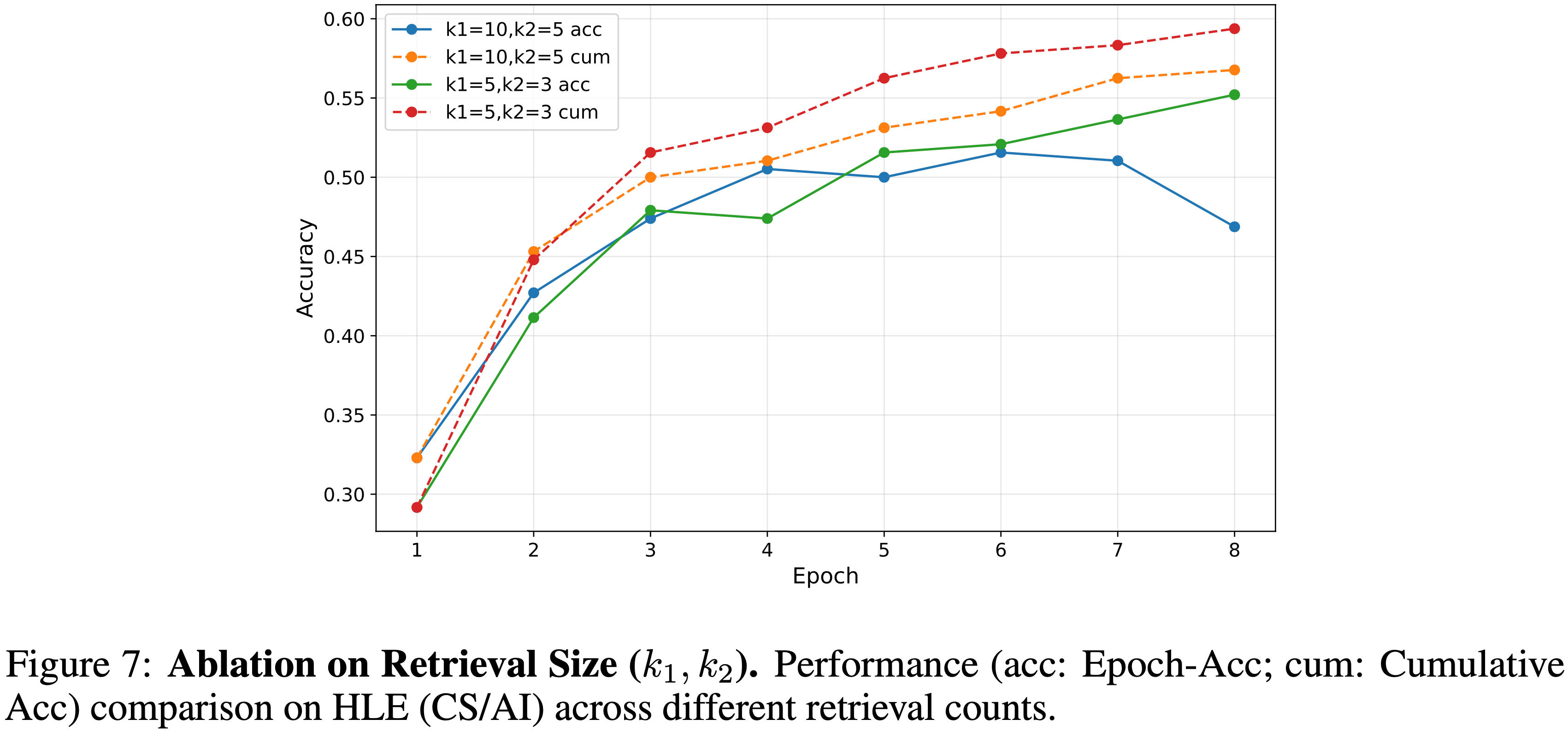
- 为了研究记忆容量对推理性能的影响,论文在 HLE 基准测试的一个子集(计算机科学/人工智能类别)上进行了消融实验
- 论文比较了两种检索配置:
- 较大的召回设置(larger recall setting) \( (k_{1} = 10, k_{2} = 5) \)
- 紧凑的召回设置(compact recall setting) \( (k_{1} = 5, k_{2} = 3) \)
- 问题:这里的 \( (k_{1}, k_{2}) \) 分别代表论文两阶段检索的候选数量
- 如图 7 所示,与较大的设置相比,紧凑的设置 \( (k_{1} = 5, k_{2} = 3) \) 实现了更优的稳定性
- 这表明对于像 HLE 这样的复杂推理任务,单纯增加上下文容量可能会引入无关噪声,干扰模型的判断
- 因此,一个更小、更高质量的检索记忆集足以保持推理精度
Discussion
- 在本节中,论文更深入地探讨驱动 MemRL 性能的机制,将实证结果与第4节提出的 Stability-plasticity 框架联系起来
MemRL as a Trajectory Verifier
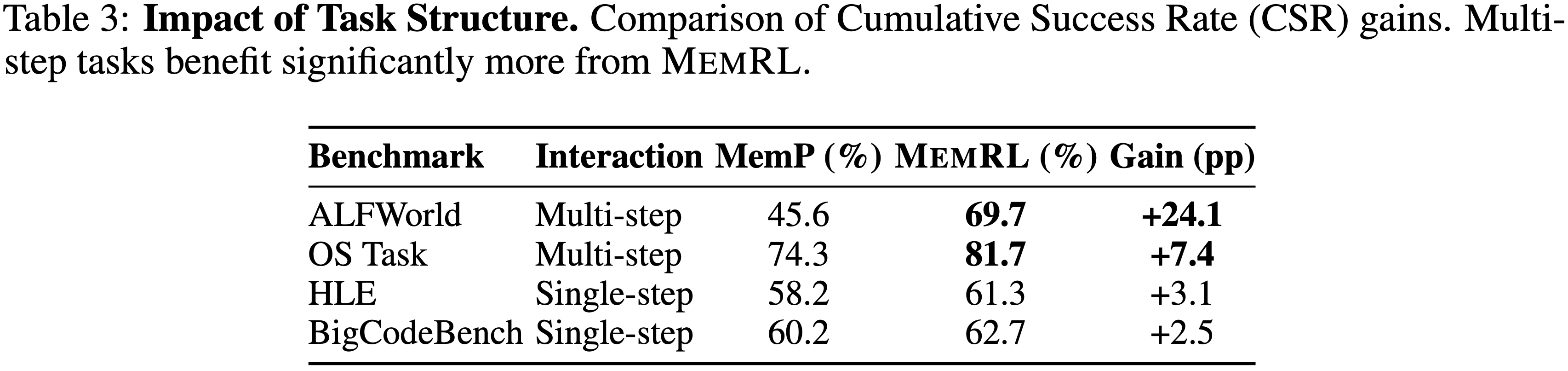
- 表 3 揭示了任务结构复杂性与性能增益之间的相关性
- 与单轮任务(例如 BigCodeBench \(+2.5\) 个百分点)相比,增益在多步骤序列任务中最为显著(例如 ALFWorld \(+24.1\) 个百分点)
- 在序列任务中,检索到的记忆必须对整个轨迹有效
- 标准的语义检索:通常会获取与初始指令匹配但后续步骤失败的记忆
- MemRL:通过将最终奖励反向传播到记忆效用 \( Q \), MemRL 有效地学习验证整个轨迹,过滤掉仅在表面上看起来正确的脆弱策略
Predictive Power of the Q-Critic
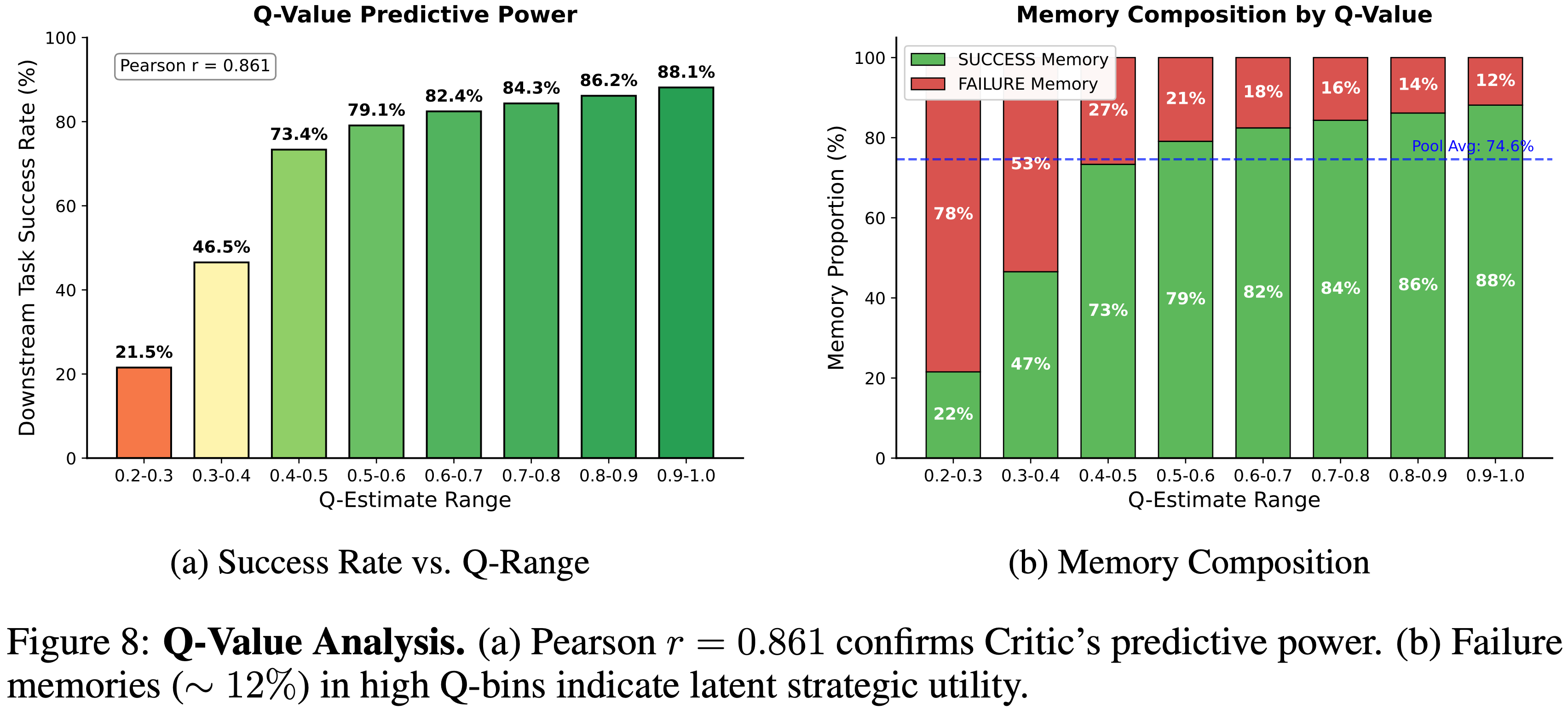
- 学习到的 Q 值是否真的反映了解决方案质量?
- 图 8a 显示了 Critic 估计的 Q 值与经验任务成功率之间存在强正相关(皮尔逊 \( r = 0.861 \))
- 成功率从最低置信度区间的 \( 21.5% \) 增加到最高区间的 \( 88.1% \)
- 这表明性能提升的主要驱动力是 Critic 根据记忆导致任务成功的可能性进行排序的能力
- 对记忆构成(图 8b)的进一步分析表明了增益的另一个来源:鲁棒性 robustness
- 即使在高 Q 值区间 (0.9-1.0),智能体仍保留一小部分标记为“失败”的记忆(约 12%)
- 这不仅不矛盾,反而符合以下解释:Q 值可以捕捉超越二元结果的效用:
- 一些不成功的轨迹在战略上仍然有用,因为它们编码了接近正确的推理和可迁移的过程性经验
- 成功率从最低置信度区间的 \( 21.5% \) 增加到最高区间的 \( 88.1% \)
- 案例研究 :一个高 Q 值“失败”记忆作为可迁移的接近成功(Case study: a high-Q “failure” memory as a transferable near-miss)
- 论文发现了一些高 Q 值的失败记忆,它们总结了一个局部的微小错误以及一个可跨任务泛化的校正启发式方法
- 这里论文用“接近成功” (near-miss) 表示大体正确但由于微小、局部错误(例如,验证疏忽或工具使用细节)而失败的轨迹
- 例如,一个 \( Q = 0.9878 \) 的失败记忆对应一个遵循了正确方法但错误地将空命令输出视为失败证据的轨迹
- 存储的反思明确指出了根本原因(误解空输出),警告了这种模式(将“无输出”等同于失败),并推荐了正确的方法(通过退出状态、错误日志或其他客观信号验证成功)
- 在后续情境中检索时,这一条“失败”记忆在论文的日志中支持了完美的下游结果(15/15 成功),证明了该记忆之所以有价值,正是因为它捕捉到了一个可修复的接近成功,而非无信息的失败
- Taken Together,这些结果表明,Critic 不仅仅是区分“成功”与“失败”,而是赋予那些提供可重用指导的记忆更高的价值
- 包括本质上属于“接近成功”的一部分高效用失败
- 通过保留和重用此类校正启发式方法,智能体可以比简单的成功重放机制更鲁棒
Stability of MemRL
- 论文通过 Stability-plasticity 困境的视角分析 MemRL 的底层机制,审视论文的框架如何平衡新能力的获取与已有知识的保留
- 卓越的 CSR(表1)表明 MemRL 有效地扩展了智能体的解决方案空间

- 与受静态相似性约束、常常检索导致重复失败的冗余最近邻的启发式基线不同,MemRL 允许智能体识别并强化不明显但有效的策略
- 这种能力使智能体能够突破传统检索方法停滞的局部最优
- 长期训练动态(图 9)揭示了一个关键的稳定性优势
- 像 MemP 这样的启发式方法,其 CSR 与当前轮次准确率之间的差距在扩大,表明新的探索无意中覆盖了有效的历史策略(灾难性遗忘)
- 相比之下,MemRL 保持了同步增长
- 论文将此归因于论文的理论保证
- 从广义 MDP 的角度(公式3),价值更新受益于标准的贝尔曼收缩性(Bellman contraction) ,\( | \mathcal{T}Q - Q^{*} |_{\infty} \leq \gamma | Q - Q^{*} |_{\infty} \) (2018),每一步都将误差缩小 \( \gamma \)
- 更具体地说,在论文的蒙特卡洛式建模下(公式8),这个过程由第4.5节保证
- 与可能随机漂移的启发式排序不同,论文的方法在数学上约束策略沿着期望奖励的变分下界攀升,确保了论文在实验中观察到的稳定、非递减的性能
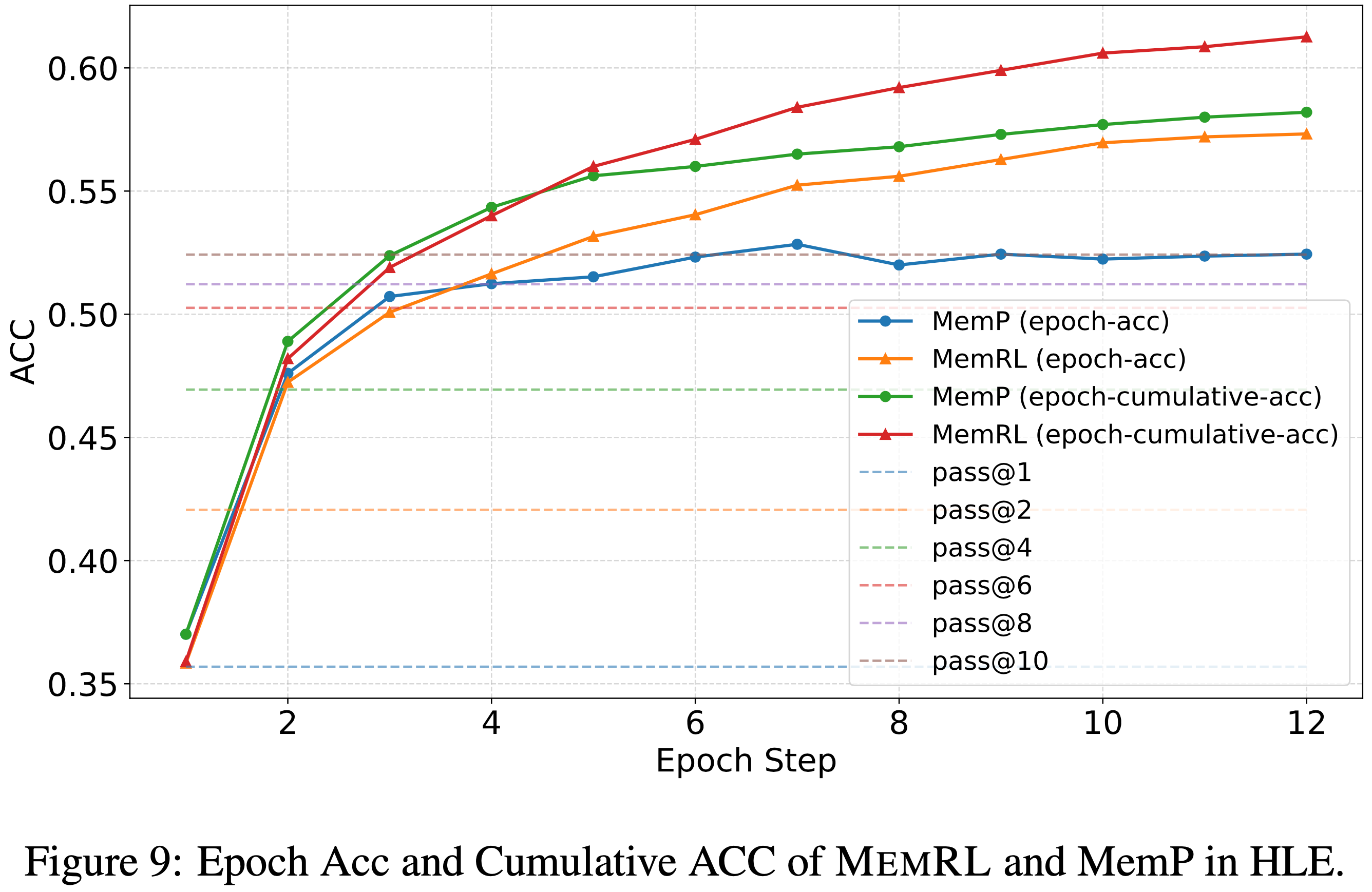
- 论文进一步使用遗忘率(Forgetting Rate)(定义为在上一轮成功而在当前轮失败的任务比例,即 成功 \( \rightarrow \) 失败)来验证这些见解
- 如图 10 所示,MemRL 实现了最低的平均遗忘率 (0.041),优于基线 MemP (0.051),并通过实验证实了论文的分析
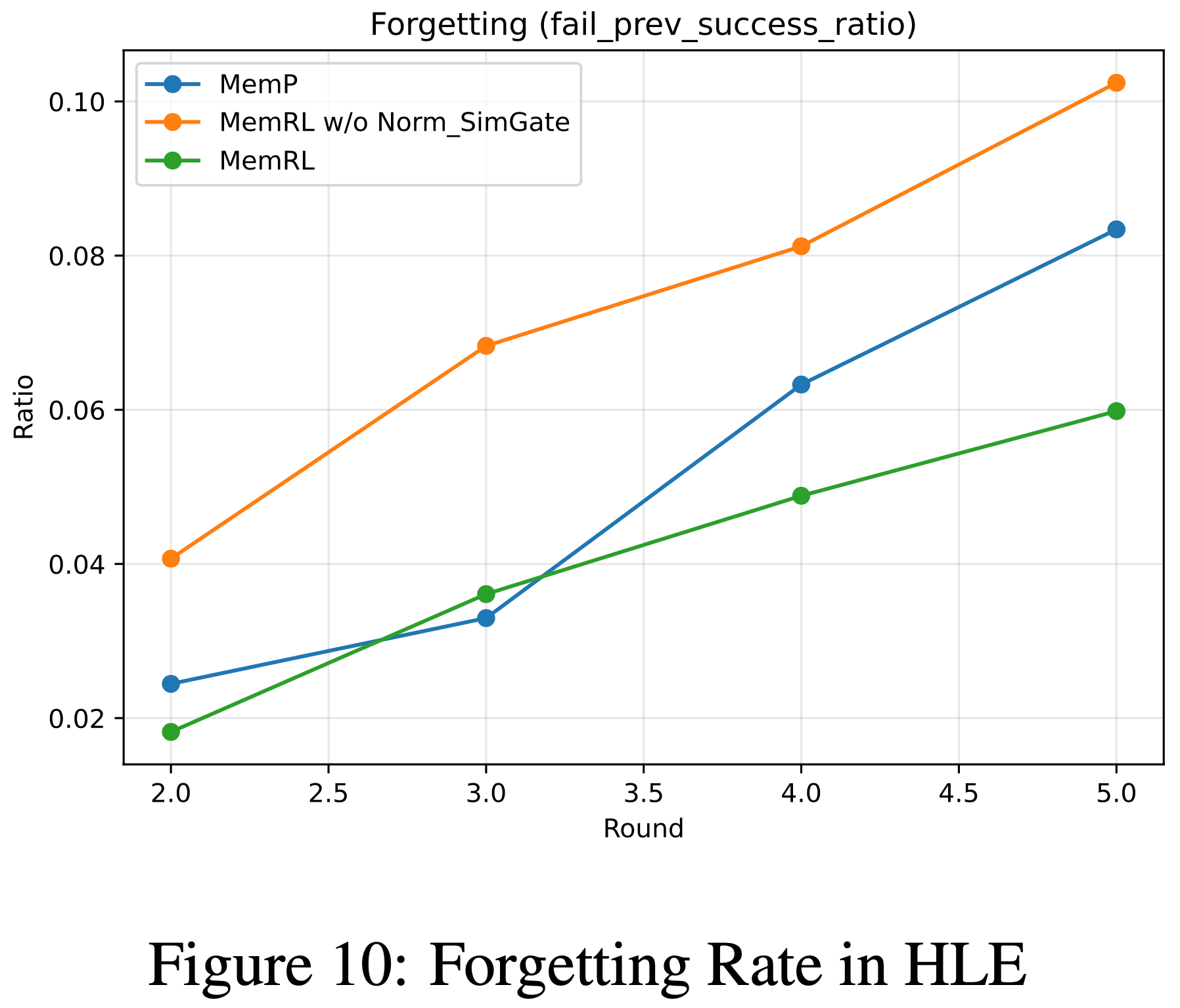
The Necessity of Normalization and Similarity Gate
- 此外,图 10 也突出了论文稳定性设计的必要性:移除归一化并降低相似性阈值(无归一化/相似性阈门)会导致平均遗忘率飙升至 0.073,这是由于不受约束的效用方差造成的
- 这表明, z-score 归一化和严格的相似性阈门对于过滤噪声至关重要,确保自进化过程在最大化正向迁移的同时保持稳定
Impact of Similarity on Memory Efficacy(任务相似性对记忆效能的影响)
- 为了理解 MemRL 发挥作用的基本条件,论文分析了数据集内语义相似性 \( \text{Sim}_{\text{intra} } \) 与论文方法提供的绝对性能增益 \( \Delta = \text{Acc}_{\text{ MemRL } } - \text{Acc}_{\text{NoMem} } \) 之间的相关性
- 如图 11 所示,论文分析了数据集内语义相似性与 MemRL 提供的绝对性能增益 \( \Delta \) 之间的相关性
- 线性回归趋势显示出普遍的正相关性:具有更高结构重复性的环境允许智能体更有效地检索和重用最优策略
- At the upper extreme,ALFWorld(相似度 0.518)充当了这种趋势的强锚点,表现出最高的重复性和相应的最大性能提升 \( \Delta = +0.229 \)
- 这证实了对于高度重复的过程性任务,记忆是通向最优轨迹的有效捷径
- 沿着回归线(Following the regression line),具有中等相似度的基准测试(例如 Lifelong-OS (0.390) 和 BigCodeBench (0.308))聚集在中间区域,显示出稳定的改进 \( \Delta \approx +0.11 \sim +0.12 \),智能体成功地在相关指令间泛化了编码模式或操作系统命令
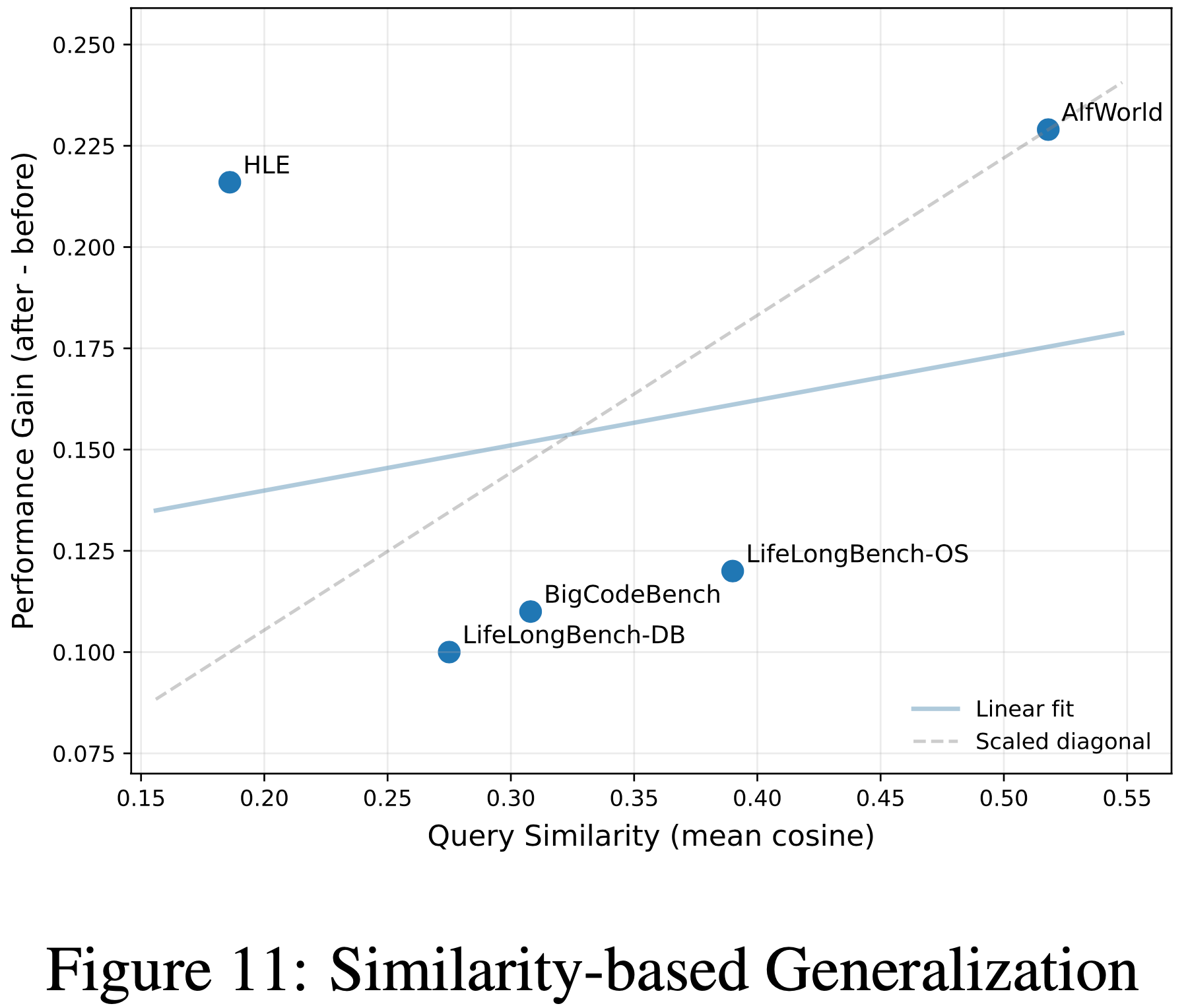
Generalization vs. Memorization
- HLE 呈现了一个独特的异常值
- 尽管由于其多样化的多学科性质具有最低的相似度 (0.186),但它却表现出惊人的高运行时增益(从 0.357 到 0.573,\( \Delta = +0.216 \))
- 这种增益的运作机制与 ALFWorld 不同
- 在高相似度基准测试中, MemRL 通过正向迁移(Positive Transfer),即将共享模式泛化到新实例中 取得成功
- In Contrast,HLE 的增益源于运行时记忆化(Runtime Memorization)
- 由于 HLE 的问题具有独特性且领域特定,智能体依赖运行时学习阶段,通过反复接触来“记忆”针对困难问题的特定解决方案
- 这种区别凸显了 MemRL 的通用性:它既支持结构化领域的模式泛化,也支持多样化领域的特定知识获取
Conclusion
- 在论文中,论文介绍了 MemRL ,这是一个新颖的框架,它使大语言模型能够通过情景记忆上的非参数强化学习实现自进化
- 针对语义检索的局限性和参数微调的不稳定性, MemRL 将记忆检索视为一个 Value-based 决策过程
- 通过将记忆组织为意图-经验-效用三元组并应用贝尔曼更新,智能体学会了区分高价值策略和语义噪声,而无需修改主干模型的权重
- 论文在从代码生成到具身导航的多样化领域进行的广泛评估表明, MemRL 在运行时学习和向未见任务的泛化方面都显著优于现有的记忆增强基线
- 理论和实证分析进一步揭示, MemRL 有效地解决了 Stability-plasticity 困境:
- 冻结的大语言模型提供了稳健的推理能力,而进化的记忆效用则充当了适应的可塑性通道
- Moreover,论文发现效用驱动的检索机制起到了轨迹 Verifier 的作用,使智能体能够在复杂、多步骤的任务中过滤掉脆弱的策略
- 作者希望这项工作为构建能够在稳定高效的方式下持续从交互中学习的自进化智能体奠定新的范式
补充:Related Works
Continous Learning
- 持续学习 (Continual learning) 处理 Stability-plasticity 困境,旨在顺序获取新知识而不遭受灾难性遗忘
- 经典方法(例如正则化、蒸馏和经验回放)通过约束参数更新或保留过去数据分布来缓解遗忘 (2017; 2017; 2017)
- 但这些参数化方法对于大语言模型来说计算成本高昂,并且通过频繁的在线更新有破坏预训练 Backbone 稳定性的风险
- 近期关于大语言模型持续学习的综述进一步系统化了这些困难,并强调了外部机制和非参数路径的重要性 (2024)
- 因此,从持续学习的角度来看,如果论文旨在让智能体在使用中改进同时保持 Backbone 的稳定性,一个更实用的方向是将可塑性从参数空间转移到外部结构和受控的经验更新通道
RL
- 强化学习已被广泛用于增强大语言模型
- 一个代表性范式是从人类反馈中构建奖励信号,并相应地优化模型策略以符合人类偏好 (2020; 2022)
- 其他近期方法利用基于规则的 Verifier 来改进大语言模型的推理能力 (2025; 2025)
- 同时,面向智能体的研究探索了交互信号如何改进工具使用和 Action 决策,并研究了语言模型在环境中执行复合 Action 的机制 (2023)
- 尽管奖励驱动的优化已被证明有效,但这些方法通常将学习置于模型参数或额外的参数化模块中,因此并未从根本上避免在线更新的成本或遗忘的风险
- 相比之下,论文的方法将记忆使用构建为一个可学习的决策问题,并对记忆应用非参数强化学习以规避该风险
Agentic Memory
- 为了绕过微调的成本,外部记忆系统已从静态的 RAG 范式发展为动态的、可治理的记忆结构 (2020; 2020)
- 早期的智能体记忆引入了反思机制和分层管理来处理长上下文经验 (2023; 2024)
- 更近期的框架系统化了记忆生命周期,专注于复杂任务的统一存储和结构化索引 (2025b; 2025; 2025; 2025)
- Furthermore,自适应方法现在探索通过反馈驱动的更新或自动增强来改进检索 (2025; 2025; 2025a; 2025)
- However,除了训练额外的可学习模块外,大多数现有方法仍然主要依赖语义相似性或启发式规则,缺乏严格的度量标准来评估记忆在最大化回报方面的实际效用
- 受记忆整合认知理论 (2007; 1980; 2000) 的启发, MemRL 通过将检索形式化为一个 Value-based 决策过程来弥合这一差距,直接从环境奖励中学习稳健的效用估计(Q 值)以区分高价值经验和噪声
附录 A:Theoretical Analysis And Proofs
- 在本节中,论文将详细推导在指数移动平均(Exponential Moving Average, EMA)更新规则下 Q 值估计的收敛性,并将分析扩展到任务分布下记忆效用(memory utility)的全局稳定性
A.1 定理 1 的证明:Convergence Of EMA Estimation
- 论文旨在证明,对于一个具有平稳奖励分布(stationary reward distribution)的固定任务-记忆对 \((s,m)\),Q 值估计 \(Q_{t}(s,m)\) 的期望会收敛到真实的平均奖励 \(\beta (s,m)\)
Assumptions
- 平稳奖励(Stationary Reward)。步骤 \(t\) 的奖励 \(r_{t}\) 取自一个具有恒定均值 \(\beta (s,m) = \mathbb{E}{[r_{t}|s,m]}\) 和有限方差 \(\sigma^{2}\) 的分布
- 更新规则(Update Rule)。效用通过学习率 \(\alpha \in (0,1)\) 的线性 EMA 规则更新:
$$Q_{t + 1} = (1 - \alpha)Q_{t} + \alpha r_{t}.$$
Derivation of Error Dynamics
- 令 \(e_{t}\triangleq Q_{t} - \beta (s,m)\) 为时间步 \(t\) 的估计误差。将 \(Q_{t} = e_{t} + \beta (s,m)\) 代入更新规则:
$$\begin{array}{rl} & e_{t + 1} + \beta (s,m) = (1 - \alpha)(e_t + \beta (s,m)) + \alpha r_t\ & \qquad e_{t + 1} = (1 - \alpha)e_t + (1 - \alpha)\beta (s,m) + \alpha r_t - \beta (s,m)\ & \qquad e_{t + 1} = (1 - \alpha)e_t + \beta (s,m) - \alpha \beta (s,m) - \beta (s,m) + \alpha r_t\ & \qquad e_{t + 1} = (1 - \alpha)e_t + \alpha (r_t - \beta (s,m)). \end{array} \tag{14}$$
Convergence Analysis
- 论文将 \(\mathcal{F}_{t}\) 定义为截至时间 \(t\) 的过滤(历史)。对公式 14 取给定 \(\mathcal{F}_{t}\) 的条件期望:
$$\mathbb{E}{[e_{t + 1}|\mathcal{F}_t]} = (1 - \alpha)e_t + \alpha (\underbrace{\mathbb{E}{[r_t|\mathcal{F}_t]}}_{\beta (s,m)} - \beta (s,m)) = (1 - \alpha)e_t.$$ - 根据迭代期望定律(Law of Iterated Expectations),取完全期望得到:
$$\mathbb{E}{[e_{t + 1}]} = \mathbb{E}{[\mathbb{E}{[e_{t + 1}|\mathcal{F}_t]}]} = (1 - \alpha)\mathbb{E}{[e_t]}.$$ - 从 \(t = 0\) 开始迭代此递推关系:
$$\mathbb{E}{[e_t]} = (1 - \alpha)^t\mathbb{E}{[e_0]}.$$ - 由于 \(0< \alpha < 1\),论文有 \(|1 - \alpha |< 1\)。因此:
$$\lim_{t\to \infty}\mathbb{E}{[e_t]} = \mathbb{E}{[e_0]}\cdot \lim_{t\to \infty}(1 - \alpha)^t = 0. \tag{15}$$ - 这证明了估计量在极限上是无偏的,即 \(\lim_{t\to \infty}\mathbb{E}{[Q_t]} = \beta (s,m)\)
A.2 Bounded Variance And Global Stability(有界方差与全局稳定性)
- 在本节中,论文将给出估计量 \(Q_{t}\) 方差界限的形式化推导
- 论文通过递归展开(recursive unrolling)明确推导有限时间方差公式,并证明其渐近收敛性,展示 Phase-A 聚类如何有助于全局稳定性
Derivation of the Variance Bound
- 令 \(\sigma^{2}\triangleq \text{Var}(r_{t}|s,m)\) 为奖励信号的方差,假设是有限的,EMA 更新规则为:
$$Q_{t + 1} = (1 - \alpha)Q_{t} + \alpha r_{t}.$$ - 由于奖励 \(r_{t}\)(当前噪声)在统计上独立于当前估计 \(Q_{t}\)(由历史 \(\mathcal{F}_{t - 1}\) 决定),和的方差是方差的和:
$$\text{Var}(Q_{t + 1}) = \text{Var}((1 - \alpha)Q_t) + \text{Var}(\alpha r_t)$$ $$= (1 - \alpha)^2\text{Var}(Q_t) + \alpha^2\sigma^2.$$ - 令 \(v_{t}\triangleq \text{Var}(Q_{t})\),论文得到一个线性递推关系
$$ v_{t + 1} = (1 - \alpha)^{2}v_{t} + \alpha^{2}\sigma^{2}$$
Recursive Unrolling
- 为了求解 \(v_{t}\),论文将递推关系从步骤 \(t\) 向后展开:
$$\begin{array}{l}{v_{t} = (1 - \alpha)^{2}v_{t - 1} + \alpha^{2}\sigma^{2} }\ {= (1 - \alpha)^{2}\left[(1 - \alpha)^{2}v_{t - 2} + \alpha^{2}\sigma^{2}\right] + \alpha^{2}\sigma^{2} }\ {= (1 - \alpha)^{4}v_{t - 2} + \alpha^{2}\sigma^{2}\left[1 + (1 - \alpha)^{2}\right]}\ {\vdots}\ {= (1 - \alpha)^{2t}v_{0} + \alpha^{2}\sigma^{2}\sum_{k = 0}^{t - 1}\left((1 - \alpha)^{2}\right)^{k}.} \end{array} \tag{16}$$ - 公式 16 明确显示,时间 \(t\) 的方差由两个部分组成:衰减的初始方差(第一项)和累积的噪声方差(第二项)
Asymptotic Convergence
- 当 \(t\to \infty\),由于学习率 \(\alpha \in (0,1)\),项 \((1 - \alpha)^{2t}\) 趋于零。求和项是一个公比为 \(r = (1 - \alpha)^{2}\) 的几何级数 \(\textstyle \sum_{k = 0}^{\infty}r^{k} = \frac{1}{1 - r}\),因此:
$$\lim_{t\to \infty}v_{t} = \alpha^{2}\sigma^{2}\cdot \frac{1}{1 - (1 - \alpha)^{2} }.$$ - 计算分母:
$$1 - (1 - \alpha)^{2} = 1 - (1 - 2\alpha +\alpha^{2}) = 2\alpha -\alpha^{2} = \alpha (2 - \alpha).$$ - 代回得到紧密的方差界限:
$$\lim_{t\to \infty}\sup \text{Var}(Q_t) = \frac{\alpha^2\sigma^2}{\alpha(2 - \alpha)} = \frac{\alpha}{2 - \alpha}\sigma^2. \tag{17}$$
Connection to Phase-A Clustering
- 这个结果为 MemRL 的稳定性提供了理论依据。虽然记忆簇 \(S(m) \triangleq \{s|\text{sim}(s,z_{m}) > \tau_{A}\}\) 内的任务可能不同,但平滑性假设(Smoothness Assumption)意味着它们的奖励取自一个方差有界 \(\sigma_{S(m)}^{2}\) 的分布
- 推导出的界限 \(\frac{\alpha}{2 - \alpha}\sigma_{S(m)}^{2}\) 保证记忆效用 \(Q(m)\) 不会发散,而是将在真实期望效用附近的一个受控范围内振荡
- 该机制有效地过滤了来自不同任务实例的高频噪声,同时保留了稳定的泛化价值
附录 B:Convergence Via Variational Inference
- 在本节中,论文为 MemRL 提供理论基础,证明论文的检索策略和更新规则保证了价值估计的收敛性
B.1 收敛目标
- 论文的最终目标是确保估计的效用 \(Q(m)\) 收敛到记忆 \(m\) 的真实期望回报(expected return),这个目标值定义为:
$$\lim_{t\to \infty}\mathbb{E}{[Q_t(m)]} = \mathbb{E}{[r|m]} = \sum_{s\in \mathcal{S}(m)}\frac{\mathbb{E}{[r|s,m]}}{\text{Stationary} }\frac{\text{Pr}(s|m)}{\text{Retrieve-Dependent} }. \tag{18}$$ - 挑战在于项 \(\operatorname *{Pr}(s|m)\),即特定状态 \(s\) 触发检索 \(m\) 的概率
- 该分布依赖于检索策略 \(\mu_t(m|s)\),而该策略本身在训练过程中会演化,从而产生一个威胁稳定性的循环依赖
B.2 带有信任区域的变分目标
- 为了解决这个问题,论文将问题表述为最大化一个全局变分目标 \(\mathcal{I}(\mu ,Q)\)
- 这个目标作为公式 18 定义的全局期望回报的一个可处理的下界,并通过一个语义信任区域进行平衡:
$$\mathcal{I}(\mu ,Q) = \mathbb{E}_{s\sim \mathcal{D} }\left[\sum_{m\in \mathcal{S}(s)}\mu (m|s)Q(s,m) - \frac{1}{\beta} D_{\text{KL} }\left(\mu (\cdot |s)| \pi_{\text{sim} }(\cdot |s)\right)\right] \tag{19}$$ - 这里,第一项直接对应于论文旨在收敛的期望效用 \(\mathbb{E}{[Q_t(m)]}\),而 \(\pi_{\text{sim} }\) 代表固定的语义先验(从 Phase-A 导出)
- KL 散度项作为一个正则化器至关重要,原因有二:
- 1)信任区域(Trust Region):它将策略约束在支持集 \(\mathcal{S}\) 内,防止智能体检索高 \(Q\) 值但语义上不相关的记忆(分布外误差)
- 2)正则化(Regularization):它在 \(Q\) 估计值嘈杂的“冷启动”阶段稳定学习动态
- 这个目标作为公式 18 定义的全局期望回报的一个可处理的下界,并通过一个语义信任区域进行平衡:
B.3 通过广义期望最大化进行优化 (GEM)
- 论文将 \(\mathcal{I}\) 的优化视为一个 GEM 过程,在策略改进(policy improvement)和价值评估(value evaluation)之间交替进行:
E-step Policy Optimization
- 固定 \(Q_t\),论文找到最大化 \(\mathcal{I}\) 的最优策略 \(\mu^*\)
- 封闭形式的解是玻尔兹曼分布(Boltzmann distribution)(Levine, 2018):
$$\mu^{*}(m|s)\propto \pi_{\text{sim} }(m|s)\exp (\beta Q_{t}(s,m))$$ - 取对数后,论文得到论文 Phase-B 检索(公式 6)中使用的特定评分函数:
$$\log \mu^{*}(m|s)\propto \underbrace{\log\pi_{\text{sim} }(m|s)}_{\approx \text{sim}(s,m)} + \beta Q_{t}(s,m)$$ - 这证明了论文的相似性和 \(Q\) 值的启发式组合在数学上等价于变分目标下的最优策略
M-step Policy Evaluation Via Error Minimization
- 虽然 E-step 基于当前估计改进了策略,但 M-step 确保这些估计是接地于现实的
- 固定策略 \(\mu_{t + 1}\),论文的目标是将变分参数 \(Q\) 与真实的环境回报对齐
- 论文将其表述为最小化估计效用与观察到的奖励目标 \(y = r\)(在论文的蒙特卡洛风格建模中)之间的均方误差(Mean Squared Error, MSE):
$$\min_{Q}\mathcal{L}(Q) = \mathbb{E}_{r\sim \mu_{t + 1} }\left[\frac{1}{2}\left(y - Q(s,m)\right)^2\right]$$ - 最小化这个误差至关重要,因为它收紧(tightens)了变分界限:
- 它确保全局目标 \(\mathcal{I}\)(公式 19)中的期望项 \(\mathbb{E}{[Q]}\) 收敛到真实期望回报 \(\mathbb{E}{[r]}\)
- 论文框架中使用的更新规则(公式 8)正好对应于对该目标的一个 SGD 步骤:
$$Q_{t + 1}(s,m)\leftarrow Q_t(s,m) - \alpha \nabla_Q\mathcal{L}(Q) = Q_t(s,m) + \alpha (y - Q_t(s,m))$$
- 通过迭代地最小化 \(\mathcal{L}(Q)\),M-step 将环境反馈传播到效用估计中,确保随后的 E-step 优化发生在一个可靠的价值格局上
Proof of Convergence
- 根据 GEM 的单调改进定理(Monotonic Improvement Theorem)(1998),序列 \((\mu_t, Q_t)\) 保证收敛到一个驻点 \((\mu^*, Q^*)\)
- 在稳态下,策略稳定 \((\mu_{t+1} \approx \mu_t)\),这意味着逆检索概率 \(\Pr(s|m)\) 变为时间不变的:
$$\Pr (s|m) = \frac{\mu^{*}(m|s)\Pr(s)}{\sum_{\mu^{\prime} }\mu^{*}(m|s^{\prime})\Pr(s^{\prime})}$$ - Consequently,公式 18 中的“依赖检索的(Retrieve-Dependent)”项被锚定
- 在固定的数据分布下,标准的贝尔曼压缩特性(Bellman contraction property)确保 \(Q_t(m)\) 收敛到唯一的固定点:
$$\lim_{t\to \infty}Q_t(m)\to \mathbb{E}_{\mu^*}[r|m] \tag{20}$$
- 在固定的数据分布下,标准的贝尔曼压缩特性(Bellman contraction property)确保 \(Q_t(m)\) 收敛到唯一的固定点:
- Thus,论文的框架从理论上保证了记忆价值在最优检索策略下收敛于真实的期望回报