Python——为什么Python中没有自增++和自减--操作?

C++和Java等语言都有++和–操作,为什么以方便自居的Python却没有这种操作呢?

Python的数值对象

a = 1
b = 1
c = 1000123
d = 1000123

print id(a)
print id(b)
print id(c)
print id(d)

## output:
# 94181316498840
# 94181316498840
# 94181323965720
# 94181323965720

Python数值对象都是不可变类型,与String一样,所以不能修改对象内部数据
C++中的i++修改内存中对象本身,数值增加1,而Python不能修改对象本身
与C++中字符串可以修改,Python中不能修改是一个道理

Python——优先队列PriorityQueue

本文介绍Python中优先队列的用法

注意: queue并不能算是Python标准库,所以在LeetCode等OJ环境中不能使用, 想要使用优先队列的话可以使用Python的标准库heapq
heapq的使用请参考 Python——heapq模块-最大堆最小堆

导入包

1
2
3

from Queue import PriorityQueue
# or
from queue import PriorityQueue

queue包名已经弃用,测试发现本地Python2.7环境可以用,但是LeetCode线上环境不能用
推荐使用Queue

使用

from Queue import PriorityQueue

pq = PriorityQueue()

pq.put((10, "start"))
pq.put((5, "b", 12, 123))
pq.put((5, "a", 6))
pq.put(1)
pq.put(4)
pq.put([0, "a"])
pq.put([8, "b"])
pq.put("avb")
pq.put(None)

# while pq.not_empty()
# while not pq.empty()
while pq.qsize():
    print pq.get()
## output:
# None
# 1
# 4
# [0, 'a']
# [8, 'b']
# avb
# (5, 'a', 6)
# (5, 'b', 12, 123)
# (10, 'start')

不能使用not pq这样的语句判断优先队列是否收敛,他不是普通的内嵌对象(list,str等是内嵌对象),除非pq == None否则,双端队列对象永远为not pq == False
下面用法最优:
1
while pq.qsize():
PriorityQueue中默认递增排序(这一点与Python中的sorted函数和sort()函数一样),每次get(),移除并返回最小的对象
PriorityQueue中,可以同时添加不同类别的对象
PriorityQueue会将对象首先按照类别排序,然后各个类别内部按照不同数值排序
若传入对象是可以直接比较大小的类型即可直接传入,包括tuple, list, str, int(long)等类型
- Python中list,tuple,str等都是可以直接比较大小的,默认使用他们的第一个元素比较大小,如果第一个元素相等,则比较第二个元素,以此类推
- 详细情况参考本文后面的说明

Python中的内嵌对象比较大小

Python中类别间也可以比较大小,默认类别间大小为:tuple > str > list > int(long) > None, 但是记不清楚的话不建议使用Python的这个特性,容易造成错误
Python中list,tuple,str等都是可以直接比较大小的,默认使用他们的第一个元素比较大小,如果第一个元素相等,则比较第二个元素,以此类推

Python中类别间也可以比较大小,默认类别间大小为:tuple > str > list > int(long) > None, 但是记不清楚的话不建议使用Python的这个特性,容易造成错误

ls = [(1, 'b'), (1, 'a'), (2, 'a'), [1, 'a'], [1, 'b'], [2, 'a'], '1a', '1b', '2a', 1, 2, 3, None]
ls.sort()
print ls
# # output
# [None, 1, 2, 3, [1, 'a'], [1, 'b'], [2, 'a'], '1a', '1b', '2a', (1, 'a'), (1, 'b'), (2, 'a')]

Python自定义对象比较大小

在做算法题时,没必要的情况下不建议使用

在做工程时建议使用这种方式

import Queue
class Node():
    def __init__(self, val):
        self.val = val

    def __lt__(self, other):
        return self.val < other.val

pq = Queue.PriorityQueue()
pq.put(Node(5))
pq.put(Node(1))

while pq.qsize():
    print pq.get().val
# # output
# 1
# 5

注意__lt__函数中是小于号,说明递增排序,大于号,说明递减排序
PriorityQueue对象不是普通Python内嵌对象,不能使用Python内嵌的len函数

Python——关于列表list的操作

Python的list有很多强大的功能,有些比较罕见的操作可能很有用,需要我们记住

list的常见操作

list子列表

注意使用子列表时是一个新对象,操作子列表与原始list无关
在快速排序和归并排序中不可将子列表传入,以期待可以从函数中修改原始列表的值

list反序子列表

list 反序列示例：

l = [1, 2, 3]
l1 = l[::-1]
print l
print l1
# # output:
# [1, 2, 3]
# [3, 2, 1]

list的罕见操作

remove(object)

移除列表中第一个与object相等的对象

l = [1, 2, 2, 3, 4]
l.remove(2)
print l

# # output:
# [1, 2, 3, 4]

pop(index)

从列表中移除一个元素,并返回该元素,index为索引

默认移除最后一个

l = [1, 2, 2, 3, 4, 5]
l.pop(0)
print l
l.pop()
print l
# # output:
# [2, 2, 3, 4, 5]
# [2, 2, 3, 4]

Python——双端队列deque

本文介绍Python中双端队列(double-ended queue, 简称为deque)的用法

导入包

1
2
from collections import deque
import collections

使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import collections
dq = collections.deque()
dq.append(3)
dq.append(4)
dq.append(1)
dq.appendleft(9)
dq.appendleft(10)
print dq
print dq.pop()
print dq
print dq.popleft()
print dq

while len(dq):
    print dq.pop()


# # output:
# deque([10, 9, 3, 4, 1])
# 1
# deque([10, 9, 3, 4])
# 10
# deque([9, 3, 4])
# 4
# 3
# 9

注意,deque没有qsize()函数,但是可以像普通队列一样使用Python内嵌的len函数

Python——自定义pip包的安装和打包

整体说明

打包本地项目为的 pip 包时，可以使用 pip install . 命令
执行 pip install . 命令时，Python 包管理工具 pip 会根据当前目录中的 setup.py 文件来安装包
- 这个过程涉及多个步骤，包括解析包的元数据、处理依赖关系、构建和安装包等
- 安装的内容包括包的所有模块、数据文件、编译文件以及命令行工具
- 默认情况下，只安装核心依赖，可选依赖需要用户显式指定

构建一个包的步骤

第一步：解析和构建

解析 setup.py (setup.py 的详细示例见附录)：
- pip 首先会查找并解析当前目录中的 setup.py 文件
- 读取包的元数据（如包名、版本、作者信息等）和安装选项（如 install_requires、extras_require 等）
构建包：
- pip 会使用 setuptools 或 distutils 来构建包
- 包的构建包括编译C扩展（如果存在）、处理包内的数据文件等
- 生成一个源代码分发包（Source Distribution，简称 sdist）或一个二进制分发包（Binary Distribution，简称 wheel）

第二步：处理依赖

安装核心依赖
- pip 会根据 setup.py 中的 install_requires 列表安装包的核心依赖
- 这些依赖是包运行所必须的
可选依赖
- 如果用户在命令中指定了可选依赖组（如 pip install .[dev]），pip 会安装对应的 extras_require 可选依赖
- 否则，默认情况下不会安装 extras_require 中的可选依赖

第三步：安装包**

导入包和模块
- pip 会将构建好的包安装到Python环境的 site-packages 目录中
- 包中的所有模块和子包都会被导入
包数据文件
- 如果 setup.py 中设置了 include_package_data=True 或指定了 package_data，这些数据文件也会被安装
命令行工具
- 如果 setup.py 中定义了 entry_points，对应的命令行工具会被安装并注册

第四步：打包内容

包和模块
- 所有通过 packages 或 find_packages() 指定的包和模块
数据文件
- 通过 package_data 或 include_package_data 指定的额外数据文件
编译文件
- 如果包中包含 C/C++ 扩展模块，这些模块会被编译并打包

附录：setup.py 文件的示例

setup.py 文件是 Python 项目中用于定义包的元数据、依赖关系及其他安装相关信息的脚本
setup.py 文件主要通过 setuptools 或 distutils 库来实现包的配置和分发

setup.py 文件示例

setup.py 文件基本结构示例：

from setuptools import setup, find_packages

setup(
    name="package_name",                # 包名
    version="0.1.0",                    # 版本号
    author="Author Name",               # 作者
    author_email="author@example.com",  # 作者邮箱
    description="A short description",  # 简短描述
    long_description=open("README.md").read(),  # 长描述（通常从README文件导入）
    long_description_content_type="text/markdown",  # 长描述类型（如Markdown）
    url="https://github.com/username/repo",  # 项目URL
    packages=find_packages(),           # 自动发现并包含所有包
    classifiers=[                      # 分类标签（如开发状态、受众、许可证）
        "Programming Language :: Python :: 3",
        "License :: OSI Approved :: MIT License",
        "Operating System :: OS Independent",
    ],
    python_requires='>=3.6',            # Python版本要求
    install_requires=[                  # 安装依赖
        "requests>=2.25.0",
        "numpy",
    ],
    extras_require={                    # 可选依赖（如开发、测试）
        "dev": ["pytest", "sphinx"],
    },
    entry_points={                      # 命令行工具入口
        "console_scripts": [
            "mycommand=mypackage.module:function",
        ],
    },
    include_package_data=True,          # 包含包内数据文件
    package_data={                      # 指定包数据文件
        "mypackage": ["data/*.dat"],
    },
    zip_safe=False,                     # 是否允许打包为zip文件
)

主要内容和功能说明

元数据：
- name ：包的名称
- version ：包的版本号，通常遵循语义版本规范（如 MAJOR.MINOR.PATCH）
- author 和 author_email ：作者的姓名和联系邮箱
- description 和 long_description ：包的简短和详细描述
- url ：项目的主页或代码仓库地址
包和模块：
- packages ：指定需要包含的包列表，通常使用 find_packages() 自动发现
- package_data ：指定需要包含的非代码文件（如数据文件、模板等）
依赖管理：
- install_requires ：安装包时需要满足的依赖列表
- extras_require ：可选依赖，按功能分组（如开发依赖、测试依赖）
Python 版本：
- python_requires ：指定包支持的Python版本范围
分类标签：
- classifiers ：用于描述包的特性和分类，帮助用户和工具识别包的适用性
命令行工具：
- entry_points ：定义包提供的命令行工具及其入口函数
数据文件：
- include_package_data ：是否包含包内的额外数据文件
打包选项：
- zip_safe ：指定包是否可以安全地打包为zip文件

附录：`setup.py` 中的 `extras_require` 使用

在 setup.py 中定义的 extras_require 提供了一种机制，可以按需安装额外的依赖项
extras_require 允许定义一些可选的依赖组，比如开发依赖、测试依赖等
举例来说，前面附录小节的示例中 extras_require 中定义了一个名为 “dev” 的组和对应的依赖
默认情况下 ，安装包时不会自动安装 extras_require 中定义的可选依赖项
- 直接使用 pip install . 或 pip install package_name 安装包即可
- 在这种情况下，只有 install_requires 中定义的核心依赖会被安装
安装可选依赖，以安装 “dev” 组的可选依赖为例：
- 使用 pip 安装时，可以通过在包名后加上 [dev] 来指定安装这些可选依赖
  1
  pip install .[dev]
- 如果包已经发布到PyPI或其他包管理平台，可以使用以下命令：
  1
  pip install package_name[dev]

Python——装饰器decorator

Python中的装饰器可以在不修改原始函数代码的基础上,在Python函数中插入一些额外操作

参考博客:https://ask.hellobi.com/blog/pythoneer

简单装饰器

装饰器定义

def decorator(func):
    def wrapper(*args, **kwargs): 
        print "decorator" # 每次函数 func 被调用时都会输出
        return func(*args, **kwargs)
    print "only once decorator" # 仅在函数定义时执行一次
    return wrapper

装饰器使用

@decorator
def add(a, b):
    print "sum: ", a+b
# 函数定义时输出：only once decorator

# just like a normal function
add(10, 20)

# output:
decorator
sum:  30

注意：函数定义时还会输出一次

装饰器是一种语法糖

实际上上面的代码等价于

def add(a, b):
    print "sum: ", a+b

add = decorator(add)

# test is a normal
add()

# output:
decorator
sum:  30

带参数的装饰器

需要对装饰器进一步的封装

def outterDecorator(tag):
    def decorator(func):
        def wrapper(*args, **kwargs):
            print "decorator: " + tag
            return func(*args, **kwargs)
        return wrapper
    return decorator

@outterDecorator(tag="123")
def test():
    print "inner test"

@outterDecorator("abc")
def add(a, b):
    print "sum: ", a+b

test()

add(10, 20)
# output
decorator: 123
inner test
decorator: abc
sum:  30

在原始的装饰器外面封装一层函数，用于接受参数，其他的不用改变

理解：
- 等价于给装饰器加了一层接受参数的外层空间
- 实际上调用的时候除了参数外，其他的都没变
- 被装饰的函数依然是被作为内层函数的参数传入装饰器中

类装饰器

类装饰器的简单示例

class Foo(object):
    def __init__(self, func):
        self._func = func

    def __call__(self):
        print ('class decorator runing')
        self._func()
        print ('class decorator ending')

@Foo
def bar():
    print ('bar')

bar()
# output
class decorator runing
bar
class decorator ending

如上述代码所示,类装饰器必须有__init__和__call__两个函数
__init__负责接受被装饰函数作为参数并存储该函数
__call__负责执行函数调用过程并执行想要插入函数的代码
被装饰的函数被调用时本质上是__call__函数被调用

类装饰器的优点

灵活度高
高内聚,不像函数一样定义在外面
封装的好,容易阅读

多个装饰器的顺序问题

@a
@b
@c
def f ():
    pass

函数可以同时被多个装饰器修饰
装饰器的顺序从靠近函数的那个开始从内向外一层层封装
1
f = a(b(c(f)))

装饰器对原始函数的属性修改

涉及到docstring,__name__等属性

# 装饰器
def logged(func):
    def with_logging(*args, **kwargs):
        print func.__name__      # 输出 'with_logging'
        print func.__doc__       # 输出 None
        return func(*args, **kwargs)
    return with_logging

# 函数
@logged
def f(x):
   """does some math"""
   return x + x * x

logged(f)

使用functools.warps装饰器可以修复原始函数的文档

from functools import wraps
def logged(func):
    @wraps(func)
    def with_logging(*args, **kwargs):
        print func.__name__      # 输出 'f'
        print func.__doc__       # 输出 'does some math'
        return func(*args, **kwargs)
    return with_logging

@logged
def f(x):
   """does some math"""
   return x + x * x

property装饰器

用于类的属性

class Student(object):
    def __init__(self, birth):
        self._birth = birth

    @property
    def birth(self):
        return self._birth

    @birth.setter
    def birth(self, value):
        self._birth = value

    @property
    def age(self):
        return 2014 - self._birth:

当加上property装饰器后,函数就变成了一个只读属性,被修饰的函数不能再当成普通函数
- 当前函数不能有参数,除非是默认参数,因为当前函数变成属性后,直接调用
  1
  s.birth(10)
  - 解析是s.birth返回一个属性值,然后,属性值不能被调用,所以抛出异常
property装饰器会生成两个新的装饰[method_name].setter和[method_name].getter,分别用于代表当前函数对应属性的的写和读功能,读的功能默认加上了,写的功能需要的话我们可以使用[method_name].setter装饰器实现
总结: property装饰器可以将类的某个属性封装起来(在不暴露类属性的情况下提供getter方法和setter方法(后者需要自己显示定义))

Python——解包与*args和**kwargs参数

整体说明

在 Python 中，*和**的主要用途有两个
- 作为解包操作符 ：用于解包（unpacking）序列或字典
- 在函数定义和调用时处理可变参数
  - * 用于接收可变数量的位置参数，被称为 “可变位置参数”（variable positional arguments）
  - ** 用于接收可变数量的关键字参数，被称为 “可变关键字参数”（variable keyword arguments）

`*`解包操作（序列解包）

*操作符用于解包可迭代对象（如列表、元组、字符串、生成器等），将其元素单独提取出来

函数调用时解包

函数调用时解包参数 Demo：

def add(a, b, c):
	return a + b + c
numbers = [1, 2, 3]
result = add(*numbers)  # 等同于 add(1, 2, 3)
print(result)  # 输出: 6

在赋值语句中解包

赋值语句中解包 Demo

a, *b, c = [1, 2, 3, 4, 5]
print(a)  # 输出: 1
print(b)  # 输出: [2, 3, 4]
print(c)  # 输出: 5

合并列表或元组

合并列表或元组时解包 Demo

# 合并列表
list1 = [1, 2]
list2 = [3, 4]
merged = [*list1, *list2]  # 等同于 [1, 2, 3, 4]
# 合并元组和列表
t = (1, 2)
l = [3, 4]
merged = [*t, *l]  # 等同于 [1, 2, 3, 4]

`**`解包操作（字典解包）

**操作符用于解包字典，将其键值对作为参数传递给函数

在函数调用时解包字典

函数调用时解包 Demo：

def greet(name, age):
	return f"Hello {name}, you are {age} years old."
person = {"name": "Alice", "age": 30}
message = greet(**person)  # 等同于 greet(name="Alice", age=30)
print(message)  # 输出: "Hello Alice, you are 30 years old."

合并字典（Python 3.5 以上版本才能使用）

合并字典解包 Demo：

1
2
3

dict1 = {"a": 1, "b": 2}
dict2 = {"c": 3, "d": 4}
merged = {**dict1, **dict2}  # 等同于 {"a": 1, "b": 2, "c": 3, "d": 4}

`*args`作为函数参数（可变位置参数）

*args用于接收任意数量的位置参数（也称为非关键字参数），并将它们作为元组处理

*args作为函数参数 Demo

def sum_numbers(*args):
	total = 0
	for num in args:
		total += num
	return total
result = sum_numbers(1, 2, 3, 4)  # args = (1, 2, 3, 4)
print(result)  # 输出: 10

说明：
- args是元组类型（解包时可以解所有序列，包括列表、元组、字符串、生成器等）
- 可以不传递参数，此时args为空元组
- 定义时*args必须放在普通参数和**kwargs之间（如def func(a, *args, **kwargs)）

`**kwargs`作为函数参数（可变关键字参数）

**kwargs用于接收任意数量的关键字参数 ，并将它们作为字典处理

**kwargs作为函数参数 Demo：

def print_info(**kwargs):
	for key, value in kwargs.items():
		print(f"{key}: {value}")
print_info(name="Bob", age=25, city="New York")
# 输出:
# name: Bob
# age: 25
# city: New York

说明：
- kwargs是字典类型
- 可以不传递参数，此时kwargs为空字典
- 必须放在参数列表的最后（如def func(a, *args, b=1, **kwargs)）

组合使用`*args`和`**kwargs`

函数可以同时接受*args和**kwargs，顺序必须是：def func(positional, *args, **kwargs)

组合使用*args和**kwargs的 Demo：

def example(a, *args, **kwargs):
	print(f"Positional: {a}")  # 必传参数
	print(f"Args: {args}")     # 可选的位置参数
	print(f"Kwargs: {kwargs}")  # 可选的关键字参数
example(1, 2, 3, x=4, y=5)
# 输出:
# Positional: 1
# Args: (2, 3)
# Kwargs: {'x': 4, 'y': 5}

说明：

普通参数也可以不传递，此时只剩下*args和**kwargs两种参数

在使用了**kwargs时，也可以继续使用关键字参数，但必须放到*args和**kwargs之间

def example(a, *args, y=10, **kwargs) 
# def example(a, *args, **kwargs, y=10) # error
``` 
* 注：函数调用时，关键字参数和`**kwargs`的顺序没有限制，但位置参数的位置不能变化
	```python
	def example(a, *args, y=10, **kwargs) 
	def example(1, 2, 3, x=4, y=5, y=10) # 关键字参数 y 的顺序变化是可以的

深入理解：放到*args和**kwargs之间的参数，必须按照关键字参数使用（定义时可以位置式的样子定义）

1
2
3

def example(a, *args, n, **kwargs)
example(1, 2, 3, n=10, x=4, y=5) # 正确，n 应该指定关键字参数使用
# example(1, 2, 3, 10, x=4, y=5) # 报错，n 应该指定关键字参数使用

常见用法

函数包装器（Decorator）透传参数

函数包装器透传参数 Demo：

def my_decorator(func):
	def wrapper(*args, **kwargs):
		print("Before function call")
		result = func(*args, **kwargs)  # 传递所有参数给原函数
		print("After function call")
		return result
	return wrapper

@my_decorator
def add(a, b):
	return a + b

继承中的参数透传

继承时参数透传 Demo：

class Parent:
	def __init__(self, name, **kwargs):
		self.name = name

class Child(Parent):
	def __init__(self, age, *args, **kwargs):
		super().__init__(*args, **kwargs)  # 传递剩余参数给父类
		self.age = age

c = Child(age=10, name="Alice")

使用注意事项

*args是非关键字参数（也称为位置参数），对应参数args为元组类型，可表示任何多个无名参数
**kwargs是关键字参数 ，对应参数kwargs为字典（dict）类型，可表示任何多个命名参数
顺序必须是：1）普通参数；2）*args；3）**kwargs的形式
- 举例：def func(a, *args, **kwargs)
- 其中普通参数、*args和**kwargs三个参数都是可选的，可以丢弃任意一个，但是相对顺序必须保障
- 放在 *args和**kwargs之间的参数一定是关键字参数

将序列解包为函数参数时要保证参数数量匹配 ：

def func(a, b):
    return a + b
args = [1, 2, 3]
func(*args)  # 报错：TypeError，参数数量不匹配

将字典解包为函数参数时要保证键名匹配 ：

def func(name, age):
    pass
kwargs = {"name": "Alice", "city": "NY"}  # 键名不匹配
func(**kwargs)  # 报错：TypeError，'city' 不是有效参数

附录：特殊用法指定参数为关键字参数

如果在函数定义时使用 *，则后面的所有参数必须通过关键字形式传入

举例：

1
2
3

# 调用 f 函数时，b 和 c 必须使用关键字传入，否则出错
def f(a, *, b=1, c=None)
	pass

RS——SENet

参考链接
- 原始论文：Squeeze-and-Excitation Networks

整体说明

SENet（Squeeze-and-Excitation Network）是一种用于图像识别等领域的神经网络架构，通过显式地建模通道之间的相互依赖关系，自适应地调整特征通道的重要性 ，从而提高模型的性能
在CV领域爆火后，近年来，SENet也被广泛应用于推荐系统中
一句话说明：SENet可以给与不同通道不同的权重，从而实现图片的重构（不同通道被乘以不同权重）

SENet整体结构

整体结构图如下：
Squeeze层（$\mathbf{F}_{sq}$）：
- 输入：特征图$U \in \mathbb{R}^{H \times W \times C}$，其中$H$、$W$、$C$分别表示特征图的高度、宽度和通道数
- 输出：一个长度为$C$的向量$z \in \mathbb{R}^{C}$
- 公式：$z_c = \mathbf{F}_{sq}(U_c)=\frac{1}{H\times W}\sum_{i=1}^{H}\sum_{j=1}^{W}U_c(i,j)$，即对每个通道的特征图进行全局平均池化，将二维的特征图压缩成一个实数，得到通道的全局统计信息
Excitation层（（$\mathbf{F}_{ex}$））：
- 输入：Squeeze层输出的向量$z$
- 输出：与输入特征图通道数相同的权重向量$s \in \mathbb{R}^{C}$，用于表示每个通道的重要性
- 公式：$s = \mathbf{F}_{ex}(z, W)= \sigma(g(z, W))=\sigma(W_2\delta(W_1z))$，其中$\sigma$是sigmoid函数，$\delta$是ReLU函数，$W_1 \in \mathbb{R}^{\frac{C}{r} \times C}$和$W_2 \in \mathbb{R}^{C \times \frac{C}{r} }$是两个全连接层的权重矩阵，$r$是一个缩减比例超参数，用于控制中间神经元的数量，减少模型复杂度
Scale层（（$\mathbf{F}_{scale}$））：也称为Reweight
- 输入：原始特征图$U$和Excitation层输出的权重向量$s$
- 输出：经过通道加权后的特征图$\tilde{U} \in \mathbb{R}^{H \times W \times C}$
- 公式：$\tilde{U}_c = \mathbf{F}_{scale}(U_c, s_c)=s_c \cdot U_c$，即将权重向量$s$与原始特征图$U$的每个通道对应相乘，实现对特征图的自适应加权
注：$\mathbf{F}_{tr}$ 是一个转换操作，跟SENet没有直接关系，在 CV 里面就是一个普通的卷积神经网络

在CV领域的使用

图像分类 ：SENet可以嵌入到各种经典的图像分类网络中，如ResNet、Inception等，通过对特征通道的自适应加权 ，能够更好地捕捉图像中的重要特征 ，抑制图片中的无关特征 ，从而提高分类准确率
目标检测 ：在目标检测任务中，SENet有助于模型更准确地定位和识别目标物体。它可以增强与目标相关的特征通道 ，使模型对目标的细节和特征更加敏感，提高检测的精度和召回率
语义分割 ：对于语义分割任务，SENet能够帮助模型更好地理解图像中的语义信息，通过调整通道权重 ，突出不同语义类别对应的特征 ，从而更精确地分割出不同的物体和区域
在 Inception 模块中的嵌入方式
在 Residual 模块中的嵌入方式

在推荐系统中的使用

特征加权 ：在推荐系统中，将用户和物品的特征类比为图像中的特征通道。SENet可以学习不同特征的重要性权重，对用户行为特征、物品属性特征等进行自适应加权，强调对推荐结果有重要影响的特征，提高推荐的准确性
- 理解：可以将SENet应用于用户的嵌入向量、物品的嵌入向量或者深度神经网络中的隐藏层输出，SENet可以对不同特征给与不同的权重（这里的特征和CV中的通道类似），相当于是一种特征重要性抽取器
- 举例：假设输入 $N \times d$ 维特征矩阵 ，有 $N$ 个特征，每个特征是 $d$ 维的 Embedding，则：
  - Squeeze层 ：将每个特征 Embedding 从 $d$ 维度降低到 1 维标量，输出 $N$ 维向量
  - Excitation层 ：用一个MLP将 $N$ 维向量先压缩到 $\frac{N}{r}$ 维再扩展为 $N$ 维
  - Scale层（Re-weight） ：将 $N$ 维向量作为权重对原始 $N \times d$ 维的特征矩阵进行加权，输出 $N \times d$ 维特征矩阵 ，此时每个特征都有自己的个性化权重
- SENet的本质是对输入 Embedding 做 field-wise 加权（这里认为每个特征就是不同的 field）
注意力机制 ：类似于在CV领域中捕捉图像中的重要信息，SENet在推荐系统中可以作为一种注意力机制，聚焦于用户和物品的关键特征，从而更好地建模用户与物品之间的交互关系，为用户提供更个性化的推荐

DL——FLOPS和FLOPs定义辨析

整体说明

FLOPS（Floating-Point Operations Per Second）和FLOPs（Floating-Point Operations）是衡量计算性能的两个相关但含义不同的术语
FLOPs 是浮点运算次数 ，是模型复杂度的评估指标，用于评估一个模型的复杂度
FLOPS 是每秒浮点运算次数 ，是硬件计算能力的单位，比如用于评估 GPU 性能

FLOPs（Floating-Point Operations）

FLOPs 是 浮点运算次数 ，即模型或算法执行的总浮点计算量（如加、减、乘、除等操作数量）
FLOPs 常用于衡量算法/模型的计算复杂度 ，举例：
- 矩阵乘法中，两个 $ n \times n $ 矩阵相乘需要 $ 2n^3 $ FLOPs（$ n \times n $个数，每个数需要 $n$ 次乘法和 $n$ 次加法操作）
- 在深度学习中，FLOPs常用来估计模型的计算开销（如卷积层的计算量）
1 GFLOPs = 10亿次运算（算法复杂度）
注：”s” 为小写，表示复数（Operations）
用法：ResNet-50 模型约需 3.8 GFLOPs（38亿次浮点运算）处理一张图像
- 注意这里的十亿用的是 G，而不是 B，两者都有十亿的含义，但不同地方用不同的值

FLOPS（Floating-Point Operations Per Second）

FLOPS 是每秒浮点运算次数 ，是硬件计算能力的单位
FLOPS 常用于衡量处理器（如CPU/GPU）的理论峰值性能。例如：
- 1 FLOPS = 1次浮点运算/秒
- 1 TFLOPS（Tera-FLOPS）= $ 10^{12} $ 次浮点运算/秒
1 GFLOPS = 10亿次运算/秒（硬件速度）
注：”S” 为大写，代表 “Second”（每秒）
用法：NVIDIA A100 GPU的峰值性能为 312 TFLOPS

一些常见错误表达

错误的写法如 “Flops” 或 “flops” 可能导致歧义，建议严格区分大小写

ML——EM算法

期望最大化(Exception Maximization Algorithm)EM算法

不同教材的不同形式

李航统计学习方法

算法步骤

输入: 观测变量数据Y
输出: 模型(参数 $\theta$)
E步: 计算 $Q(\theta, \theta^{i})$
$$
\begin{align}
Q(\theta, \theta^{i}) &= \mathbb{E}_{Z}[logP(Y,Z|\theta)|Y,\theta^{i}] \\
&= \mathbb{E}_{Z\sim P(Z|Y,\theta^{i})}[logP(Y,Z|\theta)] \\
&= \sum_{Z} P(Z|Y,\theta^{i})logP(Y,Z|\theta) \\
&= \sum_{Z} logP(Y,Z|\theta)P(Z|Y,\theta^{i})
\end{align}
$$
M步: 求使得 $Q(\theta, \theta^{i})$ 极大化的参数 $\theta=\theta^{i+1}$
$$\theta^{i+1} = \mathop{\arg\max}_{\theta}Q(\theta, \theta^{i})$$
重复E步和M步,直到收敛
理解: $Q(\theta, \theta^{i})$ 可以理解为 $Q(\theta|\theta^{i})$，表示在参数 $\theta^{i}$ 已知的情况下,对数似然函数关于隐变量后验分布的期望函数,函数的参数为 $\theta$

隐变量的期望还是分布?

参考博客:https://www.jianshu.com/p/c3ff1ae5cb66

仅考虑隐变量的期望

应用场景为k-means聚类,但是k-means聚类E步求的是最可能的 $Z$ 值(概率最大的 $Z$ 值),而不是 $Z$ 的期望

步骤	具体细节
E步	基于 $\theta^{i}$ 推断隐变量 $Z$ 的期望,记为 $Z^{i}$
M步	基于已观测变量 $Y$ 和 $Z^{i}$ 对参数 $\theta$ 做极大似然估计,得到 $\theta^{i+1}$ $$\theta^{i+1}=\mathop{\arg\max}_{\theta}P(Y,Z^{i}\mid\theta)$$

考虑隐变量的分布

应用场景为GMM模型聚类

步骤	具体细节
E步	基于 $\theta^{i}$ 推断隐变量 $Z$ 的后验分布 $P(Z\mid Y,\theta^{i})$
E步M步均可	基于隐变量的后验分布 $P(Z\mid Y,\theta^{i})$ 计算对数似然函数 $logP(Y,Z\mid\theta)$ 关于隐变量 $Z$ 的后验分布 $P(Z\mid Y,\theta^{i})$ 的期望 $Q(\theta,\theta^{i})$ $$Q(\theta,\theta^{i}) = \mathbb{E}_{P(Z\mid Y,\theta^{i})}logP(Y,Z\mid \theta)$$
M步	基于期望函数 $Q(\theta, \theta^{i})$，对参数 $\theta$ 求极值(极大似然估计),得到$$\theta^{i+1}=\mathop{\arg\max}_{\theta}Q(\theta, \theta^{i})=\mathop{\arg\max}_{\theta}\mathbb{E}_{P(Z\mid Y,\theta^{i})}logP(Y,Z\mid \theta)$$

推导

已知数据是观测数据Y,像极大似然法一样,使得似然函数最大化即可,这里为了方便计算使用对数似然
我们的终极目标与极大似然法一样,求一个使得似然函数最大(可能是极大)的参数$$\theta^{\star}=\mathop{\arg\max}_{\theta}L(\theta)$$
其中
$$
\begin{align}
L(\theta)&=logP(Y|\theta)\\
&=log\sum_{Z}P(Y,Z|\theta)\\
&=log\left(\sum_{Z}P(Y|Z,\theta)P(Z|\theta)\right)
\end{align}
$$
显然,上述似然函数比较难以求解,非凸,且涉及和(积分或加法)的对数等操作,难以展开(可能还有其他的原因)
所以我们使用EM算法迭代不断逼近原始似然函数的最优解 $\theta^{\star}$ (注意:我们只能得到局部最优,但是一般来说局部最优也够用了)
可用Jensen不等式得到 $L(\theta)$ 的下界来作为优化目标不断迭代
$$
\begin{align}
L(\theta)&=log\left(\sum_{Z}P(Y|Z,\theta)P(Z|\theta)\right)\\
&=log\left(\sum_{Z}P(Z|Y,\theta^{i})\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{i})}\right)\\
&\geq \sum_{Z}P(Z|Y,\theta^{i})log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{i})}\\
&=B(\theta,\theta^{i})
\end{align}
$$
由于此时 $B(\theta, \theta^{i})$ 是 $L(\theta)$ 的下界($B(\theta, \theta^{i})$ 是固定 $\theta^{i}$ 时关于 $\theta$ 的凸函数且容易求导,可以求极大值),所以使得前者增大的参数 $\theta$ 也能使得后者增大,为了使得后者尽可能的增大,我们对前者取极大值
- 下面的推导基于事实: 消去与 $\theta$ 无关的项,极大值点($\theta^{i+1}$)不变

$$
\begin{align}
\theta^{i+1} &= \mathop{\arg\max}_{\theta}B(\theta,\theta^{i})\\
&=\mathop{\arg\max}_{\theta}\left( \sum_{Z}P(Z|Y,\theta^{i})log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{i})}\right)\\
&=\mathop{\arg\max}_{\theta}\left( \sum_{Z}P(Z|Y,\theta^{i})logP(Y|Z,\theta)P(Z|\theta)-\sum_{Z}P(Z|Y,\theta^{i})logP(Z|Y,\theta^{i})\right)\\
&= \mathop{\arg\max}_{\theta}\left( \sum_{Z}P(Z|Y,\theta^{i})logP(Y|Z,\theta)P(Z|\theta)\right)\\
&=\mathop{\arg\max}_{\theta}Q(\theta,\theta^{i})
\end{align}
$$

由上式可知,我们的EM算法步骤中E步和M步是正确的
问题:推导第二步中为什么选择 $P(Z|Y,\theta^{i})$ 而不是其他分布呢?
- 解答: $B(\theta, \theta^{i})$ 和 $L(\theta)$ 什么时候相等呢?(前面推导中Jensen不等式什么时候能取等号呢?)
- Jensen不等式取等号当且仅当Jensen不等式中函数的值为常数,此处函数的值为 $log\frac{P(Y,Z|\theta)}{Q(Z)}$
  $$
  \begin{align}
  L(\theta)&=log\left(\sum_{Z}P(Y,Z|\theta)\right)\\
  &=log\left(\sum_{Z}Q(Z)\frac{P(Y,Z|\theta)}{Q(Z)}\right)\\
  &\geq \sum_{Z}Q(Z)log\frac{P(Y,Z|\theta)}{Q(Z)}\\
  \end{align}
  $$
- 不等式中当且仅当 $log\frac{P(Y,Z|\theta)}{Q(Z)}$ 为常数,也就是 $\frac{P(Y,Z|\theta)}{Q(Z)}=c$，c为常数,时等号成立
- 此时由于 $Q(Z)$ 是一个分布(注意:正因为 $Q(Z)$ 是一个分布才能用Jensen不等式),所以有
  $$
  \begin{align}
  Q(Z)=\frac{P(Y,Z|\theta)}{\sum_{Z}P(Y,Z|\theta)}=\frac{P(Y,Z|\theta)}{P(Y|\theta)}=P(Z|Y,\theta)
  \end{align}
  $$

吴恩达CS229

E步: 计算 $Q_{i}(Z)=P(Z|Y,\theta^{i})$
M步: 求使得原始似然函数下界极大化的参数 $\theta=\theta^{i+1}$
$$
\begin{align}
\theta^{i+1} &= \mathop{\arg\max}_{\theta}\sum_{Z}P(Z|Y,\theta^{i})log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{i})} \\
&= \mathop{\arg\max}_{\theta}\sum_{Z}Q_{i}(Z)log\frac{P(Y|Z,\theta)P(Z|\theta)}{Q_{i}(Z)}
\end{align}
$$
- 进一步消除与 $\theta$ 无关的项可以得到
  $$
  \begin{align}
  \theta^{i+1} &= \mathop{\arg\max}_{\theta}\sum_{Z}Q_{i}(Z)logP(Y|Z,\theta)P(Z|\theta)
  \end{align}
  $$
推导步骤和李航统计学习方法一样,核心是运用Jensen不等式

总结

以上两个不同课程的E步不同,但完全等价,吴恩达CS229课程中E步计算 $Q_{i}(Z)=P(Z|Y,\theta^{i})$ 就等价于计算出了李航统计学习方法中的 $Q(\theta, \theta^{i})$，二者关系如下:
$$
\begin{align}
Q(\theta, \theta^{i})&=\sum_{Z}P(Z|Y,\theta^{i})logP(Y|Z,\theta)P(Z|\theta) \\
&= \sum_{Z}Q_{i}(Z)logP(Y|Z,\theta)P(Z|\theta)
\end{align}
$$
M步中,二者本质上完全相同,但是吴恩达CS229中没消去与 $\theta$ 无关的项,所以看起来不太简洁

实例

实例一

三个硬币的抛硬币问题
- 第一次:抛硬币A,决定第二次抛C还是B,选中B的概率为 $\pi$
- 第二次:抛硬币B或C,正面为1,反面为0
(第一个硬币A抛中B的概率为隐变量)

实例二

200个人不知道男女的身高拟合问题(性别为隐变量)
这里是高斯混合模型的代表

实例三

K-Means聚类
参考<<百面机器学习>>P100-P101

进一步理解

我的理解

初始化参数 $\theta^{0}$
1.根据参数 $\theta^{i}$ 计算当前隐变量的分布函数 $Q_{i}(Z)=P(Z|Y,\theta^{i})$
- 这一步的本质是使得在参数 $\theta = \theta^i$ 时, 求得一个隐变量 $Z$ 的分布,使得原始式子中的不等式取等号
2.根据 $Q_{i}(Z)=P(Z|Y,\theta^{i})$ 得到对数似然函数下界函数 $B(\theta, \theta^{i})$ (求原始似然函数的下界B函数是因为直接对原始似然函数求极大值很难)或者 $Q(\theta,\theta^{i})$
$$\mathop{\arg\max}_{\theta}B(\theta, \theta^{i})=\mathop{\arg\max}_{\theta}Q(\theta,\theta^{i})$$
($Q(\theta,\theta^{i})$ 可以看作是 $B(\theta, \theta^{i})$ 的简化版, $B(\theta, \theta^{i})$ 才是原始似然函数的下界, $Q(\theta,\theta^{i})$ 不是原始似然函数的下界)
- 这里 $B(\theta, \theta^{i})$ 就是原始似然函数的下界(也就是不等式取到等号)
3.求使得函数 $B(\theta, \theta^{i})$ 极大化的参数 $\theta=\theta^{i+1}$
- 这一步是在固定隐变量 $Z$ 的分布时, 用极大似然求一个使得下界 $B(\theta, \theta^{i})$ 最大的参数 $\theta = \theta^{i+1}$ 使得 $B(\theta^{i+1}, \theta^{i}) = \text{max} B(\theta, \theta^{i})$
4.循环1,2,3直到收敛(相邻两次参数的变化或者是似然函数的变化足够小即可判断为收敛)
- $||\theta^{i+1}-\theta^{i}||<\epsilon_{1}$ 或者 $||Q(\theta^{i+1},\theta^{i})-Q(\theta^{i},\theta^{i})||<\epsilon_{2}$
总结:
- 在吴恩达CS229课程中: E步包含1, M步包含2,3,其中第2步中求的是 $B(\theta, \theta^{i})$
- 在李航<<统计学习方法>>中: E步包含1,2, M步包含3,其中第2步中求的是 $Q(\theta,\theta^{i})$
- 两种表达等价

图示理解

迭代图示如下图(图来自博客:https://www.cnblogs.com/xieyue/p/4384915.html)

也可参考李航<<统计学习方法>>第160页的图和解释

收敛性

参考李航<<统计学习方法>>第160页-第162页推导过程
参考<<百面机器学习>>第P099页-第P100页
- 核心思想原始函数单调有界
- 原始函数为 $L(\theta)$，函数下界为 $B(\theta,\theta^{i})$
- E步:
  - 找到使得在当前 $\theta^{i}$ 确定时,原始函数的下界 $B(\theta, \theta^{i})$，在 $\theta^{i}$ 处有
    
    $$
    \begin{align}
    L(\theta^{i}) = B(\theta,\theta^{i})
    \end{align}
    $$
- M步:
  - 找到使得函数 $B(\theta,\theta^{i})$ 取得极大值的 $\theta^{i+1}$
- i = i + 1,然后重新开始E和M步
  $$
  \begin{align}
  L(\theta^{i+1}) >= L(\theta^{i+1})
  \end{align}
  $$
- 所以函数是单调的
- 由于 $L(\theta)$ 有界(这里原始函数有界可以从似然函数的定义得到)
- 函数单调有界=>函数收敛(数学分析中的定理)

优劣性

优势

简单性
普适性

劣势

不能保证收敛到最大值,只能保证收敛到极大值
对初始值敏感,不同初始值可能收敛到不同极值点
实际使用时通常采用多次选择不同的初始值来进行迭代,最终对估计值选最好的

EM算法的推广

引入F函数

GEM1

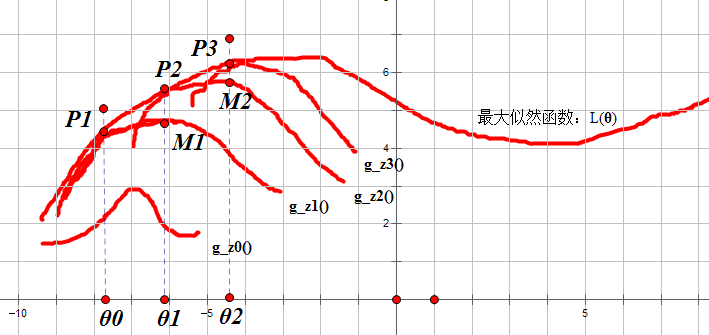
F函数极大-极大法

初始化参数 $\theta^{0}$
E步: 求使得 $F(\tilde{P},\theta^{i})$ 极大化的 $\tilde{P}^{i+1}$
M步: 求使得 $F(\tilde{P}^{i+1},\theta)$ 极大化的 $\theta^{i+1}$
重复E,M,直到收敛

GEM2

初始化参数 $\theta^{0}$
E步: 计算 $Q(\theta,\theta^{i})$
M步: 求 $\theta^{i+1}$ 使得 $Q(\theta^{i+1},\theta^{i}) > Q(\theta^{i},\theta^{i})$
重复E,M,直到收敛
总结: $Q(\theta,\theta^{i})$ 的极大化难求时,这种方法可以简化计算

GEM3

初始化参数 $\theta^{0}$
E步: 计算 $Q(\theta,\theta^{i})$
M步: 对参数 $\theta^{i}$ 的每一个维度k,固定参数的其他维度,求使得 $Q(\theta,\theta^{i})$ 极大化的 $\theta_{k}^{i+1}$，最终得到 $\theta^{i+1}$
- 使得 $Q(\theta^{i+1},\theta^{i}) > Q(\theta^{i},\theta^{i})$
重复E,M,直到收敛
总结: 一种特殊的GEM算法,将M步分解为参数 $\theta$ 的维度次来条件极大化

Joe Zhou

Stay Hungry. Stay Foolish.

GitHub E-Mail

Python的数值对象

导入包

使用

Python中的内嵌对象比较大小

Python自定义对象比较大小

list的常见操作

list子列表

list反序子列表

list的罕见操作

remove(object)

pop(index)

导入包

使用

整体说明

构建一个包的步骤

第一步：解析和构建

第二步：处理依赖

第三步：安装包**

第四步：打包内容

附录：setup.py 文件的示例

setup.py 文件示例

主要内容和功能说明

附录：setup.py 中的 extras_require 使用

简单装饰器

装饰器是一种语法糖

带参数的装饰器

类装饰器

类装饰器的优点

多个装饰器的顺序问题

装饰器对原始函数的属性修改

property装饰器

整体说明

*解包操作（序列解包）

函数调用时解包

在赋值语句中解包

合并列表或元组

**解包操作（字典解包）

在函数调用时解包字典

合并字典（Python 3.5 以上版本才能使用）

*args作为函数参数（可变位置参数）

**kwargs作为函数参数（可变关键字参数）

组合使用*args和**kwargs

常见用法

函数包装器（Decorator）透传参数

继承中的参数透传

使用注意事项

附录：特殊用法指定参数为关键字参数

整体说明

SENet整体结构

在CV领域的使用

在推荐系统中的使用

整体说明

FLOPs（Floating-Point Operations）

FLOPS（Floating-Point Operations Per Second）

一些常见错误表达

不同教材的不同形式

李航统计学习方法

算法步骤

隐变量的期望还是分布?

仅考虑隐变量的期望

考虑隐变量的分布

推导

吴恩达CS229

总结

实例

实例一

实例二

实例三

进一步理解

我的理解

图示理解

收敛性

优劣性

优势

劣势

EM算法的推广

GEM1

GEM2

GEM3

附录：`setup.py` 中的 `extras_require` 使用

`*`解包操作（序列解包）

`**`解包操作（字典解包）

`*args`作为函数参数（可变位置参数）

`**kwargs`作为函数参数（可变关键字参数）

组合使用`*args`和`**kwargs`