Hive——一些使用笔记

笔记记录，持续更新

Union操作和Union All操作

Union ：会对合并后的结果集进行去重操作，也就是会把重复的行去除，只保留其中一行
- 注意：使用Union时，同一个表的数据也会被去重
Union All ：不会进行去重操作 ，它会将所有查询结果集中的行全部保留（可存在重复的行）
特别注意：使用Union时，可能出现两个表Union后行数不如两个表分开统计行数的情况

Java——Logger变量命名规则

一般Java常量命名规范

Java中的常量名称一般用全大写，比如美团，阿里等公司均有相关要求，详情参考阿里巴巴Java开发手册.pdf

一个特殊的例子——Logger

特殊写法

Spring中Logger对象的名称使用的是小写

1	private static final Logger logger= LoggerFactory.getLogger(BeanFactory.class);

其他很多公司或者开源工具的代码也跟着这样用，比如美团的RPC开源框架mtthrift

Logger对象使用final的原因

定义成static final,logger变量不可变，读取速度快
static 修饰的变量是不管创建了new了多少个实例，也只创建一次，节省空间，如果每次都创建Logger的话比较浪费内存；final修饰表示不可更改，常量
将域定义为static,每个类中只有一个这样的域。而每一个对象对于所有的实例域却都有自己的一份拷贝，用static修饰既节约空间，效率也好。final 是本 logger 不能再指向其他 Logger 对象

为什么不适用大写

Spring开发者有自己的编程规范
- 常量引用不用大写？
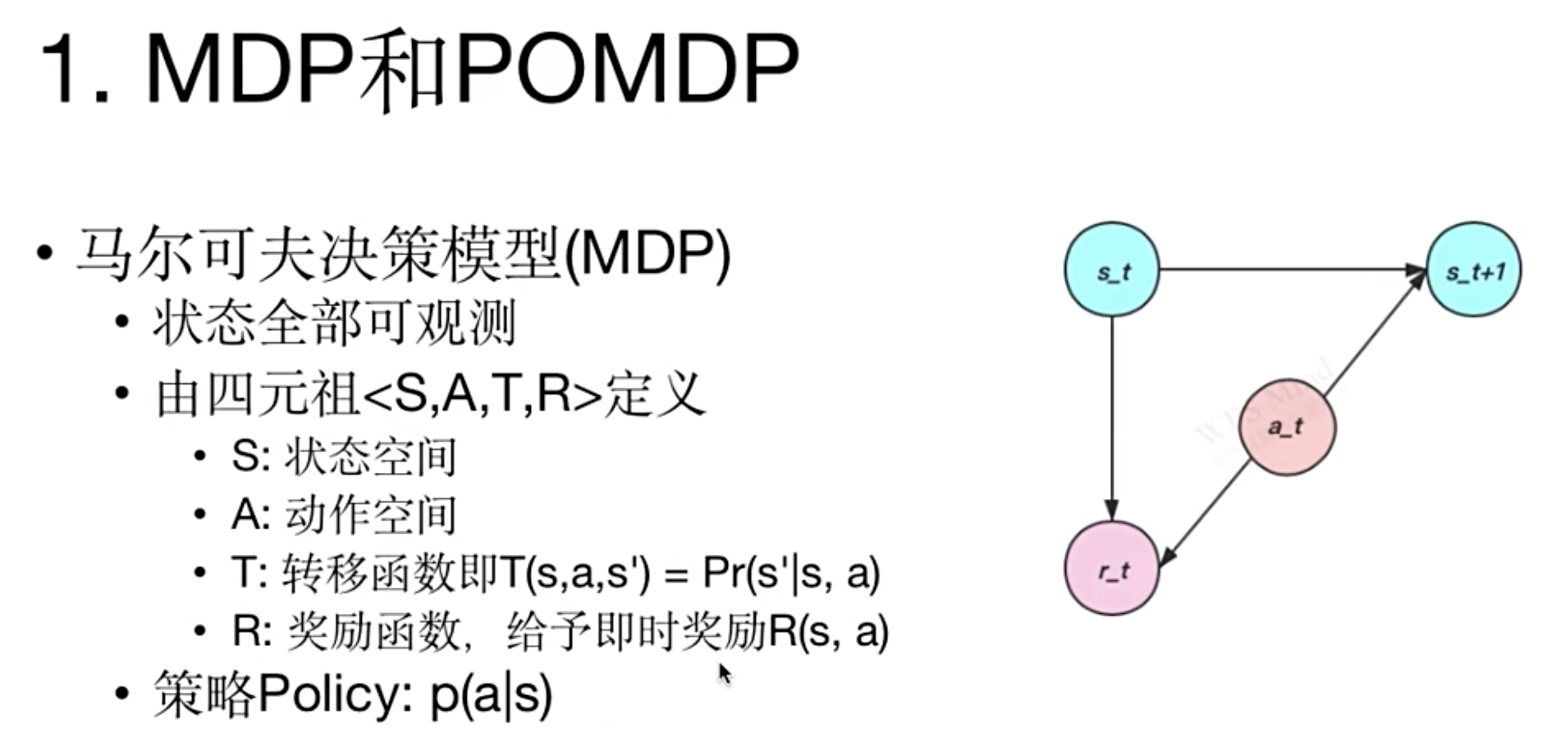
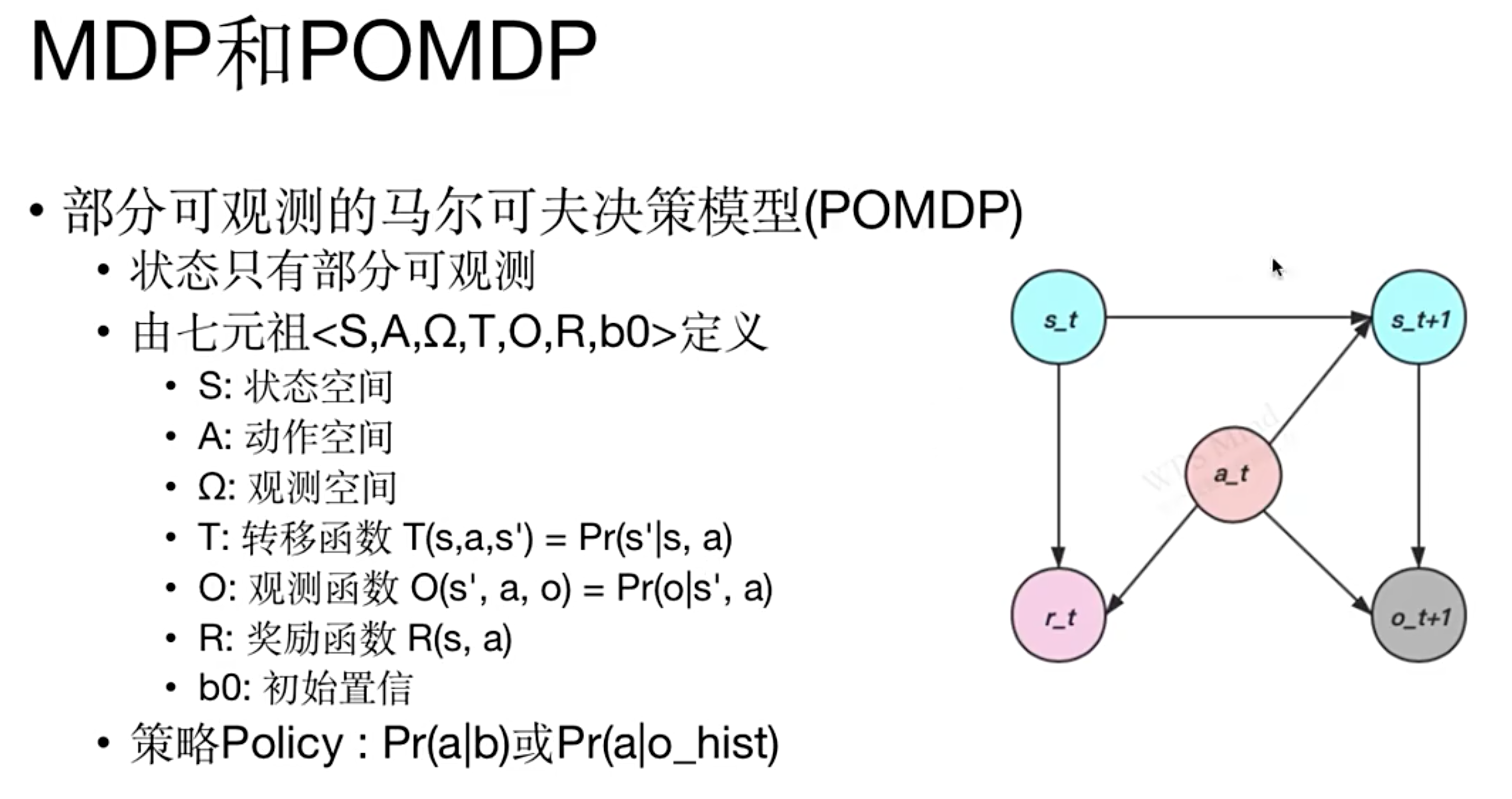
- private修饰的常量不用大写？
- Logger太特殊了，使用特殊定义，仅此一个，别无其他

RL——POMDP

本文是对POMDP这个不常见的概念的一些简单介绍，主要内容参考自POMDP讲解

参考链接：POMDP讲解

MDP 和 POMDP

马尔可夫决策模型(MDP)
- 状态全部可观测
- 由四元祖 $\langle S, A, T, R\rangle$ 定义：
  - $S$：状态空间
  - $A$：动作空间
  - $T$：转移函数即 $T(s, a, s’) = Pr(s’|s, a)$
  - $R$：奖励函数，给予即时奖励 $R(s, a)$
- 策略Policy: $p(a|s)$
部分可观测的马尔可夫决策模型(POMDP)
- 状态只有部分可观测
- 由七元祖 $\langle S, A, \Omega, T, O, R, b0\rangle$ 定义：
  - $S$：状态空间
  - $A$：动作空间
  - $\Omega$：观测空间
  - $T$：转移函数 $T(s, a, s’) = Pr(s’|s, a)$
  - $O$：观测函数 $O(s’, a, o) = Pr(o|s’, a)$
  - $R$：奖励函数 $R(s, a)$
  - $b0$：初始置信
- 策略Policy: $Pr(a|b)$ 或 $Pr(a|o_{hist})$ ，其中 $o_{hist}$ 表示单帧或多帧的历史观测信息（因为观测 $o$ 是不分更新的，可能已经不满足马尔科夫性了）
POMDP 的观测本身是不完整的系统状态信息，可能已经不满足马尔科夫性了，此时可以通过信念状态（Belief State，写作 $b$）或历史观测序列（写作 $o_{hist}$）来表示当前状态，从而保证智能体看到的观测是尽量完整的

POMDP 中的置信 Belief

Belief 的定义 ：Belief是智能体对于当前环境的状态分布估计
使用 Belief 的原因 ：因为Belief是充分统计量，也就是说做决策时只需要当前的Belief而不需要其他信息，另外观测历史也是充分统计量。在构建充分统计量后，可以将Belief理解为和MDP里的状态等价的概念，只是Belief是连续的
使用方式 ：当前置信 $b$ 情况下，在执行动作 $a$ 和得到观测 $o$ 后，需要更新置信为 $b’$
Belief 更新公式 ：
$$
\begin{align}
b’(s’) &= P_r(s’|o, a, b) = \frac{P_r(s’, o, a, b)}{P_r(o, a, b)}\\
&= \frac{P_r(o|s’, a, b)P_r(s’|a, b)}{P_r(o|a, b)}\\
&= \frac{P_r(o|s’, a)\sum_s P_r(s’|a, b, s)P_r(s|a, b)}{P_r(o|a, b)}\\
&= \frac{O(s’, a, o)\sum_s T(s, a, s’)b(s)}{P_r(o|a, b)}
\end{align}
$$

MDP 和 POMDP 的优化目标

在 MDP 里 ：在给定策略 $\pi$ 情况下
- 状态价值函数： $V_{\pi}(s) = \sum_{a\in A}\pi(a|s)Q(s, a)$
- 动作价值函数： $Q_{\pi}(s, a) = R(s, a) + \sum_{a\in A}T(s’, a, s)V_{\pi}(s’)$
- 最优价值函数： $V_{n}^{*}(s) = \max_{a}[R(s, a) + \gamma\sum_{a\in A}T(s’, a, s)V_{n - 1}^{*}(s’)]$
在 POMDP 里 ：在给定策略 $\pi$ 情况下
- 最优价值函数：
  $$
  V_{n}^{*}(b) = \max_{a\in A}[\rho(b, a) + \gamma\sum_{o\in\Omega}Pr(o|b, a)V_{n - 1}^{*}(b’)]
  $$
- 其中 $\rho(b, a)$ 是期望奖励即 $\sum_{s}b(s)R(s, a)$
- $Pr(o|b, a)$ 是在当前置信为 $b$ ，动作为 $a$ 情况下，获得观测 $o$ 的概率，且 $Pr(o|b, a) = \sum_{s’}O(s’, a, o)\sum_{s}T(s, a, s’)b(s)$

主流求解 POMDP 方法（决策规划）

离线(Offline)
- 基于点的值迭代 ：PBVI、FBVI、Perseus
- 策略迭代
在线(Online) ：POMCP、DESPOT

POMDP 于 RL

RL的设定是对于环境模型未知，常用的RL环境甚至并没有对应模型，并不一定是严格的MDP或POMDP
在假设环境模型是POMDP的强化学习情况下：
- 智能体的观测是 $o$ ，可知观测空间 $\Omega$
- 智能体的动作是 $a$ ，可知动作空间 $A$
- 状态空间 $S$ 对于智能体不可知
- 转移函数 $T$ 对于智能体不可知
- 观测函数 $O$ 对于智能体不可知
- 无法初始置信，因为 $S$ 不可知
- 智能体要学的策略是 $p(a|o)$ 或 $p(a|h)$ ， $p(a|h)$ 是因为智能体可以选择多种方法压缩多帧 $o$ 为一隐含信息 $h$ 。
传统的RL算法本身并不假设知道状态转移矩阵等，所以其实常见的RL算法可以直接用于求解POMDP，只是如果观测到的信息太少，RL不一定能保证收敛（观测不是环境的完整描述，可能不满足马尔可夫性，基于贝尔曼方程迭代的价值函数可能难以收敛）
比如策略梯度法推导过程中始终考虑的是期望收益，并不要求完整观测到环境，所以策略梯度法理论上适用于解决POMDP问题，但是观测不是环境的完整描述，可能不满足马尔可夫性，使用策略梯度法时最好使用REINFORCE方法，不使用Critic网络

附录：一些 PPT 原始介绍

以下PPT内容来自：POMDP讲解

MDP

MDP的介绍
对于确定决策，策略的概率值为1即可

POMDP

POMDP的介绍

POMDP 的求解方案

POMDP的解决方案介绍

General——深刻认识URL

你真的认识URL了吗？

URL中的`#`字符

#在URL中与服务器无关，也就是说正常访问服务器的URL不包含#
#仅仅与本地浏览器对网页的定位相关
#由于不影响对远程服务器的访问，自然也不会存在于软件包的下载连接中

URL的正则表达式

参考博客：https://blog.csdn.net/qq_25384945/article/details/81219075

Python

1	http[s]?://(?:[a-zA-Z]\|[0-9]\|[$-_@.&+]\|[!*,]\|(?:%[0-9a-fA-F][0-9a-fA-F]))+

JavaScript

1	/((([A-Za-z]{3,9}:(?:\/\/)?)(?:[\-;:&=\+\$,\w]+@)?[A-Za-z0-9\.\-]+\|(?:www\.\|[\-;:&=\+\$,\w]+@)[A-Za-z0-9\.\-]+)((?:\/[\+~%\/\.\w\-_])?\??(?:[\-\+=&;%@\.\w_])#?(?:[\.\!\/\\\w]*))?)/

Java

1	^(https?\|ftp\|file)://[-a-zA-Z0-9+&@#/%?=~_\|!:,.;]*[-a-zA-Z0-9+&@#/%=~_\|]

PyTorch——各种常用函数总结

PyTorch使用笔记，函数持续更新

torch.max()

注：torch.min与torch.max用法类似

单参数（取全局最大值）

用法
1
torch.max(input) -> Tensor
- input: 一个Tensor的对象
- return: 返回input变量中的最大值

多参数（按维度取最大值）

用法
1
torch.max(input, dim, keepdim=False, out=None) -> tuple[Tensor, Tensor]
- input: 一个Tensor的对象
- 返回是一个包含 values 和 indices 的对象，其中 values 是最大值，indices 是其索引
- dim: 指明维度，生成的结果中，indices 用于替换第 0 维度（这对应 gather() 的检索方式）
- keepdim: 是否保持输出张量的维度与输入张量一致（默认值为 False）
  - 如果为 True，输出张量在指定维度上的大小为 1；
  - 如果为 False，输出张量将减少一个维度

keepdim=False示例（包含索引使用示例）：

import torch
x = torch.tensor([[3, 2, 1],
				[4, 5, 6]])
# 获取每行的最大值
values, indices = torch.max(x, dim=1) # 默认在最后一个维度，即 dim=1 上操作，按行取最大值（生成的index是指定dim=1维度的索引）
print("values:\n", values)
print("indices:\n", indices)
# 用 indices 从 x 中检索出 values，方法一：gather 方法
retrieved_values = torch.gather(x, dim=1, index=indices.unsqueeze(1)) # 用 indices 替换 dim=1 索引维度即可抽取到对应的值
print("retrieved_values:\n", retrieved_values)
print("retrieved_values.squeeze():\n", retrieved_values.squeeze())
print("---")
# 用 indices 从 x 中检索出 values，方法二：高级索引
retrieved_values = x[torch.arange(2), indices]
print("retrieved_values:\n", retrieved_values)

# values:
#  tensor([3, 6])
# indices:
#  tensor([0, 2])
# retrieved_values:
#  tensor([[3],
#         [6]])
# retrieved_values.squeeze():
#  tensor([3, 6])
# ---
# retrieved_values:
#  tensor([3, 6])

keepdim=True示例（包含索引使用示例）：

import torch
x = torch.tensor([[3, 2, 1],
				[4, 5, 6]])
# 获取每行的最大值，保留维度
values, indices = torch.max(x, dim=1, keepdim=True) # 默认在最后一个维度，即 dim=1 上操作，按行取最大值（生成的index是指定dim=1维度的索引）
print("values:\n", values)
print("indices:\n", indices)
# 用 indices 从 x 中检索出 values，方法一：gather 方法
retrieved_values = torch.gather(x, dim=1, index=indices) # 用 indices 替换 dim=1 索引维度即可抽取到对应的值
print("retrieved_values:\n", retrieved_values)
print("---")
# 用 indices 从 x 中检索出 values，方法二：高级索引
retrieved_values = x[torch.arange(2), indices.squeeze()]
print("retrieved_values:\n", retrieved_values)
print("retrieved_values.unsqueeze(dim=1):\n", retrieved_values.unsqueeze(dim=1))

# values:
#  tensor([[3],
#         [6]])
# indices:
#  tensor([[0],
#         [2]])
# retrieved_values:
#  tensor([[3],
#         [6]])
# ---
# retrieved_values:
#  tensor([3, 6])
# retrieved_values.unsqueeze(dim=1):
#  tensor([[3],
#         [6]])

torch.backward() & torch.no_grad()

用法：

import torch
x = torch.ones(2, 2, requires_grad=True)
m = torch.ones(2, 2, requires_grad=True)
with torch.no_grad():	# 这两句合起来
	z = x + 1 			# 等价于z = x.detach() + 1
y = z * 2 + m
out = y.mean()
out.backward()
print(x.grad) # output None，因为梯度在z = x+1处断开了
print(m.grad) # output tensor([[0.2500, 0.2500],
       		  #					[0.2500, 0.2500]])
print(y.grad) # output None，因为y只是中间操作节点，不是叶子Tensor变量（leaf Tensor）

以上代码中，x不会被计算梯度，因为z = x + 1处梯度断开了，等价于z = x.detach() + 1

注意，如果调用torch.backward()时，没有任何可以计算的梯度，会报错，如下面的代码：

import torch
x = torch.ones(2, 2, requires_grad=True)
m = torch.ones(2, 2, requires_grad=True)
with torch.no_grad():	# 这两句合起来
	z = x + 1 			# 等价于z = x.detach() + 1
y = z * 2 + m.detach() # 相对上面的改动点，仅这里
out = y.mean()
out.backward()
print(x.grad) # output None，因为梯度在z = x+1处断开了
print(m.grad) # output tensor([[0.2500, 0.2500],
       		  #					[0.2500, 0.2500]])
print(y.grad) # output None，因为y只是中间操作节点，不是叶子Tensor变量（leaf Tensor）

仅修改了m.detach()后out.backward()就开始报错RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn，因为没有任何梯度可以计算了
其他说明：如果仅修改m = torch.ones(2, 2, requires_grad=True)为m = torch.ones(2, 2, requires_grad=False)，也一样会导师没有任何梯度可以计算了，执行out.backward()也会报相同错误

torch.nn.Module

直接打印torch.nn.Module类对象print(model)，默认情况下这个方法会调用model.__str__()，进一步调用model.__repr__()，这个函数会给出一个包含所有被定义为类属性的层的可读表示，但不会包括那些被定义为简单属性或方法的对象，这个方法可以用来查看模型包含哪些网络层

举例如下：

import torch
import torch.nn as nn
class MLPModel(nn.Module):
	def __init__(self):
		super(MLPModel, self).__init__()
		self.fc1 = nn.Linear(2, 2) # 会被打印
		self.fc2 = nn.Linear(2, 1) # 会被打印
		self.activation = torch.relu # 不会被打印

	def forward(self, x):
		x = self.activation(self.fc1(x))
		x = self.fc2(x)
		return x
model = MLPModel()
print(model) # 等价于print(model.__str__())和print(model.__repr__())

# MLPModel(
#     (fc1): Linear(in_features=2, out_features=2, bias=True)
#     (fc2): Linear(in_features=2, out_features=1, bias=True)
# )

tensor.item()

用于抽取一个tensor对象中的单一数值（注意，只能是单一数值，否则会报错）

import torch
# 单元素张量
tensor = torch.tensor([5])  # 形状为 (1,)
value = tensor.item()       # 提取出 Python 的 int 值
print(value)               # 输出: 5
print(type(value))         # 输出: <class 'int'>

tensor = torch.tensor([1, 2, 3])
value = tensor.item()  # 报错: ValueError: only one element tensors can be converted to Python scalars

# 强化学习中，常常用于抽取动作，方便和环境交互
action = action_dist.sample()  # 采样一个动作，action 是一个单元素张量
action_value = action.item()   # 提取出动作的标量值

torch.autograd.grad(outputs,inputs,grad_outputs)

功能：outputs对inputs求导
关键点：
- 当grad_outputs取默认值时，要求outputs必须是标量张量（一维）
- 当outputs不是标量张量时，要求grad_outputs与outputs维度一致，指明outputs中每个值对最终梯度的权重，且此时不可省略该参数（否则会报错：“RuntimeError: grad can be implicitly created only for scalar outputs”）

Demo展示:

import torch
# 创建需要梯度的张量
x = torch.tensor([2.0, 3.0], requires_grad=True)

# 定义一个多维张量 y = [x[0]**2, x[1]**3]
y = torch.stack([x[0]**2+x[1]**2, x[0]*3+x[1]**2])  # y 是一个形状为 (2,) 的张量

# 计算 y 对 x 的梯度
# 需要指定 grad_outputs 作为 y 的每个元素的权重（默认情况下，grad_outputs 是全 1 的张量）
grads = torch.autograd.grad(outputs=y, inputs=x,grad_outputs=torch.ones_like(y))

print("x:", x)
print("y:", y)
print("Gradients of y with respect to x:", grads)

### output:
# x: tensor([2., 3.], requires_grad=True)
# y: tensor([13., 15.], grad_fn=<StackBackward0>)
# Gradients of y with respect to x: (tensor([ 7., 12.]),)
# 其中 7 = 2 * x[0] + 3; 12 = 2 * x[1] + 2 * x[1]

torch.cat、stack、hstack、vstack

torch.cat和torch.stack两者都是用来拼接tensor的函数，主要区别是使用 torch.cat 在现有维度上拼接，使用 torch.stack 在新维度上拼接
- 维度变化 :
  - torch.cat 不新增维度，只在现有维度上拼接
  - torch.stack 会新增一个维度，并在该维度上拼接，torch.stack的工作需要分成两步，第一步是增加维度（比如(3,)经过dim=0会变成(1,3)），第二步是将该维度拼接
- 形状要求 :
  - torch.cat 要求非拼接维度上的形状相同
  - torch.stack 要求所有张量的形状完全一致
使用特别说明 ：一般使用 torch.cat和torch.stack就够了，torch.hstack和torch.vstack基本可以被torch.cat和torch.stack替代，所以不常用

torch.cat Demo 展示：

import torch

a = torch.tensor([[1, 2], [3, 4]])
b = torch.tensor([[5, 6], [7, 8]])

# 沿第0维拼接
c = torch.cat((a, b), dim=0)
print(c)
# 输出:
# tensor([[1, 2],
#         [3, 4],
#         [5, 6],
#         [7, 8]])

# 沿第1维拼接
d = torch.cat((a, b), dim=1)
print(d)
# 输出:
# tensor([[1, 2, 5, 6],
#         [3, 4, 7, 8]])

torch.stack Demo 展示：

import torch

a = torch.tensor([1, 2, 3])
b = torch.tensor([4, 5, 6])

# 在第0维新增维度并拼接: (3,) -> (1,3) -> (2,3)
c = torch.stack((a, b), dim=0)
print(c)
# 输出:
# tensor([[1, 2, 3],
#         [4, 5, 6]])

# 在第1维新增维度并拼接: (3,) -> (3,1) -> (3,2)
d = torch.stack((a, b), dim=1)
print(d)
# 输出:
# tensor([[1, 4],
#         [2, 5],
#         [3, 6]])

stack的动作分两步，第一步是在指定维度增加一维，比如:
- 上面的式子(3,)经过dim=0后变成(1,3)，进一步地两个(1,3)堆叠变成(2,3)
- 上面的式子(3,)经过dim=1后变成(3,1)，进一步地两个(3,1)堆叠变成(3,2)

torch.hstack和torch.vstack函数：

torch.hstack：在水平方向(dim=1)处拼接张量，不新增维度
- 对于 1 维张量会特殊处理，直接将 1 维张量变长（此时相当于在 dim=0处拼接）
torch.vstack：在垂直方向（第 0 维）拼接张量，除了原始输入为 1 维时，不新增维度
- 对于 1 维张量会特殊处理，拼接后变成 2 维（此时相当于先在dim=0增加一维再按照这个维度拼接）

不同函数在输入1维和5维向量时的Demo：

import torch
tensors_1d = [torch.tensor([1, 3, 4]), torch.tensor([1, 3, 4])]
tensors_5d = [torch.randn(1, 3, 4, 5, 6), torch.randn(1, 3, 4, 5, 6)]
# 使用 torch.stack
stacked_1d = torch.stack(tensors_1d)
stacked_5d = torch.stack(tensors_5d, dim=2)
# 使用 torch.hstack
hstacked_1d = torch.hstack(tensors_1d)
hstacked_5d = torch.hstack(tensors_5d)
# 使用 torch.vstack
vstacked_1d = torch.vstack(tensors_1d)
vstacked_5d = torch.vstack(tensors_5d)
# 使用 torch.cat
cat_1d = torch.cat(tensors_1d)
cat_5d = torch.cat(tensors_5d, dim=2)

print("tensors_1d shape:", tensors_1d[0].shape)
print("tensors_5d shape:", tensors_5d[0].shape)
print("torch.stack 1D shape:", stacked_1d.shape)
print("torch.stack 5d shape(dim=2):", stacked_5d.shape)
print("torch.hstack 1D shape:", hstacked_1d.shape)
print("torch.hstack 5d shape:", hstacked_5d.shape)
print("torch.vstack 1D shape:", vstacked_1d.shape)
print("torch.vstack 5d shape:", vstacked_5d.shape)
print("torch.cat 1D shape:", cat_1d.shape)
print("torch.cat 5d shape(dim=2):", cat_5d.shape)

# tensors_1d shape: torch.Size([3])
# tensors_5d shape: torch.Size([1, 3, 4, 5, 6])
# torch.stack 1D shape: torch.Size([2, 3])
# torch.stack 5d shape(dim=2): torch.Size([1, 3, 2, 4, 5, 6])
# torch.hstack 1D shape: torch.Size([6])
# torch.hstack 5d shape: torch.Size([1, 6, 4, 5, 6])
# torch.vstack 1D shape: torch.Size([2, 3])
# torch.vstack 5d shape: torch.Size([2, 3, 4, 5, 6])
# torch.cat 1D shape: torch.Size([6])
# torch.cat 5d shape(dim=2): torch.Size([1, 3, 8, 5, 6])

tensor.repeat()函数

基本用法
1
tensor.repeat(*sizes)
- *sizes：一个整数序列，表示每个维度上重复的次数
- 返回值：一个新的张量，其形状是原张量形状的每个维度乘以对应的重复次数
注意事项
- 新维度的顺序 ：repeat 会按照输入的顺序对每个维度进行扩展
- 内存共享 ：repeat 不会复制数据，而是通过视图（view）来实现重复。这意味着返回的张量与原始张量共享底层数据
- 维度扩展规则 ：如果输入的 sizes 长度大于张量的维度，则会在前面补充新的维度，比如(2,)的原始张量调用repeat(2,3)后，会先扩展成(1,2)的张量，再执行repeat(2,3)，但是不建议补充这个功能

函数调用Demo：

import torch
x = torch.tensor([1, 2])
print("Original tensor:", x)

# 沿第 0 维重复 3 次
result = x.repeat(3)
print("Repeated tensor(3):", result)
# 添加一个新维度，并在两个维度上重复
result = x.repeat(2, 3)
print("Repeated tensor shape(2,3):", result.shape)
print("Repeated tensor(2,3):\n", result)

x = torch.tensor([[1, 2, 3], [4, 5, 6]])
print("Original tensor:\n", x)

# 在第 0 维重复 2 次，第 1 维重复 3 次
result = x.repeat(2, 3)
print("Repeated tensor:\n", result)

# Original tensor: tensor([1, 2])
# Repeated tensor(3): tensor([1, 2, 1, 2, 1, 2])
# Repeated tensor shape(2,3): torch.Size([2, 6])
# Repeated tensor(2,3):
# tensor([[1, 2, 1, 2, 1, 2],
#         [1, 2, 1, 2, 1, 2]])
# Original tensor:
# tensor([[1, 2, 3],
#         [4, 5, 6]])
# Repeated tensor:
# tensor([[1, 2, 3, 1, 2, 3, 1, 2, 3],
#         [4, 5, 6, 4, 5, 6, 4, 5, 6],
#         [1, 2, 3, 1, 2, 3, 1, 2, 3],
#         [4, 5, 6, 4, 5, 6, 4, 5, 6]])

parameters() & named_parameters()

model.parameters()：返回模型中所有参数，不返回参数名称
model.named_parameters()：返回模型中所有参数，同时返回参数名称

Demo

# 定义一个简单的全连接神经网络
class SimpleNN(nn.Module):
	def __init__(self):
		super(SimpleNN, self).__init__()
		self.fc1 = nn.Linear(2, 2)  # 输入层到隐藏层
		self.fc2 = nn.Linear(2, 1)  # 隐藏层到输出层
		for param in self.fc2.parameters(): # 可指定设置某些参数不参与梯度更新（Frozen参数）
			param.requires_grad = False

	def forward(self, x):
		x = torch.relu(self.fc1(x)) # ReLU 激活函数
		x = self.fc2(x)
		return x

# 创建网络实例
model = SimpleNN()

# 打印模型结构
print(model)

print("\nmodel.named_parameters():")
# 遍历模型的所有参数并打印那些 requires_grad=True 的参数
for name, param in model.named_parameters():
	if param.requires_grad:
		print(f"Parameter {name} requires gradient: {param}")
	else:
		print(f"Parameter {name} don't require gradient: {param}")

print("\nmodel.parameters():")
# 遍历模型的所有参数并打印那些 requires_grad=True 的参数
for param in model.parameters():
	print(param.requires_grad)
# SimpleNN(
#     (fc1): Linear(in_features=2, out_features=2, bias=True)
# (fc2): Linear(in_features=2, out_features=1, bias=True)
# )
# 
# model.named_parameters():
# Parameter fc1.weight requires gradient: Parameter containing:
# tensor([[-0.6769,  0.7008],
#         [-0.6705,  0.2912]], requires_grad=True)
# Parameter fc1.bias requires gradient: Parameter containing:
# tensor([-0.6091, -0.2306], requires_grad=True)
# Parameter fc2.weight don't require gradient: Parameter containing:
# tensor([[ 0.5131, -0.4101]])
# Parameter fc2.bias don't require gradient: Parameter containing:
# tensor([-0.0788])
# 
# model.parameters():
# True
# True
# False
# False

torch.empty()创建变量

torch.empty() 是 PyTorch 中用于创建一个新的张量（tensor）的函数，该张量不会被初始化，即它的元素值是未定义的。这意味着张量中的元素可能是任意值，取决于分配给张量的内存块之前的状态
具体用途：
- 快速创建张量 ：当你需要一个具有特定形状的张量，但不关心初始值时，可以使用 torch.empty() 来快速创建它。这对于只需要分配内存而不必初始化数据的情况非常有用
- 占位符张量 ：在某些情况下，你可能想要创建一个张量作为占位符，稍后将用实际的数据填充它。例如，在实现算法或构建计算图时，你可能提前知道所需的空间大小，但暂时没有具体数值
- 性能优化 ：由于不需要初始化张量中的数据，torch.empty() 可以比 torch.zeros() 或 torch.ones() 更快地分配内存，因为它跳过了设置默认值的过程
- 显存管理 ：在GPU上操作时，有时会利用 torch.empty() 来预分配显存，避免后续操作中可能出现的内存碎片化问题

torch.linspace() & torch.arange()

torch.linspace 和 torch.arange 都是 PyTorch 中用于生成数值序列的函数，但它们在生成数值的方式和使用场景上有一些关键的不同
- torch.linspace : 返回一个一维张量，包含从 start 到 end（包括两端点）之间等间距分布的 steps 个点
- torch.arange : 返回一个一维张量，包含从 start 开始到 end 结束（不包括 end），以步长 step 增长的连续整数或浮点数

Demo

import torch

# 使用 linspace
linspace_tensor = torch.linspace(0, 2, steps=3)
print("Linspace:", linspace_tensor)

# 使用 arange
arange_tensor = torch.arange(0, 10, step=2)
print("Arange:", arange_tensor)

# Linspace: tensor([0.0000, 0.6667, 1.3333, 2.0000])
# Arange: tensor([0, 2, 4, 6, 8])

tensor.is_contiguous()

tensor.is_contiguous() 用于检查一个张量（Tensor）是否是连续的（contiguous）。在PyTorch中，张量的存储方式可以分为连续和非连续。一个张量被认为是连续的，如果它的元素在内存中是按行优先顺序（row-major order）依次存放的，也就是说，在内存中这些元素是连续排列的
连续排列对于需要高效访问或操作张量数据的操作非常重要，因为许多底层实现（例如，CUDNN库中的函数）要求输入的数据必须是连续存储的。如果一个张量不是连续的，即使它包含相同的数据，其内存布局也可能导致性能下降或者某些操作无法执行
当调用 tensor.is_contiguous() 方法时，如果返回值为 True，则表示该张量是连续的；如果返回 False，则表示张量当前不是以连续的方式存储的。如果你需要将一个非连续的张量转换为连续的，可以使用 .contiguous() 方法来创建一个新的、与原张量具有相同数据但存储方式为连续的张量副本

示例代码如下：

import torch

x = torch.tensor([[1, 2, 3], [4, 5, 6]])
print(x.is_contiguous())  # 输出: True

# 假设进行了转置操作，通常会导致张量变为非连续
x_t = x.t()
print(x_t.is_contiguous())  # 输出: False

# 使用 contiguous 方法将非连续张量转换为连续
x_t_contig = x_t.contiguous()
print(x_t_contig.is_contiguous())  # 输出: True

x.squeeze(dim) vs x.unsqueeze(dim)

unsqueeze：在指定维度添加一个维度，且该长度为 1
squeeze：去掉指定长度为 1 的维度
- 如果指定的不是长度为 1 的维度，则不做任何修改
- 如果不指定任何维度，则将所有长度为 1 的维度都去掉；
- 如果不指定任何维度，且没有长度为 1 的维度，则不做任何修改
unsqueeze() 有等价形式，如对于二维的张量：
- tensor.unsqueeze(dim=0) 等价于 tensor[None] 或 tensor[None,:,:]
- tensor.unsqueeze(dim=1) 等价于 tensor[:,None] 或 tensor[:,None,:]
- tensor.unsqueeze(dim=0) 等价于 tensor[:,:,None]

unsqueeze() 代码示例：

import torch
import numpy as np
x = torch.tensor([[3, 2, 1],
                  [4, 5, 6]], dtype=torch.float32)

y = x[None] # 等价于 y = x[None,:,:] 和 y = x.unsqueeze(dim=0)
print(y)
print(y.shape)

y = x[:,None] # 等价于 y = x[:,None,:] 和 y = x.unsqueeze(dim=1)
print(y)
print(y.shape)

y = x[:,:,None] # 和 y = x.unsqueeze(dim=2)
print(y)
print(y.shape)

# tensor([[[3., 2., 1.],
#          [4., 5., 6.]]])
# torch.Size([1, 2, 3])
# tensor([[[3., 2., 1.]],
#         [[4., 5., 6.]]])
# torch.Size([2, 1, 3])
# tensor([[[3.],
#          [2.],
#          [1.]],
#         [[4.],
#          [5.],
#          [6.]]])
# torch.Size([2, 3, 1])

`torch.flatten()` 和 `torch.unflatten()`

torch.flatten() 基本用法：
1
torch.flatten(input, start_dim=0, end_dim=-1)
- input：需要被展平的输入张量
- start_dim：从哪个维度开始展平，默认值为0（即从第0维开始）
- end_dim：到哪个维度结束展平，默认值为-1（即到最后一维结束）
torch.unflatten() 基本用法
1
torch.unflatten(input, dim, unflattened_size)
- input：需要被处理的输入张量
- dim：需要被拆分的维度索引
- unflattened_size：指定拆分后的维度大小，可以是元组或列表

示例

import torch

x = torch.tensor([[[[1, 2], [3, 4]], [[5, 6], [7, 8]]]])
print(x.shape)  # 输出: torch.Size([1, 2, 2, 2])

# 展平整个张量
y = torch.flatten(x)
print(y.shape)    # 输出: torch.Size([8])
print(y)          # 输出: tensor([1, 2, 3, 4, 5, 6, 7, 8])

# 展平张量的中间两个维度
z = torch.flatten(x, start_dim=1, end_dim=2)
print(z.shape)    # 输出: torch.Size([1,4,2])

# 使用 unflatten 拆分维度
w = z.unflatten(dim=1, sizes=(2,2))
print(w) # 输出: torch.Size([1, 2, 2, 2])

tensor.numpy() vs torch.from_numpy()

torch.from_numpy(ndarray)：将 NumPy 数组转换为张量，两者共享内存 ，修改NumPy变量会改变Tensor变量，反之亦然
tensor.numpy()：将张量转换为 NumPy 数组（仅限 CPU 张量），两者共享内存 ，修改NumPy变量会改变Tensor变量，反之亦然

代码示例：

import torch
import numpy as np

numpy_array = np.array([[1.0, 2, 3], [4, 5, 6]])
tensor_from_numpy = torch.from_numpy(numpy_array)
numpy_array[0, 0] = 100
print("\n修改后的 NumPy 数组:\n", numpy_array.dtype,numpy_array)
print("PyTorch 张量也会同步变化:\n", tensor_from_numpy)

tensor = torch.tensor([[7, 8, 9], [10, 11, 12]], dtype=torch.float32)
numpy_from_tensor = tensor.numpy()
tensor[0, 0] = 77
print("\n修改后的 PyTorch 张量:\n", tensor)
print("NumPy 数组也会同步变化:\n", numpy_from_tensor)


numpy_array = np.array([[1, 2, 3], [4, 5, 6]])
tensor_from_numpy = torch.Tensor(numpy_array)
numpy_array[0, 0] = 100
print("\n修改后的 NumPy 数组:\n", numpy_array)
print("PyTorch 张量不会同步变化:\n", tensor_from_numpy)

# 修改后的 NumPy 数组:
# float64 [[100.   2.   3.]
# [  4.   5.   6.]]
# PyTorch 张量也会同步变化:
# tensor([[100.,   2.,   3.],
#         [  4.,   5.,   6.]], dtype=torch.float64)
# 
# 修改后的 PyTorch 张量:
# tensor([[77.,  8.,  9.],
#         [10., 11., 12.]])
# NumPy 数组也会同步变化:
# [[77.  8.  9.]
#  [10. 11. 12.]]
# 
# 修改后的 NumPy 数组:
# [[100   2   3]
#  [  4   5   6]]
# PyTorch 张量不会同步变化:
# tensor([[1., 2., 3.],
#         [4., 5., 6.]])

特别注意（其他共享内存相关函数）
- 使用 torch.Tensor(numpy_array) 得到的变量只有在 numpy_array 的类型为 np.float32 时共享，否则不共享内存的（注意：torch.Tensor() 是无法指定数据类型的，默认类型就是 torch.float32）
- 使用 torch.tensor(numpy_array) 得到的变量总是不共享内存，都是副本

inplace参数的使用

在PyTorch中，inplace参数允许你指定操作是否直接在输入张量上进行而不需要额外的内存分配来存储结果。这对于减少内存使用特别有用，但需要注意的是，这也会覆盖原始数据。下面通过具体的例子说明如何使用inplace参数，以torch.nn.functional.relu为例：

示例代码

代码示例：

import torch
import torch.nn.functional as F

# 创建一个随机张量
input_tensor = torch.randn(2, 3)
print("Original tensor:")
print(input_tensor)

# 不使用inplace模式（默认）
output_tensor = F.relu(input_tensor)
print("\nOutput tensor (not inplace):")
print(output_tensor)
print("\nOriginal tensor after not inplace operation:")
print(input_tensor)  # 原始张量未被修改

# 使用inplace模式
F.relu(input_tensor, inplace=True)
print("\nOriginal tensor after inplace operation:")
print(input_tensor)  # 原始张量被修改，应用了ReLU

# Original tensor:
# tensor([[-0.7269, -0.2997,  0.1654],
#         [ 1.2219,  1.2698, -0.5245]])
# 
# Output tensor (not inplace):
# tensor([[0.0000, 0.0000, 0.1654],
#         [1.2219, 1.2698, 0.0000]])
# 
# Original tensor after not inplace operation:
# tensor([[-0.7269, -0.2997,  0.1654],
#         [ 1.2219,  1.2698, -0.5245]])
# 
# Original tensor after inplace operation:
# tensor([[0.0000, 0.0000, 0.1654],
#         [1.2219, 1.2698, 0.0000]])

输出解释
- 不使用inplace：当你调用F.relu(input_tensor)时，默认情况下不会修改原始的input_tensor，而是返回一个新的张量output_tensor作为ReLU操作的结果
- 使用inplace=True：当你指定inplace=True，如F.relu(input_tensor, inplace=True)，此时ReLU操作会直接作用于input_tensor本身，即它将所有负值设置为0，并且这个修改是直接在原来的张量上进行的，不会创建新的张量。因此，在执行完这个操作后，原始的input_tensor已经被修改

关于inplace的其他说明

使用inplace操作可以节省一些内存，因为不需要为输出分配新的空间
- 它会直接修改原张量的数据，在需要保留原数据的情况下要谨慎使用
- 并不是所有的函数都支持inplace参数，具体的支持情况可以查阅相关函数的文档说明
这种方式同样适用于其他许多具有inplace选项的操作，比如激活函数、归一化等，理解并正确使用inplace可以帮助更有效地管理和优化你的模型训练过程
PyTorch 中，常常用以 _ 结尾的函数实现 inplace 操作

torch.device() 和 tensor.to()函数

设备获取：torch.device('cuda')用于设备获取
tensor迁移：tensor = tensor.to(device)
模型迁移：model = model.to(device)
- 会将模型的所有可学习参数以及模型中的缓冲区移动到指定的 device 设备上
- 所有可学习参数 ：也就是模型的权重和偏置，模型的可学习参数由 model.parameters() 对象来表示（这里面包含模型的所有nn.Parameter对象）。这些参数一般是在模型的 __init__ 方法中定义的
- 模型中的缓冲区 ：即不需要反向传播更新的张量，例如 BatchNorm 层中的运行统计量，详细来说，例如 torch.nn.BatchNorm2d 层中的 running_mean 和 running_var

tensor.view() 和 tensor.reshape()

在 PyTorch 中，tensor.view() 和 tensor.reshape() 都可以用来改变张量的形状，但它们之间有一些关键的区别
tensor.view() :
- 它要求数据在内存中是连续存储的。如果 tensor 不是连续的（例如，经过 transpose、permute 或其他操作后），使用 .view() 会抛出错误。这时你需要先调用 .contiguous() 来确保 tensor 在内存中是连续的，然后才能使用 .view()
- .view() 的性能可能更好，因为它直接改变了对原始数据的视图而没有复制数据
tensor.reshape() :
- tensor.reshape() 等价于 tensor.contiguous().view()
- tensor.reshape()可以在张量不是连续的情况下工作，因为它会在必要时创建张量的一个副本
  - 如果张量是连续的，不会创建副本
- .reshape() 是自 PyTorch 0.4.0 版本引入的一个函数，旨在提供一种更一致的方式来处理形状变换。无论张量是否连续，它都可以工作
一句话总结：
- 如果确定张量是连续的 ，并且希望明确表达避免不必要的数据复制以提高性能 ，那么可以选择使用 .view()
- 然而，如果不确定张量是否连续或者你不关心额外的数据复制 ，.reshape() 提供了一个更为方便和灵活的选择
  - 在大多数情况下，为了代码的健壮性和易读性，推荐使用 .reshape()
  - 在连续存储下， .reshape() 和 .view() 是等价的，无需担心性能

tensor.topk()函数

torch.topk() 用于获取张量中指定维度上的前 k 个最大/最小值及其索引，常用于分类任务中获取 top-k 的预测结果，其函数定义如下：
1
torch.topk(input, k, dim=None, largest=True, sorted=True, *, out=None)
参数说明：
- input : 输入的张量
- k : 需要返回的最大（或最小）值的数量
- dim : 沿着哪个维度进行操作。如果未指定，则默认在最后一个维度上操作
- largest : 如果为 True，则返回最大的 k 个值；如果为 False，则返回最小的 k 个值。默认为 True
- sorted : 如果为 True，则返回的结果会按照大小排序；如果为 False，则返回的结果顺序不确定。默认为 True
- out : 可选的输出元组，用于存储结果
返回值
- values : 前 k 个最大（或最小）的值
- indices : 这些值在输入张量中的索引

用法示例

import torch
x = torch.tensor([[3, 2, 1],
				[4, 5, 6]])
# 获取每行的前 2 个最大值，下面的式子等价于 values, indices = torch.topk(x, k=2, dim=1)
values, indices = torch.topk(x, k=2) # 默认在最后一个维度，即 dim=1 上操作，按行取最大值（生成的index是指定dim=1维度的索引）
# 用 indices 从 x 中检索出 values
retrieved_values = torch.gather(x, dim=1, index=indices) # 用 indices 替换 dim=1 索引维度即可抽取到对应的值
print("values:\n", values)
print("indices:\n", indices)
print("retrieved_values:\n", retrieved_values)

print("---")
# 获取每列的前 1 个最大值
values, indices = torch.topk(x, k=1, dim=0) # 在 dim=0 上操作，生成的index是指定dim=0维度的索引
# 用 indices 从 x 中检索出 values
retrieved_values = torch.gather(x, dim=0, index=indices)
print("values:\n", values)
print("indices:\n", indices)
print("retrieved_values:\n", retrieved_values)

# values:
#  tensor([[3, 2],
#         [6, 5]])
# indices:
#  tensor([[0, 1],
#         [2, 1]])
# retrieved_values:
#  tensor([[3, 2],
#         [6, 5]])
# ---
# values:
#  tensor([[4, 5, 6]])
# indices:
#  tensor([[1, 1, 1]])
# retrieved_values:
#  tensor([[4, 5, 6]])

nn.Module.register_buffer

在PyTorch中，self.register_buffer 是一个用于向模块（nn.Module）注册持久化缓冲区（buffer）的方法。它的主要作用是告诉PyTorch某些张量是模型的一部分，但不属于可训练参数（即不需要梯度更新），但这些张量在模型保存或加载时需要被包含进来
非可训练参数：通过 register_buffer 注册的张量不会被优化器更新（不像 nn.Parameter）
- 注：在BatchNorm中，running_mean 和 running_var 是统计量，需要跟踪但不参与梯度计算，也属于这一类
持久化：注册的buffer会被包含在 model.state_dict() 中，因此当调用 torch.save 和 torch.load 时，它们会被自动保存和加载
设备移动：当调用 model.to(device) 时，这些buffer会自动移动到对应的设备（如CPU/GPU），与模型的其他参数一致
获取值：被包含在 model.state_dict()中
常见用法：一些固定常量参数或者统计量

使用示例：

class MyModel(nn.Module):
	def __init__(self):
		super().__init__()
		self.weight = nn.Parameter(torch.randn(3, 3))
		# 注册一个buffer（非可训练但需要持久化）
		self.register_buffer('buffer_a', torch.zeros(3))
model = MyModel()
print(model.state_dict())
# 输出包含：weight 和 buffer_a

PyTorch中的对数运算

以 e 为底：x.log() == torch.log(x)
以 2 为底：x.log2() == torch.log2(x)
以 10 为底：x.log10() == torch.log10(x)

以其他数字为底的通过对数换底公式实现：
$$ \log_5 x = \frac{\ln x}{\ln 5} $$

实现代码

import torch

def log5(x):
	"""计算以5为底的对数，输入为Tensor"""
	return torch.log(x) / torch.log(torch.tensor(5.0))

`torch.clip` 和 `torch.clamp`

在 PyTorch 里，torch.clip 和 torch.clamp 功能完全一样，都能用于将输入张量的数值限制在指定的区间内，从英文含义上看，两者分别是截取和限制的含义，都差不多，但理论上 clip 会更符合原本这个函数“裁剪”的含义
torch.clamp 是 PyTorch 从早期就存在的传统函数，一直被广泛运用
torch.clip 是在版本 1.7.0 时新增的函数，目的是和 NumPy 的 np.clip 保持 API 一致，方便用户从 NumPy 迁移过来
推荐使用 torch.clip，方便阅读，但为了和更早的 torch 版本兼容，还有很多人使用 clamp

`torch.allclose()` 函数

用于比较两个张量是否在给定的误差范围内“几乎相等”

基本语法

1	torch.allclose(input, other, rtol=1e-05, atol=1e-08, equal_nan=False)

特别注意：
other 与 input 形状必须相同
equal_nan：若为True，则NaN值被视为相等；若为False，则NaN会导致比较失败
若所有元素的差异都在容差范围内，则返回True；否则返回False。对于每个元素，比较条件为：
1
|input - other| ≤ atol + rtol * |other|
容易混淆的相关方法的比较（以下两个方法都是逐个元素比较，返回逐元素结果的）
- torch.isclose() ：逐元素比较两个张量是否接近，返回与输入形状相同的布尔张量（注意不是只返回一个值，是逐元素比较结果）
  1
  torch.isclose(a, b, rtol=1e-5, atol=1e-8, equal_nan=False)
- torch.eq() ：严格逐元素相等比较（不考虑容差），返回与输入形状相同的布尔张量

`torch.chuck` 函数用法

torch.chunk 是 PyTorch 中用于将张量按照指定维度拆分成多个子张量的函数，返回一个包含拆分后子张量的元组
torch.chunk 拆分后的数据与原张量共享内存（浅拷贝），修改子张量会影响原张量
函数定义为：
1
torch.chunk(input, chunks, dim=0)
- input：待拆分的输入张量（torch.Tensor）
- chunks：拆分的数量（int）。需注意：若输入张量在 dim 维度的大小不能被 chunks 整除，最后一个子张量的大小会略小（其余子张量大小相等）
- dim：指定拆分的维度（int，默认值为 0）
- 返回：一个元组（tuple），包含 chunks 个子张量（或最后一个子张量略小）
torch.chunk 与 torch.split 的区别：
- torch.chunk 按“数量”拆分（chunks 参数），子张量大小尽可能平均；
- torch.split 按“指定大小”拆分（如 split_size_or_sections=2 表示每个子张量大小为 2）

`torch.chunk` 的一些示例

基本用法（1D 张量）

import torch

# 能整除的情况
x = torch.tensor([1, 2, 3, 4, 5, 6])
chunks = torch.chunk(x, chunks=3, dim=0)  # 沿第0维拆分成3份
print(chunks)
# 输出：(tensor([1, 2]), tensor([3, 4]), tensor([5, 6]))

# 不能整除的情况
x = torch.tensor([1, 2, 3, 4, 5])
chunks = torch.chunk(x, chunks=2, dim=0)  # 5不能被2整除，最后一个子张量多1个元素
print(chunks)
# 输出：(tensor([1, 2]), tensor([3, 4, 5]))

高维张量拆分（2D 张量）示例

x = torch.arange(12).reshape(3, 4)  # 形状为 (3, 4) 的矩阵
print("原始张量：\n", x)
# 原始张量：
#  tensor([[ 0,  1,  2,  3],
#          [ 4,  5,  6,  7],
#          [ 8,  9, 10, 11]])

# 沿 dim=0（行维度）拆分成2份
chunks_dim0 = torch.chunk(x, chunks=2, dim=0)
print("沿行拆分：\n", chunks_dim0)
# 沿行拆分：
#  (tensor([[0, 1, 2, 3],
#           [4, 5, 6, 7]]), 
#   tensor([[ 8,  9, 10, 11]]))

# 沿 dim=1（列维度）拆分成2份
chunks_dim1 = torch.chunk(x, chunks=2, dim=1)
print("沿列拆分：\n", chunks_dim1)
# 沿列拆分：
#  (tensor([[0, 1],
#           [4, 5],
#           [8, 9]]), 
#   tensor([[ 2,  3],
#           [ 6,  7],
#           [10, 11]]))

`torch.where` 函数和 `tensor.where` 函数

torch.where() 是 PyTorch 中用于基于条件对张量元素进行选择性替换的方法，类似于“三目运算符”的向量版，语法如下：
1
torch.where(condition, x, y)
- condition：布尔型张量（与原张量同形状），用于判断每个元素是否满足条件
- x：当 condition 为 True 时，保留或使用 x 的值（可与原张量同形状，或为标量）
- y：当 condition 为 False 时，使用 y 的值（可与原张量同形状，或为标量）
- 返回值：一个新张量，每个元素根据 condition 从 x 或 y 中取值
注：x.where(condition, y) 是实例方法，等价于全局函数 torch.where(condition, x, y)

`tensor.where(condition, y)`（实例方法）

张量对象的实例方法，语法为：
1
result = tensor.where(condition, y)
- condition（必选）：布尔型张量（torch.BoolTensor），形状必须与 tensor 相同（或可广播为相同形状）
  - 用于判断每个元素是否满足条件，决定最终取值来源
- y（必选）：张量（与 tensor 同数据类型）或标量（如 int、float）
  - 若为张量，形状必须与 tensor 相同（或可广播为相同形状）；若为标量，会自动广播到 tensor 的形状
    - 当 condition 为 False 时，使用 y 的值（或对应位置的元素）替换 tensor 中的元素

`torch.where(condition, x, y)`（全局函数）

PyTorch 的全局函数，语法为：
1
result = torch.where(condition, x, y)
- condition（必选）：布尔型张量（torch.BoolTensor），形状必须与 x、y 相同（或可广播为相同形状）
  - 用于判断每个元素是否满足条件，决定从 x 或 y 中取值
- x（必选）：张量（与 y 同数据类型）或标量
  - 若为张量，形状必须与 condition 相同（或可广播为相同形状）；若为标量，会自动广播到对应形状
  - 当 condition 为 True 时，使用 x 的值（或对应位置的元素）
- y（必选）：张量（与 x 同数据类型）或标量
  - 若为张量，形状必须与 condition 相同（或可广播为相同形状）；若为标量，会自动广播到对应形状
  - 当 condition 为 False 时，使用 y 的值（或对应位置的元素）

示例

代码示例：

import torch

tensor = torch.tensor([1, 5, 3, 8, 2, 7]) 
condition = tensor % 2 == 0 
y = torch.tensor([-1, -1, -1, -1, -1, -1]) 

# 方法1：tensor.where(condition, y) —— 实例方法
result_instance = tensor.where(condition, y)

# 等价方法：torch.where(condition, tensor, y) —— 函数
result_function = torch.where(condition, tensor, y)

print("tensor.where() 结果：", result_instance) # tensor([-1, -1, -1,  8,  2, -1])
print("torch.where() 结果：", result_function) # tensor([-1, -1, -1,  8,  2, -1])

`torch.size()` 函数和 `tensor.size(n)`

`tensor.size()` 函数

返回张量的完整形状 ，描述张量在每个维度上的元素个数
返回值 torch.Size 可直接当作 tuple 使用（支持索引、len() 等），例如 len(t2.size()) 会返回张量的维度数（2）
等价写法：tensor.shape（属性，功能与 size() 完全一致，更简洁），例如 t2.shape 与 t2.size() 结果相同

`tensor.size(n)` 函数

返回张量第 n 维的元素个数（维度索引从 0 开始）

用法：

1	tensor.size(dim) # dim：指定维度的索引（0 表示第1维，1 表示第2维，以此类推）

如 tensor.size(1) 等价于 tensor.size()[1] 或 tensor.shape[1]

维度索引从 0 开始：
- size(0) 是第 1 维
- size(1) 是第 2 维
- size(-1) 表示最后一维（常用技巧）
若指定的维度索引超出张量的维度范围会抛出 IndexError
- 例如 1D 张量用 size(1) 会抛异常

对比 `torch.size()` 函数和 `tensor.size(n)`

size()：快速查看张量整体形状（例如确认输入数据是否符合模型要求）
size(1)：常用于提取矩阵的列数、文本张量的词向量维度等（例如 batch_size, seq_len = tensor.size(0), tensor.size(1)）

使用示例：

import torch

# 2D 张量（矩阵）整体输出
t2 = torch.tensor([[1, 2], [3, 4], [5, 6]])
print(t2.size())  # 输出: torch.Size([3, 2])，2维，3行2列

# 1D 张量：没有第1维（索引1超出范围），会报错
t1 = torch.tensor([1, 2, 3])
# print(t1.size(1))  # 报错：IndexError: Dimension out of range (expected to be in range of [-1, 0], but got 1)

# 2D 张量：第1维（索引1）是列数
print(t2.size(1))  # 输出: 2，对应 shape [3, 2] 的第2个元素（列数）
print(t2.size()[1])  # 等价写法，输出: 2

`torch.roll()` 函数

torch.roll 用于循环移位（滚动）张量元素 ，支持沿指定维度对张量元素进行循环平移，移位后超出边界的元素会从另一侧补回（类似“循环队列”的逻辑）
函数签名为：
1
torch.roll(input, shifts, dims=None) -> Tensor
- input：Tensor，输入张量（任意维度） |
- shifts：int / 序列，移位步数：
  - 正数：沿维度从后向前移（向右/向下）；
  - 负数：沿维度从前向后移（向左/向上）；
  - 序列形式（如 (2, -1)）：需与 dims 一一对应，为每个维度指定独立移位步数
- dims：int / 序列 / None，移位维度：
  - None（默认）：先将张量展平为 1D 再移位，最后恢复原形状；
  - 单个 int：仅沿该维度移位；
  - 序列形式（如 (0, 1)）：需与 shifts 长度一致，对多个维度依次移位
- 返回值：与 input 形状、数据类型完全相同的新张量（原张量不改变，除非用 in-place 版本 torch.roll_）

使用示例

1D 张量示例

import torch

x = torch.tensor([0, 1, 2, 3, 4])

# 向右移位 2 步（正数=向后移）
roll1 = torch.roll(x, shifts=2)
print(roll1)  # tensor([3, 4, 0, 1, 2])

# 向左移位 1 步（负数=向前移，等价于 shifts=len(x)-1）
roll2 = torch.roll(x, shifts=-1)
print(roll2)  # tensor([1, 2, 3, 4, 0])

2D 张量示例（注：dim=0（行方向，上下移）、dim=1（列方向，左右移））

# 仅单维度移位示例
x = torch.tensor([[1, 2, 3],
				[4, 5, 6],
				[7, 8, 9]])

# 沿 dim=0（行）向下移 1 步（最后一行绕回开头）
roll_row = torch.roll(x, shifts=1, dims=0)
print("行移位：")
print(roll_row)
# tensor([[7, 8, 9],
#         [1, 2, 3],
#         [4, 5, 6]])

# 沿 dim=1（列）向左移 1 步（第一列绕回末尾）
roll_col = torch.roll(x, shifts=-1, dims=1)
print("列移位：")
print(roll_col)
# tensor([[2, 3, 1],
#         [5, 6, 4],
#         [8, 9, 7]])

# 多维度同时移位：需保证 `shifts` 和 `dims` 长度一致，分别对应每个维度的移位步数
x = torch.tensor([[1, 2, 3],
				[4, 5, 6],
				[7, 8, 9]])

# 沿 dim=0 向下移 1 步，沿 dim=1 向右移 2 步
roll_multi = torch.roll(x, shifts=(1, 2), dims=(0, 1))
print(roll_multi)
# 步骤解析：
# 1. dim=0 移位后：[[7,8,9],[1,2,3],[4,5,6]]
# 2. 再对 dim=1 移位 2 步：[[8,9,7],[2,3,1],[5,6,4]]
# 最终结果：
# tensor([[8, 9, 7],
#         [2, 3, 1],
#         [5, 6, 4]])

dims=None（展平后移位，再恢复原来 shape）：默认将张量展平为 1D 移位，再恢复原形状，慎用（可能导致元素顺序混乱）

x = torch.tensor([[1, 2], [3, 4]])

# 展平为 [1,2,3,4]，移位 1 步 -> [4,1,2,3]，再恢复为 (2,2)
roll_flat = torch.roll(x, shifts=1, dims=None)
print(roll_flat)  # tensor([[4, 1], [2, 3]])

使用注意事项

移位步数可以超界（但不建议） ：步数会自动对维度长度取模（如长度为 5 的维度，移位 7 步等价于移位 7%5=2 步）
1
2
x = torch.tensor([0,1,2,3,4])
print(torch.roll(x, shifts=7)) # 等价于 shifts=2 -> tensor([3,4,0,1,2])
原张量不改变 ：torch.roll 是“非 in-place”操作，如需修改原张量，使用 torch.roll_（末尾加下划线）
1
2
3
x = torch.tensor([0,1,2])
x.roll_(shifts=1) # 原张量被修改
print(x) # tensor([2, 0, 1])
梯度传播 ：支持自动求导（梯度会跟随移位逻辑反向传播），可用于神经网络层中

`torch.quantile()` 函数

torch.quantile 是用于计算张量分位数的函数，支持多维张量、指定维度计算、线性插值等功能，适用于统计分析、异常值检测等场景
torch.quantile 支持多维张量、批量分位数、多种插值模式，核心是通过 dim 控制计算维度、q 指定分位数、interpolation 调整插值逻辑

torch.quantile 函数签名

torch.quantile(
	input: Tensor,
	q: Union[float, Tensor],
	dim: Optional[Union[int, Tuple[int, ...]]] = None,
	keepdim: bool = False,
	interpolation: str = 'linear',
	out: Optional[Tensor] = None
) -> Tensor

input：Tensor
- 输入张量（支持任意维度，如 1D/2D/3D 等）
q：float 或 Tensor
- 分位数（范围：[0, 1]）
- 可以是单个值（如 0.5 表示中位数）或张量（批量计算多个分位数）
dim：int 或 Tuple[int, ...]
- 计算分位数的维度（可选）。默认 None 表示对整个张量展平后计算
keepdim：bool
- 是否保留计算维度（默认 False，即压缩维度；True 则维度数不变）
interpolation：str
- 分位数插值方式（默认 'linear'），支持 5 种模式（下文详细说明）
  - 'linear'（默认），线性插值：q = i + f 时，结果 = (1-f)*x[i] + f*x[i+1]（最常用）
  - 'lower'，取下界：结果 = x[floor(i + f)]（即小于等于目标位置的最大元素）
  - 'higher'，取上界：结果 = x[ceil(i + f)]（即大于等于目标位置的最小元素）
  - 'nearest'，取最近邻：结果 = x[round(i + f)]（四舍五入到最近索引）
  - 'midpoint'，中点插值：结果 = (x[floor(i + f)] + x[ceil(i + f)]) / 2（上下界平均）

使用示例

1D 张量（展平计算），计算单个分位数（中位数）和多个分位数：

import torch

x = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0])

# 1. 计算中位数（0.5 分位数）
median = torch.quantile(x, q=0.5)
print("中位数:", median)  # 输出：tensor(3.)

# 2. 计算多个分位数（0.25、0.5、0.75 四分位数）
q_list = torch.tensor([0.25, 0.5, 0.75])
quantiles = torch.quantile(x, q=q_list)
print("四分位数:", quantiles)  # 输出：tensor([2., 3., 4.])

多维张量（指定维度计算）：对 2D 张量的行/列计算分位数，控制 dim 和 keepdim：

x = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=torch.float32)

# 1. 按列（dim=0）计算中位数，保留维度（keepdim=True）
col_median = torch.quantile(x, q=0.5, dim=0, keepdim=True)
print("按列中位数（保留维度）:\n", col_median)
# 输出：tensor([[4., 5., 6.]])（形状：[1, 3]）

# 2. 按行（dim=1）计算多个分位数（0.25、0.75），不保留维度
row_quantiles = torch.quantile(x, q=[0.25, 0.75], dim=1)
print("按行四分位数（不保留维度）:\n", row_quantiles)
# 输出：tensor([[2., 5., 8.], [3., 6., 9.]])（形状：[2, 3]）

注意事项

input 需为浮点型（float32/float64），整数型张量会自动转换为浮点型
q 必须在 [0, 1] 内，否则会抛出 ValueError
torch.quantile 的参数（如 interpolation）与 numpy.quantile 基本一致，可无缝迁移

`torch.nn.functional.pad()`（简称 `F.pad()`）

F.pad() 是用于张量填充的核心函数，支持任意维度的对称/非对称填充、多种填充模式（常数、反射、复制等），
F.pad() 函数签名
1
2
3
4
5
6
7
8
9
import torch.nn.functional as F

F.pad(
input: torch.Tensor,
pad: Sequence[int],
mode: str = 'constant',
value: float = 0.0,
**kwargs
) -> torch.Tensor
- input：torch.Tensor
  - 输入张量（支持任意维度：1D/2D/3D/4D/5D 等）
- pad：Sequence[int]
  - 填充尺寸配置（关键参数），格式为 (left0, right0, left1, right1, left2, right2, ...)，对应张量从最后一维到第一维的左右填充数
  - left0, right0 表示 dim=-1 的维度（最后一维）的左边和右边分别 pad 数量配置
  - 对于 N 维张量，pad 需包含 2*N 个整数（若某维度无需填充，填 0）
  - 每个维度的填充格式为 (left_pad, right_pad)，即 左边填充数，右边填充数
  - 示例：
    - 1D 张量（shape [L]）：pad=(left, right) ，填充后 shape [left + L + right]；
    - 2D 张量（shape [H, W]）：pad=(left_w, right_w, left_h, right_h)，填充后 shape [left_h + H + right_h, left_w + W + right_w]
    - 3D 张量（shape [D, H, W]）：pad=(left_w, right_w, left_h, right_h, left_d, right_d)，填充后 shape [left_d + D + right_d, left_h + H + right_h, left_w + W + right_w]
- mode：str
  - 填充模式（默认 'constant'），支持 6 种模式
    - 'constant'（默认）：用固定值 value 填充（如 0 填充）
    - 'reflect'，反射填充：以张量边缘为对称轴反射（不包含边缘本身）；注意，此时张量边缘是对称轴
    - 'replicate'，复制填充：用张量边缘的元素填充（重复边缘值）
    - 'circular'，循环填充：将张量视为循环结构，用对侧的元素填充（环绕填充）
    - 'edge'，等价于 'replicate'（兼容旧版本 PyTorch）
    - 'symmetric'，对称填充：以张量边缘为对称轴反射（包含边缘本身）
- value：float
  - 仅 mode='constant' 时有效，指定填充的常数（默认 0）
- **kwargs：
  - 额外参数（如 reflect/replicate 模式下的 padding_mode 兼容参数，较少用）

不同模式效果对比

以 2D 张量 [[1,2],[3,4]] 为例，左/右/上/下各填充 1 个元素，对比核心模式：

import torch
import torch.nn.functional as F

x = torch.tensor([[1,2],[3,4]], dtype=torch.float32)
pad = (1,1,1,1)  # (left_w=1, right_w=1, left_h=1, right_h=1)

# 不同模式填充结果简单对比
print("constant (value=0):")
print(F.pad(x, pad, mode='constant', value=0))
# 输出：
# tensor([[0., 0., 0., 0.],
#         [0., 1., 2., 0.],
#         [0., 3., 4., 0.],
#         [0., 0., 0., 0.]])

print("\nreflect:")
print(F.pad(x, pad, mode='reflect'))
# 输出（反射不包含边缘）：
# tensor([[4., 3., 4., 3.],
#         [2., 1., 2., 1.],
#         [4., 3., 4., 3.],
#         [2., 1., 2., 1.]])

print("\nreplicate:")
print(F.pad(x, pad, mode='replicate'))
# 输出（复制边缘）：
# tensor([[1., 1., 2., 2.],
#         [1., 1., 2., 2.],
#         [3., 3., 4., 4.],
#         [3., 3., 4., 4.]])

注意事项

pad 维度顺序 ：必须是「最后一维到第一维」的左右填充，容易混淆（如 2D 张量先 W 后 H），填错会导致尺寸异常
F.pad 是可微分操作，填充的常数部分梯度为 0，反射/复制部分梯度会反向传播到原张量边缘元素
'constant'/'replicate' 模式效率最高，'reflect'/'symmetric' 稍慢，'circular' 因循环逻辑效率较低（大张量建议提前优化）
与 nn.ZeroPad2d 等层的区别 ：nn.ZeroPad2d/nn.ReflectionPad2d 是封装好的层（仅支持特定维度），F.pad 更灵活（支持任意维度和模式），功能完全覆盖前者

`torch.unbind` 函数

torch.unbind 是 PyTorch 中用于拆分张量维度的核心函数，作用是将一个张量沿着指定维度（dim）“解绑”（拆分）为多个独立的张量，返回这些张量的元组
简单理解：假设有一个 shape 为 (batch_size, seq_len, hidden_dim) 的张量
- 沿着 dim=0（batch 维度）unbind 后，会得到 batch_size 个 shape 为 (seq_len, hidden_dim) 的张量；
- 沿着 dim=1（seq_len 维度）unbind 后，会得到 seq_len 个 shape 为 (batch_size, hidden_dim) 的张量
函数签名与核心参数
1
torch.unbind(input, dim=0) -> tuple[Tensor, ...]
- input：待拆分的输入张量（任意维度）
- dim：指定拆分的维度（默认 0，即第一个维度）
- 返回值：拆分后的张量组成的元组，元组长度 = 原张量在 dim 维度上的大小

`tensor.flip(dims)` 函数

tensor.flip(dims) 用于沿着指定维度翻转张量（reverse the order of elements），仅改变指定维度上元素的顺序，不改变张量的形状、数据类型和设备
- dims 是整数或整数元组，指定要翻转的维度（0=第1维，1=第2维，以此类推）
- 沿 dims 维度反转元素顺序，非指定维度保持不变
- 张量的 shape、dtype、device、requires_grad 均不改变
- 支持自动微分（梯度会正确传播）

注：flip 还有个实现是参数可以是可变位置参数（即展开的列表/元组）

@overload
def flip(self, dims: _size) -> Tensor: ...
@overload
def flip(self, *dims: _int) -> Tensor: ... # 可变位置参数

使用示例

import torch

# 1D 整数张量
a = torch.tensor([1, 2, 3, 4])
a_flip = a.flip(dims=[0])  # 或 a.flip(0)，沿维度0翻转（唯一维度），等价于 `tensor[::-1]`
print("1D flip结果:", a_flip)  # 输出: tensor([4, 3, 2, 1])
print("形状不变:", a_flip.shape == a.shape)  # 输出: True

# 2D 浮点数张量，可指定沿行（维度0）、列（维度1）或同时沿行列翻转
b = torch.tensor([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]])

b_flip_0 = b.flip(dims=[0])  # 沿行翻转（上下颠倒） 等价于 b.flip(0)
print("沿行翻转:\n", b_flip_0)
# 输出:
# tensor([[5., 6.],
#         [3., 4.],
#         [1., 2.]])

b_flip_1 = b.flip(dims=[1])  # 沿列翻转（左右颠倒）
print("沿列翻转:\n", b_flip_1)
# 输出:
# tensor([[2., 1.],
#         [4., 3.],
#         [6., 5.]])

b_flip_01 = b.flip(dims=[0, 1])  # 同时沿行和列翻转  等价于 b.flip(0,1)
print("沿行列翻转:\n", b_flip_01)
# 输出:
# tensor([[6., 5.],
#         [4., 3.],
#         [2., 1.]])

# 3D 张量（模拟2个2×2的图像），可指定任意维度翻转（如batch维度、高度维度、宽度维度）
c = torch.tensor([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])  # shape: (2, 2, 2)

c_flip_2 = c.flip(dims=[2])  # 沿宽度维度（第3维）翻转
print("3D沿宽度翻转:\n", c_flip_2)
# 输出:
# tensor([[[2, 1],
#         [4, 3]],
#        [[6, 5],
#         [8, 7]]])

c_flip_0 = c.flip(dims=[0])  # 沿batch维度翻转
print("3D沿batch翻转:\n", c_flip_0)
# 输出:
# tensor([[[5, 6],
#         [7, 8]],
#        [[1, 2],
#         [3, 4]]])

`torch.nn.utils.rnn.pad_sequence` 函数

torch.nn.utils.rnn.pad_sequence 是 PyTorch 中处理变长序列（Variable-length Sequences） 的工具，用于将一批长度不同的张量（序列）填充到相同长度，以便批量输入 RNN、Transformer 等模型
核心功能是将一个 张量列表（每个张量对应一条变长序列）填充为一个 统一长度的二维/高维张量 ，填充值默认是 0（可自定义）；其填充规则为：
- 短序列在 末尾（右侧） 补零（默认，可通过 batch_first 调整返回值维度顺序）；
- 最终长度由列表中 最长序列的长度 决定

函数签名

torch.nn.utils.rnn.pad_sequence(
	sequences,          # 变长序列的列表
	batch_first=False,  # 输出张量的维度顺序：是否为 (batch_size, seq_len, ...)
	padding_value=0.0   # 填充值（默认0）
) -> Tensor

sequences：List[Tensor]
- 必须是张量列表 ，每个张量的形状需满足：
  - 1D 张量：(seq_len_i,)（如单特征序列）；
  - 2D 张量：(seq_len_i, feature_dim)（如带特征维度的序列）；
  - 高维张量：(seq_len_i, d1, d2, ...)（如序列+多特征维度）；
  - 注意：所有张量的除了 第一个 维度（要求第一个维度为待对齐的序列长度）外，其余维度必须一致
batch_first：bool
- 控制输出张量的维度顺序：
  - False（默认）：输出形状 (max_seq_len, batch_size, ...)（适配 PyTorch RNN 层默认输入格式）；
  - True：输出形状 (batch_size, max_seq_len, ...)（更直观，适合自定义模型）
padding_value：float
- 虽然写的是 float，但可以填充整数，默认 0 或 0.0，（类型需与输入张量 dtype 兼容）

用法示例

1D 变长序列（单特征）

import torch
from torch.nn.utils.rnn import pad_sequence

# 生成3条长度不同的1D序列（seq_len分别为2、3、1）
seq1 = torch.tensor([1, 2])       # shape: (2,)
seq2 = torch.tensor([3, 4, 5])    # shape: (3,)
seq3 = torch.tensor([6])          # shape: (1,)
sequences = [seq1, seq2, seq3]

# 1. 默认参数（batch_first=False，padding_value=0）
padded = pad_sequence(sequences)
print("默认输出 shape:", padded.shape)  # (max_seq_len=3, batch_size=3)
print("默认输出:\n", padded)
# 输出：
# tensor([[1, 3, 6],
#         [2, 4, 0],
#         [0, 5, 0]])

2D 变长序列（带特征维度）：适用于每条序列的每个元素是一个特征向量（如词嵌入后的序列）：

# 2D序列：shape (seq_len_i, feature_dim)，feature_dim=2（统一）
seq1 = torch.tensor([[1, 10], [2, 20]])          # (2, 2)
seq2 = torch.tensor([[3, 30], [4, 40], [5, 50]]) # (3, 2)
seq3 = torch.tensor([[6, 60]])                   # (1, 2)
sequences = [seq1, seq2, seq3]

padded = pad_sequence(sequences, batch_first=True)
print("2D序列填充后 shape:", padded.shape)  # (3, 3, 2)（batch_size=3, max_seq_len=3, feature_dim=2）
print("2D序列填充后:\n", padded)
# 输出：
# tensor([[[ 1, 10],
#          [ 2, 20],
#          [ 0,  0]],  # 短序列补零（特征维度均补0）
# 
#         [[ 3, 30],
#          [ 4, 40],
#          [ 5, 50]],
# 
#         [[ 6, 60],
#          [ 0,  0],
#          [ 0,  0]]])

`torch.randperm` 函数

torch.randperm 函数的原型为：

1	torch.randperm(n, *, generator=None, out=None, dtype=torch.int64, layout=torch.strided, device=None, requires_grad=False) -> Tensor

torch.randperm 函数用于生成 0 到 n-1 的随机排列
- 返回一个长度为 n、包含不重复整数的 1D 张量 ，常用于数据打乱（如训练集 shuffle、批次采样）
- 注意返回的是索引 indices，并不改变按原始数据

`torch.argsort` 函数

torch.argsort 用于返回张量元素排序后索引的函数
- 核心作用是：不改变原张量，仅返回一个索引张量，该索引对应将原张量按指定规则排序后各元素的原始位置
torch.argsort 函数原型为：
1
torch.argsort(input, dim=-1, descending=False, stable=False, *, out=None)
- input：输入张量（任意维度，如 1D、2D、3D 等）
- dim ：指定排序的维度（负号表示倒数维度，如 dim=-1 表示最后一维）；默认 -1
- descending：是否降序排序（True 降序，False 升序）；默认 False
- stable：是否使用稳定排序（相同元素保留原始顺序，仅对 CPU 有效，GPU 不支持）；默认 False
- out：输出张量（可选，用于指定结果存储位置）；默认 None
- 返回值：一个与 input 形状完全相同的整数张量 ，元素为原张量排序后的索引

1D 张量示例：对一维张量排序，返回排序后元素的原始索引（升序/降序）

import torch

# 1D 输入张量
x = torch.tensor([3, 1, 4, 1, 5])

# 升序排序（默认 descending=False）
idx_asc = torch.argsort(x)
print("升序索引:", idx_asc)  # 输出：tensor([1, 3, 0, 2, 4])
# 验证：x[idx_asc] 即为排序后的张量
print("升序结果:", x[idx_asc])  # 输出：tensor([1, 1, 3, 4, 5])

# 降序排序（descending=True）
idx_desc = torch.argsort(x, descending=True)
print("降序索引:", idx_desc)  # 输出：tensor([4, 2, 0, 3, 1])
print("降序结果:", x[idx_desc])  # 输出：tensor([5, 4, 3, 1, 1])

结合 `torch.randperm` 函数和 `torch.argsort` 函数实现打乱再恢复

举个直观例子：
- 原索引：[0,1,2,3,4]（对应 x 的位置）
- randperm(5) 生成 shuffle_idx = [3,0,4,1,2]（随机打乱）
- x_shuffled = x[3], x[0], x[4], x[1], x[2]
- argsort(shuffle_idx) 计算：
  - 将 shuffle_idx 升序排序为 [0,1,2,3,4]，其元素对应在 shuffle_idx 中的位置是 [1,3,4,0,2]（存储为 restore_idx）
- 验证：x_shuffled[restore_idx] = x[0],x[1],x[2],x[3],x[4]（完全恢复原顺序）
通过 torch.randperm 打乱 + torch.argsort(shuffle_idx) 恢复的核心是 “索引映射的可逆性”
- 打乱：用随机索引映射到乱序；
- 恢复：用 argsort 还原该映射，与张量值无关，高效且稳定

1D 张量示例：

import torch

# 1. 生成原张量（长度为 5）
x = torch.tensor([10, 20, 30, 40, 50])  # 原张量：[10,20,30,40,50]
n = len(x)

# 2. 用 randperm 打乱顺序
shuffle_idx = torch.randperm(n)  # 生成 0~4 的随机排列（例：[3,0,4,1,2]）
x_shuffled = x[shuffle_idx]      # 打乱后的张量：x[3],x[0],x[4],x[1],x[2] -> [40,10,50,20,30]
print("打乱索引 shuffle_idx:", shuffle_idx)
print("打乱后 x_shuffled:", x_shuffled)

# 3. 用 argsort 恢复顺序（核心：对 shuffle_idx 做 argsort）
restore_idx = torch.argsort(shuffle_idx)  # 恢复索引：[1,3,4,0,2]（示例）
x_restored = x_shuffled[restore_idx]      # 恢复原张量
print("恢复索引 restore_idx:", restore_idx)
print("恢复后 x_restored:", x_restored)
print("是否完全恢复：", torch.equal(x, x_restored))  # 输出 True

注意（对 index 做排序的优点）：
- 如果原张量有重复值，直接对 x_shuffled 做 argsort 可能因值排序导致恢复失败，但对 shuffle_idx 做 argsort 不受值影响（仅依赖索引映射）

`len(dataloader)` 函数

len(dataloader) 得到的是训练数据加载器（DataLoader）的批次数（batch count），即整个训练数据集被划分为多少个批次（batch）
注：len(dataloader) 可以在任意时刻使用，不会影响 dataloader 数据集的迭代操作

示例：

import torch
from torch.utils.data import DataLoader, TensorDataset

# 构造简单数据集和dataloader
dataset = TensorDataset(torch.randn(1000, 10))  # 1000个样本
train_dataloader = DataLoader(dataset, batch_size=32, drop_last=False)

# 定义get_batch（基于dataloader迭代器）
def get_batch(loader):
	loader_iter = iter(loader)  # 每次调用都重新初始化迭代器（关键）
	return next(loader_iter)

# 第一步：调用len()
print(len(train_dataloader))  # 输出32（仅计算批次数，不碰数据）

# 第二步：正常get_batch
batch = get_batch(train_dataloader)
print(batch[0].shape)  # 输出torch.Size([32, 10])（成功获取批次，无任何影响）

`tensor.expand()` 和 `tensor.expand_as()` 函数

核心：Expand 是“视图扩展”，不是“数据复制”
expand() 和 expand_as() 的核心作用是将张量在维度上进行扩展（广播） ，但它并不会复制新的数据，而是返回原张量的一个“视图（view）”
- 扩展后的张量和原张量共享内存（修改原张量，扩展后的张量也会变；）
- 只有在维度大小为 1 的位置才能被扩展

tensor.expand() 用法

基本语法
1
tensor.expand(*sizes)
- *sizes：传入想要扩展后的张量形状（元组/多个整数）
- 规则：
  - 对于原张量中大小为 1 的维度，可以扩展为任意正整数；
  - 对于原张量中大小大于 1 的维度，必须和原维度大小一致（不能改）；
  - 可以用 -1 表示“保持原维度大小不变”；
  - 支持“维度扩展”（比如从 2D 扩展为 3D），只需在前面/后面加 1 再扩展

代码示例

import torch

# 扩展维度（可新增维度）
x = torch.tensor([1, 2, 3])  # shape: [3]
x_expand = x.expand(5, 3)    # 扩展为 [5, 3]
print("原张量x：", x)
print("扩展后x_expand：", x_expand) # 复制 5 行
print("x_expand形状：", x_expand.shape)  # torch.Size([5, 3])

# 用-1保持原维度
y = torch.tensor([[1], [2], [3]])  # shape: [3, 1]
y_expand = y.expand(3, 4)          # 扩展第2维为4，shape: [3,4]
y_expand2 = y.expand(-1, 4)        # -1 等价于保持3不变，结果和上面一致
print("\ny_expand：", y_expand)
print("y_expand2形状：", y_expand2.shape)  # torch.Size([3, 4])

# 错误示例：非1维度不能修改
z = torch.tensor([1, 2])  # shape: [2]
# z_error = z.expand(3, 4)  # 原第2维是2，不能扩展为4，会报错

tensor.expand_as() 用法

基本语法
1
tensor.expand_as(other_tensor)
- 作用：等价于 tensor.expand(other_tensor.size())，即把当前张量扩展为和 other_tensor 相同的形状
- 规则：和 expand() 完全一致，只是不需要手动写形状，直接复用另一个张量的形状

代码示例

import torch

# 原张量
a = torch.tensor([[1], [2], [3]])  # shape: [3, 1]
# 目标形状的张量
b = torch.randn(3, 4)              # shape: [3, 4]

# 扩展a为b的形状
a_expand = a.expand_as(b)
print("a_expand形状：", a_expand.shape)  # torch.Size([3, 4])
print("a_expand：", a_expand)
# 输出：
# tensor([[1, 1, 1, 1],
#         [2, 2, 2, 2],
#         [3, 3, 3, 3]])

# 等价写法
a_expand2 = a.expand(b.size())
print(torch.equal(a_expand, a_expand2))  # True（两个结果完全一致）

`torch.ge` 函数

torch.ge 是用于逐元素比较 的基础函数，核心功能是判断第一个输入张量的元素是否大于或等于第二个输入张量的对应元素，最终返回一个与输入同形状的布尔型张量（dtype=torch.bool），元素值为 True/False 表示对应位置的比较结果
完整形式：torch.ge(input, other, *, out=None)
- input：torch.Tensor（必选），第一个输入张量（比较的左操作数）
- other： torch.Tensor，数值型（int/float）（必选），第二个输入（比较的右操作数），支持广播机制
其他等价名称：torch.greater_equal（与 torch.ge 功能完全一致，可互换使用）
注意输出类型：逐元素执行 input >= other 比较，输出布尔张量（与广播后形状一致），数据类型固定为 torch.bool，每个元素对应 input 和 other 对应位置的 >= 比较结果

Centos——挖矿病毒kdevtmpfsi查杀经历

挖矿病毒kdevtmpfsi查杀经历

问题简介

服务器: 阿里云主机服务器
系统: Centos7
表现: kdevtmpfsi进程占用400%(8核心处理器)CPU
时间: 2020-01-07报警, 2020-01-08处理

查杀经过

使用clamscan命令搜索所有文件, clamav详情见我之前的博客clamav安装与杀毒
1
nohup clamscan / -r --infected -l clamscan.log > clamscan.out &
- 注：这一步比较花时间
查看扫描结果
1
cat clamscan.log | grep FOUND
/var/lib/docker/overlay/bdd049c71596d743907224a8dd6fdb3fb4ca76e3af8dfd6eee2d034de2be45a1/merged/tmp/kdevtmpfsi: Multios.Coinminer.Miner-6781728-2 FOUND
/var/lib/docker/overlay/bdd049c71596d743907224a8dd6fdb3fb4ca76e3af8dfd6eee2d034de2be45a1/merged/tmp/red2.so: Unix.Trojan.Gafgyt-6981174-0 FOUND
/var/lib/docker/overlay/bdd049c71596d743907224a8dd6fdb3fb4ca76e3af8dfd6eee2d034de2be45a1/upper/tmp/kdevtmpfsi: Multios.Coinminer.Miner-6781728-2 FOUND
/var/lib/docker/overlay/bdd049c71596d743907224a8dd6fdb3fb4ca76e3af8dfd6eee2d034de2be45a1/upper/tmp/red2.so: Unix.Trojan.Gafgyt-6981174-0 FOUND
删除这四个文件,这里直接到相关目录下查看发现../tmp目录下往往都是病毒文件(与kinsing相关,全部删除)
top查看CPU信息确定挖矿进程kdevtmpfsi的进程号[pid]
确定启动信息中启动命令,并删除(在这里查到的信息是文件已经被删除了)
1
ls /proc/[pid] -ali
查找父进程进程号
1
systemctl status [pid]
● docker-be9fcab033e6158f8ff7d6ac07d28cfd918375178c27e016aa800cbeef985161.scope - libcontainer container be9fcab033e6158f8ff7d6ac07d28cfd918375178c27e016aa800cbeef985161
Loaded: loaded (/run/systemd/system/docker-be9fcab033e6158f8ff7d6ac07d28cfd918375178c27e016aa800cbeef985161.scope; static; vendor preset: disabled)
Drop-In: /run/systemd/system/docker-be9fcab033e6158f8ff7d6ac07d28cfd918375178c27e016aa800cbeef985161.scope.d
```
      └─50-BlockIOAccounting.conf, 50-CPUAccounting.conf, 50-DefaultDependencies.conf, 50-Delegate.conf, 50-Description.conf, 50-MemoryAccounting.conf, 50-Slice.conf
```
Active: active (running) since Mon 2019-11-11 11:24:17 UTC; 1 months 27 days ago
```
  Tasks: 38
```
Memory: 2.3G
CGroup: /system.slice/docker-be9fcab033e6158f8ff7d6ac07d28cfd918375178c27e016aa800cbeef985161.scope
```
      ├─ 4475 redis-server *:6379
      ├─ 8528 sh -c /tmp/.ICEd-unix/vJhOU
      ├─ 8529 /tmp/.ICEd-unix/vJhOU
      └─22822 /tmp/kdevtmpfsi
```
Warning: Journal has been rotated since unit was started. Log output is incomplete or unavailable.
杀死不需要的相关进程,如上面的4475,8528, 8529, 22822
查看是否还有需要杀死的进程,如果有,则杀死该进程
1
ps -ef | grep kinsing
top确定挖矿进程已经被杀死

总结

查杀病毒两个小时未发现服务器有明显异常
第二天出现了,需要进一步查看,重启机器后问题没有再出现

CA——(AMA)Affine-maximizer-auction机制

参考链接：
- 其他参考论文：A Scalable Neural Network for DSIC Affine Maximizer Auction Design, NeurIPS 2023, PKU，Spotlight

AMA是什么？

仿射最大化拍卖（Affine Maximizer Auction, AMA）是一种机制设计，它旨在最大化卖家的收益同时确保买家在占优策略下报价（DSIC，Dominant Strategy Incentive Compatible）和个体理性（IR，Individually Rational）。AMA是Vickrey-Clarke-Groves (VCG) 拍卖的一种泛化形式

分配规则

假设有 $n$ 个买家竞拍一个位置，给定买家出价 $ B $，以及一组预定义的分配方案菜单 $ \mathcal{A} $，AMA选择一个分配方案 $ A^* \in \mathcal{A} $，使得如下仿射福利函数最大：
$$ A^* = \arg\max_{A \in \mathcal{A}} \left( \sum_{i=1}^{n} w_i \cdot u_i(A, B) + \lambda(A) \right) $$
- $ w_i $ 是买家 $ i $ 的权重，$ w_i \in \mathbb{R}_{+} $；
- $ u_i(A, B) $ 是买家 $ i $ 在分配方案 $ A $ 下根据出价 $ B $ 计算的效用。在其他商家出价不变时， $ u_i(A, B) $ 是关于商家自身出价 $b_i$ 是非减函数；
- $ \lambda(A) $ 是对每个分配方案 $ A $ 的增强变量（也称为仿射项），它是一个实数值

计费规则

对于每个买家 $ k $，其需要支付的价格 $ p_k $ 为她在其他买家出价情况下所带来的外部性。具体来说，买家 $ k $ 需要支付的价格为：
$$ p_k = \sum_{i \neq k} w_i \cdot u_i(A_{-k}^*, B_{-k}) + \lambda(A_{-k}^*) - \left( \sum_{i \neq k} w_i \cdot u_i(A^*, B) + \lambda(A^*) \right) $$
- $ A_{-k}^* $ 是去除买家 $ k $ 后最大化其他人仿射福利的分配方案；
- $ B_{-k} $ 表示除买家 $ k $ 外所有买家的出价集合；
- $ A^* $ 是包括买家 $ k $ 在内的最优分配方案
计费规则分析：
- 这个价格计算方法下，如果其他买家的出价保持不变，保证了即使买家 $ k $ 改变她的出价，也不会影响她实际需要支付的价格
- 此外，由于买家的真实估值不会导致负效用，所以这个机制也是个体理性的（IR）

AMA 和 VCG的比较

Vickrey-Clarke-Groves (VCG) 机制：核心目标是最大化社会福利 ，而不是直接优化卖家的收益，其分配规则选择使总效用最大化的方案，支付规则基于买家对其他买家造成的外部性来计算
Affine Maximizer Auction (AMA)机制：核心目标是最大化放射函数 ，AMA是VCG机制的一种泛化形式，它引入了仿射项（affine term）和权重参数，从而允许更灵活地设计拍卖规则，由于引入了仿射项 $ \lambda(A) $，AMA可以在保持DSIC的同时，通过适当选择 $ \lambda(A) $ 来提高卖家的收益
从理论上讲，AMA的收益上限不低于VCG ，因为：
- VCG机制是AMA的一个特例，当 $ w_i = 1 $ 且 $ \lambda(A) = 0 $ 时，AMA退化为VCG
- AMA通过调整 $ w_i $ 和 $ \lambda(A) $，可以在保持DSIC的同时探索更大的收益空间
实际收益取决于具体的买家估值分布、市场环境以及机制设计的细节：
- 如果买家估值分布较为均匀，VCG机制通常已经接近最优收益，AMA的优势可能不明显
- 如果买家估值分布不均匀或市场存在不对称性，AMA可以通过调整 $ \lambda(A) $ 来更好地提取剩余价值，从而实现更高的收益

CA——(JAMA)Joint-Bidding-in-Ad-Auctions

参考链接：
- 参考论文：Joint Bidding in Ad Auctions, pp 344–354, TAMC 2024, Meituan

前置：对文章的整体评价

提出了新颖的供应商与零售商联合拍卖场景
文章中部分内部不是很Solid，比如对原始VCG的分析不太合理
文章缺少对模型细节的详细描述

整体说明

提出问题 ：与传统拍卖方式不同，单个商品可能同时由零售商和供应商赞助，在零售商和供应商联合投标广告位这种现实场景下，传统的机制，如广义第一价格拍卖（GFP）、广义第二价格拍卖（GSP）和迈尔森拍卖，无法直接应用。此外，VCG机制在JAS中会导致负收益（存疑，待讨论）
论文工作 ：
- 论文将这种新颖的广告模式称为联合广告系统（joint advertising system，以下简称JAS）
- 论文修改了VCG的支付规则，创建了一种修正的VCG机制，以保证激励相容性、个体理性和弱预算平衡
- 论文利用仿射最大化拍卖（AMA）的结构和自动机制设计技术来训练联合AMA

讨论

论文定义了零售商和供应商对同一商品出价的全新场景
论文引入了一种创新机制，称为修正的VCG机制（revised VCG mechanism，简称RVCG），它在修改VCG支付规则的同时，满足IC、IR和WBB约束（WBB定义：平台收入不为负）
为了进一步提高收入，论文将AMA推广到联合投标场景，称为联合AMA（JAMA），并采用自动机制设计技术来训练联合AMA的参数，以提高收入
论文通过归一化和调整神经网络结构进一步限制参数的搜索空间，从而提高了模型的扩展性
- VCG机制可以最大化社会福利，而AMA最大化的是加权和 boost 后的社会福利。通过调整参数，AMA可以在保持IC和IR的同时获得比VCG更高的收入

模型与预备知识

在JAS中，有 $n$ 个零售商(Retailer) $R = \{r_1, \ldots, r_n\}$ 和 $m$个供应商(Saller) $S = \{s_1, \ldots, s_m\}$
- 零售商和供应商之间的合作关系可以用一个二分图 $G = (V, E)$ 表示，其中顶点集 $V = R \cup S$ 包含所有零售商和供应商，边集 $E$ 表示零售商和供应商之间的协作关系
- 一条边 $e = (r_i, s_j) \in E$ 意味着供应商 $j$ 为零售商 $i$ 提供商品，或者零售商 $i$ 销售供应商 $j$ 的商品
- $D(r_i) = \{s_j | (r_i, s_j) \in E\}$ 为与零售商 $r_i$ 合作的供应商集合， $C(s_j) = \{r_i | (r_i, s_j) \in E\}$ 为供应商 $s_j$ 的合作零售商集合
假设一次拍卖有$K$ 个广告位，索引为 $k \in \{1, 2, \ldots, K\}$，第k个广告位的点击率为 $\lambda_k$ ，且索引越小的广告位点击率越高，即 $\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_K \geq 0$
每个零售商 $r_i$ 对每次点击都有一个私人价值 $v_{r_i}$，供应商 $s_j$ 的点击私人价值为 $v_{s_j}$，假设 $v_{r_i}$ 和 $v_{s_j}$都是从一个公开已知的分布 $F(v)$ 中独立同分布抽取的，其概率密度函数为 $f(v)$
分别用 $\mathbf{v}^R = (v_{r_1}, \ldots, v_{r_n})$ 和 $\mathbf{v}^S = (v_{s_1}, \ldots, v_{s_m})$ 表示零售商和供应商的价值向量。用 $v = (\mathbf{v}^R, \mathbf{v}^S)$、$v_{-r_i}$、$v_{-s_j}$ 表示所有广告主的价值向量、除零售商 $i$、供应商 $j$ 之外的所有广告主的价值向量。类似地，对于出价向量，论文也使用类似的符号，例如 $\mathbf{b}^R$ 、 $\mathbf{b}^S$ 、 $\mathbf{b}$ 、 $\mathbf{b}_{-r_i}$ 和 $\mathbf{b}_{-s_j}$
在论文的模型中，一个广告商品由两方赞助：一个零售商和一个供应商。因此，对于所有 $e = (r_i, s_j) \in E$ ，论文将这样一个组合的联合投标定义为 $b_{ij} = b_{r_i} + b_{s_j}$ 。有时论文也用 “组合” 来表示一个广告商品
有了这些符号，我们可以定义JAS中的拍卖机制。一个机制 $\mathcal{M} = (\mathbf{a}(\mathbf{b}), \mathbf{p}(\mathbf{b}))$ 两部分组成：
- 分配规则：$a(\mathbf{b}) = (a_i(\mathbf{b}))_{i \in R \cup S}$
- 支付规则：$p(\mathbf{b}) = (p_i(\mathbf{b}))_{i \in R \cup S}$
- 在这里，对于任何广告主 $i$ ， $a_i(\mathbf{b}) = \sum_{k = 1}^{K} a_{ik}(\mathbf{b})\lambda_k$ 代表总点击率，其中 $a_{ik}(\mathbf{b})$ 是一个指示函数，用于决定分配到第k个广告位的广告商品是否包含广告主 $i$
由于一个广告位应分配给一个组合，且一个组合最多分配到一个广告位， $a_{ik}(\mathbf{b})$ 应满足以下可行性约束，记为$\mathcal{A}$：
$$
\sum_{k = 1}^{K}[a_{ik}(\mathbf{b}) \cdot a_{jk}(\mathbf{b})] \leq 1, \forall e = (r_i, s_j) \in E \\
\sum_{i \in R} a_{ik}(\mathbf{b}) + \sum_{j \in S} a_{jk}(\mathbf{b}) = 2, \forall k \in K \\
\sum_{i \in R} a_{ik}(\mathbf{b}) \leq 1, \sum_{j \in S} a_{jk}(\mathbf{b}) \leq 1, \forall k \in K \\
a_{ik}(\mathbf{b}) \in \{0, 1\}, \forall i \in R \cup S, k \in K
$$
- 问题：为什么是等于2？实际上就是表示各等于1吧
给定分配规则和支付规则，任何零售商或供应商 $i$ 的效用可以表示为：
$$u_i(\mathbf{b}) = v_i \cdot a_i(\mathbf{b}) - p_i(\mathbf{b})$$
拍卖机制的收入是广告主的总支付，即：
$$Rev(\mathbf{b}) = \sum_{i \in R} p_i(\mathbf{b}) + \sum_{j \in S} p_j(\mathbf{b})$$
拍卖机制的社会福利定义为广告主的总价值，即：
$$SW(\mathbf{b}) = \sum_{i \in R \cup S} v_i \cdot a_i(\mathbf{b})$$
在论文中，论文主要关注具有一些理想特性的可行机制，如激励相容性、个体理性和弱预算平衡，正式定义如下：
- 定义1（激励相容性） ：在JAS中，如果对于任何广告主 $i$ 、任何投标 $b_i’$ 和任何投标向量 $\mathbf{b}_{-i}$ ，都有 $u_i(v_i, \mathbf{b}_{-i}) \geq u_i(b_i’, \mathbf{b}_{-i})$ ，则该机制是激励相容的
- 定义2（个体理性） ：在JAS中，如果对于任何广告主 $i$ 和任何投标向量 $\mathbf{b}_{-i}$ ，都有 $u_i(v_i, \mathbf{b}_{-i}) \geq 0$ ，则该机制是个体理性的
- 定义3（弱预算平衡） ：在JAS中，如果收入总是非负的，即 $Rev(\mathbf{b}) = \sum_{i \in R} p_i(\mathbf{b}) + \sum_{j \in S} p_j(\mathbf{b}) \geq 0$ ，则该机制是弱预算平衡的
也就是说，IC和IR保证所有广告主都会如实投标并获得非负效用。WBB确保收入始终非负。在论文的其余部分，论文主要关注设计具有IC、IR和WBB的可行机制

经典拍卖机制

在本节中，论文首先主要关注经典的VCG机制，并展示它在JAS中起作用，但不能保证WBB（待讨论）。然后，论文修改VCG机制的支付规则以满足WBB，并将其称为修正的VCG机制

修正的VCG机制

在JAS中，由于一个广告位由一个零售商 $r_i$ 和与 $r_i$ 有合作关系的一个供应商 $s_j$ 组成的组合占据，分配规则更多地关注可行组合的投标。首先，论文引入分配规则（算法1），当所有广告主如实投标时，该规则可以实现最优社会福利
引理1 ：在联合广告系统中，当所有广告主如实投标时，算法1输出的分配可以实现最优社会福利
现在，论文详细阐述JAS中的VCG机制。实际上，VCG机制的分配规则遵循算法1的步骤。直观地说，VCG机制的支付规则是对每个广告主 $i$ 的外部性进行收费，即有广告主 $i$ 和没有广告主 $i$ 时所有其他广告主的社会福利之差。用 $SW^*(\mathbf{b})$ 表示投标向量 $\mathbf{b}$ 下的最优社会福利。VCG机制对广告主 $i$ 的支付可以定义为：
$$ p_i(\mathbf{b}) = SW^*(\mathbf{b}_{-i}) - [SW^*(\mathbf{b}) - a_i(\mathbf{b}) \cdot b_i] $$
不难发现，VCG机制是IR和IC的，因为任何广告主的支付都与她自己的投标无关。然而，基于联合投标的模式，当一个投标者不参加拍卖时，她的合作伙伴将失去形成组合并竞争广告位的机会，这可能会导致最优社会福利的损失。在下面的例子中，论文展示当一个投标者退出拍卖时，其他广告主的最优总价值会下降。这意味着一个广告主的支付可能为负，从而违反WBB
示例1 ：假设有两个零售商 $\{r_1, r_2\}$ 和两个供应商 $\{s_1, s_2\}$ ，只有两个合作关系 $\{(r_1, s_1), (r_2, s_2)\}$ 。设零售商和供应商的价值分别为 $(v_{r_1}, v_{r_2}) = (3, 2)$ 和 $(v_{s_1}, v_{s_2}) = (5, 1)$ 。只有一个广告位， $\lambda_1 = 1$ ，在这种情况下，VCG机制会将广告位分配给组合 $(r_1, s_1)$ ，此时社会福利为8；
- $r_1$ 的支付为 $p_{r_1}=SW_{-r_1}^* - (SW^* - \lambda_1v_{r_1}) = 1\times(0+5) - (8 - 1\times3)= 0$，直观理解就是无论是否加入 $r_1$，这个位置都会是 $s_1$ 的，所以 $r_1$ 不应该付钱
- $s_1$ 的支付为 $p_{s_1}=SW_{-s_1}^* - (SW^* - \lambda_1v_{s_1}) = 1\times(2 + 1) - (8 - 1\times5)=0$，直观理解就是无论是否加入 $s_1$，这个位置都会是 $r_1$ 的，所以 $s_1$ 不应该付钱
- $p_{s_2}=p_{r_2}=0$
- 总收益为 0，这违反了弱预算平衡的约束
- 注意：论文这里有错误，总收益写的是-2 ，且错误表达为：$r_1$ 的支付为 $p_{r_1}=SW_{-r_1}^* - (SW^* - \lambda_1v_{r_1}) = 1\times(2 + 1) - (8 - 1\times3)= - 2$（这里有错误 ：$SW_{-r_1}^*$应该是等于 $5$ 才对，$r_1$ 不参与的情况下，$s_1$ 靠自己的出价也能拿到这个位置），下面的内容也是基于错误写的：
  - 定理1 ：在联合广告系统中，VCG机制具有激励相容性、个体理性，并且可以实现最优社会福利，但不满足弱预算平衡
  - 例1中导致负收益的主要原因是，如果没有零售商 $r_1$ ，价值较高的供应商 $s_1$ 就会失去竞争机会，从而导致最优社会福利的损失。直观地说，如果论文能够保留供应商 $s_1$ 为社会福利做贡献的权利，那么零售商 $r_1$ 的支付就不会为负，进而可以保证弱预算平衡
  - 基于上述思路，论文修改VCG机制的支付规则：当关键广告商不参与拍卖时，论文假设其出价为0，并且合作关系仍然保留，而不是直接将其剔除。修改后的支付规则可以写成：
    $$p_{i}(\mathbf{b})=SW^{*}\left(0, \mathbf{b}_{-i}\right)-\left[SW^{*}(\mathbf{b})-a_{i}(\mathbf{b}) \cdot b_{i}\right]$$
  - 论文将具有上述支付规则的VCG机制定义为修正的VCG机制，并证明修正的VCG机制可以保证弱预算平衡
  - 定理2 ：在联合广告系统中，修正的VCG机制具有激励相容性、个体理性、弱预算平衡，并且可以实现最优社会福利

联合仿射最大化拍卖

在本节中，论文首先介绍仿射最大化拍卖（AMA），它是VCG机制的广义版本。然后，根据第3节中修正的VCG机制，在JAS的投标环境中扩展传统的AMA，论文将其称为联合AMA（JAMA），并概述JAMA的流程

仿射最大化拍卖概述

如前所述，修正的VCG机制可以确保平台的收入为非负。然而，平台仍然希望在保持激励相容性和个体理性等理想特性的同时，进一步提高收入。因此，论文考虑一种更广泛的机制类型，称为仿射最大化拍卖，它可以看作是VCG机制的推广
与VCG机制不同，AMA有两组参数：权重和 boost 值。每个投标者 $i $都有一个正权重 $w_{i}$ ，并且任何分配方案 $\mathbf{a} $都与一个 boost 值 $u(\mathbf{a}) $相关联。AMA的主要思想是分配物品以最大化仿射社会福利，仿射社会福利是投标者总加权价值与分配 boost 值的总和，并且一个投标者的支付被定义为所有其他投标者仿射社会福利的总减少量。直观地说，AMA可以增加收入，因为它牺牲了社会福利的最优性，使用加权社会福利来衡量投标者的外部性。正式地，给定权重和 boost 值，加权社会福利可以定义为：
$$WSW(\mathbf{b})=\sum_{i \in R \cup S} w_{i} v_{i} \cdot a_{i}(\mathbf{b})+u(\mathbf{a}(\mathbf{b}))$$
AMA的分配为 $\mathbf{a}^{*}(\mathbf{b})=\arg \max_{\mathbf{a}(\mathbf{b})} WSW(\mathbf{b})$ ，任何广告商的支付为：
$$p_{i}(\mathbf{b})=\frac{1}{w_{i}}\left(WSW^{*}\left(\mathbf{b}_{-i}\right)-\left(WSW^{*}(\mathbf{b})-w_{i} b_{i} \cdot a_{i}(\mathbf{b})\right)\right) $$
当给定权重和 boost 值时，AMA具有激励相容性和个体理性。注意，VCG机制是AMA的一种特殊情况 ，其权重为1， boost 值为零。因此，如果论文能够为AMA的参数分配合适的值，AMA的收入将高于VCG的收入
- 然而，文献证明，找到使AMA实现最大收入的最优参数是NP难问题
最近，对于多物品设置，有研究提供了一种新颖的自动机制设计方法来训练AMA的架构（Differentiable economics for randomized affine maximizer auctions），并说明了他们训练的机制在收入方面的优越性。受这种方法的启发，在本节的其余部分，论文旨在将AMA扩展到论文的联合广告系统，并提出相应的训练方法。论文将论文的AMA架构称为联合AMA。图2展示了JAMA的基本结构
论文将零售商和供应商的出价及其权重作为输入。然后根据零售商和供应商之间的合作关系计算联合出价。通过训练分配方案和相应的 boost 值，论文得到优化平台收入的最优参数集。然后输出每个零售商和供应商的分配结果和支付

JAMA架构

整体描述 ：如图2所示，JAMA中有三种可学习的参数：广告商权重 $w_{i}$ 、 boost 变量 $u(\mathbf{a}^{*})$ 以及分配方案 $\mathbf{a}^{*}$
过程：在输入阶段，零售商和供应商提交他们的出价。然后，论文分别通过将每个广告商的出价与其投标权重相结合，得到每个广告商的加权出价，之后，论文根据表示合作关系的出价二分图生成零售商和供应商之间的联合出价
分配方案 ：为了尽可能提高JAMA的收入表现，论文初始化多个分配方案。此外，论文对分配方案进行归一化处理，以满足第2节中定义的可行性约束
boost 值 ：为了得到 boost 变量，论文使用多层感知器（MLP），这是一种全连接神经网络
在得到JAMA的输出参数 $w_{i}$ 、 $\mu(\mathbf{a}^{*})$ 和 $\mathbf{a}^{*}$ 后，我们可以根据第4节中定义的公式计算分配结果并计算支付结果
优化与训练 ：由于JAMA完全具有激励相容性和个体理性，论文的目标是最大化平台的总收入。具体来说，论文将损失函数设置为负的总收入，即 $-[\sum_{i \in R} p_{i}(\mathbf{b})+\sum_{j \in S} p_{j}(\mathbf{b})]$ 。然后，论文通过梯度下降法一起学习这些参数
分配方案初始化 ：对于组合分配概率矩阵的初始化，和相关研究方法一样，论文采用两种方法：第一种是最初保留所有可行的分配。在广告商数量有限，或者合作关系结构相对简单的情况下，这种方法可以很容易地获得最优结果。另一种方法是随机初始化大量的分配，以找到带来最多收入的最佳分配，尽管实际上这些分配中只有少数会被使用。此外，在论文的实验中，获胜的分配矩阵总是确定的，这与实验设置一致
与普通拍卖不同，在联合广告中分配广告位时，论文需要考虑可行性约束（在第2节中定义），即一个组合不能出现在多个广告位中，并且单个广告位不能被重复分配。因此，论文考虑在训练过程中保持分配矩阵为双随机矩阵。论文遵循相关研究中使用的方法，通过软加操作对矩阵进行逐行和逐列归一化，并取结果的最小值
此外：
- 在训练过程中 ，论文遵循相关研究使用的方法，利用softmax函数作为max和argmax操作的可微替代函数
- 在测试时 ，论文使用常规的max运算符

CA——(JRegNet)Joint-Auction-in-the-Online-Advertising-Market

参考论文：Joint Auction in the Online Advertising Market, KDD 2024, Meituan

整体说明

联合拍卖 ：论文提出一种新颖的品牌商供应商与零售商联合拍卖的场景，一个商品可能同时有品牌商和零售商出资，目前使用的广告模式无法同时满足零售商和品牌商供应商的需求
模式建模 ：为了解决这一问题，论文创新性地提出了一种名为 “联合拍卖” 的联合广告模式，允许品牌商供应商和零售商共同竞拍广告位，以满足双方的需求
论文的方案 ：传统的广告拍卖机制并不适用于这种新场景，论文提出了JRegNet ，这是一种用于优化联合拍卖设计的神经网络架构，它可以生成能够实现最优收益，并保证（近似）占优策略激励相容和个体理性的机制
相关实验 ：论文在合成数据和真实数据上进行了多项实验，证明与已知的基线方法相比，论文提出的联合拍卖显著提高了平台的收入

联合拍卖设计

在本节中，论文首先正式介绍联合拍卖的模型，然后将最优机制设计问题转化为学习问题

联合拍卖

在联合拍卖的背景下，每当用户搜索某个关键词时，平台会返回一个包含 $ K $ 个广告位的界面，每个广告位显示一个由零售商和品牌商组成的广告捆绑（）信息。用 $\alpha_k$ 表示第 $ k $ 个广告位的点击率（CTR），其中 $ k \in \{1, \ldots, K\} $。不失一般性，假设 $ 1 > \alpha_1 \geq \cdots \geq \alpha_K > 0 $
有 $ m $ 家零售商和 $ n $ 个品牌商参与联合拍卖。对于零售商 $ i \in M = \{1, \ldots, m\} $ 和品牌商 $ j \in N = \{1, \ldots, n\} $，论文定义一个指示变量 $ \mathbf{1}_{ij} $ 来表示零售商 $ i $ 和品牌商 $ j $ 是否可以组成一个捆绑。具体来说，$ \mathbf{1}_{ij} = 1 $ 表示零售商 $ i $ 和品牌商 $ j $ 存在合作关系。此外，论文用一个矩阵来表示所有零售商和品牌商之间的捆绑关系，其中每个实体是一个定义在零售商和品牌商对上的指示变量（如图 2 示例）。在同一联合拍卖场景中，不同搜索查询样本的矩阵中的联合拍卖关系可能不同
零售商 $ i $ 单次点击价值记为 $ v_{i \cdot } $, 品牌商 $ j $ 单次点击价值记为 $ v_{ \cdot j} $（这些是零售商 $ i $或品牌商 $ j $的私有信息）。假设 $ v_{i \cdot } $ 和 $ v_{ \cdot j} $ 是从一个已知的分布中抽取的（理解：论文中假设品牌商和零售商价值服从同一个分布），取值空间为 $ V_{i \cdot } $ 和 $ V_{ \cdot j} $。价值 profile 可以表示为 $ \boldsymbol{v} = (v_{1 \cdot}, \ldots, v_{m \cdot}, v_{\cdot 1}, \ldots, v_{\cdot n}) \in \mathbb{V} $，其中 $ \mathbb{V} = V_{1 \cdot} \times \cdots \times V_{m \cdot} \times V_{\cdot 1} \times \cdots \times V_{\cdot n} $。此外，用 $ \boldsymbol{v}_{-i \cdot } $ 表示除零售商 $ i $ 之外的价值 profile ，即 $ \boldsymbol{v}_{-i \cdot } = (v_{1 \cdot}, \ldots, v_{(i-1) \cdot}, v_{(i+1) \cdot}, \ldots, v_{\cdot n}) $。类似的定义也适用于品牌商 $ j $。由于零售商（或品牌商）可能进行策略性竞价，论文用 $ b_{i \cdot } $ 和 $ b_{ \cdot j} $ 表示竞价价格。类似地，用 $ \boldsymbol{b} $、$ \boldsymbol{b}_{-i \cdot } $ 和 $ \boldsymbol{b}_{-j} $ 表示相关的竞价特征
- 问题：为什么使用 $ v_{i \cdot } $ 而不是 $ v_{i} $ 表示零售商 $i$ 的单次点击价值？
- 回答：是为了方便和品牌商 $ j $ 的单次点击价值 $ v_{ \cdot j} $ 区分开，否则下标相同无法区分（个人理解：实际上加个上标可能是最好的选择，因为这种表达容易让人觉得是一个函数，且 $\cdot$ 看起来像是另一个变量的样子，难以理解）
在联合拍卖的设置中，拍卖机制 $ \mathcal{M}(g, p) $ 包含两部分：分配规则 $ g $ 和支付规则 $ p $。具体来说，$ g = ((g_{i \cdot })_{i \in M}, (g_{ \cdot j})_{j \in N}) $，其中 $ g_{i \cdot } $ 和 $ g_{ \cdot j} $：$ \mathbb{V} \rightarrow \mathbb{R}^{+} \cup \{0\} $ 表示零售商 $ i $ 和品牌商 $ j $ 可以获得的预期点击率。即：
$$
g_{i \cdot }(\boldsymbol{b}) = \sum_{k=1}^{K} s_{i \cdot k}(\boldsymbol{b}) \alpha_k,
$$
其中 $ s_{i \cdot k}(\boldsymbol{b}) $ 表示零售商 $ i $ 被分配到第 $ k $ 个广告位的概率。支付规则 $ p = ((p_{i \cdot })_{i \in M}, (p_{ \cdot j})_{j \in N}) $ 表示零售商 $ i $ 和品牌商 $ j $ 需要支付的金额。与传统广告拍卖不同，在联合拍卖中，每个广告位最多分配给一个捆绑，每个捆绑最多获得一个广告位。换句话说，一家零售商和一个品牌商组成一个捆绑，展示在一个广告位上
每家零售商 $ i $ 和每个品牌商 $ j $ 的目标都是最大化自身效用，零售商的效用定义为拟线性形式：
$$
u_{i \cdot }(v_{i \cdot }; \boldsymbol{b}) = v_{i \cdot }(g_{i \cdot }(\boldsymbol{b})) - p_{i \cdot }(\boldsymbol{b}), \quad \forall i \in M
$$
- 理解：品牌商的效用形式类似可表示为：
  $$
  u_{\cdot j}(v_{\cdot j}; \boldsymbol{b}) = v_{\cdot j}(g_{\cdot j}(\boldsymbol{b})) - p_{\cdot j}(\boldsymbol{b}), \quad \forall j \in N
  $$

注：论文关注满足占优策略激励相容性（DSIC）和个体理性（IR）的机制

占优策略激励相容性保证对于任何竞标者，真实竞价能带来最大效用，即：
- 定义 1（DSIC） ：如果对于任何零售商 $ i $和品牌商 $ j $，无论其他竞标者如何报告，真实报告都能最大化其效用，则联合拍卖是显性策略激励相容的。即：
  $$
  \color{red}{u_{i \cdot }(v_{i \cdot }; (v_{i \cdot }, \boldsymbol{b}_{-i \cdot })) \geq u_{i \cdot }(v_{i \cdot }; (b_{i \cdot }, \boldsymbol{b}_{-i \cdot }))}, \quad \forall i \in M, v_{i \cdot } \in V_{i \cdot }, b_{i \cdot } \in V_{i \cdot }, \boldsymbol{b}_{-i \cdot } \in \mathbb{V}_{-i \cdot }
  $$
- 且：
  $$
  \color{red}{u_{ \cdot j}(v_{ \cdot j}; (v_{ \cdot j}, \boldsymbol{b}_{- \cdot j})) \geq u_{ \cdot j}(v_{ \cdot j}; (b_{ \cdot j}, \boldsymbol{b}_{- \cdot j}))}, \quad \forall j \in N, v_{ \cdot j} \in V_{ \cdot j}, b_{ \cdot j} \in V_{ \cdot j}, \boldsymbol{b}_{- \cdot j} \in \mathbb{V}_{- \cdot j}
  $$
个体理性意味着任何拍卖参与者都能获得非负效用，定义如下：
- 定义 2（IR） ：联合拍卖是事后个体理性的，如果任何零售商 $ i $（或品牌商 $ j $）在真实参与时获得非负效用，即：
  $$
  \color{red}{u_{i \cdot }(v_{i \cdot }; (v_{i \cdot }, \boldsymbol{b}_{-i \cdot })) \geq 0}, \quad \forall i \in M, \forall v_{i \cdot } \in V_{i \cdot }, \forall \boldsymbol{b}_{-i \cdot } \in \mathbb{V}_{-i \cdot },
  $$
- 且：
  $$
  \color{red}{u_{ \cdot j}(v_{ \cdot j}; (v_{ \cdot j}, \boldsymbol{b}_{- \cdot j})) \geq 0}, \quad \forall j \in N, \forall v_{ \cdot j} \in V_{ \cdot j}, \forall \boldsymbol{b}_{- \cdot j} \in \mathbb{V}_{- \cdot j}.
  $$
- 在满足 DSIC 和 IR 的联合拍卖中，平台的预期收益等于所有零售商和品牌商的总支付，定义为：
  $$
  rev := \mathbb{E}_{\boldsymbol{v} \sim F}\left[\sum_{i=1}^{m} p_{i \cdot }(\boldsymbol{v}) + \sum_{j=1}^{n} p_{ \cdot j}(\boldsymbol{v})\right],
  $$
- 其中 $ F $ 是所有零售商和品牌商价值的联合分布
最优联合拍卖设计的目标是找到一个拍卖机制 ，在满足 DSIC 和 IR 条件的同时，最大化预期收益

基于学习的联合拍卖设计问题建模

论文将设计最优联合拍卖的问题表述为一个学习问题。首先，为了满足 DSIC 条件，论文引入了事后遗憾（ex-post regret）的概念。固定其他竞标者的竞价，零售商 $ i $ 的事后遗憾是其通过虚假报告可以获得的效用最大增量，即（注：原始文章中错误的使用了 $rgt_{i \cdot }\color{red}{(\boldsymbol{v})}$，从后面的文章和RegretNet文章看，事后遗憾 $rgt_{i \cdot }$ 与 $\color{red}{(\boldsymbol{v})}$ 无关，是关于 $\color{red}{(\boldsymbol{v})} \sim F$的期望，接下来，博客内容将对该符号进行修正）：
$$
rgt_{i \cdot } = \mathbb{E}_{\boldsymbol{v} \sim F}\left[\max_{ {v’}_{i \cdot } \in V_{i \cdot } } u_{i \cdot }(v_{i \cdot }; ({v’}_{i \cdot }, \boldsymbol{v}_{-i \cdot })) - u_{i \cdot }(v_{i \cdot }; \boldsymbol{v})\right].
$$
- 品牌商 $ j $ 的事后遗憾可以类似以上定义
- 特别说明：$V_{i \cdot }$ 是价值取值空间（价值空间，包含所有可能的价值集合）
- 个人理解：$rgt_{i \cdot } \geq 0 $ 可衡量一个机制的满足 DSIC 条件的程度。任意一个 $\boldsymbol{v}$ 都是一个包含所有竞拍者真实私有价值 ，$u_{i \cdot }$ 则与机制 $\mathcal{M}(g,p)$ 有关，由于 $\boldsymbol{v}$ 是竞拍者真实私有估值（相当于都在说真话），此时满足 DSIC 条件的机制下，应该有事后遗憾 $rgt_{i \cdot } = 0 $。从更加广义的松弛视角看，机制越满足 DSIC 条件，则事后遗憾值应该越小，最小值为0
- 模型训练中，$rgt_{i \cdot }$ 越小的机制越满足 DSIC 条件
因此，拍卖机制满足 DSIC 条件当且仅当 $ rgt_{i \cdot } = 0 $ 和 $ rgt_{ \cdot j} = 0 $ 对所有零售商和品牌商成立。此外，我们可以将设计最优联合拍卖的问题表述为约束优化问题（1） ：
$$
\begin{align}
\min_{(g,p) \in \mathcal{M} } &-\mathbb{E}_{\boldsymbol{v} \sim F}\left[\sum_{i=1}^{m} p_{i \cdot }(\boldsymbol{v}) + \sum_{j=1}^{n} p_{ \cdot j}(\boldsymbol{v})\right] \\
\text{s.t.} \quad &rgt_{i \cdot } = 0, \quad i = 1, \ldots, m, \\
&rgt_{ \cdot j} = 0, \quad j = 1, \ldots, n,
\end{align}
$$
其中 $ \mathcal{M} $ 是满足 IR 的所有联合拍卖机制的集合。由于约束复杂，该优化问题通常难以直接求解。为了解决这个优化问题，论文通过参数 $ w \in \mathbb{R}^d $（其中 $ d $ 是参数 $ w $ 的维度）将拍卖机制参数化为 $ \mathcal{M}^w(g^w, p^w) \subseteq \mathcal{M}(g, p) $。然后，论文转而计算机制 $ \mathcal{M}^w(g^w, p^w) $，通过优化参数 $ w $ 来最大化预期收益 $ \mathbb{E}_{\boldsymbol{v} \sim F}\left[\sum_{i=1}^{m} p_{i \cdot }^w(\boldsymbol{v}) + \sum_{j=1}^{n} p_{ \cdot j}^w(\boldsymbol{v})\right] $，同时满足 DSIC 和 IR 条件
给定一个样本集合 $ \mathcal{L} $，包含从联合分布 $ F $ 中抽取的 $ L $ 个价值 profile 集合 $\{ (\color{blue}{v_{1\cdot}^{(\ell)},v_{2\cdot}^{(\ell)},\cdots, v_{M\cdot}^{(\ell)}}, \color{red}{v_{\cdot 1}^{(\ell)},v_{\cdot 2}^{(\ell)},\cdots, v_{\cdot N}^{(\ell)}}) \}_{l=1}^L$，其中，每个样本 $\boldsymbol{v}^{(\ell)} = (\color{blue}{v_{1\cdot}^{(\ell)},v_{2\cdot}^{(\ell)},\cdots, v_{M\cdot}^{(\ell)}}, \color{red}{v_{\cdot 1}^{(\ell)},v_{\cdot 2}^{(\ell)},\cdots, v_{\cdot N}^{(\ell)}})$ ，机制 $ \mathcal{M}^w(g^w, p^w) $ 的零售商 $ i $ 的实证事后遗憾估计为：
$$
\widehat{rgt}_{i \cdot }(w) = \frac{1}{L} \sum_{l=1}^{L} \left[\max_{ {v’}_{i \cdot } \in V_{i \cdot } } u_{i \cdot }^w(v_{i \cdot }^{(\ell)}; ({v’}_{i \cdot }, \boldsymbol{v}_{-i \cdot }^{(\ell)})) - u_{i \cdot }^w(v_{i \cdot }^{(\ell)}; \boldsymbol{v}^{(\ell)})\right].
$$
- 类似地，品牌商 $ j $ 的实证事后遗憾估计为：
  $$
  \widehat{rgt}_{ \cdot j }(w) = \frac{1}{L} \sum_{l=1}^{L} \left[\max_{ {v’}_{ \cdot j } \in V_{ \cdot j } } u_{ \cdot j }^w(v_{ \cdot j }^{(\ell)}; ({v’}_{ \cdot j }, \boldsymbol{v}_{- \cdot j }^{(\ell)})) - u_{ \cdot j }^w(v_{ \cdot j }^{(\ell)}; \boldsymbol{v}^{(\ell)})\right].
  $$
将约束优化问题 (1) 重写为：
$$
\begin{align}
\min_{w \in \mathbb{R}^{d_w} } &-\frac{1}{L} \sum_{l=1}^{L} \left[\sum_{i=1}^{m} p_{i \cdot }^w(\boldsymbol{v}^{(\ell)}) + \sum_{j=1}^{n} p_{ \cdot j}^w(\boldsymbol{v}^{(\ell)})\right] \\
\text{s.t} \quad &\widehat{rgt}_{i \cdot }(w) = 0, \quad i = 1, \ldots, m, \\
&\widehat{rgt}_{ \cdot j}(w) = 0, \quad j = 1, \ldots, n.
\end{align}
$$
此外，通过网络架构，论文确保 IR 条件成立，具体细节将在JRegNet建模中描述

JRegNet 方案

在本节中，论文将最优联合拍卖设计建模为学习问题后，提出了一种称为联合遗憾网络（JRegNet）的神经网络架构，用于最优联合拍卖设计

JRegNet 架构

本小节介绍为联合拍卖场景设计的 JRegNet 网络架构，如图 3 所示。JRegNet 架构包含两部分：编码分配规则的分配网络和编码支付规则的支付网络。两个网络的输出用于计算竞标者的效用、收益、遗憾以及整个网络的损失函数值。接下来，论文详细介绍 JRegNet 的主要组成部分
JRegNet的输入 ：在 JRegNet 中，神经网络以 $ \mathbf{1}_{ij} $、$ e_{i \cdot k} $ 和 $ e_{ \cdot jk} $ 作为输入，定义为：
$$
\begin{cases}
e_{i \cdot k} = \alpha_k b_{i \cdot }, & \forall i \in M, \forall k \in \{1, \ldots, K\}, \\
e_{ \cdot jk} = \alpha_k b_{ \cdot j}, & \forall j \in N, \forall k \in \{1, \ldots, K\},
\end{cases}
$$
- 其中 $ e_{i \cdot k} $ 和 $ e_{ \cdot jk} $ 分别表示零售商 $ i $ 和品牌商 $ j $ 在广告位 $ k $ 上的预期竞价（理解：$CPM = CTR \times Bid_\text{CPC}$）
- $ \{\mathbf{1}_{ij}\}_{i \in M, j \in N} $ 表示零售商和品牌商之间的联合关系矩阵。由于联合关系在不同搜索请求样本中可能不同（即使在同一联合拍卖场景下，即相同的零售商和品牌商），JRegNet 将 $ \{\mathbf{1}_{ij}\}_{i \in M, j \in N} $ 作为输入之一
JRegNet的输出 ：在 JRegNet 中，为了适应联合拍卖场景，JRegNet的输出分几个部分
- 分配网络首先输出捆绑的分配概率矩阵 $ A_{Q,K+1} $：矩阵 $ A $ 包含每个由零售商和品牌商组成的捆绑在每个广告位上的分配概率
- 在获得矩阵 $ A $ 后，分配网络进一步输出竞标者的分配概率矩阵 $ S_{M+N,K} $：矩阵 $ S $ 包含每个零售商和品牌商在每个广告位上的分配概率
- 随后，支付网络输出所有竞标者的支付矩阵 $ P_{M+N} $：矩阵 $ P $ 包含每个零售商竞标者和品牌商竞标者的支付金额
计算捆绑的分配概率矩阵 $ A $ ：为了计算竞标者的分配概率矩阵 $ S $，论文首先需要计算捆绑的分配概率矩阵 $ A $，因为需要通过 $ A $ 实现若干约束。然后，基于 $ A $ 计算 $ S $。此外，矩阵 $ A $ 可用于将广告位分配给由零售商和品牌商组成的捆绑。此部分的输入是通过前向传播获得的矩阵 $ C $ 和 $ R $，如图 3 中的黄色和紫色神经元所示
- 论文用 $ Q $ 表示捆绑的总数，其中捆绑 $ q \in \{1, \ldots, Q\} $ 对应于矩阵 $ \{\mathbf{1}_{ij}\} $ 中所有值为 1 的条目按行遍历后的第 $ q $ 个条目。分配概率矩阵 $ A $ 中捆绑 $ q $ 在广告位 $ k $ 上的分配概率定义为 $ a_{qk} $
- 在论文的模型中，输出矩阵 $ A $ 必须满足两个约束：
  - (a) 每个广告位最多分配给一个捆绑，即 $ \sum_{q=1}^{Q} a_{qk} \leq 1, \forall k \in \{1, \ldots, K\} $；
  - (b) 每个捆绑最多获得一个广告位，即 $ \sum_{k=1}^{K} a_{qk} \leq 1, \forall q \in \{1, \ldots, Q\} $
- 为了强制满足约束 (a) 和 (b) ，论文将分配概率矩阵 $ A $ 设计为一个双随机矩阵（bi-stochastic matrix，行和列的和都等于1的矩阵，论文和 RegretNet 中将双随机矩阵的行列和定义为小于等于1）。为了将 $ A $ 构造为双随机矩阵，需要对 $ C $ 和 $ R $ 进行一些操作。矩阵 $ C $ 通过 softmax 函数按列归一化为矩阵 $ \tilde{C} $，矩阵 $ R $ 通过 softmax 函数按行归一化为矩阵 $ \tilde{R} $。因为在联合拍卖场景中，特定的捆绑可能不会被分配到任何广告位，论文在 softmax 归一化中为每个捆绑添加了一个虚拟神经元。虚拟神经元的输出表示捆绑未被分配到任何广告位的概率。矩阵 $ \tilde{C} $ 和 $ \tilde{R} $ 中的条目分别定义为 $ \tilde{c}_{qk} $ 和 $ \tilde{r}_{qk} $。然后，论文通过以下方式计算矩阵 $ A $ 中每个捆绑的分配概率：
  $$
  a_{qk} = \min\{\tilde{c}_{qk}, \tilde{r}_{qk}\}, \quad \forall q \in \{1, \ldots, Q\}, \forall k \in \{1, \ldots, K+1\}.
  $$
  - 问题：为什么是取 $\min$?
  - 回答：可以通过引理1得到证明，取 $\min$ 以后得到的是一个双随机矩阵（bi-stochastic matrix）？
根据引理1 ，以这种方式构造的矩阵 $ A $ 是一个双随机矩阵（bi-stochastic matrix）。计算分配概率矩阵 $ A $ 的具体公式为：
$$
a_{qk} = \varphi^{BS}_{qk}(C, R) = \min \left\{ \frac{e^{c_{qk} } }{\sum_{t=1}^{Q} e^{c_{tk} } }, \frac{e^{r_{qk} } }{\sum_{t=1}^{K+1} e^{r_{qt} } } \right\},
$$
- 其中 $ \frac{e^{c_{qk} } }{\sum_{t=1}^{Q} e^{c_{tk} } } $ 和 $ \frac{e^{r_{qk} } }{\sum_{t=1}^{K+1} e^{r_{qt} } } $ 分别是 $ c_{qk} $ 的行归一化和 $ r_{qk} $ 的列归一化，索引 $ K+1 $ 对应捆绑未被分配到任何广告位的情况。这部分内容如图 3 所示
引理 1 ：矩阵 $ \varphi^{BS}_{qk}(c, r) $ 对于所有 $ c, r \in \mathbb{R}^{QK} $ 是双随机的。对于任何双随机矩阵 $ a \in [0,1]^{QK} $，存在 $ c, r \in \mathbb{R}^{QK} $ 使得 $ a = \varphi^{BS}_{qk}(c, r) $
- 注：双随机矩阵是指行和列的和都等于1的矩阵，论文和 RegretNet 中将双随机矩阵的行列和定义为小于等于1 ，所以引理1才能成立，否则是不成立的
将分配概率矩阵 $ A $ 转换为分配概率矩阵 $ S $ ：在竞标者的分配概率矩阵 $ S $ 中，零售商 $ i $ 和品牌商 $ j $ 在广告位 $ k $ 上的分配概率分别记为 $ s_{i \cdot k} $ 和 $ s_{ \cdot jk} $。在获得捆绑的分配概率矩阵 $ A $ 后，通过以下方式计算 $ S $ 中的分配概率：
$$
\begin{cases}
s_{i \cdot k} = \sum_{q \in Q_{i \cdot } } a_{qk}, & \forall k \in \{1, \ldots, K\}, \\
s_{ \cdot jk} = \sum_{q \in Q_{ \cdot j} } a_{qk}, & \forall k \in \{1, \ldots, K\},
\end{cases}
$$
- 其中 $ Q_{i \cdot } $ 和 $ Q_{ \cdot j} $ 分别表示包含零售商 $ i $ 和品牌商 $ j $ 的所有捆绑的集合。即，零售商 $ i $ 在广告位 $ k $ 上的分配概率是所有包含零售商 $ i $ 的捆绑在广告位 $ k $ 上的分配概率之和，品牌商 $ j $ 的计算类似
- 理解：原始分配时为每个捆绑 $q$ 分配概率，上述转换是在将捆绑分配概率转换给对应的零售商和品牌商，对捆绑 $q \in Q_{i \cdot } $ 做积分是因为每个品牌商和零售商可能都有多个Bundle 在同时竞争同一个位置 $k$
计算支付矩阵 $ P $ ：在获得竞标者的分配概率矩阵 $ S $ 后，论文将其传播到支付网络以计算支付矩阵 $ P $，如图 3 所示。在矩阵 $ P \in \mathbb{R}_{\geq 0}^{I+J} $ 中，前 $ m $ 行和后 $ n $ 行分别表示零售商和品牌商的支付金额。矩阵 $ P $ 中零售商 $ i $ 和品牌商 $ j $ 的支付分别记为 $ p_{i \cdot } $ 和 $ p_{ \cdot j} $。支付金额通过以下方式计算：
$$
\begin{cases}
p_{i \cdot } = \tilde{p}_{i \cdot } \left( \sum_{k=1}^{K} s_{i \cdot k} e_{i \cdot k} \right), & \forall i \in M, \\
p_{ \cdot j} = \tilde{p}_{ \cdot j} \left( \sum_{k=1}^{K} s_{ \cdot jk} e_{ \cdot jk} \right), & \forall j \in N,
\end{cases}
$$
- 其中 $ \tilde{p}_{i \cdot } \in [0,1] $ 和 $ \tilde{p}_{ \cdot j} \in [0,1] $ 是通过 sigmoid 函数计算的归一化因子，如图 3 中的绿色方块所示。在满足 DSIC 的条件下，由于 $ \tilde{p}_{i \cdot } \in [0,1] $，且零售商的效用 $ u_{i \cdot } = \sum_{k=1}^{K} s_{i \cdot k} e_{i \cdot k} - p_{i \cdot } $，每家零售商的效用必须非负，满足 IR 条件。品牌商的证明类似

问题: 实际场景位置分配

问题：实际场景中，如何根据概率分配矩阵实现位置分配？按照分配概率做采样还是做 argmax?
回答：TODO，待确认

JRegNet 的训练

本小节介绍 JRegNet 的训练过程，包括目标函数的转换、训练样本的划分、最优虚假报告的寻找以及模型参数和拉格朗日乘子的更新
从约束优化问题到无约束优化问题的转换 ：为了训练 JRegNet，论文首先需要一个目标函数。约束优化目标如式 (3) 所示。论文使用增广拉格朗日方法将约束优化问题转化为无约束优化问题，从而得到以下目标函数：
$$
\begin{align}
C_{\rho}(w; \lambda) = &-\frac{1}{L} \sum_{l=1}^{L} \left[ \sum_{i=1}^{m} p_{i \cdot }^w(\boldsymbol{v}^{(\ell)}) + \sum_{j=1}^{n} p_{ \cdot j}^w(\boldsymbol{v}^{(\ell)}) \right] \\
&+ \sum_{i=1}^{m} \lambda_{i \cdot } \widehat{rgt}_{i \cdot }(w) + \sum_{j=1}^{n} \lambda_{ \cdot j} \widehat{rgt}_{ \cdot j}(w) \\
&+ \frac{\rho}{2} \sum_{i=1}^{m} (\widehat{rgt}_{i \cdot }(w))^2 + \frac{\rho}{2} \sum_{j=1}^{n} (\widehat{rgt}_{ \cdot j}(w))^2,
\end{align}
$$
- 其中 $ \lambda \in \mathbb{R}^n $ 是拉格朗日乘子，$ \rho > 0 $ 是惩罚因子
- 问题：在训练时如何计算 $\widehat{rgt}_{i \cdot }(w)$ 和 $\widehat{rgt}_{ \cdot j}(w)$ ?
- 回答：$\widehat{rgt}_{i \cdot }(w)$ 计算公式为
  $$
  \widehat{rgt}_{i \cdot }(w) = \frac{1}{L} \sum_{l=1}^{L} \left[\max_{ {v’}_{i \cdot } \in V_{i \cdot } } u_{i \cdot }^w(v_{i \cdot }^{(\ell)}; ({v’}_{i \cdot }, \boldsymbol{v}_{-i \cdot }^{(\ell)})) - u_{i \cdot }^w(v_{i \cdot }^{(\ell)}; \boldsymbol{v}^{(\ell)})\right].
  $$
  - 类似地，品牌商 $ j $ 的实证事后遗憾$\widehat{rgt}_{ \cdot j}(w)$ 估计为：
    $$
    \widehat{rgt}_{ \cdot j }(w) = \frac{1}{L} \sum_{l=1}^{L} \left[\max_{ {v’}_{ \cdot j } \in V_{ \cdot j } } u_{ \cdot j }^w(v_{ \cdot j }^{(\ell)}; ({v’}_{ \cdot j }, \boldsymbol{v}_{- \cdot j }^{(\ell)})) - u_{ \cdot j }^w(v_{ \cdot j }^{(\ell)}; \boldsymbol{v}^{(\ell)})\right].
    $$
  - 其中 $V_{ i \cdot }, V_{ \cdot j }$ 是各自出价可能的取值集合（即取值空间），猜测可以通过随机采样几个值 ，或提前定义几个按照固定间隔采样取值，再取他们对应效用函数中的最大值即可作为近似最大效用函数
在获得训练所需的目标函数后，论文需要划分样本以训练 JRegNet
训练样本的划分 ：训练样本 $ \mathcal{L} $ 被随机划分为大小为 $ B $ 的 minibatchs。用 $ T $ 表示总迭代次数。对于每次迭代 $ t \in \{1, \ldots, T\} $，论文采样一个 minibatchs $ \mathcal{L}_t $，记为 $ \mathcal{L}_t = \{\boldsymbol{v}^{(1)}, \ldots, \boldsymbol{v}^{(B)}\} $，并将其输入 JRegNet 进行训练，直到该划分中的所有 minibatchs 都被使用。之后，训练样本 $ \mathcal{L} $ 被重新随机划分为新的 minibatchs。重复上述过程，直到完成所有迭代
在训练过程中，为了计算 $ C_{\rho}(w; \lambda) $ 中的遗憾，论文需要找到最大化遗憾的最优虚假报告
寻找最优虚假报告 ：为了计算最优虚假报告，论文使用梯度上升法。对于每个 minibatchs ，通过多次梯度上升计算每个零售商 $ i $ 或品牌商 $ j $ 以及每个价值 profile $ \ell $ 的虚假报告 $ {v’}_{i \cdot }^{(\ell)} $ 或 $ {v’}_{ \cdot j}^{(\ell)} $，并保留所有虚假报告以初始化下一轮的虚假报告。梯度上升的公式如下（其中 $ \gamma > 0 $）：
$$
\begin{cases}
{v’}_{i \cdot }^{(\ell)} = {v’}_{i \cdot }^{(\ell)} + \gamma \nabla_{ {v’}_{i \cdot } } \left. u_{i \cdot }^w(v_{i \cdot }^{(\ell)}; ({v’}_{i \cdot }, \boldsymbol{v}_{-i \cdot }^{(\ell)})) \right|_{ {v’}_{i \cdot } = {v’}_{i \cdot }^{(\ell)} }, \\
{v’}_{ \cdot j}^{(\ell)} = {v’}_{ \cdot j}^{(\ell)} + \gamma \nabla_{ {v’}_{ \cdot j} } \left. u_{ \cdot j}^w(v_{ \cdot j}^{(\ell)}; ({v’}_{ \cdot j}, \boldsymbol{v}_{- \cdot j}^{(\ell)})) \right|_{ {v’}_{ \cdot j} = {v’}_{ \cdot j}^{(\ell)} },
\end{cases}
$$
更新模型参数和拉格朗日乘子。随后，我们可以计算 $ C_{\rho}(w; \lambda) $ 的值，执行反向传播并更新神经网络参数 $ w $ 以最小化 $ C_{\rho}(w; \lambda) $。此外，在模型训练过程中，每隔固定次数的迭代更新拉格朗日乘子：
$$
\begin{cases}
\lambda_{i \cdot }^{t+1} = \lambda_{i \cdot }^t + \rho^t \widehat{rgt}_{i \cdot }(w^{t+1}), & \forall i \in M, \\
\lambda_{ \cdot j}^{t+1} = \lambda_{ \cdot j}^t + \rho^t \widehat{rgt}_{ \cdot j}(w^{t+1}), & \forall j \in N,
\end{cases}
$$
- 其中 $ t $ 表示迭代次数，$ \widehat{rgt}_{i \cdot }(w) $ 和 $ \widehat{rgt}_{ \cdot j}(w) $ 是基于式 (2) 在 minibatchs $ \mathcal{S}_t $ 上计算的实证遗憾。模型参数和拉格朗日乘子的更新交替进行。训练 JRegNet 的具体完整算法流程如算法 1 所示
对于固定的 $ \lambda^t $，$ C_{\rho} $ 关于 $ w $ 的梯度可以表示为：
$$
\begin{align}
\nabla_w C_{\rho}(w; \lambda^t) = &-\frac{1}{B} \sum_{\ell=1}^{B} \left[ \sum_{i=1}^{m} \nabla_w p_{i \cdot }^w(\boldsymbol{v}^{(\ell)}) + \sum_{j=1}^{n} \nabla_w p_{ \cdot j}^w(\boldsymbol{v}^{(\ell)}) \right] \\
&+ \sum_{\ell=1}^{B} \left[ \sum_{i=1}^{m} \lambda_{i \cdot }^t g_{\ell,i \cdot } + \sum_{j=1}^{n} \lambda_{ \cdot j}^t g_{\ell, \cdot j} \right] \\
&+ \rho \sum_{\ell=1}^{B} \left[ \sum_{i=1}^{m} \widehat{rgt}_{i \cdot }(w) g_{\ell,i \cdot } + \sum_{j=1}^{n} \widehat{rgt}_{ \cdot j}(w) g_{\ell, \cdot j} \right],
\end{align}
$$
- 其中：
  $$
  \begin{cases}
  g_{\ell,i \cdot } = \nabla_w \left[ \max_{ {v’}_{i \cdot } \in V_{i \cdot } } u_{i \cdot }^w(v_{i \cdot }^{(\ell)}; ({v’}_{i \cdot }, \boldsymbol{v}_{-i \cdot }^{(\ell)})) - u_{i \cdot }^w(v_{i \cdot }^{(\ell)}; \boldsymbol{v}^{(\ell)}) \right], \\
  g_{\ell, \cdot j} = \nabla_w \left[ \max_{ {v’}_{ \cdot j} \in V_{ \cdot j} } u_{ \cdot j}^w(v_{ \cdot j}^{(\ell)}; ({v’}_{ \cdot j}, \boldsymbol{v}_{- \cdot j}^{(\ell)})) - u_{ \cdot j}^w(v_{ \cdot j}^{(\ell)}; \boldsymbol{v}^{(\ell)}) \right].
  \end{cases}
  $$

Experiments

本节通过实证实验评估联合广告模型及JRegNet的有效性。实验运行于配备NVIDIA GPU核心的计算集群上

基线方法

论文将JRegNet与以下基线进行比较：
- RegretNet ：一种用于传统广告拍卖（仅包含零售商）的神经网络架构，可设计近似DSIC机制并实现最优收入
- 独立遗憾网络（JRegNet） ：一种广告拍卖场景下的最优机制设计神经网络架构，其中零售商与品牌商作为独立候选者竞争不同广告位（即每个广告位仅展示零售商或品牌商广告，此场景实际中不存在）
- VCG ：一种满足DSIC和IR的经典机制。实验中直接将其应用于联合广告场景
需说明的是，RegretNet的竞拍者仅为零售商；其他机制的竞拍者同时包含零售商与品牌商，其余属性均相同

评估指标

对任意给定的数据集 $ \mathcal{L} $，包含从联合分布 $ F $ 中抽取的 $ L $ 个价值 profile $\{ (\color{blue}{v_{1\cdot}^{(\ell)},v_{2\cdot}^{(\ell)},\cdots, v_{M\cdot}^{(\ell)}}, \color{red}{v_{\cdot 1}^{(\ell)},v_{\cdot 2}^{(\ell)},\cdots, v_{\cdot N}^{(\ell)}}) \}_{l=1}^L$，其中，每个样本 $\boldsymbol{v}^{(\ell)} = (\color{blue}{v_{1\cdot}^{(\ell)},v_{2\cdot}^{(\ell)},\cdots, v_{M\cdot}^{(\ell)}}, \color{red}{v_{\cdot 1}^{(\ell)},v_{\cdot 2}^{(\ell)},\cdots, v_{\cdot N}^{(\ell)}})$
采用以下指标评估各方法性能：
- 竞拍者平均经验事后遗憾值 ：
  $$
  rgt := \frac{1}{n+m}\left(\sum_{i=1}^{m} rgt_{i\cdot} + \sum_{j=1}^{n} rgt_{\cdot j}\right)
  $$
- 经验收入 ：
  $$
  rev := \frac{1}{L}\sum_{\ell=1}^{L}\left[\sum_{i=1}^{m} p_{i\cdot}^{w}\left(\boldsymbol{v}^{(\ell)}\right) + \sum_{j=1}^{n} p_{\cdot j}^{w}\left(\boldsymbol{v}^{(\ell)}\right)\right]
  $$
- 经验社会福利 ：
  $$
  sw := \frac{1}{L}\sum_{\ell=1}^{L}\left(\sum_{i=1}^{m}\sum_{k=1}^{K} s_{i.k}^{(\ell)}\alpha_{k}v_{i\cdot}^{(\ell)} + \sum_{j=1}^{n}\sum_{k=1}^{K} s_{\cdot jk}^{(\ell)}\alpha_{k}v_{\cdot j}^{(\ell)}\right)
  $$

合成数据

实现细节

为每组实验创建训练集与测试集。训练集中， minibatchs size $ B = 128 $，迭代次数为200,000， minibatchs 数量为5,000；测试集中， minibatchs size 为128， minibatchs 数量为100。因此，训练样本 size $ \mathcal{L} = 640,000 $，测试样本 size 为12,800
所有合成数据实验中，零售商与品牌商的联合关系矩阵 $\{\mathbf{1}_{ij}\}_{i\in M,j\in N}$ 为每个搜索请求样本随机生成。若某零售商（或品牌商）与任何品牌商（或零售商）无联合关系，则默认其出价为零，因其无法形成展示组合
测试JRegNet时（仅测试阶段），对每位竞拍者，在100组不同初始虚报值上执行2000次梯度上升 ，得到100组经验遗憾值 ，取最大值作为该竞拍者的经验遗憾值。RegretNet、JRegNet与JRegNet的实验结果均为测试样本上3次运行的平均值
- 问题：测试时，虚报值如何采样，均匀采样吗？
- 问题：此时时，每位竞拍者虚报值时，其他竞拍者是否固定为他们的真实出价？
- 问题：训练样本使用的是所有竞拍者的真实出价吗？还是应该包含他们各自的虚假出价？
  - 回答：训练时使用真实估值数据（至少模型会认为大家都在说真话），以计算经验事后遗憾值，训练时的目标就是让事后经验值为0

JRegNet与基线的比较

为验证联合广告模型的优越性及JRegNet的有效性，论文在以下设置中对比JRegNet生成的机制与基线：
- (A) 3 零售商、4品牌商、1广告位（CTR $\boldsymbol{\alpha} = (0.7)$），各零售商与品牌商价值独立取自均匀分布 $ U[0,1] $
- (B) 3 零售商、5品牌商、3广告位（CTRs $\boldsymbol{\alpha} = (0.5, 0.3, 0.15)$），价值分布同A
- (C) 3 零售商、5品牌商、5广告位（CTRs $\boldsymbol{\alpha} = (0.5, 0.3, 0.15, 0.1, 0.03)$），价值分布同A
- (D) 4 零售商、5品牌商、3广告位（CTRs $\boldsymbol{\alpha} = (0.5, 0.3, 0.15)$），价值分布同A
表1展示了设置A至D的实验结果。首先，在所有自动化机制设计方法中，当遗憾值小于0.001时，JRegNet生成的机制收入显著高于RegretNet与JRegNet，表明联合广告模型能较传统模型获得更高收入。此外，在联合广告场景中，JRegNet的收入亦显著优于VCG，尽管存在一定社会福利损失。这说明JRegNet生成的机制在收入方面表现优异，且JRegNet架构有效
为进一步评估联合广告模型及JRegNet性能，论文在不同价值分布、CTR及广告位数量下进行实验

不同价值分布

在设置B下，对三种价值分布重复实验：均匀分布 $ U[0,1] $、正态分布 $ N(0.5, 0.0256) $（$ v \in [0,1] $）、对数正态分布 $ LN(0.1, 1.44) $（$ v \in [0,1] $）。表2结果显示，JRegNet在三种分布下均实现最高收入，表明其机制对不同价值分布具有稳定性与鲁棒性

不同广告位CTR

基于设置B，调整CTR值并运行所有机制：
- B1 ：CTRs $\boldsymbol{\alpha} = (0.4, 0.3, 0.15)$
- B2 ：CTRs $\boldsymbol{\alpha} = (0.5, 0.4, 0.15)$
- B3 ：CTRs $\boldsymbol{\alpha} = (0.5, 0.4, 0.25)$
图4(a)显示，CTR增加时JRegNet收入随之提升，且首槽CTR变化的影响大于末槽。在所有设置中，JRegNet生成的机制收入均为最高，证明其对不同CTR仍能保持优异性能
- 【补充】CTR增加时JRegNet收入随之提升，且首槽CTR变化的影响大于末槽的证据：可以看到：图4(a)中，依次为首位CTR增大、次位CTR增大、末位CTR增大，最终曲线增长逐渐变慢

不同广告位数量

基于设置D，增减广告位数量：
- D1 ：2广告位（CTRs $\boldsymbol{\alpha} = (0.5, 0.3)$）
- D2 ：4广告位（CTRs $\boldsymbol{\alpha} = (0.5, 0.3, 0.15, 0.1)$）
- D3 ：5广告位（CTRs $\boldsymbol{\alpha} = (0.5, 0.3, 0.15, 0.1, 0.03)$）
图4(b)显示，JRegNet生成的机制在所有设置中表现最佳，且其收入随广告位数量严格递增，而其他机制未呈现此规律

真实数据集

使用美团电商平台的在线拍卖日志数据训练与评估模型。每次用户搜索查询对应一次广告拍卖。实际场景中，广告系统通过召回、粗排与精排阶段筛选约10个组合作为候选，并从中选取最多10家零售商与10个品牌商，最终通过拍卖机制分配最多5个广告位。因此，论文聚焦于10 零售商、10品牌商、5广告位的设置。由于原始数据中竞拍者数量可变，对部分记录进行截断或填充以确保每样本包含10 零售商与10品牌商（填充竞拍者的点击价值为0）。使用6912组真实样本进行测试，日志数据特征包括：每家零售商与品牌商的出价及ID、零售商与品牌商的联合关系、各广告位的预测CTR
因真实数据与模拟数据的价值函数分布差异，仅用遗憾值衡量DSIC不再适用。为此，采用以下指标评估DSIC： $$
ru := \frac{1}{L}\sum_{\ell=1}^{L}\frac{\sum_{i=1}^{m} rgt_{i\cdot}^{(\ell)} + \sum_{j=1}^{n} rgt_{\cdot j}^{(\ell)}} {\sum_{i=1}^{m} \mu_{i\cdot}^{(\ell)} + \sum_{j=1}^{n} \mu_{\cdot j}^{(\ell)}}
$$
- 其中 $ rgt_{i\cdot} := \max_{v^{\prime}_{i\cdot} \in V_{i\cdot} } u_{i\cdot}(v_{i\cdot}; (v^{\prime}_{i\cdot}, \boldsymbol{v}_{-i\cdot})) - u_{i\cdot}(v_{i\cdot}, \boldsymbol{v}) $（品牌商同理）。$ ru $ 表示虚报带来的效用增长与真实报告的效用之比。对于GSP，测试时采用枚举法[27]获取虚报值（虚报值为 $ \beta v $，$ \beta \in \{0, 0.1, \ldots, 1.9\} $），并选取该集合中能获得最大效用的虚报计算GSP的遗憾值
- 对分子的理解 ：此时也在假设商家出价是真实的，然后看修改商家出价后，商家的遗憾值多大，这个值越小，说明越满足 DSIC 条件
- 对分母的理解 ：分母上是竞拍者（品牌商和零售商）的总效用，用于归一化最终的输出，方便观察影响
使用三个不同时间段的真实数据训练JRegNet，并分别用三个时间点的数据测试。附录A.2的图5与图6展示了训练与测试所用的真实搜索查询样本数量。表3列出了所有真实数据实验中JRegNet、VCG与GSP在测试集上的性能表现（GSP为美团在联合拍卖场景中最初采用的在线机制）
表3显示，在所有真实数据实验中，当 $ ru $ 极小时，JRegNet的收入显著高于VCG；当 $ ru $ 接近时，JRegNet的收入亦显著优于GSP（配对t检验 $ p < 0.05 $）。这些实验证明了JRegNet在真实联合拍卖场景中的有效性。需注意的是，GSP不满足DSIC，导致广告主投标策略复杂化，且联合拍卖场景中其均衡状态难以预测。实验中GSP的收入基于广告主真实投标的假设计算，而均衡状态下广告主的出价低于真实值，因此GSP的实际收入低于表中所示
JRegNet可应用于实际场景。若使用1个GPU与32个CPU的服务器运行此真实设置，训练30,000次迭代约需2至4小时。由于JRegNet的训练可离线进行，尽管离线训练较慢，但调用训练好的模型进行前向传播以获取分配与支付矩阵的速度极快（每搜索查询样本约1至3毫秒），不影响在线部署与决策

未来规划

作者的未来规划：未来研究方向包括将联合拍卖应用于直播销售、多品牌商协作等其他场景
说明：如果能做城市DID实验，观察商家调价行为是否增加/是否有降价情况可能更具说服力

CA——AIGB

本文主要记录AIGB出价模型

其他参考链接：
- 原始论文：AIGB: Generative Auto-bidding via Diffusion Modeling, Alibaba & Peking University, 2024
- Decision Diffuser原始论文：Is Conditional Generative Modeling all you need for Decision-Making?, MIT, ICLR 2023

核心思路

参考Decision Diffuser方法，对该方法进行微改并应用到出价上
改动一：逆向动力学模型（Acting with Inverse-Dynamics），中使用更多的状态来生成动作，AIGB中使用 $a_t:= f_\phi(s_{t-L:t},s_{t+1})$，原始Decision Diffuser方法则仅使用 $a_t:= f_\phi(s_t,s_{t+1})$

当前存在的问题

轨迹内部的一些规律捕捉不准确，比如同一个序列内部，预算越来越低这个规律无法满足

Joe Zhou

Stay Hungry. Stay Foolish.

GitHub E-Mail

Union操作和Union All操作

一般Java常量命名规范

一个特殊的例子——Logger

特殊写法

Logger对象使用final的原因

为什么不适用大写

MDP 和 POMDP

POMDP 中的置信 Belief

MDP 和 POMDP 的优化目标

主流求解 POMDP 方法（决策规划）

POMDP 于 RL

附录：一些 PPT 原始介绍

MDP

POMDP

POMDP 的求解方案

URL中的#字符

URL的正则表达式

torch.max()

单参数（取全局最大值）

多参数（按维度取最大值）

torch.backward() & torch.no_grad()

torch.nn.Module

tensor.item()

torch.autograd.grad(outputs,inputs,grad_outputs)

torch.cat、stack、hstack、vstack

tensor.repeat()函数

parameters() & named_parameters()

torch.empty()创建变量

torch.linspace() & torch.arange()

tensor.is_contiguous()

x.squeeze(dim) vs x.unsqueeze(dim)

torch.flatten() 和 torch.unflatten()

tensor.numpy() vs torch.from_numpy()

inplace参数的使用

示例代码

关于inplace的其他说明

torch.device() 和 tensor.to()函数

tensor.view() 和 tensor.reshape()

tensor.topk()函数

nn.Module.register_buffer

PyTorch中的对数运算

torch.clip 和 torch.clamp

torch.allclose() 函数

torch.chuck 函数用法

torch.chunk 的一些示例

torch.where 函数和 tensor.where 函数

tensor.where(condition, y)（实例方法）

torch.where(condition, x, y)（全局函数）

示例

torch.size() 函数 和 tensor.size(n)

tensor.size() 函数

tensor.size(n) 函数

对比 torch.size() 函数 和 tensor.size(n)

torch.roll() 函数

使用示例

使用注意事项

torch.quantile() 函数

使用示例

注意事项

torch.nn.functional.pad()（简称 F.pad()）

不同模式效果对比

注意事项

torch.unbind 函数

tensor.flip(dims) 函数

torch.nn.utils.rnn.pad_sequence 函数

用法示例

torch.randperm 函数

torch.argsort 函数

结合 torch.randperm 函数 和 torch.argsort 函数 实现打乱再恢复

len(dataloader) 函数

tensor.expand() 和 tensor.expand_as() 函数

tensor.expand() 用法

tensor.expand_as() 用法

torch.ge 函数

挖矿病毒kdevtmpfsi查杀经历

问题简介

查杀经过

总结

AMA是什么？

分配规则

URL中的`#`字符

`torch.flatten()` 和 `torch.unflatten()`

`torch.clip` 和 `torch.clamp`

`torch.allclose()` 函数

`torch.chuck` 函数用法

`torch.chunk` 的一些示例

`torch.where` 函数和 `tensor.where` 函数

`tensor.where(condition, y)`（实例方法）

`torch.where(condition, x, y)`（全局函数）

`torch.size()` 函数和 `tensor.size(n)`

`tensor.size()` 函数

`tensor.size(n)` 函数

对比 `torch.size()` 函数和 `tensor.size(n)`

`torch.roll()` 函数

`torch.quantile()` 函数

`torch.nn.functional.pad()`（简称 `F.pad()`）

`torch.unbind` 函数

`tensor.flip(dims)` 函数

`torch.nn.utils.rnn.pad_sequence` 函数

`torch.randperm` 函数

`torch.argsort` 函数

结合 `torch.randperm` 函数和 `torch.argsort` 函数实现打乱再恢复

`len(dataloader)` 函数

`tensor.expand()` 和 `tensor.expand_as()` 函数

`torch.ge` 函数