本文主要介绍LLM-Attention优化方法中的MHA、MQA、GQA到MLA的发展历程
- 参考链接:
- MLA原始论文:DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model
- GQA原始论文:GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints
- 来自苏神的参考链接:缓存与效果的极限拉扯:从MHA、MQA、GQA到MLA
- 讲的较为清晰的原创博客:deepseek技术解读(1)-彻底理解MLA(Multi-Head Latent Attention) - 姜富春的文章 - 知乎
MHA/MQA/GQA/MLA对比和讨论
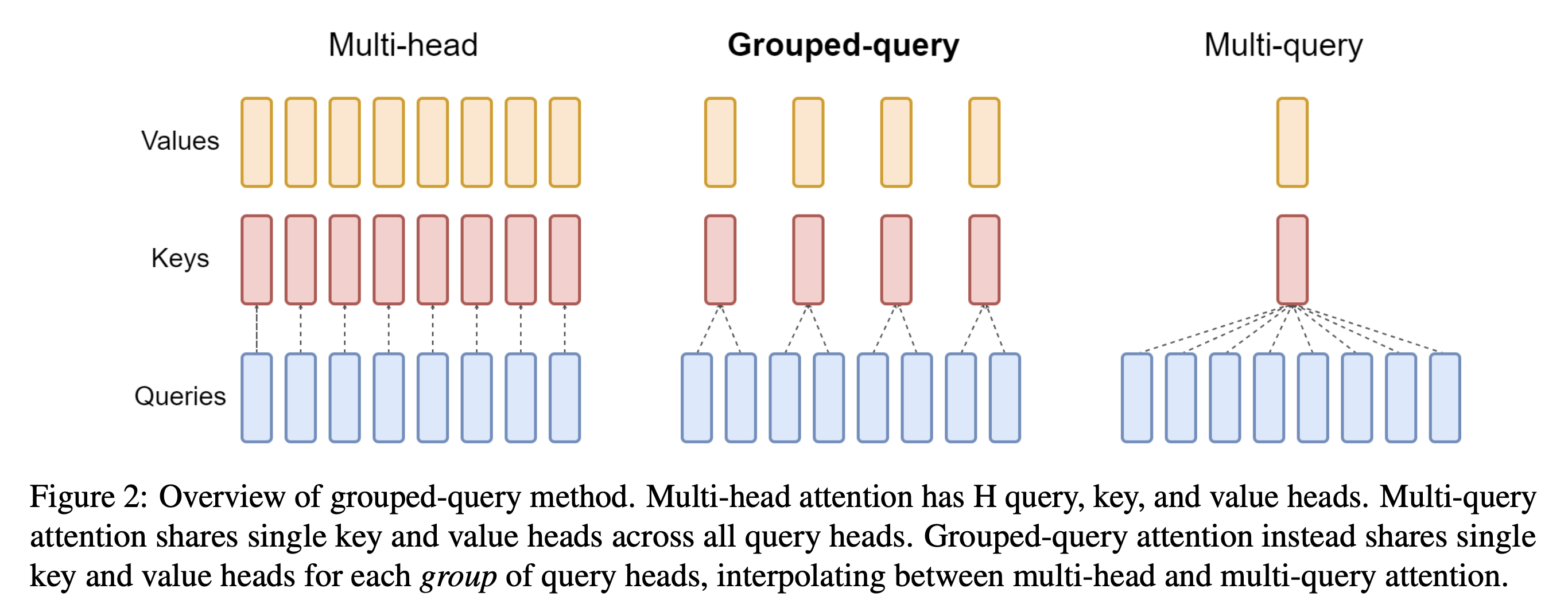
- MHA/MQA/GQA Overview(from GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints )
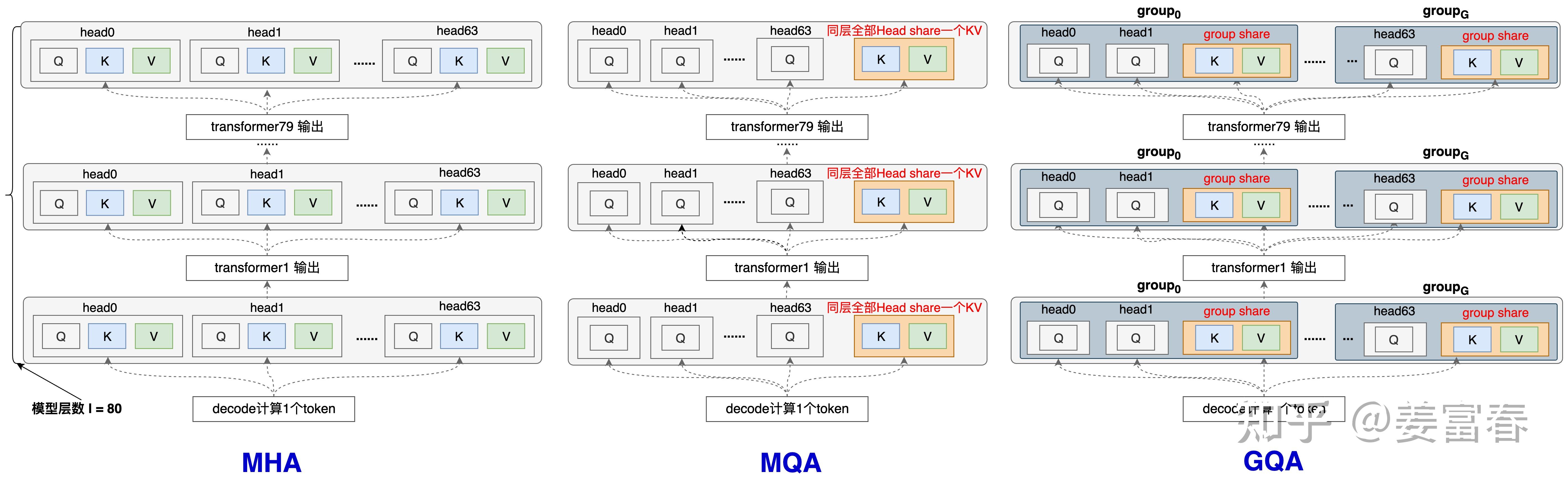
- KV-Cache示意图 (from deepseek技术解读(1)-彻底理解MLA(Multi-Head Latent Attention) - 姜富春的文章 - 知乎)
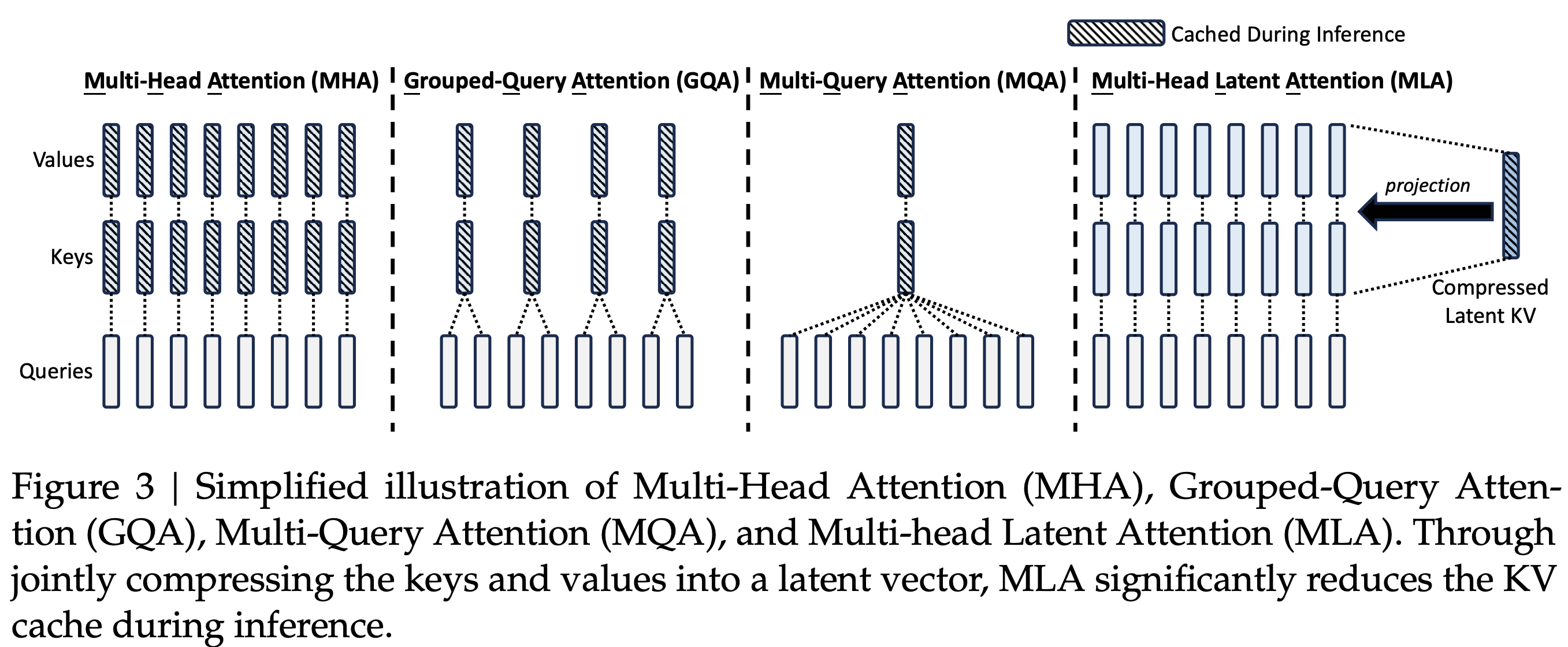
- MHA/MQA/GQA/MLA Overview(from DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model )
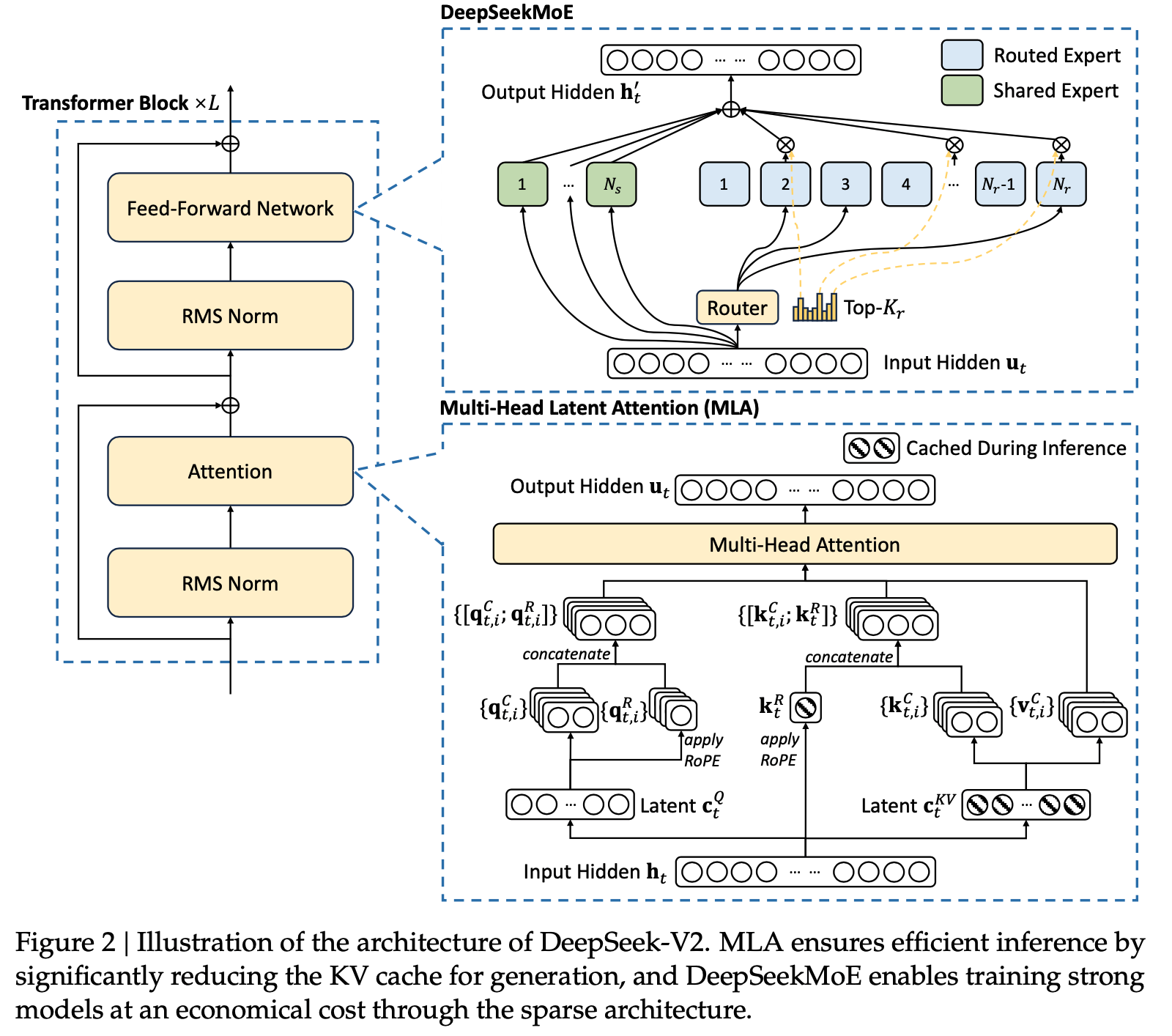
- 原始论文中,MLA的示意图
 * 核心,MLA 将 Q 和 K 拆开成 引入 RoPE 和 不引入 RoPE(NoPE)两部分,两者的 q 和 k 分别做 concat,本质是 qk 相乘以后做加法
* 核心,MLA 将 Q 和 K 拆开成 引入 RoPE 和 不引入 RoPE(NoPE)两部分,两者的 q 和 k 分别做 concat,本质是 qk 相乘以后做加法 - MHA/MQA/GQA 效果对比
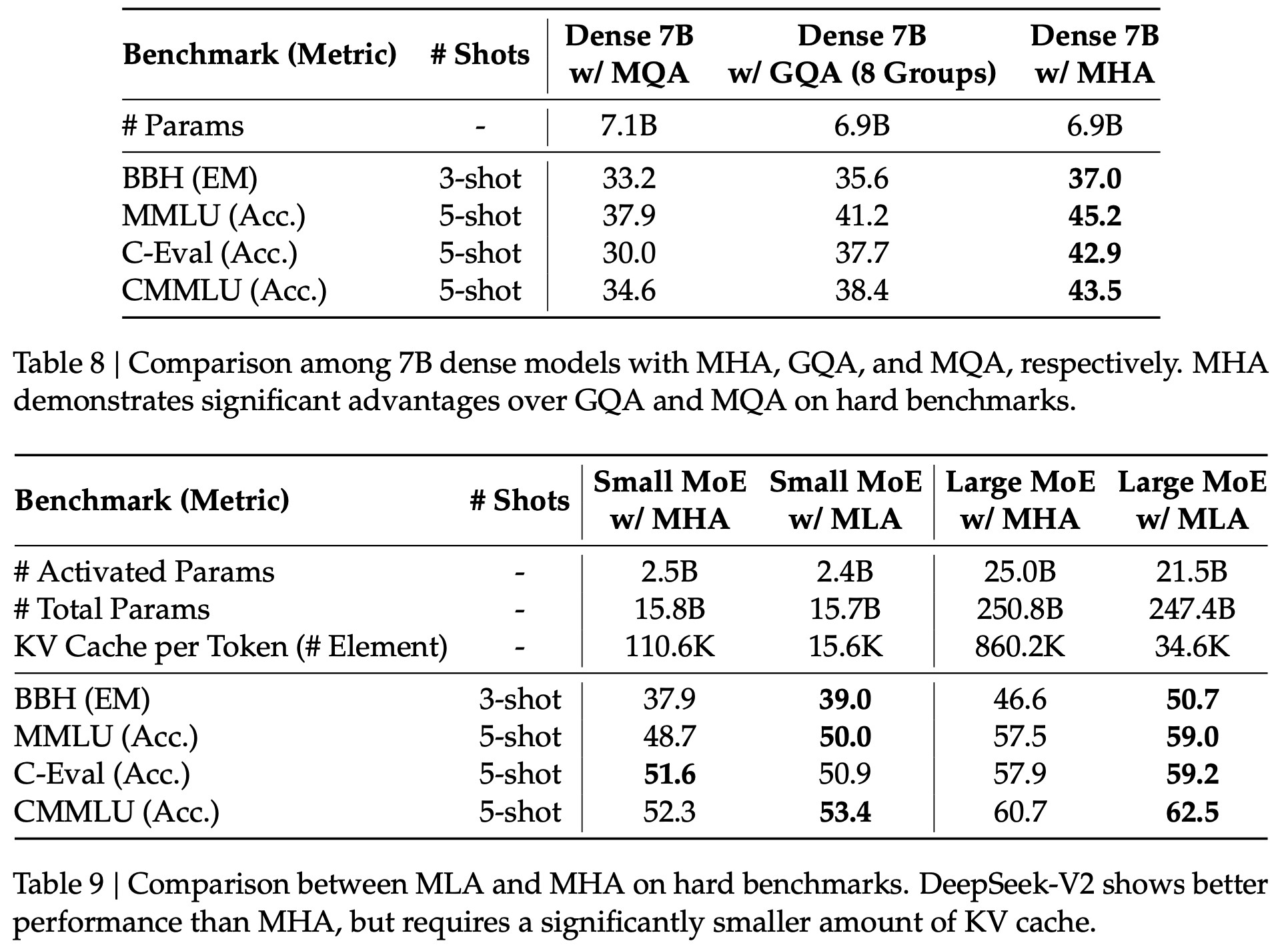
- 从上图中可以看出,整体效果为:MLA > MHA > GQA > MQA
- 问题:为什么目前在很多模型中,GQA 仍然是常客?
带RoPE的普通MHA
- 公式(from 缓存与效果的极限拉扯:从MHA、MQA、GQA到MLA):
$$
\begin{align}
\boldsymbol{o}_t &= \left[\boldsymbol{o}_t^{(1)}, \boldsymbol{o}_t^{(2)}, \cdots, \boldsymbol{o}_t^{(h)}\right] \\
\boldsymbol{o}_t^{(s)} &= Attention\left(\boldsymbol{q}_t^{(s)}, \boldsymbol{k}_{\leq t}^{(s)} ,\boldsymbol{v}_{\leq t}^{(s)}\right)\triangleq\frac{\sum_{i\leq t}\exp\left(\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top}\right)\boldsymbol{v}_i^{(s)}}{\sum_{i\leq t}\exp\left(\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top}\right)} \\
\boldsymbol{q}_i^{(s)} &= \boldsymbol{x}_i\boldsymbol{W}_q^{(s)}\color{red}{\boldsymbol{\mathcal{R}}_i}\in\mathbb{R}^{d_k},\quad \boldsymbol{W}_q^{(s)}\in\mathbb{R}^{d\times d_k}\\
\boldsymbol{k}_i^{(s)} &= \boldsymbol{x}_i\boldsymbol{W}_k^{(s)}\color{red}{\boldsymbol{\mathcal{R}}_i}\in\mathbb{R}^{d_k},\quad \boldsymbol{W}_k^{(s)}\in\mathbb{R}^{d\times d_k} \\
\boldsymbol{v}_i^{(s)} &= \boldsymbol{x}_i\boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d_v},\quad \boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d\times d_v}
\end{align}
$$
带RoPE的MLA
- 核心思想是通过将K,V降维再升维的方式,既保证了每个head有不同的K,V,又能显著降低缓存量,巧妙的减少KV-Cache存储量(仅存储降维后的中间值即可),最早由DeepSeek提出
- 此外,在训练时,将Q值也进行了降维再升维(具体优势是什么?)
- MLA公式(from 缓存与效果的极限拉扯:从MHA、MQA、GQA到MLA):
$$
\begin{align}
\boldsymbol{o}_t &= \left[\boldsymbol{o}_t^{(1)}, \boldsymbol{o}_t^{(2)}, \cdots, \boldsymbol{o}_t^{(h)}\right] \\
\boldsymbol{o}_t^{(s)} &= Attention\left(\boldsymbol{q}_t^{(s)}, \boldsymbol{k}_{\leq t}^{(s)} ,\boldsymbol{v}_{\leq t}^{(s)}\right)\triangleq\frac{\sum_{i\leq t}\exp\left(\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top}\right)\boldsymbol{v}_i^{(s)}}{\sum_{i\leq t}\exp\left(\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top}\right)} \\
\boldsymbol{q}_i^{(s)} &= \left[\boldsymbol{c}_i’\boldsymbol{W}_{qc}^{(s)}, \boldsymbol{c}_i’\boldsymbol{W}_{qr}^{(s)}\color{red}{\boldsymbol{\mathcal{R}}_i}\right]\in\mathbb{R}^{d_k + d_r},\quad \boldsymbol{W}_{qc}^{(s)}\in\mathbb{R}^{d_c’\times d_k},\boldsymbol{W}_{qr}^{(s)}\in\mathbb{R}^{d_c’\times d_r}\\
\boldsymbol{k}_i^{(s)} &= \left[\boldsymbol{c}_i\boldsymbol{W}_{kc}^{(s)}, \boldsymbol{x}_i\boldsymbol{W}_{kr}^{\color{lightgray}{\smash{\not{(s)}}}}\color{red}{\boldsymbol{\mathcal{R}}_i}\right]\in\mathbb{R}^{d_k+d_r},\quad \boldsymbol{W}_{kc}^{(s)}\in\mathbb{R}^{d_c\times d_k}, \boldsymbol{W}_{kr}^{\color{lightgray}{\smash{\not{(s)}}}}\in\mathbb{R}^{d\times d_r} \\
\boldsymbol{v}_i^{(s)} &= \boldsymbol{c}_i\boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d_v},\quad \boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d_c\times d_v} \\
\boldsymbol{c}_i’ &= \boldsymbol{x}_i \boldsymbol{W}_c’\in\mathbb{R}^{d_c’},\quad \boldsymbol{W}_c’\in\mathbb{R}^{d\times d_c’} \\
\boldsymbol{c}_i &= \boldsymbol{x}_i \boldsymbol{W}_c\in\mathbb{R}^{d_c},\quad \boldsymbol{W}_c\in\mathbb{R}^{d\times d_c} \\
\end{align}
$$ - 为了引入 RoPE,在中间向量中拼接了 RoPE 降维后的向量,该向量维度较小
原始论文中 MLA 完整公式
- MLA 完整公式如下:

- MLA 的 Q 和 K 分为 RoPE 和 非 RoPE 两部分
- 表达在 隐向量上则是 从 concat
- 表达在最终的乘积结果上泽变成 sum
- 两种表达本质是一样的(对 qk 分别做 concat 和对 qk 乘积做加法结果等价),详情见:DeepSeek-v2 MLA 原理讲解-哔哩哔哩