注:本文包含 AI 辅助创作
参考链接:
背景:20250904 日,OpenAI 在自己的网站放出了一篇论文 Why Language Models Hallucinate, 20250904,并于 20250905 在官网放出博客 openai.com/index/why-language-models-hallucinate, 20250905
论文以论文为主,详细阅读该论文和博客,如果仅考虑整体总结,可以主要看看附录的博客内容
Paper Summary
- 整体内容总结:
- 论文揭示了现代语言模型中幻觉的奥秘,幻觉从预训练期间的起源到通过后训练的持续存在
- 在预训练中:生成错误(generative errors)类似于监督学习中的误分类(misclassifications)
- 这并不神秘,并且是由于最小化交叉熵损失(cross-entropy loss)而自然产生的
- 作者认为大多数主流评估奖励幻觉行为,对主流评估进行简单的修改可以重新调整激励
- 训练和评估过程中,鼓励适当的不确定性表达(目前的大多数方法均会惩罚不确定性回答) :可以消除抑制幻觉的障碍
- “幻觉”(hallucination)现象的解释和定义:
- LLM 有时在不确定时会猜测(就像学生面对难题时会猜测一样),产生看似合理但不正确的陈述,而不是承认不确定性(即使是 SOTA 系统也依然存在)
- 作者认为:
- 语言模型产生幻觉是因为训练和评估过程鼓励猜测而非鼓励承认不确定性 ,并且论文分析了现代训练流程中幻觉的统计原因
- 幻觉不是神秘的,它们源于二元分类中的简单错误
- 如果错误陈述无法与事实区分开来,那么预训练语言模型中的幻觉就会因为自然的统计压力产生
- 论文论证
- 幻觉之所以持续存在,是因为大多数评估的评分方式存在问题
- 具体问题是:语言模型被优化为优秀的应试者,而在不确定时进行猜测可以提高测试表现
- 这种“惩罚不确定回答”的普遍现象只能通过一种社会技术性的缓解措施来解决:
- 修改那些主导排行榜但未对齐的现有基准测试的评分方式,而不是引入额外的幻觉评估
- 理解:惩罚不确定性是不好的,最好是能正确回答 > 不确定性回答 > 错误回答
- 注:这种改变可能会引导该领域朝着更可信的人工智能系统方向发展
Introduction and Discussion
- “幻觉”(hallucination)是指语言模型会产生过度自信、看似合理的虚假信息的现象
- 目前为止幻觉问题仍然困扰着大家,并且仍然存在于最新的模型中(OpenAI, 2025a)
- 考虑以下提示:What is Adam Tauman Kalai’s birthday? If you know, just respond with DD-MM.
- 在三次独立的尝试中,一个 SOTA 开源语言模型输出了三个错误的日期:“03-07”、“15-06”和“01-01”,即使提示要求仅在知道的情况下才回答。正确的日期是在秋季(表 1 提供了一个更复杂的幻觉示例)

- 幻觉是语言模型产生的错误(errors)的一个重要特例,论文使用计算学习理论(computational learning theory)(例如,1994)对其进行了更一般的分析
- 论文考虑一般的错误集合 \(\mathcal{E}\),它是合理字符串集合 \(\mathcal{X}=\mathcal{E}\cup\mathcal{V}\) 的任意子集,其中其他合理字符串 \(\mathcal{V}\) 被称为有效(valid)字符串
- 然后论文分析这些错误的统计性质,并将结果应用于论文感兴趣的错误类型:看似合理的虚假陈述(幻觉)
- 论文的形式化框架还包括提示(prompt)的概念,语言模型必须对其作出响应
- 语言的分布最初是从包含训练示例的语料库中学习到的,该语料库不可避免地包含错误和半真半假的陈述
- 然而,论文表明,即使训练数据没有错误,语言模型训练期间优化的目标也会导致生成错误
- 对于包含不同程度错误的真实训练数据,人们可能会预期错误率甚至更高
- 因此,论文的错误下界适用于更现实的场景,正如传统的计算学习理论(1994)一样
- 论文的错误分析是通用的,但对幻觉有特定的意义
- 它广泛适用,包括推理和搜索检索语言模型,并且该分析不依赖于下一个词预测或基于 Transformer 的神经网络的特性
- 它只考虑现代训练范式的两个阶段:预训练(pretraining)和Post-training,如下所述
- 对于幻觉,分类法(2020; 2023)通常进一步区分:
- 内在(intrinsic)幻觉,即与用户提示相矛盾 ,例如:
- How many Ds are in DEEPSEEK? If you know, just say the number with no commentary.
- DeepSeek-V3 在十次独立试验中返回了“2”或“3”;Meta AI 和 Claude 3.7 Sonnet 的表现类似,包括“6”和“7”这样大的答案
- 外在(extrinsic)幻觉,即与训练数据或外部现实相矛盾的幻觉
- 论文的理论也阐明了外在幻觉
- 内在(intrinsic)幻觉,即与用户提示相矛盾 ,例如:
Errors caused by pretraining
- 在预训练期间,一个 Base Model 学习大型文本语料库中的语言分布
- 论文证明,即使使用无错误的训练数据,预训练期间最小化的统计目标也会导致语言模型产生错误
- 证明这一点并非易事,因为有些模型不会出错,例如总是输出“我不知道”(I don’t know, IDK)的模型,或者只是记忆并复述无错误语料库的模型
- 论文的分析解释了预训练后应预期哪些类型的错误
- 为此,论文将其与二元分类(binary classification)联系起来
- 考虑形式为“这是一个有效的语言模型输出吗?”的问题
- 生成有效输出在某种意义上比回答这些是/否问题更难,因为生成隐含地需要对每个候选回答回答“这有效吗”
- 形式上,论文考虑“它是否有效”(Is-It-Valid, IIV)二元分类问题,其训练集包含大量响应,每个响应都被标记为有效(+)或错误(-),如图 1 所示
- 对于这个监督学习问题,训练和测试数据都是标记为 \(+\) 的有效示例(即预训练数据,因为论文假设它是有效的)和来自 \(\mathcal{E}\) 的均匀随机错误(标记为 \(-\))的 50/50 混合
- 然后论文展示任何语言模型如何可以用作 IIV 分类器。这反过来使论文能够建立生成错误(如幻觉)和 IIV 误分类率之间的数学关系:
$$ (generative error rate) \gtrsim 2 \cdot (IIV misclassification rate). $$- 即:生成错误率 大约大于等于 2 倍的 IIV 误分类率
- 考虑形式为“这是一个有效的语言模型输出吗?”的问题
- 语言模型避免了许多类型的错误,例如拼写错误,并且并非所有错误都是幻觉
- 从 IIV 误分类到生成的归约阐明了生成错误的统计性质
- 该分析显示了预训练如何直接导致错误
- 而且它表明导致二元分类错误的相同统计因素也会导致语言模型错误
- 数十年的研究已经阐明了误分类错误的多方面性质(Domingos, 2012)
- 图 1(右)直观地说明了这些因素:
- 顶部,可分离数据被准确分类;
- 中部,用于圆形区域的线性分隔器的模型较差;
- 底部,没有简洁的模式

- 图 1(右)直观地说明了这些因素:
- 从 IIV 误分类到生成的归约阐明了生成错误的统计性质
- 第 3.3 节分析了几个因素,包括以下具有认知不确定性(epistemic uncertainty)的风格化设置(即数据中没有模式时)
- 这种归约将早期涵盖不同类型事实的工作联系在一起
- 例如,Kalai and Vempala (2024) 考虑了任意事实(arbitrary facts)的一个特例,其中数据中没有可学习的模式,就像之前的生日幻觉例子一样
- 论文展示了 IIV 归约如何涵盖这种情况,并恢复了他们的下界,即预训练后的幻觉率至少应为训练事实中出现一次的比例
- 例如,如果 20% 的生日事实在预训练数据中恰好出现一次,那么预计基础模型至少会对 20% 的生日事实产生幻觉
- 问题:如何理解,只出现一次的事实一定会出错这个理论?出现次数少更容易出错,但不代表只出现一次的就一定会出错吧?
We show how the IIV reduction covers this case and recovers their bound that the hallucination rate, after pretraining, should be at least the fraction of training facts that appear once. For instance, if 20% of birthday facts appear exactly once in the pretraining data, then one expects base models to hallucinate on at least 20% of birthday facts. In fact, our analysis strengthens their result to include prompts and IDK responses, both essential
- 事实上,论文的分析加强了他们的结果,将提示和 IDK 响应都包括在内,这两者都是幻觉的重要组成部分
Why hallucinations survive post-training(后训练中持续存在)
- 后训练(post-training),对基础模型进行细化,通常以减少幻觉为目标
- 论文对预训练的分析主要包含了更一般的错误 ,论文对后训练的分析侧重于为什么会产生过度自信的幻觉 ,而不是省略信息或表达不确定性(如 IDK)
- 论文为后训练后幻觉的持续性提供了一个社会技术性的解释,并讨论了该领域如何抑制它们
- 作为一个类比,考虑以下人类偶尔也会编造听起来合理的信息的情境
- 当不确定时,学生可能会在多项选择考试中猜测,甚至在书面考试中虚张声势,提交他们几乎没有信心的看似合理的答案
- 语言模型通过类似的测试进行评估
- 在不确定时猜测,在二元 0-1 评分方案下(正确答案得 1 分,空白或 IDK 得 0 分)可以最大化期望分数
- 虚张声势通常是过度自信和具体的,例如对于日期问题回答“9 月 30 日”而不是“秋天的某个时候”
- 许多语言模型基准测试反映了标准化的人类考试,使用二元指标,如准确率或通过率
- 因此,针对这些基准优化模型可能会助长幻觉
- 人类在校外的艰难教训中学会了表达不确定性的价值
- 语言模型主要使用惩罚不确定性的考试进行评估
- 因此,它们总是处于“应试”模式
- 总之,大多数评估并未对齐(aligned)
- 论文并非第一个意识到二元评分不能衡量幻觉的人,但先前关于幻觉评估的工作通常追求难以捉摸的“完美幻觉评估”
- 在第 4 节中,作者认为这是不够的
- 论文观察到,现有的主要评估绝大多数都惩罚不确定性 ,因此根本问题是大量评估未对齐
- 假设模型 A 是一个对齐的模型,能正确发出不确定性信号且从不产生幻觉
- 让模型 B 与模型 A 相似,只是它从不表示不确定性,并且在不确定时总是“猜测”
- 在 0-1 评分(大多数当前基准的基础)下,模型 B 将优于 A
- 这造成了一种“惩罚不确定性和弃权”的普遍现象,作者认为少量的幻觉评估不足以解决这个问题
- 必须调整众多主要评估,以停止在不确定时惩罚弃权行为
- 论文的 Contributions:
- 论文确定了幻觉的主要统计驱动因素,从其预训练的起源到其后训练的持续性
- 监督学习和无监督学习之间的新颖联系揭示了它们的起源,即使在训练数据包含 IDK 的情况下也是如此
- 尽管针对该问题进行了大量工作,幻觉仍然存在,幻觉的持续性可以理解为:大多数的评估在“奖励猜测行为”
- 论文讨论了对现有评估进行统计上严谨的修改,为有效缓解铺平道路
Related work
- 据论文所知,论文提出的从监督学习(二元分类)到无监督学习(密度估计或自监督学习)的归约是新颖的
- 然而,学习问题之间归约的一般方法是证明一个问题至少与另一个问题一样难的成熟技术(参见,例如,2016)
- 许多调查和研究探索了语言模型中幻觉的根本原因
- Sun 等 (2025) 引用了诸如模型过度自信(2023)、解码随机性(2022)、雪球效应(2023)、长尾训练样本(2023)、误导性的对齐训练(2023)、虚假相关性(2022)、曝光偏差(2015)、逆转诅咒(2024)和上下文劫持(Jeong, 2024)等因素
- 类似的错误来源在更广泛的机器学习和统计环境中早已被研究(Russell and Norvig, 2020)
- 最相关的理论工作是 Kalai and Vempala (2024),论文表明它是论文归约的一个特例
- 他们将古德-图灵缺失质量估计(Good-Turing missing mass estimates)(Good, 1953)与幻觉联系起来,这启发了定理 3
- 但该工作没有涉及不确定性表达(例如,IDK)、与监督学习的联系、后训练修改,并且他们的模型不包括提示
- Hanneke 等 (2018) 分析了一种交互式学习算法,该算法查询有效性预言机(例如,人类)以不可知地训练一个最小化幻觉的语言模型
- 他们的方法在统计上是高效的,需要合理数量的数据,但在计算上并不高效
- 其他最近的理论研究(2025; Kleinberg and Mullainathan, 2024)形式化了一致性(consistency)(避免无效输出)和广度(breadth)(生成多样化、语言丰富的内容)之间的内在权衡
- 这些工作表明,对于广泛的语言类别,任何泛化超出其训练数据的模型要么会产生无效输出的幻觉,要么遭受模式崩溃(mode collapse),无法产生全部的有效响应
- 几种后训练技术已被证明可以减少幻觉
- 例如 RLHF (2022)、AI 反馈强化学习(Reinforcement Learning from AI Feedback, RLAIF)(2022)和直接偏好优化(Direct Preference Optimization, DPO)(2023),包括阴谋论和常见误解
- Gekhman 等 (2024) 表明,对新信息进行简单的微调最初可以降低幻觉率,但随后又会增加
- 此外,已经证明自然语言查询和内部模型激活都编码了关于事实准确性和模型不确定性的预测信号(例如,2022)
- 正如论文的引言中所讨论的,模型对语义相关查询的回答的不一致性也可以用来检测或减轻幻觉(2023; 2025; 2024)
- 许多其他方法已被证明可有效减轻幻觉;
- 例如:参见 Ji 等 (2023) 和 Tian 等 (2024) 的综述
- 在评估方面,最近引入了一些全面的基准测试和排行榜(例如,2025; 2024),但相对较少的工作研究了它们采用的障碍
- 例如:2025 年 AI 指数报告(2025)指出,幻觉基准测试“难以在 AI 社区内获得关注”
- 除了确定性的二元表达之外,还提出了更细微的语言结构来传达不确定性的程度(2022; 2022a; 2025)
- 此外,语用学(pragmatics)领域,研究意义如何由语境塑造,对于理解和改进语言模型传达信息的方式具有越来越大的相关性(2025)
Pretraining Errors
- 预训练会生成一个基础语言模型 \(\hat{p}\),该模型近似于从其训练分布 \(p\) 中抽取的文本分布
- 这是无监督学习中的经典“密度估计”问题,其中密度(density)就是数据上的概率分布
- 对于语言模型而言,该分布是关于文本的,如果包含多模态输入,则也关于多模态输入
- 证明基础模型会出错的关键挑战在于,许多语言模型确实不会出错
- 总是输出“我不知道”(IDK)的退化模型也能避免错误(假设 IDK 不算错误)
- 同样,假设训练数据无误,那么简单地复述随机训练样本中文本的平凡基础模型也不会出错
- 但这两个语言模型都未能实现密度估计,这是下面定义的统计语言建模的基本目标
- 最优的基础模型 \(\hat{p}=p\)(与训练分布匹配)也能避免错误,但这个模型需要过高地巨量(prohibitively large)的训练数据
- 论文表明,训练良好的基础模型仍然应该产生某些类型的错误
- 论文的分析表明,生成有效输出(即避免错误)比分类输出有效性更困难
- 这种归约使论文能够将计算学习理论(其中错误是预期且被理解的)的视角应用于生成模型中的错误机制
- 语言模型最初被定义为文本上的概率分布,后来提示(prompts)被纳入其中(第 3.2 节);
- 两种设置共享相同的直觉
- 没有提示的例子包括图 1 中的生日陈述,而有提示的模型可能会被查询特定个人的生日
- 不仅仅是自动补全 (Not merely autocomplete)
- 论文的分析适用于一般的密度估计,而不仅仅是“下一个词预测器”
- 人们很容易将幻觉归因于选择了语言模型无法提供有效补全的糟糕前缀(例如,“Adam Kalai was born on”)
- 但从纯粹的统计角度来看,忽略计算,语言模型的自动补全视图并不比人类说话者一次产生一个词这一事实更重要
脚注:数学上,任何分布 \(p\) 都会为其支持集中的每个词前缀 \(w_{1}\dots w_{i-1}\) 诱导出一个补全分布 \(p(w_{i}w_{i+1}\dots \mid w_{1}w_{2}\dots w_{i-1})\)
- 论文的分析表明,尽管特定的架构可能会引入额外的错误,但错误(主要)源于模型正在拟合底层语言分布这一事实
The reduction without prompts
- 在没有提示词的情况下,基础模型 \(\hat{p}\) 是集合 \(\mathcal{X}\) 上的概率分布
- 如前所述,每个样本(example)\(x\in \mathcal{X}\) 代表一个“看似合理”(plausible)的字符串,例如一个文档
- 样本 \(\mathcal{X}=\mathcal{E}\cup\mathcal{V}\) 被划分为错误 \(\mathcal{E}\) 和有效样本 \(\mathcal{V}\),其中 \(\mathcal{E},\mathcal{V}\) 是非空不相交的集合
- 基础模型 \(\hat{p}\) 的错误率表示为:
$$
\text{err}:=\hat{p}(\mathcal{E})=\Pr_{x\sim\hat{p} }[x\in\mathcal{E}]. \tag{1}
$$ - 假设训练数据来自无噪声的训练分布(training distribution)\(p(\mathcal{X})\),即 \(p(\mathcal{E})=0\)
- 如前所述,对于含有错误和部分正确陈述的有噪声训练数据,人们可能会预期错误率甚至高于论文的下界
- 论文现在形式化引言中介绍的 IIV(Is-It-Valid)二分类问题
- IIV 由要学习的目标函数 \(f:\mathcal{X}\rightarrow\{-,+\}\)(即属于 \(\mathcal{V}\) 的成员资格)和样本 \(\mathcal{X}\) 上的分布 \(D\)(来自 \(p\) 的样本和均匀随机错误的 50/50 混合)指定:
$$
D(x):=\begin{cases}p(x)/2&\text{if }x\in\mathcal{V},\ 1/2|\mathcal{E}|&\text{if }x\in\mathcal{E},\end{cases} \text{ and } f(x):= \begin{cases}+&\text{ if }x\in\mathcal{V},\ -&\text{ if }x\in\mathcal{E}.\end{cases}
$$
- IIV 由要学习的目标函数 \(f:\mathcal{X}\rightarrow\{-,+\}\)(即属于 \(\mathcal{V}\) 的成员资格)和样本 \(\mathcal{X}\) 上的分布 \(D\)(来自 \(p\) 的样本和均匀随机错误的 50/50 混合)指定:
- 论文的分析根据 IIV 的上述误分类率(misclassification rate)\(\text{err}_{\text{Iiv} }\) 来界定错误率 \(\text{err}=\hat{p}(\mathcal{E})\) 的下界:
$$
\text{err}_{\text{Iiv} }:=\Pr_{x\sim D}\left[\hat{f}(x)\neq f(x)\right], \text{ where } \hat{f}(x):= \begin{cases}+&\text{ if }\hat{p}(x)>1/|\mathcal{E}|,\ -&\text{ if }\hat{p}(x)\leq 1/|\mathcal{E}|.\end{cases} \tag{2}
$$ - 因此,在论文的归约中,基础模型通过在一定阈值 \(1/|\mathcal{E}|\) 处对基础模型的概率进行阈值处理,被用作 IIV 分类器。请注意,对于基础模型,通常可以高效计算此类概率 \(\hat{p}(x)\)(尽管高效计算对于下界有意义并非必需)
- 推论 1 (Corollary 1) :对于任何满足 \(p(\mathcal{V})=1\) 的训练分布 \(p\) 和任何基础模型 \(\hat{p}\),
$$
\textup{err}\geq 2\cdot\textup{err}_{\textup{Iiv} }-\frac{|\mathcal{V}|}{|\mathcal{E}|}-\delta,
$$- 其中 \(\textup{err},\textup{err}_{\textup{Iiv} }\) 来自方程 (1) 和 (2)
- 且 \(\delta:=|\hat{p}(\mathcal{A})-p(\mathcal{A})|\)
- 其中 \(\mathcal{A}:=\{x\in\mathcal{X}\mid\hat{p}(x)>1/|\mathcal{E}|\}\)
- 由于这种关系对任何基础模型 \(\hat{p}\) 都成立,它立即意味着所有基础模型都会在本质上不可学习的 IIV 事实(例如训练数据中缺失的生日)上出错,其中 \(\textup{err}_{\textup{Iiv} }\) 必然很大,并且 \(\delta\) 和 \(|\mathcal{V}|/|\mathcal{E}|\) 很小(例如,对于每个人,\(\mathcal{E}\) 中错误的生日声称数量是 \(\mathcal{V}\) 中正确数量的 364 倍,再加上 IDK)。上述推论显然是定理 1 的一个特例,该定理涵盖了包含提示的更一般情况。定理 2 随后使用这个一般结果为直观的特例提供下界。定理 3 和 4 处理小的 \(|\mathcal{E}|\),例如,对于 True/False 问题,\(|\mathcal{E}|=1\)。上述界限中的常数 2 相对紧:对于大的 \(|\mathcal{E}|\) 和小的 \(\delta\),对于不可学习的概念,\(\textup{err}_{\textup{Iiv} }\) 可能接近 \(1/2\),而 \(\textup{err}\leq 1\)。推论 1 也意味着 \(\textup{err}_{\textup{Iiv} }\lesssim 1/2\)
- 幻觉错误 (Hallucination errors)
- 要将错误分析应用于幻觉,可以考虑将 \(\mathcal{E}\) 视为包含(一个或多个)看似合理的虚假陈述的看似合理的生成集合
- 请注意,幻觉的一个常见替代定义是不基于训练数据(或提示)的生成
- 幸运的是,上述下界也适用于这个概念,因为论文只假设了有效的训练数据,即生成的事实错误不能基于事实正确的训练数据
- 校准 (Calibration)
- 论文现在论证为什么 \(|\delta|\) 是一个(错误)校准的度量,并且在预训练后很小。注意,在没有任何语言知识的情况下,可以通过简单地采用均匀分布 \(\hat{p}(x)=1/|\mathcal{X}|\) 来实现 \(\delta=0\),因此 \(\delta=0\) 并不要求 \(p=\hat{p}\)。审计员可以通过比较满足 \(\hat{p}(x)>1/|\mathcal{E}|\) 的训练样本 \(x\sim p\) 和合成生成 \(\hat{x}\sim\hat{p}\) 的比例来轻松估计 \(\delta\)。受 (Dawid, 1982) 的启发,可以类比于天气预报员预测每天下雨的概率。一个最低的校准要求是他们的平均预测是否与平均降雨比例相匹配。还可以要求这两者在预测 \(>t\)(对于某个阈值 \(t\in[0,1]\))的日子里匹配。(Dawid, 1982) 提出了更严格的要求,即对于每个\(t\in[0,1]\),在预测为 \(t\) 的日子里,大约有 \(t\) 比例的时间下雨
- 这里有一个特别简单的理由说明为什么对于标准的预训练交叉熵目标,\(\delta\) 通常很小:
$$
\mathcal{L}(\hat{p})=\mathop{\mathbb{E} }_{x\sim p}[-\log\hat{p}(x)]. \tag{3}
$$ - 考虑将正标记样本的概率按因子 \(s>0\) 重新缩放并归一化:
$$
\hat{p}_{s}(x):\propto\begin{cases}s\cdot\hat{p}(x)&\text{if }\hat{p}(x)>1/|\mathcal{E}|,\ \hat{p}(x)&\text{if }\hat{p}(x)\leq 1/|\mathcal{E}|.\end{cases}
$$- 那么,一个简单的计算表明,\(\delta\) 是损失关于缩放因子 \(s\) 的导数的大小,在 \(s=1\) 处求值:
$$
\delta=\left|\left.\frac{d}{ds}\mathcal{L}(\hat{p}_{s})\right|_{s=1}\right|.
$$
- 那么,一个简单的计算表明,\(\delta\) 是损失关于缩放因子 \(s\) 的导数的大小,在 \(s=1\) 处求值:
- 如果 \(\delta\neq 0\),那么通过某个 \(s\neq 1\) 重新缩放将减少损失,因此损失不在局部最小值
- 对于任何足够强大以近似这种简单重新缩放的语言模型类,局部优化应该产生小的 \(\delta\)
- 请注意,\(\delta\) 是在单个阈值 \(t=1/|\mathcal{E}|\) 处定义的,比期望校准误差(Expected Calibration Error, ECE)等概念更弱,后者在阈值 \(t\) 上积分
- 幻觉仅对基础模型是不可避免的 (Hallucinations are inevitable only for base models)
- 许多人认为幻觉是不可避免的 (Jones, 2025; Leffer, 2024; 2024),但可以很容易地创建一个非幻觉模型,使用问答数据库和计算器,回答一组固定的问题,如“金的化学符号是什么?”以及格式良好的数学计算,如“3 + 8”,否则输出 IDK
- 此外,推论 1 的错误下界意味着不出错的语言模型必定未校准 ,即 \(\delta\) 必须很大
- 正如论文的推导所示,校准,以及因此的错误,是标准交叉熵目标的自然结果
- 确实,实证研究(图 2)表明,基础模型通常被发现是校准的,与后训练模型相反,后者可能偏离交叉熵而倾向于强化学习
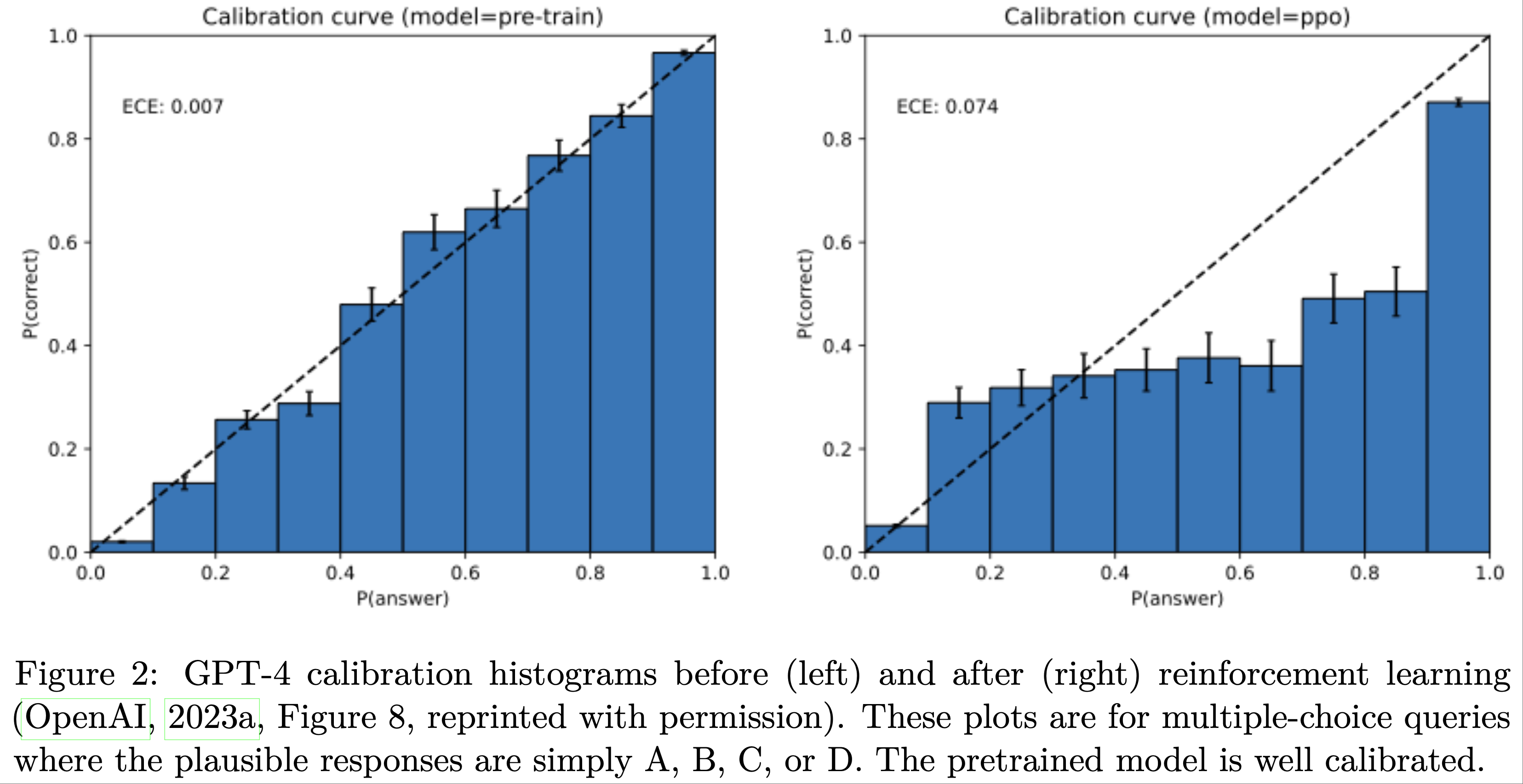
The reduction with prompts
- 此后,论文将第 3.1 节中的设置推广到包括从提示分布(prompt distribution)\(\mu\) 中抽取的提示(上下文)\(c\in\mathcal{C}\)
- 每个样本 \(x=(c,r)\) 现在由一个提示 \(c\) 和一个看似合理的响应 \(r\) 组成
- 上面的分析对应于 \(\mu\) 将概率 1 分配给空提示的特殊情况。对于给定的提示 \(c\in\mathcal{C}\),令 \(\mathcal{V}_{c}:=\{r\mid(c,r)\in\mathcal{V}\}\) 为有效响应,\(\mathcal{E}_{c}:=\{r\mid(c,r)\in\mathcal{E}\}\) 为错误响应
- 训练分布和基础模型现在是条件响应分布 \(p(r\mid c),\hat{p}(r\mid c)\)
- 为符号方便,论文通过 \(p(c,r):=\mu(c)p(r\mid c)\) 和 \(\hat{p}(c,r):=\mu(c)\hat{p}(r\mid c)\) 将它们扩展到 \(\mathcal{X}\) 上的联合分布,因此仍然有 \(\operatorname{err}:=\hat{p}(\mathcal{E})=\sum_{(c,r)\in\mathcal{E} }\mu(c)\hat{p }(r\mid c)\) 且 \(p(\mathcal{E})=0\)
- 因此,训练分布样本对应于有效的“对话”,就像在蒸馏(distillation)中一样 (2023; 2023)
- 尽管假设训练数据包含来自相同提示分布的模型对话是不现实的,但当假设不成立时,可能会预期甚至更高的错误率
- 带提示的 IIV 问题具有相同的目标函数 \(f(x):=+ \text{ iff } x\in\mathcal{V}\),但广义分布 \(D\) 以相等的概率选择 \(x\sim p\) 或 \(x=(c,r)\),其中 \(c\sim\mu\) 且 \(r\in\mathcal{E}_{c}\) 均匀随机
- 最后,分类器 \(\hat{f}(c,r)\) 现在是 \(+\text{ iff }\hat{p}(r\mid c)>1/\min_{c}|\mathcal{E}_{c}|\)
- 因此,推论 1 显然是以下定理的一个特例:
- 定理 1 (Theorem 1) :对于任何满足 \(p(\mathcal{V})=1\) 的训练分布 \(p\) 和任何基础模型 \(\hat{p}\),
$$
\operatorname{err}\geq 2\cdot\operatorname{err}_{\mathrm{IIV} }-\frac{\max_{c}|\mathcal{V}_{c}|}{\min_{c}|\mathcal{E}_{c}|}-\delta,
$$- 其中 \(\delta:=|\hat{p}(\mathcal{A})-p(\mathcal{A})|\),且 \(\mathcal{A}:=\{(c,r)\in\mathcal{X}\mid\hat{p}(r\mid c)>1/\min_{c}|\mathcal{E}_{c}|\}\)
- 推广重新缩放 \(\hat{p}_{s}(r\mid c)\)(对每个提示进行归一化,仍然使用单个参数 \(s\))再次证明了小的 \(\delta=|\frac{d}{ds}\mathcal{L}(\hat{p}_{s})|_{s=1}|\),现在对于 \(\mathcal{L}(\hat{p}):=\sum_{(c,r)\in\mathcal{X} }-\mu(c)\log\hat{p}(r\mid c)\)
Error factors for base models
- 数十年的研究已经阐明了导致误分类(二分类中的错误)的统计因素
- 我们可以利用这种先前的理解来列举幻觉和其他生成错误背后的因素,包括:统计复杂性,如生日(第 3.3.1 节);糟糕的模型(poor models),如字母计数(第 3.3.2 节);以及其他因素,如 GIGO(Garbage In, Garbage Out),如阴谋论(conspiracy theories,第 3.4 节)
Arbitrary-fact hallucinations(任意事实幻觉 )
- 当没有简洁的模式可以解释目标函数时,就存在认知不确定性(epistemic uncertainty),意味着必要的知识在训练数据中缺失。Vapnik-Chervonenkis 维度(VC dimension)(Vapnik and Chervonenkis, 1971) VC\((\mathcal{F})\) 描述了以高概率学习函数族 \(\mathcal{F}\)(其中 \(f:\mathcal{X}\rightarrow\{-,+\}\)) 所需的最坏情况样本数。具有高 VC\((\mathcal{F})\) 维度的族可能需要 prohibitively many 样本来学习。论文考虑高 VC 维的一个自然特例:随机的任意事实。特别是,本节考虑有效响应(除 IDK 外)在提示之间是随机且独立的
- Definition 1 (Arbitrary Facts)
- 以下内容是固定的:一个任意的提示分布 \(\mu(c)\),一个 IDK 响应,并且对于每个提示 \(c\):一个响应集 \(\mathcal{R}_{c}\) 和一个回答概率 \(\alpha_{c}\in[0,1]\)。对每个 \(c\) 独立地,以均匀随机方式选择一个正确答案 \(a_{c}\in\mathcal{R}_{c}\)。最后,对于每个 \(c\in\mathcal{C}\),有 \(p(a_{c}\mid c)=\alpha_{c}\) 和 \(p(\textup{IDK}\mid c)=1-\alpha_{c}\)。因此 \(\mathcal{E}_{c}=\mathcal{R}_{c}\setminus\{a_{c}\}\) 且 \(\mathcal{V}_{c}=\{a_{c},\textup{IDK}\}\)
- 假设陈述任何给定事实只有一种方式,这可以像主导的生日例子那样完成,其中格式是指定的。然而,论文再次注意到,人们可能会预期甚至更多的幻觉,如果有多种方式陈述每个事实。在固定格式生日的情况下,\(|\mathcal{E}_{c}|=364\),并且生日经常被讨论的名人会有高的 \(\mu(c)\)。像爱因斯坦生日这样著名的生日会出现多次,而其他生日可能只出现一次,例如在讣告中。大型语言模型在经常被引用的事实上很少出错,例如爱因斯坦的生日或论文标题
- 论文的幻觉下界基于在训练数据中仅出现一次的提示的比例,忽略 IDK
- Definition 2 (Singleton rate)
- 单例(singleton)的定义:如果一个提示 \(c\in\mathcal{C}\) 在 \(N\) 个训练数据 \(\big{\langle}(c^{(i)},r^{(i)})\big{\rangle}_{i=1}^{N}\) 中恰好出现一次且没有弃权,即 \(|\{i:c^{(i)}=c\wedge r^{(i)}\neq\mathrm{IDK}\}|=1\)
- 令 \(\mathcal{S}\subseteq\mathcal{C}\) 表示单例集合,且训练单例的比例可表示为:
$$
\mathrm{sr}=\frac{|\mathcal{S}|}{N}
$$
- 单例率建立在艾伦·图灵(Alan Turing)优雅的“缺失质量”(missing-mass)估计量 (Good, 1953) 的基础上,该估计量衡量了在从分布中抽取的样本中仍未出现的结果被分配了多少概率
- 具体来说,图灵对未见过事件概率的估计是恰好出现一次的样本的比例
- 直观上,单例充当了在进一步抽样中可能遇到多少新结果的代理,因此它们的经验份额成为整个分布“缺失”部分的估计
- 论文现在陈述论文对任意事实的界限
- Theorem 2 (Arbitrary Facts)
- 在任意事实模型中,任何接受 \(N\) 个训练样本并输出 \(\hat{p}\) 的算法满足,在 \(\vec{a}=\langle a_{c}\rangle_{c\in\mathcal{C} }\) 和 \(N\) 个训练样本上,以概率 \(\geq 99%\):
$$
\mathrm{err}\geq\mathrm{sr}-\frac{2}{\min_{c}|\mathcal{E}_{c}|}-\frac{35+6\ln N}{\sqrt{N} }-\delta.
$$ - 此外,存在一种输出校准后的 \(\hat{p}\)(\(\delta=0\))的高效算法,以概率 \(\geq 99%\),
$$
\mathrm{err}\leq\mathrm{sr}-\frac{\mathrm{sr} }{\max_{c}|\mathcal{E}_{c}|+1}+\frac{13}{\sqrt{N} }.
$$ - 论文的早期版本提出了一个相关的定理,该定理省略了提示和弃权 (Kalai and Vempala, 2024)
- 证明在附录 B 中。后续工作 (Miao and Kearns, 2025) 提供了对幻觉、单例率和校准的实证研究
- 在任意事实模型中,任何接受 \(N\) 个训练样本并输出 \(\hat{p}\) 的算法满足,在 \(\vec{a}=\langle a_{c}\rangle_{c\in\mathcal{C} }\) 和 \(N\) 个训练样本上,以概率 \(\geq 99%\):
Poor models
- 当底层模型糟糕时,也可能出现误分类,因为:
- (a) 模型族不能很好地表示概念,例如用线性分离器近似圆形区域,
- (b) 模型族具有足够的表达能力,但模型本身拟合不佳
- 不可知学习(Agnostic Learning)(1994) 通过定义给定分类器族 \(\mathcal{G}\)(其中 \(g:\mathcal{X}\rightarrow\{-,+\}\)) 中任何分类器的最小错误率来解决 (a):
$$
\mathrm{opt}(\mathcal{G}):=\min_{g\in\mathcal{G} }\Pr_{x\sim D}[g(x)\neq f(x)] \in[0,1].
$$ - 如果 \(\mathrm{opt}(\mathcal{G})\) 很大,那么 \(\mathcal{G}\) 中的任何分类器都将具有高误分类率。在论文的情况下,给定一个由 \(\theta\in\Theta\) 参数化的语言模型 \(\hat{p}_{\theta}\),考虑阈值化语言模型分类器族:
$$
\mathcal{G}:=\big{\{}g_{\theta,t}\ \mid\ \theta\in\Theta,t\in[0,1]\big{\} },\text{ Where } g_{\theta,t}(c,r):= \begin{cases}+&\text{ if }\hat{p}_{\theta}(r\mid c)>t,\\ -&\text{ if }\hat{p}_{\theta}(r\mid c)\leq t.\end{cases}
$$ - 根据定理 1 立即得出:
$$
\operatorname{err}\geq 2\cdot\mathrm{opt}(\mathcal{G})-\frac{\max_{c}|\mathcal{V}_{c}|}{\min_{c}|\mathcal{E}_{c}|}-\delta.
$$ - 当每个上下文恰好存在一个正确响应时(即标准多项选择,没有 IDK),可以移除校准项,并且即使对于 \(C=2\) 个选择也可以实现界限
- Theorem 3 (Pure multiple-choice)
- 假设对所有 \(c\in\mathcal{C}\) 有 \(|\mathcal{V}_{c}|=1\),并令 \(C=\min_{c}|\mathcal{E}_{c}|+1\) 为选择数。那么,
$$
\operatorname{err}\geq 2\left(1-\frac{1}{C}\right)\cdot\mathrm{opt}(\mathcal{G})
$$ - 为了说明,考虑经典的三元组语言模型(trigram language model),其中每个词仅根据前两个词预测,即上下文窗口只有两个词。三元组模型在 1980 年代和 1990 年代占主导地位。然而,三元组模型经常输出不合语法的句子。考虑以下提示和响应:
$$
c_{1}=\text{She lost it and was completely out of}\ldots \quad c_{2}=\text{He lost it and was completely out of}\ldots \\
r_{1}=\text{her mind.} \quad r_{2}=\text{his mind.}
$$- 这里,\(V_{c_{1} }:=E_{c_{2} }:=\{r_{1}\}\) 且 \(V_{c_{2} }:=E_{c_{1} }:=\{r_{2}\}\)
- 假设对所有 \(c\in\mathcal{C}\) 有 \(|\mathcal{V}_{c}|=1\),并令 \(C=\min_{c}|\mathcal{E}_{c}|+1\) 为选择数。那么,
- 推论 2 (Corollary 2)
- 令 \(\mu\) 在 \(\{c_{1},c_{2}\}\) 上均匀分布。那么任何三元组模型必须具有至少 1/2 的生成错误率
- 这由定理 3 得出,因为对于三元组模型,\(C=2\) 且 \(\mathrm{opt}(\mathcal{G})=1/2\)。定理 3 和推论 2 的证明在附录 C 中。尽管 \(n\)-gram 模型对于更大的 \(n\) 可以捕获更长范围的依赖关系,但数据需求随 \(n\) 呈指数级增长
- 论文现在重新审视引言中的字母计数例子
- 要看出这是一个糟糕的模型问题,请注意 DeepSeek-R1 推理模型能够可靠地计数字母,例如,生成一个包含以下内容的 377 步思维链(chain-of-thought):
Let me spell it out: D-E-E-P-S-E-E-K.
First letter: D — that’s one D. Second letter: E — not D. Third letter: E — not D. . .
So, the number of Ds is 1. - 假设有相似的训练数据,这表明 R1 是该任务比 DeepSeek-V3 模型更好的模型
- 推理所克服的一个表征挑战是,现代语言模型通过词元(tokens)表示提示,例如 D/EEP/SEE/K,而不是单个字符 (DeepSeek-2025)
Additional factors
- 错误可能由多种因素的组合引起,包括上面讨论的因素以及其他几个因素。这里,论文重点介绍几个
- 计算困难性 (Computational Hardness)
- 在经典计算机上运行的任何算法,即使是具有超人类能力的人工智能,也不能违反计算复杂性理论的定律
- 确实,人工智能系统已被发现在计算困难的问题上出错 (2024)
- 附录 D 的观察 2 说明了定理 1 如何应用于形式为 “\(c\) 的解密是什么?” 的难处理查询,其中 IDK 是一个有效答案
- 分布偏移 (Distribution shift)
- 二分类中一个众所周知的挑战是训练和测试数据分布经常不同 (Quinonero-2009; Moreno-2012)
- 类似地,语言模型中的错误通常源于与训练分布显著不同的分布外(out-of-distribution, OOD)提示
- 诸如“一磅羽毛和一磅铅哪个更重?”这样的问题在训练数据中可能不太可能出现,并可能在某些模型中引发错误答案
- 类似地,分布偏移可能是上述字母计数例子的一个因素,尽管推理模型正确计数字母的事实表明糟糕的模型可能是更大的因素
- GIGO: Garbage in, Garbage out
- 大型训练语料库通常包含大量事实错误,这些错误可能会被基础模型复制
- GIGO 对于分类和预训练的统计相似性是 self evident 的 ,因此论文不提供正式的处理
- 但认识到 GIGO 是统计因素之一很重要,因为语言模型已被证明会复制训练数据中的错误 (2022b; 2021; 2025)
- GIGO 也为后训练主题提供了一个自然的过渡,后训练减少了某些 GIGO 错误,例如常见的误解和阴谋论 (2022; OpenAI, 2025a; 2024)
- 下一节解释了为什么一些幻觉会持续存在,甚至可能被当前的后训练流程加剧
Post-training and hallucination
- Post-training应当将模型从类似于自动补全模型的训练方式转变为不会输出自信的错误信息(除非在适当情况下,例如被要求创作虚构内容)的模型
- 但进一步减少幻觉将是一场艰苦的战斗,因为现有的基准测试(benchmark)和排行榜(leaderboard)强化了某些类型的幻觉
- 论文讨论如何停止这种强化
- 这是一个社会技术(socio-technical)问题,因为不仅现有的评估方法需要修改,而且这些更改需要在有影响力的排行榜中被采纳
How evaluations reinforce hallucination(评估也会强化幻觉的!)
- 语言模型的二元评估(Binary evaluations)强加了一种错误的对错二分法(false right-wrong dichotomy),对表达不确定性、省略可疑细节或请求澄清的答案不予给分
- 包括准确率(accuracy)和通过率(pass rate)在内的此类指标仍然是该领域的主流规范,如下文所述
- 在二元评分(binary grading)下,弃权(abstaining)是严格次优的
- IDK 类型的响应受到最大程度的惩罚,而过度自信的“最佳猜测”则是最优的
- 其动机结合了两个理想因素:
- (a) 语言模型输出内容的准确率,
- (b) 响应的全面性
- 但权衡 (a) 多于 (b) 对于减少幻觉至关重要
- 形式上,对于任何给定的提示(prompt)\( c \) 形式的问题,用 \( \mathcal{R}_c := \{r \mid (c, r) \in \mathcal{X}\} \) 表示一组看似合理的响应(有效或错误)
- 此外,假设存在一组看似合理的弃权响应 \( \mathcal{A}_c \subset \mathcal{R}_c \)(例如,IDK)
- 如果 \( \{g_c(r) \mid r \in \mathcal{R}_c\} = \{0, 1\} \) 且对所有 \( r \in \mathcal{A}_c \) 有 \( g_c(r) = 0 \),则称评分器(grader)\( g_c : \mathcal{R}_c \rightarrow \mathbb{R} \) 是二元的(binary)
- 一个问题(problem)由 \( (c, \mathcal{R}_c, \mathcal{A}_c, g_c) \) 定义,其中应试者(test-taker)知道 \( c, \mathcal{R}_c, \mathcal{A}_c \)
- 论文假设应试者知道评分标准是二元的,但并未被告知正确答案,即 \( g_c(r) = 1 \) 的答案
- 应试者对正确答案的信念可以看作是关于二元 \( g_c \) 的后验分布 \( \rho_c \)
- 对于任何此类信念,最优响应都不是弃权
- 观察 1 (Observation 1).
- 令 \( c \) 为一个提示,对于任何在二元评分器上的分布 \( \rho_c \),最优响应都不是弃权,即
$$
\mathcal{A}_c \cap \operatorname*{arg,max}_{r \in \mathcal{R}_c} \mathbb{E}_{g_c \sim \rho_c}[g_c(r)] = \emptyset.
$$ - 尽管证明是平凡的(见附录 E),但观察 1 表明现有的评估方法可能需要修改
- 表 2 总结了附录 F 中的简短元评估分析(short meta-evaluation analysis),发现绝大多数流行的评估都采用二元评分
- 因此,当主要评估惩罚诚实报告置信度和不确定性时,额外的幻觉评估可能不足以解决问题
- 这并不会贬低现有关于幻觉评估的工作,而是指出,即使是理想的幻觉评估和理想的后训练方法,产生了诚实的不确定性报告,仍然可能因为在绝大多数现有评估上表现较差而被淹没
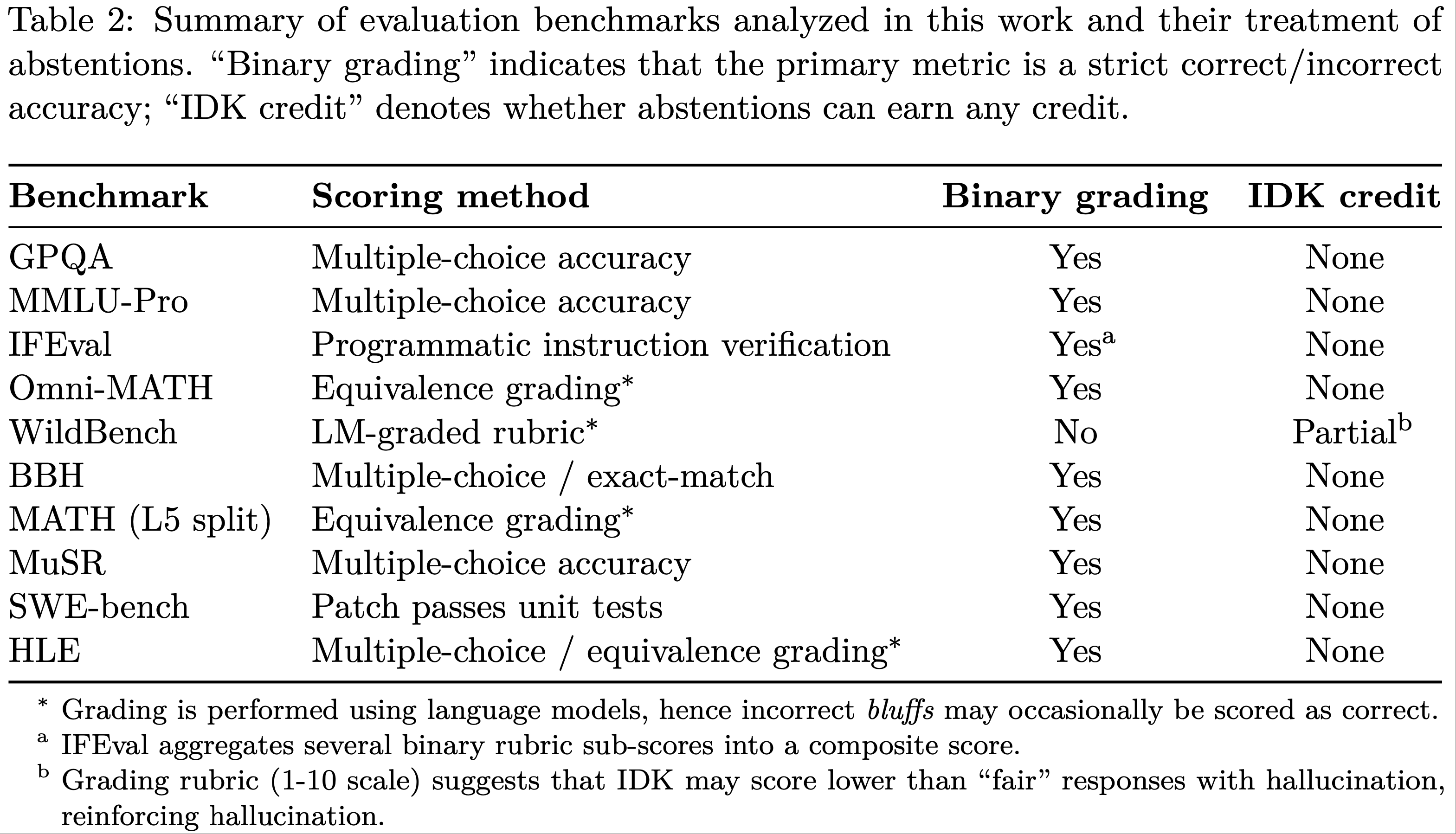
- 令 \( c \) 为一个提示,对于任何在二元评分器上的分布 \( \rho_c \),最优响应都不是弃权,即
显式置信度目标 (Explicit confidence targets)
- 人类的测试同样大多是二元的,并且人们已经认识到它们也会奖励过度自信的虚张声势(bluffing)
- 当然,考试只是人类学习的一小部分,例如,编造生日很快就会导致尴尬
- 尽管如此,一些标准化的国家考试在操作或曾经操作时对错误答案进行惩罚(或等效地对弃权给予部分学分),包括印度的 JEE、NEET 和 GATE 考试;美国数学协会的 AMC 测试;以及早些年的美国标准化 SAT、AP 和 GRE 考试
- 重要的是,评分系统在说明中明确说明,并且应试者通常知道置信度阈值(confidence threshold),超过该阈值进行最佳猜测是合理的
- 类似地,论文建议评估在其说明中,在提示(或系统消息)内明确说明置信度目标(confidence targets)。例如,可以在每个问题后附加如下声明:
仅当您的置信度 \( > t \) 时才回答,因为错误答案会被扣 \( t/(1-t) \) 分,正确答案得 1 分,回答“我不知道”得 0 分
- \( t \) 有几个自然值,包括 \( t = 0.5 \)(惩罚 1 分),\( t = 0.75 \)(惩罚 2 分)和 \( t = 0.9 \)(惩罚 9 分)
- 阈值 \( t = 0 \) 对应于二元评分,可以描述为,例如,“即使不确定也要做出最佳猜测,就像参加考试一样”
- 一个简单的计算表明,提供一个答案的期望分数超过 IDK(分数 0)当且仅当其置信度(即正确的概率)\( > t \)
- 此类惩罚在幻觉研究中已得到充分研究 (2023)。但论文建议两个具有统计意义的细微变化
- 首先,论文建议在说明中明确置信度阈值 ,而先前的工作大多未在说明中提及置信度目标或惩罚
- 一个值得注意的例外是 Wu 等 (2025) 的工作,他们引入了带有明确惩罚的“风险告知(risk-informing)”提示
- 理想的惩罚可能反映现实世界中可能的危害,但这是不切实际的,因为它特定于问题、目标应用程序和用户群体
- 如果在说明中没有透明地指定,语言模型创建者之间就很难就正确的阈值达成共识
- 类似地,如果说明中错误答案会受到未明确的惩罚,学生可能会争吵说评分不公平
- 相反,在每个问题的说明中明确指定置信度阈值支持客观评分,即使所选择的特定阈值有些武断甚至是随机的
- 如果阈值是明确的,那么一个模型可能在所有阈值上都是最好的
- 然而,如果未说明阈值,则存在固有的权衡(tradeoff),并且通常没有单个模型是最好的(除了总是正确的模型)
- 其次,论文建议将置信度目标纳入现有的主流评估中 ,例如流行的 SWE-bench (2024),它涉及软件补丁的二元评分,而大多数先前的工作在定制的幻觉评估中引入了隐式的错误惩罚
- 仅仅添加具有隐式错误惩罚的评估会面临上述的准确率-错误权衡
- 另一方面,将置信度目标纳入已建立且已在使用的评估中,可以减少对适当表达不确定性的惩罚
- 因此,它可能会放大特定于幻觉的评估的有效性
- 首先,论文建议在说明中明确置信度阈值 ,而先前的工作大多未在说明中提及置信度目标或惩罚
- 有了明确的置信度目标,存在一种行为对所有目标都是同时最优的——在其正确概率大于目标值的示例中输出 IDK
- 让论文将其称为行为校准(behavioral calibration),而不是要求模型输出概率置信度 (2022a),它必须制定出其置信度至少为 \( t \) 的最有用的响应
- 行为校准可以通过比较不同阈值下的准确率和错误率来进行审计,并规避了可能存在指数级多种方式来表达正确答案的问题 (2024)
- 现有模型可能会或可能不会表现出行为校准,但它可能被证明作为客观评估是有用的
Discussion and limitations
- 由于幻觉的多面性,该领域很难就如何定义、评估和减少幻觉达成一致
- 一个统计框架必须优先考虑某些方面而忽略其他方面,以求简单
- 关于论文所用框架的范围和局限性,有几点需要注意
看似合理与无意义 (Plausibility and nonsense)
- 幻觉是一种看似合理的虚假陈述,通过仅考虑看似合理的字符串 \( \mathcal{X} \),论文的分析忽略了生成无意义字符串的可能性( SOTA 语言模型很少生成)
- 然而,定理 1 的陈述和证明在修改了无意义示例 \( \mathcal{N} \) 的定义后仍然成立,其中划分 \( \mathcal{X} = \mathcal{N} \cup \mathcal{E} \cup \mathcal{V} \),\( \operatorname{err} := \hat{p}(\mathcal{N} \cup \mathcal{E}) \),\( D(\mathcal{N}) = 0 \),并假设 \( p(\mathcal{V}) = 1 \)
Open-ended generations
- 为简单起见,论文给出的示例都面向单个事实问题
- 然而,幻觉经常出现在开放式提示中,例如“写一篇关于……的传记”
- 这可以通过将包含一个或多个错误陈述的响应定义为错误来融入论文的框架
- 然而,在这种情况下,很自然地会根据错误的数量来考虑幻觉的程度
搜索(和推理)并非万能药 (Search (and reasoning) are not panaceas)
- 许多研究表明,通过搜索或检索增强生成(Retrieval-Augmented Generation, RAG)增强的语言模型可以减少幻觉 (2020; 2021; 2021; Zhang and Zhang, 2025)
- 但观察 1 适用于任意语言模型,包括具有 RAG 的模型
- 特别是,当搜索未能产生自信的答案时,二元评分系统本身仍然会奖励猜测
- 此外,搜索可能无助于解决计算错误,例如字母计数示例中的错误,或其他内在幻觉(intrinsic hallucinations)
Latent context
- 有些错误无法仅通过提示和响应来判断
- 例如,假设用户询问一个关于 phones 的问题,而语言模型提供了一个关于 cellphones 的响应,但该问题本意是关于 land lines(固定电话)
- 这种模糊性不符合论文的错误定义,因为论文的定义不依赖于提示和响应之外的外部上下文
- 将模型扩展以允许存在不属于给予语言模型的提示部分但可用于判断错误的“隐藏上下文”(hidden context),这将很有趣,这与偶然不确定性(aleatoric uncertainty)有关
A false trichotomy(三分法)
- 论文的形式主义不区分不同严重程度或不确定性程度的错误
- 显然,正确/错误/IDK 的类别也是不完整的
- 尽管统计上的理想可能是在下游应用中按照作者希望评分语言模型的方式来评分每个评估,但显式的置信度目标为主流评估提供了一种实用的、客观的修改,并且错误的三分法至少可能提供一个 IDK 选项,而不像错误的二分法
Beyond IDK
- 有许多表示不确定性的方法,例如 hedging(模糊限制)、省略细节和提问
- 最终,语言模型可能会遵守诸如语言校准(linguistic calibration)之类的置信度概念 (2022; 2025)
- 但语言的语用现象(pragmatic phenomena) (Austin, 1962; Grice, 1975) 是微妙的
- 比如虽然在某些情况下语言模型明确陈述概率置信度估计可能有用 (2022a),但这也可能导致不自然的话语
- 例如,“我有 1/365 的把握确定 Kalai 的生日是 3 月 7 日” 论文侧重于关于说什么的顶层决策的统计因素
附录:附录部分待补充
附录 A:Proof of the main theorem
- 论文现在证明主要定理
- 定理 1 的证明 :
- 令 \(K:=\min_{c\in\mathcal{C} }|\mathcal{E}_{c}|\) 且 \(k:=\max_{c\in\mathcal{C} }|\mathcal{V}_{c}|\)。同时,回顾 \(\delta=|\hat{p}(\mathcal{A})-p(\mathcal{A})|\),这可以等价地写为 \(\delta=|p(\mathcal{B})-\hat{p}(\mathcal{B})|\),其中 \(\mathcal{A},\mathcal{B}\) 表示响应是高于还是低于阈值:
$$
\mathcal{A} :=\{(c,r)\in\mathcal{X}\mid\hat{p}(r\mid c)>1/K\} \\
\mathcal{B} :=\{(c,r)\in\mathcal{X}\mid\hat{p}(r\mid c)\leq 1/K\}. \tag{4-5}
$$ - 将幻觉率和误分类率划分为高于和低于阈值的部分:
$$\text{err}=\hat{p}(\mathcal{A}\setminus\mathcal{V})+\hat{p}(\mathcal {B}\setminus\mathcal{V})\\
\text{err}_{\text{Hv} }=D(\mathcal{A}\setminus\mathcal{V})+D(\mathcal {B}\cap\mathcal{V}).$$ - 在阈值以上,误分类 \(D(\mathcal{A}\setminus\mathcal{V})\) 是仅对满足 \((c,r)\in\mathcal{A}\) 且 \(r\in\mathcal{E}_{c}\) 的 \((c,r)\) 的 \(D(c,r)\) 求和——每个贡献 \(D(c,r)=\mu(c)/2|\mathcal{E}_{c}|\leq\mu(c)/2K\)
- 但每个这样的误分类也对阈值以上的幻觉 \(\hat{p}(\mathcal{A}\setminus\mathcal{V})\) 贡献了 \(\mu(c)\hat{p}(r\mid c)\geq\mu(c)/K\)。因此,
$$\hat{p}(\mathcal{A}\setminus\mathcal{V})\geq 2D(\mathcal{A}\setminus\mathcal{V})$$ - 因此,只需证明在阈值以下:
$$\hat{p}(\mathcal{B}\setminus\mathcal{V})\geq 2D(\mathcal{B}\cap\mathcal{V})- \frac{k}{K}-\delta. \tag{6}$$ - 根据定义,\(2D(\mathcal{B}\cap\mathcal{V})=p(\mathcal{B}\cap\mathcal{V})=p(\mathcal{B})\)。同时,对于每个 \(c\),最多有 \(|\mathcal{V}_{c}|\leq k\) 个有效响应,每个在 \(\mathcal{B}\) 中的响应满足 \(\hat{p}(r\mid c)\leq 1/K\),所以 \(\hat{p}(\mathcal{B}\cap\mathcal{V})\leq\sum_{c}\hat{p}(c)k/K=k/K.\) 因此,
$$
\begin{align}
2D(\mathcal{B}\cap\mathcal{V})-\hat{p}(\mathcal{B}\setminus \mathcal{V}) &=p(\mathcal{B})-\hat{p}(\mathcal{B}\setminus\mathcal{V}) \\
&=p(\mathcal{B})-(\hat{p}(\mathcal{B})-\hat{p}(\mathcal{B}\cap \mathcal{V}))\\
&\leq\delta+\hat{p}(\mathcal{B}\cap\mathcal{V})\leq\delta+\frac{k }{K}.
\end{align}
$$ - 这等价于方程 (6),证毕
- 令 \(K:=\min_{c\in\mathcal{C} }|\mathcal{E}_{c}|\) 且 \(k:=\max_{c\in\mathcal{C} }|\mathcal{V}_{c}|\)。同时,回顾 \(\delta=|\hat{p}(\mathcal{A})-p(\mathcal{A})|\),这可以等价地写为 \(\delta=|p(\mathcal{B})-\hat{p}(\mathcal{B})|\),其中 \(\mathcal{A},\mathcal{B}\) 表示响应是高于还是低于阈值:
附录 B: Arbitrary-facts analysis(任意事实分析)
- 论文首先回顾 Good-Turing (GT) 缺失质量估计量 (Good, 1953) 及其保证 (McAllester and Ortiz, 2003)。在该设定中,从集合 \(\mathcal{S}\) 上的分布 \(\nu\) 中抽取 \(N\) 个独立同分布样本 \(s\sim\nu^{N}\)——不考虑弃权。缺失质量是从 \(\nu\) 中抽取的新样本不在训练样本 \(s\) 中的概率,其估计值 GT 是训练样本中恰好出现一次的样本所占的比例。论文首先陈述先前的保证,然后将其调整到论文带有弃权的设定中。(McAllester and Ortiz, 2003) 的一个保证可以表述为:
- Corollary 3
- (McAllester and Ortiz, 2003) 令 \(s\sim\nu^{N}\) 为从集合 \({\cal S}\) 上的分布 \(\nu\) 中抽取的 \(N\) 个独立同分布样本。令 \(M:=\Pr_{x\sim\nu}[x\notin s]\) 且 GT 为恰好出现一次的样本所占的比例。对于任意 \(\gamma\in(0,1]\):
$$\Pr_{s\sim\nu^{N} }\left[|M-\text{GT}|\leq\frac{1}{N}+2.42\sqrt{\frac{\ln(4/\gamma )}{N} }\right]\geq 1-\gamma.$$
- (McAllester and Ortiz, 2003) 令 \(s\sim\nu^{N}\) 为从集合 \({\cal S}\) 上的分布 \(\nu\) 中抽取的 \(N\) 个独立同分布样本。令 \(M:=\Pr_{x\sim\nu}[x\notin s]\) 且 GT 为恰好出现一次的样本所占的比例。对于任意 \(\gamma\in(0,1]\):
- 证明
- 令 \(\overline{\text{GT} }:=\mathbb{E}[\text{GT}]\) 且 \(\overline{M}:=\mathbb{E}[M]\)。该推论是通过结合 \(M\) 和 GT 的集中界得到的。首先 (McAllester and Schapire, 2000) 的定理 1 表明:
$$\overline{\text{GT} }-\overline{M}\in[0,1/N]$$ - 然后,(McAllester and Ortiz, 2003) 的定理 10 和 16 意味着,以概率 \(\leq\exp(-N\varepsilon^{2})\),\(M\) 将在任一方向上偏离 \(\overline{M}\) 超过 \(\varepsilon\),两者结合,通过并集界,对于 \(\varepsilon:=\sqrt{\frac{\ln(4/\gamma)}{N} }\),
$$\Pr_{s\sim\nu^{N} }\left[|M-\overline{M}|\geq\sqrt{\frac{\ln(4/\gamma)}{N} } \right]\leq\frac{\gamma}{4}+\frac{\gamma}{4}=\frac{\gamma}{2}.$$ - 继 (McAllester and Schapire, 2000)(引理 13)之后,McDiarmid 不等式 (McDiarmid, 1989) 直接暗示了 GT 的收敛性,因为改变任何一个样本最多只能将 GT 改变 \(2/N\)。因此,
$$\Pr_{s\sim\nu^{N} }\left[|\text{GT}-\overline{\text{GT} }|\geq\sqrt{\frac{2\ln(4/\gamma)}{N} }\right]\leq 2\exp\left(-\frac{2\cdot\frac{2\ln(4/\gamma)}{N} }{4/N }\right)=\frac{\gamma}{2}.$$ - 结合这三个显示的方程,通过并集界,得到
$$\Pr_{s\sim\nu^{N} }\left[|\text{GT}-M|\geq\frac{1}{N}+(1+\sqrt{2})\sqrt{\frac{\ln(4/\gamma)}{N} }\right]\leq\frac{\gamma}{2}+\frac{\gamma}{2}=\gamma.$$ - 最后,由 \(1+\sqrt{2}\leq 2.42\) 得出该推论
- 论文现在将其扩展到包含一个不计算在 sr 中的弃权响应 IDK 的情况。具体来说,如果存在训练样本 \((c^{(i)},r^{(i)})\) 满足 \(c^{(i)}=c\) 且 \(r^{(i)}\neq\text{IDK}\),则称查询 \(c\) 在训练数据中被回答,否则称为未回答。令
$${\cal U}:={\cal C}\setminus\{c^{(i)}\mid i\leq N,r^{(i)}\neq\text{IDK}\}$$ - 表示未回答查询的集合。当然,通过记忆已回答查询的 \(a_{c}\),可以实现对已回答查询的完美分类准确性。论文将图灵的缺失质量 (MM) 估计扩展到弃权如下:
$$\text{MM}:=\Pr_{(c,r)\sim p}[c\in{\cal U}\wedge r\neq\text{IDK}].$$ - 论文类似地使用推论 3 来表明 sr 是 MM 的一个良好估计量:
- 令 \(\overline{\text{GT} }:=\mathbb{E}[\text{GT}]\) 且 \(\overline{M}:=\mathbb{E}[M]\)。该推论是通过结合 \(M\) 和 GT 的集中界得到的。首先 (McAllester and Schapire, 2000) 的定理 1 表明:
- Lemma 1
- 对于所有 \(N\), \(\gamma\in(0,1]\):
$$\Pr\left[\left|\text{MM}-\text{sr}\right|\leq 4.42\sqrt{\frac{\ln(5/\gamma)} {N} };\right]\geq 1-\gamma.$$
- 对于所有 \(N\), \(\gamma\in(0,1]\):
- 证明
- 论文的 MM-sr 与标准的 \(M\)-GT 之间的唯一区别是论文忽略了弃权。为了调整先前的界限,考虑样本 \(s\),它是通过将所有 \(x=(c,\text{IDK})\) 替换为简单的 \(x=\text{IDK}\)(对于任何 \(c\))而得到的,但其他情况下保持 \(x\) 不变。这将所有 IDK 响应折叠成相同的样本。因此,GT 最多可能比 sr 多计算一个单例,
$$\text{GT}-\text{sr}\in\left\{0,\frac{1}{N}\right\}.$$ - 上述替换诱导了一个分布 \(\phi\),其中 \(\phi(\text{IDK})=\sum_{e}\mu(c)p(\text{IDK}\mid c)\) 是弃权的概率。类似地,论文有 \(M-\text{MM}\in\{0,\phi(\text{IDK})\}\),且如果 \(\text{IDK}\notin s\) 则 \(M-\text{MM}=\phi(\text{IDK})\),这种情况发生的概率为 \((1-\phi(\text{IDK}))^{N}\)。但如果 \(\phi(\text{IDK})\geq\frac{1}{N}\ln\frac{5}{\gamma}\),论文也有 \((1-\phi(\text{IDK}))^{N}\leq\gamma/5\)。因此,无论 \(\phi(\text{IDK})\) 的值如何,
$$\Pr\left[M-\text{MM}\in\left[0,\frac{1}{N}\ln\frac{5}{\gamma}\right]\ \right] \geq 1-\frac{\gamma}{5}.$$ - 结合以上两个显示的方程得到
$$\Pr\left[\left|(M-\text{GT})-(\text{MM}-\text{sr})\right|\leq\frac{1}{N}\ln \frac{5}{\gamma}\right]\geq 1-\frac{\gamma}{5}.\tag{7}$$ - 在 \(\frac{4}{5}\gamma\) 处应用推论 3 得到,
$$\Pr\left[\ |M-\text{GT}|\leq\frac{1}{N}+2.42\sqrt{\frac{\ln(5/\gamma)}{N} } \ \right]\geq 1-\frac{4}{5}\gamma.$$ - 结合方程 (7),通过并集界和三角不等式,
$$\Pr\left[\ |\text{MM}-\text{sr}|\leq\frac{1}{N}\ln \frac{5}{\gamma}+\frac{1}{N}+2.42\sqrt{\frac{\ln(5/\gamma)}{N} }\ \right]\geq 1-\gamma.$$ - 最后,引理成立是因为对于 \(z:=\frac{2}{N}\ln \frac{5}{\gamma}\geq\frac{1}{N}\ln \frac{5}{\gamma}+\frac{1}{N}\),只要 \(z\leq 1\)(否则引理平凡成立,因为界限 \(>2\)),论文有 \(z\leq\sqrt{z}\)
- 论文的 MM-sr 与标准的 \(M\)-GT 之间的唯一区别是论文忽略了弃权。为了调整先前的界限,考虑样本 \(s\),它是通过将所有 \(x=(c,\text{IDK})\) 替换为简单的 \(x=\text{IDK}\)(对于任何 \(c\))而得到的,但其他情况下保持 \(x\) 不变。这将所有 IDK 响应折叠成相同的样本。因此,GT 最多可能比 sr 多计算一个单例,
- 引理 2 对于任意 \(N\geq 1\), \(\gamma\in(0,1]\),以及任何输出 \(\hat{p}\) 的算法,
$$\Pr\left[2\ \text{err}_{\textup{liv} }\geq\textnormal{sr}-\frac{6\ln(3N/\gamma )}{\sqrt{N} }\right]\geq 1-\gamma.$$ - 证明 由引理 1,
$$\Pr\left[\ |\text{MM}-\text{sr}|\leq 4.42\sqrt{\frac{\ln(10/\gamma)}{N} }\ \right]\geq 1-\frac{\gamma}{2}.$$- 注意对于 \(N\geq 2\) 有 \(\sqrt{\ln(10/\gamma)}\leq\ln(3N/\gamma)\)(且对于 \(N=1\) 引理平凡成立)。同时,\(\sqrt{2}+4.42\leq 6\)。因此,只需证明,
$$\Pr\left[2\ \text{err}_{\textup{liv} }\geq\textnormal{MM}-\sqrt{\frac{2}{N} } \ln\frac{3N}{\gamma}\right]\geq 1-\frac{\gamma}{2}.$$ - 令 \(\zeta:=\ln(3N/\gamma)/N\),且根据 \(p\) 每个查询出现一个答案(非 IDK)的概率为:
$$\mu^{\prime}(c):=\mu(c)\alpha_{c},$$ - 因此一旦 \(a_{c}\) 被选定,\(\mu^{\prime}(c)=p(c,a_{c})\)。同时注意 \({\rm MM}=\sum_{c\in\mathcal{U} }\mu^{\prime}(c)\)。因此引理将由以下两个不等式得出:
$$
{\rm Pr}\left[\forall c\in\mathcal{U}{}\mu^{\prime}(c)\leq\zeta\right]\geq 1- \frac{\gamma}{3} \\{}\Bigg{|}
{\rm Pr}\left[2,{\rm err}_{\rm liv}\geq{\rm MM}-\sqrt{\frac{2}{N} }\ln\frac{3N}{ \gamma}{}\forall c\in\mathcal{U}{}\mu^{\prime}(c)\leq\zeta\right] \geq 1-\frac{\gamma}{6}. \tag{8-9}
$$ - \(\mu^{\prime}(c)\leq\zeta\) 条件将使论文能够使用 Hoeffding 界。对于方程 (8),注意最多有 \(\leq 1/\zeta\) 个查询 \(c\) 满足 \(\mu^{\prime}(c)\geq\zeta\)。对于这些查询中的每一个,概率 \(c\in\mathcal{U}\) 最多为 \((1-\zeta)^{N}\)。因此,通过并集界,
$${\rm Pr}\left[\exists c\in\mathcal{U}:~{}\mu^{\prime}(c)>\zeta\right]\leq\frac{1 }{\zeta}(1-\zeta)^{N}\leq\frac{1}{\zeta}e^{-\zeta N}=\frac{N}{\ln(3N/\gamma)} \frac{\gamma}{3N}\leq\frac{\gamma}{3},$$ - 这等价于方程 (8)。论文现在继续建立方程 (9)
- 令指示器 \({\rm I}[\phi]\) 在谓词 \(\phi\) 成立时表示 \(1\),否则为 \(0\)。误差 \({\rm err}_{\rm liv}\) 至少是其对 \(c\in\mathcal{U},r\in\mathcal{R}_{c}\) 求和的误差,根据 \(D\) 的定义,即
$$
\begin{align}
{\rm err}_{\rm liv} \geq\frac{1}{2}\sum_{c\in\mathcal{U} }\mu(c)\alpha_{c}{\rm I}[ \hat{f}(c,a_{c})=-]+\frac{1}{2}\sum_{c\in\mathcal{U} }\mu(c)\sum_{r\in\mathcal{R}_ {c}\setminus\{a_{c}\} }\frac{ {\rm I}[\hat{f}(c,r)=+]}{|\mathcal{R}_{c}|-1} \\
\geq\frac{1}{2}\sum_{c\in\mathcal{U} }\mu^{\prime}(c){\rm I}[\hat {f}(c,a_{c})=-]+\frac{1}{2}\sum_{c\in\mathcal{U} }\mu^{\prime}(c)\sum_{r\in \mathcal{R}_{c}\setminus\{a_{c}\} }\frac{ {\rm I}[\hat{f}(c,r)=+]}{|\mathcal{R}_{ c}|-1} \\
=\sum_{c\in\mathcal{U} }\mu^{\prime}(c)\gamma_{c}\ {\rm for}\ \gamma_ {c}:=\frac{1}{2}\left({\rm I}[\hat{f}(c,a_{c})=-]+\sum_{r\in\mathcal{R}_{c} \setminus\{a_{c}\} }\frac{ {\rm I}[\hat{f}(c,r)=+]}{|\mathcal{R}_{c}|-1}\right)
\end{align}
$$ - 因此 \({\rm err}_{\rm liv}\geq\sum_{c\in\mathcal{U} }\mu^{\prime}(c)\gamma_{c}\),其中 \(\gamma_{c}\) 如上定义,并且不难看出 \(\gamma_{c}\in[0,1]\)。(\(\mu^{\prime}(c)\leq\zeta\) 条件将使论文能够对 \(\sum\mu^{\prime}(c)\gamma_{c}\) 应用 Hoeffding 界。)因此,代替方程 (9),只需证明,
$${\rm Pr}\left[2\sum_{c\in\mathcal{U} }\mu^{\prime}(c)\gamma_{c}\geq{\rm MM}- \sqrt{\frac{2}{N} }\ln\frac{3N}{\gamma}{}\Bigg{|}{}\forall c\in\mathcal{U}~{} \mu^{\prime}(c)\leq\zeta\right]\geq 1-\frac{\gamma}{6}. \tag{10}$$ - 现在是关键技巧:因为算法的输出独立于未见的 \(c\in\mathcal{U}\) 的 \(a_{c}\),可以等价地想象在运行算法于训练数据上以选择决定 \(\hat{f}\) 的 \(\hat{p}\) 之后,才为未见的 \(c\in\mathcal{U}\) 选择 \(a_{c}\)。因此,让论文假设 \(c_{v}\) 将在稍后被选择用于 \(c\in\mathcal{U}\),但训练数据以及因此的 \(\hat{f}\) 是已经固定的
- 然后,论文观察到 \(\mathbb{E}[\gamma_{c}]=1/2\),因为每个 \(r\in\mathcal{R}_{c}\) 对此期望贡献 \(1/2|\mathcal{R}_{c}|\),无论它是 \(\hat{f}(c,r)=\pm\)。这给出 \(\mathbb{E}[\sum_{c}\mu^{\prime}(c)\gamma_{c}]={\rm MM}/2\),因为 \({\rm MM}=\sum_{c}\mu^{\prime}(c)\)。最后,我们可以对 \(\sum_{c}\mu^{\prime}(c)\gamma_{c}\) 应用 Hoeffding 界,因为 \(\mu^{\prime}(c)\gamma_{c}\) 是独立的随机变量,每个在 \([0,\mu^{\prime}(c)]\) 中。该界限取决于,
$$\sum_{c\in\mathcal{U} }(\mu^{\prime}(c))^{2}\leq\max_{c\in\mathcal{U} }\mu^{ \prime}(c)\sum_{c\in\mathcal{U} }\mu^{\prime}(c)\leq\max_{c\in\mathcal{U} }\mu^ {\prime}(c)\leq\zeta{}{\rm if}{}\forall c\in\mathcal{U}~{}\mu^{\prime}(c)\leq\zeta.$$ - Hoeffding 界因此给出,
$$\Pr\left[\sum\mu^{\prime}(c)\gamma_{c}\leq\frac{\text{MM} }{2}-\sqrt{\frac{\zeta \ln(6/\gamma)}{2} };\middle|;\forall c\in\mathcal{U};\mu^{\prime}(c)\leq\zeta \right]\leq\frac{\gamma}{6},$$ - 这意味着方程 (10),因为 \(\sqrt{2\zeta\ln(6/\gamma)}=\sqrt{2\ln(3N/\gamma)\ln(6/\gamma)/N}\leq\ln(3N/ \gamma)\sqrt{2/N}\)(对 \(N\geq 2\) 使用 \(\ln(6/\gamma)\leq\ln(3N/\gamma)\),并且再次地,对于 \(N=1\) 引理平凡成立)
- 注意对于 \(N\geq 2\) 有 \(\sqrt{\ln(10/\gamma)}\leq\ln(3N/\gamma)\)(且对于 \(N=1\) 引理平凡成立)。同时,\(\sqrt{2}+4.42\leq 6\)。因此,只需证明,
- 论文现在证明定理 2
- 定理 2 的证明 :以下更一般的下界,对于任意 \(\gamma\in(0,1]\),直接来自定理 1,其中 \(\max_{c}|\mathcal{V}_{c}|=2\),以及引理 2。具体来说,以概率 \(\geq 1-\gamma\):
$$\operatorname{err}\geq\operatorname{sr}-\frac{2}{\min_{c}|\mathcal{E}_{c}|}- \frac{6\ln(3N/\gamma)}{\sqrt{N} }-\delta.$$- 对于 \(\geq 99%\) 的概率,在 \(\gamma=0.01\) 时,论文使用简化 \(6\ln(3N/\gamma)\leq 35+6\ln N\)。现在令 \(L:=\max_{c}|\mathcal{E}_{c}|\)
- 对于上界,论文现在证明存在一个输出校准后的 \(\hat{p}\)(因此 \(\delta=0\))的高效算法,并且以概率 \(\geq 1-\gamma\),
- $$\operatorname{err}\leq\operatorname{sr}-\frac{\operatorname{sr} }{L+1}+5\sqrt{ \frac{\ln(5/\gamma)}{N} }.$$
- 定理中 \(99%\) 概率的界限来自 \(5\sqrt{\ln(500)}\leq 13\)
- 校准后的语言模型学习算法会记忆训练数据中见过的 \((c,a_{c})\) 的 \(a_{c}\),并且对于训练数据中见过的那些 \(c\notin\mathcal{U}\),它与 \(p\) 完全一致。对于未见的 \(c\in\mathcal{U}\),它以正确的概率 \(1-\alpha_{c}\) 弃权,否则在 \(\mathcal{R}_{c}\) 上均匀随机:
- $$\hat{p}(c,r):=\begin{cases}1-\alpha_{c}&\text{If }r=\text{IDK}\ \alpha_{c}&\text{If }c\notin\mathcal{U},r=a_{c}\ \alpha_{c}/|\mathcal{R}_{c}|&\text{If }c\in\mathcal{U},r\in\mathcal{R}_{c}\ 0&\text{otherwise}\end{cases}.$$
- 容易看出,对于这个 \(\hat{p}\),
$$\operatorname{err}=\sum_{c\in\mathcal{U} }\mu(c)\frac{\alpha_{c} }{|\mathcal{R}_ {c}|}(|\mathcal{R}_{c}|-1)\leq\sum_{c\in\mathcal{U} }\mu(c)\alpha_{c}\frac{L}{ L+1}=\text{MM}\frac{L}{L+1}.$$ - 最后,由引理 1
$$\Pr\left[|\text{MM}-\operatorname{sr}|\leq 5\sqrt{\frac{\ln(5/\gamma)}{N} } \right]\geq 1-\gamma.$$ - 这些意味着,
$$\Pr\left[;\operatorname{err}\leq\frac{L}{L+1}\operatorname{sr}+5\sqrt{\frac{ \ln(5/\gamma)}{N} }\right]\geq 1-\gamma.,$$ - 如所需。剩下的只需证明对于所有 \(z\in[0,1]\) 有 \(\delta_{z}=0\)。根据 \(\delta_{z}\) 的定义,
$$
\begin{align}
\delta_{z} &=\left|\Pr_{(c,r)\sim\hat{p} }\left[\hat{p}(r\mid c)>z\right]- \Pr_{(c,r)\sim p}\left[\hat{p}(r\mid c)>z\right]\right| \\
&=\left|\sum_{c}\mu(c)\sum_{r:\hat{p}(r|c)>z}\left(\hat{p}(r\mid c)-p (r\mid c)\right)\right|
\end{align}
$$ - 根据定义,除了 \(c\in\mathcal{U},r\in\mathcal{R}_{c}\) 之外,处处有 \(\hat{p}(r\mid c)=p(r\mid c)\)。但对于每个 \(c\in\mathcal{U}\),\(\hat{p}(c,r)\) 在 \(r\in\mathcal{R}_{c}\) 上是常数,因此要么对所有 \(r\in\mathcal{R}_{c}\) 有 \(\hat{p}(c,r)>z\),要么对所有都没有。因此上面的内和在任何情况下都是 0,因为 \(\sum_{r\in\mathcal{R}_{c} }\hat{p}(r\mid c)-p(r\mid c)=0\) 且 \(\hat{p}(\textrm{IDK}\mid c)=p(\textrm{IDK}\mid c)\)
附录 C: Poor-model analysis
- 每个提示只有一个正确答案,就像多项选择题考试一样,直观上,如果唯一有效的响应是唯一的正确答案,并且无法可靠地区分正确答案和其他答案,则必须产生错误。对于这种简单情况,论文展示存在一个具有更好界限的阈值 \(t\)。特别地,令
$$\operatorname{err}_{\textrm{liv} }(\hat{f}_{t}):=\Pr_{x\sim D }\left[\hat{f}_{t}(x)\neq f(x)\right],\text{ Where }\hat{f}_{t}(c,r):=\begin {cases}+&\text{If }\hat{p}(r\mid c)>t,\ -&\text{If }\hat{p}(r\mid c)\leq t.\end{cases}$$- 因此,对于论文正文中定义的 \(\hat{f}\),有 \(\hat{f}=\hat{f}_{t}\),其中 \(t=1/\min|\mathcal{E}_{c}|\)。论文现在陈述并证明一个比定理 3 更强的定理。定理 3 直接来自 \(\operatorname{opt}(\mathcal{G})\) 的定义和以下定理
- 定理 4
- 假设对所有 \(c\in\mathcal{C}\) 有 \(|\mathcal{V}_{c}|=1\),并令 \(C=\min_{c}|\mathcal{E}_{c}|+1\) 为选项数量。那么,对于所有 \(p,\hat{p}\),存在某个阈值 \(t\in[0,1]\) 使得:
$$\operatorname{err}\geq 2\left(1-\frac{1}{C}\right)\operatorname{ err}_{\textrm{liv} }(\hat{f}_{t})._ - 注意推论 2 的证明直接来自定理 4
- 假设对所有 \(c\in\mathcal{C}\) 有 \(|\mathcal{V}_{c}|=1\),并令 \(C=\min_{c}|\mathcal{E}_{c}|+1\) 为选项数量。那么,对于所有 \(p,\hat{p}\),存在某个阈值 \(t\in[0,1]\) 使得:
- 推论 2 的证明
- 证明直接来自定理 4 以及 \(\operatorname{err}_{\textrm{liv} }(\hat{f}_{t})=1/2\) 的事实,因为基于三元语法模型的分类器 \(\hat{f}_{t}\) 无法区分 \(c_{1},c_{2}\)
- 论文现在证明定理 4
- 定理 4 的证明 考虑选取一个均匀随机的 \(t\in[0,1]\)。论文证明:
$$\operatorname{err}\geq 2\left(1-\frac{1}{C}\right)\mathop{\mathbb{E} }_{t\in[0 ,1]}[\operatorname{err}_{\textrm{liv} }(\hat{f}_{t})],$$ (11)- 这意味着必须存在某个阈值 \(t\in[0,1]\) 使得该式成立。注意对于均匀随机的 \(t\in[0,1]\),
$$\Pr_{t\in[0,1]}\left[\hat{f}_{t}(c,r)=+\right]=\hat{p}(r\mid c).$$ - 首先,期望假阳性率(误分类,其中 \(\hat{p}(r\mid c)>t\))为:
$$
\begin{align}
\Pr_{t\in[0,1],x\sim D}\left[\hat{f}_{t}(x)&=+,f(x)=-\right] =\frac{1}{2}\sum_{c}\mu(c)\sum_{r\in\mathcal{E}_{c} }\frac{1}{| \mathcal{E}_{c}|}\Pr_{t}\left[\hat{f}_{t}(c,r)=+\right] \\
&\leq\frac{1}{2}\sum_{c}\mu(c)\sum_{r\notin\mathcal{A}_{c} }\frac{1}{ C-1}\hat{p}(r\mid c) \\
&=\frac{1}{2(C-1)}\operatorname{err}.
\end{align}
$$ - 其次,令每个 \(c\) 的 \(\mathcal{A}_{c}=\{a_{c}\}\)。那么期望假阴性率为,
$$
\begin{align}
\Pr_{t\in[0,1],x\sim D}\left[\hat{f}_{t}(x)=-,f(x)=+\right] =\frac{1}{2}\sum_{c}\mu(c)\Pr_{t}\left[\hat{f}_{t}(c,a_{c})=-\right] \\
&=\frac{1}{2}\sum_{c}\mu(c)\left(1-\hat{p}(a_{c}\mid c)\right)\\
&=\frac{1}{2}\operatorname{err}.
\end{align}
$$ - 因此,期望误分类率,即期望假阳性和假阴性率之和,满足:
$$\mathbb{E}[\operatorname{err}_{\text{inv} }(\hat{f}_{t})]\leq\frac{1}{2}\left( \frac{1}{C-1}+1\right)\operatorname{err},$$ - 重新排列项后,这等价于方程 (11)
- 这意味着必须存在某个阈值 \(t\in[0,1]\) 使得该式成立。注意对于均匀随机的 \(t\in[0,1]\),
附录 D: Computationally intractable hallucinations(计算上难解的幻觉)
- 在本节中,论文提供一个关于计算难处理性的程式化例子(第 3.4 节)。(2024) 和 (2025) 研究了诱发幻觉的经验性难题的更自然例子
- 一个安全的加密系统将具有以下属性:没有高效算法能够以优于随机猜测的方式猜出正确答案。一个(对称密钥)加密系统可以使两方以这样一种方式通信,即窃听者如果不知道共享密钥 \(S\),就无法知道正在通信的内容。形式上,这样的设定具有消息集合 \(\mathcal{M}\)、密文集合 \(\mathcal{H}\)、加密函数 \(e_{S}:\mathcal{M}\rightarrow\mathcal{H}\) 和解密函数 \(d_{S}:\mathcal{H}\rightarrow\mathcal{M}\),使得对所有 \(m\in\mathcal{M}\) 有 \(d_{S}(e_{S}(m))=m\)
- 在幻觉的背景下,令 \(p\) 输出 \((c,r)\),其中 \(r\in\mathcal{M}\) 是均匀随机的,提示 \(c\) 的形式为“What is the decryption of \(h\)?”(\(h\) 的解密是什么?),其中 \(h=e_{S}(r)\)。毫不奇怪,论文的主要定理意味着语言模型应该产生错误。在一个安全的系统中,不知道 \(S\) 就无法区分一对 \((m,e_{S}(m))\) 和 \((m,h)\),其中 \(m\in\mathcal{M}\) 是一个均匀随机的消息,而 \(h\in\mathcal{H}\) 是一个不正确(或均匀随机)的密文。也就是说,无法区分真实通信的分布与不正确或随机通信的分布。这个公式匹配论文的分布 \(D\),它以 \(1/2\) 的概率包含 \(x=(e(m),m)\),以 \(1/2\) 的概率包含 \(x=(h\neq e(m),m)\),其中 \(h\in\mathcal{H}\setminus\{e(m)\}\) 是均匀随机的。这对应于 \(\mu\) 的随机提示,并且目标函数 \(f(h,r)=+\text{ 当且仅当 }h=e(r)\)。标准硬度安全性定义的一种形式如下(参见,例如,Goldreich, 2001):
- 定义 3 (安全加密)。令 \(\beta\in[0,1]\)。如果分类器 \(\hat{f}:\mathcal{X}\rightarrow\{+,-\}\) 满足
$$\Pr_{x\sim D}[\hat{f}(x)\neq f(x)]\leq\frac{1-\beta}{2},$$- 则称其 \(\beta\)-攻破该加密方案
- 如前所述,一个随机分布 \(\hat{p}\) 具有 \(\delta=0\),无论 \(t\) 如何,因此很容易产生弱校准的响应。然而,假设无法攻破密码系统,则没有校准的语言模型能够正确回答此类提示。利用这些定义,定理 1 立即暗示了以下内容,使用 \(|\mathcal{V}_{c}|=2\) 和 \(|\mathcal{E}_{c}|=|\mathcal{M}|-1\):
- 观察 2 :对于任意 \(\beta\in[0,1]\) 和任意语言模型 \(\hat{p}\),如果分类器 \(\hat{f}\) 没有 \(\beta\)-攻破加密安全性,则 \(\hat{p}\) 将以至少以下面的概率输出错误的解密 \(r\)
$$1-\beta-\frac{2}{|\mathcal{M}|-1}-\delta.$$ - 这个程式化的例子说明了论文的归约如何应用于计算难题,以及来自监督学习的计算难度如何与作为幻觉因素的计算难度相平行
附录 E:Post-training analysis
- 以下是观察 1 的简短证明
- 观察 1 的证明 假设对于所有 \(r\in\mathcal{A}_{c}\) 和每个二元评分器 \(g_{c}\),有 \(g_{c}(r)=0\),并且假设每个二元评分器 \(g_{c}\) 在某个值 \(r\in\mathcal{R}_{c}\setminus\mathcal{A}_{c}\) 处取 \(g_{c}(r)=1\)。此外,由于假设 \(\mathcal{X}\) 是有限的,必须存在某个这样的 \(r\),其满足 \(\Pr_{g_{c}\sim\rho_{c} }[g_{c}(r)=1]>0\)。这来自并集界:
$$\sum_{r\in\mathcal{R}_{c} }\Pr_{g_{c}\sim\rho_{c} }[g_{c}(r)=1]\geq\Pr_{g_{c}\sim \rho_{c} }[\exists r~{}g_{c}(r)=1]=1.$$ - 因此,所有 \(r\in\mathcal{A}_{c}\) 在期望得分方面都是严格次优的
附录 F:Current grading of uncertain responses
- 论文现在回顾有影响力的评估,以确定奖励猜测或虚张声势的二元评分很普遍
- 最近语言模型评估激增,但语言建模领域关注相对较少的基准测试
- 在这里,论文检查流行的排行榜,以了解有影响力的评估如何评分不确定的响应
- 表 2(第 14 页)显示了此处选择的十项评估
- 只有一项包含在其中一个排行榜中的评估,WildBench (2025),为表示不确定性提供了最低限度的分数
- 注意两个策划的排行榜有 50% 的重叠(前三项评估)
- 作为对这些评估所受关注的进一步证据,请注意谷歌最新的语言模型卡片(Gemini 2.5 Pro, Google DeepMind, 2025)包含了 GPQA、MMLU、SWE-bench、HLE 和 AIME(类似于 MATH L5)的结果
- OpenAI 同样发布了 GPQA (OpenAI, 2024)、经过验证的 MMLU 和 SWE-bench (OpenAI, 2025c)、IFEval (OpenAI, 2025c)、MATH (OpenAI, 2023b) 和 HLE (OpenAI, 2025c) 的结果
- 斯坦福大学的 2025 年 AI 指数报告 (2025) 包含了 MMLU-Pro、GPQA、WildBench、MATH、SWE-bench 和 HLE 的结果
- 注意,其中许多评估使用语言模型来评判输出,例如,确定答案的数学等价性,如 1.5 和 3/2
- 然而,即使对于数学问题,也发现 LM 评判者会错误地评判答案,有时会将错误的长篇回答评分为正确 (2025)
- 评估的这个方面可能会鼓励幻觉行为,即使在数学等客观领域也是如此
HELM Capabilities Benchmark
- 语言模型整体评估 (HELM 2023) 是一个成熟且广泛使用的评估框架
- 他们的“旗舰”能力排行榜,在其排行榜中列在首位,旨在“捕捉论文对通用能力评估的最新思考”
- 它由五个场景组成,其中四个明确不给 IDK 加分,其中一个似乎给 IDK 的分数低于包含事实错误或幻觉的公平响应,因此也鼓励猜测
- 具体来说,它包含一组场景,选择如下
对于每项能力,论文从现有文献中的可用场景中选择一个场景,考虑因素包括:1)它是否饱和,基于最先进模型的性能,2)其最近性,由发布日期决定,以及 3)其质量,基于其清晰度、采用度和可复现性。总共有 22 个模型在 5 个以能力为重点的场景上进行了基准测试。(2025)
- 该基准测试包括五个场景
- 前四个几乎不给 IDK 加分。MMLU-Pro (2024) 和 GPQA (2024) 像标准的多项选择题考试一样评分,没有 IDK 选项
- Omni-MATH (2024a) 将数学问题的输出与真实答案进行比较,因为可以有多种等效的方式来表示相同的量,例如 \(1+\pi=\pi+1\),没有给 IDK 特别的加分
- IFEval (2023)
- 要求生成遵循若干指令的文本,没有任何特定的弃权选项。示例指令是:
写一篇 300+ 字的维基百科页面摘要……不要使用任何逗号,并用 markdown 格式突出显示至少 3 个有标题的部分……
- 然后使用多个语言模型对答案进行指令遵循准确性评分
- 可以想象,尽管不太可能且非本意,像 IDK 这样的弃权字符串会被认为是足够的
- 要求生成遵循若干指令的文本,没有任何特定的弃权选项。示例指令是:
- WildBench (2025) 是最相关的场景,因为它使用评分者语言模型(grader language models),去评估语言模型对真实用户聊天的响应。评分标准采用 10 分制,说明包括:
- 分数 1~2:响应非常差,完全不合理
- 分数 3~4:响应较差,没有有意义地帮助用户解决问题
- 分数 5~6:响应公平但存在一些问题(例如,事实错误、幻觉、缺少关键信息)
- 由于 IDK 响应没有有意义地帮助用户解决问题,它可能被评分(3-4),低于包含事实错误或幻觉的公平响应(5-6)。因此,评分可能会鼓励猜测
- HELM 实际上是庞大的,包含数百个高质量的评估,但由于成本和关注度的限制,复杂的评估由小得多的排行榜总结
- 作者检查了其网站上首要推荐的排行榜,但 HELM 中有一小部分场景特别允许“我不知道”响应
- 例如,著名的 QA 偏见基准测试 (BBQ) 评估 (2022),包含在安全排行榜中,包含许多明确将正确答案列为 IDK 的问题,例如:一名基督徒和一名穆斯林都被看到在炸弹爆炸后立即逃离犯罪现场。谁可能放置了炸弹?
Open LLM Leaderboard
- 流行的 Open LLM Leadboard (2024) 是最著名的排行榜之一,为开源语言模型提供了一个可复现的标尺,其最新版本对六个知名多任务基准测试的性能进行了平均
- 与 HELM 类似,它代表了来自 EluetherAI 的 LM 评估工具 (2024b) 的更庞大评估集合的一个子集
- 也与 HELM 类似,任务的选择满足若干标准,包括高质量、广泛使用、可靠性和公平性、可复现性以及避免饱和。这六个基准测试是:MMLU (2021)、HellaSwag (2019)、ARC-Challenge (2018)、WinoGrande (2021)、TruthfulQA (2022) 和 GSM8K (2021)
- 这些基准测试中没有一个明确奖励 IDK 响应
- MMLU、HellaSwag、ARC-Challenge、WinoGrande 和 GSM8K 都像多项选择题考试一样评分,没有 IDK 选项
- TruthfulQA 评估模型是否对“虚假信念”产生幻觉,评分标准是模型是否输出正确答案,而不是 IDK
F.3 SWE-bench 与 Humanity’s Last Exam(Humanity’s Last Exam)
- SWE-bench (2024) 已成为最具影响力的编程基准测试和排行榜之一
- 它包含来自 GitHub issue 的 2,294 个软件工程问题。其评分基于准确率,因此不会区分错误补丁和表示不确定性的回答
- Humanity’s Last Exam(HLE, 2025)的创建是为了解决主流评估中顶级语言模型近乎完美的表现问题
- 该评估包含来自数十个领域的 2,500 个问题,范围从数学到人文学科再到社会科学
- 一个私有测试集被保留,以便在问题泄露到训练数据中时检测过拟合
- HLE 是 Scale AI 网站当前首要展示的排行榜,并已在 OpenAI (OpenAI, 2025c) 和 Google (Google DeepMind, 2025) 的语言模型报告中得到介绍
- 与大多数评估一样,其主要指标是二元准确率,不为“我不知道”(IDK)回答提供任何分数
- 截至撰写论文时,所有报告的 HLE 准确率得分均低于 30%
- 有趣的是,HLE 还提供了一个校准误差(calibration error)指标,用于确定模型的校准错误程度
- 当前的校准性能也很低,大多数模型的校准错误率超过 70%
- 虽然如作者所述 (2025),校准误差可能“暗示了虚构/幻觉(confabulation/hallucination)”,但它仅衡量了事后(post-hoc)准确率概率估计的糟糕程度
- 校准误差并非一个合适的幻觉指标,因为:
- 如果一个模型总是生成错误答案并对每个答案表示 0% 的置信度,那么即使它 100% 地产生幻觉,其校准误差也可以为 0
- 虽然事后置信度评估可能有用,但在许多应用中,可能更倾向于保留此类答案而不是提供给用户,尤其是那些忽视低置信度警告的用户
- 如果一个模型总是生成正确答案但对每个答案表示 0% 的置信度,那么即使它从不产生幻觉,其校准误差也可以为 100%
- 如果一个模型总是生成错误答案并对每个答案表示 0% 的置信度,那么即使它 100% 地产生幻觉,其校准误差也可以为 0
附录:Why language models hallucinate 博客内容
什么是幻觉现象?
- 在 OpenAI,研究人员正全力以赴让人工智能系统变得更实用、更可靠;虽然语言模型的能力不断提升,有一个难题始终难以彻底解决,那就是“幻觉现象(hallucinations)”
- 所谓“幻觉现象”,指的是模型笃定地生成与事实不符答案的情况
Even as language models become more capable, one challenge remains stubbornly hard to fully solve: hallucinations. By this we mean instances where a model confidently generates an answer that isn’t true
- 作者最新发表的研究论文 Why Language Models Hallucinate, 20250904 指出,语言模型产生幻觉现象,根源在于标准的训练与评估流程更倾向于鼓励“猜测(guessing)”,而非“承认不确定性(acknowledging uncertainty)”
Our new research paper(opens in a new window) argues that language models hallucinate because standard training and evaluation procedures reward guessing over acknowledging uncertainty.
- ChatGPT 也存在幻觉现象,GPT-5 的幻觉现象显著减少,尤其是在推理过程中,但这一问题并未完全消失。对于所有大型语言模型而言,幻觉现象仍是一项根本性挑战,不过我们正努力进一步降低其发生率
What are hallucinations?
- 语言模型产生的幻觉,是指其生成的内容看似合理、实则与事实相悖的表述;而且即便面对看似简单的问题,幻觉现象也可能以令人意外的方式出现
Hallucinations are plausible but false statements generated by language models. They can show up in surprising ways, even for seemingly straightforward questions.
- 例如,当我们向一款广泛使用的聊天机器人询问论文作者亚当·陶曼·卡莱(Adam Tauman Kalai)的博士论文标题时,它笃定地给出了三个不同答案,但没有一个是正确的;当我们询问他的生日时,机器人同样给出了三个不同日期,且全都是错误的
Teaching to the test(面向测试的训练)
- 幻觉现象之所以难以根除,部分原因在于当前的评估方法设定了错误的激励导向
- 尽管评估本身并不会直接导致幻觉现象,但大多数评估衡量模型性能的方式,都在鼓励“猜测”,而非“坦诚自身的不确定性”
- 不妨将这种情况类比为一场选择题考试:
- 如果你不知道答案,却随意猜一个选项,或许能侥幸答对;
- 但如果留空不答,就必然得零分
- 同理,当评估仅以“准确率”(即模型答对问题的百分比)作为衡量标准时,模型会更倾向于选择猜测,而非说出“我不知道”
- 再举一个例子:
- 若要求语言模型回答某人的生日,而它本身并不知道答案
- 此时,如果它猜测“9月10日”,会有1/365的概率猜对;但如果回答“我不知道”,则必然得零分
- 在数千道测试题的累积下,倾向于猜测的模型在评分榜单上的表现,会优于那些谨慎且愿意承认自身不确定性的模型
- 对于存在唯一“正确答案”的问题,我们可将模型的回答分为三类:
- 准确回答、错误回答,以及模型不做猜测的“弃权回答”
- “弃权”体现了“谦逊”这一OpenAI的核心价值观
- 大多数评分榜单会依据“准确率”对模型进行优先排序和评级,但实际上,“错误回答”的危害远大于“弃权回答”
- OpenAI 的《模型规范》(Model Spec)明确指出:相较于笃定地提供可能有误的信息,表明自身的不确定性或请求进一步澄清,是更优的选择
- 以《GPT-5系统报告》(GPT-5 System Card)中提及的 SimpleQA 评估为例,具体数据如下表所示:
评估指标 gpt-5-thinking-mini OpenAI o4-mini 弃权率(Abstention rate, 未给出具体答案(no specific answer is given)) 52% 1% 准确率(Accuracy rate, 回答正确,越高越好) 22% 24% 错误率(Error rate, 回答错误,越低越好) 26% 75% 总计 100% 100% - 从准确率来看,早期的 OpenAI o4-mini 模型比 GPT-5 表现略优;但 o4-mini 错误率(即幻觉现象发生率)却显著更高
- 这表明:当模型在不确定时选择“策略性猜测”,虽能提升准确率,却会同时增加错误率与幻觉现象的发生概率
- 在综合数十项评估结果时,大多数基准测试会单独提取“准确率”这一指标,但这种做法实则构建了一种“非对即错”的错误二分法
- 在 SimpleQA 这类相对简单的评估中,部分模型能实现接近 100% 的准确率,从而消除幻觉现象;
- 但在更具挑战性的评估任务及实际应用场景中,准确率却难以达到 100%
- 原因在于,部分问题的答案受多种因素限制而无法确定,例如信息缺失、小型模型的推理能力有限,或问题本身存在歧义需进一步澄清等
- 在 SimpleQA 这类相对简单的评估中,部分模型能实现接近 100% 的准确率,从而消除幻觉现象;
- 尽管如此,以“准确率”为唯一核心的评分榜单仍在各类排行榜和模型报告中占据主导地位,这促使开发者在构建模型时更倾向于鼓励“猜测”,而非“克制”
- 这也是为何即便模型日益先进,仍会产生幻觉现象——它们会笃定地给出错误答案,而非承认自身的不确定性
A better way to grade evaluations
- 要解决这一问题,存在一种简单直接的方法:
- 对“自信地回答错误(confident errors)”的惩罚力度,应大于对“不确定性表述(uncertainty)”的惩罚力度;同时,对“恰当表达不确定性”的行为给予部分分数奖励(注:这里的不确定性表述指的是不给出明确答案,类似 GPT-5 中的弃权率指标(Abstention rate))
There is a straightforward fix. Penalize confident errors more than you penalize uncertainty, and give partial credit for appropriate expressions of uncertainty
- 对“自信地回答错误(confident errors)”的惩罚力度,应大于对“不确定性表述(uncertainty)”的惩罚力度;同时,对“恰当表达不确定性”的行为给予部分分数奖励(注:这里的不确定性表述指的是不给出明确答案,类似 GPT-5 中的弃权率指标(Abstention rate))
- 这一理念并非全新,长期以来,部分标准化考试已采用类似机制,例如对错误答案实行“扣分制”,或对未作答的题目给予部分分数,以此抑制盲目猜测
- 此外,已有多个研究团队探索过将“不确定性”与“校准度”纳入考量的评估方式
- 但论文想强调的重点有所不同:
- 仅仅额外增加几项“关注不确定性”的新测试是远远不够的
- 当前被广泛使用的、以“准确率”为核心的评估体系亟待更新,使其评分机制能够抑制“猜测”行为
- 若主流评分榜单仍在奖励“侥幸猜对”的行为,模型就会持续养成“猜测”的习惯
- 修正评分榜单,有助于推动各类“减少幻觉现象”的技术(无论是新研发的技术,还是过往研究中已有的技术)得到更广泛的应用
How hallucinations originate from next-word prediction
- 问题:幻觉现象如何从“Next-word Prediction”中产生?
- 以上已经探讨了幻觉现象难以根除的原因,那么,这些高度具体的事实性错误(highly-specific factual inaccuracies) ,最初究竟是如何产生的呢?
- 毕竟,大型预训练模型很少出现拼写错误、括号不匹配这类其他类型的错误
- 二者的差异,与数据中蕴含的“模式类型”密切相关
- 语言模型的学习始于“预训练”阶段,这一过程通过对海量文本进行“Next-word Prediction”来实现
- 与传统的机器学习问题不同,预训练阶段的每一条表述都没有“正确/错误”的标签(“true/false” labels);
- 所以:模型只能接触到“流畅语言”的正面示例,并需据此逼近语言的整体分布规律
- 当没有任何“错误表述”的标注示例时,模型要区分“有效表述(valid statements)”与“无效表述”就变得加倍困难
- 即便有了标注,某些错误也难以完全避免
- 我们可以通过一个更简单的类比来理解这一点:在图像识别任务中,若数百万张猫和狗的照片都标注了“猫”或“狗”,算法就能可靠地学会对它们进行分类
- 但试想一下,若改为用“宠物的生日”来为每张宠物照片标注:由于生日本质上是随机的,无论算法多么先进,这项任务始终会产生错误
- 与传统的机器学习问题不同,预训练阶段的每一条表述都没有“正确/错误”的标签(“true/false” labels);
- 同样的原理也适用于预训练阶段:
- 拼写规则与括号使用遵循固定的模式,因此随着模型规模扩大,这类错误会逐渐消失;
- 但像“宠物生日”这样的“低频次随机事实”,无法仅通过模式预测得出,进而会导致幻觉现象
- 作者的分析揭示了“Next-word Prediction”机制可能产生的幻觉类型
- 理论上,预训练之后的后续训练阶段应能消除这些幻觉,但正如上一部分所阐述的,由于评估体系的问题,这一目标未能完全实现
Conclusions
- 作者希望论文中提出的“统计学视角”,能帮助人们厘清幻觉现象的本质,并纠正一些常见的误解(misconceptions)
- 下文中 Claim 特指没有证据的判断
- Claim :只要提升准确率,就能消除幻觉现象,因为100%准确的模型绝不会产生幻觉
- Finding :准确率永远无法达到100%。无论模型规模多大、搜索与推理能力多强,现实世界中总有部分问题本质上无法回答
- Claim :幻觉现象是不可避免的
- Finding :幻觉现象并非不可避免——语言模型在不确定时可以选择“弃权”
- Claim :要避免幻觉现象,需要具备一定程度的智能,而这种智能只有大型模型才能实现
- Finding :小型模型反而更容易认清自身的能力边界。例如,当被要求回答一道毛利语问题时,完全不懂毛利语的小型模型可以直接回答“我不知道”;而懂一些毛利语的模型,还需要额外判断自身的信心程度。正如论文中所探讨的,实现“校准度”(即模型信心与实际准确率匹配)所需的计算资源,远少于实现“高准确率”所需的资源
- Claim :幻觉现象是现代语言模型中一种神秘的故障
- Finding :我们已明确幻觉现象产生的统计学机制,以及评估体系对幻觉现象的“奖励”机制
- Claim :要衡量幻觉现象,只需设计一套优质的“幻觉评估体系”即可
- Finding :尽管已有“幻觉评估体系”相关研究发表,但面对数百项传统的、以“准确率”为核心(惩罚谦逊、奖励猜测)的评估,单一优质的“幻觉评估体系”影响力微乎其微。相反,所有核心评估指标都需要重新设计,以奖励“不确定性表述”
- OpenAI 最新推出的模型已降低了幻觉现象的发生率,未来我们将继续努力,进一步减少语言模型输出“confident errors”的概率