注:本文包含 AI 辅助创作
- 参考链接:
Paper Summary
- 整体内容总结:
- 作者发现:虽然如超连接 (HC) 等工作所提出的那样扩展残差流的宽度和多样化连接可以带来性能提升,但这些连接的无约束性质会导致信号发散
- 这种破坏损害了跨层的信号能量守恒,导致训练不稳定并阻碍了深度网络的可扩展性
- 为了解决这些挑战,论文引入了是一个将残差连接空间投影到特定流形的通用框架 流形约束的超连接(Manifold-Constrained Hyper-Connections,\(m\)HC)
- 关键词:\(m\)HC, mHC
- 作者发现:虽然如超连接 (HC) 等工作所提出的那样扩展残差流的宽度和多样化连接可以带来性能提升,但这些连接的无约束性质会导致信号发散
- 背景 & 问题:
- 以超连接(Hyper-Connections,HC)为代表的研究,通过扩展残差流宽度(residual stream width)和多样化连接模式(diversifying connectivity patterns),扩展了过去十年建立的普遍存在的(ubiquitous)残差连接范式
- HC 带来了显著的性能提升,但这种多样化从根本上破坏了残差连接固有的恒等映射性质,导致严重的训练不稳定性、受限的可扩展性,并额外产生了显著的内存访问开销
- 本文解法:流形约束的超连接(\(m\)HC)
- mHC 是一个将 HC 的残差连接空间投影到特定流形以恢复恒等映射性质的通用框架,同时结合了严格的基础设施优化以确保效率
- 实证实验表明,\(m\)HC 对于大规模训练是有效的 ,提供了切实的性能改进和卓越的可扩展性
- 论文预计,\(m\)HC 作为 HC 的一个灵活且实用的扩展,将有助于更深入地理解拓扑架构设计,并为基础模型的演进指明有前景的方向
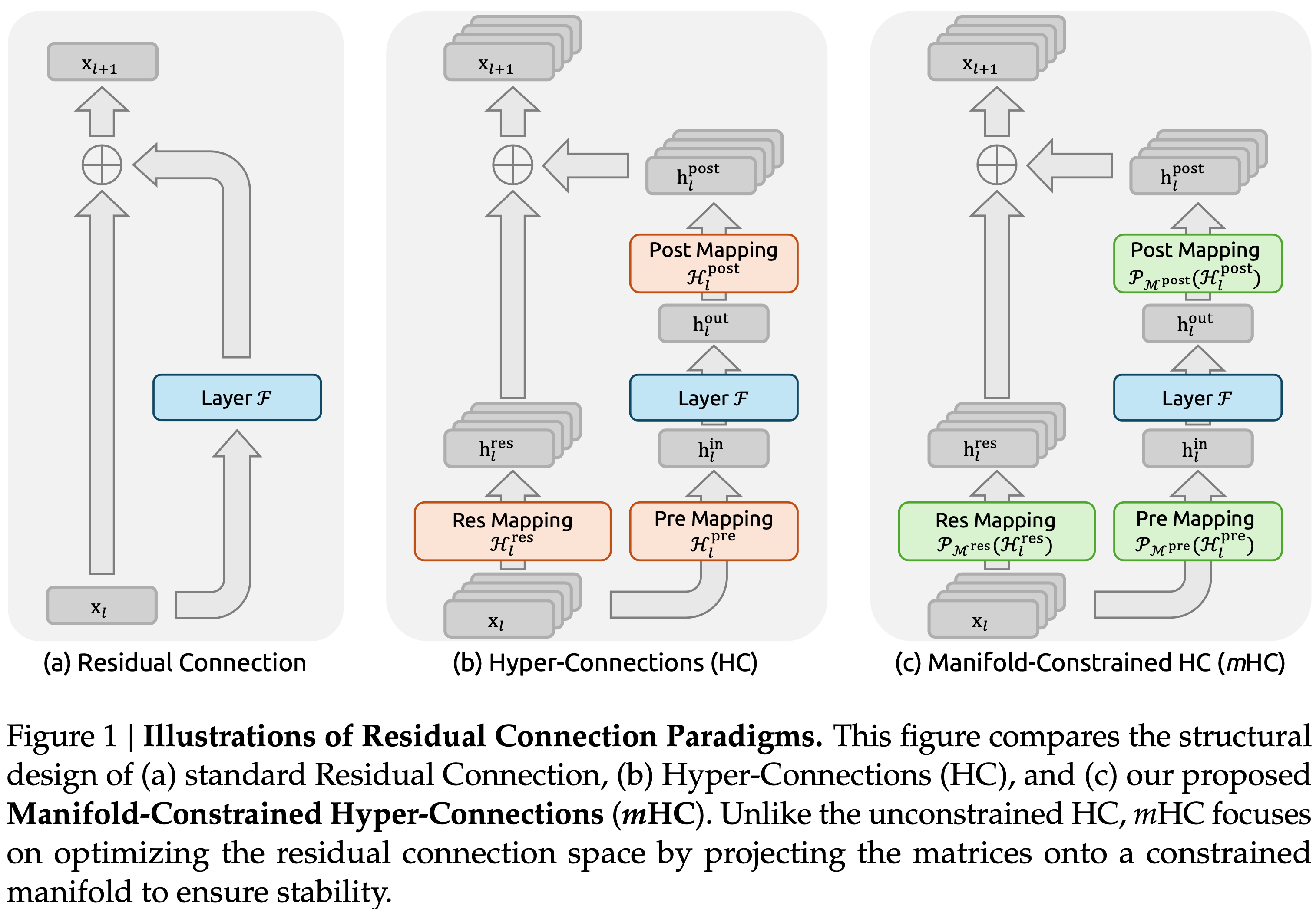
- 图 1:残差连接范式图示(Illustrations of Residual Connection Paradigms):
- (a) 标准残差连接(Standard Residual Connection)
- (b) 超连接(Hyper-Connections,HC)
- (c) mHC
- 与无约束的 HC 不同,\(m\)HC 侧重于通过将矩阵投影到约束流形上来优化残差连接空间,以确保稳定性
Introduction and Discussion
- 自 ResNets(2016a)引入以来,深度神经网络架构经历了快速演变,如图 1(a) 所示,单层的结构可以表述如下:
$$\mathbf{x}_{l+1}=\mathbf{x}_{l}+\mathcal{F}(\mathbf{x}_{l},\mathcal{W}_{l}) \tag{1}$$- \(\mathbf{x}_{l}\) 表示第 \(l\) 层的 \(C\) 维输入
- \(\mathbf{x}_{l+1}\) 表示第 \(l\) 层的 \(C\) 维输出
- \(\mathcal{F}\) 代表残差函数
- 尽管残差函数 \(\mathcal{F}\) 在过去十年中已演变为包含卷积、注意力机制和前馈网络等各种操作,但残差连接的范式保持了其原始形式
- 注:这里残差的本质是让输出等于原始输入再加一个增量
- 随着 Transformer(2017)架构的发展,该范式目前已成为 LLMs(2020;2024b;2023)的基本设计元素
- 这一成功主要归功于残差连接的简洁形式
- 更重要的是,早期研究 Identity Mappings in Deep Residual Networks, Kaiming He, Microsoft Research, 20160725 揭示了残差连接的恒等映射性质在大规模训练期间保持了稳定性和效率
- 通过跨多个层递归扩展残差连接,公式 (1) 得出:
$$\mathbf{x}_{L}=\mathbf{x}_{l}+\sum_{i=l}^{L-1}\mathcal{F}(\mathbf{x}_{i},\mathcal{W}_{i}),\tag{2}$$- 其中 \(L\) 和 \(l\) 分别对应更深层和更浅层(deeper and shallower layers)
- 术语 恒等映射(identity mapping) 指的是分量 \(\mathbf{x}_{l}\) 本身,它强调了来自浅层的信号无需任何修改直接映射到深层的性质
- Recently,以超连接(Hyper-Connections,HC)Hyper-connections, 202409 & ICLR 2025, Seed 为代表的研究为残差连接引入了新的维度,并通过实验证明了其性能潜力
- HC 的单层架构如图 1(b) 所示
- 通过扩展残差流的宽度并增强连接复杂性,HC 在不改变单个单元 FLOPs 计算开销的情况下,显著增加了拓扑复杂性
- 形式上,HC 中的单层传播定义为:
$$\mathbf{x}_{l+1}=\mathcal{H}^{\text{res} }_{l}\mathbf{x}_{l}+\mathcal{H}^{\text {post}\top }_{l}\mathcal{F}(\mathcal{H}^{\text{pre} }_{l}\mathbf{x}_{l},\mathcal{W}_{l}) \tag{3}$$ - \(\mathbf{x}_{l}\) 表示第 \(l\) 层的 \(n\times C\) 维输入
- \(\mathbf{x}_{l+1}\) 表示第 \(l\) 层的 \(n\times C\) 维输出
- 注意:
- 与公式 (1) 中的(native 残差)表述不同,\(\mathbf{x}_{l}\) 和 \(\mathbf{x}_{l+1}\) 的特征维度从 \(C\) 扩展到 \(n\times C\)
- 其中 \(n\) 是扩展率
- \(\mathcal{H}^{\text{res} }_{l}\)、\(\mathcal{H}^{\text{pre} }_{l}\) 和 \(\mathcal{H}^{\text{post} }_{l}\) 是三个可学习的映射(learnable mapping)
- \(\mathcal{H}^{\text{res} }_{l}\in\mathbb{R}^{n\times n}\) 用于混合残差流内的特征
- \(\mathcal{H}^{\text{pre} }_{l}\in\mathbb{R}^{1\times n}\) 将来自 \(nC\) 维流的特征聚合到 \(C\) 维层输入
- \(\mathcal{H}^{\text{post} }_{l}\in\mathbb{R}^{1\times n}\) 将层输出映射回流中
- 注:上述公式可对应着 图 1(b) 一起看
- 然而,随着训练规模增大,HC 引入了潜在的不稳定风险
- 主要问题在于 HC 的无约束性质在架构跨越多层时会破坏恒等映射性质
- 在包含多个并行流的架构中,理想的恒等映射作为一种守恒机制,确保跨流的平均信号强度在前向和反向传播期间保持不变
- 通过公式 (3) 将 HC 递归扩展到多层,可得:
$$\mathbf{x}_{L}=\left(\prod_{i=1}^{L-l}\mathcal{H}^{\text{res} }_{L-i}\right)\mathbf{x}_{l}+\sum_{i=l}^{L-1}\left(\prod_{j=1}^{L-1-i}\mathcal{H}^{\text{res} }_{L-j}\right)\mathcal{H}^{\text{post}\top}_{i}\mathcal{F}(\mathcal{H}^{\text{pre} }_{i}\mathbf{x}_{i},\mathcal{W}_{i}) \tag{4}$$- 其中 \(L\) 和 \(l\) 分别代表更深的层和更浅的层
- 与公式 (2) 相比,HC 中的复合映射 \(\prod_{i=1}^{L-l}\mathcal{H}^{\text{res} }_{l-i}\) 未能保持特征的全局均值
- 这种差异导致信号无限制地放大或衰减,从而在大规模训练中造成不稳定
- 进一步考虑的是,虽然 HC 在 FLOPs 方面保持了计算效率,但原始设计中未解决扩展残差流所带来的内存访问成本的硬件效率问题
- 这些因素共同限制了 HC 的实际可扩展性,阻碍了其在大规模训练中的应用
- 为应对这些挑战,论文提出了流形约束的超连接(Manifold-Constrained Hyper-Connections,\(m\)HC) ,如图 1(c) 所示,这是一个将 HC 的残差连接空间投影到特定流形以恢复恒等映射性质的通用框架,同时结合了严格的基础设施优化以确保效率
- 具体而言,\(m\)HC 利用 Sinkhorn-Knopp 算法(1967)将 \(\mathcal{H}^{\text{res} }_{l}\) 投影到 Birkhoff 多面体上
- 此操作有效地将残差连接矩阵约束在由双随机矩阵构成的流形内
- 注:Sinkhorn-Knopp(SK)通常指交替行 / 列缩放的迭代算法,用于将非负矩阵标定为满足指定行和 / 列和的矩阵(常见为双随机矩阵,行和与列和均为 1)
- 由于这些矩阵的行和与列和均等于 \(1\),操作 \(\mathcal{H}^{\text{res} }_{l} \mathbb{x}_l\) 起到输入特征凸组合的作用
- 此特性促进了条件良好的信号传播,其中特征均值得以保持,信号范数受到严格正则化,从而有效缓解信号消失或爆炸的风险
- Furthermore,由于双随机矩阵的矩阵乘法具有封闭性,复合映射 \(\prod_{i=1}^{L-l}\mathcal{H}^{\text{res} }_{l-i}\) 保留了此守恒性质
- 因此,\(m\)HC 有效地保持了任意深度之间恒等映射的稳定性
- 为确保效率,论文采用核融合并利用 TileLang(2025)开发混合精度核
- Furthermore,论文通过选择性重计算并在 DualPipe 调度(2024b)中仔细重叠通信来减少内存占用
- 具体而言,\(m\)HC 利用 Sinkhorn-Knopp 算法(1967)将 \(\mathcal{H}^{\text{res} }_{l}\) 投影到 Birkhoff 多面体上
- 在语言模型预训练上的大量实验表明,\(m\)HC 表现出卓越的稳定性和可扩展性,同时保持了 HC 的性能优势
- 内部大规模训练表明,\(m\)HC 支持大规模训练,并且在扩展率 \(n=4\) 时仅引入 6.7% 的额外时间开销
Related Works
- 深度学习的架构进展主要可分为微设计(micro-design) 和宏设计(macro-design)
- 微设计关注计算块的内部架构,指定特征如何跨空间、时间和通道维度进行处理
- In Contrast,宏设计建立块间的拓扑结构,从而规定特征表示如何在不同层间传播、路由和合并
Micro Design
- 在参数共享和平移不变性的驱动下,卷积最初主导了结构化信号的处理
- 虽然后续的变体如深度可分离卷积(depthwise separable)(2017)和分组卷积(grouped convolutions)(2017)优化了效率,但 Transformer(2017)的出现确立了注意力机制和前馈网络(Feed-Forward Networks,FFNs)作为现代架构的基本构建块
- 注意力机制促进全局信息传播,而 FFNs 增强单个特征的表示能力
- 为了平衡性能与大语言模型的计算需求,注意力机制已发展为高效变体
- 例如多查询注意力(Multi-Query Attention,MQA)(Shazeer,2019)、分组查询注意力(Grouped-Query Attention,GQA)(2023)和多头潜在注意力(Multi-Head Latent Attention,MLA)(2024b)
- 同时,FFNs 已通过 MoE 被泛化为稀疏计算范式,允许大规模参数扩展而无需成比例的计算成本
Macro Design
- 宏设计(Macro-design)控制网络的全局拓扑结构(2015)
- 继 ResNet(2016a)之后,诸如 DenseNet(2017)和 Fractal-Net(2016)等架构旨在分别通过密集连接和多路径结构增加拓扑复杂性来提高性能
- 深度层聚合(Deep Layer Aggregation,DLA)(2018)通过递归聚合不同深度和分辨率的特征进一步扩展了该范式
- 最近,宏设计的重点已转向扩展残差流的宽度(2020;2023;2025;2025;2025;2024;2025;2023;2024)
- 超连接(Hyper-Connections,HC)(2024)引入了可学习的矩阵来调制不同深度特征之间的连接强度,而残差矩阵变换器(Residual Matrix Transformer,RMT)(2025)则用外积记忆矩阵替代标准残差流以促进特征存储
- 类似地,MUDDFormer(2025)采用多路动态密集连接来优化跨层信息流
- 尽管具有潜力,但这些方法引入了一些问题:
- 这些方法破坏了残差连接固有的恒等映射性质,从而引入不稳定性并阻碍可扩展性
- 由于特征宽度扩展,这些方法还产生了显著的内存访问开销
- 在 HC 的基础上,论文提出的 \(m\)HC 将残差连接空间限制在特定流形上以恢复恒等映射性质,同时结合了严格的基础设施优化以确保效率
- 这种方法在保持扩展连接的拓扑优势的同时,增强了稳定性和可扩展性
Preliminary
- 论文首先建立本工作中使用的符号
- 在 HC 的表述中,第 \(l\) 层的输入 \(\mathbf{x}_{l}\in\mathbb{R}^{1\times C}\) 被扩展 \(n\) 倍以构建一个隐藏矩阵 \(\mathbf{x}_{l}=(\mathbf{x}_{l,0}^{\top},\ldots,\mathbf{x}_{l,n-1}^{\top})^{\top }\in\mathbb{R}^{n\times C}\),可视为 \(n\) 个流的残差
- 此操作有效地拓宽了残差流的宽度
- 为了控制该流的读出(read-out)、写入(write-in)和更新过程(updating processes),HC 引入了三个可学习的线性映射 :
- \(\mathcal{H}_{l}^{\text{pre} }\)、\(\mathcal{H}_{l}^{\text{post} }\in\mathbb{R}^{1\times n}\) 和 \(\mathcal{H}_{l}^{\text{res} }\in\mathbb{R}^{n\times n}\)
- 这些映射修改了公式 (1) 所示的标准残差连接,从而得到了公式 (3) 中的表述
- 在 HC 的表述中,可学习的映射由两部分系数组成:
- 依赖于输入的部分(Input-dependent One):称为动态映射(dynamic mappings)
- 全局部分(Global One):称为静态映射(static mappings)
- 形式上,HC 按如下方式计算系数:
$$\begin{cases}\tilde{\mathbf{x} }_{l}=\text{RMSNorm}(\mathbf{x}_{l})\\ \mathcal{H}_{l}^{\text{pre} }=\alpha_{l}^{\text{pre} }\cdot\text{tanh}(\theta_{ l}^{\text{pre} }\tilde{\mathbf{x} }_{l}^{\top})+\mathbf{b}_{l}^{\text{pre} }\\ \mathcal{H}_{l}^{\text{post} }=\alpha_{l}^{\text{post} }\cdot\text{tanh}(\theta_{l}^{\text{post} }\tilde{\mathbf{x} }_{l}^{\top})+\mathbf{b}_{l}^{\text{post} }\\ \mathcal{H}_{l}^{\text{res} }=\alpha_{l}^{\text{res} }\cdot\text{tanh}(\theta_{ l}^{\text{res} }\tilde{\mathbf{x} }_{l}^{\top})+\mathbf{b}_{l}^{\text{res} },\end{cases} \tag{5}$$- 注意:上述只是定义系数,真实的数据流动过程见 图 1
- 其中 RMSNorm(\(\cdot\))(2019)应用于最后一个维度
- 理解:相当于 \(n\))个流是相对独立做 RMSNorm 的
- 标量 \(\alpha_{l}^{\text{pre} }\)、\(\alpha_{l}^{\text{post} }\) 和 \(\alpha_{l}^{\text{res} }\in\mathbb{R}\) 是初始化为小值的可学习门控因子
- 动态映射 通过由 \(\theta^{\text{pre} }_{l}\)、\(\theta^{\text{post} }_{l}\in\mathbb{R}^{1\times C}\) 和 \(\theta^{\text{res} }_{l}\in\mathbb{R}^{n\times C}\) 参数化的线性投影得出
- 静态映射 由可学习的偏置 \(\mathbf{b}^{\text{pre} }_{l}\)、\(\mathbf{b}^{\text{post} }_{l}\in\mathbb{R}^{1\times n}\) 和 \(\mathbf{b}^{\text{res} }_{l}\in\mathbb{R}^{n\times n}\) 表示
- It is worth noting that 引入这些映射(即 \(\mathcal{H}^{\text{pre} }_{l}\)、\(\mathcal{H}^{\text{post} }_{l}\) 和 \(\mathcal{H}^{\text{res} }_{l}\))产生的计算开销可以忽略不计
- 因为典型的扩展率 \(n\)(例如 4)远小于输入维度 \(C\)
- 理解:在每一层,每个扩展(共 \(n\) 个扩展)每个系数只需要对应的一个即可
- 通过这种设计,HC 有效地将残差流的信息容量与层的输入维度(与模型的计算复杂度 FLOPs 密切相关)解耦
- 问题:这里是说,即使输入维度比较小,残差流的信息容量也可以很大?
- Consequently,HC 通过调整残差流宽度提供了一种新的扩展途径(new avenue for scaling) ,补充了预训练扩展法则(2022)中讨论的模型 FLOPs 和训练数据大小的传统扩展维度
- 算力增加:HC 需要三个映射来处理残差流和层输入之间的维度不匹配,需要更多算力
- 性能提升:表 1 所示的初步实验表明,残差映射 \(\mathcal{H}^{\text{res} }_{l}\) 带来了最显著的性能增益
- 这一发现强调了残差流内有效信息交换的至关重要性
- 注:这里的残差流宽度扩展实际上也可以看做另一种维度的 Scaling Law
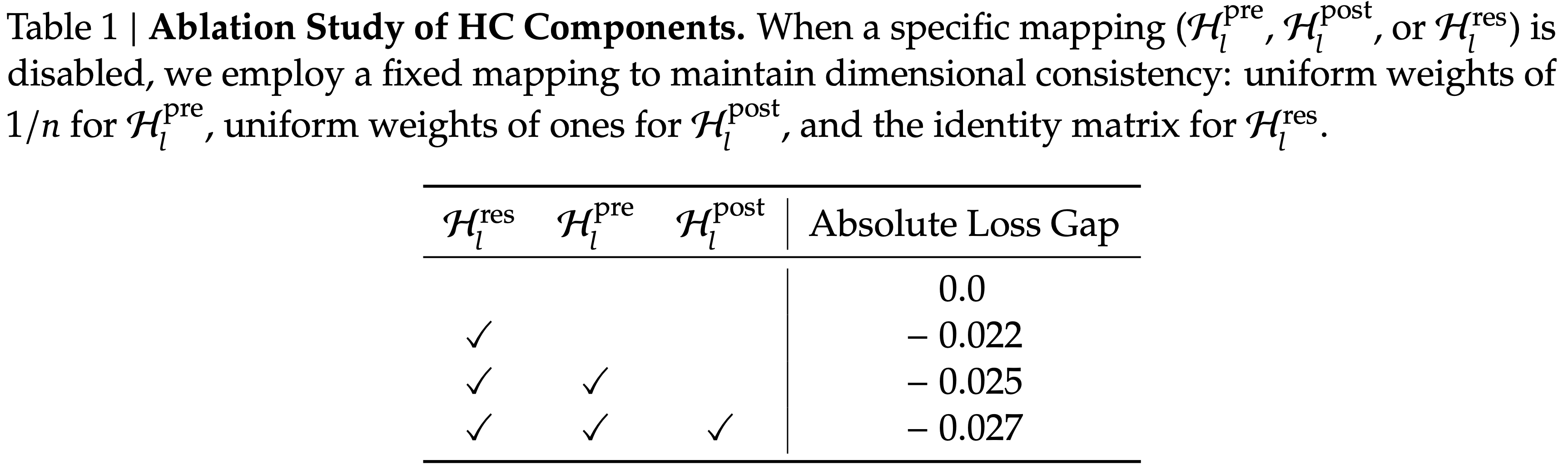
- 表 1:Ablation Study of HC Components
- 当特定映射(\(\mathcal{H}^{\text{pre} }_{l}\)、\(\mathcal{H}^{\text{post} }_{l}\) 或 \(\mathcal{H}^{\text{res} }_{l}\))被禁用时,论文采用固定映射以保持维度一致性:
- \(\mathcal{H}^{\text{pre} }_{l}\) 使用均匀权重 \(1/n\)
- \(\mathcal{H}^{\text{post} }_{l}\) 使用全一均匀权重
- \(\mathcal{H}^{\text{res} }_{l}\) 使用单位矩阵
- 当特定映射(\(\mathcal{H}^{\text{pre} }_{l}\)、\(\mathcal{H}^{\text{post} }_{l}\) 或 \(\mathcal{H}^{\text{res} }_{l}\))被禁用时,论文采用固定映射以保持维度一致性:
数值不稳定性,Numerical Instability
- 虽然残差映射 \(\mathcal{H}^{\text{res} }_{l}\) 对性能至关重要,但其顺序应用(sequential application)对数值稳定性构成重大风险
- 如公式 (4) 详述,当 HC 跨越多层扩展时,从层 \(l\) 到 \(L\) 的有效信号传播由复合映射 \(\prod_{i=1}^{L-l}\mathcal{H}^{\text{res} }_{L-i}\) 控制
- 由于可学习的映射 \(\mathcal{H}^{\text{res} }_{l}\) 是无约束的,该复合映射不可避免地偏离恒等映射
- Consequently,信号幅度在前向传递和反向传播期间都容易爆炸或消失
- 这种现象破坏了残差学习的基本前提(依赖于无阻碍的信号流),从而在更深或更大规模的模型中使训练过程不稳定
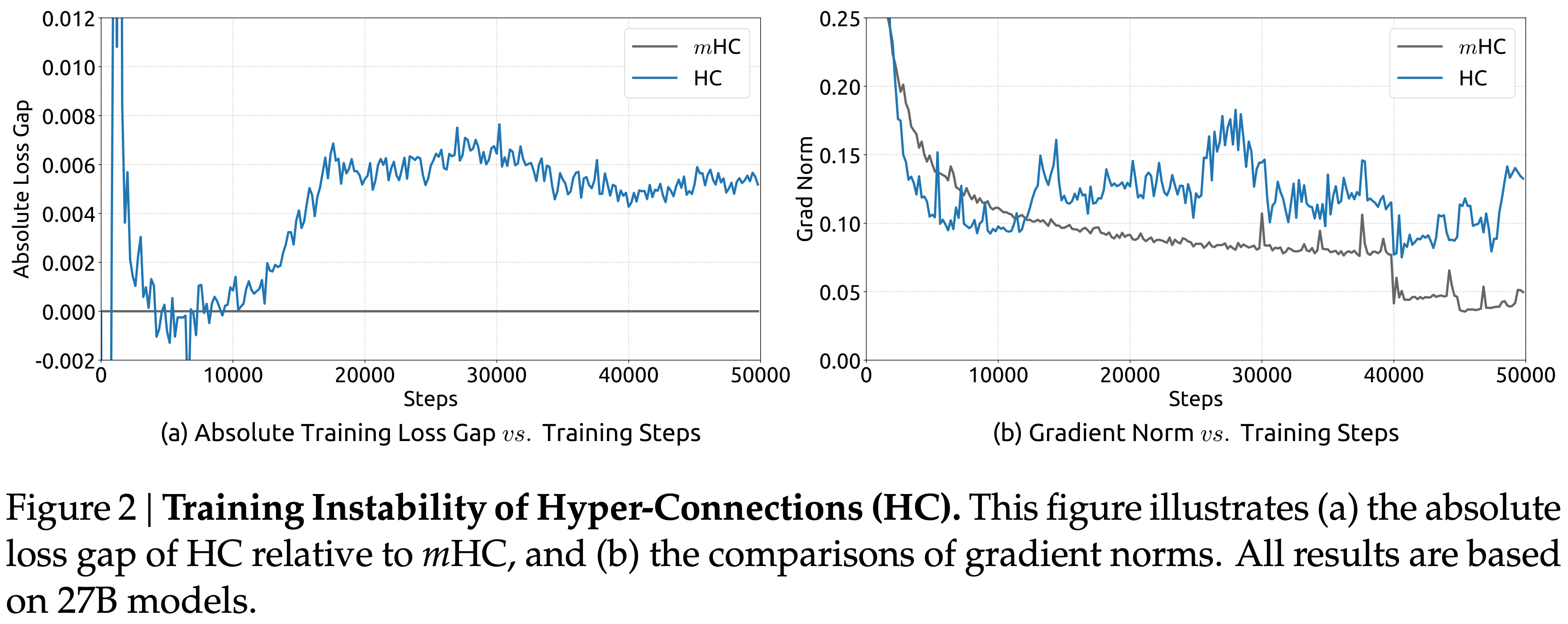
- 实证证据也支持这一分析:论文在大规模实验中观察到不稳定的损失行为,如图 2 所示
- 以 \(m\)HC 为基线,HC 在约 12k 步时表现出意外的损失激增 ,这与 梯度范数的不稳定性 高度相关
- 图 2:超连接(Hyper-Connections,HC)的训练不稳定性(Training Instability)
- 图 (a) :HC 相对于 \(m\)HC 的绝对损失差距
- 图 (b) :梯度范数的比较
- 注:所有结果基于 27B 模型
- (补充实证证据)Furthermore,对 \(\mathcal{H}^{\text{res} }_{l}\) 的分析验证了这种不稳定性的机制
- 为了量化复合映射 \(\prod_{i=1}^{L-l}\mathcal{H}^{\text{res} }_{L-i}\) 沿残差流放大信号的程度,论文利用两个指标
- 第一个基于复合映射行和的最大绝对值,捕捉前向传递中最坏情况的扩张
- 第二个基于列和的最大绝对值,对应于反向传递
- 论文将这些指标称为复合映射的最大增益幅度(Amax Gain Magnitude)
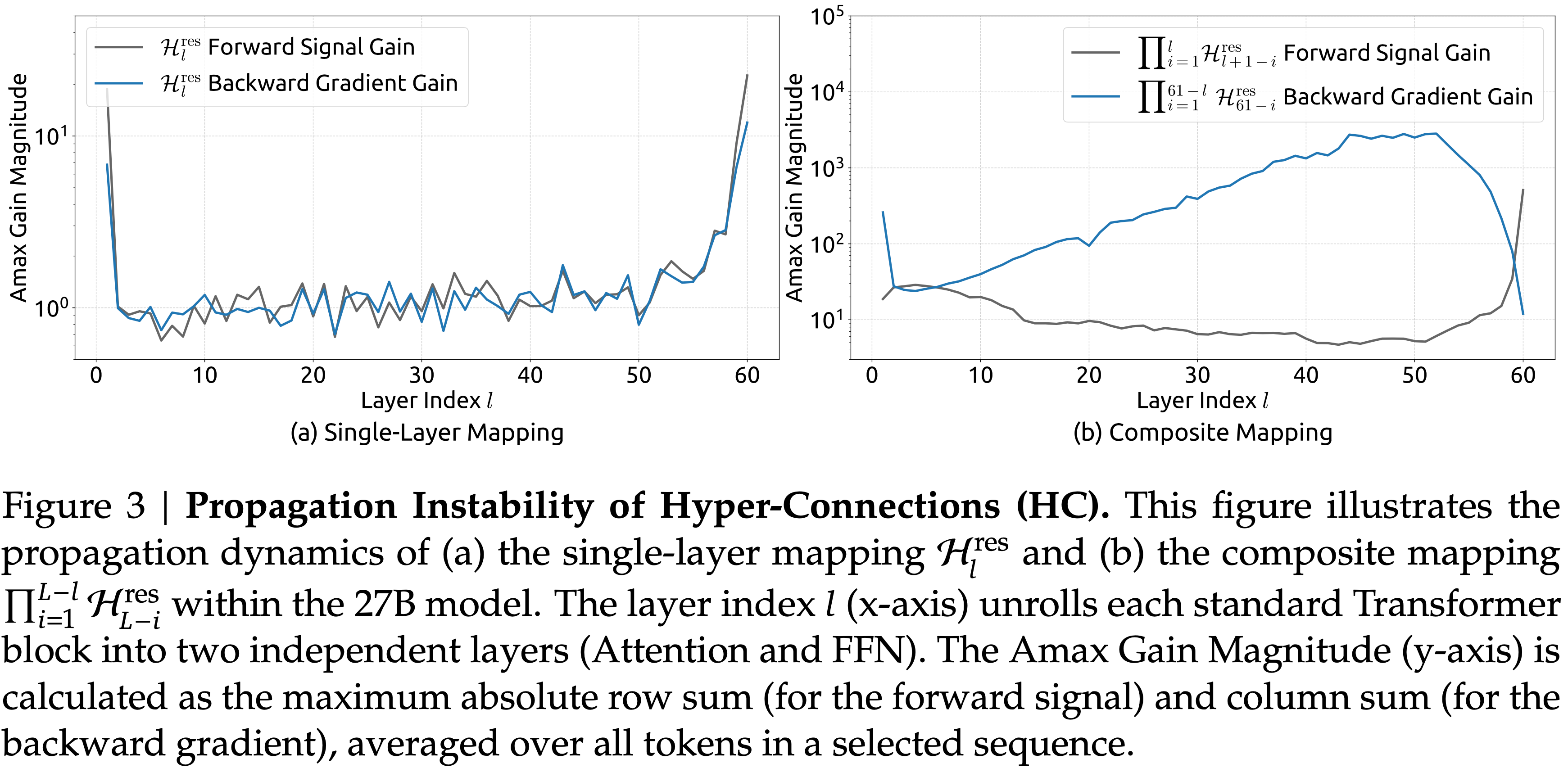
- 如图 3 (b) 所示,最大增益幅度产生了极端值,峰值达到 3000,与 1 存在巨大差异(注:恒等映射的权重系数恒为 1),这证实了残差流爆炸的存在
- 图 3:超连接(Hyper-Connections,HC)的传播不稳定性(Propagation Instability)
- 图 3(a) 展示了 27B 模型中的单层映射(Single-Layer Mapping) \(\mathcal{H}^{\text{res} }_{l}\) 的传播动态
- 图 3(b) 展示了 27B 模型中的复合映射(Composite-Layer Mapping) \(\prod_{l=1}^{L-l}\mathcal{H}^{\text{res} }_{l-l}\) 的传播动态
- Layer Index \(l\)(x 轴)将每个标准 Transformer 块展开为两个独立的层(Attention 和 FFN)
- 最大增益幅度(y 轴)计算为最大绝对行和(用于前向信号)和列和(用于反向梯度),在选定序列的所有 token 上取平均
System Overhead(系统开销)
- 由于额外映射的线性性质,HC 的计算复杂度会提升,目前为止还算可控,但系统级开销仍然构成了不可忽视的挑战
- 具体来说,内存访问(I/O)成本通常是现代模型架构中的主要瓶颈之一,被广泛称为”内存墙”(”memory wall”)(2022)
- 这一瓶颈在架构设计中经常被忽视,但它却决定性地影响运行时效率
- 着眼于广泛采用的预归一化 Transformer(2017)架构,论文分析了 HC 固有的 I/O 模式
- 表 2 总结了由 \(n\) 流残差设计在单个残差层中引入的每个 token 的内存访问开销
- 分析表明,HC 使内存访问成本增加了约与 \(n\) 成比例的倍数
- 这种过度的 I/O 需求显著降低了训练吞吐量,除非通过融合核来缓解
- Besides,由于 \(\mathcal{H}^{\text{pre} }_{l}\)、\(\mathcal{H}^{\text{post} }_{l}\) 和 \(\mathcal{H}^{\text{res} }_{l}\) 涉及可学习参数,它们的中间激活值需要用于反向传播
- 这导致 GPU 内存占用量大幅增加,通常需要梯度检查点(gradient checkpointing)来维持可行的内存使用量
- Furthermore,HC 在管道并行(pipeline parallelism)(2024)中需要 \(n\) 倍的通信成本,导致更大的气泡(bubbles)并降低训练吞吐量
- 表 2:每个 token 的内存访问成本比较(Comparison of Memory Access Costs Per Token)
- 此分析考虑了前向传递中残差流维护引入的开销,不包括层函数 \(\mathcal{F}\) 的内部 I/O
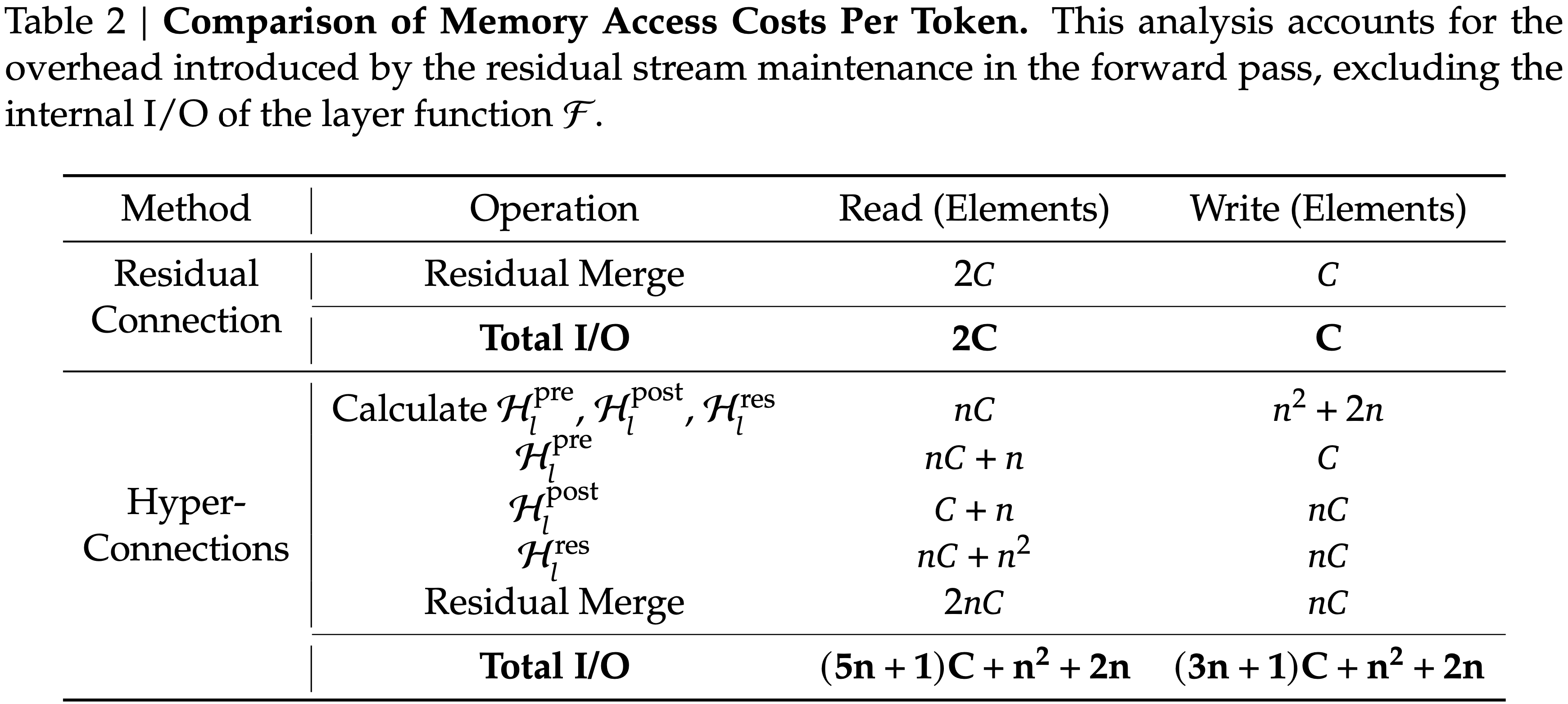
- 此分析考虑了前向传递中残差流维护引入的开销,不包括层函数 \(\mathcal{F}\) 的内部 I/O
Method
Manifold-Constrained Hyper-Connections(暂译为流形约束超连接)
- 受到恒等映射原理 (2016b) 的启发,\(m\)HC 的核心前提是 将残差映射 \(\mathcal{H}^{\text{res} }_{l}\) 约束到一个特定的流形上
- 虽然原始的恒等映射通过强制令 \(\mathcal{H}^{\text{res} }_{l}=\mathbf{I}\) 来确保稳定性,但这从根本上阻止了残差流内部的信息交换
- 而信息交换对于最大化多流架构(multi-stream architectures)的潜力至关重要
- Therefore,论文提出将残差映射投影到一个既能保持跨层信号传播稳定性、又能促进残差流之间相互作用的流形上,以保持模型的表达能力
- 为此(To this end),论文将 \(\mathcal{H}^{\text{res} }_{l}\) 限制为一个双随机矩阵(doubly stochastic matrix)
- 注:双随机矩阵是指每行每列之和为1 ,且单个元素值大于0的矩阵
- 论文中也提到:双随机矩阵是指元素非负,且行和与列和均为 1 的矩阵
- Formally,令 \(\mathcal{M}^{\text{res} }\) 表示双随机矩阵的流形(也称为 Birkhoff 多胞形)
- 多胞形是欧氏空间 \(\mathbb{R}^n\)中由有限个闭半空间的交集构成的有界凸集
- Birkhoff 多胞形(\(B_n\))是 \(\mathbb{R}^{n\times n}\) 中全体 \(n\times n\) 双随机矩阵的凸多胞形,也等价于全体 \(n\times n\) 置换矩阵的凸包
- 论文将 \(\mathcal{H}^{\text{res} }_{l}\) 约束到 \(\mathcal{P}_{\mathcal{M}^{\text{res} } }(\mathcal{H}^{\text{res} }_{l})\),其定义为:
$$\mathcal{P}_{\mathcal{M}^{\text{res} } }(\mathcal{H}^{\text{res} }_{l}):=\left\{\mathcal{H}^{\text{res} }_{l}\in\mathbb{R}^{n\times n}\mid\mathcal{H}^{\text{res} }_{l}\mathbf{1}_{n}=\mathbf{1}_{n},\mathbf{1}^{\top}_{n}\mathcal{H}^{\text{res} }_{l}=\mathbf{1}^{\top}_{n},\mathcal{H}^{\text{res} }_{l}\geqslant 0\right\} \tag{6}$$- 其中 \(\mathbf{1}_{n}\) 表示所有元素为 1 的 n 维向量
- 理解:
- \(\mathbf{1}_{n}\) 是列向量
- \(\mathcal{H}^{\text{res} }_{l}\mathbf{1}_{n}=\mathbf{1}_{n}\) 表示矩阵 \(\mathcal{H}^{\text{res} }_{l}\) 的行和为 1
- \(\mathbf{1}^{\top}_{n}\mathcal{H}^{\text{res} }_{l}=\mathbf{1}^{\top}_{n}\) 表示矩阵 \(\mathcal{H}^{\text{res} }_{l}\) 的列和为 1
- \(\mathcal{H}^{\text{res} }_{l} \ge 0\) 表示矩阵 \(\mathcal{H}^{\text{res} }_{l}\) 的元素非负
- 上述定义刚好是双随机矩阵的定义
- It is worth noting that 当 \(n=1\) 时 ,双随机条件退化为标量 1
- 此时恢复了原始的恒等映射
- 选择双随机性赋予了多个严格的理论性质,这些性质有利于大规模模型训练(The choice of double stochasticity confers several rigorous theoretical properties beneficial for large-scale model training):
- 1)范数保持 (Norm Preservation): 双随机矩阵的谱范数以 1 为界(即 \(|\mathcal{H}^{\text{res} }_{l}|_{2} \leq 1\))
- 这意味着可学习的映射是非扩张的,能有效缓解梯度爆炸问题
- 注:谱范数是矩阵范数,即:
$$
|A|_2 = \sqrt{\lambda_{\max}(A^* A)}
$$- 其中 \( \lambda_{\max} \) 表示最大特征值,\( A^* \) 是 \( A \) 的共轭转置
- 2)组合封闭性 (Compositional Closure): 双随机矩阵集合在矩阵乘法下是封闭的
- 这确保了跨越多层的复合残差映射 \(\prod_{i=1}^{L-1}\mathcal{H}^{\text{res} }_{L-i}\) 保持双随机性 ,从而在整个模型深度范围内保持稳定性
- 注:双随机矩阵的性质:两个双随机矩阵(Doubly Stochastic Matrix)的乘积仍然是双随机矩阵,推广一下,任意个双随机矩阵的乘积都是双随机矩阵
- 3)通过 Birkhoff 多胞形的几何解释 (Geometric Interpretation via the Birkhoff Polytope): 集合 \(\mathcal{M}^{\text{res} }\) 构成 Birkhoff 多胞形,它是置换矩阵集合的凸包
- 这提供了一个清晰的几何解释:残差映射充当了置换的凸组合
- 从数学上讲,重复应用此类矩阵倾向于单调地增加信息在流之间的混合,有效地充当鲁棒的特征融合机制
- 1)范数保持 (Norm Preservation): 双随机矩阵的谱范数以 1 为界(即 \(|\mathcal{H}^{\text{res} }_{l}|_{2} \leq 1\))
- 此外,论文对输入映射 \(\mathcal{H}^{\text{pre} }_{l}\) 和输出映射 \(\mathcal{H}^{\text{post} }_{l}\) 施加非负约束
- 这种约束可以防止由正负系数组合引起的信号抵消,这也可以被视为一种特殊的流形投影
Parameterization and Manifold Projection:参数化与流形投影
- 在本节中,论文将详细说明 \(m\)HC 中 \(\mathcal{H}^{\text{pre} }_{l},\mathcal{H}^{\text{post} }_{l}\) 和 \(\mathcal{H}^{\text{res} }_{l}\) 的计算过程
- 给定第 \(l\) 层的输入隐藏矩阵 \(\mathbf{x}_{l}\in\mathbb{R}^{n\times C}\),论文首先将其展平为向量 \(\vec{\mathbf{x} }_{l}=\text{vec}(\mathbf{x}_{l})\in\mathbb{R}^{1\times nC}\) 以保留完整的上下文信息
- 然后,论文遵循原始 HC 的公式来获得动态映射和静态映射:
$$\begin{cases}\vec{\mathbf{x} }^{\prime}_{l}=\text{RMSNorm}(\vec{\mathbf{x} }_{ l})\\ \tilde{\mathcal{H} }^{\text{pre} }_{l}=\alpha^{\text{pre} }_{l}\cdot(\vec{\mathbf{x} }^{\prime}_{l}\varphi^{\text{pre} }_{l})+\mathbf{b}^{\text{pre} }_{l}\\ \tilde{\mathcal{H} }^{\text{post} }_{l}=\alpha^{\text{post} }_{l}\cdot(\vec{\mathbf{x} }^{\prime}_{l}\varphi^{\text{post} }_{l})+\mathbf{b}^{\text{post} }_{l}\\ \tilde{\mathcal{H} }^{\text{res} }_{l}=\alpha^{\text{res} }_{l}\cdot\text{mat}(\vec{\mathbf{x} }^{\prime}_{l}\varphi^{\text{res} }_{l})+\mathbf{b}^{\text{res} }_{l},\end{cases} \tag{7}$$- 其中 \(\varphi^{\text{pre} }_{l},\varphi^{\text{post} }_{l}\in\mathbb{R}^{nC\times n}\) 和 \(\varphi^{\text{res} }_{l}\in\mathbb{R}^{nC\times n^{2} }\) 是用于动态映射的线性投影,而 \(\text{mat}(\cdot)\) 是将 \(\mathbb{R}^{1\times n^{2} }\) 重塑为 \(\mathbb{R}^{n\times n}\) 的函数
- 然后,通过以下方式获得最终的约束映射:
$$\begin{cases}\mathcal{H}^{\text{pre} }_{l}=\sigma(\tilde{\mathcal{H}}^{\text{pre} }_{l})\\ \mathcal{H}^{\text{post} }_{l}=2\sigma(\tilde{\mathcal{H} }^{\text{post} }_{l})\\ \mathcal{H}^{\text{res} }_{l}=\text{Sinkhorn-Knopp}(\tilde{\mathcal{H} }^{\text{res} }_{l}),\end{cases} \tag{8}$$- 其中 \(\sigma(\cdot)\) 表示 Sigmoid 函数
- \(\text{Sinkhorn-Knopp}(\cdot)\) 算子计算过程为:
- TLDR:首先通过指数算子使所有元素为正 ,然后执行迭代归一化过程 ,交替重新缩放行和列使其和为 1
- 具体来说,给定一个正矩阵 \(\mathbf{M}^{(0)}=\exp(\tilde{\mathcal{H} }^{\text{res} }_{l})\) 作为起始点,归一化迭代进行如下:
$$\mathbf{M}^{(t)}=\mathcal{T}_{r}\left(\mathcal{T}_{c}(\mathbf{M}^{(t-1)})\right) \tag{9}$$- 其中:
- \(\mathcal{T}_{r}\) 表示行归一化
- \(\mathcal{T}_{c}\) 表示列归一化
- 当 \(t_{\max}\to\infty\) 时,此过程收敛到一个双随机矩阵 \(\mathcal{H}^{\text{res} }_{l}=\mathbf{M}^{(t_{\max})}\)
- 在论文的实验中,论文选择 \(t_{\max}=20\) 作为实际值,所以得到的并不是严格的双随机矩阵
- 其中:
Efficient Infrastructure Design:高效基础设施设计
- 在本节中,论文将详细介绍为 \(m\)HC 定制的基础设施设计
- 通过严格的优化,论文将 \(m\)HC(\(n=4\))实现到大规模模型中,仅产生了 6.7% 的边际训练开销
Kernel Fusion:核融合
- 论文观察到,在 \(m\)HC 中,RMSNorm 在高维隐藏状态 \(\tilde{\mathbf{x} }_{l}\in\mathbb{R}^{1\times nC}\) 上操作时会带来显著的延迟
- 论文重新排序了除以范数的操作,使其在矩阵乘法之后进行
- 这种优化在保持数学等价性的同时提高了效率
- Furthermore
- 论文采用混合精度策略 ,在不影响速度的情况下最大化数值精度
- 并将具有共享内存访问的多个操作融合到统一的计算核中 ,以减少内存带宽瓶颈
- 基于等式 (10) 到 (13) 中详述的输入和参数,论文实现了三个专门的 \(m\)HC 核来计算 \(\mathcal{H}^{\text{pre} }_{l}\)、\(\mathcal{H}^{\text{post} }_{l}\) 和 \(\mathcal{H}^{\text{res} }_{l}\)
- 在这些核中,偏置和线性投影被整合到 \(\mathbf{b}_{l}\) 和 \(\varphi_{l}\) 中,RMSNorm 权重也被吸收到 \(\varphi_{l}\) 中
- 等式 (14) 到 (15):论文开发了一个统一的核,它融合了对 \(\tilde{\mathbf{x} }_{l}\) 的两次扫描,利用矩阵乘法单元最大化内存带宽利用率
- 反向传播——包括两个矩阵乘法——同样被整合到单个核中,消除了对 \(\tilde{\mathbf{x} }_{l}\) 的冗余重新加载
- 两个核都具有微调的流水线(加载、转换、计算、存储),以高效处理混合精度计算
- 等式 (16) 到 (18):这些对小系数的轻量级操作被适时地融合到单个核中,显著减少了核启动开销
- 等式 (19):论文在单个核内实现了 Sinkhorn-Knopp 迭代。对于反向传播,论文推导了一个定制的反向核,该核在芯片上重新计算中间结果并遍历整个迭代
$$
\begin{align}
\varphi_{l}&:\text{tfloat32} \quad [nC,n^{2}+2n]\\
\vec{\mathbf{x} }_{l}&:\text{bfloat16} \quad [1,nC]\\
\alpha^{\text{pre} }_{l},\alpha^{\text{post} }_{l},\alpha^{\text{ res} }_{l}&:\text{float32} \quad \text{Scalars}\\
\mathbf{b}_{l}&:\text{float32} \quad [1,n^{2}+2n]\\
\left[\tilde{\tilde{\mathcal{H} }}^{\text{pre} }_{l},\tilde{\tilde{\mathcal{H} } }^{\text{post } }_{l},\tilde{\tilde{\mathcal{H} }}^{\text{res} }_{l}\right]&:\text{float32} = \vec{\mathbf{x} }_{l}\varphi_{l}\\
r&:\text{float32} = |\vec{\mathbf{x} }_{l}|_{2}/\sqrt{nC}\\
\left[\tilde{\mathcal{H} }^{\text{pre} }_{l},\tilde{\mathcal{H} }^{\text{post } }_{l},\tilde{\mathcal{H} }^{\text{res} }_{l}\right]&:\text{float32} = 1/r\left[\alpha^{\text{pre} }_{l}\tilde{\tilde{\mathcal{H} }}^{\text{pre } }_{l },\alpha^{\text{post} }_{l}\tilde{\tilde{\mathcal{H} }}^{\text{post} }_{l }, \alpha^{\text{res} }_{l}\tilde{\tilde{\mathcal{H} } }^{\text{res} }_{l }\right]+\mathbf{b}_ {l}\\
\mathcal{H}^{\text{pre} }_{l}&:\text{float32} = \sigma\left(\tilde{\mathcal{H} }^{\text{pre} }_{l}\right)\\
\mathcal{H}^{\text{post} }_{l}&:\text{float32} = 2\sigma\left(\tilde{\mathcal{H} }^{\text{post} }_{l}\right)\\
\mathcal{H}^{\text{res} }_{l}&:\text{float32} = \text{Sinkhorn-Knopp}\left(\tilde{\mathcal{H} }^{\text{res} }_{l}\right)
\end{align}
\tag{10-19}
$$
- 等式 (14) 到 (15):论文开发了一个统一的核,它融合了对 \(\tilde{\mathbf{x} }_{l}\) 的两次扫描,利用矩阵乘法单元最大化内存带宽利用率
- 使用从上述核导出的系数,论文引入了两个额外的核来应用这些映射:
- 一个用于 \(\mathcal{F}_{\text{pre} }:=\mathcal{H}^{\text{pre} }_{l}\mathbf{x}_{l}\)
- 另一个用于 \(\mathcal{F}_{\text{post,res} }:=\mathcal{H}^{\text{res} }_{l}\mathbf{x}_{ l}+\mathcal{H}^{\text{posttop} }_{l}\mathcal{F}\left(\cdot,\cdot\right)\)
- 通过将 \(\mathcal{H}^{\text{post} }_{l}\) 和 \(\mathcal{H}^{\text{res} }_{l}\) 的应用与残差合并相融合,论文使该核读取的元素数量从 \((3n+1)C\) 减少到 \((n+1)C\),写入的元素数量从 \(3nC\) 减少到 \(nC\)
- 论文高效地实现了大部分核(不包括等式 (14) 到 (15)),使用 TileLang (2025)
- 该框架简化了具有复杂计算过程的核的实现,并使论文能够以最小的工程工作量充分利用内存带宽
Recomputing:重计算
- \(n\) 流残差设计在训练期间引入了大量的内存开销
- 为了缓解这个问题,论文在前向传播后丢弃 \(m\)HC 核的中间激活,并通过重新执行 \(m\)HC 核(不含繁重的层函数 \(\mathcal{F}\))在反向传播中动态地重新计算它们
- 因此,对于连续的 \(L_{r}\) 层块,论文只需要存储到第一层的输入 \(\mathbf{x}_{l_{0} }\)
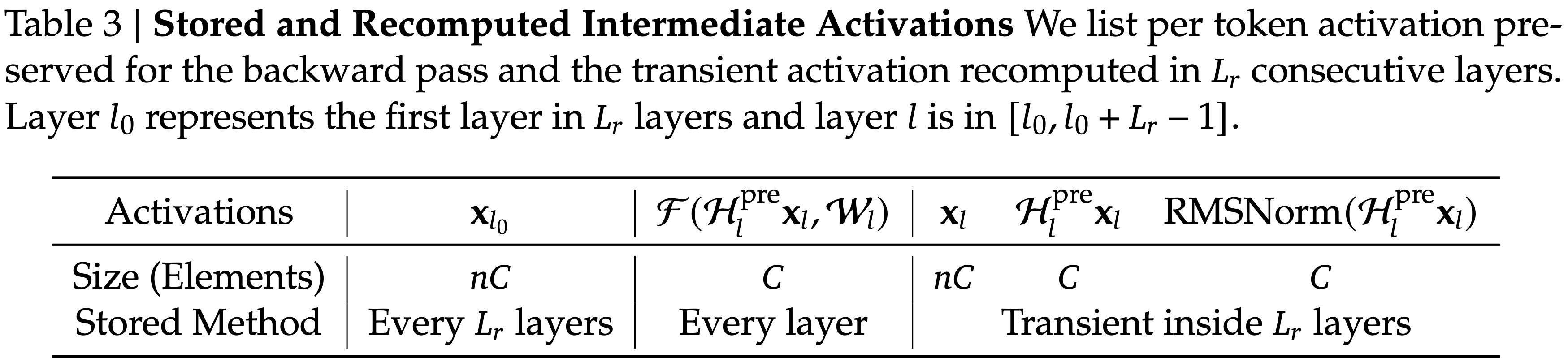
- 排除轻量级系数,同时考虑 \(\mathcal{F}\) 内的预归一化,表 3 总结了为反向传播保留的中间激活
- 由于 \(m\)HC 核的重计算是针对连续的 \(L_{r}\) 层块执行的,给定总共 \(L\) 层,论文必须为反向传播持久存储所有 \(\lceil\frac{L}{L_{r} }\rceil\) 个块的第一层输入 \(\mathbf{x}_{l_{0} }\)
- 除了这个常驻内存,重计算过程为活动块引入了 \((n+2)C\times L_{r}\) 个元素的瞬态内存开销,这决定了反向传播期间的峰值内存使用量
- 因此,论文通过最小化对应于 \(L_{r}\) 的总内存占用来确定最佳块大小 \(L^{*}_{r}\):
$$L^{*}_{r}=\arg\min_{L_{r} }\left[nC\times\left[\frac{L}{L_{r} }\right]+(n+2)C\times L_{r}\right]\approx\sqrt{\frac{nL}{n+2} } \tag{20}$$ - 此外,大规模训练中的流水线并行施加了一个约束:重计算块不得跨越流水线阶段边界
- 观察到理论最优值 \(L^{*}_{r}\) 通常与每个流水线阶段的层数一致,论文选择将重计算边界与流水线阶段同步
Overlapping Communication in DualPipe(在 DualPipe 中重叠通信)
- 在大规模训练中,流水线并行是减轻参数和梯度内存占用的标准实践
- 具体来说,论文采用 DualPipe 调度 (2024b),它有效地重叠了扩展互连通信流量,例如专家并行和流水线并行中的流量
- 然而,与单流设计相比,\(m\)HC 中提出的 \(n\) 流残差在流水线阶段之间产生了大量的通信延迟
- 此外,在阶段边界处,为所有 \(L_{r}\) 层重新计算 \(m\)HC 核引入了不可忽略的计算开销
- 为了解决这些瓶颈,论文扩展了 DualPipe 调度(见图 4),以促进在流水线阶段边界更好地重叠通信和计算
- 图 4: \(m\)HC 的通信-计算重叠 论文扩展了 DualPipe 调度以处理 \(m\)HC 引入的开销
- 每个块的长度仅为示意,不代表实际持续时间
- (F)、(B)、(W) 分别指前向传播、反向传播、权重梯度计算
- \(\mathcal{F}^{\Lambda}\) 和 \(\mathcal{F}^{M}\) 分别代表对应 Attention 和 MLP 的核
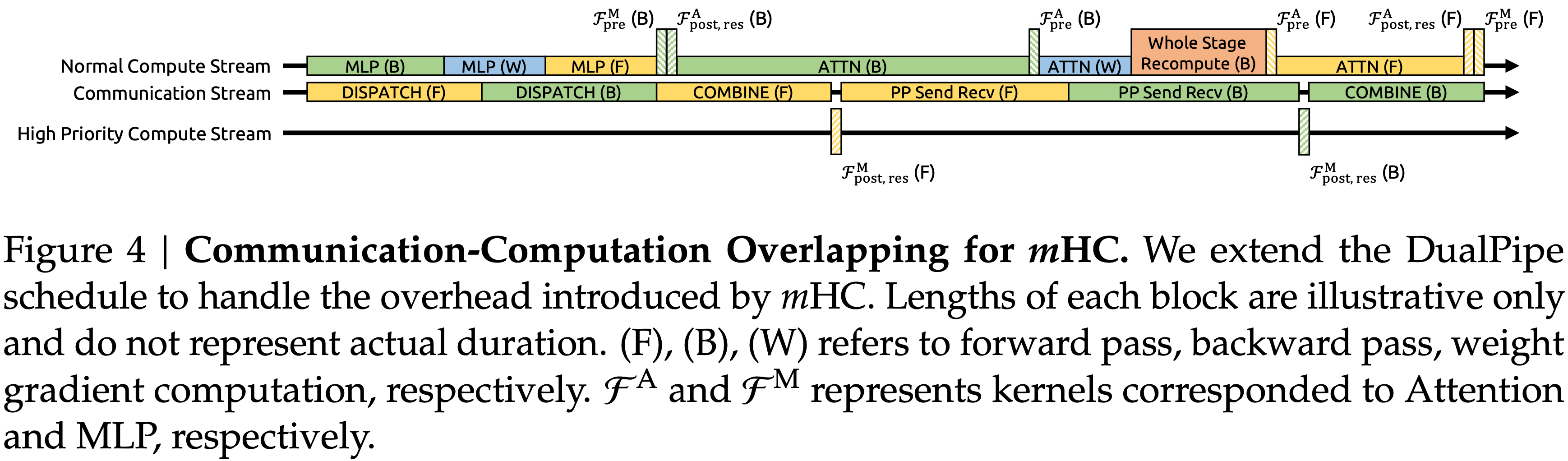
- 图 4: \(m\)HC 的通信-计算重叠 论文扩展了 DualPipe 调度以处理 \(m\)HC 引入的开销
- 值得注意的是,为了防止阻塞通信流,论文在专用高优先级计算流上执行 MLP(即 FFN)层的 \(\mathcal{F}_{\text{post,res} }\) 核
- 论文进一步避免在注意力层中对长时间运行的操作使用持久化核,从而防止长时间的停顿
- 这种设计使得可以抢占重叠的注意力计算,允许灵活的调度,同时保持计算设备处理单元的高利用率
- 此外,重计算过程与流水线通信依赖解耦,因为每个阶段的初始激活 \(\mathbf{x}_{l_{0} }\) 已本地缓存
- 表 3:存储和重计算的中间激活
- 论文列出了为反向传播保留的每 Token 激活,以及在连续的 \(L_{r}\) 层中重计算的瞬态激活
- 层 \(l_{0}\) 表示 \(L_{r}\) 层中的第一层,层 \(l\) 在 \([l_{0},l_{0}+L_{r}-1]\) 区间内
Experiments
Experimental Setup
- 论文通过语言模型预训练来验证所提出的方法,对基线、HC 和论文提出的 \(m\)HC 进行了比较分析
- 利用受 DeepSeek-V3 (2024b) 启发的 MoE 架构,论文训练了四种不同的模型变体以覆盖不同的评估机制
- Specifically,HC 和 \(m\)HC 的扩展率 \(n\) 都设置为 4
- 论文主要关注一个 27B 模型
- 其训练数据集大小与其参数成正比,这作为论文系统级主要结果的对象
- 在此基础上(Expanding on this),论文通过加入按比例数据训练的较小 3B 和 9B 模型来分析计算扩展行为
- 这使论文能够观察不同计算量下的性能趋势
- Additionally,为了专门研究 Token 扩展行为
- 论文在一个固定的 1T Token 语料库上训练了一个单独的 3B 模型
- 详细的模型配置和训练超参数在附录 A.1 中提供
Main Results
- 论文首先检查 27B 模型的训练稳定性和收敛性
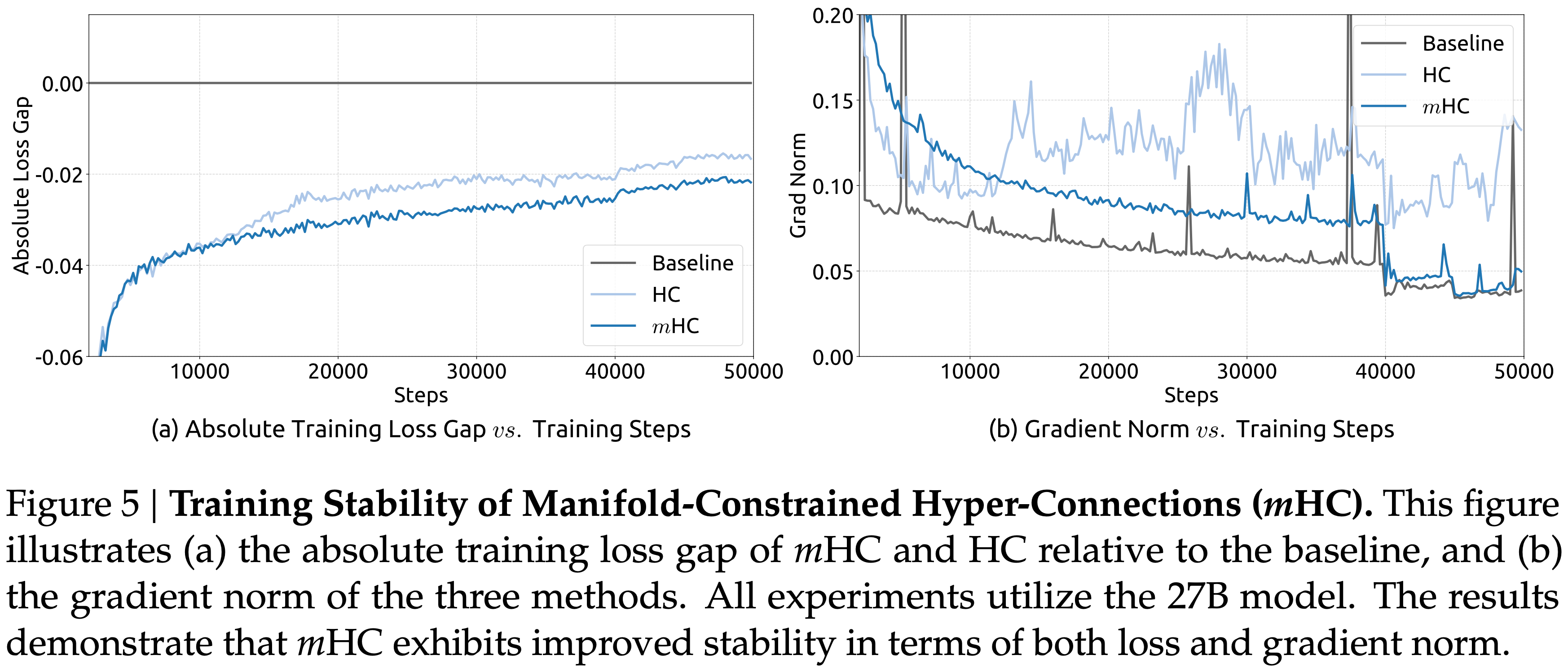
- 如图 5 (a) 所示,\(m\)HC 有效地缓解了 HC 中观察到的训练不稳定性,与基线相比最终损失减少了 0.021
- 图 5 (b) 中的梯度范数分析进一步证实了这种改进的稳定性,其中 \(m\)HC 表现出明显优于 HC 的行为,保持了与基线相当的稳定轮廓
- 图 5:流形约束超连接 (\(m\)HC) 的训练稳定性
- (a) \(m\)HC 和 HC 相对于基线的绝对训练损失差距
- (b) 三种方法的梯度范数
- 所有实验均使用 27B 模型
- 结果表明,\(m\)HC 在损失和梯度范数方面都表现出改进的稳定性
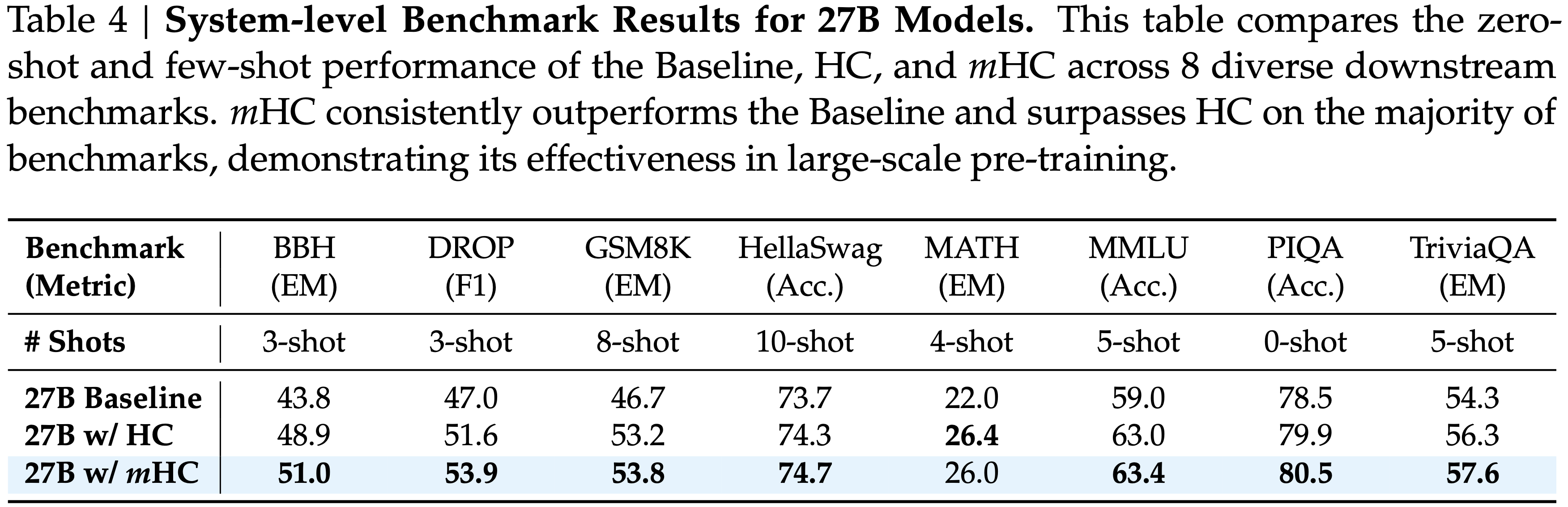
- 表 4 展示了跨多样化基准测试 (2020;2021;2020;2021;2017;2019) 的下游性能
- 比较了 Baseline、HC 和 \(m\)HC 在 8 个多样化下游基准测试上的零样本和少样本性能,\(m\)HC 带来了全面的改进,始终优于 Baseline,并在大多数任务上超过了 HC
- 值得注意的是,与 HC 相比,\(m\)HC 进一步增强了模型的推理能力,在 BBH (2022) 和 DROP (2019) 上分别带来了 2.1% 和 2.3% 的性能增益
- 在大多数基准上超越了 HC,证明了其在大规模预训练中的有效性
Scaling Experiments
- 为了评估论文方法的可扩展性,论文报告了 \(m\)HC 相对于基线在不同规模上的相对损失改进
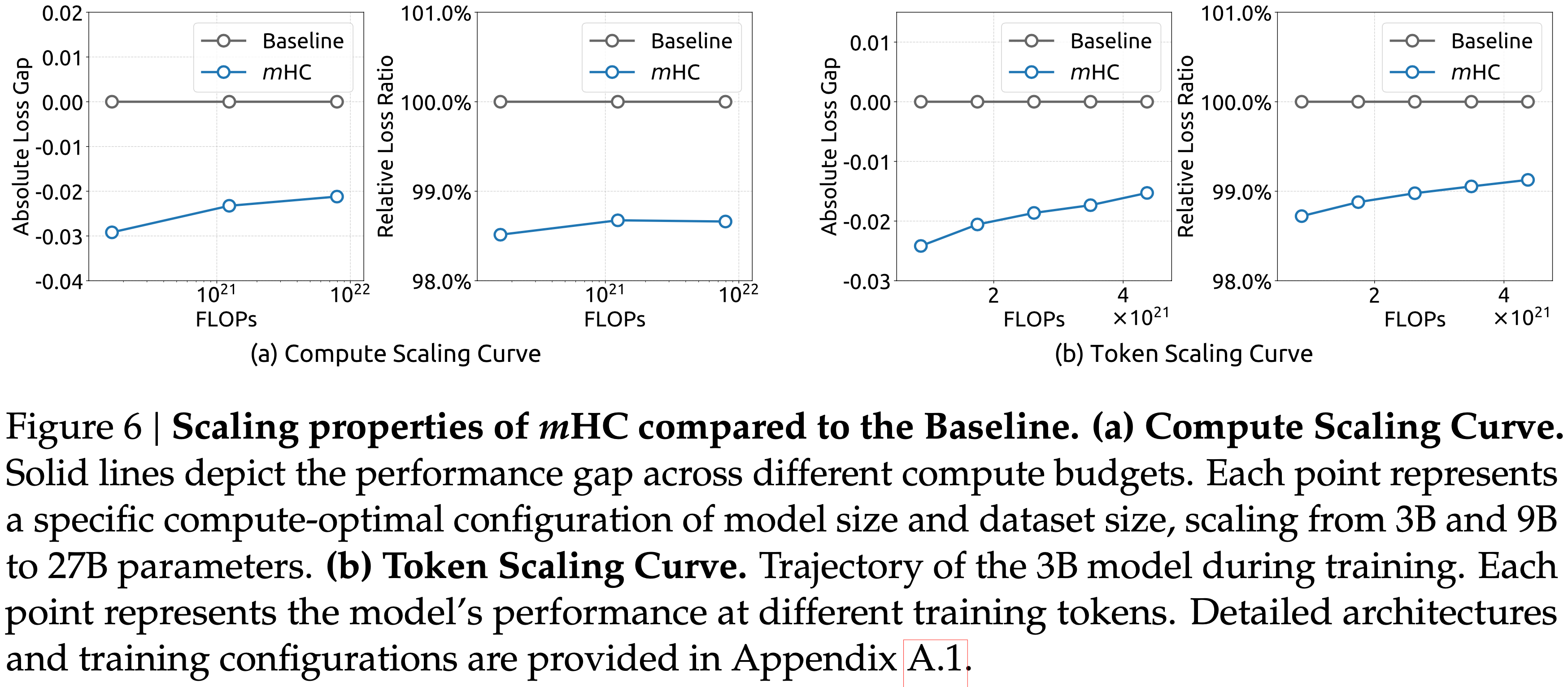
- 图 6: \(m\)HC 相比 Baseline 的扩展特性
- (a) 计算扩展曲线 实线描绘了不同计算预算下的性能差距
- 每个点代表模型大小和数据集大小的特定计算最优配置,从 3B 和 9B 扩展到 27B 参数
- 轨迹表明,即使在更高的计算预算下,性能优势也能稳健地保持,仅表现出轻微的衰减
- (b) Token 扩展曲线 3B 模型在训练期间的表现轨迹(展示了 3B 模型的 Token 扩展曲线)
- 每个点代表模型在不同训练 Token 数下的性能
- 详细的架构和训练配置见附录 A.1
- (a) 计算扩展曲线 实线描绘了不同计算预算下的性能差距
- 总的来说,这些发现验证了 \(m\)HC 在大规模场景中的有效性
- 论文的内部大规模训练实验进一步证实了这一结论
Stability Analysis
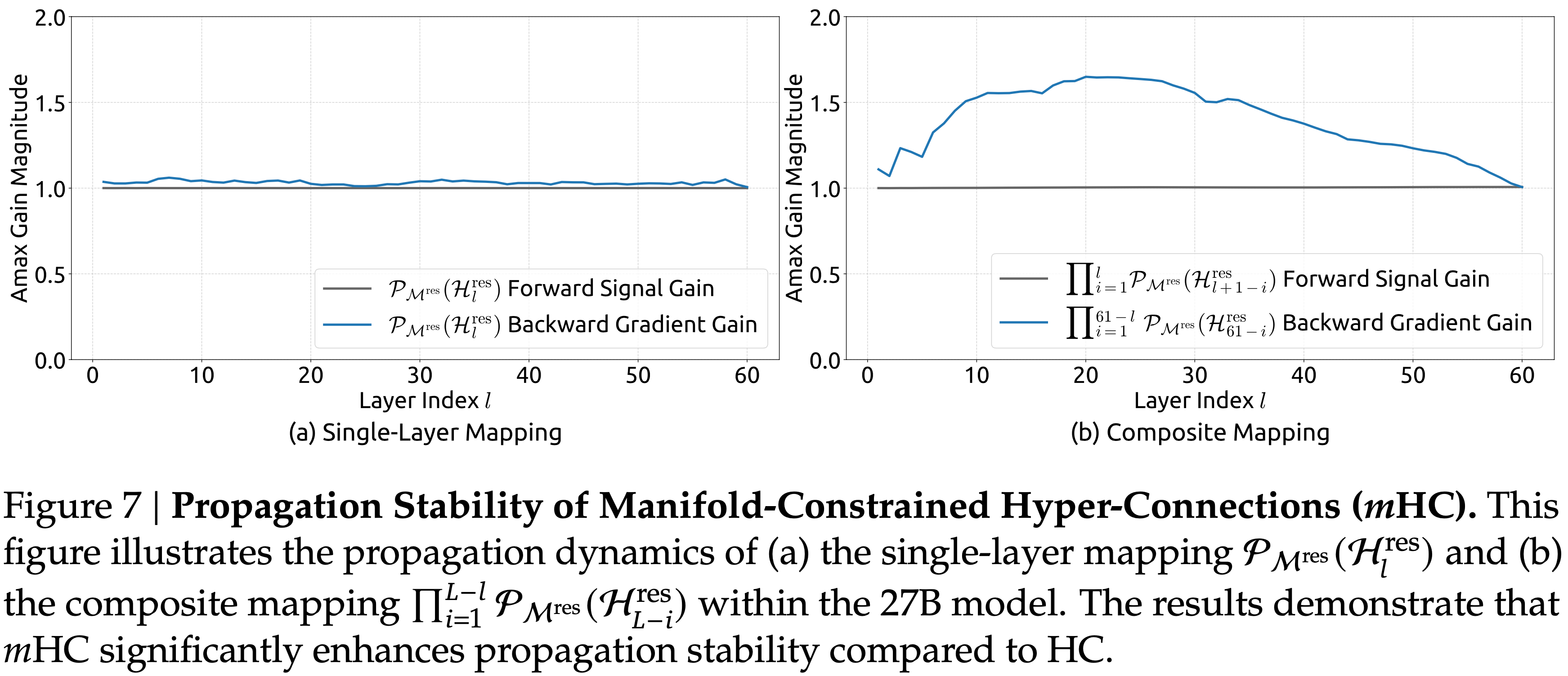
- 与图 3 类似,图 7 展示了 \(m\)HC 的传播稳定性
- Ideally,单层映射满足双随机约束,这意味着前向信号增益和后向梯度增益都应等于 1
- However,实际中使用 Sinkhorn-Knopp 算法的实现必须限制迭代次数以实现计算效率
- 故而论文使用 20 次迭代来获得近似解
- Consequently,图 7 展示了如下结果:
- 如图 7(a) 所示,后向梯度增益略微偏离 1
- 在图 7(b) 所示的复合情况下,偏差增加但仍保持有界,最大值约为 1.6
- Notably,与 HC 中近 3000 的最大增益幅度相比,\(m\)HC 将其降低了三个数量级
- 这些结果表明,与 HC 相比,\(m\)HC 显著增强了传播稳定性,确保了稳定的前向信号和后向梯度流
- 图 7: 流形约束超连接 (\(m\)HC) 的传播稳定性 本图展示了
- (a) 单层映射 \(\mathcal{P}_{\mathcal{M}^{\text{res} } }(\mathcal{H}_{l}^{\text{res} })\)
- (b) 复合映射 \(\prod_{i=1}^{L-l}\mathcal{P}_{\mathcal{M}^{\text{res} } }(\mathcal{H}_{l-i}^{\text {res} })\) 在 27B 模型内的传播动态
- 结果表明,与 HC 相比,\(m\)HC 显著增强了传播稳定性
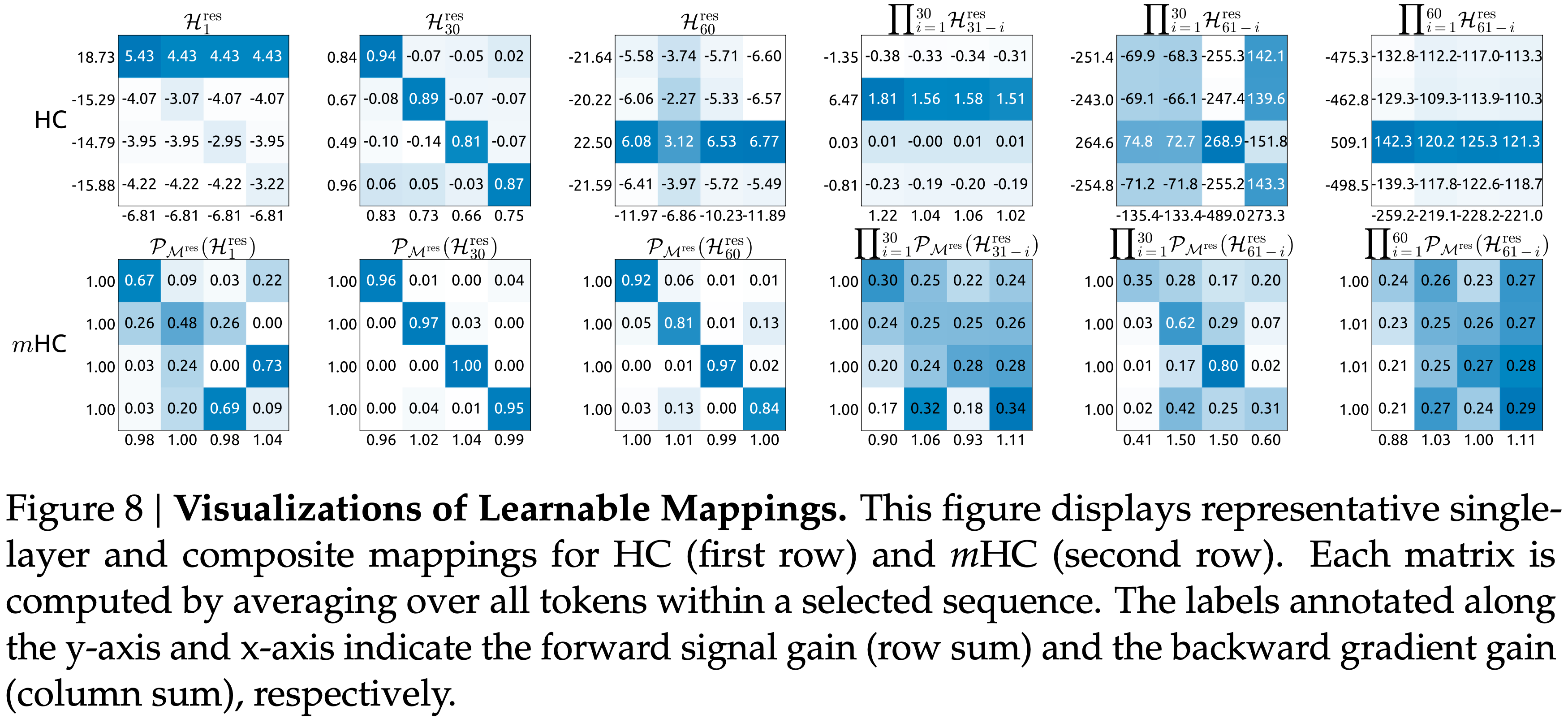
- Additionally,图 8 展示了代表性的映射
- 论文观察到,对于 HC,当最大增益很大时,其他值往往也很大,这表明所有传播路径普遍存在不稳定性
- In Contrast,\(m\)HC 始终产生稳定的结果
- 图 8: 可学习映射的可视化 本图展示了 HC(第一行)和 \(m\)HC(第二行)的代表性单层和复合映射
- 每个矩阵通过平均选定序列内所有 Token 计算得出
- 标注在 y 轴和 x 轴上的标签分别表示前向信号增益(行和)和后向梯度增益(列和)
Outlook
- 作为 HC 范式的通用扩展,\(m\)HC 为未来的研究开辟了几条有前景的途径
- 尽管这项工作利用双随机矩阵来确保稳定性,但该框架允许探索针对特定学习目标定制的多样化流形约束
- 论文预计,对不同几何约束的进一步研究可能会产生新的方法,以更好地优化可塑性和稳定性之间的权衡
- 此外,作者希望 \(m\)HC 能重新激发社区对宏观架构设计的兴趣
- 通过深化对拓扑结构如何影响优化和表示学习的理解,\(m\)HC 将有助于解决当前的局限性,并可能为下一代基础架构的演进照亮新的途径
附录 A.1:详细模型规格和超参数
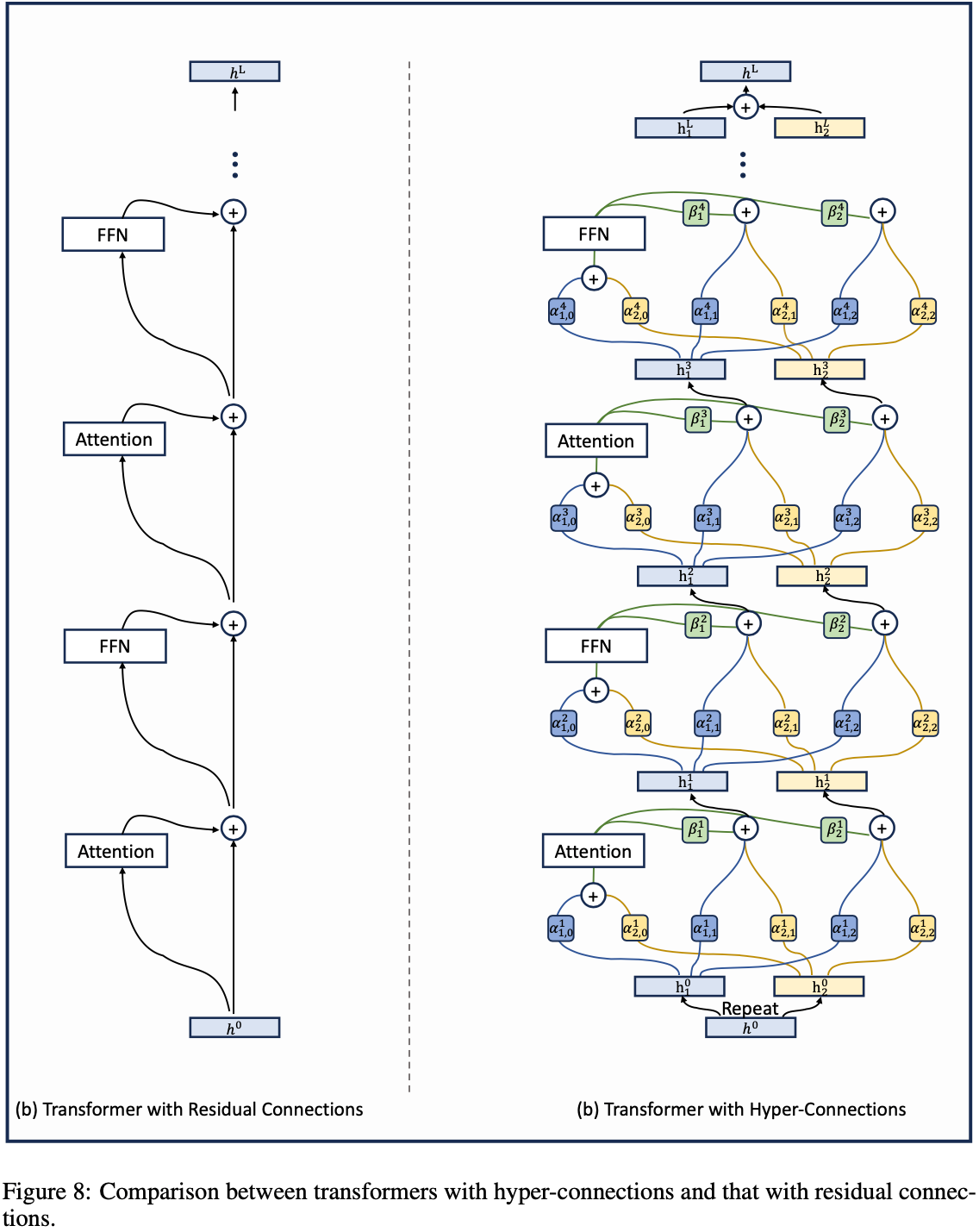
- 表 5: 详细模型规格和超参数
- 本表展示了基于 DeepSeek-V3 (2024b) 架构的 3B、9B 和 27B 模型的架构配置
- 它概述了 mHC 和 HC 的特定超参数,包括残差流扩展和 Sinkhorn-Knopp 设置,以及实验中使用的优化和训练方案
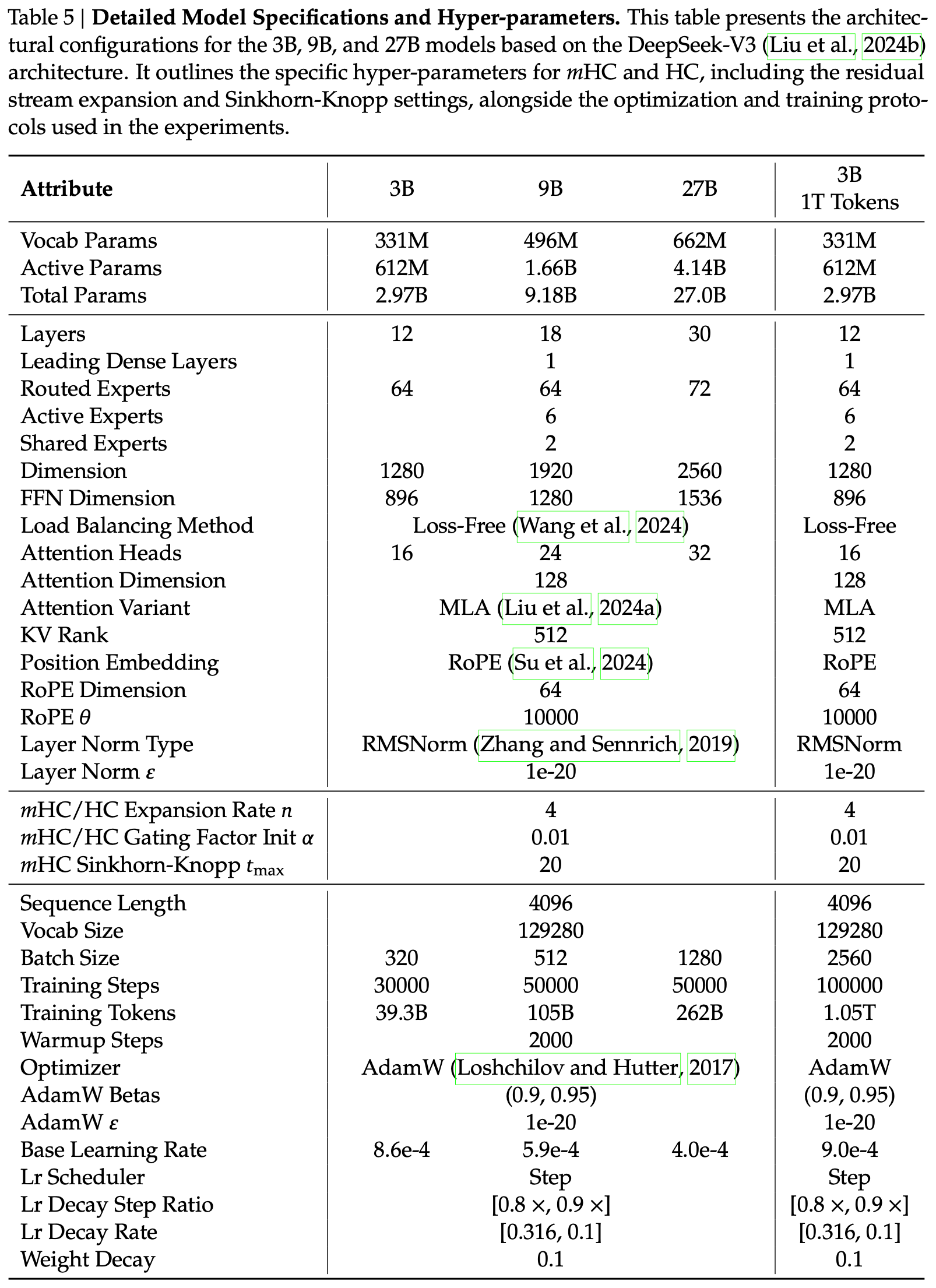
附录:关于 HC 的一些细节
Figure 2:Expansion rate \(n=2\) 的 HC 示意图
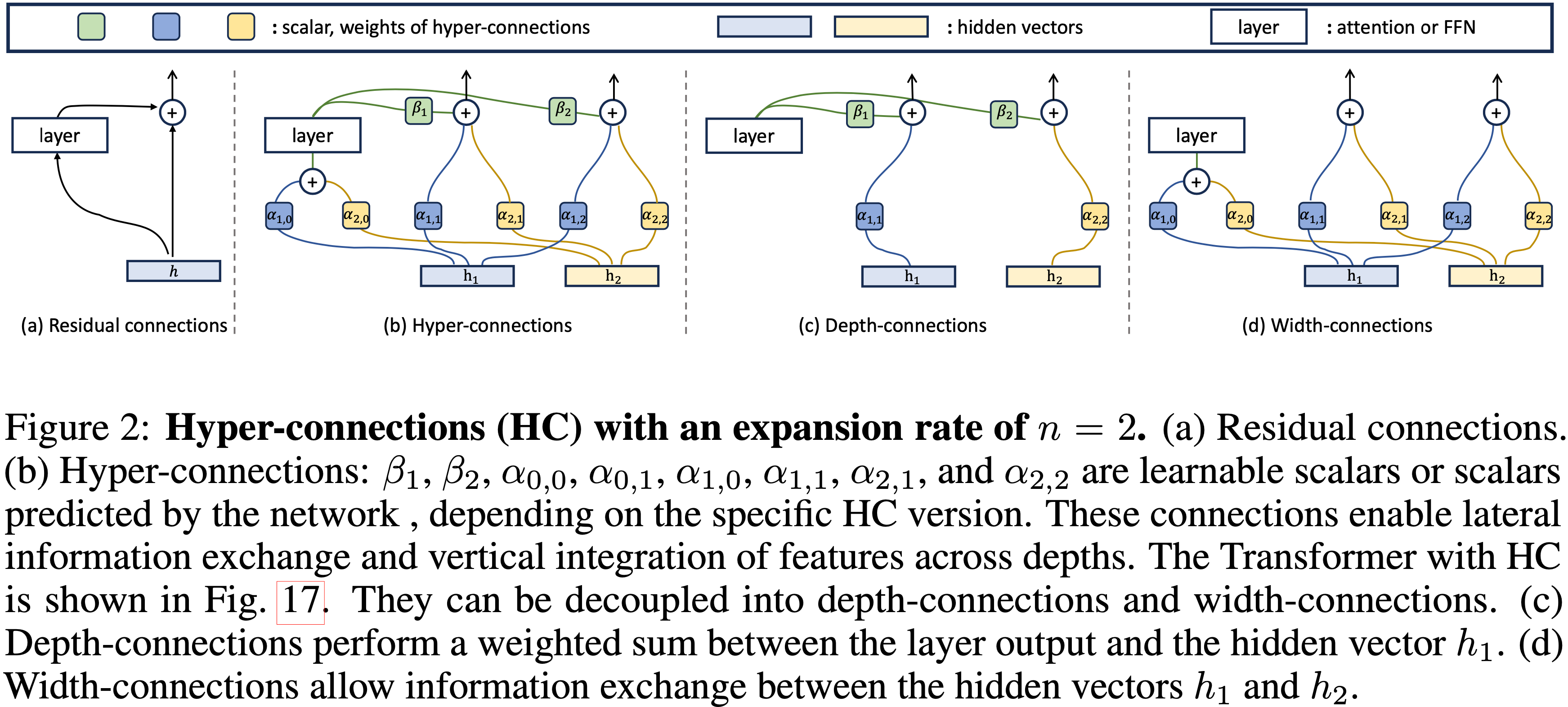
Figure 8: Transformer HC 形式
Algorithm 2:Pseudocode of hyper-connections in a PyTorch-like style.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43# h: hyper hidden matrix (BxLxNxD)
class HyperConnection(nn.Module):
def __init__(self, dim, rate, layer_id, dynamic, device=None):
super(HyperConnection, self).__init__()
self.rate = rate
self.layer_id = layer_id
self.dynamic = dynamic
self.static_beta = nn.Parameter(torch.ones((rate,), device=device))
init_alpha0 = torch.zeros((rate, 1), device=device)
init_alpha0[layer_id % rate, 0] = 1.
self.static_alpha = nn.Parameter(torch.cat([init_alpha0, torch.eye((rate), device=device)], dim=1))
if self.dynamic:
self.dynamic_alpha_fn = nn.Parameter(torch.zeros((dim, rate+1), device=device))
self.dynamic_alpha_scale = nn.Parameter(torch.ones(1, device=device) * 0.01)
self.dynamic_beta_fn = nn.Parameter(torch.zeros((dim, ), device=device))
self.dynamic_beta_scale = nn.Parameter(torch.ones(1, device=device) * 0.01)
self.layer_norm = LayerNorm(dim)
def width_connection(self, h):
# get alpha and beta
if self.dynamic:
norm_h = self.layer_norm(h)
if self.dynamic:
wc_weight = norm_h @ self.dynamic_alpha_fn
wc_weight = F.tanh(wc_weight)
dynamic_alpha = wc_weight * self.dynamic_alpha_scale
alpha = dynamic_alpha + self.static_alpha[None, None, ...]
else:
alpha = self.static_alpha[None, None, ...]
if self.dynamic:
dc_weight = norm_h @ self.dynamic_beta_fn
dc_weight = F.tanh(dc_weight)
dynamic_beta = dc_weight * self.dynamic_beta_scale
beta = dynamic_beta + self.static_beta[None, None, ...]
else:
beta = self.static_beta[None, None, ...]
# width connection
mix_h = alpha.transpose(-1, -2) @ h
return mix_h, beta
def depth_connection(self, mix_h, h_o, beta):
h = torch.einsum("blh,bln->blnh", h_o, beta) + mix_h[..., 1:, :]
return hAlgorithm3:Pseudocode of transformer with hyper-connections in a PyTorch-like style.
1
2
3
4
5
6
7
8
9
10
11
12
13# h: hyper hidden matrix (BxLxNxD)
# atten_hyper_connection, ffn_hyper_connection: hyper-connection modules
# attn_norm, ffn_norm: normalization modules
# Attention Block
mix_h, beta = atten_hyper_connection.width_connection(h)
h = attn_norm(mix_h[...,0,:])
h = self_attention(h)
h = atten_hyper_connection.depth_connection(mix_h, dropout(h), beta)
# FFN Block
mix_h, beta = ffn_hyper_connection.width_connection(h)
h = ffn_norm(mix_h[...,0,:])
h = ffn(h)
h = ffn_hyper_connection.depth_connection(mix_h, dropout(h), beta)
附录:Manifold(流形)
- 在数学和理论计算机科学(如几何深度学习、流形学习)中,Manifold(流形)是一个核心概念,它是局部欧几里得的拓扑空间
- 一个 \(n\) 维流形( \(n\)-dimensional manifold) \(M\) 是满足以下条件的豪斯多夫拓扑空间(Hausdorff topological space):
- 存在一个开覆盖 \(\{U_\alpha\}_{\alpha\in A}\),即 \(M = \bigcup_{\alpha\in A} U_\alpha\)
- 对每个 \(U_\alpha\),存在一个同胚 (Homeomorphism)(即连续双射且逆连续) \(\phi_\alpha: U_\alpha \to V_\alpha\),其中 \(V_\alpha\) 是 \(\mathbb{R}^n\) 中的开集
- 注:豪斯多夫拓扑空间 :也称为 \(T_2\) 空间,是拓扑学中最基础且应用最广泛的一类拓扑空间,其核心特征是空间中任意两个不同的点,都可以被两个不相交的开集分别 “包围”
- 注:同胚 是拓扑学中的核心概念,描述的是两个拓扑空间之间的一种 “连续且可逆的连续” 映射关系,直观上可以理解为:两个空间可以通过连续的拉伸、扭曲、弯曲(但不能撕裂、粘连或打孔)相互转化
- 这个二元组 \((U_\alpha, \phi_\alpha)\) 称为坐标卡(chart),所有坐标卡的集合 \({(U_\alpha, \phi_\alpha)}_{\alpha\in A}\) 称为图册(atlas)
关于 Manifold 的关键数学表达式
(1)局部欧几里得性的形式化
- 对任意 \(p \in M\),存在 \(p\) 的开邻域 \(U \subset M\) 和同胚映射 \(\phi: U \to \phi(U) \subset \mathbb{R}^n\),即
$$
\phi: U \xrightarrow{\text{同胚}} \phi(U) \subset \mathbb{R}^n
$$- 其中 \(\phi(U)\) 是 \(\mathbb{R}^n\) 中的开集,\(n\) 称为流形 \(M\) 的维数
(2)坐标卡的相容性(光滑流形的附加条件)
- 若流形 \(M\) 是光滑流形 ,则其图册中任意两个重叠的坐标卡 \((U_\alpha, \phi_\alpha)\) 和 \((U_\beta, \phi_\beta)\)(满足 \(U_\alpha \cap U_\beta \neq \emptyset\))的转移映射
$$
\phi_{\beta\alpha} = \phi_\beta \circ \phi_\alpha^{-1}: \phi_\alpha(U_\alpha \cap U_\beta) \to \phi_\beta(U_\alpha \cap U_\beta)
$$- 是 \(\mathbb{R}^n\) 上的光滑函数( \(C^\infty\) 函数)
(3)流形的嵌入(示例:黎曼流形)
- 若 \(M\) 是黎曼流形 ,则它配备了一个光滑的正定对称二阶协变张量场 \(g\)(黎曼度量,Riemannian Metric),对任意 \(p \in M\) 和切向量 \(v, w \in T_pM\)( \(p\) 点的切空间(Tangent Space)),黎曼度量给出内积
$$
g_p(v, w) = \langle v, w \rangle_p
$$ - 满足正定性 \(g_p(v, v) \geq 0\),且等号当且仅当 \(v = 0\) 成立
Manifold 在 NLP/LLM 中的应用场景
- 在大模型相关研究中,流形的核心应用是流形假设(Manifold Hypothesis):
- 高维数据(如词嵌入、句嵌入)实际上分布在低维流形上,而非整个高维欧几里得空间
- 公式化表述:若 \(X \subset \mathbb{R}^D\) 是高维数据空间,存在 \(n \ll D\) 维流形 \(M\),使得 \(X \subset M\)
- 这一假设是对比学习、降维算法(如 t-SNE、UMAP)和几何深度学习的理论基础