NLP——LLM位置编码

本文主要介绍LLM的各种编码方式

• 参考链接：
  • 再论大模型位置编码及其外推性（万字长文）
  • 十分钟读懂旋转编码（RoPE）
  • 位置编码之路：SIN->ALiBi->RoPE ->PI->NKT->YARN
  • 旋转式位置编码 (RoPE) 知识总结 - Soaring的文章 - 知乎
  • Transformer升级之路：10、RoPE是一种β进制编码
  • 从ROPE到Yarn, 一条通用公式速通长文本大模型中的位置编码 - Whisper的文章 - 知乎

---

整体介绍

• 位置编码 ：Position Encoding，一些地方也叫作 Positional Encoding，由于一般是一个向量的形式，所以在很多文章中也叫作Postion Embedding，一般简写为PE
  • 个人理解：可学习时使用Postion Embedding合适，不可学习时使用Postion Encoding合适
• 常用位置编码 ：当前常用的位置编码方式有固定位置编码、正弦位置编码(Sinusoidal)、旋转位置编码(RoPE)、相对位置编码(AliBi)等
• 外推性含义 ：是指模型在预测时，处理超过模型训练长度的能力。外推性越好，则模型对于长度越不敏感，即可以在更长/未训练过的长度上预测

---

为什么需要位置编码？

• 根据Self-Attention的基本逻辑，Self-Attention不关注顺序，只关注表示q,k,v向量本身
• 在没有位置编码的情况下：
  • 假设输入是 \([a^0,b^0,c^0,d^0]\)，那么第1次Self-Attention的输出是 \([a^1,b^1,c^1,d^1]\)，同理，第t次Attention的输出是 \([a^t,b^t,c^t,d^t]\)
  • 假设输入是 \([a^0,c^0,b^0,d^0]\)，那么第1次Self-Attention的输出是 \([a^1,c^1,b^1,d^1]\)，同理，第t次Attention的输出是 \([a^t,c^t,b^t,d^t]\)
• 显然， \([a^0,b^0,c^0,d^0]\) 和 \([a^0,c^0,b^0,d^0]\) 无数次Self-Attention以后的结果只有序的差别，而Transformer本身主要就是许多层的Self-Attention组成的
• 如果在模型的最后一层我们增加了一个全连接层去实现一个文本分类，显然对模型来说想学到两者的序的差别是困难的（注意不是完全学不到，只是比较困难）
• 如果在Self-Attention之前或Self-Attention的过程中就考虑位置，那么 \([a^0,b^0,c^0,d^0]\) 和 \([a^0,c^0,b^0,d^0]\) 每次Self-Attention后的结果都会差异较大，随着Self-Attention次数的增多，模型可以用复杂的参数学到位置信息
• Causal Decoder（Transformer的Decoder部分）模型中，由于存在Mask，此时的Self-Attention不再是对称的，此时每一层Masked Self-Attention自然就有一定的位置信息。（因此有些研究文章也提到Causal Decoder不需要位置编码）
• Transformer中Encoder和Decoder都有位置编码
• 个人理解：
  • 增加位置编码至少不会带来坏处
  • 即使模型能区分位置，也不代表增加位置编码没有收益，因为显示增加位置编码会降低模型学习的难度（相当于是一个强特征，这对模型很重要）

---

固定位置编码

• 具体实现：对每个位置 \(i\) 初始化一个可学习的参数向量 \(\boldsymbol{p}_i\)，然后在输入的向量 \(\boldsymbol{x}_i\) 中加入这个向量，训练过程中更新位置向量
  $$
  \boldsymbol{x}_i = \boldsymbol{x}_i + \boldsymbol{p}_i
  $$
  • 由于是可学习的向量，也叫作Position Embedding
  • 注：在很多文献中，也称正弦位置编码为固定位置编码
• BERT 中使用了这种编码方式，这种位置编码方式，最大的缺点是无法外推

---

正弦位置编码

• 正弦位置编码，即Sinusoidal Positional Encoding（由于此处位置编码是不可学习的向量，所以使用Encoding而不是Embedding），最早在 Transformer 原始论文中提出
• 由于正弦位置编码实际上每个位置也是固定的，所以很多文献也称正弦位置编码为固定位置编码
• Transformer的原生位置编码方式
• 每个token的位置的编码是提前固定的，不可学习的
• 使用了Sinusoidal函数，即正弦曲线函数，所以也叫作也叫作Sinusoidal位置编码
• 具体来说把每个位置编码为一个向量 \(\boldsymbol{p}_i\)：
  $$
  p_{pos,2i} = sin\left(\frac{pos}{10000^{2i/\text{d_model}}}\right) \\
  p_{pos,2i+1} = cos\left(\frac{pos}{10000^{2i/\text{d_model}}}\right) \\
  $$
  • \(pos \in [0,\text{seq_len}]\) 是 token 的位置，表示第 \(pos\) 个 token，为了方便书写和理解，下文中也使用 \(t\) 表示位置
  • \(i \in [0,\frac{d}{2}]\) 是 Embedding 维度，表示第 \(i\) 个 Embedding 维度
• 展开来看有：
  $$
  \begin{equation} \boldsymbol{p}_{pos} = \begin{pmatrix}\sin (pos\cdot\theta_0) \\ \cos (pos\cdot\theta_0) \\ \sin (pos\cdot\theta_1) \\ \cos (pos\cdot\theta_1) \\ \vdots \\ \sin (pos\cdot\theta_{d/2-1}) \\ \cos (pos\cdot\theta_{d/2-1})
  \end{pmatrix}, \quad \theta_i = \frac{1}{10000^{2i/\text{d_model}}}
  \end{equation}
  $$
• 在输入层将位置向量添加到输入中
  $$
  \boldsymbol{x}_t = \boldsymbol{x}_t + \boldsymbol{p}_t
  $$
• 特点1：位置向量 \(\boldsymbol{p}_{t+k}\) 可以由 \(\boldsymbol{p}_{i}\) 和 \(\boldsymbol{p}_{k}\) 表示得到（使用三角函数的性质即可证明），以下证明来源于：再论大模型位置编码及其外推性（万字长文）（注：文章中认为 “其中u, v为关于k的常数，所以可以证明PE(t+k)可以由PE(i)线性表示。”这句话理解有误，实际上位置向量 \(\boldsymbol{p}_{t+k}\) 需要由 \(\boldsymbol{p}_{i}\) 和 \(\boldsymbol{p}_{k}\) 共同表示）
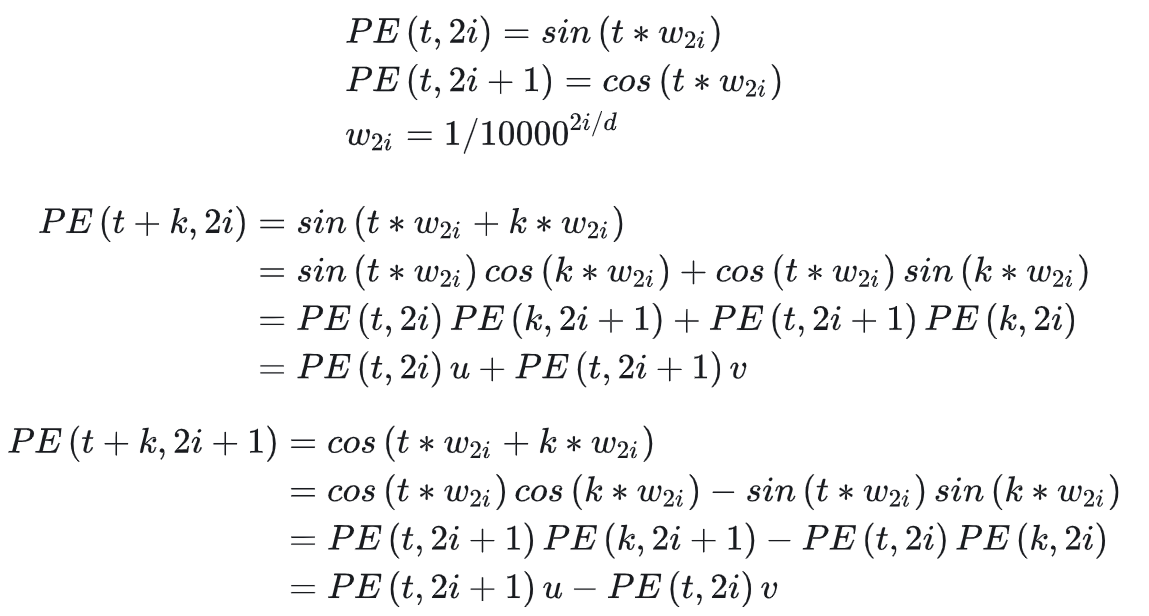
• 特点2：任意两个位置向量的乘积只与他们之间的距离有关 ：以下证明最后一步可以通过下面的三角函数公式 \(cos(\alpha-\beta)=cos\alpha \cdot cos\beta+sin\alpha \cdot sin\beta\) 得到（注：三角函数的变换公式可参考：考生必记：三角函数公式汇总+记忆（没有比这更全））
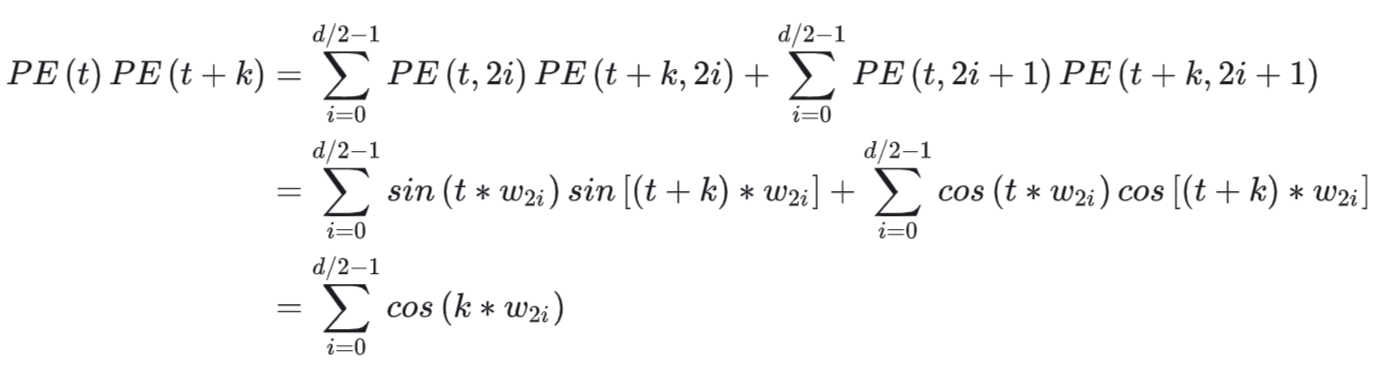
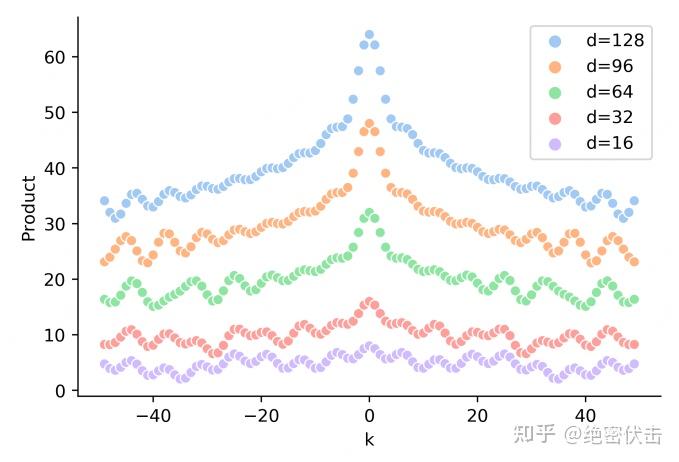
• 特点3：随着相对距离增加，位置向量的内积逐渐减小，有衰减趋势（这里是波动衰减，不是单调的），下图参考自再论大模型位置编码及其外推性（万字长文）
• 训练/预估时同一个批次的队列的token长度需要相同，不足最大长度的需要padding
  • 仔细观察原始公式可以知道，对于固定的位置 \(pos\)，随着维度 \(i \in [0,\frac{d}{2}-1]\) 的逐步增大 \(i = 0 \rightarrow \frac{d}{2}\)（注：取不到\(\frac{d}{2}\)），角度变化为：
    $$
    \begin{align}
    2i/\text{d_model} &\in [0,1), \quad 0 \rightarrow 1\\
    10000^{2i/\text{d_model}} &\in [1,10000), \quad 1 \rightarrow 10000\\
    \frac{pos}{10000^{2i/\text{d_model}}} &\in [pos,\frac{pos}{10000}), \quad pos \rightarrow \frac{pos}{10000}
    \end{align}
    $$
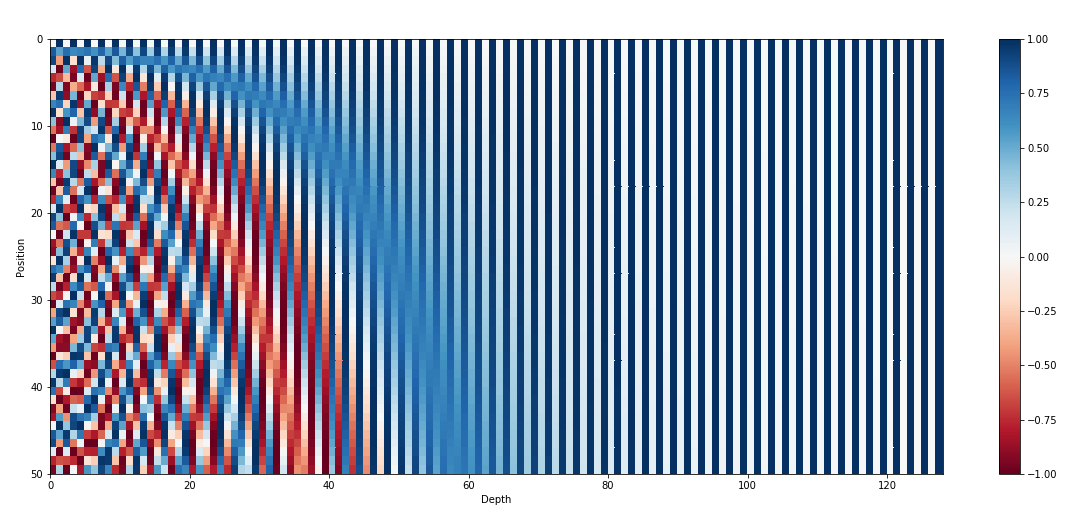
  • 按照行（位置）作比较来看，不同行（位置）的表示角度范围不同（这里指 sin/cos 内部角度的范围），位置越大，角度范围越大，经历的周期越多
  • 按照列（d_model维度）作比较来看，不同列的周期不同，列对应的维度位置 \(i\) 越高，频率越低，周期越小
  • 同一列内部来看，sin/cos函数的角度 \(\frac{pos}{10000^{2i/\text{d_model}}}\) 从上往下单调递增 ，（ \(pos\) 单调递增，导致 \(\frac{pos}{10000^{2i/\text{d_model}}}\) 单调递增）
  • 同一行内部来看，sin/cos函数的角度 \(\frac{pos}{10000^{2i/\text{d_model}}}\) 从左往右单调递减 ，（ \(i\) 单调递增，导致 \(\frac{pos}{10000^{2i/\text{d_model}}}\) 单调递减）
• \(\frac{pos}{10000^{2i/\text{d_model}}}\) 中的base=10000，base的取值实际上决定的是周期，base越大，周期越大，频率越小
  • 再论大模型位置编码及其外推性（万字长文）中提到，base越大，编码中的重复值越少，有一定的道理。但是换个角度想，只要base不是特别小，不同位置的向量都会不同，不会出现两个位置的编码重复即可

---

相对位置编码

• 原始论文：Self-Attention with Relative Position Representations, 2018, Google
• 核心思路：把相对位置信息加到 V 上或 K 上
• 原始 Attention：
  $$\alpha_{i,j} = \text{Softmax}(\boldsymbol{q}_i \boldsymbol{k}_j^\top)\\
  \boldsymbol{o}_i = \sum_j \alpha_{i,j} \boldsymbol{v}_j\\$$
• 相对位置编码下的 Attention，相对位置信息加到 V 上（为了方便解释，使用的符号和原始论文不完全相同）：
  $$\alpha_{i,j} = \text{Softmax}(\boldsymbol{q}_i \boldsymbol{k}_j^\top)\\
  \boldsymbol{o}_i = \sum_j \alpha_{i,j} (\boldsymbol{x}_j \boldsymbol{W}^V + \boldsymbol{R}_{i,j}^V)$$
  • 其中 \(\boldsymbol{R}_{i,j}^V\) 是一个与相对位置 \(i-j\) 有关的矩阵
  • 本质是把位置编码增加到了 V 上，作为对比，原始 Attention 的输出为：\(\boldsymbol{o}_i = \sum_j \alpha_{i,j}(\boldsymbol{x}_j \boldsymbol{W}^V)\)
• 相对位置编码下的 Attention，相对位置信息加到 K 上：
  $$\alpha_{i,j} = \text{Softmax}(\boldsymbol{q}_i (\boldsymbol{x}_j \boldsymbol{W}^K + \boldsymbol{R}_{i,j}^K)^\top)\\
  \boldsymbol{o}_i = \sum_j \alpha_{i,j} \boldsymbol{v}_j\\$$
  • 其中 \(\boldsymbol{R}_{i,j}^K\) 是一个与相对位置 \(i-j\) 有关的矩阵

---

RoPE-旋转位置编码

• RoPE，Rotary Position Embedding，旋转位置编码
• 论文只是简单介绍，详细情况参见：NLP——旋转位置编码-RoPE

基本思想

• 基本思路：通过将旋转位置编码（对每个位置的token输入向量进行旋转，旋转角度与位置有关），实现相对位置编码的能力
• 本质：不再将位置向量直接加到原始输入向量中，而是在Attention的时候同时考虑位置，根据不同的两个位置进行不同的Attention（实际上是在Attention中Query和Key的内积中考虑位置信息）
  • 理解：这个思路其实没问题，因为当前我们输入向量都要经过Attention的，只要Attention中考虑了位置，就能保证模型能考虑到位置

位置嵌入过程

• 旋转位置编码(RoPE)的核心思想 ：通过旋转矩阵将绝对位置信息融入Self-Attention机制中
• 基本定义 ：对于位置\( m \)的词向量\( \boldsymbol{x}_m \in \mathbb{R}^d \)，通过线性变换得到查询向量\( \boldsymbol{q}_m \)和键向量\( \boldsymbol{k}_n \)：
  $$
  \boldsymbol{q}_m = W_q \boldsymbol{x}_m, \quad \boldsymbol{k}_n = W_k \boldsymbol{x}_n
  $$
• 旋转操作 ：将\( \boldsymbol{q}_m \)和\( \boldsymbol{k}_n \)划分为\( d/2 \)个复数对（每组2维），对第\( i \)组复数应用旋转矩阵：
  $$
  \begin{aligned}
  \boldsymbol{q}_m^{(i)} &= \begin{pmatrix}
  q_{m,2i} \\
  q_{m,2i+1}
  \end{pmatrix}, \quad
  \boldsymbol{k}_n^{(i)} = \begin{pmatrix}
  k_{n,2i} \\
  k_{n,2i+1}
  \end{pmatrix} \\
  R_{\theta_i}^m &= \begin{pmatrix}
  \cos m\theta_i & -\sin m\theta_i \\
  \sin m\theta_i & \cos m\theta_i
  \end{pmatrix}, \quad \theta_i = 10000^{-2i/d}
  \end{aligned}
  $$
  • 注意：位置为 \(m\) 的旋转矩阵对应正余弦角度为 \(\color{red}{m}\theta_i\)
• 旋转后的向量 ：旋转后的查询和键向量为：
  $$
  \begin{aligned}
  \boldsymbol{q}_m’ = \bigoplus_{i=0}^{d/2-1} R_{\theta_i}^m \boldsymbol{q}_m^{(i)}, \quad
  \boldsymbol{k}_n’ = \bigoplus_{i=0}^{d/2-1} R_{\theta_i}^n \boldsymbol{k}_n^{(i)}
  \end{aligned}
  $$
  • 其中\( \oplus \)表示向量拼接：
    $$\bigoplus_{i=0}^{d/2-1} R_{\theta_i}^m \boldsymbol{q}_m^{(i)} = \text{Concat}(\{ R_{\theta_i}^m \boldsymbol{q}_m^{(i)}\}_{i=0}^{d/2-1})$$
• 旋转后的Attention权重变化
  $$
  \begin{equation}
  (\boldsymbol{\mathcal{R}}_m \boldsymbol{q}_m)^{\top}(\boldsymbol{\mathcal{R}}_n \boldsymbol{k}_n) = \boldsymbol{q}_m^{\top} \boldsymbol{\mathcal{R}}_m^{\top}\boldsymbol{\mathcal{R}}_n \boldsymbol{k}_n = \boldsymbol{q}_m^{\top} \boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{k}_n
  \end{equation}
  $$
  • 位置为 \(m\) 的向量 \(\boldsymbol{q}_m\) 乘以矩阵 \(\boldsymbol{\mathcal{R}}_m\)；位置为 \(n\) 的向量 \(\boldsymbol{k}_n\) 乘以矩阵 \(\boldsymbol{\mathcal{R}}_n\)（注意角标）
  • 上面的式子中等式是恒成立的（详细证明见 NLP——旋转位置编码-RoPE），右边的 \(\boldsymbol{\mathcal{R}}_{n-m}\)仅与相对位置 \(n-m\) 有关，体现了相对位置编码的核心要义
    • 注：\(\boldsymbol{\mathcal{R}}_{m-n}\) 和 \(\boldsymbol{\mathcal{R}}_{n-m}\) 不相等，旋转角度相同，但方向相反
• 展开成矩阵相乘的形式为（refer to Transformer升级之路：2、博采众长的旋转式位置编码）：
  $$
  \begin{equation}\scriptsize{\underbrace{\begin{pmatrix}
  \cos m\theta_0 & -\sin m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\
  \sin m\theta_0 & \cos m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\
  0 & 0 & \cos m\theta_1 & -\sin m\theta_1 & \cdots & 0 & 0 \\
  0 & 0 & \sin m\theta_1 & \cos m\theta_1 & \cdots & 0 & 0 \\
  \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
  0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2-1} & -\sin m\theta_{d/2-1} \\
  0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2-1} & \cos m\theta_{d/2-1} \\
  \end{pmatrix}}_{\boldsymbol{\mathcal{R}}_m} \begin{pmatrix}q_0 \\ q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_{d-2} \\ q_{d-1}\end{pmatrix}}\end{equation}
  $$
• 由于旋转矩阵是一个稀疏矩阵，所以旋转过程可以改进为如下等价实现：
  $$
  \begin{equation}\begin{pmatrix}q_0 \\ q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_{d-2} \\ q_{d-1}
  \end{pmatrix}\otimes\begin{pmatrix}\cos m\theta_0 \\ \cos m\theta_0 \\ \cos m\theta_1 \\ \cos m\theta_1 \\ \vdots \\ \cos m\theta_{d/2-1} \\ \cos m\theta_{d/2-1}
  \end{pmatrix} + \begin{pmatrix}-q_1 \\ q_0 \\ -q_3 \\ q_2 \\ \vdots \\ -q_{d-1} \\ q_{d-2}
  \end{pmatrix}\otimes\begin{pmatrix}\sin m\theta_0 \\ \sin m\theta_0 \\ \sin m\theta_1 \\ \sin m\theta_1 \\ \vdots \\ \sin m\theta_{d/2-1} \\ \sin m\theta_{d/2-1}
  \end{pmatrix}\end{equation}
  $$
  • 其中 \(\otimes\) 是按位相乘
• RoPE下的Attention公式总结 ：（旋转位置编码的核心公式）
  $$
  \begin{aligned}
  \text{Attention}(\boldsymbol{x}) &= \text{softmax}\left(\frac{(\boldsymbol{q}’)^\top \boldsymbol{k}’}{\sqrt{d} }\right)V
  \end{aligned}
  $$

旋转体现在哪里？

• 旋转体现在 \(\boldsymbol{q}_m\)（或\(\boldsymbol{k}_n\)） 的每两个维度组成的向量 \(\boldsymbol{q}_m^{(i)} = \begin{pmatrix} q_{m,2i} \\ q_{m,2i+1} \end{pmatrix}\) 经过 RoPE 变换前后，他们的向量长度不变，即：
  $$
  \begin{pmatrix}cos(m\theta_1) &-sin(m\theta_1) \\ sin(m\theta_1) &cos(m\theta_1)\end{pmatrix} \begin{pmatrix}q_{m,2i} \\ q_{m,2i+1}\end{pmatrix} = \begin{pmatrix}q_{m,2i}\cdot cos(m\theta_1) -q_{m,2i+1}\cdot sin(m\theta_1) \\ q_{m,2i}\cdot sin(m\theta_1)+ q_{m,2i+1}\cdot cos(m\theta_1) \end{pmatrix} \\
  $$
• 进一步，由于 \((cos(m\theta_1))^2 + (sin(m\theta_1))^2 = 1\) 有
  $$
  \begin{align}
  \left|\begin{pmatrix}q_{m,2i}\cdot cos(m\theta_1) -q_{m,2i+1}\cdot sin(m\theta_1) \\ q_{m,2i}\cdot sin(m\theta_1)+ q_{m,2i+1}\cdot cos(m\theta_1) \end{pmatrix} \right| &= \sqrt{\left(q_{m,2i}\cdot cos(m\theta_1) -q_{m,2i+1}\cdot sin(m\theta_1)\right)^2 + \left(q_{m,2i}\cdot sin(m\theta_1)+ q_{m,2i+1}\cdot cos(m\theta_1)\right)^2} \\
  &= \sqrt{(q_{m,2i})^2 + (q_{m,2i+1})^2}
  \end{align}
  $$
• 也就是说： \(\boldsymbol{q}_m\)（或\(\boldsymbol{k}_n\)）相邻两两维度在变换前后的向量长度并没有变化，是一个旋转操作

如何改进 RoPE 以实现绝对位置编码？

• 当前的设计仅能实现相对位置编码（因为 Query 和 Key 的内积只与他们的相对位置有关，与绝对位置无关），但如果在 Value 上也施加位置编码则能实现绝对位置编码的能力
• 让研究人员绞尽脑汁的Transformer位置编码中苏神提到：

  这样一来，我们得到了一种融绝对位置与相对位置于一体的位置编码方案，从形式上看它有点像乘性的绝对位置编码，通过在 \(\boldsymbol{q},\boldsymbol{k}\) 中施行该位置编码，那么效果就等价于相对位置编码，而如果还需要显式的绝对位置信息，则可以同时在 \(\boldsymbol{v}\) 上也施行这种位置编码。总的来说，我们通过绝对位置的操作，可以达到绝对位置的效果，也能达到相对位置的效果

---

T5 Bias-可学习的相对位置编码

• TLDR：T5 Bias 是一种相对位置编码，通过在 Self-Attention 机制中加入一个可学习的偏置项来实现

---

AliBi-相对位置编码

• AliBi, Attention With Linear Biases
• 原始论文链接：TRAIN SHORT, TEST LONG: ATTENTION WITH LINEAR BIASES ENABLES INPUT LENGTH EXTRAPOLATION - ICLR 2022

基本思想

• 在位置上增加一个偏执，距离越远，相关度惩罚越大
• 不同head以不同的坡度去进行衰减

详细方案

• 将Attention中的softmax修改为如下的形式
  $$
  Softmax\left(\boldsymbol{q}_i\boldsymbol{K}^T + m \cdot [-(i-1), \cdots ,-2, -1, 0]\right)
  $$
  • 上式中， \(\boldsymbol{K}\) 是行数为 \(i\) 的矩阵（偏置项 \(m \cdot [-(i-1), \cdots ,-2, -1, 0]\) 的长度也为 \(i\)），因为在 Decoder-only 场景中，对于 \(\boldsymbol{q}_i\)，仅需要与前 \(i\) 个 Key 向量做交叉即可，后面的都不需要考虑
    • 换句话说，当 \(i < j\) 时 \(\boldsymbol{q}_i\boldsymbol{k}_j\) 不需要加偏置（反正看不到）
    • ALiBi 实际上是对隔得远的位置添加压制，让离得远的位置 Attention Score 变小（符合隔得越远，越不相关的常识）
• 在MHA中，每个头对应的 \(m\) 取值不同，对于N个head的情况，第n个head的取值为
  $$
  m_n = 2^{\frac{-8}{n}}
  $$
• 原始论文中的方法图示：
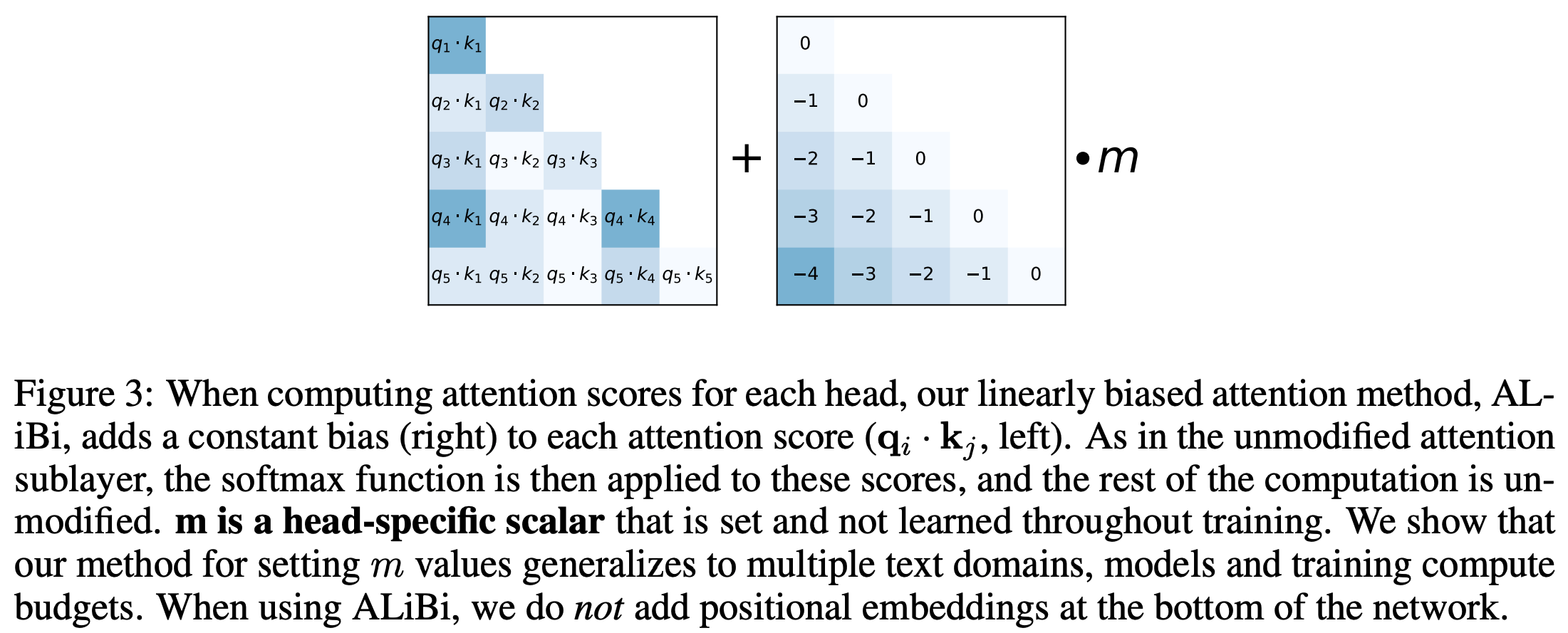
• 原始论文中对ALiBi方法的讲解：

一些简单讨论

• ALiBi具有极强的外推能力：在推理时能处理远超训练长度的序列（如从8K扩展到32K），且无需微调
  • 因为ALiBi的本质是对离得远的位置进行 Attention Score 压制，这个压制值可以多，也可以少，队列越长，压制越大就行
• ALiBi计算效率高：仅需在 Attention 计算时添加偏置，不增加额外参数
• 缺点：容易完全忽略远程的一些关系，ALiBi的线性偏置会显著降低远距离token的注意力分数，使模型难以捕捉超远举例的依赖
• 目前使用AliBi编码的模型有：Baichuan13B

---

位置编码的外推性

外推性定义

• 外推性含义 ：是指模型在预测时，处理超过模型训练长度的能力。外推性越好，则模型对于长度越不敏感，即可以在更长/未训练过的长度上预测
• 外推性不好带来的问题 ：如果模型的外推性不好，那么在预测时，超出训练时指定的长度就容易出现性能不佳的现象，这会影响模型在多轮会话上的表现
• 外推性的评估指标 ：常用困惑度（Perplexity）

不同位置编码外推性比较

• 下面是 ALiBi 原始论文 ALiBi 的实验结论：
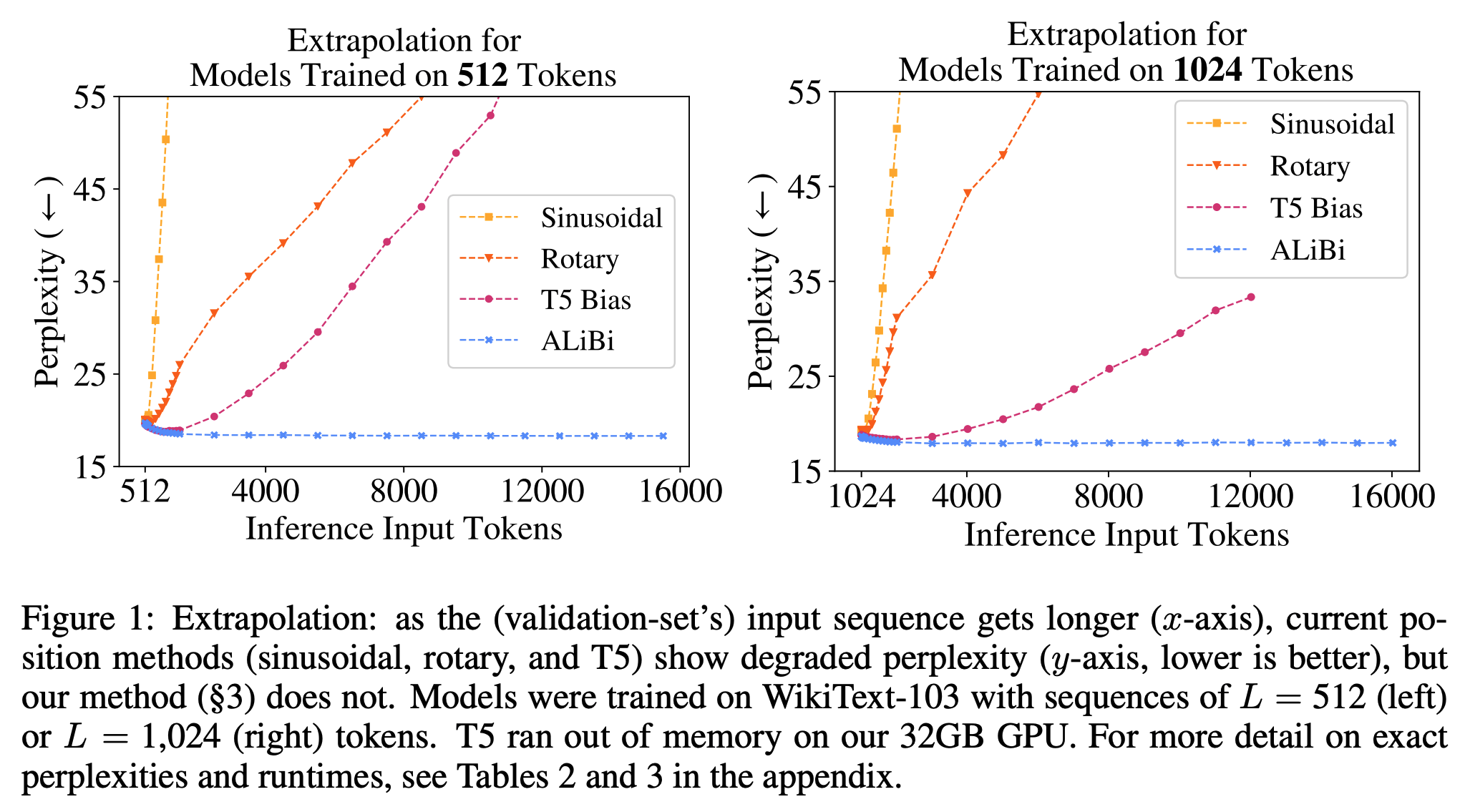
• 从图中可以看出外推性能：ALiBi > T5 Bias > RoPE > Sinusoidal
• ALiBi 不添加位置 Embedding，而是在 Q,K 点积后添加静态、非学习的线性偏差，ALiBi的本质是对离得远的位置进行 Attention Score 压制，这个压制值可以多，也可以少，队列越长，压制越大就行
• RoPE 理论上可以实现外推，但存在多个问题：
  • 问题一：某些维度上遇到未见过的旋转角度。RoPE中 Embedding 向量靠前的部分被旋转的次数多（维度 \(i\) 越靠前，对应的角度 \(\theta_i\) 越大，周期越小），只需要很短的序列就能旋转一周，训练很充分；但靠后的部分被旋转次数少，需要训练很长序列才能旋转一周，训练时没见过的旋转角度，如果在推理时出现了，模型难以处理（这个问题 NTK-aware Scaled RoPE 也没有彻底解决，是 YaRN 引入 NTK-by-parts Interpolation 才解决的）
  • 问题二：RoPE是基于正余弦三角式位置编码改进的，正余弦三角式位置编码本身外推性存在缺点，虽不需要训练就能推演无限长度位置编码，但远处位置信息因周期性函数的特性，在位置衰减后趋于直线震荡 ，位置信息区分度变差 ，RoPE 基于正余弦三角式位置编码改进 ，也受到了一定影响
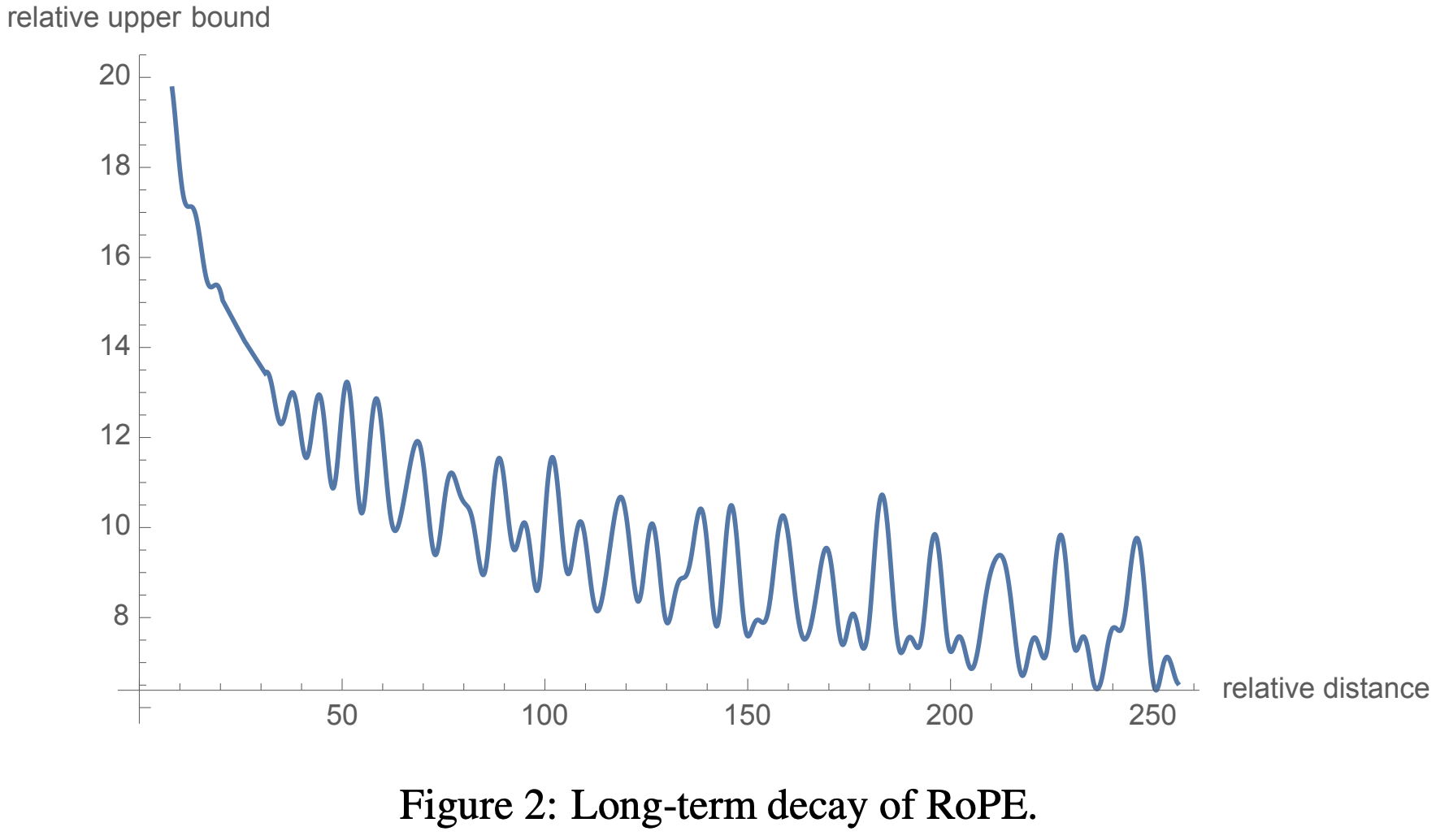
• Sinusoidal 理论上可以实现外推，但存在以下问题：
  • 问题一：虽然 Sinusoidal Q,K 点积的值仅与相对位置有关，但 Sinusoidal 是绝对位置编码，修改了原始 Embedding 向量的值，这个修改会影响后续的每一个模块，如果模型没有见过某个绝对位置编码，模型表现是未知的（增加一个模型没有见过的位置编码很危险）
  • 问题二：也与RoPE一样，存在远程震荡衰减现象，远程震荡导致位置信息区分度变差
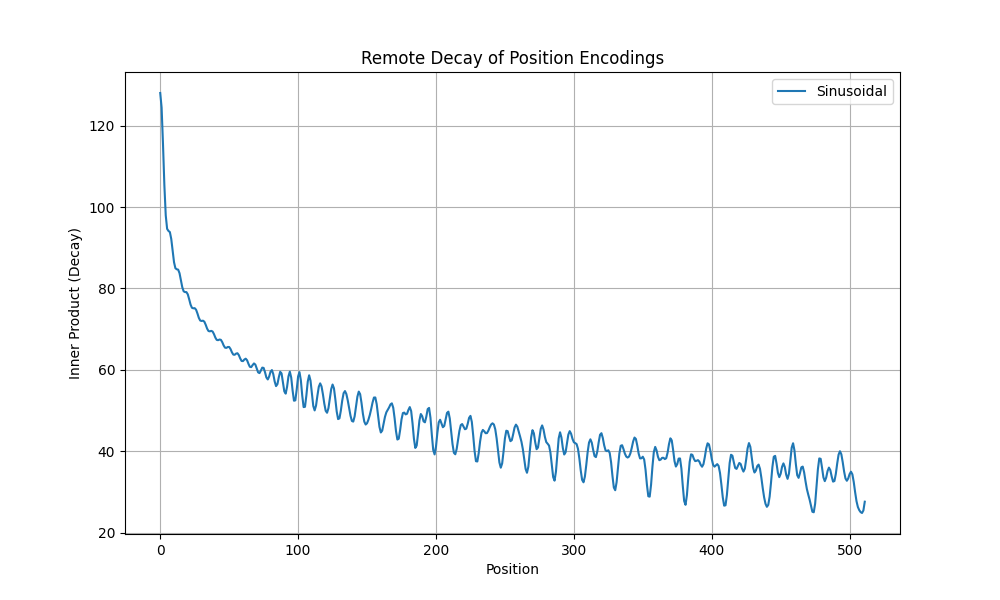
• 注：Sinusoidal 虽然看着能有相对位置编码的思维，但是本质是绝对位置编码，模型对未见过的位置编码是难以外推的，所以直观上看，RoPE 理论上有比 Sinusoidal 更好的外推性

---

RoPE的外推性优化

RoPE 的直接外推

• 直接外推方法 ：不对模型做任何处理，直接使用模型推理超出训练长度的场景，实现上下文长度扩展
• 理论支撑 ：RoPE 通过旋转矩阵编码绝对位置信息来融入相对位置信息，理论上有外推能力
• 缺点 ：短队列下，Embedding 后半部分旋转角度训练不足；存在远程震荡衰减现象，远程震荡导致位置信息区分度变差，所以直接外推方法仅限于较小的扩展
• 实验结论 ：直接外推法对非外推部分友好，对外推部分不友好，推理时遇到没见过的外推位置，效果难以保障；实际上，也可以通过继续微调实现外推到更长的上下文，但是需要的训练量较大

RoPE 的线性内插

• 线性内插，也称为位置内插（Position Interpolation，PI），原始论文 (Position Interpolation)EXTENDING CONTEXT WINDOW OF LARGE LANGUAGE MODELS VIA POSITION INTERPOLATION, 2023, Meta
• 具体方法可以简单理解为保证原始旋转角度不变化的情况下扩展上下文长度，具体地，此时的 Attention 如下形式：
  $$
  \begin{equation}
  (\boldsymbol{\mathcal{R}}_{\color{red}{\frac{m}{k}}} \boldsymbol{q}_m)^{\top}(\boldsymbol{\mathcal{R}}_{\color{red}{\frac{n}{k}}} \boldsymbol{k}_n) = \boldsymbol{q}_m^{\top} \boldsymbol{\mathcal{R}}_{\color{red}{\frac{m}{k}}}^{\top}\boldsymbol{\mathcal{R}}_{\color{red}{\frac{n}{k}}} \boldsymbol{k}_n = \boldsymbol{q}_m^{\top} \boldsymbol{\mathcal{R}}_{(\color{red}{\frac{n}{k}}-\color{red}{\frac{m}{k}})} \boldsymbol{k}_n
  \end{equation}
  $$
  • 此时，位置为 \(m\) 的向量 \(\boldsymbol{q}_m\) 乘以矩阵 \(\boldsymbol{\mathcal{R}}_{\color{red}{\frac{m}{k}}}\)；位置为 \(n\) 的向量 \(\boldsymbol{k}_n\) 乘以矩阵 \(\boldsymbol{\mathcal{R}}_{\color{red}{\frac{n}{k}}}\)（注意角标）
  • 上述方法从而实现了将最大长度为 \(L\) 的模型扩展到了 \(L’ = k\cdot L\)，此时有 \(k\) 的取值为：
    $$ k = \frac{L’}{L} $$
  • 由于这种扩展保证了原始旋转角度不变化的情况下扩展长度，这样做法理论上保证了不存在直接外推中遇到的Embedding 后半部分旋转角度训练不足问题
• PI方法示例：
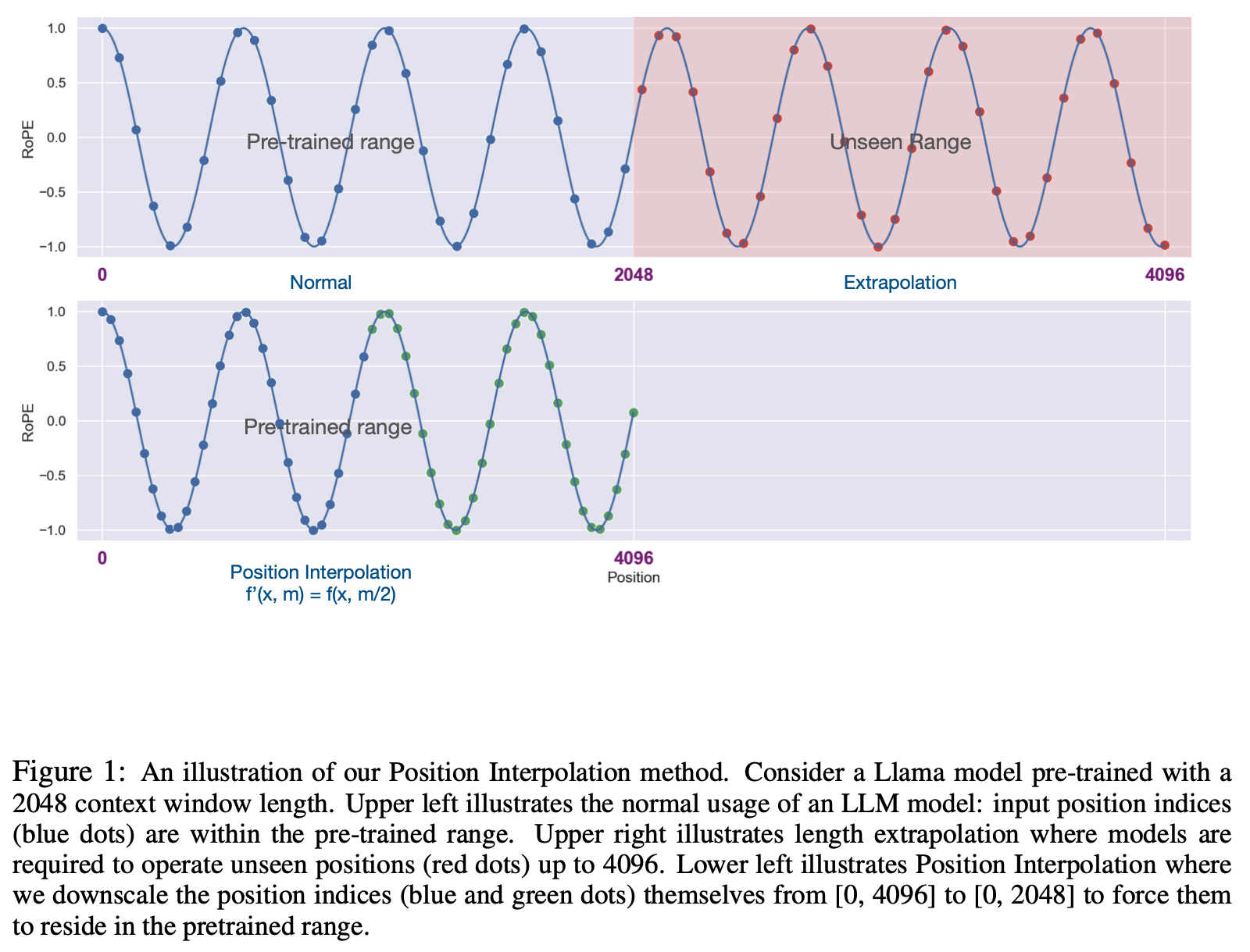
• 实验结果：

  refer to 旋转式位置编码 (RoPE) 知识总结 - Soaring的文章 - 知乎
  这样做的效果如何呢? 实验发现, 在没有额外训练的情况下, 线性内插 的效果比 直接外推 的效果要差; 如果额外训练 1000 步, 线性内插 的效果和原本效果是接近的

  • 问题：在不增加训练的情况下，为什么位置内插效果反而不如直接外推？
  • 理解：这里效果不好主要是针对非外推部分（即距离较近的部分），这种做法理论上会影响模型在已经训练的不错的近距离上的效果
  • 实验结论 ：线性内插后需要额外训练才能保证非外推部分的效果，但是对于外推部分，线性内插方案比直接外推方案需要的微调步数更少 ，能跟快适应新的位置编码

    refer to Transformer升级之路：10、RoPE是一种β进制编码
    当然，有读者会说外推方案也可以微调。是的，但内插方案微调所需要的步数要少得多，因为很多场景（比如位置编码）下，相对大小（或许说序信息）更加重要

• 进一步分析，从角度变化的角度看，位置插入的方法也可以理解为如下变化（可以证明两种表示形式完全等价）：
  $$ \theta_i = 10000^{-2i/d} \cdot k^{-1} $$

NTK-aware Scaled RoPE

• NTK-aware Scaled RoPE 方法最早被 bloc97 提出于博客 NTK-aware Scaled RoPE 中

• 注：NTK 名称的来源是 Neural Tangent Kernel 的缩写，原始博客中有提到：

  Basically if you apply Neural Tangent Kernel (NTK) theory to this problem, it becomes clear that simply interpolating the RoPE’s fourier space “linearly” is very sub-optimal, as it prevents the network to distinguish the order and positions of tokens that are very close by.

• Transformer升级之路：10、RoPE是一种β进制编码中给出了编码进制的理解思路

• 位置内插（线性内插）的问题：常规的位置内插是线性内插，即是通过修改行映射来实现均匀内插，该均匀体现在两个方面：

  • 对每一行（或者说每个位置 \(m\)），放缩相同的比例 \(m \rightarrow \frac{m}{k}\)
  • 对每一列（或者说 Embedding 的每个2维子矩阵 \(i\)），不管高频低频，放缩相同的比例 \(m \rightarrow \frac{m}{k}\)
    • 注：高频对应低维 Embedding 部分，角度旋转多；低频对应高维 Embedding部分，角度旋转少
  • 总结来说：位置内插方法是降低整体分辨率

• 位置内插会导致高频（Embedding 低维）的旋转值的绝对值发生较大变化（即使是训练范围内的序列长度），这时候可以考虑一种非均匀的插值方法，在训练时见过的长度上，低维（高频）旋转角度变化小，高维（低频）旋转角度变化大（但角度的绝对值变化不大），这个方法就是 NTK-aware Scaled RoPE 方法（更多细节讨论见附录）

  refer to 上下文长度扩展：从RoPE到YARN - barely的文章 - 知乎
  简而言之，PI存在的问题是：根据NTK理论，输入特征中高频分量的分布对模型十分重要 ，而PI的做法导致输入中的高频分量的分布发生了较大的变化，对模型的性能有损害

• 除了 NTK理论外，RoPE中，高频维度的重要性解释还有：高频维度（短波长）负责编码局部位置的细微差异（如邻近 token 的相对位置）。若直接插值，会压缩这些高频波长，导致模型难以分辨近距离 token 的顺序

• NTK-aware Scaled RoPE 通过修改 base（原始值为10000）来实现非均匀的内插 ，其核心思路是：高频外推，低频内插（基本理论：从 NTK 理论可知，模型对高频分量的分布敏感，需要尽量保持高频分量不要变化）
  $$
  \begin{align}
  \theta_i &= (10000\cdot k^{d/(d-2)})^{-2i/d} \\
  &= 10000^{-2i/d} \cdot k^{-2i/(d-2)}
  \end{align}
  $$

  • \(k = \frac{L’}{L}\) 是外推比例，一些常见文献中也会使用 \(s = \frac{L’}{L}\) 表示外推比例
  • 以上使用 \(k^{d/(d-2)}\) 的原因是为了保证 \(i=\frac{d}{2}-1\) 时，刚好是 \(k^{-1}\) 用于内插
  • 理解：其实在 \(d\) 较大的情况下，使用 \(k\) 替换 \(k^{d/(d-2)}\) 应该也没什么问题

• 假设将原始 RoPE 的旋转角度固定为：
  $$ \theta_i^{\text{fix}} = 10000^{-2i/d} $$

• 则 NTK-aware Scaled RoPE 的角度变化还可以简写为下面的形式
  $$ \theta_i = k^{-2i/(d-2)} \cdot \theta_i^{\text{fix}} $$

• 此外，在部分博客中，常用 \(D\) 表示模型 Embedding 维度，而用 \(d\) 表示维度索引，此时，公式应该如下：
  $$
  \theta_d^{\text{fix}} = 10000^{-2d/D}\\
  \theta_i = k^{-2d/(D-2)} \cdot \theta_d^{\text{fix}}
  $$

• 原始博客中还给出了原始实现代码 NTKAwareScaledRotaryEmbedding.ipynb，其中，核心代码只有几行，详情如下（完整代码见附录）：

  from transformers import AutoModelForCausalLM, AutoTokenizer, GenerationConfig
  import torch
  import transformers
  
  ### NTK-aware Scaled RoPE 核心代码开始
  old_init = transformers.models.llama.modeling_llama.LlamaRotaryEmbedding.__init__
  def ntk_scaled_init(self, dim, max_position_embeddings=2048, base=10000, device=None):
  	#The method is just these three lines
  	max_position_embeddings = 16384
  	a = 8 #Alpha value
  	base = base * a ** (dim / (dim-2)) #Base change formula
  	old_init(self, dim, max_position_embeddings, base, device)
  transformers.models.llama.modeling_llama.LlamaRotaryEmbedding.__init__ = ntk_scaled_init
  ### NTK-aware Scaled RoPE 核心代码完
  ### 其他

• NTK-aware Scaled RoPE 方法实现了不需要增加微调训练的上下文长度扩展，在Transformer升级之路：10、RoPE是一种β进制编码中给出了以下结论：

  1、直接外推的效果不大行；
  2、内插如果不微调，效果也很差；
  3、NTK-RoPE不微调就取得了非平凡（但有所下降）的外推结果；

NTK-aware Scaled RoPE 的 Dynamic Scaling 改进

• Dynamic Scaling 进一步动态调整 \(k\) 以适配不同上下文长度
  $$
  \begin{align}
  \theta_i &= (10000\cdot (\alpha k - \alpha + 1)^{d/(d-2)})^{-2i/d} \\
  &= (10000)^{-2i/d} \cdot (\alpha k - \alpha + 1)^{-2i/(d-2)}
  \end{align}
  $$
  • \(k = \frac{L’}{L}\) 是外推比例 （代码中使用 base = self.base * ((self.scaling_factor * seq_len / self.max_position_embeddings) - (self.scaling_factor - 1)) ** (self.dim / (self.dim - 2))）
  • \(\alpha > 1\) 是一个超参数，作者通过实验取 \(\alpha = 2\)
• 可参考：旋转式位置编码 (RoPE) 知识总结 和 从ROPE到Yarn, 一条通用公式速通长文本大模型中的位置编码 - Whisper的文章 - 知乎
• 注：Llama中也是用了这种形式：

ReRoPE

• 本节内容主要参考自：旋转式位置编码 (RoPE) 知识总结
• ReRoPE，即 Rectified Rotary Position Embedding，其名称跟 ReLU (Rectified Linear Unit) 中的 Rectified 含义相似
• ReRoPE的基本思想是，使用分段函数实现对相对位置超过一定长度的旋转进行截断，具体来说有：
  $$
  \mathrm{score}(\boldsymbol{q}_m, \boldsymbol{k}_n)=
  \begin{cases}
  \boldsymbol{q}_m^{\mathrm{T} }\cdot\boldsymbol{R}_{n - m}\cdot\boldsymbol{k}_n & (m - n < w) \\
  \boldsymbol{q}_m^{\mathrm{T} }\cdot\boldsymbol{R}_{-w}\cdot\boldsymbol{k}_n & (m - n \geq w)
  \end{cases}
  $$
  • 其核心思想是：如果 Query 向量 \(\boldsymbol{q}\) 和 Key 向量 \(\boldsymbol{k}\) 的相对位置超过 \(w\)，那么就进行截断，直接将其设置为 \(w\)
• 进一步地，论文还可以仿照 Leaky ReLU，将向量 \(\boldsymbol{q}\) 和 \(\boldsymbol{k}\) 的相对位置超过 \(w\) 的部分用斜率为 \(\frac{1}{k}\) 的函数进行光滑处理：
  $$
  \mathrm{score}(\boldsymbol{q}_m, \boldsymbol{k}_n)=
  \begin{cases}
  \boldsymbol{q}_m^{\mathrm{T} }\cdot\boldsymbol{R}_{n - m}\cdot\boldsymbol{k}_n & (m - n < w) \\
  \boldsymbol{q}_m^{\mathrm{T} }\cdot\boldsymbol{R}_{-w^*}\cdot\boldsymbol{k}_n & (m - n \geq w)
  \end{cases}
  $$
  • 其中，\(w^*\) 的公式如下：
    $$
    w^* = \frac{m - n - w}{k}+w
    $$
    • 注意这里的 \(k\) 不是之前的序列长度比值了

      不再和序列长度挂钩，只要大于 1，且相对位置都在预训练的范围内即可。苏剑林的实验发现，如果预训练是 512，推理是 4096，\(k\) 的值设置为 16 最好

• 旋转式位置编码 (RoPE) 知识总结中其他更多表述：

  • 在公式中，\(m - n\) 就是相对位置，\(m - n - w\) 就是除去 \(w\) 后的长度。论文将这种方式称为 Leaky ReRoPE
  • 根据苏剑林大佬的实验，NTK-aware 方案有 5% 的性能下降，而 ReRoPE 的性能下降在 1% 以内 \(w\) 设置成预训练最大长度的一半，而且 ReRoPE 理论上可以处理任意长度，属于比较完美的方案
  • 但是，这个方案有一个很大的问题：推理成本。在 NTK-aware 的方案中，我们可以通过改 \(\theta_i\) 函数来实现长度外推，增加的推理成本几乎可以忽略；但是在 ReRoPE 中，Attention 的运算规则都发生了变化 (分段函数)，此时的推理成本会增加非常多
  • 于是，苏剑林大佬又想到一个办法，在预训练时采用 Leaky RoPE，而在推理时采用原始的 RoPE，不过公式变成：
    $$
    w^* = -(k(m - n - w)+w)
    $$
  • 这样的好处是：Train Short, Test Long。如果预训练的最大长度是 2048，\(k\) 值是 16，那么推理时的最大长度是 \(2048×16 = 32768\)。经过实验，这样做性能下降也是在 1% 以内。如果你有资源重新训练大模型，这会是一个很好的方案。

NTK-by-parts Interpolation

• NTK-by-parts Interpolation 是 YaRN 作者在 https://github.com/jquesnelle/yarn/pull/1中提出的，YaRN 原始论文中有方案介绍 YaRN: Efficient Context Window Extension of Large Language Models, ICLR 2024,
• NTK-by-parts Interpolation ，顾名思义，即部分 NTK 插值方法，基于波长局部分段插值
• 截止目前的外推方法主要面临问题和讨论 ：
  • 背景：前面提到，原始 RoPE 中 Embedding 向量靠前的部分被旋转的次数多（维度 \(i\) 越靠前，对应的角度 \(\theta_i\) 越大，周期越小），只需要很短的序列就能旋转一周，训练很充分；但靠后的部分被旋转次数少，需要训练很长序列才能旋转一周，训练时没见过的旋转角度，如果在推理时出现了，模型难以处理
  • 线性内插 保证了原始旋转角度不变化的情况下扩展长度，理论上保证了不存在直接外推中遇到的Embedding 后半部分旋转角度训练不足问题，但高频部分维度也被修改了（NTK 理论告诉我们高频部分不应该修改）
  • NTK-aware Scaled RoPE 通过非线性的插值，直观上看对高频（低维）做到了几乎不调整 ，对低频（高维）做到了接近线性内插（在最后一维时完全等于线性内插），
  • 问题：NTK-aware Scaled RoPE 真的解决未见过的角度这个问题了吗？答案是没有彻底解决，两边的维度都没问题了（高频部分角度变化够大，早已超过了\(2\pi\)；低频部分做线性内插，不会出现超过角度问题），但依然会有部分中间维度出现超过训练时旋转角度的情况，详细证明见附录：NTK-aware Scaled RoPE 外推分量推导
• 回顾 NTK-aware Scaled RoPE 修改了 base 从而实现了非线性的插值：
  $$
  \begin{align}
  \theta_i &= (10000\cdot k^{d/(d-2)})^{-2i/d} \\
  &= 10000^{-2i/d} \cdot k^{-2i/(d-2)}
  \end{align}
  $$
  • \(k = \frac{L’}{L}\) 是外推比例，一些常见文献中也会使用 \(s = \frac{L’}{L}\) 表示外推比例
  • 我们将原始 RoPE 的旋转角度固定为：
    $$ \theta_i^{\text{fix}} = 10000^{-2i/d} $$
  • 则 NTK-aware Scaled RoPE 的角度变化还可以简写为下面的形式
    $$ \theta_i = k^{-2i/(d-2)} \cdot \theta_i^{\text{fix}} $$
• NTK-by-parts Interpolation 的思路：NTK理论告诉我们高频部分不应该进行插值；从分析看低频部分不能直接外推（会导致遇到没见过的旋转角度）
  • NTK-by-parts Interpolation 是根据不同波长分段实现插值，其中波长的定义为
    $$\lambda_i = \frac{2\pi}{\theta_i^{\text{fix}}} = 2\pi \cdot 10000^{2i/d}$$
  • 对波长短（高频）的维度不进行插值（直接外推）；
  • 对波长长（低频）维度进行线性内插（PI）；
  • 对中间维度，以不超过旋转角度的范围内进行插值
• 具体来说，NTK-by-parts Interpolation 使用下面的公式来实现分段非线性插值：
  $$
  \begin{align}
  \theta_i = (1-\gamma(r_i))\frac{\theta_i^{\text{fix}}}{k} + \gamma(r_i)\theta_i^{\text{fix}}\\
  \end{align}
  $$
  • 其中 \(r_i = \frac{L}{\lambda_i}\) 是序列长度和波长的比值，且：
    $$
    \gamma(r_i) = \gamma(i) =
    \begin{cases}
    1, & \text{if } r_i>\beta \\
    \frac{r_i-\alpha}{\beta - \alpha}, & \text{if } \alpha\leq r_i<\beta \\
    0, & \text{if } r_i<\alpha
    \end{cases}
    $$
• 公式解读为：不同波长 \(\lambda_i\) 类型维度 \(i\) 的插值策略不同 ，使用序列长度和波长的比值 \(r_i = \frac{L}{\lambda_i}\) 来圈定（\(r_i\) 与波长 \(\lambda_i\) 成反比）
  • 高频维度（\(r_i>\beta\)）：波长短，高频低维，不做任何插值。一方面满足NTK原理要求（模型对高频特征敏感），另一方面这样也能不破坏相邻序列之间的细节关系（局部位置关系）
  • 低频维度（\(r(d)<\alpha\)）：波长长，低频高维，对低频维度进行线性插值，避免角度外推带来的位置混淆
  • 中间维度（\(\alpha\leq r_i<\beta\)）：波长中间，在原始频率和拉伸后的频率之间进行线性插值，插值程度由\(\frac{r_i-\alpha}{\beta - \alpha}\)决定
• \(\alpha,\beta\) 的设置一般是：

  The values of α and β should be tuned on a case-by-case basis. For example, we have found experimentally that for the Llama family of models, good values for \(\alpha\) and \(\beta\) are \(\alpha=1\) and \(\beta=32\)

YaRN

• 原始论文：YaRN: Efficient Context Window Extension of Large Language Models
  • YaRN 原始论文中对各种方法有统一介绍和梳理，值得一看
  • 吐槽以下：YaRN 取名很随意（Yet another RoPE extensioN method），且 YaRN 论文里面的符号于之前其他论文（比如原始 Transformer）中不一致，容易造成误解，论文处于一致性考虑，仍使用原始 Transformer 和其他社区常用的符号
  • 注：YaRN 中，用 \(D\) 表示 Embedding 维度（论文用 \(d\)），用 \(d\) 表示维度索引/分量（论文用 \(i\)），用 \(s\) 表示外推比例（论文用 \(k\)）
• YaRN = NTK-by-parts Interpolation + attention-scaling ，也就是说，YaRN 是基于 NTK-by-parts Interpolation 的，在此基础上还加入了 预 Softmax 缩放机制（也称为 attention-scaling 机制）：
  $$ \text{softmax}\left(\frac{\boldsymbol{q}_m^\top \boldsymbol{k}_n}{t\sqrt{d}}\right) \\
  \sqrt{\frac{1}{t}} = 0.1\ln(k) + 1
  $$
  • \(k = \frac{L’}{L}\) 是外推比例
• 关于温度系数 \(t\) 的理解：
  • 温度系数越大，注意力分布越平均
  • 温度系数越小，注意力分布越集中
  • \(\sqrt{\frac{1}{t}} = 0.1\ln(k) + 1\) 是通过大量的实验验证出来的，这里可以看出扩展长度越长（\(k\) 越大），需要的温度系数就越小，即此时需要让注意力分布更集中
  • 直观上理解，该定义下，当 \(k > e\) 时，\(\sqrt{\frac{1}{t}} = 0.1\ln(k) + 1 > 1\)，此时有 \(t < 1\)，也就是说，attention-scaling 机制 是在通过温度系数 \(t\)，使得 Softmax 注意力更集中
    • 注：一些博客中的解释是用于缓解锐化，促进平均，在 \(k > e\) 时，这个观点是错误的（现实中扩展往往是4倍以上）
  • 实现时，可以通过将 Embedding 缩放为原来的 \(\frac{1}{\sqrt{t}}\) 来实现 attention-scaling 机制
• YaRN 的优点总结：
  • 仅需要少量微调即可
  • 性能由于其他扩展方法
• 注：YaRN 已经是 LLMs 领域的标配技术， DeepSeek R1 用于 YaRN 技术从 DeepSeek-V3-Base (4K上下文) 扩展到 128K 上下文使用的技术，通过两阶段扩展（4K -> 32K -> 128K）完成上下文长度扩展

问题：为什么扩展长度越长，需要的温度系数越小呢？

• 参考1：YaRN 原始论文3.4节简单提到这个问题，附录A.2中有实验支撑，但没有非常理论的证明
• 参考2：

  refer to 【LLM理论系列】LLM上下文长度扩展：YaRN - LLMCat的文章 - 知乎
  较小的 \(t\) 值会使注意力分布更加”尖锐”，增强模型对长距离依赖的捕捉能力
  较大的 \(t\) 值则会使注意力分布更加”平滑”，有助于保持模型的稳定性

• 个人理解：
  • 这里温度系数是为了中高频率维度考虑：一方面，高频维度负责编码局部位置的细微差异，不能插值，会导致模型难以分辨近距离 token 的顺序；实际上，在序列扩展特别长时，中高频被插值影响太大了，对模型效果也有损（模型难以区分中远距离的 token 顺序）
  • NTK-aware Scaled RoPE 中对高频做了较小的插值；
  • NTK-by-parts Interpolation 对超高频不插值，中高的频率维度做较小插值，低频做线性插值
  • NTK-by-parts Interpolation 不对超高频插值，彻底解决了超高频问题，但是中间频率问题没有解决，且随着扩展长度增加，中间频率被放缩的越多
  • 中频维度负责编码中远距离位置的细微差异，此时需要使用更小的温度系数，让 Attention 更关注中远距离的 token（注：因为 RoPE 的Attention 权重有远程衰减特性，固更小的温度系数会将注意力更集中到更近的距离）

LongRoPE

• Microsoft Research原始论文：LongRoPE: Extending LLM Context Window Beyond 2 Million Tokens - arXiv 2024
• 微软亚研知乎：LongRoPE：超越极限，将大模型上下文窗口扩展超过200万tokens
• 其相对RoPE的改进点有:

  refer to LongRoPE：超越极限，将大模型上下文窗口扩展超过200万tokens

  • 精细化非均匀位置插值 ：目前的大模型通常采用 RoPE 旋转位置编码，对 RoPE 位置编码进行插值是解决上述挑战中第一个问题的一种常见方法。这种方法将新位置索引缩小到预训练范围内。在已有的相关工作中，位置插值（position interpolation，PI）会通过扩展比例来线性插值 RoPE 的旋转角度。NTK-aware 位置编码插值方法提出，利用公式对每个RoPE维度进行经验性重新缩放，YaRN 会将 RoPE 维度分成三组，并分别针对三组 RoPE 维度进行不同的缩放（即直接外推，NTK-aware 插值和线性插值）。然而，这些方法主要基于启发式经验插值，未充分利用 RoPE 中的复杂非均匀性，导致关键信息在位置编码插值后丢失，从而限制了上下文窗口的大小。研究员们经过实验发现，有效的位置编码插值应考虑两种非均匀性：不同的 RoPE 维度和 token 位置。低维 RoPE 和初始 token 位置存储着关键信息，因此需要进行更少程度的插值。相比之下，高维 RoPE 存储的信息相对较为稀疏，可进行较大程度的插值。为了充分利用这些非均匀性，研究员们提出了一种基于进化算法的方法，允许搜索 RoPE 每个维度以及不同 token 位置的旋转角度缩放因子，有效地保留了原始 RoPE 位置编码中的信息。这种方法最大程度地减小了位置插值引起的信息损失，从而为微调提供了更好的初始化。此外，这种方法还允许在不微调的情况下实现8倍的扩展
  • 渐进式扩展策略 ：在非均匀位置编码插值的基础上，LongRoPE 采取了高效的渐进式扩展策略，从而在无需直接对极长文本进行微调的情况下，有效实现了2048k上下文窗口的目标。具体策略如下：首先在预训练的大模型上搜索256k上下文窗口对应的位置编码插值方案，并在此长度下进行微调。其次，由于 LongRoPE 的非均匀插值允许在不微调的情况下进行8倍扩展，所以研究员们对已扩展的微调后的大模型进行了二次非均匀插值搜索，最终达到了2048k上下文窗口
  • 调整LongRoPE以恢复短上下文窗口性能 ：在将上下文窗口扩展到极长的2048k后，研究员们注意到原始上下文窗口内的性能出现了下降。这是位置插值的一个已知问题，因为它导致原始上下文窗口内的位置被压缩在更窄的区域内，从而对大模型的性能产生了负面影响。为了解决这一问题，研究员们在扩展后的大模型上对8k长度内的 RoPE 缩放因子进行了重新搜索，旨在引导在较短长度上进行较少的位置插值，来恢复短上下文窗口的性能。在推理过程中，大模型可根据输入长度动态调整相应的 RoPE 缩放因子

RoPE ABF

• 参考链接： Effective Long-Context Scaling of Foundation Models, arXiv preprint 2023, GenAI, Meta
• RoPE ABF（RoPE with Adjusted Base Frequency）的核心改进是：通过调整基础频率降低远距离 Token 的衰减效应
• 传统RoPE位置编码 ：通过旋转向量实现位置信息嵌入，其核心公式为：
  $$
  f^{\text{RoPE}}(x, t)_j = (x_{2j} + ix_{2j+1}) e^{i b^{-\frac{2j}{d}} t}
  $$
  • 其中，\(b\) 为基础频率（默认值为10,000），\(d\) 为模型维度，\(t\) 为Token位置，\(j\) 为维度索引
  • RoPE的衰减问题源于旋转角度随位置 \(t\) 增大而快速变化，导致远距离Token的注意力分数显著下降
• RoPE ABF的改进 ：通过增大基础频率 \(b\)（如从10,000调整为500,000），减少旋转角度，从而降低远距离Token的衰减。调整后的公式为：
  $$
  f^{\text{RoPE ABF}}(x, t)_j = (x_{2j} + ix_{2j+1}) e^{i (\beta b)^{-\frac{2j}{d}} t}
  $$
  • 其中，\(\beta\)为缩放因子（文中取\(\beta = 50\)），通过增大\(\beta b\)，使得位置编码对远距离Token的区分度更高，衰减更平缓
• RoPE ABF方法 和 NTK-aware Scaled RoPE 方法基本一致，两者都是对频率（原始值为10000）进行调整
  • NTK-aware Scaled RoPE 方法是动态（根据需要外推的倍数进行调整）；RoPE ABF 方法是固定调整（比如论文第四节提到直接从 10000 变成 500000）
  • NTK-aware Scaled RoPE 方法更偏向于无需继续微调训练；RoPE ABF 方法更倾向于需要继续微调训练
• 注：这篇文章发表晚于 NTK-aware Scaled RoPE 方法的提出，但并没有和 NTK-aware Scaled RoPE 方法作比较（其实就是同一个，甚至不如 NTK-aware Scaled RoPE 方法精巧）

  We propose a simple modification to the default RoPE encoding to reduce the decaying effect – increasing the “base frequency b” of ROPE from 10,000 to 500,000, which essentially reduces the rotation angles of each dimension. The idea is also concurrently suggested in the Reddit r/LocalLLaMa community and Rozière et al. (2023).

DCA

• 参考链接 Training-Free Long-Context Scaling of Large Language Models
• 双块注意力（Dual Chunk Attention, DCA）是一种无需训练的大语言模型长上下文扩展框架
• DCA 通过将长序列的注意力计算分解为块内（Intra-Chunk）、块间（Inter-Chunk）和连续块（Successive-Chunk）三种注意力机制，有效捕捉短程和长程依赖关系
• DCA 可保证位置编码不会超过预训练 ：通过重新设计相对位置矩阵 \( M \) 反映 tokens 间的真实相对位置，避免传统方法（如位置插值PI、NTK）对引入未见过的位置信息
• 保留预训练的位置编码，每个块的大小 \( s \) 小于模型预训练长度 \( c \)，确保块内相对位置不超过预训练范围的降维损失
• DCA 可同时与 Flash Attention 结合实现高效计算
• 实验表明 DCA 在长上下文中的表现显著优于传统位置插值方法，如 PI 和 NTK-aware Scored RoPE
• 更多详情参考：NLP——LLM位置编码-DCA

其他与上下文扩展相关的优化

Attention-E

• 在中提到使用下面的Attention变体称为“Attention-E”（Entropy Invariance）有利于上下文泛化（外推）：
  $$ \begin{equation}Attention(Q,K,V) = softmax\left(\frac{\log_{512} {n}}{\sqrt{d}}QK^{\top}\right)V\end{equation} $$
  • 其中 \(n\) 为最大序列长度，外推到多大，这里的 \(n\) 就取对应的值（注意：训练训练长度是固定的，此时 \(n\) 是也固定的）
  • 以 \(512\) 为底主要是作者提出这个方案前，大部分模型训练最大长度都是 \(512\)，作者想在 \(n=512\) 时退化到原始 Attention
  • 注：这 Attention-E 实现下，在不外推时，效果其实不如原始的 Attention；外推时效果则相对原始的 Attention 较好

---

各种编码方式总结

• 参考链接
  • 大模型面试准备（四）：必会的位置编码（绝对位置编码sinusoidal，旋转位置编码RoPE，以及相对位置编码ALiBi）
• 固定位置编码和正弦位置编码（Sinusoidal）都是绝对位置编码
• RoPE是旋转位置编码，实际上是在 \(\boldsymbol{q},\boldsymbol{k}\) 做内积前将他们旋转，可以证明，RoPE算是相对位置编码，仅仅与他们的相对位置有关
• T5 Bias是带偏置的Attention，其偏置项是可学习的
• ALiBi是带偏置的Attention，实际上是在 \(\boldsymbol{q},\boldsymbol{k}\) 做内积后在他们的内积上加一个负偏置，相对位置越远，偏置越大，本质上是相对位置编码
• ALiBi论文中跟各种方法，特别是 Sinusoidal 进行了比较，在固定长度的短序列（1024,2048）训练下，ALiBi 和 Sinusoidal 的性能及效果都差不多，但是外推性上，ALiBi 好很多
• LongRoPE是RoPE的改进版本，采用插值+微调来实现长文本，目前最长可扩展到200W+（2048k）上下文窗口
• AliBi和LongRoPE都有很强的外推性，都适合长文本

---

附录：推理速度讨论

• 下面是 ALiBi 原始论文 ALiBi 的实验结论：
• RoPE 需要的存储更多是因为需要存储更大的位置编码矩阵（即使进存储简化后的矩阵，不同位置也需要分别存储）
• 存储消耗：RoPE > T5 Bias > ALiBi > Sinusoidal
• 训练速度：Sinusoidal ~ ALiBi > RoPE > T5 Bias
• 推理退镀：Sinusoidal ~ ALiBi > RoPE > T5 Bias

---

附录：为什么ALiBi不如RoPE流行

• 问题：为什么 RoPE 在训练/推理效率、存储消耗、外推性等方面都不如 AliBi，RoPE 却是当前开源大模型主流的位置编码方案（截止到25年）?
• 有以下原因：
  • RoPE 训练更稳定：RoPE 对注意力分布的影响更平滑，适合大规模预训练
  • RoPE 生态兼容性：主流推理框架（如 vLLM、Ollama）对 RoPE 支持更好，RoPE 与 FlashAttention、vLLM 等优化库兼容，相比 ALiBi 在混合精度训练（如 bfloat16）下更稳定

---

附录：NTK-aware Scaled RoPE详细代码示例

• 原始实现代码 NTKAwareScaledRotaryEmbedding.ipynb：

  from transformers import AutoModelForCausalLM, AutoTokenizer, GenerationConfig
  import torch
  import transformers
  
  ### NTK-aware Scaled RoPE 核心代码开始
  old_init = transformers.models.llama.modeling_llama.LlamaRotaryEmbedding.__init__
  def ntk_scaled_init(self, dim, max_position_embeddings=2048, base=10000, device=None):
  	#The method is just these three lines
  	max_position_embeddings = 16384
  	a = 8 #Alpha value
  	base = base * a ** (dim / (dim-2)) #Base change formula
  	old_init(self, dim, max_position_embeddings, base, device)
  transformers.models.llama.modeling_llama.LlamaRotaryEmbedding.__init__ = ntk_scaled_init
  ### NTK-aware Scaled RoPE 核心代码完
  
  model_path = "TheBloke/OpenAssistant-SFT-7-Llama-30B-HF"
  tokenizer = AutoTokenizer.from_pretrained(model_path)
  model = AutoModelForCausalLM.from_pretrained(model_path, torch_dtype=torch.float16, device_map="auto")
  generation_config = GenerationConfig(
  	temperature=0.0,
  	top_k=20,
  	repetition_penalty=1.2,
  )
  print("Prompt token length:", len(tokenizer(prompt, return_tensors="pt")["input_ids"][0]))
  def print_predict(prompt):
  	prompt = "<|prompter|>" + prompt + "</s><|assistant|>"
  	encoding = tokenizer(prompt, return_tensors="pt")
  	input_ids = encoding["input_ids"].to("cuda")
  
  	with torch.inference_mode():
  		result = model.generate(
  			input_ids=input_ids,
  			generation_config=generation_config,
  			return_dict_in_generate=False,
  			output_scores=False,
  			max_new_tokens=512,
  		)
  
  	decoded_output = tokenizer.decode(result[0][len(input_ids[0]):])
  	print(decoded_output)
  prompt_question = prompt + "\nPlease give me a brief summary of this research paper in a few bullet points."
  print_predict(prompt_question)
  prompt_question = prompt + "\nPlease write me the abstract for this paper."
  print_predict(prompt_question)
  prompt_question = prompt + "\nHow many steps was the model fine tuned for the final results? Give a short answer."
  print_predict(prompt_question)
  prompt_question = prompt + "\nHow big is the interpolation bound compared to the extrapolation bound? Give a short answer."
  print_predict(prompt_question)

---

附录：不同插值方法的可视化比较

• d_model=32，序列长度为10下的不同外推方法旋转角度 \(\theta\) 可视化如下（图中每个节点）：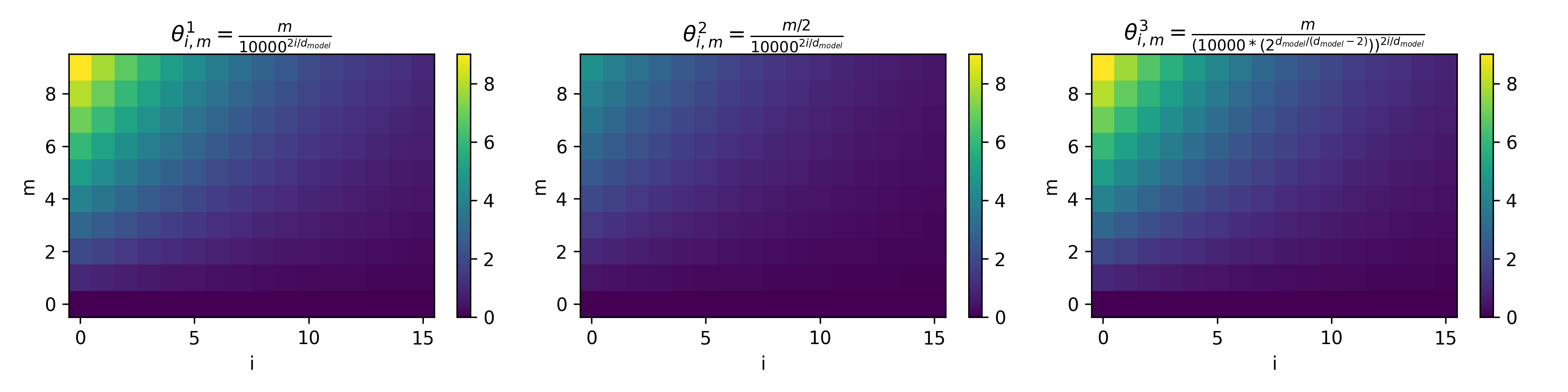
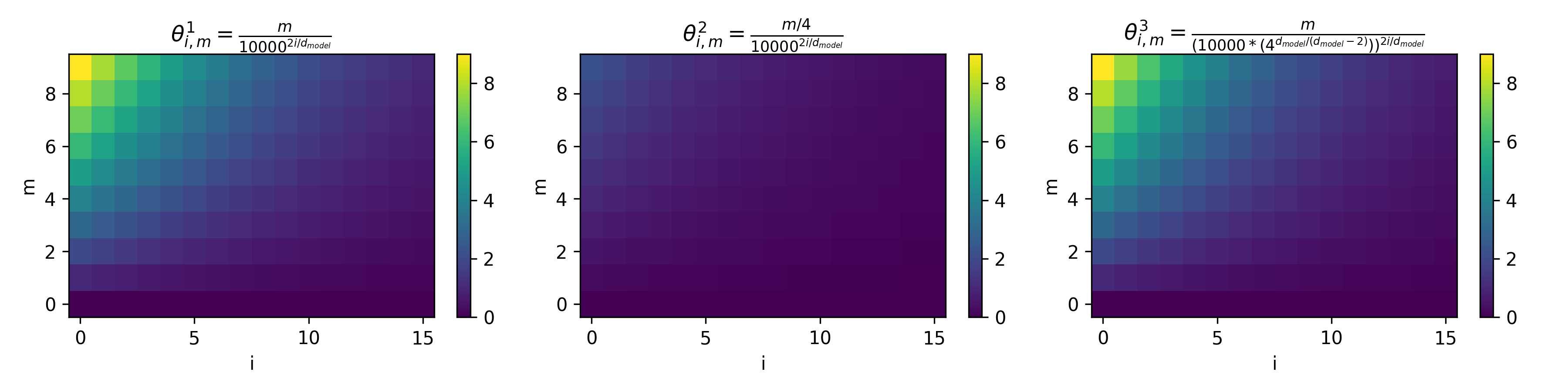
• 上图的解读如下：
  • 图中第一行、第二行分别为 k=2 和 k=4 的外推场景
  • 每一行从左到右依次是 直接外推方法、位置插值法（PI）、NTK-aware Scaled RoPE 三种方法下的角度变化
  • 每个小图中，横轴是维度 \(i \in [0,15]\)，纵轴是位置 \(m \in [0,9]\)
  • 为了方便，论文画出的每个图 \(m\) 范围是一样的
    • 以第一行为例，可以理解为训练长度是 5，泛化长度是 10，也就是说第一行的图中，泛化出来的是 \(m \in [5,9]\)
    • 以第二行为例，可以理解为训练长度是 2，泛化长度是 8，也就是说第一行的图中，泛化出来的是 \(m \in [2,7]\) （多余两个行忽略即可）
  • 显然，对第一行，若只观察未泛化的位置 \(m \in [0,4]\) 的情况，可以做如下分析：
    • 直接外推法不影响原始训练长度内（\(m \in [0,4]\)）的旋转角度；
    • 位置内插方法低维和高维的值都发生了较大改变，特别是低维的范围变化绝对值太大；
    • NTK-aware Scaled RoPE 方法则几乎不改变低维上的旋转角度范围（和直接外推法基本一样），高维的角度有变化，但是因为绝对值不大而管差不出来
• RoPE中，高频对应低维 Embedding 部分，角度旋转多；低频对应高维 Embedding部分，角度旋转少：
  • 位置内插会导致高频（Embedding 低维）的旋转值的绝对值发生较大变化（即使是训练范围内的序列长度）
  • NTK-aware Scaled RoPE是一种非均匀的插值方法，在训练时见过的长度上，低维（高频）旋转角度变化小，高维（低频）旋转角度变化大（但角度的绝对值变化不大）
  • 注：高频维度（短波长）负责编码局部位置的细微差异（如邻近 token 的相对位置）。若直接插值，会压缩这些高频波长，导致模型难以分辨近距离 token 的顺序
• 补充，上述图像生成的代码如下：
  >>>点击展开折叠内容...

  import numpy as np
  import matplotlib.pyplot as plt
  
  # Original（直接外推法）
  def theta_1(i, m, d_model=128):
  	return m / (10000 ** (2 * i / d_model))
  
  # Position Interpolation
  def theta_2(i, m, d_model=128):
  	return (m / 2) / (10000 ** (2 * i / d_model))
  
  # NTK-aware Scaled RoPE
  def theta_3(i, m, d_model=128):
  	denominator_base = 10000 * (2 ** (d_model / (d_model - 2)))
  	return m / (denominator_base ** (2 * i / d_model))
  
  d_model = 32
  seq_len = 10
  i_values = np.arange(0, d_model // 2, 1)
  m_values = np.arange(0, seq_len, 1)
  
  matrix_1 = np.zeros((len(m_values), len(i_values)))
  matrix_2 = np.zeros((len(m_values), len(i_values)))
  matrix_3 = np.zeros((len(m_values), len(i_values)))
  
  for idx_m, m in enumerate(m_values):
  	for idx_i, i in enumerate(i_values):
  		matrix_1[idx_m, idx_i] = theta_1(i, m)
  		matrix_2[idx_m, idx_i] = theta_2(i, m)
  		matrix_3[idx_m, idx_i] = theta_3(i, m)
  
  # 确定统一的颜色标尺
  vmin = min(matrix_1.min(), matrix_2.min(), matrix_3.min())
  vmax = max(matrix_1.max(), matrix_2.max(), matrix_3.max())
  
  plt.rcParams['figure.dpi'] = 300
  fig, axes = plt.subplots(1, 3, figsize=(12, 3))
  
  im1 = axes[0].imshow(matrix_1, origin='lower', aspect='auto', cmap='viridis', vmin=vmin, vmax=vmax)
  axes[0].set_title(r'$\theta^1_{i,m} = \frac{m}{10000^{2i/d_{model}}}$')
  axes[0].set_xlabel('i')
  axes[0].set_ylabel('m')
  fig.colorbar(im1, ax=axes[0])
  
  im2 = axes[1].imshow(matrix_2, origin='lower', aspect='auto', cmap='viridis', vmin=vmin, vmax=vmax)
  axes[1].set_title(r'$\theta^2_{i,m} = \frac{m/2}{10000^{2i/d_{model}}}$')
  axes[1].set_xlabel('i')
  axes[1].set_ylabel('m')
  fig.colorbar(im2, ax=axes[1])
  
  im3 = axes[2].imshow(matrix_3, origin='lower', aspect='auto', cmap='viridis', vmin=vmin, vmax=vmax)
  axes[2].set_title(r'$\theta^3_{i,m} = \frac{m}{(10000*(2^{d_{model}/(d_{model}-2)}))^{2i/d_{model}}}$')
  axes[2].set_xlabel('i')
  axes[2].set_ylabel('m')
  fig.colorbar(im3, ax=axes[2])
  
  plt.tight_layout()
  plt.savefig("./demo.png")
  plt.show()

---

附录：NTK-aware Scaled RoPE 外推分量推导

• 参考：上下文长度扩展：从RoPE到YARN - barely的文章 - 知乎