注:本文包含 AI 辅助创作
- 参考链接:
Paper Summary
- 整体总结:
- 本文提出了一种新的框架:Gated DeltaNet
- vs Mamba2:能够实现更好的键值关联学习
- vs DeltaNet:具有更强的自适应内存清除能力
- 本文提出了一种新的框架:Gated DeltaNet
- 背景 & 问题:
- 线性 Transformer (Linear Transformers) 作为标准 Transformer 的高效替代方案获得了关注,但它们在检索和长上下文任务中的性能有限
- 为了解决这些限制,最近的工作探索了两种不同的机制:
- 用于自适应内存控制的门控 (gating for adaptive memory control)
- 用于精确内存修改的 Delta 更新规则 (delta update rule for precise memory modifications)
- 论文观察到这些机制是互补的,门控支持快速内存擦除,而 Delta 规则促进定向更新
- 基于这一见解,论文引入了门控 Delta 规则 (gated delta rule),并开发了一种针对现代硬件优化的并行训练算法
- 论文提出新的架构 Gated DeltaNet
- 在包括语言建模、常识推理、上下文检索、长度外推和长上下文理解在内的多个基准测试中,超越了 Mamba2 和 DeltaNet 等现有模型
- 作者通过开发将 Gated DeltaNet 层与滑动窗口注意力 (sliding window attention) 或 Mamba2 层相结合的混合架构,进一步提升了性能,实现了改进的训练效率和卓越的任务性能
Introduction and Discussion
- Transformer 架构显著提升了 LLM 的能力,由于其有效的注意力机制,在各种任务上展现出卓越的性能
- 该机制在精确序列建模方面表现出色,并在训练期间利用了现代 GPU 的并行处理能力
- 但自注意力 (self-attention) 组件的计算复杂度随序列长度呈二次方增长,导致巨大的计算需求,给训练和推理都带来了挑战
- 为了缓解这些问题,研究人员探索了诸如线性 Transformer (2020a) 等替代方案,它们用基于核化点积的线性注意力 (kernelized dot-product-based linear attention) 取代了传统的基于 softmax 的注意力,通过将其重构为具有矩阵值状态的线性 RNN,显著减少了推理期间的内存需求
- 虽然早期版本的线性 Transformer 在语言建模任务中表现不如标准 Transformer,但最近的增强已经显示出有前景的改进
- 例如结合类似于 LSTM 中的数据依赖门控机制,以 GLA (2024a) 和 Mamba2 (2024a) 等模型为例
- 然而,在管理长序列信息方面仍然存在挑战,特别是在上下文检索任务中,传统 Transformer 仍保持其优势 (2023a; 2024;)
- 这种现象并不令人惊讶:
- 线性 Transformer 可以被解释为实现了一种基于外积 (outer-product) 的键值关联记忆,让人联想到张量积表示 (1990)
- 但它们可以存储的正交键值对的数量受到模型维度的限制
- 当序列长度超过这个维度时,“记忆碰撞 (memory collisions)”将不可避免,阻碍精确检索 (2021a)
- Mamba2 通过引入一个简单的门控更新规则来解决这个限制:
$$ \mathbf{S}_{t}=\alpha_{t}\mathbf{S}_{t-1}+\boldsymbol{v}_{t}\boldsymbol{k}^{\mathrm{T} }_{t}$$- 该规则在每个时间步通过一个动态比率 \(\alpha_t \in (0,1)\) 统一衰减所有键值关联
- 但这种方法没有考虑不同键值关联的重要性差异,可能导致内存利用效率低下
- 如果模型需要忘记一个特定的键值关联,所有键值关联都会被同等程度地遗忘 ,使得这个过程缺乏针对性和效率
- 相比之下,采用 Delta 规则 (1960) 的线性 Transformer,即 DeltaNet (2021a; 2024b),通过(软性地)用传入的新键值对替换旧的键值对来选择性更新记忆
- 这种方法在上下文检索的合成基准测试中展示了令人印象深刻的性能
- 但由于这个过程((一次只修改一个键值对)),模型缺乏快速清除过时或无关信息的能力 ,尤其是在需要擦除先前数据的上下文切换期间
- 因此,人们发现 DeltaNet 在现实世界任务中表现一般 (2024b),这很可能是因为缺乏强大的内存清除机制
- 认识到门控更新规则和 Delta 规则在内存管理方面的互补优势,论文提出了门控 Delta 规则 (gated delta rule)
- 这是一种简单直观的机制,结合了两种方法
- 这个统一的规则实现了灵活的内存控制:
- 可以通过设置 \(\alpha_{t}\to 0\) 来迅速清除内存
- 同时可以通过设置 \(\alpha_{t}\to 1\) 来选择性更新特定内容而不影响其他信息(有效地切换到纯 Delta 规则)
- 剩下的挑战在于以硬件高效的方式实现门控 Delta 规则
- 基于 (2024b) 使用 WY 表示 (1985) 并行化 Delta 规则计算的高效算法,论文仔细扩展了他们的方法以纳入门控项
- 论文的扩展保留了分块并行 (chunkwise parallelism) 的优势 (2022a; 2023a; 2024a),实现了硬件高效的训练
- 论文最终的架构 Gated DeltaNet,在一套全面的基准测试中,包括语言建模、常识推理、上下文检索、长度外推和长上下文理解,持续优于 Mamba2 和 DeltaNet
- 基于这些结果,作者还开发了混合架构,策略性地将 Gated DeltaNet 层与滑动窗口注意力或 Mamba2 层相结合,进一步提升了训练效率和模型性能
Preliminary
Mamba2:带衰减的线性注意力 (Mamba2: Linear Attention with decay)
- 众所周知,线性 Transformer (2020a) 在排除归一化和查询/键激活的情况下,可以表述为以下线性递归:
$$
\begin{align}
\mathbf{S}_{t}&=\mathbf{S}_{t-1}+\boldsymbol{v}_{t}\boldsymbol{k}_{t}^{\intercal} \in\mathbb{R}^{d_{v}\times d_{k} },\\
\boldsymbol{o}_{t}&=\mathbf{S}_{t}\boldsymbol{q}_ {t}\in\mathbb{R}^{d_{v} }
\end{align}
$$- 其中 \(d_{k}\) 和 \(d_{v}\) 分别代表查询/键 (query/key) 和值 (value) 的(头)维度
- 通过展开递归,我们可以将其表示为向量形式(左)和矩阵形式(右)如下:
$$
\begin{align}
\boldsymbol{o}_{t}&=\sum_{i=1}^{t}(\boldsymbol{v}_{i}\boldsymbol{k}_{i}^{\intercal})\boldsymbol{q }_{t}=\sum_{i=1}^{t}\boldsymbol{v}_{i}(\boldsymbol{k}_{i}^{\intercal}\boldsymbol{q}_{t})\in\mathbb{R}^{d_{v} },\\
\mathbf{O}&=(\mathbf{Q}\mathbf{K}^{\intercal}\odot\mathbf{M}) \mathbf{V}\in\mathbb{R}^{L\times d_{v} }
\end{align}
$$- 其中 \(L\) 是序列长度,\(\mathbf{M}\in\mathbb{R}^{L\times L}\) 是由 \(\mathbf{M}_{ij}=0\)(当 \(i< j\))和 \(1\)(其他情况)定义的因果掩码 (causal mask)
- 然而,这种普通的线性注意力在语言建模中表现远不如 Transformer
- 理解:本质上 \(\sum_{i=1}^{t}\boldsymbol{v}_{i}(\boldsymbol{k}_{i}^{\intercal}\boldsymbol{q}_{t})\in\mathbb{R}^{d_{v} }\) 也有了一定的按照 Q 和 K 的相似度对 V 进行加权的思想,但这里主要差异在于 Transformer 是 Softmax 的 Attention 权重:
$$Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\frac{\boldsymbol{Q}\boldsymbol{K}^{\top}}{\sqrt{d_k}}\right)\boldsymbol{V}$$ - 理解:线性 Attention 和 Softmax Attention 都是 QK 内积越大,V 权重越大,但两者有本质区别:
- 线性 Attention 未实现归一化,仅仅累加所有 Token 的 V,理论上会导致越靠后的 Token,方差是越大的
- Softmax Attention 的权重是 \(e^{qk}\) 加权归一化,本质与线性归一化是不同的
- 问题:如果线性 Attention 中使用 \(e^{qk}\) 作为累加,是否基本上可以实践 Softmax 的等价实现?
- 回答:不可以,因为 Softmax Attention 中的 权重是 \(e^{qk}\),而线性 Attention 累加的对象是 \(kv\),重点:即使使用 \(e^{kv}\) 累加,累加对象也不同,反而导致含义变了!线性 Attention 的形式导致了他们无法实现 Softmax Attention 这样的 \(e^{qk}\) 加权平均
- 理解:本质上 \(\sum_{i=1}^{t}\boldsymbol{v}_{i}(\boldsymbol{k}_{i}^{\intercal}\boldsymbol{q}_{t})\in\mathbb{R}^{d_{v} }\) 也有了一定的按照 Q 和 K 的相似度对 V 进行加权的思想,但这里主要差异在于 Transformer 是 Softmax 的 Attention 权重:
- 为了解决这个问题,通常添加一个衰减项来遗忘历史信息
- 这里论文以 Mamba2 (2024a) 为例,它可以表示为以下线性递归(取决于具体的参数化):
$$
\begin{align}
\mathbf{S}_{t}&=\alpha_{t}\mathbf{S}_{t-1}+\boldsymbol{v}_{t}\boldsymbol{k}_{t}^ {\intercal},\\
\boldsymbol{o}_{t}&=\mathbf{S}_{t}\boldsymbol{q}_{t}
\end{align}
$$ - 其中 \(\alpha_{t}\in(0,1)\) 是一个数据依赖的标量值衰减项,随 \(t\) 变化
- 这里论文以 Mamba2 (2024a) 为例,它可以表示为以下线性递归(取决于具体的参数化):
- 定义累积衰减乘积
$$\gamma_{j}=\prod_{i=1}^{j}\alpha_{i}$$ - 并通过展开递归,我们可以将结果表示为向量形式(左)和矩阵并行形式(右):
$$
\begin{align}
\boldsymbol{o}_{t}&=\sum_{i=1}^{t}\left(\frac{\gamma_{t} }{\gamma_{i} }\boldsymbol{v }_{i}\boldsymbol{k}_{i}^{\intercal}\right)\boldsymbol{q}_{t}=\sum_{i=1}^{t}\boldsymbol{v}_{i}\left( \frac{\gamma_{t} }{\gamma_{i} }\boldsymbol{k}_{i}^{\intercal}\boldsymbol{q}_{t}\right),\\
\mathbf{O}&=((\mathbf{Q}\mathbf{K}^{\intercal})\odot\Gamma),\mathbf{V}
\end{align}
$$- 这里,\(\Gamma\in\mathbb{R}^{L\times L}\) 是一个衰减感知的因果掩码,其中 \(\Gamma_{ij}=\frac{\gamma_{i} }{\gamma_{j} }\)(如果 \(i\geq j\)),否则 \(\Gamma_{ij}=0\)
- 这种并行形式和递归形式之间的等价性也被称为 状态空间对偶性 (state space duality, SSD) (2024a)
- 这种递归结构也出现在其他几种架构中,包括 Gated RFA (2021)、xLSTM (2024) 和 Gated RetNet (2023a)
- 当 \(\gamma_{t}\) 与数据无关时(data-independent),该公式简化为 RetNet (2023a) 和 Lightning-Attention (2024a)
- 此外,如果 \(\gamma_{t}\) 扩展为矩阵值而非标量值,当使用外积结构参数化时,高效的训练算法仍然是可能的,正如 (2024a) 所展示并被 (2024b;2024;2025 等) 所使用的 分块训练 (Chunkwise training)
- 但递归形式和并行形式对于高效训练来说都不是理想的 (2022a; 2024a),这促使了使用分块并行形式 (2022a; 2023a) 进行硬件高效的线性时间训练,如下所述
- 总结来说,分块并行形式将输入和输出分割成几个大小为 \(C\) 的块 (chunk),并根据前一个块的最终状态以及当前块的查询/键/值块来计算每个块的输出
- 遵循 (2023a); (2024a) 的符号,论文以查询块 \(\boldsymbol{q}\) 为例
- 论文将
- \(\mathbf{Q}_{[t]}:={\boldsymbol{q} }_{tC+1:(t+1)C+1}\) 表示为块 \(t\) 的查询块
- \({\boldsymbol{q} }_{[t]}^{r}:={\boldsymbol{q} }_{tC+r}\) 表示为块 \(t\) 内的第 \(r\) 个查询块
- \(t\) 的初始状态定义为 \(\mathbf{S}_{[t]}:=\mathbf{S}_{[t]}^{0}=\mathbf{S}_{[t-1]}^{C}\)
- 通过部分展开递归,论文有
$$
\begin{align}
\mathbf{S}_{[t]}^{r}&=\mathbf{S}_{[t]}+\sum_{i=1}^{r}\boldsymbol{v}_{[t]}^{i}\boldsymbol{k}_{[t ]}^{i\tau}\in\mathbb{R}^{d_{v}\times d_{k} },\\
\boldsymbol{\sigma}_{[t]}^{r}&=\mathbf{S }_{[t]}^{r}{\boldsymbol{q} }_{[t]}^{r}=\mathbf{S}_{[t]}{\boldsymbol{q} }_{[t]}^{r}+\sum_{i=1}^{r} \boldsymbol{v}_{[t]}^{i}\left(\boldsymbol{k}_{[t]}^{i\tau}{\boldsymbol{q} }_{[t]}^{r}\right)\in\mathbb{R}^ {d_{v} }
\end{align}
$$ - 等价地,以矩阵形式表示:
$$
\begin{align}
\mathbf{S}_{[t+1]}&=\mathbf{S}_{[t]}+\mathbf{V}_{[t]}\mathbf{K}_{[t]}^{\tau} \in\mathbb{R}^{d_{v}\times d_{k} },\\
\mathbf{O}_{[t]}&=\mathbf{Q}_{[t]}{ \mathbf{S} }_{[t]}^{\tau}+\left(\mathbf{Q}_{[t]}\mathbf{K}_{[t]}^{\tau}\odot \mathbf{M}\right)\mathbf{V}_{[t]}\in\mathbb{R}^{C\times d_{v} }
\end{align}
$$- 其中 \(\mathbf{M}\in\mathbb{R}^{C\times C}\) 是因果掩码
- 上述等式富含矩阵乘法 (matmuls),允许基于张量核心 (tensor-core) 的硬件优化
- 这个分块算法可以轻松扩展到带衰减的线性注意力:
$$
\begin{align}
\mathbf{S}_{[t+1]}&=\overrightarrow{\mathbf{S}_{[t]} }+\mathbf{V}_{[t]}^{\tau} \overrightarrow{\mathbf{K}_{[t]} }\in\mathbb{R}^{d_{v}\times d_{k} },\\
\mathbf {O}_{[t]}&=\overleftarrow{\mathbf{Q}_{[t]}\mathbf{S}_{[t]}^{\tau} }+\left( \mathbf{Q}_{[t]}\mathbf{K}_{[t]}^{\tau}\odot\Gamma_{[t]}\right)\mathbf{V}_{[t ]}\in\mathbb{R}^{C\times d_{v} }
\end{align} \tag{1}
$$- 其中有
$$(\Gamma_{[t]})_{ij}=\frac{\gamma_{[t]}^{i} }{\gamma_{[t]}^{j} },\gamma_{[t]}^{j}= \prod_{j=tC+1}^{tC+j}\alpha_{j} $$- 注:这里论文稍微滥用了 \(\gamma\) 的符号来表示每个块的累积乘积(分别从每个块的第一个位置开始),而不是整个序列
- 这里论文使用左箭头 (\(\overset{\leftarrow}{\cdot}\)) 或右箭头 (\(\overset{\rightarrow}{\cdot}\)) 分别表示衰减到每个块第一个位置和最后一个位置的变量,
$$
\begin{align}
\overleftarrow{ {\boldsymbol{q} }_{[t]}^{r} }&=\gamma_{[t]}^{r}{\boldsymbol{q} }_{[t]}^{r} \text{ 将每个向量衰减到块 t 的第一个位置 (decaying each vector to the first position of chunk t)}\\
\overleftarrow{ {\boldsymbol{k} }_{[t]}^{r} }&=\frac{\gamma_{[t]}^{C} }{ \gamma_{[t]}^{c} }\boldsymbol{k}_{[t]}^{r} \text{ 将每个向量衰减到块 t 的最后一个位置 (decaying each vector to the last position of chunk t)} \\
\overrightarrow{\mathbf{S}_{[t]} }&=\gamma_{[t]}^{C}\mathbf{S}_{[t]} \text{ 在整个块 t 上衰减状态矩阵 (decaying the state matrix over the entire chunk t)} \tag{2}
\end{align}
$$- 其他变量(例如 \(\overrightarrow{\boldsymbol{v} }\))也类似
- 其中有
- Mamba2 中引入的 SSD 分解算法在很大程度上等同于这种分块算法
- 对于更通用的方法, (2024a) 提出了一种扩展的分块算法,用于线性注意力,该算法结合了细粒度的衰减机制
Delta Networks: Linear Attention with Delta Rule
- Delta 更新规则(Delta Update Rule) (1960; 2021a) 动态地擦除与当前输入键 (\(\boldsymbol{k}_{t}\)) 关联的旧值 (\(\boldsymbol{v}_{t}^{\text{old} }\)) ,并写入一个新值 (\(\boldsymbol{v}_{t}^{\text{new} }\)) ,该新值是基于“写入强度” \(\beta_{t}\in(0,1)\) 的当前输入值和旧值的线性组合 (可以将 \(\beta_{t}\in(0,2)\) 设置为允许负特征值,以解锁 DeltaNet 的状态跟踪能力 (2024; 2025))
$$
\begin{align}
\mathbf{S}_{t}&=\mathbf{S}_{t-1}-\underbrace{(\mathbf{S}_{t-1}\boldsymbol{k}_{t})}_{\boldsymbol {v}_{t}^{\text{old} } }\boldsymbol{k}_{t}^{\top}+\underbrace{(\beta_{t}\boldsymbol{v}_{t}+(1-\beta_{t})\mathbf{S}_{t-1}\boldsymbol{k}_{t}))}_{\boldsymbol{v}_{t}^{\text{new} } }\boldsymbol{k}_{t}^{\top} \\
&= \mathbf{S}_{t-1}\left(\mathbf{I}-\beta_{t}\boldsymbol{k}_{t}\boldsymbol{k}_{t}^{\top}\right)+ \beta_{t}\boldsymbol{v}_{t}\boldsymbol{k}_{t}^{\top}
\end{align}
$$- 如上所示,DeltaNet 实现了具有广义 Householder 转移矩阵 (\(\mathbf{I}-\beta_{t}\boldsymbol{k}_{t}\boldsymbol{k}_{t}^{\mathsf{T} }\)) 的一阶线性递归
- 尽管在关联回忆和语言建模性能上表现出色 (2021a),但由于计算效率低下,DeltaNet 受到的关注有限,直到 (2024b) 引入了一种硬件高效的分块训练算法,详情如下
- 分块并行形式 (Chunkwise parallel form)。通过部分展开递归,论文有
$$\mathbf{S}_{[t]}^{r}=\mathbf{S}_{[t]}\underbrace{\left(\prod_{i=1}^{r} \mathbf{I}-\beta_{[t]}^{i}\boldsymbol{k}_{[t]}^{i}\boldsymbol{k}_{[t]}^{i\mathsf{T} }\right)}_{:= \mathbf{P}_{[t]}^{r} }+\underbrace{\sum_{i=1}^{r}\left(\beta_{[t]}^{i}\boldsymbol{v}_{[t ]}^{i}\boldsymbol{k}_{[t]}^{i\mathsf{T} }\prod_{j=i+1}^{r}\left(\mathbf{I}-\beta_{[t]}^{ j}\boldsymbol{k}_{[t]}^{j}\boldsymbol{k}_{[t]}^{j\mathsf{T} }\right)\right)}_{:=\mathbf{H}_{[t]}^{r} } \tag{3}$$ - 其中 \(\mathbf{P}_{[t]}^{j}\) 涉及广义 Householder 矩阵的累积乘积,可以通过经典的 WY 表示 (1985) 进行优化:
$$\mathbf{P}_{[t]}^{r}=\mathbf{I}-\sum_{i=1}^{r}\mathbf{w}_{[t]}^{i}\boldsymbol{k}_{[t]}^{ i\mathsf{T} }\in\mathbb{R}^{d_{k}\times d_{k} }\qquad\mathbf{w}_{[t]}^{r}=\beta_{ [t]}^{r}\left(\boldsymbol{k}_{[t]}^{r}-\sum_{i=1}^{r-1}\left(\mathbf{w}_{[t]}^{i}(\boldsymbol{k}_ {[t]}^{i\mathsf{T} }\boldsymbol{k}_{[t]}^{r})\right)\right)\in\mathbb{R}^{d_{k} } \tag{4}$$ - 同样,\(\mathbf{H}_{[t]}^{r}\) 可以表示为:
$$\mathbf{H}_{[t]}^{r}=\sum_{i=1}^{r}\mathbf{u}_{[t]}^{i}\boldsymbol{k}_{[t]}^{i\mathsf{T } }\in\mathbb{R}^{d_{v}\times d_{k} }\qquad\mathbf{u}_{[t]}^{r}=\beta_{[t]}^{r} \left(\boldsymbol{v}_{[t]}^{r}-\sum_{i=1}^{r-1}\left(\mathbf{u}_{[t]}^{i}(\boldsymbol{k}_{[t]}^{ i\mathsf{T} }\boldsymbol{k}_{[t]}^{r})\right)\right)\in\mathbb{R}^{d_{v} } \tag{5}$$ - 并以矩阵形式表示:\(\mathbf{P}_{[t]}=\mathbf{I}-\mathbf{W}_{[t]}^{\top}\mathbf{K}_{[t]}\in\mathbb{R }^{d_{k}\times d_{k} }\),\(\mathbf{H}_{[t]}=\mathbf{U}_{[t]}^{\top}\mathbf{K}_{[t]}\in\mathbb{R}^{d_{v} \times d_{k} }\)。通过使用 UT 变换 (2006),我们可以进一步将 \(\mathbf{W}\) 和 \(\mathbf{U}\) 写成矩阵形式:
$$\mathbf{T}_{[t]} =\left[\mathbf{I}+\text{strictLower}\left(\text{diag}(\beta_{[t]} )\mathbf{K}_{[t]}\mathbf{K}_{[t]}^{\mathsf{T} }\right)\right]^{-1}\text{ diag}\left(\beta_{[t]}\right)\in\mathbb{R}^{C\times C} \\
\mathbf{W}_{[t]} =\mathbf{T}_{[t]}\mathbf{K}_{[t]}\in\mathbb{R}^{C\times d_{k} }, \qquad\mathbf{U}_{[t]}=\mathbf{T}_{[t]}\mathbf{V}_{[t]}\in\mathbb{R}^{C \times d_{v} }\tag{6-7}$$ - 将这些代回方程 3,得到了一个硬件高效的 DeltaNet 分块算法,该算法利用了矩阵乘法,实现了基于张量核心的 GPU 优化:
$$\mathbf{S}_{[t+1]} =\mathbf{S}_{[t]}\mathbf{P}_{[t]}+\mathbf{H}_{[t]}=\mathbf{S}_{[t ]}+\left(\mathbf{U}_{[t]}-\mathbf{W}_{[t]}\mathbf{S}_{[t]}^{\mathsf{T} }\right)^ {\mathsf{T} }\mathbf{K}_{[t]} \in\mathbb{R}^{d_{v}\times d_{k} } \\
\mathbf{O}_{[t]} =\mathbf{Q}_{[t]}\mathbf{S}_{[t]}^{\mathsf{T} }+(\mathbf{Q}_{[t]} \mathbf{K}_{[t]}^{\mathsf{T} }\odot\mathbf{M})\left(\mathbf{U}_{[t]}-\mathbf{W }_{[t]}\mathbf{S}_{[t]}^{\mathsf{T} }\right) \in\mathbb{R}^{C\times d_{v} } \tag{8-9}$$
Gated Delta Networks
Formulation: Gated Delta Rule
- 论文提出的门控 Delta 规则简单而有效:
$$\mathbf{S}_{t}=\mathbf{S}_{t-1}\left(\alpha_{t}(\mathbf{I}-\beta_{t}\boldsymbol{k}_{t }\boldsymbol{k}_{t}^{\mathsf{T} })\right)+\beta_{t}\boldsymbol{v}_{t}\boldsymbol{k}_{t}^{\mathsf{T} } \tag{10}$$- 其中数据依赖的门控项 \(\alpha_{t}\in(0,1)\) 控制状态衰减
- 这个公式统一了门控机制和 Delta 规则的优势:门控项支持自适应内存管理,而 Delta 更新结构促进有效的键值关联学习
- 论文通过 Liu 等 (2024) 引入的在线学习框架的视角,对门控 Delta 规则进行了正式分析
- 在这个框架中,循环状态更新作为在线学习问题的闭式解出现,如表 1 所示
- 最近的线性 RNN 架构通常在其在线学习目标中包含一个正则化项,以防止状态偏离先前的值,从而实现记忆保留
- 但当状态被信息饱和时,这种保留机制会变得有问题。在这种情况下,每个状态将对多个信息片段进行编码,使得精确检索变得困难
- 为了解决这个限制,Mamba2 和 Gated DeltaNet 引入了一个自适应缩放因子 \(\alpha_{t}\),它放松了正则化项,允许 \(\mathbf{S}_{t}\) 和 \(\mathbf{S}_{t-1}\) 之间的受控偏差
- 这个修改通过选择性遗忘实现了动态内存管理,这在过滤无关信息时可能很有用(见 章节3.2)

- 这个修改通过选择性遗忘实现了动态内存管理,这在过滤无关信息时可能很有用(见 章节3.2)
- 另一方面,线性注意力 (Linear Attention, LA) 和 Mamba2 使用简单的负内积损失 -\(\langle\mathbf{S}_{t}\boldsymbol{k}_{t},\boldsymbol{v}_{t}\rangle\),而 Longhorn (2024) 使用更具表达力的在线回归目标 \(|\mathbf{S}_{t}\boldsymbol{k}_{t}-\boldsymbol{v}_{t}|^{2}\) 来更好地建模键值关联。由此产生的 Longhorn 更新规则与 Delta 更新规则非常相似,这表明(门控)Delta 规则在上下文关联回忆方面优于 Mamba2
- Longhorn 更新规则与 Delta 更新规则理论上的区别在于优化方法:Longhorn 使用隐式在线学习 (2010) 来推导闭式的全局最优更新,而 DeltaNet 通过一步显式梯度下降来优化相同的目标,正如 (2024) 所指出的
- 从快速权重编程 (fast weight programming) (2022a)、测试时训练 (test-time training) (2024a) 和回归 (2025) 的角度来看,隐藏状态 \(\mathbf{S}\) 可以被解释为一个(快速)权重矩阵,Delta 规则通过测试时随机梯度下降 (stochastic gradient descent, SGD) 优化在线回归目标 \(\mathcal{L}(\mathbf{S}_{t})=\frac{1}{2}|\mathbf{S}_{t}\boldsymbol{k}_{t}-\boldsymbol{v}_{t}|^{2}\):
$$\mathbf{S}_{t+1}=\mathbf{S}_{t}-\beta_{t}\nabla\mathcal{L}(\mathbf{S}_{t})= \mathbf{S}_{t}-\beta_{t}(\mathbf{S}_{t}\boldsymbol{k}_{t}-\boldsymbol{v}_{t})\boldsymbol{k}_{t}^{\top}= \mathbf{S}_{t}\left(\mathbf{I}-\beta_{t}\boldsymbol{k}_{t}\boldsymbol{k}_{t}^{\top}\right)+\beta_{t}\boldsymbol{v}_{t}\boldsymbol{k}_{t}^{\top}$$- 其中 \(\beta_{t}\) 代表(自适应)学习率。从这个角度来看,门控 Delta 规则可以被视为将自适应权重衰减项 \(\alpha_{t}\) 纳入 SGD 更新中,这是一种在深度学习中广泛使用的技术 (1991; 2023)
- 同时,Titans (2024) 证明了在 RNN 测试时 SGD 更新中结合权重衰减机制的有效性
Case study: Single Needle in a Haystack, S-NIAH,大海捞针
- 为了更好地理解 Delta 规则和门控规则之间的互补优势,论文提供了一个关于来自 RULER (2024) 的“大海捞针”基准测试套件的案例研究,其中一个键值对充当“大海”(上下文)中的“针”,模型必须在给定键时回忆起值

- 表 2 展示了结果,论文得出三个主要观察:
- 衰减损害记忆保留 (Decay hurts memory retention)
- 在最简单的 S-NIAH-1 设置中,具有重复的合成上下文,模型记忆的信息最少,测试长期保留能力
- DeltaNet 在所有序列长度上都实现了接近完美的性能
- Mamba2 在超过 2K 序列后性能显著下降,因为它衰减历史信息太快,而 Gated DeltaNet 的下降不那么严重,这得益于使用了 Delta 规则
- 门控促进过滤 (Gating facilitates filtering)
- 在具有真实世界文章上下文的 S-NIAH-2/3 中,模型存储所有潜在相关信息,测试高效的内存管理
- 在固定状态大小的情况下,缺乏清除会导致内存碰撞,信息变得叠加且无法区分
- DeltaNet 的性能在较长序列时显著下降,原因是内存清除能力差
- Mamba2 和 Gated DeltaNet 通过过滤无关信息的门控机制保持了更好的性能
- Delta 规则有助于记忆 (Delta rule helps memorization)
- 在 S-NIAH-3 中,值从数字变为 UUID,测试复杂模式记忆
- Mamba2 的性能迅速下降,而 Gated DeltaNet 表现更好,验证了 Delta 规则确实具有更好的记忆能力
- 衰减损害记忆保留 (Decay hurts memory retention)
Algorithm: Hardware-efficient Chunkwise training
- 在本小节中,论文推导出用于训练 Gated DeltaNet 的硬件高效分块算法。通过部分展开方程 10 中的递归,论文有
$$\mathbf{S}_{[t]}^{r}=\underbrace{\mathbf{S}_{[t]}\left(\prod_{i=1}^{ r}\alpha_{[t]}^{i}\left(\mathbf{I}-\beta_{[t]}^{i}\boldsymbol{k}_{[t]}^{i} \boldsymbol{k}_{[t]}^{i\mathsf{T} }\right)\right)}_{\text{:=F}_{[t]}^{r} }+\underbrace {\sum_{i=1}^{r}\left(\beta_{[t]}^{i}\boldsymbol{v}_{[t]}^{i}\boldsymbol{k}_{[t]} ^{i\mathsf{T} }\prod_{j=i+1}^{r}\alpha_{[t]}^{j}\left(\mathbf{I}-\beta_{[t]}^{j }\boldsymbol{k}_{[t]}^{j}\boldsymbol{k}_{[t]}^{j\mathsf{T} }\right)\right)}_{ \text{:=G}_{[t]}^{r} }$$- 很容易看出 \(\mathbf{F}_{[t]}^{r}=\gamma_{[t]}^{r}\mathrm{P}_{[t]}^{r}=\hat{\overline{\mathbf {P} }_{[t]}^{r} }\)
- 至于 \(\mathbf{G}_{[t]}^{r}\),论文调整方程 5 如下:
$$\mathbf{G}_{[t]}^{r}=\sum_{i=1}^{r}\frac{\gamma_{[t]}^{r} }{\gamma_{[t]}^{i} }\tilde{\mathbf{u} }_{[t]}^{i}\boldsymbol{k}_{[t]}^{i\mathsf{T} }\in \mathbb{R}^{d_{v}\times d_{k} }\qquad\tilde{\mathbf{u} }_{[t]}^{r}=\beta_{[t]}^{r }\left(\boldsymbol{v}_{[t]}^{r}-\sum_{i=1}^{r-1}\left(\tilde{\mathbf{u} }_{[t]}^ {i}(\frac{\gamma_{[t]}^{r} }{\gamma_{[t]}^{i} }\boldsymbol{k}_{[t]}^{i\mathsf{T } }\boldsymbol{k}_{[t]}^{r})\right)\right)\in\mathbb{R}^{d_{v} }$$- (证明见附录 A)
- 通过 UT 变换,论文得到矩阵形式:
$$\widetilde{\mathbf{U} }_{[t]}^{-}=\left[\mathbf{I}+\text{strictLower}\left( \operatorname{diag}\left(\beta_{[t]}\right)(\Gamma_{[t]}\odot\mathbf{K}_{[t]} \mathbf{K}_{[t]}^{\mathsf{T} })\right)\right]^{-1}\operatorname{diag}\left( \beta_{[t]}\right)\mathbf{V}_{[t]}\qquad\in\mathbb{R}^{C\times d_{v} }$$
- 类似于 Mamba2 扩展线性注意力的方式(方程 1),我们可以调整 DeltaNet 的分块算法(方程 8-9)用于 Gated DeltaNet,以实现硬件高效训练,如下所示:
$$
\begin{align}
\mathbf{S}_{[t+1]}&=\overrightarrow{\mathbf{S}_{[t]} }+\left( \overrightarrow{\mathbf{U} }_{[t]}-\overleftarrow{\mathbf{W} }_{[t]}\mathbf{S}_{[ t]}^{\mathsf{T} }\right)^{\mathsf{T} }\overrightarrow{\mathbf{K} }_{[t]} \in\mathbb{R}^{d_{v}\times d_{k} } \\
\mathbf{O}_{[t]}&=\overleftarrow{\mathbf{O} }_{[t]}\mathbf{S}_{[t]} ^{\mathsf{T} }+\left(\mathbf{Q}_{[t]}\mathbf{K}_{[t]}^{\mathsf{T} }\odot \mathbf{M}\right)\left(\overrightarrow{\mathbf{U} }_{[t]}-\overleftarrow{ \mathbf{W} }_{[t]}\mathbf{S}_{[t]}^{\mathsf{T} }\right)\in\mathbb{R}^{C\times d_ {v} }
\end{align}
$$- 其中 \(\overleftarrow{\boldsymbol{q} }_{[t]}^{r}=\gamma_{[t]}^{r}\boldsymbol{q}_{[t]}^ {r}\), \(\overleftarrow{\mathbf{w} }_{[t]}^{r}=\gamma_{[t]}^{r}\mathbf{w}_{[t]}^{r}\), \(\overleftarrow{\boldsymbol{k} }_{[t]}^{r}=\frac{\gamma_{[t]}^{C} }{\gamma_{[t]} } \boldsymbol{k}_{[t]}^{r}\), 并且 \(\overrightarrow{\mathbf{S} }_{[t]}\neq\gamma_{[t]}^{C}\mathbf{S}_{[t]}\) 如同论文在方程 2 中的定义
Gated Delta Networks and Hybrid Models
- Token 混合器块 (Token mixer block)
- 基本的 Gated DeltaNet 遵循 Llama 的宏观架构,将 Token 混合器层与 SwiGLU MLP 层堆叠,但用门控 Delta 规则 Token 混合取代了自注意力
- 图 1(右)显示了其块设计
- 对于门控 Delta 规则(方程 10),查询、键和值 \(\{\boldsymbol{q},\boldsymbol{k},\boldsymbol{v}\}\) 通过线性投影、短卷积 (short convolution) 和 SiLU 生成,并对 \(\boldsymbol{q},\boldsymbol{k}\) 应用 L2 归一化以保持训练稳定性。\(\alpha,\beta\) 仅使用线性投影(论文对 \(\alpha\) 使用 Mamba2 的参数化,但为简洁起见省略了细节)
- 遵循 Sun 等 (2023a),输出在应用输出投影之前通过归一化和门控处理
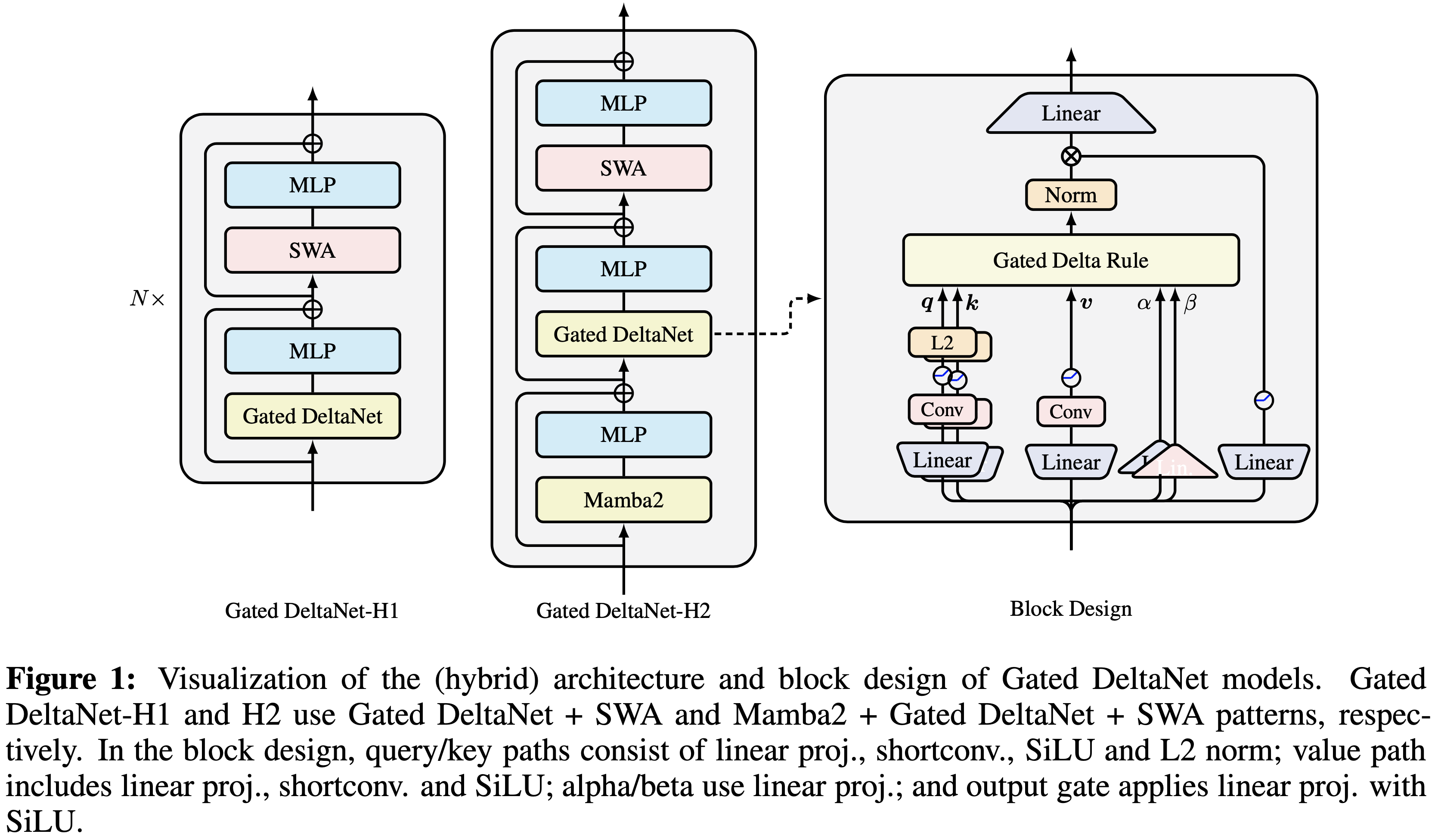
- 混合模型 (Hybrid models)
- 线性 Transformer 在建模局部偏移和比较方面存在局限性,并且其固定状态大小使得检索任务变得困难 (2023a)
- 遵循最近的混合架构,如 Griffin (2024) 和 Samba (2024),论文将线性循环层与滑动窗口注意力 (sliding window attention, SWA) 相结合,产生了 GatedDeltaNet-H1
- 论文还堆叠了 Mamba2、GatedDeltaNet 和 SWA,产生了 GatedDeltaNet-H2
Experiments
Setup
- 论文的实验包括对最近最先进架构的全面比较,包括纯 Transformer 模型、基于 RNN 的方法和混合架构
- 论文针对以下基线进行评估:RetNet (2023a)、HGRN2 (2024b)、Mamba (2023)、Mamba2 (2024a)、Samba (2024) 和 DeltaNet (2024b)
- 为了公平比较,所有模型都在相同条件下训练,具有 1.3B 参数,使用从 FineWeb-Edu 数据集 (2024) 中采样的 100B Token
- 论文使用 AdamW 优化器,峰值学习率为 4e-4,权重衰减为 0.1,梯度裁剪为 1.0
- 学习率遵循余弦退火调度,具有 1B Token 的预热期 和 0.5M Token 的批次大小
- 所有模型都使用词表为 32,000 的 Llama2 分词器
- 对于序列建模,论文将训练长度设置为 4K Token ,Samba 和论文的混合模型使用 2K 的滑动窗口大小
- 评估设置见附录 B.1,消融研究见附录 B.2
Common-sense reasoning
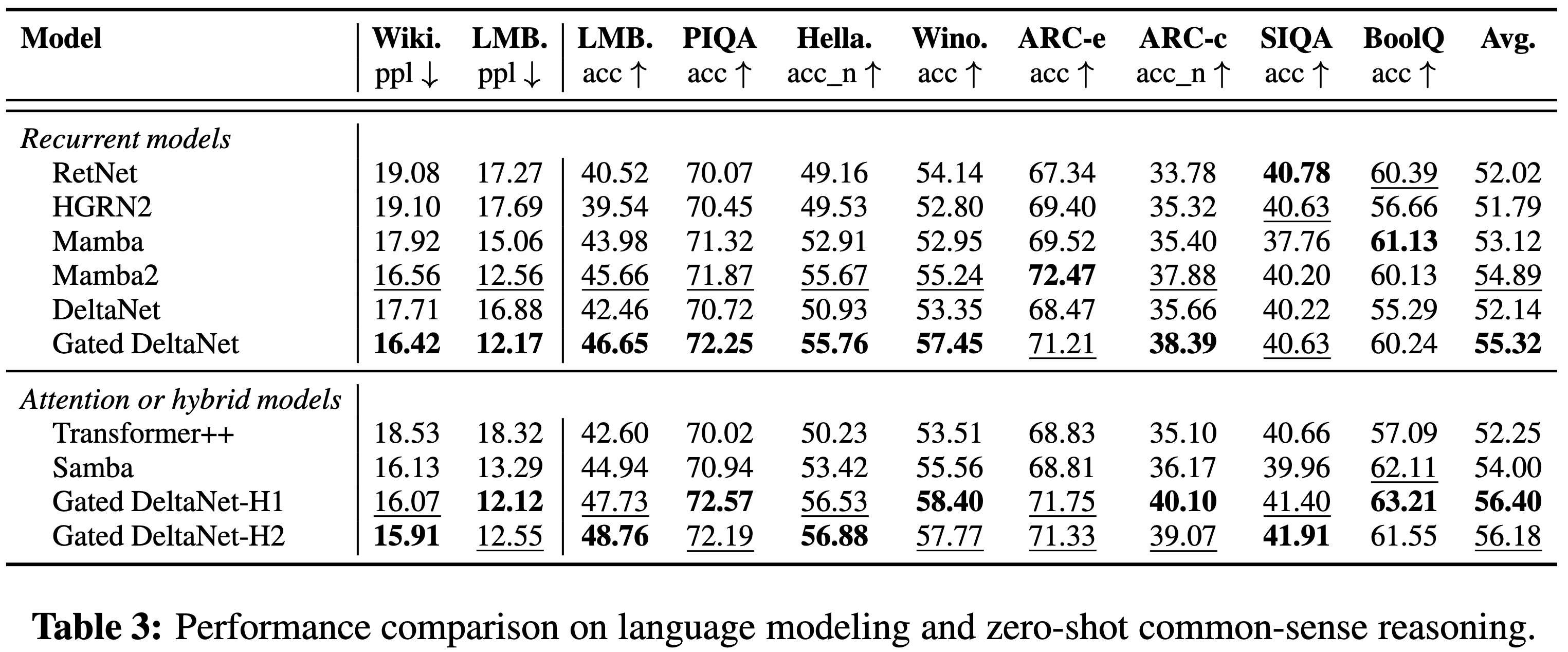
- 在表 3 中,论文展示了具有 0.4B 和 1.3B 参数模型的语言建模困惑度以及在常识推理基准测试上的零样本准确率
- Gated DeltaNet 在两个规模上都持续优于其他线性模型,包括 RetNet、HGRN2、Mamba、Mamba2 和 DeltaNet
- 正如预期的那样,混合变体进一步提升了性能
In-context retrieval on real-world data
- 表 4 展示了在 Arora 等 (2023a) 使用的真实世界回忆密集型任务上的结果
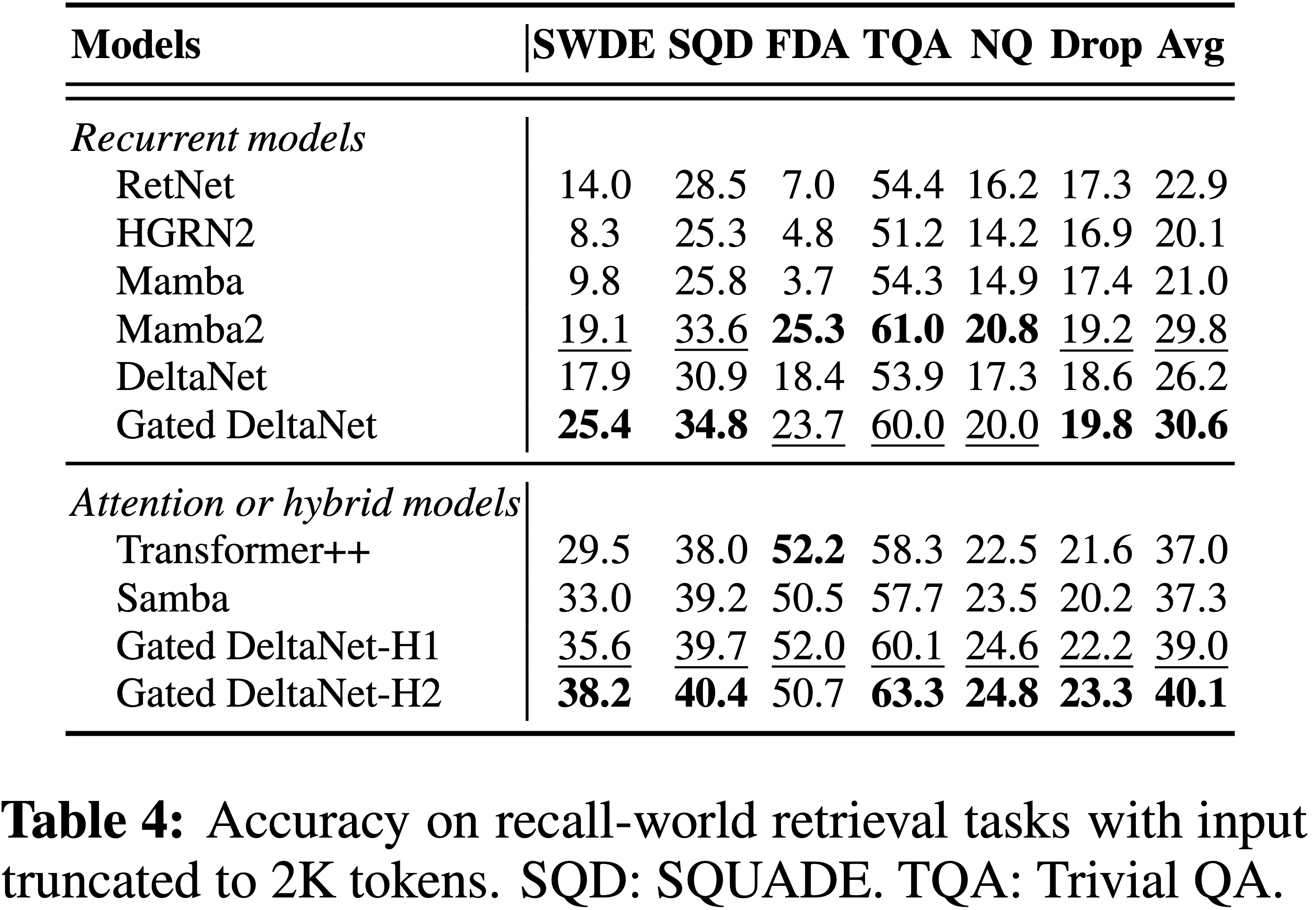
- 正如预期的那样,线性循环模型与 Transformer 相比显示出显著的性能差距,而结合线性循环和注意力的混合模型在检索任务中优于纯注意力模型
- 对于纯循环模型,尽管 DeltaNet 在合成的上下文检索任务上表现出色 (2024b),但其真实世界的检索性能落后于 Mamba2,这与论文在 S-NIAH-2 和 S-NIAH-3 中的观察一致(表 2)

- Gated DeltaNet 由于其门控 Delta 规则,性能优于 DeltaNet 和 Mamba2,尽管改进幅度小于表 2
- 论文将这种性能差距的缩小归因于未进行指令调优的小型语言模型容易产生重复错误,这些错误是这些任务中错误的主要来源(参见 Arora 等 (2023a, 附录 E))
- 由于这个问题在很大程度上与更新规则的选择无关,因此模型之间的性能差异与表 2 相比不那么明显
Length extrapolation on long sequences
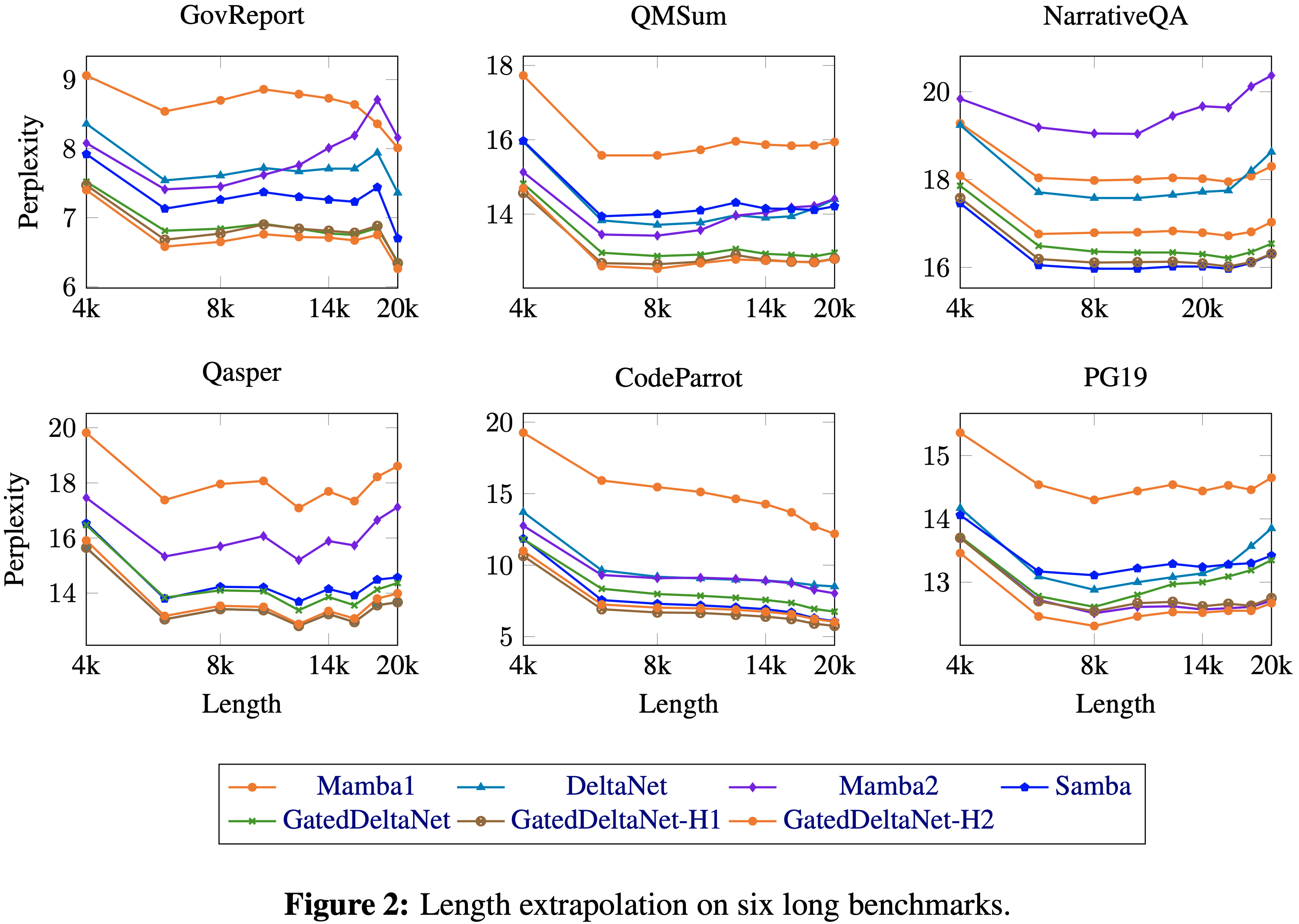
- 如图 2 所示,论文评估了模型在六个长上下文基准测试中外推到长达 20K Token 序列的能力
- 在 RNN 模型中,Gated DeltaNet 在所有任务中实现了最低的整体困惑度
- 虽然论文在长度外推中观察到结果好坏参半,但 Gated DeltaNet 表现出相对更稳健的性能,表明其具有更好的内存管理能力
- 混合模型通过利用注意力进行局部上下文建模,进一步改善了这一点,从而减轻了其循环组件在内存管理上的负担
- 未来的工作将探索这些模型在更长序列上的能力
Long context understanding
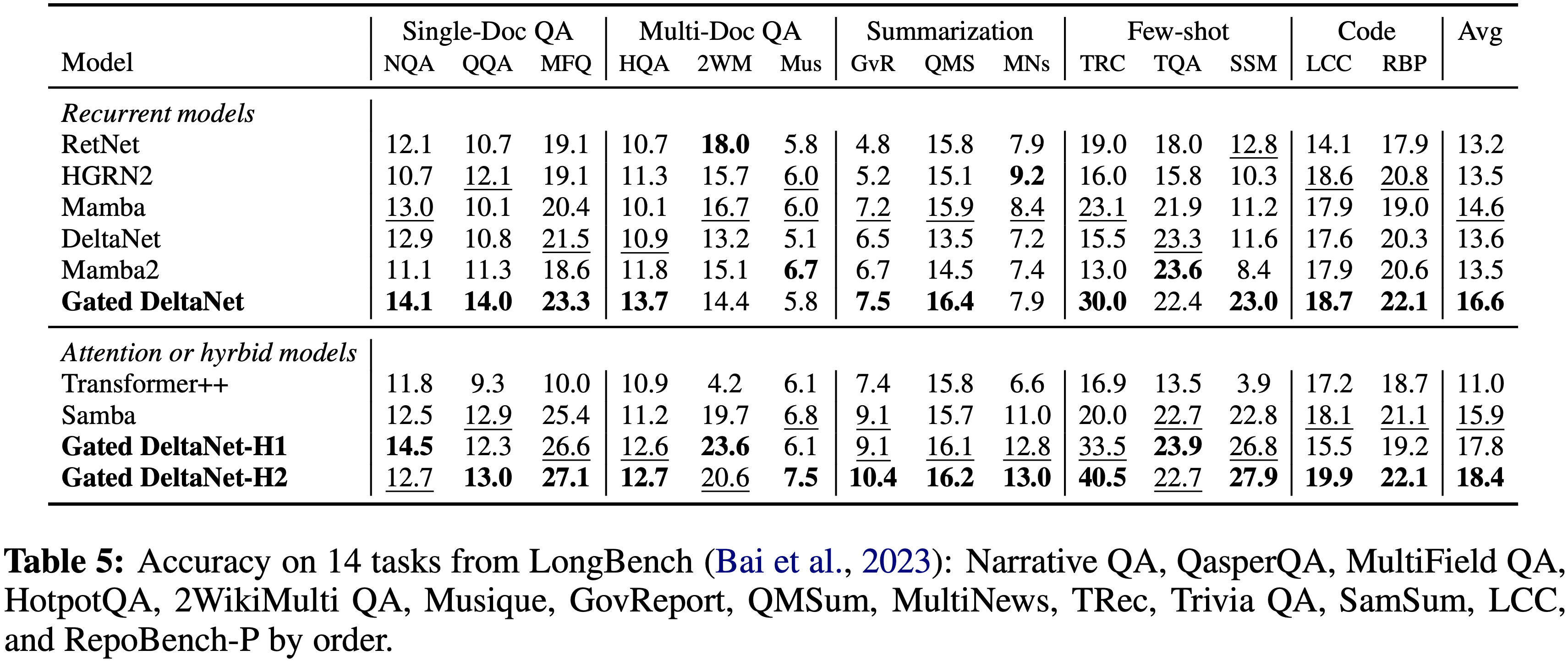
- 如表 5 所示,论文评估了模型在 LongBench (2023) 上的性能
- 在循环模型中,Gated DeltaNet 显示出持续的优势,特别是在单文档问答、少样本上下文学习和代码任务中,分别展示了其在检索、上下文学习和状态跟踪方面的卓越能力
Throughput Comparison
- 不同模型的训练吞吐量对比如图 3 所示
- 正如论文的分析所示,论文提出的门控 delta 规则 (gated delta rule) 与原始 delta 规则相比仅引入了微小的开销,Gated DeltaNet 的吞吐量与 DeltaNet 基本相同
- 由于它们具有更具表达力的转移矩阵 (transition matrices),两者都比 Mamba2 稍慢(约慢 2–3K tokens/sec)
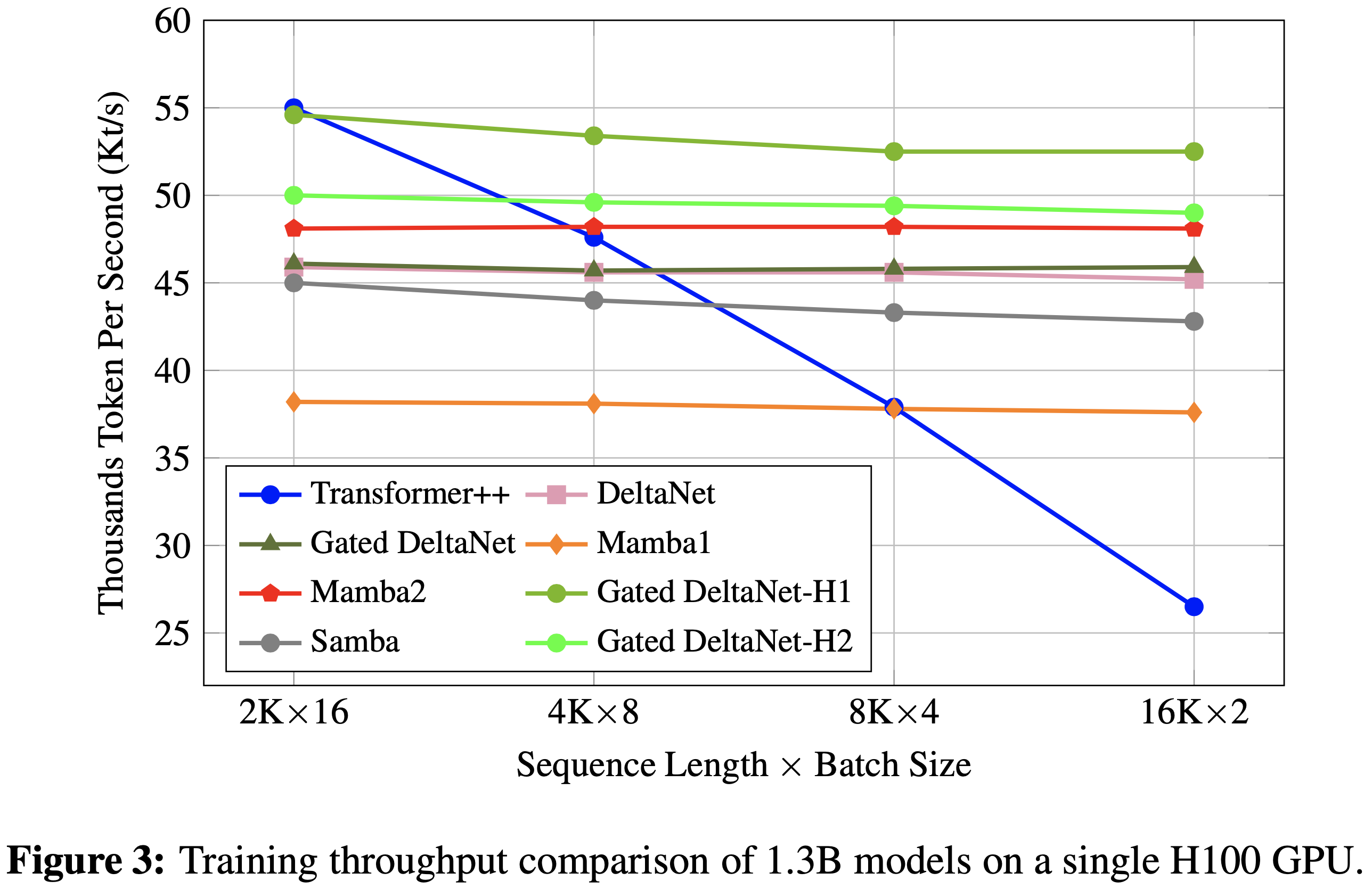
- 正如论文的分析所示,与原始 Delta 规则相比,提出的门控 Delta 规则仅引入了边际开销,Gated DeltaNet 实现了与 DeltaNet 基本相同的吞吐量
- 由于它们具有更具表达力的转移矩阵,两者都比 Mamba2(2-3K Token /秒)稍慢
- Transformer++ 在 2K 上下文窗口领域实现了最佳性能
- 这得益于高度优化的 Flash-Attention-2 内核 (2023)
- 因此,将 2K 窗口大小的滑动窗口注意力 (sliding window attention, SWA) 与其他令牌混合器 (token mixer) 相结合的混合方法,其吞吐量高于独立的混合器:Samba 优于 Mamba,而 Gated DeltaNet-H1 和 Gated DeltaNet-H2 优于 Gated DeltaNet
- 值得注意的是,Gated DeltaNet-H1 在所有序列长度上均保持了可观的训练吞吐量,即使在短序列上也是如此
Related Work
Gated linear RNN
- 大型线性循环语言模型因其训练和推理效率而备受关注
- 线性循环神经网络领域已经从使用数据无关的衰减机制迅速发展为在更近期的架构中融入数据相关的衰减机制
- 数据无关的衰减机制:例如 S4 (2022)、S5 (2023)、LRU (2023)、RWKV4/5 (2023) 和 RetNet (2023a) 等模型所例证
- 数据相关的衰减机制:例如 HGRN1/2 (2023a; 2024b)、Mamba1/2 (2023; 2024a)、RWKV6 (2024)、GSA (2024)
- 这一转变源于门控/遗忘机制(在 Mamba 中称为选择性机制)被证实的优势,这是一个源于门控循环神经网络文献 (2000) 的经典概念,其重要性一直被反复确认 (2015; 2018; 2023b; 2024b)
- 现代遗忘门与传统设计(如 LSTM 中的遗忘门)的不同之处在于,它移除了对先前隐藏状态的依赖,仅依赖于输入数据
- 这种修改使得在序列长度上能够实现高效的并行性 (2018; 2023b)
- 缺乏遗忘门一直是 DeltaNet 的一个显著局限,而论文的门控扩展以一种自然、有效且硬件高效的方式弥补了这一差距
- 论文也注意到最近的一项并行工作 RWKV-7 使用了类似的想法,但采用了更宽松的使用对角加低秩转移的形式化表示:
$$\mathbf{S}_{t}=\mathbf{S}_{t-1}(\mathrm{diag}(\mathbf{d}_{t})-\mathbf{a}_{t}\mathbf{b}_{t}^{\top})+v_{t}\boldsymbol{k}_{t}^{\top}$$ - 其中 \(\mathbf{d}_{t},\mathbf{a}_{t},\mathbf{b}_{t}\in\mathbb{R}^{d_{k} }\)
- 分块算法可以类似地适用于这种情况,正如在 Flash Linear Attention (2024) 中所实现的那样
Delta rule
- Delta 学习规则在记忆容量上表现出优于赫布学习规则 (1988; 1989),DeltaNet 利用了这一点,而线性 Transformer 则依赖于类赫布规则
- 这种记忆容量优势在合成上下文学习任务中表现明显,并延伸到语言建模 (2021; 2024b)、强化学习 (2022b) 和图像生成 (2023)
- (2024b) 将 delta 规则计算并行化,并证明了 DeltaNet 的数据相关的单位加低秩结构 (\(\mathbf{I}-\beta_{t}\boldsymbol{k}_{t}\boldsymbol{k}_{t}^{\top}\)) 比 Mamba2 的数据相关的对角矩阵 (\(\alpha_{\mathbf{I} }\)) 提供了更大的灵活性
- 这种结构优势可能实现复杂的推理,包括正则语言识别 (2024; 2024) 和超越 TC’ 复杂度的状态跟踪 (2024),这对于编码和推理应用至关重要
- 尽管有这些显著优势,delta 规则面临理论局限 (2023) 并且在真实世界数据集上表现中等 (2024b),表明仍有改进空间
- 先前通过非线性循环 (2021, 2022a) 来增强表达力的尝试解决了一些局限,但牺牲了训练并行性,造成了性能-效率的权衡
- 最近的工作提出了一些不损害并行性的增强方法,以获得更好的状态跟踪性能,包括使用负特征值 (2024) 和使用多个户主转移矩阵的乘积 (2025),这实现了高秩变换
- 这些方法可以无缝应用于 Gated DeltaNet
- 从(在线)学习目标的角度来看,替代的公式化可以进一步扩展表达力:
- 非线性回归 (\(\mathcal{L}(\mathbf{S}_{t})=\frac{1}{2}||\boldsymbol{f}_{\mathbf{S}_{t} }(\boldsymbol{k}_{t})-\boldsymbol{v}_{t}||^{2}\)),如 TTT (2024a) 和 Titans (2024) 中那样,其中 \(\boldsymbol{f}_{\mathbf{S} }\) 是由 \(\mathbf{S}\) 参数化的非线性函数;
- 或者考虑整个历史的回归 (\(\mathcal{L}(\mathbf{S}_{t})=\frac{1}{2}\sum_{i=1}^{d}||\mathbf{S}_{t}\boldsymbol{k}_{i}-\boldsymbol{v}_{t}||^{2}\)),如 Mesa 层 (von 2024) 中那样——类似于最小均方算法和递归最小二乘算法之间的区别
- 然而,这些更具表达力的变体引入了非线性循环,并且需要变通方法,例如在处理完整个分块后才执行非线性更新(如在 TTT 和 Titans 中);或者近似非线性循环方法,如 (2024; 2024; 2025)
Hybrid models
- 在这项工作中,论文探索了在层间交错混合注意力层,这在诸如 MiniMax-01 (2025) 和 Hybrid Mamba2-Attention (2024) 中常用
- 研究在单个层内混合线性/softmax 注意力也很有趣 (2022a; 2024; 2025)