- 参考链接:
原始 Transformer
基本 Attention 公式
- 在标准的Transformer模型中,自注意力机制(Self-Attention)的公式是核心组成部分
- 给定查询矩阵 \( Q \)、键矩阵 \( K \) 和值矩阵 \( V \),注意力输出计算为:
$$
\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k} }\right)V
$$- \( Q \in \mathbb{R}^{n \times d_k} \), \( K \in \mathbb{R}^{m \times d_k} \), \( V \in \mathbb{R}^{m \times d_v} \)(\( n \)是目标序列长度,\( m \)是源序列长度)
- \( d_k \) 是键/查询向量的维度
- \( \sqrt{d_k} \) 用于缩放点积,防止梯度消失
Multi-Head Attention
- Transformer使用多头注意力扩展基本注意力:
$$
\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h)W^O
$$ - 每个头的计算为:
$$
\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)
$$- \( W_i^Q \in \mathbb{R}^{d_{\text{model} } \times d_k} \), \( W_i^K \in \mathbb{R}^{d_{\text{model} } \times d_k} \), \( W_i^V \in \mathbb{R}^{d_{\text{model} } \times d_v} \)
- \( W^O \in \mathbb{R}^{hd_v \times d_{\text{model} } } \) 是输出投影矩阵
- \( h \) 是头的数量,通常满足 \( d_k = d_v = \frac{d_{\text{model} } }{h} \)
加入位置编码(仅修改输入即可)
- 在Transformer中,输入会加上正弦位置编码 \( P \in \mathbb{R}^{d_{\text{model}}} \):
$$
X = \text{Embedding}(x) + P
$$- 其中 \( P \in \mathbb{R}^{d_{\text{model}}} \) 的每个元素为:
$$
P_{pos, 2i} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model} } } }\right), \quad
P_{pos, 2i+1} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model} } } }\right)
$$
- 其中 \( P \in \mathbb{R}^{d_{\text{model}}} \) 的每个元素为:
Self-Attention 完整公式(以单头为例)
- 对于一个输入序列 \( X \in \mathbb{R}^{n \times d_{\text{model} } } \):
$$
\begin{aligned}
Q &= XW^Q, \quad K = XW^K, \quad V = XW^V \\
\text{Attention}(X) &= \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k} } + M\right)V
\end{aligned}
$$- \( M \) 是可选的掩码矩阵(如解码器的因果掩码)
- 注:实际实现时,也可以直接在进入 Softmax 操作前,将 \(\frac{QK^\top}{\sqrt{d_k} }\) 的结果置为最小值 \(-e^9\),效果是等价的
Self-Attention 简单实现
- Self-Attention的Python代码简单实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64# 单头Attention
class ScaledDotProductAttention(nn.Module):
def__init__(self, d_k):
super().__init__()
self.d_k = d_k
def forward(self, Q, K, V, mask=None):
# Q, K, V shape: (batch_size, seq_len, d_k(or d_v))
scores = torch.matmul(Q, K.transpose(-2, -1)) / (self.d_k ** 0.5)
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
attn_weights = F.softmax(scores, dim=-1)
output = torch.matmul(attn_weights, V)
return output
# 多头Attention
class MultiHeadAttention(nn.Module):
def __init__(self, d_model, num_heads):
super().__init__()
assert d_model % num_heads == 0, "d_model must be divisible by num_heads"
self.d_model = d_model
self.num_heads = num_heads
self.d_k = d_model // num_heads
self.W_q = nn.Linear(d_model, d_model)
self.W_k = nn.Linear(d_model, d_model)
self.W_v = nn.Linear(d_model, d_model)
self.W_o = nn.Linear(d_model, d_model)
# 使用单头Attention
self.attention = ScaledDotProductAttention(self.d_k)
def split_heads(self, x):
"""
x shape: (batch_size, seq_len, d_model)
return shape: (batch_size, num_heads, seq_len, d_k)
"""
batch_size, seq_len, _ = x.size()
return x.view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)
def combine_heads(self, x):
"""
x shape: (batch_size, num_heads, seq_len, d_k)
return shape: (batch_size, seq_len, d_model)
"""
batch_size, _, seq_len, _ = x.size()
return x.transpose(1, 2).contiguous().view(batch_size, seq_len, self.d_model)
def forward(self, Q, K, V, mask=None):
Q = self.W_q(Q)
K = self.W_k(K)
V = self.W_v(V)
Q = self.split_heads(Q)
K = self.split_heads(K)
V = self.split_heads(V)
# 如果需要,扩展mask以匹配多头(这里假设了mask是为单头准备的)
if mask is not None:
mask = mask.unsqueeze(1) # (batch_size, 1, seq_len) -> (batch_size, 1, 1, seq_len)
attn_output = self.attention(Q, K, V, mask)
output = self.combine_heads(attn_output)
output = self.W_o(output)
return output
固定位置编码实现
- 固定位置编码,比如正弦位置编码,直接在 Attention 之前将位置编码向量加入到原始向量 \(X\) 中,Attention代码不需要做任何修改
Rotary Position Embedding, RoPE
- 本节符号和原始论文 (RoPE) RoFormer: Enhanced Transformer with Rotary Position Embedding, Arxiv 2023 & Neurocomputing 2024, 追一科技 符号保持一致
- 旋转位置编码(RoPE)的核心思想 :通过旋转矩阵将位置信息融入Self-Attention 机制中
- 基本定义 :对于位置\( m \)的词向量\( \boldsymbol{x}_m \in \mathbb{R}^d \),通过线性变换得到查询向量\( \boldsymbol{q}_m \)和键向量\( \boldsymbol{k}_n \):
$$
\boldsymbol{q}_m = W_q \boldsymbol{x}_m, \quad \boldsymbol{k}_n = W_k \boldsymbol{x}_n
$$ - 旋转操作 :将\( \boldsymbol{q}_m \)和\( \boldsymbol{k}_n \)划分为\( d/2 \)个复数对(每组2维,RoPE要求维度必须是偶数,这一般都能满足),对第\( i \)组复数应用旋转矩阵:
$$
\begin{aligned}
\boldsymbol{q}_m^{(i)} &= \begin{pmatrix}
q_{m,2i} \\
q_{m,2i+1}
\end{pmatrix}, \quad
\boldsymbol{k}_n^{(i)} = \begin{pmatrix}
k_{n,2i} \\
k_{n,2i+1}
\end{pmatrix} \\
R_{\theta_i}^m &= \begin{pmatrix}
\cos m\theta_i & -\sin m\theta_i \\
\sin m\theta_i & \cos m\theta_i
\end{pmatrix}, \quad \theta_i = 10000^{-2i/d}
\end{aligned}
$$- 注意:位置为 \(m\) 的旋转矩阵对应正余弦角度为 \(\color{red}{m}\theta_i\)
- 理解:旋转矩阵 \(R_{\theta_i}^m\) 可以将目标向量进行旋转,\(R_{\theta_i}^m \boldsymbol{x}\) 相当于将 \( \boldsymbol{x}\) 向逆时针方向旋转 \(m\theta_i\) 度(注意:只是旋转,并不修改原始向量的模长,因为 \(R_{\theta_i}^m\) 是正交矩阵),详情见附录
- 旋转后的向量 :旋转后的查询和键向量为:
$$
\begin{aligned}
\boldsymbol{q}_m’ = \bigoplus_{i=0}^{d/2-1} R_{\theta_i}^m \boldsymbol{q}_m^{(i)}, \quad
\boldsymbol{k}_n’ = \bigoplus_{i=0}^{d/2-1} R_{\theta_i}^n \boldsymbol{k}_n^{(i)}
\end{aligned}
$$- 其中\( \oplus \)表示向量拼接:
$$\bigoplus_{i=0}^{d/2-1} R_{\theta_i}^m \boldsymbol{q}_m^{(i)} = \text{Concat}(\{ R_{\theta_i}^m \boldsymbol{q}_m^{(i)}\}_{i=0}^{d/2-1})$$
- 其中\( \oplus \)表示向量拼接:
- 旋转后的Attention权重变化
$$
\begin{equation}
(\boldsymbol{\mathcal{R}}_m \boldsymbol{q}_m)^{\top}(\boldsymbol{\mathcal{R}}_n \boldsymbol{k}_n) = \boldsymbol{q}_m^{\top} \boldsymbol{\mathcal{R}}_m^{\top}\boldsymbol{\mathcal{R}}_n \boldsymbol{k}_n = \boldsymbol{q}_m^{\top} \boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{k}_n
\end{equation}
$$- 位置为 \(m\) 的向量 \(\boldsymbol{q}_m\) 乘以矩阵 \(\boldsymbol{\mathcal{R}}_m\);位置为 \(n\) 的向量 \(\boldsymbol{k}_n\) 乘以矩阵 \(\boldsymbol{\mathcal{R}}_n\)(注意角标)
- 上面的式子中等式是恒成立的(\( \boldsymbol{\mathcal{R}}_m^{\top}\boldsymbol{\mathcal{R}}_n = \boldsymbol{\mathcal{R}}_{\color{red}{n-m}}\)的详细证明见附录),右边的 \(\boldsymbol{\mathcal{R}}_{\color{red}{n-m}}\)仅与相对位置 \(n-m\) 有关,体现了相对位置编码的核心要义
- 注:\(\boldsymbol{\mathcal{R}}_{m-n}\) 和 \(\boldsymbol{\mathcal{R}}_{n-m}\) 不相等,旋转角度相同,但方向相反
- 展开成矩阵相乘的形式为(refer to Transformer升级之路:2、博采众长的旋转式位置编码):
$$
\begin{equation}\scriptsize{\underbrace{\begin{pmatrix}
\cos m\theta_0 & -\sin m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\
\sin m\theta_0 & \cos m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\
0 & 0 & \cos m\theta_1 & -\sin m\theta_1 & \cdots & 0 & 0 \\
0 & 0 & \sin m\theta_1 & \cos m\theta_1 & \cdots & 0 & 0 \\
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2-1} & -\sin m\theta_{d/2-1} \\
0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2-1} & \cos m\theta_{d/2-1} \\
\end{pmatrix}}_{\boldsymbol{\mathcal{R}}_m} \begin{pmatrix}q_0 \\ q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_{d-2} \\ q_{d-1}\end{pmatrix}}\end{equation}
$$ - 由于旋转矩阵是一个稀疏矩阵,所以旋转过程可以改进为如下等价实现:
$$
\begin{equation}\begin{pmatrix}q_0 \\ q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_{d-2} \\ q_{d-1}
\end{pmatrix}\otimes\begin{pmatrix}\cos m\theta_0 \\ \cos m\theta_0 \\ \cos m\theta_1 \\ \cos m\theta_1 \\ \vdots \\ \cos m\theta_{d/2-1} \\ \cos m\theta_{d/2-1}
\end{pmatrix} + \begin{pmatrix}-q_1 \\ q_0 \\ -q_3 \\ q_2 \\ \vdots \\ -q_{d-1} \\ q_{d-2}
\end{pmatrix}\otimes\begin{pmatrix}\sin m\theta_0 \\ \sin m\theta_0 \\ \sin m\theta_1 \\ \sin m\theta_1 \\ \vdots \\ \sin m\theta_{d/2-1} \\ \sin m\theta_{d/2-1}
\end{pmatrix}\end{equation}
$$- 其中 \(\otimes\) 是按位相乘
- RoPE下的Attention公式总结 :(旋转位置编码的核心公式)
$$
\begin{aligned}
\text{Attention}(\boldsymbol{x}) &= \text{softmax}\left(\frac{(\boldsymbol{q}’)^\top \boldsymbol{k}’}{\sqrt{d} }\right)V
\end{aligned}
$$- 注:\(V\) 是 Attention 中的 Value 矩阵,中不需要位置编码信息
- 这里使用 \((\boldsymbol{q}’)^\top \boldsymbol{k}’\),转置在 \(\boldsymbol{q}’\) 上,和原始论文表达方式一致,实际上这种表示是OK的,数学中常用这种表示 ,这种表示下,向量为列向量;原始 Transformer 论文中的符号转置在 Key 上,此时向量为行向量
- 原始论文中的RoPE示意图:
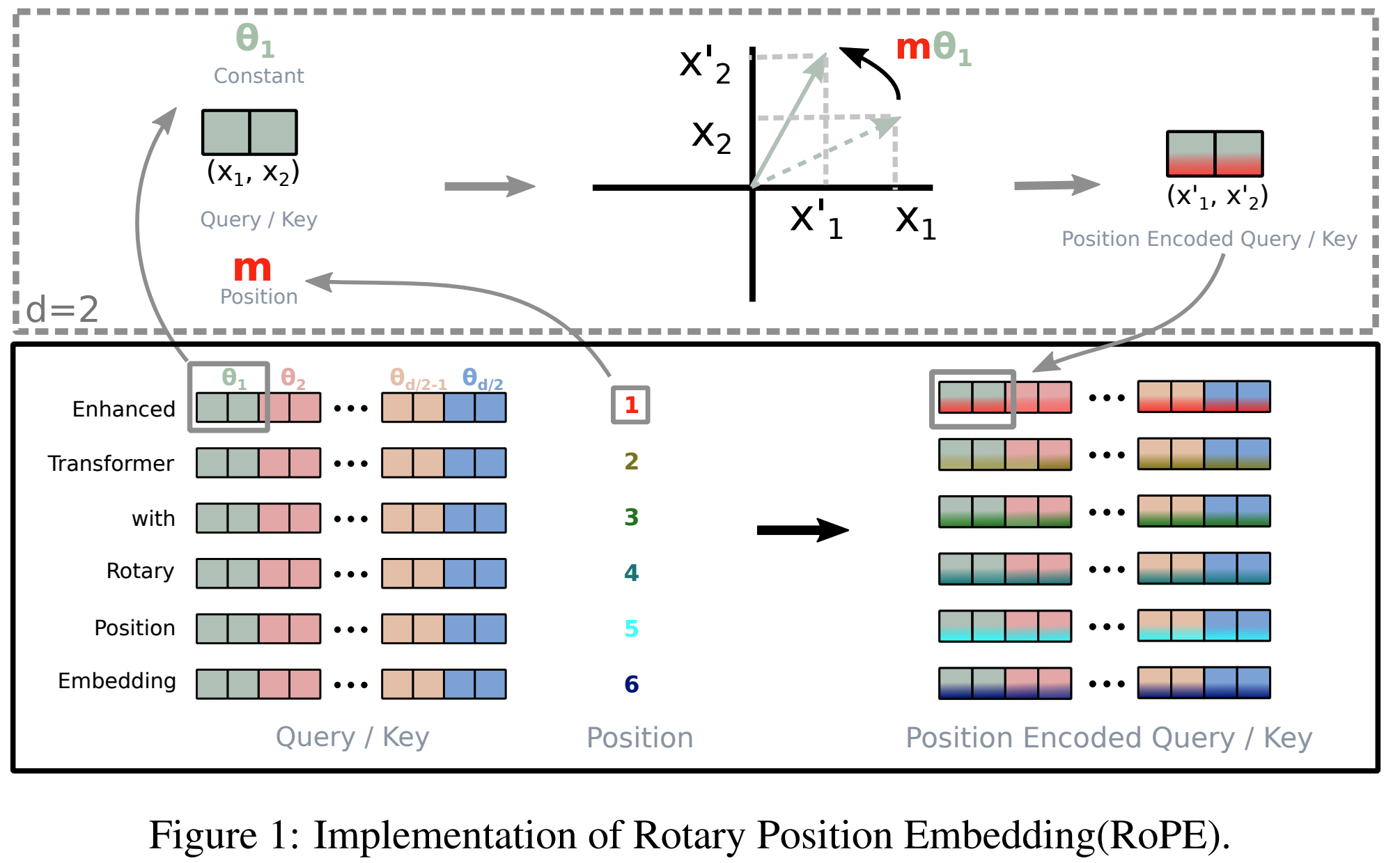
多头注意力下的 RoPE
- 为了跟传统的 Transformer 符号对齐,本节改用 \(Q,K,V\)表示矩阵,与 RoPE 原始论文符号不再一致
- 给定输入序列 \( X \in \mathbb{R}^{n \times d_{\text{model} } } \),先投影到查询、键、值空间:
$$
Q = XW^Q, \quad K = XW^K, \quad V = XW^V
$$- 其中 \( W^Q, W^K \in \mathbb{R}^{d_{\text{model} } \times d_k} \), \( W^V \in \mathbb{R}^{d_{\text{model} } \times d_v} \)
- 应用旋转位置编码(RoPE) :对 \( Q \) 和 \( K \) 的每个位置 \( m \) 和 \( n \) 的分量应用旋转矩阵 \( R_{\theta}^m \) 和 \( R_{\theta}^n \):
$$
\begin{aligned}
Q’ &= \text{RoPE}(Q) = \bigoplus_{i=0}^{d_k/2-1} R_{\theta_i}^m Q^{(i)} \\
K’ &= \text{RoPE}(K) = \bigoplus_{i=0}^{d_k/2-1} R_{\theta_i}^n K^{(i)}
\end{aligned}
$$- \( Q^{(i)} \in \mathbb{R}^2 \) 和 \( K^{(i)} \in \mathbb{R}^2 \) 是 \( Q \) 和 \( K \) 的第 \( i \) 个二维分量
- \( \oplus \)表示向量拼接:
$$\bigoplus_{i=0}^{d_k/2-1} R_{\theta_i}^m Q^{(i)} = \text{Concat}(\{R_{\theta_i}^m Q^{(i)}\}_{i=0}^{d_k/2-1} )$$
- 旋转矩阵 \( R_{\theta_i}^m \) 定义为:
$$
R_{\theta_i}^m = \begin{pmatrix}
\cos m\theta_i & -\sin m\theta_i \\
\sin m\theta_i & \cos m\theta_i
\end{pmatrix}, \quad \theta_i = 10000^{-2i/d_k}
$$ - 多头注意力输出
$$
\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \dots, \text{head}_H) W^O \\
\text{head}_h = \text{Softmax}\left(\frac{Q^{\prime}_h {K^{\prime}_h}^\top}{\sqrt{d_k} }\right) V_h
$$- 其中 \( W^O \in \mathbb{R}^{H d_v \times d_{\text{model} } } \) 是输出投影矩阵
- 多头注意力下的 RoPE 的 Attention 公式总结 :
$$
\begin{aligned}
\text{Attention}(Q,K,V) &= \text{softmax}\left(\frac{(\text{RoPE}(Q))(\text{RoPE}(K))^\top}{\sqrt{d_k} }\right)V \\
\text{where} \quad \text{RoPE}(X) &= \bigoplus_{i=0}^{d/2-1} R_{\theta_i}^m X^{(i)}
\end{aligned}
$$
多头注意力下的 RoPE 实现
- 多头注意力下的RoPE PyTorch 实现 (待补充)
- 注:多头注意力下,每个头是独立编码的(每个头维度从 0 开始),且使用的旋转矩阵一样,即旋转矩阵的维度 \(d = d_{\text{head}} = d_{\text{model}}/h\)
关于 RoPE 的一些讨论
- RoPE 传统 Transformer 的区别 :
- 传统Transformer:位置编码是加性的(\( X + P \))
- RoPE:位置编码是乘性的(通过旋转矩阵直接修改 \( Q \) 和 \( K \))
- 相对位置保持性 :
- 旋转后的注意力分数 \( [Q’ K’^\top]_{m,n} \) 仅依赖于相对位置 \( m-n \),满足线性注意力性质
- 远程衰减性 :(注:如下图所示的远距离衰减,会导致太远的距离下,难以区分位置,效果不好,外推性变差?)
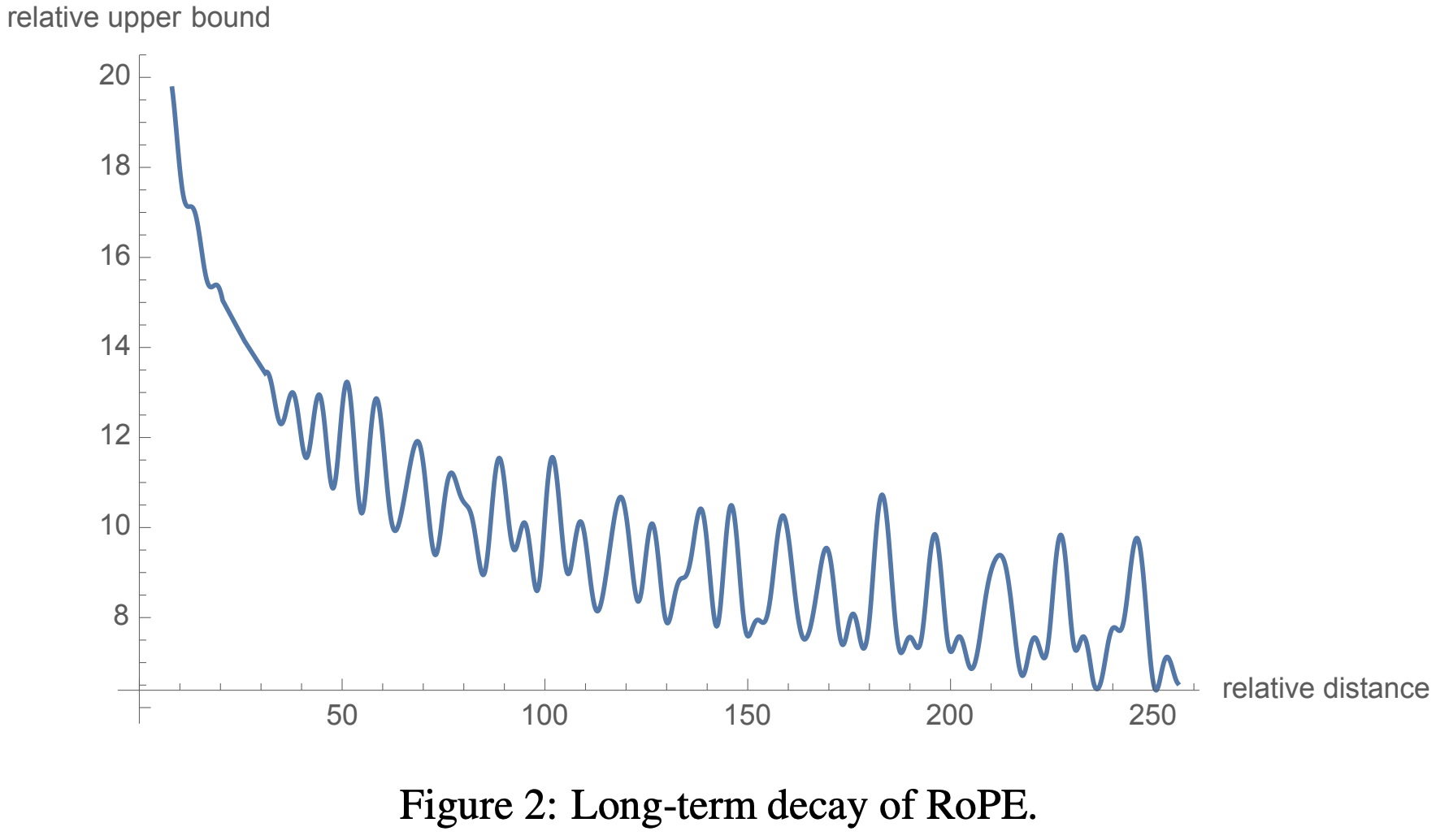
附录:相对位置旋转公式证明
- 目标:证明 \( \boldsymbol{\mathcal{R}}_m^{\top}\boldsymbol{\mathcal{R}}_n = \boldsymbol{\mathcal{R}}_{\color{red}{n-m}}\)
- 考虑到 \(\boldsymbol{\mathcal{R}}_m\) 是以二维子矩阵为单位的“对角”矩阵,故只要证明 \((R_{\theta_i}^m)^\top R_{\theta_i}^n = R_{\theta_i}^{\color{red}{n-m}}\) 即可,证明过程如下:
- 给定旋转矩阵 \( R_{\theta_i}^m \) 定义为:
$$
R_{\theta_i}^m = \begin{pmatrix}
\cos m\theta_i & -\sin m\theta_i \\
\sin m\theta_i & \cos m\theta_i
\end{pmatrix}
$$ - 其转置矩阵为:
$$
(R_{\theta_i}^m)^\top = \begin{pmatrix}
\cos m\theta_i & \sin m\theta_i \\
-\sin m\theta_i & \cos m\theta_i
\end{pmatrix}
$$ - 计算 \((R_{\theta_i}^m)^\top R_{\theta_i}^n\)
$$
(R_{\theta_i}^m)^\top R_{\theta_i}^n = \begin{pmatrix}
\cos m\theta_i & \sin m\theta_i \\
-\sin m\theta_i & \cos m\theta_i
\end{pmatrix}
\begin{pmatrix}
\cos n\theta_i & -\sin n\theta_i \\
\sin n\theta_i & \cos n\theta_i
\end{pmatrix}
$$ - 回顾三角函数和差角公式:
$$
\sin(A \pm B) = \sin A \cos B \pm \cos A \sin B \\
\cos(A \pm B) = \cos A \cos B \mp \sin A \sin B
$$ - 计算矩阵乘积的每个元素:
- 左上角元素:
$$
\begin{align}
\cos m\theta_i \cdot \cos n\theta_i + \sin m\theta_i \cdot \sin n\theta_i &= \cos(n\theta_i - m\theta_i) \\
&= \cos((n - m)\theta_i) \\
\end{align}
$$ - 右上角元素:
$$
\begin{align}
\cos m\theta_i \cdot (-\sin n\theta_i) + \sin m\theta_i \cdot \cos n\theta_i &= -\cos m\theta_i \sin n\theta_i + \sin m\theta_i \cos n\theta_i \\
&= \sin m\theta_i \cos n\theta_i - \cos m\theta_i \sin n\theta_i\\
& = \sin((m-n)\theta_i) \\
& = - \sin((n-m)\theta_i)
\end{align}
$$ - 左下角元素:
$$
\begin{align}
-\sin m\theta_i \cdot \cos n\theta_i + \cos m\theta_i \cdot \sin n\theta_i &= -\sin m\theta_i \cos n\theta_i + \cos m\theta_i \sin n\theta_i \\
&= \sin n\theta_i \cos m\theta_i - \cos n\theta_i \sin m\theta_i \\
&= \sin((n - m)\theta_i)
\end{align}
$$ - 右下角元素:
$$
\begin{align}
-\sin m\theta_i \cdot (-\sin n\theta_i) + \cos m\theta_i \cdot \cos n\theta_i &= \sin m\theta_i \sin n\theta_i + \cos m\theta_i \cos n\theta_i \\
&= \sin m\theta_i \sin n\theta_i + \cos m\theta_i \cos n\theta_i \\
&= \cos((n - m)\theta_i)
\end{align}
$$
- 左上角元素:
- 因此,乘积矩阵为:
$$
(R_{\theta_i}^m)^\top R_{\theta_i}^n = \begin{pmatrix}
\cos((n - m)\theta_i) & -\sin((n - m)\theta_i) \\
\sin((n - m)\theta_i) & \cos((n - m)\theta_i)
\end{pmatrix} = R_{\theta_i}^{\color{red}{n-m}}
$$ - 至此,我们证明了:
$$
(R_{\theta_i}^m)^\top R_{\theta_i}^n = R_{\theta_i}^{\color{red}{n-m}}
$$ - 证毕
附录:不同参数下 RoPE 对 Attention 的影响
- RoPE原始论文已经说明了随着距离的增长,Attention Score 有越来越小的趋势(且长距离部分会波动)
- 下面是固定
query_index下,Attention Score 随key_index(横轴)变化的图像(代码参考链接修改的 旋转式位置编码 (RoPE) 知识总结 - Soaring的文章 - 知乎)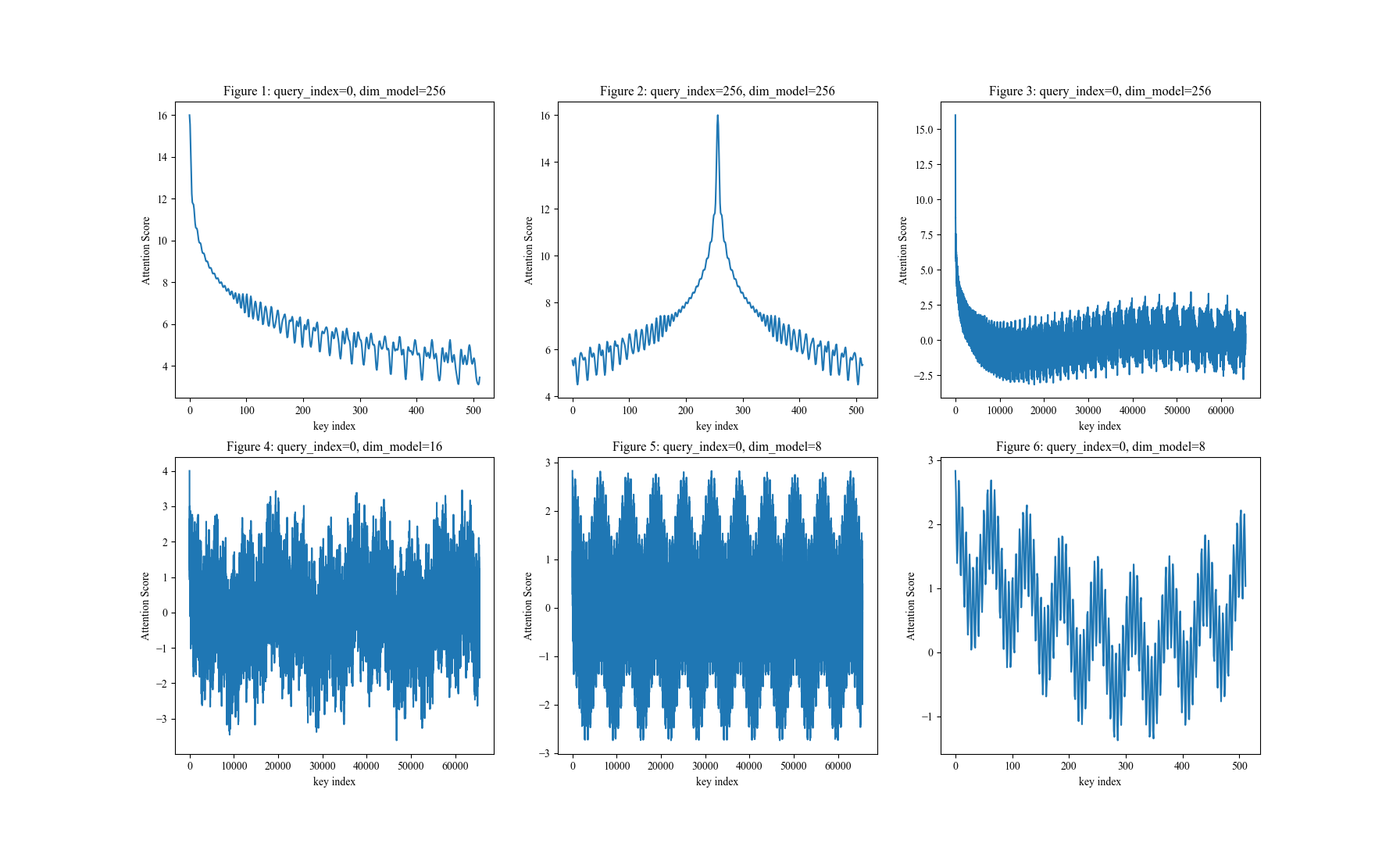
- 从上图可以观察到:
- 图1:RoPE确实有远距离衰减趋势(震荡递减),且
dim_model=256时,q,k 距离为500时Attention值已经衰减的较小了 - 图2:与图1类似,RoPE的衰减是对称的(图2展示的是当
query_index=256时的图像);- 注:注意虽然 Attention Score 是对称相等的,但是旋转角度是相反的,即 \(\boldsymbol{\mathcal{R}}_{m-n}\) 和 \(\boldsymbol{\mathcal{R}}_{n-m}\) 旋转角度相同,但方向是相反的
- 图3:RoPE 在拉到足够长的距离后,不会一直衰减(从后续的图可以知道实际上还是周期函数,只是周期很大)
- 图4+图5:与图1对比可以发现,RoPE 在拉到足够长的距离后,实际上还是周期函数,只不过周期与
d_model相关(d_model越大,周期越长),图4说明了当d_model=8时,周期是 10000 左右 - 图6:缩小了图5的横轴区间,将图5的前半部分图像放大了看,是在小周期上震荡的,且还存在图5所示的大周期
- 图1:RoPE确实有远距离衰减趋势(震荡递减),且
- 附上图的代码:
>>>点击展开折叠内容...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57# refer to: [旋转式位置编码 (RoPE) 知识总结 - Soaring的文章 - 知乎](https://zhuanlan.zhihu.com/p/662790439)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.axes import Axes
def create_sin_cos_table_cache(max_num_tokens, dim_model):
# 所有pos下对应的cos/sin值分别存储为矩阵
theta = 10000 ** (-np.arange(0, dim_model, 2) / dim_model)
theta = theta.reshape(-1, 1).repeat(2, axis=1).flatten()
pos = np.arange(0, max_num_tokens)
table = pos.reshape(-1, 1) @ theta.reshape(1, -1) # [max_num_tokens, dim_model]
sin_table_cache = np.sin(table)
sin_table_cache[:, ::2] = -sin_table_cache[:, ::2]
cos_table_cache = np.cos(table)
return sin_table_cache, cos_table_cache
def rotate_half(q_vec):
# 将q_vec的值两个一组分组并在分组内对调,实现从[q_0,q_1,q_2,q_3,...,q_{d-1},q_d]到的转换[q_1,q_0,q_3,q_2,...,q_d,q_{d-1}]
return q_vec.reshape(-1, 2)[:, ::-1].flatten()
def rotary(vec, pos, sin_table, cos_table):
# 原始论文中的公式
return vec * cos_table[pos] + rotate_half(vec) * sin_table[pos]
def plot(plt_obj: Axes, pic_index, query_index=0, dim_model=256, max_num_tokens=8192, step=1):
# q_vec 和 k_vec 都设定为1,仅关注 RoPE 引发的Attention Score的变化
q_vec = np.ones(dim_model)
k_vec = np.ones(dim_model)
sin_table, cos_table = create_sin_cos_table_cache(max_num_tokens, dim_model)
rotated_q_vec = rotary(q_vec, query_index, sin_table, cos_table)
k_indices = np.arange(0, max_num_tokens, step)
rotated_k_vecs = rotary(k_vec, k_indices, sin_table, cos_table)
attn_scores = (rotated_k_vecs @ rotated_q_vec) / np.sqrt(dim_model) # 未经过Softmax的Attention权重,用于展示RoPE对原始Attention Score
plt_obj.plot(k_indices, attn_scores)
plt_obj.set_title(f"Figure {pic_index}: query_index={query_index}, dim_model={dim_model}")
plt_obj.set_xlabel("key index")
plt_obj.set_ylabel("Attention Score")
plt.rcParams.update({
"font.sans-serif": ["Times New Roman", ],
"font.size": 10
})
_, axes = plt.subplots(nrows=2, ncols=3, figsize=(10, 10))
plot(axes[0, 0], 1, query_index=0, max_num_tokens=512)
plot(axes[0, 1], 2, query_index=256, max_num_tokens=512)
plot(axes[0, 2], 3, query_index=0, dim_model=256, max_num_tokens=65535)
# plot(axes[1, 0], 4, query_index=0, dim_model=32, max_num_tokens=65535)
plot(axes[1, 0], 4, query_index=0, dim_model=16, max_num_tokens=65535)
plot(axes[1, 1], 5, query_index=0, dim_model=8, max_num_tokens=65536)
plot(axes[1, 2], 6, query_index=0, dim_model=8, max_num_tokens=512)
plt.show()
附录:如何改进 RoPE 以实现绝对位置编码?
- 当前的设计仅能实现相对位置编码(因为 Query 和 Key 的内积只与他们的相对位置有关,与绝对位置无关),但如果在 Value 上也施加位置编码则能实现绝对位置编码的能力
- 让研究人员绞尽脑汁的Transformer位置编码中苏神提到:
这样一来,我们得到了一种融绝对位置与相对位置于一体的位置编码方案,从形式上看它有点像乘性的绝对位置编码,通过在 \(\boldsymbol{q},\boldsymbol{k}\) 中施行该位置编码,那么效果就等价于相对位置编码,而如果还需要显式的绝对位置信息,则可以同时在 \(\boldsymbol{v}\) 上也施行这种位置编码。总的来说,我们通过绝对位置的操作,可以达到绝对位置的效果,也能达到相对位置的效果
附录:旋转体现在哪里?
- 旋转体现在 \(\boldsymbol{q}_m\)(或\(\boldsymbol{k}_n\)) 的每两个维度组成的向量 \(\boldsymbol{q}_m^{(i)} = \begin{pmatrix} q_{m,2i} \\ q_{m,2i+1} \end{pmatrix}\) 经过 RoPE 变换前后,他们的向量长度不变,即:
$$
\begin{pmatrix}cos(m\theta_1) &-sin(m\theta_1) \\ sin(m\theta_1) &cos(m\theta_1)\end{pmatrix} \begin{pmatrix}q_{m,2i} \\ q_{m,2i+1}\end{pmatrix} = \begin{pmatrix}q_{m,2i}\cdot cos(m\theta_1) -q_{m,2i+1}\cdot sin(m\theta_1) \\ q_{m,2i}\cdot sin(m\theta_1)+ q_{m,2i+1}\cdot cos(m\theta_1) \end{pmatrix} \\
$$ - 进一步,由于 \((cos(m\theta_1))^2 + (sin(m\theta_1))^2 = 1\) 有
$$
\begin{align}
\left|\begin{pmatrix}q_{m,2i}\cdot cos(m\theta_1) -q_{m,2i+1}\cdot sin(m\theta_1) \\ q_{m,2i}\cdot sin(m\theta_1)+ q_{m,2i+1}\cdot cos(m\theta_1) \end{pmatrix} \right| &= \sqrt{\left(q_{m,2i}\cdot cos(m\theta_1) -q_{m,2i+1}\cdot sin(m\theta_1)\right)^2 + \left(q_{m,2i}\cdot sin(m\theta_1)+ q_{m,2i+1}\cdot cos(m\theta_1)\right)^2} \\
&= \sqrt{(q_{m,2i})^2 + (q_{m,2i+1})^2}
\end{align}
$$ - 也就是说: \(\boldsymbol{q}_m\)(或\(\boldsymbol{k}_n\))相邻两两维度在变换前后的向量长度并没有变化,是一个旋转操作
附录:可视化RoPE旋转过程
- 旋转矩阵 \(R_{\theta_i}^m\) 的定义如下:
$$
\begin{aligned}
R_{\theta_i}^m &= \begin{pmatrix}
\cos m\theta_i & -\sin m\theta_i \\
\sin m\theta_i & \cos m\theta_i
\end{pmatrix}, \quad \theta_i = 10000^{-2i/d}
\end{aligned}
$$ - 旋转矩阵 \(R_{\theta_i}^m\) 可以将目标向量进行旋转,\(R_{\theta_i}^m \boldsymbol{x}\) 相当于将 \( \boldsymbol{x}\) 向逆时针方向旋转 \(m\theta_i\) 度
- 当 \(m\theta_i = \frac{\pi}{4}\) 时,其旋转可视化结果如下:
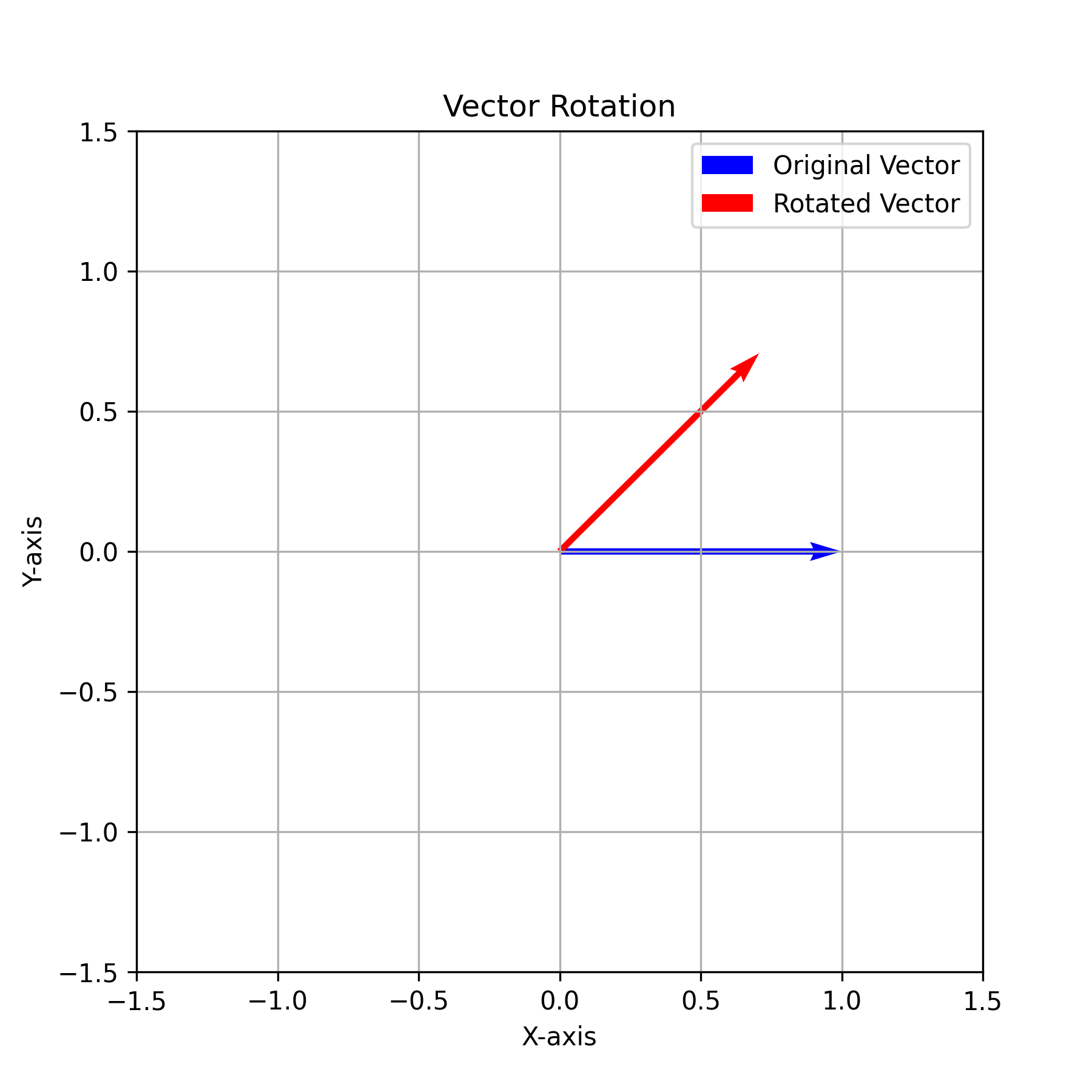
- 实现上述旋转的代码如下
>>>点击展开折叠内容...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34import numpy as np
import matplotlib.pyplot as plt
# 设定原始向量 x
x = np.array([1, 0])
# 角度转换为弧度
angle = np.radians(45)
# 旋转矩阵定义
R = np.array([[np.cos(angle), -np.sin(angle)],
[np.sin(angle), np.cos(angle)]])
# 矩阵惩罚实现旋转向量
x_rotated = R @ x
plt.rcParams['figure.dpi'] = 300
plt.figure(figsize=(6, 6))
plt.quiver(0, 0, x[0], x[1], angles='xy', scale_units='xy', scale=1, color='b', label='Original Vector')
plt.quiver(0, 0, x_rotated[0], x_rotated[1], angles='xy', scale_units='xy', scale=1, color='r', label='Rotated Vector')
plt.xlim(-1.5, 1.5)
plt.ylim(-1.5, 1.5)
plt.grid(True)
plt.legend()
plt.title('Vector Rotation')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.savefig("./demo.png")
plt.show()
附录:RoPE的诞生历史
- RoPE方案来自苏神原始博客:
- 2021年2月在让研究人员绞尽脑汁的Transformer位置编码中提出想法
- 2023年3月在Transformer升级之路:2、博采众长的旋转式位置编码中给出详细方案和推导,同时提交论文到arXiv上
- 原始论文:Roformer: Enhanced Transformer With Rotray Position Embedding,该论文24年发表于Neurocomputing期刊上(《Neurocomputing》是国际知名期刊,被列为中科院SCI二区top期刊,CCF-C类期刊)
- 随后,各种开源大模型开始使用RoPE,RoPE逐渐成为大模型的标配
附录:RoPE的高维扩展
- 论文介绍当前的是一维 RoPE,每 2 维为一组,旋转矩阵为 \(2\times 2\),在二维 RoPE 场景中,可以每 4 维为一组,旋转矩阵变成 \(4\times 4\) 即可,详情见 旋转式位置编码 (RoPE) 知识总结
- 将四个维度作为一组:
$$
\boldsymbol{R}_{m_1,m_2} =
\begin{bmatrix}
\cos m_1 \theta & -\sin m_1 \theta & 0 & 0 \\
\sin m_1 \theta & \cos m_1 \theta & 0 & 0 \\
0 & 0 & \cos m_2 \theta & -\sin m_2 \theta \\
0 & 0 & \sin m_2 \theta & \cos m_2 \theta
\end{bmatrix}
$$ - 上述分组下满足:
$$
\mathbf{R}_{m_1,m_2}^{\top} \cdot \mathbf{R}_{n_1,n_2} = \mathbf{R}_{n_1 - m_1,n_2 - m_2}
$$ - 注:更高维度的可以继续扩展,比如三维的扩展为每 6 维为一组,旋转矩阵为 \(6\times 6\) 即可
附录:RoPE中的复数和旋转矩阵等价性证明
问题定义
- 定义二维旋转矩阵和向量如下:
$$
\begin{align}
R_{\theta_i}^m &= \begin{pmatrix}
\cos m\theta_i & -\sin m\theta_i \\
\sin m\theta_i & \cos m\theta_i
\end{pmatrix} \\
\boldsymbol{x} &= \begin{pmatrix} x_1 \\ x_2
\end{pmatrix}
\end{align}
$$ - 目标:证明下面的等式
$$R_{\theta_i}^m \boldsymbol{x} = z e^{i m\theta_i}$$- 其中 \( z = x_1 + i x_2 \) 是向量 \(\boldsymbol{x} = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}\) 的复数形式
- 即目标是证明:旋转矩阵 \( R_{\theta_i}^m \) 作用在 \(\boldsymbol{x}\) 上相当于将复数 \( z \) 乘以旋转因子 \( e^{i m\theta_i} \)
证明
方程左边展开
$$
R_{\theta_i}^m \boldsymbol{x} = \begin{pmatrix}
\cos m\theta_i & -\sin m\theta_i \\
\sin m\theta_i & \cos m\theta_i
\end{pmatrix}
\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} =
\begin{pmatrix}
x_1 \cos m\theta_i - x_2 \sin m\theta_i \\
x_1 \sin m\theta_i + x_2 \cos m\theta_i
\end{pmatrix}
$$- 这个结果对应的复数为:
$$
R_{\theta_i}^m \boldsymbol{x} = (x_1 \cos m\theta_i - x_2 \sin m\theta_i) + i (x_1 \sin m\theta_i + x_2 \cos m\theta_i)
$$
- 这个结果对应的复数为:
等方程右边展开
- 右边的 \(\boldsymbol{x} e^{i m\theta_i}\) 表示将复数 \( z = x_1 + i x_2 \) 乘以 \( e^{i m\theta_i} \),即:
$$
z e^{i m\theta_i} = (x_1 + i x_2)(\cos m\theta_i + i \sin m\theta_i)
$$ - 可以重新整理为:
$$ z e^{i m\theta_i} = (x_1 \cos m\theta_i - x_2 \sin m\theta_i) + i (x_1 \sin m\theta_i + x_2 \cos m\theta_i) $$ - 展开后与旋转矩阵作用的结果完全一致
- 右边的 \(\boldsymbol{x} e^{i m\theta_i}\) 表示将复数 \( z = x_1 + i x_2 \) 乘以 \( e^{i m\theta_i} \),即:
结论: 在复数表示下,旋转矩阵 \( R_{\theta_i}^m \) 作用在向量 \(\boldsymbol{x}\) 上等价于将对应的复数 \( z \) 乘以旋转因子 \( e^{i m\theta_i} \)。因此,等式成立:
$$
\color{red}{R_{\theta_i}^m \boldsymbol{x} = \boldsymbol{x} e^{i m\theta_i}}
$$
附录:旋转位置编码的其他推导过程
- 下面的推导过程来自通俗易懂-大模型的关键技术之一:旋转位置编码rope(2)和通俗易懂-大模型的关键技术之一:旋转位置编码rope (3),推导过程看过,基本没有问题,先截图,以后有时间再手打一遍
- \(q,k\) 向量旋转后再进行Attention,注意图中 \(e^{im\theta}\) 的 \(i\) 是虚数的意思,这里使用二维向量 \((\boldsymbol{W}_q\boldsymbol{x}_m)\) 乘以一个虚数的本质是想表达向量内积的意思(虚数可以展开成二维向量),此外,\(a_{m,n}\) 表示 Attention 权重,在不考虑权重时值为 Softmax,Element-wise看:\(a_{m,n} =\frac{\exp(\frac{q^T_m k_n}{\sqrt{d_k}})}{\sum_{j=1}^N \exp(\frac{q^T_m k_j}{\sqrt{d_k}})}\),注:下图中的表达有误,实际上应该是 \(a_{m,n}=\frac{\exp(\frac{ {x^{\prime}_m}^T x^{\prime}_n}{\sqrt{d_k} })}{\sum_{j=1}^N \exp(\frac{ {x^{\prime}_m}^T x^{\prime}_j}{\sqrt{d_k} })}\)(详情见原始论文:(RoPE) RoFormer: Enhanced Transformer with Rotary Position Embedding, Arxiv 2023 & Neurocomputing 2024, 追一科技 )
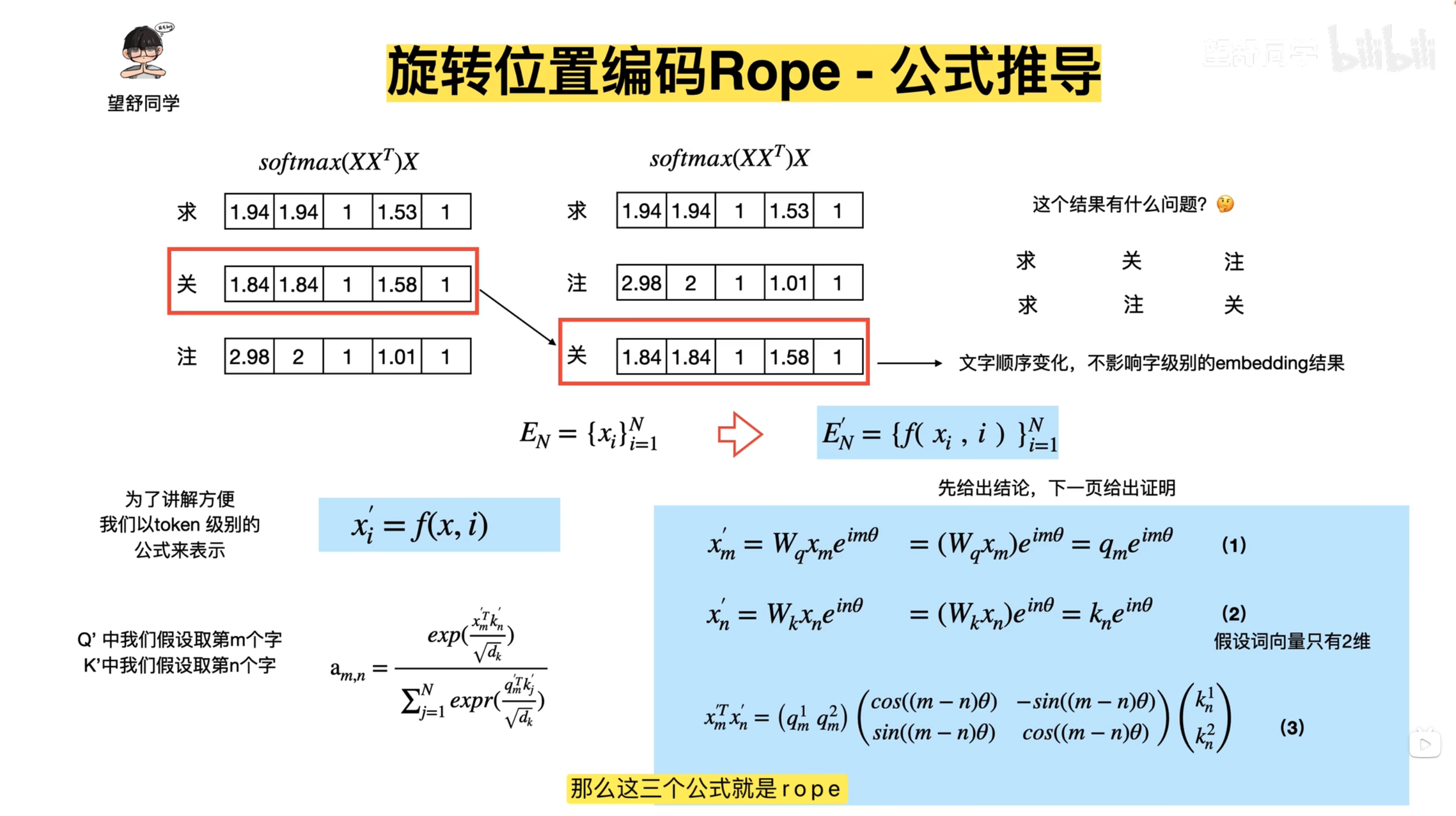
- 公式1,2,推导出公式3的过程(内积角度)
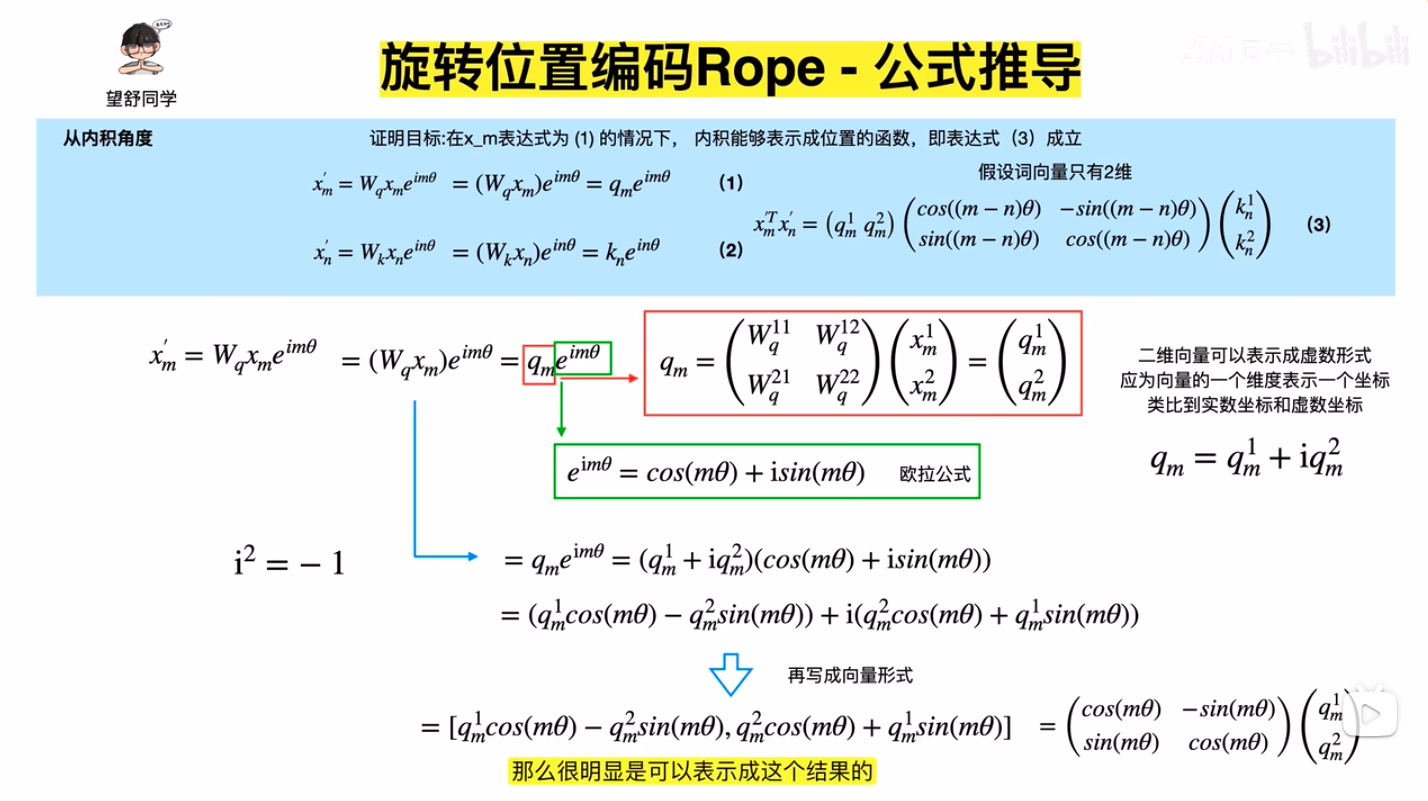


- 公式1,2,推导出公式3的过程(公式角度)
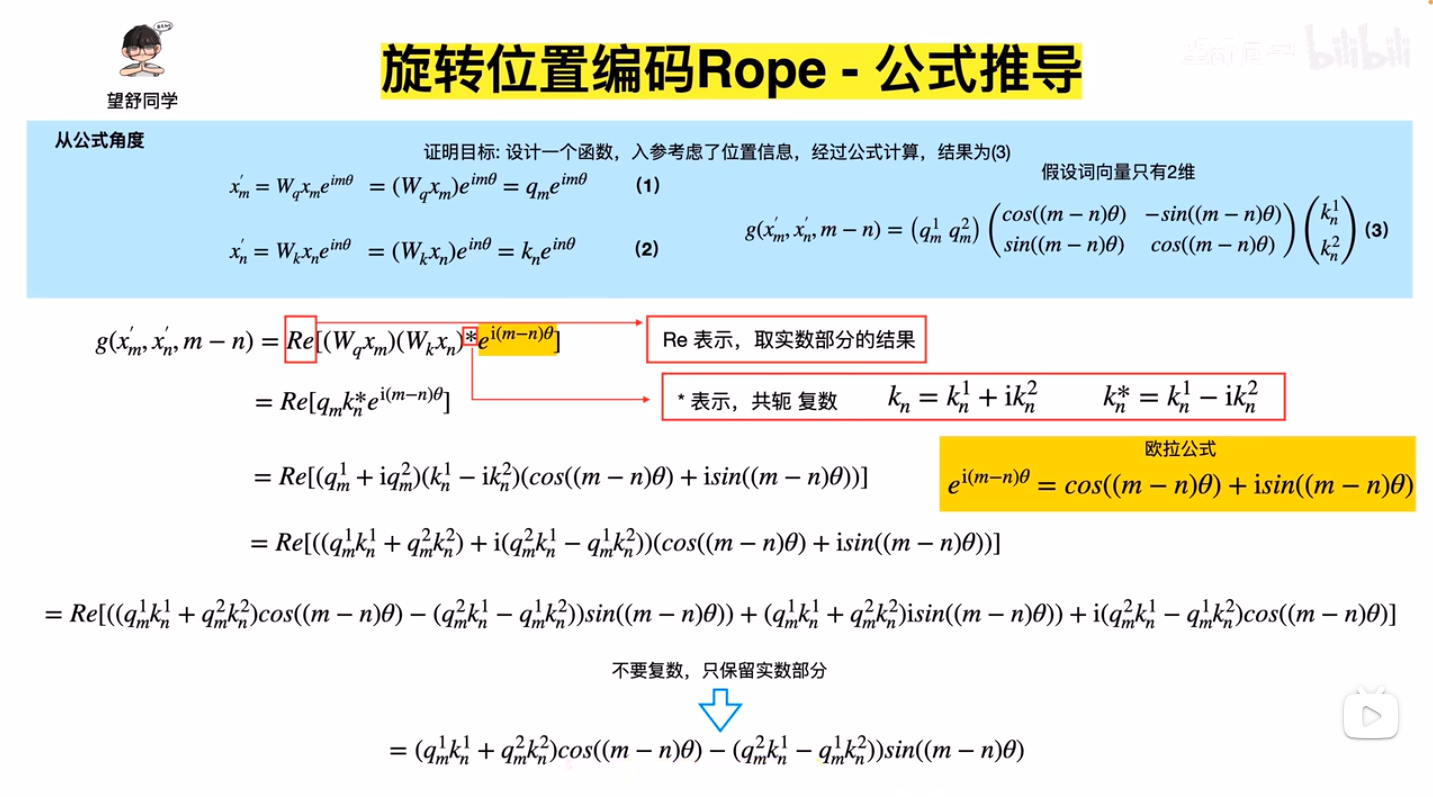
- 内积角度和公式角度推导结果可以对齐
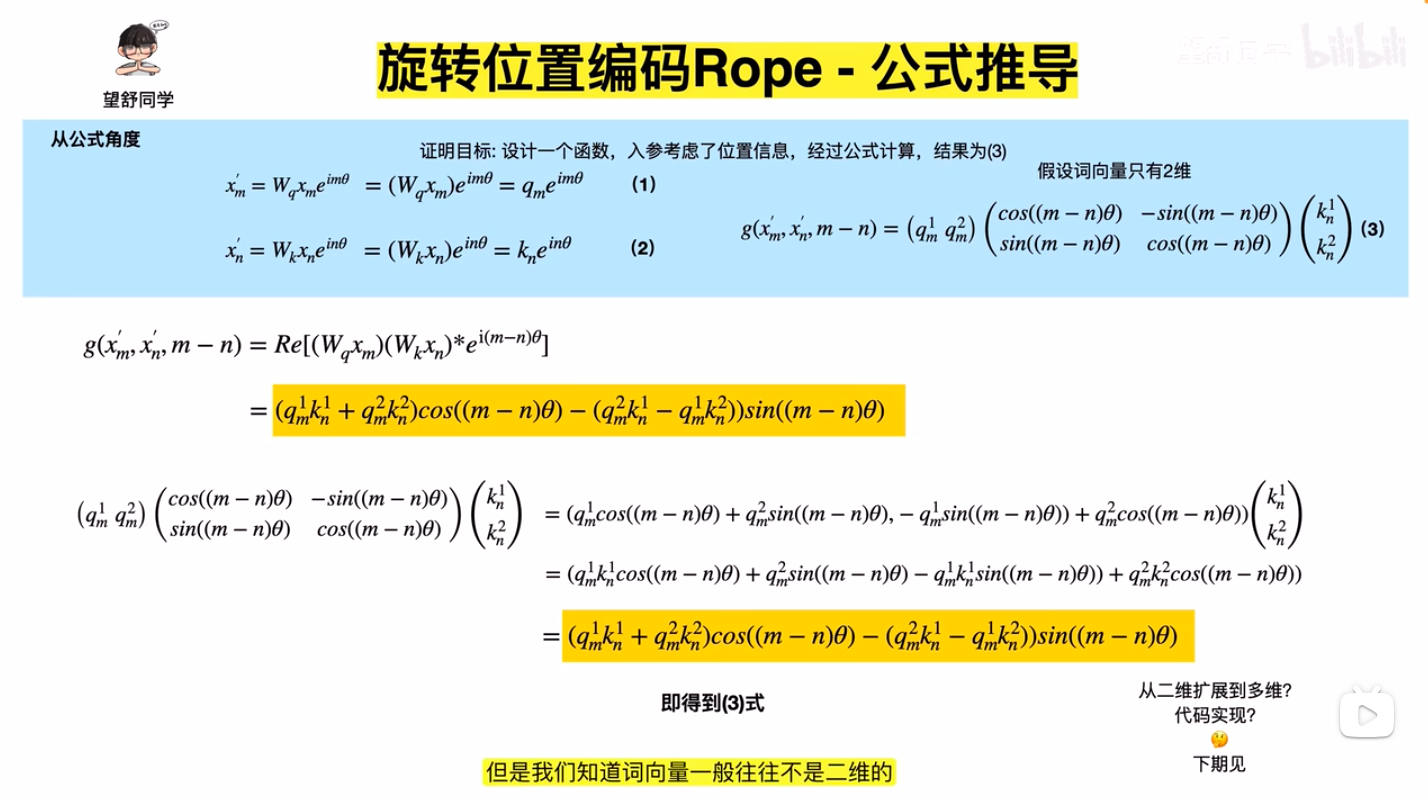
- 扩展到多维的方式,将模型
d_model维度按照两两一组分(注意这里不是序列两两分,序列本来做Attention就是两两做内积的),这里要求模型维度是偶数的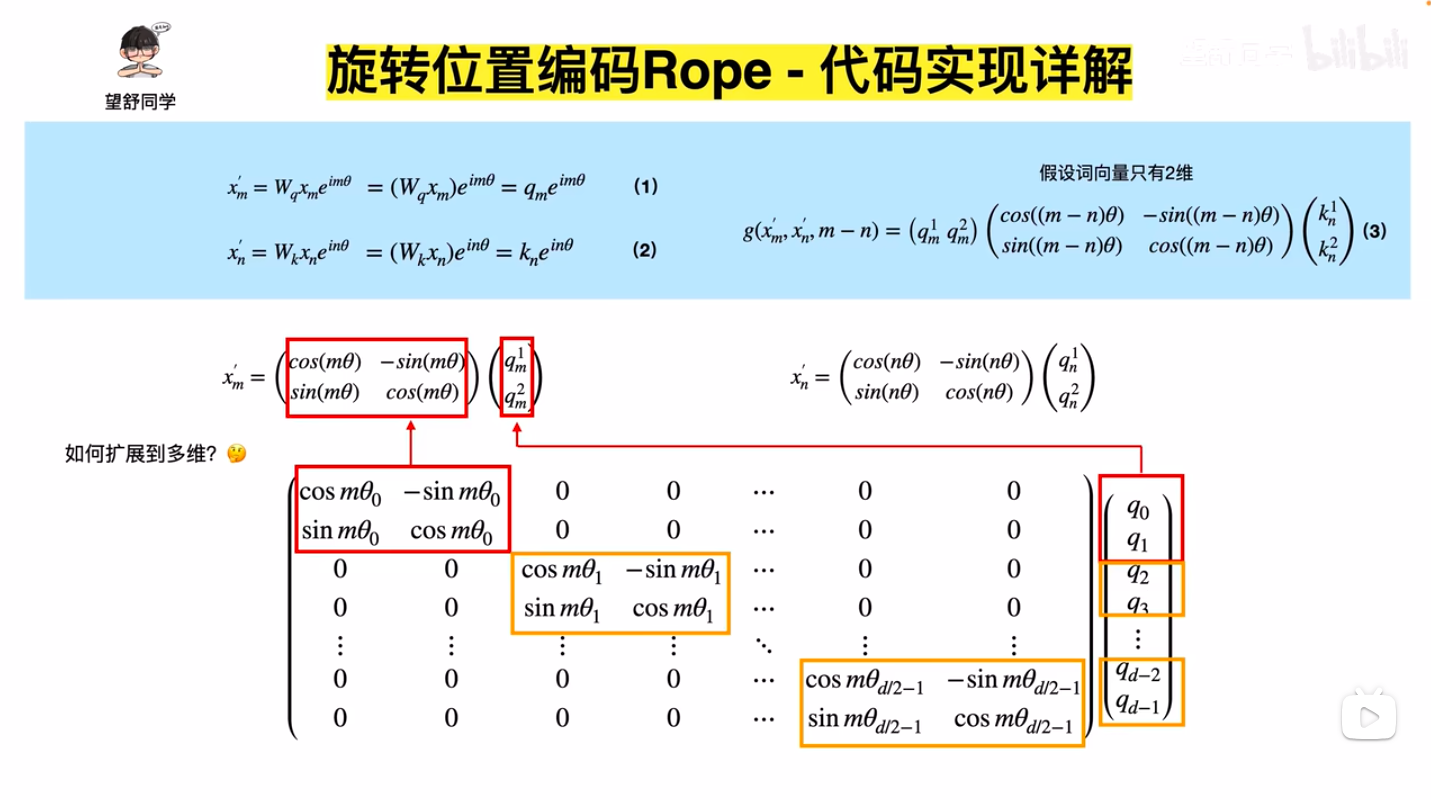
- 公式化简
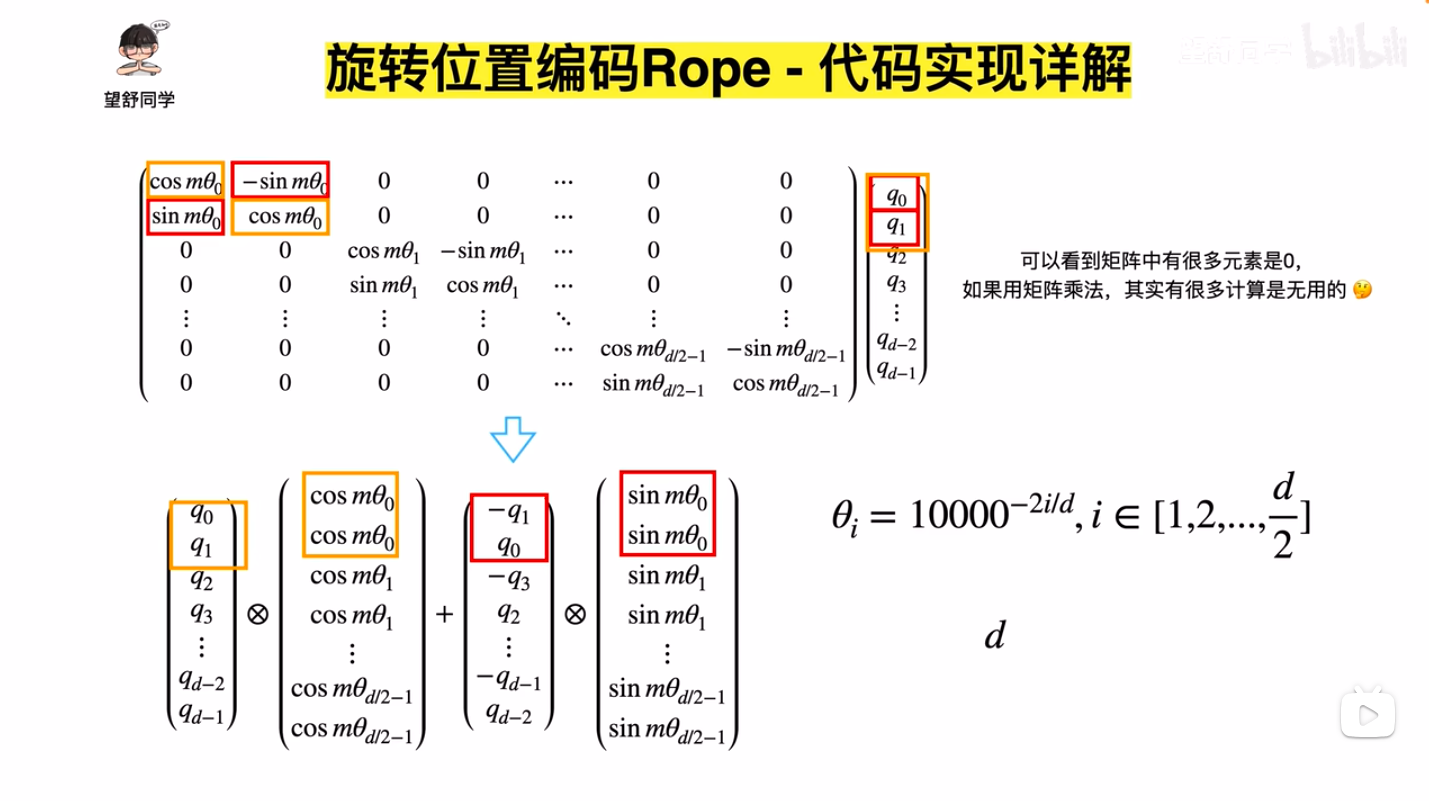
- 代码实现
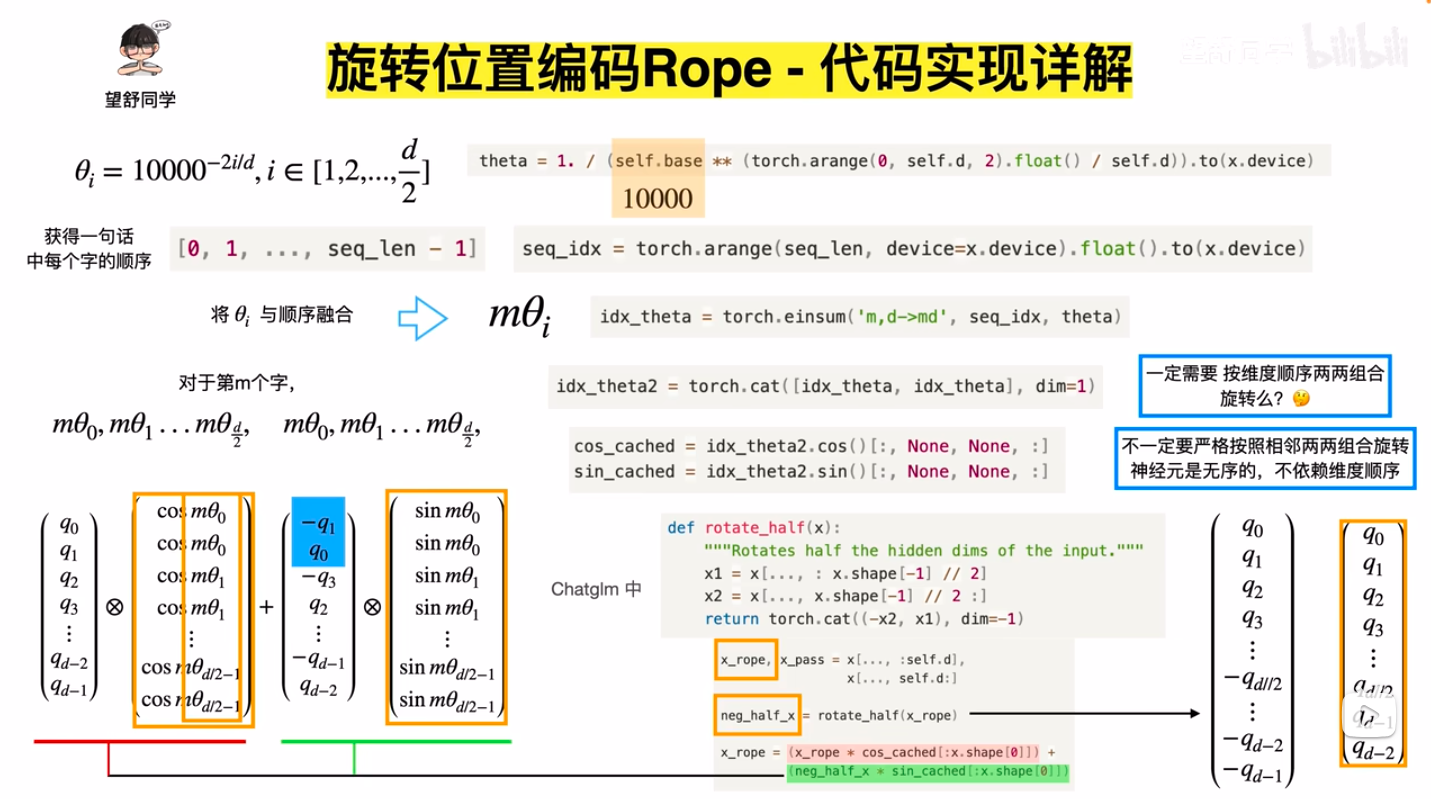
- 上述实现中使用了
torch.einsum,本质是爱因斯坦求和约定 ,是矩阵乘法的一种表示,C = torch.einsum("n,d->md", A,B)表示矩阵C[m,d] = A[n]*B[d],,这是个很常用的省略写法,更详细的可以看看图学 AI:einsum 爱因斯坦求和约定到底是怎么回事?
- 上述实现中使用了