NLP——LLM对齐微调-Self-Rewarding-RubricRL

注：本文包含 AI 辅助创作

• 参考链接：
  • 原始论文：(Self-Rewarding-RubricRL) Self-Rewarding Rubric-Based Reinforcement Learning for Open-Ended Reasoning, 20250919, Ant Group

Paper Summary

• 整体说明：
  • 论文介绍了一种轻量级的训练范式 用于开放域推理的 Rubric-based RL Self-rewarding 强化学习(Self-Rewarding Rubric-Based Reinforcement Learning for Open-Ended Reasoning) ，在基于 Rubric 验证的奖励下，用策略模型本身替代了单独的奖励模型
    • 这种方法在降低训练成本的同时，提升了在困难任务上的性能
  • 核心创新点：自己作为自己的 Grader，不断“互相”进化（循环进化）
  • 注意：这项工作的实验仅限于医疗领域的 HealthBench
    • 作者相信该方法对其他开放域任务也会有效，未来的工作应探索更广泛的领域
  • 阅读问题：
    • 在数据分析阶段，全文包含了许多图片和文字描述不一致的情况！深究下去比较浪费时间，不建议深究，仅关注论文的核心贡献是 Self-Rewarding 即可
• 背景 & 问题：
  • 开放式评估对于在现实世界场景中部署大语言模型至关重要
  • 在研究 HealthBench 时，作者观察到使用模型自身作为 Grader 并生成 Rubric-based 奖励信号，能显著提高推理性能（训练后的模型也会成为更强的 Grader ）
• Motivated by this，论文提出了 Self-Rewarding Rubric-Based Reinforcement Learning for Open-Ended Reasoning
  • 一个轻量级框架，能够实现更快、更高效的资源利用训练，同时超越 Baseline 方法
  • 在 Qwen3-32B 模型上，仅使用 4000 个样本的 HealthBench Easy 子集进行训练，就足以获得一个在 HealthBench Hard 上性能超过 GPT-5 的模型
  • 加入少量由教师（Teacher）评分的数据可以进一步提升能力较弱模型的性能

---

Introduction and Discussion

• 随着 OpenAI o1 (2024) 的发布和 DeepSeek R1 (2025) 的开源，基于 RLVR 的推理模型已迅速成为社区关注的焦点，为大型语言模型引入了第二个可扩展性维度
• 早期的研究主要集中在提升数学和编码能力，而最近的开源模型如 Kimi K2 (2025) 和 GLM-4.5 (2025) 则将注意力转向训练智能体能力
  • 与开放式（Open-Ended）推理相比，这些场景下的奖励信号相对明确
• 在实际应用中，用户通过多轮对话与模型交互，并提出开放式问题，这与基准测试类型的任务有很大不同
  • 因此，用于评估和强化学习的可靠奖励信号要难以获取得多
• 这一挑战在医疗保健领域（healthcare domain）尤为突出（Particularly pronounced） ，因为用户期望获得值得信赖且可靠的回答
  • 为解决此问题，OpenAI 引入了一个名为 HealthBench (2025) 的开源基准
    • HealthBench 是一个基于对话的开放式评估基准，旨在评估语言模型在医学领域的能力
    • HealthBench 采用 LLM-as-a-Judge (2023) 框架，并使用基于详细 Rubric 的评分系统，针对特定任务的标准来评估模型性能
• 为应对这一挑战，论文专注于 HealthBench 基准测试，并提出Self-rewarding Rubric-based 的开放式推理强化学习 ，
  • 该方法直接利用 Rubric-based 评估信号进行训练，并整合了模型的自我评分（self-grading）
• 论文的方法显著降低了资源消耗，提高了训练效率，同时提升了性能

---

Background and Preliminary Experiments

Background on Open-Ended Evaluation

• 自从将 RLVR 引入训练以来，LLMs 在具有客观可验证事实依据的任务上取得了显著进步，例如：
  • 数学领域的 AIME 和 FrontierMath (2025)；
  • 编码领域的 SWE-bench (2024) 和 Aider Polyglot (2025)；
  • 用于指令遵循或工具使用的 BrowseComp (2025) 和 Tau2-bench (2025)
  • 这展示了强大的推理时 Scaling 能力（inference-time scaling capabilities.）
  • 这些进步主要归因于在强化训练期间，此类任务中存在定义明确的奖励信号
• By Contrast，针对大语言模型的开放式评估基准相对较少
  • 代表性的例子包括 LMSYS Chatbot Arena (2023)、 MT-Bench (2023) 和 AlpacaEval (2023)，但这些基准通常依赖于 LLMs 或人类专家作为 Grader ，这带来了潜在的偏见和可扩展性问题
• HealthBench 是一个医学领域的开放式评估基准，包含 5000 个对话实例，其模型回答根据 Task-specific Rubric 进行评估，论文主要关注 HealthBench ，原因如下：
  • HealthBench 的基准数据由具有临床实践经验的医师标注，确保了正确性和领域专业知识，因此与 LMSYS Chatbot Arena (2025) 相比减少了偏见
  • HealthBench 包含一个由 1000 个问题组成的 HealthBench Hard 子集，前沿模型在该子集上的得分尚未超过 50% ，这使其适合研究开放式回答中的推理
  • HealthBench 提供了一个元评估（在论文中称为 HealthBench Meta ），该评估使用宏观 F1 分数来量化 LLM Grader 与人类医师之间的差异

Meta Evaluation of Open-Source Models on HealthBench

• HealthBench 依赖闭源模型 GPT-4.1 进行评分，这对评估的可重复性和训练的可行性提出了挑战
  • 因此，论文使用不同规模的开源模型进行 HealthBench 评估
  • 论文使用 simple-evals 进行评估，采样参数详见附录 A.1
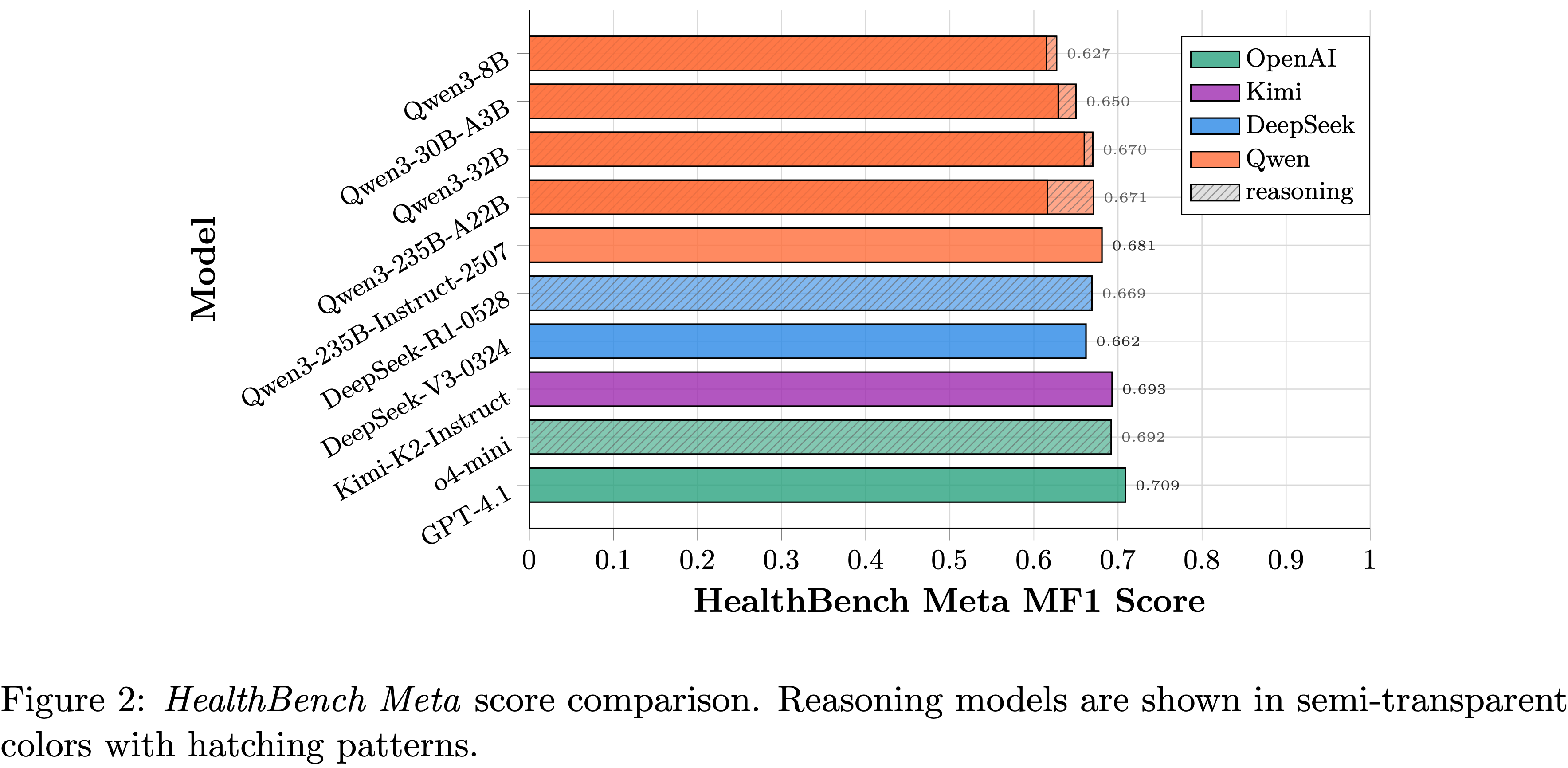
• 如图 2 所示，虽然 GPT-4.1 仍然是最强的 Grader （0.709），但开源模型正在逐步追赶
  • 例如 Kimi-K2-Instruct (0.693) 和 Qwen3-235B-Instruct-2507 (0.681)，并且呈现出模型越大得分越高的趋势
  • Notably，对于 Qwen3 的混合推理模型，无思考模式（nothink mode）的得分低于思考模式（think mode）
    • 这种性能下降在 MoE 模型中尤为明显，Qwen3-235B-A22B 下降了 0.055
    • 理解：
      • 图 2 中，nothink/think 是在同一个图上的， 模型也相同，只是灵活取消了 think 作为 nothink
      • 这里的 nothink 主要是只同一个模型既可以 think 又可以不 think 时的 nothink 选项；与传统的 nonthinking 模型不完全一致
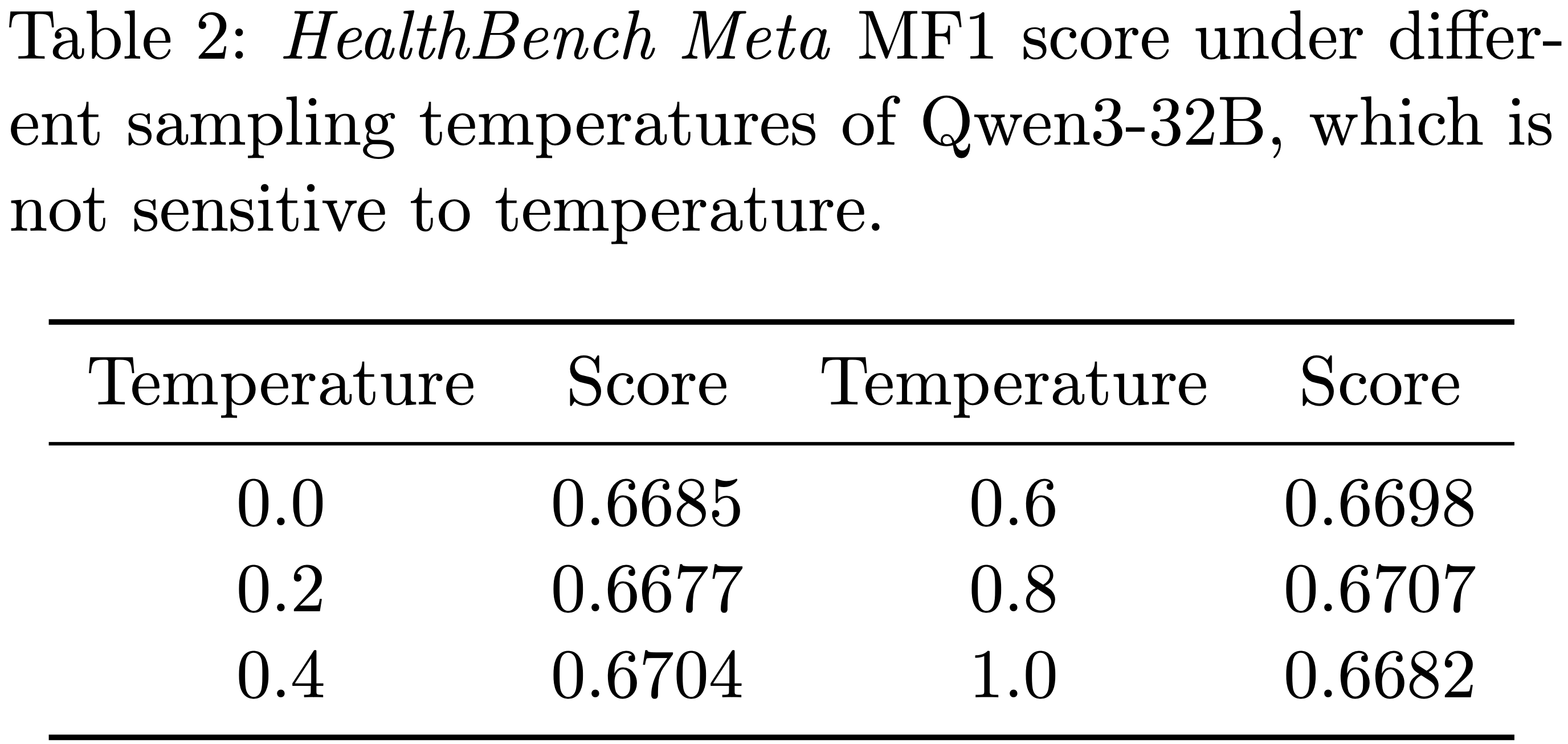
• 论文还测试了 Qwen3-32B 在不同采样温度下的评分能力，如表 2 所示
  • 结果表明，Qwen3-32B 在评分能力上对采样温度不敏感，得分在 0.670 左右波动
  • 理解：这里给了个很好的实例，调整模型的采样温度实际上不一定影响很大（表 2 中从 0.0 到 1.0 都试了，分数几乎没有太大变化）
• Furthermore，论文使用 GPT-4.1、Kimi-K2-Instruct 和 Qwen3-32B 自身分别作为 Grader ，以思考模式评估 Qwen3-32B 作为采样模型
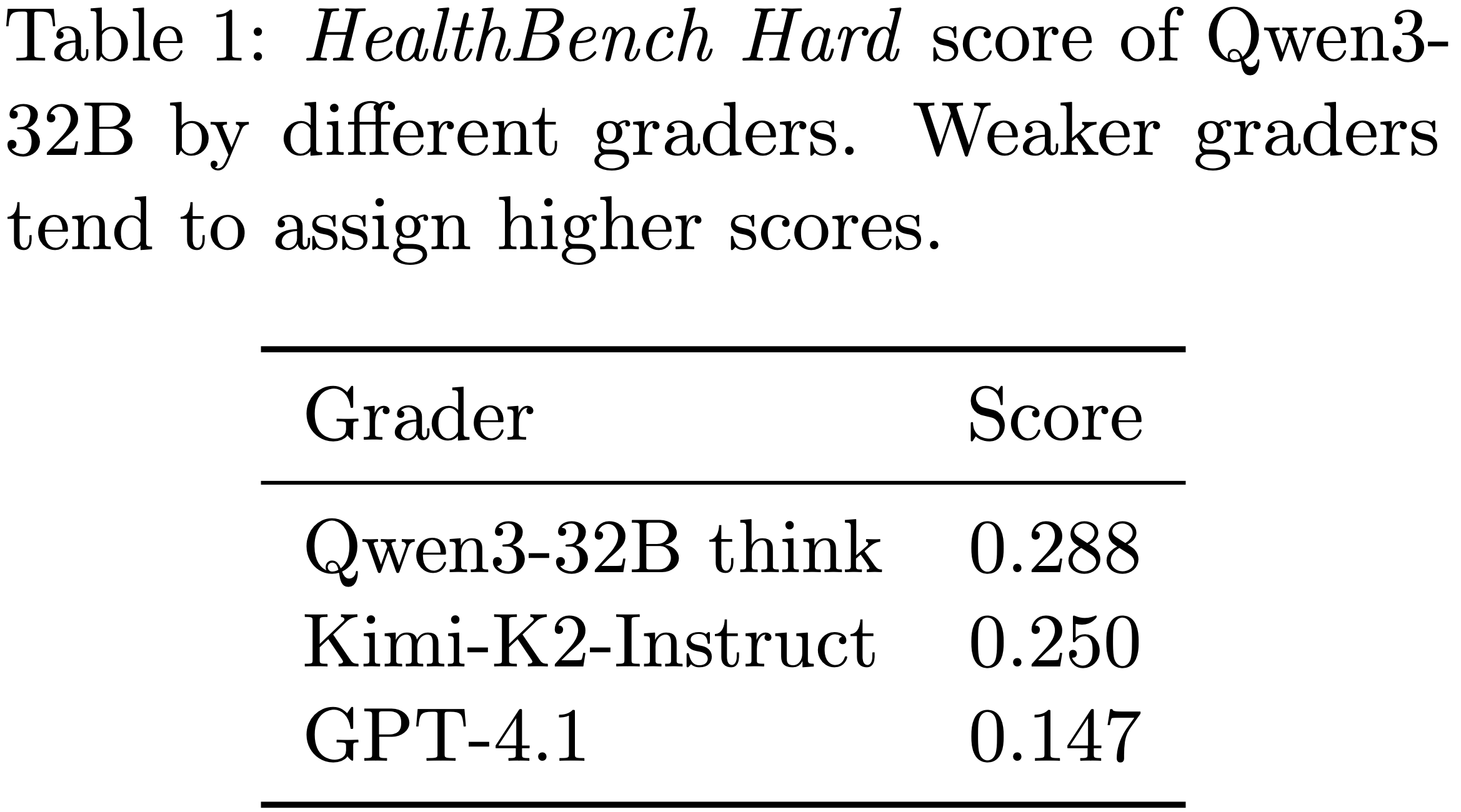
  • 如表 1 所示，随着 Grader 能力的增强，Qwen3-32B 在 HealthBench Hard 上的得分降低，这表明较弱的 Grader 往往会由于评估错误而给出更高的分数

Preliminary Experiments

• 论文进行了初步实验，以研究使用开源模型作为 Grader 来训练开放式推理任务的可行性
• 除非另有说明(Unless otherwise specified)，后续章节中的实验训练数据和参数均与本节介绍的一致

Models and Datasets

• 如图 2 和表 1 所示，Qwen3-32B 是一个合理的选择
• 在后续的 Self-rewarding 实验中，论文验证了即使是较弱的 Qwen3-8B 也能取得良好的性能
• 对于训练数据，论文将其分为两类：
  • 一类是基准和合成数据，其中每个 Prompt 都附带 Rubric 及其对应的分数；
  • 另一类是论文收集的 GPT-4.1 评分数据，用于判断特定 Response 是否满足特定 Rubric
• 在整篇论文中，论文使用以下数据集术语：
  • Easy data ：4000 个 HealthBench Easy 样本，除非另有说明，否则用于训练
  • Synthetic data ：4000 个与 Easy 数据类似的合成生成样本
  • Scoring data ：1000 个论文从先前评估中收集的 GPT-4.1 评分样本
  • Mixed data ：Easy 数据和 Scoring 数据的组合，总计 5000 个样本
• 在本节中，论文主要使用 Easy 数据进行训练，并在 HealthBench Hard 的 1000 个问题上评估模型的推理能力
  • 在后续的 Self-rewarding 实验中，论文也使用合成数据进行训练，但这并非论文重点

Training Details

• SFT ：
  • 由于 HealthBench 为大多数样本提供了理想的完成结果，论文首先在 Easy 数据集上进行 SFT。论文使用批大小为 64，学习率为 1e-5，序列长度为 4096，训练 3 个轮次
• RL ：
  • 论文使用 GRPO 算法，并采用 DAPO 的大部分参数
  • 论文通过 verl 实现，最大 Prompt 长度为 2048 个 token，最大 Response 长度为 6144 个 token，训练 Prompt 批大小为 32，每个 Prompt 生成 4 个 Response，训练 10 个轮次
    • 其他详细参数在附录 A.3 中提供
  • 论文使用生成式奖励模型（generative reward model，GRM）来评判每个 Rubric 是否被满足并相应赋分 ，奖励计算详见第 3.4.1 节
    • 本节实验中，GRM 是处于思考模式的静态 Qwen3-32B 模型

Reward Formulation for Reinforcement Learning

• RL 的训练目标与 DAPO 类似，采用 clip-higher 策略、token 级别的梯度损失，并省略了 KL 惩罚项，其目标函数如下：
  $$
  \mathcal{J}(\theta)= \mathbb{E}_{(q,\mathcal{R})\sim\mathcal{D},\{o_{i}\}_{i=1}^{G} \sim\pi_{\theta_{\text{old} } }(\cdot|q)}
  \left[\frac{1}{\sum_{i=1}^{G}|o_{i}|}\sum_{i=1}^{G}\sum_{t=1}^{|o_{i}|}\min \left(w_{i,t}(\theta)\hat{A}_{i,t},\text{clip}\left(w_{i,t}(\theta), 1-\varepsilon_{\text{low} },1+\varepsilon_{\text{high} }\right)\hat{A}_{i,t}\right)\right] \tag{1}
  $$
  • \(\pi_{\theta}\) 是语言模型
  • \(q\) 是从 Prompt 集 \(\mathcal{D}\) 中采样的 Prompt
  • \(\mathcal{R}\) 是 \(q\) 对应的特定 Rubric 集
  • 每个 Prompt 生成 \(G\) 个样本的组
  • \(w_{i,t}=\frac{\pi_{\theta}(o_{i,t}|q,o_{i,< t})}{\pi_{\theta_{\text{old} } }(o_{i,t}|q,o_{i,< t})}\) 是重要性采样比率
• Importantly，优势估计通过下式进行：
  $$
  \hat{A}_{i,t}=\frac{S_{i}-\text{mean}(\{S_{i}\}_{i=1}^{G})}{\text{std}(\{S_{i}\}_{i=1}^{G})} \tag{2}
  $$
  • 其中 \(S_{i}\) 是组中第 \(i\) 个样本的奖励分数
• 对于每个样本，奖励分数 \(S\) 的计算方法是：
  • 对满足的每个 Rubric \(r_i \in \mathcal{R}\) ，由 \(\color{red}{\pi_{\theta_{\text{old} } } }\) 以生成方式进行判断（Prompt 模板与 HealthBench 相同），并赋予分数点 \(p_i\)，将所有赋分累加，然后除以可能的总正分数点，最后将分数裁剪到 [0, 1] 范围
    $$
    S=\frac{\sum_{r_{i}\in\mathcal{R} }p_{i}\cdot\mathbb{I}(\color{red}{\pi_{\theta_{\text{old} } }}(r_{i}\text{ criteria_met}))}{\sum_{r_{i}\in\mathcal{R} }p_{i}\cdot\mathbb{I}(p_{i}>0)} \tag{3}
    $$
    • 特别注意：这里使用的 Rubric Verifier 是策略自身，即 \(\color{red}{\pi_{\theta_{\text{old} } } }\)
• 这种方法与先前工作有两点主要不同：
  • 1）它使用针对任务的大量且多样化的特定 Rubric ，而非通用原则（rather than general principles）；
  • 2）每个 Rubric 由 GRM 独立评分，提供了清晰、细粒度的（fine-grained）奖励信号
  • 奖励过程受原始 HealthBench 评估协议的启发

Preliminary Results

SFT degrades open-ended reasoning without chain-of-thought(不包含思维链的 SFT 会降低开放式推理能力)

• 论文观察到，虽然训练损失持续下降，但验证损失在一个轮次后迅速增加，如图 8 所示（附录 A.2）
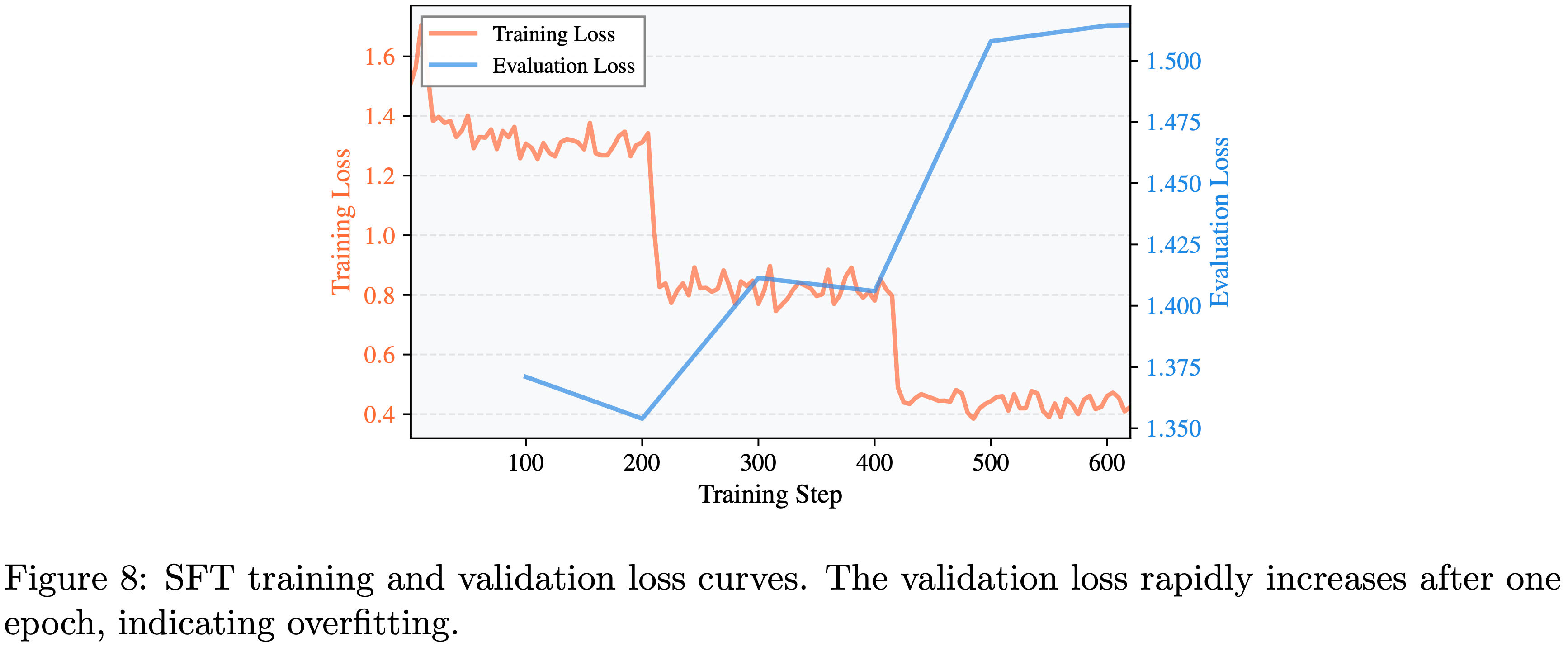
• 使用 Kimi-K2-Instruct 作为 Grader ，论文发现 SFT 模型在 HealthBench Hard 上的得分，在验证损失最低的检查点（200 步后），从基础模型的 0.1988 下降到 0.0004，两者均在无思考模式下评估
  • 注意：0.1988 下降到 0.0004 这个分数在 图 8 中没有找到，是其他地方显示的吗？
• 这一发现与之前的研究 (2024, 2025) 一致，特别是当 SFT 中未包含思维链推理时，模型即使在分布内的挑战性问题上也未能泛化

RL consistently enhances model performance even with limited data(数据有限的情况下，RL 也能持续提升模型性能)

• 如图 3 所示，训练期间模型的 Response 长度自发增加，奖励持续提升直至达到最大 Response 长度
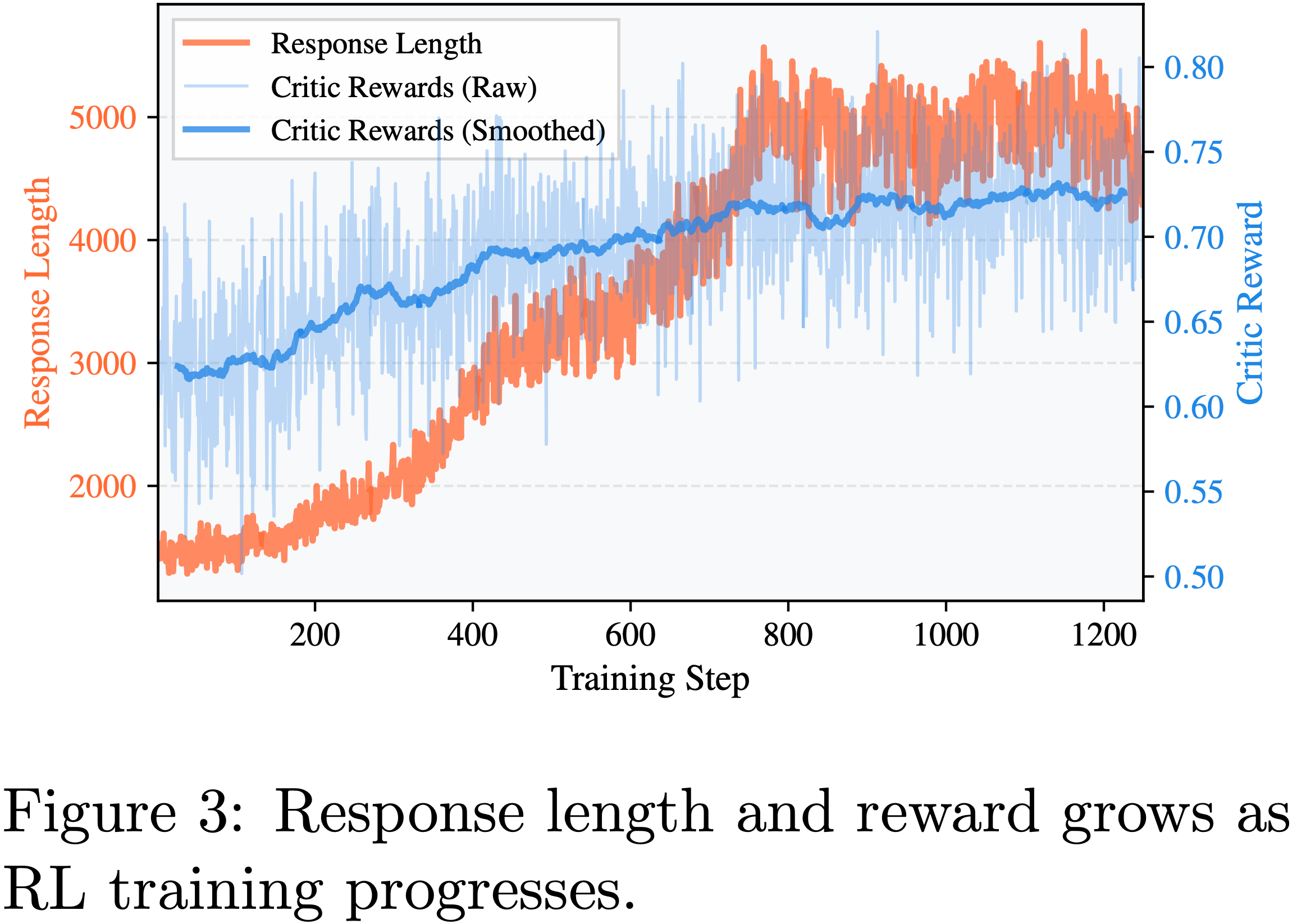
• Simultaneously，在 HealthBench Hard 评估中，模型性能持续提升，最终达到 0.446，显著超过 OpenAI o3 的 0.32 分，如图 4 所示
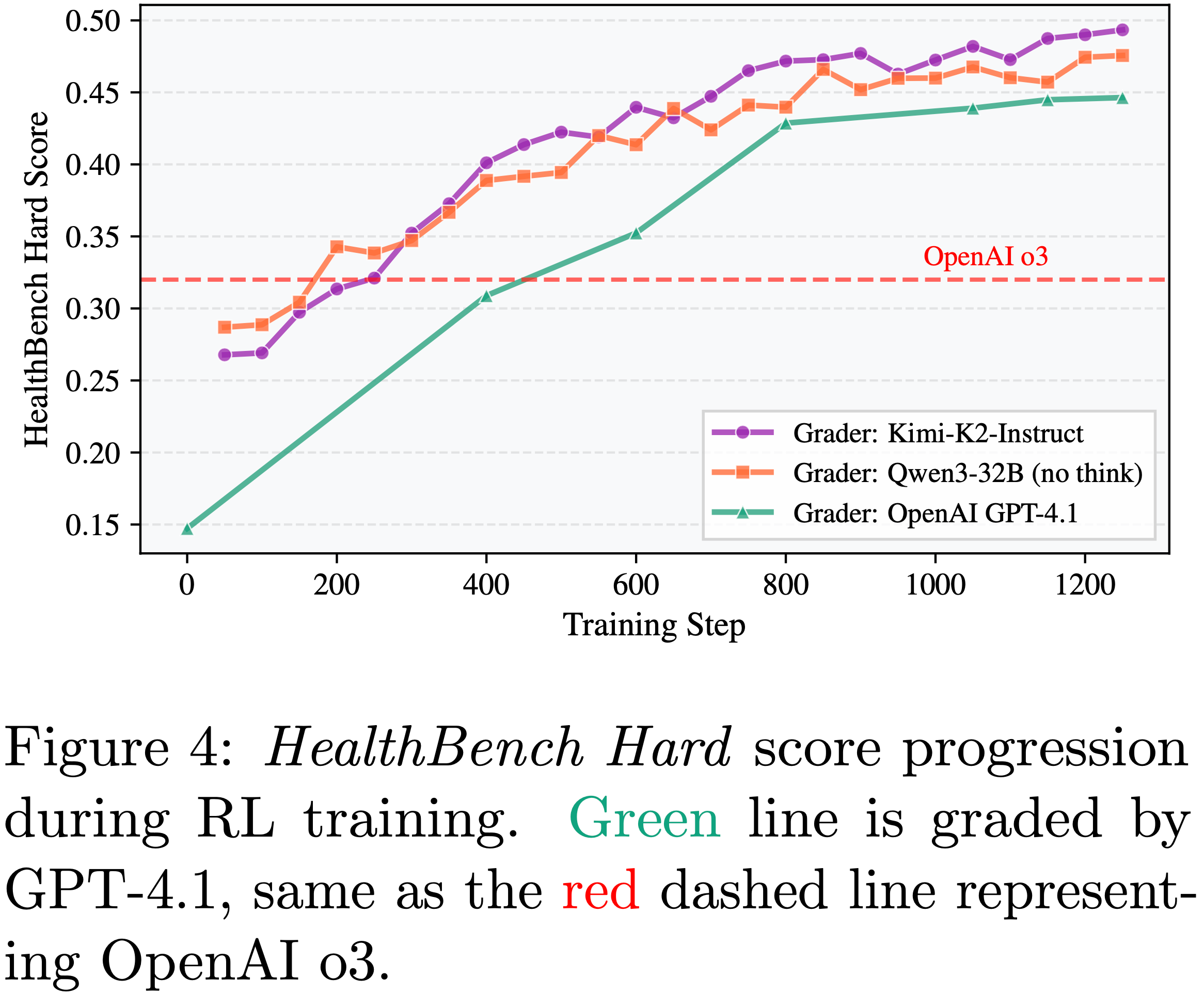
• 论文观察到，虽然使用 Kimi-K2-Instruct 或 Qwen3-32B 作为 Grader 会得到更高的分数，但趋势保持一致
• 因此，在后续实验中，论文主要使用开源模型作为 Grader 以降低 API 成本
• 问题：这里的 RL 训练趋势中，Kimi-K2-Instruct 和 Qwen3-32B 的效果比 GPT4.1 还好，跟前面表 1 中（原始模型能力）的结论看起来不一致，是不是有问题？

Grading ability preserves after RL training

• 论文评估了 RL 后模型的 HealthBench Meta 分数，发现思考和无思考模式的分数均有轻微提升，如表 3 所示
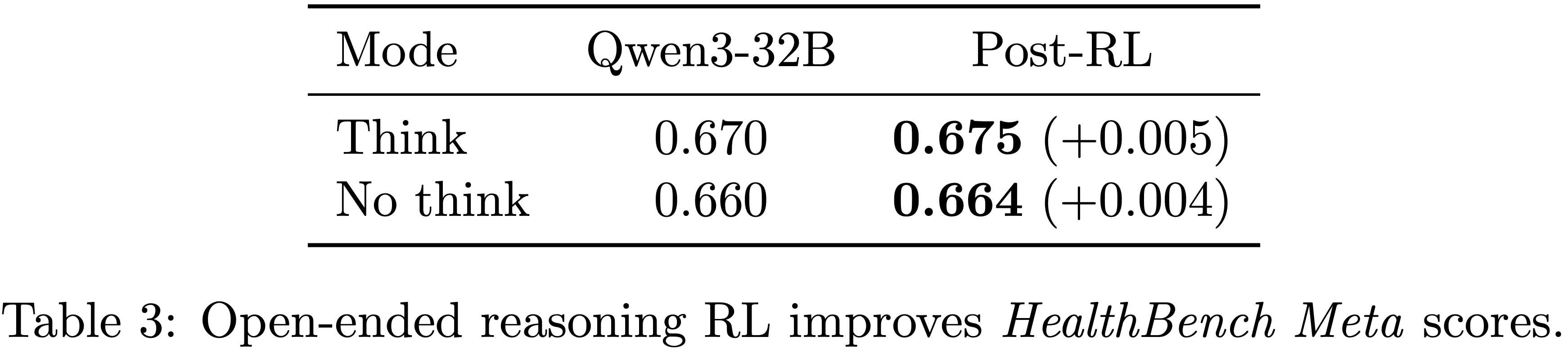
• 这一观察结果自然引导论文考虑使用模型自身作为强化学习的 Grader

---

Method

• 第 3.3 节验证了使用 Rubric-based RL 奖励来训练开放域推理任务的有效性

• however，可能存在两个限制：

• 训练效率瓶颈 (Training Efficiency Bottleneck)

  • 由于在 verl 中实现的 GRPO 采用 on-policy 训练方法，actor 训练必须等待所有样本的奖励计算完成
    • 这极其耗时：
      • 一方面，GRM 评分本身就很慢；
      • 另一方面，每个 Rubric 都需要进行判断，每个样本平均有 11 个 Rubrics，再加上每个样本采样 4 个 Responses
    • 在论文之前的实验中，论文部署了与训练 GPU 数量相同的 SGLang router 服务来进行 GRM 推理
      • 由于性能限制，单步训练时间中大约有 70-80% 消耗在奖励计算上

• GRM 能力限制 (GRM Capability Constraints)

  • 一个自然的担忧是 GRM 自身的能力可能会限制 RL 训练的效果
  • 出于可扩展性的考虑，作者希望在不依赖比策略模型更大的模型的情况下取得更好的结果
    • 其背后的直觉与 (2024) 类似

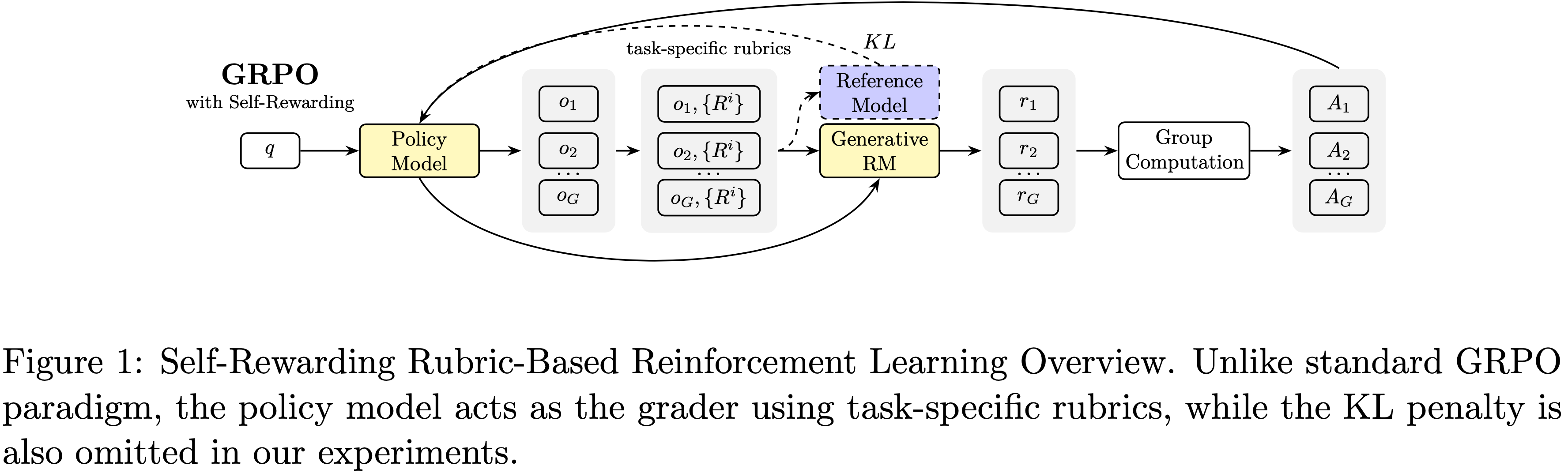
• 根据论文初步实验观察到的模型评分能力在 RL 训练期间没有下降的现象，论文提出了 用于开放域推理的 Rubric-based RL Self-rewarding 强化学习 (Self-Rewarding Rubric-Based Reinforcement Learning for Open-Ended Reasoning) ，如图 1 和算法 1 所示

  • 与原始 GRPO 的关键区别在于，论文通过 Task-specific Rubrics 使奖励信号可验证，并使用模型自身作为奖励模型，在保持有效性的同时大大减少了评分时间
  • 通过使用模型自身作为奖励评估器，这种方法有两个优点：
    • 优点1：减少了训练所需的计算资源
      • 在使用相同数量 GPU 且无需额外推理资源的情况下，单步训练时间最多可减少 30%
    • 优点2：使得训练出的模型能够超越 Baseline 性能

• 前文公式补充：
  $$
  \mathcal{J}(\theta)= \mathbb{E}_{(q,\mathcal{R})\sim\mathcal{D},\{o_{i}\}_{i=1}^{G} \sim\pi_{\theta_{\text{old} } }(\cdot|q)}
  \left[\frac{1}{\sum_{i=1}^{G}|o_{i}|}\sum_{i=1}^{G}\sum_{t=1}^{|o_{i}|}\min \left(w_{i,t}(\theta)\hat{A}_{i,t},\text{clip}\left(w_{i,t}(\theta), 1-\varepsilon_{\text{low} },1+\varepsilon_{\text{high} }\right)\hat{A}_{i,t}\right)\right] \tag{1}
  $$

  $$
  \hat{A}_{i,t}=\frac{S_{i}-\text{mean}(\{S_{i}\}_{i=1}^{G})}{\text{std}(\{S_{i}\}_{i=1}^{G})} \tag{2}
  $$

  $$
  S=\frac{\sum_{r_{i}\in\mathcal{R} }p_{i}\cdot\mathbb{I}(\color{red}{\pi_{\theta_{\text{old} } }}(r_{i}\text{ criteria_met}))}{\sum_{r_{i}\in\mathcal{R} }p_{i}\cdot\mathbb{I}(p_{i}>0)} \tag{3}
  $$

---

Results

Self-Rewarding Effectiveness

The model’s scoring ability improves as response length increases(模型的评分能力随着 Response 长度增加而提高)

• 论文在与第 3.3 节 Baseline 相同的训练设置下，对 Qwen3-32B 进行了 Self-rewarding 实验，使用模型自身作为 Grader （这是一个移动的目标）
  • 注：这里说的 Baseline 是 3.3 节（Preliminary Experiments）中提到的使用开源模型作为 Grader 的方案
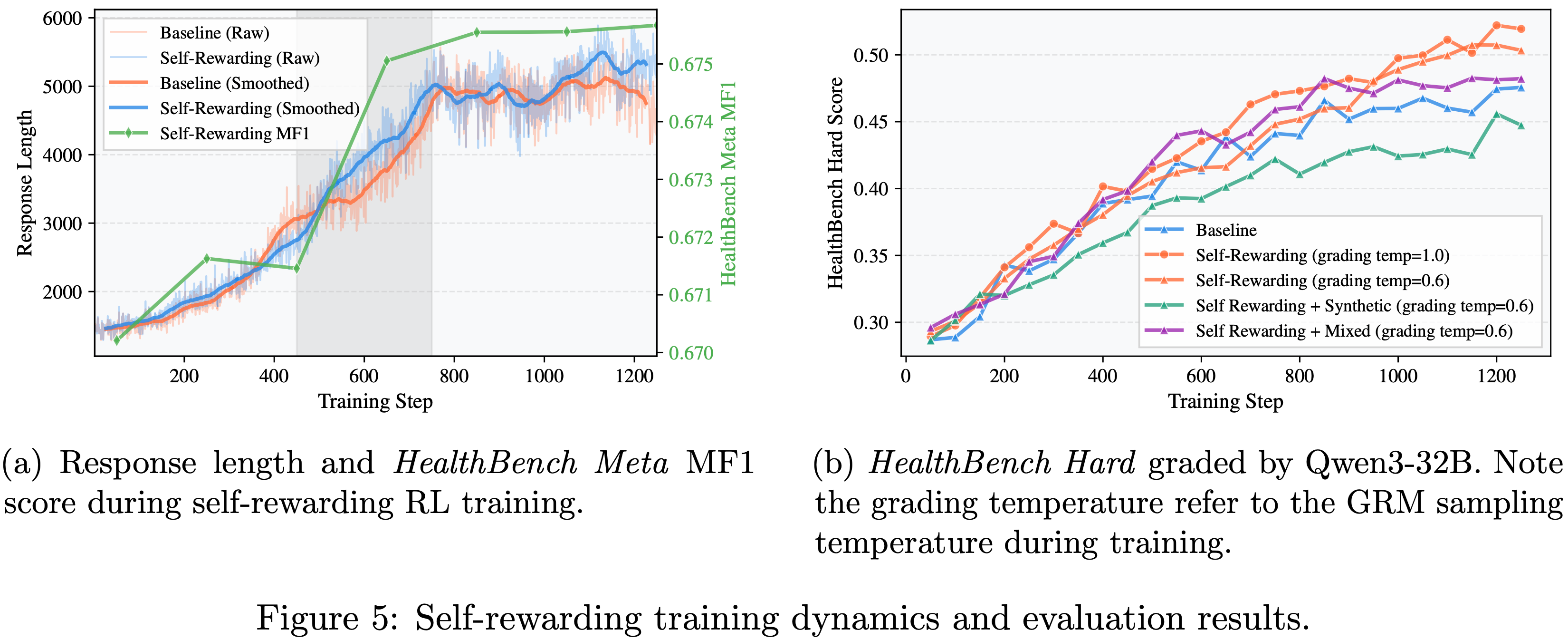
• 由于训练集奖励或验证集分数是由不同的 Grader 评分的，论文无法直接与 Baseline 进行比较，因此论文在图 5a 中提供了 Response 长度的变化过程及其 HealthBench MF1 分数
  • 问题：找一个相同 Grader 来评分不旧好了？
  • 问题：MF1 分数是什么？
    • 回答：HealthBench 的 MF1 分数 是 Macro F1 score（宏 F1，Macro-F1） ，是该医疗评估基准中用于衡量模型分级器（grader）与人类医师评分一致性的核心指标，取值范围为 0 到 1，越接近 1 代表一致性越高，详情见论文附录部分
• 从图 5 中可以看出：
  • 尽管论文没有显式地训练模型的评分能力，但评分能力并未下降，而是与 Response 长度同步变化，这反过来又提供了更高质量的奖励信号，形成了一个良性循环
    • 理解：其实看起来 MF1 分数的提升很小，累计只有 0.005 左右，其实不能算是看到了持续提升， 更像是持平
  • Especially，图 5a 中的灰色区域表明，与 Baseline 相比，它帮助模型生成了更长的输出
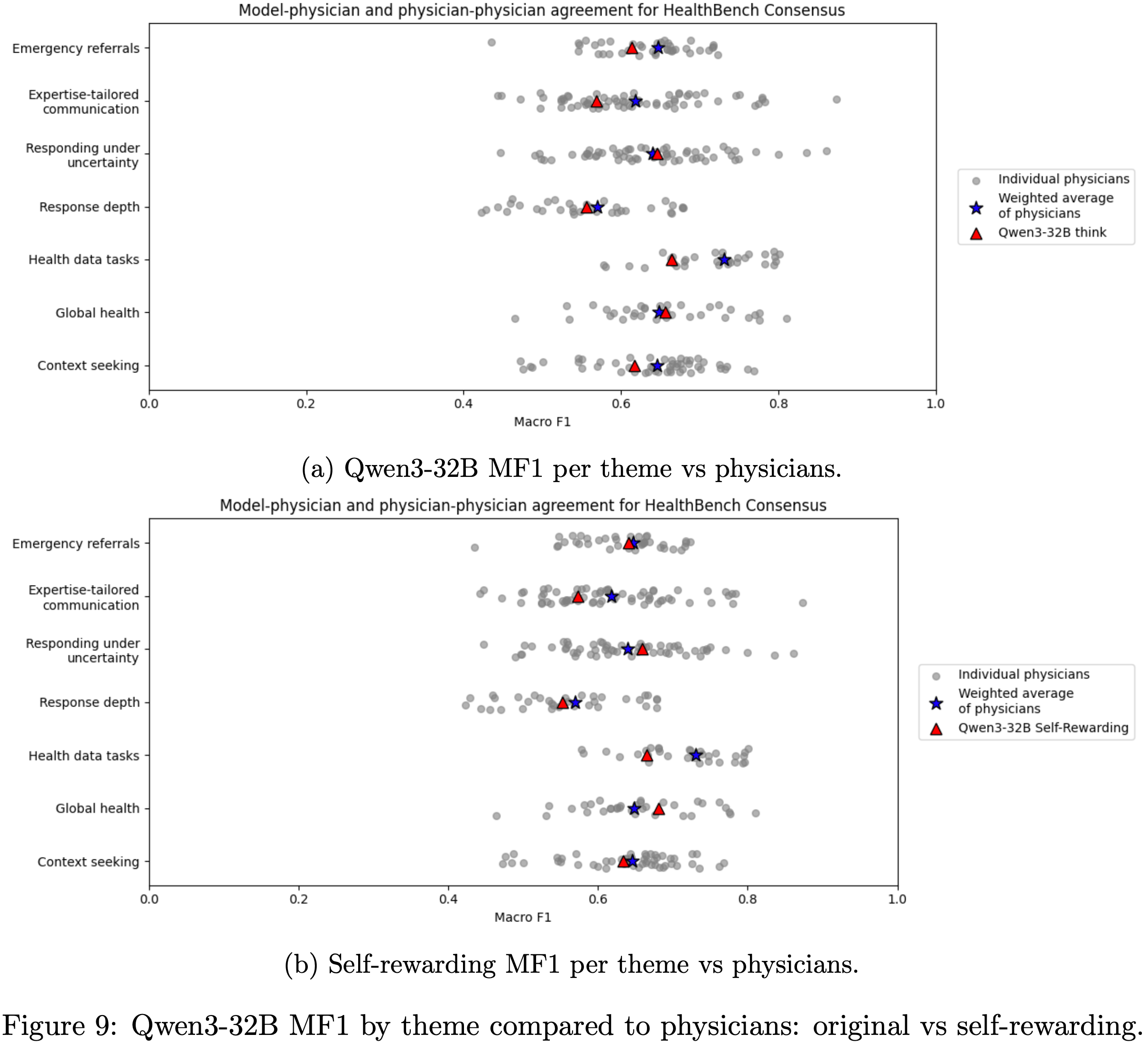
  • Additionally，通过与医生按主题比较 MF1，论文发现模型在大多数主题上都优于原始的 Qwen3-32B；
  • Notably，模型在全球健康和不确定性下响应 (Global Health and Responding Under Uncertainty) 方面超过了医生的加权平均值（见附录 A.4 的图 9）

Once the response length reaches its limit, self-rewarding further enhances the model’s reasoning performance(Response 长度达到限制后， Self-rewarding 能进一步提升推理性能)

• 论文使用 Qwen3-32B 模型作为 Grader ，在 HealthBench Hard 上评估了实验，结果如图 5b 所示
  • 其中一次 Self-rewarding 运行的评分温度 (grading temperature) 设为 1.0（与 rollout 温度相同），而其他运行则保持建议的 0.6
    • 注：如表 2 所示，温度不应该影响评分性能
• 最终结果显示所有配置都持续优于 Baseline ，而将评分温度设置为 1.0 时取得了最佳性能
  • 如图 5a 所示， Self-rewarding 比 Baseline 更早达到最大 Response 长度（均在 700-800 步内）；
  • 然而，其在图 5b 中显示的 HealthBench Hard 分数持续增加，从而获得了相对于 Baseline 更好的最终结果
  • 理解： Baseline 的配置见 3.3 节（Preliminary Experiments）中提到的使用开源模型作为 Grader 的方案
• 最后，论文使用 GPT-4.1 作为 Grader 进行了更准确的评估，结果如表 4 所示
  • 论文观察到所有 Self-rewarding 方法都优于 Baseline ，甚至超过了 GPT-5 的性能
• 此外，论文发现将评分温度设置为与 rollout 温度相匹配会得到更好的结果，这与 Qwen3-32B 评估结果一致，达到了 0.500 的分数

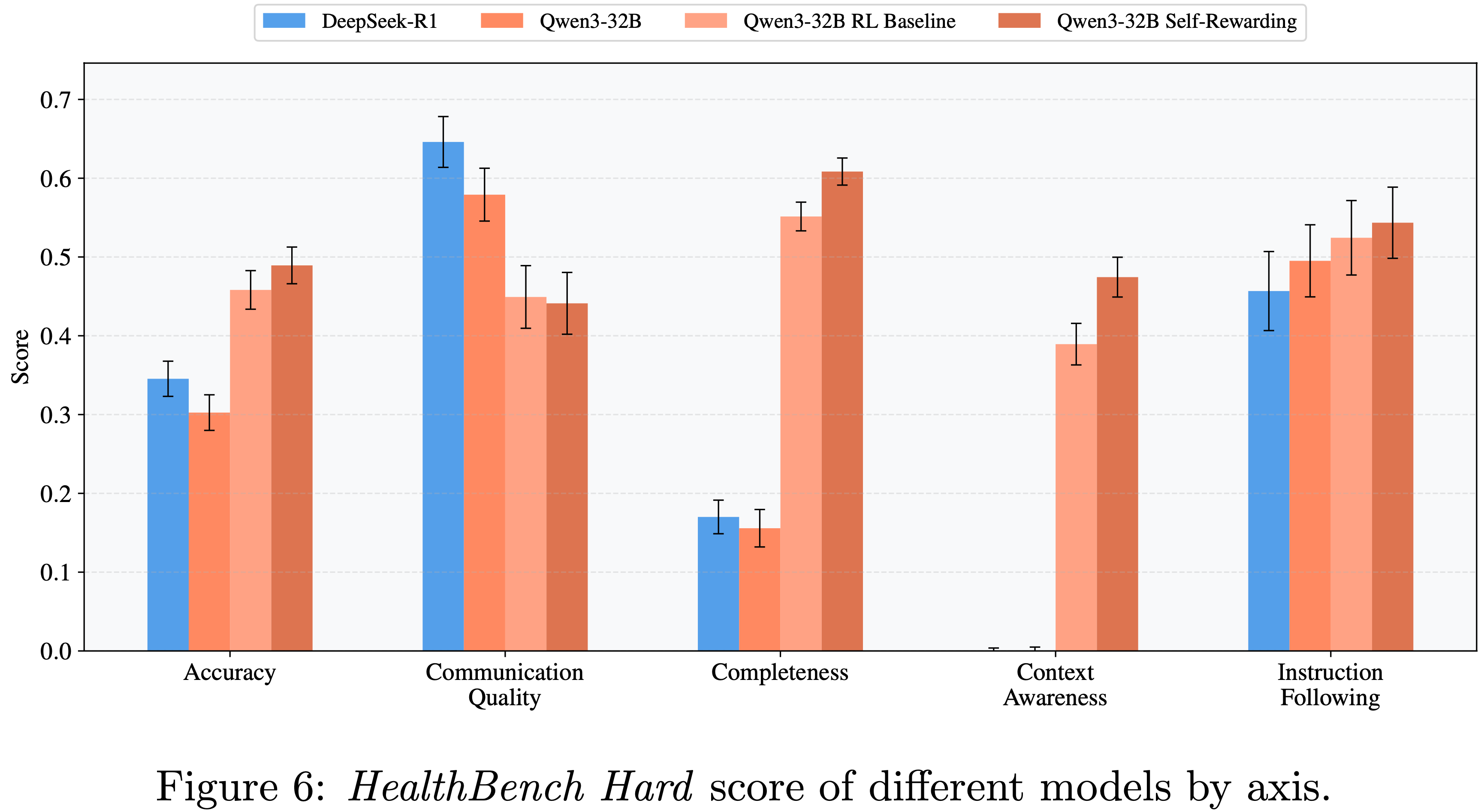
Improvements are observed across most evaluation dimensions

• 论文分析了不同维度的分数变化，发现在完整性和上下文感知 (context awareness) 方面有显著改善，这对大多数模型来说都具有挑战性
• 后者尤其要求模型“恰当地响应存在的上下文线索”，需要强大的上下文理解能力
• 然而，随着输出内容变长，沟通质量 (communication quality) 方面出现了一个负面副作用
  • 即模型的表达变得不够简洁、清晰和易读
  • 这凸显了在开放性问题中需要进行权衡，并表明仍有大量的研究机会
• 论文比较了原始 Qwen3-32B 模型和 Self-rewarding 模型的分数，发现 82.5% 的样本有所改进
  • 在改进的样本中，与其余样本相比，上下文感知 Rubric 的比例从 20.6% 下降到 17.5%，而沟通质量的比例从 6.0% 增加到 9.1%
  • 相关案例见附录 A.5

Training Efficiency

• 论文分析了 Self-rewarding 方法相比于 Baseline 方法的训练效率
• 如表 5 所示，在早期阶段，较短的 average rollouts 使得奖励计算在单步时间中占比较大，而在后期阶段，较长的 rollouts 降低了奖励时间的相对比例
• Self-rewarding 在单步时间和奖励计算时间上均实现了显著的加速（各阶段均减少约 50%），展示了论文方法的计算优势
• 请注意， Baseline 训练使用 32 个 GPU 进行训练，另外 32 个 GPU 用于 GRM 推理，而 Self-rewarding 总共只使用 32 个 GPU，所有其他配置保持不变
• Importantly，观察到的训练效率提升与实现细节密切相关；因此，论文仅报告论文配置下的相对效果

Dataset Influence

Using scoring data further enhances the model’s grading ability（使用评分数据可进一步提升模型的评分能力）

• 为了进一步评估改进的评分能力如何影响不同规模的训练，论文从前期的 GPT-4.1 评估中构建了一个评分数据集，并使用可验证的奖励目标进行训练
• 当仅在评分数据上训练时（图 7a），Qwen3-8B 的 HealthBench MF1 从 0.627 提升到 0.651，而 Qwen3-32B 的则从 0.670 提升到 0.684
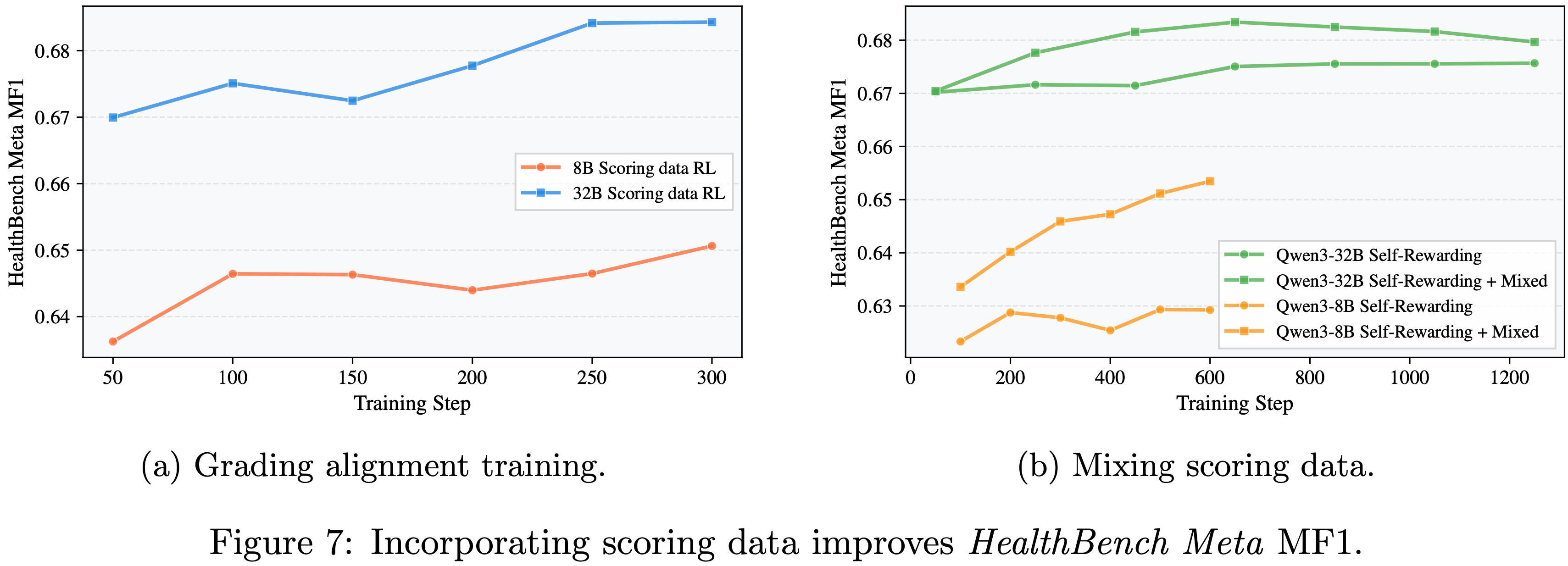
• 在混合目标 (mixed-objective) 设置下（图 7b），评分能力进一步提升；
  • 然而，对于 Qwen3-8B，整个训练过程中分数持续增加，而对于 Qwen3-32B，则出现了过拟合
• 值得注意的是，由于重复输出，Qwen3-8B 的训练在大约 600 步后崩溃，而 Qwen3-32B 的训练则非常稳定
• 问题：从图 7(a) 看，300 步内，看着整体还是呈现上升状态的，600 步后的崩溃没有给出图像说明
  • 图 7(b) 中给出了 Qwen3-8B 到 600 步以后就没有分数了，看起来像是 Mixed 和 非 Mixed 都同时崩溃？

Mixed-objective training benefits weaker models but not stronger ones（混合目标训练对较弱模型有益，但对较强模型无效）

• 当使用混合数据 (mixed data) 训练时，Qwen3-8B 的 HealthBench Hard 分数（由 Qwen3-32B 评分）从 0.354 增加到 0.380，而 Qwen3-32B 的性能则如图 5b 所示有所下降
  • 问题：似乎没看到下降，始终高于不适用混合数据的训练方案；只是自身在提升后随着训练的进行有下降趋势（仍始终高于非混合数据方案）
• 结合图 7b 中观察到的过拟合现象，论文假设较强模型的评分能力对于自我训练已经足够，而混合目标干扰了原始目标
• 因此，论文建议对较强的模型使用纯 Rubric-based RL 训练目标

Synthetic data remain effective, but underperform expert data

• 合成数据仍然有效，但表现不及专家数据
• 同样，像 easy set 这样的专家精心策划的数据收集成本高昂，因此论文评估了合成数据的有效性
• 如图 5b 所示，使用合成数据进行训练是有效的（effective），但落后于专家数据的 Baseline
  • 这符合预期：更高质量的专家数据为学习提供了更强的指导
  • 问题：合成数据的训练明显是所有方案中 HealthBench Hard 得分最低的，怎么能说是有效的呢？作者是不是看错了？

---

补充：Related Works

• 自演进（self-evolving）大语言模型的概念既引人入胜，也在迅速发展
  • 在此，论文总结最相关的研究方向

Reinforcement Learning from AI Feedback，RLAIF

• RLAIF 最初是作为 RLHF 的替代方案提出的，用于训练模型使其有用、诚实且无害 (2022)
  • 其主要优点是不需要人类标注者，而是依赖于一个标量奖励模型 (2022)
• (2024) 进一步证明，当奖励模型和策略模型规模相当时，RLAIF 可以达到与 RLHF 相当甚至更优的结果
  • 他们还提出了一种变体，直接 RLAIF（direct-RLAIF），即直接使用更小的通用 LLM 作为 Grader ，其性能可以超越同规模的奖励模型
• 论文的工作借鉴了这一观点（特别是，生成式奖励模型可能更有效）
  • 通过利用训练好的策略模型本身作为奖励模型来生成奖励信号

Rubrics as Rewards，RaR

• 同样受 HealthBench (2025) 启发，同时期的工作 (2025) 也探索了使用 Rubric-based 评分信号进行训练
  • However，他们的方法依赖于更强的专有模型作为 Grader
• In Contrast，论文的工作并不专注于自动构建 Rubric 数据集
  • 因为论文的实验表明，由专家定制的 Rubric 数据在训练效果上具有显著优势

Self-Rewarding Language Models

• Self-Rewarding Language Models (2025) 首次引入了这种范式，通过对模型自身的回答进行评分，并构建成对偏好数据用于直接偏好优化（DPO）训练
• However，(2024) 指出这种训练可能会积累偏见，导致优化目标漂移
• Kimi K2 (2025) 提出了自批判 Rubric 奖励机制（Self-Critique Rubric Reward），该机制针对一组有限的 Rubric 进行成对评估
• 论文的方法主要采用点式复合奖励（point-wise composite rewards）和广泛的 Task-specific Rubric 来减轻奖励破解（reward hacking），并证明相对较小的开源模型能在困难的开放式推理任务上达到最先进的结果

---

附录 A：更多细节

A.1 Sampling Parameters for Evaluation

• 关于采样器（Samplers），对于所有开源模型，max_tokens 均设置为 32768
• 关于 Graders ，对于非推理模型设置为 4096，启用思考模式时设置为 8192
  • 对于 GPT-4.1，参数与原始代码库中提供的保持一致
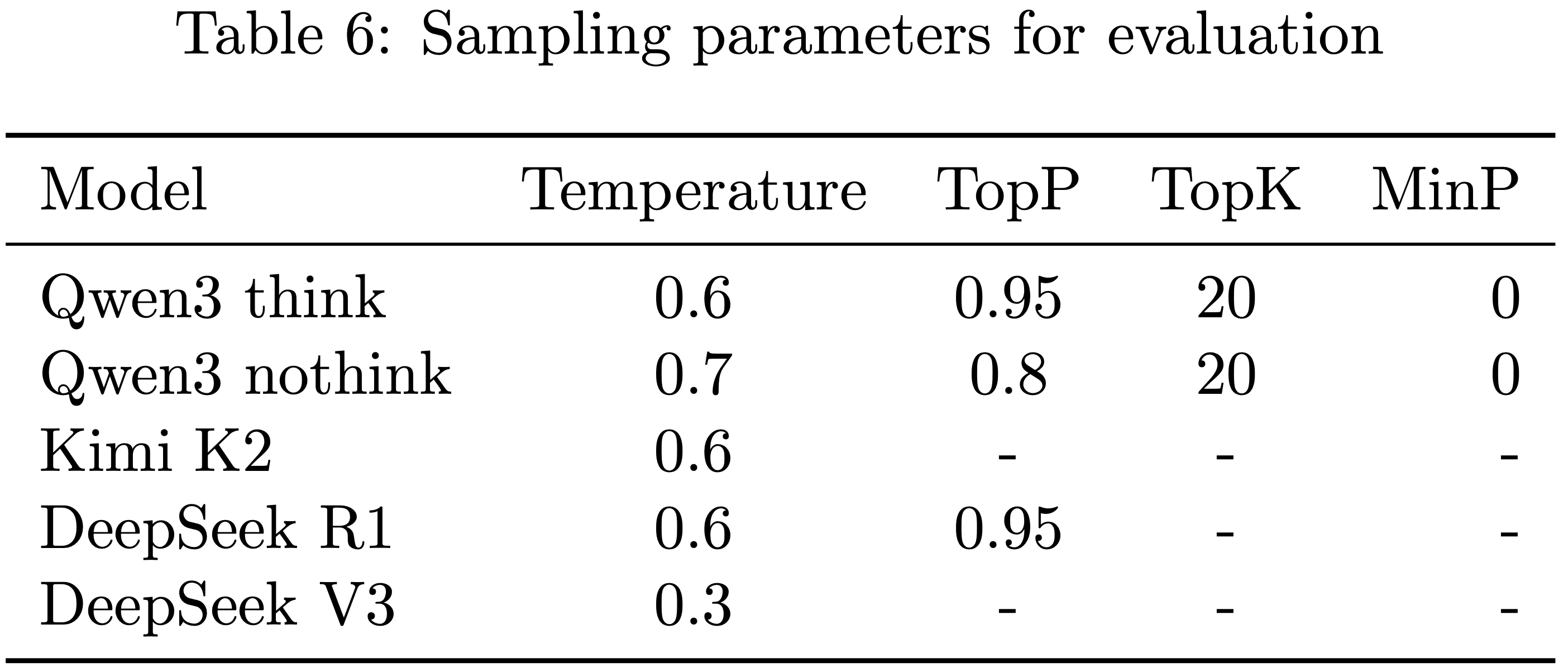
  • 其他采样参数总结在表 6 中

A.2 SFT Loss Curves

• Figure 8：

A.3 强化学习的训练细节

• 由于 verl 中参数和配置的复杂性，论文在此仅列出关键设置；完整的训练脚本将在开源代码库准备就绪后提供
• 后端（Backends） 论文使用 Megatron 进行 Actor 训练，使用 vLLM 进行 Rollout，但 GRM/评估使用 SGLang 路由器部署
• 并行策略（Parallelism Strategy） 对于 Qwen3-32B，论文使用 4 路张量并行和 2 路流水线并行进行训练，使用 4 路张量并行进行 Rollout。对于 Qwen3-8B，论文使用 4 路张量并行进行训练
• ** Baseline SGLang 设置** 每个节点以 8 路数据并行初始化，并通过具有自动负载均衡的 SGLang 路由器连接
• verl 的特定参数（Specific parameters for verl）
  • 除了混合数据实验外，所有实验的 train_batch_size=32，ppo_mini_batch_size=32；混合数据实验的这些值都设为 40，以保持每步的 Rubric 数据一致
  • max_prompt_length=2k，max_response_length=6k
  • rollout.n=4，rollout.max_model_len=16k
  • rollout.temperature=1.0，rollout.top_p=1.0，rollout.top_k=-1
  • clip_ratio_low=0.2，clip_ratio_high=0.28

A.4 Comparision to Physicians

• Figure 9：

A.5 案例研究

A.5.1 Performance Improvement Case

• 详情见原文

A.5.2 Performance Drop Case

• 详情见原文

---

附录：HealthBench MF1 指标介绍

• HealthBench 是 OpenAI 推出的医疗大模型评估基准，核心以医生编写的细粒度评分标准为核心，从 5 大行为维度与 7 大场景主题对模型回复打分，用标准化方式衡量医疗大模型在真实临床交互中的安全性、准确性与实用性
• HealthBench 原始论文：HealthBench: Evaluating Large Language Models Towards Improved Human Health, OpenAI, 20250513
• HealthBench HuggingFace：huggingface.co/datasets/openai/healthbench
• HealthBench 博客链接：Introducing HealthBench, OpenAI, 20250512
• MF1（Macro F1 分数）是用于二分类任务的性能评估指标，核心是对正类（met）和负类（not-met）的 F1 分数进行无加权平均，能平衡两类结果的评估敏感度，尤其适合类别不平衡的场景（如医疗评分中部分标准极少被触发）
• 先明确二分类任务中的核心统计量：
  • \( TP_{pos} \)：正类真阳性（模型判定“符合标准”且实际符合）
  • \( FP_{pos} \)：正类假阳性（模型判定“符合标准”但实际不符合）
  • \( FN_{pos} \)：正类假阴性（模型判定“不符合标准”但实际符合）
  • \( TP_{neg} \)：负类真阳性（模型判定“不符合标准”且实际不符合）
  • \( FP_{neg} \)：负类假阳性（模型判定“不符合标准”但实际符合）
  • \( FN_{neg} \)：负类假阴性（模型判定“符合标准”但实际不符合）
• 单类 F1 分数计算
  • F1 分数是精确率（Precision）和召回率（Recall）的调和平均数，公式为：
    $$ F1 = 2 \times \frac{\text{Precision} \times \text{Recall} }{\text{Precision} + \text{Recall} } $$
  • 分别计算正类和负类的 F1 分数：
    • 正类 F1 分数（\( F1_{pos} \)）：
      $$ F1_{pos} = 2 \times \frac{TP_{pos} }{2 \times TP_{pos} + FP_{pos} + FN_{pos} } $$
    • 负类 F1 分数（\( F1_{neg} \)）：
      $$ F1_{neg} = 2 \times \frac{TP_{neg} }{2 \times TP_{neg} + FP_{neg} + FN_{neg} } $$
• MF1 最终计算
  • MF1 是正类与负类 F1 分数的无加权平均值，公式为：
    $$ MF1 = 0.5 \times (F1_{pos} + F1_{neg}) $$

一些简答说明

• 无加权特性：无论正类、负类样本数量差异多大，两类 F1 分数在计算中权重相同，避免少数类表现被掩盖
• 医疗场景适配性：在 HealthBench 中，MF1 用于衡量模型评分与医师判断的一致性，能同时捕捉“漏判重要医疗标准”（假阴性）和“误判无关标准”（假阳性），贴合医疗评估的严谨性需求