NLP——LLM对齐微调-Reflect-Retry-Reward

注：本文包含 AI 辅助创作

Paper Summary

  • 整体总结：
    • 论文展示了通过训练模型改进 Self-reflection （注意不是训练特定任务），可以显著提升 LLM 的性能
    • 这种间接方法仅依赖于一个验证器（validator），用于检测模型响应是否正确
      • 注：特别适用于响应易于验证的任务（例如 JSON 输出格式是否正确、生成的代码是否可执行或方程约束是否满足）
    • 论文通过在 APIGen 函数调用和 Countdown 数学方程求解数据集上的实验验证了方法的有效性
    • 研究核心发现：
      • 通过 GRPO 训练的 Self-reflection 模型在函数调用测试集和 Countdown 数学方程数据集上均有不错的提升
      • 较小的 Self-reflection 训练模型可以超越更大的未训练模型；例如：
        • 经过训练的 Qwen-2-7B Instruct 在函数调用上表现优于未训练的 Qwen2-72B Instruct
        • 经过训练的 Qwen2.5-7B Instruct 在 Countdown 数学方程上表现优于 Qwen2.5-72B Instruct
      • 论文的模型还对灾难性遗忘表现出鲁棒性
    • 特别发现：尽管论文仅训练模型改进 Self-reflection，但论文发现即使不需要 Self-reflection（即第一次尝试就成功），模型的表现也显著提升
      • 作者猜测这是因为通过专注于 Self-reflection 而非特定任务，模型可能更普遍地提升了其推理能力
    • 局限性：本文未研究 Self-reflection 训练是否可以泛化到不同任务
    • 总结：论文提供了一种更实用、更可靠的新范式，能够在有限的外部反馈下提升性能
  • 论文探索了一种通过 Self-reflection 和 RL 提升 LLM 性能的方法
    • 论文通过激励模型在其回答错误时生成更好的 Self-reflection
    • 论文证明了在无法生成合成数据（synthetic data）且仅能获得二元反馈（binary feedback）的条件下，模型解决复杂可验证任务的能力也能得到提升
  • 论文的框架分为两个阶段：
    • 第一阶段，当模型未能完成任务时，它会生成一段 Self-reflection 评论来分析之前的尝试；
    • 第二阶段，模型将这段 Self-reflection 纳入上下文后重新尝试完成任务，如果后续尝试成功，则对 Self-reflection 阶段生成的 token 进行奖励
  • 实验表明该方法在各种模型架构上均取得了显著的性能提升
    • 数学方程编写的性能提升高达 34.7%
    • 函数调用的性能提升达 18.1%
  • 特别地：经过微调的 1.5B 至 7B 参数的小模型在相同模型家族中表现优于参数规模大 10 倍的模型

Introduction and Discussion

  • LLM 在自然语言处理任务（2023）、数学（2023; 2024）和推理（2023）等领域展现了令人印象深刻的能力
  • 但当前模型仍存在盲点，且无法保证一个模型在成功完成某项任务后，能够成功完成另一项类似任务（2023; 2024）
    • 解决方案一：针对失败任务的数据重新训练或微调模型，但如果此类数据集不存在，则可能无法实现
      • 特别地，在最先进的超大模型也难以完成任务的情况下（某些情况下是可能出现的），此时我们无法利用它们生成合成训练数据（2024）
    • 解决方案二：提示模型解释其推理过程或反思失败原因，比如
      • CoT 范式（2022）表明，如果模型被提示展示其推理过程而不仅仅是提供答案，其在算术、常识和推理任务中的表现会显著提升
      • Self-reflection 遵循类似的原理：如果能检测到大语言模型提供了错误答案，可以提示其反思推理中的缺陷并尝试重新回答（2023; 2024）
      • 以上这些方法的主要优势在于不需要额外的训练数据，但其效果直接依赖于推理或反思提示的有效性

Self-reflection

Self-reflection in LLMs
  • Self-reflection，也称为自省（introspection），是一种元提示策略（metaprompting strategy），语言模型通过分析自身的推理过程来识别和纠正潜在错误
  • Self-reflection 范式在大语言模型研究中获得了广泛关注，被视为提升多步推理和问题解决能力的有效手段，尤其是在算术、常识推理和问答等领域（2022; 2023; 2024; 2023）
  • 典型的 Self-reflection 流程包括生成初始答案、生成自然语言反馈以批判该答案，然后基于反馈优化回答
  • 这一过程可以进行迭代，通常使用同一模型生成和评估解决方案，并可能包含记忆缓冲区或显式的元指令模块（2025; 2025）
    • 注：Reflexion 其实是 Self-reflection 的一种实现？
Approaches and Limitations
  • 大语言模型的 Self-reflection 方法在多个维度上存在差异
    • 一些方法仅对失败或低置信度的查询进行自我纠正
    • 另一些方法则对每个回答都应用 Self-reflection；
  • 反馈可以是标量分数、外部标注或自然语言形式，并可能由人类、外部模型或大语言模型自身生成（2022; 2023; 2022; 2024）
  • 在许多场景中提示大语言模型进行 Self-reflection 确实能提高准确性，但最近的研究表明，其效果高度依赖于上下文：挑战包括
    • 在没有真实标签或外部验证的情况下无法可靠识别自身错误、重复反思的收益递减
    • 对于简单提示或高性能基础模型可能导致性能下降的风险（2024; 2024; 2023）
  • 特别是，当初始准确率较低、问题难度较高且存在外部验证时，Self-reflection 的效果最为显著
    • 大语言模型有时可能无法识别自身错误 ，在存在外部监督的情况下能从反馈中受益（2024; 2023）
Training-Based Methods
  • 最近的研究方向聚焦于在模型训练阶段融入自我提升能力，例如通过微调自我纠正轨迹或将流程建模为多轮强化学习问题（2024; 2024; 2025）
  • 这些基于训练的方法表明，在训练过程中利用模型自身的批判能够带来持久的改进——即使在没有 test-time Self-reflection 的情况下
  • 这些方法通常依赖于更大的教师模型生成数据或提供监督，这可以被视为一种知识蒸馏（2015）
本篇论文的方法
  • 基于先前研究的观点，论文提出仅针对外部验证器识别的失败案例进行纠正，将其二元反馈转化为 Self-reflection 提示，并训练模型利用 Self-reflection 在第二次尝试中取得成功
  • 这种基于验证器的条件计算利用了训练时的 benefits 以减少测试时的开销（overhead），并且能够保证性能提升或至少保持不变
    • 因为论文的纠正仅应用到初始错误的样本
  • 在训练中，论文采用了 GRPO
  • 特别说明：该方法仅从模型自身的输出中自举（bootstraps），无需依赖外部大语言模型

Reinforcement Learning for Language Models

GRPO（Group Relative Policy Optimization）
  • 分组相对策略优化（Group Relative Policy Optimization, GRPO）是一种基于结果的强化学习方法，旨在解决 LLM 在复杂数学推理任务中面临的独特挑战（2024）
  • 与传统方法如近端策略优化（Proximal Policy Optimization, PPO）（2017）不同，GRPO 摒弃了单独的价值（评论）网络，而是通过比较一组采样生成的结果直接估计优势
  • 这使得 GRPO 特别适用于监督信号稀疏且仅在生成结束时可用的情况
    • 例如，仅能通过标量奖励反映输出质量或正确性的任务
    • 在这种环境中，模型必须在接收到任何反馈之前生成完整的序列
  • GRPO 的优势函数可以表示为：
    $$
    A(s, a) = R(s, a) - \frac{1}{|G|} \sum_{a’ \in G} R(s, a’)
    $$
    • 其中 \( A(s, a) \) 是状态 \( s \) 和动作 \( a \) 的优势值，\( R(s, a) \) 是奖励函数，\( G \) 是一组采样生成的动作
本篇论文的方法
  • 论文采用 GRPO 作为唯一的强化学习机制，不涉及额外的监督微调阶段
  • 最近的研究表明，调整 GRPO 的奖励结构可以有效鼓励模型在失败后继续尝试，例如通过奖励失败后的重试行为，从而促进自我纠正和鲁棒性（2025）
  • GRPO 在需要复杂行为监督的相关领域也展现出潜力，包括工具使用和高级数学问题求解，为多样化的大语言模型应用提供了灵活高效的优化策略（2025; 2025）

Reflect, Retry, Reward

  • 论文的新颖 Reflect, Retry, Reward（反思、重试、奖励）方法按以下方式运行，如图 1 所示
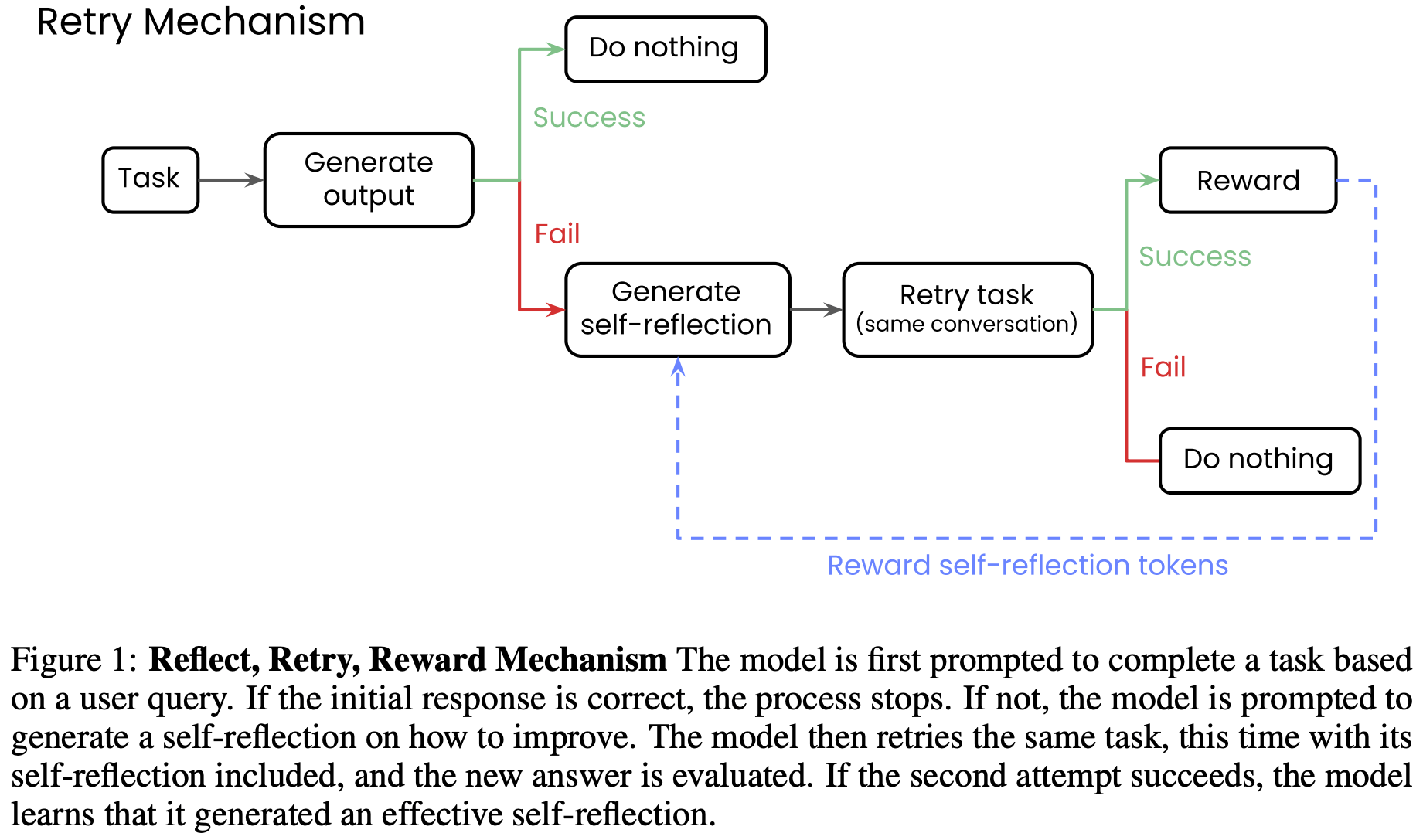
  • 具体步骤如下：
    • 第一步 ：模型在提示完成一项任务
      • 如果成功 ，论文不做任何操作，因为模型已经满足需求
      • 如果失败 ，论文会提示模型生成一段 Self-reflection，分析可能出错的原因
        • 这需要一个验证器（validator）来自动评估响应是成功还是失败（二元判断）
        • 虽然在某些任务中可以定义不依赖真实标签的验证器（例如基本的 API 函数调用（API 调用是否返回有效响应？）、数学方程（方程是否计算为目标答案？）或代码（生成的代码是否能执行？）），但某些任务类型可能需要真实的目标答案作为验证标准
    • 第二步 ：生成 Self-reflection 后，模型会利用对话历史中的反思内容进行第二次尝试
      • 如果仍然失败 ，论文不做任何操作；因为 Self-reflection 不足以将失败转化为成功
      • 如果成功 ，论文会使用 GRPO 仅奖励在 Self-reflection 阶段生成的 token
        • 通过将所有其他生成 token 的优势项（advantage terms）设为零来实现
        • 理解：其他生成 Token 肯定包含了第二步失败的 Token，但是包含了第一步成功的吗？【应该不包含吧？】
      • 论文这样做是因为作者希望模型学会更普遍地进行 Self-reflection，而不是针对特定任务进行专门优化
      • 换句话说，论文不奖励正确答案，只奖励 Self-reflection

Experiments

  • 论文通过两个不同任务的实验证明了方法的有效性：函数调用（function calling）和数学方程（math equations）

Function Calling

  • 论文使用 APIGen 数据集（2024b）进行函数调用实验
  • APIGen 是一个包含 60,000 个高质量函数调用的数据集，每个数据点包括用户查询（纯文本）、可能用于回答查询的工具列表（JSON）以及正确格式化的函数调用（JSON）
  • 数据集中共有 4,211 个特有的工具，每个工具平均有 2.3 个参数，每个用户查询平均有 2.8 个可选工具（1-8 个）
    • 只有当模型不仅选择了正确的工具，还生成了正确的参数和值时，才被认为正确
    • 下面是一个挑选两个工具的示例
  • 为了保持实验的完整性，论文仅评估在 APIGen 数据集发布（2024 年 6 月）之前发布的模型
    • 论文报告了 Qwen2（1.5B/7B Instruct）（2024）、Llama3.1（8B Instruct）（2024）和 Phi3.5-mini Instruct（2024）的结果
    • 论文还报告了 Qwen2-72B Instruct、Llama3.1-70B Instruct 和 Writer 的 Palmyra X4（2024）的基线性能
      • 论文是 Writer 公司发表的，所以选了他们的模型
  • 因为不同模型家族有不同的建议 tool-calling 方法，作者为每个模型家族都测试了不同的模版并最终选择最好的模版
  • 对于函数调用验证器，论文要求模型输出与数据集中的正确答案完全匹配（即基于真实标签）。论文使用以下提示生成失败函数调用尝试的 Self-reflection：

    You tried performing the task, but failed in generating the correct tool call. Reflect on what went wrong and write a short explanation that will help you do better next time.

    • 基本思路是：告诉模型未能生成正确的工具调用，让模型反思出错原因，并写一段简短的说明，以帮助模型下次做得更好

Countdown Math Equations

  • 论文使用 TinyZero 项目引入的 Countdown 数据集（2025a, 2025b）进行数学方程实验
    • Countdown 数据集包含 450k 组 3-4 个数字和一个目标数字
    • 目标是通过对数字应用基本算术运算，给定一组数字和目标值，仅用加减乘除构造等于目标的等式，每个数字仅用一次，常作为推理 / 强化学习的训练任务
    • 只有当模型使用了所有数字（顺序不限）且最终方程成功计算为目标数字时，才被认为正确
    • 示例如下：

      Using the numbers [4, 73, 4, 23], create an equation that equals 76. You can use basic arithmetic operations (+, -, *, /) and each number can only be used once.

  • 同样，为了保持实验完整性，论文仅评估在 Countdown 数据集公开（2025 年 1 月）之前发布或知识截止日期早于该日期的模型
    • 论文报告了 Qwen2.5（1.5B/3B/7B Instruct）（2025）、Llama3.1（8B Instruct）、Llama3.2（3B Instruct）和 Writer 的 Palmyra 1.7B 的结果
    • 论文还报告了 Qwen2.5-32B Instruct、Qwen2.5-72B Instruct、Llama3.1-70B Instruct 和 Palmyra X4（2024）的基线性能
  • 对于数学方程验证器，论文要求生成的方程与提示中的目标答案匹配（即不需要真实标签）。论文使用以下提示生成失败 Countdown 数学方程的 Self-reflection：

    You tried solving the problem and got the wrong answer. Reflect on what went wrong and write a short explanation that will help you do better next time.

    • 基本思路是：告诉模型尝试解决问题但得到了错误答案，让模型反思出错原因，并写一段简短的说明，以帮助下次做得更好

A Dataset of Failures

  • 出于效率和分析考虑，论文没有在完整的函数调用和数学方程训练集上训练模型，而是选择首先为每个任务创建一个失败数据集
    • 论文为每个任务的每个模型生成最多 64 个响应（根据模型大小调整），并仅保留模型失败的查询（基于任务相关的验证器）
    • 论文通常为较大的模型生成更多响应，因为它们失败频率较低，否则会得到更少的训练样本
  • 这种方法有几个优点
    • 第一：它节省时间，因为模型已经能成功处理的查询是无法从中学习的
    • 第二：通过为每个查询生成多个响应，数据更具鲁棒性
    • 第三：通过仅包含失败案例，我们可以精确确定模型需要多少样本才能收敛到最佳 Self-reflection

Multi-Step GRPO

  • 论文以 TRL 框架（2020）为基础，实现了多步 GRPO 算法（即从 Self-reflection 后的第二次尝试中学习）
  • 论文扩展了 GRPOTrainer，并修改其 _prepare_inputs 函数以调用 second_step 函数
    • 该函数在 GRPOTrainer 生成的补全基础上执行另一步生成，而不影响 GRPOTrainer 已计算的掩码（mask）
    • 由于论文在失败数据集上操作，模型生成的 Self-reflection 文本的掩码对应其 token
    • 这样，我们可以在初始补全上执行任意数量的后续步骤，并仅奖励初始补全对应的 token（通过 GRPOTrainer 生成的掩码）
  • 论文在失败数据集上训练模型，最多 1,750 步，有效批次大小为 256 个失败样本（尽管大多数模型收敛得更快）
    • 例如，Llama-3.1-8B Instruct 的函数调用实验仅需 100 个训练步骤，使用了不到 2,000 个独特查询
    • 所有函数调用实验平均使用了不到 25,000 个独特查询，数学方程实验平均使用了约 15,000 个独特问题
  • 论文使用了标准 GRPO 训练参数（2024），并进行了超参数实验
    • 最终实验中，KL 散度系数设为 0.001，学习率为 5e-7，采用余弦退火调度和 0.03 的预热比例
    • 每个模型使用 4 到 8 个 H100 GPU 进行训练。由于 GRPO 的计算效率和可扩展性问题（2025），论文将实验限制在 1.5B 到 8B 亿参数的模型
  • 除了以上实验结果外，作者还在一些小模型上进行实验，论文没有 Report 这部分实验：
    • 这些实验速度快，但是他们生成正确答案和 self-reflect 的能力非常有限（比如 Qwen2/Qwen2.5 0.5B Instruct and Llama3.2-1B Instruct）
    • 相似地，尽管微软的 Phi 3.5 小模型也能完成 Function Calling，但在 equation writing 方面能力不行

Experimental Results

  • 论文的主要实验结果如表 1 和表 2 所示
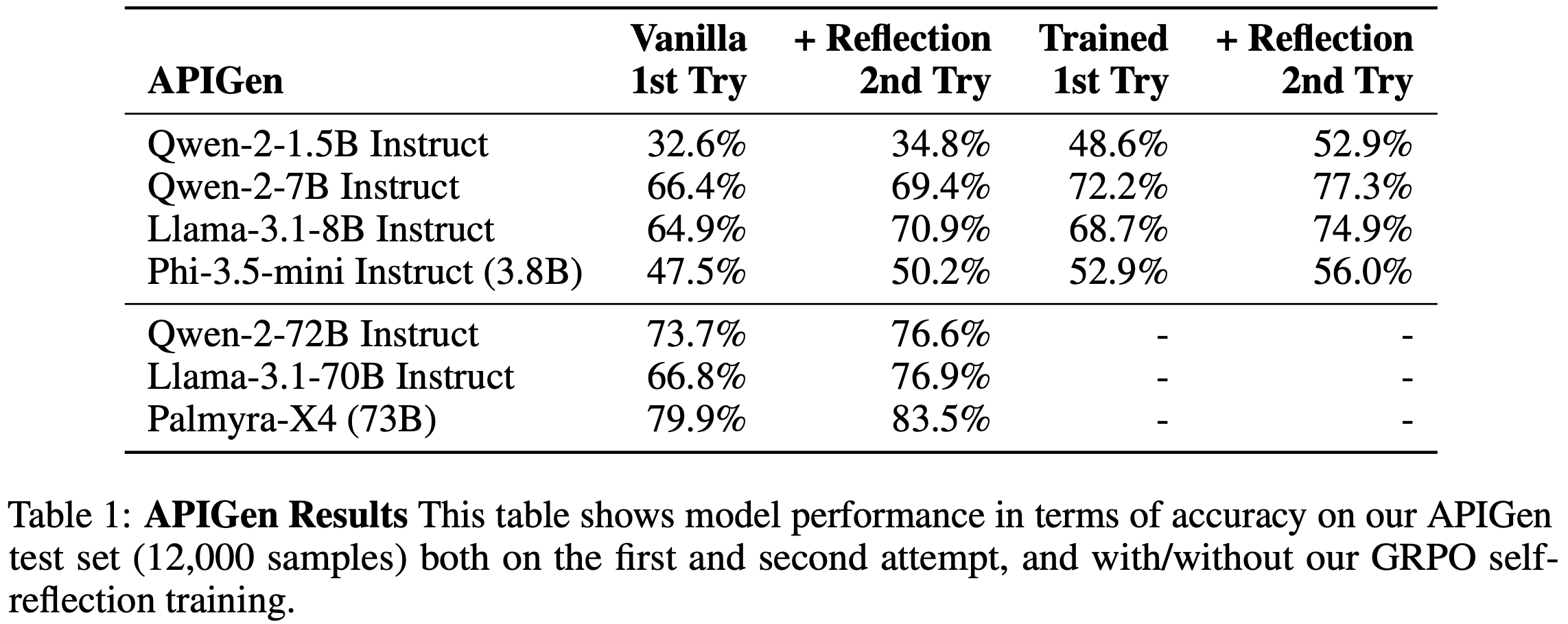
    • 表 1 展示了各模型在 APIGen 测试集（12,000 个样本）上第一次和第二次尝试的表现（包括训练前后的对比）
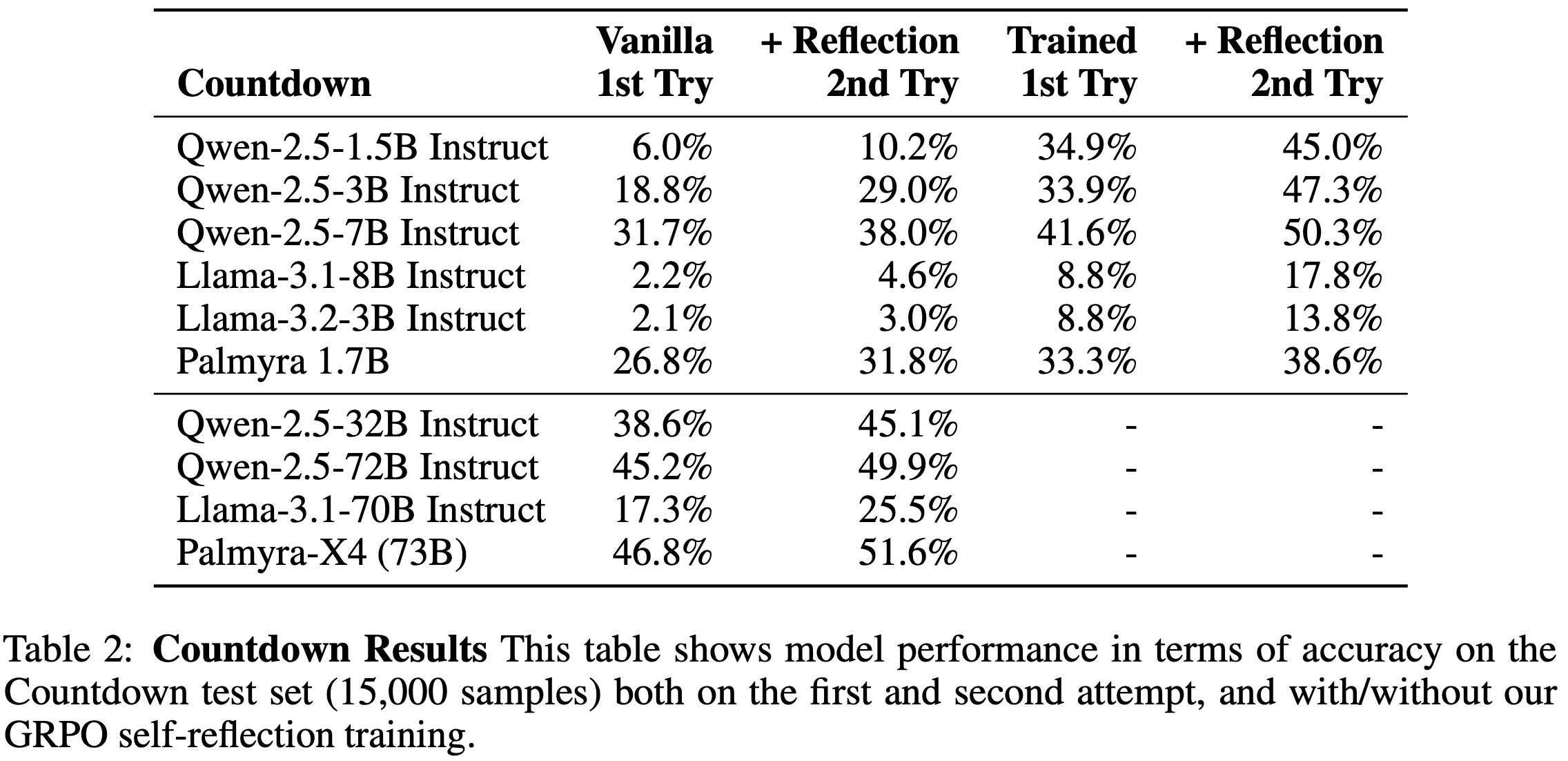
    • 表 2 展示了在 Countdown 测试集（15,000 个样本）上的相同数据
  • 在 APIGen 方面
    • 第一次尝试的表现与模型大小完全正相关（符合预期）
      • 包括 Vanilla 1st Try 和 Trained 1st Try
    • 通过 Self-reflection 的第二次尝试，模型表现平均提升了 4.5%，这与之前的研究一致
    • 最大的提升出现在 GRPO 训练之后：
      • 尽管论文仅奖励 Self-reflection 生成的 token ，几乎所有 Trained 模型在一次尝试后就能超越 Vanilla 模型两次尝试的表现
      • 理解：这说明训练是非常有用的
      • 作者猜测这是因为 Self-reflection 的 token 通常有助于模型推理，因此即使不需要显式生成 Self-reflection，模型也能受益
    • 尽管如此， Self-reflection 在训练后仍然有帮助，当模型可以通过 Self-reflection 进行第二次尝试时，表现平均进一步提升了 4.7%
    • 特别地，经过 GRPO 训练的 Qwen-2-7B 模型（在两次尝试后），其表现甚至超越了未训练的 Qwen-2-72B 模型（在两次尝试后），尽管后者规模是前者的 10 倍
  • 在 Countdown 方面
    • 整体表现较低，尤其是未训练的 Llama 模型（包括 Llama-3.1 和 Llama-3.2）在这一任务上表现非常糟糕
    • Llama-3.1-70B 模型的表现甚至不及 Qwen-2.5-3B 模型（规模小 20 倍的）
    • 性能提升的模式与 APIGen 实验类似，但幅度略高：
      • Self-reflection 在训练前和训练后分别平均提升了 5.3% 和 8.6%
      • 作者猜测这些更大的提升是因为模型的初始基线较低，因此有更多的学习空间
  • 论文的发现不仅验证了之前关于 Self-reflection 益处的研究，还展示了通过 GRPO 优化 Self-reflection 可以进一步提升性能

Better Self-reflections

  • 为了展示 Self-reflection 训练如何改进 Self-reflection 的质量，论文在图 2 中提供了一个定性示例，对比了未训练模型和经过 GRPO 训练的模型生成的 Self-reflection
  • 可以明显看出，未训练的 Self-reflection 更长、更冗长且重复，而训练后的 Self-reflection 更简洁、清晰且通用
  • 尽管这直观上合理（人类也更喜欢简短、清晰的指令），但这一发现与思维链（Chain-of-Thought）式输出的观点形成对比，后者被认为表现更好恰恰是因为其更冗长
  • 论文将其作为一个开放问题：何时生成简洁或冗长的输出对模型更有利
  • 理解：图2 展示的是 self-reflection 的内容，经过 GRPO 训练后，给出的 self-reflection内容都很简单且直接，而且不包含 CoT；而训练前的内容一般是非常冗长的
    • 一个猜测是因为问题不够复杂，简单的提示就够了，或者模型的 CoT 反而容易引入错误，导致模型学到在 self-reflection 时不要加入过多的 CoT 内容

Low Catastrophic Forgetting

  • 微调模型时的一个常见问题是灾难性遗忘（catastrophic forgetting），即模型在某一任务上过度专业化而牺牲其他任务的性能（2016; 2017; 2024）
  • 论文的 Self-reflection 训练旨在以任务无关的方式提升性能，论文在多个多样化基准（MMLU-Pro、GSM8K、Hellaswag 和 MATH）上评估模型，以衡量其在语言理解、数学问题解决和常识推理方面的能力
  • 论文使用常见的评估框架 lm-eval（2024）进行测试
  • 作者的假设是：性能应保持相对稳定，因为论文从未针对特定任务进行优化，而是优化通用的 Self-reflection 推理能力
  • 表 3 中展示了实验结果
    • 性能在 Self-reflection 训练后确实保持稳定
    • 在大多数情况下，与基础模型相比，性能下降不到 1%，甚至有些模型表现更好
    • 例如，Qwen-2.5-1.5B 在 MMLU-Pro 和 MATH 上的表现分别提升了 0.6% 和 0.8%
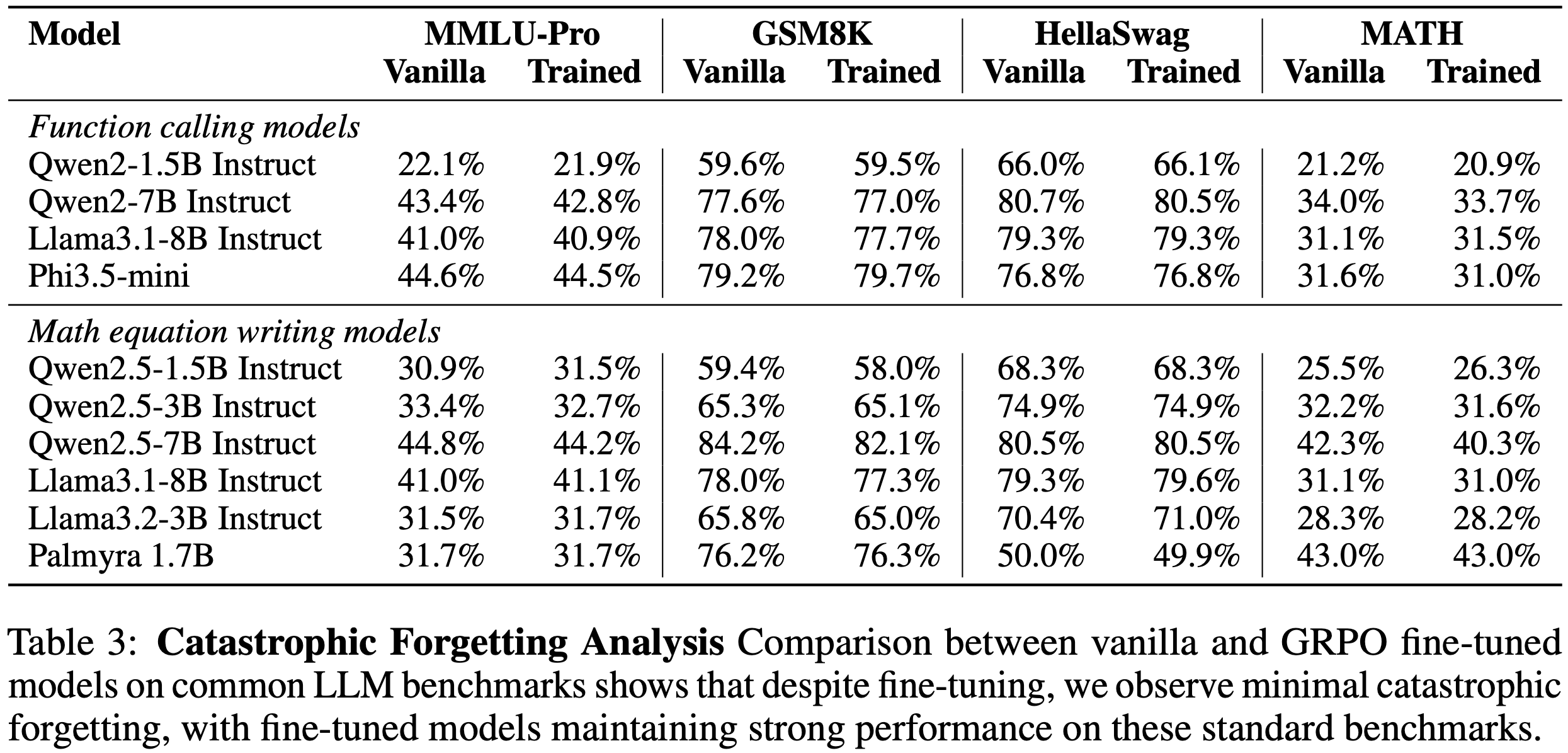
  • 基于以上实验结果，作者认为论文的方法对灾难性遗忘具有鲁棒性

Limitations

  • 并非所有任务都能轻松定义二元成功/失败验证器
  • 论文开发这一方法时假设标注训练数据可能稀缺，但也认识到如果有可用的真实标签，可以将其用作验证器
  • 也可以使用更大的模型作为评判者（2023）
  • 论文还发现，论文的方法并非适用于所有模型和任务；模型必须具备执行任务、 Self-reflection 和学习的基本能力，才能通过提升自我修正能力发挥作用
    • 例如，Llama3.2-3B Instruct 无法在函数调用任务上学会自我修正

附录 A Prompt Templates

  • 为便于复现和清晰理解，论文提供了训练期间使用的提示模板细节
  • 论文尽可能遵循模型提供方的推荐提示方式，并通过迭代优化确保每个模型在每项任务上达到合理的基线表现

A.1 Function Calling

  • Qwen 2 系列模型 对于 Qwen 2 系列模型的函数调用任务，论文采用以下提示风格
    • 首先，提供系统提示：

      你是一个能够回答问题并协助完成任务的助手

      \# 工具
      你可以调用一个或多个函数来协助完成用户查询

      函数签名位于 <tools></tools> XML 标签内：
      <tools>
      {工具列表，每行一个工具}
      </tools>

      对于每个函数调用，返回一个包含函数名称和参数的 JSON 对象，并将其放在 <tool_call></tool_call> XML 标签内：
      <tool_call>
      {"name": <函数名称>, "arguments": <参数 JSON 对象>}
      </tool_call>

    • 随后，以用户角色提供数据集中的查询。模型会生成首次任务尝试。如果尝试失败，则提示生成 Self-reflection ：

      你尝试完成任务，但未能生成正确的工具调用。请反思问题所在，并写一段简短的说明以帮助下次改进

    • 生成 Self-reflection 后，再次提供系统提示和用户查询，为模型的第二次尝试做准备
  • Llama 3.1 和 Phi 3.5 模型
    • 论文遵循 Llama 3.1 推荐的工具调用格式。Phi 模型使用 Llama 模板效果更佳。系统提示如下：

      当你收到工具调用响应时，请使用输出内容回答原始用户问题

      你是一个具备工具调用能力的助手
      以用户角色提供工具和查询：
      根据以下函数，请以 JSON 格式返回一个函数调用及其参数，以最佳方式回答给定提示

      响应格式为 {"name": 函数名称, "parameters": 参数字典}。不要使用变量

      {工具列表，每行一个工具}
      问题：{用户查询}

    • 模型生成首次尝试后，提示 Self-reflection ：

      你尝试完成任务，但未能生成正确的工具调用。请反思问题所在，并写一段简短的说明以帮助下次改进

    • 随后仅提供用户查询，为第二次尝试做准备

A.2 ountdown Math Equations

  • 系统提示如下：

    请逐步推理，并将最终答案放在 \(\boxed{}\) 中

  • 用户提示为：

    使用数字 {数字列表} 创建一个等于 {目标值} 的方程。你可以使用基本算术运算（+、-、*、/），且每个数字只能使用一次。请逐步推理，并将最终答案放在 \(\boxed{}\) 中

  • 模型生成首次尝试后，若失败则提示 Self-reflection ：

    你尝试解决问题但得到了错误答案。请反思问题所在，并写一段简短的说明以帮助下次改进

  • 生成 Self-reflection 后，重复用户提示，为第二次尝试做准备

附录 B Error Analysis

  • 论文对训练前后模型的错误进行分类，以更好地理解模型在这些任务中容易犯的错误类型，以及哪些错误可以通过 Self-reflection 训练缓解
  • 论文仅分析首次尝试任务时的错误（pass@1）

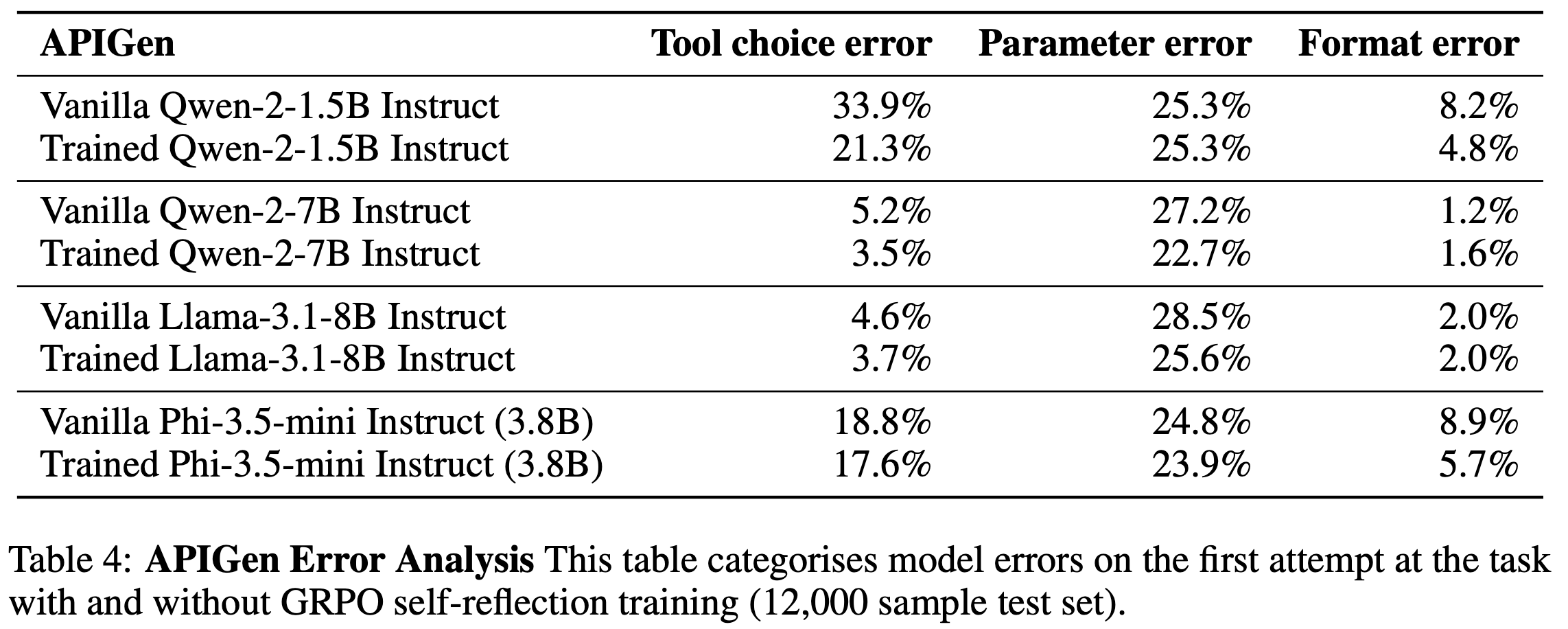
B.1 Function Calling

  • 将错误分为三类：工具选择错误、参数名称或值错误、格式错误
  • 参数选择比工具选择更具挑战性
  • 小模型（如 Qwen-2-1.5B Instruct 和 Phi-3.5-mini Instruct） ：未经训练时在工具选择上表现较差，训练后对参数值的改进有限
  • 大模型（7-80 亿参数） ：未经训练时工具选择已较准确，训练主要提升参数选择能力

B.2 Math Countdown Equations

  • 将错误分为三类：无效方程（含非法字符）、使用非提供数字（错误数字）、方程结果未达目标值（未命中目标）
  • 所有模型 ：主要问题集中在未能仅使用允许的数字
    • 训练显著减少了此类错误（除 Qwen-2.5-7B Instruct 外）
  • Qwen-2.5-7B Instruct ：训练后更倾向于命中目标值，即使使用了错误数字