NLP——LLM对齐微调-RLOO

本文是 RLOO（REINFORCE Leave-One-Out） 原始论文的阅读笔记，尽量详细阅读论文细节，并加入了自己的理解
注：本文包含 AI 辅助创作

• 参考链接：
  • 原始论文：Back to Basics: Revisiting REINFORCE Style Optimization for Learning from Human Feedback in LLMs, 2024, Cohere For AI
  • 注：RLOO 方法中基线评估方法最早是在论文 Buy 4 reinforce samples, get a baseline for free!, ICLR 2019, University of Amsterdam 中提出的

Paper Summary

• 整体总结：
  • 论文视角较高，认为在 LLM 的微调场景中，基于优质 SFT 模型的策略初始化策略，结合 Prompt 的进一步条件化，能够避开传统 Deep-RL 中高方差和大动作空间的历史性问题
  • 论文通过实证结果支持了这一观点，表明尽管在传统 Deep-RL 场景中因高方差问题而鲜少使用基于 REINFORCE 的普通策略梯度（Vanilla PG） ，但这种 REINFORCE 方法在 LLM 微调中优于 PPO 方法
  • 论文重新审视了如何建模从人类偏好中学习的问题，并通过实验证明，尽管 REINFORCE Estimator 简单，但它能够实现高质量的奖励优化
• 背景 & 问题：
  • RLHF 形式的 AI 对齐已逐渐成为实现高性能 LLM 的关键要素，而 PPO 是 RLHF 中强化学习部分的经典方法，但它既涉及高计算成本，又需要敏感的超参数调优
• 本文解法：
  • 作者认为 PPO 的设计本身并不与 RLHF 完全对齐，论文主张采用一种计算成本较低的方法（该方法能保持甚至提高性能）
  • 在 RL 的背景下重新审视了基于人类偏好的对齐公式，以简单性为指导原则，证明了 PPO 的许多组件在 RLHF 环境中是不必要的，而且简单得多的 REINFORCE-style 优化变体的性能优于 PPO 和新提出的 “RL-free” 方法（如 DPO 和 RAFT）
  • 论文的工作表明，仔细适应 LLM 的对齐特性能够以低成本从在线 RL 优化中获益
• 论文的实验表明，作为 REINFORCE 的多样本扩展，REINFORCE Leave-One-Out（RLOO）在性能上优于 RAFT、DPO 和 PPO，同时相对于 RAFT 等迭代微调方法保持了更高的鲁棒性

---

Introduction and Discussion

• 文章中引用的一句话：
  • 原话：I suppose it is tempting, if the only tool you have is a hammer, to treat everything as if it were a nail. — Abraham Maslow, 1966.
  • 直译：”我想，如果一个人唯一拥有的工具是锤子，那么把一切都当作钉子来对待是很诱人的”
  • 含义：”如果你唯一的工具是锤子，那么你很可能会把所有东西都当作钉子来对待”，这是在暗示 PPO 算法是锤子，直接用 PPO 去做 RLHF 是不合适的
• 当前 SOTA LLM 通常在包含 trillions of tokens 的海量文本上进行预训练，这些训练语料库通常包含许多复杂的偏好、关系和意图（preferences， relations， and intentions），但并非所有特性都是 LLM 应当展现的
  • 研究界和更广泛的从业者群体都非常感兴趣的一个问题是，如何使这些模型与人类偏好保持一致？
• 尽管已经有大量研究工作投入，但对于实现这一目标的最佳方法尚未达成共识
  • RLHF 是最广泛认可的对齐方法之一，直接借鉴了传统的 RL 方法，并使用诸如 PPO 等技术来最大化奖励模型产生的奖励分数，该奖励模型通常被训练为对人类注释者标注的补全（completions）对进行二元分类
• 虽然 PPO 通过其在 RLHF 的开创性文献中的应用已成为一种经典方法，但对于非 RL 专家来说，让 PPO 在实践中发挥作用并非易事，并且存在已知的问题：
  • 计算成本（Computational Cost） ：PPO 通常需要同时加载多达4个模型：生成器（Generator）、参考模型（reference，用于KL估计）、Critic 模型和奖励模型（reward model，RM），其中生成模型和 Critic 模型的训练是交替进行的，模型多 和 现代 LLM 的规模大进一步加剧了这个计算成本问题
  • 优化挑战（Optimization challenges） ：Online RL 优化的不稳定性和敏感性（理解：参数敏感），以及 PPO 相对较高的算法复杂性，需要专业知识才能进行良好的调优（详情可参考 Implementation matters in deep policy gradients: A case study on ppo and trpo, ICLR 2020, Two Sigma）
• 近期出现了一些 “RL-free” 方法：
  • DPO：包含偏好（正负）样本对的监督微调方法
  • IPO：A General Theoretical Paradigm to Understand Learning from Human Preferences, 2023, Google DeepMind，与 DPO 方法类似（通过比较两个样本的优劣来构造损失函数并训练模型），发表于 DPO 之后，号称可以缓解 DPO 中过拟合问题
  • 迭代微调方法（Iterative fine-tuning）：用于 LLM 偏好训练的 Iterative fine-tuning（2023等）
    • 补充：迭代微调方法的基本思路是：1）收集数据；2）评估样本优劣；3）挑选优质样本微调模型；4）迭代循环1,2,3步
  • 但这些工作无法质疑 “在 RL 范式内是否存在更简单的解决方案“，相反地，所有这些方法都试图通过从 RLHF 中剥离所有 RL 组件来回答这个问题，困难也随之而来；
    • 迭代微调技术仅依靠强大的奖励模型来识别训练样本子集（理解：迭代微调技术会在每一轮挑选优质的样本）
    • DPO 和 IPO 则通过直接从人类反馈中学习来避免强化学习和训练单独的奖励模型
• 与这些方法不同，论文仍然保持在强化学习范式中，但回归基础
  • 本工作的核心问题是：论文能否在保持性能的同时，避免PPO的计算和优化复杂性？
  • 论文梳理出传统 Deep-RL 设定（Settings）与典型的 LLM 人类偏好学习设定之间的几个关键差异
  • 论文注意到，PPO 作为一种方法，强调跨迭代的稳定性，旨在通过 小而稳定的更新（small, stable updates） 来训练有效的策略
  • PPO 是为 off-policy 梯度更新足够大以至于引入不稳定的场景（regime）设计的，这种场景在传统 Deep-RL 基准测试中占主导地位（2020;2017）
  • 在本研究中，作者认为 RLHF 的场景（对 pre-trained LLM 进行 fine-tuning）缺乏这些特性
• 与传统 Deep-RL 环境不同，策略的初始化（以预训练和 SFT 模型的形式）远非随机参数化
  • 尽管可想象的搜索空间非常庞大，但由于预训练和 SFT 阶段，概率质量集中在少数 token 上，因此只有一小部分 token 可能被生成
  • 因此，传统 Deep-RL 环境需要强正则化来降低梯度 Estimator 的高方差；而论文通过实验观察到，这在 RLHF 中并不是一个实际的问题，因此论文提出了一种计算成本更低且保持鲁棒性的方法（2018;2021）
• 此外，论文重新审视了在强化学习背景下如何形式化（formulated）人类偏好的学习问题
  • 之前的建模：
    • 生成每个 token 被建模为一个 action
    • 每个从 Prompt 开始的局部序列被视为一个 state
    • 在实践中，对 PPO 方法来说，这种建模假设常常被忽略
  • 作者认为并证明，在这种仅对 完整生成（full generations） 赋予奖励而对中间 token 没有真实奖励的场景中，对局部序列建模是不必要的
  • 论文的建模：将整个生成建模为单个动作，初始状态由 Prompt 决定（作者认为这是更合适且高效的方法）
• 基于这些观察，论文以简洁性为指导原则，探索了使用 REINFORCE estimator（1992）及其多样本扩展 REINFORCE Leave-One-Out（RLOO）（2019）来优化序列级目标
  • 论文拆解了PPO，并展示了最基础的策略梯度算法（Vanilla Policy Gradient REINFORCE），在性能上持续优于 PPO
  • 对于预训练 LLM 的环境，PPO 显得过于复杂
  • 与 PPO 不同，我们可以使用 REINFORCE 直接优化完整轨迹（序列）的回报，并结合无偏基线，而 Actor-Critc 算法（如 PPO）（1999）则通过自举中间状态价值函数来减少方差，但代价是在 estimator 中引入了偏差
• 论文在多个模型（包括 Llama（2023）、Pythia（2023））和数据集（如Anthropic Helpful & Harmless（2022）和 TL;DR Summarize（2020））上得出一致的结论：
  • PPO 不是 RLHF 中进行 RL 的合适工具（PPO is not the right tool for doing RL in RLHF）
    • 论文拆解了 PPO，并展示了最”基础”的策略梯度算法（Vanilla Policy Gradient REINFORCE（2020）在胜率上持续优于 PPO），幅度从 3.2% 到 20.3%，覆盖所有数据集和基础模型配对
  • RLOO 优于关键基线方法（RLOO outperforms key baselines）
    • 基于 REINFORCE 的 RLOO 能够使用多个在线样本，论文通过实验证明其在所有数据集和模型上持续优于 PPO、DPO（Rafailov 等, 2023）以及 RAFT（Dong 等, 2023）。论文还展示了 RLOO 比 RAFT 更有效地利用在线样本，同时对噪声和 KL 惩罚的鲁棒性更高
  • 建模局部 completions 是不必要的（Modeling partial completions is not necessary）
    • 论文有效地证明了为 LLM 偏好训练建模局部序列是不必要的任务
    • 相反，建模完整生成在保持性能的同时降低了强化学习阶段的复杂性，并显著加速了学习过程
  • RLOO 对噪声和 KL 惩罚敏感性相对鲁棒（RLOO is relatively robust to noise and KL penalty sensitivity）
    • 论文还通过多维度分析（包括语言流畅性、多样性和对噪声的鲁棒性）验证了结果
    • 论文展示了 RLOO 相对于 RAFT 在噪声和 KL 惩罚程度上的鲁棒性

---

Background

• 传统的 RLHF 流程（for LLM）由 Ziegler 等人（2020）提出，包含以下三个阶段：
  • (1) SFT 阶段 ：一个预训练的语言模型（LM）通过指令微调数据集进行训练，数据集通常包含给定的指令 Prompt 和人工撰写的 completion 文本。语言模型（策略）通过仅对 completion 文本部分的交叉熵损失进行训练。通常，监督微调模型 \(\pi^{\text{sft} }\) 会用于初始化奖励模型和 RLHF 策略
  • (2) 奖励模型（RM）阶段 ：RLHF 方法利用奖励模型 \(r_{\phi}(x, y)\)，该模型通过偏好数据集 \(\mathcal{D} = \{(x, y_{+}, y_{-})\}_{i=1}^{N}\) 训练，其中 \(y_{+}\) 和 \(y_{-}\) 分别表示针对 Prompt \(x\) 的偏好和非偏好 completion 文本。奖励模型作为二元分类器训练，其损失函数如下：
    $$
    \mathcal{L}_{RM} = -\log \sigma(\log(r_{\phi}(x, y_{+}) - \log(r_{\phi}(x, y_{-}))
    $$
    • 其中 \(\sigma\) 表示逻辑函数
  • (3) RL 阶段 ：在此阶段，奖励模型用于提供在线反馈，以优化策略，目标函数如下：
    $$
    \max_{\pi_{\theta} } \mathbb{E}_{x \sim \mathcal{D}, y \sim \pi_{\theta}(\cdot|x)} [r_{\phi}(x, y) - \beta D_{\text{KL} }(\pi_{\theta}(\cdot|x) || \pi_{\text{ref} }(\cdot|x)]
    $$
    • 其中 \(\beta\) 用于控制优化过程中与初始策略 \(\pi_{\text{ref} }\) 的距离，如 Stiennon 等人（2022）所提出
    • KL 惩罚至关重要，因为无惩罚的奖励模型优化会导致模型连贯性下降。优化此目标等价于最大化以下 KL 形奖励的期望：
      $$
      R(x, y) = r_{\phi}(x, y) - \beta \log \frac{\pi_{\theta}(y|x)}{\pi_{\text{ref} }(y|x)}
      $$
• 尽管 RL 方法共享上述组件，但技术在奖励的表述上有所不同。为了理解这些差异，论文在以下章节中介绍 PPO 及其替代方法，如 REINFORCE 和 REINFORCE Leave-One-Out（RLOO）

PPO

• 在 RL 阶段使用 PPO 时，初始状态由 Prompt 确定，每个生成的 Token 被建模为一个动作，部分序列被视为状态，并使用折扣因子 \(\gamma \in [0, 1]\) 为 1。在此框架中，只有生成 <EOS> Token 时才会获得奖励，该奖励由奖励模型输出并与 KL 惩罚结合，而对于词汇表中的其他 Token，只有 KL 部分是非零的：
  $$
  R(x, y) = \sum_{t=1}^{T} R_{t}(x, y_{t})
  $$
  • \(y_{t}\) 表示 \(y\) 的第 \(t\) 个 Token
  • \(T\) 是轨迹中的 Token 数量，\(R_{t}\) 是对应的形奖励
• 在实践中，PPO 使用以下 Token 级裁剪目标：
  $$
  \min \left( f(y_{t}|s_{t}) \hat{A}_{\lambda}(y_{t}, s_{t}), \text{clip}_{1-\epsilon}^{1+\epsilon}(f(y_{t}|s_{t})) \hat{A}_{\lambda}(y_{t}, s_{t}) \right) \text{ 其中 } f(y_{t}|s_{t}) = \frac{\pi_{\theta}(y_{t}|s_{t})}{\pi_{\text{old} }(y_{t}|s_{t})}, \tag{5}
  $$
  • \(s_{t} = \{y_{ < t}, x\}\) 表示状态，即在生成步骤 \(t\) 时的上下文，由生成的 Token 历史 \(y_{ < t}\) 和给定 Prompt \(x\) 组成
  • \(\pi_{\text{old} }\) 是一个较旧的策略（与 \(\pi_{\text{ref} }\) 不同），
  • \(\hat{A}(y_{t}, s_{t})\) 是在生成步骤 \(t-1\) 时生成 Token（动作）\(y_{t}\) 的估计优势函数（优势函数使用广义优势估计（GAE）进行估计（2018））
  • \(\epsilon\) 是裁剪比例

REINFORCE

• 在 LLM 应用中，\(r(x, y)\) 仅在完整序列的末尾获得，因此将整个生成建模为单个动作可能更为合适，而不是每个 Token
• 尽管在 LLM 对齐的背景下尚未探索，但将完整 completion 建模为单个动作（如 bandit 问题中的表述）允许使用 REINFORCE Estimator（2017；2017a；1992）。这使得可以通过离散动作（生成）空间进行反向传播，并直接优化整个序列的 KL 形奖励目标
  $$
  \mathbb{E}_{x \sim \mathcal{D}, y \sim \pi_{\theta}(\cdot|x)} [R(y, x) \nabla_{\theta} \log \pi_{\theta}(y|x)]
  $$
  • 注意：在论文里面，这里的奖励 \(R(y, x)\) 和更新策略 \(\pi_{\theta}(y|x)\)都是 Response 粒度的，也就是说一个 Response 只有一个状态和一个动作，论文刻意将这个点与 Vanilla PG 方法（Response 的 每个 Token 都对应一个状态和动作）做比较
  • 特别说明：实际的 RL 中，REINFORCE 方法和 Vanilla PG 方法几乎是一样的（都是每个时间步有一个状态），REINFORCE 就是 Vanilla PG 的一种简单实现，只是说 Vanilla PG 是更广泛的框架，可能在累计收益上减去基线
• 为了改进学习，可以通过减去一个与随机梯度估计高度协方差的基线 \(b\) 来减少公式 6 中 Estimator 的方差，同时保持其无偏性（1992；2014）：
  $$
  \mathbb{E}_{x \sim \mathcal{D}, y \sim \pi_{\theta}(\cdot|x)} [(R(y, x) - b) \nabla_{\theta} \log \pi_{\theta}(y|x)]
  $$
• 一个强大的无参数基线选择是训练过程中所有奖励的移动平均值（1992）：
  $$
  b_{\text{MA} } = \frac{1}{S} \sum_{s} R(x^{s}, y^{s}) \tag{8}
  $$
  • 其中 \(S\) 是训练步数（理解：是模型 update 的时间步，不是策略 rollout 的时间步），\((x^{s}, y^{s})\) 是第 \(s\) 步的 prompt-completion 对

REINFORCE Leave-One-Out（RLOO）

• 公式 8 中的基线实现简单且计算成本低。然而，如果论文能够访问多个 online 样本，则可以进一步进行无偏方差减少：
  • （1）每个样本的奖励可以作为其他样本的基线；
  • （2）策略更新可以基于每个样本的梯度估计的平均值，从而得到一个方差减少的多样本蒙特卡洛（MC）估计
• 以上就是 REINFORCE Leave-One-Out（RLOO）Estimator 的核心思想（2019）：
  $$
  \frac{1}{k} \sum_{i=1}^{k} \left[ R(y_{(i)}, x) - \frac{1}{k-1} \sum_{j \neq i} R(y_{(j)}, x) \right] \nabla \log \pi(y_{(i)}|x) \text{，其中 } y_{(1)}, …, y_{(k)} \overset{i.i.d}{\sim} \pi_{\theta}(\cdot|x)
  $$
  • 其中 \(k\) 表示生成的在线样本数量
• \(\text{RLOO}_{k}\) 单独考虑每个 \(y_{(i)}\)，并使用剩余的 \(k-1\) 个样本为 Prompt 创建一个无偏的期望回报估计，类似于一个无参数的价值函数，但在每个训练步骤中动态估计
• 实验表明，这种基线比 \(b_{\text{MA} }\) 更有效，因为它为每个样本和每个训练步骤即时创建，但代价是训练期间采样时间增加
• 论文注意到，已有 Concurrent 工作（ReMax, 2023, ICML 2024, 香港中文大学，南京大学）提出通过生成额外样本进行方差减少，但论文专注于 RLOO，因为它能充分利用所有样本，具有更高的效率优势

偏好训练中替代 RL 的方法

• 在 RLHF 的背景下，大量研究提出了 “RL-free” 方法，这些方法不涉及第三阶段
• 论文将 PPO、REINFORCE 和 RLOO 等 RL 方法与 “直接偏好优化（DPO）” 和 RAFT（2023）等替代方法进行基准测试，以下简要介绍这两种方法
• 迭代微调（Iterative Fine-tuning） ：迭代微调方法使用训练好的奖励模型对在线或离线采样的 Prompt 的 Completions 进行排序，然后在选定的子集上迭代微调策略（2023；2023）
  • 论文注意到，这种将 Reinforcement/Bandit Learning 的奖励与监督学习目标结合的方法，在 NLP 问题的离线强化学习中已被证明有效（2018；2018）
• 论文以 RAFT（Reward rAnked FineTuning；2023）为基准，该方法使用简单的交叉熵损失对基于 \(R(x, y)\) 或 \(r(x, y)\) 从 \(k\) 个在线样本中排名最高的 completion 文本进行优化
  • 需要注意的是，RAFT 并未充分利用所有样本，因为它仅优化经过过滤的排名靠前的样本
  • 相比之下，RLOO 充分利用了构建基线和多样本 MC 估计的策略梯度
• 直接偏好优化（DPO） ：与其他方法不同，DPO（2023）跳过了传统 RLHF 流程中的奖励建模阶段，直接使用偏好对优化策略，其损失函数如下：
  $$
  -\log \sigma \left( \beta \log \frac{\pi_{\theta}(y_{+}|x)}{\pi_{\text{ref} }(y_{+}|x)} - \beta \log \frac{\pi_{\theta}(y_{-}|x)}{\pi_{\text{ref} }(y_{-}|x)} \right)
  $$

---

从 PPO 到 REINFORCE

• 论文仔细研究了 PPO 的各个组件，认为它们并不完全适合 RLHF。论文从理论起源出发，结合 LLM RLHF 的实际条件，并通过初步实验提供实证支持

重新审视低方差 Estimator 的必要性

• Actor-critic 算法（如 PPO）的提出源于传统强化学习环境中观察到的高方差问题
• PPO 通过利用总轨迹回报的低方差 Estimator 来改进学习
  • 这些 Estimator 通过自举状态价值函数构建（1999；2018；2020）
  • 尽管自举减少了方差，但其代价是引入了偏差，可能导致优化偏向有偏的奖励
• 相比之下，REINFORCE 使用无偏的蒙特卡洛 Estimator 来估计轨迹回报，理论上可能具有高方差，尤其是在仅用单样本近似时，传统 Deep-RL 环境中并不常使用 REINFORCE
• 近期研究提供了大量证据表明，REINFORCE 在高方差和大动作空间（如 NLP）的情况下表现不佳（2016；2017；2020；等）
  • 然而，论文注意到这些发现基于从随机或弱初始化开始训练的场景 ，而不是从强大的预训练模型热启动
• 在此，作者质疑这些实证证据是否适用于 RLHF
  • 作者认为，在微调 LLM 的场景中，这并不是一个实际问题，因为策略的初始化（即预训练的 LLM）非常强大
  • 与传统 Deep-RL 设置不同，预训练和 SFT 模型的初始化远非随机参数化
  • 尽管搜索空间巨大，但由于预训练和 SFT 阶段，概率质量集中在少数可能的 Token 上
  • 因此，传统 Deep-RL 需要强正则化以减少梯度估计的高方差；而论文通过实证观察到，在 RLHF 中这并非实际关切，并由此提出一种计算成本更低且保持鲁棒性的方法（2018；2021）
• 实证支撑（Empirical support） ：为了验证这一假设，论文调整了方差最小化和偏差引入的权重
  • 在 2.1 节的 PPO 表述中，GAE（2018）用于在估计真实优势函数时权衡偏差和方差
  • GAE 引入了一个超参数 \(\lambda \in [0, 1]\)，用于平衡构造 Estimator 的偏差和方差：\(\lambda\) 越接近 1，观察到的方差越高；在高度随机的环境中，以偏差为代价最小化方差是值得的；然而，在方差已经较低的稳定环境中，引入偏差是不必要的
• 在极端情况下，当 \(\lambda = 1\) 时（以方差为代价最小化偏差），优势项简化为 Vanilla Policy Gradient（PG）REINFORCE 中使用的回报 Estimator，该 Estimator 直接基于 REINFORCE Estimator，Vanilla PG 方法 优化从生成中每个 Token 开始的轨迹回报（注：阅读原文时这里可能会有误解，在论文情景中，实际上这里是指 Vanilla PG 方法（多状态建模 MDP），和论文前面提到的 REINFORCE 方法（单状态 MPD）不同）：
  $$
  \sum_{t=t}^{T} \gamma^{T-i-1} R_{t}(x, y_{t}) - b_{\phi}(s_{t})
  $$
  • 其中 \(b_{\phi}(s_{t})\) 是一个学习的基线状态 \(s_{t}\)，类似于传统强化学习中价值网络的学习方式，使用标准 MLE 损失
    $$\frac{1}{2} \left( \sum_{i=t}^{T} \gamma^{T-i-1} R_{i}(x, y_{i}) - b_{\psi}(s_{t}) \right)^{2}$$
  • Vanilla PG 与论文中提到的 REINFORCE 的关键区别在于：
    • Vanilla PG 将 REINFORCE Estimator 应用于由 Prompt 和 partial completion 形成的上下文开始的轨迹回报
    • REINFORCE Estimator 应用于完整轨迹回报（2.2 节）
    • 论文将在结果部分 5.1 节中重新讨论这一区别，以评估在 RLHF 中评估 partial completion 是否必要
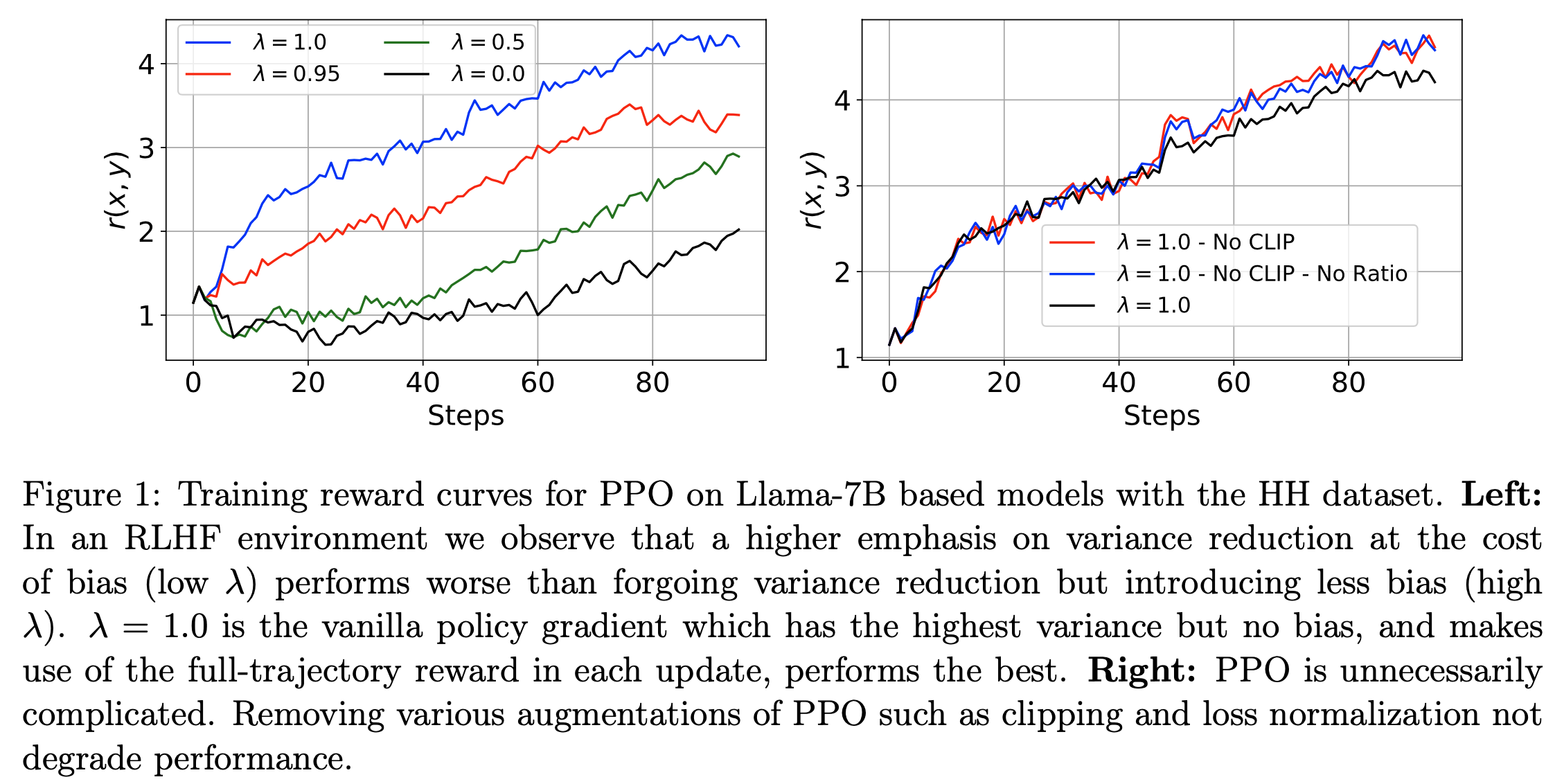
• 在 图1 中，论文展示了评估 PPO 在不同 \(\lambda\) 值下的奖励结果
  • 变体（\(\hat{A}_{\lambda=1.00}\)（即上述 Vanilla PG）和 \(\hat{A}_{\lambda=0.95}\)）最小化偏差但引入高方差
  • 变体（\(\hat{A}_{\lambda=0.0}\) 和 \(\hat{A}_{\lambda=0.5}\)）以偏差为代价最小化方差
  • 图1 绘制了奖励曲线，观察到最极端的变体 Vanilla PG（无偏的 \(\hat{A}_{\lambda=1.0}\)）表现最佳，因为它没有偏差但存在高方差风险
  • 随着 \(\lambda\) 的减小，奖励单调递减，这支持了论文的假设：在 RLHF 设置中，以偏差为代价减少方差是不必要的，因为环境的默认属性已经足够稳定

Clipping is Rarely Necessary in RLHF（裁剪在 RLHF 中几乎很少是必要的）

• 本节讨论裁剪比例 \(\epsilon\)（见公式 5），它用于防止当 \(\frac{\pi_{\theta} }{\pi_{\text{old} } }\) 偏离 1 过大时策略更新过大，即防止与当前策略偏离过远的更新（2017）
• 在 图1 中，论文比较了独立 PPO 训练在有裁剪和无裁剪情况下的奖励曲线
  • 需要注意的是，在这组实验中，论文也关闭了价值网络的裁剪（移除这些组件对学习的影响微乎其微），这在传统 Deep-RL 环境中对学习有明显影响（2020）
  • 论文通过实证发现，在 RLHF 设置中，每个批次中损失被裁剪的平均时间不到 5%，这表明学习机制接近于“on-policy”状态，策略在迭代之间变化缓慢
• 为了进一步验证这一点，论文将 PPO 损失简化为 Vanilla PG 的损失 ：
  • 完全关闭裁剪
  • 移除比例 \(\frac{\pi_{\theta} }{\pi_{\text{old} } }\)
  • 设 \(\lambda = 1\)
• 结果显示，移除裁剪甚至略微提升了性能 ，验证了论文的假设：在优化机制中，大的 off-policy 更新很少见，并且不会像传统 Deep-RL 中那样对学习产生灾难性影响

建模 partial completion 是不必要的

• 如第 2 节所述，PPO 将每个 Token 建模为一个动作，而 REINFORCE 将整个生成建模为单个动作
  • RLHF (for LLM) 中的 \(r(x, y)\) 仅归属于 <EOS> Token
  • 对于其他 Token，只有 \(\log \frac{\pi(y_{t}|s_{t})}{\pi_{\text{ref} }(y_{t}|s_{t})}\) 构成 \(R_{t}(x, y)\)，这并无实际意义
• 从 pure RL 角度来看，环境动态是完全确定的（\(P_{D}(\{y_{ < t+1}, x\}|s_{t}, y_{t}) = 1 \)），这意味着论文的环境（上下文）会根据新预测的 Token/Action 确定性变化
  • 因此，问题可以简化为一个 bandit 问题，其中马尔可夫决策过程（MDP）仅包含由 Prompt 确定的初始状态和生成后始终到达的终止状态（2017；2017b）
  • 需要注意的是，将整个生成建模为单个动作是 REINFORCE 明确实现的，但迭代微调方法也隐式实现了这一点，这些方法首先生成完整 completion 文本，然后使用奖励模型进行过滤
• 在结果部分 5.1 节中，论文将明确比较 REINFORCE 和 RLOO（两者均建模完整轨迹回报）与 PPO 和 Vanilla PG（两者均建模 partial completion）
• 论文提出的问题是：在 RLHF 中，将整个生成建模为单个动作是否足以实现相同或更好的性能？

---

Experimental Setup

Training Details

• 数据集（Datasets） ：论文在 TL;DR Summarize（2020）和 Anthropic Helpful and Harmless Dialogue（2022a）数据集上 Report 结果
  • TL;DR Summarize 数据集的训练集包含 116k 条人工编写的指令和 93k 条人工标注的偏好对
  • 预处理后的 Anthropic-HH 数据集包含 112k 条训练偏好对
• 模型（Models） ：对于这两个数据集，论文使用 Pythia-6.9B（2023）作为预训练的基础模型
  • 为了研究预训练模型质量对人类偏好学习的影响，论文还使用 Llama-7B（2023a）和 Anthropic-HH 数据集进行了实验
• 为了确保所有方法的公平比较，论文在 SFT 和奖励模型训练阶段均使用 512 个 token 的上下文长度
  • 除非另有说明，否则奖励模型和策略均使用相应的 SFT 检查点进行初始化
• 实验细节 ：
  • 对于 TL;DR Summarize 数据集，论文使用专用的 SFT 分割
  • 由于原始 Anthropic-HH 数据集未包含单独的 SFT 分割，论文与之前的工作（2023；2023；2023）类似，在 SFT 阶段使用二元比较中的 Prompt 和 preferred responses
  • 在偏好训练阶段（理解：就是 RLHF 对齐微调阶段），论文使用与 SFT 阶段相同的 Prompt 生成补全
  • 更多实验设置和超参数的细节见附录C

Evaluation

• 优化质量（Optimization Quality） ：对于所有在线方法（除 DPO 外的所有方法），为了衡量方法优化内在目标的效果，论文 Report 测试集上 1000 个样本的平均奖励（使用奖励模型评估）
  • 为了衡量每种方法优化外在目标（将模型与人类偏好对齐）的效果，论文在相同的测试样本上，根据 Alpacafarm 框架（2024）Report 模拟胜率，其中论文使用 GPT-4 作为人类评估的代理
    • 理解：胜率的定义是，在人类 annotator 的选择上，待评估模型的输出 战胜 参考模型输出 的概率；模拟胜率则是使用高级 LLM 取代替人类 annotator 的情况
  • 对于 TL;DR 数据集，论文测量与 reference SFT completions 的胜率（win-rates）；对于 HH 数据集，测量与 preferred completions 的胜率。在评估时，除非另有说明，否则论文使用贪心采样
    • 问题：在评估 HH 数据集时，preferred completions 是哪个模型产生的？测量的是谁与谁的的胜率？
    • 回答：这里 preferred completions 不是模型产生的，是 HH 数据集自带的，HH 数据集包含两列，分别是 chosen 列和 rejected 列，每列都包含完整的对话（两列对话仅最后一轮不同），详情见 Anthropic/hh-rlhf
• 对齐税（Alignment Tax） ：RLHF 微调通常伴随着多样性和语言流畅性的下降，这被称为对齐税（2021；2024），因此，论文还 Report 了作为流畅性和多样性代理的指标，与 Dong 等人（2023）类似
  • 为了测量流畅性，论文使用测试集中的 preferred completions 计算困惑度（PPL）
  • 最后，论文使用平均补全长度和平均 n-gram 多样性（2016）来测量多样性

---

Results and Discussion

Reward Optimization

• RLOO、带（移动平均）基线的 REINFORCE、RAFT、PPO 和 Vanilla PG 的目标是最大化奖励分数，因此论文比较每种方法的优化效果。在每个数据集和基础模型对上，论文为所有方法使用相同的奖励模型，因此它们的测试奖励分数可以直接比较
• 建模部分补全与完整生成 ：如 图2 所示，论文发现不建模部分补全的方法（如带基线（移动平均）的 REINFORCE 和 RLOO）在奖励优化上始终优于将每个 token 建模为动作的 Vanilla PG 和 PPO（即建模部分补全）
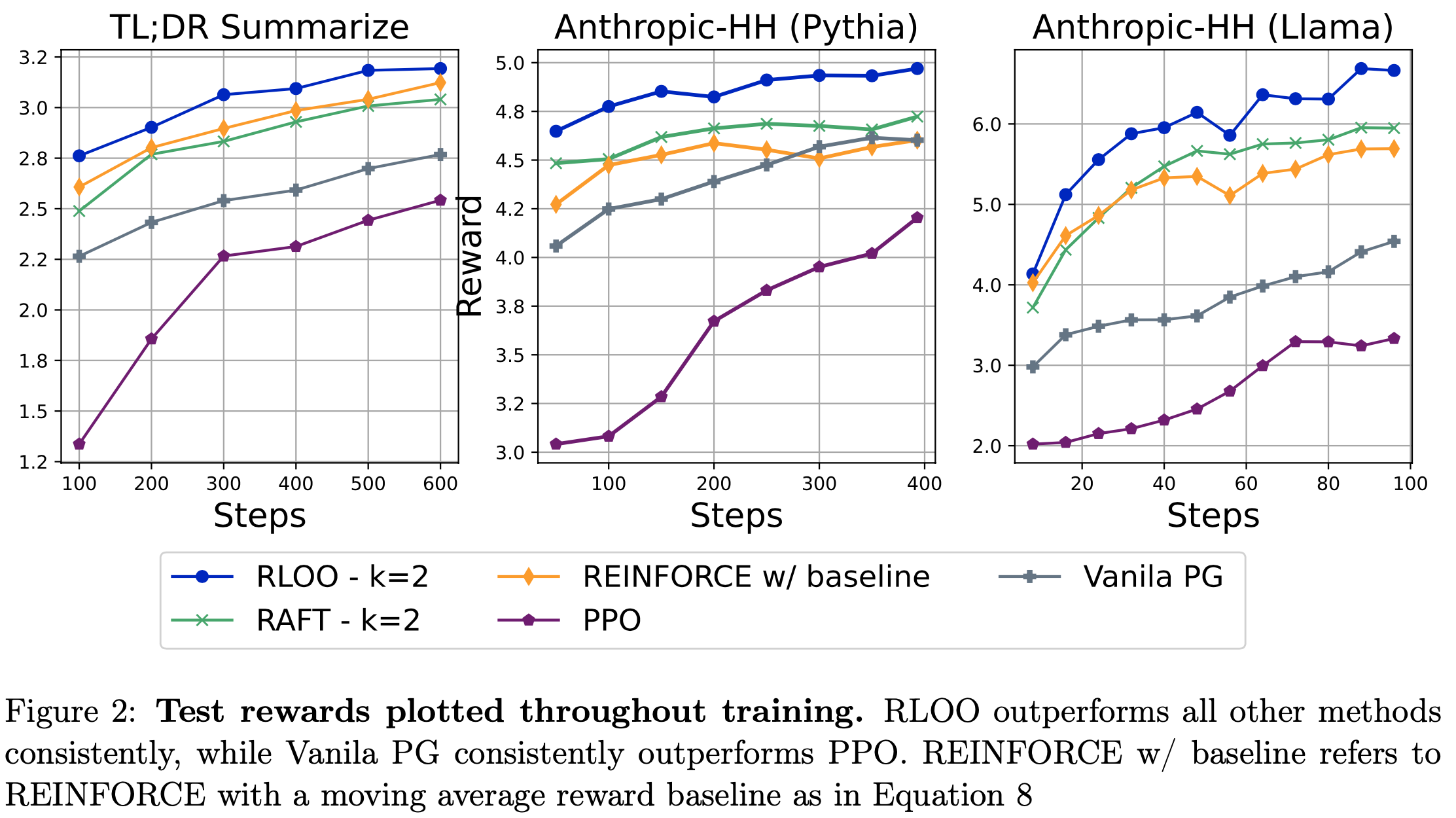
  • 此外，除了在奖励优化上的优越性能外，这些方法相比 Vanilla PG 和 PPO 需要加载的模型副本少一个，并且创建基线的方式也不同。这是因为它们消除了训练学习基线和价值网络的需求（Vanilla PG 需要价值网络作为基线，PPO 分别需要价值网络计算 GAE）。这表明在 RLHF 上下文中，建模部分序列是不必要的
• 采样效率 ：在相同的采样 Budget（每个 Prompt 生成 \(k\) 个在线样本）下，RLOO 在整个训练过程中始终优于 RAFT（如 图3 所示）
  • 值得注意的是，尽管采样 Budget 较小，RLOO \(k=2\) 在所有数据集和模型上的表现与 RAFT \(k=4\) 相当甚至更好。在这种情况下，RLOO 使用的在线样本 Budget 仅为 RAFT 的一半（步数相同）
  • 注：采样 Budget 越大，效果越好
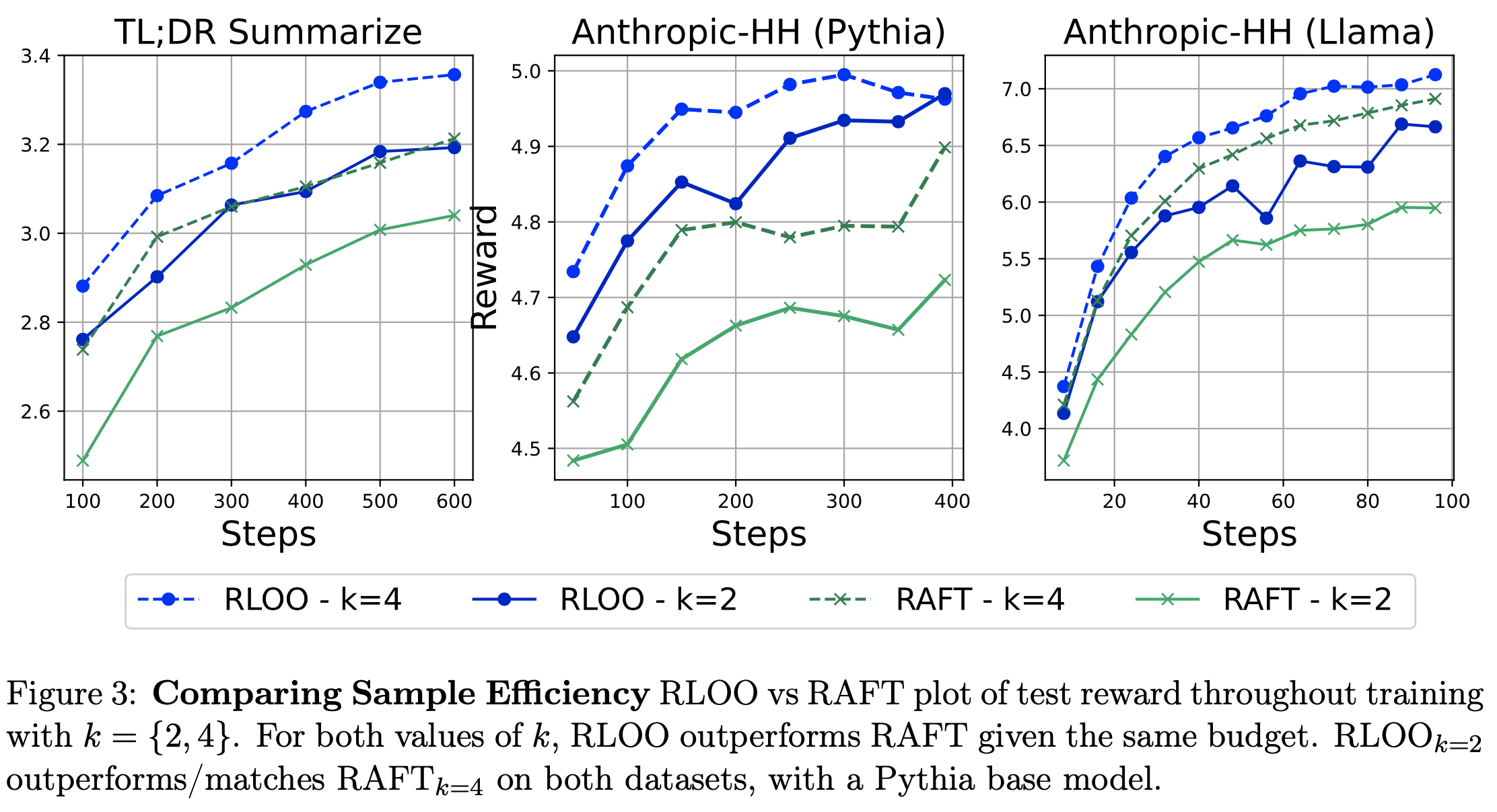
• 这证实了 RLOO 通过利用所有生成的样本实现了更好的优化，而 RAFT 仅使用排名最高的样本进行微调。图4 展示了相同的发现，它绘制了训练过程中生成的样本数量与奖励的关系（不考虑 \(k\) 值）
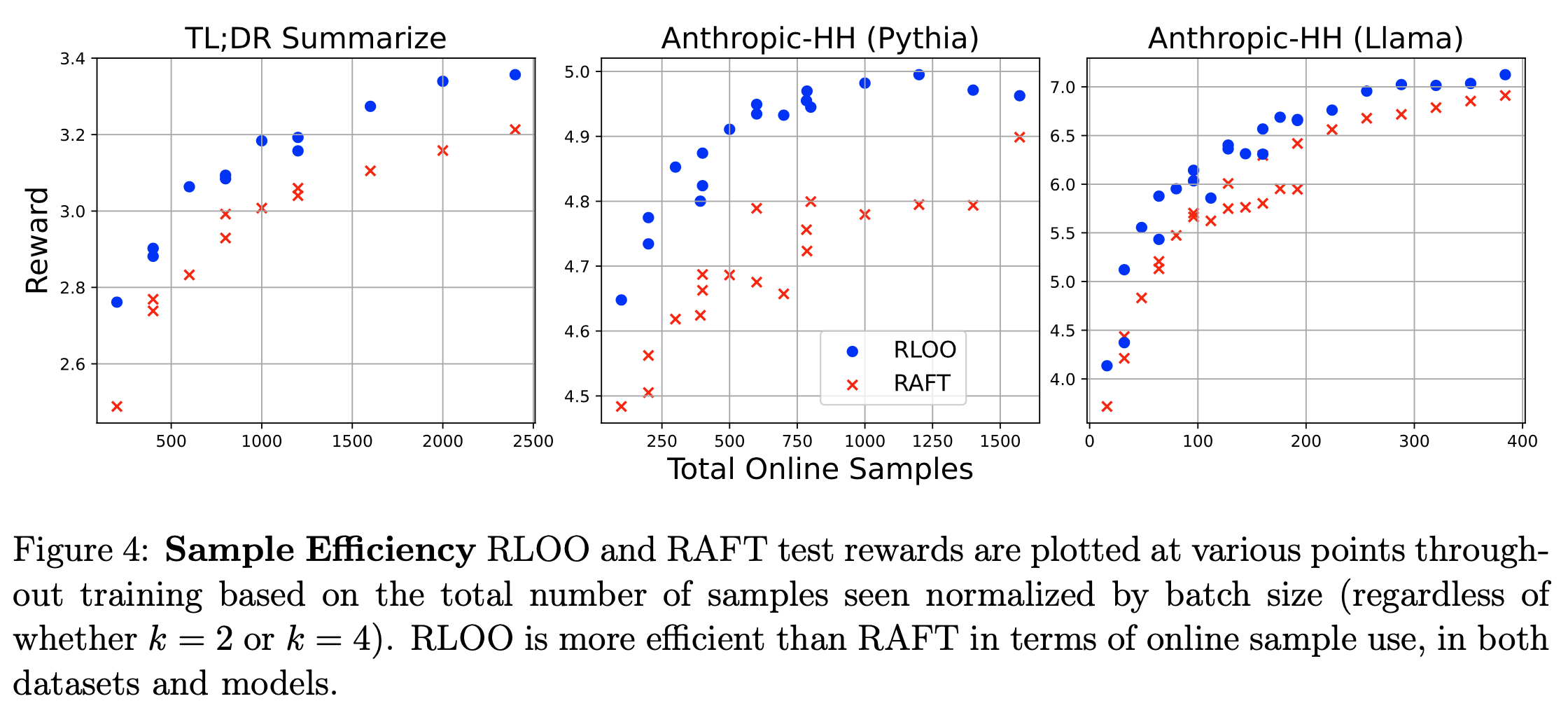
  • 结论：相同样本数量下，RLOO 效果更好，即 RLOO 样本效率更高

Simulated win-rates

• 表1 展示了 TL;DR Summarize 和 Anthropic-HH 数据集中每种方法相对于原始补全的胜率。这里论文还包含了 DPO
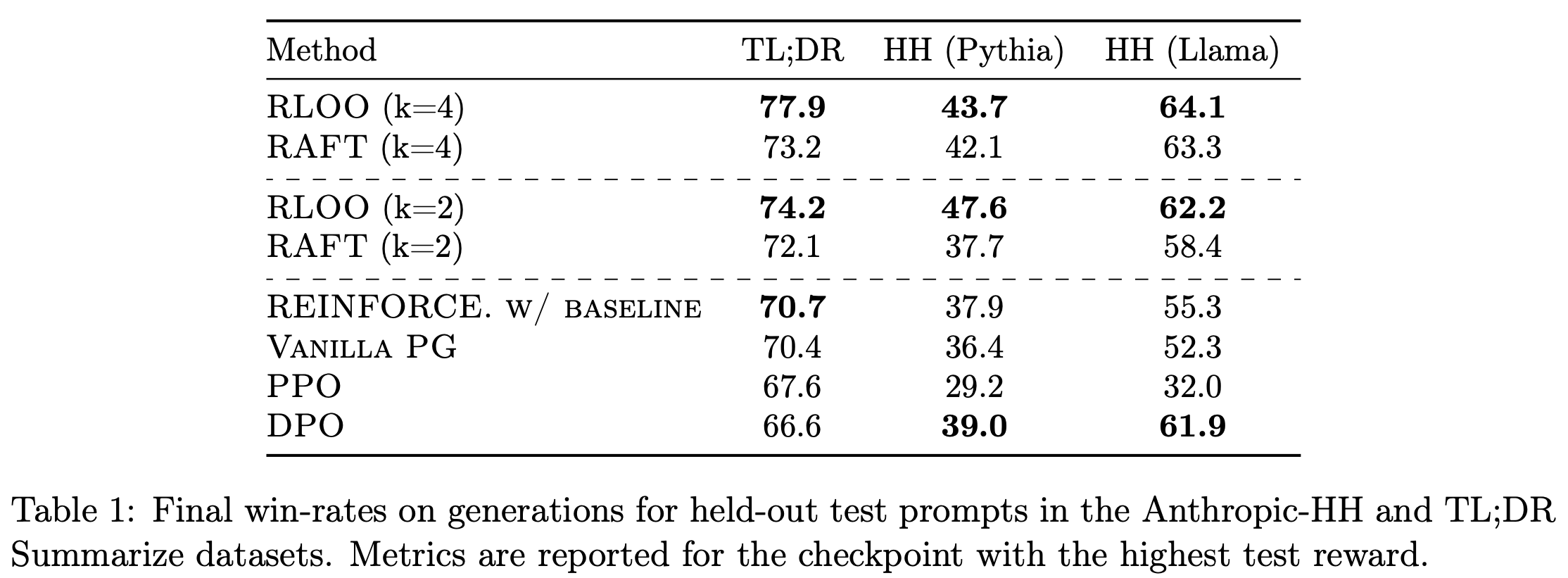
• 建模部分补全是不必要的（Modeling partial completions is not necessary） ：回顾 Vanilla PG 和 REINFORCE 的关键区别在于，Vanilla PG 将每个 token 视为动作 ，而 REINFORCE 将整个生成视为一个动作
  • 如 表1 所示，在使用 Pythia 基础模型时，带基线（移动平均）的 REINFORCE 在 TL;DR（70.7 vs 70.4）和 HH（37.9 vs 36.4）数据集上的表现与 Vanilla PG 相当
  • 此外，在使用 Llama 基础模型的 HH 数据集中，带基线（移动平均）的 REINFORCE 胜率更高（55.3 vs 52.3），优于 Vanilla PG
  • 这证实了仅建模完整生成而不建模部分补全的有效性，即使在 RLHF 中不使用多个样本时也是如此
  • 注：采样 Budget 越大，效果越好，但是 Pythia 在 HH 评估上胜率提升 采样预算 \(k=2 \to k=4\) 后，效果反而变差了，原因是波动导致？
• 胜率与测试奖励分数一致（Win-rates are inline with test reward scores） ：RLOO \(k=4\) 实现了最高的胜率，在 TL;DR、HH（Pythia）和 HH（Llama）上分别比 PPO 高出 10.3、14.5 和 32.1 个百分点。唯一的例外是 RLOO \(k=2\) 在 HH 数据集上的胜率最高
• RLOO 比 RAFT 样本效率更高（RLOO is more sample efficient than RAFT） ：在相同的采样 Budget \(k\) 下，RLOO 在所有数据集和模型上的表现始终优于 RAFT
  • 当在三个数据集和模型对上取平均值时，RLOO 在 \(k=2\) 和 \(k=4\) 时的胜率分别为 61.3 和 61.9，而 RAFT 分别为 56.1 和 59.5
  • 值得注意的是，RLOO 在 HH 数据集上（\(k=2\) 和 Pythia 基础模型）的胜率提升最大，比 RAFT 高出 9.9 个百分点（表1 第二列）

Alignment Tax

• 表2 展示了 Anthropic-HH 数据集中 Llama 基础模型的各种内在评估指标，包括困惑度和多样性分数
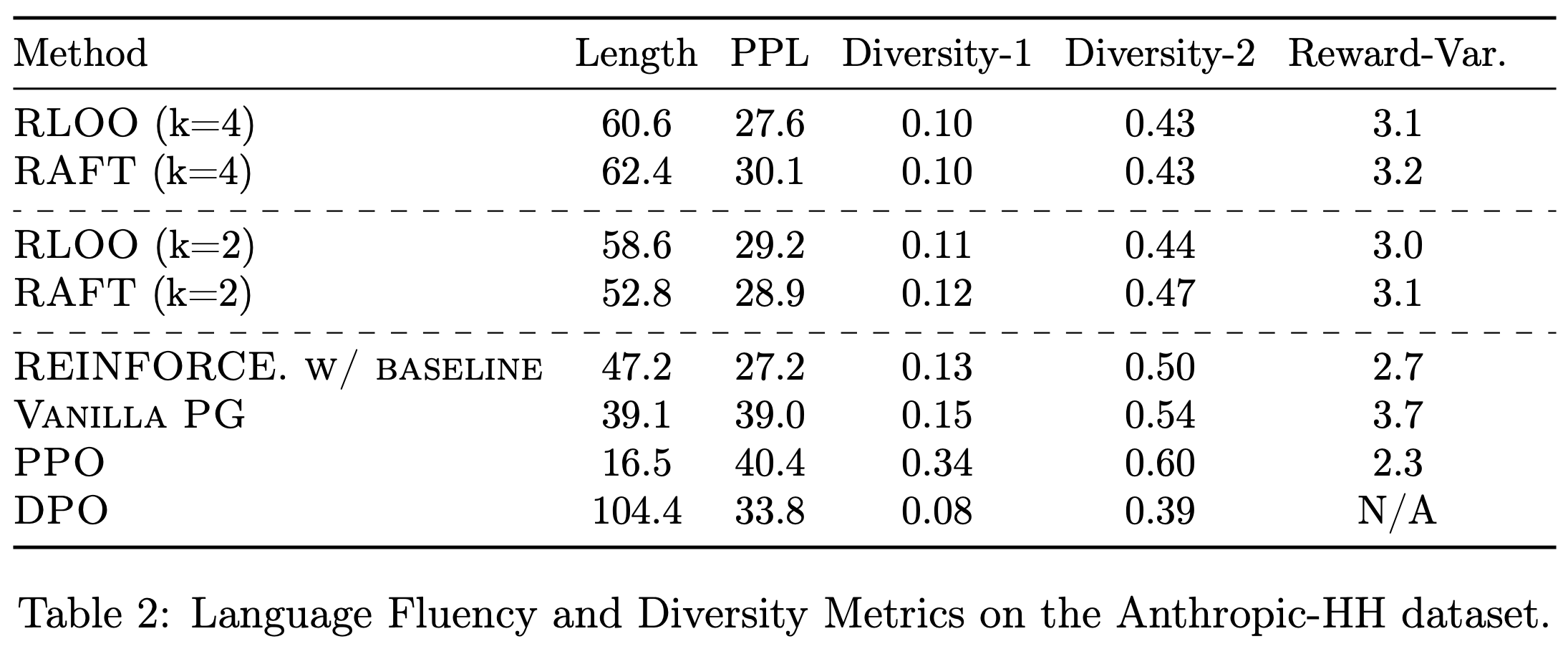
• 生成长度（Length of Generations） ：值得注意的是，DPO 训练的模型往往过于冗长（平均生成长度为 104 个 token），而 PPO 训练的模型生成较短（平均仅 16 个 token）。论文在附录 E 中提供了示例响应
• 困惑度与多样性（Perplexity and Diversity） ：如表2 所示
  • RLOO、RAFT 和带基线（移动平均）的 REINFORCE 的困惑度（PPL）分数较为接近，且三者均显著低于 PPO 和 Vanilla PG
  • 在多样性方面，RLOO、RAFT、带基线（移动平均）的 REINFORCE 和 Vanilla PG 的 Diversity-1 分数相似。Diversity-2 分数在奖励优化较高的方法中略有下降（2021）。这并不意外，因为它们的生成长度与其他方法相比存在显著差异
  • 总体而言，RLOO 和带基线（移动平均）的 REINFORCE 在保持生成流畅性和多样性的同时 ，实现了更高的奖励分数和胜率
• 奖励方差 ：较低的奖励方差对于安全和无害性等应用是理想的，因为这些应用中生成低奖励样本的风险较高
  • 表2 的结果显示，在相同的 \(k\) 值下，RLOO 的生成奖励方差略低于 RAFT（后者是奖励优化方面与 RLOO 最具竞争力的方法）
  • Vanilla PG 的奖励方差最高
  • 带基线（移动平均）的 REINFORCE 在奖励优化和胜率上与 Vanilla PG 相当甚至更好，但其奖励方差比 Vanilla PG 低 27%
  • 问题：为什么 DPO 没有评估方差？
    • 回答：因为这里的方差是训练过程中采样的奖励方差，DPO 训练过程中不需要采样，所以作者没评估？

Robustness

• 如前所述，RAFT 的一个主要缺点是它仅优化排名最高的样本，而丢弃其余在线样本。因此，可能导致最佳补全排名不准确的因素也会显著阻碍学习。论文通过展示下面两项指标证明了这种脆弱性
  • 1）KL 项的高 \(\beta\) 值
  • 2）插入的奖励噪声对 RAFT 的影响（与 RLOO 相比）
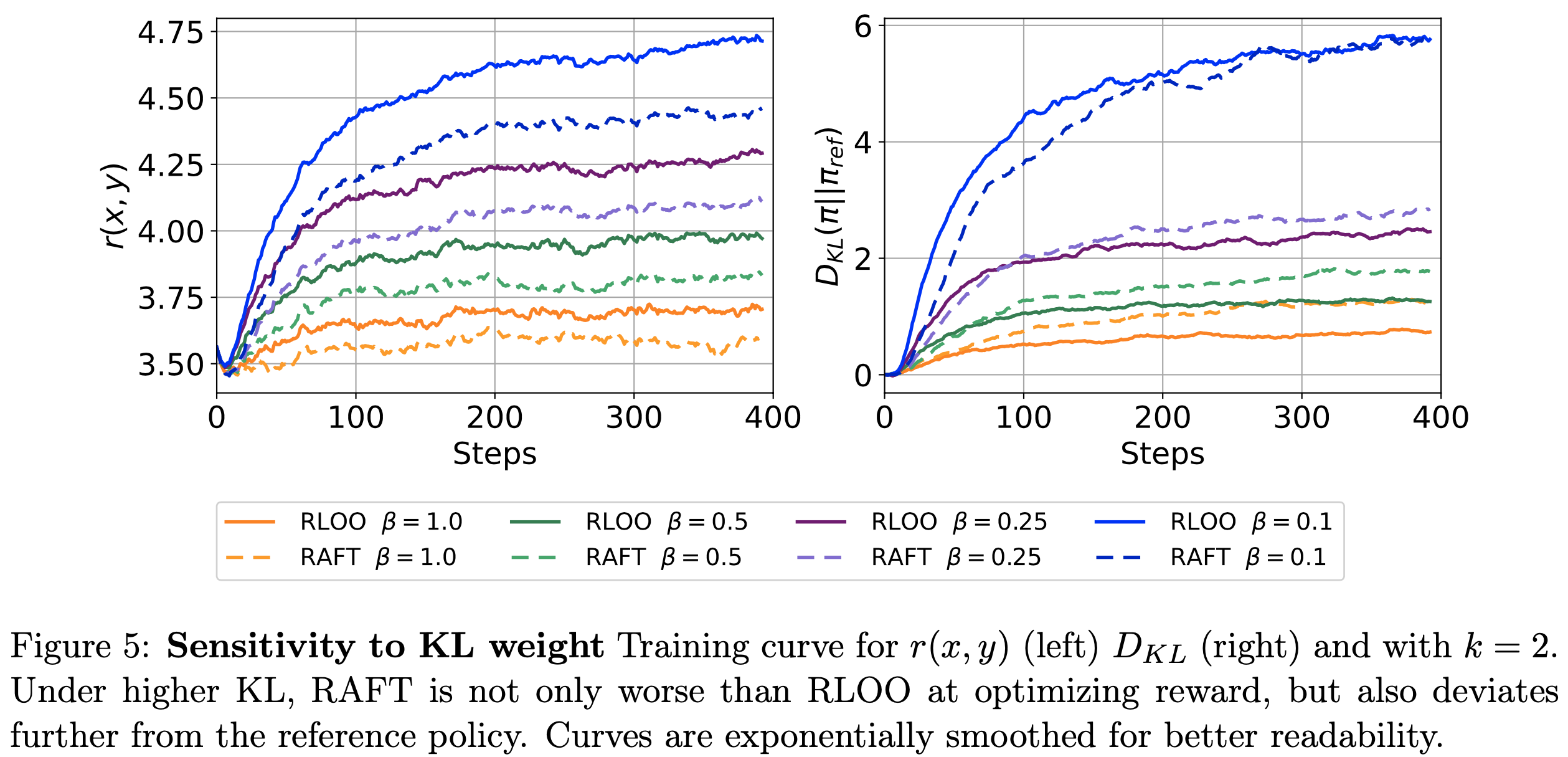
• KL 惩罚不匹配（Mismatch from KL-penalty） ：在图5 中，论文展示了 RLOO 和 RAFT 在 HH 数据集上（使用 Pythia 基础模型，\(k=2\)）训练过程中 KL 距离和测试奖励曲线 \(r(x,y)\) 的变化
  • 论文使用 \(\beta=\{0.25, 0.5, 1\}\) 来调整 KL 正则化。在这里，\(R(x,y)\) 中较大的 KL 惩罚（较高的 \(\beta\)）可能会增加 \(k\) 个在线样本之间的排名不匹配
    • 问题：如何理解排名不匹配？
    • 回答（个人理解）：由于奖励中包含了 KL 散度，若 KL 散度的权重 \(\beta\) 过高，可能会导致排序上不是真实奖励最大的排在前面（即 increase mismatches between rankings of the k online samples）
  • \(\beta\) 的选择通常取决于数据和基础模型输出 logits 的分布等多种因素，即使使用 early-stopping 也可能不允许 \(\beta\) 值太低
    • 理解：太低的 \(\beta\) 值可能导致模型没有限制，突然就跑飞了
  • 论文发现 RAFT 对较高的 KL 正则化更为敏感（注意：RAFT 中也是在奖励中使用了 KL 散度的）
    • 在低正则化情况下（\(\beta=\{0.1\}\)），RLOO 和 RAFT 收敛到与参考策略相同的 KL 距离，但 RLOO 实现了更高的奖励
    • 随着正则化增强（\(\beta=\{0.25, 0.5, 1.0\}\)），RAFT 不仅在奖励优化上表现更差，而且偏离参考策略的程度也更大
• 奖励噪声不匹配（Mismatch from Reward Noise） ：由于人类偏好的固有噪声性质，奖励模型本身是奖励信号的噪声代理（2017b；2018）
  • 受贝叶斯深度学习中建模偶然性不确定性（Aleatoric Uncertainty）的文献启发（2017；2021），为了模拟不同程度的噪声效应，论文对每个 Prompt 的奖励添加噪声。具体来说，论文在二元分类器的输出 logits 上添加噪声 \(\epsilon\)：
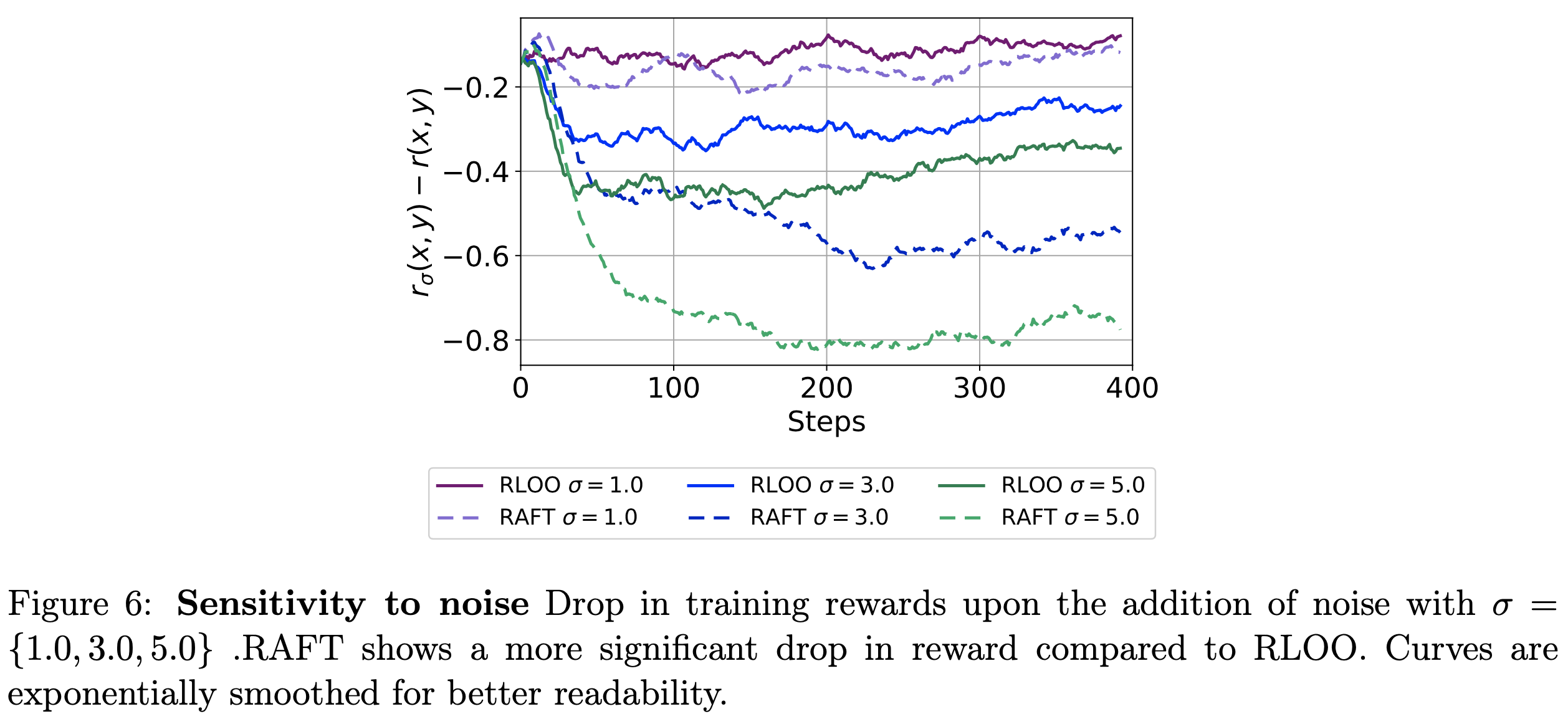
    $$ r_{\sigma}(x,y) = r(x,y) + \epsilon \quad \text{其中} \quad \epsilon \sim \mathcal{N}(0,\sigma^{2}) $$
  • 图6 显示了在不同噪声水平 \(\sigma=\{1.0, 3.0, 5.0\}\) 下奖励的下降情况
    • 正如预期的那样，训练奖励在 RLOO 和 RAFT 中均有所下降
    • 对于 RAFT，当 \(\sigma=\{3.0, 5.0\}\) 时，奖励下降更为明显（这是由于奖励噪声的添加影响了相对排名，从而影响了训练奖励）
    • RLOO 在噪声奖励信号下表现出相对稳健的奖励优化

---

Limitations

• 本研究的局限性之一是论文未研究奖励模型（Reward Model, RM）的过优化（over-optimization）问题
  • 该问题是指代理奖励（proxy reward）的优化轨迹与“黄金”奖励目标（gold reward objective）发生偏离的现象（2022）
  • 这一方面在 RAFT 等迭代微调方法中也尚未得到充分研究，值得未来专门探讨
• 另一局限性在于，论文未探索在单 Token 动作框架中使用 Leave-One-Out（LOO）Baseline的情况，即建模部分序列并提供中间奖励（intermediary rewards）
  • 在本研究中，论文证明了在奖励仅针对完整序列的 RLHF 上下文中，建模部分序列（completion）是不必要的任务
• 最后，论文的实验使用了基于 GPT-4 的 LLM 模拟胜率（simulated win-rates），而未测量其与最终人类评估偏好（human evaluation preferences）的相关性（PS：其实其他论文（如 Secrets of RLHF in Large Language Models Part I: PPO, Fudan & ByteDance）有测试过，一致性挺好的）
  • 同时，论文也未探索使用其他奖励指标（如 ROUGE、BLEU 或其他自然语言处理（NLP）中常用指标）进行强化学习训练（问题：有必要吗？）

---

附录A Effective Conditioning

• 为了验证”概率质量高度集中且条件作用显著缩小了可能的生成空间”这一假设，论文实证研究了输出分布和每个生成步骤的特性。论文使用了结果部分 HH 实验中采用的Llama SFT 模型
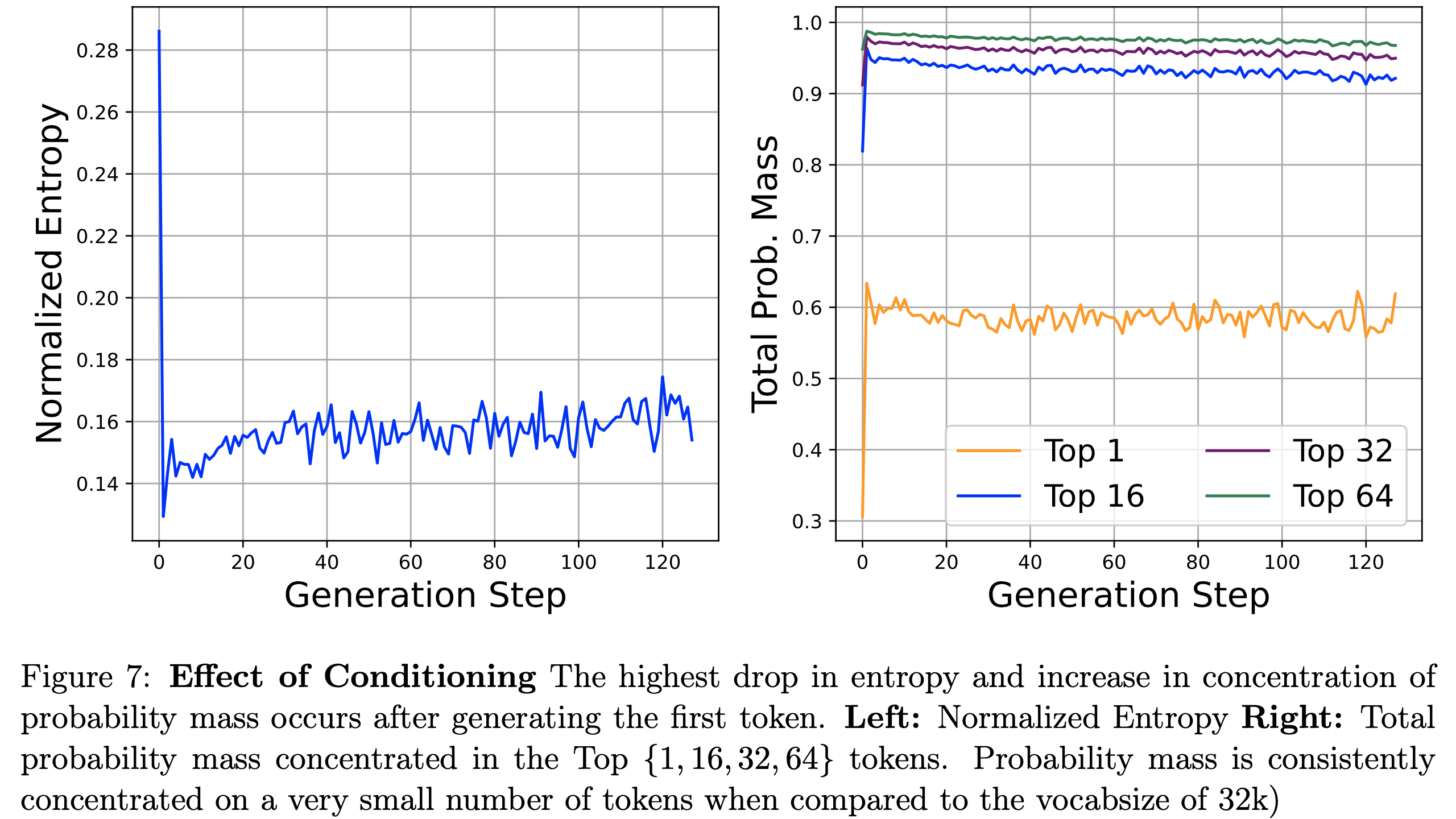
• 概率质量集中（Probability Mass Concentration） ：图7（右）绘制了前 \{1,16,32,64\} 个 token 所集中的总概率质量（mass）。在生成第一个 token 后 ，总概率质量出现了显著跃升，这表明从第一个 token 和 Prompt 开始的条件作用非常有效
  • 第一个 Token 生成后，后续的 Token 约 60% 的概率质量集中在单个最可能的 token 上，超过 90% 的总质量集中在前 16 个 token ，而前 32 和 64 个 token 的增量增长则趋于平缓
    • 理解：注意需要先生成第一个 Token，再开始统计，Prompt 后输出的第一个 Token 随机性较大（下文也会描述，第一个 Token 的熵比较大）
  • 这一实证证据直接支持了论文反复强调的观点：尽管每个步骤的可行搜索（动作）空间巨大，但实际上由于 SFT 模型和 Prompt 的条件作用，大部分概率质量仅分布在可能 token 的一小部分上
• 低熵值（Low Entropy） ：图7（左）绘制了归一化熵 \(\hat{H}(X)=\frac{H(X)}{H_{max}(X)}\)，其中 \(H_{max}(X)\) 是词汇表大小下均匀分布的熵
  • 与图7右中概率质量的跃升类似，正如预期的那样，熵的最大下降发生在生成第一个token之后，仅略微上升直至生成结束，且始终保持低位
  • 这进一步支持了生成空间高度偏斜的证据，并自然表明由于生成过程中的熵持续较低，生成概率的方差也较低。这进一步支持了单动作建模的合理性，因为它表明生成中的第一个条件作用最具影响力

---

附录B RLOO 与对比损失的关联（RLOO’s Connection to Contrastive Loss）

• 其他多项迭代微调工作（2023；2023）通过根据奖励模型确定的权重，上调正样本的对数概率并下调负样本的概率，使用了对比式损失：
  $$
  \mathcal{L}_{c}^{k=2}=-\log\pi(y_{+}|x)+\log\pi(y_{-}|x)
  $$
• 论文也有与 原文 2.3 节的方程对应的 \(k=2\) 损失：
  $$
  \mathcal{L}_{\text{RLOO} }^{k=2}=\frac{\left(R(y_{+},x)-R(y_{-},x)\right)}{2}(-\log\pi(y_{+}|x)+\log\pi(y_{-}|x))
  $$
• 显然，\(\text{RLOO}_{k=2}\) 损失正是对比损失，但按绝对分数差异加权（\(\frac{1}{k}\) 因子已合并到学习率中）

---

附录C Training Details

• 以下是关于训练和数据预处理的更多细节
• 数据预处理（Data-preprocessing） ：
  • 对于每个数据集，论文过滤掉超过预设长度的 Prompt，以减少不包含 <EOS> token 的生成的出现
  • 对于 TL;DR 数据集：滤掉超过 448 个 token 的 Prompt
  • 对于 HH 数据集：滤掉超过 348 个 token 的 Prompt
• SFT 训练 ：
  • 对于 TL;DR Summarize 数据集，论文使用专用的 SFT 分割
  • 对于Anthropic-HH，由于原始数据集不包含单独的 SFT 分割，论文在 SFT 阶段使用来自二元比较的 Prompt 和首选响应（preferred responses）。这与之前的工作（2023；）一致
  • 在训练超参数方面
    • 对于 Pythia 模型，与之前的工作（2023a；2022a）类似，论文在摘要和对话任务中训练 2 个epoch，初始学习率为 2e-5
    • 对于Anthropic-HH 数据集，由于论文没有 SFT 集，论文使用构成HH数据集的二元比较中的首选响应。这与之前的工作（2023；）一致
    • 对于摘要数据集，论文使用初始数据集指定的专用 SFT 集
    • 对于 Llama 模型，论文发现 SFT 阶段 1 个 epoch 已足够
• RM 训练 ：
  • 在 RM 阶段，论文训练 RM 1 个 epoch，初始学习率为 1e-5
  • 对于 RM 和 SFT 训练，论文使用 cosine decay learning schedule（2016）和 0.03 的 warm-up ratio（注：warm-up 阶段（学习率上升阶段）步数占总训练阶段步数的 3%，这个数字是实验过的？一般是 5% 到 10%吧？）
• 偏好训练（Preference Training）
  • 对于仅使用 Pythia 模型的 TL;DR Summarize 数据集，论文训练每个变体 600 步，rollout batch size为 512，step batch size 为 256。论文使用 \(\beta\) 值为 0.03
  • 对于 Anthropic-HH，论文训练 Pythia 模型 393 步，batch size 配置与 TL;DR 摘要相同
  • 对于 Llama 模型，论文遵循（Dong等人，2023）的设置，在 2 个 epoch 中使用 2048 的 rollout 和 step batch size
  • 除非另有说明，否则所有 Anthropic-HH 实验使用 \(\beta=0.10\)
  • 对于 TL;DR 和 HH 数据集，论文都使用与 SFT 阶段相同的 Prompt 进行在线生成
  • 在两个数据集和所有模型中，论文使用 \(1e-6\) 的恒定学习率和占总步数 3% 的线性预热时间
  • 学习率是在对 RAFT 和 RLOO 的 \{1×10^{-6}, 1×10^{-5}, 2×10^{-5}\} 以及对 PPO 和 Vanilla PG 的 \{1×10^{-6}, 1×10^{-5}\} 进行扫描（sweep）后选择的
    • 这里是说，学习率是经过了简单的挑选的，具体挑选的方式是在几个常见的学习率上来选择，论文最终选择了 \(1e-6\)
  • 对于所有算法，论文对每个批次进行 2次 梯度步
    问题：这里是说收集一次数据更新两次吗？是否会破坏 REINFORCE on-policy 的设定呢？

---

附录D GPT-4 评估 Prompt

• 注：（详情见原始论文附录D，这里给出中文翻译仅供参考，可借用于自己的任务上）

• TL;DR Summarize:

  以下哪个摘要更好地总结了给定论坛帖子中最重要的点，而不包含不重要或不相关的细节？一个好的摘要既精确又简洁
  帖子：{instruction}
  摘要（A）：{output_1}
  摘要（B）：{output_2}
  首先提供一个一句话的比较，解释你更喜欢哪个摘要及其原因。其次，在新的一行中，仅注明"摘要（A）"或"摘要（B）"以表明你的选择。你的回答应使用以下格式：
  比较：<一句话的比较和解释> 首选：<"摘要（A）"或"摘要（B）">

• Anthropic-HH:

  对于以下对聊天机器人助手的查询，哪个响应更有帮助？
  查询：instruction
  响应（A）：{output_1}
  响应（B）：{output_2}
  首先提供一个一句话的比较，解释你认为哪个响应更有帮助。其次，在新的一行中，仅注明"响应（A）"或"响应（B）"以表明哪个响应更有帮助。如果它们同样好或差，注明"Neither"。你的回答应使用以下格式：
  比较：<一句话的比较和解释> 首选：<"响应（A）"或"响应（B）"或"Neither">

---

附录E 示例响应

E.1 TL;DR Summarize（Pythia）

• 详情见原论文附录，给出了每个模型在不同设定下的输出

E.2 HH（Llama）

• 详情见原论文附录，给出了每个模型在不同设定下的输出