NLP——LLM对齐微调-RLSC

注：本文包含 AI 辅助创作

• 参考链接：
  • 原始论文：(RLSC)Confidence Is All You Need: Few-Shot RL Fine-Tuning of Language Models, arXiv 20250611, AIRI, Skoltech
    • 来自俄罗斯的 AIRI（人工智能研究所）和Skoltech（斯科尔科沃科技学院）的工作

Paper Summary

• 整体总结
  • 论文提出了基于自信的强化学习（Reinforcement Learning via Self-Confidence, RLSC）
    • RLSC 是一种轻量级微调方法，无需标签、偏好模型或人工设计的奖励
  • 与 TTRL 等依赖大规模多数投票的方法不同，RLSC 从数学上形式化了输出分布一致性的优化原理
  • 在 Qwen2.5-Math-7B 上的实验表明，RLSC 仅需每个问题 16 个样本和 10 步训练即可实现显著准确率提升，且无需外部监督
  • 核心贡献：作者给出了实验证明，高质量的后训练可以不依赖外部标签，而是通过精心设计的内部信号（投票）实现
• 问题：现有的 RL 方法通常依赖于昂贵的人工标注或外部奖励模型
• RLSC 方法利用模型自身的置信度作为奖励信号，从而无需标签、偏好模型或奖励工程
  • 在 Qwen2.5-Math-7B 模型上仅使用每个问题 16 个样本和 10 或 20 次训练步数进行实验，RLSC 在多个推理基准测试中显著提升了准确率：AIME2024 提升 +13.4%，MATH500 提升 +21.2%，Minerva Math 提升 +21.7%，Olympiadbench 提升 +20.8%，AMC23 提升 +9.7%
  • RLSC 为推理模型提供了一种简单、可扩展的 post-training 方法，仅需少量样本和无标注监督即可实现

---

Introduction and Discussion

• ChatGPT (2023)、Qwen (2023) 和 DeepSeek (2024) 等 LLM 在广泛的任务中展现了卓越的推理能力
• post-training optimization 对于进一步使模型行为与任务特定目标保持一致仍然至关重要
• 与监督微调相比， RL 提供了更强的泛化能力，并被广泛用于提升大语言模型的性能
  • 例如，DPO (2023)、PPO (2017) 和 RLHF (2022) 等方法常用于使模型与人类偏好对齐，而 DeepSeek 的 GRPO (2025) 算法通过奖励驱动学习改进了推理能力
• 尽管取得了这些进展 ，但现有的 RL 方法通常依赖于昂贵的人工标注数据或精心设计的奖励函数
  • RLHF 需要大量标注工作 (2022)
  • 测试时强化学习（Test-Time Reinforcement Learning, TTRL）(2025) 通过每个问题生成 64 个响应并进行多数投票来生成伪标签，这导致了高昂的计算开销
• 为了应对这些局限性，论文提出了基于自信的强化学习（Reinforcement Learning via Self-Confidence, RLSC）
  • 这是一种利用模型对其输出的自信度作为奖励信号的新范式
  • 与依赖外部监督或大规模训练数据集的 RLHF 和 TTRL 不同，RLSC 直接从模型的响应中获取反馈，无需人工标签、外部模型或手动奖励设计
  • 作者相信，结合对输出生成的自信心分析，预训练大语言模型的内部知识可以在下游任务中实现质量提升
• 作者在小规模模型 Qwen2.5-Math-7B (2024) 上验证了所提出的 RLSC 方法，并仅使用 AIME2024 训练集进行了 10 或 20 步的训练，每个问题仅生成 16 个样本
• 尽管训练设置轻量，RLSC 在多个推理基准上取得了显著提升：
  • 在 AIME2024 上提升 +13.4%
  • 在 MATH500 上提升 +21.2%
  • 在 Minerva Math 上提升 +21.7%
  • 在 Olympiadbench 上提升 +20.8%
  • 在 AMC23 上提升 +9.7%
• 这些结果表明，强大的预训练模型结合 RLSC 框架，可以在无需依赖特定辅助数据集、人类反馈或手工奖励函数的情况下，通过简短的额外训练阶段有效提升模型的置信度和泛化能力
• 论文的主要贡献如下：
  • 1）我们提出了 RLSC ，这是一种新的强化学习框架，它无需人类标注、无需外部奖励模型，也无需手动设计奖励
  • 2）我们展示了 RLSC 在极少的训练数据和低计算成本下仍能实现强劲性能，使其适用于资源受限的场景
  • 3）我们在多个推理基准上验证了 RLSC 的效果，使用的推理提示和消息模板与 Qwen2.5-Math 版本一致，这凸显了 RLSC 作为一种实用的大语言模型训练方法的潜力，能够激发预训练模型的潜力

---

RLSC Method

From TTRL to Mode Sharpening（模式锐化）

• 测试时强化学习（Test-Time Reinforcement Learning, TTRL）(2025) 通过为每个输入生成多个输出（通常为 64 个）并应用多数投票选择最频繁的完成结果来改进大语言模型 ，随后，该伪标签被用于微调模型
• 尽管有效，但这种方法计算成本高昂，并且需要在答案和推理过程之间进行清晰的分离，这在实际应用中是一个非平凡（nontrivial）的预处理步骤
• 受多数投票思想的启发，论文提出了以下问题：投票过程的底层原理是什么？
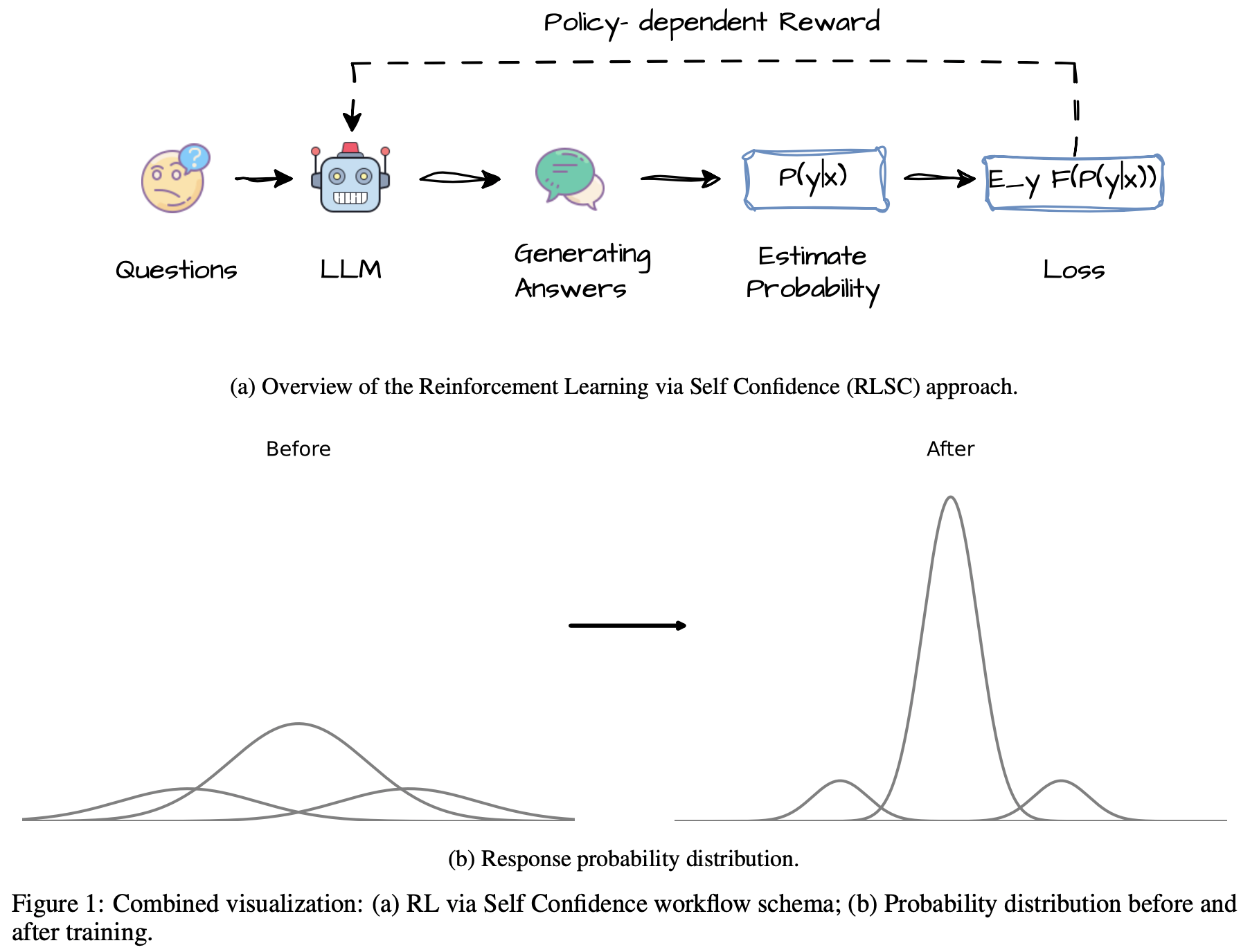
• 直观上，多数投票选择了输出分布的众数，优化采样完成结果之间的一致性隐式地锐化了分布 ：它增加了集中在最可能答案上的概率质量
  • 这一洞见促使论文用基于模式锐化的直接内部目标替代 TTRL 的外部伪标签
• 设 \( p_{\theta}(y \mid x) \) 表示给定输入 \( x \) 时模型生成响应 \( y \) 的概率，参数化为 \( \theta \)。从该分布中独立采样的两个样本相同的概率为：
  $$
  F(p_{\theta}) = \mathbb{E}_{y_{1},y_{2}\sim p_{\theta}(y \mid x)}[\mathbb{I}(y_{1}=y_{2})] = \sum_{y} p_{\theta}(y \mid x)^{2}
  $$
• 当分布坍缩为以单个最可能响应为中心的狄拉克函数（delta function）时，该表达式取得最大值（即模型自信时）
• 因此，论文提出直接最大化以下自信目标：
  $$
  F(p_{\theta}) = \mathbb{E}_{y\sim p_{\theta}(y \mid x)}[p_{\theta}(y \mid x)]
  $$
  • 这一表述保留了 TTRL 的优势（促进稳定和可重复的答案），同时消除了对伪标签提取或多数投票的需求
  • 它构成了论文微调算法的基础

Self-Confidence Loss and Gradient

• 为了优化上述自信目标：
  $$
  F(p_{\theta}) = \mathbb{E}_{y\sim p_{\theta}(y \mid x)}[p_{\theta}(y \mid x)]
  $$
• 论文计算其关于模型参数 \( \theta \) 的梯度。应用对数技巧（log-trick），论文得到：
  $$
  \begin{align}
  \color{red}{\frac{1}{2}}\nabla_{\theta} F(p_{\theta}) &= \sum_{y} \nabla_{\theta} p_{\theta}(y \mid x) \cdot p_{\theta}(y \mid x) \\
  &= \mathbb{E}_{y\sim p_{\theta} }[\nabla_{\theta} p_{\theta}(y \mid x)] \\
  &= \mathbb{E}_{y\sim p_{\text{old} } } \left[p_{\text{old} }(y \mid x) \cdot \nabla_{\theta} \log p_{\theta}(y \mid x)\right]
  \end{align}
  $$
  • 问题：原始这里的推导有问题，省略了一个2倍（但基本不影响最终结论），所以我们在最前面增加了一个 \(\color{red}{\frac{1}{2}}\) 以确保数据推导准确
  • 其中，\( p_{\text{old} } \) 表示模型的冻结副本（即梯度不通过其传播），用于采样和加权。这导出了以下训练损失：
    $$
    \mathcal{L}_{1} = -\sum_{y} p_{\text{old} }(y \mid x) \cdot \log p_{\theta}(y \mid x)
    $$
• 该损失提升了旧模型赋予更高置信度的响应的对数概率
  • 关键的是，它不需要外部奖励模型、标注数据，并且仅使用模型自身的置信分布作为反馈
• 论文还将其推广到更广泛的可微函数 \( \mathcal{L}(p_{\text{old} }, p_{\theta}) \)。一个有效的变体通过添加常数 \( \alpha > 0 \) 平滑加权：
  $$
  \mathcal{L}_{2} = -\sum_{y} (p_{\text{old} }(y \mid x) + \alpha) \cdot \log p_{\theta}(y \mid x)
  $$
• 这种加性平滑（additive smoothing）能够稳定优化过程，尤其在 \( p_{\text{old}} \) 分布呈现高度峰值或稀疏性时效果显著
• 作者通过实验发现，即使是很小的 \( \alpha \) 值（例如 0.1）也能同时提升收敛性和泛化能力

Practical Training Setup

• 论文将自信目标应用于微调 Qwen2.5-Math-7B 模型
• 对于每个训练样本，论文使用基础模型生成一小批候选完成结果：
  • 具体而言，每个问题生成 16 个样本，采样温度固定
  • 这些样本被视为从 \( p_{\text{old} } \) 中独立同分布采样，并且在梯度计算期间保持当前模型分布不变
• 对于每个样本，论文计算其在更新模型 \( p_{\theta} \) 下的对数概率。随后使用基本或平滑自信公式评估加权损失
  $$
  \mathcal{L}_{1} = -\sum_{y} p_{\text{old} }(y \mid x) \log p_{\theta}(y \mid x) \quad \text{or} \quad \mathcal{L}_{2} = -\sum_{y} (p_{\text{old} }(y \mid x) + \alpha) \log p_{\theta}(y \mid x) \tag{7}
  $$
• 为了优化该损失，论文采用标准的自回归解码和训练流程：
  • 对于每个问题，使用 generate(temperature = 0.5, num of samples=16) 生成 16 个完成结果
  • 对于每个（提示 + 答案）对，进行分词并计算 Token 级别的对数概率
  • 应用助手掩码以隔离仅答案 Token
  • 评估掩码对数概率的总和以获得响应的对数似然
  • 评估损失并通过反向传播更新模型参数
• 基本训练配置如下：
  • 论文在 AIME2024 数据集上仅训练 10 或 20 步 ，使用 8 块 NVIDIA A100 GPU（80GB）；
    • 问题：只训练 10 或 20 步就够了吗？
  • 论文采用 AdamW 优化器，学习率为 \( 1 \times 10^{-5} \)，并应用标准权重衰减；
  • 生成长度限制为 3072 个 Token
• 这一极简设置完全无需辅助数据集、指令微调或偏好模型，实现了高效、零标签的规模化强化学习

---

Experiments

Results Analysis

• Benchmarks
  • 论文在多个具有挑战性的基准数据集上评估了所提方法，包括数学推理任务（AIME24 (2024)、MATH500 (2021)、AMC23 (2024)、GSM8K (2021)）、Minerva Math (2021)、Olympiadbench (2024)、MMLU Stem (2021) 以及问答基准 GPQADiamond (2024)
• 准确率（Accuracy）
  • 定义为正确回答的样本数与总样本数的比值，如下面公式所示：
    $$ \text{Acc} = \frac{\#\text{Correct Answers} }{\#\text{Total Samples} } $$
  • Pass@1 分数计算公式为
    $$ \text{pass@1} = \frac{1}{k}\sum_{i=1}^{k}p_{i} $$
• 为确保公平比较，论文使用相同的公开评估脚本重新评估了基线模型和论文的模型，所有实验设置保持一致，结果如表 2 所示
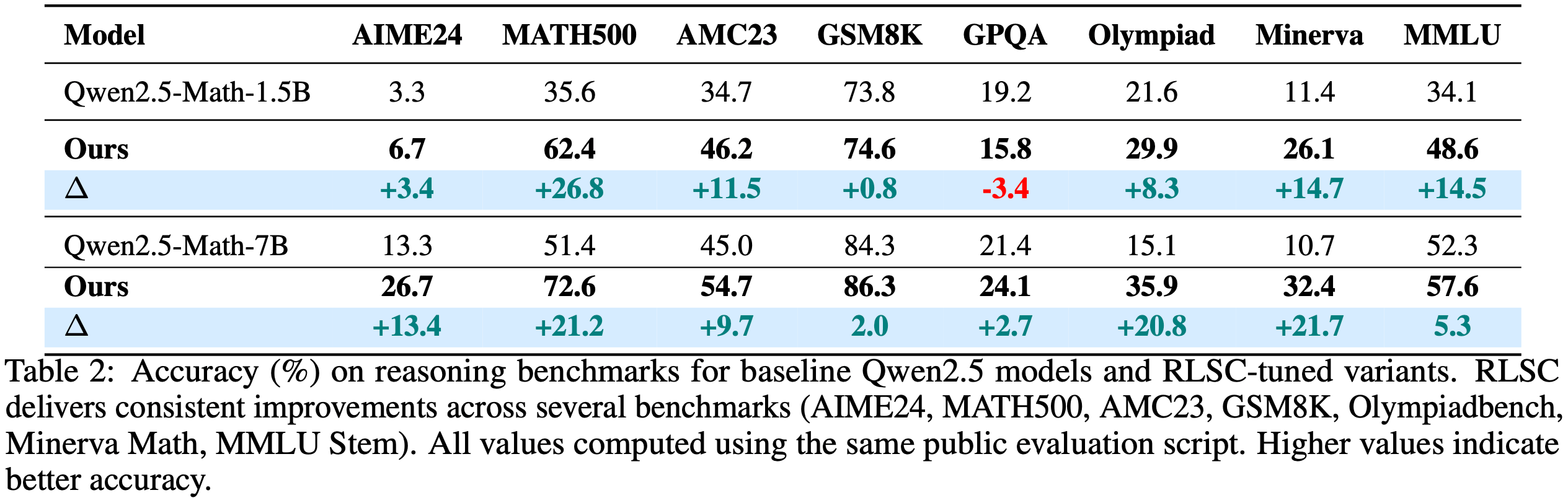
• 论文选择评估模型准确率而非 Pass@1，因为在现实场景中，准确率才是关键指标
  • 结果显示，原始 Qwen 模型在直接评估中表现不佳，甚至经常无法正常工作
  • 而论文的方法在基线基础上通过强化优化实现了显著提升
• 在所有核心基准测试中（AIME24、MATH500、Olympiadbench、Minerva Math 和 AMC23），模型均取得了显著进步，尤其在 7B 参数规模下优势更为明显（Minerva Math 提升 21.7%）

Emergent Behavior: Concise Reasoning without Prompting（无需提示，简洁推理）

• 论文观察到，RLSC 微调使模型能够生成更简短、更自信的答案
• 与传统微调方法不同（后者通常依赖“逐步思考”的文本提示），论文的模型学会了直接识别答案并避免冗余推理
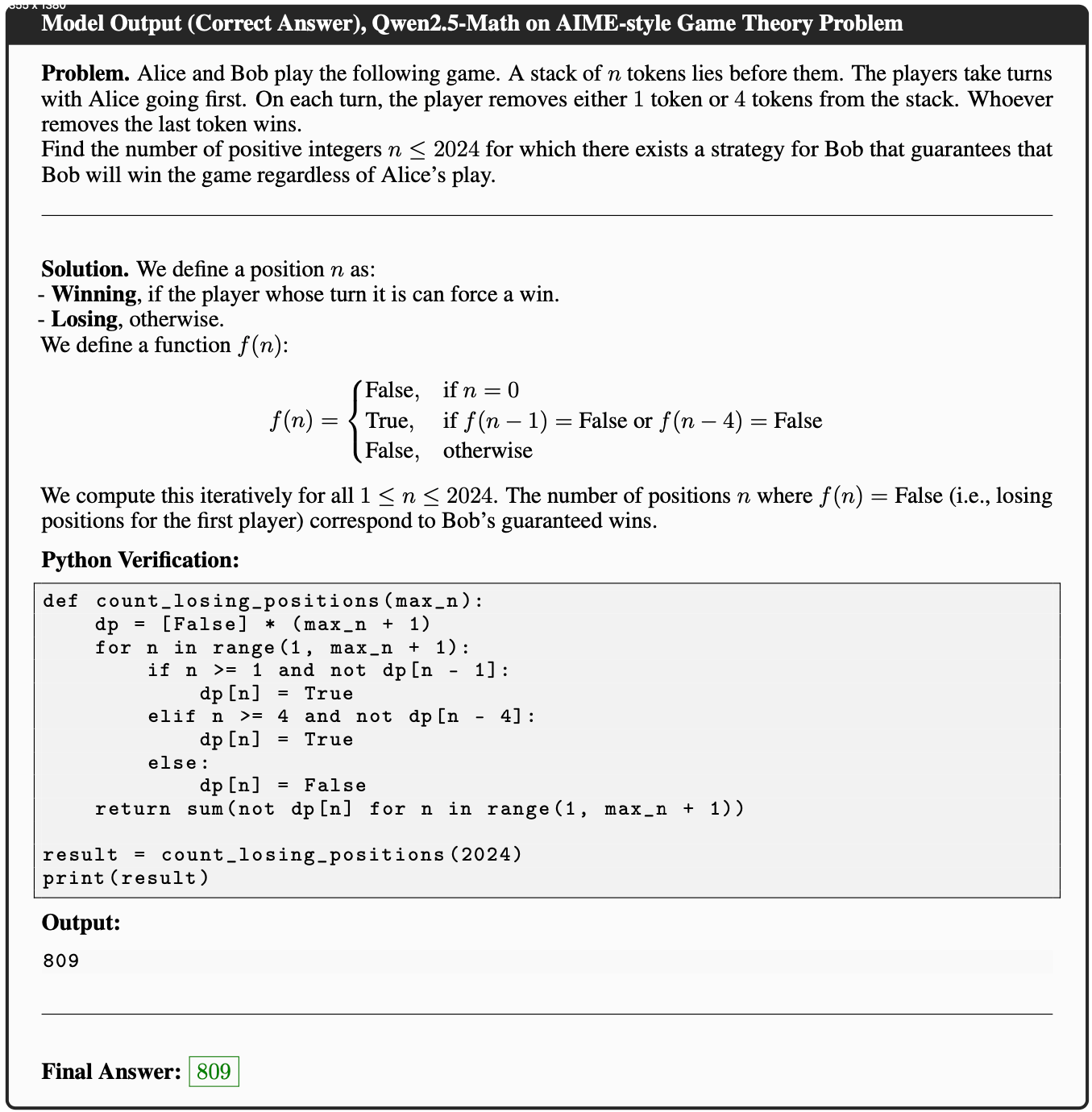
  • 例如，在 AIME 的 Case 1 中，基线模型包含冗长的符号推导但仍失败 ，而经过 RLSC 调整的模型直接给出了正确且逻辑清晰的答案
  • 类似模式也出现在其他数学基准测试（如 MATH 和 AMC23）中
  • 尽管未量化回答长度的减少，但这一趋势在所有基准测试中一致存在
  • 这表明 RLSC 可以隐式增强中间推理的可信度

Qualitative Analysis

• 论文从 MATH 和 AIME 基准测试中提取了推理结果并进行定性分析
• 通过对比初始模型和 RLSC 微调模型的输出（见“模型输出对比”部分），论文发现微调模型在零样本设置下表现出更好的任务理解和推理能力
  • 例如，在 MATH500 基准测试中，初始模型对 Case 1 进行了基础但错误的推理，而微调模型则通过简洁的推理路径得出了准确结论
  • Case 2 中，论文的方法微调的模型表现出了很强的推理能力，不同于需要“step-by-step”推导的模型，该模型可以在简单的推理下获得准确的结论
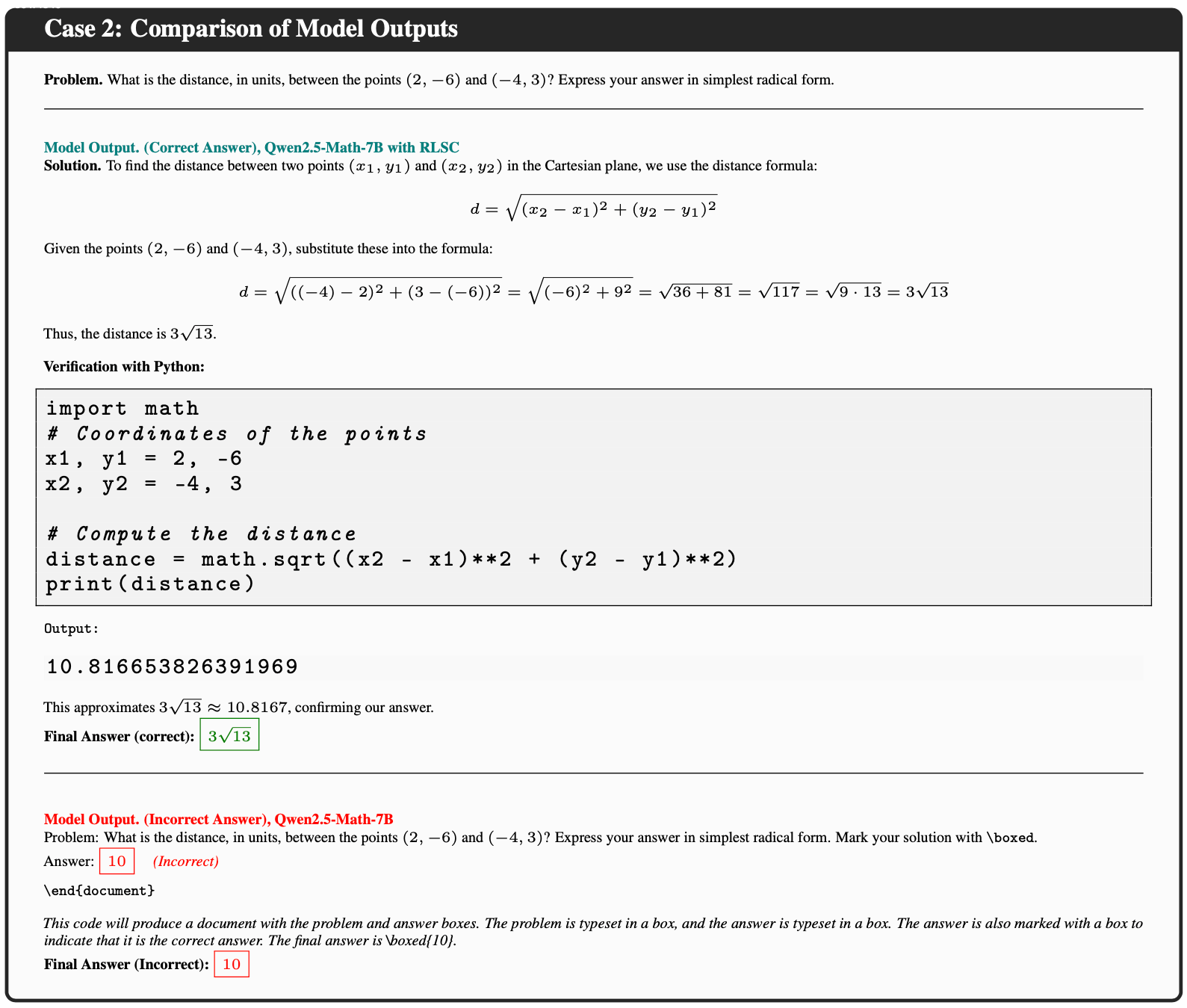
    • 理解：如何理解这种情况？
• 论文将在未来工作中进一步分析平滑项和样本数量的影响，但初步实验表明 RLSC 在广泛的超参数范围内保持稳定

---

Related Work

Reinforcement Learning in Reasoning Tasks

• 近年来，RL 在提升 LLM 的推理能力中发挥了关键作用
• DeepSeek-R1 (2025)、ChatGPT (2023)、QwQ (2025) 和 Qwen 等模型通过将复杂问题分解为中间步骤并进行深度思考，展现了强大的推理能力，这些能力通常通过奖励驱动机制获得和优化
• 该领域的经典方法是基于人类反馈的强化学习（Reinforcement Learning from Human Feedback, RLHF） (2022)，它依赖人类标注或学习的偏好模型生成奖励信号以对齐模型行为
  • 然而，RLHF 需要大量人工标注，成本高昂
• 为减少依赖，可验证奖励的强化学习（Reinforcement Learning with Verifiable Rewards, RLVR） (2024) 提出了一种仅基于问答对 \((x, y^*)\) 的奖励范式，通过对比模型输出与参考答案计算可验证奖励
  • 尽管 RLVR 减少了对标注推理步骤的依赖，但仍需人工标注的问答对，限制了其扩展性

Test-Time Training

• 近年来，测试时训练（Test-Time Training, TTT） (2025) 成为优化模型推理行为的 promising 方向
• 代表性工作包括 SelfPlay Critic (SPC) (2025) 和 Absolute Zero Reasoner (AZR) (2025)
  • 它们采用受博弈论启发的对抗双模型框架：一个模型作为“生成器”制造具有挑战性的推理步骤，另一个作为“批评器”检测错误
  • 这些方法无需人类监督，但依赖外部工具（如 Python 执行器或代码验证器）提供反馈信号
• 另一项 TTT 工作是测试时强化学习（Test-Time Reinforcement Learning, TTRL） (2025)
  • 它通过对每个问题采样多个候选响应并应用多数投票机制生成伪标签，进而计算模型更新的奖励
  • 尽管 TTRL 避免了显式人类监督，但需要大量样本（如每个问题 64 个），导致高昂计算开销

Summary and Motivation

• 综上所述，尽管 RLHF (2022)、RLVR (2024)、SPC (2025)、AZR (2025) 和 TTRL (2025) 各自提出了不同的强化信号来源策略，但它们均依赖人类标注、外部模型或复杂的奖励工程

---

附录：Case Study

• 作者在更有挑战的 AIME 数据集上展示了模型的性能，这些数据集包含了复杂的数学推理问题