NLP——LLM对齐微调-ORPO

注：本文包含 AI 辅助创作

参考链接：
- 原始论文：ORPO: Monolithic Preference Optimization without Reference Model, arXiv 20240314, KAIST AI：截止到20250616日，cited by 244
  - 注：KAIST AI 是韩国科学技术院（KAIST）的一个机构
- 模型开源权重
  - https://huggingface.co/kaist-ai/mistral-orpo-alpha
  - https://huggingface.co/kaist-ai/mistral-orpo-beta

Paper Summary

整体总结：
- 论文通过重新审视和理解 SFT 阶段在偏好对齐中的价值，提出了一种无需参考模型的单步偏好对齐方法 ORPO（本质是一种 SFT 方法）
- ORPO 在多个规模上均被微调后的奖励模型偏好于 SFT 和 RLHF，并且随着模型规模的增大，其对 DPO 的胜率也逐渐提高
- 论文通过 2.7B 和 7B 的预训练语言模型验证了 ORPO 的可扩展性，其在 AlpacaEval 上的表现超过了更大规模的先进指令跟随语言模型
- 特别说明：作者发布了 Mistral-ORPO-$\alpha$ 和 Mistral-ORPO-$\beta$ 的微调代码和模型 checkpoint 以促进可复现性
背景：
- 尽管最近的 LLM 偏好对齐算法已展现出有希望的结果，但 SFT 对于实现成功收敛仍然至关重要
- 论文研究了 SFT 在偏好对齐中的关键作用，强调只需对不受欢迎的生成风格施加轻微惩罚即可实现偏好对齐的 SFT
基于此，论文提出了一种简单而创新的 无需参考模型的 单一（monolithic） 几率比偏好优化算法（Odds Ratio Preference Optimization, ORPO），消除了额外偏好对齐阶段的需求
论文通过实证和理论证明，在 125M 到 7B 的不同规模模型上，几率比（odds ratio）是对比 SFT 中受欢迎和不受欢迎风格的合理选择
仅使用 UltraFeedback 数据集对 Phi-2（2.7B）、Llama-2（7B）和 Mistral（7B）进行 ORPO 微调，其性能超过了参数规模超过 7B 和 13B 的最先进语言模型：
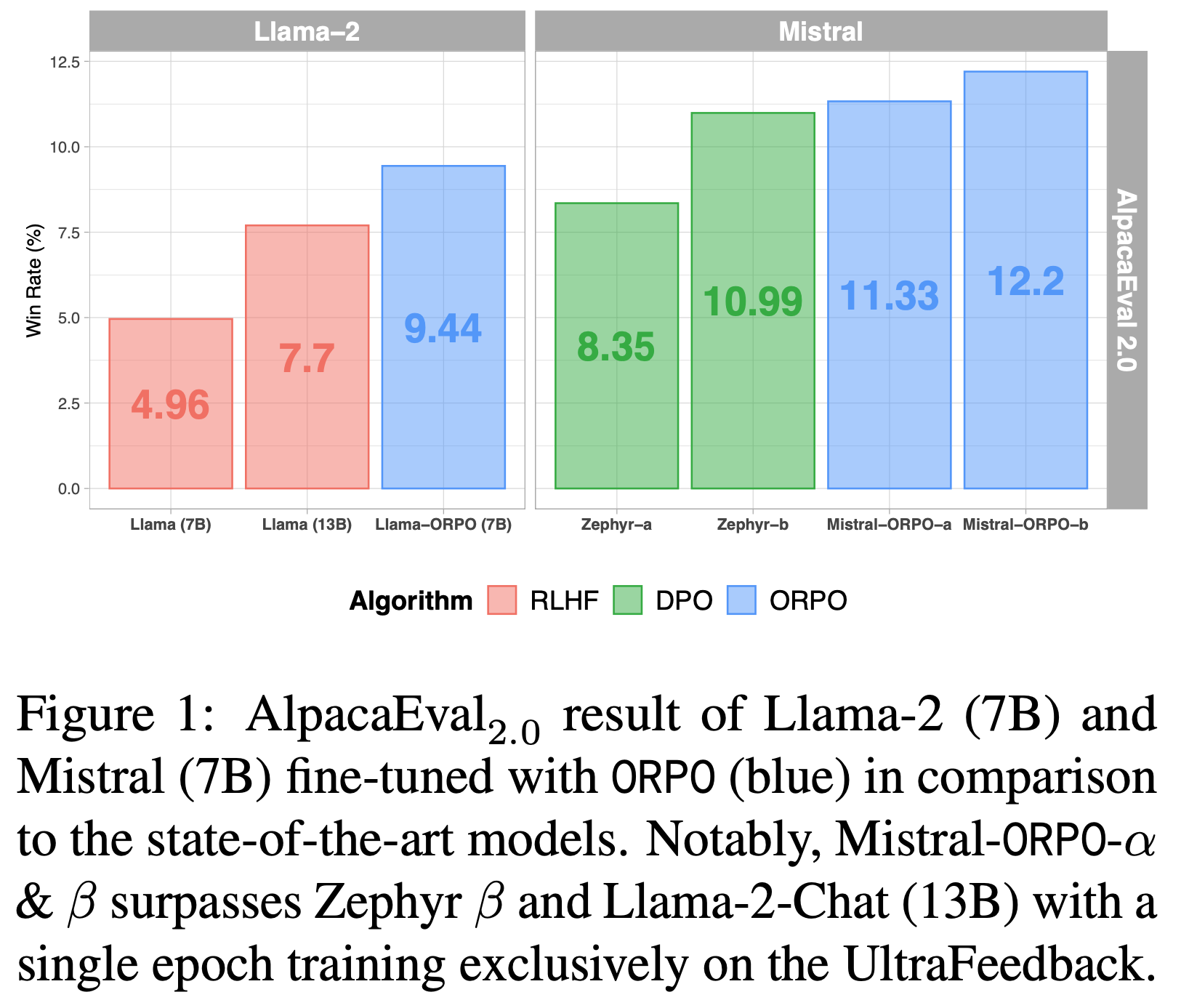
- 在 AlpacaEval$_{2.0}$ 上达到 12.20%（图1），在 IFEval（指令级宽松评估）上达到 66.19%（表 6），在 MT-Bench 上达到 7.32（图12）
论文发布了 Mistral-ORPO-$\alpha$（7B）和 Mistral-ORPO-$\beta$（7B）的代码和模型 checkpoints

Introduction and Discussion

预训练语言模型（Pre-trained Language Models, PLMs）通过大规模训练语料（如网络文本 (2020) 或教科书 (2023)）展现了在多样化自然语言处理（NLP）任务中的卓越能力 (2020; 2022; 2023)
- 但这些模型需要通过进一步调优才能适用于通用领域应用，通常通过指令微调（instruction tuning）和偏好对齐（preference alignment）等过程实现
指令微调 (2022; 2023) 训练模型遵循自然语言描述的任务，使其能够很好地泛化到未见过的任务
- 尽管模型能够遵循指令，但它们可能生成有害或不道德的输出 (2021; 2023)
- 为了进一步将这些模型与人类价值观对齐，需要使用成对偏好数据进行额外训练，例如基于人类反馈的强化学习（Reinforcement Learning from Human Feedback, RLHF）(2020; 2022) 和直接偏好优化（Direct Preference Optimization, DPO）(2023)
偏好对齐方法在多个下游任务中展现了成功，例如提升事实性 (2023)、基于代码的问答 (2022) 和机器翻译 (2023)
- 对齐算法在广泛下游任务中的多功能性凸显了理解对齐过程并进一步改进算法效率和性能的必要性
- 但现有的偏好对齐方法通常是一个多阶段过程，如图2 所示，通常需要第二个参考模型和单独的 SFT 预热阶段 (2020; 2023)
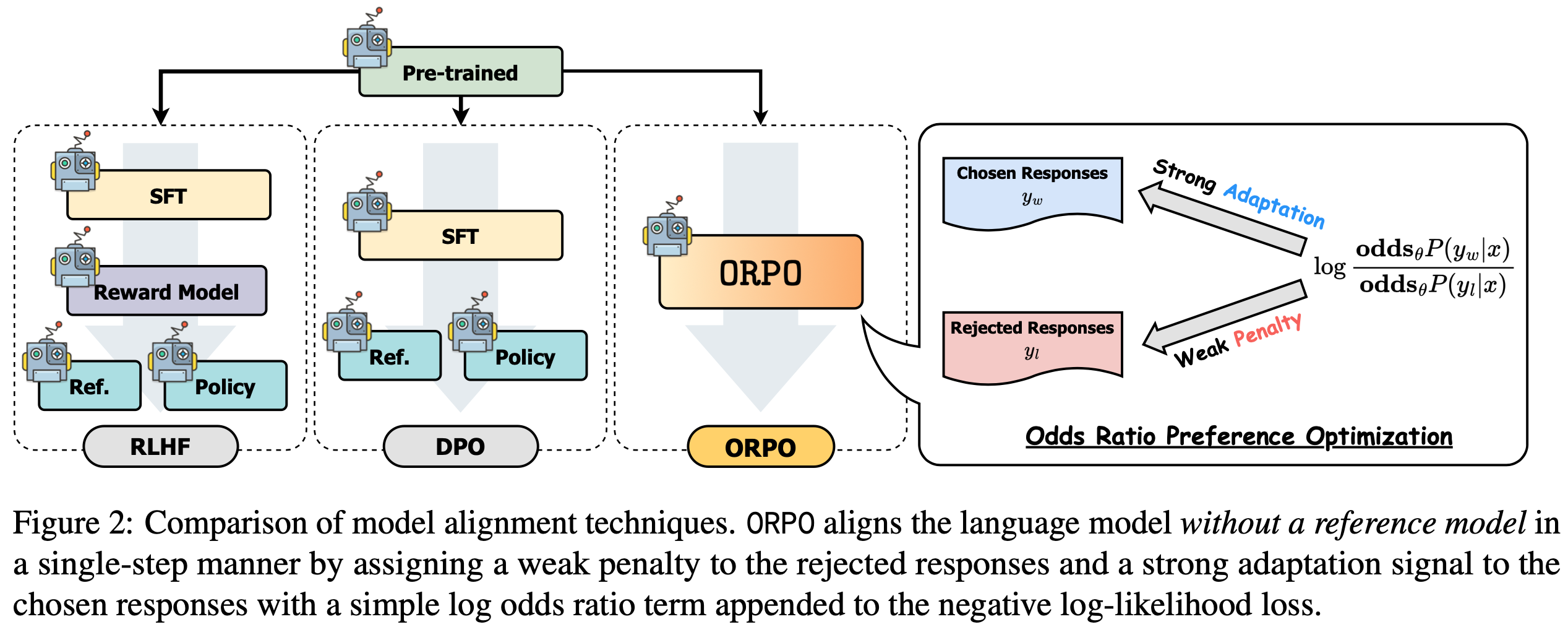
论文中，论文在第 3 节研究了成对偏好数据集中 SFT 的作用和影响，并在第 4 节提出了一种简单而新颖的对齐方法 ORPO，它能在 SFT 期间高效惩罚模型学习不期望的生成风格
与之前的工作不同，论文的方法既不需要 SFT 预热阶段 ，也不需要参考模型 ，从而实现了资源高效的偏好对齐模型开发
论文在第 6.1 和 6.2 节通过微调 Phi-2（2.7B）、Llama-2（7B）和 Mistral（7B）评估了模型对齐任务和流行排行榜的有效性
在第 6.3 节中，论文通过控制实验将 ORPO 与模型对齐的经典方法（RLHF 和 DPO）在不同数据集和模型规模上进行比较
结合第 6.4 节生成多样性的后验分析，论文在第 7.3 节中阐述了在单一偏好对齐中使用几率比的理论、实证和计算依据
论文发布了 Mistral-ORPO-$\alpha$（7B）和 Mistral-ORPO-$\beta$（7B）的训练代码和 checkpoint
这些模型在 MT-Bench 上分别达到 7.24 和 7.32，在 AlpacaEval$_{2.0}$ 上达到 11.33% 和 12.20%，在 IFEval 指令级宽松准确率上达到 61.63% 和 66.19%

The Role of Supervised Fine-tuning

论文通过分析 SFT 的损失函数以及实证研究训练后的 SFT 模型对偏好的理解能力，探讨了 SFT 作为偏好对齐方法初始阶段的作用（2020；2023）
SFT 在将预训练语言模型（PLM）适配到目标领域方面发挥了重要作用（2023a；2024），它通过增加相关 Token 的对数概率来实现这一点
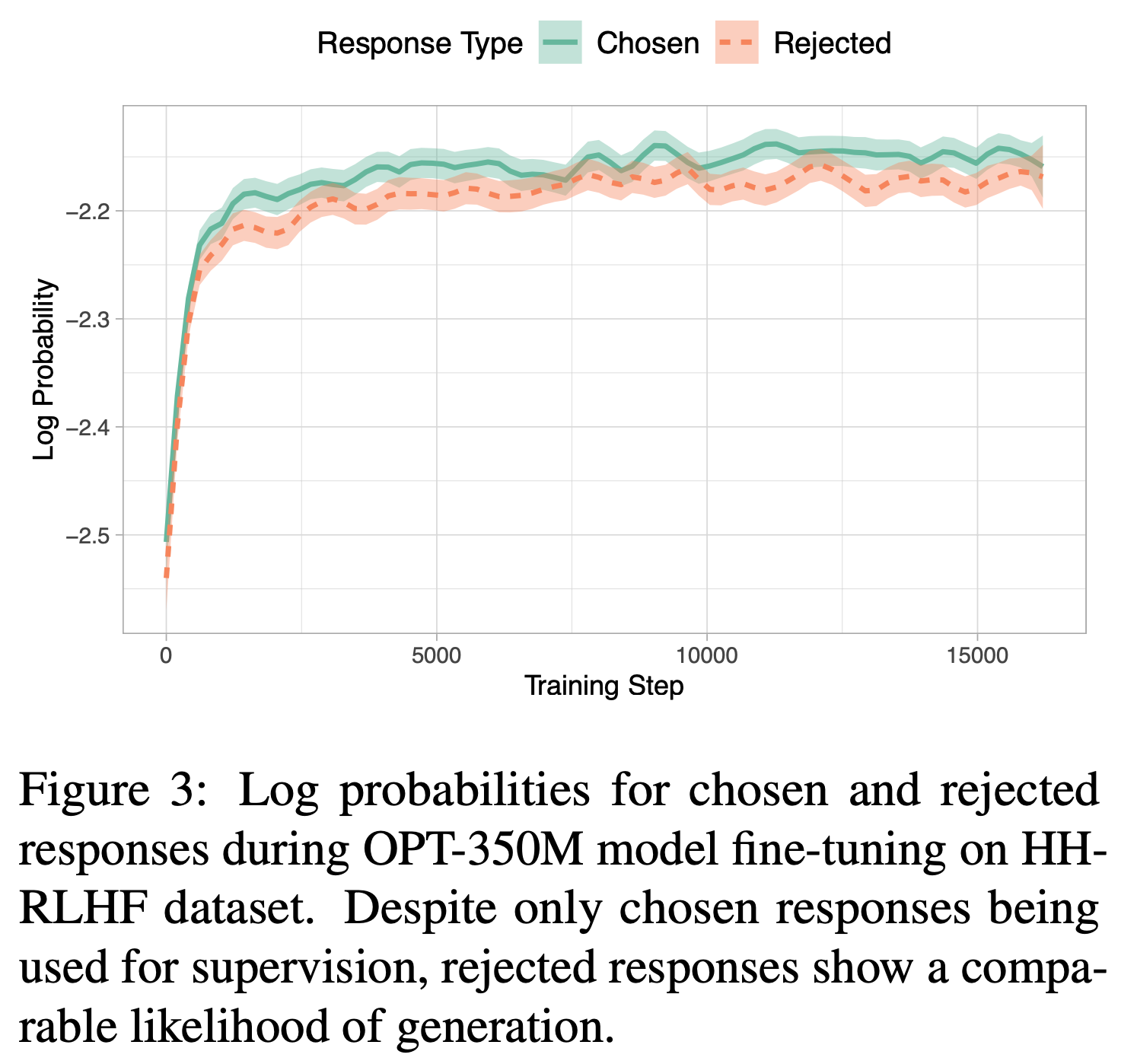
- 但这一过程也无意中提高了生成不良风格 Token 的可能性，如图3 所示
- 因此，有必要开发一种方法，能够在保留 SFT 领域适配作用的同时，识别并抑制不良生成风格

Absence of Penalty in Cross-Entropy Loss

交叉熵损失微调的目标是惩罚模型对参考答案的预测对数概率较低的情况，如公式（2）所示：
$$
\begin{align}
\mathcal{L} &= -\frac{1}{m} \sum_{k=1}^{m} \log P(\mathbf{x}^{(k)}, \mathbf{y}^{(k)}) \tag{1} \\
&= -\frac{1}{m} \sum_{k=1}^{m} \sum_{i=1}^{|V|} y_i^{(k)} \cdot \log(p_i^{(k)}) \tag{2}
\end{align}
$$
- $ y_i $ 是一个布尔值，表示词汇集 $ V $ 中的第 $ i $ 个 Token 是否为标签 Token
- $ p_i $ 表示第 $i$ 个 Token 的概率
- $ m $ 是序列长度
- 单独使用交叉熵时，由于 $ y_i $ 会被设置为0，因此对非答案 Token 的对数概率没有直接的惩罚或补偿（2017）
- 虽然交叉熵在领域适配中通常有效（2023），但在偏好对齐的视角下，它缺乏对拒绝响应的惩罚机制
  - 因此，拒绝响应中的 Token 对数概率会与选择响应中的 Token 对数概率同步增加，这是不理想的

Generalization over Both Response Styles

论文通过一项初步研究实证展示了仅使用监督微调时选择响应和拒绝响应的校准问题
论文在 HH-RLHF 数据集（2022a）上对 OPT-350M（2022）进行微调，仅使用选择响应
训练过程中，论文监测每个批次中拒绝响应的对数概率，结果如图3 所示。选择响应和拒绝响应的对数概率同时增加，这可以从两个角度解释：
- 1）交叉熵损失有效地引导模型适应目标领域（例如对话）
- 2）由于缺乏对不良生成的惩罚，拒绝响应的对数概率有时甚至高于选择响应
- 问题：为什么缺乏惩罚就会增加拒绝影响的 Token 对数概率？
- 回答：因为拒绝响应和选择响应都是相同领域的，所以概率同时增大了

Penalizing Undesired Generations

在损失函数中添加“不似然”惩罚项已被证明可以有效减少模型的不良退化特征（2019；2020）
例如，为了防止重复，可以通过在损失函数中添加 $ (1 - p_i^{(k)}) $ 项来抑制最近上下文中的不良 Token 集 $ k \in \mathcal{C}_{recent} $
受SFT中拒绝响应 Token 概率升高的启发（图3）以及抑制不良特征的有效性，论文设计了一种单步偏好对齐方法，能够动态惩罚每个查询中的不良响应，而无需手动构造拒绝 Token 集

ORPO

论文提出了一种新颖的偏好对齐算法——比值比偏好优化（Odds Ratio Preference Optimization, ORPO）
该算法在传统的负对数似然（Negative Log-Likelihood, NLL）损失基础上，引入了一个基于比值比的惩罚项，用于区分偏好响应和非偏好响应的生成风格

Preliminary

给定输入序列 $ x $，生成输出序列 $ y $（长度为 $ m $ 个 Token ）的平均对数似然如公式（3）所示。生成输出序列 $ y $ 的比值（odds）定义为公式（4）：
$$
\begin{align}
\log P_{\theta}(y|x) &= \frac{1}{m} \sum_{t=1}^{m} \log P_{\theta}(y_t | x, y_{ < t}) \tag{3} \\
\text{odds}_{\theta}(y|x) &= \frac{P_{\theta}(y|x)}{1 - P_{\theta}(y|x)} \tag{4}
\end{align}
$$
直观上，$ \text{odds}_{\theta}(y|x) = k $ 表示模型 $ \theta $ 生成输出序列 $ y $ 的可能性是不生成它的 $ k $ 倍。因此，选择响应 $ y_w $ 相对于拒绝响应 $ y_l $ 的比值比 $ \text{OR}_{\theta}(y_w, y_l) $ 表示模型 $ \theta $ 在给定输入 $ x $ 时生成 $ y_w $ 而非 $ y_l $ 的相对可能性，定义如公式（5）：
$$
\text{OR}_{\theta}(y_w, y_l) = \frac{\text{odds}_{\theta}(y_w|x)}{\text{odds}_{\theta}(y_l|x)} \tag{5}
$$

Objective Function of ORPO

ORPO 的目标函数如公式（6）所示，包含两个部分：
- 1） SFT 损失 $ \mathcal{L}_{SFT} $；
- 2）相对比值损失 $ \mathcal{L}_{OR} $
  $$
  \mathcal{L}_{ORPO} = \mathbb{E}_{(x,y_w,y_l)} \left[ \mathcal{L}_{SFT} + \lambda \cdot \mathcal{L}_{OR} \right] \tag{6}
  $$
- $ \mathcal{L}_{SFT} $ 遵循传统的因果语言建模负对数似然（NLL）损失函数，用于最大化生成参考 Token 的似然，如第3节所述
- 公式（7）中的 $ \mathcal{L}_{OR} $ 通过最大化生成偏好响应 $ y_w $ 和非偏好响应 $ y_l $ 的比值比，将对数比值比包裹在log-sigmoid函数中，使得通过增加 $ y_w $ 和 $ y_l $ 之间的对数比值比可以最小化 $ \mathcal{L}_{OR} $
  $$
  \mathcal{L}_{OR} = -\log \sigma \left( \log \frac{\text{odds}_{\theta}(y_w|x)}{\text{odds}_{\theta}(y_l|x)} \right) \tag{7}
  $$
  - 通过加权组合 $ \mathcal{L}_{SFT} $ 和 $ \mathcal{L}_{OR} $，预训练语言模型能够适配到目标领域的特定子集，同时抑制生成拒绝响应集中的内容

Gradient of ORPO

$ \mathcal{L}_{Ratio} $ 的梯度进一步证明了使用比值比损失的合理性。它包含两项：一项惩罚错误预测，另一项在选择响应和拒绝响应之间形成对比，如公式（8）所示，其中 $ d = (x, y_l, y_w) \sim D $
$$
\begin{align}
\nabla_{\theta} \mathcal{L}_{OR} &= \delta(d) \cdot h(d) \tag{8} \\
\delta(d) &= \left[ 1 + \frac{\text{odds}_{\theta} P(y_w|x)}{\text{odds}_{\theta} P(y_l|x)} \right]^{-1} \tag{9} \\
h(d) &= \frac{\nabla_{\theta} \log P_{\theta}(y_w|x)}{1 - P_{\theta}(y_w|x)} - \frac{\nabla_{\theta} \log P_{\theta}(y_l|x)}{1 - P_{\theta}(y_l|x)} \tag{10}
\end{align}
$$
当偏好响应的比值相对高于非偏好响应时，公式（9）中的 $ \delta(d) $ 会收敛到 0
- 这表明 $ \delta(d) $ 扮演了惩罚项的角色，如果模型更倾向于生成拒绝响应，则会加速参数更新
同时，公式（10）中的 $ h(d) $ 表示来自选择响应和拒绝响应的梯度的加权对比
- 具体来说，分母中的 $ 1 - P(y|x) $ 在对应似然 $ P(y|x) $ 较低时放大了梯度
- 对于选择响应，随着似然的增加，这会加速模型向选择响应分布的适配

Experimental Settings

Training Configurations

模型（Models） ：论文训练了一系列参数规模从 125M 到 1.3B 的 OPT 模型（2022），比较了 SFT，PPO，DPO，ORPO
- PPO 和 DPO 模型基于 TRL 库（2020）在 SFT 模型上进行微调
- 遵循 Rafailov 等（2023）和 Tunstall 等（2023）的方法，这些 SFT 模型在选定响应上训练了一个 epoch
- 论文在每种算法前添加“+”以作区分（例如，+DPO）
- 此外，论文还训练了 Phi-2（2.7B）（2023），这是一个在下游任务中表现优异的预训练语言模型（2023），以及 Llama-2（7B）（2023）和 Mistral（7B）（2023）
- 每种方法的详细训练配置见附录C
数据集（Datasets） ：论文在两个数据集上测试了每种训练配置和模型：
- 1）Anthropic 的 HH-RLHF（2022a）；
- 2）二值化的 UltraFeedback（2023）。论文过滤掉了 $y_w = y_l$ 或 $y_w = \emptyset$ 或 $y_l = \emptyset$ 的实例
奖励模型（Reward Models） ：论文在每个数据集上训练了 OPT-350M 和 OPT-1.3B 作为奖励模型，目标函数为公式（11）（2020）
- OPT-350M 奖励模型用于 PPO，OPT-1.3B 奖励模型用于评估微调模型的生成结果
- 在第 6 节中，论文将这些奖励模型分别称为 RM-350M 和 RM-1.3B
  $$
  -\mathbb{E}_{(x,y_l,y_w)} \left[ \log \sigma \left( r(x, y_w) - r(x, y_l) \right) \right] \tag{11}
  $$

Leaderboard Evaluation

在第 6.1 节中，论文使用 AlpacaEval1.0 和 AlpacaEval2.0（2023b）基准评估模型，将 ORPO 与官方排行榜中报告的其他指令微调模型进行比较，包括 Llama-2 Chat（7B 和 13B）（2023）以及 Zephyr $\alpha$ 和 $\beta$（2023）
类似地，在第 6.2 节中，论文使用 MT-Bench（2023）评估模型，并报告结果及官方排行榜中相同模型的分数
在 AlpacaEval1.0 中，论文使用 GPT-4（2023）作为评估器，判断训练模型的响应是否优于 text-davinci-003 生成的响应
对于 AlpacaEval2.0，论文按照默认设置使用 GPT-4-turbo，评估生成的响应是否优于 GPT-4 的响应
在 MT-Bench 中，论文使用 GPT-4 作为评估器，测试模型在多轮对话中是否能够遵循包含复杂答案的指令

Results and Analysis

在第 6.1 节和第 6.2 节中通过比较不同偏好对齐算法评估模型的通用指令遵循能力
在第 6.3 节中，论文使用 OPT 1.3B 作为奖励模型，测量 ORPO 训练模型相对于其他对齐方法的胜率
在第 6.4 节中，论文测量了 ORPO 和 DPO 训练模型的词汇多样性

Single-turn Instruction Following

Phi-2（2.7B） ：ORPO 通过仅使用 UltraFeedback 作为指令微调数据集，将预训练的 Phi-2 性能提升至超过 Llama-2 Chat 指令遵循语言模型，如表1 所示
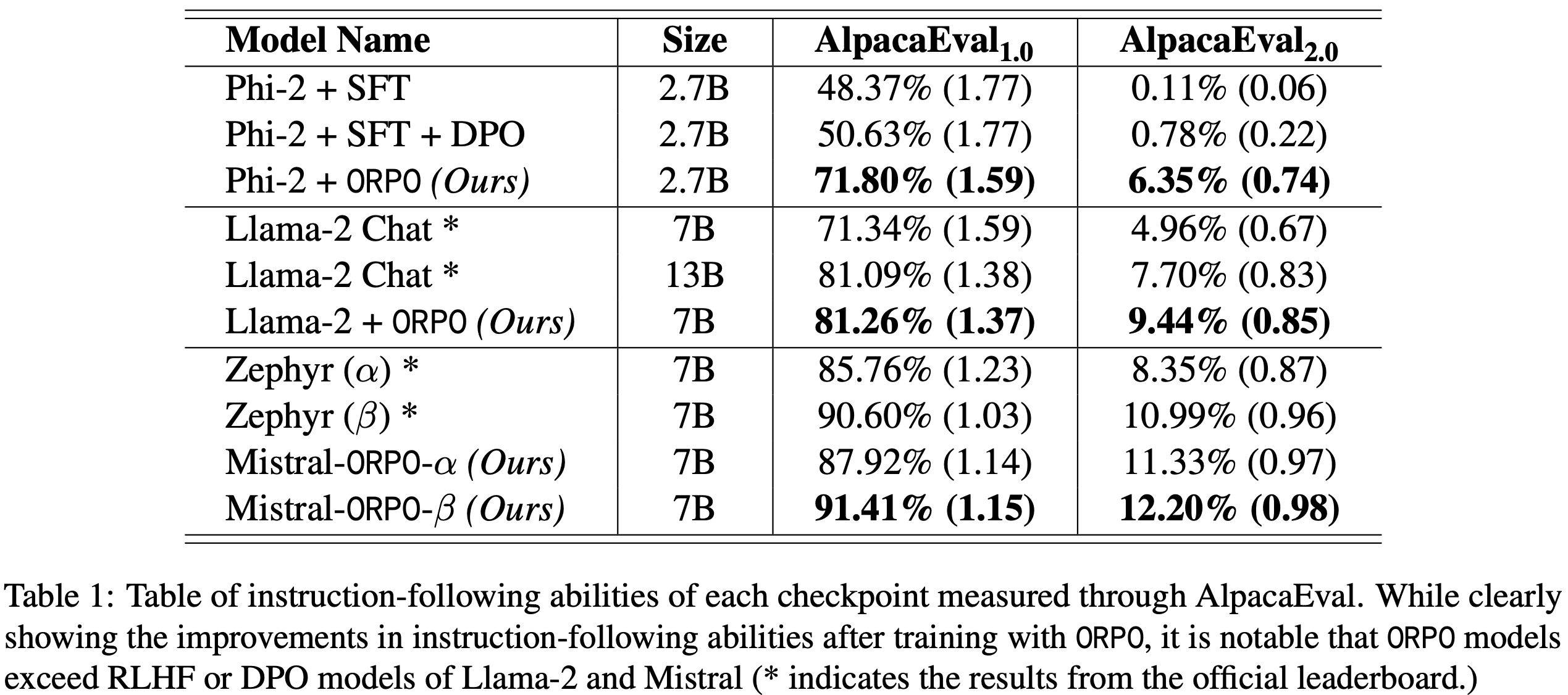
- Phi-2 的 $\lambda$ 设置为 0.25，在 AlpacaEval 中分别达到 71.80% 和 6.35%
Llama-2（7B） ：值得注意的是，UltraFeedback 和 ORPO（$\lambda = 0.2$）在 Llama-2（7B）上的 AlpacaEval 分数高于通过 RLHF 训练的 7B 和 13B 版本的聊天模型，最终在两个 AlpacaEval 中分别达到 81.26% 和 9.44%
- 相比之下，在论文的对照实验中，按照 Tunstall 等（2023）和 Rafailov 等（2023）的方法进行一个 epoch 的 SFT 和三个 epoch 的 DPO 训练后，Llama-2 + SFT 和 Llama-2 + SFT + DPO 生成的输出无法被评估
- 这支持了 ORPO 的有效性，即模型能够在有限数据下快速学习目标领域和偏好，这与论文在第 4.3 节中对方法梯度 $h(d)$ 的分析一致
Mistral-ORPO-$\alpha$（7B） ：此外，使用单轮对话数据集 UltraFeedback 和 ORPO（$\lambda = 0.1$）对 Mistral（7B）进行微调后，其性能超过了 Zephyr 系列模型
- Zephyr 是基于 Mistral（7B）的模型，通过 SFT 在 20K UltraChat（2023）和 DPO 在完整 UltraFeedback 上微调得到
- 如表1 所示，Mistral-ORPO-$\alpha$（7B）在 AlpacaEval2.0 中达到 87.92% 和 11.33%，分别超过 Zephyr $\alpha$ 1.98% 和 Zephyr $\beta$ 0.34%。样本响应及 GPT-4 的参考响应见附录I
Mistral-ORPO-$\beta$（7B） ：使用与 Mistral-ORPO-$\alpha$（7B）相同的配置，论文进一步比较了在清洗版 UltraFeedback 上微调的 Mistral，以展示数据质量的影响
- 虽然数据集的实际规模相近，但 ORPO 从数据质量中获得了额外优势，在 AlpacaEval 中得分超过 91% 和 12%，如表1 所示
- 关于两个 Mistral 模型在 IFEval（2023c）上的指令遵循评估结果见附录D

Multi-turn Instruction Following

使用论文的最佳模型 Mistral-ORPO-$\alpha$（7B）和 Mistral-ORPO-$\beta$（7B），论文还通过 MT-Bench 评估了模型在确定性答案（如数学问题）上的多轮指令遵循能力
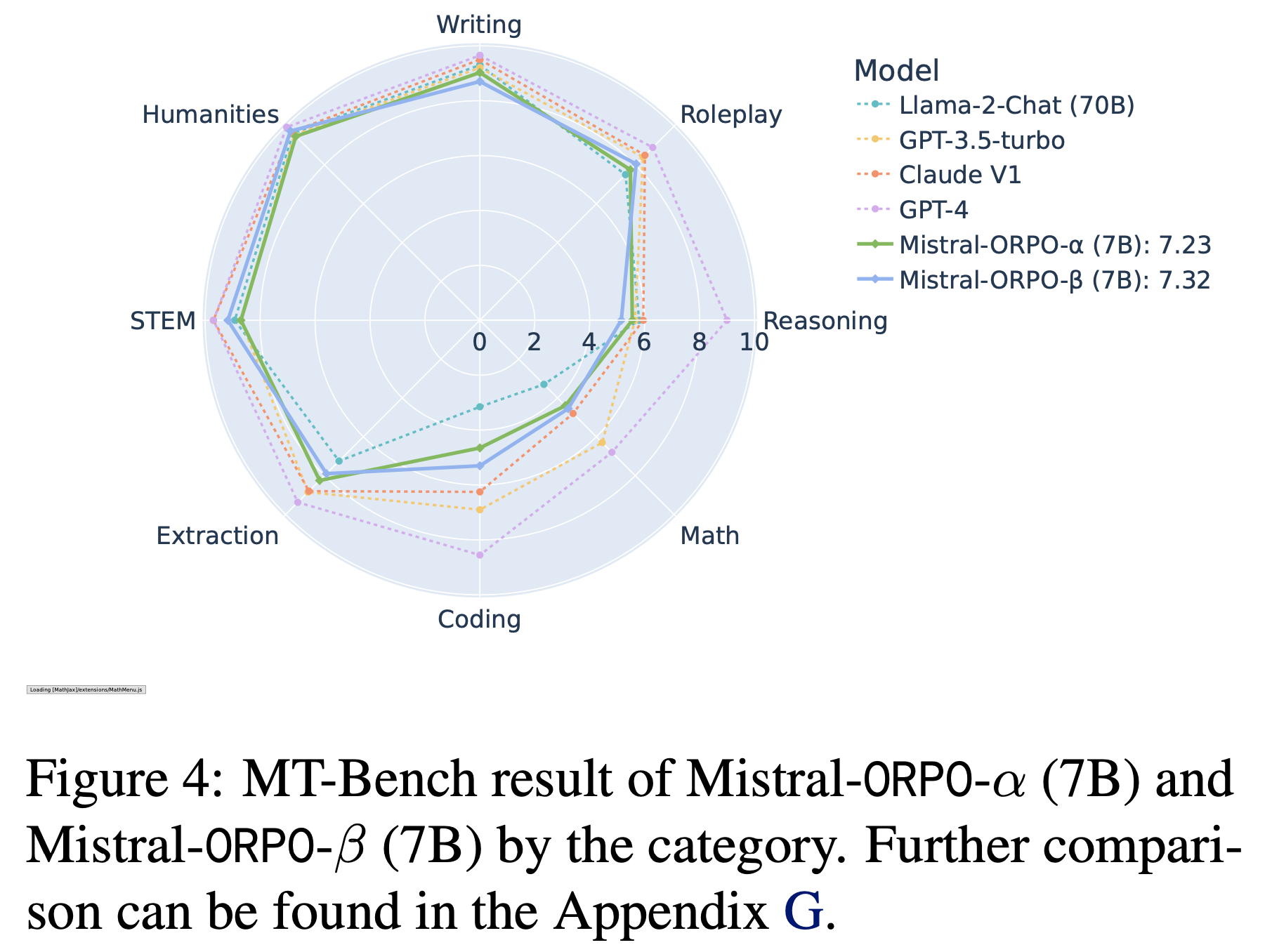
如图4 所示，ORPO-Mistral（7B）系列的结果与更大规模或专有模型（如 Llama-2-Chat（70B）和 Claude）相当。最终，Mistral-ORPO-$\alpha$（7B）和 Mistral-ORPO-$\beta$（7B）在训练期间未接触多轮对话数据集的情况下，在 MT-Bench 中分别获得 7.23 和 7.32 分

Reward Model Win Rate

论文使用 RM-1.3B 评估 ORPO 相对于其他偏好对齐方法（包括 SFT、PPO 和 DPO）的胜率，以理解 ORPO 的有效性和可扩展性（表2 和表3）。此外，论文通过可视化验证 ORPO 能够有效提升预期奖励（图5）
HH-RLHF ：在表2 中，ORPO 在所有模型规模上均优于 SFT 和 PPO。模型规模越大，ORPO 对 SFT 和 PPO 的最高胜率分别为 78.0% 和 79.4%。同时，ORPO 对 DPO 的胜率与模型规模相关，最大模型的胜率最高（70.9%）
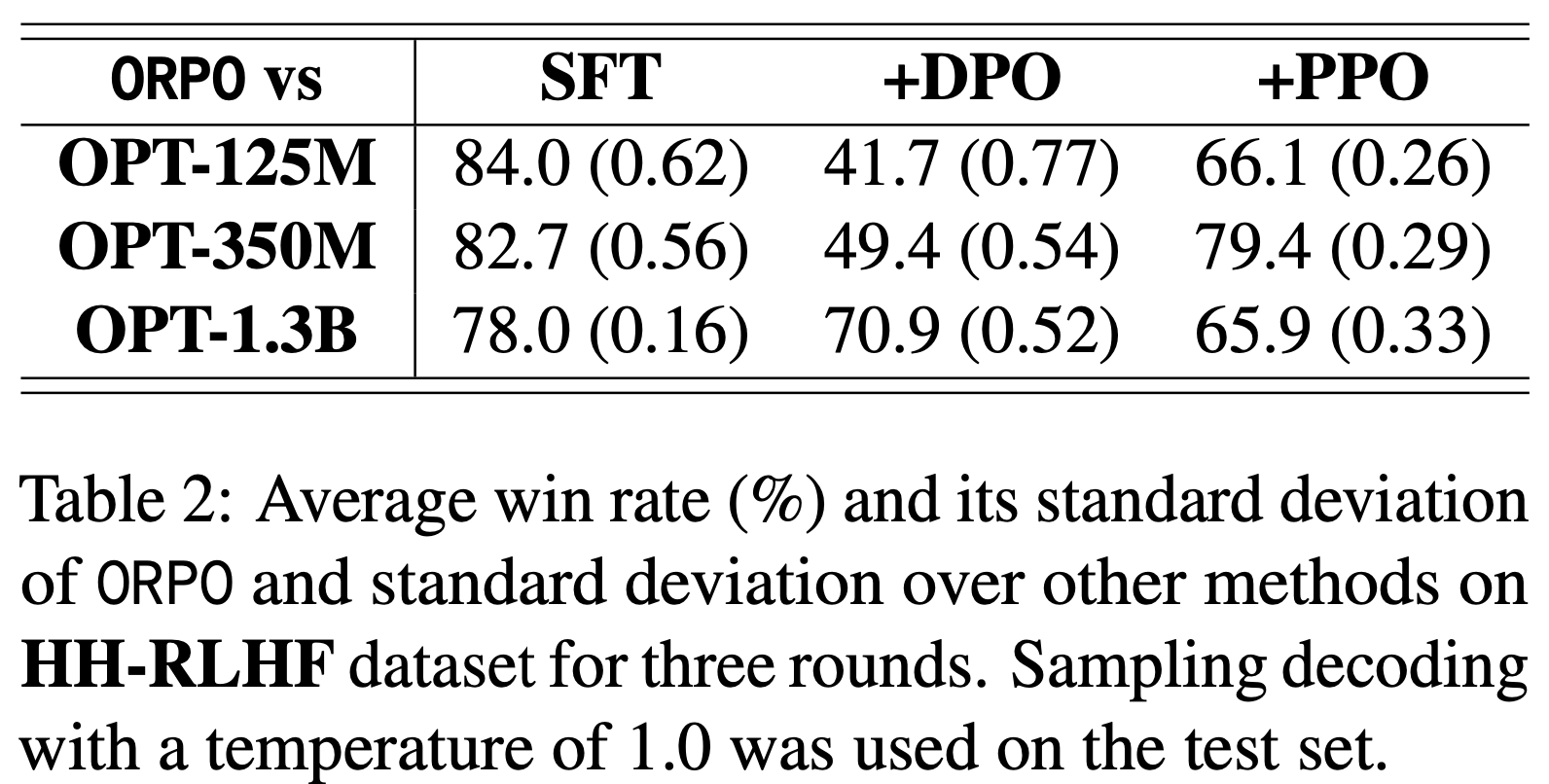
- 问题：在小模型上的胜率不如 DPO？为什么 DPO 在小模型上胜率如此之好？是不是超参数没调好
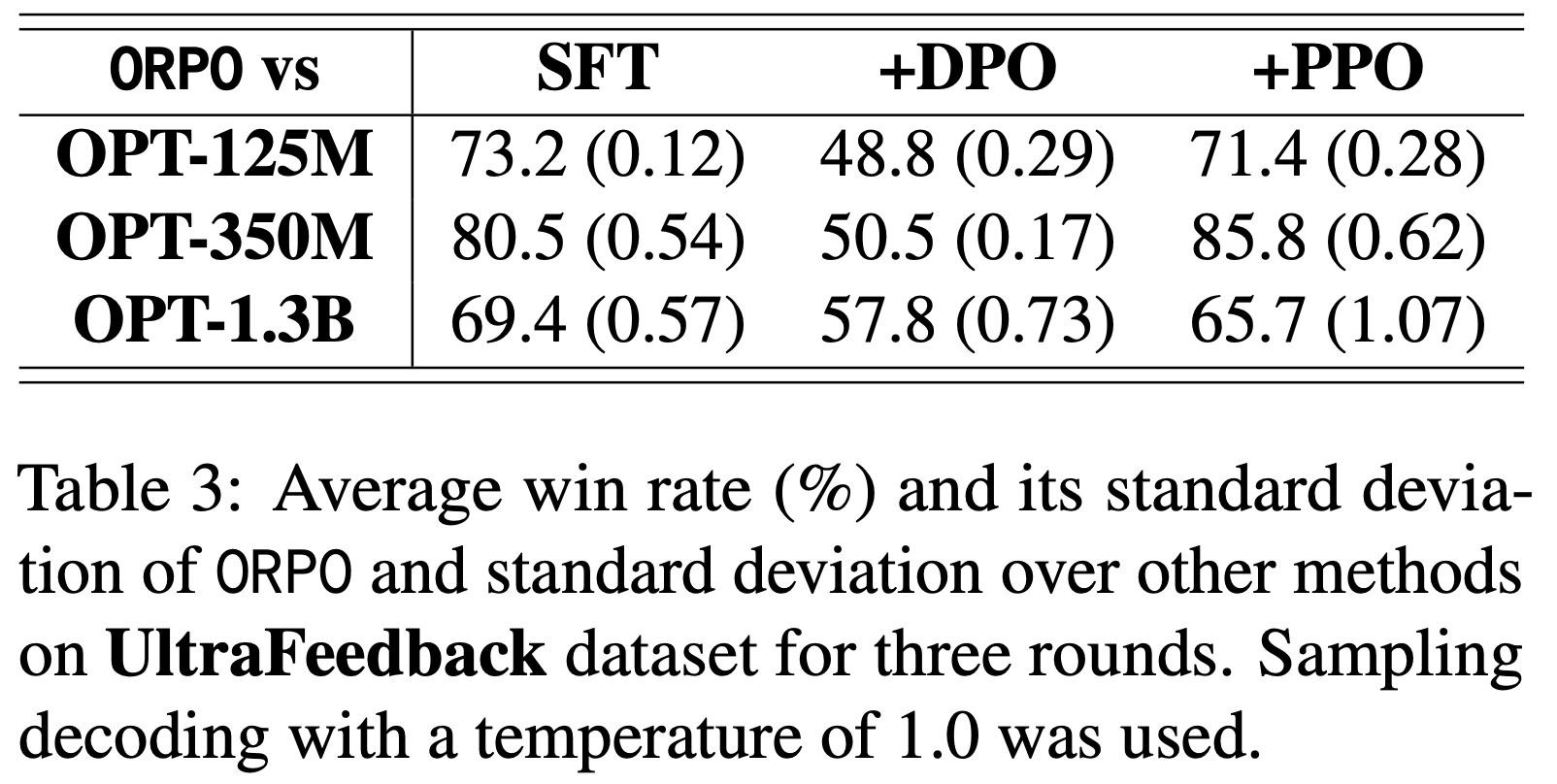
UltraFeedback ：UltraFeedback 中的胜率趋势与 HH-RLHF 报告的结果相似（表3）。ORPO 对 SFT 和 PPO 的最高胜率分别为 80.5% 和 85.8%。虽然 ORPO 始终优于 SFT 和 PPO，但对 DPO 的胜率随着模型规模的增加而逐步提升。这种规模趋势将在第 6.1 节中通过 2.7B 模型进一步展示
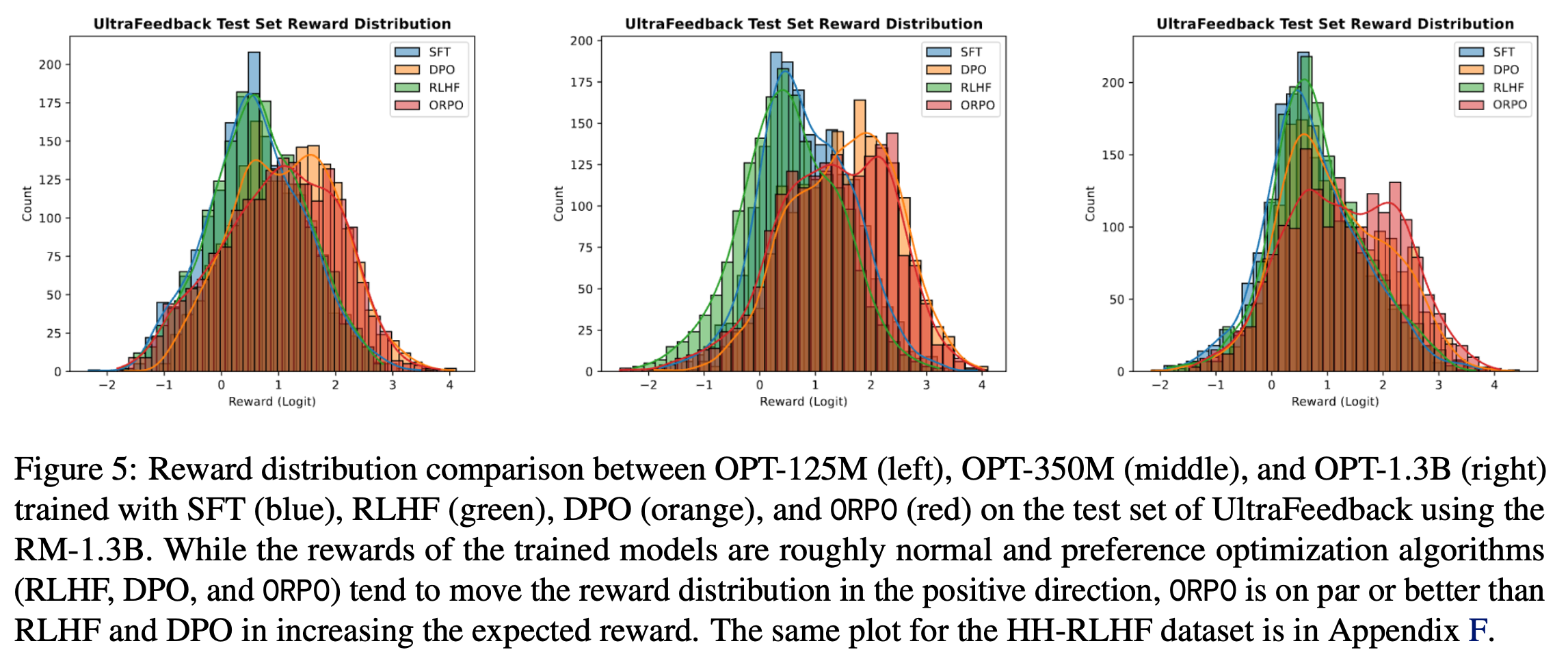
整体奖励分布（Overall Reward Distribution） ：除了胜率外，论文还比较了 UltraFeedback 数据集测试集上生成响应的奖励分布（图5）和 HH-RLHF 数据集的奖励分布（附录F）
- 以 SFT 奖励分布为基准，PPO、DPO 和 ORPO 在两个数据集中均对其进行了调整。然而，每种算法的奖励调整幅度不同
在图5 中，RLHF（即 SFT + PPO）的分布具有一些异常特性，预期奖励较低
- 论文将其归因于 RLHF 的不稳定性和奖励不匹配问题（2023；2022；2023），因为 RLHF 模型使用 RM-350M 训练，而评估使用 RM-1.3B
- 值得注意的是，ORPO 分布（红色）主要位于每个子图的右侧，表明其预期奖励更高
- 结合偏好对齐方法的目标，图5 中的分布表明 ORPO 在所有模型规模上均能有效实现偏好对齐的目标

Lexical Diversity

先前的研究（2024）探讨了偏好对齐语言模型的词汇多样性
论文通过使用 Gemini-Pro（Gemini 团队等，2023）作为嵌入模型扩展了 Kirk 等（2024）提出的 单输入多样性（Per Input Diversity，PID） 和 跨输入多样性（Across Input Diversity，AID） 概念
给定一组采样响应，多样性度量定义为公式（13）：

$$
\mathcal{O}_{\theta}^{i} := \{y_j \sim \theta(y|x_i) | j = 1, 2, …, K\} \tag{12}
$$

$$
D(\mathcal{O}_{\theta}^{i}) = \frac{1}{2} \cdot \frac{\sum_{i=1}^{N-1} \sum_{j=i+1}^{N} \cos(h_i, h_j)}{N \cdot (N-1)} \tag{13}
$$

其中，$\cos(h_i, h_j)$ 表示嵌入 $h_i$ 和 $h_j$ 之间的余弦相似度
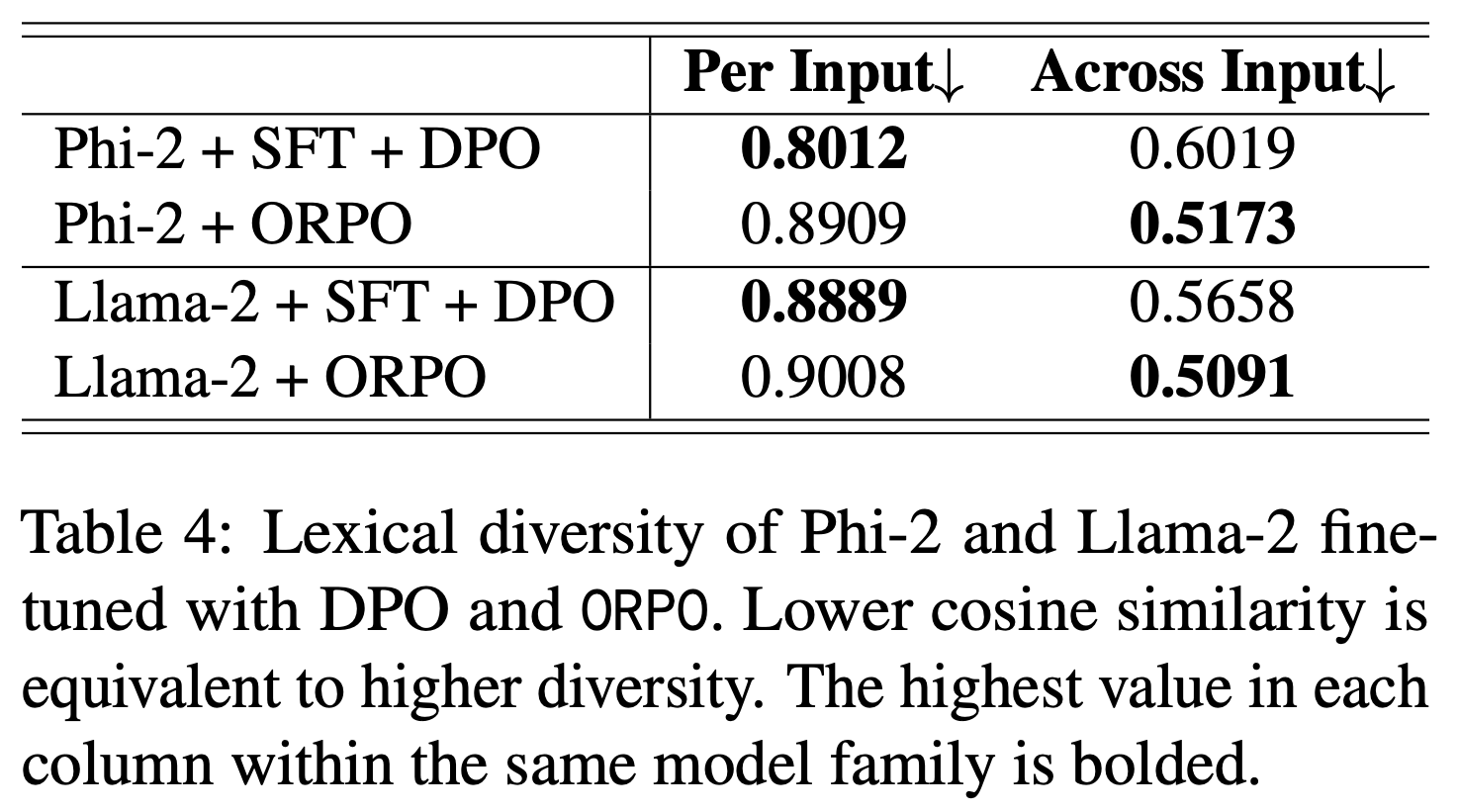
论文在 AlpacaEval 的 160 个查询中采样了 5 个不同的响应（即 $K=5, N=160$），使用 ORPO 和 DPO 训练的 Phi-2 和 Llama-2 模型，结果如表4 所示
单输入多样性（Per Input Diversity，PID）
- 论文通过公式（14）计算输入间生成样本的平均余弦相似度，评估单输入多样性。在表4 中，ORPO 模型在第一列中的平均余弦相似度最高，表明其单输入多样性最低。这说明 ORPO 通常为期望的 token 分配高概率，而 DPO 的 logit 分布相对平滑
  $$
  \text{PID}_{D}(\theta) = \frac{1}{N} \sum_{i=1}^{N} D(\mathcal{O}_{\theta}^{i}) \tag{14}
  $$
跨输入多样性（Across Input Diversity，AID）
- 论文为每个输入采样第一个响应，并通过公式（15）计算其间的余弦相似度，评估跨输入多样性
- 与单输入多样性不同，值得注意的是，Phi-2（ORPO）在表4 的第二行中平均余弦相似度较低
- 我们可以推断，ORPO 促使模型生成更多与指令相关的响应，而 DPO 则相对泛化
  $$
  \text{AID}_{D}(\theta) = D\left( \bigcup_{i=1}^{N} \mathcal{O}_{\theta,j=1}^{i} \right) \tag{15}
  $$

Discussion

在本节中，论文详细阐述了 ORPO 的理论和计算细节
ORPO 的理论分析将在第 7.1 节中讨论，并通过第 7.2 节的实证分析加以支持
论文在第 7.3 节中比较了 DPO 和 ORPO 的计算负载

Comparison to Probability Ratio

选择几率比（odds ratio）而非概率比（probability ratio）的原因在于其稳定性。给定输入序列 $ x $，生成偏好响应 $ y_w $ 相对于非偏好响应 $ y_l $ 的概率比可以定义为：
$$
\textbf{PR}_{\theta}(y_w, y_l) = \frac{P_{\theta}(y_w|x)}{P_{\theta}(y_l|x)} \tag{16}
$$
虽然这一公式在先前需要 SFT 前置的偏好对齐方法中已被使用 (2023; 2023)，但在将偏好对齐融入 SFT 的场景中，几率比是更优的选择，因为它对模型偏好理解的敏感性更高
- 换句话说，概率比会导致对非偏好响应的极端区分，而几率比则更为温和
论文通过采样分布可视化这一点
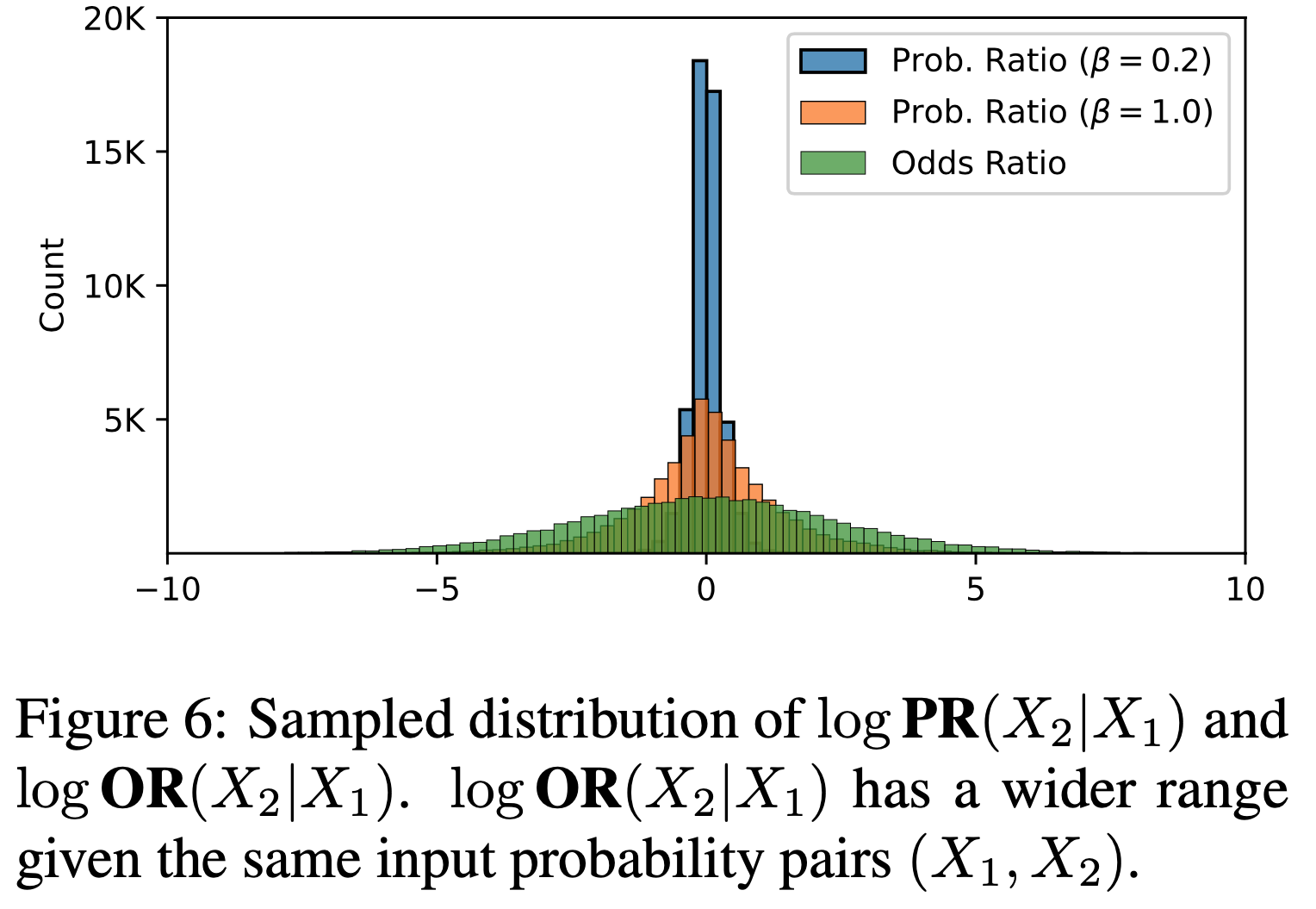
- 从均匀分布 $ X_1, X_2 \sim \text{Unif}(0,1) $ 中采样 50,000 个样本，并绘制对数概率比 $ \log \textbf{PR}(X_2|X_1) $ 和对数几率比 $ \log \textbf{OR}(X_2|X_1) $ 的分布，如图6 所示
- 概率比乘以系数 $ \beta $（如概率比方法中的常见做法），并报告 $ \beta = 0.2 $ 和 $ \beta = 1.0 $ 的情况
回想一下，对数 sigmoid 函数被应用于对数概率比和对数几率比，每种比例的尺度决定了在损失最小化时偏好与非偏好风格之间的预期边际
- 从这个意义上说，当输入 $ \textbf{PR}(X_2|X_1) $ 而非 $ \textbf{OR}(X_2|X_1) $ 到对数 sigmoid 函数时，为了最小化损失，对比需要相对极端
- 考虑到 $ \log \textbf{PR}(X_2|X_1) $ 的尖锐分布（如图6 所示），这种过度对比可能导致在融入 SFT 的场景中，对非偏好响应的 token 对数概率的过度抑制，从而引发退化问题

最小化 $ \mathcal{L}_{OR} $

论文证明了通过 ORPO 训练的模型能够在整个训练过程中反映偏好
论文监测了偏好和非偏好响应的对数概率以及对数几率比（$ \lambda = 1.0 $）
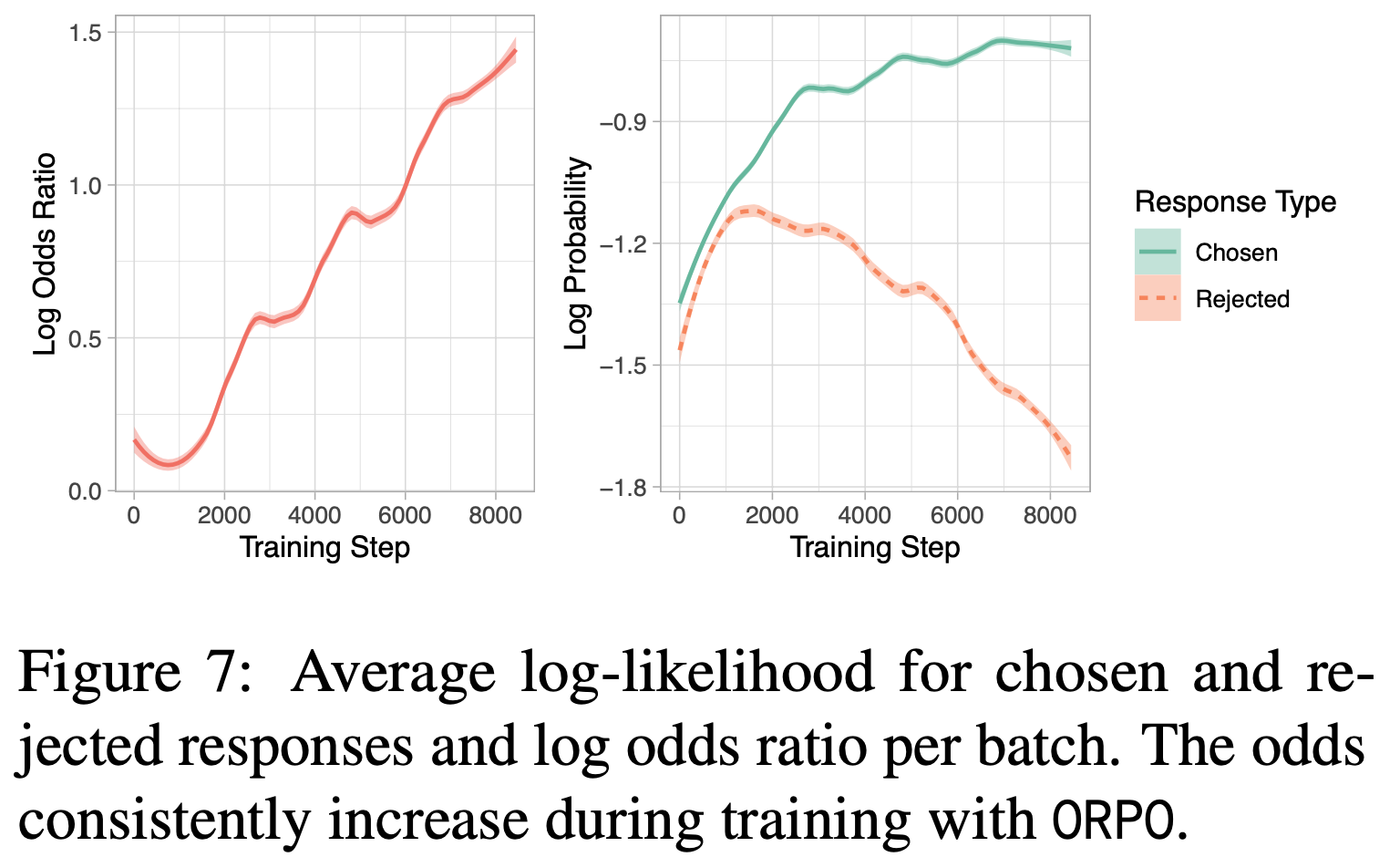
使用与图3 相同的数据集和模型，图7 显示，随着对数几率比的增加，非偏好响应的对数概率逐渐降低，而偏好响应的对数概率与图3 相当
这表明 ORPO 在保留 SFT 领域适应作用的同时，通过惩罚项 $ \mathcal{L}_{OR} $ 诱导模型降低非偏好生成的可能性
论文在附录E 中讨论了 $ \lambda $ 的影响，研究了偏好与非偏好响应之间对数概率边际随 $ \lambda $ 变化的趋势

Computational Efficiency

如图2 所示，ORPO 不需要参考模型（reference model），这与 RLHF 和 DPO 不同。从这个意义上说，ORPO 在两个方面比 RLHF 和 DPO 更具计算效率：
- 1）内存分配；
- 2）每批次的 FLOPs 更少
在 RLHF 和 DPO 的上下文中，参考模型 $ \pi_{SFT} $ 表示通过 SFT 训练的模型，它将作为 RLHF 或 DPO 更新参数的基线模型 (2020; 2023)
- 因此，在训练过程中需要两个 $ \pi_{SFT} $：一个冻结的参考模型和一个正在调优的模型
此外，理论上，每个模型需要两次前向传播来计算偏好和非偏好响应的 logits
- 换句话说，每个批次总共需要进行四次前向传播
- 而 ORPO 不需要参考模型，因为 $ \pi_{SFT} $ 是直接更新的
- 这使得训练期间每个批次所需的前向传播次数减少了一半

Limitations

尽管论文对包括 DPO 和 RLHF 在内的多种偏好对齐方法进行了全面分析，但并未涵盖更广泛的偏好对齐算法
论文将与其他方法的更广泛比较以及将论文的方法扩展到 7B 以上模型作为未来工作
此外，论文计划将微调数据集扩展到更多领域和质量水平，从而验证论文的方法在各种 NLP 下游任务中的通用性
最后，作者希望研究论文的方法对预训练语言模型的内部影响，将偏好对齐过程的理解扩展到不仅包括监督微调阶段，还包括后续的偏好对齐算法

Alignment with RL

基于人类反馈的强化学习（RLHF）通常应用 Bradley-Terry 模型 (1952) 来估计两个独立评估实例之间成对竞争的概率
训练一个额外的奖励模型来评分实例，并使用近端策略优化（Proximal Policy Optimization, PPO）(2017) 等强化学习算法训练模型以最大化所选响应的奖励模型分数，从而得到基于人类偏好训练的语言模型 (2020; 2022)
值得注意的是，(2022) 证明了 RLHF 对指令遵循语言模型的可扩展性和多功能性
扩展方法如基于语言模型反馈的强化学习（RLAIF）可能是人类反馈的可行替代方案 (2022; 2023)
但由于 PPO 的不稳定性 (2023) 和奖励模型的敏感性 (2022; 2024)，RLHF 面临广泛的超参数搜索挑战。因此，开发稳定的偏好对齐算法至关重要

Alignment without Reward Model

一些偏好对齐技术避免了强化学习的需要 (2023; 2023; 2023; 2024)
(2023) 提出了直接策略优化（DPO），将奖励建模阶段合并到偏好学习阶段
(2023) 通过恒等偏好优化（Identity Preference Optimization, IPO）防止了 DPO 中潜在的过拟合问题
(2024) 和 (2023) 分别提出了卡尼曼-特沃斯基优化（KTO）和统一语言模型对齐（ULMA），这些方法不需要成对偏好数据集，与 RLHF 和 DPO 不同
(2023) 进一步建议将参考响应集的 softmax 值合并到负对数似然损失中，以融合监督微调和偏好对齐

Alignment with Supervised Fine-tuning

RL 中的偏好对齐方法通常利用 SFT 来确保活动策略相对于旧策略的稳定更新 (2017)
这是因为在 RLHF 的上下文中，SFT 模型是旧策略 (2020)
此外，实证结果表明，即使在非 RL 对齐方法中，SFT 模型对于实现期望结果的收敛也至关重要 (2023; 2023)
相比之下，也有通过仅使用过滤数据集进行 SFT 来构建人类对齐语言模型的方法 (2023; 2023; 2024; 2023)
(2023) 表明，通过细粒度过滤和精心策划的小规模数据进行的 SFT 足以构建有用的语言模型助手
此外，(2023) 和 (2024) 提出了一种迭代过程，通过细粒度选择对齐生成后，用其自身生成进一步微调监督微调的语言模型，(2023) 提出偏好数据集的策划子集足以实现对齐
尽管这些工作强调了 SFT 在对齐中的影响和重要性，但 SFT 的实际作用以及将偏好对齐纳入 SFT 的理论背景仍未得到充分研究

附录A 基于比值比（Odds Ratio）的 $\nabla_\theta \mathcal{L}_{OR}$ 推导

假设 $g(x, y_l, y_w) = \frac{\text{odds}_\theta P(y_w|x)}{\text{odds}_\theta P(y_l|x)}$，则：
$$
\begin{align}
\nabla_\theta \mathcal{L}_{OR} &= \nabla_\theta \log \sigma \left( \log \frac{\text{odds}_\theta P(y_w|x)}{\text{odds}_\theta P(y_l|x)} \right)
\tag{20} \\
&= \frac{\sigma’ (\log g(x, y_l, y_w))}{\sigma (\log g(x, y_l, y_w))}
\tag{21} \\
&= \sigma (-\log g(x, y_l, y_w)) \cdot \nabla_\theta \log g(x, y_l, y_w)
\tag{22} \\
&= \frac{\sigma (-\log g(x, y_l, y_w))}{g(x, y_l, y_w)} \cdot \nabla_\theta g(x, y_l, y_w)
\tag{23} \\
&= \sigma (-\log g(x, y_l, y_w)) \cdot \nabla_\theta \log g(x, y_l, y_w)
\tag{24} \\
&= \left( 1 + \frac{\text{odds}_\theta P(y_w|x)}{\text{odds}_\theta P(y_l|x)} \right)^{-1} \cdot \nabla_\theta \log \frac{\text{odds}_\theta P(y_w|x)}{\text{odds}_\theta P(y_l|x)}
\tag{25}
\end{align}
$$
在公式 (25) 中，剩余的导数可通过替换 $\text{odds}_\theta(y|x)$ 中的 $1 - P_\theta(y|x)$ 项进一步简化（其中 $P(y|x) = \prod_{t=1}^N P_\theta(y_t|x, y_{ < t})$）：
$$
\begin{align}
\nabla_\theta \log (1 - P_\theta(y|x)) &= \frac{\nabla_\theta (1 - P_\theta(y|x))}{1 - P_\theta(y|x)}
\tag{26}\\
&= -\frac{\nabla_\theta P_\theta(y|x)}{1 - P_\theta(y|x)}
\tag{27}\\
&= -\frac{P_\theta(y|x)}{1 - P_\theta(y|x)} \cdot \nabla_\theta \log P_\theta(y|x)
\tag{28}\\
&= \text{odds}_\theta(y|x) \cdot \nabla_\theta \log P_\theta(y|x)
\tag{29}\\
\nabla_\theta \log \frac{\text{odds}_\theta P(y_w|x)}{\text{odds}_\theta P(y_l|x)} &= \nabla_\theta \log \frac{P_\theta(y_w|x)}{P_\theta(y_l|x)} - \left( \nabla_\theta \log(1 - P_\theta(y_w|x)) - \nabla_\theta \log(1 - P_\theta(y_l|x)) \right)
\tag{30}\\
&= (1 + \text{odds}_\theta P(y_w|x)) \nabla_\theta \log P_\theta(y_w|x) - (1 + \text{odds}_\theta P(y_l|x)) \nabla_\theta \log P_\theta(y_l|x)
\tag{31}
\end{align}
$$
因此，$\nabla_\theta \mathcal{L}_{OR}$ 的最终形式为：
$$
\begin{align}
\nabla_\theta \mathcal{L}_{OR} &= \frac{1 + \text{odds}_\theta P(y_w|x)}{1 + \frac{\text{odds}_\theta P(y_w|x)}{\text{odds}_\theta P(y_l|x)} } \cdot \nabla_\theta \log P_\theta(y_w|x) - \frac{1 + \text{odds}_\theta P(y_l|x)}{1 + \frac{\text{odds}_\theta P(y_w|x)}{\text{odds}_\theta P(y_l|x)} } \cdot \nabla_\theta \log P_\theta(y_l|x)
\tag{32}\\
&= \left( 1 + \frac{\text{odds}_\theta P(y_w|x)}{\text{odds}_\theta P(y_l|x)} \right)^{-1} \cdot \left( \frac{\nabla_\theta \log P_\theta(y_w|x)}{1 - P(y_w|x)} - \frac{\nabla_\theta \log P_\theta(y_l|x)}{1 - P(y_l|x)} \right)
\tag{33}
\end{align}
$$

附录B 概率比（Probability Ratio）与比值比（Odds Ratio）的消融实验

本部分延续第7.1节的讨论，通过实验比较在 UltraFeedback 数据集上使用概率比和比值比训练时，模型对优选和非优选响应对数概率的影响
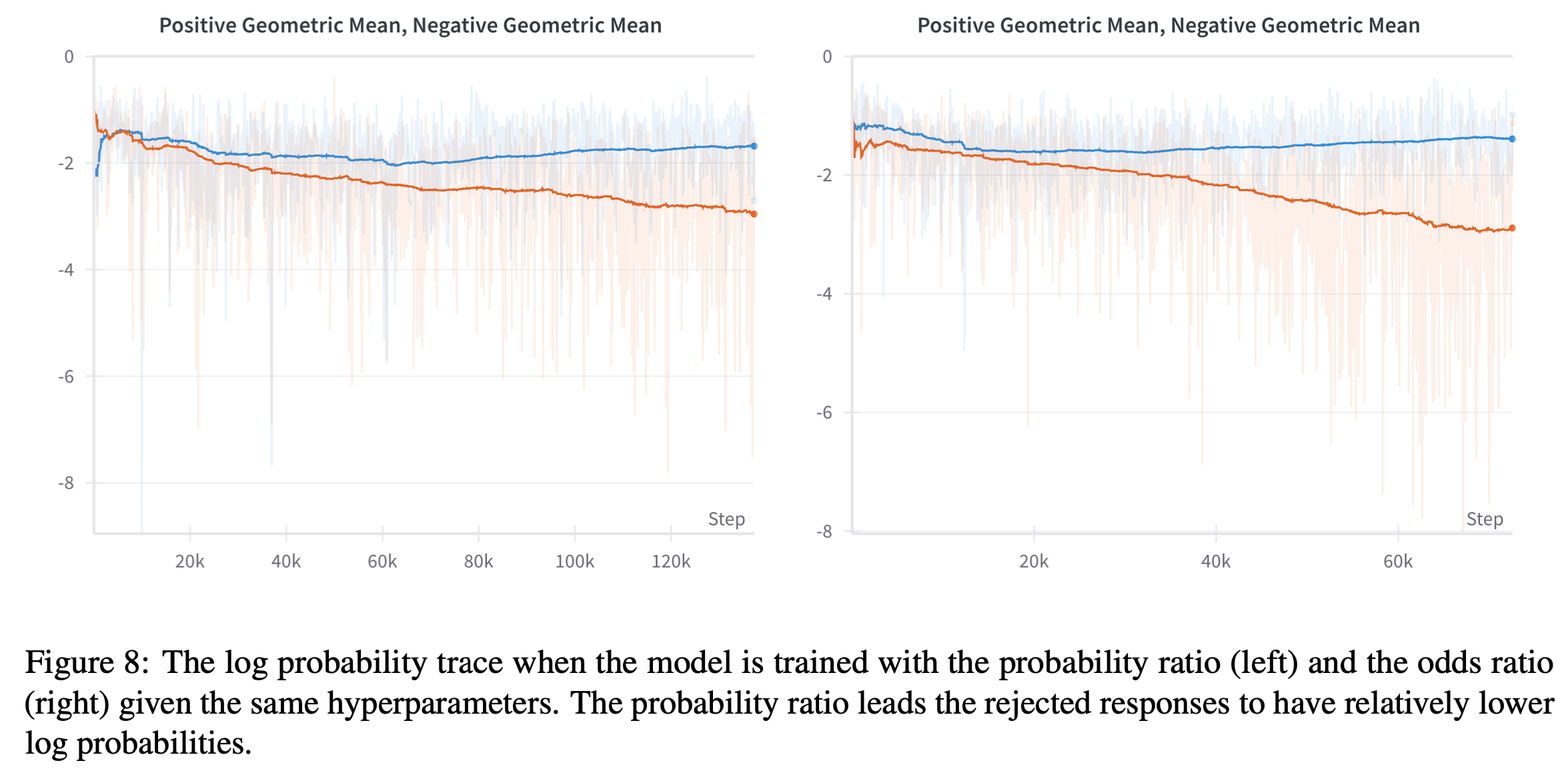
如第7.1节所述，概率比预计会以更大的幅度降低非优选响应的对数概率
图8展示了这一现象：使用概率比训练时（左图），非优选响应的对数概率迅速降至-4以下（问题：没看出来）；而使用比值比时（右图），过拟合后才会出现类似现象

附录C 实验细节

所有预训练模型均采用 Flash-Attention 2（2023）以提升计算效率。具体配置如下：
硬件：
- OPT系列和 Phi-2（2.7B）使用 DeepSpeed ZeRO 2（2020）；
- Llama-2（7B）和 Mistral（7B）使用 Fully Sharded Data Parallel（FSDP）（2023）
- 7B 和 2.7B 模型分别在 4块和 2块 NVIDIA A100 上训练
- 其余模型使用 4块 NVIDIA A6000
优化器 ：采用 AdamW（2019）或分页AdamW（2023），学习率使用线性预热与余弦衰减策略
输入长度 ：HH-RLHF 和 UltraFeedback 数据集分别截断或填充至 1024 和 2048 个 Token
- 为确保模型充分学习生成合理响应，过滤了提示超过 1024 Token 的样本

SFT

最大学习率设为 1e-5，训练 epoch 为 1（遵循2023年的研究）

RLHF

UltraFeedback 的超参数见表5。HH-RLHF 数据集的输出最小和最大长度分别设为64和256

DPO

$\beta$ 设为0.1，学习率5e-6，训练 3个 epoch ，根据验证损失选择最佳模型（通常前两个 epoch 表现最佳）

ORPO

最大学习率设为 8e-6，训练 10个 epoch ，基于验证损失选择最佳模型（适用于 OPT 系列、Phi-2 和 Llama-2）

附录D Mistral-ORPO-$\alpha$ 和 Mistral-ORPO-$\beta$ 的 IFEval 结果

除第6.1节的 AlpacaEval 结果外，表6展示了 Mistral-ORPO-$\alpha$ 和 Mistral-ORPO-$\beta$ 在 IFEval（2023）上的表现（使用2023年的代码计算）

附录E 权重值 $\lambda$ 的消融实验

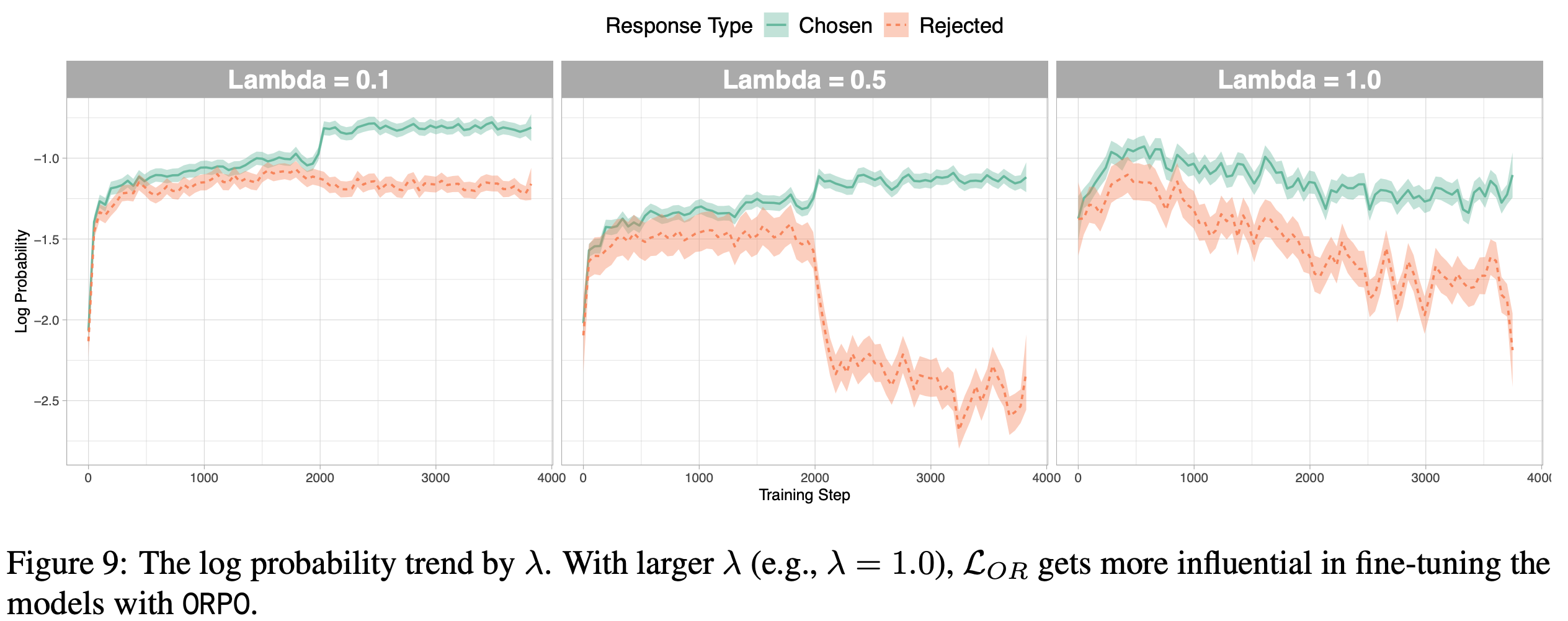
针对公式6中的权重值 $\lambda$，论文以 Mistral（7B）和 UltraFeedback 为基础，对 $\lambda \in \{0.1, 0.5, 1.0\}$ 进行消融研究

E.1 对数概率趋势

图9显示，较大的 $\lambda$（如1.0）会增强 $\mathcal{L}_{OR}$ 在微调中的影响力。具体表现为：
- $\lambda = 0.1$：优选和非优选响应的对数概率保持接近
- $\lambda = 0.5$：优选响应的对数概率上升，非优选响应下降
- $\lambda = 1.0$：两者对数概率均下降，但差距扩大

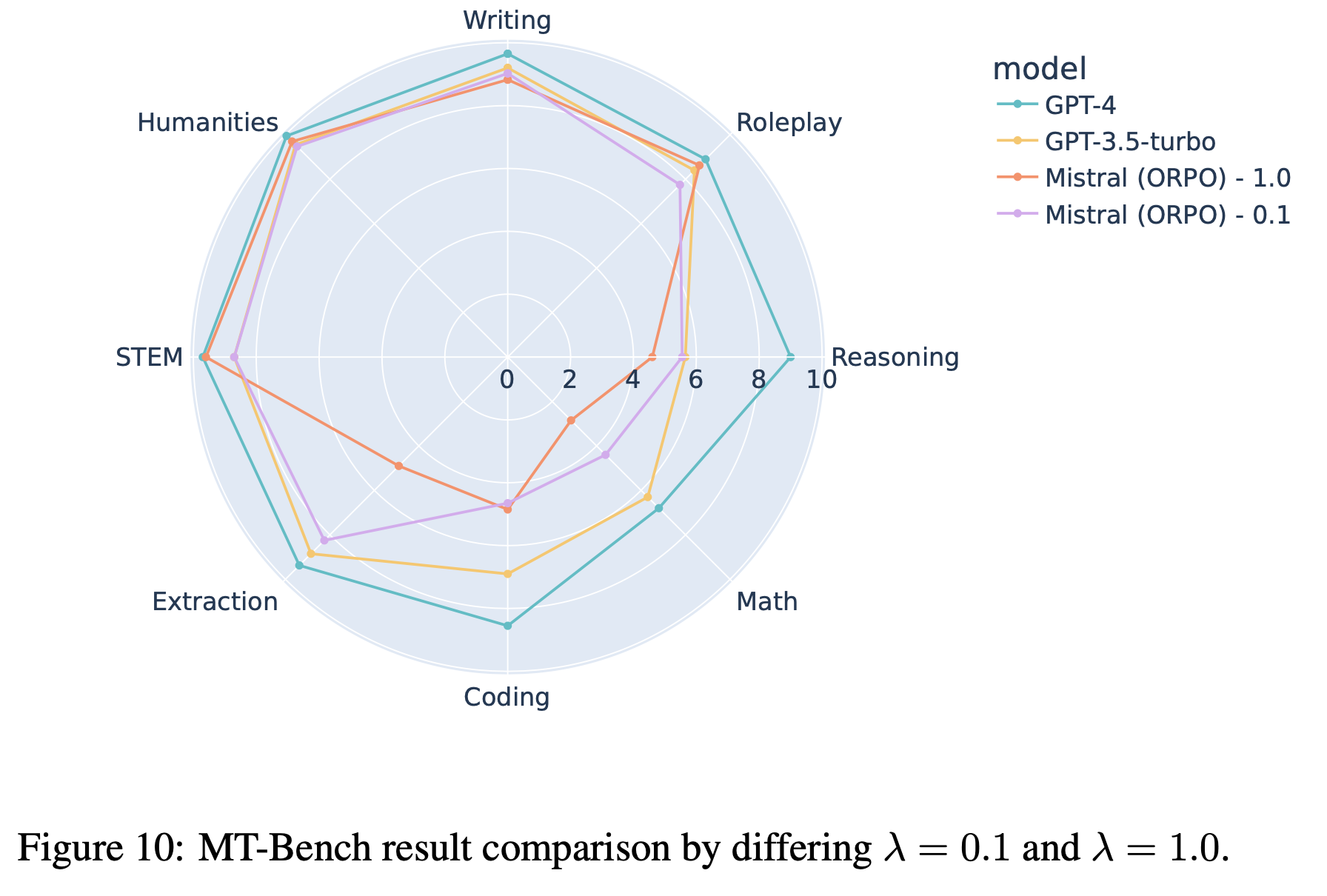
E.2 MT-Bench 表现

图10显示，$\lambda = 1.0$ 在需要确定性答案的类别（如数学、推理）上表现较差，但在开放性任务（如STEM、人文学科）上更优。这表明高 $\lambda$ 可能导致模型过度适应训练数据中的优选响应集

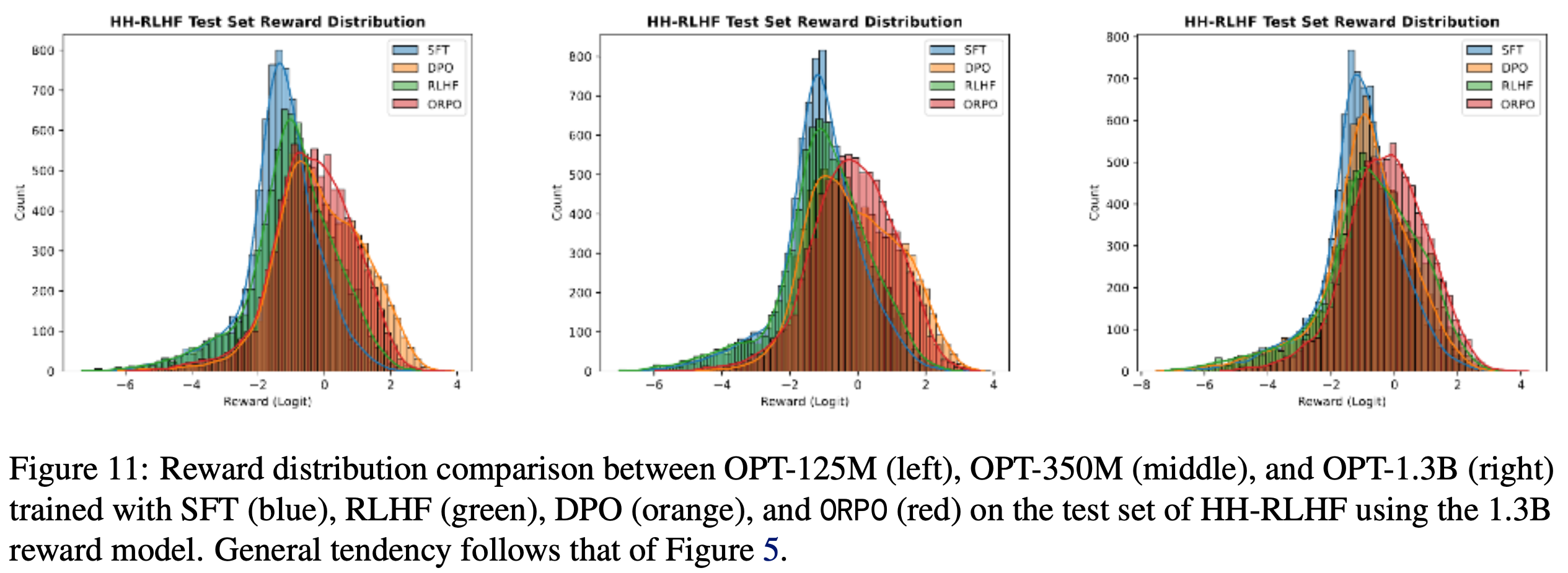
附录F HH-RLHF 测试集的奖励分布

图11展示了 OPT2-125M、OPT2-350M 和 OPT2-1.3B 在 HH-RLHF 数据集上的奖励分布。如第6.3节所述，ORPO 始终将 SFT 的奖励分布向右推移

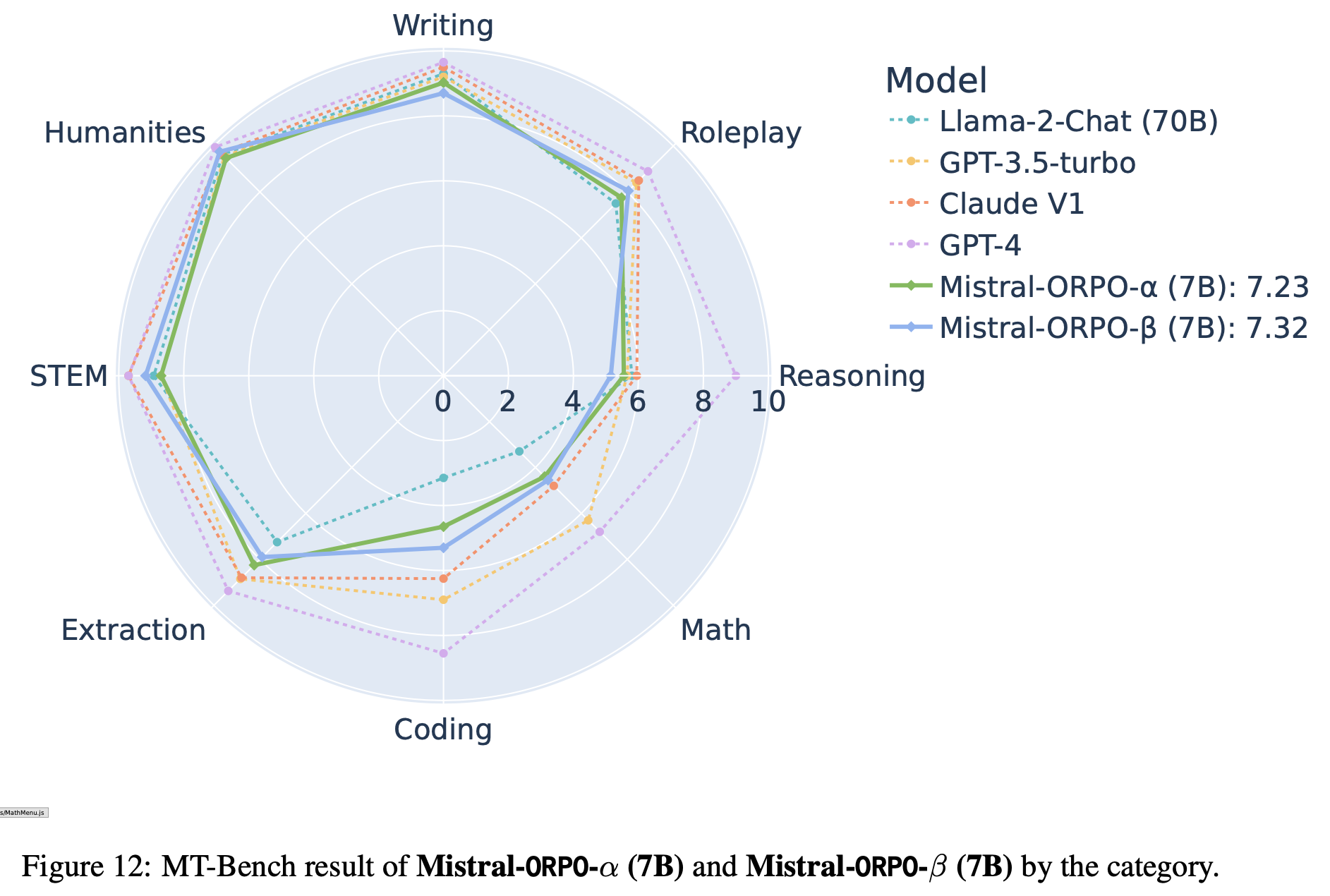
附录G Mistral-ORPO-$\alpha$ 和 Mistral-ORPO-$\beta$ 的 MT-Bench 结果

图12显示，Mistral-ORPO-$\beta$（7B）在多数类别上超越 Llama-2 Chat（13B/70B），并与 GPT-3.5-turbo 在描述性任务上表现相当。但在编码和数学类任务上较弱，推测是由于训练数据不足（仅使用61k UltraFeedback 样本）

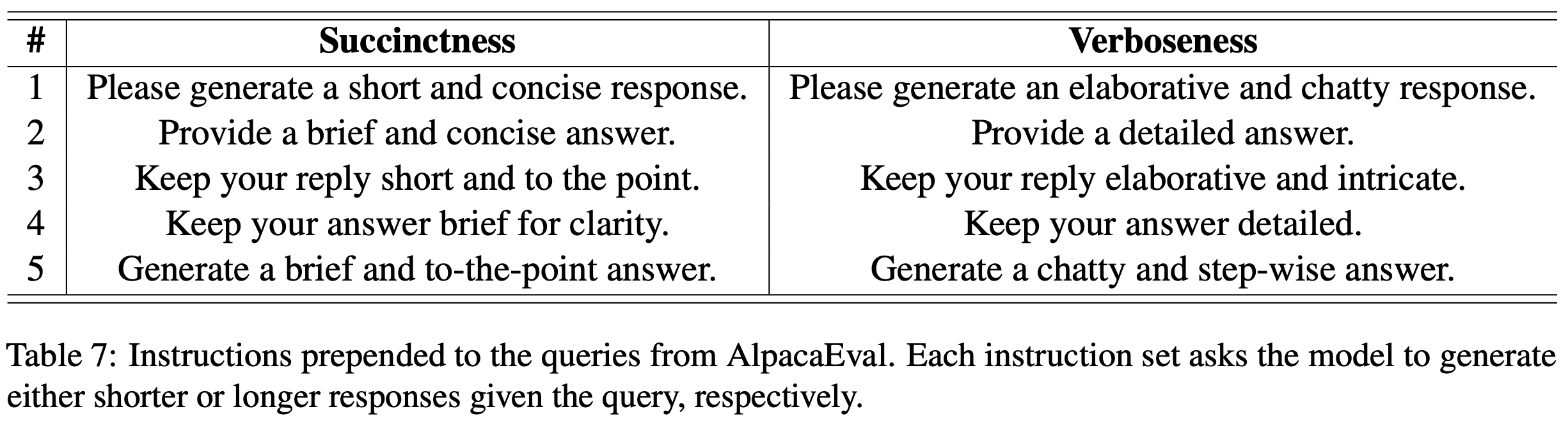
附录H 用于冗余性评估的特殊指令

表7列出了为简洁性和冗余性评估生成的5组指令（通过 ChatGPT 生成），每批次随机选择一条以避免词汇偏差

附录I Mistral-ORPO-$\alpha$（7B）的生成样本

本节展示 Mistral-ORPO-$\alpha$（7B）在 AlpacaEval 上的两个生成样本（温度=0.7），包括一个优于 GPT-4 的案例和一个 GPT-4 更优的案例

Query 1（GPT-4 胜出）

书籍简述 ：Matilda
GPT-4 ：详细介绍了《Matilda》的情节、主题及影响
Mistral-ORPO-$\beta$ ：简要概括了书籍的核心内容和主题

Query 2（Mistral-ORPO-$\beta$ 胜出）

对 ChatGPT 的看法
GPT-4 ：中立描述 ChatGPT 的功能与局限性
Mistral-ORPO-$\beta$ ：在肯定技术价值的同时，更强调批判性使用的重要性

Introduction and Discussion

The Role of Supervised Fine-tuning

Absence of Penalty in Cross-Entropy Loss

Generalization over Both Response Styles

Penalizing Undesired Generations

ORPO

Preliminary

Objective Function of ORPO

Gradient of ORPO

Experimental Settings

Training Configurations

Leaderboard Evaluation

Results and Analysis

Single-turn Instruction Following

Multi-turn Instruction Following

Reward Model Win Rate

Lexical Diversity

Discussion

Comparison to Probability Ratio

最小化 \( \mathcal{L}_{OR} \)

Computational Efficiency

Limitations

补充：Related Works

Alignment with RL

Alignment without Reward Model

Alignment with Supervised Fine-tuning

附录A 基于比值比（Odds Ratio）的 \(\nabla_\theta \mathcal{L}_{OR}\) 推导

附录B 概率比（Probability Ratio）与比值比（Odds Ratio）的消融实验

附录C 实验细节

SFT

RLHF

DPO

ORPO

附录D Mistral-ORPO-\(\alpha\) 和 Mistral-ORPO-\(\beta\) 的 IFEval 结果

附录E 权重值 \(\lambda\) 的消融实验

E.1 对数概率趋势

E.2 MT-Bench 表现

附录F HH-RLHF 测试集的奖励分布

附录G Mistral-ORPO-\(\alpha\) 和 Mistral-ORPO-\(\beta\) 的 MT-Bench 结果

附录H 用于冗余性评估的特殊指令

附录I Mistral-ORPO-\(\alpha\)（7B）的生成样本

Query 1（GPT-4 胜出）

Query 2（Mistral-ORPO-\(\beta\) 胜出）