注:本文包含 AI 辅助创作
Paper Summary
- 整体说明:
- 论文提出 VAPO(Value-model-based Augmented Proximal Policy Optimization) 框架/算法,利用 Qwen2.5-32B 模型在 AIME24 基准上实现了 SOTA 性能
- VAPO 通过在 PPO 之上引入七项新技术(包含 VC-PPO 和 DAPO 相关的优化),这些技术专注于改进价值学习和平衡探索,论文的基于 Value Model 的方法优于当代 value-model-free 方法,如 GRPO 和 DAPO
- 评价:论文更偏实践,很多优化点是来自已有的工作,如 VC-PPO 和 DAPO 等
- VAPO 是一种专为 value-model-based paradigm 的推理模型量身定制的框架
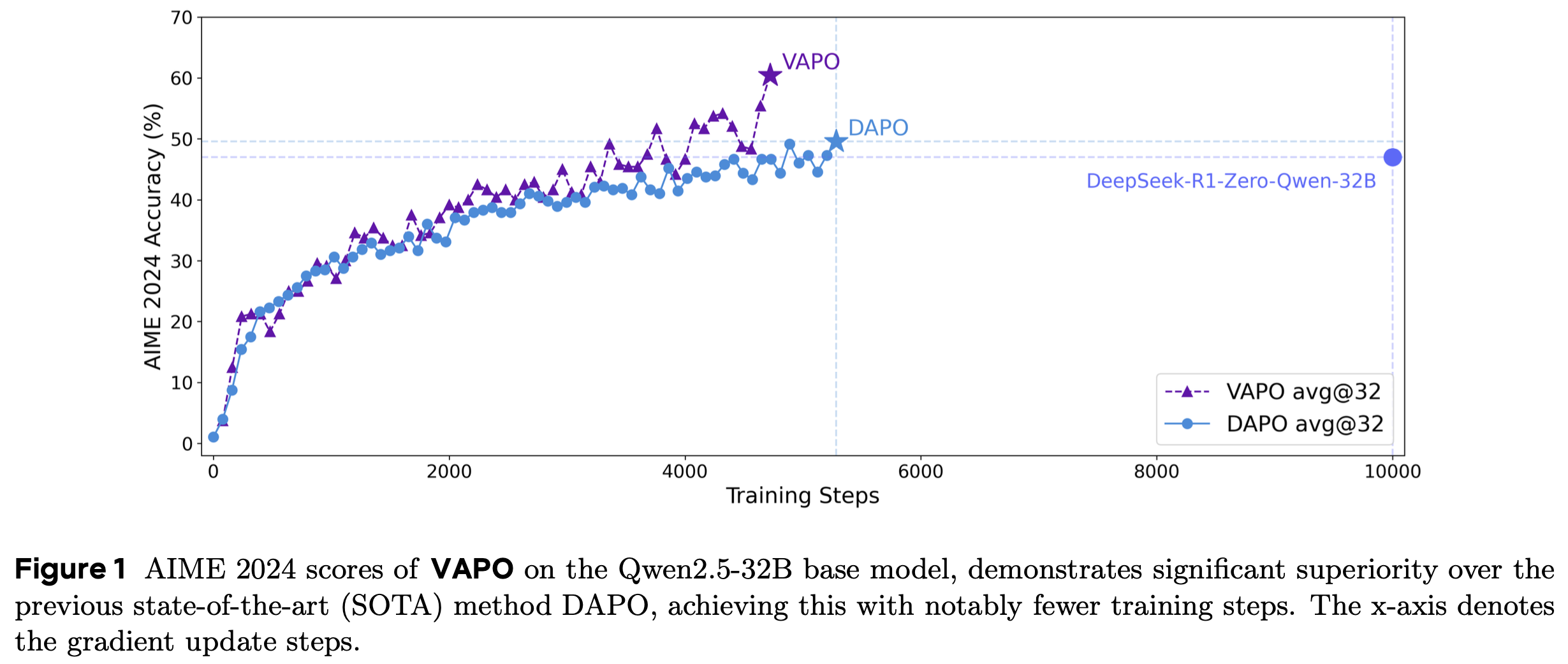
- 在 AIME 2024 数据集上进行基准测试时,基于 Qwen 32B 预训练模型构建的 VAPO 取得了 60.4 的 SOTA 性能
- 在相同的实验设置下直接比较,VAPO 比 DeepSeek-R1-Zero-Qwen-32B 和 DAPO 的结果高出 10分 以上
- VAPO 的训练过程稳定且高效:
- 仅在 5,000 步内就达到了 SOTA 性能;
- 在多次独立运行中,没有发生训练崩溃
- 本研究使用 Value-model-based 强化学习框架深入研究长思维链(long-CoT)推理
- 论文指出了困扰 Value-model-based 方法的三个关键挑战:
- Value Model 偏差(value model bias)
- 存在异质序列长度(the presence of heterogeneous sequence lengths)
- 奖励信号稀疏 (the sparsity of reward signals)
- 通过系统设计,VAPO 提供了一个集成解决方案,有效地缓解了这些挑战,从而在 long-CoT 推理任务中实现了性能提升
Introduction and Discussion
- 诸如 OpenAI o1 和 DeepSeek R1 等推理模型在数学推理等复杂任务中表现出卓越性能,这些任务需要在测试时通过长思维链(long-CoT)进行逐步分析和问题解决,从而极大地推动了人工智能的发展
- RL 在这些模型的成功中起着关键作用。它通过在可验证问题上不断探索通向正确答案的推理路径,逐步提高模型的性能,实现了前所未有的推理能力
- 在 LLM 的 RL 训练中,像 GRPO 和 DAPO 这样的 value-model-free 方法已证明具有显著效果
- 这些方法消除了学习 Value Model 的计算开销,而是仅基于整个轨迹的最终奖励来计算优势
- Trajectory-level 优势被直接分配为序列中每个位置的 Token-level 优势
- 当训练可靠的 Value Model 特别具有挑战性时, value-model-free 方法通过对一组内的多个轨迹的奖励进行平均,为优势计算提供了准确且稳定的基线
- 这种基于组的奖励聚合减轻了对显式价值估计的需求,而显式价值估计在复杂任务中往往不稳定
- 因此, value-model-free 方法在解决 long-CoT 推理等难题方面获得了显著关注,大量研究工作致力于优化其框架
- 尽管 value-model-free 方法取得了显著成功,但作者认为,如果能够解决 Value Model 训练中的挑战,基于 Value Model 的方法具有更高的性能上限
- 首先, Value Model 通过准确追踪每个动作对后续回报的影响 ,实现更精确的信用分配 ,从而促进更精细的优化
- 这对于复杂推理任务尤为关键 ,在这些任务中,单个步骤的细微错误往往会导致灾难性失败,而在value-model-free 框架下进行模型优化仍然具有挑战性
- 其次,与 value-model-free 方法中从蒙特卡罗方法得出的优势估计不同, Value Model 可以为每个 Token 提供方差更低的价值估计,从而增强训练稳定性
- 此外,训练良好的 Value Model 表现出固有的泛化能力,能够更有效地利用在线探索过程中遇到的样本。这显著提升了强化学习算法的优化上限
- 问题:这一点有点牵强吧,不一定需要 Value 模型啊
- 因此,尽管在复杂问题中训练 Value Model 面临巨大挑战,但克服这些困难的潜在收益是巨大的
- 首先, Value Model 通过准确追踪每个动作对后续回报的影响 ,实现更精确的信用分配 ,从而促进更精细的优化
- 然而,在 long-CoT 任务中训练完美的 Value Model 存在重大挑战
- 首先,鉴于长轨迹和以自举方式学习价值的不稳定性,学习低偏差的 Value Model 并非易事
- 其次,同时处理短响应和长响应也具有挑战性,因为它们在优化过程中可能对偏差-方差权衡表现出截然不同的偏好
- 最后,验证器的奖励信号的稀疏性因 long-CoT 模式而进一步加剧,这本质上需要更好的机制来平衡探索和利用
- 为了应对上述挑战并充分释放基于 Value Model 的方法在推理任务中的潜力,论文提出了 VAPO(Value-model-based Augmented Proximal Policy Optimization)
- 这是一个基于 Value Model 的RL训练框架
- VAPO 从 VC-PPO 和 DAPO 等先前研究工作中汲取灵感,并进一步扩展了它们的概念
- 论文总结了论文的主要贡献如下:
- 1)论文引入了VAPO,这是第一个在 long-CoT 任务上显著优于 value-model-free 方法的基于 Value Model 的RL训练框架
- VAPO不仅在性能方面表现出显著优势,还展示了增强的训练效率,简化了学习过程,并强调了其作为该领域新基准的潜力
- 2)论文提出了长度自适应广义优势估计(Length-adaptive GAE),它基于响应长度在GAE计算中自适应调整 \(\lambda\) 参数
- 这种做法有效地满足了与高度可变长度的响应相关的不同偏差-方差权衡要求
- 结果显示,优化了优势估计过程的准确性和稳定性(特别是在数据序列长度变化很大的场景中)
- 3)论文系统地整合了先前工作中的技术(论文还通过消融研究进一步验证了它们的必要性),如:
- DAPO 的 Clip-Higher 和 Token-level Loss
- VC-PPO 的 Value-Pretraining 和 Decoupled-GAE
- SIL 的自我模仿学习(self-imitation learning)
- GRPO 的 Group-Sampling
- 1)论文引入了VAPO,这是第一个在 long-CoT 任务上显著优于 value-model-free 方法的基于 Value Model 的RL训练框架
- VAPO是一个有效的强化学习系统,它汇集了这些改进
- 这些增强功能协同工作,产生的综合结果优于各个部分的总和
- 论文使用 Qwen2.5-32B 预训练模型进行实验,确保在任何实验中都不引入 SFT 数据,以保持与相关工作(DAPO 和 DeepSeek-R1-Zero-Qwen-32B)的可比性
- VAPO的性能从原始 PPO 的 5分 提高到 60分,超过了之前的最先进 value-model-free 方法 DAPO(+10分)
- 特别地,VAPO 非常稳定(论文在训练期间没有观察到任何崩溃,并且多次运行的结果始终相似)
Preliminaries
- 本节将介绍论文提出算法的基础概念和符号表示
- 论文首先探讨如何将语言生成任务建模为强化学习问题,随后介绍近端策略优化(Proximal Policy Optimization, PPO)和广义优势估计(Generalized Advantage Estimation, GAE)
将语言生成建模为 Token-level 的马尔可夫决策过程
- 强化学习的核心是学习一种策略,使得智能体在与环境交互时能够最大化累积奖励
- 在本研究中,论文将语言生成任务建模为马尔可夫决策过程(Markov Decision Process, MDP)(1998)
- 设输入的 Prompt为 \( x \),生成的Response为 \( y \)
- 两者均可分解为一系列 token 的序列
- 例如: Prompt \( x \) 可表示为 \( x = (x_0, \ldots, x_m) \),其中 token 来自固定的离散词汇表 \( \mathcal{A} \)
- 论文将 Token-level 的 MDP 定义为元组 \( \mathcal{M} = (\mathcal{S}, \mathcal{A}, \mathbb{P}, R, d_0, \omega) \),各组成部分的详细说明如下:
- 状态空间(State Space, \( \mathcal{S} \)) :该空间包含所有可能的状态,每个状态由当前已生成的 token 序列构成。在时间步 \( t \),状态 \( s_t \) 定义为 \( s_t = (x_0, \ldots, x_m, y_0, \ldots, y_t) \)
- 动作空间(Action Space, \( \mathcal{A} \)) :对应固定的离散词汇表,生成过程中从中选择 token 作为动作
- 状态转移(Dynamics, \( \mathbb{P} \)) :表示 token 之间的确定性转移模型。给定状态 \( s_t = (x_0, \ldots, x_m, y_0, \ldots, y_t) \)、动作 \( a = y_{t+1} \) 和下一状态 \( s_{t+1} = (x_0, \ldots, x_m, y_0, \ldots, y_t, y_{t+1}) \),转移概率 \( \mathbb{P}(s_{t+1}|s_t, a) = 1 \)
- 终止条件(Termination Condition) :当执行终止动作 \( \omega \)(通常是句子结束 token)时,语言生成过程结束
- 奖励函数(Reward Function, \( R(s, a) \)) :该函数提供标量反馈,用于评估智能体在状态 \( s \) 下执行动作 \( a \) 的表现。在RLHF (2022) 中,奖励函数可以从人类偏好中学习,或根据任务规则定义
- 初始状态分布(Initial State Distribution, \( d_0 \)) :是 Prompt \( x \) 的概率分布。初始状态 \( s_0 \) 由 Prompt \( x \) 的 token 序列构成
RLHF 目标
- 论文将优化问题建模为带 KL 散度正则化的强化学习任务。目标是逼近最优的 KL 正则化策略,其数学表示为:
$$
\pi^* = \arg \max_{\pi} \mathbb{E}_{\pi, s_0 \sim d_0} \left[ \sum_{t=0}^{H} \left( R(s_t, a_t) - \beta \text{KL} \left( \pi(\cdot|s_t) | \pi_{\text{ref} }(\cdot|s_t) \right) \right) \right]
$$- \( H \) 表示决策步的总数
- \( s_0 \) 是从数据集中采样的 Prompt
- \( R(s_t, a_t) \) 是从奖励函数中获得的 Token-level 奖励
- \( \beta \) 是控制 KL 正则化强度的系数
- \( \pi_{\text{ref} } \) 是初始策略
- 在传统的 RLHF 和大多数 LLM 相关任务中,奖励是稀疏的,仅在终止动作 \( \omega \)(即句子结束 token <eos>)时分配
PPO
- PPO (2017) 使用带裁剪的替代目标函数来更新策略。其核心思想是限制每一步策略更新的幅度,避免因策略变化过大而导致训练不稳定
- 设 \( \pi_\theta(a|s) \) 为参数化策略,\( \pi_{\theta_{\text{old} } }(a|s) \) 为上一轮迭代的旧策略。PPO 的替代目标函数定义为:
$$
\mathcal{L}^{CLIP}(\theta) = \hat{\mathbb{E} }_t \left[ \min \left( r_t(\theta) \hat{A}_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) \hat{A}_t \right) \right]
$$- \( r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{\text{old} } }(a_t|s_t)} \) 是概率比
- \( \hat{A}_t \) 是时间步 \( t \) 的优势估计
- \( \epsilon \) 是控制裁剪范围的超参数
- 广义优势估计 (GAE) 是一种用于在 PPO 中更准确估计优势函数的技术
- 它结合多步自举(bootstrapping)来降低优势估计的方差
- 对于长度为 \( T \) 的轨迹,时间步 \( t \) 的优势估计 \( \hat{A}_t \) 计算如下:
$$
\hat{A}_t = \sum_{l=0}^{T-t-1} (\gamma \lambda)^l \delta_{t+l}
$$- \( \gamma \) 是折扣因子
- \( \lambda \in [0,1] \) 是 GAE 参数
- \( \delta_t = R(s_t, a_t) + \gamma V(s_{t+1}) - V(s_t) \) 是时序差分(Temporal-Difference, TD)误差
- 这里 \( R(s_t, a_t) \) 是时间步 \( t \) 的奖励,\( V(s) \) 是价值函数
- 注:在 RLHF 中通常设置折扣因子 \( \gamma = 1.0 \),为简化表示,论文后续章节将省略 \( \gamma \)
long-CoT RL推理任务中的挑战
- long-CoT 任务给 RL 训练带来了独特的挑战,特别是对于采用 Value Model 来减少方差的方法
- 在本节中,论文系统地分析了由序列长度动态、价值函数不稳定性和奖励稀疏性引起的技术问题
Value Model Bias over Long Sequences(长序列上的 Value Model 偏差)
- 如 VC-PPO 中所指出的,用奖励模型初始化 Value Model 会引入显著的初始化偏差
- 这种正偏差源于两个模型之间的目标不匹配
- 奖励模型被训练为在<eos> Token 上评分,这促使它由于上下文不完整而给早期 Token 分配较低的分数
- 注:Value Model 估计在给定策略下所有先于<eos>的 Token 的预期累积奖励
- 在训练的早期阶段,鉴于 GAE 的反向计算,每个时间步t都会存在正偏差,该偏差沿轨迹累积
- 另一个使用 \(\lambda=0.95\) 的 GAE 的标准做法可能会加剧这个问题
- 终止 Token 处的奖励信号 \(R(s_{T},<eos>)\) 作为 \(\lambda^{T-t} R(s_{T},<eos>)\) 反向传播到第 \(t\) 个 Token
- 对于 \(T-t \gg 1\) 的长序列,这种折扣将有效奖励信号降低到接近零
- 理解:最准确的那个值(最后一个 Token 输出)反而被赋予了很小的权重
- 因此,价值更新几乎完全以自举方式进行,依赖于高度偏差的估计,这削弱了 Value Model 作为可靠方差减少基线的作用
Heterogeneous Sequence Lengths during Training(异质序列长度)
- 在 long-CoT 对得出正确答案至关重要的复杂推理任务中,模型通常会生成长度高度可变的响应
- 这种可变性要求算法足够稳健,能够管理从非常短到极长的序列。因此,具有固定 \(\lambda\) 参数的常用 GAE 方法面临重大挑战
- 即使 Value Model 是完美的,静态 \(\lambda\) 可能无法有效适应不同长度的序列
- 对于短长度的响应,通过 GAE 获得的估计往往具有高方差:
- GAE 代表了偏差和方差之间的权衡:在短响应的情况下,估计偏向于方差主导的一侧(理解:方差较大的一侧)
- 理解:短的响应中,对每个 Token 来说,需要预估的未来 Token 不多,更像是蒙特卡罗采样得到的?
- 另一方面,对于长长度的响应,GAE 由于自举而往往导致高偏差
- GAE 的递归性质依赖于未来状态值,在长序列上累积误差,加剧了偏差问题
- 这些限制深深植根于 GAE 计算框架的指数衰减性质
Sparsity of Reward Signal in Verifier-based Tasks(奖励信号的稀疏性)
- 复杂推理任务经常部署验证器作为奖励模型,基于验证器的奖励模型通常提供二进制反馈
- 这与提供密集信号(如-4到4的连续值)的传统基于语言模型的奖励模型不同,如 0 和 1
- 理解:其实传统 RL 中很多也是二值反馈,这没什么大不了的
- long-CoT 推理进一步加剧了奖励信号的稀疏性
- 由于CoT显著延长了输出长度,它不仅增加了计算时间,还减少了接收非零奖励的频率
- 在策略优化中,具有正确答案的采样响应可能极其稀缺和宝贵
- 这种情况提出了一个独特的探索-利用困境
- 一方面,模型必须保持相对较高的不确定性 ,使其能够采样多样化的响应范围,增加为给定 Prompt 生成正确答案的可能性
- 另一方面,算法需要有效地利用通过艰苦探索获得的正确采样响应 ,以提高学习效率
- 如果不能在探索和利用之间取得适当的平衡,模型可能会因过度利用而陷入次优解,或者在无成效的探索上浪费计算资源
VAPO:Addressing the Challenges in Long-CoT RL
Mitigating Value Model Bias over Long Sequences(缓解长序列上的 Value Model 偏差)
- 基于原文 3.1节 中对基于 Value Model 的模型的分析,论文提出使用 Value-Pretraining 和 decoupled-GAE 来解决长序列上 Value Model 偏差的关键挑战
- 注:这两种技术都借鉴了 VC-PPO 中先前引入的方法
- Value-Pretraining 旨在缓解价值初始化偏差
- 将 PPO 应用于 long-CoT 任务会导致失败,例如输出长度崩溃和性能下降:
- 原因是 Value Model 从奖励模型初始化,而奖励模型与 Value Model 的目标不匹配
- 这种现象首先在 VC-PPO 中被识别和解决,在论文中,论文遵循Value-Pretraining技术,具体步骤如下:
- 1)通过从固定策略(例如 \(\pi_{sft}\) )采样连续生成响应,并使用蒙特卡罗回报更新 Value Model
- 2)训练 Value Model,直到关键训练指标(包括价值损失和解释方差)达到足够低的值
- 3)保存价值检查点,并加载此检查点用于后续实验
- 将 PPO 应用于 long-CoT 任务会导致失败,例如输出长度崩溃和性能下降:
- Decoupled-GAE 在 VC-PPO 中被证明是有效的
- 该技术将价值和策略的优势计算解耦(主要是使用不同的 \(\lambda\))
- 对于价值更新,建议使用 \(\lambda=1.0\) 计算价值更新目标
- 这种选择导致无偏梯度下降优化,有效解决了 long-CoT 任务中的奖励衰减问题
- 对于策略更新,在计算和时间限制下,使用较小的 \(\lambda\) 来加速策略收敛
- 问题:为什么较小的 \(\lambda\) 能加速策略收敛?
- 在 VC-PPO 中,这是通过在优势计算中使用不同的系数来实现的:
- \(\lambda_{critic}=1.0\) 和 \(\lambda_{policy}=0.95\)
- 在论文中,论文采用了 Decoupled-GAE 计算的核心思想
Managing Heterogeneous Sequence Lengths during Training
- 为了应对训练中异构序列长度的挑战,论文提出了 长度自适应广义优势估计(Length-Adaptive GAE)
- 该方法根据序列长度动态调整 GAE 参数,从而实现对不同长度序列的自适应优势估计
- 此外,为了增强混合长度序列的训练稳定性,论文将传统的样本级策略梯度损失替换为 Token-Level 策略梯度损失(Token-Level Policy Gradient Loss)
- Length-Adaptive GAE :专门用于解决不同长度序列对 \(\lambda_{\text{policy} }\) 最优值的需求不一致问题
- 在 VC-PPO (2025) 中,\(\lambda_{\text{policy} }\) 被固定为 0.95。但对于长度 \(l > 100\) 的长序列,奖励对应的 TD 误差系数为 \(0.95^{100} \approx 0.006\),实际上接近于零
- 这里的 \(\lambda\) 是 GAE 计算公式中的超参,详情见 VC-PPO 论文:(VC-PPO)What’s Behind PPO’s Collapse in Long-CoT? Value Optimization Holds the Secret, Seed, arXiv 20250303
- 因此,固定 \(\lambda_{\text{policy} }=0.95\) 会导致 GAE 计算被潜在的有偏自举 TD 误差主导,无法有效处理极长序列
- 为了解决这一问题,论文提出以下公式动态调整 \(\lambda_{\text{policy} }\):
$$
\sum_{t=0}^{\infty}\lambda_{\text{policy} }^{t} \approx \frac{1}{1-\lambda_{\text{policy} } } = \alpha l,
$$- 其中 \(\alpha\) 是控制偏差-方差权衡的超参数
- 通过求解上式,论文得到长度自适应的 \(\lambda_{\text{policy} }\) 公式:
$$
\lambda_{\text{policy} } = 1 - \frac{1}{\alpha l}
$$ - 这种方法使得 GAE 计算能够更均匀地分配 TD 误差,从而优化长短序列的处理效果
- 在 VC-PPO (2025) 中,\(\lambda_{\text{policy} }\) 被固定为 0.95。但对于长度 \(l > 100\) 的长序列,奖励对应的 TD 误差系数为 \(0.95^{100} \approx 0.006\),实际上接近于零
- Token-Level Policy Gradient Loss :参考 DAPO (2025),论文修改了策略梯度损失的计算方法,以调整长思维链场景中的损失权重分配。传统实现中,策略梯度损失的计算如下:
$$
\mathcal{L}_{\text{PPO} }(\theta) = -\frac{1}{G}\sum_{i=1}^{G}\frac{1}{|o_{i}|}\sum_{t=1}^{|o_{i}|}\min\left(r_{i,t}(\theta)\hat{A}_{i,t},\text{clip}\left(r_{i,t}(\theta),1-\varepsilon,1+\varepsilon\right)\hat{A}_{i,t}\right),
$$- 其中 \(G\) 是训练批次大小,\(o_{i}\) 是第 \(i\) 个样本的轨迹
- 这种损失计算方式会导致长序列中的 Token 对最终损失的贡献被稀释,从而可能引发训练不稳定甚至崩溃
- 为了解决这一问题,论文将损失函数修正为以下形式:
$$
\mathcal{L}_{\text{PPO} }(\theta) = -\frac{1}{\sum_{i=1}^{G}|o_{i}|}\sum_{i=1}^{G}\sum_{t=1}^{|o_{i}|}\min\left(r_{i,t}(\theta)\hat{A}_{i,t},\text{clip}\left(r_{i,t}(\theta),1-\varepsilon,1+\varepsilon\right)\hat{A}_{i,t}\right),
$$ - 通过为批次中的所有 Token 分配均匀权重,模型能够更高效地处理长序列问题
Dealing with Sparsity of Reward Signal in Verifier-based Tasks
- 如第 3.3 节所述,在奖励信号高度稀疏的场景下,提升强化学习中探索-利用的平衡效率至关重要
- 为此,论文采用了三种方法:Clip-Higher、正例语言模型损失(Positive Example LM Loss) 和 分组采样(Group-Sampling) :
- Clip-Higher :用于缓解 PPO 和 GRPO 训练中遇到的熵崩溃问题,该方法首次由 DAPO (2025) 提出,论文将裁剪范围解耦为 \(\varepsilon_{\text{low} }\) 和 \(\varepsilon_{\text{high} }\):
$$
\mathcal{L}_{\text{PPO} }(\theta) = -\frac{1}{\sum_{i=1}^{G}|o_{i}|}\sum_{i=1}^{G}\sum_{t=1}^{|o_{i}|}\min\left(r_{i,t}(\theta)\hat{A}_{i,t},\text{clip}\left(r_{i,t}(\theta),1-\varepsilon_{\text{low} },1+\varepsilon_{\text{high} }\right)\hat{A}_{i,t}\right),
$$- 通过增大 \(\varepsilon_{\text{high} }\),论文为低概率 Token 提供了更多增长空间,同时保持较小的 \(\varepsilon_{\text{low} }\) 以避免采样空间崩溃
- Positive Example LM Loss :旨在提升强化学习中对正样本的利用效率
- 在复杂推理任务中,许多训练样本的答案错误,传统策略优化效率低下。为了最大化正确样本的效用,论文引入负对数似然(NLL)损失:
$$
\mathcal{L}_{\text{NLL} }(\theta) = -\frac{1}{\sum_{o_{i}\in\mathcal{T} }|o_{i}|}\sum_{o_{i}\in\mathcal{T} }\sum_{t=1}^{|o_{i}|}\log\pi_{\theta}\left(a_{t}|s_{t}\right),
$$- 其中 \(\mathcal{T}\) 表示正确答案集合
- 最终损失通过权重系数 \(\mu\) 与策略梯度损失结合:
$$
\mathcal{L}(\theta) = \mathcal{L}_{\text{PPO} }(\theta) + \mu * \mathcal{L}_{\text{NLL} }(\theta).
$$
- 在复杂推理任务中,许多训练样本的答案错误,传统策略优化效率低下。为了最大化正确样本的效用,论文引入负对数似然(NLL)损失:
- Group-Sampling :用于在同一 Prompt 下采样具有区分性的正负样本
- 在固定计算预算下,论文观察到减少批次中 Prompt 数量并增加重复生成次数能够略微提升性能,原因是其引入了更丰富的对比信号,从而增强了策略模型的学习能力
Experiments
Training Details
- 论文通过基于 Qwen-32B 模型对 PPO 算法进行各种修改来增强模型的数学性能
- 这些技术对其他推理任务(如与代码相关的任务)也有效
- 对于 basic PPO:
- 使用 AdamW 作为优化器
- Actor 学习率设置为 \(1×10^{-6}\)
- Critic 学习率设置为 \(2×10^{-6}\) (因为 Critic 需要更快地更新以跟上策略变化)
- 学习率采用 warmup-constant 调度器
- 问题:warmup-constant 调度器是什么?
- Batch Size 为 8192 个 Prompt ,每个 Prompt 采样一次,每个 Mini-Batch Size 设置为 512
- 价值网络使用奖励模型初始化
- GAE \(\lambda\) 设置为 0.95
- \(\gamma\) 设置为 1.0
- 使用 Sample-level loss
- \(\epsilon\) 设置为 0.2
- 与 vanilla PPO 相比,VAPO 进行了以下参数调整:
- 1)在开始策略训练之前,基于奖励模型(RM)对价值网络进行了 50步 的预热(对应 Value-Pretraining)
- 2)利用Decoupled-GAE ,其中价值网络从使用 \(\lambda=1.0\) 估计的回报中学习,而策略网络从使用单独 \(\lambda\) 获得的优势中学习
- 3)根据序列长度自适应设置优势估计的 \(\lambda\),遵循公式:
$$ \lambda_{policy}=1-\frac{1}{\alpha l}$$- 其中 \(\alpha=0.05\)
- 4)将裁剪范围调整为 \(\epsilon_{high}=0.28\) 和 \(\epsilon_{low}=0.2\)
- 5)采用 Token-level 策略梯度损失
- 6)在策略梯度损失中添加 Positive Example LM Loss ,权重为 0.1
- 7)每个采样使用 512 个 Prompt ,每个 Prompt 采样 16 次,并将小批量大小设置为 512
- 论文还将展示从 VAPO 中单独移除这七项修改中的每一项的最终效果
- 对于评估指标,论文使用 AIME24 在 32次采样上的平均通过率
- 采样参数设置为 \(topp=0.7\) 和 \(temperature=1.0\)
Ablation Results
- 在 Qwen-32b 上,使用 GRPO 的 DeepSeek R1 在 AIME24 上达到 47 分,而 DAPO 在 50% 的更新步骤中达到 50分
- 在图1中,论文提出的 VAPO 仅使用 DAPO 步骤的 60% 就达到了这一性能,并在仅 5,000 步内实现了 60.4 的新 SOTA 分数,证明了 VAPO 的效率
- 此外,VAPO 保持稳定的熵(既不崩溃也不过高),并且在三次重复实验中始终达到 60-61 的峰值分数,突出了论文算法的可靠性
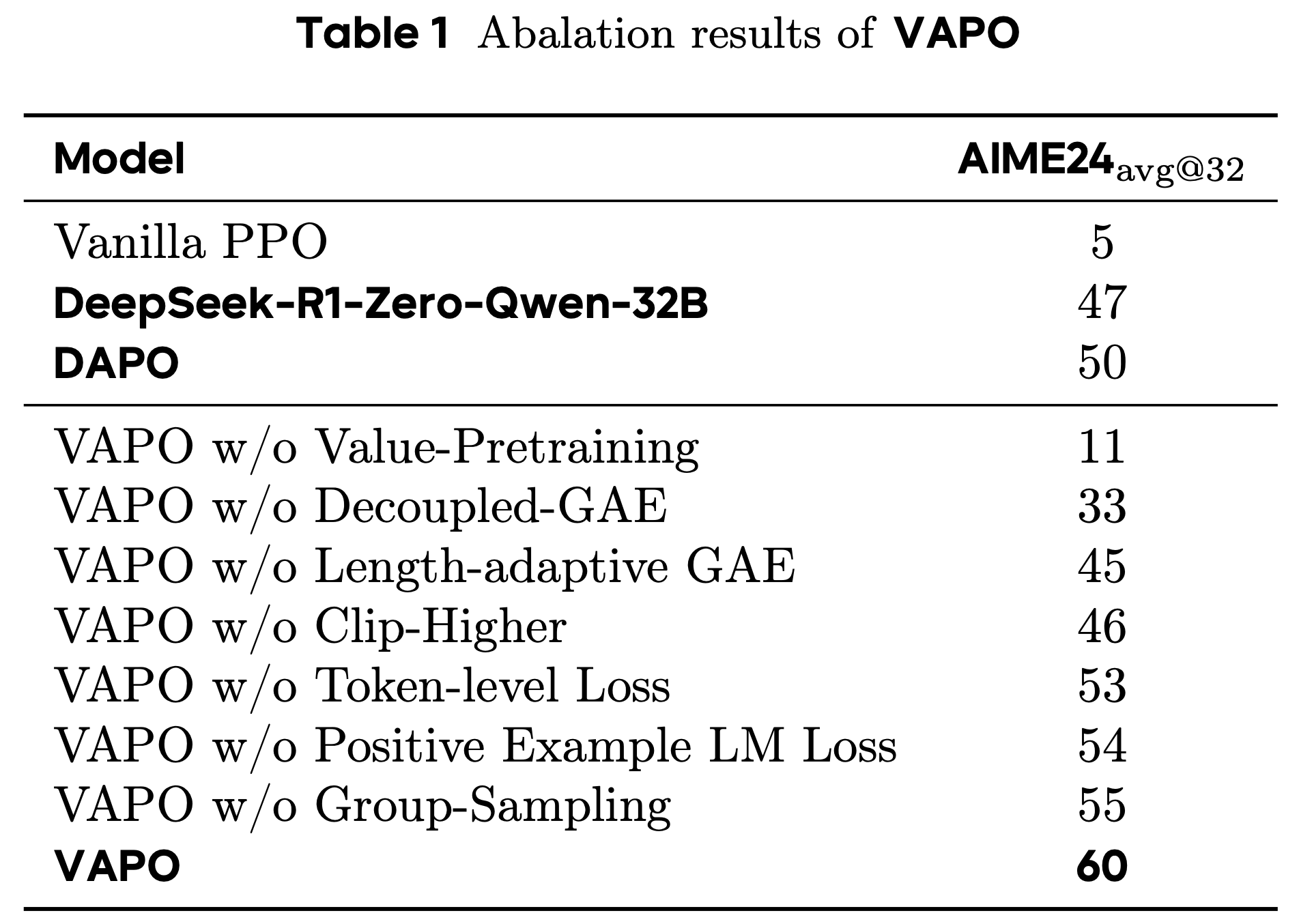
- 表1 系统地呈现了论文的实验结果:
- 原始PPO方法由于 Value Model 学习崩溃,在训练后期仅达到 5分,其特征是响应长度急剧减少,模型直接回答问题而不进行推理
- 论文的 VAPO方法 最终达到 60分,这是一个显著的改进
- 论文通过单独消融七项提出的修改进一步验证了它们的有效性:
- 1)没有 Value-Pretraining:模型在训练期间经历与原始 PPO 相同的崩溃,收敛到最大值约 11分
- 2)移除Decoupled-GAE :会导致奖励信号在反向传播期间指数衰减,阻止模型充分优化长形式响应,并导致 27分 的下降
- 3)Adaptive GAE:平衡了对短响应和长响应的优化,产生了 15分 的改进
- 4)Clip higher:鼓励彻底的探索和利用;移除它将模型的最大收敛限制为 46分
- 5)Token-level loss:隐含地增加了长响应的权重,贡献了 7分 的增益
- 6)结合 Positive Example LM Loss 将模型提高了近 6分
- 7)使用 Group-Sampling 生成更少的 Prompt 但更多的重复也导致了 5分的改进
Training Dynamics
- RL 训练期间生成的曲线提供了训练稳定性的实时 insights,不同曲线之间的比较可以突出算法差异
- 通常认为,更平滑的变化和更快的增长是这些曲线的理想特征
- 通过比较 VAPO 和 DAPO 的训练过程,论文做出了以下 observations:
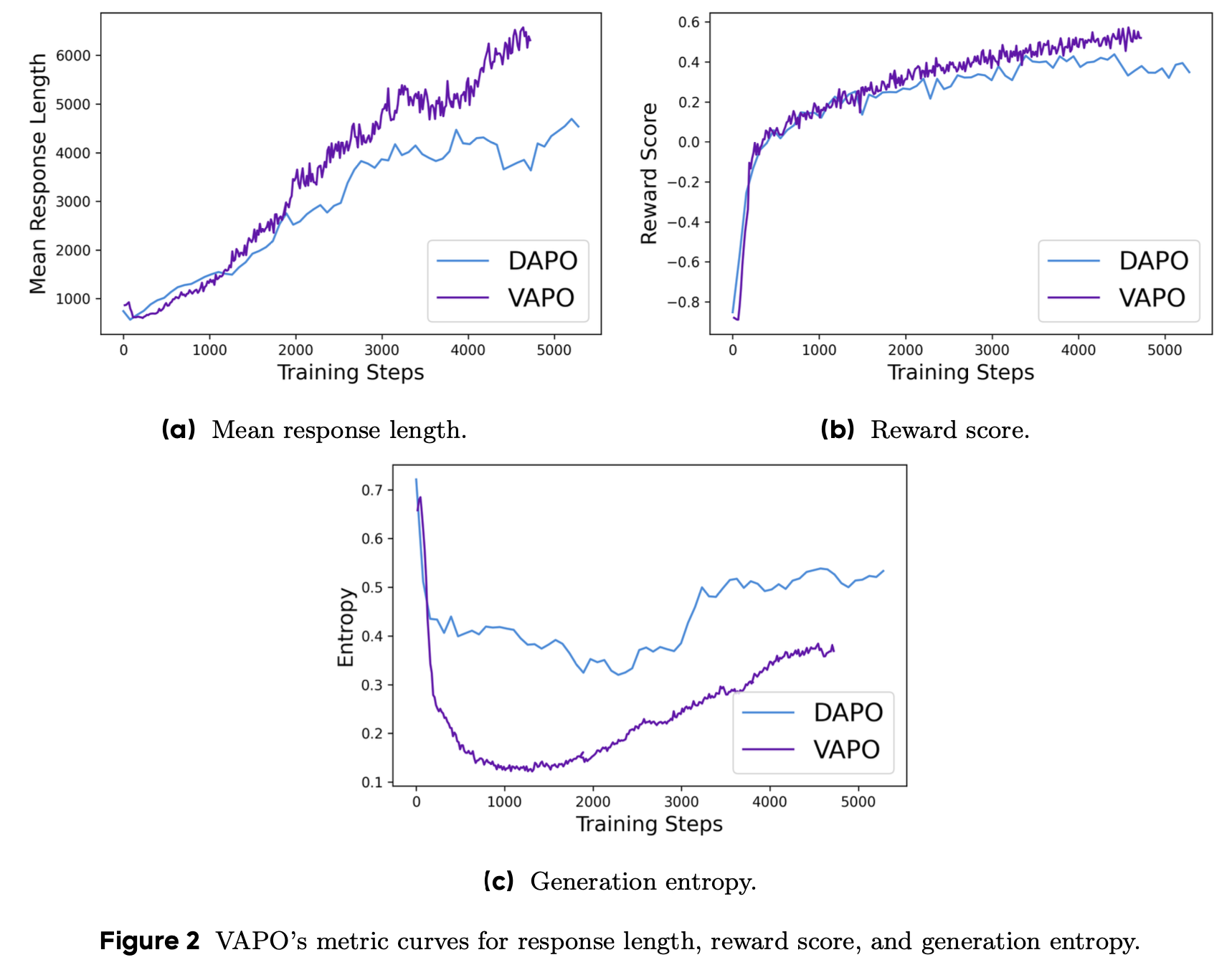
- 图2 显示 VAPO 的训练曲线比 DAPO 的更平滑,表明 VAPO 中的算法优化更稳定
- 如图2a 所示,与 DAPO 相比,VAPO 表现出更好的长度缩放:在现代背景下,更好的长度缩放被广泛认为是模型性能提高的标志,因为它增强了模型的泛化能力
- 图2b 表明 VAPO 的分数增长比 DAPO 快,因为 Value Model 为模型提供了更细粒度的信号来加速优化
- 根据图2c,VAPO 的熵在训练后期比 DAPO 的下降得更低,这是一把双刃剑:
- 一方面,它可能阻碍探索
- 另一方面,它提高了模型稳定性
- 从 VAPO 的最终结果来看,较低的熵对性能的负面影响最小,而可重复性和稳定性被证明是非常有利的
Related Work
- OpenAI o1 在 LLM 中引入了深刻的范式转变,其特点是在提供最终响应之前进行扩展推理
- DeepSeek R1 开源了其训练算法(value-model-free 的 GRPO)和模型权重,其性能可与 o1 媲美
- DAPO 识别了在 value-model-free LLM RL 扩展期间遇到的先前未公开的挑战,如熵崩溃,并提出了四种有效技术来克服这些挑战,实现了 SOTA 行业级性能
- 最近,Dr.GRPO 移除了 GRPO 中的长度和 std 归一化项
- 另一方面,ORZ 遵循 PPO 并使用 Value Model 进行优势估计,提出蒙特卡罗估计而不是广义优势估计
- 然而,它们只能达到与 GRPO 和 DAPO 等 value-model-free 方法相当的性能
- 在论文中,论文也遵循基于 Value Model 的方法并提出 VAPO,其性能优于 SOTA value-model-free 算法 DAPO